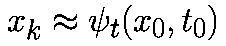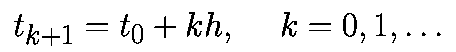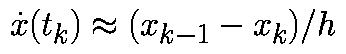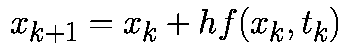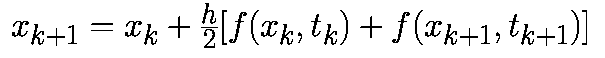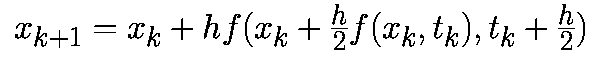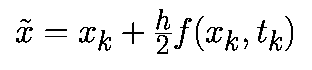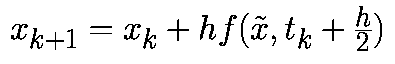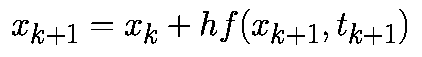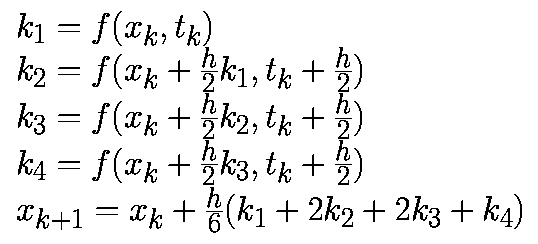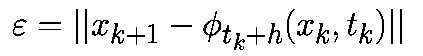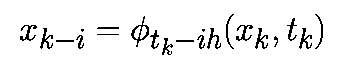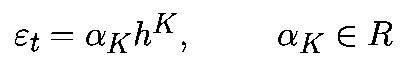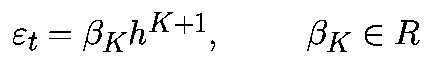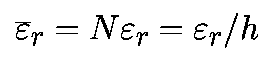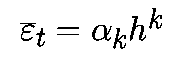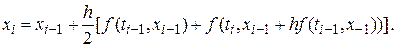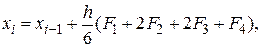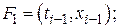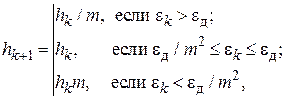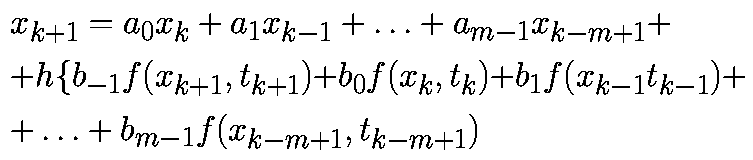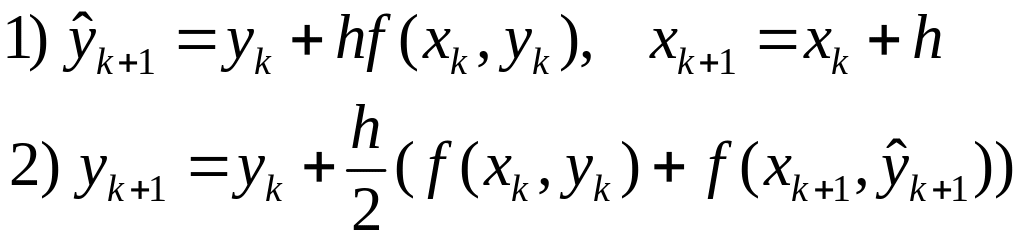Локальная ошибка усечения

From Wikipedia, the free encyclopedia

Truncation errors in numerical integration are of two kinds:

local truncation errors – the error caused by one iteration, and
global truncation errors – the cumulative error caused by many iterations.

Definitions[edit]

Suppose we have a continuous differential equation

$y'=f(t,y),\qquad y(t_{0})=y_{0},\qquad t\geq t_{0}$

and we wish to compute an approximation y_n of the true solution $y(t_{n})$ at discrete time steps $t_{1},t_{2},\ldots ,t_{N}$ . For simplicity, assume the time steps are equally spaced:

$h=t_{n}-t_{{n-1}},\qquad n=1,2,\ldots ,N.$

Suppose we compute the sequence y_n with a one-step method of the form

$y_{n}=y_{{n-1}}+hA(t_{{n-1}},y_{{n-1}},h,f).$

The function is called the increment function, and can be interpreted as an estimate of the slope ${\frac {y(t_{n})-y(t_{n-1})}{h}}$ .

Local truncation error[edit]

The local truncation error $\tau _{n}$ is the error that our increment function, , causes during a single iteration, assuming perfect knowledge of the true solution at the previous iteration.

More formally, the local truncation error, $\tau _{n}$ , at step is computed from the difference between the left- and the right-hand side of the equation for the increment $y_{n}\approx y_{{n-1}}+hA(t_{{n-1}},y_{{n-1}},h,f)$ :

$\tau _{n}=y(t_{n})-y(t_{{n-1}})-hA(t_{{n-1}},y(t_{{n-1}}),h,f).$

^[1]^[2]

The numerical method is consistent if the local truncation error is o(h) (this means that for every $\varepsilon >0$ there exists an such that $|\tau _{n}|<\varepsilon h$ for all h<H ; see little-o notation). If the increment function is continuous, then the method is consistent if, and only if, .^[3]

Furthermore, we say that the numerical method has order if for any sufficiently smooth solution of the initial value problem, the local truncation error is $O(h^{{p+1}})$ (meaning that there exist constants and such that $|\tau _{n}|<Ch^{{p+1}}$ for all h<H ).^[4]

Global truncation error[edit]

The global truncation error is the accumulation of the local truncation error over all of the iterations, assuming perfect knowledge of the true solution at the initial time step.^{[citation needed]}

More formally, the global truncation error, $e_{n}$ , at time t_n is defined by:

${\begin{aligned}e_{n}&=y(t_{n})-y_{n}\\&=y(t_{n})-{\Big (}y_{0}+hA(t_{0},y_{0},h,f)+hA(t_{1},y_{1},h,f)+\cdots +hA(t_{{n-1}},y_{{n-1}},h,f){\Big )}.\end{aligned}}$

^[5]

The numerical method is convergent if global truncation error goes to zero as the step size goes to zero; in other words, the numerical solution converges to the exact solution: $\lim _{{h\to 0}}\max _{n}|e_{n}|=0$ .^[6]

Relationship between local and global truncation errors[edit]

Sometimes it is possible to calculate an upper bound on the global truncation error, if we already know the local truncation error. This requires our increment function be sufficiently well-behaved.

The global truncation error satisfies the recurrence relation:

$e_{{n+1}}=e_{n}+h{\Big (}A(t_{n},y(t_{n}),h,f)-A(t_{n},y_{n},h,f){\Big )}+\tau _{{n+1}}.$

This follows immediately from the definitions. Now assume that the increment function is Lipschitz continuous in the second argument, that is, there exists a constant such that for all and $y_{1}$ and $y_{2}$ , we have:

$|A(t,y_{1},h,f)-A(t,y_{2},h,f)|\leq L|y_{1}-y_{2}|.$

Then the global error satisfies the bound

$|e_{n}|\leq {\frac {\max _{j}\tau _{j}}{hL}}\left({\mathrm {e}}^{{L(t_{n}-t_{0})}}-1\right).$

^[7]

It follows from the above bound for the global error that if the function in the differential equation is continuous in the first argument and Lipschitz continuous in the second argument (the condition from the Picard–Lindelöf theorem), and the increment function is continuous in all arguments and Lipschitz continuous in the second argument, then the global error tends to zero as the step size approaches zero (in other words, the numerical method converges to the exact solution).^[8]

Extension to linear multistep methods[edit]

Now consider a linear multistep method, given by the formula

$\begin{align} & y_{n+s} + a_{s-1} y_{n+s-1} + a_{s-2} y_{n+s-2} + \cdots + a_0 y_n \\ & \qquad {} = h \bigl( b_s f(t_{n+s},y_{n+s}) + b_{s-1} f(t_{n+s-1},y_{n+s-1}) + \cdots + b_0 f(t_n,y_n) \bigr), \end{align}$

Thus, the next value for the numerical solution is computed according to

$y_{n+s}=-\sum _{k=0}^{s-1}a_{k}y_{n+k}+h\sum _{k=0}^{s}b_{k}f(t_{n+k},y_{n+k}).$

The next iterate of a linear multistep method depends on the previous s iterates. Thus, in the definition for the local truncation error, it is now assumed that the previous s iterates all correspond to the exact solution:

$\tau _{n}=y(t_{n+s})+\sum _{k=0}^{s-1}a_{k}y(t_{n+k})-h\sum _{k=0}^{s}b_{k}f(t_{n+k},y(t_{n+k})).$

^[9]

Again, the method is consistent if $\tau _{n}=o(h)$ and it has order p if $\tau _{n}=O(h^{{p+1}})$ . The definition of the global truncation error is also unchanged.

The relation between local and global truncation errors is slightly different from in the simpler setting of one-step methods. For linear multistep methods, an additional concept called zero-stability is needed to explain the relation between local and global truncation errors. Linear multistep methods that satisfy the condition of zero-stability have the same relation between local and global errors as one-step methods. In other words, if a linear multistep method is zero-stable and consistent, then it converges. And if a linear multistep method is zero-stable and has local error $\tau _{n}=O(h^{{p+1}})$ , then its global error satisfies $e_{n}=O(h^{p})$ .^[10]

Notes[edit]

^ Gupta, G. K.; Sacks-Davis, R.; Tischer, P. E. (March 1985). «A review of recent developments in solving ODEs». Computing Surveys. 17 (1): 5–47. CiteSeerX 10.1.1.85.783. doi:10.1145/4078.4079.
^ Süli & Mayers 2003, p. 317, calls $\tau _{n}/h$ the truncation error.
^ Süli & Mayers 2003, pp. 321 & 322
^ Iserles 1996, p. 8; Süli & Mayers 2003, p. 323
^ Süli & Mayers 2003, p. 317
^ Iserles 1996, p. 5
^ Süli & Mayers 2003, p. 318
^ Süli & Mayers 2003, p. 322
^ Süli & Mayers 2003, p. 337, uses a different definition, dividing this by essentially by h
^ Süli & Mayers 2003, p. 340

References[edit]

Iserles, Arieh (1996), A First Course in the Numerical Analysis of Differential Equations, Cambridge University Press, ISBN 978-0-521-55655-2.
Süli, Endre; Mayers, David (2003), An Introduction to Numerical Analysis, Cambridge University Press, ISBN 0521007941.

External links[edit]

Notes on truncation errors and Runge-Kutta methods^{[dead link]}
Truncation error of Euler’s method^{[dead link]}

Источник

Иллюстрация метода Эйлера. Неизвестная кривая выделена синим цветом, а ее полигональная аппроксимация — красным.

В математике и вычислительной технике используется метод Эйлера (также называемый прямой метод Эйлера ) — это числовая процедура первого порядка для решения обыкновенных дифференциальных уравнений (ОДУ) с заданным начальным значением. Это самый простой явный метод для численного интегрирования обыкновенных дифференциальных уравнений и простейший метод Рунге – Кутта. Метод Эйлера назван в честь Леонарда Эйлера, который рассмотрел его в своей книге Institutionum Calculi Integratedis (опубликовано в 1768–1870 гг.).

Метод Эйлера является первым порядок, что означает, что локальная ошибка (ошибка на шаг) пропорциональна квадрату размера шага, а глобальная ошибка (ошибка в данный момент времени) пропорциональна размеру шага. Метод Эйлера часто служит основой для построения более сложных методов, например, метод предиктора – корректора.

Содержание

1 Неформальное геометрическое описание
2 Пример
- 2.1 Использование размера шага, равного 1 ( h = 1)
- 2.2 Пример кода MATLAB
- 2.3 Пример кода R
- 2.4 Использование других размеров шага
3 Деривация
4 Локальная ошибка усечения
5 Глобальная ошибка усечения
6 Числовой стабильность
7 Ошибки округления
8 Модификации и расширения
9 В популярной культуре
10 См. также
11 Примечания
12 Ссылки
13 Внешние ссылки

Неформальное геометрическое описание

Рассмотрим задачу вычисления формы неизвестной кривой, которая начинается в заданной точке и удовлетворяет заданному дифференциальному уравнению. Здесь дифференциальное уравнение можно представить как формулу, по которой угол наклона касательной линии к кривой может быть вычислен в любой точке кривой, если положение этой точка была рассчитана.

Идея состоит в том, что, хотя кривая изначально неизвестна, ее начальная точка, которую мы обозначаем A 0, {\ displaystyle A_ {0},} $A_ {0},$ , известна (см. рисунок вверху справа). Затем из дифференциального уравнения можно вычислить наклон кривой в A 0 {\ displaystyle A_ {0}} $A_{0}$ и, следовательно, касательную.

Сделайте небольшой шаг по касательной до точки A 1. {\ displaystyle A_ {1}.} $A_ {1}.$ Вдоль этого небольшого шага наклон не слишком сильно меняется, поэтому A 1 {\ displaystyle A_ {1}} $A_ {1}$ будет близко к кривой. Если мы сделаем вид, что A 1 {\ displaystyle A_ {1}} $A_ {1}$ все еще на кривой, рассуждения будут те же, что и для точки A 0 {\ displaystyle A_ {0}} $A_{0}$ выше можно использовать. После нескольких шагов многоугольная кривая A 0 A 1 A 2 A 3… {\ displaystyle A_ {0} A_ {1} A_ {2} A_ {3} \ dots} $A_ {0} A_ {1} A_ {2} A_ {3} \ dots$ вычисляется. В общем, эта кривая не отклоняется слишком далеко от исходной неизвестной кривой, и ошибку между двумя кривыми можно сделать небольшой, если размер шага достаточно мал и интервал вычислений конечен:

y ′ (t) = f (t, y (t)), y (t 0) = y 0. {\ displaystyle y ‘(t) = f (t, y (t)), \ qquad y (t_ {0}) = y_ {0}.} $y'(t)=f(t,y(t)),\qquad y(t_{0})=y_{0}.$

Выберите значение h {\ displaystyle h}для размера каждого шага и установите tn = t 0 + nh {\ displaystyle t_ {n} = t_ {0} + nh} $t_{n}=t_{0}+nh$ . Теперь один шаг метода Эйлера от tn {\ displaystyle t_ {n}} $t_ {n}$ до tn + 1 = tn + h {\ displaystyle t_ {n + 1} = t_ { n} + h} $t_{n+1}=t_{n}+h$ :

yn + 1 = yn + hf (tn, yn). {\ displaystyle y_ {n + 1} = y_ {n} + hf (t_ {n}, y_ {n}).} $y_ {n + 1} = y_ {n} + hf (t_ {n }, y_ {n}).$

Значение yn {\ displaystyle y_ {n}} $y_ {n}$ — аппроксимация решения ОДУ в момент времени tn {\ displaystyle t_ {n}} $t_ {n}$ : yn ≈ y (tn) {\ displaystyle y_ {n} \ приблизительно y (t_ {n})} $y_ {n} \ приблизительно y (t_ {n})$ . Метод Эйлера явный, то есть решение yn + 1 {\ displaystyle y_ {n + 1}} $y_ { n + 1}$ является явной функцией от yi {\ displaystyle y_ {i}} $y_ {i}$ для i ≤ n {\ displaystyle i \ leq n} $i \ leq n$ .

Хотя метод Эйлера интегрирует ОДУ первого порядка, любое ОДУ порядка N может быть представлено как система ОДУ первого порядка: для обработки уравнения

y (N) (t) = f (t, y (t), y ′ (t),…, y (N — 1) (t)) {\ displaystyle y ^ {(N)} (t) = f (t, y (t), y ‘(t), \ ldots, y ^ {(N-1)} (t))} $y^{(N)}(t)=f(t,y(t),y'(t),\ldots,y^{(N-1)}(t))$

вводим вспомогательные переменные z 1 (t) = y (t), z 2 (t) = y ′ (t),…, z N (t) = y (N — 1) (t) {\ displaystyle z_ {1 } (t) = y (t), z_ {2} (t) = y ‘(t), \ ldots, z_ {N} (t) = y ^ {(N-1)} (t)} $z_{1}(t)=y(t),z_{2}(t)=y'(t),\ldots,z_{N}(t)=y^{(N-1)}(t)$ и получим эквивалентное уравнение:

z ′ (t) = (z 1 ′ (t) ⋮ z N — 1 ′ (t) z N ′ (t)) = (y ′ (t) ⋮ y (N — 1) (t) y (N) (t)) = (z 2 (t) ⋮ z N (t) f (t, z 1 (t),…, z N (t))) { \ Displaystyle \ mathbf {z} ‘(t) = {\ begin {pmatrix} z_ {1}’ (t) \\\ vdots \\ z_ {N-1} ‘(t) \\ z_ {N} ‘(t) \ end {pmatrix}} = {\ begin {pmatrix} y’ (t) \\\ vdots \\ y ^ {(N-1)} (t) \\ y ^ {(N)} (t) \ end {pmatrix}} = {\ begin {pmatrix} z_ {2} (t) \\\ vdots \\ z_ {N} (t) \\ f (t, z_ { 1} (t), \ ldots, z_ {N} (t)) \ end {pmatrix}}} $\mathbf {z} '(t)={\begin{pmatrix}z_{1}'(t)\\\vdots \\z_{N-1}'(t)\\z_{N}'(t)\end{pmatrix}}={\begin{pmatrix}y'(t)\\\vdots \\y^{(N-1)}(t)\\y^{(N)}(t)\end{pmatrix}}={\begin{pmatrix}z_{2}(t)\\\vdots \\z_{N}(t)\\f(t,z_{1}(t),\ldots,z_{N}(t))\end{pmatrix}}$

Это система первого порядка по переменной z (t) {\ displaystyle \ mathbf { z} (t)} $\ mathbf {z} (t)$ и может обрабатываться методом Эйлера или, фактически, любой другой схемой для систем первого порядка.

Пример

Учитывая начальное проблема стоимости

y ′ = y, y (0) = 1, {\ displaystyle y ‘= y, \ quad y (0) = 1,} $y'=y,\quad y(0)=1,$

мы хотели бы использовать метод Эйлера для аппроксимации y (4) {\ displaystyle y (4)} y(4) .

Использование размера шага, равного 1 (h = 1)

Иллюстрация численного интегрирования для уравнения

y ′ = y, y (0) = 1. {\ displaystyle y ‘= y, y (0) = 1.}

Синий — метод Эйлера; зеленый — метод средней точки ; красный, точное решение,

y = e t. {\ displaystyle y = e ^ {t}.}

$y=e^{t}.$ Размер шага h = 1,0.

Метод Эйлера:

y n + 1 = y n + h f (t n, y n). {\ displaystyle y_ {n + 1} = y_ {n} + hf (t_ {n}, y_ {n}). \ qquad \ qquad} $y_ {n + 1} = y_ {n} + hf (t_ {n}, y_ {n}). \ Qquad \ qquad$

поэтому сначала мы должны вычислить f (t 0, y 0) {\ displaystyle f (t_ {0}, y_ {0})} $f(t_{0},y_{0})$ . В этом простом дифференциальном уравнении функция f {\ displaystyle f}определяется как f (t, y) = y {\ displaystyle f (t, y) = y}. У нас есть

f (t 0, y 0) = f (0, 1) = 1. {\ displaystyle f (t_ {0}, y_ {0}) = f (0,1) = 1. \ Qquad \ qquad} $f (t_ {0}, y_ {0}) = f (0,1) = 1. \ qquad \ qquad$

Выполнив описанный выше шаг, мы нашли наклон прямой, касательной к кривой решения в точке (0, 1) {\ displaystyle (0,1)} (0,1) . Напомним, что наклон определяется как изменение в y {\ displaystyle y}, деленное на изменение в t {\ displaystyle t}или Δ y / Δ t {\ displaystyle \ Delta y / \ Delta t} $\ Delta y / \ Delta t$ .

Следующий шаг — умножить указанное выше значение на размер шага h {\ displaystyle h}, который мы приравняйте к единице здесь:

час ⋅ е (y 0) = 1 ⋅ 1 = 1. {\ displaystyle h \ cdot f (y_ {0}) = 1 \ cdot 1 = 1. \ qquad \ qquad} $h \ cdot f (y_ {0}) = 1 \ cdot 1 = 1. \ qquad \ qquad$

Так как размер шага — это изменение t {\ displaystyle t}, когда мы умножаем размер шага и наклон касательной, мы получаем изменение y {\ displaystyle y}значение. Затем это значение добавляется к начальному значению y {\ displaystyle y}, чтобы получить следующее значение, которое будет использоваться для вычислений.

y 0 + hf (y 0) = y 1 = 1 + 1 ⋅ 1 = 2. {\ displaystyle y_ {0} + hf (y_ {0}) = y_ {1} = 1 + 1 \ cdot 1 = 2. \ Qquad \ qquad} $y_ {0} + hf (y_ {0}) = y_ {1} = 1 + 1 \ cdot 1 = 2. \ qquad \ qquad$

Чтобы найти y 2 {\ displaystyle y_ {2}} $y_ {2}$ , y 3 {\ displaystyle y_ {3}}<243, необходимо повторить описанные выше действия.>и y 4 {\ displaystyle y_ {4}} $y_ {4 }$ .

y 2 = y 1 + hf (y 1) = 2 + 1 ⋅ 2 = 4, y 3 = y 2 + hf (y 2) = 4 + 1 ⋅ 4 = 8, y 4 = y 3 + hf (y 3) = 8 + 1 ⋅ 8 = 16. {\ displaystyle {\ begin {align} y_ {2} = y_ {1} + hf ( y_ {1}) = 2 + 1 \ cdot 2 = 4, \\ y_ {3} = y_ {2} + hf (y_ {2}) = 4 + 1 \ cdot 4 = 8, \\ y_ {4 } = y_ {3} + hf (y_ {3}) = 8 + 1 \ cdot 8 = 16. \ end {align}}} ${\ begin {выровнено } y_ {2} = y_ {1} + hf (y_ {1}) = 2 + 1 \ cdot 2 = 4, \\ y_ {3} = y_ {2} + hf (y_ {2}) = 4 + 1 \ cdot 4 = 8, \\ y_ {4} = y_ {3} + hf (y_ {3}) = 8 + 1 \ cdot 8 = 16. \ End {align}}$

Из-за повторяющегося характера этого алгоритма может быть полезно организовать вычисления в виде диаграммы, как показано ниже, чтобы избежать ошибок.

n {\ displaystyle n}	yn {\ displaystyle y_ {n}} $y_ {n}$	tn {\ displaystyle t_ {n}} $t_ {n}$	f (tn, yn) {\ displaystyle f (t_ {n) }, y_ {n})} $f (t_ {n}, y_ {n})$	h {\ displaystyle h}	Δ y {\ displaystyle \ Delta y} $\ Delta y$	yn + 1 {\ displaystyle y_ {n + 1}} $y_ { n + 1}$
0	1	0	1	1	1	2
1	2	1	2	1	2	4
2	4	2	4	1	4	8
3	8	3	8	1	8	16

Результат этого вычисления состоит в том, что y 4 = 16 {\ displaystyle y_ {4} = 16} $y_ {4} = 16$ . Точное решение дифференциального уравнения: y (t) = et {\ displaystyle y (t) = e ^ {t}} $y (t) = e ^ {t}$ , поэтому y (4) = e 4 ≈ 54,598 {\ displaystyle y (4) = e ^ {4} \ приблизительно 54,598} $y (4) = e ^ {4} \ приблизительно 54,598$ . Хотя приближение метода Эйлера не было очень точным в этом конкретном случае, особенно из-за большого размера шага h {\ displaystyle h}, его поведение качественно правильное, как показано на рисунке.

пример кода MATLAB

clear; clc; закрыть все'); y0 = 1; t0 = 0; h = 1; % try: h = 0,01 tn = 4; % равно: t0 + h * n, где n число шагов [t, y] = Эйлера (t0, y0, h, tn); сюжет (t, y, 'b'); % точное решение (y = e ^ t): tt = (t0: 0,001: tn); yy = ехр (tt); Оставайтесь на линии'); сюжет (tt, yy, 'r'); откладывать'); легенда ('Эйлер', 'Точный'); функция [t, y] = Euler (t0, y0, h, tn) fprintf ('% 10s% 10s% 10s% 15s \ n', 'i', 'yi', 'ti', 'f (yi, ti) '); fprintf ('% 10d% + 10.2f% + 10.2f% + 15.2f \ n', 0, y0, t0, f (y0, t0)); t = (t0: h: tn) '; y = нули (размер (t)); у (1) = у0; для i = 1: 1: length (t) - 1 y (i + 1) = y (i) + h * f (y (i), t (i)); fprintf ('% 10d% + 10.2f% + 10.2f% + 15.2f \ n', i, y (i + 1), t (i + 1), f (y (i + 1), t (i + 1))); end end% в этом случае f (y, t) = f (y) function dydt = f (y, t) dydt = y; конец% ВЫХОД:% i yi ti f (yi, ti)% 0 +1.00 +0.00 +1.00% 1 +2.00 +1.00 +2.00% 2 +4.00 +2.00 +4.00% 3 +8.00 +3.00 +8.00% 4 +16.00 +4.00 +16.00% ПРИМЕЧАНИЕ: Код также выводит график сравнения

Пример кода R

Графический вывод кода языка программирования R для представленного примера

Ниже приведен код примера в R язык программирования.

# ============ # РЕШЕНИЕ # y '= y, где y' = f (t, y) # затем: f <- function(ti,y) y # INITIAL VALUES: t0 <- 0 y0 <- 1 h <- 1 tn <- 4 # Euler's method: function definition Euler <- function(t0, y0, h, tn, dy.dt) { # dy.dt: derivative function # t sequence: tt <- seq(t0, tn, by=h) # table with as many rows as tt elements: tbl <- data.frame(ti=tt) tbl$yi <- y0 # Initializes yi with y0 tbl$Dy.dt[1] <- dy.dt(tbl$ti[1],y0) # derivative for (i in 2:nrow(tbl)) { tbl$yi[i] <- tbl$yi[i-1] + h*tbl$Dy.dt[i-1] # For next iteration: tbl$Dy.dt[i] <- dy.dt(tbl$ti[i],tbl$yi[i]) } return(tbl) } # Euler's method: function application r <- Euler(t0, y0, h, tn, f) rownames(r) <- 0:(nrow(r)-1) # to coincide with index n # Exact solution for this case: y = exp(t) # added as an additional column to r r$y <- exp(r$ti) # TABLE with results: print(r) plot(r$ti, r$y, type="l", col="red", lwd=2) lines(r$ti, r$yi, col="blue", lwd=2) grid(col="black") legend("top", legend = c("Exact", "Euler"), lwd=2, col = c("red", "blue")) # OUTPUT: # # ti yi Dy.dt y # 0 0 1 1 1.000000 # 1 1 2 2 2.718282 # 2 2 4 4 7.389056 # 3 3 8 8 20.085537 # 4 4 16 16 54.598150 # NOTE: Code also outputs a comparison plot

Использование других размеров шага

Та же иллюстрация для h = 0,25.

Как предлагается во введении, метод Эйлера более точен, если размер шага h {\ displaystyle h}меньше. В таблице ниже показан результат с разными размерами шага. Верхняя строка соответствует примеру из предыдущего раздела, а вторая строка проиллюстрирована на рисунке.

размер шага	результат метода Эйлера	ошибка
1	16.00	38.60
0.25	35.53	19,07
0,1	45,26	9,34
0,05	49,56	5,04
0,025	51,98	2,62
0,0125	53,26	1,34

Ошибка, записанная в последнем столбце таблицы, представляет собой разницу между точным решением при t = 4 {\ displaystyle t = 4} t = 4 и приближение Эйлера. В нижней части таблицы размер шага составляет половину размера шага в предыдущей строке, а ошибка также составляет примерно половину ошибки в предыдущей строке. Это говорит о том, что ошибка примерно пропорциональна размеру шага, по крайней мере, для довольно малых значений размера шага. В целом это верно и для других уравнений; подробнее см. в разделе Глобальная ошибка усечения.

Другие методы, такие как метод средней точки, также проиллюстрированный на рисунках, ведут себя более благоприятно: глобальная ошибка метода средней точки примерно пропорциональна квадрату размера шага. По этой причине метод Эйлера называется методом первого порядка, а метод средней точки — методом второго порядка.

Мы можем экстраполировать из приведенной выше таблицы, что размер шага, необходимый для получения ответа, который является правильным с точностью до трех десятичных знаков, составляет приблизительно 0,00001, что означает, что нам нужно 400 000 шагов. Такое большое количество шагов влечет за собой большие вычислительные затраты. По этой причине люди обычно используют альтернативные методы более высокого порядка, такие как методы Рунге – Кутта или линейные многоступенчатые методы, особенно если требуется высокая точность.

Вывод

Метод Эйлера можно получить несколькими способами. Во-первых, это геометрическое описание выше.

Другая возможность — рассмотреть разложение Тейлора функции y {\ displaystyle y}около t 0 {\ displaystyle t_ {0 }} $t_ {0}$ :

y (t 0 + h) = y (t 0) + hy ′ (t 0) + 1 2 h 2 y ″ (t 0) + O (h 3). {\ displaystyle y (t_ {0} + h) = y (t_ {0}) + hy ‘(t_ {0}) + {\ frac {1} {2}} h ^ {2} y’ ‘(t_ {0}) + O (h ^ {3}).} $y(t_{0}+h)=y(t_{0})+hy'(t_{0})+{\frac {1}{2}}h^{2}y''(t_{0})+O(h^{3}).$

Дифференциальное уравнение утверждает, что y ′ = f (t, y) {\ displaystyle y ‘= f (t, y)}. Если это подставить в разложение Тейлора и игнорировать квадратичные члены и члены более высокого порядка, возникает метод Эйлера. Расширение Тейлора используется ниже для анализа ошибки, допущенной методом Эйлера, и его можно расширить для получения методов Рунге – Кутты.

Близким к этому выводом является замена прямой конечной разности формула для производной,

y ′ (t 0) ≈ y (t 0 + h) — y (t 0) h {\ displaystyle y ‘(t_ {0}) \ приблизительно {\ frac {y (t_ { 0} + h) -y (t_ {0})} {h}}} $y'(t_{0})\approx {\frac {y(t_{0}+h)-y(t_{0})}{h}}$

в дифференциальном уравнении y ′ = f (t, y) {\ displaystyle y ‘= f (t, y) }. Опять же, это дает метод Эйлера. Аналогичное вычисление приводит к методу средней точки и обратному методу Эйлера.

Наконец, можно интегрировать дифференциальное уравнение из t 0 {\ displaystyle t_ {0}}От $t_ {0}$ до t 0 + h {\ displaystyle t_ {0} + h} $t_ {0} + h$ и примените фундаментальную теорему исчисления, чтобы получить:

y (t 0 + h) — y (t 0) знак равно ∫ t 0 t 0 + hf (t, y (t)) dt. {\ displaystyle y (t_ {0} + h) -y (t_ {0}) = \ int _ {t_ {0}} ^ {t_ {0} + h} f (t, y (t)) \, \ mathrm {d} t.} $y (t_ {0} + h) -y (t_ {0}) = \ int _ {t_ {0}} ^ {t_ {0} + h} f (t, y (t)) \, \ mathrm {d} t.$

Теперь аппроксимируем интеграл с помощью метода левого прямоугольника (только с одним прямоугольником):

∫ t 0 t 0 + hf (t, y ( t)) dt ≈ hf (t 0, y (t 0)). {\ displaystyle \ int _ {t_ {0}} ^ {t_ {0} + h} f (t, y (t)) \, \ mathrm {d} t \ приблизительно hf (t_ {0}, y (t_ {0})).} $\ int _ {t_ { 0}} ^ {t_ {0} + h} f (t, y (t)) \, \ mathrm {d} t \ приблизительно hf (t_ {0}, y (t_ {0})).$

Комбинируя оба уравнения, можно снова найти метод Эйлера. Эту мысль можно продолжить, чтобы прийти к различным линейным многоступенчатым методам.

ошибка локального усечения метода Эйлера — это ошибка, сделанная за один шаг. Это разница между численным решением после одного шага, y 1 {\ displaystyle y_ {1}} $y_ {1}$ , и точным решением в момент времени t 1 = t 0 + h {\ стиль отображения t_ {1} = t_ {0} + h} $t_ {1} = t_ {0} + h$ . Численное решение дается формулой

y 1 = y 0 + h f (t 0, y 0). {\ displaystyle y_ {1} = y_ {0} + hf (t_ {0}, y_ {0}). \ quad} $y_ {1} = y_ {0} + hf (t_ {0}, y_ {0}). \ Quad$

Для точного решения мы используем разложение Тейлора, упомянутое в разделе Вывод выше:

y (t 0 + h) = y (t 0) + hy ‘(t 0) + 1 2 h 2 y ″ (t 0) + O (h 3). {\ displaystyle y (t_ {0} + h) = y (t_ {0}) + hy ‘(t_ {0}) + {\ frac {1} {2}} h ^ {2} y’ ‘(t_ {0}) + O (h ^ {3}).} $y(t_{0}+h)=y(t_{0})+hy'(t_{0})+{\frac {1}{2}}h^{2}y''(t_{0})+O(h^{3}).$

Локальная ошибка усечения (LTE), вносимая методом Эйлера, определяется разницей между этими уравнениями:

LTE = y (t 0 + h) — y 1 = 1 2 h 2 y ″ (t 0) + O (h 3). {\ displaystyle \ mathrm {LTE} = y (t_ {0} + h) -y_ {1} = {\ frac {1} {2}} h ^ {2} y » (t_ {0}) + O (h ^ {3}).} $\mathrm {LTE} =y(t_{0}+h)-y_{1}={\frac {1}{2}}h^{2}y''(t_{0})+O(h^{3}).$

Этот результат действителен, если y {\ displaystyle y}имеет ограниченную третью производную.

Это показывает, что для малых h {\ displaystyle h}, локальная ошибка усечения приблизительно пропорциональна h 2 {\ displaystyle h ^ {2}} $h ^ {2}$ . Это делает метод Эйлера менее точным (для малых h {\ displaystyle h}), чем другие методы более высокого порядка, такие как методы Рунге-Кутты и линейный многоступенчатый методы, для которых локальная ошибка усечения пропорциональна большей степени размера шага.

Несколько иную формулировку локальной ошибки усечения можно получить, используя форму Лагранжа для остаточного члена в теореме Тейлора. Если y {\ displaystyle y}имеет непрерывную вторую производную, то существует ξ ∈ [t 0, t 0 + h] {\ displaystyle \ xi \ in [t_ { 0}, t_ {0} + h]} $\ xi \ in [t_ {0}, t_ {0} + h ]$ такие, что

LTE = y (t 0 + h) — y 1 = 1 2 h 2 y ″ (ξ). {\ displaystyle \ mathrm {LTE} = y (t_ {0} + h) -y_ {1} = {\ frac {1} {2}} h ^ {2} y » (\ xi).} $\mathrm {LTE} =y(t_{0}+h)-y_{1}={\frac {1}{2}}h^{2}y''(\xi).$

В приведенных выше выражениях для ошибки вторую производную неизвестного точного решения y {\ displaystyle y}можно заменить выражением, содержащим правую часть дифференциального уравнения. Действительно, из уравнения y ′ = f (t, y) {\ displaystyle y ‘= f (t, y)}следует

y ″ (t 0) = ∂ f ∂ t (t 0, y (t 0)) + ∂ f ∂ y (t 0, y (t 0)) f (t 0, y (t 0)). {\ displaystyle y » (t_ {0}) = {\ partial f \ over \ partial t} (t_ {0}, y (t_ {0})) + {\ partial f \ over \ partial y} (t_ {0}, y (t_ {0})) \, f (t_ {0}, y (t_ {0})).} $y''(t_{0})={\partial f \over \partial t}(t_{0},y(t_{0}))+{\partial f \over \partial y}(t_{0},y(t_{0}))\,f(t_{0},y(t_{0})).$

Глобальная ошибка усечения

Глобальная ошибка усечения — это ошибка в фиксированное время t {\ displaystyle t}, после того, сколько шагов необходимо предпринять методам, чтобы достичь этого времени из начального момента. Глобальная ошибка усечения — это совокупный эффект локальных ошибок усечения, совершаемых на каждом шаге. Количество шагов легко определяется как (t — t 0) / h {\ displaystyle (t-t_ {0}) / h} $(t-t_ {0}) / h$ , что пропорционально 1 / h {\ displaystyle 1 / h} 1 / h , а ошибка, совершаемая на каждом этапе, пропорциональна h 2 {\ displaystyle h ^ {2}} $h ^ {2}$ (см. предыдущий раздел). Таким образом, следует ожидать, что глобальная ошибка усечения будет пропорциональна h {\ displaystyle h}.

. Это интуитивное рассуждение можно сделать точным. Если решение y {\ displaystyle y}имеет ограниченную вторую производную и f {\ displaystyle f}является непрерывным по Липшицу в своем второй аргумент, то глобальная ошибка усечения (GTE) ограничена

| GTE | ≤ час M 2 L (е L (t — t 0) — 1) {\ displaystyle | {\ text {GTE}} | \ leq {\ frac {hM} {2L}} (e ^ {L (t-t_ {0})} — 1) \ qquad \ qquad} $| {\ text {GTE}} | \ leq {\ frac {hM} {2L}} (e ^ {L (t-t_ {0})} - 1) \ qquad \ qquad$

где M {\ displaystyle M}— верхняя граница второй производной от y {\ displaystyle y}.на данном интервале, а L {\ displaystyle L}— константа Липшица для f {\ displaystyle f}.

Точная форма этой границы: имеет небольшое практическое значение, так как в большинстве случаев граница значительно переоценивает действительную ошибку, допущенную методом Эйлера. Важно то, что он показывает, что глобальная ошибка усечения (приблизительно) пропорциональна h {\ displaystyle h}. По этой причине метод Эйлера считается методом первого порядка.

Числовая устойчивость

Решение

y ′ = — 2.3 y {\ displaystyle y ‘= — 2.3y}

вычислено методом Эйлера с размером шага

h = 1 {\ displaystyle h = 1}

h = 1 (синие квадраты) и

h = 0,7 {\ displaystyle h = 0,7}

h=0.7 (красные кружки). Черная кривая показывает точное решение.

Метод Эйлера также может быть численно нестабильным, особенно для жестких уравнений, что означает, что численное решение становится очень большим для уравнений, в которых точное решение нет. Это можно проиллюстрировать с помощью линейного уравнения

y ′ = — 2.3 y, y (0) = 1. {\ displaystyle y ‘= — 2.3y, \ qquad y (0) = 1.} $y'=-2.3y,\qquad y(0)=1.$

Точное решением является y (t) = e — 2.3 t {\ displaystyle y (t) = e ^ {- 2.3t}} $y (t) = e ^ {- 2.3t}$ , которое убывает до нуля при t → ∞ {\ displaystyle t \ to \ infty} $t \ to \ infty$ . Однако, если к этому уравнению применить метод Эйлера с размером шага h = 1 {\ displaystyle h = 1} h = 1 , то численное решение качественно неверно: оно колеблется и растет (см. Рисунок). Вот что значит быть нестабильным. Если используется меньший размер шага, например h = 0,7 {\ displaystyle h = 0,7} ${\ displaystyle h = 0.7}$ , численное решение действительно затухает до нуля.

Розовый диск показывает область устойчивости для метода Эйлера.

Если метод Эйлера применяется к линейному уравнению y ′ = ky {\ displaystyle y ‘= ky} y'=ky , тогда численное решение будет неустойчивым, если произведение hk {\ displaystyle hk}находится за пределами области

{z ∈ C ∣ | z + 1 | ≤ 1}, {\ displaystyle \ {z \ in \ mathbf {C} \ mid | z + 1 | \ leq 1 \},} $\ {z \ in \ mathbf {C} \ mid | z + 1 | \ leq 1 \},$

показано справа. Эта область называется (линейной) областью устойчивости. В этом примере k {\ displaystyle k}равно −2,3, поэтому, если h = 1 {\ displaystyle h = 1} h = 1 , то hk = — 2.3 {\ displaystyle hk = -2.3}, который находится за пределами области стабильности, и, следовательно, численное решение нестабильно.

Это ограничение — наряду с медленной сходимостью ошибки с h — означает, что метод Эйлера используется нечасто, за исключением простого примера численного интегрирования.

Ошибки округления

В ходе обсуждения до сих пор игнорировались последствия ошибки округления. На шаге n метода Эйлера ошибка округления примерно равна величине εy n, где ε — машинный эпсилон. Предполагая, что все ошибки округления имеют примерно одинаковый размер, общая ошибка округления за N шагов будет примерно Nεy 0, если все ошибки указывают в одном направлении. Поскольку количество шагов обратно пропорционально размеру шага h, общая ошибка округления пропорциональна ε / h. В действительности, однако, крайне маловероятно, что все ошибки округления указывают в одном направлении. Если вместо этого предполагается, что ошибки округления являются независимыми случайными величинами, то ожидаемая общая ошибка округления пропорциональна ε / h {\ displaystyle \ varepsilon / {\ sqrt {h}}} $\ varepsilon / {\ sqrt {h}}$ .

Таким образом, для чрезвычайно При малых значениях размера шага ошибка усечения будет небольшой, но влияние ошибки округления может быть большим. Большей части эффекта ошибки округления можно легко избежать, если использовать компенсированное суммирование в формуле для метода Эйлера.

Модификации и расширения

Простая модификация Метод Эйлера, который устраняет проблемы устойчивости, отмеченные в предыдущем разделе, — это обратный метод Эйлера :

yn + 1 = yn + hf (tn + 1, yn + 1). {\ displaystyle y_ {n + 1} = y_ {n} + hf (t_ {n + 1}, y_ {n + 1}).} $y_ {n + 1} = y_ {n} + hf (t_ {n + 1}, y_ {n + 1}).$

Он отличается от (стандартного или прямого) метода Эйлера тем, что функция f {\ displaystyle f}оценивается в конечной точке шага, а не в начальной точке. Обратный метод Эйлера — это неявный метод, что означает, что формула обратного метода Эйлера имеет yn + 1 {\ displaystyle y_ {n + 1}} $y_ { n + 1}$ с обеих сторон, поэтому при применении обратного метода Эйлера мы должны решить уравнение. Это удорожает реализацию.

Другие модификации метода Эйлера, которые помогают с устойчивостью, дают экспоненциальный метод Эйлера или полунеявный метод Эйлера.

Более сложные методы позволяют достичь более высокого порядка (и больше точности). Одна из возможностей — использовать больше функциональных оценок. Это иллюстрируется методом средней точки, который уже упоминался в этой статье:

yn + 1 = yn + hf (tn + 1 2 h, yn + 1 2 hf (tn, yn)) { \ displaystyle y_ {n + 1} = y_ {n} + hf {\ Big (} t_ {n} + {\ tfrac {1} {2}} h, y_ {n} + {\ tfrac {1} {2 }} hf (t_ {n}, y_ {n}) {\ Big)}} ${\ displaystyle y_ {n + 1} = y_ {n} + hf {\ Big (} t_ {n} + {\ tfrac {1} {2}} h, y_ {n} + {\ tfrac {1} { 2}} hf (t_ {n}, y_ {n}) {\ Big)}}$

Это приводит к семейству методов Рунге – Кутта.

Другая возможность — использовать больше прошлых значений, так как иллюстрируется двухэтапным методом Адамса – Башфорта:

yn + 1 = yn + 3 2 hf (tn, yn) — 1 2 hf (tn — 1, yn — 1). {\ displaystyle y_ {n + 1} = y_ {n} + {\ tfrac {3} {2}} hf (t_ {n}, y_ {n}) — {\ tfrac {1} {2}} hf ( t_ {n-1}, y_ {n-1}).} $y_ {n + 1} = y_ {n} + {\ tfrac {3} {2}} hf (t_ {n}, y_ {n}) - {\ tfrac {1} {2}} hf (t_ {n-1}, y_ { n-1}).$

Это приводит к семейству линейных многоступенчатых методов. Существуют и другие модификации, которые используют методы сжатия данных для минимизации использования памяти

В популярной культуре

В фильме Скрытые фигуры, Кэтрин Гобл прибегает к методу Эйлера при вычислении входа в атмосферу космонавта Джона Гленна с околоземной орбиты.

См. также

метод Кранка – Николсона
градиентный спуск аналогично использует конечные шагов, здесь можно найти минимум функций
Список методов Рунге-Кутта
Линейный многоступенчатый метод
Численное интегрирование (для вычисления определенных интегралов)
Численные методы для обыкновенных дифференциальных уравнений

Примечания

Ссылки

Аткинсон, Кендалл А. (1989). Введение в численный анализ (2-е изд.). Нью-Йорк: John Wiley Sons. ISBN 978-0-471-50023-0 .
Ascher, Uri M.; Петцольд, Линда Р. (1998). Компьютерные методы решения обыкновенных дифференциальных и дифференциально-алгебраических уравнений. Филадельфия: Общество промышленной и прикладной математики. ISBN 978-0-89871-412-8 .
Мясник, Джон К. (2003). Численные методы решения обыкновенных дифференциальных уравнений. Нью-Йорк: John Wiley Sons. ISBN 978-0-471-96758-3 .
Хайрер, Эрнст; Норсетт, Сиверт Пол; Ваннер, Герхард (1993). Решение обыкновенных дифференциальных уравнений I: нежесткие задачи. Берлин, Нью-Йорк: Springer-Verlag. ISBN 978-3-540-56670-0 .
Исерлес, Арье (1996). Первый курс численного анализа дифференциальных уравнений. Издательство Кембриджского университета. ISBN 978-0-521-55655-2 .
Стоер, Йозеф; Булирш, Роланд (2002). Введение в численный анализ (3-е изд.). Берлин, Нью-Йорк: Springer-Verlag. ISBN 978-0-387-95452-3 .
Лакоба, Тарас И. (2012), Простой метод Эйлера и его модификации (PDF) (Конспекты лекций для MATH334), Университет Вермонта, получено 29 февраля 2012 г.
Унни, М. П. (2017). «Сокращение памяти для численного решения дифференциальных уравнений с использованием сжатия». 13-й Международный коллоквиум по обработке сигналов и ее применению (CSPA), 2017 г.. С. 79–84. doi : 10.1109 / CSPA.2017.8064928. ISBN 978-1-5090-1184-1 . S2CID 13082456.

Внешние ссылки

СМИ, связанные с Метод Эйлера на Wikimedia Commons
Реализации метода Эйлера на разных языках по Код Розетты
, Энциклопедия математики, EMS Press, 2001 [ 1994]

Источник

Ошибки усечения при численном интегрировании бывают двух видов:

локальные ошибки усечения — ошибка, вызванная одной итерацией, и
глобальные ошибки усечения — совокупная ошибка, вызванная множеством итераций.

Определения

Предположим, у нас есть непрерывное дифференциальное уравнение

$y '= f (t, y), \ qquad y (t_ {0}) = y_ {0}, \ qquad t \ geq t_ {0}$

и мы хотим вычислить приближение истинного решения с дискретными временными шагами . Для простоты предположим, что временные шаги равномерно распределены:
y_n $y (t_ {n})$ $t_ {1}, t_ {2}, \ ldots, t_ {N}$

$h = t_ {n} -t _ {{n-1}}, \ qquad n = 1,2, \ ldots, N.$

Предположим, мы вычисляем последовательность одношаговым методом вида
y_n

$y_ {n} = y _ {{n-1}} + hA (t _ {{n-1}}, y _ {{n-1}}, h, f).$

Эта функция называется функцией приращения , и ее можно интерпретировать как оценку наклона .
${\ displaystyle {\ frac {y (t_ {n}) - y (t_ {n-1})} {h}}}$

Ошибка локального усечения

Локальная ошибка усечения является ошибкой , что наше приращение функции, вызывает в течение одной итерации, предполагая , что совершенное знание истинного решения на предыдущей итерации.
$\ тау _ {п}$

Более формально локальная ошибка усечения на шаге вычисляется из разницы между левой и правой частями уравнения для приращения :
$\ тау _ {п}$ $y_ {n} \ приблизительно y _ {{n-1}} + hA (t _ {{n-1}}, y _ {{n-1}}, h, f)$

$\ tau _ {n} = y (t_ {n}) - y (t _ {{n-1}}) - hA (t _ {{n-1}}, y (t _ {{n-1}}), з, е).$

Численный метод является непротиворечивым, если локальная ошибка усечения равна (это означает, что для каждого существует такая, что для всех ; см. Небольшие обозначения ). Если функция приращения непрерывна, то метод непротиворечив, если и только если ,.
ой) $\ varepsilon> 0$ ЧАС $| \ tau _ {n} | <\ varepsilon h$ h <H

Кроме того, мы говорим, что численный метод имеет порядок, если для любого достаточно гладкого решения задачи начального значения локальная ошибка усечения равна (это означает, что существуют константы и такие, что для всех ).
$О (ч ^ {{р + 1}})$ ЧАС $| \ tau _ {n} | <Ch ^ {{p + 1}}$ h <H

Глобальная ошибка усечения

Глобальная ошибка усечения является накоплением локальной погрешности усечения за все итерации, предполагая совершенное знание истинного решения на начальном этапе времени.

Более формально глобальная ошибка усечения во времени определяется следующим образом:
$e_ {n}$ t_n

${\ begin {align} e_ {n} & = y (t_ {n}) - y_ {n} \\ & = y (t_ {n}) - {\ Big (} y_ {0} + hA (t_ { 0}, y_ {0}, h, f) + hA (t_ {1}, y_ {1}, h, f) + \ cdots + hA (t _ {{n-1}}, y _ {{n-1 }}, h, f) {\ Big)}. \ end {align}}$

Численный метод сходится, если глобальная ошибка усечения стремится к нулю, когда размер шага стремится к нулю; другими словами, численное решение сходится к точному решению: .
$\ lim _ {{h \ to 0}} \ max _ {n} | e_ {n} | = 0$

Связь между локальными и глобальными ошибками усечения

Иногда можно вычислить верхнюю границу глобальной ошибки усечения, если мы уже знаем локальную ошибку усечения. Для этого требуется, чтобы наша функция приращения работала достаточно хорошо.

Глобальная ошибка усечения удовлетворяет рекуррентному соотношению:

$e _ {{n + 1}} = e_ {n} + h {\ Big (} A (t_ {n}, y (t_ {n}), h, f) -A (t_ {n}, y_ {n) }, h, f) {\ Big)} + \ tau _ {{n + 1}}.$

Это сразу следует из определений. Теперь предположим, что функция приращения липшицева по второму аргументу, то есть существует такая константа , что для всех и и мы имеем:
$г_ {1}$ $г_ {2}$

$| A (t, y_ {1}, h, f) -A (t, y_ {2}, h, f) | \ leq L | y_ {1} -y_ {2} |.$

Тогда глобальная ошибка удовлетворяет оценке

$| e_ {n} | \ leq {\ frac {\ max _ {j} \ tau _ {j}} {hL}} \ left ({\ mathrm {e}} ^ {{L (t_ {n} -t_ {0})}} - 1 \ вправо).$

Из приведенной выше оценки глобальной ошибки следует, что если функция в дифференциальном уравнении непрерывна по первому аргументу и липшицева по второму аргументу (условие из теоремы Пикара – Линделёфа ), а функция приращения непрерывна во всех аргументы и непрерывность Липшица во втором аргументе, то глобальная ошибка стремится к нулю, когда размер шага приближается к нулю (другими словами, численный метод сходится к точному решению).
час

Расширение линейных многоступенчатых методов

Теперь рассмотрим линейный многоступенчатый метод , задаваемый формулой

$\ begin {align} & y_ {n + s} + a_ {s-1} y_ {n + s-1} + a_ {s-2} y_ {n + s-2} + \ cdots + a_0 y_n \\ & \ qquad {} = h \ bigl (b_s f (t_ {n + s}, y_ {n + s}) + b_ {s-1} f (t_ {n + s-1}, y_ {n + s}) -1}) + \ cdots + b_0 f (t_n, y_n) \ bigr), \ end {align}$

Таким образом, следующее значение численного решения вычисляется согласно

${\ displaystyle y_ {n + s} = - \ sum _ {k = 0} ^ {s-1} a_ {k} y_ {n + k} + h \ sum _ {k = 0} ^ {s} b_ {k} f (t_ {n + k}, y_ {n + k}).}$

Следующая итерация линейного многоступенчатого метода зависит от предыдущих итераций s . Таким образом, в определении локальной ошибки усечения теперь предполагается, что все предыдущие s итерации соответствуют точному решению:

${\ displaystyle \ tau _ {n} = y (t_ {n + s}) + \ sum _ {k = 0} ^ {s-1} a_ {k} y (t_ {n + k}) - час \ сумма _ {k = 0} ^ {s} b_ {k} f (t_ {n + k}, y (t_ {n + k})).}$

Опять же, метод непротиворечив, если и имеет порядок p, если . Не изменилось и определение глобальной ошибки усечения.
$\ тау _ {п} = о (ч)$ $\ tau _ {n} = O (h ^ {{p + 1}})$

Связь между локальными и глобальными ошибками усечения немного отличается от более простой настройки одношаговых методов. Для линейных многошаговых методов требуется дополнительная концепция, называемая нулевой стабильностью, чтобы объяснить связь между локальными и глобальными ошибками усечения. Линейные многоступенчатые методы, удовлетворяющие условию нулевой устойчивости, имеют такое же соотношение между локальными и глобальными ошибками, что и одношаговые методы. Другими словами, если линейный многоступенчатый метод устойчив к нулю и непротиворечив, то он сходится. И если линейный многоступенчатый метод устойчив к нулю и имеет локальную ошибку , то его глобальная ошибка удовлетворяет .
$\ tau _ {n} = O (h ^ {{p + 1}})$ $e_ {n} = O (h ^ {p})$

Смотрите также

Порядок точности
Численное интегрирование
Численные обыкновенные дифференциальные уравнения
Ошибка усечения

Ноты

Ссылки

Изерлес, Ари (1996), Первый курс численного анализа дифференциальных уравнений , Cambridge University Press , ISBN 978-0-521-55655-2.
Сули, Эндре; Майерс, Дэвид (2003), Введение в численный анализ , Cambridge University Press , ISBN 0521007941.

внешние ссылки

Примечания к ошибкам усечения и методам Рунге-Кутта
Ошибка усечения метода Эйлера

Источник

Локальная и глобальная ошибки дискретизации при численном интегрировании дифференциальных уравнений

последовательностью точек x₀,x₁. в соответствующие моменты времени t₀,t₁. Значения точек должны удоволетворять приближенному равенству

Если специально не оговорено иное, то предполагается, что моменты времени выбираются через равные интервалы с величиной шага h>0, то есть

Аппроксимируем производную в момент времени t_k соотношением

При такой аппроксимации уравнение (1) примет вид:

Формула (2) известна как прямой метод Эйлера.

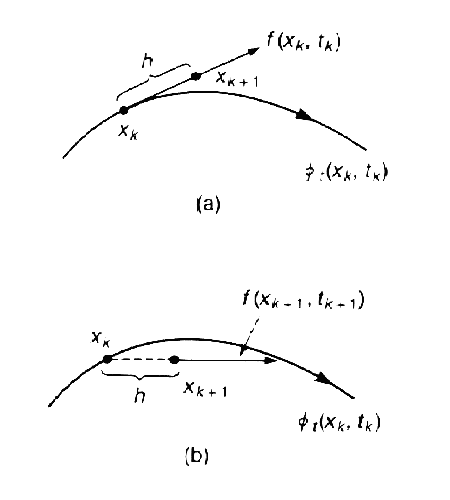
На рис.1(a) показана графическая интерпретация прямого метода Эйлера. На (k+1)-ом шаге векторное поле предполагается (локально) постоянным со значением f(x_k,t_k).

Рис.1 Иллюстрация алгоритмов (а) прямого метода Эйлера, (b) обратного метода Эйлера

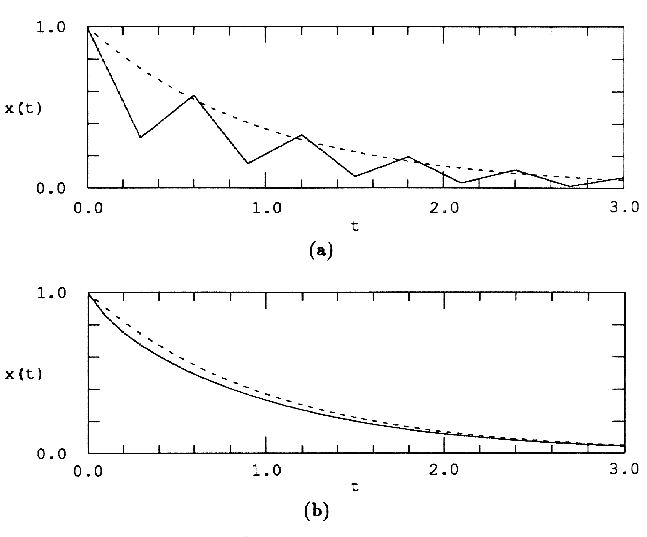
Меньшее значение величины шага h в итоге дает точки аппроксимации чаще и, как демонстрирует рис.2, приводит к большей точности интегрирования, что приобретает математический смысл, поскольку (2) стремится к (1) при h->0.

Рис.2 Влияние величины шага. Уравнение dx/dt=-6x+5t -t интегрируется от x=1 прямым методом Эйлера при h=0.3 (а) и при h=0.1 (b). Точное решение показано штриховой линией.

Обратный метод Эйлера подобен прямому, но есть одно отличие в аппроксимации для производной

Такая аппроксимация дает формулу обратного метода Эйлера:

На рис.1(b) показана геометрическая интерпретация обратного метода Эйлера. На (k+1)-ом шаге векторное поле предполагается (локально) постоянным со значением f(x_k+1,t_k+1).

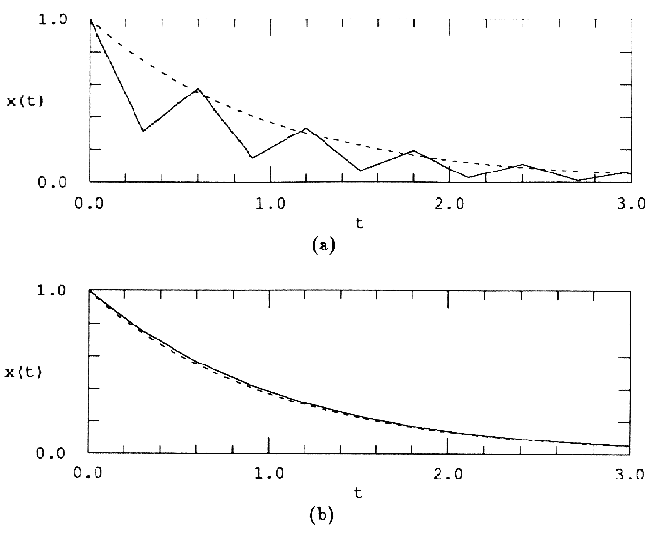
Обратный метод Эйлера — это пример неявного алгоритма интегрирования , где x_k+1 является функцией от самой себя. И напротив, прямой метод Эйлера представляет собой явный алгоритм. В неявных алгоритмах для определения x_k+1 требуются дополнительные вычисления, но они по сравнению с аналогичными прямыми алгоритмами более устойчивы и дают более высокую точность вычислений (см. рис.3). Возможно это обусловлено наличием члена x_k+1 в правой части формулы, что может рассматриваться как вид обратной связи.

Рис.3 Та же система, что и на рис.2 проинтегрирована от x₀=1.0 с h=0.3 (a) прямым методом Эйлера, (b) обратным методом Эйлера. Точное решение показано штриховой линией.

Трапецеидальный алгоритм имеет вид:

Имеется целое семейство уравнений Рунге-Кутта второго порядка. Мы рассмотрим модифицированный алгоритм Эйлера-Коши, заданный соотношением:

Из этой формулы следует, что модифицированный алгоритм Эйлера-Коши включает два этапа. На первом этапе с помощью прямого метода Эйлера происходит перемещение на пол шага вперед к моменту времени (t_k+h/2):

На втором этапе это промежуточное значение используется для аппроксимации векторного поля с помощью итераций Эйлера прямого типа:

Как и в случае алгоритма второго порядка метод Рунге-Кутта четвертого порядка относится к явным алгоритмам. Он использует промежуточные моменты времени для для вычисления состояния в момент времени t_k+1. Следующие формулы определяют алгоритм Рунге-Кутта четвертого порядка:

Для определенных выше алгоритмов на каждом шаге требуется только одна начальная точка x_k. Такие алгоритмы называются одношаговыми. Одношаговые алгоритмы высокого порядка имеют высокую точность, но они не эффективны, если велики затраты на вычисление f. Например, алгоритм Рунге-Кутта четвертого порядка требует на шаге четыре значения f. Кроме того, на текущем шаге не выполняются оценки функций с целью их использования на последующих шагах.
В отличие от одношаговых алгоритмов, многошаговые алгоритмы повторно используют предыдущую информацию о траектории. В m-шаговом алгоритме для определения x_k+1 используют m предыдущих точек x_k, x_k-1. x_k-m+1 и значения f в этих точках. Общая формула m-шагового алгоритма имеет вид

Локальная ошибка определяется как ошибка на шаге алгоритма:

Для m-шаговых алгоритмов предполагается, что предыдущие m точек x_k-i при i=0. m-1 являются точно заданными, т.е.

Ошибка усечения — это локальная ошибка, которая получилась бы в результате выполнения алгоритма на компьютере с бесконечной точностью.
Другими словами, подразумевается, что эта локальная ошибка возникает помимо ошибки округления. Также важно помнить, что для m-шаговых алгоритмов предыдущие m точек x_k. x_k-m+1 предполагаются точно заданными.
Ошибка усечения берет свое название от алгоритмов, основанных на рядах Тейлора (например, Рунге-Кутта). Эти алгоритмы были бы точными, если бы использовались полные (бесконечные) ряды. Ошибка возникает при усечении ряда до конечного числа членов.
Ошибка усечения зависит только от алгоритма. Она не зависит от используемого компьютера и, следовательно, может быть проанализирована. Для алгоритмов Рунге-Кутта K-го порядка, при подходящих условиях, локальная ошибка усечения представляет собой

где «альфа» зависит от K, f и x_k, но не зависит от h. Для многошагового алгоритма K-го порядка локальная ошибка усечения имеет вид

Глобальнае ошибка округления — это простое накопление локальных ошибок округления. Если локальная ошибка составляет «эпсилон», то ошибка округления на единичном интервале будет

Подобно ошибке округления, локальная ошибка усечения также накапливается с каждым шагом. Для одношаговых алгоритмов K-го порядка локальная ошибка усечения составляет

Если пренебречь зависимостью a_k от x_k, то на единичном интервале времени ошибка усечения будет:

Порядок метода интегрирования.

Дата добавления: 2015-06-12 ; просмотров: 3180 ; Нарушение авторских прав

Главный вопрос при использовании любого численного метода состоит в оценке точности приближенных вычислений 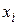. В разд. 3.2.1 уже отмечалось, что существуют два источника погрешности при выполнении шага интегрирования:

· ошибка дискретизации, возникающая в результате замены дифференциального уравнения (3.1) разностной аппроксимацией (3.2);

· ошибка округления, накопившаяся при выполнении арифметических операций.

При этом доминирующей является, как правило, ошибка дискретизации.

Будем считать, что все вычисления проводятся точно. Интуитивно ясно, что при 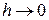ошибка дискретизации также должна стремиться к нулю и это действительно имеет место для любого метода. Однако взаимосвязь скорости уменьшения ошибки от скорости уменьшения для разных методов интегрирования различна.

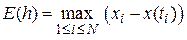
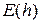
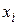
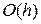
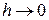
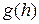
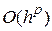
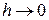
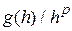
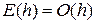
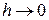
Введем величину , называемую глобальной ошибкой дискретизации. Отметим, что зависит от величины шага, поскольку предполагается, что значения вычисляются при определенном . Воспользуемся также стандартным обозначением для величины, стремящейся к нулю при с той же скоростью, что и . В общем случае будем говорить, что функция равна , если при величина ограничена. Проведя анализ можно показать [23], что для метода Эйлера . Это, обычно, выражают утверждением, что метод Эйлера имеет первый порядок. Практическим следствием этого факта является то, что при уменьшении приближенное решение будет все более точным, и при будет сходиться к точному решению с линейной скоростью по , т.е. при уменьшении шага вдвое ошибка дискретизации уменьшится примерно в 2 раза. Столь медленная сходимость служит препятствием использования простых методов первого порядка.

Очевидно, что повышение порядка метода позволяет повысить точность интегрирования при той же величине шага интегрирования . Способы повышения порядка могут быть различными.

Рассмотрим, например, явный одношаговый метод Хьюна (или метод Рунге – Кутты второго порядка). Он определяется формулой

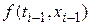
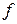
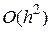
Сравнивая его с методом Эйлера легко заметить, что значение заменено на среднее значений функции , вычисленных в двух различных точках. Данный метод имеет ошибку дискретизации .

Наиболее знаменитым из методов Рунге – Кутты, а возможно и из всех методов численного интегрирования, является классический метод четвертого порядка, задаваемый формулой

где

;

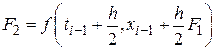
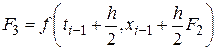
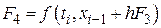
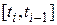
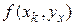
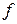
Суть метода в том, что вектор-функция правых частей системы ОДУ определяется не только в узлах сетки, но и в промежуточных точках интервала , а величина в методе Эйлера заменена на взвешенное среднее значений , вычисленных в четырех различных точках.

Как видно, повышение порядка метода связано с повышением затрат на вычисление значений функции 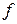. При нелинейной связи между ростом точности метода и объемом вычислений можно ожидать, что для каждой схемы интегрирования существует некоторый оптимальный порядок метода.

Для многошаговых методов порядок напрямую связан с объемом информации, используемой на каждом шаге. В частности, двух и трехшаговые методы Адамса – Бишфорта, задаваемые формулами (3.10) и (3.11) имеют второй и третий порядок, соответственно.

3.2.6. Процедуры численного моделирования
с автоматическим выбором шага

Данный раздел касается не выбора того или иного метода интегрирования, а реализации самой процедуры интегрирования на ЭВМ.

Выше уже отмечалось, что выбор шага интегрирования связан с динамическими свойствами моделируемого объекта. Для явных методов он должен быть меньше минимальной постоянной времени объекта, с тем, чтобы обеспечить устойчивость и позволить моделировать самые высокочастотные составляющие процесса. Неявные методы позволяют использовать больший шаг, но общий характер зависимости остается тем же самым. В то же время, на интервале моделирования характер моделируемых процессов может меняться. Например, в большинстве реальных систем высокочастотные составляющие переходного процесса затухают быстрее, чем низкочастотные, и процесс со временем приобретает более плавный характер. Это наводит на мысль организовать процедуру моделирования таким образом, чтобы шаг интегрирования менялся в процессе работы алгоритма. Там, где решение меняется плавно, можно вести интегрирование с относительно большим шагом. В областях же, где решение изменяется резко, необходимо считать с маленьким шагом. Проблема заключается в том, как определить величину шага, с которым следует начать следующий шаг интегрирования.

На выбор шага, как обычно влияют два фактора – точность и устойчивость. Шаг целесообразно поддерживать таким, чтобы погрешность интегрирования не превышала допустимого значения и величина шага при этом была максимально возможной.

Обычный подход состоит в оценке локальной ошибки дискретизации и, в зависимости от ее величины, уменьшении или увеличении текущего значения шага.

Два простых способа состоят либо в прохождении последнего шага интегрирования с половинным шагом и сравнении двух полученных результатов, либо в использовании двух методов интегрирования, имеющих разный порядок. Оба эти способа требуют дополнительных вычислений значений .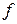

Первый способ реализует правило Рунге [29, 23], при котором ошибка дискретизации определяется по формуле

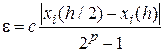
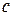
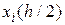
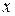
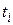
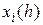
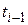
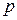
где – некоторая константа;

– значение фазовой переменной , полученной в точке тем же методом, что и , но только за два шага интегрирования от точки , каждый из которых в два раза меньше обычного шага ;

– порядок метода интегрирования.

Для метода Эйлера формула Рунге дает

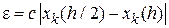
для метода Рунге – Кутты 4-го порядка

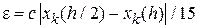
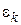
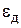
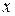
Величина погрешности аппроксимации на каждом шаге не должна превышать допускаемой погрешности . Обычно полагают, что она составляет от 0,01 до 0,001 от текущего значения определяемой фазовой координаты .

При автоматическом выборе шага наиболее популярным является алгоритм «трех зон» [29]:

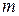
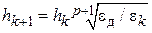
где – коэффициент изменения шага, обычно равный 2, позволяет дискретно менять шаг в процессе интегрирования. Другим вариантом является алгоритм плавного изменения шага интегрирования

где 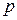– порядок метода интегрирования.

3.2.7. Особенности численного интегрирования
технических систем

Обширный набор методов численного интегрирования, которым обладают современные пакеты моделирования, позволяет эффективно решать самые различные задачи исследования технических систем, но при этом возникает проблема выбора наиболее подходящего метода
и правильного задания его параметров. Очень часто пользователь задает только интервал интегрирования и не обращает внимания на другие опции решателя. При решении простых задач с умеренной точностью такой подход вполне допустим, однако при решении сложных задач неудачный выбор метода либо неправильное задание его параметров может привести к неоправданно большим затратам машинного времени либо, вообще, к невозможности получить правильное решение.

Таким образом, для профессиональной работы с любым моделирующим программным обеспечением пользователь должен обладать некоторыми знаниями о реализованных в нем численных методах
и применимости их к требуемому кругу задач.

Практика показала, что наличие в технических системах объектов различной физической природы приводит к тому, что процессы в них характеризуются разнотемповостью, т.е. наличием быстрых и медленных составляющих движения. Кроме того, возможно одновременное присутствие как монотонных, так и медленно затухающих гармонических составляющих. Свойство системы содержать в своем переходном процессе существенно различные по своим спектральным характеристикам составляющие принято называть жесткостью[27].

Примером жесткой системы может служить робототехническая система, в которой быстрые составляющие связаны с включением тормозных устройств и демпферов, взятием или освобождением груза.

Жесткость часто является следствием избыточности модели, связанной с введением в нее малозначащих составляющих. Однако на этапе предварительных исследований такой избыточности трудно избежать. С другой стороны, часто жесткость имеет принципиальный характер и неучет быстрых движений может привести к неадекватности модели.

Жесткие системы требуют особого подхода к процедуре численного интегрирования, так как наличие быстрых и медленных составляющих в спектре движений предъявляет совершенно разные требования к методам интегрирования. Необходимо уметь оценивать характеристики жесткости и использовать эти оценки для выбора или настройки процедуры интегрирования.

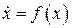
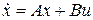
Пусть исследуемая система является линейной и может быть описана матричными уравнениями состояния

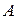
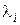
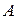
Матрица называется матрицей состояния или матрицей Якоби. Собственные значения матрицы определяют устойчивость и характер переходных процессов в исследуемой системе.

Составляющие движения (обычно называемые модами), связанные с собственными значениями 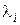, лежащими в левой полуплоскости далеко от мнимой оси, соответствуют быстро протекающим и, обычно, быстро затухающим процессам в системе. Собственные значения малые по модулю, лежащие близко к мнимой оси, определяют основное движение системы.

Исходя из распределения собственных значений матрицы Якоби на комплексной плоскости, можно назвать жесткой системой ОДУ такую систему, у которой матрица Якоби имеет различающиеся на несколько порядков максимальное и минимальное по модулю собственные значения.

Оценкой жесткости системы ОДУ обычно считается число обусловленности матрицы Якоби

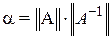
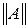
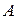
где – норма матрицы .

Для целей управления процессом моделирования под числом обусловленности чаще понимают отношение модулей максимального и минимального собственных значений матрицы

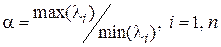
К жестким относят системы ОДУ, у которых 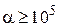. Их также называют плохо обусловленными, хотя, чаще, этот термин относится к системам алгебраических уравнений.

Для нелинейной системы матрицу Якоби можно определить после ее линеаризации в рабочей точке, как это описано в разд. 3.2.2.

Элементами матрицы Якоби являются частные производные от
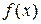
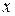
нелинейной вектор функции по переменным состояния системы . Для нелинейных систем жесткость, в общем случае, не является постоянной величиной и меняется в процессе интегрирования.

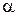
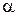
При умеренных значениях числа обусловленности (нежесткие задачи) интегрирование обычно выполняется традиционными явными методами и требует небольших вычислительных затрат. Трудности возникают при больших значениях , когда для получения правильного решения бывает необходимо выбирать очень малый шаг интегрирования.

При моделировании такой системы в начальный момент времени инициируются все, или большинство мод, как быстрых так и медленных. Однако через некоторое время быстрые моды затухают и решение сходится к медленному движению.

Исследователя могут интересовать и быстрые и медленные составляющие движения. В этом случае, целесообразно использование явных методов в сочетании с эффективной процедурой изменения величины шага интегрирования в зависимости от состояния моделируемой системы. Это позволит достаточно точно смоделировать быстрые движения и избежать чрезмерных затрат машинного времени, так как явные методы требуют минимальных временных затрат на каждый шаг интегрирования.

Если исследователя мало интересуют быстро затухающие движения, но отбросить их на этапе формирования модели у него нет достаточных оснований, предпочтительными являются неявные методы, которые в сумме способны дать меньшее время интегрирования при удовлетворительном качестве. Такие методы подавляют все составляющие решения, соответствующие большим по модулю собственным значениям (если только шаг не выбран очень малым).

Изложенные рекомендации по выбору методов интегрирования жестких систем предполагают, что исследователь хорошо знаком с особенностями объекта. Например, если речь идет о проектировании или оптимизации системы управления некоторого хорошо изученного объекта, то выбор метода интегрирования может быть проведен путем сравнения нескольких вариантов. Если же объект недостаточно исследован, то эффективными могут оказаться процедуры, обладающие элементами адаптации к особенностям объекта.

Некоторые современные моделирующие программные комплексы содержат наборы методов, расчетные формулы которых настраиваются на решаемую задачу, используя для этого оценки некоторых параметров, обычно, собственных значений якобиана. Особенно перспективными считаются явные адаптивные методы, не требующие при своей реализации вычисления матрицы Якоби и решения алгебраических уравнений [27]. Такие методы есть, в частности, среди решателей ОДУ программного комплекса «МВТУ».

3.3. Моделирование гибридных (событийно-управляемых)
технических систем

Технические системы, по определению, относятся к сложным техническим системам. Одной из особенностей этих систем является то, что поведение многих из них определяется событиями, происходящими как внутри этих систем, так и в окружающей среде. Соответственно, они обладают как непрерывной, так и дискретной динамикой, находящимися в сложном взаимодействии. Подобные системы часто называют гибридными системами [20, 21]. В отечественной литературе также используются синонимы – непрерывно-дискретные, системы с переменной структурой, реактивные, событийно-управляемые.

Примерами гибридных технических систем могут служить системы управления, используемые в промышленности (автоматизированные технологические процессы), в быту (сложные бытовые приборы), в военной области (высокотехнологичные виды вооружений), в сфере космонавтики, транспорта и связи.

Гибридное поведение может быть связано со следующими факторами:

· совместное функционирование непрерывных и дискретных объектов. Подобное поведение является типовым для непрерывных объектов (механических, гидравлических и т.д.) управляемых цифровыми регуляторами, например, для ИСЗ. Управление может формироваться как в фиксированные моменты времени, так и асинхронно, в зависимости от изменения фазовых координат объекта;

· гибридное поведение, связанное с особенностями физических процессов в непрерывных объектах. Например, учет в моделях механических систем таких эффектов как сухое трение или люфт может быть реализован в виде некоторых логических условий, меняющих модель системы;

· гибридное поведение, обусловленное изменением состава системы.

Все перечисленные факторы являются типичными для технических систем.

Учет дискретной динамики приводит к тому, что фазовое пространство гибридных систем разбивается на области с различным поведением, при этом фазовая траектория в зависимости от происходящих событий оказывается то в одной области фазового пространства, то в другой. Достижение фазовой траекторией границы областей является событием, приводящим к смене поведения.

События могут быть как внутренними, так и внешними. Например, при моделировании робота-манипулятора внутренние события могут быть связаны с типовыми нелинейностями механической части, а внешние – являться следствием взаимодействия со средой.

Очевидной и удобной моделью систем, управляемых событиями, является конечно-автоматная модель. Например, можно использовать конечный автомат, чтобы описать автоматическую передачу автомобиля. Передача имеет ряд состояний: парковка, нейтраль, движение, реверс и т.д. Система переходит из одного состояния в другое, когда водитель перемещает рычаг из одной позиции в другую, например, из позиции парковка в нейтральное положение.

При всей ее простоте и наглядности конечно-автоматная модель достаточно строга и формальна. Однако классическое графическое представление конечных автоматов обладает рядом недостатков. Главным недостатком является отсутствие понятия времени, что предполагает статичность состояний. Другие недостатки – отсутствие иерархии состояний, обобщения переходов, средств выражения прерываний
и продолжения нормальной работы после их обработки [11].

Для полноценного компьютерного моделирования физики процессов необходимо обеспечить сопряжение непрерывной составляющей поведения системы и логики работы управляющих ей устройств (дискретная компонента). Математический аппарат описания в данном случае – это система уравнений, но не дифференциальных, а дифференциально-алгебраическо-логических, для которых отсутствует стройная теория и единый подход.

В настоящее время для моделирования систем, управляемых событиями, широко используется предложенный Д. Харелом [7] визуальный формализм – Statechart (карты состояний и переходов). Карты состояния были разработаны применительно к моделированию дискретных систем, однако они могут служить хорошей основой и для моделирования гибридных систем, т.е. с их помощью можно описать поведение системы как в дискретном, так и в непрерывном времени [8]. Основные
неграфические компоненты таких диаграмм – это событие и действие, основные графические компоненты – состояние и переход.

Событие – нечто, происходящее вне рассматриваемой системы, возможно требующее некоторых ответных действий. События могут быть вызваны поступлением некоторых данных или некоторых задающих сигналов со стороны человека или некоторой другой части системы. События считаются мгновенными.

Действия –это реакции моделируемой системы на события. Подобно событиям, действия принято считать мгновенными.

Состояние –условия, в которых моделируемая система пребывает некоторое время, в течение которого она ведет себя одинаковым образом. В диаграмме переходов состояния представлены прямоугольными полями со скругленными углами.

Переход – изменение состояния, обычно вызываемое некоторым событием. Как правило, состояние соответствует промежутку времени между двумя такими событиями. Переходы показываются в диаграммах переходов линиями со стрелками, указывающими направление перехода. Каждому переходу могут быть сопоставлены условия, при выполнении которых переход осуществляется.

С каждым переходом и каждым состоянием могут быть соотнесены некоторые действия. Действия могут дополнительно обозначаться как действия, выполняемые однократно при входе в состояние; действия, выполняемые многократно внутри некоторого состояния; действия, выполняемые однократно при выходе из состояния.

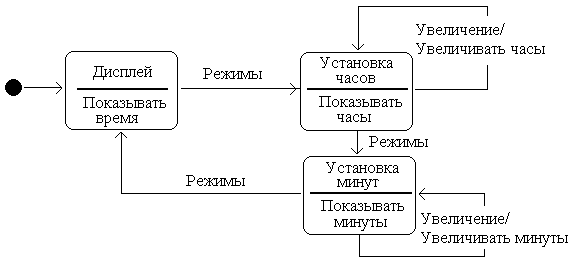
В [25] качестве примера простой дискретной системы (частного случая гибридной системы) рассмотрена диаграмма (карта) состояний и переходов цифровых часов, представленная на рис. 3.4.

Рис. 3.4. Диаграмма состояний и переходов цифровых часов

На часах имеется две кнопки: Кнопка Режима и Кнопка Увеличения. Нажатие любой из них генерирует событие, которое может вызывать переход из одного состояния в другое. Имеются три состояния: Дисплей, Установка Часов и Установка Минут. Состояние Дисплей – начальное состояние (что обозначается стрелкой, направленной от блока перехода по умолчанию в виде черного круга). Нажатие кнопки Режимы в состоянии Дисплей вызывает появление события Режимы и переход в состояние Установка часов. В состоянии Установка Часов, событие Режимы вызывает переход к состоянию Установка Минут, тогда как событие Увеличение увеличивает текущее время (число часов), которое отображается на экране, причем это происходит без изменения состояния. Каждому состоянию часов соответствует действие, записанное ниже горизонтальной линии. Оно начинает выполняться после того, как переход в это состояние произошел.

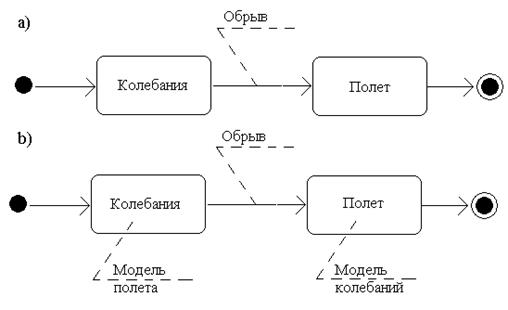
В [21] в качестве примера рассмотрена модель, которая описывает поведение маятника в виде шарика на нити, у которого в некоторый момент времени (событие «Обрыв») рвется нить. У этой модели два состояния – «Колебания» и «Полет». Оба описываются системами дифференциальных уравнений, каждая из которых является динамической системой. Карта поведений представляет собой совокупность состояний и переходов. В любой момент времени только одно состояние является текущим.

На рис. 3.5, а показана карта состояний обрывающегося маятника, на которой кроме двух обычных состояний помещены два особых состояния – начальное и конечное.

Рис. 3.5. Карта состояний и карта поведений обрывающегося маятника

В общем случае для состояния могут быть определены входные воздействия, выходные воздействия, а также локальная деятельность. Последовательность входных воздействий выполняется при каждом входе в состояние, последовательность выходных действий – при каждом выходе. Локальные действия выполняются все время, пока состояние является текущим.

Рис. 3.5, а отражает качественное поведение маятника. Для получения количественной картины необходимо связать с каждым состоянием локальное действие, в частности, интегрирование систем уравнений «Модель колебаний» и «Модель полета», как это сделано на рис. 3.5, b. Карта состояний, дополненная моделями состояний, названа в [20] картой поведения гибридной системы.

Одна из доступных реализаций концепции гибридного моделирования реализована в пакете StateFlow среды MATLAB, который кратко описан в главе 5. Также следует выделить отечественный пакет Model Vision Studium, ориентированный на моделирование сложных поведений [19].

Глава 4
Автоматизированное моделирование
технических объектов

Исторический экскурс. Необходимость автоматизации процессов моделирования технических объектов возникла практически одновременно с появлением вычислительных машин. Однако, исторически, разные этапы моделирования автоматизировались в разное время. Первым этапом следует считать создание библиотек численных методов исследования систем. Сами численные методы были разработаны задолго до появления ЭВМ и предназначались, прежде всего, для решения задач небесной механики. Так как первоначально расчеты велись вручную, алгоритмы методов были хорошо отлажены и оптимизированы. К концу 70-х годов прошлого столетия были созданы специализированные коллекции численных методов практически для всех областей численного анализа.

Дальнейшие шаги на пути автоматизации моделирования были связаны с разработкой систем автоматизированного проектирования (САПР) и систем автоматизации вычислительного эксперимента – пакетов прикладных программ. Автоматизации подлежали стандартные расчеты и оформление результатов экспериментов. Как правило, эти системы создавались под определенную предметную область, прежде всего, в наукоемких отраслях (космическая, авиация и т.д.). Для создания большинства пакетов прикладных программ для численных расчетов использовался язык Фортран, хорошо приспособленный именно для этих целей. Подобные пакеты создавались годами, их модификация и развитие требовали специальных знаний в предметной области, численных методах и программировании.

Наиболее трудно автоматизируемым этапом явился процесс построения модели. Ручная подготовка модели сложного технического объекта связана с большим объемом преобразований, в которых легко допустить ошибку. Использование систем автоматизации моделирования (САМ) позволило существенно повысить производительность труда, снизить число ошибок и, во многих случаях, исключить необходимость привлечение программистов к решению конкретных предметных задач. Опираясь на САМ, специалист в предметной (прикладной) области может самостоятельно создавать достаточно сложные модели.

При использовании системы автоматизированного моделирования исследователь формулирует математическую модель исследуемой системы на формальном входном языке моделирования. На ранних этапах развития САМ, когда отсутствовали возможности прямого изображения структуры модели на экране монитора, использовались методы кодирования структурной информации [1, 6]. Программа модели представляла собой последовательность вызовов процедур, каждая из которых являлась моделью структурного компонента. После связывания с модулями исполняющей системы пакета моделирования список компонентов преобразовывался в независимую исполняемую программу.

В современных системах автоматизированного моделирования, исходя из соображений удобства восприятия человеком, используются, как правило, графические средства задания исходной информации о модели. Переход к изображению структуры системы на экране монитора позволил исключить этап ручного кодирования схемы, однако потребовал разработки нового принципа организации самого процесса численных расчетов – принципа Data Flow, или принципа потока данных.

Можно отметить следующие факторы, способствующие внедрению систем автоматизированного моделирования:

· трудоемкость получения математической модели сложных технических объектов, связанная с опасностью совершить ошибку в многочисленных преобразованиях модельных выражений;

· необходимость многовариантного моделирования, при котором необходимо иметь для одного объекта несколько моделей, отличающихся по сложности;

· желание иметь дружественный интерфейс с программой и возможность оперативно вносить изменения в модель, что проще всего на основе использования графических языков задания исходной информации.

4.1. Особенности современных систем
автоматизированного моделирования

Современные профессиональные САМ имеют следующие отличительные черты [31]:

· поддержка иерархического проектирования как сверху – вниз, так и снизу – вверх, за счет реализации многоуровневого моделирования и метода локальной детализации модели;

· компонентное моделирование на основе использования библиотек, содержащих большое число графических и функциональных описаний компонентов, причем эти библиотеки открыты для добавления в них новых описаний, которые может сделать сам пользователь;

· графический пользовательский интерфейс, сочетающий графические средства формирования визуального образа исследуемого технического устройства с автоматической генерацией модели всей схемы по ее структурному описанию;

· наличие интерактивной рабочей среды проектирования (управляющей оболочки, монитора), т.е. специальной программы, из которой можно запускать все или большинство других программ пакета, не обращаясь к услугам штатной операционной системы;

· наличие в современных САПР и САМ постпроцессоров моделирования, что позволяет не только просматривать в удобной для пользователя форме результаты моделирования, но и обрабатывать эти результаты;

· наличие встроенных средств численного моделирования рабочего процесса в режиме реального времени или в режиме масштабирования модельного времени;

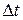
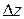
· реализация механизмов продвижения модельного времени, основанных как на принципе , так и на принципе ;

· интегрируемость с другими пакетами аналогичного назначения, которая обеспечивается соответствующими программами – конверторами, позволяющими импортировать и экспортировать данные из одной системы в другую;

· наличие средств, обеспечивающие формирование виртуальных аналогов измерительно-управляющей аппаратуры.

Если САМ предназначена для решения исследовательских задач, то к перечисленным качествам добавляются возможности активного вычислительного эксперимента [21]. В частности:

· визуализация результатов во время эксперимента;

· возможность интерактивного вмешательства в ход моделирования;

· возможность использования 2D и 3D анимации.

4.2. Иерархическое проектирование
и многоуровневое моделирование технических систем

С точки зрения инженера, основное назначение моделирования – поддержка процедур проектирования технических объектов и систем. Процедуры проектирования работают с моделями объектов реального мира и должны быть подстроены под их свойства.

Сложные системы имеют, как правило, иерархическую структуру. Естественные возможности человека позволяют оперативно обрабатывать не более 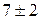единиц информации одновременно. В процессе проектирования исследователю удобно сосредотачиваться сначала на поведении отдельных компонентов системы, а затем на их взаимодействии [21]. При необходимости модели компонентов могут детализироваться или, наоборот, укрупняться.

Такой подход, известный как иерархическое проектирование [21, 31], является типовым при разработке сложных технических объектов и заключается в разбиении исходной задачи на подзадачи.

В процессе проектирования сложной системы формируются определенные представления о системе, отражающие ее существенные свойства с той или иной степенью подробности. В этих представлениях можно выделить составные части – уровни проектирования. В один уровень, как правило, включаются представления, имеющие общую физическую основу и допускающие для своего описания использование одного и того же математического аппарата. Уровни проектирования можно выделять по степени подробности, с какой отражаются свойства проектируемого объекта. Тогда их называют горизонтальными (иерархическими) уровнями проектирования.

В результате такого подхода объект проектирования декомпозируется на фрагменты (подсхемы) и проектирование каждого из них ведется в определенном смысле самостоятельно. На каждом уровне иерархии этот принцип применяется вновь, что позволяет заменить решение одной сложной задачи многократным решением задач меньшей размерности.

При иерархическом проектировании разработчику достаточно держать в поле зрения лишь один фрагмент объекта. Остальные части лишь имитируют внешнюю среду, т.е. взаимодействие проектируемого фрагмента с другими частями объекта.

Использование принципа иерархического проектирования позволяет ограничить текущую сложность проекта на приемлемом уровне, за счет того, что в каждый момент времени разработчик имеет дело только с двумя смежными уровнями декомпозиции объекта – структурным описанием проектируемого в данный момент фрагмента и функциональным описанием внешней среды.

Инструментальной поддержкой иерархического проектирования является многоуровневое моделирование.При многоуровневом моделировании различные фрагменты представляются на различных уровнях иерархии, т.е. с разной степенью детальности. Например, проектируемая в настоящий момент времени часть объекта раскрыта до уровня элементарных динамических компонентов и имитируется структурной моделью, а остальные фрагменты представлены на соседнем более высоком уровне в виде функциональных моделей.

Завершив проектирование одного фрагмента, разработчик может свернуть его в функциональный блок и перейти к детальной модели следующего фрагмента, с которым он собирается работать. Эта процедура повторяется многократно, на разных уровнях иерархии проектируемого объекта. Достоинством такого подхода является то, что в поле зрения разработчика находится в каждый момент времени минимум
необходимой информации, не перегруженной лишними деталями. Описанный метод проектирования называется методом локальной детализации объекта.

Программной поддержкой многоуровневого моделирования, реализованной в большинстве языков графического программирования, является процедура инкапсуляции, которая позволяет «свернуть» любой смысловой фрагмент графического представления в единичный блок. Кроме того, что инкапсуляция служит основой получения иерархически структурированных моделей, она так же позволяет расширить библиотеку базовых блоков блоками пользователя, которые, впоследствии, можно многократно использовать (например, типовые динамические звенья).

Такой возможностью обладает, в частности, пакет LabVIEW, пакет Simulink и основанные на нем пакеты SimMechanics и SimPower. Пакеты IDEF-моделирования (ERWIN, BPWIN) принципиально основаны на многоуровневом изображении объектов.

4.4. Архитектура программ
автоматизированного моделирования

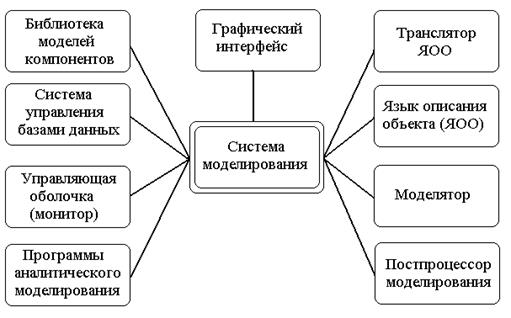
Существующие инструментальные средства автоматизированного моделирования могут относиться к разным предметным областям и существенно различаться по своим возможностям, но их модульные структуры мало отличаются друг от друга. На рис. 4.1 представлена типовая структура современного пакета визуального компонентного моделирования. Рассмотрим более детально назначение и особенности основных элементов этой структуры.

4.4.1. Графический интерфейс программ математического
моделирования динамических систем

Графический интерфейс является в настоящее время стандартным компонентом современной САМ. Он создает дружественный интерфейс между пользователем и программой, дает возможность оперировать с графическими образами вместо аналитических выражений. Это значительно облегчает работу в САМ и снижает вероятность ошибок при вводе информации о системе.

Рис. 4.1. Модульная структура
системы автоматизированного моделирования

Графический пользовательский интерфейс позволяет вводить информацию об исследуемой системе путем «рисования» на экране монитора проектируемой схемы в виде, понятном широкому кругу специалистов. Формой графического представления информации о моделируемой системе могут быть [16]:

· операторно-структурные схемы, принятые в ТАУ;

· функциональные и принципиальные схемы различных физических устройств;

· кинематические схемы механизмов;

· блок-схемы алгоритмов и другие графические модели.

Однако простым «рисованием» роль графического интерфейса не ограничивается. Задачами графического интерфейса, кроме того, могут быть [16]:

· контроль за соблюдением некоторых правил в процессе создания графического изображения на экране монитора (обычно накладываются ограничения на способы соединения компонентов и т.п.);

· преобразование информации о схеме в команды для моделирующей программы (моделятора);

· контроль за процессом моделирования, визуализация результатов моделирования.

П.5. Локальные и глобальные погрешности одношаговых методов решения ДУ

(метода Эйлера и методов Рунге-Кутта 2го, 4го порядка).

Теорема 6.1:

Если локальная погрешность метода , то глобальная .

как и при численном интегрировании, при переходе от локальной погрешности к глобальной, точность метода уменьшается на порядок. (6.8):

Методы	Локальная	Глобальная
Эйлер	const*h 2	const*h
Р.–К. 2го порядка по времени	const*h 3	const*h 2
Р.–К. 2го порядка по производной	const*h 3	const*h 2
Р.–К. 4го порядка	const*h 5	const*h 4

Как и при численном интегрировании, порядок метода – степень h в глобальной погрешности.

П.6. Многошаговые методы решения ДУ и СДУ.

Все рассмотренные ранее методы – одношаговые, т.к. для нахождения мы использовали только лишь значения с предыдущего шага. В многошаговых методах для нахождения используется не только лишь одно , но и предыдущие значения.

В k-шаговом методе используются значения с k предыдущих шагов.

Многошаговые методы, как правило, дают лучший результат, чем одношаговые, в силу того, что более устойчивы к вычислительным погрешностям. Многошаговых методов много, самый распространенный среди них – метод Милна.

Формулы метода Милна:

(6.9)

Метод Милна – 4х шаговый (т.к. использует 4 предыдущих значения) и имеет 4-ый порядок точности. Перед применением метода Милна нам надо знать 4y, следовательно, необходимо сделать хотя бы 3 шага каким-нибудь одношаговым методом.

П.7. Оценка погрешности решения ДУ и СДУ методом двойного пересчета. Коррекция решения.

Используя такую же идею, как и в численном интегрировании, находим решение ДУ на [a,b] дважды с шагом h и с шагом h/2. Получим следующую картину:

Сравниваем попарно, если расхождение между для метода 2го порядка, для метода 4го порядка, то в качестве точного решения берём . Если же точность не достигнута, то шаг h уменьшаем вдвое и т.д., пока она не будет достигнута.

Метод двойного пересчёта при решении ДУ и СДУ практически единственный имеет возможность для оценки погрешностей, так как иные формулы очень сложны и требуют оценок различных производных.

Как и при ЧИ, при решении ДУ и СДУ после 2го пересчёта в качестве точного решения выгодно брать не , а .

— для второго порядка

Метод двойного пересчёта применим не только лишь при ЧИ, при решении ДУ и СДУ, но и при решении других численных методов.

П.7. Краевые задачи для дифференциальных уравнений.

Выше рассматривалось решение ДУ и СДУ с начальными условиями, заданными в одной точке, так называемую задачу Коши, но для ДУ высших порядков часто бывает необходимо решить не з. Коши, а так называемую краевую задачу, т.е. начальные условия, которые заданы в разных точках.

Рассмотрим простейшую краевую задачу для ДУ 2го порядка:

(6.10)

А мы умеем решать:

(6.11),

В (6.11) нам известно , поэтому для решения задачи (6.10) мы будем подбирать в (6.11), с тем, чтобы у(b) = у₁

Метод стрельб

После пристрелки и определения интервала [a,b],

где идёт смена знака, запускаем МПД или МХ.

На практике это выглядит так, как будто мы

решаем уравнение , где возвращает

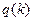
решение задачи Коши (6.11) в точке b при

П.9. Что делать, если ДУ не может быть разрешено относительно старшей производной?

Так как ДУ не может быть решено относительно старшей производной, то тогда на каждом шаге решаем нелинейное уравнение относительно y ( n) (все остальные неизвестные y,y’,y”,…, y ( n-1) -к этому моменту уже известны).

Решать уравнение относительно старшей производной любым методом(Хорд, МПД, Ньютона).

Замечание:

Таким образом, если ДУ не разрешается относительно старшей производной, то у нас возникает дополнительный цикл (самый внутренний) при написании программы.

Типы и классификация ошибок численного интегрирования

Современный численный метод одновременно с решением задачи Коши должен вычислять значение или оценку ошибки. Первый такой метод был предложен Мсрсоном в 1959 году (метод Рунгс-Кутта-Мсрсона). Теоретически таких методов описано достаточно много. Однако хороших практических реализаций в виде алгоритмов или прикладных программ мало. Рассмотрим причины возникновения ошибки при решении задачи Коши. Эта ошибка складывается из следующих компонент.

1. Неустранимая погрешность исходных данных. На нее повлиять нельзя, но учесть необходимо.
2. Локальная ошибка метода. Ее величина определяется порядком р используемого метода и зависит от шага: е,

()(h p *’). Эта ошибка связана с отбрасыванием остатка ряда при разложении точного решения в ряд по шагу при условии, что вес исходные данные заданы точно и вычисления проводятся без ошибок округления.

3. Ошибка переноса, которая возникает из-за того, что ошибка, сделанная на предыдущем шаге, переносится на следующий шаг с каким- то коэффициентом.

4. Ошибка округления, сопровождающая любые расчеты. Она возникает как при выполнении арифметических операций, так и при использовании алгоритмов вычисления значений многих элементарных функций (тригонометрических, показательных и других).

Если производить расчет на малом отрезке интегрирования, то ошибкой округления можно пренебречь, и преобладающей становится ошибка метода. Но когда количество шагов велико, ошибки округления накапливаются и становятся преобладающими. Экспериментально устаО а

количестве шагов взаимодействуют, в результате возникает общая ошибка, накопленная на веем отрезке интегрирования при применении данного метода. Эта общая ошибка ?_г называется глобальной ошибкой. Известно, что при интегрировании на отрезке |0; Т|

Здесь множитель Т)(Т) зависит только от вида функции f(x) и нс зависит от шага интегрирования. Соотношение (7.9) называют правилом Рунге.

Общая ошибка ?у, порожденная всеми составляющими, сеть их сумма (рис. 7.1). Существует оптимальное значение шага /Г, обеспечивающее наименьшую суммарную ошибку. В случае, изображенном на рис. 7.1, отклонение от этого оптимального значения нс вызывает силь-

„ _ , „ , ного изменения ошибки. Возможно, однако, си-

Рнс.7.1. Суммарная ошибка

численного интегрирования туация, когда график суммарной ошибки столь крут, что даже малое изменение шага вызывает резкий рост суммарной ошибки. Такая ситуация характеризует вычислительную неустойчивость процесса интегрирования.

Полученную в результате интегрирования ошибку нужно уметь оценивать. Кроме того, полезно иметь возможность сознательно так выбирать шаг интегрирования, чтобы влиять на величину ошибки.

Наиболее популярный метод вычисления локальной ошибки основан на разложении решения в ряд по шагу. Если используется метод порядка р. то остаток ряда начинается с члена, содержащего

Очевидно, именно этот член и характеризует величину ошибки. Значит, следует оценить значение величины R. Будем считать, что при малом /| на протяжении шага R = const. Пусть на некотором шаге с номером г выбрана точка t е [t_r‘,t_nl]. Тогда x(t’) — точное, а х*/, — вычисленное при интегрировании с шагом /; значение искомой функции. Можно считать, что на шаге

Теперь разобьем шаг на два, длины —. и вычислим то же значение,

выполнив два шага интегрирования. Будем считать, что величина R при этом нс изменилась. Получим:

Вычитая уравнения, можно получить

И можно считать, что при интегрировании с постоянным шагом И верно соотношение

Таким образом, схема выбора величины /г на шаге для достижения заданной точности Очакова:

1. при известном х, с шагом /г вычислить т_г+/;

источники:

http://life-prog.ru/2_14935_poryadok-metoda-integrirovaniya.html

http://megalektsii.ru/s20945t2.html

http://bstudy.net/718789/ekonomika/tipy_klassifikatsiya_oshibok_chislennogo_integrirovaniya

Источник

Ошибка метода Эйлера

Представленный
метод аппроксимации решения задачи
Коши называется разностным. Решение
представляет собой совокупность
отдельных точек, называемых узловыми.

При
использовании разностных методов
существует два источника ошибок: ошибка
дискретизации, возникающая в результаты
замены дифференциального уравнения
разностной аппроксимацией (2.5), и ошибка
округления, накопившаяся при выполнении
арифметических операций. Будем считать,
что значения

вычисляются точно, так что погрешности
обусловлены только ошибкой дискретизации.
Введем величину, равную наибольшему
отклонению аппроксимации от точного
решения на отрезке

(3.1)

называемую
глобальной
ошибкой дискретизации
(иногда эту величину называют глобальной
ошибкой усечения).
Отметим, что

зависит от величины шага

,
поскольку предполагается, что приближения

вычисляют при заданном значении

.
Интуитивно ожидаем, что при уменьшении

ошибка дискретизации будет убывать и,
в частности, при стремлении

к нулю, так же будет стремиться к нулю.

Теорема
(ошибка дискретизации метода Эйлера).
Если функция

имеет ограниченную частную производную
по второй переменной и если решение
задачи Коши имеет ограниченную вторую
производную, то глобальная ошибка
дискретизации метода Эйлера

.

Порядок
метода численного интегрирования
показывает, от какой степени шага зависит
величина ошибки.

Локальная
(или шаговая)
ошибка метода – это ошибка, совершаемая
на одном шаге. Очевидно, что от шага к
шагу, т. е. при многократном применении
формулы метода, возможно наложение
ошибок. За

шагов, т. е. в точке

,
образуется глобальная
ошибка.

Порядок
глобальной ошибки (относительно шага

)
на единицу ниже, чем порядок локальной
ошибки, а порядком глобальной ошибки и
определяется порядок соответствующего
численного процесса решения задачи
Коши.

Глобальная
ошибка метода Эйлера есть

,
т. е. данный метод имеет первый порядок.
Иными словами, размер шага и ошибка для
метода Эйлера связаны линейно. Практическим
следствием этого факта является ожидание
того, что при уменьшении

приближенное решение будет все более
точным и при стремлении

к нулю будет стремиться к точному решению
с линейной скоростью

;
т.е. ожидаем, что при уменьшении шага

вдвое ошибка уменьшится примерно в два
раза. Такое поведение ошибки демонстрируется
на следующем примере.

Поскольку
в методе Эйлера ошибка достаточно велика
и от шага к шагу накапливается, а точность
пропорциональна количеству вычислений,
то метод Эйлера обычно применяют для
грубых расчетов, для оценки поведения
системы в принципе. Для точных
количественных расчетов применяют
более точные методы.

Метод Хьюна

Следующий
подход представляет новую идею построения
алгоритмов решения задачи Коши. Пусть

на
отрезке

с начальным условием

Для
получения решения в точке

,
можем воспользоваться теоремой о
вычислнии определенного интеграла:

где
первообразная от

является
искомой функцией

.
Если разрешить уравнение последнее
уравнение относительно

,
получим

Теперь
можно применить численные методы
нахождения интеграла. Воспользуемся
методом трапеций с шагом

,
получим:

Правая
часть формулы включает в себя еще не
найденное значение

.
Для его нахождения воспользуемся методом
Эйлера. Получим конечную формулу,
именуемую методом
Хьюна (синонимы:
метод
Хойна,
метод
Эйлера-Коши):

Продолжая
процесс, получим последовательность
точек, аппроксимирующих кривую решения

.
Метод Хьюна относится к классу методов
прогноза-коррекции. На каждом шаге метод
Эйлера используется для предсказания,
а метод трапеций для уточнения конечного
значения. Общие формулы для шага метода
Хьюна:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Definitions[edit]

Local truncation error[edit]

Global truncation error[edit]

Relationship between local and global truncation errors[edit]

Extension to linear multistep methods[edit]

See also[edit]

Notes[edit]

References[edit]

External links[edit]

Содержание

Неформальное геометрическое описание

Пример

Использование размера шага, равного 1 (h = 1)

пример кода MATLAB

Пример кода R

Использование других размеров шага

Вывод