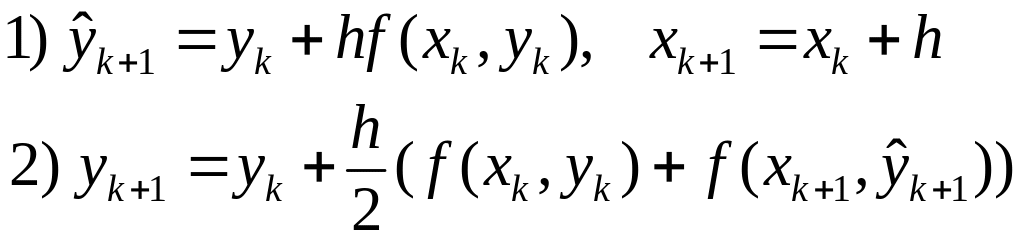Локальная и глобальная ошибка

Ошибка метода Эйлера

Представленный
метод аппроксимации решения задачи
Коши называется разностным. Решение
представляет собой совокупность
отдельных точек, называемых узловыми.

При
использовании разностных методов
существует два источника ошибок: ошибка
дискретизации, возникающая в результаты
замены дифференциального уравнения
разностной аппроксимацией (2.5), и ошибка
округления, накопившаяся при выполнении
арифметических операций. Будем считать,
что значения

вычисляются точно, так что погрешности
обусловлены только ошибкой дискретизации.
Введем величину, равную наибольшему
отклонению аппроксимации от точного
решения на отрезке

(3.1)

называемую
глобальной
ошибкой дискретизации
(иногда эту величину называют глобальной
ошибкой усечения).
Отметим, что

зависит от величины шага

,
поскольку предполагается, что приближения

вычисляют при заданном значении

.
Интуитивно ожидаем, что при уменьшении

ошибка дискретизации будет убывать и,
в частности, при стремлении

к нулю, так же будет стремиться к нулю.

Теорема
(ошибка дискретизации метода Эйлера).
Если функция

имеет ограниченную частную производную
по второй переменной и если решение
задачи Коши имеет ограниченную вторую
производную, то глобальная ошибка
дискретизации метода Эйлера

.

Порядок
метода численного интегрирования
показывает, от какой степени шага зависит
величина ошибки.

Локальная
(или шаговая)
ошибка метода – это ошибка, совершаемая
на одном шаге. Очевидно, что от шага к
шагу, т. е. при многократном применении
формулы метода, возможно наложение
ошибок. За

шагов, т. е. в точке

,
образуется глобальная
ошибка.

Порядок
глобальной ошибки (относительно шага

)
на единицу ниже, чем порядок локальной
ошибки, а порядком глобальной ошибки и
определяется порядок соответствующего
численного процесса решения задачи
Коши.

Глобальная
ошибка метода Эйлера есть

,
т. е. данный метод имеет первый порядок.
Иными словами, размер шага и ошибка для
метода Эйлера связаны линейно. Практическим
следствием этого факта является ожидание
того, что при уменьшении

приближенное решение будет все более
точным и при стремлении

к нулю будет стремиться к точному решению
с линейной скоростью

;
т.е. ожидаем, что при уменьшении шага

вдвое ошибка уменьшится примерно в два
раза. Такое поведение ошибки демонстрируется
на следующем примере.

Поскольку
в методе Эйлера ошибка достаточно велика
и от шага к шагу накапливается, а точность
пропорциональна количеству вычислений,
то метод Эйлера обычно применяют для
грубых расчетов, для оценки поведения
системы в принципе. Для точных
количественных расчетов применяют
более точные методы.

Метод Хьюна

Следующий
подход представляет новую идею построения
алгоритмов решения задачи Коши. Пусть

на отрезке с начальным условием

Для
получения решения в точке

,
можем воспользоваться теоремой о
вычислнии определенного интеграла:

где
первообразная от

является
искомой функцией

.
Если разрешить уравнение последнее
уравнение относительно

,
получим

Теперь
можно применить численные методы
нахождения интеграла. Воспользуемся
методом трапеций с шагом

,
получим:

Правая
часть формулы включает в себя еще не
найденное значение

.
Для его нахождения воспользуемся методом
Эйлера. Получим конечную формулу,
именуемую методом
Хьюна (синонимы:
метод
Хойна,
метод
Эйлера-Коши):

Продолжая
процесс, получим последовательность
точек, аппроксимирующих кривую решения

.
Метод Хьюна относится к классу методов
прогноза-коррекции. На каждом шаге метод
Эйлера используется для предсказания,
а метод трапеций для уточнения конечного
значения. Общие формулы для шага метода
Хьюна:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

The truncation error does not satisfy that equation, it’s just its definition.

Consider two following problems:

• The first is an ODE.
  $$
  y'(t) = f(t, y(t))\\
  y(0) = a.
  $$
  Its solution is some smooth function $y(t)$.
• The second is a difference equation
  $$
  \frac{z_{i+1} — z_i}{h} = f(t_i, z_i)\\
  z_0 = a.
  $$
  Its solution is some discrete function $z_i$.

I’ve intentionally used different letters to denote those two solutions. They are quite different, the former is a smooth function while the latter is a discrete one. One needs to be careful even to compare those two. Usually the third function is introduced. It is defined as a restriction of the smooth $y(t)$ to the grid $t_i$, where the discrete function $z_i$ is defined. Let’s denote the restriction as $w_i$:
$$
w_i \equiv y(t_i).
$$

The function $w_i$ is discrete just like $z_i$ and $w_i$ coincide with $y(t)$ at grid points. Since now $w_i$ and $z_i$ are functions of the same class we can easily compare them:
$$
e_i = w_i — z_i \equiv y(t_i) — z_i.
$$
So, roughly speaking, the global error shows how close are $y(t)$ and $z_i$ (by restricting the former to the grid). When someone is solving some problem numerically the global error is what he is interesting in. Anyway, direct computation of global error is almost impossible, since we often simply do not have the exact values of $w_i = y(t_i)$ (
in contradistinction to $z_i$, which we can compute easily).

And the local truncation error concept comes to the rescue. Note that previously we’ve compared the solutions. Now we’re going to compare problems. Take $z_i$. It is the solution to the second problem. Plugging $z_i$ into it makes it a valid identity
$$
\frac{z_{i+1} — z_i}{h} = f(t_i, z_i)\\
z_0 = a.
$$
But if we now take $w_i$ and try to plug it into the difference scheme we wont get an identity. Instead we’ll get a residual:
$$
\frac{w_{i+1} — w_i}{h} = f(t_i, w_i) \color{red}{{}+ d_i}\\
w_0 = a \color{red}{{} + d_0}.
$$
If we are very lucky, some residuals may vanish, like $d_0$, but often it is not the case.

So why is $d_i$ interesting while it also is defined in terms of $w_i$ (the unknown solution to the original problem)? It turns out that we can estimate the $d_i$ without knowing the exact values of $w_i$ by just knowing the original problem.
$$
d_i = \frac{w_{i+1} — w_i}{h} — f(t_i, w_i) \equiv
\frac{y(t_{i+1}) — y(t_i)}{h} — f(t_i, y(t_i)) = \\ =
y'(t_i) + h \frac{y»(t_i)}{2} + O(h^2) — f(t_i, y(t_i)) = \\ =
\color{blue}{\left[y'(t_i) — f(t_i, y(t_i))\right]} + \color{red}{h \frac{y»(t_i)}{2} + O(h^2)}
$$
The blue term in braces is exactly the original ODE, and $y(t)$ is exactly its solution. So the term is equal to zero.
$$
d_i = h \frac{y»(t_i)}{2} + O(h^2).
$$
Similar result may be obtained if using different form of Taylor’s formula:
$$
d_i = h \frac{y»(\xi_i)}{2}, \qquad \xi_i \in [t_{i}, t_{i+1}].
$$

So now we can estimate the local truncation error, but we’re interested in the global error.

To relate them we need to introduce another concept of stability. Consider the two discrete problems
$$
\begin{aligned}
&\frac{z_{i+1} — z_i}{h} = f(t_i, z_i)\\
&z_0 = a
\end{aligned}
\qquad\text{and}\qquad
\begin{aligned}
&\frac{w_{i+1} — w_i}{h} = f(t_i, w_i) \color{green}{{} + d_i}\\
&w_0 = a \color{green}{{} + d_0}
\end{aligned}.
$$
Pretend that we know $d_i$. Let’s view the second problem as a perturbation of the first one. That’s reasonable, since $d_i$ is a small value of $O(h)$ magnitude. A difference problem is called stable if such small perturbations result in small changes of the solution. For this case this means that the difference $z_i — w_i$ will also be small. Precisely
$$
\max_i |z_i — w_i| \leq C \max_i |d_i|
$$
where $C$ is called the stability constant of the method. For the explicit Euler method it can be shown that for Lipschitz-continuous $f$
$$
C \leq e^{LT}
$$
with $L$ being the Lipschitz constant of $f$ and $T$ is the total integration time $T = \max_i t_i$.

Finally we can relate the global error and the local truncation error by
$$
|e_i| \leq C \max_i |d_i|
$$

If the local truncation error tends to zero when the discrete mesh is refined the numerical method is called consistent. The Lax theorem states that a stable consistent method converges, in sense that $e_i \to 0$ when the mesh is refined.

Численные методы решения задачи Коши

Основные понятия и определения

Обыкновенным дифференциальным уравнением называется уравнение, связывающее независимую переменную [math]x[/math], неизвестную функцию [math]y(x)[/math] этой независимой переменной и ее производные [math]y'(x),y»(x),\ldots,y^{(n)}(x)\colon[/math]

[math]F \bigl(x,y(x), y'(x),\ldots,y^{(n)}(x)\bigr)=0,\qquad \mathsf{(6.1)}[/math]

где [math]F(x,y, y’,\ldots,y^{(n)})[/math] — функция указанных аргументов, заданная в некоторой области их изменения.

Порядком дифференциального уравнения называется порядок старшей производной, входящей в уравнение.

Если в соотношении (6.1) функция [math]F[/math] такова, что его можно представить в виде

[math]y^{(n)}= f \bigl(x,y(x),\ldots,y^{(n-1)}(x)\bigr),\qquad \mathsf{(6.2)}[/math]

то уравнение называется обыкновенным дифференциальным уравнением л-го порядка, разрешенным относительно старшей производной.

Уравнение называется линейным, если функция [math]f[/math] линейна относительно искомой функции и ее производных, т.е. если уравнение может быть записано в виде

где [math]a_n(x),a_{n-1}(x),\ldots,a_0(x),f(x)[/math] — известные в общем случае нелинейные функции от [math]x[/math].

Решением дифференциального уравнения n-го порядка называется функция [math]y(x)[/math], непрерывная на некотором интервале [math](a,b)[/math] вместе со своими производными до [math](n-1)[/math] порядка включительно, имеющая производную [math]y^{(n)}(x)[/math] и такая, что подстановка [math]y(x)[/math] в уравнение обращает его в тождество.

График решения дифференциального уравнения называется интегральной кривой.

Одной из важнейших задач в теории и приложениях дифференциальных уравнений является задана Коши (начальная задана), в которой требуется найти решение дифференциального уравнения, удовлетворяющее заданным начальным условиям. Для уравнения (6.2) она записывается следующим образом:

где [math]x_0\in (a,b),~ y_0,y’_0,\ldots,y_0^{(n-1)}[/math] — заданные числа.

Теорема 6.1 (о существовании и единственности решения задачи Коши (6.4)). Пусть выполнены следующие условия:

а) функция [math]f(x,y,\ldots,y^{(n-1)})[/math] определена и непрерывна в некоторой замкнутой области [math]\overline{D}[/math], а также имеет в [math]\overline{D}[/math] ограниченные частные производные по переменным [math]y,y’,\ldots,y^{(n-1)}[/math];

б) точка [math](x_0,y_0,y’_0,\ldots,y_0^{(n-1)})[/math] лежит внутри области [math]\overline{D}[/math].

Тогда решение задачи Коши (6.4) существует и единственно.

Общим решением дифференциального уравнения л-го порядка в области [math]G\subset \overline{D}[/math] ([math]\overline{D}[/math] — область, в которой выполнены условия теоремы 6.1) называется функция [math]y=y(x,C_1,\ldots,C_n)[/math], зависящая от [math]n[/math] произвольных постоянных, и такая, что при подстановке в уравнение она обращает его в тождество при любых значениях [math]C_1,\ldots,C_n[/math]. Геометрически общее решение в области [math]G[/math] представляет собой семейство непересекающихся интегральных кривых, полностью покрывающих всю область.

Общим интегралом дифференциального уравнения называется соотношение вида [math]\varphi(x,y,C_1,\ldots,C_n)=0[/math], неявно определяющее общее решение.

При конкретных значениях [math]C_1,\ldots,C_n[/math], включая [math]\pm\infty[/math], из общего решения выделяется частное решение, а общий интефал становится частным интегралом. В каждой точке [math](x,y)[/math] частного решения или частного интефала выполняются условия теоремы 6.1.

Наряду с проблемой решения дифференциальных уравнений л-го порядка на практике возникает проблема решения систем обыкновенных дифференциальных уравнений первого порядка, связывающих независимую переменную [math]x[/math], неизвестные функции [math]y_1(x),\ldots, y_n(x)[/math] и их производные [math]y’_1(x),\ldots, y’_n(x)[/math].

В случае, если уравнения разрешимы относительно производных, систему можно записать в нормальной форме Коши (где [math]f_i(x,y_1,\ldots,y_n),~ i=\overline{1,n}[/math] — известные функции):

Решением системы (6.5) называется совокупность [math]n[/math] функций [math]y_1(x),\ldots, y_n(x)[/math], непрерывных на некотором интервале (д,6), такая, что подстановка этих функций в (6.5) обращает все уравнения в тождества.

Задача Коши для системы (6.5) состоит в нахождении решения системы, удовлетворяющего начальным условиям (где [math]y_{1\,0},y_{2\,0},\ldots,y_{n\,0}[/math] — известные числа):

В векторной форме задача Коши (6.5),(6.6) имеет вид

где [math]Y=(y_1,\ldots,y_n)^T,~ F(x,Y)= \bigl(f_1(x,Y),\ldots, f_n(x,Y)\bigr)^T,~ Y_0= \bigl(y_{1\,0},\ldots, y_{n\,0}\bigr)^T[/math].

Теорема 6.2 (о существовании и единственности решения задачи Коши (6.5),(6.6)). Пусть выполнены следующие условия:

а) функции [math]f_i(x,y_1,\ldots,y_n),~ i=\overline{1,n}[/math], определены и непрерывны в некоторой замкнутой области [math]\overline{D}[/math], а также имеют в [math]\overline{D}[/math] ограниченные частные производные по переменным [math]y_1,\ldots,y_n[/math];

б) точка [math](x_0,y_{1\,0},y_{2\,0},\ldots,y_{n\,0})[/math] лежит внутри области [math]\overline{D}[/math].

Тогда решение задачи Коши (6.5),(6.6) существует и единственно.

Замечания.

1. Во многих практических приложениях независимая переменная обозначается через [math]t[/math] и имеет смысл времени, поэтому задача Коши называется начальной задачей.

2. Понятия общего и частного решений, общего и частного интегралов для уравнения первого порядка и систем совпадают по форме, если заменить функцию [math]y(x)[/math] на вектор-функцию [math]Y(x),~ f(x,y)[/math] на [math]F(x,Y)[/math], а [math]y_0[/math] — на [math]Y_0[/math].

Численные методы, рассматриваемые в данном разделе, пригодны для решения задач Коши, записанных в форме (6.5),(6.6). Чтобы решить задачу Коши (6.4) этими методами, ее необходимо привести к системе [math]n[/math] уравнений первого порядка, т.е. к виду (6.5),(6.6).

Обозначая [math]y_1(x)=y(x),~ y_2(x)= y'(x),~\ldots,~ y_n(x)= y^{(n-1)}(x)[/math], получаем

Получим точное решение модельного примера, используемого далее для демонстрации применения различных численных методов.

Пример 6.1. Найти аналитическое решение задачи Коши [math]Ty’+y=1,~ y(0)=0[/math], где [math]T>0[/math] — известное число, называемое постоянной времени.

Решение

Пример 6.2. Записать дифференциальное уравнение второго порядка [math]2y»+y’+4y=6\sin{x},~ y(0)=1,~ y'(0)=2[/math], в виде системы дифференциальных уравнений в нормальной форме Коши.

Решение

Численные и приближенно-аналитические методы решения задачи Коши в отличие от аналитических методов позволяют найти искомую функцию [math]y(x)[/math] лишь приближенно. Но при этом численные методы являются более универсальными, так как с их помощью можно приближенно решать многие из задач, точные решения которых аналитическими методами не могут быть найдены. Аналитическими методами в основном решаются только линейные задачи и некоторые типы нелинейных задач, в то время как для численных методов эти ограничения отсутствуют.

Чтобы упростить изложение и в силу того, что численные методы легко обобщаются на системы уравнений, в дальнейшем будем рассматривать решение задачи Коши для уравнения первого порядка

Численное решение задачи ищется в узлах сетки [math]\Omega_n= \{x_0,x_1,\ldots,x_n\}[/math], где [math]h_{i+1}=x_{i+1}-x_{i},~ i=\overline{0,n-1}[/math] — расстояние между соседними узлами, называемое шагом интегрирования (параметром сетки). Если [math]h_{i+1}=h=\text{const}[/math], сетка называется равномерной (регулярной), а если [math]h_{i+1}=\text{var}[/math] — неравномерной (нерегулярной). В случае равномерной сетки узлы находятся по формуле [math]x_{i}= x_0+ih,~ i=\overline{0,n}[/math], а в случае неравномерной (где [math]\delta_{i+1}= \frac{h_{i+1}}{h_{i}}[/math] — параметр нерегулярности):

[math]x_1=x_0+h_1,\quad x_2=x_1+h_2=x_1+\delta_2h_1,\quad \ldots,\quad x_{i+1}=x_{i}+ \delta_{i+1}h_{i},\quad\ldots, \quad x_n=x_{n-1}+\delta_{n}h_{n-1}.[/math]

Решение находится в виде последовательности значений [math]\widehat{y}_0,\widehat{y}_1, \widehat{y}_2,\ldots, \widehat{y}_n[/math], являющихся приближением значений [math]y_0,y(x_1),y(x_2),\ldots,y(x_n)[/math] точного решения [math]y(x)[/math] в узлах сетки [math]\Omega_{n}[/math] (рис. 6.1).

Сеточное представление [math]y(x_i),~i=\overline{0,n}[/math], известной функции [math]y(x)[/math] (точного решения задачи Коши) называется проекцией [math]y(x)[/math] на сетку [math]\Omega_n[/math].

---

Дискретные и непрерывно-дискретные методы

Численные методы решения обыкновенных дифференциальных уравнений делятся на две группы:

– дискретные методы, позволяющие найти решение только в узлах сетки. Эти методы называются еще разностными методами или методами сеток;

– непрерывно-дискретные методы, основанные на использовании дискретных методов и сплайн-функций для восполнения численных результатов. Они позволяют найти непрерывные решения дифференциальных уравнений.

Дискретные методы (методы сеток) подразделяются на явные и неявные. Значение [math]\widehat{y}_{i+1}[/math], на (i+1)-м шаге может определяться явно:

где [math]\Phi(.)[/math] — некоторая функция, зависящая от конкретного метода (кроме последней рассчитанной точки [math](x_{i},\widehat{y}_{i})[/math] могут использоваться еще [math](k-1)[/math] предыдущих точек), или неявно:

где искомая величина [math]\widehat{y}_{i+1}[/math] входит одновременно и в левую, и в правую часть.

Явные и неявные методы делятся также на одношаговые и многошаговые (k-шаговые). В одношаговых методах для расчета очередной точки [math](x_{i+1},\widehat{y}_{i+1})[/math] требуется информация только о последней рассчитанной точке [math](x_{i},\widehat{y}_{i})[/math]. В k-шаговых методах для нахождения точки [math]x_{i+1},\widehat{y}_{i+1}[/math] требуется информация о [math]k[/math] предыдущих точках (рис. 6.2).

Формулы (6.10),(6.11) в общем случае представляют собой нелинейные уравнения относительно [math]\widehat{y}_{i+1}[/math] и называются разностными схемами.

Численный алгоритм (метод) называется устойчивым, если численные результаты непрерывно зависят от входных данных и если погрешность остается ограниченной при заданных пределах изменения параметров численного алгоритма (шагов сетки, числа итераций и др.).

Сходимость приближенных методов является основной проблемой, от успешного преодоления которой зависит точность решения всей задачи. Численный алгоритм называется сходящимся, если при стремлении его параметров к определенным предельным значениям, например, при [math]h\to0[/math] (или при [math]s\to\infty[/math], где [math]s[/math] — число итераций), результаты стремятся к точному решению.

При известном точном решении некоторой модельной задачи сходимость может быть проверена следующим образом. Фиксируется некоторая точка [math]x>x_0[/math] и строится последовательность сеток [math]\Omega_{n}[/math], таких, что [math]h\to0,[/math] [math]x=x_{n}= x_{0}+nh[/math]. Здесь для простоты считаем, что все сетки, образующие указанную последовательность, являются равномерными. Тогда, если [math]|\widehat{y}_{n}-y(x_{n})|\to0[/math] при [math]h\to0~ (n\to\infty)[/math], то метод является сходящимся в точке [math]x[/math]. Если метод сходится в каждой точке [math]x\in[c,d]\subset (a,b)[/math], то он сходящийся на [math][c,d][/math].

---

Локальная и глобальная ошибки

Локальной ошибкой численного метода на (i+1) -м шаге называется величина

[math]\varepsilon_{i+1}(h)= \widehat{y}_{i+1}-y(x_{i+1}),[/math]

где [math]y(x_{i+1})[/math] — значение точного решения при [math]x=x_{i+1}[/math], а [math]\widehat{y}_{i+1}[/math] — приближенное решение, получаемое по формуле (6.10) или (6.11) при условии, что вместо приближенных значений [math]\widehat{y}_{i}, \widehat{y}_{i-1},\ldots, \widehat{y}_{i-k+1}[/math] используются значения, соответствующие точному решению, т.е. [math]y(x_{i}), y(x_{i-1}),\ldots, y(x_{i-k-1})[/math].

Глобальной ошибкой называется величина [math]e_{n}(h)= \widehat{y}_{n}-y(x_{n})[/math], где [math]\widehat{y}_{n}[/math] — значение, получаемое по формулам (6.10) или (6.11) при [math]i=n-1[/math].

Глобальная ошибка определяется:

а) ошибками округления и ошибками арифметических действий, обусловленными числом разрядов компьютера и характером выполняемых операций для расчета значения искомой функции в очередной точке [math]x_{i+1}[/math];

б) методическими ошибками, определяемыми выбранным алгоритмом;

в) переходными ошибками, обусловленными тем, что при расчете значения р/+1 вместо точных значений [math]y(x_{i}), y(x_{i-1}),\ldots, y(x_{i-k-1})[/math] берутся приближенные значения [math]\widehat{y}_{i}, \widehat{y}_{i-1},\ldots, \widehat{y}_{i-k+1}[/math], полученные на предыдущих шагах.

Локальные ошибки «переносятся» в точку [math]x_n[/math] и формируют глобальную ошибку.

Число [math]p[/math] называется порядком (точностью) численного метода, если его глобальная ошибка есть [math]O[/math] большое от [math]h^p[/math], то есть [math]e_n(h)= O(h^p)[/math].

На практике в качестве характеристики точности метода часто используется величина [math]\varepsilon(h)= \max_{i=0,1,\ldots,n}\bigl|\widehat{y}_{i}-y(x_{i})\bigr|[/math].

Рассмотрим введенные понятия более подробно на примере явных одношаговых методов, построенных для задачи (6.9). При этом формулу (6.10) представим в виде

[math]\widehat{y}_{i+1}= \widehat{y}_{i}+h\cdot \Psi(\widehat{y}_{i},x_{i},h),[/math]

где [math]\Psi(\widehat{y}_{i},x_{i},h)[/math] — некоторая функция, определяемая конструкцией того или иного метода.

Обозначим [math]y(x,x_{i},\widehat{y}_{i})[/math] — решение задачи Коши [math]u’=f(x,u),~ u(x_{i})= \widehat{y}_{i}[/math]. Тогда локальная ошибка определяется выражением

[math]\varepsilon_{i+1}(h)= \widehat{y}_{i}+ h\cdot \Psi(\widehat{y}_{i},x_{i},h)-y(x_{i+1}, x_{i}, \widehat{y}_{i}).[/math]

Геометрическая интерпретация возникновения локальных и глобальной ошибок изображена на рис. 6.3.

Можно показать, что если локальная ошибка имеет порядок [math](p+1)[/math], то есть [math]\varepsilon_{i+1}(h)= O(h^{p+1})[/math], то глобальная погрешность имеет на единицу меньший порядок, т.е. [math]e_{n}(h)= O(h^p)[/math].

Перейдем теперь к рассмотрению устойчивости численных методов. Она проверяется на «тестовом примере»

где [math]\mu[/math] — в общем случае комплексная константа. Дифференциальное уравнение в (6.12) является простейшим линейным уравнением, и для него можно получить значимые критерии устойчивости в явной форме.

---

Устойчивость методов решения задачи Коши

Метод называется устойчивым (ограниченно устойчивым), если существует такое число [math]h_{\text{kr}}>0[/math], что при использовании метода для решения задачи (6.12), где [math]\operatorname{Re}\mu<0[/math], с шагом [math]0<h<h_{\text{kr}}[/math] при [math]i\to\infty[/math] глобальная ошибка ограничена. Величина [math]h_{\text{kr}}[/math] называется критическим шагом. Если [math]h>h_{\text{kr}}[/math], глобальная ошибка может неограниченно возрастать.

В ограниченно устойчивых методах при задании величины шага [math]h[/math] необходимо учитывать значение критического шага [math]h_{\text{kr}}[/math]. Для сложных дифференциальных уравнений и систем нахождение [math]h_{\text{kr}}[/math] является самостоятельной задачей, а свойство ограниченной устойчивости предупреждает вычислителя о возможных проблемах. Поэтому на практике становится актуальной задача конструирования таких методов, которые были бы устойчивы при любом значении шага, а его величина выбиралась бы только исходя из желаемой точности расчетов (при этом класс решаемых задач может быть ограничен).

Метод называется A-устойчивым, если при его применении с любым фиксированным положительным шагом [math]h[/math] все численные решения задачи (6.12) с комплексной константой [math]\mu~(\operatorname{Re}\mu<0)[/math] стремятся к нулю при [math]i\to\infty[/math].

Область A-устойчивости — совокупность значений [math]h[/math] и [math]\mu[/math], удовлетворяющих условию [math]\operatorname{Re}(h\mu)<0[/math]. Она изображена на рис. 6.4,а. Выполнение свойства A-устойчивости является желательным, поскольку если решение задачи (6.12) асимптотически устойчиво (в силу условия [math]\operatorname{Re}\mu<0[/math] корень характеристического уравнения находится в левой полуплоскости), то погрешность численного решения стремится к нулю при любой величине шага [math]h>0[/math].

При исследовании устойчивости численного метода необходимо использовать соответствующую ему разностную схему для решения задачи (6.12) и привести ее к линейному разностному уравнению с постоянными коэффициентами:

[math]a_ny(i+n)+ a_{n-1}y(i+n-1)+\ldots+a_0y(i)=g(i),\quad i=0,1,2,\ldots[/math]

Известно, что критерием устойчивости решения линейного разностного уравнения является требование расположения корней [math]\lambda_{i}[/math] соответствующего характеристического уравнения [math]a_n \lambda^n+ a_{n-1}\lambda^{n-1}+ \ldots+a_0=0[/math] внутри круга единичного радиуса с центром в начале координат, т.е.

Замечания

1. Численные методы, которые можно представить в виде (где |[math]|\alpha_0|+|\beta_0|\ne0,~ f_{i+1-j}= f(x_{i+1-j}, \widehat{y}_{i+1-j})[/math] называются линейными k-шаговыми методами)

Обозначим [math]\textstyle{\rho(\xi)= \sum\limits_{j=0}^{k} \alpha_{j}\xi^{k-j},~ \sigma(\xi)= \sum\limits_{j=0}^{k} \beta_{j}\xi^{k-j}}[/math]. Линейный многошаговый метод является устойчивым, если для фиксированного значения [math]h\mu[/math] корни уравнения

лежат внутри круга единичного радиуса с центром в начале координат.

2. Для ограниченно устойчивых методов важной задачей является нахождение величины критического шага [math]h_{\text{kr}}[/math]. Если константа [math]\mu[/math] в уравнении (6.12) действительная, то можно найти интервал устойчивости.

3. Существуют определения, смягчающие свойство A-устойчивости. Приведем одно из них. Метод называется A(α)-устойчивым, [math]\alpha\in(0,\pi\!\!\not{\phantom{|}}\,2)[/math], если при его применении все численные решения уравнения (6.12) с фиксированным положительным шагом [math]h[/math] стремятся к нулю при [math]i\to\infty[/math] для всех [math]\mu[/math], удовлетворяющих условию [math]|\arg(-\mu)|<\alpha,~ |\mu|\ne0[/math], где [math]\arg(-\mu)[/math] — аргумент комплексного числа [math](-\mu)[/math]. Область A(α)-устойчивости показана на рис. 6.4,5. Это условие применимо и для линейных систем с постоянными коэффициентами [math]y’=Ay[/math], где [math]A[/math] — матрица коэффициентов, имеющая собственные значения [math]\lambda_{i},~ i=\overline{1,n}[/math]. Геометрическая интерпретация изображена на рис. 6.4,в.

4. Можно показать, что явные линейные многошаговые методы не могут быть A-устойчивыми.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

При рассмотрении численных методов решения задачи Коши выделяют следующие погрешности

1) локальную (ошибку);

2) глобальную (ошибку);

3) вычислений на ЭВМ;

4) общую.

Локальная погрешность – это погрешность, допущенная на данном шаге , при условии, что предыдущие значения вычислены точно и отсутствуют ошибки округления. Другими словами, решается задача Коши:

где известно точное значение . Тогда локальная погрешность  равна:

,

где  – решение разностной задачи в отсутствие ошибок округления, а  – значение точного решения дифференциальной задачи в точке .

Глобальная погрешность – это разность между вычисленным решением разностной задачи в отсутствии ошибок округления и точным решением. То есть, решается задача Коши:

Глобальная погрешность R равна:

,

где  – вычисленное в отсутствие ошибок округления решение разностной задачи в точке ;            – точное решение задачи Коши в этой же точке.

Для частного случая, когда функция  не зависит от y, то есть , глобальная погрешность равна сумме локальных погрешностей.

В общем случае для устойчивых дифференциальных задач Коши глобальная погрешность будет меньше суммы локальных погрешностей, но для неустойчивых дифференциальных задач Коши глобальная погрешность больше суммы локальных погрешностей.

Общая погрешность – это сумма глобальной погрешности и погрешности вычислений на ЭВМ. Другими словами, общая погрешность – это разность между вычисленным и точным решениями с учетом ошибок округления на ЭВМ.

При оценке точности численного метода решения задачи Коши важной характеристикой является порядок метода. Разностная задача имеет порядок k по h, если для глобальной погрешности справедливо: . Для локальной погрешности в этом случае справедливо равенство . Условия для глобальной и локальной погрешности можно записать в эквивалентном виде:

,          ,

где c, c₁ – положительные константы, не зависящие от h.

1. Речевые ошибки и коммуникативный подходи

Лекция 11

2. Исправление глобальных ошибок

• Марина Берт убедительно доказывает, что
деление ошибок на глобальные и локальные
это наиболее распространяющийся критерий
для определения коммуникативной ошибки
(Error analysis in the adult ESL classroom,
TESOL Quarterly 9, c. 53-63, с. 58)
• утверждает, что исправление одной
глобальной ошибки в предложении
проясняет замысел высказывания больше,
чем исправление нескольких локальных
ошибок в том же предложении
• пишет о том, что сведение коррекции к
исправлению только коммуникативных ошибок
позволяет повысить мотивацию студентов
и повышает их самооценку успешности
относительно изучаемого языка.
• полагает, что только тогда когда
речепорождение на изучаемом языке
освобождается от глобальных ошибок,
студентам следует сосредотачиваться на
исправлении локальных ошибок, если
предполагается, что они должны достигнуть
беглости близкой речи носителя языка. (С.58)

3. Альберт Валдман

• http://frit.indiana.edu/faculty/valdman.shtml
• Исследуя последствия коррекции ошибок при обучении
студентов уровня Proficiency письменной речи, Альберт
Валдман усовершенствовал концепцию разделения БертКипарски на глобальные/ локальные ошибки.
• Learner’s system and error analysis. In Gilbert A.Jarvis (ed.) A New
Freedom.Skokie, IL: National Textbook company, 219 – 258

4. Глобальные и локальные ошибки у А.Вальдмана

• определил глобальную
ошибку как
коммуникативную ошибку,
которая приводит к тому, что
говорящий на иностранном
языке либо неправильно
понимает содержание
устного или письменного
высказывания, либо
считает его малопонятным
в данном контексте
• Локальная ошибка – это
языковая ошибка, которая
делает данную языковую
форму или структуру в
предложении
затруднительной для
понимания, но, тем не
менее, но незначительно
или совсем не затрудняет
понимание замысла
высказывания с учетом
контекста.

5. Причины локальных ошибок

• Большинство локальных
ошибок было обусловлено
неправильным
употреблением или
пропуском предлогов,
нарушением или
отсутствием субъектнопредикативных отношений
(subject – verb agreement)
неправильным написанием
слов или неверным
выбором слов
• ( Hendrikson, Error analysis
and selective correction in the
adult ESL classroom: An
experiment. ERIC: Center for
Applied liguistics, Arlington VA
EDRS: ED 135 260)