In mathematical logic, a tautology (from Greek: ταυτολογία) is a formula or assertion that is true in every possible interpretation. An example is «x=y or x≠y». Similarly, «either the ball is green, or the ball is not green» is always true, regardless of the colour of the ball.
The philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921, borrowing from rhetoric, where a tautology is a repetitive statement. In logic, a formula is satisfiable if it is true under at least one interpretation, and thus a tautology is a formula whose negation is unsatisfiable. In other words, it cannot be false. It cannot be untrue.
Unsatisfiable statements, both through negation and affirmation, are known formally as contradictions. A formula that is neither a tautology nor a contradiction is said to be logically contingent.
Such a formula can be made either true or false based on the values assigned to its propositional variables. The double turnstile notation 
is used to indicate that S is a tautology. Tautology is sometimes symbolized by «Vpq«, and contradiction by «Opq«. The tee symbol 
is sometimes used to denote an arbitrary tautology, with the dual symbol 
(falsum) representing an arbitrary contradiction; in any symbolism, a tautology may be substituted for the truth value «true», as symbolized, for instance, by «1».[1]
Tautologies are a key concept in propositional logic, where a tautology is defined as a propositional formula that is true under any possible Boolean valuation of its propositional variables.[2] A key property of tautologies in propositional logic is that an effective method exists for testing whether a given formula is always satisfied (equiv., whether its negation is unsatisfiable).
The definition of tautology can be extended to sentences in predicate logic, which may contain quantifiers—a feature absent from sentences of propositional logic.[3]
Indeed, in propositional logic, there is no distinction between a tautology and a logically valid formula. In the context of predicate logic, many authors define a tautology to be a sentence that can be obtained by taking a tautology of propositional logic, and uniformly replacing each propositional variable by a first-order formula (one formula per propositional variable). The set of such formulas is a proper subset of the set of logically valid sentences of predicate logic (i.e., sentences that are true in every model).
History[edit]
The word tautology was used by the ancient Greeks to describe a statement that was asserted to be true merely by virtue of saying the same thing twice, a pejorative meaning that is still used for rhetorical tautologies. Between 1800 and 1940, the word gained new meaning in logic, and is currently used in mathematical logic to denote a certain type of propositional formula, without the pejorative connotations it originally possessed.
In 1800, Immanuel Kant wrote in his book Logic:
The identity of concepts in analytical judgments can be either explicit (explicita) or non-explicit (implicita). In the former case analytic propositions are tautological.
Here, analytic proposition refers to an analytic truth, a statement in natural language that is true solely because of the terms involved.
In 1884, Gottlob Frege proposed in his Grundlagen that a truth is analytic exactly if it can be derived using logic. However, he maintained a distinction between analytic truths (i.e., truths based only on the meanings of their terms) and tautologies (i.e., statements devoid of content).
In his Tractatus Logico-Philosophicus in 1921, Ludwig Wittgenstein proposed that statements that can be deduced by logical deduction are tautological (empty of meaning), as well as being analytic truths. Henri Poincaré had made similar remarks in Science and Hypothesis in 1905. Although Bertrand Russell at first argued against these remarks by Wittgenstein and Poincaré, claiming that mathematical truths were not only non-tautologous but were synthetic, he later spoke in favor of them in 1918:
Everything that is a proposition of logic has got to be in some sense or the other like a tautology. It has got to be something that has some peculiar quality, which I do not know how to define, that belongs to logical propositions but not to others.
Here, logical proposition refers to a proposition that is provable using the laws of logic.
During the 1930s, the formalization of the semantics of propositional logic in terms of truth assignments was developed. The term «tautology» began to be applied to those propositional formulas that are true regardless of the truth or falsity of their propositional variables. Some early books on logic (such as Symbolic Logic by C. I. Lewis and Langford, 1932) used the term for any proposition (in any formal logic) that is universally valid. It is common in presentations after this (such as Stephen Kleene 1967 and Herbert Enderton 2002) to use tautology to refer to a logically valid propositional formula, but to maintain a distinction between «tautology» and «logically valid» in the context of first-order logic (see below).
Background[edit]
Propositional logic begins with propositional variables, atomic units that represent concrete propositions. A formula consists of propositional variables connected by logical connectives, built up in such a way that the truth of the overall formula can be deduced from the truth or falsity of each variable. A valuation is a function that assigns each propositional variable to either T (for truth) or F (for falsity). So by using the propositional variables A and B, the binary connectives 
and 
representing disjunction and conjunction respectively, and the unary connective 
representing negation, the following formula can be obtained:
.
A valuation here must assign to each of A and B either T or F. But no matter how this assignment is made, the overall formula will come out true. For if the first conjunction 
is not satisfied by a particular valuation, then one of A and B is assigned F, which will make one of the following disjunct to be assigned T.
Definition and examples[edit]
A formula of propositional logic is a tautology if the formula itself is always true, regardless of which valuation is used for the propositional variables. There are infinitely many tautologies. Examples include:
(«A or not A«), the law of excluded middle. This formula has only one propositional variable, A. Any valuation for this formula must, by definition, assign A one of the truth values true or false, and assign A the other truth value. For instance, «The cat is black or the cat is not black».- («if A implies B, then not-B implies not-A«, and vice versa), which expresses the law of contraposition. For instance, «If it’s a book, it is blue; if it’s not blue, it’s not a book.»
- («if not-A implies both B and its negation not-B, then not-A must be false, then A must be true»), which is the principle known as reductio ad absurdum. For instance, «If it’s not blue, it’s a book, if it’s not blue, it’s also not a book, so it is blue.»
- («if not both A and B, then not-A or not-B«, and vice versa), which is known as De Morgan’s law. «If it is not both blue and a book, then it’s either not a book or it’s not blue»
- («if A implies B and B implies C, then A implies C«), which is the principle known as syllogism. «If it’s a book, then it’s blue and if it’s blue, then it’s on that shelf, then if it’s a book, it’s on that shelf.»
- («if at least one of A or B is true, and each implies C, then C must be true as well»), which is the principle known as proof by cases. «Books and blue things are on that shelf. If it’s either a book or it’s blue, it’s on that shelf.»
A minimal tautology is a tautology that is not the instance of a shorter tautology.
Verifying tautologies[edit]
The problem of determining whether a formula is a tautology is fundamental in propositional logic. If there are n variables occurring in a formula then there are 2n distinct valuations for the formula. Therefore, the task of determining whether or not the formula is a tautology is a finite and mechanical one: one needs only to evaluate the truth value of the formula under each of its possible valuations. One algorithmic method for verifying that every valuation makes the formula to be true is to make a truth table that includes every possible valuation.[2]
For example, consider the formula
There are 8 possible valuations for the propositional variables A, B, C, represented by the first three columns of the following table. The remaining columns show the truth of subformulas of the formula above, culminating in a column showing the truth value of the original formula under each valuation.
 |
 |
 |
 |
 |
 |
 |
|
|---|---|---|---|---|---|---|---|
| T | T | T | T | T | T | T | T |
| T | T | F | T | F | F | F | T |
| T | F | T | F | T | T | T | T |
| T | F | F | F | T | T | T | T |
| F | T | T | F | T | T | T | T |
| F | T | F | F | T | F | T | T |
| F | F | T | F | T | T | T | T |
| F | F | F | F | T | T | T | T |
Because each row of the final column shows T, the sentence in question is verified to be a tautology.
It is also possible to define a deductive system (i.e., proof system) for propositional logic, as a simpler variant of the deductive systems employed for first-order logic (see Kleene 1967, Sec 1.9 for one such system). A proof of a tautology in an appropriate deduction system may be much shorter than a complete truth table (a formula with n propositional variables requires a truth table with 2n lines, which quickly becomes infeasible as n increases). Proof systems are also required for the study of intuitionistic propositional logic, in which the method of truth tables cannot be employed because the law of the excluded middle is not assumed.
Tautological implication[edit]
A formula R is said to tautologically imply a formula S if every valuation that causes R to be true also causes S to be true. This situation is denoted 
. It is equivalent to the formula 
being a tautology (Kleene 1967 p. 27).
For example, let 
be 
. Then is not a tautology, because any valuation that makes false will make false. But any valuation that makes true will make true, because 
is a tautology. Let 
be the formula 
. Then , because any valuation satisfying will make true—and thus makes true.
It follows from the definition that if a formula is a contradiction, then tautologically implies every formula, because there is no truth valuation that causes to be true, and so the definition of tautological implication is trivially satisfied. Similarly, if is a tautology, then is tautologically implied by every formula.
Substitution[edit]
There is a general procedure, the substitution rule, that allows additional tautologies to be constructed from a given tautology (Kleene 1967 sec. 3). Suppose that S is a tautology and for each propositional variable A in S a fixed sentence SA is chosen. Then the sentence obtained by replacing each variable A in S with the corresponding sentence SA is also a tautology.
For example, let S be the tautology
- .
Let SA be 
and let SB be 
.
It follows from the substitution rule that the sentence
Semantic completeness and soundness[edit]
An axiomatic system is complete if every tautology is a theorem (derivable from axioms). An axiomatic system is sound if every theorem is a tautology.
Efficient verification and the Boolean satisfiability problem[edit]
The problem of constructing practical algorithms to determine whether sentences with large numbers of propositional variables are tautologies is an area of contemporary research in the area of automated theorem proving.
The method of truth tables illustrated above is provably correct – the truth table for a tautology will end in a column with only T, while the truth table for a sentence that is not a tautology will contain a row whose final column is F, and the valuation corresponding to that row is a valuation that does not satisfy the sentence being tested. This method for verifying tautologies is an effective procedure, which means that given unlimited computational resources it can always be used to mechanistically determine whether a sentence is a tautology. This means, in particular, the set of tautologies over a fixed finite or countable alphabet is a decidable set.
As an efficient procedure, however, truth tables are constrained by the fact that the number of valuations that must be checked increases as 2k, where k is the number of variables in the formula. This exponential growth in the computation length renders the truth table method useless for formulas with thousands of propositional variables, as contemporary computing hardware cannot execute the algorithm in a feasible time period.
The problem of determining whether there is any valuation that makes a formula true is the Boolean satisfiability problem; the problem of checking tautologies is equivalent to this problem, because verifying that a sentence S is a tautology is equivalent to verifying that there is no valuation satisfying 
. It is known that the Boolean satisfiability problem is NP complete, and widely believed that there is no polynomial-time algorithm that can perform it. Consequently, tautology is co-NP-complete. Current research focuses on finding algorithms that perform well on special classes of formulas, or terminate quickly on average even though some inputs may cause them to take much longer.
Tautologies versus validities in first-order logic[edit]
The fundamental definition of a tautology is in the context of propositional logic. The definition can be extended, however, to sentences in first-order logic.[4] These sentences may contain quantifiers, unlike sentences of propositional logic. In the context of first-order logic, a distinction is maintained between logical validities, sentences that are true in every model, and tautologies (or, tautological validities), which are a proper subset of the first-order logical validities. In the context of propositional logic, these two terms coincide.
A tautology in first-order logic is a sentence that can be obtained by taking a tautology of propositional logic and uniformly replacing each propositional variable by a first-order formula (one formula per propositional variable). For example, because 
is a tautology of propositional logic, 
is a tautology in first order logic. Similarly, in a first-order language with a unary relation symbols R,S,T, the following sentence is a tautology:
It is obtained by replacing with 
, with 
, and with 
in the propositional tautology .
Not all logical validities are tautologies in first-order logic. For example, the sentence
is true in any first-order interpretation, but it corresponds to the propositional sentence 
which is not a tautology of propositional logic.
See also[edit]
Normal forms[edit]
- Algebraic normal form
- Conjunctive normal form
- Disjunctive normal form
- Logic optimization
[edit]
|
|
References[edit]
- ^ Weisstein, Eric W. «Tautology». mathworld.wolfram.com. Retrieved 2020-08-14.
- ^ a b «tautology | Definition & Facts». Encyclopedia Britannica. Retrieved 2020-08-14.
- ^ «Tautology (logic)». wikipedia.org.
- ^ «New Members». Naval Engineers Journal. 114 (1): 17–18. January 2002. doi:10.1111/j.1559-3584.2002.tb00103.x. ISSN 0028-1425.
Further reading[edit]
- Bocheński, J. M. (1959) Précis of Mathematical Logic, translated from the French and German editions by Otto Bird, Dordrecht, South Holland: D. Reidel.
- Enderton, H. B. (2002) A Mathematical Introduction to Logic, Harcourt/Academic Press, ISBN 0-12-238452-0.
- Kleene, S. C. (1967) Mathematical Logic, reprinted 2002, Dover Publications, ISBN 0-486-42533-9.
- Reichenbach, H. (1947). Elements of Symbolic Logic, reprinted 1980, Dover, ISBN 0-486-24004-5
- Wittgenstein, L. (1921). «Logisch-philosophiche Abhandlung», Annalen der Naturphilosophie (Leipzig), v. 14, pp. 185–262, reprinted in English translation as Tractatus logico-philosophicus, New York City and London, 1922.
External links[edit]
- «Tautology», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
In mathematical logic, a tautology (from Greek: ταυτολογία) is a formula or assertion that is true in every possible interpretation. An example is «x=y or x≠y». Similarly, «either the ball is green, or the ball is not green» is always true, regardless of the colour of the ball.
The philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921, borrowing from rhetoric, where a tautology is a repetitive statement. In logic, a formula is satisfiable if it is true under at least one interpretation, and thus a tautology is a formula whose negation is unsatisfiable. In other words, it cannot be false. It cannot be untrue.
Unsatisfiable statements, both through negation and affirmation, are known formally as contradictions. A formula that is neither a tautology nor a contradiction is said to be logically contingent.
Such a formula can be made either true or false based on the values assigned to its propositional variables. The double turnstile notation is used to indicate that S is a tautology. Tautology is sometimes symbolized by «Vpq«, and contradiction by «Opq«. The tee symbol is sometimes used to denote an arbitrary tautology, with the dual symbol (falsum) representing an arbitrary contradiction; in any symbolism, a tautology may be substituted for the truth value «true», as symbolized, for instance, by «1».[1]
Tautologies are a key concept in propositional logic, where a tautology is defined as a propositional formula that is true under any possible Boolean valuation of its propositional variables.[2] A key property of tautologies in propositional logic is that an effective method exists for testing whether a given formula is always satisfied (equiv., whether its negation is unsatisfiable).
The definition of tautology can be extended to sentences in predicate logic, which may contain quantifiers—a feature absent from sentences of propositional logic.[3]
Indeed, in propositional logic, there is no distinction between a tautology and a logically valid formula. In the context of predicate logic, many authors define a tautology to be a sentence that can be obtained by taking a tautology of propositional logic, and uniformly replacing each propositional variable by a first-order formula (one formula per propositional variable). The set of such formulas is a proper subset of the set of logically valid sentences of predicate logic (i.e., sentences that are true in every model).
History[edit]
The word tautology was used by the ancient Greeks to describe a statement that was asserted to be true merely by virtue of saying the same thing twice, a pejorative meaning that is still used for rhetorical tautologies. Between 1800 and 1940, the word gained new meaning in logic, and is currently used in mathematical logic to denote a certain type of propositional formula, without the pejorative connotations it originally possessed.
In 1800, Immanuel Kant wrote in his book Logic:
The identity of concepts in analytical judgments can be either explicit (explicita) or non-explicit (implicita). In the former case analytic propositions are tautological.
Here, analytic proposition refers to an analytic truth, a statement in natural language that is true solely because of the terms involved.
In 1884, Gottlob Frege proposed in his Grundlagen that a truth is analytic exactly if it can be derived using logic. However, he maintained a distinction between analytic truths (i.e., truths based only on the meanings of their terms) and tautologies (i.e., statements devoid of content).
In his Tractatus Logico-Philosophicus in 1921, Ludwig Wittgenstein proposed that statements that can be deduced by logical deduction are tautological (empty of meaning), as well as being analytic truths. Henri Poincaré had made similar remarks in Science and Hypothesis in 1905. Although Bertrand Russell at first argued against these remarks by Wittgenstein and Poincaré, claiming that mathematical truths were not only non-tautologous but were synthetic, he later spoke in favor of them in 1918:
Everything that is a proposition of logic has got to be in some sense or the other like a tautology. It has got to be something that has some peculiar quality, which I do not know how to define, that belongs to logical propositions but not to others.
Here, logical proposition refers to a proposition that is provable using the laws of logic.
During the 1930s, the formalization of the semantics of propositional logic in terms of truth assignments was developed. The term «tautology» began to be applied to those propositional formulas that are true regardless of the truth or falsity of their propositional variables. Some early books on logic (such as Symbolic Logic by C. I. Lewis and Langford, 1932) used the term for any proposition (in any formal logic) that is universally valid. It is common in presentations after this (such as Stephen Kleene 1967 and Herbert Enderton 2002) to use tautology to refer to a logically valid propositional formula, but to maintain a distinction between «tautology» and «logically valid» in the context of first-order logic (see below).
Background[edit]
Propositional logic begins with propositional variables, atomic units that represent concrete propositions. A formula consists of propositional variables connected by logical connectives, built up in such a way that the truth of the overall formula can be deduced from the truth or falsity of each variable. A valuation is a function that assigns each propositional variable to either T (for truth) or F (for falsity). So by using the propositional variables A and B, the binary connectives and representing disjunction and conjunction respectively, and the unary connective representing negation, the following formula can be obtained:.
A valuation here must assign to each of A and B either T or F. But no matter how this assignment is made, the overall formula will come out true. For if the first conjunction is not satisfied by a particular valuation, then one of A and B is assigned F, which will make one of the following disjunct to be assigned T.
Definition and examples[edit]
A formula of propositional logic is a tautology if the formula itself is always true, regardless of which valuation is used for the propositional variables. There are infinitely many tautologies. Examples include:
- («A or not A«), the law of excluded middle. This formula has only one propositional variable, A. Any valuation for this formula must, by definition, assign A one of the truth values true or false, and assign A the other truth value. For instance, «The cat is black or the cat is not black».
- («if A implies B, then not-B implies not-A«, and vice versa), which expresses the law of contraposition. For instance, «If it’s a book, it is blue; if it’s not blue, it’s not a book.»
- («if not-A implies both B and its negation not-B, then not-A must be false, then A must be true»), which is the principle known as reductio ad absurdum. For instance, «If it’s not blue, it’s a book, if it’s not blue, it’s also not a book, so it is blue.»
- («if not both A and B, then not-A or not-B«, and vice versa), which is known as De Morgan’s law. «If it is not both blue and a book, then it’s either not a book or it’s not blue»
- («if A implies B and B implies C, then A implies C«), which is the principle known as syllogism. «If it’s a book, then it’s blue and if it’s blue, then it’s on that shelf, then if it’s a book, it’s on that shelf.»
- («if at least one of A or B is true, and each implies C, then C must be true as well»), which is the principle known as proof by cases. «Books and blue things are on that shelf. If it’s either a book or it’s blue, it’s on that shelf.»
A minimal tautology is a tautology that is not the instance of a shorter tautology.
Verifying tautologies[edit]
The problem of determining whether a formula is a tautology is fundamental in propositional logic. If there are n variables occurring in a formula then there are 2n distinct valuations for the formula. Therefore, the task of determining whether or not the formula is a tautology is a finite and mechanical one: one needs only to evaluate the truth value of the formula under each of its possible valuations. One algorithmic method for verifying that every valuation makes the formula to be true is to make a truth table that includes every possible valuation.[2]
For example, consider the formula
There are 8 possible valuations for the propositional variables A, B, C, represented by the first three columns of the following table. The remaining columns show the truth of subformulas of the formula above, culminating in a column showing the truth value of the original formula under each valuation.
|
|
|
|
|
|
|
|
|---|---|---|---|---|---|---|---|
| T | T | T | T | T | T | T | T |
| T | T | F | T | F | F | F | T |
| T | F | T | F | T | T | T | T |
| T | F | F | F | T | T | T | T |
| F | T | T | F | T | T | T | T |
| F | T | F | F | T | F | T | T |
| F | F | T | F | T | T | T | T |
| F | F | F | F | T | T | T | T |
Because each row of the final column shows T, the sentence in question is verified to be a tautology.
It is also possible to define a deductive system (i.e., proof system) for propositional logic, as a simpler variant of the deductive systems employed for first-order logic (see Kleene 1967, Sec 1.9 for one such system). A proof of a tautology in an appropriate deduction system may be much shorter than a complete truth table (a formula with n propositional variables requires a truth table with 2n lines, which quickly becomes infeasible as n increases). Proof systems are also required for the study of intuitionistic propositional logic, in which the method of truth tables cannot be employed because the law of the excluded middle is not assumed.
Tautological implication[edit]
A formula R is said to tautologically imply a formula S if every valuation that causes R to be true also causes S to be true. This situation is denoted . It is equivalent to the formula being a tautology (Kleene 1967 p. 27).
For example, let be . Then is not a tautology, because any valuation that makes false will make false. But any valuation that makes true will make true, because is a tautology. Let be the formula . Then , because any valuation satisfying will make true—and thus makes true.
It follows from the definition that if a formula is a contradiction, then tautologically implies every formula, because there is no truth valuation that causes to be true, and so the definition of tautological implication is trivially satisfied. Similarly, if is a tautology, then is tautologically implied by every formula.
Substitution[edit]
There is a general procedure, the substitution rule, that allows additional tautologies to be constructed from a given tautology (Kleene 1967 sec. 3). Suppose that S is a tautology and for each propositional variable A in S a fixed sentence SA is chosen. Then the sentence obtained by replacing each variable A in S with the corresponding sentence SA is also a tautology.
For example, let S be the tautology
- .
Let SA be and let SB be .
It follows from the substitution rule that the sentence
Semantic completeness and soundness[edit]
An axiomatic system is complete if every tautology is a theorem (derivable from axioms). An axiomatic system is sound if every theorem is a tautology.
Efficient verification and the Boolean satisfiability problem[edit]
The problem of constructing practical algorithms to determine whether sentences with large numbers of propositional variables are tautologies is an area of contemporary research in the area of automated theorem proving.
The method of truth tables illustrated above is provably correct – the truth table for a tautology will end in a column with only T, while the truth table for a sentence that is not a tautology will contain a row whose final column is F, and the valuation corresponding to that row is a valuation that does not satisfy the sentence being tested. This method for verifying tautologies is an effective procedure, which means that given unlimited computational resources it can always be used to mechanistically determine whether a sentence is a tautology. This means, in particular, the set of tautologies over a fixed finite or countable alphabet is a decidable set.
As an efficient procedure, however, truth tables are constrained by the fact that the number of valuations that must be checked increases as 2k, where k is the number of variables in the formula. This exponential growth in the computation length renders the truth table method useless for formulas with thousands of propositional variables, as contemporary computing hardware cannot execute the algorithm in a feasible time period.
The problem of determining whether there is any valuation that makes a formula true is the Boolean satisfiability problem; the problem of checking tautologies is equivalent to this problem, because verifying that a sentence S is a tautology is equivalent to verifying that there is no valuation satisfying . It is known that the Boolean satisfiability problem is NP complete, and widely believed that there is no polynomial-time algorithm that can perform it. Consequently, tautology is co-NP-complete. Current research focuses on finding algorithms that perform well on special classes of formulas, or terminate quickly on average even though some inputs may cause them to take much longer.
Tautologies versus validities in first-order logic[edit]
The fundamental definition of a tautology is in the context of propositional logic. The definition can be extended, however, to sentences in first-order logic.[4] These sentences may contain quantifiers, unlike sentences of propositional logic. In the context of first-order logic, a distinction is maintained between logical validities, sentences that are true in every model, and tautologies (or, tautological validities), which are a proper subset of the first-order logical validities. In the context of propositional logic, these two terms coincide.
A tautology in first-order logic is a sentence that can be obtained by taking a tautology of propositional logic and uniformly replacing each propositional variable by a first-order formula (one formula per propositional variable). For example, because is a tautology of propositional logic, is a tautology in first order logic. Similarly, in a first-order language with a unary relation symbols R,S,T, the following sentence is a tautology:
It is obtained by replacing with , with , and with in the propositional tautology .
Not all logical validities are tautologies in first-order logic. For example, the sentence
is true in any first-order interpretation, but it corresponds to the propositional sentence which is not a tautology of propositional logic.
See also[edit]
Normal forms[edit]
- Algebraic normal form
- Conjunctive normal form
- Disjunctive normal form
- Logic optimization
[edit]
|
|
References[edit]
- ^ Weisstein, Eric W. «Tautology». mathworld.wolfram.com. Retrieved 2020-08-14.
- ^ a b «tautology | Definition & Facts». Encyclopedia Britannica. Retrieved 2020-08-14.
- ^ «Tautology (logic)». wikipedia.org.
- ^ «New Members». Naval Engineers Journal. 114 (1): 17–18. January 2002. doi:10.1111/j.1559-3584.2002.tb00103.x. ISSN 0028-1425.
Further reading[edit]
- Bocheński, J. M. (1959) Précis of Mathematical Logic, translated from the French and German editions by Otto Bird, Dordrecht, South Holland: D. Reidel.
- Enderton, H. B. (2002) A Mathematical Introduction to Logic, Harcourt/Academic Press, ISBN 0-12-238452-0.
- Kleene, S. C. (1967) Mathematical Logic, reprinted 2002, Dover Publications, ISBN 0-486-42533-9.
- Reichenbach, H. (1947). Elements of Symbolic Logic, reprinted 1980, Dover, ISBN 0-486-24004-5
- Wittgenstein, L. (1921). «Logisch-philosophiche Abhandlung», Annalen der Naturphilosophie (Leipzig), v. 14, pp. 185–262, reprinted in English translation as Tractatus logico-philosophicus, New York City and London, 1922.
External links[edit]
- «Tautology», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
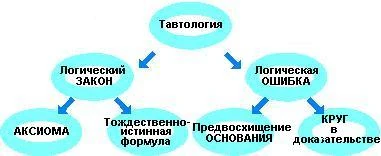
Логические
погрешности текста возникают по различным
причи-нам: это и нечеткость мышления, и
неоформленность темы, и про-стой
недосмотр, и неучет нежелательных
побочных ассоциаций и интерпретаций
[40. С. 294].
Логики
выделяют три причины логических ошибок:
1) пси-хические нарушения, 2) сокращенное
умозаключение и 3) плохое владе-ние
языком. Первые две причины порождают
ошибки в умозаключе-ниях, а третья —
ошибки в речи, ведущие к нарушениям
логики [4. С. 164]. А. Н. Беззубов делит
логические ошибки на два класса:
1)
ошибки собственно логические, ошибки
мышления, ошиб-ки плана содержания;
2)
ошибки речи, ошибки плана выражения,
вторичные логиче-ские ошибки [4. С. 165].
Такая
классификация, на наш взгляд, совершенно
оправдана. Первый тип ошибок связан с
нарушением четырех законов формальной
логики, о чем мы писали выше, второй тип
— с нарушением языковой, стилевой нормы.
А.
Н. Беззубов выделяет лексиче-ские и
синтаксические речевые ошибки. Лексические
ошибки он рассматривает в разде-ле
«Нормативно-языковые ошибки», отмечая,
что они возникают по двум причинам: или
из-за незнания значения сло-ва, или из-за
небрежного словоупотребления, но в
любом случае они создают некую логическую
неувязку, часто комического свойства: Он
облокотился спиной на холодную батарею (В.
Катаев). Облокотиться можно только
локтем, а спиной прислониться. Этот
пример А. Н. Беззубов приводит как
типичный случай сме-шения словосочетаний,
относя его к ошибкам по небрежности, по
невнимательности, а не по незнанию.
Исследователь
замечает, что небрежность, приблизительность
словоупотребления — час-тое явление в
газете, которое распространяется и на
газетную метафору. Он упоминает старый
термин — «ломаная
метафора»,
— обо-значающий логическую несочетаемость
двух метафор: Пусть
акулы империализма не протягивают к
нам свои лапы (Из
газет 20-х годов).
К
логическим дефектам речи А. Н. Беззубов
относит и речевые излишества на
основе плеоназма,
многие из которых выглядят достаточно
безобидно: самый
лучший, толпа людей, сжатый кулак, идти
пешком, в общем и целом и
т. д. Они стали штампами, и не так-то
просто доказать иному автору необходимость
редактирования таких словосочетаний.
Однако возможен и комический эф-фект,
понятный любому: Он
был в берете, напяленном на правое ухо
головы(газета), Приемный
пункт по приему стеклотары (вывеска).
По
мнению А. Н. Беззубова, особый тип
плеоназма связан с неточным знанием
значения иноязычного слова. Это уже
несомненные ошибки — и грубые: своя
автобиография (авто и
есть своя), памятный
сувенир (сувенир — подарок
на память), период
времени (период —
промежуток времени), прейску-рант
цен (прейскурант —
текущая цена)
и т. п. Отмечает автор и «узаконенные
ошибки», вошедшие в употребление и не
рассматриваемые сегодня как ошибки: пойти
ва-банк от
французского va banque — идет
банк (из
речи картежников).
Самой
грубой лексической логической ошиб-кой,
по мнению А. Н. Беззубова, является так
называемый логический
скачок.
Вот пример из литературоведческой
статьи: Сложный
и оригинальный внутренний облик Катерины
нашел свое отражение в ее языке, самом
ярком среди всех действующих
лиц «Грозы». Язык
оказался среди действующих лиц: автор
соединил понятия из разных логических
рядов, это и есть логиче-ский скачок.
Разновидностью
логического скачка считает А. Н. Беззубов
и неправиль-ное употребление конструкций
с предлогами «кроме», «наряду», «вместе»,
«помимо» и подобными. Например: (брачное
объявление в германской газете
(перевод)):Ищу
мужа. Я еще молода. Рост высокий, талия
тон-кая. В хозяйстве, кроме того, имеется
трактор.
Отмечает
исследователь и ошибку, которую предлагает
назвать повествовательным
алогизмом.
Чаще всего это связано с тем, что
повествователь (писатель или журналист)
отличается такой небрежностью, что не
помнит, что он написал в предыдущей
фразе. В
лесу было тихо. Рядом пела звонким
голосом лирическую песню, перелетая с
дерева на дерево, иволга. Где-то далеко
куковала невидимая кукушка (Газета).
Не очень-то тихо было в лесу.
Одним
из частных случаев логических ошибок
можно считать амфиболию. Амфиболия (от
греч. ?мцйвплЯб — двусмысленность,
неясность) — двойственность или
двусмысленность, получающаяся от того
или иного расположения слов или от
употребления их в различных смыслах,
смешение понятий.
Классический
пример амфиболии — фраза «Казнить нельзя
помиловать», где смысл меняется в
зависимости от места паузы после или
перед словом «нельзя». Многочисленные
примеры амфиболий дают греческие легенды
об оракулах. Амфиболия может возникнуть
при таком построении предложения, когда
подлежащее в именительном падеже трудно
отличить от прямого дополнения в
винительном падеже.
|
Вид |
Ошибочное |
|
|
1.Утверждение |
Всем |
|
|
2.Смешение |
В |
|
|
3.Смешение |
Кругом, |
|
|
4.Неверное |
Отсутствие |
|
|
5.Неправильный
— между
— между |
Сейчас
Человечеству |
|
Мы
считаем, что примеры, показанные в
таблице, можно классифицировать как
первичные логические ошибки:
1.
Закон противоречия — дуэт баянистов,
но перечисляется три
фамилии.
Тогда трио баянистов;
2.
Закон тождества — Татьяну Ларину не
понимали, поэтому она сидела у окна?;
3.
Языковая, стилевая ошибка, т.е. «ломаная
метафора» — трупы не живые души;
4.
Закон достаточного основания — почему
из-за отсутствия спортивных площадок
подростки портят стены?;
5.
Закон достаточного основания предлог а в
первом примере и предлог но во
втором примере не делает выводов.
Логичность
как общее коммуникативное качество
свойственно текстам любых функциональных
стилей. Но проявляется это речевое
качество весьма
специфично
— в зависимости от конкретных условий
коммуникации. Требования, предъявляемые
речи со стороны ее логичности, особенно
высоки в научном стиле, однако и при
создании текстов публицистического
стиля, призванных выполнять информирующую
и воздействующую функции, необходимо
строго соблюдать законы логики. В
противном случае задачи журналиста
будут не выполнены.
В
следующей главе мы рассмотрим логические
ошибки, мешающие восприятию текста,
обнаруженные нами при анализе районных
газет.
22.
Классификация логических ошибок
Логические
ошибки (Л) –
связаны с нарушением логической
правильности речи. Они возникают в
результате нарушения законов логики,
допущенного как в пределах одного
предложения, суждения, так и на уровне
целого текста.
|
-
Работа
редактора над фактическим материалом:
определение поняия факт в редактировании;
основные функции фактов; оценка
значимости фактов.
Факт –
предмет журналистского исследования.
Теоретики журналистики рассматривают
факт с позиций теории познания как
фрагмент действительности и метафорически,
наблюдая, как осваивается в процессе
журналистского творчества его отвлечённое
значение, как происходит его типизация,
даётся образная трактовка. Для
журналиста факт всегда соотнесён с
суждением о событии, служащим
утверждению истинности или ложности
определённых положений, выяснению
связей и отношений между явлениями,
между предметом и его свойствами.1
Теория
редактирования предлагает свою трактовку
этой важнейшей для журналистского
творчества проблемы, исследуя то, как
факт воплощён в тексте литературного
произведения, как он передан средствами
языка. Понятие фактический
материал, которое
принято в редактировании, охватывает
все опорные для текста элементы,
передающие смысл и предметные
отношения.2 При
правке текста они не должны подвергнуться
изменениям или выпасть. Фактический
материал реализуется в текстовых
конструкциях, которые обозначают не
только события, но и «кусочки
действительности» – вещные элементы
предметного ряда, свойства, качества,
состояния, наименования лиц, отношений,
количества.
Фактический
материал может быть привлечён журналистом
как собственно
информация, как аргумент в процессе
логического доказательства и основание
для общих утверждений и, наконец, как
иллюстрация, дополняющая то или иное
наблюдение. Приёмы
изложения всегда обусловлены
функциональным назначением фактического
материала.
Любая
неясность в журналистском тексте
неприемлема. Поэтому так важна
правильность передачи информации,
сквозная оценка и точная разработка
фактического материала. Наблюдения
над газетной практикой убеждают в том,
насколько важна для автора помощь
редактора.
Уместно
напомнить, что именно «горячий» материал,
когда времени на детальную выверку
сведений нет, требует от редактора
профессионального навыка выделить
из текста фактический материал, подлежащий
проверке, и сделать это быстро и
чётко. Профессиональное контролирующее
мышление редактора должно быть нацелено
на соотнесение данных внутри текста
и оценку их достоверности. Если бы это
требование было выполнено, вряд ли бы
мы прочитали в одной и той же заметке:
«несколько вагонов, в том числе цистерна»,
а чуть ниже: «четыре вагона и три
цистерны».
Не
менее важно для контролирующего мышления
редактора умение конкретно представить,
как происходили события, о которых
говорится в тексте.
Не
была достигнута при редактировании и
терминологическая точность, необходимая
в информационном материале.
Работая
над материалами публицистики, редактор
должен представлять сложность
диалектических отношений между мыслью
и фактом в журналистском творчестве,
когда непосредственный контакт с
действительностью стимулирует развитие
мысли, а сформировавшееся суждение
предопределяет отбор фактов и разработку
деталей и фактический материал входит
в текст как элемент логического
построения, основание для вывода.
Еще
В.Г. Белинский говорил, что не нужно
выдумывать факты, стоит только обратить
внимание преимущественно на те факты,
которые подтверждают заранее составленное
мнение, закрывая глаза на те, что
противоречат этому мнению. Факты можно
искажать и не выдумывая лжи. Предпринимая
расследование, журналист не претендует
на бесспорность своих выводов, но он
всегда привлекает внимание к найденным
им фактам, к судьбам людей, их поступкам
и отношениям между ними. Форма, в которую
суждения журналиста облечены, приёмы,
к которым он прибегает, конструируя эти
суждения, должны быть оценены редактором
не только с узкопрофессиональных, но и
с более широких, этических, позиций.
Насколько
тесно связаны в журналистском творчестве
проблемы литературного мастерства
и этики при обработке фактического
материала – убеждают многие публикации.
Фактический
материал в функции иллюстрации –
относительно свободный элемент
текста. Его включение в текст не
обусловлено требованиями логической
конструкции. Он дополняет, уточняет
смысловую основу материала, часто
рассчитан на эмоциональное воздействие,
пробуждение читательского интереса. И
тем не менее связь фактов-иллюстраций
с содержанием текста должна быть для
читателя очевидной. «Описательство»
как явление не характерно для публицистики
наших дней, тем не менее очерк, подобный
тому, отрывок из неотредактированного
варианта которого мы приводим ниже,
может встретиться редактору и сегодня.
Проверка
фактического материала
Традиционное
суждение по поводу обязанностей редактора
состоит в том, что он должен устранить
фактические ошибки, однако эта
очевидная и элементарная, на первый
взгляд, задача часто вынуждает его
провести самостоятельное исследование,
которое заставляет мысленно повторить
весь путь автора в его работе над фактом.
Ответственность редактора за точность
и достоверность публикуемого
фактического материала не вызывает
сомнений. Редакционная практика даёт
нам много примеров того, как остро
реагирует читатель на любую фактическую
неточность.
Известно,
например, как ревниво относятся люди к
рассказу о своей профессии, и если
журналист проявит здесь малейшую
неосведомлённость, это воспринимается
как неуважение к ней.
Для
редактора не существует неточностей
больших и малых, ошибок значительных и
незначительных. Все неточности и ошибки
надо вовремя заметить и устранить. И
пусть иногда ошибка кажется совсем
безобидной, не угрожает смыслу, но
читатель всегда проверит нас. Малейшая
небрежность в передаче факта создаст
психологическую предпосылку для сомнения
в истинности суждений автора. Даже
опытный и творчески работающий редактор
не может сравняться по эрудиции с автором
– специалистом в своей области. Тем
большее значение для редактора
приобретает методика профессиональной
работы с фактическим материалом: умение
быстро и точно найти нужную справку,
проверить правильность данных, знание
широкого круга справочных пособий,
навык ориентироваться в них, владение
приёмами анализа текста.
Пособия
по методике редактирования рекомендуют три
вида проверки фактического материала:
внутреннюю проверку, сличение с
авторитетным источником, официальное
подтверждение.
Методика
внутренней проверки основывается на
соотнесении фактического материала в
пределах редактируемого текста и его
конкретизации. Для выбора авторитетного
источника существуют специальные
правила. Так, при работе с опубликованными
данными фактический материал проверяют
только по изданиям, из которых он
заимствован. Источников косвенных
следует избегать. При необходимости
обратиться к справочным пособиям
предпочитают издание, последнее по
времени. Энциклопедии представляют
систематизированную информацию по всем
отраслям знания. Отраслевые пособия –
отраслевые энциклопедии, справочники
по специальностям, справочно-информационные
издания, официальные материалы –
содержат сведения по одной отрасли
знания и практической деятельности.
В
том случае, когда ни сличение с авторитетным
источником, ни внутренняя проверка не
дают возможности убедиться в достоверности
и точности фактического материала,
прибегают к консультации авторитетных
специальных учреждений. Их официальное
подтверждение – достаточное основание
для публикации оригинального фактического
материала.
-
Приёмы
поверки и обработки различных типов
фактического материала.
Что
вообще должно быть в ответе: РАБОТА
РЕДАКТОРА С ФАКТИЧЕСКИМ МАТЕРИАЛОМ
ТЕКСТА, ПРИЕМЫ ПРОВЕРКИ И ОБРАБОТКИ
(ТОЧНОСТЬ НОМИНАЦИИ, ИСТОРИЧЕСКИХ И
БЫТОВЫХ ФАКТОВ, СИТУАЦИЙ СОВРЕМЕННОЙ
ДЕЙСТВИТЕЛЬНОСТИ; ПРАВИЛЬНОСТЬ ЦИФР,
ССЫЛОК И ЦИТАТ). Техника сверки цитат с
первоисточником. Оформление ссылок на
источники. Принципы единообразия и
написания имен, фамилий, дат, географических
названия, наименования и терминов.
Что
ещё есть в книге. Факт – предмет
журналистского исследования. Теоретики
журналистики рассматривают факт с
позиций теории познания как фрагмент
действительности и метафорически,
наблюдая, как осваивается в процессе
журналистского творчества его отвлечённое
значение, как происходит его типизация,
даётся образная трактовка. Для журналиста
факт всегда соотнесён с суждением о
событии, служащим утверждению
истинности или ложности определённых
положений, выяснению связей и отношений
между явлениями, между предметом и его
свойствами.1
Теория
редактирования предлагает свою трактовку
этой важнейшей для журналистского
творчества проблемы, исследуя то, как
факт воплощён в тексте литературного
произведения, как он передан средствами
языка. Понятие фактический материал,
которое принято в редактировании,
охватывает все опорные для текста
элементы, передающие смысл и предметные
отношения.2 При правке текста они не
должны подвергнуться изменениям или
выпасть. Фактический материал может
быть привлечён журналистом как собственно
информация, как аргумент в процессе
логического доказательства и основание
для общих утверждений и, наконец, как
иллюстрация, дополняющая то или иное
наблюдение. Любая неясность в журналистском
тексте неприемлема. Поэтому так важна
правильность передачи информации,
сквозная оценка и точная разработка
фактического материала. Что в подобной
ситуации зависело от литературного
редактора? Ведь на месте событий он не
был, оснований заведомо не верить
корреспонденту у него нет. И всё же
уместно напомнить, что именно «горячий»
материал, когда времени на детальную
выверку сведений нет, требует от редактора
профессионального навыка выделить из
текста фактический материал, подлежащий
проверке, и сделать это быстро и
чётко. Профессиональное контролирующее
мышление редактора должно быть нацелено
на соотнесение данных внутри текста и
оценку их достоверности. Не менее важно
для контролирующего мышления редактора
умение конкретно представить, как
происходили события, о которых говорится
в тексте. Редактор должен предусмотреть
и возможность субъективной трактовки
читателем фактов, представленных
автором, следить за тем, чтобы картина
действительности не была разрушена, а
смысловые связи не были искажены. Пусть
ситуация подана журналистом как
случайная, прогнозировать, как она может
быть истолкована читателем, необходимо
Фактический
материал в функции иллюстрации –
относительно свободный элемент текста.
Его включение в текст не обусловлено
требованиями логической конструкции.
Он дополняет, уточняет смысловую основу
материала, часто рассчитан на эмоциональное
воздействие, пробуждение читательского
интереса. И тем не менее связь
фактов-иллюстраций с содержанием текста
должна быть для читателя очевидной.
Для
редактора не существует неточностей
больших и малых, ошибок значительных и
незначительных. Все неточности и ошибки
надо вовремя заметить и устранить. И
пусть иногда ошибка кажется совсем
безобидной, не угрожает смыслу, но
читатель всегда проверит нас. Малейшая
небрежность в передаче факта создаст
психологическую предпосылку для сомнения
в истинности суждений автора.
Пособия
по методике редактирования рекомендуют
три вида проверки фактического
материала: внутреннюю
проверку, сличение с авторитетным
источником, официальное подтверждение.
Методика
внутренней проверки основывается на
соотнесении фактического материала в
пределах редактируемого текста и его
конкретизации. Для выбора авторитетного
источника существуют специальные
правила. Так, при работе с опубликованными
данными фактический материал проверяют
только по изданиям, из которых он
заимствован. Источников косвенных
следует избегать. При необходимости
обратиться к справочным пособиям
предпочитают издание, последнее по
времени. Энциклопедии представляют
систематизированную информацию по всем
отраслям знания. Отраслевые пособия –
отраслевые энциклопедии, справочники
по специальностям, справочно-информационные
издания, официальные материалы –
содержат сведения по одной отрасли
знания и практической деятельности.
В
том случае, когда ни сличение с авторитетным
источником, ни внутренняя проверка не
дают возможности убедиться в достоверности
и точности фактического материала,
прибегают к консультации авторитетных
специальных учреждений. Их официальное
подтверждение – достаточное основание
для публикации оригинального фактического
материала.
Методика
работы редактора над текстом не
безразлична к тому, что представляет
собой фактический материал: имена и
фамилии людей, географические наименования,
факты истории, реалии действительности,
цитаты, цифры, даты.
Оценка
элементов номинации. Причиной ошибок
номинации может послужить недостаточная
осведомлённость автора, неадекватность
действительности его представлений,
бедность языка, техническая неточность
воспроизведения текста. Требование
точности номинации в первую очередь
определяет работу редактора над именами
собственными, терминами и в широком
смысле охватывает оценку точности
словоупотребления в целом.
Факты
истории. Прошлое и настоящее всегда
взаимосвязаны, и дело публициста –
сделать эту связь зримой для современников.
Публикации, сообщающие факты истории,
могут послужить примером того, как важна
помощь редактора при оценке точности
фактического материала, приёмов его
разработки и включения в текст. Неумелое
его использование разрушает конструкцию
текста, препятствует точной передаче
последовательности событий, перегружает
текст сведениями, не делающими суждения
автора более убедительными.
Оценка
ситуаций современной действительности.
Основа журналистского выступления –
это, прежде всего, факты действительности,
события современности, разнообразие и
характер которых предусмотреть заранее
невозможно, а сверить часто не с чем. Да
и всё ли надо проверять? Точнее, всё ли
может проверить редактор? По всей
вероятности, нет. Ведь если допустить,
что сведения, не проверенные нами, не
могут быть сообщены читателю, огромное
количество материалов никогда не попало
бы в печать, приток информации значительно
бы сократился. И тем большая ответственность
ложится на редактора: он должен определить,
какую смысловую нагрузку несут факты.
Умение
оценить, правильно осмыслить явления
и события редактору необходимо в не
меньшей мере, чем автору, но объектом
редакторской оценки является не только
сам факт действительности, но и то, как
эта действительность автором изображена.
Поэтому редакторский анализ фактического
материала идёт всегда в двух направлениях.
Определяя, насколько точен был автор,
строя фактическую основу материала,
редактор своим опытом, профессиональными
знаниями, своим восприятием первого
читателя проверяет автора. Рассматривая
роль факта в общей структуре журналистского
выступления как литературного
произведения, редактор судит о способах
разработки и подачи фактического
материала, он оценивает приёмы и
литературное мастерство автора. Оставляя
за автором право сообщить свои наблюдения,
редактор разделяет с ним ответственность
за те выводы, которые предлагаются
читателю. Новизна сообщения, быстрота
редакции не снимают ни с автора, ни с
редактора ответственность за серьёзность
каждого сообщения. Оно должно
соответствовать современному уровню
знаний о предмете. Оперативность не
может служить оправданием при появлении
на страницах газеты сенсаций, способных
ввести читателя в заблуждение.
В
небрежно отредактированном материале
факты нередко предстают перед читателем
в искажённом виде, логические связи
нарушены, выводы автора необоснованы.
Вправе
ли журналист домысливать факты, писать
о том, что могло бы произойти, но чего в
действительности не было? В какой степени
в своём стремлении найти в единичном
отражение всеобщего журналист может
реконструировать действительность? И
если домысел возможен, каковы его
границы?
На
эти вопросы обычно отвечают так: если
журналист говорит о конкретных ситуациях,
называет имена и фамилии реальных людей,
домысел недопустим, если в публикации
представлены лишь обобщённые,
«безадресные» суждения, – домысел
ситуаций и эпизодов не противопоказан.
Цифры
в тексте. Цифра – символ иной, чем слово,
знаковой системы. Как обозначению числа
ей изначально присуща точность, обобщение,
концентрированность информации. Этот
сложный для редактирования материал
требует особого внимания редактора.
Начать следует с того, чтобы убедиться,
легко ли прочитать текст вслух. Так,
заголовок «1 100 000 000-й гражданин» наверняка
представит трудности для многих
читателей. Конструктивные возможности
имён числительных, которыми в языке
передаются значения количества, в
некоторых случаях оказываются
ограниченными, и мы неизбежно сталкиваемся
с трудностями словообразования. Многие
порядковые числительные, числительные
в составе сложных слов, сочетания
числительного со словами, употребляющимися
только в форме множественного числа, –
далеко не полный перечень таких
затруднений (22 сутки экспедиция провела
в горах.., …вчера в очередь записался
36 124 человек). Мы встречаем словообразование
«71-летний старик», но никто не скажет:
«однолетний ребёнок», «однолетний
отпуск».
Издательская
практика выработала специальные
рекомендации для обозначения чисел в
тексте.4 Числа от 1 до 9 включительно
принято обозначать словом, когда они
не имеют при себе единиц измерения и
стоят в косвенном падеже. Это необходимо,
чтобы избежать остановки при прочтении
цифры, которая воспринимается первоначально
всегда в форме именительного падежа.
(Сравните: с четырьмя книгами – с 4
книгами; у пяти студентов – у 5 студентов).
Словом обозначаются числа при стечении
нескольких цифровых обозначений
(семнадцать 19-летних военнослужащих
оказались на больничных койках), но
лучшим вариантом в этом случае будет
изменение фразы, позволяющее избежать
стечения количественных понятий. Словом
обозначают количественное числительное,
когда им начато предложение. В противном
случае границы между предложениями
стираются. Цифрой принято обозначать
однозначные числа, когда они находятся
в одном ряду с многозначными, а также
когда они имеют при себе единицы
измерения. Цифровая форма предпочтительна
для многозначных чисел. Она более
отчётлива и лучше воспринимается.
Выбор
между цифровой и различными вариантами
словесной формы для обозначения
количества зачастую приобретает для
редактора принципиальное значение.
Перед ним может встать вопрос, что
предпочесть: «25%», «одна четвёртая
часть»; «четверть» или конкретное
обозначение количества цифрой, например:
«Общая протяжённость топливных артерий
достигает в республике более шести
тысяч километров. К концу нынешнего
года она увеличится на четверть». Был
ли прав редактор, когда обозначил
количество существительным «четверть»?
Очевидно, текст выиграл в выразительности,
но проиграл в точности (сравните:
«протяжённость … увеличится на 1500 км»).
Выбор между цифрой и словом каждый раз
должен быть мотивирован.
Включение
цифр в текст – одно из наиболее
рациональных средств сообщения информации
и действенное средство убеждения.
Печатая сводки, экономические обозрения,
материалы изучения общественного
мнения, предоставляя слово экономистам,
статистикам, социологам, политикам,
специалистам промышленности и сельского
хозяйства, журналист разговаривает с
читателем языком цифр.
Цифра
всегда останавливает на себе внимание.
Строго определённое её значение как
знака математического предопределяет
первое и главное требование редактора
к этому виду фактического материала.
Цифра в тексте должна быть точна
независимо от того, какую функцию –
информации, аргумента или иллюстрации
– она выполняет. Редактору важно знать
основные критерии выбора необходимых
и выразительных цифр, способы аналитической
их обработки и специфические приёмы
редакторской оценки и обработки
статистического материала, полезно
выработать навык соотнесения числовых
значений, владеть методикой построения
системных рядов, знать правила округления
величин, уметь проверить вычисления.
Включённая
в словесный текст, цифра входит в систему
существующих в нём смысловых связей,
её надо уметь вписать в него. Цифра,
неумело включённая в текст, создает
лишь иллюзию точной информации. Редактор
не только оценивает реальное значение
каждой цифры, но и соотносит его со
значением других элементов текста: дата
должна быть не только проверена, но и
соотнесена с обозначением события и
отдельных реалий, числа осознаны в ряду
определённых закономерностей. Это
поможет избежать досадных ошибок и
неточностей, которые всегда вызывают
резкую и справедливую реакцию читателей.
Обилие цифр и дат никогда не идёт на
пользу газетной публикации. Перегружать
ими текст нельзя, необходимость каждой
должна быть очевидна. И, наконец, приём
конкретизации цифры, очень важный для
работы над публицистическим материалом.
Он заключается в том, чтобы, пусть в
общих чертах, представить реальное
значение цифры. Затруднения неизбежно
возникнут, если цифра включена в текст
необдуманно, механически перенесена в
него из статистического отчёта.
Попробуйте, например, конкретизировать
цифру, входящую в количественно-именное
сочетание 20,5 коровы! («На сто гектаров
угодий хозяйство имеет 54 головы крупного
рогатого скота, в том числе 20,5 коровы»).
Эта цифра нелепо выглядит на газетной
полосе в журналистской публикации.
Правда, Глеб Успенский один из своих
очерков назвал «Четверть лошади», но
если в очерке Успенского число – образ,
в приведённом нами отрывке – это
результат небрежной обработки редактором
статистического материала.
Обработка
таблиц. Таблица – форма обобщения
фактического (главным образом,
статистического) материала, традиционная
для экономики, статистики, точных наук.
Благодаря приёмам группировки по общим
признакам, показатели таблицы выглядят
рельефно, их легко сравнивать, достигается
возможность наглядно представить
операции с данными. Они располагаются
в таблице по вертикальным колонкам —
графам, снабжённым заголовками и
отделённым друг от друга вертикальными
линейками (при публикации в газете
вертикальные линейки часто опускают).
Основные части таблицы: тематический
заголовок, головка, боковик, прографка.
Если таблиц несколько, они могут иметь
также нумерационный заголовок.
При
воспроизведении текста высокой печатью
газеты редко публиковали таблицы,
требовавшие по условиям технологического
процесса ручного набора. Современная
полиграфическая техника расширила
возможности графического оформления
фактического материала. Таблицы стали
часто появляться на газетной полосе.
Таблицы
различаются по своим целям. Справочные
— это так называемые рабочие таблицы
или таблицы сведений. Газеты регулярно
печатают таблицы курса валют, результатов
и дат спортивных состязаний, таблицы
выигрышей. Задача редактора в этом
случае – проверить правильность данных
и облегчить читателю пользование
таблицей: сведения должны быть расположены
в определённом порядке, например, по
алфавиту, во временной последовательности,
в порядке возрастания или убывания
величин.
Аналитические
таблицы – итог счётной и статистической
работы. Такая таблица сводит воедино
данные по нескольким объектам наблюдений,
фиксирует результат классификации
данных, их группировки, подсчётов,
вычислений, выявляет и делает очевидными
связи между явлениями. Для журналиста
включение в текст аналитической таблицы
– экономный и выразительный способ
представить сложный фактический
материал.
Эти
данные показательны для читателей
журнала, представляют они интерес и для
специалистов – историков печати и
социологов, но построение таблицы нельзя
назвать удачным. Если рассматривать её
только как справочную, найти нужные
сведения удастся не сразу: названия
изданий расположены беспорядочно. Никак
не помогает таблица и анализу ситуации,
несмотря на то, что работа, необходимая
для этого, была проведена: в таблицу
включены не только абсолютные цифровые
значения (количество подписчиков за
два года), но и процентное отношение
этих данных. Читателю трудно зрительно
сопоставить цифры. Наиболее красноречивые
данные теряются в ряду менее показательных.
Ни расположением их, ни средствами
графики отношения меньше – больше не
выявлены. Нарушено и важнейшее для
всякой аналитической таблицы требование
сопоставимости величин. Объединять в
одной графе сведения об изданиях разных
типов – газетах и журналах, среди которых
даже один толстый литературно-художественный
журнал, неправомерно. О небрежности
оформления таблицы свидетельствуют
пустая графа в головке таблицы,
формулировка её тематического заголовка,
оформление размерности показателей.
Перестроенная
таблица выявляет тенденции, которые
нашли своё развитие в дальнейшем. Через
год, комментируя предварительные данные
о подписке уже на 1991 г., еженедельник
АиФ констатировал не только всеобщее
снижение тиражей, причиной которого
послужило повышение цен на газеты и
журналы, но и то, что многих читателей
перестало удовлетворять качество
информации, её направленность, оценка
событий и фактов. Подписка на центральные
издания сократилась, перестали практически
пользоваться спросом многие партийные
коммунистические газеты и журналы –
все эти процессы способны отразить
цифры, сведённые в таблицу.
Обычно,
обращаясь к таблицам, журналист имеет
дело с фактами, уже обработанными
специалистом и сгруппированными
определённым образом. Такие таблицы
подробны, содержат много данных,
группировка которых продиктована
специальными задачами. Для журналиста
– это лишь исходный материал, но тем не
менее надо уметь прочитать любую, даже
самую сложную, таблицу, сопоставляя
данные друг с другом, выявляя логические
связи между величинами, понять принцип
их группировки. Это необходимо, чтобы
помочь автору упростить таблицу,
освободить её от лишних данных и правильно
оформить. Редактор проверяет достоверность,
существенность, сопоставимость
показателей, точность формулировок,
оценивает построение и оформление
таблицы, судит о том, насколько наглядно
представлены в ней данные и связи между
ними.9
В
основе логической структуры таблицы
лежит суждение. Её цель – выявить
логические связи между его субъектом
и предикатом, между величинами и их
характеристикой. Если данных в таблице
немного и она проста по построению, в
газете её включают в текст после двоеточия
в виде вывода (без линеек). В других
случаях таблица сохраняет свою
традиционную форму, но никогда в
журналистском материале основной текст
не должен повторять таблицу, он лишь
комментирует её, формулирует выводы,
следующие из данных, которые в этом
случае играют роль аргументов.
Чтобы
проверить содержание таблицы, рекомендуется
провести выборочную проверку величин,
оценить авторитетность источника, из
которого заимствованы данные, убедиться
в строгости следования избранному
принципу группировки данных. Важно,
чтобы общие признаки, на основании
которых ведётся группировка, были
найдены правильно. Следует проверить,
сопоставимы ли данные по существу и по
их количественному значению, специально
обращая внимание на единицы измерения
и их написание, на то, сопоставимы ли
отрезки времени, в течение которых
велось наблюдение.
Таблица
должна наглядно проявить для читателя
взаимозависимость величин. Полезно
знать, что сравнивать их легче, когда
они расположены по вертикали, причём
напомним, как важно точно расположить
цифры – разряд под разрядом. Простой,
но эффективный способ выявить взаимосвязь
величин, стоящих в боковике, – система
отступов. В таблице не должно быть
повторов, пустых граф – они свидетельствуют
о непродуманности построения таблицы:
комбинация вертикальных граф и
горизонтальных строк наглядно проявляет
смысл суждений. В таблице не должно быть
лишних граф и строк (например, графы «№
по порядку»), нумерации граф, строк,
содержащих итоги вычислений («Всего…»,
«Итого…») Примечания должны быть
вынесены вниз таблицы отдельной строкой.
Сложный,
содержащий большое количество данных,
табличный материал, оформленный как
вывод, воспринимается с трудом. Если по
техническим причинам вертикальные
линейки поставить нельзя, пробелы между
графами следует увеличить. Теряет в
наглядности таблица, завёрстанная в
газете с переходом на другую полосу,
трудно прочитать головку таблицы, когда
строки в ней расположены по вертикали.
Даже
при публикации официальных статистических
данных, уже представленных в исходных
материалах в виде таблиц, в которых
редактор не вправе что-либо изменить
по существу, необходимо обработать
их с учётом особенностей восприятия
читателем газетного текста, требований
наглядности и технических возможностей
газетной вёрстки.
Работа
с литературными цитатами. Для журналиста
обращение к цитатам – экономный и
убедительный приём, позволяющий
представить читателю факты, обобщить
их, подтвердить своё мнение ссылкой на
авторитетный источник. В публицистическом
тексте это средство не только убеждения,
но и эмоционального воздействия. Как
один из видов фактического материала,
цитаты должны удовлетворять предъявляемым
к нему общим требованиям, на первом
месте среди которых стоит требование
точности. Цитата – по известному
определению – дословно приведённая
выдержка из текста. Требование точности
воспроизведения цитаты охватывает не
только слова, но и знаки препинания,
шрифтовое оформление.10 Это в равной
мере относится к выдержке из официального
документа, несущей читателю содержательную
информацию, и к эмоционально насыщенной
цитате из художественного произведения.
В газете не принято давать подробные
ссылки на источник цитаты, читатель
принимает её на веру, и редактор полностью
ответственен за то, чтобы в тексте не
было искажений. Поэтому он обязан
тщательно выверить цитату, не передоверяя
это техническим работникам.
Известно,
что автор иногда цитирует по памяти.
Редактор не должен позволять себе этого.
Авторитет публикации может подорвать
даже незначительная ошибка. Если она
пройдёт незамеченной, текст может
быть истолкован неверно. Даже признанный
в своей области специалист не застрахован
от ошибок при цитировании по памяти.
Точность
цитирования трактуется редактированием
широко. Она предусматривает оценку
цитаты по существу, правомерность её
выбора, оценку приёмов, которыми она
введена в текст. Редактор должен уточнить,
из какого источника цитата извлечена,
кем, когда, в связи с какими обстоятельствами
создан цитируемый текст. Это особенно
существенно потому, что объём журналистского
материала невелик и не допускает
включения большого количества пространных
цитат. Отбор их должен быть обоснованным,
а обработка текста цитаты, которую нет
возможности привести полностью, требует
особой тщательности: каждый пропуск в
цитате следует обозначить, сокращения
не должны исказить смысл. Чтобы решить,
допустимо ли сокращение, предложенное
автором, редактор должен восстановить
текст цитаты, и только после этого,
сравнив полный и сокращённый варианты,
он определяет, допустимы ли сделанные
автором купюры. Особого внимания требуют
цитаты из художественной литературы.
Если эти цитаты удачно найдены и точно
вписаны в текст журналистского материала,
они способны обогатить его, открыть для
читателя новые стороны явления.
Цитата
может быть представлена одним или
несколькими предложениями, частью
предложения, даже одним словом. Но во
всех случаях это «чужой» фрагмент в
структуре текста. Войдя в него, став его
частью, цитата продолжает сохранять
содержательные и экспрессивные качества,
которые были присущи ей в тексте,
послужившем источником цитирования.
Так возникает своеобразная перекличка
двух литературных произведений, их
внутренних миров, открывающая широкие
возможности для образного освоения
публицистом действительности. И в то
же время двойственная природа цитаты
может послужить причиной досадных
редакторских просчётов.
В
публицистическом тексте цитатам
отводится особая роль, возрастает
значение комментария, содержащего
авторскую оценку цитаты. Между цитатой
и комментарием возникают своеобразные
типы связи. Опытный редактор знает, как
важен в этом случае выбор приёмов
комментирования и как серьезны могут
быть последствия любой небрежности при
обработке такого текста.
Только
точный и глубокий комментарий может
сообщить современное звучание цитатам
из классической литературы, к которым
часто обращаются журналисты. Достичь
этого, включая ту или иную цитату в текст
просто как подходящую к случаю, невозможно.
Ни привлекательность цитируемых строк,
ни доверительный тон комментария не
помогут скрыть поверхностность
рассуждений журналиста.
Острым
публицистическим выступлениям свойственна
полемичность, активное отношение к
своему материалу. Особенности
комментирования цитат зачастую
определяются противопоставлением
двух позиций – автора и его оппонента.
Цитаты представляют в этом случае
суждения оппонента, комментарий содержит
авторскую оценку этих суждений. Он может
предшествовать цитате или идти после
неё, может быть введён внутрь цитаты,
но никогда не должен сводиться к её
пересказу. В нём может быть дана оценка
содержания цитаты, её литературной
формы, уточнены смысловые акценты,
выявлены намерения автора. Цитата –
материал исследования публициста,
комментарий – инструмент этого
исследования. Приспосабливать цитату
к комментарию, разрывая её – приём
недобросовестный. Так называемый
«монтажный метод», когда взятые в кавычки
части цитаты включаются в авторский
текст, сливаясь с ним, создаёт лишь
видимость достоверного цитирования.
Целостность цитаты разрушается, исчезают
границы между мыслями автора и его
оппонента, и оппонент лишается слова.
Вырвав из текста одну фразу, нельзя
спешить со своими выводами и обобщениями,
на которые приведённая цитата права не
даёт. Распространённым явлением в
литературной практике журналистов
стало включение в текст так называемых
«раскавыченных цитат» – графически не
выделенных фрагментов текста литературных
произведений. Особенно часто к этому
приёму прибегают в заголовках. Точность
цитирования при этом не преследуется.
Цитату «приспосабливают» к новому
контексту, изменения при этом могут
быть значительными: сокращения, при
которых выпадают даже существенные для
мысли автора части, изменения и замена
слов. Лингвисты склонны рассматривать
цитирование без кавычек в ряду явлений,
характерных для демократизации языка,
как элемент некой «игры», присущей
мироощущению современного человека,
как путь к формированию нового класса
речений, который занимает промежуточное
положение между крылатыми словами и
обычными свободными сочетаниями слов.
Другой
тип освоения литературной цитаты –
полное её подчинение новому контексту.
В последнее время газетные публикации
часто включают строку из стихотворения
А. Ахматовой «Творчество». Напомним
текст стихотворения:
Когда
б вы знали, из какого сора
Растут
стихи, не ведая стыда,
Как
жёлтый одуванчик у забора,
Как
лопухи и лебеда.
Приведём
газетный текст, в который включена
цитата без кавычек: «Когда б вы знали,
из какого сора творит Зайцев высокую
моду. Из габардина фабрики П. Алексеева».
Эта же строка послужила заголовком к
заметке в другой газете о том, как в
Петропавловске-Камчатском местные
умельцы шили кожаные куртки из обложек
к партбилетам. Оторванная от первичного
контекста стихотворная строка потеряла
свои поэтические свойства. Остался лишь
отголосок ритма, а те, кто знает
стихотворение, ощутят бестактность
подобного обращения с поэтическим
текстом. Это не содержащее смысла и не
завершённое по форме высказывание не
станет пословицей, не будет причислено
к крылатым словам. Оно на наших глазах
превращается в речевой штамп.
Оценить
конкретное цитатное вкрапление можно
только исходя из анализа текста, вновь
создаваемого и первичного, того, откуда
цитата взята. Это правило цитирования,
известное каждому редактору, остаётся
в силе и тогда, когда он имеет дело с
«раскавыченными цитатами». Сегодня
журналист имеет практически неограниченные
возможности обращаться к разнообразным
литературным источникам – от Библии
до произведений новейших литературных
школ и направлений. Встреча с новым,
часто нетрадиционным материалом требует
от редактора точных знаний, понимания
процессов, происходящих в языке,
ответственного отношения к слову.
25.Таблица
как с вид фактического материала, как
способ оформления статистических
данных.
Таблицы
Распространённой
формой представления фактических
цифровых данных являются таблицы,
которые могут использоваться как в
тексте работы, так и в приложении к ней.
Таблица
является формой систематизации
фактического материала, включающей
главным образом цифровые данные. Следует
помнить о назначении таблиц, которые
подразделяются на справочные и
аналитические: первые включают сведения,
расположенные в определённом порядке
с целью облегчения поиска информации,
вторые – классифицированные данные,
являющиеся результатом анализа связей
между явлениями и группирующие наблюдения
по нескольким объектам.
Следует
помнить, что таблицу не рекомендуется
перегружать сведениями, словесные
формулировки должны быть лаконичными
и ясными.
Наконец,
основное правило использования таблиц
заключается в том, что основной текст
работы комментирует таблицу, формулирует
на её основании выводы, но ни в коем
случае не повторяет таблицу.
Для
схем, диаграмм и других видов графического
материала применимы те же правила.
26.Цитаты
как с вид фактического материала.
.
Цитаты и цитирование
Своеобразным
видом фактического материала, как уже
отмечалось, являются цитаты — части
текста, выписанные из другой книги или
статьи без всяких изменений. Трудно
назвать такой вид литературы, в котором
не использовались бы цитаты.
При
редакторском анализе цитат приходится
решать две задачи.
Во-первых,
надо установить, нужны ли цитаты для
разработки темы, нет ли возможности
сократить число приведенных высказываний,
какие из них надо обязательно оставить.
Обильное
цитирование не всегда оправдано
интересами дела, иногда оно продиктовано
мотивами, весьма далекими от научной
принципиальности. Вот характерный
диалог между редактором и автором,
приводимый работником белорусского
издательства «Народна асвета»:
«—
Зачем Вы обильно цитируете? Ведь у самого
есть ценный материал, удачные исследования.
Вы полшага сделаете самостоятельно и
тут же торопитесь стать в чужой след,
оставленный «маститой ногой»,
пересказываете мысли «великих». Зачем
же тогда нужна Ваша книга?
— Ну,
ладно, — идет на уступку автор, — ссылку
на Рубинштейна снимите: его нет в живых,
не обидится. А вот Щукину, пожалуйста,
оставьте. И Люблинскую тоже, и Божович,
и Менчинскую, пожалуй. Еще подумают, что
я не признаю их работ, и мою книгу
раздраконят…».
Во-вторых,
редактор должен установить, соответствуют
ли цитаты источнику, не допущены ли
ошибки в ходе цитирования.
Решая
первую задачу, естественно, надо учитывать
характер текста. Различают цитаты
иллюстративные, т. е. подтверждающие
какую-либо мысль, и аналитические,
составляющие часть анализируемого
материала. Во многих случаях число
иллюстративных цитат без ущерба для
содержания может быть сокращено.
Относительно аналитических цитат такой
вывод был бы неправильным. Например, в
работах, посвященных разбору конкретных
произведений — художественных, научных,
публицистических, цитирование этих
сочинений в широких масштабах не только
возможно, но и обязательно. Вместе с тем
и здесь редактор нередко встречает
случаи, когда несколько цитат подтверждают
одно и то же положение и, значит, можно
без труда их число сократить. Бесспорно,
что цитата не нужна и там, где положение
аксиоматично, очевидно само по себе.
Вторая
задача состоит в том, чтобы установить,
правильно ли цитирует автор, не допускает
ли он искажения мысли, содержащейся в
источнике.
Бывают
случаи, когда положения, взятые в
авторитетном источнике, искажаются,
так сказать, несознательно, вследствие
непонимания того, как надо цитировать.
Факты такого рода, к сожалению, не так
уж редки.
Немало
ошибок связано, например, с тем, что в
качестве цитаты дается произвольно
взятая часть фразы.
Наконец,
встречается и такой ошибочный прием —
высказывание по конкретному поводу
рассматривается как всеобъемлющее, ему
придается весьма широкий смысл.
Из
сказанного ясно, что простой сверки
процитированных слов с текстом, откуда
они взяты, совсем недостаточно для
ответа на вопрос, правильно ли цитирует
автор. Здесь необходим анализ не только
самих цитат, но и всего контекста, а
также сопоставлениезаконченного
раздела рукописи с первоисточником,
частью которого является цитата.
Например,
во время суда над бывшим президентом
Югославии Слабоданом Милошевичем,
подсудимый в качестве обвинения
американцев во всём происходящем в
Сербии использовал материалы немецкой
кинохроники, которые сами немцы приводили
для доказательства преступной деятельности
Милошевича. Создалась весьма любопытная
ситуация, когда один и тот же материал
служил и в качестве обвинения, и в
качестве оправдания в зависимости от
трактовки.
Таким
образом, предметом редакторского
внимания на этой стадии работы должны
стать не только сами цитаты, но и их
текстовое обрамление, а также приемы
цитирования. Анализ цитат и фактического
материала в целом есть важная составная
часть разбора содержания рукописи; он
позволяет оценить существенные аспекты
разработки темы.
-
Цифра
как вид фактического материала и
элемент текста.
Цифры
в тексте
Факт
– предмет журналистского исследования.
Для
журналиста факт всегда соотнесён с
суждением о событии, служащим
утверждению истинности или ложности
определённых положений, выяснению
связей и отношений между явлениями,
между предметом и его свойствами
Понятие
фактический материал, которое принято
в редактировании, охватывает все опорные
для текста элементы, передающие смысл
и предметные отношения.2 При правке
текста они не должны подвергнуться
изменениям или выпасть. Фактический
материал реализуется в текстовых
конструкциях, которые обозначают не
только события, но и «кусочки
действительности» – вещные элементы
предметного ряда, свойства, качества,
состояния, наименования лиц, отношений,
количества.
Любая
неясность в журналистском тексте
неприемлема. Поэтому так важна правильность
передачи информации, сквозная оценка
и точная разработка фактического
материала. Наблюдения над газетной
практикой убеждают в том, насколько
важна для автора помощь редактора.
Не
менее важно для контролирующего мышления
редактора умение конкретно представить,
как происходили события, о которых
говорится в тексте.
В
небрежно отредактированном материале
факты нередко предстают перед читателем
в искажённом виде, логические связи
нарушены, выводы автора необоснованы.
Поверхностность
суждений непростительна для журналиста,
и редактору следует особенно внимательно
отнестись к выигрышным, на первый взгляд,
материалам.
Цифры
в тексте. Цифра – символ иной, чем слово,
знаковой системы. Как обозначению числа
ей изначально присуща точность, обобщение,
концентрированность информации. Этот
сложный для редактирования материал
требует особого внимания редактора.
Начать следует с того, чтобы убедиться,
легко ли прочитать текст вслух. Так,
заголовок «1 100 000 000-й гражданин» наверняка
представит трудности для многих
читателей. Конструктивные возможности
имён числительных, которыми в языке
передаются значения количества, в
некоторых случаях оказываются
ограниченными, и мы неизбежно сталкиваемся
с трудностями словообразования.
Издательская
практика выработала специальные
рекомендации для обозначения чисел в
тексте.4 Числа от 1 до 9 включительно
принято обозначать словом, когда они
не имеют при себе единиц измерения и
стоят в косвенном падеже. Это необходимо,
чтобы избежать остановки при прочтении
цифры, которая воспринимается первоначально
всегда в форме именительного падежа.Цифрой
принято обозначать однозначные числа,
когда они находятся в одном ряду с
многозначными, а также когда они имеют
при себе единицы измерения. Цифровая
форма предпочтительна для многозначных
чисел. Она более отчётлива и лучше
воспринимается.Выбор между цифровой и
различными вариантами словесной формы
для обозначения количества зачастую
приобретает для редактора принципиальное
значение. Перед ним может встать вопрос,
что предпочесть: «25%», «одна четвёртая
часть»; «четверть» или конкретное
обозначение количества цифрой.
Включение
цифр в текст – одно из наиболее
рациональных средств сообщения информации
и действенное средство убеждения.
Печатая сводки, экономические обозрения,
материалы изучения общественного
мнения, предоставляя слово экономистам,
статистикам, социологам, политикам,
специалистам промышленности и сельского
хозяйства, журналист разговаривает с
читателем языком цифр.
Цифра
всегда останавливает на себе внимание.
Строго определённое её значение как
знака математического предопределяет
первое и главное требование редактора
к этому виду фактического материала.
Цифра в тексте должна быть точна
независимо от того, какую функцию –
информации, аргумента или иллюстрации
– она выполняет. Редактору важно знать
основные критерии выбора необходимых
и выразительных цифр, способы аналитической
их обработки и специфические приёмы
редакторской оценки и обработки
статистического материала, полезно
выработать навык соотнесения числовых
значений, владеть методикой построения
системных рядов, знать правила округления
величин, уметь проверить вычисления.
Значения
меньше – больше, ближе – дальше, раньше
– позже и т. п. должны быть подтверждены
в тексте.
Включённая
в словесный текст, цифра входит в систему
существующих в нём смысловых связей,
её надо уметь вписать в него. Цифра,
неумело включённая в текст, создает
лишь иллюзию точной информации. Редактор
не только оценивает реальное значение
каждой цифры, но и соотносит его со
значением других элементов текста: дата
должна быть не только проверена, но и
соотнесена с обозначением события и
отдельных реалий, числа осознаны в ряду
определённых закономерностей. Это
поможет избежать досадных ошибок и
неточностей, которые всегда вызывают
резкую и справедливую реакцию читателей.
Обилие
цифр и дат никогда не идёт на пользу
газетной публикации. Перегружать ими
текст нельзя, необходимость каждой
должна быть очевидна. Даты, не связанные
по смыслу с предметом публикации, не
следует включать в текст.
Существенно,
чтобы перевод количественных понятий
в разряд конкретных представлений был
по силам читателю. Прежде всего, это
касается обозначения больших количеств
и приблизительных величин. Когда в
погоне за эффектом авторы злоупотребляют
ими, кроме самого общего представления,
запёчатлённого в сознании как много,
мало, хорошо, плохо, читатель никакой
другой информации из текста не извлекает.
Редактору следует помнить, что имена
существительные со значением числа,
такие как тысяча, миллион, миллиард,
которыми мы пользуемся для обозначения
больших количеств, мыслятся, прежде
всего, как предметно-собирательные
значения множества, и конкретизации их
в тексте следует уделить специальное
внимание.
И,
наконец, приём конкретизации цифры,
очень важный для работы над публицистическим
материалом. Он заключается в том, чтобы,
пусть в общих чертах, представить
реальное значение цифры. Затруднения
неизбежно возникнут, если цифра включена
в текст необдуманно, механически
перенесена в него из статистического
отчёта.
Тавтология (от греч. ταὐτός – тот же самый и λόγος – слово), термин классической формальной логики, означающий формулу (суждение, высказывание), которая остаётся тождественно истинной для любого набора истинностных значений ее переменных. Тождественная истинность такой формулы обусловлена исключительно её логической структурой.
-
-
- Например, в логике предикатов 1-го порядка любая атомарная формула A вида a = a (где a суть терм (термин)) является тавтологией: если a = МАСЛО, то атомарная формула A имеет вид
-
-
-
-
-
-
-
- МАСЛО = МАСЛО («Масло масленное»).
-
-
-
-
-
-
-
- Например, в логике предикатов 1-го порядка любая атомарная формула A вида a = a (где a суть терм (термин)) является тавтологией: если a = МАСЛО, то атомарная формула A имеет вид
-
Это значение термина «тавтология» было введено Л.Витгенштейном, а позднее сфера его применения была расширена: «тавтологией» стали называть вообще логически истинные формулы классических логических исчислений – законы классической логики. В соответствии с этим термин «тавтология» естественно относить не к «чистым», а к прикладным формальным исчислениям, в которых зафиксирована область изменения переменных (предметная область рассмотрения или универсум), не смотря на то, что тавтология не зависит от того, каков этот универсум.
Почему? Потому что известна область интерпретации абстрактной формулы: вы всегда имеете возможность проверки её тождественной истинности, а не просто выполнимости в какой-то части универсума.
В классической формальной логике термины «тавтология», «логический закон», «тождественно истинная формула» являются синонимами. Одновременно в классической формальной логике термин «тавтология» используется в качестве особой разновидности логической ошибки.
Позиция автора статьи[]
Витгенштейн, назвав «тавтологией» любую тождественно истинную формулу или логический закон формального исчисления, фактически закрепил уже применяемую десятилетиями многими логиками и философами лексику. Так Г.В.Ф.Гегель применял термин «тавтология» именно в смысле логического закона. Широко известна данная им характеристика для классической формальной логики: «Эта логика ничего кроме формальных тавтологий дать не в состоянии…»
Двусмысленность понятия «Тавтология» в обыденной речи[]
В обыденной речи (в отличие от, например, текстов юридических законов или инструкций по эксплуатации) достаточно часто используются тавтологичные конструкции, которые, однако, не вводят в заблуждение, так как верификация высказываний осуществляется в «режиме реального времени». В этом случае мы легко различаем, какой смысл «здесь и сейчас» (тавтология это логический закон или логическая ошибка) имеет понятие «Тавтология»:
-
-
-
-
-
-
-
-
-
-
-
-
-
-
- Тавтология как логическая ОШИБКА:
-
-
-
-
-
-
-
-
-
-
-
-
-
1) крайний случай логической ошибки «предвосхищение основания» (лат. peti-tio principii), а именно: когда нечто определяется или доказывается тем же самым (лат. idem per idem).
2) “п о р о ч н ы й круг”, т. е. когда тезис обосновывается аргументами, а аргументы обосновываются этим же тезисом.
-
-
-
-
-
-
- Например, “Опиум усыпляет потому, что имеет усыпляющую силу”.
-
-
-
-
-
В среде формализованного языка (будь то формальная или содержательная логика), очевидно, что такая двусмысленность не допустима, так как верификация суждения осуществляется «наедине с текстом».
Тавтологии диалектической логики[]
Диалектическими противоположностями в марксизме традиционно являются следующие пары:
сущность и явление, качество и количество, пространство и время, причина и следствие, необходимость и случайность, действительность и возможность, материя и сознание, объект и субъект и др.
Будучи диалектическими противоположностями эти категории образуют диалектически тождественные пары (диады), которые являются элементарными тавтологиями диалектической логики:
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
- СУЩНОСТЬ
ЯВЛЕНИЕ
- СУЩНОСТЬ
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
- КАЧЕСТВО
КОЛИЧЕСТВО
- КАЧЕСТВО
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
- ЕДИНСТВО
БОРЬБА
- ЕДИНСТВО
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
- МАТЕРИЯ
СОЗНАНИЕ
- МАТЕРИЯ
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
- ПРИЧИНА
СЛЕДСТВИЕ
- ПРИЧИНА
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
- НЕОБХОДИМОСТЬ
СЛУЧАЙНОСТЬ
- НЕОБХОДИМОСТЬ
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
- Производительные СИЛЫ
Производственные ОТНОШЕНИЯ
- Производительные СИЛЫ
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
- Потребительная СТОИМОСТЬ
Меновая СТОИМОСТЬ
- Потребительная СТОИМОСТЬ
-
-
-
-
-
-
-
-
-
-
-
-
-
-
- Здесь символ «
» суть знак диалектической тождественности.
- Здесь символ «
-
-
Тавтологиями Гегель и Маркс в собственных логиках считали также триады. При этом необходимо учитывать, что эти триады никогда не проходили интерсубъективной верификации, а считались эпигонами безусловно истинными как результаты божественного откровения. В марксистско-ленинской диалектике истинной считается единственная гегелевская триада:
При этом не может не возникнуть вопрос: как это в диалектико-материалистическую идеализацию мог попасть как тождественно истинный логический закон из диаметрально противоположной диалектико-идеалистической идеализации? Как это стало возможным? Подумайте!!!
-
-
-
-
-
-
-
-
-
-
- Всё предельно элементарно: гегелевские суждения становятся правдоподобными тогда, когда Гегель забывает о своём Принципе препозиции (ИДЕЯ — первична, МАТЕРИЯ — вторична), а мыслит в соответствие с реальным развитием процесса, т.е. материалистически…
-
-
-
-
-
-
-
-
-
Тавтология в Дианомике[]
Тавтология (от греч. tauto — то же самое и logos — слово) суть категория Дианомики — логически истинная формула, логический закон. Категория ТАВТОЛОГИЯ суть результат диалектического отрицания категории ПАРАДОКС. В своей экзогенной сети категория ТАВТОЛОГИЯ суть акциденция категории РАЗРЕШЕНИЕ.
Тавтологией в Дианомической логике является любая диада, триада, а также любое суждение, которое корректно образовано из категорий с помощью логических операций и принадлежащее Диалектической сети.
Тавтология и парадокс[]
-
-
-
-
-
-
-
-
- Краткий миг торжества… между двумя бесконечностями времени…
-
-
-
-
-
-
-
Из энциклопедических словарей:[]
- Википедия
- Философия: Энциклопедический словарь. — М.: Гардарики. Под редакцией А.А. Ивина. 2004.
- БСЭ, 1969-1978
См. также[]
- Логическая истинность
- Апория
- АНТИНОМИЯ
- Парадокс логический
- Вопрос
- Категории АПОРИЯ и АНТИНОМИЯ, ПАРАДОКС и ТАВТОЛОГИЯ
- Диалектическая логика
Литература[]
- Л.Витгенштейн. Логико-философский трактат
- Чёрч Α., Введение в математическую логику, пер. с англ., [т.] 1, [M.], 1960, § 15, 19, 23.
- Никлас Луман. Тавтология и парадокс в самоописаниях современного общества.
Ссылки[]
Обобщить
понятие
— значит
перейти от понятия с меньшим объемом,
но с большим содержанием к понятию с
большим объемом, но с меньшим содержанием.
Например, обобщая понятие «Министерство
юстиции Российской Федерации», мы
переходим к понятию «министерство
юстиции»,которое более шире по объёму.
Ограничить
понятие
— значит
перейти от понятия с большим объемом,
но с меньшим содержанием к понятию с
меньшим объемом, но большим содержанием.
Иначе говоря, чтобы ограничить понятие
«юрист», мы переходим к понятию
«следователь», которое в свою очередь
можем ограничить, образовав понятие
«следователь прокуратуры». Пределом
ограничения понятия является
единичное
понятие.
Обобщение-переход
от единичного к общему,а ограничение-от
общего к единичному.
8. Определение понятий. Правила и ошибки определения.
Логическая
операция, раскрывающая содержание
понятия,
называется определением понятий.
Правила определения:
1. Определение
должно быть соразмерным.
Правило соразмерности
требует, чтобы объем определяемого
понятия был равен объему определяющего.
Иначе говоря,
эти понятия должны находиться в отношении
равнообъемности.
2. Определение
не должно заключать в себе круга.
Если при определении
мы прибегаем к другому понятию, которое,
в свою очередь, определяется при помощи
первого, то такое определение содержит
в себе круг. Разновидностью круга в
определении является
тавтология
— ошибочное
определение, в котором определяющее
понятие повторяет определяемое.
Тавтология, отличается от круга в
определении меньшей сложностью
построения. Определяющее понятие
является повторением определяемого.
3. Определение
должно быть ясным.
Оно должно указывать
на известные признаки, не нуждающиеся
в определении и не содержащие
двусмысленности. Если же понятие
определяется через другое понятие,
признаки которого неизвестны и которое
само нуждается в определении, то это
ведет к ошибке, называемой
определением
неизвестного через неизвестное, или
определением х через
у.
4. Определение
не должно быть отрицательным. Отрицательное
определение не раскрывает определяемого
понятия. Оно указывает, чем не является
предмет, не указывая, чем он является.
Ошибки
определения:
а)
широкое определение, когда определяющее
понятие по объему шире, чем определяемое
понятие. Такая ошибка содержится в
следующих определениях: “Лампа — источник
света”.
б)
узкое определение, когда определяющее
понятие по объему уже, чем определяемое
понятие. Например, “совесть — это
осознание человеком ответственности
перед самим собой за свои действия и
поступки” (а перед обществом?);
в)
определение в одном отношении широкое,
в другом — узкое. Например, “бочка — сосуд
для хранения жидкостей”. С одной стороны,
это широкое определение, так как сосудом
для хранения жидкостей может быть и
ведро, а с другой стороны, это узкое
определение, так как бочка пригодна для
хранения и твердых тел, а не только
жидкостей.
9. Деление понятий. Правила деления. Ошибки в делении.
Логическая операция,
раскрывающая объем понятия,
называется делением.
В операции деления
следует различать
делимое
понятие—
объем которого
следует раскрыть,
члены
деления
— соподчиненные
виды, на которые делится понятие, и
основание
деления
— признак,
по которому производится деление.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Юлия Валерьевна Шульгина
Эксперт по предмету «Логика»
преподавательский стаж — 10 лет
Предложить статью
Тавтология как речевая ошибка
Определение 1
Логические тавтологии – это выражения, остающиеся истинными независимо от конкретных объектов, о которых идет речь («всегда истинные выражения»).
В речи тавтология рассматривается как ошибка.
Определение 2
Речевая тавтология – это повтор в предложении (словосочетании) однокоренных слов (или одного и того же слова).
Термин «тавтология» имеет греческое происхождение. Он возник от слияния двух слов:
- «тавто», что можно перевести как «то же самое»,
- «логос» — «слово».
Тавтология является одной из разновидностей плеоназма.
Определение 3
Плеоназмом называют употребление лишних (не несущих смысловой нагрузки) слов.
Примеры плеоназмов:
- прайс-лист цен (по своей сути прайс-лист – это список товаров с указанием цен, слово «прайс» переводится с английского как «цена»);
- своя автобиография (автобиография всегда «своя»; если человек пишет чужую биографию, она не называется «авто»);
- коллеги по работе (слово «коллеги» уже означает общность профессиональной или трудовой деятельности, уточнение «по работе» не требуется).
В тавтологии слова не просто лишние, но еще и однокоренные или повторяющиеся.
Примеры тавтологий:
- подарить в дар;
- объединиться воедино;
- написанное писателем.
Иногда употребление однокоренных слов в словосочетании не является тавтологией; некоторые подобные словосочетания даже стали устойчивыми: «варить варенье», «писать письма», «белое белье».
В риторике не разделяют понятие тавтологии и плеоназма; тавтологию рассматривают более обобщенно, без обязательного требования на неиспользование однокоренных слов.
Определение 4
Тавтология в риторике – это необоснованное повторение одних и тех же, однокоренных или близких по смыслу слов.
«Логические тавтологии» 👇
Тавтология при умелом использовании из ошибки превращается в стилистический прием, создающий образность, эмоциональность и выразительность художественного произведения.
Примеры тавтологий в пословицах и поговорках:
- Дружба дружбой, а служба службой.
- Без вины виноватый.
Иногда тавтологии приобретают дополнительный смысл, определяемый контекстом.
Пример 1
В честь павшего в битве капитана Ла Паллиса солдаты сложили песню «За четверть часа до смерти он был еще живой». Любой человек до смерти (за любое время) является живым. Но эта тавтология подчеркивает внезапность, неожиданность момента смерти, бренность человеческой жизни. Речь идет о том, что всего за 15 минут до смерти этот капитан не собирался умирать, строил планы, активно действовал.
Логические законы как тавтологии
Логические законы представляют собой важный элемент механизма мышления, что определяет их неразрывную связь с другими элементами этого механизма, и в первую очередь – с понятием логического следования, центральным понятием логики как науки. В современной логике эта связь выражается следующим образом: доказать утверждение – это значит показать, что оно логически следует из других утверждений, определенно истинных. Логическое следование заключения из принятых посылок определяется логическими законами. Если нет логического закона, разрушается логическое следование и сам принцип доказательства.
Все логические законы представляют собой логические тавтологии. Если заменить в формуле, представляющей закон, переменные на любые постоянные выражения (подходящей категории), эта формула станет истинным высказыванием:
- закон тождества («если А, то А»): «Если светит солнце, то светит солнце», «Если сейчас зима, то сейчас зима», «Если я иду, значит, я иду»;
- закон исключенного третьего («А или не-А»): «Сейчас идет дождь или не идет дождь», «Два плюс два равно два или два плюс два не равно два»;
- закон противоречия («Неверно, что А и не-А»): «Неверно, что дважды два четыре и дважды два не четыре»;
- закон двойного отрицания («Если неверно, что А неверно, то А верно»): «Если неверно, что сейчас не идет дождь, то сейчас идет дождь».
Все полученные подстановкой сложные высказывания истинны. Они не зависят от рассматриваемой предметной области.
Тавтологический характер логических законов может стать отправной точкой для спекуляций. Тавтология не дает нам новой информации. Так, из высказывания «Сейчас идет дождь или не идет дождь» нельзя понять, какая погода на улице и нужно ли брать с собой зонт. Тавтологию нельзя рассматривать как описание реального положения вещей, поскольку она совместима с любой ситуацией; тавтологию нельзя опровергнуть. Эти специфические особенности логической тавтологии послужили основанием для предположения об отсутствии связи между законами логики и действительностью. Однако подобное предположение неверно. Дело в том, что законы логики занимают «исключительное положение» среди всех высказываний. Они являются априорными, известными до любого опыта истины. Они не бессмысленны – но при том не имеют содержательного смысла; они не могут быть ни подтверждены, ни опровергнуты эмпирическим путем.
Если бы законы логики не несли никакой информации, они бы по своей сути отличались от других научных законов (которые описывают действительность, сообщают какие-то сведения о ней). Основой мысли об информационной пустоте законов логики является узость толкования опыта, который может подтвердить или опровергнуть научный закон. Опыт нельзя сводить к изолированным, фрагментарным ситуациям и фактам. Такого опыта недостаточно для того, чтобы судить об истинности теоретических обобщений, имеющих абстрактный характер и опирающихся на систематический, совокупный опыт. Даже в естественных науках – физике, биологии – нельзя обосновать закон простой ссылкой на наблюдаемые факты. Тем более нельзя это сделать для законов логики, имеющих большую степень абстракции. Законы логики черпают свое обоснование из максимально расширенного опыта теоретической мыслительной деятельности. Конечно, за законами логики тоже стоит опыт – как и за остальными научными законами – но это конденсированный опыт, сложившийся за всю историю познания действительности человеком.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
ЛОГИЧЕСКИЕ ТАВТОЛОГИИ
ЛОГИЧЕСКИЕ ТАВТОЛОГИИ
В обычном языке слово «тавтология» означает повторение того, что уже было сказано; «Жизнь есть жизнь» или «Не повезет так не повезет».
Тавтологии бессодержательны и пусты, они не несут никакой информации. От них стремятся избавиться как от ненужного балласта, загромождающего речь и затрудняющего общение.
Иногда, правда, случается, что тавтология наполняется вдруг каким-то чужим содержанием. Попадая в определенный контекст, она как бы принимается светить отраженным светом.
Французский капитан Ла Паллис пал в битве при Павии в 1525 году. В его честь солдаты сложили дошедшую до наших дней песню «За четверть часа до смерти он был еще живой…». Понятая буквально, эта строка песни, ставшая ее названием, является тавтологией. Как таковая она совершенно пуста. Всякий человек до самой своей смерти жив. Сказать о ком-то, что он был жив за день до своей смерти или за четверть часа до нее, значит, ровным счетом ничего о нем не сказать.
И тем не менее какая-то мысль, какое-то содержание за этой строкой стоит. Оно каким-то образом напоминает о бренности человеческой жизни и особенно жизни солдата, о случайности и, так сказать, неожидаемости момента смерти и о чем-то еще другом.
Один писатель сказал о своем герое: он дожил до самой смерти, а потом умер. Козьме Пруткову принадлежит афоризм: «Не будь цветов, все ходили бы в одноцветных одеяниях». Буквально говоря, это тавтологии и пустота. Но на самом деле смысл здесь все-таки есть, хотя это и не собственный смысл данных фраз, а отражаемый или навеваемый ими смысл.
С легкой руки Л. Витгенштейна слово «тавтология» стало широко использоваться для характеристики законов логики.
Став логическим термином, оно получило строгие определения применительно к отдельным разделам логики. В общем случае логическая тавтология — это выражение, остающееся истинным независимо от того, о какой области объектов идет речь, или «всегда истинное выражение».
Все законы логики являются логическими тавтологиями. Если в формуле, представляющей закон, заменить переменные любыми постоянными выражениями соответствующей категории, эта формула превратится в истинное высказывание.
Например, в формулу «А или не-А», представляющую закон исключенного третьего, вместо переменной А должны подставляться высказывания, то есть выражения языка, являющиеся истинными или ложными. Результаты таких подстановок: «Дождь идет или не идет», «Два плюс два равно нулю или не равно нулю», «Бог существует или его нет» и тому подобное. Каждое из этих сложных высказываний является истинным. И какие бы дальнейшие высказывания ни подставлялись вместо А — как истинные, так и ложные, — результат будет тем же — полученное высказывание будет истинным.
Аналогично в случае формул, представляющих закон противоречия, закон тождества, закон двойного отрицания и т. д. «Неверно, что бог существует и не существует; что дождь идет и не идет; что я иду быстро и не иду быстро» — все это высказывания, полученные из формулы: «Неверно, что А и не-А», и все они являются истинными. «Если бога нет, то его нет; если я иду быстро, то я иду быстро; если два равно нулю, то два равно нулю» — это результаты подстановок в формулу «Если А, то А» и опять-таки истинные высказывания.
Тавтологический характер законов логики послужил отправным пунктом для многих спекуляций по их поводу.
Из тавтологии «Дождь идет или не идет» мы ничего не можем узнать о погоде. Тавтология «Неверно, что бог есть и его нет» ровным счетом ничего не говорит о существовании бога. Ни одна тавтология не несет содержательной информации о мире.
Тавтология не описывает никакого реального положения вещей. Она совместима с любым таким положением. Немыслима ситуация, сопоставлением с которой можно было бы тавтологию опровергнуть.
Эти специфические особенности тавтологий были истолкованы как несомненное доказательство отсутствия какой-либо связи законов логики с действительностью.
Такое «исключительное положение» законов логики среди всех предложений подразумевает прежде всего, что законы логики представляют собой априорные, известные до всякого опыта истины. Они не являются бессмысленными, но вместе с тем не имеют и содержательного смысла. Их невозможно ни подтвердить, ни опровергнуть ссылкой на опыт.
Действительно ли законы логики не несут никакой информации?
Если бы это было так, они по самой своей природе решительно отличались бы от законов других наук, описывающих действительность и что-то говорящих о ней.
Мысль об информационной пустоте логических законов является, конечно, ошибочной. В основе ее лежит крайне узкое истолкование опыта, способного подтверждать научные утверждения и законы. Этот опыт сводится к фрагментарным, изолированным ситуациям или фактам. Они достаточны для проверки истинности элементарных описательных утверждений типа «Идет дождь» или «Я иду быстро». Но явно недостаточны для суждения об истинности абстрактных теоретических обобщений, опирающихся не на отдельные, разрозненные факты, а на совокупный, систематический опыт. Даже законы опытных наук, подобных биологии или физике, нельзя обосновать простой ссылкой на факты и конкретику. Тем более это невозможно сделать в случае самых абстрактных из всех законов — законов логики. Они должны черпать свое обоснование из предельно широкого опыта мыслительной, теоретической деятельности. За законами логики стоит, конечно, опыт, и в этом они сходны со всеми иными научными законами. Но опыт не в форме каких-то изолированных, доступных наблюдению ситуаций, а конденсированный опыт всей истории человеческого познания.
Тавтологии обычного языка нередко наполняются содержанием, пришедшим со стороны, и светят отраженным светом. Так же обстоит дело и с логическими тавтологиями.
Изолированная от других тавтологий, оторванная от языка и от истории познания, логическая тавтология блекнет и создает впечатление отсутствия всякого содержания.
Это еще раз подтверждает мысль, что рассуждения о смысле и значении отдельных выражений языка, изъятых из среды своего существования, допустимы и справедливы только в ограниченных пределах. Нужно постоянно иметь в виду, что язык — это единый, целостный организм, части которого взаимосвязаны, взаимообусловлены и не способны действовать вне его.
Кроме того, сам язык не является некой самодостаточной системой. Он погружен в более широкую среду — среду познания и социальной жизни, когда-то создавшей его и с тех пор постоянно его воссоздающей.
Данный текст является ознакомительным фрагментом.
Читайте также
§ 6. Логические операции с понятиями
§ 6. Логические операции с понятиями
Основными логическими операциями с понятиями являются: обобщение и ограничение понятий, их определение и деление. В основе данных операций лежат родо-видовые отношения между понятиями.Логические операции обобщения и ограничения
А. Логические формы мыслей
А. Логические формы мыслей
1. Что такое логическая форма
Каким же образом логика может выполнить свою задачу? Как она может установить общие условия правильности всех мыслей? Ведь мыслей существует бесчисленное множество, и они очень разнообразны: мысли о музыке, о дне
4. Логические операции с теориями
4. Логические операции с теориями
По аналогии с понятиями и суждениями, — только, разумеется, тоже в более высоком смысле, — можно говорить о логических операциях с теориями. И здесь налицо определенное сходство.Прежде всего следует выделить логические операции
Глава IV. Логические операции с суждениями
Глава IV. Логические операции с суждениями
1. Преобразование суждений
Преобразование простых атрибутивных суждений1. Определите, какие виды преобразования суждений использованы в следующих примерах:
«Все учебники — книги» — «Некоторые книги — учебники».
«Все учебники
§ 3. Логические свойства отношений в умозаключениях
§ 3. Логические свойства отношений в умозаключениях
Многие из умозаключений, рассмотренных нами в предыдущих главах, можно рассматривать как умозаключения, которые зависят от природы отношений включения или исключения классов. Мы кратко отметим то, почему логические
§ 1. Логические ошибки
§ 1. Логические ошибки
Обычно каждый учебник по логике содержит главу, посвященную ошибкам в рассуждении. В целом данные ошибки классифицируются следующим образом: А) чисто логические, или формальные, В) полулогические, или вербальные, С) материальные.A. Формальные
ЛОГИЧЕСКИЕ ЗАКОНЫ
ЛОГИЧЕСКИЕ ЗАКОНЫ
«…Практическая деятельность человека миллиарды раз должна была приводить сознание человека к повторению разных логических фигур, дабы эти фигуры могли получить значение аксиом».
В. И. Ленин
«Свои способности человек может узнать, только шлифуя их».
ГЛАВА 9 ЛОГИЧЕСКИЕ СЛОВА И ЛОЖЬ
ГЛАВА 9
ЛОГИЧЕСКИЕ СЛОВА И ЛОЖЬ
В предшествующей главе мы имели дело с истиной нашей веры и наших предложений в случаях, когда это зависит только от наблюдений, а не от выводов из прежде полученного знания. В этой главе мы должны начать исследование предложений тех видов,
12. Логические приемы образования понятий
12. Логические приемы образования понятий
Для человека, занимающегося научными изысканиями, постоянно необходимо получать новую информацию. Для этого ученый читает множество литературы по избранному предмету, ведет наблюдение, делает опыты. Однако вся эта деятельность
1. Логические приемы образования понятий
1. Логические приемы образования понятий
Для человека, занимающегося научными изысканиями, постоянно необходимо получать новую информацию. Для этого ученый читает множество литературы по избранному предмету, ведет наблюдение, делает опыты. Однако вся эта деятельность
ЛЕКЦИЯ № 14 Логические законы
ЛЕКЦИЯ № 14
Логические законы
1. Понятие логических законов
Законы логики известны еще с античных времен — закон тождества, непротиворечия и исключенного третьего. Все они были открыты Аристотелем. Закон достаточного основания был открыт Лейбницем. Они имеют большое
ЛЕКЦИЯ № 23 Софизмы. Логические парадоксы
ЛЕКЦИЯ № 23
Софизмы. Логические парадоксы
1. Софизмы. Понятие, примеры
Раскрывая данный вопрос, необходимо сказать, что любой софизм является ошибкой. В логике выделяют также паралогизмы. Отличие этих двух видов ошибок состоит в том, что первая (софизм) допущена умышленно,
ЛОГИЧЕСКИЕ УМОЗАКЛЮЧЕНИЯ
ЛОГИЧЕСКИЕ УМОЗАКЛЮЧЕНИЯ
Подавляющее большинство рассуждений, претендующих на то, чтобы считаться логичными, таковыми на самом деле не являются. Они являются псевдологичными, логичнообразными или в лучшем случае лишь частично логичными. Логичными являются рассуждения
9. СЛУЧАЙ «ОПИСАНИЯ», «ТАВТОЛОГИИ» И «ОБЪЯСНЕНИЯ»
9. СЛУЧАЙ «ОПИСАНИЯ», «ТАВТОЛОГИИ» И «ОБЪЯСНЕНИЯ»
Люди высоко ценят и описание, и объяснение, но этот пример двойной информации отличается от большинства других случаев, рассмотренных в этой главе, тем, что объяснение не содержит новой информации, отличной от уже