Закон противоречия и ошибки, связанные с его нарушением
Соблюдение
закона
противоречия
обеспечивает такие смысловые качества
текста, как последовательность и
непротиворечивость. Этот закон работает
на уровне суждений и формулируется
следующим образом: не
могут быть одновременно истинны два
противоположных суждения об одном и
том же предмете, взятые в одном и том же
отношении в одно и то же время.
Иными словами, не могут считаться
истинными два высказывания, из которых
одно что-либо утверждает, а другое,
наоборот, то же самое отрицает. Формулировка
«в одном и том же отношении» означает,
что предмет характеризуется с одной
точки зрения. Оговорка «в одно и то же
время» введена в формулировку закона
в связи с тем, что со временем ситуация
может меняться и истинное ранее становится
ложным. Графически нарушение этого
закона можно представить так: А есть Б;
А не есть Б.
Задача
редактора состоит в том, чтобы выявить
и устранить возможные противоречия.
Например:
«Члены
жюри решили, что самой высокой оценки
достойна работа студента Е. К. Петрова.
Не менее высокую оценку заслуживает
работа студента К.Е.Сидорова» (См.:
Рахманин Л. В. Стилистика деловой речи
и редактирование служебных документов:
Учеб. пособие. — 4-е изд. — М., 1998).
В первом предложении говорится о том,
что самой высокой оценки достойна одна
работа, во втором предложении
говорится, что другая работа тоже
заслуживает высокой оценки. Противоречие
заключается в том, что лишь одна из работ
заслуживает самой высокой оценки.
Опираясь на закон противоречия, можно
сделать вывод, что одно из суждений
следует считать истинным, второе —
ложным.
Предложение
«Шум
вокруг романа В. Сорокина, поднятый
„Идущими вместе»,
такой, что писатель, вероятно, автоматически
попадет в мировую
сокровищницу
русской
литературы»
содержит именно такие противоречивые
тезисы: сокровищница
мировая — сокровищница
русской литературы.
Кроме
формально-логических
противоречий,
в журналистском
тексте
могут возникнуть и
образные
противоречия.
Формально-логические
противоречия обнаруживаются
при
сопоставлении в тексте суждений, а
образные проявляются на уровне наглядных
представлений. Обычно такую ошибку
называют — двоение
образа.
Например: «Дом, словно
ласточкино гнездо, прилепился
на самом уютном месте, стоит прочно,
кажется, врос в землю». Автор,
нарисовав портрет, предмет, дает их
второе «изображение», несовместимое с
первым. В результате читатель не может
представить себе облик такого героя,
образ такого дома. А. К. Толстой о
непредусмотренных автором образных
противоречиях писал, что они «насилуют
воображение».
Механизм
работы редактора с противоречиями
можно представить следующей схемой:
противоречие
—>
формально-логическое или образное
—> преднамеренное или непреднамеренное
—> разрешимое или неразрешимое. Только
после такой последовательной оценки
зафиксированного противоречия можно
определить дальнейшую стратегию работы
с текстом.
Закон исключенного третьего и ошибки, связанные с его нарушением
Закон
противоречия помогает обнаружить
непоследовательность изложения, найти
противоположные суждения разных видов,
закон
же исключенного третьего,
работающий совместно с законом
противоречия, помогает определить,
какое из противоположных суждений
истинно, и соответствующим образом
править текст. Формулируется он так: из
двух противоположных суждений об одном
и том же предмете, взятых одновременно
в одном и том же отношении, одно непременно
истинно. Третьего не дано.
Задача
редактора — найти это истинное суждение
и опираться на него и время правки.
Покажем это на примере правки некоторых
ранее отмеченных противоречий (курсивом
отмечены выправленные фрагменты).
В
следующем предложении автор
противопоставляет качества, которые
не исключают друг друга: «Человек на
деле может быть мягким
и деликатным,
а
в полете — собранным,
волевым». Часто
нарушение закона исключенного третьего
обнаруживается в альтернативных
ситуациях, когда высказывание строится
с опорой на модель «либо
– либо». «Настоящий
мужик не должен себя жалеть. Он может
либо
поступать правильно и за это уважать
себя, либо ругать себя за ошибки и тут
же их исправлять, после чего начинать
уважать за самокритичность. Все,
третьего не дано». В этом высказывании
сопоставление должно
быть
проведено по линии либо
поступать
правильно —
либо
совершать ошибки (а уже потом ругать
себя за это).
Закон
исключенного третьего действителен в
следующих случаях:
1)
когда одно из суждений что-либо утверждает,
а второе то же самое отрицает относительно
единичного предмета или явления.
Например:
«Новый секретарь оформил этот документ
не совсем правильно».
Это суждение по содержанию совпадает
с суждением: «Новый
секретарь оформил этот документ
неправильно».
Конечно, высказывание: «Новый
секретарь оформил этот документ не
совсем правильно»,
— может быть высказано самостоятельно,
если при этом не заменяет суждение:
«Новый
секретарь оформил этот документ
неправильно»;
2)
когда одно из суждений что-либо утверждает
относительно целого класса предметов
или явлений, а другое то же самое отрицает
в отношении части предметов или явлений
данного класса. Например:
«Все члены коллектива единогласно
проголосовали за принятие данного
решения. Сидоров и Петров проголосовали
против принятия данного решения».
Эти
высказывания прямо противоположны
друг другу. Истинным может быть только
одно из них, второе при этом будет ложным.
Если
вы сталкиваетесь с какими-либо
противоречащими друг другу суждениями,
то сначала надо установить, какое из
них является истинным, а какое —
ложным. Если вам предлагается вопрос,
требующий однозначного ответа, то
необходимо дать ответ на данный вопрос,
не отвлекаясь при этом от темы. Например:
«Присутствовал
ли на совещании начальник стройки?»
Это вопрос требует однозначного
ответа. Ответ может быть либо да,
либо
нет.
Высказывания
типа «Начальник
не смог прийти, так как ему срочно
понадобилось выехать на объект»;
«Начальник стройки выступал с докладом
о ходе строительства»
и другие не заменят ответа на вопрос,
хотя при этом могут считаться важными
или просто интересными.
Часто
нарушение закона исключенного третьего
обнаруживается в альтернативных
ситуациях, когда высказывание строится
с опорой на модель «либо
– либо». «Настоящий
мужик не должен себя жалеть. Он может
либо
поступать правильно и за это уважать
себя, либо ругать себя за ошибки и тут
же их исправлять, после чего начинать
уважать за самокритичность. Все,
третьего не дано». В этом высказывании
сопоставление должно
быть
проведено по линии либо
поступать
правильно —
либо
совершать ошибки (а уже потом ругать
себя за это).
Существует
также закон
достаточного основания, который
утверждает: должны
быть достаточные основания для признания
суждения о предмете истинным.
Истинность выдвигаемых положений
необходимо доказывать, так как
бездоказательные утверждения нельзя
принимать на веру.
Закон
достаточного основания требует
последовательности и аргументированности
высказываний. Если высказывание
недостаточно аргументировано, то не
может считаться убедительным. А если
вы решили опровергнуть высказывание
оппонента, то должны привести достаточные
основания для того, чтобы аргументы
оппонента были признаны неправильными.
Закон
достаточного основания касается обычно
установления причинно-следственных
отношений между частями изложения. При
невозможности соотнести части как
причину и следствие возникает алогизм:
«Остановлюсь на одной примечательной
актерской судьбе. Выпускница Щукинского
театрального училища Екатерина Быстрова
была приглашена работать в Театр юного
зрителя. Стали ее вводить на несколько
ролей сразу. Катя показала себя натурой
незаурядной, самостоятельной. Тут
уж было чему удивляться и порадоваться».
Автор
не сообщил достаточных фактов, чтобы
«подвести» читателя к выводу было
чему удивляться и порадоваться.
Обычно
причинно-следственные отношения
оформляются в
языке
с помощью слов вот,
и это, поэтому, следовательно, итак и
т. п. Редактору следует фиксировать
особое внимание на той части фразы,
которая
предшествует
им.
Алогизмы,
возникшие в результате нарушений законов
логики, могут быть контактными,
т.е.
проявлять себя на уровне
предложения,
высказывания, словосочетания (о них шла
речь выше), и дистантными.
Дистантные
алогизмы обнаруживают себя при
сопоставлении отдельных фрагментов
текста, текста и заголовка, рубрики и
текста и т. п.
7
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
19.05.20156.67 Mб7Рекомендации.rtf
- #
- #
- #
Урок 5. Логические законы и противоречия

Во введении к курсу было сказано, что логика – это нормативная наука о формах и приёмах рациональной познавательной деятельности. Как и любая другая наука, логика также формулирует свои законы. Однако в отличие от других наук, законы эти являются нормативными, то есть они не описывают процесс человеческого мышления, а предписывают, как человек должен мыслить, если он хочет, чтобы его рассуждение было корректным. Таким образом, логические законы представляют собой некие общие принципы, которыми люди должны руководствоваться в процессе рассуждения.
Если попытаться дать более строгое определение, то:
Логический закон – это определённая логическая форма, благодаря которой высказывание в целом принимает значение «истина», независимо от конкретного содержания его частей.
По этой причине логические законы также иногда называют логическими тавтологиями: о чём бы мы не говорили, высказывания, имеющие форму логических законов, всегда оказываются истинными. К тому же они кажутся «бесплодными», потому что мы не можем извлечь из них никакой реальной информации о мире.
Логические противоречия – полная противоположность логическим законам, то есть это такая логическая форма, при которой высказывание в целом всегда принимает значение «ложь», независимо от содержания его частей.
Содержание:
- Таблицы истинности
- Логические законы
- Закон тождества
- Закон противоречия
- Закон исключения третьего
- Проверочные вопросы на усвоение материала
Таблицы истинности
Как же определить, что определённое высказывание всегда принимает значение «истина» или «ложь»? Логики придумали для этого очень удобный метод, который получил название «таблиц истинности». Как понятно из названия, они представляют собой таблицы, в которых в верхнюю строку записывается логическая форма высказываний, а в столбцы под каждым компонентом записываются их истинностные значения. Давайте построим таблицу истинности для высказывания «Идёт дождь».
Здесь всё довольно ясно: «Идёт дождь» – это простое высказывание, которое может принимать значение либо «истина», либо «ложь». Обычно для удобства логики сокращают значения до «и» и «л», а само высказывание записывают маленькой буквой латинского алфавита: p, q, r, s и т.д. Поэтому в классическом виде таблица истинности для одного простого высказывания будет выглядеть так:
Давайте теперь представим, что у нас есть два высказывания: «Идёт дождь» и «Светит солнце». Пока они никаким образом не связаны между собой. Однако поскольку их уже два, то у нас возможны уже не две, а четыре комбинации: оба высказывания истинны, оба высказывания ложны, истинно либо первое, либо второе высказывание. Таблица истинности для них будет включать уже четыре строки для значений.
Если у нас есть три высказывания («Идёт дождь», «Светит солнце», «Трава зеленеет»), то таблица будет включать уже восемь строк для значений, так как в таком случае возможны восемь комбинаций.
|
p |
q |
r |
|
и |
и |
и |
|
и |
и |
л |
|
и |
л |
и |
|
и |
л |
л |
|
л |
и |
и |
|
л |
и |
л |
|
л |
л |
и |
|
л |
л |
л |
Чем больше разных высказываний вы хотите рассмотреть, тем больше комбинаций из значений возможно. Число этих комбинаций для n высказываний вычисляется по формуле 2n. Так для четырёх высказываний, число комбинаций – шестнадцать, для пяти – тридцать два и т.д.
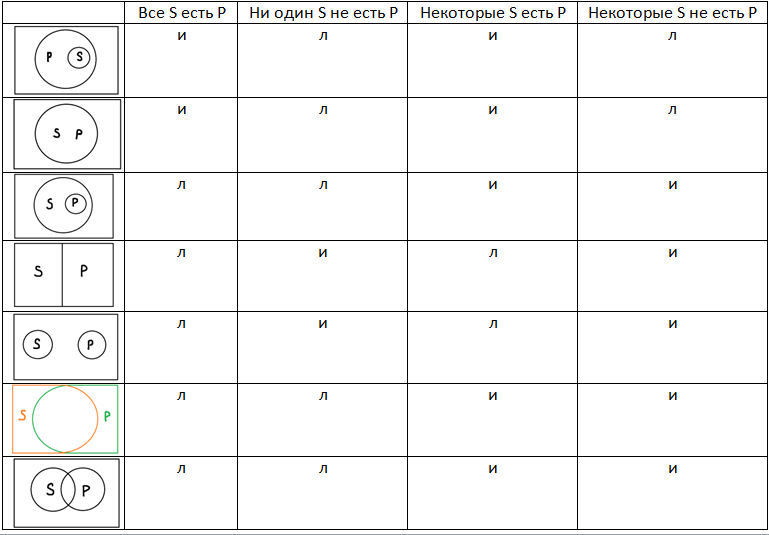
Таблицы истинности строятся и в силлогистике, однако выглядят они немного иначе. В левый столбец обычно помещается диаграмма, изображающая то или иное отношение между терминами S и P, а справа помещаются различные типы высказываний и их истинностные значения.
Это сводная таблица истинности для всех типов атрибутивных высказываний, которые мы обсуждали в прошлом уроке (единичные высказывания не включены отдельно, так как их условия истинности приравниваются к условиям истинности для общих высказываний).
Далее, понятно, что обычно в рассуждении высказывания каким-то образом связаны между собой с помощью пропозициональных связок. Мы зададим истинностные значения для основных связок, которые используются чаще всего в естественном языке.
Логическое отрицание используется, когда в высказывании отрицается наличие некоторой ситуации в мире, говорится об её отсутствии. Например, «Дождь не идёт», «Комната была небольшой», «Неправда, что они друзья». В логике обычно передается через выражения «неверно, что p» или просто «не-p».
Как видно из таблицы, если высказывание истинно, то его отрицание будет принимать значение «ложь», если же высказывание само по себе ложно, то – «истина». Предположим, что вместо p мы имеем высказывание «Маргарет Тэтчер была первой и на настоящий момент единственной женщиной-премьер-министром Великобритании». Это истинное высказывание. Соответственно, если взять его отрицание: «Маргарет Тэтчер не была первой и на настоящий момент единственной женщиной-премьер-министром Великобритании», то оно будет ложным. Если же взять высказывание «Все болезни от нервов», которое является ложным, то его отрицание «Неверно, что все болезни от нервов» будет истинным.
Конъюнкция представляет собой одновременное утверждение наличия двух ситуаций. В естественном языке она обычно передаётся союзами «и», «а», «но» и конструкциями типа «в то же время», «одновременно», «вместе» и т.д. Примеры конъюнкции можно увидеть в высказываниях «Пошёл дождь, и я спрятался под навес», «Витя хотел пойти в кино, а я хотел поиграть в футбол», «Белкин ждал директора целый час, но так и не дождался». Как видно, конъюнкция соединяет два или более простых высказываний в одно сложное.
|
p |
q |
p и q |
|
и |
и |
и |
|
и |
л |
л |
|
л |
и |
л |
|
л |
л |
л |
Конъюнктивное высказывание может быть истинным, только если все его части истинны. Если хотя бы одно простое высказывание, входящее в её состав ложно, то тогда и конъюнкция в целом ложна. Пример истинной конъюнкции: «44-го президента США зовут Барак, а его жену – Мишель». Все следующие высказывания будут ложными: «44-го президента США зовут Барак, а его жену – Мэгги», «44-го президента США зовут Борат, а его жену – Мишель», «44-го президента США зовут Джон, а его жену – Элен».
Дизъюнкция утверждает, что хотя бы одна из двух или более ситуаций имеет место. В естественном языке она выражается словами «или» и «либо». Примеры дизъюнктивных высказываний: «Маша была замужем за Анатолием или за Николаем», «Он работает над проектом ИК-25 либо ПФ-40». Хотя это не так очевидно, как в случае с конъюнкцией, дизъюнкция также объединяет в одно сложное высказывание два или более простых высказывания. Если мы выявляем логическую форму, то правильной была бы запись: «Маша была замужем за Анатолием, или Маша была замужем за Николаем».
|
p |
q |
p или q |
|
и |
и |
и |
|
и |
л |
и |
|
л |
и |
и |
|
л |
л |
л |
Из таблицы понятно, что дизъюнкция ложна, только когда все простые высказывания, входящие в её состав ложны. К примеру, ложным будет высказывание «Уганда находится в Центральной Америке или Западной Европе». Когда хотя бы одна из частей дизъюнкции истина, она в целом также будет истинной. Например, истинным является высказывание «Нот всего семь или шесть». При этом важно отметить, что выражение «хотя бы одна» подразумевает, что и обе части могут быть истинными. Иллюстрацией может служить следующее высказывание: «Велосипеды бывают двухколёсными или трёхколесными». Велосипеды бывают и такими, и другими, поэтому высказывание истинно. Однако нередки случаи, когда мы хотим указать, что лишь одна из альтернатив истинна, но никак не обе вместе. Рассмотрим высказывание «Картина “Герника” принадлежит кисти Пикассо или Тициана». Здесь либо одно, либо другое. Они даже не могли написать её вместе, так как жили в разных веках. В таких ситуациях говорят о строгой дизъюнкции, которая будет истинна исключительно при истинности одного из её членов. Обычно она выражается словами «либо, либо».
|
p |
q |
либо p, либо q |
|
и |
и |
л |
|
и |
л |
и |
|
л |
и |
и |
|
л |
л |
л |
Материальная импликация – это связка, которая передаёт отношения причинно-следственной связи между высказываниями. Она выражается словами «если, то». «Если Люся – полная отличница, то и по математике у неё должна быть пятёрка». Смысл импликации состоит в том, что если первое простое высказывание верно, то и второе тоже будет верным.
|
p |
q |
Если p, то q |
|
и |
и |
и |
|
и |
л |
л |
|
л |
и |
и |
|
л |
л |
и |
Попробуем разобраться с этой таблицей. Проблема в том, что истинностные значения материальной импликации, в отличие от значений других пропозициональных связок, совсем не являются интуитивными. С первой строкой всё ясно: если первое высказывание верно, и второе высказывание верно, то импликация в целом тоже верна. Пример: «Если птицы улетают на юг, то, значит, наступила осень». Со второй строкой тоже всё более или менее понятно: если первое высказывание истинно, а второе ложно, то отношения следования между ними нет. Вспомните отрывок из «Золотого ключика», в котором Мальвина пытается научить Буратино арифметике:
– Предположим у вас в кармане два яблока, и некто забрал у вас одно из них. Сколько у вас останется яблок?
– Два.
– Но почему?
– Ведь я не отдам Некту яблоко, пусть он и дерись!
Рассуждения Буратино можно представить в виде высказывания «Если некто забрал одно из имеющихся у меня двух яблок, у меня всё равно осталось два яблока». Если первая часть истинна, то вторая, безусловно, ложна, а потому и импликация в целом ложна. Способностей к арифметике у Буратино, действительно, не было.
С последними двумя строчками дело обстоит сложнее. Проблема в том, что для них сложно придумать пример на естественном языке. Когда логики формулировали значение материальной импликации, они пользовались математическим примером. Они взяли высказывание «Для всякого числа верно, что если оно кратно 4, то оно кратно и двум». Если это высказывание верно для всякого числа, то оно должно быть верным и для любого конкретного числа: 5, 6, 8, 12 и т.д. Если подставить в высказывание 8, то получим: «если 8 кратно 4, то оно кратно и 2». Здесь и первая, и вторая части истинны. Мы получили первую строку. Если подставить число 6, «если 6 кратно 4, то оно кратно и 2», то мы получаем третью строку (первая часть ложна, а вторая истинна). Если подставить 5, «если 5 кратно 4, то 5 кратно и двум», то выходит последняя строка (обе части ложны). Однако мы всё же можем подобрать примеры для всех этих ситуации, поэтому импликация истинна. Но вот для второй строки пример подобрать нельзя: нет такого числа, которое было бы кратно 4, но некратно 2. Поэтому вторая строка ложна.
Итак, мы разобрали истинностные значения основных связок, теперь мы можем посмотреть, какие их комбинации приведут к тому, что высказывание подобной формы будет всегда истинным, независимо от его содержания, другими словами – будет логическим законом.
Логические законы
Сразу стоит оговориться, что логических законов довольно много. Кроме того, обычно они формулируются в рамках конкретной логической системы: логики высказываний, логики предикатов, силлогистики, модальной логики и т.д. То, что является законом в одной системе, совсем необязательно будет законом в другой системе. Однако существует несколько основных законов, которые будут верны в любой логической системе. О них мы и расскажем.
1
Закон тождества
Закон тождества обычно формулируется в виде формулы «А есть А» или «Если А, то А».
Проверим этот закон с помощью таблицы истинности. Во-первых, у нас всего одно выражение – А, поэтому таблица будет включать только две комбинации: А истинно и А ложно. Во-вторых, связка «Если …, то …» выступает как знак материальной импликации. Таким образом, мы должны взять первую и последнюю строку из таблицы для материальной импликации.
|
А |
Если А |
то А |
Истинностное значение импликации |
|
и |
и |
и |
и |
|
л |
л |
л |
и |
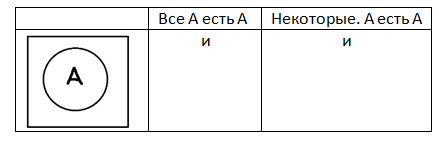
Закон тождества также может быть сформулирован и в силлогистике для высказываний «Все А есть А» и «Некоторые А есть А»:
Какой бы термин мы не подставили на место А, высказывания, имеющие эти формы, всегда будут истинными: «Все кошки – это кошки», «Все туфли – это туфли», «Некоторые автомобили – это автомобили», «Некоторые дома – это дома» и т.п.
Как понятно из названия этого закона, он говорит о том, что А тождественно самому себе. Что это означает? Смысл этого закона состоит в утверждении того, что языковые выражения (будь то термин или целое высказывание) не могут менять своё значение в процессе рассуждения. Языковые знаки должны трактоваться однозначно, их употребление должно быть стабильным. Если я утверждаю, что какое-то высказывание истинно, например, что высказывание «Красота спасёт мир» истинно, я не могу следующим шагом утверждать, что оно ложно. И наоборот, если я утверждаю, что какое-то высказывание ложно, оно не может вдруг ни с того ни с сего превратиться в истинное. Рассуждение должно быть последовательным.
Чаще всего закон тождества нарушается при так называемой подмене понятий: в ходе рассуждения используется один и тот же термин, но значения в него вкладываются каждый раз разные. К примеру, возьмём следующее рассуждение: «Знание – сила. Сила – это векторная физическая величина, мера интенсивности воздействия на данное тело других тел и полей. Следовательно, знание – это векторная физическая величина, мера интенсивности воздействия на данное тело других тел и полей». Такое рассуждение не может быть верным, так как здесь нарушен принцип тождества: термин «сила» употребляется в первом и втором предложении в разных значениях.
2
Закон противоречия
Закон противоречия гласит: неверно, что А и не-А.
Построим таблицу истинности.
|
А |
Неверно, что |
А |
и |
не-А |
|
и |
и |
и |
л |
л |
|
л |
и |
л |
л |
и |
В первом столбце даны значения А («истина» и «ложь»). Соответственно, мы просто копируем эти значения в третий столбец. Значения для не-А в пятом столбце будут прямо обратными для значений А, поэтому получаем «ложь», «истина». В четвёртом столбце располагается конъюнкция между А и не-А. Она не может быть истинной ни в одном из случаев. Поэтому её значение всегда «ложь». Наконец, второй столбец представляет значение выражения полностью – это отрицание конъюнкции между А и не-А. Поскольку конъюнкция ложна, то её отрицание будет истинным. В итоге, мы видим, что выражение в целом всегда истинно.
Если же мы возьмём выражение типа «А и не-А», то оно как раз будет представлять собой противоречие. Из таблицы мы видим, что такое выражение всегда будет принимать значение «ложь».
Согласно закону противоречия (иногда его называют законом непротиворечия) невозможно, чтобы одновременно оказались истинными высказывание и его прямое отрицание: неверно, что снег идёт и в то же время не идёт, неверно, что Катя любит ананасы и не любит ананасы. Важно сделать следующее замечание: противоречия возникает только тогда, когда утверждение и отрицание делаются об одном и том же объекте, в одно и то же время, в одном и тот же отношении. Например, высказывания «Снег идёт на Северном полюсе, но снег не идёт в Зимбабве», «Толя ходил в кино вчера, а сегодня не ходил», «Катя любит ананасы, а Петя не любит ананасы», «Вася любит кататься на коньках и не любит кататься на лыжах» не являются противоречиями. Все они говорят либо о разных предметах, либо о разных временных отрезках, либо о разных аспектах одного предмета. Поэтому не всё, что выглядит как противоречие, действительно является таковым. Такие кажущиеся противоречия называют мнимыми. Пример мнимого противоречия можно найти в дзенской притче «Бокудзю и ручей»:
Один дзэнский монах, Бокудзю, говорил: «Иди и пересеки ручей, но не позволяй воде прикоснуться к тебе».
А через ручей около его монастыря не было никакого моста. Многие пытались сделать это, но когда они пересекали ручей, то, конечно же, вода прикасалась к ним. Поэтому однажды один монах пришел к нему и сказал:
— Вы задали нам неразрешимую задачу. Мы пытаемся пересечь этот ручей; через него нет никакого моста. Если бы был мост, то мы, конечно же, пересекли бы ручей, и вода не прикоснулась бы к нам. Но мы вынуждены идти через поток, и вода прикасается к нам.
И Бокудзю сказал:
— Я пойду и пересеку его, а вы наблюдайте.
И Бокудзю пересёк ручей. Вода, конечно, прикоснулась к его ногам, и они сказали:
— Смотрите, вода прикоснулась к вам!
Бокудзю сказал:
— Насколько я знаю, она не прикоснулась ко мне. Я был просто свидетелем. Вода прикоснулась к моим ногам, но не ко мне. Я был просто свидетельствующим.
Между тем, чтобы пересечь ручей без моста и не позволить воде прикоснуться к себе, нет противоречия, потому что в данном случае человеческое я рассматривает в разных отношениях: как тело, и как дух. Тело проходит через ручей и намокает, но дух остаётся безмятежным и не затронутым водой.
Как и закон тождества, закон противоречия требует от нас быть последовательными в рассуждениях. Либо мы принимаем, что высказывание истинно, либо мы принимаем, что оно ложно, но не то и другое вместе. Смешение истины и лжи приводит к тому, что всё рассуждение обесценивается, так как мы уже не можем быть уверены в сделанном выводе. Противоречия опасны потому, что с точки зрения логики из них можно вывести всё что угодно, то есть высказывание формы «Если А и не-А, то В» всегда будет истинным. Вы можете сами проверить это с помощью таблицы истинности. «Если дождь идёт, и дождь не идёт, то Чехов – автор “Войны и мира”». Если допускать противоречия, подобное «рассуждение» оказывается возможным. Поэтому логика ставит запрет на противоречия.
Нужно сказать, что противоречия бывают не только явными, но и скрытыми. Очевидно, что чаще всего никто старается не допускать в своём рассуждении наличия двух прямо противоположных высказываний. Однако, не редки случаи, когда противоречие прячется за вроде бы правильными формулировками. Приведём несколько примеров, которые хорошо это иллюстрируют: «Мы заставим их стать свободными», «Мы будем бороться за мир, и камня на камне не останется от нашей борьбы». Понятно, что идея свободы предполагает, что человека не заставляют, а он сам принимает решения, а идея мира предполагает отсутствия борьбы или войны.
Обычно появление противоречия – это знак того, что в рассуждение где-то закралась ошибка. Исправление этой ошибки, снимет и противоречие. Ошибка может скрываться в сделанных умозаключениях, но может содержаться и в изначально избранных посылках. По этой причине приведение к противоречию играет ключевую роль в так называемых доказательствах от противного. Наверное, все помнят их со школьных уроков геометрии. Доказательство от противного строится на том, что нужно обосновать какой-то тезис, но прямое его доказательство найти не получается. Тогда берётся его отрицание, и в определённый момент рассуждения мы наталкиваемся на противоречие, а это знак того, что отрицание тезиса было неверным. Так что противоречие может играть и позитивную роль в рассуждении.
В заключение, добавим, что в советской философии, превозносившей Маркса и Гегеля, появилось целое направление под названием «диалектическая логика», которая якобы допускала наличие противоречий и даже оценивала их положительно. Такая точка зрения строилась на том, что противоречия – это источник движения и развития, а потому это хорошо, если мы сталкиваемся с ними. Ещё и сегодня можно встретить людей, которые придерживаются подобного мнения. Однако нужно понимать, что речь здесь не идёт о противоречии в логическом смысле (как форме высказывания, которое при любой интерпретации принимает значение «ложь»). Скорее, под противоречием тут следует мыслить несовместимость, плохую сочетаемость ситуаций, феноменов, характеров и т.д. Так во Франции конца XVIII века желание буржуазии участвовать в политической жизни страны плохо сочеталось с формой правления абсолютной монархии, что в итоге привело к буржуазной революции. Можно сказать, что между ними возникло противоречие, но это не имеет никакого отношения к логике.
3
Закон исключённого третьего
Закон исключённого третьего имеет следующую форму: А или неверно, что А.
Построим таблицу истинности:
|
А |
или |
неверно, что А |
|
и |
и |
л |
|
л |
и |
и |
Если А принимает значение «истина» и «ложь», то «неверно, что А» соответственно будет принимать значения «ложь» и «истина». Их дизъюнкция всегда будет истинной.
Закон исключённого третьего очень похож на закон противоречия, потому что он точно также утверждает, что высказывание и его отрицание не могут быть одновременно истинными. Истинно либо одно, либо другое, и третьего не дано. Истинно или высказывание «Глинка был композитором», или его отрицание «Глинка не был композитором», но они не могут быть истинными одновременно. Опять же здесь также стоит следить за тем, чтобы высказывания относились к одному и тому же предмету, говорили о нём в одном и том же отношении и в одно и то же время.
Нужно отметить, что законом исключённого третьего часто пользуются в качестве уловки, пытаясь представить какую-либо сложную ситуацию в виде простой оппозиции. К примеру: «Ты с нами или ты против нас», «Женщины бывают либо умными, либо красивыми», «Они либо патриоты, либо предатели». Особенно часто этим приёмом любят пользоваться политики, пытаясь представить, будто их оппоненты защищают какую-то радикальную позицию, которой те на самом деле не придерживаются. Отчасти эта склонность сводить всё многообразие фактов и позиций к двум противоположностям обусловлена чисто психологическими механизмами работы человеческого мышления. Всё дело в том, что наше мышление работает по так называемому принципу когнитивной экономии: вместо того, чтобы тратить время и энергию на анализ всей сложности ситуации, мы предпочитаем представить её в виде грубой полярной схемы. Поэтому если ваш собеседник или демагог из телевизора говорит вам, что «третьего не дано», подумайте, так ли это: не заключается ли между двумя членами оппозиции целый спектр разнообразных возможностей.
Кроме того, с законом исключённого третьего нужно быть аккуратными ещё и потому, что значения высказываний во многих случаях определяются относительно конкретного контекста. Помните Ивана и его детей из прошлого урока? Вполне можно было бы сказать в соответствии с законом исключённого третьего: «Дети Ивана либо лысы, либо нет, третьего не дано». Но ни одна из этих альтернатив не может нас удовлетворить, так как у Ивана нет детей. Таким образом, прежде чем применять закон исключённого третьего, сверьтесь с контекстом высказывания.
Законы тождества, противоречия и исключённого третьего фундаментальны и выполняются в любых логических системах. Без соблюдения этих законов невозможно делать правильные умозаключения. Иногда к ним присоединяют ещё так называемый закон достаточного основания. Этот закон гласит, что любое утверждение должно быть корректно обосновано. Хотя это очень важный принцип, на котором должны базироваться любые рассуждения, законом в собственно логическом смысле он не является, так как не представим в виде логической формы, которая при любой трактовке принимала бы значение «истина». Скорее, это общее требование, вытекающее из самой идеи логичного рассуждения, целью которого как раз и является обоснование тезиса путём правильных умозаключений. О том, как правильно делать умозаключения, мы начнём рассказывать в следующем уроке.
Проверьте свои знания
Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.
← 4 Суждение в логике6 Умозаключения →
Самые распространенные логические ошибки
Уровень сложности
Простой
Время на прочтение
11 мин
Количество просмотров 37K
Логическая ошибка — это ошибка, допущенная в связи с нарушением логической правильности умозаключений.
Всякий раз, когда я просматриваю внутренний документ о принятии решения, предложение о стратегическом развитии, отчет об эксперименте, инвестиционную декларацию или какой-либо другой документ, который может оказать значительное влияние на результаты деятельности компании, я проверяю, имеет ли аргумент смысл с точки зрения логики.
Другими словами, я исследую, подтверждается ли вывод предшествующими ему утверждениями и посылками. Любые противоречия и несоответствия я продолжаю изучать дальше. Изучение логических ошибок помогает развить мышление и навыки аргументации.
School of Thought проделала отличную работу, описав на простом английском языке 24 наиболее распространенные логические ошибки. Их можно изучить на их интерактивном сайте или в этой статье.
1. Подмена тезиса
Эта логическая ошибка основана на искажении одного из аргументов оппонента и последующем его опровержении.
Преувеличивая, искажая или просто подменяя аргументы оппонента, гораздо легче представить свою собственную позицию как разумную, но такая нечестность негативно сказывается на рациональности дискуссии.
Пример: Уилл высказал мнение, что необходимо вкладывать больше денег в здравоохранение и образование. Уоррен сказал в ответ, что он удивлен тем, насколько же Уилл ненавидит страну, что хочет оставить ее беззащитной, сократив военные расходы.
2. Корреляция не равно причинно-следственная связь
Предположение, что реальная или предполагаемая связь между вещами означает, что одно является причиной другого.
Многие путают корреляцию (то, что происходит вместе или последовательно) с причинно-следственной связью (при которой одно вызывает другое). Иногда корреляция является случайной, или же она может быть обусловлена общей причиной.
Пример: Роджер утверждает, указывая на причудливую диаграмму, что последние несколько столетий температура повышалась, в то же время количество пиратов уменьшалось. Из чего следует, что пираты способствуют похолоданию, а глобальное потепление — это обман.
3. Апелляция к эмоциям
Попытка манипулировать эмоциональной реакцией вместо использования обоснованных и убедительных аргументов.
Апелляция к эмоциям предполагает обращение к эмоциям оппонента: страху, зависти, злости, жалости, гордости и т. д. Важно отметить, что иногда логичный аргумент может вызвать эмоции или включать в себя эмоциональный аспект. Проблема и ошибка возникают, когда эмоции используются вместо логического аргумента или для сокрытия того факта, что для подтверждения позиции не существует убедительных рациональных причин. Все люди, кроме социопатов, подвержены влиянию эмоций, и поэтому апелляция к эмоциям — очень распространенная и эффективная тактика построения аргументации. Но в конечном итоге она несовершенна и нечестна.
Пример: Люк не хотел есть овечьи мозги с рубленой печенью и брюссельской капустой. На что отец сказал ему подумать о бедных голодающих детях в странах третьего мира, у которых вообще нет никакой еды.
4. Аргумент от заблуждения
Предположение о том, что поскольку утверждение было плохо аргументировано, или было допущено заблуждение, то само утверждение должно быть неверным.
Вполне реально сделать ложное утверждение и при этом логически обосновать его, так же как возможно сделать истинное утверждение и обосновать его с помощью различных заблуждений и плохих аргументов.
Пример: Алиса поняла, что Аманда совершила ошибку в аргументации, когда утверждала, что нужно есть здоровую пищу, потому что диетолог сказал, что это популярно. Поэтому Алиса парировала, что нужно есть двойные чизбургеры с беконом каждый день.
5. Тенденциозность / «скользкий уклон»
Утверждение, что если позволить случиться А, то в конце концов случится и Б, поэтому А не должно случаться.
Проблема такого рассуждения заключается в том, что оно позволяет избежать рассмотрения самого вопроса, а вместо этого переключает внимание на крайние неправдоподобные гипотезы. Поскольку нет никаких доказательств того, что такие крайние гипотезы произойдут на самом деле, эта ошибка близка к ошибке «апелляции к эмоциям», нагнетая страх. В результате рассматриваемое утверждение несправедливо опошляется необоснованными предположениями.
Пример: Колин Клозет утверждает, что если мы разрешим однополым парам вступать в брак, то в следующий раз мы разрешим людям жениться на своих родителях, машинах и даже обезьянах.
6. Апелляция к личности / «переход на личности»
Обращение к характеру или личным качествам оппонента как попытка подорвать его аргументацию, вместо указания на несостоятельность самого аргумента.
Апелляция к личности может принимать форму открытых нападок на кого-либо или более тонко выраженных сомнений в его характере или личных качествах как способ дискредитации аргументов. Результатом такой атаки может быть подрыв аргументов без необходимости вступать с оппонентом в диалог.
Пример: После того как Салли представила красноречивый и убедительный аргумент в пользу более справедливой системы налогообложения, Сэм спрашивает аудиторию, должны ли мы верить чему-либо от женщины, которая не замужем, однажды была арестована и странно пахнет.
7. Апелляция к лицемерию / «ты тоже»
Ответ на критику критикой, который помогает избежать необходимости отвечать на критику оппонента.
Латинское название “tu quoque” произносится как “too-kwo-kwee” и буквально переводится как «ты тоже»/«посмотри на себя». Эта ошибка также известна как апелляция к лицемерию/ханжеству. Обычно ее используют в качестве отвлекающего маневра — она снимает напряжение с того, кому приходится защищать свои аргументы, и вместо этого переключает внимание на критикующего.
Пример: Николь определила и сказала, что Ханна совершила логическую ошибку. Вместо того, чтобы ответить по существу ее утверждения, Ханна обвинила Николь в том, что та совершила ошибку ранее в их разговоре.
8. Невежество
При этой ошибке вы, если вам что-то показалось сложным для понимания или вы не знаете, как это работает, делаете вид, что это, скорее всего, неправда.
Сложные предметы для обсуждения, например, биологическая эволюция посредством естественного отбора, требуют определенного понимания, прежде чем человек сможет вынести обоснованное суждение об этом предмете. Ошибка обычно используется вместо этого понимания.
Пример: Кирк нарисовал рисунок рыбы и человека и с нескрываемой надменностью спросил Ричарда, действительно ли он считает нас настолько глупыми, чтобы поверить, что рыба каким-то образом превратилась в человека в результате случайных событий, происходящих с течением времени.
9. Ситуативная надстройка
Придумывание новых условий или исключений в случае, если утверждение оказалось ложным.
Люди — забавные существа и испытывают глупое отвращение к тому факту, что иногда ошибаются. Многие цепляются за старые убеждения вместо того, чтобы оценить преимущества возможности изменить свое мнение благодаря лучшему пониманию. Часто для этого используется пост-рационализация причины, по которой то, что они считали истинным, должно оставаться истинным. Обычно очень легко найти причину верить во что-то, что нас устраивает, и требуется честность и искренность с самим собой, чтобы исследовать собственные убеждения и мотивы, не попадая в ловушку оправдания существующих способов видения себя и окружающего мира.
Пример: Эдвард Джонс утверждал, что является экстрасенсом. Однако во время проверки в надлежащих условиях научного эксперимента его «способности» не проявились. Эдвард объяснил это тем, что для того, чтобы его способности работали, нужно в них верить.
10. Провокационный вопрос
Постановка вопроса, в который заложено предположение. На такой вопрос не получится ответить, не показавшись виноватым.
Ошибки с провокационным вопросом особенно эффективны для срыва рациональных дебатов из-за их подстрекательского характера — получатель такого вопроса вынужден защищаться и может показаться взволнованным или отстающим в дискуссии.
Пример: Грейс и Хелен обе влюблены в Брэда. Однажды, когда Брэд сидел в пределах слышимости, Грейс пытливым тоном спросила Хелен, не страдает ли она все еще от наркотической зависимости.
11. Бремя доказательства / негативное доказательство
Утверждение, что бремя доказывания лежит не на том, кто делает утверждение, а на том, кто его опровергает.
Бремя доказывания лежит на том, кто делает утверждение, и никто другой не обязан его опровергать. Неспособность или нежелание опровергнуть утверждение не делает его действительным.
Пример: Берт заявляет, что в этот самый момент на орбите вокруг Солнца между Землей и Марсом находится чайник, и поскольку никто не может доказать его неправоту, его утверждение является обоснованным.
12. Двусмысленность
Использование двойного смысла или языковой двусмысленности, чтобы ввести в заблуждение или исказить истину.
Часто использование двусмысленности, которая вводит в заблуждение, можно заметить за политиками. Впоследствии, если эта ситуация обращает на себя внимание, они в оправдание говорят, что технически это не было ложью. Двусмысленность квалифицируется как ошибка, потому что она по своей сути вводит в заблуждение.
Пример: Когда судья спросил обвиняемого, почему он не оплатил штраф за парковку, тот ответил, что он не должен был его оплачивать, поскольку на знаке было написано «Парковка здесь — это нормально» (англ. “Fine for parking here”), и поэтому он предположил, что парковаться здесь нормально.
13. Ошибка игрока / ложный вывод Монте-Карло
Убеждение, что в рамках статистически независимых явлений, таких как вращение колеса рулетки, случаются крупные удачи.
Можно сказать, что это распространенная ошибка помогла построить целый город в пустыне штата Невада. Хотя вероятность «сорвать куш» может быть низкой, каждое вращение колеса рулетки само по себе независимо от предыдущего. Поэтому, хотя вероятность того, что при подбрасывании монеты 20 раз подряд выпадет орел, может быть очень мала, шансы выпадения орла при каждом отдельном подбрасывании остаются 50/50, и на них не влияет то, что произошло раньше.
Пример: На колесе рулетки шесть раз подряд выпало красное, поэтому Грег думал, что почти наверняка следующим выпадет черное. При таком мышлении он вскоре потерял все свои сбережения, пострадав от экономической формы естественного отбора.
14. Распространенное заблуждение
Апелляция к популярности рассматриваемого объекта/явления/идеи.
Изъян этого аргумента в том, что популярность идеи не имеет никакого отношения к ее обоснованности. Если бы это было так, то Земля на протяжении большей части истории была бы плоской, чтобы соответствовать этому популярному убеждению.
Пример: Шамус, будучи пьяным, попросил Шона объяснить, почему столько людей верят в лепреконов, если они всего лишь старое глупое суеверие. Шон, однако, сам выпил слишком много «Гиннесса» и упал со стула.
15. Апелляция к авторитету
Предположение, что если авторитет убежден в состоятельности рассматриваемой идеи/явления, то это действительно должно быть правдой.
Важно отметить, что эта ошибка не должна использоваться для отрицания утверждений экспертов или научного консенсуса. Апелляция к авторитету не является веским аргументом, но и пренебрегать утверждениями экспертов, обладающих глубокими знаниями, неразумно, если у человека нет аналогичного уровня понимания и/или доступа к эмпирическим доказательствам. Однако вполне возможно, что мнение авторитетного лица или учреждения ошибочно. Поэтому авторитет, которым обладает такое лицо или учреждение, не имеет подлинного отношения к тому, правдивы их утверждения или нет.
Пример: Не в состоянии защитить свою позицию, что эволюция — это не факт, Боб говорит, что он знает ученого, который также сомневается в эволюции (и предположительно не является приматом).
16. Ошибка деления / от частного к целому
Предположение, что одна часть чего-то должна применяться ко всем или другим его частям; или что целое должно применяться к своим частям.
Часто, когда что-то верно для части, это также применимо и к целому, или наоборот. Но решающее различие заключается в том, существуют ли веские доказательства того, что это так. Поскольку мы склонны замечать закономерности в происходящем, есть риск стать предвзятыми и начать полагать, что закономерность существует там, где ее нет.
Пример: Дэниел был одаренным ребенком и любил логику. Он рассуждал, что атомы невидимы, и поскольку он сам состоит из атомов, он тоже невидим. К сожалению, несмотря на свои неординарные мыслительные способности, игру в прятки он проиграл.
17. Игнорирование контрпримера или апелляция к истинности / «Ни один настоящий шотландец»
Совершение апелляции к «правильности» как способ отбросить критику или недостатки аргумента.
При такой форме ошибочного рассуждения утверждение становится нефальсифицируемым, поскольку независимо от убедительности доказательств, человек просто меняет условия так, чтобы они не применялись к якобы «истинному» примеру. Подобная пост-рационализация — это способ избежать обоснованной критики своих аргументов.
Пример: Ангус заявляет, что шотландцы не кладут сахар в кашу, на что Лахлан указывает, что он шотландец и кладет сахар в кашу. В ярости, как настоящий шотландец, Ангус кричит, что ни один настоящий шотландец не кладет сахар в кашу.
18. Генетическая ошибка / ошибка происхождения
Оценка чего-либо как хорошего или плохого на основании того, откуда или от кого оно произошло.
Эта ошибка позволяет избежать необходимости приводить настоящие аргументы, переключая внимание на происхождение обсуждаемого предмета/явления. Это похоже на ошибку апелляции к личности: человек использует существующее негативное восприятие, чтобы выставить чей-то аргумент в плохом свете, не предоставляя реальную аргументацию, почему сам аргумент не заслуживает внимания.
Пример: Одного депутата в выпуске новостей обвинили в коррупции и получении взяток. На это он сказал, что нужно очень осторожно относиться к тому, что говорят в СМИ, потому что «все мы знаем, насколько они ненадежны».
19. Черно-белое
Представление только двух состояний как единственно возможных, хотя на самом деле вариантов существует больше.
Эта коварная тактика, известная также как ложная дилемма. Внешне она выглядит как логический аргумент, но при ближайшем рассмотрении становится очевидно, что существует больше возможностей, чем представленный выбор «или-или». Бинарное черно-белое мышление не позволяет учесть множества различных переменных, условий и контекстов, в которых может существовать больше, чем только две представленные возможности. Это вводит в заблуждение и препятствует рациональному, честному обсуждению.
Пример: В рамках поддержки своего плана по ограничению прав граждан Верховный Лидер сказал людям, что они либо на его стороне, либо на стороне врага.
20. Предвосхищение основания
Использование кругового аргумента, в котором заключение включено в посылку.
Такая логически бессвязная аргументация часто возникает в ситуациях существования глубоко укоренившегося предположения, которое воспринимается как данность. Круговая аргументация плоха главным образом потому, что она не очень хороша.
Пример: Слово Зорбо Великого безупречно и совершенно. Мы знаем это, потому что так сказано в «Великой и непогрешимой книге лучших и самых истинных вещей Зорбо, которые безусловно верны и не должны подвергаться сомнению».
21. Апелляция к природе вещей
Утверждение, что все «естественное» обосновано, оправдано, неизбежно, хорошо или идеально.
Многие «естественные» вещи считаются «хорошими», и это может искажать наше мышление; но сама по себе естественность не делает что-то хорошим или плохим. Например, убийство может выглядеть вполне естественным, но это не означает, что оно хорошо или оправданно.
Пример: В город приехал знахарь и стал продавать различные природные средства, например, особую простую воду. Он сказал, что вполне естественно, что люди должны опасаться «искусственных» лекарств, таких как антибиотики.
22. Эпизодическое свидетельство (Anecdotal evidence)
Использование личного опыта или единичного частного примера вместо обоснованного аргумента.
Зачастую людям гораздо проще поверить чьему-то свидетельству, чем разбираться в сложных данных. Количественные научные показатели почти всегда более точны, чем личное восприятие и опыт, но мы склонны верить тому, что для нас осязаемо, и/или слову человека, которому мы доверяем, а не более «абстрактным» статистическим данным.
Пример: Джейсон сказал, что исследования это круто и все такое, но его дед выкуривал около 30 сигарет в день и прожил до 97 лет — так что не стоит верить всему, что вы читаете о мета-анализах методологически обоснованных исследований, демонстрирующих доказанные причинно-следственные связи.
23. Ошибка меткого стрелка
Подбор сходных данных и/или поиск закономерности, которые подтвердят предположение.
Это заблуждение было выведено после комичной истории: один стрелок беспорядочно стрелял по сараям, а затем рисовал мишени-«яблочки» в том месте, где было больше всего пулевых отверстий, тем самым создавая впечатление, что он действительно хорошо стреляет. Сходные данные иногда появляются, но это не обязательно указывает на наличие причинно-следственной связи.
Пример: Производители сахаросодержащих напитков ссылаются на результаты исследований, согласно которым из пяти стран, где сахаросодержащие напитки продаются больше всего, три входят в десятку самых здоровых стран Земли. Следовательно, сахаросодержащие напитки полезны для здоровья.
24. Апелляция к умеренности / ложный компромисс
Утверждение, что истиной должен быть компромисс или средняя точка между двумя крайностями.
В большинстве случаев истина действительно лежит между двумя крайними точками, но этот факт может исказить наше мышление: иногда что-то просто неправда и компромисс с ней — тоже неправда. Середина между правдой и ложью — это все равно ложь.
Пример: Холли утверждала, что прививки вызывают аутизм у детей, но ее научно подкованный друг Калеб сказал, что это утверждение было развенчано и доказано как ложное. Их подруга Элис предложила компромиссный вариант: прививки вызывают некоторый аутизм, но не всякий.
Знание о существовании логических ошибок (как говорится, «знай врага в лицо») является важной составляющей развитого критического мышления. Критическое мышление помогает принимать взвешенные решения как в личной жизни, так и в рабочих ситуациях, структурировать информацию и вести переговоры.
Также в принятии качественных решений нам помогает системное мышление. Применение этого навыка может быть сложным для менеджеров, особенно в контексте изменчивой деятельности людей. На открытом уроке мы рассмотрим инструменты, которые QA лиды могут использовать для выявления системных проблем и поиска их причин. На уроке подробно рассмотрим паттерны поведения систем, метод для поиска причин «5 почему» и CLD диаграммы (Casual Loop Diagrams). Записаться можно по ссылке.
Как думаете, какие логические ошибки не попали в этот список? Пишите в комментариях.
Перевела: Ксения Мосеенкова
Логические ошибки – это то, что встречается у каждого из нас. В данной статье мы рассмотрим примеры логических ошибок, которые, так или иначе, встречаются в нашей повседневной жизни.
Основы логики мы рассматривали отдельно. Настоятельно рекомендуем ознакомиться с ними и узнать 4 главных закона логики. Также обратите внимание на когнитивные искажения, или распространенные ошибки мышления. Очень интересно!
Но сейчас мы будем говорить только о логических ошибках.
Подмена тезиса – это логическая ошибка в доказательстве, состоящая в том, что начав доказывать некоторый тезис, постепенно в ходе доказательства переходят к доказательству другого положения, сходного с тезисом, но имеющего совершенно иное значение.
Другая популярная логическая ошибка – «предвосхищение основания». Она заключается в том, что в качестве аргументов используются недоказанные, как правило, произвольно взятые положения: ссылаются на слухи, на ходячие мнения, высказанные кем-то предположения или даже на собственный вымысел, выдавая их за аргументы, якобы обосновывающие тезис.
В действительности же доброкачественность таких доводов лишь предвосхищается, но не устанавливается с несомненностью. Обычно подобные лже-аргументы сопровождаются фразами: «Как абсолютно всем известно…», «Кто же будет спорить с тем, что…», «Само собой разумеется, что…», «Каждому известно, что…», дабы рассеять возможные сомнения у простого слушателя.
Что такое Логическая Ошибка
Логическая ошибка – в логике, философии и прочих науках, изучающих познание, ошибка, связанная с нарушением логической правильности умозаключений.
Ошибочность обусловлена каким-либо логическим недочётом в доказательстве, что делает доказательство неверным в целом.
Если человеку, который смотрит на уходящие вдаль рельсы железной дороги, кажется, что они сходятся на горизонте в одной точке, то он ошибается. Ошибается тот, кому кажется, что падение одного зерна на землю не производит ни малейшего шума, что пушинка не имеет веса и т. д.
Можно ли назвать эти ошибки логическими? Нет. Они связаны с обманом зрения, слуха и т. д., это ошибки чувственного восприятия.
Логические же ошибки относятся к мыслям. Причем не к мыслям как таковым, а к тому, как связывается одна мысль с другой, к отношениям между различными мыслями.
Нарушение закона тождества
В нашей повседневной жизни часто приходится наблюдать нарушение одного из главных законов логики – закона тождества. Взять, например, такой разговор.
– Можно мне взять твои книги?
– Возьми.
– А я не хочу их брать.
– Тогда не бери.
– Он запретил мне брать свои книги.
Здесь в выражении «не бери» смешиваются два разных суждения: «не бери» в смысле «можешь не брать» и «не бери» в смысле «нельзя брать», в результате чего нарушается закон тождества и неизбежно возникает недоразумение.
Часто самые незначительные изменения во фразе, например, перенос ударения, могут совершенно изменить ее логический смысл.
Вспомним недоразумение, которое возникло в связи с высказыванием Исаака Ньютона: «Гипотез не сочиняю». Многих удивляло, что Ньютон, несмотря на это заявление, сам выдвигал много гипотез.
В действительности же оснований для удивления нет. И те, кто усматривает здесь противоречие, просто нарушают закон тождества. В приведенном высказывании Ньютона нужно поставить логическое ударение на слове «сочиняю». И тогда оно будет иметь смысл: «Гипотез не сочиняю, но выдвигаю их на основе фактов».
Некоторые истолковали, его иначе и, поставив логическое ударение на слове «гипотез». Вложили в это высказывание совсем иной смысл: «Гипотез не выдвигаю, то есть, не создаю их вообще». На основе этого был сделан вывод, что Ньютон – противник всяких гипотез.
Нарушение закона исключенного третьего
Также нередко встречаются логические ошибки, связанные с нарушением закона исключенного третьего. Приведем классический пример.
В одной бане, вывешено объявление следующего содержания:
В камеру хранения принимаются:
- верхняя одежда,
- головные уборы,
- обувь,
- деньги и ценные вещи.
Не принимаются на хранение:
- огнестрельное и холодное оружие,
- горючие вещества,
- продукты,
- молотки и ножи.
В баню приходит гражданин, который хочет сдать вместе с одеждой связку книг. Гардеробщица отказывается брать книги, мотивируя тем, что их нет в списке вещей, принимающихся на хранение. Гражданин настаивает, ссылаясь на то, что и в списке предметов, не принимающихся на хранение, книги не указаны.
На основании указанного объявления суждение «книги принимаются» отрицается так же, как и суждение «книги не принимаются».
Логические ошибки мышления
В рассмотренных примерах противоречие возникает между двумя разными суждениями. Но законы мышления могут быть нарушены и внутри одного суждения.
Это бывает в тех случаях, когда из одного суждения вытекает другое, ему противоречащее. Например, древнегреческие софисты выдвинули утверждение «истинных суждений не существует».
Это утверждение опроверг Аристотель следующим образом.
Утверждение «истинных суждений не существует» является суждением. Если все суждения неистинны, то неистинно также и это суждение, то есть неистинно, что истинных суждений нет. А это значит, что истинные суждения существуют.
Такого же рода внутренне противоречивое суждение высказывает Пигасов в романе Тургенева «Рудин».
– Прекрасно! – промолвил Рудин, – стало быть, по-вашему, убеждений нет?
– Нет – и не существует.
– Это ваше убеждение?
– Да.
– Как же вы говорите, что их нет? Вот вам уже одно на первый случай.
Логика Галилея
В истории науки были случаи, когда казавшиеся безусловно истинными суждения опровергались впоследствии. Путем обнаружения их внутренней логической несостоятельности.
Так, по вопросу о падении тел в физике в свое время считалась общепризнанной точка зрения. Согласно которой скорость падающих тел тем больше, чем больше вес тела. Эту точку зрения опроверг Галилео Галилей. Найдя в ней логическую ошибку. Сделал он это при помощи следующего рассуждения.
Пусть большой камень падает с какой-то определенной скоростью. Тогда другой камень, поменьше, будет падать с меньшей скоростью.
Теперь предположим, что мы сложили эти камни. С какой скоростью будет падать новый камень, вес которого равен весу двух первых?
- С одной стороны, эта скорость должна быть меньше скорости первого камня, поскольку мы присоединили к нему камень, падающий с меньшей скоростью, и этим самым уменьшили скорость падения первого камня.
- С другой стороны, вес камня, получившегося от сложения двух камней, больше веса каждого из них, поэтому и скорость его падения должна быть больше скорости каждого отдельного камня.
- Получается противоречие: скорость двойного камня одновременно и меньше и больше скоростей каждого из двух первых камней, что противоречит закону исключенного третьего.
Чтобы устранить это противоречие, говорит Галилей, нужно сделать допущение, что все тела падают с одинаковым ускорением.
Таким образом, по неправильности суждений можно судить об их неистинности. Если два или более утверждения противоречат друг другу, то это значит, что в них заключена какая-то ложь.
К слову сказать, это обстоятельство используется на суде для уличения преступника. Запутавшись в противоречивых показаниях, преступник бывает вынужден сознаться в своем преступлении.
Софизмы
Если законы логики нарушаются умышленно, то мы имеем дело с софизмами (от греч. sophisma – «измышление, хитрость»), которые представляют собой внешне правильные доказательства ложных мыслей.
Приведем несколько популярных софизмов.
Разные числа
Числа 3 и 4 – это два разных числа, 3 и 4 – это 7, следовательно, 7 – это два разных числа.
В данном внешне правильном и убедительном рассуждении смешиваются или отождествляются различные, нетождественные вещи: простое перечисление чисел (первая часть рассуждения) и математическая операция сложения (вторая часть рассуждения); между первым и вторым нельзя поставить знак равенства, т. е. налицо нарушение закона тождества.
Женщина – не человек
Или вот еще один пример софизма, где ловко прячется простая логическая ошибка.
Любой мужчина – человек. Женщина не мужчина. Следовательно, женщина – не человек.
Знаешь то, чего не знаешь
– Знаешь ли ты, о чём я хочу тебя спросить?
– Нет.
– Знаешь ли ты, что добродетель есть добро?
– Знаю.
– Об этом я и хотел тебя спросить. А ты, выходит, не знаешь то, что знаешь.
Лекарство
Лекарство, принимаемое больным, есть добро. Чем больше делать добра, тем лучше. Значит, лекарств нужно принимать как можно больше.
Вор
Вор не желает приобрести ничего дурного. Приобретение хорошего есть дело хорошее. Следовательно, вор желает хорошего.
Как разоблачать софизмы
Для разоблачения софизма необходимо найти в рассуждении два объекта, которые умышленно и незаметно отождествляются.
При этом стоит заметить, что сделать это далеко не всегда просто. Именно поэтому так важно развивать логическое мышление.
Паралогизмы
От софизмов следует отличать паралогизмы (от греч. paralogismus – «неправильное рассуждение») – логические ошибки, допускаемые непроизвольно, в силу незнания, невнимательности или иных причин. Рассмотрим несколько примеров.
- Один человек пожилого возраста доказывает, что сила его, несмотря на преклонные годы, ничуть не уменьшилась:
– В юности и молодости я не мог поднять штангу весом 200 кг. Сейчас я тоже не могу ее поднять, стало быть, сила моя осталась прежней.
- В одной китайской семье родилась девочка. Когда ей исполнился год, к ее родителям пришел сосед и стал сватать девочку за своего двухлетнего сына. Отец сказал:
– Моей девочке всего год, а твоему мальчику целых два, т. е. он в два раза старше ее, значит, когда моей дочери будет 20 лет, твоему сыну будет уже 40. Зачем же мне выдавать свою дочь за старого жениха?!
Эти слова услышала жена и возразила:
– Сейчас нашей дочке год, а мальчику два, однако через год ей будет тоже два и они станут ровесниками, так что вполне можно в будущем выдать нашу девочку за соседского мальчика.
- Маленький мальчик спрашивает:
– Мама, что от нас дальше – Луна или Африка?
– Конечно же Африка, ведь Луну отсюда видно, а Африку – нет!
Логические парадоксы
Также от софизмов следует отличать логические парадоксы (греч. paradoxes – «неожиданный, странный»).
Парадокс в широком смысле слова – это нечто необычное и удивительное, то, что расходится с привычными ожиданиями, здравым смыслом и жизненным опытом.
Логический парадокс – это такая необычная и удивительная ситуация, когда два противоречащих суждения не только являются одновременно истинными (что невозможно в силу логических законов противоречия и исключенного третьего), но еще и вытекают друг из друга, друг друга обуславливают.
Если софизм – это всегда какая-либо уловка, преднамеренная логическая ошибка, которую можно обнаружить, разоблачить и устранить, то парадокс представляет собой неразрешимую ситуацию.
Это своего рода мыслительный тупик, «камень преткновения» в логике: за всю ее историю было предложено множество разнообразных способов преодоления и устранения парадоксов, однако ни один из них до сих пор не является исчерпывающим.
Парадокс лжеца
Наиболее известный логический парадокс – это парадокс «лжеца». Часто его называют «королем логических парадоксов». Он был открыт еще в Древней Греции.
По преданию, философ Диодор Кронос дал обет не есть до тех пор, пока не разрешит этот парадокс. В конечном счете, он умер от голода, так и не сумев решить эту логическую головоломку. Другой мыслитель – Филет Косский впал в отчаяние от невозможности найти решение парадокса «лжеца» и покончил с собой, бросившись со скалы в море.
Существует несколько формулировок парадокса лжеца. Наиболее коротко и просто он формулируется в ситуации, когда человек произносит простую фразу: Я лжец.
Анализ этого элементарного и бесхитростного на первый взгляд высказывания приводит к ошеломляющему результату. Как известно, любое высказывание (в том числе и вышеприведенное) может быть или истинным или ложным.
Рассмотрим последовательно оба случая. В первом из которых это высказывание является истинным, а во втором – ложным.
- Допустим, что фраза «Я лжец» истинна, т. е. человек, который произнес ее, сказал правду. Но в этом случае он действительно лжец, следовательно, произнеся данную фразу, он солгал.
- Теперь предположим, что фраза «Я лжец» ложна, т. е. человек, который произнес ее, солгал, но в этом случае он не лжец, а правдолюб. Следовательно, произнеся данную фразу, он сказал правду.
Получается нечто удивительное и даже невозможное: если человек сказал правду, то он солгал; а если он солгал, то он сказал правду. Два противоречащих суждения не только одновременно истинны, но и вытекают друг из друга.
Парадокс деревенского парикмахера
Другой известный логический парадокс, обнаруженный в начале 20 века английским философом, логиком и математиком Бертраном Расселом, – это парадокс «деревенского парикмахера».
Представим себе, что в некой деревне есть только один парикмахер, бреющий тех ее жителей, которые не бреются сами. Анализ этой незамысловатой ситуации приводит к необыкновенному выводу.
Зададимся вопросом: может ли деревенский парикмахер брить самого себя? Рассмотрим оба варианта, в первом из которых он сам себя бреет, а во втором – не бреет.
- Допустим, что деревенский парикмахер сам себя бреет, но тогда он относится к тем жителям деревни, которые бреются сами и которых не бреет парикмахер, следовательно, в этом случае, он сам себя не бреет.
- Теперь предположим, что деревенский парикмахер сам себя не бреет, но тогда он относится к тем жителям деревни, которые не бреются сами и которых бреет парикмахер, следовательно, в этом случае он сам себя бреет.
Как видим, получается невероятное: если деревенский парикмахер сам себя бреет, то он сам себя не бреет; а если он сам себя не бреет, то он сам себя бреет (два противоречащих суждения являются одновременно истинными и взаимообуславливают друг друга).
Парадоксы «лжеца» и «деревенского парикмахера» вместе с другими подобными им парадоксами также называют антино́миями (греч. antinomia – «противоречие в законе»), т. е. рассуждениями, в которых доказывается, что два высказывания, отрицающие друг друга, вытекают одно из другого.
Считается, что антиномии представляют собой наиболее крайнюю форму парадоксов. Однако довольно часто термины «логический парадокс» и «антиномия» рассматриваются как синонимы.
Протагор и Эватл
Менее удивительную формулировку, но не меньшую известность, чем парадоксы «лжеца» и «деревенского парикмахера», имеет парадокс «Протагор и Эватл», также появившийся в Древней Греции.
В основе этого логического парадокса лежит незатейливая на первый взгляд история, которая заключается в том, что у софиста Протагора был ученик Эватл, бравший у него уроки логики и риторики.
Учитель и ученик договорились, что Эватл заплатит Протагору гонорар за обучение только в том случае, если выиграет свой первый судебный процесс.
Однако по завершении обучения Эватл не стал участвовать ни в одном процессе. И денег учителю, разумеется, не платил. Протагор пригрозил ему, что подаст на него в суд. И тогда Эватлу в любом случае придется заплатить.
– Тебя или присудят к уплате гонорара, или не присудят, – сказал ему Протагор, – если тебя присудят к уплате, ты должен будешь заплатить по приговору суда; если же тебя не присудят к уплате, то ты, как выигравший свой первый судебный процесс, должен будешь заплатить по нашему уговору.
На это Эватл ему ответил:
– Все правильно: меня или присудят к уплате гонорара, или не присудят; если меня присудят к уплате, то я, как проигравший свой первый судебный процесс, не заплачу по нашему уговору; если же меня не присудят к уплате, то я не заплачу по приговору суда.
Таким образом, вопрос о том, должен Эватл заплатить Протагору гонорар или нет, является неразрешимым.
Договор учителя и ученика, несмотря на его вполне невинный внешний вид. Является внутренне, или логически, противоречивым. Так как он требует выполнения невозможного действия: Эватл должен и заплатить за обучение, и не заплатить одновременно.
В силу этого сам договор между Протагором и Эватлом, а также вопрос об их тяжбе представляет собой не что иное, как логический парадокс.
Решить этот спор можно было бы лишь в том случае, если бы обе стороны соблюдали закон тождества. И в качестве основания для уплаты или неуплаты брали что-нибудь одно: либо решение суда, либо свой договор.
Как избегать логических ошибок
Как же научиться не делать логических ошибок, то есть мыслить правильно, во всех случаях, по каким угодно вопросам, знакомым или впервые встретившимся, о каких угодно предметах, привычных и непривычных?
Повседневная жизненная практика, «здравый смысл», как уже говорилось, во многих случаях помогают избежать логических ошибок. Однако отнюдь не гарантируют избавление от них.
Конечно, чем шире практика, чем с большим количеством разнообразных предметов и видов деятельности сталкивается человек, тем больше возможностей он имеет для развития у себя правильного мышления.
Расширение кругозора, углубление фактических знаний, знакомство с самыми различными рассуждениями, несомненно, способствуют развитию мышления вообще.
Широко образованный, развитой человек быстрее заметит логическую ошибку в рассуждении. Даже и тогда, когда она не касается непосредственно его специальности, его обычных, повседневных занятий.
Поэтому изучение различных наук имеет большое значение. Ведь каждая наука так или иначе, в той или иной степени связана с рассуждениями.
Использованная литература:
Авенир Уемов «Логические ошибки»,
Дмитрий Гусев «Удивительная логика».
Будем благодарны за Вашу поддержку!
Е.А. Иванов
Источник
Раздел шестой. Основные законы мышления
Анализ наиболее общих форм мышления – понятий, суждений и др. – будет неполным, если не рассмотреть еще основных законов мышления, действующих в них и пронизывающих всю их ткань.
Неосновные законы, о которых говорилось в соответствующих местах, – закон обратного отношения между содержанием и объемом понятия, законы распределенности терминов в простых суждениях, законы соединения простых суждений в сложные и их взаимоотношений между собой, законы различных типов, видов и разновидностей умозаключений и т. д. – связаны лишь с определенной формой мышления и, следовательно, действуют в ограниченной сфере.
Важнейшая особенность основных законов мышления состоит в том, что они носят здесь универсальный характер, т. е. лежат в основе функционирования всего мышления в целом. Можно сказать без преувеличения, что без этих законов процесс мышления в целом был бы попросту невозможен. Ведь в них отражаются фундаментальные – наиболее общие и глубокие свойства, связи и отношения объективного мира, постигаемого нашим мышлением. Вот почему они рассматриваются нами после анализа всех конкретных мыслительных форм.
Основные законы мышления, в свою очередь, подразделяются на два типа: формально-логические законы и законы диалектической логики, находящиеся в определенном соотношении между собой.
Изучение тех и других законов необходимо и важно для понимания сложных глубинных процессов, протекающих в мышлении естественным образом, независимо от нашего осознания их и воли; а также для использования этих законов в практике мыслительной деятельности.
Глава I. Основные формально-логические законы
Основными в формальной логике считаются четыре закона – тождества, противоречия, исключенного третьего и достаточного основания. Они освящены многовековой традицией логической науки и играют важную роль в любом, в том числе современном, мышлении. Знание этих законов необходимо для использования их в практике как научного, так и повседневного мышления и, конечно, в юридической практике.
Исходным в ряду формально-логических законов выступает закон тождества. Вот почему наш анализ начинается именно с него.
1. Закон тождества
Объективный характер и сущность закона тождества. С действием этого закона связано такое коренное свойство правильного мышления, как его определенность.
Что же послужило объективным основанием для возникновения и действия этого закона в мышлении? Как уже отмечалось ранее, одним из фундаментальных свойств окружающего нас мира выступает качественная определенность самих предметов и явлений действительности, отражаемых в мышлении. Это означает, что, несмотря на непрерывно происходящие в них изменения, они до поры до времени остаются теми же самыми, тождественными себе. Например, после долгих лет отлучки мы посетили родные места, где прошло наше детство. Мы видим, что многое вокруг изменилось. И все же мы узнаём свой дом, улицу, школу, родных и близких. Почему? Да потому, что при всех многообразных изменениях они сохранили свой неповторимый облик, то, что делало их данными, а не иными, они не утратили тождества с собой. И даже риторический вопрос Евгения Онегина: «Ужель та самая Татьяна..?» – лишь подчеркивает наличие тождества: конечно, та самая, хотя и прошло столько времени.
Подобную диалектику самой действительности выразил в своих стихах А. Блок:
: Идут века, шумит война,
: Встает мятеж, горят деревни,
: А ты все та ж, моя страна,
: В красе заплаканной и древней.
Даже в той парадоксальной ситуации, созданной воображением Льюиса Кэрролла, когда Алиса в течение дня несколько раз сильно меняется – то вдруг вырастает, то уменьшается в размерах, она все же остается той же самой Алисой и не превращается в других обитателей Страны чудес. Иначе повествование о ней было бы невозможным50.
Но если действительность именно такова, если предметы и явления определенны и эта определенность более или менее длительно сохраняется, то какой будет мысль о них, каким свойством она будет обладать, коль в ней верно отражаются эти предметы и явления? Она будет тоже определенной, тождественной себе.
Вот эту определенность мысли о качественно определенном предмете и отражает формально-логический закон тождества. Честь открытия этого закона принадлежит Аристотелю. Он писал: «…Невозможно что-либо мыслить, если не мыслят что-то одно…»51.
Правда, Аристотель не дал ему своего названия. Оно появилось в логике позднее. Сам же закон в разные эпохи у разных авторов получал неоднозначное толкование и весьма различные формулировки. Воспользуемся этим обстоятельством и дадим ему следующую формулировку: мысль о качественно определенном предмете, если она соответствует ему, не может не быть определенной, однозначной, тождественной себе.
Отсюда – наименование самого закона: закон тождества. Его наиболее общая формула: «А есть А» или «А = А», где под «А» разумеется всякая мысль вообще.
Закон тождества есть закон функционирования отдельно взятой мысли. Но, как и во всяком законе, в нем так или иначе выражается внутренняя, существенная, необходимая связь, повторяющаяся всегда и всюду при определенных условиях. В данном случае это отношение тождества мысли с самой собой, сколько бы раз она ни появлялась в рассуждении и в какие бы взаимоотношения ни вступала с другими мыслями. Иначе это будет уже другая мысль.
Исторически закон тождества в качестве формально-логического закона явился обобщением практики оперирования понятиями и выражающими их словами или словосочетаниями. И в настоящее время он действует прежде всего в сфере понятий и проявляется уже в процессе их образования. Как известно, любое понятие может быть образовано правильно и неправильно. Если в одно и то же понятие объединяются разнородные элементы, то оно оказывается расплывчатым, смутным, неопределенным, а действительность в нем искажается. Например, так будет в том случае, когда в понятие «мебель» мы включим столы, кастрюльки, ложки и т. д. Если же понятие охватывает лишь такие предметы, которые едины, общи, тождественны в том или ином отношении, то оно будет четким и ясным, будет иметь определенное содержание и определенный объем. Например: мебель – это столы, стулья, шкафы и т. п. Закон тождества обнаруживает свое действие и в процессе использования уже готовых понятий. Если бы в них не было определенности, однозначности, тождественности, если бы они то и дело неуловимо меняли свое содержание и свой объем, то мы попросту не могли бы их применять. Так, лишь зная точное содержание понятия «товар», мы можем твердо, однозначно, категорично ответить, являются ли, например, сапоги товаром или нет: если они произведены для продажи, то это товар, если для себя, то нет.
Если бы понятия не были определенными по своему содержанию и объему, то мы не смогли бы выделять их виды, устанавливать отношения между ними, производить над ними логические операции – определения, деления, обобщения и ограничения.
Действие закона тождества простирается и на суждения. Определенность понятий, из которых они образуются, служит важнейшей предпосылкой их определенности. Но этим действие закона тождества не исчерпывается. Ведь наиболее глубокая сущность суждений – в отражаемых ими связях и отношениях действительности. И если эти связи и отношения определенны, то и суждение, верно отражающее их, не может не быть определенным.
Пожалуй, наиболее рельефно закон тождества проявляется в суждениях типа: «Солнце есть Солнце», «Война есть война» и др., упоминавшихся выше. В них непосредственно раскрывается тождество предмета с самим собой. И такие суждения нередки в практике мышления. Вспомним слова поэта: «Осел останется ослом, хотя осыпь его звездами». Или высказывания других авторов: «Факты есть факты, и по вашему желанию они никуда не исчезнут»; «Прибыль есть прибыль, как бы мала она ни была»; «Джентльмен всегда джентльмен». А вот заголовки из современных газет: «Мастер – он и в глубинке мастер»; «Ложь всегда есть ложь»; «Преступность везде преступность». Вспомним народную мудрость: «Что в лоб, что по лбу»; «Как был дураком, так им и остался» и др.
Разновидностью подобных суждений, выражающих объективное тождество, служат суждения типа: «Отрицательный результат тоже результат»; «Мировой судья есть судья»; «Суров закон, но он закон». Здесь налицо тождество рода и вида (в том смысле, что вид заключает в себе все признаки рода, хотя и не наоборот).
Обобщая, можно сказать, что любое суждение – будь то атрибутивное или реляционное, – фиксируя то или иное тождество свойств предметов или отношений между предметами, является утверждением или отрицанием и в силу этого может быть истинным или ложным. В свою очередь, каждое простое суждение, вступая в связи с другими, образуя конъюнкцию, дизъюнкцию и т. д., сохраняет в них свой определенный, однозначный смысл. Без этого было бы тоже невозможно выяснять значение истинности или ложности сложного суждения, включать его в еще более сложные мыслительные конструкции.
Действие закона тождества распространяется и на обширную область умозаключений. Так, простой категорический силлогизм возможен, в частности, потому, что средний термин, связывающий большую и меньшую посылки, сохраняет в них один и тот же смысл. А больший и меньший термины не только сохраняют свой смысл в посылках и заключении, но если они не распределены в посылках, то не могут быть распределены и в заключении. В противном случае силлогизм оказывается неправильным.
В доказательстве, если оно тоже правильное, закон тождества проявляется в том, что и тезис, и основания сохраняют свою определенность на протяжении всей данной логической процедуры. Без этого доказательство не состоялось бы или было бы неправильным.
Наконец, теория может возникнуть и успешно развиваться, если исходное знание – факты или аксиомы – определенны и сохраняют свой смысл на протяжении более или менее длительного времени. Точно также производное знание – теоремы, принципы, законы – имеет значение постольку, поскольку оно тоже определенно, однозначно, тождественно себе.
Из этого краткого обзора видно, что закон тождества универсален в смысле охвата всех без исключения форм мышления, всякой мысли вообще.
Требования закона тождества и логические ошибки из-за их нарушения. Из объективно действующего в нашем мышлении закона тождества вытекают определенные требования. Это логические нормы, установки, предписания или правила, которые формулируются самими людьми на основе закона и которые необходимо соблюдать, чтобы мышление было правильным, ведущим к истине. Их можно свести к следующим двум.
1. Каждое понятие, суждение и т. д. должны употребляться в одном и том же, определенном смысле и сохранять его в процессе всего рассуждения.
2. Нельзя отождествлять различные мысли и нельзя тождественные мысли принимать за различные.
Требуя определенности, однозначности мысли, закон тождества в то же время направлен против всякой нечеткости, неточности, размытости наших понятий. По Ф. Бэкону, если понятия неотчетливы, то нет ничего прочного в том, что на них построено52.
В тех случаях, когда требования закона тождества нарушаются, возникают многочисленные логические ошибки. Они называются по-разному: «амфиболия» (двусмысленность, т. е. употребление одного и того же слова-омонима одновременно в,разных смыслах), «смешение понятий», «путаница в понятиях», «подмена одного понятия другим», «подмена тезиса» и т. д.
Аналогичная ситуация нередко возникает во сне. Вот что рассказывал один психолог: «Припоминаю, что однажды я видел себя во сне куда-то едущим: сначала я ехал в пролетке, потом немедленно за этим ехал в санях и еще через мгновение был уже в лодке на какой-то реке, и эта быстрая смена способов передвижения меня нисколько не удивила». Действительно, во сне мы зачастую не сознаем, что это алогичность. Но если мы проснулись и понимаем, что так не бывает, то это значит, что в нашем мышлении действует закон тождества. Ибо если мы едем в пролетке, то это именно пролетка, и она не может быть через мгновение санями или лодкой.
Отождествление нетождественного во сне хорошо описал Л. Толстой в романе «Анна Каренина». Облонский, просыпаясь, вспоминает сонные видения: «Да, как это было? Да! Алабин давал обед в Дармштадте; нет, не в Дармштадте, а что-то американское. Да, но там Дармштадт был в Америке. Да, Алабин давал обед на стеклянных столах, да, – и столы пели: И mio tesoro (мое сокровище), и не II mio tesoro, а что-то лучше, и какие-то маленькие графинчики, и они же женщины». Здесь налицо несколько сбоев мысли о случившемся: Дармштадт не Дармштадт, поющие столы, графинчики-женщины…
Подобная неопределенность мышления возможна и в состоянии бодрствования. Вспомним классический образ Хлестакова в пьесе Н. Гоголя «Ревизор». Сам Гоголь обрисовал его так. Он не в состоянии остановить постоянного внимания на какой-нибудь мысли. Речь его отрывиста, и слова вылетают из уст его совершенно неожиданно. В самой пьесе, нарисовав яркую картину вранья Хлестакова, Гоголь показал, как раздваивается его мысль, теряет определенность и становится непонятной, бессмысленной. Он безбожно путает разных людей – Смирдина с Брамбеусом, Маврушку с посланниками и т. д. А когда, делая предложение дочери городничего Марье Антоновне, он вдруг делает аналогичное предложение его жене Анне Андреевне, та произносит знаменательную фразу: «Но позвольте, я еще не понимаю значения слов». Это верный показатель того, что мышление Хлестакова окончательно запутывается, требования закона тождества не выполняются.
Яркие примеры нелогичного мышления, вызванного нарушениями требований закона тождества – двусмыслицами, неожиданными переосмыслениями слов и т. д., дает Л. Кэрролл в «Приключениях Алисы в Стране чудес». Вот лишь один из них:
«– Совершенно верно, – согласилась Герцогиня. – Фламинго кусаются не хуже горчицы. А мораль отсюда такова: это птицы одного полета!
– Только горчица совсем не птица, – заметила Алиса…
– Кажется, горчица – минерал, – продолжала Алиса задумчиво.
– Конечно, минерал, – подтвердила Герцогиня… – Минерал огромной взрывчатой силы. Из нее делают мины и закладывают при подкопах… А мораль отсюда такова: хорошая мина при плохой игре – самое главное!
– Вспомнила, – сказала вдруг Алиса… – Горчица – это овощ. Правда, на овощ она не похожа – и все-таки это овощ!
– Я совершенно с тобой согласна, – сказала Герцогиня. – А мораль отсюда такова: всякому овощу свое время! Или, хочешь, я это сформулирую попроще: никогда не думай, что ты иная, чем могла бы быть иначе, чем будучи иной в тех случаях, когда иначе нельзя не быть»53.
Это апофеоз бессмыслицы: мысль Герцогини окончательно запутывается и теряет всякую определенность.
Подобное бывает и в реальной практике мышления. Вот что писал по этому поводу Г. Плеханов. «Иногда людям приходится вести долгие споры просто потому, что они употребляют слова в разных смыслах. Это скучные и бесплодные споры. Но еще несравненно скучнее и еще несравненно бесплоднее такие споры, в которых один человек связывает с данными словами определенное понятие, а у его противника с теми же словами не связывается ровно никаких определенных понятий, вследствие чего он и получает возможность играть ими как ему вздумается»54.
Иногда подмена понятия, использование одного и того же слова одновременно в разных смыслах осуществляется сознательно – в качестве основы для остроты. Вспомним рекламу: «Мы не в Находке, мы в Москве, но мы находка для вас». Или: «Шли дождь и два студента». Но этим не отрицается, а лишь подтверждается действие закона тождества в нормально протекающем, не парадоксальном мышлении.
Значение закона тождества. Знание закона тождества и его использование в практике мышления имеет принципиальное значение, так как позволяет сознательно и четко отделять правильное рассуждение от неправильного, находить логические ошибки – двусмысленность, подмену понятий и т. д. – в рассуждениях других людей и избегать в своих собственных.
В любой речи – письменной или устной – следует в соответствии с законом тождества добиваться ясности изложения, а она предполагает использование слов и выражений в одном и том же смысле, понятном для других, и в естественных сочетаниях с другими словами.
Очень важно соблюдать требования закона тождества в дискуссиях, спорах и т. д. Чтобы спор не был беспредметным, необходимо всегда точно определить предмет спора и точно выяснить ключевые понятия в нем. Для равнозначных понятий можно и нужно использовать слова-синонимы. Они, как уже отмечалось, обогащают речь. Следует лишь помнить, что синонимия носит относительный характер (слова, являющиеся синонимами в одном отношении, не являются ими в другом). А под видом синонимов иногда употребляются совершенно разные понятия. Если же применяются слова-омонимы, то требуется точно выяснить тот смысл, в котором они в данном случае берутся.
Неоценимо значение требований закона тождества в деятельности юриста. Надо учитывать, что даже в законодательных актах, над которыми, как правило, ведется особенно тщательная работа, нередко встречаются неясности и просто двусмысленности. А это очень опасно, так как неизбежно ведет к различному толкованию одного и того же закона и, следовательно, к его неоднозначному применению.
На требованиях закона тождества основано такое важное следственное действие, как опознание.
В ст. 193 УПК РФ «Предъявление для опознания» говорится, что следователь может предъявить для опознания лицо или предмет свидетелю, потерпевшему, подозреваемому или обвиняемому. Для опознания может быть предъявлен и труп. А далее тщательно раскрывается механизм этой процедуры.
В следственной практике широко используется также идентификация (отождествление). Ее задача – установление тождества тех или иных вещей, людей, документов и т. д., которые до этого мыслились раздельно. Например, идентификация подозреваемого в разных преступлениях, идентификация ножа, которым был ранен или убит человек, и ножа, найденного у подозреваемого. Для этого применяются так называемые «идентификационные свойства». Идентификация живых лиц может производиться на основе их анатомических признаков – роста, строения, пальцевых узоров, по признакам почерка, фотоснимкам и пр. Идентификация вещей – по их следам: на пулях, гильзах и т. п.
Иногда идентификация представляет собой сложнейший процесс с привлечением самых различных специалистов. Вспомним идентификацию останков последнего российского царя Николая II и его семьи, расстрелянных в Екатеринбурге.
В ходе расследования и на самом суде важно выяснить точный смысл, в котором употребляются слова обвиняемым, свидетелем; не подменять их, иначе цель не будет достигнута, а дело приостановлено из-за возникших неясностей. В самом приговоре или решении особенно важны точность понятий, их определенность и однозначность, исключающие всякую недоговоренность, неясность, неточность.
2. Закон противоречия
С законом тождества органически связан закон противоречия. Можно сказать так: если бы не было первого, то не могло бы быть и второго. В то же время закон противоречия носит самостоятельный характер. Если закон тождества обусловливает такую коренную черту правильного мышления, как определенность, то действие закона противоречия обеспечивает его последовательность, непротиворечивость.
Объективная основа закона противоречия и его сущность. Как уже показано, основу закона тождества составляет качественная определенность предметов и явлений, сохраняющаяся в процессе их взаимодействия на протяжении более или менее длительного времени. Отсюда следует, что если такой предмет существует, то он не может в то же время не существовать; он не может вместе обладать тем или иным качественно определенным свойством и не обладать им, находиться в том или ином отношении с другими предметами и не находиться в этом отношении.
Эта фундаментальная особенность окружающего мира и составляет объективную основу закона противоречия как закона мышления. Аристотель, открывший этот закон, дал ему свою формулировку. Он сознательно исходил из объективной предпосылки мышления: «Невозможно, чтобы одно и то же в одно и то же время было и не было присуще одному и тому же в одном и том же отношении»55. А существо самого закона противоречия кратко выразил так: «Невозможно что-либо вместе утверждать и отрицать»56.
Почему же этот закон позднее получил наименование закона противоречия? Потому что в нем отражена закономерность, действующая в сфере логического противоречия.
Но что такое логическое противоречие? Очевидно, что это два несовместимых, взаимоисключающих высказывания о чем-либо. Однако далеко не всякие подобные высказывания оказываются логическим противоречием. Рассмотрим с этой целью ряд пар суждений.
Например: «Ночь длинная» – «День короткий». Здесь налицо два противоположных высказывания, но они касаются разных предметов. Такие два высказывания могут быть одновременно истинными. Следовательно, никакого логического противоречия здесь нет: есть лишь отражение противоположных свойств, присущих дню и ночи.
А если мы выскажем два противоположных суждения об одном и том же предмете? Могут ли они быть одновременно истинными? Да, но при условии, если предмет рассматривается в разное время. Например: «Октябрьский день короткий» – «Июньский день длинный». Здесь тоже нет логического противоречия.
Могут ли, далее, быть одновременно истинными противоположные высказывания об одном и том же предмете, взятом в одно и то же время? Да, но при новом условии: если он рассматривается в разных отношениях. Например: «Октябрьский день короткий по сравнению с июньским» – «Октябрьский день длинный по сравнению с январским».
Возьмем, наконец, последний случай. Могут ли быть одновременно истинными два противоположных суждения об одном и том же предмете, взятом в одно и то же время и в одном и том же отношении? Нет. Октябрьский день по сравнению с июньским не может быть и длинным и коротким. Если мы будем рассуждать так, то допустим логическое противоречие. Это и есть такой феномен мышления, когда высказываются два взаимоисключающих суждения об одном и том же предмете,, который рассматривается в одно и то же время и в одном и том же отношении.
Что же характерно для логического противоречия? Какая в нем скрыта закономерность? Как мы могли убедиться, в отличие от других высказываний здесь два таких высказывания не могут быть одновременно истинными.
Вот эта объективная закономерность и нашла свое отражение в формально-логическом законе противоречия: два противоположных или противоречащих суждения об одном и том же предмете, который взят в одно и то же время и в одном и том же отношении, не могут быть одновременно истинными. Одно из них по необходимости ложное.
Формула такого закона: «Неверно, что А и не-А». Иногда говорят, что это лишь отрицательная формула закона тождества. Но в этом отрицании есть свой собственный глубокий смысл.
Какова же сфера действия закона противоречия? Она тоже весьма широка. Этот закон представляет собой прежде всего обобщение практики оперирования суждениями. В нем отражается закономерное отношение между двумя суждениями – утвердительным и отрицательным; отношение несовместимости их по истинности: если одно истинно, то другое непременно ложно.
Поскольку суждения делятся на утвердительные и отрицательные, а они – в свою очередь, на истинные и ложные, то этим объясняется универсальный характер закона противоречия. Естественно, что поскольку из простых суждений образуются сложные, то закон противоречия действует и здесь, если они находятся в отношении отрицания.
Этот закон распространяется также на понятия, а именно на отношения между ними. Это отношения несовместимости. Так, если лес «хвойный», то он не может быть «лиственным» (отношение соподчинения); если человек «щедрый», то он не может быть в то же время «нещедрым» (отношение противоречия) или «скупым» (отношение противоположности). Конечно, все это проявляется в процессе функционирования понятий.
Закон противоречия обнаруживается и в умозаключениях. На нем основаны, например, непосредственные умозаключения через превращение суждений. Эта операция, как мы помним, возможна лишь потому, что предмет мысли не может одновременно принадлежать и не принадлежать к одному и тому же классу предметов («Все адвокаты – юристы» – это значит, что «Ни один адвокат не может быть неюристом»). В противном случае будет логическое противоречие. В умозаключениях через отношение суждений в логическом квадрате действие закона противоречия сказывается в том, что если какое-либо суждение истинно, то противоречащее или противоположное ему будет ложным. Иными словами, они не могут быть одновременно истинными.
Закон противоречия действует также в доказательстве. Он лежит в основе одного из правил оснований доказательства: они не должны противоречить друг другу. Без действия этого закона было бы невозможным опровержение. Доказав истинность одного тезиса, мы не смогли бы заключить отсюда о ложности противоположного или противоречащего ему тезиса.
Наконец, действие закона противоречия простирается и на всю безграничную сферу теории. Говоря об этой форме мышления и требованиях, предъявляемых к формам развития научного знания – фактам, проблемам, гипотезам – мы много раз фиксировали внимание на их отношении к логическому противоречию.
Требование непротиворечивости мысли и его нарушения в практике мышления. Действие объективного закона противоречия в мышлении предъявляет человеку важное требование – непротиворечивости в его рассуждениях, в связях между мыслями. Чтобы наши мысли были истинными, они должны быть последовательными, непротиворечивыми. Или: в процессе любого рассуждения нельзя противоречить себе, отвергать свои собственные высказывания, признаваемые за истинные.
Вот почему закон противоречия называют иногда «законом непротиворечия». Но подобное наименование основано на недоразумении. Ведь сам закон и требование, вытекающее из него, – это разные вещи. Объективный закон называется законом противоречия потому, что он действует лишь там, где есть логическое противоречие, где образующие его суждения объективно не могут быть вместе истинными. Называть его законом непротиворечия – значит отождествлять его с требованием, которое формулируют сами люди на его основе («принцип непротиворечивости»).
С нарушением требований закона противоречия тоже связаны логические ошибки. Они весьма разнообразны, но их общее наименование – «логические противоречия». Правда, бывают ситуации, когда один человек всегда противоречит другим. Он проникнут, как говорят, духом противоречия и, соответственно, поступает наперекор им. Таков, например, лермонтовский Печорин, который сам заявляет о себе: «У меня врожденная страсть противоречить». Подобные люди могут быть правы или не правы, быть гениальными или с отклонениями в психике, но логического противоречия тут нет. Иначе никакие споры были бы невозможны. Логическое противоречие допускается тогда, когда одним и тем же человеком два взаимоисключающих высказывания принимаются за истинные.
Образ такого человека, впадающего в логические противоречия, т. е. в противоречия с самим собой, многократно высмеян в художественной литературе. Классический пример мы находим в романе И. Тургенева «Рудин».
« – …Всякий толкует о своих убеждениях и еще уважения к ним требует, носится с ними… Эх!
И Пигасов потряс кулаком в воздухе…
– Прекрасно! – промолвил Рудин, – стало быть, по-вашему, убеждений нет?
– Нет – и не существует.
– Это ваше убеждение?
– Да.
– Как же вы говорите, что их нет? Вот вам уже одно на первый случай.
Все в комнате улыбнулись и переглянулись».
«Убеждения не существуют» и «Убеждения существуют» – одновременное признание того и другого одним и тем же человеком и есть логическое противоречие.
Образцом непоследовательности, когда по одному и тому же поводу высказываются взаимоисключающие, несовместимые положения, служат рассуждения полицейского надзирателя Очумелова в рассказе А. Чехова «Хамелеон». Меняются предположения о хозяине, которому могла бы принадлежать собака, укусившая человека за палец, – и вместе с этим меняются на прямо противоположные его оценки происшедшего. Отсюда и характерное название рассказа.
Пример логической противоречивости дает следующая сказка о ходже Насреддине. Однажды он попросил своего богатого и скупого соседа дать ему на время котел. Сосед дал, хотя и неохотно. Возвращая котел хозяину, Насреддин вместе с ним дал еще и кастрюльку, сказав, что эту кастрюльку родил котел. Сосед согласился с таким объяснением и кастрюльку взял. В следующий раз Насреддин вновь взял котел, но уже не вернул. А когда сосед потребовал котел обратно, то ответил: «С удовольствием возвратил бы тебе котел, да не могу, потому что он умер». – «Как! – возмутился сосед, – что ты говоришь чепуху – разве котел может умереть?» – «Отчего же, – ответил Насреддин, – котел не может умереть, если он может родить кастрюльку?»
Сознательное использование логических противоречий служит одним из распространенных средств создания анекдотов, острот, шуток и т. д. Так, в габровском анекдоте «Реклама», созвучном нашему времени, говорится:
«– Значит, это самая новая ткань?
– Только вчера получил, прямо с фабрики!
– А она не линючая?
– Да что вы! Больше месяца висела на витрине, и ничего ей не сделалось!»
Современный анекдот. Милиционеры поймали мужика. Притащили в дежурку.
– Да я не виновен.
– Прошлый раз тоже говорил, что невиновен.
– Да вы что! Это моя первая кража.
Логические противоречия нередко допускаются в научном познании. Они носят здесь самый разнообразный характер. Это может быть противоречие в самом сочетании слов. И тогда оно называется contradictio in adjecto. В этом случае говорят: «Жареный лед», «Круглый квадрат», «Круглый стол с острыми углами», «Громкая тишина».
Иногда такое сочетание взаимоисключающих слов или понятий используется вполне осознанно для придания художественному образу большей выразительности. Достаточно сослаться на такие названия произведений искусства: «Живой труп» Л. Толстого; «Без вины виноватые» А. Островского, «Оптимистическая трагедия» Н. Погодина; «Горячий снег» Ю. Бондарева, «Зияющие высоты» А. Зиновьева.
Это могут быть противоречия между отдельными положениями, между более или менее законченными рассуждениями или целыми теориями; между естественнонаучными (или общественно-политическими) взглядами и философскими позициями; в рамках целостной философской системы между ее частями (например, между системой и методом Гегеля).
Люди зачастую противоречат себе в обыденной жизни. Словом, логическое противоречие – довольно распространенная ошибка.
Значение закона противоречия. Хотя мириться с логическими противоречиями нельзя ни в каком рассуждении, даже в самом простом, особенно важно учитывать действие закона противоречия в науке. Ведь логические противоречия способны разрушить любое, сколь угодно сложное умственное построение. А здесь они далеко не так просты и очевидны, как те, что приводятся (для наглядности) в учебных целях. Поскольку всякое научное рассуждение – более или менее обстоятельное, подробное, взаимоисключающие мысли могут находиться в разных его местах и их попросту трудно обнаружить. Тем более затруднительно это сделать, если рассуждения разделены во времени: то, что утверждалось в одно время, может незаметно для самого говорящего отрицаться в другое. Но от этого логические противоречия не утрачивают своего вреда. Они представляют собой интеллектуальный «шлак», засоряющий наши рассуждения и требующий постоянного очищения их, чтобы можно было успешно двигаться к истине. Вот почему в науке придается принципиальное значение предупреждению или устранению в ней логических противоречий.
Одно из важнейших условий построения теоретической системы, как уже подчеркивалось, – это непротиворечивость исходных данных («непротиворечивость системы аксиом»).
Другое условие – непротиворечивость вытекающих из них теоретических построений («непротиворечивость самой теоретической системы»). Если в науке обнаруживается какое-либо противоречие логического порядка, то его всячески стремятся устранить как помеху на пути познания истины.
Конечно, закон противоречия ничего не говорит да и не может сказать о том, какое из двух взаимоисключающих положений истинно, а какое ложно. Но он дает тревожный сигнал о неблагополучии в каком-либо пункте рассуждений и мобилизует усилия на поиск и устранение ложного высказывания.
Логические противоречия нетерпимы и в повседневной речи. Человека перестают уважать, если он по одному и тому же поводу сегодня говорит одно, а завтра другое. Это человек без принципов.
Особое внимание логическим противоречиям отводится в юридической области. К сожалению, они нередки и здесь. Это могут быть противоречия внутри одного и того же закона (между его разными статьями); противоречия между отдельными законами, действующими одновременно; между вновь принимаемыми законами и старыми; между законами и подзаконными актами; между законами и Конституцией; между законами той или иной страны и международными правовыми нормами.
Одним из средств их разрешения служит кодификация законодательства. Она предполагает не только переработку действующих норм с целью большего соответствия их жизни, восполнение пробелов, отмену устаревших норм, но и устранение противоречий одних норм другим, приведение всего законодательства в более стройную, внутренне согласованную систему.
Другим средством выступает использование принципа приоритета высших законов перед низшими. Так, установлено, что Конституция Российской Федерации имеет высшую юридическую силу. Причем в ней самой есть своя «шкала ценностей». В разделе первом, в главе 1 изложены «Основы конституционного строя», а далее подчеркнуто, что никакие другие положения Конституции не могут противоречить этим основам. Законы и другие правовые акты, действовавшие на территории Федерации до вступления в силу новой Конституции, применяются лишь в той части, которая не противоречит ей.
Характерно, что нижестоящие нормативные правовые акты должны разрабатываться в соответствии с вышестоящими. Если же они были изданы ранее, то должны приводиться в соответствие с вновь принятыми.
В случае, если обнаруживается противоречие между отдельными звеньями в иерархии законов, то всякий раз действуют вышестоящие законы. Так, если это противоречие между подзаконным актом и соответствующим законом, то действует закон; если противоречие между законом субъекта РФ и федеральным законом, действует федеральный закон; если, наконец, противоречие между федеральным законом и конституцией, действует конституция.
Общепризнанные принципы и нормы международного права и международные договоры Российской Федерации являются составной частью ее правовой системы. Если международным договором Российской Федерации установлены иные правила, чем предусмотрены законом, то применяются правила международного договора.
О том, насколько важна проблема недопустимости логических противоречий в законодательстве, ярко свидетельствует, например, Трудовой кодекс РФ. В нем есть особая статья 5 «Трудовое законодательство и иные нормативные правовые акты, содержащие нормы трудового права», где тщательнейшим образом расписано, как должны соотноситься между собой нормативные акты трудового права разных уровней с точки зрения логического закона противоречия. Здесь, в частности, сказано, что нормы трудового права, содержащиеся в иных законах, должны соответствовать настоящему Кодексу. Указы Президента Российской Федерации, содержащие нормы трудового права, не должны противоречить настоящему Кодексу и иным федеральным законам. Постановления Правительства Российской Федерации, содержащие нормы трудового права, не должны противоречить настоящему Кодексу, иным федеральным законам и указам Президента Российской Федерации (и т. д. и т. п., вплоть до соответствующих актов местных органов).
В случае противоречий между настоящим Кодексом и иными федеральными законами, содержащими нормы трудового права, применяется настоящий Кодекс.
Все это имеет не чисто абстрактное значение трогательной заботы о логической «чистоте» и строгости в сложнейшей иерархии законов страны. Логические противоречия между законами заключают в себе вполне конкретную, и притом грозную, опасность правового нигилизма. И действительно, если один закон требует одного, а другой – противоположного, то можно не выполнять ни того, ни другого.
Закон противоречия имеет большое значение в судебной практике.
В ст. 7 УПК РФ говорится, что суд, прокурор, следователь, органы дознания не вправе применять федеральный закон, противоречащий настоящему Кодексу. Суд, установив в ходе производства по уголовному делу несоответствие федерального закона или иного нормативного правового акта настоящему Кодексу, принимает решение в соответствии с настоящим Кодексом.
На действии этого закона основано алиби. Доказывание его как раз и состоит в установлении того, что данный человек во время преступления был в другом месте. И если это истинно, то не может быть одновременно истинно обратное, что он был на месте преступления.
Одно из эффективных средств опровержения, часто используемое на суде, – это выявление противоречий в рассуждениях оппонента. Тем самым демонстрируется несостоятельность всей его речи. Но, разумеется, надо тщательно следить за тем, чтобы не допускать противоречий в собственных рассуждениях, ибо они обесценивают сказанное. Тем более недопустимы противоречия в приговоре или решении суда. При их наличии тот или другое могут быть опротестованы.
3. Закон исключенного третьего
С законом противоречия, в свою очередь, тесно связан закон исключенного третьего.
Как установлено выше, закон противоречия гласит, что утверждение и отрицание одного и того же не могут быть вместе истинными: одно из них непременно ложно. Но могут ли они быть одновременно ложными? Об этом закон противоречия ничего не говорит.
На этот вопрос отвечает закон исключенного третьего. В этом смысле его можно считать дополнением к закону противоречия (а следовательно, и к закону тождества). Его действием также обусловлена так или иначе определенность мышления, его последовательность, непротиворечивость. Но он обладает относительной самостоятельностью, имеет свою сферу действия и свое предназначение в мышлении.
Объективный источник и существо закона исключенного третьего. Подобно законам тождества и противоречия, этот закон имеет объективный источник. В нем отражается та же качественная определенность предметов и явлений действительного мира, сохраняющаяся до поры до времени в процессе их изменения и развития. А это означает, что нечто существует или не существует, входит в какой-то класс предметов или не входит, ему что-то присуще или не присуще, оно находится в каком-то отношении или не находится.
Поэтому в той мере, в какой мир альтернативен, раздвоен на «наличие – отсутствие», мышление, если оно верно отражает его, не может не быть тоже альтернативным. В нем неизбежно действует закон исключенного третьего.
Открытый Аристотелем, этот закон гласит: «Не может быть ничего промежуточного между двумя членами противоречия, а относительно чего-то одного необходимо что бы то ни было одно либо утверждать, либо отрицать»57. И в другом месте: «О чем бы то ни было истинно или утверждение, или отрицание…»58.
Обосновывая неизбежность действия этого закона и невозможность его отрицания, Аристотель приводил ряд (семь!) доводов в его пользу. В более позднее время он получил название закона исключенного третьего, хотя формулировки ему давались самые различные. Наиболее общей из них является следующая: два противоречащих высказывания об одном и том же предмете не могут быть вместе ложными: одно из них по необходимости истинно. Формула этого закона: «А или не-А».
Чтобы понять действие закона, приведем две пары несовместимых высказываний:
1) «Байкал глубокий» – «Байкал мелкий»;
2) «Байкал глубокий» – «Байкал неглубокий».
Обратим внимание, что в первой паре предикатами выступают противоположные понятия («глубокий» – «мелкий»), а во второй – противоречащие понятия («глубокий» – «неглубокий»). Между ними, как мы помним, имеется не только сходство, но и различие. Противоположные отрицают друг друга, но не исчерпывают объема родового понятия. Спрашивается: могут ли два высказывания с противоположными предикатами быть одновременно истинными? Нет. Об этом говорит закон противоречия. Но могут ли они быть одновременно ложными? Да, потому что не исчерпывают всех возможных вариантов. Может статься, что «Байкал средней глубины». Закон исключенного третьего здесь не действует.
Что же касается противоречащих понятий («глубокий» – «неглубокий»), то они не только отрицают друг друга, но и исчерпывают объем родового понятия. Возникают те же вопросы. Могут ли оба суждения с подобными предикатами быть одновременно истинными? Нет. Это опять-таки следует из закона противоречия. А могут ли они быть одновременно ложными? Вот тут-то и «зарыта собака». В отличие от первой пары они не могут быть и одновременно ложными. Ведь третьего здесь попросту нет, так как озеро либо глубокое, либо неглубокое. Одно из них непременно истинно. Эта закономерность, свойственная подобным суждениям, и нашла свое отражение в законе исключенного третьего.
Теперь нетрудно понять, какова сфера действия этого закона. Она тоже весьма широка. В общей форме можно сказать так: не всюду там, где действует закон противоречия, действует и закон исключенного третьего. Но всюду, где он проявляет свою силу, проявляется и закон противоречия.
Как и закон противоречия, закон исключенного третьего – результат обобщения практики применения суждений. Но если в законе противоречия выражаются их отношения по истинности, то в законе исключенного третьего – по ложности. Он действует в отношениях между противоречащими (контрадикторными) суждениями (А – О, Е – I).
Но он не действует во взаимоотношениях между противоположными (контрарными) суждениями (А – Е), хотя закон противоречия действует и здесь: они не могут быть вместе истинными, но могут быть одновременно ложными. Действие закона исключенного третьего обнаруживается и в сложных суждениях (например, в строгой дизъюнкции, когда составляющие ее суждения взаимно исключают друг друга, а следовательно, не могут быть вместе не только истинными, но и ложными).
Закон исключенного третьего проявляется также в умозаключениях и доказательстве. Например, он лежит в основе непосредственных умозаключений через превращение суждений и через отношение противоречащих (контрадикторных) суждений в логическом квадрате. Без его действия было бы невозможно косвенное доказательство. Устанавливая ложность какого-либо тезиса, мы тем самым доказываем истинность противоречащего ему тезиса, поскольку оба они не могут быть вместе ложными.
Требования закона исключенного третьего и их нарушения. На основе этого закона можно сформулировать определенные требования к мышлению. Чтобы понять их принципиальный смысл, вспомним историю с буридановым ослом. Как гласит легенда, он сдох с голоду, ибо так и не смог выбрать одну из двух совершенно одинаковых охапок сена. Перед человеком нередко тоже встает дилемма, но уже иная: выбирать не из одинаковых, а из взаимоотрицающих высказываний. Закон исключенного третьего как раз и предъявляет требование выбора – одного из двух – по принципу «или – или», tertium non datur (третьего не дано). Он означает, что при решении альтернативного вопроса нельзя уклоняться от определенного ответа; нельзя искать что-то промежуточное, среднее, третье.
С такого рода альтернативами человек сталкивается довольно часто. Еще в Древнем Риме родилась крылатая фраза: «Aut Caesar, aut nihil» (буквально «Или Цезарь, или ничто»), которую иногда употребляют в обобщенном смысле: «Все или ничего». Подобную интеллектуальную ситуацию гениально выразил У. Шекспир, вложив в уста Гамлета слова, ставшие тоже крылатыми: «Быть или не быть?» У А. Пушкина мы находим: «Она меня зовет: поеду или нет?» Ясно, что из этих вариантов приходится выбирать: ничего третьего нет.
И в современных условиях возникают альтернативы, требующие однозначного выбора. Вот лишь несколько примеров из газет: «Либо общими усилиями будет спасен весь мир, либо погибнет вся цивилизация»; «Или дальнейшее утверждение политической целесообразности, или утверждение закона в России».
Нарушение требования выбора проявляется в разных формах. Иногда сам вопрос сформулирован неальтернативно. Вспомним: «Перестал ли ты бить своего отца?» Как правильно ответить? Если «перестал», значит, бил. Если же «не перестал», значит, продолжаешь бить. Тут как раз возможно третье: «Я его не бил и не бью». Или на вопрос: «Любишь ли ты его?» нередко нельзя ответить по формуле «или – или». Ведь можно кого-то любить, можно презирать или ненавидеть, а можно просто проявлять безразличие или равнодушие.
Но если вопрос сформулирован правильно, то уклонение от определенного ответа на него, поиски чего-то третьего будут ошибкой. Она свойственна людям нерешительным, неуверенным в себе или просто беспринципным.
Значение закона исключенного третьего. Конечно, как и закон противоречия, этот закон не может точно указать, какое именно из двух противоречащих суждений истинно. Но его-значение состоит в том, что он устанавливает для нас вполне определенные интеллектуальные границы, в которых возможен поиск истины. Эта истина заключена в одном из двух отрицающих друг друга высказываний. За этими пределами искать ее не имеет смысла. Сам же выбор одного из суждений в качестве истинного обеспечивается средствами той или иной науки и практики.
Какое значение имеет закон исключенного третьего в юридическом отношении? Можно сказать, что именно здесь он празднует свой триумф. На принципе «или – или» основана, по существу, вся юридическая практика. Еще в афинском суде было установлено двойное голосование судей: первым определялась виновность или невиновность, а вторым – мера наказания. Этим достигалась большая точность в рассмотрении дел.
И в настоящее время суды постоянно сталкиваются с альтернативами. Так, в уголовном судопроизводстве – имело место событие преступления или не имело, находился на месте преступления подозреваемый или не находился, признает он себя виновным или не признает, виновен обвиняемый на самом деле или не виновен, правилен приговор суда или неправилен. Вспомним, что в соответствии со ст. 74 УПК РФ суд, прокурор, следователь, дознаватель «устанавливает наличие или отсутствие обстоятельств, подлежащих доказыванию …» Ничего третьего нет.
Аналогично и в гражданских делах. Например, если ответчик не признает своего отцовства, то суд может назначить судебно-медицинскую экспертизу, и эксперт либо исключает то, что ребенок мог родиться от данного человека, либо допускает такую возможность. Правда, подобное заключение используется в качестве доказательства лишь в совокупности с другими. Но само решение суда остается однозначным.
В законодательной практике решаются свои альтернативные вопросы. Так, на заседании Государственной Думы либо есть кворум, либо его нет, вопрос вносится в повестку дня или не вносится, то или иное решение принято или не принято. Вспомним электронное табло в зале заседаний депутатов, которое мы не раз наблюдали по телевидению и на котором всякий раз однозначно высвечивались результаты голосования: либо «решение принято», либо «решение не принято».
4. Закон достаточного основания
Важное место среди формально-логических законов мышления занимает закон достаточного основания. Он тоже находится в неразрывной связи с остальными. И действительно, если мысль обладает определенностью (закон тождества), то это открывает возможность для установления ее истинности или ложности во взаимоотношениях с другими мыслями (закон противоречия и закон исключенного третьего). Само же установление истинности или ложности мысли невозможно без соответствующего обоснования.
Отсюда – действие закона достаточного основания. Им обусловлена еще одна коренная черта правильного мышления наряду с определенностью и последовательностью, непротиворечивостью – его обоснованность, доказательность.
Объективные предпосылки и смысл закона достаточного основания. Качественно определенные предметы, известным образом соотносящиеся между собой (о чем уже говорилось выше), так или иначе возникают из других предметов и сами, в свою очередь, порождают третьи, изменяются и развиваются в процессе взаимодействия между собой. Следовательно, все в окружающем мире имеет свои основания в другом.
Такая объективно существующая универсальная зависимость одних предметов от других и служит важнейшей предпосылкой возникновения и функционирования в нашем мышлении закона достаточного основания. Этот закон был открыт и впервые сформулирован Г. Лейбницем. Он писал: «Ни одно явление не может оказаться истинным или действительным, ни одно утверждение справедливым – без достаточного основания, почему именно дело обстоит так, а не иначе…»59
Правда, у Лейбница он дан как универсальный закон и бытия, и познания – закон причинности. Применительно лишь к мышлению ему можно дать следующую формулировку: ни одно суждение не может быть признано истинным без достаточного основания. Отсюда – название самого закона. Но почему идет речь именно о «достаточном» основании? Достаточными являются такие фактические и теоретические основания, из которых данное суждение следует с логической необходимостью. Примерная формула закона: «А истинно, потому что есть достаточное основание В».
Логическое основание неразрывно связано с объективным, но в то же время и отлично от него. Объективным основанием служит причина, а результат ее действия – следствие. Логическим же основанием может выступать ссылка как на причину, так и на следствие. Классический пример. Дождь прошел. Это объективное основание (причина) того, что крыши домов мокрые (следствие), но не наоборот. Логических же оснований в рассуждении об этой причинно-следственной связи может быть два: «Крыши домов мокрые, потому что прошел дождь» и «Прошел дождь, потому что крыши домов мокрые». Почему это возможно? Потому что причина и следствие связаны между собой необходимым образом. Если есть причина, то есть и следствие, и наоборот: если есть следствие, то есть и причина. Надо только учитывать фактор «множественности причин» или «множественности следствий» (см. об этом выше).
Какова сфера действия закона достаточного основания? Если закон тождества явился обобщением прежде всего практики оперирования понятиями, а закон противоречия и исключенного третьего – практики функционирования суждений, то закон достаточного основания есть результат обобщения практики получения выводного знания. В нем выражено отношение одних истинных мыслей к другим – отношение логического следования, обеспечивающего в конечном счете их соответствие действительности. Этот закон означает, что в правильном рассуждении вывод всегда достаточно обоснован.
Следовательно, в сферу действия этого закона входят прежде всего умозаключения. Когда, например, из двух посылок: «Все живое смертно» и «Люди – живые существа» мы делаем вывод, что «Все люди смертны», то это означает: «Все люди смертны» потому, что «Все живое смертно». Подведение того или иного предмета мысли под общее понятие служит достаточным основанием для распространения на него всех тех свойств, которые присущи всему классу предметов, мыслимому в этом понятии. Вспомним аксиому простого категорического силлогизма: Dictum de omni et de nullo.
В сфере действия закона достаточного основания находятся также доказательства. Уже само их существование есть показатель того, что такой закон существует. Кроме того, одно из важнейших правил доказательства – правило не только необходимости, но и достаточности оснований – прямо обусловлено действием этого закона. Например, существует объективная связь между ясным мышлением и ясным изложением. Поэтому если мы хотим обосновать, почему человек ясно излагает свои мысли, то можем сослаться на то, что он ясно мыслит. Это достаточное основание. Впрочем, можно сказать и наоборот: «Он ясно мыслит, потому что ясно излагает». Это тоже достаточное логическое основание.
Требования, вытекающие из закона достаточного основания, и ошибки, связанные с их нарушением. Будучи объективным, закон достаточного основания предъявляет к нашему мышлению важные требования: всякая истинная мысль должна быть обоснованной (У Лейбница это требование выражено в отрицательной форме так: «Ничто не должно утверждаться без основания» (там же, с. 124). Или: нельзя признать высказывание истинным, если для него нет достаточных оснований. Иными словами, ничего нельзя принимать на веру: надо основываться на достоверных фактах и ранее доказанных положениях. Этот закон направлен против бессвязных, хаотичных, бездоказательных рассуждений; голого, необоснованного теоретизирования; неоправданных, неубедительных выводов. Он враг всяких догм, пустых верований, суеверий и предрассудков.
Важнейшей логической ошибкой, связанной с нарушением требований закона достаточного основания, выступает «поп sequitur» («не следует») – ошибка «мнимого следования». Она обнаруживается там, где нет достаточной логической связи между посылками и заключением, между тезисом и основаниями, доводами и выводами. Пример такой ошибки содержится в известном произведении Н. Гоголя «Повесть о том, как поссорился Иван Иванович с Иваном Никифоровичем». Вот какое обоснование злостных намерений И. Н. Довгочхуна дает И. И. Перерепенко: «Вышеизображенный дворянин, которого уже самое имя и фамилия внушает всякое омерзение, питает в душе злостное намерение поджечь меня в собственном доме. Несомненные чему признаки из нижеследующего явствуют: во-первых, оный злокачественный дворянин начал выходить часто из своих покоев, чего прежде никогда, по причине своей лености и гнусной тучности тела, не предпринимал; во-вторых, в людской его, примыкающей о самый забор, ограждающий мою собственную, полученную мною от покойного родителя моего, блаженной памяти Ивана, Онисиева сына, Перерепенка, землю, ежедневно и в необычайной продолжительности горит свет, что уже явное есть к тому доказательство, ибо до сего, по скаредной его скупости, всегда не только сальная свеча, но даже каганец был потушаем».
Итак, если человек начал часто выходить из своих покоев и в людской его ежедневно и подолгу горит свет – значит, имеется намерение поджечь соседа. Здесь явно нет достаточного основания: вывод не следует из доводов.
Образцом подобной нелогичности служит рассуждение философов-лилипутов в произведении Джонатана Свифта «Путешествие Лемюэля Гулливера»: «Вы утверждаете, правда, что на свете существуют другие королевства и государства, где живут такие же гиганты, как вы. Однако наши философы сильно сомневаются в этом… Ведь не подлежит никакому сомнению, что сто человек вашего роста могут за самое короткое время истребить все плоды и весь скот во владениях его величества. Кроме того, у нас есть летописи. Они заключают в себе описание событий за время в шесть тысяч лун, но ни разу не упоминают ни о каких других странах, кроме двух великих империй – Лилипутии и Блефуску».
Здесь снова вывод не вяжется с доводами. Если в летописях нет упоминания о каком-либо событии, то это еще не значит, что его не было на самом деле. Существование события не связано необходимым образом с летописями.
В обращении «К читателю» этого учебника уже приводился классический пример с Катюшей Масловой из романа Л. Толстого «Воскресение». Отмечалось, что в связи с убийством (отравлением) купца Смелькова Маслова была приговорена к каторжным работам и что сделано это вследствие не только судебной, но и логической ошибки. Теперь уместно сказать, что ею как раз и была ошибка под названием non sequitur («не следует»). Если бы в решении суда присяжных было записано: «Виновна, но без умысла ограбления и без намерения лишить жизни», Маслова была бы оправдана.
По сути эта же логическая ошибка была допущена и в уголовном деле упоминавшегося там же А. Кравченко, который был отправлен на тот свет за преступление, совершенное другим человеком – Чикатило.
Ошибка «мнимого следования» иногда сознательно допускается для создания комичной ситуации, шутки и т. п. Мы находим, например, у бессмертного Козьмы Пруткова: «Я поэт, поэт даровитый! Я в этом убедился; убедился, читая других: если они поэты, так и я тоже». Или: «Смерть для того поставлена в конце жизни, чтобы удобнее к ней приготовиться».
В законодательстве Российской Федерации есть специальные статьи, направленные на предотвращение логической ошибки «мнимого следования» или ее устранения, если она уже допущена. Так, в УПК РФ имеется ст. 379, где излагаются основания отмены или изменения судебного решения в кассационном порядке. Среди этих оснований на первом месте стоит «несоответствие выводов суда, изложенных в приговоре, фактическим обстоятельствам уголовного дела, установленным судом первой или апелляционной инстанции». А следующая, ст. 380 целиком посвящена случаям этого несоответствия. В статье сказано, что приговор признается несоответствующим фактическим обстоятельствам уголовного дела, если:
«1) выводы не подтверждаются доказательствами, рассмотренными в судебном заседании;
2) суд не учел обстоятельства, которые могли существенно повлиять на выводы суда;
3) при наличии противоречивых доказательств, имеющих существенное значение для Выводов суда, в приговоре не указано, по каким основаниям суд принял одни из этих доказательств и отверг другие;
4) выводы суда, изложенные в приговоре, содержат существенные противоречия, которые повлияли или могли повлиять на решение вопроса о виновности или невиновности осужденного или оправданного, на правильность применения уголовного закона или определения меры наказания».
Значение закона достаточного основания. Этот закон, разумеется, ничего не говорит о том, какие конкретно основания для данного вывода являются достаточными. Он только дисциплинирует наше мышление, направляя его на поиск таких оснований, на обеспечение обоснованности вывода.
Это особенно важно в научном познании, прежде всего в теоретических науках, где велика роль выводного знания. Вот почему Г. Лейбниц придавал фундаментальное значение не только принципу противоречия, но и принципу достаточного основания. Он имеет большое значение, в частности, в связи с коренным вопросом теории познания – о критерии истинности наших знаний. Установлено, что таким критерием служит прежде всего общественная практика – материально-производственная, общественно-политическая деятельность, практика научных наблюдений и экспериментов. Именно она позволяет надежно отделять истинные знания от ложных. Однако далеко не все знания возможно и необходимо проверять непосредственно на практике. Если мы знаем, что существует закон всемирного тяготения, то нет надобности каждый раз проверять, упадет предмет или нет, когда мы его выпустим из рук. Это можно сделать и логическим путем: вывести одно знание из другого, уже проверенного на практике и получившего статус истинного. Следовательно, наряду с коренным, практическим критерием истинности наших знаний есть и другой – производный, логический критерий. Весь вопрос только в том, достаточны ли логические основания для того или иного вывода. На правильное решение этого вопроса и ориентирует нас закон достаточного основания.
В практической деятельности тоже важно руководствоваться этим законом. Так, известный русский социолог Питирим Сорокин (с 1922 г. – в эмиграции), выступая против извращений в строительстве социализма в нашей стране, заявлял: «Можно и должно звать всех к производительной работе по возрождению страны, но ниоткуда не следует, что эта работа может и должна совершаться только по штампам и циркулярам в качестве агентов власти и чиновников, или обратно – должна быть непременно работой, низвергающей власть»60.
Таким образом, автор отмечал известное отсутствие последовательности в определенных тогдашних практических действиях власти в стране. И позднее не было достаточных оснований для того, чтобы в экономике страны десятилетиями игнорировать мировой опыт развития рыночных отношений. Но и в настоящее время, когда произошла смена власти, многие ее действия представляются тоже недостаточно обоснованными, правда, уже в ином социальном смысле. Так, нередко опыт предшествующего развития страны огульно отрицается лишь на том основании, что он в конечном счете не удался. Однако это еще не достаточное основание для подобного нигилизма.
Против аналогичного необоснованного поведения, но уже в литературе, в свое время выступал М. Шолохов. «Добротно написанная книга, – отвечал он на вопросы одного корреспондента, – живет долго, а все живущее нельзя отвергать без достаточных к тому оснований»61.
Закон достаточного основания имеет прямое отношение к юридической практике. В законодательстве довольно широко распространено само понятие «достаточные основания» (или «законные основания» или просто «основания»). Так, в ст. 10 УПК РФ закреплено: «Никто не может быть задержан по подозрению в совершении преступления или заключен под стражу при отсутствии на то законных оснований, предусмотренных настоящим Кодексом». В ст. 24 сказано, что уголовное дело не может быть возбуждено, а возбужденное уголовное дело подлежит прекращению по следующим основаниям (и далее следуют сами эти основания). В ст. 297 УПК РФ говорится: «Приговор суда должен быть законным, обоснованным и справедливым».
В гражданском законодательстве говорится, что гражданские права и обязанности возникают из предусмотренных законом оснований.
В повседневной речи, говоря о том, что многие законы не действуют, мы приводим в качестве основания то, что нет процедуры их применения и т. д.
Рассмотренные выше основные формально-логические законы мышления открыты традиционной логикой. Как относится к ним символическая логика? Она основывается на них в своих построениях и процедурах, но в целях решения собственных специфических задач вносит в них необходимые уточнения и дает им свою символику. Так, раскрывая их единство в определенном отношении, она рассматривает их в качестве тождественно-истинных формул. Что это значит? Многие логические формулы, используемые в символической логике (логике высказываний), оказываются при одних логических значениях своих переменных истинными, а при других – ложными. Тождественно-истинные формулы тем и отличаются, что они имеют логическое значение «истина» при всех логических значениях своих переменных. Истинность таких формул обусловлена их логической структурой. Поэтому они называются еще логически-истинными формулами. В конечном счете их истинность определяется тем, что в их структуре отражаются наиболее глубокие и общие связи самого объективного мира. Посредством этих формул и выражаются законы логики.
Так, закон тождества выражается логической формулой
A ≡ А (А равносильно А) или А → А («Если А, то А»).
Закон противоречия выражается формулой ˥(А∧˥А) («Неверно, что А и не-А).
Закон исключенного третьего – A∨˥А (А или не-А).
Оба последних закона в символической логике относятся лишь к противоречащим высказываниям и потому могут быть выведены друг из друга.
Считается, что закон достаточного основания символически выразить нельзя, так как это исключительно содержательный закон.
Приведем пример толкования подобных формул. Так, сложные высказывания типа: «Закон принят, или закон не принят», «Решение суда правильное, или решение суда неправильное», имея формулу A∨˥А (закон исключенного третьего), истинны независимо от того, истинны или ложны образующие их элементарные суждения. Вот таблица истинности этой формулы:
Наряду с тождественно-истинными формулами есть еще тождественно-ложные формулы. Ими выражаются логические противоречия.
Благодаря табличному способу символическая логика (логика высказываний) в состоянии эффективно выявлять как тождественно-истинные формулы, так и тождественно-ложные формулы – законы логики и логические противоречия. В этом ее громадный шаг вперед по сравнению с традиционной логикой.
Глава II. Соотношение законов формальной и диалектической логики
Основные формально-логические законы – при всей их значимости и широте действия – не исчерпывают всех фундаментальных закономерностей мышления. Кроме них действуют еще диалектические законы мышления, изучаемые диалектической логикой..
Что же представляют собой такие законы? И как они соотносятся с законами формальной логики? Ответ на эти вопросы позволяет не только глубже понять место и роль основных формально-логических законов в общей системе мышления, но и более правильно пользоваться ими в познании и общении.
1. Сфера действия диалектических законов мышления
Как и громадное большинство законов природы и общества, основные формально-логические законы мышления носят относительный характер. Это означает, что они действуют в определенных условиях, а именно когда рассматривается «готовый» предмет, до поры до времени сохраняющий свою качественную определенность, проявляющий в том или ином определенном отношении то или иное определенное свойство.
Но как только мы начинаем исследовать предмет диалектически – всесторонне, во взаимодействии с остальным миром, а следовательно, с точки зрения его возникновения, изменения и развития, его превращения в новое качественное состояние, одних формально-логических законов оказывается недостаточно. Здесь вступают в силу новые, в известном смысле слова более высокие, диалектические законы мышления.
Не ставя перед собой задачи дать более или менее полный анализ этих законов62, приведем ряд ситуаций, демонстрирующих их необходимость, характер и сферу действия.
Отражение в мышлении переходных (промежуточных) состояний. Пока предмет – например, стекло – сохраняет свое агрегатное состояние или качество твердого тела, мы можем безошибочно подвести его под соответствующее общее понятие – «твердое тело». В этом, как мы видели, и состоит действие закона тождества в его традиционном смысле. Но вместе с ним действуют и остальные из основных формально-логических законов. Так, если мы назвали стекло «твердым телом», то мы уже не можем, в силу действия закона противоречия, назвать его одновременно и «нетвердым телом» или «жидкостью». При этом, в силу закона исключенного третьего, мы стоим перед дилеммой: стекло либо твердое тело, либо нетвердое тело; третье решение здесь исключено. И наконец, для подведения стекла под понятие «твердого тела» у нас есть достаточные основания. Стекло обладает свойствами сохранять определенную форму, занимать определенный объем и т. д. А именно подобные признаки и входят в содержание понятия «твердое тело». Этим оно отличается от жидкости, которая способна принимать форму соответствующего сосуда, и газа, способного занимать весь его объем.
Но как обстоит дело с логической операцией подведения под понятие в такой ситуации, когда стекло, будучи расплавленным, лишь приобретает свою качественную определенность твердого тела, т. е. не является «ставшим», оформившимся, «готовым», а находится в процессе становления? Можем ли мы и в этом случае дать определенный, однозначный, категорический ответ: «Да, это твердое тело», «Нет, это нетвердое тело» («жидкость»)? Оказывается, по самому существу дела такого ответа дать уже нельзя. Затвердевание расплавленного (жидкого) стекла – более или менее длительный процесс. Он совершается постепенно, незаметно, через множество промежуточных ступеней, так что никакой определенной границы, которая четко отделяла бы твердое состояние от жидкого, нет. Поэтому мы в силу объективных оснований не можем точно сказать, когда застывающее стекло «еще жидкое», а когда «уже твердое». В этом случае правильным будет сказать: стекло «и жидкое, и не жидкое», «и нетвердое, и твердое»; оно «уже не жидкое, но еще не твердое»; его нельзя назвать «ни жидким, ни нежидким», «ни твердым, ни нетвердым».
Но что означают подобные формулы? Это не словесная эквилибристика. Они как раз и означают, что тут действуют уже иные, диалектические законы мышления. Налицо диалектика тождества и различия, их единство, поскольку в затвердевающем стекле уже нельзя фиксировать лишь абстрактное тождество жидкости с самой собой и отвлечься от имеющихся в ней различий. Ведь подобные различия, нарастая, становятся все более существенными, ибо жидкость все более перестает быть жидкостью. Они выступают формой проявления изменений, происходящих в процессе затвердевания, и их результатом – признаками твердого тела.
Здесь действует общий диалектический закон соединения (сочетания) противоположностей. Ведь затвердевающее стекло – это переходное (промежуточное) состояние. А всякий переход объективно отличается противоречивостью, единством бытия и небытия, исчезновением одних свойств (в данном случае – жидкого тела) и возникновением других (твердого).
Здесь проявляет свою силу закон перехода количественных изменений в качественные (и обратно). Именно постепенные количественные изменения при переходе от одного качества к другому и делают возможным нечто промежуточное, среднее, третье, требующее соответствующего отражения в понятиях.
Здесь, наконец, обнаруживается закон отрицания и преемственности. Ибо стекло при всех преобразованиях не перестало быть стеклом. Произошло лишь отрицание одной качественно определенной формы (жидкость) другой (твердое тело). А это потребовало соответствующего сочетания понятий.
Пример со стеклом – не единичный. Все аморфные тела превращаются из одного агрегатного состояния в другое именно подобным образом. Следовательно, во всех случаях такого превращения неизбежно будут действовать диалектические законы мышления. Этим определяется одна из сфер их действия.
Аналогичный пример – из области живой природы. В громадном большинстве случаев мы точно, ясно, определенно можем сказать: «Это ребенок», «Это подросток», «Это юноша» и т. д. Объективным основанием для этого служат качественные различия между стадиями развития человека. В противном случае мы не могли бы образовать самих понятий «ребенок», «подросток», «юноша» и др.
Но можем ли мы во всех без исключения случаях безошибочно определить, какой перед нами человек? Нет. Ведь ребенок рано или поздно превращается в подростка, подросток в юношу и т. п. Причем это тоже процесс постепенных количественных изменений, приводящих незаметно к новому качеству. Здесь не бывает так, что вечером человек лег спать еще подростком, а утром проснулся уже юношей.
Чтобы правильно отразить подобный процесс превращения одного качества в другое, мы вновь вынуждены прибегать к диалектическим формулам: данный человек «не только подросток и не только юноша»; он «уже не подросток, но еще не юноша»; он «ни подросток, ни не подросток в отдельности, но и то и другое вместе». Следовательно, вместо формулы «или – или» мы используем формулу «как то, так и другое».
Отражение изменений предмета во времени. Диалектические законы мышления действуют при отражении не только переходных (промежуточных) состояний. Они проявляют свою силу и там, где рассматривается «ставший», сложившийся, качественно определенный предмет, но оценивается не в данный конкретный момент времени, а в целом, с учетом разных этапов его проявления и развития. Так, на конкретный вопрос: «Может ли нормальный человек в молодости овладеть в совершенстве иностранным языком?» – мы можем однозначно ответить: «Да, может». – «А в глубокой старости?» – «Нет, не может». Но если мы поставим вопрос в принципе, следовательно, в обобщенной форме: «Может ли человек вообще в совершенстве овладеть иностранным языком?», тогда ответ будет неизбежно диалектическим: «И может, и не может». А сама эта формула потребует конкретизации применительно к определенному возрасту.
Вспомним классический пример с дождем: «Полезен или вреден дождь для урожая?» В обобщенной форме на него возможен лишь диалектический ответ: «Дождь и полезен, и вреден». Но если ответ конкретизируется применительно к определенному времени, то он примет однозначную форму: «Дождь полезен весной, когда зерно уже в земле», но «Дождь вреден осенью, когда идет уборка урожая».
С точки зрения диалектики любой предмет, существуя более или менее длительное время, претерпевает те или иные изменения, развивается, поэтому в разное время проявляет разные, в том числе противоположные, свойства. Их адекватное, точное, верное отражение и происходит на основе действия законов диалектической логики.
Отражение предмета в его различных взаимоотношениях с другими. Диалектические законы мышления проявляют свою силу и тогда, когда один и тот же качественно определенный предмет, взятый в один и тот же отрезок времени, рассматривается всесторонне, в разных отношениях к другим, с которыми он так или иначе связан.
Существует притча. Восковые фигурки, находившиеся близко к огню, предчувствуя свою гибель, обратились к нему с жалобой: «Ты несправедлив по отношению к нам: этим фарфоровым вазам ты придаешь твердость, а нас расплавляешь». Огонь ответил: «Я остаюсь огнем. Пеняйте на свою собственную природу».
И действительно, будучи качественно определенным, огонь тем не менее в разных отношениях проявляет себя по-разному, обнаруживает различные, даже противоположные свойства.
Каким же законам будет подчиняться отражение этих свойств одного и того же явления? Если мы будем рассматривать его в каком-либо одном отношении, то достаточно действия одних формально-логических законов. Например: «По отношению к фарфоровым вазам огонь способен придавать им твердость». Если же мы будем говорить об огне всесторонне, в общей форме, независимо от одного какого-либо отношения, с учетом всех его возможных взаимоотношений, то неизбежно действие диалектических законов: «Огонь и способен придавать телам твердость, и не способен».
Другой пример. На вопрос: «Стекло твердое или не твердое?» – можно отвечать двояко. Оно может быть твердым, острым по отношению к живой ткани, но мягким, податливым по отношению к алмазу. А в общей форме мы обязаны ответить по формуле: «И то и другое вместе». «Стекло и твердое, и нетвердое».
Сказанное также относится ко всякому предмету вообще. Ведь его свойства не создаются отношением к другому предмету, а лишь проявляются в таком отношении. А так как любой предмет взаимодействует с множеством других предметов, то он неизбежно обнаруживает разные, в том числе противоположные, свойства. Их всесторонняя оценка возможна лишь на базе законов диалектической логики.
2. Действие формально-логических законов мышления в обобщенной форме
Формы проявления законов мышления. Означает ли сказанное, что в случае действия диалектических законов мышления его формально-логические законы вовсе перестают действовать?» Нет, не означает. Дело в том, что одни и те же законы, будь то законы природы или общества, в разных условиях могут проявляться по-разному, а следовательно, принимать различные формы.
С этой точки зрения основные формально-логические законы мышления перестают действовать в своей простой форме, проявляющейся лишь в определенных условиях, но с изменением этих условий продолжают действовать уже в иной, более сложной и общей форме. Если простая форма этих законов давно открыта традиционной логикой, то их другая, более общая и сложная форма – лишь в процессе становления диалектической логики.
Так, будучи в ряде случаев не в состоянии однозначно ответить, имеем ли мы дело с подростком или юношей, мы находим выход в том, что называем такого человека «и подростком, и юношей». Ясно, что требования закона тождества, а следовательно, и других формально-логических законов в их обычной, простой, традиционной форме не выполняются.
Но разве тем самым наша мысль утрачивает определенность, последовательность (непротиворечивость), обоснованность (доказательность)? Отнюдь нет. Говоря «и подросток, и не подросток», мы на самом деле наиболее точно отражаем действительность – именно такой, какова она есть. Следовательно, мы мыслим тоже нечто определенное, отличное от всякой иной мысли, но слагающееся уже из двух определенных мыслей: о подростке и юноше одновременно. Таким образом, закон тождества как закон определенности мысли продолжает действовать и здесь. Он только меняет форму своего проявления. Эта форма оказывается применительно к более сложным условиям более сложной.
Сохраняет свою силу и закон противоречия, но он тоже принимает иную, более общую форму. Ибо если данный человек «и подросток, и юноша», то мы уже не можем, не насилуя логики, не впадая в логическое противоречие, т. е. противоречие с самим собой, одновременно утверждать: «Этот человек только подросток» (или: «Этот человек только юноша»). Такие утверждения не могут быть одновременно истинными. Что-нибудь одно из них непременно ложно: или диалектическая формула, выраженная сложным суждением, или однозначная формула, выраженная простым суждением.
То же самое с законом исключенного третьего. Он продолжает действовать и здесь, но тоже в обобщенной форме. Его требование сохраняется: или «Данный человек и подросток, и юноша», или «Данный человек только подросток» («только юноша»). Ничего третьего между ними нет и не может быть. Следовательно, они не могут быть вместе ложными: что-то одно из них непременно истинно: или сложное, диалектическое суждение, или простое.
Наконец, действие закона достаточного основания – причем тоже в особой форме, с учетом особых условий – сказывается в том, что для переходного явления недостаточно подвести его под какое-то одно понятие: «подросток», «юноша». Наоборот, необходимым и достаточным будет подведение под оба понятия сразу, одновременно.
Вред абсолютизации законов формальной и диалектической логики. Каково же в целом отношение формально-логических законов мышления к законам диалектической логики? Они, как можно сделать вывод из сказанного, и исключают друг друга, и не исключают. Все зависит от того, в каком виде рассматриваются формально-логические законы – простом, традиционном или сложном. Формально-логические законы необходимы в любом мышлении, будь то недиалектическое или диалектическое. В известных пределах – в рамках «домашнего обихода» – ими можно вполне ограничиться, чтобы обеспечить правильность мышления.
Но при определенных условиях они оказываются недостаточными. Требуется действие диалектических законов мышления. Однако и в этих условиях формально-логические законы не прекращают своего действия. Они лишь неизбежно меняют свою форму. Взаимодействуя с диалектическими законами, они и здесь обеспечивают определенность, последовательность (непротиворечивость), обоснованность (доказательность) диалектического мышления, которое тоже не может не быть правильным, если оно ведет к истине.
Раскрывая существо законов формальной и диалектической логики, мы особо подчеркивали, что и те, и другие законы не имеют абсолютного характера, что они действуют лишь при определенных условиях. За этими пределами они утрачивают свою силу.
Отсюда следует, что, с одной стороны, нельзя абсолютизировать законы формальной логики, пытаться, например, давать однозначные ответы там, где речь идет о переходных явлениях, о рассмотрении предмета в разное время или в разных отношениях. Абсолютизация формально-логических законов служит одним из источников неопределенности, путаницы и непоследовательности в мышлении.
С другой стороны, нельзя абсолютизировать и диалектические законы мышления, применять их требования там, где требуется однозначный ответ: существует нечто или не существует, присуще ему какое-либо свойство или не присуще. Жонглирование диалектическими формулами, выход за пределы их действительной применимости – все это способно привести не только к логическим противоречиям, но и к полной неопределенности мысли.
Как же избежать абсолютизации требований формальной и диалектической логики? Есть один фундаментальный критерий для этого: соответствие наших мыслей действительности. Например, если единству взаимоисключающих понятий соответствует нечто в объективной действительности, то в данном случае имеет место диалектическое суждение, выражающее диалектическое, жизненное противоречие. Если же такому единству нет соответствия, нет аналога в действительности, если сущность предмета искажается, то налицо логическое противоречие.
Все это имеет значение для всякого мышления, включая и юридическое.
50
См.: Кэрролл Л. Соч.: В 4 т. Т. 1. М., 1975. С. 127.
51
Аристотель. Соч.: В 4 т. Т. 1.М., 1975. С. 12.
52
См.: Бекон Ф. Соч.: В 2 т. Т. 2. М, 1978. С. 14.
53
Кэрролл Л. Приключения Алисы в Стране чудес… М., 1978. С. 74.
54
Плеханов Г. В. Избранные философские произведения. В 5 т. М., 1957. Т. 3. С. 240.
55
Аристотель. Соч. М., 1975. Т. 1. С. 125.
56
Там же. Т. 2 С. 276.
57
Аристотель. Соч. Т. 1. С. 141.
58
Там же. Т. 2. С. 257.
59
Лейбниц Г. Соч.: В 4 т. Т. 3. М., 1984. С. 377.
60
Философские науки. М., 1992. № 1. С. 7.
61
Русские писатели – лауреаты Нобелевской премии. М. Шолохов. М., 1991. С. 329.
62
Подробнее о них см.: Иванов Е. А. О соотношении законов формальной и диалектической логики в процессе оперирования понятиями. М., 1963.
Источник: Логика: учебник для студентов юридических вузов и факультетов / Е. А. Иванов. — Изд. 3-е, перераб. и доп. — Москва: Волтерс Клувер, 2007. — 405 с. — (Библиотека студентв).; ISBN 5-466-00105-8
Комментарии для сайта Cackle