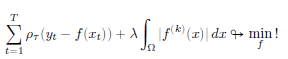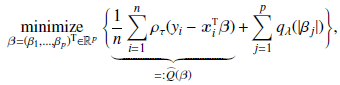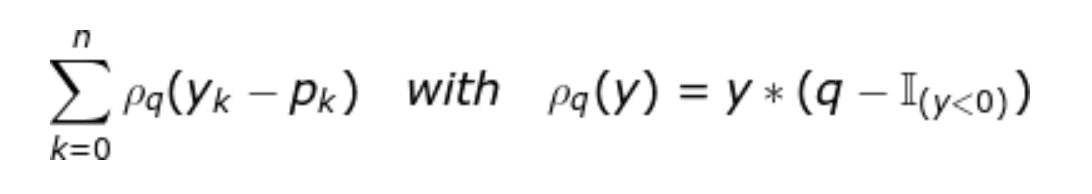Квантильная ошибка формула

Квантильная регрессия, от линейных моделей до деревьев к глубокому обучению

  Перевод

  Ссылка на автора

Предположим, что аналитик по недвижимости хочет прогнозировать цены на жилье на основе таких факторов, как возраст дома и расстояние от центров занятости. Типичная цель будет генерировать лучшую цену на домточечная оценкаучитывая те факторы, где «наилучший» часто относится к оценке, которая сводит к минимуму квадратичные отклонения от реальности.

Но что, если они хотят предсказать не только одну оценку, но и вероятный диапазон? Это называетсяинтервал прогнозированияи общий способ их получения известен какквантильная регрессия, В этом посте я опишу, как эта проблема формализована; как реализовать это в шести линейных, древовидных методах и методах глубокого обучения (в Python — вот блокнот Jupyter); и как они работают с реальными наборами данных.

Квантильная регрессия минимизирует квантильную потерю

Подобно тому, как регрессии минимизируют функцию потерь в квадрате ошибок для прогнозирования оценки по одной точке, квантильные регрессии минимизируютквантильная потеряв прогнозировании определенного квантиля. Самым популярным квантилем является медиана, или 50-й процентиль, и в этом случае квантильная потеря — это просто суммаабсолютныйошибки. Другие квантили могут дать конечные точки интервала прогнозирования; например, средний-80-процентный диапазон определяется 10-м и 90-м процентилями. Потери в квантиле различаются в зависимости от оцененного квантиля, так что больше отрицательных ошибок штрафуется больше для более высоких квантилей, а более положительные ошибки штрафуются больше для более низких квантилей.

Прежде чем углубиться в формулу, предположим, что мы сделали прогноз для одной точки с истинным значением ноль, и наши прогнозы варьируются от -1 до +1; то есть наши ошибки также варьируются от -1 до +1. Этот график показывает, как квантильная потеря изменяется с ошибкой, в зависимости от квантиля.

Давайте посмотрим на каждую строку отдельно:

• Средняя синяя линия показывает медиану, который симметричен относительно нуля, где все потери равны нулю, потому что прогноз был идеальным. До сих пор выглядит хорошо: медиана стремится разделить пополам набор прогнозов, поэтому мы хотим взвешивать недооценки в равной степени и завышенные. Как мы скоро увидим, потеря квантиля около медианы составляет половину абсолютного отклонения, то есть 0,5 при -1 и +1 и 0 при 0.
• Голубая линия показывает 10-й процентиль, который назначает меньшую потерю отрицательным ошибкам и большую потерю положительным ошибкам. 10-й процентиль означает, что мы считаем, что существует 10-процентная вероятность того, что истинное значение будет ниже прогнозируемого значения, поэтому имеет смысл назначать меньшие потери недооценкам, чем переоценкам.
• Синяя линия показывает 90-й процентиль,что является обратной моделью от 10-го процентиля.

Мы также можем посмотреть на это по квантилям для заниженных и завышенных прогнозов. Чем выше квантиль, тем больше функция потерь квантиля штрафует недооценки и тем меньше штрафов завышает.

Учитывая эту интуицию, вот формула квантильных потерь (источник):

И в коде Python, где мы можем заменить разветвленную логику наmaximumзаявление:

def quantile_loss(q, y, f):
  # q: Quantile to be evaluated, e.g., 0.5 for median.
  # y: True value.
  # f: Fitted (predicted) value.
  e = y - f
  return np.maximum(q * e, (q - 1) * e)

Далее мы рассмотрим шесть методов — OLS, линейная квантильная регрессия, случайные леса, повышение градиента, Keras и TensorFlow — и посмотрим, как они работают с некоторыми реальными данными.

Данные

Этот анализ будет использовать Бостонский корпус данных, который содержит 506 наблюдений, представляющих города в районе Бостона. Она включает в себя 13 объектов наряду с медианной стоимостью домов, занимаемых владельцами. Таким образом, квантильная регрессия предсказывает долю городов (не домов) с медианными значениями дома ниже значения.

Я тренирую модели на 80 процентов и проверяю оставшиеся 20 процентов. Для упрощения визуализации первый набор моделей использует одну функцию:AGEдоля домов, занятых собственниками, построенных до 1940 года. Как и следовало ожидать, города с более старыми домами имеют более низкую стоимость жилья, хотя отношения являются шумными.

Для каждого метода мы прогнозируем 10-й, 30-й, 50-й, 70-й и 90-й процентили в тестовом наборе.

Обычные наименьшие квадраты

Хотя OLS прогнозирует среднее значение, а не медиану, мы все же можем рассчитать интервалы прогнозирования на основе стандартных ошибок и обратного нормального CDF:

def ols_quantile(m, X, q):
  # m: OLS statsmodels model.
  # X: X matrix.
  # q: Quantile.
  mean_pred = m.predict(X)
  se = np.sqrt(m.scale)
  return mean_pred + norm.ppf(q) * se

Этот базовый подход создает линейные и параллельные квантили с центром вокруг среднего значения (которое прогнозируется как медиана). Хорошо настроенная модель покажет около 80 процентов точек между верхней и нижней линиями. Обратите внимание, что точки отличаются от первого графика рассеяния, так как здесь мы показываем набор тестов для оценки прогнозов вне выборки.

Линейная квантильная регрессия

Линейные модели простираются выше среднего до среднего и других квантилей. Линейная квантильная регрессия предсказывает заданное квантильное, расслабляющее предположение параллельного тренда OLS, в то же время налагая линейность (под капотом минимизируется потеря квантилей) Это просто сstatsmodels:

sm.QuantReg(train_labels, X_train).fit(q=q).predict(X_test)
# Provide q.

Случайные леса

Наш первый отход от линейных моделей случайные леса, коллекция деревьев. Хотя эта модель не предсказывает квантили в явном виде, мы можем рассматривать каждое дерево как возможное значение и вычислять квантили, используя его эмпирический CDF (Андо Саабас написал больше об этом):

def rf_quantile(m, X, q):
  # m: sklearn random forests model.
  # X: X matrix.
  # q: Quantile.
  rf_preds = []
  for estimator in m.estimators_:
    rf_preds.append(estimator.predict(X))
    # One row per record.
    rf_preds = np.array(rf_preds).transpose()
  return np.percentile(rf_preds, q * 100, axis=1)

Это сходит с ума в этом случае, предлагая переоснащение. Так как случайные леса чаще используются для многомерных наборов данных, мы вернемся к ним после добавления дополнительных функций в модель.

Повышение градиента

Другой древовидный метод повышение градиента,scikit-learn«s реализация которых поддерживает явное квантильное предсказание:

ensemble.GradientBoostingRegressor(loss='quantile', alpha=q)

Хотя он и не такой нервный, как случайные леса, он не слишком хорош для однофункциональной модели.

Керас (глубокое обучение)

Keras является дружественной оболочкой для наборов инструментов нейронной сети, включая TensorFlow, Мы можем использовать глубокие нейронные сети для прогнозирования квантилей, передавая функцию потерь квантилей. Код несколько сложен, поэтому проверьте Блокнот Jupyter или читать больше из Сачин Абейвардана чтобы увидеть, как это работает.

В основе большинства глубоких сетей лежат линейные модели с изломами (называемыевыпрямленные линейные единицы, илиReLUs), что мы можем увидеть здесь визуально: Keras предсказывает более скученную стоимость домов для городов, около 70 процентов которых построено до 1940 года, в то же время все больше и больше в очень низких и очень высоких возрастах. Похоже, это хороший прогноз, основанный на подборе данных испытаний.

TensorFlow

Одним из недостатков Keras является то, что каждый квантиль должен обучаться отдельно. Чтобы использовать шаблоны, общие для квантилей, мы должны перейти к самому TensorFlow. Увидеть Блокнот Jupyter а также Джейкоб Цвейг «s статья чтобы узнать больше об этом.

Мы можем видеть это совместное обучение по квантилям в его предсказаниях, где модель изучает общий излом, а не отдельные для каждого квантиля. Похоже, это хороший выбор в стиле Оккама.

Который сделал лучше всего?

Взгляд в глаза предполагает, что глубокое обучение хорошо, линейные модели — хорошо, а методы на основе дерева — плохо, но можем ли мы определить, какой из них лучше? Да, мы можем, используя квантильные потери в тестовом наборе.

Напомним, что квантильные потери различаются в зависимости от квантиля. Поскольку мы рассчитали пять квантилей, у нас есть пять квантильных потерь для каждого наблюдения в тестовом наборе. Усреднение по всем квантильным наблюдениям подтверждает визуальную интуицию: случайные леса показали худшие результаты, а TensorFlow — лучшие.

Мы также можем разбить это на квантиль, обнаружив, что древовидные методы особенно плохо работали на 90-м процентиле, тогда как глубокое обучение лучше всего работало на нижних квантилях.

Большие наборы данных дают больше возможностей для улучшения по сравнению с OLS

Так что случайные леса были ужасны для этого однофункционального набора данных, но это не то, для чего они созданы. Что произойдет, если мы добавим 12 других функций к модели жилья в Бостоне?

Древовидные методы вернулись, и хотя OLS улучшился, разрыв между OLS и другими не древовидными методами увеличился.

Взглянем на квантильную регрессию

Свежий пакет «conquer».

Базовым пакетом для квантильной регрессии является пакет quantreg, про который очень хорошо было написано вот тут.

Но сегодня мы поговорим о пакете, который был презентован 1 ноября.

Немного математики

Если есть выборка размера n, и классическая матрица признаки-ответы (X-Y), то задача квантильной регрессии для квантиля τ записывается как

Оценки коэффициентов β вычисляются по формуле

Развитие методов регуляризации в обычной регрессии логичным образом перешло и в квантильную регрессию. Постановка задачи регуляризации в квантильной регрессии такая же, как и в обычной:

Более полно эту задачу можно расписать как

Решение этого функционала сводится к задаче квадратичного программирования. В 1994 году было показано, что можно убрать квадрат из штрафной функции, заменив ее задачей

Разница между получающимися функциями представлена на рисунке ниже

Фактически, последняя формула повторяет постановку задачи лассо-регрессии, в которой берется модуль от некоторого оценщика. Еще одно ее преимущество – вычислительная простота, поскольку конкретные значения коэффициентов можно получить в результате решения задачи линейного программирования.

Последующее развитие постановки задачи привело ее к виду

где степень производной k предполагалось выбирать в зависимости от свойств данных:

— если функция f(x) предполагает наличие мгновенных скачков, то выбирается k=1

— если функция f(x) непрерывна, но имеет точки перегиба, то k=2

— если функция f(x) непрерывна и дифференцируема, то k=3

Далее усилия теоретиков были направлены на определение оптимального значения параметра λ. Как правило, для этого используется алгоритм перекрестной проверки (кросс-валидация с разбиением на несколько групп)

В сентябре 2021 года коллектив китайских ученых выпустил препринт статьи (https://arxiv.org/abs/2109.05640), в котором предложил способ борьбы с систематическими ошибками, которые дает лассо-регуляризация в квантильной регрессии

Постановка задачи нахождения коэффициентов квантильной регрессии записывается теперь так:

где q_λ – некоторая функция от λ

Кроме того, первое слагаемое функции потерь заменяется ими на ядро K(ž), и предлагается общий итеративный алгоритм нахождения коэффициентов квантильной регрессии. Именно он и используется в новом пакете conquer

Немного расчетов

Для расчетов возьмем базу данных Schooling из пакета Ecdat. В ней представлены данные о зарплате американских рабочих. Опрос был проведен в 1976 году.

В качестве зависимой переменной выберем заработную плату, независимых – количество лет образования, возраст, результаты теста iq и опыт работы.

Простую модель квантильной регрессии можно построить с помощью команды conquer(), которая содержит следующие параметры:

X, Y – матрица независимых и вектор зависимого признаков

tau – квантиль (при tau = 0.5 получается медианная регрессия)

kernel  — определяет, какое ядро сглаживания K(ž) используется (выбор из следующий значений: «Gaussian», «logistic», «uniform», «parabolic», «triangular»)

ci – параметр, определяющий необходимость расчета доверительных интервалов коэффициентов регрессии

h, checkSing, tol, iteMax, alpha – параметры алгоритма расчета

library(Ecdat)
library(tidyverse)
library(conquer)
Base1<-na.omit(Ecdat::Schooling)
glimpse(Base1)
Y <- Base1$wage76
X <- as.matrix(Base1[,c(7,9,25,28)])
mod_1<-conquer(X,Y,tau=0.9)
mod_1$coeff

В итоге выводятся коэффициенты регрессии в порядке следования параметров, первое число – значение свободного члена

Также по результатам расчетов можно вывести:

ite — Число итераций до сходимости.

residual — Вектор полученных моделью значений

perCI, pivCI, normCI – Доверительные интервалы коэффициентов регрессии

 Посчитаем модель с другим ядром и выведем доверительные интервалы

Как видно, коэффициенты, во-первых, отличаются не сильно, и, во-вторых, относительно устойчивы (доверительные интервалы не включают 0)

Функция conquer.cv.reg – позволяет реализовать квантильную регрессию с применением методов регуляризации (за это отвечает параметр penalty, которое может принимать одно из трех значений: «lasso», «scad», «mcp») и кросс-валидации (параметр kfolds отвечает за число блоков). Посчитаем квантильную регрессию с лассо-регуляризацией (придется подождать, считает дольше)

Как видно, регуляризация посчитала, что последнюю переменную можно не учитывать.

Также крайне удобна функция conquer.process. Она позволяет посчитать сразу целый блок квантильных регрессий для разных значений квантиля:

tau_t <- seq(0.1, 0.9, by = 0.05)
mod_3 <-conquer.process(X,Y,tauSeq = tau_t)
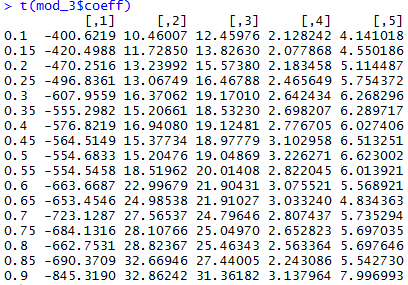
colnames(mod_3$coeff) <- tau_t
t(mod_3$coeff)

Собственно, это показывает, что для разных квантилей коэффициенты регрессии могут сильно отличаться

Кроме того, с небольшой модификацией можно использовать эти функции для отбора признаков. Посмотрим, как будут меняться коэффициенты функции при разных значениях λ

lambda_v <- 10^(seq(-4, -1, by = 0.1))
Res <- matrix(0, nrow = 31, ncol = 5)
for(i in 1:31) { 
mod_4 <- conquer.reg(X,Y,lambda = lambda_v[i],tau = 0.9, penalty = c("lasso"))
Res[i,]<-mod_4$coeff}
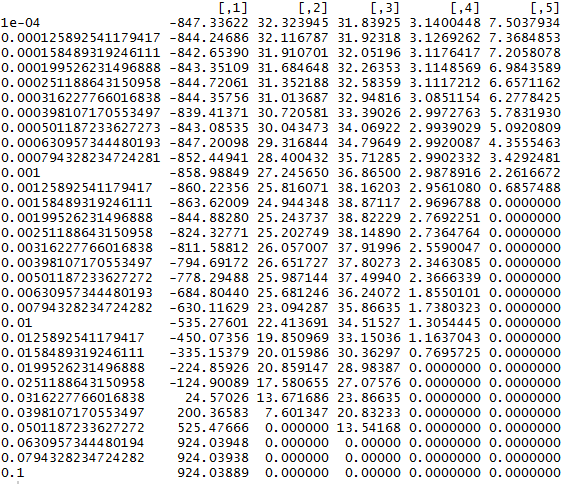
rownames(Res)<-lambda_v
Res

Эту динамику значений вполне можно использовать как характеристику важности переменных. Таким образом, ранжирование переменных по значимости будет выглядеть так: возраст → количество лет учебы → результаты теста iq → опыт работы.

Предположим, аналитик по недвижимости хочет спрогнозировать цены на жилье на основе таких факторов, как возраст дома и расстояние до центров занятости. Типичной целью будет получение точечной оценки наилучшей цены на жилье с учетом этих факторов, где «наилучшая» часто относится к оценке, которая сводит к минимуму квадратичные отклонения от реальности.

Но что, если они хотят спрогнозировать не только одну оценку, но и вероятный диапазон? Это называется интервалом прогнозирования, а общий метод их получения известен как квантильная регрессия. В этом посте я опишу, как формализуется эта проблема; как реализовать это в шести линейных, древовидных и глубоких методах обучения (в Python — вот блокнот Jupyter); и как они работают с реальными наборами данных.

Квантильная регрессия минимизирует квантильные потери

Подобно тому, как регрессии минимизируют функцию потерь квадрата ошибок для прогнозирования одноточечной оценки, квантильные регрессии минимизируют квантильные потери при прогнозировании определенного квантиля. Самый популярный квантиль — это медиана или 50-й процентиль, и в этом случае потеря квантиля — это просто сумма абсолютных ошибок. Другие квантили могут давать конечные точки интервала прогнозирования; например, средний 80-процентный диапазон определяется 10-м и 90-м процентилями. Потери квантилей различаются в зависимости от оцениваемого квантиля, так что большее количество отрицательных ошибок наказывается больше для более высоких квантилей, а более положительные ошибки наказываются больше для более низких квантилей.

Прежде чем углубляться в формулу, предположим, что мы сделали прогноз для одной точки с истинным значением нуля, и наши прогнозы находятся в диапазоне от -1 до +1; то есть наши ошибки также варьируются от -1 до +1. Этот график показывает, как квантильные потери меняются с ошибкой в ​​зависимости от квантиля.

Давайте посмотрим на каждую строку отдельно:

• Средняя синяя линия показывает медиану, которая симметрична относительно нуля, где все потери равны нулю, потому что прогноз был идеальным. Пока все выглядит хорошо: медиана направлена ​​на то, чтобы разделить набор прогнозов пополам, поэтому мы хотим взвесить заниженные оценки наравне с завышенными. Как мы скоро увидим, потеря квантиля вокруг медианы составляет половину абсолютного отклонения, поэтому 0,5 при -1 и +1 и 0 при 0.
• Голубая линия показывает 10-й процентиль, который определяет меньшие потери для отрицательных ошибок и более высокие потери для положительных ошибок. 10-й процентиль означает, что, по нашему мнению, существует 10-процентная вероятность того, что истинное значение ниже этого прогнозируемого значения, поэтому имеет смысл приписывать меньший убыток заниженным оценкам, чем завышенным.
• Темно-синяя линия показывает 90-й процентиль, который является обратной схемой 10-го процентиля.

Мы также можем посмотреть на это по квантилю для заниженных и завышенных прогнозов. Чем выше квантиль, тем больше функция потерь квантиля штрафует заниженные оценки и тем меньше штрафует завышенные оценки.

Учитывая эту интуицию, вот формула квантильной потери (источник):

И в коде Python, где мы можем заменить разветвленную логику оператором maximum:

def quantile_loss(q, y, f):
  # q: Quantile to be evaluated, e.g., 0.5 for median.
  # y: True value.
  # f: Fitted (predicted) value.
  e = y - f
  return np.maximum(q * e, (q - 1) * e)

Далее мы рассмотрим шесть методов — OLS, линейную квантильную регрессию, случайные леса, повышение градиента, Keras и TensorFlow — и посмотрим, как они работают с некоторыми реальными данными.

Данные

В этом анализе будет использоваться Набор данных о жилищном строительстве Бостона, который содержит 506 наблюдений, представляющих города в районе Бостона. Он включает 13 характеристик наряду с целевой средней стоимостью домов, занимаемых владельцами. Таким образом, квантильная регрессия позволяет прогнозировать долю городов (не домов) со средней стоимостью жилья ниже значения.

Я обучаю модели на 80 процентах и ​​тестирую оставшиеся 20 процентов. Для упрощения визуализации в первом наборе моделей используется одна особенность: AGE, доля занятых владельцами единиц, построенных до 1940 года. Как и следовало ожидать, в городах со старыми домами стоимость домов ниже, хотя соотношение между ними довольно шумное.

Для каждого метода мы прогнозируем 10-й, 30-й, 50-й, 70-й и 90-й процентили в тестовой выборке.

Обычный метод наименьших квадратов

Хотя OLS предсказывает среднее, а не медианное значение, мы все же можем вычислять интервалы предсказания на его основе на основе стандартных ошибок и обратного нормального CDF:

def ols_quantile(m, X, q):
  # m: OLS statsmodels model.
  # X: X matrix.
  # q: Quantile.
  mean_pred = m.predict(X)
  se = np.sqrt(m.scale)
  return mean_pred + norm.ppf(q) * se

Этот базовый подход дает линейные и параллельные квантили, центрированные вокруг среднего (которое прогнозируется как медиана). Хорошо настроенная модель покажет около 80 процентов точек между верхней и нижней линиями. Обратите внимание, что точки отличаются от первого графика рассеяния, так как здесь мы показываем набор тестов для оценки прогнозов вне выборки.

Линейная квантильная регрессия

Линейные модели выходят за рамки среднего значения до медианы и других квантилей. Линейная квантильная регрессия предсказывает данный квантиль, ослабляя допущение о параллельном тренде OLS, в то же время сохраняя линейность (под капотом это минимизирует квантильные потери). Это просто с statsmodels:

sm.QuantReg(train_labels, X_train).fit(q=q).predict(X_test)
# Provide q.

Случайные леса

Наш первый отход от линейных моделей — это случайные леса, набор деревьев. Хотя эта модель не предсказывает квантили явным образом, мы можем рассматривать каждое дерево как возможное значение и вычислять квантили, используя его эмпирический CDF (Андо Саабас написал об этом больше):

def rf_quantile(m, X, q):
  # m: sklearn random forests model.
  # X: X matrix.
  # q: Quantile.
  rf_preds = []
  for estimator in m.estimators_:
    rf_preds.append(estimator.predict(X))
  # One row per record.
  rf_preds = np.array(rf_preds).transpose()
  return np.percentile(rf_preds, q * 100, axis=1)

В данном случае это выглядит немного сумасшедшим, предполагая переоснащение. Поскольку случайные леса чаще используются для многомерных наборов данных, мы вернемся к ним после добавления дополнительных функций в модель.

Повышение градиента

Другой древовидный метод — это повышение градиента, scikit-learn реализация которого поддерживает явное квантильное предсказание:

ensemble.GradientBoostingRegressor(loss='quantile', alpha=q)

Хотя он и не такой резкий, как случайные леса, он не очень хорош и для одноэлементной модели.

Керас (глубокое обучение)

Keras — удобная оболочка для нейросетевых инструментов, включая TensorFlow. Мы можем использовать глубокие нейронные сети для прогнозирования квантилей, передавая функцию квантильных потерь. Код в некоторой степени сложен, поэтому посмотрите Блокнот Jupyter или прочтите больше Сачина Абейвардана, чтобы увидеть, как он работает.

В основе наиболее глубоких сетей лежат линейные модели с изгибами (называемые выпрямленными линейными единицами или ReLU), которые мы можем увидеть здесь визуально: Керас предсказывает большее скопление ценностей домов для городов около 70 процентов из них было построено до 1940 года, при этом разветвляется больше на очень низком и очень высоком конце возраста. Это хороший прогноз, основанный на подборе тестовых данных.

TensorFlow

Одним из недостатков Keras является то, что каждый квантиль необходимо обучать отдельно. Чтобы использовать шаблоны, общие для квантилей, нам нужно обратиться к самому TensorFlow. См. Блокнот Jupyter и статью Джейкоба Цвейга, чтобы узнать об этом больше.

Мы можем видеть это совместное обучение по квантилям в своих прогнозах, где модель изучает общий излом, а не отдельные изломы для каждого квантиля. Похоже, это хороший выбор, вдохновленный Оккамом.

Что лучше всего?

Наблюдения показывают, что глубокое обучение работает хорошо, линейные модели — плохо, а древовидные методы — плохо, но можем ли мы количественно определить, какой из них лучше? Да, мы можем, используя квантильные потери по тестовой выборке.

Напомним, что квантильные потери различаются в зависимости от квантиля. Поскольку мы рассчитали пять квантилей, у нас есть пять квантильных потерь для каждого наблюдения в тестовой выборке. Усреднение по всем наблюдениям квантилей подтверждает визуальную интуицию: случайные леса показали худшие результаты, а TensorFlow — лучше всех.

Мы также можем разбить это на квантиль, показывая, что древовидные методы особенно плохо работали на 90-м процентиле, в то время как глубокое обучение показало лучшие результаты на более низких квантилях.

Большие наборы данных дают больше возможностей для улучшения по сравнению с OLS

Случайные леса были ужасны для этого набора данных с одним признаком, но они созданы не для этого. Что произойдет, если мы добавим еще 12 функций к модели жилья в Бостоне?

Древовидные методы вернулись, и хотя OLS улучшилась, разрыв между OLS и другими не-древовидными методами увеличился.

Проблемы реального мира часто выходят за рамки средств прогнозирования. Возможно, разработчика приложения интересует не только ожидаемое использование пользователями, но и их вероятность стать суперпользователями. Или компания по автострахованию хочет знать вероятность того, что водитель предъявит претензию на крупную сумму при разных порогах. Экономисты могут захотеть стохастически вменять информацию из одного набора данных в другой, выбирая из CDF, чтобы обеспечить правильную вариацию (пример, который я рассмотрю в следующей статье).

Квантильная регрессия полезна для каждого из этих вариантов использования, и инструменты машинного обучения часто могут превосходить линейные модели, особенно простые в использовании древовидные методы. Попробуйте это на своих данных и дайте мне знать, как это происходит!

В задачах классификации можно получить распределение вероятностей набора классов. Однако в задачах регрессии модели машинного обучения всегда предсказывают одно значение без какого-либо способа измерить достоверность этого значения. В большинстве случаев очень важно уметь сопоставить прогноз с его вероятностью. Например, Qucit Parking, решение, разработанное в Qucit, прогнозирует время, необходимое для поиска парковочного места, до 12 часов вперед. Совершенно очевидно, что существует критическая разница между предсказанием с вероятностью 95% правильности до пяти минут и потенциальной ошибкой в ​​несколько часов! Следовательно, очень важно уметь измерять уровень достоверности прогноза. Отсюда интервалы прогнозирования: интервалы, внутри которых почти наверняка будет истинное значение цели.

Квантильная регрессия, стандартный способ построения интервалов прогноза

В области машинного обучения доверительные интервалы обычно строятся с помощью квантильной регрессии. Этот подход направлен на оценку условных квантилей (наиболее распространенным является медиана) переменной отклика, в отличие от метода наименьших квадратов, который оценивает условное среднее. Учитывая случайную переменную (например, прогнозируемое время стоянки) и значение в [0, 1], соответствующий квантиль представляет собой такое значение, что P (Y ‹= q) = p. Например, медиана — квантиль 0,5. Например, предположим, что прогнозная модель, которая вычисляет время парковки на завтрашнее утро в центре Бордо, оценивает 22 минуты как квантиль 0,95. Это означает, что вероятность того, что время парковки будет меньше или равно 22 минутам, составляет 95% (очевидно, это просто вымышленный пример, особенно если вы живете в таком городе, как Париж, и читаете этот пост в воскресенье!).

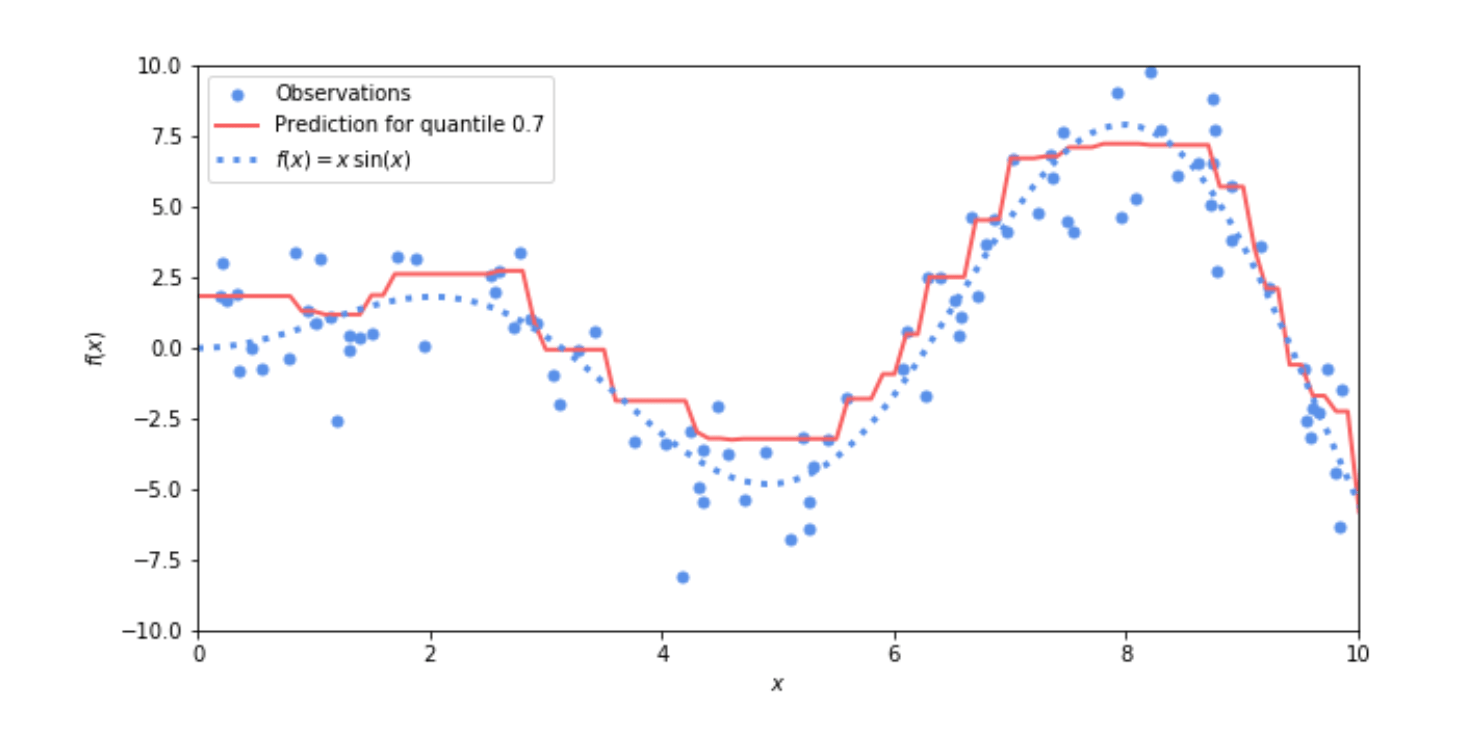
Рис. 1 Пример квантильной регрессии: вероятность того, что предсказанное значение (красная линия) больше или равно фактическим выборкам (синие точки), составляет 70%

Использование квантильной регрессии для вычисления интервалов прогнозирования довольно просто. Комбинируя два квантильных регрессора, можно построить интервал, окруженный двумя наборами прогнозов, созданных этими двумя моделями.

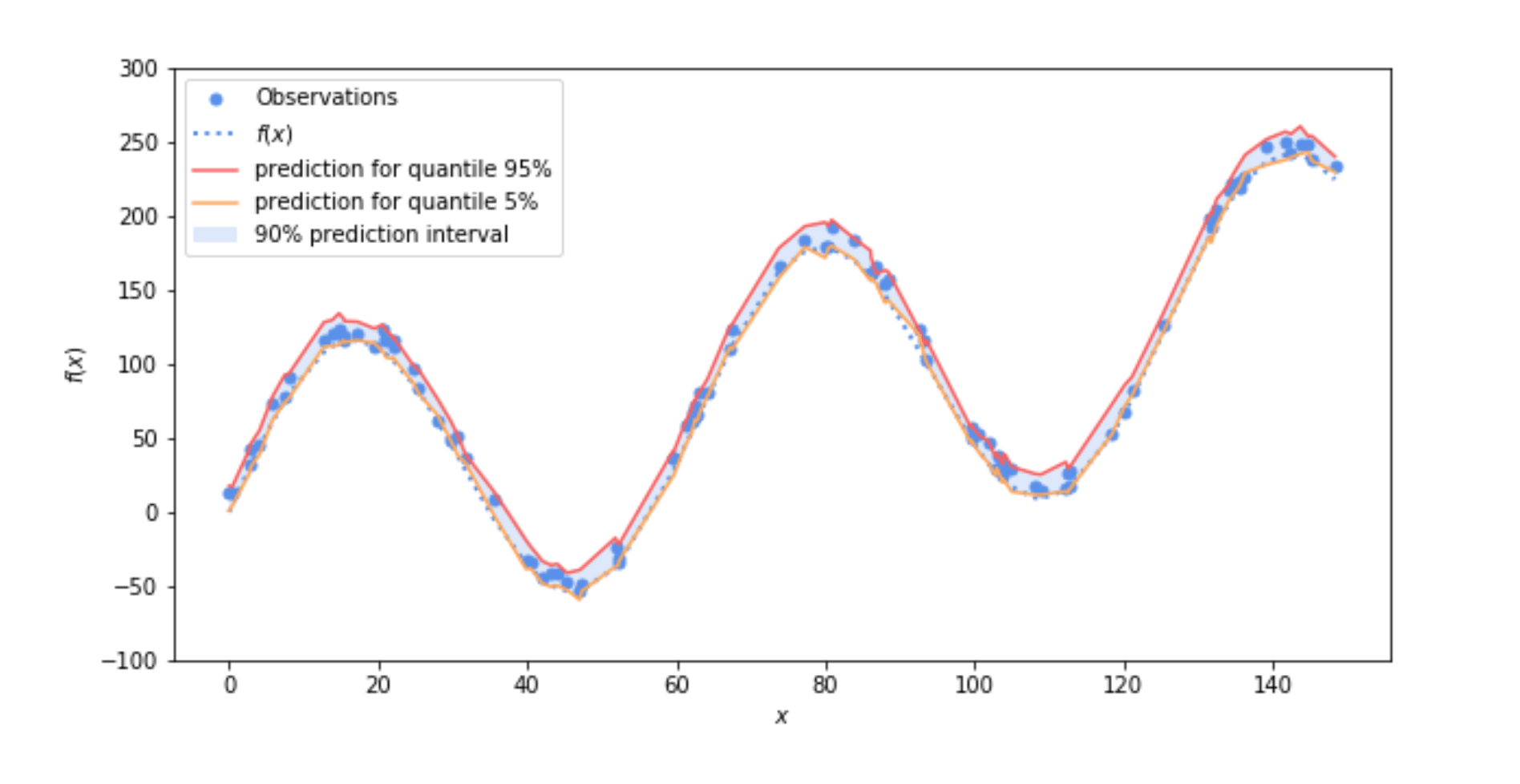
На следующем рисунке (рис. 2) показано, как квантили 0,05 и 0,95 используются для вычисления интервала прогнозирования 0,9. Используя предсказания квантильного регрессора 0,05 в качестве нижней границы и предсказания квантильного регрессора 0,95 в качестве верхней, по построению вероятность того, что значение принадлежит интервалу между верхней и нижней границей, составляет: P (l ‹= X ‹= U) = P (X‹ = u) — P (X ‹= l) = 0,95–0,05 = 0,9

Грубо говоря, это означает, что интервал прогнозирования будет содержать примерно 90% выборок.

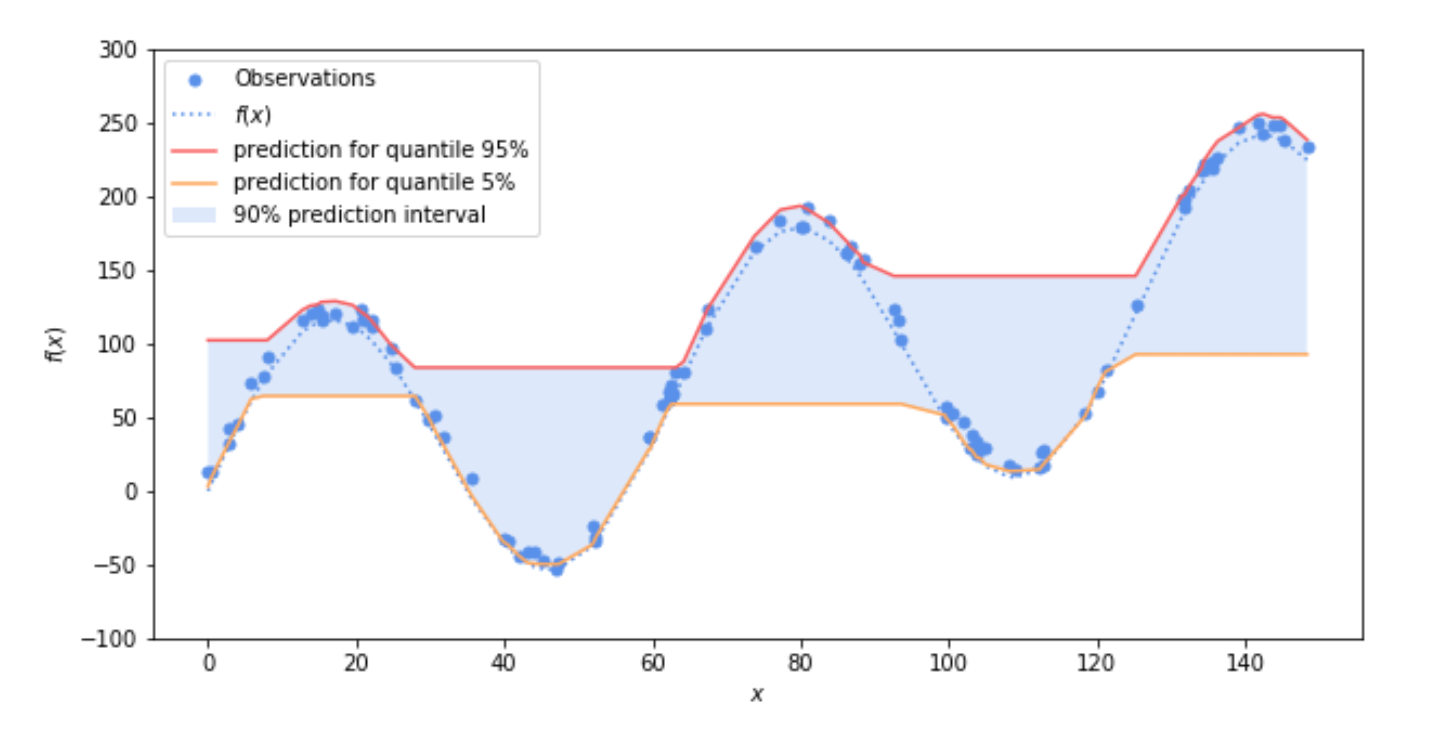
Рис. 2 Пример интервала прогноза 0,9: вероятность того, что фактические наблюдения функции (синяя точка) принадлежат интервалу прогноза (область, закрашенная синим), составляет 90%.

Квантильная регрессия на практике

Квантильная регрессия — это классический метод, и некоторые широко распространенные пакеты машинного обучения уже реализуют его, например scikit-learn в python.

Действительно, в scikit-learn уже доступен Регрессор повышения градиента, который позволяет квантильную регрессию и может давать отличные результаты. Здесь вы можете найти пример его использования.

Однако градиентные регрессоры и квантильная регрессия в целом имеют некоторые практические недостатки.

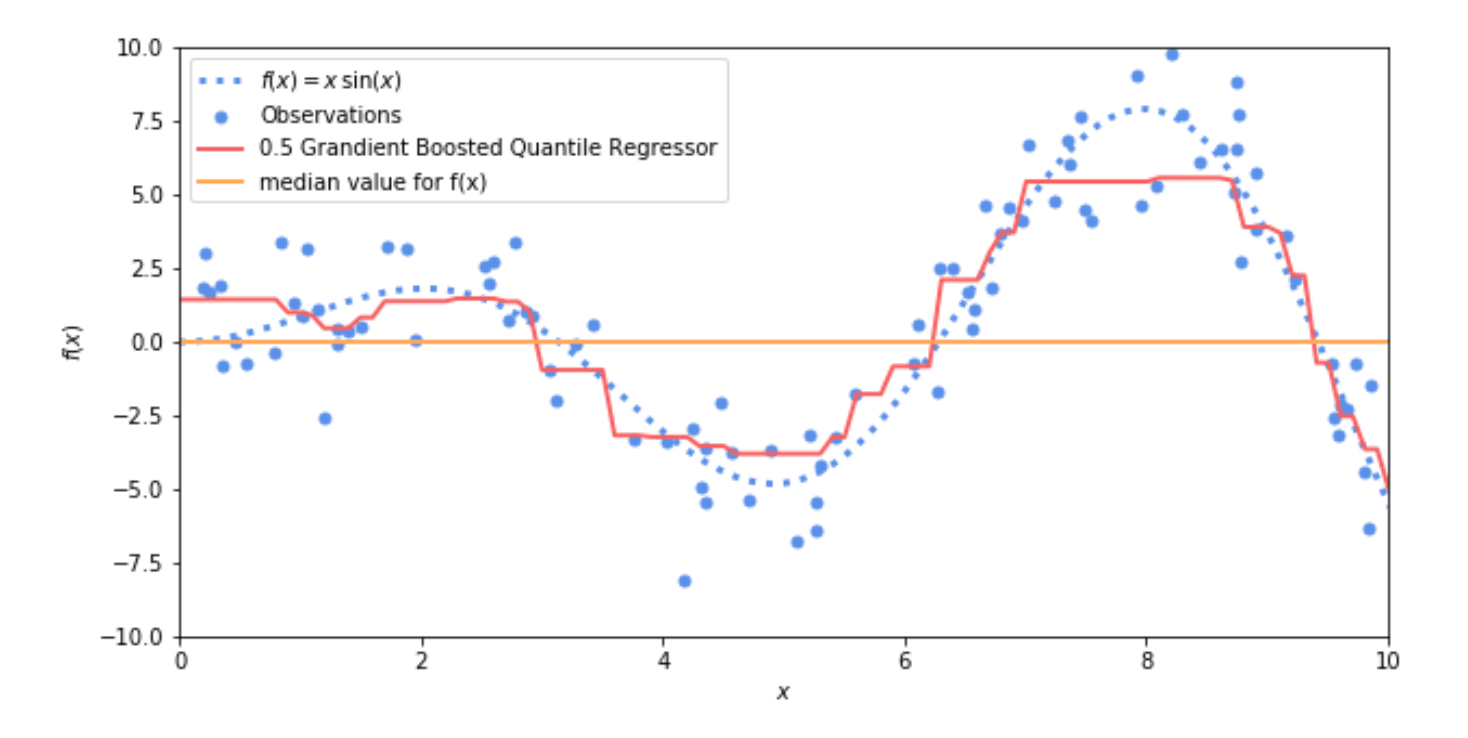
При представлении крайних квантилей (очень низких или очень высоких) Регрессор повышения градиента имеет тенденцию создавать интервалы, которые очень далеки от истинных значений. Вы можете наблюдать это на рисунке 2, где прогнозы 0,05 и 0,95 вычисляются двумя регуляторами градиентного усиления. Как вы видите на рисунке, это не означает, что квантили неверны, но на практике мы предпочитаем квантили, которые наиболее близки к реальным данным. Давайте посмотрим на следующую картинку (рис. 3). Оранжевая линия представляет собой медианное значение подчиненной функции f (x), используемой для генерации наблюдения. Красная линия представляет собой прогноз, полученный с помощью квантильного регрессора с градиентным усилением 0,5. Обе линии разделяют наблюдение пополам, то есть вероятность того, что наблюдение превышает прогнозируемое значение для всего набора данных, составляет 50%. Однако на практике значение статической медианы менее полезно. Фактически, он имеет более высокую дисперсию и не соответствует данным. Вернемся к примеру с парковкой и предположим, что среднее время парковки в вашем городе составляет 10 минут. Модель, которая всегда прогнозирует 10 минут, будь то ночью, когда время парковки близко к 0, или утром, когда время парковки может стать очень большим, совершенно бесполезна по сравнению с моделью, которая может адаптироваться к контексту.

Рис. 3 Среднее значение f (x) (оранжевая линия) против 0,5 градиентного регрессора (красная линия). Оба они разделяют наблюдение пополам, то есть вероятность того, что наблюдение превышает прогнозируемое значение, составляет 50%, но медиана менее полезна в реальных приложениях.

Еще один недостаток заключается в том, что каждому квантилю нужен собственный регрессор. В зависимости от конечного приложения потребность в точности может варьироваться, и иногда мы хотим оценить все распределение прогнозов. Возможное решение — обучить модель для каждого возможного квантиля, но это неуклюжее и дорогое решение. Допустим, нам нужна оценка для каждого процентного квантиля (0,01, 0,02, 0,03 и т. Д. До 0,99). Эти решения предполагают обучение и управление 99 моделями. Напротив, наличие одной модели, способной оценить все базовое распределение, подразумевает обучение и управление только одной моделью.

Наконец, квантильная регрессия доступна не для всех типов регрессионных моделей. В scikit-learn единственная модель, которая реализует это, — это Регрессор с градиентным усилением. Иногда, например, в случае XGBoost, вы можете настроить функцию стоимости модели для получения квантильного регрессора. Подробнее о том, как это сделать, читайте здесь.

В общем, это сложный процесс, требующий глубокого понимания алгоритмов, которые нужно настраивать, и их реализации. Чтобы решить эти проблемы, здесь, в Qucit, мы создали оценщик распространения.

Оценщик распределения

Оценщик распределения — это обученная модель, которая может вычислять квантильную регрессию для любой заданной вероятности без необходимости повторного обучения или калибровки.

В отличие от стандартной квантильной регрессии, которая предсказывает один квантиль на значение вероятности (0,1, 0,2, 0,5 и т. Д.), Этот оценщик предсказывает все распределение предсказаний. Такой подход сводит весь процесс к обучению отдельной модели для каждой цели, что делает ее менее затратной в вычислительном отношении и упрощает ее обслуживание.

Как мы можем предсказать распределение?

Основное предположение, лежащее в основе оценки распределения Qucit, заключается в том, что желаемый прогноз следует нормальному распределению. Сначала это кажется сильным предположением, но, как мы покажем далее, на практике это предположение приводит к удовлетворительным результатам.

Следовательно, оценщик распределения работает, производя прогноз и ошибку оценки для этого прогноза. По этим двум значениям он оценивает распределение как гауссову функцию, сосредоточенную на предсказании, со стандартным отклонением, равным оцененной ошибке. Другими словами, модель (в дальнейшем называемая базовой моделью) предсказывает среднее значение гауссовского распределения, тогда как оцененная ошибка дает нам стандартное отклонение распределения.

Есть две основные стратегии получения значений и прогнозов ошибок:

Обучение модели машинного обучения предсказанию значений и использование ее RMSE для вычисления ошибки.

Первая стратегия предполагает, что стандартное отклонение нормального распределения постоянно. Первая регрессионная модель, базовая модель, обучается на обучающем наборе, и ее среднеквадратичная ошибка оценивается на проверочном наборе и используется в качестве оценки стандартного отклонения.

Вот пример фрагмента кода для этого:

# split the data into a train and validation sets X1, X2, y1, y2 = train_test_split(X_train, y_train, test_size=0.5) # base_model can be any regression modelbase_mode.fit(X1, y1) base_prediction = base_model.predict(X2) #compute the RMSE value error = mean_squared_error(base_prediction, y2) ** 0.5 # compute the mean and standard deviation of the distribution mean = base_model.predict(X_test) st_dev = error

Обучение модели машинного обучения предсказанию значений и ошибок

На практике ошибка не всегда постоянна (зависит от особенностей). Следовательно, в качестве улучшения мы можем подобрать модель для изучения самой ошибки.

Как и раньше, базовая модель изучается на основе данных обучения. Затем вторая модель (модель ошибок) обучается на проверочном наборе для прогнозирования квадрата разницы между предсказаниями и реальными значениями.

Стандартное отклонение распределения вычисляется путем извлечения корня из ошибки, предсказанной моделью ошибок. Опять же, вот пример кода для этого:

# split the data in train a validation set X1, X2, y1, y2 = train_test_split(X, y, test_size=0.5) # base_model can be any regression model, a # sklearn.ensemble.GradientBoostingRegressor for instance base_model.fit(X1, y1) base_prediction = base_model.predict(X2) # compute the prediction error vector on the validation set validation_error = (base_prediction - y2) ** 2 error_model.fit(X2, validation_error) # compute the mean and standard deviation of the distribution mean = base_model.predict(X_test) st_dev = error_model.predict(X_test)**0.5

Полученные результаты

Чтобы протестировать наши модели и сравнить их со стандартным квантильным регрессором с градиентным усилением, мы обучили несколько оценщиков распределения на игрушечном наборе данных.

Однако для более содержательной оценки мы изменили некоторые детали того, как создается набор данных. Чтобы провести краш-тест нашего предположения, что ошибка предсказания является гауссовой, мы заменили гауссовский шум на однородный. Более того, чтобы получить более реалистичный набор данных, мы обучили модели на 50 000 выборок, а не только на 1000.

Для оценки использовались следующие модели:

• Квантильный регрессор с градиентным усилением
• Оценщик распределения с фиксированной ошибкой на основе стандартного градиентного регрессора (называемого оценщиком распределения RMSE GBR)
• Оценщик распределения, состоящий из базовой модели градиентного регрессора и модели ошибок градиентного регрессора (называемый оценщиком распределения GBR)
• Оценщик распределения, состоящий из базовой модели K ближайшего соседа и модели ошибки K ближайшего соседа (называемой оценщиком распределения KNN)

По определению, оценщикам распределения требуется меньше ресурсов для обучения и использования, чем для квантильного регрессора с градиентным усилением (только две модели вместо одной на квантиль).

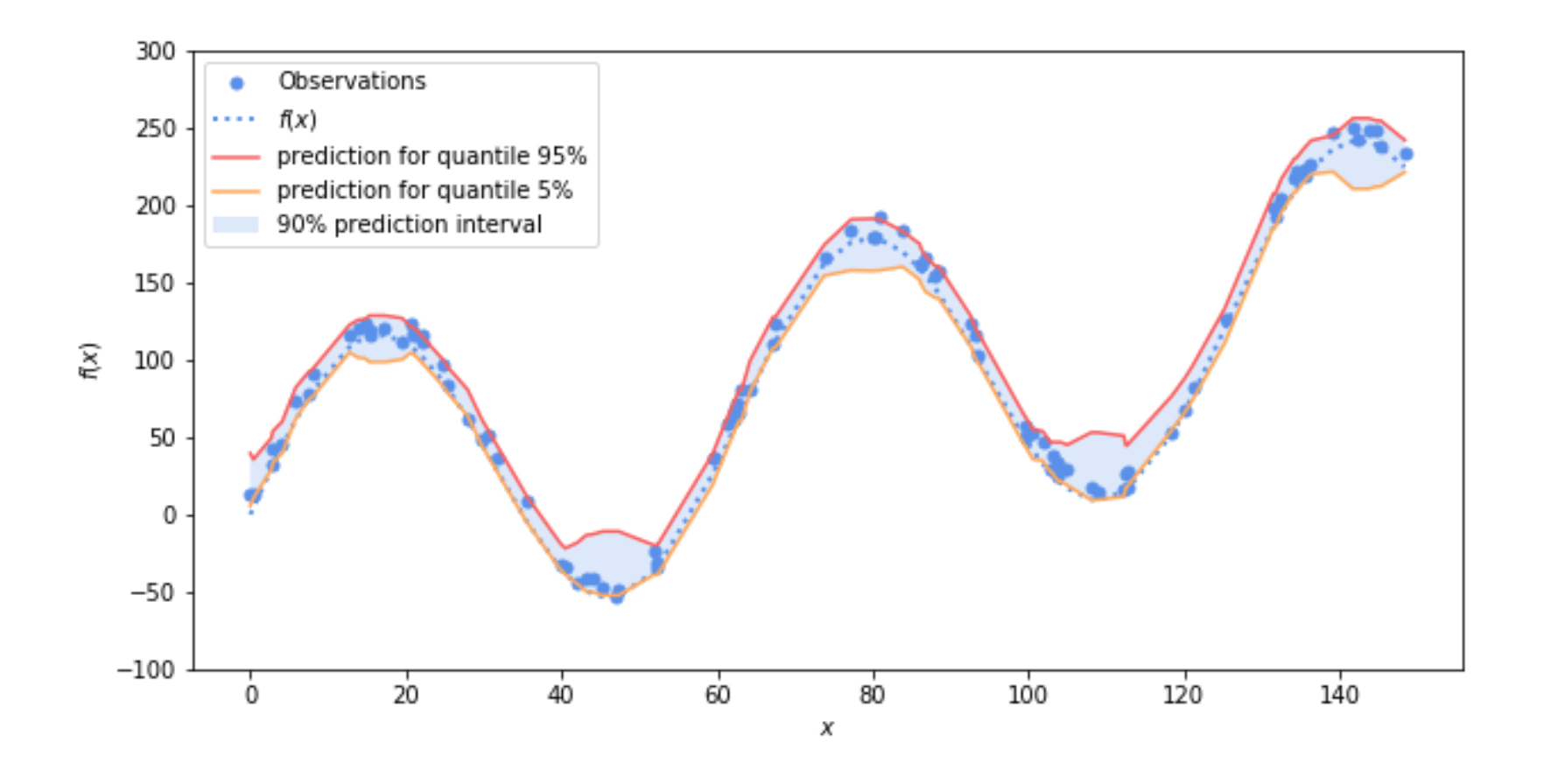
Что еще более интересно, они, как правило, дают более узкие интервалы прогнозирования (более низкую дисперсию), чем стандартные квантильные регрессоры. На следующем рисунке показан 90% интервал прогнозирования, оцененный оценщиком распределения, базовая модель и модель ошибки которого являются двумя регрессорами с градиентным усилением:

Рис. 4. 90% -ный интервал прогнозирования, оцененный с помощью оценщика распределения, базовая модель и модель ошибки которого представляют собой два регрессора с усилением градиентов

Еще одним преимуществом оценщика распределений является возможность их построения с помощью любой модели машинного обучения. Например, оценка распределения, основанная на моделях KNN, дает довольно удивительно хорошие результаты, как вы можете видеть на рисунке ниже.

Рисунок 5: 90% -ный интервал прогноза, оцененный оценщиком распределения, базовая модель и модель ошибки которого являются двумя оценщиками KNN

Чтобы завершить оценку, мы сравнили фактическую производительность различных моделей. Мы использовали проигрыш в пинболе. Это стандартная функция потерь, используемая в контексте квантильной регрессии. Вот формула для данной вероятности q и прогнозов p_ {k}:

Ключевым моментом является то, что модель, которая минимизирует потери пинбола, дает оптимальный квантиль. Если вам интересно, вы можете узнать больше об этой потере и ее связи с квантильной регрессией.

Мы вычислили потери для каждого квантиля с помощью наших четырех моделей, отображаемых на следующем графике:

Рисунок 6: Сравнение потерь для различных моделей квантильной регрессии. Координата x соответствует вероятности (в%), а координата y — соответствующему проигрышу.

Обратите внимание, что модели, использующие оценки распределения (красный, оранжевый и зеленый графики), имеют меньшие потери, чем модель простой регрессии (синяя на графике выше) для разных вероятностей. Модели Оценщика распределения, использующие две обученные модели (одна с обучающими данными, другая с ошибкой), также лучше, чем модель, оценивающая ошибку с помощью RMSE.

Заключение

Несмотря на кажущуюся простоту и предположение Гаусса, оценщик распределения оказался очень мощным инструментом, который можно эффективно использовать в рамках квантильной регрессии.

Мы показали, что применительно к игрушечному примеру он превосходит стандартный квантильный регрессор с градиентным усилением, реализованный в scikit learn. Надо признать, что такой прирост производительности вкупе с простотой модели может показаться немного волшебным. Тем не менее, мы используем его в производстве некоторых наших продуктов, и это дает отличные результаты. Если в будущем мы найдем больше доказательств эффективности этого подхода или некоторых примеров использования, в которых наша оценка распределения дает сбой, мы опубликуем новую статью об этом.

Первоначально опубликовано на https://qucit.com 6 апреля 2018 г.