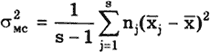Лекция №6
Систематические
погрешности и их классификация
В
настоящее время, особенно после введения
одного из основополагающих метрологических
стандартов — ГОСТ 8.009-84 ТСИ. Нормируемые
метрологические характеристики средств
измерений», понятие «систематическая
погрешность» несколько изменилось
по отношению к определению, данному
ГОСТ 16263-70 «ГСИ. Метрология. Термины
и определения». Систематическая
погрешность считается специфической,
«вырожденной» случайной величиной,
обладающей некоторыми, но не всеми
свойствами случайной величины, изучаемой
в теории вероятностей и математической
статистике. Свойства систематической
погрешности, которые необходимо учитывать
при объединении составляющих погрешности,
отражаются такими же характеристиками,
что и свойства «настоящих» случайных
величин — дисперсией (СКО) и коэффициентом
взаимной корреляции.
Систематическая погрешность представляет
собой определенную функцию влияющих
факторов, состав которых зависит от
физиче-ских, конструктивных и
технологических особеннрстей СИ, условий
их применения, а также индивидуальных
качеств наблюдателя. В метрологической
практике при оценке систематических
погрешностей должно учитываться влияние
следующих основных факторов:
1. Объект измерения. Перед измерением
он должен быть достаточно хорошо изучен
с целью корректного выбора его модели.
Чем полнее модель соответствует
исследуемому объекту, тем точнее могут
быть получены результаты измерения.
Например, кривизна земной поверхности
может не учитываться при измерении
площади сельскохозяйственных угодий,
так как она не вносит ощутимой погрешности,
однако при измерении площади океанов
ею пренебрегать уже нельзя.
2. Субъект измерения. Его вклад в
погрешность измерения необходимо
уменьшать путем подбора операторов
высокой квалификации и соблюдения
требований эргономики при разработке
СИ.
3. Метод и средство измерений.
Чрезвычайно важен их правильный выбор,
который производится на основе априорной
информации об объекте измерения. Чем
больше априорной информации, тем точнее
может быть проведено измерение. Основной
вклад в систематическую погрешность
вносит, как правило, методическая
погрешность.
4. Условия измерения. Обеспечение и
стабилизация нормальных условий являются
необходимыми требованиями для минимизации
дополнительной погрешности, которая
по своей природе, как правило, является
систематической.
Систематические
погрешности принято классифицировать
по двум признакам. По характеру изменения
во времени они делятся на постоянные и
переменные. Постоянными называются
такие погрешности измерения, которые
остаются неизменными в течение всей
серии измерений. Например, погрешность
от того, что неправильно установлен
ноль стрелочного электроизмерительного
прибора, погрешность от постоянного
дополнительного веса на чашке весов и
т.д. Переменными называются погрешности,
изменяющиеся в процессе измерения. Они
делятся на монотонно изменяющиеся,
периодические и изменяющиеся по сложному
закону. Если в процессе измерения
систематическая погрешность монотонно
возрастает или убывает, ее называют
монотонно изменяющейся. Например, она
имеет место при постепенном разряде
батареи, питающей средство измерений.
Периодической называется погрешность,
значение которой является периодической
функцией времени. Примером может служить
погрешность, обусловленная суточными
колебаниями напряжения силовой питающей
сети, температуры окружающей среды и
др. Систематические погрешности могут
изменяться и по более сложному закону,
обусловленному какими-либо внешними
причинами.
Способы обнаружения и устранения
систематических погрешностей
Результаты
наблюдений, полученные при наличии
систематической погрешности, называются
неисправленными. При проведении измерений
стараются в максимальной степени
исключить или учесть влияние систематических
погрешностей. Это может быть достигнуто
следующими путями:
—
устранением источников погрешностей
до начала измерений. В большинстве
областей измерений известны главные
источники систематических погрешностей
и разработаны методы, исключающие их
возникновение или устраняющие их влияние
на результат измерения. В связи с этим
в практике измерений стараются устранить
систематические погрешности не путем
обработки экспериментальных данных, а
применением СИ, реализующих соответствующие
методы измерений;
—
определением поправок и внесением их
в результат измерения;
—
оценкой границ неисключенных
систематических погрешностей.
Постоянная
систематическая погрешность не может
быть найдена методами совместной
обработки результатов измерений. Однако
она не искажает ни показатели точности
измерений, характеризующие случайную
погрешность, ни результат нахождения
переменной составляющей систематической
погрешности. Действительно, результат
одного измерения
где
xи — истинное значение
измеряемой величины;
i
— i-я случайная погрешность;
i
— i-я систематическая погрешность. После
устранения результатов многократных
измерении получаем среднее арифметическое
значение измеряемой величины
Если
систематическая погрешность постоянна
во всех измерениях, т.е.
i=
,то
Таким
образом, постоянная систематическая
погрешность не устраняется при
многократных измерениях.
Постоянные
систематические погрешности могут быть
обнаружены лишь путем сравнения
результатов измерений с другими,
полученными с помощью более высокоточных
методов и средств. Иногда эти погрешности
могут быть устранены специальными
приемами проведения процесса измерений.
Эти методы рассмотрены ниже.
Наличие
существенной переменной систематической
погрешности искажает оценки характеристик
случайной погрешности и аппроксимацию
ее распределения. Поэтому она должна
обязательно выявляться и исключаться
из результатов измерений.
Для
устранения постоянных систематических
погрешностей применяют следующие
методы:
—
Метод замещения, представляющий собой
разновидность метода сравнения, когда
сравнение осуществляется заменой
измеряемой величины известной величиной,
причем так, что при этом в состоянии и
действии всех используемых средств
измерений не происходит никаких
изменений. Этот метод дает наиболее
полное решение задачи. Для его реализации
необходимо иметь регулируемую меру,
величина которой однородна измеряемой.
Например, взвешивание по методу Борда,
измерение сопротивления посредством
моста постоянного тока и мер сопротивления.
—
Метод противопоставления, являющийся
разновидностью метода сравнения, при
котором измерение выполняется дважды
и проводится так, чтобы в обоих случаях
причина постоянной погрешности оказывала
разные, но известные по закономерности
воздействия на результаты наблюдений.
Например, способ взвешивания Гаусса.
—
Метод компенсации погрешности по знаку
(метод изменения знака систематической
погрешности), предусматривающий измерение
с двумя наблюдениями, выполняемыми так,
чтобы постоянная систематическая
погрешность входила в результат каждого
из них с разными знаками.
—
Метод рандомизации — наиболее
универсальный способ исключения
неизвестных постоянных систематических
погрешностей. Суть его состоит в том,
что одна и та же величина измеряется
различными методами (приборами).
Систематические погрешности каждого
из них для всей совокупности являются
разными случайными величинами. -Вследствие
этого при увеличении числа используемых
методов (приборов) систематические
погрешности взаимно компенсируются.
Для
устранения переменных и монотонно
изменяющихся систематических погрешностей
применяют следующие приемы и методы.
—
Анализ знаков неисправленных случайных
погрешностей. Если знаки неисправленных
случайных погрешностей чередуются с
какой-либо закономерностью, то наблюдается
переменная систематическая погрешность.
Если последовательность знаков «+»
у случайных погрешностей сменяется
последовательностью знаков «-» или
наоборот, то присутствует монотонно
изменяющаяся систематическая погрешность.
Если группы знаков «+» и «-» у
случайных погрешностей чередуются, то
присутствует периодическая систематическая
погрешность.
—
Графический метод. Он является одним
из наиболее простых способов обнаружения
переменной систематической погрешности
в ряду результатов наблюдений и
заключается в построении графика
последовательности неисправленных
значений результатов наблюдений. На
графике через построенные точки проводят
плавную кривую, которая выражает
тенденцию результата измерения, если
она существует. Если тенденция не
прослеживается, то переменную
систематическую погрешность считают
практически отсутствующей.
—
Метод симметричных наблюдений.
Рассмотрим сущность этого метода на
примере измерительного преобразователя,
передаточная функция которого имеет
вид y=kx+y0 , где х, у — входная
и выходная величины преобразователя;
k — коэффициент, погрешность которого
изменяется во времени по линейному
закону; у0 — постоянная.
Для
устранения систематической погрешности
трижды измеряется выходная величина у
через равные промежутки времени At. При
первом и третьем измерениях на вход
преобразователя подается сигнал х0 от
образцовой меры. В результате измерений
получается система уравнений:
Ее
решение позволяет получить значение
х, свободное от переменной систематической
погрешности, обусловленной изменением
коэффициента k:
Специальные
статистические методы. К ним относятся
способ последовательных разностей,
дисперсионный анализ, и др. Рассмотрим
подробнее некоторые из них.
Способ
последовательных разностей (критерий
Аббе). Применяется для обнаружения
изменяющейся во времени систематической
погрешности и состоит в следующем.
Дисперсию результатов наблюдений можно
оценить двумя способами: обычным
и
вычислением суммы квадратов последовательных
(в порядке проведения измерений) разностей
( xi+1 — xi)2
Если
в процессе измерений происходило
смещение центра группирования результатов
наблюдений, т.е. имела место переменная
систематическая погрешность, то
2[x]
дает преувеличенную оценку дисперсии
результатов наблюдений. Это объясняется
тем, что на
2[x]
влияют вариации
.
В то же время изменения центра группирования
весьма
мало сказываются на значениях
последовательных разностей d
i=x i+1-x i,
поэтому смещения
почти
не отразятся на значении Q 2[x].
Отношение
является
критерием для обнаружения систематических
смещений центра группирования результатов
наблюдений. Критическая область для
этого критерия (критерия Аббе) определяется
как
,
где q = 1-Р — уровень значимости, Р
— доверительная вероятность. Значения
vq для различных уровней
значимости q и числа наблюдений n
приведены в таблице. Если полученное
значение критерия Аббе меньше при
заданных q и n, то гипотеза о
постоянстве центра группирования
результатов наблюдений отвергается,
т.е. обнаруживается переменная
систематическая погрешность результатов
измерений.
|
n |
vq |
n |
vq |
||||
|
0.001 |
0.01 |
0.05 |
0.001 |
0.01 |
0.05 |
||
|
4 |
0.295 |
0.313 |
0.390 |
13 |
0.295 |
0.431 |
0.578 |
|
5 |
0.208 |
0.269 |
0.410 |
14 |
0.311 |
0.447 |
0.591 |
|
6 |
0.182 |
0.281 |
0.445 |
15 |
0.327 |
0.461 |
0.603 |
|
7 |
0.185 |
0.307 |
0.468 |
16 |
0.341 |
0.474 |
0.614 |
|
8 |
0.202 |
0.331 |
0.491 |
17 |
0.355 |
0.487 |
0.624 |
|
9 |
0.221 |
0.354 |
0.512 |
18 |
0.368 |
0.499 |
0.633 |
|
10 |
0.241 |
0.376 |
0.531 |
19 |
0.381 |
0.510 |
0.642 |
|
11 |
0.260 |
0.396 |
0.548 |
20 |
0.393 |
0.520 |
0.650 |
|
12 |
0.278 |
0.414 |
0.564 |
Дисперсионный
анализ (критерий Фишера). В практике
измерений часто бывает необходимо
выяснить наличие систематической
погрешности результатов наблюдений,
обусловленной влиянием какого-либо
постоянно действующего фактора, или
определить, вызывают ли изменения этого
фактора систематическое смещение
результатов измерений. В данном случае
проводят многократные измерения,
состоящие из достаточного числа серий,
каждая из которых соответствует
определенным (пусть неизвестным, но
различным) значениям влияющего фактора.
Влияющими факторами, по которым
производится объединение результатов
наблюдений по сериям, могут быть внешние
условия (температура, давление и т.д.),
временная последовательность проведения
измерений и т.п.
После
проведения N измерений их разбивают
на s серий (s > 3) по nj
результатов наблюдений ( snj
= N ) в каждой серии и затем устанавливают,
имеется или отсутствует систематическое
расхождение между результатами наблюдений
в различных сериях. При этом должно быть
установлено, что результаты в сериях
распределены нормально. Рассеяние
результатов наблюдений в пределах
каждой серии отражает только случайные
влияния, характеризует лишь случайные
погрешности измерений в пределах этой
серии.
Характеристикой
совокупности случайных внутрисерийных
погрешностей будет средняя сумма
дисперсий результатов наблюдений,
вычисленных раздельно для каждой серии,
т.е.
где
xji — результат i-го измерения
в j-й серии.
Внутрисерийная
дисперсия
2BC
характеризует случайные погрешности
измерений, так как только случайные
влияния обусловливают те различия
(отклонения результатов наблюдений),
на которых она основана. В то же время
рассеяние
j
различных серий обусловливается не
только случайными погрешностями
измерений, но и систематическими
различиями (если они существуют) между
результатами наблюдений, сгруппированными
по сериям. Следовательно, усредненная
межсерийная дисперсия
где
,
выражает силу действия фактора,
вызывающего систематические различия
между сериями.
Таким
образом,
2BC /(
2BC+
2MC) характеризует
долю дисперсии всех результатов
наблюдений, обусловленную наличием
случайных погрешностей измерений, а
2MC
/(
2BC+
2MC) — долю дисперсии,
обусловленную межсерийными различиями
результатов наблюдений. Первую из них
называют коэффициентом ошибки,
вторую — показателем дифференциации.
Чем больше отношение показателя
дифференциации к коэффициенту ошибки,
тем сильнее действие фактора, по которому
группировались серии, и тем больше
систематическое различие между ними.
Критерием
оценки наличия систематических
погрешностей в данном случае является
дисперсионный критерий Фишера F=
2MC
2BC. Критическая область
для критерия Фишера соответствует
P(F>Fq)=q.
Значения
Fq для различных уровней
значимости q, числа измерений N и
числа серий s приведены в приложении
1, где k2=N-s , k1=s-1.
Если полученное значение критерия
Фишера больше Fq (при
заданных q, N и s), то гипотеза об отсутствии
систематических смещений результатов
наблюдений по сериям отвергается, т.е.
обнаруживается систематическая
погрешность, вызываемая тем фактором,
по которому группировались результаты
наблюдений.
Из
всех рассмотренных способов обнаружения
систематических погрешностей дисперсионный
анализ является наиболее эффективным
и достоверным, так как позволяет не
только установить факт наличия
погрешности, но и дает возможность
проанализировать источники ее
возникновения.
Критерий
Вилкоксона. Если закон распределения
результатов измерений неизвестен, то
для обнаружения систематической
погрешности применяют статистический
критерий Вилкоксона.
Из
двух групп результатов измерений x1,
x2,…, xn и y1,
y2,…, ym ,
n>=m>=5 , составляется вариационный
ряд, в котором все n+m значений x1,
x2,…, xn и y1,
y2,…, ym
располагают в порядке их возрастания
и приписывают им ранги — порядковые
номера членов вариационного ряда.
Различие средних значений каждого из
рядов можно считать допустимым, если
выполняется неравенство
где
Ri — ранг (номер) члена xi,
равный его номеру в вариационном ряду
T —q и T
+q — нижнее и верхнее
критические значения для выбранного
уровня значимости q. При m<15 эти
критические значения определяются по
таблице. При m>15 они рассчитываются
по формулам:
где
zp — квантиль нормированной
функции Лапласа.
Таблица. Критические значения Tq—
и Tq+ при q=0.05 и 0,01
|
n |
m |
q=0.05 |
q=0.01 |
||
|
Tq— |
Tq+ |
Tq— |
Tq+ |
||
|
8 |
8 |
49 |
87 |
43 |
93 |
|
10 |
53 |
99 |
47 |
105 |
|
|
15 |
65 |
127 |
56 |
136 |
|
|
9 |
9 |
62 |
109 |
56 |
115 |
|
15 |
79 |
146 |
69 |
156 |
|
|
10 |
10 |
78 |
132 |
71 |
139 |
|
15 |
94 |
166 |
84 |
176 |
|
|
12 |
12 |
115 |
185 |
105 |
195 |
|
15 |
127 |
209 |
115 |
221 |
|
|
14 |
14 |
160 |
246 |
147 |
259 |
|
15 |
164 |
256 |
151 |
268 |
|
|
15 |
15 |
184 |
282 |
171 |
294 |
Соседние файлы в папке Лекции по метрологии
- #
- #
- #
- #
- #
- #
- #
- #
- #
Систематические погрешности и способы их обнаружения
и устранения.
В зависимости от характера измерения систематические погрешности подразделяются на постоянные и переменные [3].
Постоянные погрешности – погрешности, которые длительное время сохраняют свое значение, например, в течение времени выполнения всего ряда измерений. Они встречаются наиболее часто.
Переменные погрешности делятся на прогрессивные, периодические и погрешности, изменяющиеся по сложному закону
Прогрессивные погрешности – непрерывно возрастающие или убывающие погрешности. К ним относятся, например, погрешности вследствие износа измерительных наконечников, контактирующих с деталью при контроле ее прибором активного контроля.
Периодические погрешности – погрешности, значение которых является периодической функцией времени.
Погрешности, изменяющиеся по сложному закону, происходят вследствие совместного действия нескольких систематических погрешностей.
Измерения, содержащие систематические погрешности, называются неисправленными, а те, в которых систематическая погрешность стремится к нулю – правильными. Обнаружить и исключить систематические погрешности – это достаточно сложная задача, которая обычно достигается следующими путями [19]:
• устранением источников погрешностей и исключение их еще до начала измерений;
• определением поправки и внесение ее в результат измерения, если исключить систематическую погрешность не удается;
• если первый и второй пути не возможны, то оцениваются границы неисключенных систематических погрешностей, которые учитываются при обработке результатов измерений.
Постоянные систематические погрешности обнаруживаются лишь сравнением результатов измерений с другими, результатами, полученными с помощью более высокоточных методов и средств. К наиболее распространенным методам обнаружения постоянных систематических погрешностей можно отнести такие, как метод замещения, метод рандомизации и др.
Метод замещения заключается в замене неизвестной измеряемой величины известной величиной, как правило, воспроизводимой мерой.
При использовании метода рандомизации искомая величина измеряется различными приборами, при этом с увеличением количества приборов систематические погрешности взаимно компенсируются.
Для обнаружения переменных систематических погрешностей используются различные статистические способы, например, способ последовательных разностей, дисперсионный анализ и др.
Способ последовательных разностей
(критерий Аббе)
Суть данного метода заключается в следующем. Дисперсия результатов измерений оценивается двумя способами:
обычным:
(25)
и вычислением суммы квадратов последовательных разностей:
(26)
Определяется расчетное значение критерия Аббе:
(27)
Если расчетное значение критерия Аббе меньше критического q, то в результатах измерений обнаруживается переменная систематическая погрешность. Критические значения критерия Аббе приведены в табл. 13.
Таблица 13
Значения критерия Аббе q
n
q при q, равном
0,001
0,01
0,05
9
0,221
0,354
0,512
10
0,241
0,376
0,531
11
0,26
0,396
0,548
12
0,278
0,414
0,564
13
0,295
0,431
0,578
14
0,311
0,447
0,591
15
0,327
0,461
0,603
16
0,341
0,474
0,614
17
0,355
0,487
0,624
18
0,368
0,499
0,633
19
0,381
0,51
0,642
20
0,393
0,52
0,65
Дисперсионный анализ (критерий Фишера)
Суть данного метода состоит в следующем. Проводится N измерений, после чего их необходимо разбить на s серий (s > 3), по nj результатов измерений в каждой серии. Затем устанавливается, имеется или отсутствует систематическое расхождение между результатами наблюдение в различных сериях. Рассеяние результатов измерений в пределах каждой серии отражает только случайные влияния и характеризует лишь случайные погрешности измерений в пределах этой серии. Характеристикой случайных внутрисерийных погрешностей будет средняя сумма дисперсий результатов измерений, вычисленных отдельно для каждой серии, т. е.
(31)
где xij – результат i-го измерения в j-й серии. При этом рассеяние различных серий обусловливается не только случайными погрешностями измерений, но и систематическими различиями (если они существуют) между результатами измерений, сгруппированными по сериям. Таким образом, усредненная межсерийная дисперсия
(32)
где , выражает силу действия фактора, вызывающего систематические различия между сериями.
Критерием оценки наличия систематических погрешностей является дисперсионный критерий Фишера
(33)
В случае если расчетное значение критерия F будет больше критического Fq, то в результатах измерения присутствует переменная систематическая погрешность. Значения Fq для различной доверительной вероятности приводятся в табл. 15.
Таблица 15
Значения критерия Фишера
k2
Fq при k1, равном
1
2
3
4
5
6
8
12
16
2
18,51
19,00
19,16
19,25
19,30
19,33
19,37
19,41
19,43
4
7,71
6,94
6,59
6,39
6,26
6,16
6,04
5,91
5,84
6
5,99
5,14
4,76
4,53
4,39
4,28
4,15
4,00
3,92
8
5,32
4,46
4,07
3,84
3,69
3,58
3,44
3,28
3,20
10
4,96
4,10
3,71
3,48
3,33
3,22
3,07
2,91
2,82
12
4,75
3,88
3,49
3,26
3,11
3,00
2,85
2,69
2,60
14
4,60
3,74
3,34
3,11
2,96
2,85
2,70
2,53
2,44
16
4,49
3,63
3,24
3,01
2,85
2,74
2,59
2,42
2,33
18
4,41
3,55
3,16
2,93
2,77
2,66
2,51
2,34
2,25
20
4,35
3,49
3,10
2,87
2,71
2,60
2,45
2,28
2,18
30
4,17
3,32
2,92
2,69
2,53
2,42
2,27
2,09
1,99
Примечание: k1 = s – 1, k2 = N – s.
Грубые погрешности и способы их исключения
Грубая погрешность – это погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда [3]. Иногда вместо термина грубая погрешность измерений применяют термин «промах». Промахи как правило связаны с ошибками, неправильными действиями операторов. Грубую погрешность при однократном измерении обнаружить невозможно, ее можно обнаружить после проведения многократных измерений с последующей математической обработкой полученных результатов наблюдений с использованием специальных критериев, например, критерий «трех сигм», критерий Шовенэ, Романовского, Шарлье, Диксона, Граббса.
Критерий Романовского
Критерий Романовского применяется, если число измерений n < 20. При этом вычисляется отношение
, (38)
где – проверяемое значение, – среднее арифметическое значение измеряемой величины, Sx – среднее квадратическое отклонение.
Далее расчетное значение сравнивается с критерием т, выбранным по табл. 17. Если т, то результат xi считается промахом и отбрасывается.
Таблица 17
Значения критерия Романовского т=f(n)
q
n = 4
n = 6
n = 8
n = 10
n = 12
n = 15
n = 20
0,01
1,73
2,16
2,43
2,62
2,75
2,90
3,08
0,02
1,72
2,13
2,37
2,54
2,66
2,80
2,96
0,05
1,71
2,10
2,27
2,41
2,53
2,64
2,78
0,10
1,69
2,00
2,17
2,29
2,39
2,49
2,62
Критерий Шарлье
Критерий Шарлье используется, если число измерений велико (n > 20). Пользуясь данным критерием, отбрасывается результат, для значения которого выполняется неравенство
Значения критерия Шарлье
n
5
10
20
30
40
50
100
Кш
1,3
1,65
1,96
2,13
2,24
2,32
2,58
Критерий Диксона
При использовании данного критерия полученные результаты измерений записываются в вариационный возрастающий ряд x1
50 для идентификации закона распределения используется критерий Пирсона. При 50 > n > 15 для проверки нормальности закона распределения применяется составной критерий. При n < 15 принадлежность экспериментального распределения к нормальному не проверяется.
4. Определение доверительных границ случайной погрешности
Если удалось идентифицировать закон распределения результатов измерений, то с его использованием находится квантильный множитель zp при заданном значении доверительной вероятности Р. В этом случае доверительные границы случайной погрешности Здесь – СКО среднего арифметического значения. При n < 30 часто используется распределение Стьюдента, при этом доверительные границы случайной погрешности
Здесь tP – коэффициент Стьюдента, приведенный в табл. 22, n – количество измерений.
Таблица 22
Величина tP при различных уровнях значимости
n
Уровни значимости
0,2
0,1
0,05
0,02
0,01
0,005
0,002
0,001
2
3,08
6,31
12,71
31,82
63,66
127,32
318,30
636,61
3
1,84
2,92
4,30
6,96
9,99
14,09
22,33
31,60
4
1,64
2,35
3,18
4,54
5,84
7,45
10,21
12,92
5
1,53
2,13
2,78
3,75
4,60
5,60
7,17
8,61
6
1,48
2,02
2,57
3,36
4,03
4,77
5,89
6,87
7
1,44
1,94
2,45
3,14
3,71
4,32
5,21
5,96
8
1,41
1,89
2,36
3,00
3,50
4,03
4,74
5,41
9
1,40
1,80
2,31
2,90
3,36
3,83
4,50
5,04
10
1,38
1,83
2,26
2,82
3,25
3,64
4,30
4,78
11
1,37
1,81
2,23
2,76
3,17
3,50
4,14
4,59
1. Определение границ неисключенной систематической погрешности
результата измерения
Под этими границами понимаются найденные нестатистическими методами границы интервала, внутри которого находится неисключенная систематическая погрешность. На практике, как правило, границы неисключеной систематической погрешности принимаются равными пределам допускаемых основных и дополнительных погрешностей средств измерений, если их случайные составляющие пренебрежимо малы.
2. Определение доверительных границ погрешности
результата измерения
Данная операция осуществляется путем суммирования границ случайной составляющей и границ неисключенной систематической составляющей θ в зависимости от соотношения .
7. Запись результата измерения
Результат измерения записывается в виде при доверительной вероятности Р = Рд.
Результат любого измерения не определён однозначно и имеет случайную составляющую.
Поэтому адекватным языком для описания погрешностей является язык вероятностей.
Тот факт, что значение некоторой величины «случайно», не означает, что
она может принимать совершенно произвольные значения. Ясно, что частоты, с которыми
возникает те или иные значения, различны. Вероятностные законы, которым
подчиняются случайные величины, называют распределениями.
2.1 Случайная величина
Случайной будем называть величину, значение которой не может быть достоверно определено экспериментатором. Чаще всего подразумевается, что случайная величина будет изменяться при многократном повторении одного и того же эксперимента. При интерпретации результатов измерений в физических экспериментах, обычно случайными также считаются величины, значение которых является фиксированным, но не известно экспериментатору. Например смещение нуля шкалы прибора. Для формализации работы со случайными величинами используют понятие вероятности. Численное значение вероятности того, что какая-то величина примет то или иное значение определяется либо как относительная частота наблюдения того или иного значения при повторении опыта большое количество раз, либо как оценка на основе данных других экспериментов.
Замечание.
Хотя понятия вероятности и случайной величины являются основополагающими, в литературе нет единства в их определении. Обсуждение формальных тонкостей или построение строгой теории лежит за пределами данного пособия. Поэтому на начальном этапе лучше использовать «интуитивное» понимание этих сущностей. Заинтересованным читателям рекомендуем обратиться к специальной литературе: [5].
Рассмотрим случайную физическую величину x, которая при измерениях может
принимать непрерывный набор значений. Пусть
P[x0,x0+δx] — вероятность того, что результат окажется вблизи
некоторой точки x0 в пределах интервала δx: x∈[x0,x0+δx].
Устремим интервал
δx к нулю. Нетрудно понять, что вероятность попасть в этот интервал
также будет стремиться к нулю. Однако отношение
w(x0)=P[x0,x0+δx]δx будет оставаться конечным.
Функцию w(x) называют плотностью распределения вероятности или кратко
распределением непрерывной случайной величины x.
Замечание. В математической литературе распределением часто называют не функцию
w(x), а её интеграл W(x)=∫w(x)𝑑x. Такую функцию в физике принято
называть интегральным или кумулятивным распределением. В англоязычной литературе
для этих функций принято использовать сокращения:
pdf (probability distribution function) и
cdf (cumulative distribution function)
соответственно.
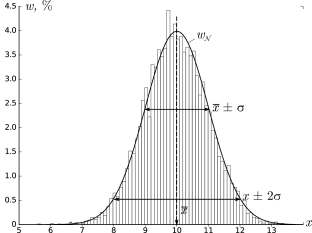
Гистограммы.
Проиллюстрируем наглядно понятие плотности распределения. Результат
большого числа измерений случайной величины удобно представить с помощью
специального типа графика — гистограммы.
Для этого область значений x, размещённую на оси абсцисс, разобьём на
равные малые интервалы — «корзины» или «бины» (англ. bins)
некоторого размера h. По оси ординат будем откладывать долю измерений w,
результаты которых попадают в соответствующую корзину. А именно,
пусть k — номер корзины; nk — число измерений, попавших
в диапазон x∈[kh,(k+1)h]. Тогда на графике изобразим «столбик»
шириной h и высотой wk=nk/n.
В результате получим картину, подобную изображённой на рис. 2.1.
σ=1,0, h=0,1, n=104)
Высоты построенных столбиков будут приближённо соответствовать значению
плотности распределения w(x) вблизи соответствующей точки x.
Если устремить число измерений к бесконечности (n→∞), а ширину корзин
к нулю (h→0), то огибающая гистограммы будет стремиться к некоторой
непрерывной функции w(x).
Самые высокие столбики гистограммы будут группироваться вблизи максимума
функции w(x) — это наиболее вероятное значение случайной величины.
Если отклонения в положительную и отрицательную стороны равновероятны,
то гистограмма будет симметрична — в таком случае среднее значение ⟨x⟩
также будет лежать вблизи этого максимума. Ширина гистограммы будет характеризовать разброс
значений случайной величины — по порядку величины
она, как правило, близка к среднеквадратичному отклонению sx.
Свойства распределений.
Из определения функции w(x) следует, что вероятность получить в результате
эксперимента величину x в диапазоне от a до b
можно найти, вычислив интеграл:
| Px∈[a,b]=∫abw(x)𝑑x. | (2.1) |
Согласно определению вероятности, сумма вероятностей для всех возможных случаев
всегда равна единице. Поэтому интеграл распределения w(x) по всей области
значений x (то есть суммарная площадь под графиком w(x)) равен единице:
Это соотношение называют условием нормировки.
Среднее и дисперсия.
Вычислим среднее по построенной гистограмме. Если размер корзин
h достаточно мал, все измерения в пределах одной корзины можно считать примерно
одинаковыми. Тогда среднее арифметическое всех результатов можно вычислить как
Переходя к пределу, получим следующее определение среднего значения
случайной величины:
где интегрирование ведётся по всей области значений x.
В теории вероятностей x¯ также называют математическим ожиданием
распределения.
Величину
| σ2=(x-x¯)2¯=∫(x-x¯)2w𝑑x | (2.3) |
называют дисперсией распределения. Значение σ есть
срекднеквадратичное отклонение в пределе n→∞. Оно имеет ту
же размерность, что и сама величина x и характеризует разброс распределения.
Именно эту величину, как правило, приводят как характеристику погрешности
измерения x.
Доверительный интервал.
Обозначим как P|Δx|<δ вероятность
того, что отклонение от среднего Δx=x-x¯ составит величину,
не превосходящую по модулю значение δ:
| P|Δx|<δ=∫x¯-δx¯+δw(x)𝑑x. | (2.4) |
Эту величину называют доверительной вероятностью для
доверительного интервала |x-x¯|≤δ.
2.2 Нормальное распределение
Одним из наиболее примечательных результатов теории вероятностей является
так называемая центральная предельная теорема. Она утверждает,
что сумма большого количества независимых случайных слагаемых, каждое
из которых вносит в эту сумму относительно малый вклад, подчиняется
универсальному закону, не зависимо от того, каким вероятностным законам
подчиняются её составляющие, — так называемому нормальному
распределению (или распределению Гаусса).
Доказательство теоремы довольно громоздко и мы его не приводим (его можно найти
в любом учебнике по теории вероятностей). Остановимся
кратко на том, что такое нормальное распределение и его основных свойствах.
Плотность нормального распределения выражается следующей формулой:
| w𝒩(x)=12πσe-(x-x¯)22σ2. | (2.5) |
Здесь x¯ и σ
— параметры нормального распределения: x¯ равно
среднему значению x, a σ —
среднеквадратичному отклонению, вычисленным в пределе n→∞.
Как видно из рис. 2.1, распределение представляет собой
симметричный
«колокол», положение вершины которого
соответствует x¯ (ввиду симметрии оно же
совпадает с наиболее вероятным значением — максимумом
функции w𝒩(x)).
При значительном отклонении x от среднего величина
w𝒩(x)
очень быстро убывает. Это означает, что вероятность встретить отклонения,
существенно большие, чем σ, оказывается пренебрежимо
мала. Ширина «колокола» по порядку величины
равна σ — она характеризует «разброс»
экспериментальных данных относительно среднего значения.
Замечание. Точки x=x¯±σ являются точками
перегиба графика w(x) (в них вторая производная по x
обращается в нуль, w′′=0), а их положение по высоте составляет
w(x¯±σ)/w(x¯)=e-1/2≈0,61
от высоты вершины.
Универсальный характер центральной предельной теоремы позволяет широко
применять на практике нормальное (гауссово) распределение для обработки
результатов измерений, поскольку часто случайные погрешности складываются из
множества случайных независимых факторов. Заметим, что на практике
для приближённой оценки параметров нормального распределения
случайной величины используются выборочные значения среднего
и дисперсии: x¯≈⟨x⟩, sx≈σx.
Вычислим некоторые доверительные вероятности (2.4) для нормально Замечание. Значение интеграла вида ∫e-x2/2𝑑x Вероятность того, что результат отдельного измерения x окажется Вероятность отклонения в пределах x¯±2σ: а в пределах x¯±3σ: Иными словами, при большом числе измерений нормально распределённой Пример. В сообщениях об открытии бозона Хиггса на Большом адронном коллайдере Полученные значения доверительных вероятностей используются при означает, что измеренное значение лежит в диапазоне (доверительном Замечание. Хотя нормальный закон распределения встречается на практике довольно Теперь мы можем дать количественный критерий для сравнения двух измеренных Пусть x1 и x2 (x1≠x2) измерены с Допустим, одна из величин известна с существенно большей точностью: Пусть погрешности измерений сравнимы по порядку величины: Замечание. Изложенные здесь соображения применимы, только если x¯ иx-x0σ2=2w(x)σ1=1
Доверительные вероятности.
распределённых случайных величин.
(его называют интегралом ошибок) в элементарных функциях не выражается,
но легко находится численно.
в пределах x¯±σ оказывается равна
P|Δx|<σ=∫x¯-σx¯+σw𝒩𝑑x≈0,68.
величины можно ожидать, что лишь треть измерений выпадут за пределы интервала
[x¯-σ,x¯+σ]. При этом около 5%
измерений выпадут за пределы [x¯-2σ;x¯+2σ],
и лишь 0,27% окажутся за пределами
[x¯-3σ;x¯+3σ].
говорилось о том, что исследователи ждали подтверждение результатов
с точностью «5 сигма». Используя нормальное распределение (2.5)
нетрудно посчитать, что они использовали доверительную вероятность
P≈1-5,7⋅10-7=0,99999943. Такую точность можно назвать фантастической.
стандартной записи результатов измерений. В физических измерениях
(в частности, в учебной лаборатории), как правило, используется P=0,68,
то есть, запись
интервале) x∈[x¯-δx;x¯+δx] с
вероятностью 68%. Таким образом погрешность ±δx считается
равной одному среднеквадратичному отклонению: δx=σ.
В технических измерениях чаще используется P=0,95, то есть под
абсолютной погрешностью имеется в виду удвоенное среднеквадратичное
отклонение, δx=2σ. Во избежание разночтений доверительную
вероятность следует указывать отдельно.
часто, стоит помнить, что он реализуется далеко не всегда.
Полученные выше соотношения для вероятностей попадания значений в
доверительные интервалы можно использовать в качестве простейшего
признака нормальности распределения: в частности, если количество попадающих
в интервал ±σ результатов существенно отличается от 2/3 — это повод
для более детального исследования закона распределения ошибок.Сравнение результатов измерений.
величин или двух результатов измерения одной и той же величины.
погрешностями σ1 и σ2 соответственно.
Ясно, что если различие результатов |x2-x1| невелико,
его можно объяснить просто случайными отклонениями.
Если же теория предсказывает, что вероятность обнаружить такое отклонение
слишком мала, различие результатов следует признать значимым.
Предварительно необходимо договориться о соответствующем граничном значении
вероятности. Универсального значения здесь быть не может,
поэтому приходится полагаться на субъективный выбор исследователя. Часто
в качестве «разумной» границы выбирают вероятность 5%,
что, как видно из изложенного выше, для нормального распределения
соответствует отклонению более, чем на 2σ.
σ2≪σ1 (например, x1 — результат, полученный
студентом в лаборатории, x2 — справочное значение).
Поскольку σ2 мало, x2 можно принять за «истинное»:
x2≈x¯. Предполагая, что погрешность измерения
x1 подчиняется нормальному закону с и дисперсией σ12,
можно утверждать, что
различие считают будет значимы, если
σ1∼σ2. В теории вероятностей показывается, что
линейная комбинация нормально распределённых величин также имеет нормальное
распределение с дисперсией σ2=σ12+σ22
(см. также правила сложения погрешностей (2.7)). Тогда
для проверки гипотезы о том, что x1 и x2 являются измерениями
одной и той же величины, нужно вычислить, является ли значимым отклонение
|x1-x2| от нуля при σ=σ12+σ22.
Пример. Два студента получили следующие значения для теплоты испарения
некоторой жидкости: x1=40,3±0,2 кДж/моль и
x2=41,0±0,3 кДж/моль, где погрешность соответствует
одному стандартному отклонению. Можно ли утверждать, что они исследовали
одну и ту же жидкость?
Имеем наблюдаемую разность |x1-x2|=0,7 кДж/моль,
среднеквадратичное отклонение для разности
σ=0,22+0,32=0,36 кДж/моль.
Их отношение |x2-x1|σ≈2. Из
свойств нормального распределения находим вероятность того, что измерялась
одна и та же величина, а различия в ответах возникли из-за случайных
ошибок: P≈5%. Ответ на вопрос, «достаточно»
ли мала или велика эта вероятность, остаётся на усмотрение исследователя.
его стандартное отклонение σ получены на основании достаточно
большой выборки n≫1 (или заданы точно). При небольшом числе измерений
(n≲10) выборочные средние ⟨x⟩ и среднеквадратичное отклонение
sx сами имеют довольно большую ошибку, а
их распределение будет описываться не нормальным законом, а так
называемым t-распределением Стъюдента. В частности, в зависимости от
значения n интервал ⟨x⟩±sx будет соответствовать несколько
меньшей доверительной вероятности, чем P=0,68. Особенно резко различия
проявляются при высоких уровнях доверительных вероятностей P→1.
2.3 Независимые величины
Величины x и y называют независимыми если результат измерения одной
из них никак не влияет на результат измерения другой. Для таких величин вероятность того, что x окажется в некоторой области X, и одновременно y — в области Y,
равна произведению соответствующих вероятностей:
Обозначим отклонения величин от их средних как Δx=x-x¯ и
Δy=y-y¯.
Средние значения этих отклонений равны, очевидно, нулю: Δx¯=x¯-x¯=0,
Δy¯=0. Из независимости величин x и y следует,
что среднее значение от произведения Δx⋅Δy¯
равно произведению средних Δx¯⋅Δy¯
и, следовательно, равно нулю:
| Δx⋅Δy¯=Δx¯⋅Δy¯=0. | (2.6) |
Пусть измеряемая величина z=x+y складывается из двух независимых
случайных слагаемых x и y, для которых известны средние
x¯ и y¯, и их среднеквадратичные погрешности
σx и σy. Непосредственно из определения (1.1)
следует, что среднее суммы равно сумме средних:
Найдём дисперсию σz2. В силу независимости имеем
| Δz2¯=Δx2¯+Δy2¯+2Δx⋅Δy¯≈Δx2¯+Δy2¯, |
то есть:
Таким образом, при сложении независимых величин их погрешности
складываются среднеквадратичным образом.
Подчеркнём, что для справедливости соотношения (2.7)
величины x и y не обязаны быть нормально распределёнными —
достаточно существования конечных значений их дисперсий. Однако можно
показать, что если x и y распределены нормально, нормальным
будет и распределение их суммы.
Замечание. Требование независимости
слагаемых является принципиальным. Например, положим y=x. Тогда
z=2x. Здесь y и x, очевидно, зависят друг от друга. Используя
(2.7), находим σ2x=2σx,
что, конечно, неверно — непосредственно из определения
следует, что σ2x=2σx.
Отдельно стоит обсудить математическую структуру формулы (2.7).
Если одна из погрешностей много больше другой, например,
σx≫σy,
то меньшей погрешностью можно пренебречь, σx+y≈σx.
С другой стороны, если два источника погрешностей имеют один порядок
σx∼σy, то и σx+y∼σx∼σy.
Эти обстоятельства важны при планирования эксперимента: как правило,
величина, измеренная наименее точно, вносит наибольший вклад в погрешность
конечного результата. При этом, пока не устранены наиболее существенные
ошибки, бессмысленно гнаться за повышением точности измерения остальных
величин.
Пример. Пусть σy=σx/3,
тогда σz=σx1+19≈1,05σx,
то есть при различии двух погрешностей более, чем в 3 раза, поправка
к погрешности составляет менее 5%, и уже нет особого смысла в учёте
меньшей погрешности: σz≈σx. Это утверждение
касается сложения любых независимых источников погрешностей в эксперименте.
2.4 Погрешность среднего
Выборочное среднее арифметическое значение ⟨x⟩, найденное
по результатам n измерений, само является случайной величиной.
Действительно, если поставить серию одинаковых опытов по n измерений,
то в каждом опыте получится своё среднее значение, отличающееся от
предельного среднего x¯.
Вычислим среднеквадратичную погрешность среднего арифметического
σ⟨x⟩.
Рассмотрим вспомогательную сумму n слагаемых
Если {xi} есть набор независимых измерений
одной и той же физической величины, то мы можем, применяя результат
(2.7) предыдущего параграфа, записать
| σZ=σx12+σx22+…+σxn2=nσx, |
поскольку под корнем находится n одинаковых слагаемых. Отсюда с
учётом ⟨x⟩=Z/n получаем
Таким образом, погрешность среднего значения x по результатам
n независимых измерений оказывается в n раз меньше погрешности
отдельного измерения. Это один из важнейших результатов, позволяющий
уменьшать случайные погрешности эксперимента за счёт многократного
повторения измерений.
Подчеркнём отличия между σx и σ⟨x⟩:
величина σx — погрешность отдельного
измерения — является характеристикой разброса значений
в совокупности измерений {xi}, i=1..n. При
нормальном законе распределения примерно 68% измерений попадают в
интервал ⟨x⟩±σx;
величина σ⟨x⟩ — погрешность
среднего — характеризует точность, с которой определено
среднее значение измеряемой физической величины ⟨x⟩ относительно
предельного («истинного») среднего x¯;
при этом с доверительной вероятностью P=68% искомая величина x¯
лежит в интервале
⟨x⟩-σ⟨x⟩<x¯<⟨x⟩+σ⟨x⟩.
2.5 Результирующая погрешность опыта
Пусть для некоторого результата измерения известна оценка его максимальной
систематической погрешности Δсист и случайная
среднеквадратичная
погрешность σслуч. Какова «полная»
погрешность измерения?
Предположим для простоты, что измеряемая величина в принципе
может быть определена сколь угодно точно, так что можно говорить о
некотором её «истинном» значении xист
(иными словами, погрешность результата связана в основном именно с
процессом измерения). Назовём полной погрешностью измерения
среднеквадратичное значения отклонения от результата измерения от
«истинного»:
Отклонение x-xист можно представить как сумму случайного
отклонения от среднего δxслуч=x-x¯
и постоянной (но, вообще говоря, неизвестной) систематической составляющей
δxсист=x¯-xист=const:
Причём случайную составляющую можно считать независимой от систематической.
В таком случае из (2.7) находим:
| σполн2=⟨δxсист2⟩+⟨δxслуч2⟩≤Δсист2+σслуч2. | (2.9) |
Таким образом, для получения максимального значения полной
погрешности некоторого измерения нужно квадратично сложить максимальную
систематическую и случайную погрешности.
Если измерения проводятся многократно, то согласно (2.8)
случайная составляющая погрешности может быть уменьшена, а систематическая
составляющая при этом остаётся неизменной:
Отсюда следует важное практическое правило
(см. также обсуждение в п. 2.3): если случайная погрешность измерений
в 2–3 раза меньше предполагаемой систематической, то
нет смысла проводить многократные измерения в попытке уменьшить погрешность
всего эксперимента. В такой ситуации измерения достаточно повторить
2–3 раза — чтобы убедиться в повторяемости результата, исключить промахи
и проверить, что случайная ошибка действительно мала.
В противном случае повторение измерений может иметь смысл до
тех пор, пока погрешность среднего
σ⟨x⟩=σxn
не станет меньше систематической.
Замечание. Поскольку конкретная
величина систематической погрешности, как правило, не известна, её
можно в некотором смысле рассматривать наравне со случайной —
предположить, что её величина была определена по некоторому случайному
закону перед началом измерений (например, при изготовлении линейки
на заводе произошло некоторое случайное искажение шкалы). При такой
трактовке формулу (2.9) можно рассматривать просто
как частный случай формулы сложения погрешностей независимых величин
(2.7).
Подчеркнем, что вероятностный закон, которому подчиняется
систематическая ошибка, зачастую неизвестен. Поэтому неизвестно и
распределение итогового результата. Из этого, в частности, следует,
что мы не можем приписать интервалу x±Δсист какую-либо
определённую доверительную вероятность — она равна 0,68
только если систематическая ошибка имеет нормальное распределение.
Можно, конечно, предположить,
— и так часто делают — что, к примеру, ошибки
при изготовлении линеек на заводе имеют гауссов характер. Также часто
предполагают, что систематическая ошибка имеет равномерное
распределение (то есть «истинное» значение может с равной вероятностью
принять любое значение в пределах интервала ±Δсист).
Строго говоря, для этих предположений нет достаточных оснований.
Пример. В результате измерения диаметра проволоки микрометрическим винтом,
имеющим цену деления h=0,01 мм, получен следующий набор из n=8 значений:
Вычисляем среднее значение: ⟨d⟩≈386,3 мкм.
Среднеквадратичное отклонение:
σd≈9,2 мкм. Случайная погрешность среднего согласно
(2.8):
σ⟨d⟩=σd8≈3,2
мкм. Все результаты лежат в пределах ±2σd, поэтому нет
причин сомневаться в нормальности распределения. Максимальную погрешность
микрометра оценим как половину цены деления, Δ=h2=5 мкм.
Результирующая полная погрешность
σ≤Δ2+σd28≈6,0 мкм.
Видно, что σслуч≈Δсист и проводить дополнительные измерения
особого смысла нет. Окончательно результат измерений может быть представлен
в виде (см. также правила округления
результатов измерений в п. 4.3.2)
d=386±6мкм,εd=1,5%.
Заметим, что поскольку случайная погрешность и погрешность
прибора здесь имеют один порядок величины, наблюдаемый случайный разброс
данных может быть связан как с неоднородностью сечения проволоки,
так и с дефектами микрометра (например, с неровностями зажимов, люфтом
винта, сухим трением, деформацией проволоки под действием микрометра
и т. п.). Для ответа на вопрос, что именно вызвало разброс, требуются
дополнительные исследования, желательно с использованием более точных
приборов.
Пример. Измерение скорости
полёта пули было осуществлено с погрешностью δv=±1 м/c.
Результаты измерений для n=6 выстрелов представлены в таблице:
Усреднённый результат ⟨v⟩=162,0м/с,
среднеквадратичное отклонение σv=13,8м/c, случайная
ошибка для средней скорости
σv¯=σv/6=5,6м/с.
Поскольку разброс экспериментальных данных существенно превышает погрешность
каждого измерения, σv≫δv, он почти наверняка связан
с реальным различием скоростей пули в разных выстрелах, а не с ошибками
измерений. В качестве результата эксперимента представляют интерес
как среднее значение скоростей ⟨v⟩=162±6м/с
(ε≈4%), так и значение σv≈14м/с,
характеризующее разброс значений скоростей от выстрела к выстрелу.
Малая инструментальная погрешность в принципе позволяет более точно
измерить среднее и дисперсию, и исследовать закон распределения выстрелов
по скоростям более детально — для этого требуется набрать
бо́льшую статистику по выстрелам.
Пример. Измерение скорости
полёта пули было осуществлено с погрешностью δv=10 м/c. Результаты
измерений для n=6 выстрелов представлены в таблице:
Усреднённый результат ⟨v⟩=163,3м/с,
σv=12,1м/c, σ⟨v⟩=5м/с,
σполн≈11,2м/с. Инструментальная
погрешность каждого измерения превышает разброс данных, поэтому в
этом опыте затруднительно сделать вывод о различии скоростей от выстрела
к выстрелу. Результат измерений скорости пули:
⟨v⟩=163±11м/с,
ε≈7%. Проводить дополнительные выстрелы при такой
большой инструментальной погрешности особого смысла нет —
лучше поработать над точностью приборов и методикой измерений.
2.6 Обработка косвенных измерений
Косвенными называют измерения, полученные в результате расчётов,
использующих результаты прямых (то есть «непосредственных»)
измерений физических величин. Сформулируем основные правила пересчёта
погрешностей при косвенных измерениях.
2.6.1 Случай одной переменной
Пусть в эксперименте измеряется величина x, а её «наилучшее»
(в некотором смысле) значение равно x⋆ и оно известно с
погрешностью σx. После чего с помощью известной функции
вычисляется величина y=f(x).
В качестве «наилучшего» приближения для y используем значение функции
при «наилучшем» x:
Найдём величину погрешности σy. Обозначая отклонение измеряемой
величины как Δx=x-x⋆, и пользуясь определением производной,
при условии, что функция y(x) — гладкая
вблизи x≈x⋆, запишем
где f′≡dydx — производная фукнции f(x), взятая в точке
x⋆. Возведём полученное в квадрат, проведём усреднение
(σy2=⟨Δy2⟩,
σx2=⟨Δx2⟩), и затем снова извлечём
корень. В результате получим
Пример. Для степенной функции
y=Axn имеем σy=nAxn-1σx, откуда
σyy=nσxx,или εy=nεx,
то есть относительная погрешность степенной функции возрастает пропорционально
показателю степени n.
Пример. Для y=1/x имеем ε1/x=εx
— при обращении величины сохраняется её относительная
погрешность.
Упражнение. Найдите погрешность логарифма y=lnx, если известны x
и σx.
Упражнение. Найдите погрешность показательной функции y=ax,
если известны x и σx. Коэффициент a задан точно.
2.6.2 Случай многих переменных
Пусть величина u вычисляется по измеренным значениям нескольких
различных независимых физических величин x, y, …
на основе известного закона u=f(x,y,…). В качестве
наилучшего значения можно по-прежнему взять значение функции f
при наилучших значениях измеряемых параметров:
Для нахождения погрешности σu воспользуемся свойством,
известным из математического анализа, — малые приращения гладких
функции многих переменных складываются линейно, то есть справедлив
принцип суперпозиции малых приращений:
где символом fx′≡∂f∂x обозначена
частная производная функции f по переменной x —
то есть обычная производная f по x, взятая при условии, что
все остальные аргументы (кроме x) считаются постоянными параметрами.
Тогда пользуясь формулой для нахождения дисперсии суммы независимых
величин (2.7), получим соотношение, позволяющее вычислять
погрешности косвенных измерений для произвольной функции
u=f(x,y,…):
| σu2=fx′2σx2+fy′2σy2+… | (2.11) |
Это и есть искомая общая формула пересчёта погрешностей при косвенных
измерениях.
Отметим, что формулы (2.10) и (2.11) применимы
только если относительные отклонения всех величин малы
(εx,εy,…≪1),
а измерения проводятся вдали от особых точек функции f (производные
fx′, fy′ … не должны обращаться в бесконечность).
Также подчеркнём, что все полученные здесь формулы справедливы только
для независимых переменных x, y, …
Остановимся на некоторых важных частных случаях формулы
(2.11).
Пример. Для суммы (или разности) u=∑i=1naixi имеем
σu2=∑i=1nai2σxi2.
(2.12)
Пример. Найдём погрешность степенной функции:
u=xα⋅yβ⋅…. Тогда нетрудно получить,
что
σu2u2=α2σx2x2+β2σy2y2+…
или через относительные погрешности
εu2=α2εx2+β2εy2+…
(2.13)
Пример. Вычислим погрешность произведения и частного: u=xy или u=x/y.
Тогда в обоих случаях имеем
εu2=εx2+εy2,
(2.14)
то есть при умножении или делении относительные погрешности складываются
квадратично.
Пример. Рассмотрим несколько более сложный случай: нахождение угла по его тангенсу
u=arctgyx.
В таком случае, пользуясь тем, что (arctgz)′=11+z2,
где z=y/x, и используя производную сложной функции, находим
ux′=uz′zx′=-yx2+y2,
uy′=uz′zy′=xx2+y2, и наконец
σu2=y2σx2+x2σy2(x2+y2)2.
Упражнение. Найти погрешность вычисления гипотенузы z=x2+y2
прямоугольного треугольника по измеренным катетам x и y.
По итогам данного раздела можно дать следующие практические рекомендации.
-
•
Как правило, нет смысла увеличивать точность измерения какой-то одной
величины, если другие величины, используемые в расчётах, остаются
измеренными относительно грубо — всё равно итоговая погрешность
скорее всего будет определяться самым неточным измерением. Поэтому
все измерения имеет смысл проводить примерно с одной и той же
относительной погрешностью. -
•
При этом, как следует из (2.13), особое внимание
следует уделять измерению величин, возводимых при расчётах в степени
с большими показателями. А при сложных функциональных зависимостях
имеет смысл детально проанализировать структуру формулы
(2.11):
если вклад от некоторой величины в общую погрешность мал, нет смысла
гнаться за высокой точностью её измерения, и наоборот, точность некоторых
измерений может оказаться критически важной. -
•
Следует избегать измерения малых величин как разности двух близких
значений (например, толщины стенки цилиндра как разности внутреннего
и внешнего радиусов): если u=x-y, то абсолютная погрешность
σu=σx2+σy2
меняется мало, однако относительная погрешность
εu=σux-y
может оказаться неприемлемо большой, если x≈y.
Систематическая погрешность (или, на физическом жаргоне, систематика) характеризует неточность измерительного инструмента или метода обработки данных. Если точнее, то она показывает наше ограниченное знание этой неточности: ведь если инструмент «врет», но мы хорошо знаем, насколько именно, то мы сможем скорректировать его показания и устранить инструментальную неопределенность результата. Слово «систематическая» означает, что вы можете повторять какое-то измерение на этой установке миллионы раз, но если у нее «сбит прицел», то вы систематически будете получать значение, отличающееся от истинного.
Конечно, систематические погрешности хочется взять под контроль. Поскольку это чисто инструментальный эффект, ответственность за это целиком лежит на экспериментаторах, собиравших, настраивавших и работающих на этой установке. Они прилагают все усилия для того, чтобы, во-первых, корректно определить эти погрешности, а во-вторых, их минимизировать. Собственно, они этим начинают заниматься с самых первых дней работы установки, даже когда еще собственно научная программа исследований и не началась.
Возможные источники систематических погрешностей
Современный коллайдерный эксперимент очень сложен. В нём есть место огромному количеству источников систематических погрешностей на самых разных стадиях получения экспериментального результата. Вот некоторые из них.
Погрешности могут возникать на уровне «железа», при получении сырых данных:
- дефектные или неработающие отдельные регистрирующие компоненты или считывающие элементы. В детекторе миллионы отдельных компонентов, и даже если 1% из них оказался дефектным, это может ухудшить «зоркость» детектора и четкость регистрации сигналов. Надо подчеркнуть, что, даже если при запуске детектор работает на все 100%, постоянное детектирование частиц (это же жесткая радиация!) с течением времени выводит из строя отдельные компоненты, так что следить за поведением детектора абсолютно необходимо;
- наличие «слепых зон» детектора; например, если частица вылетает близко к оси пучков, то она улетит в трубу и детектор ее просто не заметит.
Погрешности могут возникать на этапе распознавания сырых данных и их превращение в физическое событие:
- погрешность при измерении энергии частиц в калориметре;
- погрешность при измерении траектории частиц в трековых детекторах, из-за которой неточно измеряется точка вылета и импульс частицы;
- неправильная идентификация типа частицы (например, система неудачно распознала след от π-мезона и приняла его за K-мезон). Более тонкий вариант: неправильное объединение адронов в одну адронную струю и неправильная оценка ее энергии;
- неправильный подсчет числа частиц (две частицы случайно вылетели так близко друг к другу, что детектор «увидел» только один след и посчитал их за одну).
Наконец, новые систематические погрешности добавляются на этапе позднего анализа события:
- неточность в измерении светимости пучков, которая влияет на пересчет числа событий в сечение процесса;
- наличие посторонних процессов рождения частиц, которые отличаются с физической точки зрения, но, к сожалению, выглядят для детектора одинаковыми. Такие процессы порождают неустранимый фон, который часто мешает разглядеть искомый эффект;
- необходимость моделировать процессы (в особенности, адронизацию, превращение кварков в адроны), опираясь частично на теорию, частично на прошлые эксперименты. Несовершенство того и другого привносит неточности и в новый экспериментальный результат. По этой причине теоретическую погрешность тоже часто относят к систематике.
В отдельных случаях встречаются источники систематических погрешностей, которые умудряются попасть сразу во все категории, они совмещают в себе и свойства детекторного «железа», и методы обработки и интерпретации данных. Например, если вы хотите сравнить друг с другом количество рожденных частиц и античастиц какого-то сорта (например, мюонов и антимюонов), то вам не стоит забывать, что ваш детектор состоит из вещества, а не из антивещества! Этот «перекос» в сторону вещества может привести к тому, что детектор будет видеть мюонов меньше, чем антимюонов, подробности см. в заметке Немножко про CP-нарушение, или Как жаль, что у нас нет детекторов из антивещества!.
Всю эту прорву источников потенциальных проблем надо распознать и оценить их влияние на выполняемый анализ. Здесь никаких абсолютно универсальных алгоритмов нет; исследователь должен сам понять, на какие погрешности надо обращать внимание и как грамотно их оценить. Конечно, тут на помощь приходят разные калибровочные измерения, выполненные в первые год-два работы детектора, и программы моделирования, которые позволяют виртуально протестировать поведение детектора в тех или иных условиях. Но главным в этом искусстве всё же является физическое чутье экспериментатора, его квалификация и накопленный опыт.
Почему важна грамотная оценка систематики
Беспечная оценка систематических погрешностей может привести к двум крайностям, причем обе очень нежелательны.
Заниженная погрешность — то есть неоправданная уверенность экспериментатора в том, что погрешности в его детекторе маленькие, хотя они на самом деле намного больше, — исключительно опасна, поскольку она может привести к совершенно неправильным научным выводам. Например, экспериментатор может на их основании решить, что измерения отличаются от теоретических предсказаний на уровне статистической значимости 10 стандартных отклонений (сенсация!), хотя истинная причина расхождения может просто состоять в том, что он проглядел источник ошибок, в 10 раз увеличивающий неопределенность измерения, и никакого расхождения на самом деле нет.
В борьбе с этой опасностью есть соблазн впасть в другую крайность: «А вдруг там есть еще какие-то погрешности? Может, я что-то не учел? Давай-ка я на всякий случай увеличу погрешности измерения в 10 раз для пущей безопасности.» Такая крайность плоха тем, что она обессмысливает измерение. Неоправданно завышая погрешность, вы рискуете получить результат, который будет, конечно, правильным, но очень неопределенным, ничем не лучше тех результатов, которые уже были получены до вас на гораздо более скромных установках. Такой подход, фактически, перечеркивает всю работу по разработке технологий, по изготовлению компонентов, по сборке детектора, все затраты на его работу и на анализ результатов.
Грамотный и ответственный анализ систематики должен удерживать оптимальный баланс (максимальная достоверность при максимальной научной ценности), не допуская таких крайностей. Это очень тонкая и сложная работа, и первые страницы в большинстве современных экспериментальных статей по физике частиц посвящены тщательному обсуждению систематических (а также статистических) погрешностей.
Мы не будем обсуждать подробности того, как обсчитывать систематические погрешности. Подчеркнем только, что это серьезная наука с множеством тонкостей и подводных камней. В качестве примера умеренно простого обсуждения некоторых вопросов см. статью Systematic Errors: facts and fictions.
Систематические погрешности при повторных измерениях остаются постоянными или изменяются по определенному закону.
Когда судят о погрешности, подразумевают не значение, а интервал значений, в котором с заданной вероятностью находится истинное значение. Поэтому говорят об оценке погрешности. Если бы погрешность оказалась измеренной, т.е. стали бы известны её знак и значение, то её можно было бы исключить из действительного значения измеряемой физической величины и получить истинное значение.
Для получения результатов, минимально отличающихся от истинного значения измеряемой физической величины, проводят многократные наблюдения и проводят математическую обработку полученного массива с целью определения и минимизации случайной составляющей погрешности.
Минимизация систематической погрешности в процессе наблюдений выполняется следующими методами: метод замещения (состоит в замещении измеряемой величины мерой), метод противопоставления (состоит в двух поочерёдных измерениях при замене местами меры и измеряемого объекта), метод компенсации погрешности по знаку (состоит в двух поочерёдных измерениях, при которых влияющая величина становится противоположной).
При многократных наблюдениях возможно апостериорное (после выполнения наблюдений) исключение систематической погрешности в результате анализа рядов наблюдений. Рассмотрим графический анализ. При этом результаты последовательных наблюдений представляются функцией времени либо ранжируются в порядке возрастания погрешности.
Рассмотрим временную зависимость. Будем проводить наблюдения через одинаковые интервалы времени. Результаты последовательных наблюдений являются случайной функцией времени. В серии экспериментов, состоящих из ряда последовательных наблюдений, получаем одну реализацию этой функции. При повторении серии получаем новую реализацию, отличающуюся от первой.
Реализации отличаются преимущественно из-за влияния факторов, определяющих случайную погрешность, а факторы, определяющие систематическую погрешность, одинаково проявляются для соответствующих моментов времени в каждой реализации. Значение, соответствующее каждому моменту времени, называется сечением случайной функции времени. Для каждого сечения можно найти среднее по всем реализациям значение. Очевидно, что эта составляющая и определяет систематическую погрешность. Если через значения систематической погрешности для всех моментов времени провести плавную кривую, то она будет характеризовать временную закономерность изменения погрешности. Зная закономерность изменения, можем определить поправку для исключения систематической погрешности. После исключения систематической погрешности получаем «исправленный ряд результатов наблюдений».
Известен ряд способов исключения систематических погрешностей, которые условно можно разделить па 4 основные группы:
- устранение источников погрешностей до начала измерений;
- исключение почетностей в процессе измерения способами замещения, компенсации погрешностей по знаку, противопоставления, симметричных наблюдений;
- внесение известных поправок в результат измерения (исключение погрешностей начислением);
- оценка границ систематических погрешностей, если их нельзя исключить.
По характеру проявления систематические погрешности подразделяют на постоянные, прогрессивные и периодические.
Постоянные систематические погрешности сохраняют свое значение в течение всего времени измерений (например, погрешность в градуировке шкалы прибора переносится на все результаты измерений).
Прогрессивные погрешности – погрешности, которые в процессе измерении подрастают или убывают (например, погрешности, возникающие вследствие износа контактирующих деталей средств измерения).
И группу систематических погрешностей можно отнести: инструментальные погрешности; погрешности из-за неправильной установки измерительного устройства; погрешности, возникающие вследствие внешних влияний; погрешности метода измерения (теоретические погрешности); субъективные погрешности.