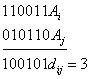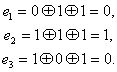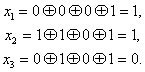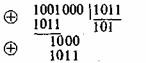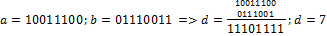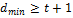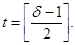Число обнаруживаемых или исправляемых ошибок.
При применении двоичных кодов учитывают
только дискретные искажения, при которых
единица переходит в нуль (1 → 0) или нуль
переходит в единицу (0 → 1). Переход 1 →
0 или 0 → 1 только в одном элементе кодовой
комбинации называют единичной ошибкой
(единичным искажением). В общем случае
под кратностью ошибки подразумевают
число позиций кодовой комбинации, на
которых под действием помехи одни
символы оказались заменёнными на другие.
Возможны двукратные (t= 2) и многократные (t> 2) искажения элементов в кодовой
комбинации в пределах 0 <t<n.
Минимальное кодовое расстояние является
основным параметром, характеризующим
корректирующие способности данного
кода. Если код используется только для
обнаружения ошибок кратностью t0,
то необходимо и достаточно, чтобы
минимальное кодовое расстояние было
равно
dmin
> t0
+ 1. (13.10)
В этом случае никакая комбинация из t0ошибок не может перевести одну разрешённую
кодовую комбинацию в другую разрешённую.
Таким образом, условие обнаружения всех
ошибок кратностьюt0можно записать в виде:
t0≤ dmin — 1. (13.11)
Чтобы можно было исправить все ошибки
кратностью tии менее, необходимо иметь минимальное
расстояние, удовлетворяющее условию:
. (13.12)
В этом случае любая кодовая комбинация
с числом ошибок tиотличается от каждой разрешённой
комбинации не менее чем вtи+ 1 позициях. Если условие (13.12) не выполнено,
возможен случай, когда ошибки кратностиtисказят переданную
комбинацию так, что она станет ближе к
одной из разрешённых комбинаций, чем к
переданной или даже перейдёт в другую
разрешённую комбинацию. В соответствии
с этим, условие исправления всех ошибок
кратностью не болееtиможно записать в виде:
tи
≤(dmin
— 1) / 2 . (13.13)
Из (13.10) и (13.12) следует, что если код
исправляет все ошибки кратностью tи,
то число ошибок, которые он может
обнаружить, равноt0= 2∙tи. Следует
отметить, что соотношения (13.10) и (13.12)
устанавливают лишь гарантированное
минимальное число обнаруживаемых или
исправляемых ошибок при заданномdminи не ограничивают возможность обнаружения
ошибок большей кратности. Например,
простейший код с проверкой на чётность
сdmin= 2 позволяет обнаруживать не только
одиночные ошибки, но и любое нечётное
число ошибок в пределахt0<n.
Корректирующие возможности кодов.
Вопрос о минимально необходимой
избыточности, при которой код обладает
нужными корректирующими свойствами,
является одним из важнейших в теории
кодирования. Этот вопрос до сих пор не
получил полного решения. В настоящее
время получен лишь ряд верхних и нижних
оценок (границ), которые устанавливают
связь между максимально возможным
минимальным расстоянием корректирующего
кода и его избыточностью.
Так, граница Плоткинадаёт верхнюю
границу кодового расстоянияdminпри заданном числе разрядовnв
кодовой комбинации и числе информационных
разрядовm, и для
двоичных кодов:
(13.14)
или
при
. (13.15)
Верхняя граница Хеммингаустанавливает
максимально возможное число разрешённых
кодовых комбинаций (2m)
любого помехоустойчивого кода при
заданных значенияхnиdmin:

где
—
число сочетаний изnэлементов поiэлементам.
Отсюда можно получить выражение для
оценки числа проверочных символов:

Для значений (dmin/n)
≤ 0,3 разница между границей Хемминга и
границей Плоткина сравнительно невелика.
Граница Варшамова-Гильбертадля
больших значенийnопределяет нижнюю
границу для числа проверочных разрядов,
необходимого для обеспечения заданного
кодового расстояния:

Отметим, что для некоторых частных
случаев Хемминг получил простые
соотношения, позволяющие определить
необходимое число проверочных символов:
дляdmin= 3,
дляdmin= 4.
Блочные коды с dmin= 3 и 4 в литературе обычно называют кодами
Хемминга.
Все приведенные выше оценки дают
представление о верхней границе числаdminпри фиксированных значенияхnиmили оценку снизу числа проверочных
символовkпри заданныхmиdmin.
Существующие методы построения избыточных
кодов решают в основном задачу нахождения
такого алгоритма кодирования и
декодирования, который позволял бы
наиболее просто построить и реализовать
код с заданным значением dmin.
Поэтому различные корректирующие коды
при одинаковыхdminсравниваются по сложности кодирующего
и декодирующего устройств. Этот критерий
является в ряде случаев определяющим
при выборе того или иного кода.
Соседние файлы в папке ЛБ_3
- #
- #
14.04.2015937 б75KodHemmig.m
- #
14.04.20150 б67ЛБ_3.exe
Число обнаруживаемых или исправляемых ошибок.
При применении двоичных кодов учитывают
только дискретные искажения, при которых
единица переходит в нуль (1 → 0) или нуль
переходит в единицу (0 → 1). Переход 1 →
0 или 0 → 1 только в одном элементе кодовой
комбинации называют единичной ошибкой
(единичным искажением). В общем случае
под кратностью ошибки подразумевают
число позиций кодовой комбинации, на
которых под действием помехи одни
символы оказались заменёнными на другие.
Возможны двукратные (t= 2) и многократные (t> 2) искажения элементов в кодовой
комбинации в пределах 0 <t<n.
Минимальное кодовое расстояние является
основным параметром, характеризующим
корректирующие способности данного
кода. Если код используется только для
обнаружения ошибок кратностью t0,
то необходимо и достаточно, чтобы
минимальное кодовое расстояние было
равно
dmin
> t0
+ 1. (13.10)
В этом случае никакая комбинация из t0ошибок не может перевести одну разрешённую
кодовую комбинацию в другую разрешённую.
Таким образом, условие обнаружения всех
ошибок кратностьюt0можно записать в виде:
t0≤ dmin — 1. (13.11)
Чтобы можно было исправить все ошибки
кратностью tии менее, необходимо иметь минимальное
расстояние, удовлетворяющее условию:
. (13.12)
В этом случае любая кодовая комбинация
с числом ошибок tиотличается от каждой разрешённой
комбинации не менее чем вtи+ 1 позициях. Если условие (13.12) не выполнено,
возможен случай, когда ошибки кратностиtисказят переданную
комбинацию так, что она станет ближе к
одной из разрешённых комбинаций, чем к
переданной или даже перейдёт в другую
разрешённую комбинацию. В соответствии
с этим, условие исправления всех ошибок
кратностью не болееtиможно записать в виде:
tи
≤(dmin
— 1) / 2 . (13.13)
Из (13.10) и (13.12) следует, что если код
исправляет все ошибки кратностью tи,
то число ошибок, которые он может
обнаружить, равноt0= 2∙tи. Следует
отметить, что соотношения (13.10) и (13.12)
устанавливают лишь гарантированное
минимальное число обнаруживаемых или
исправляемых ошибок при заданномdminи не ограничивают возможность обнаружения
ошибок большей кратности. Например,
простейший код с проверкой на чётность
сdmin= 2 позволяет обнаруживать не только
одиночные ошибки, но и любое нечётное
число ошибок в пределахt0<n.
Корректирующие возможности кодов.
Вопрос о минимально необходимой
избыточности, при которой код обладает
нужными корректирующими свойствами,
является одним из важнейших в теории
кодирования. Этот вопрос до сих пор не
получил полного решения. В настоящее
время получен лишь ряд верхних и нижних
оценок (границ), которые устанавливают
связь между максимально возможным
минимальным расстоянием корректирующего
кода и его избыточностью.
Так, граница Плоткинадаёт верхнюю
границу кодового расстоянияdminпри заданном числе разрядовnв
кодовой комбинации и числе информационных
разрядовm, и для
двоичных кодов:
(13.14)
или
при
. (13.15)
Верхняя граница Хеммингаустанавливает
максимально возможное число разрешённых
кодовых комбинаций (2m)
любого помехоустойчивого кода при
заданных значенияхnиdmin:

где
—
число сочетаний изnэлементов поiэлементам.
Отсюда можно получить выражение для
оценки числа проверочных символов:

Для значений (dmin/n)
≤ 0,3 разница между границей Хемминга и
границей Плоткина сравнительно невелика.
Граница Варшамова-Гильбертадля
больших значенийnопределяет нижнюю
границу для числа проверочных разрядов,
необходимого для обеспечения заданного
кодового расстояния:

Отметим, что для некоторых частных
случаев Хемминг получил простые
соотношения, позволяющие определить
необходимое число проверочных символов:
дляdmin= 3,
дляdmin= 4.
Блочные коды с dmin= 3 и 4 в литературе обычно называют кодами
Хемминга.
Все приведенные выше оценки дают
представление о верхней границе числаdminпри фиксированных значенияхnиmили оценку снизу числа проверочных
символовkпри заданныхmиdmin.
Существующие методы построения избыточных
кодов решают в основном задачу нахождения
такого алгоритма кодирования и
декодирования, который позволял бы
наиболее просто построить и реализовать
код с заданным значением dmin.
Поэтому различные корректирующие коды
при одинаковыхdminсравниваются по сложности кодирующего
и декодирующего устройств. Этот критерий
является в ряде случаев определяющим
при выборе того или иного кода.
Соседние файлы в папке ЛБ_3
- #
- #
14.04.2015937 б70KodHemmig.m
- #
14.04.20150 б62ЛБ_3.exe
Оценка корректирующей способности блокового (n, k) кода
Кодовое (хемминговое) расстояние — число несовпадающих разрядов двух кодовых комбинаций.
Минимальное кодовое расстояние (d) — минимальное расстояние, взятое по всем парам разрешенных кодовых комбинаций.
Кратность ошибки (r) — число искаженных символов кодовой комбинации.
Вес кодовой комбинации — число единиц в двоичной кодовой комбинации.
Вектор ошибки — двоичный код, содержащий 1 в искаженных и 0 в остальных разрядах.
Доля обнаруживаемых ошибок 2k(2n-2k)/(2k2n) = 1 — 2k—n
Число кодовых комбинаций: любых 2n , разрешенных 2к, запрещенных 2n — 2k .

Рекомендуемые материалы
Доля исправляемых ошибок среди обнаруживаемых 2k(2n—k-1)/2k(2n-2k)=2—k. Запрещенную кодовую комбинацию заменяют ближайшей разрешенной комбинацией. Ближайшими к разрешенной комбинации являются 2n-k-1 запрещенных кодовых комбинаций. Ошибка будет исправлена, если принятая запрещенная комбинация окажется «ближайшей» к переданной разрешенной комбинации. Число таких случаев 2k(2n-k-1).

Вместе с этой лекцией читают «3.6 Точечные случайные процессы. Формула Ито для считающих процессов. Компенсаторы».
d ³ r + 1 для обнаружения ошибки кратности r,
d ³ 2s + 1 для исправления ошибки кратности s,
d ³ r + s + 1 (r ³ s) для обнаружения и одновременного исправления ошибок кратности r и s.
Для исправления ошибки контрольная кодовая комбинация должна указывать место ошибки. Следовательно, число различных контрольных кодовых комбинаций должно быть не менее количества различных ошибок.. Число ошибок кратности r равно числу сочетаний Сnr . При s = 1 (исправление ошибки кратности 1) должно выполняться условие 2n—k-1 > Cn1 = n, при s = 2 — условие 2n—k-1 > Cn1+ Cn2, в общем случае – условие
Эта оценка Хемминга определяет минимальную избыточность, необходимую для исправления ошибок. Коды с минимальной избыточностью, для которых неравенство превращается в равенство, называются совершенными.
Содержание
- 1 Исправление ошибок в помехоустойчивом кодировании
- 2 Параметры помехоустойчивого кодирования
- 3 Контроль чётности
- 4 Классификация помехоустойчивых кодов
- 5 Код Хэмминга
- 5.1 Декодирование кода Хэмминга
- 5.2 Расстояние Хэмминга
- 6 Помехоустойчивые коды
- 6.1 Компромиссы при использовании помехоустойчивых кодов
- 6.2 Необходимость чередования (перемежения)
Назначение помехоустойчивого кодирования – защита информации от помех и ошибок при передаче и хранении информации. Помехоустойчивое кодирование необходимо для устранения ошибок, которые возникают в процессе передачи, хранения информации. При передачи информации по каналу связи возникают помехи, ошибки и небольшая часть информации теряется.
Без использования помехоустойчивого кодирования было бы невозможно передавать большие объемы информации (файлы), т.к. в любой системе передачи и хранении информации неизбежно возникают ошибки.
Рассмотрим пример CD диска. Там информация хранится прямо на поверхности диска, в углублениях, из-за того, что все дорожки на поверхности, часто диск хватаем пальцами, елозим по столу и из-за этого без помехоустойчивого кодирования, информацию извлечь не получится.
Использование кодирования позволяет извлекать информацию без потерь даже с поврежденного CD/DVD диска, когда какая либо область становится недоступной для считывания.
В зависимости от того, используется в системе обнаружение или исправление ошибок с помощью помехоустойчивого кода, различают следующие варианты:
- запрос повторной передачи (Automatic Repeat reQuest, ARQ): с помощью помехоустойчивого кода выполняется только обнаружение ошибок, при их наличии производится запрос на повторную передачу пакета данных;
- прямое исправление ошибок (Forward Error Correction, FEC): производится декодирование помехоустойчивого кода, т. е. исправление ошибок с его помощью.
Возможен также гибридный вариант, чтобы лишний раз не гонять информацию по каналу связи, например получили пакет информации, попробовали его исправить, и если не смогли исправить, тогда отправляется запрос на повторную передачу.
Исправление ошибок в помехоустойчивом кодировании
Любое помехоустойчивое кодирование добавляет избыточность, за счет чего и появляется возможность восстановить информацию при частичной потере данных в канале связи (носителе информации при хранении). В случае эффективного кодирования убирали избыточность, а в помехоустойчивом кодировании добавляется контролируемая избыточность.
Простейший пример – мажоритарный метод, он же многократная передача, в котором один символ передается многократно, а на приемной стороне принимается решение о том символе, количество которых больше.
Допустим есть 4 символа информации, А, B, С,D, и эту информацию повторяем несколько раз. В процессе передачи информации по каналу связи, где-то возникла ошибка. Есть три пакета (A1B1C1D1|A2B2C2D2|A3B3C3D3), которые должны нести одну и ту же информацию.
Но из картинки справа, видно, что второй символ (B1 и C1) они отличаются друг от друга, хотя должны были быть одинаковыми. То что они отличаются, говорит о том, что есть ошибка.
Необходимо найти ошибку с помощью голосования, каких символов больше, символов В или символов С? Явно символов В больше, чем символов С, соответственно принимаем решение, что передавался символ В, а символ С ошибочный.
Для исправления ошибок нужно, как минимум 3 пакета информации, для обнаружения, как минимум 2 пакета информации.
Параметры помехоустойчивого кодирования
Первый параметр, скорость кода R характеризует долю информационных («полезных») данных в сообщении и определяется выражением: R=k/n=k/m+k
- где n – количество символов закодированного сообщения (результата кодирования);
- m – количество проверочных символов, добавляемых при кодировании;
- k – количество информационных символов.
Параметры n и k часто приводят вместе с наименованием кода для его однозначной идентификации. Например, код Хэмминга (7,4) значит, что на вход кодера приходит 4 символа, на выходе 7 символов, Рида-Соломона (15, 11) и т.д.
Второй параметр, кратность обнаруживаемых ошибок – количество ошибочных символов, которые код может обнаружить.
Третий параметр, кратность исправляемых ошибок – количество ошибочных символов, которые код может исправить (обозначается буквой t).
Контроль чётности
Самый простой метод помехоустойчивого кодирования это добавление одного бита четности. Есть некое информационное сообщение, состоящее из 8 бит, добавим девятый бит.
Если нечетное количество единиц, добавляем 0.
1 0 1 0 0 1 0 0 | 0
Если четное количество единиц, добавляем 1.
1 1 0 1 0 1 0 0 | 1
Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.
1 1 0 0 0 1 0 0 | 1
Под кратностью понимается, всевозможные ошибки, которые можно обнаружить. В этом случае, кратность исправляемых ошибок 0, так как мы не можем исправить ошибки, а кратность обнаруживаемых 1.
Есть последовательность 0 и 1, и из этой последовательности составим прямоугольную матрицу размера 4 на 4. Затем для каждой строки и столбца посчитаем бит четности.
Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:
И если в процессе передачи информации допустим ошибку (ошибка нолик вместо единицы, желтым цветом), начинаем делать проверку. Нашли ошибку во втором столбце, третьей строке по координатам. Чтобы исправить ошибку, просто инвертируем 1 в 0, тем самым ошибка исправляется.
Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные.
Рассчитаем скорость кода для:
- 1 1 0 0 0 1 0 0 | 1
Здесь R=8/9=0,88
- И для прямоугольного кода:
Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)
Более эффективный с точки зрения скорости является первый вариант, но зато мы не можем с помощью него исправлять ошибки, а с помощью прямоугольного кода можно. Сейчас на практике прямоугольный код не используется, но логика работы многих помехоустойчивых кодов основана именно на прямоугольном коде.
Классификация помехоустойчивых кодов
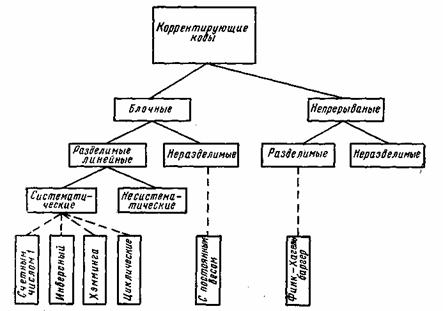
- Непрерывные — процесс кодирования и декодирования носит непрерывный характер. Сверточный код является частным случаем непрерывного кода. На вход кодера поступил один символ, соответственно, появилось несколько на выходе, т.е. на каждый входной символ формируется несколько выходных, так как добавляется избыточность.
- Блочные (Блоковые) — процесс кодирования и декодирования осуществляется по блокам. С точки зрения понимания работы, блочный код проще, разбиваем код на блоки и каждый блок кодируется в отдельности.
По используемому алфавиту:
- Двоичные. Оперируют битами.
- Не двоичные (код Рида-Соломона). Оперируют более размерными символами. Если изначально информация двоичная, нужно эти биты превратить в символы. Например, есть последовательность 110 110 010 100 и нужно их преобразовать из двоичных символов в не двоичные, берем группы по 3 бита — это будет один символ, 6, 6, 2, 4 — с этими не двоичными символами работают не двоичные помехоустойчивые коды.
Блочные коды делятся на
- Систематические — отдельно не измененные информационные символы, отдельно проверочные символы. Если на входе кодера присутствует блок из k символов, и в процессе кодирования сформировали еще какое-то количество проверочных символов и проверочные символы ставим рядом к информационным в конец или в начало. Выходной блок на выходе кодера будет состоять из информационных символов и проверочных.
- Несистематические — символы исходного сообщения в явном виде не присутствуют. На вход пришел блок k, на выходе получили блок размером n, блок на выходе кодера не будет содержать в себе исходных данных.
В случае систематических кодов, выходной блок в явном виде содержит в себе, то что пришло на вход, а в случае несистематического кода, глядя на выходной блок нельзя понять что было на входе.
Смотря на картинку выше, код 1 1 0 0 0 1 0 0 | 1 является систематическим, на вход поступило 8 бит, а на выходе кодера 9 бит, которые в явном виде содержат в себе 8 бит информационных и один проверочный.
Код Хэмминга
Код Хэмминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Позволяет устранить одну ошибку и находить двойную.
Код Хэмминга (7,4) — 4 бита на входе кодера и 7 на выходе, следовательно 3 проверочных бита. С 1 по 4 информационные биты, с 6 по 7 проверочные (см. табл. выше). Пятый проверочный бит y5, это сумма по модулю два 1-3 информационных бит. Сумма по модулю 2 это вычисление бита чётности.
Декодирование кода Хэмминга
Декодирование происходит через вычисление синдрома по выражениям:
Синдром это сложение бит по модулю два. Если синдром не нулевой, то исправление ошибки происходит по таблице декодирования:
Расстояние Хэмминга
Расстояние Хэмминга — число позиций, в которых соответствующие символы двух кодовых слов одинаковой длины различны. Если рассматривать два кодовых слова, (пример на картинке ниже, 1 0 1 1 0 0 1 и 1 0 0 1 1 0 1) видно что они отличаются друг от друга на два символа, соответственно расстояние Хэмминга равно 2.
Кратность исправляемых ошибок и обнаруживаемых, связано минимальным расстоянием Хэмминга. Любой помехоустойчивый код добавляет избыточность с целью увеличить минимальное расстояние Хэмминга. Именно минимальное расстояние Хэмминга определяет помехоустойчивость.
Помехоустойчивые коды
Современные коды более эффективны по сравнению с рассматриваемыми примерами. В таблице ниже приведены Коды Боуза-Чоудхури-Хоквингема (БЧХ)
Из таблицы видим, что там один класс кода БЧХ, но разные параметры n и k.
- n — количество символов на входе.
- k — количество символов на выходе.
- t — кратность исправляемых ошибок.
- Отношение k/n — скорость кода.
- G (энергетический выигрыш) — величина, показывающая на сколько можно уменьшить отношение сигнал/шум (Eb/No) для обеспечения заданной вероятности ошибки.
Несмотря на то, что скорость кода близка, количество исправляемых ошибок может быть разное. Количество исправляемых ошибок зависит от той избыточности, которую добавим и от размера блока. Чем больше блок, тем больше ошибок он исправляет, даже при той же самой избыточности.
Пример: помехоустойчивые коды и двоичная фазовая манипуляция (2-ФМн). На графике зависимость отношения сигнал шум (Eb/No) от вероятности ошибки. За счет применения помехоустойчивых кодов улучшается помехоустойчивость.
Из графика видим, код Хэмминга (7,4) на сколько увеличилась помехоустойчивость? Всего на пол Дб это мало, если применить код БЧХ (127, 64) выиграем порядка 4 дБ, это хороший показатель.
Компромиссы при использовании помехоустойчивых кодов
Чем расплачиваемся за помехоустойчивые коды? Добавили избыточность, соответственно эту избыточность тоже нужно передавать. Нужно: увеличивать пропускную способность канала связи, либо увеличивать длительность передачи.
Компромисс:
- Достоверность vs полоса пропускания.
- Мощность vs полоса пропускания.
- Скорость передачи данных vs полоса пропускания
Необходимость чередования (перемежения)
Все помехоустойчивые коды могут исправлять только ограниченное количество ошибок t. Однако в реальных системах связи часто возникают ситуации сгруппированных ошибок, когда в течение непродолжительного времени количество ошибок превышает t.
Например, в канале связи шумов мало, все передается хорошо, ошибки возникают редко, но вдруг возникла импульсная помеха или замирания, которые повредили на некоторое время процесс передачи, и потерялся большой кусок информации. В среднем на блок приходится одна, две ошибки, а в нашем примере потерялся целый блок, включая информационные и проверочные биты. Сможет ли помехоустойчивый код исправить такую ошибку? Эта проблема решаема за счет перемежения.
Пример блочного перемежения:
На картинке, всего 5 блоков (с 1 по 25). Код работает исправляя ошибки в рамках одного блока (если в одном блоке 1 ошибка, код его исправит, а если две то нет). В канал связи отдается информация не последовательно, а в перемешку. На выходе кодера сформировались 5 блоков и эти 5 блоков будем отдавать не по очереди а в перемешку. Записали всё по строкам, но считывать будем, чтобы отправлять в канал связи, по столбцам. Информация в блоках перемешалась. В канале связи возникла ошибка и мы потеряли большой кусок. В процессе приема, мы опять составляем таблицу, записываем по столбцам, но считываем по строкам. За счет того, что мы перемешали большое количество блоков между собой, групповая ошибка равномерно распределится по блокам.
Добавил:
Andrew1992
Факультет ИКСС, группа ИКВТ-61
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
vlss16up_motpk.pdf
Скачиваний:
258
Добавлен:
20.11.2018
Размер:
830.71 Кб
Скачать

ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
Федеральное государственное бюджетное образовательное учреждение высшего образования «САНКТ-ПЕТЕРБУРГСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ им. проф. М. А. БОНЧ-БРУЕВИЧА»
С. С. Владимиров
МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ
Учебное пособие
Санкт-Петербург
2016
УДК 621.391(075.8) ББК 32.88173
В 57
Рецензенты профессор кафедры СС и ПД, доктор технических наук О. С. Когновицкий;
ведущий инженер ЗАО «НПП «ИСТА-Системс», кандидат технических наук А. А. Березкин
Утверждено редакционно-издательским советом СПбГУТ в качестве учебного пособия
Владимиров, С. С.
В 57 Математические основы теории помехоустойчивого кодирования : учебное пособие / С. С. Владимиров ; СПбГУТ. — СПб, 2016. — 96 с.
ISBN 978-5-89160-131-4
Настоящее учебное пособие призвано ознакомить студентов старших курсов с математическими основами теории помехоустойчивого кодирования.
Предназначено для студентов, обучающихся по направлениям 11.03.02 «Инфокоммуникационные технологии и системы связи» и 09.03.01 «Информатика и вычислительная техника».
УДК 621.391(075.8) ББК 32.88173
|
ISBN 978-5-89160-131-4 |
c |
|
Владимиров С. С., 2016 |
|
|
c |
|
|
Федеральное государственное бюджетное |
|
|
образовательное учреждение высшего образования |
|
|
«Санкт-Петербургский государственный |
|
|
университет телекоммуникаций |
|
|
им. проф. М. А. Бонч-Бруевича», 2016 |
СОДЕРЖАНИЕ
Предисловие . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
1. Помехоустойчивое кодирование . . . . . . . . . . . . . . . . . 6
1.1.Основные параметры помехоустойчивых кодов. . . . . . . . . . 7
1.2.Классификация помехоустойчивых кодов . . . . . . . . . . . . 8
Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . 10
2. Элементы двоичной алгебры . . . . . . . . . . . . . . . . . . 11
2.1.Понятие системы счисления. Основные системы счисления. . . . 11
2.2.Перевод чисел между системами счисления . . . . . . . . . . . 13
2.3.Операции над двоичными числами . . . . . . . . . . . . . . . . 17
|
Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . |
26 |
|
3. Матрицы и действия над ними . . . . . . . . . . . . . . . . . |
27 |
|
3.1. Понятие матрицы . . . . . . . . . . . . . . . . . . . . . . . . |
27 |
|
3.2. Операции с матрицами . . . . . . . . . . . . . . . . . . . . . |
29 |
|
Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . |
31 |
|
4. Элементы комбинаторики . . . . . . . . . . . . . . . . . . . . |
32 |
|
Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . |
32 |
|
5. Полиномы и действия над ними . . . . . . . . . . . . . . . . . |
33 |
|
5.1. Операции с полиномами . . . . . . . . . . . . . . . . . . . . . |
34 |
|
Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . |
35 |
6. Понятие группы, кольца и поля . . . . . . . . . . . . . . . . . 36 6.1. Группа . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
6.2.Подгруппы и смежные классы . . . . . . . . . . . . . . . . . . 38
6.3.Кольцо . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
6.4.Поле . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . 41
7. Математика полей Галуа . . . . . . . . . . . . . . . . . . . . 42 7.1. Поле Галуа и его свойства . . . . . . . . . . . . . . . . . . . . 42 7.2. Основные действия над элементами поля . . . . . . . . . . . . 47 7.3. Алгоритмы для проведения расчетов в двоичных полях Галуа и их реализации . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . 66
3
8. Элементы теории графов . . . . . . . . . . . . . . . . . . . . 67
8.1.Основные понятия. . . . . . . . . . . . . . . . . . . . . . . . 67
8.2.Матричное представление графа. . . . . . . . . . . . . . . . . 70
8.3.Линейные графы сигналов и передача графа . . . . . . . . . . . 73
Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . 77
9. Модели каналов передачи данных . . . . . . . . . . . . . . . 78
9.1.Параметры моделей каналов ПД . . . . . . . . . . . . . . . . . 79
9.2.Двоичный симметричный канал . . . . . . . . . . . . . . . . . 80
9.3.Двоичный симметричный канал со стираниями. . . . . . . . . . 82
9.4.Двоичный несимметричный канал (Z-канал) . . . . . . . . . . . 83
9.5.Канал Гилберта–Эллиотта. . . . . . . . . . . . . . . . . . . . 84
|
9.6. Модель канала Поля . . . . . . . . . . . . . . . . . . . . . . |
86 |
|
9.7. Канал с аддитивным белым гауссовским шумом . . . . . . . . . |
88 |
|
Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . |
89 |
|
Заключение. . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
90 |
|
Список литературы. . . . . . . . . . . . . . . . . . . . . . . . . |
91 |
4
ПРЕДИСЛОВИЕ
При разработке систем передачи данных одним из важнейших этапов является выбор методов повышения достоверности при передаче информационных сообщений по каналам связи. Использование избыточных помехоустойчивых кодов является одним из наиболее эффективных методов борьбы с ошибками при передаче дискретных сообщений по каналам связи. Соответственно, вопросам изучения теории помехоустойчивого кодирования придается большое внимание в программах подготовки бакалавров и магистров, обучающихся по специальностям из области телекоммуникаций.
В настоящем пособии приведены основы математического аппарата, который используется при изучении теории помехоустойчивого кодирования, исследовании алгоритмов кодирования и декодирования, разработке и построении кодеров и декодеров приемопередающих устройств.
Пособие состоит из девяти разделов. В разд. 1 рассмотрены основные понятия и классификация помехоустойчивых кодов. Разд. 2 посвящен основам двоичной алгебры и реализации основных операций над двоичными числами. В разд. 3 описаны матрицы и основные действия над ними. В разд. 4 приводятся основные понятия комбинаторики. В разд. 5 — полиномы и основные операции с полиномами. Разд. 6 посвящен понятиям группы, кольца и поля, а в разд. 7 описан основной математический аппарат блочных помехоустойчивых кодов (Боуза–Чоудхури–Хоквингема и Рида–Соломона) — двоичные поля Галуа. В разд. 8 приводятся основы теории графов. В разд. 9 рассмотрены основные модели каналов передачи данных.
5
1. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ
Помехоустойчивое кодирование (англ. Error Correcting Coding, ECC) — процесс преобразования информации, предоставляющий возможность обнаружить и исправить ошибки, возникающие при передаче информации по каналам передачи данных.
Под ошибкой при этом понимают ситуацию, когда в результате действия помех и искажений в канале передачи данных приемник принимает неверное решение, отождествляя принятый сигнал не с фактически переданным символом, а с каким-либо другим [1].
Процесс помехоустойчивого кодирования заключается во введении избыточности, т. е. для передачи информации используется код, у которого используются не все возможные комбинации, а только некоторые из них. Такие коды называют избыточными или корректирующими.
Соответственно, процесс введения избыточности (преобразование информационных символов в кодовое слово) называется кодированием, а обратный процесс восстановления информации из кодового слова, возможно содержащего ошибки, — декодированием.
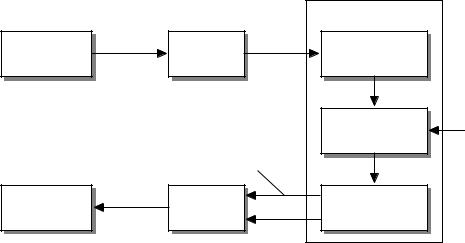
В рамках цифровой системы передачи данных задачи кодирования и декодирования возложены на кодер и декодер соответственно. Структура цифровой системы передачи данных показана на рис. 1.1 [2].
|
Двоичные |
Дискретный канал |
||
|
Источник |
данные |
Модулятор |
|
|
данных |
Кодер |
||
|
S(t) |
|||
|
Информация |
Физический |
Помехи |
|
|
канал |
n(t) |
||
|
о надежности |
ˆ |
||
|
Двоичные |
S(t) |
||
|
Получатель |
данные |
Демодулятор |
|
|
данных |
Декодер |
||
Рис. 1.1. Структура цифровой системы передачи данных
Часто декодеру доступна информация, указывающая на надежность решений, принимаемых о различных символах кодового слова. Такая информация может быть использована для упрощения процесса декодирования, либо для улучшения его характеристик [2].
В целом, способность помехоустойчивых кодов определять и исправлять ошибки — их корректирующие свойства — зависит от правил постро-
6
ения этих кодов и параметров кода (числа разрядов, избыточности и др.), а также от используемых алгоритмов декодирования.
1.1. Основные параметры помехоустойчивых кодов
Основными параметрами, характеризующими корректирующие свойства кодов являются:
1)избыточность кода;
2)кодовое расстояние;
3)кратность гарантированно обнаруживаемых ошибок;
4)кратность гарантированно исправляемых ошибок.
1.1.1.Избыточность корректирующего кода
Избыточность корректирующего кода может быть абсолютной и относительной. Под абсолютной избыточностью понимают число вводимых дополнительных разрядов
r = n k;
где n — число кодовых символов на выходе кодера, соответствующих k информационным символам на его входе.
Относительной избыточностью корректирующего кода называют величину
|
R |
отн |
= |
r |
= |
n k |
= |
k |
: |
|
|
n n |
1 n |
С ней связана так называемая относительная скорость передачи информации или скорость кода, которая показывает, какую часть общего числа символов кодовой комбинации составляют информационные символы.
k = 1 Rотн:
n
Если производительность источника равна H символов в секунду, то скорость передачи после кодирования этой информации будет равна
R = H k : n
1.1.2. Кодовое расстояние
Кодовое расстояние d или расстояние Хемминга характеризует cтепень различия любых двух кодовых комбинаций. Оно выражается числом разрядов, в которых комбинации отличаются одна от другой.
Чтобы получить кодовое расстояние между двумя комбинациями двоичного кода, достаточно подсчитать число единиц в поразрядной сумме этих
7

комбинаций по модулю 2:
10011 11001 = 01010 ) d = 2:
Кодовое расстояние может быть различным. Так, в первичном натуральном безызбыточном коде это расстояние для различных комбинаций может различаться от единицы до n, где n — длина (значность) кода.
Для помехоустойчивого кода наиболее важным является минимальное кодовое расстояние dmin — наименьшее кодовое расстояние из всех между всеми парами кодовых комбинаций.
В безызбыточном коде все комбинации являются разрешенными, dmin = 1. Поэтому искажение хотя бы одного символа в комбинации будет приводить к получению ошибочного сообщения.
1.1.3. Кратности гарантированно обнаруживаемых и гарантированно исправляемых ошибок
Эти параметры напрямую зависят от минимального кодового расстояния. Под кратностью понимается количество поражённых ошибками символов кодовой комбинации.
В общем случае при необходимости обнаруживать ошибки кратности tобн минимальное кодовое расстояние должно быть, по крайней мере, на единицу больше tобн, т. е.
dmin tобн + 1:
Соответственно, кратность гарантированно обнаруживаемых кодом ошибок равна
tобн dmin 1:
Кратность гарантированно исправляемых кодом ошибок вычисляется по формуле
t dmin 1:
2
Таким образом, код, имеющий минимальное кодовое расстояние dmin = 3, позволяет гарантированно обнаружить tобн = 2 и менее ошибок и гарантированно исправить t = 1 ошибку.
1.2. Классификация помехоустойчивых кодов
Помехоустойчивые коды классифицируются по различным признакам. Одной из основных классификаций является деление кодов на блочные и непрерывные.
8
Блочный (блоковый) код является кодом без памяти. Кодер блочного кода отображает подающийся на вход блок информационных символов длиной k в кодовую последовательность из n выходных символов. Термин «без памяти» указывает, что каждый блок из n символов зависит только от соответствующего блока из k символов и не зависит от других блоков [2].
Основыми параметрами блочных кодов являются длина информационного блока k, длина кодового слова n, скорость кода nk и минимальное кодовое расстояние dmin.
Непрерывные или древовидные коды — это помехоустойчивые коды использующие непрерывную, или последовательную, обработку информации короткими фрагментами (блоками). Кодер древовидного кода является устройством с памятью. На его вход поступают наборы из k входных информационных символов, а на выходе появляются наборы из n кодовых символов. Каждый набор n кодовых символов зависит от текущего входного набора и от v предыдущих входных символов. Следовательно кодер должен содержать устройство памяти на m = k + v входных символов. Параметр m часто называют длиной кодового ограничения кода [2].
Также непрерывные коды характеризуются скоростью кода nk и свободным расстоянием dсв [2].
Чаще всего используются линейные древовидные коды, называемые
сверточными.
Особое место в классификации помехоустойчивых кодов занимают каскадные коды и турбо коды, представляющие из себя комбинации блочных и/или непрерывных кодов [3].
Другой подход к классификации делит коды на линейные и нелинейные. Линейные коды образуют векторное пространство, в котором два кодовых слова при сложении по определенному правилу дают в результате третье кодовое слово [2].
Практически все применяемые на практике схемы кодирования основаны на использовании линейных кодов. Двоичные линейные блоковые коды часто называют групповыми кодами, так как их кодовые слова образуют математическую структуру, называемую группа [2].
Нелинейные коды применяются гораздо реже линейных. К нелинейным кодам относится код с контрольным суммированием, в котором проверочные разряды являются записью суммы единиц в кодовой комбинации [1].
По способу кодирования коды делятся на систематические и несистематические. В первом случае информационные символы передаются на выход декодера без изменения и к ним добавляются проверочные символы. В
9
случае несистематического кодирования информационные символы в явном виде в кодовом слове отсутствуют.
Большинство помехоустойчивых кодов может быть использовано как для обнаружения, так и для исправления ошибок, хотя есть коды, которые позволяют лишь обнаруживать ошибки. Поскольку избыточность, требуемая для обнаружения ошибок, меньше избыточности для исправления ошибок, то коды с обнаружением ошибок часто используют в системах с обратной связью [1].
Ещё одним вариантом деления помехоустойчивых кодов является разделение их на коды, исправляющие случайные ошибки, и коды, исправляющие пакеты (пачки) ошибок. Хотя для исправления пачек ошибок было разработано большое количество кодов с хорошими характеристиками, часто оказывается выгодным использовать коды, исправляющие случайные ошибки, совместно с устройствами перемежения/деперемежения [2]. Также стоит отметить, что существуют алгоритмы декодирования, позволяющие использовать коды, рассчитанные на исправление случайных ошибок, для исправления пачек ошибок без использования перемежителей. К таким алгоритмам относится, например, мажоритарное декодирование на основе двойственного базиса [4].
Контрольные вопросы
1.Что такое помехоустойчивое кодирование?
2.Опишите структуру цифровой системы передачи данных.
3.Дайте понятие избыточности корректирующего кода. Что такое абсолютная и относительная избыточности? Как определяется скорость кода?
4.Что такое кодовое расстояние? Как оно определяется?
5.Как рассчитываются кратности гарантированно обнаруживаемых и гарантированно исправляемых ошибок?
6.Приведите классификацию помехоустойчивых кодов.
10
Соседние файлы в предмете Математические Основы Теории Помехоустойчивого Кодирования
- #
20.11.201816.44 Кб10meggit_s_obnulenia.circ
- #
- #
- #
- #
- #
- #
- #
20.11.2018760.56 Кб17Козырев А. Б..odt
Все помехоустойчивые коды делятся на блоковые и непрерывные (их называют также цепные или рекуррентные). При блоковом кодировании данные передаются отдельными блоками (словами, кодовыми комбинациями). При этом поступающие в кодер символы, разбиваются на блоки по k информационных символов. В кодере этот блок информационных символов преобразуется в блок из кодовых символов, где п называется длиной кода. Добавленные при кодировании r = n – k символов являются проверочными. Такой блоковый код принято обозначать как (n, k) – код. Величину R = k / n называют скоростью кода, а величину, обратную скорости, Rи = n / k называют избыточностью кода.
Проверочные символы являются избыточными, они необходимы для обнаружения и (или) исправления ошибок, возникших при передаче. Существуют безызбыточные (примитивные) коды. У этих кодов проверочных символов нет (n = k), поэтому у них самая высокая скорость кода R = 1, но они не способны обнаруживать ошибки.
Ошибки при передаче кодового слова возникают потому, что некоторые из переданных символов могут быть приняты неверно. Принцип обнаружения ошибок заключается в следующем. Если блоковый (n, k) – код имеет основание (количество символов в используемом алфавите) q, то возможно Q = qn различных кодовых слов. Для передачи же используются только Qр = qk кодовых слов, которые называются разрешенными. Остальные Qз = Q – Qр слов априорно для передачи не используются и называются запрещенными.
В дальнейшем будут рассматриваться только двоичные коды, у которых алфавит состоит из двух символов 0 и 1, т. е. с основанием q = 2.
В памяти кодера и декодера хранится таблица разрешенных слов. Работа кодера заключается в выборе разрешенного кодового слова, соответствующего поступившему информационному слову. Приходящее в декодер кодовое слово сравнивается с таблицей разрешенных слов и, если происходит совпадение, то потребитель получает информационное слово, соответствующее данному разрешенному слову. Если же совпадение не наступает, то слово считается запрещенным, а потребитель получает сообщение об ошибке. Однако если совокупность ошибок превратит одно разрешенное слово в другое разрешенное, то возникшие ошибки не могут быть обнаружены.
Пример 1. Требуется передача сообщения о наступлении одного из четырех возможных событий A, B, C, D. Эти события представлены информационными словами 00, 01, 10, 11 соответственно. При передаче этих слов безызбыточным кодом все возможные комбинации являются разрешенными. Поэтому достаточно искажения хотя бы одного символа, чтобы сообщение было принято неверно. Так, если передавалось сообщение A в виде кодового слова 00, а принято было слово 01, то декодер, найдя в таблице такое разрешенное слово, вынесет решение о приеме сообщения B.
Если к вышеперечисленным информационным словам добавить по одному избыточному символу, поставив в соответствие разрешенные слова 000, 011, 101, 110, то искажение одного символа в переданном слове можно обнаружить. Так, если передавалось сообщение A в виде кодового слова 000, а принято было слово 001, то декодер, не найдя в таблице такого разрешенного слова, объявит принятое слово запрещенным и сообщит об обнаружении ошибки в слове. Однако если было принято слово 011, то декодер вынесет решение о приеме сообщения B.
Для сравнения слов необходимо задать метрику, т. е. способ измерения расстояний между кодовыми словами. Известно несколько способов выбора метрики, из которых наиболее распространенным является метрика Хэмминга. Расстоянием Хэмминга между двумя кодовыми словами называется количество несовпадающих символов в этих словах. Важнейшей характеристикой блочного кода является кодовое расстояние – d, оно равно наименьшему расстоянию из всех возможных для данного кода.
Пример 2. Для передачи используются три разрешенных слова 000, 100, 111. Расстояние между первым и вторым словами равно 1, между вторым и третьим словами – 2, а между первым и вторым – 3. Кодовое расстояние для данного кода d = 1.
Очевидно, что у безызбыточного кода d = 1, так как между любой парой его слов расстояние равно единице. Этот код не позволяет обнаруживать ошибки. Приведенный в примере 1 избыточный код (он называется кодом с проверкой на четность) имеет d = 2. Он позволяет гарантировано обнаружить однократную ошибку.
Кратностью ошибки называется количество неправильно принятых символов в кодовом слове. Если искажения символов возникают независимо друг от друга, то ошибки меньшей кратности более вероятны, чем ошибки большей кратности. Следовательно, прежде всего требуется вести борьбу с ошибками малой кратности.
Можно заметить, что максимальная кратность гарантировано обнаруживаемой ошибки tо = d – 1. Действительно, при возникновении необнаруженной ошибки одно разрешенное слово должно превратиться в другое разрешенное слово. А для этого надо, чтобы кратность возникшей ошибки была не менее d, поскольку все разрешенные слова по определению кодового расстояния различаются не менее, чем на d символов. Если же принятое кодовое слово хотя бы на один символ отличается от разрешенных кодовых слов, то будет зафиксировано появление ошибки.
При декодировании вместо обнаружения ошибок возможно их исправление. Так, если было принято запрещенное кодовое слово, то можно не отбрасывать его, а найти наиболее похожее разрешенное слово и объявить его принятым. Таким образом, возникшие при передаче ошибки считаются исправленными, и потребитель получает не сообщение об ошибке, а очередное информационное слово. При декодировании с исправлением ошибок решение принимается по минимуму расстояния Хэмминга, т. е. переданным считается то разрешенное кодовое слово, которое отличается от принятого слова наименьшим количеством несовпадающих символов.
Пример 3. Для передачи используется два разрешенных кодовых слова 000 и 111. Было принято слово 001, на беглый взгляд оно больше похоже на 000, чем на 111. Действительно, слово 001 от первого разрешенного слова отличается на один символ, а от второго на два. Так как однократная ошибка вероятнее двукратной, то скорее всего было передано первое слово и в нем исказился один символ. Декодер принимает решение по минимуму расстояния Хэмминга и объявляет принятым разрешенное слово 000.
В
рассмотренном примере код имеет d = 3, он позволяет гарантировано исправлять однократную ошибку. Можно заметить, что максимальная кратность гарантировано исправляемой ошибки :
где [x] –целая часть числа x.
Существует так называемый прием со стиранием. Это частный случай приема с мягким решением. Его особенность состоит в том, что решающее устройство имеет область неопределенности, в которую попадают все сигналы, не превысившие установленный порог. Решающее устройство выдает при этом специальный символ, заменяющий неуверенно принятый сигнал. Этот символ оказывается, таким образом, «стертым». Так, при передаче двоичным кодом на выходе решающего устройства появляется один из трех символов: 0, 1 и символ стирания Х.
Восстановить стертые знаки часто оказывается легче, чем исправить ошибочные. Это обусловлено тем, что местонахождение стертых знаков известно, так как оно обозначено символом стирания Х, тогда как местоположение ошибок неизвестно, и каждый из знаков 0 или 1 может быть как верным, так и неверным.
Для сохранения различимости кодовых комбинаций при стирании не более s знаков кодовое расстояние d должно удовлетворять условию:
Для того, чтобы код мог одновременно исправлять t ошибок и восстанавливать s стертых символов кодовое расстояние должно быть:
Преимущество кодов со стираниями очевидно: например, при d = 3 такой код может как и обычный исправить одиночную ошибку, но может восстановить два стертых символа.
Описанный выше метод кодирования и декодирования, основанный на запоминании таблицы разрешенных слов, называется универсальным, поскольку годится для всех блочных кодов. Однако этот метод практически не применяется из-за сложности реализации и низкого быстродействия. Если длина информационного слова достаточно велика, то требуется большой объем памяти для хранения всех разрешенных слов. Кроме того, сравнение принятого слова со всей таблицей может продолжаться очень долго, что недопустимо при работе в режиме реального времени. Поэтому созданы другие методы кодирования и декодирования блочных кодов, в которых используется не поиск разрешенных слов, а математические операции над информационными и проверочными символами.
Чаще всего применяются систематические коды. Систематическим называется такой блочный код, у которого информационные и проверочные символы расположены на одних и тех же позициях во всех кодовых словах
В примере 1 был рассмотрен избыточный код с проверкой на четность. При его кодировании к информационному слову добавляется один проверочный символ так, чтобы количество единиц в кодовом слове было четным. При декодировании проверяется выполнение этого условия. Если количество единиц в принятом слове нечетно, то слово является запрещенным. Таким образом, можно обойтись без запоминания таблицы разрешенных слов.
Если в кодере используются лишь линейные операции над поступающими информационными символами, то код называется линейным. Принцип кодирования и декодирования линейного кода заключается в системе линейных уравнений, в которую входят информационные и проверочные символы. Для каждого кода эта система своя. Рассмотрим её на примере кода (7, 4), имеющего d = 3.
a1 а2 а3 а5 = 0
а2 а3 а4 а6 = 0
а1 а2 а4 а7 = 0
где — знак сложения по модулю 2, символы а1, а2, а3, а4 являются информационными, а символы а5, а6, а7 – проверочными. При кодировании проверочные символы вычисляются из информационных так, чтобы они удовлетворяли системе уравнений. При декодировании символы принятого слова подставляются в систему уравнений и вычисляется её правая часть. Эта правая часть представляет собой вектор, который называется исправляющим вектором или синдромом. Анализ синдрома позволяет исправлять ошибки. Каждому возможному синдрому соответствует номер искаженного символа.
|
Синдром |
Номер искаженного символа |
|
000 |
Ошибок не обнаружено |
|
101 |
1 |
|
111 |
2 |
|
110 |
3 |
|
011 |
4 |
Проверочные символы вычисляются с помощью производящей (порождающей) матрицы. Производящая матрица G – это таблица, у которой k строк и n столбцов, в которой записаны k линейно независимых разрешенных комбинаций данного кода. По ней можно построить все остальные разрешенные кодовые комбинации, складывая поразрядно по модулю 2 строки производящей матрицы во всех возможных сочетаниях. В памяти кодера достаточно иметь производящую матрицу. С помощью набора сумматоров можно получить любую разрешенную кодовую комбинацию.
Производящую матрицу принято представлять в каноническом виде. Для рассматриваемого кода она будет:

Где левая часть матрицы — единичная матрица, соответствующая информационным символам, а правая часть матрицы соответствует проверочным символам. Схема кодирования строится на основе производящей матрицы. Кодер состоит из k-элементного регистра для информационного слова и n – k сумматоров по модулю 2. Элементы правой части производящей матрицы pij отвечают за вычисление проверочных символов. Они показывают связь i-ой ячейки регистра с j-м сумматором. Если pij = 1, то связь есть, если pij = 0 , то связи нет.
Д
ля декодирования требуется проверочная матрица H, содержащая n – k строк и n столбцов. В каждой строке этой матрицы единицы находятся в тех разрядах, которые входят в соответствующее проверочное уравнение. Для рассмотренного кода Хэмминга (7, 4) проверочная матрица будет иметь вид:
Существует особый класс блочных линейных кодов – циклические коды. Они отличаются тем, что всякая циклическая перестановка символов разрешенного кодового слова приводит также к разрешенному слову. Все кодовые комбинации можно получить циклическим сдвигом одного слова. Поэтому важным достоинством циклических кодов является то, что операции кодировании и декодирования легко реализуются на сдвигающих регистрах.
Содержание
- 1 Исправление ошибок в помехоустойчивом кодировании
- 2 Параметры помехоустойчивого кодирования
- 3 Контроль чётности
- 4 Классификация помехоустойчивых кодов
- 5 Код Хэмминга
- 5.1 Декодирование кода Хэмминга
- 5.2 Расстояние Хэмминга
- 6 Помехоустойчивые коды
- 6.1 Компромиссы при использовании помехоустойчивых кодов
- 6.2 Необходимость чередования (перемежения)
Назначение помехоустойчивого кодирования – защита информации от помех и ошибок при передаче и хранении информации. Помехоустойчивое кодирование необходимо для устранения ошибок, которые возникают в процессе передачи, хранения информации. При передачи информации по каналу связи возникают помехи, ошибки и небольшая часть информации теряется.
Без использования помехоустойчивого кодирования было бы невозможно передавать большие объемы информации (файлы), т.к. в любой системе передачи и хранении информации неизбежно возникают ошибки.
Рассмотрим пример CD диска. Там информация хранится прямо на поверхности диска, в углублениях, из-за того, что все дорожки на поверхности, часто диск хватаем пальцами, елозим по столу и из-за этого без помехоустойчивого кодирования, информацию извлечь не получится.
Использование кодирования позволяет извлекать информацию без потерь даже с поврежденного CD/DVD диска, когда какая либо область становится недоступной для считывания.
В зависимости от того, используется в системе обнаружение или исправление ошибок с помощью помехоустойчивого кода, различают следующие варианты:
- запрос повторной передачи (Automatic Repeat reQuest, ARQ): с помощью помехоустойчивого кода выполняется только обнаружение ошибок, при их наличии производится запрос на повторную передачу пакета данных;
- прямое исправление ошибок (Forward Error Correction, FEC): производится декодирование помехоустойчивого кода, т. е. исправление ошибок с его помощью.
Возможен также гибридный вариант, чтобы лишний раз не гонять информацию по каналу связи, например получили пакет информации, попробовали его исправить, и если не смогли исправить, тогда отправляется запрос на повторную передачу.
Исправление ошибок в помехоустойчивом кодировании
Любое помехоустойчивое кодирование добавляет избыточность, за счет чего и появляется возможность восстановить информацию при частичной потере данных в канале связи (носителе информации при хранении). В случае эффективного кодирования убирали избыточность, а в помехоустойчивом кодировании добавляется контролируемая избыточность.
Простейший пример – мажоритарный метод, он же многократная передача, в котором один символ передается многократно, а на приемной стороне принимается решение о том символе, количество которых больше.
Допустим есть 4 символа информации, А, B, С,D, и эту информацию повторяем несколько раз. В процессе передачи информации по каналу связи, где-то возникла ошибка. Есть три пакета (A1B1C1D1|A2B2C2D2|A3B3C3D3), которые должны нести одну и ту же информацию.
Но из картинки справа, видно, что второй символ (B1 и C1) они отличаются друг от друга, хотя должны были быть одинаковыми. То что они отличаются, говорит о том, что есть ошибка.
Необходимо найти ошибку с помощью голосования, каких символов больше, символов В или символов С? Явно символов В больше, чем символов С, соответственно принимаем решение, что передавался символ В, а символ С ошибочный.
Для исправления ошибок нужно, как минимум 3 пакета информации, для обнаружения, как минимум 2 пакета информации.
Параметры помехоустойчивого кодирования
Первый параметр, скорость кода R характеризует долю информационных («полезных») данных в сообщении и определяется выражением: R=k/n=k/m+k
- где n – количество символов закодированного сообщения (результата кодирования);
- m – количество проверочных символов, добавляемых при кодировании;
- k – количество информационных символов.
Параметры n и k часто приводят вместе с наименованием кода для его однозначной идентификации. Например, код Хэмминга (7,4) значит, что на вход кодера приходит 4 символа, на выходе 7 символов, Рида-Соломона (15, 11) и т.д.
Второй параметр, кратность обнаруживаемых ошибок – количество ошибочных символов, которые код может обнаружить.
Третий параметр, кратность исправляемых ошибок – количество ошибочных символов, которые код может исправить (обозначается буквой t).
Контроль чётности
Самый простой метод помехоустойчивого кодирования это добавление одного бита четности. Есть некое информационное сообщение, состоящее из 8 бит, добавим девятый бит.
Если нечетное количество единиц, добавляем 0.
1 0 1 0 0 1 0 0 | 0
Если четное количество единиц, добавляем 1.
1 1 0 1 0 1 0 0 | 1
Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.
1 1 0 0 0 1 0 0 | 1
Под кратностью понимается, всевозможные ошибки, которые можно обнаружить. В этом случае, кратность исправляемых ошибок 0, так как мы не можем исправить ошибки, а кратность обнаруживаемых 1.
Есть последовательность 0 и 1, и из этой последовательности составим прямоугольную матрицу размера 4 на 4. Затем для каждой строки и столбца посчитаем бит четности.
Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:
И если в процессе передачи информации допустим ошибку (ошибка нолик вместо единицы, желтым цветом), начинаем делать проверку. Нашли ошибку во втором столбце, третьей строке по координатам. Чтобы исправить ошибку, просто инвертируем 1 в 0, тем самым ошибка исправляется.
Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные.
Рассчитаем скорость кода для:
- 1 1 0 0 0 1 0 0 | 1
Здесь R=8/9=0,88
- И для прямоугольного кода:
Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)
Более эффективный с точки зрения скорости является первый вариант, но зато мы не можем с помощью него исправлять ошибки, а с помощью прямоугольного кода можно. Сейчас на практике прямоугольный код не используется, но логика работы многих помехоустойчивых кодов основана именно на прямоугольном коде.
Классификация помехоустойчивых кодов
- Непрерывные — процесс кодирования и декодирования носит непрерывный характер. Сверточный код является частным случаем непрерывного кода. На вход кодера поступил один символ, соответственно, появилось несколько на выходе, т.е. на каждый входной символ формируется несколько выходных, так как добавляется избыточность.
- Блочные (Блоковые) — процесс кодирования и декодирования осуществляется по блокам. С точки зрения понимания работы, блочный код проще, разбиваем код на блоки и каждый блок кодируется в отдельности.
По используемому алфавиту:
- Двоичные. Оперируют битами.
- Не двоичные (код Рида-Соломона). Оперируют более размерными символами. Если изначально информация двоичная, нужно эти биты превратить в символы. Например, есть последовательность 110 110 010 100 и нужно их преобразовать из двоичных символов в не двоичные, берем группы по 3 бита — это будет один символ, 6, 6, 2, 4 — с этими не двоичными символами работают не двоичные помехоустойчивые коды.
Блочные коды делятся на
- Систематические — отдельно не измененные информационные символы, отдельно проверочные символы. Если на входе кодера присутствует блок из k символов, и в процессе кодирования сформировали еще какое-то количество проверочных символов и проверочные символы ставим рядом к информационным в конец или в начало. Выходной блок на выходе кодера будет состоять из информационных символов и проверочных.
- Несистематические — символы исходного сообщения в явном виде не присутствуют. На вход пришел блок k, на выходе получили блок размером n, блок на выходе кодера не будет содержать в себе исходных данных.
В случае систематических кодов, выходной блок в явном виде содержит в себе, то что пришло на вход, а в случае несистематического кода, глядя на выходной блок нельзя понять что было на входе.
Смотря на картинку выше, код 1 1 0 0 0 1 0 0 | 1 является систематическим, на вход поступило 8 бит, а на выходе кодера 9 бит, которые в явном виде содержат в себе 8 бит информационных и один проверочный.
Код Хэмминга
Код Хэмминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Позволяет устранить одну ошибку и находить двойную.
Код Хэмминга (7,4) — 4 бита на входе кодера и 7 на выходе, следовательно 3 проверочных бита. С 1 по 4 информационные биты, с 6 по 7 проверочные (см. табл. выше). Пятый проверочный бит y5, это сумма по модулю два 1-3 информационных бит. Сумма по модулю 2 это вычисление бита чётности.
Декодирование кода Хэмминга
Декодирование происходит через вычисление синдрома по выражениям:
Синдром это сложение бит по модулю два. Если синдром не нулевой, то исправление ошибки происходит по таблице декодирования:
Расстояние Хэмминга
Расстояние Хэмминга — число позиций, в которых соответствующие символы двух кодовых слов одинаковой длины различны. Если рассматривать два кодовых слова, (пример на картинке ниже, 1 0 1 1 0 0 1 и 1 0 0 1 1 0 1) видно что они отличаются друг от друга на два символа, соответственно расстояние Хэмминга равно 2.
Кратность исправляемых ошибок и обнаруживаемых, связано минимальным расстоянием Хэмминга. Любой помехоустойчивый код добавляет избыточность с целью увеличить минимальное расстояние Хэмминга. Именно минимальное расстояние Хэмминга определяет помехоустойчивость.
Помехоустойчивые коды
Современные коды более эффективны по сравнению с рассматриваемыми примерами. В таблице ниже приведены Коды Боуза-Чоудхури-Хоквингема (БЧХ)
Из таблицы видим, что там один класс кода БЧХ, но разные параметры n и k.
- n — количество символов на входе.
- k — количество символов на выходе.
- t — кратность исправляемых ошибок.
- Отношение k/n — скорость кода.
- G (энергетический выигрыш) — величина, показывающая на сколько можно уменьшить отношение сигнал/шум (Eb/No) для обеспечения заданной вероятности ошибки.
Несмотря на то, что скорость кода близка, количество исправляемых ошибок может быть разное. Количество исправляемых ошибок зависит от той избыточности, которую добавим и от размера блока. Чем больше блок, тем больше ошибок он исправляет, даже при той же самой избыточности.
Пример: помехоустойчивые коды и двоичная фазовая манипуляция (2-ФМн). На графике зависимость отношения сигнал шум (Eb/No) от вероятности ошибки. За счет применения помехоустойчивых кодов улучшается помехоустойчивость.
Из графика видим, код Хэмминга (7,4) на сколько увеличилась помехоустойчивость? Всего на пол Дб это мало, если применить код БЧХ (127, 64) выиграем порядка 4 дБ, это хороший показатель.
Компромиссы при использовании помехоустойчивых кодов
Чем расплачиваемся за помехоустойчивые коды? Добавили избыточность, соответственно эту избыточность тоже нужно передавать. Нужно: увеличивать пропускную способность канала связи, либо увеличивать длительность передачи.
Компромисс:
- Достоверность vs полоса пропускания.
- Мощность vs полоса пропускания.
- Скорость передачи данных vs полоса пропускания
Необходимость чередования (перемежения)
Все помехоустойчивые коды могут исправлять только ограниченное количество ошибок t. Однако в реальных системах связи часто возникают ситуации сгруппированных ошибок, когда в течение непродолжительного времени количество ошибок превышает t.
Например, в канале связи шумов мало, все передается хорошо, ошибки возникают редко, но вдруг возникла импульсная помеха или замирания, которые повредили на некоторое время процесс передачи, и потерялся большой кусок информации. В среднем на блок приходится одна, две ошибки, а в нашем примере потерялся целый блок, включая информационные и проверочные биты. Сможет ли помехоустойчивый код исправить такую ошибку? Эта проблема решаема за счет перемежения.
Пример блочного перемежения:
На картинке, всего 5 блоков (с 1 по 25). Код работает исправляя ошибки в рамках одного блока (если в одном блоке 1 ошибка, код его исправит, а если две то нет). В канал связи отдается информация не последовательно, а в перемешку. На выходе кодера сформировались 5 блоков и эти 5 блоков будем отдавать не по очереди а в перемешку. Записали всё по строкам, но считывать будем, чтобы отправлять в канал связи, по столбцам. Информация в блоках перемешалась. В канале связи возникла ошибка и мы потеряли большой кусок. В процессе приема, мы опять составляем таблицу, записываем по столбцам, но считываем по строкам. За счет того, что мы перемешали большое количество блоков между собой, групповая ошибка равномерно распределится по блокам.
Все помехоустойчивые коды делятся на блоковые и непрерывные (их называют также цепные или рекуррентные). При блоковом кодировании данные передаются отдельными блоками (словами, кодовыми комбинациями). При этом поступающие в кодер символы, разбиваются на блоки по k информационных символов. В кодере этот блок информационных символов преобразуется в блок из кодовых символов, где п называется длиной кода. Добавленные при кодировании r = n – k символов являются проверочными. Такой блоковый код принято обозначать как (n, k) – код. Величину R = k / n называют скоростью кода, а величину, обратную скорости, Rи = n / k называют избыточностью кода.
Проверочные символы являются избыточными, они необходимы для обнаружения и (или) исправления ошибок, возникших при передаче. Существуют безызбыточные (примитивные) коды. У этих кодов проверочных символов нет (n = k), поэтому у них самая высокая скорость кода R = 1, но они не способны обнаруживать ошибки.
Ошибки при передаче кодового слова возникают потому, что некоторые из переданных символов могут быть приняты неверно. Принцип обнаружения ошибок заключается в следующем. Если блоковый (n, k) – код имеет основание (количество символов в используемом алфавите) q, то возможно Q = qn различных кодовых слов. Для передачи же используются только Qр = qk кодовых слов, которые называются разрешенными. Остальные Qз = Q – Qр слов априорно для передачи не используются и называются запрещенными.
В дальнейшем будут рассматриваться только двоичные коды, у которых алфавит состоит из двух символов 0 и 1, т. е. с основанием q = 2.
В памяти кодера и декодера хранится таблица разрешенных слов. Работа кодера заключается в выборе разрешенного кодового слова, соответствующего поступившему информационному слову. Приходящее в декодер кодовое слово сравнивается с таблицей разрешенных слов и, если происходит совпадение, то потребитель получает информационное слово, соответствующее данному разрешенному слову. Если же совпадение не наступает, то слово считается запрещенным, а потребитель получает сообщение об ошибке. Однако если совокупность ошибок превратит одно разрешенное слово в другое разрешенное, то возникшие ошибки не могут быть обнаружены.
Пример 1. Требуется передача сообщения о наступлении одного из четырех возможных событий A, B, C, D. Эти события представлены информационными словами 00, 01, 10, 11 соответственно. При передаче этих слов безызбыточным кодом все возможные комбинации являются разрешенными. Поэтому достаточно искажения хотя бы одного символа, чтобы сообщение было принято неверно. Так, если передавалось сообщение A в виде кодового слова 00, а принято было слово 01, то декодер, найдя в таблице такое разрешенное слово, вынесет решение о приеме сообщения B.
Если к вышеперечисленным информационным словам добавить по одному избыточному символу, поставив в соответствие разрешенные слова 000, 011, 101, 110, то искажение одного символа в переданном слове можно обнаружить. Так, если передавалось сообщение A в виде кодового слова 000, а принято было слово 001, то декодер, не найдя в таблице такого разрешенного слова, объявит принятое слово запрещенным и сообщит об обнаружении ошибки в слове. Однако если было принято слово 011, то декодер вынесет решение о приеме сообщения B.
Для сравнения слов необходимо задать метрику, т. е. способ измерения расстояний между кодовыми словами. Известно несколько способов выбора метрики, из которых наиболее распространенным является метрика Хэмминга. Расстоянием Хэмминга между двумя кодовыми словами называется количество несовпадающих символов в этих словах. Важнейшей характеристикой блочного кода является кодовое расстояние – d, оно равно наименьшему расстоянию из всех возможных для данного кода.
Пример 2. Для передачи используются три разрешенных слова 000, 100, 111. Расстояние между первым и вторым словами равно 1, между вторым и третьим словами – 2, а между первым и вторым – 3. Кодовое расстояние для данного кода d = 1.
Очевидно, что у безызбыточного кода d = 1, так как между любой парой его слов расстояние равно единице. Этот код не позволяет обнаруживать ошибки. Приведенный в примере 1 избыточный код (он называется кодом с проверкой на четность) имеет d = 2. Он позволяет гарантировано обнаружить однократную ошибку.
Кратностью ошибки называется количество неправильно принятых символов в кодовом слове. Если искажения символов возникают независимо друг от друга, то ошибки меньшей кратности более вероятны, чем ошибки большей кратности. Следовательно, прежде всего требуется вести борьбу с ошибками малой кратности.
Можно заметить, что максимальная кратность гарантировано обнаруживаемой ошибки tо = d – 1. Действительно, при возникновении необнаруженной ошибки одно разрешенное слово должно превратиться в другое разрешенное слово. А для этого надо, чтобы кратность возникшей ошибки была не менее d, поскольку все разрешенные слова по определению кодового расстояния различаются не менее, чем на d символов. Если же принятое кодовое слово хотя бы на один символ отличается от разрешенных кодовых слов, то будет зафиксировано появление ошибки.
При декодировании вместо обнаружения ошибок возможно их исправление. Так, если было принято запрещенное кодовое слово, то можно не отбрасывать его, а найти наиболее похожее разрешенное слово и объявить его принятым. Таким образом, возникшие при передаче ошибки считаются исправленными, и потребитель получает не сообщение об ошибке, а очередное информационное слово. При декодировании с исправлением ошибок решение принимается по минимуму расстояния Хэмминга, т. е. переданным считается то разрешенное кодовое слово, которое отличается от принятого слова наименьшим количеством несовпадающих символов.
Пример 3. Для передачи используется два разрешенных кодовых слова 000 и 111. Было принято слово 001, на беглый взгляд оно больше похоже на 000, чем на 111. Действительно, слово 001 от первого разрешенного слова отличается на один символ, а от второго на два. Так как однократная ошибка вероятнее двукратной, то скорее всего было передано первое слово и в нем исказился один символ. Декодер принимает решение по минимуму расстояния Хэмминга и объявляет принятым разрешенное слово 000.
В
рассмотренном примере код имеет d = 3, он позволяет гарантировано исправлять однократную ошибку. Можно заметить, что максимальная кратность гарантировано исправляемой ошибки :
где [x] –целая часть числа x.
Существует так называемый прием со стиранием. Это частный случай приема с мягким решением. Его особенность состоит в том, что решающее устройство имеет область неопределенности, в которую попадают все сигналы, не превысившие установленный порог. Решающее устройство выдает при этом специальный символ, заменяющий неуверенно принятый сигнал. Этот символ оказывается, таким образом, «стертым». Так, при передаче двоичным кодом на выходе решающего устройства появляется один из трех символов: 0, 1 и символ стирания Х.
Восстановить стертые знаки часто оказывается легче, чем исправить ошибочные. Это обусловлено тем, что местонахождение стертых знаков известно, так как оно обозначено символом стирания Х, тогда как местоположение ошибок неизвестно, и каждый из знаков 0 или 1 может быть как верным, так и неверным.
Для сохранения различимости кодовых комбинаций при стирании не более s знаков кодовое расстояние d должно удовлетворять условию:
Для того, чтобы код мог одновременно исправлять t ошибок и восстанавливать s стертых символов кодовое расстояние должно быть:
Преимущество кодов со стираниями очевидно: например, при d = 3 такой код может как и обычный исправить одиночную ошибку, но может восстановить два стертых символа.
Описанный выше метод кодирования и декодирования, основанный на запоминании таблицы разрешенных слов, называется универсальным, поскольку годится для всех блочных кодов. Однако этот метод практически не применяется из-за сложности реализации и низкого быстродействия. Если длина информационного слова достаточно велика, то требуется большой объем памяти для хранения всех разрешенных слов. Кроме того, сравнение принятого слова со всей таблицей может продолжаться очень долго, что недопустимо при работе в режиме реального времени. Поэтому созданы другие методы кодирования и декодирования блочных кодов, в которых используется не поиск разрешенных слов, а математические операции над информационными и проверочными символами.
Чаще всего применяются систематические коды. Систематическим называется такой блочный код, у которого информационные и проверочные символы расположены на одних и тех же позициях во всех кодовых словах
В примере 1 был рассмотрен избыточный код с проверкой на четность. При его кодировании к информационному слову добавляется один проверочный символ так, чтобы количество единиц в кодовом слове было четным. При декодировании проверяется выполнение этого условия. Если количество единиц в принятом слове нечетно, то слово является запрещенным. Таким образом, можно обойтись без запоминания таблицы разрешенных слов.
Если в кодере используются лишь линейные операции над поступающими информационными символами, то код называется линейным. Принцип кодирования и декодирования линейного кода заключается в системе линейных уравнений, в которую входят информационные и проверочные символы. Для каждого кода эта система своя. Рассмотрим её на примере кода (7, 4), имеющего d = 3.
a1 а2 а3 а5 = 0
а2 а3 а4 а6 = 0
а1 а2 а4 а7 = 0
где — знак сложения по модулю 2, символы а1, а2, а3, а4 являются информационными, а символы а5, а6, а7 – проверочными. При кодировании проверочные символы вычисляются из информационных так, чтобы они удовлетворяли системе уравнений. При декодировании символы принятого слова подставляются в систему уравнений и вычисляется её правая часть. Эта правая часть представляет собой вектор, который называется исправляющим вектором или синдромом. Анализ синдрома позволяет исправлять ошибки. Каждому возможному синдрому соответствует номер искаженного символа.
|
Синдром |
Номер искаженного символа |
|
000 |
Ошибок не обнаружено |
|
101 |
1 |
|
111 |
2 |
|
110 |
3 |
|
011 |
4 |
Проверочные символы вычисляются с помощью производящей (порождающей) матрицы. Производящая матрица G – это таблица, у которой k строк и n столбцов, в которой записаны k линейно независимых разрешенных комбинаций данного кода. По ней можно построить все остальные разрешенные кодовые комбинации, складывая поразрядно по модулю 2 строки производящей матрицы во всех возможных сочетаниях. В памяти кодера достаточно иметь производящую матрицу. С помощью набора сумматоров можно получить любую разрешенную кодовую комбинацию.
Производящую матрицу принято представлять в каноническом виде. Для рассматриваемого кода она будет:

Где левая часть матрицы — единичная матрица, соответствующая информационным символам, а правая часть матрицы соответствует проверочным символам. Схема кодирования строится на основе производящей матрицы. Кодер состоит из k-элементного регистра для информационного слова и n – k сумматоров по модулю 2. Элементы правой части производящей матрицы pij отвечают за вычисление проверочных символов. Они показывают связь i-ой ячейки регистра с j-м сумматором. Если pij = 1, то связь есть, если pij = 0 , то связи нет.
Д
ля декодирования требуется проверочная матрица H, содержащая n – k строк и n столбцов. В каждой строке этой матрицы единицы находятся в тех разрядах, которые входят в соответствующее проверочное уравнение. Для рассмотренного кода Хэмминга (7, 4) проверочная матрица будет иметь вид:
Существует особый класс блочных линейных кодов – циклические коды. Они отличаются тем, что всякая циклическая перестановка символов разрешенного кодового слова приводит также к разрешенному слову. Все кодовые комбинации можно получить циклическим сдвигом одного слова. Поэтому важным достоинством циклических кодов является то, что операции кодировании и декодирования легко реализуются на сдвигающих регистрах.
Назначение помехоустойчивого кодирования – защита информации от помех и ошибок при передаче и хранении информации. Помехоустойчивое кодирование необходимо для устранения ошибок, которые возникают в процессе передачи, хранения информации. При передачи информации по каналу связи возникают помехи, ошибки и небольшая часть информации теряется.
Без использования помехоустойчивого кодирования было бы невозможно передавать большие объемы информации (файлы), т.к. в любой системе передачи и хранении информации неизбежно возникают ошибки.
Рассмотрим пример CD диска. Там информация хранится прямо на поверхности диска, в углублениях, из-за того, что все дорожки на поверхности, часто диск хватаем пальцами, елозим по столу и из-за этого без помехоустойчивого кодирования, информацию извлечь не получится.
Использование кодирования позволяет извлекать информацию без потерь даже с поврежденного CD/DVD диска, когда какая либо область становится недоступной для считывания.
В зависимости от того, используется в системе обнаружение или исправление ошибок с помощью помехоустойчивого кода, различают следующие варианты:
- запрос повторной передачи (Automatic Repeat reQuest, ARQ): с помощью помехоустойчивого кода выполняется только обнаружение ошибок, при их наличии производится запрос на повторную передачу пакета данных;
- прямое исправление ошибок (Forward Error Correction, FEC): производится декодирование помехоустойчивого кода, т. е. исправление ошибок с его помощью.
Возможен также гибридный вариант, чтобы лишний раз не гонять информацию по каналу связи, например получили пакет информации, попробовали его исправить, и если не смогли исправить, тогда отправляется запрос на повторную передачу.
Исправление ошибок в помехоустойчивом кодировании
Любое помехоустойчивое кодирование добавляет избыточность, за счет чего и появляется возможность восстановить информацию при частичной потере данных в канале связи (носителе информации при хранении). В случае эффективного кодирования убирали избыточность, а в помехоустойчивом кодировании добавляется контролируемая избыточность.
Простейший пример – мажоритарный метод, он же многократная передача, в котором один символ передается многократно, а на приемной стороне принимается решение о том символе, количество которых больше.
Допустим есть 4 символа информации, А, B, С,D, и эту информацию повторяем несколько раз. В процессе передачи информации по каналу связи, где-то возникла ошибка. Есть три пакета (A1B1C1D1|A2B2C2D2|A3B3C3D3), которые должны нести одну и ту же информацию.
Но из картинки справа, видно, что второй символ (B1 и C1) они отличаются друг от друга, хотя должны были быть одинаковыми. То что они отличаются, говорит о том, что есть ошибка.
Необходимо найти ошибку с помощью голосования, каких символов больше, символов В или символов С? Явно символов В больше, чем символов С, соответственно принимаем решение, что передавался символ В, а символ С ошибочный.
Для исправления ошибок нужно, как минимум 3 пакета информации, для обнаружения, как минимум 2 пакета информации.
Параметры помехоустойчивого кодирования
Первый параметр, скорость кода R характеризует долю информационных («полезных») данных в сообщении и определяется выражением: R=k/n=k/m+k
- где n – количество символов закодированного сообщения (результата кодирования);
- m – количество проверочных символов, добавляемых при кодировании;
- k – количество информационных символов.
Параметры n и k часто приводят вместе с наименованием кода для его однозначной идентификации. Например, код Хэмминга (7,4) значит, что на вход кодера приходит 4 символа, на выходе 7 символов, Рида-Соломона (15, 11) и т.д.
Второй параметр, кратность обнаруживаемых ошибок – количество ошибочных символов, которые код может обнаружить.
Третий параметр, кратность исправляемых ошибок – количество ошибочных символов, которые код может исправить (обозначается буквой t).
Контроль чётности
Самый простой метод помехоустойчивого кодирования это добавление одного бита четности. Есть некое информационное сообщение, состоящее из 8 бит, добавим девятый бит.
Если нечетное количество единиц, добавляем 0.
1 0 1 0 0 1 0 0 | 0
Если четное количество единиц, добавляем 1.
1 1 0 1 0 1 0 0 | 1
Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.
1 1 0 0 0 1 0 0 | 1
Под кратностью понимается, всевозможные ошибки, которые можно обнаружить. В этом случае, кратность исправляемых ошибок 0, так как мы не можем исправить ошибки, а кратность обнаруживаемых 1.
Есть последовательность 0 и 1, и из этой последовательности составим прямоугольную матрицу размера 4 на 4. Затем для каждой строки и столбца посчитаем бит четности.
Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:
И если в процессе передачи информации допустим ошибку (ошибка нолик вместо единицы, желтым цветом), начинаем делать проверку. Нашли ошибку во втором столбце, третьей строке по координатам. Чтобы исправить ошибку, просто инвертируем 1 в 0, тем самым ошибка исправляется.
Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные.
Рассчитаем скорость кода для:
- 1 1 0 0 0 1 0 0 | 1
Здесь R=8/9=0,88
- И для прямоугольного кода:
Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)
Более эффективный с точки зрения скорости является первый вариант, но зато мы не можем с помощью него исправлять ошибки, а с помощью прямоугольного кода можно. Сейчас на практике прямоугольный код не используется, но логика работы многих помехоустойчивых кодов основана именно на прямоугольном коде.
Классификация помехоустойчивых кодов
- Непрерывные — процесс кодирования и декодирования носит непрерывный характер. Сверточный код является частным случаем непрерывного кода. На вход кодера поступил один символ, соответственно, появилось несколько на выходе, т.е. на каждый входной символ формируется несколько выходных, так как добавляется избыточность.
- Блочные (Блоковые) — процесс кодирования и декодирования осуществляется по блокам. С точки зрения понимания работы, блочный код проще, разбиваем код на блоки и каждый блок кодируется в отдельности.
По используемому алфавиту:
- Двоичные. Оперируют битами.
- Не двоичные (код Рида-Соломона). Оперируют более размерными символами. Если изначально информация двоичная, нужно эти биты превратить в символы. Например, есть последовательность 110 110 010 100 и нужно их преобразовать из двоичных символов в не двоичные, берем группы по 3 бита — это будет один символ, 6, 6, 2, 4 — с этими не двоичными символами работают не двоичные помехоустойчивые коды.
Блочные коды делятся на
- Систематические — отдельно не измененные информационные символы, отдельно проверочные символы. Если на входе кодера присутствует блок из k символов, и в процессе кодирования сформировали еще какое-то количество проверочных символов и проверочные символы ставим рядом к информационным в конец или в начало. Выходной блок на выходе кодера будет состоять из информационных символов и проверочных.
- Несистематические — символы исходного сообщения в явном виде не присутствуют. На вход пришел блок k, на выходе получили блок размером n, блок на выходе кодера не будет содержать в себе исходных данных.
В случае систематических кодов, выходной блок в явном виде содержит в себе, то что пришло на вход, а в случае несистематического кода, глядя на выходной блок нельзя понять что было на входе.
Смотря на картинку выше, код 1 1 0 0 0 1 0 0 | 1 является систематическим, на вход поступило 8 бит, а на выходе кодера 9 бит, которые в явном виде содержат в себе 8 бит информационных и один проверочный.
Код Хэмминга
Код Хэмминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Позволяет устранить одну ошибку и находить двойную.
Код Хэмминга (7,4) — 4 бита на входе кодера и 7 на выходе, следовательно 3 проверочных бита. С 1 по 4 информационные биты, с 6 по 7 проверочные (см. табл. выше). Пятый проверочный бит y5, это сумма по модулю два 1-3 информационных бит. Сумма по модулю 2 это вычисление бита чётности.
Декодирование кода Хэмминга
Декодирование происходит через вычисление синдрома по выражениям:
Синдром это сложение бит по модулю два. Если синдром не нулевой, то исправление ошибки происходит по таблице декодирования:
Расстояние Хэмминга
Расстояние Хэмминга — число позиций, в которых соответствующие символы двух кодовых слов одинаковой длины различны. Если рассматривать два кодовых слова, (пример на картинке ниже, 1 0 1 1 0 0 1 и 1 0 0 1 1 0 1) видно что они отличаются друг от друга на два символа, соответственно расстояние Хэмминга равно 2.
Кратность исправляемых ошибок и обнаруживаемых, связано минимальным расстоянием Хэмминга. Любой помехоустойчивый код добавляет избыточность с целью увеличить минимальное расстояние Хэмминга. Именно минимальное расстояние Хэмминга определяет помехоустойчивость.
Помехоустойчивые коды
Современные коды более эффективны по сравнению с рассматриваемыми примерами. В таблице ниже приведены Коды Боуза-Чоудхури-Хоквингема (БЧХ)
Из таблицы видим, что там один класс кода БЧХ, но разные параметры n и k.
- n — количество символов на входе.
- k — количество символов на выходе.
- t — кратность исправляемых ошибок.
- Отношение k/n — скорость кода.
- G (энергетический выигрыш) — величина, показывающая на сколько можно уменьшить отношение сигнал/шум (Eb/No) для обеспечения заданной вероятности ошибки.
Несмотря на то, что скорость кода близка, количество исправляемых ошибок может быть разное. Количество исправляемых ошибок зависит от той избыточности, которую добавим и от размера блока. Чем больше блок, тем больше ошибок он исправляет, даже при той же самой избыточности.
Пример: помехоустойчивые коды и двоичная фазовая манипуляция (2-ФМн). На графике зависимость отношения сигнал шум (Eb/No) от вероятности ошибки. За счет применения помехоустойчивых кодов улучшается помехоустойчивость.
Из графика видим, код Хэмминга (7,4) на сколько увеличилась помехоустойчивость? Всего на пол Дб это мало, если применить код БЧХ (127, 64) выиграем порядка 4 дБ, это хороший показатель.
Компромиссы при использовании помехоустойчивых кодов
Чем расплачиваемся за помехоустойчивые коды? Добавили избыточность, соответственно эту избыточность тоже нужно передавать. Нужно: увеличивать пропускную способность канала связи, либо увеличивать длительность передачи.
Компромисс:
- Достоверность vs полоса пропускания.
- Мощность vs полоса пропускания.
- Скорость передачи данных vs полоса пропускания
Необходимость чередования (перемежения)
Все помехоустойчивые коды могут исправлять только ограниченное количество ошибок t. Однако в реальных системах связи часто возникают ситуации сгруппированных ошибок, когда в течение непродолжительного времени количество ошибок превышает t.
Например, в канале связи шумов мало, все передается хорошо, ошибки возникают редко, но вдруг возникла импульсная помеха или замирания, которые повредили на некоторое время процесс передачи, и потерялся большой кусок информации. В среднем на блок приходится одна, две ошибки, а в нашем примере потерялся целый блок, включая информационные и проверочные биты. Сможет ли помехоустойчивый код исправить такую ошибку? Эта проблема решаема за счет перемежения.
Пример блочного перемежения:
На картинке, всего 5 блоков (с 1 по 25). Код работает исправляя ошибки в рамках одного блока (если в одном блоке 1 ошибка, код его исправит, а если две то нет). В канал связи отдается информация не последовательно, а в перемешку. На выходе кодера сформировались 5 блоков и эти 5 блоков будем отдавать не по очереди а в перемешку. Записали всё по строкам, но считывать будем, чтобы отправлять в канал связи, по столбцам. Информация в блоках перемешалась. В канале связи возникла ошибка и мы потеряли большой кусок. В процессе приема, мы опять составляем таблицу, записываем по столбцам, но считываем по строкам. За счет того, что мы перемешали большое количество блоков между собой, групповая ошибка равномерно распределится по блокам.
7.1. Классификация корректирующих кодов
7.2. Принципы помехоустойчивого кодирования
7.3. Систематические коды
7.4. Код с четным числом единиц. Инверсионный код
7.5. Коды Хэмминга
7.6. Циклические коды
7.7. Коды с постоянным весом
7.8. Непрерывные коды
7.1. Классификация корректирующих кодов
В каналах с помехами эффективным средством повышения достоверности передачи сообщений является помехоустойчивое кодирование. Оно основано на применении специальных кодов, которые корректируют ошибки, вызванные действием помех. Код называется корректирующим, если он позволяет обнаруживать или обнаруживать и исправлять ошибки при приеме сообщений. Код, посредством которого только обнаруживаются ошибки, носит название обнаруживающего кода. Исправление ошибки при таком кодировании обычно производится путем повторения искаженных сообщений. Запрос о повторении передается по каналу обратной связи. Код, исправляющий обнаруженные ошибки, называется исправляющим, кодом. В этом случае фиксируется не только сам факт наличия ошибок, но и устанавливается, какие кодовые символы приняты ошибочно, что позволяет их исправить без повторной передачи. Известны также коды, в которых исправляется только часть обнаруженных ошибок, а остальные ошибочные комбинации передаются повторно.
Для того чтобы «од обладал корректирующими способностями, в кодовой последовательности должны содержаться дополнительные (избыточные) символы, предназначенные для корректирования ошибок. Чем больше избыточность кода, тем выше его корректирующая способность.
Помехоустойчивые коды могут быть построены с любым основанием. Ниже рассматриваются только двоичные коды, теория которых разработана наиболее полно.
В настоящее время известно большое количество корректирующих кодов, отличающихся как принципами построения, так и основными характеристиками. Рассмотрим их простейшую классификацию, дающую представление об основных группах, к которым принадлежит большая часть известных кодов [12]. На рис. 7.1 показана схема, поясняющая классификацию, проведенную по способам построения корректирующих кодов.
Все известные в настоящее время коды могут быть разделены
на две большие группы: блочные и непрерывные. Блочные коды характеризуются тем, что последовательность передаваемых символов разделена на блоки операции кодирования и декодирования в каждом блоке производятся отдельно. Отличительной особенностью непрерывных кодов является то, что первичная последовательность символов, несущих информацию, непрерывно преобразуется по определенному закону в другую последовательность, содержащую избыточное число символов. Здесь процессы кодирования и декодирования не требуют деления кодовых символов на блоки.
Рис. 7.1. Классификация корректирующих кодов
Разновидностями как блочных, так и непрерывных кодов являются разделимые и неразделимые коды. В разделимых кодах всегда можно выделить информационные символы, содержащие передаваемую информацию, и контрольные (проверочные) символы, которые являются избыточными и служат ‘исключительно для коррекции ошибок. В неразделимых кодах такое разделение символов провести невозможно.
Наиболее многочисленный класс разделимых кодов составляют линейные коды. Основная их особенность состоит в том, что контрольные символы образуются как линейные комбинации информационных символов.
В свою очередь, линейные коды могут быть |разбиты на два подкласса: систематические и несистематические. Все двоичные систематические коды являются групповыми. Последние характеризуются принадлежностью кодовых комбинаций к группе, обладающей тем свойством, что сумма по модулю два любой пары комбинаций снова дает комбинацию, принадлежащую этой группе. Линейные коды, которые не могут быть отнесены к подклассу систематических, называются несистематическими. Вертикальными прямоугольниками на схеме рис. 7.1 представлены некоторые конкретные коды, описанные в последующих параграфах.
7.2. Принципы помехоустойчивого кодирования
В теории помехоустойчивого кодирования важным является вопрос об использовании избыточности для корректирования возникающих при передаче ошибок. Здесь удобно рассмотреть блочные моды, в которых всегда имеется возможность выделить отдельные кодовые комбинации. Напомним, что для равномерных кодов, которые в дальнейшем только и будут изучаться, число возможных комбинаций равно M=2n, где п — значность кода. В обычном некорректирующем коде без избыточности, например в коде Бодо, число комбинаций М выбирается равным числу сообщений алфавита источника М0и все комбинации используются для передачи информации. Корректирующие коды строятся так, чтобы число комбинаций М превышало число сообщений источника М0. Однако в.этом случае лишь М0комбинаций из общего числа используется для передачи информации. Эти комбинации называются разрешенными, а остальные М—М0комбинаций носят название запрещенных. На приемном конце в декодирующем устройстве известно, какие комбинации являются разрешенными и какие запрещенными. Поэтому если переданная разрешенная комбинация в результате ошибки преобразуется в некоторую запрещенную комбинацию, то такая ошибка будет обнаружена, а при определенных условиях исправлена. Естественно, что ошибки, приводящие к образованию другой разрешенной комбинации, не обнаруживаются.
Различие между комбинациями равномерного кода принято характеризовать расстоянием, равным числу символов, которыми отличаются комбинации одна от другой. Расстояние d между двумя комбинациями
и
определяется количеством единиц в сумме этих комбинаций по модулю два. Например,
Для любого кода d. Минимальное расстояние между разрешенными комбинациями ,в данном коде называется кодовым расстоянием d.
Расстояние между комбинациями и
условно обозначено на рис. 7.2а, где показаны промежуточные комбинации, отличающиеся друг от друга одним символом. B общем случае некоторая пара разрешенных комбинаций
и
, разделенных кодовым расстоянием d, изображается на прямой рис. 7.2б, где точками указаны запрещенные комбинации. Для того чтобы в результате ошибки комбинация
преобразовалась в другую разрешенную комбинацию
, должно исказиться d символов.
Рис. 7.2. Геометрическое представление разрешенных и запрещенных кодовых комбинаций
При искажении меньшего числа символов комбинация перейдет в запрещенную комбинацию и ошибка будет обнаружена. Отсюда следует, что ошибка всегда обнаруживается, если ее кратность, т. е. число искаженных символов в кодовой комбинации,
(7.1)
Если g>d, то некоторые ошибки также обнаруживаются. Однако полной гарантии обнаружения ошибок здесь нет, так как ошибочная комбинация ib этом случае может совпасть с какой-либо разрешенной комбинацией. Минимальное кодовое расстояние, при котором обнаруживаются любые одиночные ошибки, d=2.
Процедура исправления ошибок в процессе декодирования сводится к определению переданной комбинации по известной принятой. Расстояние между переданной разрешенной комбинацией и принятой запрещенной комбинацией d0 равно кратности ошибок g. Если ошибки в символах комбинации происходят независимо относительно друг друга, то вероятность искажения некоторых g символов в n-значной комбинации будет равна:
(7.2)
где — вероятность искажения одного символа. Так как обычно
<<1, то вероятность многократных ошибок уменьшается с увеличением их кратности, при этом более вероятны меньшие расстояния d0. В этих условиях исправление ошибок может производиться по следующему правилу. Если принята запрещенная комбинация, то считается переданной ближайшая разрешенная комбинация. Например, пусть образовалась запрещенная комбинация
(см.рис.7.2б), тогда принимается решение, что была передана комбинация
. Это .правило декодирования для указанного распределения ошибок является оптимальным, так как оно обеспечивает исправление максимального числа ошибок. Напомним, что аналогичное правило используется в теории потенциальной помехоустойчивости при оптимальном приеме дискретных сигналов, когда решение сводится к выбору того переданного сигнала, который ib наименьшей степени отличается от принятого. Нетрудно определить, что при таком правиле декодирования будут исправлены все ошибки кратности
(7.3)
Минимальное значение d, при котором еще возможно исправление любых одиночных ошибок, равно 3.
Возможно также построение таких кодов, в которых часть ошибок исправляется, а часть только обнаруживается. Так, в соответствии с рис. 7.2в ошибки кратности исправляются, а ошибки, кратность которых лежит в пределах
только обнаруживаются. Что касается ошибок, кратность которых сосредоточена в пределах
, то они обнаруживаются, однако при их исправлении принимается ошибочное решение — считается переданной комбинация А
вместо A
или наоборот.
Существуют двоичные системы связи, в которых решающее устройство выдает, кроме обычных символов 0 и 1, еще так называемый символ стирания . Этот символ соответствует приему сомнительных сигналов, когда затруднительно принять определенное решение в отношении того, какой из символов 0 или 1 был передан. Принятый символ в этом случае стирается. Однако при использовании корректирующего кода возможно восстановление стертых символов. Если в кодовой комбинации число символов
оказалось равным gc, причем
(7.4)
а остальные символы приняты без ошибок, то такая комбинация полностью восстанавливается. Действительно, для восстановления всех символов необходимо перебрать всевозможные сочетания из gc символов типа 0 и 1. Естественно, что все эти сочетания, за исключением одного, будут неверными. Но так как в неправильных сочетаниях кратность ошибок
, то согласно неравенству (7.1) такие ошибки обнаруживаются. Другими словами, в этом случае неправильно восстановленные сочетания из gc символов совместно с правильно принятыми символами образуют запрещенные комбинации и только одно- сочетание стертых символов даст разрешенную комбинацию, которую и следует считать как правильно восстановленную.
Если , то при восстановлении окажется несколько разрешенных комбинаций, что не позволит принять однозначное решение.
Таким образом, при фиксированном кодовом расстоянии максимально возможная кратность корректируемых ошибок достигается в кодах, которые обнаруживают ошибки или .восстанавливают стертые символы. Исправление ошибок представляет собой более трудную задачу, практическое решение которой сопряжено с усложнением кодирующих и декодирующих устройств. Поэтому исправляющие «оды обычно используются для корректирования ошибок малой кратности.
Корректирующая способность кода возрастает с увеличением d. При фиксированном числе разрешенных комбинаций Мувеличение d возможно лишь за счет роста количества запрещенных комбинаций:
(7.5)
что, в свою очередь, требует избыточного числа символов r=n—k, где k — количество символов в комбинации кода без избыточности. Можно ввести понятие избыточности кода и количественно определить ее по аналогии с (6.12) как
(7.6)
При независимых ошибках вероятность определенного сочетания g ошибочных символов в n-значной кодовой комбинации выражается ф-лой ((7.2), а количество всевозможных сочетаний g ошибочных символов в комбинации зависит от ее длины и определяется известной формулой числа сочетаний
Отсюда полная вероятность ошибки кратности g, учитывающая все сочетания ошибочных символов, равняется:
(7.7)
Используя (7.7), можно записать формулы, определяющие вероятность отсутствия ошибок в кодовой комбинации, т. е. вероятность правильного приема
и вероятность правильного корректирования ошибок
Здесь суммирование ‘Производится по всем значениям кратности ошибок g, которые обнаруживаются и исправляются. Таким образом, вероятность некорректируемых ошибок равна:
(7.8)
Анализ ф-лы (7.8) показывает, что при малой величине Р0и сравнительно небольших значениях п наиболее вероятны ошибки малой кратности, которые и необходимо корректировать в первую очередь.
Вероятность Р, избыточность
и число символов n являются основными характеристиками корректирующего кода, определяющими, насколько удается повысить помехоустойчивость передачи дискретных сообщений и какой ценой это достигается.
Общая задача, которая ставится при создании кода, заключается, в достижении наименьших значений Р и
. Целесообразность применения того или иного кода зависит также от сложности кодирующих и декодирующих устройств, которая, в свою очередь, зависит от п. Во многих практических случаях эта сторона вопроса является решающей. Часто, например, используются коды с большой избыточностью, но обладающие простыми правилами кодирования и декодирования.
В соответствии с общим принципом корректирования ошибок, основанным на использовании разрешенных и запрещенных комбинаций, необходимо сравнивать принятую комбинацию со всеми комбинациями данного кода. В результате М сопоставлений и принимается решение о переданной комбинации. Этот способ декодирования логически является наиболее простым, однако он требует сложных устройств, так как в них должны запоминаться все М комбинаций кода. Поэтому на практике чаще всего используются коды, которые позволяют с помощью ограниченного числа преобразований принятых кодовых символов извлечь из них всю информацию о корректируемых ошибках. Изучению таких кодов и посвящены последующие разделы.
7.3. Систематические коды
Изучение конкретных способов помехоустойчивого кодирования начнем с систематических кодов, которые в соответствии с классификацией (рис. 7.1) относятся к блочным разделимым кодам, т. е. к кодам, где операции кодирования осуществляются независимо в пределах каждой комбинации, состоящей из информационных и контрольных символов.
Остановимся кратко на общих принципах построения систематических кодов. Если обозначить информационные символы буквами с, а контрольные — буквами е, то любую кодовую комбинацию, содержащую k информационных и r контрольных символов, можно представить последовательностью:, где с и е в двоичном коде принимают значения 0 или 1.
Процесс кодирования на передающем конце сводится к образованию контрольных символов, которые выражаются в виде линейной функции информационных символов:
(7.9)
Здесь — коэффициенты, равные 0 или 1, а
и
— знаки суммирования по модулю два. Значения
выбираются по определенным правилам, установленным для данного вида кода. Иными словами, символы е представляют собой суммы по модулю два информационных символов в различных сочетаниях. Процедура декодирования принятых комбинаций может осуществляться различными» методами. Один из них, так называемый метод контрольных чисел, состоит в следующем. Из информационных символов принятой кодовой комбинации
образуется по правилу (7.9) вторая группа контрольных символов
Затем производится сравнение обеих групп контрольных символов путем их суммирования по модулю два:
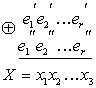
Полученное число X называется контрольным числом или синдромом. С его помощью можно обнаружить или исправить часть ошибок. Если ошибки в принятой комбинации отсутствуют, то все суммы, а следовательно, и контрольное число X будут равны .нулю. При появлении ошибок некоторые значения х могут оказаться равным 1. В этом случае
, что и позволяет обнаружить ошибки. Таким образом, контрольное число Х определяется путем r проверок на четность.
Для исправления ошибок знание одного факта их возникновения является недостаточным. Необходимо указать номер ошибочно принятых символов. С этой целью каждому сочетанию исправляемых ошибок в комбинации присваивается одно из контрольных чисел, что позволяет по известному контрольному числу определить место положения ошибок и исправить их.
Контрольное число X записывается в двоичной системе, поэтому общее количество различных контрольных чисел, отличающихся от нуля, равно. Очевидно, это количество должно быть не меньше числа различных сочетаний ошибочных символов, подлежащих исправлению. Например, если код предназначен для исправления одиночных ошибок, то число различных вариантов таких ошибок равно
. В этом случае должно выполняться условие
(7.11)
Формула (7.11) позволяет при заданном количестве информационных символов k определить необходимое число контрольных символов r, с помощью которых исправляются все одиночные ошибки.
7.4. Код с чётным числом единиц. Инверсионный код
Рассмотрим некоторые простейшие систематические коды, применяемые только для обнаружения ошибок. Одним из кодов подобного типа является код с четным числом единиц. Каждая комбинация этого кода содержит, помимо информационных символов, один контрольный символ, выбираемый равным 0 или 1 так, чтобы сумма единиц в комбинации всегда была четной. Примером могут служить пятизначные комбинации кода Бодо, к которым добавляется шестой контрольный символ: 10101,1 и 01100,0. Правило вычисления контрольного символа можно выразить на
основании (7.9) в следующей форме: . Отсюда вытекает, что для любой комбинации сумма всех символов по модулю два будет равна нулю (
— суммирование по модулю):
(7.12)
Это позволяет в декодирующем устройстве сравнительно просто производить обнаружение ошибок путем проверки на четность. Нарушение четности имеет место при появлении однократных, трехкратных и в общем, случае ошибок нечетной кратности, что и дает возможность их обнаружить. Появление четных ошибок не изменяет четности суммы (7.12), поэтому такие ошибки не обнаруживаются. На основании ,(7.8) вероятность необнаруженной ошибки равна:
К достоинствам кода следует отнести простоту кодирующих и декодирующих устройств, а также малую .избыточность , однако последнее определяет и его основной недостаток — сравнительно низкую корректирующую способность.
Значительно лучшими корректирующими способностями обладает инверсный код, который также применяется только для обнаружения ошибок. С принципом построения такого кода удобно ознакомиться на примере двух комбинаций: 11000, 11000 и 01101, 10010. В каждой комбинации символы до запятой являются информационными, а последующие — контрольными. Если количество единиц в информационных символах четное, т. е. сумма этих
символов
(7.13)
равна нулю, то контрольные символы представляют собой простое повторение информационных. В противном случае, когда число единиц нечетное и сумма (7.13) равна 1, контрольные символы получаются из информационных посредством инвертирования, т. е. путем замены всех 0 на 1, а 1 на 0. Математическая форма записи образования контрольных символов имеет вид . При декодировании происходит сравнение принятых информационных и контрольных символов. Если сумма единиц в принятых информационных символах четная, т. е.
, то соответствующие друг другу информационные и контрольные символы суммируются по модулю два. В противном случае, когда c‘
=1, происходит такое же суммирование, но с инвертированными контрольными символами. Другими словами, в соответствии с (7.10) производится r проверок на четность:
. Ошибка обнаруживается, если хотя бы одна проверка на четность дает 1.
Анализ показывает, что при наименьшая кратность необнаруживаемой ошибки g=4. Причем не обнаруживаются только те ошибки четвертой кратности, которые искажают одинаковые номера информационных и контрольных символов. Например, если передана комбинация 10100, 10100, а принята 10111, 10111, то такая четырехкратная ошибка обнаружена не будет, так как здесь все значения
равны 0. Вероятность необнаружения ошибок четвертой кратности определяется выражением
Для g>4 вероятность необнаруженных ошибок еще меньше. Поэтому при достаточно малых вероятностях ошибочных символов ро можно полагать, что полная вероятность необнаруженных ошибок
Инверсный код обладает высокой обнаруживающей способностью, однако она достигается ценой сравнительно большой избыточности, которая, как нетрудно определить, составляет величину =0,5.
7.5. Коды Хэмминга
К этому типу кодов обычно относят систематические коды с расстоянием d=3, которые позволяют исправить все одиночные ошибки (7.3).
Рассмотрим построение семизначного кода Хэмминга, каждая комбинация которого содержит четыре информационных и триконтрольных символа. Такой код, условно обозначаемый (7.4), удовлетворяет неравенству (7.11) и имеет избыточность
Если информационные символы с занимают в комбинация первые четыре места, то последующие три контрольных символа образуются по общему правилу (7.9) как суммы:
(7.14)
Декодирование осуществляется путем трех проверок на четность (7.10):
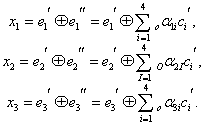
Так как х равно 0 или 1, то всего может быть восемь контрольных чисел Х=х1х2х3: 000, 100, 010, 001, 011, 101, 110 и 111. Первое из них имеет место в случае правильного приема, а остальные семь появляются при наличии искажений и должны использоваться для определения местоположения одиночной ошибки в семизначной комбинации. Выясним, каким образом устанавливается взаимосвязь между контрольными числами я искаженными символами. Если искажен один из контрольных символов: или
, то, как следует из (7.15), контрольное число примет соответственно одно из трех значений: 100, 010 или 001. Остальные четыре контрольных числа используются для выявления ошибок в информационных символах.
Таблица 7.1
Порядок присвоения контрольных чисел ошибочным информационным символам может устанавливаться любой, например, как показано в табл. 7.1. Нетрудно показать, что этому распределению контрольных чисел соответствуют коэффициенты , приведенные в табл. 7.2.
Таблица 7.2
Если подставить коэффициенты в выражение (7.15), то получим:
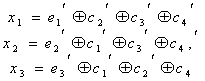
При искажении одного из информационных символов становятся равными единице те суммы х, в которые входит этот символ. Легко проверить, что получающееся в этом случае контрольное число согласуется с табл. 7.1.Нетрудно заметить, что первые четыре контрольные числа табл. 7.1 совпадают со столбцами табл. 7.2. Это свойство дает возможность при выбранном распределении контрольных чисел составить таблицу коэффициентов
. Таким образом, при одиночной ошибке можно вычислить контрольное число, позволяющее по табл. 7.1 определить тот символ кодовой комбинации, который претерпел искажения. Исправление искаженного символа двоичной системы состоит в простой замене 0 на 1 или 1 на 0. B качестве примера рассмотрим передачу комбинации, в которой информационными символами являются
, Используя ф-лу (7.14) и табл. 7.2, вычислим контрольные символы:
Передаваемая комбинация при этом будет . Предположим, что принята комбинация — 1001, 010 (искажен символ
). Подставляя соответствующие значения в (7.16), получим:
Вычисленное таким образом контрольное число 110 позволяет согласно табл. 7.1 исправить ошибку в символе.
Здесь был рассмотрен простейший способ построения и декодирования кодовых комбинаций, в которых первые места отводились информационным символам, а соответствие между контрольными числами и ошибками определялось таблице. Вместе с тем существует более изящный метод отыскания одиночных ошибок, предложенный впервые самим Хэммингом. При этом методе код строится так, что контрольное число в двоичной системе счисления сразу указывает номер искаженного символа. Правда, в этом случае контрольные символы необходимо располагать среди информационных, что усложняет процесс кодирования. Для кода (7.4) символы в комбинации должны размещаться в следующем порядке: , а контрольное число вычисляться по формулам:
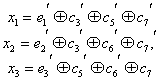
Так, если произошла ошибка в информационном символе с’5 то контрольное число , что соответствует числу 5 в двоичной системе.
В заключение отметим, что в коде (7.4) при появлении многократных ошибок контрольное число также может отличаться от нуля. Однако декодирование в этом случае будет проведено неправильно, так как оно рассчитано на исправление лишь одиночных ошибок.
7.6. Циклические коды
Важное место среди систематических кодов занимают циклические коды. Свойство цикличности состоит в том, что циклическая перестановка всех символов кодовой комбинации дает другую комбинацию
также принадлежащую этому коду. При такой перестановке символы кодовой комбинации перемещаются слева направо на одну позицию, причем крайний правый символ переносится на место крайнего левого символа. Например,
.
Комбинации циклического кода, выражаемые двоичными числами, для удобства преобразований обычно определяют в виде полиномов, коэффициенты которых равны 0 или 1. Примером этому может служить следующая запись:
Помимо цикличности, кодовые комбинации обладают другим важным свойством. Если их представить в виде полиномов, то все они делятся без остатка на так называемый порождающий полином G(z) степени , где k—значность первичного кода без избыточности, а п-значность циклического кода
Построение комбинаций циклических кодов возможно путем умножения комбинации первичного кода A*(z) ,на порождающий полином G(z):
A(z)=A*(z)G(z).
Умножение производится по модулю zn и в данном случае сводится к умножению по обычным правилам с приведением подобных членов по модулю два.
В полученной таким способом комбинации A(z) в явном виде не содержатся информационные символы, однако они всегда могут быть выделены в результате обратной операции: деления A(z) на G(z).
Другой способ кодирования, позволяющий представить кодовую комбинацию в виде информационных и контрольных символов, заключается в следующем. К комбинации первичного кода дописывается справа г нулей, что эквивалентно повышению полинома A*(z) на ,г разрядов, т. е. умножению его на гг. Затем произведение zrA*(z) делится на порождающий полином. B общем случае результат деления состоит из целого числа Q(z) и остатка R(z). Отсюда
Вычисленный остаток К(г) я используется для образования комбинации циклического кода в виде суммы
A(z)=zrA*(z)@R(z).
Так как сложение и вычитание по модулю два дают один и тот же результат, то нетрудно заметить, что A(z) = Q(z)G(z), т. е. полученная комбинация удовлетворяет требованию делимости на порождающий полином. Степень полинома R{z) не превышает r—1, поэтому он замещает нули в комбинации zA*(z).
Для примера рассмотрим циклический код c n = 7, k=4, r=3 и G(z)=z3-z+1=1011. Необходимо закодировать комбинацию A*(z)=z*+1 = 1001. Тогда zA*(z)=z
+z
= 1001000. Для определения остатка делим z3A*(z) на G(z):
Окончательно получаем
В А(z) высшие четыре разряда занимают информационные символы, а остальные при — контрольные.
Контрольные символы в циклическом коде могут быть вычислены по общим ф-лам (7.9), однако здесь определение коэффициентов затрудняется необходимостью выполнять требования делимости А(z) на порождающий полином G(z).
Процедура декодирования принятых комбинаций также основана на использовании полиномов G(z). Если ошибок в процессе передачи не было, то деление принятой комбинации A(z) на G(z) дает целое число. При наличии корректируемых ошибок в результате деления образуется остаток, который и позволяет обнаружить или исправить ошибки.
Кодирующие и декодирующие устройства циклических кодов в большинстве случаев обладают сравнительной простотой, что следует считать одним из основных их преимуществ. Другим важным достоинством этих кодов является их способность корректировать пачки ошибок, возникающие в реальных каналах, где действуют импульсные и сосредоточенные помехи или наблюдаются замирания сигнала.
В теории кодирования весом кодовых комбинаций принято называть .количество единиц, которое они содержат. Если все комбинации кода имеют одинаковый вес, то такой код называется кодом с постоянным весом. Коды с постоянным весом относятся к классу блочных неразделимых кодов, так как здесь не представляется возможным выделить информационные и контрольные символы. Из кодов этого типа наибольшее распространение получил обнаруживающий семизначный код 3/4, каждая разрешенная комбинация которого имеет три единицы и четыре нуля. Известен также код 2/5. Примером комбинаций кода 3/4 могут служить следующие семизначные последовательности: 1011000, 0101010, 0001110 и т. д.
Декодирование принятых комбинаций сводится к определению их веса. Если он отличается от заданного, то комбинация принята с ошибкой. Этот код обнаруживает все ошибки нечетной краткости и часть ошибок четной кратности. Не обнаруживаются только так называемые ошибки смещения, сохраняющие неизменным вес комбинации. Ошибки смещения характеризуются тем, что число искаженных единиц всегда равно числу искаженных нулей. Можно показать, что вероятность необнаруженной ошибки для кода 3/4 равна:
при
(7.18)
В этом коде из общего числа комбинаций М = 27=128 разрешенными являются лишь , поэтому в соответствии с (7.6) коэффициент избыточности
Код 3/4 находит применение при частотной манипуляции в каналах с селективными замираниями, где вероятность ошибок смещения невелика.
7.8. Непрерывные коды
Из непрерывных кодов, исправляющих ошибки, наиболее известны коды Финка—Хагельбаргера, в которых контрольные символы образуются путем линейной операции над двумя или более информационными символами. Принцип построения этих кодов рассмотрим на примере простейшего цепного кода. Контрольные символы в цепном коде формируются путем суммирования двух информационных символов, расположенных один относительно другого на определенном расстоянии:
;
(7.19)
Расстояние между информационными символами l=k—i определяет основные свойства кода и называется шагом сложения. Число контрольных символов при таком способе кодирования равно числу информационных символов, поэтому избыточность кода =0,5. Процесс образования последовательности контрольных символов показан на рис.7. символы разметаются между информационными символами с задержкой на два шага сложения.
Рис. 7.3. Образование и размещение контрольных символов в цепном коде Финка—Хагельбаргера
При декодировании из принятых информационных символов по тому же правилу (7.19) формируется вспомогательная последовательность контрольных символов е», которая сравнивается с принятой последовательностью контрольных символов е’ (рис. 7.36). Если произошла ошибка в информационном символе, например, c‘k, то это вызовет искажения сразу двух символов e«k и e«km, что и обнаружится в результате их сравнения с и e‘km. Отсюда по общему индексу k легко определить и исправить ошибочно принятый информационный символ с’
Ошибка в принятом контрольном символе, например, e‘k приводит к несовпадению контрольных последовательностей лишь в одном месте. Исправление такой ошибки не требуется.
Важное преимущество непрерывных кодов состоит в их способности исправлять не только одиночные ошибки, но я группы (пакеты) ошибок. Если задержка контрольных символов выбрана равной 2l, то можно показать, что максимальная длина исправляемого пакета ошибок также равна 2l при интервале между пакетами не менее 6l+1. Таким образом, возможность исправления длинных пакетов связана с увеличением шага сложения, а следовательно, и с усложнением кодирующих и декодирующих устройств.
Вопросы для повторения
1. Как могут быть классифицированы корректирующие коды?
2. Каким образом исправляются ошибки в кодах, которые только их обнаруживают?
3. В чем состоят основные принципы корректирования ошибок?
4. Дайте определение кодового расстояния.
5. При каких условиях код может обнаруживать или исправлять ошибки?
6. Как используется корректирующий код в системах со стиранием?
7. Какие характеристики определяют корректирующие способности кода?
8. Как осуществляется построение кодовых комбинаций в систематических кодах?
9. На чем основан принцип корректирования ошибок с использованием контрольного числа?
10. Объясните метод построения кода с четным числом единиц.
11. Как осуществляется процедура кодирования в семизначном коде Хэмминга?
12. Почему семизначный код 3/4 не обнаруживает ошибки смещения?
13. Каким образом производится непрерывное кодирование?
14. От чего зависит длина пакета исправляемых ошибок в коде Финка—Хагельбаргера?
Добавил:
Andrew1992
Факультет ИКСС, группа ИКВТ-61
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
vlss16up_motpk.pdf
Скачиваний:
295
Добавлен:
20.11.2018
Размер:
830.71 Кб
Скачать

ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
Федеральное государственное бюджетное образовательное учреждение высшего образования «САНКТ-ПЕТЕРБУРГСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ им. проф. М. А. БОНЧ-БРУЕВИЧА»
С. С. Владимиров
МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ
Учебное пособие
Санкт-Петербург
2016
УДК 621.391(075.8) ББК 32.88173
В 57
Рецензенты профессор кафедры СС и ПД, доктор технических наук О. С. Когновицкий;
ведущий инженер ЗАО «НПП «ИСТА-Системс», кандидат технических наук А. А. Березкин
Утверждено редакционно-издательским советом СПбГУТ в качестве учебного пособия
Владимиров, С. С.
В 57 Математические основы теории помехоустойчивого кодирования : учебное пособие / С. С. Владимиров ; СПбГУТ. — СПб, 2016. — 96 с.
ISBN 978-5-89160-131-4
Настоящее учебное пособие призвано ознакомить студентов старших курсов с математическими основами теории помехоустойчивого кодирования.
Предназначено для студентов, обучающихся по направлениям 11.03.02 «Инфокоммуникационные технологии и системы связи» и 09.03.01 «Информатика и вычислительная техника».
УДК 621.391(075.8) ББК 32.88173
|
ISBN 978-5-89160-131-4 |
c |
|
Владимиров С. С., 2016 |
|
|
c |
|
|
Федеральное государственное бюджетное |
|
|
образовательное учреждение высшего образования |
|
|
«Санкт-Петербургский государственный |
|
|
университет телекоммуникаций |
|
|
им. проф. М. А. Бонч-Бруевича», 2016 |
СОДЕРЖАНИЕ
Предисловие . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
1. Помехоустойчивое кодирование . . . . . . . . . . . . . . . . . 6
1.1.Основные параметры помехоустойчивых кодов. . . . . . . . . . 7
1.2.Классификация помехоустойчивых кодов . . . . . . . . . . . . 8
Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . 10
2. Элементы двоичной алгебры . . . . . . . . . . . . . . . . . . 11
2.1.Понятие системы счисления. Основные системы счисления. . . . 11
2.2.Перевод чисел между системами счисления . . . . . . . . . . . 13
2.3.Операции над двоичными числами . . . . . . . . . . . . . . . . 17
|
Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . |
26 |
|
3. Матрицы и действия над ними . . . . . . . . . . . . . . . . . |
27 |
|
3.1. Понятие матрицы . . . . . . . . . . . . . . . . . . . . . . . . |
27 |
|
3.2. Операции с матрицами . . . . . . . . . . . . . . . . . . . . . |
29 |
|
Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . |
31 |
|
4. Элементы комбинаторики . . . . . . . . . . . . . . . . . . . . |
32 |
|
Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . |
32 |
|
5. Полиномы и действия над ними . . . . . . . . . . . . . . . . . |
33 |
|
5.1. Операции с полиномами . . . . . . . . . . . . . . . . . . . . . |
34 |
|
Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . |
35 |
6. Понятие группы, кольца и поля . . . . . . . . . . . . . . . . . 36 6.1. Группа . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
6.2.Подгруппы и смежные классы . . . . . . . . . . . . . . . . . . 38
6.3.Кольцо . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
6.4.Поле . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . 41
7. Математика полей Галуа . . . . . . . . . . . . . . . . . . . . 42 7.1. Поле Галуа и его свойства . . . . . . . . . . . . . . . . . . . . 42 7.2. Основные действия над элементами поля . . . . . . . . . . . . 47 7.3. Алгоритмы для проведения расчетов в двоичных полях Галуа и их реализации . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . 66
3
8. Элементы теории графов . . . . . . . . . . . . . . . . . . . . 67
8.1.Основные понятия. . . . . . . . . . . . . . . . . . . . . . . . 67
8.2.Матричное представление графа. . . . . . . . . . . . . . . . . 70
8.3.Линейные графы сигналов и передача графа . . . . . . . . . . . 73
Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . 77
9. Модели каналов передачи данных . . . . . . . . . . . . . . . 78
9.1.Параметры моделей каналов ПД . . . . . . . . . . . . . . . . . 79
9.2.Двоичный симметричный канал . . . . . . . . . . . . . . . . . 80
9.3.Двоичный симметричный канал со стираниями. . . . . . . . . . 82
9.4.Двоичный несимметричный канал (Z-канал) . . . . . . . . . . . 83
9.5.Канал Гилберта–Эллиотта. . . . . . . . . . . . . . . . . . . . 84
|
9.6. Модель канала Поля . . . . . . . . . . . . . . . . . . . . . . |
86 |
|
9.7. Канал с аддитивным белым гауссовским шумом . . . . . . . . . |
88 |
|
Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . |
89 |
|
Заключение. . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
90 |
|
Список литературы. . . . . . . . . . . . . . . . . . . . . . . . . |
91 |
4
ПРЕДИСЛОВИЕ
При разработке систем передачи данных одним из важнейших этапов является выбор методов повышения достоверности при передаче информационных сообщений по каналам связи. Использование избыточных помехоустойчивых кодов является одним из наиболее эффективных методов борьбы с ошибками при передаче дискретных сообщений по каналам связи. Соответственно, вопросам изучения теории помехоустойчивого кодирования придается большое внимание в программах подготовки бакалавров и магистров, обучающихся по специальностям из области телекоммуникаций.
В настоящем пособии приведены основы математического аппарата, который используется при изучении теории помехоустойчивого кодирования, исследовании алгоритмов кодирования и декодирования, разработке и построении кодеров и декодеров приемопередающих устройств.
Пособие состоит из девяти разделов. В разд. 1 рассмотрены основные понятия и классификация помехоустойчивых кодов. Разд. 2 посвящен основам двоичной алгебры и реализации основных операций над двоичными числами. В разд. 3 описаны матрицы и основные действия над ними. В разд. 4 приводятся основные понятия комбинаторики. В разд. 5 — полиномы и основные операции с полиномами. Разд. 6 посвящен понятиям группы, кольца и поля, а в разд. 7 описан основной математический аппарат блочных помехоустойчивых кодов (Боуза–Чоудхури–Хоквингема и Рида–Соломона) — двоичные поля Галуа. В разд. 8 приводятся основы теории графов. В разд. 9 рассмотрены основные модели каналов передачи данных.
5

1. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ
Помехоустойчивое кодирование (англ. Error Correcting Coding, ECC) — процесс преобразования информации, предоставляющий возможность обнаружить и исправить ошибки, возникающие при передаче информации по каналам передачи данных.
Под ошибкой при этом понимают ситуацию, когда в результате действия помех и искажений в канале передачи данных приемник принимает неверное решение, отождествляя принятый сигнал не с фактически переданным символом, а с каким-либо другим [1].
Процесс помехоустойчивого кодирования заключается во введении избыточности, т. е. для передачи информации используется код, у которого используются не все возможные комбинации, а только некоторые из них. Такие коды называют избыточными или корректирующими.
Соответственно, процесс введения избыточности (преобразование информационных символов в кодовое слово) называется кодированием, а обратный процесс восстановления информации из кодового слова, возможно содержащего ошибки, — декодированием.
В рамках цифровой системы передачи данных задачи кодирования и декодирования возложены на кодер и декодер соответственно. Структура цифровой системы передачи данных показана на рис. 1.1 [2].
|
Двоичные |
Дискретный канал |
||
|
Источник |
данные |
Модулятор |
|
|
данных |
Кодер |
||
|
S(t) |
|||
|
Информация |
Физический |
Помехи |
|
|
канал |
n(t) |
||
|
о надежности |
ˆ |
||
|
Двоичные |
S(t) |
||
|
Получатель |
данные |
Демодулятор |
|
|
данных |
Декодер |
||
Рис. 1.1. Структура цифровой системы передачи данных
Часто декодеру доступна информация, указывающая на надежность решений, принимаемых о различных символах кодового слова. Такая информация может быть использована для упрощения процесса декодирования, либо для улучшения его характеристик [2].
В целом, способность помехоустойчивых кодов определять и исправлять ошибки — их корректирующие свойства — зависит от правил постро-
6
ения этих кодов и параметров кода (числа разрядов, избыточности и др.), а также от используемых алгоритмов декодирования.
1.1. Основные параметры помехоустойчивых кодов
Основными параметрами, характеризующими корректирующие свойства кодов являются:
1)избыточность кода;
2)кодовое расстояние;
3)кратность гарантированно обнаруживаемых ошибок;
4)кратность гарантированно исправляемых ошибок.
1.1.1.Избыточность корректирующего кода
Избыточность корректирующего кода может быть абсолютной и относительной. Под абсолютной избыточностью понимают число вводимых дополнительных разрядов
r = n k;
где n — число кодовых символов на выходе кодера, соответствующих k информационным символам на его входе.
Относительной избыточностью корректирующего кода называют величину
|
R |
отн |
= |
r |
= |
n k |
= |
k |
: |
|
|
n n |
1 n |
С ней связана так называемая относительная скорость передачи информации или скорость кода, которая показывает, какую часть общего числа символов кодовой комбинации составляют информационные символы.
k = 1 Rотн:
n
Если производительность источника равна H символов в секунду, то скорость передачи после кодирования этой информации будет равна
R = H k : n
1.1.2. Кодовое расстояние
Кодовое расстояние d или расстояние Хемминга характеризует cтепень различия любых двух кодовых комбинаций. Оно выражается числом разрядов, в которых комбинации отличаются одна от другой.
Чтобы получить кодовое расстояние между двумя комбинациями двоичного кода, достаточно подсчитать число единиц в поразрядной сумме этих
7

комбинаций по модулю 2:
10011 11001 = 01010 ) d = 2:
Кодовое расстояние может быть различным. Так, в первичном натуральном безызбыточном коде это расстояние для различных комбинаций может различаться от единицы до n, где n — длина (значность) кода.
Для помехоустойчивого кода наиболее важным является минимальное кодовое расстояние dmin — наименьшее кодовое расстояние из всех между всеми парами кодовых комбинаций.
В безызбыточном коде все комбинации являются разрешенными, dmin = 1. Поэтому искажение хотя бы одного символа в комбинации будет приводить к получению ошибочного сообщения.
1.1.3. Кратности гарантированно обнаруживаемых и гарантированно исправляемых ошибок
Эти параметры напрямую зависят от минимального кодового расстояния. Под кратностью понимается количество поражённых ошибками символов кодовой комбинации.
В общем случае при необходимости обнаруживать ошибки кратности tобн минимальное кодовое расстояние должно быть, по крайней мере, на единицу больше tобн, т. е.
dmin tобн + 1:
Соответственно, кратность гарантированно обнаруживаемых кодом ошибок равна
tобн dmin 1:
Кратность гарантированно исправляемых кодом ошибок вычисляется по формуле
t dmin 1:
2
Таким образом, код, имеющий минимальное кодовое расстояние dmin = 3, позволяет гарантированно обнаружить tобн = 2 и менее ошибок и гарантированно исправить t = 1 ошибку.
1.2. Классификация помехоустойчивых кодов
Помехоустойчивые коды классифицируются по различным признакам. Одной из основных классификаций является деление кодов на блочные и непрерывные.
8
Блочный (блоковый) код является кодом без памяти. Кодер блочного кода отображает подающийся на вход блок информационных символов длиной k в кодовую последовательность из n выходных символов. Термин «без памяти» указывает, что каждый блок из n символов зависит только от соответствующего блока из k символов и не зависит от других блоков [2].
Основыми параметрами блочных кодов являются длина информационного блока k, длина кодового слова n, скорость кода nk и минимальное кодовое расстояние dmin.
Непрерывные или древовидные коды — это помехоустойчивые коды использующие непрерывную, или последовательную, обработку информации короткими фрагментами (блоками). Кодер древовидного кода является устройством с памятью. На его вход поступают наборы из k входных информационных символов, а на выходе появляются наборы из n кодовых символов. Каждый набор n кодовых символов зависит от текущего входного набора и от v предыдущих входных символов. Следовательно кодер должен содержать устройство памяти на m = k + v входных символов. Параметр m часто называют длиной кодового ограничения кода [2].
Также непрерывные коды характеризуются скоростью кода nk и свободным расстоянием dсв [2].
Чаще всего используются линейные древовидные коды, называемые
сверточными.
Особое место в классификации помехоустойчивых кодов занимают каскадные коды и турбо коды, представляющие из себя комбинации блочных и/или непрерывных кодов [3].
Другой подход к классификации делит коды на линейные и нелинейные. Линейные коды образуют векторное пространство, в котором два кодовых слова при сложении по определенному правилу дают в результате третье кодовое слово [2].
Практически все применяемые на практике схемы кодирования основаны на использовании линейных кодов. Двоичные линейные блоковые коды часто называют групповыми кодами, так как их кодовые слова образуют математическую структуру, называемую группа [2].
Нелинейные коды применяются гораздо реже линейных. К нелинейным кодам относится код с контрольным суммированием, в котором проверочные разряды являются записью суммы единиц в кодовой комбинации [1].
По способу кодирования коды делятся на систематические и несистематические. В первом случае информационные символы передаются на выход декодера без изменения и к ним добавляются проверочные символы. В
9
случае несистематического кодирования информационные символы в явном виде в кодовом слове отсутствуют.
Большинство помехоустойчивых кодов может быть использовано как для обнаружения, так и для исправления ошибок, хотя есть коды, которые позволяют лишь обнаруживать ошибки. Поскольку избыточность, требуемая для обнаружения ошибок, меньше избыточности для исправления ошибок, то коды с обнаружением ошибок часто используют в системах с обратной связью [1].
Ещё одним вариантом деления помехоустойчивых кодов является разделение их на коды, исправляющие случайные ошибки, и коды, исправляющие пакеты (пачки) ошибок. Хотя для исправления пачек ошибок было разработано большое количество кодов с хорошими характеристиками, часто оказывается выгодным использовать коды, исправляющие случайные ошибки, совместно с устройствами перемежения/деперемежения [2]. Также стоит отметить, что существуют алгоритмы декодирования, позволяющие использовать коды, рассчитанные на исправление случайных ошибок, для исправления пачек ошибок без использования перемежителей. К таким алгоритмам относится, например, мажоритарное декодирование на основе двойственного базиса [4].
Контрольные вопросы
1.Что такое помехоустойчивое кодирование?
2.Опишите структуру цифровой системы передачи данных.
3.Дайте понятие избыточности корректирующего кода. Что такое абсолютная и относительная избыточности? Как определяется скорость кода?
4.Что такое кодовое расстояние? Как оно определяется?
5.Как рассчитываются кратности гарантированно обнаруживаемых и гарантированно исправляемых ошибок?
6.Приведите классификацию помехоустойчивых кодов.
10
Соседние файлы в предмете Математические Основы Теории Помехоустойчивого Кодирования
- #
20.11.201816.44 Кб12meggit_s_obnulenia.circ
- #
- #
- #
- #
- #
- #
- #
20.11.2018760.56 Кб20Козырев А. Б..odt
Теория кодирования возникла в конце 40-х годов с появлением работ Голея, Хэмминга и Шеннона. Истоками теории являются инженерные задачи, но ее развитие приводит к все более утонченным математическим методам. Первые два автора заложили основу алгебраическим методам кодирования, Шеннон предложил и исследовал понятие случайного кодирования.
1. ВВЕДЕНИЕ 4
2. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ 5
3. ПРАКТИЧЕСКАЯ ЧАСТЬ 10
4. ЗАКЛЮЧЕНИЕ 13
5. СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 14
Файлы: 1 файл
Казанский Государственный Технический Университет им. А.Н. Туполева
Институт радиоэлектроники и телекоммуникаций
Кафедра Радиоэлектронных и Телекоммуникационных систем
______________________________ ______________________________ ______
Пояснительная записка к курсовой работе по курсу
ТЕОРИЯ ЭЛЕКТРИЧЕСКОЙ СВЯЗИ
Выполнил:
Студент группы 4404
Супрунов Д.О.
Проверил:
Доцент кафедры РТС
Коробков А.А.
Задание
2. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ 5
ТеорИнф Lecture3
3. ПРАКТИЧЕСКАЯ ЧАСТЬ 10
4. ЗАКЛЮЧЕНИЕ 13
5. СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 14
ВВЕДЕНИЕ
Теория кодирования возникла в конце 40-х годов с появлением работ Голея, Хэмминга и Шеннона. Истоками теории являются инженерные задачи, но ее развитие приводит к все более утонченным математическим методам. Первые два автора заложили основу алгебраическим методам кодирования, Шеннон предложил и исследовал понятие случайного кодирования.
В современных информационных системах важнейшей задачей является обеспечение информационной безопасности, связанной с методами криптографии, теоретические основы которой заложил Шеннон во второй своей важнейшей работе.
В течение большей части второй половины прошлого века математики и специалисты по аппаратным и программным средствам ЭВМ и проблемам передачи данных упорно бились над тем, чтобы выработать технологию, позволяющую кодировать информацию таким образом, чтобы
при разрушении случайно выбранных ее блоков, эти блоки можно было восстановить. После того, как была заложена математическая основа для кодирования, разработаны эффективные алгоритмы кодирования и декодирования, технология ближе к концу прошлого века стала более
или менее устоявшейся. Технология применяется при приеме / передаче данных в сетях и при чтении / записи данных на большинстве носителей информации, «на лету» обнаруживая и по возможности исправляя искаженные блоки данных. В связи с бурным развитием хакерской мысли эта технология является весьма актуальной в настоящее время.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Теория помехоустойчивого кодирования базируется на результатах исследований, проведенных Клодом Шенноном. Он сформулировал теорему для дискретного канала с шумом: при любой скорости передачи двоичных символов, меньшей, чем пропускная способность канала, существует такой код, при котором вероятность ошибочного декодирования будет сколь угодно мала.
Построение такого кода достигается ценой введения избыточности. То есть, применяя для передачи информации код, у которого используются не все возможные комбинации, а только некоторые из них, можно повысить помехоустойчивость приема. Такие коды называют избыточными или корректирующими. Корректирующие свойства избыточных кодов зависят от правил построения этих кодов и параметров кода (длительности символов, числа разрядов, избыточности и др.).
Коды Рида-Соломона. Кодирование на примере 8-ричного кода с кодовым расстоянием 5.
В настоящее время наибольшее внимание уделяется двоичным равномерным корректирующим кодам. Они обладают хорошими корректирующими свойствами и их реализация сравнительно проста.
Помехоустойчивое кодирование [2] — кодирование, состоящее в целенаправленном введении избыточных символов, с целью обеспечения возможности обнаружения и исправления ошибок.
Обнаружить ошибку [2] — зафиксировать факт, что в данной кодовой комбинации присутствует ошибка.
Исправить ошибку [2] — точно указать разряд в кодовой комбинации, в котором произошла ошибка и исправить её (инвертировать разряд с ошибкой).
Основой помехоустойчивого кода является простой двоичный код. Расчёт количества разрядов необходимых для кодирования конечного числа сообщений в простом коде производится по формуле (1) [3, стр.22], где N-количество кодируемых сообщений, m-используемая, при кодировании, система исчисления.
Источник: www.yaneuch.ru
Основы теории помехоустойчивого кодирования. Понятие кодового расстояния, минимальное расстояние кода.
Основной задачей помехоустойчивого кодирования является решение проблемы обеспечения высокой достоверности передаваемых данных за счет применения устройств кодирования/декодирования в составе системы передачи цифровой информации.
Помехоустойчивое кодирование стало неотъемлемой частью современных систем передачи и хранения информации.
Кодовое расстояние по Хемингу-если имеются две кодовые комбинации одинаковой длины 
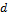




Наименьшее расстояние кода — наименьшее из всех возможных кодовое расстояние для кодов а и b.
Исправляющая способность помехоустойчивого кода.
Кратность ошибки- число искаженных разрядов при передачи.
Исправляющая способность кода- кратность обнаруживаемых ошибок и кратность исправляемых ошибок.
Если между двумя разрешенными 1 запрещенная, то можно только обнаружить ее. А для исправления ошибки между двумя разрешенными 2 запрещенных.
– обнаружение ошибки.
– исправление ошибки.
Структура ПЭВМ. Назначение основных блоков.
Цп — центральный процессор.
ОП – оперативная память.
ВУ — внешнее устройство, имеют меньшее быстродействие чем цп или сп.
К – контролер, специализированный процессор.
Kt – контролер таймера. Таймер – формирование программно-задаваемых временных задержок.
КПДП — контролер прямого доступа к памяти — позволяет выполнять обмен между внешними устройствами и оперативной памятью без участия цп, во время этого обмена цп может выполнять программы загруженные в его внутреннюю память, таким образом обеспечивается параллельное выполнение нескольких процессов. Эффективен при обмене блоками данных.
ПКП — программируемый контролер прерывания, на вход поступают запросы на прерывание ВУ.
ПЗУ — постоянное запоминающее устройство (храниться BIOS.
1.Тестирование компьютера при включении(post).
2.SETUP — задание конфигурации.
3.функция ввода вывода.
СMOS — элементарный метал-окисел полупроводник — используется в устройствах, требующих длительное хранилище без особых затрат энергии. Состоит из 2 частей:
1.часы реального времени.
2.память, в которой таблица конфигурации компьютера.
Параметры ПЭВМ.
1. Быстродействие.
· — тактовая частота.
– тактовый интервал.
тактовый интервал — время выполнения 1 микрооперации.
· — время обращения к памяти.
· — ширина выборки — какое количество данных можно получить или записать за одно обращение. За одно обращение 128-256 бит.
2. Потребляемая мощность.
– информационная емкость памяти.
3. Надежность.
· время безотказной работы.
Источник: poisk-ru.ru
Мажоритарное декодирование циклических кодов
Декодирование циклических мажоритарных кодов с повторением. При декодировании циклических кодов, допускающих мажоритарную обработку, процесс декодирования может быть осуществлен только после приема всей комбинации циклического (п, k) – кода. Для кодов с повторением мажоритарная обработка заканчивается после приема всех повторений комбинации. Использование для помехоустойчивого кодирования сообщений одновременно циклических мажоритарных кодов и метода многократных повторений позволяет обеспечить требуемые характеристики по достоверности и надежности передачи информации при использовании каналов связи низкого качества.
На рис. 2 изображена функциональная схема декодирующего устройства для циклических мажоритарных кодов с повторением. Устройство содержит регистр сдвига 1, сумматоры по модулю два 2, распределитель 3, счетчики мажоритарных проверок 4 – 1, 4–2,…, 4 – k, блок запоминания 5, блок, сравнения 6 и дешифратор 7.
Регистр сдвига установлен для записи п элементов одной кодовой комбинации циклического (п, k) – кода и перезаписи комбинации по цепи обратной связи при формировании результатов мажоритарных проверок.
Сумматоры по модулю два 2 предназначены для вычисления мажоритарных проверок путем суммирования импульсов с различных ячеек регистра сдвига 1 с целью получения серии импульсов, из которых затем по большинству определяется значение информационного элемента. Входы сумматоров подключены к ячейкам регистра сдвига в соответствии с системой мажоритарных проверок для конкретного циклического кода.
Распределитель 3 служит для направления результатов мажоритарных проверок с выходов сумматоров в счетчик того информационного элемента, которому соответствуют эти проверки.
Счетчики мажоритарных проверок 4–1, 4–2,…. 4-k используются для подсчета результатов мажоритарных проверок. Они выполнены по схеме с несколькими порогами срабатывания. Каждый порог определяется числом принятых кодовых комбинаций, по результатам мажоритарных проверок которых вычисляются информационные элементы.
В общем случае число счетчиков равняется числу информационных элементов k в исходной кодовой комбинации. Если l – число мажоритарных проверок для одного информационного элемента за одно повторение, то минимальный порог определится величиной 0,5l (l – четное) или 0,5 (l+ 1). где l – нечетное. За m повторений порог определится величиной 0,5 lm или 0,5 (1m + 1). За все N повторений порог определится величиной 0,5 lm или 0,5 (lm + 1). Так, для циклического (7,3) – кода с трехкратным повторением l = 4, минимальный порог за одно повторение равен двум, порог за два повторения равен четырем и порог за все повторения равен 6.
При этом счетчик мажоритарных проверок для одного информационного элемента (рис. 3) будет состоять из трех двоичных разрядов и значение информационного элемента для минимального порога определится состоянием второго разряда счетчика после обработки первого повторения, для второго порога – состоянием третьего разряда счетчика после обработки двух повторений и для третьего порога за все повторения – состоянием второго и третьего разрядов счетчика после обработки трех повторений.
В частном случае порогов срабатывания может быть два: первый порог за одно или часть повторений определяет первый этап обработки, второй порог за все повторения определяет второй этап обработки.
Счетчики мажоритарных проверок 4–1, 4–2,…, 4-t выполнены по схеме с двумя порогами и соответственно имеют по два выхода.
Блок запоминания 5 служит для поочередного запоминания результатов мажоритарной обработки, соответствующих реализованным порогам срабатывания счетчиков 4–1, 4–2,…, 4-к.
Блок сравнения 6 первый результат мажоритарной обработки выдает для исполнения, сравнивает каждый последующий результат с предыдущим и при их несовпадении выдает сигнал на прекращение исполнения предыдущего решения и выдает для исполнения последующее решение.
Дешифратор 7 анализирует результаты мажоритарных обработок и при выявлении запрещенной комбинации блокирует ее выдачу до окончания приема всех повторений. К запрещенным комбинациям могут быть отнесены сообщения, исполнение которых приводит к необратимым процессам у получателя и которые не могут быть скорректированы последующими результатами мажоритарных проверок.
В частном случае для систем, в которых отсутствуют запрещенные комбинации, дешифратор 7 будет отсутствовать. Работа устройства происходит следующим образом.
Принимаемая n-разрядная кодовая комбинация вводится в регистр сдвига 1. Далее, в течение к тактов при помощи регистра сдвига 1 и сумматоров 2 формируются результаты мажоритарных проверок для каждого из к информационных элементов, которые через распределитель 3 вводятся в соответствующий счетчик мажоритарных проверок 4–1, 4–2,…, 4-k. Вся процедура декодирования осуществляется за время , где V – скорость модуляции для принимаемой кодовой комбинации. Аналогично обрабатывается каждое повторение циклического кода. После приема и обработки т повторений, определяющих первый порог срабатывания, информационные элементы с первых выходов счетчиков мажоритарных проверок поступают одновременно в блок запоминания 5 и блок сравнения 6. Из блока сравнения 6 декодированная комбинация поступает в дешифратор 7, который анализирует и не препятствует выдаче для исполнения разрешенной комбинации, или подачей сигнала в блок сравнения 6 блокирует выдачу запрещенной комбинации.
После приема и обработки m повторений, определяющих второй порог срабатывания, информационные элементы со вторых выходов счетчиков мажоритарных проверок поступают одновременно в блок запоминания 5 и блок сравнения 6. Поступившие информационные элементы вытесняют из блока запоминания 5 в блок сравнения 6 ранее запомненный результат. В блоке сравнения 6 сравниваются результаты первого и второго этапов обработки. При их совпадении продолжает исполняться сообщение, декодированное на первом этапе. При несовпадении блок сравнения 6 выдает сигнал на прекращение исполнения сообщения, декодированного на первом этапе и выдает для исполнения сообщение, декодированное на втором этапе. В случае имевшей место на первом этапе блокировки блок сравнения 6 выдает для исполнения сообщение, декодированное на втором этапе. Выбором соответствующего значения m обеспечивается то, что в абсолютном большинстве случаев сообщения, декодированные на первом и втором этапах, будут совпадать и время приема определится величиной
что в раз меньше, чем время приема в известных устройствах.
Если – реализуемое кодовое расстояние циклического мажоритарного М (n, k) – кода [7, 115], которое аналогично минимальному расстоянию, то кратность гарантийно исправляемых ошибок определяется соотношением
В общем виде реализуемое расстояние определяется выражением


Реализуемое кодовое расстояние, соответствующее т повторениям первого этапа обработки,
а кратность исправляемых ошибок
(19)
Второй этап обработки характеризуется приемом N повторений, реализуемое кодовое расстояние которых
а кратность исправляемых ошибок
(20)
Характеристики (19) и (20) позволяют определить достоверность информации первого и второго этапов обработки по методике (п. 3.3).
Таким образом, можно отметить, что наряду с разработанными процедурами обнаружения и исправления ошибок циклические коды хорошо совместимы с процедурой поэтапного принятия решений, что повышает эффективность их использования при передаче информации в информационных системах.
Модели организации как закрытой, открытой, частично открытой системы: Закрытая система имеет жесткие фиксированные границы, ее действия относительно независимы.
Как вы ведете себя при стрессе?: Вы можете самостоятельно управлять стрессом! Каждый из нас имеет право и возможность уменьшить его воздействие на нас.
Почему 1285321 студент выбрали МегаОбучалку.
Система поиска информации
Источник: megaobuchalka.ru
кодовое расстояние-это количество мест где есть различие между символами, те 10 01, а 11 00 не считаеся.
на выходе кодера канала при использовании кода (6,5).


5)
Четное число единиц на 6-ти интервалах
№2Выберите подходящее правило формирования проверочного символа кода (6,5)
с общей проверкой на четность.
2) b6= b1Å b2 Å b3 Å b4Å b5.
3) Проверочный символ равен сумме по модулю 2 значений информационных символов кодовой комбинации.
4) Проверочный символ устанавливается таким, чтобы общее число «1»в выходной кодовой комбинации стало чётным.
№3Выберите подходящие цели помехоустойчивого кодирования.
1) Обнаружение и исправление ошибок в принятых сообщениях
2) Исправление ошибок в принятых сообщениях
3) Уменьшение числа ошибок в принятых сообщениях
№4Выберите подходящие определения кодового расстояния.
1) Минимальный вес ненулевых кодовых комбинаций
2) Минимальное число «1» в ненулевых кодовых комбинациях
3) Минимальное число разрядов, в которых различаются разные кодовые комбинациии
4) Минимальное расстояние (по Хэммингу) между различными кодовыми комбинациями
№5Выберите верные варианты кратности обнаруживаемых и исправляемых ошибок кодом с кодовым расстоянием 5
1) Обнаруживаются любые ошибки с кратностью < 5
2) Исправляются любые ошибки с кратностью < 3
3) Обнаруживаются любые ошибки с кратностью 3
4) Исправляются любые однократные и двукратные ошибки
№6Выберите тройки кодовых комбинаций с весами < 6
Вес-это число единиц в строке(это число должно быть меньше 6)
Приер неправ ответа:
0111001011 здесь 6 единиц
№7Выберите пары кодовых комбинаций c расстояниями между ними > 4
Ответ: кодовое расстояние-это количество мест где есть различие между символами, те 10 01, а 11 00 не считаеся.
1001011001 код расст 5
0100111000 код раст 8
№8Выберите пары кодовых комбинаций с весами < 5
Ответ: Вес-это число единиц в строке(это число должно быть меньше 5)
1) 1001000010 вес 3
0010111000 вес 4
№9Выберите пары кодовых комбинаций c расстояниями между ними < 5
кодовое расстояние-это количество мест где есть различие между символами, те 10 01, а 11 00 не считаеся.
0111000000 код раст 3
№10Выберите верные варианты трактовки параметров блочного линейного систематического кода (n, k, d)
1) стандарт в учебнике стр 244 см
k-число иформационных символов в кодовых комбинациях.
d — кодовое расстояние
2) n — разрядность блоков на выходе кодера,
k — разрядность блоков на входе кодера,
d — кодовое расстояние
3) n — разрядность кодовых комбинаций,
k — число информационных символов в кодовых комбинациях,
d — кодовое расстояние
4) n — разрядность блоков на выходе кодера,
k — разрядность блоков на входе кодера,
d — минимальное расстояние между кодовыми комбинациями
№11Выберите верные варианты трактовки параметров блочного линейного систематического кода (n, k)
1) n — длина кода,
k — разрядность кода на входе кодера,
(n — k)- число проверочных символов в кодовых комбинациях.
n — разрядность кода на выходе кодера,
k — разрядность кода на входе кодера,
(n — k)/n — избыточность кода.
3) n — длина кода,
k — число информационных символов в кодовых комбинациях,
(n — k)– число проверочных символов в кодовых комбинациях.
4) n — разрядность кода на выходе кодера,
k — разрядность кода на входе кодера,
(n — k)- число проверочных символов в кодовых комбинациях.
№12Выберите верные описания линейного кода и процедуры кодирования на матричной основе.
— вектор-строка i-ой входной
— вектор-строка i-ой выходной
В — матрица всех разрешенных комбинаций,
ВИ — матрица информационных кодовых последовательностей,
Р — подматрица проверочных символов.
В — матрица всех разрешенных комбинаций,
ВИ — матрица информационных кодовых последовательностей,
G — порождающая матрица.
G — порождающая матрица.
№13Выберите верные операции процедуры декодирования линейного кода на матричной основе.
— i-ый синдром,
H — проверочная матрица.
1) Вычисляют синдром путем умножения вектора принятой кодовой комбинации на транспонированную проверочную матрицу.
2) Инвертируют символ принятой комбинации, на который указывает синдром.
— i-ый синдром,
— вектор-строка i-ой принятой
H — проверочная матрица.
— i-ый синдром,
— вектор переданной комбинации.
H — проверочная матрица
№14Выберите верные описания процедуры кодирования линейного кода (n, k) на полиномиальной основе.
b(x) = a(x)·g(x)
b(x) — полином кодовой комбинации,
a(x) — информационный полином,
g(x) — порождающий полином.
2) Полином кодовой комбинации получают умножением полинома информационной комбинации на порождающий полином.
3) b(x) = b(x)·x n-k +
+ [a(x)·x n-k mod g(x)]
b(x) — полином кодовой комбинации,
a(x) — информационный полином,
g(x) — порождающий полином.
4) b(x) = g(x)·a(x)
b(x) — полином кодовой комбинации,
a(x) — информационный полином,
g(x) — порождающий полином.
№15Выберите верные операции процедуры декодирования линейного кода (n, k) на полиномиальной основе.
s(x) — синдромный полином,
— полином принятой кодовой
g(x) — порождающий полином.
2) 1) Вычисляют синдромный полином путем вычисления остатка от деления полинома принятой кодовой комбинации на порождающий полином.
2) Инвертируют символ принятой комбинации, на который указывает синдром.
s(x) — синдромный полином,
— полином принятой кодовой комбинации,
g(x) — порождающий полином.
4) 1) Вычисляют синдромный полином
путем деления полинома принятой кодовой комбинации по модулю порождающего полинома.
2) Инвертируют символ принятой комбинации, на который указывает синдром.
№16 Выберите верные цели использования перемежения при помехоустойчивом кодировании.
1) Для борьбы с пакетами ошибок при использовании помехоустойчивых кодов, испрвляющих независимые ошибки.
2) Для преобразования зависимых ошибок в почти независимые.
3)Для декорреляции ошибок
4)Для преобразования многократных ошибок одной кодовой комбинации в однократные ошибки многих кодовых комбинаций.
№17Определите вес кодовой комбинации 10010110.
№18Определите вес кодовой комбинации 0110101011.
№19Определите расстояние (по Хэммингу) между кодовыми комбинациями
№20Определите расстояние (по Хэммингу) между кодовыми комбинациями
№21 Оределите максимальную кратность гарантированно исправляемых ошибок кодом с кодовым расстоянием 13.
Ответ: см стр 241: 132=6, 5 следов ответ=6
№22 Определите число разрешенных кодовых комбинаций кода (8, 7).
Ответ: 2 в 7 степени: 128
№23Определите число разрешенных кодовых комбинаций кода (15, 11).
№24Определите число запрещенных кодовых комбинаций кода (7, 4).
Ответ: 2 в 7-ой минус 2 в 4-ой:
№25Определите число запрещенных кодовых комбинаций кода (7, 6).
№26Порождающий полином несистематического линейного кода (7, 4) g(x) = x 3 + x + 1.
На входе кодера информационная комбинация 0101.
Определите кодовую комбинацию на выходе кодера.
Ответ: см таблицу на стр 249: 0101100
№27Порождающий полином систематического линейного кода (7, 4) g(x) = x 3 + x + 1.
На входе кодера информационная комбинация 1101.
Определите кодовую комбинацию на выходе кодера
№28Порождающий полином линейного кода (7, 4) g(x) = x 3 + x + 1.
Определите синдром для кодовой комбинации 1001001.
\синдром=X6+X3+1 mod g(x) : x2+x+1
№29Порождающий полином кода (7, 3) g(x) = x 4 + x 2 + x + 1.
Определите синдром для кодовой комбинации 1001010.
№30По порождающей матрице G линейного кода (7, 4) и информационной комбинации 0111 на входе кодера определите кодовую комбинацию на выходе кодера.
Ответ: см стр 247:0111010
№ 31По порождающей матрице G линейного кода (7, 4) и информационной комбинации 1010 на входе кодера определите кодовую комбинацию на выходе кодера.
№32 Определите синдром для принятой комбинации 1001111 линейного кода (7, 4) с проверочной матрицей H.
№33Определите синдром для принятой комбинации 1010001 линейного кода (7, 4) с проверочной матрицей H.
Воспользуйтесь поиском по сайту:
Источник: megalektsii.ru
3. Оценка помехоустойчивости кода
п где С ч п =——-биномиальный коэффициент.
Вероятность ошибки на этапе обнаружения
а вероятность ошибки на этапе исправления
При экспериментальной оценке вероятности р появления некоторого события проводится N независимых испытаний и используют формулу непосредственного подсчета вероятности
где М — число испытаний , в которых произошло данное событие. Следует иметь в виду, что при больших М и N-M в силу центральной предельной теоремы распределение вероятностей возможных значений оценки приближенно описывается нормальным законом с математическим ожиданием и среднеквадратическим значением соответственно
т р=р> °i, =(p(1-p)/n) 1/2 > (7Л9)
поэтому для получения точных оценок нужно проводить много испытаний.
Например, число испытаний, требуемое для достижения относительной среднеквадратической ошибки в 10%, определим из (7.19) как
4. Лабораторная установка
Лабораторная установка содержит основные элементы (или их имитаторы) одноканальной двоичной системы передачи информации.
Генератор тактовых импульсов вырабатывает последовательность импульсов с периодом, определяющим длительность двоичного символа 7=т=2 мкс.
Распределитель импульсов синхронизирует работу всех остальных элементов схемы и для этого вырабатывает синхроимпульсы следующих видов:
- 1) тактовые импульсы через Г=2 мкс;
- 2) импульсы синхронизации КК тКк=7т;
- 3) импульсы введения паузы между словами тп=13т.
В качестве имитатора источника информации использованы шесть тумблеров КОД ВХ., при помощи которых можно ввести любую комбинацию из шести информационных символов кода (7,6). При исследовании циклического кода (7,4) для ввода информационных символов используются первые четыре тумблера.
Кодер (7,6)-кода выполнен по схеме рис. 7.1, а кодер (7,4)-кода — по схеме рис.7.3. Выбор кода осуществляется переключателем (7,4)-(7,6).
Имитатор двоичного симметричного канала с ошибками содержит сумматор по mod 2, на один вход которого подается последовательность символов с выхода кодера, а на другой вход — последовательность двоичных символов вектора ошибки. Установлены два режима введения ошибок: ручной и от генератора ошибок, причем выбор режима производится тумблером РУЧН-ГЕН.
В первом режиме семь элементов вектора ошибки набираются при помощи семи тумблеров ОШИБКА. Во втором режиме в передаваемые символы вводятся случайные независимые ошибки от генератора случайной двоичной импульсной последовательности. Требуемое значение вероятности р появления ошибки в одном символе может быть установлено переключателем «-log2P», при этом р примерно равно одному из следующих значений: 1/2, 1/4, 1/8. 1/256 (более точная оценка истинного значенияр определяется экспериментально).
Визуальная индикация КК на выходе канала осуществляется при помощи семи светодиодов ВЫХОД.
Декодер циклического кода выполнен по схеме рис. 7.4. Обнаружение ошибки осуществляется к моменту окончания приема КК (первые семь тактов), а пауза в передаче (следующие семь тактов) используется для выяснения номера ошибочного символа.
Декодер кода с проверкой на четность также производит обнаружение ошибки к концу приема КК. Поскольку код с проверкой на четность не способен исправлять ошибки, пауза является для него холостой.
Компаратор последовательно сравнивает каждую переданную КК с тем, что получилось на выходе канала или на выходе декодера и в зависимости от результата сравнения выдает или не выдает положительный импульс на разъем ЧАСТ.
Выбор одного из четырех возможных режимов работы компаратора производится переключателем ВИД ОШ., при этом частотомер (счетчик импульсов) 43-32, подключенный к разъему ЧАСТ., в зависимости от выбранного режима, фиксирует одну из следующих величин:
- 1) количество переданных кодовых комбинаций;
- 2) количество КК, в которых в канале произошли ошибки;
- 3) количество КК на выходе декодера с необнаруженными ошибками;
- 4) количество КК на выходе декодера с неисправленными ошибками.
Последний режим используется только при применении циклического кода.
Включение макета производится тумблером СЕТЬ ВКЛ. Синхроимпульсы, соответствующие началу каждой КК, подаются на осциллограф с разъема СИНХР. Контроль напряжений в характерных точках схемы производится при помощи контрольной колодки, на гнезда которой подаются:
А1 — кодовая комбинация (КК) с выхода кодера;
А2 — вектор ошибки;
АЗ — КК с выхода канала с ошибками;
А4 — сигнал с выхода счетного триггера декодера кода с проверкой на чётность;
А5 — сигнал с выхода счетчика импульсов (параллельно разъему ЧАСТ.);
А6 — сигнал с выхода схемы совпадения, индицирующей появление комбинации ООО в регистре декодера кода (7,4);
А7 — сигнал с выхода схемы совпадения, индицирующей появление комбинации 100 в регистре декодера кода (7,4).
- 5. Рекомендуемый порядок лабораторных исследований
- 5.1. Изучить краткие сведения из теории корректирующих кодов и продумать ответы на контрольные вопросы.
- 5.2. Уяснить принципы построения кодирующих и декодирующих устройств для кода с проверкой на четность (7,6 ) и циклического кода (7,4). Освоить методику кодирования и декодирования.
- 5.3. Для кода (7,6):
- 1) для заданной преподавателем последовательности информационных символов вычислить КК;
- 2) определить кодовое расстояние dKoa, кратности гарантированно обнаруживаемых q0 и исправляемых qn ошибок, избыточность кода R;
- 3) сравнить с тем, что наблюдается на макете, зарисовав осциллограммы напряжений в контрольных точках лабораторного макета для двух случаев: без ошибки и с одиночной ошибкой, вводимой вручную.
- 5.4. Для кода (7,4):
- 1) для заданной преподавателем комбинации информационных символов вычислить КК на выходе кодера V всеми известными способами и объяснить, почему не всегда получается одна и та же комбинация;
- 2) определить кодовое расстояние, кратности гарантированно обнаруживаемых и исправляемых ошибок, избыточность кода;
- 3) выполнить операции декодирования для вычисленных КК для случаев: без ошибки и вводя одиночную ошибку в один из информационных символов. Деление выполнить алгебраически и с помощью регистра с обратными связями. Привести таблицы, поясняющие процесс декодирования с обнаружением и исправлением ошибки (см. пример табл. 7.2 и 7.3);
- 4) результаты, полученные вычислением, сравнить с наблюдаемыми на макете, зарисовав осциллограммы напряжений в контрольных точках лабораторного макета для случаев: без ошибки и с одиночной ошибкой, вводимой вручную.
- 5.5. Пользуясь ручным вводом ошибок, определить, какой кратности ошибки способен обнаруживать и исправлять каждый из кодов. Для циклического кода отметить факты, когда обнаруживаются некоторые из трехкратных ошибок. Объяснить полученные результаты.
- 5.6. Экспериментально определить, как способность кода обнаруживать и исправлять ошибки зависит от вероятности появления ошибки в одном символе. Сопоставить с результатами аналитических расчетов.
- 5.7. Проанализировать, как обнаруживающая способность кода зависит от его избыточности при разных уровнях помех.
- 5.8. Отчет должен содержать:
- 1) результаты выполнения индивидуального домашнего задания;
- 2) функциональные схемы кодеров и декодеров;
- 3) осциллограммы напряжений в характерных точках схемы;
- 4) результаты измерений, графики, расчеты;
- 5) необходимые выводы.
- 6. Контрольные вопросы
- 6.1. Какой канал называют двоичным симметричным?
- 6.2. Что такое вектор ошибки?
- 6.3. Что называют обнаружением ошибки?
- 6.4. Почему при коррекции ошибок наиболее важно обнаруживать и исправлять ошибки малых кратностей?
- 6.5. Что называют кодовым расстоянием?
- 6.6. Как кратность обнаруживаемых и исправляемых ошибок зависит от величины кодового расстояния?
- 6.7. Чему равно кодовое расстояние для кодов с проверкой на четность?
- 6.8. Почему линейный блочный код иногда называют кодом с многократными проверками на четность?
- 6.9. Укажите способы задания циклических кодов.
- 6.10. Запишите производящую и проверочную матрицы для кода с проверкой на четность (7,6) и циклического кода (7,4)).
- 6.11. Какими корректирующими способностями обладают код с проверкой на четность (7,6) и циклический код (7,4)?
- 6.12. Нарисуйте схему кодера для циклического кода (7,4).
- 6.13. Сформулируйте принцип декодирования циклических кодов.
- 6.14. Нарисуйте схему декодера для циклического кода (7,4).
- 6.15. Зависит ли вероятность ошибочного декодирования от того, какая КК, принадлежащая линейному блочному коду, была передана? Обоснуйте.
- 6.16. В чем заключается преимущество циклических кодов по сравнению с другими разновидностями линейных блочных кодов?
Источник: ozlib.com
Все помехоустойчивые коды делятся на блоковые и непрерывные (их называют также цепные или рекуррентные). При блоковом кодировании данные передаются отдельными блоками (словами, кодовыми комбинациями). При этом поступающие в кодер символы, разбиваются на блоки по k информационных символов. В кодере этот блок информационных символов преобразуется в блок из кодовых символов, где п называется длиной кода. Добавленные при кодировании r = n – k символов являются проверочными. Такой блоковый код принято обозначать как (n, k) – код. Величину R = k / n называют скоростью кода, а величину, обратную скорости, Rи = n / k называют избыточностью кода.
Проверочные символы являются избыточными, они необходимы для обнаружения и (или) исправления ошибок, возникших при передаче. Существуют безызбыточные (примитивные) коды. У этих кодов проверочных символов нет (n = k), поэтому у них самая высокая скорость кода R = 1, но они не способны обнаруживать ошибки.
Ошибки при передаче кодового слова возникают потому, что некоторые из переданных символов могут быть приняты неверно. Принцип обнаружения ошибок заключается в следующем. Если блоковый (n, k) – код имеет основание (количество символов в используемом алфавите) q, то возможно Q = qn различных кодовых слов. Для передачи же используются только Qр = qk кодовых слов, которые называются разрешенными. Остальные Qз = Q – Qр слов априорно для передачи не используются и называются запрещенными.
В дальнейшем будут рассматриваться только двоичные коды, у которых алфавит состоит из двух символов 0 и 1, т. е. с основанием q = 2.
В памяти кодера и декодера хранится таблица разрешенных слов. Работа кодера заключается в выборе разрешенного кодового слова, соответствующего поступившему информационному слову. Приходящее в декодер кодовое слово сравнивается с таблицей разрешенных слов и, если происходит совпадение, то потребитель получает информационное слово, соответствующее данному разрешенному слову. Если же совпадение не наступает, то слово считается запрещенным, а потребитель получает сообщение об ошибке. Однако если совокупность ошибок превратит одно разрешенное слово в другое разрешенное, то возникшие ошибки не могут быть обнаружены.
Пример 1. Требуется передача сообщения о наступлении одного из четырех возможных событий A, B, C, D. Эти события представлены информационными словами 00, 01, 10, 11 соответственно. При передаче этих слов безызбыточным кодом все возможные комбинации являются разрешенными. Поэтому достаточно искажения хотя бы одного символа, чтобы сообщение было принято неверно. Так, если передавалось сообщение A в виде кодового слова 00, а принято было слово 01, то декодер, найдя в таблице такое разрешенное слово, вынесет решение о приеме сообщения B.
Если к вышеперечисленным информационным словам добавить по одному избыточному символу, поставив в соответствие разрешенные слова 000, 011, 101, 110, то искажение одного символа в переданном слове можно обнаружить. Так, если передавалось сообщение A в виде кодового слова 000, а принято было слово 001, то декодер, не найдя в таблице такого разрешенного слова, объявит принятое слово запрещенным и сообщит об обнаружении ошибки в слове. Однако если было принято слово 011, то декодер вынесет решение о приеме сообщения B.
Для сравнения слов необходимо задать метрику, т. е. способ измерения расстояний между кодовыми словами. Известно несколько способов выбора метрики, из которых наиболее распространенным является метрика Хэмминга. Расстоянием Хэмминга между двумя кодовыми словами называется количество несовпадающих символов в этих словах. Важнейшей характеристикой блочного кода является кодовое расстояние – d, оно равно наименьшему расстоянию из всех возможных для данного кода.
Пример 2. Для передачи используются три разрешенных слова 000, 100, 111. Расстояние между первым и вторым словами равно 1, между вторым и третьим словами – 2, а между первым и вторым – 3. Кодовое расстояние для данного кода d = 1.
Очевидно, что у безызбыточного кода d = 1, так как между любой парой его слов расстояние равно единице. Этот код не позволяет обнаруживать ошибки. Приведенный в примере 1 избыточный код (он называется кодом с проверкой на четность) имеет d = 2. Он позволяет гарантировано обнаружить однократную ошибку.
Кратностью ошибки называется количество неправильно принятых символов в кодовом слове. Если искажения символов возникают независимо друг от друга, то ошибки меньшей кратности более вероятны, чем ошибки большей кратности. Следовательно, прежде всего требуется вести борьбу с ошибками малой кратности.
Можно заметить, что максимальная кратность гарантировано обнаруживаемой ошибки tо = d – 1. Действительно, при возникновении необнаруженной ошибки одно разрешенное слово должно превратиться в другое разрешенное слово. А для этого надо, чтобы кратность возникшей ошибки была не менее d, поскольку все разрешенные слова по определению кодового расстояния различаются не менее, чем на d символов. Если же принятое кодовое слово хотя бы на один символ отличается от разрешенных кодовых слов, то будет зафиксировано появление ошибки.
При декодировании вместо обнаружения ошибок возможно их исправление. Так, если было принято запрещенное кодовое слово, то можно не отбрасывать его, а найти наиболее похожее разрешенное слово и объявить его принятым. Таким образом, возникшие при передаче ошибки считаются исправленными, и потребитель получает не сообщение об ошибке, а очередное информационное слово. При декодировании с исправлением ошибок решение принимается по минимуму расстояния Хэмминга, т. е. переданным считается то разрешенное кодовое слово, которое отличается от принятого слова наименьшим количеством несовпадающих символов.
Пример 3. Для передачи используется два разрешенных кодовых слова 000 и 111. Было принято слово 001, на беглый взгляд оно больше похоже на 000, чем на 111. Действительно, слово 001 от первого разрешенного слова отличается на один символ, а от второго на два. Так как однократная ошибка вероятнее двукратной, то скорее всего было передано первое слово и в нем исказился один символ. Декодер принимает решение по минимуму расстояния Хэмминга и объявляет принятым разрешенное слово 000.
В
рассмотренном примере код имеет d = 3, он позволяет гарантировано исправлять однократную ошибку. Можно заметить, что максимальная кратность гарантировано исправляемой ошибки :
где [x] –целая часть числа x.
Существует так называемый прием со стиранием. Это частный случай приема с мягким решением. Его особенность состоит в том, что решающее устройство имеет область неопределенности, в которую попадают все сигналы, не превысившие установленный порог. Решающее устройство выдает при этом специальный символ, заменяющий неуверенно принятый сигнал. Этот символ оказывается, таким образом, «стертым». Так, при передаче двоичным кодом на выходе решающего устройства появляется один из трех символов: 0, 1 и символ стирания Х.
Восстановить стертые знаки часто оказывается легче, чем исправить ошибочные. Это обусловлено тем, что местонахождение стертых знаков известно, так как оно обозначено символом стирания Х, тогда как местоположение ошибок неизвестно, и каждый из знаков 0 или 1 может быть как верным, так и неверным.
Для сохранения различимости кодовых комбинаций при стирании не более s знаков кодовое расстояние d должно удовлетворять условию:
Для того, чтобы код мог одновременно исправлять t ошибок и восстанавливать s стертых символов кодовое расстояние должно быть:
Преимущество кодов со стираниями очевидно: например, при d = 3 такой код может как и обычный исправить одиночную ошибку, но может восстановить два стертых символа.
Описанный выше метод кодирования и декодирования, основанный на запоминании таблицы разрешенных слов, называется универсальным, поскольку годится для всех блочных кодов. Однако этот метод практически не применяется из-за сложности реализации и низкого быстродействия. Если длина информационного слова достаточно велика, то требуется большой объем памяти для хранения всех разрешенных слов. Кроме того, сравнение принятого слова со всей таблицей может продолжаться очень долго, что недопустимо при работе в режиме реального времени. Поэтому созданы другие методы кодирования и декодирования блочных кодов, в которых используется не поиск разрешенных слов, а математические операции над информационными и проверочными символами.
Чаще всего применяются систематические коды. Систематическим называется такой блочный код, у которого информационные и проверочные символы расположены на одних и тех же позициях во всех кодовых словах
В примере 1 был рассмотрен избыточный код с проверкой на четность. При его кодировании к информационному слову добавляется один проверочный символ так, чтобы количество единиц в кодовом слове было четным. При декодировании проверяется выполнение этого условия. Если количество единиц в принятом слове нечетно, то слово является запрещенным. Таким образом, можно обойтись без запоминания таблицы разрешенных слов.
Если в кодере используются лишь линейные операции над поступающими информационными символами, то код называется линейным. Принцип кодирования и декодирования линейного кода заключается в системе линейных уравнений, в которую входят информационные и проверочные символы. Для каждого кода эта система своя. Рассмотрим её на примере кода (7, 4), имеющего d = 3.
a1 а2 а3 а5 = 0
а2 а3 а4 а6 = 0
а1 а2 а4 а7 = 0
где — знак сложения по модулю 2, символы а1, а2, а3, а4 являются информационными, а символы а5, а6, а7 – проверочными. При кодировании проверочные символы вычисляются из информационных так, чтобы они удовлетворяли системе уравнений. При декодировании символы принятого слова подставляются в систему уравнений и вычисляется её правая часть. Эта правая часть представляет собой вектор, который называется исправляющим вектором или синдромом. Анализ синдрома позволяет исправлять ошибки. Каждому возможному синдрому соответствует номер искаженного символа.
|
Синдром |
Номер искаженного символа |
|
000 |
Ошибок не обнаружено |
|
101 |
1 |
|
111 |
2 |
|
110 |
3 |
|
011 |
4 |
Проверочные символы вычисляются с помощью производящей (порождающей) матрицы. Производящая матрица G – это таблица, у которой k строк и n столбцов, в которой записаны k линейно независимых разрешенных комбинаций данного кода. По ней можно построить все остальные разрешенные кодовые комбинации, складывая поразрядно по модулю 2 строки производящей матрицы во всех возможных сочетаниях. В памяти кодера достаточно иметь производящую матрицу. С помощью набора сумматоров можно получить любую разрешенную кодовую комбинацию.
Производящую матрицу принято представлять в каноническом виде. Для рассматриваемого кода она будет:

Где левая часть матрицы — единичная матрица, соответствующая информационным символам, а правая часть матрицы соответствует проверочным символам. Схема кодирования строится на основе производящей матрицы. Кодер состоит из k-элементного регистра для информационного слова и n – k сумматоров по модулю 2. Элементы правой части производящей матрицы pij отвечают за вычисление проверочных символов. Они показывают связь i-ой ячейки регистра с j-м сумматором. Если pij = 1, то связь есть, если pij = 0 , то связи нет.
Д
ля декодирования требуется проверочная матрица H, содержащая n – k строк и n столбцов. В каждой строке этой матрицы единицы находятся в тех разрядах, которые входят в соответствующее проверочное уравнение. Для рассмотренного кода Хэмминга (7, 4) проверочная матрица будет иметь вид:
Существует особый класс блочных линейных кодов – циклические коды. Они отличаются тем, что всякая циклическая перестановка символов разрешенного кодового слова приводит также к разрешенному слову. Все кодовые комбинации можно получить циклическим сдвигом одного слова. Поэтому важным достоинством циклических кодов является то, что операции кодировании и декодирования легко реализуются на сдвигающих регистрах.
Назначение помехоустойчивого кодирования – защита информации от помех и ошибок при передаче и хранении информации. Помехоустойчивое кодирование необходимо для устранения ошибок, которые возникают в процессе передачи, хранения информации. При передачи информации по каналу связи возникают помехи, ошибки и небольшая часть информации теряется.
Без использования помехоустойчивого кодирования было бы невозможно передавать большие объемы информации (файлы), т.к. в любой системе передачи и хранении информации неизбежно возникают ошибки.
Рассмотрим пример CD диска. Там информация хранится прямо на поверхности диска, в углублениях, из-за того, что все дорожки на поверхности, часто диск хватаем пальцами, елозим по столу и из-за этого без помехоустойчивого кодирования, информацию извлечь не получится.
Использование кодирования позволяет извлекать информацию без потерь даже с поврежденного CD/DVD диска, когда какая либо область становится недоступной для считывания.
В зависимости от того, используется в системе обнаружение или исправление ошибок с помощью помехоустойчивого кода, различают следующие варианты:
- запрос повторной передачи (Automatic Repeat reQuest, ARQ): с помощью помехоустойчивого кода выполняется только обнаружение ошибок, при их наличии производится запрос на повторную передачу пакета данных;
- прямое исправление ошибок (Forward Error Correction, FEC): производится декодирование помехоустойчивого кода, т. е. исправление ошибок с его помощью.
Возможен также гибридный вариант, чтобы лишний раз не гонять информацию по каналу связи, например получили пакет информации, попробовали его исправить, и если не смогли исправить, тогда отправляется запрос на повторную передачу.
Исправление ошибок в помехоустойчивом кодировании
Любое помехоустойчивое кодирование добавляет избыточность, за счет чего и появляется возможность восстановить информацию при частичной потере данных в канале связи (носителе информации при хранении). В случае эффективного кодирования убирали избыточность, а в помехоустойчивом кодировании добавляется контролируемая избыточность.
Простейший пример – мажоритарный метод, он же многократная передача, в котором один символ передается многократно, а на приемной стороне принимается решение о том символе, количество которых больше.
Допустим есть 4 символа информации, А, B, С,D, и эту информацию повторяем несколько раз. В процессе передачи информации по каналу связи, где-то возникла ошибка. Есть три пакета (A1B1C1D1|A2B2C2D2|A3B3C3D3), которые должны нести одну и ту же информацию.
Но из картинки справа, видно, что второй символ (B1 и C1) они отличаются друг от друга, хотя должны были быть одинаковыми. То что они отличаются, говорит о том, что есть ошибка.
Необходимо найти ошибку с помощью голосования, каких символов больше, символов В или символов С? Явно символов В больше, чем символов С, соответственно принимаем решение, что передавался символ В, а символ С ошибочный.
Для исправления ошибок нужно, как минимум 3 пакета информации, для обнаружения, как минимум 2 пакета информации.
Параметры помехоустойчивого кодирования
Первый параметр, скорость кода R характеризует долю информационных («полезных») данных в сообщении и определяется выражением: R=k/n=k/m+k
- где n – количество символов закодированного сообщения (результата кодирования);
- m – количество проверочных символов, добавляемых при кодировании;
- k – количество информационных символов.
Параметры n и k часто приводят вместе с наименованием кода для его однозначной идентификации. Например, код Хэмминга (7,4) значит, что на вход кодера приходит 4 символа, на выходе 7 символов, Рида-Соломона (15, 11) и т.д.
Второй параметр, кратность обнаруживаемых ошибок – количество ошибочных символов, которые код может обнаружить.
Третий параметр, кратность исправляемых ошибок – количество ошибочных символов, которые код может исправить (обозначается буквой t).
Контроль чётности
Самый простой метод помехоустойчивого кодирования это добавление одного бита четности. Есть некое информационное сообщение, состоящее из 8 бит, добавим девятый бит.
Если нечетное количество единиц, добавляем 0.
1 0 1 0 0 1 0 0 | 0
Если четное количество единиц, добавляем 1.
1 1 0 1 0 1 0 0 | 1
Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.
1 1 0 0 0 1 0 0 | 1
Под кратностью понимается, всевозможные ошибки, которые можно обнаружить. В этом случае, кратность исправляемых ошибок 0, так как мы не можем исправить ошибки, а кратность обнаруживаемых 1.
Есть последовательность 0 и 1, и из этой последовательности составим прямоугольную матрицу размера 4 на 4. Затем для каждой строки и столбца посчитаем бит четности.
Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:
И если в процессе передачи информации допустим ошибку (ошибка нолик вместо единицы, желтым цветом), начинаем делать проверку. Нашли ошибку во втором столбце, третьей строке по координатам. Чтобы исправить ошибку, просто инвертируем 1 в 0, тем самым ошибка исправляется.
Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные.
Рассчитаем скорость кода для:
- 1 1 0 0 0 1 0 0 | 1
Здесь R=8/9=0,88
- И для прямоугольного кода:
Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)
Более эффективный с точки зрения скорости является первый вариант, но зато мы не можем с помощью него исправлять ошибки, а с помощью прямоугольного кода можно. Сейчас на практике прямоугольный код не используется, но логика работы многих помехоустойчивых кодов основана именно на прямоугольном коде.
Классификация помехоустойчивых кодов
- Непрерывные — процесс кодирования и декодирования носит непрерывный характер. Сверточный код является частным случаем непрерывного кода. На вход кодера поступил один символ, соответственно, появилось несколько на выходе, т.е. на каждый входной символ формируется несколько выходных, так как добавляется избыточность.
- Блочные (Блоковые) — процесс кодирования и декодирования осуществляется по блокам. С точки зрения понимания работы, блочный код проще, разбиваем код на блоки и каждый блок кодируется в отдельности.
По используемому алфавиту:
- Двоичные. Оперируют битами.
- Не двоичные (код Рида-Соломона). Оперируют более размерными символами. Если изначально информация двоичная, нужно эти биты превратить в символы. Например, есть последовательность 110 110 010 100 и нужно их преобразовать из двоичных символов в не двоичные, берем группы по 3 бита — это будет один символ, 6, 6, 2, 4 — с этими не двоичными символами работают не двоичные помехоустойчивые коды.
Блочные коды делятся на
- Систематические — отдельно не измененные информационные символы, отдельно проверочные символы. Если на входе кодера присутствует блок из k символов, и в процессе кодирования сформировали еще какое-то количество проверочных символов и проверочные символы ставим рядом к информационным в конец или в начало. Выходной блок на выходе кодера будет состоять из информационных символов и проверочных.
- Несистематические — символы исходного сообщения в явном виде не присутствуют. На вход пришел блок k, на выходе получили блок размером n, блок на выходе кодера не будет содержать в себе исходных данных.
В случае систематических кодов, выходной блок в явном виде содержит в себе, то что пришло на вход, а в случае несистематического кода, глядя на выходной блок нельзя понять что было на входе.
Смотря на картинку выше, код 1 1 0 0 0 1 0 0 | 1 является систематическим, на вход поступило 8 бит, а на выходе кодера 9 бит, которые в явном виде содержат в себе 8 бит информационных и один проверочный.
Код Хэмминга
Код Хэмминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Позволяет устранить одну ошибку и находить двойную.
Код Хэмминга (7,4) — 4 бита на входе кодера и 7 на выходе, следовательно 3 проверочных бита. С 1 по 4 информационные биты, с 6 по 7 проверочные (см. табл. выше). Пятый проверочный бит y5, это сумма по модулю два 1-3 информационных бит. Сумма по модулю 2 это вычисление бита чётности.
Декодирование кода Хэмминга
Декодирование происходит через вычисление синдрома по выражениям:
Синдром это сложение бит по модулю два. Если синдром не нулевой, то исправление ошибки происходит по таблице декодирования:
Расстояние Хэмминга
Расстояние Хэмминга — число позиций, в которых соответствующие символы двух кодовых слов одинаковой длины различны. Если рассматривать два кодовых слова, (пример на картинке ниже, 1 0 1 1 0 0 1 и 1 0 0 1 1 0 1) видно что они отличаются друг от друга на два символа, соответственно расстояние Хэмминга равно 2.
Кратность исправляемых ошибок и обнаруживаемых, связано минимальным расстоянием Хэмминга. Любой помехоустойчивый код добавляет избыточность с целью увеличить минимальное расстояние Хэмминга. Именно минимальное расстояние Хэмминга определяет помехоустойчивость.
Помехоустойчивые коды
Современные коды более эффективны по сравнению с рассматриваемыми примерами. В таблице ниже приведены Коды Боуза-Чоудхури-Хоквингема (БЧХ)
Из таблицы видим, что там один класс кода БЧХ, но разные параметры n и k.
- n — количество символов на входе.
- k — количество символов на выходе.
- t — кратность исправляемых ошибок.
- Отношение k/n — скорость кода.
- G (энергетический выигрыш) — величина, показывающая на сколько можно уменьшить отношение сигнал/шум (Eb/No) для обеспечения заданной вероятности ошибки.
Несмотря на то, что скорость кода близка, количество исправляемых ошибок может быть разное. Количество исправляемых ошибок зависит от той избыточности, которую добавим и от размера блока. Чем больше блок, тем больше ошибок он исправляет, даже при той же самой избыточности.
Пример: помехоустойчивые коды и двоичная фазовая манипуляция (2-ФМн). На графике зависимость отношения сигнал шум (Eb/No) от вероятности ошибки. За счет применения помехоустойчивых кодов улучшается помехоустойчивость.
Из графика видим, код Хэмминга (7,4) на сколько увеличилась помехоустойчивость? Всего на пол Дб это мало, если применить код БЧХ (127, 64) выиграем порядка 4 дБ, это хороший показатель.
Компромиссы при использовании помехоустойчивых кодов
Чем расплачиваемся за помехоустойчивые коды? Добавили избыточность, соответственно эту избыточность тоже нужно передавать. Нужно: увеличивать пропускную способность канала связи, либо увеличивать длительность передачи.
Компромисс:
- Достоверность vs полоса пропускания.
- Мощность vs полоса пропускания.
- Скорость передачи данных vs полоса пропускания
Необходимость чередования (перемежения)
Все помехоустойчивые коды могут исправлять только ограниченное количество ошибок t. Однако в реальных системах связи часто возникают ситуации сгруппированных ошибок, когда в течение непродолжительного времени количество ошибок превышает t.
Например, в канале связи шумов мало, все передается хорошо, ошибки возникают редко, но вдруг возникла импульсная помеха или замирания, которые повредили на некоторое время процесс передачи, и потерялся большой кусок информации. В среднем на блок приходится одна, две ошибки, а в нашем примере потерялся целый блок, включая информационные и проверочные биты. Сможет ли помехоустойчивый код исправить такую ошибку? Эта проблема решаема за счет перемежения.
Пример блочного перемежения:
На картинке, всего 5 блоков (с 1 по 25). Код работает исправляя ошибки в рамках одного блока (если в одном блоке 1 ошибка, код его исправит, а если две то нет). В канал связи отдается информация не последовательно, а в перемешку. На выходе кодера сформировались 5 блоков и эти 5 блоков будем отдавать не по очереди а в перемешку. Записали всё по строкам, но считывать будем, чтобы отправлять в канал связи, по столбцам. Информация в блоках перемешалась. В канале связи возникла ошибка и мы потеряли большой кусок. В процессе приема, мы опять составляем таблицу, записываем по столбцам, но считываем по строкам. За счет того, что мы перемешали большое количество блоков между собой, групповая ошибка равномерно распределится по блокам.
Кратность ошибки
Предмет
Электроника, электротехника, радиотехника
Разместил
🤓 yanast26
👍 Проверено Автор24
число неверных разрядов в данной кодовой комбинации.
Научные статьи на тему «Кратность ошибки»
Код Хэмминга
, а также ошибки при хранении информации….
То есть при обнаружении ошибки делается попытка исправления ошибки, и если попытка оказалась неудачной…
Величина кратности обнаруженных ошибок….
То есть число символов с ошибками, которое код способен определить….
Величина кратности исправленных ошибок.

Статья от экспертов
Норменное декодирование БЧХ-кодов с первой нулевой компонентой синдрома
Работа посвящена развитию метода сжатия норм синдромов путем приведения к нулю первой компоненты синдрома. Приведены исследования для БЧХ-кодов длиной, корректирующих ошибки кратности.
Проектирование собственного кода, исправляющего ошибки
Определение 1
Проектирование собственного кода, исправляющего ошибки — это методика коррекции…
При нахождении ошибки выполняется операция по её исправлению, но если ошибку исправить не удалось, то…
Значение кратности выявления ошибок….
Значение кратности скорректированных ошибок….
двойной ошибки.

Статья от экспертов
Экспериментальные исследования двоичных кодов с суммированием
Проведен анализ двоичных кодов с суммированием с точки зрения обнаружения искажений информационных разрядов в кодовых словах. Выявлены новые свойства кодов с суммированием
Повышай знания с онлайн-тренажером от Автор24!
- Напиши термин
- Выбери определение из предложенных или загрузи свое
-
Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных
карточек
Оценка корректирующей способности блокового (n, k) кода
Кодовое (хемминговое) расстояние — число несовпадающих разрядов двух кодовых комбинаций.
Минимальное кодовое расстояние (d) — минимальное расстояние, взятое по всем парам разрешенных кодовых комбинаций.
Кратность ошибки (r) — число искаженных символов кодовой комбинации.
Вес кодовой комбинации — число единиц в двоичной кодовой комбинации.
Вектор ошибки — двоичный код, содержащий 1 в искаженных и 0 в остальных разрядах.
Доля обнаруживаемых ошибок 2k(2n-2k)/(2k2n) = 1 — 2k—n
Число кодовых комбинаций: любых 2n , разрешенных 2к, запрещенных 2n — 2k .

Рекомендуемые материалы
Доля исправляемых ошибок среди обнаруживаемых 2k(2n—k-1)/2k(2n-2k)=2—k. Запрещенную кодовую комбинацию заменяют ближайшей разрешенной комбинацией. Ближайшими к разрешенной комбинации являются 2n-k-1 запрещенных кодовых комбинаций. Ошибка будет исправлена, если принятая запрещенная комбинация окажется «ближайшей» к переданной разрешенной комбинации. Число таких случаев 2k(2n-k-1).

Вместе с этой лекцией читают «3.6 Точечные случайные процессы. Формула Ито для считающих процессов. Компенсаторы».
d ³ r + 1 для обнаружения ошибки кратности r,
d ³ 2s + 1 для исправления ошибки кратности s,
d ³ r + s + 1 (r ³ s) для обнаружения и одновременного исправления ошибок кратности r и s.
Для исправления ошибки контрольная кодовая комбинация должна указывать место ошибки. Следовательно, число различных контрольных кодовых комбинаций должно быть не менее количества различных ошибок.. Число ошибок кратности r равно числу сочетаний Сnr . При s = 1 (исправление ошибки кратности 1) должно выполняться условие 2n—k-1 > Cn1 = n, при s = 2 — условие 2n—k-1 > Cn1+ Cn2, в общем случае – условие
Эта оценка Хемминга определяет минимальную избыточность, необходимую для исправления ошибок. Коды с минимальной избыточностью, для которых неравенство превращается в равенство, называются совершенными.
Содержание
- 1 Исправление ошибок в помехоустойчивом кодировании
- 2 Параметры помехоустойчивого кодирования
- 3 Контроль чётности
- 4 Классификация помехоустойчивых кодов
- 5 Код Хэмминга
- 5.1 Декодирование кода Хэмминга
- 5.2 Расстояние Хэмминга
- 6 Помехоустойчивые коды
- 6.1 Компромиссы при использовании помехоустойчивых кодов
- 6.2 Необходимость чередования (перемежения)
Назначение помехоустойчивого кодирования – защита информации от помех и ошибок при передаче и хранении информации. Помехоустойчивое кодирование необходимо для устранения ошибок, которые возникают в процессе передачи, хранения информации. При передачи информации по каналу связи возникают помехи, ошибки и небольшая часть информации теряется.
Без использования помехоустойчивого кодирования было бы невозможно передавать большие объемы информации (файлы), т.к. в любой системе передачи и хранении информации неизбежно возникают ошибки.
Рассмотрим пример CD диска. Там информация хранится прямо на поверхности диска, в углублениях, из-за того, что все дорожки на поверхности, часто диск хватаем пальцами, елозим по столу и из-за этого без помехоустойчивого кодирования, информацию извлечь не получится.
Использование кодирования позволяет извлекать информацию без потерь даже с поврежденного CD/DVD диска, когда какая либо область становится недоступной для считывания.
В зависимости от того, используется в системе обнаружение или исправление ошибок с помощью помехоустойчивого кода, различают следующие варианты:
- запрос повторной передачи (Automatic Repeat reQuest, ARQ): с помощью помехоустойчивого кода выполняется только обнаружение ошибок, при их наличии производится запрос на повторную передачу пакета данных;
- прямое исправление ошибок (Forward Error Correction, FEC): производится декодирование помехоустойчивого кода, т. е. исправление ошибок с его помощью.
Возможен также гибридный вариант, чтобы лишний раз не гонять информацию по каналу связи, например получили пакет информации, попробовали его исправить, и если не смогли исправить, тогда отправляется запрос на повторную передачу.
Исправление ошибок в помехоустойчивом кодировании
Любое помехоустойчивое кодирование добавляет избыточность, за счет чего и появляется возможность восстановить информацию при частичной потере данных в канале связи (носителе информации при хранении). В случае эффективного кодирования убирали избыточность, а в помехоустойчивом кодировании добавляется контролируемая избыточность.
Простейший пример – мажоритарный метод, он же многократная передача, в котором один символ передается многократно, а на приемной стороне принимается решение о том символе, количество которых больше.
Допустим есть 4 символа информации, А, B, С,D, и эту информацию повторяем несколько раз. В процессе передачи информации по каналу связи, где-то возникла ошибка. Есть три пакета (A1B1C1D1|A2B2C2D2|A3B3C3D3), которые должны нести одну и ту же информацию.
Но из картинки справа, видно, что второй символ (B1 и C1) они отличаются друг от друга, хотя должны были быть одинаковыми. То что они отличаются, говорит о том, что есть ошибка.
Необходимо найти ошибку с помощью голосования, каких символов больше, символов В или символов С? Явно символов В больше, чем символов С, соответственно принимаем решение, что передавался символ В, а символ С ошибочный.
Для исправления ошибок нужно, как минимум 3 пакета информации, для обнаружения, как минимум 2 пакета информации.
Параметры помехоустойчивого кодирования
Первый параметр, скорость кода R характеризует долю информационных («полезных») данных в сообщении и определяется выражением: R=k/n=k/m+k
- где n – количество символов закодированного сообщения (результата кодирования);
- m – количество проверочных символов, добавляемых при кодировании;
- k – количество информационных символов.
Параметры n и k часто приводят вместе с наименованием кода для его однозначной идентификации. Например, код Хэмминга (7,4) значит, что на вход кодера приходит 4 символа, на выходе 7 символов, Рида-Соломона (15, 11) и т.д.
Второй параметр, кратность обнаруживаемых ошибок – количество ошибочных символов, которые код может обнаружить.
Третий параметр, кратность исправляемых ошибок – количество ошибочных символов, которые код может исправить (обозначается буквой t).
Контроль чётности
Самый простой метод помехоустойчивого кодирования это добавление одного бита четности. Есть некое информационное сообщение, состоящее из 8 бит, добавим девятый бит.
Если нечетное количество единиц, добавляем 0.
1 0 1 0 0 1 0 0 | 0
Если четное количество единиц, добавляем 1.
1 1 0 1 0 1 0 0 | 1
Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.
1 1 0 0 0 1 0 0 | 1
Под кратностью понимается, всевозможные ошибки, которые можно обнаружить. В этом случае, кратность исправляемых ошибок 0, так как мы не можем исправить ошибки, а кратность обнаруживаемых 1.
Есть последовательность 0 и 1, и из этой последовательности составим прямоугольную матрицу размера 4 на 4. Затем для каждой строки и столбца посчитаем бит четности.
Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:
И если в процессе передачи информации допустим ошибку (ошибка нолик вместо единицы, желтым цветом), начинаем делать проверку. Нашли ошибку во втором столбце, третьей строке по координатам. Чтобы исправить ошибку, просто инвертируем 1 в 0, тем самым ошибка исправляется.
Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные.
Рассчитаем скорость кода для:
- 1 1 0 0 0 1 0 0 | 1
Здесь R=8/9=0,88
- И для прямоугольного кода:
Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)
Более эффективный с точки зрения скорости является первый вариант, но зато мы не можем с помощью него исправлять ошибки, а с помощью прямоугольного кода можно. Сейчас на практике прямоугольный код не используется, но логика работы многих помехоустойчивых кодов основана именно на прямоугольном коде.
Классификация помехоустойчивых кодов
- Непрерывные — процесс кодирования и декодирования носит непрерывный характер. Сверточный код является частным случаем непрерывного кода. На вход кодера поступил один символ, соответственно, появилось несколько на выходе, т.е. на каждый входной символ формируется несколько выходных, так как добавляется избыточность.
- Блочные (Блоковые) — процесс кодирования и декодирования осуществляется по блокам. С точки зрения понимания работы, блочный код проще, разбиваем код на блоки и каждый блок кодируется в отдельности.
По используемому алфавиту:
- Двоичные. Оперируют битами.
- Не двоичные (код Рида-Соломона). Оперируют более размерными символами. Если изначально информация двоичная, нужно эти биты превратить в символы. Например, есть последовательность 110 110 010 100 и нужно их преобразовать из двоичных символов в не двоичные, берем группы по 3 бита — это будет один символ, 6, 6, 2, 4 — с этими не двоичными символами работают не двоичные помехоустойчивые коды.
Блочные коды делятся на
- Систематические — отдельно не измененные информационные символы, отдельно проверочные символы. Если на входе кодера присутствует блок из k символов, и в процессе кодирования сформировали еще какое-то количество проверочных символов и проверочные символы ставим рядом к информационным в конец или в начало. Выходной блок на выходе кодера будет состоять из информационных символов и проверочных.
- Несистематические — символы исходного сообщения в явном виде не присутствуют. На вход пришел блок k, на выходе получили блок размером n, блок на выходе кодера не будет содержать в себе исходных данных.
В случае систематических кодов, выходной блок в явном виде содержит в себе, то что пришло на вход, а в случае несистематического кода, глядя на выходной блок нельзя понять что было на входе.
Смотря на картинку выше, код 1 1 0 0 0 1 0 0 | 1 является систематическим, на вход поступило 8 бит, а на выходе кодера 9 бит, которые в явном виде содержат в себе 8 бит информационных и один проверочный.
Код Хэмминга
Код Хэмминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Позволяет устранить одну ошибку и находить двойную.
Код Хэмминга (7,4) — 4 бита на входе кодера и 7 на выходе, следовательно 3 проверочных бита. С 1 по 4 информационные биты, с 6 по 7 проверочные (см. табл. выше). Пятый проверочный бит y5, это сумма по модулю два 1-3 информационных бит. Сумма по модулю 2 это вычисление бита чётности.
Декодирование кода Хэмминга
Декодирование происходит через вычисление синдрома по выражениям:
Синдром это сложение бит по модулю два. Если синдром не нулевой, то исправление ошибки происходит по таблице декодирования:
Расстояние Хэмминга
Расстояние Хэмминга — число позиций, в которых соответствующие символы двух кодовых слов одинаковой длины различны. Если рассматривать два кодовых слова, (пример на картинке ниже, 1 0 1 1 0 0 1 и 1 0 0 1 1 0 1) видно что они отличаются друг от друга на два символа, соответственно расстояние Хэмминга равно 2.
Кратность исправляемых ошибок и обнаруживаемых, связано минимальным расстоянием Хэмминга. Любой помехоустойчивый код добавляет избыточность с целью увеличить минимальное расстояние Хэмминга. Именно минимальное расстояние Хэмминга определяет помехоустойчивость.
Помехоустойчивые коды
Современные коды более эффективны по сравнению с рассматриваемыми примерами. В таблице ниже приведены Коды Боуза-Чоудхури-Хоквингема (БЧХ)
Из таблицы видим, что там один класс кода БЧХ, но разные параметры n и k.
- n — количество символов на входе.
- k — количество символов на выходе.
- t — кратность исправляемых ошибок.
- Отношение k/n — скорость кода.
- G (энергетический выигрыш) — величина, показывающая на сколько можно уменьшить отношение сигнал/шум (Eb/No) для обеспечения заданной вероятности ошибки.
Несмотря на то, что скорость кода близка, количество исправляемых ошибок может быть разное. Количество исправляемых ошибок зависит от той избыточности, которую добавим и от размера блока. Чем больше блок, тем больше ошибок он исправляет, даже при той же самой избыточности.
Пример: помехоустойчивые коды и двоичная фазовая манипуляция (2-ФМн). На графике зависимость отношения сигнал шум (Eb/No) от вероятности ошибки. За счет применения помехоустойчивых кодов улучшается помехоустойчивость.
Из графика видим, код Хэмминга (7,4) на сколько увеличилась помехоустойчивость? Всего на пол Дб это мало, если применить код БЧХ (127, 64) выиграем порядка 4 дБ, это хороший показатель.
Компромиссы при использовании помехоустойчивых кодов
Чем расплачиваемся за помехоустойчивые коды? Добавили избыточность, соответственно эту избыточность тоже нужно передавать. Нужно: увеличивать пропускную способность канала связи, либо увеличивать длительность передачи.
Компромисс:
- Достоверность vs полоса пропускания.
- Мощность vs полоса пропускания.
- Скорость передачи данных vs полоса пропускания
Необходимость чередования (перемежения)
Все помехоустойчивые коды могут исправлять только ограниченное количество ошибок t. Однако в реальных системах связи часто возникают ситуации сгруппированных ошибок, когда в течение непродолжительного времени количество ошибок превышает t.
Например, в канале связи шумов мало, все передается хорошо, ошибки возникают редко, но вдруг возникла импульсная помеха или замирания, которые повредили на некоторое время процесс передачи, и потерялся большой кусок информации. В среднем на блок приходится одна, две ошибки, а в нашем примере потерялся целый блок, включая информационные и проверочные биты. Сможет ли помехоустойчивый код исправить такую ошибку? Эта проблема решаема за счет перемежения.
Пример блочного перемежения:
На картинке, всего 5 блоков (с 1 по 25). Код работает исправляя ошибки в рамках одного блока (если в одном блоке 1 ошибка, код его исправит, а если две то нет). В канал связи отдается информация не последовательно, а в перемешку. На выходе кодера сформировались 5 блоков и эти 5 блоков будем отдавать не по очереди а в перемешку. Записали всё по строкам, но считывать будем, чтобы отправлять в канал связи, по столбцам. Информация в блоках перемешалась. В канале связи возникла ошибка и мы потеряли большой кусок. В процессе приема, мы опять составляем таблицу, записываем по столбцам, но считываем по строкам. За счет того, что мы перемешали большое количество блоков между собой, групповая ошибка равномерно распределится по блокам.