Вариации
оценок параметров будут, в конечном
счете, определять точность уравнения
множественной регрессии. Для их измерения
в многомерном регрессионном анализе
рассматривают так называемую
ковариационную
матрицу К,
являющуюся
матричным аналогом дисперсии одной
переменной:

где
элементы
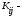
(или
корреляционные
моменты) оценок
параметров
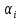
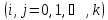
Ковариация
двух переменных определяется как
математическое ожидание произведения
отклонений этих переменных от их
математических ожиданий [Ссылка]. Поэтому
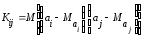
где
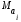
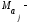
ожидания соответственно для параметров
и
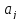
Ковариация
характеризует как степень рассеяния
значений двух переменных относительно
их математических ожиданий, так и
взаимосвязь этих переменных.
В
силу того, что оценки
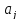
полученные методом наименьших квадратов,
являются несмещенными оценками параметров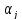
т.е.
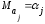
выражение(13.28)
примет
вид:
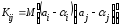
Рассматривая
ковариационную матрицу К,
легко
заметить, что на ее главной диагонали
находятся дисперсии опенок параметров
регрессии, ибо
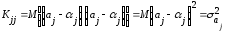
(13.29)
В
сокращенном виде ковариационная матрица
К
имеет
вид:
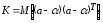
(13.30)
Учитывая
(13.28)
мы
можем записать
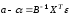
Тогда
выражение (12.30) примет вид:
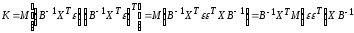
(13.31)
ибо
элементы матрицы X
—неслучайные
величины.
Матрица
представляет
собой ковариационную матрицу
вектора возмущений
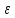
в
которой все элементы, не лежащие на
главной диагонали, равны нулю в силу
предпосылки 4
о
некоррелированности возмущений
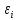
и
между
собой,
а
все элементы, лежащие на главной
диагонали, в силу предпосылок 2
и
3
регрессионного
анализа
равны
одной и той же дисперсии

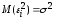
Поэтому
матрица
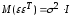
где
единичная
матрица
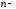
порядка.
Следовательно, в силу (13.31)
ковариационная
матрица вектора
оценок
параметров:
Так
как
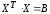
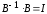
то окончательно получим:
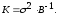
Таким
образом, с
помощью обратной матрицы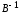
уравнении регрессии
определяется
не только сам вектор

параметров (13.28),
но
и дисперсии и ковариации его компонент.
Входящая
в (13.32)
дисперсия
возмущений неизвестна. Заменив ее
выборочной остаточной дисперсией
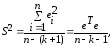
по
(13.32)
получаем
выборочную оценку ковариационной
матрицы К.
(В
знаменателе выражения (13.33)
стоит
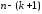
а
не
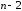
как
это было выше в (13.6).
Это
связано с тем, что теперь
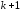
свободы (а не две) теряются при определении
неизвестных параметров, число которых
вместе со свободным членом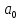
4.10. Определение доверительных интервалов для коэффициентов и функции множественной регрессии
Перейдем
теперь к оценке значимости коэффициентов
регрессии
и
построению доверительного интервала
для параметров регрессионной модели
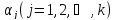
В
силу (13.29),
(13.32) и
изложенного выше оценка дисперсии
коэффициента регрессии
определится
по формуле:
где
несмещенная
оценка параметра
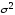
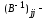
элемент матрицы
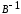
Среднее
квадратическое отклонение (стандартная
ошибка) коэффициента регрессии
примет
вид:
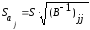
(13.34)
Значимость
коэффициента регрессии
можно
проверить, если учесть, что статистика
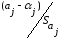
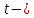
Стьюдента с
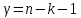
свободы. Поэтому
значимо
отличается от нуля на уровне
значимости
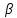
если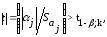
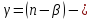
интервал для параметра
есть
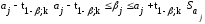
(13.35)
Наряду
с интервальным оцениванием коэффициентов
регрессии по (13.35)
весьма
важным для оценки точности определения
зависимой переменной (прогноза) является
построение доверительного
интервала для функции регрессии или
для условного математического
ожидания зависимой переменной
найденного в предположении, что
объясняющие переменные
приняли
значения, задаваемые вектором
такой интервал получен для уравнения
парной регрессии (см. (13.13)
и
(13.12)).
Обобщая
соответствующие выражения на случай
множественной регрессии, можно получить
доверительный интервал для
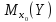
где
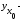
средняя, определяемая по уравнению
регрессии,
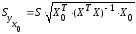
— ее
стандартная ошибка.
При
обобщении формул (13.15)
и
(13.14)
аналогичный
доверительный
интервал для индивидуальных значений
зависимой переменной
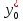
вид:
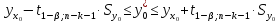
где
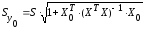
(13.38)
Доверительный
интервал для дисперсии возмущений
в
множественной регрессии с надежностью
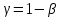
по формуле(13.20)
с
соответствующим изменением числа
степеней свободы критерия
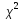
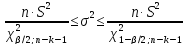
Пример
13.6.
По
данным примера 13.4
оценить
сменную добычу
угля на одного рабочего для шахт с
мощностью пласта 8 м и уровнем механизации
работ 6%; найти 95%-ные доверительные
интервалы для индивидуального и среднего
значений сменной добычи угля на 1
рабочего для таких же шахт. Проверить
значимость коэффициентов регрессии и
построить для них 95%-ные доверительные
интервалы. Найти с надежностью 0,95
интервальную оценку для дисперсии
возмущений
Решение.
В примере 13.4
уравнение
регрессии получено в виде:
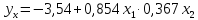
По
условию надо оценить
где
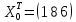
Выборочной оценкой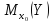
является
групповая средняя, которую найдем по
уравнению регрессии:
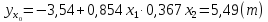
Для построения доверительного
интервала для М (у) необходимо знать
дисперсию его оценки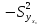
Для
ее вычисления обратимся к табл. 13.7
(точнее к ее двум последним столбцам,
при составлении которых учтено, что
групповые средние определяются по
полученному уравнению регрессии).
Теперь
по (13.37):
и
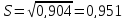
Определяем
стандартную ошибку групповой средней
г> по формуле (13.41).
Вначале
найдем
Теперь
(т).
По
табл. IV приложений при числе степеней
свободы
находим
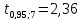
По
(13.40)
доверительный
интервал для
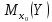
равен
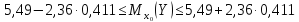
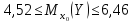
Итак,
с надежностью 0,95
средняя
сменная добыча угля на одного рабочего
для шахт с мощностью пласта 8
м
и уровнем механизации работ 6%
находится
в пределах от 4,52
до
6,46
т.
Сравнивая
новый доверительный интервал для функции
регрессии
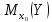
полученный
с учетом двух объясняющих переменных,
с аналогичным интервалом с учетом одной
объясняющей переменной (см. пример
13.1),
можно
заметить уменьшение его величины. Это
связано с тем, что включение в модель
новой объясняющей переменной позволяет
несколько повысить точность модели
за счет увеличения взаимосвязи зависимой
и объясняющей переменных (см. ниже).
Найдем
доверительный интервал для индивидуального
значения
при
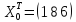
(13.43):
(т)
и по (13.42):
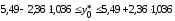
т. е.
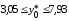
Итак,
с надежностью 0,95
индивидуальное
значение сменной добычи угля в шахтах
с мощностью пласта 8
м
и уровнем механизации работ 6%
находится
в пределах от 3,05
до
7,93
(т).
Проверим
значимость коэффициентов регрессии
и
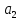
В
примере 13.4
получены
и
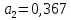
Стандартная
ошибка
в
соответствии с (13.38)
равна:
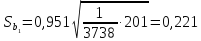
Так
как
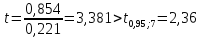
то
коэффициент
значим.
Аналогично вычисляем
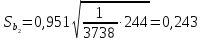
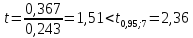
незначим
на 5%-ном уровне.
Доверительный
интервал имеет смысл построить только
для значимого коэффициента регрессии
по
(13.39)
или
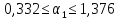
Итак,
с надежностью 0,95 за счет изменения на
1 м мощности пласта
(при
неизменном
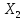
сменная
добыча угля на одного рабочего У
будет изменяться в пределах от 0,332 до
1,376 т.
Найдем
95%-ный доверительный интервал для
параметра ст2.
Учитывая, что
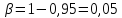
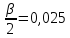
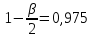
V
приложений при
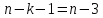
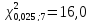
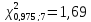
Таким
образом, с надежностью 0,95 дисперсия
возмущений заключена в пределах от
0,565 до 5,35, а их стандартное отклонение
— от 0,751 до 2,31 (т).
Формально
переменные, имеющие незначимые
коэффициенты регрессии, могут быть
исключены из рассмотрения. В экономических
исследованиях исключению переменных
из регрессии должен предшествовать
тщательный качественный
анализ.
Поэтому может оказаться целесообразным
все же оставить в регрессионной модели
одну или несколько объясняющих
переменных, не оказывающих существенного
(значимого) влияния на зависимую
переменную.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
27.03.20162.81 Mб142Учебник Туристское ресурсоведение.rtf
- #
- #
- #
- #
- #
- #
27.03.20164.24 Mб200Физика Яковлев.pdf
количественные характеристики ее элементов с более или менее приемлемой точностью априорно предсказать практически невозможно. Вследствие этого обобщенные МНК и ММП для оценки значений коэффициентов эконометрической модели в прямом виде не могут быть реализованы. В
таком случае исследователи обычно применяют некоторые приемы,
позволяющие получить более или менее удовлетворительную оценку ковариационной матрицы ошибки, ее некоторое приближение, которое можно было бы использовать в обобщенных методах оценивания. Некоторые из таких приемов будут рассмотрены в данном разделе на примере МНК.
Можно выделить два основных практических подхода к оценке недиагональной ковариационной матрицы ошибок эконометрической модели, отражающей существование корреляционной зависимости между ее значениями. Первый из них не требует использования предварительной
информации относительно характера взаимосвязей между ее последовательными значениями t, t+1, t+2,… . Согласно этому подходу матрица Cov(e), рассматриваемая как оценка ковариационной матрицы истинной ошибки модели Cov( ), находится эмпирически путем
последовательного приближения по результатам этапов расчетов по построению промежуточных вариантов эконометрических моделей.
Первый этап полностью соответствует процедуре построения эконометрической модели, рассмотренной в главах 1 и 2. Согласно ему, на основании исходных данных – вектора у и матрицы Х – формируется уравнение эконометрической модели, затем с помощью МНК оцениваются ее коэффициенты, определяется вектор фактической ошибки е, значения которого проверяются, например, с помощью критерия Дарбина-Уотсона на наличие автокорреляции.
В том случае если факт корреляции установлен, то на основе эмпирического ряда ошибки е1, е2,…, еТ оцениваются элементы ее ковариационной или корреляционной матрицы на основе следующих общих выражений:

|
) |
T k |
||||||||
|
cov( |
et |
, |
et |
et k |
|||||
|
et 1 |
|||||||||
|
t 1 |
|||||||||
|
cov( |
et |
, |
) |
||||||
|
rk |
et 1 |
; |
|||||||
|
2 |
|||||||||
|
e |
|||||||||
|
k 1,2,… |
На практике обычно бывает достаточно оценить два-три выборочных коэффициента корреляции, поскольку взаимосвязь между значениями ошибки с увеличением сдвига k резко ослабевает и значения коэффициентов r4, r5,… cтановятся практически не отличимыми от нуля.
На втором этапе определенную таким образом либо ковариационную матрицу фактической ошибки e, либо ее корреляционную матрицу e
используют для оценки коэффициентов той же эконометрической модели с помощью обобщенного МНК (выражения (3.11), (3.13)). Далее вычисляется новый ряд фактической ошибки, происходит его проверка на наличие автокорреляции и, в случае подтверждения этой гипотезы, определяются новые матрицы e или e. Затем с помощью обобщенного МНК строится третий вариант эконометрической модели и т. д.
Процедура построения модели завершается, если критерий Дарбина-
Уотсона не подтверждает наличие автокорреляции в ряду фактической ошибки очередного варианта эконометрической модели. На практике для получения варианта модели с некоррелированной ошибкой часто достаточно провести одну итерацию. Вследствие этого такой подход получил название
“двухшагового МНК”.
Подтверждением эффективности такого подхода является уменьшение дисперсий коэффициентов эконометрической модели каждого следующего варианта по сравнению с предыдущим, обычно наблюдаемое на практике.
Напомним, что значения этих дисперсий рассчитываются как диагональные элементы матриц, определяемых выражениями (2.18) и (3.15).

Явление уменьшения дисперсий коэффициентов последовательных вариантов эконометрической модели может быть обнаружено на основе использования критерия Фишера для сумм элементов ковариационных матриц оценок коэффициентов модели двух последовательных ее вариантов.
Дело в том, что сумма элементов матрицы Cov(a), рассчитываемой согласно выражениям (2.18) для МНК и (3.15) для обобщенного МНК, выражает дисперсию суммы оценок коэффициентов модели. В этом случае, если выполняется условие
F*(T–n–1, T–n–1, p*),
(3.24)
где sm2 – сумма элементов ковариационной матрицы оценок Cov(a) на m-м
шаге расчетов; F*(T–n–1, T– n–1, p*) – табличное значение критерия Фишера для числа степеней свободы 1= 2=T– n–1 и уровне доверительной вероятности p*, то гипотезу о том, что дисперсия суммы оценок коэффициентов модели уменьшилась на m-м шаге расчетов по сравнению с m–1, следует считать подтвержденной.
Заметим, что на практике вместо суммы элементов ковариационной матрицы оценок коэффициентов модели при определении их эффективности можно использовать фактическую дисперсию модели. Например, для МНК
Cov(a)= e2 (Х Х)–1. Поскольку матрица Х Х постоянна, то отличия дисперсий коэффициентов полностью определяются значением e2.
При сопоставлении дисперсий оценок коэффициентов, полученных с помощью обобщенного МНК, подобную замену теоретически нельзя использовать, поскольку в формировании их ковариационной матрицы принимает участие корреляционная матрица ошибок (Cov(a)= e2 (Х –1Х)–1).
Однако, если допустить, что на m-м шаге расчетов значения коэффициентов корреляции изменились не слишком значительно по сравнению m–1-м
шагом, то данной некорректностью можно пренебречь.

Другая группа подходов к построению эконометрических моделей с эффективными оценками коэффициентов при невыполнении условия
Cov( )= 2 Е основана на использовании априорной информации относительно возможного вида ковариационной матрицы ошибок. Эта информация может вытекать из анализа закономерностей измерения переменных модели, характера их взаимосвязей, формы самой модели и т. п.
Достаточно часто, предвидя появление ошибки спецификации модели
(например, исходя из некоторого несоответствия ее уравнения эмпирическому графику входящих в нее переменных), исследователи заранее предполагают, что значения ошибки связаны между собой автокорреляционной зависимостью первого порядка
где 1 – коэффициент автокорреляции ошибки t первого порядка; t –
ошибка модели (3.25) с нулевым средним и конечной дисперсией 2, которая неизвестна.
В отношении ошибки t обычно предполагают выполнение следующих свойств на интервале (1,Т):
– 2= const;
|
– Cov( ) = 2 Е; |
(3.26) |
|
Несложно показать, что при выполнении условия (3.25) |
ковариационная |
матрица ошибки эконометрической модели будет иметь следующий вид:
|
1 |
1 |
12 … |
1T 1 |
|
1 |
1 |
1 … |
1T 2 |
|
Cov( ) = = 2 = 2 … |
. (3.27) |
||
|
… |
… |
… |
|
|
1T 1 |
1T 2 |
1T 3… |
1 |

Чтобы показать справедливость выражения (3.27), последовательно
|
определим ковариации ряда t |
с рядами t–1, t–2 и т. д. |
Для сначала этого |
|||||||||
|
умножим левую и правую части выражения (3.25) на |
t–1, полученный |
||||||||||
|
результат просуммируем |
по t |
и далее разделим на T–2. В итоге с учетом |
|||||||||
|
независимости переменных t–1 |
и t |
получим |
|||||||||
|
T 1 |
T 1 |
2 |
T 1 |
||||||||
|
t |
t 1 |
t 1 t |
|||||||||
|
t 1 |
|||||||||||
|
t 2 |
t 2 |
t 2 |
|||||||||
|
T 2 |
1 |
T 2 |
T 2 |
||||||||
|
cov( t , t– 1)= 1 2. |
(3.28) |
Проведем аналогичную операцию, умножив левую и правую части
|
выражения (3.25) на t–2. Получим |
|
|
cov( t , t–2)= 1 cov( t , t–1)= 12 2 |
(3.29) |
|
и т. д. |
|
|
cov( t , t–k )= 1k 2. |
Таким образом, при выполнении условия (3.25) корреляционная матрица истинной ошибки эконометрической модели оказывается определенной следующим выражением:
|
1 |
1 |
12 … |
1T 1 |
|
|
1 |
1 |
1 … |
1T 2 |
(3.30) |
|
= … |
, |
|||
|
… |
… |
… |
||
|
1T 1 |
1T 2 |
1T 3… |
1 |
в котором величина 1 однако остается неизвестной.
Вместе с тем, очевидно, что “хорошая” оценка r1 коэффициента корреляции 1 должна обеспечивать получение эффективных оценок
Если r10
значение r10
коэффициентов эконометрической модели a0, a1,… an. Если предположить,
что: а) как и ранее, эффективные оценки характеризуются минимальным значением суммы элементов ковариационной матрицы Cov(a); б) эта сумма
(дисперсия) является непрерывной выпуклой функцией по r1, минимум которой соответствует “хорошей” оценке коэффициента 1, то теоретически эту оценку, как и эффективные оценки a0, a1,… an, можно определить с помощью несложной итеративной процедуры, в основе которой лежит обобщенный МНК. Ее суть состоит в следующем. Задается начальное
и на его основе (согласно выражению (3.27)) определяется
Cov0( ). Далее с использованием обобщенного МНК (выражение (3.16))
определяются оценки a00, a10,… an0 и их ковариационная матрица Cov0(a)
(выражение (3.15)).
На втором шаге определяется значение r11=r10+ r, где r – выбранный прирост оценки коэффициента автокорреляции, а затем повторяется последовательность расчетов первого шага.
не являлось искомым оптимальным значением коэффициента автокорреляции, то при правильно выбранном знаке r сумма элементов
Cov1(a) будет меньше соответствующей характеристики матрицы Cov0(a).
Однако изложенная процедура практически не применяется. Причинами этого являются неизвестный характер зависимости суммы элементов ковариационной матрицы Cov(a) от значений r1 (эта характеристика вообще может быть не слишком чувствительна к изменениям r1); неизбежные ошибки округления, которые приводят к смещению находимых оценок коэффициентов a00, a10,… an0; большой объем вычислений по каждому этапу процедуры. Все это делает ее трудно реализуемой даже на современных компьютерных системах.
В эконометрике обычно для получения эффективных оценок коэффициентов модели с коррелирующими остатками в предположении о справедливости зависимости (3.25) используются несколько другие подходы,
предполагающие необходимость преобразования уравнения самой модели.
Рассмотрим эти подходы более подробно.
Представим эконометрическую модель с учетом условия (3.25) в виде следующей системы уравнений:
|
уt = 0+ 1x1t +…+ n xnt+ t ; |
|
|
t= 1 t–1+ t. |
(3.31) |
Поскольку t–1=уt–1– 0– 1x1,t–1–…– nxn,t–1, то систему (3.31) можно выразить единым уравнением
уt = 1уt–1+(1– 1) 0 + 1 x1t – 1 1x1,t–1+…+ n xnt – 1 n xn,t–1+ t . (3.32)
Критерием при определении неизвестных параметров выражения (3.31)
является минимум суммы квадратов t .
Обозначим произведения коэффициентов (1– 1) 0, 1 1,…, 1 n как 0,
1,… n. Тогда вместо выражения (3.32) можно записать
|
уt = 1уt–1+ 0 + 1 x1t – 1 x1,t– 1+…+ n xnt – n xn, t– 1+ t, |
(3.33) |
|
где 0 =(1– 1) 0, 1 = 1 1,…, n = 1 n . |
(3.34) |
Из выражения (3.33) непосредственно вытекает, что, поскольку обычный МНК в общем случае не гарантирует выполнения условия (3.34), для оценки коэффициентов этой модели должен быть применен МНК, учитывающий эти нелинейные соотношения. МНК, учитывающий ограничения на параметры,
да еще нелинейного вида, достаточно трудоемок с вычислительной точки зрения.
Вследствие этого на практике в таких ситуациях более широкое применение нашел так называемый двухшаговый метод наименьших
квадратов, предложенный Дарбином (двухшаговый МНК Дарбина). Его суть состоит в следующем. На первом шаге, применяя обыкновенный МНК для оценки коэффициентов модели (3.33), определяют r1 – оценку коэффициента при уt–1. Далее формируются новые зависимая и независимые переменные ut=уt –r1уt–1; vit=xit –r1xi,t–1 , i=1,2,…, n; t=1,2,…, T–1, зависимость между которыми выражается линейной эконометрической моделью следующего вида:
|
ut=b0+ a1v1t +…+anvnt +wt . |
(3.35) |
где коэффициенты b0, a1,…, an являются оценками соответствующих коэффициентов модели 0, 1,…, n, wt – фактическая ошибка модели.
Эти оценки определяются с помощью обычного МНК на втором шаге расчетов.
Метод Дарбина легко распространяется на ситуации, характеризующиеся наличием автокорреляционной зависимости между значениями ошибки более высокого порядка. Например, для автокорреляции второго порядка модель, связывающая текущие значения ошибки с двумя предыдущими,
представляется в следующем виде:
|
t= 1 t–1+ 2 t–2+ t. |
(3.36) |
где 1 и 2 – коэффициенты модели автокорреляции, отражающие характер зависимости текущего значения ошибки t от ее предшествующих значенийt–1 и t–2. Оценки этих коэффициентов с1 и с2 определяются на основании значений выборочных коэффициентов автокорреляции r1 и r2 – первого и второго порядка соответственно.
В этом случае по аналогии с выражением (3.32) можно записать
уt =с1уt–1+с2уt– 2+a1x1t+…+anxnt+(1–с1–с2)a0–с1a1x1,t–1–…–с1anxn,t–-1 – –с2a1x1,t–2 –
…–с2anxn,t–2+wt. (3.37)
Применение двухшагового метода Дарбина к оценке коэффициентов модели (3.37) позволяет с помощью обыкновенного МНК на первом шаге определить оценки коэффициентов с1 и с2 при переменных уt–1 и уt–2 этой модели. Далее, как и в предыдущем случае, формируются новые
переменные ut=уt–с1уt–1–с2уt–2; vit=xit–с1xi,t–1–с2xi,t–2, i=1,2,…, n; t=1,2,…, T–1,
и на втором шаге оценки коэффициентов исходной модели и a0, a1,… an
находятся опять же с помощью обыкновенного МНК, как и коэффициенты модели (3.35).
Отметим, что автокорреляционная зависимость ошибок с порядком более двух практически не встречается. В большинстве случаев порядок автокорреляции равен единице.
Заметим также, что корректность построенной модели в данном случае может быть определена на основе критерия Дарбина-Уотсона,
рассчитываемого для остатков модели (3.35).
3.2.2. Эконометрические модели с гетероскедастичными ошибками
Причиной непостоянства дисперсии (гетероскедастичность ошибки)
эконометрической модели часто является ее зависимость от масштаба рассматриваемых явлений. В эконометрическую модель ошибка входит как аддитивная переменная (слагаемое). В то же время часто она имеет относительный характер и определяется по отношению к измеренному уровню рассматриваемых факторов. Вследствие этого, если на интервале
(1,Т) переменная у, увеличивается в 5 и более раз, то можно ожидать, что даже при правильно выбранной форме зависимости этой переменной от объясняющих факторов ошибка модели увеличится примерно во столько же раз.
Гипотеза о гетероскедастичности ошибки модели обычно проверяется с использованием теста, рассмотренного в разделе 2.2.1. В случае ее подтверждения для оценки коэффициентов эконометрической модели может
быть применена процедура последовательных этапов расчетов как и в случае автокорреляции между ошибками модели. Для этого на первом этапе по результатам применения обыкновенного МНК должны сформированы оценки 12, 22,…, Т2 матрицы Cov(е) (выражение 3.4). Сделать это на основе значений фактической ошибки e1, e2, …, eТ для каждой точки t=1,2,…, T
невозможно, вследствие чего в данном случае приходится привлекать на помощь некоторые дополнительные гипотезы относительно характера изменения дисперсии ошибки, например, гипотезу о линейном законе ее изменения.
При таком предположении оценки дисперсий 12,…, T2 могут быть определены следующим образом. Для двух непересекающихся интервалов (1,
|
Т1) и (Т2, Т) по значениям рядов фактической ошибки е1 |
,…, |
еТ 1 |
и еТ 2 |
,…, |
еТ |
могут |
быть получены оценки дисперсий k2 и m2, которые соотносятся к моментам t=k и t=m, являющимся серединами этих рядов. Далее на основе этих двух значений строится линейная зависимость 2(t), аппроксимирующая изменение дисперсии на интервале (1, Т), каждое из значений которой t2
будет представлять собой оценку соответствующего элемента диагональной матрицы (выражение (3.4)). Эта матрица затем должна использоваться на втором этапе вычислений оценок коэффициентов следующего варианта эконометрической модели с помощью обобщенного МНК.
Справедливость выдвинутой гипотезы о гетероскедастичности ошибки подтверждается (или отвергается) сопоставлением дисперсий сумм оценок коэффициентов модели, рассчитанных для оценок обычного и обобщенного МНК. Эти суммы определяются на основе элементов соответствующих ковариационных матриц оценок, определенных согласно выражениям (2.27)
и (3.15) соответственно.
Подобная процедура может быть реализована для любых приемлемых
(правдоподобных) вариантов закономерностей изменения дисперсий ошибок,
например, для квадратичной, логарифмической и т. п. зависимостей.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Фильтр Калмана — это легко
Время на прочтение
18 мин
Количество просмотров 51K
Много людей, в первый раз сталкивающихся в работе с датчиками, склонны считать, что получаемые показания — это точные значения. Некоторые вспоминают, что в показаниях всегда есть погрешности и ошибки. Чтобы ошибки в измерениях не приводили к ошибкам в функционировании системы в целом, данные датчиков необходимо обрабатывать. На ум сразу приходит словосочетание “фильтр Калмана”. Но слава этого “страшного” алгоритма, малопонятные формулы и разнообразие используемых обозначений отпугивают разработчиков. Постараемся разобраться с ним на практическом примере.
Об алгоритме
Что же нам потребуется для работы фильтра Калмана?
- Нам потребуется модель системы.
- Модель должна быть линейной (об этом чуть позже).
- Нужно будет выбрать переменные, которые будут описывать состояние системы (“вектор состояния”).
- Мы будем производить измерения и вычисления в дискретные моменты времени (например, 10 раз в секунду). Нам потребуется модель наблюдения.
- Для работы фильтра достаточно данных измерений в текущий момент времени и результатов вычислений с предыдущего момента времени.
Алгоритм работает итеративно. На каждом шаге алгоритм берёт данные датчиков (с шумом и другими проблемами), вектор состояния с предыдущего шага и по этим данным оценивает состояние системы на текущем шаге. Кроме того, он еще отслеживает насколько мы можем быть уверены, что наш текущий вектор состояний соответствует истинному положению дел (разброс значений для каждой переменной в векторе).
Обычно используются следующие обозначения:
— вектор состояния;
— мера неопределенности вектора состояния. Представляет из себя ковариационную матрицу (об этом позже — это будет, наверное, самая сложная часть).
Содержимое вектора состояния зависит от фантазии разработчика и решаемой задачи. Например, мы можем отслеживать координаты объекта, а также его скорость и ускорение. В этом случае получается вектор из трёх переменных: {позиция, скорость, ускорение} (для одномерного случая; для 3D мира будет по одному такому набору для каждой оси, то есть, 9 значений в векторе)
По сути, речь идёт о совместном распределении случайных величин
В фильтре Калмана мы предполагаем, что все погрешности и ошибки (как во входных данных, так и в оценке вектора состояния) имеют нормальное распределение. А для многомерного нормального распределения его полностью определяют два параметра: математическое ожидание вектора и его ковариационная матрица.
Математическая модель системы / процесса
Мы имеем дело с динамической системой, т.е. состояние системы меняется со временем. Имея модель системы, фильтр Калмана может предугадывать, каким будет состояние системы в следующий момент времени. Именно это позволяет фильтру так эффективно устранять шум и оценивать параметры, которые не наблюдаются (не измеряются) напрямую.
Фильтр Калмана накладывает ограничения на используемые модели: это должны быть дискретные модели в пространстве состояний. А ещё они должны быть линейными.
Дискретные и линейные?
Дискретность означает для нас то, что модель работает “шагами”. На каждом шаге мы вычисляем новое состояние системы по вектору состояния с предыдущего шага. Обычно, модели такого рода задаются системой разностных уравнений.
По поводу линейности: каждое уравнение системы является линейным уравнением, задающим новое значение переменной состояния. Т.е. никаких косинусов, синусов, возведений в степень и даже сложений с константой.
Такую модель удобно представлять в виде разностного матричного уравнения:
Давайте разберём это уравнение подробно. В первую очередь, нас интересует первое слагаемое () — это как раз модель эволюции процесса. А матрица
(также встречаются обозначения
,
) — называется матрицей процесса (state transition matrix). Она задаёт систему линейных уравнений, описывающих, как получается новое состояние системы из предыдущего.
Например, для равноускоренного движения матрица будет выглядеть так:
Первая строка матрицы — хорошо знакомое уравнение . Аналогично, вторая строка матрицы описывает изменение скорости. Третья строка описывает изменение ускорения.
А что же с остальными слагаемыми?
В некоторых случаях, мы напрямую управляем процессом (например, управляем квадракоптером с помощью пульта Д/У) и нам достоверно известны задаваемые параметры (заданная на пульте скорость полёта). Второе слагаемое — это модель управления. Матрица называется матрицей управления, а вектор
— вектор управляющих воздействий. В случаях когда мы только наблюдаем за процессом, это слагаемое отсутствует.
Последнее слагаемое — — это вектор ошибки модели. Модель равноускоренного движения абсолютно точно описывает положение объекта. Однако в реальном мире есть множество случайных факторов — дороги неровные, дует ветер, и т.п. Иногда, процесс сложен и приходится использовать упрощённую модель, которая не учитывает все аспекты. Именно так возникает ошибка модели.
То, что мы записываем это слагаемое, не означает, что мы знаем ошибку на каждом шаге или описываем её аналитически. Однако фильтр Калмана делает важное предположение — ошибка имеет нормальное распределение с нулевым математическим ожиданием и ковариационной матрицей . Эта матрица очень важна для стабильной работы фильтра и мы её рассмотрим позже.
Модель наблюдения
Не всегда получается так, что мы измеряем интересующие нас параметры напрямую (например, мы измеряем скорость вращения колеса, хотя нас интересует скорость автомобиля). Модель наблюдения описывает связь между переменными состояния и измеряемыми величинами:
— это вектор измерения/наблюдения.Это значения, получаемые с датчиков системы.
Первое слагаемое — модель, связывающая вектор состояния
с соответствующими ему показаниями датчиков. (Такой выбор модели может показаться странным, ведь наша задача — получить
из
, а эта модель получает
из
. Но это действительно так. В частности, это необходимо потому, что некоторые переменные состояния из
могут отсутствовать в
).
Второе слагаемое — это вектор ошибок измерения. Как и в случае с предыдущими ошибками, предполагается, что она имеет нормальное распределение с нулевым математическим ожиданием.
— ковариационная матрица, соответствующая вектору
.
Вернёмся к нашему примеру. Пусть у нас на роботе установлен один единственный датчик — GPS приёмник (“измеряет” положение). В этом случае матрица будет выглядеть следующим образом:
Строки матрицы соответствуют переменным в векторе состояния, столбцы — элементам вектора измерений. В первой строке матрицы находится значение “1” так как единица измерения положения в векторе состояния совпадает с единицей измерения значения в векторе измерений. Остальные строки содержат “0” потому что переменные состояния соответствующие этим строкам не измеряются датчиком.
Что будет, если датчик и модель используют разные единицы измерения? А если датчиков несколько?
Например, модель использует метры, а датчик — количество оборотов колеса. В этом случае матрица будет выглядеть так:
Количество датчиков ничем (кроме здравого смысла) не ограничено.
Например, добавим спидометр:
Второй столбец матрицы соответствует нашему новому датчику.
Несколько датчиков могут измерять один и тот же параметр. Добавим ещё один датчик скорости:
Ковариационные матрицы и где они обитают
Для настройки фильтра нам потребуется заполнить несколько ковариационных матриц:
,
и
.
Ковариационные матрицы?
Для нормально распределенной случайной величины её математическое ожидание и дисперсия полностью определяют её распределение. Дисперсия — это мера разброса случайной величины. Чем больше дисперсия — тем сильнее может отклоняться случайная величина от её математического ожидания. Ковариационная матрица — это многомерный аналог дисперсии, для случая, когда у нас не одна случайная величина, а случайный вектор.
В одной статье сложно уместить всю теорию вероятностей, поэтому ограничимся сугубо практическими свойствами ковариационных матриц. Это симметричные квадратные матрицы, на главной диагонали которой располагаются дисперсии элементов вектора. Остальные элементы матрицы — ковариации между компонентами вектора. Ковариация показывает, насколько переменные зависят друг от друга.
Проиллюстрируем влияние мат. ожидания, дисперсии и ковариации.
Начнём с одномерного случая. Функция плотности вероятности нормального распределения — знаменитая колоколообразная кривая. Горизонтальная ось — значение случайной величины, а вертикальная ось — сравнительная вероятность того что случайная величина примет это значение:
Чем меньше дисперсия — тем меньше ширина колокола.
Понятие ковариации возникает для совместного распределения нескольких случайных величин. Когда случайные величины независимы, то ковариация равна нулю:
Ненулевое значение ковариации означает, что существует связь между значениями случайных величин:
На каждом шаге фильтр Калмана строит предположение о состоянии системы, исходя из предыдущей оценки состояния и данных измерений. Если неопределенности вектора состояния выше, чем ошибка измерения, то фильтр будет выбирать значения ближе к данным измерений. Если ошибка измерения больше оценки неопределенности состояния, то фильтр будет больше “доверять” данным моделирования. Именно поэтому важно правильно подобрать значения ковариационных матриц — основного инструмента настройки фильтра.
Рассмотрим каждую матрицу подробнее:
— ковариационная матрица состояния
Квадратная матрица, порядок матрицы равен размеру вектора состояния
Как уже было сказано выше, эта матрица определяет “уверенность” фильтра в оценке переменных состояния. Алгоритм самостоятельно обновляет эту матрицу в процессе работы. Однако нам нужно установить начальное состояние, вместе с исходным предположением о векторе состояния.
Во многих случаях нам неизвестны значения ковариации между переменными для изначального состояния (элементы матрицы, расположенные вне главной диагонали). Поэтому можно проигнорировать их, установив равными 0. Фильтр самостоятельно обновит значения в процессе работы. Если же значения ковариации известны, то, конечно же, стоит использовать их.
Дисперсию же проигнорировать не выйдет. Необходимо установить значения дисперсии в зависимости от нашей уверенности в исходном векторе состояния. Для этого можно воспользоваться правилом трёх сигм: значение случайной величины попадает в диапазон с вероятностью 99.7%.
Пример
Допустим, нам нужно установить дисперсию для переменной состояния — скорости робота. Мы знаем что максимальная скорость передвижения робота — 10 м/с. Но начальное значение скорости нам неизвестно. Поэтому, мы выберем изначальное значение переменной — 0 м/с, а среднеквадратичное отклонение ;
Соответственно, дисперсия
.
— ковариационная матрица шума измерений
Квадратная матрица, порядок матрицы равен размеру вектора наблюдения (количеству измеряемых параметров).
Во многих случаях можно считать, что измерения не коррелируют друг с другом. В этом случае матрица будет являться диагональной матрицей, где все элементы вне главной диагонали равны нулю. Достаточно будет установить значения дисперсии для каждого измеряемого параметра. Иногда эти данные можно найти в документации к используемым датчика. Однако, если справочной информации нет, то можно оценить дисперсию, измеряя датчиком заранее известное эталонное значение, или воспользоваться правилом трёх сигм.
— ковариационная матрица ошибки модели
Квадратная матрица, порядок матрицы равен размеру вектора состояния.
С этой матрицей обычно возникает наибольшее количество вопросов. Что означает ошибка модели? Каков смысл этой матрицы и за что она отвечает? Как заполнять эту матрицу? Рассмотрим всё по порядку.
Каждый раз, когда фильтр предсказывает состояние системы, используя модель процесса, он увеличивает неуверенность в оценке вектора состояния. Для одномерного случая формула выглядит приблизительно следующим образом:
Если установить очень маленькое значение , то этап предсказания будет слабо увеличивать неопределенность оценки. Это означает, что мы считаем, что наша модель точно описывает процесс.
Если же установить большое значение , то этап предсказания будет сильно увеличивать неопределенность оценки. Таким образом, мы показываем что модель может содержать неточности или неучтенные факторы.
Для многомерного случая формула выглядит несколько сложнее, но смысл схожий. Однако, есть важное отличие: эта матрица указывает, на какие переменные состояния будут в первую очередь влиять ошибки модели и неучтённые факторы.
Допустим, мы отслеживаем перемещение робота, используя модель равноускоренного движения, и вектор состояния содержит следующие переменные: положение x, скорость v и ускорение a. Однако, наша модель не учитывает, что на дороге встречаются неровности.
Когда робот проходит неровность, показания датчиков и предсказание модели начнут расходиться. Структура матрицы будет определять, как фильтр отреагирует на это расхождение.
Мы можем выдвинуть различные предположения относительно природы шума. Для нашего примера с равноускоренным движением логично было бы предположить, что неучтённые факторы (неровность дороги) в первую очередь влияют на ускорение. Этот подход применим ко многим структурам модели, где в векторе состояния присутствует переменная и несколько её производных по времени (например, положение и производные: скорость и ускорение). Матрица выбирается таким образом, чтобы наибольшее значение соответствовало самому высокому порядку производной.
Так как же заполняется матрица Q?
Обычно используют модель-приближение. Рассмотрим на примере модели равноускоренного движения:
Модель непрерывного белого шума
Мы предполагаем, что ускорение постоянно на каждом шаге. Но из-за неровностей дороги ускорение, на самом деле, постоянно изменяется. Мы можем предположить, что изменение ускорения происходит под воздействием непрерывного белого шума с нулевым математическим ожиданием (т.е. усреднив все небольшие изменения ускорения за время движения робота мы получаем 0)
В этой модели матрица Q рассчитывается следующим образом
Мы формируем матрицу Qc в соответствии со структурой вектора состояния. Наивысшему порядку производной соответствует правый нижний элемент матрицы. В случае, если в векторе состояния несколько таких переменных, то каждая из них учитывается в матрице.
Для нашей модели равноускоренного движения матрица будет выглядеть так:
— спектральная плотность мощности белого шума
Подставляем матрицу процесса, соответствующую нашей модели:
После перемножения и интегрирования получаем:
Модель “кусочного” белого шума
Мы предполагаем, что ускорение на самом деле постоянно в течение каждого шага моделирования, но дискретно и независимо меняется между шагами. Выглядит очень похоже на предыдущую модель, но небольшая разница есть
— мощность шума
— наивысший порядок производной, используемой в модели (т.е. ускорение для вышеописанной модели)
В этой модели матрица определяется следующим образом:
Из матрицы процесса F
берём столбец с наивысшим порядком производной
и подставляем в формулу. В итоге получаем:
Обе модели являются приближениями того, что происходит на самом деле в реальности. На практике, приходится экспериментировать и выяснять, какая модель подходит лучше в каждом отдельном случае. Плюсом второй модели является то, что мы оперируем дисперсией шума, с которой уже хорошо умеем работать.
Простейший подход
В некоторых случаях прибегают к грубому упрощению: устанавливают все элементы матрицы равными нулю, за исключением элементов, соответствующих максимальным порядкам производных переменных состояния.
Действительно, если рассчитать по одному из приведённых выше методов, при достаточно малых значениях
, значения элементов матрицы
оказываются очень близкими к нулю.
Т.е. для нашей модели равноускоренного движения можно взять матрицу следующего вида:
И хотя такой подход не совсем корректен, его можно использовать в качестве первого приближения или для экспериментов. Без сомнения, не стоит выбирать матрицу таким образом для любых важных задач без весомых причин.
Важное замечание
Во всех примерах выше используется вектор состояния и может показаться, что во всех случаях дисперсия, соответствующая наивысшему порядок производной, находится в правом нижнем углу матрицы. Это не так.
Рассмотрим вектор состояния
Матрица будет представлять собой блочную матрицу, где отдельные блоки 3х3 элементов будут соответствовать группам
и
. Остальные элементы матрицы будут равны нулю.
Дисперсия, соответствующая наивысшим порядкам производных и
, будет находиться на 3-ей и 5-ой позициях на главной диагонали матрицы.
Однако, на практике нет никакого смысла перемешивать порядок переменных состояния таким образом, чтобы порядки производных шли не по очереди — это просто неудобно.
Пример кода
Нет смысла изобретать велосипед и писать свою собственную реализацию фильтра Калмана, когда существует множество готовых библиотек. Я выбрал язык python и библиотеку filterpy для примера.
Чтобы не загромождать пример, возьмем одномерный случай. Одномерный робот оборудован одномерным GPS, который определяет положение с некоторой погрешностью.
Моделирование данных датчиков
Начнём с равномерного движения:
Simulator.py
import numpy as np
import numpy.random
# Моделирование данных датчика
def simulateSensor(samplesCount, noiseSigma, dt):
# Шум с нормальным распределением. мат. ожидание = 0, среднеквадратичное отклонение = noiseSigma
noise = numpy.random.normal(loc = 0.0, scale = noiseSigma, size = samplesCount)
trajectory = np.zeros((3, samplesCount))
position = 0
velocity = 1.0
acceleration = 0.0
for i in range(1, samplesCount):
position = position + velocity * dt + (acceleration * dt ** 2) / 2.0
velocity = velocity + acceleration * dt
acceleration = acceleration
trajectory[0][i] = position
trajectory[1][i] = velocity
trajectory[2][i] = acceleration
measurement = trajectory[0] + noise
return trajectory, measurement # Истинное значение и данные "датчика" с шумом
Визуализируем результаты моделирования:
Код
import matplotlib.pyplot as plt
dt = 0.01
measurementSigma = 0.5
trajectory, measurement = simulateSensor(1000, measurementSigma, dt)
plt.title("Данные датчика")
plt.plot(measurement, label="Измерение", color="#99AAFF")
plt.plot(trajectory[0], label="Истинное значение", color="#FF6633")
plt.legend()
plt.show()

Реализация фильтра
Для начала выберем модель системы. Я решил взять 3 переменных состояния: положение, скорость и ускорение. В качестве модели процесса возьмем модель равноускоренного движения:
У нас единственный датчик, который напрямую измеряет положение. Поэтому модель наблюдения получается очень простой:
Мы предполагаем, что наш робот находится в точке 0 и имеет нулевые скорость и ускорение в начальный момент времени:
Однако, мы не уверены, что это именно так. Поэтому установим матрицу ковариации для начального состояния с большими значениями на главной диагонали:
Я воспользовался функцией библиотеки filterpy для расчёта ковариационной матрицы ошибки модели: filterpy.common.Q_discrete_white_noise. Эта функция использует модель непрерывного белого шума.
Код
import filterpy.kalman
import filterpy.common
import matplotlib.pyplot as plt
import numpy as np
import numpy.random
from Simulator import simulateSensor # моделирование датчиков
dt = 0.01 # Шаг времени
measurementSigma = 0.5 # Среднеквадратичное отклонение датчика
processNoise = 1e-4 # Погрешность модели
# Моделирование данных датчиков
trajectory, measurement = simulateSensor(1000, measurementSigma, dt)
# Создаём объект KalmanFilter
filter = filterpy.kalman.KalmanFilter(dim_x=3, # Размер вектора стостояния
dim_z=1) # Размер вектора измерений
# F - матрица процесса - размер dim_x на dim_x - 3х3
filter.F = np.array([ [1, dt, (dt**2)/2],
[0, 1.0, dt],
[0, 0, 1.0]])
# Матрица наблюдения - dim_z на dim_x - 1x3
filter.H = np.array([[1.0, 0.0, 0.0]])
# Ковариационная матрица ошибки модели
filter.Q = filterpy.common.Q_discrete_white_noise(dim=3, dt=dt, var=processNoiseVariance)
# Ковариационная матрица ошибки измерения - 1х1
filter.R = np.array([[measurementSigma*measurementSigma]])
# Начальное состояние.
filter.x = np.array([0.0, 0.0, 0.0])
# Ковариационная матрица для начального состояния
filter.P = np.array([[10.0, 0.0, 0.0],
[0.0, 10.0, 0.0],
[0.0, 0.0, 10.0]])
filteredState = []
stateCovarianceHistory = []
# Обработка данных
for i in range(0, len(measurement)):
z = [ measurement[i] ] # Вектор измерений
filter.predict() # Этап предсказания
filter.update(z) # Этап коррекции
filteredState.append(filter.x)
stateCovarianceHistory.append(filter.P)
filteredState = np.array(filteredState)
stateCovarianceHistory = np.array(stateCovarianceHistory)
# Визуализация
plt.title("Kalman filter (3rd order)")
plt.plot(measurement, label="Измерение", color="#99AAFF")
plt.plot(trajectory[0], label="Истинное значение", color="#FF6633")
plt.plot(filteredState[:, 0], label="Оценка фильтра", color="#224411")
plt.legend()
plt.show()
Бонус — сравнение различных порядков моделей
Сравним поведение фильтра с моделями разного порядка. Для начала, смоделируем более сложный сценарий поведения робота. Пусть робот находится в покое первые 20% времени, затем движется равномерно, а затем начинает двигаться равноускоренно:
Simulator.py
# Моделирование данных датчика
def simulateSensor(samplesCount, noiseSigma, dt):
# Шум с нормальным распределением. мат. ожидание = 0, среднеквадратичное отклонение = noiseSigma
noise = numpy.random.normal(loc = 0.0, scale = noiseSigma, size = samplesCount)
trajectory = np.zeros((3, samplesCount))
position = 0
velocity = 0.0
acceleration = 0.0
for i in range(1, samplesCount):
position = position + velocity * dt + (acceleration * dt ** 2) / 2.0
velocity = velocity + acceleration * dt
acceleration = acceleration
# Переход на равномерное движение
if(i == (int)(samplesCount * 0.2)):
velocity = 10.0
# Переход на равноускоренное движение
if (i == (int)(samplesCount * 0.6)):
acceleration = 10.0
trajectory[0][i] = position
trajectory[1][i] = velocity
trajectory[2][i] = acceleration
measurement = trajectory[0] + noise
return trajectory, measurement # Истинное значение и данные "датчика" с шумомВ предыдущем примере мы использовали модель, содержащую переменную (положение) и две производных её по времени (скорость и ускорение). Посмотрим, что будет, если избавиться от одной или обеих производных:
2-й порядок
# Создаём объект KalmanFilter
filter = filterpy.kalman.KalmanFilter(dim_x=2, # Размер вектора стостояния
dim_z=1) # Размер вектора измерений
# F - матрица процесса - размер dim_x на dim_x - 2х2
filter.F = np.array([ [1, dt],
[0, 1.0]])
# Матрица наблюдения - dim_z на dim_x - 1x2
filter.H = np.array([[1.0, 0.0]])
filter.Q = [[dt**2, dt],
[ dt, 1.0]] * processNoise
# Начальное состояние.
filter.x = np.array([0.0, 0.0])
# Ковариационная матрица для начального состояния
filter.P = np.array([[8.0, 0.0],
[0.0, 8.0]])1-й порядок
# Создаём объект KalmanFilter
filter = filterpy.kalman.KalmanFilter(dim_x=1, # Размер вектора стостояния
dim_z=1) # Размер вектора измерений
# F - матрица процесса - размер dim_x на dim_x - 1х1
filter.F = np.array([ [1.0]])
# Матрица наблюдения - dim_z на dim_x - 1x1
filter.H = np.array([[1.0]])
# Ковариационная матрица ошибки модели
filter.Q = processNoise
# Ковариационная матрица ошибки измерения - 1х1
filter.R = np.array([[measurementSigma*measurementSigma]])
# Начальное состояние.
filter.x = np.array([0.0])
# Ковариационная матрица для начального состояния
filter.P = np.array([[8.0]])
Сравним результаты:
На графиках сразу заметно, что модель первого порядка начинает отставать от истинного значения на участках равномерного движения и равноускоренного движения. Модель второго порядка успешно справляется с участком равномерного движения, но так же начинает отставать на участке равноускоренного движения. Модель третьего порядка справляется со всеми тремя участками.
Однако, это не означает что нужно использовать модели высокого порядка во всех случаях. В нашем примере, модель третьего порядка справляется с участком равномерного движения несколько хуже модели второго порядка, т.к. фильтр интерпретирует шум сенсора как изменение ускорения. Это приводит к колебанию оценки фильтра. Стоит подбирать порядок модели в соответствии с планируемыми режимами работы фильтра.
Нелинейные модели и фильтр Калмана
Почему фильтр Калмана не работает для нелинейных моделей и что делать
Всё дело в нормальном распределении. При применении линейных преобразованийк нормально распределенной случайной величине, результирующее распределение будет представлять собой нормальное распределение, или будет пропорциональным нормальному распределению. Именно на этом принципе и строится математика фильтра Калмана.
Есть несколько модификаций алгоритма, которые позволяют работать с нелинейными моделями.
Например:
Extended Kalman Filter (EKF) — расширенный фильтр Калмана. Этот подход строит линейное приближение модели на каждом шаге. Для этого требуется рассчитать матрицу вторых частных производных функции модели, что бывает весьма непросто. В некоторых случаях, аналитическое решение найти сложно или невозможно, и поэтому используют численные методы.
Unscented Kalman Filter (UKF). Этот подход строит приближение распределения получающегося после нелинейного преобразования при помощи сигма-точек. Преимуществом этого метода является то, что он не требует вычисления производных.
Мы рассмотрим именно Unscented Kalman Filter
Unscented Kalman Filter и почему он без запаха
Основная магия этого алгоритма заключается в методе, который строит приближение распределения плотности вероятности случайной величины после прохождения через нелинейное преобразование. Этот метод называется unscented transform — сложнопереводимое на русский язык название. Автор этого метода, Джеффри Ульман, не хотел, чтобы его разработку называли “Фильтр Ульмана”. Согласно интервью, он решил назвать так свой метод после того как увидел дезодорант без запаха (“unscented deodorant”) на столе в лаборатории, где он работал.
Этот метод достаточно точно строит приближение функции распределения случайной величины, но что более важно — он очень простой.
Для использования UKF не придётся реализовывать какие-либо дополнительные вычисления, за исключением моделей системы. В общем виде, нелинейная модель не может быть представлена в виде матрицы, поэтому мы заменяем матрицы и
на функции
и
. Однако смысл этих моделей остаётся тем же.
Реализуем unscented Kalman filter для линейной модели из прошлого примера:
Код
import filterpy.kalman
import filterpy.common
import matplotlib.pyplot as plt
import numpy as np
import numpy.random
from Simulator import simulateSensor, CovarianceQ
dt = 0.01
measurementSigma = 0.5
processNoiseVariance = 1e-4
# Функция наблюдения - аналог матрицы наблюдения
# Преобразует вектор состояния x в вектор измерений z
def measurementFunction(x):
return np.array([x[0]])
# Функция процесса - аналог матрицы процесса
def stateTransitionFunction(x, dt):
newState = np.zeros(3)
newState[0] = x[0] + dt * x[1] + ( (dt**2)/2 ) * x[2]
newState[1] = x[1] + dt * x[2]
newState[2] = x[2]
return newState
trajectory, measurement = simulateSensor(1000, measurementSigma)
# Для unscented kalman filter необходимо выбрать алгоритм выбора сигма-точек
points = filterpy.kalman.JulierSigmaPoints(3, kappa=0)
# Создаём объект UnscentedKalmanFilter
filter = filterpy.kalman.UnscentedKalmanFilter(dim_x = 3,
dim_z = 1,
dt = dt,
hx = measurementFunction,
fx = stateTransitionFunction,
points = points)
# Ковариационная матрица ошибки модели
filter.Q = filterpy.common.Q_discrete_white_noise(dim=3, dt=dt, var=processNoiseVariance)
# Ковариационная матрица ошибки измерения - 1х1
filter.R = np.array([[measurementSigma*measurementSigma]])
# Начальное состояние.
filter.x = np.array([0.0, 0.0, 0.0])
# Ковариационная матрица для начального состояния
filter.P = np.array([[10.0, 0.0, 0.0],
[0.0, 10.0, 0.0],
[0.0, 0.0, 10.0]])
filteredState = []
stateCovarianceHistory = []
for i in range(0, len(measurement)):
z = [ measurement[i] ]
filter.predict()
filter.update(z)
filteredState.append(filter.x)
stateCovarianceHistory.append(filter.P)
filteredState = np.array(filteredState)
stateCovarianceHistory = np.array(stateCovarianceHistory)
plt.title("Unscented Kalman filter")
plt.plot(measurement, label="Измерение", color="#99AAFF")
plt.plot(trajectory[0], label="Истинное значение", color="#FF6633")
plt.plot(filteredState[:, 0], label="Оценка фильтра", color="#224411")
plt.legend()
plt.show()
Разница в коде минимальна. Мы заменили матрицы F и H на функции f(x) и h(x). Это позволяет использовать нелинейные модели системы и/или наблюдения:
# Функция наблюдения - аналог матрицы наблюдения
# Преобразует вектор состояния x в вектор измерений z
def measurementFunction(x):
return np.array([x[0]])
# Функция процесса - аналог матрицы процесса
def stateTransitionFunction(x, dt):
newState = np.zeros(3)
newState[0] = x[0] + dt * x[1] + ( (dt**2)/2 ) * x[2]
newState[1] = x[1] + dt * x[2]
newState[2] = x[2]
return newStateТакже, появилась строчка, устанавливающая алгоритм генерации сигма-точек
points = filterpy.kalman.JulierSigmaPoints(3, kappa=0)
Этот алгоритм определяет точность оценки распределения вероятности при прохождении через нелинейное преобразование. К сожалению, существуют только общие рекомендации относительно генерации сигма-точек. Поэтому для каждой отдельной задачи значения параметров алгоритма подбираются экспериментальным путём.
Ожидаемый результат — график оценки положения практически не отличается от обычного фильтра Калмана.
В этом примере используется линейная модель. Однако мы могли бы использовать нелинейные функции. Например, мы могли бы использовать следующую реализацию:
g = 9.8
# Вектор состояния - угол наклона
# Вектор измерений - ускорение вдоль осей X и Y
def measurementFunction(x):
measurement = np.zeros(2)
measurement[0] = math.sin(x[0]) * g
measurement[1] = math.cos(x[0]) * g
return measurementТакую модель измерений было бы невозможно использовать в случае с линейным фильтром Калмана
Вместо заключения
За рамками статьи остались теоретические основы фильтра Калмана. Однако объем материала по этой теме ошеломляет. Сложно выбрать хороший источник. Я бы хотел рекомендовать замечательную книгу от автора библиотеки filterpy Roger Labbe (на английском языке). В ней доступно описаны принципы работы алгоритма и сопутствующая теория. Книга представляет собой документ Jupyter notebook, который позволяет в интерактивном режиме экспериментировать с примерами.
Литература
→ Roger Labbe — Kalman and Bayesian Filters in Python
→ Wikipedia
Battery state-of-power evaluation methods
Shunli Wang, … Zonghai Chen, in Battery System Modeling, 2021
7.4.4 Main charge-discharge condition test
The initial value of the error covariance matrix P0 can be determined from the X0 error of the initial state. In the application, the initial value should be as small as possible to speed up the tracking speed of the algorithm. Two important parameters are processed noise variance matrix Q and observation noise variance matrix R. As can be known from theoretical formula derivation, the dispose to Q and R plays a key role in improving the estimation effect by using this algorithm. Because it affects the size of the Kalman gain matrix K directly, the value of error covariance matrix P can be described as shown in Eq. (7.61):
(7.61)Rk=Eυk2=συ2
It is the expression of the observation noise variance, which is mainly derived from the distribution of observation error of experimental instruments and sensors, as shown in Eq. (7.62):
(7.62)Qk=Eω1k2Eω1kω2kEω2kω1kEω2k2=σω1,12σω1,22σω2,12σω2,22
It is the relationship between the system noise variance and the processing noise covariance. The two states in the system are generally unrelated and the covariance value is zero. Therefore, the diagonal variance can have a small value. The variance Q of processing noise is mainly derived from the error of the established equivalent model, which is difficult to be obtained by theoretical methods or means. A reasonable value range can be obtained through continuous debugging through simulation, and it is usually a small amount.
To verify the applicable range and stability of the algorithm, the input of different working conditions is used to observe the estimation accuracy of the algorithm. In this simulation, two working conditions are used: the constant-current working condition and the Beijing bus dynamic street test working condition. For the constant-current condition, only a constant value needs to be set in the program. To increase the complexity of the condition, two shelved stages are added to the constant-current input list to verify the tracking effect of Ah and the extended Kalman filtering. The following code is generated for the current.
The experimental data should be used to simulate the algorithm under its operating conditions. The current input module is realized in the environment under Beijing bus dynamic street test operating conditions. It is the time integration module, whose output is the capacity change of the working condition, and the lower part is the working condition data output module. It outputs the current into the workspace at the minimum time interval of the sampling measurement. The data onto the workspace are a time-series type and the current data need to be extracted. The data extraction and transformation can be performed in the main program, wherein the working condition is the Simulink module. The current is the time-series data, including the current output. S_Est is the algorithm program module, whose input is the initial S_Est_init and current data onto the estimated state value.
The current data are input into the program module of the extended Kalman filtering algorithm based on the model, and the initial values of other parameters have been determined in the program. The program finally outputs the ampere hour time integral and the state estimation curve of the extended Kalman filtering through the minimum time interval of 10 times as the sampling time. The current curve of the experimental test can be obtained as shown in Fig. 7.13.
Fig. 7.13. Pulse current operating current curve for the experimental test. (A) Main charge working condition. (B) Main discharge experimental test.
The unscented Kalman filtering algorithm is programmed by writing scripts to realize algorithm simulation to compare the output effect. The specific implementation process conforms to the processing requirements, and the main simulation program can be constructed. The program takes 10 times the minimum time interval as the sampling time and simulates the three methods of the state estimation, including ampere hour time integration, extended Kalman filtering, and unscented Kalman filtering, to compare the following situation of the three methods of the state over time. The program simultaneously outputs the state variation curve and estimation error curve with time, so that the tracking effect and error variation on the three methods can be obtained visually. Its implementation process is consistent with script. Different modules are used to replace the code block. The integration advantage of the environment is used in the graphical interface to obtain the same stimulation effect.
The operation logic is ensured by the unchanged intuitive presentation of the calculation process. Based on script implementation, the modular simulation is built accordingly. The experiment data are used as the input current, and the state prediction is obtained by the state prediction module. The forecast and model parameters are calculated. After that, the equivalent model can be used to predict the completion status value of Up as well as the output voltage. The input of the algorithm includes the update module, output state correction, and error covariance matrix update as the basis of the forecast. It takes the ampere hour integral result as the minimum time interval of the current data, which is taken as the reference value of the measured state.
The estimation effect of ampere hour and extended Kalman filtering is compared when the minimum time interval can be set as 10 times as the sampling period. The stability of the extended Kalman filtering algorithm is evaluated under working conditions. The state variable needs to accept the last estimated value as the basis of the next state prediction, in which the predicted value Up_pre is directly input into the corresponding position of the resistance-capacitance circuit modeling to conduct the terminal voltage prediction of the current polarization voltage. The functions of each part are realized in a more modular way for the complete structure and clear hierarchy.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780323904728000044
Dynamic Model Development
P.W. Oxby, … T.A. Duever, in Computer Aided Chemical Engineering, 2003
3.2 An Optimality Property of the Determinant Criterion
Equation (12) can be generalized by replacing the inverse of the estimate of the error covariance matrix,
Σ^εn−1, with an arbitrary symmetric positive definite weight matrix, W:
(14)Δθ^(k)=(XTWX)−1XTWz(θ^(k))
The estimate of the parameter covariance is:
(15)Σ^θ=(XTWX)−1XTWΣ^εn(XTWX)−1
If the determinant of the estimate of the parameter covariance matrix,
|Σ^θ|, is minimized with respect to the elements of W, the solution is independent of X and is simply
(16)W=Σ^εn−1
Substitution of (16) back into (14) gives (12) which, as has been shown, is equivalent to the determinant criterion. Therefore of all weighting schemes in the form of (14), it is the one equivalent to the determinant criterion that minimizes
|Σ^θ|, the determinant of the estimate of the parameter covariance matrix when the error covariance is unknown. This appears to be a rather strong result in support of the determinant criterion. It might also be noted that, unlike derivations based on likelihood, this result does not depend on the measurement errors being normally distributed. But it will be shown that the practical usefulness of the result does depend on the assumption that the residual covariance
Z(θ^)Z(θ^)T/n, is a good estimate of the true error covariance. Ideally one would want W to be the inverse of the error covariance matrix. The determinant in effect makes a compromise and substitutes an estimate of it. The potential problem here is that if the data set is not large, the residual covariance matrix may be a poor estimate of the error covariance matrix. A poor estimate of the error covariance matrix will lead to a poor estimate of the parameter covariance matrix. Therefore, although the determinant criterion gives the minimum determinant of the estimate of the parameter covariance matrix, if this estimate is poor, then the optimality property may be of little significance. This suggests that the optimality of the determinant criterion may be more relevant for large data sets than small ones. The simulation studies presented in Section 4 will confirm this to be true.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/S1570794603800706
Kalman Filters and Nonlinear Filters
Vytas B. Gylys, in Encyclopedia of Physical Science and Technology (Third Edition), 2003
IV.B Square Root Filtering
By far the greatest trouble spot in computer mechanization of the KF is the updating of state error covariance matrix P, that is, the computation of Pk∣k according to Eq. (18). As the estimation process progresses, the elements of Pk∣k typically continue to decrease in magnitude and so matrix Pk∣k keeps approaching the zero matrix, although theoretically it should forever remain positive definite, no matter how small in magnitude its elements become. Hence, unless special measures are taken, accumulation of roundoff error in the repetitive use of Eq. (18) may cause the computed Pk∣k to lose its positive definiteness. As suggested by the matrix inversion operation appearing on the right-hand side of Eq. (16) for computing the Kalman gain, this situation is aggravated if several components of the measurement vector are very accurate and consequently the positive definite measurement error covariance matrix R is ill conditioned, that is, if R has eigenvalues of both relatively very large and small magnitudes.
Let A be a nonnegative definite symmetric matrix; then there exists a matrix S such that A = SST. Matrix S is often called the square root of A. The Cholesky decomposition algorithm provides a method of constructing from A the matrix S so that S is lower triangular; that is, all elements of S above the main diagonal are zero. Square root filtering is motivated by the observations that, if the state error covariance matrix P = SST, then (a) since SST is always nonnegative definite, matrix P expressed as SST cannot become negative definite, and (b) matrix S is generally less ill conditioned than matrix P.
Several versions of the square root filtering algorithm are known. The earliest form was developed by J. E. Potter in 1964 for applications in which the process noise is absent (i.e., covariance matrix Q is zero) and the measurements are sequentially processed as scalars. In 1967 J. F. Bellantoni and K. W. Dodge extended Potter’s results to vector-valued measurements. A. Andrews in 1968 and then S. F. Schmidt in 1970 published two alternative procedures for handling the process noise. In 1973 N. A. Carlson described a procedure that considerably improved the speed and decreased the memory requirements of square root filtering and in which, as in Potter’s algorithm, vector-valued measurements are processed sequentially as scalars. Finally, the so-called UDUT covariance factorization method is the most recent major milestone in numerical handling of KFs. This method, developed by G. J. Bierman and C. L. Thornton, represents the state error covariances before and after the measurement update step asPk|k−1=Uk|k−1Dk|k−1Uk|k−1TandPk|k=Uk|kDk|kUk|kT,with D being a diagonal matrix and U an upper triangular matrix with 1’s on its main diagonal. In this method, the square root of the covariance matrix, which now would correspond to UD1/2, is never computed explicitly, which avoids numerical computation of square roots. Like Carlson’s algorithm, the UDUT factorization method maintains the covariance matrix in factored form and so (like Carlson’s algorithm) is considerably more efficient in processor time and storage than the original Potter algorithm.
As a quick comparison of computational efficiency, the conventional Kalman method, the less efficient form of Carlson’s algorithm, and the UDUT factorization method are roughly equal: The processing of each time step (consisting of one time propagation and one measurement update) requires of the order of 16[9ns3 + 9ns2nm + 3ns2nw] adds and about the same number of multiplies, plus a relatively modest number of divides and square roots (square roots are required only in some, as in Potter’s or Carlson’s square root algorithms). Here, as before, ns is the length of the state vector, nm the length of the measurement vector, and nw the lenght of the process noise vector w. The faster version of Carlson’s algorithm is more efficient and requires only of the order of 16[5ns3 + 9ns2nm + 3ns2nw] adds and 16[5ns3 + 12ns2nm + 3ns2nw] multiplies, plus 2nsnm divides and nsnm square roots, at each time point. The stable (Joseph) form of the KF [as given by Eq. (18′)] fares more poorly: At each time step, it requires of the order of 16[18ns3 + 15ns2nm + 3ns2nw] adds and about the same number of multiplies.
As a summary, (a) a square root filter is a numerically stable form for performing the KF covariance–gain processing defined by Eqs. (15), (16), and (18); (b) the efficiency of its more recent versions roughly compares with that of these three equations; (c) the increased stability allows one to use relatively low-precision arithmetic in the KF gain–covariance processing, with a possible exception of some dot products.
Real-time implementation of a filter involves additional issues that are unimportant in the non-real-time environment. Besides the adequacy of functional performance, the most important of these issues is the requirement to produce timely responses to external stimuli. Thus, resorting to a parallel or concurrent processing may be the only way out. This usually implies the use of special hardware architectures such as parallel, vector pipelined, or systolic processors.
As one example, consider the use of a filter in the tracking of multiple objects in a hard real-time environment characterized by strict deadlines. In such a case one may want to maintain simultaneously many estimation processes, each handling a single object. Parallel processors may seem to be a suitable hardware architecture for this problem, but if separate estimation processes in such an application progress at different rates and at any time some of them require a great amount of special handling, then parallel architecture, such as a single-instruction multiple-data stream computer, may not be the best choice. As another example, consider a KF to be implemented as part of a navigation system on a small airborne computer (uniprocessor). Suppose that the navigation measurements come at a certain fixed rate. If the filtering process cannot keep up with the arrival rate of measurements and so not all of them can be utilized, the estimation performance may deteriorate. In this problem, if there is an upper bound on hardware resources, the only solution may be to decompose the estimation algorithm into concurrently executable processes. For instance, the time-propagation step (which, say, is to be executed at a relatively high rate) may constitute one process and the measurement-update step (which needs to be executed only at some lower rate, say, at the rate of measurement arrivals) may constitute another. Such a decomposition of an estimation algorithm into concurrent procedures often creates a surrogate algorithm that performs more poorly than the original algorithm.
The effects of the finite-length word computing is another issue that must be considered in filter implementation for real-time applications. The computer on which a filter is developed and validated through successive off-line simulations is often more powerful and uses higher-precision arithmetic and number representations than the ultimate real-time processor. Hence, one must in advance determine in advance what effect a shorter word length will have on performance.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B0122274105003574
Computer Techniques and Algorithms in Digital Signal Processing
K. Giridhar, … Ronald A. Iltis, in Control and Dynamic Systems, 1996
A Appendix – Time Updates for the Blind MAPSD Algorithm
In this Appendix, we derive the one-step time updates of the channel estimate and the associated error covariance matrix for the blind MAP symbol detector developed in Section 4.2. Recall from Eq. (51) that
(A.1)pfk+1|dik+1,Nf,rk=∑j:djk,Nf∈dik+1,Nfαjp(fk+1|djk,Nf,rk)
where αj is given by Eq. (52). Using Eq. (49), this Gaussian sum can be explicitly written as follows:
(A.2)pfk+1|dik+1,Nf,rk=∑j:djk,Nf∈dik+1,NfαjNfk+1;Ff^jk|k,FPjk|kFH+Q
which defines the one-step prediction of the mean vector f^ik+1|k and the covariance matrix Pik+1|k. Some basic results about sums of Gaussian p.d.f.s can be used to derive these one-step predictions.
Lemma: Let the p.d.f. of the random vector x be a weighted sum of N multivariate Gaussian p.d.f.s as follows:
(A.3)px=∑j=1NαjNx;xj,Pj
where αj , xj, and Pj are, respectively, the jth weight, mean, and covariance. (i) The mean value of x is given by
(A.4)xa=∑j=1Nαjxj.
(ii) The error covariance is given by
(A.5)Pa=∑j=1NαjPj+xa–xjxa–xjH.
Proof: The first part of the lemma is easily proved from the definition of xa, i.e.,
(A.6)xa=Ex=∫xx∑j=1NαjNx;xj,Pjdx=∑j=1Nαjxj.
To prove the second part of the lemma, consider
(A.7)Pa=Ex−xax−xaH=∑j=1Nαj∫xxxHNjdx+xaxaH−∫xxxaHNjdx−∫xxaxHNjdx
where, for convenience, we have used the notation Nj to represent the p.d.f. N(x; xj, Pĵ). Observe that ∫xxaHNjdx=xjxaHand∫xaxHNjdx=xaxjH. By adding and subtracting the term xjxjH to the expression inside the square brackets, we obtain
(A.8)Pa=∑j=1Nαj∫xxxHNjdx−xjxjH+xaxaH−xjxaH−xaxjH+xjxjH=∑j=1Nαj∫xxxHNjdx−xjxjH+xa−xjxa−xjH..
It is straightforward to show that
(A.9)∑j=1Nαj∫xxxHNjdx−xjxjH=∑j=1Nαj∫xx−xj(x−xj)HNjdx=∑j=1NαjPj.
Substituting this result into Eq. (A.8 ), we obtain the result in Eq. (A.5 ) for the error covariance Pa, which completes the proof.
To obtain the one-step predicted mean vector of the blind MAPSD algorithm, Eq. (A.4 ) is used with xj=Ff^jk|k. The summation is performed over the M predecessor subsequences djk,Nf, yielding
(A.10)f^ik+1|k)=∑j:djk,Nf∈dik+1,NfαjFf^jk|k.
By substituting αj=pdjk,Nf|rk−1/qik, the final expression in Eq. (53) is obtained. Similarly, the one-step error covariance update in Eq. (54) is obtained by substituting FPjk|kFH+Q=Pj and
(A.11)νj,ikνj,iHk=xa−xjxa−xjH
into Eq. (A.5 ) where xa=f^ik+1|k (and xj=Ff^jk|k as above).
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/S0090526796800454
State Estimation
Jay Farrell, in The Electrical Engineering Handbook, 2005
4.3 Recursive State Estimation
Equations 4.4 through 4.5 provide the mean and the covariance of the state through time based only on the initial mean state vector and its error covariance matrix. When measurements y(k) are available, the measurements can be used to improve the accuracy of an estimate of the state vector at time k. The symbols xˆ−(k) and xˆ+(k) are used to denote the estimate of x(k) before and after incorporating the measurement, respectively.
Similarly, the symbols Pxˆ−(k) and Pxˆ+(k) are used to denote the error covariance matrices corresponding to xˆ−(k) and xˆ+(k), respectively. This section presents the time propagation and measurement update equations for both the state estimate and its error covariance. The equations are presented in a form that is valid for any linear unbiased measurement correction. These equations contain a gain matrix K that determines the estimator performance. The choice of K to minimize the error covariance Pxˆ+(k) will be of interest.
For an unbiased linear measurement, the update will have the form:
(4.8)xˆ+(k)=xˆ−(k)+K(k)(y(k)−yˆ−(k)),
where yˆ−(k)=H(k)xˆ−(k).. The error covariance of xˆ+(k) is the following:
(4.9)Pxˆ+(k)=(I−K(k)H(k))Pxˆ−(k)(I−K(k)H(k))T +K(k)R(k)KT(k).
K(k) is a possibly time-varying state estimation gain vector to be designed. If no measurement is available at time k, then K(k) = 0, which yields xˆ+(k)=xˆ−(k) and Pxˆ+(k)=Pxˆ−(k). If a measurement is available, and the state estimator is designed well, then Pxˆ+(k)≤Pxˆ−(k). In either case, the time propagation of the state estimate and its error covariance matrix is achieved by:
(4.10)xˆ−(k+1)=Φ(k)xˆ+(k)+Γˆuu(k)
(4.11)Pxˆ−(k+1)=Φ(k)Pxˆ+(k)ΦT(k)+ΓωQd(k)ΓωT.
At least two issues are of interest relative to the state estimation problem. First, does there exist a state estimation gain vector K(k) such that xˆ is guaranteed to converge to x regardless of initial condition and the sequence u(k)? Second, how should the designer select the gain vector K(k)?
The first issue raises the question of observability. A linear time-invariant system is observable if the following matrix has rank n:
[HT, ΦTHT, …,( ΦT)nHT].
When a system is observable, then it is guaranteed that a stabilizing gain vector K exists. Assuming that the system of interest is observable, the remainder of this chapter discusses the design and analysis of state estimators.
Figure 4.1 portrays the state estimator in conjunction with the system of interest. The system of interest is depicted in the upper left. The state estimator is superimposed on a gray background in the lower right.
FIGURE 4.1. State Estimation System Block Diagram
This interconnected system will be referred to as the state estimation system. The figure motivates several important comments. First, although the state estimator has only n states, the state estimation system has 2n states. Second, the inputs to the state estimation system are the deterministic input u and the stochastic inputs ω and v. Third, the inputs to the state estimator are the deterministic input u and the measured plant output y. The state space model for the state estimation system is the following:
(4.12)[x(k+1)xˆ−(k+1)]=[Φx0LHxΦ−LH][x(k)xˆ−(k)]+[ΓuΓω0Γˆu0L][u(k)ω(k)v(k)],
where L = ΦK.
Based on this state-space model, with the assumption that the system is time invariant, the transfer function from v to yˆ is as written here:
(4.13)Gv(z)=H[zI−(Φ−LH)]−1L,
where z is the discrete-time unit advance operator. Assuming that H = Hx, the transfer function from u to r is as follows:
(4.14)Gu(z)=H[zI−(Φ−LH)]−1 [(zI−Φ)(zI−Φx)−1Γu−(zI−Φx)(zI−Φx)−1Γˆu].
Therefore, if Γu=Γˆu and Φx = Φ, then this transfer function is identically zero. Assuming again that H = Hx, the transfer function from ω to r is the following:
(4.15)Gω(z)=H[zI−(Φ−LH)]−1[zI−Φ][zI−Φx]−1Γω.
In the special case where, in addition, Φx = Φ, the transfer function Gω(z) has n identical poles and zeros. This transfer functions is often stated as:
(4.16)Gω(z)=H[zI−(Φ−LH)]−1Γω,
where n pole and zero cancellations have occurred. These pole-zero cancellations and therefore the validity of equation 4.16 are dependent on the exact modeling assumption and the stability of the canceled poles.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780121709600500815
Data Assimilation in Numerical Weather Prediction and Sample Applications
Andrew S. Jones, Steven J. Fletcher, in Solar Energy Forecasting and Resource Assessment, 2013
13.3.5 Ensemble DA
The ensemble Kalman filter (EnsKF) is a sequential filter that forecasts the state vector, xf, as well as the model-error covariance matrix, Pf, toward a future time step (Evensen, 1994). This is a linear process, but it can employ nonlinear models within the system; no adjoints are required. For example, the forward state is given by the propagation of the model forward in time
(13.29)xf(ti)=Mi−1[xa(ti−1)]
as well as its associated forecast-error covariance matrix
(13.30)Pf(ti)=Mi−1Pa(ti−1)Mi−1T+Q(ti−1)
This is followed by an analysis step that updates (or readjusts) the state information and the forecast-error covariance information
(13.31)xa(ti)=xf(ti)+Kidi
(13.32)Pa(ti)=(I−KiHi)Pf(ti)
where the innovation vector, di, is given by
(13.33)di=yio−Hi[xf(ti)]
It is important to note that M and H are linearizations of the gradients of M and H with respect to the control vector, x. The Kalman gain, Ki, is given by
(13.34)Ki=Pf(ti)HiT[HiPf(ti)HiT+Ri]−1
where Pf(ti) is now approximated by the mean ensemble estimate
(13.35)Pf(ti)≈1K−2∑K≠lK[xf(tk)−x¯f(tl)][xf(tk)−x¯f(tl)]T
K is the number of ensemble-model runs required to generate the estimate, and a reference model state, l, is used to define the mean ensemble estimate of the forecast error covariance matrix. In addition to the approach in equation 13.35, other EnsKF variants are used by the NWP DA community. The analysis stage that propagates the forecast error covariance matrix is a powerful feature of EnsKF. Additional improvements in EnsKF performance can be achieved by improving sampling behaviors—for example, using sampling strategies and square root schemes, some of which also allow for a low-rank representation of the observational-error covariance matrix (Evensen, 2004).
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123971777000139
The Basics of Analytical Mechanics, Optimization, Control and Estimation
Kyle T. Alfriend, … Louis S. Breger, in Spacecraft Formation Flying, 2010
3.8 Kalman Filtering
In 1960, Robert Kalman introduced a new approach for minimum mean-square error filtering that used state-space methods [80]. The Kalman Filter (KF) is a recursive scheme that propagates a current estimate of a state and the error covariance matrix of that state forward in time. The filter optimally blends the new information introduced by the measurements with old information embodied in the prior state with a Kalman gain matrix. The gain matrix balances uncertainty in the measurements with the uncertainty in the dynamics model. The KF is guaranteed to be the optimal filter (in the sense of minimizing the 2-norm-squared of the estimation error) for a linear system with linear measurements [81]. However, few systems can be accurately modeled with linear dynamics. Shortly after its inception, improvements on the Kalman filter to handle nonlinear systems were proposed. One of the most popular choices, the Extended Kalman Filter (EKF), was applied to relative navigation filters in LEO [43]. We will demonstrate how to use the EKF for relative spacecraft state estimation in Chapter 12.
The discrete EKF is as a state estimator for systems whose state dynamics model, measurement model, or both may be nonlinear, as in Eqs. (3.48) and (3.53) [81]. The dynamics model provides the equations to propagate xˆk, the estimate of the state x at time k, to time step k+1, producing xˆk+1. The measurement model then incorporates the new sensor information to update this estimate, updating the a priori estimate xˆk+1− to the a posteriori estimate, xˆk+1+. This process is illustrated in Fig. 3.1.
FIGURE 3.1. A Kalman filter process.
The continuous state x is governed by the dynamics
(3.48)ẋ(tk)=f(x,u,tk)+w(tk)
where u is a known control input, and w(t) is an additive white noise that models the error accumulated by uncertainty in the dynamics during the time step. The power spectral density of this zero mean, white noise process is
(3.49)Q=E[w(t)w(t)T]
To proceed, linear expressions for the dynamics and measurement equations must be formed. In general, this requires knowledge of the probability density function [81], but the EKF approximates the nonlinear function by expanding it in a Taylor series, at each time step, about the current estimate,
(3.50)Fk=∂f∂x|x=xˆk
The dynamics are discretized with time step Δt by forming the state transition matrix,
(3.51)Φk=eFkΔt
The cumulative effect of the white noise process w(t) over the time step is captured in the discrete process noise covariance matrix
(3.52)Qk=∫0ΔteFkτQ(eFkτ)Tdτ
The vector of measurements, y,
(3.53)y=h(x,t)+vk
is modeled as a nonlinear function of the state and time, with an additive white noise process v(t) that accounts for uncertainty in the sensors and their models. The measurement noise covariance matrix is defined by
(3.54)Rk=E[vkvkT]
The nonlinear measurement equation is also linearized about the current estimate,
(3.55)Hk=∂h∂x|x=xˆk−
Because approximations must be made in the linearization, the EKF is a suboptimal filter, in the sense that its stability and performance are not guaranteed. Fortunately, the dynamics of orbital motion are fairly simple, and the EKF can have very good performance in space navigation applications. The discrete, linear representation of the system dynamics are
(3.56)xk=Φk−1xk−1+wk−1+uk−1
The confidence in the current estimate is captured in the state error covariance matrix, P,
(3.57)Pk=E[x̃kx̃kT]=E[(xˆk−xk)(xˆk−xk)T]
where x̃k=xˆk−xk is the estimation error. The first step in the EKF involves propagating the state and error covariance forward in time. Equation (3.56), with zero process noise, is used to propagate the state estimate. The error covariance is propagated forward using
(3.58)Pk−=Φk−1Pk−1+Φk−1T+Qk−1
An alternate approach to the time propagation step involves using the nonlinear dynamics equations to propagate the state. A 4th-order Runge–Kutta integration scheme uses the nonlinear state dynamics equation
(3.59)xˆ̇(t)=f(xˆ(t),u(t))for t=tk−1→tk
to find xˆk. The state covariance is still propagated with Eq. (3.58), so the state transition matrix Φk−1 must be calculated regardless of whether the linear or nonlinear state propagation is chosen.
The second step of the filter uses the measurement equation to update the a priori state xˆk− to the a posteriori state xˆk+. When a measurement becomes available, the new information provided by the measurement and the previous information captured in the state estimate are combined to form an updated state estimate. The Kalman gain K is the blending gain matrix that is used to weight the importance of the old and new information. The optimum gain matrix is formulated by minimizing the trace of the a posteriori state error covariance matrix Pk+, which essentially minimizes the estimation error vector at each time step [81]. The terms in the gain matrix equation include the previous state estimate, the linearized measurement matrix, and the expected noise of the new measurements,
(3.60)Kk=Pk−HkT(HkPk−HkT+Rk)−1
The nonlinear measurement equation is used to update the state estimate
(3.61)xˆk+=xˆk−−Kk(yk−hk(xˆk−))
Note that the computation of the gain matrix Kk requires the linear measurement matrix Hk. The covariance is updated after the measurement with
(3.62)Pk+=(I−KkHk)Pk−(I−KkHk)T+KkRkKkT
which is the Joseph form of the covariance update whose inherent symmetry makes it numerically stable [82].
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780750685337002086
Static State Estimation
Soliman Abdel-hady Soliman Ph.D., Ahmad M. Al-Kandari Ph.D., in Electrical Load Forecasting, 2010
2.3 Properties of Least Error Squares Estimation
Least error squares estimation results are easy to compute and possess a number of interesting properties. The least squares are the best estimates (maximum likelihood) when the measurement errors follow a Gaussian or normal distribution and the weighting matrix is equal to the inverse of the error covariance matrix. The least error squares estimates can be easily calculated.
Where the measurement error distribution does not follow a Gaussian distribution and the number of measurements greatly exceeds the number of unknown parameters, the method of least error squares yields very good estimates. However, there are many estimation problems for which the error distribution is not a Gaussian and the number of measurements does not greatly exceed the number of unknown parameters. In such cases, the least error squares estimations are adversely affected by bad data. This problem has been recognized and addressed by several researchers who have proposed different ways of refining the least error squares method to make estimation less affected by the presence of bad data. In the next section, we discuss an alternative technique to the LES estimation. This technique is based on least absolute value approximation.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123815439000026
Principles of meteorology and numerical weather prediction
Sue Ellen Haupt, … Branko Kosović, in Renewable Energy Forecasting, 2017
1.2.2.2 Variational assimilation
Variational assimilation techniques are a form of statistical interpolation. All statistical interpolation techniques require an estimation of the error covariances between variables in the background state, as well as error covariances between the observed variables. These techniques find the optimal analysis by globally minimizing a cost function that incorporates the distance between the analysis and observations within the assimilation window. This method also requires the observation error covariance matrix and the background error covariance matrix (e.g., Talagrand, 1997; Kalnay, 2003), which at times may be difficult to compute accurately. In three-dimensional variational DA (3D-Var) schemes, these error covariance matrices come from a static climatology, and all observations within a given assimilation window are assumed to be valid at the analysis time. These assumptions reduce the computational burden. In contrast, four-dimensional variational DA (4D-Var) schemes seek to minimize the cost function, subject to the NWP model equations, to find the best model trajectory through the entire assimilation window, rather than just at the analysis time. In addition, the error covariance matrices are flow-dependent in 4D-Var. These differences make 4D-Var significantly more computationally intensive than 3D-Var, but also more accurate (e.g., Klinker et al., 2000; Yang et al., 2009).
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780081005040000019
Smart grids: control and cybersecurity
Magdi S. Mahmoud, … Mutaz M. Hamdan, in Cyberphysical Infrastructures in Power Systems, 2022
2.2.3 Cyberattack minimization in smart grids
A recursive KF estimator (RKFE) is constructed to operate on observation information in order to produce the optimal state estimation. The forecasted system-state estimate is expressed as follows:
(2.8)xˆr(k)=Adxˆ(k−1)+Bdu(k−1),
where xˆ(k−1) is the previous state estimate. Then the forecasted error covariance matrix is given by
(2.9)Pr(k)=AdP(k−1)AdT+Qw(k−1),
where P(k−1) is the previously estimated error covariance matrix. The observation innovation residual d(k) is given by
(2.10)d(k)=yrd(k)−Cxˆr(k),
where yrd(k) is the dequantized and demodulated output bit sequence. The Kalman gain matrix can be written as
(2.11)K(k)=Pr(k)CT[CPr(k)CT+Rv(k)]−1.
This yields the updated state estimation as
(2.12)xˆ(k)=xˆr(k)−K(k)d(k),
along with the updated estimated error-covariance matrix
(2.13)P(k)=Pr(k)−K(k)CPr(k).
After estimating the system state, the proposed control strategy is applied for regulating the MG states as shown in the next section.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780323852616000117
Вариации
оценок параметров будут, в конечном
счете, определять точность уравнения
множественной регрессии. Для их измерения
в многомерном регрессионном анализе
рассматривают так называемую
ковариационную
матрицу К,
являющуюся
матричным аналогом дисперсии одной
переменной:

где
элементы
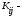
(или
корреляционные
моменты) оценок
параметров
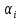
Ковариация
двух переменных определяется как
математическое ожидание произведения
отклонений этих переменных от их
математических ожиданий [Ссылка]. Поэтому
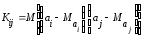
где
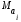
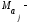
ожидания соответственно для параметров
и
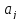
Ковариация
характеризует как степень рассеяния
значений двух переменных относительно
их математических ожиданий, так и
взаимосвязь этих переменных.
В
силу того, что оценки
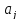
полученные методом наименьших квадратов,
являются несмещенными оценками параметров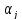
т.е.
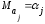
выражение(13.28)
примет
вид:
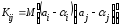
Рассматривая
ковариационную матрицу К,
легко
заметить, что на ее главной диагонали
находятся дисперсии опенок параметров
регрессии, ибо
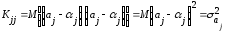
(13.29)
В
сокращенном виде ковариационная матрица
К
имеет
вид:
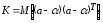
(13.30)
Учитывая
(13.28)
мы
можем записать
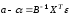
Тогда
выражение (12.30) примет вид:
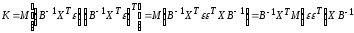
(13.31)
ибо
элементы матрицы X
—неслучайные
величины.
Матрица
представляет
собой ковариационную матрицу
вектора возмущений
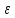
в
которой все элементы, не лежащие на
главной диагонали, равны нулю в силу
предпосылки 4
о
некоррелированности возмущений
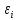
и
между
собой,
а
все элементы, лежащие на главной
диагонали, в силу предпосылок 2
и
3
регрессионного
анализа
равны
одной и той же дисперсии

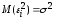
Поэтому
матрица
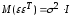
где
единичная
матрица
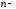
порядка.
Следовательно, в силу (13.31)
ковариационная
матрица вектора
оценок
параметров:
Так
как
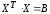
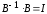
то окончательно получим:
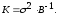
Таким
образом, с
помощью обратной матрицы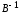
уравнении регрессии
определяется
не только сам вектор

параметров (13.28),
но
и дисперсии и ковариации его компонент.
Входящая
в (13.32)
дисперсия
возмущений неизвестна. Заменив ее
выборочной остаточной дисперсией
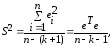
по
(13.32)
получаем
выборочную оценку ковариационной
матрицы К.
(В
знаменателе выражения (13.33)
стоит
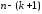
а
не
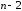
как
это было выше в (13.6).
Это
связано с тем, что теперь
свободы (а не две) теряются при определении
неизвестных параметров, число которых
вместе со свободным членом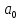
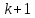
4.10. Определение доверительных интервалов для коэффициентов и функции множественной регрессии
Перейдем
теперь к оценке значимости коэффициентов
регрессии
и
построению доверительного интервала
для параметров регрессионной модели
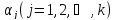
В
силу (13.29),
(13.32) и
изложенного выше оценка дисперсии
коэффициента регрессии
определится
по формуле:
где
несмещенная
оценка параметра
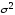
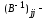
элемент матрицы
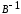
Среднее
квадратическое отклонение (стандартная
ошибка) коэффициента регрессии
примет
вид:
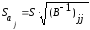
(13.34)
Значимость
коэффициента регрессии
можно
проверить, если учесть, что статистика
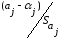
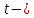
Стьюдента с
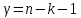
свободы. Поэтому
значимо
отличается от нуля на уровне
значимости
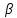
если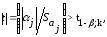
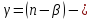
интервал для параметра
есть
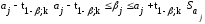
(13.35)
Наряду
с интервальным оцениванием коэффициентов
регрессии по (13.35)
весьма
важным для оценки точности определения
зависимой переменной (прогноза) является
построение доверительного
интервала для функции регрессии или
для условного математического
ожидания зависимой переменной
найденного в предположении, что
объясняющие переменные
приняли
значения, задаваемые вектором
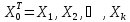
такой интервал получен для уравнения
парной регрессии (см. (13.13)
и
(13.12)).
Обобщая
соответствующие выражения на случай
множественной регрессии, можно получить
доверительный интервал для
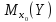
где
средняя, определяемая по уравнению
регрессии,
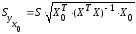
— ее
стандартная ошибка.
При
обобщении формул (13.15)
и
(13.14)
аналогичный
доверительный
интервал для индивидуальных значений
зависимой переменной
вид:
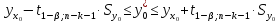
где
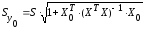
(13.38)
Доверительный
интервал для дисперсии возмущений
в
множественной регрессии с надежностью
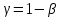
по формуле(13.20)
с
соответствующим изменением числа
степеней свободы критерия
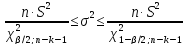
Пример
13.6.
По
данным примера 13.4
оценить
сменную добычу
угля на одного рабочего для шахт с
мощностью пласта 8 м и уровнем механизации
работ 6%; найти 95%-ные доверительные
интервалы для индивидуального и среднего
значений сменной добычи угля на 1
рабочего для таких же шахт. Проверить
значимость коэффициентов регрессии и
построить для них 95%-ные доверительные
интервалы. Найти с надежностью 0,95
интервальную оценку для дисперсии
возмущений
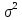
Решение.
В примере 13.4
уравнение
регрессии получено в виде:
По
условию надо оценить
где
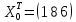
Выборочной оценкой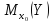
является
групповая средняя, которую найдем по
уравнению регрессии:
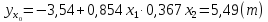
Для построения доверительного
интервала для М (у) необходимо знать
дисперсию его оценки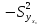
Для
ее вычисления обратимся к табл. 13.7
(точнее к ее двум последним столбцам,
при составлении которых учтено, что
групповые средние определяются по
полученному уравнению регрессии).
Теперь
по (13.37):
и
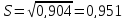
Определяем
стандартную ошибку групповой средней
г> по формуле (13.41).
Вначале
найдем
Теперь
(т).
По
табл. IV приложений при числе степеней
свободы
находим
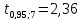
По
(13.40)
доверительный
интервал для
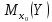
равен
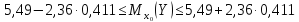
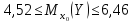
Итак,
с надежностью 0,95
средняя
сменная добыча угля на одного рабочего
для шахт с мощностью пласта 8
м
и уровнем механизации работ 6%
находится
в пределах от 4,52
до
6,46
т.
Сравнивая
новый доверительный интервал для функции
регрессии
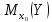
полученный
с учетом двух объясняющих переменных,
с аналогичным интервалом с учетом одной
объясняющей переменной (см. пример
13.1),
можно
заметить уменьшение его величины. Это
связано с тем, что включение в модель
новой объясняющей переменной позволяет
несколько повысить точность модели
за счет увеличения взаимосвязи зависимой
и объясняющей переменных (см. ниже).
Найдем
доверительный интервал для индивидуального
значения
при
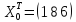
(13.43):
(т)
и по (13.42):
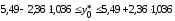
т. е.
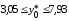
Итак,
с надежностью 0,95
индивидуальное
значение сменной добычи угля в шахтах
с мощностью пласта 8
м
и уровнем механизации работ 6%
находится
в пределах от 3,05
до
7,93
(т).
Проверим
значимость коэффициентов регрессии
и
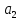
В
примере 13.4
получены
и
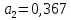
Стандартная
ошибка
в
соответствии с (13.38)
равна:
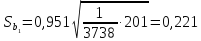
Так
как
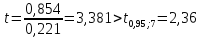
то
коэффициент
значим.
Аналогично вычисляем
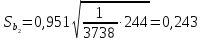
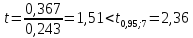
незначим
на 5%-ном уровне.
Доверительный
интервал имеет смысл построить только
для значимого коэффициента регрессии
по
(13.39)
или
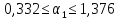
Итак,
с надежностью 0,95 за счет изменения на
1 м мощности пласта
(при
неизменном
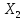
сменная
добыча угля на одного рабочего У
будет изменяться в пределах от 0,332 до
1,376 т.
Найдем
95%-ный доверительный интервал для
параметра ст2.
Учитывая, что
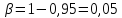
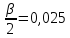
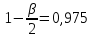
V
приложений при
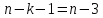
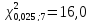
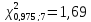
Таким
образом, с надежностью 0,95 дисперсия
возмущений заключена в пределах от
0,565 до 5,35, а их стандартное отклонение
— от 0,751 до 2,31 (т).
Формально
переменные, имеющие незначимые
коэффициенты регрессии, могут быть
исключены из рассмотрения. В экономических
исследованиях исключению переменных
из регрессии должен предшествовать
тщательный качественный
анализ.
Поэтому может оказаться целесообразным
все же оставить в регрессионной модели
одну или несколько объясняющих
переменных, не оказывающих существенного
(значимого) влияния на зависимую
переменную.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
27.03.20162.81 Mб141Учебник Туристское ресурсоведение.rtf
- #
- #
- #
- #
- #
- #
27.03.20164.24 Mб196Физика Яковлев.pdf
Battery state-of-power evaluation methods
Shunli Wang, … Zonghai Chen, in Battery System Modeling, 2021
7.4.4 Main charge-discharge condition test
The initial value of the error covariance matrix P0 can be determined from the X0 error of the initial state. In the application, the initial value should be as small as possible to speed up the tracking speed of the algorithm. Two important parameters are processed noise variance matrix Q and observation noise variance matrix R. As can be known from theoretical formula derivation, the dispose to Q and R plays a key role in improving the estimation effect by using this algorithm. Because it affects the size of the Kalman gain matrix K directly, the value of error covariance matrix P can be described as shown in Eq. (7.61):
(7.61)Rk=Eυk2=συ2
It is the expression of the observation noise variance, which is mainly derived from the distribution of observation error of experimental instruments and sensors, as shown in Eq. (7.62):
(7.62)Qk=Eω1k2Eω1kω2kEω2kω1kEω2k2=σω1,12σω1,22σω2,12σω2,22
It is the relationship between the system noise variance and the processing noise covariance. The two states in the system are generally unrelated and the covariance value is zero. Therefore, the diagonal variance can have a small value. The variance Q of processing noise is mainly derived from the error of the established equivalent model, which is difficult to be obtained by theoretical methods or means. A reasonable value range can be obtained through continuous debugging through simulation, and it is usually a small amount.
To verify the applicable range and stability of the algorithm, the input of different working conditions is used to observe the estimation accuracy of the algorithm. In this simulation, two working conditions are used: the constant-current working condition and the Beijing bus dynamic street test working condition. For the constant-current condition, only a constant value needs to be set in the program. To increase the complexity of the condition, two shelved stages are added to the constant-current input list to verify the tracking effect of Ah and the extended Kalman filtering. The following code is generated for the current.
The experimental data should be used to simulate the algorithm under its operating conditions. The current input module is realized in the environment under Beijing bus dynamic street test operating conditions. It is the time integration module, whose output is the capacity change of the working condition, and the lower part is the working condition data output module. It outputs the current into the workspace at the minimum time interval of the sampling measurement. The data onto the workspace are a time-series type and the current data need to be extracted. The data extraction and transformation can be performed in the main program, wherein the working condition is the Simulink module. The current is the time-series data, including the current output. S_Est is the algorithm program module, whose input is the initial S_Est_init and current data onto the estimated state value.
The current data are input into the program module of the extended Kalman filtering algorithm based on the model, and the initial values of other parameters have been determined in the program. The program finally outputs the ampere hour time integral and the state estimation curve of the extended Kalman filtering through the minimum time interval of 10 times as the sampling time. The current curve of the experimental test can be obtained as shown in Fig. 7.13.
Fig. 7.13. Pulse current operating current curve for the experimental test. (A) Main charge working condition. (B) Main discharge experimental test.
The unscented Kalman filtering algorithm is programmed by writing scripts to realize algorithm simulation to compare the output effect. The specific implementation process conforms to the processing requirements, and the main simulation program can be constructed. The program takes 10 times the minimum time interval as the sampling time and simulates the three methods of the state estimation, including ampere hour time integration, extended Kalman filtering, and unscented Kalman filtering, to compare the following situation of the three methods of the state over time. The program simultaneously outputs the state variation curve and estimation error curve with time, so that the tracking effect and error variation on the three methods can be obtained visually. Its implementation process is consistent with script. Different modules are used to replace the code block. The integration advantage of the environment is used in the graphical interface to obtain the same stimulation effect.
The operation logic is ensured by the unchanged intuitive presentation of the calculation process. Based on script implementation, the modular simulation is built accordingly. The experiment data are used as the input current, and the state prediction is obtained by the state prediction module. The forecast and model parameters are calculated. After that, the equivalent model can be used to predict the completion status value of Up as well as the output voltage. The input of the algorithm includes the update module, output state correction, and error covariance matrix update as the basis of the forecast. It takes the ampere hour integral result as the minimum time interval of the current data, which is taken as the reference value of the measured state.
The estimation effect of ampere hour and extended Kalman filtering is compared when the minimum time interval can be set as 10 times as the sampling period. The stability of the extended Kalman filtering algorithm is evaluated under working conditions. The state variable needs to accept the last estimated value as the basis of the next state prediction, in which the predicted value Up_pre is directly input into the corresponding position of the resistance-capacitance circuit modeling to conduct the terminal voltage prediction of the current polarization voltage. The functions of each part are realized in a more modular way for the complete structure and clear hierarchy.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780323904728000044
Dynamic Model Development
P.W. Oxby, … T.A. Duever, in Computer Aided Chemical Engineering, 2003
3.2 An Optimality Property of the Determinant Criterion
Equation (12) can be generalized by replacing the inverse of the estimate of the error covariance matrix,
Σ^εn−1, with an arbitrary symmetric positive definite weight matrix, W:
(14)Δθ^(k)=(XTWX)−1XTWz(θ^(k))
The estimate of the parameter covariance is:
(15)Σ^θ=(XTWX)−1XTWΣ^εn(XTWX)−1
If the determinant of the estimate of the parameter covariance matrix,
|Σ^θ|, is minimized with respect to the elements of W, the solution is independent of X and is simply
(16)W=Σ^εn−1
Substitution of (16) back into (14) gives (12) which, as has been shown, is equivalent to the determinant criterion. Therefore of all weighting schemes in the form of (14), it is the one equivalent to the determinant criterion that minimizes
|Σ^θ|, the determinant of the estimate of the parameter covariance matrix when the error covariance is unknown. This appears to be a rather strong result in support of the determinant criterion. It might also be noted that, unlike derivations based on likelihood, this result does not depend on the measurement errors being normally distributed. But it will be shown that the practical usefulness of the result does depend on the assumption that the residual covariance
Z(θ^)Z(θ^)T/n, is a good estimate of the true error covariance. Ideally one would want W to be the inverse of the error covariance matrix. The determinant in effect makes a compromise and substitutes an estimate of it. The potential problem here is that if the data set is not large, the residual covariance matrix may be a poor estimate of the error covariance matrix. A poor estimate of the error covariance matrix will lead to a poor estimate of the parameter covariance matrix. Therefore, although the determinant criterion gives the minimum determinant of the estimate of the parameter covariance matrix, if this estimate is poor, then the optimality property may be of little significance. This suggests that the optimality of the determinant criterion may be more relevant for large data sets than small ones. The simulation studies presented in Section 4 will confirm this to be true.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/S1570794603800706
Kalman Filters and Nonlinear Filters
Vytas B. Gylys, in Encyclopedia of Physical Science and Technology (Third Edition), 2003
IV.B Square Root Filtering
By far the greatest trouble spot in computer mechanization of the KF is the updating of state error covariance matrix P, that is, the computation of Pk∣k according to Eq. (18). As the estimation process progresses, the elements of Pk∣k typically continue to decrease in magnitude and so matrix Pk∣k keeps approaching the zero matrix, although theoretically it should forever remain positive definite, no matter how small in magnitude its elements become. Hence, unless special measures are taken, accumulation of roundoff error in the repetitive use of Eq. (18) may cause the computed Pk∣k to lose its positive definiteness. As suggested by the matrix inversion operation appearing on the right-hand side of Eq. (16) for computing the Kalman gain, this situation is aggravated if several components of the measurement vector are very accurate and consequently the positive definite measurement error covariance matrix R is ill conditioned, that is, if R has eigenvalues of both relatively very large and small magnitudes.
Let A be a nonnegative definite symmetric matrix; then there exists a matrix S such that A = SST. Matrix S is often called the square root of A. The Cholesky decomposition algorithm provides a method of constructing from A the matrix S so that S is lower triangular; that is, all elements of S above the main diagonal are zero. Square root filtering is motivated by the observations that, if the state error covariance matrix P = SST, then (a) since SST is always nonnegative definite, matrix P expressed as SST cannot become negative definite, and (b) matrix S is generally less ill conditioned than matrix P.
Several versions of the square root filtering algorithm are known. The earliest form was developed by J. E. Potter in 1964 for applications in which the process noise is absent (i.e., covariance matrix Q is zero) and the measurements are sequentially processed as scalars. In 1967 J. F. Bellantoni and K. W. Dodge extended Potter’s results to vector-valued measurements. A. Andrews in 1968 and then S. F. Schmidt in 1970 published two alternative procedures for handling the process noise. In 1973 N. A. Carlson described a procedure that considerably improved the speed and decreased the memory requirements of square root filtering and in which, as in Potter’s algorithm, vector-valued measurements are processed sequentially as scalars. Finally, the so-called UDUT covariance factorization method is the most recent major milestone in numerical handling of KFs. This method, developed by G. J. Bierman and C. L. Thornton, represents the state error covariances before and after the measurement update step asPk|k−1=Uk|k−1Dk|k−1Uk|k−1TandPk|k=Uk|kDk|kUk|kT,with D being a diagonal matrix and U an upper triangular matrix with 1’s on its main diagonal. In this method, the square root of the covariance matrix, which now would correspond to UD1/2, is never computed explicitly, which avoids numerical computation of square roots. Like Carlson’s algorithm, the UDUT factorization method maintains the covariance matrix in factored form and so (like Carlson’s algorithm) is considerably more efficient in processor time and storage than the original Potter algorithm.
As a quick comparison of computational efficiency, the conventional Kalman method, the less efficient form of Carlson’s algorithm, and the UDUT factorization method are roughly equal: The processing of each time step (consisting of one time propagation and one measurement update) requires of the order of 16[9ns3 + 9ns2nm + 3ns2nw] adds and about the same number of multiplies, plus a relatively modest number of divides and square roots (square roots are required only in some, as in Potter’s or Carlson’s square root algorithms). Here, as before, ns is the length of the state vector, nm the length of the measurement vector, and nw the lenght of the process noise vector w. The faster version of Carlson’s algorithm is more efficient and requires only of the order of 16[5ns3 + 9ns2nm + 3ns2nw] adds and 16[5ns3 + 12ns2nm + 3ns2nw] multiplies, plus 2nsnm divides and nsnm square roots, at each time point. The stable (Joseph) form of the KF [as given by Eq. (18′)] fares more poorly: At each time step, it requires of the order of 16[18ns3 + 15ns2nm + 3ns2nw] adds and about the same number of multiplies.
As a summary, (a) a square root filter is a numerically stable form for performing the KF covariance–gain processing defined by Eqs. (15), (16), and (18); (b) the efficiency of its more recent versions roughly compares with that of these three equations; (c) the increased stability allows one to use relatively low-precision arithmetic in the KF gain–covariance processing, with a possible exception of some dot products.
Real-time implementation of a filter involves additional issues that are unimportant in the non-real-time environment. Besides the adequacy of functional performance, the most important of these issues is the requirement to produce timely responses to external stimuli. Thus, resorting to a parallel or concurrent processing may be the only way out. This usually implies the use of special hardware architectures such as parallel, vector pipelined, or systolic processors.
As one example, consider the use of a filter in the tracking of multiple objects in a hard real-time environment characterized by strict deadlines. In such a case one may want to maintain simultaneously many estimation processes, each handling a single object. Parallel processors may seem to be a suitable hardware architecture for this problem, but if separate estimation processes in such an application progress at different rates and at any time some of them require a great amount of special handling, then parallel architecture, such as a single-instruction multiple-data stream computer, may not be the best choice. As another example, consider a KF to be implemented as part of a navigation system on a small airborne computer (uniprocessor). Suppose that the navigation measurements come at a certain fixed rate. If the filtering process cannot keep up with the arrival rate of measurements and so not all of them can be utilized, the estimation performance may deteriorate. In this problem, if there is an upper bound on hardware resources, the only solution may be to decompose the estimation algorithm into concurrently executable processes. For instance, the time-propagation step (which, say, is to be executed at a relatively high rate) may constitute one process and the measurement-update step (which needs to be executed only at some lower rate, say, at the rate of measurement arrivals) may constitute another. Such a decomposition of an estimation algorithm into concurrent procedures often creates a surrogate algorithm that performs more poorly than the original algorithm.
The effects of the finite-length word computing is another issue that must be considered in filter implementation for real-time applications. The computer on which a filter is developed and validated through successive off-line simulations is often more powerful and uses higher-precision arithmetic and number representations than the ultimate real-time processor. Hence, one must in advance determine in advance what effect a shorter word length will have on performance.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B0122274105003574
Computer Techniques and Algorithms in Digital Signal Processing
K. Giridhar, … Ronald A. Iltis, in Control and Dynamic Systems, 1996
A Appendix – Time Updates for the Blind MAPSD Algorithm
In this Appendix, we derive the one-step time updates of the channel estimate and the associated error covariance matrix for the blind MAP symbol detector developed in Section 4.2. Recall from Eq. (51) that
(A.1)pfk+1|dik+1,Nf,rk=∑j:djk,Nf∈dik+1,Nfαjp(fk+1|djk,Nf,rk)
where αj is given by Eq. (52). Using Eq. (49), this Gaussian sum can be explicitly written as follows:
(A.2)pfk+1|dik+1,Nf,rk=∑j:djk,Nf∈dik+1,NfαjNfk+1;Ff^jk|k,FPjk|kFH+Q
which defines the one-step prediction of the mean vector f^ik+1|k and the covariance matrix Pik+1|k. Some basic results about sums of Gaussian p.d.f.s can be used to derive these one-step predictions.
Lemma: Let the p.d.f. of the random vector x be a weighted sum of N multivariate Gaussian p.d.f.s as follows:
(A.3)px=∑j=1NαjNx;xj,Pj
where αj , xj, and Pj are, respectively, the jth weight, mean, and covariance. (i) The mean value of x is given by
(A.4)xa=∑j=1Nαjxj.
(ii) The error covariance is given by
(A.5)Pa=∑j=1NαjPj+xa–xjxa–xjH.
Proof: The first part of the lemma is easily proved from the definition of xa, i.e.,
(A.6)xa=Ex=∫xx∑j=1NαjNx;xj,Pjdx=∑j=1Nαjxj.
To prove the second part of the lemma, consider
(A.7)Pa=Ex−xax−xaH=∑j=1Nαj∫xxxHNjdx+xaxaH−∫xxxaHNjdx−∫xxaxHNjdx
where, for convenience, we have used the notation Nj to represent the p.d.f. N(x; xj, Pĵ). Observe that ∫xxaHNjdx=xjxaHand∫xaxHNjdx=xaxjH. By adding and subtracting the term xjxjH to the expression inside the square brackets, we obtain
(A.8)Pa=∑j=1Nαj∫xxxHNjdx−xjxjH+xaxaH−xjxaH−xaxjH+xjxjH=∑j=1Nαj∫xxxHNjdx−xjxjH+xa−xjxa−xjH..
It is straightforward to show that
(A.9)∑j=1Nαj∫xxxHNjdx−xjxjH=∑j=1Nαj∫xx−xj(x−xj)HNjdx=∑j=1NαjPj.
Substituting this result into Eq. (A.8 ), we obtain the result in Eq. (A.5 ) for the error covariance Pa, which completes the proof.
To obtain the one-step predicted mean vector of the blind MAPSD algorithm, Eq. (A.4 ) is used with xj=Ff^jk|k. The summation is performed over the M predecessor subsequences djk,Nf, yielding
(A.10)f^ik+1|k)=∑j:djk,Nf∈dik+1,NfαjFf^jk|k.
By substituting αj=pdjk,Nf|rk−1/qik, the final expression in Eq. (53) is obtained. Similarly, the one-step error covariance update in Eq. (54) is obtained by substituting FPjk|kFH+Q=Pj and
(A.11)νj,ikνj,iHk=xa−xjxa−xjH
into Eq. (A.5 ) where xa=f^ik+1|k (and xj=Ff^jk|k as above).
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/S0090526796800454
State Estimation
Jay Farrell, in The Electrical Engineering Handbook, 2005
4.3 Recursive State Estimation
Equations 4.4 through 4.5 provide the mean and the covariance of the state through time based only on the initial mean state vector and its error covariance matrix. When measurements y(k) are available, the measurements can be used to improve the accuracy of an estimate of the state vector at time k. The symbols xˆ−(k) and xˆ+(k) are used to denote the estimate of x(k) before and after incorporating the measurement, respectively.
Similarly, the symbols Pxˆ−(k) and Pxˆ+(k) are used to denote the error covariance matrices corresponding to xˆ−(k) and xˆ+(k), respectively. This section presents the time propagation and measurement update equations for both the state estimate and its error covariance. The equations are presented in a form that is valid for any linear unbiased measurement correction. These equations contain a gain matrix K that determines the estimator performance. The choice of K to minimize the error covariance Pxˆ+(k) will be of interest.
For an unbiased linear measurement, the update will have the form:
(4.8)xˆ+(k)=xˆ−(k)+K(k)(y(k)−yˆ−(k)),
where yˆ−(k)=H(k)xˆ−(k).. The error covariance of xˆ+(k) is the following:
(4.9)Pxˆ+(k)=(I−K(k)H(k))Pxˆ−(k)(I−K(k)H(k))T +K(k)R(k)KT(k).
K(k) is a possibly time-varying state estimation gain vector to be designed. If no measurement is available at time k, then K(k) = 0, which yields xˆ+(k)=xˆ−(k) and Pxˆ+(k)=Pxˆ−(k). If a measurement is available, and the state estimator is designed well, then Pxˆ+(k)≤Pxˆ−(k). In either case, the time propagation of the state estimate and its error covariance matrix is achieved by:
(4.10)xˆ−(k+1)=Φ(k)xˆ+(k)+Γˆuu(k)
(4.11)Pxˆ−(k+1)=Φ(k)Pxˆ+(k)ΦT(k)+ΓωQd(k)ΓωT.
At least two issues are of interest relative to the state estimation problem. First, does there exist a state estimation gain vector K(k) such that xˆ is guaranteed to converge to x regardless of initial condition and the sequence u(k)? Second, how should the designer select the gain vector K(k)?
The first issue raises the question of observability. A linear time-invariant system is observable if the following matrix has rank n:
[HT, ΦTHT, …,( ΦT)nHT].
When a system is observable, then it is guaranteed that a stabilizing gain vector K exists. Assuming that the system of interest is observable, the remainder of this chapter discusses the design and analysis of state estimators.
Figure 4.1 portrays the state estimator in conjunction with the system of interest. The system of interest is depicted in the upper left. The state estimator is superimposed on a gray background in the lower right.
FIGURE 4.1. State Estimation System Block Diagram
This interconnected system will be referred to as the state estimation system. The figure motivates several important comments. First, although the state estimator has only n states, the state estimation system has 2n states. Second, the inputs to the state estimation system are the deterministic input u and the stochastic inputs ω and v. Third, the inputs to the state estimator are the deterministic input u and the measured plant output y. The state space model for the state estimation system is the following:
(4.12)[x(k+1)xˆ−(k+1)]=[Φx0LHxΦ−LH][x(k)xˆ−(k)]+[ΓuΓω0Γˆu0L][u(k)ω(k)v(k)],
where L = ΦK.
Based on this state-space model, with the assumption that the system is time invariant, the transfer function from v to yˆ is as written here:
(4.13)Gv(z)=H[zI−(Φ−LH)]−1L,
where z is the discrete-time unit advance operator. Assuming that H = Hx, the transfer function from u to r is as follows:
(4.14)Gu(z)=H[zI−(Φ−LH)]−1 [(zI−Φ)(zI−Φx)−1Γu−(zI−Φx)(zI−Φx)−1Γˆu].
Therefore, if Γu=Γˆu and Φx = Φ, then this transfer function is identically zero. Assuming again that H = Hx, the transfer function from ω to r is the following:
(4.15)Gω(z)=H[zI−(Φ−LH)]−1[zI−Φ][zI−Φx]−1Γω.
In the special case where, in addition, Φx = Φ, the transfer function Gω(z) has n identical poles and zeros. This transfer functions is often stated as:
(4.16)Gω(z)=H[zI−(Φ−LH)]−1Γω,
where n pole and zero cancellations have occurred. These pole-zero cancellations and therefore the validity of equation 4.16 are dependent on the exact modeling assumption and the stability of the canceled poles.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780121709600500815
Data Assimilation in Numerical Weather Prediction and Sample Applications
Andrew S. Jones, Steven J. Fletcher, in Solar Energy Forecasting and Resource Assessment, 2013
13.3.5 Ensemble DA
The ensemble Kalman filter (EnsKF) is a sequential filter that forecasts the state vector, xf, as well as the model-error covariance matrix, Pf, toward a future time step (Evensen, 1994). This is a linear process, but it can employ nonlinear models within the system; no adjoints are required. For example, the forward state is given by the propagation of the model forward in time
(13.29)xf(ti)=Mi−1[xa(ti−1)]
as well as its associated forecast-error covariance matrix
(13.30)Pf(ti)=Mi−1Pa(ti−1)Mi−1T+Q(ti−1)
This is followed by an analysis step that updates (or readjusts) the state information and the forecast-error covariance information
(13.31)xa(ti)=xf(ti)+Kidi
(13.32)Pa(ti)=(I−KiHi)Pf(ti)
where the innovation vector, di, is given by
(13.33)di=yio−Hi[xf(ti)]
It is important to note that M and H are linearizations of the gradients of M and H with respect to the control vector, x. The Kalman gain, Ki, is given by
(13.34)Ki=Pf(ti)HiT[HiPf(ti)HiT+Ri]−1
where Pf(ti) is now approximated by the mean ensemble estimate
(13.35)Pf(ti)≈1K−2∑K≠lK[xf(tk)−x¯f(tl)][xf(tk)−x¯f(tl)]T
K is the number of ensemble-model runs required to generate the estimate, and a reference model state, l, is used to define the mean ensemble estimate of the forecast error covariance matrix. In addition to the approach in equation 13.35, other EnsKF variants are used by the NWP DA community. The analysis stage that propagates the forecast error covariance matrix is a powerful feature of EnsKF. Additional improvements in EnsKF performance can be achieved by improving sampling behaviors—for example, using sampling strategies and square root schemes, some of which also allow for a low-rank representation of the observational-error covariance matrix (Evensen, 2004).
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123971777000139
The Basics of Analytical Mechanics, Optimization, Control and Estimation
Kyle T. Alfriend, … Louis S. Breger, in Spacecraft Formation Flying, 2010
3.8 Kalman Filtering
In 1960, Robert Kalman introduced a new approach for minimum mean-square error filtering that used state-space methods [80]. The Kalman Filter (KF) is a recursive scheme that propagates a current estimate of a state and the error covariance matrix of that state forward in time. The filter optimally blends the new information introduced by the measurements with old information embodied in the prior state with a Kalman gain matrix. The gain matrix balances uncertainty in the measurements with the uncertainty in the dynamics model. The KF is guaranteed to be the optimal filter (in the sense of minimizing the 2-norm-squared of the estimation error) for a linear system with linear measurements [81]. However, few systems can be accurately modeled with linear dynamics. Shortly after its inception, improvements on the Kalman filter to handle nonlinear systems were proposed. One of the most popular choices, the Extended Kalman Filter (EKF), was applied to relative navigation filters in LEO [43]. We will demonstrate how to use the EKF for relative spacecraft state estimation in Chapter 12.
The discrete EKF is as a state estimator for systems whose state dynamics model, measurement model, or both may be nonlinear, as in Eqs. (3.48) and (3.53) [81]. The dynamics model provides the equations to propagate xˆk, the estimate of the state x at time k, to time step k+1, producing xˆk+1. The measurement model then incorporates the new sensor information to update this estimate, updating the a priori estimate xˆk+1− to the a posteriori estimate, xˆk+1+. This process is illustrated in Fig. 3.1.
FIGURE 3.1. A Kalman filter process.
The continuous state x is governed by the dynamics
(3.48)ẋ(tk)=f(x,u,tk)+w(tk)
where u is a known control input, and w(t) is an additive white noise that models the error accumulated by uncertainty in the dynamics during the time step. The power spectral density of this zero mean, white noise process is
(3.49)Q=E[w(t)w(t)T]
To proceed, linear expressions for the dynamics and measurement equations must be formed. In general, this requires knowledge of the probability density function [81], but the EKF approximates the nonlinear function by expanding it in a Taylor series, at each time step, about the current estimate,
(3.50)Fk=∂f∂x|x=xˆk
The dynamics are discretized with time step Δt by forming the state transition matrix,
(3.51)Φk=eFkΔt
The cumulative effect of the white noise process w(t) over the time step is captured in the discrete process noise covariance matrix
(3.52)Qk=∫0ΔteFkτQ(eFkτ)Tdτ
The vector of measurements, y,
(3.53)y=h(x,t)+vk
is modeled as a nonlinear function of the state and time, with an additive white noise process v(t) that accounts for uncertainty in the sensors and their models. The measurement noise covariance matrix is defined by
(3.54)Rk=E[vkvkT]
The nonlinear measurement equation is also linearized about the current estimate,
(3.55)Hk=∂h∂x|x=xˆk−
Because approximations must be made in the linearization, the EKF is a suboptimal filter, in the sense that its stability and performance are not guaranteed. Fortunately, the dynamics of orbital motion are fairly simple, and the EKF can have very good performance in space navigation applications. The discrete, linear representation of the system dynamics are
(3.56)xk=Φk−1xk−1+wk−1+uk−1
The confidence in the current estimate is captured in the state error covariance matrix, P,
(3.57)Pk=E[x̃kx̃kT]=E[(xˆk−xk)(xˆk−xk)T]
where x̃k=xˆk−xk is the estimation error. The first step in the EKF involves propagating the state and error covariance forward in time. Equation (3.56), with zero process noise, is used to propagate the state estimate. The error covariance is propagated forward using
(3.58)Pk−=Φk−1Pk−1+Φk−1T+Qk−1
An alternate approach to the time propagation step involves using the nonlinear dynamics equations to propagate the state. A 4th-order Runge–Kutta integration scheme uses the nonlinear state dynamics equation
(3.59)xˆ̇(t)=f(xˆ(t),u(t))for t=tk−1→tk
to find xˆk. The state covariance is still propagated with Eq. (3.58), so the state transition matrix Φk−1 must be calculated regardless of whether the linear or nonlinear state propagation is chosen.
The second step of the filter uses the measurement equation to update the a priori state xˆk− to the a posteriori state xˆk+. When a measurement becomes available, the new information provided by the measurement and the previous information captured in the state estimate are combined to form an updated state estimate. The Kalman gain K is the blending gain matrix that is used to weight the importance of the old and new information. The optimum gain matrix is formulated by minimizing the trace of the a posteriori state error covariance matrix Pk+, which essentially minimizes the estimation error vector at each time step [81]. The terms in the gain matrix equation include the previous state estimate, the linearized measurement matrix, and the expected noise of the new measurements,
(3.60)Kk=Pk−HkT(HkPk−HkT+Rk)−1
The nonlinear measurement equation is used to update the state estimate
(3.61)xˆk+=xˆk−−Kk(yk−hk(xˆk−))
Note that the computation of the gain matrix Kk requires the linear measurement matrix Hk. The covariance is updated after the measurement with
(3.62)Pk+=(I−KkHk)Pk−(I−KkHk)T+KkRkKkT
which is the Joseph form of the covariance update whose inherent symmetry makes it numerically stable [82].
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780750685337002086
Static State Estimation
Soliman Abdel-hady Soliman Ph.D., Ahmad M. Al-Kandari Ph.D., in Electrical Load Forecasting, 2010
2.3 Properties of Least Error Squares Estimation
Least error squares estimation results are easy to compute and possess a number of interesting properties. The least squares are the best estimates (maximum likelihood) when the measurement errors follow a Gaussian or normal distribution and the weighting matrix is equal to the inverse of the error covariance matrix. The least error squares estimates can be easily calculated.
Where the measurement error distribution does not follow a Gaussian distribution and the number of measurements greatly exceeds the number of unknown parameters, the method of least error squares yields very good estimates. However, there are many estimation problems for which the error distribution is not a Gaussian and the number of measurements does not greatly exceed the number of unknown parameters. In such cases, the least error squares estimations are adversely affected by bad data. This problem has been recognized and addressed by several researchers who have proposed different ways of refining the least error squares method to make estimation less affected by the presence of bad data. In the next section, we discuss an alternative technique to the LES estimation. This technique is based on least absolute value approximation.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123815439000026
Principles of meteorology and numerical weather prediction
Sue Ellen Haupt, … Branko Kosović, in Renewable Energy Forecasting, 2017
1.2.2.2 Variational assimilation
Variational assimilation techniques are a form of statistical interpolation. All statistical interpolation techniques require an estimation of the error covariances between variables in the background state, as well as error covariances between the observed variables. These techniques find the optimal analysis by globally minimizing a cost function that incorporates the distance between the analysis and observations within the assimilation window. This method also requires the observation error covariance matrix and the background error covariance matrix (e.g., Talagrand, 1997; Kalnay, 2003), which at times may be difficult to compute accurately. In three-dimensional variational DA (3D-Var) schemes, these error covariance matrices come from a static climatology, and all observations within a given assimilation window are assumed to be valid at the analysis time. These assumptions reduce the computational burden. In contrast, four-dimensional variational DA (4D-Var) schemes seek to minimize the cost function, subject to the NWP model equations, to find the best model trajectory through the entire assimilation window, rather than just at the analysis time. In addition, the error covariance matrices are flow-dependent in 4D-Var. These differences make 4D-Var significantly more computationally intensive than 3D-Var, but also more accurate (e.g., Klinker et al., 2000; Yang et al., 2009).
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780081005040000019
Smart grids: control and cybersecurity
Magdi S. Mahmoud, … Mutaz M. Hamdan, in Cyberphysical Infrastructures in Power Systems, 2022
2.2.3 Cyberattack minimization in smart grids
A recursive KF estimator (RKFE) is constructed to operate on observation information in order to produce the optimal state estimation. The forecasted system-state estimate is expressed as follows:
(2.8)xˆr(k)=Adxˆ(k−1)+Bdu(k−1),
where xˆ(k−1) is the previous state estimate. Then the forecasted error covariance matrix is given by
(2.9)Pr(k)=AdP(k−1)AdT+Qw(k−1),
where P(k−1) is the previously estimated error covariance matrix. The observation innovation residual d(k) is given by
(2.10)d(k)=yrd(k)−Cxˆr(k),
where yrd(k) is the dequantized and demodulated output bit sequence. The Kalman gain matrix can be written as
(2.11)K(k)=Pr(k)CT[CPr(k)CT+Rv(k)]−1.
This yields the updated state estimation as
(2.12)xˆ(k)=xˆr(k)−K(k)d(k),
along with the updated estimated error-covariance matrix
(2.13)P(k)=Pr(k)−K(k)CPr(k).
After estimating the system state, the proposed control strategy is applied for regulating the MG states as shown in the next section.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780323852616000117
Battery state-of-power evaluation methods
Shunli Wang, … Zonghai Chen, in Battery System Modeling, 2021
7.4.4 Main charge-discharge condition test
The initial value of the error covariance matrix P0 can be determined from the X0 error of the initial state. In the application, the initial value should be as small as possible to speed up the tracking speed of the algorithm. Two important parameters are processed noise variance matrix Q and observation noise variance matrix R. As can be known from theoretical formula derivation, the dispose to Q and R plays a key role in improving the estimation effect by using this algorithm. Because it affects the size of the Kalman gain matrix K directly, the value of error covariance matrix P can be described as shown in Eq. (7.61):
(7.61)Rk=Eυk2=συ2
It is the expression of the observation noise variance, which is mainly derived from the distribution of observation error of experimental instruments and sensors, as shown in Eq. (7.62):
(7.62)Qk=Eω1k2Eω1kω2kEω2kω1kEω2k2=σω1,12σω1,22σω2,12σω2,22
It is the relationship between the system noise variance and the processing noise covariance. The two states in the system are generally unrelated and the covariance value is zero. Therefore, the diagonal variance can have a small value. The variance Q of processing noise is mainly derived from the error of the established equivalent model, which is difficult to be obtained by theoretical methods or means. A reasonable value range can be obtained through continuous debugging through simulation, and it is usually a small amount.
To verify the applicable range and stability of the algorithm, the input of different working conditions is used to observe the estimation accuracy of the algorithm. In this simulation, two working conditions are used: the constant-current working condition and the Beijing bus dynamic street test working condition. For the constant-current condition, only a constant value needs to be set in the program. To increase the complexity of the condition, two shelved stages are added to the constant-current input list to verify the tracking effect of Ah and the extended Kalman filtering. The following code is generated for the current.
The experimental data should be used to simulate the algorithm under its operating conditions. The current input module is realized in the environment under Beijing bus dynamic street test operating conditions. It is the time integration module, whose output is the capacity change of the working condition, and the lower part is the working condition data output module. It outputs the current into the workspace at the minimum time interval of the sampling measurement. The data onto the workspace are a time-series type and the current data need to be extracted. The data extraction and transformation can be performed in the main program, wherein the working condition is the Simulink module. The current is the time-series data, including the current output. S_Est is the algorithm program module, whose input is the initial S_Est_init and current data onto the estimated state value.
The current data are input into the program module of the extended Kalman filtering algorithm based on the model, and the initial values of other parameters have been determined in the program. The program finally outputs the ampere hour time integral and the state estimation curve of the extended Kalman filtering through the minimum time interval of 10 times as the sampling time. The current curve of the experimental test can be obtained as shown in Fig. 7.13.
Fig. 7.13. Pulse current operating current curve for the experimental test. (A) Main charge working condition. (B) Main discharge experimental test.
The unscented Kalman filtering algorithm is programmed by writing scripts to realize algorithm simulation to compare the output effect. The specific implementation process conforms to the processing requirements, and the main simulation program can be constructed. The program takes 10 times the minimum time interval as the sampling time and simulates the three methods of the state estimation, including ampere hour time integration, extended Kalman filtering, and unscented Kalman filtering, to compare the following situation of the three methods of the state over time. The program simultaneously outputs the state variation curve and estimation error curve with time, so that the tracking effect and error variation on the three methods can be obtained visually. Its implementation process is consistent with script. Different modules are used to replace the code block. The integration advantage of the environment is used in the graphical interface to obtain the same stimulation effect.
The operation logic is ensured by the unchanged intuitive presentation of the calculation process. Based on script implementation, the modular simulation is built accordingly. The experiment data are used as the input current, and the state prediction is obtained by the state prediction module. The forecast and model parameters are calculated. After that, the equivalent model can be used to predict the completion status value of Up as well as the output voltage. The input of the algorithm includes the update module, output state correction, and error covariance matrix update as the basis of the forecast. It takes the ampere hour integral result as the minimum time interval of the current data, which is taken as the reference value of the measured state.
The estimation effect of ampere hour and extended Kalman filtering is compared when the minimum time interval can be set as 10 times as the sampling period. The stability of the extended Kalman filtering algorithm is evaluated under working conditions. The state variable needs to accept the last estimated value as the basis of the next state prediction, in which the predicted value Up_pre is directly input into the corresponding position of the resistance-capacitance circuit modeling to conduct the terminal voltage prediction of the current polarization voltage. The functions of each part are realized in a more modular way for the complete structure and clear hierarchy.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780323904728000044
Dynamic Model Development
P.W. Oxby, … T.A. Duever, in Computer Aided Chemical Engineering, 2003
3.2 An Optimality Property of the Determinant Criterion
Equation (12) can be generalized by replacing the inverse of the estimate of the error covariance matrix,
Σ^εn−1, with an arbitrary symmetric positive definite weight matrix, W:
(14)Δθ^(k)=(XTWX)−1XTWz(θ^(k))
The estimate of the parameter covariance is:
(15)Σ^θ=(XTWX)−1XTWΣ^εn(XTWX)−1
If the determinant of the estimate of the parameter covariance matrix,
|Σ^θ|, is minimized with respect to the elements of W, the solution is independent of X and is simply
(16)W=Σ^εn−1
Substitution of (16) back into (14) gives (12) which, as has been shown, is equivalent to the determinant criterion. Therefore of all weighting schemes in the form of (14), it is the one equivalent to the determinant criterion that minimizes
|Σ^θ|, the determinant of the estimate of the parameter covariance matrix when the error covariance is unknown. This appears to be a rather strong result in support of the determinant criterion. It might also be noted that, unlike derivations based on likelihood, this result does not depend on the measurement errors being normally distributed. But it will be shown that the practical usefulness of the result does depend on the assumption that the residual covariance
Z(θ^)Z(θ^)T/n, is a good estimate of the true error covariance. Ideally one would want W to be the inverse of the error covariance matrix. The determinant in effect makes a compromise and substitutes an estimate of it. The potential problem here is that if the data set is not large, the residual covariance matrix may be a poor estimate of the error covariance matrix. A poor estimate of the error covariance matrix will lead to a poor estimate of the parameter covariance matrix. Therefore, although the determinant criterion gives the minimum determinant of the estimate of the parameter covariance matrix, if this estimate is poor, then the optimality property may be of little significance. This suggests that the optimality of the determinant criterion may be more relevant for large data sets than small ones. The simulation studies presented in Section 4 will confirm this to be true.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/S1570794603800706
Kalman Filters and Nonlinear Filters
Vytas B. Gylys, in Encyclopedia of Physical Science and Technology (Third Edition), 2003
IV.B Square Root Filtering
By far the greatest trouble spot in computer mechanization of the KF is the updating of state error covariance matrix P, that is, the computation of Pk∣k according to Eq. (18). As the estimation process progresses, the elements of Pk∣k typically continue to decrease in magnitude and so matrix Pk∣k keeps approaching the zero matrix, although theoretically it should forever remain positive definite, no matter how small in magnitude its elements become. Hence, unless special measures are taken, accumulation of roundoff error in the repetitive use of Eq. (18) may cause the computed Pk∣k to lose its positive definiteness. As suggested by the matrix inversion operation appearing on the right-hand side of Eq. (16) for computing the Kalman gain, this situation is aggravated if several components of the measurement vector are very accurate and consequently the positive definite measurement error covariance matrix R is ill conditioned, that is, if R has eigenvalues of both relatively very large and small magnitudes.
Let A be a nonnegative definite symmetric matrix; then there exists a matrix S such that A = SST. Matrix S is often called the square root of A. The Cholesky decomposition algorithm provides a method of constructing from A the matrix S so that S is lower triangular; that is, all elements of S above the main diagonal are zero. Square root filtering is motivated by the observations that, if the state error covariance matrix P = SST, then (a) since SST is always nonnegative definite, matrix P expressed as SST cannot become negative definite, and (b) matrix S is generally less ill conditioned than matrix P.
Several versions of the square root filtering algorithm are known. The earliest form was developed by J. E. Potter in 1964 for applications in which the process noise is absent (i.e., covariance matrix Q is zero) and the measurements are sequentially processed as scalars. In 1967 J. F. Bellantoni and K. W. Dodge extended Potter’s results to vector-valued measurements. A. Andrews in 1968 and then S. F. Schmidt in 1970 published two alternative procedures for handling the process noise. In 1973 N. A. Carlson described a procedure that considerably improved the speed and decreased the memory requirements of square root filtering and in which, as in Potter’s algorithm, vector-valued measurements are processed sequentially as scalars. Finally, the so-called UDUT covariance factorization method is the most recent major milestone in numerical handling of KFs. This method, developed by G. J. Bierman and C. L. Thornton, represents the state error covariances before and after the measurement update step asPk|k−1=Uk|k−1Dk|k−1Uk|k−1TandPk|k=Uk|kDk|kUk|kT,with D being a diagonal matrix and U an upper triangular matrix with 1’s on its main diagonal. In this method, the square root of the covariance matrix, which now would correspond to UD1/2, is never computed explicitly, which avoids numerical computation of square roots. Like Carlson’s algorithm, the UDUT factorization method maintains the covariance matrix in factored form and so (like Carlson’s algorithm) is considerably more efficient in processor time and storage than the original Potter algorithm.
As a quick comparison of computational efficiency, the conventional Kalman method, the less efficient form of Carlson’s algorithm, and the UDUT factorization method are roughly equal: The processing of each time step (consisting of one time propagation and one measurement update) requires of the order of 16[9ns3 + 9ns2nm + 3ns2nw] adds and about the same number of multiplies, plus a relatively modest number of divides and square roots (square roots are required only in some, as in Potter’s or Carlson’s square root algorithms). Here, as before, ns is the length of the state vector, nm the length of the measurement vector, and nw the lenght of the process noise vector w. The faster version of Carlson’s algorithm is more efficient and requires only of the order of 16[5ns3 + 9ns2nm + 3ns2nw] adds and 16[5ns3 + 12ns2nm + 3ns2nw] multiplies, plus 2nsnm divides and nsnm square roots, at each time point. The stable (Joseph) form of the KF [as given by Eq. (18′)] fares more poorly: At each time step, it requires of the order of 16[18ns3 + 15ns2nm + 3ns2nw] adds and about the same number of multiplies.
As a summary, (a) a square root filter is a numerically stable form for performing the KF covariance–gain processing defined by Eqs. (15), (16), and (18); (b) the efficiency of its more recent versions roughly compares with that of these three equations; (c) the increased stability allows one to use relatively low-precision arithmetic in the KF gain–covariance processing, with a possible exception of some dot products.
Real-time implementation of a filter involves additional issues that are unimportant in the non-real-time environment. Besides the adequacy of functional performance, the most important of these issues is the requirement to produce timely responses to external stimuli. Thus, resorting to a parallel or concurrent processing may be the only way out. This usually implies the use of special hardware architectures such as parallel, vector pipelined, or systolic processors.
As one example, consider the use of a filter in the tracking of multiple objects in a hard real-time environment characterized by strict deadlines. In such a case one may want to maintain simultaneously many estimation processes, each handling a single object. Parallel processors may seem to be a suitable hardware architecture for this problem, but if separate estimation processes in such an application progress at different rates and at any time some of them require a great amount of special handling, then parallel architecture, such as a single-instruction multiple-data stream computer, may not be the best choice. As another example, consider a KF to be implemented as part of a navigation system on a small airborne computer (uniprocessor). Suppose that the navigation measurements come at a certain fixed rate. If the filtering process cannot keep up with the arrival rate of measurements and so not all of them can be utilized, the estimation performance may deteriorate. In this problem, if there is an upper bound on hardware resources, the only solution may be to decompose the estimation algorithm into concurrently executable processes. For instance, the time-propagation step (which, say, is to be executed at a relatively high rate) may constitute one process and the measurement-update step (which needs to be executed only at some lower rate, say, at the rate of measurement arrivals) may constitute another. Such a decomposition of an estimation algorithm into concurrent procedures often creates a surrogate algorithm that performs more poorly than the original algorithm.
The effects of the finite-length word computing is another issue that must be considered in filter implementation for real-time applications. The computer on which a filter is developed and validated through successive off-line simulations is often more powerful and uses higher-precision arithmetic and number representations than the ultimate real-time processor. Hence, one must in advance determine in advance what effect a shorter word length will have on performance.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B0122274105003574
Computer Techniques and Algorithms in Digital Signal Processing
K. Giridhar, … Ronald A. Iltis, in Control and Dynamic Systems, 1996
A Appendix – Time Updates for the Blind MAPSD Algorithm
In this Appendix, we derive the one-step time updates of the channel estimate and the associated error covariance matrix for the blind MAP symbol detector developed in Section 4.2. Recall from Eq. (51) that
(A.1)pfk+1|dik+1,Nf,rk=∑j:djk,Nf∈dik+1,Nfαjp(fk+1|djk,Nf,rk)
where αj is given by Eq. (52). Using Eq. (49), this Gaussian sum can be explicitly written as follows:
(A.2)pfk+1|dik+1,Nf,rk=∑j:djk,Nf∈dik+1,NfαjNfk+1;Ff^jk|k,FPjk|kFH+Q
which defines the one-step prediction of the mean vector f^ik+1|k and the covariance matrix Pik+1|k. Some basic results about sums of Gaussian p.d.f.s can be used to derive these one-step predictions.
Lemma: Let the p.d.f. of the random vector x be a weighted sum of N multivariate Gaussian p.d.f.s as follows:
(A.3)px=∑j=1NαjNx;xj,Pj
where αj , xj, and Pj are, respectively, the jth weight, mean, and covariance. (i) The mean value of x is given by
(A.4)xa=∑j=1Nαjxj.
(ii) The error covariance is given by
(A.5)Pa=∑j=1NαjPj+xa–xjxa–xjH.
Proof: The first part of the lemma is easily proved from the definition of xa, i.e.,
(A.6)xa=Ex=∫xx∑j=1NαjNx;xj,Pjdx=∑j=1Nαjxj.
To prove the second part of the lemma, consider
(A.7)Pa=Ex−xax−xaH=∑j=1Nαj∫xxxHNjdx+xaxaH−∫xxxaHNjdx−∫xxaxHNjdx
where, for convenience, we have used the notation Nj to represent the p.d.f. N(x; xj, Pĵ). Observe that ∫xxaHNjdx=xjxaHand∫xaxHNjdx=xaxjH. By adding and subtracting the term xjxjH to the expression inside the square brackets, we obtain
(A.8)Pa=∑j=1Nαj∫xxxHNjdx−xjxjH+xaxaH−xjxaH−xaxjH+xjxjH=∑j=1Nαj∫xxxHNjdx−xjxjH+xa−xjxa−xjH..
It is straightforward to show that
(A.9)∑j=1Nαj∫xxxHNjdx−xjxjH=∑j=1Nαj∫xx−xj(x−xj)HNjdx=∑j=1NαjPj.
Substituting this result into Eq. (A.8 ), we obtain the result in Eq. (A.5 ) for the error covariance Pa, which completes the proof.
To obtain the one-step predicted mean vector of the blind MAPSD algorithm, Eq. (A.4 ) is used with xj=Ff^jk|k. The summation is performed over the M predecessor subsequences djk,Nf, yielding
(A.10)f^ik+1|k)=∑j:djk,Nf∈dik+1,NfαjFf^jk|k.
By substituting αj=pdjk,Nf|rk−1/qik, the final expression in Eq. (53) is obtained. Similarly, the one-step error covariance update in Eq. (54) is obtained by substituting FPjk|kFH+Q=Pj and
(A.11)νj,ikνj,iHk=xa−xjxa−xjH
into Eq. (A.5 ) where xa=f^ik+1|k (and xj=Ff^jk|k as above).
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/S0090526796800454
State Estimation
Jay Farrell, in The Electrical Engineering Handbook, 2005
4.3 Recursive State Estimation
Equations 4.4 through 4.5 provide the mean and the covariance of the state through time based only on the initial mean state vector and its error covariance matrix. When measurements y(k) are available, the measurements can be used to improve the accuracy of an estimate of the state vector at time k. The symbols xˆ−(k) and xˆ+(k) are used to denote the estimate of x(k) before and after incorporating the measurement, respectively.
Similarly, the symbols Pxˆ−(k) and Pxˆ+(k) are used to denote the error covariance matrices corresponding to xˆ−(k) and xˆ+(k), respectively. This section presents the time propagation and measurement update equations for both the state estimate and its error covariance. The equations are presented in a form that is valid for any linear unbiased measurement correction. These equations contain a gain matrix K that determines the estimator performance. The choice of K to minimize the error covariance Pxˆ+(k) will be of interest.
For an unbiased linear measurement, the update will have the form:
(4.8)xˆ+(k)=xˆ−(k)+K(k)(y(k)−yˆ−(k)),
where yˆ−(k)=H(k)xˆ−(k).. The error covariance of xˆ+(k) is the following:
(4.9)Pxˆ+(k)=(I−K(k)H(k))Pxˆ−(k)(I−K(k)H(k))T +K(k)R(k)KT(k).
K(k) is a possibly time-varying state estimation gain vector to be designed. If no measurement is available at time k, then K(k) = 0, which yields xˆ+(k)=xˆ−(k) and Pxˆ+(k)=Pxˆ−(k). If a measurement is available, and the state estimator is designed well, then Pxˆ+(k)≤Pxˆ−(k). In either case, the time propagation of the state estimate and its error covariance matrix is achieved by:
(4.10)xˆ−(k+1)=Φ(k)xˆ+(k)+Γˆuu(k)
(4.11)Pxˆ−(k+1)=Φ(k)Pxˆ+(k)ΦT(k)+ΓωQd(k)ΓωT.
At least two issues are of interest relative to the state estimation problem. First, does there exist a state estimation gain vector K(k) such that xˆ is guaranteed to converge to x regardless of initial condition and the sequence u(k)? Second, how should the designer select the gain vector K(k)?
The first issue raises the question of observability. A linear time-invariant system is observable if the following matrix has rank n:
[HT, ΦTHT, …,( ΦT)nHT].
When a system is observable, then it is guaranteed that a stabilizing gain vector K exists. Assuming that the system of interest is observable, the remainder of this chapter discusses the design and analysis of state estimators.
Figure 4.1 portrays the state estimator in conjunction with the system of interest. The system of interest is depicted in the upper left. The state estimator is superimposed on a gray background in the lower right.
FIGURE 4.1. State Estimation System Block Diagram
This interconnected system will be referred to as the state estimation system. The figure motivates several important comments. First, although the state estimator has only n states, the state estimation system has 2n states. Second, the inputs to the state estimation system are the deterministic input u and the stochastic inputs ω and v. Third, the inputs to the state estimator are the deterministic input u and the measured plant output y. The state space model for the state estimation system is the following:
(4.12)[x(k+1)xˆ−(k+1)]=[Φx0LHxΦ−LH][x(k)xˆ−(k)]+[ΓuΓω0Γˆu0L][u(k)ω(k)v(k)],
where L = ΦK.
Based on this state-space model, with the assumption that the system is time invariant, the transfer function from v to yˆ is as written here:
(4.13)Gv(z)=H[zI−(Φ−LH)]−1L,
where z is the discrete-time unit advance operator. Assuming that H = Hx, the transfer function from u to r is as follows:
(4.14)Gu(z)=H[zI−(Φ−LH)]−1 [(zI−Φ)(zI−Φx)−1Γu−(zI−Φx)(zI−Φx)−1Γˆu].
Therefore, if Γu=Γˆu and Φx = Φ, then this transfer function is identically zero. Assuming again that H = Hx, the transfer function from ω to r is the following:
(4.15)Gω(z)=H[zI−(Φ−LH)]−1[zI−Φ][zI−Φx]−1Γω.
In the special case where, in addition, Φx = Φ, the transfer function Gω(z) has n identical poles and zeros. This transfer functions is often stated as:
(4.16)Gω(z)=H[zI−(Φ−LH)]−1Γω,
where n pole and zero cancellations have occurred. These pole-zero cancellations and therefore the validity of equation 4.16 are dependent on the exact modeling assumption and the stability of the canceled poles.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780121709600500815
Data Assimilation in Numerical Weather Prediction and Sample Applications
Andrew S. Jones, Steven J. Fletcher, in Solar Energy Forecasting and Resource Assessment, 2013
13.3.5 Ensemble DA
The ensemble Kalman filter (EnsKF) is a sequential filter that forecasts the state vector, xf, as well as the model-error covariance matrix, Pf, toward a future time step (Evensen, 1994). This is a linear process, but it can employ nonlinear models within the system; no adjoints are required. For example, the forward state is given by the propagation of the model forward in time
(13.29)xf(ti)=Mi−1[xa(ti−1)]
as well as its associated forecast-error covariance matrix
(13.30)Pf(ti)=Mi−1Pa(ti−1)Mi−1T+Q(ti−1)
This is followed by an analysis step that updates (or readjusts) the state information and the forecast-error covariance information
(13.31)xa(ti)=xf(ti)+Kidi
(13.32)Pa(ti)=(I−KiHi)Pf(ti)
where the innovation vector, di, is given by
(13.33)di=yio−Hi[xf(ti)]
It is important to note that M and H are linearizations of the gradients of M and H with respect to the control vector, x. The Kalman gain, Ki, is given by
(13.34)Ki=Pf(ti)HiT[HiPf(ti)HiT+Ri]−1
where Pf(ti) is now approximated by the mean ensemble estimate
(13.35)Pf(ti)≈1K−2∑K≠lK[xf(tk)−x¯f(tl)][xf(tk)−x¯f(tl)]T
K is the number of ensemble-model runs required to generate the estimate, and a reference model state, l, is used to define the mean ensemble estimate of the forecast error covariance matrix. In addition to the approach in equation 13.35, other EnsKF variants are used by the NWP DA community. The analysis stage that propagates the forecast error covariance matrix is a powerful feature of EnsKF. Additional improvements in EnsKF performance can be achieved by improving sampling behaviors—for example, using sampling strategies and square root schemes, some of which also allow for a low-rank representation of the observational-error covariance matrix (Evensen, 2004).
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123971777000139
The Basics of Analytical Mechanics, Optimization, Control and Estimation
Kyle T. Alfriend, … Louis S. Breger, in Spacecraft Formation Flying, 2010
3.8 Kalman Filtering
In 1960, Robert Kalman introduced a new approach for minimum mean-square error filtering that used state-space methods [80]. The Kalman Filter (KF) is a recursive scheme that propagates a current estimate of a state and the error covariance matrix of that state forward in time. The filter optimally blends the new information introduced by the measurements with old information embodied in the prior state with a Kalman gain matrix. The gain matrix balances uncertainty in the measurements with the uncertainty in the dynamics model. The KF is guaranteed to be the optimal filter (in the sense of minimizing the 2-norm-squared of the estimation error) for a linear system with linear measurements [81]. However, few systems can be accurately modeled with linear dynamics. Shortly after its inception, improvements on the Kalman filter to handle nonlinear systems were proposed. One of the most popular choices, the Extended Kalman Filter (EKF), was applied to relative navigation filters in LEO [43]. We will demonstrate how to use the EKF for relative spacecraft state estimation in Chapter 12.
The discrete EKF is as a state estimator for systems whose state dynamics model, measurement model, or both may be nonlinear, as in Eqs. (3.48) and (3.53) [81]. The dynamics model provides the equations to propagate xˆk, the estimate of the state x at time k, to time step k+1, producing xˆk+1. The measurement model then incorporates the new sensor information to update this estimate, updating the a priori estimate xˆk+1− to the a posteriori estimate, xˆk+1+. This process is illustrated in Fig. 3.1.
FIGURE 3.1. A Kalman filter process.
The continuous state x is governed by the dynamics
(3.48)ẋ(tk)=f(x,u,tk)+w(tk)
where u is a known control input, and w(t) is an additive white noise that models the error accumulated by uncertainty in the dynamics during the time step. The power spectral density of this zero mean, white noise process is
(3.49)Q=E[w(t)w(t)T]
To proceed, linear expressions for the dynamics and measurement equations must be formed. In general, this requires knowledge of the probability density function [81], but the EKF approximates the nonlinear function by expanding it in a Taylor series, at each time step, about the current estimate,
(3.50)Fk=∂f∂x|x=xˆk
The dynamics are discretized with time step Δt by forming the state transition matrix,
(3.51)Φk=eFkΔt
The cumulative effect of the white noise process w(t) over the time step is captured in the discrete process noise covariance matrix
(3.52)Qk=∫0ΔteFkτQ(eFkτ)Tdτ
The vector of measurements, y,
(3.53)y=h(x,t)+vk
is modeled as a nonlinear function of the state and time, with an additive white noise process v(t) that accounts for uncertainty in the sensors and their models. The measurement noise covariance matrix is defined by
(3.54)Rk=E[vkvkT]
The nonlinear measurement equation is also linearized about the current estimate,
(3.55)Hk=∂h∂x|x=xˆk−
Because approximations must be made in the linearization, the EKF is a suboptimal filter, in the sense that its stability and performance are not guaranteed. Fortunately, the dynamics of orbital motion are fairly simple, and the EKF can have very good performance in space navigation applications. The discrete, linear representation of the system dynamics are
(3.56)xk=Φk−1xk−1+wk−1+uk−1
The confidence in the current estimate is captured in the state error covariance matrix, P,
(3.57)Pk=E[x̃kx̃kT]=E[(xˆk−xk)(xˆk−xk)T]
where x̃k=xˆk−xk is the estimation error. The first step in the EKF involves propagating the state and error covariance forward in time. Equation (3.56), with zero process noise, is used to propagate the state estimate. The error covariance is propagated forward using
(3.58)Pk−=Φk−1Pk−1+Φk−1T+Qk−1
An alternate approach to the time propagation step involves using the nonlinear dynamics equations to propagate the state. A 4th-order Runge–Kutta integration scheme uses the nonlinear state dynamics equation
(3.59)xˆ̇(t)=f(xˆ(t),u(t))for t=tk−1→tk
to find xˆk. The state covariance is still propagated with Eq. (3.58), so the state transition matrix Φk−1 must be calculated regardless of whether the linear or nonlinear state propagation is chosen.
The second step of the filter uses the measurement equation to update the a priori state xˆk− to the a posteriori state xˆk+. When a measurement becomes available, the new information provided by the measurement and the previous information captured in the state estimate are combined to form an updated state estimate. The Kalman gain K is the blending gain matrix that is used to weight the importance of the old and new information. The optimum gain matrix is formulated by minimizing the trace of the a posteriori state error covariance matrix Pk+, which essentially minimizes the estimation error vector at each time step [81]. The terms in the gain matrix equation include the previous state estimate, the linearized measurement matrix, and the expected noise of the new measurements,
(3.60)Kk=Pk−HkT(HkPk−HkT+Rk)−1
The nonlinear measurement equation is used to update the state estimate
(3.61)xˆk+=xˆk−−Kk(yk−hk(xˆk−))
Note that the computation of the gain matrix Kk requires the linear measurement matrix Hk. The covariance is updated after the measurement with
(3.62)Pk+=(I−KkHk)Pk−(I−KkHk)T+KkRkKkT
which is the Joseph form of the covariance update whose inherent symmetry makes it numerically stable [82].
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780750685337002086
Static State Estimation
Soliman Abdel-hady Soliman Ph.D., Ahmad M. Al-Kandari Ph.D., in Electrical Load Forecasting, 2010
2.3 Properties of Least Error Squares Estimation
Least error squares estimation results are easy to compute and possess a number of interesting properties. The least squares are the best estimates (maximum likelihood) when the measurement errors follow a Gaussian or normal distribution and the weighting matrix is equal to the inverse of the error covariance matrix. The least error squares estimates can be easily calculated.
Where the measurement error distribution does not follow a Gaussian distribution and the number of measurements greatly exceeds the number of unknown parameters, the method of least error squares yields very good estimates. However, there are many estimation problems for which the error distribution is not a Gaussian and the number of measurements does not greatly exceed the number of unknown parameters. In such cases, the least error squares estimations are adversely affected by bad data. This problem has been recognized and addressed by several researchers who have proposed different ways of refining the least error squares method to make estimation less affected by the presence of bad data. In the next section, we discuss an alternative technique to the LES estimation. This technique is based on least absolute value approximation.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123815439000026
Principles of meteorology and numerical weather prediction
Sue Ellen Haupt, … Branko Kosović, in Renewable Energy Forecasting, 2017
1.2.2.2 Variational assimilation
Variational assimilation techniques are a form of statistical interpolation. All statistical interpolation techniques require an estimation of the error covariances between variables in the background state, as well as error covariances between the observed variables. These techniques find the optimal analysis by globally minimizing a cost function that incorporates the distance between the analysis and observations within the assimilation window. This method also requires the observation error covariance matrix and the background error covariance matrix (e.g., Talagrand, 1997; Kalnay, 2003), which at times may be difficult to compute accurately. In three-dimensional variational DA (3D-Var) schemes, these error covariance matrices come from a static climatology, and all observations within a given assimilation window are assumed to be valid at the analysis time. These assumptions reduce the computational burden. In contrast, four-dimensional variational DA (4D-Var) schemes seek to minimize the cost function, subject to the NWP model equations, to find the best model trajectory through the entire assimilation window, rather than just at the analysis time. In addition, the error covariance matrices are flow-dependent in 4D-Var. These differences make 4D-Var significantly more computationally intensive than 3D-Var, but also more accurate (e.g., Klinker et al., 2000; Yang et al., 2009).
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780081005040000019
Smart grids: control and cybersecurity
Magdi S. Mahmoud, … Mutaz M. Hamdan, in Cyberphysical Infrastructures in Power Systems, 2022
2.2.3 Cyberattack minimization in smart grids
A recursive KF estimator (RKFE) is constructed to operate on observation information in order to produce the optimal state estimation. The forecasted system-state estimate is expressed as follows:
(2.8)xˆr(k)=Adxˆ(k−1)+Bdu(k−1),
where xˆ(k−1) is the previous state estimate. Then the forecasted error covariance matrix is given by
(2.9)Pr(k)=AdP(k−1)AdT+Qw(k−1),
where P(k−1) is the previously estimated error covariance matrix. The observation innovation residual d(k) is given by
(2.10)d(k)=yrd(k)−Cxˆr(k),
where yrd(k) is the dequantized and demodulated output bit sequence. The Kalman gain matrix can be written as
(2.11)K(k)=Pr(k)CT[CPr(k)CT+Rv(k)]−1.
This yields the updated state estimation as
(2.12)xˆ(k)=xˆr(k)−K(k)d(k),
along with the updated estimated error-covariance matrix
(2.13)P(k)=Pr(k)−K(k)CPr(k).
After estimating the system state, the proposed control strategy is applied for regulating the MG states as shown in the next section.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780323852616000117
В предыдущих параграфах данной главы мы рассматривали случай отказа от одной предпосылки классической линейной модели множественной регрессии. Теперь мы расширим наш анализ и откажемся сразу от двух предпосылок: от предпосылок №№4-5 (о постоянстве дисперсии случайной ошибки и о некоррелированности разных случайных ошибок между собой). В техническом смысле этот параграф несколько сложнее предыдущих (в частности, тут более широко используется линейная алгебра). Поэтому, если вы заинтересованы в том, чтобы разобраться только в прикладных аспектах множественной регрессии, а в соответствующих вычислениях готовы полностью довериться эконометрическому пакету, можете его пропустить.
Отказ от указанных двух предпосылок означает, что ковариационная матрица вектора случайных ошибок (таблица, в которой записаны все ковариации между (varepsilon_{i}) и (varepsilon_{j}), см. параграф 3.3) больше не является диагональной матрицей с одинаковыми числами на главной диагонали, как это было в первоначальной классической модели. Теперь ковариационная матрица вектора случайных ошибок Ω — это произвольная ковариационная матрица (разумеется, так как это не совсем любая матрица, а именно ковариационная матрица, то по своим свойствам она является симметричной и положительно определенной).
Модель, в которой сохранены только первые три предпосылки классической линейной модели множественной регрессии, называется обобщенной линейной моделью множественной регрессии.
Проанализируем, к каким последствиям приводит отказ от предпосылок №№4-5.
Во-первых, полученная обычным методом наименьших квадратов оценка ({widehat{beta} = left( {X^{‘}X} right)^{- 1}}X’y) остается несмещенной (это свойство мы доказывали, опираясь как раз лишь на первые три предпосылки).
Во-вторых, МНК-оценки хоть и остаются несмещенными, но больше не являются эффективными.
В-третьих, если мы оцениваем ковариационную матрицу вектора оценок коэффициентов (которая нужна для тестирования всевозможных гипотез), то оценка (widehat{V}{{(widehat{beta})} = left( {X^{‘}X} right)^{- 1}}S^{2}) смещена и больше не является корректной.
Чтобы убедиться в этом, посчитаем ковариационную матрицу от (widehat{beta}) в условиях обобщенной модели (при этом мы используем свойства ковариационной матрицы, перечисленные в параграфе 3.3):
(V{left( widehat{beta} right) = V}{leftlbrack {{({X^{‘}X})}^{- 1}X’y} rightrbrack = V}{leftlbrack {{({X^{‘}X})}^{- 1}X'{({mathit{Xbeta} + varepsilon})}} rightrbrack =})
({}V{leftlbrack {{({{({X^{‘}X})}^{- 1}X’})}varepsilon} rightrbrack = left( {X^{‘}X} right)^{- 1}}X^{‘}Vlbrackvarepsilonrbrack{left( {left( {X^{‘}X} right)^{- 1}X^{‘}} right)^{‘} = {({X^{‘}X})}^{- 1}}X^{‘}Omega{left( {left( {X^{‘}X} right)^{- 1}X^{‘}} right)^{‘} = {({X^{‘}X})}^{- 1}}X^{‘}Omega X{({X^{‘}X})}^{- 1})
Так выглядит ковариационная матрица вектора МНК-оценок в обобщенной модели. Ясно, что она не может быть корректно оценена стандартной оценкой (left( {X^{‘}X} right)^{- 1}S^{2}). Следовательно, прежней формулой пользоваться нельзя: если мы будем использовать стандартные ошибки, рассчитанные по обычной формуле (предполагая выполнение предпосылок классической линейной модели), то получим некорректные стандартные ошибки, что может привести нас к неверным выводам по поводу значимости или незначимости тех или иных регрессоров.
Таким образом, последствия перехода к обобщенной модели аналогичны тем, что мы наблюдали для случая гетероскедастичности. Это неудивительно, так как гетероскедастичность — частный случай обобщенной линейной модели.
Поэтому для получения эффективных оценок обычный МНК не подойдет, и придется воспользоваться альтернативным методом — обобщенным МНК (ОМНК, generalized least squares, GLS). Формулу для расчета оценок коэффициентов при помощи ОМНК позволяет получить специальная теорема.
Теорема Айткена
Если
- модель линейна по параметрам и правильно специфицирована
({y = {mathit{Xbeta} + varepsilon}},) - матрица Х — детерминированная матрица, имеющая максимальный ранг k,
- (E{(varepsilon) = overrightarrow{0}}),
- (V{(varepsilon) = Omega}) — произвольная положительно определенная и симметричная матрица,
то оценка вектора коэффициентов модели ({{widehat{beta}}^{} = {({X’Omega^{- 1}X})}^{- 1}}X’Omega^{- 1}y) является:
- несмещенной
- и эффективной, то есть имеет наименьшую ковариационную матрицу в классе всех несмещенных и линейных по y оценок.
Предпосылки теоремы Айткена — это предпосылки обобщенной линейной модели множественной регрессии. Из них первые три — стандартные, как в классической модели, а четвертая ничего особого не требует (у вектора случайных ошибок может быть любая ковариационная матрица без каких-либо дополнительных специальных ограничений). Сама теорема Айткена является аналогом теоремы Гаусса — Маркова для случая обобщенной модели.
Докажем эту теорему.
Из линейной алгебры известно: если матрица (Omega) симметрична и положительно определена, то существует такая матрица P, что
(P’bullet{P = Omega^{- 1}}) ⇔ ({P^{‘} = Omega^{- 1}}bullet P^{- 1})
А раз такое представление возможно, то воспользуемся им для замены переменных. От вектора значений зависимой переменной (y), перейдем к вектору (Pbullet y), обозначив его как вектор ({y^{} = P}bullet y). Аналогичным образом введем матрицу ({X^{} = P}bullet X) и вектор ошибок ({varepsilon^{} = P}bulletvarepsilon).
Вернемся к исходной модели, параметры которой нас и интересуют:
({y = X}{beta + varepsilon})
Умножим левую и правую части равенства на матрицу (P):
({mathit{Py} = mathit{PX}}{beta + mathit{Pvarepsilon}})
С учетом новых обозначений это равенство можно записать так:
({y^{} = X^{}}{beta + varepsilon^{}})
Для новой модели (со звездочками) выполняются предпосылки теоремы Гаусса-Маркова. Чтобы в этом убедиться, достаточно показать, что математическое ожидание вектора случайных ошибок является нулевым вектором (третья предпосылка классической модели) и ковариационная матрица вектора случайных ошибок является диагональной с одинаковыми элементами на главной диагонали (четвертая и пятая предпосылки).
Для этого вычислим математическое ожидание нового вектора ошибок:
(E{left( varepsilon^{} right) = E}{left( mathit{Pvarepsilon} right) = P}bullet E{(varepsilon) = P}bullet{overrightarrow{0} = overrightarrow{0}})
Теперь вычислим ковариационную матрицу вектора (varepsilon^{}):
(V{left( varepsilon^{} right) = V}{left( {Pbulletvarepsilon} right) = P}bullet V(varepsilon)bullet{P^{‘} = P}bulletOmegabullet{P^{‘} = P}bulletOmegabulletOmega^{- 1}bullet{P^{- 1} = I_{n}})
Здесь (I_{n}) обозначает единичную матрицу размера n на n.
Следовательно, для модели со звездочками выполняются все предпосылки теоремы Гаусса — Маркова. Поэтому получить несмещенную и эффективную оценку вектора коэффициентов можно, применив к этой измененной модели обычный МНК:
({{widehat{beta}}^{} = left( {{X^{}}^{‘}X^{}} right)^{- 1}}{X^{}}^{‘}y^{})
Теперь осталось вернуться к исходным обозначениям, чтобы получить формулу несмещенной и эффективной оценки интересующего нас вектора в терминах обобщенной модели:
({{widehat{beta}}^{} = left( {{X^{}}^{‘}X^{}} right)^{- 1}}{X^{}}^{‘}{y^{} = left( {{(mathit{PX})}^{‘}mathit{PX}} right)^{- 1}}left( mathit{PX} right)^{‘}{mathit{Py} = left( {X’P’mathit{PX}} right)^{- 1}}X^{‘}P^{‘}{mathit{Py} =}left( {X’Omega^{- 1}P^{- 1}mathit{PX}} right)^{- 1}X’Omega^{- 1}P^{- 1}{mathit{Py} = {({X’Omega^{- 1}X})}^{- 1}}X’Omega^{- 1}y)
Что и требовалось доказать.
Взвешенный МНК, который мы обсуждали ранее, — это частный вариант обобщенного МНК (для случая, когда только предпосылка №4 нарушена, а предпосылка №5 сохраняется).
Как и при использовании взвешенного МНК в ситуации применения ОМНК коэффициент R-квадрат не обязан лежать между нулем и единицей и не может быть интерпретирован стандартным образом.
Слабая сторона ОМНК состоит в том, что для его реализации нужно знать не только матрицу регрессоров X с вектором значений зависимой переменной y, но и ковариационную матрицу вектора случайных ошибок (Omega). На практике, однако, эта матрица почти никогда не известна. Поэтому в прикладных исследованиях практически всегда вместо ОМНК используется, так называемый, доступный ОМНК (его ещё называют практически реализуемый ОМНК, feasible GLS). Идея доступного ОМНК состоит в том, что следует сначала оценить матрицу (Omega) (традиционно обозначим её оценку (widehat{Omega})), а уже затем получить оценку вектора коэффициентов модели, заменив в формуле ОМНК (Omega) на (widehat{Omega}):
({{widehat{beta}}^{} = {({X'{widehat{Omega}}^{- 1}X})}^{- 1}}X'{widehat{Omega}}^{- 1}y.)
Применение этого подхода осложняется тем, что (widehat{Omega}) не может быть оценена непосредственно без дополнительных предпосылок, так как в ней слишком много неизвестных элементов. Действительно, в матрице размер (n) на (n) всего (n^{2}) элементов, и оценить их все, имея всего (n) наблюдений, представляется слишком амбициозной задачей. Даже если воспользоваться тем, что матрица (Omega) является симметричной, в результате чего достаточно оценить только элементы на главной диагонали и над ней, мы все равно столкнемся с необходимостью оценивать (left( {n + 1} right){n/2}) элементов, что всегда больше числа доступных нам наблюдений.
Поэтому процедура доступного ОМНК устроена так:
- Делаются некоторые предпосылки по поводу того, как устроена ковариационная матрица вектора случайных ошибок (Omega). На основе этих предпосылок оценивается матрица (widehat{Omega}).
- После этого по формуле ({({X'{widehat{Omega}}^{- 1}X})}^{- 1}X'{widehat{Omega}}^{- 1}y) вычисляется вектор оценок коэффициентов модели.
Из сказанного следует, что доступный ОМНК может быть реализован только в ситуации, когда есть разумные основания сформулировать те или иные предпосылки по поводу матрицы (widehat{Omega}). Рассмотрим некоторые примеры таких ситуаций.
Пример 5.4. Автокорреляция и ОМНК-оценка
Рассмотрим линейную модель ({y = X}{beta + varepsilon}), для которой дисперсия случайных ошибок постоянна, однако наблюдается так называемая автокорреляция первого порядка:
(varepsilon_{i} = {{rho ast varepsilon_{i — 1}} + u_{i}})
Здесь (u_{i}) — независимые и одинаково распределенные случайные величины с дисперсией (sigma_{u}^{2}), а (rhoin{({{- 1},1})}) — коэффициент автокорреляции.
(а) Найдите ковариационную матрицу вектора случайных ошибок для представленной модели.
(б) Запишите в явном виде формулу ОМНК-оценки вектора коэффициентов модели, предполагая, что коэффициент (rho) известен.
Примечание: в отличие от гетероскедастичности, автокорреляция случайных ошибок обычно наблюдается не в пространственных данных, а во временных рядах. Для временных рядов вполне естественна подобная связь будущих случайных ошибок с предыдущими их значениями.
Решение:
(а) Используя условие о постоянстве дисперсии случайной ошибки, то есть условие (mathit{var}{{(varepsilon_{i})} = mathit{var}}{(varepsilon_{i — 1})}), найдем эту дисперсию:
(mathit{var}{{(varepsilon_{i})} = mathit{var}}{({{rho ast varepsilon_{i — 1}} + u_{i}})})
(mathit{var}{{(varepsilon_{i})} = rho^{2}}mathit{var}{{(varepsilon_{i — 1})} + mathit{var}}{(u_{i})})
(mathit{var}{{(varepsilon_{i})} = rho^{2}}mathit{var}{{(varepsilon_{i})} + sigma_{u}^{2}})
(mathit{var}{left( varepsilon_{i} right) = frac{sigma_{u}^{2}}{1 — rho^{2}}}.)
Тем самым мы нашли элементы, которые будут стоять на главной диагонали ковариационной матрицы вектора случайных ошибок. Теперь найдем элементы, которые будут находиться непосредственно на соседних с главной диагональю клетках:
(mathit{cov}{left( {varepsilon_{i},varepsilon_{i — 1}} right) = mathit{cov}}{left( {{{rho ast varepsilon_{i — 1}} + u_{i}},varepsilon_{i — 1}} right) = {rho ast mathit{cov}}}{left( {varepsilon_{i — 1},varepsilon_{i — 1}} right) + mathit{cov}}{left( {u_{i},varepsilon_{i — 1}} right) = {rho ast mathit{var}}}{{left( varepsilon_{i — 1} right) + 0} = frac{rho ast sigma_{u}^{2}}{1 — rho^{2}}})
По аналогии легко убедиться, что
(mathit{cov}{left( {varepsilon_{i},varepsilon_{i — k}} right) = frac{rho^{k} ast sigma_{u}^{2}}{1 — rho^{2}} = frac{sigma_{u}^{2} ast rho^{k}}{1 — rho^{2}}}.)
Следовательно, ковариационная матрица вектора случайных ошибок имеет вид:
({Omega = frac{sigma_{u}^{2}}{1 — rho^{2}}}begin{pmatrix} begin{matrix} 1 & rho rho & 1 end{matrix} & ldots & begin{matrix} rho^{n — 2} & rho^{n — 1} rho^{n — 3} & rho^{n — 2} end{matrix} ldots & ldots & ldots begin{matrix} rho^{n — 2} & rho^{n — 3} rho^{n — 1} & rho^{n — 2} end{matrix} & ldots & begin{matrix} 1 & rho rho & 1 end{matrix} end{pmatrix})
(б) Вектор ОМНК-оценок коэффициентов имеет вид:
({{widehat{beta}}^{} = {({X’Omega^{- 1}X})}^{- 1}}X^{‘}Omega^{- 1}{y =}{left( {X’begin{pmatrix} begin{matrix} 1 & rho rho & 1 end{matrix} & ldots & begin{matrix} rho^{n — 2} & rho^{n — 1} rho^{n — 3} & rho^{n — 2} end{matrix} ldots & ldots & ldots begin{matrix} rho^{n — 2} & rho^{n — 3} rho^{n — 1} & rho^{n — 2} end{matrix} & ldots & begin{matrix} 1 & rho rho & 1 end{matrix} end{pmatrix}^{- 1}X} right)^{- 1} ast}X’begin{pmatrix} begin{matrix} 1 & rho rho & 1 end{matrix} & ldots & begin{matrix} rho^{n — 2} & rho^{n — 1} rho^{n — 3} & rho^{n — 2} end{matrix} ldots & ldots & ldots begin{matrix} rho^{n — 2} & rho^{n — 3} rho^{n — 1} & rho^{n — 2} end{matrix} & ldots & begin{matrix} 1 & rho rho & 1 end{matrix} end{pmatrix}^{- 1}y)
Обратите внимание, что дробь (frac{sigma_{u}^{2}}{1 — rho^{2}}) при расчете представленной оценки сокращается. Поэтому для вычисления оценки знать величину (sigma_{u}^{2}) не нужно.
Примечание: если коэффициент автокорреляции (rho) неизвестен, то его можно легко оценить. Например, для этого можно применить обычный МНК к исходной регрессии, получить вектор остатков и оценить регрессию ({widehat{e}}_{i} = {widehat{rho} ast e_{i — 1}}). Полученной оценки (widehat{rho}) достаточно, чтобы вычислить ОМНК-оценку вектора параметров модели. Тем самым в представленном примере для применения доступного ОМНК достаточно оценить всего один параметр ковариационной матрицы вектора оценок коэффициентов.
Пример 5.5. Гетероскедастичность и ОМНК-оценка
Рассмотрим линейную модель ({y = X}{beta + varepsilon}), для которой выполнены все предпосылки классической линейной модели множественной регрессии за одним исключением: дисперсия случайной ошибки прямо пропорциональна квадрату некоторой известной переменной
(mathit{var}{left( varepsilon_{i} right) = sigma_{i}^{2} = sigma_{0}^{2}}{z_{i}^{2} > 0}.)
(а) Найдите ковариационную матрицу вектора случайных ошибок для представленной модели.
(б) Запишите в явном виде формулу ОМНК-оценки вектора коэффициентов модели.
Решение:
(а) Так как в этом случае нарушена только четвертая предпосылка классической линейной модели множественной регрессии, то вне главной диагонали ковариационной матрицы вектора случайных ошибок будут стоять нули.
(Omega = begin{pmatrix} begin{matrix} {sigma_{0}^{2}z_{1}^{2}} & 0 0 & {sigma_{0}^{2}z_{2}^{2}} end{matrix} & begin{matrix} ldots & 0 ldots & 0 end{matrix} begin{matrix} ldots & ldots 0 & 0 end{matrix} & begin{matrix} ldots & ldots ldots & {sigma_{0}^{2}z_{n}^{2}} end{matrix} end{pmatrix})
(б) Обратите внимание, что при подстановке в общую формулу для ОМНК-оценки величина (sigma_{0}^{2}) сокращается, следовательно, для оценки вектора коэффициентов знать её не нужно:
({{widehat{beta}}^{} = {({X’Omega^{- 1}X})}^{- 1}}X^{‘}Omega^{- 1}{y =}left( {X’begin{pmatrix} begin{matrix} z_{1}^{2} & 0 0 & z_{2}^{2} end{matrix} & begin{matrix} ldots & 0 ldots & 0 end{matrix} begin{matrix} ldots & ldots 0 & 0 end{matrix} & begin{matrix} ldots & ldots ldots & z_{n}^{2} end{matrix} end{pmatrix}^{- 1}X} right)^{- 1}X’begin{pmatrix} begin{matrix} z_{1}^{2} & 0 0 & z_{2}^{2} end{matrix} & begin{matrix} ldots & 0 ldots & 0 end{matrix} begin{matrix} ldots & ldots 0 & 0 end{matrix} & begin{matrix} ldots & ldots ldots & z_{n}^{2} end{matrix} end{pmatrix}^{- 1}y)
* * *
Ещё одна важная ситуация, когда с успехом может быть применен доступный ОМНК — это модель со случайными эффектами, которую мы рассмотрим в главе, посвященной панельным данным.
Допустим, что наша оценка представляет собой точку минимума в пространстве без ограничений для некоторой целевой функции 





Допустим, что мы слегка изменили данные, заменив 



Раскладывая левую часть 


так что приблизительно

где, как обычно, 
Искомая ковариационная матрица 

так что

Величины 




где 

Если мы предположим, что вектор 




Эта формула применяется к любой целевой функции независимо от статистических обоснований для ее выбора. Более специальные результаты можно получить, когда целевая функция зависит только от матрицы моментов 





где

При допущениях, подобных тем, какие делались при выводе равенства 


Подставляя 


Вывод, аналогичный тому, какой дается в приложении 




Предполагая, что наблюдения имеют стандартное отклонение а, в случае единственного уравнения наименьших квадратов мы имеем:

так что равенство 

Его сравнение с равенством 

Когда дисперсия 

Приведем теперь результаты для некоторых функций правдоподобия, которые были рассмотрены в разделе 5.9.
1. Нормальное распределение с известной матрицей 
В соответствии со строкой 1 табл. 



2. Как и в пункте 1, но матрица 






Для широкого класса оценок максимального правдоподобия с нормальными распределениями мы тогда имеем

Качество такой аппроксимации возрастает по мере того, как дисперсия измерений убывает и достигается лучшее соответствие модели и данных наблюдения.
Для оценок максимального правдоподобия без ограничений в большинстве случаев можцр показать 

Вычисление требуемого математического ожидания очень утомительно, если только вообще возможно; поэтому мы обычно заменяем математическое ожидание на наиболее вероятное значение, т. е. на значение в точке 

Приведенные здесь и далее оценки для 
Как иллюстрируется примерами раздела 7.22, эти колебания могут быть довольно большими даже тогда, когда может быть достигнуто хорошее соответствие модели и данных. Мы сами не будем здесь касаться вычисления выборочных дисперсий для 

Тот факт, что эти аппроксимации рушатся, когда подгонка модели плоха, не должен нас чрезмерно беспокоить, поскольку в этом случае мы так или иначе не слишком доверяем модели и будем пытаться улучшать либо модель, либо данные. Даже очень грубая аппроксимация для 

Многие статистические задачи требуют оценки ковариационной матрицы совокупности, которую можно рассматривать как оценку формы диаграммы разброса набора данных. В большинстве случаев такая оценка должна выполняться на выборке, свойства которой (размер, структура, однородность) имеют большое влияние на качество оценки. Пакет sklearn.covariance предоставляет инструменты для точной оценки ковариационной матрицы для данной популяции в различных условиях.
Мы предполагаем, что наблюдения независимы и одинаково распределены (iid).
2.6.1. Эмпирическая ковариация
Ковариационная матрица набора данных хорошо аппроксимируется классической оценкой максимального правдоподобия (или «эмпирической ковариацией») при условии, что количество наблюдений достаточно велико по сравнению с количеством признаков (переменных, описывающих наблюдения). Точнее, оценщик максимального правдоподобия выборки — это асимптотически несмещенный оценщик ковариационной матрицы соответствующей совокупности.
Эмпирическая ковариационная матрица выборки может быть вычислена с использованием empirical_covariance функции пакета или путем подгонки EmpiricalCovariance объекта к выборке данных с помощью EmpiricalCovariance.fit метода. Будьте осторожны, чтобы результаты зависели от центрирования данных, поэтому можно использовать assume_centered параметр точно. Точнее, если assume_centered=False, то предполагается, что тестовый набор имеет тот же средний вектор, что и обучающий набор. В противном случае оба должны быть центрированы пользователем и assume_centered=True использоваться.
Примеры
- См. В разделе Оценка ковариации усадки: LedoitWolf против OAS и максимальное правдоподобие пример того, как подогнать
EmpiricalCovarianceобъект к данным.
2.6.2. Уменьшение ковариации
2.6.2.1. Базовая усадка
Несмотря на то, что он является асимптотически несмещенным оценщиком ковариационной матрицы, оценщик максимального правдоподобия не является хорошим оценщиком собственных значений ковариационной матрицы, поэтому матрица точности, полученная в результате ее обращения, не является точной. Иногда даже оказывается, что эмпирическая ковариационная матрица не может быть инвертирована по числовым причинам. Для того, чтобы избежать такой проблемы инверсии, преобразование эмпирической ковариационной матрицы было введено: shrinkage.
В scikit-learn это преобразование (с определяемым пользователем коэффициентом усадки) можно напрямую применить к предварительно вычисленной ковариации с помощью shrunk_covariance метода. Кроме того, сжатая оценка ковариации может быть адаптирована к данным с помощью ShrunkCovariance объекта и его ShrunkCovariance.fit метода. Опять же, результаты зависят от того, центрированы ли данные, поэтому можно использовать assume_centered параметр точно.
Математически это сжатие состоит в уменьшении отношения между наименьшим и наибольшим собственными значениями эмпирической ковариационной матрицы. Это можно сделать, просто сдвинув каждое собственное значение в соответствии с заданным смещением, что эквивалентно нахождению оценщика максимального правдоподобия со штрафом l2 ковариационной матрицы. На практике усадка сводится к простому выпуклому преобразованию: $Sigma_{rm shrunk} = (1-alpha)hat{Sigma} + alphafrac{{rm Tr}hat{Sigma}}{p}rm Id$.
Выбирая величину усадки, $alpha$ сводится к установлению компромисса смещения/дисперсии и обсуждается ниже.
Примеры
- См. В разделе Оценка ковариации усадки: LedoitWolf против OAS и максимальное правдоподобие пример того, как подогнать
ShrunkCovarianceобъект к данным.
2.6.2.2. Усадка Ледуа-Вольфа
В своей статье 1 2004 г. О. Ледуа и М. Вольф предлагают формулу для расчета оптимального коэффициента усадки.α который минимизирует среднеквадратичную ошибку между оценочной и реальной ковариационной матрицей.
Оценщик Ледойта-Вольфа ковариационной матрицы может быть вычислен на выборке с ledoit_wolf функцией sklearn.covariance пакета, или ее можно получить иным способом, подгоняя LedoitWolf объект к той же выборке.
Примечание Случай, когда ковариационная матрица популяций изотропна
Важно отметить, что когда количество образцов намного превышает количество элементов, можно ожидать, что усадка не потребуется. Интуиция, лежащая в основе этого, заключается в том, что если ковариация совокупности имеет полный ранг, когда количество выборок растет, ковариация выборки также станет положительно определенной. В результате усадка не потребуется, и метод должен делать это автоматически.
Однако это не так в процедуре Ледуа-Вольфа, когда ковариация совокупности оказывается кратной единичной матрице. В этом случае оценка усадки Ледуа-Вольфа приближается к 1 по мере увеличения количества образцов. Это указывает на то, что оптимальная оценка ковариационной матрицы в смысле Ледуа-Вольфа кратна единице. Поскольку ковариация населения уже кратна единичной матрице, решение Ледуа-Вольфа действительно является разумной оценкой.
Примеры
- См. В разделе Оценка ковариации усадки: LedoitWolf против OAS и максимальное правдоподобие пример того, как подогнать
LedoitWolfобъект к данным и визуализировать характеристики оценщика Ледуа-Вольфа с точки зрения правдоподобия.
Рекомендации
О. Ледойт и М. Вольф, «Хорошо обусловленная оценка для многомерных ковариационных матриц», Журнал многомерного анализа, том 88, выпуск 2, февраль 2004 г., страницы 365-411.
2.6.2.3. Приблизительная усадка Oracle
Предполагая, что данные распределены по Гауссу, Chen et al. 2 выведена формула, направленная на выбор коэффициента усадки, который дает меньшую среднеквадратичную ошибку, чем та, которая дается формулой Ледуа и Вольфа. Результирующая оценка известна как оценка ковариации Oracle Shrinkage Approximating.
Оценщик OAS ковариационной матрицы может быть вычислен на выборке с помощью oas функции sklearn.covariance пакета, или он может быть получен иным образом путем подгонки OAS объекта к той же выборке.
Компромисс смещения и дисперсии при установке усадки: сравнение вариантов оценок Ледуа-Вольфа и OAS
Рекомендации
Чен и др., «Алгоритмы сжатия для оценки ковариации MMSE», IEEE Trans. на знак. Proc., Volume 58, Issue 10, October 2010.
Примеры
- См. В разделе Оценка ковариации усадки: LedoitWolf против OAS и максимальное правдоподобие пример того, как подогнать
OASобъект к данным. - См. Оценку Ледуа-Вольфа и OAS для визуализации разницы среднеквадратических ошибок между a
LedoitWolfиOASоценкой ковариации.
2.6.3. Редкая обратная ковариация
Матрица, обратная ковариационной матрице, часто называемая матрицей точности, пропорциональна матрице частичной корреляции. Это дает частичную независимость отношениям. Другими словами, если два признака независимы друг от друга условно, соответствующий коэффициент в матрице точности будет равен нулю. Вот почему имеет смысл оценивать матрицу разреженной точности: оценка ковариационной матрицы лучше обусловлена изучением отношений независимости от данных. Это называется ковариационным отбором .
В ситуации с малой выборкой, в которой n_samples порядок n_features или меньше, разреженные оценки обратной ковариации, как правило, работают лучше, чем оценки сжатой ковариации. Однако в противоположной ситуации или для сильно коррелированных данных они могут быть численно нестабильными. Кроме того, в отличие от оценщиков усадки, разреженные оценщики могут восстанавливать недиагональную структуру.
Оценщик GraphicalLasso использует l1 штраф для обеспечения разреженности на высокоточной матрице: тем выше его alpha параметр, тем более разреженной прецизионную матрицу. Соответствующий GraphicalLassoCV объект использует перекрестную проверку для автоматической установки alpha параметра.
Сравнение максимального правдоподобия, усадки и разреженных оценок ковариации и матрицы точности в настройках очень малых выборок.
Примечание Восстановление структуры
Восстановление графической структуры из корреляций в данных — непростая задача. Если вы заинтересованы в таком восстановлении, имейте в виду, что:
- Восстановление легче из корреляционной матрицы, чем из ковариационной матрицы: стандартизируйте свои наблюдения перед запуском
GraphicalLasso - Если в нижележащем графе есть узлы с гораздо большим количеством соединений, чем в среднем узле, алгоритм пропустит некоторые из этих соединений.
- Если количество ваших наблюдений невелико по сравнению с количеством ребер в вашем нижележащем графе, вы не сможете его восстановить.
- Даже если вы находитесь в благоприятных условиях восстановления, альфа-параметр, выбранный путем перекрестной проверки (например, с использованием
GraphicalLassoCVобъекта), приведет к выбору слишком большого количества ребер. Однако соответствующие ребра будут иметь больший вес, чем нерелевантные.
Математическая формулировка следующая:
$$hat{K} = mathrm{argmin}_K big( mathrm{tr} S K — mathrm{log} mathrm{det} K + alpha |K|_1 big)$$
Где $K$ — матрица точности, которую необходимо оценить, и $S$ — это выборочная ковариационная матрица. $|K|_1$ — сумма модулей недиагональных коэффициентов $K$. Для решения этой проблемы используется алгоритм GLasso из статьи Friedman 2008 Biostatistics. Это тот же алгоритм, что и в glasso пакете R.
Примеры
- Оценка разреженной обратной ковариации: пример синтетических данных, показывающих восстановление структуры и сравнение с другими оценками ковариации.
- Визуализация структуры фондового рынка: пример реальных данных фондового рынка, определение наиболее связанных символов.
Рекомендации
- Фридман и др., «Оценка разреженной обратной ковариации с помощью графического лассо» , Biostatistics 9, стр. 432, 2008 г.
2.6.4. Оценка робастной ковариации
Реальные наборы данных часто подвержены ошибкам измерения или записи. Регулярные, но необычные наблюдения также могут появляться по разным причинам. Наблюдения, которые случаются очень редко, называются выбросами. Эмпирическая оценка ковариации и сжатая оценка ковариации, представленные выше, очень чувствительны к наличию выбросов в данных. Следовательно, следует использовать надежные оценщики ковариации для оценки ковариации реальных наборов данных. В качестве альтернативы можно использовать робастные оценщики ковариации для обнаружения выбросов и отбрасывания / уменьшения веса некоторых наблюдений в соответствии с дальнейшей обработкой данных.
В sklearn.covariance пакете реализована надежная оценка ковариации, определитель минимальной ковариации 3 .
2.6.4.1. Определитель минимальной ковариации
Оценщик, определяющий минимальную ковариацию, — это надежный оценщик ковариации набора данных, представленный PJ Rousseeuw в 3 . Идея состоит в том, чтобы найти заданную пропорцию (h) «хороших» наблюдений, которые не являются выбросами, и вычислить их эмпирическую ковариационную матрицу. Эта эмпирическая ковариационная матрица затем масштабируется, чтобы компенсировать выполненный выбор наблюдений («этап согласованности»). Вычислив оценку определителя минимальной ковариации, можно присвоить веса наблюдениям в соответствии с их расстоянием Махаланобиса, что приведет к повторной оценке ковариационной матрицы набора данных («этап повторного взвешивания»).
Rousseeuw и Van Driessen 4 разработали алгоритм FastMCD для вычисления определителя минимальной ковариации. Этот алгоритм используется в scikit-learn при подгонке объекта MCD к данным. Алгоритм FastMCD также одновременно вычисляет надежную оценку местоположения набора данных.
Сырые оценки могут быть доступны как raw_location_ и raw_covariance_ атрибутами из MinCovDet надежного объекта ковариационной оценивани.
Рекомендации
- 3 PJ Rousseeuw. Наименьшая медиана квадратов регрессии. Дж. Ам Стат Асс, 79: 871, 1984.
- 4 Быстрый алгоритм для определения определителя минимальной ковариации, 1999, Американская статистическая ассоциация и Американское общество качества, TECHNOMETRICS.
Примеры
- См. Пример надежной и эмпирической ковариационной оценки, чтобы узнать, как подогнать
MinCovDetобъект к данным, и посмотрите, насколько оценка остается точной, несмотря на наличие выбросов. - См оценку ковариационной Robust и Махаланобиса расстояния Актуальность визуализировать разницу между
EmpiricalCovarianceиMinCovDetковариации оценок с точки зрения расстояния Махаланобиса (так мы получим более точную оценку точности матрицы тоже).
Авторы
Гай Е.В.
Организация
ГНЦ РФ – Физико-энергетический институт имени А.И. Лейпунского, Обнинск, Россия
Аннотация
Обработка экспериментальных данных методами математической статистики позволяет оценить лежащие в их основе физические закономерности или, по крайней мере, построить непрерывную аппроксиманту этих данных. Обычно при такой обработке используются декларированные статистические и систематические погрешности экспериментальных данных. В классической математической статистике проверка согласованности этих погрешностей с наблюдаемым разбросом данных осуществляется с помощью критерия χ2. В настоящей работе показано, что при большом числе экспериментальных точек погрешность оценки определяется систематическими погрешностями этих точек, но значение критерия χ2 от них не зависит и поэтому он не замечает несоответствия между их декларирированными и наблюдаемыми значениями.
Ключевые слова
критерий χ2, погрешности, МНК, функция правдоподобия, дисперсия экспериментальных данных, систематические ошибки
Полная версия статьи (PDF, 3996 кб)
Список литературы
УДК 539.17
Вопросы атомной науки и техники. Cер. Ядерные константы, 2011-2012, вып. 1-2, c. 8-26
В предыдущих параграфах данной главы мы рассматривали случай отказа от одной предпосылки классической линейной модели множественной регрессии. Теперь мы расширим наш анализ и откажемся сразу от двух предпосылок: от предпосылок №№4-5 (о постоянстве дисперсии случайной ошибки и о некоррелированности разных случайных ошибок между собой). В техническом смысле этот параграф несколько сложнее предыдущих (в частности, тут более широко используется линейная алгебра). Поэтому, если вы заинтересованы в том, чтобы разобраться только в прикладных аспектах множественной регрессии, а в соответствующих вычислениях готовы полностью довериться эконометрическому пакету, можете его пропустить.
Отказ от указанных двух предпосылок означает, что ковариационная матрица вектора случайных ошибок (таблица, в которой записаны все ковариации между (varepsilon_{i}) и (varepsilon_{j}), см. параграф 3.3) больше не является диагональной матрицей с одинаковыми числами на главной диагонали, как это было в первоначальной классической модели. Теперь ковариационная матрица вектора случайных ошибок Ω — это произвольная ковариационная матрица (разумеется, так как это не совсем любая матрица, а именно ковариационная матрица, то по своим свойствам она является симметричной и положительно определенной).
Модель, в которой сохранены только первые три предпосылки классической линейной модели множественной регрессии, называется обобщенной линейной моделью множественной регрессии.
Проанализируем, к каким последствиям приводит отказ от предпосылок №№4-5.
Во-первых, полученная обычным методом наименьших квадратов оценка ({widehat{beta} = left( {X^{‘}X} right)^{- 1}}X’y) остается несмещенной (это свойство мы доказывали, опираясь как раз лишь на первые три предпосылки).
Во-вторых, МНК-оценки хоть и остаются несмещенными, но больше не являются эффективными.
В-третьих, если мы оцениваем ковариационную матрицу вектора оценок коэффициентов (которая нужна для тестирования всевозможных гипотез), то оценка (widehat{V}{{(widehat{beta})} = left( {X^{‘}X} right)^{- 1}}S^{2}) смещена и больше не является корректной.
Чтобы убедиться в этом, посчитаем ковариационную матрицу от (widehat{beta}) в условиях обобщенной модели (при этом мы используем свойства ковариационной матрицы, перечисленные в параграфе 3.3):
(V{left( widehat{beta} right) = V}{leftlbrack {{({X^{‘}X})}^{- 1}X’y} rightrbrack = V}{leftlbrack {{({X^{‘}X})}^{- 1}X'{({mathit{Xbeta} + varepsilon})}} rightrbrack =})
({}V{leftlbrack {{({{({X^{‘}X})}^{- 1}X’})}varepsilon} rightrbrack = left( {X^{‘}X} right)^{- 1}}X^{‘}Vlbrackvarepsilonrbrack{left( {left( {X^{‘}X} right)^{- 1}X^{‘}} right)^{‘} = {({X^{‘}X})}^{- 1}}X^{‘}Omega{left( {left( {X^{‘}X} right)^{- 1}X^{‘}} right)^{‘} = {({X^{‘}X})}^{- 1}}X^{‘}Omega X{({X^{‘}X})}^{- 1})
Так выглядит ковариационная матрица вектора МНК-оценок в обобщенной модели. Ясно, что она не может быть корректно оценена стандартной оценкой (left( {X^{‘}X} right)^{- 1}S^{2}). Следовательно, прежней формулой пользоваться нельзя: если мы будем использовать стандартные ошибки, рассчитанные по обычной формуле (предполагая выполнение предпосылок классической линейной модели), то получим некорректные стандартные ошибки, что может привести нас к неверным выводам по поводу значимости или незначимости тех или иных регрессоров.
Таким образом, последствия перехода к обобщенной модели аналогичны тем, что мы наблюдали для случая гетероскедастичности. Это неудивительно, так как гетероскедастичность — частный случай обобщенной линейной модели.
Поэтому для получения эффективных оценок обычный МНК не подойдет, и придется воспользоваться альтернативным методом — обобщенным МНК (ОМНК, generalized least squares, GLS). Формулу для расчета оценок коэффициентов при помощи ОМНК позволяет получить специальная теорема.
Теорема Айткена
Если
- модель линейна по параметрам и правильно специфицирована
({y = {mathit{Xbeta} + varepsilon}},) - матрица Х — детерминированная матрица, имеющая максимальный ранг k,
- (E{(varepsilon) = overrightarrow{0}}),
- (V{(varepsilon) = Omega}) — произвольная положительно определенная и симметричная матрица,
то оценка вектора коэффициентов модели ({{widehat{beta}}^{} = {({X’Omega^{- 1}X})}^{- 1}}X’Omega^{- 1}y) является:
- несмещенной
- и эффективной, то есть имеет наименьшую ковариационную матрицу в классе всех несмещенных и линейных по y оценок.
Предпосылки теоремы Айткена — это предпосылки обобщенной линейной модели множественной регрессии. Из них первые три — стандартные, как в классической модели, а четвертая ничего особого не требует (у вектора случайных ошибок может быть любая ковариационная матрица без каких-либо дополнительных специальных ограничений). Сама теорема Айткена является аналогом теоремы Гаусса — Маркова для случая обобщенной модели.
Докажем эту теорему.
Из линейной алгебры известно: если матрица (Omega) симметрична и положительно определена, то существует такая матрица P, что
(P’bullet{P = Omega^{- 1}}) ⇔ ({P^{‘} = Omega^{- 1}}bullet P^{- 1})
А раз такое представление возможно, то воспользуемся им для замены переменных. От вектора значений зависимой переменной (y), перейдем к вектору (Pbullet y), обозначив его как вектор ({y^{} = P}bullet y). Аналогичным образом введем матрицу ({X^{} = P}bullet X) и вектор ошибок ({varepsilon^{} = P}bulletvarepsilon).
Вернемся к исходной модели, параметры которой нас и интересуют:
({y = X}{beta + varepsilon})
Умножим левую и правую части равенства на матрицу (P):
({mathit{Py} = mathit{PX}}{beta + mathit{Pvarepsilon}})
С учетом новых обозначений это равенство можно записать так:
({y^{} = X^{}}{beta + varepsilon^{}})
Для новой модели (со звездочками) выполняются предпосылки теоремы Гаусса-Маркова. Чтобы в этом убедиться, достаточно показать, что математическое ожидание вектора случайных ошибок является нулевым вектором (третья предпосылка классической модели) и ковариационная матрица вектора случайных ошибок является диагональной с одинаковыми элементами на главной диагонали (четвертая и пятая предпосылки).
Для этого вычислим математическое ожидание нового вектора ошибок:
(E{left( varepsilon^{} right) = E}{left( mathit{Pvarepsilon} right) = P}bullet E{(varepsilon) = P}bullet{overrightarrow{0} = overrightarrow{0}})
Теперь вычислим ковариационную матрицу вектора (varepsilon^{}):
(V{left( varepsilon^{} right) = V}{left( {Pbulletvarepsilon} right) = P}bullet V(varepsilon)bullet{P^{‘} = P}bulletOmegabullet{P^{‘} = P}bulletOmegabulletOmega^{- 1}bullet{P^{- 1} = I_{n}})
Здесь (I_{n}) обозначает единичную матрицу размера n на n.
Следовательно, для модели со звездочками выполняются все предпосылки теоремы Гаусса — Маркова. Поэтому получить несмещенную и эффективную оценку вектора коэффициентов можно, применив к этой измененной модели обычный МНК:
({{widehat{beta}}^{} = left( {{X^{}}^{‘}X^{}} right)^{- 1}}{X^{}}^{‘}y^{})
Теперь осталось вернуться к исходным обозначениям, чтобы получить формулу несмещенной и эффективной оценки интересующего нас вектора в терминах обобщенной модели:
({{widehat{beta}}^{} = left( {{X^{}}^{‘}X^{}} right)^{- 1}}{X^{}}^{‘}{y^{} = left( {{(mathit{PX})}^{‘}mathit{PX}} right)^{- 1}}left( mathit{PX} right)^{‘}{mathit{Py} = left( {X’P’mathit{PX}} right)^{- 1}}X^{‘}P^{‘}{mathit{Py} =}left( {X’Omega^{- 1}P^{- 1}mathit{PX}} right)^{- 1}X’Omega^{- 1}P^{- 1}{mathit{Py} = {({X’Omega^{- 1}X})}^{- 1}}X’Omega^{- 1}y)
Что и требовалось доказать.
Взвешенный МНК, который мы обсуждали ранее, — это частный вариант обобщенного МНК (для случая, когда только предпосылка №4 нарушена, а предпосылка №5 сохраняется).
Как и при использовании взвешенного МНК в ситуации применения ОМНК коэффициент R-квадрат не обязан лежать между нулем и единицей и не может быть интерпретирован стандартным образом.
Слабая сторона ОМНК состоит в том, что для его реализации нужно знать не только матрицу регрессоров X с вектором значений зависимой переменной y, но и ковариационную матрицу вектора случайных ошибок (Omega). На практике, однако, эта матрица почти никогда не известна. Поэтому в прикладных исследованиях практически всегда вместо ОМНК используется, так называемый, доступный ОМНК (его ещё называют практически реализуемый ОМНК, feasible GLS). Идея доступного ОМНК состоит в том, что следует сначала оценить матрицу (Omega) (традиционно обозначим её оценку (widehat{Omega})), а уже затем получить оценку вектора коэффициентов модели, заменив в формуле ОМНК (Omega) на (widehat{Omega}):
({{widehat{beta}}^{} = {({X'{widehat{Omega}}^{- 1}X})}^{- 1}}X'{widehat{Omega}}^{- 1}y.)
Применение этого подхода осложняется тем, что (widehat{Omega}) не может быть оценена непосредственно без дополнительных предпосылок, так как в ней слишком много неизвестных элементов. Действительно, в матрице размер (n) на (n) всего (n^{2}) элементов, и оценить их все, имея всего (n) наблюдений, представляется слишком амбициозной задачей. Даже если воспользоваться тем, что матрица (Omega) является симметричной, в результате чего достаточно оценить только элементы на главной диагонали и над ней, мы все равно столкнемся с необходимостью оценивать (left( {n + 1} right){n/2}) элементов, что всегда больше числа доступных нам наблюдений.
Поэтому процедура доступного ОМНК устроена так:
- Делаются некоторые предпосылки по поводу того, как устроена ковариационная матрица вектора случайных ошибок (Omega). На основе этих предпосылок оценивается матрица (widehat{Omega}).
- После этого по формуле ({({X'{widehat{Omega}}^{- 1}X})}^{- 1}X'{widehat{Omega}}^{- 1}y) вычисляется вектор оценок коэффициентов модели.
Из сказанного следует, что доступный ОМНК может быть реализован только в ситуации, когда есть разумные основания сформулировать те или иные предпосылки по поводу матрицы (widehat{Omega}). Рассмотрим некоторые примеры таких ситуаций.
Пример 5.4. Автокорреляция и ОМНК-оценка
Рассмотрим линейную модель ({y = X}{beta + varepsilon}), для которой дисперсия случайных ошибок постоянна, однако наблюдается так называемая автокорреляция первого порядка:
(varepsilon_{i} = {{rho ast varepsilon_{i — 1}} + u_{i}})
Здесь (u_{i}) — независимые и одинаково распределенные случайные величины с дисперсией (sigma_{u}^{2}), а (rhoin{({{- 1},1})}) — коэффициент автокорреляции.
(а) Найдите ковариационную матрицу вектора случайных ошибок для представленной модели.
(б) Запишите в явном виде формулу ОМНК-оценки вектора коэффициентов модели, предполагая, что коэффициент (rho) известен.
Примечание: в отличие от гетероскедастичности, автокорреляция случайных ошибок обычно наблюдается не в пространственных данных, а во временных рядах. Для временных рядов вполне естественна подобная связь будущих случайных ошибок с предыдущими их значениями.
Решение:
(а) Используя условие о постоянстве дисперсии случайной ошибки, то есть условие (mathit{var}{{(varepsilon_{i})} = mathit{var}}{(varepsilon_{i — 1})}), найдем эту дисперсию:
(mathit{var}{{(varepsilon_{i})} = mathit{var}}{({{rho ast varepsilon_{i — 1}} + u_{i}})})
(mathit{var}{{(varepsilon_{i})} = rho^{2}}mathit{var}{{(varepsilon_{i — 1})} + mathit{var}}{(u_{i})})
(mathit{var}{{(varepsilon_{i})} = rho^{2}}mathit{var}{{(varepsilon_{i})} + sigma_{u}^{2}})
(mathit{var}{left( varepsilon_{i} right) = frac{sigma_{u}^{2}}{1 — rho^{2}}}.)
Тем самым мы нашли элементы, которые будут стоять на главной диагонали ковариационной матрицы вектора случайных ошибок. Теперь найдем элементы, которые будут находиться непосредственно на соседних с главной диагональю клетках:
(mathit{cov}{left( {varepsilon_{i},varepsilon_{i — 1}} right) = mathit{cov}}{left( {{{rho ast varepsilon_{i — 1}} + u_{i}},varepsilon_{i — 1}} right) = {rho ast mathit{cov}}}{left( {varepsilon_{i — 1},varepsilon_{i — 1}} right) + mathit{cov}}{left( {u_{i},varepsilon_{i — 1}} right) = {rho ast mathit{var}}}{{left( varepsilon_{i — 1} right) + 0} = frac{rho ast sigma_{u}^{2}}{1 — rho^{2}}})
По аналогии легко убедиться, что
(mathit{cov}{left( {varepsilon_{i},varepsilon_{i — k}} right) = frac{rho^{k} ast sigma_{u}^{2}}{1 — rho^{2}} = frac{sigma_{u}^{2} ast rho^{k}}{1 — rho^{2}}}.)
Следовательно, ковариационная матрица вектора случайных ошибок имеет вид:
({Omega = frac{sigma_{u}^{2}}{1 — rho^{2}}}begin{pmatrix} begin{matrix} 1 & rho \ rho & 1 \ end{matrix} & ldots & begin{matrix} rho^{n — 2} & rho^{n — 1} \ rho^{n — 3} & rho^{n — 2} \ end{matrix} \ ldots & ldots & ldots \ begin{matrix} rho^{n — 2} & rho^{n — 3} \ rho^{n — 1} & rho^{n — 2} \ end{matrix} & ldots & begin{matrix} 1 & rho \ rho & 1 \ end{matrix} \ end{pmatrix})
(б) Вектор ОМНК-оценок коэффициентов имеет вид:
({{widehat{beta}}^{} = {({X’Omega^{- 1}X})}^{- 1}}X^{‘}Omega^{- 1}{y =}{left( {X’begin{pmatrix} begin{matrix} 1 & rho \ rho & 1 \ end{matrix} & ldots & begin{matrix} rho^{n — 2} & rho^{n — 1} \ rho^{n — 3} & rho^{n — 2} \ end{matrix} \ ldots & ldots & ldots \ begin{matrix} rho^{n — 2} & rho^{n — 3} \ rho^{n — 1} & rho^{n — 2} \ end{matrix} & ldots & begin{matrix} 1 & rho \ rho & 1 \ end{matrix} \ end{pmatrix}^{- 1}X} right)^{- 1} ast}X’begin{pmatrix} begin{matrix} 1 & rho \ rho & 1 \ end{matrix} & ldots & begin{matrix} rho^{n — 2} & rho^{n — 1} \ rho^{n — 3} & rho^{n — 2} \ end{matrix} \ ldots & ldots & ldots \ begin{matrix} rho^{n — 2} & rho^{n — 3} \ rho^{n — 1} & rho^{n — 2} \ end{matrix} & ldots & begin{matrix} 1 & rho \ rho & 1 \ end{matrix} \ end{pmatrix}^{- 1}y)
Обратите внимание, что дробь (frac{sigma_{u}^{2}}{1 — rho^{2}}) при расчете представленной оценки сокращается. Поэтому для вычисления оценки знать величину (sigma_{u}^{2}) не нужно.
Примечание: если коэффициент автокорреляции (rho) неизвестен, то его можно легко оценить. Например, для этого можно применить обычный МНК к исходной регрессии, получить вектор остатков и оценить регрессию ({widehat{e}}_{i} = {widehat{rho} ast e_{i — 1}}). Полученной оценки (widehat{rho}) достаточно, чтобы вычислить ОМНК-оценку вектора параметров модели. Тем самым в представленном примере для применения доступного ОМНК достаточно оценить всего один параметр ковариационной матрицы вектора оценок коэффициентов.
Пример 5.5. Гетероскедастичность и ОМНК-оценка
Рассмотрим линейную модель ({y = X}{beta + varepsilon}), для которой выполнены все предпосылки классической линейной модели множественной регрессии за одним исключением: дисперсия случайной ошибки прямо пропорциональна квадрату некоторой известной переменной
(mathit{var}{left( varepsilon_{i} right) = sigma_{i}^{2} = sigma_{0}^{2}}{z_{i}^{2} > 0}.)
(а) Найдите ковариационную матрицу вектора случайных ошибок для представленной модели.
(б) Запишите в явном виде формулу ОМНК-оценки вектора коэффициентов модели.
Решение:
(а) Так как в этом случае нарушена только четвертая предпосылка классической линейной модели множественной регрессии, то вне главной диагонали ковариационной матрицы вектора случайных ошибок будут стоять нули.
(Omega = begin{pmatrix} begin{matrix} {sigma_{0}^{2}z_{1}^{2}} & 0 \ 0 & {sigma_{0}^{2}z_{2}^{2}} \ end{matrix} & begin{matrix} ldots & 0 \ ldots & 0 \ end{matrix} \ begin{matrix} ldots & ldots \ 0 & 0 \ end{matrix} & begin{matrix} ldots & ldots \ ldots & {sigma_{0}^{2}z_{n}^{2}} \ end{matrix} \ end{pmatrix})
(б) Обратите внимание, что при подстановке в общую формулу для ОМНК-оценки величина (sigma_{0}^{2}) сокращается, следовательно, для оценки вектора коэффициентов знать её не нужно:
({{widehat{beta}}^{} = {({X’Omega^{- 1}X})}^{- 1}}X^{‘}Omega^{- 1}{y =}left( {X’begin{pmatrix} begin{matrix} z_{1}^{2} & 0 \ 0 & z_{2}^{2} \ end{matrix} & begin{matrix} ldots & 0 \ ldots & 0 \ end{matrix} \ begin{matrix} ldots & ldots \ 0 & 0 \ end{matrix} & begin{matrix} ldots & ldots \ ldots & z_{n}^{2} \ end{matrix} \ end{pmatrix}^{- 1}X} right)^{- 1}X’begin{pmatrix} begin{matrix} z_{1}^{2} & 0 \ 0 & z_{2}^{2} \ end{matrix} & begin{matrix} ldots & 0 \ ldots & 0 \ end{matrix} \ begin{matrix} ldots & ldots \ 0 & 0 \ end{matrix} & begin{matrix} ldots & ldots \ ldots & z_{n}^{2} \ end{matrix} \ end{pmatrix}^{- 1}y)
* * *
Ещё одна важная ситуация, когда с успехом может быть применен доступный ОМНК — это модель со случайными эффектами, которую мы рассмотрим в главе, посвященной панельным данным.
Фильтр Калмана — это легко +64
Алгоритмы, Блог компании Singularis
Рекомендация: подборка платных и бесплатных курсов таргетированной рекламе — https://katalog-kursov.ru/
Много людей, в первый раз сталкивающихся в работе с датчиками, склонны считать, что получаемые показания — это точные значения. Некоторые вспоминают, что в показаниях всегда есть погрешности и ошибки. Чтобы ошибки в измерениях не приводили к ошибкам в функционировании системы в целом, данные датчиков необходимо обрабатывать. На ум сразу приходит словосочетание “фильтр Калмана”. Но слава этого “страшного” алгоритма, малопонятные формулы и разнообразие используемых обозначений отпугивают разработчиков. Постараемся разобраться с ним на практическом примере.
Об алгоритме
Что же нам потребуется для работы фильтра Калмана?
- Нам потребуется модель системы.
- Модель должна быть линейной (об этом чуть позже).
- Нужно будет выбрать переменные, которые будут описывать состояние системы (“вектор состояния”).
- Мы будем производить измерения и вычисления в дискретные моменты времени (например, 10 раз в секунду). Нам потребуется модель наблюдения.
- Для работы фильтра достаточно данных измерений в текущий момент времени и результатов вычислений с предыдущего момента времени.
Алгоритм работает итеративно. На каждом шаге алгоритм берёт данные датчиков (с шумом и другими проблемами), вектор состояния с предыдущего шага и по этим данным оценивает состояние системы на текущем шаге. Кроме того, он еще отслеживает насколько мы можем быть уверены, что наш текущий вектор состояний соответствует истинному положению дел (разброс значений для каждой переменной в векторе).
Обычно используются следующие обозначения:
— вектор состояния;
— мера неопределенности вектора состояния. Представляет из себя ковариационную матрицу (об этом позже — это будет, наверное, самая сложная часть).
Содержимое вектора состояния зависит от фантазии разработчика и решаемой задачи. Например, мы можем отслеживать координаты объекта, а также его скорость и ускорение. В этом случае получается вектор из трёх переменных: {позиция, скорость, ускорение} (для одномерного случая; для 3D мира будет по одному такому набору для каждой оси, то есть, 9 значений в векторе)
По сути, речь идёт о совместном распределении случайных величин
В фильтре Калмана мы предполагаем, что все погрешности и ошибки (как во входных данных, так и в оценке вектора состояния) имеют нормальное распределение. А для многомерного нормального распределения его полностью определяют два параметра: математическое ожидание вектора и его ковариационная матрица.
Математическая модель системы / процесса
Мы имеем дело с динамической системой, т.е. состояние системы меняется со временем. Имея модель системы, фильтр Калмана может предугадывать, каким будет состояние системы в следующий момент времени. Именно это позволяет фильтру так эффективно устранять шум и оценивать параметры, которые не наблюдаются (не измеряются) напрямую.
Фильтр Калмана накладывает ограничения на используемые модели: это должны быть дискретные модели в пространстве состояний. А ещё они должны быть линейными.
Дискретные и линейные?
Дискретность означает для нас то, что модель работает “шагами”. На каждом шаге мы вычисляем новое состояние системы по вектору состояния с предыдущего шага. Обычно, модели такого рода задаются системой разностных уравнений.
По поводу линейности: каждое уравнение системы является линейным уравнением, задающим новое значение переменной состояния. Т.е. никаких косинусов, синусов, возведений в степень и даже сложений с константой.
Такую модель удобно представлять в виде разностного матричного уравнения:
Давайте разберём это уравнение подробно. В первую очередь, нас интересует первое слагаемое (
) — это как раз модель эволюции процесса. А матрица
(также встречаются обозначения
,
) — называется матрицей процесса (state transition matrix). Она задаёт систему линейных уравнений, описывающих, как получается новое состояние системы из предыдущего.
Например, для равноускоренного движения матрица будет выглядеть так:
Первая строка матрицы — хорошо знакомое уравнение
. Аналогично, вторая строка матрицы описывает изменение скорости. Третья строка описывает изменение ускорения.
А что же с остальными слагаемыми?
В некоторых случаях, мы напрямую управляем процессом (например, управляем квадракоптером с помощью пульта Д/У) и нам достоверно известны задаваемые параметры (заданная на пульте скорость полёта). Второе слагаемое — это модель управления. Матрица
называется матрицей управления, а вектор
— вектор управляющих воздействий. В случаях когда мы только наблюдаем за процессом, это слагаемое отсутствует.
Последнее слагаемое —
— это вектор ошибки модели. Модель равноускоренного движения абсолютно точно описывает положение объекта. Однако в реальном мире есть множество случайных факторов — дороги неровные, дует ветер, и т.п. Иногда, процесс сложен и приходится использовать упрощённую модель, которая не учитывает все аспекты. Именно так возникает ошибка модели.
То, что мы записываем это слагаемое, не означает, что мы знаем ошибку на каждом шаге или описываем её аналитически. Однако фильтр Калмана делает важное предположение — ошибка имеет нормальное распределение с нулевым математическим ожиданием и ковариационной матрицей
. Эта матрица очень важна для стабильной работы фильтра и мы её рассмотрим позже.
Модель наблюдения
Не всегда получается так, что мы измеряем интересующие нас параметры напрямую (например, мы измеряем скорость вращения колеса, хотя нас интересует скорость автомобиля). Модель наблюдения описывает связь между переменными состояния и измеряемыми величинами:
— это вектор измерения/наблюдения.Это значения, получаемые с датчиков системы.
Первое слагаемое
— модель, связывающая вектор состояния
с соответствующими ему показаниями датчиков. (Такой выбор модели может показаться странным, ведь наша задача — получить
из
, а эта модель получает
из
. Но это действительно так. В частности, это необходимо потому, что некоторые переменные состояния из
могут отсутствовать в
).
Второе слагаемое
— это вектор ошибок измерения. Как и в случае с предыдущими ошибками, предполагается, что она имеет нормальное распределение с нулевым математическим ожиданием.
— ковариационная матрица, соответствующая вектору
.
Вернёмся к нашему примеру. Пусть у нас на роботе установлен один единственный датчик — GPS приёмник (“измеряет” положение). В этом случае матрица
будет выглядеть следующим образом:
Строки матрицы соответствуют переменным в векторе состояния, столбцы — элементам вектора измерений. В первой строке матрицы находится значение “1” так как единица измерения положения в векторе состояния совпадает с единицей измерения значения в векторе измерений. Остальные строки содержат “0” потому что переменные состояния соответствующие этим строкам не измеряются датчиком.
Что будет, если датчик и модель используют разные единицы измерения? А если датчиков несколько?
Например, модель использует метры, а датчик — количество оборотов колеса. В этом случае матрица будет выглядеть так:
Количество датчиков ничем (кроме здравого смысла) не ограничено.
Например, добавим спидометр:
Второй столбец матрицы соответствует нашему новому датчику.
Несколько датчиков могут измерять один и тот же параметр. Добавим ещё один датчик скорости:
Ковариационные матрицы и где они обитают
Для настройки фильтра нам потребуется заполнить несколько ковариационных матриц:
,
и
.
Ковариационные матрицы?
Для нормально распределенной случайной величины её математическое ожидание и дисперсия полностью определяют её распределение. Дисперсия — это мера разброса случайной величины. Чем больше дисперсия — тем сильнее может отклоняться случайная величина от её математического ожидания. Ковариационная матрица — это многомерный аналог дисперсии, для случая, когда у нас не одна случайная величина, а случайный вектор.
В одной статье сложно уместить всю теорию вероятностей, поэтому ограничимся сугубо практическими свойствами ковариационных матриц. Это симметричные квадратные матрицы, на главной диагонали которой располагаются дисперсии элементов вектора. Остальные элементы матрицы — ковариации между компонентами вектора. Ковариация показывает, насколько переменные зависят друг от друга.
Проиллюстрируем влияние мат. ожидания, дисперсии и ковариации.
Начнём с одномерного случая. Функция плотности вероятности нормального распределения — знаменитая колоколообразная кривая. Горизонтальная ось — значение случайной величины, а вертикальная ось — сравнительная вероятность того что случайная величина примет это значение:
Чем меньше дисперсия — тем меньше ширина колокола.
Понятие ковариации возникает для совместного распределения нескольких случайных величин. Когда случайные величины независимы, то ковариация равна нулю:
Ненулевое значение ковариации означает, что существует связь между значениями случайных величин:
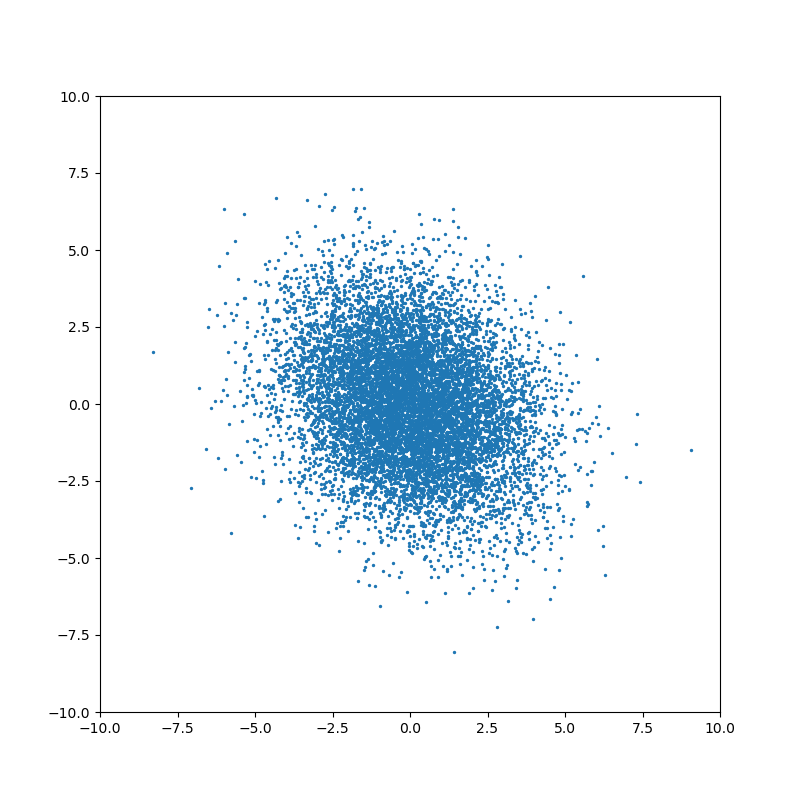
На каждом шаге фильтр Калмана строит предположение о состоянии системы, исходя из предыдущей оценки состояния и данных измерений. Если неопределенности вектора состояния выше, чем ошибка измерения, то фильтр будет выбирать значения ближе к данным измерений. Если ошибка измерения больше оценки неопределенности состояния, то фильтр будет больше “доверять” данным моделирования. Именно поэтому важно правильно подобрать значения ковариационных матриц — основного инструмента настройки фильтра.
Рассмотрим каждую матрицу подробнее:
— ковариационная матрица состояния
Квадратная матрица, порядок матрицы равен размеру вектора состояния
Как уже было сказано выше, эта матрица определяет “уверенность” фильтра в оценке переменных состояния. Алгоритм самостоятельно обновляет эту матрицу в процессе работы. Однако нам нужно установить начальное состояние, вместе с исходным предположением о векторе состояния.
Во многих случаях нам неизвестны значения ковариации между переменными для изначального состояния (элементы матрицы, расположенные вне главной диагонали). Поэтому можно проигнорировать их, установив равными 0. Фильтр самостоятельно обновит значения в процессе работы. Если же значения ковариации известны, то, конечно же, стоит использовать их.
Дисперсию же проигнорировать не выйдет. Необходимо установить значения дисперсии в зависимости от нашей уверенности в исходном векторе состояния. Для этого можно воспользоваться правилом трёх сигм: значение случайной величины попадает в диапазон
с вероятностью 99.7%.
Пример
Допустим, нам нужно установить дисперсию для переменной состояния — скорости робота. Мы знаем что максимальная скорость передвижения робота — 10 м/с. Но начальное значение скорости нам неизвестно. Поэтому, мы выберем изначальное значение переменной — 0 м/с, а среднеквадратичное отклонение
;
Соответственно, дисперсия
.
— ковариационная матрица шума измерений
Квадратная матрица, порядок матрицы равен размеру вектора наблюдения (количеству измеряемых параметров).
Во многих случаях можно считать, что измерения не коррелируют друг с другом. В этом случае матрица
будет являться диагональной матрицей, где все элементы вне главной диагонали равны нулю. Достаточно будет установить значения дисперсии для каждого измеряемого параметра. Иногда эти данные можно найти в документации к используемым датчика. Однако, если справочной информации нет, то можно оценить дисперсию, измеряя датчиком заранее известное эталонное значение, или воспользоваться правилом трёх сигм.
— ковариационная матрица ошибки модели
Квадратная матрица, порядок матрицы равен размеру вектора состояния.
С этой матрицей обычно возникает наибольшее количество вопросов. Что означает ошибка модели? Каков смысл этой матрицы и за что она отвечает? Как заполнять эту матрицу? Рассмотрим всё по порядку.
Каждый раз, когда фильтр предсказывает состояние системы, используя модель процесса, он увеличивает неуверенность в оценке вектора состояния. Для одномерного случая формула выглядит приблизительно следующим образом:
Если установить очень маленькое значение
, то этап предсказания будет слабо увеличивать неопределенность оценки. Это означает, что мы считаем, что наша модель точно описывает процесс.
Если же установить большое значение
, то этап предсказания будет сильно увеличивать неопределенность оценки. Таким образом, мы показываем что модель может содержать неточности или неучтенные факторы.
Для многомерного случая формула выглядит несколько сложнее, но смысл схожий. Однако, есть важное отличие: эта матрица указывает, на какие переменные состояния будут в первую очередь влиять ошибки модели и неучтённые факторы.
Допустим, мы отслеживаем перемещение робота, используя модель равноускоренного движения, и вектор состояния содержит следующие переменные: положение x, скорость v и ускорение a. Однако, наша модель не учитывает, что на дороге встречаются неровности.
Когда робот проходит неровность, показания датчиков и предсказание модели начнут расходиться. Структура матрицы
будет определять, как фильтр отреагирует на это расхождение.
Мы можем выдвинуть различные предположения относительно природы шума. Для нашего примера с равноускоренным движением логично было бы предположить, что неучтённые факторы (неровность дороги) в первую очередь влияют на ускорение. Этот подход применим ко многим структурам модели, где в векторе состояния присутствует переменная и несколько её производных по времени (например, положение и производные: скорость и ускорение). Матрица
выбирается таким образом, чтобы наибольшее значение соответствовало самому высокому порядку производной.
Так как же заполняется матрица Q?
Обычно используют модель-приближение. Рассмотрим на примере модели равноускоренного движения:
Модель непрерывного белого шума
Мы предполагаем, что ускорение постоянно на каждом шаге. Но из-за неровностей дороги ускорение, на самом деле, постоянно изменяется. Мы можем предположить, что изменение ускорения происходит под воздействием непрерывного белого шума с нулевым математическим ожиданием (т.е. усреднив все небольшие изменения ускорения за время движения робота мы получаем 0)
В этой модели матрица Q рассчитывается следующим образом
Мы формируем матрицу Qc в соответствии со структурой вектора состояния. Наивысшему порядку производной соответствует правый нижний элемент матрицы. В случае, если в векторе состояния несколько таких переменных, то каждая из них учитывается в матрице.
Для нашей модели равноускоренного движения матрица будет выглядеть так:
— спектральная плотность мощности белого шума
Подставляем матрицу процесса, соответствующую нашей модели:
После перемножения и интегрирования получаем:
Модель “кусочного” белого шума
Мы предполагаем, что ускорение на самом деле постоянно в течение каждого шага моделирования, но дискретно и независимо меняется между шагами. Выглядит очень похоже на предыдущую модель, но небольшая разница есть
— мощность шума
— наивысший порядок производной, используемой в модели (т.е. ускорение для вышеописанной модели)
В этой модели матрица
определяется следующим образом:
Из матрицы процесса F
берём столбец с наивысшим порядком производной
и подставляем в формулу. В итоге получаем:
Обе модели являются приближениями того, что происходит на самом деле в реальности. На практике, приходится экспериментировать и выяснять, какая модель подходит лучше в каждом отдельном случае. Плюсом второй модели является то, что мы оперируем дисперсией шума, с которой уже хорошо умеем работать.
Простейший подход
В некоторых случаях прибегают к грубому упрощению: устанавливают все элементы матрицы
равными нулю, за исключением элементов, соответствующих максимальным порядкам производных переменных состояния.
Действительно, если рассчитать
по одному из приведённых выше методов, при достаточно малых значениях
, значения элементов матрицы
оказываются очень близкими к нулю.
Т.е. для нашей модели равноускоренного движения можно взять матрицу
следующего вида:
И хотя такой подход не совсем корректен, его можно использовать в качестве первого приближения или для экспериментов. Без сомнения, не стоит выбирать матрицу
таким образом для любых важных задач без весомых причин.
Важное замечание
Во всех примерах выше используется вектор состояния
и может показаться, что во всех случаях дисперсия, соответствующая наивысшему порядок производной, находится в правом нижнем углу матрицы. Это не так.
Рассмотрим вектор состояния
Матрица
будет представлять собой блочную матрицу, где отдельные блоки 3х3 элементов будут соответствовать группам
и
. Остальные элементы матрицы будут равны нулю.
Дисперсия, соответствующая наивысшим порядкам производных
и
, будет находиться на 3-ей и 5-ой позициях на главной диагонали матрицы.
Однако, на практике нет никакого смысла перемешивать порядок переменных состояния таким образом, чтобы порядки производных шли не по очереди — это просто неудобно.
Пример кода
Нет смысла изобретать велосипед и писать свою собственную реализацию фильтра Калмана, когда существует множество готовых библиотек. Я выбрал язык python и библиотеку filterpy для примера.
Чтобы не загромождать пример, возьмем одномерный случай. Одномерный робот оборудован одномерным GPS, который определяет положение с некоторой погрешностью.
Моделирование данных датчиков
Начнём с равномерного движения:
Simulator.py
import numpy as np
import numpy.random
# Моделирование данных датчика
def simulateSensor(samplesCount, noiseSigma, dt):
# Шум с нормальным распределением. мат. ожидание = 0, среднеквадратичное отклонение = noiseSigma
noise = numpy.random.normal(loc = 0.0, scale = noiseSigma, size = samplesCount)
trajectory = np.zeros((3, samplesCount))
position = 0
velocity = 1.0
acceleration = 0.0
for i in range(1, samplesCount):
position = position + velocity * dt + (acceleration * dt ** 2) / 2.0
velocity = velocity + acceleration * dt
acceleration = acceleration
trajectory[0][i] = position
trajectory[1][i] = velocity
trajectory[2][i] = acceleration
measurement = trajectory[0] + noise
return trajectory, measurement # Истинное значение и данные "датчика" с шумом
Визуализируем результаты моделирования:
Код
import matplotlib.pyplot as plt
dt = 0.01
measurementSigma = 0.5
trajectory, measurement = simulateSensor(1000, measurementSigma, dt)
plt.title("Данные датчика")
plt.plot(measurement, label="Измерение", color="#99AAFF")
plt.plot(trajectory[0], label="Истинное значение", color="#FF6633")
plt.legend()
plt.show()
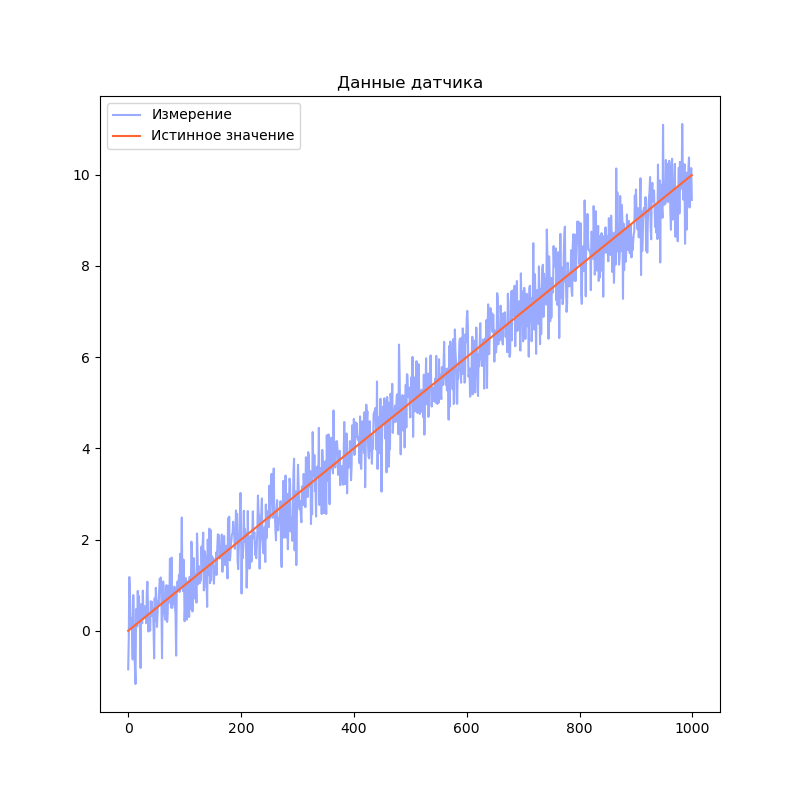
Реализация фильтра
Для начала выберем модель системы. Я решил взять 3 переменных состояния: положение, скорость и ускорение. В качестве модели процесса возьмем модель равноускоренного движения:
У нас единственный датчик, который напрямую измеряет положение. Поэтому модель наблюдения получается очень простой:
Мы предполагаем, что наш робот находится в точке 0 и имеет нулевые скорость и ускорение в начальный момент времени:
Однако, мы не уверены, что это именно так. Поэтому установим матрицу ковариации для начального состояния с большими значениями на главной диагонали:
Я воспользовался функцией библиотеки filterpy для расчёта ковариационной матрицы ошибки модели: filterpy.common.Q_discrete_white_noise. Эта функция использует модель непрерывного белого шума.
Код
import filterpy.kalman
import filterpy.common
import matplotlib.pyplot as plt
import numpy as np
import numpy.random
from Simulator import simulateSensor # моделирование датчиков
dt = 0.01 # Шаг времени
measurementSigma = 0.5 # Среднеквадратичное отклонение датчика
processNoise = 1e-4 # Погрешность модели
# Моделирование данных датчиков
trajectory, measurement = simulateSensor(1000, measurementSigma, dt)
# Создаём объект KalmanFilter
filter = filterpy.kalman.KalmanFilter(dim_x=3, # Размер вектора стостояния
dim_z=1) # Размер вектора измерений
# F - матрица процесса - размер dim_x на dim_x - 3х3
filter.F = np.array([ [1, dt, (dt**2)/2],
[0, 1.0, dt],
[0, 0, 1.0]])
# Матрица наблюдения - dim_z на dim_x - 1x3
filter.H = np.array([[1.0, 0.0, 0.0]])
# Ковариационная матрица ошибки модели
filter.Q = filterpy.common.Q_discrete_white_noise(dim=3, dt=dt, var=processNoiseVariance)
# Ковариационная матрица ошибки измерения - 1х1
filter.R = np.array([[measurementSigma*measurementSigma]])
# Начальное состояние.
filter.x = np.array([0.0, 0.0, 0.0])
# Ковариационная матрица для начального состояния
filter.P = np.array([[10.0, 0.0, 0.0],
[0.0, 10.0, 0.0],
[0.0, 0.0, 10.0]])
filteredState = []
stateCovarianceHistory = []
# Обработка данных
for i in range(0, len(measurement)):
z = [ measurement[i] ] # Вектор измерений
filter.predict() # Этап предсказания
filter.update(z) # Этап коррекции
filteredState.append(filter.x)
stateCovarianceHistory.append(filter.P)
filteredState = np.array(filteredState)
stateCovarianceHistory = np.array(stateCovarianceHistory)
# Визуализация
plt.title("Kalman filter (3rd order)")
plt.plot(measurement, label="Измерение", color="#99AAFF")
plt.plot(trajectory[0], label="Истинное значение", color="#FF6633")
plt.plot(filteredState[:, 0], label="Оценка фильтра", color="#224411")
plt.legend()
plt.show()
Бонус — сравнение различных порядков моделей
Сравним поведение фильтра с моделями разного порядка. Для начала, смоделируем более сложный сценарий поведения робота. Пусть робот находится в покое первые 20% времени, затем движется равномерно, а затем начинает двигаться равноускоренно:
Simulator.py
# Моделирование данных датчика
def simulateSensor(samplesCount, noiseSigma, dt):
# Шум с нормальным распределением. мат. ожидание = 0, среднеквадратичное отклонение = noiseSigma
noise = numpy.random.normal(loc = 0.0, scale = noiseSigma, size = samplesCount)
trajectory = np.zeros((3, samplesCount))
position = 0
velocity = 0.0
acceleration = 0.0
for i in range(1, samplesCount):
position = position + velocity * dt + (acceleration * dt ** 2) / 2.0
velocity = velocity + acceleration * dt
acceleration = acceleration
# Переход на равномерное движение
if(i == (int)(samplesCount * 0.2)):
velocity = 10.0
# Переход на равноускоренное движение
if (i == (int)(samplesCount * 0.6)):
acceleration = 10.0
trajectory[0][i] = position
trajectory[1][i] = velocity
trajectory[2][i] = acceleration
measurement = trajectory[0] + noise
return trajectory, measurement # Истинное значение и данные "датчика" с шумомВ предыдущем примере мы использовали модель, содержащую переменную (положение) и две производных её по времени (скорость и ускорение). Посмотрим, что будет, если избавиться от одной или обеих производных:
2-й порядок
# Создаём объект KalmanFilter
filter = filterpy.kalman.KalmanFilter(dim_x=2, # Размер вектора стостояния
dim_z=1) # Размер вектора измерений
# F - матрица процесса - размер dim_x на dim_x - 2х2
filter.F = np.array([ [1, dt],
[0, 1.0]])
# Матрица наблюдения - dim_z на dim_x - 1x2
filter.H = np.array([[1.0, 0.0]])
filter.Q = [[dt**2, dt],
[ dt, 1.0]] * processNoise
# Начальное состояние.
filter.x = np.array([0.0, 0.0])
# Ковариационная матрица для начального состояния
filter.P = np.array([[8.0, 0.0],
[0.0, 8.0]])1-й порядок
# Создаём объект KalmanFilter
filter = filterpy.kalman.KalmanFilter(dim_x=1, # Размер вектора стостояния
dim_z=1) # Размер вектора измерений
# F - матрица процесса - размер dim_x на dim_x - 1х1
filter.F = np.array([ [1.0]])
# Матрица наблюдения - dim_z на dim_x - 1x1
filter.H = np.array([[1.0]])
# Ковариационная матрица ошибки модели
filter.Q = processNoise
# Ковариационная матрица ошибки измерения - 1х1
filter.R = np.array([[measurementSigma*measurementSigma]])
# Начальное состояние.
filter.x = np.array([0.0])
# Ковариационная матрица для начального состояния
filter.P = np.array([[8.0]])
Сравним результаты:
На графиках сразу заметно, что модель первого порядка начинает отставать от истинного значения на участках равномерного движения и равноускоренного движения. Модель второго порядка успешно справляется с участком равномерного движения, но так же начинает отставать на участке равноускоренного движения. Модель третьего порядка справляется со всеми тремя участками.
Однако, это не означает что нужно использовать модели высокого порядка во всех случаях. В нашем примере, модель третьего порядка справляется с участком равномерного движения несколько хуже модели второго порядка, т.к. фильтр интерпретирует шум сенсора как изменение ускорения. Это приводит к колебанию оценки фильтра. Стоит подбирать порядок модели в соответствии с планируемыми режимами работы фильтра.
Нелинейные модели и фильтр Калмана
Почему фильтр Калмана не работает для нелинейных моделей и что делать
Всё дело в нормальном распределении. При применении линейных преобразованийк нормально распределенной случайной величине, результирующее распределение будет представлять собой нормальное распределение, или будет пропорциональным нормальному распределению. Именно на этом принципе и строится математика фильтра Калмана.
Есть несколько модификаций алгоритма, которые позволяют работать с нелинейными моделями.
Например:
Extended Kalman Filter (EKF) — расширенный фильтр Калмана. Этот подход строит линейное приближение модели на каждом шаге. Для этого требуется рассчитать матрицу вторых частных производных функции модели, что бывает весьма непросто. В некоторых случаях, аналитическое решение найти сложно или невозможно, и поэтому используют численные методы.
Unscented Kalman Filter (UKF). Этот подход строит приближение распределения получающегося после нелинейного преобразования при помощи сигма-точек. Преимуществом этого метода является то, что он не требует вычисления производных.
Мы рассмотрим именно Unscented Kalman Filter
Unscented Kalman Filter и почему он без запаха
Основная магия этого алгоритма заключается в методе, который строит приближение распределения плотности вероятности случайной величины после прохождения через нелинейное преобразование. Этот метод называется unscented transform — сложнопереводимое на русский язык название. Автор этого метода, Джеффри Ульман, не хотел, чтобы его разработку называли “Фильтр Ульмана”. Согласно интервью, он решил назвать так свой метод после того как увидел дезодорант без запаха (“unscented deodorant”) на столе в лаборатории, где он работал.
Этот метод достаточно точно строит приближение функции распределения случайной величины, но что более важно — он очень простой.
Для использования UKF не придётся реализовывать какие-либо дополнительные вычисления, за исключением моделей системы. В общем виде, нелинейная модель не может быть представлена в виде матрицы, поэтому мы заменяем матрицы
и
на функции
и
. Однако смысл этих моделей остаётся тем же.
Реализуем unscented Kalman filter для линейной модели из прошлого примера:
Код
import filterpy.kalman
import filterpy.common
import matplotlib.pyplot as plt
import numpy as np
import numpy.random
from Simulator import simulateSensor, CovarianceQ
dt = 0.01
measurementSigma = 0.5
processNoiseVariance = 1e-4
# Функция наблюдения - аналог матрицы наблюдения
# Преобразует вектор состояния x в вектор измерений z
def measurementFunction(x):
return np.array([x[0]])
# Функция процесса - аналог матрицы процесса
def stateTransitionFunction(x, dt):
newState = np.zeros(3)
newState[0] = x[0] + dt * x[1] + ( (dt**2)/2 ) * x[2]
newState[1] = x[1] + dt * x[2]
newState[2] = x[2]
return newState
trajectory, measurement = simulateSensor(1000, measurementSigma)
# Для unscented kalman filter необходимо выбрать алгоритм выбора сигма-точек
points = filterpy.kalman.JulierSigmaPoints(3, kappa=0)
# Создаём объект UnscentedKalmanFilter
filter = filterpy.kalman.UnscentedKalmanFilter(dim_x = 3,
dim_z = 1,
dt = dt,
hx = measurementFunction,
fx = stateTransitionFunction,
points = points)
# Ковариационная матрица ошибки модели
filter.Q = filterpy.common.Q_discrete_white_noise(dim=3, dt=dt, var=processNoiseVariance)
# Ковариационная матрица ошибки измерения - 1х1
filter.R = np.array([[measurementSigma*measurementSigma]])
# Начальное состояние.
filter.x = np.array([0.0, 0.0, 0.0])
# Ковариационная матрица для начального состояния
filter.P = np.array([[10.0, 0.0, 0.0],
[0.0, 10.0, 0.0],
[0.0, 0.0, 10.0]])
filteredState = []
stateCovarianceHistory = []
for i in range(0, len(measurement)):
z = [ measurement[i] ]
filter.predict()
filter.update(z)
filteredState.append(filter.x)
stateCovarianceHistory.append(filter.P)
filteredState = np.array(filteredState)
stateCovarianceHistory = np.array(stateCovarianceHistory)
plt.title("Unscented Kalman filter")
plt.plot(measurement, label="Измерение", color="#99AAFF")
plt.plot(trajectory[0], label="Истинное значение", color="#FF6633")
plt.plot(filteredState[:, 0], label="Оценка фильтра", color="#224411")
plt.legend()
plt.show()
Разница в коде минимальна. Мы заменили матрицы F и H на функции f(x) и h(x). Это позволяет использовать нелинейные модели системы и/или наблюдения:
# Функция наблюдения - аналог матрицы наблюдения
# Преобразует вектор состояния x в вектор измерений z
def measurementFunction(x):
return np.array([x[0]])
# Функция процесса - аналог матрицы процесса
def stateTransitionFunction(x, dt):
newState = np.zeros(3)
newState[0] = x[0] + dt * x[1] + ( (dt**2)/2 ) * x[2]
newState[1] = x[1] + dt * x[2]
newState[2] = x[2]
return newStateТакже, появилась строчка, устанавливающая алгоритм генерации сигма-точек
points = filterpy.kalman.JulierSigmaPoints(3, kappa=0)
Этот алгоритм определяет точность оценки распределения вероятности при прохождении через нелинейное преобразование. К сожалению, существуют только общие рекомендации относительно генерации сигма-точек. Поэтому для каждой отдельной задачи значения параметров алгоритма подбираются экспериментальным путём.
Ожидаемый результат — график оценки положения практически не отличается от обычного фильтра Калмана.
В этом примере используется линейная модель. Однако мы могли бы использовать нелинейные функции. Например, мы могли бы использовать следующую реализацию:
g = 9.8
# Вектор состояния - угол наклона
# Вектор измерений - ускорение вдоль осей X и Y
def measurementFunction(x):
measurement = np.zeros(2)
measurement[0] = math.sin(x[0]) * g
measurement[1] = math.cos(x[0]) * g
return measurementТакую модель измерений было бы невозможно использовать в случае с линейным фильтром Калмана
Вместо заключения
За рамками статьи остались теоретические основы фильтра Калмана. Однако объем материала по этой теме ошеломляет. Сложно выбрать хороший источник. Я бы хотел рекомендовать замечательную книгу от автора библиотеки filterpy Roger Labbe (на английском языке). В ней доступно описаны принципы работы алгоритма и сопутствующая теория. Книга представляет собой документ Jupyter notebook, который позволяет в интерактивном режиме экспериментировать с примерами.
Литература
> Roger Labbe — Kalman and Bayesian Filters in Python
> Wikipedia
В течение последних лет методы
нестационарной (во времени) фильтрации и сглаживания широко использовались в
различных задачах. Задачи фильтрации и сглаживания подразумевают оценивание сигнала
по наблюдениям, состоящим из аддитивной смеси сигнала и шума. Различие этих
двух задач состоит в моментах времени оценки сигнала и в интервалах времени
наблюдения. В задачах фильтрации оценку получают в конце интервала наблюдения,
при сглаживании сигнал оценивается в некоторые моменты внутри интервала
наблюдения. В гл. 7 и § 8.2, 8 3 эти проблемы основательно обсуждены.
Две трудности
препятствуют практическому использованию уравнений фильтрации и сглаживания –
это выбор математической модели вектора состояний оцениваемого сигнала и выбор
соответствующих ковариационных матриц сигнала и наблюдения, используемых при
решении этих задач. Желательно, чтобы модель сигнала описывала его достаточно
полно и в то же время была проста настолько, чтобы алгоритмы фильтрации
поддавались численному решению Матрицы ковариаций для сигнала и шума измерений
также желательно иметь такие, чтобы они соответствовали реальным процессам. К сожалению,
полное статистическое описание подобных процессов, как правило, невозможно.
Основным показателем расхождения
(модели и сигнала и матриц ковариаций является анализ чувствительности
ковариационной матрицы ошибок оценивания. Анализ чувствительности в задачах
фильтрации при больших ошибках был рассмотрен для случая дискретных наблюдений
в [60], [87], [173], [174], а для непрерывного времени в [175] Детальный анализ
чувствительности в задачах сглаживания дан в [82], [84] В этом разделе
построим алгоритмы, необходимые для анализа чувствительности в задачах
сглаживания и фильтрации. Эти алгоритмы будут получены для задач сглаживания в
фиксированной точке и сглаживания на временном фиксированном интервале. Отсюда
как частные случаи будут получены алгоритмы чувствительности задач фильтрации.
Анализ ошибок и чувствительности уравнений
фильтрации и сглаживания на фиксированном интервале при непрерывное времени. Рассмотрим несколько примеров,
иллюстрирующих применение разработанных ранее алгоритмов вычисления ковариационных
матриц ошибок оценивания и дифференциальных матричных функций чувствительности
в малом и большом.
Предположим,
что процесс описывается моделью
(8.178)
и
предположим, что измерения (наблюдения) могут быть представлены в линейной
форме
(8.179)
Будем считать также, что шумы
нормальные белые с нулевыми средними и матрицами интенсивностей и
соответственно. Как и в гл.
6, черта сверху указывает, что эти величины предполагаемые и могут не быть равными
их действительным значениям. Оптимальный фильтр, минимизирующий
среднеювадратическую ошибку
(8.180)
может быть описан уравнениями,
содержащимися в табл 7.4.
(8.181)
(8.182)
(8.182 а)
где — оптимальная оценка вектора состояний в
момент t при предполагаемых параметрах .
Дифференциальное
уравнение для оценки сглаживания на фиксированном интервале, полученное
минимизацией выражения
(8.183)
дано в табл. 8.3. Оценка вектора
состояний удовлетворяет уравнению
. (8.184)
Ковариационная
матрица ошибок также удовлетворяет некоторому дифференциальному уравнению, но
только в том случае, когда модель процесса и априорные данные достоверны. Это
дифференциальное уравнение имеет вид

Начальные условия
для (8.185)
вытекают из решения задачи фильтрации. Как уже известно, ур-ния (8.184) и (8 185) решаются в обратном времени
для всех и
решением является оценка сглаживания, а также соответствующая ковариационная
матрица ошибок В ажио отметить, что для того чтобы найти оценку сглаживания,
нет необходимости вычислять (ковариационную’ матрицу ошибок.
Указанные
алгоритмы оптимальной фильтрации и сглаживания обеспечивают минимальный риск
только в том случае, если модель совпадает с реальным процессом. Если же этого
не происходит, то матрица
ковариаций ошибок оценивания уже не является истинной (ковариационной матрицей
ошибок Таким образом, действительная ковариационная матрица ошибок может
выявлять ошибки, возникающие в результате использования некорректной модели.
Поэтому эта матрица играет первостепенную роль в любом анализе ошибок и
исследовании чувствительности алгоритмов фильтрации и сглаживания Как сейчас
будет показано, для действительной матрицы ковариаций можно получить
специальное дифференциальное уравнение
Сначала предположим,
что реальный физический процесс точно описывается уравнением
(8.187)
а вектор измерений равен
(8.188)
и величины и
являются точными. Теперь
найдем уравнения для действительной ошибки фильтрации
(8.189)
и ошибки сглаживания
(8.190)
Используя
введенные соотношения, можно получить дифференциальные уравнения, которым
должны удовлетворять ошибки оценивания. В случае фильтрации имеем
(8.191)
а для сглаживания
(8.192)
где
(8.193)
В ур-ниях (8 191) и (8.192) для
упрощения записи у некоторых функций не указан аргумент (время) Образовывая
новый вектор состояний, можно векторные дифференциальные уравнения для
действительной ошибки фильтрации сглаживания и ошибки модели свести в одно
дифференциальное уравнении. Этот вектор можно определить как

а новый входной вектор
. (8.195)
Тогда новое уравнение для вектора
состояний можно записать как
(8.196)


Теперь, внося
операцию усреднения под знак дифференциального оператора, можно найти
уравнение для «ковариационной матрицы процесса .
Дифференциальное
уравнение для имеет
следующее решение

где — переходная матрица состояний (8.199). Используя
(8.196) и (8.199), а также свойство дельта-функции, имеем


Для того чтобы
двигаться дальше, следует вычислить взаимные ковариационные члены в (8 200). В
следующем ниже примере, который читатель, интересующийся только конечным
результатом, может пропустить, показано, как вычисляются взаимные кавариации.
Пример
8.2. Взаимная ковариационная матрица в (8.200) может быть
выражена в такой форме, что для ее нахождения можно использовать только одио
дифференциальное уравнение Такая форма позволяет найти выражение для и упрощает
вычисление ковариационной матрицы действительных ошибок оценивания. Матрица может быть разбита
на подматрицы, поскольку

a может быть представлена следующим
образом

где
—
подматрица размером .
Подматрицы ур ния (1) определяются из векторного дифференциального
уравнения
(3)
где


Решение
ур-ния (3) может быть записано в виде

где
и
.
выражение
для можно
найти, усредняя произведение в правой части ур-ння (6) и и учитывая то, что при
начальном условии сигнал
и шум наблюдения независимы. Тогда имеем

Можно
упростить это выражение, если, поменяв местами операции интегрирования и
усреднения, выполнить интегрирование с учетом соотношения

и
свойств дельта-функции Результирующее уравнение можно представить в виде
(8)
Поскольку
есть
компонента вектора , то, следовательно, соотношения
верны.
Далее
.
Если эти выражения подставить в правую часть (1) и
результирующую матрицу умножить слева на правую часть ур-ния (2), то получим
(9)
где
(10)

здесь — подматрица
. Если матрицу перехода
обозначить через ,
то, как известно,.
Это свойство может быть использовано для редукции к выражениям следующего вида
(11)
Если
уравнение записано
в составной форме, то, как легко видеть, уравнение
(12)
Следовательно
.
Два
выражения из (10) еще содержат компоненты . Эти компоненты равны:
(13)
(14)
Их можно вычислить, если определить матрицу . Последнюю можно найти однако, только в случае, когда
иайдеиы дифференциальные уравнения для и
. Сначала возьмем производную от ур-иия (14). Это дает
(15)
Как
было показано выше, удовлетворяет
дифференциальному уравнению
.
Следовательно,
(16)
Но должно
удовлетворять дифференциальному уравнению , откуда видно, что
(17)
Следовательно,
если (16) и (17) подставить в (15), то получим
(18)
Аналогично можно найти дифференциальное уравнение и для , если сначала
взять производную от ур-ния (15) и проделать все указанные процедуры. Тогда
(19)
Начальные условия для этих уравнений имеют вид .
Тогда . Теперь все компоненты уравнения определены через
известные величины или величины, которые могут быть найдены решением ур ний
(15) и (19)
Расширяя матрицу ковариаций для получим

где В алгоритмах фильтрации действительная
ковариационная матрица ошибок оценивания определяется решением
дифференциального матричного уравнения

где удовлетворяет условию
(8.204)
а условию
(8.205)
Эти соотношения легко получить
методами, развитыми в § 3.5. Начальными условиями для предыдущих уравнений
являются
(8.206)
Если матрицы и
одинаковы для модели и
действительного физического процесса, то ур-ние (8.203) приобретает такой вид,
что для его решения не нужны ур-ния (8.204) и (8.205). Наконец, если и
то (8.203) переходит в
(8.183), являющееся строгим уравнением для ковариационной матрицы ошибок, если
модель и априорные данные верны.
Дополнительные дифференциальные
уравнения:



(8.210)
(8.211)
с начальными условиями:

должны быть решены в том случае,
если в задаче сглаживания необходимо найти ковариационную матрицу
действительных ошибок сглаживания. Вычисление по этим соотношениям следует
непосредственно и предоставляется читателю в качестве упражнения.
Два из предыдущих
дифференциальных уравнений могут быть исключены. Это можно сделать путем
следующего определения матриц:
(8.213)
(8.214)
Поскольку правые части этих тождеств удовлетворяют
дифференциальным уравнениям и начальным условиям левой часть, то указанные
тождества справедливы. Использование этих тождеств в ур-нии (8.207) дает

что является эквивалентным выражением для полученных
ранее соотношений (8.207) — (8.209). Для нахождения ковариационной матрицы
сглаживания ур-ния (8 210), (8.211) и (8.215) должны решаться в обратном
времени для всех .
Если модель действительно отражает реальный физический процесс, то ур-ние
(8.215) переходит в (8.186).
Если
ковариационная матрица действительной ошибки найдена, то матричные функции
чувствительности в большом определяются соотношениями:
(8.216)
для случаев фильтрации и сглаживания соответственно; — разность между значением параметра модели,
используемой для оценивания, и параметра действительного процесса. Величины и
вычисляются при действительном значении параметра
, a
и
— при
предполагаемом его значении .
Действительный риск как для фильтрации, так и для
сглаживания может быть записан в виде , где
— оценка сигнала в случае фильтрации
или сглаживания. Таким образом, по матрице ковариаций функции чувствительности
в большом мы можем определить чувствительность в большом функции риска из
соотношений:
(8.217)
Ecли различия между моделью и действительным процессом
невелики, то полезным оказывается анализ чувствительности дифференциального
типа или чувствительности в малом.Матрица чувствительности в малом для алгоритмов
фильтрации определяется как

где — истинный параметр, a
— предполагаемое его значение. Прямое вычисление полученного выше
выражения в задачах, связанных с чувствительностью в большом, «может оказаться
затруднительным, поавольку аналитические выражения для ковариационных матриц
обычно не существуют. Однако можно найти матричное дифференциальное уравнение
для матричной функции чувствительности, пригодное для изменений первого
порядка.
Если взять
частную производную от обеих частей ур-ния (8.203), поменять порядок
дифференцирования и множество параметров действительного процесса заменить на
множество параметров модели фильтрации, то получим дифференциальное уравнение
для чувствительности в малом, которое имеет вид
(8.219)
где

Начальным условием для этого выражения является
соотношение

Подобное начальное условие позволит нам вычислить
чувствительность действительной ковариационной матрицы и разности начальных
дисперсий модели и действительного процесса. Заметим, что матричная функция
чувствительности в малом может быть вычислена легче, чем чувствительность в
большом. Однако последняя более полезна.
Матричная функция
чувствительности
в малом позволяет найти еще две величины,
представляющие интерес. Можно найти матрицу разности между действительной
ковариационной матрицей и ковариационной матрицей моде

где — число компонент вектора
, a
—
дифференциальный оператор. Матрицу чувствительности в малом можно использовать
также для нахождения чувствительности в малом функции риска тем же методом,
который использовался при анализе чувствительности в большом. В результате
чувствительность функции риска равна
(8.223)
Полученное выше выражение для
чувствительности функции риска имеет такой же вид, который использовался в
[202].
Для задач сглаживания
также можно определить матричную функцию чувствительности

Так же, как и в случае фильтрации,
«можно получить для этой функции следующие дифференциальные уравнения:
(8.225)

где
(8.227)
Кроме того,

Начальными условиями являются:
(8.229)
Аналогичные результаты для анализа
чувствительности в малом можно получить и для алгоритмов сглаживания на
фикшрован ном интервале. В табл. 8.9 ,и 8.10 приведены алгоритмы анализа ошибок
и чувствительности для задач фильтрации и сглаживания на фиксированном
интервале в непрерывном времени. Используя ту же методику, можно получить и
дискретный аналог выведенных алгоритмов. Без вывода они даны в табл. 8.11 и
8.12.
Таблица 8.9. Алгоритм
анализа ошибок и чувствительности для фильтрации в непрерывном времени
|
Предполагаемая
|
|
Предполагаемая модель наблюдения
|
|
Алгоритм
|
|
Вычисление
|
|
Вычисление предполагаемой ковариационной матрицы ошибок
|
|
Предполагаемые априорные данные
|
|
Действительные априорные данные
|
|
Действительная
|
|
Вычисление действительной ковариационной матрицы ошибок
|
|
Вычисление моментов
|
|
Начальные условия
|
|
Вычисление
|
|
Вычисление
|
Таблица 8.10. Анализ ошибок и чувствительности алгоритмов
сглаживания на фиксированном интервале в непрерывном времени (алгоритмы
фильтрации табл. 8.9 составляют общую часть алгоритмов этой таблицы)
|
Алгоритм сглаживания
|
|
Предполагаемая ковариационная матрица ошибок
|
|
Действительная ошибка сглаживания
|
|
Действительная
|
|
Вычисление моментов |
|
Граничные условия
|
|
Вычисление чувствительности в
|
|
Вычисление
|
Таблица 8.11. Дискретные
алгоритмы анализа ошибок и чувствительности фильтрации
|
Предполагаемая
|
|
Предполагаемая
|
|
Алгоритм
|
|
Алгоритм
|
|
Вычисление
|
|
Предполагаемая
|
|
Предполагаемая |
|
Вычисление
|
|
Предполагаемые
|
|
Действительные
|
|
Вычисление
|
|
Вычисление
|
|
Вычисление
|
|
Вычисление
|
|
Вычисление
|
|
Начальные
|
|
Вычисление
|
|
Вычисление
|
Таблица 8.12. Дискретные алгоритмы анализа ошибок
и чувствительности для сглаживания на фиксированном интервале (алгоритмы
фильтрации табл. 8 11 составляют общую часть алгоритмов этой таблицы)
|
Алгоритм
|
|
Вычисление коэффициента усиления
|
|
Вычисление предполагаемой ковариационной матрицы ошибок
|
|
Вычисление
|
|
Вычисление действительной |
|
Вычисление
|
|
Начальные
|
|
Чувствительность
|
|
Чувствительность
|
Поскольку получение предыдущих результатов заняло много места и времени,
мы рассмотрим один простой пример, чтобы продемонстрировать разработанные идеи.
Более сложные примеры можно найти в [82, 84].
Пример 8.3. Рассмотрим
простой пример, в котором предположим, что модель процесса
описывается соотношениями:
где предполагаемая дисперсия шума
равна , а
начальная дисперсия состояния есть Эта модель может описывать движение
объекта на постоянной высоте, данные о которой снимаются с альтиметра и
искажены белым шумом.
Уравнение для ковариационной матрицы ошибок фильтрации имеет вид Решение этого
уравнения 
следовательно, коэффициент усиления 
Если
предположить, что параметры и
являются
действительными, то ур-ние (8.203) для действительной ковариационной матрицы
ошибок примет вид
где удовлетворяет уравнению
и . Ho
есть
дисперсия состояния и . Начальные условия
. Решение приведенных
уравнений дает:
Непосредственное
использование (8.216) дает выражение для чувствительности в большом алгоритмов
фильтрации:
Дифференциальные уравнения
матричных функций чувствительности в малом можно получить из (8.219) н (8.220)
в виде
где соответствует
,
или
,
при этом
с начальными условиями . Эти дифференциальные
уравнения первого порядка легко решаются:
Эти соотношения можно
также получить из действительной ковариационной матрицы, используя определение
чувствительности.
На рис. 8.1 и 8.2
приведены для данного примера функции чувствительности в большом и в малом.
Здесь выражения для чувствительностей в большом и малом одинаковы для исходной
и вычисленной ковариационной матриц.
Рис. 8.1. Функции
чувствительности дисперсии ошибки в зависимости от изменений начальной дисперсии
ошибки и дисперсии измерений: фильтрация; ______ — сглаживание;
Рис. 8.2. Функции
чувствительности при изменении константы измерений:
Зависимость чувствительности от параметра приведена на рис. 8.3,
иллюстрирующем различие между чувствительностью в малом и большом.
В этом примере ковариационная
матрица ошибок сглаживания при конечном условии
. Отсюда следует, что
ковариационная матрица ошибок не зависит от времени и получается из (8.203) для
момента времени .
Значения чувствительностей также постоянны и равны чувствительностям для
фильтра в момент .
Пунктирные кривые на рис. 8,1 представляют две функции чувствительности для
задачи сглаживания.
Рис.
8.3. Сравнение чувствительности в большом и малом при изменении константы
измерений.
«Вычисляемая»
дисперсия ошибки фильтрации всегда уменьшается при увеличении времени
наблюдения. Для численного анализа выражений для действительной дисперсии
положим .
Тогда «вычисленная» дисперсия ошибки равна , а следовательно, «вычисленная» дисперсия
сглаживания и,
как и следовало ожидать, от не зависит. В этом случае действительная
дисперсия ошибки фильтрации определится выражением 
, то это выражение совпадает с
выражением для минимума дисперсии ошибки .
Интересно
отметить, что действительная ошибка (дисперсия) не достигает нуля при больших t до тех пор, пока не станет равным
нулю, что означает отсутствие ошибки в модели наблюдения. Для больших приближенно можно
считать, что действительная дисперсия ошибки равна . На рис. 8.4 приведены графики
действительных дисперсий ошибок и «вычисленных» дисперсий для случая, когда
априорная статистика задана верно .
Если
модель наблюдения не содержит ошибок, , то дисперсия ошибки
. Если отношение
, то имеем минимум дисперсии
ошибки, соответствующий .
Анализ
ошибок и чувствительности линейных алгоритмов сглаживания в фиксированной
точке.
Предположим,
что непрерывный процесс может быть задан векторным дифференциальным уравнением
(8.178), а модель наблюдения линейна [см. (8.179)]
Рис. 8.4. Дисперсия ошибки фильтрации при разных ,
;
Оценка
сглаживания в фиксированной точке удовлетворяет дифференциальному уравнению
(8.230)
где
, (8.231)
а — матрица (обозначенная
так для удобства), которая удовлетворяет уравнению
(8.232)
Начальным
условием служит оценка фильтрации в момент
и
. (8.233)
Ковариационная
матрица ошибки оценивания может быть получена из уравнения
(8.234)
Эта матрица ошибок удовлетворяет
ур-нию (8.234) только в том случае,
если модель и ее априорные характеристики совпадают с действительным процессом
и его характеристиками. На практике обычно это условие не выполняется.
Поскольку действительная ковариационная матрица ошибок оценивания позволяет
выявить ошибки при использовании неадэкватной модели, она играет основную роль в анализе ошибок и чувствительности алгоритмов сглаживания
В непрерывном времени
действительная ковариационная матрица вычисляется следующим образом. Сначала
постулируем модель для действительного процесса в том же виде, что и в ур-ниях
(8.178), (8.179), за исключением того, что не ставим черты сверху. Далее
находим дифференциальное уравнение для действительной ошибки оценивания
подстановкой соотношений:
(8.235)
в (8.230), где
действительные ошибки оценок фильтрации и сглаживания определены выражениями:
(8.236)
Тогда результирующее
дифференциальное уравнение для ошибки оценивания имеет вид
(8.237)
Для простоты обозначений
зависимость матриц от временного параметра не указана; определяется как разность
между и
. Следующий шаг
состоит в образовании нового дифференциального уравнения для вектора приращений
с использованием предыдущего уравнения, уравнения для действительной
ошибки оценивания в случае фильтрации, которую мы рассмотрели в предыдущем
параграфе, и дифференциального уравнения для действительного процесса:
, (8.238)
где

Матрицы и
были определены в предыдущем
параграфе. Далее выпишем решение ур-ния (8.238):

где удовлетворяет матричному
дифференциальному уравнению
. (8.241)
Затем необходимо усреднить
произведение вектора на транспонированный вектор
. Тогда получим

В последнем выражении два средних
(внутренних) интеграла равны нулю, так как среднее в подынтегральных выражениях
для всех , больших
равно нулю.
Среднее в последнем члене (8.242) можно представить в виде

Если взять внутренний
интеграл в последнем слагаемом (8.242), то, используя свойства дельта-функции,
можно получить

Члены этого уравнения
содержат искомые ковариационные матрицы. Однако численное решение этого
уравнения затруднительно. Эти трудности можно обойти, если найти дифференциальное
уравнение для .
Его можно получить следующим образом. Сначала берется производная от обеих
частей ур-ния (8.244). Далее в полученное уравнение подставляется ур-ние
(8.241). Наконец используя (8.240), находим
(8.245)
По определению
имеем

где
(8.247)
а определено соотношением (8.204).
Дифференциальное уравнение для действительной ковариационной матрицы ошибки
сглаживания имеет вид
(8.248)
где и
удовлетворяют уравнениям:
(8.249)
(8.250)
Начальными условиями являются:

Дифференциальные уравнения для ,
и
даны в предыдущем разделе
совместно с результатами фильтрации.
Как только действительные
ковариационные матрицы ошибок найдены, матричные функции чувствительности в
большом можно определить из соотношения
(8.252)
По определению есть разность между
параметрами действительного процесса и параметрами модели, используемой для
нахождения оценки сглаживания. Так же, как и в случае сглаживания на
фиксированном интервале, функции чувствительности могут быть использованы для
нахождения чувствительности в большом функции риска.
Дифференциальная матричная
функция чувствительности (чувствительность в малом) ‘находится из выражения

Символом обозначено множество
параметров действительного процесса; — соответствующее множество параметров
модели оценивания;
-й элемент множества
. Если разности между
истинными параметрами и параметрами модели малы, то функции чувствительности в
малом могут быть использованы для нахождения матрицы разностей между
ковариационными матрицами модели и процесса. Эта матрица определяется как 
— число
параметров множества , а
— дифференциал
-го параметра множества
.
Прямое вычисление (8.254) если
не невозможно, то затруднительно, потому что почти не существует аналитических
решений для действительных матриц ковариаций. Если взять частную производную от
обеих частей ур-ния (8.248), то можно найти дифференциальные уравнения,
решением которых является искомая функция чувствительности. Если после этого поменять
порядок дифференцирования, то получим

где и
удовлетворяют уравнениям:


В ур-нии (8 255) член появляется в
результате анализа чувствительности в малом задачи фильтрации, а ур-ние (8.219)
представляет алгоритм для его вычисления. Для указанных трех уравнений
начальными условиями являются:
(2.857)
Пример 8.4. Рассмотрим упрощенную
модель, в которой принимаемый амплитудно модулированный сигнал аддитивно
взаимодействует с белым шумом. Пусть полезный сигнал имеет вид где
и
— нормальные случайные величины
с нулевыми средними и дисперсиями и
соответственно. Этот сигнал модулирует
несущую, так что наблюдаемое колебание имеет вид Здесь предполагается, что
— белый нормальный шум с нулевым
средним и интенсивностью . Необходимо оценить сигнал в момент t по наблюдаемой реализации на
интервале от нуля до . Задачу можно решить методом сглаживания
в фиксированной точке, формулируя ее в терминах состояний. Такое
переопределение задачи приводит в конечном счете к векторному дифференциальному
уравнению.
где элемент есть сигнал
. Вектор измерений
равен
На рис. 8.5-8.7 представлены
результаты некоторых вычислений. Здесь дисперсии величин и
равны
единице, а дисперсия шума равна 0,25. Частоты сигнала и несущей равны 6,28 и
62,8 1/с соответственно. В этих предположениях дисперсия ошибок иллюстрируется
рис. 8.5.
Рис. 8.5. Дисперсия
ошибок оценки сигнала с момента 0,2 с для различных значений дисперсии шума
наблюдений: 1 — действительная дисперсия; 2 — предполагаемая дисперсия
Рис. 8.6.
Чувствительность дисперсии ошибки оценки сигнала к 10%-ному изменению несущей
частоты в зависимости от времени наблюдения
Рис. 8 7. Дисперсия
ошибки оценки сигнала для различных значений несущей частоты: 1— действительная
дисперсия; 2 — предполагаемая дисперсия
Здесь дисперсия ошибки предсказания
сигнала в момент 0,2 с [вычисленная по (8.248)] приведена как функция времени,
при котором появляются иовые наблюдения. На рис 8 6 представлен график функции
чувствительности в большом дисперсии ошибки оценки для случая, когда истинная
частота сигнала на 10% выше предполагаемой. Влияние ошибки в выборе частоты
несущей показано на рис. 8.7.
Алгоритмы анализа для
сглаживания в фиксированной точке в непрерывном времени сведены в табл. 8ЛЗ, а
для дискретного случая в табл. 8.14.
Таблица 8.13. Алгоритмы анализа ошибок и
чувствительности для сглаживания в фиксированной точке в непрерывном времени (алгоритмы фильтрации табл. 8.9 составляют
общую часть алгоритмов этой таблицы)
|
Алгоритмы
|
|
Вычисление
|
|
Вычисление
|
|
Вычисление
|
|
Действительная
|
|
Действительная
|
|
Вычисление
|
|
Начальные
|
|
Чувствительность
|
|
Чувствительность
[см |
Таблица 8.14.Алгоритмы анализа ошибок и
чувствительности алгоритмов сглаживания в фиксированной точке в дискретном
времени (алгоритмы фильтрации табл 8.11 составляют общую часть алгоритмов этой
таблицы)
|
Алгоритм
|
|
Вычисление
|
|
Вычисление
|
|
Вычисление
|
|
Вычисление
|
|
Вычисление
|
|
Начальные
|
|
Чувствительность
|
|
Чувствительность
Дифференциальное |
Вычисление соответствующих
алгоритмов для сглаживания с фиксированной задержкой мы оставляем в качестве
упражнения для заинтересованного читателя. Теперь основное внимание будет
уделено вычислению границ ошибок для ковариационных матриц ошибок фильтрации и
сглаживания.
Границы ошибок. Нишимурой [175] были
найдены границы дисперсии ошибок при использовании алгоритма фильтрации
Калмана — Бьюси. Основной результат содержится в следующей теореме:
если и
для всех
из интервала
, то
(8.258)
для всех . Элементы
и
являются диагональными
элементами матриц и
соответственно.
Знак означает,
что матрица левее этого знака положительно полуопределена.
Следовательно, если приведенные
выше соотношения выполняются, то существует верхняя грань дисперсии ошибки
сглаживания в точке даже в том случае, если дисперсия истинного процесса
‘неизвестна. Теорема, данная выше, применима только к непрерывным уравнениям
сглаживания в точке. Однако, поскольку время произвольно и может принимать любые
значения внутри интервала то результат этой теоремы оказывается справедливым
и для уравнений сглаживания на заданном интервале и с фиксированной задержкой.
Конечно, можно установить соответствующие условия и для дискретных алгоритмов
сглаживания.
Проверить указанную
теорему можно, выписав дифференциальные уравнения, которым должны удовлетворять
действительные ковариационные матрицы. Для алгоритмов фильтрации— это ур-ние (8.203) при условии, что :
(8.259)
где и
матрицы размера
и
, определяемые моделью (8.178),
а -мерный
вектор измерения ,
где матрица размера
, а
— матрица
коэффициентов усиления фильтра Калмана размера . Предполагается, что реальный процесс
представляется той же самой моделью, за исключением того, что процессы и
заменяются
на и
.
В такой ситуации, когда
единственным отличием модели оценки от реального процесса является различие в
ковариационных матрицах, (8.248) сводится к уравнению
(8.260)
где . Матрицы
и
удовлетворяют ур-ниям (8.249)
и (8.232). Поскольку модели сообщения и наблюдения не содержат ошибок, то из (8.250) равно
нулю. Определим

а затем для найдем дифференциальное уравнение
(8.262)
где


Далее, если определено как
, то
,
,
и можно найти уравнение для
, представляющей разность
между матрицами и
:
(8.264)
Решение этого уравнения можно записать в виде

где
(8.266)
Теперь, если и
для всех
из интервала наблюдения
, то
и, следовательно,
матрица, представляющая интегральный член ур-ния (8.265), должна быть
положительно полуопределена. Если , то
и
тогда первый член в правой части (8.265) тоже положительно полуопределенная
матрица. Отсюда следует, что матрица тоже положительно полуопределена. Но
верхние диагональные элементы откуда следуют ур-ние (8.178) и
справедливость указанной теоремы.
Пример 8.5. Предположим,
что необходимо передать сигнал известной частоты с неизвестной амплитудой и
фазой. Принимаемый сигнал может быть записан в виде,
экспоненциально-коррелированный шум, а
белый шум. Шум
моделирует случайный
процесс, возникающий при передаче, а
шум
приемника. Мы хотим оценить сигнал на некотором интервале времени Запишем
сигнал в виде Модель
состояний для такого сигнала и аддитивного шума можно определить следующим
образом:
здесь представляет записанный в измененном
виде сигнал, есть
, а
.
Оптимальная оценка сигнала не обязательно
является оптимальной оценкой амплитуды и фазы, но обязательно является
оптимальной оценкой мгновенных значений сигнала. Предполагаемые параметры
модели состояний и наилучшие оценки априорных дисперсий равны,
,
и
. В этом примере
предполагается, что сигнал не связан с шумом. Для получения оценок из ур-ния
(8.58) используются параметры, значения которых равны четырехкратным значениям
тех параметров, которые были выбраны в качестве априорных дисперсий.
Рис. 8.8. Дисперсии ошибок для
различных ;
1 – предполагаемая, 2,3,4 – действительная:
фильтрация, ______
сглаживание; —
;
;
Рис. 8 9 Дисперсия
ошибки оценки при различных :
фильтрация, ______ сглаживание
На рис. 8.8 приведены графики вычисленной и истинной
дисперсии ошибок оценки сигнала (сигнала ) для случаев оптимальной фильтрации и
сглаживания на фиксированном интервале. Три нижние кривые получены варьированием
начального значения дисперсии действительного процесса На рис. 8.9 представлены
графики действительной дисперсии ошибок оценки сигнала для различных значений
дисперсий белого шума В этом примере дисперсия ошибки оценки сигнала почти не
зависит от изменений действительной дисперсии процесса , поэтому мы не приводим эту
зависимость. Значительные ошибки при выборе априорных дисперсий и
вызывают существенные
увеличения дисперсий ошибки оценивания реального сигнала, которые намного
больше оптимального значения дисперсии. Но в силу сформулированной выше теоремы
действительные дисперсии все равно находятся ниже уровня, определяемого верхней
гранью вычисленных дисперсий ошибок оценивания.
From Wikipedia, the free encyclopedia
In statistics, sometimes the covariance matrix of a multivariate random variable is not known but has to be estimated. Estimation of covariance matrices then deals with the question of how to approximate the actual covariance matrix on the basis of a sample from the multivariate distribution. Simple cases, where observations are complete, can be dealt with by using the sample covariance matrix. The sample covariance matrix (SCM) is an unbiased and efficient estimator of the covariance matrix if the space of covariance matrices is viewed as an extrinsic convex cone in Rp×p; however, measured using the intrinsic geometry of positive-definite matrices, the SCM is a biased and inefficient estimator.[1] In addition, if the random variable has a normal distribution, the sample covariance matrix has a Wishart distribution and a slightly differently scaled version of it is the maximum likelihood estimate. Cases involving missing data, heteroscedasticity, or autocorrelated residuals require deeper considerations. Another issue is the robustness to outliers, to which sample covariance matrices are highly sensitive.[2][3][4]
Statistical analyses of multivariate data often involve exploratory studies of the way in which the variables change in relation to one another and this may be followed up by explicit statistical models involving the covariance matrix of the variables. Thus the estimation of covariance matrices directly from observational data plays two roles:
-
- to provide initial estimates that can be used to study the inter-relationships;
- to provide sample estimates that can be used for model checking.
Estimates of covariance matrices are required at the initial stages of principal component analysis and factor analysis, and are also involved in versions of regression analysis that treat the dependent variables in a data-set, jointly with the independent variable as the outcome of a random sample.
Estimation in a general context[edit]
Given a sample consisting of n independent observations x1,…, xn of a p-dimensional random vector X ∈ Rp×1 (a p×1 column-vector), an unbiased estimator of the (p×p) covariance matrix
is the sample covariance matrix
where 
is the sample mean.
This is true regardless of the distribution of the random variable X, provided of course that the theoretical means and covariances exist. The reason for the factor n − 1 rather than n is essentially the same as the reason for the same factor appearing in unbiased estimates of sample variances and sample covariances, which relates to the fact that the mean is not known and is replaced by the sample mean (see Bessel’s correction).
In cases where the distribution of the random variable X is known to be within a certain family of distributions, other estimates may be derived on the basis of that assumption. A well-known instance is when the random variable X is normally distributed: in this case the maximum likelihood estimator of the covariance matrix is slightly different from the unbiased estimate, and is given by
A derivation of this result is given below. Clearly, the difference between the unbiased estimator and the maximum likelihood estimator diminishes for large n.
In the general case, the unbiased estimate of the covariance matrix provides an acceptable estimate when the data vectors in the observed data set are all complete: that is they contain no missing elements. One approach to estimating the covariance matrix is to treat the estimation of each variance or pairwise covariance separately, and to use all the observations for which both variables have valid values. Assuming the missing data are missing at random this results in an estimate for the covariance matrix which is unbiased. However, for many applications this estimate may not be acceptable because the estimated covariance matrix is not guaranteed to be positive semi-definite. This could lead to estimated correlations having absolute values which are greater than one, and/or a non-invertible covariance matrix.
When estimating the cross-covariance of a pair of signals that are wide-sense stationary, missing samples do not need be random (e.g., sub-sampling by an arbitrary factor is valid).[citation needed]
Maximum-likelihood estimation for the multivariate normal distribution[edit]
A random vector X ∈ Rp (a p×1 «column vector») has a multivariate normal distribution with a nonsingular covariance matrix Σ precisely if Σ ∈ Rp × p is a positive-definite matrix and the probability density function of X is
where μ ∈ Rp×1 is the expected value of X. The covariance matrix Σ is the multidimensional analog of what in one dimension would be the variance, and
normalizes the density 
Suppose now that X1, …, Xn are independent and identically distributed samples from the distribution above. Based on the observed values x1, …, xn of this sample, we wish to estimate Σ.
First steps[edit]
The likelihood function is:
It is fairly readily shown that the maximum-likelihood estimate of the mean vector μ is the «sample mean» vector:
See the section on estimation in the article on the normal distribution for details; the process here is similar.
Since the estimate 
and then seek the value of Σ that maximizes the likelihood of the data (in practice it is easier to work with log 
The trace of a 1 × 1 matrix[edit]
Now we come to the first surprising step: regard the scalar 
where


Using the spectral theorem[edit]
It follows from the spectral theorem of linear algebra that a positive-definite symmetric matrix S has a unique positive-definite symmetric square root S1/2. We can again use the «cyclic property» of the trace to write
Let B = S1/2 Σ −1 S1/2. Then the expression above becomes
The positive-definite matrix B can be diagonalized, and then the problem of finding the value of B that maximizes
Since the trace of a square matrix equals the sum of eigenvalues («trace and eigenvalues»), the equation reduces to the problem of finding the eigenvalues λ1, …, λp that maximize
This is just a calculus problem and we get λi = n for all i. Thus, assume Q is the matrix of eigen vectors, then
i.e., n times the p×p identity matrix.
Concluding steps[edit]
Finally we get
i.e., the p×p «sample covariance matrix»
is the maximum-likelihood estimator of the «population covariance matrix» Σ. At this point we are using a capital X rather than a lower-case x because we are thinking of it «as an estimator rather than as an estimate», i.e., as something random whose probability distribution we could profit by knowing. The random matrix S can be shown to have a Wishart distribution with n − 1 degrees of freedom.[5] That is:
Alternative derivation[edit]
An alternative derivation of the maximum likelihood estimator can be performed via matrix calculus formulae (see also differential of a determinant and differential of the inverse matrix). It also verifies the aforementioned fact about the maximum likelihood estimate of the mean. Re-write the likelihood in the log form using the trace trick:
The differential of this log-likelihood is
It naturally breaks down into the part related to the estimation of the mean, and to the part related to the estimation of the variance. The first order condition for maximum, 



which leads to the maximum likelihood estimator
This lets us simplify
as defined above. Then the terms involving 

The first order condition 


which of course coincides with the canonical derivation given earlier.
Dwyer[6] points out that decomposition into two terms such as appears above is «unnecessary» and derives the estimator in two lines of working. Note that it may be not trivial to show that such derived estimator is the unique global maximizer for likelihood function.
Intrinsic covariance matrix estimation[edit]
Intrinsic expectation[edit]
Given a sample of n independent observations x1,…, xn of a p-dimensional zero-mean Gaussian random variable X with covariance R, the maximum likelihood estimator of R is given by
The parameter 
![{\displaystyle \mathrm {E} [{\hat {\mathbf {R} }}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7d2b38d1494210ca33b439b935b3432a7b21712)


where
are the exponential map and inverse exponential map, respectively, «exp» and «log» denote the ordinary matrix exponential and matrix logarithm, and E[·] is the ordinary expectation operator defined on a vector space, in this case the tangent space of the manifold.[1]
Bias of the sample covariance matrix[edit]
The intrinsic bias vector field of the SCM estimator 
The intrinsic estimator bias is then given by 
For complex Gaussian random variables, this bias vector field can be shown[1] to equal
where
and ψ(·) is the digamma function. The intrinsic bias of the sample covariance matrix equals
and the SCM is asymptotically unbiased as n → ∞.
Similarly, the intrinsic inefficiency of the sample covariance matrix depends upon the Riemannian curvature of the space of positive-definite matrices.
Shrinkage estimation[edit]
If the sample size n is small and the number of considered variables p is large, the above empirical estimators of covariance and correlation are very unstable. Specifically, it is possible to furnish estimators that improve considerably upon the maximum likelihood estimate in terms of mean squared error. Moreover, for n < p (the number of observations is less than the number of random variables) the empirical estimate of the covariance matrix becomes singular, i.e. it cannot be inverted to compute the precision matrix.
As an alternative, many methods have been suggested to improve the estimation of the covariance matrix. All of these approaches rely on the concept of shrinkage. This is implicit in Bayesian methods and in penalized maximum likelihood methods and explicit in the Stein-type shrinkage approach.
A simple version of a shrinkage estimator of the covariance matrix is represented by the Ledoit-Wolf shrinkage estimator.[7][8][9][10] One considers a convex combination of the empirical estimator (



Various shrinkage targets have been proposed:
- the identity matrix, scaled by the average sample variance;
- the single-index model;
- the constant-correlation model, where the sample variances are preserved, but all pairwise correlation coefficients are assumed to be equal to one another;
- the two-parameter matrix, where all variances are identical, and all covariances are identical to one another (although not identical to the variances);
- the diagonal matrix containing sample variances on the diagonal and zeros everywhere else;
- the identity matrix.[8]
The shrinkage estimator can be generalized to a multi-target shrinkage estimator that utilizes several targets simultaneously.[11] Software for computing a covariance shrinkage estimator is available in R (packages corpcor[12] and ShrinkCovMat[13]), in Python (scikit-learn library [1]), and in MATLAB.[14]
See also[edit]
- Propagation of uncertainty
- Sample mean and sample covariance
- Variance components
References[edit]
- ^ a b c Smith, Steven Thomas (May 2005). «Covariance, Subspace, and Intrinsic Cramér–Rao Bounds». IEEE Trans. Signal Process. 53 (5): 1610–1630. doi:10.1109/TSP.2005.845428. S2CID 2751194.
- ^ Robust Statistics, Peter J. Huber, Wiley, 1981 (republished in paperback, 2004)
- ^ «Modern applied statistics with S», William N. Venables, Brian D. Ripley, Springer, 2002, ISBN 0-387-95457-0, ISBN 978-0-387-95457-8, page 336
- ^ Devlin, Susan J.; Gnanadesikan, R.; Kettenring, J. R. (1975). «Robust Estimation and Outlier Detection with Correlation Coefficients». Biometrika. 62 (3): 531–545. doi:10.1093/biomet/62.3.531.
- ^
K.V. Mardia, J.T. Kent, and J.M. Bibby (1979) Multivariate Analysis, Academic Press. - ^ Dwyer, Paul S. (June 1967). «Some applications of matrix derivatives in multivariate analysis». Journal of the American Statistical Association. 62 (318): 607–625. doi:10.2307/2283988. JSTOR 2283988.
- ^ O. Ledoit and M. Wolf (2004a) «A well-conditioned estimator for large-dimensional covariance matrices Archived 2014-12-05 at the Wayback Machine» Journal of Multivariate Analysis 88 (2): 365—411.
- ^ a b A. Touloumis (2015) «Nonparametric Stein-type shrinkage covariance matrix estimators in high-dimensional settings» Computational Statistics & Data Analysis 83: 251—261.
- ^ O. Ledoit and M. Wolf (2003) «Improved estimation of the covariance matrix of stock returns with an application to portofolio selection Archived 2014-12-05 at the Wayback Machine» Journal of Empirical Finance 10 (5): 603—621.
- ^ O. Ledoit and M. Wolf (2004b) «Honey, I shrunk the sample covariance matrix Archived 2014-12-05 at the Wayback Machine» The Journal of Portfolio Management 30 (4): 110—119.
- ^
T. Lancewicki and M. Aladjem (2014) «Multi-Target Shrinkage Estimation for Covariance Matrices», IEEE Transactions on Signal Processing, Volume: 62, Issue 24, pages: 6380-6390. - ^ corpcor: Efficient Estimation of Covariance and (Partial) Correlation, CRAN, 16 September 2021
{{citation}}: CS1 maint: location missing publisher (link) - ^ ShrinkCovMat: Shrinkage Covariance Matrix Estimators, CRAN, 30 July 2019
{{citation}}: CS1 maint: location missing publisher (link) - ^ MATLAB code for shrinkage targets: scaled identity, single-index model, constant-correlation model, two-parameter matrix, and diagonal matrix.

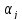
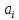
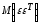
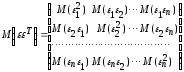
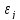
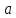
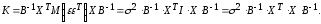
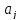
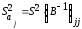
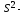
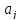
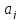
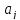
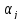
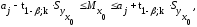
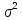
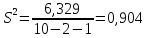
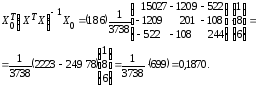
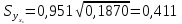
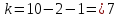
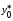
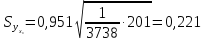
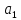
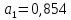
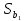
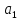
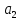
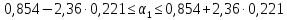
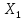
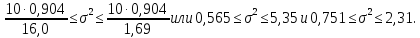


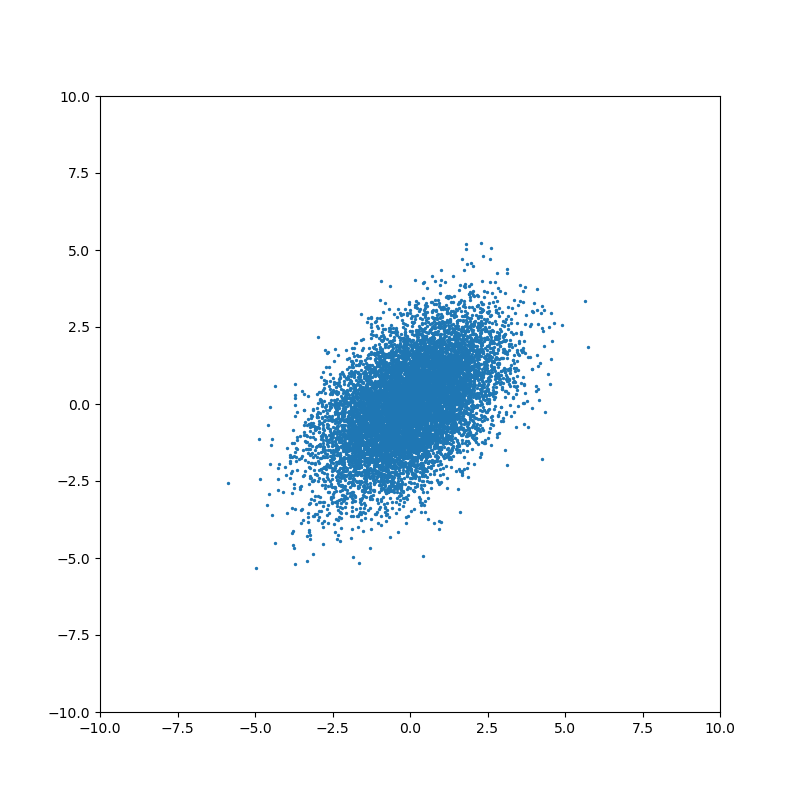
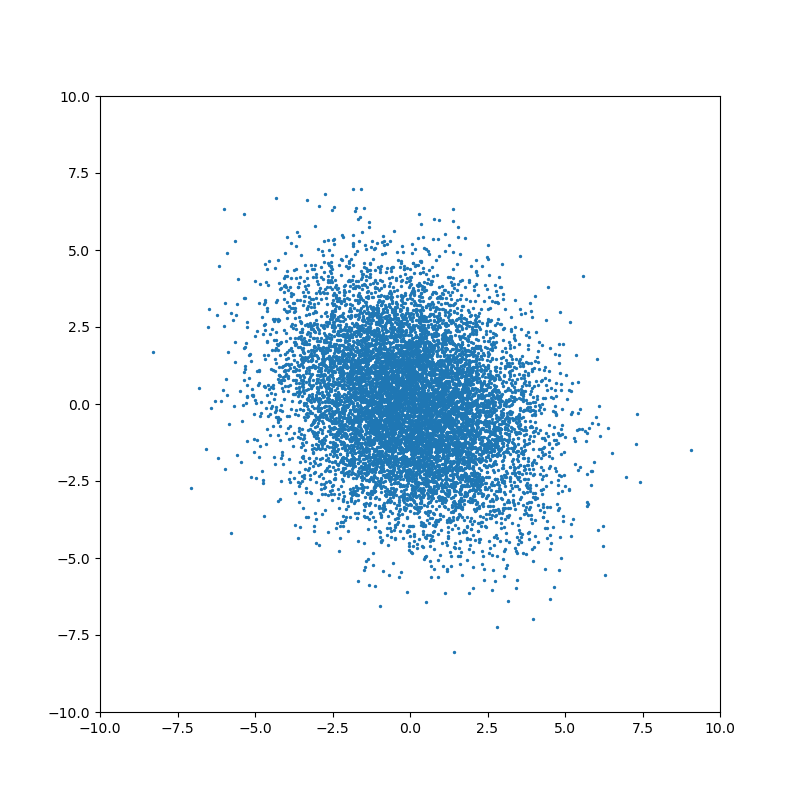
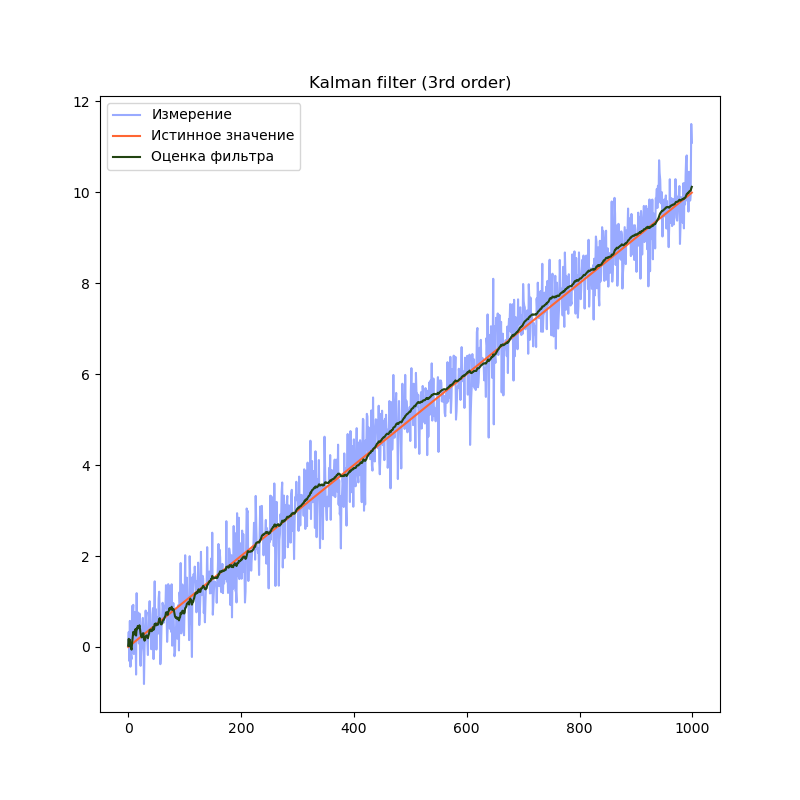
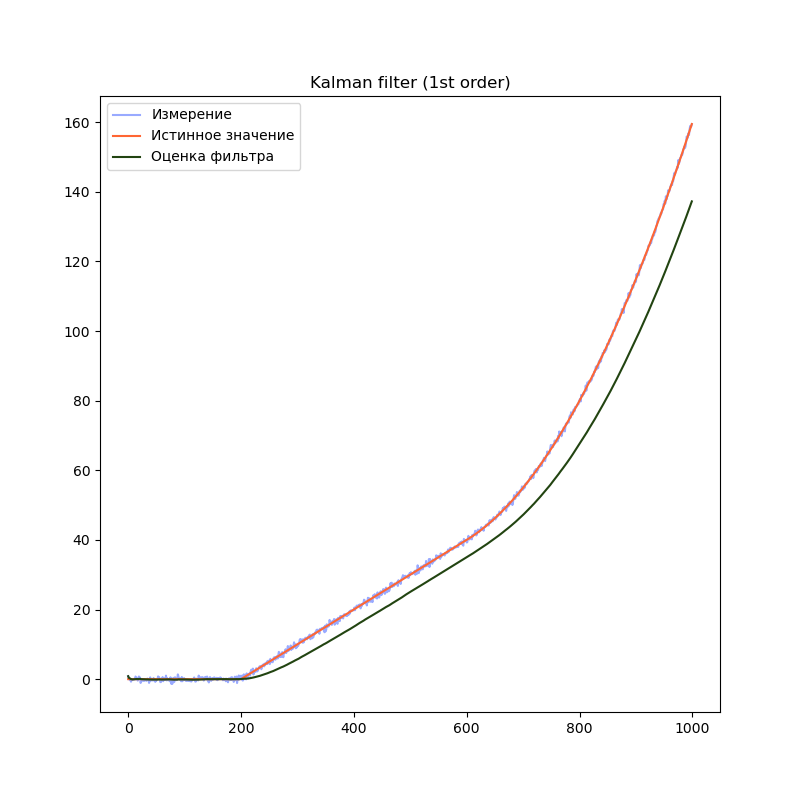
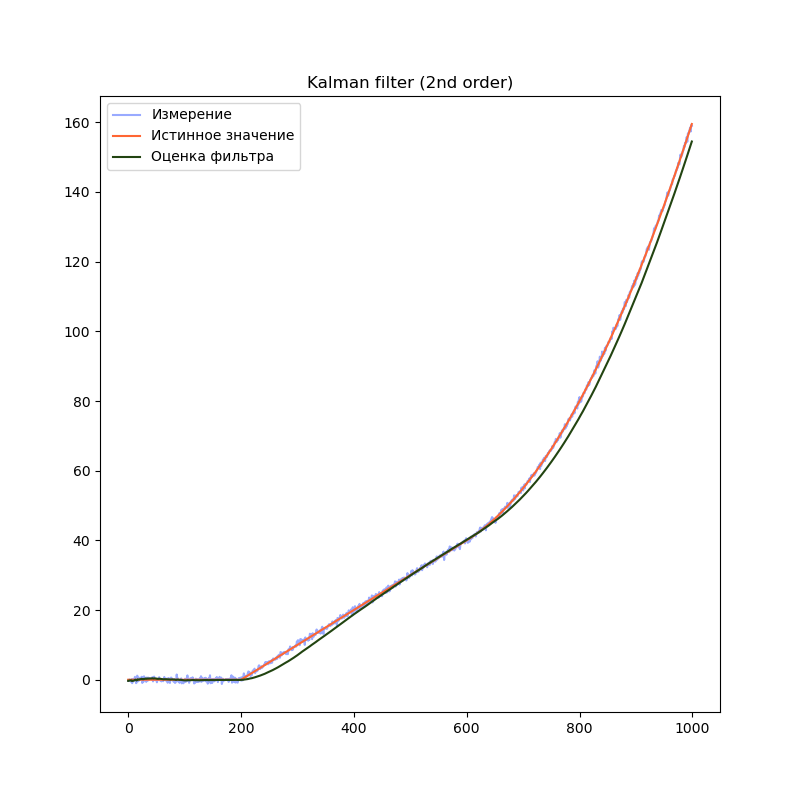







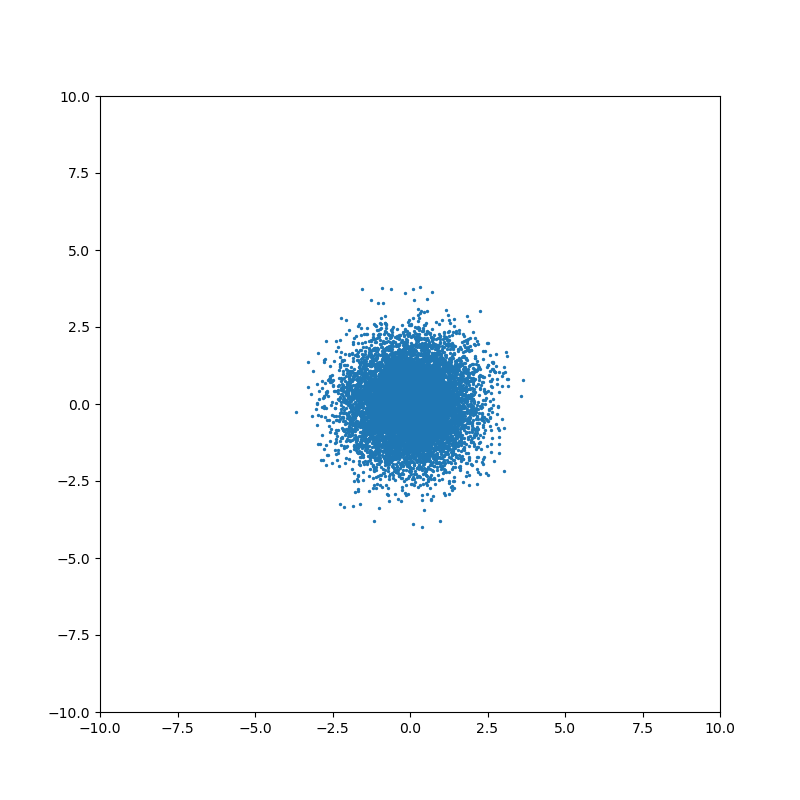


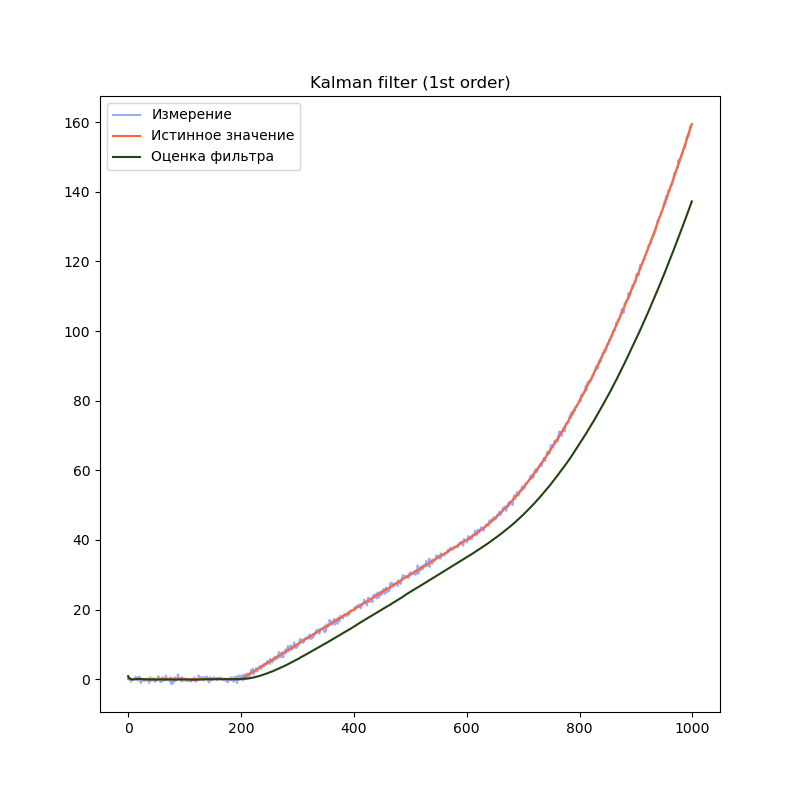
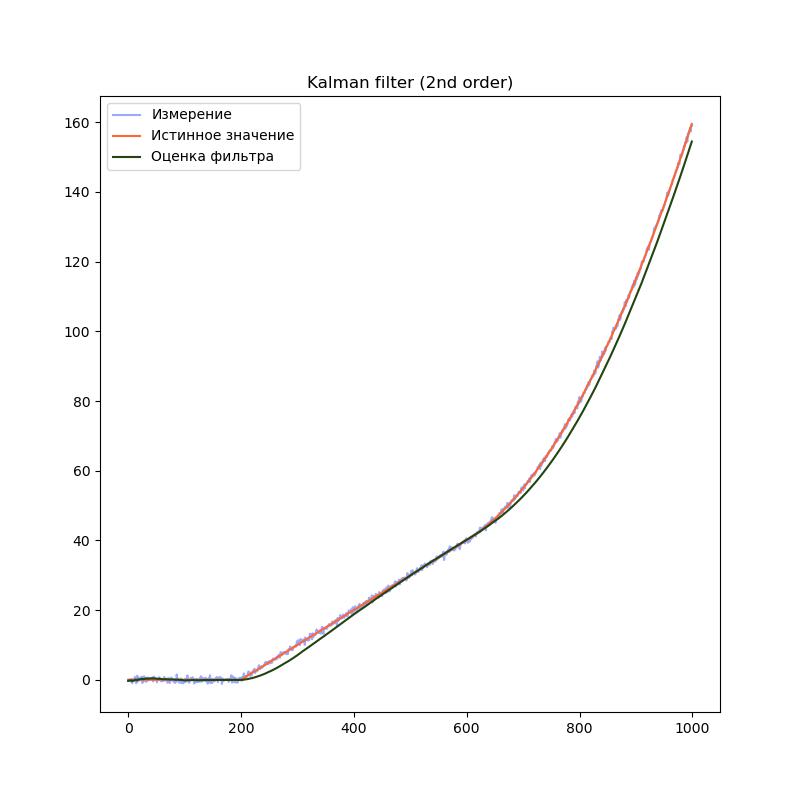


 (8.203)
(8.203)
 (8.207)
(8.207)
 (8 2166)
(8 2166)
































![{\displaystyle \operatorname {\Sigma } =\operatorname {E} \left[\left(X-\operatorname {E} [X]\right)\left(X-\operatorname {E} [X]\right)^{\mathrm {T} }\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdd1400b2d5e8baf3d9a79011f1452bb1d83c274)


















![\ln {\mathcal {L}}(\mu ,\Sigma )=\operatorname {const}-{n \over 2}\ln \det(\Sigma )-{1 \over 2}\operatorname {tr}\left[\Sigma ^{{-1}}\sum _{{i=1}}^{n}(x_{i}-\mu )(x_{i}-\mu )^{{\mathrm {T}}}\right].](https://wikimedia.org/api/rest_v1/media/math/render/svg/19a132ab3db51593d7fba1786566392c2089f173)
![{\displaystyle d\ln {\mathcal {L}}(\mu ,\Sigma )=-{\frac {n}{2}}\operatorname {tr} \left[\Sigma ^{-1}\left\{d\Sigma \right\}\right]-{1 \over 2}\operatorname {tr} \left[-\Sigma ^{-1}\{d\Sigma \}\Sigma ^{-1}\sum _{i=1}^{n}(x_{i}-\mu )(x_{i}-\mu )^{\mathrm {T} }-2\Sigma ^{-1}\sum _{i=1}^{n}(x_{i}-\mu )\{d\mu \}^{\mathrm {T} }\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e05b9dbd637f1304a2e7781fa63fb813f8a5f3d)



![-{1 \over 2}\operatorname {tr}\left(\Sigma ^{{-1}}\left\{d\Sigma \right\}\left[nI_{p}-\Sigma ^{{-1}}S\right]\right).](https://wikimedia.org/api/rest_v1/media/math/render/svg/1724960e30912702239cb54b5d90b71c4f89ce07)


![{\mathrm {E}}_{{{\mathbf {R}}}}[{\hat {{\mathbf {R}}}}]\ {\stackrel {{\mathrm {def}}}{=}}\ \exp _{{{\mathbf {R}}}}{\mathrm {E}}\left[\exp _{{{\mathbf {R}}}}^{{-1}}{\hat {{\mathbf {R}}}}\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/71ec1f6bcb105144b3b61dc03f28d46445b83064)


![{\mathbf {B}}({\hat {{\mathbf {R}}}})=\exp _{{{\mathbf {R}}}}^{{-1}}{\mathrm {E}}_{{{\mathbf {R}}}}\left[{\hat {{\mathbf {R}}}}\right]={\mathrm {E}}\left[\exp _{{{\mathbf {R}}}}^{{-1}}{\hat {{\mathbf {R}}}}\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3e09f12f16b646e19a2737456dce7e5f5c89472)


