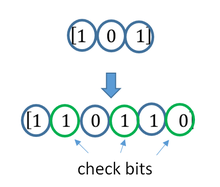
Каждому устройству, использующему флэш-память NAND, необходим код с исправлением случайных битов (известный как «мягкая» ошибка). Это потому что много электрический шум производится внутри чипа NAND, а уровни сигналов битов, проходящих через цепочку чипов NAND, очень слабые.

Один из способов, которым NAND память стали самый дешевый всего, потому что это требует, чтобы исправление ошибок было выполнено от элемента вне самого чипа NAND; В случае SSD, ECC выполняется на контроллере .
Такое же исправление ошибок также помогает исправить битовые ошибки из-за носить на Память сами клетки , Истощение может вызвать «застревание» битов в том или ином состоянии (известное как «жесткая» ошибка или жесткая ошибка) и может увеличить частоту «мягких» ошибок.
Хотя это понятие не является слишком широким, сопротивление флэш-памяти является мерой того, сколько циклов стирания / записи может выдержать блок флэш-памяти, прежде чем начнут появляться «серьезные» ошибки. Очень часто эти сбои происходят только в отдельных битах, и очень редко происходит сбой всего блока. При достаточно высоком числе стирания / записи «мягкая» частота ошибок также увеличивается из-за ряда других механизмов в самом SSD.
If ECC может быть используемый чтобы исправить эти «жесткие» ошибки, а «мягкие» ошибки не увеличиваются, срок службы всего блока значительно удлиняется, что значительно превышает сопротивление, указанное производителем.
Давайте рассмотрим пример: допустим, что неиспользуемый чип NAND имеет достаточно «мягких» ошибок, чтобы требовать 8 бит ECC, то есть при каждом считывании страницы может быть до 8 бит, которые были случайно повреждены (обычно из-за электрических помех, которые мы говорили о). вначале). ECC, используемый в этом чипе, может исправлять 12-битные ошибки, так что ECC не может решить эту проблему мы должны найти 8 «мягких» ошибок, связанных с электрическим шумом, плюс еще 5 «мягких» из-за износа.
Теперь производители флэш-памяти гарантируют, что первый из этих 5 сбоев произойдет через некоторое время после спецификации прочности SSD. Это означает, что ни один бит не выйдет из строя из-за износа, пока не будут превышены циклы стирания / записи, указанные производителем. Теперь имейте в виду, что спецификации не достаточно точны, чтобы предсказать, когда следующий бит выйдет из строя, и на самом деле это может занять несколько тысяч циклов стирания / записи выше спецификации, чтобы это произошло; помните, что производитель гарантирует, что это не произойдет до X циклов, но не тогда, когда это произойдет после их превышения.
Это означает, что это может занять много времени, прежде чем блок становится настолько коррумпированным что его необходимо удалить из службы (а также для этого на SSD обычно есть «дополнительные» блоки для замены поврежденных), что, в свою очередь, означает, что сопротивление исправлен от ошибок блок может быть во много раз больше указанного сопротивления, в зависимости от количества избыточных ошибок, которые ECC предназначен для исправления.
Какое влияние оказывает код исправления ошибок на SSD?
Как мы объясняли ранее, флэш-память настолько дешева, потому что она не включает в себя ECC в самих чипах, но интегрирована в другое внешнее оборудование, и, как вы предположите, это имеет свою цену. Более сложный ECC требует большей вычислительной мощности на контроллере и может быть медленнее, если алгоритмы не очень современные. Кроме того, количество ошибок, которые могут быть исправлены, будет зависеть от того, насколько большой сектор памяти исправляется, поэтому контроллер SSD со сложным алгоритмом ECC, вероятно, будет использовать много ресурсов, снижение общий SSD производительность , Эти улучшения также делают контроллер дороже .
Алгоритмы ECC имеют свое собственное математическое состояние в зависимости от контроллера (другими словами, нет никакого стандарта), и даже самые базовые кодировки ECC (Рида-Соломона и LDPC) довольно сложны для понимания. Когда кто-то говорит о пределе Шеннона (максимальное количество битов, которое может быть исправлено), это величина, которую, как вы не знаете от производителя в технических характеристиках, чрезвычайно сложно вычислить.
Просто придерживайтесь этого: большее количество корректирующих битов увеличивает срок службы SSD, но также оказывает некоторое влияние на производительность или даже цену продукта, так как требует более мощный контроллер.
Оглавление
- Вступление
- Коррекция ошибок
- Финансовая сторона
- Тестовый стенд
- Методика тестирования
- Результаты тестирования
- Тест памяти
- 3DMark
- 7Zip
- Cinebench
- CrystalMark
- Fritz
- LinX
- wPrime
- AIDA64 Extreme
- Заключение
Вступление
На сегодняшний день на просторах Рунета можно встретить открытые темы на форумах с вопросами – стоит ли брать рабочую станцию с ECC-памятью или можно обойтись обычной? В данных ветках можно прочесть множество противоречивых утверждений, и часть из них говорит о том, что коррекция ошибок сильно замедляет память, а следовательно и ЦП. Но мало кто это проверял на деле на современных процессорах.
Сегодня мы разберемся в этом вопросе и сравним производительность серверного процессора с обоими типами памяти. Но для начала небольшой экскурс.
Коррекция ошибок
Для чего необходима коррекция? И почему в работе памяти возникают ошибки? Перед ответом на эти вопросы следует разделить ошибки на два типа:
- Аппаратные ошибки;
- Случайные ошибки.
Причиной появления аппаратных ошибок является дефектная микросхема DRAM, а случайные ошибки возникают под воздействием излучения, альфа-частиц, элементарных частиц и прочего. Соответственно, первые в принципе неисправимы – если чип дефектный, то поможет только его замена; а вот вторые могут быть исправлены.
Почему же так необходима коррекция ошибок в рабочих станциях и серверах? Однобитовая ошибка в 64-битном слове меняет содержимое ячейки памяти, а в конечном итоге на жесткий диск может быть записано другое число, другие данные, при этом компьютер не зафиксирует эту подмену. А изменение бита в оперативной памяти может вызвать сбой программы, что для рабочей станции и сервера недопустимо.
рекомендации
3060 дешевле 30тр в Ситилинке
3070 Gigabyte Gaming за 50 тр с началом
<b>13900K</b> в Регарде по СТАРОМУ курсу 62
3070 Gainward Phantom дешевле 50 тр
10 видов <b>4070 Ti</b> в Ситилинке — все до 100 тр
13700K дешевле 40 тр в Регарде
MSI 3050 за 25 тр в Ситилинке
13600K дешевле 30 тр в Регарде
4080 почти за 100тр — дешевле чем по курсу 60
12900K за 40тр с началом в Ситилинке
RTX 4090 за 140 тр в Регарде
Компьютеры от 10 тр в Ситилинке
3060 Ti Gigabyte дешевле 40 тр в Регарде
3070 дешевле 50 тр в Ситилинке
-7% на 4080 Gigabyte Gaming
Для обнаружения изменения битов памяти можно использовать метод подсчета контрольной суммы, но он позволяет лишь обнаруживать ошибки без их исправления.
В свое время было предложено много различных способов решения данной проблемы, но на сегодняшний день наибольшее распространение получил метод коррекции ошибок или ECC (Error-Correcting Code). Данный метод позволяет автоматически исправлять однобитовые ошибки в 64-битном слове – SEC (Single Error Correction) и детектировать двухбитовые – DED (Double Error Detection).
Физическая реализация ECC заключается в размещении дополнительной микросхемы памяти на модуле ОЗУ – соответственно, при одностороннем дизайне модуля памяти вместо восьми чипов располагается девять, а при двустороннем вместо шестнадцати – восемнадцать. Таким образом, ширина модуля становится не 64 бита, а 72 бита.
Метод коррекции ошибок работает следующим образом: при записи 64 бит данных в ячейку памяти происходит подсчет контрольной суммы, составляющей 8 бит. Когда процессор обращается к этим данным и производит считывание, проводится повторный подсчет контрольной суммы и сравнение с исходной. Если суммы не совпадают – произошла ошибка. Если она однобитовая, то неправильный бит исправляется автоматически, если двухбитовая – детектируется и сообщается ОС.
Финансовая сторона
Прежде чем приступить к тестированию, необходимо затронуть финансовый вопрос.
Стоимость обычного модуля памяти DDR3-1600 с напряжением 1.35 В и объемом 8 Гбайт составляет около 3600 рублей, а с коррекцией ошибок – 4800 рублей. На первый взгляд ECC-память выходит на 30-35% дороже, что, в целом, не позволяет их сравнивать в силу существенно большей стоимости последней. Но почему же тогда такой вопрос возникает при сборке рабочей станции? Все просто – необходимо смотреть на данный вопрос шире, а именно – смотреть на общую стоимость рабочей станции.
Ценник однопроцессорной станции на базе четырехъядерного восьмипоточного Xeon (настольные процессоры серий i5 и i7 не поддерживают ECC-память) с 32 Гбайтами памяти, материнской платы с чипсетом C222/С224/С226 (десктопные наборы логики Z87/Z97 и другие также не поддерживают память с коррекцией ошибок) будет превышать 70 000 рублей (при условии, что устанавливаются серверные SSD с повышенным ресурсом). А если включить в эту стоимость и дискретную видеокарту, и прочие сопутствующие компоненты, например, ИБП, то ценник из пятизначного превратится в шестиизначный, перевалив планку в 100 000 рублей.
Покупка 32 Гбайт памяти с коррекцией ошибок потребует дополнительных 4-6 тысяч рублей, что по отношению к общей стоимости рабочей станции не превышает 5%, то есть не является критичным. Также переход от десктопного к серверному железу предоставит и другие преимущества, например: интегрированные графические карты P4600 в процессорах Intel Xeon E3-1200 третьего поколения получили оптимизированные драйверы, которые должны повышать производительность в профессиональных приложениях, например, в CAD; поддержка технологии Intel VT-d, которая позволяет пробрасывать устройства в виртуальную среду, например, видеокарты; прочие серверные технологии – Intel AMT или IPMI, WatchDog и другие, которые также могут оказаться полезными.
Таким образом, хоть и сама ECC-память стоит заметно дороже обычной, в общей стоимости рабочей станции данная статья затрат является несущественной, и переплата не превышает 5%.
Тестовый стенд
Для данного обзора использовалась следующая конфигурация:
- Материнская плата: Supermicro X10SAE (Intel C226, LGA 1150);
- Процессор: Xeon E3-1245V3 (Turbo Boost – off, EIST – off, HT – on);
- Оперативная память:
- 2x Kingston DDR3-1600 ECC 8 Гбайт (KVR16LE11/8 CL11, 1.35 В);
- 2x Kingston DDR3-1600 8 Гбайт (KVR16LN11/8 CL11, 1.35 В);
- ОС: Windows 8.1 Pro 64-bit.
Методика тестирования
В рамках тестирования были произведены замеры производительности как при одноканальном режиме работы ИКП, так и при двухканальном. Суммарный объем ОЗУ составил 8 (один модуль) и 16 Гбайт (два модуля) соответственно.
Программное обеспечение:
- 3DMark 2006 1.2;
- 7Zip 9.20;
- AIDA64 Extreme 5.20.3400;
- Cinebench R15;
- CrystalMark 2004R3;
- Fritz 4.20;
- LinX 0.6.5;
- wPrime 2.10.
Результаты тестирования
Тест памяти
Перед тем, как приступить к тестированию, проведем замер пропускной способности памяти и латентности.
При изучении результатов можно заключить, что производительность ECC- и non-ECC- памяти находится на одном и том же уровне в рамках погрешности.
Если в предыдущем тесте от замера к замеру выигрывал то один, то другой тип памяти, то при замере латентности ECC-память постоянно показывает большие задержки. Но разница несущественна – всего лишь 1 нс.
Таким образом, замер ПС и латентности памяти не показал особых различий между ECC- и non-ECC-памятью. Посмотрим, повторится ли это в последующих тестах.
3DMark
Тестовый пакет 3DMark содержит подтесты как для процессора, так и для графической карты. Здесь и кроется самое интересное – давно известно, что встроенному видеоядру не хватает существующей ПСП в 25.6 Гбайт/с, поэтому именно в графических подтестах можно выявить негативное влияние коррекции ошибок, если оно вообще есть,…
… но разницы нет – что ECC, что non-ECC. Ни процессор, ни интегрированное ядро никак не реагируют на замену обычной памяти на DDR с коррекцией ошибок – результаты одинаковы в рамках погрешности. Среднеарифметическая разница составила 0.02% в пользу ECC-памяти для одноканального режима и 1.6% для двухканального режима.
При этом нельзя сказать, что встроенная видеокарта P4600 не зависит от скорости ОЗУ – при одноканальном доступе общий результат почти на 30% ниже, чем при двухканальном. Другими словами, скорость ОЗУ критична для графического ядра, но сами по себе «ECC-версии» не влияют ни на скорость ОЗУ, ни на видеокарту.
7Zip
Архиваторы, как известно, чувствительны к памяти, поэтому, возможно, здесь получится зафиксировать влияние типа памяти на производительность.
Ситуация с архивацией неоднозначная: с одной стороны – в одноканальном режиме (как при распаковке, так и при сжатии) ECC-память уверенно оказывается медленнее на 2%; с другой – в двухканальном режиме при сжатии ECC-память уверенно быстрее, а при распаковке – медленнее, а среднее арифметическое – быстрее на 0.65%.
Скорее всего, причина в следующем – пропускной способности памяти при одноканальном доступе процессору явно недостаточно, и поэтому чуть большая латентность ECC-памяти сказывается на производительности; а при двухканальном доступе ПСП полностью покрывает нужды CPU и поэтому чуть большая латентность памяти с коррекцией ошибок не сказывается на производительности. В любом случае зафиксировать существенного влияния на скорость архивации не получилось.
Cinebench
Тестовый пакет Cinebench содержит подтест как процессора, так и видеокарты.
Но ни первый, ни вторая никак не отреагировали на ECC-память.
Зато налицо явная зависимость видеокарты от ПСП – при одноканальном доступе результат в OpenGL оказался на 25% ниже, чем при двухканальном. Вспоминая результаты 3DMark и смотря на нынешние, можно заключить, что производительность интегрированной видеокарты хоть и зависит от ПСП, но ECC-память не оказывает на нее негативного влияния.
Ошибки при хранении
информации в памяти неизбежны. Они
обычно классифицируются как отказы и
нерегулярные ошибки (сбои). Если нормально
функционирующая микросхема вследствие,
например, физического повреждения
начинает работать неправильно, то все
происходящее и называется постоянным
отказом. Чтобы устранить этот тип отказа,
обычно требуется заменить некоторую
часть аппаратных средств памяти, например
неисправную микросхему SIMM или DIMM.
Другой, более
коварный тип отказа
нерегулярная ошибка (сбой). Это непостоянный
отказ, который не происходит при
повторении условий функционирования
или через регулярные интервалы.
Приблизительно
20 лет назад сотрудники Intel
установили, что причиной сбоев являются
альфа-частицы. Поскольку альфа-частицы
не могут проникнуть даже через тонкий
лист бумаги, выяснилось, что их источником
служит вещество, используемое в
полупроводниках. При исследовании были
обнаружены частицы тория и урана в
пластмассовых и керамических корпусах
микросхем, применявшихся в те годы.
Изменив технологический процесс,
производители памяти избавились от
этих примесей.
В настоящее время
производители памяти почти полностью
устранили источники альфа-частиц. И
многие стали думать, что проверка
четности не нужна вовсе. Например, сбои
в памяти емкостью 16 Мбайт из-за альфа-частиц
случаются в среднем только один раз за
16 лет! Однако сбои памяти происходят
значительно чаще.
Сегодня самая
главная причина нерегулярных ошибок
космические лучи. Поскольку они имеют
очень большую проникающую способность,
от них практически нельзя защититься
с помощью экранирования.
К сожалению,
производители персональных компьютеров
не признали это причиной погрешностей
памяти; случайную природу сбоя намного
легче оправдать разрядом электростатического
электричества, большими выбросами
мощности или неустойчивой работой
программного обеспечения (например,
использованием новой версии операционной
системы или большой прикладной программы).
Хотя космические
лучи и радиация являются причиной
большинства программных ошибок памяти,
существуют и другие факторы.
-
Скачки в
энергопотреблении или шум на линии.
Причиной может быть неисправный блок
питания или настенная розетка. -
Использование
неверного типа или параметра быстродействия
памяти. Тип
памяти должен поддерживаться конкретным
набором микросхем и обладать определенной
этим набором скоростью доступа. -
Радиочастотная
интерференция.
Связана с расположением радиопередатчиков
рядом с компьютером, что иногда приводит
к генерированию паразитных электрических
сигналов в монтажных соединениях и
схемах компьютера. Беспроводные сети,
мыши и клавиатуры увеличивают риск
появления радиочастотной интерференции. -
Статические
разряды.
Вызывают моментальные скачки в
энергоснабжении, что может повлиять
на целостность данных. -
Ошибки
синхронизации. Не
поступившие своевременно данные могут
стать причиной появления программных
ошибок. Зачастую причина заключается
в неверных параметрах BIOS,
оперативной памяти, быстродействие
которой ниже, чем требуется системой,
«разогнанных» процессорах и прочих
ситемных компонентах.
Большинство
системных проблем не приводят к
прекращению работы микросхем памяти,
однако могут повлиять на хранимые
данные.
Игнорирование
сбоев, конечно, не лучший способ борьбы
с ними. К сожалению, именно этот способ
сегодня выбрали многие производители
компьютеров. Лучше было бы увеличить
отказоустойчивость систем. Для этого
необходимы механизмы обнаружения и,
возможно, исправления ошибок в памяти
персонального компьютера. В основном
для повышения отказоустойчивости в
современных компьютерах применяются
следующие методы:
-
контроль четности;
-
коды коррекции
ошибок (ECC).
Соседние файлы в папке Сватов лабы
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Контроль четности и коды коррекции ошибок (ECC).
Ошибки при хранении информации в памяти неизбежны. Они обычно классифицируются как отказы и нерегулярные ошибки (сбои). Если нормально функционирующая микросхема вследствие, например, физического повреждения начинает работать неправильно, то все происходящее и называется постоянным отказом. Чтобы устранить этот тип отказа, обычно требуется заменить некоторую часть аппаратных средств памяти, например неисправную микросхему памяти.
Другой, более коварный тип отказа — нерегулярная ошибка (сбой). Это непостоянный отказ, который не происходит при повторении условий функционирования или через регулярные интервалы.
Приблизительно 20 лет назад сотрудники Intel установили, что причиной сбоев являются альфа-частицы. Поскольку альфа-частицы не могут проникнуть даже через тонкий лист бумаги, выяснилось, что их источником служит вещество, используемое в полупроводниках. При исследовании были обнаружены частицы тория и урана в пластмассовых и керамических корпусах микросхем, применявшихся в те годы. Изменив технологический процесс, производители памяти избавились от этих примесей.
В настоящее время производители памяти почти полностью устранили источники альфачастиц. И многие стали думать, что проверка четности не нужна вовсе. Например, сбои в памяти емкостью 16 Мбайт из-за альфа-частиц случаются в среднем только один раз за 16 лет! Однако сбои памяти происходят значительно чаще.
Сегодня самая главная причина нерегулярных ошибок — космические лучи. Поскольку они имеют очень большую проникающую способность, от них практически нельзя защититься с помощью экранирования.
Эксперимент, проверяющий степень влияния космических лучей на появление ошибок в работе микросхем, показал, что соотношение “сигнал–ошибка” (signal-to-error ratio — SER) для некоторых модулей DRAM составило 5950 единиц интенсивности отказов (failure units — FU) на миллиард часов наработки для каждой микросхемы. Измерения проводились в условиях, приближенных к реальной жизни, с учетом длительности в несколько миллионов машиночасов. В среднестатистическом компьютере это означало бы появление программной ошибки памяти примерно каждые шесть месяцев. В серверных системах или мощных рабочих станциях с большим объемом установленной оперативной памяти подобная статистика указывает на одну ошибку (или даже более) в работе памяти каждый месяц! Когда тестовая система с теми же модулями DIMM была размещена в надежном убежище на глубине более 15 метров каменной породы, что полностью устраняет влияние космических лучей, программные ошибки в работе памяти вообще не были зафиксированы. Эксперимент продемонстрировал не только опасность влияния космических лучей, но и доказал, насколько эффективно устранять влияние альфалучей и радиоактивных примесей в оболочках модулей памяти.
К сожалению, производители ПК не признали это причиной погрешностей памяти; случайную природу сбоя намного легче оправдать разрядом электростатического электричества, большими выбросами мощности или неустойчивой работой программного обеспечения (например, использованием новой версии операционной системы или большой прикладной программы). Исследования показали, что для систем ECC доля программных ошибок в 30 раз больше, чем аппаратных. Это неудивительно, учитывая вредное влияние космических лучей. Количество ошибок зависит от числа установленных модулей памяти и их объема. Программные ошибки могут случаться и раз в месяц, и несколько раз в неделю, и даже чаще!
Хотя космические лучи и радиация являются причиной большинства программных ошибок памяти, существуют и другие факторы:
1. Скачки в энергопотреблении или шум на линии. Причиной может быть неисправный блок питания или настенная розетка.
2. Использование неверного типа или параметра быстродействия памяти. Тип памяти
должен поддерживаться конкретным набором микросхем и обладать определенной
этим набором скоростью доступа.
3. Электромагнитные помехи. Возникают при расположении радиопередатчиков рядом с
компьютером, что иногда приводит к генерированию паразитных электрических сигна-
лов в монтажных соединениях и схемах компьютера. Имейте в виду, что беспроводные
сети, мыши и клавиатуры увеличивают риск появления электромагнитных помех.
4. Статические разряды. Вызывают моментальные скачки в энергоснабжении, что может
повлиять на целостность данных.
5. Ошибки синхронизации. Не поступившие своевременно данные могут стать причиной
появления программных ошибок. Зачастую причина заключается в неверных парамет-
рах BIOS, оперативной памяти, быстродействие которой ниже, чем требуется систе-
мой, “разогнанных” процессорах и прочих системных компонентах.
Большинство описанных проблем не приводят к прекращению работы микросхем памяти (хотя некачественное энергоснабжение или статическое электричество могут физически повредить микросхемы), однако могут повлиять на хранимые данные.
Игнорирование сбоев, конечно, не лучший способ борьбы с ними. К сожалению, именно этот способ сегодня выбрали многие производители компьютеров. Лучше было бы повысить отказоустойчивость систем. Для этого необходимы механизмы определения и, возможно, исправления ошибок в памяти ПК. В основном для повышения отказоустойчивости в современных компьютерах применяются следующие методы:
— контроль четности;
— коды коррекции ошибок (ECC).
Системы без контроля четности вообще не обеспечивают отказоустойчивости данных. Единственная причина, по которой они используются, — их минимальная базовая стоимость. При этом, в отличие от других технологий (ECC и контроль четности), не требуется дополнительная оперативная память.
Байт данных с контролем четности включает в себя 9, а не 8 бит, поэтому стоимость памяти с контролем четности выше примерно на 12,5%. Кроме того, контроллеры памяти, не требующие логических мостов для подсчета данных четности или ECC, обладают упрощенной внутренней архитектурой. Портативные системы, для которых вопрос минимального энергопотребления особенно важен, выигрывают от уменьшенного энергопотребления памяти благодаря использованию меньшего количества микросхем DRAM. И наконец, шина данных памяти без контроля четности имеет меньшую разрядность, что выражается в сокращении количества буферов данных. Статистическая вероятность возникновения ошибок памяти в современных настольных компьютерах составляет примерно одну ошибку в несколько месяцев. При этом количество ошибок зависит от объема и типа используемой памяти. Подобный уровень ошибок может быть приемлемым для обычных компьютеров, не используемых для работы с важными приложениями. В этом случае цена играет основную роль, а дополнительная стоимость модулей памяти с поддержкой контроля четности и кода ECC себя не оправдывает.
Применение не отказоустойчивых к ошибкам компьютеров рискованно и предполагает отсутствие ошибок памяти при эксплуатации систем. При этом также учитывается, что совокупная стоимость потерь, вызванная ошибками в работе памяти, будет меньше, чем затраты на приобретение дополнительных аппаратных устройств для определения таковых ошибок.
Тем не менее ошибки памяти вполне могут стать причиной серьезных проблем: например, представьте себе указание неверного значения суммы в банковском чеке. Ошибки в работе оперативной памяти серверных систем зачастую приводят к “зависанию” последних и отключению всех клиентских компьютеров, соединенных с серверами по локальной сети. Наконец, отследить причину возникновения проблем в компьютерах, не поддерживающих контроль четности или код ECC, крайне сложно. Последние технологии по крайней мере однозначно укажут на оперативную память как на источник проблемы, тем самым экономя время и усилия системных администраторов.
Контроль четности
Это один из стандартов, введенных IBM, в соответствии с которым информация в банках памяти хранится фрагментами по девять битов, причем восемь из них (составляющих один байт) предназначены собственно для данных, а девятый является битом четности (parity). Использование девятого бита позволяет схемам управления памятью на аппаратном уровне контролировать целостность каждого байта данных. Если обнаруживается ошибка, работа компьютера останавливается и на экран выводится сообщение о неисправности.
Технология контроля четности не позволяет исправлять системные ошибки, однако дает возможность их обнаружить пользователю компьютера, что имеет следующие преимущества:
— контроль четности оберегает от последствий проведения неверных вычислений на базе некорректных данных;
— контроль четности точно указывает на источник возникновения ошибок, помогая разобраться с проблемой и улучшая степень эксплутационной надежности компьютера.
Для реализации поддержки памяти с контролем четности или без него не требуется особых усилий. В частности, внедрить поддержку контроля четности для системной платы не составит никакого труда. Основная стоимость внедрения относится к цене самих модулей памяти с контролем четности. Если покупатели нуждаются в контроле четности для работы с определенными приложениями, поставщики компьютеров могут без проблем предложить соответствующие системы.
Компания Intel и прочие производители наборов микросхем системной логики внедрили поддержку контроля четности и кода ECC в большинстве своих продуктов (особенно в наборах микросхем, ориентированных на рынок высокопроизводительных серверов). В то же время наборы микросхем низшей ценовой категории, как правило, не поддерживают эти технологии. Пользователям, требовательным к надежности выполняемых приложений, следует обращать особое внимание на поддержку контроля четности и ECC.
Код коррекции ошибок
Коды коррекции ошибок (Error Correcting Code — ECC) позволяют не только обнаружить ошибку, но и исправить ее в одном разряде. Поэтому компьютер, в котором используются подобные коды, в случае ошибки в одном разряде может работать без прерывания, причем данные не будут искажены. Коды коррекции ошибок в большинстве ПК позволяют только обнаруживать, но не исправлять ошибки в двух разрядах. Но приблизительно 98% сбоев памяти вызвано именно ошибкой в одном разряде, т.е. она успешно исправляется с помощью данного типа кодов. Данный тип ECC получил название SEC)DED (single-bit error-correction double-bit error detection — одноразрядная коррекция, двухразрядное обнаружение ошибок). В кодах коррекции ошибок этого типа для каждых 32 бит требуется дополнительно семь контрольных разрядов при 4-байтовой и восемь — при 8-байтовой организации (64-разрядные процессоры Athlon/Pentium). Реализация кода коррекции ошибок при 4-байтовой организации, очевидно, дороже реализации проверки нечетности или четности, но при 8-байтовой организации стоимость реализации кода коррекции ошибок не превышает стоимости реализации проверки четности.
Для использования кодов коррекции ошибок необходим контроллер памяти, вычисляющий контрольные разряды при операции записи в память. При чтении из памяти такой контроллер сравнивает прочитанные и вычисленные значения контрольных разрядов и при необходимости исправляет испорченный бит (или биты). Стоимость дополнительных логических схем для реализации кода коррекции ошибок в контроллере памяти не очень высока, но это может значительно снизить быстродействие памяти при операциях записи. Это происходит потому, что при операциях записи и чтения необходимо ждать, когда завершится вычисление контрольных разрядов. При записи части слова вначале следует прочитать полное слово, затем перезаписать изменяемые байты и только после этого — новые вычисленные контрольные разряды.
В большинстве случаев сбой памяти происходит в одном разряде, и потому такие ошибки успешно исправляются кодом коррекции ошибок. Использование отказоустойчивой памяти обеспечивает высокую надежность компьютера. Память с кодом ECC предназначена для серверов, рабочих станций или приложений, для которых последствия потенциальных ошибок памяти менее желательны, чем дополнительные затраты на приобретение добавочных модулей памяти и вычислительные затраты на коррекцию ошибок. Если данные имеют особое значение и компьютеры применяются для решения важных задач, без памяти ECC не обойтись. По сути, ни один уважающий себя системный инженер не будет использовать сервер, даже самый неприхотливый, без памяти ECC.
Пользователи имеют выбор между системами без контроля четности, с контролем четности и с ECC, т.е. между желательным уровнем отказоустойчивости компьютера и степенью ценности используемых данных.
«Interleaver» redirects here. For the fiber-optic device, see optical interleaver.
In computing, telecommunication, information theory, and coding theory, an error correction code, sometimes error correcting code, (ECC) is used for controlling errors in data over unreliable or noisy communication channels.[1][2] The central idea is the sender encodes the message with redundant information in the form of an ECC. The redundancy allows the receiver to detect a limited number of errors that may occur anywhere in the message, and often to correct these errors without retransmission. The American mathematician Richard Hamming pioneered this field in the 1940s and invented the first error-correcting code in 1950: the Hamming (7,4) code.[2]
ECC contrasts with error detection in that errors that are encountered can be corrected, not simply detected. The advantage is that a system using ECC does not require a reverse channel to request retransmission of data when an error occurs. The downside is that there is a fixed overhead that is added to the message, thereby requiring a higher forward-channel bandwidth. ECC is therefore applied in situations where retransmissions are costly or impossible, such as one-way communication links and when transmitting to multiple receivers in multicast. Long-latency connections also benefit; in the case of a satellite orbiting around Uranus, retransmission due to errors can create a delay of five hours. ECC information is usually added to mass storage devices to enable recovery of corrupted data, is widely used in modems, and is used on systems where the primary memory is ECC memory.
ECC processing in a receiver may be applied to a digital bitstream or in the demodulation of a digitally modulated carrier. For the latter, ECC is an integral part of the initial analog-to-digital conversion in the receiver. The Viterbi decoder implements a soft-decision algorithm to demodulate digital data from an analog signal corrupted by noise. Many ECC encoders/decoders can also generate a bit-error rate (BER) signal, which can be used as feedback to fine-tune the analog receiving electronics.
The maximum fractions of errors or of missing bits that can be corrected are determined by the design of the ECC code, so different error correcting codes are suitable for different conditions. In general, a stronger code induces more redundancy that needs to be transmitted using the available bandwidth, which reduces the effective bit-rate while improving the received effective signal-to-noise ratio. The noisy-channel coding theorem of Claude Shannon can be used to compute the maximum achievable communication bandwidth for a given maximum acceptable error probability. This establishes bounds on the theoretical maximum information transfer rate of a channel with some given base noise level. However, the proof is not constructive, and hence gives no insight of how to build a capacity achieving code. After years of research, some advanced ECC systems as of 2016[3] come very close to the theoretical maximum.
Forward error correction[edit]
In telecommunication, information theory, and coding theory, forward error correction (FEC) or channel coding[4][3] is a technique used for controlling errors in data transmission over unreliable or noisy communication channels. The central idea is that the sender encodes the message in a redundant way, most often by using an ECC.
The redundancy allows the receiver to detect a limited number of errors that may occur anywhere in the message, and often to correct these errors without re-transmission. FEC gives the receiver the ability to correct errors without needing a reverse channel to request re-transmission of data, but at the cost of a fixed, higher forward channel bandwidth. FEC is therefore applied in situations where re-transmissions are costly or impossible, such as one-way communication links and when transmitting to multiple receivers in multicast. FEC information is usually added to mass storage (magnetic, optical and solid state/flash based) devices to enable recovery of corrupted data, is widely used in modems, is used on systems where the primary memory is ECC memory and in broadcast situations, where the receiver does not have capabilities to request re-transmission or doing so would induce significant latency. For example, in the case of a satellite orbiting Uranus, a re-transmission because of decoding errors would create a delay of at least 5 hours.
FEC processing in a receiver may be applied to a digital bit stream or in the demodulation of a digitally modulated carrier. For the latter, FEC is an integral part of the initial analog-to-digital conversion in the receiver. The Viterbi decoder implements a soft-decision algorithm to demodulate digital data from an analog signal corrupted by noise. Many FEC coders can also generate a bit-error rate (BER) signal which can be used as feedback to fine-tune the analog receiving electronics.
The maximum proportion of errors or missing bits that can be corrected is determined by the design of the ECC, so different forward error correcting codes are suitable for different conditions. In general, a stronger code induces more redundancy that needs to be transmitted using the available bandwidth, which reduces the effective bit-rate while improving the received effective signal-to-noise ratio. The noisy-channel coding theorem of Claude Shannon answers the question of how much bandwidth is left for data communication while using the most efficient code that turns the decoding error probability to zero. This establishes bounds on the theoretical maximum information transfer rate of a channel with some given base noise level. His proof is not constructive, and hence gives no insight of how to build a capacity achieving code. However, after years of research, some advanced FEC systems like polar code[3] achieve the Shannon channel capacity under the hypothesis of an infinite length frame.
How it works[edit]
ECC is accomplished by adding redundancy to the transmitted information using an algorithm. A redundant bit may be a complex function of many original information bits. The original information may or may not appear literally in the encoded output; codes that include the unmodified input in the output are systematic, while those that do not are non-systematic.
A simplistic example of ECC is to transmit each data bit 3 times, which is known as a (3,1) repetition code. Through a noisy channel, a receiver might see 8 versions of the output, see table below.
| Triplet received | Interpreted as |
|---|---|
| 000 | 0 (error-free) |
| 001 | 0 |
| 010 | 0 |
| 100 | 0 |
| 111 | 1 (error-free) |
| 110 | 1 |
| 101 | 1 |
| 011 | 1 |
This allows an error in any one of the three samples to be corrected by «majority vote», or «democratic voting». The correcting ability of this ECC is:
- Up to 1 bit of triplet in error, or
- up to 2 bits of triplet omitted (cases not shown in table).
Though simple to implement and widely used, this triple modular redundancy is a relatively inefficient ECC. Better ECC codes typically examine the last several tens or even the last several hundreds of previously received bits to determine how to decode the current small handful of bits (typically in groups of 2 to 8 bits).
Averaging noise to reduce errors[edit]
ECC could be said to work by «averaging noise»; since each data bit affects many transmitted symbols, the corruption of some symbols by noise usually allows the original user data to be extracted from the other, uncorrupted received symbols that also depend on the same user data.
- Because of this «risk-pooling» effect, digital communication systems that use ECC tend to work well above a certain minimum signal-to-noise ratio and not at all below it.
- This all-or-nothing tendency – the cliff effect – becomes more pronounced as stronger codes are used that more closely approach the theoretical Shannon limit.
- Interleaving ECC coded data can reduce the all or nothing properties of transmitted ECC codes when the channel errors tend to occur in bursts. However, this method has limits; it is best used on narrowband data.
Most telecommunication systems use a fixed channel code designed to tolerate the expected worst-case bit error rate, and then fail to work at all if the bit error rate is ever worse.
However, some systems adapt to the given channel error conditions: some instances of hybrid automatic repeat-request use a fixed ECC method as long as the ECC can handle the error rate, then switch to ARQ when the error rate gets too high;
adaptive modulation and coding uses a variety of ECC rates, adding more error-correction bits per packet when there are higher error rates in the channel, or taking them out when they are not needed.
Types of ECC[edit]
A block code (specifically a Hamming code) where redundant bits are added as a block to the end of the initial message
A continuous code convolutional code where redundant bits are added continuously into the structure of the code word
The two main categories of ECC codes are block codes and convolutional codes.
- Block codes work on fixed-size blocks (packets) of bits or symbols of predetermined size. Practical block codes can generally be hard-decoded in polynomial time to their block length.
- Convolutional codes work on bit or symbol streams of arbitrary length. They are most often soft decoded with the Viterbi algorithm, though other algorithms are sometimes used. Viterbi decoding allows asymptotically optimal decoding efficiency with increasing constraint length of the convolutional code, but at the expense of exponentially increasing complexity. A convolutional code that is terminated is also a ‘block code’ in that it encodes a block of input data, but the block size of a convolutional code is generally arbitrary, while block codes have a fixed size dictated by their algebraic characteristics. Types of termination for convolutional codes include «tail-biting» and «bit-flushing».
There are many types of block codes; Reed–Solomon coding is noteworthy for its widespread use in compact discs, DVDs, and hard disk drives. Other examples of classical block codes include Golay, BCH, Multidimensional parity, and Hamming codes.
Hamming ECC is commonly used to correct NAND flash memory errors.[5]
This provides single-bit error correction and 2-bit error detection.
Hamming codes are only suitable for more reliable single-level cell (SLC) NAND.
Denser multi-level cell (MLC) NAND may use multi-bit correcting ECC such as BCH or Reed–Solomon.[6][7] NOR Flash typically does not use any error correction.[6]
Classical block codes are usually decoded using hard-decision algorithms,[8] which means that for every input and output signal a hard decision is made whether it corresponds to a one or a zero bit. In contrast, convolutional codes are typically decoded using soft-decision algorithms like the Viterbi, MAP or BCJR algorithms, which process (discretized) analog signals, and which allow for much higher error-correction performance than hard-decision decoding.
Nearly all classical block codes apply the algebraic properties of finite fields. Hence classical block codes are often referred to as algebraic codes.
In contrast to classical block codes that often specify an error-detecting or error-correcting ability, many modern block codes such as LDPC codes lack such guarantees. Instead, modern codes are evaluated in terms of their bit error rates.
Most forward error correction codes correct only bit-flips, but not bit-insertions or bit-deletions.
In this setting, the Hamming distance is the appropriate way to measure the bit error rate.
A few forward error correction codes are designed to correct bit-insertions and bit-deletions, such as Marker Codes and Watermark Codes.
The Levenshtein distance is a more appropriate way to measure the bit error rate when using such codes.
[9]
Code-rate and the tradeoff between reliability and data rate[edit]
The fundamental principle of ECC is to add redundant bits in order to help the decoder to find out the true message that was encoded by the transmitter. The code-rate of a given ECC system is defined as the ratio between the number of information bits and the total number of bits (i.e., information plus redundancy bits) in a given communication package. The code-rate is hence a real number. A low code-rate close to zero implies a strong code that uses many redundant bits to achieve a good performance, while a large code-rate close to 1 implies a weak code.
The redundant bits that protect the information have to be transferred using the same communication resources that they are trying to protect. This causes a fundamental tradeoff between reliability and data rate.[10] In one extreme, a strong code (with low code-rate) can induce an important increase in the receiver SNR (signal-to-noise-ratio) decreasing the bit error rate, at the cost of reducing the effective data rate. On the other extreme, not using any ECC (i.e., a code-rate equal to 1) uses the full channel for information transfer purposes, at the cost of leaving the bits without any additional protection.
One interesting question is the following: how efficient in terms of information transfer can an ECC be that has a negligible decoding error rate? This question was answered by Claude Shannon with his second theorem, which says that the channel capacity is the maximum bit rate achievable by any ECC whose error rate tends to zero:[11] His proof relies on Gaussian random coding, which is not suitable to real-world applications. The upper bound given by Shannon’s work inspired a long journey in designing ECCs that can come close to the ultimate performance boundary. Various codes today can attain almost the Shannon limit. However, capacity achieving ECCs are usually extremely complex to implement.
The most popular ECCs have a trade-off between performance and computational complexity. Usually, their parameters give a range of possible code rates, which can be optimized depending on the scenario. Usually, this optimization is done in order to achieve a low decoding error probability while minimizing the impact to the data rate. Another criterion for optimizing the code rate is to balance low error rate and retransmissions number in order to the energy cost of the communication.[12]
Concatenated ECC codes for improved performance[edit]
Classical (algebraic) block codes and convolutional codes are frequently combined in concatenated coding schemes in which a short constraint-length Viterbi-decoded convolutional code does most of the work and a block code (usually Reed–Solomon) with larger symbol size and block length «mops up» any errors made by the convolutional decoder. Single pass decoding with this family of error correction codes can yield very low error rates, but for long range transmission conditions (like deep space) iterative decoding is recommended.
Concatenated codes have been standard practice in satellite and deep space communications since Voyager 2 first used the technique in its 1986 encounter with Uranus. The Galileo craft used iterative concatenated codes to compensate for the very high error rate conditions caused by having a failed antenna.
Low-density parity-check (LDPC)[edit]
Low-density parity-check (LDPC) codes are a class of highly efficient linear block
codes made from many single parity check (SPC) codes. They can provide performance very close to the channel capacity (the theoretical maximum) using an iterated soft-decision decoding approach, at linear time complexity in terms of their block length. Practical implementations rely heavily on decoding the constituent SPC codes in parallel.
LDPC codes were first introduced by Robert G. Gallager in his PhD thesis in 1960,
but due to the computational effort in implementing encoder and decoder and the introduction of Reed–Solomon codes,
they were mostly ignored until the 1990s.
LDPC codes are now used in many recent high-speed communication standards, such as DVB-S2 (Digital Video Broadcasting – Satellite – Second Generation), WiMAX (IEEE 802.16e standard for microwave communications), High-Speed Wireless LAN (IEEE 802.11n),[13] 10GBase-T Ethernet (802.3an) and G.hn/G.9960 (ITU-T Standard for networking over power lines, phone lines and coaxial cable). Other LDPC codes are standardized for wireless communication standards within 3GPP MBMS (see fountain codes).
Turbo codes[edit]
Turbo coding is an iterated soft-decoding scheme that combines two or more relatively simple convolutional codes and an interleaver to produce a block code that can perform to within a fraction of a decibel of the Shannon limit. Predating LDPC codes in terms of practical application, they now provide similar performance.
One of the earliest commercial applications of turbo coding was the CDMA2000 1x (TIA IS-2000) digital cellular technology developed by Qualcomm and sold by Verizon Wireless, Sprint, and other carriers. It is also used for the evolution of CDMA2000 1x specifically for Internet access, 1xEV-DO (TIA IS-856). Like 1x, EV-DO was developed by Qualcomm, and is sold by Verizon Wireless, Sprint, and other carriers (Verizon’s marketing name for 1xEV-DO is Broadband Access, Sprint’s consumer and business marketing names for 1xEV-DO are Power Vision and Mobile Broadband, respectively).
Local decoding and testing of codes[edit]
Sometimes it is only necessary to decode single bits of the message, or to check whether a given signal is a codeword, and do so without looking at the entire signal. This can make sense in a streaming setting, where codewords are too large to be classically decoded fast enough and where only a few bits of the message are of interest for now. Also such codes have become an important tool in computational complexity theory, e.g., for the design of probabilistically checkable proofs.
Locally decodable codes are error-correcting codes for which single bits of the message can be probabilistically recovered by only looking at a small (say constant) number of positions of a codeword, even after the codeword has been corrupted at some constant fraction of positions. Locally testable codes are error-correcting codes for which it can be checked probabilistically whether a signal is close to a codeword by only looking at a small number of positions of the signal.
Interleaving[edit]
«Interleaver» redirects here. For the fiber-optic device, see optical interleaver.
A short illustration of interleaving idea
Interleaving is frequently used in digital communication and storage systems to improve the performance of forward error correcting codes. Many communication channels are not memoryless: errors typically occur in bursts rather than independently. If the number of errors within a code word exceeds the error-correcting code’s capability, it fails to recover the original code word. Interleaving alleviates this problem by shuffling source symbols across several code words, thereby creating a more uniform distribution of errors.[14] Therefore, interleaving is widely used for burst error-correction.
The analysis of modern iterated codes, like turbo codes and LDPC codes, typically assumes an independent distribution of errors.[15] Systems using LDPC codes therefore typically employ additional interleaving across the symbols within a code word.[16]
For turbo codes, an interleaver is an integral component and its proper design is crucial for good performance.[14][17] The iterative decoding algorithm works best when there are not short cycles in the factor graph that represents the decoder; the interleaver is chosen to avoid short cycles.
Interleaver designs include:
- rectangular (or uniform) interleavers (similar to the method using skip factors described above)
- convolutional interleavers
- random interleavers (where the interleaver is a known random permutation)
- S-random interleaver (where the interleaver is a known random permutation with the constraint that no input symbols within distance S appear within a distance of S in the output).[18]
- a contention-free quadratic permutation polynomial (QPP).[19] An example of use is in the 3GPP Long Term Evolution mobile telecommunication standard.[20]
In multi-carrier communication systems, interleaving across carriers may be employed to provide frequency diversity, e.g., to mitigate frequency-selective fading or narrowband interference.[21]
Example[edit]
Transmission without interleaving:
Error-free message: aaaabbbbccccddddeeeeffffgggg Transmission with a burst error: aaaabbbbccc____deeeeffffgggg
Here, each group of the same letter represents a 4-bit one-bit error-correcting codeword. The codeword cccc is altered in one bit and can be corrected, but the codeword dddd is altered in three bits, so either it cannot be decoded at all or it might be decoded incorrectly.
With interleaving:
Error-free code words: aaaabbbbccccddddeeeeffffgggg Interleaved: abcdefgabcdefgabcdefgabcdefg Transmission with a burst error: abcdefgabcd____bcdefgabcdefg Received code words after deinterleaving: aa_abbbbccccdddde_eef_ffg_gg
In each of the codewords «aaaa», «eeee», «ffff», and «gggg», only one bit is altered, so one-bit error-correcting code will decode everything correctly.
Transmission without interleaving:
Original transmitted sentence: ThisIsAnExampleOfInterleaving Received sentence with a burst error: ThisIs______pleOfInterleaving
The term «AnExample» ends up mostly unintelligible and difficult to correct.
With interleaving:
Transmitted sentence: ThisIsAnExampleOfInterleaving... Error-free transmission: TIEpfeaghsxlIrv.iAaenli.snmOten. Received sentence with a burst error: TIEpfe______Irv.iAaenli.snmOten. Received sentence after deinterleaving: T_isI_AnE_amp_eOfInterle_vin_...
No word is completely lost and the missing letters can be recovered with minimal guesswork.
Disadvantages of interleaving[edit]
Use of interleaving techniques increases total delay. This is because the entire interleaved block must be received before the packets can be decoded.[22] Also interleavers hide the structure of errors; without an interleaver, more advanced decoding algorithms can take advantage of the error structure and achieve more reliable communication than a simpler decoder combined with an interleaver[citation needed]. An example of such an algorithm is based on neural network[23] structures.
Software for error-correcting codes[edit]
Simulating the behaviour of error-correcting codes (ECCs) in software is a common practice to design, validate and improve ECCs. The upcoming wireless 5G standard raises a new range of applications for the software ECCs: the Cloud Radio Access Networks (C-RAN) in a Software-defined radio (SDR) context. The idea is to directly use software ECCs in the communications. For instance in the 5G, the software ECCs could be located in the cloud and the antennas connected to this computing resources: improving this way the flexibility of the communication network and eventually increasing the energy efficiency of the system.
In this context, there are various available Open-source software listed below (non exhaustive).
- AFF3CT(A Fast Forward Error Correction Toolbox): a full communication chain in C++ (many supported codes like Turbo, LDPC, Polar codes, etc.), very fast and specialized on channel coding (can be used as a program for simulations or as a library for the SDR).
- IT++: a C++ library of classes and functions for linear algebra, numerical optimization, signal processing, communications, and statistics.
- OpenAir: implementation (in C) of the 3GPP specifications concerning the Evolved Packet Core Networks.
List of error-correcting codes[edit]
| Distance | Code |
|---|---|
| 2 (single-error detecting) | Parity |
| 3 (single-error correcting) | Triple modular redundancy |
| 3 (single-error correcting) | perfect Hamming such as Hamming(7,4) |
| 4 (SECDED) | Extended Hamming |
| 5 (double-error correcting) | |
| 6 (double-error correct-/triple error detect) | Nordstrom-Robinson code |
| 7 (three-error correcting) | perfect binary Golay code |
| 8 (TECFED) | extended binary Golay code |
- AN codes
- BCH code, which can be designed to correct any arbitrary number of errors per code block.
- Barker code used for radar, telemetry, ultra sound, Wifi, DSSS mobile phone networks, GPS etc.
- Berger code
- Constant-weight code
- Convolutional code
- Expander codes
- Group codes
- Golay codes, of which the Binary Golay code is of practical interest
- Goppa code, used in the McEliece cryptosystem
- Hadamard code
- Hagelbarger code
- Hamming code
- Latin square based code for non-white noise (prevalent for example in broadband over powerlines)
- Lexicographic code
- Linear Network Coding, a type of erasure correcting code across networks instead of point-to-point links
- Long code
- Low-density parity-check code, also known as Gallager code, as the archetype for sparse graph codes
- LT code, which is a near-optimal rateless erasure correcting code (Fountain code)
- m of n codes
- Nordstrom-Robinson code, used in Geometry and Group Theory[24]
- Online code, a near-optimal rateless erasure correcting code
- Polar code (coding theory)
- Raptor code, a near-optimal rateless erasure correcting code
- Reed–Solomon error correction
- Reed–Muller code
- Repeat-accumulate code
- Repetition codes, such as Triple modular redundancy
- Spinal code, a rateless, nonlinear code based on pseudo-random hash functions[25]
- Tornado code, a near-optimal erasure correcting code, and the precursor to Fountain codes
- Turbo code
- Walsh–Hadamard code
- Cyclic redundancy checks (CRCs) can correct 1-bit errors for messages at most
bits long for optimal generator polynomials of degree
, see Mathematics of cyclic redundancy checks#Bitfilters
See also[edit]
- Code rate
- Erasure codes
- Soft-decision decoder
- Burst error-correcting code
- Error detection and correction
- Error-correcting codes with feedback
References[edit]
- ^ Glover, Neal; Dudley, Trent (1990). Practical Error Correction Design For Engineers (Revision 1.1, 2nd ed.). CO, USA: Cirrus Logic. ISBN 0-927239-00-0.
- ^ a b Hamming, Richard Wesley (April 1950). «Error Detecting and Error Correcting Codes». Bell System Technical Journal. USA: AT&T. 29 (2): 147–160. doi:10.1002/j.1538-7305.1950.tb00463.x. S2CID 61141773.
- ^ a b c Maunder, Robert (2016). «Overview of Channel Coding».
- ^ Charles Wang; Dean Sklar; Diana Johnson (Winter 2001–2002). «Forward Error-Correction Coding». Crosslink. The Aerospace Corporation. 3 (1). Archived from the original on 14 March 2012. Retrieved 5 March 2006.
How Forward Error-Correcting Codes Work
- ^ «Hamming codes for NAND flash memory devices» Archived 21 August 2016 at the Wayback Machine. EE Times-Asia. Apparently based on «Micron Technical Note TN-29-08: Hamming Codes for NAND Flash Memory Devices». 2005. Both say: «The Hamming algorithm is an industry-accepted method for error detection and correction in many SLC NAND flash-based applications.»
- ^ a b «What Types of ECC Should Be Used on Flash Memory?» (Application note). Spansion. 2011.
Both Reed–Solomon algorithm and BCH algorithm are common ECC choices for MLC NAND flash. … Hamming based block codes are the most commonly used ECC for SLC…. both Reed–Solomon and BCH are able to handle multiple errors and are widely used on MLC flash.
- ^ Jim Cooke (August 2007). «The Inconvenient Truths of NAND Flash Memory» (PDF). p. 28.
For SLC, a code with a correction threshold of 1 is sufficient. t=4 required … for MLC.
- ^ Baldi, M.; Chiaraluce, F. (2008). «A Simple Scheme for Belief Propagation Decoding of BCH and RS Codes in Multimedia Transmissions». International Journal of Digital Multimedia Broadcasting. 2008: 1–12. doi:10.1155/2008/957846.
- ^ Shah, Gaurav; Molina, Andres; Blaze, Matt (2006). «Keyboards and covert channels». USENIX. Retrieved 20 December 2018.
- ^ Tse, David; Viswanath, Pramod (2005), Fundamentals of Wireless Communication, Cambridge University Press, UK
- ^ Shannon, C. E. (1948). «A mathematical theory of communication» (PDF). Bell System Technical Journal. 27 (3–4): 379–423 & 623–656. doi:10.1002/j.1538-7305.1948.tb01338.x. hdl:11858/00-001M-0000-002C-4314-2.
- ^ Rosas, F.; Brante, G.; Souza, R. D.; Oberli, C. (2014). «Optimizing the code rate for achieving energy-efficient wireless communications». Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC). pp. 775–780. doi:10.1109/WCNC.2014.6952166. ISBN 978-1-4799-3083-8.
- ^ IEEE Standard, section 20.3.11.6 «802.11n-2009» Archived 3 February 2013 at the Wayback Machine, IEEE, 29 October 2009, accessed 21 March 2011.
- ^ a b Vucetic, B.; Yuan, J. (2000). Turbo codes: principles and applications. Springer Verlag. ISBN 978-0-7923-7868-6.
- ^ Luby, Michael; Mitzenmacher, M.; Shokrollahi, A.; Spielman, D.; Stemann, V. (1997). «Practical Loss-Resilient Codes». Proc. 29th Annual Association for Computing Machinery (ACM) Symposium on Theory of Computation.
- ^ «Digital Video Broadcast (DVB); Second generation framing structure, channel coding and modulation systems for Broadcasting, Interactive Services, News Gathering and other satellite broadband applications (DVB-S2)». En 302 307. ETSI (V1.2.1). April 2009.
- ^ Andrews, K. S.; Divsalar, D.; Dolinar, S.; Hamkins, J.; Jones, C. R.; Pollara, F. (November 2007). «The Development of Turbo and LDPC Codes for Deep-Space Applications». Proceedings of the IEEE. 95 (11): 2142–2156. doi:10.1109/JPROC.2007.905132. S2CID 9289140.
- ^ Dolinar, S.; Divsalar, D. (15 August 1995). «Weight Distributions for Turbo Codes Using Random and Nonrandom Permutations». TDA Progress Report. 122: 42–122. Bibcode:1995TDAPR.122…56D. CiteSeerX 10.1.1.105.6640.
- ^ Takeshita, Oscar (2006). «Permutation Polynomial Interleavers: An Algebraic-Geometric Perspective». IEEE Transactions on Information Theory. 53 (6): 2116–2132. arXiv:cs/0601048. Bibcode:2006cs……..1048T. doi:10.1109/TIT.2007.896870. S2CID 660.
- ^ 3GPP TS 36.212, version 8.8.0, page 14
- ^ «Digital Video Broadcast (DVB); Frame structure, channel coding and modulation for a second generation digital terrestrial television broadcasting system (DVB-T2)». En 302 755. ETSI (V1.1.1). September 2009.
- ^ Techie (3 June 2010). «Explaining Interleaving». W3 Techie Blog. Retrieved 3 June 2010.
- ^ Krastanov, Stefan; Jiang, Liang (8 September 2017). «Deep Neural Network Probabilistic Decoder for Stabilizer Codes». Scientific Reports. 7 (1): 11003. arXiv:1705.09334. Bibcode:2017NatSR…711003K. doi:10.1038/s41598-017-11266-1. PMC 5591216. PMID 28887480.
- ^ Nordstrom, A.W.; Robinson, J.P. (1967), «An optimum nonlinear code», Information and Control, 11 (5–6): 613–616, doi:10.1016/S0019-9958(67)90835-2
- ^ Perry, Jonathan; Balakrishnan, Hari; Shah, Devavrat (2011). «Rateless Spinal Codes». Proceedings of the 10th ACM Workshop on Hot Topics in Networks. pp. 1–6. doi:10.1145/2070562.2070568. hdl:1721.1/79676. ISBN 9781450310598.
Further reading[edit]
- MacWilliams, Florence Jessiem; Sloane, Neil James Alexander (2007) [1977]. Written at AT&T Shannon Labs, Florham Park, New Jersey, USA. The Theory of Error-Correcting Codes. North-Holland Mathematical Library. Vol. 16 (digital print of 12th impression, 1st ed.). Amsterdam / London / New York / Tokyo: North-Holland / Elsevier BV. ISBN 978-0-444-85193-2. LCCN 76-41296. (xxii+762+6 pages)
- Clark, Jr., George C.; Cain, J. Bibb (1981). Error-Correction Coding for Digital Communications. New York, USA: Plenum Press. ISBN 0-306-40615-2.
- Arazi, Benjamin (1987). Swetman, Herb (ed.). A Commonsense Approach to the Theory of Error Correcting Codes. MIT Press Series in Computer Systems. Vol. 10 (1 ed.). Cambridge, Massachusetts, USA / London, UK: Massachusetts Institute of Technology. ISBN 0-262-01098-4. LCCN 87-21889. (x+2+208+4 pages)
- Wicker, Stephen B. (1995). Error Control Systems for Digital Communication and Storage. Englewood Cliffs, New Jersey, USA: Prentice-Hall. ISBN 0-13-200809-2.
- Wilson, Stephen G. (1996). Digital Modulation and Coding. Englewood Cliffs, New Jersey, USA: Prentice-Hall. ISBN 0-13-210071-1.
- «Error Correction Code in Single Level Cell NAND Flash memories» 2007-02-16
- «Error Correction Code in NAND Flash memories» 2004-11-29
- Observations on Errors, Corrections, & Trust of Dependent Systems, by James Hamilton, 2012-02-26
- Sphere Packings, Lattices and Groups, By J. H. Conway, Neil James Alexander Sloane, Springer Science & Business Media, 2013-03-09 – Mathematics – 682 pages.
External links[edit]
- Morelos-Zaragoza, Robert (2004). «The Correcting Codes (ECC) Page». Retrieved 5 March 2006.
- lpdec: library for LP decoding and related things (Python)
Прослеживание лекарственных препаратов обеспечивается путем оптического считывания маркировки при помощи технологии машинного зрения (рис. 1) и регистрации результатов считывания в соответствующих базах данных.
Рис. 1. Считывание Data Matrix-кода при помощи камеры машинного зрения
В рамках данной статьи будут рассмотрены аспекты нанесения и надежного считывания маркировки ЛП, вызывающие наибольшее количество вопросов и споров среди участников фармацевтического рынка. Особое внимание будет уделено верификации качества кода, а также инженерной проблематике использования машинного зрения на этапах сериализации и агрегации ЛП на фармацевтическом производстве.
Маркировка лекарств как объект оптического контроля
В соответствии с утвержденным Правительством РФ Постановлением, маркировка ЛП при нанесении на вторичную (потребительскую) упаковку (а в случае ее отсутствия — на первичную упаковку лекарственного препарата) должна соответствовать следующим требованиям:
- двумерный штриховой код наносится точечными символами в соответствии с требованиями ГОСТ Р ИСО/МЭК 16022-2008 «Автоматическая идентификация. Кодирование штриховое. Спецификация символики Data Matrix»;
- двумерный штриховой код наносится с уровнем класса качества C или выше в соответствии с требованиями ГОСТ Р ИСО/МЭК 15415-2012 «Информационные технологии. Технологии автоматической идентификации и сбора данных. Спецификация испытаний символов штрихового кода для оценки качества печати. Двумерные символы»;
- двумерный штриховой код наносится печатью с использованием метода коррекции ошибок ЕСС-200 в соответствии с требованиями ГОСТ Р ИСО/МЭК 16022-2008 «Автоматическая идентификация. Кодирование штриховое. Спецификация символики Data Matrix»;
- при нанесении средства идентификации лекарственного препарата используется ASCII-кодирование на основе ГОСТ Р ИСО/МЭК 16022-2008 «Автоматическая идентификация. Кодирование штриховое. Спецификация символики Data Matrix».
Грейд — класс качества кода
Качество маркировки ЛП с точки зрения надежности ее оптического считывания зависит от множества факторов: скорости движения ЛП в ходе маркировки, типа используемого принтера (в том числе количества печатающих головок), вида упаковки, физического размера и т. п.
Для оценки качественного уровня нанесенной маркировки существует понятие «грейд» (Grade), означающее класс, сорт или категорию. Значение грейда варьируется от A до F, где A — самый высокий класс, а F — самый низкий (рис. 2).
Рис. 2. Класс качества кодов по ИСО/МЭК 15415
Качество кода определяется по следующим критериям:
- Контраст элементов кода — разница между значениями самых светлых и темных элементов, а также между «свободной» зоной и элементами периметра (рис. 3).
Рис. 3. Код с плохим контрастом элементов
- Осевая неоднородность — величина отклонения по основным осям элементов кода (рис. 4).
Рис. 4. Проблема осевой неоднородности
- Модуляция — однородность светлых и темных элементов по всему коду (рис. 5).
Рис. 5. Код с плохой модуляцией, вызванной нерегулярными темными областями
- Неоднородность сетки — отклонение ячейки кода от сетки теоретически «идеального» кода (рис. 6).
Рис. 6. Проблема неравномерности сетки
- Неиспользуемая коррекция ошибок — количество доступных исправлений ошибок в коде.
Рис. 7. Повреждение фиксированного шаблона
- Повреждения фиксированных шаблонов — измеряет и оценивает любое повреждение шаблона, «свободной» зоны и направляющих кода (рис. 7).
Рис. 8. Слишком большой рост печати
- Уровень печати — отклонение фактического размера элемента от его предполагаемого размера из-за проблем с печатью (рис. 8, 9).
Рис. 9. Потеря печати
Введение криптозащиты существенно усложнило достижение требуемого Постановлением грейда С и выше. К ранее кодируемой в Data Matrix информации о ЛП добавились дополнительные 92 символа (четыре символа ключа проверки и 88 символов электронной подписи), что привело к существенному уплотнению наносимого кода. В условиях высоких скоростей движения ЛП на линии и ограничений по размеру упаковки класс качества печати значительно снизился.
Кроме того, как показывает практика, при движении ЛП от производителя до конечного потребителя маркировка последовательно теряет свое качество примерно на один уровень, что обусловлено физическими факторами при транспортировке и складировании. Поэтому следует уделять особое внимание исходному качеству нанесения маркировки ЛП.
Валидация, оценка качества и верификация кода
После нанесения маркировки на упаковку ЛП необходимо удостовериться, что она нанесена корректно и с должным классом качества. Выделяют три уровня такой проверки.
Первый уровень — валидация, в ходе которой проверяют соответствие содержания данных маркировки выданному на печать заданию. Для решения задачи валидации на производственной линии могут быть использованы простые оптические считыватели — сканеры кодов.
Второй уровень проверки оценивает качество печати маркировки (грейд). Бюджетные сканеры чаще всего не способны выполнять такую оценку. Поэтому для оценки грейда на производственных линиях применяются либо смарт-камеры, либо специальные аппаратно-программные инструменты машинного зрения. В последнем случае подразумевается использование камеры машинного зрения и специализированных программных библиотек, предназначенных для анализа изображений. Примером такой библиотеки служит программное обеспечение Cognex VisionPro.
Для абсолютной оценки качества нанесенной маркировки ЛП (третий уровень) применяют так называемые верификаторы (рис. 10). Они проверяют соответствие качества кодов международным стандартам. Для уверенной безошибочной работы верификатора требуется калибровка и точное позиционирование элементов подсветки. Сам процесс верификации занимает более длительное время, нежели просто считывание кодов, поэтому верификаторы, как правило, используются не для сквозной, а для выборочной проверки качества маркировки.
Рис. 10. Верификатор Cognex DataMan 8072V
Инструменты машинного зрения для решения задач прослеживания ЛП
Печать и проверка качества нанесенной на каждую упаковку ЛП маркировки проводятся на этапе сериализации. Для оценки качества необходимо выполнить считывание уникального кода упаковки и проверку его соответствия стандарту ISO 15415.
Рис. 11. Агрегация ЛП
При агрегации осуществляется привязка кода третичной (транспортной) упаковки ЛП к кодам находящихся в ней сериализованных индивидуальных упаковок. На этом этапе необходимо выполнять множественное считывание кодов с нескольких слоев короба (рис. 11).
Рис. 12. Сканер Cognex серии DataMan 300/360
Для считывания кодов на этапах сериализации и агрегации применяют сканеры кодов, смарт-камеры или системы на базе камер машинного зрения. Имея большой опыт разработки систем машинного зрения для разных отраслей, в том числе систем прослеживания продукции, мы обобщили наше видение преимуществ и недостатков каждого из инструментов (табл., рис. 12–14). Для примера в таблице представлено оборудование машинного зрения Cognex, чьим дистрибьютором и партнером-интегратором является наша компания «Малленом Системс».
Рис. 13. Смарт-камера Cognex серии In-Sight 7000
Рис. 14. Камера машинного зрения Cognex CIC
С точки зрения выбора и настройки оборудования машинного зрения этап агрегации имеет больше нюансов, нежели этап сериализации. Поэтому ниже приведены дополнительные рекомендации по настройке оборудования для этапа агрегации:
- Расчет разрешающей способности камеры производится на основании максимальных размеров короба, количества слоев (высоты короба) и размеров кода. Как правило, для агрегации достаточным является разрешение от 5 Мп (752×480) до 20 Мп (5472×3648). В ряде случаев при работе с широкой зоной контроля для ее покрытия используют несколько камер.
- При послойной агрегации крайне важно обеспечить большую глубину резкости, что достигается объективом с большим фокусным расстоянием. Однако следует учитывать, что использование таких объективов требует увеличения физического расстояния от камеры до упаковок в коробе.
- Также при расчете параметров камеры и объектива необходимо учитывать, что зона контроля в нижней части короба будет больше зоны контроля в верхней части, соответственно, расчет нужного разрешения следует выполнять по двум условиям:
- верхняя часть короба полностью видна камерой;
- разрешения камеры достаточно для надежного считывания всех кодов в нижней части.
Таблица. Сравнение инструментов машинного зрения, используемых при сериализации и агрегации
|
Устройство |
Сериализация |
Агрегация |
|
Стационарный оптический сканер кодов Разрешение от 0,3 Мп (752×480) до 3 Мп (2048×1536) |
Преимущества:
Недостатки:
|
Преимущества:
Недостатки:
|
|
Смарт-камера Разрешение от 0,3 Мп (640×480) до 12 Мп (4096×3000) |
Преимущества:
Недостатки:
|
Преимущества:
Недостатки:
|
|
Камера машинного зрения Разрешение от 0,3 Мп (640×480) до 29 Мп (6576×4384) |
Преимущества:
Недостатки:
|
Преимущества:
Недостатки:
|
Готовое решение от компании «Малленом Системс»
В нашей собственной разработке для фармацевтической отрасли — системе маркировки лекарственных средств «ВИСКОНТ.Фарма», представленной в ноябре прошлого года на выставке Pharmtech & Ingredients, — используются камеры машинного зрения как на этапе сериализации, так и на этапе агрегации для послойного считывания сериализованных упаковок в гофрокоробе. Существует также ручная версия системы на основе оптических сканеров кодов.
Выбор инструментов машинного зрения для «ВИСКОНТ.Фарма» обусловлен несколькими причинами. Прежде всего, мы стремились создать максимально гибкое решение и обеспечить возможность его использования как при создании новых технологических линий, так и для модернизации существующих, с ручной, полуавтоматической либо автоматической агрегацией. Кроме того, для нас важно было предложить весь требуемый функционал системы прослеживания, включая возможность проверки грейда, без переплат за использование дорогостоящих смарт-камер.
Представленная на выставке версия системы «ВИСКОНТ.Фарма» для высокоскоростных производственных линий на основе конвейера с прижимным механизмом упаковок включает стол подачи, разгонный фидер, регулируемый конвейер и стол агрегации (рис. 15).
Рис. 15. Оборудование для сериализации и агрегации ЛП «ВИСКОНТ.Фарма»
Регулируемый конвейер оснащен узлом печати, обеспечивающим высоту печати до 12,7 мм. Понимая, что именно от конструкции узла печати и выбора принтера зависит получаемый класс качества маркировки, мы проработали различные варианты и в итоге добились стабильного получения грейда не ниже В.
Проверка качества печати маркировки осуществляется в «ВИСКОНТ.Фарма» с помощью камеры Cognex и осветителя. При прохождении упаковки с маркировкой ненадлежащего качества система подает сигнал пневматическому отбраковщику на удаление данной упаковки с линии (рис. 16).
Рис. 16. Экранная форма программного обеспечения системы «ВИСКОНТ.Фарма»
Успешно прошедшие проверку упаковки попадают на стол агрегации, где оператор вручную формирует слои в гофрокоробе. Над столом агрегации расположена еще одна камера Cognex и осветители. Камера непрерывно сканирует маркировку упаковок в слое гофрокороба. В зависимости от особенностей технологического процесса возможны как установка камеры в фиксированном положении, так и использование сервопривода для подъема/опускания камеры при послойной агрегации.
Процесс агрегации можно видеть на мониторе. При успешной агрегации слоя система выдает сообщение «Слой завершен», и так для каждого слоя в гофрокоробе. После агрегации последнего слоя система посылает команду на печать стикера гофрокороба. Стикер наклеивается вручную, и гофрокороб поступает на дальнейшую упаковку и формирование палет.
Заключение
Чтобы обеспечить прослеживание ЛП в ходе производства, требуется решить множество непростых инженерных задач как на этапе сериализации ЛП, так и на этапе их агрегации. В статье мы поделились опытом и постарались выделить некоторые важные, на наш взгляд, особенности использования оборудования машинного зрения применительно к данной задаче. Надеемся, что этот материал будет полезен широкому кругу интеграторов, разработчиков, заказчиков и пользователей подобных систем в сфере фармацевтического производства.
Текст ГОСТ Р ИСО/МЭК 16022-2008 Автоматическая идентификация. Кодирование штриховое. Спецификация символики Data Matrix
ГОСТ Р ИСО/МЭК 16022-2008
Группа П85
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Автоматическая идентификация
КОДИРОВАНИЕ ШТРИХОВОЕ
Спецификация символики Data Matrix
Automatic identification. Bar coding. Data Matrix symbology specification
ОКС 35.040
Дата введения 2010-01-01
Предисловие
Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. N 184-ФЗ «О техническом регулировании», а правила применения национальных стандартов Российской Федерации — ГОСТ Р 1.0-2004 «Стандартизация в Российской Федерации. Основные положения»*
____________
* На территории Российской Федерации документ не действует. Действует ГОСТ Р 1.0-2012. — .
Сведения о стандарте
1 ПОДГОТОВЛЕН Ассоциацией автоматической идентификации «ЮНИСКАН/ГС1 РУС» совместно с Обществом с ограниченной ответственностью (ООО) НПЦ «Интелком» на основе аутентичного перевода стандарта, указанного в пункте 4, выполненного ООО НПЦ «Интелком»
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 355 «Автоматическая идентификация»
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 18 декабря 2008 г. N 509-ст
4 Настоящий стандарт идентичен международному стандарту ИСО/МЭК 16022:2006* «Информационные технологии. Технологии автоматической идентификации и сбора данных. Спецификация символики штрихового кода Data Matrix» (ISO/IEC 16022:2006 «Information technology — Automatic identification and data capture techniques — Data Matrix bar code symbology specification»), за исключением приложения U, содержащего сведения о соответствии терминов на русском и английском языках, приложения V, включающего в себя сведения о наборах знаков по ИСО/МЭК 646, ИСО/МЭК 8859-1 и ИСО/МЭК 8859-5. В приложении М приведены исправления в соответствии со списком технических опечаток 1 (Technical Corrigendum 1) к ISO/IEC 16022.1:2006.
________________
* Доступ к международным и зарубежным документам, упомянутым здесь и далее по тексту, можно получить перейдя по ссылке на сайт . —
Наименование национального стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2004* (подраздел 3.5) и учета его принадлежности к группе стандартов «Автоматическая идентификация».
_______________
* На территории Российской Федерации документ не действует. Действует ГОСТ Р 1.5-2012. — .
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных (региональных) стандартов соответствующие им национальные стандарты, сведения о которых приведены в дополнительном приложении W
5 ВВЕДЕН ВПЕРВЫЕ
ВНЕСЕНО Изменение N 1, утвержденное и введенное в действие Приказом Росстандарта от 26.09.2013 N 1112-ст c 01.01.2014
Изменение N 1 внесено изготовителем базы данных по тексту ИУС N 1, 2014 год
Информация об изменениях к настоящему стандарту публикуется в ежегодно издаваемом информационном указателе «Национальные стандарты», а текст изменений и поправок — в ежемесячно издаваемых информационных указателях «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе «Национальные стандарты». Соответствующая информация, уведомления и тексты размещаются также в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет
Введение
Data Matrix — двухмерная матричная символика, состоящая из квадратных модулей, упорядоченных внутри периметра шаблона поиска. В настоящем документе представление символа и его описание приведено, главным образом, для темных модулей на светлом фоне. Тем не менее, символы Data Matrix также могут быть напечатаны в виде светлых модулей на темном фоне.
Производителям оборудования и пользователям технологии штрихового кодирования необходима общедоступная стандартная спецификация символики, на которую они могли бы ссылаться при разработке оборудования и стандартов по применению. С этой целью и был разработан настоящий стандарт.
Следует обратить внимание на возможность того, что некоторые элементы, включенные в настоящий стандарт, могут быть объектом патентного права, и организации ИСО и МЭК не берут на себя ответственность за определение некоторых или всех подобных патентных прав.
Сноски в тексте стандарта, выделенные курсивом, приведены для пояснения текста стандарта.
1 Область применения
1 Область применения
Настоящий стандарт устанавливает требования к символике Data Matrix*, а также параметры символики, кодирование знаков данных, форматы символов, требования к размерам и качеству печати, правила исправления ошибок, алгоритм декодирования и прикладные параметры, выбираемые пользователем.
________________
* Название символики произносится как Дата Матрикс, что в переводе на русский язык — «матрица данных».
Настоящий стандарт распространяется на все символы символики Data Matrix, напечатанные или нанесенные каким-либо другим способом.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты и другие нормативные документы*, которые необходимо учитывать при использовании настоящего стандарта. В случае ссылок на документы, у которых указана дата утверждения, необходимо пользоваться только указанной редакцией. В случае, когда дата утверждения не приведена, следует пользоваться последней редакцией ссылочных документов, включая любые поправки и изменения к ним:
_______________
* Таблицу соответствия национальных стандартов международным см. по ссылке. — .
ИСО/МЭК 15424 Информационные технологии. Технологии автоматической идентификации и сбора данных. Идентификаторы носителей данных (включая идентификаторы символик) (Information technology — Automatic identification and data capture techniques — Data Carrier Identifiers (including Symbology Identifiers)
ИСО/МЭК 19762-1 Информационные технологии. Технологии автоматической идентификации и сбора данных. Гармонизированный словарь. Часть 1. Общие термины, связанные с автоматической идентификацией и сбором данных (Information technology — Automatic identification and data capture (AIDC) techniques — Harmonized vocabulary — Part 1: General terms relating to AIDC)
ИСО/МЭК 19762-2 Информационные технологии. Технологии автоматической идентификации и сбора данных. Гармонизированный словарь. Часть 2. Средства для оптического считывания (Information technology — Automatic identification and data capture (AIDC) techniques — Harmonized vocabulary — Part 2: Optically readable media (ORM))
ИСО/МЭК 15415 Информационные технологии. Технологии автоматической идентификации и сбора данных. Спецификация испытаний качества печати символов штрихового кода. Двумерные символы (Information technology — Automatic identification and data capture techniques — Bar code print quality test specification — Two-dimensional symbols)
ИСО/МЭК 15416 Информационные технологии. Технологии автоматической идентификации и сбора данных. Спецификация испытаний качества печати символов штрихового кода. Линейные символы (Information technology — Automatic identification and data capture techniques — Bar code print quality test specification — Linear symbols)
ИСО/МЭК 646:1991 Информационные технологии. Набор 7-битовых кодированных знаков ИСО для обмена информацией (Information technology — ISO 7-bit coded character set for information interchange)
ИСО/МЭК 8859-1 Информационные технологии. Наборы 8-битовых однобайтных кодированных графических знаков. Часть 1. Латинский алфавит N 1 (Information technology — 8-bit single-byte coded graphic character sets — Part 1: Latin alphabet N 1)
ИСО/МЭК 8859-5:1999 Информационные технологии. Наборы 8-битовых однобайтных кодированных графических знаков. Часть 5. Латинский/кирилловский алфавит (Information technology — 8-bit single-byte coded graphic character sets — Part 5: Latin/Cyrillic alphabet)
AIM Inc. ITS/04-001 Международный технический стандарт. Интерпретации в расширенном канале. Часть 1. Схемы идентификации и протокол (AIM Inc. ITS/04-001 International Technical Standard: Extended Channel Interpretations — Part 1: Identification Schemes and Protocol)
3 Термины, определения, символы и математические/логические обозначения
3.1 Термины и определения
В данном документе используются термины, определенные в ИСО/МЭК 19762-1, ИСО/МЭК 19762-2, а также следующие:
3.1.1 кодовое слово (codeword): Значение знака символа, формируемое на промежуточном уровне кодирования в процессе преобразования исходных данных в их графическое представление в символе.
3.1.2 модуль (module): Отдельная ячейка матричной символики, используемая для кодирования одного бита информации и имеющая номинально квадратную форму в символах Data Matrix.
3.1.3 сверточное кодирование (convolutional coding): Алгоритм контроля и исправления ошибок, преобразующий множество битов на входе во множество битов на выходе, которое может быть восстановлено после повреждения, путем кодирования с разделением множества входящих битов на блоки с последующим проведением операции свертки каждого входящего блока с регистром сдвига со множеством состояний для получения защищенных на выходе блоков.
Примечание — Такие алгоритмы кодирования могут быть реализованы с помощью аппаратных средств путем использования входных и выходных коммутаторов, регистров сдвига и вентилей исключающих ИЛИ*.
________________
* Международное обозначение операции исключающее ИЛИ: exclusive-or — XOR.
3.1.4 шаблонная рандомизация (pattern randomising): Процедура, с помощью которой исходный набор битов превращают в другой набор битов путем инвертирования отдельных битов с целью уменьшения вероятности повторения в символе одинаковых наборов.
3.2 Символы
В данном документе, если иное не предусмотрено в особых случаях, применяют следующие математические символы:
|
— число кодовых слов исправления ошибок; |
|||
|
— число стираний; |
|||
|
— (для версии ЕСС 000-140) число битов в полном сегменте на входе в конечный автомат для генерирования сверточного кода; (для версии ЕСС 200) общее число кодовых слов исправления ошибок; |
|||
|
— порядок памяти сверточного кода; |
|||
|
— (для версии ЕСС 000-140) число битов в полном сегменте, сгенерированных конечным автоматом, порождающим сверточный код; (для версии ЕСС 200) общее число кодовых слов данных; |
|||
|
— числовое основание в схеме кодирования; |
|||
|
— число кодовых слов, зарезервированных для обнаружения ошибок; |
|||
|
— знак символа; |
|||
|
— число ошибок; |
|||
|
— сегмент битов на входе в конечный автомат, принимающий битов за единицу времени; |
|||
|
— сегмент битов на выходе из конечного автомата, генерирующего битов за единицу времени; |
|||
|
— горизонтальный и вертикальный размеры модуля; |
|||
|
— кодовое слово исправления ошибок. |
3.3 Математические обозначения
В настоящем стандарте используются следующие обозначения и математические операции:
|
div |
— оператор деления на целое число; |
||
|
mod |
— остаток при делении на целое число; |
||
|
XOR |
— исключающее ИЛИ (exclusive-or) — логическая функция или операция, результатом которой является единица только в случае неэквивалентности двух входов; |
||
|
LSB |
— младший значащий разряд (Least Significant Bit); |
||
|
MSB |
— старший значащий разряд (Most Significant Bit). |
4 Описание символов
4.1 Основные параметры
Data Matrix представляет собой двумерную матричную символику.
Существуют две версии символики Data Matrix:
— версия, обозначаемая ЕСС 200, в которой используют алгоритм исправления ошибок Рида-Соломона. Версия ЕСС 200 рекомендуется для разработки любого нового применения;
— версия, обозначаемая ЕСС 000-140, с несколькими доступными уровнями сверточного исправления ошибок, такими как ЕСС 000, ЕСС 050, ЕСС 080, ЕСС 100 и ЕСС 140. Версию ЕСС 000-140 следует использовать только для замкнутых прикладных систем, в которых одна и та же сторона контролирует создание и считывание символов и обеспечивает функционирование всей системы.
Символика Data Matrix имеет следующие параметры:
a) кодируемый набор знаков:
1) знаки набора ASCII (версии КОИ-7) по ИСО/МЭК 646* (согласно национальной версии США**) (далее — знаки ASCII (КОИ-7)) с десятичными значениями от 0 до 127.
________________
* Набор знаков ASCII (версия КОИ-7) по ИСО/МЭК 646 приведен в приложении V.
** Набор знаков по ANSI INCITS 4-1986 (R2007) Information Systems — Coded Character Sets — 7-Bit American National Standard Code for Information Interchange (7-Bit ASCII) (Информационные системы — Кодированные наборы знаков — 7-битовый американский национальный стандартный код для обмена информацией (7-битовый ASCII).
Примечание 1 — Указанная версия ASCII (КОИ-7) состоит из набора знаков G0 по ИСО/МЭК 646 и С0 по ИСО/МЭК 6429, в котором знаки с десятичными значениями от 28 до 31 соответствуют знакам FS, GS, RS и US соответственно;
2) знаки расширенного набора ASCII (версия КОИ-8) по ИСО/МЭК 8859-1* (далее — знаки расширенного набора ASCII (КОИ-8)) с десятичными значениями от 128 до 255;
b) представление данных: темный модуль соответствует двоичной единице, светлый — двоичному нулю.
________________
* Набор знаков расширенного набора ASCII (КОИ-8) приведен в приложении V.
Примечание 2 — Настоящий стандарт определяет символы Data Matrix как темные модули, расположенные на светлом фоне. Однако в 4.2 предусмотрено, что символы могут также быть образованы с заменой цвета на противоположный, и для таких символов положения настоящего стандарта в отношении темных модулей должны применяться к светлым модулям и наоборот;
c) размеры символа в модулях (без учета свободной зоны):
— для версии ЕСС 200 — от 10х10 до 144х144, только четные значения;
— для версии ЕСС 000-140 — от 9х9 до 49 на 49, только нечетные значения;
d) число знаков данных в символе (для символа максимального размера версии ЕСС 200):
1) алфавитно-цифровые данные — до 2335 знаков,
2) в 8-битовых байтах — 1555 знаков,
3) числовые данные — 3116 числовых разрядов;
e) задаваемое исправление ошибок:
— для версии ЕСС 200 — исправление ошибок Рида-Соломона;
— для версии ЕСС 000-140 — четыре уровня исправления ошибок на основе сверточного кода плюс (по выбору) только обнаружение ошибки;
f) тип кода: матричный;
g) независимость от ориентации: присутствует.
4.2 Дополнительные свойства
Символика Data Matrix обладает следующими дополнительными, неотъемлемыми или устанавливаемыми по выбору свойствами:
a) обратимость изображения (неотъемлемое свойство). Символы предназначены для считывания как напечатанные темным на светлом фоне, так и светлым на темном фоне (рисунок 1). Положения настоящего стандарта установлены для темного изображения на светлом фоне, следовательно указания о темных или светлых модулях должны рассматриваться как указания о светлых или темных модулях соответственно для символов с обращением изображения;
b) интерпретации в расширенном канале (только для версии ЕСС 200, свойство по выбору). Данный механизм позволяет использовать знаки из иных наборов (например, знаки арабского, кирилловского, греческого, еврейского алфавитов) и иных различных интерпретаций данных или представлять их в соответствии с особыми отраслевыми требованиями;
c) прямоугольная форма символов (только для версии ЕСС 200, свойство по выбору). Установлены шесть форматов символа прямоугольной формы;
d) структурированное соединение (только для версии ЕСС 200, свойство по выбору). Позволяет представить один документ в виде нескольких (до 16) символов Data Matrix. Исходные данные могут быть восстановлены вне зависимости от порядка сканирования символов.
Рисунок 1 — Пример кодирования сообщения «A1B2C3D4E5F6G7H8I9J0K1L2» в символе версии ЕСС 200 и уровня ЕСС
а) темное изображение на светлом фоне для версии ЕСС 200
b) светлое изображение на темном фоне для версии ЕСС 200
с) темное изображение на светлом фоне для уровня ЕСС 140
Рисунок 1 — Пример кодирования сообщения «A1B2C3D4E5F6G7H8I9J0K1L2» в символе версии ЕСС 200 (рисунки а) и b)) и уровня ЕСС 140 (рисунок с))
4.3 Структура символов
Каждый символ Data Matrix состоит из областей данных, составленных из номинально квадратных модулей, структурированных в регулярную матрицу. В больших символах версии ЕСС 200 области данных отделены направляющими шаблонами. Область данных окружена шаблоном поиска, вокруг которого со всех четырех сторон должна быть свободная зона. На рисунке 1 приведен пример символа уровня ЕСС 140 и два примера символа версии ЕСС 200.
4.3.1 Шаблон поиска
Шаблоном поиска является периметр области данных шириной в один модуль. Две смежные стороны — левая и нижняя, являются сплошными темными линиями и формируют L-образную границу. Они используются, прежде всего, для определения реального размера, ориентации и искажений символа. Две противоположные стороны состоят из чередующихся темных и светлых модулей. Они используются, прежде всего, для определения структуры символа, состоящей из ячеек, но также могут применяться для определения физического размера и искажений символа. Наличие свободной зоны обозначено на рисунке 1 угловыми метками.
4.3.2 Размеры и емкость символов
Символы версии ЕСС 200 состоят из четного числа строк и четного числа столбцов. Символы версии ЕСС 200 могут быть квадратной формы с размерами (в модулях) от 10х10 до 144х144 без учета свободных зон, либо прямоугольной формы размерами (в модулях) от 8х18 до 16х48 без учета свободных зон. Все символы версии ЕСС 200 можно распознать по светлому модулю в правом верхнем углу. Полный перечень атрибутов символа версии ЕСС 200 приведен в 5.5 (таблица 7).
Символы версии ЕСС 000-140 состоят из нечетного числа строк и нечетного числа столбцов. Символы версии ЕСС 000-140 имеют квадратную форму размерами от 9х9 до 49х49 модулей без учета свободных зон. Данные символы можно распознать по темному модулю в правом верхнем углу. Полный перечень атрибутов символов версии ЕСС 000-140 приведен в приложении G.
5.1 Основные положения процедуры кодирования
Настоящий раздел содержит общие сведения о процедуре кодирования. В следующих разделах приведено более детальное рассмотрение указанной процедуры. Пример кодирования для символа версии ЕСС 200 приведен в приложении О. Преобразование данных пользователя в символ версии ЕСС 200 происходит в следующей последовательности:
Этап 1. Кодирование данных
Анализируют поток данных для определения разнообразия типов различных знаков, подлежащих кодированию. Символы версии ЕСС 200 содержат различные схемы кодирования, которые позволяют найденные множества знаков преобразовать в кодовые слова более эффективно по сравнению со схемой кодирования, принятой по умолчанию. Вводят дополнительные кодовые слова для переключения между схемами кодирования и для выполнения других функций. Добавляют необходимое количество знаков-заполнителей для образования требуемого числа кодовых слов. Если пользователь не установил размер матрицы, то выбирают наименьший размер, в котором могут быть размещены данные. Полный перечень размеров матриц приведен в 5.5 (таблица 7).
Этап 2. Формирование кодовых слов проверки и исправления ошибок
Для символов, содержащих более 255 кодовых слов, поток кодовых слов подразделяют на чередующиеся блоки, чтобы дать возможность обработки алгоритмами исправления ошибок (приложение А). Для каждого блока формируют кодовые слова исправления ошибок. Результатом этого процесса является удлинение потока кодовых слов на число кодовых слов исправления ошибок. Кодовые слова исправления ошибок помещают после кодовых слов данных.
Этап 3. Размещение модулей в матрице
Модули кодовых слов размещают в матрице. В матрицу вставляют модули направляющих шаблонов (при их наличии). Вокруг матрицы добавляют модули шаблона поиска.
5.2 Кодирование данных
5.2.1 Общие положения
Данные можно кодировать с использованием любой комбинации из шести схем кодирования (таблица 1), при этом кодирование по схеме ASCII (КОИ-7/КОИ-8) является основной схемой. Остальные схемы кодирования вызываются из схемы кодирования ASCII (КОИ-7/КОИ-8) с последующим возвратом к этой же схеме. Следует учитывать эффективность уплотнения (число битов на знак данных), приведенную в таблице 1. Лучшей схемой для выбранного набора данных может оказаться не та, у которой на знак данных приходится наименьшее число битов. Если требуется наибольшая степень уплотнения, то надо принимать в расчет служебную информацию для переключения между схемами кодирования и наборами знаков внутри одной схемы кодирования (приложение Р). Следует также учитывать, что даже если число кодовых слов минимизировано, поток кодовых слов может нуждаться в расширении для полного заполнения символа. Дополнение осуществляют путем использования знаков-заполнителей.
Таблица 1 — Схемы кодирования для символов версии ЕСС 200
|
Наименование схемы кодирования |
Знаки |
Число битов на один знак данных |
|
ASCII |
Сдвоенные разряды чисел |
4 |
|
(КОИ-7/ |
Знаки ASCII (КОИ-7) с десятичными значениями от 0 до 127 |
8 |
|
КОИ-8) |
Знаки расширенного набора ASCII (КОИ-8) с десятичными значениями от 128 до 255 |
16 |
|
С40 |
Цифры и прописные латинские буквы |
5,33 |
|
Специальные знаки и строчные латинские буквы |
10,66* |
|
|
Text |
Цифры и строчные латинские буквы |
5,33 |
|
Специальные знаки и прописные латинские буквы |
10,66** |
|
|
ANSI X12 |
Набор знаков данных для электронного обмена данными по ANSI X12 EDI |
5,33 |
|
EDIFACT |
Знаки ASCII (КОИ-7) с десятичными значениями от 32 до 94 |
6 |
|
По основанию 256 |
Любые байты с десятичными значениями от 0 до 255 |
8 |
|
* Кодируют как два значения в схеме кодирования С40 с использованием знака регистра (Shift). ** Кодируют как два значения в схеме кодирования Text с использованием знака регистра (Shift). |
5.2.2 Интерпретация знаков по умолчанию
Интерпретация знаков по умолчанию для знаков с десятичными значениями от 0 до 127 должна соответствовать версии КОИ-7 по ИСО/МЭК 646, а для знаков с десятичными значениями от 128 до 255 — версии КОИ-8 по ИСО 8859-1 «Латинский алфавит N 1». Графические представления знаков данных, приведенных в настоящем стандарте, соответствуют интерпретации по умолчанию. Эта интерпретация может быть изменена с помощью переключающих последовательностей интерпретации в расширенном канале (5.4). Интерпретацией по умолчанию является ECI 000003.
5.2.3 Схема кодирования ASCII (КОИ-7/КОИ-8)
Схема кодирования ASCII (КОИ-7/КОИ-8) представляет собой набор знаков по умолчанию для первого знака символа в символах любого размера. С помощью указанной схемы кодируют знаки ASCII (КОИ-7) и расширенного набора ASCII (КОИ-8), числовые данные двойной плотности и управляющие знаки символики. Управляющие знаки символики включают в себя функциональные знаки, знак-заполнитель и знаки-переключатели на другие кодовые наборы. Знаки данных ASCII (КОИ-7) кодируют как кодовые слова с десятичными значениями от 1 до 128 (десятичное значение знака КОИ-7 плюс 1). Знаки данных расширенного набора ASCII (КОИ-8) с десятичными значениями от 128 до 255 кодируют с использованием управляющего знака верхнего регистра (Upper Shift) (5.2.4.2). Пары цифр от 00 до 99 кодируют кодовыми словами от 130 до 229 (числовое значение плюс 130). Присвоенные значения кодовых слов для схемы кодирования ASCII (КОИ-7/КОИ-8) приведены в таблице 2.
Таблица 2 — Значения кодовых слов в схеме кодирования ASCII (КОИ-7/КОИ-8)
|
Значение кодового слова |
Знак данных или функция |
|
1-128 |
Знаки данных ASCII (КОИ-7) (десятичное значение знака +1) |
|
129 |
Знак-заполнитель |
|
130-229 |
Пары цифр от 00 до 99 (числовое значение +130) |
|
230 |
Знак фиксации схемы кодирования С40 |
|
231 |
Знак фиксации схемы кодирования по основанию 256 |
|
232 |
Знак FNC1 |
|
233 |
Знак структурированного соединения |
|
234 |
Знак программирования устройства считывания |
|
235 |
Знак верхнего регистра (переход к расширенному набору ASCII (КОИ-8)) |
|
236 |
Знак Макро 05 |
|
237 |
Знак Макро 06 |
|
238 |
Знак фиксации схемы кодирования Х12 |
|
239 |
Знак фиксации схемы кодирования Text |
|
240 |
Знак фиксации схемы кодирования EDIFACT |
|
241 |
Знак интерпретации в расширенном канале (ECI) |
|
242-255 |
Не подлежит использованию в схеме кодирования ASCII (КОИ-7/КОИ-8) |
5.2.4 Управляющие знаки символики
В символах версии ЕСС 200 есть несколько специальных управляющих знаков символики, имеющих особое значение для схемы кодирования. Эти знаки должны использоваться для сообщения команды декодеру на выполнение определенных функций или передачи управляющему компьютеру специальных данных (5.2.4.1-5.2.4.9). Эти управляющие знаки символики, за исключением знаков с десятичными значениями от 242 до 255, присутствуют в кодовом наборе ASCII (КОИ-7/КОИ-8) (таблица 2).
5.2.4.1 Знаки фиксации схемы кодирования (Latch)
Для переключения из схемы кодирования ASCII (КОИ-7/КОИ-8) в любую иную схему кодирования используют знаки фиксации. Все кодовые слова после знака фиксации должны кодироваться в соответствии с новой схемой кодирования. Различные схемы кодирования имеют свои способы возврата к кодовому набору ASCII (КОИ-7/КОИ-8).
5.2.4.2 Знак верхнего регистра (Upper Shift)
Знак верхнего регистра используется в комбинации с знаком ASCII (КОИ-7) для кодирования знака расширенного набора ASCII (КОИ-8) с десятичными значениями от 128 до 255. Знак расширенного набора ASCII (КОИ-8), кодируемый в схемах кодирования ASCII (КОИ-7/КОИ-8), С40 или Text, требует наличия предшествующего знака верхнего регистра, после которого стоит знак ASCII (КОИ-7), десятичное значение которого уменьшено на 128. Эту пару кодируют в соответствии с правилами схемы кодирования. В схеме кодирования ASCII (КОИ-7/КОИ-8) знак верхнего регистра представлен кодовым словом со значением 235. Уменьшенное десятичное значение знака данных (т.е. десятичное значение знака расширенного набора ASCII (КОИ-8) минус 128) преобразуют в значение кодового слова путем прибавления к его значению единицы. Например, для кодирования знака (ДЕНЕЖНЫЙ ЗНАК ИЕНЫ, десятичное значение которого равно 165) следует после знака верхнего регистра (кодовое слово со значением 235) поставить знак ASCII (КОИ-7) с десятичным значением 37 (165-128), которое кодируется как кодовое слово со значением 38. При наличии протяженных последовательностей знаков данных расширенного набора ASCII (КОИ-8), более эффективное кодирование может быть достигнуто путем использования знака фиксации схемы кодирования по основанию 256.
5.2.4.3 Знак-заполнитель (Pad)
Если кодируемых данных, независимо от используемой схемы кодирования, не хватает для полного заполнения символа для данных, то оставшаяся часть символа для данных должна быть заполнена знаками-заполнителями. Знаки-заполнители должны использоваться исключительно для указанной цели. Перед вводом знака-заполнителя необходимо вернуться к схеме кодирования ASCII (КОИ-7/КОИ-8) из любой другой используемой схемы кодирования.
Алгоритм рандомизации с шаблоном из 253 состояний применяют к знакам-заполнителям, ко всей последовательности знаков-заполнителей, начиная со второго знака-заполнителя и до конца символа (приложение В.1).
5.2.4.4 Знак интерпретации в расширенном канале (ECI)
Знак интерпретации в расширенном канале (ECI) используют для смены интерпретации, принятой по умолчанию, на иную интерпретацию, применяемую для кодирования данных. Протокол интерпретации в расширенном канале является общим для многих символик и его применение к символике версии ЕСС 200 более полно определено в 5.4. После знака ECI обязательно должны следовать одно, два или три кодовых слова, которые идентифицируют конкретную активизируемую ECI. Новая ECI действует до конца кодируемых данных или до тех пор, пока другой знак ECI не вызовет иную интерпретацию.
5.2.4.5 Знаки регистра (Shift) в схемах кодирования С40 и Text
В схемах кодирования С40 и Text используют три специальных знака, называемые знаками регистра, в качестве префикса к одному из 40 значений для кодирования примерно трех четвертей набора знаков ASCII (КОИ-7). Это позволяет добиться более компактного кодирования оставшихся знаков ASCII (КОИ-7) с помощью одиночных значений*.
________________
* Без предшествующего знака «Регистр» перед каждым знаком.
5.2.4.6 Знак FNC1 как идентификатор альтернативного типа данных
Для кодирования данных, соответствующих специальным международным отраслевым стандартам, одобренных AIM Inc, знак FNC1 должен присутствовать в позиции первого или второго знака символа (либо пятой или шестой позиции данных в первом символе структурированного соединения символов). Знак FNC1, кодируемый в позиции любого иного знака символа, используют как разделитель полей, и он подлежит передаче как управляющий знак (знак ASCII (КОИ-7) с десятичным значением 29).
5.2.4.7 Знаки Макро (Macro)
Символика Data Matrix обеспечивает представление специальных международных отраслевых головной и конечной меток в одном знаке символа, которое сокращает число знаков символа, необходимых для кодирования данных в символе при использовании установленных структурированных форматов. Любой знак Макро применяют только в позиции первого знака символа. Эти знаки не должны использоваться вместе со структурированным соединением (Structured Append). Функции знаков Макро приведены в таблице 3. Головная метка должна быть включена в передаваемый поток данных в виде префикса, а конечная метка — суффикса*. Если используют идентификатор символики, то он должен предшествовать головной метке.
________________
* Суффикс является завершающим дополнением к потоку данных.
Таблица 3 — Функции знаков Макро
|
Значение кодового слова знака Макро |
Обозначение знака |
Интерпретация метки |
|
|
Головная метка |
Конечная метка |
||
|
236 |
Макро 05 |
|
|
|
237 |
Макро 06 |
|
|
________________
* Знаки КОИ-7 (ASCII) с десятичными значениями 91, 41, 62, 30, 48, 53, 29.
** Знаки КОИ-7 (ASCII) с десятичными значениям 30, 4.
*** Знаки КОИ-7 (ASCII) с десятичными значениями 91, 41, 62, 30, 48, 54, 29.
5.2.4.8 Знак структурированного соединения (Structured Append)
Знак структурированного соединения используют для указания того, что символ является частью последовательности символов структурированного соединения в соответствии с 5.6.
5.2.4.9 Знак программирования устройства считывания
Знак программирования устройства считывания указывает на то, что в символе закодировано сообщение, предназначенное для программирования устройства считывания. Знак программирования устройства считывания должен быть первым кодовым словом символа и не подлежит использованию совместно со структурированным соединением.
5.2.5 Схема кодирования С40
Схему кодирования С40 применяют для оптимизации кодирования данных, состоящих из последовательности, включающей прописные буквы латинского алфавита и числа (включая знак ПРОБЕЛ). Данная схема позволяет также кодировать и другие знаки путем использования знаков регистра в комбинации с другими знаками данных.
Знаки данных в схеме кодирования С40 разделены на четыре набора. Знаки из первого набора, называемого основным набором, содержат три специальных знака регистра, знак ПРОБЕЛ и знаки ASCII (КОИ-7) c A по Z и с 0 по 9. Каждому знаку данных соответствует единственное значение схемы кодирования С40 (далее — значение С40). Знаки других наборов присваивают одному из трех знаков регистра, которые указывают на один из трех оставшихся наборов и сопровождаются одним из значений С40 (приложение С, таблица С.1).
В результате первого этапа кодирования каждый знак данных преобразуют в одно значение С40 или в пару значений С40. Затем полную строку значений С40 разбивают на группы по три значения (если в конце данных остается одно или два значения, то применяют специальные правила, приведенные в 5.2.5.2.). После этого три значения (С1, С2, С3) кодируют как одно 16-битовое значение по формуле (1600хС1)+(40хС2)+С3+1. В завершение каждое 16-битовое значение кодируют в двух кодовых словах, представляющих собой восемь старших битов и восемь младших битов.
5.2.5.1 Переключение на схему кодирования С40 и обратно
На схему кодирования С40 можно переключиться из схемы кодирования ASCII (КОИ-7/КОИ-8), используя соответствующее кодовое слово фиксации схемы кодирования С40 со значением 230. Кодовое слово со значением 254, непосредственно следующее за парой кодовых слов в схеме кодирования С40, действует как отказ от фиксации (Unlatch) для возврата к схеме кодирования ASCII (КОИ-7/КОИ-8). В противном случае кодирование по схеме кодирования С40 сохраняется до окончания данных, закодированных в символе.
5.2.5.2 Правила кодирования С40
Каждая пара кодовых слов представляет собой 16-битовое значение, в котором первое кодовое слово соответствует восьми старшим битам, а второе — восьми младшим битам. Три значения С40 (С1, С2, С3) кодируют по формуле (1600хС1)+(40хС2)+С3+1.
В результате получают значения от 1 до 64000. Уплотнение трех значений С40 в два кодовых слова представлено на рисунке 2.
Рисунок 2 — Пример кодирования по схеме кодирования С40
|
Исходные знаки данных |
AIM |
|
Полученные значения С40 |
14, 22, 26 |
|
Вычисление 16-битового значения |
(1600х14)+(40х22)+26+1=23307 |
|
Определение первого кодового слова: (16-битовое значение) div 256 |
23307 div 256=91 |
|
Определение второго кодового слова: (16-битовое значение) mod 256 |
23307 mod 256=11 |
|
Итоговые кодовые слова |
91, 11 |
Рисунок 2 — Пример кодирования по схеме кодирования С40
Для кодирования знаков, принадлежащих наборам Регистр 1 (Shift 1), Регистр 2 (Shift 2) и Регистр 3 (Shift 3), сначала следует закодировать соответствующий знак регистра, а затем — значение С40 для данных. Кодирование по схеме С40 может действовать до окончания кодовых слов символа, кодирующих данные.
В случае, если в символе остается только один или два знака символа до начала следования кодовых слов исправления ошибки, то следует придерживаться следующих правил:
a) если остаются два знака символа и кодированию подлежат три оставшихся значения С40 (которые могут включать как знаки данных, так и знаки регистра (Shift)), то эти три значения С40 кодируют в двух последних знаках символа. Заключительного кодового слова отказа от фиксации схемы кодирования (Unlatch) не требуется;
b) если остаются два знака символа и кодированию подлежат два оставшихся значения С40 (первое из которых может быть знаком регистра (Shift) или знаком данных, а второе должно представлять знак данных), то эти два оставшиеся значения С40 кодируют с добавлением значения заполнителя С40, равного 0 (из набора Регистр 1) в двух последних знаках символа. Кодового слова отказа от фиксации схемы кодирования (Unlatch) также не требуется;
c) если остаются два знака символа для кодирования одного оставшегося значения С40 (знака данных), то в первом из двух оставшихся знаков символа (предпоследнем знаке символа) кодируют отказ от фиксации схемы кодирования (Unlatch), а в последнем знаке символа кодируют знак данных по схеме кодирования ASCII (КОИ-7/КОИ-8);
d) если остается один знак символа для кодирования одного оставшегося значения С40 (знака данных), то в последнем знаке символа кодируют знак данных по схеме кодирования ASCII (КОИ-7/КОИ-8). Знак отказа от фиксации схемы кодирования (Unlatch) не кодируют, его наличие подразумевается перед последним знаком символа.
Во всех остальных случаях либо используют знак отказа от фиксации схемы кодирования (Unlatch) для выхода из схемы кодирования С40 перед окончанием символа, либо применяют символ большего размера для кодирования данных.
5.2.5.3 Использование знака верхнего регистра (Upper Shift) в схеме кодирования С40
В схеме кодирования С40 знак верхнего регистра (Upper Shift) не является функциональным знаком символики, а используется как знак регистра (Shift) внутри данного кодового набора. Для кодирования знаков расширенного набора ASCII (КОИ-8) с десятичными значениями от 128 до 255 необходимо закодировать три или четыре значения С40 в соответствии со следующими требованиями.
Если [десятичное значение знака расширенного набора ASCII (КОИ-8) минус 128] принадлежит основному набору, то используют запись:
[1 (значение знака Регистр 2 (Shift))] [30 (значение знака верхнего регистра (UperShift))] [V (десятичное значение знака расширенного набора ASCII (КОИ-8) минус 128)].
В противном случае запись приобретает следующий вид:
[1 (значение знака Регистр 2)] [30 (значение знака верхнего регистра)] [0, 1 или 2 (значения знаков Регистр 1, 2 или 3)] [V (десятичное значение знака расширенного набора ASCII (КОИ-8) минус 128)].
В данных записях число, приведенное в квадратных скобках, соответствует значению согласно приложению С.1, соответствующее значение С40 обозначено V.
5.2.6 Схема кодирования Text
Схема кодирования Text предназначена для кодирования обычного печатного текста, состоящего в основном из знаков нижнего регистра (строчных букв латинского алфавита, цифр, знака ПРОБЕЛ). По структуре она похожа на кодовый набор, используемый в схеме кодирования С40, за исключением того, что строчные буквы нижнего регистра кодируют напрямую (без переключения регистра). Знаки верхнего регистра (прописные буквы латинского алфавита, цифры, специальные графические знаки и знак ПРОБЕЛ) предваряют знаком регистра 3. Полный кодовый набор знаков схемы кодирования Text приведен в приложении С (таблица С.2).
5.2.6.1 Переключение на схему кодирования Text и обратно
На схему кодирования Text можно переключиться из схемы кодирования ASCII (КОИ-7/КОИ-8), используя соответствующее кодовое слово фиксации схемы кодирования с десятичным значением 239. Кодовое слово значением 254, непосредственно следующее за парой кодовых слов в схеме кодирования Text, действует как кодовое слово отказа от фиксации (Unlatch) для возврата в схему кодирования ASCII (КОИ-7/КОИ-8). В противном случае схема кодирования Text действует до окончания данных, кодируемых в символе.
5.2.6.2 Правила кодирования в схеме кодирования Text
Применяют те же правила, что и в схеме кодирования С40.
5.2.7 Схема кодирования ANSI X12
Схему кодирования ANSI X12 применяют для кодирования знаков, используемых при стандартном электронном обмене данными по ANSI X12, в которой три знака данных размещают с уплотнением в двух кодовых словах и которая в некоторой степени подобна схеме кодирования С40. Схема кодирования ANSI Х12 позволяет кодировать буквы верхнего регистра (прописные латинские буквы), цифры, знак ПРОБЕЛ и три стандартных ограничительных и разделительных знака в соответствии с ANSI X12. Соответствие кодов по ANSI X12 приведено в таблице 4. В наборе кодируемых знаков по ANSI X12 отсутствуют знаки регистра (Shift).
Таблица 4 — Набор кодируемых знаков по ANSI X12
|
Значение знака Х12 |
Кодируемые знаки |
Десятичные значения знака ASCII (КОИ-7) |
|
0 |
Х12 ограничитель сегмента <CR> |
13 |
|
1 |
Х12 разделитель сегментов * (ЗВЕЗДОЧКА) |
42 |
|
2 |
Х12 разделитель подэлементов > (БОЛЬШЕ) |
62 |
|
3 |
ПРОБЕЛ |
32 |
|
4-13 |
от 0 до 9 |
48-57 |
|
14-39 |
от А до Z |
65-90 |
________________
Управляющий знак CR соответствует обозначению знака ВК «ВОЗВРАТ КАРЕТКИ» по ГОСТ 27465-87 «Системы обработки информации. Символы. Классификация, наименование и обозначение».
5.2.7.1 Переключение на схему кодирования ANSI X12 и обратно
На схему кодирования ANSI X12 можно переключиться из схемы кодирования ASCII (КОИ-7/КОИ-8), используя соответствующее кодовое слово фиксации схемы кодирования (Latch) (значение 238). Кодовое слово значением 254, непосредственно следующее за парой кодовых слов схемы кодирования ANSI X12, действует как кодовое слово отказа от фиксации (Unlatch) для возврата в схему кодирования ASCII (КОИ-7/КОИ-8). В противном случае схема кодирования ANSI X12 действует до окончания данных, кодируемых в символе.
5.2.7.2 Правила кодирования в соответствии со схемой кодирования ANSI X12
Применяют правила, установленные для схемы кодирования С40. Исключение составляет окончание кодирования данных ANSI X12. Если знаки данных не полностью заполняют пары кодовых слов, то сразу за последней полной парой кодовых слов следует использовать переключение в схему кодирования ASCII (КОИ-7/КОИ-8) с помощью кодового слова значением 254 и продолжить использование схемы кодирования ASCII (КОИ-7/КОИ-8) за исключением случая, когда остается единственный конечный знак символа (кодовое слово) перед первым кодовым словом исправления ошибки. Этот единственный знак символа кодируется по схеме кодирования ASCII (КОИ-7/КОИ-8) без использования кодового слова отказа от фиксации (Unlatch).
5.2.8 Схема кодирования EDIFACT
Схема кодирования EDIFACT включает в себя 63 знака КОИ-7 (ASCII) с десятичными значениями от 32 до 94, а также знак отказа от фиксации (двоичное значение 011111) для возврата в схему кодирования ASCII (КОИ-7/КОИ-8). Схема кодирования EDIFACT позволяет кодировать четыре знака данных в трех кодовых словах. Знаки данных включают в себя все цифры, буквы латинского алфавита и специальные графические знаки (знаки пунктуации), определенные в наборе знаков «EDIFACT Level А» без знаков регистра (Shift), используемых в схеме кодирования С40.
5.2.8.1 Переключение на схему кодирования EDIFACT и обратно
На схему кодирования EDIFACT можно переключиться из схемы кодирования ASCII (КОИ-7/КОИ-8), используя соответствующее кодовое слово фиксации схемы кодирования (Latch) значением 240. Знак отказа от фиксации в схеме кодирования EDIFACT следует использовать в качестве ограничителя окончания схемы кодирования EDIFACT для возврата в схему кодирования ASCII (КОИ-7/КОИ-8).
5.2.8.2 Правила кодирования в соответствии со схемой кодирования EDIFACT
Набор знаков в схеме кодирования EDIFACT приведен в приложении С, таблица С.З. Существует простое соответствие между 6-битовыми значениями знаков по EDIFACT и 8-битовыми байтами знака расширенного набора ASCII (КОИ-8). При построении 6-битового значения знака по EDIFACT исключают два бита старших разрядов 8-битового байта в соответствии с рисунком 3. Строки из четырех знаков со значениями по EDIFACT кодируют в три кодовых слова. В процессе простого кодирования два бита старших разрядов удаляют из 8-битового байта. Оставшийся 6-битовый байт является значением по EDIFACT и должен быть непосредственно закодирован в кодовом слове (рисунок 4).
Рисунок 3 — Соответствие значений знаков по EDIFACT и значений 8-битовых байтов
|
Знак данных |
Значение знака расширенного набора ASCII (КОИ-8) |
Значение знака по EDIFACT |
|
|
Десятичное значение |
8-битовое двоичное значение |
||
|
А |
65 |
01000001 |
000001 |
|
9 |
57 |
00111001 |
111001 |
|
Примечание — В процессе декодирования, если начальный бит (6-й разряд) равен 1, то для построения 8-битового байта требуется вставить в качестве префикса биты 00. Если начальный бит (6-й разряд) равен нулю, то для построения 8-битового байта надо вставить в качестве префикса биты 01. Исключением является знак со значением по EDIFACT 011111, который является управляющим знаком символики отказа от фиксации (Unlatch) для возврата в схему кодирования ASCII (КОИ-7/КОИ-8). |
Рисунок 3 — Соответствие значений знаков по EDIFACT и значений 8-битовых байтов
Рисунок 4 — Пример кодирования по EDIFACT
|
Знаки данных |
D |
А |
Т |
А |
|||||||||||
|
Исходные двоичные значения (по таблице С.3) |
00 |
01 |
00 |
00 |
00 |
01 |
01 |
01 |
00 |
00 |
00 |
01 |
|||
|
Разделение по три 8-битовых байта |
00 |
01 |
00 |
00 |
00 |
01 |
01 |
01 |
00 |
00 |
00 |
01 |
|||
|
Итоговые значения кодовых слов |
16 |
21 |
1 |
Рисунок 4 — Пример кодирования по EDIFACT
Когда кодирование EDIFACT завершается знаком отказа от фиксации схемы кодирования (Unlatch), любые биты, оставшиеся в одиночном знаке символа, следует заполнять нулями. Схема кодирования ASCII (КОИ-7/КОИ-8) начинается со следующего знака символа. Если схема кодирования EDIFACT действует до конца символа, и до первого знака исправления ошибки осталось закодировать только одно или два кодовых слова, оставшихся за последним триплетом кодовых слов по схеме кодирования EDIFACT, их следует кодировать по схеме кодирования ASCII (КОИ-7/КОИ-8) без использования знака отказа от фиксации (Unlatch).
5.2.9 Схема кодирования по основанию 256
Схему кодирования по основанию 256 используют для кодирования любых 8-битовых байтов данных, включая интерпретации в расширенном канале (ECI), и двоичных данных. Интерпретация, используемая по умолчанию, определена в 5.2.2. Алгоритм рандомизации с шаблоном из 255 состояний применяют к каждой последовательности по основанию 256, встречающейся в закодированных данных (приложение В.2). Схема начинает действовать после знака фиксации схемы кодирования по основанию 256 и заканчивается на последнем знаке, определенном длиной поля в схеме кодирования по основанию 256.
5.2.9.1 Переключение на схему кодирования по основанию 256 и обратно
На схему кодирования по основанию 256 можно переключиться из схемы кодирования ASCII (КОИ-7/КОИ-8), используя соответствующее кодовое слово фиксации схемы кодирования значением 231. По окончании данных, закодированных в соответствии со схемой кодирования по основанию 256, возврат к схеме кодирования ASCII (КОИ-7/КОИ-8) осуществляется автоматически. Обращение к интерпретации в расширенном канале (ECI), отличающейся от принятой по умолчанию, должно быть выполнено до переключения на схему кодирования по основанию 256. Последовательность ECI не требуется располагать непосредственно перед переключением в схему кодирования по основанию 256.
5.2.9.2 Правила кодирования в соответствии со схемой кодирования по основанию 256
После переключения на схему кодирования по основанию 256 первые одно () или два (, ) кодовых слова устанавливают длину поля данных в байтах. Определение степени соответствия между длиной поля и значениями и приведено в таблице 5. Далее записываются значения данных в байтах.
Таблица 5 — Длина поля в схеме кодирования по основанию 256
|
Длина поля |
Значения , |
Допустимые значения |
|
До конца символа |
0 |
0 |
|
От 1 до 249 |
заданная длина |
от 1 до 249 |
|
От 250 до 1555 |
(заданная длина DIV 250)+249 |
от 250 до 255 |
|
заданная длина MOD 250 |
от 0 до 249 |
5.3 Рекомендации пользователям
Символика версии ЕСС 200 предлагает гибкие способы кодирования данных. К альтернативным наборам знаков следует обращаться с использованием протокола интерпретации в расширенном канале (ECI). Данные могут быть закодированы в символ квадратной или прямоугольной формы. Если длина сообщения превышает емкость символа, то оно может быть закодировано с использованием последовательности структурированного соединения нескольких (до 16) отдельных, но логически связанных символов версии ЕСС 200 (5.6).
5.3.1 Выбор пользователем интерпретации в расширенном канале (ECI)
Использование альтернативной интерпретации в расширенном канале (ECI) для задания определенной кодовой страницы (набора) или более специфичной интерпретации данных требует вызова дополнительных кодовых слов для активизации этой возможности. Использование протокола интерпретации в расширенном канале (ECI) (5.4) обеспечивает возможность кодирования в данных знаков алфавитов, отличающихся от латинского (по ИСО/МЭК 8859-1 Латинский алфавит N 1), поддерживаемого интерпретацией по умолчанию (последовательность ECI 000003).
5.3.2 Выбор пользователем формы и размера символа
Версия ЕСС 200 имеет двадцать четыре квадратных и шесть прямоугольных конфигураций символа. Можно выбрать подходящий размер и форму символа, в зависимости от требований к его практическому применению; технические требования к данным конфигурациям приведены в 5.5.
5.4 Интерпретация в расширенном канале
Протокол интерпретации в расширенном канале (ECI) позволяет включать в выходной поток данных знаки различных интерпретаций, отличающиеся от набора знаков по умолчанию. Протокол ECI единообразно определен для ряда символик. В символике Data Matrix поддерживаются четыре распространенных типа интерпретаций:
a) международные наборы знаков (или кодовые страницы);
b) интерпретации общего назначения, такие как шифрование и уплотнение;
c) определяемые пользователем интерпретации для замкнутых систем применения;
d) управляющая информация для структурированного соединения в небуферизованном режиме.
Протокол интерпретации в расширенном канале полностью установлен в стандарте AIM Inc. ITS/04-001 «Интерпретации в расширенном канале. Часть 1» («International Technical Specification — Extended Channel Interpretation — Parth 1»). Протокол обеспечивает последовательный метод установления специфических интерпретаций значений байтов перед печатью и после декодирования. Конкретную интерпретацию в расширенном канале идентифицируют с помощью 6-разрядного числа, которое в символике Data Matrix кодируют знаком ECI, за которым следует от одного до трех кодовых слов. Специальные интерпретации приведены в документе AIM Inc. «Интерпретации в расширенном канале. Часть 3» («Extended Chanel Interpretations — Part 3 — Register»). Интерпретация в расширенном канале может использоваться только с устройствами считывания, позволяющими передавать идентификаторы символики. Устройства считывания, которые не могут передавать идентификаторы символики, не обеспечивают передачу данных из любого символа, содержащего ECI. Исключение может быть сделано только в случае, если интерпретация в расширенном канале может быть полностью обработана самим устройством считывания.
Протокол интерпретации в расширенном канале используют только в символах версии ЕСС 200. Заданная интерпретация в расширенном канале может быть вызвана в любом месте закодированного сообщения.
5.4.1 Кодирование интерпретации в расширенном канале
Разнообразные схемы кодирования символики Data Matrix версии ЕСС 200 (таблица 1) могут применяться при любой интерпретации в расширенном канале. Вызов ECI может быть осуществлен только из схемы кодирования ASCII (КОИ-7/КОИ-8), после которого допускается переключение между любыми схемами кодирования. Используемый способ кодирования строго определен 8-битовыми значениями данных и он не зависит от действующей ECI. Например последовательность знаков с десятичными значениями в диапазоне от 48 до 57 может быть наиболее эффективно закодирована в цифровом режиме, даже если они не будут интерпретироваться как числа. Назначение ECI вводят с помощью кодового слова значением 241 (знак ECI) в схеме кодирования ASCII (КОИ-7/КОИ-8). Одно, два или три дополнительных кодовых слова используют для кодирования номера назначения ECI (ECI Assignment member). Правила кодирования приведены в таблице 6.
Таблица 6 — Кодирование номеров назначения ECI в символике версии ЕСС 200
|
Номер назначения ECI |
Последовательность кодовых слов |
Значения кодовых слов |
Область значений |
|
От 000000 до 000126 |
241 |
||
|
ЕСI_nо +1* |
(от 1 до 127) |
||
|
От 000127 до 016382 |
241 |
||
|
(ЕСI_no — 127)div254+128 |
(от 128 до 191) |
||
|
(ЕСI_nо — 127) mod 254+1 |
(от 1 до 254) |
||
|
От 0016383 до 999999 |
241 |
||
|
(ЕС1_no — 16383)div64516+192 |
(от 192 до 207) |
||
|
[(ЕСI_no — 16383) div 254] mod 254+1 |
(от 1 до 254) |
||
|
(ЕСI_no — 16383) mod 254+1 |
(от 1 до 254) |
________________
* ECl_nо +1 — заданный номер назначения ECI.
Следующие примеры приведены для иллюстрации кодирования:
номер назначения ECI=015000
Кодовые слова:
[241][(15000-127) div 254+128][(15000-127) mod 254+1]=[241][58+128][141+1]=[241][186][142]
номер назначения ECI=090000
Кодовые слова:
[241][(90000-16383) div 64516+192][((90000-16383) div 254) mod 254+1][(90000-16383) mod 254+1]=[241][1+192][289 mod 254+1][211+1]=[241][193][36][212]
5.4.2 ECI и структурированное соединение
ECI могут появляться в любом месте сообщения, закодированного в одиночном символе или в символе структурированного соединения (5.6) набора символов Data Matrix. Любая активизированная ECI сохраняет действие либо до конца закодированных данных, либо до появления другой ECI. Таким образом, интерпретация в заданной ECI может распространяться на два или более символов.
5.4.3 Протокол после декодирования
Протокол передачи данных ECI определен в 11.4. При применении интерпретаций в расширенном канале следует использовать идентификаторы символики (11.5) и соответствующий идентификатор символики должен передаваться перед декодированными данными.
5.5 Атрибуты символа версии ЕСС 200
5.5.1 Размер и емкость символа
В символике версии ЕСС 200 доступны 24 квадратных и 6 прямоугольных символов, указанные в таблице 7.
Таблица 7 — Атрибуты символов ЕСС 200
|
Размер* |
Область данных |
Размер коор- |
Общее число кодовых слов |
Число кодовых слов в блоке Рида- |
Число чере- |
Максимальная емкость символа для данных |
Кодо- |
Мак- |
|||||||
|
Число строк |
Число столб- |
Раз- |
Чис- |
дан- |
исп- |
дан- |
исп- |
чис- |
число латин- |
чис- |
|||||
|
Символы квадратной формы |
|||||||||||||||
|
10 |
10 |
8×8 |
1 |
8×8 |
3 |
5 |
3 |
5 |
1 |
6 |
3 |
1 |
62,5 |
2/0 |
|
|
12 |
12 |
10×10 |
1 |
10×10 |
5 |
7 |
5 |
7 |
1 |
10 |
6 |
3 |
58,3 |
3/0 |
|
|
14 |
14 |
12×12 |
1 |
12×12 |
8 |
10 |
8 |
10 |
1 |
16 |
10 |
6 |
55,6 |
5/7 |
|
|
16 |
16 |
14×14 |
1 |
14×14 |
12 |
12 |
12 |
12 |
1 |
24 |
16 |
10 |
50 |
6/9 |
|
|
18 |
18 |
16×16 |
1 |
16×16 |
18 |
14 |
18 |
14 |
1 |
36 |
25 |
16 |
43,8 |
7/11 |
|
|
20 |
20 |
18×18 |
1 |
18×18 |
22 |
18 |
22 |
18 |
1 |
44 |
31 |
20 |
45 |
9/15 |
|
|
22 |
22 |
20×20 |
1 |
20×20 |
30 |
20 |
30 |
20 |
1 |
60 |
43 |
28 |
40 |
10/17 |
|
|
24 |
24 |
22×22 |
1 |
22×22 |
36 |
24 |
36 |
24 |
1 |
72 |
52 |
34 |
40 |
12/21 |
|
|
26 |
26 |
24×24 |
1 |
24×24 |
44 |
28 |
44 |
28 |
1 |
88 |
64 |
42 |
38,9 |
14/25 |
Контроль четности и коды коррекции ошибок (ECC).
Ошибки при хранении информации в памяти неизбежны. Они обычно классифицируются как отказы и нерегулярные ошибки (сбои). Если нормально функционирующая микросхема вследствие, например, физического повреждения начинает работать неправильно, то все происходящее и называется постоянным отказом. Чтобы устранить этот тип отказа, обычно требуется заменить некоторую часть аппаратных средств памяти, например неисправную микросхему памяти.
Другой, более коварный тип отказа — нерегулярная ошибка (сбой). Это непостоянный отказ, который не происходит при повторении условий функционирования или через регулярные интервалы.
Приблизительно 20 лет назад сотрудники Intel установили, что причиной сбоев являются альфа-частицы. Поскольку альфа-частицы не могут проникнуть даже через тонкий лист бумаги, выяснилось, что их источником служит вещество, используемое в полупроводниках. При исследовании были обнаружены частицы тория и урана в пластмассовых и керамических корпусах микросхем, применявшихся в те годы. Изменив технологический процесс, производители памяти избавились от этих примесей.
В настоящее время производители памяти почти полностью устранили источники альфачастиц. И многие стали думать, что проверка четности не нужна вовсе. Например, сбои в памяти емкостью 16 Мбайт из-за альфа-частиц случаются в среднем только один раз за 16 лет! Однако сбои памяти происходят значительно чаще.
Сегодня самая главная причина нерегулярных ошибок — космические лучи. Поскольку они имеют очень большую проникающую способность, от них практически нельзя защититься с помощью экранирования.
Эксперимент, проверяющий степень влияния космических лучей на появление ошибок в работе микросхем, показал, что соотношение “сигнал–ошибка” (signal-to-error ratio — SER) для некоторых модулей DRAM составило 5950 единиц интенсивности отказов (failure units — FU) на миллиард часов наработки для каждой микросхемы. Измерения проводились в условиях, приближенных к реальной жизни, с учетом длительности в несколько миллионов машиночасов. В среднестатистическом компьютере это означало бы появление программной ошибки памяти примерно каждые шесть месяцев. В серверных системах или мощных рабочих станциях с большим объемом установленной оперативной памяти подобная статистика указывает на одну ошибку (или даже более) в работе памяти каждый месяц! Когда тестовая система с теми же модулями DIMM была размещена в надежном убежище на глубине более 15 метров каменной породы, что полностью устраняет влияние космических лучей, программные ошибки в работе памяти вообще не были зафиксированы. Эксперимент продемонстрировал не только опасность влияния космических лучей, но и доказал, насколько эффективно устранять влияние альфалучей и радиоактивных примесей в оболочках модулей памяти.
К сожалению, производители ПК не признали это причиной погрешностей памяти; случайную природу сбоя намного легче оправдать разрядом электростатического электричества, большими выбросами мощности или неустойчивой работой программного обеспечения (например, использованием новой версии операционной системы или большой прикладной программы). Исследования показали, что для систем ECC доля программных ошибок в 30 раз больше, чем аппаратных. Это неудивительно, учитывая вредное влияние космических лучей. Количество ошибок зависит от числа установленных модулей памяти и их объема. Программные ошибки могут случаться и раз в месяц, и несколько раз в неделю, и даже чаще!
Хотя космические лучи и радиация являются причиной большинства программных ошибок памяти, существуют и другие факторы:
1. Скачки в энергопотреблении или шум на линии. Причиной может быть неисправный блок питания или настенная розетка.
2. Использование неверного типа или параметра быстродействия памяти. Тип памяти
должен поддерживаться конкретным набором микросхем и обладать определенной
этим набором скоростью доступа.
3. Электромагнитные помехи. Возникают при расположении радиопередатчиков рядом с
компьютером, что иногда приводит к генерированию паразитных электрических сигна-
лов в монтажных соединениях и схемах компьютера. Имейте в виду, что беспроводные
сети, мыши и клавиатуры увеличивают риск появления электромагнитных помех.
4. Статические разряды. Вызывают моментальные скачки в энергоснабжении, что может
повлиять на целостность данных.
5. Ошибки синхронизации. Не поступившие своевременно данные могут стать причиной
появления программных ошибок. Зачастую причина заключается в неверных парамет-
рах BIOS, оперативной памяти, быстродействие которой ниже, чем требуется систе-
мой, “разогнанных” процессорах и прочих системных компонентах.
Большинство описанных проблем не приводят к прекращению работы микросхем памяти (хотя некачественное энергоснабжение или статическое электричество могут физически повредить микросхемы), однако могут повлиять на хранимые данные.
Игнорирование сбоев, конечно, не лучший способ борьбы с ними. К сожалению, именно этот способ сегодня выбрали многие производители компьютеров. Лучше было бы повысить отказоустойчивость систем. Для этого необходимы механизмы определения и, возможно, исправления ошибок в памяти ПК. В основном для повышения отказоустойчивости в современных компьютерах применяются следующие методы:
— контроль четности;
— коды коррекции ошибок (ECC).
Системы без контроля четности вообще не обеспечивают отказоустойчивости данных. Единственная причина, по которой они используются, — их минимальная базовая стоимость. При этом, в отличие от других технологий (ECC и контроль четности), не требуется дополнительная оперативная память.
Байт данных с контролем четности включает в себя 9, а не 8 бит, поэтому стоимость памяти с контролем четности выше примерно на 12,5%. Кроме того, контроллеры памяти, не требующие логических мостов для подсчета данных четности или ECC, обладают упрощенной внутренней архитектурой. Портативные системы, для которых вопрос минимального энергопотребления особенно важен, выигрывают от уменьшенного энергопотребления памяти благодаря использованию меньшего количества микросхем DRAM. И наконец, шина данных памяти без контроля четности имеет меньшую разрядность, что выражается в сокращении количества буферов данных. Статистическая вероятность возникновения ошибок памяти в современных настольных компьютерах составляет примерно одну ошибку в несколько месяцев. При этом количество ошибок зависит от объема и типа используемой памяти. Подобный уровень ошибок может быть приемлемым для обычных компьютеров, не используемых для работы с важными приложениями. В этом случае цена играет основную роль, а дополнительная стоимость модулей памяти с поддержкой контроля четности и кода ECC себя не оправдывает.
Применение не отказоустойчивых к ошибкам компьютеров рискованно и предполагает отсутствие ошибок памяти при эксплуатации систем. При этом также учитывается, что совокупная стоимость потерь, вызванная ошибками в работе памяти, будет меньше, чем затраты на приобретение дополнительных аппаратных устройств для определения таковых ошибок.
Тем не менее ошибки памяти вполне могут стать причиной серьезных проблем: например, представьте себе указание неверного значения суммы в банковском чеке. Ошибки в работе оперативной памяти серверных систем зачастую приводят к “зависанию” последних и отключению всех клиентских компьютеров, соединенных с серверами по локальной сети. Наконец, отследить причину возникновения проблем в компьютерах, не поддерживающих контроль четности или код ECC, крайне сложно. Последние технологии по крайней мере однозначно укажут на оперативную память как на источник проблемы, тем самым экономя время и усилия системных администраторов.
Контроль четности
Это один из стандартов, введенных IBM, в соответствии с которым информация в банках памяти хранится фрагментами по девять битов, причем восемь из них (составляющих один байт) предназначены собственно для данных, а девятый является битом четности (parity). Использование девятого бита позволяет схемам управления памятью на аппаратном уровне контролировать целостность каждого байта данных. Если обнаруживается ошибка, работа компьютера останавливается и на экран выводится сообщение о неисправности.
Технология контроля четности не позволяет исправлять системные ошибки, однако дает возможность их обнаружить пользователю компьютера, что имеет следующие преимущества:
— контроль четности оберегает от последствий проведения неверных вычислений на базе некорректных данных;
— контроль четности точно указывает на источник возникновения ошибок, помогая разобраться с проблемой и улучшая степень эксплутационной надежности компьютера.
Для реализации поддержки памяти с контролем четности или без него не требуется особых усилий. В частности, внедрить поддержку контроля четности для системной платы не составит никакого труда. Основная стоимость внедрения относится к цене самих модулей памяти с контролем четности. Если покупатели нуждаются в контроле четности для работы с определенными приложениями, поставщики компьютеров могут без проблем предложить соответствующие системы.
Компания Intel и прочие производители наборов микросхем системной логики внедрили поддержку контроля четности и кода ECC в большинстве своих продуктов (особенно в наборах микросхем, ориентированных на рынок высокопроизводительных серверов). В то же время наборы микросхем низшей ценовой категории, как правило, не поддерживают эти технологии. Пользователям, требовательным к надежности выполняемых приложений, следует обращать особое внимание на поддержку контроля четности и ECC.
Код коррекции ошибок
Коды коррекции ошибок (Error Correcting Code — ECC) позволяют не только обнаружить ошибку, но и исправить ее в одном разряде. Поэтому компьютер, в котором используются подобные коды, в случае ошибки в одном разряде может работать без прерывания, причем данные не будут искажены. Коды коррекции ошибок в большинстве ПК позволяют только обнаруживать, но не исправлять ошибки в двух разрядах. Но приблизительно 98% сбоев памяти вызвано именно ошибкой в одном разряде, т.е. она успешно исправляется с помощью данного типа кодов. Данный тип ECC получил название SEC)DED (single-bit error-correction double-bit error detection — одноразрядная коррекция, двухразрядное обнаружение ошибок). В кодах коррекции ошибок этого типа для каждых 32 бит требуется дополнительно семь контрольных разрядов при 4-байтовой и восемь — при 8-байтовой организации (64-разрядные процессоры Athlon/Pentium). Реализация кода коррекции ошибок при 4-байтовой организации, очевидно, дороже реализации проверки нечетности или четности, но при 8-байтовой организации стоимость реализации кода коррекции ошибок не превышает стоимости реализации проверки четности.
Для использования кодов коррекции ошибок необходим контроллер памяти, вычисляющий контрольные разряды при операции записи в память. При чтении из памяти такой контроллер сравнивает прочитанные и вычисленные значения контрольных разрядов и при необходимости исправляет испорченный бит (или биты). Стоимость дополнительных логических схем для реализации кода коррекции ошибок в контроллере памяти не очень высока, но это может значительно снизить быстродействие памяти при операциях записи. Это происходит потому, что при операциях записи и чтения необходимо ждать, когда завершится вычисление контрольных разрядов. При записи части слова вначале следует прочитать полное слово, затем перезаписать изменяемые байты и только после этого — новые вычисленные контрольные разряды.
В большинстве случаев сбой памяти происходит в одном разряде, и потому такие ошибки успешно исправляются кодом коррекции ошибок. Использование отказоустойчивой памяти обеспечивает высокую надежность компьютера. Память с кодом ECC предназначена для серверов, рабочих станций или приложений, для которых последствия потенциальных ошибок памяти менее желательны, чем дополнительные затраты на приобретение добавочных модулей памяти и вычислительные затраты на коррекцию ошибок. Если данные имеют особое значение и компьютеры применяются для решения важных задач, без памяти ECC не обойтись. По сути, ни один уважающий себя системный инженер не будет использовать сервер, даже самый неприхотливый, без памяти ECC.
Пользователи имеют выбор между системами без контроля четности, с контролем четности и с ECC, т.е. между желательным уровнем отказоустойчивости компьютера и степенью ценности используемых данных.
Ошибки
при хранении информации в памяти
неизбежны. Они обычно классифицируются
как
отказы и нерегулярные ошибки (сбои).
Если
нормально функционирующая микросхема
вследствие, например, физического
повреждения
начинает работать неправильно, то все
происходящее и называется постоянным
отказом. Чтобы устранить этот тип отказа,
обычно требуется заменить некоторую
часть аппаратных
средств памяти, например неисправную
микросхему SIMM
или
DIMM.
Другой,
более коварный тип отказа — нерегулярная
ошибка (сбой). Нерегулярная ошибка —
это непостоянный отказ, который не
происходит при повторении условий
функционирования
или через регулярные интервалы.
Контроль
четности — это
один из стандартов, введенных фирмой
IBM,
в
соответствии с которым информация в
банках
памяти хранится фрагментами по девять
битов, причем восемь из них (составляющих
один
байт) предназначены собственно для
данных, а девятый является битом
четности (parity).
Использование
девятого бита позволяет схемам управления
памятью на аппаратном уровне контролировать
целостность каждого байта данных. Если
обнаруживается ошибка, работа компьютера
останавливается и на экран выводится
сообщение о неисправности. Если вы
работаете на компьютере
под управлением Windows
или
OS/2, то при возникновении ошибки контроля
четности
сообщение, возможно, не появится, а
просто произойдет блокировка системы.
Модули
SIMM
бывают
как с битом четности, так и без него. До
недавнего времени во всех PC-совместимых
компьютерах для повышения надежности
предусматривался контроль четности.
Однако в компьютерах многих других фирм
он никогда не использовался.
Как
все это делается? В большинстве новых
системных плат предусмотрена возможность
отключения
схем контроля четности для того, чтобы
на них можно было устанавливать модули
SIMM
без
бита четности. В старых системных платах
можно было использовать только модули
SIMM
с
битом четности, поскольку отключить
схему контроля было нельзя. Сейчас на
одних системных платах устанавливается
перемычка для включения и отключения
схемы контроля,
а в других в программу установки
параметров BIOS
введен
соответствующий параметр.
Кроме того, в некоторых компьютерах
автоматически проверяется существование
разряда
четности, и, если его нет хотя бы в одном
банке, схема контроля отключается.
Появление
ошибок четности является первым
признаком, неисправности системы,
поэтому отсутствие разряда четности
в большинстве новых компьютеров не
радует.
Некоторые
системы вообще не поддерживают контроль
четности. Данный факт
ставит под сомнение четкую работу
системы с критическими приложениями,
требующими
контроля четности.
При
разработке схемы контроля четности
фирма IBM
установила,
что значение бита четности
задается таким, чтобы количество единиц
во всех девяти разрядах (восемь разрядов
данных
и разряд четности) было нечетным.
Другими
словами, когда байт (8 бит) данных
заносится
в память, специальная схема контроля
четности (микросхема, установленная на
сие- t
темной
плате или на плате памяти) подсчитывает
количество единиц в байте. Если оно
четное,
на выходе микросхемы формируется сигнал
логической единицы, который сохраняется
в соответствующем разряде памяти как
девятый бит (бит четности). Количество
единиц во всех девяти
разрядах при этом становится нечетным.
Если же количество единиц в восьми
разрядах
исходных данных нечетное, то бит четности
равен 0 и сумма двоичных цифр в девяти
разрядах
также остается нечетной.
Рассмотрим
конкретный пример (имейте в виду, что
разряды в байте нумеруются, начиная с
нуля, т.е. О, 1, 2,…, 7):
Разряд
данных: 01234567
Бит
четности
Значение
бита: 10110011
О
В
данном случае общее число единичных
битов данных нечетное (5), поэтому бит
четности должен
быть равен нулю, чтобы количество единиц
во всех девяти разрядах было нечетным.
Рассмотрим
еще один пример:
Разряд
данных: 01234567
Бит
четности
Значение
бита: 00110011
1
В
этом примере общее число единичных
битов данных четное (4), поэтому бит
четности должен быть равен единице,
чтобы количество единиц во всех девяти
разрядах, как и в предыдущем
примере, было нечетным.
При
считывании из памяти та же самая
микросхема проверяет информацию на
четность. Если в 9-разрядном байте число
единиц четное и бит четности также равен
единице, значит, при
считывании или записи данных произошла
ошибка. Определить, в каком разряде она
произошла,
невозможно (нельзя даже выяснить
количество испорченных разрядов). Более
того,
если сбой произошел в трех разрядах (в
нечетном их количестве), то ошибка будет
зафиксирована; однако при двух
ошибочных разрядах (или четном их
количестве) сбой не регистрируется.
При
обнаружении ошибки схема контроля
четности на системной плате формирует
немаскируемое
прерывание (Non-maskable
Interrupt— NMI), по
которому основная работа прекращается
и инициируется специальная процедура,
записанная в BIOS.
В
результате ее выполнения
экран очищается и в левом верхнем углу
выводится сообщение об ошибке. Текст
сообщения
зависит от типа компьютера. В некоторых
старых компьютерах фирмы IBM
при
выполнении
указанной процедуры приостанавливается
работа процессора, компьютер блокируется
и пользователю приходится перезапускать
его с помощью кнопки сброса или выключать
и через некоторое время вновь включать
питание. При этом, естественно, теряется
вся несохраненная
информация. (Немаскируемое прерывание
— это системное предупреждение, которое
программы не могут проигнорировать.)
Соседние файлы в папке тси на Kot_434_
- #
- #
- #
- #
Всем привет! Тема сегодняшней публикации — поддержка ECC оперативной памяти: что это такое, как работает данная функция, зависит ли от процессора ее использование на ПК.
Что такое ЕСС память
Аббревиатура происходит от английского названия error correcting code memory, то есть память с коррекцией ошибок кода. Такая ОЗУ распознает и устраняет спонтанно возникающие изменения в битах памяти, которых быть не должно.
Как правило, такая память может исправить изменения в одном бите одного машинного слова. При его чтении будет опознано то же значение, что и было записано, несмотря на возникающие «глюки».
Обычная память, то есть non-ECC, этого делать не умеет.
Этот тип памяти используется в компьютерах, для которых важна бесперебойная работа, включая крупные серверные станции. Для использования такого режима необходима поддержка контроллером ОЗУ – как встраиваемого в чипсет, так и реализованном на кристалле вместе с ядрами.
Базовый алгоритм, который используется чаще всего, основан на коде Хемминга – самоконтролирующемся двоичном коде, названном в честь предложившего такую систему американского математика.
Существуют алгоритмы, способные исправлять более одной ошибки, но используются они реже. С технологической точки зрения такая система предполагает использование модулей ОЗУ, в которых на каждые 8 микросхем памяти приходится один компонент, хранящий ЕСС-коды (то есть 8 бит на каждые 64 бита).
Причины появления ошибок в ОЗУ
Главная проблема для любого электронного устройства – невидимые космические лучи, от которых земная атмосфера не защищает должным образом. Элементарные частицы, которые пребывают в этом потоке, способны влиять на работу электроники.
А так как любой компьютер на самом «глубинном» уровне проводит все вычисления с помощью двоичных кодов, нарушения свойств электронных компонентов и провоцируют ошибки в работе.
Характерно, что чем выше от уровня моря, тем меньше плотность воздуха и соответственно, интенсивнее космическое излучение. Компьютерные системы, которые работают на большой высоте, требуют более эффективной защиты. Советую также почитать «Что такое ОЗУ в компьютере: из чего состоит и для чего служит?»(уже на сайте).
Стоит ли использовать ЕСС память
Объективных причин для использования такой ОЗУ на домашнем ПК нет.
Несмотря на то, что земной диск медленно дрейфует по Космическому океану, покоясь на спинах трех китов, вероятность искажения данных под воздействием вредоносных лучей, на самом-то деле крайне мала. При этом самое страшное, что может случиться при таких неполадках – вылет операционной системы в синий экран.
Впрочем, это может быть действительно страшно – например, в случае, если вы в течение пары часов монтировали видеоролик, забывая сохраняться в процессе, или же у вас последний и решительный бой, от которого зависит судьба клана, в какой-нибудь ММОРПГ.
Такая память работает медленнее обычной – в среднем, на 2-3%, так как для проверки контрольных сумм необходим один дополнительный такт контроллера. Такой режим работы требует больше логических ресурсов.
Как уже сказано выше, в основном такая память почти всегда регистровая (Registered), то есть имеет дополнительный регистр для считывания и хранения двоичных кодов. Существуют модули ECC памяти без регистров (UDIMM), которые можно использовать в домашних ПК.
Однако учтите, что такое удовольствие обойдется дороже, так как цена на такие модули ОЗУ обычно выше. Кроме того, требуется наличие материнской платы, чипсета и процессора (к слову, такие модели есть и у Intel, и у AMD), поддерживающих ЕСС память. Стоят они внезапно тоже, как правило, дороже.
И если вы решили проапгрейдить комп для использования ЕСС памяти, проверьте спецификации упомянутых выше компонентов. Если в описании написано что нет поддержки такого режима, деталь придется менять на более подходящую, что значит дополнительные расходы.
Не исключено, что придется менять и мать, и «камень», и планки оперативки. При сборке нового компьютера несколько проще: можно сразу купить соответствующие компоненты. Однако, на мой взгляд, это уже лишнее – страховка от мнимых сбоев не стоит потери быстродействия.
Также советую на эту тему ознакомиться с публикациями «Влияние тактовой частоты оперативной памяти в компьютере»(уже на блоге) и «Тайминги и частота оперативной памяти: кто важнее и влиятельней?». Буду признателен всем, кто расшарит эту статью в социальных сетях. До завтра!
С уважением, автор блога Андрей Андреев.
«Interleaver» redirects here. For the fiber-optic device, see optical interleaver.
In computing, telecommunication, information theory, and coding theory, forward error correction (FEC) or channel coding[1][2][3] is a technique used for controlling errors in data transmission over unreliable or noisy communication channels.
The central idea is that the sender encodes the message in a redundant way, most often by using an error correction code or error correcting code (ECC).[4][5] The redundancy allows the receiver not only to detect errors that may occur anywhere in the message, but often to correct a limited number of errors. Therefore a reverse channel to request re-transmission may not be needed. The cost is a fixed, higher forward channel bandwidth.
The American mathematician Richard Hamming pioneered this field in the 1940s and invented the first error-correcting code in 1950: the Hamming (7,4) code.[5]
FEC can be applied in situations where re-transmissions are costly or impossible, such as one-way communication links or when transmitting to multiple receivers in multicast.
Long-latency connections also benefit; in the case of a satellite orbiting Uranus, retransmission due to errors can create a delay of five hours. FEC is widely used in modems and in cellular networks, as well.
FEC processing in a receiver may be applied to a digital bit stream or in the demodulation of a digitally modulated carrier. For the latter, FEC is an integral part of the initial analog-to-digital conversion in the receiver. The Viterbi decoder implements a soft-decision algorithm to demodulate digital data from an analog signal corrupted by noise. Many FEC decoders can also generate a bit-error rate (BER) signal which can be used as feedback to fine-tune the analog receiving electronics.
FEC information is added to mass storage (magnetic, optical and solid state/flash based) devices to enable recovery of corrupted data, and is used as ECC computer memory on systems that require special provisions for reliability.
The maximum proportion of errors or missing bits that can be corrected is determined by the design of the ECC, so different forward error correcting codes are suitable for different conditions. In general, a stronger code induces more redundancy that needs to be transmitted using the available bandwidth, which reduces the effective bit-rate while improving the received effective signal-to-noise ratio. The noisy-channel coding theorem of Claude Shannon can be used to compute the maximum achievable communication bandwidth for a given maximum acceptable error probability. This establishes bounds on the theoretical maximum information transfer rate of a channel with some given base noise level. However, the proof is not constructive, and hence gives no insight of how to build a capacity achieving code. After years of research, some advanced FEC systems like polar code[3] come very close to the theoretical maximum given by the Shannon channel capacity under the hypothesis of an infinite length frame.
Method[edit]
ECC is accomplished by adding redundancy to the transmitted information using an algorithm. A redundant bit may be a complicated function of many original information bits. The original information may or may not appear literally in the encoded output; codes that include the unmodified input in the output are systematic, while those that do not are non-systematic.
A simplistic example of ECC is to transmit each data bit 3 times, which is known as a (3,1) repetition code. Through a noisy channel, a receiver might see 8 versions of the output, see table below.
| Triplet received | Interpreted as |
|---|---|
| 000 | 0 (error-free) |
| 001 | 0 |
| 010 | 0 |
| 100 | 0 |
| 111 | 1 (error-free) |
| 110 | 1 |
| 101 | 1 |
| 011 | 1 |
This allows an error in any one of the three samples to be corrected by «majority vote», or «democratic voting». The correcting ability of this ECC is:
- Up to 1 bit of triplet in error, or
- up to 2 bits of triplet omitted (cases not shown in table).
Though simple to implement and widely used, this triple modular redundancy is a relatively inefficient ECC. Better ECC codes typically examine the last several tens or even the last several hundreds of previously received bits to determine how to decode the current small handful of bits (typically in groups of 2 to 8 bits).
Averaging noise to reduce errors[edit]
ECC could be said to work by «averaging noise»; since each data bit affects many transmitted symbols, the corruption of some symbols by noise usually allows the original user data to be extracted from the other, uncorrupted received symbols that also depend on the same user data.
- Because of this «risk-pooling» effect, digital communication systems that use ECC tend to work well above a certain minimum signal-to-noise ratio and not at all below it.
- This all-or-nothing tendency – the cliff effect – becomes more pronounced as stronger codes are used that more closely approach the theoretical Shannon limit.
- Interleaving ECC coded data can reduce the all or nothing properties of transmitted ECC codes when the channel errors tend to occur in bursts. However, this method has limits; it is best used on narrowband data.
Most telecommunication systems use a fixed channel code designed to tolerate the expected worst-case bit error rate, and then fail to work at all if the bit error rate is ever worse.
However, some systems adapt to the given channel error conditions: some instances of hybrid automatic repeat-request use a fixed ECC method as long as the ECC can handle the error rate, then switch to ARQ when the error rate gets too high;
adaptive modulation and coding uses a variety of ECC rates, adding more error-correction bits per packet when there are higher error rates in the channel, or taking them out when they are not needed.
Types of ECC[edit]
The two main categories of ECC codes are block codes and convolutional codes.
- Block codes work on fixed-size blocks (packets) of bits or symbols of predetermined size. Practical block codes can generally be hard-decoded in polynomial time to their block length.
- Convolutional codes work on bit or symbol streams of arbitrary length. They are most often soft decoded with the Viterbi algorithm, though other algorithms are sometimes used. Viterbi decoding allows asymptotically optimal decoding efficiency with increasing constraint length of the convolutional code, but at the expense of exponentially increasing complexity. A convolutional code that is terminated is also a ‘block code’ in that it encodes a block of input data, but the block size of a convolutional code is generally arbitrary, while block codes have a fixed size dictated by their algebraic characteristics. Types of termination for convolutional codes include «tail-biting» and «bit-flushing».
There are many types of block codes; Reed–Solomon coding is noteworthy for its widespread use in compact discs, DVDs, and hard disk drives. Other examples of classical block codes include Golay, BCH, Multidimensional parity, and Hamming codes.
Hamming ECC is commonly used to correct NAND flash memory errors.[6]
This provides single-bit error correction and 2-bit error detection.
Hamming codes are only suitable for more reliable single-level cell (SLC) NAND.
Denser multi-level cell (MLC) NAND may use multi-bit correcting ECC such as BCH or Reed–Solomon.[7][8] NOR Flash typically does not use any error correction.[7]
Classical block codes are usually decoded using hard-decision algorithms,[9] which means that for every input and output signal a hard decision is made whether it corresponds to a one or a zero bit. In contrast, convolutional codes are typically decoded using soft-decision algorithms like the Viterbi, MAP or BCJR algorithms, which process (discretized) analog signals, and which allow for much higher error-correction performance than hard-decision decoding.
Nearly all classical block codes apply the algebraic properties of finite fields. Hence classical block codes are often referred to as algebraic codes.
In contrast to classical block codes that often specify an error-detecting or error-correcting ability, many modern block codes such as LDPC codes lack such guarantees. Instead, modern codes are evaluated in terms of their bit error rates.
Most forward error correction codes correct only bit-flips, but not bit-insertions or bit-deletions.
In this setting, the Hamming distance is the appropriate way to measure the bit error rate.
A few forward error correction codes are designed to correct bit-insertions and bit-deletions, such as Marker Codes and Watermark Codes.
The Levenshtein distance is a more appropriate way to measure the bit error rate when using such codes.
[10]
Code-rate and the tradeoff between reliability and data rate[edit]
The fundamental principle of ECC is to add redundant bits in order to help the decoder to find out the true message that was encoded by the transmitter. The code-rate of a given ECC system is defined as the ratio between the number of information bits and the total number of bits (i.e., information plus redundancy bits) in a given communication package. The code-rate is hence a real number. A low code-rate close to zero implies a strong code that uses many redundant bits to achieve a good performance, while a large code-rate close to 1 implies a weak code.
The redundant bits that protect the information have to be transferred using the same communication resources that they are trying to protect. This causes a fundamental tradeoff between reliability and data rate.[11] In one extreme, a strong code (with low code-rate) can induce an important increase in the receiver SNR (signal-to-noise-ratio) decreasing the bit error rate, at the cost of reducing the effective data rate. On the other extreme, not using any ECC (i.e., a code-rate equal to 1) uses the full channel for information transfer purposes, at the cost of leaving the bits without any additional protection.
One interesting question is the following: how efficient in terms of information transfer can an ECC be that has a negligible decoding error rate? This question was answered by Claude Shannon with his second theorem, which says that the channel capacity is the maximum bit rate achievable by any ECC whose error rate tends to zero:[12] His proof relies on Gaussian random coding, which is not suitable to real-world applications. The upper bound given by Shannon’s work inspired a long journey in designing ECCs that can come close to the ultimate performance boundary. Various codes today can attain almost the Shannon limit. However, capacity achieving ECCs are usually extremely complex to implement.
The most popular ECCs have a trade-off between performance and computational complexity. Usually, their parameters give a range of possible code rates, which can be optimized depending on the scenario. Usually, this optimization is done in order to achieve a low decoding error probability while minimizing the impact to the data rate. Another criterion for optimizing the code rate is to balance low error rate and retransmissions number in order to the energy cost of the communication.[13]
Concatenated ECC codes for improved performance[edit]
Classical (algebraic) block codes and convolutional codes are frequently combined in concatenated coding schemes in which a short constraint-length Viterbi-decoded convolutional code does most of the work and a block code (usually Reed–Solomon) with larger symbol size and block length «mops up» any errors made by the convolutional decoder. Single pass decoding with this family of error correction codes can yield very low error rates, but for long range transmission conditions (like deep space) iterative decoding is recommended.
Concatenated codes have been standard practice in satellite and deep space communications since Voyager 2 first used the technique in its 1986 encounter with Uranus. The Galileo craft used iterative concatenated codes to compensate for the very high error rate conditions caused by having a failed antenna.
Low-density parity-check (LDPC)[edit]
Low-density parity-check (LDPC) codes are a class of highly efficient linear block
codes made from many single parity check (SPC) codes. They can provide performance very close to the channel capacity (the theoretical maximum) using an iterated soft-decision decoding approach, at linear time complexity in terms of their block length. Practical implementations rely heavily on decoding the constituent SPC codes in parallel.
LDPC codes were first introduced by Robert G. Gallager in his PhD thesis in 1960,
but due to the computational effort in implementing encoder and decoder and the introduction of Reed–Solomon codes,
they were mostly ignored until the 1990s.
LDPC codes are now used in many recent high-speed communication standards, such as DVB-S2 (Digital Video Broadcasting – Satellite – Second Generation), WiMAX (IEEE 802.16e standard for microwave communications), High-Speed Wireless LAN (IEEE 802.11n),[14] 10GBase-T Ethernet (802.3an) and G.hn/G.9960 (ITU-T Standard for networking over power lines, phone lines and coaxial cable). Other LDPC codes are standardized for wireless communication standards within 3GPP MBMS (see fountain codes).
Turbo codes[edit]
Turbo coding is an iterated soft-decoding scheme that combines two or more relatively simple convolutional codes and an interleaver to produce a block code that can perform to within a fraction of a decibel of the Shannon limit. Predating LDPC codes in terms of practical application, they now provide similar performance.
One of the earliest commercial applications of turbo coding was the CDMA2000 1x (TIA IS-2000) digital cellular technology developed by Qualcomm and sold by Verizon Wireless, Sprint, and other carriers. It is also used for the evolution of CDMA2000 1x specifically for Internet access, 1xEV-DO (TIA IS-856). Like 1x, EV-DO was developed by Qualcomm, and is sold by Verizon Wireless, Sprint, and other carriers (Verizon’s marketing name for 1xEV-DO is Broadband Access, Sprint’s consumer and business marketing names for 1xEV-DO are Power Vision and Mobile Broadband, respectively).
Local decoding and testing of codes[edit]
Sometimes it is only necessary to decode single bits of the message, or to check whether a given signal is a codeword, and do so without looking at the entire signal. This can make sense in a streaming setting, where codewords are too large to be classically decoded fast enough and where only a few bits of the message are of interest for now. Also such codes have become an important tool in computational complexity theory, e.g., for the design of probabilistically checkable proofs.
Locally decodable codes are error-correcting codes for which single bits of the message can be probabilistically recovered by only looking at a small (say constant) number of positions of a codeword, even after the codeword has been corrupted at some constant fraction of positions. Locally testable codes are error-correcting codes for which it can be checked probabilistically whether a signal is close to a codeword by only looking at a small number of positions of the signal.
Interleaving[edit]
«Interleaver» redirects here. For the fiber-optic device, see optical interleaver.
Interleaving is frequently used in digital communication and storage systems to improve the performance of forward error correcting codes. Many communication channels are not memoryless: errors typically occur in bursts rather than independently. If the number of errors within a code word exceeds the error-correcting code’s capability, it fails to recover the original code word. Interleaving alleviates this problem by shuffling source symbols across several code words, thereby creating a more uniform distribution of errors.[15] Therefore, interleaving is widely used for burst error-correction.
The analysis of modern iterated codes, like turbo codes and LDPC codes, typically assumes an independent distribution of errors.[16] Systems using LDPC codes therefore typically employ additional interleaving across the symbols within a code word.[17]
For turbo codes, an interleaver is an integral component and its proper design is crucial for good performance.[15][18] The iterative decoding algorithm works best when there are not short cycles in the factor graph that represents the decoder; the interleaver is chosen to avoid short cycles.
Interleaver designs include:
- rectangular (or uniform) interleavers (similar to the method using skip factors described above)
- convolutional interleavers
- random interleavers (where the interleaver is a known random permutation)
- S-random interleaver (where the interleaver is a known random permutation with the constraint that no input symbols within distance S appear within a distance of S in the output).[19]
- a contention-free quadratic permutation polynomial (QPP).[20] An example of use is in the 3GPP Long Term Evolution mobile telecommunication standard.[21]
In multi-carrier communication systems, interleaving across carriers may be employed to provide frequency diversity, e.g., to mitigate frequency-selective fading or narrowband interference.[22]
Example[edit]
Transmission without interleaving:
Error-free message: aaaabbbbccccddddeeeeffffgggg Transmission with a burst error: aaaabbbbccc____deeeeffffgggg
Here, each group of the same letter represents a 4-bit one-bit error-correcting codeword. The codeword cccc is altered in one bit and can be corrected, but the codeword dddd is altered in three bits, so either it cannot be decoded at all or it might be decoded incorrectly.
With interleaving:
Error-free code words: aaaabbbbccccddddeeeeffffgggg Interleaved: abcdefgabcdefgabcdefgabcdefg Transmission with a burst error: abcdefgabcd____bcdefgabcdefg Received code words after deinterleaving: aa_abbbbccccdddde_eef_ffg_gg
In each of the codewords «aaaa», «eeee», «ffff», and «gggg», only one bit is altered, so one-bit error-correcting code will decode everything correctly.
Transmission without interleaving:
Original transmitted sentence: ThisIsAnExampleOfInterleaving Received sentence with a burst error: ThisIs______pleOfInterleaving
The term «AnExample» ends up mostly unintelligible and difficult to correct.
With interleaving:
Transmitted sentence: ThisIsAnExampleOfInterleaving... Error-free transmission: TIEpfeaghsxlIrv.iAaenli.snmOten. Received sentence with a burst error: TIEpfe______Irv.iAaenli.snmOten. Received sentence after deinterleaving: T_isI_AnE_amp_eOfInterle_vin_...
No word is completely lost and the missing letters can be recovered with minimal guesswork.
Disadvantages of interleaving[edit]
Use of interleaving techniques increases total delay. This is because the entire interleaved block must be received before the packets can be decoded.[23] Also interleavers hide the structure of errors; without an interleaver, more advanced decoding algorithms can take advantage of the error structure and achieve more reliable communication than a simpler decoder combined with an interleaver[citation needed]. An example of such an algorithm is based on neural network[24] structures.
Software for error-correcting codes[edit]
Simulating the behaviour of error-correcting codes (ECCs) in software is a common practice to design, validate and improve ECCs. The upcoming wireless 5G standard raises a new range of applications for the software ECCs: the Cloud Radio Access Networks (C-RAN) in a Software-defined radio (SDR) context. The idea is to directly use software ECCs in the communications. For instance in the 5G, the software ECCs could be located in the cloud and the antennas connected to this computing resources: improving this way the flexibility of the communication network and eventually increasing the energy efficiency of the system.
In this context, there are various available Open-source software listed below (non exhaustive).
- AFF3CT(A Fast Forward Error Correction Toolbox): a full communication chain in C++ (many supported codes like Turbo, LDPC, Polar codes, etc.), very fast and specialized on channel coding (can be used as a program for simulations or as a library for the SDR).
- IT++: a C++ library of classes and functions for linear algebra, numerical optimization, signal processing, communications, and statistics.
- OpenAir: implementation (in C) of the 3GPP specifications concerning the Evolved Packet Core Networks.
List of error-correcting codes[edit]
| Distance | Code |
|---|---|
| 2 (single-error detecting) | Parity |
| 3 (single-error correcting) | Triple modular redundancy |
| 3 (single-error correcting) | perfect Hamming such as Hamming(7,4) |
| 4 (SECDED) | Extended Hamming |
| 5 (double-error correcting) | |
| 6 (double-error correct-/triple error detect) | Nordstrom-Robinson code |
| 7 (three-error correcting) | perfect binary Golay code |
| 8 (TECFED) | extended binary Golay code |
- AN codes
- Algebraic geometry code
- BCH code, which can be designed to correct any arbitrary number of errors per code block.
- Barker code used for radar, telemetry, ultra sound, Wifi, DSSS mobile phone networks, GPS etc.
- Berger code
- Constant-weight code
- Convolutional code
- Expander codes
- Group codes
- Golay codes, of which the Binary Golay code is of practical interest
- Goppa code, used in the McEliece cryptosystem
- Hadamard code
- Hagelbarger code
- Hamming code
- Latin square based code for non-white noise (prevalent for example in broadband over powerlines)
- Lexicographic code
- Linear Network Coding, a type of erasure correcting code across networks instead of point-to-point links
- Long code
- Low-density parity-check code, also known as Gallager code, as the archetype for sparse graph codes
- LT code, which is a near-optimal rateless erasure correcting code (Fountain code)
- m of n codes
- Nordstrom-Robinson code, used in Geometry and Group Theory[25]
- Online code, a near-optimal rateless erasure correcting code
- Polar code (coding theory)
- Raptor code, a near-optimal rateless erasure correcting code
- Reed–Solomon error correction
- Reed–Muller code
- Repeat-accumulate code
- Repetition codes, such as Triple modular redundancy
- Spinal code, a rateless, nonlinear code based on pseudo-random hash functions[26]
- Tornado code, a near-optimal erasure correcting code, and the precursor to Fountain codes
- Turbo code
- Walsh–Hadamard code
- Cyclic redundancy checks (CRCs) can correct 1-bit errors for messages at most
bits long for optimal generator polynomials of degree
, see Mathematics of cyclic redundancy checks#Bitfilters
See also[edit]
- Code rate
- Erasure codes
- Soft-decision decoder
- Burst error-correcting code
- Error detection and correction
- Error-correcting codes with feedback
- Linear code
- Quantum error correction
References[edit]
- ^ Charles Wang; Dean Sklar; Diana Johnson (Winter 2001–2002). «Forward Error-Correction Coding». Crosslink. The Aerospace Corporation. 3 (1). Archived from the original on 14 March 2012. Retrieved 5 March 2006.
- ^ Charles Wang; Dean Sklar; Diana Johnson (Winter 2001–2002). «Forward Error-Correction Coding». Crosslink. The Aerospace Corporation. 3 (1). Archived from the original on 14 March 2012. Retrieved 5 March 2006.
How Forward Error-Correcting Codes Work]
- ^ a b Maunder, Robert (2016). «Overview of Channel Coding».
- ^ Glover, Neal; Dudley, Trent (1990). Practical Error Correction Design For Engineers (Revision 1.1, 2nd ed.). CO, USA: Cirrus Logic. ISBN 0-927239-00-0.
- ^ a b Hamming, Richard Wesley (April 1950). «Error Detecting and Error Correcting Codes». Bell System Technical Journal. USA: AT&T. 29 (2): 147–160. doi:10.1002/j.1538-7305.1950.tb00463.x. S2CID 61141773.
- ^ «Hamming codes for NAND flash memory devices» Archived 21 August 2016 at the Wayback Machine. EE Times-Asia. Apparently based on «Micron Technical Note TN-29-08: Hamming Codes for NAND Flash Memory Devices». 2005. Both say: «The Hamming algorithm is an industry-accepted method for error detection and correction in many SLC NAND flash-based applications.»
- ^ a b «What Types of ECC Should Be Used on Flash Memory?» (Application note). Spansion. 2011.
Both Reed–Solomon algorithm and BCH algorithm are common ECC choices for MLC NAND flash. … Hamming based block codes are the most commonly used ECC for SLC…. both Reed–Solomon and BCH are able to handle multiple errors and are widely used on MLC flash.
- ^ Jim Cooke (August 2007). «The Inconvenient Truths of NAND Flash Memory» (PDF). p. 28.
For SLC, a code with a correction threshold of 1 is sufficient. t=4 required … for MLC.
- ^ Baldi, M.; Chiaraluce, F. (2008). «A Simple Scheme for Belief Propagation Decoding of BCH and RS Codes in Multimedia Transmissions». International Journal of Digital Multimedia Broadcasting. 2008: 1–12. doi:10.1155/2008/957846.
- ^ Shah, Gaurav; Molina, Andres; Blaze, Matt (2006). «Keyboards and covert channels». USENIX. Retrieved 20 December 2018.
- ^ Tse, David; Viswanath, Pramod (2005), Fundamentals of Wireless Communication, Cambridge University Press, UK
- ^ Shannon, C. E. (1948). «A mathematical theory of communication» (PDF). Bell System Technical Journal. 27 (3–4): 379–423 & 623–656. doi:10.1002/j.1538-7305.1948.tb01338.x. hdl:11858/00-001M-0000-002C-4314-2.
- ^ Rosas, F.; Brante, G.; Souza, R. D.; Oberli, C. (2014). «Optimizing the code rate for achieving energy-efficient wireless communications». Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC). pp. 775–780. doi:10.1109/WCNC.2014.6952166. ISBN 978-1-4799-3083-8.
- ^ IEEE Standard, section 20.3.11.6 «802.11n-2009» Archived 3 February 2013 at the Wayback Machine, IEEE, 29 October 2009, accessed 21 March 2011.
- ^ a b Vucetic, B.; Yuan, J. (2000). Turbo codes: principles and applications. Springer Verlag. ISBN 978-0-7923-7868-6.
- ^ Luby, Michael; Mitzenmacher, M.; Shokrollahi, A.; Spielman, D.; Stemann, V. (1997). «Practical Loss-Resilient Codes». Proc. 29th Annual Association for Computing Machinery (ACM) Symposium on Theory of Computation.
- ^ «Digital Video Broadcast (DVB); Second generation framing structure, channel coding and modulation systems for Broadcasting, Interactive Services, News Gathering and other satellite broadband applications (DVB-S2)». En 302 307. ETSI (V1.2.1). April 2009.
- ^ Andrews, K. S.; Divsalar, D.; Dolinar, S.; Hamkins, J.; Jones, C. R.; Pollara, F. (November 2007). «The Development of Turbo and LDPC Codes for Deep-Space Applications». Proceedings of the IEEE. 95 (11): 2142–2156. doi:10.1109/JPROC.2007.905132. S2CID 9289140.
- ^ Dolinar, S.; Divsalar, D. (15 August 1995). «Weight Distributions for Turbo Codes Using Random and Nonrandom Permutations». TDA Progress Report. 122: 42–122. Bibcode:1995TDAPR.122…56D. CiteSeerX 10.1.1.105.6640.
- ^ Takeshita, Oscar (2006). «Permutation Polynomial Interleavers: An Algebraic-Geometric Perspective». IEEE Transactions on Information Theory. 53 (6): 2116–2132. arXiv:cs/0601048. Bibcode:2006cs……..1048T. doi:10.1109/TIT.2007.896870. S2CID 660.
- ^ 3GPP TS 36.212, version 8.8.0, page 14
- ^ «Digital Video Broadcast (DVB); Frame structure, channel coding and modulation for a second generation digital terrestrial television broadcasting system (DVB-T2)». En 302 755. ETSI (V1.1.1). September 2009.
- ^ Techie (3 June 2010). «Explaining Interleaving». W3 Techie Blog. Retrieved 3 June 2010.
- ^ Krastanov, Stefan; Jiang, Liang (8 September 2017). «Deep Neural Network Probabilistic Decoder for Stabilizer Codes». Scientific Reports. 7 (1): 11003. arXiv:1705.09334. Bibcode:2017NatSR…711003K. doi:10.1038/s41598-017-11266-1. PMC 5591216. PMID 28887480.
- ^ Nordstrom, A.W.; Robinson, J.P. (1967), «An optimum nonlinear code», Information and Control, 11 (5–6): 613–616, doi:10.1016/S0019-9958(67)90835-2
- ^ Perry, Jonathan; Balakrishnan, Hari; Shah, Devavrat (2011). «Rateless Spinal Codes». Proceedings of the 10th ACM Workshop on Hot Topics in Networks. pp. 1–6. doi:10.1145/2070562.2070568. hdl:1721.1/79676. ISBN 9781450310598.
Further reading[edit]
- MacWilliams, Florence Jessiem; Sloane, Neil James Alexander (2007) [1977]. Written at AT&T Shannon Labs, Florham Park, New Jersey, USA. The Theory of Error-Correcting Codes. North-Holland Mathematical Library. Vol. 16 (digital print of 12th impression, 1st ed.). Amsterdam / London / New York / Tokyo: North-Holland / Elsevier BV. ISBN 978-0-444-85193-2. LCCN 76-41296. (xxii+762+6 pages)
- Clark, Jr., George C.; Cain, J. Bibb (1981). Error-Correction Coding for Digital Communications. New York, USA: Plenum Press. ISBN 0-306-40615-2.
- Arazi, Benjamin (1987). Swetman, Herb (ed.). A Commonsense Approach to the Theory of Error Correcting Codes. MIT Press Series in Computer Systems. Vol. 10 (1 ed.). Cambridge, Massachusetts, USA / London, UK: Massachusetts Institute of Technology. ISBN 0-262-01098-4. LCCN 87-21889. (x+2+208+4 pages)
- Wicker, Stephen B. (1995). Error Control Systems for Digital Communication and Storage. Englewood Cliffs, New Jersey, USA: Prentice-Hall. ISBN 0-13-200809-2.
- Wilson, Stephen G. (1996). Digital Modulation and Coding. Englewood Cliffs, New Jersey, USA: Prentice-Hall. ISBN 0-13-210071-1.
- «Error Correction Code in Single Level Cell NAND Flash memories» 2007-02-16
- «Error Correction Code in NAND Flash memories» 2004-11-29
- Observations on Errors, Corrections, & Trust of Dependent Systems, by James Hamilton, 2012-02-26
- Sphere Packings, Lattices and Groups, By J. H. Conway, Neil James Alexander Sloane, Springer Science & Business Media, 2013-03-09 – Mathematics – 682 pages.
External links[edit]
- Morelos-Zaragoza, Robert (2004). «The Correcting Codes (ECC) Page». Retrieved 5 March 2006.
- lpdec: library for LP decoding and related things (Python)
Каждому устройству, использующему флэш-память NAND, необходим код с исправлением случайных битов (известный как «мягкая» ошибка). Это потому что много электрический шум производится внутри чипа NAND, а уровни сигналов битов, проходящих через цепочку чипов NAND, очень слабые.

Один из способов, которым NAND память стали самый дешевый всего, потому что это требует, чтобы исправление ошибок было выполнено от элемента вне самого чипа NAND; В случае SSD, ECC выполняется на контроллере .
Такое же исправление ошибок также помогает исправить битовые ошибки из-за носить на Память сами клетки , Истощение может вызвать «застревание» битов в том или ином состоянии (известное как «жесткая» ошибка или жесткая ошибка) и может увеличить частоту «мягких» ошибок.
Хотя это понятие не является слишком широким, сопротивление флэш-памяти является мерой того, сколько циклов стирания / записи может выдержать блок флэш-памяти, прежде чем начнут появляться «серьезные» ошибки. Очень часто эти сбои происходят только в отдельных битах, и очень редко происходит сбой всего блока. При достаточно высоком числе стирания / записи «мягкая» частота ошибок также увеличивается из-за ряда других механизмов в самом SSD.
If ECC может быть используемый чтобы исправить эти «жесткие» ошибки, а «мягкие» ошибки не увеличиваются, срок службы всего блока значительно удлиняется, что значительно превышает сопротивление, указанное производителем.
Давайте рассмотрим пример: допустим, что неиспользуемый чип NAND имеет достаточно «мягких» ошибок, чтобы требовать 8 бит ECC, то есть при каждом считывании страницы может быть до 8 бит, которые были случайно повреждены (обычно из-за электрических помех, которые мы говорили о). вначале). ECC, используемый в этом чипе, может исправлять 12-битные ошибки, так что ECC не может решить эту проблему мы должны найти 8 «мягких» ошибок, связанных с электрическим шумом, плюс еще 5 «мягких» из-за износа.
Теперь производители флэш-памяти гарантируют, что первый из этих 5 сбоев произойдет через некоторое время после спецификации прочности SSD. Это означает, что ни один бит не выйдет из строя из-за износа, пока не будут превышены циклы стирания / записи, указанные производителем. Теперь имейте в виду, что спецификации не достаточно точны, чтобы предсказать, когда следующий бит выйдет из строя, и на самом деле это может занять несколько тысяч циклов стирания / записи выше спецификации, чтобы это произошло; помните, что производитель гарантирует, что это не произойдет до X циклов, но не тогда, когда это произойдет после их превышения.
Это означает, что это может занять много времени, прежде чем блок становится настолько коррумпированным что его необходимо удалить из службы (а также для этого на SSD обычно есть «дополнительные» блоки для замены поврежденных), что, в свою очередь, означает, что сопротивление исправлен от ошибок блок может быть во много раз больше указанного сопротивления, в зависимости от количества избыточных ошибок, которые ECC предназначен для исправления.
Какое влияние оказывает код исправления ошибок на SSD?
Как мы объясняли ранее, флэш-память настолько дешева, потому что она не включает в себя ECC в самих чипах, но интегрирована в другое внешнее оборудование, и, как вы предположите, это имеет свою цену. Более сложный ECC требует большей вычислительной мощности на контроллере и может быть медленнее, если алгоритмы не очень современные. Кроме того, количество ошибок, которые могут быть исправлены, будет зависеть от того, насколько большой сектор памяти исправляется, поэтому контроллер SSD со сложным алгоритмом ECC, вероятно, будет использовать много ресурсов, снижение общий SSD производительность , Эти улучшения также делают контроллер дороже .
Алгоритмы ECC имеют свое собственное математическое состояние в зависимости от контроллера (другими словами, нет никакого стандарта), и даже самые базовые кодировки ECC (Рида-Соломона и LDPC) довольно сложны для понимания. Когда кто-то говорит о пределе Шеннона (максимальное количество битов, которое может быть исправлено), это величина, которую, как вы не знаете от производителя в технических характеристиках, чрезвычайно сложно вычислить.
Просто придерживайтесь этого: большее количество корректирующих битов увеличивает срок службы SSD, но также оказывает некоторое влияние на производительность или даже цену продукта, так как требует более мощный контроллер.
Оглавление
- Вступление
- Коррекция ошибок
- Финансовая сторона
- Тестовый стенд
- Методика тестирования
- Результаты тестирования
- Тест памяти
- 3DMark
- 7Zip
- Cinebench
- CrystalMark
- Fritz
- LinX
- wPrime
- AIDA64 Extreme
- Заключение
Вступление
На сегодняшний день на просторах Рунета можно встретить открытые темы на форумах с вопросами – стоит ли брать рабочую станцию с ECC-памятью или можно обойтись обычной? В данных ветках можно прочесть множество противоречивых утверждений, и часть из них говорит о том, что коррекция ошибок сильно замедляет память, а следовательно и ЦП. Но мало кто это проверял на деле на современных процессорах.
Сегодня мы разберемся в этом вопросе и сравним производительность серверного процессора с обоими типами памяти. Но для начала небольшой экскурс.
Коррекция ошибок
Для чего необходима коррекция? И почему в работе памяти возникают ошибки? Перед ответом на эти вопросы следует разделить ошибки на два типа:
- Аппаратные ошибки;
- Случайные ошибки.
Причиной появления аппаратных ошибок является дефектная микросхема DRAM, а случайные ошибки возникают под воздействием излучения, альфа-частиц, элементарных частиц и прочего. Соответственно, первые в принципе неисправимы – если чип дефектный, то поможет только его замена; а вот вторые могут быть исправлены.
Почему же так необходима коррекция ошибок в рабочих станциях и серверах? Однобитовая ошибка в 64-битном слове меняет содержимое ячейки памяти, а в конечном итоге на жесткий диск может быть записано другое число, другие данные, при этом компьютер не зафиксирует эту подмену. А изменение бита в оперативной памяти может вызвать сбой программы, что для рабочей станции и сервера недопустимо.
рекомендации
3060 дешевле 30тр в Ситилинке
3070 Gigabyte Gaming за 50 тр с началом
<b>13900K</b> в Регарде по СТАРОМУ курсу 62
3070 Gainward Phantom дешевле 50 тр
10 видов <b>4070 Ti</b> в Ситилинке — все до 100 тр
13700K дешевле 40 тр в Регарде
MSI 3050 за 25 тр в Ситилинке
13600K дешевле 30 тр в Регарде
4080 почти за 100тр — дешевле чем по курсу 60
12900K за 40тр с началом в Ситилинке
RTX 4090 за 140 тр в Регарде
Компьютеры от 10 тр в Ситилинке
3060 Ti Gigabyte дешевле 40 тр в Регарде
3070 дешевле 50 тр в Ситилинке
-7% на 4080 Gigabyte Gaming
Для обнаружения изменения битов памяти можно использовать метод подсчета контрольной суммы, но он позволяет лишь обнаруживать ошибки без их исправления.
В свое время было предложено много различных способов решения данной проблемы, но на сегодняшний день наибольшее распространение получил метод коррекции ошибок или ECC (Error-Correcting Code). Данный метод позволяет автоматически исправлять однобитовые ошибки в 64-битном слове – SEC (Single Error Correction) и детектировать двухбитовые – DED (Double Error Detection).
Физическая реализация ECC заключается в размещении дополнительной микросхемы памяти на модуле ОЗУ – соответственно, при одностороннем дизайне модуля памяти вместо восьми чипов располагается девять, а при двустороннем вместо шестнадцати – восемнадцать. Таким образом, ширина модуля становится не 64 бита, а 72 бита.
Метод коррекции ошибок работает следующим образом: при записи 64 бит данных в ячейку памяти происходит подсчет контрольной суммы, составляющей 8 бит. Когда процессор обращается к этим данным и производит считывание, проводится повторный подсчет контрольной суммы и сравнение с исходной. Если суммы не совпадают – произошла ошибка. Если она однобитовая, то неправильный бит исправляется автоматически, если двухбитовая – детектируется и сообщается ОС.
Финансовая сторона
Прежде чем приступить к тестированию, необходимо затронуть финансовый вопрос.
Стоимость обычного модуля памяти DDR3-1600 с напряжением 1.35 В и объемом 8 Гбайт составляет около 3600 рублей, а с коррекцией ошибок – 4800 рублей. На первый взгляд ECC-память выходит на 30-35% дороже, что, в целом, не позволяет их сравнивать в силу существенно большей стоимости последней. Но почему же тогда такой вопрос возникает при сборке рабочей станции? Все просто – необходимо смотреть на данный вопрос шире, а именно – смотреть на общую стоимость рабочей станции.
Ценник однопроцессорной станции на базе четырехъядерного восьмипоточного Xeon (настольные процессоры серий i5 и i7 не поддерживают ECC-память) с 32 Гбайтами памяти, материнской платы с чипсетом C222/С224/С226 (десктопные наборы логики Z87/Z97 и другие также не поддерживают память с коррекцией ошибок) будет превышать 70 000 рублей (при условии, что устанавливаются серверные SSD с повышенным ресурсом). А если включить в эту стоимость и дискретную видеокарту, и прочие сопутствующие компоненты, например, ИБП, то ценник из пятизначного превратится в шестиизначный, перевалив планку в 100 000 рублей.
Покупка 32 Гбайт памяти с коррекцией ошибок потребует дополнительных 4-6 тысяч рублей, что по отношению к общей стоимости рабочей станции не превышает 5%, то есть не является критичным. Также переход от десктопного к серверному железу предоставит и другие преимущества, например: интегрированные графические карты P4600 в процессорах Intel Xeon E3-1200 третьего поколения получили оптимизированные драйверы, которые должны повышать производительность в профессиональных приложениях, например, в CAD; поддержка технологии Intel VT-d, которая позволяет пробрасывать устройства в виртуальную среду, например, видеокарты; прочие серверные технологии – Intel AMT или IPMI, WatchDog и другие, которые также могут оказаться полезными.
Таким образом, хоть и сама ECC-память стоит заметно дороже обычной, в общей стоимости рабочей станции данная статья затрат является несущественной, и переплата не превышает 5%.
Тестовый стенд
Для данного обзора использовалась следующая конфигурация:
- Материнская плата: Supermicro X10SAE (Intel C226, LGA 1150);
- Процессор: Xeon E3-1245V3 (Turbo Boost – off, EIST – off, HT – on);
- Оперативная память:
- 2x Kingston DDR3-1600 ECC 8 Гбайт (KVR16LE11/8 CL11, 1.35 В);
- 2x Kingston DDR3-1600 8 Гбайт (KVR16LN11/8 CL11, 1.35 В);
- ОС: Windows 8.1 Pro 64-bit.
Методика тестирования
В рамках тестирования были произведены замеры производительности как при одноканальном режиме работы ИКП, так и при двухканальном. Суммарный объем ОЗУ составил 8 (один модуль) и 16 Гбайт (два модуля) соответственно.
Программное обеспечение:
- 3DMark 2006 1.2;
- 7Zip 9.20;
- AIDA64 Extreme 5.20.3400;
- Cinebench R15;
- CrystalMark 2004R3;
- Fritz 4.20;
- LinX 0.6.5;
- wPrime 2.10.
Результаты тестирования
Тест памяти
Перед тем, как приступить к тестированию, проведем замер пропускной способности памяти и латентности.
При изучении результатов можно заключить, что производительность ECC- и non-ECC- памяти находится на одном и том же уровне в рамках погрешности.
Если в предыдущем тесте от замера к замеру выигрывал то один, то другой тип памяти, то при замере латентности ECC-память постоянно показывает большие задержки. Но разница несущественна – всего лишь 1 нс.
Таким образом, замер ПС и латентности памяти не показал особых различий между ECC- и non-ECC-памятью. Посмотрим, повторится ли это в последующих тестах.
3DMark
Тестовый пакет 3DMark содержит подтесты как для процессора, так и для графической карты. Здесь и кроется самое интересное – давно известно, что встроенному видеоядру не хватает существующей ПСП в 25.6 Гбайт/с, поэтому именно в графических подтестах можно выявить негативное влияние коррекции ошибок, если оно вообще есть,…
… но разницы нет – что ECC, что non-ECC. Ни процессор, ни интегрированное ядро никак не реагируют на замену обычной памяти на DDR с коррекцией ошибок – результаты одинаковы в рамках погрешности. Среднеарифметическая разница составила 0.02% в пользу ECC-памяти для одноканального режима и 1.6% для двухканального режима.
При этом нельзя сказать, что встроенная видеокарта P4600 не зависит от скорости ОЗУ – при одноканальном доступе общий результат почти на 30% ниже, чем при двухканальном. Другими словами, скорость ОЗУ критична для графического ядра, но сами по себе «ECC-версии» не влияют ни на скорость ОЗУ, ни на видеокарту.
7Zip
Архиваторы, как известно, чувствительны к памяти, поэтому, возможно, здесь получится зафиксировать влияние типа памяти на производительность.
Ситуация с архивацией неоднозначная: с одной стороны – в одноканальном режиме (как при распаковке, так и при сжатии) ECC-память уверенно оказывается медленнее на 2%; с другой – в двухканальном режиме при сжатии ECC-память уверенно быстрее, а при распаковке – медленнее, а среднее арифметическое – быстрее на 0.65%.
Скорее всего, причина в следующем – пропускной способности памяти при одноканальном доступе процессору явно недостаточно, и поэтому чуть большая латентность ECC-памяти сказывается на производительности; а при двухканальном доступе ПСП полностью покрывает нужды CPU и поэтому чуть большая латентность памяти с коррекцией ошибок не сказывается на производительности. В любом случае зафиксировать существенного влияния на скорость архивации не получилось.
Cinebench
Тестовый пакет Cinebench содержит подтест как процессора, так и видеокарты.
Но ни первый, ни вторая никак не отреагировали на ECC-память.
Зато налицо явная зависимость видеокарты от ПСП – при одноканальном доступе результат в OpenGL оказался на 25% ниже, чем при двухканальном. Вспоминая результаты 3DMark и смотря на нынешние, можно заключить, что производительность интегрированной видеокарты хоть и зависит от ПСП, но ECC-память не оказывает на нее негативного влияния.
Ошибки при хранении
информации в памяти неизбежны. Они
обычно классифицируются как отказы и
нерегулярные ошибки (сбои). Если нормально
функционирующая микросхема вследствие,
например, физического повреждения
начинает работать неправильно, то все
происходящее и называется постоянным
отказом. Чтобы устранить этот тип отказа,
обычно требуется заменить некоторую
часть аппаратных средств памяти, например
неисправную микросхему SIMM или DIMM.
Другой, более
коварный тип отказа
нерегулярная ошибка (сбой). Это непостоянный
отказ, который не происходит при
повторении условий функционирования
или через регулярные интервалы.
Приблизительно
20 лет назад сотрудники Intel
установили, что причиной сбоев являются
альфа-частицы. Поскольку альфа-частицы
не могут проникнуть даже через тонкий
лист бумаги, выяснилось, что их источником
служит вещество, используемое в
полупроводниках. При исследовании были
обнаружены частицы тория и урана в
пластмассовых и керамических корпусах
микросхем, применявшихся в те годы.
Изменив технологический процесс,
производители памяти избавились от
этих примесей.
В настоящее время
производители памяти почти полностью
устранили источники альфа-частиц. И
многие стали думать, что проверка
четности не нужна вовсе. Например, сбои
в памяти емкостью 16 Мбайт из-за альфа-частиц
случаются в среднем только один раз за
16 лет! Однако сбои памяти происходят
значительно чаще.
Сегодня самая
главная причина нерегулярных ошибок
космические лучи. Поскольку они имеют
очень большую проникающую способность,
от них практически нельзя защититься
с помощью экранирования.
К сожалению,
производители персональных компьютеров
не признали это причиной погрешностей
памяти; случайную природу сбоя намного
легче оправдать разрядом электростатического
электричества, большими выбросами
мощности или неустойчивой работой
программного обеспечения (например,
использованием новой версии операционной
системы или большой прикладной программы).
Хотя космические
лучи и радиация являются причиной
большинства программных ошибок памяти,
существуют и другие факторы.
-
Скачки в
энергопотреблении или шум на линии.
Причиной может быть неисправный блок
питания или настенная розетка. -
Использование
неверного типа или параметра быстродействия
памяти. Тип
памяти должен поддерживаться конкретным
набором микросхем и обладать определенной
этим набором скоростью доступа. -
Радиочастотная
интерференция.
Связана с расположением радиопередатчиков
рядом с компьютером, что иногда приводит
к генерированию паразитных электрических
сигналов в монтажных соединениях и
схемах компьютера. Беспроводные сети,
мыши и клавиатуры увеличивают риск
появления радиочастотной интерференции. -
Статические
разряды.
Вызывают моментальные скачки в
энергоснабжении, что может повлиять
на целостность данных. -
Ошибки
синхронизации. Не
поступившие своевременно данные могут
стать причиной появления программных
ошибок. Зачастую причина заключается
в неверных параметрах BIOS,
оперативной памяти, быстродействие
которой ниже, чем требуется системой,
«разогнанных» процессорах и прочих
ситемных компонентах.
Большинство
системных проблем не приводят к
прекращению работы микросхем памяти,
однако могут повлиять на хранимые
данные.
Игнорирование
сбоев, конечно, не лучший способ борьбы
с ними. К сожалению, именно этот способ
сегодня выбрали многие производители
компьютеров. Лучше было бы увеличить
отказоустойчивость систем. Для этого
необходимы механизмы обнаружения и,
возможно, исправления ошибок в памяти
персонального компьютера. В основном
для повышения отказоустойчивости в
современных компьютерах применяются
следующие методы:
-
контроль четности;
-
коды коррекции
ошибок (ECC).
Соседние файлы в папке Сватов лабы
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Контроль четности и коды коррекции ошибок (ECC).
Ошибки при хранении информации в памяти неизбежны. Они обычно классифицируются как отказы и нерегулярные ошибки (сбои). Если нормально функционирующая микросхема вследствие, например, физического повреждения начинает работать неправильно, то все происходящее и называется постоянным отказом. Чтобы устранить этот тип отказа, обычно требуется заменить некоторую часть аппаратных средств памяти, например неисправную микросхему памяти.
Другой, более коварный тип отказа — нерегулярная ошибка (сбой). Это непостоянный отказ, который не происходит при повторении условий функционирования или через регулярные интервалы.
Приблизительно 20 лет назад сотрудники Intel установили, что причиной сбоев являются альфа-частицы. Поскольку альфа-частицы не могут проникнуть даже через тонкий лист бумаги, выяснилось, что их источником служит вещество, используемое в полупроводниках. При исследовании были обнаружены частицы тория и урана в пластмассовых и керамических корпусах микросхем, применявшихся в те годы. Изменив технологический процесс, производители памяти избавились от этих примесей.
В настоящее время производители памяти почти полностью устранили источники альфачастиц. И многие стали думать, что проверка четности не нужна вовсе. Например, сбои в памяти емкостью 16 Мбайт из-за альфа-частиц случаются в среднем только один раз за 16 лет! Однако сбои памяти происходят значительно чаще.
Сегодня самая главная причина нерегулярных ошибок — космические лучи. Поскольку они имеют очень большую проникающую способность, от них практически нельзя защититься с помощью экранирования.
Эксперимент, проверяющий степень влияния космических лучей на появление ошибок в работе микросхем, показал, что соотношение “сигнал–ошибка” (signal-to-error ratio — SER) для некоторых модулей DRAM составило 5950 единиц интенсивности отказов (failure units — FU) на миллиард часов наработки для каждой микросхемы. Измерения проводились в условиях, приближенных к реальной жизни, с учетом длительности в несколько миллионов машиночасов. В среднестатистическом компьютере это означало бы появление программной ошибки памяти примерно каждые шесть месяцев. В серверных системах или мощных рабочих станциях с большим объемом установленной оперативной памяти подобная статистика указывает на одну ошибку (или даже более) в работе памяти каждый месяц! Когда тестовая система с теми же модулями DIMM была размещена в надежном убежище на глубине более 15 метров каменной породы, что полностью устраняет влияние космических лучей, программные ошибки в работе памяти вообще не были зафиксированы. Эксперимент продемонстрировал не только опасность влияния космических лучей, но и доказал, насколько эффективно устранять влияние альфалучей и радиоактивных примесей в оболочках модулей памяти.
К сожалению, производители ПК не признали это причиной погрешностей памяти; случайную природу сбоя намного легче оправдать разрядом электростатического электричества, большими выбросами мощности или неустойчивой работой программного обеспечения (например, использованием новой версии операционной системы или большой прикладной программы). Исследования показали, что для систем ECC доля программных ошибок в 30 раз больше, чем аппаратных. Это неудивительно, учитывая вредное влияние космических лучей. Количество ошибок зависит от числа установленных модулей памяти и их объема. Программные ошибки могут случаться и раз в месяц, и несколько раз в неделю, и даже чаще!
Хотя космические лучи и радиация являются причиной большинства программных ошибок памяти, существуют и другие факторы:
1. Скачки в энергопотреблении или шум на линии. Причиной может быть неисправный блок питания или настенная розетка.
2. Использование неверного типа или параметра быстродействия памяти. Тип памяти
должен поддерживаться конкретным набором микросхем и обладать определенной
этим набором скоростью доступа.
3. Электромагнитные помехи. Возникают при расположении радиопередатчиков рядом с
компьютером, что иногда приводит к генерированию паразитных электрических сигна-
лов в монтажных соединениях и схемах компьютера. Имейте в виду, что беспроводные
сети, мыши и клавиатуры увеличивают риск появления электромагнитных помех.
4. Статические разряды. Вызывают моментальные скачки в энергоснабжении, что может
повлиять на целостность данных.
5. Ошибки синхронизации. Не поступившие своевременно данные могут стать причиной
появления программных ошибок. Зачастую причина заключается в неверных парамет-
рах BIOS, оперативной памяти, быстродействие которой ниже, чем требуется систе-
мой, “разогнанных” процессорах и прочих системных компонентах.
Большинство описанных проблем не приводят к прекращению работы микросхем памяти (хотя некачественное энергоснабжение или статическое электричество могут физически повредить микросхемы), однако могут повлиять на хранимые данные.
Игнорирование сбоев, конечно, не лучший способ борьбы с ними. К сожалению, именно этот способ сегодня выбрали многие производители компьютеров. Лучше было бы повысить отказоустойчивость систем. Для этого необходимы механизмы определения и, возможно, исправления ошибок в памяти ПК. В основном для повышения отказоустойчивости в современных компьютерах применяются следующие методы:
— контроль четности;
— коды коррекции ошибок (ECC).
Системы без контроля четности вообще не обеспечивают отказоустойчивости данных. Единственная причина, по которой они используются, — их минимальная базовая стоимость. При этом, в отличие от других технологий (ECC и контроль четности), не требуется дополнительная оперативная память.
Байт данных с контролем четности включает в себя 9, а не 8 бит, поэтому стоимость памяти с контролем четности выше примерно на 12,5%. Кроме того, контроллеры памяти, не требующие логических мостов для подсчета данных четности или ECC, обладают упрощенной внутренней архитектурой. Портативные системы, для которых вопрос минимального энергопотребления особенно важен, выигрывают от уменьшенного энергопотребления памяти благодаря использованию меньшего количества микросхем DRAM. И наконец, шина данных памяти без контроля четности имеет меньшую разрядность, что выражается в сокращении количества буферов данных. Статистическая вероятность возникновения ошибок памяти в современных настольных компьютерах составляет примерно одну ошибку в несколько месяцев. При этом количество ошибок зависит от объема и типа используемой памяти. Подобный уровень ошибок может быть приемлемым для обычных компьютеров, не используемых для работы с важными приложениями. В этом случае цена играет основную роль, а дополнительная стоимость модулей памяти с поддержкой контроля четности и кода ECC себя не оправдывает.
Применение не отказоустойчивых к ошибкам компьютеров рискованно и предполагает отсутствие ошибок памяти при эксплуатации систем. При этом также учитывается, что совокупная стоимость потерь, вызванная ошибками в работе памяти, будет меньше, чем затраты на приобретение дополнительных аппаратных устройств для определения таковых ошибок.
Тем не менее ошибки памяти вполне могут стать причиной серьезных проблем: например, представьте себе указание неверного значения суммы в банковском чеке. Ошибки в работе оперативной памяти серверных систем зачастую приводят к “зависанию” последних и отключению всех клиентских компьютеров, соединенных с серверами по локальной сети. Наконец, отследить причину возникновения проблем в компьютерах, не поддерживающих контроль четности или код ECC, крайне сложно. Последние технологии по крайней мере однозначно укажут на оперативную память как на источник проблемы, тем самым экономя время и усилия системных администраторов.
Контроль четности
Это один из стандартов, введенных IBM, в соответствии с которым информация в банках памяти хранится фрагментами по девять битов, причем восемь из них (составляющих один байт) предназначены собственно для данных, а девятый является битом четности (parity). Использование девятого бита позволяет схемам управления памятью на аппаратном уровне контролировать целостность каждого байта данных. Если обнаруживается ошибка, работа компьютера останавливается и на экран выводится сообщение о неисправности.
Технология контроля четности не позволяет исправлять системные ошибки, однако дает возможность их обнаружить пользователю компьютера, что имеет следующие преимущества:
— контроль четности оберегает от последствий проведения неверных вычислений на базе некорректных данных;
— контроль четности точно указывает на источник возникновения ошибок, помогая разобраться с проблемой и улучшая степень эксплутационной надежности компьютера.
Для реализации поддержки памяти с контролем четности или без него не требуется особых усилий. В частности, внедрить поддержку контроля четности для системной платы не составит никакого труда. Основная стоимость внедрения относится к цене самих модулей памяти с контролем четности. Если покупатели нуждаются в контроле четности для работы с определенными приложениями, поставщики компьютеров могут без проблем предложить соответствующие системы.
Компания Intel и прочие производители наборов микросхем системной логики внедрили поддержку контроля четности и кода ECC в большинстве своих продуктов (особенно в наборах микросхем, ориентированных на рынок высокопроизводительных серверов). В то же время наборы микросхем низшей ценовой категории, как правило, не поддерживают эти технологии. Пользователям, требовательным к надежности выполняемых приложений, следует обращать особое внимание на поддержку контроля четности и ECC.
Код коррекции ошибок
Коды коррекции ошибок (Error Correcting Code — ECC) позволяют не только обнаружить ошибку, но и исправить ее в одном разряде. Поэтому компьютер, в котором используются подобные коды, в случае ошибки в одном разряде может работать без прерывания, причем данные не будут искажены. Коды коррекции ошибок в большинстве ПК позволяют только обнаруживать, но не исправлять ошибки в двух разрядах. Но приблизительно 98% сбоев памяти вызвано именно ошибкой в одном разряде, т.е. она успешно исправляется с помощью данного типа кодов. Данный тип ECC получил название SEC)DED (single-bit error-correction double-bit error detection — одноразрядная коррекция, двухразрядное обнаружение ошибок). В кодах коррекции ошибок этого типа для каждых 32 бит требуется дополнительно семь контрольных разрядов при 4-байтовой и восемь — при 8-байтовой организации (64-разрядные процессоры Athlon/Pentium). Реализация кода коррекции ошибок при 4-байтовой организации, очевидно, дороже реализации проверки нечетности или четности, но при 8-байтовой организации стоимость реализации кода коррекции ошибок не превышает стоимости реализации проверки четности.
Для использования кодов коррекции ошибок необходим контроллер памяти, вычисляющий контрольные разряды при операции записи в память. При чтении из памяти такой контроллер сравнивает прочитанные и вычисленные значения контрольных разрядов и при необходимости исправляет испорченный бит (или биты). Стоимость дополнительных логических схем для реализации кода коррекции ошибок в контроллере памяти не очень высока, но это может значительно снизить быстродействие памяти при операциях записи. Это происходит потому, что при операциях записи и чтения необходимо ждать, когда завершится вычисление контрольных разрядов. При записи части слова вначале следует прочитать полное слово, затем перезаписать изменяемые байты и только после этого — новые вычисленные контрольные разряды.
В большинстве случаев сбой памяти происходит в одном разряде, и потому такие ошибки успешно исправляются кодом коррекции ошибок. Использование отказоустойчивой памяти обеспечивает высокую надежность компьютера. Память с кодом ECC предназначена для серверов, рабочих станций или приложений, для которых последствия потенциальных ошибок памяти менее желательны, чем дополнительные затраты на приобретение добавочных модулей памяти и вычислительные затраты на коррекцию ошибок. Если данные имеют особое значение и компьютеры применяются для решения важных задач, без памяти ECC не обойтись. По сути, ни один уважающий себя системный инженер не будет использовать сервер, даже самый неприхотливый, без памяти ECC.
Пользователи имеют выбор между системами без контроля четности, с контролем четности и с ECC, т.е. между желательным уровнем отказоустойчивости компьютера и степенью ценности используемых данных.
«Interleaver» redirects here. For the fiber-optic device, see optical interleaver.
In computing, telecommunication, information theory, and coding theory, an error correction code, sometimes error correcting code, (ECC) is used for controlling errors in data over unreliable or noisy communication channels.[1][2] The central idea is the sender encodes the message with redundant information in the form of an ECC. The redundancy allows the receiver to detect a limited number of errors that may occur anywhere in the message, and often to correct these errors without retransmission. The American mathematician Richard Hamming pioneered this field in the 1940s and invented the first error-correcting code in 1950: the Hamming (7,4) code.[2]
ECC contrasts with error detection in that errors that are encountered can be corrected, not simply detected. The advantage is that a system using ECC does not require a reverse channel to request retransmission of data when an error occurs. The downside is that there is a fixed overhead that is added to the message, thereby requiring a higher forward-channel bandwidth. ECC is therefore applied in situations where retransmissions are costly or impossible, such as one-way communication links and when transmitting to multiple receivers in multicast. Long-latency connections also benefit; in the case of a satellite orbiting around Uranus, retransmission due to errors can create a delay of five hours. ECC information is usually added to mass storage devices to enable recovery of corrupted data, is widely used in modems, and is used on systems where the primary memory is ECC memory.
ECC processing in a receiver may be applied to a digital bitstream or in the demodulation of a digitally modulated carrier. For the latter, ECC is an integral part of the initial analog-to-digital conversion in the receiver. The Viterbi decoder implements a soft-decision algorithm to demodulate digital data from an analog signal corrupted by noise. Many ECC encoders/decoders can also generate a bit-error rate (BER) signal, which can be used as feedback to fine-tune the analog receiving electronics.
The maximum fractions of errors or of missing bits that can be corrected are determined by the design of the ECC code, so different error correcting codes are suitable for different conditions. In general, a stronger code induces more redundancy that needs to be transmitted using the available bandwidth, which reduces the effective bit-rate while improving the received effective signal-to-noise ratio. The noisy-channel coding theorem of Claude Shannon can be used to compute the maximum achievable communication bandwidth for a given maximum acceptable error probability. This establishes bounds on the theoretical maximum information transfer rate of a channel with some given base noise level. However, the proof is not constructive, and hence gives no insight of how to build a capacity achieving code. After years of research, some advanced ECC systems as of 2016[3] come very close to the theoretical maximum.
Forward error correction[edit]
In telecommunication, information theory, and coding theory, forward error correction (FEC) or channel coding[4][3] is a technique used for controlling errors in data transmission over unreliable or noisy communication channels. The central idea is that the sender encodes the message in a redundant way, most often by using an ECC.
The redundancy allows the receiver to detect a limited number of errors that may occur anywhere in the message, and often to correct these errors without re-transmission. FEC gives the receiver the ability to correct errors without needing a reverse channel to request re-transmission of data, but at the cost of a fixed, higher forward channel bandwidth. FEC is therefore applied in situations where re-transmissions are costly or impossible, such as one-way communication links and when transmitting to multiple receivers in multicast. FEC information is usually added to mass storage (magnetic, optical and solid state/flash based) devices to enable recovery of corrupted data, is widely used in modems, is used on systems where the primary memory is ECC memory and in broadcast situations, where the receiver does not have capabilities to request re-transmission or doing so would induce significant latency. For example, in the case of a satellite orbiting Uranus, a re-transmission because of decoding errors would create a delay of at least 5 hours.
FEC processing in a receiver may be applied to a digital bit stream or in the demodulation of a digitally modulated carrier. For the latter, FEC is an integral part of the initial analog-to-digital conversion in the receiver. The Viterbi decoder implements a soft-decision algorithm to demodulate digital data from an analog signal corrupted by noise. Many FEC coders can also generate a bit-error rate (BER) signal which can be used as feedback to fine-tune the analog receiving electronics.
The maximum proportion of errors or missing bits that can be corrected is determined by the design of the ECC, so different forward error correcting codes are suitable for different conditions. In general, a stronger code induces more redundancy that needs to be transmitted using the available bandwidth, which reduces the effective bit-rate while improving the received effective signal-to-noise ratio. The noisy-channel coding theorem of Claude Shannon answers the question of how much bandwidth is left for data communication while using the most efficient code that turns the decoding error probability to zero. This establishes bounds on the theoretical maximum information transfer rate of a channel with some given base noise level. His proof is not constructive, and hence gives no insight of how to build a capacity achieving code. However, after years of research, some advanced FEC systems like polar code[3] achieve the Shannon channel capacity under the hypothesis of an infinite length frame.
How it works[edit]
ECC is accomplished by adding redundancy to the transmitted information using an algorithm. A redundant bit may be a complex function of many original information bits. The original information may or may not appear literally in the encoded output; codes that include the unmodified input in the output are systematic, while those that do not are non-systematic.
A simplistic example of ECC is to transmit each data bit 3 times, which is known as a (3,1) repetition code. Through a noisy channel, a receiver might see 8 versions of the output, see table below.
| Triplet received | Interpreted as |
|---|---|
| 000 | 0 (error-free) |
| 001 | 0 |
| 010 | 0 |
| 100 | 0 |
| 111 | 1 (error-free) |
| 110 | 1 |
| 101 | 1 |
| 011 | 1 |
This allows an error in any one of the three samples to be corrected by «majority vote», or «democratic voting». The correcting ability of this ECC is:
- Up to 1 bit of triplet in error, or
- up to 2 bits of triplet omitted (cases not shown in table).
Though simple to implement and widely used, this triple modular redundancy is a relatively inefficient ECC. Better ECC codes typically examine the last several tens or even the last several hundreds of previously received bits to determine how to decode the current small handful of bits (typically in groups of 2 to 8 bits).
Averaging noise to reduce errors[edit]
ECC could be said to work by «averaging noise»; since each data bit affects many transmitted symbols, the corruption of some symbols by noise usually allows the original user data to be extracted from the other, uncorrupted received symbols that also depend on the same user data.
- Because of this «risk-pooling» effect, digital communication systems that use ECC tend to work well above a certain minimum signal-to-noise ratio and not at all below it.
- This all-or-nothing tendency – the cliff effect – becomes more pronounced as stronger codes are used that more closely approach the theoretical Shannon limit.
- Interleaving ECC coded data can reduce the all or nothing properties of transmitted ECC codes when the channel errors tend to occur in bursts. However, this method has limits; it is best used on narrowband data.
Most telecommunication systems use a fixed channel code designed to tolerate the expected worst-case bit error rate, and then fail to work at all if the bit error rate is ever worse.
However, some systems adapt to the given channel error conditions: some instances of hybrid automatic repeat-request use a fixed ECC method as long as the ECC can handle the error rate, then switch to ARQ when the error rate gets too high;
adaptive modulation and coding uses a variety of ECC rates, adding more error-correction bits per packet when there are higher error rates in the channel, or taking them out when they are not needed.
Types of ECC[edit]
A block code (specifically a Hamming code) where redundant bits are added as a block to the end of the initial message
A continuous code convolutional code where redundant bits are added continuously into the structure of the code word
The two main categories of ECC codes are block codes and convolutional codes.
- Block codes work on fixed-size blocks (packets) of bits or symbols of predetermined size. Practical block codes can generally be hard-decoded in polynomial time to their block length.
- Convolutional codes work on bit or symbol streams of arbitrary length. They are most often soft decoded with the Viterbi algorithm, though other algorithms are sometimes used. Viterbi decoding allows asymptotically optimal decoding efficiency with increasing constraint length of the convolutional code, but at the expense of exponentially increasing complexity. A convolutional code that is terminated is also a ‘block code’ in that it encodes a block of input data, but the block size of a convolutional code is generally arbitrary, while block codes have a fixed size dictated by their algebraic characteristics. Types of termination for convolutional codes include «tail-biting» and «bit-flushing».
There are many types of block codes; Reed–Solomon coding is noteworthy for its widespread use in compact discs, DVDs, and hard disk drives. Other examples of classical block codes include Golay, BCH, Multidimensional parity, and Hamming codes.
Hamming ECC is commonly used to correct NAND flash memory errors.[5]
This provides single-bit error correction and 2-bit error detection.
Hamming codes are only suitable for more reliable single-level cell (SLC) NAND.
Denser multi-level cell (MLC) NAND may use multi-bit correcting ECC such as BCH or Reed–Solomon.[6][7] NOR Flash typically does not use any error correction.[6]
Classical block codes are usually decoded using hard-decision algorithms,[8] which means that for every input and output signal a hard decision is made whether it corresponds to a one or a zero bit. In contrast, convolutional codes are typically decoded using soft-decision algorithms like the Viterbi, MAP or BCJR algorithms, which process (discretized) analog signals, and which allow for much higher error-correction performance than hard-decision decoding.
Nearly all classical block codes apply the algebraic properties of finite fields. Hence classical block codes are often referred to as algebraic codes.
In contrast to classical block codes that often specify an error-detecting or error-correcting ability, many modern block codes such as LDPC codes lack such guarantees. Instead, modern codes are evaluated in terms of their bit error rates.
Most forward error correction codes correct only bit-flips, but not bit-insertions or bit-deletions.
In this setting, the Hamming distance is the appropriate way to measure the bit error rate.
A few forward error correction codes are designed to correct bit-insertions and bit-deletions, such as Marker Codes and Watermark Codes.
The Levenshtein distance is a more appropriate way to measure the bit error rate when using such codes.
[9]
Code-rate and the tradeoff between reliability and data rate[edit]
The fundamental principle of ECC is to add redundant bits in order to help the decoder to find out the true message that was encoded by the transmitter. The code-rate of a given ECC system is defined as the ratio between the number of information bits and the total number of bits (i.e., information plus redundancy bits) in a given communication package. The code-rate is hence a real number. A low code-rate close to zero implies a strong code that uses many redundant bits to achieve a good performance, while a large code-rate close to 1 implies a weak code.
The redundant bits that protect the information have to be transferred using the same communication resources that they are trying to protect. This causes a fundamental tradeoff between reliability and data rate.[10] In one extreme, a strong code (with low code-rate) can induce an important increase in the receiver SNR (signal-to-noise-ratio) decreasing the bit error rate, at the cost of reducing the effective data rate. On the other extreme, not using any ECC (i.e., a code-rate equal to 1) uses the full channel for information transfer purposes, at the cost of leaving the bits without any additional protection.
One interesting question is the following: how efficient in terms of information transfer can an ECC be that has a negligible decoding error rate? This question was answered by Claude Shannon with his second theorem, which says that the channel capacity is the maximum bit rate achievable by any ECC whose error rate tends to zero:[11] His proof relies on Gaussian random coding, which is not suitable to real-world applications. The upper bound given by Shannon’s work inspired a long journey in designing ECCs that can come close to the ultimate performance boundary. Various codes today can attain almost the Shannon limit. However, capacity achieving ECCs are usually extremely complex to implement.
The most popular ECCs have a trade-off between performance and computational complexity. Usually, their parameters give a range of possible code rates, which can be optimized depending on the scenario. Usually, this optimization is done in order to achieve a low decoding error probability while minimizing the impact to the data rate. Another criterion for optimizing the code rate is to balance low error rate and retransmissions number in order to the energy cost of the communication.[12]
Concatenated ECC codes for improved performance[edit]
Classical (algebraic) block codes and convolutional codes are frequently combined in concatenated coding schemes in which a short constraint-length Viterbi-decoded convolutional code does most of the work and a block code (usually Reed–Solomon) with larger symbol size and block length «mops up» any errors made by the convolutional decoder. Single pass decoding with this family of error correction codes can yield very low error rates, but for long range transmission conditions (like deep space) iterative decoding is recommended.
Concatenated codes have been standard practice in satellite and deep space communications since Voyager 2 first used the technique in its 1986 encounter with Uranus. The Galileo craft used iterative concatenated codes to compensate for the very high error rate conditions caused by having a failed antenna.
Low-density parity-check (LDPC)[edit]
Low-density parity-check (LDPC) codes are a class of highly efficient linear block
codes made from many single parity check (SPC) codes. They can provide performance very close to the channel capacity (the theoretical maximum) using an iterated soft-decision decoding approach, at linear time complexity in terms of their block length. Practical implementations rely heavily on decoding the constituent SPC codes in parallel.
LDPC codes were first introduced by Robert G. Gallager in his PhD thesis in 1960,
but due to the computational effort in implementing encoder and decoder and the introduction of Reed–Solomon codes,
they were mostly ignored until the 1990s.
LDPC codes are now used in many recent high-speed communication standards, such as DVB-S2 (Digital Video Broadcasting – Satellite – Second Generation), WiMAX (IEEE 802.16e standard for microwave communications), High-Speed Wireless LAN (IEEE 802.11n),[13] 10GBase-T Ethernet (802.3an) and G.hn/G.9960 (ITU-T Standard for networking over power lines, phone lines and coaxial cable). Other LDPC codes are standardized for wireless communication standards within 3GPP MBMS (see fountain codes).
Turbo codes[edit]
Turbo coding is an iterated soft-decoding scheme that combines two or more relatively simple convolutional codes and an interleaver to produce a block code that can perform to within a fraction of a decibel of the Shannon limit. Predating LDPC codes in terms of practical application, they now provide similar performance.
One of the earliest commercial applications of turbo coding was the CDMA2000 1x (TIA IS-2000) digital cellular technology developed by Qualcomm and sold by Verizon Wireless, Sprint, and other carriers. It is also used for the evolution of CDMA2000 1x specifically for Internet access, 1xEV-DO (TIA IS-856). Like 1x, EV-DO was developed by Qualcomm, and is sold by Verizon Wireless, Sprint, and other carriers (Verizon’s marketing name for 1xEV-DO is Broadband Access, Sprint’s consumer and business marketing names for 1xEV-DO are Power Vision and Mobile Broadband, respectively).
Local decoding and testing of codes[edit]
Sometimes it is only necessary to decode single bits of the message, or to check whether a given signal is a codeword, and do so without looking at the entire signal. This can make sense in a streaming setting, where codewords are too large to be classically decoded fast enough and where only a few bits of the message are of interest for now. Also such codes have become an important tool in computational complexity theory, e.g., for the design of probabilistically checkable proofs.
Locally decodable codes are error-correcting codes for which single bits of the message can be probabilistically recovered by only looking at a small (say constant) number of positions of a codeword, even after the codeword has been corrupted at some constant fraction of positions. Locally testable codes are error-correcting codes for which it can be checked probabilistically whether a signal is close to a codeword by only looking at a small number of positions of the signal.
Interleaving[edit]
«Interleaver» redirects here. For the fiber-optic device, see optical interleaver.
A short illustration of interleaving idea
Interleaving is frequently used in digital communication and storage systems to improve the performance of forward error correcting codes. Many communication channels are not memoryless: errors typically occur in bursts rather than independently. If the number of errors within a code word exceeds the error-correcting code’s capability, it fails to recover the original code word. Interleaving alleviates this problem by shuffling source symbols across several code words, thereby creating a more uniform distribution of errors.[14] Therefore, interleaving is widely used for burst error-correction.
The analysis of modern iterated codes, like turbo codes and LDPC codes, typically assumes an independent distribution of errors.[15] Systems using LDPC codes therefore typically employ additional interleaving across the symbols within a code word.[16]
For turbo codes, an interleaver is an integral component and its proper design is crucial for good performance.[14][17] The iterative decoding algorithm works best when there are not short cycles in the factor graph that represents the decoder; the interleaver is chosen to avoid short cycles.
Interleaver designs include:
- rectangular (or uniform) interleavers (similar to the method using skip factors described above)
- convolutional interleavers
- random interleavers (where the interleaver is a known random permutation)
- S-random interleaver (where the interleaver is a known random permutation with the constraint that no input symbols within distance S appear within a distance of S in the output).[18]
- a contention-free quadratic permutation polynomial (QPP).[19] An example of use is in the 3GPP Long Term Evolution mobile telecommunication standard.[20]
In multi-carrier communication systems, interleaving across carriers may be employed to provide frequency diversity, e.g., to mitigate frequency-selective fading or narrowband interference.[21]
Example[edit]
Transmission without interleaving:
Error-free message: aaaabbbbccccddddeeeeffffgggg Transmission with a burst error: aaaabbbbccc____deeeeffffgggg
Here, each group of the same letter represents a 4-bit one-bit error-correcting codeword. The codeword cccc is altered in one bit and can be corrected, but the codeword dddd is altered in three bits, so either it cannot be decoded at all or it might be decoded incorrectly.
With interleaving:
Error-free code words: aaaabbbbccccddddeeeeffffgggg Interleaved: abcdefgabcdefgabcdefgabcdefg Transmission with a burst error: abcdefgabcd____bcdefgabcdefg Received code words after deinterleaving: aa_abbbbccccdddde_eef_ffg_gg
In each of the codewords «aaaa», «eeee», «ffff», and «gggg», only one bit is altered, so one-bit error-correcting code will decode everything correctly.
Transmission without interleaving:
Original transmitted sentence: ThisIsAnExampleOfInterleaving Received sentence with a burst error: ThisIs______pleOfInterleaving
The term «AnExample» ends up mostly unintelligible and difficult to correct.
With interleaving:
Transmitted sentence: ThisIsAnExampleOfInterleaving... Error-free transmission: TIEpfeaghsxlIrv.iAaenli.snmOten. Received sentence with a burst error: TIEpfe______Irv.iAaenli.snmOten. Received sentence after deinterleaving: T_isI_AnE_amp_eOfInterle_vin_...
No word is completely lost and the missing letters can be recovered with minimal guesswork.
Disadvantages of interleaving[edit]
Use of interleaving techniques increases total delay. This is because the entire interleaved block must be received before the packets can be decoded.[22] Also interleavers hide the structure of errors; without an interleaver, more advanced decoding algorithms can take advantage of the error structure and achieve more reliable communication than a simpler decoder combined with an interleaver[citation needed]. An example of such an algorithm is based on neural network[23] structures.
Software for error-correcting codes[edit]
Simulating the behaviour of error-correcting codes (ECCs) in software is a common practice to design, validate and improve ECCs. The upcoming wireless 5G standard raises a new range of applications for the software ECCs: the Cloud Radio Access Networks (C-RAN) in a Software-defined radio (SDR) context. The idea is to directly use software ECCs in the communications. For instance in the 5G, the software ECCs could be located in the cloud and the antennas connected to this computing resources: improving this way the flexibility of the communication network and eventually increasing the energy efficiency of the system.
In this context, there are various available Open-source software listed below (non exhaustive).
- AFF3CT(A Fast Forward Error Correction Toolbox): a full communication chain in C++ (many supported codes like Turbo, LDPC, Polar codes, etc.), very fast and specialized on channel coding (can be used as a program for simulations or as a library for the SDR).
- IT++: a C++ library of classes and functions for linear algebra, numerical optimization, signal processing, communications, and statistics.
- OpenAir: implementation (in C) of the 3GPP specifications concerning the Evolved Packet Core Networks.
List of error-correcting codes[edit]
| Distance | Code |
|---|---|
| 2 (single-error detecting) | Parity |
| 3 (single-error correcting) | Triple modular redundancy |
| 3 (single-error correcting) | perfect Hamming such as Hamming(7,4) |
| 4 (SECDED) | Extended Hamming |
| 5 (double-error correcting) | |
| 6 (double-error correct-/triple error detect) | Nordstrom-Robinson code |
| 7 (three-error correcting) | perfect binary Golay code |
| 8 (TECFED) | extended binary Golay code |
- AN codes
- BCH code, which can be designed to correct any arbitrary number of errors per code block.
- Barker code used for radar, telemetry, ultra sound, Wifi, DSSS mobile phone networks, GPS etc.
- Berger code
- Constant-weight code
- Convolutional code
- Expander codes
- Group codes
- Golay codes, of which the Binary Golay code is of practical interest
- Goppa code, used in the McEliece cryptosystem
- Hadamard code
- Hagelbarger code
- Hamming code
- Latin square based code for non-white noise (prevalent for example in broadband over powerlines)
- Lexicographic code
- Linear Network Coding, a type of erasure correcting code across networks instead of point-to-point links
- Long code
- Low-density parity-check code, also known as Gallager code, as the archetype for sparse graph codes
- LT code, which is a near-optimal rateless erasure correcting code (Fountain code)
- m of n codes
- Nordstrom-Robinson code, used in Geometry and Group Theory[24]
- Online code, a near-optimal rateless erasure correcting code
- Polar code (coding theory)
- Raptor code, a near-optimal rateless erasure correcting code
- Reed–Solomon error correction
- Reed–Muller code
- Repeat-accumulate code
- Repetition codes, such as Triple modular redundancy
- Spinal code, a rateless, nonlinear code based on pseudo-random hash functions[25]
- Tornado code, a near-optimal erasure correcting code, and the precursor to Fountain codes
- Turbo code
- Walsh–Hadamard code
- Cyclic redundancy checks (CRCs) can correct 1-bit errors for messages at most
bits long for optimal generator polynomials of degree
, see Mathematics of cyclic redundancy checks#Bitfilters
See also[edit]
- Code rate
- Erasure codes
- Soft-decision decoder
- Burst error-correcting code
- Error detection and correction
- Error-correcting codes with feedback
References[edit]
- ^ Glover, Neal; Dudley, Trent (1990). Practical Error Correction Design For Engineers (Revision 1.1, 2nd ed.). CO, USA: Cirrus Logic. ISBN 0-927239-00-0.
- ^ a b Hamming, Richard Wesley (April 1950). «Error Detecting and Error Correcting Codes». Bell System Technical Journal. USA: AT&T. 29 (2): 147–160. doi:10.1002/j.1538-7305.1950.tb00463.x. S2CID 61141773.
- ^ a b c Maunder, Robert (2016). «Overview of Channel Coding».
- ^ Charles Wang; Dean Sklar; Diana Johnson (Winter 2001–2002). «Forward Error-Correction Coding». Crosslink. The Aerospace Corporation. 3 (1). Archived from the original on 14 March 2012. Retrieved 5 March 2006.
How Forward Error-Correcting Codes Work
- ^ «Hamming codes for NAND flash memory devices» Archived 21 August 2016 at the Wayback Machine. EE Times-Asia. Apparently based on «Micron Technical Note TN-29-08: Hamming Codes for NAND Flash Memory Devices». 2005. Both say: «The Hamming algorithm is an industry-accepted method for error detection and correction in many SLC NAND flash-based applications.»
- ^ a b «What Types of ECC Should Be Used on Flash Memory?» (Application note). Spansion. 2011.
Both Reed–Solomon algorithm and BCH algorithm are common ECC choices for MLC NAND flash. … Hamming based block codes are the most commonly used ECC for SLC…. both Reed–Solomon and BCH are able to handle multiple errors and are widely used on MLC flash.
- ^ Jim Cooke (August 2007). «The Inconvenient Truths of NAND Flash Memory» (PDF). p. 28.
For SLC, a code with a correction threshold of 1 is sufficient. t=4 required … for MLC.
- ^ Baldi, M.; Chiaraluce, F. (2008). «A Simple Scheme for Belief Propagation Decoding of BCH and RS Codes in Multimedia Transmissions». International Journal of Digital Multimedia Broadcasting. 2008: 1–12. doi:10.1155/2008/957846.
- ^ Shah, Gaurav; Molina, Andres; Blaze, Matt (2006). «Keyboards and covert channels». USENIX. Retrieved 20 December 2018.
- ^ Tse, David; Viswanath, Pramod (2005), Fundamentals of Wireless Communication, Cambridge University Press, UK
- ^ Shannon, C. E. (1948). «A mathematical theory of communication» (PDF). Bell System Technical Journal. 27 (3–4): 379–423 & 623–656. doi:10.1002/j.1538-7305.1948.tb01338.x. hdl:11858/00-001M-0000-002C-4314-2.
- ^ Rosas, F.; Brante, G.; Souza, R. D.; Oberli, C. (2014). «Optimizing the code rate for achieving energy-efficient wireless communications». Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC). pp. 775–780. doi:10.1109/WCNC.2014.6952166. ISBN 978-1-4799-3083-8.
- ^ IEEE Standard, section 20.3.11.6 «802.11n-2009» Archived 3 February 2013 at the Wayback Machine, IEEE, 29 October 2009, accessed 21 March 2011.
- ^ a b Vucetic, B.; Yuan, J. (2000). Turbo codes: principles and applications. Springer Verlag. ISBN 978-0-7923-7868-6.
- ^ Luby, Michael; Mitzenmacher, M.; Shokrollahi, A.; Spielman, D.; Stemann, V. (1997). «Practical Loss-Resilient Codes». Proc. 29th Annual Association for Computing Machinery (ACM) Symposium on Theory of Computation.
- ^ «Digital Video Broadcast (DVB); Second generation framing structure, channel coding and modulation systems for Broadcasting, Interactive Services, News Gathering and other satellite broadband applications (DVB-S2)». En 302 307. ETSI (V1.2.1). April 2009.
- ^ Andrews, K. S.; Divsalar, D.; Dolinar, S.; Hamkins, J.; Jones, C. R.; Pollara, F. (November 2007). «The Development of Turbo and LDPC Codes for Deep-Space Applications». Proceedings of the IEEE. 95 (11): 2142–2156. doi:10.1109/JPROC.2007.905132. S2CID 9289140.
- ^ Dolinar, S.; Divsalar, D. (15 August 1995). «Weight Distributions for Turbo Codes Using Random and Nonrandom Permutations». TDA Progress Report. 122: 42–122. Bibcode:1995TDAPR.122…56D. CiteSeerX 10.1.1.105.6640.
- ^ Takeshita, Oscar (2006). «Permutation Polynomial Interleavers: An Algebraic-Geometric Perspective». IEEE Transactions on Information Theory. 53 (6): 2116–2132. arXiv:cs/0601048. Bibcode:2006cs……..1048T. doi:10.1109/TIT.2007.896870. S2CID 660.
- ^ 3GPP TS 36.212, version 8.8.0, page 14
- ^ «Digital Video Broadcast (DVB); Frame structure, channel coding and modulation for a second generation digital terrestrial television broadcasting system (DVB-T2)». En 302 755. ETSI (V1.1.1). September 2009.
- ^ Techie (3 June 2010). «Explaining Interleaving». W3 Techie Blog. Retrieved 3 June 2010.
- ^ Krastanov, Stefan; Jiang, Liang (8 September 2017). «Deep Neural Network Probabilistic Decoder for Stabilizer Codes». Scientific Reports. 7 (1): 11003. arXiv:1705.09334. Bibcode:2017NatSR…711003K. doi:10.1038/s41598-017-11266-1. PMC 5591216. PMID 28887480.
- ^ Nordstrom, A.W.; Robinson, J.P. (1967), «An optimum nonlinear code», Information and Control, 11 (5–6): 613–616, doi:10.1016/S0019-9958(67)90835-2
- ^ Perry, Jonathan; Balakrishnan, Hari; Shah, Devavrat (2011). «Rateless Spinal Codes». Proceedings of the 10th ACM Workshop on Hot Topics in Networks. pp. 1–6. doi:10.1145/2070562.2070568. hdl:1721.1/79676. ISBN 9781450310598.
Further reading[edit]
- MacWilliams, Florence Jessiem; Sloane, Neil James Alexander (2007) [1977]. Written at AT&T Shannon Labs, Florham Park, New Jersey, USA. The Theory of Error-Correcting Codes. North-Holland Mathematical Library. Vol. 16 (digital print of 12th impression, 1st ed.). Amsterdam / London / New York / Tokyo: North-Holland / Elsevier BV. ISBN 978-0-444-85193-2. LCCN 76-41296. (xxii+762+6 pages)
- Clark, Jr., George C.; Cain, J. Bibb (1981). Error-Correction Coding for Digital Communications. New York, USA: Plenum Press. ISBN 0-306-40615-2.
- Arazi, Benjamin (1987). Swetman, Herb (ed.). A Commonsense Approach to the Theory of Error Correcting Codes. MIT Press Series in Computer Systems. Vol. 10 (1 ed.). Cambridge, Massachusetts, USA / London, UK: Massachusetts Institute of Technology. ISBN 0-262-01098-4. LCCN 87-21889. (x+2+208+4 pages)
- Wicker, Stephen B. (1995). Error Control Systems for Digital Communication and Storage. Englewood Cliffs, New Jersey, USA: Prentice-Hall. ISBN 0-13-200809-2.
- Wilson, Stephen G. (1996). Digital Modulation and Coding. Englewood Cliffs, New Jersey, USA: Prentice-Hall. ISBN 0-13-210071-1.
- «Error Correction Code in Single Level Cell NAND Flash memories» 2007-02-16
- «Error Correction Code in NAND Flash memories» 2004-11-29
- Observations on Errors, Corrections, & Trust of Dependent Systems, by James Hamilton, 2012-02-26
- Sphere Packings, Lattices and Groups, By J. H. Conway, Neil James Alexander Sloane, Springer Science & Business Media, 2013-03-09 – Mathematics – 682 pages.
External links[edit]
- Morelos-Zaragoza, Robert (2004). «The Correcting Codes (ECC) Page». Retrieved 5 March 2006.
- lpdec: library for LP decoding and related things (Python)