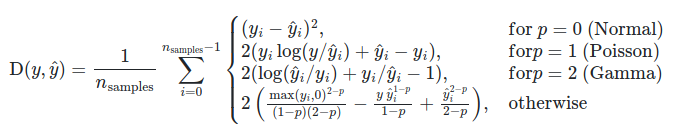Есть 3 различных API для оценки качества прогнозов модели:
- Метод оценки оценщика : у оценщиков есть
scoreметод, обеспечивающий критерий оценки по умолчанию для проблемы, для решения которой они предназначены. Это обсуждается не на этой странице, а в документации каждого оценщика. - Параметр оценки: инструменты оценки модели с использованием перекрестной проверки (например,
model_selection.cross_val_scoreиmodel_selection.GridSearchCV) полагаются на внутреннюю стратегию оценки . Это обсуждается в разделе Параметр оценки: определение правил оценки модели . - Метрические функции : В
sklearn.metricsмодуле реализованы функции оценки ошибки прогноза для конкретных целей. Эти показатели подробно описаны в разделах по метрикам классификации , MultiLabel ранжирования показателей , показателей регрессии и показателей кластеризации .
Наконец, фиктивные оценки полезны для получения базового значения этих показателей для случайных прогнозов.
3.3.1. В scoring параметрах: определение правил оценки моделей
Выбор и оценка модели с использованием таких инструментов, как model_selection.GridSearchCV и model_selection.cross_val_score, принимают scoring параметр, который контролирует, какую метрику они применяют к оцениваемым оценщикам.
3.3.1.1. Общие случаи: предопределенные значения
Для наиболее распространенных случаев использования вы можете назначить объект подсчета с помощью scoring параметра; в таблице ниже показаны все возможные значения. Все объекты счетчика следуют соглашению о том, что более высокие возвращаемые значения лучше, чем более низкие возвращаемые значения . Таким образом, метрики, которые измеряют расстояние между моделью и данными, например metrics.mean_squared_error, доступны как neg_mean_squared_error, которые возвращают инвертированное значение метрики.
| Подсчет очков | Функция | Комментарий |
| Классификация | ||
| ‘accuracy’ | metrics.accuracy_score |
|
| ‘balanced_accuracy’ | metrics.balanced_accuracy_score |
|
| ‘top_k_accuracy’ | metrics.top_k_accuracy_score |
|
| ‘average_precision’ | metrics.average_precision_score |
|
| ‘neg_brier_score’ | metrics.brier_score_loss |
|
| ‘f1’ | metrics.f1_score |
для двоичных целей |
| ‘f1_micro’ | metrics.f1_score |
микро-усредненный |
| ‘f1_macro’ | metrics.f1_score |
микро-усредненный |
| ‘f1_weighted’ | metrics.f1_score |
средневзвешенное |
| ‘f1_samples’ | metrics.f1_score |
по многопозиционному образцу |
| ‘neg_log_loss’ | metrics.log_loss |
требуетсяpredict_probaподдержка |
| ‘precision’ etc. | metrics.precision_score |
суффиксы применяются как с ‘f1’ |
| ‘recall’ etc. | metrics.recall_score |
суффиксы применяются как с ‘f1’ |
| ‘jaccard’ etc. | metrics.jaccard_score |
суффиксы применяются как с ‘f1’ |
| ‘roc_auc’ | metrics.roc_auc_score |
|
| ‘roc_auc_ovr’ | metrics.roc_auc_score |
|
| ‘roc_auc_ovo’ | metrics.roc_auc_score |
|
| ‘roc_auc_ovr_weighted’ | metrics.roc_auc_score |
|
| ‘roc_auc_ovo_weighted’ | metrics.roc_auc_score |
|
| Кластеризация | ||
| ‘adjusted_mutual_info_score’ | metrics.adjusted_mutual_info_score |
|
| ‘adjusted_rand_score’ | metrics.adjusted_rand_score |
|
| ‘completeness_score’ | metrics.completeness_score |
|
| ‘fowlkes_mallows_score’ | metrics.fowlkes_mallows_score |
|
| ‘homogeneity_score’ | metrics.homogeneity_score |
|
| ‘mutual_info_score’ | metrics.mutual_info_score |
|
| ‘normalized_mutual_info_score’ | metrics.normalized_mutual_info_score |
|
| ‘rand_score’ | metrics.rand_score |
|
| ‘v_measure_score’ | metrics.v_measure_score |
|
| Регрессия | ||
| ‘explained_variance’ | metrics.explained_variance_score |
|
| ‘max_error’ | metrics.max_error |
|
| ‘neg_mean_absolute_error’ | metrics.mean_absolute_error |
|
| ‘neg_mean_squared_error’ | metrics.mean_squared_error |
|
| ‘neg_root_mean_squared_error’ | metrics.mean_squared_error |
|
| ‘neg_mean_squared_log_error’ | metrics.mean_squared_log_error |
|
| ‘neg_median_absolute_error’ | metrics.median_absolute_error |
|
| ‘r2’ | metrics.r2_score |
|
| ‘neg_mean_poisson_deviance’ | metrics.mean_poisson_deviance |
|
| ‘neg_mean_gamma_deviance’ | metrics.mean_gamma_deviance |
|
| ‘neg_mean_absolute_percentage_error’ | metrics.mean_absolute_percentage_error |
Примеры использования:
>>> from sklearn import svm, datasets >>> from sklearn.model_selection import cross_val_score >>> X, y = datasets.load_iris(return_X_y=True) >>> clf = svm.SVC(random_state=0) >>> cross_val_score(clf, X, y, cv=5, scoring='recall_macro') array([0.96..., 0.96..., 0.96..., 0.93..., 1. ]) >>> model = svm.SVC() >>> cross_val_score(model, X, y, cv=5, scoring='wrong_choice') Traceback (most recent call last): ValueError: 'wrong_choice' is not a valid scoring value. Use sorted(sklearn.metrics.SCORERS.keys()) to get valid options.
Примечание
Значения, перечисленные в виде ValueError исключения, соответствуют функциям измерения точности прогнозирования, описанным в следующих разделах. Объекты счетчика для этих функций хранятся в словаре sklearn.metrics.SCORERS.
3.3.1.2. Определение стратегии выигрыша от метрических функций
Модуль sklearn.metrics также предоставляет набор простых функций, измеряющих ошибку предсказания с учетом истинности и предсказания:
- функции, заканчивающиеся на,
_scoreвозвращают значение для максимизации, чем выше, тем лучше. - функции, заканчивающиеся на
_errorили_lossвозвращающие значение, которое нужно минимизировать, чем ниже, тем лучше. При преобразовании в объект счетчика с использованиемmake_scorerустановите дляgreater_is_betterпараметра значениеFalse(Trueпо умолчанию; см. Описание параметра ниже).
Метрики, доступные для различных задач машинного обучения, подробно описаны в разделах ниже.
Многим метрикам не даются имена для использования в качестве scoring значений, иногда потому, что они требуют дополнительных параметров, например fbeta_score. В таких случаях вам необходимо создать соответствующий объект оценки. Самый простой способ создать вызываемый объект для оценки — использовать make_scorer. Эта функция преобразует метрики в вызываемые объекты, которые можно использовать для оценки модели.
Один из типичных вариантов использования — обернуть существующую метрическую функцию из библиотеки значениями, отличными от значений по умолчанию для ее параметров, такими как beta параметр для fbeta_score функции:
>>> from sklearn.metrics import fbeta_score, make_scorer
>>> ftwo_scorer = make_scorer(fbeta_score, beta=2)
>>> from sklearn.model_selection import GridSearchCV
>>> from sklearn.svm import LinearSVC
>>> grid = GridSearchCV(LinearSVC(), param_grid={'C': [1, 10]},
... scoring=ftwo_scorer, cv=5)
Второй вариант использования — создание полностью настраиваемого объекта скоринга из простой функции Python с использованием make_scorer, которая может принимать несколько параметров:
- функция Python, которую вы хотите использовать (
my_custom_loss_funcв примере ниже) - возвращает ли функция Python оценку (
greater_is_better=True, по умолчанию) или потерю (greater_is_better=False). В случае потери результат функции python аннулируется объектом скоринга в соответствии с соглашением о перекрестной проверке, согласно которому скоринтеры возвращают более высокие значения для лучших моделей. - только для показателей классификации: требуется ли для предоставленной вами функции Python постоянная уверенность в принятии решений (
needs_threshold=True). Значение по умолчанию неверно. - любые дополнительные параметры, такие как
betaилиlabelsвf1_score.
Вот пример создания пользовательских счетчиков очков и использования greater_is_better параметра:
>>> import numpy as np >>> def my_custom_loss_func(y_true, y_pred): ... diff = np.abs(y_true - y_pred).max() ... return np.log1p(diff) ... >>> # score will negate the return value of my_custom_loss_func, >>> # which will be np.log(2), 0.693, given the values for X >>> # and y defined below. >>> score = make_scorer(my_custom_loss_func, greater_is_better=False) >>> X = [[1], [1]] >>> y = [0, 1] >>> from sklearn.dummy import DummyClassifier >>> clf = DummyClassifier(strategy='most_frequent', random_state=0) >>> clf = clf.fit(X, y) >>> my_custom_loss_func(y, clf.predict(X)) 0.69... >>> score(clf, X, y) -0.69...
3.3.1.3. Реализация собственного скорингового объекта
Вы можете сгенерировать еще более гибкие модели скоринга, создав свой собственный скоринговый объект с нуля, без использования make_scorer фабрики. Чтобы вызываемый может быть бомбардиром, он должен соответствовать протоколу, указанному в следующих двух правилах:
- Его можно вызвать с параметрами (estimator, X, y), где estimator это модель, которая должна быть оценена, X это данные проверки и y основная истинная цель для (в контролируемом случае) или None (в неконтролируемом случае).
- Он возвращает число с плавающей запятой, которое количественно определяет
estimatorкачество прогнозированияXсо ссылкой наy. Опять же, по соглашению более высокие числа лучше, поэтому, если ваш секретарь сообщает о проигрыше, это значение следует отменить.
Примечание Использование пользовательских счетчиков в функциях, где n_jobs> 1
Хотя определение пользовательской функции оценки вместе с вызывающей функцией должно работать из коробки с бэкэндом joblib по умолчанию (loky), его импорт из другого модуля будет более надежным подходом и будет работать независимо от бэкэнда joblib.
Например, чтобы использовать n_jobsбольше 1 в примере ниже, custom_scoring_function функция сохраняется в созданном пользователем модуле ( custom_scorer_module.py) и импортируется:
>>> from custom_scorer_module import custom_scoring_function >>> cross_val_score(model, ... X_train, ... y_train, ... scoring=make_scorer(custom_scoring_function, greater_is_better=False), ... cv=5, ... n_jobs=-1)
3.3.1.4. Использование множественной метрической оценки
Scikit-learn также позволяет оценивать несколько показателей в GridSearchCV, RandomizedSearchCV и cross_validate.
Есть три способа указать несколько показателей оценки для scoring параметра:
- Как итерация строковых показателей:
>>> scoring = ['accuracy', 'precision']
- В качестве
dictсопоставления имени секретаря с функцией подсчета очков:
>>> from sklearn.metrics import accuracy_score
>>> from sklearn.metrics import make_scorer
>>> scoring = {'accuracy': make_scorer(accuracy_score),
... 'prec': 'precision'}
Обратите внимание, что значения dict могут быть либо функциями счетчика, либо одной из предварительно определенных строк показателей.
- Как вызываемый объект, возвращающий словарь оценок:
>>> from sklearn.model_selection import cross_validate
>>> from sklearn.metrics import confusion_matrix
>>> # A sample toy binary classification dataset
>>> X, y = datasets.make_classification(n_classes=2, random_state=0)
>>> svm = LinearSVC(random_state=0)
>>> def confusion_matrix_scorer(clf, X, y):
... y_pred = clf.predict(X)
... cm = confusion_matrix(y, y_pred)
... return {'tn': cm[0, 0], 'fp': cm[0, 1],
... 'fn': cm[1, 0], 'tp': cm[1, 1]}
>>> cv_results = cross_validate(svm, X, y, cv=5,
... scoring=confusion_matrix_scorer)
>>> # Getting the test set true positive scores
>>> print(cv_results['test_tp'])
[10 9 8 7 8]
>>> # Getting the test set false negative scores
>>> print(cv_results['test_fn'])
[0 1 2 3 2]
3.3.2. Метрики классификации
В sklearn.metrics модуле реализованы несколько функций потерь, оценки и полезности для измерения эффективности классификации. Некоторые метрики могут потребовать оценок вероятности положительного класса, значений достоверности или значений двоичных решений. Большинство реализаций позволяют каждой выборке вносить взвешенный вклад в общую оценку с помощью sample_weight параметра.
Некоторые из них ограничены случаем двоичной классификации:
precision_recall_curve(y_true, probas_pred, *) |
Вычислите пары точности-отзыва для разных пороговых значений вероятности. |
roc_curve(y_true, y_score, *[, pos_label, …]) |
Вычислить рабочую характеристику приемника (ROC). |
det_curve(y_true, y_score[, pos_label, …]) |
Вычислите частоту ошибок для различных пороговых значений вероятности. |
Другие также работают в случае мультикласса:
balanced_accuracy_score(y_true, y_pred, *[, …]) |
Вычислите сбалансированную точность. |
cohen_kappa_score(y1, y2, *[, labels, …]) |
Каппа Коэна: статистика, измеряющая согласованность аннотаторов. |
confusion_matrix(y_true, y_pred, *[, …]) |
Вычислите матрицу неточностей, чтобы оценить точность классификации. |
hinge_loss(y_true, pred_decision, *[, …]) |
Средняя потеря петель (нерегулируемая). |
matthews_corrcoef(y_true, y_pred, *[, …]) |
Вычислите коэффициент корреляции Мэтьюза (MCC). |
roc_auc_score(y_true, y_score, *[, average, …]) |
Вычислить площадь под кривой рабочих характеристик приемника (ROC AUC) по оценкам прогнозов. |
top_k_accuracy_score(y_true, y_score, *[, …]) |
Top-k Рейтинг по классификации точности. |
Некоторые также работают в многоярусном регистре:
accuracy_score(y_true, y_pred, *[, …]) |
Классификационная оценка точности. |
classification_report(y_true, y_pred, *[, …]) |
Создайте текстовый отчет, показывающий основные показатели классификации. |
f1_score(y_true, y_pred, *[, labels, …]) |
Вычислите оценку F1, также известную как сбалансированная оценка F или F-мера. |
fbeta_score(y_true, y_pred, *, beta[, …]) |
Вычислите оценку F-beta. |
hamming_loss(y_true, y_pred, *[, sample_weight]) |
Вычислите среднюю потерю Хэмминга. |
jaccard_score(y_true, y_pred, *[, labels, …]) |
Оценка коэффициента сходства Жаккара. |
log_loss(y_true, y_pred, *[, eps, …]) |
Потеря журнала, также известная как потеря логистики или потеря кросс-энтропии. |
multilabel_confusion_matrix(y_true, y_pred, *) |
Вычислите матрицу неточностей для каждого класса или образца. |
precision_recall_fscore_support(y_true, …) |
Точность вычислений, отзыв, F-мера и поддержка для каждого класса. |
precision_score(y_true, y_pred, *[, labels, …]) |
Вычислите точность. |
recall_score(y_true, y_pred, *[, labels, …]) |
Вычислите отзыв. |
roc_auc_score(y_true, y_score, *[, average, …]) |
Вычислить площадь под кривой рабочих характеристик приемника (ROC AUC) по оценкам прогнозов. |
zero_one_loss(y_true, y_pred, *[, …]) |
Потеря классификации нулевая единица. |
А некоторые работают с двоичными и многозначными (но не мультиклассовыми) проблемами:
В следующих подразделах мы опишем каждую из этих функций, которым будут предшествовать некоторые примечания по общему API и определению показателей.
3.3.2.1. От бинарного до мультиклассового и многозначного
Некоторые метрики по существу определены для задач двоичной классификации (например f1_score, roc_auc_score). В этих случаях по умолчанию оценивается только положительная метка, предполагая по умолчанию, что положительный класс помечен 1 (хотя это можно настроить с помощью pos_label параметра).
При расширении двоичной метрики на задачи с несколькими классами или метками данные обрабатываются как набор двоичных задач, по одной для каждого класса. Затем есть несколько способов усреднить вычисления двоичных показателей по набору классов, каждый из которых может быть полезен в некотором сценарии. Если возможно, вы должны выбрать одно из них с помощью average параметра.
"macro"просто вычисляет среднее значение двоичных показателей, придавая каждому классу одинаковый вес. В задачах, где редкие занятия тем не менее важны, макро-усреднение может быть средством выделения их производительности. С другой стороны, предположение, что все классы одинаково важны, часто неверно, так что макро-усреднение будет чрезмерно подчеркивать обычно низкую производительность для нечастого класса."weighted"учитывает дисбаланс классов, вычисляя среднее значение двоичных показателей, в которых оценка каждого класса взвешивается по его присутствию в истинной выборке данных."micro"дает каждой паре выборка-класс равный вклад в общую метрику (за исключением результата взвешивания выборки). Вместо того, чтобы суммировать метрику для каждого класса, это суммирует дивиденды и делители, составляющие метрики для каждого класса, для расчета общего частного. Микро-усреднение может быть предпочтительным в настройках с несколькими ярлыками, включая многоклассовую классификацию, когда класс большинства следует игнорировать."samples"применяется только к задачам с несколькими ярлыками. Он не вычисляет меру для каждого класса, вместо этого вычисляет метрику по истинным и прогнозируемым классам для каждой выборки в данных оценки и возвращает их (sample_weight— взвешенное) среднее значение.- Выбор
average=Noneвернет массив с оценкой для каждого класса.
В то время как данные мультикласса предоставляются метрике, как двоичные цели, в виде массива меток классов, данные с несколькими метками указываются как индикаторная матрица, в которой ячейка [i, j] имеет значение 1, если у образца i есть метка j, и значение 0 в противном случае.
3.3.2.2. Оценка точности
Функция accuracy_score вычисляет точность , либо фракции ( по умолчанию) или количество (нормализует = False) правильных предсказаний.
В классификации с несколькими ярлыками функция возвращает точность подмножества. Если весь набор предсказанных меток для выборки строго соответствует истинному набору меток, то точность подмножества равна 1,0; в противном случае — 0, 0.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец и $y_i$ — соответствующее истинное значение, тогда доля правильных прогнозов по сравнению с $n_{samples}$ определяется как
$$texttt{accuracy}(y, hat{y}) = frac{1}{n_text{samples}} sum_{i=0}^{n_text{samples}-1} 1(hat{y}_i = y_i)$$
где $1(x)$- индикаторная функция .
>>> import numpy as np >>> from sklearn.metrics import accuracy_score >>> y_pred = [0, 2, 1, 3] >>> y_true = [0, 1, 2, 3] >>> accuracy_score(y_true, y_pred) 0.5 >>> accuracy_score(y_true, y_pred, normalize=False) 2
В многопозиционном корпусе с бинарными индикаторами меток:
>>> accuracy_score(np.array([[0, 1], [1, 1]]), np.ones((2, 2))) 0.5
Пример:
- См. В разделе Проверка с перестановками значимости классификационной оценки пример использования показателя точности с использованием перестановок набора данных.
3.3.2.3. Рейтинг точности Top-k
Функция top_k_accuracy_score представляет собой обобщение accuracy_score. Разница в том, что прогноз считается правильным, если истинная метка связана с одним из kнаивысших прогнозируемых баллов. accuracy_score является частным случаем k = 1.
Функция охватывает случаи двоичной и многоклассовой классификации, но не случай многозначной классификации.
Если $hat{f}_{i,j}$ прогнозируемый класс для $i$-й образец, соответствующий $j$-й по величине прогнозируемый результат и $y_i$ — соответствующее истинное значение, тогда доля правильных прогнозов по сравнению с $n_{samples}$ определяется как
$$texttt{top-k accuracy}(y, hat{f}) = frac{1}{n_text{samples}} sum_{i=0}^{n_text{samples}-1} sum_{j=1}^{k} 1(hat{f}_{i,j} = y_i)$$
где k допустимое количество предположений и 1(x)- индикаторная функция.
>>> import numpy as np >>> from sklearn.metrics import top_k_accuracy_score >>> y_true = np.array([0, 1, 2, 2]) >>> y_score = np.array([[0.5, 0.2, 0.2], ... [0.3, 0.4, 0.2], ... [0.2, 0.4, 0.3], ... [0.7, 0.2, 0.1]]) >>> top_k_accuracy_score(y_true, y_score, k=2) 0.75 >>> # Not normalizing gives the number of "correctly" classified samples >>> top_k_accuracy_score(y_true, y_score, k=2, normalize=False) 3
3.3.2.4. Сбалансированный показатель точности
Функция balanced_accuracy_score вычисляет взвешенную точность , что позволяет избежать завышенных оценок производительности на несбалансированных данных. Это макросреднее количество оценок отзыва по классу или, что то же самое, грубая точность, где каждая выборка взвешивается в соответствии с обратной распространенностью ее истинного класса. Таким образом, для сбалансированных наборов данных оценка равна точности.
В двоичном случае сбалансированная точность равна среднему арифметическому чувствительности (истинно положительный показатель) и специфичности (истинно отрицательный показатель) или площади под кривой ROC с двоичными прогнозами, а не баллами:
$$texttt{balanced-accuracy} = frac{1}{2}left( frac{TP}{TP + FN} + frac{TN}{TN + FP}right )$$
Если классификатор одинаково хорошо работает в любом классе, этот термин сокращается до обычной точности (т. е. Количества правильных прогнозов, деленного на общее количество прогнозов).
Напротив, если обычная точность выше вероятности только потому, что классификатор использует несбалансированный набор тестов, тогда сбалансированная точность, при необходимости, упадет до $frac{1}{n_classes}$.
Оценка варьируется от 0 до 1 или, когда adjusted=True используется, масштабируется до диапазона $frac{1}{1 — n_classes}$ до 1 включительно, с произвольной оценкой 0.
Если yi истинная ценность $i$-й образец, и $w_i$ — соответствующий вес образца, затем мы настраиваем вес образца на:
$$hat{w}_i = frac{w_i}{sum_j{1(y_j = y_i) w_j}}$$
где $1(x)$- индикаторная функция . Учитывая предсказанный $hat{y}_i$ для образца $i$, сбалансированная точность определяется как:
$$texttt{balanced-accuracy}(y, hat{y}, w) = frac{1}{sum{hat{w}_i}} sum_i 1(hat{y}_i = y_i) hat{w}_i$$
С adjusted=True сбалансированной точностью сообщает об относительном увеличении от $texttt{balanced-accuracy}(y, mathbf{0}, w) =frac{1}{n_classes}$. В двоичном случае это также известно как * статистика Юдена * , или информированность .
Примечание
Определение мультикласса здесь кажется наиболее разумным расширением метрики, используемой в бинарной классификации, хотя в литературе нет определенного консенсуса:
- Наше определение: [Mosley2013] , [Kelleher2015] и [Guyon2015] , где [Guyon2015] принимает скорректированную версию, чтобы гарантировать, что случайные предсказания имеют оценку 0 а точные предсказания имеют оценку 1..
- Точность балансировки классов, как описано в [Mosley2013] : вычисляется минимум между точностью и отзывом для каждого класса. Затем эти значения усредняются по общему количеству классов для получения сбалансированной точности.
- Сбалансированная точность, как описано в [Urbanowicz2015] : среднее значение чувствительности и специфичности вычисляется для каждого класса, а затем усредняется по общему количеству классов.
Рекомендации:
- Гийон 2015 ( 1 , 2 ) И. Гайон, К. Беннет, Г. Коули, Х. Дж. Эскаланте, С. Эскалера, Т. К. Хо, Н. Масиа, Б. Рэй, М. Саид, А. Р. Статников, Э. Вьегас, Дизайн конкурса ChaLearn AutoML Challenge 2015 , IJCNN 2015 г.
- Мосли 2013 ( 1 , 2 ) Л. Мосли, Сбалансированный подход к проблеме мультиклассового дисбаланса , IJCV 2010.
- Kelleher2015 Джон. Д. Келлехер, Брайан Мак Нейме, Аойф Д’Арси, Основы машинного обучения для прогнозной аналитики данных: алгоритмы, рабочие примеры и тематические исследования , 2015.
- Урбанович2015 Urbanowicz RJ, Moore, JH ExSTraCS 2.0: описание и оценка масштабируемой системы классификаторов обучения , Evol. Intel. (2015) 8:89.
3.3.2.5. Каппа Коэна
Функция cohen_kappa_score вычисляет каппа-Коэна статистику. Эта мера предназначена для сравнения меток, сделанных разными людьми-аннотаторами, а не классификатором с достоверной информацией.
Показатель каппа (см. Строку документации) представляет собой число от -1 до 1. Баллы выше 0,8 обычно считаются хорошим совпадением; ноль или ниже означает отсутствие согласия (практически случайные метки).
Оценка Каппа может быть вычислена для двоичных или многоклассовых задач, но не для задач с несколькими метками (за исключением ручного вычисления оценки для каждой метки) и не более чем для двух аннотаторов.
>>> from sklearn.metrics import cohen_kappa_score >>> y_true = [2, 0, 2, 2, 0, 1] >>> y_pred = [0, 0, 2, 2, 0, 2] >>> cohen_kappa_score(y_true, y_pred) 0.4285714285714286
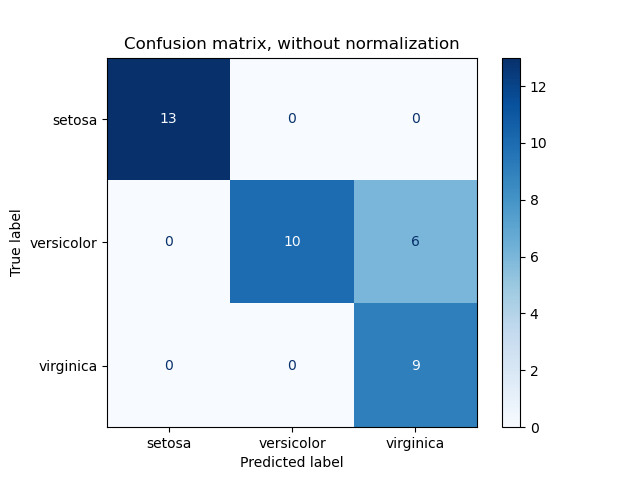
3.3.2.6. Матрица неточностей ¶
Точность функции confusion_matrix вычисляет классификацию пути вычисления матрицы путаницы с каждой строкой , соответствующей истинный классом (Википедия и другие ссылки могут использовать различные конвенции для осей).
По определению запись i,j в матрице неточностей — количество наблюдений в группе i, но предполагается, что он будет в группе j. Вот пример:
>>> from sklearn.metrics import confusion_matrix
>>> y_true = [2, 0, 2, 2, 0, 1]
>>> y_pred = [0, 0, 2, 2, 0, 2]
>>> confusion_matrix(y_true, y_pred)
array([[2, 0, 0],
[0, 0, 1],
[1, 0, 2]])
plot_confusion_matrix может использоваться для визуального представления матрицы неточностей, как показано в примере матрицы неточностей, который создает следующий рисунок:
Параметр normalize позволяет сообщать коэффициенты вместо подсчетов. Матрица путаница может быть нормализована в 3 различными способами: 'pred', 'true'и 'all' которые будут делить счетчики на сумму каждого столбца, строки или всей матрицы, соответственно.
>>> y_true = [0, 0, 0, 1, 1, 1, 1, 1]
>>> y_pred = [0, 1, 0, 1, 0, 1, 0, 1]
>>> confusion_matrix(y_true, y_pred, normalize='all')
array([[0.25 , 0.125],
[0.25 , 0.375]])
Для двоичных задач мы можем получить подсчет истинно отрицательных, ложноположительных, ложноотрицательных и истинно положительных результатов следующим образом:
>>> y_true = [0, 0, 0, 1, 1, 1, 1, 1] >>> y_pred = [0, 1, 0, 1, 0, 1, 0, 1] >>> tn, fp, fn, tp = confusion_matrix(y_true, y_pred).ravel() >>> tn, fp, fn, tp (2, 1, 2, 3)
Пример:
- См. В разделе Матрица неточностей пример использования матрицы неточностей для оценки качества выходных данных классификатора.
- См. В разделе Распознавание рукописных цифр пример использования матрицы неточностей для классификации рукописных цифр.
- См. Раздел Классификация текстовых документов с использованием разреженных функций для примера использования матрицы неточностей для классификации текстовых документов.
3.3.2.7. Отчет о классификации
Функция classification_report создает текстовый отчет , показывающий основные показатели классификации. Вот небольшой пример с настраиваемыми target_names и предполагаемыми ярлыками:
>>> from sklearn.metrics import classification_report
>>> y_true = [0, 1, 2, 2, 0]
>>> y_pred = [0, 0, 2, 1, 0]
>>> target_names = ['class 0', 'class 1', 'class 2']
>>> print(classification_report(y_true, y_pred, target_names=target_names))
precision recall f1-score support
class 0 0.67 1.00 0.80 2
class 1 0.00 0.00 0.00 1
class 2 1.00 0.50 0.67 2
accuracy 0.60 5
macro avg 0.56 0.50 0.49 5
weighted avg 0.67 0.60 0.59 5
Пример:
- См. В разделе Распознавание рукописных цифр пример использования отчета о классификации рукописных цифр.
- См. Раздел Классификация текстовых документов с использованием разреженных функций, где приведен пример использования отчета о классификации для текстовых документов.
- См. Раздел « Оценка параметров с использованием поиска по сетке с перекрестной проверкой», где приведен пример использования отчета о классификации для поиска по сетке с вложенной перекрестной проверкой.
3.3.2.8. Потеря Хэмминга
hamming_loss вычисляет среднюю потерю Хэмминга или расстояние Хемминга между двумя наборами образцов.
Если $hat{y}_j$ прогнозируемое значение для $j$-я этикетка данного образца, $y_j$ — соответствующее истинное значение, а $n_{labels}$ — количество классов или меток, то потеря Хэмминга $L_{Hamming}$ между двумя образцами определяется как:
$$L_{Hamming}(y, hat{y}) = frac{1}{n_text{labels}} sum_{j=0}^{n_text{labels} — 1} 1(hat{y}_j not= y_j)$$
где $1(x)$- индикаторная функция .
>>> from sklearn.metrics import hamming_loss >>> y_pred = [1, 2, 3, 4] >>> y_true = [2, 2, 3, 4] >>> hamming_loss(y_true, y_pred) 0.25
В многопозиционном корпусе с бинарными индикаторами меток:
>>> hamming_loss(np.array([[0, 1], [1, 1]]), np.zeros((2, 2))) 0.75
Примечание
В мультиклассовой классификации потери Хэмминга соответствуют расстоянию Хэмминга между y_true и, y_pred что аналогично функции потерь нуля или единицы . Однако, в то время как потеря нуля или единицы наказывает наборы предсказаний, которые не строго соответствуют истинным наборам, потеря Хэмминга наказывает отдельные метки. Таким образом, потеря Хэмминга, ограниченная сверху потерей нуля или единицы, всегда находится между нулем и единицей включительно; и прогнозирование надлежащего подмножества или надмножества истинных меток даст исключительную потерю Хэмминга от нуля до единицы.
3.3.2.9. Точность, отзыв и F-меры
Интуитивно, точность — это способность классификатора не маркировать как положительный образец, который является отрицательным, а отзыв — это способность классификатора находить все положительные образцы.
F-мера ($F_beta$ а также $F_1$ меры) можно интерпретировать как взвешенное гармоническое среднее значение точности и полноты. А $F_beta$ мера достигает своего лучшего значения на уровне 1 и худшего результата на уровне 0. С $beta = 1$, $F_beta$ а также $F_1$ эквивалентны, а отзыв и точность одинаково важны.
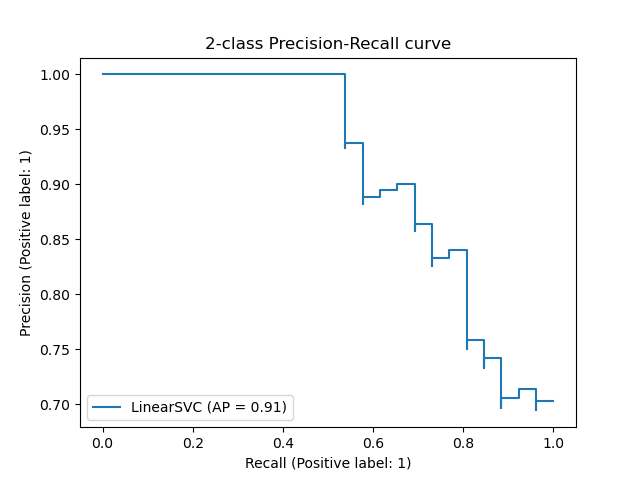
precision_recall_curve вычисляет кривую точности-отзыва на основе наземной метки истинности и оценки, полученной классификатором путем изменения порога принятия решения.
Функция average_precision_score вычисляет среднюю точность (AP) от оценки прогнозирования. Значение от 0 до 1 и выше — лучше. AP определяется как
$$text{AP} = sum_n (R_n — R_{n-1}) P_n$$
где $P_n$ а также $R_n$- точность и отзыв на n-м пороге. При случайных прогнозах AP — это доля положительных образцов.
Ссылки [Manning2008] и [Everingham2010] представляют альтернативные варианты AP, которые интерполируют кривую точности-отзыва. В настоящее время average_precision_score не реализован какой-либо вариант с интерполяцией. Ссылки [Davis2006] и [Flach2015] описывают, почему линейная интерполяция точек на кривой точности-отзыва обеспечивает чрезмерно оптимистичный показатель эффективности классификатора. Эта линейная интерполяция используется при вычислении площади под кривой с помощью правила трапеции в auc.
Несколько функций позволяют анализировать точность, отзыв и оценку F-мер:
average_precision_score(y_true, y_score, *) |
Вычислить среднюю точность (AP) из оценок прогнозов. |
f1_score(y_true, y_pred, *[, labels, …]) |
Вычислите оценку F1, также известную как сбалансированная оценка F или F-мера. |
fbeta_score(y_true, y_pred, *, beta[, …]) |
Вычислите оценку F-beta. |
precision_recall_curve(y_true, probas_pred, *) |
Вычислите пары точности-отзыва для разных пороговых значений вероятности. |
precision_recall_fscore_support(y_true, …) |
Точность вычислений, отзыв, F-мера и поддержка для каждого класса. |
precision_score(y_true, y_pred, *[, labels, …]) |
Вычислите точность. |
recall_score(y_true, y_pred, *[, labels, …]) |
Вычислите рекол. |
Обратите внимание, что функция precision_recall_curve ограничена двоичным регистром. Функция average_precision_score работает только в двоичном формате классификации и MultiLabel индикатора. В функции plot_precision_recall_curve графики точности вспомнить следующим образом .
Примеры:
- См. Раздел Классификация текстовых документов с использованием разреженных функций для примера использования
f1_scoreдля классификации текстовых документов. - См. Раздел « Оценка параметров с использованием поиска по сетке с перекрестной проверкой», где приведен пример
precision_scoreиrecall_scoreиспользование для оценки параметров с помощью поиска по сетке с вложенной перекрестной проверкой. - См. В разделе Precision-Recall пример использования
precision_recall_curveдля оценки качества вывода классификатора.
Рекомендации:
- [Manning2008] г. CD Manning, P. Raghavan, H. Schütze, Introduction to Information Retrieval , 2008.
- [Everingham2010] М. Эверингем, Л. Ван Гул, CKI Уильямс, Дж. Винн, А. Зиссерман, Задача классов визуальных объектов Pascal (VOC) , IJCV 2010.
- [Davis2006] Дж. Дэвис, М. Гоадрич, Взаимосвязь между точным воспроизведением и кривыми ROC , ICML 2006.
- [Flach2015] П.А. Флэч, М. Кулл, Кривые точности-отзыва-выигрыша: PR-анализ выполнен правильно , NIPS 2015.
3.3.2.9.1. Бинарная классификация
В задаче бинарной классификации термины «положительный» и «отрицательный» относятся к предсказанию классификатора, а термины «истинный» и «ложный» относятся к тому, соответствует ли этот прогноз внешнему суждению ( иногда известное как «наблюдение»). Учитывая эти определения, мы можем сформулировать следующую таблицу:
| Фактический класс (наблюдение) | ||
| Прогнозируемый класс (ожидание) | tp (истинно положительный результат) Правильный результат | fp (ложное срабатывание) Неожиданный результат |
| Прогнозируемый класс (ожидание) | fn (ложноотрицательный) Отсутствует результат | tn (истинно отрицательное) Правильное отсутствие результата |
В этом контексте мы можем определить понятия точности, отзыва и F-меры:
$$text{precision} = frac{tp}{tp + fp},$$
$$text{recall} = frac{tp}{tp + fn},$$
$$F_beta = (1 + beta^2) frac{text{precision} times text{recall}}{beta^2 text{precision} + text{recall}}.$$
Вот несколько небольших примеров бинарной классификации:
>>> from sklearn import metrics >>> y_pred = [0, 1, 0, 0] >>> y_true = [0, 1, 0, 1] >>> metrics.precision_score(y_true, y_pred) 1.0 >>> metrics.recall_score(y_true, y_pred) 0.5 >>> metrics.f1_score(y_true, y_pred) 0.66... >>> metrics.fbeta_score(y_true, y_pred, beta=0.5) 0.83... >>> metrics.fbeta_score(y_true, y_pred, beta=1) 0.66... >>> metrics.fbeta_score(y_true, y_pred, beta=2) 0.55... >>> metrics.precision_recall_fscore_support(y_true, y_pred, beta=0.5) (array([0.66..., 1. ]), array([1. , 0.5]), array([0.71..., 0.83...]), array([2, 2])) >>> import numpy as np >>> from sklearn.metrics import precision_recall_curve >>> from sklearn.metrics import average_precision_score >>> y_true = np.array([0, 0, 1, 1]) >>> y_scores = np.array([0.1, 0.4, 0.35, 0.8]) >>> precision, recall, threshold = precision_recall_curve(y_true, y_scores) >>> precision array([0.66..., 0.5 , 1. , 1. ]) >>> recall array([1. , 0.5, 0.5, 0. ]) >>> threshold array([0.35, 0.4 , 0.8 ]) >>> average_precision_score(y_true, y_scores) 0.83...
3.3.2.9.2. Мультиклассовая и многозначная классификация
В задаче классификации по нескольким классам и меткам понятия точности, отзыва и F-меры могут применяться к каждой метке независимо. Есть несколько способов , чтобы объединить результаты по этикеткам, указанных в average аргументе к average_precision_score (MultiLabel только) f1_score, fbeta_score, precision_recall_fscore_support, precision_score и recall_score функция, как описано выше . Обратите внимание, что если включены все метки, «микро» -усреднение в настройке мультикласса обеспечит точность, отзыв и $F$ все они идентичны по точности. Также обратите внимание, что «взвешенное» усреднение может дать оценку F, которая не находится между точностью и отзывом.
Чтобы сделать это более явным, рассмотрим следующие обозначения:
- $y$ набор предсказанных ($sample$, $label$) пары
- $hat{y}$ набор истинных ($sample$, $label$) пары
- $L$ набор лейблов
- $S$ набор образцов
- $y_s$ подмножество $y$ с образцом $s$, т.е $y_s := left{(s’, l) in y | s’ = sright}$.
- $y_l$ подмножество $y$ с этикеткой $l$
- по аналогии, $hat{y}_s$ а также $hat{y}_l$ являются подмножествами $hat{y}$
- $P(A, B) := frac{left| A cap B right|}{left|Aright|}$ для некоторых наборов $A$ и $B$
- $R(A, B) := frac{left| A cap B right|}{left|Bright|}$ (Условные обозначения различаются в зависимости от обращения $B = emptyset$; эта реализация использует $R(A, B):=0$, и аналогичные для $P$.)
- $$F_beta(A, B) := left(1 + beta^2right) frac{P(A, B) times R(A, B)}{beta^2 P(A, B) + R(A, B)}$$
Тогда показатели определяются как:
| average | Точность | Отзывать | F_beta |
| «micro» | $P(y, hat{y})$ | $R(y, hat{y})$ | $F_beta(y, hat{y})$ |
| «samples» | $frac{1}{left|Sright|} sum_{s in S} P(y_s, hat{y}_s)$ | $frac{1}{left|Sright|} sum_{s in S} R(y_s, hat{y}_s)$ | $frac{1}{left|Sright|} sum_{s in S} F_beta(y_s, hat{y}_s)$ |
| «macro» | $frac{1}{left|Lright|} sum_{l in L} P(y_l, hat{y}_l)$ | $frac{1}{left|Lright|} sum_{l in L} R(y_l, hat{y}_l)$ | $frac{1}{left|Lright|} sum_{l in L} F_beta(y_l, hat{y}_l)$ |
| «weighted» | $frac{1}{sum_{l in L} left|hat{y}lright|} sum{l in L} left|hat{y}_lright| P(y_l, hat{y}_l)$ | $frac{1}{sum_{l in L} left|hat{y}lright|} sum{l in L} left|hat{y}_lright| R(y_l, hat{y}_l)$ | $frac{1}{sum_{l in L} left|hat{y}lright|} sum{l in L} left|hat{y}lright| Fbeta(y_l, hat{y}_l)$ |
| None | $langle P(y_l, hat{y}_l) | l in L rangle$ | $langle R(y_l, hat{y}_l) | l in L rangle$ | $langle F_beta(y_l, hat{y}_l) | l in L rangle$ |
>>> from sklearn import metrics >>> y_true = [0, 1, 2, 0, 1, 2] >>> y_pred = [0, 2, 1, 0, 0, 1] >>> metrics.precision_score(y_true, y_pred, average='macro') 0.22... >>> metrics.recall_score(y_true, y_pred, average='micro') 0.33... >>> metrics.f1_score(y_true, y_pred, average='weighted') 0.26... >>> metrics.fbeta_score(y_true, y_pred, average='macro', beta=0.5) 0.23... >>> metrics.precision_recall_fscore_support(y_true, y_pred, beta=0.5, average=None) (array([0.66..., 0. , 0. ]), array([1., 0., 0.]), array([0.71..., 0. , 0. ]), array([2, 2, 2]...))
Для мультиклассовой классификации с «отрицательным классом» можно исключить некоторые метки:
>>> metrics.recall_score(y_true, y_pred, labels=[1, 2], average='micro') ... # excluding 0, no labels were correctly recalled 0.0
Точно так же метки, отсутствующие в выборке данных, могут учитываться при макро-усреднении.
>>> metrics.precision_score(y_true, y_pred, labels=[0, 1, 2, 3], average='macro') 0.166...
3.3.2.10. Оценка коэффициента сходства Жаккара
Функция jaccard_score вычисляет среднее значение коэффициентов сходства Jaccard , также называемый индексом Jaccard, между парами множеств меток.
Коэффициент подобия Жаккара i-ые образцы, с набором меток наземной достоверности yi и прогнозируемый набор меток y^i, определяется как
$$J(y_i, hat{y}_i) = frac{|y_i cap hat{y}_i|}{|y_i cup hat{y}_i|}.$$
jaccard_score работает как precision_recall_fscore_support наивно установленная мера, применяемая изначально к бинарным целям, и расширена для применения к множественным меткам и мультиклассам за счет использования average(см. выше ).
В двоичном случае:
>>> import numpy as np >>> from sklearn.metrics import jaccard_score >>> y_true = np.array([[0, 1, 1], ... [1, 1, 0]]) >>> y_pred = np.array([[1, 1, 1], ... [1, 0, 0]]) >>> jaccard_score(y_true[0], y_pred[0]) 0.6666...
В многопозиционном корпусе с бинарными индикаторами меток:
>>> jaccard_score(y_true, y_pred, average='samples') 0.5833... >>> jaccard_score(y_true, y_pred, average='macro') 0.6666... >>> jaccard_score(y_true, y_pred, average=None) array([0.5, 0.5, 1. ])
Задачи с несколькими классами преобразуются в двоичную форму и обрабатываются как соответствующая задача с несколькими метками:
>>> y_pred = [0, 2, 1, 2] >>> y_true = [0, 1, 2, 2] >>> jaccard_score(y_true, y_pred, average=None) array([1. , 0. , 0.33...]) >>> jaccard_score(y_true, y_pred, average='macro') 0.44... >>> jaccard_score(y_true, y_pred, average='micro') 0.33...
3.3.2.11. Петля лосс
Функция hinge_loss вычисляет среднее расстояние между моделью и данными с использованием петля лосс, односторонний показателем , который учитывает только ошибки прогнозирования. (Потери на шарнирах используются в классификаторах максимальной маржи, таких как опорные векторные машины.)
Если метки закодированы с помощью +1 и -1, $y$: истинное значение, а $w$ — прогнозируемые решения на выходе decision_function, тогда потери на шарнирах определяются как:
$$L_text{Hinge}(y, w) = maxleft{1 — wy, 0right} = left|1 — wyright|_+$$
Если имеется более двух ярлыков, hinge_loss используется мультиклассовый вариант, разработанный Crammer & Singer. Вот статья, описывающая это.
Если $y_w$ прогнозируемое решение для истинного лейбла и $y_t$ — это максимум предсказанных решений для всех других меток, где предсказанные решения выводятся функцией принятия решений, тогда потеря шарнира в нескольких классах определяется следующим образом:
$$L_text{Hinge}(y_w, y_t) = maxleft{1 + y_t — y_w, 0right}$$
Вот небольшой пример, демонстрирующий использование hinge_loss функции с классификатором svm в задаче двоичного класса:
>>> from sklearn import svm >>> from sklearn.metrics import hinge_loss >>> X = [[0], [1]] >>> y = [-1, 1] >>> est = svm.LinearSVC(random_state=0) >>> est.fit(X, y) LinearSVC(random_state=0) >>> pred_decision = est.decision_function([[-2], [3], [0.5]]) >>> pred_decision array([-2.18..., 2.36..., 0.09...]) >>> hinge_loss([-1, 1, 1], pred_decision) 0.3...
Вот пример, демонстрирующий использование hinge_loss функции с классификатором svm в мультиклассовой задаче:
>>> X = np.array([[0], [1], [2], [3]]) >>> Y = np.array([0, 1, 2, 3]) >>> labels = np.array([0, 1, 2, 3]) >>> est = svm.LinearSVC() >>> est.fit(X, Y) LinearSVC() >>> pred_decision = est.decision_function([[-1], [2], [3]]) >>> y_true = [0, 2, 3] >>> hinge_loss(y_true, pred_decision, labels) 0.56...
3.3.2.12. Лог лосс
Лог лосс, также называемые потерями логистической регрессии или кросс-энтропийными потерями, определяются на основе оценок вероятности. Он обычно используется в (полиномиальной) логистической регрессии и нейронных сетях, а также в некоторых вариантах максимизации ожидания и может использоваться для оценки выходов вероятности ( predict_proba) классификатора вместо его дискретных прогнозов.
Для двоичной классификации с истинной меткой $y in {0,1}$ и оценка вероятности $p = operatorname{Pr}(y = 1)$, логарифмическая потеря на выборку представляет собой отрицательную логарифмическую вероятность классификатора с истинной меткой:
$$L_{log}(y, p) = -log operatorname{Pr}(y|p) = -(y log (p) + (1 — y) log (1 — p))$$
Это распространяется на случай мультикласса следующим образом. Пусть истинные метки для набора выборок будут закодированы размером 1 из K как двоичная индикаторная матрица $Y$, т.е. $y_{i,k}=1$ если образец $i$ есть ярлык $k$ взят из набора $K$ этикетки. Пусть $P$ — матрица оценок вероятностей, с $p_{i,k} = operatorname{Pr}(y_{i,k} = 1)$. Тогда потеря журнала всего набора равна
$$L_{log}(Y, P) = -log operatorname{Pr}(Y|P) = — frac{1}{N} sum_{i=0}^{N-1} sum_{k=0}^{K-1} y_{i,k} log p_{i,k}$$
Чтобы увидеть, как это обобщает приведенную выше потерю двоичного журнала, обратите внимание, что в двоичном случае $p_{i,0} = 1 — p_{i,1}$ и $y_{i,0} = 1 — y_{i,1}$, поэтому разложив внутреннюю сумму на $y_{i,k} in {0,1}$ дает двоичную потерю журнала.
В log_loss функции вычисляет журнал потеря дана список меток приземной истины и матриц вероятностей, возвращенный оценщик predict_proba методом.
>>> from sklearn.metrics import log_loss >>> y_true = [0, 0, 1, 1] >>> y_pred = [[.9, .1], [.8, .2], [.3, .7], [.01, .99]] >>> log_loss(y_true, y_pred) 0.1738...
Первое [.9, .1] в y_pred означает 90% вероятность того, что первая выборка будет иметь метку 0. Лог лос неотрицательны.
3.3.2.13. Коэффициент корреляции Мэтьюза
Функция matthews_corrcoef вычисляет коэффициент корреляции Матфея (MCC) для двоичных классов. Цитата из Википедии:
«Коэффициент корреляции Мэтьюза используется в машинном обучении как мера качества двоичных (двухклассных) классификаций. Он учитывает истинные и ложные положительные и отрицательные результаты и обычно рассматривается как сбалансированная мера, которую можно использовать, даже если классы очень разных размеров. MCC — это, по сути, значение коэффициента корреляции между -1 и +1. Коэффициент +1 представляет собой идеальное предсказание, 0 — среднее случайное предсказание и -1 — обратное предсказание. Статистика также известна как коэффициент фи ».
В бинарном (двухклассовом) случае $tp$, $tn$, $fp$ а также $fn$ являются соответственно количеством истинно положительных, истинно отрицательных, ложноположительных и ложноотрицательных результатов, MCC определяется как
$$MCC = frac{tp times tn — fp times fn}{sqrt{(tp + fp)(tp + fn)(tn + fp)(tn + fn)}}.$$
В случае мультикласса коэффициент корреляции Мэтьюза может быть определен в терминах confusion_matrix C для Kклассы. Чтобы упростить определение, рассмотрим следующие промежуточные переменные:
- $t_k=sum_{i}^{K} C_{ik}$ количество занятий k действительно произошло,
- $p_k=sum_{i}^{K} C_{ki}$ количество занятий k был предсказан,
- $c=sum_{k}^{K} C_{kk}$ общее количество правильно спрогнозированных образцов,
- $s=sum_{i}^{K} sum_{j}^{K} C_{ij}$ общее количество образцов.
Тогда мультиклассовый MCC определяется как:
$$MCC = frac{ c times s — sum_{k}^{K} p_k times t_k }{sqrt{ (s^2 — sum_{k}^{K} p_k^2) times (s^2 — sum_{k}^{K} t_k^2) }}$$
Когда имеется более двух меток, значение MCC больше не будет находиться в диапазоне от -1 до +1. Вместо этого минимальное значение будет где-то между -1 и 0 в зависимости от количества и распределения наземных истинных меток. Максимальное значение всегда +1.
Вот небольшой пример, иллюстрирующий использование matthews_corrcoef функции:
>>> from sklearn.metrics import matthews_corrcoef >>> y_true = [+1, +1, +1, -1] >>> y_pred = [+1, -1, +1, +1] >>> matthews_corrcoef(y_true, y_pred) -0.33...
3.3.2.14. Матрица путаницы с несколькими метками
Функция multilabel_confusion_matrix вычисляет класс-накрест ( по умолчанию) или samplewise (samplewise = True) MultiLabel матрицы спутанности для оценки точности классификации. Multilabel_confusion_matrix также обрабатывает данные мультикласса, как если бы они были многоклассовыми, поскольку это преобразование, обычно применяемое для оценки проблем мультикласса с метриками двоичной классификации (такими как точность, отзыв и т. д.).
При вычислении классовой матрицы путаницы с несколькими метками $C$, количество истинных негативов для класса i является $C_{i,0,0}$, ложноотрицательные $C_{i,1,0}$, истинные положительные стороны $C_{i,1,1}$ а ложные срабатывания $C_{i,0,1}$.
Вот пример, демонстрирующий использование multilabel_confusion_matrix функции с вводом многозначной индикаторной матрицы:
>>> import numpy as np
>>> from sklearn.metrics import multilabel_confusion_matrix
>>> y_true = np.array([[1, 0, 1],
... [0, 1, 0]])
>>> y_pred = np.array([[1, 0, 0],
... [0, 1, 1]])
>>> multilabel_confusion_matrix(y_true, y_pred)
array([[[1, 0],
[0, 1]],
[[1, 0],
[0, 1]],
[[0, 1],
[1, 0]]])
Или можно построить матрицу неточностей для каждой метки образца:
>>> multilabel_confusion_matrix(y_true, y_pred, samplewise=True)
array([[[1, 0],
[1, 1]],
[[1, 1],
[0, 1]]])
Вот пример, демонстрирующий использование multilabel_confusion_matrix функции с многоклассовым вводом:
>>> y_true = ["cat", "ant", "cat", "cat", "ant", "bird"]
>>> y_pred = ["ant", "ant", "cat", "cat", "ant", "cat"]
>>> multilabel_confusion_matrix(y_true, y_pred,
... labels=["ant", "bird", "cat"])
array([[[3, 1],
[0, 2]],
[[5, 0],
[1, 0]],
[[2, 1],
[1, 2]]])
Вот несколько примеров, демонстрирующих использование multilabel_confusion_matrix функции для расчета отзыва (или чувствительности), специфичности, количества выпадений и пропусков для каждого класса в задаче с вводом многозначной индикаторной матрицы.
Расчет отзыва (также называемого истинно положительным коэффициентом или чувствительностью) для каждого класса:
>>> y_true = np.array([[0, 0, 1], ... [0, 1, 0], ... [1, 1, 0]]) >>> y_pred = np.array([[0, 1, 0], ... [0, 0, 1], ... [1, 1, 0]]) >>> mcm = multilabel_confusion_matrix(y_true, y_pred) >>> tn = mcm[:, 0, 0] >>> tp = mcm[:, 1, 1] >>> fn = mcm[:, 1, 0] >>> fp = mcm[:, 0, 1] >>> tp / (tp + fn) array([1. , 0.5, 0. ])
Расчет специфичности (также называемой истинно отрицательной ставкой) для каждого класса:
>>> tn / (tn + fp) array([1. , 0. , 0.5])
Расчет количества выпадений (также называемый частотой ложных срабатываний) для каждого класса:
>>> fp / (fp + tn) array([0. , 1. , 0.5])
Расчет процента промахов (также называемого ложноотрицательным показателем) для каждого класса:
>>> fn / (fn + tp) array([0. , 0.5, 1. ])
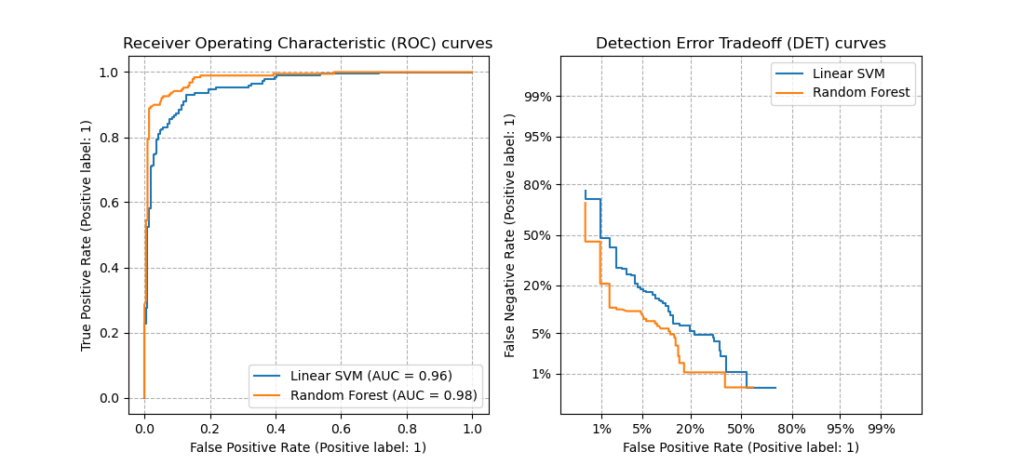
3.3.2.15. Рабочая характеристика приемника (ROC)
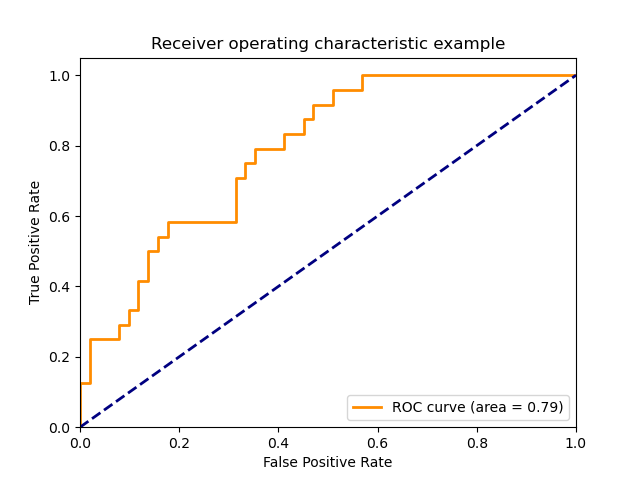
Функция roc_curve вычисляет рабочую характеристическую кривую приемника или кривую ROC . Цитата из Википедии:
«Рабочая характеристика приемника (ROC), или просто кривая ROC, представляет собой графический график, который иллюстрирует работу системы двоичного классификатора при изменении ее порога дискриминации. Он создается путем построения графика доли истинных положительных результатов из положительных (TPR = частота истинных положительных результатов) по сравнению с долей ложных положительных результатов из отрицательных (FPR = частота ложных положительных результатов) при различных настройках пороговых значений. TPR также известен как чувствительность, а FPR — это единица минус специфичность или истинно отрицательный показатель ».
Для этой функции требуется истинное двоичное значение и целевые баллы, которые могут быть либо оценками вероятности положительного класса, либо значениями достоверности, либо двоичными решениями. Вот небольшой пример использования roc_curve функции:
>>> import numpy as np >>> from sklearn.metrics import roc_curve >>> y = np.array([1, 1, 2, 2]) >>> scores = np.array([0.1, 0.4, 0.35, 0.8]) >>> fpr, tpr, thresholds = roc_curve(y, scores, pos_label=2) >>> fpr array([0. , 0. , 0.5, 0.5, 1. ]) >>> tpr array([0. , 0.5, 0.5, 1. , 1. ]) >>> thresholds array([1.8 , 0.8 , 0.4 , 0.35, 0.1 ])
На этом рисунке показан пример такой кривой ROC:
Функция roc_auc_score вычисляет площадь под операционной приемника характеристика (ROC) кривой, которая также обозначается через ППК или AUROC. При вычислении площади под кривой roc информация о кривой суммируется в одном номере. Для получения дополнительной информации см. Статью в Википедии о AUC.
По сравнению с такими показателями, как точность подмножества, потеря Хэмминга или оценка F1, ROC не требует оптимизации порога для каждой метки.
3.3.2.15.1. Двоичный регистр
В двоичном случае вы можете либо предоставить оценки вероятности, используя classifier.predict_proba() метод, либо значения решения без пороговых значений, заданные classifier.decision_function() методом. В случае предоставления оценок вероятности следует указать вероятность класса с «большей меткой». «Большая метка» соответствует classifier.classes_[1] и, следовательно classifier.predict_proba(X) [:, 1]. Следовательно, параметр y_score имеет размер (n_samples,).
>>> from sklearn.datasets import load_breast_cancer >>> from sklearn.linear_model import LogisticRegression >>> from sklearn.metrics import roc_auc_score >>> X, y = load_breast_cancer(return_X_y=True) >>> clf = LogisticRegression(solver="liblinear").fit(X, y) >>> clf.classes_ array([0, 1])
Мы можем использовать оценки вероятностей, соответствующие clf.classes_[1].
>>> y_score = clf.predict_proba(X)[:, 1] >>> roc_auc_score(y, y_score) 0.99...
В противном случае мы можем использовать значения решения без порога.
>>> roc_auc_score(y, clf.decision_function(X)) 0.99...
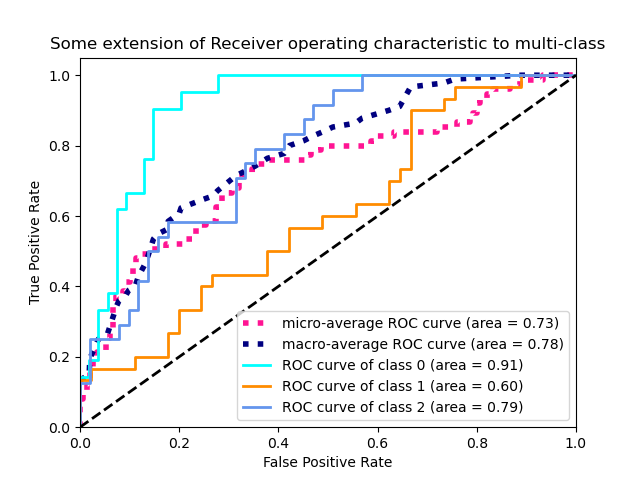
3.3.2.15.2. Мультиклассовый кейс
Функция roc_auc_score также может быть использована в нескольких классах классификации . В настоящее время поддерживаются две стратегии усреднения: алгоритм «один против одного» вычисляет среднее попарных оценок AUC ROC, а алгоритм «один против остальных» вычисляет среднее значение оценок ROC AUC для каждого класса по сравнению со всеми другими классами. В обоих случаях предсказанные метки предоставляются в виде массива со значениями от 0 до n_classes, а оценки соответствуют оценкам вероятности того, что выборка принадлежит определенному классу. Алгоритмы OvO и OvR поддерживают равномерное взвешивание ( average='macro') и по распространенности ( average='weighted').
Алгоритм «один против одного» : вычисляет средний AUC всех возможных попарных комбинаций классов. [HT2001] определяет метрику AUC мультикласса, взвешенную равномерно:
$$frac{1}{c(c-1)}sum_{j=1}^{c}sum_{k > j}^c (text{AUC}(j | k) + text{AUC}(k | j))$$
где $c$ количество классов и $text{AUC}(j | k)$ AUC с классом $j$ как положительный класс и класс $k$ как отрицательный класс. В общем, $text{AUC}(j | k) neq text{AUC}(k | j))$ в случае мультикласса. Этот алгоритм используется, установив аргумент ключевого слова , multiclass чтобы 'ovo' и average в 'macro'.
[HT2001] мультиклассируют AUC метрика может быть расширена , чтобы быть взвешены по распространенности:
$$frac{1}{c(c-1)}sum_{j=1}^{c}sum_{k > j}^c p(j cup k)( text{AUC}(j | k) + text{AUC}(k | j))$$
где cколичество классов. Этот алгоритм используется, установив аргумент ключевого слова , multiclass чтобы 'ovo' и average в 'weighted'. В 'weighted' опции возвращает распространенность усредненные , как описано в [FC2009] .
Алгоритм «один против остальных» : вычисляет AUC каждого класса относительно остальных [PD2000] . Алгоритм функционально такой же, как и в случае с несколькими этикетками. Чтобы включить этот алгоритм, установите для аргумента ключевого слова multiclass значение 'ovr'. Как и OvO, OvR поддерживает два типа усреднения: 'macro' [F2006] и 'weighted' [F2001] .
В приложениях , где высокий процент ложных срабатываний не терпимый параметр max_fpr из roc_auc_score может быть использовано , чтобы суммировать кривую ROC до заданного предела.
3.3.2.15.3. Кейс с несколькими метками
В классификации несколько меток, функция roc_auc_score распространяются путем усреднения меток , как выше . В этом случае вы должны указать y_score форму . Таким образом, при использовании оценок вероятности необходимо выбрать вероятность класса с большей меткой для каждого выхода.(n_samples, n_classes)
>>> from sklearn.datasets import make_multilabel_classification >>> from sklearn.multioutput import MultiOutputClassifier >>> X, y = make_multilabel_classification(random_state=0) >>> inner_clf = LogisticRegression(solver="liblinear", random_state=0) >>> clf = MultiOutputClassifier(inner_clf).fit(X, y) >>> y_score = np.transpose([y_pred[:, 1] for y_pred in clf.predict_proba(X)]) >>> roc_auc_score(y, y_score, average=None) array([0.82..., 0.86..., 0.94..., 0.85... , 0.94...])
И значения решений не требуют такой обработки.
>>> from sklearn.linear_model import RidgeClassifierCV >>> clf = RidgeClassifierCV().fit(X, y) >>> y_score = clf.decision_function(X) >>> roc_auc_score(y, y_score, average=None) array([0.81..., 0.84... , 0.93..., 0.87..., 0.94...])
Примеры:
- См. В разделе « Рабочие характеристики приемника» (ROC) пример использования ROC для оценки качества выходных данных классификатора.
- См. В разделе « Рабочие характеристики приемника» (ROC) с перекрестной проверкой пример использования ROC для оценки качества выходных данных классификатора с помощью перекрестной проверки.
- См. В разделе Моделирование распределения видов пример использования ROC для моделирования распределения видов.
- HT2001 ( 1 , 2 ) Рука, DJ и Тилль, RJ, (2001). Простое обобщение области под кривой ROC для задач классификации нескольких классов. Машинное обучение, 45 (2), стр. 171-186.
- FC2009 Ферри, Сезар и Эрнандес-Оралло, Хосе и Модройу, Р. (2009). Экспериментальное сравнение показателей эффективности для классификации. Письма о распознавании образов. 30. 27-38.
- PD2000 Провост Ф., Домингос П. (2000). Хорошо обученные ПЭТ: Улучшение деревьев оценки вероятностей (Раздел 6.2), Рабочий документ CeDER № IS-00-04, Школа бизнеса Стерна, Нью-Йоркский университет.
- F2006 Фосетт, Т., 2006. Введение в анализ ROC. Письма о распознавании образов, 27 (8), стр. 861-874.
- F2001Фосетт, Т., 2001. Использование наборов правил для максимизации производительности ROC в интеллектуальном анализе данных, 2001. Труды Международной конференции IEEE, стр. 131-138.
3.3.2.16. Компромисс при обнаружении ошибок (DET)
Функция det_curve вычисляет кривую компенсации ошибок обнаружения (DET) [WikipediaDET2017] . Цитата из Википедии:
«График компромисса ошибок обнаружения (DET) — это графическая диаграмма частоты ошибок для систем двоичной классификации, отображающая частоту ложных отклонений по сравнению с частотой ложных приемов. Оси x и y масштабируются нелинейно по их стандартным нормальным отклонениям (или просто с помощью логарифмического преобразования), в результате получаются более линейные кривые компромисса, чем кривые ROC, и большая часть области изображения используется для выделения важных различий в критический рабочий регион ».
Кривые DET представляют собой вариацию кривых рабочих характеристик приемника (ROC), где ложная отрицательная скорость нанесена на ось y вместо истинной положительной скорости. Кривые DET обычно строятся в масштабе нормального отклонения путем преобразования $phi^{-1}$ (с участием $phi$ — кумулятивная функция распределения). Полученные кривые производительности явно визуализируют компромисс типов ошибок для заданных алгоритмов классификации. См. [Martin1997], где приведены примеры и мотивация.
На этом рисунке сравниваются кривые ROC и DET двух примеров классификаторов для одной и той же задачи классификации:
Характеристики:
- Кривые DET образуют линейную кривую по шкале нормального отклонения, если оценки обнаружения нормально (или близки к нормальному) распределены. В [Navratil2007] было показано, что обратное не обязательно верно, и даже более общие распределения могут давать линейные кривые DET.
- При обычном преобразовании масштаба с отклонением точки распределяются таким образом, что занимает сравнительно большее пространство графика. Следовательно, кривые с аналогичными характеристиками классификации легче различить на графике DET.
- С ложноотрицательной скоростью, «обратной» истинной положительной скорости, точкой совершенства для кривых DET является начало координат (в отличие от верхнего левого угла для кривых ROC).
Приложения и ограничения:
Кривые DET интуитивно понятны для чтения и, следовательно, позволяют быстро визуально оценить работу классификатора. Кроме того, кривые DET можно использовать для анализа пороговых значений и выбора рабочей точки. Это особенно полезно, если требуется сравнение типов ошибок.
С другой стороны, кривые DET не представляют свою метрику в виде единого числа. Поэтому для автоматической оценки или сравнения с другими задачами классификации лучше подходят такие показатели, как производная площадь под кривой ROC.
Примеры:
- См. Кривую компенсации ошибок обнаружения (DET) для примера сравнения кривых рабочих характеристик приемника (ROC) и кривых компенсации ошибок обнаружения (DET).
Рекомендации:
- ВикипедияDET2017 Авторы Википедии. Компромисс ошибки обнаружения. Википедия, свободная энциклопедия. 4 сентября 2017 г., 23:33 UTC. Доступно по адресу: https://en.wikipedia.org/w/index.php?title=Detection_error_tradeoff&oldid=798982054 . По состоянию на 19 февраля 2018 г.
- Мартин 1997 А. Мартин, Дж. Доддингтон, Т. Камм, М. Ордовски и М. Пшибоцки, Кривая DET в оценке эффективности задач обнаружения , NIST 1997.
- Навратил2007 Дж. Наврактил и Д. Клусачек, « О линейных DET », 2007 г. Международная конференция IEEE по акустике, обработке речи и сигналов — ICASSP ’07, Гонолулу, Гавайи, 2007 г., стр. IV-229-IV-232.
3.3.2.17. Нулевой проигрыш
Функция zero_one_loss вычисляет сумму или среднее значение потери 0-1 классификации ($L_{0−1}$) над $n_{samples}$. По умолчанию функция нормализуется по выборке. Чтобы получить сумму $L_{0−1}$, установите normalize значение False.
В классификации по zero_one_loss нескольким меткам подмножество оценивается как единое целое, если его метки строго соответствуют прогнозам, и как ноль, если есть какие-либо ошибки. По умолчанию функция возвращает процент неправильно спрогнозированных подмножеств. Чтобы вместо этого получить количество таких подмножеств, установите normalize значение False
Если $hat{y}_i$ прогнозируемое значение $i$-й образец и $y_i$ — соответствующее истинное значение, тогда потеря 0-1 $L_{0−1}$ определяется как:
$$L_{0-1}(y_i, hat{y}_i) = 1(hat{y}_i not= y_i)$$
где $1(x)$- индикаторная функция.
>>> from sklearn.metrics import zero_one_loss >>> y_pred = [1, 2, 3, 4] >>> y_true = [2, 2, 3, 4] >>> zero_one_loss(y_true, y_pred) 0.25 >>> zero_one_loss(y_true, y_pred, normalize=False) 1
В случае с несколькими метками с двоичными индикаторами меток, где первый набор меток [0,1] содержит ошибку:
>>> zero_one_loss(np.array([[0, 1], [1, 1]]), np.ones((2, 2))) 0.5 >>> zero_one_loss(np.array([[0, 1], [1, 1]]), np.ones((2, 2)), normalize=False) 1
Пример:
- См. В разделе « Рекурсивное исключение функции с перекрестной проверкой» пример использования нулевой потери для выполнения рекурсивного исключения функции с перекрестной проверкой.
3.3.2.18. Потеря очков по Брайеру
Функция brier_score_loss вычисляет оценку Шиповник для бинарных классов [Brier1950] . Цитата из Википедии:
«Оценка Бриера — это правильная функция оценки, которая измеряет точность вероятностных прогнозов. Это применимо к задачам, в которых прогнозы должны назначать вероятности набору взаимоисключающих дискретных результатов ».
Эта функция возвращает среднеквадратичную ошибку фактического результата. y∈{0,1} и прогнозируемая оценка вероятности $p=Pr(y=1)$ ( pred_proba ) как выведено :
$$BS = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}} — 1}(y_i — p_i)^2$$
Потеря по шкале Бриера также составляет от 0 до 1, и чем ниже значение (средняя квадратичная разница меньше), тем точнее прогноз.
Вот небольшой пример использования этой функции:
>>> import numpy as np >>> from sklearn.metrics import brier_score_loss >>> y_true = np.array([0, 1, 1, 0]) >>> y_true_categorical = np.array(["spam", "ham", "ham", "spam"]) >>> y_prob = np.array([0.1, 0.9, 0.8, 0.4]) >>> y_pred = np.array([0, 1, 1, 0]) >>> brier_score_loss(y_true, y_prob) 0.055 >>> brier_score_loss(y_true, 1 - y_prob, pos_label=0) 0.055 >>> brier_score_loss(y_true_categorical, y_prob, pos_label="ham") 0.055 >>> brier_score_loss(y_true, y_prob > 0.5) 0.0
Балл Бриера можно использовать для оценки того, насколько хорошо откалиброван классификатор. Однако меньшая потеря по шкале Бриера не всегда означает лучшую калибровку. Это связано с тем, что по аналогии с разложением среднеквадратичной ошибки на дисперсию смещения потеря оценки по Бриеру может быть разложена как сумма потерь калибровки и потерь при уточнении [Bella2012]. Потеря калибровки определяется как среднеквадратическое отклонение от эмпирических вероятностей, полученных из наклона ROC-сегментов. Потери при переработке можно определить как ожидаемые оптимальные потери, измеренные по площади под кривой оптимальных затрат. Потери при уточнении могут изменяться независимо от потерь при калибровке, таким образом, более низкие потери по шкале Бриера не обязательно означают более качественную калибровку модели. «Только когда потеря точности остается неизменной, более низкая потеря по шкале Бриера всегда означает лучшую калибровку» [Bella2012] , [Flach2008] .
Пример:
- См. Раздел « Калибровка вероятности классификаторов», где приведен пример использования потерь по шкале Бриера для выполнения калибровки вероятности классификаторов.
Рекомендации:
- Brier1950 Дж. Брайер, Проверка прогнозов, выраженных в терминах вероятности , Ежемесячный обзор погоды 78.1 (1950)
- Bella2012 ( 1 , 2 ) Белла, Ферри, Эрнандес-Оралло и Рамирес-Кинтана «Калибровка моделей машинного обучения» в Хосров-Пур, М. «Машинное обучение: концепции, методологии, инструменты и приложения». Херши, Пенсильвания: Справочник по информационным наукам (2012).
- Flach2008 Флак, Питер и Эдсон Мацубара. «О классификации, ранжировании и оценке вероятности». Дагштульский семинар. Schloss Dagstuhl-Leibniz-Zentrum от Informatik (2008).
3.3.3. Метрики ранжирования с несколькими ярлыками
В многоэлементном обучении с каждой выборкой может быть связано любое количество меток истинности. Цель состоит в том, чтобы дать высокие оценки и более высокий рейтинг наземным лейблам.
3.3.3.1. Ошибка покрытия
Функция coverage_error вычисляет среднее число меток , которые должны быть включены в окончательном предсказании таким образом, что все истинные метки предсказанные. Это полезно, если вы хотите знать, сколько меток с наивысшими баллами вам нужно предсказать в среднем, не пропуская ни одной истинной. Таким образом, наилучшее значение этого показателя — среднее количество истинных ярлыков.
Примечание
Оценка нашей реализации на 1 больше, чем оценка, приведенная в Tsoumakas et al., 2010. Это расширяет ее для обработки вырожденного случая, когда экземпляр имеет 0 истинных меток.
Формально, учитывая двоичную индикаторную матрицу наземных меток истинности $y in left{0, 1right}^{n_text{samples} times n_text{labels}}$ и оценка, связанная с каждой меткой $hat{f} in mathbb{R}^{n_text{samples} times n_text{labels}}$ покрытие определяется как
$$coverage(y, hat{f}) = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}} — 1} max_{j:y_{ij} = 1} text{rank}_{ij}$$
с участием $text{rank}{ij} = left|left{k: hat{f}{ik} geq hat{f}_{ij} right}right|$. Учитывая определение ранга, связи y_scores разрываются путем присвоения максимального ранга, который был бы присвоен всем связанным значениям.
Вот небольшой пример использования этой функции:
>>> import numpy as np >>> from sklearn.metrics import coverage_error >>> y_true = np.array([[1, 0, 0], [0, 0, 1]]) >>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]]) >>> coverage_error(y_true, y_score) 2.5
3.3.3.2. Средняя точность ранжирования метки
В label_ranking_average_precision_score функции реализует маркировать ранжирование средней точности (LRAP). Этот показатель связан с average_precision_score функцией, но основан на понятии ранжирования меток, а не на точности и отзыве.
Средняя точность ранжирования меток (LRAP) усредняет по выборкам ответ на следующий вопрос: для каждой основной метки истинности какая доля меток с более высоким рейтингом была истинной? Этот показатель эффективности будет выше, если вы сможете лучше ранжировать метки, связанные с каждым образцом. Полученная оценка всегда строго больше 0, а наилучшее значение равно 1. Если имеется ровно одна релевантная метка для каждой выборки, средняя точность ранжирования меток эквивалентна среднему обратному рангу .
Формально, учитывая двоичную индикаторную матрицу наземных меток истинности $y in left{0, 1right}^{n_text{samples} times n_text{labels}}$ и оценка, связанная с каждой меткой $hat{f} in mathbb{R}^{n_text{samples} times n_text{labels}}$, средняя точность определяется как
$$LRAP(y, hat{f}) = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}} — 1} frac{1}{||y_i||0} sum{j:y_{ij} = 1} frac{|mathcal{L}{ij}|}{text{rank}{ij}}$$
где $mathcal{L}{ij} = left{k: y{ik} = 1, hat{f}{ik} geq hat{f}{ij} right}$, $text{rank}{ij} = left|left{k: hat{f}{ik} geq hat{f}_{ij} right}right|$, |cdot| вычисляет мощность набора (т. е. количество элементов в наборе), и $||cdot||_0$ это $ell_0$ «Norm» (который вычисляет количество ненулевых элементов в векторе).
Вот небольшой пример использования этой функции:
>>> import numpy as np >>> from sklearn.metrics import label_ranking_average_precision_score >>> y_true = np.array([[1, 0, 0], [0, 0, 1]]) >>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]]) >>> label_ranking_average_precision_score(y_true, y_score) 0.416...
3.3.3.3. Потеря рейтинга
Функция label_ranking_loss вычисляет ранжирование потери , которые в среднем более образцы числа пар меток, которые неправильно упорядочены, т.е. истинные метки имеют более низкую оценку , чем ложные метки, взвешенную по обратной величине числа упорядоченных пар ложных и истинных меток. Наименьшая возможная потеря рейтинга равна нулю.
Формально, учитывая двоичную индикаторную матрицу наземных меток истинности $y in left{0, 1right}^{n_text{samples} times n_text{labels}}$ и оценка, связанная с каждой меткой $hat{f} in mathbb{R}^{n_text{samples} times n_text{labels}}$ потеря ранжирования определяется как
$$ranking_loss(y, hat{f}) = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}} — 1} frac{1}{||y_i||0(ntext{labels} — ||y_i||0)} left|left{(k, l): hat{f}{ik} leq hat{f}{il}, y{ik} = 1, y_{il} = 0 right}right|$$
где $|cdot|$ вычисляет мощность набора (т. е. количество элементов в наборе) и $||cdot||_0$ это $ell_0$ «Norm» (который вычисляет количество ненулевых элементов в векторе).
Вот небольшой пример использования этой функции:
>>> import numpy as np >>> from sklearn.metrics import label_ranking_loss >>> y_true = np.array([[1, 0, 0], [0, 0, 1]]) >>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]]) >>> label_ranking_loss(y_true, y_score) 0.75... >>> # With the following prediction, we have perfect and minimal loss >>> y_score = np.array([[1.0, 0.1, 0.2], [0.1, 0.2, 0.9]]) >>> label_ranking_loss(y_true, y_score) 0.0
Рекомендации:
- Цумакас, Г., Катакис, И., и Влахавас, И. (2010). Майнинг данных с несколькими метками. В справочнике по интеллектуальному анализу данных и открытию знаний (стр. 667-685). Springer США.
3.3.3.4. Нормализованная дисконтированная совокупная прибыль
Дисконтированный совокупный выигрыш (DCG) и Нормализованный дисконтированный совокупный выигрыш (NDCG) — это показатели ранжирования, реализованные в dcg_score и ndcg_score; они сравнивают предсказанный порядок с оценками достоверности, такими как релевантность ответов на запрос.
Со страницы Википедии о дисконтированной совокупной прибыли:
«Дисконтированная совокупная прибыль (DCG) — это показатель качества ранжирования. При поиске информации он часто используется для измерения эффективности алгоритмов поисковой системы или связанных приложений. Используя шкалу градуированной релевантности документов в наборе результатов поисковой системы, DCG измеряет полезность или выгоду документа на основе его позиции в списке результатов. Прирост накапливается сверху вниз в списке результатов, причем прирост каждого результата дисконтируется на более низких уровнях »
DCG упорядочивает истинные цели (например, релевантность ответов на запросы) в предсказанном порядке, затем умножает их на логарифмическое убывание и суммирует результат. Сумма может быть усечена после первогоKрезультатов, и в этом случае мы называем это DCG @ K. NDCG или NDCG @ $K$ — это DCG, деленная на DCG, полученную с помощью точного прогноза, так что оно всегда находится между 0 и 1. Обычно NDCG предпочтительнее DCG.
По сравнению с потерей ранжирования, NDCG может принимать во внимание оценки релевантности, а не ранжирование на основе фактов. Таким образом, если основополагающая информация состоит только из упорядочивания, предпочтение следует отдавать потере ранжирования; если основополагающая информация состоит из фактических оценок полезности (например, 0 для нерелевантного, 1 для релевантного, 2 для очень актуального), можно использовать NDCG.
Для одного образца, учитывая вектор непрерывных значений истинности для каждой цели $y in R^M$, где $M$ это количество выходов, а прогноз $hat{y}$, что индуцирует функцию ранжирования $f$, оценка DCG составляет
$$sum_{r=1}^{min(K, M)}frac{y_{f(r)}}{log(1 + r)}$$
а оценка NDCG — это оценка DCG, деленная на оценку DCG, полученную для $y$.
Рекомендации:
- Запись в Википедии о дисконтированной совокупной прибыли
- Джарвелин, К., и Кекалайнен, Дж. (2002). Оценка IR методов на основе накопленного коэффициента усиления. Транзакции ACM в информационных системах (TOIS), 20 (4), 422-446.
- Ван, Ю., Ван, Л., Ли, Ю., Хе, Д., Чен, В., и Лю, Т. Ю. (2013, май). Теоретический анализ показателей рейтинга NDCG. В материалах 26-й ежегодной конференции по теории обучения (COLT 2013)
- МакШерри Ф. и Наджорк М. (2008, март). Эффективность вычислений при поиске информации измеряется эффективно при наличии связанных оценок. В Европейской конференции по поиску информации (стр. 414-421). Шпрингер, Берлин, Гейдельберг.
3.3.4. Метрики регрессии
В sklearn.metrics модуле реализованы несколько функций потерь, оценки и полезности для измерения эффективности регрессии. Некоторые из них были расширены , чтобы обработать случай multioutput: mean_squared_error, mean_absolute_error, explained_variance_score и r2_score.
У этих функций есть multioutput аргумент ключевого слова, который определяет способ усреднения результатов или проигрышей для каждой отдельной цели. По умолчанию используется значение 'uniform_average', которое определяет равномерно взвешенное среднее значение по выходным данным. Если передается ndarrayформа shape (n_outputs,), то ее записи интерпретируются как веса, и возвращается соответствующее средневзвешенное значение. Если multioutputесть 'raw_values'указан, то все неизменные индивидуальные баллы или потери будут возвращены в массиве формы (n_outputs,).
r2_score и explained_variance_score принять дополнительное значение 'variance_weighted' для multioutput параметра. Эта опция приводит к взвешиванию каждой индивидуальной оценки по дисперсии соответствующей целевой переменной. Этот параметр определяет количественно зафиксированную немасштабированную дисперсию на глобальном уровне. Если целевые переменные имеют разную шкалу, то этот балл придает большее значение хорошему объяснению переменных с более высокой дисперсией. multioutput='variance_weighted' — значение по умолчанию r2_score для обратной совместимости. В будущем это будет изменено на uniform_average.
3.3.4.1. Оценка объясненной дисперсии
explained_variance_score вычисляет объясненной дисперсии регрессии балл.
Если $hat{y}$ — расчетный целевой объем производства, y соответствующий (правильный) целевой результат, и $Var$- Дисперсия , квадрат стандартного отклонения, то объясненная дисперсия оценивается следующим образом:
$$explained_{}variance(y, hat{y}) = 1 — frac{Var{ y — hat{y}}}{Var{y}}$$
Наилучшая возможная оценка — 1.0, более низкие значения — хуже.
Вот небольшой пример использования explained_variance_score функции:
>>> from sklearn.metrics import explained_variance_score >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> explained_variance_score(y_true, y_pred) 0.957... >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> explained_variance_score(y_true, y_pred, multioutput='raw_values') array([0.967..., 1. ]) >>> explained_variance_score(y_true, y_pred, multioutput=[0.3, 0.7]) 0.990...
3.3.4.2. Максимальная ошибка
Функция max_error вычисляет максимальную остаточную ошибку , показатель , который фиксирует худшую ошибку случае между предсказанным значением и истинным значением. В идеально подобранной модели регрессии с одним выходом он max_error будет находиться 0 в обучающем наборе, и хотя это маловероятно в реальном мире, этот показатель показывает степень ошибки, которую имела модель при подборе.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец, и $y_i$ — соответствующее истинное значение, тогда максимальная ошибка определяется как
$$text{Max Error}(y, hat{y}) = max(| y_i — hat{y}_i |)$$
Вот небольшой пример использования функции max_error:
>>> from sklearn.metrics import max_error >>> y_true = [3, 2, 7, 1] >>> y_pred = [9, 2, 7, 1] >>> max_error(y_true, y_pred) 6
max_error не поддерживает multioutput.
3.3.4.3. Средняя абсолютная ошибка
Функция mean_absolute_error вычисляет среднюю абсолютную погрешность , риск метрики , соответствующей ожидаемого значение абсолютной потери или ошибок $l1$-нормальная потеря.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец, и $y_i$ — соответствующее истинное значение, тогда средняя абсолютная ошибка (MAE), оцененная за $n_{samples}$ определяется как
$$text{MAE}(y, hat{y}) = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}}-1} left| y_i — hat{y}_i right|.$$
Вот небольшой пример использования функции mean_absolute_error:
>>> from sklearn.metrics import mean_absolute_error >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> mean_absolute_error(y_true, y_pred) 0.5 >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> mean_absolute_error(y_true, y_pred) 0.75 >>> mean_absolute_error(y_true, y_pred, multioutput='raw_values') array([0.5, 1. ]) >>> mean_absolute_error(y_true, y_pred, multioutput=[0.3, 0.7]) 0.85...
3.3.4.4. Среднеквадратичная ошибка
Функция mean_squared_error вычисляет среднюю квадратическую ошибку , риск метрики , соответствующую ожидаемое значение квадрата (квадратичной) ошибки или потерю.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец, и $y_i$ — соответствующее истинное значение, тогда среднеквадратичная ошибка (MSE), оцененная на $n_{samples}$ определяется как
$$text{MSE}(y, hat{y}) = frac{1}{n_text{samples}} sum_{i=0}^{n_text{samples} — 1} (y_i — hat{y}_i)^2.$$
Вот небольшой пример использования функции mean_squared_error:
>>> from sklearn.metrics import mean_squared_error >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> mean_squared_error(y_true, y_pred) 0.375 >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> mean_squared_error(y_true, y_pred) 0.7083...
Примеры:
- См. В разделе Регрессия повышения градиента пример использования среднеквадратичной ошибки для оценки регрессии повышения градиента.
3.3.4.5. Среднеквадратичная логарифмическая ошибка
Функция mean_squared_log_error вычисляет риск метрики , соответствующий ожидаемому значению квадрата логарифмической (квадратичной) ошибки или потери.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец, и $y_i$ — соответствующее истинное значение, тогда среднеквадратичная логарифмическая ошибка (MSLE), оцененная на $n_{samples}$ определяется как
$$text{MSLE}(y, hat{y}) = frac{1}{n_text{samples}} sum_{i=0}^{n_text{samples} — 1} (log_e (1 + y_i) — log_e (1 + hat{y}_i) )^2.$$
Где $log_e (x)$ означает натуральный логарифм $x$. Эту метрику лучше всего использовать, когда цели имеют экспоненциальный рост, например, численность населения, средние продажи товара в течение нескольких лет и т. Д. Обратите внимание, что эта метрика штрафует за заниженную оценку больше, чем за завышенную оценку.
Вот небольшой пример использования функции mean_squared_log_error:
>>> from sklearn.metrics import mean_squared_log_error >>> y_true = [3, 5, 2.5, 7] >>> y_pred = [2.5, 5, 4, 8] >>> mean_squared_log_error(y_true, y_pred) 0.039... >>> y_true = [[0.5, 1], [1, 2], [7, 6]] >>> y_pred = [[0.5, 2], [1, 2.5], [8, 8]] >>> mean_squared_log_error(y_true, y_pred) 0.044...
3.3.4.6. Средняя абсолютная ошибка в процентах
mean_absolute_percentage_error (MAPE), также известный как среднее абсолютное отклонение в процентах (МАПД), является метрикой для оценки проблем регрессии. Идея этой метрики — быть чувствительной к относительным ошибкам. Например, он не изменяется глобальным масштабированием целевой переменной.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец и $y_i$ — соответствующее истинное значение, тогда средняя абсолютная процентная ошибка (MAPE), оцененная за $n_{samples}$ определяется как
$$text{MAPE}(y, hat{y}) = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}}-1} frac{{}left| y_i — hat{y}_i right|}{max(epsilon, left| y_i right|)}$$
где $epsilon$ — произвольное маленькое, но строго положительное число, чтобы избежать неопределенных результатов, когда y равно нулю.
В функции mean_absolute_percentage_error опоры multioutput.
Вот небольшой пример использования функции mean_absolute_percentage_error:
>>> from sklearn.metrics import mean_absolute_percentage_error >>> y_true = [1, 10, 1e6] >>> y_pred = [0.9, 15, 1.2e6] >>> mean_absolute_percentage_error(y_true, y_pred) 0.2666...
В приведенном выше примере, если бы мы использовали mean_absolute_error, он бы проигнорировал небольшие значения магнитуды и только отразил бы ошибку в предсказании максимального значения магнитуды. Но эта проблема решена в случае MAPE, потому что он вычисляет относительную процентную ошибку по отношению к фактическому выходу.
3.3.4.7. Средняя абсолютная ошибка
Это median_absolute_error особенно интересно, потому что оно устойчиво к выбросам. Убыток рассчитывается путем взятия медианы всех абсолютных различий между целью и прогнозом.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец и $y_i$ — соответствующее истинное значение, тогда средняя абсолютная ошибка (MedAE), оцененная на $n_{samples}$ определяется как
$$text{MedAE}(y, hat{y}) = text{median}(mid y_1 — hat{y}_1 mid, ldots, mid y_n — hat{y}_n mid).$$
median_absolute_error Не поддерживает multioutput.
Вот небольшой пример использования функции median_absolute_error:
>>> from sklearn.metrics import median_absolute_error >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> median_absolute_error(y_true, y_pred) 0.5
3.3.4.8. R² балл, коэффициент детерминации
Функция r2_score вычисляет коэффициент детерминации , как правило , обозначенный как R².
Он представляет собой долю дисперсии (y), которая была объяснена независимыми переменными в модели. Он обеспечивает показатель степени соответствия и, следовательно, меру того, насколько хорошо невидимые выборки могут быть предсказаны моделью через долю объясненной дисперсии.
Поскольку такая дисперсия зависит от набора данных, R² не может быть значимо сопоставимым для разных наборов данных. Наилучшая возможная оценка — 1,0, и она может быть отрицательной (потому что модель может быть произвольно хуже). Постоянная модель, которая всегда предсказывает ожидаемое значение y, игнорируя входные характеристики, получит оценку R² 0,0.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец и $y_i$ соответствующее истинное значение для общего n образцов, расчетный R² определяется как:
$$R^2(y, hat{y}) = 1 — frac{sum_{i=1}^{n} (y_i — hat{y}i)^2}{sum{i=1}^{n} (y_i — bar{y})^2}$$
где $bar{y} = frac{1}{n} sum_{i=1}^{n} y_i$ и $sum_{i=1}^{n} (y_i — hat{y}i)^2 = sum{i=1}^{n} epsilon_i^2$.
Обратите внимание, что r2_score вычисляется нескорректированное R² без поправки на смещение выборочной дисперсии y.
Вот небольшой пример использования функции r2_score:
>>> from sklearn.metrics import r2_score >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> r2_score(y_true, y_pred) 0.948... >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> r2_score(y_true, y_pred, multioutput='variance_weighted') 0.938... >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> r2_score(y_true, y_pred, multioutput='uniform_average') 0.936... >>> r2_score(y_true, y_pred, multioutput='raw_values') array([0.965..., 0.908...]) >>> r2_score(y_true, y_pred, multioutput=[0.3, 0.7]) 0.925...
Пример:
- См. В разделе « Лассо и эластичная сеть для разреженных сигналов» приведен пример использования показателя R² для оценки лассо и эластичной сети для разреженных сигналов.
3.3.4.9. Средние отклонения Пуассона, Гаммы и Твиди
Функция mean_tweedie_deviance вычисляет среднюю ошибку Deviance Tweedie с powerпараметром ($p$). Это показатель, который выявляет прогнозируемые ожидаемые значения целей регрессии.
Существуют следующие особые случаи:
- когда
power=0это эквивалентноmean_squared_error. - когда
power=1это эквивалентноmean_poisson_deviance. - когда
power=2это эквивалентноmean_gamma_deviance.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец и $y_i$ — соответствующее истинное значение, тогда средняя ошибка отклонения Твиди (D) для мощности $p$, оценивается более $n_{samples}$ определяется как
Отклонение от твиди — однородная функция степени 2-power. Таким образом, гамма-распределение power=2 означает, что одновременно масштабируется y_true и y_pred не влияет на отклонение. Для распределения Пуассона power=1 отклонение масштабируется линейно, а для нормального распределения ( power=0) — квадратично. В общем, чем выше, powerтем меньше веса придается крайним отклонениям между истинными и прогнозируемыми целевыми значениями.
Например, давайте сравним два прогноза 1.0 и 100, которые оба составляют 50% от их соответствующего истинного значения.
Среднеквадратичная ошибка ( power=0) очень чувствительна к разнице прогнозов второй точки:
>>> from sklearn.metrics import mean_tweedie_deviance >>> mean_tweedie_deviance([1.0], [1.5], power=0) 0.25 >>> mean_tweedie_deviance([100.], [150.], power=0) 2500.0
Если увеличить powerдо 1:
>>> mean_tweedie_deviance([1.0], [1.5], power=1) 0.18... >>> mean_tweedie_deviance([100.], [150.], power=1) 18.9...
разница в ошибках уменьшается. Наконец, установив power=2:
>>> mean_tweedie_deviance([1.0], [1.5], power=2) 0.14... >>> mean_tweedie_deviance([100.], [150.], power=2) 0.14...
мы получим идентичные ошибки. Таким образом, отклонение when power=2чувствительно только к относительным ошибкам.
3.3.5. Метрики кластеризации
В модуле sklearn.metrics реализованы несколько функций потерь, оценки и полезности. Для получения дополнительной информации см. Раздел « Оценка производительности кластеризации » для кластеризации экземпляров и « Оценка бикластеризации» для бикластеризации.
3.3.6. Фиктивные оценки
При обучении с учителем простая проверка работоспособности состоит из сравнения своей оценки с простыми практическими правилами. DummyClassifier реализует несколько таких простых стратегий классификации:
stratifiedгенерирует случайные прогнозы, соблюдая распределение классов обучающего набора.most_frequentвсегда предсказывает наиболее частую метку в обучающем наборе.priorвсегда предсказывает класс, который максимизирует предыдущий класс (какmost_frequent) иpredict_probaвозвращает предыдущий класс.uniformгенерирует предсказания равномерно в случайном порядке.constantвсегда предсказывает постоянную метку, предоставленную пользователем. Основная мотивация этого метода — оценка F1, когда положительный класс находится в меньшинстве.
Обратите внимание, что со всеми этими стратегиями predict метод полностью игнорирует входные данные!
Для иллюстрации DummyClassifier сначала создадим несбалансированный набор данных:
>>> from sklearn.datasets import load_iris >>> from sklearn.model_selection import train_test_split >>> X, y = load_iris(return_X_y=True) >>> y[y != 1] = -1 >>> X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
Далее сравним точность SVC и most_frequent:
>>> from sklearn.dummy import DummyClassifier >>> from sklearn.svm import SVC >>> clf = SVC(kernel='linear', C=1).fit(X_train, y_train) >>> clf.score(X_test, y_test) 0.63... >>> clf = DummyClassifier(strategy='most_frequent', random_state=0) >>> clf.fit(X_train, y_train) DummyClassifier(random_state=0, strategy='most_frequent') >>> clf.score(X_test, y_test) 0.57...
Мы видим, что SVC это не намного лучше, чем фиктивный классификатор. Теперь давайте изменим ядро:
>>> clf = SVC(kernel='rbf', C=1).fit(X_train, y_train) >>> clf.score(X_test, y_test) 0.94...
Мы видим, что точность увеличена почти до 100%. Для лучшей оценки точности рекомендуется стратегия перекрестной проверки, если она не требует слишком больших затрат на ЦП. Для получения дополнительной информации см. Раздел « Перекрестная проверка: оценка производительности оценщика ». Более того, если вы хотите оптимизировать пространство параметров, настоятельно рекомендуется использовать соответствующую методологию; подробности см. в разделе « Настройка гиперпараметров оценщика ».
В более общем плане, когда точность классификатора слишком близка к случайной, это, вероятно, означает, что что-то пошло не так: функции бесполезны, гиперпараметр настроен неправильно, классификатор страдает от дисбаланса классов и т. Д.
DummyRegressor также реализует четыре простых правила регрессии:
meanвсегда предсказывает среднее значение тренировочных целей.medianвсегда предсказывает медианное значение тренировочных целей.quantileвсегда предсказывает предоставленный пользователем квантиль учебных целей.constantвсегда предсказывает постоянное значение, предоставляемое пользователем.
Во всех этих стратегиях predict метод полностью игнорирует входные данные.
Обновлено: 09.04.2023
Для оценки качества прогноза принято использовать такие характеристики как надёжность, точность, достоверность, ошибки прогноза.
Под надёжностью прогнозных расчётов понимается мера неопределённости поведения объекта прогнозирования во времени.
Достоверность прогноза определяется вероятностью осуществления прогноза для заданного варианта или доверительного интервала.
Точность прогноза характеризует интервальный разброс прогнозных траекторий при фиксированном уровне достоверности.
Ошибки прогноза представляют собой меру отклонения прогнозных оценок от реальных значений состояния прогнозируемого объекта.
Рис. 8. Факторы, влияющие на качество прогноза.
Качество исходной информации, в свою очередь, определяется:
— точностью экономических измерений;
— отсутствием ошибок согласования (данные ошибки возникают в тех случаях, когда исходная информация для проведения прогнозных расчётов подготавливается различными специалистами, использующими разные методологические подходы).
Погрешности, связанные с выбором модели прогноза, возникают в результате упрощения, несовершенства теоретических построений или неадекватности моделей прогнозируемым социально-экономическим процессам. Иногда для прогнозирования процессов, протекающих в нашей стране, используются модели разработанные зарубежными специалистами и хорошо себя зарекомендовавшие для прогнозирования аналогичных процессов в других странах. Однако следует помнить о том, что данные модели могут быть неадекватны социально-экономическим процессам, происходящим в нашей стране и их использование может привести к серьезным ошибкам и просчетам.
Наиболее часто на практике для анализа адекватности модели прогноза исследуемым социально-экономическим процессам используются абсолютные показатели, позволяющие количественно определить величину ошибки моделирования в единицах измерения прогнозируемого объекта. К ним относятся:
— абсолютная ошибка, определяемая как разность между фактическим значением показателя и его расчётным значением ;
— средняя абсолютная ошибка ;
Следует отметить, что абсолютные показатели малопригодны для сравнения и анализа точности моделирования разнородных объектов, так как их значения существенно зависят от масштаба измерения исследуемых явлений. В этих случаях используются относительные показатели:
— средняя относительная ошибка .
Прогнозирование численности населения с помощью методов скользящей средней, наименьших квадратов и экспоненциального сглаживания. Построение графика потребления электроэнергии, определения сезонных колебаний и поквартальный прогноз объема потребления.
| Рубрика | Экономико-математическое моделирование |
| Вид | задача |
| Язык | русский |
| Дата добавления | 30.12.2010 |
| Размер файла | 58,3 K |
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Государственное образовательное учреждение
Высшего профессионального образования
Уральский государственный экономический университет
По дисциплине Прогнозирование национальной экономики
Задание 1. Имеются данные размера ввода в действие общей площади жилых домов в городе за 1989-1999 гг., тыс. м 2
2. Постройте график фактического и расчетных показателей.
3. Рассчитайте ошибки полученных прогнозов при использовании каждого метода.
4. Сравните результаты.
Скользящая средняя (n = 3):
Ввод в действие общей площади жилых домов, тыс. м 2 . Уt
Скользящая средняя m
Расчет средней относительной ошибки |Уф — Ур| Уф * 100
Рис. 1 График фактических (чёрная линия) и расчетных (серая линия) показателей. (Составлено по таблице 1)
Прогноз на 2000 г.: У2000=806,7+(652-865)/3=735,7
Прогноз на 2001 г.: У2001=750,9+(735,7-652)/3=778,8 и т.д. (Таблица 1).
Средняя относительная ошибка: ?=42,6/9=4,7
Метод экспоненциального сглаживания:
Значение параметра сглаживания: 2/(n+1)=2/(11+1)=0,2=0,17
Начальное значение Uo двумя способами:
1 способ (средняя арифметическая): Uo = 16262/11 = 1478,4
2 способ (принимаем первое значение базы прогноза): Uo = 2360
Ввод в действие общей площади жилых домов, тыс. м 2 .
Экспоненциально взвешенная средняя Ut
Расчет средней относительной ошибки
Рис. 2 График фактических и расчетных показателей экспоненциально взвешенных средних 1 и 2 способ. (Составлено по таблице 2, 3)
Экспоненциально взвешенная средняя для каждого года:
U1989 = 2360*0,17+(1-0,17) * 1478,4=1628,272 1 способ
U1989 = 2360*0,17+(1-0,17) * 2360=2360 2 способ
(Остальное приведено в таблице до 2009 года с целью прогноза на 2007, 2008 годы)
Средняя относительная ошибка:
? = 442,945295/11 = 40,27% (1 способ)
? = 563,561351/11 = 51,23% (2 способ)
прогнозирование экспоненциальный сглаживание
Задание 2. Имеются данные потребления электроэнергии в городе за 2003-2006 гг., млн. кВт·ч
1. Постройте график исходных данных и определите наличие сезонных колебаний.
2. Постройте прогноз объема потребления электроэнергии в городе на 2007-2008 гг. с разбивкой по кварталам.
3. Рассчитайте ошибки прогноза.
I 1 = 102,5714108
I 2 = 134,6464502
I 3 = 90,91831558
I 4 = 73,11296966
Средняя относительная ошибка: 297,09/16=18,57%
потребления электроэнергии в городе., млн. кВт*ч Уф
потребления электроэнергии в городе., млн. кВт*ч
Подобные документы
Использование принципа дисконтирования информации в методах статистического прогнозирования. Общая формула расчета экспоненциальной средней. Определение значения параметра сглаживания. Ретроспективный прогноз и средняя квадратическая ошибка отклонений.
реферат [9,8 K], добавлен 16.12.2011
Сущность социально-экономического прогнозирования. Роль сахара в жизни человека. Математический аппарат, используемый при прогнозировании потребления. Регрессионный анализ. Методы наименьших квадратов и моментов. Оценка качества моделей прогнозирования.
курсовая работа [1,5 M], добавлен 26.11.2012
Сущность, содержание и цели экономического прогнозирования. Классификация и обзор базовых методов прогнозирования спроса. Основные показатели динамики экономических процессов. Моделирование сезонных колебаний при использовании фиктивных переменных.
дипломная работа [372,5 K], добавлен 29.11.2014
Основные задачи и принципы экстраполяционного прогнозирования, его методы и модели. Экономическое прогнозирование доходов ООО «Уфа-Аттракцион» с помощью экстраполяционных методов. Анализ особенностей применения метода экспоненциального сглаживания Хольта.
курсовая работа [1,7 M], добавлен 21.02.2015
Планирование деятельности предприятия по производству продуктов питания. Прогнозирование объема продаж продукции на заданный период времени, построение графика изменения, используя метод трехчленной скользящей средней; расчет доверительных интервалов.
контрольная работа [668,5 K], добавлен 02.01.2012
Порядок и особенности расчета прогнозных значений урожайности озимой пшеницы в Волгоградский области. Общая характеристика основных методов прогнозирования — аналитического выравнивания, экспоненциального сглаживания, скользящих средних и рядов Фурье.
контрольная работа [2,3 M], добавлен 11.07.2010
Построение поля корреляции, оценка тесноты связи с помощью показателей корреляции и детерминации, адекватности линейной модели. Статистическая надёжность нелинейных моделей по критерию Фишера. Модель сезонных колебаний и расчёт прогнозных значений.
практическая работа [145,7 K], добавлен 13.05.2014
В каждой формуле буквой Ф обозначено фактическое значение, а буквой П — прогнозное. Каждая ошибка прогнозирования (кроме последней!), может использоваться для нахождения общей точности прогнозирования некоторого списка позиций, по типу того, что изображен ниже (либо для любого другого подобной детализации):
Алгоритм для нахождения любой из ошибок прогнозирования для такого списка примерно одинаковый: сначала находим ошибку прогнозирования по одной позиции, а затем рассчитываем общую. Итак, основные ошибки прогнозирования!
MPE — Mean Percent Error
MPE — средняя процентная ошибка прогнозирования. Основная проблема данной ошибки заключается в том, что в нестабильном числовом ряду с большими выбросами любое незначительное колебание факта или прогноза может значительно поменять показатель ошибки и, как следствие, точности прогнозирования. Помимо этого, ошибка является несимметричной: одинаковые отклонения в плюс и в минус по-разному влияют на показатель ошибки.
- Для каждой позиции рассчитывается ошибка прогноза (из факта вычитается прогноз) — Error
- Для каждой позиции рассчитывается процентная ошибка прогноза (ошибка прогноза делится на фактический показатель) — Percent Error
- Находится среднее арифметическое всех процентных ошибок прогноза (процентные ошибки суммируются и делятся на количество) — Mean Percent Error
MAPE — Mean Absolute Percent Error
MAPE — средняя абсолютная процентная ошибка прогнозирования. Основная проблема данной ошибки такая же, как и у MPE — нестабильность.
- Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта по модулю) — Absolute Error
- Для каждой позиции рассчитывается абсолютная процентная ошибка прогноза (абсолютная ошибка прогноза делится на фактический показатель) — Absolute Percent Error
- Находится среднее арифметическое всех абсолютных процентных ошибок прогноза (абсолютные процентные ошибки суммируются и делятся на количество) — Mean Absolute Percent Error
Вместо среднего арифметического всех абсолютных процентных ошибок прогноза можно использовать медиану числового ряда (MdAPE — Median Absolute Percent Error), она наиболее устойчива к выбросам.
WMAPE / MAD-Mean Ratio / WAPE — Weighted Absolute Percent Error
- Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта, по модулю) — Absolute Error
- Находится сумма всех фактов по всем позициям (общий фактический объем)
- Сумма всех абсолютных ошибок делится на сумму всех фактов — WAPE
Данная ошибка прогнозирования является симметричной и наименее чувствительна к искажениям числового ряда.
Рекомендуется к использованию при расчете точности прогнозирования. Более подробно читать здесь.
RMSE (as %) / nRMSE — Root Mean Square Error
RMSE — среднеквадратичная ошибка прогнозирования. Примерно такая же проблема, как и в MPE и MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня. Но так как MSE дает расчетные единицы измерения в квадрате, то использовать данную ошибку будет немного неправильно.
MASE — Mean Absolute Scaled Error
MASE — средняя абсолютная масштабированная ошибка прогнозирования. Согласно Википедии, является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени.
Важно! Если предыдущие ошибки прогнозирования мы могли использовать для нахождения точности прогнозирования некого списка номенклатур, где каждой из которых соответствует фактическое и прогнозное значение (как было в примере в начале статьи), то данная ошибка для этого не предназначена: MASE используется для расчета точности прогнозирования одной единственной позиции, основываясь на предыдущих показателях факта и прогноза, и чем больше этих показателей, тем более точно мы сможем рассчитать показатель точности. Вероятно, из-за этого ошибка не получила широкого распространения.
Здесь данная формула представлена исключительно для ознакомления и не рекомендуется к использованию.
Суть формулы заключается в нахождении среднего арифметического всех масштабированных ошибок, что при упрощении даст нам следующую конечную формулу:
Также, хочу отметить, что существует ошибка RMMSE (Root Mean Square Scaled Error — Среднеквадратичная масштабированная ошибка), которая примерно похожа на MASE, с теми же преимуществами и недостатками.
Это основные ошибки прогнозирования, которые могут использоваться для расчета точности прогнозирования. Но не все! Их очень много и, возможно, чуть позже я добавлю еще немного информации о некоторых из них. А примеры расчетов уже описанных ошибок прогнозирования будут выложены через некоторое время, пока что я подготавливаю пример, ожидайте.
Работая с научными публикациями, сталкиваюсь с различными показателями ошибок прогнозирования временных рядов. Среди всех встречающихся оценок ошибки прогнозирования стоит отметить две, которые в настоящее время, являются самыми популярными: MAE и MAPE. Пусть ошибка есть разность:
,
где Z(t) – фактическое значение временного ряда, а – прогнозное.
Тогда формулы для оценок ошибки прогнозирования временных рядов для N отчетов можно записать в следующем виде.
MAPE – средняя абсолютная ошибка в процентах
.
Данная оценка применяется для временных рядов, фактические значения которых значительно больше 1. Например, оценки ошибки прогнозирования энергопотребления почти во всех статьях приводятся как значения MAPE.
Если же фактические значения временного ряда близки к 0, то в знаменателе окажется очень маленькое число, что сделает значение MAPE близким к бесконечности – это не совсем корректно. Например, фактическая цена РСВ = 0.01 руб/МВт.ч, a прогнозная = 10 руб/МВт.ч, тогда MAPE = (0.01 – 10)/0.01 = 999%, хотя в действительности мы не так уж сильно ошиблись, всего на 10 руб/МВт.ч. Для рядов, содержащих значения близкие к нулю, применяют следующую оценку ошибки прогноза.
MAE – средняя абсолютная ошибка
.
Для оценки ошибки прогнозирования цен РСВ и индикатора БР корректнее использовать MAE.
Кроме указанных иногда используют другие оценки ошибки, менее популярные, но также применимые. Подробнее об этих оценках ошибки прогноза читайте указанные статьи в Википедии.
MSE – среднеквадратичная ошибка
.
RMSE – квадратный корень из среднеквадратичной ошибки
.
ME – средняя ошибка
.
SD – стандартное отклонение
Связь точности и ошибки прогнозирования
Точность прогнозирования есть понятие прямо противоположное ошибке прогнозирования. Если ошибка прогнозирования велика, то точность мала и наоборот, если ошибка прогнозирования мала, то точность велика. По сути дела оценка ошибки прогноза MAPE есть обратная величина для точности прогнозирования — зависимость здесь простая.
Точность прогноза в % = 100% – MAPE
Величину точности оценивать не принято, говоря о прогнозировании всегда оценивают, то есть определяют значение именно ошибки прогноза, то есть величину MAPE и/или MAE. Однако нужно понимать, что если MAPE = 5%, то точность прогнозирования = 95%. Говоря о высокой точности, мы всегда говорим о низкой ошибки прогноза и в этой области недопонимания быть не должно. Вы практически не найдете материалов о прогнозировании, в которых приведены оценки именно точности прогноза, хотя с точки зрения здравого маркетинга корректней говорить именно о высокой точности. В рекламных статьях всегда будет написано о высокой точности.
При этом величина MAPE является количественной оценкой именно ошибки, и эта величина нам ясно говорит и о точности прогнозирования, исходя из приведенной выше простой формулы. Таким образом, оценивая ошибку, мы всегда оцениваем точность прогнозирования.
Читайте также:
- Аппаратурные методы вольтамперометрии реферат
- Организация самостоятельной деятельности детей реферат
- Реферат шахматы увлекательная игра
- Реферат на тему праздники
- Реферат женщины и насилие
Есть 3 различных API для оценки качества прогнозов модели:
- Метод оценки оценщика : у оценщиков есть
scoreметод, обеспечивающий критерий оценки по умолчанию для проблемы, для решения которой они предназначены. Это обсуждается не на этой странице, а в документации каждого оценщика. - Параметр оценки: инструменты оценки модели с использованием перекрестной проверки (например,
model_selection.cross_val_scoreиmodel_selection.GridSearchCV) полагаются на внутреннюю стратегию оценки . Это обсуждается в разделе Параметр оценки: определение правил оценки модели . - Метрические функции : В
sklearn.metricsмодуле реализованы функции оценки ошибки прогноза для конкретных целей. Эти показатели подробно описаны в разделах по метрикам классификации , MultiLabel ранжирования показателей , показателей регрессии и показателей кластеризации .
Наконец, фиктивные оценки полезны для получения базового значения этих показателей для случайных прогнозов.
3.3.1. В scoring параметрах: определение правил оценки моделей
Выбор и оценка модели с использованием таких инструментов, как model_selection.GridSearchCV и model_selection.cross_val_score, принимают scoring параметр, который контролирует, какую метрику они применяют к оцениваемым оценщикам.
3.3.1.1. Общие случаи: предопределенные значения
Для наиболее распространенных случаев использования вы можете назначить объект подсчета с помощью scoring параметра; в таблице ниже показаны все возможные значения. Все объекты счетчика следуют соглашению о том, что более высокие возвращаемые значения лучше, чем более низкие возвращаемые значения . Таким образом, метрики, которые измеряют расстояние между моделью и данными, например metrics.mean_squared_error, доступны как neg_mean_squared_error, которые возвращают инвертированное значение метрики.
| Подсчет очков | Функция | Комментарий |
| Классификация | ||
| ‘accuracy’ | metrics.accuracy_score |
|
| ‘balanced_accuracy’ | metrics.balanced_accuracy_score |
|
| ‘top_k_accuracy’ | metrics.top_k_accuracy_score |
|
| ‘average_precision’ | metrics.average_precision_score |
|
| ‘neg_brier_score’ | metrics.brier_score_loss |
|
| ‘f1’ | metrics.f1_score |
для двоичных целей |
| ‘f1_micro’ | metrics.f1_score |
микро-усредненный |
| ‘f1_macro’ | metrics.f1_score |
микро-усредненный |
| ‘f1_weighted’ | metrics.f1_score |
средневзвешенное |
| ‘f1_samples’ | metrics.f1_score |
по многопозиционному образцу |
| ‘neg_log_loss’ | metrics.log_loss |
требуетсяpredict_probaподдержка |
| ‘precision’ etc. | metrics.precision_score |
суффиксы применяются как с ‘f1’ |
| ‘recall’ etc. | metrics.recall_score |
суффиксы применяются как с ‘f1’ |
| ‘jaccard’ etc. | metrics.jaccard_score |
суффиксы применяются как с ‘f1’ |
| ‘roc_auc’ | metrics.roc_auc_score |
|
| ‘roc_auc_ovr’ | metrics.roc_auc_score |
|
| ‘roc_auc_ovo’ | metrics.roc_auc_score |
|
| ‘roc_auc_ovr_weighted’ | metrics.roc_auc_score |
|
| ‘roc_auc_ovo_weighted’ | metrics.roc_auc_score |
|
| Кластеризация | ||
| ‘adjusted_mutual_info_score’ | metrics.adjusted_mutual_info_score |
|
| ‘adjusted_rand_score’ | metrics.adjusted_rand_score |
|
| ‘completeness_score’ | metrics.completeness_score |
|
| ‘fowlkes_mallows_score’ | metrics.fowlkes_mallows_score |
|
| ‘homogeneity_score’ | metrics.homogeneity_score |
|
| ‘mutual_info_score’ | metrics.mutual_info_score |
|
| ‘normalized_mutual_info_score’ | metrics.normalized_mutual_info_score |
|
| ‘rand_score’ | metrics.rand_score |
|
| ‘v_measure_score’ | metrics.v_measure_score |
|
| Регрессия | ||
| ‘explained_variance’ | metrics.explained_variance_score |
|
| ‘max_error’ | metrics.max_error |
|
| ‘neg_mean_absolute_error’ | metrics.mean_absolute_error |
|
| ‘neg_mean_squared_error’ | metrics.mean_squared_error |
|
| ‘neg_root_mean_squared_error’ | metrics.mean_squared_error |
|
| ‘neg_mean_squared_log_error’ | metrics.mean_squared_log_error |
|
| ‘neg_median_absolute_error’ | metrics.median_absolute_error |
|
| ‘r2’ | metrics.r2_score |
|
| ‘neg_mean_poisson_deviance’ | metrics.mean_poisson_deviance |
|
| ‘neg_mean_gamma_deviance’ | metrics.mean_gamma_deviance |
|
| ‘neg_mean_absolute_percentage_error’ | metrics.mean_absolute_percentage_error |
Примеры использования:
>>> from sklearn import svm, datasets >>> from sklearn.model_selection import cross_val_score >>> X, y = datasets.load_iris(return_X_y=True) >>> clf = svm.SVC(random_state=0) >>> cross_val_score(clf, X, y, cv=5, scoring='recall_macro') array([0.96..., 0.96..., 0.96..., 0.93..., 1. ]) >>> model = svm.SVC() >>> cross_val_score(model, X, y, cv=5, scoring='wrong_choice') Traceback (most recent call last): ValueError: 'wrong_choice' is not a valid scoring value. Use sorted(sklearn.metrics.SCORERS.keys()) to get valid options.
Примечание
Значения, перечисленные в виде ValueError исключения, соответствуют функциям измерения точности прогнозирования, описанным в следующих разделах. Объекты счетчика для этих функций хранятся в словаре sklearn.metrics.SCORERS.
3.3.1.2. Определение стратегии выигрыша от метрических функций
Модуль sklearn.metrics также предоставляет набор простых функций, измеряющих ошибку предсказания с учетом истинности и предсказания:
- функции, заканчивающиеся на,
_scoreвозвращают значение для максимизации, чем выше, тем лучше. - функции, заканчивающиеся на
_errorили_lossвозвращающие значение, которое нужно минимизировать, чем ниже, тем лучше. При преобразовании в объект счетчика с использованиемmake_scorerустановите дляgreater_is_betterпараметра значениеFalse(Trueпо умолчанию; см. Описание параметра ниже).
Метрики, доступные для различных задач машинного обучения, подробно описаны в разделах ниже.
Многим метрикам не даются имена для использования в качестве scoring значений, иногда потому, что они требуют дополнительных параметров, например fbeta_score. В таких случаях вам необходимо создать соответствующий объект оценки. Самый простой способ создать вызываемый объект для оценки — использовать make_scorer. Эта функция преобразует метрики в вызываемые объекты, которые можно использовать для оценки модели.
Один из типичных вариантов использования — обернуть существующую метрическую функцию из библиотеки значениями, отличными от значений по умолчанию для ее параметров, такими как beta параметр для fbeta_score функции:
>>> from sklearn.metrics import fbeta_score, make_scorer
>>> ftwo_scorer = make_scorer(fbeta_score, beta=2)
>>> from sklearn.model_selection import GridSearchCV
>>> from sklearn.svm import LinearSVC
>>> grid = GridSearchCV(LinearSVC(), param_grid={'C': [1, 10]},
... scoring=ftwo_scorer, cv=5)
Второй вариант использования — создание полностью настраиваемого объекта скоринга из простой функции Python с использованием make_scorer, которая может принимать несколько параметров:
- функция Python, которую вы хотите использовать (
my_custom_loss_funcв примере ниже) - возвращает ли функция Python оценку (
greater_is_better=True, по умолчанию) или потерю (greater_is_better=False). В случае потери результат функции python аннулируется объектом скоринга в соответствии с соглашением о перекрестной проверке, согласно которому скоринтеры возвращают более высокие значения для лучших моделей. - только для показателей классификации: требуется ли для предоставленной вами функции Python постоянная уверенность в принятии решений (
needs_threshold=True). Значение по умолчанию неверно. - любые дополнительные параметры, такие как
betaилиlabelsвf1_score.
Вот пример создания пользовательских счетчиков очков и использования greater_is_better параметра:
>>> import numpy as np >>> def my_custom_loss_func(y_true, y_pred): ... diff = np.abs(y_true - y_pred).max() ... return np.log1p(diff) ... >>> # score will negate the return value of my_custom_loss_func, >>> # which will be np.log(2), 0.693, given the values for X >>> # and y defined below. >>> score = make_scorer(my_custom_loss_func, greater_is_better=False) >>> X = [[1], [1]] >>> y = [0, 1] >>> from sklearn.dummy import DummyClassifier >>> clf = DummyClassifier(strategy='most_frequent', random_state=0) >>> clf = clf.fit(X, y) >>> my_custom_loss_func(y, clf.predict(X)) 0.69... >>> score(clf, X, y) -0.69...
3.3.1.3. Реализация собственного скорингового объекта
Вы можете сгенерировать еще более гибкие модели скоринга, создав свой собственный скоринговый объект с нуля, без использования make_scorer фабрики. Чтобы вызываемый может быть бомбардиром, он должен соответствовать протоколу, указанному в следующих двух правилах:
- Его можно вызвать с параметрами (estimator, X, y), где estimator это модель, которая должна быть оценена, X это данные проверки и y основная истинная цель для (в контролируемом случае) или None (в неконтролируемом случае).
- Он возвращает число с плавающей запятой, которое количественно определяет
estimatorкачество прогнозированияXсо ссылкой наy. Опять же, по соглашению более высокие числа лучше, поэтому, если ваш секретарь сообщает о проигрыше, это значение следует отменить.
Примечание Использование пользовательских счетчиков в функциях, где n_jobs> 1
Хотя определение пользовательской функции оценки вместе с вызывающей функцией должно работать из коробки с бэкэндом joblib по умолчанию (loky), его импорт из другого модуля будет более надежным подходом и будет работать независимо от бэкэнда joblib.
Например, чтобы использовать n_jobsбольше 1 в примере ниже, custom_scoring_function функция сохраняется в созданном пользователем модуле ( custom_scorer_module.py) и импортируется:
>>> from custom_scorer_module import custom_scoring_function >>> cross_val_score(model, ... X_train, ... y_train, ... scoring=make_scorer(custom_scoring_function, greater_is_better=False), ... cv=5, ... n_jobs=-1)
3.3.1.4. Использование множественной метрической оценки
Scikit-learn также позволяет оценивать несколько показателей в GridSearchCV, RandomizedSearchCV и cross_validate.
Есть три способа указать несколько показателей оценки для scoring параметра:
- Как итерация строковых показателей:
>>> scoring = ['accuracy', 'precision']
- В качестве
dictсопоставления имени секретаря с функцией подсчета очков:
>>> from sklearn.metrics import accuracy_score
>>> from sklearn.metrics import make_scorer
>>> scoring = {'accuracy': make_scorer(accuracy_score),
... 'prec': 'precision'}
Обратите внимание, что значения dict могут быть либо функциями счетчика, либо одной из предварительно определенных строк показателей.
- Как вызываемый объект, возвращающий словарь оценок:
>>> from sklearn.model_selection import cross_validate
>>> from sklearn.metrics import confusion_matrix
>>> # A sample toy binary classification dataset
>>> X, y = datasets.make_classification(n_classes=2, random_state=0)
>>> svm = LinearSVC(random_state=0)
>>> def confusion_matrix_scorer(clf, X, y):
... y_pred = clf.predict(X)
... cm = confusion_matrix(y, y_pred)
... return {'tn': cm[0, 0], 'fp': cm[0, 1],
... 'fn': cm[1, 0], 'tp': cm[1, 1]}
>>> cv_results = cross_validate(svm, X, y, cv=5,
... scoring=confusion_matrix_scorer)
>>> # Getting the test set true positive scores
>>> print(cv_results['test_tp'])
[10 9 8 7 8]
>>> # Getting the test set false negative scores
>>> print(cv_results['test_fn'])
[0 1 2 3 2]
3.3.2. Метрики классификации
В sklearn.metrics модуле реализованы несколько функций потерь, оценки и полезности для измерения эффективности классификации. Некоторые метрики могут потребовать оценок вероятности положительного класса, значений достоверности или значений двоичных решений. Большинство реализаций позволяют каждой выборке вносить взвешенный вклад в общую оценку с помощью sample_weight параметра.
Некоторые из них ограничены случаем двоичной классификации:
precision_recall_curve(y_true, probas_pred, *) |
Вычислите пары точности-отзыва для разных пороговых значений вероятности. |
roc_curve(y_true, y_score, *[, pos_label, …]) |
Вычислить рабочую характеристику приемника (ROC). |
det_curve(y_true, y_score[, pos_label, …]) |
Вычислите частоту ошибок для различных пороговых значений вероятности. |
Другие также работают в случае мультикласса:
balanced_accuracy_score(y_true, y_pred, *[, …]) |
Вычислите сбалансированную точность. |
cohen_kappa_score(y1, y2, *[, labels, …]) |
Каппа Коэна: статистика, измеряющая согласованность аннотаторов. |
confusion_matrix(y_true, y_pred, *[, …]) |
Вычислите матрицу неточностей, чтобы оценить точность классификации. |
hinge_loss(y_true, pred_decision, *[, …]) |
Средняя потеря петель (нерегулируемая). |
matthews_corrcoef(y_true, y_pred, *[, …]) |
Вычислите коэффициент корреляции Мэтьюза (MCC). |
roc_auc_score(y_true, y_score, *[, average, …]) |
Вычислить площадь под кривой рабочих характеристик приемника (ROC AUC) по оценкам прогнозов. |
top_k_accuracy_score(y_true, y_score, *[, …]) |
Top-k Рейтинг по классификации точности. |
Некоторые также работают в многоярусном регистре:
accuracy_score(y_true, y_pred, *[, …]) |
Классификационная оценка точности. |
classification_report(y_true, y_pred, *[, …]) |
Создайте текстовый отчет, показывающий основные показатели классификации. |
f1_score(y_true, y_pred, *[, labels, …]) |
Вычислите оценку F1, также известную как сбалансированная оценка F или F-мера. |
fbeta_score(y_true, y_pred, *, beta[, …]) |
Вычислите оценку F-beta. |
hamming_loss(y_true, y_pred, *[, sample_weight]) |
Вычислите среднюю потерю Хэмминга. |
jaccard_score(y_true, y_pred, *[, labels, …]) |
Оценка коэффициента сходства Жаккара. |
log_loss(y_true, y_pred, *[, eps, …]) |
Потеря журнала, также известная как потеря логистики или потеря кросс-энтропии. |
multilabel_confusion_matrix(y_true, y_pred, *) |
Вычислите матрицу неточностей для каждого класса или образца. |
precision_recall_fscore_support(y_true, …) |
Точность вычислений, отзыв, F-мера и поддержка для каждого класса. |
precision_score(y_true, y_pred, *[, labels, …]) |
Вычислите точность. |
recall_score(y_true, y_pred, *[, labels, …]) |
Вычислите отзыв. |
roc_auc_score(y_true, y_score, *[, average, …]) |
Вычислить площадь под кривой рабочих характеристик приемника (ROC AUC) по оценкам прогнозов. |
zero_one_loss(y_true, y_pred, *[, …]) |
Потеря классификации нулевая единица. |
А некоторые работают с двоичными и многозначными (но не мультиклассовыми) проблемами:
В следующих подразделах мы опишем каждую из этих функций, которым будут предшествовать некоторые примечания по общему API и определению показателей.
3.3.2.1. От бинарного до мультиклассового и многозначного
Некоторые метрики по существу определены для задач двоичной классификации (например f1_score, roc_auc_score). В этих случаях по умолчанию оценивается только положительная метка, предполагая по умолчанию, что положительный класс помечен 1 (хотя это можно настроить с помощью pos_label параметра).
При расширении двоичной метрики на задачи с несколькими классами или метками данные обрабатываются как набор двоичных задач, по одной для каждого класса. Затем есть несколько способов усреднить вычисления двоичных показателей по набору классов, каждый из которых может быть полезен в некотором сценарии. Если возможно, вы должны выбрать одно из них с помощью average параметра.
"macro"просто вычисляет среднее значение двоичных показателей, придавая каждому классу одинаковый вес. В задачах, где редкие занятия тем не менее важны, макро-усреднение может быть средством выделения их производительности. С другой стороны, предположение, что все классы одинаково важны, часто неверно, так что макро-усреднение будет чрезмерно подчеркивать обычно низкую производительность для нечастого класса."weighted"учитывает дисбаланс классов, вычисляя среднее значение двоичных показателей, в которых оценка каждого класса взвешивается по его присутствию в истинной выборке данных."micro"дает каждой паре выборка-класс равный вклад в общую метрику (за исключением результата взвешивания выборки). Вместо того, чтобы суммировать метрику для каждого класса, это суммирует дивиденды и делители, составляющие метрики для каждого класса, для расчета общего частного. Микро-усреднение может быть предпочтительным в настройках с несколькими ярлыками, включая многоклассовую классификацию, когда класс большинства следует игнорировать."samples"применяется только к задачам с несколькими ярлыками. Он не вычисляет меру для каждого класса, вместо этого вычисляет метрику по истинным и прогнозируемым классам для каждой выборки в данных оценки и возвращает их (sample_weight— взвешенное) среднее значение.- Выбор
average=Noneвернет массив с оценкой для каждого класса.
В то время как данные мультикласса предоставляются метрике, как двоичные цели, в виде массива меток классов, данные с несколькими метками указываются как индикаторная матрица, в которой ячейка [i, j] имеет значение 1, если у образца i есть метка j, и значение 0 в противном случае.
3.3.2.2. Оценка точности
Функция accuracy_score вычисляет точность , либо фракции ( по умолчанию) или количество (нормализует = False) правильных предсказаний.
В классификации с несколькими ярлыками функция возвращает точность подмножества. Если весь набор предсказанных меток для выборки строго соответствует истинному набору меток, то точность подмножества равна 1,0; в противном случае — 0, 0.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец и $y_i$ — соответствующее истинное значение, тогда доля правильных прогнозов по сравнению с $n_{samples}$ определяется как
$$texttt{accuracy}(y, hat{y}) = frac{1}{n_text{samples}} sum_{i=0}^{n_text{samples}-1} 1(hat{y}_i = y_i)$$
где $1(x)$- индикаторная функция .
>>> import numpy as np >>> from sklearn.metrics import accuracy_score >>> y_pred = [0, 2, 1, 3] >>> y_true = [0, 1, 2, 3] >>> accuracy_score(y_true, y_pred) 0.5 >>> accuracy_score(y_true, y_pred, normalize=False) 2
В многопозиционном корпусе с бинарными индикаторами меток:
>>> accuracy_score(np.array([[0, 1], [1, 1]]), np.ones((2, 2))) 0.5
Пример:
- См. В разделе Проверка с перестановками значимости классификационной оценки пример использования показателя точности с использованием перестановок набора данных.
3.3.2.3. Рейтинг точности Top-k
Функция top_k_accuracy_score представляет собой обобщение accuracy_score. Разница в том, что прогноз считается правильным, если истинная метка связана с одним из kнаивысших прогнозируемых баллов. accuracy_score является частным случаем k = 1.
Функция охватывает случаи двоичной и многоклассовой классификации, но не случай многозначной классификации.
Если $hat{f}_{i,j}$ прогнозируемый класс для $i$-й образец, соответствующий $j$-й по величине прогнозируемый результат и $y_i$ — соответствующее истинное значение, тогда доля правильных прогнозов по сравнению с $n_{samples}$ определяется как
$$texttt{top-k accuracy}(y, hat{f}) = frac{1}{n_text{samples}} sum_{i=0}^{n_text{samples}-1} sum_{j=1}^{k} 1(hat{f}_{i,j} = y_i)$$
где k допустимое количество предположений и 1(x)- индикаторная функция.
>>> import numpy as np >>> from sklearn.metrics import top_k_accuracy_score >>> y_true = np.array([0, 1, 2, 2]) >>> y_score = np.array([[0.5, 0.2, 0.2], ... [0.3, 0.4, 0.2], ... [0.2, 0.4, 0.3], ... [0.7, 0.2, 0.1]]) >>> top_k_accuracy_score(y_true, y_score, k=2) 0.75 >>> # Not normalizing gives the number of "correctly" classified samples >>> top_k_accuracy_score(y_true, y_score, k=2, normalize=False) 3
3.3.2.4. Сбалансированный показатель точности
Функция balanced_accuracy_score вычисляет взвешенную точность , что позволяет избежать завышенных оценок производительности на несбалансированных данных. Это макросреднее количество оценок отзыва по классу или, что то же самое, грубая точность, где каждая выборка взвешивается в соответствии с обратной распространенностью ее истинного класса. Таким образом, для сбалансированных наборов данных оценка равна точности.
В двоичном случае сбалансированная точность равна среднему арифметическому чувствительности (истинно положительный показатель) и специфичности (истинно отрицательный показатель) или площади под кривой ROC с двоичными прогнозами, а не баллами:
$$texttt{balanced-accuracy} = frac{1}{2}left( frac{TP}{TP + FN} + frac{TN}{TN + FP}right )$$
Если классификатор одинаково хорошо работает в любом классе, этот термин сокращается до обычной точности (т. е. Количества правильных прогнозов, деленного на общее количество прогнозов).
Напротив, если обычная точность выше вероятности только потому, что классификатор использует несбалансированный набор тестов, тогда сбалансированная точность, при необходимости, упадет до $frac{1}{n_classes}$.
Оценка варьируется от 0 до 1 или, когда adjusted=True используется, масштабируется до диапазона $frac{1}{1 — n_classes}$ до 1 включительно, с произвольной оценкой 0.
Если yi истинная ценность $i$-й образец, и $w_i$ — соответствующий вес образца, затем мы настраиваем вес образца на:
$$hat{w}_i = frac{w_i}{sum_j{1(y_j = y_i) w_j}}$$
где $1(x)$- индикаторная функция . Учитывая предсказанный $hat{y}_i$ для образца $i$, сбалансированная точность определяется как:
$$texttt{balanced-accuracy}(y, hat{y}, w) = frac{1}{sum{hat{w}_i}} sum_i 1(hat{y}_i = y_i) hat{w}_i$$
С adjusted=True сбалансированной точностью сообщает об относительном увеличении от $texttt{balanced-accuracy}(y, mathbf{0}, w) =frac{1}{n_classes}$. В двоичном случае это также известно как * статистика Юдена * , или информированность .
Примечание
Определение мультикласса здесь кажется наиболее разумным расширением метрики, используемой в бинарной классификации, хотя в литературе нет определенного консенсуса:
- Наше определение: [Mosley2013] , [Kelleher2015] и [Guyon2015] , где [Guyon2015] принимает скорректированную версию, чтобы гарантировать, что случайные предсказания имеют оценку 0 а точные предсказания имеют оценку 1..
- Точность балансировки классов, как описано в [Mosley2013] : вычисляется минимум между точностью и отзывом для каждого класса. Затем эти значения усредняются по общему количеству классов для получения сбалансированной точности.
- Сбалансированная точность, как описано в [Urbanowicz2015] : среднее значение чувствительности и специфичности вычисляется для каждого класса, а затем усредняется по общему количеству классов.
Рекомендации:
- Гийон 2015 ( 1 , 2 ) И. Гайон, К. Беннет, Г. Коули, Х. Дж. Эскаланте, С. Эскалера, Т. К. Хо, Н. Масиа, Б. Рэй, М. Саид, А. Р. Статников, Э. Вьегас, Дизайн конкурса ChaLearn AutoML Challenge 2015 , IJCNN 2015 г.
- Мосли 2013 ( 1 , 2 ) Л. Мосли, Сбалансированный подход к проблеме мультиклассового дисбаланса , IJCV 2010.
- Kelleher2015 Джон. Д. Келлехер, Брайан Мак Нейме, Аойф Д’Арси, Основы машинного обучения для прогнозной аналитики данных: алгоритмы, рабочие примеры и тематические исследования , 2015.
- Урбанович2015 Urbanowicz RJ, Moore, JH ExSTraCS 2.0: описание и оценка масштабируемой системы классификаторов обучения , Evol. Intel. (2015) 8:89.
3.3.2.5. Каппа Коэна
Функция cohen_kappa_score вычисляет каппа-Коэна статистику. Эта мера предназначена для сравнения меток, сделанных разными людьми-аннотаторами, а не классификатором с достоверной информацией.
Показатель каппа (см. Строку документации) представляет собой число от -1 до 1. Баллы выше 0,8 обычно считаются хорошим совпадением; ноль или ниже означает отсутствие согласия (практически случайные метки).
Оценка Каппа может быть вычислена для двоичных или многоклассовых задач, но не для задач с несколькими метками (за исключением ручного вычисления оценки для каждой метки) и не более чем для двух аннотаторов.
>>> from sklearn.metrics import cohen_kappa_score >>> y_true = [2, 0, 2, 2, 0, 1] >>> y_pred = [0, 0, 2, 2, 0, 2] >>> cohen_kappa_score(y_true, y_pred) 0.4285714285714286
3.3.2.6. Матрица неточностей ¶
Точность функции confusion_matrix вычисляет классификацию пути вычисления матрицы путаницы с каждой строкой , соответствующей истинный классом (Википедия и другие ссылки могут использовать различные конвенции для осей).
По определению запись i,j в матрице неточностей — количество наблюдений в группе i, но предполагается, что он будет в группе j. Вот пример:
>>> from sklearn.metrics import confusion_matrix
>>> y_true = [2, 0, 2, 2, 0, 1]
>>> y_pred = [0, 0, 2, 2, 0, 2]
>>> confusion_matrix(y_true, y_pred)
array([[2, 0, 0],
[0, 0, 1],
[1, 0, 2]])
plot_confusion_matrix может использоваться для визуального представления матрицы неточностей, как показано в примере матрицы неточностей, который создает следующий рисунок:
Параметр normalize позволяет сообщать коэффициенты вместо подсчетов. Матрица путаница может быть нормализована в 3 различными способами: 'pred', 'true'и 'all' которые будут делить счетчики на сумму каждого столбца, строки или всей матрицы, соответственно.
>>> y_true = [0, 0, 0, 1, 1, 1, 1, 1]
>>> y_pred = [0, 1, 0, 1, 0, 1, 0, 1]
>>> confusion_matrix(y_true, y_pred, normalize='all')
array([[0.25 , 0.125],
[0.25 , 0.375]])
Для двоичных задач мы можем получить подсчет истинно отрицательных, ложноположительных, ложноотрицательных и истинно положительных результатов следующим образом:
>>> y_true = [0, 0, 0, 1, 1, 1, 1, 1] >>> y_pred = [0, 1, 0, 1, 0, 1, 0, 1] >>> tn, fp, fn, tp = confusion_matrix(y_true, y_pred).ravel() >>> tn, fp, fn, tp (2, 1, 2, 3)
Пример:
- См. В разделе Матрица неточностей пример использования матрицы неточностей для оценки качества выходных данных классификатора.
- См. В разделе Распознавание рукописных цифр пример использования матрицы неточностей для классификации рукописных цифр.
- См. Раздел Классификация текстовых документов с использованием разреженных функций для примера использования матрицы неточностей для классификации текстовых документов.
3.3.2.7. Отчет о классификации
Функция classification_report создает текстовый отчет , показывающий основные показатели классификации. Вот небольшой пример с настраиваемыми target_names и предполагаемыми ярлыками:
>>> from sklearn.metrics import classification_report
>>> y_true = [0, 1, 2, 2, 0]
>>> y_pred = [0, 0, 2, 1, 0]
>>> target_names = ['class 0', 'class 1', 'class 2']
>>> print(classification_report(y_true, y_pred, target_names=target_names))
precision recall f1-score support
class 0 0.67 1.00 0.80 2
class 1 0.00 0.00 0.00 1
class 2 1.00 0.50 0.67 2
accuracy 0.60 5
macro avg 0.56 0.50 0.49 5
weighted avg 0.67 0.60 0.59 5
Пример:
- См. В разделе Распознавание рукописных цифр пример использования отчета о классификации рукописных цифр.
- См. Раздел Классификация текстовых документов с использованием разреженных функций, где приведен пример использования отчета о классификации для текстовых документов.
- См. Раздел « Оценка параметров с использованием поиска по сетке с перекрестной проверкой», где приведен пример использования отчета о классификации для поиска по сетке с вложенной перекрестной проверкой.
3.3.2.8. Потеря Хэмминга
hamming_loss вычисляет среднюю потерю Хэмминга или расстояние Хемминга между двумя наборами образцов.
Если $hat{y}_j$ прогнозируемое значение для $j$-я этикетка данного образца, $y_j$ — соответствующее истинное значение, а $n_{labels}$ — количество классов или меток, то потеря Хэмминга $L_{Hamming}$ между двумя образцами определяется как:
$$L_{Hamming}(y, hat{y}) = frac{1}{n_text{labels}} sum_{j=0}^{n_text{labels} — 1} 1(hat{y}_j not= y_j)$$
где $1(x)$- индикаторная функция .
>>> from sklearn.metrics import hamming_loss >>> y_pred = [1, 2, 3, 4] >>> y_true = [2, 2, 3, 4] >>> hamming_loss(y_true, y_pred) 0.25
В многопозиционном корпусе с бинарными индикаторами меток:
>>> hamming_loss(np.array([[0, 1], [1, 1]]), np.zeros((2, 2))) 0.75
Примечание
В мультиклассовой классификации потери Хэмминга соответствуют расстоянию Хэмминга между y_true и, y_pred что аналогично функции потерь нуля или единицы . Однако, в то время как потеря нуля или единицы наказывает наборы предсказаний, которые не строго соответствуют истинным наборам, потеря Хэмминга наказывает отдельные метки. Таким образом, потеря Хэмминга, ограниченная сверху потерей нуля или единицы, всегда находится между нулем и единицей включительно; и прогнозирование надлежащего подмножества или надмножества истинных меток даст исключительную потерю Хэмминга от нуля до единицы.
3.3.2.9. Точность, отзыв и F-меры
Интуитивно, точность — это способность классификатора не маркировать как положительный образец, который является отрицательным, а отзыв — это способность классификатора находить все положительные образцы.
F-мера ($F_beta$ а также $F_1$ меры) можно интерпретировать как взвешенное гармоническое среднее значение точности и полноты. А $F_beta$ мера достигает своего лучшего значения на уровне 1 и худшего результата на уровне 0. С $beta = 1$, $F_beta$ а также $F_1$ эквивалентны, а отзыв и точность одинаково важны.
precision_recall_curve вычисляет кривую точности-отзыва на основе наземной метки истинности и оценки, полученной классификатором путем изменения порога принятия решения.
Функция average_precision_score вычисляет среднюю точность (AP) от оценки прогнозирования. Значение от 0 до 1 и выше — лучше. AP определяется как
$$text{AP} = sum_n (R_n — R_{n-1}) P_n$$
где $P_n$ а также $R_n$- точность и отзыв на n-м пороге. При случайных прогнозах AP — это доля положительных образцов.
Ссылки [Manning2008] и [Everingham2010] представляют альтернативные варианты AP, которые интерполируют кривую точности-отзыва. В настоящее время average_precision_score не реализован какой-либо вариант с интерполяцией. Ссылки [Davis2006] и [Flach2015] описывают, почему линейная интерполяция точек на кривой точности-отзыва обеспечивает чрезмерно оптимистичный показатель эффективности классификатора. Эта линейная интерполяция используется при вычислении площади под кривой с помощью правила трапеции в auc.
Несколько функций позволяют анализировать точность, отзыв и оценку F-мер:
average_precision_score(y_true, y_score, *) |
Вычислить среднюю точность (AP) из оценок прогнозов. |
f1_score(y_true, y_pred, *[, labels, …]) |
Вычислите оценку F1, также известную как сбалансированная оценка F или F-мера. |
fbeta_score(y_true, y_pred, *, beta[, …]) |
Вычислите оценку F-beta. |
precision_recall_curve(y_true, probas_pred, *) |
Вычислите пары точности-отзыва для разных пороговых значений вероятности. |
precision_recall_fscore_support(y_true, …) |
Точность вычислений, отзыв, F-мера и поддержка для каждого класса. |
precision_score(y_true, y_pred, *[, labels, …]) |
Вычислите точность. |
recall_score(y_true, y_pred, *[, labels, …]) |
Вычислите рекол. |
Обратите внимание, что функция precision_recall_curve ограничена двоичным регистром. Функция average_precision_score работает только в двоичном формате классификации и MultiLabel индикатора. В функции plot_precision_recall_curve графики точности вспомнить следующим образом .
Примеры:
- См. Раздел Классификация текстовых документов с использованием разреженных функций для примера использования
f1_scoreдля классификации текстовых документов. - См. Раздел « Оценка параметров с использованием поиска по сетке с перекрестной проверкой», где приведен пример
precision_scoreиrecall_scoreиспользование для оценки параметров с помощью поиска по сетке с вложенной перекрестной проверкой. - См. В разделе Precision-Recall пример использования
precision_recall_curveдля оценки качества вывода классификатора.
Рекомендации:
- [Manning2008] г. CD Manning, P. Raghavan, H. Schütze, Introduction to Information Retrieval , 2008.
- [Everingham2010] М. Эверингем, Л. Ван Гул, CKI Уильямс, Дж. Винн, А. Зиссерман, Задача классов визуальных объектов Pascal (VOC) , IJCV 2010.
- [Davis2006] Дж. Дэвис, М. Гоадрич, Взаимосвязь между точным воспроизведением и кривыми ROC , ICML 2006.
- [Flach2015] П.А. Флэч, М. Кулл, Кривые точности-отзыва-выигрыша: PR-анализ выполнен правильно , NIPS 2015.
3.3.2.9.1. Бинарная классификация
В задаче бинарной классификации термины «положительный» и «отрицательный» относятся к предсказанию классификатора, а термины «истинный» и «ложный» относятся к тому, соответствует ли этот прогноз внешнему суждению ( иногда известное как «наблюдение»). Учитывая эти определения, мы можем сформулировать следующую таблицу:
| Фактический класс (наблюдение) | ||
| Прогнозируемый класс (ожидание) | tp (истинно положительный результат) Правильный результат | fp (ложное срабатывание) Неожиданный результат |
| Прогнозируемый класс (ожидание) | fn (ложноотрицательный) Отсутствует результат | tn (истинно отрицательное) Правильное отсутствие результата |
В этом контексте мы можем определить понятия точности, отзыва и F-меры:
$$text{precision} = frac{tp}{tp + fp},$$
$$text{recall} = frac{tp}{tp + fn},$$
$$F_beta = (1 + beta^2) frac{text{precision} times text{recall}}{beta^2 text{precision} + text{recall}}.$$
Вот несколько небольших примеров бинарной классификации:
>>> from sklearn import metrics >>> y_pred = [0, 1, 0, 0] >>> y_true = [0, 1, 0, 1] >>> metrics.precision_score(y_true, y_pred) 1.0 >>> metrics.recall_score(y_true, y_pred) 0.5 >>> metrics.f1_score(y_true, y_pred) 0.66... >>> metrics.fbeta_score(y_true, y_pred, beta=0.5) 0.83... >>> metrics.fbeta_score(y_true, y_pred, beta=1) 0.66... >>> metrics.fbeta_score(y_true, y_pred, beta=2) 0.55... >>> metrics.precision_recall_fscore_support(y_true, y_pred, beta=0.5) (array([0.66..., 1. ]), array([1. , 0.5]), array([0.71..., 0.83...]), array([2, 2])) >>> import numpy as np >>> from sklearn.metrics import precision_recall_curve >>> from sklearn.metrics import average_precision_score >>> y_true = np.array([0, 0, 1, 1]) >>> y_scores = np.array([0.1, 0.4, 0.35, 0.8]) >>> precision, recall, threshold = precision_recall_curve(y_true, y_scores) >>> precision array([0.66..., 0.5 , 1. , 1. ]) >>> recall array([1. , 0.5, 0.5, 0. ]) >>> threshold array([0.35, 0.4 , 0.8 ]) >>> average_precision_score(y_true, y_scores) 0.83...
3.3.2.9.2. Мультиклассовая и многозначная классификация
В задаче классификации по нескольким классам и меткам понятия точности, отзыва и F-меры могут применяться к каждой метке независимо. Есть несколько способов , чтобы объединить результаты по этикеткам, указанных в average аргументе к average_precision_score (MultiLabel только) f1_score, fbeta_score, precision_recall_fscore_support, precision_score и recall_score функция, как описано выше . Обратите внимание, что если включены все метки, «микро» -усреднение в настройке мультикласса обеспечит точность, отзыв и $F$ все они идентичны по точности. Также обратите внимание, что «взвешенное» усреднение может дать оценку F, которая не находится между точностью и отзывом.
Чтобы сделать это более явным, рассмотрим следующие обозначения:
- $y$ набор предсказанных ($sample$, $label$) пары
- $hat{y}$ набор истинных ($sample$, $label$) пары
- $L$ набор лейблов
- $S$ набор образцов
- $y_s$ подмножество $y$ с образцом $s$, т.е $y_s := left{(s’, l) in y | s’ = sright}$.
- $y_l$ подмножество $y$ с этикеткой $l$
- по аналогии, $hat{y}_s$ а также $hat{y}_l$ являются подмножествами $hat{y}$
- $P(A, B) := frac{left| A cap B right|}{left|Aright|}$ для некоторых наборов $A$ и $B$
- $R(A, B) := frac{left| A cap B right|}{left|Bright|}$ (Условные обозначения различаются в зависимости от обращения $B = emptyset$; эта реализация использует $R(A, B):=0$, и аналогичные для $P$.)
- $$F_beta(A, B) := left(1 + beta^2right) frac{P(A, B) times R(A, B)}{beta^2 P(A, B) + R(A, B)}$$
Тогда показатели определяются как:
| average | Точность | Отзывать | F_beta |
| «micro» | $P(y, hat{y})$ | $R(y, hat{y})$ | $F_beta(y, hat{y})$ |
| «samples» | $frac{1}{left|Sright|} sum_{s in S} P(y_s, hat{y}_s)$ | $frac{1}{left|Sright|} sum_{s in S} R(y_s, hat{y}_s)$ | $frac{1}{left|Sright|} sum_{s in S} F_beta(y_s, hat{y}_s)$ |
| «macro» | $frac{1}{left|Lright|} sum_{l in L} P(y_l, hat{y}_l)$ | $frac{1}{left|Lright|} sum_{l in L} R(y_l, hat{y}_l)$ | $frac{1}{left|Lright|} sum_{l in L} F_beta(y_l, hat{y}_l)$ |
| «weighted» | $frac{1}{sum_{l in L} left|hat{y}lright|} sum{l in L} left|hat{y}_lright| P(y_l, hat{y}_l)$ | $frac{1}{sum_{l in L} left|hat{y}lright|} sum{l in L} left|hat{y}_lright| R(y_l, hat{y}_l)$ | $frac{1}{sum_{l in L} left|hat{y}lright|} sum{l in L} left|hat{y}lright| Fbeta(y_l, hat{y}_l)$ |
| None | $langle P(y_l, hat{y}_l) | l in L rangle$ | $langle R(y_l, hat{y}_l) | l in L rangle$ | $langle F_beta(y_l, hat{y}_l) | l in L rangle$ |
>>> from sklearn import metrics >>> y_true = [0, 1, 2, 0, 1, 2] >>> y_pred = [0, 2, 1, 0, 0, 1] >>> metrics.precision_score(y_true, y_pred, average='macro') 0.22... >>> metrics.recall_score(y_true, y_pred, average='micro') 0.33... >>> metrics.f1_score(y_true, y_pred, average='weighted') 0.26... >>> metrics.fbeta_score(y_true, y_pred, average='macro', beta=0.5) 0.23... >>> metrics.precision_recall_fscore_support(y_true, y_pred, beta=0.5, average=None) (array([0.66..., 0. , 0. ]), array([1., 0., 0.]), array([0.71..., 0. , 0. ]), array([2, 2, 2]...))
Для мультиклассовой классификации с «отрицательным классом» можно исключить некоторые метки:
>>> metrics.recall_score(y_true, y_pred, labels=[1, 2], average='micro') ... # excluding 0, no labels were correctly recalled 0.0
Точно так же метки, отсутствующие в выборке данных, могут учитываться при макро-усреднении.
>>> metrics.precision_score(y_true, y_pred, labels=[0, 1, 2, 3], average='macro') 0.166...
3.3.2.10. Оценка коэффициента сходства Жаккара
Функция jaccard_score вычисляет среднее значение коэффициентов сходства Jaccard , также называемый индексом Jaccard, между парами множеств меток.
Коэффициент подобия Жаккара i-ые образцы, с набором меток наземной достоверности yi и прогнозируемый набор меток y^i, определяется как
$$J(y_i, hat{y}_i) = frac{|y_i cap hat{y}_i|}{|y_i cup hat{y}_i|}.$$
jaccard_score работает как precision_recall_fscore_support наивно установленная мера, применяемая изначально к бинарным целям, и расширена для применения к множественным меткам и мультиклассам за счет использования average(см. выше ).
В двоичном случае:
>>> import numpy as np >>> from sklearn.metrics import jaccard_score >>> y_true = np.array([[0, 1, 1], ... [1, 1, 0]]) >>> y_pred = np.array([[1, 1, 1], ... [1, 0, 0]]) >>> jaccard_score(y_true[0], y_pred[0]) 0.6666...
В многопозиционном корпусе с бинарными индикаторами меток:
>>> jaccard_score(y_true, y_pred, average='samples') 0.5833... >>> jaccard_score(y_true, y_pred, average='macro') 0.6666... >>> jaccard_score(y_true, y_pred, average=None) array([0.5, 0.5, 1. ])
Задачи с несколькими классами преобразуются в двоичную форму и обрабатываются как соответствующая задача с несколькими метками:
>>> y_pred = [0, 2, 1, 2] >>> y_true = [0, 1, 2, 2] >>> jaccard_score(y_true, y_pred, average=None) array([1. , 0. , 0.33...]) >>> jaccard_score(y_true, y_pred, average='macro') 0.44... >>> jaccard_score(y_true, y_pred, average='micro') 0.33...
3.3.2.11. Петля лосс
Функция hinge_loss вычисляет среднее расстояние между моделью и данными с использованием петля лосс, односторонний показателем , который учитывает только ошибки прогнозирования. (Потери на шарнирах используются в классификаторах максимальной маржи, таких как опорные векторные машины.)
Если метки закодированы с помощью +1 и -1, $y$: истинное значение, а $w$ — прогнозируемые решения на выходе decision_function, тогда потери на шарнирах определяются как:
$$L_text{Hinge}(y, w) = maxleft{1 — wy, 0right} = left|1 — wyright|_+$$
Если имеется более двух ярлыков, hinge_loss используется мультиклассовый вариант, разработанный Crammer & Singer. Вот статья, описывающая это.
Если $y_w$ прогнозируемое решение для истинного лейбла и $y_t$ — это максимум предсказанных решений для всех других меток, где предсказанные решения выводятся функцией принятия решений, тогда потеря шарнира в нескольких классах определяется следующим образом:
$$L_text{Hinge}(y_w, y_t) = maxleft{1 + y_t — y_w, 0right}$$
Вот небольшой пример, демонстрирующий использование hinge_loss функции с классификатором svm в задаче двоичного класса:
>>> from sklearn import svm >>> from sklearn.metrics import hinge_loss >>> X = [[0], [1]] >>> y = [-1, 1] >>> est = svm.LinearSVC(random_state=0) >>> est.fit(X, y) LinearSVC(random_state=0) >>> pred_decision = est.decision_function([[-2], [3], [0.5]]) >>> pred_decision array([-2.18..., 2.36..., 0.09...]) >>> hinge_loss([-1, 1, 1], pred_decision) 0.3...
Вот пример, демонстрирующий использование hinge_loss функции с классификатором svm в мультиклассовой задаче:
>>> X = np.array([[0], [1], [2], [3]]) >>> Y = np.array([0, 1, 2, 3]) >>> labels = np.array([0, 1, 2, 3]) >>> est = svm.LinearSVC() >>> est.fit(X, Y) LinearSVC() >>> pred_decision = est.decision_function([[-1], [2], [3]]) >>> y_true = [0, 2, 3] >>> hinge_loss(y_true, pred_decision, labels) 0.56...
3.3.2.12. Лог лосс
Лог лосс, также называемые потерями логистической регрессии или кросс-энтропийными потерями, определяются на основе оценок вероятности. Он обычно используется в (полиномиальной) логистической регрессии и нейронных сетях, а также в некоторых вариантах максимизации ожидания и может использоваться для оценки выходов вероятности ( predict_proba) классификатора вместо его дискретных прогнозов.
Для двоичной классификации с истинной меткой $y in {0,1}$ и оценка вероятности $p = operatorname{Pr}(y = 1)$, логарифмическая потеря на выборку представляет собой отрицательную логарифмическую вероятность классификатора с истинной меткой:
$$L_{log}(y, p) = -log operatorname{Pr}(y|p) = -(y log (p) + (1 — y) log (1 — p))$$
Это распространяется на случай мультикласса следующим образом. Пусть истинные метки для набора выборок будут закодированы размером 1 из K как двоичная индикаторная матрица $Y$, т.е. $y_{i,k}=1$ если образец $i$ есть ярлык $k$ взят из набора $K$ этикетки. Пусть $P$ — матрица оценок вероятностей, с $p_{i,k} = operatorname{Pr}(y_{i,k} = 1)$. Тогда потеря журнала всего набора равна
$$L_{log}(Y, P) = -log operatorname{Pr}(Y|P) = — frac{1}{N} sum_{i=0}^{N-1} sum_{k=0}^{K-1} y_{i,k} log p_{i,k}$$
Чтобы увидеть, как это обобщает приведенную выше потерю двоичного журнала, обратите внимание, что в двоичном случае $p_{i,0} = 1 — p_{i,1}$ и $y_{i,0} = 1 — y_{i,1}$, поэтому разложив внутреннюю сумму на $y_{i,k} in {0,1}$ дает двоичную потерю журнала.
В log_loss функции вычисляет журнал потеря дана список меток приземной истины и матриц вероятностей, возвращенный оценщик predict_proba методом.
>>> from sklearn.metrics import log_loss >>> y_true = [0, 0, 1, 1] >>> y_pred = [[.9, .1], [.8, .2], [.3, .7], [.01, .99]] >>> log_loss(y_true, y_pred) 0.1738...
Первое [.9, .1] в y_pred означает 90% вероятность того, что первая выборка будет иметь метку 0. Лог лос неотрицательны.
3.3.2.13. Коэффициент корреляции Мэтьюза
Функция matthews_corrcoef вычисляет коэффициент корреляции Матфея (MCC) для двоичных классов. Цитата из Википедии:
«Коэффициент корреляции Мэтьюза используется в машинном обучении как мера качества двоичных (двухклассных) классификаций. Он учитывает истинные и ложные положительные и отрицательные результаты и обычно рассматривается как сбалансированная мера, которую можно использовать, даже если классы очень разных размеров. MCC — это, по сути, значение коэффициента корреляции между -1 и +1. Коэффициент +1 представляет собой идеальное предсказание, 0 — среднее случайное предсказание и -1 — обратное предсказание. Статистика также известна как коэффициент фи ».
В бинарном (двухклассовом) случае $tp$, $tn$, $fp$ а также $fn$ являются соответственно количеством истинно положительных, истинно отрицательных, ложноположительных и ложноотрицательных результатов, MCC определяется как
$$MCC = frac{tp times tn — fp times fn}{sqrt{(tp + fp)(tp + fn)(tn + fp)(tn + fn)}}.$$
В случае мультикласса коэффициент корреляции Мэтьюза может быть определен в терминах confusion_matrix C для Kклассы. Чтобы упростить определение, рассмотрим следующие промежуточные переменные:
- $t_k=sum_{i}^{K} C_{ik}$ количество занятий k действительно произошло,
- $p_k=sum_{i}^{K} C_{ki}$ количество занятий k был предсказан,
- $c=sum_{k}^{K} C_{kk}$ общее количество правильно спрогнозированных образцов,
- $s=sum_{i}^{K} sum_{j}^{K} C_{ij}$ общее количество образцов.
Тогда мультиклассовый MCC определяется как:
$$MCC = frac{ c times s — sum_{k}^{K} p_k times t_k }{sqrt{ (s^2 — sum_{k}^{K} p_k^2) times (s^2 — sum_{k}^{K} t_k^2) }}$$
Когда имеется более двух меток, значение MCC больше не будет находиться в диапазоне от -1 до +1. Вместо этого минимальное значение будет где-то между -1 и 0 в зависимости от количества и распределения наземных истинных меток. Максимальное значение всегда +1.
Вот небольшой пример, иллюстрирующий использование matthews_corrcoef функции:
>>> from sklearn.metrics import matthews_corrcoef >>> y_true = [+1, +1, +1, -1] >>> y_pred = [+1, -1, +1, +1] >>> matthews_corrcoef(y_true, y_pred) -0.33...
3.3.2.14. Матрица путаницы с несколькими метками
Функция multilabel_confusion_matrix вычисляет класс-накрест ( по умолчанию) или samplewise (samplewise = True) MultiLabel матрицы спутанности для оценки точности классификации. Multilabel_confusion_matrix также обрабатывает данные мультикласса, как если бы они были многоклассовыми, поскольку это преобразование, обычно применяемое для оценки проблем мультикласса с метриками двоичной классификации (такими как точность, отзыв и т. д.).
При вычислении классовой матрицы путаницы с несколькими метками $C$, количество истинных негативов для класса i является $C_{i,0,0}$, ложноотрицательные $C_{i,1,0}$, истинные положительные стороны $C_{i,1,1}$ а ложные срабатывания $C_{i,0,1}$.
Вот пример, демонстрирующий использование multilabel_confusion_matrix функции с вводом многозначной индикаторной матрицы:
>>> import numpy as np
>>> from sklearn.metrics import multilabel_confusion_matrix
>>> y_true = np.array([[1, 0, 1],
... [0, 1, 0]])
>>> y_pred = np.array([[1, 0, 0],
... [0, 1, 1]])
>>> multilabel_confusion_matrix(y_true, y_pred)
array([[[1, 0],
[0, 1]],
[[1, 0],
[0, 1]],
[[0, 1],
[1, 0]]])
Или можно построить матрицу неточностей для каждой метки образца:
>>> multilabel_confusion_matrix(y_true, y_pred, samplewise=True)
array([[[1, 0],
[1, 1]],
[[1, 1],
[0, 1]]])
Вот пример, демонстрирующий использование multilabel_confusion_matrix функции с многоклассовым вводом:
>>> y_true = ["cat", "ant", "cat", "cat", "ant", "bird"]
>>> y_pred = ["ant", "ant", "cat", "cat", "ant", "cat"]
>>> multilabel_confusion_matrix(y_true, y_pred,
... labels=["ant", "bird", "cat"])
array([[[3, 1],
[0, 2]],
[[5, 0],
[1, 0]],
[[2, 1],
[1, 2]]])
Вот несколько примеров, демонстрирующих использование multilabel_confusion_matrix функции для расчета отзыва (или чувствительности), специфичности, количества выпадений и пропусков для каждого класса в задаче с вводом многозначной индикаторной матрицы.
Расчет отзыва (также называемого истинно положительным коэффициентом или чувствительностью) для каждого класса:
>>> y_true = np.array([[0, 0, 1], ... [0, 1, 0], ... [1, 1, 0]]) >>> y_pred = np.array([[0, 1, 0], ... [0, 0, 1], ... [1, 1, 0]]) >>> mcm = multilabel_confusion_matrix(y_true, y_pred) >>> tn = mcm[:, 0, 0] >>> tp = mcm[:, 1, 1] >>> fn = mcm[:, 1, 0] >>> fp = mcm[:, 0, 1] >>> tp / (tp + fn) array([1. , 0.5, 0. ])
Расчет специфичности (также называемой истинно отрицательной ставкой) для каждого класса:
>>> tn / (tn + fp) array([1. , 0. , 0.5])
Расчет количества выпадений (также называемый частотой ложных срабатываний) для каждого класса:
>>> fp / (fp + tn) array([0. , 1. , 0.5])
Расчет процента промахов (также называемого ложноотрицательным показателем) для каждого класса:
>>> fn / (fn + tp) array([0. , 0.5, 1. ])
3.3.2.15. Рабочая характеристика приемника (ROC)
Функция roc_curve вычисляет рабочую характеристическую кривую приемника или кривую ROC . Цитата из Википедии:
«Рабочая характеристика приемника (ROC), или просто кривая ROC, представляет собой графический график, который иллюстрирует работу системы двоичного классификатора при изменении ее порога дискриминации. Он создается путем построения графика доли истинных положительных результатов из положительных (TPR = частота истинных положительных результатов) по сравнению с долей ложных положительных результатов из отрицательных (FPR = частота ложных положительных результатов) при различных настройках пороговых значений. TPR также известен как чувствительность, а FPR — это единица минус специфичность или истинно отрицательный показатель ».
Для этой функции требуется истинное двоичное значение и целевые баллы, которые могут быть либо оценками вероятности положительного класса, либо значениями достоверности, либо двоичными решениями. Вот небольшой пример использования roc_curve функции:
>>> import numpy as np >>> from sklearn.metrics import roc_curve >>> y = np.array([1, 1, 2, 2]) >>> scores = np.array([0.1, 0.4, 0.35, 0.8]) >>> fpr, tpr, thresholds = roc_curve(y, scores, pos_label=2) >>> fpr array([0. , 0. , 0.5, 0.5, 1. ]) >>> tpr array([0. , 0.5, 0.5, 1. , 1. ]) >>> thresholds array([1.8 , 0.8 , 0.4 , 0.35, 0.1 ])
На этом рисунке показан пример такой кривой ROC:
Функция roc_auc_score вычисляет площадь под операционной приемника характеристика (ROC) кривой, которая также обозначается через ППК или AUROC. При вычислении площади под кривой roc информация о кривой суммируется в одном номере. Для получения дополнительной информации см. Статью в Википедии о AUC.
По сравнению с такими показателями, как точность подмножества, потеря Хэмминга или оценка F1, ROC не требует оптимизации порога для каждой метки.
3.3.2.15.1. Двоичный регистр
В двоичном случае вы можете либо предоставить оценки вероятности, используя classifier.predict_proba() метод, либо значения решения без пороговых значений, заданные classifier.decision_function() методом. В случае предоставления оценок вероятности следует указать вероятность класса с «большей меткой». «Большая метка» соответствует classifier.classes_[1] и, следовательно classifier.predict_proba(X) [:, 1]. Следовательно, параметр y_score имеет размер (n_samples,).
>>> from sklearn.datasets import load_breast_cancer >>> from sklearn.linear_model import LogisticRegression >>> from sklearn.metrics import roc_auc_score >>> X, y = load_breast_cancer(return_X_y=True) >>> clf = LogisticRegression(solver="liblinear").fit(X, y) >>> clf.classes_ array([0, 1])
Мы можем использовать оценки вероятностей, соответствующие clf.classes_[1].
>>> y_score = clf.predict_proba(X)[:, 1] >>> roc_auc_score(y, y_score) 0.99...
В противном случае мы можем использовать значения решения без порога.
>>> roc_auc_score(y, clf.decision_function(X)) 0.99...
3.3.2.15.2. Мультиклассовый кейс
Функция roc_auc_score также может быть использована в нескольких классах классификации . В настоящее время поддерживаются две стратегии усреднения: алгоритм «один против одного» вычисляет среднее попарных оценок AUC ROC, а алгоритм «один против остальных» вычисляет среднее значение оценок ROC AUC для каждого класса по сравнению со всеми другими классами. В обоих случаях предсказанные метки предоставляются в виде массива со значениями от 0 до n_classes, а оценки соответствуют оценкам вероятности того, что выборка принадлежит определенному классу. Алгоритмы OvO и OvR поддерживают равномерное взвешивание ( average='macro') и по распространенности ( average='weighted').
Алгоритм «один против одного» : вычисляет средний AUC всех возможных попарных комбинаций классов. [HT2001] определяет метрику AUC мультикласса, взвешенную равномерно:
$$frac{1}{c(c-1)}sum_{j=1}^{c}sum_{k > j}^c (text{AUC}(j | k) + text{AUC}(k | j))$$
где $c$ количество классов и $text{AUC}(j | k)$ AUC с классом $j$ как положительный класс и класс $k$ как отрицательный класс. В общем, $text{AUC}(j | k) neq text{AUC}(k | j))$ в случае мультикласса. Этот алгоритм используется, установив аргумент ключевого слова , multiclass чтобы 'ovo' и average в 'macro'.
[HT2001] мультиклассируют AUC метрика может быть расширена , чтобы быть взвешены по распространенности:
$$frac{1}{c(c-1)}sum_{j=1}^{c}sum_{k > j}^c p(j cup k)( text{AUC}(j | k) + text{AUC}(k | j))$$
где cколичество классов. Этот алгоритм используется, установив аргумент ключевого слова , multiclass чтобы 'ovo' и average в 'weighted'. В 'weighted' опции возвращает распространенность усредненные , как описано в [FC2009] .
Алгоритм «один против остальных» : вычисляет AUC каждого класса относительно остальных [PD2000] . Алгоритм функционально такой же, как и в случае с несколькими этикетками. Чтобы включить этот алгоритм, установите для аргумента ключевого слова multiclass значение 'ovr'. Как и OvO, OvR поддерживает два типа усреднения: 'macro' [F2006] и 'weighted' [F2001] .
В приложениях , где высокий процент ложных срабатываний не терпимый параметр max_fpr из roc_auc_score может быть использовано , чтобы суммировать кривую ROC до заданного предела.
3.3.2.15.3. Кейс с несколькими метками
В классификации несколько меток, функция roc_auc_score распространяются путем усреднения меток , как выше . В этом случае вы должны указать y_score форму . Таким образом, при использовании оценок вероятности необходимо выбрать вероятность класса с большей меткой для каждого выхода.(n_samples, n_classes)
>>> from sklearn.datasets import make_multilabel_classification >>> from sklearn.multioutput import MultiOutputClassifier >>> X, y = make_multilabel_classification(random_state=0) >>> inner_clf = LogisticRegression(solver="liblinear", random_state=0) >>> clf = MultiOutputClassifier(inner_clf).fit(X, y) >>> y_score = np.transpose([y_pred[:, 1] for y_pred in clf.predict_proba(X)]) >>> roc_auc_score(y, y_score, average=None) array([0.82..., 0.86..., 0.94..., 0.85... , 0.94...])
И значения решений не требуют такой обработки.
>>> from sklearn.linear_model import RidgeClassifierCV >>> clf = RidgeClassifierCV().fit(X, y) >>> y_score = clf.decision_function(X) >>> roc_auc_score(y, y_score, average=None) array([0.81..., 0.84... , 0.93..., 0.87..., 0.94...])
Примеры:
- См. В разделе « Рабочие характеристики приемника» (ROC) пример использования ROC для оценки качества выходных данных классификатора.
- См. В разделе « Рабочие характеристики приемника» (ROC) с перекрестной проверкой пример использования ROC для оценки качества выходных данных классификатора с помощью перекрестной проверки.
- См. В разделе Моделирование распределения видов пример использования ROC для моделирования распределения видов.
- HT2001 ( 1 , 2 ) Рука, DJ и Тилль, RJ, (2001). Простое обобщение области под кривой ROC для задач классификации нескольких классов. Машинное обучение, 45 (2), стр. 171-186.
- FC2009 Ферри, Сезар и Эрнандес-Оралло, Хосе и Модройу, Р. (2009). Экспериментальное сравнение показателей эффективности для классификации. Письма о распознавании образов. 30. 27-38.
- PD2000 Провост Ф., Домингос П. (2000). Хорошо обученные ПЭТ: Улучшение деревьев оценки вероятностей (Раздел 6.2), Рабочий документ CeDER № IS-00-04, Школа бизнеса Стерна, Нью-Йоркский университет.
- F2006 Фосетт, Т., 2006. Введение в анализ ROC. Письма о распознавании образов, 27 (8), стр. 861-874.
- F2001Фосетт, Т., 2001. Использование наборов правил для максимизации производительности ROC в интеллектуальном анализе данных, 2001. Труды Международной конференции IEEE, стр. 131-138.
3.3.2.16. Компромисс при обнаружении ошибок (DET)
Функция det_curve вычисляет кривую компенсации ошибок обнаружения (DET) [WikipediaDET2017] . Цитата из Википедии:
«График компромисса ошибок обнаружения (DET) — это графическая диаграмма частоты ошибок для систем двоичной классификации, отображающая частоту ложных отклонений по сравнению с частотой ложных приемов. Оси x и y масштабируются нелинейно по их стандартным нормальным отклонениям (или просто с помощью логарифмического преобразования), в результате получаются более линейные кривые компромисса, чем кривые ROC, и большая часть области изображения используется для выделения важных различий в критический рабочий регион ».
Кривые DET представляют собой вариацию кривых рабочих характеристик приемника (ROC), где ложная отрицательная скорость нанесена на ось y вместо истинной положительной скорости. Кривые DET обычно строятся в масштабе нормального отклонения путем преобразования $phi^{-1}$ (с участием $phi$ — кумулятивная функция распределения). Полученные кривые производительности явно визуализируют компромисс типов ошибок для заданных алгоритмов классификации. См. [Martin1997], где приведены примеры и мотивация.
На этом рисунке сравниваются кривые ROC и DET двух примеров классификаторов для одной и той же задачи классификации:
Характеристики:
- Кривые DET образуют линейную кривую по шкале нормального отклонения, если оценки обнаружения нормально (или близки к нормальному) распределены. В [Navratil2007] было показано, что обратное не обязательно верно, и даже более общие распределения могут давать линейные кривые DET.
- При обычном преобразовании масштаба с отклонением точки распределяются таким образом, что занимает сравнительно большее пространство графика. Следовательно, кривые с аналогичными характеристиками классификации легче различить на графике DET.
- С ложноотрицательной скоростью, «обратной» истинной положительной скорости, точкой совершенства для кривых DET является начало координат (в отличие от верхнего левого угла для кривых ROC).
Приложения и ограничения:
Кривые DET интуитивно понятны для чтения и, следовательно, позволяют быстро визуально оценить работу классификатора. Кроме того, кривые DET можно использовать для анализа пороговых значений и выбора рабочей точки. Это особенно полезно, если требуется сравнение типов ошибок.
С другой стороны, кривые DET не представляют свою метрику в виде единого числа. Поэтому для автоматической оценки или сравнения с другими задачами классификации лучше подходят такие показатели, как производная площадь под кривой ROC.
Примеры:
- См. Кривую компенсации ошибок обнаружения (DET) для примера сравнения кривых рабочих характеристик приемника (ROC) и кривых компенсации ошибок обнаружения (DET).
Рекомендации:
- ВикипедияDET2017 Авторы Википедии. Компромисс ошибки обнаружения. Википедия, свободная энциклопедия. 4 сентября 2017 г., 23:33 UTC. Доступно по адресу: https://en.wikipedia.org/w/index.php?title=Detection_error_tradeoff&oldid=798982054 . По состоянию на 19 февраля 2018 г.
- Мартин 1997 А. Мартин, Дж. Доддингтон, Т. Камм, М. Ордовски и М. Пшибоцки, Кривая DET в оценке эффективности задач обнаружения , NIST 1997.
- Навратил2007 Дж. Наврактил и Д. Клусачек, « О линейных DET », 2007 г. Международная конференция IEEE по акустике, обработке речи и сигналов — ICASSP ’07, Гонолулу, Гавайи, 2007 г., стр. IV-229-IV-232.
3.3.2.17. Нулевой проигрыш
Функция zero_one_loss вычисляет сумму или среднее значение потери 0-1 классификации ($L_{0−1}$) над $n_{samples}$. По умолчанию функция нормализуется по выборке. Чтобы получить сумму $L_{0−1}$, установите normalize значение False.
В классификации по zero_one_loss нескольким меткам подмножество оценивается как единое целое, если его метки строго соответствуют прогнозам, и как ноль, если есть какие-либо ошибки. По умолчанию функция возвращает процент неправильно спрогнозированных подмножеств. Чтобы вместо этого получить количество таких подмножеств, установите normalize значение False
Если $hat{y}_i$ прогнозируемое значение $i$-й образец и $y_i$ — соответствующее истинное значение, тогда потеря 0-1 $L_{0−1}$ определяется как:
$$L_{0-1}(y_i, hat{y}_i) = 1(hat{y}_i not= y_i)$$
где $1(x)$- индикаторная функция.
>>> from sklearn.metrics import zero_one_loss >>> y_pred = [1, 2, 3, 4] >>> y_true = [2, 2, 3, 4] >>> zero_one_loss(y_true, y_pred) 0.25 >>> zero_one_loss(y_true, y_pred, normalize=False) 1
В случае с несколькими метками с двоичными индикаторами меток, где первый набор меток [0,1] содержит ошибку:
>>> zero_one_loss(np.array([[0, 1], [1, 1]]), np.ones((2, 2))) 0.5 >>> zero_one_loss(np.array([[0, 1], [1, 1]]), np.ones((2, 2)), normalize=False) 1
Пример:
- См. В разделе « Рекурсивное исключение функции с перекрестной проверкой» пример использования нулевой потери для выполнения рекурсивного исключения функции с перекрестной проверкой.
3.3.2.18. Потеря очков по Брайеру
Функция brier_score_loss вычисляет оценку Шиповник для бинарных классов [Brier1950] . Цитата из Википедии:
«Оценка Бриера — это правильная функция оценки, которая измеряет точность вероятностных прогнозов. Это применимо к задачам, в которых прогнозы должны назначать вероятности набору взаимоисключающих дискретных результатов ».
Эта функция возвращает среднеквадратичную ошибку фактического результата. y∈{0,1} и прогнозируемая оценка вероятности $p=Pr(y=1)$ ( pred_proba ) как выведено :
$$BS = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}} — 1}(y_i — p_i)^2$$
Потеря по шкале Бриера также составляет от 0 до 1, и чем ниже значение (средняя квадратичная разница меньше), тем точнее прогноз.
Вот небольшой пример использования этой функции:
>>> import numpy as np >>> from sklearn.metrics import brier_score_loss >>> y_true = np.array([0, 1, 1, 0]) >>> y_true_categorical = np.array(["spam", "ham", "ham", "spam"]) >>> y_prob = np.array([0.1, 0.9, 0.8, 0.4]) >>> y_pred = np.array([0, 1, 1, 0]) >>> brier_score_loss(y_true, y_prob) 0.055 >>> brier_score_loss(y_true, 1 - y_prob, pos_label=0) 0.055 >>> brier_score_loss(y_true_categorical, y_prob, pos_label="ham") 0.055 >>> brier_score_loss(y_true, y_prob > 0.5) 0.0
Балл Бриера можно использовать для оценки того, насколько хорошо откалиброван классификатор. Однако меньшая потеря по шкале Бриера не всегда означает лучшую калибровку. Это связано с тем, что по аналогии с разложением среднеквадратичной ошибки на дисперсию смещения потеря оценки по Бриеру может быть разложена как сумма потерь калибровки и потерь при уточнении [Bella2012]. Потеря калибровки определяется как среднеквадратическое отклонение от эмпирических вероятностей, полученных из наклона ROC-сегментов. Потери при переработке можно определить как ожидаемые оптимальные потери, измеренные по площади под кривой оптимальных затрат. Потери при уточнении могут изменяться независимо от потерь при калибровке, таким образом, более низкие потери по шкале Бриера не обязательно означают более качественную калибровку модели. «Только когда потеря точности остается неизменной, более низкая потеря по шкале Бриера всегда означает лучшую калибровку» [Bella2012] , [Flach2008] .
Пример:
- См. Раздел « Калибровка вероятности классификаторов», где приведен пример использования потерь по шкале Бриера для выполнения калибровки вероятности классификаторов.
Рекомендации:
- Brier1950 Дж. Брайер, Проверка прогнозов, выраженных в терминах вероятности , Ежемесячный обзор погоды 78.1 (1950)
- Bella2012 ( 1 , 2 ) Белла, Ферри, Эрнандес-Оралло и Рамирес-Кинтана «Калибровка моделей машинного обучения» в Хосров-Пур, М. «Машинное обучение: концепции, методологии, инструменты и приложения». Херши, Пенсильвания: Справочник по информационным наукам (2012).
- Flach2008 Флак, Питер и Эдсон Мацубара. «О классификации, ранжировании и оценке вероятности». Дагштульский семинар. Schloss Dagstuhl-Leibniz-Zentrum от Informatik (2008).
3.3.3. Метрики ранжирования с несколькими ярлыками
В многоэлементном обучении с каждой выборкой может быть связано любое количество меток истинности. Цель состоит в том, чтобы дать высокие оценки и более высокий рейтинг наземным лейблам.
3.3.3.1. Ошибка покрытия
Функция coverage_error вычисляет среднее число меток , которые должны быть включены в окончательном предсказании таким образом, что все истинные метки предсказанные. Это полезно, если вы хотите знать, сколько меток с наивысшими баллами вам нужно предсказать в среднем, не пропуская ни одной истинной. Таким образом, наилучшее значение этого показателя — среднее количество истинных ярлыков.
Примечание
Оценка нашей реализации на 1 больше, чем оценка, приведенная в Tsoumakas et al., 2010. Это расширяет ее для обработки вырожденного случая, когда экземпляр имеет 0 истинных меток.
Формально, учитывая двоичную индикаторную матрицу наземных меток истинности $y in left{0, 1right}^{n_text{samples} times n_text{labels}}$ и оценка, связанная с каждой меткой $hat{f} in mathbb{R}^{n_text{samples} times n_text{labels}}$ покрытие определяется как
$$coverage(y, hat{f}) = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}} — 1} max_{j:y_{ij} = 1} text{rank}_{ij}$$
с участием $text{rank}{ij} = left|left{k: hat{f}{ik} geq hat{f}_{ij} right}right|$. Учитывая определение ранга, связи y_scores разрываются путем присвоения максимального ранга, который был бы присвоен всем связанным значениям.
Вот небольшой пример использования этой функции:
>>> import numpy as np >>> from sklearn.metrics import coverage_error >>> y_true = np.array([[1, 0, 0], [0, 0, 1]]) >>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]]) >>> coverage_error(y_true, y_score) 2.5
3.3.3.2. Средняя точность ранжирования метки
В label_ranking_average_precision_score функции реализует маркировать ранжирование средней точности (LRAP). Этот показатель связан с average_precision_score функцией, но основан на понятии ранжирования меток, а не на точности и отзыве.
Средняя точность ранжирования меток (LRAP) усредняет по выборкам ответ на следующий вопрос: для каждой основной метки истинности какая доля меток с более высоким рейтингом была истинной? Этот показатель эффективности будет выше, если вы сможете лучше ранжировать метки, связанные с каждым образцом. Полученная оценка всегда строго больше 0, а наилучшее значение равно 1. Если имеется ровно одна релевантная метка для каждой выборки, средняя точность ранжирования меток эквивалентна среднему обратному рангу .
Формально, учитывая двоичную индикаторную матрицу наземных меток истинности $y in left{0, 1right}^{n_text{samples} times n_text{labels}}$ и оценка, связанная с каждой меткой $hat{f} in mathbb{R}^{n_text{samples} times n_text{labels}}$, средняя точность определяется как
$$LRAP(y, hat{f}) = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}} — 1} frac{1}{||y_i||0} sum{j:y_{ij} = 1} frac{|mathcal{L}{ij}|}{text{rank}{ij}}$$
где $mathcal{L}{ij} = left{k: y{ik} = 1, hat{f}{ik} geq hat{f}{ij} right}$, $text{rank}{ij} = left|left{k: hat{f}{ik} geq hat{f}_{ij} right}right|$, |cdot| вычисляет мощность набора (т. е. количество элементов в наборе), и $||cdot||_0$ это $ell_0$ «Norm» (который вычисляет количество ненулевых элементов в векторе).
Вот небольшой пример использования этой функции:
>>> import numpy as np >>> from sklearn.metrics import label_ranking_average_precision_score >>> y_true = np.array([[1, 0, 0], [0, 0, 1]]) >>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]]) >>> label_ranking_average_precision_score(y_true, y_score) 0.416...
3.3.3.3. Потеря рейтинга
Функция label_ranking_loss вычисляет ранжирование потери , которые в среднем более образцы числа пар меток, которые неправильно упорядочены, т.е. истинные метки имеют более низкую оценку , чем ложные метки, взвешенную по обратной величине числа упорядоченных пар ложных и истинных меток. Наименьшая возможная потеря рейтинга равна нулю.
Формально, учитывая двоичную индикаторную матрицу наземных меток истинности $y in left{0, 1right}^{n_text{samples} times n_text{labels}}$ и оценка, связанная с каждой меткой $hat{f} in mathbb{R}^{n_text{samples} times n_text{labels}}$ потеря ранжирования определяется как
$$ranking_loss(y, hat{f}) = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}} — 1} frac{1}{||y_i||0(ntext{labels} — ||y_i||0)} left|left{(k, l): hat{f}{ik} leq hat{f}{il}, y{ik} = 1, y_{il} = 0 right}right|$$
где $|cdot|$ вычисляет мощность набора (т. е. количество элементов в наборе) и $||cdot||_0$ это $ell_0$ «Norm» (который вычисляет количество ненулевых элементов в векторе).
Вот небольшой пример использования этой функции:
>>> import numpy as np >>> from sklearn.metrics import label_ranking_loss >>> y_true = np.array([[1, 0, 0], [0, 0, 1]]) >>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]]) >>> label_ranking_loss(y_true, y_score) 0.75... >>> # With the following prediction, we have perfect and minimal loss >>> y_score = np.array([[1.0, 0.1, 0.2], [0.1, 0.2, 0.9]]) >>> label_ranking_loss(y_true, y_score) 0.0
Рекомендации:
- Цумакас, Г., Катакис, И., и Влахавас, И. (2010). Майнинг данных с несколькими метками. В справочнике по интеллектуальному анализу данных и открытию знаний (стр. 667-685). Springer США.
3.3.3.4. Нормализованная дисконтированная совокупная прибыль
Дисконтированный совокупный выигрыш (DCG) и Нормализованный дисконтированный совокупный выигрыш (NDCG) — это показатели ранжирования, реализованные в dcg_score и ndcg_score; они сравнивают предсказанный порядок с оценками достоверности, такими как релевантность ответов на запрос.
Со страницы Википедии о дисконтированной совокупной прибыли:
«Дисконтированная совокупная прибыль (DCG) — это показатель качества ранжирования. При поиске информации он часто используется для измерения эффективности алгоритмов поисковой системы или связанных приложений. Используя шкалу градуированной релевантности документов в наборе результатов поисковой системы, DCG измеряет полезность или выгоду документа на основе его позиции в списке результатов. Прирост накапливается сверху вниз в списке результатов, причем прирост каждого результата дисконтируется на более низких уровнях »
DCG упорядочивает истинные цели (например, релевантность ответов на запросы) в предсказанном порядке, затем умножает их на логарифмическое убывание и суммирует результат. Сумма может быть усечена после первогоKрезультатов, и в этом случае мы называем это DCG @ K. NDCG или NDCG @ $K$ — это DCG, деленная на DCG, полученную с помощью точного прогноза, так что оно всегда находится между 0 и 1. Обычно NDCG предпочтительнее DCG.
По сравнению с потерей ранжирования, NDCG может принимать во внимание оценки релевантности, а не ранжирование на основе фактов. Таким образом, если основополагающая информация состоит только из упорядочивания, предпочтение следует отдавать потере ранжирования; если основополагающая информация состоит из фактических оценок полезности (например, 0 для нерелевантного, 1 для релевантного, 2 для очень актуального), можно использовать NDCG.
Для одного образца, учитывая вектор непрерывных значений истинности для каждой цели $y in R^M$, где $M$ это количество выходов, а прогноз $hat{y}$, что индуцирует функцию ранжирования $f$, оценка DCG составляет
$$sum_{r=1}^{min(K, M)}frac{y_{f(r)}}{log(1 + r)}$$
а оценка NDCG — это оценка DCG, деленная на оценку DCG, полученную для $y$.
Рекомендации:
- Запись в Википедии о дисконтированной совокупной прибыли
- Джарвелин, К., и Кекалайнен, Дж. (2002). Оценка IR методов на основе накопленного коэффициента усиления. Транзакции ACM в информационных системах (TOIS), 20 (4), 422-446.
- Ван, Ю., Ван, Л., Ли, Ю., Хе, Д., Чен, В., и Лю, Т. Ю. (2013, май). Теоретический анализ показателей рейтинга NDCG. В материалах 26-й ежегодной конференции по теории обучения (COLT 2013)
- МакШерри Ф. и Наджорк М. (2008, март). Эффективность вычислений при поиске информации измеряется эффективно при наличии связанных оценок. В Европейской конференции по поиску информации (стр. 414-421). Шпрингер, Берлин, Гейдельберг.
3.3.4. Метрики регрессии
В sklearn.metrics модуле реализованы несколько функций потерь, оценки и полезности для измерения эффективности регрессии. Некоторые из них были расширены , чтобы обработать случай multioutput: mean_squared_error, mean_absolute_error, explained_variance_score и r2_score.
У этих функций есть multioutput аргумент ключевого слова, который определяет способ усреднения результатов или проигрышей для каждой отдельной цели. По умолчанию используется значение 'uniform_average', которое определяет равномерно взвешенное среднее значение по выходным данным. Если передается ndarrayформа shape (n_outputs,), то ее записи интерпретируются как веса, и возвращается соответствующее средневзвешенное значение. Если multioutputесть 'raw_values'указан, то все неизменные индивидуальные баллы или потери будут возвращены в массиве формы (n_outputs,).
r2_score и explained_variance_score принять дополнительное значение 'variance_weighted' для multioutput параметра. Эта опция приводит к взвешиванию каждой индивидуальной оценки по дисперсии соответствующей целевой переменной. Этот параметр определяет количественно зафиксированную немасштабированную дисперсию на глобальном уровне. Если целевые переменные имеют разную шкалу, то этот балл придает большее значение хорошему объяснению переменных с более высокой дисперсией. multioutput='variance_weighted' — значение по умолчанию r2_score для обратной совместимости. В будущем это будет изменено на uniform_average.
3.3.4.1. Оценка объясненной дисперсии
explained_variance_score вычисляет объясненной дисперсии регрессии балл.
Если $hat{y}$ — расчетный целевой объем производства, y соответствующий (правильный) целевой результат, и $Var$- Дисперсия , квадрат стандартного отклонения, то объясненная дисперсия оценивается следующим образом:
$$explained_{}variance(y, hat{y}) = 1 — frac{Var{ y — hat{y}}}{Var{y}}$$
Наилучшая возможная оценка — 1.0, более низкие значения — хуже.
Вот небольшой пример использования explained_variance_score функции:
>>> from sklearn.metrics import explained_variance_score >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> explained_variance_score(y_true, y_pred) 0.957... >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> explained_variance_score(y_true, y_pred, multioutput='raw_values') array([0.967..., 1. ]) >>> explained_variance_score(y_true, y_pred, multioutput=[0.3, 0.7]) 0.990...
3.3.4.2. Максимальная ошибка
Функция max_error вычисляет максимальную остаточную ошибку , показатель , который фиксирует худшую ошибку случае между предсказанным значением и истинным значением. В идеально подобранной модели регрессии с одним выходом он max_error будет находиться 0 в обучающем наборе, и хотя это маловероятно в реальном мире, этот показатель показывает степень ошибки, которую имела модель при подборе.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец, и $y_i$ — соответствующее истинное значение, тогда максимальная ошибка определяется как
$$text{Max Error}(y, hat{y}) = max(| y_i — hat{y}_i |)$$
Вот небольшой пример использования функции max_error:
>>> from sklearn.metrics import max_error >>> y_true = [3, 2, 7, 1] >>> y_pred = [9, 2, 7, 1] >>> max_error(y_true, y_pred) 6
max_error не поддерживает multioutput.
3.3.4.3. Средняя абсолютная ошибка
Функция mean_absolute_error вычисляет среднюю абсолютную погрешность , риск метрики , соответствующей ожидаемого значение абсолютной потери или ошибок $l1$-нормальная потеря.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец, и $y_i$ — соответствующее истинное значение, тогда средняя абсолютная ошибка (MAE), оцененная за $n_{samples}$ определяется как
$$text{MAE}(y, hat{y}) = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}}-1} left| y_i — hat{y}_i right|.$$
Вот небольшой пример использования функции mean_absolute_error:
>>> from sklearn.metrics import mean_absolute_error >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> mean_absolute_error(y_true, y_pred) 0.5 >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> mean_absolute_error(y_true, y_pred) 0.75 >>> mean_absolute_error(y_true, y_pred, multioutput='raw_values') array([0.5, 1. ]) >>> mean_absolute_error(y_true, y_pred, multioutput=[0.3, 0.7]) 0.85...
3.3.4.4. Среднеквадратичная ошибка
Функция mean_squared_error вычисляет среднюю квадратическую ошибку , риск метрики , соответствующую ожидаемое значение квадрата (квадратичной) ошибки или потерю.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец, и $y_i$ — соответствующее истинное значение, тогда среднеквадратичная ошибка (MSE), оцененная на $n_{samples}$ определяется как
$$text{MSE}(y, hat{y}) = frac{1}{n_text{samples}} sum_{i=0}^{n_text{samples} — 1} (y_i — hat{y}_i)^2.$$
Вот небольшой пример использования функции mean_squared_error:
>>> from sklearn.metrics import mean_squared_error >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> mean_squared_error(y_true, y_pred) 0.375 >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> mean_squared_error(y_true, y_pred) 0.7083...
Примеры:
- См. В разделе Регрессия повышения градиента пример использования среднеквадратичной ошибки для оценки регрессии повышения градиента.
3.3.4.5. Среднеквадратичная логарифмическая ошибка
Функция mean_squared_log_error вычисляет риск метрики , соответствующий ожидаемому значению квадрата логарифмической (квадратичной) ошибки или потери.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец, и $y_i$ — соответствующее истинное значение, тогда среднеквадратичная логарифмическая ошибка (MSLE), оцененная на $n_{samples}$ определяется как
$$text{MSLE}(y, hat{y}) = frac{1}{n_text{samples}} sum_{i=0}^{n_text{samples} — 1} (log_e (1 + y_i) — log_e (1 + hat{y}_i) )^2.$$
Где $log_e (x)$ означает натуральный логарифм $x$. Эту метрику лучше всего использовать, когда цели имеют экспоненциальный рост, например, численность населения, средние продажи товара в течение нескольких лет и т. Д. Обратите внимание, что эта метрика штрафует за заниженную оценку больше, чем за завышенную оценку.
Вот небольшой пример использования функции mean_squared_log_error:
>>> from sklearn.metrics import mean_squared_log_error >>> y_true = [3, 5, 2.5, 7] >>> y_pred = [2.5, 5, 4, 8] >>> mean_squared_log_error(y_true, y_pred) 0.039... >>> y_true = [[0.5, 1], [1, 2], [7, 6]] >>> y_pred = [[0.5, 2], [1, 2.5], [8, 8]] >>> mean_squared_log_error(y_true, y_pred) 0.044...
3.3.4.6. Средняя абсолютная ошибка в процентах
mean_absolute_percentage_error (MAPE), также известный как среднее абсолютное отклонение в процентах (МАПД), является метрикой для оценки проблем регрессии. Идея этой метрики — быть чувствительной к относительным ошибкам. Например, он не изменяется глобальным масштабированием целевой переменной.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец и $y_i$ — соответствующее истинное значение, тогда средняя абсолютная процентная ошибка (MAPE), оцененная за $n_{samples}$ определяется как
$$text{MAPE}(y, hat{y}) = frac{1}{n_{text{samples}}} sum_{i=0}^{n_{text{samples}}-1} frac{{}left| y_i — hat{y}_i right|}{max(epsilon, left| y_i right|)}$$
где $epsilon$ — произвольное маленькое, но строго положительное число, чтобы избежать неопределенных результатов, когда y равно нулю.
В функции mean_absolute_percentage_error опоры multioutput.
Вот небольшой пример использования функции mean_absolute_percentage_error:
>>> from sklearn.metrics import mean_absolute_percentage_error >>> y_true = [1, 10, 1e6] >>> y_pred = [0.9, 15, 1.2e6] >>> mean_absolute_percentage_error(y_true, y_pred) 0.2666...
В приведенном выше примере, если бы мы использовали mean_absolute_error, он бы проигнорировал небольшие значения магнитуды и только отразил бы ошибку в предсказании максимального значения магнитуды. Но эта проблема решена в случае MAPE, потому что он вычисляет относительную процентную ошибку по отношению к фактическому выходу.
3.3.4.7. Средняя абсолютная ошибка
Это median_absolute_error особенно интересно, потому что оно устойчиво к выбросам. Убыток рассчитывается путем взятия медианы всех абсолютных различий между целью и прогнозом.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец и $y_i$ — соответствующее истинное значение, тогда средняя абсолютная ошибка (MedAE), оцененная на $n_{samples}$ определяется как
$$text{MedAE}(y, hat{y}) = text{median}(mid y_1 — hat{y}_1 mid, ldots, mid y_n — hat{y}_n mid).$$
median_absolute_error Не поддерживает multioutput.
Вот небольшой пример использования функции median_absolute_error:
>>> from sklearn.metrics import median_absolute_error >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> median_absolute_error(y_true, y_pred) 0.5
3.3.4.8. R² балл, коэффициент детерминации
Функция r2_score вычисляет коэффициент детерминации , как правило , обозначенный как R².
Он представляет собой долю дисперсии (y), которая была объяснена независимыми переменными в модели. Он обеспечивает показатель степени соответствия и, следовательно, меру того, насколько хорошо невидимые выборки могут быть предсказаны моделью через долю объясненной дисперсии.
Поскольку такая дисперсия зависит от набора данных, R² не может быть значимо сопоставимым для разных наборов данных. Наилучшая возможная оценка — 1,0, и она может быть отрицательной (потому что модель может быть произвольно хуже). Постоянная модель, которая всегда предсказывает ожидаемое значение y, игнорируя входные характеристики, получит оценку R² 0,0.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец и $y_i$ соответствующее истинное значение для общего n образцов, расчетный R² определяется как:
$$R^2(y, hat{y}) = 1 — frac{sum_{i=1}^{n} (y_i — hat{y}i)^2}{sum{i=1}^{n} (y_i — bar{y})^2}$$
где $bar{y} = frac{1}{n} sum_{i=1}^{n} y_i$ и $sum_{i=1}^{n} (y_i — hat{y}i)^2 = sum{i=1}^{n} epsilon_i^2$.
Обратите внимание, что r2_score вычисляется нескорректированное R² без поправки на смещение выборочной дисперсии y.
Вот небольшой пример использования функции r2_score:
>>> from sklearn.metrics import r2_score >>> y_true = [3, -0.5, 2, 7] >>> y_pred = [2.5, 0.0, 2, 8] >>> r2_score(y_true, y_pred) 0.948... >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> r2_score(y_true, y_pred, multioutput='variance_weighted') 0.938... >>> y_true = [[0.5, 1], [-1, 1], [7, -6]] >>> y_pred = [[0, 2], [-1, 2], [8, -5]] >>> r2_score(y_true, y_pred, multioutput='uniform_average') 0.936... >>> r2_score(y_true, y_pred, multioutput='raw_values') array([0.965..., 0.908...]) >>> r2_score(y_true, y_pred, multioutput=[0.3, 0.7]) 0.925...
Пример:
- См. В разделе « Лассо и эластичная сеть для разреженных сигналов» приведен пример использования показателя R² для оценки лассо и эластичной сети для разреженных сигналов.
3.3.4.9. Средние отклонения Пуассона, Гаммы и Твиди
Функция mean_tweedie_deviance вычисляет среднюю ошибку Deviance Tweedie с powerпараметром ($p$). Это показатель, который выявляет прогнозируемые ожидаемые значения целей регрессии.
Существуют следующие особые случаи:
- когда
power=0это эквивалентноmean_squared_error. - когда
power=1это эквивалентноmean_poisson_deviance. - когда
power=2это эквивалентноmean_gamma_deviance.
Если $hat{y}_i$ прогнозируемое значение $i$-й образец и $y_i$ — соответствующее истинное значение, тогда средняя ошибка отклонения Твиди (D) для мощности $p$, оценивается более $n_{samples}$ определяется как
Отклонение от твиди — однородная функция степени 2-power. Таким образом, гамма-распределение power=2 означает, что одновременно масштабируется y_true и y_pred не влияет на отклонение. Для распределения Пуассона power=1 отклонение масштабируется линейно, а для нормального распределения ( power=0) — квадратично. В общем, чем выше, powerтем меньше веса придается крайним отклонениям между истинными и прогнозируемыми целевыми значениями.
Например, давайте сравним два прогноза 1.0 и 100, которые оба составляют 50% от их соответствующего истинного значения.
Среднеквадратичная ошибка ( power=0) очень чувствительна к разнице прогнозов второй точки:
>>> from sklearn.metrics import mean_tweedie_deviance >>> mean_tweedie_deviance([1.0], [1.5], power=0) 0.25 >>> mean_tweedie_deviance([100.], [150.], power=0) 2500.0
Если увеличить powerдо 1:
>>> mean_tweedie_deviance([1.0], [1.5], power=1) 0.18... >>> mean_tweedie_deviance([100.], [150.], power=1) 18.9...
разница в ошибках уменьшается. Наконец, установив power=2:
>>> mean_tweedie_deviance([1.0], [1.5], power=2) 0.14... >>> mean_tweedie_deviance([100.], [150.], power=2) 0.14...
мы получим идентичные ошибки. Таким образом, отклонение when power=2чувствительно только к относительным ошибкам.
3.3.5. Метрики кластеризации
В модуле sklearn.metrics реализованы несколько функций потерь, оценки и полезности. Для получения дополнительной информации см. Раздел « Оценка производительности кластеризации » для кластеризации экземпляров и « Оценка бикластеризации» для бикластеризации.
3.3.6. Фиктивные оценки
При обучении с учителем простая проверка работоспособности состоит из сравнения своей оценки с простыми практическими правилами. DummyClassifier реализует несколько таких простых стратегий классификации:
stratifiedгенерирует случайные прогнозы, соблюдая распределение классов обучающего набора.most_frequentвсегда предсказывает наиболее частую метку в обучающем наборе.priorвсегда предсказывает класс, который максимизирует предыдущий класс (какmost_frequent) иpredict_probaвозвращает предыдущий класс.uniformгенерирует предсказания равномерно в случайном порядке.constantвсегда предсказывает постоянную метку, предоставленную пользователем. Основная мотивация этого метода — оценка F1, когда положительный класс находится в меньшинстве.
Обратите внимание, что со всеми этими стратегиями predict метод полностью игнорирует входные данные!
Для иллюстрации DummyClassifier сначала создадим несбалансированный набор данных:
>>> from sklearn.datasets import load_iris >>> from sklearn.model_selection import train_test_split >>> X, y = load_iris(return_X_y=True) >>> y[y != 1] = -1 >>> X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
Далее сравним точность SVC и most_frequent:
>>> from sklearn.dummy import DummyClassifier >>> from sklearn.svm import SVC >>> clf = SVC(kernel='linear', C=1).fit(X_train, y_train) >>> clf.score(X_test, y_test) 0.63... >>> clf = DummyClassifier(strategy='most_frequent', random_state=0) >>> clf.fit(X_train, y_train) DummyClassifier(random_state=0, strategy='most_frequent') >>> clf.score(X_test, y_test) 0.57...
Мы видим, что SVC это не намного лучше, чем фиктивный классификатор. Теперь давайте изменим ядро:
>>> clf = SVC(kernel='rbf', C=1).fit(X_train, y_train) >>> clf.score(X_test, y_test) 0.94...
Мы видим, что точность увеличена почти до 100%. Для лучшей оценки точности рекомендуется стратегия перекрестной проверки, если она не требует слишком больших затрат на ЦП. Для получения дополнительной информации см. Раздел « Перекрестная проверка: оценка производительности оценщика ». Более того, если вы хотите оптимизировать пространство параметров, настоятельно рекомендуется использовать соответствующую методологию; подробности см. в разделе « Настройка гиперпараметров оценщика ».
В более общем плане, когда точность классификатора слишком близка к случайной, это, вероятно, означает, что что-то пошло не так: функции бесполезны, гиперпараметр настроен неправильно, классификатор страдает от дисбаланса классов и т. Д.
DummyRegressor также реализует четыре простых правила регрессии:
meanвсегда предсказывает среднее значение тренировочных целей.medianвсегда предсказывает медианное значение тренировочных целей.quantileвсегда предсказывает предоставленный пользователем квантиль учебных целей.constantвсегда предсказывает постоянное значение, предоставляемое пользователем.
Во всех этих стратегиях predict метод полностью игнорирует входные данные.
Качество исходной информации Модель прогноза Метод прогнозирования
Качество прогноза
Рис.
2.2. Факторы, влияющие на качество прогноза
Качество
исходной информации, в свою очередь,
определяется:
-
точностью
экономических измерений; -
качеством
выборки; -
отсутствием
ошибок согласования (данные ошибки
возникают в тех случаях, когда исходная
информация для проведения прогнозных
расчётов подготавливается различными
специалистами, использующими разные
методологические подходы).
Наибольшие
погрешности (стратегические ошибки
прогнозирования) возникают в результате
неудачного выбора метода прогнозирования.
Например, на основании прогнозов
социально-экономического развития
СССР, проводимых в 1960-е годы, Генеральный
секретарь Коммунистической партии
Н.С.Хрущёв заверил, что к 1980 году «СССР
догонит и перегонит Америку». Стратегическая
ошибка прогнозирования была обусловлена
тем, что для долгосрочного прогнозирования
применялись методы экстраполяции
которые, как мы уже знаем, целесообразно
использовать для краткосрочного
прогнозирования.
Погрешности,
связанные с выбором модели прогноза,
возникают в результате упрощения,
несовершенства теоретических построений
или неадекватности моделей прогнозируемым
социально-экономическим процессам.
Иногда для прогнозирования процессов,
протекающих в нашей стране, используются
модели разработанные зарубежными
специалистами и хорошо себя зарекомендовавшие
для прогнозирования аналогичных
процессов в других странах. Однако
следует помнить о том, что данные модели
могут быть неадекватны по отношению к
социально-экономическим процессам,
происходящим в нашей стране, и их
использование может привести к серьезным
ошибкам и просчетам.
Результат
прогноза, разработанного формализованным
методом, чаще всего выражается
количественным показателем, которому
может быть дана точечная ()
и (или) интервальная оценка ().
Точечная
оценка ()
— это единичная оценка прогнозного
параметра. Точечные значения экономических
величин лишены содержания, так как имеют
нулевую вероятность. Для устранения
этого недостатка прогноз должен быть
дан в виде интервала значений.
Интервальная
оценка ()
— это числовой интервал (доверительный
интервал), в котором, вероятно, находится
прогнозный параметр.
Точность
прогноза
тем выше, чем меньше величина ошибки,
которая представляет собой разность
между прогнозируемыми и фактическими
значениями исследуемой величины. Понятие
точности прогноза и методы ее оценки
отличаются от точности исходных данных.
Точность исходных данных может быть
однозначно оценена на этапе сбора
информации как степень приближения
результатов измерений к истинному
значению измеряемой величины. На практике
часто количественную оценку точности
заменяют указанием ошибки измерения
(погрешности), которая определяется как
разница между оцениваемым результатом
и результатом, полученным более точным
методом. В прогнозных значениях (до
наступления прогнозируемого события)
точность обычно также выражается как
погрешность, но с помощью вероятностных
пределов отклонения фактической величины
от прогнозируемого значения, которые
принято называть доверительным
интервалом.
Заметим,
что прогнозируемые значения должны
реализоваться в соответствующее время
с указанной вероятностью и лежать внутри
некоторой доверительной области, ширина
которой зависит от заданной вероятности.
Математическая
вероятность ()
случайной величины равна отношению
числа событий, благоприятствующих ее
появлению (т.е. свершению прогноза) к
общему числу событий (благоприятных и
неблагоприятных). Численное значение
вероятности прогноза лежит в пределах
от 0 до 1.
Очевидно,
что точность прогноза максимальна при
построении точечного прогноза. Но
построить его с высокой степенью
вероятности часто не представляется
возможным.
В
то же время границы доверительного
интервала можно задать такими широкими,
что прогнозируемое значение попадет
туда с любой вероятностью, включая Р
= 0 и Р
= 1. Такой
прогноз называется абсолютно достоверным.
Однако границы доверительного интервала
будут столь широкими, что полученный
прогноз не будет иметь практической
ценности для принятия управленческих
решений. На практике достаточно иметь
вероятность прогноза 0,7-0,95.
Под
достоверностью
прогноза
понимается вероятность осуществления
прогноза в заданном доверительном
интервале
.
Условная
графическая интерпретация доверительного
интервала показателя у
при заданной
вероятности Р
представлена
на рис. 2.3.
Рис.
2.3. Графическая интерпретация границ
доверительного интервала
Существуют
неформальный и формальный способы
определения доверительного интервала.
Неформально доверительный интервал
может быть определен экспертами с учетом
степени изменчивости фактических
значений показателей вокруг расчетных
(теоретических) значений в прошлом и
возможности деформации в будущем. При
этом экспертам может быть предложено
оценить суммарную величину ошибки или
степень влияния различных составляющих
на точность прогноза. Суммарная ошибка
решения прогнозной задачи определяется
по формуле
,
(2.10)
где
— суммарная ошибка;
—ошибки
информации, обусловленные неадекватностью
описания объекта, погрешностями получения
и обработки информации;
—ошибки
метода прогнозирования, вызванные
невозможностью идеального выбора метола
для данного объекта, а также обязательной
схематичностью метода;
—ошибки
вычислительных процедур;
—ошибки,
допущенные человеком и обусловленные
субъективными факторами (низкая
квалификация, восторженность, пессимизм);
—нерегулярная
составляющая ошибки, обусловленная
возможностью появления непредсказуемых
изменений в объекте.
Формально
границы доверительного интервала можно
определить на основе оценки изменчивости
уровней ряда. Чем выше эта изменчивость,
тем менее точной может быть расчетная
величина и тем шире должен быть
доверительный интервал при одной и той
же вероятности прогноза.
На
практике, получая прогнозный результат
в виде точечного значения
,
необходимо указать и возможную величину
ошибки,
т.е. перейти к интервальному прогнозу
по формуле
,
(2.11)
где
— точечное значение прогнозной
характеристики;
—интервальное
значение прогнозной характеристики;
—вероятная
ошибка прогноза.
Для
определения границ доверительного
интервала используется выражение
,
(2.12)
где
—
среднеквадратическое отклонение;
— критерий
Стьюдента.
Величина
среднеквадратического отклонения
рассчитывается по формуле
,
(2.13)
где
— фактическое
значение исследуемой характеристики
на участке ретроспекции;
—расчетное
значение исследуемой характеристики
на участке ретроспекции;
п
— число
наблюдений (размер выборки).
Среднеквадратическое
отклонение характеризует, насколько
точно теоретическая кривая описывает
поведение исследуемой характеристики
в прошлом. Величина
определяет минимальную ошибку прогноза.
Она зависит, с одной стороны, от
корректности модели, с другой — от
стабильности исследуемой характеристики
в прошлом.
—критерий
Стьюдента, значение которого зависит
от размера выборочной совокупности и
заданной вероятности прогноза,
использование этого коэффициента
определяется ограниченностью выборки
(табличные значения критерия Стьюдента
приведены в приложении. Критерий
Стьюдента позволяет учесть то
обстоятельство, что чем выше заданная
вероятность прогноза и чем меньше размер
выборки, тем шире должны быть границы
доверительного интервала.
После
наступления прогнозируемого события
ошибка прогноза определяется как
разность между фактическим и прогнозным
значением показателя. Существует
несколько способов количественной
оценки ошибки прогноза, например, ошибка
прогноза или погрешность для каждого
момента времени, в котором рассматривается
прогноз:
,
(2.14)
где
— ошибка
прогноза в момент времени t,
—фактическое
значение в момент времени t,
—прогнозное
значение в момент времени t.
Для обобщенной
оценки метода прогнозирования на
практике вместе с показателем
среднеквадратического отклонения могут
быть использованы и другие способы
оценки средней ошибки прогноза
(погрешности):
-
среднее
абсолютное отклонение (mean absolute derivation,
MAD). Использование
этого показателя имеет смысл, когда
исследователю необходимо оценить
ошибку в тех же единицах, что и исходный
ряд:
;
(2.15)
-
средняя
процентная ошибка (mean percentage error, МРЕ)
позволяет
оценить возможное смещение прогноза,
когда полученный прогноз окажется
завышенным или заниженным. При несмещенном
прогнозе имеем величину ошибки, близкую
к нулю, при завышенном — большое
положительное процентное значение,
при заниженном — большое отрицательное:
;
(2.16)
-
средняя
абсолютная ошибка в процентах (mean
absolute percentage error, MAPE):
.
(2.17)
Приведенные
выше способы оценки качества прогноза
позволяют осуществить сравнение
результатов, полученных различными
методами прогнозирования, и выбрать
наиболее приемлемый метод для решения
прогнозной задачи.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Прогнозирование и планирование
1 2 3 4 5 6 7 8 9 10 11
 По учету прогнозного фона различают прогнозы:
По учету прогнозного фона различают прогнозы:
Некоторые ответы приведены ниже. Для гарантированной сдачи тестов можете заказать у нас полное прохождение тестов.
| Номер вопроса: | 2 | 5 | 6 |
| Ответ: | 1 | 3 | 1 |
Заказать прохождение тестов
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное
учреждение высшего образования
«Тульский государственный университет»
Кафедра «Финансы и менеджмент»
КОНСПЕКТ ЛЕКЦИЙ
по дисциплине
«ПЛАНИРОВАНИЕ И ПРОГНОЗИРОВАНИЕ В
УСЛОВИЯХ РЫНКА»
Направление подготовки: 080100 «Экономика»
Профили подготовки: «Финансы и кредит», «Бухгалтерский учет, анализ и
аудит», «Налоги и налогообложение»
Квалификация (степень) выпускника: 62 бакалавр
Тула 2014
2
Основные понятия прогнозирования, планирования и программирования
в системе государственного регулирования рыночной экономики
1.1. Понятие прогнозирования и планирования
1.2. Организация экономического прогнозирования в РФ
1.3. Предпосылки экономического прогнозирования
1.4. Классификация прогнозов и планов
1.5. Функции, условия и методология прогнозирования и планирования
2. Основы методологии прогнозирования и планирования
2.1. Теоретическая база методов планирования и прогнозирования.
2.2. Принципы прогнозирования и планирования
2.3. Технология прогнозирования
3. Понятие временного ряда в экономическом прогнозировании
3.1. Определение и основные виды моделей динамики данных.
3.2. Математико-статистический анализ социально-экономических
процессов
3.3. Методы выравнивания временного ряда
4. Система методов прогнозирования
4.1. Классификация методов прогнозирования.
4.2. Оценка качества количественных прогнозов
4.3. Методы экспертных оценок
4.4. Методы экстраполяции
4.5. Методы моделирования
5. Система методов планирования
5.1.
Нормативный метод планирования
5.2.
Программно-целевой метод планирования
5.3.
Индикативное планирование
5.4.
Балансовый метод планирования
5.5.
Графический метод планирования
5.6.
Принятие решений в условиях неопределенности
6. Макроэкономическое (государственное) планирование и прогнозирование
6.1.
Государственное прогнозирование, планирование и программирование социально-экономического развития
6.2.
Прогнозирование и формирование темпов, пропорций и структуры экономики в условиях рынка
6.3.
Прогнозирование уровня жизни населения
7. Планирование и прогнозирование на микроэкономическом уровне
(предприятие, фирма)
7.1.
Основы стратегического планирования
7.2.
Прогнозирование рынка сбыта продукции предприятия
7.3.
Назначение, цель и задачи бюджетирования
3
7.4.
7.5.
7.6.
7.7.
Условия формирования системы эффективного бюджетного
управления
Период бюджетирования
Технология разработки бюджетов
Внутрифирменный контроль за исполнением бюджетов
4
Раздел 1. Основные понятия прогнозирования, стратегического планирования и программирования в системе государственного регулирования рыночной экономики
1.1 Понятие прогнозирования и планирования
Задача данного учебного курса состоит в рассмотрении комплекса теоретических, методологических и организационных вопросов прогнозирования и
планирования развития экономики на современном этапе.
Теория прогнозирования и планирования является составной частью экономической науки. Теория прогнозирования и планирования экономики базируется на экономической теории. Если последняя изучает глубинные процессы
экономического развития, устанавливает их суть, движущие силы для любых
общественно-экономических формаций, то прогнозирование и планирование
являются рабочим инструментом определения величин экономических показателей, позволяют выявить наиболее эффективные методы регулирования социально-экономических процессов в обществе и одновременно выступают в качестве методологической основы при рассмотрении вопросов прогнозирования и
планирования отраслевых экономик, таких, как экономика промышленности,
экономика транспорта, экономика строительства и др. Таким образом, место
теории прогнозирования и планирования в системе экономических дисциплин
определяется тем, что она является как бы связующим звеном экономической
теории, с одной стороны, и отраслевыми экономиками — с другой. Данная наука
имеет тесную связь со статистикой, от которой она заимствует методы анализа
и необходимые сведения для расчетов. Прогнозирование и планирование использует достижения естественных, биологических и других наук, особенно
математики.
Главным объектом, применительно к которому будут анализироваться
процессы прогнозирования и стратегического планирования, являются крупные
социально-экономические системы, взаимодействующие между собой в масштабах глобального мирового сообщества.
В центре анализа находится социально-экономическая система России и
возможные траектории ее изменений в контексте общемировых тенденций.
В социально-экономической системе России в свою очередь в центр рассмотрения ставится ее национальная экономика как структурная целостность
образующих ее отраслей, регионов, кластеров, разнообразных хозяйственных
систем.
Предвидение — самая общая характеристика круга явлений, связанных с
ожиданиями будущего. В общем случае предвидение может быть представлено
в виде трех его форм — гипотеза, прогноз, план.
Прогноз — система научно обоснованных представлений о возможных состояниях объекта в будущем, об альтернативных путях его развития. Процесс
разработки прогноза называется прогнозированием.
5
Гипотеза относится к научно-исследовательской фазе осуществления
предвидения, когда данные о будущем выдвигаются в порядке предположений,
с опорой на интуицию и чисто теоретические конструкции.
Сценарий — гипотетическая последовательность событий, которая показывает, как из существующей или некой заданной ситуации может развертываться шаг за шагом будущее состояние объекта, интересующего разработчика.
Планирование — процесс научного или эмпирического обоснования целей и приоритетов социально-экономического развития с определением путей и
средств их достижения. Соответственно план — это документ, который содержит систему показателей и набор различных мероприятий по решению социально-экономических задач. В нем отражаются как цели и приоритеты, так и
ресурсы, источники их обеспечения, порядок и сроки выполнения.
Главная отличительная черта плана – определенность заданий, в нем
предвидение получает наибольшую конкретность и определенность. Представляют интерес трактовки понятия планирования отечественными и зарубежными
учеными, из множества которых можно выделить определение сущности планирования как самого процесса.
A.M. Ковалевский определяет планирование как научное предвидение
хода развития и определение конкретных путей осуществления расширенного
воспроизводства, базирующееся на экономической теории, результатах научнотехнического прогресса, передового опыта, направленное на достижение поставленных целей.
В.А. Грузинов подчеркивает, что «планирование есть непрерывный процесс, в ходе которого устанавливаются и постоянно уточняются во времени цели и задачи развития предприятия, определяются стратегия и политика по их
достижению…».
Общие черты прогнозов и планов – опережающий характер содержащейся в них информации, что отличает предвидение от экономического анализа и статистики. Прогнозирование и планирование могут использовать одинаковые методы и показатели, строиться на основе общей информационной базы.
Взаимосвязь между прогнозом и планом заключается, прежде всего, в
том, что прогнозирование – это исследовательская база планирования. Традиционно прогноз предшествует разработке плана, но он может также следовать
за ним, определяя возможности достижения запланированных ориентиров.
Различия между ними обусловлены тем, что прогнозирование по своему
существу носит характер исследования, научного описания будущего (предсказания), а план – характер целеполагания (предуказания).
1. Прогноз носит вероятностный характер, а план – нормативный.
2. Прогноз имеет вариантное содержание, в то время как план представляет собой однозначное решение, даже если он разработан на вариантной основе.
3. Прогнозирование существует независимо от планирования, хотя может
быть составной частью процесса планирования.
4. Непременное требование к планам – их ресурсная обеспеченность, в то
6
время как прогнозы могут предсказывать вероятность достижения цели при неполном обеспечении ресурсами.
5. В процессе планирования в большей степени проявляется влияние
субъективного фактора – воли, желаний, устремлений человека, принимающего
решения в постановке цели, в выборе способов ее достижения.
Формы планирования:
— Директивное планирование, т.е. обязательное, жесткое, подлежащее
исполнению,
предполагает
применение,
прежде
всего,
командноадминистративных рычагов для обязательного претворения в жизнь установленных целей и задач. Условие обязательности реализуется через издание соответствующих административно-распорядительных документов — законов, указов, приказов, распоряжений, после чего осуществляются практическая реализация установленных заданий, текущий и конечный контроль степени выполнения с применением мер административного и другого воздействия к исполнителям.
— Стратегическое планирование — процесс определения целей и значений экономических показателей по основным, наиболее важным направлениям
социально-экономического развития страны (отрасли, объединения, предприятия и др.), как правило, на средний срок и длительную перспективу и формирование механизма их реализации. Оно предполагает учет факторов внешней
среды. Представляет собой адаптивный процесс, в результате которого происходит регулярная (ежегодная) корректировка решений, оформленных в виде
программ, прогнозов, планов, дополнений и изменений системы мер по их выполнению на основе непрерывного контроля и оценки происходящих изменений в экономическом развитии государства, государств-партнеров и мирового
сообщества. Его назначение — сделать оперативные и текущие управленческие
решения обоснованными не только с точки зрения сложившейся конъюнктуры,
но в первую очередь с позиций завтрашнего дня.
— Индикативное планирование является основным рабочим инструментом по реализации целей, поставленных в стратегическом плане развития с учетом конкретно складывающейся экономической ситуации. Индикативный планпрогноз дополняет стратегический и выступает в качестве практического инструмента в развитии экономики на кратко- и среднесрочный периоды.
Индикативный план включает в себя концептуальную (концепция социально-экономического
развития);
прогнозную
(прогноз
социальноэкономического развития); планово-регулирующую (система экономических
регуляторов и государственные целевые комплексные программы) части.
Программирование — процесс формирования тех или иных программ социально-экономического и научно-технического развития. Речь может идти о
комплексных программах развития страны (региона), национальных программах и проектах по реализации избранных приоритетов или о конкретных целевых программах по осуществлению прорывов в тех или иных областях либо о
более узких отраслевых или региональных программах и др.
7
Мероприятие — намеченная к реализации конкретная мера воздействия
для решения поставленной задачи. Как правило, носит локальный характер и
выступает в качестве составной части прогноза, плана или аналогичных им
экономических категорий.
Программа — документ, представляющий собой увязанный по ресурсам,
исполнителям и срокам осуществления комплекс социально-экономических и
других заданий и мероприятий, направленных на решение определенной проблемы. Чаще всего программы являются составной частью прогноза или плана
и призваны выделить приоритетные проблемы развития народного хозяйства
(обеспечение населения важнейшими видами продуктов, развитие отдельных
видов транспорта, промышленного производства и др.). Иногда программы
имеют и самостоятельное значение.
Целевая программа — это система взаимоувязанных по целям, ресурсам
и срокам мероприятий, обеспечивающая реализацию приоритета социального,
экономического, научно-технического или экологического развития в заданные
сроки и с наилучшим эффектом.
Глобальное программирование — широкая цепь прогнозно-плановых
проработок и управленческих мероприятий, направленных на перевод макроэкономической системы страны (или региона) в качественно новое состояние в
будущем. В таком контексте, очевидно, понятие «программирование» становится близким по смыслу понятию «долгосрочное стратегическое планирование» развития макросистем.
Концепция — руководящая идея, общий замысел, т.е. основной путь следования для достижения поставленной цели в прогнозе, плане или программе.
1.2. Организация экономического прогнозирования в РФ
Понятие «организация прогнозирования» включает в себя три составляющие:
во-первых, это формирование определенной организационной структуры, предназначенной для разработки прогнозов;
во-вторых, определение состава прогнозных документов, порядка и
сроков их разработки, исполнителей;
в-третьих, определение последовательности процедур и методов,
применяемых при разработке конкретного прогноза, так называемая технология
прогнозирования.
Основные элементы организационной структуры — субъект прогнозирования, заказчик и потребитель прогноза.
Субъект прогнозирования — организация, предприятие, учреждение
или отдельное лицо, осуществляющее разработку прогноза.
Заказчик прогноза — организация, предприятие или отдельное лицо,
выдающее задание на прогноз, выступающее инициатором его разработки.
Потребитель прогноза — организация, предприятие или отдельное лицо, использующее его результаты в своей деятельности. В отдельных случаях
8
потребителем прогноза может являться заказчик.
Обычно выделяют систему частного инициативного прогнозирования и
государственную систему прогнозирования.
Система частного инициативного прогнозирования представлена сетью независимых, конкурирующих между собой фирм, которые выполняют заказы на разработку прогнозов по интересующим потребителя проблемам микро- и макроуровня. Организации этой системы часто обладают значительным
научным потенциалом и не только решают конкретные исследовательские задачи, но и вносят серьезный вклад в развитие методов прогнозирования. Среди
зарубежных организаций стоит назвать Мюнхенский институт конъюнктуры,
Японский центр экономических исследований, Лондонскую школу бизнеса,
Кембриджскую группу экономической политики. Среди отечественных организаций и центров отметим Институт народнохозяйственного прогнозирования
Российской академии наук, Центр ситуационного анализа и прогнозирования
ЦЭМИ РАН, Центр экономической конъюнктуры при Правительстве Российской Федерации, Институт экономики переходного периода. Инициативные
прогнозы могут выполнять предприятия и организации самостоятельно, используя научный потенциал собственных специалистов для оценки перспектив
собственного развития.
В последние годы ведется активная прогнозная деятельность по разработке глобальных прогнозов международными исследовательскими центрами.
Государственная система прогнозирования более сильна в тех странах,
где государство уделяет большое внимание регулированию экономики (например, Япония, Франция). Прогнозы, разрабатываемые в рамках этой системы, —
основа разрабатываемых мер прямого и косвенного регулирования экономики,
формирования национальных программ и планов.
Федеральный закон от 20 июля 1995 г. № 115-ФЗ «О государственном
прогнозировании и программах социально-экономического развития Российской Федерации» определяет состав, назначение и содержание прогнозных документов, порядок их разработки.
К числу основных планово-прогнозных документов, разрабатываемых в
нашей стране, относятся прогнозы, концепция и программа социальноэкономического развития Российской Федерации. Прогнозы как система научно обоснованных представлений о направлениях социально-экономического
развития Российской Федерации разрабатываются на долгосрочную, среднесрочную и краткосрочную перспективу по Российской Федерации в целом, народно-хозяйственным комплексам и регионам. Отдельно выделяется прогноз
развития государственного сектора экономики.
Прогнозы – основа для формирования концепции социальноэкономического развития Российской Федерации на долгосрочную и среднесрочную перспективу. Концепция определяет цели социально-экономического
развития Российской Федерации, конкретизирует его варианты, пути и средства
достижения целей. Первое после вступления в должность Президента Российской Федерации Послание, с которым Президент обращается к Федеральному
9
Собранию, содержит специальный раздел, посвященный Концепции социально-экономического развития Российской Федерации на среднесрочную перспективу. Исходя из положений Концепции Правительство Российской Федерации разрабатывает Программу социально-экономического развития Российской Федерации, которая представляется в Совет Федерации и Государственную Думу.
В Программе должны быть отражены:
оценка итогов социально-экономического развития Российской Федерации за предыдущий период и характеристика состояния экономики Российской Федерации;
концепция Программы социально-экономического развития Российской Федерации на среднесрочную перспективу (р нее входят макроэкономическая политика, институциональные преобразования, инвестиционная и структурная, социальная, аграрная, экологическая, региональная экономическая и
внешнеэкономическая политика).
Прогнозные документы на краткосрочную перспективу должны конкретизировать формирование и распределение бюджетных ресурсов.
1.3. Предпосылки экономического прогнозирования
Прогнозирование – важнейшее связующее звено между теорией и практикой во всех областях жизни общества. Оно выполняет две функции – предсказательную (описательную) и предуказательную (предписательную). Предсказание подразумевает описание возможных или желательных состояний, решений, альтернатив. Предуказание означает использование информации о будущем в целенаправленной деятельности. Предсказательная функция отражает
теоретико-познавательный аспект прогнозирования, а предуказательная –
управленческий.
Начало систематического применения экономического прогнозирования
относится к первой четверти XX в., первоначально применялись принципы и
методы естественно-научных прогнозов.
Примечательно, что значительный вклад в развитие теоретических и методических основ социально-экономического прогнозирования внесли наши
соотечественники. В частности, ученые конъюнктурного института, возглавляемого Н.Д. Кондратьевым (1892–1938), в 1920-е гг. успешно занимались решением проблем экономического прогнозирования рыночного хозяйства, этот
ученый сформулировал основы теории предвидения в серии работ («Проблемы
предвидения», «Основные проблемы экономической статики и динамики»,
«Большие циклы конъюнктуры»). Исследователь исходил из того, что динамика общества поддается прогнозированию, что оно развивается по определенным законам, познание которых дает возможность предвидеть будущие тенденции.
Позднее условия для развития прогнозирования в нашей стране значительно усложнились. Причина заключалась в господствовавшем представлении
10
о плане как основном методе регулирования социалистической экономики и в
противопоставлении прогноза и плана – прогнозирование рассматривалось
только как предплановая стадия, аксиомой считалось утверждение, что директивные планы однозначно определяют ход социально-экономического развития.
На Западе прогностические исследования стали активно развиваться с
конца 1940-х гг. В это время начали создаваться правительственные и неправительственные организации, основной задачей которых стало научное обеспечение разнообразных программ и проектов.
«Бум прогнозов» пришелся на 1960–1970-е гг. В это время появились
многочисленные публикации в области теории, методологии научного предвидения, ведутся активные дискуссии ученых о соотношении прогнозирования и
планирования. Учитывая последствия воздействия многочисленных прогнозов,
особенно пессимистичных, на психологию людей, в 1970 г. Тофлер ввел понятие «футурошок» (боязнь будущего) и заявил о необходимости обучения переменам, считая, что людей необходимо готовить к будущему, а для этого нужна
теория адаптации к будущему.
С начала 1980-х гг. в нашей стране прогнозирование стало рассматриваться как обязательный начальный этап процесса планирования. Этому способствовала и разработка в середине 1980-х комплексной программы социально-экономического и научно-технического развития СССР, которая потребовала более активного применения известных методов прогнозирования для обоснования ее положений.
В первые годы рыночных реформ в России наивные представления о
возможностях регулирования экономики «невидимой рукой рынка» препятствовали системному применению экономического прогнозирования, что часто
приводило к принятию непродуманных решений. В 1995 г. был принят Федеральный закон «О государственном прогнозировании и программах социальноэкономического развития Российской Федерации», определивший цели и содержание системы государственных прогнозов социально-экономического развития Российской Федерации и порядок их разработки.
Необходимость прогнозирования социально-экономических событий и
явлений определяется тем, что любая экономическая организация в своей деятельности неизбежно сталкивается с подвижностью, неопределенностью внешней среды. Подвижность (изменчивость, нестабильность) среды в зарубежной
экономике объясняется в первую очередь высокой насыщенностью потребительского рынка, его разнообразным, быстро изменяющимся характером. В
российской экономике подвижность среды обусловлена, кроме того, нестабильностью социальной, политической и правовой сферы. В этих условиях для
принятия коммерческих решений нужно опираться на постоянное обновление
данных о внешней среде, их анализ и прогноз.
Неопределенность внешней среды означает, что фирма не обладает достаточно полными данными о своем настоящем и будущем, она не в состоянии
предугадать все изменения, которые могут произойти во внешней среде. Про-
11
гнозирование и является одним из способов предвидения внутренних и внешних условий деятельности. Прогнозирование как метод снижения рисков, вызванных неопределенностью, позволяет узнать наиболее вероятное состояние
внешней среды в будущем (политической, научно-технической, финансовой,
экологической, социальной). Так, менеджеров организации могут интересовать
вопросы: какие изменения налогового законодательства возможны в прогнозируемой перспективе; изменится ли таможенное регулирование ввоза (вывоза)
готовой продукции и сырья; следует ли ожидать активизации экологического
либо других общественных движений, способных изменить требования к технологии производства и качеству продукции предприятия?
Кроме того, прогнозирование дает возможность оценки ближайших и отдаленных последствий принимаемых решений. Например, менеджеров организации могут интересовать вопросы: как изменится прибыль организации в ближайшей и отдаленной перспективе в результате диверсификации производства,
изменения организационной структуры предприятия; каких затрат потребует
освоение нового вида продукции?
Возможность прогнозирования обеспечивается тем, что экономические
явления происходят под влиянием экономических законов, закономерностей,
причинно-следственных связей между явлениями. Экономические законы, как
и общественные вообще, существенно отличаются от законов в естественных
науках. Главное отличие заключается в том, что экономические законы, являясь
объективными, проявляют себя через субъективный фактор, т.е. через волю и
сознание людей. Следовательно, эти законы не имеют таких точных зависимостей между переменными, как это наблюдается в законах природы.
Экономические законы от естественных отличаются также по форме своего действия и выражения. Большинство законов природы представляют собой
обобщения преимущественно однозначных причинно-следственных связей –
одна причина обусловливает одно следствие. Кроме того, зависимость между
переменными может носить совершенно определенный характер – такой, что ее
можно представить в виде точной формулы. Как это, например, выглядит в
формулировках закона всемирного тяготения, закона относительности и др.
Что же касается экономических законов, то они являются обобщениями
многозначных статистических причинно-следственных связей. Другими словами, та или иная причина непременно вызовет соответствующее ей следствие.
Но оно появится не в совершенно точной величине, а в среднем, в каких-то
пределах возможных колебаний, как тенденция. Так, в частности, согласно закону спроса, при увеличении цены будет падать его объем, но на сколько –
точно определить никак нельзя, только примерно, только в среднем. В отличие
от законов естественно-научных экономические законы проявляются через
случайности. Этот факт не позволяет надеяться на однозначное, абсолютно
точное предвидение будущего, но позволяет утверждать, что чем более стабильно развитие какого-либо процесса, чем устойчивее взаимосвязи между
изучаемыми явлениями, тем большая вероятность получения достоверного прогноза.
12
В прогнозировании, по мнению Н.Д. Кондратьева, важно основываться на
познанных закономерностях статики, цикличной динамики и социогенетики.
Статика дает возможность исследовать функциональную и морфологическую
структуру системы с точки зрения обеспечения равновесия и равновесного
движения, нормального функционирования с учетом строго определенных пропорций между отдельными составными частями, причем в разных соотношениях этих пропорций.
Ученый проводил серьезные исследования закономерностей динамики
социально-экономических явлений и выявил длинные волны, получившие
позднее название волн Кондратьева. Эти волны – долгосрочные циклы динамики общества (48–55 лет). Они вызывают глубокие изменения в обществе, приводящие к радикальным преобразованиям, кризисам, которые могут завершаться распадом системы, сменой одной системы другой. Закономерности социогенетики проявляются в наследственной изменчивости и отборе, который может
быть целенаправленным или стихийным.
Важная предпосылка, определяющая возможность научного прогнозирования, – степень познания экономических законов, закономерностей, взаимосвязей между явлениями. Поверхностные знания логики развития экономических процессов могут привести к ошибочным выводам относительно будущего.
Кроме того, развитию экономических и социальных явлений присуща в
той или иной степени инерционность, сохранение сложившихся свойств в течение некоторого времени, постепенная реакция на происходящие изменения.
Это обстоятельство позволяет предположить, что динамические характеристики объекта, сложившиеся в прошлом, можно перенести на прогнозируемый период.
Оценка эффективности прогнозирования может быть осуществлена
методом «от противного» – оценивается ущерб, возникающий при выработке и
принятии управленческих решений по результатам анализа текущих ситуаций и
выявления уже возникших проблем, без предварительной прогнозной проработки, эффект прогноза принимается равным величине предотвращенного
ущерба. Следовательно, чтобы прогнозирование было экономически целесообразно, необходимо соблюдение ряда условий:
■ во-первых, осуществлять прогнозирование тенденций динамики внешней среды и объекта управления и результатов развития объекта управления;
■ во-вторых, обеспечить достоверность разрабатываемых прогнозов;
■ в-третьих, своевременно принять управленческие решения, использующие полученную прогнозную информацию.
1.4. Классификация прогнозов и планов
В практике социально-экономического прогнозирования существует
множество подходов к классификации прогнозов и планов. В зависимости от
целей исследования объединение прогнозов в группы может производиться по
одному из критериев. Остановимся подробнее на следующей классификации.
Природа объекта прогнозирования
13
Экономический; социальный; научно-технический; экологический
Подход к прогнозированию
Нормативный; поисковый; комплексный
По подходу к прогнозированию различают поисковые, нормативные и
комплексные прогнозы. Перед поисковым прогнозом ставится задача определения перспектив, возможных состояний развития объекта прогнозирования в
будущем и вероятностей их достижения. Нормативный прогноз определяет пути и способы достижения тех или иных альтернатив, рассматривая сами альтернативы как заданные. Комплексный прогноз сочетает в себе два предыдущих.
Рассмотрим пример подготовки организацией решения о выпуске новой
продукции. В первую очередь руководство организации будут интересовать ответы на такие вопросы: какими качественными характеристиками должен обладать наш товар, чтобы привлечь внимание покупателей; каким может быть наиболее вероятный спрос на наш товар при определенных качественных параметрах и цене? Ответить на эти вопросы – задача поискового прогнозирования.
Определив наиболее вероятные альтернативные варианты качественных характеристик и спроса, руководство предприятия должно выяснить, каких затрат
потребует реализация каждой альтернативы. Ответы на эти вопросы дает нормативный прогноз.
Дальность прогнозирования
Оперативный – до 1 месяца; краткосрочный – от 1 месяца до 1 года;
среднесрочный – от 1 года до 5 лет; долгосрочный — от 5 до 15 лет; дальнесрочный – свыше 15 лет
Уровень (масштаб, глобальность) объекта прогнозирования
Глобальный; межгосударственный; общегосударственный; межрегиональный; региональный; локальный
Размерность характеристик
Одномерный; многомерный
По размерности характеристик объекта прогнозирования различают одномерные и многомерные прогнозы. Одномерные дают описание перспектив
развития объекта одной характеристикой, например, прогноз курса акций или
валют, цены товара или объема продаж конкретного товара; многомерные прогнозы описывают перспективы развития объекта прогнозирования несколькими
характеристиками. К многомерным можно отнести прогнозы рынка труда, здоровья нации, конъюнктуры рынка, финансового состояния предприятия. Каждый из них может содержать несколько показателей. Выбор между многомерными и одномерными прогнозами осуществляется с учетом сложности объекта
прогнозирования и его целей, так как они задают степень детализации прогнозных расчетов.
14
Учет прогнозного фона
Безусловный; условный
По учету прогнозного фона различают условные и безусловные прогнозы. В первые десятилетия специалисты в области экономического прогнозирования пытались давать точную, однозначную количественную характеристику
объекта прогнозирования, например, объемы производства и продаж на определенную дату, точную величину цены на конкретный товар и т.п. Задача эта,
сложно разрешимая в прошлом, с повышением нестабильности, изменчивости
экономической среды в настоящее время становится нереальной. Осознание
этого обстоятельства привело к распространению условных прогнозов.
Безусловным называют прогноз, в котором будущее состояние объекта
прогнозируют без учета возможных будущих состояний прогнозного фона. Полученный таким образом прогноз основан либо на сложившейся в прошлом динамике объекта, либо на выявленных в прошлом взаимосвязях. Чем выше степень неопределенности и изменчивости прогнозного фона, тем менее достоверным становится прогноз.
Прогнозный фон – совокупность внешних по отношению к объекту прогнозирования условий, существенно влияющих на развитие объекта. Описание
прогнозного фона может включать наиболее значимые для развития объекта
прогнозирования характеристики макро- и микросреды.
Условный прогноз учитывает возможные состояния прогнозного фона и
поэтому разрабатывается в нескольких вариантах. Состояние объекта прогнозирования ставится в зависимость от состояния прогнозного фона. Логика разработки такого прогноза следующая. Если в прогнозном периоде состояние
прогнозного фона будет характеризоваться параметрами А (а1, а2, a3…), то развитие объекта прогнозирования, вероятно, будет характеризоваться параметрами хА (х1, х2, х3, …), если состояние прогнозного фона будет характеризовать
другие параметры, то они будут задавать другие условия развития объекта прогнозирования и состояние объекта прогнозирования будет описываться системой параметров у (у1, у2, у3, …).
С понятием условных прогнозов тесно связана современная интерпретация принципа вариантности прогнозирования. Она понимается как разработка
прогнозов, учитывающих возможность возникновения нескольких качественно
различных ситуаций, соответственно нескольких альтернативных вариантов
развития объекта прогнозирования. Наряду с позитивными вариантами следует
разрабатывать предупредительные профилактические прогнозы, так называемые прогнозы катастроф. Их цель – предусмотреть, какие условия могут привести объект прогнозирования (предприятие, организацию, город, регион, страну) к катастрофе и какие меры позволят предупредить ее. К профилактическим
прогнозам могут быть отнесены прогнозы банкротства предприятий, прогноз
экологической катастрофы, прогноз полного исчерпания необходимых предприятию ресурсов и др.
15
Точность характеристик
Точечный; интервальный
По точности прогнозных характеристик принято выделять точечные прогнозы и интервальные. В точечном прогнозе содержится одно количественное
значение искомой характеристики. Следует иметь в виду, что этот прогноз
практически никогда не совпадает с результатом. Относительно количественных точечных прогнозов должно быть задано вероятностное определение соответствия прогнозов действительным величинам. Например, можно принять
требование, что вероятность превышения действительных данных равна вероятности их занижения по прогнозу. В этом случае у нас получится точечный
прогноз типа медианы. Интервальные прогнозы выражают количественное значение искомого показателя в виде «вилки» возможных значений.
Следует отметить, что существует определенная взаимосвязь между различными классификационными группами. Так, существует определенная зависимость между глобальностью объекта прогнозирования и дальностью разрабатываемого прогноза. Чем крупнее объект, тем более инертен он в своем развитии, тем медленнее накапливаются и проявляются в нем изменения, но тем
серьезнее они по возможным последствиям. Поэтому необходимо заблаговременно предвидеть вероятные тенденции его динамики. Управление локальными
объектами часто сталкивается с проблемой оперативного получения информации о ближайших перспективах (изменение спроса и цен на фондовом, товарном и валютном рынках, перспективы достижения намеченных ориентиров в
предпринимательской деятельности и т.п.). Подобная логика лежит в основе
взаимозависимости между глобальностью объектов прогнозирования и точностью прогнозных характеристик, между точностью прогнозных характеристик
и дальностью прогнозирования.
Планы классифицируется по содержанию, по объекту планирования, по
времени действия, по степени точности.
По содержанию выделяют технико-экономическое, оперативнопроизводственное, бизнес-планирование и др.
Технико-экономическое планирование предусматривает разработку и количественное определение технико-экономических показателей, характеризующих развитие социально-экономической системы. В ходе техникоэкономического планирования могут обосновываться оптимальные объемы
производства товаров, выбираться необходимые ресурсы и устанавливаться
нормы их расхода, определяться конечные финансово-экономические показатели и т.д.
В ходе оперативно-производственного планирования устанавливаются
текущие задания структурам и службам, осуществляются организационноуправленческие воздействия с целью корректировки плана в соответствии с изменяющейся обстановкой.
При разработке бизнес-плана проводятся расчеты технологической и эко-
16
номической эффективности конкретного направления развития предприятия.
В зависимости от объекта планирования выделяют план предприятия,
план цеха, план участка, план рабочего места и др.
По времени действия планирование разделяется на оперативное, краткосрочное, среднесрочное и долгосрочное.
По степени точности планирование может быть укрупненным и уточненным.
1.4. Функции, условия и методология прогнозирования и планирования
Прогнозирование в социально-экономической области сочетает три группы функций: теоретико-познавательную, предсказательную и управленческую.
Функции прогнозирования:
Предвидение тенденций развития прогнозируемого объекта (экономика страны, региона, предприятия, рынка и т.п.) в силу воздействующих на его
динамику факторов.
Предвидение реакции этого объекта на то или иное плановое или рыночное решение, возможные последствия реализации этого решения (строительства нового предприятия, выхода с новым товаром на рынок, изменения
ставки налога и т.п.).
После того, как решение принято и начало осуществляться, нужно
продолжать прогнозировать ход и последствия его выполнения, чтобы вовремя
скорректировать или отменить решение, если условия его реализации радикально изменились.
При разработке плана необходимо соблюдать ряд требований, важнейшими из которых являются:
1. Оптимальность, предполагающая такой вариант плана, когда потребности в ресурсах наименьшие, а конечный результат по финансовым и другим
критериям лучший и, как правило, сроки осуществления события минимальные.
2. Определенность, при которой установленные показатели и другие условия должны быть конкретизированы по величине и срокам выполнения,
обоснованными и реализуемыми.
3. В плане должны быть четко определены цели и задачи. План оформляется в виде специального документа. После его принятия соответствующим органом управления начинается организационная работа по практической реализации плана.
Требования, которым должны удовлетворять прогнозы:
а) вариантность прогноза;
б) высокая степень объективности и достоверности прогнозных оценок;
в) комплексность прогноза с охватом характеристик всех важнейших
сфер экономики и социальной жизни;
17
г) сбалансированность оценок, содержащихся в различных структурных
блоках прогноза, между собой;
д) непрерывность прогнозирования, опирающаяся на сопряженность информационную, функциональную и методологическую — прогнозов, относящихся к различным периодам прогнозирования.
Функции целевого программирования — выявление узловых точек (приоритетов) социально-экономического развития, позволяющих решать крупные
проблемы; концентрация сил и средств на решении ограниченного числа стратегических задач; взаимная увязка программ между собой и с остальными блоками экономики.
Условия и факторы развития роли прогнозирования, планирования и
программирования в регулировании экономики:
1. Усиление зависимости процессов в каждой отдельной стране от экономических и социально-политических процессов во внешнем мире существенно
повышает значение взаимодействия национальных центров прогнозноплановой работы с аналогичными центрами общемировой ориентации.
2. Резкое обострение в мировых масштабах проблемы дефицита энергетических и иных природных ресурсов — освоение глубинного потенциала новых
знаний и научно-технологических инноваций, позволяющих задействовать ресурсоэкономные технологии и многократно повысить конечную эффективность
экономики — научно-технологическое прогнозирование.
3. Взаимодействие государственной и частной форм власти во всех вопросах стратегического регулирования развития.
4. Развитие транснациональных корпораций (ТНК) и иных предпринимательских структур национального и регионального масштаба.
5. Проявление региональных особенностей социально-экономической политики.
Изыскательский
(генетический)
подход
Нормативный
(телеологический)
подход
Потенциал
знаний и
технологий.
Законы развития
Цели
Потребности
Проблемы
Ресурсы
Варианты стратегических
решений
ПРОГНОЗЫ
Методологии прогнозирования:
— генетического (изыскательского) прогнозирования и
— методологии нормативного (телеологического) прогнозирования (см.
рис. 1.1).
Концепции
Стратегии
Планы
Программы
18
Рис. 1.1. Взаимодействие изыскательского и нормативного подходов при прогнозировании, стратегическом планировании и программировании социальноэкономического развития
Генетический (изыскательский) подход исходит из анализа предыстории развития объекта (макроэкономической системы), фиксирует его основополагающие факторы, определяет особенности развития, выводит устойчивые
тенденции и закономерности, и на этой основе выстраиваются гипотезы и выводы относительно прогнозируемого объекта в будущем.
Нормативный (телеологический) подход отражает возможность и необходимость целенаправленного влияния на прогнозируемые макроэкономические процессы, исходя из понимания потребностей общества, выдвигаемых целей и ресурсной базы.
Метод прогнозирования — это способ, алгоритм разработки прогноза.
Применительно к социально-хозяйственной системе (например, к национальной экономике в целом или к ее региональным блокам) выделяют три основные
группы методов прогнозирования:
1) эвристические (базирующиеся на исследовании и раскрытии ранее неизвестного), среди которых наиболее используемыми являются методы экспертных оценок;
2) фактологические (базирующиеся на логическом анализе фактов, статистических данных и прогнозных оценок с использованием, например, математических моделей);
3) комплексные (комбинированные).
В условиях рыночной экономики при разработке любого прогноза учитываются:
1. Формы организации материальных потоков. Преобладающая часть
всех видов продукции реализуется свободно. В связи с этим разработать достоверный прогноз загрузки мощностей в том или ином производстве можно только на основе детальной информации о конъюнктуре на товарных рынках.
2. Способы формирования денежных потоков. Финансовые ресурсы в
преобладающей части вышли из сферы прямого государственного регулирования. Поэтому важно определить, каких объемов достигнет частный капитал и
куда он будет направлен.
3. Динамика цен и их влияние на производство и распределение. Сейчас
нельзя получить ни одной достоверной прогнозной оценки по производству, не
зная конъюнктуры цен.
4. Внутренняя конвертируемость рубля. Известно, в каких отраслях зарабатывается валюта, а в каких она нужна для импорта. Прогноз определяет ее
движение, переход от одних собственников к другим.
Раздел 2. Методология прогнозирования и планирования
19
2.1. Основы методологии прогнозирования и планирования
Методология прогнозирования и планирования развития экономики определяет основные принципы, подходы и методы проведения прогнозных и
плановых расчетов, раскрывает и характеризует логику формирования прогнозов, планов и их осуществления.
Принципы — это основополагающие правила прогнозирования и планирования, т.е. исходные положения формирования прогнозов и обоснования
планов с точки зрения их целенаправленности, системности, структуры, логики
и организации разработки. Это основные требования, которые должны выполняться при разработке прогнозов и планов.
Методы — это способы, приемы, используемые при разработке прогнозов,
планов, программ. Они выступают в качестве инструмента, позволяющего реализовывать методологические принципы прогнозирования и планирования.
Логика — упорядоченная последовательность действий при проведении
прогнозных расчетов и обосновании плановых решений.
Составной частью методологии является методика. Она носит частный
характер и находится в соподчинении с методологией. Методика представляет
собой совокупность конкретных способов и приемов, используемых для проведения конкретных прогнозных или плановых расчетов. Примером могут служить методики Международного валютного фонда по прогнозированию макроэкономических показателей или методики определения эффективности внедрения научно-технических мероприятий, расчета показателей на микроуровне.
Общеметодологический
подход
к
исследованию
социальноэкономических процессов определяет диалектический метод, который позволяет проникать в суть изучаемых явлений и фактов, относящихся к исследуемым объектам, устанавливать связи между явлениями. Он реализуется на основе использования как общих научных подходов и методов исследования, так и
специфических.
Среди общих подходов можно выделить следующие:
— исторический, суть которого заключается в рассмотрении каждого явления во взаимосвязи его исторических форм;
— комплексный — включает рассмотрение явлений в их связи и зависимости
с другими процессами и явлениями;
— системно-структурный — предполагает, с одной стороны, рассмотрение
экономической системы в качестве динамически развивающегося целого, с
другой — расчленение системы на составляющие структурные элементы в их
взаимодействии.
В рамках комплексного подхода выделяются: генетический и целевой
подходы. Сущность генетического подхода состоит в том, чтобы проследить
возможные направления и этапы будущего развития, опираясь на оценку исходного уровня настоящего и выявленные исследованием закономерности развития. Этот подход учитывает инерционные моменты, возникшие в прошлом,
20
настоящем и оказывающие влияние на будущее. При данном подходе связь и
последовательность явлений рассматривается от прошлого и настоящего к будущему. Генетический подход позволяет рассматривать объект, выявляя тенденции его развития и возможные результаты без влияния на этот объект.
При целевом подходе определяется цель и возможные пути ее достижения, т.е. он исходит из определенного результата, который должен быть достигнут в будущем. При этом подходе связь явлений рассматривается от будущего к настоящему.
Эти два подхода используются во взаимосвязи, потому что важно получить сведения о развитии объекта, не влияя на него и, задав цель, определить
пути ее достижения.
Научными основами методологии прогнозирования и планирования экономики служат законы развития общества и экономическая теория.
Прогностические функции выполняют законы диалектики: закон единства и борьбы противоположностей, закон взаимного перехода количественных
и качественных изменений, закон отрицания отрицания.
Теоретической основой разработки научных представлений о будущем
развитии экономики является экономическая теория:
А) Кейнсианская теория делает упор на совокупные расходы (совокупный
спрос) и их компоненты: внутреннее потребление в частном секторе; государственные расходы; инвестиции; экспорт товаров и услуг; импорт товаров и услуг. В состоянии равновесия левая часть (совокупные расходы) равна правой
части (объему производства в стране). Спрос обеспечивает сбалансированный
рост. На этой модели базируется методика расчета ВНП, возможных инвестиционных потоков, экспорта и импорта товаров и услуг.
Б) Представителем монетарной теории является М. Фридмен. Главный
параметр стабилизационной политики, согласно данной теории, — объем денежного предложения, т.е. монетаризм делает упор на деньги. Монетарная политика — один из основных макроэкономических инструментов, опирающихся на
способность денежно-кредитной системы влиять на денежное предложение и
соответственно на ставку процента.
В) Среди важнейших положений марксистской теории необходимо выделить следующие: деление общественного производства на две сферы — сферу
материального производства, где производятся материальные блага и услуги, и
непроизводственную сферу, оказывающую различные нематериальные услуги;
деление производственной сферы на два подразделения: I подразделение —
производство средств производства, II — производство предметов потребления;
деление совокупного общественного продукта и любого вида продукции (товара) по стоимости на две части: стоимость израсходованных средств производства (с) и вновь созданную стоимость (v + т), где v — стоимость необходимого
продукта и т — стоимость прибавочного продукта; положение о прибавочном
продукте как источнике накопления и о накоплении как источнике расширенного воспроизводства. Эти положения имеют важное значение при формировании (установлении) общеэкономических пропорций на прогнозируемый (пла-
21
новый) период. На их основе выделяются приоритеты, обосновываются соотношения между фондами потребления и накопления, производством и потреблением и другие пропорции.
2.2. Принципы прогнозирования и планирования
Разработка прогнозов и планов должна основываться на методологических принципах.
1. Основополагающим принципом прогнозирования является принцип
альтернативности, который требует проведения многовариантных прогнозных разработок (альтернатив). В основу используемого прогноза должен быть
положен наилучший вариант из двух или нескольких возможных. Развитие
экономики и ее звеньев возможно по разным траекториям.
2. Принцип системности предполагает исследование количественных и
качественных закономерностей в экономических системах, построение такой
логической цепочки исследования, согласно которой процесс выработки и
обоснования любого решения должен отталкиваться от определения общей цели системы и подчинять деятельность всех подсистем достижению этой цели.
Он позволяет расчленить любую систему на множество подсистем (экономика
делится на комплексы, последние — на подкомплексы и т.д.).
3. В связи с непрерывностью экономического развития, совершенствованием производства на базе развития науки и техники должен соблюдаться
принцип непрерывности планирования, т.е. преемственности прогнозов,
планов. Должны разрабатываться прогнозы и планы различного временного аспекта и увязываться между собой. Так, среднесрочные планы должны разрабатываться на основе перспективных направлений, отражаемых в долгосрочных
планах, краткосрочные — исходя из показателей среднесрочных планов. Долгосрочные планы должны корректироваться и продлеваться на соответствующий период. Это обусловлено возникновением новых потребностей общества,
крупными изменениями в технике и другими причинами.
4. Принцип целенаправленности и приоритетности требует, чтобы каждый план носил целевой характер, т.е. был направлен на достижение определенных целей, а в качестве приоритетов выделялись отрасли экономики и социально-экономические проблемы, от развития и решения которых зависит развитие экономики в целом. Этот принцип позволяет сосредоточить ресурсы на
главных направлениях развития экономики и решении проблем общегосударственного значения.
5. Принцип приоритетности реализуется в тесной связи с принципом
комплексности, предполагающим рассмотрение всех сторон объекта исследования в его связи и зависимости с другими процессами и явлениями. При обеспечении приоритета в развитии важнейших отраслей должно предусматриваться соответствующее развитие всех других отраслей.
6. С этими принципами в тесной связи должен реализовываться принцип
социальной ориентации, требующий обеспечения приоритетного решения социальных проблем.
22
7. С целью обеспечения наиболее эффективного функционирования экономики должен соблюдаться принцип оптимальности. Оптимальность непосредственно связана с повышением эффективности производства. Оптимальный — это такой вариант развития экономики, который предусматривает максимальное удовлетворение нужд народного хозяйства и населения при имеющихся ресурсах с учетом их рационального использования.
8. Принцип адекватности целесообразно в большей мере рассматривать
применительно к моделированию социально-экономических процессов. Экономико-математические модели, используемые в процессе прогнозирования
развития экономики и оптимального планирования, должны быть адекватными,
т.е. отражать реальные процессы. От этого во многом зависят результаты прогнозных и плановых расчетов.
9. Сбалансированное и пропорциональное развитие экономики возможно
при учете в процессе разработки прогнозов и планов принципа сбалансированности и пропорциональности. Сущность этого принципа заключается в
балансовой увязке различных показателей, установлении пропорций и обеспечении их соблюдения.
10. Принцип сочетания отраслевого и регионального аспектов планирования требует, чтобы отраслевые планы разрабатывались с учетом интересов данной территории и рационального использования местных ресурсов. Отраслевое планирование позволяет осуществлять единую техническую политику
в каждой отрасли, выявлять спрос на продукцию отрасли, поддерживать необходимые пропорции (внутриотраслевые, межотраслевые), использовать передовой опыт и решать другие задачи. Территориальное планирование позволяет
обеспечить комплексное развитие хозяйства регионов, рациональное размещение производства, решение социальных и экологических проблем. Соблюдение
этого принципа способствует повышению эффективности общественного производства, росту благосостояния народа и улучшению состояния окружающей
среды.
2.3. Технология прогнозирования
Технология прогнозирования включает в себя ряд последовательных этапов, описанных в табл. 2.1. Содержание работ на каждом этапе будет определяться и спецификой объекта исследования, и избранными методами прогнозирования.
Таблица 2.1
Процедурная схема прогнозирования
Этап
Содержание работ
Прогнозная ориентация Совокупность работ, включающая определение цели, объекта и
(программа исследова- задач прогнозирования, периода упреждения (перспективного пения)
риода) и периода основания (ретроспективного периода) прогноза,
заданной точности и вероятности прогноза. Завершается разработкой задания па прогноз
Прогнозная ретроспек- Исследование истории развития объекта прогнозирования и про-
23
ция
гнозного фона с целью получения их системного описания (сбор
информации о развитии объекта прогнозирования и прогнозного
фона в ретроспективном периоде)
Прогнозный диагноз
Обобщение и систематизация полученной па предыдущем этапе
информации, построение динамических рядов показателей для выявления тенденций развития объекта прогнозирования и прогнозного фона, выбора (разработки) моделей и методов их прогнозирования. Качественная и количественная оценка сложившихся в
прошлом закономерностей
Прогнозная проспекция Разработка альтернативных вариантов прогноза развития объекта
прогнозирования, конкретизация пессимистического, оптимистического, инерционного и реального вариантов
Верификация прогноза Оценка достоверности и точности прогноза
Корректировка прогно- Уточнение прогноза на основании его верификации и (или) дополза
нительной информации
Далее мы подробно рассмотрим подсистемы, обеспечивающие процесс
прогнозирования.
Организационное обеспечение будет различным при разработке прогноза самостоятельно менеджером, использующим его результаты для принятия
управленческих решений, собственными службами предприятия либо специализированными организациями.
Информационное обеспечение в значительной степени определяет возможность использования тех или иных методов прогнозирования. Виды и источники информации, требования к информационному обеспечению прогнозирования рассматриваются в следующей главе.
Техническое обеспечение создает материальную базу для применения
аппарата математического моделирования, обработки больших массивов информации, использования современных справочно-поисковых систем.
Кадровое обеспечение включает специалистов по организации и технологии прогнозирования, а при применении интуитивных методов — компетентных экспертов. Они определяют выбор методов и инструментария прогнозирования, оценивают качество исходной и прогнозной информации, дают содержательную интерпретацию полученных результатов.
Программное обеспечение характеризуется в последние годы огромным
влиянием на развитие прогнозирования через разработку пакетов прикладных
программ, специально предназначенных для применения различных методов
прогнозирования. Они позволяют оперативно проводить расчеты, необходимые
для обоснования будущего.
Для специалиста при разработке прогноза представляют интерес два типа
компьютерных пакетов. Во-первых, это статистические пакеты, позволяющие
проводить регрессионный анализ, анализ временных рядов и т.п. Типичной
программой, позволяющей использовать статистические пакеты, является
Microsoft Excel. Во-вторых, это пакеты, специально созданные для прогнозирования. В настоящее время их число постоянно растет, а внутреннее наполнение
совершенствуется в направлении усовершенствования математического аппа-
24
рата и максимального упрощения их использования и интерпретации результатов.
Методическое обеспечение включает совокупность методов прогнозирования, из которых необходимо выбрать наиболее адекватный задачам прогнозирования и собранной информации. Специалисты считают, что метод прогнозирования должен вызывать доверие у менеджеров, принимающих решение
на основе прогноза, поэтому не всегда оправдано усложнение прогнозных моделей. Процедура прогнозирования должна приносить прибыль, которая как
минимум покрывала бы издержки на выполнение прогноза.
Методы прогнозирования — это совокупность приемов и способов
мышления, позволяющих на основе анализа ретроспективных данных об исследуемом объекте вывести суждения определенной достоверности относительно
будущего развития объекта.
3. Понятие временного ряда в экономическом прогнозировании
3.1.
Определение и основные виды моделей динамики данных.
Для разработки прогнозов определенный интерес представляют данные о
развитии объекта в течение времени. Задача состоит в изучении таких данных с
последующим перенесением сложившейся тенденции на будущий период. Прогнозы, основанные на экстраполяции данных, считают развитие объекта инерционным, сохраняющим в будущем периоде траекторию движения.
Любая характеристика, которая собрана или зафиксирована через последовательные промежутки времени, называется временным, или динамическим,
рядом. Выбор метода прогнозирования для временного ряда определяется типом моделей динамики данных.
Выделяют четыре основных типа моделей динамики данных.
Горизонтальную модель используют, если наблюдения колеблются относительно постоянного уровня или среднего значения, в этом случае временной ряд называют стационарным. Внешние воздействия относительно постоянны. Прогнозирование включает использование его предыстории для оценки
среднего значения, которое становится прогнозным. Для оценки будущей динамики могут быть использованы методы наивного прогнозирования, простого
среднего, скользящего среднего, простое экспоненциальное сглаживание.
Трендовая модель применяется, если значения временного ряда возрастают или убывают в течение некоторого, достаточно большого промежутка
времени. Методы прогнозирования должны дать возможность выявить закономерность и рассчитать параметры средней теоретической линии развития объекта. Эта задача может быть решена методами прогнозной экстраполяции, для
оценки одного будущего значения используют методы скользящей средней и
линейного экспоненциального сглаживания.
Сезонная модель используется, если на данные наблюдений влияют не
только общие закономерности развития, но и сезонные факторы. В прогнозировании могут быть использованы модели экстраполяции с аддитивной и мульти-
25
пликативной компонентой.
Циклическая модель применяется, если данные характеризуются подъемами и спадами, не зависящими от времени. Циклическая компонента обычно
имеет причиной общие закономерности экономического развития (жизненный
цикл продукции, деловой цикл, бизнес-цикл). Методы прогнозирования — экономические индикаторы, эконометрические модели, многомерная регрессия.
Временной (или динамический) ряд — это упорядоченная во времени
совокупность измерений одной из характеристик исследуемого объекта ( y t ),
t — порядковый номер анализируемого периода.
Временные ряды отличаются от простых статистических выборок в фиксированный момент времени следующими признаками:
последовательные во времени показатели временных рядов являются
взаимозависимыми, особенно это относится к близко расположенным наблюдениям;
в зависимости от момента наблюдения показатели временного ряда
обладают разной информативностью: информационная ценность наблюдений
убывает по мере их удаления от текущего момента времени;
с увеличением количества показателей временного ряда точность статистических характеристик не будет увеличиваться пропорционально числу наблюдений, а при появлении новых закономерностей развития она может даже
уменьшаться.
В зависимости от того, отражают ли элементы временного ряда состояние
объекта за определенный промежуток времени или фиксируют в строго установленные моменты, различают интервальные и моментные ряды. Они могут
задаваться в табличной или графической форме.
Интервальный временной ряд — это совокупность показателей, каждый из которых характеризует развитие объекта исследования за определенный
период времени (год, квартал, месяц, сутки и т.п.).
Моментный временной ряд — это совокупность показателей, характеризующих состояние объекта на определенную дату, например на первое число
каждого месяца, на первое января каждого года и т.п.
В зависимости от способа построения исследуемых характеристик возможно построение временных рядов, состоящих из абсолютных, относительных и средних величин. Относительные уровни можно получить делением абсолютных или средних значений на один и тот же элемент ряда, принятый за
базу. Возможно также получение относительных величин при сравнении каждого значения показателей временного ряда с предыдущим. Выбор вида ряда
определяется задачами прогноза.
Основное правило построения временных рядов — необходимость обеспечения сопоставимости его отдельных показателей. Для этого все элементы
должны характеризовать изучаемое явление за равные промежутки времени
или фиксировать состояние признака через равные интервалы. Каждое значение показателя во временном ряду необходимо рассчитывать по единой методике и выражать в одних и тех же единицах измерения. Количество измерений
26
должно быть достаточно представительным, чтобы выявить устойчивую тенденцию. В то же время следует учитывать, что использование слишком большого количества ретроспективных значений может привести к преувеличению
прошлых тенденций, нечувствительности тренда к переменам. Для построения
экономического прогноза рекомендуется использовать 5—20 измерений исследуемой характеристики в ретроспективном периоде. Количество анализируемой информации зависит также от длины перспективного периода, т.е. периода
времени, на который вы намереваетесь строить прогноз. Экстраполяция может
дать хорошие результаты, если ваши выводы о будущем развитии объекта прогнозирования основываются на информации о развитии исследуемого объекта
за ретроспективный период, в 3 раза превышающий период упреждения прогноза.
3.2.
Математико-статистический
анализ
социально-
экономических процессов
Непосредственно до этапа прогнозирования экономических показателей
объект прогнозирования необходимо проанализировать.
В процессе анализа могут быть рассчитаны следующие средние показатели динамики:
средний уровень ряда, или средняя хронологическая;
средний абсолютный прирост;
средний темп роста;
средний темп прироста.
Средний уровень ряда показывает, какая средняя величина уровня характерна для всего анализируемого периода. К его расчету прибегают для рядов, состояние или изменение которых стабильно в течение большого периода
времени, и рядов с уровнями, колеблющимися в короткие промежутки времени.
Показатель рассчитывается различно для интервальных и моментных рядов.
Для интервального ряда сумма значений фактических показателей временного ряда делится на число показателей:
n
y
y
t
t 1
n
(2.1)
Для моментного ряда расчет осуществляется по формуле (2.2). Следует
учесть, что значения первого и последнего показателей временного ряда берутся в половинном размере, поэтому в знаменателе количество показателей
уменьшается на единицу.
1
1
y1 y 2 … yt … y n
2
y 2
n 1
(2.2)
Средний абсолютный прирост ряда показывает скорость развития явления и рассчитывается по формуле
27
y n y1
,
(2.3)
n 1
где y1 — первый зарегистрированный показатель временного ряда;
y n — последний зарегистрированный показатель временного ряда;
п — число показателей временного ряда.
Средний темп роста может быть рассчитан по формуле средней геометрической, при сравнении последнего показателя временного ряда с первым расчет осуществляется по формуле
y
T p n1 n *100%.
y1
(2.4)
Средний темп прироста определяется по формуле
T пр Т р 100% .
(2.5)
Следует учесть, что средние показатели можно использовать только для
равномерно меняющихся явлений.
y
3.3.
Методы выравнивания временного ряда
Одним из подготовительных этапов прогнозирования выступает процедура выравнивания временного ряда.
Для начала напомним основные статистические инструменты, которые
могут быть использованы для целей выравнивания временного ряда.
Скользящее среднее порядка k — это среднее значение k последовательных наблюдений:
y
y1 y 2 … y k
,
k
(2.6)
где k — количество наблюдений в скользящем среднем.
Величина k может принимать произвольно выбранное значение (3, 4, 5 и
т.д.). Заметим, что величина k зависит от размера изучаемой совокупности, чем
большее количество наблюдений анализируется, тем большее значение она
может принимать.
Метод простого скользящего среднего может быть применен к стабильным данным, при незначительных колебаниях. В случае однонаправленных изменений исследуемого показателя (повышения или понижения) может быть использован метод двойного скользящего среднего.
Метод двойного скользящего среднего представляет более сложную
двухэтапную процедуру усреднения. Сначала временной ряд сглаживается методом простого скользящего среднего, а потом повторяется процедура усреднения для рассчитанных значений.
Для описания динамики многих экономических явлений и процессов используют процедуры, приближающие фактические значения временного ряда к
28
тренду. Для решения этой задачи используется сглаживание, близкое по технике расчетов к расчетам скользящей средней.
Сглаживание представляет собой усреднение значений временного ряда.
Оно может быть выполнено по разным методикам: как средние арифметические или средние геометрические, по четному или нечетному количеству точек.
Ниже приводятся формулы сглаживания по трем или пяти точкам по средней
арифметической.
Формулы сглаживания по трем точкам:
1
~
y 0 ( y 1 y 0 y 1 );
3
1
~
y 1 (5 y 1 2 y 0 y 1 );
6
1
~
y 1 ( y 1 2 y 0 5 y 1 ).
6
(2.7)
1
~
y0 ( y 2 y 1 y0 y 1 y 2 );
5
1
~
y 1 (4 y 2 3 y 1 2 y0 y 1 );
10
1
~
y 1 ( y 1 2 y0 3 y 1 4 y 2 );
10
1
~
y 2 (3 y 2 2 y 1 y 0 y 1 );
5
1
~
y 2 ( y 2 y0 2 y 1 3 y 2 ).
5
(2.8)
где y 0 , ~y 0 — значения исходной и сглаженной функции в средней точке;
y 1 , ~
y 1 — значения исходной и сглаженной функции в левой от средней
точки;
y 1 , ~
y 1 — значение исходной и сглаженной функции в правой от средней
точки.
Формулы ~y 1 , ~y 1 применяются только по краям интервала.
Формулы сглаживания по пяти точкам:
Процедура сглаживания может быть простой или рекуррентной. При рекуррентном сглаживании первоначально рассчитывается значение в первой
точке временного ряда по простой средней, а при расчете значений в последующих точках в формулу подставляется сглаженное значение в предыдущей.
Следует учесть также, что чем короче исходный временной ряд, тем
меньшее количество усреднений следует использовать. Процедура сглаживания
повторяется от одного до трех раз. Степень сглаживания проверяется визуально
или рассчитывается в соответствии с принятым критерием. Объективным критерием оценки целесообразности сглаживания может быть величина абсолютного отклонения сглаженных значений от фактических:
y t ~y t ,
(2.9)
29
где — положительное число, выбираемое из соображений точности
представления данных и точности последующих алгоритмов обработки.
Сглаженные значения, рассчитанные по разным методикам, как правило,
не совпадают, но это не мешает решить основные задачи предварительного
этапа прогнозирования – оценить возможность применения методов прогнозной экстраполяции (будут рассмотрены далее) и выбрать вид функции, способный описать рассматриваемый процесс.
4. Система методов прогнозирования
4.1.
Классификация методов прогнозирования.
На сегодняшний день в теории и практике прогнозирования разработано
большое число методов прогнозирования (по оценкам специалистов известно
свыше 150). Они различаются по назначению, по виду используемой информации, по реализации формальных процедур получения прогнозов и т.д.
В специальной литературе, изучающей методологические основы прогнозирования, предлагаются различные подходы к проведению классификации методов прогнозирования. Однако наибольшее распространение нашла трехуровневая классификация (см. рис. 2.1), на каждом уровне которой разделение осуществляется в соответствии со своим классификационным признаком:
1 уровень – степень формализации;
2 уровень – общий принцип действия;
3 уровень – способ получения прогнозной информации.
Так по степени формализации (степени использования математического
аппарата) все методы можно разделить на две больших группы – экспертные
методы прогнозирования и формализованные методы прогнозирования.
Методы
прогнозирования
Экспертные методы
прогнозирования
Методы
индивидуальных эксэкспертных
оценок
Методы
коллективных
экспертных
оценок
Интервью
Комиссий
Формализованные методы
прогнозирования
Сценарный метод прогнози-
Методы
экстраполяции
Методы
моделирования
Экстраполяция по
темпу
прироста
Экономикостатистиче-
30
рования
ское
Анкетного опроса
Мозговой атаки
Метод
морфологического
анализа
Экстраполяция по
темпу роста
Структурное
Аналитических записок
Суда
Метод
прогнозирования по
аналогии
Аппроксимация
динамического ряда
Оптимизационное
Адаптивные методы
Имитационное
Метод
подбора
функций
Модели
теории
игр
Рис. 2.1. Классификация методов прогнозирования
4.2.
Оценка качества количественных прогнозов
Для оценки качества прогноза, разработанного с применением формализованных методов, принято использовать такие характеристики как надёжность, точность, достоверность, ошибки прогноза.
Под надёжностью прогнозных расчётов понимается мера неопределённости поведения объекта прогнозирования во времени.
Достоверность прогноза определяется вероятностью осуществления
прогноза для заданного варианта или доверительного интервала.
Точность прогноза характеризует интервальный разброс прогнозных траекторий при фиксированном уровне достоверности.
Ошибки прогноза представляют собой меру отклонения прогнозных оценок от реальных значений состояния прогнозируемого объекта.
Однако, описать такие характеристики как надёжность, точность, достоверность, вычислить ошибки прогноза априори не представляется возможным,
поскольку прогнозные результаты не с чем сравнивать. Поэтому и на сегодняшний день перед разработчиками прогнозов встаёт проблема: «Как оценить
качество прогноза ещё до его реализации?». Определённые шаги в сторону
улучшения качества прогноза можно сделать, изучив факторы, влияющие на
показатели качества прогноза (рис. 2.2).
Качество исходной информации
Модель
прогноза
Метод прогнозирования
31
Качество
прогноза
Рис. 2.2. Факторы, влияющие на качество прогноза
Качество исходной информации, в свою очередь, определяется:
— точностью экономических измерений;
— качеством выборки;
— отсутствием ошибок согласования (данные ошибки возникают в тех
случаях, когда исходная информация для проведения прогнозных расчётов подготавливается различными специалистами, использующими разные методологические подходы).
Наибольшие погрешности (стратегические ошибки прогнозирования)
возникают в результате неудачного выбора метода прогнозирования. Например, на основании прогнозов социально-экономического развития СССР, проводимых в 1960-е годы, Генеральный секретарь Коммунистической партии
Н.С.Хрущёв заверил, что к 1980 году «СССР догонит и перегонит Америку».
Стратегическая ошибка прогнозирования была обусловлена тем, что для долгосрочного прогнозирования применялись методы экстраполяции которые, как
мы уже знаем, целесообразно использовать для краткосрочного прогнозирования.
Погрешности, связанные с выбором модели прогноза, возникают в результате упрощения, несовершенства теоретических построений или неадекватности моделей прогнозируемым социально-экономическим процессам. Иногда для прогнозирования процессов, протекающих в нашей стране, используются модели разработанные зарубежными специалистами и хорошо себя зарекомендовавшие для прогнозирования аналогичных процессов в других странах.
Однако следует помнить о том, что данные модели могут быть неадекватны по
отношению к социально-экономическим процессам, происходящим в нашей
стране, и их использование может привести к серьезным ошибкам и просчетам.
Результат прогноза, разработанного формализованным методом, чаще
всего выражается количественным показателем, которому может быть дана то^
чечная ( y i ) и (или) интервальная оценка ( y i ).
Точечная оценка ( y i ) — это единичная оценка прогнозного параметра.
Точечные значения экономических величин лишены содержания, так как имеют нулевую вероятность. Для устранения этого недостатка прогноз должен
быть дан в виде интервала значений.
32
^
Интервальная оценка ( y i ) — это числовой интервал (доверительный
интервал), в котором, вероятно, находится прогнозный параметр.
Точность прогноза тем выше, чем меньше величина ошибки, которая
представляет собой разность между прогнозируемыми и фактическими значениями исследуемой величины. Понятие точности прогноза и методы ее оценки
отличаются от точности исходных данных. Точность исходных данных может
быть однозначно оценена на этапе сбора информации как степень приближения
результатов измерений к истинному значению измеряемой величины. На практике часто количественную оценку точности заменяют указанием ошибки измерения (погрешности), которая определяется как разница между оцениваемым
результатом и результатом, полученным более точным методом. В прогнозных
значениях (до наступления прогнозируемого события) точность обычно также
выражается как погрешность, но с помощью вероятностных пределов отклонения фактической величины от прогнозируемого значения, которые принято называть доверительным интервалом.
Заметим, что прогнозируемые значения должны реализоваться в соответствующее время с указанной вероятностью и лежать внутри некоторой доверительной области, ширина которой зависит от заданной вероятности.
Математическая вероятность ( Pi ) случайной величины равна отношению числа событий, благоприятствующих ее появлению (т.е. свершению прогноза) к общему числу событий (благоприятных и неблагоприятных). Численное значение вероятности прогноза лежит в пределах от 0 до 1.
Очевидно, что точность прогноза максимальна при построении точечного
прогноза. Но построить его с высокой степенью вероятности часто не представляется возможным.
В то же время границы доверительного интервала можно задать такими
широкими, что прогнозируемое значение попадет туда с любой вероятностью,
включая Р = 0 и Р = 1. Такой прогноз называется абсолютно достоверным. Однако границы доверительного интервала будут столь широкими, что полученный прогноз не будет иметь практической ценности для принятия управленческих решений. На практике достаточно иметь вероятность прогноза 0,7-0,95.
Под достоверностью прогноза понимается вероятность осуществления
прогноза в заданном доверительном интервале 2 .
Условная графическая интерпретация доверительного интервала показателя у при заданной вероятности Р представлена на рис. 2.3.
33
Рис. 2.3. Графическая интерпретация границ доверительного интервала
Существуют неформальный и формальный способы определения доверительного интервала. Неформально доверительный интервал может быть определен экспертами с учетом степени изменчивости фактических значений показателей вокруг расчетных (теоретических) значений в прошлом и возможности
деформации в будущем. При этом экспертам может быть предложено оценить
суммарную величину ошибки или степень влияния различных составляющих
на точность прогноза. Суммарная ошибка решения прогнозной задачи определяется по формуле
Ñ È Ì Â × Í ,
(2.10)
где Ñ — суммарная ошибка;
È — ошибки информации, обусловленные неадекватностью описания
объекта, погрешностями получения и обработки информации;
Ì — ошибки метода прогнозирования, вызванные невозможностью идеального выбора метола для данного объекта, а также обязательной схематичностью метода;
 — ошибки вычислительных процедур;
× — ошибки, допущенные человеком и обусловленные субъективными
факторами (низкая квалификация, восторженность, пессимизм);
Í — нерегулярная составляющая ошибки, обусловленная возможностью
появления непредсказуемых изменений в объекте.
Формально границы доверительного интервала можно определить на основе оценки изменчивости уровней ряда. Чем выше эта изменчивость, тем менее точной может быть расчетная величина и тем шире должен быть доверительный интервал при одной и той же вероятности прогноза.
На практике, получая прогнозный результат в виде точечного значения
y i , необходимо указать и возможную величину ошибки , т.е. перейти к интервальному прогнозу по формуле
^
yi yi ,
где y i — точечное значение прогнозной характеристики;
^
y i — интервальное значение прогнозной характеристики;
— вероятная ошибка прогноза.
(2.11)
34
Для определения границ доверительного интервала используется выражение
t ,
(2.12)
где — среднеквадратическое отклонение; t — критерий Стьюдента.
Величина среднеквадратического отклонения рассчитывается по формуле
(y
i
yi ) 2
n
,
(2.13)
где yi — фактическое значение исследуемой характеристики на участке
ретроспекции;
yi — расчетное значение исследуемой характеристики на участке ретроспекции;
п — число наблюдений (размер выборки).
Среднеквадратическое отклонение характеризует, насколько точно теоретическая кривая описывает поведение исследуемой характеристики в прошлом.
Величина определяет минимальную ошибку прогноза. Она зависит, с одной
стороны, от корректности модели, с другой — от стабильности исследуемой
характеристики в прошлом.
t — критерий Стьюдента, значение которого зависит от размера выборочной совокупности и заданной вероятности прогноза, использование этого
коэффициента определяется ограниченностью выборки (табличные значения
критерия Стьюдента приведены в приложении. Критерий Стьюдента позволяет
учесть то обстоятельство, что чем выше заданная вероятность прогноза и чем
меньше размер выборки, тем шире должны быть границы доверительного интервала.
После наступления прогнозируемого события ошибка прогноза определяется как разность между фактическим и прогнозным значением показателя.
Существует несколько способов количественной оценки ошибки прогноза, например, ошибка прогноза или погрешность для каждого момента времени, в котором рассматривается прогноз:
et y t y t ,
(2.14)
где et — ошибка прогноза в момент времени t,
yt — фактическое значение в момент времени t,
yt — прогнозное значение в момент времени t.
Для обобщенной оценки метода прогнозирования на практике вместе с
показателем среднеквадратического отклонения могут быть использованы и
другие способы оценки средней ошибки прогноза (погрешности):
среднее абсолютное отклонение (mean absolute derivation, MAD). Использование этого показателя имеет смысл, когда исследователю необходимо
оценить ошибку в тех же единицах, что и исходный ряд:
MAD
1
yi yi ;
n
(2.15)
35
средняя процентная ошибка (mean percentage error, МРЕ) позволяет
оценить возможное смещение прогноза, когда полученный прогноз окажется
завышенным или заниженным. При несмещенном прогнозе имеем величину
ошибки, близкую к нулю, при завышенном — большое положительное процентное значение, при заниженном — большое отрицательное:
MPE
1 ( yi yi )
y 100% ;
n
i
(2.16)
средняя абсолютная ошибка в процентах (mean absolute percentage
error, MAPE):
MAPE
yi yi
1
100% .
n
yi
(2.17)
Приведенные выше способы оценки качества прогноза позволяют осуществить сравнение результатов, полученных различными методами прогнозирования, и выбрать наиболее приемлемый метод для решения прогнозной задачи.
4.3.
Методы экспертных оценок
Основная идея прогнозирования на основе экспертных оценок заключается в построении рациональной процедуры интуитивно-логического мышления
человека в сочетании с количественными методами оценки и обработки получаемых результатов.
Сущность методов экспертных оценок заключается в том, что в основу
прогноза закладывается мнение специалиста или коллектива специалистов, основанное на профессиональном, научном и практическом опыте.
Индивидуальные экспертные оценки — основаны на использовании
мнений экспертов-специалистов соответствующего профиля.
1. Метод «интервью» предполагает беседу прогнозиста с экспертом по
схеме «вопрос-ответ», в процессе которой прогнозист в соответствии с заранее
разработанной программой ставит перед экспертом вопросы относительно перспектив развития прогнозируемого объекта. Успех такой оценки в значительной степени зависит от способности эксперта экспромтом давать заключение
по самым различным вопросам.
2. Метод анкетного опроса заключается в том, что эксперту предлагается для заполнения анкета (опросный лист), содержащая перечень вопросов, каждый из которых логически связан с задачей исследования.
В анкете могут использоваться следующие типы вопросов:
открытые – ответы на данные вопросы могут быть сформулированы в
любой форме;
закрытого типа – предлагаются варианты ответов, один из которых
должен выбрать эксперт.
Использование в анкете вопросов закрытого типа предпочтительней, так
как упрощает статистическую обработку результатов ответа и облегчает работу
эксперта при заполнении анкеты. С другой стороны, перечень ответов на вопрос может и не содержать мнение эксперта. Поэтому при формировании пе-
36
речня вариантов ответов на некоторые вопросы следует предусматривать возможность выдвижения экспертом своего варианта ответа или уклонение от ответа
3. Аналитический метод (аналитических записок) предусматривает
тщательную самостоятельную работу эксперта над анализом тенденций, оценкой состояния и путей развития прогнозируемого объекта. Эксперт может использовать всю необходимую ему информацию об объекте прогноза. Свои выводы он оформляет в виде докладной записки. Основное преимущество этого
метода — возможность максимального использования индивидуальных способностей эксперта. Однако он мало пригоден для прогнозирования сложных
систем и выработки стратегии из-за ограниченности знаний одного специалиста-эксперта в смежных областях знаний.
Основное преимущество методов индивидуальных экспертных оценок
состоит в возможности максимального использования индивидуальных способностей экспертов. Однако данные методы мало пригодны для прогнозирования наиболее общих стратегий из-за ограниченности знаний одного эксперта
о развитии смежных областей науки и практики.
Примером использования экспертных оценок при планировании развития
социально-экономических систем может служить многокритериальная задача
выбора варианта решения, которая на сегодняшний день актуальна во многих
сферах деятельности человека.
Процедура многокритериального выбора включает в себя следующие
этапы:
1. Выявление наиболее существенных показателей (критериев), характеризующих исследуемый объект;
2. Определение способа количественной оценки показателей;
3. Определение допустимых границ изменения показателей;
4. Выбор метода поиска наилучшего варианта;
5. Решение задачи и анализ результатов.
В качестве целевой функции для оценки вариантов решений чаще всего
используется аддитивная свертка критериев:
n
I i f i max или min ,
(2.18)
i 1
где i — весовые коэффициенты, характеризующие значимость критерия
f i . Численные значения i определяются экспертами, при этом, желательно соблюдение следующего условия:
n
i 1 .
(2.19)
i 1
Если критерии f1 , f 2 ,… f n имеют различные единицы измерения, то их необходимо привести к единому безразмерному масштабу так, чтобы выполнялись следующие неравенства:
0 fi ;
(2.20)
f i 1.
(2.21)
37
Пример. По мнению экспертов, основными показателями экономического
и социального развития региона являются:
валовый внутренний (региональный) продукт;
уровень занятости населения;
среднемесячная заработная плата.
Экспертная оценка значимости критериев по десятибалльной шкале
представлена в табл. 2.2.
Руководству региона предложено четыре целевые программы развития
региона, направленные на первоочередное финансирование:
1. Агропромышленного комплекса;
2. Предприятий пищевой промышленности;
3. Отраслей социально-культурной сферы;
4. Жилищного строительства.
Ожидаемые значения основных показателей, получаемые при реализации
рассматриваемых целевых программ, приведены в табл. 2.3.
Таблица 2.2
Результаты экспертной оценки
Показатель
Эксперт
Валовый проУровень за- Среднемесячная
дукт
нятости
заработная плата
1
10
5
4
2
10
6
5
3
7
4
3
Средняя арифметическая
оценка
9
5
4
Таблица 2.3
Ожидаемые значения основных социально-экономических
показателей развития региона
Значение показателей
Целевая программа Валовый про- Уровень занятости,
Среднемесячная
дукт,
%
заработная плата,
млн.руб
руб
1
2000
80
2000
2
2500
70
800
3
1500
80
1000
4
2000
90
1500
Необходимо определить наиболее целесообразную программу развития
региона.
Решение:
Определим значения весовых коэффициентов:
1
9
5
4
0,5 ; 2
0, 278 ; 3
0,222 .
954
95 4
954
38
Таким образом, в результате обработки экспертных оценок целевая
функция имеет следующий вид:
I 0,5 f1 0,278 f 2 0, 222 f 3 max .
Учитывая, что целевая программа №3 заведомо неэффективна по сравнению с программой №2 (1500<2000; 80=80; 1000<2000), удалим её из матрицы
возможных решений:
2000 80 2000
2500 70 800
2000 90 1500
Так как значения показателей имеют различную размерность, то их необходимо привести к единому безразмерному масштабу. Это достигается делением элементов каждого столбца на максимальную величину в столбце:
0,8 0,889
1
1 0,778 0,4
0,8
1
0,75
На заключительном этапе определим значение целевой функции для
предложенных программ:
1. I 0,5 0,8 0,278 0,889 0,222 1 0,869;
2. I 0,5 1 0,278 0,778 0,222 0,4 0,805;
4. I 0,5 0,8 0,278 1 0,222 0,75 0,845.
Максимальное значение целевой функции соответствует программе №1.
Следовательно, реализация данной программы наиболее целесообразна.
Наиболее достоверными являются коллективные экспертные оценки предполагают определение степени согласованности мнений экспертов по перспективным направлениям развития объекта прогнозирования, сформулированным отдельными специалистами.
Для организации проведения экспертных оценок создаются рабочие
группы, в функции которых входят проведение опроса, обработка материалов и
анализ результатов коллективной экспертной оценки. Рабочая группа назначает
экспертов, которые дают ответы на поставленные вопросы, касающиеся перспектив развития данного объекта.
1. Суть метода коллективной генерации идей (мозговой атаки) состоит
в использовании творческого потенциала специалистов при мозговой атаке
проблемной ситуации, реализующей вначале генерацию идей, а затем их структурирование, анализ и критику с выдвижением контридей и выработкой согласованной точки зрения.
Метод коллективной генерации идей предполагает реализацию следую-
39
щих этапов:
1. формирование группы участников «мозговой атаки» по решению определенной проблемы. Оптимальная численность группы находится эмпирическим путем. Наиболее продуктивными признаны группы, состоящие из 10—15
человек.
2. Группа анализа составляет проблемную записку, в которой формулируется проблемная ситуация и содержится описание метода и проблемной ситуации.
3. Этап генерации идей. Каждый участник имеет право выступать много
раз. Критика предыдущих выступлений и скептические замечания не допускаются. Ведущий корректирует процесс, приветствует усовершенствование или
комбинацию идей, оказывает поддержку, освобождая участников от скованности. Продолжительность «мозговой атаки» — не менее 20 мин и не более 1 ч в зависимости от активности участников.
4. Систематизация идей, высказанных на этапе генерации. Формируется
перечень идей, выделяются признаки, по которым идеи могут быть объединены, идеи объединяются в группы согласно выделенным признакам.
5. На пятом этапе осуществляется деструктурирование (разрушение) систематизированных идей. Каждая идея подвергается всесторонней критике со
стороны группы высококвалифицированных специалистов в составе 20-25 человек.
6. На шестом этапе дается оценка критических замечаний и составляется
список практически реализуемых идей.
Метод «635» — одна из разновидностей «мозговой атаки». Цифры б, 3, 5
обозначают 6 участников, каждый из которых должен записать 3 идеи в течение 5 мин. Лист ходит по кругу. Таким образом, за полчаса каждый запишет в
свой актив 18 идей, а все вместе — 108. Структура идей четко определена. Возможны модификации метода. Этот метод широко используется в зарубежных
странах (особенно в Японии) для отбора из множества идей наиболее оригинальных и прогрессивных по решению определенных проблем.
2. Метод «Дельфи». Цель метода — разработка программы последовательных многотуровых индивидуальных опросов. Индивидуальный опрос экспертов обычно проводится в форме анкет-вопросников. Затем осуществляется
их статистическая обработка на ЭВМ и формируется коллективное мнение
группы, выявляются и обобщаются аргументы в пользу различных суждений.
Обработанная на ЭВМ информация сообщается экспертам, которые могут корректировать оценки, объясняя при этом причины своего несогласия с коллективным суждением. Эта процедура может повторяться до 3-4 раз. В результате
происходит сужение диапазона оценок и вырабатывается согласованное суждение относительно перспектив развития объекта.
Особенности метода «Дельфи»:
а) анонимность экспертов — взаимодействие членов группы при заполнении анкет полностью исключается;
б) возможность использования результатов предыдущего тура опроса;
40
в) статистическая характеристика группового мнения.
3. Метод «комиссий» — основан на работе специальных комиссий. Группы экспертов за «круглым столом» обсуждают ту или иную проблему с целью
согласования точек зрения и выработки единого мнения. Недостаток этого метода заключается в том, что группа экспертов в своих суждениях руководствуется в основном логикой компромисса.
Метод экспертных комиссий может быть организован в одной из следующих форм:
обсуждение и открытое голосование;
обсуждение и закрытое голосование;
высказывание мнений и обсуждение без голосования.
Как показала практика, метод «комиссий» имеет существенные недостатки:
большое влияние такого психологического фактора как мнение авторитетных экспертов, к которому присоединяются остальные эксперты, не высказывая своей точки зрения;
нежелание экспертов публично отказываться от ранее высказанных
ими мнений;
при работе комиссий чаще всего происходит спор двух или трех наиболее авторитетных экспертов, в результате чего другие эксперты в дискуссии
участие или не принимают или не учитываются высказанные ими мнения.
4. Метод суда – основан на организации работы коллектива экспертов в
форме ведения судебного процесса. Использование этого метода целесообразно
при наличии нескольких групп экспертов, каждая из которых отстаивает свою
точку зрения. В данном случае в качестве «подсудимого» выступает объект
прогнозирования. Лидеры групп, высказывающих альтернативные точки зрения, выступают в качестве обвинения и защиты (прокурор, адвокат). Отдельные
эксперты играют роль свидетелей, предоставляя суду необходимую для принятия решения информацию. Роль судьи играет заинтересованное лицо (группа
лиц). Так, например, в телевизионной передаче «Процесс», основанной на использовании метода суда для анализа и прогнозирования развития различных
социально-экономических процессов, роль судьи играли зрители, голосуя в
процессе передачи телефонными звонками за ту точку зрения, которую они
поддерживали.
Метод морфологического анализа предполагает выбор наиболее приемлемого решения проблемы из числа возможных. Его целесообразно использовать при прогнозировании фундаментальных исследований. Метод включает
ряд приемов, предполагающих систематизированное рассмотрение характеристик объекта. Исследование проводится по методу «морфологического ящика»,
который строится в виде дерева целей или матрицы, в клетки которой вписаны
соответствующие параметры. Последовательное соединение параметра первого
уровня с одним из параметров последующих уровней представляет собой возможное решение проблемы. Общее количество возможных решений равно произведению числа всех параметров, представленных в «ящике», взятых по стро-
41
кам. Путем перестановок и различных сочетаний можно выработать вероятностные характеристики объектов.
Метод написания сценария — основан на определении логики процесса
или явления во времени при различных условиях. Он предполагает установление последовательности событий, развивающихся при переходе от существующей ситуации к будущему состоянию объекта. Прогнозный сценарий определяет стратегию развития прогнозируемого объекта. Он должен отражать генеральную цель развития объекта, критерии оценки верхних уровней «дерева целей», приоритеты проблем и ресурсы для достижения основных целей. В сценарии отображаются последовательное решение задачи, возможные препятствия. При этом используются необходимые материалы по развитию объекта
прогнозирования.
Прогнозный граф — это фигура, состоящая из точек-вершин, соединенных
отрезками-ребрами. «Дерево целей» — это граф-дерево, выражающее отношение
между вершинами-этапами или проблемами достижения цели. Каждая вершина
представляет собой цель для всех исходящих из нее ветвей. «Дерево целей»
предполагает выделение нескольких структурных или иерархических уровней.
Построение «дерева целей» требует решения многих задач: прогноза развития объекта в целом; формулирования сценария прогнозируемой цели, определение уровней и вершин «дерева», критериев и их весов в ранжировании
вершин. Эти задачи могут решаться при необходимости методами экспертных
оценок. Следует отметить, что данной цели как объекту прогноза может соответствовать множество разнообразных сценариев.
Сценарий обычно носит многовариантный характер и освещает три линии поведения: оптимистическую — развитие системы в наиболее благоприятной ситуации; пессимистическую — развитие системы в наименее благоприятной ситуации; рабочую — развитие системы с учетом противодействия отрицательным факторам, появление которых наиболее вероятно. В рамках прогнозного сценария целесообразно прорабатывать резервную стратегию на случай
непредвиденных ситуаций.
Сценарий в готовом виде должен быть подвергнут анализу. На основании
анализа информации, признанной пригодной для предстоящего прогноза, формулируются цели, определяются критерии, рассматриваются альтернативные
решения.
4.4. Методы экстраполяции
Сущность экстраполяции заключается в изучении сложившихся в прошлом и настоящем устойчивых тенденций развития объекта прогноза и переносе их на будущее.
При прогнозной экстраполяции фактическое развитие увязывается с
гипотезами о динамике исследуемого процесса с учетом изменений влияния
различных факторов в перспективе.
Основу экстраполяционных методов прогнозирования составляет изучение динамических рядов. Динамический ряд — это множество наблюдений, по-
42
лученных последовательно во времени.
В экономическом прогнозировании широко применяется метод математической экстраполяции, в математическом смысле означающий распространение закона изменения функции из области ее наблюдения на область, лежащую вне отрезка наблюдения. Тенденция, описанная некоторой функцией от
времени, называется трендом. Тренд — это длительная тенденция изменения
экономических показателей. Функция представляет собой простейшую математико-статистическую (трендовую) модель изучаемого явления.
Выделяют следующие методы экстраполяции:
метод подбора функций;
экстраполяция по абсолютному приросту;
экстраполяция по темпу роста;
аппроксимация динамического ряда аналитическими функциями;
адаптивные методы прогнозирования.
I. Метод подбора функций — выбор оптимального вида функции, описывающей эмпирический ряд. Задача выбора функции заключается в подборе по
фактическим данным формы зависимости (линии) так, чтобы отклонения данных исходного ряда, от соответствующих расчетных, находящихся на линии,
были наименьшими. После этого можно продолжить эту линию и получить
прогноз.
II. Экстраполяция по абсолютному приросту.
В данном случае возможно применение нескольких вариантов расчета
значения прогнозируемого параметра.
Вариант А. Прогнозное значение определяется по формуле:
y y t y ,
(2.22)
где — абсолютный прирост, который находится из выражения:
y y t yt 1 ,
(2.23)
здесь y t — значение показателя текущего периода;
y t 1 — значение показателя предыдущего периода.
Вариант Б. Если имеется динамика за ряд предшествующих периодов, то
можно использовать средний абсолютный прирост:
y n y1
;
n 1
y y t y .
y
(2.24)
(2.25)
III. Экстраполяция по темпу роста.
Возможны два варианта экстраполяции по темпу роста.
Вариант А. Прогнозное значение определяется по формуле:
y yt k p ,
(2.26)
где k p — коэффициент роста, который находится из выражения:
kP
yt
,
y t 1
(2.27)
43
Вариант Б. Если имеется динамика за ряд предшествующих периодов, то
можно использовать усредненный коэффициент роста:
k P n 1
yn
,
y1
y y t TP .
(2.28)
(2.29)
IV. Аппроксимация динамического ряда аналитическими функциями – расчет параметров (а, b, с) для конкретной функциональной зависимости.
Параметры модели тренда должны минимизировать отклонения расчетных значений от соответствующих значений исходного ряда. Выбор модели осуществляется с помощью специально разработанных программ. Есть программы, предусматривающие возможность моделирования экономических рядов по 16-ти
функциям: линейной (y = а + b * х), гиперболической различных типов (у = а +
b / х), экспоненциальной, степенной, логарифмической и др. Каждая из них может иметь свою, специфическую область применения при прогнозировании
экономических явлений.
Так, линейная функция применяется для описания процессов, равномерно
развивающихся во времени. Параметр b (коэффициент регрессии) показывает
скорость изменения прогнозируемого у при изменении х. Гиперболы хорошо
описывают процессы, характеризующиеся насыщением, когда существует фактор, сдерживающий рост прогнозируемого показателя.
Модель выбирается, во-первых, визуально, на основе сопоставления вида
кривой, ее специфических свойств и качественной характеристики тенденции
экономического явления; во-вторых, исходя из значения критерия. В качестве
критерия чаще всего используется сумма квадратов отклонений – из совокупности функций выбирается та, которой соответствует ее минимальное значение.
Для окончательного выбора вида функции нужно исследовать логику
протекания процесса в целом, в том числе гипотезы его протекания в перспективе. Игнорирование этого этапа приводит к ошибочным, а иногда к парадоксальным выводам. Вы должны ответить на следующие вопросы:
является ли исследуемый показатель величиной монотонно возрастающей, монотонно убывающей, стабильной или периодической;
ограничен ли сверху или снизу исследуемый показатель каким-либо
пределом;
имеет ли функция, определяющая процесс, точку перегиба;
обладает ли функция, описывающая процесс, свойством симметричности;
имеет ли процесс четкое ограничение развития во времени?
Если в ходе предварительной обработки информации и содержательного анализа выявлено отсутствие инерционности в развитии объекта, то
использование прогнозной экстраполяции недопустимо!
Выбор функции, применяемой для описания явления, зависит от типа ди-
44
намики процесса. Далее будут приведены основные элементарные функции
прогнозной экстраполяции.
Прогноз предполагает продление тенденции прошлого, выражаемой выбранной функцией, в будущее, т.е. экстраполяцию динамического ряда. Программным путем на ЭВМ определяется значение прогнозируемого показателя.
Для этого в формулу, описывающую процесс, подставляется величина периода,
на который необходимо получить прогноз.
В связи с тем, что этот метод исходит из инерционности экономических
явлений и предпосылок, что общие условия, определяющие развитие в прошлом, не претерпят существенных изменений в будущем, его целесообразно
использовать при разработке краткосрочных прогнозов обязательно в сочетании с методами экспертных оценок. Причем динамический ряд может строиться на основании данных не по годам, а по месяцам, кварталам.
При аппроксимации динамического ряда известными аналитическими
функциями предполагается, что для прогнозирования будет использована
функция, у которой форма кривой ближе всего подходит к графическому тренду. Самый простой способ выбора функции – визуальный, на основе графического изображения динамического ряда. Чаще всего для аппроксимации используются:
— линейная функция y a bt ;
— парабола y a bt ct 2 ;
b
t
— гипербола y a ;
—
логарифмическая функция y a b ln t ;
экспоненциальная функция y ae bt ;
степенная функция y at b .
показательная ó àât .
Каждая функция имеет свою сферу применения. Например, линейная
функция используется для описания равномерно развивающихся процессов, а
гипербола хорошо описывает процессы, для которых характерно насыщение
рынка.
Для определения значений эмпирических коэффициентов a, b и c обычно
используется метод наименьших квадратов. Суть данного метода заключается в определении таких значений эмпирических коэффициентов, которые минимизируют сумму квадратов отклонений расчётных и фактических значений
динамического ряда:
n
f ( y t yt ) 2 min ,
t 1
где y t и y t — расчетные и фактические значения;
n — число наблюдений.
Так для линейной функции имеем:
(2.30)
45
n
f (a bt y t ) 2 min .
(2.31)
t 1
Известно, что функция имеет экстремум, если её производная равна нулю. Дифференцируя функцию по искомым переменным и приравнивая производную нулю, получаем систему линейных уравнений, решая которую найдем
неизвестные эмпирические коэффициенты:
n
n
n
df
2(a bt y t ) 0; или na b t y t ;
da t 1
t 1
t 1
n
n
n
ï
df
2
2(a bt y t )t 0,
a t b t y t t.
db t 1
t 1
t 1
t 1
(2.32)
(2.33)
При прогнозировании исследуемого процесса в аналитическую зависимость подставляют вместо параметра t порядковый номер следующего прогнозного периода и получают точечное значение прогнозируемого параметра.
Так как прогнозируемые процессы носят вероятностный характер, то помимо
точечного прогноза, как правило, определяют границы возможного изменения
прогнозируемого показателя – доверительные интервалы. Ширину доверительного интервала рассчитывают по формуле:
t ,
(2.34)
где t — коэффициент доверия по распределению Стьюдента, выбирается в соответствии с принятым уровнем доверительной вероятности (табл. 2.4);
— среднеквадратическое отклонение от тренда,
(ó
t
ót ) 2
;
(ï ò )
(2.35)
ò — число параметров аналитической зависимости.
Таблица 2.4
Значения коэффициента доверия по распределению Стьюдента
Уровень доверительной вероятности, 0,683 0,95 0,99 0,997
1
1,96 2,576
3
Коэффициент доверия, t
Для параболы y a bt ct 2 система уравнений, решая которую необходимо определить коэффициенты а , b и c , имеет вид:
n
n
n
na b t c t 2 y t ;
t 1
n
t 1
n
(2.36)
t 1
n
ï
a t b t 2 c t 3 ty t ;
t 1
ï
t 1
t 1
n
t 1
ï
ï
à t 2 b t 3 ñ t 4 t 2 ót .
t 1
t 1
t 1
t 1
Адаптивные методы прогнозирования.
Метод экспоненциально-взвешенного среднего.
46
Все адаптивные методы основаны на идее экспоненциально-взвешенного
среднего (ЭВС):
ut d t ( 1 ) u t 1 ,
(2.37)
где d t — фактическое значение показателя, соответствующее текущему
моменту времени t;
— параметр сглаживания;
u t 1 — предыдущее значение ЭВС в момент времени t-1. В момент времени t=1 предыдущее значение ЭВС определяют на основе экспертной оценки.
или
f t 1 u t 1 et ,
(2.38)
где f t 1 — прогноз на следующий момент времени,
et d t u t 1 — текущее значение ошибки прогноза.
Метод адаптивной скорости реакции.
Если в изменении показателя предполагаются переходы среднего значения на новый уровень и дальнейшие колебания относительно нового уровня, то
для прогнозирования показателя можно использовать метод адаптивной скорости реакции. Этот метод основан на адаптации к поступающим данным. В качестве параметра сглаживания здесь используется не постоянная величина , а
рассчитываемое для каждого момента времени значение трекинг-сигнала:
Tt e t MAD t ,
(2.39)
где et — экспоненциально взвешенная ошибка:
et et ( 1 ) et 1 ,
(2.40)
et 1 — предыдущее значение экспоненциально взвешенной ошибки (в момент времени t=1 предыдущее значение экспоненциально взвешенной ошибки
принимается равным нулю),
MADt — среднее абсолютное отклонение ошибки (Mean Absolute
Deviation):
MADt et ( 1 ) MADt 1 ,
(2.41)
MADt 1 — предыдущее значение среднего абсолютного отклонения ошибки (в момент времени t=1 предыдущее значение среднего абсолютного отклонения принимается равным 0,1 u t 1 .
Прогноз на следующий момент времени по модели адаптивной скорости
реакции рассчитывается следующим образом:
f t 1 Tt d t ( 1 Tt ) f t ,
(2.42)
где f t — значение текущего прогноза показателя (в момент времени t=1
текущее значение прогноза определяется на основе экспертной оценки).
47
Метод Холта.
Если среднее значение прогнозируемого показателя с течением времени
меняется в соответствии с линейной функцией, то прогноз на моментов времени вперед можно рассчитать по методу Холта:
f t u t bt ,
(2.43)
где u t — оценка стационарного фактора:
u t A d t ( 1 A ) ( u t 1 bt 1 ) ,
(2.44)
bt — оценка линейного роста:
bt B ( u t u t 1 ) ( 1 B ) bt 1 ,
(2.45)
bt 1 — предыдущее значение оценки линейного роста (в момент времени
t=1 предыдущее значение оценки линейного роста принимается равным нулю),
u t 1 — предыдущее значение стационарного фактора (в момент времени
t=1 предыдущее значение стационарного фактора определяется на основе экспертной оценки).
Холт рекомендует следующие значения констант: А=0,1, В=0,01. Однако
при рассмотрении конкретных экономических показателей значения констант
могут корректироваться.
В условиях сильного линейного роста метод Холта дает заниженные значения прогноза.
Метод двойного сглаживания Брауна.
Этот метод используется, как и предыдущий, в условиях линейного роста
показателя, однако является более точным.
Прогноз на моментов времени вперед определяется по формуле
f t f t bt ,
(2.46)
где f t 2 u t u t ,
(2.47)
u t — экспоненциально-взвешенное среднее, рассчитанное по формуле
(2.37),
u t — двойное экспоненциально-взвешенное среднее:
u t ut ( 1 ) ut 1 ,
(2.48)
ut 1 — предыдущее значение двойного ЭВС (в момент времени t=1 предыдущее значение двойного ЭВС принимают равным нулю),
bt
( ut ut )
1
.
(2.49)
Если период упреждения =1, прогноз можно рассчитать по формуле
( 2 ) ut ut
f t 1
1
.
(2.50)
48
Метод адаптивного сглаживания Брауна (взвешенный метод наименьших квадратов).
Этот метод, как правило, дает наилучшие результаты прогнозирования в
условиях линейного роста прогнозируемого показателя.
Прогноз на моментов времени вперед:
f t u t bt ,
(2.51)
2
где u t ut 1 bt 1 ( 1 ) et ,
bt bt 1 ( 1 ) 2 et ,
(2.52)
(2.53)
et d t f t ,
(2.54)
В момент времени t=1 предыдущее значение стационарного фактора u t 1
определяют на основе экспертной оценки, предыдущее значение оценки линейного роста bt 1 принимают равным нулю.
Браун рекомендует выбирать =0,8. Для конкретных случаев прогнозирования этот параметр можно корректировать.
Сезонно-декомпозиционная модель Холта-Винтера.
Используется для описания комбинации линейного и сезонноаддитивного тренда. Модель предполагает, что характеристики временного ряда – стационарность, линейность и сезонность – могут быть разделены, изучены и оценены изолированно. Окончательный прогноз осуществляется сведением прогнозов различных элементов в один.
а) Оценка стационарного фактора:
d
u t A t ( 1 A )( u t 1 bt 1 )
Ft L
,
(2.55)
б) Оценка линейного роста:
bt B ( u t u t 1 ) ( 1 B ) bt ,
(2.56)
в) Оценка сезонного фактора:
d
Ft C t ( 1 C ) Ft L
ut
,
(2.57)
где Ft — коэффициент сезонности, соответствующий моменту времени t,
Ft L — коэффициент сезонности, соответствующий моменту времени t-L,
то есть сдвинутому на L моментов времени назад. L – длина сезонного цикла
или количество временных отрезков в цикле (для месяцев L=12, для кварталов
L=4).
Коэффициент сезонности представляет собой отношение значения текущего наблюдения к среднестационарному значению показателя. Коэффициент
сезонности можно найти по формуле
49
Ft
dt
ut ,
(2.58)
при этом для расчета стационарного фактора u t можно использовать
формулу (2.37), если среднее значение показателя за год меняется незначительно, и по формулам (2.44), (2.52), если среднее значение показателя имеет тенденцию к росту.
Рекомендуемые значения констант для формул (2.55) – (2.57): А=0,2;
В=0,2; С=0,5.
Прогноз на моментов времени вперед, составляющие которого определены по формулам (2.55) – (2.57), рассчитывается по формуле
f t ( u t bt t ) Ft L .
(2.59)
При использовании модели Холта-Винтера рекомендуется следующий
алгоритм расчета. По данным динамики показателя за предыдущий год рассчитывают оценки коэффициентов сезонности (2.58). В качестве момента времени
t=1 принимают значение показателя в январе или I квартале года, предшествующего текущему. Затем по формулам (2.55) – (2.57) находят оценки стационарного фактора, линейного роста и коэффициентов сезонности для текущего
года. Прогноз осуществляется на базе найденных составляющих элементов по
формуле (2.59), где обозначение коэффициента сезонности Ft L соответствует коэффициенту сезонности для того же месяца или квартала, но предыдущего
года, например, делая прогноз на май 2013 года, необходимо использовать значение коэффициента сезонности, рассчитанное для мая 2012 года.
4.5. Методы моделирования
В настоящее время моделирование считается наиболее эффективным методом прогнозирования. Алгоритм построения экономико-математической модели включает следующие этапы:
1. формулировка цели прогнозного исследования;
2. выделение в объекте прогнозирования структурных элементов, оказывающих влияние на характер и динамику его развития;
3. выявление внешних факторов, влияющих на развитие объекта прогнозирования;
4. логическое описание взаимосвязей между элементами объекта прогнозирования, внешними и результирующими факторами (построение информационной модели);
5. формализация (математическое описание) взаимосвязей между элементами объекта прогнозирования, внешними и результирующими факторами
(показателями);
6. проведение расчетов, корректировка и уточнение модели.
Экономико-математические модели имеют следующие преимущества:
50
— возможность отражения многосторонних связей между результирующими и
влияющими факторами;
— возможность использования экономико-математических моделей при управлении экономическими процессами и при поиске наиболее эффективных
(оптимальных) управленческих решений.
В соответствии с математической формой построения выделяют следующие типы экономико-математических моделей:
— экономико-статистические;
— структурные;
— оптимизационные;
— имитационные и др.
В зависимости от уровня управления экономическими и социальными
процессами различают макроэкономические, межотраслевые, межрайонные,
отраслевые, региональные модели и модели микроуровня (модели развития
фирмы).
По аспектам развития экономики выделяют модели прогнозирования
воспроизводства основных фондов, трудовых ресурсов, цен и др.
Экономико-статистические модели представляют собой вид моделей,
описывающих с помощью уравнений регрессии зависимости между входными
и результирующими факторами. Различают однофакторные и многофакторные
модели. Многофакторные модели позволяют изучать влияние на объект прогнозирования нескольких факторов, однофакторные – одного. Начальным этапом построения модели является отбор влияющих факторов. Влияние факторов
может описываться уравнениями следующих видов:
— линейные у а0 а1 х1 а2 х2 … ап х п ;
— степенные у а0 х1а х2а … хпа ;
— логарифмические ln y a0 a1 ln x1 a2 ln x2 … an ln xn .
Основным объектом прогнозирования в рыночной экономике является
спрос населения на товары потребления. Среди факторов, обусловливающих
спрос, можно выделить среднедушевой денежный доход потребителей и цену
товара. Существует большое количество экономико-статистических моделей
спроса ( у ) как функции цены единицы товара ( р ) и среднедушевого денежного
дохода ( d ). Например, для товаров длительного пользования часто используются следующие модели:
— у а0 а1 ln p а2 ln d a3 ln p ln d ;
— у а0 а1d a 2 p .
Однако применение данных моделей затруднено тем, что, зачастую отсутствуют статистические данные об уровнях дохода и ценах, относящиеся к
одному временному периоду. В этом случае используются однофакторные модели спроса от цены или среднедушевого дохода. Установлено, что при неизменном уровне душевого дохода для большинства товаров спрос увеличивается
с уменьшением цены. В свою очередь рост среднедушевого дохода, как прави1
2
п
51
ло, вызывает рост спроса на товары и услуги (за исключением дешёвых и низкокачественных).
Экономико-статистические модели являются одним из основных инструментов управления социально-экономическими процессами и часто используются при поиске наиболее эффективных решений.
Пример. Фабрика «Первомайская» является крупным производителем мяса
птицы в регионе. Статистическая информация об объёмах реализации продукции фабрикой за первые 3 квартала 2010 года представлена в табл. 2.5. Определить цену реализации мяса птицы, оптимизирующую прибыль предприятия, если прямые затраты на производство 1 кг. составляют 29 руб.
Таблица 2.5
Объём реализации мяса птицы за первые 3 квартала 2008 г.
Квартал
Объём реализаЦена реализации
ции,
мяса птицы,
кг.
руб./кг.
1
800000
40
2
490000
52
3
650000
45
Решение:
Для описания влияния цены продукции ( Ц ) на объем её реализации ( у )
используем линейную экономико-статистическую модель вида: у а0 а1 Ц .
Параметры модели а0 и а1 определим с помощью метода наименьших
квадратов:
n
f (a0 a1 Ц i уфi ) 2 min,
(2.37)
i 1
n
df
2(a0 a1 Ц i у фi ) 0,
da
0 i 1
или
n
df
2(a a1 Ц i у фi ) Ц i 0.
da1 i 1 0
n
n
na
a
Ц
yфi 0,
1
i
i 1
i 1
n
n
n
a Ц a Ц 2 y Ц 0.
1
i
фi i
0 i 1 i
i 1
i 1
Расчёты сведём в табл. 2.6.
Таблица 2.6
Квартал, i
1
2
Результаты расчёта параметров модели
Объём реализации Цена реализаЦ i2
мяса птицы, у фi
ции, Ц i
800000
40
1600
490000
52
2704
у фi Ц i
32000000
25480000
52
3
Всего,
650000
1940000
45
137
2025
6329
29250000
86730000
После подстановки результатов расчетов в систему уравнений, имеем:
3а0 137 а1 1940000 0,
137 а0 6329а1 86730000 0.
Решая
систему уравнений, находим
а1 25642,2. Окончательно, модель имеет вид:
коэффициенты:
а0 1817660,6,
у 1817660,6 25642,2 Ц .
Выручка от реализации продукции определяется как произведение цены
на объем реализации:
ВЦу.
(2.38)
Или, подставляя вместо объема реализации полученную экономикостатистическую модель, имеем:
В (1817660,6 25642,2 Ц ) Ц 1817660,6 Ц 25642, 2 Ц 2 .
Общие затраты на производство продукции (Со ) складываются из постоянных (Сс ) и переменных (Сп с у ) затрат, где с — прямые затраты на изготовление единицы продукции (в нашем случае с 29 руб.). Таким образом, общие
затраты на производство продукции:
С о Сс с у С с 29 у С с 29(1817660,6 25642,2 Ц ) .
Прибыль фабрики находится как разность между выручкой и затратами на
производство:
П В Со
1817660,6 Ц 25642, 2 Ц 2 С с 29(1817660,6 25642, 2 Ц )
или, после преобразований: П 2561284,4 Ц 25642,2 Ц 2 С с 52712157 .
Известно, что функция имеет экстремум если её производная по искомому параметру равна нулю. В нашем случае искомым параметром является цена
реализации продукции, поэтому:
П
2561284,4 51284,4 Ц 0 ,
Ц
и оптимальная цена реализации продукции:
Ц
2561284,4
50 руб.
51284,4
Прогнозируемый объем реализации мяса птицы при цене 50 руб./кг.:
у 1817660,6 25642,2 Ц 1817660,6 25642,2 50 535551 кг.
Приведенный выше пример иллюстрирует использование самой простой
– линейной однофакторной модели. На практике же широкое применение нашли более сложные – многофакторные модели. Соответственно и применение
многофакторных моделей для решения практических задач требует более громоздких расчетов, (осуществляемых, как правило, с использованием вычислительной техники) и более высокой квалификации разработчиков.
53
Структурные (эконометрические) модели используются для анализа и
прогнозирования сложных экономических объектов на макроэкономическом
или микроэкономическом уровне и представляют собой систему регрессионных
уравнений и тождеств, описывающих взаимосвязи основных параметров и характеристик развития объекта прогнозирования.
Структурные модели имеют следующие достоинства:
— позволяют исследовать комплексное воздействие различных факторов на
развитие объекта прогнозирования;
— дают возможность получения взаимосбалансированных прогнозов по большому числу показателей;
— при использовании вычислительной техники появляется возможность проведения многовариантных расчетов.
К недостаткам структурных моделей следует отнести:
— высокую стоимость работ, обусловленную необходимостью привлечения
высококвалифицированных специалистов для формирования и обработки
больших массивов исходной информации;
— структурная модель более пригодна для прогнозирования устоявшихся процессов и малопригодна для прогнозирования процессов, развитие которых
носит циклический характер.
Начальным этапом структурного моделирования является построение
информационной модели. Например, при прогнозировании развития предприятия основным плановым показателем является прибыль, и соответственно, укрупненная информационная модель может иметь вид представленный на рис.
2.4.
Вторым этапом моделирования является формализация (математическое
описание) взаимосвязей между параметрами модели. Введем обозначения: прибыль – П; выручка – В; затраты – З; Объем реализованной продукции – О; цена
продукции – Ц; затраты на материалы – М; затраты на заработную плату – З;
затраты на рекламу – Р; прочие затраты – Пр; показатель качества продукции –
К; доходы населения – Д. Эмпирические коэффициенты уравнений регрессии
обозначим аi и вi .
Для математического описания взаимосвязей между параметрами модели
будем использовать линейные модели.
Прибыль
Выручка
Объем
Затраты
Материалы
Цена
Зарплата
Качество
54
Реклама
Доходы
населения
Прочие
Рис. 2.4. Информационная модель формирования прибыли предприятия
Система уравнений, описывающая взаимосвязи между параметрами модели и внешними влияющими факторами будет иметь следующий вид:
П В З;
В О Ц ;
З М ЗП Р Пр;
К а а М а ЗП ;
1
2
О в0 в1 Р в2 Ц в3 К в 4 Д .
На третьем этапе на основе обработки статистической информации определяются значения эмпирических коэффициентов аi и вi .
На заключительном этапе, подставляя в уравнения внешний фактор – доходы населения и изменяя цену реализации продукции, рекламные расходы и
материалы изготовления продукции (т.е. материальные затраты) проводятся
многовариантные расчеты таких параметров как прибыль, качество продукции,
ожидаемый объем реализации. Полученная в ходе расчетов информация анализируется, после чего выбирается наиболее рациональный вариант развития
предприятия.
Разработка структурных моделей — очень трудозатратный и дорогостоящий процесс но, несмотря на это, структурные модели находят все большее
применение в разных сферах деятельности (в основном благодаря интенсивному развитию вычислительной техники, произошедшему за последнее десятилетие).
Оптимизационная модель представляет собой модель математического
программирования, состоящую из целевой функции и системы ограничений в
форме уравнений или неравенств, и направлена на поиск наиболее эффективного (оптимального) управленческого решения при соблюдении установленных
ограничений.
Целевая функция описывает цель оптимизации и представляет собой зависимость показателя, по которому ведётся оптимизация, от искомых переменных. На макроуровне критерием оптимальности может являться максимум валового национального дохода, максимум среднедушевого денежного дохода.
На микроуровне: максимум прибыли предприятия, минимум затрат и др.
Например, общий вид модели для расчета оптимального варианта производства продукции на предприятии:
55
n
Целевая функция:
I ( Ц j З j ) X j max,
j 1
Система ограничений:
ограничения по сбыту
X j min X j X j max ,
ограничения по мощности
bij X j Bi ,
n
j 1
n
ограничения по снабжению mkj X j M k ,
j 1
условие неотрицательности X j 0,
где Ц j — цена реализации единицы товара j -го вида;
З j — затраты на изготовление единицы товара j -го вида;
X j — количество товара j -го вида, подлежащее изготовлению;
X j min — обязательный минимальный объем производства товара j -го вида,
обусловленный необходимостью выполнения уже заключённых договоров или
необходимостью сохранения своего присутствия с минимальным предложением на рынках, привлекательных в долгосрочном периоде;
X j max — максимально возможный объём реализации товара j -го вида;
bij — норма затрат времени по изготовлению единицы товара j -го вида на
оборудовании i -го вида;
Bi — фонд рабочего времени на оборудовании i -го вида;
mkj — нора затрат материала k -го вида на изготовление единицы товара j го вида;
M k — имеющийся фонд k -го вида сырья.
Оптимизационные модели могут носить детерминированный и стохастический характер. В детерминированных моделях результат решения однозначно
зависит от входных параметров. Стохастические (вероятностные) модели в отличие от детерминированных описывают случайные процессы, в которых результат всегда остаётся неопределённым. В настоящее время разработано
большое количество программных пакетов, позволяющих решать сложные оптимизационные задачи на основе ЭВМ.
Пример. Малое предприятие изготавливает и реализует два вида продукции. Количество ресурсов, имеющихся на складе предприятия и нормы их затрат на изготовление продукции представлены в табл. 2.7:
Таблица 2.7
Ресурсы предприятия и нормы их затрат
Норма затрат ресурсов, кг Количество
Ресурс
Продукция
Продукция ресурсов, кг
1-го вида
2-го вида
1
2
2
1200
2
1
2
800
56
3
4
4
4
1600
1200
Прибыль от реализации продукции 1-го вида – 2 руб/шт., 2-го вида – 3
руб/шт. Сколько продукции каждого вида следует изготовить, чтобы получить
максимально возможную прибыль.
Решение:
Обозначим искомое количество продукции первого вида Х 1 , а второго
вида Х 2 , тогда целевая функция, максимизирующая прибыль предприятия будет иметь вид:
I 2 X 1 3 X 2 max,
Система ограничений:
1) 2 Х 1 2 Х 2 1200,
2) 1Х 1 2 Х 2 800,
3) 4 Х 1 1600 или Х 1 400,
4) 4 Х 2 1200 или Х 2 300,
5) Х 1 , Х 2 0.
Наиболее простой и быстрый путь решения данной задачи – использование средств ЭВМ. Более трудоёмкий способ решения – графический.
По осям отложим количество продукции Х 1 и Х 2 . Построим линии ограничения (на графике они пронумерованы соответственно номерам неравенств в
модели). Область возможных значений объёмов производства продукции заштрихована пунктирными линиями. Оптимальному варианту производства
продукции соответствуют либо координаты точки А или координаты точки К
(рис. 2.5).
600
400
300
1
К
А
2
Х1
Рис. 2.5. Графическое решение оптимизационной задачи
400
600
800
57
Найдем координаты точек А и К.
Для точки А: Х 1 400 , подставляя в неравенство 1 или 2 имеем
2 Х 2 400 Х 2 200 .
Прибыль I 2 X 1 3 X 2 2 400 3 200 1400 руб.
Для точки К Х 2 300 , подставляя в неравенство 2 имеем Х 1 200 .
Прибыль I 2 200 3 300 1300 руб.
Наибольшая прибыль соответствует точке А.
Ответ: Необходимо изготовить 400 единиц продукции первого вида и 200
второго.
Особенностью оптимизационных моделей с которой приходится считаться при их использовании является однокритериальность. То есть поиск лучшего
решения осуществляется по одному критерию. В то же время большинство социально-экономических процессов характеризуется системой показателей. Поэтому при математическом описании сложных, протекающих во времени экономических процессов, характеризуемых несколькими показателями часто используются имитационные модели.
Имитационными называются модели, воспроизводящие реальные соотношения между экономическими показателями, описывающими прогнозируемый объект.
В настоящее время имитационные модели разрабатываются как программы для ЭВМ, позволяющие с помощь средств вычислительной техники «проигрывать» (проводить много вариантные расчёты) развития сложных систем.
Имитационная модель учитывает временной фактор и наряду с математическими моделями, имитирующими прогнозируемый процесс, содержит блоки, в которых решения принимаются человеком (прогнозистом). Имитация процессов
организуется в форме диалога и у прогнозиста имеется возможность на каждом
этапе принятия решения, анализируя и оценивая последствия принятия того
или иного решения выбрать самое рациональное, по его мнению, решение.
В последние годы имитационные модели находят все более широкое
применение для имитации экономических процессов, в которых сталкиваются
различные интересы, типа конкуренции на рынке.
Имитационные модели, как и структурные модели, требуют больших
трудозатрат на их разработку и высокой квалификации специалистов.
Модели теории игр направлены на математическое описание и выбор
решений в конфликтных ситуациях, при которых интересы участников либо
противоположны (антагонистические игры), либо не совпадают, хота и не противоположны (игры с противоположными интересами). Для конфликтных ситуаций характерно то, что ни одна из сторон не может полностью контролировать ситуацию и эффективность решений, принимаемых в ходе конфликта каждой из сторон, зависит от действий другой стороны.
Теория игр впервые была систематически изложена О.Моргенштерном и
Дж. фон Нейманом в 1944 году и содержала в основном экономические приме-
58
ры, поскольку экономическому конфликту легче всего придать численную
форму. Во время второй мировой войны и сразу после неё теорией игр серьёзно
заинтересовались военные, которые увидели в ней аппарат для исследования
стратегических решений. В СССР аппарат теории игр для разрешения экономических конфликтов практически не использовался, так как, директивная система планирования исключала наличие конфликтных ситуаций в экономике. С
переходом к рыночным отношениям применение моделей теории игр для оценки конфликтных ситуаций и принятия решений в условиях неопределённости
стало актуальным.
Содержание игры заключается в том, что каждый из её участников выбирает такую стратегию действий, которая, как он полагает, обеспечивает ему
максимальный выигрыш (минимальный проигрыш). Стратегию игрока называют оптимальной, если при её применении выигрыш данного игрока не уменьшается, какими бы стратегиями не пользовался его противник. Результаты принимаемых решений заносятся в специальную таблицу, которая называется матрицей игры или платёжной матрицей. При поиске оптимальных стратегий в
теории игр игроки опираются на принцип максимальной осторожности. Данный принцип гласит, что каждый игрок, считая партнёра по игре высоко интеллектуальным соперником, выбирает свою стратегию в предположении о том,
что соперник не упустит ни единой возможности использовать его ошибку в
своих интересах.
В экономической практике часто приходится придавать игровую форму
таким ситуациям, в которых один из участников безразличен к результату игры.
Такие игры называют статистическими или играми с «природой», понимая под
«природой» всю совокупность внешних обстоятельств. В играх с «природой»
степень неопределённости для сознательного игрока возрастает, так как «природа», будучи индеферентной в отношении выигрыша, может предпринимать и
такие ответные действия, которые ей совершенно не выгодны.
Рассмотрим игровую ситуацию, в которой игроки А и В должны принять
с каждой стороны по одному решению из трёх возможных. Результаты принимаемых решений (выигрыши игрока А ) занесены в платёжную матрицу (табл.
2.8).
Действия игрока А :
1. Определяется для каждого решения минимальное значение аi , ожидаемого
выигрыша аi min aij . Для нашего случая а1 7, а 2 4, а3 0 .
2. Из всех возможных выигрышей аi игрок А выбирает максимальное значение а max ai , т.е. а max min aij . Это a 7 .
Число a называется нижней чистой ценой игры.
Действия игрока В :
1. Определяется для каждого решения максимально возможный проигрыш
j max aij . Для нашего случая 1 14, 2 7, 3 8 .
59
2. Из всех проигрышей игрок В выбирает минимальное значение min j ,
т.е. min max aij . Это 7 .
Число называется верхней чистой ценой игры.
Таблица 2.8
Платёжная матрица
Аi
аi
Вj
В1
В2
В3
9
8
7
7
11
6
4
4
14
3
i
14
8
7
Таким образом, в нашей игровой ситуации имеется «седловая» точка
аij max min aij min max aij 7 — наименьшая в строке и наибольшая в столбце, и
соответственно, игроку А следует принять 1 решение, а игроку В — 2.
Однако на практике достаточно часто возникают игровые ситуации, не
имеющие чётко выраженных «седловых» точек. Платёжная матрица такой ситуации представлена в табл. 2.9.
Таблица 2.9
Платёжная матрица
А1
А2
А3
Ai
аi
Вj
В1
В2
3
10
3
8
5
5
8
10
В этом случае игрокам необходимо использовать смешанные стратегии.
Обозначим через pi вероятности, с которыми игрок А принимает свои решения
( pi 0, pi 1 ). Обозначим через q j вероятности, с которыми игрок В приниА1
А2
i
i
мает свои решения ( q j 0, q j 1 ). Тогда величина выигрыша будет являться
j
функцией от вероятностей принимаемых решений:
f ( p, q ) aij pi q j .
i
(2.45)
j
Для нашего случая:
f ( p, q ) 3 p1q1 10 p1q2 8 p2 q1 5 p2 q2 .
Обозначим оптимальные смешанные стратегии:
p
p1
p2
;
q
q1
q2
.
По аналогии с предыдущей ситуацией для «седловой» точки (наименьшая
в строке и наибольшая в столбце) должно выполняться неравенство:
f ( p, q ) f ( p , q ) f ( p , q ).
(2.46)
60
«Седловую» точку при оптимальных смешанных стратегиях называют
ценой игры: v f ( p , q ) , т.е.:
(2.47)
аij pi q j v aij pi q j .
Проведём преобразования:
aij pi q j pi aij q j 1 aij q j ;
i
j
j
aij pi q j q j aij pi 1 aij pi ;
j
i
i
aij q j v aij pi .
j
i
Разделим обе части неравенства на цену игры v :
aij
j
Введём обозначения:
qj
v
q j
v
1 aij
i
pi
.
v
pi
xi .
v
yj,
Тогда неравенство будет иметь следующий вид:
aij y j 1 aij xi .
j
i
Таким образом, наша игровая ситуация сводится к решению оптимизационной задачи. Игрок А , стремясь увеличить свой выигрыш, должен минимизировать величину обратную своему выигрышу:
xi
i
i
pi 1
1
pi min .
v v i
v
(2.48)
При выполнении ограничений:
aij xi 1 .
(2.49)
i
Игрок В , наоборот, стремится сделать свой проигрыш меньше, а значит
1
больше. Для игрока В задача запишется в следующем виде:
v
(2.50)
у j max ,
величину
j
aij y j 1 .
(2.51)
j
Для игрока А в рассматриваемой игровой ситуации:
х1 х2 min,
3 x1 8 x2 1,
10 x1 5 x2 1,
x1 0, x2 0.
Решая данную задачу, получаем х1 0,046 , х2 0,108 .
1
v
xi 0,046 0,108 0,154 . v
i
1
6,5 .
0,154
Оптимальная смешанная стратегия:
p
p1 x1v 0,046 6,5 0,3
p2 x2 v 0,108 6,5 0,7
.
61
Пример Фермерское хозяйство выращивает картофель и пшеницу на
площади 100 Га. Прибыль, получаемая от реализации 1 тонны картофеля –500
руб., от 1 т. пшеницы – 3000 руб. Урожайность культур зависит от погодных
условий. В засушливое лето урожайность картофеля – 15 т/га, пшеницы – 3 т/га.
В дождливое лето урожайность картофеля – 24 т/га, пшеницы – 2 т/га. Определить какую площадь фермерскому хозяйству необходимо отвести под картофель и пшеницу.
Решение:
1. Если на площади 100 Га посадить только картофель, то ожидаемая прибыль
составляет:
— в засушливое лето П 100 15 500 750000 руб.,
— в дождливое лето П 100 24 500 1200000 руб.
2. Если на площади 100 Га посадить только пшеницу, то ожидаемая прибыль
составляет:
— в засушливое лето П 100 3 3000 900000 руб.,
— в дождливое лето П 100 2 3000 600000 руб.
Заполним платёжную матрицу (табл. 2.10).
Если был посажен картофель, и сложилось дождливое лето, наш проигрыш будет равен 0 (мы приняли наилучший вариант решения для сложившихся
погодных условий).
Если был посажен картофель, и сложилось засушливое лето, наш проигрыш составит 750000 900000 150000 руб. (был принят не лучший вариант решения, при посадке пшеницы в засушливое лето мы получили бы 900000 руб.
прибыли, а так только – 750000 руб.).
Если была посажена пшеница, и сложилось дождливое лето, наш проигрыш составит 600000 1200000 600000 руб. (при посадке картофеля мы получили бы 1200000 руб.).
Если была посажена пшеница, и сложилось дождливое лето, наш проигрыш будет равен 0.
Таблица 2.10
Платёжная матрица
Вариант решения
Картофель
Пшеница
Погодные условия
Дождливое лето
Засушливое
лето
-150000
-600000
Произведём преобразование матрицы — для того чтобы избавиться от отрицательных чисел прибавим к каждому её элементу 600000:
600000 450000
4 3
, и разделим на 150000
.
600000
0 4
62
Целевая функция: I x1 x2 min ,
Ограничения:
1) 4 x1 0 x 2 1 ,
2) 3 x1 4 x2 1 .
Из первого ограничения имеем: х1 0,25 , подставим значение х1 во второе
ограничение:
0,25
0,0625 .
4
1
3,2 .
хi 0,25 0,0625 0,3125 , v
0,3125
i
p1 0,25 3,2 0,8
p
p 2 0,0625 3, 2 0, 2
4 х2 1 3 0,25 0,25 х2
Таким образом, картофелем следует засадить 100 p1 100 0,8 80 Га, а
пшеницей 100 p2 100 0,2 20 Га.
Теория игр нашла широкое применение для теоретического описания таких процессов как конкуренция на рынке. Однако, практика показывает, что
основной принцип, которым оперирует теория игр (принцип максимальной осторожности, т.е. мы при выборе или поиске своего решения исходим из того,
что наш конкурент является высокоинтеллектуальным человеком, принимающим лучшие решения) реализуется, по оценкам экспертов, на 20%. В основном,
наши конкуренты принимают далеко не самые эффективные решения.
Раздел 3. Методология планирования
5. Система методов планирования
Планирование можно рассматривать с одной стороны как процесс обработки информации с целью упрощения выбора и принятия наилучшего планового решения, а с другой как процесс разработки плана или плановых документов с их последующей корректировкой.
Методы планирования представляют собой совокупность способов и
приёмов с помощью которых обеспечивается разработка и обоснование плановых документов. Система методов планирования включает в себя: нормативный, программно-целевой, балансовый и графический методы.
5.1. Нормативный метод планирования
Нормативный метод основан на определении и использовании в процессе
планирования системы норм и нормативов.
Норма – это научно обоснованная мера затрат ресурса на изготовление
единицы продукции в конкретных производственно-технических условиях.
Нормативы отражают общественные требования к результатам деятельности и характеризуют необходимый уровень использования ресурса.
63
Комплекс норм и нормативов, используемых для разработки плановых
документов, называется нормативной базой.
Сам по себе нормативный метод самый лёгкий и простой в применении
из всех остальных методов планирования. Так, например, если норма времени
на изготовление изделия – 10 часов ( n 10 ), а годовой объем производства –
200 шт. ( Q 200 ), то трудоёмкость составит T n Q 10 200 2000 часов. При
использовании для изготовления изделий одних и тех же технологий величина
нормы остаётся постоянной.
Основная сложность при применении нормативного метода заключается
в определении величины нормы. Существуют следующие основные методы
разработки норм и нормативов:
1. научного обоснования;
2. аналитически-расчетный;
3. аналитически-исследовательский;
4. опытный;
5. отчетно-статистический.
Метод научного обоснования нормы позволяет находить оптимальное
значение нормы с учетом действия технических, экономических, социальных и
других факторов, оказывающих влияние на ее величину.
Пример. Магазин закупает хлеб на хлебозаводе по цене 10 рублей за батон, а продает по 11 руб. Если хлеб не будет реализован в день завоза, то на
следующий день его продают по 8 рублей за батон (с одой стороны это связано
с ухудшением качества продукции, а с другой стороны, присутствует определённый элемент рекламы). Необходимо определить ежедневную норму завоза
хлеба, обеспечивающую максимум прибыли. Данные об объемах реализации
хлеба в течение прошлой недели представлены в табл. 3.1.
Таблица 3.1
Объемы реализации хлеба в течение недели
Исследуемый параметр
День недели
Пн. Вт. Ср. Чт. Пт. Сб. Вс.
Количество проданных буханок хлеба, шт.
120 146 114 155 141 132 137
Решение.
Прежде всего, рассчитаем средний объем реализации хлеба за день:
120 146 114 155 141 132 137
135 шт.
7
Номинальная прибыль от реализации хлеба составляет: П 11 10 1 руб.
Х
В том случае, когда хлеб не продается в день его завоза, магазин несёт убыток с
каждой буханки: У 10 8 2 руб. Если бы номинальная прибыль и потери, связанные с не реализацией хлеба были бы одинаковы, то ежедневная норма завоза
хлеба была бы равна среднему объёму продаж за день, т.е. 135 буханок. Однако
убыток, связанный с не реализацией превышает прибыль, получаемую в ре-
64
зультате продажи буханки хлеба, а значит, норма завоза должна быть меньше
135 буханок.
Обозначим вероятность продажи x -вой буханки хлеба — p(x) . Тогда ожидаемая прибыль, получаемая от реализации x -вой буханки будет равна:
П х П р( х) 1 р( х) .
(3.1)
С другой стороны, ожидаемый убыток связанный с не реализацией (а
значит с ухудшением качества) х -вой буханки хлеба:
У х У (1 р ( х )) 2 (1 р( х )) ,
(3.2)
где (1 р ( х)) — вероятность того, что х -вая буханка хлеба не будет реализована в
день её завоза.
Для определения оптимальной нормы завоза необходимо уравновесить
ожидаемую прибыль и убыток:
П х У х , или 1 р( х) 2 (1 р( х)) .
Отсюда, вероятность реализации хлеба:
р( х)
2
2
0,67 .
2 1 3
Значит, ежедневная норма завоза хлеба должна составлять такое количество буханок, вероятность продажи которых равна 0,67 или 67%.
Будем считать, что исследуемое нами явление, как и большинство других
экономических процессов подчиняется нормальному закону распределения.
Тогда с ростом нормы завоза хлеба вероятность реализации всего завоза будет
уменьшаться по зависимости изображенной на рис. 3.1.
t p
Вероятность
1
0,67
0,5
Ф
65
135 3
135
135 3
норма, шт.
Рис. 3.1. Зависимость вероятности реализации заказа от его размера
Таким образом, величину нормы можно определить из выражения:
п 135 t p ,
где t p — коэффициент нормального распределения, зависящий от значения
функции Лапласа – Ф , при Ф 0,67 0,5 0,17 t p 0,44 (приложение 1);
— среднее квадратическое отклонение, для нашего случая:
(120 135) 2 (146 135) 2 (114 135) 2 (155 135) 2
(141 135) 2 (132 135) 2 (137 135) 2
7 1
14,35
Соответственно, ежедневная норма завоза хлеба:
п 135 0,44 14,35 129 .
Существует достаточно большое количество разнообразных примеров
применения метода научного обоснования нормы. При этом, с целью определения оптимальной (по определенному критерию) нормы могут использоваться
экономико-статистические, оптимизационные и другие модели.
Аналитически-расчётный метод основан на разделении выполняемых
работ на составные элементы с последующим их анализом и проектированием
рациональных вариантов использования материальных ресурсов, оборудования
и рабочей силы.
Пример. Из прутка стандартной длины — 3 метра нарезаются заготовки
вида А — 80 см и вида Б — 52 см. Применяемость данных заготовок в изделии: А
– 2 шт., Б – 2 шт. Масса 1 метра погонного прутка 2,4 кг. Ширина распила –
5мм. Определить норму расхода материала на изделие.
Решение. Рассмотрим возможные варианты распила прутка. Первоначально попытаемся нарезать как можно больше заготовок вида А (так как они
самые длинные), а из оставшегося материала заготовки меньшей длины – Б. В
последующих вариантах будем уменьшать количество нарезаемых заготовок
вида А на одну единицу.
Вариант 1. 3 А и 1 Б, Отходы материала:
300 3 (80 0,5) (52 0,5) 6см.
Вариант 2. 2 А и 2 Б, Отходы материала:
300 2 (80 0,5) 2 (52 0,5) 34см.
Вариант 3. 1 А и 4 Б, Отходы материала:
300 (80 0,5) 4 (52 0,5) 9,5см.
Вариант 4. 0 А и 5 Б, Отходы материала:
300 5 (52 0,5) 37,5см.
На первый взгляд самым подходящим является вариант №2. Из одного
прутка данным способом можно вырезать 2 заготовки вида А и 2 вида Б, т.е.,
66
комплект заготовок на одно изделие. Следовательно, норма затрат материала –
3 метра погонных на изделие, или 3 2,4 7,2кг. , в зависимости от того в какой
размерности установлена цена на материал. Однако проанализируем возможность комбинации различных вариантов распила прутка.
а) Рассмотрим сочетание 1 и 3-го вариантов. Обозначим х — долю прутков,
разрезаемых 1-м способом, тогда (1 х) — доля прутков, разрезаемых 3-м способом. Количество заготовок вида А и Б, а также долю х определим из выражений:
N A 3 x 1(1 x ) 1 2 x ;
N Б 1х 4(1 х ) 4 3 х .
N Б 4 3х
1 , 4 3х 1 2 х
N А 1 2х
и
х
3
0,6 .
5
Значит, при сочетании 1 и 3 вариантов из 5 прутков — 3 следует разрезать
1-м способом, а 2 прутка 3-м способом. В этом случае мы получаем:
N А 3 3 2 1 11 ,
N Б 3 1 2 4 11 , т.е. из 10 прутков можно
вырезать по 22 заготовки каждого вида, а это — 11 изделий.
Норма: п
10 3
2,73 м.пог/шт, или п 2,73 2,4 6,55 кг/шт.
11
б) Рассмотрим сочетание 1 и 4-го вариантов. Обозначим х — долю прутков, разрезаемых 1-м способом, (1 х) — доля прутков, разрезаемых 4-м способом, тогда:
N A 3 x 0(1 x) 3x ;
N Б 1х 5(1 х) 5 4 х .
N Б 5 4х
1 , 5 4 х 3х
NА
3х
и
х
5
.
7
Это значит, что из 7 прутков 1-м вариантом разрезаем 5, а 2-м – 2 прутка.
Количество заготовок: N А 5 3 15 , N Б 5 1 2 5 15 , т.е. из 14 прутков можно вырезать по 30 заготовок каждого вида и, соответственно, получить 15 изделий.
Норма: п
14 3
2,8 м.пог/шт, или п 2,8 2,4 6,72 кг/шт.
15
Анализ возможных вариантов распила прутков показывает, что наиболее
целесообразным является сочетание 1 и 3 вариантов, так как в этом случае норма расхода материалов будет наименьшей ( п 2,73 м.пог/шт, или 6,55 кг/шт).
Аналитически-исследовательский метод основан на определении норм
путем проведения наблюдений и экспериментов. Данный метод нашел широкое
применение на действующих производствах. С помощью наблюдений, как правило, определяются нормы затрат времени на выполнение технологических
операций.
Часто в ходе наблюдений и экспериментов изучается возможность и оценивается целесообразность внедрения различных вспомогательных приспособлений, снижающих затраты времени на выполнение операций.
67
Таким
образом,
практическое
применение
аналитическоисследовательского метода направлено не только на определение значений
нормируемых параметров, но и на совершенствование технологического процесса.
Отчётно-статистический метод заключается в том, что нормы затрат
производственных ресурсов устанавливаются на основе отчётных или статистических данных за прошедшие периоды.
Пример. Имеются отчетные данные по энергопотреблению цехом, выпускающим продукцию двух наименований (табл. 3.2).
Определить нормы затрат электроэнергии на изготовление продукции вида А и Б, а также, затраты на освещение цеха.
Таблица 3.2
Затраты электроэнергии на выпуск продукции
Месяц
Количество продукции, шт.
Затраты электроэнергии, кВтч.
Продукция
Продукция
вида А
вида Б
Январь
10000
25000
800000
Февраль
15000
25000
900000
Март
20000
20000
920000
Решение.
Обозначим нормы затрат электроэнергии на изготовление продукции вида А, Б и затраты на освещение — па , пб и пс , соответственно. Тогда по имеющимся данным за прошедшие месяцы (январь, февраль, март) можно составить
следующую систему уравнений:
10000 п а 25000 пб пс 800000;
15000 п а 25000 пб пс 900000;
20000 п 20000 п п 920000.
а
б
с
Из второго уравнения вычитаем первое и получаем: 5000 п а 100000, отсюда норма затрат на изготовление изделия А — па 20 кВтч. Вычитая из третьего уравнения второе, имеем: 5000 20 5000 пб 20000 , и пб 16 кВтч. Для вычисления постоянных затрат на освещение цеха подставим полученные величины
норм па и пб в первое уравнение: пс 800000 100000 20 25000 16 200000 кВтч.
Для дальнейшего планирования энергопотребления можно использовать
следующее выражение:
W 20 X a 16 X б 200000 .
После подстановки в данное выражение планируемого выпуска продукции вида А ( Х а ) и вида Б ( Х б ) получим плановые затраты электроэнергии.
Опытный метод основан на определении норм путем опроса технологов,
мастеров цеха или других опытных специалистов.
Как видно из приведенных выше примеров, определение норм связано со
сравнительно большими временными затратами (либо на проведение матема-
68
тических расчетов, либо на проведение наблюдений и экспериментов). В условиях единичного производства такие затраты зачастую являются нецелесообразными. Поэтому при планировании материальных затрат и затрат на оплату
труда используются нормы установленные экспертным путем. Точность данных норм не столь высока, однако удается избежать временных затрат, связанных с определением величин норм с использованием математического аппарата.
5.2. Программно-целевой метод планирования
Программно-целевой метод используется для планирования развития
сложных систем и процессов, в которых возможно выделение ряда структурных (иерархических) уровней. Информационная модель программно-целевого
метода изображена на рис. 3.2.
Программно-целевой метод нашел широкое применение при разработке
целевых комплексных программ. По своему содержанию выделяют социальноэкономические, научно-технические, экологические и др. комплексные программы.
Разработка целевых комплексных программ осуществляется поэтапно. На
первом этапе формулируется важная проблема, требующая решения (генеральная цель). На втором этапе выделяют отдельные взаимоувязанные мероприятия
(цели первого уровня), направленные на достижение генеральной цели в намеченные сроки, назначаются ответственные исполнители, несущие административную ответственность за выполнение работ, определяются затраты на финансирование мероприятий и т.д.
Генеральная цель
Ц
И
Ц
И
Ц
И
С
Ф
С
Ф
С
Ф
Ц
И
Ц
И
С
Ф
С
Ф
Цели 1 уровня
Цели 2 уровня
Ц – цель работы или ее содержание;
И – ответственный исполнитель;
С – срок выполнения работы;
Ф – размер финансирования.
Рис. 3.2. Информационная модель программно-целевого метода планирования
69
5.4. Балансовый метод планирования
Балансовый метод заключается в уравновешивании результатов производственной деятельности с одной стороны и затрачиваемых ресурсов с другой.
Различают материальные, стоимостные и трудовые балансы.
Центральное место в системе экономических балансов занимают материальные балансы. По виду используемой балансовой модели балансы бывают
однопродуктовыми и межпродуктовыми. Однопродуктовые балансы разрабатываются по конкретному виду продукции. Многопродуктовые балансы увязывают производство продукции и потребление ресурсов между отраслями экономики.
Разработка материальных балансов начинается с определения потребностей общества в продукции каждого вида. Для определения потребности общества в продукции того или иного вида чаще всего используется нормативный
метод. Например, потребность в молокопродуктах определяется произведением
рациональной нормы потребления молокопродуктов, приходящейся на одного
человека, на численность населения. После определения потребностей в продукции формируется ресурсная часть баланса.
Широкое распространение для анализа межотраслевых связей и формирования структуры национальной экономики получили межотраслевые балансы
в стоимостном и материальном выражении. Информационная модель межотраслевого баланса в стоимостном выражении представлена в табл. 3.3.
Межотраслевой баланс в стоимостном выражении состоит из четырёх
квадрантов.
В первом квадранте отражаются финансовые потоки между отраслями
производителями и отраслями потребителями материальных ресурсов. Также в
этом квадранте определяется промежуточное потребление и промежуточные
затраты на производство продукции отраслями.
Во втором квадранте характеризуется потребление конечного продукта,
который включает конечное потребление продукции в домашних хозяйствах,
валовое накопление, сальдо экспортно-импортных операций.
В третьем квадранте приводятся данные об амортизационных отчислениях, заработной плате, прибыли и налогах по отраслям.
В четвёртом квадранте отражается перераспределение национального дохода.
Исходя из условия равенства валового выпуска и затрат получаем следующие уравнения:
xij yij xij vij
i
i
j
(3.3)
j
или, например, для первой отрасли имеем:
х11 х12 … х1n y11 y12 y13 x11 x 21 … x n1 v11 v 21 v 31 v 41
(3.4)
Таблица 3.3
70
1
2
…
п
Промежуточные
затраты
Амортизация
Заработная плата
Прибыль
Налоги
Добавленная
стоимость:
Валовые затраты
х11
х12
х 21
х 22
…
…
х п1
хп 2
хi1
хi 2
v11
v12
v 21
v22
v31
v32
v41
v42
vi1
x1
…
…
…
…
…
х1п
х2п
…
х пп
хin
vi 2
…
…
…
…
…
vin
x2
…
xn
v1n
v2 n
v3n
v4 n
Промежуточное
потребление
х1 j
х2 j
…
хnj
хij
Конечный продукт
Валовое
накопление
Сальдо экспор-таимпорта
Итого
Отрасли потребления
п
1
2
Конечное
потребле-
Отрасли производства
у11
у12
у13
у 21
y 22
у 23
…
…
…
уп1
уп2
у п3
уi1
уi 2
yi 3
y1 j
y2 j
…
ynj
yij
Валовый выпуск
Информационная модель межотраслевого баланса в стоимостном выражении
х1
х2
…
хп
хi
v1 j
v2 j
v3 j
v4 n
vij
Алгоритм использования балансового метода для макроэкономического
планирования можно представить в виде следующих взаимосвязанных этапов:
1. Расчет конечного потребления различных видов продукции;
2. Определение технологических коэффициентов;
3. Расчет валового производства отраслей;
4. Определение норм затрат трудовых ресурсов и «справедливых» цен
реализации продукции;
Недостатком использования балансового метода является его «инертность». Так, например, если прогнозы конечного потребления продукции населением были неточны, то продукция, пользующаяся повышенным спросом,
полностью раскупалась, и возникал дефицит. Внести же коррективы в план
можно только в следующем плановом периоде.
5.5. Графический метод планирования
Графический метод планирования заключается в изображении планируемого процесса в виде графика. Впервые данный метод был применен в начале
20-го века американскими инженерами Ф.У.Тейлором и Г.Л.Гантом.
Наиболее широкое применение на практике нашли линейные и сетевые
графики.
Линейные графики строятся в прямоугольной системе координат. По оси
абсцисс откладывают время протекания планируемого процесса (часы, смены и
др.), по оси ординат – вид выполняемой работы. Каждая работа характеризуется затрачиваемыми на ее выполнение материальными и трудовыми ресурсами.
Изменяя очередность выполнения работ во времени, определяется наиболее це-
71
лесообразный график выполнения работ, обеспечивающий равномерную загрузку оборудования и рабочей силы. Линейные графики широко применяются
при оперативно-производственном планировании деятельности предприятий.
Сетевой график устанавливает и наглядно представляет взаимосвязи выполнения комплекса работ. Основными элементами сетевого графика являются
работа и событие. Работа в сетевом графике изображается стрелкой, событие –
кружком. Сетевые графики широко используются при планировании научных
разработок, строительства сложных объектов и т.п.
5.6. Принятие решений в условиях неопределенности
Для рыночной экономики характерно постоянное колебание цен на ресурсы. В подобных условиях использование традиционных методов планирования показателей производственно-хозяйственной деятельности, основанных
на обработке детерминированной информации, может привести к значительным просчетам. В связи с этим, для принятия решений при неопределенности
исходной информации могут быть использованы следующие критерии:
1. Минимум средних затрат.
n
S
min
i 1
n
ij
,
(3.5)
здесь j – вариант стратегии;
i – вариант условий.
Недостаток данного критерия – предположение о равной вероятности появления всех условий, что может не соответствовать действительности.
2. Критерий минимаксных затрат
min max Sij .
(3.6)
3. Критерий минимаксного риска (критерий Севиджа)
min max Sij , Sij Sij min Sij ,
(3.7)
где S ij — показатель риска.
Недостаток второго и третьего критериев состоит в ориентации на появление самых худших условий. Данные критерии предохраняют от наибольших
потерь.
4. Критерий пессимизма-оптимизма (критерий Гурвица)
min ( max Sij (1 ) min Sij ) ,
здесь — взвешивающий множитель.
(3.8)
5. Обобщенный критерий
1
min ( ( max Sij min Sij Sij )) ,
3
где Sij — среднеарифметическое значение затрат.
(3.9)
72
В том случае, если использование перечисленных выше критериев приводит к различным результатам, принимается компромиссное решение.
Рассмотрим пример.
Зависимость себестоимости единицы продукции имеет следующий вид:
S 1C A 2CB ,
(3.10)
где C A и C B — цена единицы ресурсов A и B (труд и капитал).
Диапазоны изменения цен на ресурсы представлены в табл. 3.4.
Рассматриваются три стратегии использования ресурсов:
1 0,6; 2 0,5.
2. 1 0,4; 2 0,9.
3. 1 0,7; 2 0,3.
1.
Необходимо определить наиболее целесообразную стратегию (взвешивающий множитель 0,4).
Таблица 3.4
Результаты экспертного прогноза
Ресурс Минимальный уровень цен, руб.
Максимальный уровень цен, руб.
A
B
150
70
210
120
Решение:
По результатам расчетов себестоимости, в зависимости от стратегии и
уровня цен, составляется платежная матрица (см. табл. 3.5).
Таблица 3.5
Матрица себестоимости единицы продукции
Стратегия
Себестоимость единицы продукции при различном сочетании
цен на ресурсы
min C A
min CB
min C A
max CB
max C A
min CB
max C A
max CB
1
125
150
161
186
2
123
168
147
192
3
126
141
168
183
Данная платежная матрица обрабатывается с применением приведенных
выше критериев (см. табл. 3.6).
Таблица 3.6
Результаты расчета критериев
СтратеКритерии
гия
МиниМинимакс- Минимаксно- ПессимизОбобщенмум
ных затрат
го риска
маный
средних
оптимизма
73
1
2
3
затрат
155,5
157,5
154,5
186
192
183
61
69
57
149,4
150,6
148,8
155,5
157,5
154,5
По результатам обработки можно сделать вывод, что по всем критериям в
рассматриваемом примере целесообразно принять стратегию под номером 3.
6. Макроэкономическое (государственное) планирование и прогнозирование
6.1. Государственное прогнозирование, планирование и программирование социально-экономического развития
Индикативное планирование является наиболее распространенным средством государственного прогнозирования и планирования социальноэкономического развития в условиях рыночной экономики. Оно представляет
собой механизм координации интересов и деятельности государства, предприятий, домохозяйств в условиях рынка.
Существуют различные подходы к индикативному планированию. Можно выделить четыре основных подхода, которые нашли применение в практике
прогнозирования и регулирования социально-экономического развития в условиях рынка.
Первый подход основывается на представлении об индикативном планировании как макроэкономическом планировании при самостоятельно хозяйствующих субъектах — предприятиях. Например, китайские экономисты считают, что планирование в Китае носит не директивный, а индикативный характер,
поскольку деятельность государственных предприятий осуществляется в условиях экономической самостоятельности. Оно представляет собой макроэкономическое планирование, основанное на сочетании частного и государственного
секторов экономики при доминировании государственного сектора.
При таком подходе индикативное планирование представляет собой процесс формирования системы индикаторов — параметров, характеризующих
развитие экономики страны, соответствующих определенной государственной
социально-экономической политике, и системы мер государственного воздействия на социальные и экономические процессы с целью достижения указанных параметров.
Второй подход основан на том, что индикативное планирование выполняет информационно-ориентирующие и мотивационные функции. Индикативное планирование состоит в том, что государство в интересах всего общества, с
учетом потребностей регионов, а также субъектов рынка разрабатывает планы
экономического развития всего народного хозяйства, включая частный сектор,
устанавливает конкретные хозяйственные ориентиры, включая макроэкономические параметры и обеспеченные ресурсами структурные показатели. Тем са-
74
мым государство с помощью индикативного планирования мотивирует заинтересованное участие как предпринимателей всех форм собственности, так и регионов страны в реализации планов, важных для общества.
Такой подход к индикативному планированию нашел распространение в
ряде развитых стран. Например, в Японии общегосударственное экономическое
планирование носит индикативный характер. В стране разрабатываются общегосударственные планы социально-экономического развития, которые формально не являются законами, а представляют собой программы, ориентирующие и мобилизующие отдельные звенья экономической структуры на выполнение этих программ в общенациональных интересах.
Третий подход, нашедший применение во многих странах, основывается
на том, что индикативный план содержит обязательные задания для государства и госсектора. Частные предприятия ориентируются на индикаторы плана и
на планы самого мощного хозяйствующего субъекта в рыночной системе — государства, несмотря на то, что это для них не обязательно. Соответственно государственный план представляет собой систему показателей как для централизованного управления, так и для косвенного регулирования различных секторов
экономики. Она включает в себя ориентирующие показатели — контрольные
цифры, имеющие информационное значение для предприятий, отраслей и регионов, а также директивные показатели в форме государственных заказов и
экономических регуляторов, включая цены, налоги, процентные ставки, экономические нормативы.
Четвертый подход основывается на том, что индикативное планирование
— это механизм координации действий и интересов государства и других субъектов экономики. Помимо информации хозяйствующих субъектов такое планирование выполняет координационную роль, оно предполагает согласование
деятельности центральных органов, регионов и предприятий в процессе самостоятельной разработки каждым из них своих планов.
Этот подход распространен в практике индикативного планирования во
Франции. Правительство воздействует на экономическое развитие в большей
степени путем координации и обеспечения информацией, чем путем принятия
решений и выдачи указаний. Французская практика основывается на обмене
планами и информацией между правительством и частными предпринимателями, в ходе которого выявляется схема экономического роста, включающая взаимно совместимые по линии правительственных организаций планы.
Многие французские экономисты считают, что переход к индикативному
планированию позволил на демократической основе координировать позиции
государства и частного бизнеса. Планирование, основанное на принципах консультирования и согласования, включающее участие на равноправных началах
представителей различных групп — госслужащих, предпринимателей, профсоюзов, союзов потребителей, позволяет получить план в результате многоступенчатых уточнений. В реализации такого плана заинтересованы все участники
его создания. Вместе с тем плановые показатели не являются обязательными, а
75
выступают в качестве экономических индикаторов — носителей информации
относительно ожидаемой экономической конъюнктуры.
Индикативное планирование в такой форме выступает одновременно и
институтом государственного регулирования экономики, и институтом саморегулирования, корректируя как дефекты рыночного механизма, так и изъяны
прямого государственного вмешательства в экономику.
На саморегулирование как важнейший результат индикативного планирования обычно обращают внимание при изучении опыта Японии. Опыт Японии характеризуется тем, что планово-прогнозные расчеты основываются на
исследованиях реального состояния экономики. В процессе исследований выявляется система макроэкономических и микроэкономических показателей,
факторов, определяющих эффективность капитала, труда и научнотехнического прогресса. В результате находят удачное сочетание этих факторов на уровне всей экономики, в каждой отрасли, а также в регионах и в системе свободного предпринимательства.
Индикативное планирование — это механизм координации интересов и деятельности государства и самостоятельно хозяйствующих субъектов,
сочетающий государственное регулирование с рыночным саморегулированием,
механизм, который основан на разработке системы индикаторов социальноэкономического развития и включает определение его общенациональных приоритетов, целеполагание, прогнозирование, бюджетирование, программирование, контрактацию и другие процедуры согласования решений на макро- и
микроуровне.
Индикативное планирование включает налоговые и иные меры государственной поддержки хозяйствующих субъектов, участвующих в реализации
плана. В нем принимают участие институты местного самоуправления, управленческие органы корпораций, финансово-промышленных групп и других хозяйствующих единиц.
Исторически первой формой индикативного планирования стала конъюнктурная форма, связанная с усилением влияния бюджета на темпы и пропорции экономического роста. Структурная перестройка экономики в развитых
странах во второй половине XX в. вызвала необходимость согласования бюджетов с показателями народнохозяйственных прогнозов, на которых основывались оценки налоговых поступлений. Это привело к разработке среднесрочных
и долгосрочных прогнозов.
Примерами могут служить «Десятилетний план удвоения национального
дохода» на 1961 — 1970 гг. в Японии, план под названием «Выбор путей экономического роста» на 1976—1985 гг. в Канаде, Прогноз Министерства труда
на 1986—1995 гг. в США. В 60-е годы во многих странах с рыночной экономикой начали создавать специальные плановые органы. Во Франции был создан
Генеральный комиссариат по планированию, в Канаде — Экономический совет, в Японии — Экономический консультативный совет.
Вовлечение в систему индикативных планов частных предприятий и территориальных властей с использованием налоговых льгот, льготных кредитов,
76
государственных программ и иных мер в рамках структурной политики породило структурную форму индикативного планирования.
Структурную форму индикативного планирования успешно использовали
в Японии. На ее основе был разработан первый план комплексного территориально-отраслевого развития страны на 1960-1970 гг. Эта тенденция сохранялась
в последующих планах.
Целенаправленные структурные изменения, включая развитие наукоемких отраслей и территориальное размещение производства, оставались главным
направлением государственной экономической политики Японии четверть века.
После либерализации в начале 80-х годов финансовой системы Япония не отказалась от проведения активной структурной долгосрочной политики. В действующем «Четвертом комплексном плане национального развития», рассчитанном на период до конца XX столетия, как и в трех предыдущих планах, сформулированы основные цели развития всех областей жизни страны.
Главная цель японского планирования состоит в том, чтобы исходя из
существующих проблем страны и необходимости обеспечения ее безопасности
добиться многополярности использования ее специфических возможностей.
Достижение этой цели предполагает ликвидацию чрезмерной концентрации населения, хозяйства, административных функций государства в основных районах страны, многополярность развития территории в целях углубления связей
между отдельными районами, взаимодействия в международном масштабе.
Эволюция к структурной форме планирования прослеживается во Франции. С начала 70-х годов «индикативный план рассматривается как план государства, производящего общественные блага, и метод координации действий
зависящих от государственной политики доходов и расходов отраслевых и региональных подсистем экономики. Другими словами, обязательные и прогнозные аспекты плана более четко разделены».
Под влиянием кризиса развития 70—80-х годов, который был связан со
сменой доминирующих технологических укладов и углублением постиндустриальных тенденций развития, индикативное планирование в развитых странах
трансформируется в стратегическую форму, для которой характерна гибкость, необходимая при быстрых эволюционных изменениях в экономике. В
стратегическом планировании по сравнению со структурным планированием
значительно сократилась регламентация действий субъектов, сроков и количественных показателей планирования.
Во Франции идея стратегического планирования, суть которой — выбор
главных приоритетов развития национальной экономики, впервые получила
воплощение в десятом индикативном плане на 1989-1992 гг. В этом плане было
установлено шесть главных направлений развития: укрепление национальной
валюты и обеспечение занятости, образование, научные исследования, социальная защита населения, обустройство территории, обновление государственных служб. Каждое из направлений получило статус целевой государственной
программы, обеспеченной системой финансирования.
77
Американские власти определяют индикативное стратегическое планирование как «поиск новых решений для достижения успешной конкуренции, развития всестороннего сотрудничества, максимального содействия продуктивности экономической политики, основанной на полном доверии и финансовой
поддержке штатных и местных властей».
В 80-90-х годах масштабы структурного индикативного планирования в
развитых странах стали быстро сокращаться. Это было обусловлено недостаточной гибкостью сложившейся формы структурного планирования. Кроме того, структурное планирование в известной мере способствовало развитию лоббирования интересов старых сокращающихся отраслей и неэффективно работающих государственных предприятий.
Финансовые кризисы второй половины 90-х годов показали, что усиление
роли рыночных механизмов по мере интернационализации рынков увеличивает
проблемы национальных кредитно-финансовых систем. В связи с этим усиливается необходимость координации действий хозяйствующих субъектов не
только на национальном, но и на международном уровне. Поэтому многие экономисты прогнозируют усиление роли планирования экономики развитых
стран в ближайшей перспективе.
Эволюция форм индикативного планирования от «конъюнктурной» к
«структурной», а затем к «стратегической» в развитых странах заняла несколько
десятилетий. В Российской Федерации пока используются отдельные элементы,
обычно входящие в конъюнктурную, структурную и стратегическую формы
планирования. Термин «индикативное планирование» в законодательстве пока
не используется. Прогнозирование и планирование в различных сферах деятельности государства и государственного регулирования пока не объединены
в общую систему.
Меры государственного воздействия на социально-экономическое развитие могут осуществляться вне системы индикативного планирования, но они
несравнимо более эффективны в системе индикативного планирования.
Многие экономисты считают, что формирование системы индикативного
планирования в структурной форме представляется остро необходимым направлением развития хозяйственного механизма. Но они допускают возможность перехода к либеральной, стратегической форме индикативного планирования лишь после преодоления экономического кризиса и завершения периода
технологической и институциональной модернизации российской экономики.
С этим нельзя согласиться. Как известно, именно в условиях кризиса и
быстрых структурных изменений многие страны были вынуждены отказываться от неповоротливых, негибких систем и процедур структурного планирования. Наиболее эффективными оказались методы стратегического управления.
Гибкость стратегического управления, принципы которого — невысокий уровень регламентации и незамедлительное принятие решений в ответ на возникающие опасности и выявляющиеся возможности, диктует необходимость использовать в российских условиях стратегическую форму индикативного пла-
78
нирования, в рамках которой целесообразно применять и элементы структурного планирования.
Государство в условиях современного рынка осуществляет свою деятельность по следующим основным направлениям:
установление и взимание налогов на производство и оборот товаров,
доходы и имущество юридических и физических лиц, на использование природных ресурсов;
осуществление бюджетных расходов на содержание государственного
аппарата, закупки продукции для государственных нужд, на помощь отраслям,
регионам и иностранным государствам, на поддержку отдельных категорий
граждан;
привлечение, погашение и обслуживание государственных займов;
приобретение, продажа и использование государственного имущества;
планирование деятельности государственных предприятий.
Разработка бюджета на будущий год должна основываться на достоверных оценках доходов и расходов налогоплательщиков и получателей средств из
бюджета. Поскольку развитие разных рынков, отраслей, регионов и предприятий взаимосвязано, учитывать эти взаимосвязи следует при прогнозировании
налогового потенциала и бюджетных потребностей. Бюджетные расходы, налоговые ставки и другие нормативы, государственные заимствования воздействуют на спрос и предложение, на эффективность производства и на занятость.
Поэтому должно быть учтено их влияние на налоговые поступления.
Налоговые поступления, доходы от использования государственной собственности определяют общий размер и структуру бюджетных расходов, в том
числе средства целевых бюджетных и некоторых внебюджетных фондов. Средства страховых фондов, собираемые и используемые на выплаты пенсий, пособий по нетрудоспособности или безработице и на иные аналогичные нужды,
также воздействуют на спрос и предложение.
Таким образом, существует комплекс взаимосвязей процессов в экономике и возможностей формирования бюджетов. Поэтому народнохозяйственный
прогноз и бюджет образуют единую систему, состоящую из прогнозных показателей развития экономики и бюджетных показателей. Исполнение бюджетных показателей, как известно, является обязательным. Если процедуры разработки бюджетов и экономических прогнозов взаимосвязаны и адекватны реальным экономическим процессам, они составляют макроэкономический план,
в котором бюджетные показатели имеют директивный, а остальные — прогнозный, информационный характер.
Прогноз развития экономики разрабатывается не только для использования в бюджетном процессе. На основе прогнозов принимаются многие макроэкономические решения как административного, так и нормативного характера.
На данные прогнозов ориентируются все субъекты, действующие в экономике.
Поэтому данные прогнозов должны быть для них доступны.
79
Государственное программирование в развитых странах в настоящее время играет роль важного инструмента стратегического планирования. Государственные программы формируются по приоритетным направлениям стратегии
развития (обычно выделяют не более десятка). В рамках этих программ государство часто выступает в роли заказчика, организатора и координатора в решении крупных общественно значимых проблем, например, таких, как полет
человека в космос, освоение какого-либо источника энергии, создание новых
видов вооружений, развитие отстающих территорий или привлечение зарубежных инвестиций. Для достижения соответствующей конечной цели оказывается
необходимым в течение длительного периода решать комплекс взаимосвязанных задач.
В таких случаях возникает необходимость принятия решений о финансировании работ по достижению данной цели до начала разработки бюджетов на
каждый финансовый год. Для преодоления этого противоречия используется
программно-целевой подход. В соответствии со сложившейся практикой применения программно-целевого подхода для достижения конкретной цели принимается нормативный акт, закон, в котором определяются: 1) органы государственного управления как заказчики и исполнители; 2) прочие организацииисполнители; 3) порядок взаимодействия исполнителей; 4) перечень задач —
подцелей, подлежащих решению, качественных, стоимостных параметров и
сроков получения, оценки и приемки результатов; 5) эффект от выполнения
программы.
В государственной целевой программе считается важным взаимосвязанность целей и возможность оптимизации затрат времени и ресурсов на реализацию программы. Во взаимосвязи с бюджетным планированием целевые программы — это комплексы локализованных во времени и пространстве непротиворечивых мер в области социальной, структурно-инвестиционной, финансовокредитной, налоговой, бюджетной, ценовой, внешнеэкономической, аграрной,
научно-технической, институциональной политики, ориентированных на достижение качественно и количественно определенных целей социальноэкономического развития.
Разработка и утверждение целевой программы осуществляются путем поэтапного согласования с учетом интересов заказчиков и исполнителей, макроэкономической ситуации и прогнозируемых бюджетных возможностей. Для
координации бюджетов и программирования важно, чтобы решения об ассигнованиях на программу принимал орган власти, утверждающий бюджет.
Государственное регулирование рыночной экономики может осуществляться административными методами. Они просты, но могут затруднять развитие эффективных процессов самоорганизации в экономике и создавать основу
для коррупции.
При использовании административных методов по каждой проблеме
управляющий орган принимает конкретное решение. К административным методам относятся: предоставление индивидуальных налоговых, монетарных и
таможенных льгот; проведение конкурсов на поставку товаров для государст-
80
венных нужд и приватизационных конкурсов; осуществление процедур банкротства; зачет дебиторской задолженности предприятий в погашение их просроченных долговых обязательств; лицензирование и квотирование предприятий и видов хозяйственной деятельности и др.
Нормативное регулирование заключается в том, что государство устанавливает совокупность нормативов, параметров, связывающих одни экономические величины с другими, обязательных для всех субъектов, и контролирует их
исполнение. У хозяйствующих субъектов сохраняется большая свобода действий, а государство при этом оказывается в состоянии изменять макроэкономические пропорции, варьируя общие нормативы.
В числе нормативов регулирования следующие:
налоговые ставки и другие параметры, определяющие размеры налоговых платежей;
монетарные нормативы, в частности ставка рефинансирования, нормы
обязательных резервов, нормативы резервов по ссудам и другие параметры,
обеспечивающие функционирование банковской системы;
нормативы распределения дохода по уровням бюджетной системы;
нормативы заработной платы в бюджетных организациях, а также
обеспеченности их работников производственными помещениями и другими
ресурсами;
социальные нормативы, определяющие размеры и структуру социальных расходов, а также процедуры их индексации в зависимости от темпов инфляции и роста заработной платы;
нормативы обеспечения военнослужащих и сотрудников правоохранительных органов помещениями, амуницией, военной техникой и вооружением, другие нормативы, регулирующие деятельность вооруженных сил и правоохранительных органов;
льготы различным категориям граждан и организаций, влияющие на
их налоговые обязательства, на их потребности в трансфертах — пособиях из
бюджета или на цены потребляемых ими благ во взаимосвязи с необходимыми
для этого субсидиями из бюджета.
Нормативное регулирование экономики, способное обеспечить эффективное достижение целей индикативного планирования, может основываться на
принципах децентрализованности, равновесности, системности, обусловленности.
Принцип децентрализованности состоит в том, что выбор хозяйственных альтернатив и принятие стратегических решений субъекты экономики
осуществляют самостоятельно, руководствуясь лишь нормативами, задающими
распределение чистого дохода, и другими нормативами, связывающими между
собой затраты и результаты деятельности. Экономические субъекты разрабатывают и реализуют прогнозы и планы своей деятельности самостоятельно, без
вмешательства государственных органов.
Принцип равновесности означает, что должны устанавливаться некоторые равновесные значения экономических нормативов, обеспечивающие эф-
81
фективное достижение целей, намеченных правительством. Например, налоговые ставки должны устанавливаться на уровне, обеспечивающем планируемый
объем собираемых налогов. Ставка рефинансирования центрального банка
должна устанавливаться на уровне, обеспечивающем планируемый объем кредитования.
Произвольное задание нормативов, к сожалению, можно наблюдать очень
часто. Например, часто завышаются ставки налогов. При сильной государственной власти экономические субъекты подчиняются такому давлению, но отвечают на него пассивным сопротивлением, выражающимся в снижении деловой активности, эмиграции, вывозе капитала за рубеж. В результате страна отстает в соревновании с другими странами по показателям эффективности производства, как это было с Францией 70-х годов. В слабом государстве экономические субъекты, кроме того, не платят налоги, развивается теневая экономика.
Принцип системности. Поскольку равновесные значения нормативов,
как правило, взаимосвязаны, то их выбор должен осуществляться по определенной системе. Эта система определяет выбор траекторий развития экономики, соответствующей сочетанию выбранных нормативов.
Выбор системы нормативов представляет собой сложную задачу, поскольку улучшение одних показателей может сопровождаться ухудшением
других. Главной проблемой выбора является согласование интересов. Экономические субъекты могут повлиять на цели и методы нормативного регулирования лоббистскими средствами. Кроме того, в условиях интернационализации
и глобализации рынков государствам приходится иметь дело с очень мощными
субъектами, например многонациональными компаниями.
Принцип обусловленности. Нормативы можно подразделить на безусловные, действительные для всех случаев и субъектов данного типа, и обусловленные, определяемые выполнением субъектами определенных требований.
Такими требованиями могут быть, например, превышение фондом оплаты труда уровня, определяемого установленным законодательством минимальным
размером заработной платы более чем в некоторое число раз, что влечет взимание налога на прибыль с суммы превышения.
Государственные закупки представляют собой один из важнейших инструментов регулирования рыночной экономики, поскольку государство выступает крупнейшим заказчиком, покупателем на рынке продукции, работ и услуг.
Решение задач планирования государственных закупок может осуществляться на основе сочетания макроэкономического прогнозирования, а также
процедур поэтапного согласования крупных срочных контрактов по государственным программам.
6.2. Прогнозирование и формирование темпов, пропорций и структуры экономики в условиях рынка
Прогнозирование темпов роста, пропорций, структуры и эффективности
экономики страны или отдельного региона осуществляется на основе системы
82
национальных счетов или системы региональных счетов и эконометрических
моделей.
При разработке прогнозов создаются математические модели, переменные моделей определяются в рамках системы национальных счетов, взаимосвязи переменных устанавливаются в виде тождеств и функциональных структурных уравнений. Предварительно определяют вид уравнений, отражающих причинно-следственные связи между переменными, а затем с помощью эконометрических методов оцениваются параметры.
Получаемая таким образом эконометрическая модель описывает количественное изменение переменных, вызванное изменениями в других переменных, характеризующих экономическую политику и внешние условия функционирования экономической системы.
Модель позволяет определить значения переменных экономической политики, которые отражают желаемое изменение переменных разрабатываемого
плана. Модели включают экзогенные — внешние и эндогенные — внутренние
переменные.
Экзогенные переменные разделяются на заданные переменные, например объем мировой торговли, численность населения, и переменные экономической политики, например государственные расходы, процентные ставки.
Вначале определяются значения экзогенных переменных, причем заданные переменные, а также переменные экономической политики не являются независимыми. После этого рассчитывают параметры уравнений модели и в результате одновременного решения уравнений модели находят значения эндогенных переменных, например валовой национальный продукт, занятость, цены.
Эндогенные переменные, тесно связанные с экономической политикой,
называются переменными плана. Поскольку переменные плана зависят от переменных экономической политики, то органы, ответственные за экономическую политику, могли бы получать желательные прогнозируемые значения переменных плана при соответствующих величинах переменных экономической
политики.
Параметры моделей разделяют на две группы. Некоторые параметры могут устанавливаться органами власти, например ставки налогов, и называются
параметрами экономической политики. Другие параметры уравнений моделей принято называть структурными параметрами.
Прогнозирование и планирование с помощью эконометрических моделей
связано с тем, что предсказываемые величины эндогенных переменных зависят
от вводимых значений экзогенных переменных. Поэтому различные величины
экзогенных переменных порождают различные величины эндогенных переменных.
Количественные ошибки в экзогенных переменных и параметрах могут
быть выявлены по расхождениям между величинами эндогенных переменных,
рассчитанных с помощью модели, и их известными значениями. В случае за-
83
метных расхождений следует уточнить значения экзогенных переменных и параметров уравнений модели на основе новой информации. Таким образом,
можно постоянно улучшать модель и совершенствовать проводимую экономическую политику.
В условиях кризисов и неустойчивости развития в моделях могут наблюдаться не только количественные ошибки. Изменение структуры и траектории
развития экономической системы может привести к необходимости изменения
структуры и количества уравнений модели для обеспечения удовлетворительной точности прогнозов.
Система национальных счетов, как и система региональных счетов, основываясь на агрегировании экономических показателей, не охватывает всех деталей экономической реальности. В системе счетов находят отражение макроэкономические процессы и процессы, наблюдаемые в масштабах отраслей. В
ней отражаются масштабные явления, происхождение которых относится к более или менее отдаленному прошлому и которые во многих случаях потеряли
свою динамичность. В развитии могут наблюдаться менее масштабные факты
— предвестники будущих тенденций.
Потому особенно в условиях неустойчивого развития необходимо, с одной стороны, сокращать горизонты прогнозирования и планирования, основанного на применении национальных счетов и эконометрических моделей, с другой стороны — дополнять процедуры прогнозирования, планирования анализом ситуации и перспектив развития, используя экспертные методы, методы
теории катастроф, выявление скрытых факторов.
Прогнозирование темпов роста, пропорций, структуры и эффективности
экономики на основе системы национальных счетов и эконометрических моделей делится на долгосрочное, среднесрочное и текущее, макроэкономическое и
балансовое. На практике модели этих прогнозов должны сочетаться. В сочетании моделей эндогенные переменные одних моделей могут быть экзогенными
переменными других моделей.
Прогнозирование темпов роста, пропорций, структуры экономики регионов строится на основе системы региональных счетов.
Модели долгосрочных макроэкономических прогнозов предназначаются
для оценки экономического развития во времени на максимально возможную
по длительности перспективу и перспективного планирования. Для их построения необходимы временные ряды данных национальных счетов и других показателей за длительные периоды. Длина этих рядов может быть сопоставима с
периодом циклов Н.Кондратьева, продолжительность которых, как известно,
составляет порядка 50 лет.
Долгосрочные модели различаются по степени детализации описания
экономической системы и, соответственно, по степени агрегации переменных.
Типичными примерами таких моделей могут служить первые модели
японской экономики, построенные при доработке «Десятилетнего плана удвоения национального дохода» на 1961—1970 гг. в Японии. При этом были полу-
84
чены две долгосрочные модели, которые использовались для прогнозирования
на период до 1975 и 1985 гг.
Макроэкономические модели могут использоваться для среднесрочных
счетов национального дохода при заданной совокупности условий и средств
экономической политики. Их используют для оценки движения цен и уровней
заработной платы, соответствующего прогнозу счетов. С их помощью контролируют расхождения между целями, предусмотренными планом, и ситуацией,
которая может сложиться в ходе выполнения плана.
Особенности таких моделей прогнозов можно видеть на примере макроэкономической модели среднесрочного прогноза, построенной при доработке
«Десятилетнего плана удвоения национального дохода» на 1961-1970 гг. в Японии. При создании этой модели ставилась задача разработать прогноз уровней
различных статей национальных счетов в текущих ценах, сохраняя баланс между четырьмя основными секторами экономики: производством, домашним хозяйством, правительственным и внешним секторами.
Использование номинальных величин вместо величин в неизменных ценах обеспечивало возможность оценки величин государственных доходов и
расходов — главные переменные экономической политики, а также возможность анализа денежного хозяйства, изучения спроса и предложения на денежном рынке. Были введены шесть коэффициентов пересчета, чтобы связать текущие затраты в данной модели с уровнем реальных расходов, реальным эффективным спросом, а также с уровнем производства и занятости.
В прогнозировании и планировании могут быть использованы межотраслевые балансовые модели. Это метод прогнозирования, известный под названием «затраты-выпуск», создан в 20-е годы В.Леонтьевым. Позднее метод развит,
усовершенствован и распространен его автором в развитых странах. В связи с
распространением этого метода в состав систем национальных и региональных
счетов введены отраслевые разделы.
Международные стандарты систем национальных счетов начиная с 1968
г. включают счета потоков фондов, балансов продуктов, имущества в натуральной и стоимостной формах по отраслям. Эти счета при наличии данных* позволяют строить межотраслевые балансовые модели.
Особенности межотраслевых балансовых моделей прогнозов можно видеть на примере модели среднесрочного прогноза, построенной японскими
учеными в 1962 г.
6.3. Прогнозирование уровня жизни населения
Среди методов, чаще других применяемых в прогнозировании социального развития и уровня жизни населения, можно выделить следующие: метод
экспертных оценок; метод экономического анализа; нормативный метод; балансовый метод; метод экстраполяции; метод экономико-математического моделирования; метод корреляционно-регрессионного анализа; экспоненциального сглаживания и др.
85
В практике прогнозирования, планирования и регулирования социального
развития используются следующие основные модели:
— структура минимального и рационального потребления;
— динамика объема и макроструктуры ресурсов для потребления;
— динамика объема личного и индивидуального потребления;
— динамика роста жилищного строительства;
— дифференцированный баланс доходов и расходов населения и др.
Экономико-математические методы и модели, применяемые в прогнозировании социального развития и повышения уровня жизни, позволяют определить основные тенденции развития степени удовлетворения жизненных потребностей населения, учитывать динамику их изменения на перспективу.
Кроме того, они позволяют осуществлять количественный и качественный анализ конкретных составляющих социального развития и уровня жизни.
Специфика прогнозирования социального развития и уровня жизни проявляется в том, что не всегда удается адекватно выразить процессы, происходящие вне сферы материального производства. Используя даже систему моделей и прогнозов можно описать и проанализировать лишь отдельные стороны
такой экономической категории, как уровень жизни.
Рассмотрим на примере прогнозирования спроса и розничного товарооборота методические аспекты построения прогноза. При прогнозировании
спроса и розничного товарооборота используются различные методы в зависимости от направления прогноза и его характера. Так, например, балансовый метод применяется при определении уровней перспективного потребления основных продовольственных и непродовольственных товаров.
Метод экономического анализа используется для качественного описания
и определения развития потребностей, как в настоящем, так и в прогнозируемом периоде.
Нормативный метод в среднесрочном прогнозировании спроса и розничного товарооборота базируется на использовании норм рационального и минимального потребления продуктов питания и непродовольственных товаров, а
также на использовании нормативов обеспеченности товарами длительного
пользования.
Методы экономико-математического моделирования применяются для
определения количественных характеристик возможной структуры спроса и товарооборота в среднесрочном прогнозировании.
Метод экспертных оценок основан на получении информации о будущем
состоянии спроса и предложения и розничного товарооборота на основе мнений отдельных экспертов и последующей обработки результатов индивидуальных оценок в обобщенную экспертную оценку.
Широко используются при прогнозировании динамики многих показателей социального развития и уровня жизни населения метод регрессионного
анализа. Его использование возможно при обеспечении следующих условий:
-базовый период, на основе которого разрабатывается прогноз, должен
быть характерен для будущего периода развития спроса;
86
-должна быть достаточно полная и постоянная теснота связей между коррелирующими величинами;
-взаимосвязь прошлого с будущим осуществляется с введением в уравнение регрессии дополнительных переменных величин (например, фактора времени).
7. Планирование и прогнозирование на микроэкономическом уровне
(предприятие, фирма)
7.1. Основы стратегического планирования
Стратегическое планирование представляет собой комплекс решений и
действий по разработке стратегий, необходимых для достижения целей организации, предприятия. Современное стратегическое планирование является инструментом управления, помогающим высшему управленческому персоналу
предприятия принимать основополагающие решения.
Главная задача стратегического планирования — обеспечить гибкость и
нововведения в деятельности организации, необходимые для достижения целей
в изменяющейся среде. Стратегическое планирование — один из инструментов
воспроизведения предприятием предпринимательского поведения.
В рамках стратегического планирования решаются четыре основные задачи: распределение ресурсов, адаптация к внешней среде, внутренняя координация и формирование стратегической организационной культуры.
Распределение ресурсов. Этот процесс включает распределение ограниченных ресурсов предприятия, таких, как дефицитные кадры — управленческий персонал и специалисты, технологии, производственные фонды, финансовые ресурсы. Например, в апреле 1994 г. корпорация «Сони» реорганизовала свою структуру. Вместо 27 подразделений она, перераспределив ресурсы,
создала 8 самостоятельных компаний. Компании возглавили президенты, ответственные перед корпорацией за стратегии своих компаний.
Адаптация к внешней среде представляет собой действия стратегического характера, которые улучшают отношения компании с ее окружением.
Компаниям необходимо адаптироваться к благоприятным внешним возможностям, опасностям, выявить адекватные варианты деятельности — альтернативы и обеспечить эффективное приспособление стратегии к окружающим условиям.
Проникновение АО «ГАЗ» на рынок мини-грузовиков и микроавтобусов
— пример адаптации к окружающим условиям. Предприятие изучило внутренние и внешние возможности и опасности и предложило рынку модели «Газель»
и «Соболь».
Внутренняя координация. Координация стратегической деятельности
должна вестись с целью достижения эффективной интеграции внутри предприятия с учетом сильных и слабых сторон предприятия. Обеспечение эффективных внутренних операций в организациях является важнейшим фактором планирования.
87
Стратегическая организационная культура предполагает систематическое развитие мышления управленческого персонала путем формирования
структуры организации, стиля деятельности, нацеленных на постоянные поиски, изменения, усвоение опыта прошлых стратегических решений.
Способность учиться на опыте дает возможность своевременно корректировать направление деятельности, повышать корпоративный профессионализм в области стратегического управления.
Стратегическое планирование реализуется последовательно по этапам:
— Формулировка миссии организации
— Постановка целей
— Оценка и анализ внешней среды
— Управленческое обследование организации
— Анализ стратегических альтернатив
— Выбор стратегии
Реализация стратегии и последующая оценка результатов завершают
цикл стратегического управления. Циклы управления, включающие стратегическое планирование, периодически повторяются. На любом этапе возможен
возврат к любому предыдущему этапу планирования. Основной тенденцией последних десятилетий является сокращение периодов изменения стратегий и переход к непрерывному стратегическому планированию.
Стратегия представляет собой детальный всесторонний комплексный
план, предназначенный для того, чтобы обеспечить осуществление миссии организации и достижение ее целей. Стратегический план обосновывается исследованиями и фактическими данными. Предприятие должно постоянно заниматься сбором и анализом информации об отрасли, рынке, конкуренции и других факторах.
Стратегические планы должны быть целостными в течение длительного
времени, но достаточно гибкими, чтобы при необходимости можно было осуществить их переориентацию.
Исследования крупнейших в мире компаний по рейтингу журнала американских деловых кругов «Форчун-500» позволили выявить основные особенности практики стратегического планирования.
1.За стратегическое планирование отвечают плановый отдел корпорации
и отделы в ее стратегических хозяйственных подразделениях.
2.Основные элементы стратегического плана формируются на совещаниях высшего руководства корпорации, проводимых ежегодно или чаще.
3.Годовой стратегический план объединяется с годовым финансовым
планом, их совокупность и образует внутрифирменный план.
На крупных предприятиях, занимающихся сложным формальным стратегическим планированием, планы оформляются в письменном виде, существуют
тысячи документов, разрабатываемых в процессе планирования.
7.2. Прогнозирование рынка сбыта продукции предприятия
88
Важнейшим направлением прогнозирования рынков сбыта продукции
предприятия является определение величин спроса и показателей рыночной доли для конкретных рынков — рыночных сегментов. В основе процесса выбора
целевых рынков — сегментов рынка лежит изучение рыночного спроса.
Рыночный спрос — это общий объем продаж на определенном рынке определенной марки товара или совокупности марок товара за определенный период.
На величину спроса оказывают влияние факторы внешней среды и маркетинговые усилия конкурирующих фирм. В зависимости от уровня маркетинговых усилий различают первичный спрос, рыночный потенциал и текущий рыночный спрос.
Первичный или не стимулированный спрос — это суммарный
спрос на все марки данного продукта, реализуемые без использования маркетинга.
Рыночный потенциал — это предел, к которому стремится рыночный
спрос при приближении затрат на маркетинг в отрасли к такой величине, что их
дальнейшее увеличение уже не приводит к росту спроса при неизменных условиях внешней среды.
Приближенно рыночным потенциалом можно считать спрос, соответствующий его максимальному значению на кривой жизненного цикла продукта
для стабильного рынка. При этом предполагается, что конкурирующие фирмы
для поддержания спроса прилагают максимально возможные маркетинговые
усилия.
Выделяют абсолютный потенциал рынка, который понимают как предел рыночного потенциала при нулевой цене. Это понятие позволяет оценить
порядок величины экономических возможностей, которые открывает данный
рынок. Например, абсолютный потенциал рынка легковых автомобилей может
определяться общей численностью населения, начиная с возраста получения
водительских прав. Изменение абсолютного рыночного потенциала обусловлено внешними факторами, такими, как уровень доходов и цен, привычки потребителей, культурные ценности, государственное регулирование. Иногда предприятия могут оказать косвенное влияние на эти внешние факторы, например
путем лоббирования принятия определенных законов. Основные усилия предприятий направлены на предвидение изменений внешней среды.
Текущий рыночный спрос, характеризующий объем продаж за определенный период в определенных условиях внешней среды при определенном
уровне маркетинговых усилий предприятий отрасли.
По степени влияния маркетинговой деятельности на величину спроса выделяют два крайних типа рынка: расширяющийся рынок и не расширяющийся
рынок. Первый реагирует на применение инструментов маркетинга, второй —
не реагирует.
Доля рынка. Важным показателем, величину которого необходимо определять и прогнозировать, является доля рынка. Рыночная доля — это отношение объема продаж определенного товара данной организации к суммарному
89
объему продаж данного товара, осуществленному всеми организациями, действующими на данном рынке.
Этот показатель является ключевым при оценке конкурентной позиции
организации. Поскольку организация с высоким показателем рыночной доли
больше производит и реализует продукта, то себестоимость единицы продукта
этой организации ниже по сравнению с конкурентами. Позиции организации с
большей долей рынка в конкурентной борьбе предпочтительны.
Спрос на многие товары может быть оценен по данным официальной статистики, поскольку собирается и публикуется информация об объемах проданной продукции и оказанных услугах в самых различных аспектах: для международных рынков, рынков отдельных стран и регионов, в разрезе отдельных
отраслей и предприятий.
Для многих видов товаров детальная, надежная статистическая информация отсутствует. Поэтому для определения и прогнозирования величин спроса
и других рыночных характеристик требуется проводить специальные маркетинговые исследования.
Текущий рыночный спрос в денежном выражении определяется как
Q = n • с • р,
(6.1)
где n — число покупателей данного вида товара на данном рынке; с —
средняя цена данного товара; р — число покупок покупателя за исследуемый
период времени.
При оценке спроса необходимо учитывать дополнительные факторы, определяющие спрос на эти товары. Так, при определении спроса на товары длительного пользования в результате проведения маркетинговых исследований
необходимо оценить спрос на замену. Для этого нужны следующие данные:
объем имеющегося у потребителей парка исследуемого товара длительного
пользования, распределение этого парка по сроку службы, темп замены товара,
возможность появления новых альтернатив замены.
Темп прекращения срока службы связан обратной зависимостью с длительностью этого срока. Например, средний срок службы равен 5 годам, средний темп прекращения этого срока составляет: (1 : 5) * 100 = 20%.
Спрос на замену находится в прямой зависимости от размера парка и срока службы товара длительного пользования. Темп замены необязательно совпадает с темпом прекращения срока службы, под которым понимается доля товаров длительного пользования, прекращающих существование. Товар может устареть потому, что его экономические показатели стали неудовлетворительными или потому, что он просто вышел из моды.
Некоторые данные, необходимые для оценки спроса, например данные об
имеющемся парке товара и его возрастном распределении, могут быть получены из анализа прошлых продаж. Необходимая оценка распределения по срокам
службы может быть найдена на основе выборочного исследования владельцев
товара, например тех, которые заняты заменой имеющегося у них изделия. Значительная часть продаж товаров длительного пользования соответствует спросу
на замену, особенно в развитых странах.
90
Текущий рыночный спрос можно определять на основе нормативного
подхода. Этот подход предполагает последовательную декомпозицию потенциала рынка вплоть до нахождения оценки спроса на конкретный товар или
марку на основе использования нормативов и долевых показателей.
Например, предприятие производит и продает пищевой консервант,
предназначенный для применения в производстве газированных напитков. Поскольку многие предприятия пока еще не используют такую добавку, требуется
оценить текущий и возможный потенциал рынка, а также реальный уровень
спроса в определенной географической зоне. Расчет производится следующим
образом.
На основе отчетной, нормативной и статистической информации был установлен объем производства напитков всеми фирмами определенного региона,
например — 100 млн. л, норма расхода консерванта — 0,1 мг/л; доля фирм,
применяющих консерванты, — 70%. Возможный потенциал рынка:
100 млн. л • 0,1 мг/л • 0,70 = 7000 кг.
Исследования показали, что доля фирм, применяющих консервант предприятия, равна 50%. На основе этих данных определяется суммарный текущий
рыночный спрос:
7000 кг • 0,50 = 3500 кг.
Если цель предприятия — добиться доли рынка в 70%, то продажи товара
в данном регионе, то есть текущий рыночный спрос для предприятия, должны
быть доведены до 4900 кг.
Трудность подхода состоит в нахождении соответствующих нормативов
и долевых показателей. Их получение обычно требует проведения специальных
исследований.
Более углубленный анализ спроса направлен на обнаружение самых важных факторов и определение их относительного влияния на объем продаж;
наиболее часто анализируются такие факторы, как цены, уровень дохода,
структура потребителей и влияние различных методов продвижения продукта.
При проведении такого анализа используются методы математической и прикладной статистики.
Рынки потребительских товаров и продукция производственнотехнического назначения изучаются главным образом на основе использования
следующих подходов: 1) посредством анализа вторичной информации; 2) путем
изучения мотивации и поведения потребителей.
Анализ вторичной информации. В рамках этого подхода изучаются все
документы, представляющие интерес для предприятия, изданные статистическими органами, различными министерствами, торгово-промышленными палатами, региональными органами управления, а также являющиеся результатом
специальных, не относящихся к сфере маркетинговых исследований. Такая информация часто достаточно дешева, бесплатна, относительно легко доступна. В
результате изучения документов можно получить общую картину импорта и
экспорта, структуры производства, а также структуры потребления по видам
продукции и отраслям.
91
Однако информация может оказаться закрытой, неполной, недостаточно
детализированной. Номенклатура продукции обычно слишком укрупнена. Изучение документов не может дать и оперативной информации. Поэтому эту информацию порой невозможно использовать для нужд предприятия.
Изучение мотивации и поведения потребителей и анализ выпускаемой и
реализуемой продукции осуществляются путем проведения маркетинговых исследований. Исследование мотивации, поведения потребителей, их отношения
к продукции предприятия проводится путем специальных обследований — организации интервью, собеседований, заполнения анкет. В качестве опрашиваемых выступают люди, хорошо разбирающиеся в проблеме: пользователи,
влияющие на выбор продавца, покупатели, которые потребляют продукт. Для
проведения исследований необходимо хорошо знать соответствующий рынок и
исследуемый продукт, обладать информацией о компаниях-производителях и
посреднических организациях.
Следует иметь в виду, что мотивация покупок продукции производственно-технического назначения является рациональной и в существенно меньшей
степени эмоциональной по сравнению с покупкой потребительских товаров.
Выборка в случае изучения продукции производственно-технического назначения охватывает не отдельных людей, а предприятия. Когда проводят анкетирование в промышленной сфере, то выборка, как правило, невелика. Исключение составляют так называемые атомизированные рынки, где потенциальные потребители представлены большим количеством предприятий. Замены в
промышленной сфере часто невозможны, так как существуют компании, которые надо обязательно опросить, например крупные предприятия — лидеры отрасли.
В случае атомизированных рынков существует практика формирования
выборки предприятии на репрезентативной основе, включающей предприятия
разных размеров и уровня рыночной деятельности.
При обследовании продукции производственно-технического назначения
необходимо учитывать, что в процессе подготовки и принятия решения о покупке принимают участие различные специалисты и руководители предприятия, иногда входящие в состав постоянно действующей закупочной комиссии.
Но часто эти комиссии могут действовать на неформальной основе.
Помимо изучения мнений потребителей изучается также мнение руководителей и специалистов посреднических, дистрибьюторских организаций, а
также предприятий-производителей. Спрос на продукцию производственнотехнического назначения является производным от спроса на конечные потребительские товары, при изготовлении которых она используется. Поэтому в целях прогнозирования необходимо изучать существующих и потенциальных потребителей не только продукции производственно-технического назначения, но
и соответствующих конечных товаров.
В промышленной среде очень распространено недоверие к анкетированию, особенно среди тех, на деятельность которых могут повлиять полученные
результаты. На предприятиях-производителях — это производственники, ра-
92
ботники конструкторских бюро, а часто и руководство предприятия. Это объясняется рядом причин: в промышленной среде зачастую предпочтение отдают
производству и оперируют такими понятиями, как количество, качество, себестоимость.
Технические специалисты, как правило, не имеют экономического образования, не знакомы со спецификой маркетинга продукции производственнотехнического назначения. Поэтому они часто проявляют коммерческую близорукость, полагая, что все знают о своей продукции, ее высокое качество представляется им достаточным условием, чтобы найти покупателя. Маркетинговые
исследования они недооценивают, поскольку те не дают таких точных количественных результатов, на которые специалисты привыкли рассчитывать в решении технических задач.
Изучение мнений руководителей и специалистов посреднических торговых организаций, получение у них необходимой информации зачастую оказывается еще более сложной задачей, чем проведение исследований на предприятиях-изготовителях. Здесь возникают проблемы сохранения коммерческой
тайны, связанные с предоставлением информации о продукции, об отношениях
потребителей, объемах продаж и фирм-конкурентов. Многое зависит от умения
маркетолога «добыть» необходимую информацию даже в неблагоприятных условиях.
При проведении маркетинговых исследований, особенно когда трудно
получить надежную количественную информацию на основе одного из рассмотренных подходов, следует сочетать все указанные подходы. Конечные результаты, например величина спроса, показатель рыночной доли, могут представлять средние или средневзвешенные оценки, полученные разными путями
и из разных источников.
При проведении исследований обычно стараются получить ответы на
следующие основные вопросы:
Какова емкость рынка в физическом и денежном выражении?
Какова емкость отдельных рыночных сегментов?
Какова доля фирмы на рынке и отдельных рыночных сегментах?
Какова тенденция рынка и его сегментов — рост, стагнация, спад?
Каково среднее потребление на душу населения, семью, клиента? Каково
значение уровня насыщения рынка? Какова степень оснащенности семьи или
фирмы товарами? Каков средний срок службы товара?
Какая доля продаж обусловлена спросом на замену? Имеют ли продажи
сезонную структуру? Каковы товары-заменители, выполняющие ту же функцию? Какие нововведения могут изменить отношение к товару? Разумеется, это
неполный перечень вопросов. Он лишь указывает, информацию какого типа
следует отыскивать.
На крупных предприятиях прогнозы сбыта готовят отделы, ответственные за изучение конъюнктуры рынка под руководством и наблюдением главного руководителя по маркетингу или главного коммерческого руководителя. В
небольших фирмах прогноз подготавливает руководитель сбыта, коммерческий
93
руководитель. Независимо от титула «главный человек» по сбыту должен обеспечить своевременную подготовку надежного прогноза.
Продолжительность прогнозируемого периода зависит от назначения и
цели прогноза. Прогнозы должны составляться в соответствии с потребностями
предприятия, с учетом выпускаемой продукции и условий производства. Прогнозы на предприятиях подразделяют на краткосрочные, среднесрочные и долгосрочные.
Краткосрочные прогнозы. Большинство предприятий готовят прогнозы годового объема сбыта для операций за финансовый или календарный год.
Этот прогноз сбыта используется в качестве основы для планирования всех потребностей в ресурсах. Если спрос на продукцию предприятия подвержен сезонным колебаниям, то готовятся прогнозы по месяцам, сезонам.
Некоторые фирмы ограничивают период прогноза продолжительностью
одного операционного цикла, период которого измеряется длительностью одного оборота оборотных средств. Если для превращения сырья в готовую продукцию и ее реализации требуется 6 месяцев, то краткосрочный прогноз сбыта
охватывает полугодовой период. В торговле обычно за год совершается больше
оборотов оборотных средств — от 6-ти до 15-ти. Поэтому кратчайший горизонт
прогноза составит от 2 месяцев до 25 дней.
Среднесрочные прогнозы. Среднесрочные прогнозы могут охватывать период от 2 до 5 лет. Эти прогнозы часто основываются на предположении
о сохранении существующих тенденций в будущем с учетом воздействия предполагаемых изменений численности населения, конъюнктуры рынка и других
факторов. Они используются для установления сроков мероприятий, из которых складывается стратегия сбыта, предвидения трудностей и возможностей в
определенных районах сбыта.
Например, предприятие только что предложило рынку новый продукт.
Сбыт невелик из-за сильной конкуренции. Руководство предвидело эту проблему, текущий годовой прогноз сбыта этого продукта был верным. Но необходимо знать, сколько времени потребуется для того, чтобы продукт вышел на
этап роста сбыта, когда этот продукт получит признание, и какой степени признания можно ожидать. Среднесрочный прогноз дает руководству представление о вероятном проникновении продукта на рынок в течение следующих 2—5
лет и позволяет составлять планы производства и сбыта.
Долгосрочные прогнозы составляются на срок свыше 3—5 лет. Многие крупные предприятия заглядывают далеко вперед и составляют прогнозы с
горизонтом до 50 лет. Значение долгосрочного прогноза зависит от сферы деятельности предприятия. Например, предприятия, занятые добычей полезных
ископаемых, часто планируют разработку дополнительных ресурсов и нового
оборудования за десятилетия до того, как они понадобятся.
Долгосрочные прогнозы позволяют руководству заранее подготовиться к
созданию новых продуктов и технологий. Когда наступает время реализации
мероприятий долгосрочных планов, предприятие сможет опираться на многолетнюю подготовку: к этому времени будет проведена большая научно-
94
исследовательская работа, будут разработаны финансовые планы, производственные возможности будут увязаны с новыми планами сбыта.
Методы прогнозирования сбыта. На практике наибольшее распространение получили следующие методы прогнозирования сбыта.
Мнение группы руководителей. На небольших предприятиях руководитель маркетинга готовит общий расчет будущего сбыта. Затем группа руководителей обсуждает и оценивает прогноз. Они могут предложить пересмотреть прогноз. Если их предложения аргументированы, основаны на новой информации или на знании каких-то специфических обстоятельств, руководитель
маркетинга может изменить свою оценку.
Окончательное решение принимает группа в составе руководителя маркетинга, руководителя производства, сотрудника, отвечающего за финансы, и
руководителя предприятия.
Метод используют на предприятиях, не имеющих опыта прогнозирования
и планирования, в условиях, когда у руководителей нет статистики сбыта и статистических данных о рынке.
Комбинация мнений работников службы сбыта. Этот метод использует комбинацию оценок отдельных торговых агентов и руководителей
сбыта. Торговые агенты подготавливают оценки, которые рассматриваются и
обобщаются их руководителями. Обобщенные оценки представляются руководителю службы маркетинга. Руководитель службы маркетинга готовит сводный
прогноз, основанный на отчетах работников сбыта. Он может представить свой
предварительный прогноз другим руководителям предприятия для дальнейшего уточнения.
Метод применим в областях, для которых большое значение имеет знание
мнений клиентов, например в сбыте промышленного оборудования.
Прошлый товарооборот. При этом методе используются данные о
сбыте за прошлый период в качестве основы для предсказания вероятного сбыта в будущем. Делающий прогноз предполагает, что товарооборот следующего
года будет отличаться от текущего так же, как товарооборот текущего года отличается от прошлогоднего:
Товарооборот следующего года =
= (товарооборот текущего года) •
• (товарооборот текущего года)/
/(товарооборот прошлого года).
(6.2)
Этот элементарный метод широко применяется в краткосрочном прогнозировании из-за простоты и наглядности. Его применение возможно на предприятиях в стабильных условиях, например в сфере коммунального хозяйства.
Анализ тенденций и циклов. При прогнозировании методом анализа
тенденций и циклов изучается несколько основных факторов. Это прежде всего
долгосрочные тенденции роста фирмы, циклические колебания деловой активности, сезонные изменения сбыта компании и возможные нерегулярные влияния забастовок, технических изменений и появления новых конкурентов. На
основе изучения влияния этих факторов даются количественные оценки, гото-
95
вятся диаграммы или графики, характеризующие показатели будущего сбыта.
Этот метод требует подбора и обработки статистических данных, использования статистических методов.
Метод может быть использован для долгосрочных прогнозов в отраслях,
развитие которых тесно связано с общей экономической конъюнктурой.
Математические модели. Этот метод основывается на использовании
регрессионных, структурных и имитационных моделей. Используя этот метод
пытаются выявить симптомы в экономике и характеристики деятельности
предприятия, связанные с вероятным будущим объемом сбыта. Прогнозы основываются на оценках влияния выявленных таким образом факторов.
Прогнозируемый объем сбыта может зависеть от разных явных и скрытых факторов. Это могут быть такие факторы, как численность, доходы населения, уровень цен в регионе, неравномерность распределения доходов, количество магазинов, торгующих товаром, интенсивность рекламы. Например, если
компания продает нефтепродукты через сеть станций, то в числе факторов роста сбыта увеличение регистрация автомобилей в регионе. Однако необходимо
объективно выявить и оценить это влияние. Для оценки влияния факторов
нужно:
определить наличие и тесноту корреляционной связи между объемом
сбыта и показателями, характеризующими те или иные факторы;
определить временные лаги, то есть сдвиги во времени, которые определяют, когда изменения факторов станут сказываться на объеме сбыта;
получить регрессионные или структурные модели, характеризующие
влияние различных факторов на сбыт.
Корреляция между сбытом и остальными факторами наблюдается не всегда, степень корреляции меняется по различным типам продуктов.
Например, при прогнозировании сбыта потребительских товаров часто
рассматривают такой фактор, как расходуемая часть дохода населения.
Это наиболее современный и точный метод. Но применение его в нестабильных условиях, когда характер взаимосвязей в экономике меняется, может
ввести в заблуждение. Ошибки будут иметь место, если возможность изменений не отражается в используемых математических моделях.
Рынок для товаров данной отрасли производства и ваша доля на
рынке. Этот метод состоит в том, что делается прогноз сбыта всей отрасли, а
потом оценивается доля рынка, которую может получить предприятие. Если
предприятию доступны отраслевые прогнозы, то этот метод может упростить
подготовку прогнозов сбыта.
Например, известно, что в предшествующие годы было продано столькото кусков мыла, холодильников, автомобилей. Ваше предприятие продавало
определенные доли этих продуктов. Для получения оценки будущего сбыта необходимо использовать отраслевые прогнозы и дать прогноз вероятной доли
вашего предприятия в сбыте всей данной отрасли. Доля предприятия определяется на основе планируемых действий предприятия и оценки всех конкурирующих факторов в данной отрасли производства.
96
Метод применим на предприятиях, действующих в отраслях с развитой
системой отраслевой статистики.
Анализ конечного использования. Прогноз основывается на предсказываемом объеме сбыта продукции, в производства которой используются
товары промышленного назначения, на изучении экономического положения
потребляющих отраслей.
Например, этот метод может применять фирма, которая производит синтетические волокна. Она продает волокно фабрикам, которые производят ткани
для одежды, предметов домашнего обихода или обивки, материал для производства фетра, ковров, канатов, автомобильных шин. Специалисты компании
оценивают вероятных клиентов по каждой отрасли, обобщают все прогнозы и
получают окончательную оценку будущего сбыта для всех потребителей.
Метод применяется при прогнозировании сбыта товаров промышленного
назначения, таких, как сырье, материалы, комплектующие, промышленное оборудование.
Анализ ассортимента товаров. Многие предприятия производят разнообразные продукты для сбыта предприятиям только одной или нескольких
отраслей промышленности. Поэтому им приходится делать прогноз по каждому
продукту. Затем они сводят прогнозы по отдельным продуктам для получения
общего итога по всему производству. Для упрощения этого процесса компания,
производящая большую номенклатуру изделий, объединяет аналогичные изделия в группы.
Например, компания может производить столовую посуду, оптическое
стекло, лабораторное оборудование, электролампы, кинескопы, части электронных устройств. Все эти продукты продаются различным отраслям. Поэтому делается прогноз и оценивается сбыт по каждому продукту. Для получения
прогноза сбыта компании полученные оценки суммируются.
Метод применяется на предприятиях, которые производят товары для
различных отраслей и сфер хозяйства.
На практике в большинстве случаев сочетают применение различных методов.
Оценка и пересмотр прогнозов. Для того чтобы учесть изменившиеся условия и исправить ошибки, часто бывает необходимо прогнозы проверять и пересматривать. Необходимость и периодичность оценки и пересмотра прогнозов
зависят от компании, отрасли и продукта. Некоторые эксперты считают, что
разница между предполагаемым и фактическим сбытом величиной 5% на любом этапе требует немедленного повторного прогноза. Но решения по пересмотру и повторению прогнозов следует принимать в том случае, если это различие создает трудности — приводит к накоплению дорогостоящих запасов
или увеличению производственных издержек.
Сверять прогноз и фактические результаты сбытовой деятельности следует в конце каждого планового периода. Важность такой проверки состоит в
том, что она позволяет оценивать использованные данные. При этом выявляются ошибки, новые отношения и новые факты. Кроме того, можно получить
97
представление о том, что делать и чего не делать при составлении будущих
прогнозов.
Непрерывное прогнозирование. При непрерывном внутрифирменном
планировании предприятия пересматривают и разрабатывают прогнозы на плановый период ежемесячно, то есть прогнозирование ведется непрерывно.
Например, при годовом плановом периоде прогноз охватывает плановый
период с января по декабрь. В конце декабря прогноз как основа плана перерабатывается и составляется прогноз на период с января по декабрь следующего
года. В конце января прогноз перерабатывается, составляется прогноз на период с февраля по январь следующего года. И так далее.
Этот процесс создает непрерывный квартальный и годовой прогноз. Основой для непрерывного планирования служат соответствующие системы учета
и компьютерные системы маркетинговой информации.
Система маркетинговой информации. Это — набор банков данных и эффективных методов анализа маркетинговой информации и проблем маркетинга.
Эта система нашла широкое распространение в таких корпорациях, как «Дженерал моторе», «Дженерал электрик», а затем и во многих крупных и сравнительно небольших фирмах.
Основу любой системы анализа маркетинговой информации составляют
наряду с банком данных статистический банк и банк моделей.
7.3. Назначение, цель и задачи бюджетирования
Разработка различных финансовых планов (в форме бюджетов) составляет основу финансового управления предприятием и реализуется в процессе
бюджетирования.
Как показывает практика развитых стран, использование планирования
создает для корпораций следующие преимущества:
делает возможным подготовиться к использованию будущих благоприятных условий на товарном и финансовом рынках;
проясняет многие возникающие проблемы;
стимулирует менеджеров к реализации своих решений в дальнейшей
работе;
улучшает координацию действий между структурными подразделениями предприятия; увеличивает возможности в обеспечении его специалистов
полезной для них информацией;
способствует более эффективному распределению ресурсов и усилению контроля в корпорации.
Финансовый план — обобщенный плановый документ, отражающий поступление и расходование денежных ресурсов предприятия на текущий (до одного года) и долгосрочный (свыше одного года) периоды. Он может включать в
себя прогноз финансовых ресурсов на два-три года (например, в рамках инвестиционного плана).
98
Бюджет — оперативный финансовый план, составленный, как правило, в
рамках до одного года (на декаду, месяц, квартал), отражающий расходы и поступления средств по текущей, инвестиционной и финансовой деятельности
предприятия.
Он является инструментом финансового планирования (прогнозирования)
и контроля за деятельностью компании и ее структурных подразделений.
Бюджетирование — процесс разработки конкретных бюджетов в соответствии с целями оперативного планирования (например, платежный баланс на
предстоящий месяц).
Бюджетирование капитала — процесс разработки отдельного бюджета по
управлению капиталом предприятия, источникам формирования капитала (пассивы баланса) и их размещению (активы баланса). Например, прогноз баланса
активов и пассивов (на конец предстоящего квартала, полугодия, года).
Бюджетный контроль — текущий контроль за исполнением отдельных
показателей доходов и расходов, активов и пассивов, определенных плановым
бюджетом.
Смета — форма планового расчета, определяющая потребность предприятия в денежных ресурсах на предстоящий период и последовательность действий по исчислению показателей. Например, смета затрат на производство и
реализацию продукции, составляемая на год с поквартальной разбивкой показателей. Данный термин широко использовался в плановой экономике при разработке техпром-финплана предприятия.
Ключевая цель бюджетирования — обеспечение производственнокоммерческого процесса необходимыми как по объему, так и по структуре денежными ресурсами. Для достижения этой главной цели должны быть решены
следующие основные задачи:
определение объектов бюджетирования;
разработка системы бюджетов — операционных и финансовых;
вычисление соответствующих показателей бюджетов;
расчет необходимого объема денежных ресурсов, обеспечивающих
финансовую устойчивость, платежеспособность и ликвидность баланса предприятия;
определение величины внутреннего и внешнего финансирования, выявление резервов их дополнительного привлечения;
прогноз доходов, расходов и капитала предприятия;
анализ и оценка деятельности отдельных подразделений осуществляют
на базе показателей, утвержденных для каждого из них.
В общей системе бюджетов выделяют основной (консолидированный) и
локальные бюджеты. Основной бюджет — это финансовое, количественно определенное выражение маркетинговых и производственных планов, необходимых для достижения поставленных целей. На практике его часто называют мастер-бюджетом.
Мастер-бюджет — финансовый план развития предприятия, с помощью
которого регулируют, координируют и контролируют во временном аспекте
99
использование материальных, трудовых и финансовых ресурсов, все основные
фазы производственного цикла: план закупок, производственную программу,
план продаж и др.
Локальные бюджеты служат исходной информационной базой для разработки основного бюджета.
Процесс бюджетирования носит непрерывный или скользящий характер.
Исходя из плановых финансовых показателей в течение текущего финансового
года (до наступления планового периода) разрабатывают систему квартальных
бюджетов. В рамках квартальных бюджетов составляют месячные бюджеты (с
подекадной разбивкой показателей). Такое скользящее бюджетирование гарантирует непрерывность оперативного финансового планирования на предприятии.
Основная идея системы бюджетирования состоит в том, что ключевые
параметры экономической деятельности предприятия уточняют на уровне его
отдельных структурных подразделений (филиалов) по информации о видах доходов и расходов. Для этого создают соответствующие центры ответственности: доходов, расходов, прибыли и инвестиций.
Центр ответственности — это набор статей бюджета предприятия (объединенных по общему признаку), за планирование и выполнение которых несет
ответственность один из ведущих менеджеров фирмы или руководитель структурного подразделения.
На российских предприятиях могут быть выделены следующие типы центров ответственности:
• центр затрат (место их возникновения);
• центр доходов и затрат (или центр финансового учета);
• центр прибыли (центр финансовой ответственности);
• центр инвестиций (отдел капитального строительства).
В рамках процесса бюджетирования руководитель центра ответственности отвечает за:
• организацию планирования и нормирования вверенного ему набора
статей;
• правильность расчета соответствующих статей бюджета;
• контроль по выполнению плановых параметров статей бюджета;
• принятие решений по устранению отклонений плановых статей бюджета от фактических параметров (если такие отклонения превышают 5%).
Преимущества бюджетирования:
• определяет деятельность предприятия в целом путем координации работы ведущих специалистов, отделов и служб;
• оказывает положительное воздействие на мотивацию и настрой коллектива;
• позволяет усовершенствовать процесс распределения ресурсов;
• позволяет менеджерам низового звена понять свою роль на предприятии;
100
• предоставляет пользователям более реальную информацию за счет помесячного планирования показателей бюджетов структурных подразделений
(об объеме доходов, расходов, прибыли и др.), чем бухгалтерская и статистическая отчетность;
• в рамках утвержденных месячных бюджетов структурным подразделениям предприятия предоставлена большая самостоятельность в использовании
средств;
• минимизация числа показателей бюджетов позволяет снизить затраты
рабочего времени персонала финансово-экономических служб предприятия;
• позволяет более эффективно расходовать денежные ресурсы предприятия, что особенно важно в условиях их дефицита.
При внедрении системы бюджетирования у предприятия могут возникнуть определенные трудности:
• высокие затраты на разработку и реализацию данной системы;
• конфликты между менеджерами структурных подразделений и специалистами финансово-экономических служб;
• стремление получить больше ресурсов для реализации бюджета;
• распространение недостоверной информации о бюджетах по неформальным каналам и др.
Роль бюджетов в финансовом управлении и принятии решений определяется следующими аспектами:
• помощь в планировании хозяйственных операций;
• координация в деятельности различных подразделений и обеспечение
гармоничности их развития;
• необходимость в доведении планов до руководителей’ различных центров ответственности;
• стимулирование (мотивация) труда руководителей (ведущих менеджеров) по достижению целей предприятия;
• оценка эффективности работы руководителей и специалистов.
101
Классификация и содержание бюджетов
Система бюджетирования на предприятии состоит из двух ключевых
подсистем:
1.бюджетов структурных подразделений (цехов, участков, отделов, служб
и т.д.);
2.сквозного (сводного, главного) бюджета, характеризующего деятельность предприятия в целом.
Систему бюджетов подразделяют также на операционные и финансовые.
Основные составляющие главного бюджета и их взаимосвязи рассмотрим
с помощью схемы.
Бюджет продаж
Бюджет капитальных затрат
Бюджет коммерческих продаж
Производственный бюджет
Бюджет закупки материалов
Прогноз себестоимости продукции
Бюджет (смета)
денежных
средств
Бюджет трудовых затрат
Бюджет общепроизв. расходов
Прогнозный
отчет о прибылях и убытках
Прогноз бухгалтерского баланса
Бюджет общехозяйственных расходов
Операционный бюджет
Финансовый бюджет
Операционный бюджет включает в себя сводный бюджет доходов и расходов, базой для разработки которого являются более частные (локальные)
бюджеты: производства, продажи продукции, закупок материалов, прочих до-
102
ходов и расходов, затрат на материалы и энергию, оплаты труда, амортизационных отчислений, общепроизводственных и общехозяйственных расходов,
налоговый и др.
Финансовый бюджет состоит из бюджета движения денежных средств и
прогнозного баланса активов и пассивов (бюджета по балансовому листу).
При этом наряду с главным операционным и финансовым бюджетами освещают и другие их виды. Например, дополнительный бюджет предусматривает финансирование мероприятий, не включенных в основной бюджет. Приростный бюджет формируют путем простой индексации (в процентах) предыдущего бюджета без пересмотра его статей. Добавочный бюджет предусматривает изучение предыдущих бюджетов и их корректировку под текущие параметры: темпы инфляции, изменения в штатном расписании, в ассортименте выпускаемой продукции и др. Целевой бюджет выражает основные направления расходования средств и связывает их с ключевыми задачами подразделений (филиалов) компании.
Стратегический бюджет интегрирует элементы стратегического финансового планирования и контроля. Он необходим в периоды нестабильности и неопределенности деятельности компании. Руководитель подразделения вправе
распространить бюджет рекурсивным образом на период, следующий за отчетным. Новый период добавляют к оставшимся и получают новый бюджет. Преимущество непрерывного бюджетирования заключается в улучшении планирования, учете данных истекших периодов и возникающих изменений.
Разрабатывают также бюджеты с нулевым уровнем, которые составляют
каждый раз заново, с нуля, что требует дополнительных усилий и времени. Однако они предотвращают повторение одних и тех же ошибок, которые могут
присутствовать в преемственных бюджетах.
Многовариантный бюджет предполагает несколько сценариев развития
событий, и в зависимости от складывающейся ситуации выбирают наиболее реальный вариант. В этом случае отдельные статьи бюджета доходов я расходов
имеют несколько значений, из которых в итоге выбирается одно.
Бюджеты можно формировать по принципу «снизу вверх» и «сверху
вниз».
Бюджеты, составленные по принципу «снизу вверх», предусматривают
сбор ин передачу информации от исполнителей к менеджерам нижнего уровня
и далее руководству предприятия. Основным недостатком таких бюджетов считается, что много сил и времени уходит на их согласование, а руководство компании лишено возможности вникнуть во все детали исходной информации.
Бюджеты, построенные по принципу «сверху вниз», функционируют по
обратной процедуре. Недостатком этого вида бюджетов служит то, что не учитывают мнение непосредственных исполнителей. Руководство предприятия
часто не обладает полной информацией, необходимой для разработки бюджетов. На практике, как правило, используют комбинированные варианты, содержащие в себе элементы различных типов бюджетов.
103
Составление бюджета доходов и расходов является отправной точкой
процесса сквозного бюджетирования на любом предприятии. Данный бюджет
представляет собой расчетную оценку доходов и расходов, а также их структуру на предстоящий период (квартал, год). Доходную и расходную части бюджета вычисляют отдельно, а затем сводят в единую таблицу. Доходную часть
бюджета разделяют на три составляющие:
1)доходы от реализации продукции (услуг);
2)доходы от прочей текущей деятельности;
3)доходы от финансовой деятельности.
Расходная часть состоит из текущих (эксплуатационных) расходов, связанных с производством и реализацией продукции; расходов на выплату налогов; расходов по финансовой деятельности.
Пересмотр бюджета доходов и расходов возможен в случаях:
• его дефицита (превышения расходов над доходами);
• если плановая рентабельность продаж, активов и собственного капитала находится, по мнению руководства, на недостаточном уровне (отношение
профицита бюджета к объему продаж, активов и собственного капитала), что не
позволяет в полной мере реализовать финансовую гибкость предприятия.
Финансовая гибкость — способность фирмы оперативно формировать
необходимый объем денежных ресурсов при неожиданном возникновении высокоэффективных финансовых предложений или новых возможностей ускорения производственного, научно-технического и социального развития.
Концентрация всех видов денежных поступлений и платежей (денежных
потоков) получает отражение в специальном финансовом документе — бюджете движения денежных средств. Основной целью разработки этого бюджета является прогнозирование во времени денежных потоков предприятия в разрезе
отдельных видов его хозяйственной деятельности (текущей, инвестиционной и
финансовой) и обеспечение платежеспособности на приемлемом уровне (недопущение кассовых разрывов) в течение всего планового периода. Бюджет движения денежных средств составляют в несколько этапов:
• бюджет поступлений от реализации продукции (он необходим также
для разработки
• бюджета доходов и расходов);
• бюджет прочих поступлений;
• бюджет закупок сырья и материалов;
• бюджет платежей по оплате труда;
• бюджет выплат по общепроизводственным расходам;
• бюджет выплат по общехозяйственным расходам;
• бюджет налоговых платежей (включая косвенные налоги);
• бюджет поступлений и выплат по инвестиционной деятельности;
• бюджет поступлений и выплат по финансовой деятельности;
• сводный бюджет движения денежных средств.
Ожидаемое сальдо денежных средств на конец планируемого месяца
(квартала) сравнивают с их минимальной величиной, которая должна поддер-
104
живаться предприятием. Если ожидаемое сальдо меньше минимальной суммы
денежных средств, то дефицит денежной наличности покрывают за счет банковского или коммерческого кредита. Оптимальное соотношение между отдельными видами денежных потоков достигается в случае, когда основным источником поступлений средств является текущая деятельность предприятия.
Средства, полученные от этой деятельности, направляют на финансирование
реальных инвестиций (на капитальные вложения).
Финансовая деятельность призвана увеличивать денежные ресурсы предприятия и создавать дополнительные источники финансирования текущей и
инвестиционной деятельности. Сводный бюджет движения денежных средств
обычно детализируют по центрам финансовой ответственности (центрам финансового учета), которые генерируют основной объем притока и оттока денежных средств. Таким образом, практическое значение бюджета движения денежных средств заключается в следующем:
• обеспечение постоянной платежеспособности предприятия в течение
всего года;
• изучение взаимосвязи полученного финансового результата и изменения величины денежных средств;
• осуществление рациональной кредитной политики;
• эффективное размещение свободных денежных средств, временно не
участвующих в хозяйственном обороте;
• контроль за деятельностью центров финансовой ответственности (центров финансового учета).
Сравнительно новый расчет в практике финансового планирования на
предприятиях России — разработка планового баланса активов и пассивов на
конец прогнозного периода (квартала, года). Составление данного баланса
(бюджета по балансовому листу) в разрезе укрупненной номенклатуры статей
может оказать существенное влияние на пересмотр финансовой стратегии и
тактики предприятия. Если предварительные расчеты показывают, что не достигается необходимая финансовая устойчивость и платежеспособность фирмы,
то возможны значительные корректировки чистой прибыли, направляемой на
выплату дивидендов, и цели развития, оборотных активов и краткосрочных
обязательств. Прогнозный баланс позволяет:
• выявить возможные неблагоприятные для предприятия последствия
финансовых решений, принимаемых на планируемый период;
• проверить математическую правильность процесса бюджетирования в
целом. Например, достоверность составленного бюджета движения денежных
средств;
• осуществить анализ финансового состояния предприятия в будущем на
основе расчета финансовых коэффициентов по балансовым статьям и оценить
их уровень с позиции требований финансового рынка;
• установить будущую структуру капитала и активов (имущества) предприятия;
105
• определить наиболее мобильную часть источников собственных
средств в форме чистого оборотного капитала.
При разработке бюджета по балансовому листу следует иметь в виду, что
некоторые показатели баланса имеются в результате составления бюджета доходов и расходов и бюджета движения денежных средств (денежные средства
на счетах в банках и в кассе). Ряд показателей берут из предыдущего баланса
(например, уставный, резервный и добавочный капиталы).
7.4. Условия формирования системы эффективного бюджетного
управления
Процесс бюджетирования на многих предприятиях протекает в условиях
экономической нестабильности и отсутствия четких перспектив развития. Прежде всего, данный процесс должен иметь организационное, информационное и
кадровое обеспечение, а также возможность оперативного проведения аналитических процедур (быстрый сбор и анализ собираемых данных), на что специалисты предприятия затрачивают много времени.
Наиболее характерный недостаток бюджетов — слабая вовлеченность
конкретных исполнителей в процесс бюджетирования и управления (принятие
решений), сложность формирования гибкой системы оценки результатов деятельности структурных подразделений (цехов, отделов, служб и др.).
Основные проблемы, возникающие при построении системы бюджетирования на предприятии:
• четко не обозначена концепция финансового управления;
• отсутствует управленческий (производственный) учет;
• основой бюджетирования служат фактические данные бухгалтерского
учета;
• процедуры учета, анализа, планирования и контроля не формализованы, не разграничена ответственность должностных лиц;
• не определены принципы централизации и децентрализации управленческих функций.
Следовательно, для успешного формирования и функционирования системы бюджетного управления необходимо соблюдение ряда обязательных условий.
1.
Целесообразно создание новой организационной структуры управления предприятием, определяющей права и ответственность руководителей
структурных подразделений, а также структуры бизнес-процессов, влияющих
на скорость и качество внутрифирменного планирования. В данную структуру
управления обычно включают: функции подразделений, процедуры взаимодействия между ними, систему ответственности и др. Нормативным обеспечением
организационной структуры служат:
• положение об организационной структуре;
106
• положение о должностных обязанностях руководителей и специалистов высшего и среднего звена управления, а также менеджеров отделов, служб
и др.;
• штатное расписание.
2.Обязательная интеграция бюджетирования с организационной и информационной структурами предприятия и системой исполнения бизнеспроцессов (производством товаров). Наиболее предпочтительным является
подход, когда происходит закрепление организационной структуры в соответствии с целями и задачами предприятия, а также ситуацией во внешней среде.
После этого определяют правила движения информации (документов, регистров, отчетов и др.), которая отражает результаты деятельности предприятия в
целом и его подразделений (филиалов).
3.Для успешного планирования целесообразно стандартизировать учетные данные с целью их совместного использования»всеми структурными подразделениями (бизнес-центрами, центрами ответственности и т. д.).
В этих целях необходимо разработать следующие внутренние нормативные документы:
• положение о конвертизации и консолидации данных бухгалтерского
учета;
• план счетов налогового учета;
• положение о формировании налоговой отчетности;
• положение о системе управленческого учета и отчетности;
• классификатор первичных элементов производственной логистики,
идентифицированных во времени и пространстве;
• классификатор первичных планово-учетных единиц бюджетного
управления;
• положение о маркетинговом учете (о порядке сбора и систематизации
ин формации о состоянии рынка продуктов и услуг и отдельных его сегментов).
Основным документом, закрепляющим способ ведения бухгалтерского и
налогового учета на предприятии, является приказ об учетной политике.
Стандартные формы бюджетной отчетности должны содержать информацию, необходимую для:
• маржинального анализа;
• план-факт анализа;
• анализа безубыточности выпуска отдельных изделий (построение графиков безубыточности).
Обязательным условием формирования системы бюджетирования является разработка регламента, определяющего последовательность построения
бюджетов, поскольку каждый из них требует согласования не только со смежными бюджетами, но и другими функциями управления предприятием.
7.5. Период бюджетирования
Подготовительная работа к составлению бюджетов на следующий год
должна начинаться за несколько месяцев до начала этого года. Если бюджет
107
основан на календарном годе, то предварительные разработки целесообразно
начинать с 1 октября. Бюджет может охватывать любой временной период. Однако чем больший временной лаг выражает бюджет, тем менее он надежен.
Краткосрочный бюджет (в пределах календарного года) более надежен и
отражает содержание оперативных планов и тактических действий предприятия. Период бюджетирования зависит от тактических задач и необходимости
применения бюджетирования для их решения. Он зависит от объемов производства и продаж, технологии и цикла производства, достоверности данных об
ассортименте продукции, сезонности, оборачиваемости запасов, наличия ресурсов (материальных, трудовых и финансовых), резервов производственных
мощностей (в случае расширения масштабов производства), уровня предпринимательского риска, государственного регулирования экономики (налоговые
ставки, тарифы взносов в государственные внебюджетные фонды, учетная
ставка Центрального банка РФ) и др.
Сезонные колебания возникают под влиянием ряда факторов объективного характера (климатические условия, возможности транспортировки сырья и
материалов, поставки энергоресурсов и т. д.) и могут значительно влиять на покупательский спрос, поставки материальных ресурсов и состояние производственных запасов на предприятии.
Детализированный бюджет для каждого структурного подразделения
(филиала, центра ответственности и др.) обычно разрабатывают на определенный период. Годовой бюджет можно разделить на двенадцать месяцев. Он может быть также распределен по месяцам на первые три месяца и по кварталам
на оставшиеся девять месяцев. В течение года квартальные бюджеты делят на
месячные. Последние из них могут быть детализированы по декадам и пятидневкам. Например, в течение первого квартала с появлением новой информации могут быть изменены бюджеты на последующие три квартала и будет подготовлен план на первый квартал следующего года.
Данный процесс называют непрерывным или скользящим составлением
бюджета, что гарантирует наличие двенадцатимесячного бюджета, к которому
добавляют бюджет на предстоящий квартал, как только истекает срок бюджета
предыдущего квартала. В течение года период, на который составлен бюджет,
будет сокращаться, и так до тех пор, пока не будет составлен бюджет на следующий год.
Таким образом, скользящие бюджеты гарантируют непрерывность планирования — это не единовременное событие, а последовательный процесс, когда руководители чувствуют необходимость заглядывать вперед и пересматривать планы на будущее. Более того, вполне вероятно, что фактические результаты будут сопоставлены с более реалистичными плановыми параметрами, поскольку операционные бюджеты систематически пересматривают и корректируют. Поскольку бюджеты пересматривают в конце каждого квартала или месяца, то существует опасность, что руководители структурных подразделений
не будут уделять достаточного внимания подготовке бюджетов на следующий
период, так как знают, что они, возможно, изменятся в процессе ежекварталь-
108
ного пересмотра. Однако данный негативный фактор блокируют необходимостью соблюдать должностные обязанности и инструкции на каждом предприятии, что предусматривают в соответствующих положениях по бюджетному
управлению.
Непрерывность бюджетирования в значительной мере обеспечивают с
помощью применения различных компьютерных технологий. Они полагают
быстро и точно выполнять финансовые расчеты, проводить необходимые сравнения и постоянно отслеживать результаты отклонений от планов. Моделируя
различные ситуации, руководитель (ведущий специалист) выбирает из набора
альтернатив наилучший способ действий. Если его не устраивают результативные показатели, то он вправе изменить свои решения и установки.
7.6. Технология разработки бюджетов
Бюджет является высокоэффективным инструментом внутрифирменного
финансового планирования и позволяет оперативно координировать и оценивать деятельность структурных подразделений предприятия. С бюджета начинается процесс постановки конкретных целей и задач коммерческой деятельности (например, увеличение объема продаж, рост рыночной стоимости предприятия, максимизация прибыли, оптимизация структуры капитала и обеспечение
финансовой устойчивости и платежеспособности фирмы и т. д.). Отклонения от
плановых показателей* в процессе исполнения краткосрочных бюджетов служат сигналом руководителям для принятия действенных мер по устранению негативных отклонений.
В состав процедур финансового управления включают: бюджетирование,
привлечение заемных средств и размещение временно свободных денежных
средств на финансовом рынке. По отношению к бюджетированию две последние процедуры занимают подчиненное положение. Это вызвано тем, что без
четкого управления и контроля за денежными потоками внутри предприятия
действия по привлечению и размещению денежных средств могут оказаться неэффективными и не приведут к укреплению финансовой устойчивости и платежеспособности субъекта хозяйствования.
Процесс бюджетирования должен быть стандартизирован с помощью
бюджетных форм, инструкций и процедур, разработанных самим предприятием. В западных корпорациях данный процесс включает:
• определение общей цели (миссии);
• установление задач подразделениям (филиалам) компании;
• оценку ключевых направлений финансовой деятельности (потребность
в капитале, величина объема продаж, финансовое положение и т. д.);
• подготовку бюджетов: по доходам от продаж, издержкам производства,
движению денежных средств, активам и пассивам баланса и др.;
• подготовку бюджетов подразделений и сводного (консолидированного)
бюджета по корпорации в целом;
• проверку бюджетов на предмет внесения необходимых изменений; разработку ежемесячных отчетов об исполнении бюджетов;
109
• определение отклонений между фактическими и запланированными
статья ми доходов и расходов, активов и пассивов баланса;
• подготовку рекомендаций по улучшению будущей деятельности.
В России процесс бюджетирования включает следующие примерные этапы:
1)первоочередную подготовку бюджетов;
2)обсуждение бюджета с вышестоящим руководством;
3)координацию и анализ рассмотренных бюджетов;
4)окончательное принятие бюджета;
5)последующий анализ и контроль бюджета.
На этапе первоначальной подготовки бюджета управление процессом
бюджетирования обычно начинают с назначения директора но бюджету. Он отвечает за подготовительный процесс, стандартизацию плановых форм, сбор и
анализ данных, проверку информации и представление отчетов. Руководителем
по бюджету обычно назначают финансового директора (заместителя генерального директора по экономике и финансам). Он выступает в качестве штатного
эксперта и координирует деятельность отделов и служб.
Комитет по бюджету — это составленная из руководителей верхнего звена управления предприятием консультативная группа, которая может включать
и внешних консультантов. Данный комитет — постоянно действующий орган,
который занимается тщательной проверкой стратегических и текущих производственных и финансовых планов, дает рекомендации, разрешает разногласия
и оперативно вносит коррективы в деятельность предприятия (с согласия генерального директора).
В западных компаниях подобное структурное подразделение может быть
названо группой стратегического планирования или группой финансового анализа и планирования.
Руководство по бюджету представляет собой набор инструкций и положений, отражающих финансовую политику, организационную структуру предприятия, распределение прав, обязанностей и ответственности исполнителей.
Эти инструкции выполняют роль свода правил и рекомендаций для разработки
бюджетных программ. На первоначальном этапе руководители, отвечающие за
выполнение плановых показателей, обязаны составлять бюджеты для тех областей деятельности, которые они контролируют. Процесс подготовки бюджета
должен осуществляться снизу вверх. Это означает, что бюджет начинают составлять на низшем уровне руководства, а совершенствовать и координировать
— на более высоком уровне. Подобный подход позволяет руководителям подразделений (центров ответственности) принимать участие в подготовке своих
бюджетов и повышает вероятность того, что они будут стремиться достичь запланированных целен.
Однозначного метода количественного определения конкретной статьи
бюджета не существует. Отчетные данные можно использовать как отправную
точку для составления бюджета, но это не означает, что его разрабатывают исходя из предположения, что если событие имело место в прошлом, то оно про-
110
изойдет и в будущем. Целесообразно учитывать в бюджетном процессе изменение условий в будущем, а информация о прошлом может быть полезной в
дальнейшей работе. Кроме того, руководители, составляя свои бюджеты, могут
придерживаться указаний высшего руководства. Например, специальных инструкций по изменению цен на приобретаемые сырье, материалы и услуги. В
производственной деятельности можно ориентироваться на нормативные затраты как основу калькулирования себестоимости выпускаемой продукции,
предусматриваемой в бюджете.
При подготовке бюджетов руководители всех уровней должны принять
во внимание влияние следующих факторов:
• вида продуктов и услуг;
• числа занятых рабочих и их квалификацию;
• возможности производства и ограничения по мощностям;
• стабильности производственного цикла;
• цен на закупаемые материальные ресурсы и энергию, а также продажных цен на готовые продукты (услуги);
• наличия производственных запасов и необходимости их пополнения;
• скорости оборота текущих активов (например, счетов к получению);
• цикличности производства;
• технологических аспектов, включая наличие физически и морально изношенного оборудования;
• контроля качества продукции и сервисных возможностей;
• деловой ситуации на товарном и финансовом рынках; потребностей в
финансировании и др.
При разработке бюджета следует иметь в виду, что грамотно составленный плановый документ отличается следующими свойствами:
1. имеет возможности по прогнозированию абсолютных и относительных показателей;
2. обладает четкими каналами движения информации, распределением
полномочий и ответственности;
3. содержит ясную, подробную и достоверную информацию о деятельности подразделения (филиала);
4. представляет возможности сравнения показателей в историческом аспекте;
5. поддерживается всеми заинтересованными лицами внутри предприятия, и прежде всего его руководством.
На этапе обсуждения бюджета с вышестоящим руководством руководители подразделений обязаны не только составлять свои бюджеты, но и представлять их на утверждение вышестоящему руководителю. Он, в свою очередь,
объединяет все бюджеты, за которые отвечает, и становится ответственным за
составление бюджета на своем уровне.
Технологию разработки бюджетов можно представить как цепочку последовательных действий:
111
1. установление целей и стратегии их достижения по нисходящей —
сверху вниз;
2. подготовка бюджета по восходящей — снизу вверх;
3. утверждение составленных бюджетов снова по нисходящей — от
высшего руководства до руководителей структурных подразделений.
Важное значение при подготовке бюджетов имеет четкое разграничение
функций и обязанностей менеджеров структурных подразделений предприятия.
Так, например, менеджер по закупкам планирует закупки в физическом и стоимостном выражении. Закупки могут быть запланированы в разрезе отдельных
поставщиков.
Менеджер по производству проектирует будущие затраты на выпуск всей
продукции и в разрезе отдельных изделий. Он обязан составить график выпуска
продукции, чтобы производственный процесс не прерывался. Менеджер по
производству несет ответственность за качество производимой продукции и ее
ассортимент, увеличение (снижение) объемов производства, нахождение оптимального режима организации работ, эксплуатации, ремонта и замены оборудования. Он обязан также определить допустимый уровень брака на основе
практического опыта прошлых периодов.
Менеджер по качеству оценивает качество продукции, выявляет причины
снижения качества изделий и формирует требования по контролю качества.
Менеджер по продажам проектирует будущие объемы продаж товаров и услуг,
цены реализации и прибыль с учетом сегментов рынка и покупателей. Он должен также рассчитать соответствующие затраты: на оплату труда, комиссионные вознаграждения посредникам, на продвижение и транспортировку товаров,
представительские расходы и др.
Менеджер по кредитному контролю несет ответственность за расширение
объема продаж с помощью привлечения кредита (если это оправдано) при одновременном снижении безнадежных долгов покупателей. Он обязан добиваться роста объема продаж и одновременно — снижения просроченной дебиторской задолженности.
После приведения всех бюджетов в соответствие с требованиями финансовой, ценовой, инвестиционной, снабженческо-сбытовой политики предприятия необходимо свести их в один (главный) бюджет и представить высшему
руководству на утверждение. Предварительно бюджеты обсуждаются исполнителями и их непосредственными руководителями и после снятия спорных вопросов должны быть приняты обеими сторонами.
Следовательно, включенные в бюджет показатели являются результатом
обсуждения между лицами, ответственными за данный бюджет, и его руководителем. Представляется важным аспектом, чтобы составители бюджета участвовали в принятии его окончательного варианта, а руководитель не пересматривал статьи этого документа без учета доводов подчиненных лиц. В ином случае исполнители вряд ли будут заинтересованы в исполнении бюджета, которого они не принимали. Необходимо также следить за тем, чтобы лица, ответственные за составление бюджета, не пытались преднамеренно добиться приня-
112
тия легко выполнимых заданий или занизить бюджетные показатели в надежде
на то, что исполнение окончательного бюджета — легко достигаемая цель.
Обсуждение — очень важный процесс подготовки бюджета, так как в ходе этого процесса можно установить, станет ли он действительно эффективным
средством управления или будет просто техническим приемом. Если руководитель подразделения (центра ответственности) достиг успеха в установлении доверительных отношений со своими подчиненными, то процесс обсуждения позволит внести значительные улучшения в подготовку бюджета.
На этапе координации и анализа рассмотренных бюджетов проводят следующую работу. По мере продвижения бюджета снизу вверх — от нижестоящего руководителя к вышестоящему — в процессе обсуждения целесообразно
изучать параметры бюджета. Такое изучение может показать, что некоторые
бюджеты не сбалансированы с другими бюджетами и нуждаются в серьезной
корректировке. При этом должны быть приняты во внимание другие условия,
ограничения и планы, о которых руководитель подразделения не знает и не
может на них влиять. Например, генеральный директор предприятия может потребовать от подчиненных ему лиц замены оборудования, когда достаточных
средств для этого нет. Финансовый менеджер обязан выявлять такие несоответствия и ставить в известность своего руководителя. Вносить в бюджет любые
изменения должно лицо, ответственное за его подготовку, а это может потребовать прохождения планового документа снизу вверх во второй или даже в третий раз, до тех пор, пока все бюджеты не будут скоординированы и не станут
приемлемыми для всех заинтересованных сторон.
В процессе координации целесообразно составлять бюджет доходов и
расходов, бюджет движения денежных средств и бюджет по балансовому листу, чтобы гарантировать их целостность и приемлемость для исполнения.
На этапе окончательного принятия бюджета все плановые документы
сводят в обобщенный (сводный) бюджет по предприятию в целом. После его
утверждения все локальные бюджеты направляют подразделениям (центрам
ответственности) для исполнения.
Следует подчеркнуть, что процедура выбора системы бюджетирования
касается в основном операционных бюджетов. Предприятие самостоятельно,
исходя из специфики своей деятельности и выбранной стратегии развития, определяет необходимость построения того или иного бюджета, а также решает
проблему консолидации всех или части бюджетов с учетом своей финансовой
структуры.
На заключительном этапе — «Последующий анализ и контроль бюджета»
— процесс составления бюджетов не должен завершаться их согласованием.
Фактические результаты деятельности подразделений сравнивают с плановыми. Сравнение должно производиться ежемесячно, и до середины следующего
месяца отчет по результатам сравнения предоставляют составителям бюджетов,
чтобы активизировать их деятельность. Это позволяет руководителям подразделений определить, какие позиции бюджета не выполнены, и выяснить причины отклонений от плана. Если проблема отклонений находится в сфере компе-
113
тенции руководителей подразделений (центров ответственности), то следует
принять меры, чтобы предотвратить существенные отклонения в будущем. Если возникают какие-либо объективные изменения реальных условий по сравнении с запланированными, то бюджет подлежит уточнению, что входит в компетенцию руководства предприятия.
Итак, бюджетирование целесообразно начинать с разработки операционных бюджетов — в первую очередь с бюджета продаж. На базе этого планового
документа формируют бюджеты производства, снабженческо-заготовительной,
операционной, сбытовой и других видов деятельности. Параллельно (или вслед
за операционным) составляют бюджет движения денежных средств. Он позволяет наладить учет и контроль за платежеспособностью и обеспечивает текущую финансовую устойчивость предприятия. Бюджет движения денежных
средств наиболее локален и требует минимума внешней информации.
Завершающий шаг — разработка бюджета доходов и расходов и бюджета
по балансовому листу. Первый из них позволяет управлять важнейшим финансовым результатом деятельности — прибылью, а второй выражает обязательства и вложения предприятия по основным статьям активов и пассивов. Таким
образом, окончательным результатом процесса бюджетирования является разработка трех ключевых бюджетов: доходов и расходов, движения денежных
средств и по балансовому листу. Они могут быть составлены с большей или
меньшей степенью детализации, но отсутствие одного из них нарушает комплексность финансового планирования на предприятии.
7.7. Внутрифирменный контроль за исполнением бюджетов
Контроль, с одной стороны, является одной из завершающих стадий
управления финансами предприятий, а с другой — он выступает необходимым
условием управления ими. Финансовый контроль имманентно присущ контрольной функции финансов и тесно с ней взаимосвязан. Контроль определяет
все стадии индивидуального кругооборота фондов, начиная с авансирования
средств в производственные запасы и заканчивая процессом реализации продукции и поступления выручки па счета предприятия в банках. Финансовый
контроль как понятие субъективное представляет собой метод управления финансовыми ресурсами и денежными потоками хозяйствующих субъектов.
Западные экономисты выделяют следующие фундаментальные принципы
внутреннего финансового контроля.
1. Разделение обязанностей. Ответственность между персоналом компании распределяют таким образом, чтобы ни один служащий не нес ответственности за операцию в целом. Основное мотив состоит в том, что лицо, разрешающее операцию не несет ответственности за участвующие в ней активы и за
регистрацию данной операции. Конечно, за финансовое состояние компании в
целом отвечает финансовый директор.
2. Разрешение и одобрение. Данный принцип заключается в том, что все
операции, связанные с движением денежных средств, реальных и финансовых
активов, должны быть одобрены финансовым директором в пределах тех объе-
114
мов финансовых ресурсов, на которые он имеет полномочия. В акционерных
обществах работу правления контролируют совет директоров ревизионная комиссия и общее собрание акционеров.
3. Физический контроль предполагает право доступа проверяющего к активам и документам компании. Чтобы эффективно управлять контрольной работой, руководство должно составить план ее организации. Данный план должен содержать четкие инструкции, права и обязанности различных официальных лиц, чтобы исключить бесполезное дублирование в их контрольной работе.
4. Важность свидетельства. Основной частью системы контроля является свидетельство выполнения работы, заверенное подписью контролера. Для
снижения риска неудовлетворительной работы проверяющих лиц руководство
обязано регулярно проверять их с целью определения эффективности их деятельности и точности исправления ошибок. В крупных компаниях потенциальные преимущества регулярного финансового контроля часто окупают расходы
по созданию отдела внутреннего аудита. Важным критерием его работы служит
снижение потенциальных убытков.
Система контроля предназначена для помощи руководителям предприятий в вопросах: выбора между различными альтернативными действиями,
планирования действий, которые должны быть приняты в течение определенного периода времени; выявления ошибок конкретных исполнителей. Они могут заключаться в установлении нереальных планов при наличии точных прогнозов или в невыполнении тех действий, которые должны быть предприняты
для реализации конкретных маркетинговых, инвестиционных и иных решений;
осуществления действий для исправления ошибок и закрепления успеха.
Объектом финансового контроля выступают показатели бюджетов предприятия. Для осуществления контроля за исполнением бюджетов Минэкономразвития России рекомендует использовать двухуровневую систему. Нижний
уровень — контроль за исполнением бюджетов структурных подразделений
предприятия, который осуществляют их руководители. Верхний уровень —
контроль за исполнением бюджетов всех структурных подразделений (включая
контроль составляющих их бюджетов по элементам затрат), проводимый финансово-экономической службой и бухгалтерией предприятия.
Ключевыми элементами системы контроля являются:
• объекты контроля — бюджеты структурных подразделений;
• предметы контроля — отдельные показатели бюджетов (соблюдение
лимитов фонда оплаты труда, расходов сырья, материалов и энергии, накладных расходов и т.д.);
• субъекты контроля — руководители структурных подразделений и финансово-экономических служб предприятия;
• методы контроля бюджетов — осуществление процедур, необходимых
для определения отклонения фактических показателей бюджетов от плановых в
абсолютных суммах и в относительном выражении (в процентах); построение
динамических рядов этих отклонений. Контроль за выполнением доходной части сводного бюджета призван обеспечить бесперебойность финансирования те-
115
кущей (операционной) и инвестиционной деятельности предприятия. Его осуществляет финансовая служба. Контроль за соблюдением расходной части консолидированного бюджета является важной проблемой, от решения которой зависит эффективность финансово-хозяйственной деятельности предприятия.
Для успешного решения данной проблемы рекомендуют устанавливать и
соблюдать четкий порядок проведения управленческих процедур, который
обеспечивает:
1. оперативный анализ фактических отклонений от плановых функциональных и сводного бюджетов (за месяц, квартал, год);
2. разработку мероприятий по устранению непроизводительных расходов и потерь, а также удорожающих факторов, выявленных в ходе анализа;
3. оформление и представление дирекции предприятия аналитических
мате риалов по исполнению сводного и функциональных бюджетов с предложениями по корректировке их доходной и расходной части.
Рекомендуют использовать метод пересмотра расходов бюджета, основанный на принятой системе приоритетов финансирования (оплаты) операционных расходов предприятия. В качестве приоритетных предлагают следующие
расходы бюджета:
1) оплата труда работников в расчете на производственную программу;
2) взносы в государственные внебюджетные фонды;
3) выплата налогов в федеральный, региональный и местный бюджеты;
4) оплата закупок материальных ресурсов и энергии, коммунальные платежи;
5) все остальные расходы.
Целесообразно на каждом предприятии создавать и внедрять комплексную автоматизированную систему бюджетного планирования (на базе локальной компьютерной сети), что позволяет оперативно (ежедневно) получать информацию об исполнении бюджетов и своевременно вносить коррективы в доходную и расходную части в целях повышения эффективности управления финансами предприятий.
116
Библиографический список
1. Данилов Н.Н. Курс математической экономики : учеб. пособие для вузов /
Н.Н.Данилов .— М. : Высш. шк, 2006 .— 407с. : ил. (7)
2. Елисеева И.И. Эконометрика : учебник для вузов / И.И.Елисеева [и др].; под
ред. И.И. Елисеевой .— 2-е изд., перераб.и доп. — М. : Финансы и статистика,
2008 .— 576с. : ил. (12)
3. Кузык Б.Н. Прогнозирование, стратегическое планирование и национальное
программирование : учебник / Б.Н. Кузык, В.И. Кушлин, Ю.В. Яковец .— 2-е
изд., перераб. и доп. — М. : Экономика, 2008 .— 575 с. : ил. (12)
4. Строгалев В.П. Имитационное моделирование : учеб. пособие для вузов /
В.П. Строгалев, И.О. Толкачева .— М. : Изд-во МГТУ им. Н.Э. Баумана, 2008.
— 280с. : ил. (5)
117