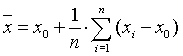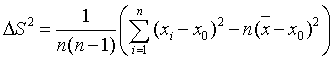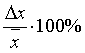Коэффициент Стьюдента
|
n |
a |
||||||||
|
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
0,95 |
0,98 |
0,99 |
0,999 |
|
|
3 |
0,82 |
1,06 |
1,3 |
1,9 |
2,9 |
4,3 |
7,0 |
9,9 |
31,6 |
|
5 |
0,74 |
0,94 |
1,2 |
1,5 |
2,1 |
2,8 |
3,7 |
4,6 |
8,6 |
|
10 |
0,7 |
0,88 |
1,1 |
1,4 |
1,8 |
2,3 |
2,8 |
3,3 |
4,8 |
Таким образом,
порядок расчета случайной ошибки
измерения должен быть следующим:
а)
производят n измерений искомой физической
величины и вычисляют ее среднее значение

б) находят абсолютные
погрешности отдельных измерений
;
в)
рассчитывают среднюю квадратическую
погрешность среднего арифметического

г)
по заданной доверительной вероятности
и числу измерений n
находят из табл. 1.1 коэффициент Стьюдента
;
д) рассчитывают
доверительный интервал
;
е) окончательный
результат записывают в виде
при
.
Замечания.
Так как при малом числе измерений
является
случайной величиной и определяется с
большой погрешностью, то при записи
числового значения доверительного
интерваланеобходимо
учитывать это обстоятельство. В теории
ошибок доказано, что при числе измеренийn
10
в числовом значении
достаточно
оставить одну значащую цифру, если она
больше трех (),
и две, если первая из них меньше четырех
().
Затем числовое значение <X
>
округляют до разряда ошибки, например:
.
Точность вычислений
при обработке результатов измерений
нужно согласовать с точностью самих
измерений, ошибка вычислений должна
быть на порядок меньше ошибки измерений.
Систематические ошибки. Соотношение случайной и систематической ошибок
Систематические
ошибки могут существенно исказить
результат измерения, поэтому перед
началом измерений необходимо выявить
систематические ошибки и, если возможно,
исключить их. С этой целью проверяют
исправность используемых приборов,
правильность их установки, анализируют
метод измерения и т. д. Чаще всего
источником систематических погрешностей
являются неточности, допущенные при
изготовлении измерительных приборов,
такие погрешности называют инструментальными,
или приборными. Эти ошибки при изготовлении
приборов не определяют, а лишь
устанавливают, не превышают ли они
допустимые пределы. Предельная погрешность
обычно указывается в паспорте или
обозначается соответствующим условным
знаком на шкале прибора. Например, для
микрометра предельная погрешность
равна 0,004 мм,
для штангенциркуля –
0,05 мм
и
т. д.
Таким
образом, в результате обработки данных,
полученных при измерении, мы находим
случайную ошибку, величина которой
определяется полушириной доверительного
интервала
,
и ситематическую ошибку, равную предельной
погрешности:Если предельная допустимая погрешность
измерительного прибора не указана, то∆Хпр
берут равной половине цены наименьшего
деления шкалы прибора.
К
какому же отношению между величинами
случайной и систематической погрешностей
следует стремиться при проведении
измерений? По-видимому, определяющей
должна быть систематическая ошибка,
т.е., выбирая метод измерения и необходимое
число измерений, нужно добиваться, чтобы
была
меньше.
Если,
то пренебрегают систематической ошибкой,
прирассматривают только систематическую
ошибку. Может оказаться, что случайная
ошибка сравнима по величине с
систематической, тогда находят суммарную
ошибку
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Коэффициент Стьюдента является одной из самых важных статистических мер и используется для оценки статистической значимости различий между двумя сравниваемыми группами или средними значениями. Он был разработан английским статистиком Уильямом Госсетом, известным под псевдонимом Стьюдент, в начале 20 века. Коэффициент Стьюдента позволяет оценить степень различий между группами и определить, насколько вероятно, что эти различия являются реальными и не случайными.
Применение коэффициента Стьюдента широко распространено в различных областях науки, включая медицину, психологию, экономику, биологию и другие. Например, он используется для оценки эффективности лекарственных препаратов, сравнения результатов клинических исследований, анализа данных опросов и много других задач. При помощи коэффициента Стьюдента можно обнаружить статистически значимые различия между группами и принять обоснованные решения на основе полученных результатов.
Расчет коэффициента Стьюдента основан на сравнении двух групп и оценке различия между их средними значениями. Для этого нужно знать значения средних, стандартных отклонений и размеров выборок обеих групп. По результату расчета получается значение t-статистики, которое сравнивается с соответствующим доверительным интервалом и позволяет принять решение о статистической значимости различий. Чем больше значение t-статистики, тем больше различия между группами и тем более значимыми они являются.
Содержание
- История и суть коэффициента Стьюдента
- Применение коэффициента Стьюдента
- Как рассчитать коэффициент Стьюдента
- Значение и интерпретация коэффициента Стьюдента
- Статистическая значимость и коэффициент Стьюдента
- Альтернативные методы оценки статистической значимости
- Ошибки и предостережения при использовании коэффициента Стьюдента
- Вопрос-ответ
- Зачем нужен коэффициент Стьюдента?
- Как рассчитывается коэффициент Стьюдента?
- В каких областях применяется коэффициент Стьюдента?
- Как интерпретировать значение коэффициента Стьюдента?
История и суть коэффициента Стьюдента
Коэффициент Стьюдента, также известный как t-критерий, был разработан английским статистиком Уильямом Стьюдентом в 1908 году. Стьюдент работал под руководством Рональда Фишера, одного из основоположников современной статистики, и проводил исследования в области оценки среднего значения и дисперсии выборки.
Основная идея коэффициента Стьюдента заключается в том, чтобы оценить разницу между средними значениями двух выборок и определить, насколько эта разница статистически значима. Коэффициент Стьюдента является мерой отношения разницы между выборочным средним и гипотетическим средним к стандартной ошибке разности.
В основе расчета коэффициента Стьюдента лежит распределение Стьюдента, которое является вариацией нормального распределения и зависит от объема выборки и степеней свободы. Степени свободы определяются по числу наблюдений в выборке.
Коэффициент Стьюдента широко используется в статистике для проверки гипотез о различиях между средними значениями выборок. Он позволяет определить, является ли разница между выборочными средними статистически значимой или возникла случайно. Коэффициент Стьюдента также применяется при оценке доверительных интервалов и проведении регрессионного анализа.
Важно отметить, что использование коэффициента Стьюдента предполагает выполнение определенных предпосылок, таких как нормальность распределения и однородность дисперсий выборок. В противном случае результаты теста могут быть недостоверными.
Применение коэффициента Стьюдента
Коэффициент Стьюдента является важным инструментом статистического анализа данных. Он используется для определения статистической значимости различий между двумя наборами данных и для оценки достоверности полученных результатов. Применение коэффициента Стьюдента часто встречается в различных областях, таких как экономика, медицина, психология и других.
В основе применения коэффициента Стьюдента лежит предположение о нормальном распределении данных. Он используется для определения того, насколько различия в данных являются статистически значимыми или случайными. Если различия между двумя наборами данных являются статистически значимыми, это означает, что вероятность того, что эти различия могут быть получены случайно, очень низкая.
Применение коэффициента Стьюдента позволяет сравнить средние значения двух выборок и определить, есть ли между ними значимое различие. Обычно это делается с помощью t-теста, который вычисляет значение t-статистики и сравнивает его со значениями из таблицы распределения Стьюдента. Если значение t-статистики попадает в область отклонения, то различия считаются статистически значимыми, если нет — различия считаются случайными.
Применение коэффициента Стьюдента также распространено при оценке достоверности результатов и интервалов доверия. Коэффициент Стьюдента позволяет учесть случайную погрешность выборки и предсказать, насколько точными могут быть полученные результаты. Интервалы доверия, вычисленные с использованием коэффициента Стьюдента, позволяют определить диапазон значений, в которых с определенной вероятностью можно ожидать истинное значение показателя.
Таким образом, применение коэффициента Стьюдента является важным инструментом для проведения статистического анализа данных. Он позволяет определить статистическую значимость различий между выборками, оценить достоверность результатов и интервалы доверия. Умение правильно применять коэффициент Стьюдента позволяет сделать более обоснованные выводы на основе статистического анализа данных.
Как рассчитать коэффициент Стьюдента
Коэффициент Стьюдента (t-статистика) представляет собой стандартизированную меру разницы между средними значениями двух групп. Он используется для проверки статистической значимости различий между двумя группами данных.
Чтобы рассчитать коэффициент Стьюдента, необходимо выполнить следующие шаги:
- Провести две группы экспериментов или исследований, для которых хочется сравнить средние значения.
- Определить среднее значение и стандартное отклонение (СКО) для каждой группы.
- Вычислить разницу между средними значениями двух групп.
- Рассчитать стандартную ошибку разницы между средними значениями (стандартное отклонение разницы) с помощью формулы:
SE_diff = sqrt((SD_1^2 / n_1) + (SD_2^2 / n_2))
где SE_diff — стандартная ошибка разницы, SD_1 и SD_2 — стандартные отклонения для групп, а n_1 и n_2 — размеры групп.
- Рассчитать t-статистику с помощью формулы:
t = (M_1 — M_2) / SE_diff
где t — коэффициент Стьюдента, M_1 и M_2 — средние значения для групп, а SE_diff — стандартная ошибка разницы.
Полученное значение t-статистики может быть сравнено с табличными значениями для определения статистической значимости различий. Если значение t-статистики выше критического значения, то различия между группами считаются статистически значимыми.
Рассчет коэффициента Стьюдента может быть выполнен с помощью программного обеспечения для статистического анализа, такого как SPSS или Microsoft Excel, или с использованием специальных онлайн-калькуляторов.
Значение и интерпретация коэффициента Стьюдента
Коэффициент Стьюдента является одним из основных показателей статистической значимости и используется для определения значимости различий между двумя выборками. Значение коэффициента Стьюдента позволяет судить о том, насколько различаются две выборки и насколько эти различия статистически значимы.
Интерпретация значения коэффициента Стьюдента основывается на его показателях статистической значимости, которые выражаются в виде p-значения.
1. Если p-значение меньше заданного уровня значимости (обычно принимается уровень значимости 0,05 или 0,01), то различия между выборками считаются статистически значимыми. Это означает, что есть достаточно оснований полагать, что различия не случайны.
2. Если p-значение больше заданного уровня значимости, то различия между выборками не считаются статистически значимыми. Это означает, что различия могут быть случайными и не имеют статистической значимости.
Таким образом, значение коэффициента Стьюдента в сочетании с p-значением позволяет делать выводы о статистической значимости различий между выборками. Это является важным инструментом при проведении статистического анализа и позволяет выявлять закономерности и различия в исследуемой группе.
Статистическая значимость и коэффициент Стьюдента
Статистическая значимость – это показатель, который позволяет определить, является ли полученный результат статистически значимым или случайным. Она используется в статистике для оценки степени уверенности в полученных результатах и сравнении различных групп или выборок.
Коэффициент Стьюдента, или t-значение, является одним из наиболее распространенных показателей для оценки статистической значимости. Он позволяет определить разницу между средними значениями двух выборок и оценить вероятность того, что эта разница является статистически значимой.
Для расчета коэффициента Стьюдента необходимо знать средние значения и стандартные отклонения двух выборок, а также размер каждой выборки. После расчета коэффициента Стьюдента можно сопоставить полученное значение с табличным значением для определенного уровня значимости. Если полученное значение больше табличного, то разница считается статистически значимой.
Коэффициент Стьюдента является нормированной величиной и может принимать положительные и отрицательные значения. Знак коэффициента показывает, в какой группе среднее значение выше: если коэффициент положителен, то среднее значение в первой группе выше, если отрицателен – то во второй группе. Величина коэффициента позволяет определить степень разницы между группами: чем больше значение коэффициента, тем значительнее разница между группами.
Коэффициент Стьюдента широко используется в медицинских исследованиях, психологии, социологии и других областях, где требуется статистический анализ данных и сравнение групп или выборок. Он помогает определить, насколько вероятно, что различия между группами не случайны, и основываясь на этой информации, принять решение или сделать выводы.
Альтернативные методы оценки статистической значимости
Коэффициент Стьюдента является одним из наиболее распространенных инструментов для оценки статистической значимости различий между двумя выборками. Однако, существуют и другие методы, которые могут быть использованы для этой цели.
Метод Манна-Уитни — это непараметрический тест, который позволяет оценить статистическую значимость различий между двумя независимыми выборками. В отличие от коэффициента Стьюдента, данный метод не требует предположения о нормальном распределении данных. Вместо этого, он основан на рангах значений в выборках.
Метод Манна-Уитни вычисляет статистику U, которая представляет собой сумму ранжированных значений в одной из выборок. Тест проводится на основе гипотезы о том, что случайная величина в одной выборке статистически равна случайной величине в другой выборке. Если значение U статистически значимо отличается от ожидаемого, это может указывать на наличие различий между выборками.
Перестановочный тест — это еще один непараметрический тест, который может быть использован для оценки статистической значимости различий между выборками. В этом тесте значения из обеих выборок перемешиваются случайным образом, чтобы создать новые выборки. Затем вычисляется статистика на основе различий между новыми выборками.
Перестановочный тест позволяет оценить вероятность получения наблюдаемых различий между выборками в нулевой гипотезе, которая заключается в отсутствии различий. Если вероятность статистически низкая, то это указывает на наличие статистически значимых различий между выборками.
Анализ дисперсии (ANOVA) — это метод, который позволяет сравнивать средние значения трех или более независимых выборок. ANOVA предполагает, что данные имеют нормальное распределение и одинаковую дисперсию. Однако, существует и непараметрическая версия ANOVA, которая не требует этих предположений.
ANOVA вычисляет F-статистику, которая представляет собой отношение между объясненной и необъясненной дисперсией. Если F-статистика статистически значима, то это указывает на наличие различий между средними значениями выборок.
В заключение, коэффициент Стьюдента является важным инструментом для оценки статистической значимости различий между выборками. Однако, существуют и другие методы, такие как метод Манна-Уитни, перестановочный тест и ANOVA, которые могут быть использованы в случае, когда данные не соответствуют предположениям коэффициента Стьюдента.
Ошибки и предостережения при использовании коэффициента Стьюдента
1. Несоблюдение предпосылок:
Для применения коэффициента Стьюдента необходимо соблюдение определенных предпосылок. В случае их нарушения, результаты могут быть неверными или искаженными. Важно убедиться, что распределение данных является нормальным и выборки независимы друг от друга.
2. Размер выборки:
Коэффициент Стьюдента чувствителен к размеру выборки. При маленьком размере выборки может возникнуть нехватка информации для достоверного вычисления и интерпретации результатов. Идеально использовать коэффициент Стьюдента при выборках больших размеров (обычно более 30).
3. Значимость результатов:
Важно помнить, что коэффициент Стьюдента говорит о статистической значимости различий между группами, но не о практической значимости этих различий. При интерпретации результатов необходимо учитывать не только статистическую значимость, но и практическую значимость полученных результатов.
4. Учет множественных сравнений:
При проведении множественных сравнений с использованием коэффициента Стьюдента возникает риск ложных положительных результатов (ошибка первого рода). При таких сравнениях следует применять поправку на уровень значимости (например, метод Бонферрони), чтобы уменьшить этот риск.
5. Возможные проблемы с выборкой:
При выборочной работе могут возникнуть различные проблемы, связанные с некорректным выбором статистической единицы, исключением выбросов, пропусками данных и другими факторами. Если выборка не представляет всю популяцию или имеет проблемы, это может привести к неверным или необобщаемым результатам при использовании коэффициента Стьюдента.
6. Несоответствие другим методам:
Существуют и другие методы и тесты, которые можно использовать для сравнения групп или оценки статистической значимости. В некоторых случаях, использование коэффициента Стьюдента может быть неоптимальным. Поэтому всегда имеет смысл ознакомиться с альтернативными методами и выбрать подходящий для конкретного исследования.
7. Переоценка результатов:
Нельзя полагаться только на коэффициент Стьюдента и его результаты без учета других факторов и проверки предпосылок. Некорректное толкование результатов может привести к ошибочным выводам и неправильным решениям. Всегда важно анализировать данные с учетом контекста и других факторов.
Использование коэффициента Стьюдента требует аккуратности и внимания к деталям. Важно учитывать указанные предостережения, чтобы избежать неправильных результатов и ошибок в интерпретации.
Вопрос-ответ
Зачем нужен коэффициент Стьюдента?
Коэффициент Стьюдента используется для определения статистической значимости различий между средними значениями двух групп. Он позволяет оценить, насколько различия между группами статистически значимы.
Как рассчитывается коэффициент Стьюдента?
Коэффициент Стьюдента рассчитывается с использованием формулы: t = (X — μ) / (s / √n), где X — среднее значение выборки, μ — гипотетическое среднее значение генеральной совокупности, s — стандартное отклонение выборки, n — объем выборки. В зависимости от задачи используются различные формулы для расчета коэффициента Стьюдента.
В каких областях применяется коэффициент Стьюдента?
Коэффициент Стьюдента широко используется в статистике для анализа данных, сравнения средних значений, проверки гипотез и оценки статистической значимости различий между группами. Он применяется в различных областях, включая социологию, экономику, медицину, психологию и другие науки.
Как интерпретировать значение коэффициента Стьюдента?
Значение коэффициента Стьюдента позволяет судить о статистической значимости различий между группами. Если полученное значение t-статистики является большим, то различия между группами являются статистически значимыми. В противном случае, различия между группами считаются незначительными.
Погрешность вычислительного эксперимента.
Для оценки погрешности используют различные числовые характеристики:
Пусть x1, х2, … хnобозначают n результатов измерений величины, истинное значение которой X:
1. Среднее значение
Среднее значение величины находится по формуле:
Это среднее значение принимают за приближенное (наиболее вероятное) значение измеряемой величины.
2. Дисперсия
Дисперсия – среднеквадратичная погрешность. Рассеяние результатов измерений относительно среднего значения принято характеризовать дисперсией ΔS2:
3. Стандартное отклонение
4.
Абсолютная погрешность
Абсолютная погрешность результата – доверительный интервал – Δх – характеризует попадание случайной величины в доверительный интервал с доверительной вероятностью α:
,
где tα – коэффициент Стьюдента зависит от доверительной вероятности и числа проведенных экспериментов. В математической статистике коэффициент Стьюдента вычислен для различных значений, и его можно найти в таблице:
Таблица коэффициентов Стьюдента.
n α
0.80
0.90
0.95
0.98
0.99
0.995
0.998
0.999
1
3.0770
6.3130
12.7060
31.820
63.656
127.656
318.306
636.619
2
1.8850
2.9200
4.3020
6.964
9.924
14.089
22.327
31.599
3
1.6377
2.35340
3.182
4.540
5.840
7.458
10.214
12.924
4
1.5332
2.13180
2.776
3.746
4.604
5.597
7.173
8.610
5
1.4759
2.01500
2.570
3.649
4.0321
4.773
5.893
6.863
6
1.4390
1.943
2.4460
3.1420
3.7070
4.316
5.2070
5.958
7
1.4149
1.8946
2.3646
2.998
3.4995
4.2293
4.785
5.4079
8
1.3968
1.8596
2.3060
2.8965
3.3554
3.832
4.5008
5.0413
9
1.3830
1.8331
2.2622
2.8214
3.2498
3.6897
4.2968
4.780
10
1.3720
1.8125
2.2281
2.7638
3.1693
3.5814
4.1437
4.5869
Для n = 5 (число измерений) и α = 0.95, коэффициент Стьюдента — 2.570
Обычно для расчетов доверительного интервала пользуются значениями a=0,95; иногда достаточно a=0,90, но при ответственных измерениях требуется более высокая надежность (a = 0,99).
5.
Относительная погрешность
Относительная погрешность:
назад