Классической теории ошибок - Решение и исправление самых разных ошибок на TopOshibok.ru

Что такое ТМОГИ

16.05.2022

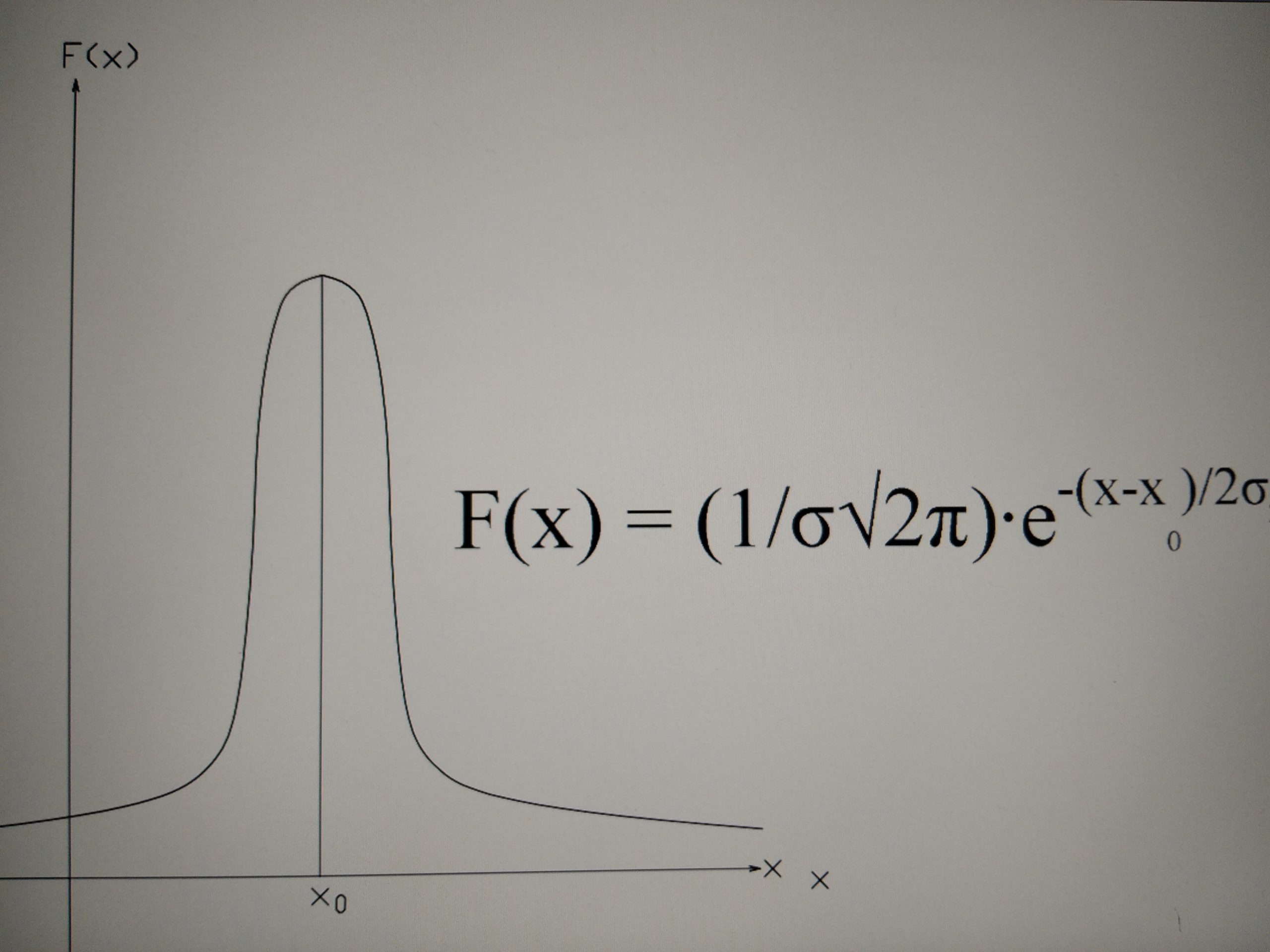
Теория математической обработки геодезических измерений.

Понятия и определения.

Измерения и наблюдения.

Каждый набор наблюдений называют выборкой. В результате наблюдений получают ограниченное число (n) значений случайной величины – это называется случайная выборка. Число n называют объёмом выборки. В зависимости от объема выборки применяются два метода обработки:

1. Метод индивидуальной обработки основан на применении формул теории вероятности. Его применяют тогда, когда объем наблюдений n < 50. Когда n > 50, применяется

2. Групповой метод обработки (в этом курсе не рассматривается).

Неисправленный результат наблюдения — результат наблюдения до введения поправок с целью устранения систематических погрешностей.

Исправленный результат наблюдения — результат наблюдения, получаемый после внесения поправок в неисправленный результат наблюдения.

Группа результатов наблюдений — совокупность результатов наблюдений, полученная при условиях, которые в соответствии с целью измерения необходимы для получения результата измерения с заданной точностью.

Неисправленный результат измерения — среднее арифметическое результатов наблюдений до введения поправок с целью устранения систематических погрешностей.

Исправленный результат измерений — результат измерения, получаемый после внесения поправок в неисправленный результат измерения.

Основными характеристиками измерений являются: 1) принцип, 2) метод, 3) погрешность, 4) точность, 5) правильность и 6) достоверность измерений.

1. Принцип измерений – это физическое явление или совокупность явлений, составляющих основу измерений. Например, определение массы тела взвешиванием основано на использовании пропорциональности массы (m) и силы тяжести (F_Т).

2. Метод измерений – совокупность приёмов использования принципов и средств измерений. Метод измерений представляет собой обязательный порядок действий, определяющий данный тип измерений независимо от принципа действия.

3. Погрешность измерений – отклонение результата измерения от истинного значения измеряемой величины.

4. Точность измерений – характеристика измерений, отражающая близость их результатов к истинному значению измеряемой величины.

5. Правильность измерений – качество измерений, отражающее близость к нулю систематической погрешности.

6. Достоверность измерений – степень доверия к результатам измерений. Измерения, для которых известны вероятностные характеристики отклонения результатов от истинного значения, относятся к категории достоверных.

Наряду с основными характеристиками измерений применяются понятия сходимости и воспроизводимости измерений. Сходимость измерений отражает близость друг к другу результатов измерений, выполненных в одинаковых условиях. Воспроизводимость измерений отражает близость друг к другу результатов измерений, выполненных при различных условиях (в разное время, в разных местах и т. д.).

Метод геодезических измерений – это совокупность приемов использования технологических принципов и технических средств измеренийгеодезических величин. В качестве геодезических величин выступают физические величины, значения которых определяются в результате выполнения геодезических измерений, а именно: длина линии (стороны); горизонтальный угол; вертикальный угол (зенитное расстояние или угол наклона); азимут; превышение; высота (отметка); координаты (приращения координат) точки.

Одна из главных задач измерений в процессе производства геодезических работ состоит не только в получении результата измерений, но и в оценке его достоверности. Этой задаче подчинена технология геодезических работ, обязательным условием построения которой является наличие избыточных измерений, обеспечивающих не только контроль работ, но и возможность количественной оценки их качества и надежности. Непосредственной целью измерений является определение истинных значений постоянной или изменяющейся измеряемой величины.

Результат измерений является реализацией случайной величины, равной сумме истинного значения измеряемой величины и погрешности-ошибки измерений. Чтобы узнать истинное значение измеряемой величины, нужно найти и исключить ошибки измерений.

Как правило, истинное значение измеряемой физической величины мы не знаем и никогда не узнаем, следовательно, и погрешность измерения мы не знаем и никогда не узнаем. Однако погрешность измерения можно охарактеризовать и оценить.

Происхождение ошибок измерений — объективное, закономерности их возникновения и действия изучаются в теории ошибок измерений и во всех геодезических дисциплинах; в геодезии это называется ТМОГИ — теория математической обработки геодезических измерений.

Теория ошибок решает следующие основные задачи:

Изучение законов распределения ошибок наблюдений.
Оценка точности непосредственно полученных результатов наблюдений и их функций.
Отыскание наиболее надежного значения определяемой величины и характеристики точности.
Установление допусков, ограничивающих использование результатов наблюдений в заданных пределах точности.

Ошибки подразделяются на грубые, систематические и случайные.

Грубые ошибки — это промахи (ляпы) в измерениях, вызванные невнимательностью наблюдателя, неисправностью инструмента или неучётом влияния внешней среды, которое не является пренебрегаемо малым. По своей природе промах − это случайная ошибка, но появляется она настолько редко, что её нельзя оценить, используя стандартные алгоритмы статистической обработки, и приходится применять свои особые методы. Их выявляют при обработке результатов измерений и исключают из рассмотрения, пользуясь определёнными правилами. Задача наблюдателя состоит в надлежащей организации контроля работ с целью своевременного устранения грубых ошибок из результатов измерений.

Систематические ошибки — происходят от определенного источника и имеют определенные знак и величину. Влияние такого рода ошибок может быть выражено функцией, связывающей результат измерений с каким-либо физическим фактором (например, с температурой). Систематические ошибки повторяются из опыта в опыт, от наблюдения к наблюдению, и имеют одно и то же значение. Из них можно выделить: поправки (уточняющие теорию, постоянные воздействия, и т.п.), неизвестного происхождения (недостаточно разработанная теория, сложный эксперимент) и, наконец, класс точности приборов. Чаще всего класс точности приборов считается основным источником систематических ошибок. Здесь задача наблюдателя состоит в том, чтобы исключить основную часть систематических ошибок из результатов измерений, а остаточное их влияние свести к пренебрегаемо малым величинам.

Случайные ошибки — ошибки измерений, закономерности которых проявляются в массе, и которые обусловлены точностью инструмента, квалификацией наблюдателя, неучтенными колебаниями внешних условий. Если систематическая ошибка может быть исключена из единичного измерения, то случайные ошибки, поскольку они являются одним из наиболее ярких примеров случайной величины, и их закономерности обнаруживаются только в массовом проявлении, — не могут быть устранены из единичного измерения. Их влияние можно лишь ослабить, повышая качество и количество измерений, а также надлежащей математической обработкой результатов измерений. Под величиной случайной ошибки имеют в виду разность между наблюдённым значением случайной величины и её истинным (точным) значением при условии исключения систематических ошибок.

Причин возникновения случайных ошибок измерений много: влияние внешних условий, неточности изготовления и юстировки приборов, неточности выполнения операций наблюдателем и т.д. Очевидно, что случайные ошибки являются результатом суммирования большого числа независимых элементарных ошибок. На основании центральной предельной теоремы Ляпунова можно считать, что случайные ошибки измерений подчиняются нормальному закону распределения (закону Гаусса): F(x) = (1/σ√2π)∙e^-(^x^—^x₀^)/2^σ², здесь х – случайная величина, х₀ – истинное или среднее значение (или математическое ожидание m_x), σ — среднее квадратичное отклонение.

Закон распределения Гаусса отражает следующие положения теории случайных погрешностей:

1) случайные погрешности обоих знаков встречаются одинаково часто;

2) меньшие случайные погрешности встречаются чаще, чем большие;

3) очень большие погрешности маловероятны.

Закон распределения Гаусса является типичным статистическим законом. Он подергался многократным экспериментальным проверкам, которые показали, что этот закон выполняется тем точнее, чем больше проведено наблюдений. Закон Гаусса имеет основополагающее значение для разработки критериев оценок точности измерений, а также при обработке результатов физических измерений.

Понятие о центральной предельной теореме.

Теорема, устанавливающая условия, при которых возникает нормальный закон, как предельный закон, известна в теории вероятностей под названием «центральной предельной теоремы», или теоремы А.М. Ляпунова.

Теорема Ляпунова может быть сформулирована так: если некоторая случайная величина есть сумма достаточно большого числа других случайных независимых величин, отклоняющихся от своих математических ожиданий на малые величины по сравнению с отклонением суммарной величины, то закон распределения этой суммарной случайной величины будет близок к нормальному. Теорема Ляпунова имеет большое значение для теории ошибок измерений. Можно полагать, что основные требования центральной предельной теоремы выполняются в отношении природы образования случайных ошибок измерений. В классической теории ошибок измерений принимают следующие два постулата:

1. считают, что при любых измерениях грубые ошибки отсутствуют, основная часть систематических ошибок исключена из результатов измерений, а остаточные систематические ошибки ничтожно малы, т.е. измерения сопровождаются только случайными ошибками Δ = х_i – X, (где х_i — результат измерений, Х — истинное значение измеряемой величины). Очевидно, что M(Δ) = 0, а M(х) = X, — центр распределения случайной величины х_i совпадает с истинным значением величины Х, то есть с её математическим ожиданием M(х) = X;

2. полагают также, что случайные ошибки измерений подчиняются нормальному закону распределения.

Примечание (8.207—ГОСТ—76): При числе результатов наблюдений n ≤ 15 принадлежность их к нормальному распределению не проверяют.

Ошибки абсолютные и относительные.

Абсолютная погрешность (абсолютная ошибка) измерения – отклонение результата измерения от истинного значения измеряемой величины.

Относительная погрешность (относительная ошибка) измерения – отношение абсолютной погрешности к истинному значению измеряемой величины X (если X неизвестно, его заменяют результатом измерения x). Относительную ошибку обычно выражают в виде дроби с числителем, равным 1, например: 1/m. Часто она выражается также в процентах.

Абсолютная ошибка измеряемой величины x имеет размерность величины x. Относительная ошибка вводится для оценки качества измерения; она, очевидно, безразмерна.

Поскольку мы никогда не знаем значения физической величины, значение абсолютной и относительной погрешностей нам также неизвестны. Под самой физической величиной понимают её наиболее вероятное значение, а под абсолютной и относительной погрешностями – их наиболее вероятные оценки.

В случае наличия серии прямых физических измерений за наиболее вероятное значение принимается среднее арифметическое значение.

По точности геодезические измерения различаются в широком диапазоне: относительная погрешность от 1-3*10^-3 до 0,5-2*10^-6. В топографо-геодезическом производстве точность измерений определяют классом выполняемых работ: ходы 1, 2 разрядов и повышенной точности.

Принято также измерения делить на: высокоточные, точные (средней точности), технические (малой точности), что связано с типом применяемых средств измерений. С классификацией измерений по точности тесно связаны понятия равноточные и неравноточные измерения.

В зависимости от количества (объема) получаемой информации геодезические измерения подразделяют на необходимые и избыточные. При необходимых измерениях располагают количеством измерений, достаточным для (однократного) однозначного нахождения значения геодезической величины. Избыточными называют измерения, выполненные сверх необходимого их количества. Наличие избыточных измерений является принципиальной особенностью геодезических измерений. Это позволяет не только повысить надежность результатов измерений, но и оценить их точность. Необходимыми называют величины, которые нужно знать (измерить), чтобы однократно найти значения искомых величин. Например, чтобы найти все шесть элементов плоского треугольника, необходимо измерить три его элемента, в числе которых была бы, по крайней мере, одна сторона. При математической обработке геодезических измерений необходимые величины называют необходимыми неизвестными (или параметрами).

Необходимые неизвестные, как и необходимые измеренные величины, можно выбирать, руководствуясь тем, чтобы последующие вычисления были возможно более простыми. Между необходимыми величинами никаких математических соотношений существовать не может.

Избыточными называют величины, измеренные сверх необходимых. Избыточно измеренные величины в геодезических построениях — засечки, ходы, сети — позволяют многократно находить значения искомых величин. Каждая избыточно измеренная величина непременно влечет появление математических соотношений между измеренными величинами. В этих соотношениях при подстановке в них измеренных значений величины, из-за неизбежных малых ошибок измерений будут возникать невязки.

Избыточные измерения позволяют обнаруживать промахи и просчёты, судить о точности измерений и найденных значений искомых величин.

На практике все величины всегда измеряются многократно, и в геодезических сетях всегда предусматриваются обязательные измерения избыточных величин. Поэтому в практике геодезических вычислений возникает и более общая задача — задача совместной обработки измерений, выполненных для определения не одной, а многих неизвестных величин. Получение наиболее надежных значений этих величин и их оценка точности составляют задачу т.н. уравнительных вычислений (уравнивания). Уравнивание выполняют по методу наименьших квадратов (МНК), согласно которому измеренные величины получают поправки v, удовлетворяющие условию [pv²] = min, гдеp — вес измерения. Карлом Гауссом и русским математиком А. Марковым доказано, что этот принцип приводит к наилучшим результатам для искомых неизвестных: они, при условии отсутствия систематических ошибок в измерениях, являются несмещёнными и обладают минимальной дисперсией (теория Гаусса-Маркова). Это утверждение справедливо и для любых функций уравненных неизвестных.

Задача уравнивания возникает именно потому, что число измерений n в геодезических построениях всегда больше числа необходимых неизвестных k, для определения которых и выполняют работы. Наличие избыточных измерений, число которых r = n — k, позволяет:

— выполнить контроль измерений,

— оценить их точность, и

— повысить точность уравненных неизвестных и их функций.

Погрешности вычислений.

При проведении расчётов приходится обычно работать с приближёнными числами. Математические действия над приближёнными значениями величин называются приближёнными вычислениями. При этом важно уметь оценивать точность полученных результатов. Погрешность получившегося результата зависит от многих причин. Погрешности, встречающиеся при расчётах, могут быть в основном подразделены на пять групп.

1. Погрешности, связанные с самой постановкой задачи. Математические модели отображают реальные явления с некоторой погрешностью, так как в процессе исследования приходится принимать некоторые упрощающие задачу предположения. Такие погрешности называют погрешностями задачи.

Иногда бывает и так, что решить задачу в точной постановке трудно или даже невозможно. Тогда её заменяют некоторой приближённой задачей. При этом возникает погрешность, которую можно называть погрешностью метода.

2. Погрешности, связанные с наличием бесконечных процессов в математическом анализе. Функции, применяемые в формулах, часто задаются

в виде бесконечных последовательностей или рядов. Многие уравнения можно решить, лишь описав бесконечные процессы, пределы которых и являются искомыми решениями. Так как бесконечный процесс, вообще говоря, не может быть завершён за конечное число шагов, то мы вынуждены остановиться на некотором члене последовательности, считая его приближением к искомому решению. Понятно, что такой обрыв процесса вызывает погрешность, которую называют обычно остаточной погрешностью.

3. Погрешности, связанные с наличием в расчётных зависимостях числовых параметров, значения которых могут быть определены лишь приближённо. Таковы, например, все физические константы, или результаты, получаемые при использовании всевозможных приборов. Такие погрешности называют начальными или неустранимыми.

4. Погрешности, связанные с системой исчисления или с конечностью разрядов чисел, используемых при вычислениях, называют погрешностью округления. Справа от запятой может быть бесконечное число цифр (например, может получиться бесконечная десятичная периодическая дробь). При вычислениях, очевидно, можно использовать лишь конечное число этих цифр. Приходится округлять также промежуточные и конечные результаты, если число значащих цифр в них больше, чем позволяет разрядность вычислительной машины. Так возникает погрешность округления.

5. Погрешности, связанные с действиями над приближёнными числами (погрешности действий). Понятно, что производя вычисления с приближёнными числами, погрешности исходных данных в какой-то мере мы переносим в результат вычислений. Конечно, при решении конкретной задачи те или иные погрешности иногда отсутствуют, или же влияние их ничтожно. Но, вообще говоря, для полного анализа погрешностей следует учитывать все их виды.

Запись приближённых чисел, т.е. приближённых численных значений величин, производится так, чтобы сам вид записи говорил о степени точности. Обычно их записывают так, что все цифры верны, кроме последней, сомнительной, в которой допускается ошибка не больше чем на единицу. К примеру, в равенствах R=100.35Ω и R=100.3500Ω для сопротивления есть огромная разница, поскольку эти записи свидетельствуют, что первое вычисление производилось с точностью до 0.01, а второе − до 0.0001Ω.

Округление результатов физических измерений начинается с погрешности.

Абсолютная погрешность Δх округляется до одной значащей цифры, если эта цифра больше 3, и до двух значащих цифр во всех остальных случаях (то есть, если эта цифра 1, 2 или 3). Например, если Δх = 0,523, то погрешность после округления содержит одну значащую цифру: Δх = 0,5. Если Δх = 0,123, то в результате округления погрешность содержит две значащие цифры: Δх = 0,12.

Знáчащими цифрами числá называют все цифры в его записи, начиная с первой ненулевой слева. Значащие цифры нумеруются слева направо. Например, в числах α = 0.03045, α = 0.0304500 значащими цифрами являются подчёркнутые цифры. Число значащих цифр в первом случае равно 4, во втором 6. Значащую цифру называют верной в широком смысле, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего этой цифре, или верной в узком смысле, если абсолютная погрешность числа не превосходит половины единицы разряда, соответствующего этой цифре.

Округление к ближайшему целому.

Округление к ближайшему целому — наиболее часто используемое округление, при котором число округляется до целого, модуль разности с которым у этого числа минимален. В общем случае, когда число в десятичной системе округляют до N-го знака, правило может быть сформулировано следующим образом: если N+1 знак < 5, то N-й знак сохраняют, а N+1 и все последующие обнуляют; если N+1 знак ≥ 5, то N-й знак увеличивают на единицу, а N+1 и все последующие обнуляют.

Например: 11,9 → 12; −0,9 → −1; −1,1 → −1; 2,5 → 3. Максимальная дополнительная абсолютная погрешность, вносимая при таком округлении (погрешность округления), составляет ±0,5 последнего сохраняемого разряда.

Но округление строго половины – к ближайшему чётному: 2,50 → 2; 5,50 → 6. Есть, правда, варианты.

Варианты округления 0,5 к ближайшему целому.

Отдельные правила округления существуют для специального случая, когда (N+1)-й знак = 5, а последующие знаки равны нулю («строгая» половина). Если во всех остальных случаях округление до ближайшего целого обеспечивает меньшую погрешность округления, то данный частный случай характерен тем, что для однократного округления формально безразлично, производить его «вверх» или «вниз» — в обоих случаях вносится погрешность ровно в 1/2 младшего разряда. Существуют следующие варианты правила округления до ближайшего целого для данного случая:

Математическое округление (описано выше) — округление всегда в бо́льшую по модулю сторону (предыдущий разряд всегда увеличивается на единицу).

Округление до ближайшего чётного (в английском языке известно под названием banker’s rounding — «округление банкира») — округление для этого случая происходит к ближайшему чётному числу, то есть 2,5 → 2; 3,5 → 4.

Случайное округление — округление происходит в меньшую или большую сторону в случайном порядке, но с равной вероятностью (может использоваться в статистике).

Чередующееся округление — округление происходит в меньшую или большую сторону поочерёдно.

Во всех вариантах в случае, когда (N+1)-й знак не равен 5 или последующие знаки не равны нулю, округление происходит по обычным правилам: 2,49 → 2; 2,51 → 3.

Математическое округление просто формально соответствует общему правилу округления. Его недостатком является то, что при округлении большого числа значений, которые далее будут обрабатываться совместно, может происходить накопление ошибки округления. Типичный пример: округление до целых рублей денежных сумм, выражаемых в рублях и копейках. В реестре из 10 000 строк (если считать копеечную часть каждой суммы случайным числом с равномерным распределением, что обычно вполне допустимо) окажется в среднем около 100 строк с суммами, содержащими в части копеек значение 50. При округлении всех таких строк по правилам математического округления «вверх» сумма «итого» по округлённому реестру окажется на 50 рублей больше точной. Три остальных варианта как раз и придуманы для того, чтобы уменьшить общую погрешность суммы при округлении большого количества значений. Округление «до ближайшего чётного» исходит из предположения, что при большом числе округляемых значений, имеющих 0,5 в округляемом остатке, в среднем половина из них окажется слева, а половина — справа от ближайшего чётного, таким образом, ошибки округления взаимно погасятся. Строго говоря, предположение это верно лишь тогда, когда набор округляемых чисел обладает свойствами случайного ряда, что обычно верно в бухгалтерских приложениях, где речь идёт о ценах, суммах на счетах и так далее. Если же предположение будет нарушено, то и округление «до чётного» может приводить к систематическим ошибкам. Для таких случаев лучше работают два следующих метода.

Два последних варианта округления гарантируют, что примерно половина специальных значений будет округлена в одну сторону, половина — в другую. Но реализация таких методов на практике требует дополнительных усилий по организации вычислительного процесса. Округление в случайную сторону требует для каждой округляемой строки генерировать случайное число. При использовании псевдослучайных чисел, создаваемых линейным рекуррентным методом, для генерации каждого числа требуется операция умножения, сложения и деления по модулю, что для больших объёмов данных может существенно замедлить расчёты. Чередующееся округление требует хранить флаг, показывающий, в какую сторону последний раз округлялось специальное значение, и при каждой операции переключать значение этого флага.

Правила оценки предельных погрешностей при выполнении операции над приближёнными числами:

1. При сложении или вычитании чисел их абсолютные погрешности складываются. Относительная погрешность суммы заключена между наибольшим и наименьшим значениями относительных погрешностей слагаемых, на практике принимается наибольшее значение.

2. При умножении или делении чисел друг на друга их относительные погрешности складываются. При возведении в степень приближённого числа его относительная погрешность умножается на показатель степени.

Критерии точности измерений.

Основным и наилучшим критерием точности результатов измерений является средняя квадратическая ошибка m — оценка среднего квадратического отклонения. Известно, что мерой разброса случайной величины вблизи центра распределения служат: её дисперсия и среднее квадратическое отклонение.

По определению среднее квадратическое отклонение равно корню квадратному из дисперсии: σ = √D, а D = Σ(х-х₀)²/n. Дисперсия D характеризует отклонение случайной величины от их общего среднего, и тем самым дает оценку общей надежности наблюдательного материала. Если результат отдельного измерения физической величины X есть нормально распределённая случайная величина, то, проводя измерения n раз, и, используя в качестве оценки истинного значения выборочное среднее в X, вычисленное по всем n измерениям, мы уменьшаем погрешность измерений в n раз.

Предельной ошибкой Δпред называют такую ошибку, больше которой в ряде измерений ошибок не должно быть. В качестве предельных выбирают величины, определяемые по правилу: Δпред=2m (для практических целей) и Δпред=3m (для исследовательских работ). Введение понятия предельной ошибки позволяет исключать из обработки результаты измерений с грубыми ошибками.

О точности вычислений.

Точность обработки числового материала должна быть согласована с точностью самих измерений. Вычисления, проведенные с бóльшим числом знаков, чем это необходимо, создают ложное впечатление о большой точности измерений. В то же время не следует ухудшать результаты измерений, грубо округляя измерения. Во всех случаях необходимо придерживаться правила: ошибка, получающаяся в результате вычислений должна быть на порядок (т.е. в 10 раз) меньше общей ошибки измерений.

Относительная погрешность всегда округляется до двух значащих цифр. И последнее. При расчёте необходимо оставлять (переписывать с калькулятора) минимум на один порядок больше, чем будет произведено последующее округление.

Источник

Основные
понятия теории ошибок.
Оценка точности
наблюдений.

Для
последующей ясности, в этой статье, под
наблюдениями будем подразумевать
совокупность одиночных измерений
определенной величины: разница в блеске,
показание шкалы микрометра и прочее.
Это величина называется измеряемой или
наблюдаемой. По особенности проведения,
все наблюдения можно разделить на две
группы: равноточные и неравноточные. К
первой категории относятся такие
наблюдения, которые были выполнены
одним человеком, на одном приборе
(инструменте) в сравнительно короткий
промежуток времени (то есть одинаковое
воздействие внешних факторов). Во вторую
категорию, естественно, попадают те
наблюдения, которые не соответствуют
одному, нескольким или всем условиям
принадлежности к равноточным наблюдениям.
В этой статье не будут описаны точностные
расчеты для наблюдений второй категории,
они более сложны и громоздки, и применяются
чаще в обработке геодезических измерений
и при комплексных астронаблюдениях.
Планируется подробно остановится на
неравноточных измерениях в следующей
статье из этого цикла, которая будет
содержать основные принципы совместного
уравнивания результатов наблюдений по
способу наименьших квадратов.

Типы
погрешностей наблюдений и особенности
их учета

Любое
измерение в реальных условиях производится
с погрешностью, которую можно разделить
на две составляющие — систематическую
и случайную. Систематическая погрешность
возникает в основном из-за ограниченной
точности измерительных приборов,
отчетных механизмов, а так же в связи с
отсутствием учета второстепенных
факторов, влияющих на измерения, или,
если этот учет ведется не корректно.
Систематические погрешности ведут к
одностороннему искажению результатов
наблюдений (постоянное завышение или
занижение значения измеряемой величины).
Их главная особенность — в ходе поверок
инструментов и тестовых измерений
вполне реально выявить такие погрешности
(найти их численные значения и знаки),
и тем самым свести их влияние на результаты
наблюдений к минимуму. Случайные
погрешности появляются из-за
непредсказуемых, хаотичных причин,
искажающих результаты наблюдений. Их
особенность в том, что они приводят к
получению разных значений измерений
при их многократных повторах, проведенных
в одинаковых условиях. Выявить случайные
погрешности из отдельных замеров
практически невозможно, но зато при
достаточном количестве однородных
измерений вполне реально «свести на
нет» их совокупное влияние на результаты
наблюдений. Такое минимизирование
случайных искажений данных основано
на ряде процедур, которые в свою очередь
базируются на выводах и следствиях
теории ошибок. Теория ошибок — математическая
дисциплина, изучающая законы и особенности
«поведения» погрешностей (ошибок)
измерений. Например, нормальное
распределение, эффект взаимной компенсации
по знакам и так далее. Возникла эта
дисциплина, как одно из многочисленных
«ответвлений» от Теории Вероятностей.
Математическая обработка различна для
обоих видов погрешностей. Учет
систематической составляющей есть
процесс почти уникальный для каждого
типа приборов и инструментов, для
различных природных и прочих факторов,
в том числе для каждого отдельного
наблюдателя (так называемая личная
ошибка, которую обычно классифицируют
как подтип систематической составляющей).
Случайные ошибки подчиняются универсальным
законам, которые можно применять не
только при наблюдениях разных объектов
и измерениях разных величин, но и в
разных науках — будь то астрономия,
физика или геодезия. Основные принципы
обработки везде одни и те же. Впрочем
существует еще один класс погрешностей
— грубая ошибка, или ложное измерение.

Точностной
расчет для серии равноточных наблюдений

Рассмотрим
алгоритм первичной обработки серии
равноточных наблюдений. Пусть мы получили
массив замеров измеряемой величины
«Х», который имеет вид: X1, X2, …, Xn,
где n — количество замеров на сеансе.

Находим
среднее арифметическое значение «Х»
на сеансе:

Xs
= ( X1 + X2 + … + Xn ) / n

Рассчитываем
отклонения среднего значения от
измеренных:

d1
= X1 — Xs, d2 = X2 — Xs, …, dn = Xn — Xs

Определяем
среднюю квадратическую погрешность
одного измерения, это параметр, который
характеризует среднюю точность
проведения одного замера:

MX
= SQR ( ( d1 ^ 2 + d2 ^ 2 + … + dn ^ 2 ) / ( n — 1 ) )

Находим
среднюю квадратическую ошибку среднего
арифметического, которая определяет
надежность полученного результата:

MXs
= MX / SQR ( n )

Рассчитываем
относительную погрешность результата
наблюдений:

U
( в процентах ) = ( MXs * 100% ) / Xs

Таким
образом, получаем, что наиболее вероятное
значение измеряемой величины на сеансе
имеет значение:

Xsv
= Xs + MXs

Особенности
точностного расчета для прямых и
косвенных измерений

По
признаку анализирования получаемой
при наблюдении информации, измерения
делятся на прямые и косвенные. При прямых
измерениях значение исследуемой величины
измеряют непосредственно, например
момент или промежуток времени. При
косвенных измерениях, искомую величину
рассчитывают по определенной формуле,
в которую входят величины, измеряемые
непосредственно, а так же заданные
значения вспомогательных величин и
констант, то есть можем записать: Y = F (
X1, X2, …, Xn ), где Y — искомая величина, а X1,
X2, …, Xn — ее аргументы, измеряемые
непосредственно. Пример косвенного
измерения: исходя из снятых отчетов по
окулярному микрометру, впоследствии
переходим к координатам объекта. Важной
задачей при обработке косвенных
наблюдений является определение
погрешности искомой величины по известным
погрешностям величин ее составляющих.
Формула, которая связывает эти параметры,
имеет следующий вид:

MY
= SQR ( ( ( dY / dX1 ) ^ 2 ) * MX1 ^ 2 + ( dY / dX2 ) ^ 2 ) * MX2 ^ 2
+ …
… +
( dY / dXn ) ^ 2 ) * MXn ^ 2 ),

где
( Di / dXi ) — частная производная функции Y
= F ( X1, X2, …, Xn ) по аргументу Xi, вычисленная
в точке Xi.

Пример:
А теперь еще раз «пробежимся» по
описанной выше методики оценки точности
проведенных наблюдений, но уже на базе
конкретного случая. При наблюдениях
деталей на диске Юпитера, на протяжении
ночи были сделаны несколько
зарисовок/фотографий. 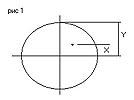На
всех рисунках/фотографиях отмечено
точечное образование, находящееся в
южном полушарии и медленно передвигающееся
параллельно экватору за счет суточного
вращения планеты. Задача: определить
широту наблюдаемого образования — по
всей видимости ядра нового мощного
антициклона, на которые богата бурная
юпитерианская атмосфера. С изображения
Юпитера снимем два линейных значения:
расстояние от экватора (его легко
прочертить учитывая значительное сжатие
планеты) до полюса — Y и расстояние от
экватора до зафиксированного образования.
(см. рис 1). Так как масштаб зарисовок/фотографий
может быть разным, вычислим для всех
изображений относительные значения
величины Х ( Y приравняем к единице).
Далее приводится таблица с примером
вычисления средних квадратических
погрешностей одного наблюдения и всего
результата.

Xs
= 2.88 / 8 = 0.360
MX = SQR ( 0.0114 / 8 — 1 ) = 0.040
MXs =
0.040 / SQR ( 8 ) = 0.014
U = ( 0.014 * 100% ) / 0.360 =
3.889%
Xsv = 0.360 + 0.014, или: 0.346 <= Xsv <= 0.374

Но,
результат получен в относительной
линейной мере. Переход к широте в градусах
осуществляется по формуле: B = ARCSIN ( X / Y
), а с учетом того, что Y — единичный
отрезок: Bs = ARCSIN ( X ) = ARCSIN ( 0.360 ) = 21.1002° =
21° 06.01′ Для вычисления средней квадратической
погрешности определения широты объекта
в градусной мере, воспользуемся выражением
описанным в параграфе о прямых и косвенных
наблюдениях, принимая во внимание, что
Y — константа ( Y = 1 ). Находим производную
функции B ( X ): ( dB / dX ) = 1 / SQR ( 1 — X ^ 2 ).
Вычисляем погрешность результата
наблюдений в градусной мере: MBsv = ( r * MXs
) / SQR ( 1 — Xs ^ 2 ), где r — коэффициент перехода
из радианной меры в градусную ( r = 57.2958
). MBsv = (r * 0.014 ) / SQR ( 1 — 0.360 ^ 2 ) = 0.8598° = 51.59′. U
=( 0.8598 * 100% ) / 21.002 = 4.094%

Итог:
Средняя вероятная широта образования,
зафиксированного на диске Юпитера,
составляет: Bsv = 21° 06.01′ + 51.59′, или: 20°14.42′
<= Bsv <= 21°57.60′.

Все
описанные в этой статье этапы обработки
легко программируются (для нахождения
частных производных можно воспользоваться
одним из численных методов, например
Рунге — Кутта), и поэтому впоследствии
не будут отнимать почти никакого времени
— необходимо только создать массив или
файл исходных данных — значений измеренных
величин. Стоит еще добавить, что точностной
расчет проведенных измерений помимо
своего основного назначения (оценка
надежности исследований) имеет еще и
другую немаловажную роль. Проводя изо
дня в день, из месяца в месяц определенный
вид работ, наблюдатель может следить,
как в динамике прогрессирует (или
регрессирует) достоверность и качество
информации, источником которой он
является, то есть проводить своеобразный
самоконтроль. И будет очень неплохо,
если последняя в этой статье фраза в
скобках так и останется «закрытой».

5.
В технических характеристиках приборов
приведены различные данные диапазонов
измерения
и отображения.
В диапазонах
измерения
наших приборов
представлены пределы измерений
с учетом внешних активных сопротивлений
измерительных проводников стандартной
…

Соседние файлы в папке Лабораторные работы

#
#
#
#
02.05.201416.9 Кб31Расчеты к лабе2.xls

Источник

Тео́рия оши́бок, раздел математической статистики, посвящённый построению выводов о численных значениях приближённо измеренных величин и об ошибках (погрешностях) измерений. Повторные измерения одной и той же постоянной величины дают, как правило, различные результаты, т. к. каждое измерение содержит некоторую ошибку. Различают три основных вида ошибок: систематические, грубые и случайные. Систематические ошибки постоянно либо преувеличивают, либо преуменьшают результаты измерений и происходят от определённых причин (неправильной установки измерительных приборов, влияния окружающей среды и т. д.), систематически влияющих на результаты измерений и изменяющих их в одном направлении. Оценка систематических ошибок производится с помощью методов, выходящих за пределы математической статистики. Например, в астрономии при измерении величины угла между направлением на светило и плоскостью горизонта систематическая ошибка является суммой двух ошибок: систематической ошибки, которую даёт прибор при отсчёте данного угла (инструментальная ошибка) и систематической ошибки, обусловленной преломлением лучей света в атмосфере (рефракция). Инструментальная ошибка учитывается с помощью таблицы или графика поправок для данного прибора; ошибку, связанную с рефракцией (для углов, меньших 80°), можно достаточно точно вычислить теоретически. Грубые ошибки возникают в результате просчёта, неправильного чтения показаний измерительного прибора и т. п. Результаты измерений, содержащие грубые ошибки, как правило, сильно отличаются от других результатов измерений и поэтому часто бывают хорошо заметны. Случайные ошибки происходят от различных случайных причин, действующих при каждом из отдельных измерений непредсказуемым образом то в сторону уменьшения, то в сторону увеличения результата.

Теория ошибок занимается изучением лишь случайных и грубых ошибок. Основные задачи теории ошибок: определение законов распределения случайных ошибок, построение статистических оценок неизвестных величин по результатам измерений, вычисление погрешностей таких оценок и устранение грубых ошибок.

Пусть в результате nn независимых измерений некоторой неизвестной величины μ\mu получены значения X1,X2,…,XnX_1,X_2,\dots,X_n. Разности

δ1=X1−μ, δ2=X2−μ, …, δn=Xn−μ\delta_1=X_1-\mu,\, \delta_2=X_2-\mu, \,\dots, \, \delta_n=X_n-\muназываются истинными ошибками; в терминах вероятностной теории ошибок все δi\delta_i рассматриваются как случайные величины, независимость измерений понимается как взаимная независимость случайных величин δ1,…,δn\delta_1, \dots, \delta_n. При этом измерения называются равноточными (в широком смысле), если эти величины имеют одно и то же распределение. Т. о., истинные ошибки равноточных измерений суть независимые одинаково распределённые случайные величины. При этом математическое ожидание истинных ошибок b=Eδ1=…=Eδnb=\text{E}\delta_1=\ldots =\text{E}\delta_n называется систематической ошибкой, а разности δ1−b,…,δn−b\delta_1-b,\dots,\delta_n-b – случайными ошибками. Отсутствие систематической ошибки означает, что b=0b=0, в этом случае δ1,…,δn\delta_1,\dots,\delta_n суть случайные ошибки. Величину 1/(2σ)1/(\sqrt{2}\sigma), где σ\sigma – квадратичное отклонение ошибок δ1,…,δn\delta_1,\dots,\delta_n, называют мерой точности (при наличии систематической ошибки мера точности есть 1/2(b2+σ2)1/\sqrt{2(b^2+\sigma^2)}. Равноточность измерений в узком смысле понимается как одинаковость меры точности всех результатов измерений. Наличие грубых ошибок означает нарушение равноточности (как в широком, так и в узком смысле) для некоторых отдельных измерений.

В качестве оценки неизвестной величины μ \mu обычно берут арифметическое среднее из результатов измерений X1,…,XnX_1,\dots,X_n:

X‾=1n∑i=1nXi,\displaystyle\overline X=\frac{1}{n}\sum^n_{i=1}X_i,а разности Δ1=X1−X‾,…,Δn−X‾\Delta_1=X_1- \overline X, \dots, \Delta_n — \overline X называются кажущимися ошибками. Выбор X‾\overline X в качестве оценки для μ\mu основан на том, что при достаточно большом числе nn равноточных измерений, лишённых систематической ошибки, оценка X‾\overline X с вероятностью, сколь угодно близкой к единице, сколь угодно мало отличается от неизвестной величины μ\mu (это связано с Законом больших чисел); оценка X‾\overline X лишена систематической ошибки (оценки с таким свойством называются несмещёнными оценками); дисперсия этой оценки есть

DX‾=E(X‾−μ)2=σ2/n.\text D\overline X=\text E(\overline X-\mu)^2=\sigma^2/n.Опыт показывает, что практически очень часто случайные ошибки имеют распределения, близкие к нормальным (это объясняется центральной предельной теоремой). В этом случае распределение величины X‾\overline X мало отличается от нормального распределения с математическим ожиданием μ\mu и дисперсией σ2/n\sigma^2/n. Если распределение величин δ1,…,δn\delta_1,\dots,\delta_n в точности нормально, то дисперсия всякой другой несмещённой оценки для μ\mu, например медианы, не меньше DX‾\text D\overline X. Если же распределение величин δ1,…,δn\delta_1,\dots,\delta_n отлично от нормального, то последнее свойство может не иметь места.

Если дисперсия σ2\sigma^2 отдельных измерений заранее неизвестна, то для её оценки пользуются величиной

s2=1n−1∑i=1nΔi2;\displaystyle s^2=\frac{1}{n-1}\sum^n_{i=1}\Delta^2_i;

s2s^2 – несмещённая оценка для σ2\sigma^2, т. к. Es2=σ2\text E s^2=\sigma^2.

Если случайные ошибки δ1,…,δn\delta_1,\dots,\delta_n имеют нормальное распределение, то отношение

t=(X‾−μ)nst=\dfrac{(\overline X -\mu)\sqrt{n}}{s}имеет распределение Стьюдента с n−1n-1 степенью свободы. Этим можно воспользоваться для оценки погрешности приближённого равенства μ≈X‾\mu \approx \overline X (см. Метод наименьших квадратов). Величина

χ2=(n−1)s2σ2\chi^2=\dfrac{(n-1)s^2}{\sigma^2}при тех же предположениях имеет распределение хи-квадрат с n−1n-1 степенью свободы. Это позволяет оценить погрешность приближённого равенства σ≈s\sigma \approx s. Относительная погрешность ∣s−σ∣/s|s-\sigma|/s не превосходит числа qq с вероятностью

ω=F(z2,n−1)−F(z1,n−1),\omega=F(z^2,n-1)-F(z_1,n-1),
где F(z,n−1)F(z, n-1) – функция распределения хи-квадрат, а

z1=n−11+q,z2=n−11−q.z_1=\dfrac{\sqrt{n-1}}{1+q},\quad z_2 = \dfrac{\sqrt{n-1}}{1-q}.

Опубликовано 1 августа 2022 г. в 13:27 (GMT+3). Последнее обновление 1 августа 2022 г. в 13:27 (GMT+3).

Источник

На чтение 9 мин Просмотров 2к. Опубликовано 03.10.2021

Теория ошибок измерений изучает свойства ошибок и законы их распределения, методы обработки измерений с учетом их ошибок, а также способы вычисления числовых характеристик точности измерений. При многократных измерениях одной и той же величины результаты измерений получаются неодинаковыми. Этот очевидный факт говорит о том, что измерения сопровождаются разными по величине и по знаку ошибками. Задача теории ошибок – нахождение наиболее надежного значения измеренной величины, оценка точности результатов измерений и их функций и установление допусков, ограничивающих использование результатов обработки измерений.

По своей природе ошибки бывают грубые, систематические и случайные.

Грубые ошибки являются результатом промахов и просчетов. Их можно избежать при внимательном и аккуратном отношении к работе и организации надежного полевого контроля измерений. В теории ошибок грубые ошибки не изучаются.

Систематические ошибки имеют определенный источник, направление и величину. Если источник систематической ошибки обнаружен и изучен, то можно получить формулу влияния этой ошибки на результат измерения и затем ввести в него поправку; это исключит влияние систематической ошибки. Пока источник какой-либо систематической ошибки не найден, приходится считать ее случайной ошибкой, ухудшающей качество измерений.

Случайные ошибки измерений обусловлены точностью способа измерений (строгостью теории), точностью измерительного прибора, квалификацией исполнителя и влиянием внешних условий. Закономерности случайных ошибок проявляются в массе, то-есть, при большом количестве измерений; такие закономерности называют статистическими. Освободить результат единичного измерения от случайных ошибок невозможно; невозможно также предсказать случайную ошибку единичного измерения. Теория ошибок занимается в основном изучением случайных ошибок.

Случайная истинная ошибка измерения Δ – это разность между измеренным значением величины l и ее истинным значением X:
(1.25)

Свойства случайных ошибок. Случайные ошибки подчиняются некоторым закономерностям:

1. при данных условиях измерений абсолютные значения случайных ошибок не превосходят некоторого предела; если какая-либо ошибка выходит за этот предел, она считается грубой,
2. положительные и отрицательные случайные ошибки равновозможны,
3. среднее арифметическое случайных ошибок стремится к нулю при неограниченном возрастании числа измерений. Третье свойство случайных ошибок записывается так:
(1.26)
4. малые по абсолютной величине случайные ошибки встречаются чаще, чем большие.

Кроме того, во всей массе случайных ошибок не должно быть явных закономерностей ни по знаку, ни по величине. Если закономерность обнаруживается, значит здесь сказывается влияние какой-то систематической ошибки.

Средняя квадратическая ошибка одного измерения. Для оценки точности измерений можно применять разные критерии; в геодезии таким критерием является средняя квадратическая ошибка. Это понятие было введено Гауссом; он же разработал основные положения теории ошибок. Средняя квадратическая ошибка одного измерения обозначается буквой m и вычисляется по формуле Гаусса:
(1.27)

где: ;
n – количество измерений одной величины.

Средняя квадратическая ошибка очень чувствительна к большим по абсолютной величине ошибкам, так как каждая ошибка возводится в квадрат. В то же время она является устойчивым критерием для оценки точности даже при небольшом количество измерений; начиная с некоторого n дальнейшее увеличение числа измерений почти не изменяет значения m; доказано, что уже при n = 8 значение m получается достаточно надежным.

Предельная ошибка ряда измерений обозначается Δпред; она обычно принимается равной 3*m при теоретических исследованиях и 2*m или 2.5*m при практических измерениях. Считается, что из тысячи измерений только три ошибки могут достигать или немного превосходить значение Δпред = 3*m.

Отношение mx/X называется средней квадратической относительной ошибкой; для некоторых видов измерений относительная ошибка более наглядна, чем m. Относительная ошибка выражается дробью с числителем, равным 1, например, mx/X = 1/10 000.

Средняя квадратическая ошибка функции измеренных величин. Выведем формулу средней квадратической ошибки функции нескольких аргументов произвольного вида:

F = f( X, Y, Z … ), (1.28)

здесь: X, Y, Z … – истинные значения аргументов,
F – истинное значение функции.

В результате измерений получены измеренные значения аргументов lX, lY, lZ, при этом:
(1.29)

где ΔX, ΔY, ΔZ – случайные истинные ошибки измерения аргументов.

Функцию F можно выразить через измеренные значения аргуметов и их истинные ошибки:

Разложим функцию F в ряд Тейлора, ограничившись первой степенью малых приращений ΔX, ΔY, ΔZ:
(1.30)

Разность является случайной истинной ошибкой функции с противоположным знаком, поэтому:
(1.31)

Если выполнить n измерений аргументов X, Y, Z, то можно записать n уравнений вида (1.31). Возведем все эти уравнения в квадрат и сложим их; суммарное уравнение разделим на n и получим

В силу третьего свойства случайных ошибок члены, содержащие произведения случайных ошибок, будут незначительными по величине, и их можно не учитывать; таким образом,
(1.32)

Как частные случаи формулы (1.32) можно написать выражения для средней квадратической ошибки некоторых функций:

Если функция имеет вид произведения нескольких аргументов,

F = x * y * z,

то для нее можно записать выражение относительной ошибки функции:
(1.33)

которое в некоторых случаях оказывается более удобным, чем формула (1.32).

Принцип равных влияний. В геодезии часто приходится определять средние квадратические ошибки аргументов по заданной средней квадратической ошибке функции. Если аргумент всего один, то решение задачи не представляет трудности. Если число аргументов t больше одного, то возникает задача нахождения t неизвестных из одного уравнения, которую можно решить, применяя принцип равных влияний. Согласно этому принципу все слагаемые правой части формулы (1.32) или (1.33) считаются равными между собой.

Арифметическая середина. Пусть имеется n измерений одной величины X, то-есть,
(1.34)

Сложим эти равенства, суммарное уравнение разделим на n и получим:
(1.35)

Величина (1.36)

называется средним арифметическим или простой арифметической серединой. Запишем (1.35) в виде

по третьему свойству ошибок (1.26) можно написать:

что означает, что при неограниченном возрастании количества измерений простая арифметическая середина стремится к истинному значению измеряемой величины. При ограниченном количестве измерений арифметическая середина является наиболее надежным и достоверным значением измеряемой величины.

Запишем формулу (1.36) в виде

и подсчитаем среднюю квадратическую ошибку арифметической середины, которая обозначается буквой M. Согласно формуле (1.32) напишем:

или

Но ml1 = ml2 = … = mln= m по условию задачи, так как величина X измеряется при одних и тех же условиях. Тогда в квадратных скобках будет n * m2, одно n сократится и в итоге получим:

M2 = m2/n

или
(1.37)

то-есть, средняя квадратическая ошибка арифметической середины в корень из n раз меньше ошибки одного измерения.

Вычисление средней квадратической ошибки по уклонениям от арифметической середины. Формулу Гаусса (1.27) применяют лишь в теоретических выкладках и при исследованиях приборов и методов измерений, когда известно истинное значение измеряемой величины. На практике оно, как правило, неизвестно, и оценку точности выполняют по уклонениям от арифметической середины.

Пусть имеется ряд равноточных измерений величины X:

l1, l2 , …, ln .

Вычислим арифметическую середину X0 = [1]/n и образуем разности:
(1.38)

Сложим все разности и получим [l] – n * X0 = [V]. По определению арифметической середины n * X0 = [l], поэтому:

[V] = 0. (1.39)

Величины V называют вероятнейшими ошибками измерений; именно по их значениям и вычисляют на практике среднюю квадратическую ошибку одного измерения, используя для этого формулу Бесселя:
(1.40)

Приведем вывод этой формулы. Образуем разности случайных истинных ошибок измерений Δ и вероятнейших ошибок V:
(1.41)

Разность (X0 – X) равна истинной ошибке арифметической середины; обозначим ее Δ0 и перепишем уравнения (1.41):
(1.42)
Возведем все уравнения (1.42) в квадрат, сложим их и получим:
.

Второе слагаемое в правой части этого выражения равно нулю по свойству (1.39), следовательно,
.

Разделим это уравнение на n и учтя, что [Δ2]/n =m2, получим:
(1.43)

Заменим истинную ошибку арифметической середины Δ0 ее средней квадратической ошибкой ; такая замена практически не изменит правой части формулы (1.43). Итак,

,
откуда ;

после перенесения (n-1) в правую часть и извлечения квадратного корня получается формула Бесселя (1.40).

Для вычисления средней квадратической ошибки арифметической середины на основании (1.37) получается формула:
(1.44)

Веса измерений. Измерения бывают равноточные и неравноточные. Например, один и тот же угол можно измерить точным или техническим теодолитом, и результаты таких измерений будут неравноточными. Или один и тот же угол можно измерить разным количеством приемов; результаты тоже будут неравноточными. Понятно, что средние квадратические ошибки неравноточных измерений будут неодинаковы. Из опыта известно, что измерение, выполненное с большей точностью (с меньшей ошибкой), заслуживает большего доверия.

Вес измерения – это условное число, характеризующее надежность измерения, степень его доверия; вес обозначается буквой p. Значение веса измерения получают по формуле:

p = C/m2 (1.45)

где C – в общем случае произвольное положительное число.

При неравноточных измерениях одной величины наиболее надежное ее значение получают по формуле средневесовой арифметической середины:
(1.46)
или X0 = [l*p] / [p] .

Ошибку измерения, вес которого равен 1, называют средней квадратической ошибкой единицы веса; она обозначается буквой m. Из формулы (1.45) получаем

откуда (1.47)

то-есть, за число C принимают квадрат ошибки единицы веса.

Подсчитаем вес P средневесовой арифметической середины. По определению веса имеем:
(1.48)

Согласно (1.46) и (1.32) напишем:

Подставим сюда вместо mli2 их выражения через вес m2 = C/p , тогда:

Подставим это выражение в формулу (1.48) и получим,

P = [p], (1.49)

то-есть, вес средневесовой арифметической середины равен сумме весов отдельных измерений.

В случае равноточных измерений, когда веса всех измерений одинаковы и равны единице, формула (1.49) принимает вид:

P = n. (1.50)

При обработке больших групп измерений (при уравнивании геодезических построений по МНК) вычисляются значение ошибки единицы веса, веса измерений и других элементов после уравнивания, а ошибка любого уравненного элемента подсчитывается по формуле:
(1.51)

где pi – вес i-того элемента.

Источник