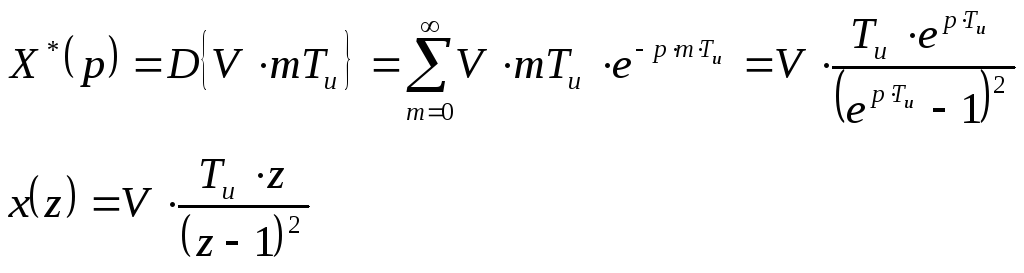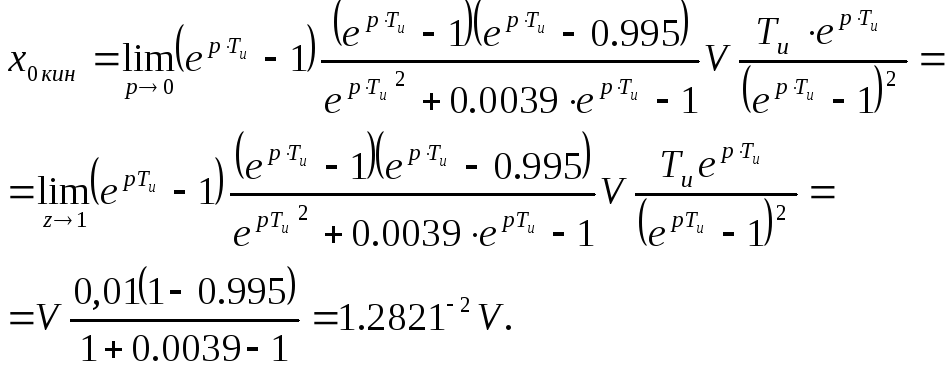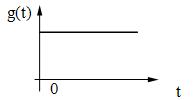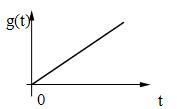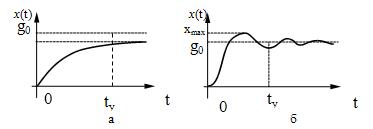-
Определение статической и кинетической ошибки замкнутой импульсной сау.
Передаточная
функция системы относительно ошибки
равна:
Тогда статистическая
ошибка при
:
Кинетическая
ошибка имеет место, когда входной
является функция, изменяющаяся по
линейному закону:
или
Дискретное
преобразование Лапласа указанного
сигнала:
С учетом этого
кинетическая ошибка будет равна:
Оглавление
Студент 1
Преподаватель 1
Задание
на расчет. 2
1 Преобразовать
исходную структурную схему к типовому
виду; определить непрерывную
передаточную функцию приведенной
непрерывной части разомкнутой импульсной
системы ; 2
2 По найти дискретную
передаточную функцию разомкнутой
импульсной системы ; 2
3 Построить годограф
разомкнутой импульсной САУ: 2
a.) По выражению
; 2
b.) По годографу 2
4 Оценить устойчивость
замкнутой импульсной САУ и найти
предельный коэффициент усиления: 2
a.) По критерию
Найквиста; 2
b.) По критерию
Гурвица; 2
c.) По корням
характеристического уравнения 2
5 Построить
переходной процесс для замкнутой
импульсной САУ. 2
6 Определить
статическую и кинетическую ошибки
замкнутой импульсной САУ. 2
7 Провести сравнение
расчетных результатов с данными,
полученными на основе пакета прикладных
программ. 2
1 Преобразование
исходной структурной схемы к типовому
виду; определение непрерывной
передаточной функции приведенной
непрерывной части разомкнутой импульсной
системы . 3
2 Нахождение
дискретной передаточной функции
разомкнутой импульсной системы по . 4
3 Построение
годографа разомкнутой импульсной
САУ: 4
a.) По выражению
; 4
b.) По годографу 5
4 Оценка устойчивости
замкнутой импульсной САУ и нахождение
предельного коэффициента усиления: 6
a.) По критерию
Найквиста; 6
b.) По критерию
Гурвица; 7
5 Построение
переходного процесса для замкнутой
импульсной САУ при К=0.9137. 8
6 Определение
статической и кинетической ошибки
замкнутой импульсной САУ. 10
Соседние файлы в папке Вариант № 90
- #
- #
24.02.2016187.27 Кб59Программа.xmcd
-
Определение статической и кинетической ошибки замкнутой импульсной сау.
Передаточная
функция системы относительно ошибки
равна:
Тогда статистическая
ошибка при
:
Кинетическая
ошибка имеет место, когда входной
является функция, изменяющаяся по
линейному закону:
или
Дискретное
преобразование Лапласа указанного
сигнала:
С учетом этого
кинетическая ошибка будет равна:
Оглавление
Студент 1
Преподаватель 1
Задание
на расчет. 2
1 Преобразовать
исходную структурную схему к типовому
виду; определить непрерывную
передаточную функцию приведенной
непрерывной части разомкнутой импульсной
системы ; 2
2 По найти дискретную
передаточную функцию разомкнутой
импульсной системы ; 2
3 Построить годограф
разомкнутой импульсной САУ: 2
a.) По выражению
; 2
b.) По годографу 2
4 Оценить устойчивость
замкнутой импульсной САУ и найти
предельный коэффициент усиления: 2
a.) По критерию
Найквиста; 2
b.) По критерию
Гурвица; 2
c.) По корням
характеристического уравнения 2
5 Построить
переходной процесс для замкнутой
импульсной САУ. 2
6 Определить
статическую и кинетическую ошибки
замкнутой импульсной САУ. 2
7 Провести сравнение
расчетных результатов с данными,
полученными на основе пакета прикладных
программ. 2
1 Преобразование
исходной структурной схемы к типовому
виду; определение непрерывной
передаточной функции приведенной
непрерывной части разомкнутой импульсной
системы . 3
2 Нахождение
дискретной передаточной функции
разомкнутой импульсной системы по . 4
3 Построение
годографа разомкнутой импульсной
САУ: 4
a.) По выражению
; 4
b.) По годографу 5
4 Оценка устойчивости
замкнутой импульсной САУ и нахождение
предельного коэффициента усиления: 6
a.) По критерию
Найквиста; 6
b.) По критерию
Гурвица; 7
5 Построение
переходного процесса для замкнутой
импульсной САУ при К=0.9137. 8
6 Определение
статической и кинетической ошибки
замкнутой импульсной САУ. 10
Соседние файлы в папке Вариант № 90
- #
- #
24.02.2016187.27 Кб58Программа.xmcd
Точность систем управления является
важнейшим показателем их качества. Чем выше точность, тем выше качество
системы. Однако предъявление повышенных требований к точности вызывает
неоправданное удорожание системы, усложняет ее конструкцию. Недостаточная
точность может привести к несоответствию характеристик системы условиям
функционирования и необходимости ее повторной разработки. Поэтому на этапе
проектирования системы должно быть проведено тщательное обоснование требуемых
показателей точности.
В этом разделе рассматриваются методы
определения ошибок, возникающих при работе систем управления с детерминированными
входными воздействиями. Вначале анализируются ошибки систем в переходном
режиме. Затем особое внимание уделено простым способам расчета ошибок систем в
установившемся режиме. Будет показано, что все системы управления можно разделить
по величине установившихся ошибок на системы без памяти, так называемые статические
системы, и системы, обладающие памятью, – астатические
системы управления.
Типовые
входные воздействия
Для оценки качества работы систем
управления рассматривают их поведение при некоторых типовых воздействиях.
Обычно такими воздействиями служат следующие три основные вида функций:
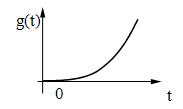
а) ступенчатое воздействие: g(t) = 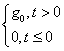
;
б) линейное воздействие: g(t) = t , t > 0
; ;
в) квадратичное воздействие:
/2 , t > 0 ;
g(p) = .
В
некоторых случаях рассматривают обобщенное полиномиальное воздействие:
, t > 0.
Ступенчатое воздействие является одним
из простейших, но именно с его помощью определяется ряд важных свойств систем
управления, связанных с видом переходного процесса. Линейное и квадратичное
воздействия часто бывают связаны с задачами слежения за координатами
движущегося объекта. Тогда линейное воздействие соответствует движению объекта
с постоянной скоростью; квадратичное — движению объекта с постоянным ускорением.
Переходные процессы при типовых
воздействиях можно построить следующим образом. Пусть задана передаточная
функция замкнутой системы управления W(p). Тогда
x(p)
= W(p) g(p),
где g(p) – изображение соответствующего воздействия.
Например, если , то
и для g(t) = g0
получим .
С помощью вычетов или по таблицам
находим обратное преобразование Лапласа и получаем вид переходного процесса x(t)
для заданного входного воздействия:
,
где Res
x(p)
– вычет функции x(p)
в точке a.
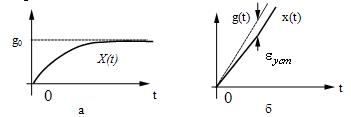
Обычно реакция системы на ступенчатое
воздействие имеет вид, показанный на рис. 21,а или рис. 21,б.
Рис.
21.
Переходный процесс,
как правило, характеризуют двумя параметрами – длительностью переходного
процесса (временем установления) и величиной перерегулирования.
Под временем установления tу
понимают временной интервал, по истечении которого отклонение |x(t) — xуст
| выходного процесса от установившегося значения xуст не
превышает определенную величину, например, 0,1gо. Время
установления является важным параметром САУ, позволяющим оценить ее быстродействие.
Величину tу можно оценить приближенно по амплитудно-частотной
характеристике системы. При заданной частоте среза . Для оценки качества системы
используется также величина перерегулирования, определяемая соотношением .
В зависимости от
характера собственных колебаний системы переходный процесс в ней может быть
колебательным, как это показано на рис. 21, б, или плавным гладким, называемым
апериодическим (рис. 21,а). Если корни характеристического уравнения системы
действительны, то переходный процесс в ней апериодический. В случае
комплексных корней характеристического уравнения собственные колебания
устойчивой системы управления являются затухающими гармоническими и переходный
процесс в системе имеет колебательный характер.
При малом запасе устойчивости САУ ее
собственные колебания затухают медленно, и перерегулирование в переходном режиме
получается значительным. Как следствие, величина перерегулирования может
служить мерой запаса устойчивости системы. Для многих систем запас
устойчивости считается достаточным, если величина перерегулирования .
Установившийся
режим
При проектировании систем управления
часто требуется оценить ошибку слежения в установившемся режиме . В зависимости от
вида воздействия и свойств системы эта ошибка может быть нулевой, постоянной
или бесконечно большой величиной.
Очень важно, что величина
установившейся ошибки может быть легко найдена с помощью теоремы о предельном
значении оригинала: .
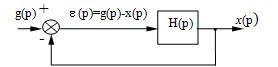
При использовании этой теоремы нужно
выразить величину ошибки e (p) через g(p). Для этого рассмотрим
структурную схему замкнутой системы управления (рис. 22).
Рис.
22
Очевидно, e (p) = g(p) — x(p)
= g(p) — H(p)e(p). Отсюда или e (p) = He(p)g(p)
, где He(p) = называется передаточной функцией
системы управления от входного воздействия g(p) к ошибке слежения e(p).
Таким образом, величину установившейся ошибки можно найти с помощью следующего
соотношения:
,
где He(p) = 1/(1+H(p));
g(p) — изображение типового входного воздействия.
Пример 1. Рассмотрим
систему управления, в составе которой нет интеграторов, например,
.
Найдем величину установившейся
ошибки при ступенчатом входном воздействии g(t) = g0, t ³ 0.
В этом случае
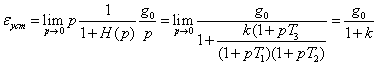
Предположим теперь, что входное
воздействие изменяется линейно t или
.
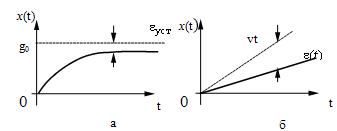
Тогда . Соответствующие входные воздействия и
переходные процессы можно представить графиками на рис. 23,а и б.
Рис.
23
Пример 2. Рассмотрим
теперь систему, содержащую один интегратор. Типичным примером может быть
система сервопривода (рис. 6) с .
Для ступенчатого воздействия g(t) = g0
или g(p) = получим
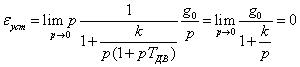
При линейном входном воздействии
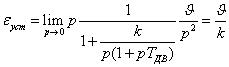
Такие процессы можно проиллюстрировать
соответствующими кривыми на рис.24, а и б.
Рис.
24
Пример 3.
Рассмотрим систему с двумя интеграторами. Пусть, например, . При ступенчатом
воздействии 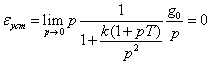
При линейном 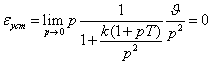
Наконец, если входное воздействие
квадратичное g(t) = at2/2 (g(p) = a/p3),
то
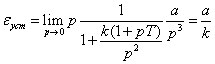
Таким образом, в системе с двумя
интеграторами может осуществляться слежение за квадратичным входным
воздействием при конечной величине установившейся ошибки. Например, можно
следить за координатами объекта, движущегося с постоянным ускорением.
Статические
и астатические системы управления
Анализ рассмотренных примеров
показывает, что системы управления, содержащие интегрирующие звенья, выгодно
отличаются от систем без интеграторов. По этому признаку все системы делятся на
статические системы, не содержащие интегрирующих звеньев, и астатические
системы, которые содержат интеграторы. Системы с одним интегратором называются
системами с астатизмом первого порядка. Системы с двумя интеграторами –
системами с астатизмом второго порядка и т.д.
Для статических систем даже при
неизменяющемся воздействии g(t) = g0 установившаяся ошибка имеет
конечную величину g(t) = g0 . В системах с астатизмом первого
порядка при ступенчатом воздействии установившаяся ошибка равна нулю, но при линейно
изменяющемся воздействии . Наконец, в системах с астатизмом
второго порядка ненулевая установившаяся ошибка появляется только при
квадратичных входных воздействиях g(t) = at2 /2 и
составляет величину eуст =
a/k.
Какие же физические причины лежат в
основе таких свойств астатических систем управления?
Рассмотрим систему управления с
астатизмом второго порядка (рис. 25)
Рис.
25
Пусть входной сигнал системы управления
изменяется линейно:
t. Как было
установлено, в такой системе установившаяся ошибка равна нулю, т.е. e
(t) =0. Каким же образом система работает при нулевом сигнале ошибки? Если x(t)
= t , то на
входе второго интегратора должен быть сигнал . Действительно, при нулевом
рассогласовании e (t) =0 в системе с интеграторами
возможно существование ненулевого выходного сигнала первого интегратора . Первый интегратор
после окончания переходного процесса «запоминает» скорость изменения входного
воздействия и в дальнейшем работа системы управления осуществляется по
«памяти». Таким образом, физическим объяснением такого значительного различия
статических и астатических систем является наличие памяти у астатических систем
управления.
*
* *
Итак, существуют простые возможности
определения важнейшего показателя систем управления – величины их динамических
ошибок. Детальный анализ переходных процессов в системах управления обычно
выполняют с помощью моделирования на ПЭВМ. Вместе с тем величины
установившихся ошибок легко находятся аналитически. При этом астатические
системы управления, т.е. системы с интеграторами, имеют существенно лучшие
показатели качества по сравнению со статическими системами.
Точность систем автоматического управления
1. Точность САУ
Точность САУ оценивается в установившемся режиме по величине установившейся ошибки при типовых воздействиях. При анализе точности систем рассматривается установившийся режим, так как текущее значение ошибки резко меняется вследствие наличия переходных процессов и не может быть мерой точности.
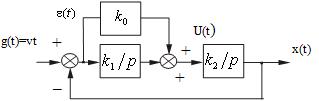
Рассмотрим систему представленную на рис. 1.
 |
На схеме приняты следующие обозначения: Kу(p) – передаточная функция устройства управления; K0(p) – передаточная функция объекта управления; f – возмущающее воздействие; x – задающее воздействие; y – регулируемая величина.
Ошибка по задающему воздействию равна e(t) = x(t) – y(t).
Изображение ошибки равно
(1)
Установившееся значение ошибки определяется с помощью теоремы о конечном значении функции
(2)
Ошибка по возмущению воздействию равна e(t) = – y(t), т.е. равна изменению регулируемой величины под действием возмущения при отсутствии входного воздействия.
В общем случае как задающее, так и возмущающее воздействия являются сложными функциями времени. При определении ошибок пользуются типовыми воздействиями, которые с одной стороны соответствуют наиболее тяжелым режимам работы системы и, вместе с тем, достаточно просты для аналитических исследований.
Кроме того, типовые воздействия удобны для сравнительного анализа различных систем, и соответствуют наиболее часто применяемым законам изменения управляющих и возмущающих воздействий.
2. Типы ошибок
Различают следующие типы ошибок:
– статическая ошибка (ошибка по положению) – ошибка, возникающая в системе при отработке единичного воздействия;
– кинетическая ошибка (ошибка по скорости) – ошибка, возникающая в системе при отработке линейно – возрастающего воздействия;
– инерционная ошибка (ошибка по ускорению) – ошибка, возникающая в системе при отработке квадратичного воздействия.
С точки зрения ошибок, системы можно классифицировать на статические и астатические.
Передаточная функция статической системы имеет вид
(3)
Передаточная функция астатической системы имеет вид
(4)
где K*(p) – передаточная функция, не содержащая интегрирующих звеньев а s – порядок астатизма.
Рассмотрим статическую систему (s = 0). Определим выражения для соответствующих ошибок.
1. Статическая ошибка определяется следующим соотношением
(5)
2. Кинетическая ошибка определяется следующим соотношением
(6)
3. Инерционная ошибка определяется следующим соотношением
(7)
Эта система не может быть использована как синхронно – следящая, так как кинетическая ошибка стремится к бесконечности.
Пример 1. Для заданной системы (рис. 2) определить установившиеся ошибки
 |
Решение: Определим установившиеся ошибки.
1. Статическая ошибка определяется следующим соотношением
2. Кинетическая ошибка определяется следующим соотношением
3. Инерционная ошибка определяется следующим соотношением
На графиках это можно изобразить следующим образом (рис. 3)
Рассмотрим астатическую систему первого порядка (s = 1).
Определим выражения для установившихся ошибок.
1. Статическая ошибка определяется следующим соотношением
(8)
2. Кинетическая ошибка определяется следующим соотношением
(9)
3. Инерционная ошибка определяется следующим соотношением
(10)
Эта система может быть использована как синхронно – следящая, так как кинетическая ошибка равна нулю.
Пример 2. Для заданной системы (рис. 4) определить ошибки
 |
Решение: Определим выражения для ошибок.
1. Статическая ошибка определяется следующим соотношением
2. Кинетическая ошибка определяется следующим соотношением
Т.е. ошибка является функцией скорости изменения входного воздействия и коэффициента усиления системы.
3. Инерционная ошибка определяется следующим соотношением
Графики изменения ошибок приведены на рис. 5.
 |
 |
Рассмотрим астатическую систему второго порядка (s = 2).
Определим выражения для ошибок.
1. Статическая ошибка определяется следующим соотношением
(11)
2. Кинетическая ошибка определяется следующим соотношением
(12)
3. Инерционная ошибка определяется следующим соотношением
(13)
Инерционная ошибка является функцией ускорения изменения входного воздействия и коэффициента усиления системы.
Эта система может быть использована как синхронно – следящая, так как кинетическая ошибка равна нулю.
Пример 3. Для заданной системы (рис. 6) определить установившиеся ошибки
 |
Решение: Определим выражения для ошибок.
1. Статическая ошибка определяется следующим соотношением
2. Кинетическая ошибка определяется следующим соотношением
3. Инерционная ошибка определяется следующим соотношением
На графиках это можно изобразить следующим образом (рис. 7)
 |
|||

Для повышения точности САУ необходимо увеличивать коэффициент усиления системы и порядок астатизма, но это может привести к неустойчивости, т.е. требования по точности и устойчивости противоречивы.
Определение ошибок по виду частотных характеристик САУ
О характере ошибок можно судить по низкочастотной ветви любой частотной характеристики (АФХ, ЛАЧХ, ФЧХ), так как низкочастотная ветвь характеризует статику системы. Частотные характеристики систем с различным порядком астатизма приведены в таблице 1.
Таблица 1
| АФХ | ЛАЧХ | ФЧХ | |
| s = 0; ec = x0/(1+k); eк = ¥; eи = ¥. |
+j -1 + |
||
| s = 1; ec = 0; eк = v/kv; eи = ¥. |
+j -1 + |
||
| s = 1; ec = 0; eк = 0; eи = a/ka. |
+j -1 + |
3. Ошибки по возмущению
Установившаяся ошибка по возмущению равна

Рассмотрим примеры
Пример 4. Для заданной системы (рис. 9) со статическим регулятором определить ошибку по возмущению.
 |
Решение: Пусть f(p) = f0 /p, при этом ошибка равна

При статическом регуляторе установившаяся ошибка по возмущению зависит от амплитуды воздействия и коэффициента усиления регулятора т.е. ef = f(f0, k1).
Пример 5. Для заданной системы (рис. 10) с астатическим регулятором, определить ошибку по возмущению.
 |
Решение: Пусть f(p) = f0 /p, при этом ошибка равна

При астатическом регуляторе ошибка по возмущению равна нулю.
Литература
1. Вероятностные методы в вычислительной технике. Под ред. А.Н. Лебедева и Е.А. Чернявского – М.: Высш. Шк., 1986. -312 с.
2. Зайцев Г.Ф. Теория автоматического управления и регулирования. – 2-е изд., перераб. и доп. Киев, Издательство Выща школа Головное издательство, 198
3. Справочник по теории автоматического управления. /Под ред. А.А. Красовского – М.: Наука, 1987. – 712 с.
4. Теория автоматического управления: Учебник для вузов. Ч1 / Под ред. А.А. Воронова – М.: Высш. Шк., 1986. – 367 с.
5. Теория автоматического управления: Учебник для вузов. Ч2 / Под ред. А.А. Воронова – М.: Высш. Шк., 1986. -504 с.
6. Шандров Б.В. Технические средства автоматизации: учебник для студентов высших учебных заведений. Москва, Издательский центр «Академия», 2007.
Система автоматического управления. Состав САУ. Составление структурной схемы системы. Определение передаточных функций звеньев
Страницы работы
Фрагмент текста работы
Содержание:
1. Анализ исходных
данных.
2. Описание работы
системы.
3. Составление
структурной схемы системы.
4. Определение
передаточных функций звеньев.
5. Определение
передаточных функций системы.
6. Синтез
корректирующих звеньев.
7. Анализ показателей
качества синтезированной системы по результатам моделирования
Исходные данные
1. Назначение
Система
автоматического управления (далее по тексту САУ, или «система») предназначена
для линейного перемещения горизонтального стола применительно к станкам
фрезерной или координатно-расточной групп.
2.
Состав САУ
Блок-схема
системы автоматического управления приведена на рис. 1, а комбинированная
схема силовой части — на рис. 2. САУ построена как система подчиненного
регулирования, выполненная по контурам напряжения (тока), скорости, положения.
В контуре напряжения (тока) имеется нелинейный элемент (на схеме не показан).
На
рисунках приняты следующие обозначения:
—
управляющее воздействие;
—
управляемая (регулируемая) координата;
—
ошибка системы;
—
сигнал задания по управляющему воздействию;
—
сигнал главной обратной связи по
регулируемой координате;
—
сигнал по ошибке;
ЧЭ —
чувствительный элемент;
РП —
регулятор положения;
У, КЗ —
усилитель и корректирующее звено в контуре положения;
РС —
регулятор скорости;
РН —
регулятор напряжения (тока);
ТП-
транзисторный (тиристорный) преобразователь;
М —
исполнительный двигатель;
Р1 —
механический редуктор силовой;
МП —
механическая передача (шариковинтовая передача (ШВП));
Н —
нагрузка (стол с деталью);
ДН, У —
датчик напряжения, усилитель;
ТГ —
тахогенератор;
Р2 —
механический редуктор, приборный;
ДОС —
датчик обратной связи;
ВТ —
вращающийся трансформатор;
ПФН —
преобразователь фаза-напряжение;
U1, U2,U3, UЯ — промежуточные
координаты (управляющие напряжения соответственно РС, РН, ТП, ИД);
jД, j1, j2 —
промежуточные координаты (угол поворота соответственно ИД, ШВП, ВТ);
,
—
выходное напряжение, соответственно, ТГ и ВТ.
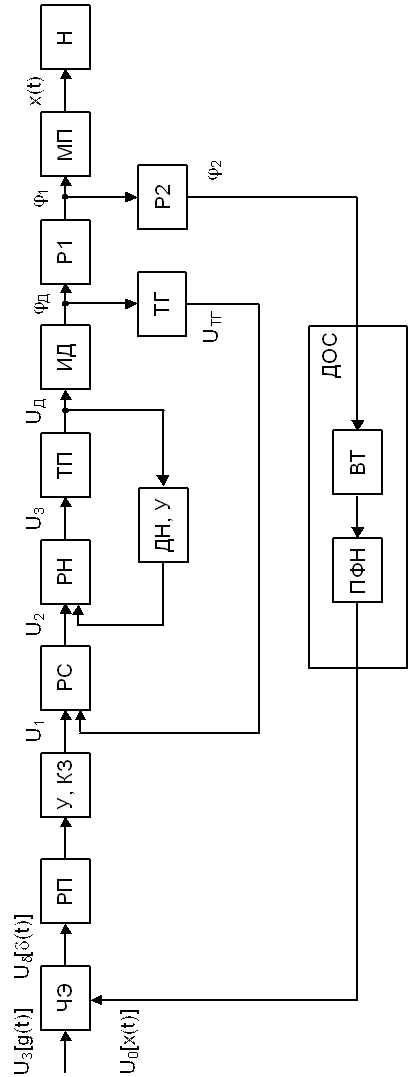 |
Рис.1 Блок-схема
системы автоматического управления.
Рис.2
Комбинированная схема силовой части САУ
I. Анализ исходных данных
При
проектировании всех технических устройств и систем исходным документом является
техническое задание (ТЗ). Аналогом ТЗ при выполнении настоящей работы являются
исходные данные, приведенные выше. В пояснительной записке необходимо привести
все данные согласно пунктам раздела «Исходные данные». Взятые из таблиц
сведения даются в следующей форме: название параметра (характеристики),
условное обозначение, единицы измерения, числовое значение.
Характеристики
системы автоматического управления
1. Характеристики системы автоматического управления
1.1. Характеристики исполнительного
двигателя:
— мощность двигателя
Р, кВт 1.0
— частота вращения n, об/мин 1500
— напряжение на
якоре Uя, В 110
— ток якоря Iя, А 9,1
— активное
сопротивление якорной цепи двигателя Rя, Ом 1,2
— индуктивность
якоря цепи Lя, мГн. 1,87
— момент инерции
собственных вращающихся частей
двигателя Jя, кгм2 0,75
*10-3
1.2. Тип и параметр преобразователя:
— тип управляемый
выпрямитель
— частота питания
преобразователя F, Гц 400
— напряжение
управления Uу, В 15
— число фаз n 1
— активное
сопротивление тиристорного преобразователя Rтп, Ом 0,48
— индуктивность
тиристорного преобразователя Lтп, мГн 2,4
1.3. Вид и параметры регуляторов
контуров:
— регулятор
положения пропорциональный; К2=5
— регулятор скорости
пропорциональный; К4=3
— регулятор
напряжения пропорционально-интегральный;
0,03+1/p
1.4. Параметры схемы:
— максимальное
перемещение Xmax, мм 250
— шаг винта ШВП γ,
мм 6
— цена оборота ДОС
β, мм 1
— цена импульса Δ,
мм 0,001
1.5. Параметры управляющего воздействия,
динамические характеристики САУ:
— максимальная
скорость Vмакс, м/мин 15
— кинетическая
ошибка δк, мм 2
— перерегулирование
σ, % 35
— время переходного
процесса tпп, с 0,075
— число
перерегулирования n 3
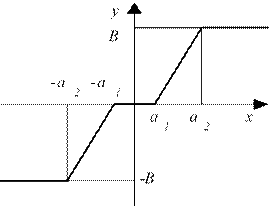
Параметры нелинейных элементов а1 =
0,1
а2 =
0,7
В =
0,6
 |
II. Описание работы системы.
Входной
сигнал подается на ЧЭ, на котором сравнивается с сигналом обратной связи. Затем сигнал подается на РП, представляющий
собой звено с ПФН и ВТ после которого усиливается и корректируется на
КЗ. Далее сигнал поступает на РС, служащий для поддержания постоянной скорости
передвижения исполнительного механизма, затем после РС поступает на РН,
контролирующий напряжение. Он позволяет
регулировать скорость двигателя в широком диапазоне за счет ширины выдаваемых
прямоугольных импульсов ИД через регулятор Р1 вращает механизм передачи,
являющийся ШВП. Для контроля перемещения ШВП стоит ВТ,
соединенный с винтом передачи с помощью редуктора Р2.
III. Составление структурной схемы
системы
В соответствии с исходной блок-схемой приведена структурная схема системы
(на рисунке 3). Общие правила ее составления следующие:
3.1. Система представляется
в виде совокупности звеньев и их взаимосвязи согласно заданной блок-схеме.
3.2. Элементы,
формирующие сигнал единичной обратной связи с единицей измерения управляющего
для (системы) контура сигнала, показываются в цепи обратной связи. Далее при
описании замкнутой системы коэффициент передачи звена (совокупности звеньев)
принимается равным единице.
3.3. Элемент,
выполняющий сравнение (вычитание) сигналов задания и главной обратной связи,
вносится в прямой тракт в виде автономного элемента или в совокупности с
элементами, формирующими сигнал главной обратной связи. На схеме дается
условное обозначение элемента сравнения, его коэффициент передачи принимается
равным единице.
3.4. При замыкании
внутренних контуров местной единичной обратной связью поступают аналогично пп.
3.2 и 3.3.
3.5. Нумерация
передаточных функций дается в индексах, порядок нумерации слева направо.
3.6. Показываются
входная и выходная координаты, ошибка и необходимые для использования в
расчетах промежуточные координаты.
Приводится
структурная схема системы, и дается расшифровка обозначения
Похожие материалы
- Анализ САУ бесцентрово-шлифовального станка
- Разработка общей конструкции изделия. Детальная разработка всех вопросов, связанных с воплощением принципиальной схемы в реальную конструкцию
- Скребкові конвеєри. Розрахунок та вибір робочого та тягового органу машини. Розрахунок основних вузлів машини