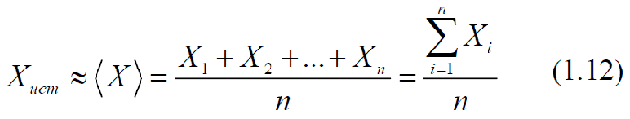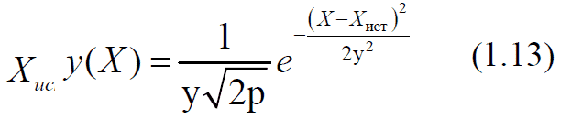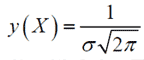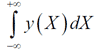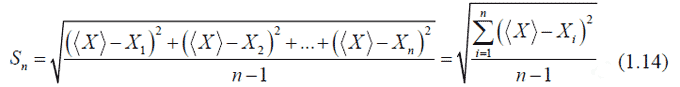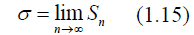Средняя квадратичная ошибка.
При ответственных
измерениях, когда необходимо знать
надежность полученных результатов,
используется средняя квадратичная
ошибка (или
стандартное отклонение), которая
определяется формулой
(5)
Величина
характеризует отклонение отдельного
единичного измерения от истинного
значения.
Если мы вычислили
по n
измерениям среднее значение
по формуле (2), то это значение будет
более точным, то есть будет меньше
отличаться от истинного, чем каждое
отдельное измерение. Средняя квадратичная
ошибка среднего значения
равна
(6)
где — среднеквадратичная
ошибка каждого отдельного измерения,
n
– число
измерений.
Таким образом,
увеличивая число опытов, можно уменьшить
случайную ошибку в величине среднего
значения.
В настоящее время
результаты научных и технических
измерений принято представлять в виде
(7)
Как показывает
теория, при такой записи мы знаем
надежность полученного результата, а
именно, что истинная величина Х с
вероятностью 68% отличается от
не более, чем на
.
При использовании
же средней арифметической (абсолютной)
ошибки (формула 2) о надежности результата
ничего сказать нельзя. Некоторое
представление о точности проведенных
измерений в этом случае дает относительная
ошибка (формула 4).
При выполнении
лабораторных работ студенты могут
использовать как среднюю абсолютную
ошибку, так и среднюю квадратичную.
Какую из них применять указывается
непосредственно в каждой конкретной
работе (или указывается преподавателем).
Обычно если число
измерений не превышает 3 – 5, то
можно использовать среднюю абсолютную
ошибку. Если число измерений порядка
10 и более, то следует использовать более
корректную оценку с
помощью средней квадратичной ошибки
среднего (формулы 5 и 6).
Учет систематических ошибок.
Увеличением числа
измерений можно уменьшить только
случайные ошибки опыта, но не
систематические.
Максимальное
значение систематической ошибки обычно
указывается на приборе или в его паспорте.
Для измерений с помощью обычной
металлической линейки систематическая
ошибка составляет не менее 0,5 мм; для
измерений штангенциркулем –
0,1 – 0,05 мм;
микрометром – 0,01 мм.
Часто в качестве
систематической ошибки берется половина
цены деления прибора.
На шкалах
электроизмерительных приборов указывается
класс точности. Зная класс точности К,
можно вычислить систематическую ошибку
прибора ∆Х по формуле
где К – класс
точности прибора, Хпр – предельное
значение величины, которое может быть
измерено по шкале прибора.
Так, амперметр
класса 0,5 со шкалой до 5А измеряет ток с
ошибкой не более
Среднее значение
полной погрешности складывается из
случайной и систематической
погрешностей.
Ответ с учетом
систематических и случайных ошибок
записывается в виде
Погрешности косвенных измерений
В физических
экспериментах чаще бывает так, что
искомая физическая величина сама на
опыте измерена быть не может, а является
функцией других величин, измеряемых
непосредственно. Например, чтобы
определить объём цилиндра, надо измерить
диаметр D и высоту h, а затем вычислить
объем по формуле
Величины D и h будут измерены с
некоторой ошибкой. Следовательно,
вычисленная величина
V
получится также с некоторой ошибкой.
Надо уметь выражать погрешность
вычисленной величины через погрешности
измеренных величин.
Как и при прямых
измерениях можно вычислять среднюю
абсолютную (среднюю арифметическую)
ошибку или среднюю квадратичную ошибку.
Общие правила
вычисления ошибок для обоих случаев
выводятся с помощью дифференциального
исчисления.
Пусть искомая
величина φ является функцией нескольких
переменных Х,
У, Z…
φ(Х,
У, Z…).
Путем прямых
измерений мы можем найти величины
,
а также оценить их средние абсолютные
ошибки
…
или средние квадратичные ошибки Х,
У,
Z…
Тогда средняя
арифметическая погрешность
вычисляется по формуле
где
— частные
производные от φ по
Х, У, Z. Они
вычисляются для средних значений
…
Средняя квадратичная
погрешность вычисляется по формуле
Пример.
Выведем формулы погрешности для
вычисления объёма цилиндра.
а) Средняя
арифметическая погрешность.
Величины
D и h
измеряются соответственно с ошибкой
D
и h.
Погрешность
величины объёма будет равна
б) Средняя
квадратичная погрешность.
Величины
D и h
измеряются соответственно с ошибкой
D, h.
Погрешность
величины объёма будет равна
Если формула
представляет выражение удобное для
логарифмирования (то есть произведение,
дробь, степень), то удобнее вначале
вычислять относительную погрешность.
Для этого (в случае средней арифметической
погрешности) надо проделать следующее.
1. Прологарифмировать
выражение.
2. Продифференцировать
его.
3. Объединить
все члены с одинаковым дифференциалом
и вынести его за скобки.
4. Взять выражение
перед различными дифференциалами по
модулю.
5. Заменить
значки дифференциалов d
на значки абсолютной погрешности .
В итоге получится
формула для относительной погрешности
Затем,
зная ,
можно вычислить абсолютную погрешность
=
Пример.
Аналогично можно
записать относительную среднюю
квадратичную погрешность
Правила
представления результатов измерения
следующие:
-
погрешность должна
округляться до одной значащей цифры:
правильно = 0,04,
неправильно —
= 0,0382;
-
последняя значащая
цифра результата должна быть того же
порядка величины, что и погрешность:
правильно
= 9,830,03,
неправильно —
= 9,8260,03;
-
если результат
имеет очень большую или очень малую
величину, необходимо использовать
показательную форму записи — одну и ту
же для результата и его погрешности,
причем запятая десятичной дроби должна
следовать за первой значащей цифрой
результата:
правильно —
= (5,270,03)10-5,
неправильно —
= 0,00005270,0000003,
= 5,2710-50,0000003,
=
= 0,0000527310-7,
= (5273)10-7,
= (0,5270,003)
10-4.
-
Если результат
имеет размерность, ее необходимо
указать:
правильно – g=(9,820,02)
м/c2,
неправильно – g=(9,820,02).
Соседние файлы в папке Отчеты_Погрешность
- #
- #
- #
- #
- #
From Wikipedia, the free encyclopedia
In statistics, the mean squared error (MSE)[1] or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the actual value. MSE is a risk function, corresponding to the expected value of the squared error loss.[2] The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate.[3] In machine learning, specifically empirical risk minimization, MSE may refer to the empirical risk (the average loss on an observed data set), as an estimate of the true MSE (the true risk: the average loss on the actual population distribution).
The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the error approaches zero.
The MSE is the second moment (about the origin) of the error, and thus incorporates both the variance of the estimator (how widely spread the estimates are from one data sample to another) and its bias (how far off the average estimated value is from the true value).[citation needed] For an unbiased estimator, the MSE is the variance of the estimator. Like the variance, MSE has the same units of measurement as the square of the quantity being estimated. In an analogy to standard deviation, taking the square root of MSE yields the root-mean-square error or root-mean-square deviation (RMSE or RMSD), which has the same units as the quantity being estimated; for an unbiased estimator, the RMSE is the square root of the variance, known as the standard error.
Definition and basic properties[edit]
The MSE either assesses the quality of a predictor (i.e., a function mapping arbitrary inputs to a sample of values of some random variable), or of an estimator (i.e., a mathematical function mapping a sample of data to an estimate of a parameter of the population from which the data is sampled). The definition of an MSE differs according to whether one is describing a predictor or an estimator.
Predictor[edit]
If a vector of 



In other words, the MSE is the mean 

In matrix notation,
where 



The MSE can also be computed on q data points that were not used in estimating the model, either because they were held back for this purpose, or because these data have been newly obtained. Within this process, known as cross-validation, the MSE is often called the test MSE,[4] and is computed as
Estimator[edit]
The MSE of an estimator 

This definition depends on the unknown parameter, but the MSE is a priori a property of an estimator. The MSE could be a function of unknown parameters, in which case any estimator of the MSE based on estimates of these parameters would be a function of the data (and thus a random variable). If the estimator 
The MSE can be written as the sum of the variance of the estimator and the squared bias of the estimator, providing a useful way to calculate the MSE and implying that in the case of unbiased estimators, the MSE and variance are equivalent.[5]
Proof of variance and bias relationship[edit]
An even shorter proof can be achieved using the well-known formula that for a random variable 



But in real modeling case, MSE could be described as the addition of model variance, model bias, and irreducible uncertainty (see Bias–variance tradeoff). According to the relationship, the MSE of the estimators could be simply used for the efficiency comparison, which includes the information of estimator variance and bias. This is called MSE criterion.
In regression[edit]
In regression analysis, plotting is a more natural way to view the overall trend of the whole data. The mean of the distance from each point to the predicted regression model can be calculated, and shown as the mean squared error. The squaring is critical to reduce the complexity with negative signs. To minimize MSE, the model could be more accurate, which would mean the model is closer to actual data. One example of a linear regression using this method is the least squares method—which evaluates appropriateness of linear regression model to model bivariate dataset,[6] but whose limitation is related to known distribution of the data.
The term mean squared error is sometimes used to refer to the unbiased estimate of error variance: the residual sum of squares divided by the number of degrees of freedom. This definition for a known, computed quantity differs from the above definition for the computed MSE of a predictor, in that a different denominator is used. The denominator is the sample size reduced by the number of model parameters estimated from the same data, (n−p) for p regressors or (n−p−1) if an intercept is used (see errors and residuals in statistics for more details).[7] Although the MSE (as defined in this article) is not an unbiased estimator of the error variance, it is consistent, given the consistency of the predictor.
In regression analysis, «mean squared error», often referred to as mean squared prediction error or «out-of-sample mean squared error», can also refer to the mean value of the squared deviations of the predictions from the true values, over an out-of-sample test space, generated by a model estimated over a particular sample space. This also is a known, computed quantity, and it varies by sample and by out-of-sample test space.
In the context of gradient descent algorithms, it is common to introduce a factor of 
Examples[edit]
Mean[edit]
Suppose we have a random sample of size 




which has an expected value equal to the true mean 
where 
For a Gaussian distribution, this is the best unbiased estimator (i.e., one with the lowest MSE among all unbiased estimators), but not, say, for a uniform distribution.
Variance[edit]
The usual estimator for the variance is the corrected sample variance:
This is unbiased (its expected value is 
where 

However, one can use other estimators for 

then we calculate:
This is minimized when
For a Gaussian distribution, where 



Further, while the corrected sample variance is the best unbiased estimator (minimum mean squared error among unbiased estimators) of variance for Gaussian distributions, if the distribution is not Gaussian, then even among unbiased estimators, the best unbiased estimator of the variance may not be 
Gaussian distribution[edit]
The following table gives several estimators of the true parameters of the population, μ and σ2, for the Gaussian case.[9]
| True value | Estimator | Mean squared error |
|---|---|---|
 |
 = the unbiased estimator of the population mean, = the unbiased estimator of the population mean,  |

|
 |
 = the unbiased estimator of the population variance, = the unbiased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
Interpretation[edit]
An MSE of zero, meaning that the estimator 

Values of MSE may be used for comparative purposes. Two or more statistical models may be compared using their MSEs—as a measure of how well they explain a given set of observations: An unbiased estimator (estimated from a statistical model) with the smallest variance among all unbiased estimators is the best unbiased estimator or MVUE (Minimum-Variance Unbiased Estimator).
Both analysis of variance and linear regression techniques estimate the MSE as part of the analysis and use the estimated MSE to determine the statistical significance of the factors or predictors under study. The goal of experimental design is to construct experiments in such a way that when the observations are analyzed, the MSE is close to zero relative to the magnitude of at least one of the estimated treatment effects.
In one-way analysis of variance, MSE can be calculated by the division of the sum of squared errors and the degree of freedom. Also, the f-value is the ratio of the mean squared treatment and the MSE.
MSE is also used in several stepwise regression techniques as part of the determination as to how many predictors from a candidate set to include in a model for a given set of observations.
Applications[edit]
- Minimizing MSE is a key criterion in selecting estimators: see minimum mean-square error. Among unbiased estimators, minimizing the MSE is equivalent to minimizing the variance, and the estimator that does this is the minimum variance unbiased estimator. However, a biased estimator may have lower MSE; see estimator bias.
- In statistical modelling the MSE can represent the difference between the actual observations and the observation values predicted by the model. In this context, it is used to determine the extent to which the model fits the data as well as whether removing some explanatory variables is possible without significantly harming the model’s predictive ability.
- In forecasting and prediction, the Brier score is a measure of forecast skill based on MSE.
Loss function[edit]
Squared error loss is one of the most widely used loss functions in statistics[citation needed], though its widespread use stems more from mathematical convenience than considerations of actual loss in applications. Carl Friedrich Gauss, who introduced the use of mean squared error, was aware of its arbitrariness and was in agreement with objections to it on these grounds.[3] The mathematical benefits of mean squared error are particularly evident in its use at analyzing the performance of linear regression, as it allows one to partition the variation in a dataset into variation explained by the model and variation explained by randomness.
Criticism[edit]
The use of mean squared error without question has been criticized by the decision theorist James Berger. Mean squared error is the negative of the expected value of one specific utility function, the quadratic utility function, which may not be the appropriate utility function to use under a given set of circumstances. There are, however, some scenarios where mean squared error can serve as a good approximation to a loss function occurring naturally in an application.[10]
Like variance, mean squared error has the disadvantage of heavily weighting outliers.[11] This is a result of the squaring of each term, which effectively weights large errors more heavily than small ones. This property, undesirable in many applications, has led researchers to use alternatives such as the mean absolute error, or those based on the median.
See also[edit]
- Bias–variance tradeoff
- Hodges’ estimator
- James–Stein estimator
- Mean percentage error
- Mean square quantization error
- Mean square weighted deviation
- Mean squared displacement
- Mean squared prediction error
- Minimum mean square error
- Minimum mean squared error estimator
- Overfitting
- Peak signal-to-noise ratio
Notes[edit]
- ^ This can be proved by Jensen’s inequality as follows. The fourth central moment is an upper bound for the square of variance, so that the least value for their ratio is one, therefore, the least value for the excess kurtosis is −2, achieved, for instance, by a Bernoulli with p=1/2.
References[edit]
- ^ a b «Mean Squared Error (MSE)». www.probabilitycourse.com. Retrieved 2020-09-12.
- ^ Bickel, Peter J.; Doksum, Kjell A. (2015). Mathematical Statistics: Basic Ideas and Selected Topics. Vol. I (Second ed.). p. 20.
If we use quadratic loss, our risk function is called the mean squared error (MSE) …
- ^ a b Lehmann, E. L.; Casella, George (1998). Theory of Point Estimation (2nd ed.). New York: Springer. ISBN 978-0-387-98502-2. MR 1639875.
- ^ Gareth, James; Witten, Daniela; Hastie, Trevor; Tibshirani, Rob (2021). An Introduction to Statistical Learning: with Applications in R. Springer. ISBN 978-1071614174.
- ^ Wackerly, Dennis; Mendenhall, William; Scheaffer, Richard L. (2008). Mathematical Statistics with Applications (7 ed.). Belmont, CA, USA: Thomson Higher Education. ISBN 978-0-495-38508-0.
- ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ Steel, R.G.D, and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, page 288.
- ^ Mood, A.; Graybill, F.; Boes, D. (1974). Introduction to the Theory of Statistics (3rd ed.). McGraw-Hill. p. 229.
- ^ DeGroot, Morris H. (1980). Probability and Statistics (2nd ed.). Addison-Wesley.
- ^ Berger, James O. (1985). «2.4.2 Certain Standard Loss Functions». Statistical Decision Theory and Bayesian Analysis (2nd ed.). New York: Springer-Verlag. p. 60. ISBN 978-0-387-96098-2. MR 0804611.
- ^ Bermejo, Sergio; Cabestany, Joan (2001). «Oriented principal component analysis for large margin classifiers». Neural Networks. 14 (10): 1447–1461. doi:10.1016/S0893-6080(01)00106-X. PMID 11771723.
Загрузить PDF
Загрузить PDF
После сбора данных их нужно проанализировать. Обычно нужно найти среднее значение, квадратичное отклонение и погрешность. Мы расскажем вам, как это сделать.
-
1
Запишите числовые значения, которые вы собираетесь анализировать. Мы проанализируем случайно подобранные числовые значения в качестве примера.
- Например, 5 школьникам был предложен письменный тест. Их результаты (в баллах по 100 бальной системе): 12, 55, 74, 79 и 90 баллов.
Реклама
-
1
Для того чтобы посчитать среднее значение, нужно сложить все имеющиеся числовые значения и разделить получившееся число на их количество.
- Среднее значение (μ) = Σ/N, где Σ сумма всех числовых значений, а N количество значений.
- То есть, в нашем случае μ равно (12+55+74+79+90)/5 = 62.
-
1
Мы будем считать среднее отклонение. Среднее отклонение = σ = квадратный корень из [(Σ((X-μ)^2))/(N)].
- Для вышеуказанного примера это квадратный корень из [((12-62)^2 + (55-62)^2 + (74-62)^2 + (79-62)^2 + (90-62)^2)/(5)] = 27,4. (Обратите внимание, что если это выборочное среднеквадратическое отклонение, то делить нужно на N-1, где N количество значений.)
Реклама
-
1
Считаем среднюю погрешность (среднего значения). Это оценка того, насколько сильно округляется общее среднее значение. Чем больше числовых значений, тем меньше средняя погрешность, тем точнее среднее значение. Для расчета погрешности надо разделить среднее отклонение на корень квадратный от N. Стандартная погрешность = σ/кв.корень(n).
- Если в нашем примере 5 школьников, а всего в классе 50 школьников, и среднее отклонение, посчитанное для 50 школьников равно 17 (σ = 21), средняя погрешность = 17/кв. корень(5) = 7.6.
Советы
- Расчеты среднего значения, среднего отклонения и погрешности годятся для анализа равномерно распределенных данных. Среднее отклонение математического среднего значения распределения относится приблизительно к 68% данных, 2 средних отклонения – к 95% данных, а 3 – к 99.7% данных. Стандартная погрешность же уменьшается при увеличении количества значений.
- Простой в использовании калькулятор для расчета среднего отклонения.
Реклама
Предупреждения
- Считайте дважды. Все делают ошибки.
Реклама
Об этой статье
Эту страницу просматривали 67 118 раз.
Была ли эта статья полезной?
Среднее арифметическое значение серии измерений <X> определяется как частное от деления арифметической суммы всех результатов измерений в серии Xi на общее число измерений в серии n:
При увеличении n среднее значение <X> стремится к истинному значению измеряемой величины Xист. Поэтому, за наиболее вероятное значение измеряемой величины следует принять ее среднее арифметическое значение, если ошибки подчиняются нормальному закону распределения ошибок —закону Гаусса.
Формула Гаусса может быть выведена из следующих предположений:
- ошибки измерений могут принимать непрерывный ряд значений;
- при большом числе наблюдений ошибки одинаковой величины, но разного знака встречаются одинаково часто;
- вероятность, то есть относительная частота появления ошибок, уменьшается с увеличением величины ошибки. Иначе говоря, большие ошибки встречаются реже, чем малые.
Нормальный закон распределения описывается следующей функцией:
где σ – средняя квадратичная ошибка; σ2 – дисперсия измерения; Хист – истинное значение измеряемой величины.
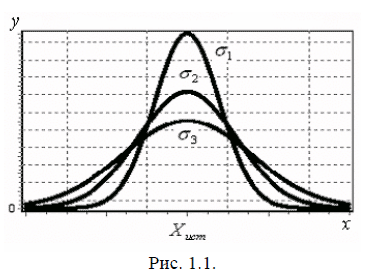
Анализ формулы (1.13) показывает, что функция нормального распределения симметрична относительно прямой X = Xист и имеет максимум при X = Xист. Значение ординаты этого максимума найдем, поставив в правую часть уравнения (1.13) Xист вместо X. Получим
,
откуда следует, что с уменьшением σ возрастает y(X). Площадь под кривой
должна оставаться постоянной и равной 1, так как вероятность того, что измеренное значение величины Х будет заключено в интервале от -∞ до +∞ равно 1 (это свойство называется условием нормировки вероятности).
На рис. 1.1 приведены графики трех функций нормального распределения для трех значений σ (σ3 > σ2 > σ1) и одном Хист. Нормальное распределение характеризуется двумя параметрами: средним значением случайной величины, которая при бесконечно большом количестве измерений (n → ∞) совпадает с ее истинным значением, и дисперсией σ. Величина σ характеризует разброс погрешностей относительно среднего значения принимаемого за истинное. При малых значениях σ кривые идут более круто и большие значения ΔХ менее вероятны, то есть отклонение результатов измерений от истинного значения величины в этом случае меньше.
Для оценки величины случайной ошибки измерения существует несколько способов. Наиболее распространена оценка с помощью стандартной или среднеквадратичной ошибки. Иногда применяется средняя арифметическая ошибка.
Стандартная ошибка (среднеквадратическая) среднего в серии из n измерений определяется по формуле:
.
Если число наблюдений очень велико, то подверженная случайным случайным колебаниям величина Sn стремится к некоторому постоянному значению σ, которое называется статистическим пределом Sn:
Именно этот предел и называется средней квадратичной ошибкой. Как уже было отмечено выше, квадрат этой величины называется дисперсией измерения, которая входит в формулу Гаусса (1.13).
Величина σ имеет большое практическое значение. Пусть в результате измерений некоторой физической величины нашли среднее арифметическое <Х> и некоторую ошибку ΔX. Если измеряемая величина подвержена случайной ошибке, то нельзя безоговорочно считать, что истинное значение измеряемой величины лежит в интервале (<Х> – ΔХ, <Х> + ΔХ) или (<Х> – ΔХ) < Х < (<Х> + ΔХ)). Всегда существует некоторая вероятность того, что истинное значение лежит за пределами этого интервала.
Доверительным интервалом называется интервал значений (<Х> – ΔХ, <Х> + ΔХ) величины X, в который по определению попадает ee истинное значение Хист с заданной вероятностью.
Надежностью результата серии измерений называют вероятность того, что истинное значение измеряемой величины попадает в данный доверительный интервал. Надежность результата измерения или доверительная вероятность выражается в долях единицы или процентах.
Пусть α означает вероятность того, что результат измерений отличается от истинного значения на величину, не большую, чем ΔХ. Это принято записывать в виде:
Р((<Х> – ΔХ) < Х < (<Х> + ΔХ)) = α
(1.16).
Выражение (1.16) означает, что с вероятностью, равной α, результат измерений не выходит за пределы доверительного интервала от <Х> – ΔХ до <Х> + ΔХ. Чем больше доверительный интервал, то есть чем больше задаваемая погрешность результата измерений ΔХ, тем с большей надежностью искомая величина Х попадает в этот интервал. Естественно, что величина α зависит от числа n произведенных измерений. а также от задаваемой погрешности ΔХ.
Таким образом, для характеристики величины случайной ошибки, необходимо задать два числа, а именно:
- величину самой ошибки (или доверительный интервал);
- величину доверительной вероятности (надежности).
Указание одной только величины ошибки без указания соответствующей ей доверительной вероятности в значительной мере лишено смысла, так как при этом мы не знаем, сколь надежны наши данные. Знание доверительной вероятности позволяет оценить степень надежности полученного результата.
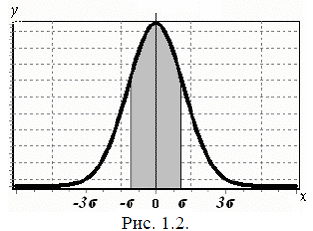
Необходимая степень надежности задается характером проводимых изменений. Средней квадратичной ошибке Sn соответствует доверительная вероятность 0.68, удвоенной средней квадратичной ошибке (2σ) – доверительная вероятность 0.95, утроенной (3σ) – 0.997.
Если в качестве доверительного интервала выбран интервал (X – σ, X + σ), то мы можем сказать, что из ста результатов измерений 68 будут обязательно находиться внутри этого интервала (рис. 1.2). Если при измерении абсолютная погрешность ∆Х > 3σ, то это измерение стоит отнести к грубым погрешностям или промаху. Величину 3σ обычно принимают за предельную абсолютную погрешность отдельного измерения (иногда вместо 3σ берут абсолютную погрешность измерительного прибора).
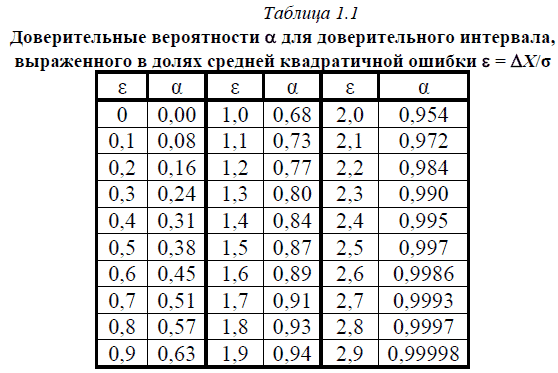
Для любой величины доверительного интервала по формуле Гаусса может быть рассчитана соответствующая доверительная вероятность. Эти вычисления проведены и их результаты сведены в табл. 1.1.
Доверительные вероятности α для доверительного интервала, выраженного а долях средней квадратичной ошибки ε = ΔX/σ:

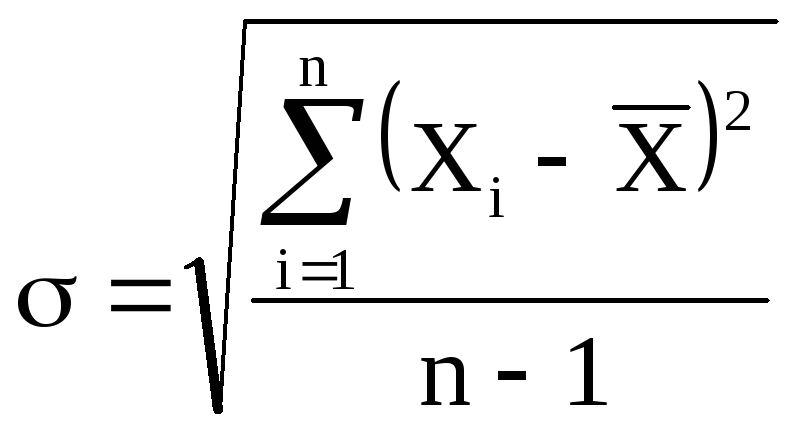
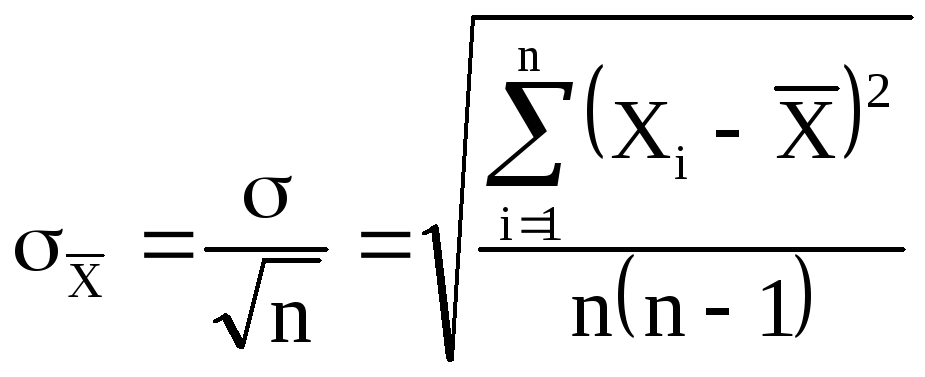
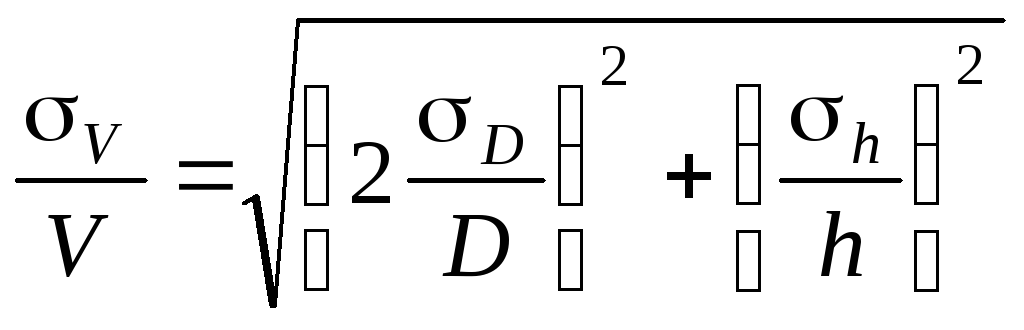



![{\displaystyle \operatorname {MSE} ({\hat {\theta }})=\operatorname {E} _{\theta }\left[({\hat {\theta }}-\theta )^{2}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a0e1b3bac58f9ba2d2f4ff8b85b2e35a8f4bf78)

![{\displaystyle {\begin{aligned}\operatorname {MSE} ({\hat {\theta }})&=\operatorname {E} _{\theta }\left[({\hat {\theta }}-\theta )^{2}\right]\\&=\operatorname {E} _{\theta }\left[\left({\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]+\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)^{2}\right]\\&=\operatorname {E} _{\theta }\left[\left({\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]\right)^{2}+2\left({\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]\right)\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)+\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)^{2}\right]\\&=\operatorname {E} _{\theta }\left[\left({\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]\right)^{2}\right]+\operatorname {E} _{\theta }\left[2\left({\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]\right)\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)\right]+\operatorname {E} _{\theta }\left[\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)^{2}\right]\\&=\operatorname {E} _{\theta }\left[\left({\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]\right)^{2}\right]+2\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)\operatorname {E} _{\theta }\left[{\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]\right]+\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)^{2}&&\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta ={\text{const.}}\\&=\operatorname {E} _{\theta }\left[\left({\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]\right)^{2}\right]+2\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\operatorname {E} _{\theta }[{\hat {\theta }}]\right)+\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)^{2}&&\operatorname {E} _{\theta }[{\hat {\theta }}]={\text{const.}}\\&=\operatorname {E} _{\theta }\left[\left({\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]\right)^{2}\right]+\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)^{2}\\&=\operatorname {Var} _{\theta }({\hat {\theta }})+\operatorname {Bias} _{\theta }({\hat {\theta }},\theta )^{2}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ac524a751828f971013e1297a33ca1cc4c38cd6)
![{\displaystyle {\begin{aligned}\operatorname {MSE} ({\hat {\theta }})&=\mathbb {E} [({\hat {\theta }}-\theta )^{2}]\\&=\operatorname {Var} ({\hat {\theta }}-\theta )+(\mathbb {E} [{\hat {\theta }}-\theta ])^{2}\\&=\operatorname {Var} ({\hat {\theta }})+\operatorname {Bias} ^{2}({\hat {\theta }},\theta )\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a89b110dd50aaf64585bb22b53b45f92d39adbf9)

![{\displaystyle \operatorname {MSE} \left({\overline {X}}\right)=\operatorname {E} \left[\left({\overline {X}}-\mu \right)^{2}\right]=\left({\frac {\sigma }{\sqrt {n}}}\right)^{2}={\frac {\sigma ^{2}}{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4647a2cc4c8f9a4c90b628faad2dcf80c4aae84)



![{\displaystyle {\begin{aligned}\operatorname {MSE} (S_{a}^{2})&=\operatorname {E} \left[\left({\frac {n-1}{a}}S_{n-1}^{2}-\sigma ^{2}\right)^{2}\right]\\&=\operatorname {E} \left[{\frac {(n-1)^{2}}{a^{2}}}S_{n-1}^{4}-2\left({\frac {n-1}{a}}S_{n-1}^{2}\right)\sigma ^{2}+\sigma ^{4}\right]\\&={\frac {(n-1)^{2}}{a^{2}}}\operatorname {E} \left[S_{n-1}^{4}\right]-2\left({\frac {n-1}{a}}\right)\operatorname {E} \left[S_{n-1}^{2}\right]\sigma ^{2}+\sigma ^{4}\\&={\frac {(n-1)^{2}}{a^{2}}}\operatorname {E} \left[S_{n-1}^{4}\right]-2\left({\frac {n-1}{a}}\right)\sigma ^{4}+\sigma ^{4}&&\operatorname {E} \left[S_{n-1}^{2}\right]=\sigma ^{2}\\&={\frac {(n-1)^{2}}{a^{2}}}\left({\frac {\gamma _{2}}{n}}+{\frac {n+1}{n-1}}\right)\sigma ^{4}-2\left({\frac {n-1}{a}}\right)\sigma ^{4}+\sigma ^{4}&&\operatorname {E} \left[S_{n-1}^{4}\right]=\operatorname {MSE} (S_{n-1}^{2})+\sigma ^{4}\\&={\frac {n-1}{na^{2}}}\left((n-1)\gamma _{2}+n^{2}+n\right)\sigma ^{4}-2\left({\frac {n-1}{a}}\right)\sigma ^{4}+\sigma ^{4}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf22322412b8454c706d78671e5d94208675a6e0)