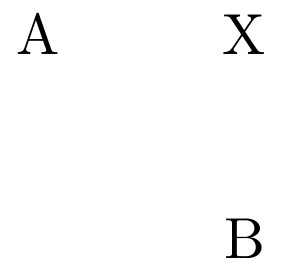Pgfplots: краткое руководство
О пакете
Пакет pgfplots представляет собой мощный инструмент, предназначенный для создания научных графиков. Он создан на базе tikz, не менее прекрасного пакета, который позволяет создавать векторную графику прямо на латехе.
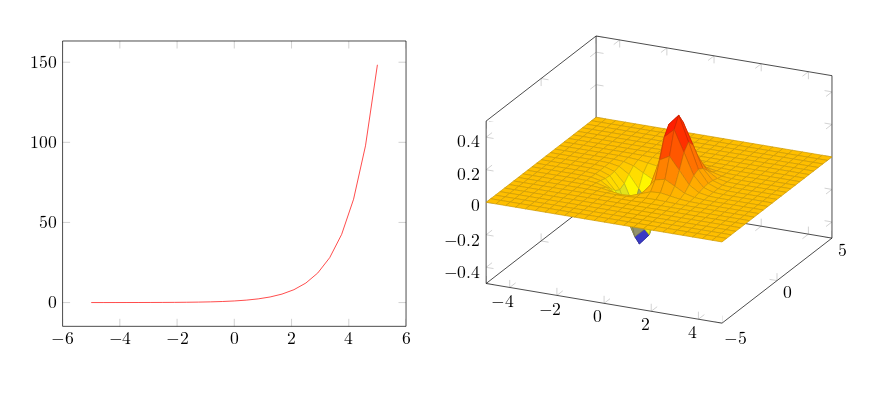
Если вы сомневаетесь в необходимости использования pgfplots или tikz, посмотрите на простые графики, созданные с помощью этих пакетов:
Много небольших примеров применения можно посмотреть в галерее pgfplots 1.
Основная идея pgfplots — упрощение включения графиков в документ. Задача пользователя — задать формулу или данные, а остальным занимается pgfplots. Так, код графиков (см. пример на overleaf), приведенных выше (без преамбулы) выглядит так:
% Код первого графика
begin{tikzpicture}
begin{axis}
addplot[color=red]{exp(x)};
end{axis}
end{tikzpicture}% Код второго графика
begin{tikzpicture}
begin{axis}
addplot3[surf] {exp(-x^2-y^2)*x};
end{axis}
end{tikzpicture}Заметьте, от пользователя в простейшем случае не потребовалось практически ничего, кроме задания функции и вида её отображения. Разумеется, можно и вручную задать пределы построения функции и многое
другое.
Оглавление
- 0. Введение в pgfplots
- 0.1. Преамбула
- 0.2. Окружение осей
- 0.3. Пакет standalone: графики в отдельных файлах
- 1. Математика в pgfplots
- 1.1. Стандартные операторы
- 1.2. Стандартные функции
- 1.3. Генерация случайных чисел
- 2. Объявление новых функций
- 2.1. Составление функции Хевисайда. Ступенька произвольной длины
- 3. Настройка осей и сетки
- 3.1. Оси и их подписи. Настройка
- 3.2. «Тики» (метки на осях) и их подписи
- 3.2.1. Дополнительные тики
- 3.2.2. Промежуточные тики (minor ticks)
- 3.3. Максимальные и минимальные значения на графике. Масштаб осей
- 3.4. Сетка. Единицы измерения в LaTeX
- 3.4.1. Сетка через основные и промежуточные тики
- 3.4.2. Сетка через дополнительные (extra) тики
- 4. Легенда графика
- 5. Построение графика
- 5.1. Чтение данных из таблицы
- 5.1.2. Создание новых стоблцов таблицы
- 5.2. Отметки на линии графика (marks)
- 5.3. Прямоугольники ошибок
- 5.3.1. Постоянная абсолютная или относительная погрешность
- 5.3.2. Абсолютная или относительная погрешность из файла
- 5.4. Настройка линии графика
- 5.4.1. Толщина и цвет линии графика
- 5.4.2. Тип линии графика
- 5.1. Чтение данных из таблицы
- 6. Особенности построения графиков
- 6.1. Построение графиков, терпящих бесконечный скачок
- 6.2. Циклы в pgfplots и построение асимптот. Системы координат рисунка
- 6.3. Использование команд TikZ на графиках Pgfplots
- The End. Рекомендуемые источники
0. Введение в pgfplots
0.1. Преамбула
Подключается пакет стандартным образом. Вставьте этот код в преамбулу (до begin{document}):
Так же можно сразу в преамбуле сделать некоторые настройки. Во-первых, можно задать используемую версию pgfplots. Так как пакет динамично развивается, то некоторые вещи становятся несовместимыми от версии к версии. Наиболее разумным является использование текущей версии указанием параметра
pgfplotsset{width=10cm,compat=newest}но после окончания работы неплохо бы указать текущую версию вручную, чтобы если вдруг у вас будет такая функциональность, что не будет работать в следующих версиях, это не помешало бы компилировать график спустя длительное время.
Параметр width задает ширину графика. Также можно задать и высоту height. Надо заметить, что это нововведение по сравнению с tikz: в tikz картинки изменяют свой размер соответственно содержимому, pgfplots же может подогнать содержимое (масштабом осей) под график. Надо заметить, что возможно и обратное — задавать вручную масштаб осей, тогда высота и ширина будут определяться ими и содержимым, а параметры width, height будут игнорироваться.
0.2. Окружение осей
Поскольку pgfplots основан на tikz, график должен находиться в окружении tikzpicture. Сам график строится в осях (полотно графика с системой координат и некоторым масштабом).
Оси задаются окружением begin{axis} ... end{axis}. У осей могут быть свои параметры:
begin{tikzpicture}
begin{axis}[
%axis, % Обычные оси
%semilogxaxis, % По оси x логарифмический масштаб
%semilogyaxis, % По оси y логарифмический масштаб
%loglogaxis, % По обоим осям логарифмический масштаб
enlargelimits=true, % Делать размер осей чуть больше графика
]
addplot[color=red]{ln(x)};
end{axis}
end{tikzpicture}Булев параметр enlargelimits, если он включен, делает размер рисунка немного больше, так, чтобы нарисованные графики не касались края рисунка, а оставалось некоторое расстояние. По умолчанию он включен, и отключать его почти никогда не требуется.
Здесь они закомментированы. Достаточно одного из параметров, причем параметр axis используется по умолчанию, и его можно не указывать.
Чтобы добавить график, используется команда
addplot[color=red]{ln(x)};Внутри квадратных скобок могут быть переданы некоторые параметры, например здесь указан цвет линии графика. Квадратные скобки обязательны, если не передано ни одного параметра, нужно оставить между ними пробел.
Важно, что все команды (эта необходимость тянется из пакета tikz) должны заканчиваться точкой с запятой.
Внутри фигурных скобок размещается функция, задающая график. О её составлении рассказано ниже.
Так же более подробно о настройке осей и сетки см. раздел 3 «Настройка осей и сетки»
Самое подробное описание (на английском) можно найти в мануале по pgfplots 2.
0.3. Пакет standalone: графики в отдельных файлах
Компиляция графиков pgfplots может быть долгой. Особенно это касается случаев, когда строится функция с большим числом точек, уходящая на бесконечность или обрабатываются большие экспериментальные данные из файла.
В таком случае разумно, чтобы сократить время компиляции, создавать каждый рисунок как отдельный pdf-документ, а затем подключать его как картинку. С одной стороны, увеличивается скорость компиляции, с другой, документ становится проще за счет выноса длинного кода в отдельные файлы, а структура документа становится более гибкой: отдельный график можно использовать в других проектах.
Настоятельно рекомендуется использовать именно этот способ. Для него достаточно указать классом документа standalone, и документ будет компилироваться в pdf файл, причем так, что поле документа будет обрезано до размеров графика.
Стоит отметить, что этот пакет конфликтует с пакетом geometry, и последний использовать в документах класса standalone не нужно.
Дочерний документ (например, это файл img/ris1.tex):
documentclass{standalone}
usepackage[utf8]{inputenc}
usepackage{pgfplots}
pgfplotsset{width=10cm,compat=1.9}
begin{document}
begin{tikzpicture}
begin{axis}
addplot[color=red]{exp(x)};
end{axis}
end{tikzpicture}
end{document}Вставка картинки в основной документ:
begin{figure}[h!]
centering
includegraphics[scale=1]{img/ris1}
caption{Наш отдельный график}
label{fig:ris1}
end{figure}1. Математика в pgfplots
Математический аппарат pgfplots-а принадлежит пакету более низкого уровня pgf. Математические возможности pgf достаточно велики, и мы рассмотрим только некоторые аспекты составления сложных функций для построения различных графиков.
1.1. Стандартные операторы
- Без пояснения:
+,-,*,/,^ - Сравнение:
>,>=,<=,==,!= - Оператор факториала:
x!аналогичен вызову функцииfactorial(x)
Отдельно стоит сказать об условном операторе x ? y : z. Он вернет y, если x истина, и z, если ложь. Это можно использовать, например, для построения функций Хевисайда, о чем будет сказано ниже.
1.2. Стандартные функции
div(x,y)— целочисленное делениеmod(x,y)— остаток от деленияsign(x)— знак числа
Также ряд функций, не нуждающихся в объяснениях:
factorial(x),
sqrt(x),
exp(x),
ln(x),
log10(x),
log2(x),
abs(x)
Функции округления
round(x)— округлит до ближайшего целого, большего по модулю чем округляемое, числа: 1.5->2, -1.5->-2floor(x)— округлит х до ближайшего целого числа в большую сторонуceil(x)— округлит х до ближайшего целого числа в меньшую сторонуint(x)— просто вернет целую частьxfrac(x)— вернет дробную частьx
Целочисленные функции
iseven(x),isodd(x)— проверяет четность (нечетность) числа, в случае успеха вернет 1, в случае неудачи 1isprime(x)— проверяет, простое ли число (аналогично вернет 1/0)
Тригонометрические функции
sin,cos,tan,sec,cosec,cot,asin,acos,atan
Важно заметить, что все тригонометрические функции принимают на вход число в градусах, а для перевода из радиан в градусы служит функция deg, а обратно — rad. Это поведение по умолчанию, его можно поменять:
pgfkeys{/pgf/trig format=rad|deg}Кроме того, можно использовать радианы и не изменяя поведение по умолчанию — указать, что аргумент дан в радианах: cos(pi/2 r) ->0.
Гиперболические функции
sinh,cosh,tanh
1.3. Генерация случайных чисел
Присутствует и возможность генерации случайных чисел: вызов rnd вернет случайное число от 0 до 1, rand от -1 до 1.
Более подробно о функциях и операторах можно почитать в руководстве по pgf, 1000-1011 страницы 3.
2. Объявление новых функций
begin{tikzpicture}[
declare function={
myfun(x,t) = (x*t);
}
]
begin{axis}
addplot[color=red, domain=0:4, samples=300]{myfun(x,2)};
end{axis}
end{tikzpicture}Объявляется новая функция для всего рисунка. Все должно быть понятно из примера.
2.1. Составление функции Хевисайда. Ступенька произвольной длины
Используя условный оператор, несложно составить функцию Хевисайда:
Очевидно, она будет равна множителю перед скобкой при x>0 и нулю в отрицательной области. Из двух функций Хевисайда можно составить и прямоугольный импульс:
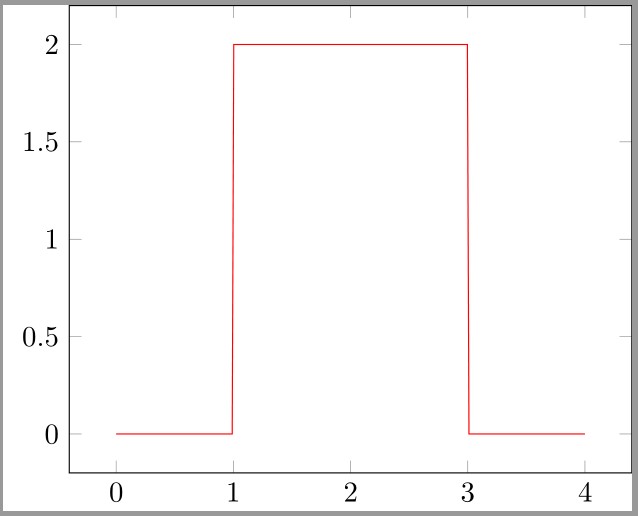
1*(x>0 ? 1 : 0)-1*(x>1 ? 1 : 0)Это прямоугольный импульс, начинающийся от нуля. Однако, можно создать функцию с аргументами высоты, ширины и начала ступеньки:
Нажмите для просмотра результата
begin{tikzpicture}[
declare function={
impuls(h,w,b,x) = h*((x>b ? 1 : 0)-(x>(b+w) ? 1 : 0));
}
]
begin{axis}
addplot[color=red, domain=0:4, samples=300]{impuls(2,2,1,x)};
end{axis}
end{tikzpicture}Заметим, что в общем случае, например для построения кусочно-гладких функций, необязательно создавать громоздкую функцию, которая будет включать в себя все остальные с помощью условного оператора.
Если заранее известно, что функция будет без скачков (скачок сам по себе можно построить, но особого смысла нет), то можно воспользоваться тем, что команда addplot имеет параметр области построения графика domain=start:end и использовать несколько плотов:
begin{tikzpicture}
begin{axis}
addplot[color=red, domain=0:1, samples=300]{x^2};
addplot[color=red, domain=1:4, samples=300]{2*x};
end{axis}
end{tikzpicture}samples здесь — количество точек графика. График не может строиться абсолютно непрерывно и берется в некотором числе точек, которые соединяются отрезками: чем выше число точек, тем качественнее картинка, но и медленнее её компиляция и отрисовка. Разумно делать это число меньше для медленно меняющихся графиков и много больше для быстро меняющихся, особенно для таких, как в предыдущем примере — со скачком.
По мере чтения руководства читатель может заметить появление новых параметров без объяснения. Предполагается, что они могут быть интуитивно понятны.
3. Настройка осей и сетки
3.1. Оси и их подписи. Заголовок графика.
Рассмотрим базовый пример настройки осей. По умолчанию, вместо координатных осей рисуется прямоугольник координат (axis lines = box), как это часто принято в научных статьях. Однако никто не мешает использовать оси-стрелки, или вообще отключить оси:
begin{tikzpicture}
begin{axis}[
axis lines = middle, % привычные оси со стрелочками с пересечением в нуле
% возможные значения: box, left, middle, center, right, none
xlabel = {$x$}, % подпись оси x
ylabel = {$f(x)$}, % подпись оси y
title={Мой первый график $f(x)=x^2 - 2cdot x - 1$},
]
addplot[domain=-10:10, samples=100, color=red] {x^2 - 2*x - 1};
end{axis}
end{tikzpicture}Обратите внимание на то, что у нас появился параметр title, задающий заголовок графику. Как правило, при использовании пакета standalone, это не нужно — заголовок графика задается командой caption в окружении figure.
Вообще говоря, положение осей можно применять и по отдельности:
axis x line=center,
axis y line=left,Можно задать и определенные правила отрисовки осей, например цвет, или сделать их пунктиром (dashed):
x axis line style ={black!40, dashed},
y axis line style ={red},Заметьте, как здесь указывается цвет. Это обозначение black!40!red означает смешение цветов, в соотношении 40% black 60% red, если цвет справа не указан, то он берется белым: значит, black!40 даст нам серый цвет. Таким образом из базовых цветов можно составить любой цвет.
Также можно перенести подписи осей к стрелкам на осях:
xlabel style={below right},
ylabel style={above left, red, scale=1.5},Здесь появился новый параметр scale, подпись к оси y будет в полтора раза больше, чем к оси x, очевидно.
Подразумевается, что все приведенные выше параметры подставляются в параметры окружения axis.
3.2. «Тики» (метки на осях) и их подписи
Когда график не качественный, важно наиболее удобно показать подписи (числа) к осям. За них отвечают ticks (тики) — маленькие перпендикулярные черты к осям с численной подписью.
Настройка расстояния между тиками:
xtick distance=1,
ytick distance=2Также можно вручную указать список основных тиков:
xtick={0,20,40,60,80,100},
ytick={0,20,40,60,80,100,120}А при необходимости, можно задать и подписи к ним (по умолчанию подпись — это координата тика):
ytick={1.5707,0.7853,1},
yticklabels={$frac{pi}{2},$, $frac{pi}{4}$, 1}, По умолчанию pgfplots пытается подобрать наиболее разумное расположение тиков.
3.2.1. Дополнительные тики
Иногда требуется специально показать положение чего-либо на осях. Для этого можно использовать дополнительные тики, задав им координаты и их подписи:
extra y ticks={-9/16,-6/16}, % положение дополнительных тиков
extra y tick labels={ % их подписи
{$U_{min}$}, {$U_{min}+Delta U$}
}, Для x аналогично.
3.2.2. Промежуточные тики (minor ticks)
Часто кроме основных меток на осях, ставят промежуточные: так, например, на линейке отмечены сантиметры рисками с подписями, а миллиметры просто рисками без подписей.
Такое задается с помощью minor ticks:
Этот параметр задает количество таких тиков (эквидистантных) между основными (major) тиками для обоих осей одинаково. А можно задать и для каждой оси отдельно:
minor x tick num=3,
minor y tick num=8,3.3. Максимальные и минимальные значения на графике. Масштаб осей
Масштаб осей задан в виде <длина орта x> <длина орта y>:
unit vector ratio = 1 1,
xmax = 8,
xmin=-2,
ymax=1.5,
ymin=-0.2,Максимальные и минимальные значения заданы очевидным образом.
3.4. Сетка. Единицы измерения в LaTeX
3.4.1. Сетка через основные и промежуточные тики
Сетка всегда проходит через тики на осях. Она может проходить как через основные (major) так и через промежуточные (minor) тики:
grid=major, % м.б. еще both - и там и там
grid style={dotted, cyan},Причем стиль можно задать как всей сетке (и основной major и промежуточной minor), так и по отдельности:
minor grid style={dashed,red, line width=0.2pt},
major grid style={solid,black, line width=0.1pt},Обратите внимание на используемые единицы измерения. em — это высота одной буквы шрифта 10pt:
pt называется типографским пунктом.
По умолчанию, сетка автоматически проведет линии и через пользовательские (дополнительные) тики, но этот стиль можно модифицировать:
extra tick style={grid=major, grid style={dotted, cyan}},Здесь мы скопировали стиль основных линий сетки и модифицировали его, сделав в точечку (dotted) и голубым (cyan).
4. Легенда графика
Для того, чтобы сопоставить какому-либо графику, который строится с помощью addplot, элемент легенды, есть специальная команда addlegendentry, которую нужно разместить после addplot:
begin{tikzpicture}
begin{axis}[
axis lines = middle,
xlabel = {$x$},
ylabel = {$f(x)$},
title={Мой первый график $f(x)=x^2 - 2cdot x - 1$},
legend pos={south west},
]
addplot[domain=-10:10, samples=100, color=red] {x^2+2*x};
addlegendentry{$x^+2cdot x$};
end{axis}
end{tikzpicture}Здесь появился параметр legend pos, который задает положение легенды на графике:
legend pos=south west|south east|north west|north east5. Построение графика
В самом начале мы рассмотрели и далее неоднократно употребляли построение графика заданной функции (y=f(x)). Однако, часто требуется построить не такой (или не только такой график), а покоординатный график (или, как это говорят математики, функция задана таблично, а не аналитически).
Обычно такая задача возникает при обработке экспериментальных данных. Есть два способа: записать данные непосредественно в график, или записать их в текстовую таблицу (tsv или csv). Рассмотрим такие случаи.
5.1. Чтение данных из таблицы
Важно: для чтения из таблицы нужно подключить пакет:
usepackage{pgfplotstable}Рассмотрим такой пример: пусть у нас есть файл data.tsv, лежащий в той же папке, что и рисунок:
Fr Uin err
15 7.446 0.1
25 7.532 0.1
40 7.512 0.1
100 7.412 0.1
200 7.41 0.1
300 7.32 0.1
400 7.27 0.1
500 7.236 0.1
1000 7.3 0.1
2000 7.282 0.1
3000 7.27 0.1Тогда его можно построить командой:
addplot +[blue, dashed]
plot table [
x=Fr,
y=Uin
]{data.tsv};В этом примере все просто. В первых квадратных скобках пишутся параметры, управляющие отрисованным графиком, построением прямоугольников ошибок и т.п., а во вторых — параметры чтения из таблицы, создание новых столбцов таблицы путем математического выражения, составленного из существующих столбцов, о чем написано ниже.
5.1.2. Создание новых стоблцов таблицы
Рассмотрим простой пример, на основе приведенного выше файла данных. В нем в первой столбце стоит частота в герцах, но допустим, что мы хотим построить график от круговой частоты, т.е. домножить на (2pi):
addplot +[blue, dashed]
plot table [
create on use/omega/.style={
create col/expr={
thisrow{Fr}*2*pi
}
},
x=omega,
y=Uin
]{data.tsv};Здесь видно, как несложно оперировать созданием новых столбцов. При этом применима вся математика, рассмотренная в разделе выше.
5.2. Маркеры на линии графика
Часто требуется не просто соединить экспериментальные точки линией, а указать каждую конкретную точку маркером (mark), а то и вовсе составить график только из маркеров. Для этого предыдущий пример несложно модифицируется:
addplot +[blue, mark=*, mark size=1.5pt, only marks]
plot table [
create on use/omega/.style={
create col/expr={
thisrow{Fr}*2*pi
}
},
x=omega,
y=Uin
]{data.tsv};Параметр only marks принуждает рисовать только маркеры, без линии их соединяющих, mark size размер маркера, mark тип маркера.
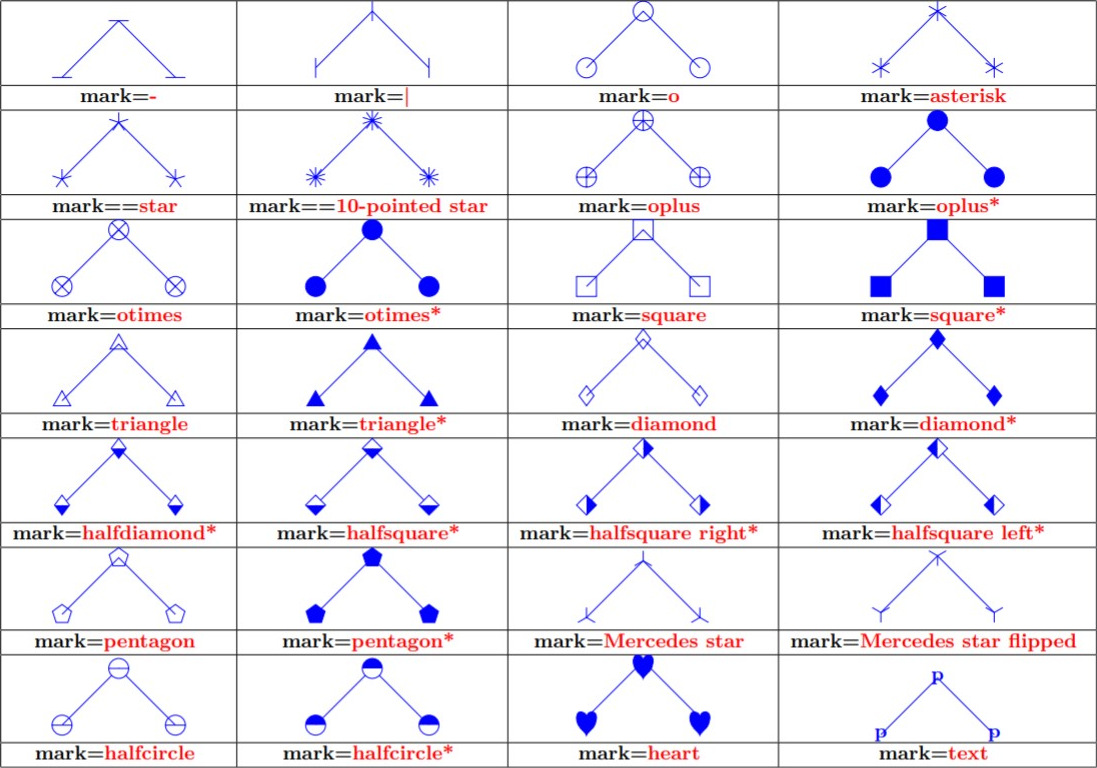
Существует достаточно много типов:
Эта картинка взята из руководства по tikz в картинках 4.
Для маркеров можно сразу задать несколько параметров: вместо размера задать масштаб (второй способ изменить размер маркера, иногда более удобный), основной цвет (draw) и цвет заливки (fill
addplot +[
mark=*,
mark options={
scale=2,
fill=blue,
draw=red,
},
only marks
] plot table [
create on use/omega/.style={
create col/expr={
thisrow{Fr}*2*pi
}
},
x=omega,
y=Uin
]{data.tsv};5.3. Прямоугольники ошибок
Для начала рассмотрим простейший случай постоянной ошибки. Параметры прямоугольников ошибок пишутся в параметры команды plot. Рассматривать будем все на примере ошибки по y, по другим осям анологично с точностью до замены y->x,z.
Для включения прямоугольников ошибки и возможности их настройки перед последующими рассмотренными параметрами нужно вставлять параметр error bars/.cd.
5.3.1. Постоянная абсолютная или относительная погрешность
Сначала нужно определить, какая будет ошибка: строго положительная, отрицательная или в обе стороны. За это отвечает параметр y dir=minus|plus|both.
addplot +[
mark=*,
only marks,
] plot[
error bars/.cd,
y dir=both,
y fixed=0.1,
% y fixed relative=0.1,
] table [
x=Fr,
y=Uin
]{data.tsv};Здесь указана сразу абсолютная погрешность для всех значений. Аналогично можно задать сразу относительную параметром y fixed relative.
5.3.2. Абсолютная или относительная погрешность из файла
Необходимо явно указать, что ожидается чтение данных ошибки из файла, указать в каком столбце (y error=err) записана ошибка и тип ошибки:
addplot +[
mark=*,
only marks,
] plot[
error bars/.cd,
y dir=both,
y explicit relative,
] table [
x=Fr,
y=Uin,
y error=err,
]{data.tsv};Для абсолютной ошибки параметр y explicit, для относительной y explicit relative.
5.4. Настройка линии графика
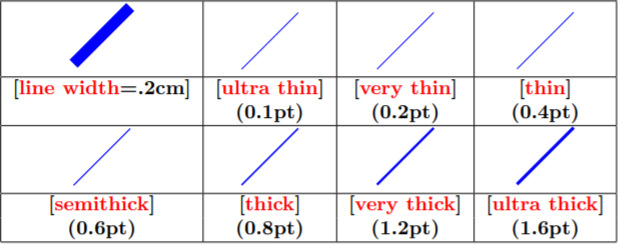
5.4.1. Толщина и цвет линии графика
Толщина линии управляется либо параметром line width=, либо словесными алиасами (рекомендуется использовать именно их):
Цвет линии сам является параметром:
addplot +[
thick,
blue!20!black
] plot table [
x=Fr,
y=Uin,
]{data.tsv};О составлении цветов сказано ранее в разделе ().
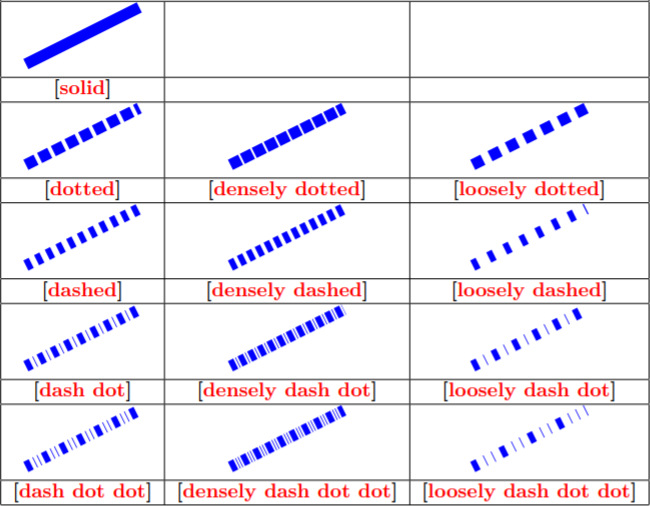
5.4.2. Тип линии графика
Как и цвет, тип линии графика сам по себе параметр:
addplot +[
thick,
blue!20!black,
dashed
] plot table [
x=Fr,
y=Uin,
]{data.tsv};Существует несколько типов линий:
6. Особенности построения графиков
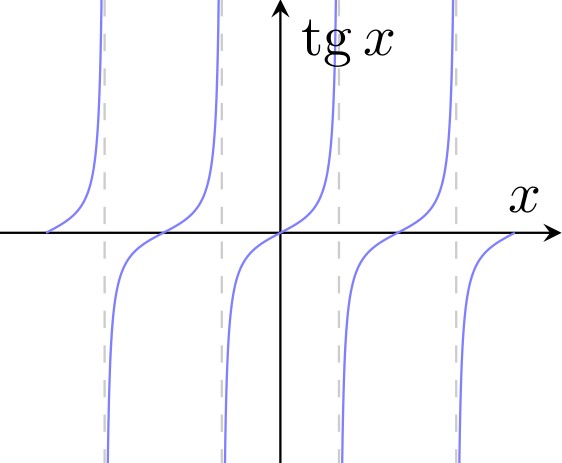
6.1. Построение графиков, терпящих бесконечный скачок
Рассмотрим построение графика с бесконечным скачком на примере построения (tan(x)).
Расчет функций, которые уходят на бесконечность, может привести к ошибкам компиляции. Чтобы этого избежать, можно указать в параметрах принудительное вписывание в пределы расчетов: выйдя за эти пределы, математический движок pgf просто будет пропускать эти значения, пока опять не войдет в пределы:
restrict y to domain=-20:20,Разумно выбирать эти пределы немного больше заданного предела осей xmin,xmax,ymin,ymax.
Кроме того, можно сказать pgfplots-у, как вести себя при получении бесконечности в расчетах, и не ограничивая расчет:
unbounded coords=discard|jumpЭтот ключ настраивает, что делать, если одна или несколько координат одной точки неограничена, или, например, при чтении из файла на этом месте стоит nan или ничего не стоит.
discard (по умолчанию) отбрасывает точку завершения, и в логе компиляции выдается предупреждение. При этом график строится, как если бы неограниченная точка не произошла: pgfplots интерполирует между ограниченными ближайшими точками.
jump просто пропустит значения, которые уходят на бесконечность, и график станет с разрывом.
Однако, как это ни странно, в случае тангенса это все не так: для стандартных функций с разрывом разработчики постарались, и они строятся без дополнительных усилий. Но при этом (+infty) и (-infty) точки графика соединяются, что не всегда может быть полезно: например, обычно в этом месте строят линии асимптот.
Все же придется вернуться к первоначальному определению:
documentclass[tikz,10pt]{standalone}
usepackage[T2A]{fontenc}
usepackage[utf8x]{inputenc}
usepackage[russian]{babel}
usepackage{amsmath,amssymb,cmap,pgfplots,pgfplotstable}
usetikzlibrary{arrows,calc,intersections}
pgfplotsset{compat=newest}
begin{document}
begin{tikzpicture}
begin{axis}[
xlabel={$x$},
ylabel={$tg x$},
axis lines=middle,
ymax = 10,
ymin = -10,
enlargelimits=true,
xmin=-4*pi/2,
xmax=4*pi/2,
restrict y to domain=-20:20,
xtick=empty,
ytick=empty,
]
addplot[blue!50,domain={-4*pi/2:4*pi/2},samples=1000] {tan(deg(x))};
pgfplotsinvokeforeach{-2,-1,...,2}{%
draw[dashed, black!20]
({{pi/2+pi*#1},0} |- {rel axis cs:0,0})
-- ({{pi/2+pi*#1},0}|-{rel axis cs:0,1});
}
end{axis}
end{tikzpicture}
end{document}Здесь есть интересный код для построения асимптот. Рассмотрим его подробнее.
6.2. Циклы в pgfplots и построение асимптот. Системы координат рисунка
Стандартный цикл tikz-а, к сожалению, в pgfplots не работает. Приходится использовать его более низкоуровневый аналог:
pgfplotsinvokeforeach{-2,-1,...,2}{%
% Выражение в цикле. Счетчик цикла - #1
}Счетчик пробегает указанные значения. Можно указывать их как список {0,1,2,3},а можно указать первое значение, второе, троеточие, последнее: из первого и второго рассчитается шаг и счетчик пробежит нужные значения. Они могут быть дробными.
Теперь подробнее, как же работает код построения вертикальной асимптоты. В tikz есть интересный способ расчета координаты в угле. Если задана такая координата X: (A -| B), то она находится в точке, которая образована пересечением горизонтальной линии через A и вертикальной через B:
Можно наоборот, (B -| A), соотв. вертикальная через А и горизонтальная через B.
По умолчанию используется система координат осей, в которой начало и орты отвечают нарисованным на графике.
Есть еще так называемая rel axis cs — система координат рисунка: в ней точка (0,0) это левый нижний угол рисунка, а (1,1) — верхний правый.
Со всей этой информацией теперь нетрудно должно быть понять, как работает асимптота через точку x:
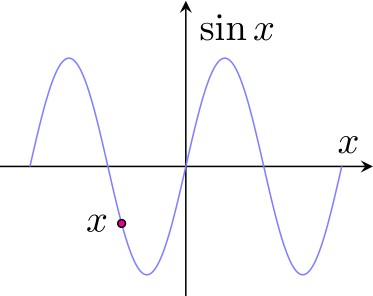
({x},0} |- {rel axis cs:0,0}) -- ({x},0}|-{rel axis cs:0,1});6.3. Использование команд TikZ на графиках Pgfplots
Ровно в предыдущем параграфе рассмотрено применение команд tikz для построения асимптот в осях графика.
Часто возникает еще потребность подписать какие-либо точки на кривой. Для этого можно создать ноду на кривой, где положение ноды задается от 0 до 1 — 0 в начале кривой, 1 в конце. Эдакие криволинейные координаты.
addplot[blue!50,domain={-4*pi/2:4*pi/2},samples=1000] {sin(deg(x))}
node[pos=0.3] (1) {}
node[pos=.3,left,black]{$x$};
draw[fill=magenta] (1) circle (1pt);Здесь мы специально создали пустую ноду с координатой (1), в которой потом можно нарисовать точку, а вторая нода уже рисует текст.
Для понимания это может быть затруднено, если вы не изучали tikz. Тогда можно просто использовать этот пример, не заботясь принципами его работы.
На кривую так можно поместить сколько угодно точек, главное, в конце списка должна стоять точка с запятой.
6.3. Качественные графики: удаление меток с осей
Достаточно добавить два параметра к окружению axis:
xtick=empty,
ytick=empty,The End. Рекомендуемые источники
Наконец, прочитав небольшое руководство по использованию pgfplots, вы почти готовы к тому, чтобы применить его для своих работ. В этом нелегком (поначалу) труде смогут помочь некоторые источники.
Дипломные работы, курсовые, контрольные, рефераты на заказ
Методические рекомендации особенности физических наблюдений.(4 часа)
Подобный материал:
- Методические рекомендации по проведению Единого Всекубанского классного часа, 33.75kb.
- Методические рекомендации «Педагогические особенности использования мультимедиа в образовании», 698.02kb.
- Постановлением Президиума Ростовского областного суда 6 августа 2004 года методические, 89.43kb.
- Методические рекомендации для учителей предметников по использованию цор в своей педагогической, 1201.3kb.
- Методические рекомендации по подготовке проекта муниципального правового акта органа, 154.99kb.
- Методические рекомендации и учебные материалы для проведения единого классного часа, 148.78kb.
- Методика преподавания темы «Многочлены» в профильной школе Методические рекомендации, 72.18kb.
- Основы метрологии в физике, 146.66kb.
- С. И. Сай «17» февраля 2003 года методические рекомендации, 234.96kb.
- Академия оценки и строительства казахстанская республиканская палата оценщиков особенности, 1159.14kb.
6/10. Определение погрешности измерений. Прямоугольник ошибок.
Дать понятие о погрешности измерений, ее влияние на вывод эмпирических зависимостей. Виды погрешностей. Погрешность измерительного прибора. Абсолютная погрешность. Погрешность отсчета. Прямоугольник ошибок.
Демонстрации
- Измерение объема колбы мензурками с разной ценой деления.
- Измерение длины нескольких тетрадных листов одной линейкой и определение среднего значения длины тетрадного листа.
— 8 —
- Определение толщины нити с помощью линейки с миллиметровыми делениями.
- Измерение длины парты линейкой, длина которой не превышает 30 см.
- Определение погрешности скорости равномерного движения математическими методами.
- Погрешность, вызываемая округлением величин.
- Построить график зависимости силы тяжести от массы, определить цену деления динамометра, точность измерения массы и указать на графике прямоугольник ошибок.
Лабораторные работы и опыты
- При измерении длины с помощью ученической линейки может быть допущена ошибка за счет неправильного расположения глаза. Как измерять правильно? Чем вызывается ошибка при таких измерениях?
- Дана таблица измерений приложенной нагрузки от положения конца образца. Постройте график этой зависимости и проанализируйте погрешности измерений на разных его участках.
| 0 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 | 1100 | Нагрузка |
| 0 | 2,1 | 4,2 | 6,3 | 8,5 | 10,6 | 12,6 | 14,6 | 16,6 | 18,6 | 20,5 | 22,3 | Растяжение |
Самостоятельные работы
- Рассмотрите шприц и охарактеризуйте его как измерительный прибор.. Определите погрешность, верхний и нижний пределы его измерений.
- Определите с земли высоту дерева, телеграфного столба или любого другого предмета, имея только небольшую линейку. Предложите несколько способов. Оцените погрешность каждого способа.
- Измерить площадь фигуры неправильной формы и подсчитать погрешность своих измерений.
7/11. Измерение коэффициента упругости пружин различной жесткости с помощью графика.
Графическая зависимость силы упругости от растяжения. Расчет коэффициента упругости с помощью графика.
Демонстрации Измерение растяжения пружин разной жесткости под действием различных сил.
Лабораторные работы и опыты
Измерение коэффициента упругости пружин различной жесткости с помощью графика.
Самостоятельные работы
Начертить график зависимости силы упругости от деформации на миллиметровой бумаге, подсчитать погрешность опыта, построить прямоугольник ошибок и вычислить коэффициент упругости пружины.
8/12. Сила трения. Измерение коэффициента трения.
Сила трения покоя, скольжения, качения. Зависимость силы трения от силы нормального давления. Коэффициент трения. Шероховатости соприкасающихся поверхностей, взаимодействие молекул. Жидкое трение.
Демонстрации
— 9 —
- Трение скольжения, покоя и качения. Равновесие тела на вращающемся диске.
- Смазывание трущихся поверхностей уменьшает трение. Почему же труднее удерживать рукоятку топора сухой рукой, чем влажной?
Лабораторные работы и опыты
Изучение зависимости силы трения скольжения от силы давления. Результат получить аналитически и графически.
Самостоятельные работы
- Карандаш удерживают на столе в вертикальном положении заостренным концом вниз. После того как его отпустили, он начинает падать, как движется при этом острие карандаша в зависимости от коэффициента трения? Оторвется ли острие карандаша от стола (в отличие от случая, когда в результате скольжения место заточки карандаша в конце концов соприкоснется со столом )?
- Карандаш находится в горизонтальном положении, опираясь концами на два моих указательных пальца. Пока я медленно сдвигаю пальцы, чтобы они встретились под центром стержня, он скользит либо по одному, либо по другому пальцу. Почему он так движется?
9/13. Закон инерции. Законы взаимодействия.
Фундаментальные законы взаимодействия. Их значение для становления физики как науки. Связь действующей силы с изменением скорости. Движение с постоянной скоростью.
Демонстрации
- Расположите на столе близко друг к другу два алюминиевых бруска. Свяжите ножки пинцета и поместите его между брусками. Пережгите нить. Почему бруски приходят в движение? Одинаковы ли их скорости? Массы?
- Повторите опыт, взяв бруски одинакового объема, но разных масс. Одинаковы ли их скорости?
- Демонстрация законов инерции.
Приборы и материалы. Бумажная тарелка, ножницы, бумажный шарик.
Ход работы.
- Отрежьте от тарелки одну половину.
- Поместите шарик на кромку отрезанной части.
- Поставьте тарелку на стол и слегка наклоните ее, чтобы шарик быстро покатился по выемке тарелки.
Шарик скатывается с тарелки и удаляется от нее по прямой.
Вывод. Предметы движутся по прямой, если на них не действуют никакие силы.
- Положите лист картона так, чтобы он опирался на две книги. На середину листа положите мешочек с песком. Резко поднимите лист вместе с мешочком. Почему изменилась его форма?
— 10 —
- Действие равно противодействию. Но почему тело движется, ведь какую бы силу мы не приложили, появится противодействующая сила. Где здесь ошибка в рассуждениях?
Лабораторные работы и опыты
- Положите шарик на лист бумаги. Отметьте положение шарика относительно стола. Выдерните лист резким движением. Изменилось ли положение шарика?
- Подвесите алюминиевый и медный цилиндры на нить к лапке штатива. Отклоните их в разные стороны и проследите, что с ними происходит после удара.
- Зацепите крючками два динамометра и слегка разведите их в стороны. Заметьте их показания.
Самостоятельные работы
- Придумайте и проделайте опыты, при помощи которых можно показать проявление инерции у покоящихся и движущихся тел.
- Придумайте опыты, при помощи которых можно показать зависимость инертности тел от массы.
- Висящий на нити, привязанной к потолку каюты, груз отклонился в сторону, хотя на него ничто не действовало. Нет ли здесь противоречия с законом инерции?
- Свойством инерции обладают не только твердые, но также жидкие и газообразные тела. Придумайте и проделайте опыты, при помощи которых можно показать проявление инерции жидких тел.
- Предмет покоится на краю горизонтального стола. Его толкают и он падает с другой стороны стола, ширина которого 1 м, через 2 с. Есть ли у предмета колеса?
10/14. Скорость равномерного движения. Относительность движения.
Мгновенная скорость. Скорость равномерного движения. Относительность движения. Относительная скорость тел. Расчет скорости движения для равномерного движения. Средняя скорость.
Демонстрации
- Самолет, летящий со скоростью 900 км/ч, во время полета заправляется горючим от другого самолета. С какой скоростью движется при этом самолет-заправщик?
- Демонстрация относительности движения на примере тележки и вращающегося диска, установленного на штативе.
- Демонстрация теневой проекции вращения тела, лежащего на горизонтально расположенном диске.
- Автомобиль проехал 60 км за 1 ч, а потом еще 240 км за 5 ч. Какова средняя скорость на всем пути?
- Двигаясь по шоссе, велосипедист проехал 900 м со скоростью 15 м/с, а затем по плохой дороге 400 м со скоростью 10 м/с. С какой средней скоростью он проехал весь путь?
- Минутная стрелка настенных часов вдвое длиннее, чем часовая. В какой момент после полуночи конец минутной стрелки будет удаляться от конца часовой стрелки с наибольшей скоростью?
Лабораторные работы и опыты
- Положите линейку на лист бумаги. Один конец линейки зажмите и с помощью карандаша переместите на некоторый угол. Определите траекторию, скорость и перемещение относительно линейки и листа бумаги.
- Положите деревянный брусок на лист бумаги. Медленно потяните за край листа. В каком состоянии относительно стола находится лист бумаги и брусок? В каком состоянии относительно листа бумаги находился брусок?
— 11 —
- Положите брусок на лист бумаги и резко потяните за край листа. В каком состоянии относительно стола находился лист бумаги? В каком состоянии относительно бумаги находился стол? В каком состоянии относительно стола находился брусок?
- Можно ли сказать, что брусок движется относительно стола в опытах, указанных в предыдущих задачах?
Самостоятельные работы
- Подсчитайте скорость своего подъема по лестнице.
- Определите среднюю скорость движения автобуса между остановками и переведите ее в м/с.
- Определите скорость, с которой перемещается конец минутной стрелки ваших часов.
- Голодный паук приготовился поймать насекомое, если оно окажется в паутинке, которая натянута между ним и стеной. Длина нити 1 м. на нить попала гусеница. Увидев паука, она стала уползать от него к стене со скоростью ν1= 1мм/с относительно нити, а паук , оставаясь на месте, стал вытягивать свой конец нити со скоростью ν0= 1 см/с, считая, что нить может растягиваться без ограничений. Доползет ли гусеница до стены? Как изменится решение предыдущей задачи, если паук не сидит на месте, а удаляется от стены, увлекая за собой конец нити?
11/15. Перемещение при равномерном движении.
Траектория. Перемещение. Путь. Связь пути и перемещения при прямолинейном равномерном движении.
Демонстрации
Сравнить движение стрелок часов; нитяного маятника; равномерное движение тележки, привязанной к грузу, подвешенному к ней через блок. На тележке стоит капельница, с помощью которой отмечаются величины перемещений за равные промежутки времени. Вращение диска с закрепленной осью.
Лабораторные работы и опыты
Расположите резиновую трубку, заполненную водой, вертикально. Перевернув трубку, проследите за движением пузырька воздуха в ней. Отмерив одинаковые расстояния, проследите за тем, соответствуют ли ударам метронома прохождение пузырьком сделанных вами меток.
Самостоятельные работы
- Определите путь и перемещение минутной стрелки часов за 10 минут, 30 минут и 1 час.
- В движущемся вагоне в любой момент времени есть точки, движущиеся в сторону, обратную движению вагона. Какие это точки?
- Две одинаковые шайбы А и В скользят без трения по льду озера. Они соединены легкой, нерастяжимой, но упругой нитью длиной √2L. В момент времени t = 0 шайба А покоится в точке с координатами (0,0), а шайба В, которая находится в точке с координатами (L,0), сообщают скорость v вдоль оси y в положительном направлении. Определите координаты и скорости шайб А и В в моменты времени t1 = 2L/v и t2 = 100L /v.
12/16. Графики зависимости скорости и перемещения от времени.
Научить строить и читать графики равномерного движения.
1. Получены данные о движения автомобиля:
| Длительность движения,ч | 0,1 | 0,4 | 0,2 |
| Скорость, км/ч | 20 | 60 | 20 |
— 12 —
- Какой путь пройдет автомобиль за первый промежуток времени?
- Какова общая длина пути, пройденного автомобилем?
- Постройте график зависимости скорости от времени для этой поездки
- За какое время автомобиль пройдет первые 14 км пути?
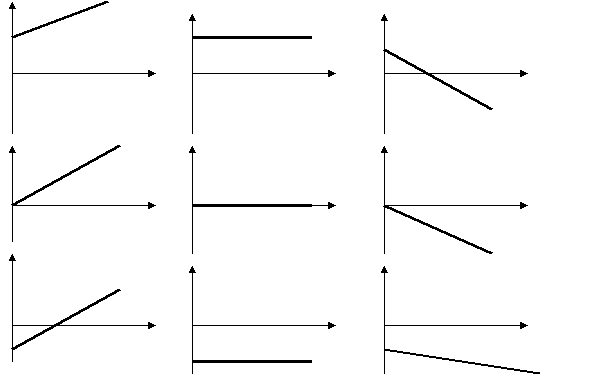
- Укажите площадь на вашем графике, соответствующую первым 14 км пути.
2. Проанализируем графики, приведенные ниже. Какие из них могут соответствовать графикам зависимости перемещения от времени и почему? Какие из них могут соответствовать графикам зависимости скорости равномерного движения от времени и почему?
Лабораторные работы и опыты
Проследим, как движутся пузырьки воздуха со дна водоема. Проанализируем фотографии, сделанные за одинаковые промежутки времени. Измеряя перемещения пузырьков, запишем результаты в таблицу.
| x, cм | ||||
| t, c |
По полученным данным построим график зависимости перемещения от времени.
Самостоятельные работы
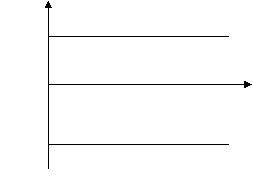
На рисунке представлены графики проекций скоростей двух автомобилей, движущихся по одной прямой. Что можно сказать о направлении движения автомобилей? Меняются ли их скорости со временем? Какой из автомобилей движется быстрее?
— 13 —
13/17. Координатный метод описания движения.
Движение-это изменение положения тела относительно данного тела отсчета и связанной с ним системы координат с течением времени. Система отсчета и система координат. Положение тела в одномерной, двумерной и трехмерной системе координат. Угловая система координат.
Демонстрации
- Все вы знаете стихотворение А. С. Пушкина «У лукоморья дуб зеленый…». Что является телом отсчета для описания движения кота?
- Определим координаты люстры в классе, выбрав за тело отсчета входную дверь.
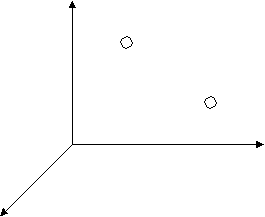
- На рисунке изображено положение двух точек в пространстве относительно координатных осей. Определить:
Цену деления осей
Координаты точки А.
Координаты точки В.
Лабораторные работы и опыты
На рисунке показано положение трех точек А, В и С, соединенных между собой кривой линией. Эта линия является траекторией движения точки из А в С. Определить:
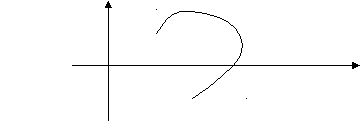
- Цену деления осей координат
- Координаты точек А, В и С.
- Проекции вектора АВ, ВС и АС.
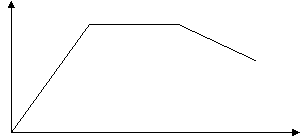
На рисунке изображен график координаты тела от времени. Определите:
- Цену деления осей.
- Время движения по оси ох
- Время остановки
- Время движения против оси ох
- Пройденный путь
- Среднюю скорость движения
- Скорость до остановки
- Скорость после остановки
- Величину перемещения
— 14 —
X,м
Самостоятельные работы
С помощью рулетки или сантиметровой измерительной ленты определите координаты точки подвеса комнатного светильника по отношению к системе отсчета, связанной с одним из нижних углов комнаты. Координаты оси направьте вдоль стен комнаты.
14/18. Движение с ускорением.
Движение с изменяющейся во времени скоростью. Ускорение. Перемещение при прямолинейном равноускоренном движении. Изменение скорости по направлению при вращении стрелок часов.
Демонстрации
1. Видеофильм «Основы кинематики». Элемент технологии критического мышления И.Д.Е.А.Л.
- Формулировка проблемы (все ли тела движутся равномерно)
- Формулировка проблемы в виде вопроса (как можно описать движение тел, отличающихся от равномерного)
- Генерирование как можно большего числа решений вопроса
- Выбор наилучших вариантов
- Характер изменения физические величины при движении со скоростью, меняющейся во времени
Оформление решения проблемы
2. Конический маятник.
3. Проделайте опыт Г.Галилея: убедитесь в том, что пути, проходимые в последовательные равные промежутки времени, относятся как последовательный ряд нечетных чисел. Положив шарик вверху желоба, отпустите его и карандашом отметьте местоположения шарика под удары метронома. Пути, проходимые при равноускоренном движении за последовательные равные промежутки времени, определите по миллиметровой шкале на линейке. Наклонная плоскость должна составлять малый угол с плоскостью стола, для того чтобы шарик скатывался медленно.
Лабораторные работы и опыты
Определите среднюю скорость шарика, скатывающегося с наклонной плоскости. Как она зависит от угла наклона плоскости? От чего зависит точность ваших измерений? Как определить конечную скорость шарика? Как она зависит от угла наклонной плоскости и ее длины?
Самостоятельные работы
Пластиковый пузырек с подкрашенной жидкостью поставить на тележку и открыть отверстие в дне сосуда. Измерить расстояния между каплями, оставленными на бумажной ленте, положенной на демонстрационный стол, при скатывании тележки с наклонной плоскости, а также общее время движения и интервалы времени, соответствующие отметкам на ленте. Подсчитать среднюю скорость движения.
— 15 —
15/19. Свободное падение тел.
Движение тела из состояния покоя под действием силы тяжести. Постоянство ускорения свободного падения для данного места на земной поверхности. Измерение ускорения свободного падения.
Демонстрации
- Определите экспериментально ускорение, с которым шарик скатывается по наклонному желобу. Как изменяется ускорение шарика при увеличении угла наклона желоба?
- Шарик упал со стола. С каким ускорением он двигался? Сколько времени длилось падение шарика? Какой была скорость шарика в момент, когда он коснулся пола? Какова высота стола?
Лабораторные работы и опыты
- Пронаблюдайте за падением тел разной массы, но одинакового объема; разной формы. Сделайте вывод.
- Придумать опыт, доказывающий, что свободно падающий шарик движется по вертикали.
Самостоятельные работы
- Определите ускорение свободного падения, пользуясь отвесом, секундомером и камнями различной формы и объема. Местом проведения опыта может быть высокий мост, глубокий овраг или балкон многоэтажного дома. Возьмите округленный камень небольших размеров и под счет “раз, два, пуск” предоставьте ему возможность падать. Секундомером измерьте время падения камня, а затем по известной формуле найдите ускорение свободного падения. Повторите опыт несколько раз с разными телами и убедитесь в том, что ускорение свободного падения не зависит от массы падающего тела. Как влияет на результат расчета ускорения свободного падения погрешность измерения времени и время реакции человека?
- Маленький шарик В лежит на краю стола высотой 1 м, другой такой же шарик А подвешен на нити длинной 1 м и представляет собой математический маятник. Если нить с шариком А привести в горизонтальное положение и отпустить, то между шариками произойдет упругое столкновение. Рассматривая движение шарика В только до момента его падения на землю, ответьте на вопросы: а) какой шарик дольше находится в движении; б) у какого шарика больше длина траектории?
16/20. График скорости от времени при равноускоренном движении.
График скорости от времени при равномерном движении (повторение). Отличие графика скорости неравномерного движения от графика скорости для равномерного движения. Физический смысл угла наклона графика. График скорости свободно падающего тела. Угол наклона графика скорости тела, движущегося под действием силы тяжести.
Основной материал
- В таблице приведены значения мгновенной скорости автомобиля от времени:
| Время,с | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Скорость, м/с | 10,0 | 12,4 | 14,8 | 17,2 | 19,6 | 22,0 | 24,4 |
Постройте график скорости от времени для этой поездки и ответьте на вопросы:
- С какой скоростью двигался автомобиль в моменты времени 2,6 с и 4,8 с?
- Какой путь прошел автомобиль между этими двумя моментами времени?
2. Дан график скорости от времени.
— 16 —
V,м/c
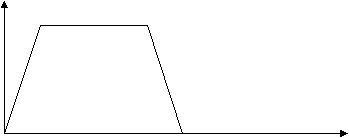
Разобрать, как меняется скорость движения велосипедиста по графику. Какое время он двигался равномерно? Какое расстояние он проехал, двигаясь с постоянной скоростью, при разгоне и при торможении?
Лабораторные работы и опыты
По графику скорости найдите ускорение и среднюю скорость за первые две секунды его
движения.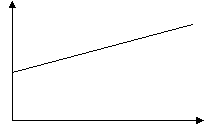
Самостоятельные работы
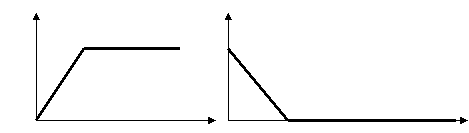
Определите ускорение и среднюю скорость тел, пользуясь графиками скорости от времени.
Дипломные работы, курсовые, контрольные, рефераты на заказ
Методические рекомендации особенности физических наблюдений.(4 часа)
Подобный материал:
- Методические рекомендации по проведению Единого Всекубанского классного часа, 33.75kb.
- Методические рекомендации «Педагогические особенности использования мультимедиа в образовании», 698.02kb.
- Постановлением Президиума Ростовского областного суда 6 августа 2004 года методические, 89.43kb.
- Методические рекомендации для учителей предметников по использованию цор в своей педагогической, 1201.3kb.
- Методические рекомендации по подготовке проекта муниципального правового акта органа, 154.99kb.
- Методические рекомендации и учебные материалы для проведения единого классного часа, 148.78kb.
- Методика преподавания темы «Многочлены» в профильной школе Методические рекомендации, 72.18kb.
- Основы метрологии в физике, 146.66kb.
- С. И. Сай «17» февраля 2003 года методические рекомендации, 234.96kb.
- Академия оценки и строительства казахстанская республиканская палата оценщиков особенности, 1159.14kb.
6/10. Определение погрешности измерений. Прямоугольник ошибок.
Дать понятие о погрешности измерений, ее влияние на вывод эмпирических зависимостей. Виды погрешностей. Погрешность измерительного прибора. Абсолютная погрешность. Погрешность отсчета. Прямоугольник ошибок.
Демонстрации
- Измерение объема колбы мензурками с разной ценой деления.
- Измерение длины нескольких тетрадных листов одной линейкой и определение среднего значения длины тетрадного листа.
— 8 —
- Определение толщины нити с помощью линейки с миллиметровыми делениями.
- Измерение длины парты линейкой, длина которой не превышает 30 см.
- Определение погрешности скорости равномерного движения математическими методами.
- Погрешность, вызываемая округлением величин.
- Построить график зависимости силы тяжести от массы, определить цену деления динамометра, точность измерения массы и указать на графике прямоугольник ошибок.
Лабораторные работы и опыты
- При измерении длины с помощью ученической линейки может быть допущена ошибка за счет неправильного расположения глаза. Как измерять правильно? Чем вызывается ошибка при таких измерениях?
- Дана таблица измерений приложенной нагрузки от положения конца образца. Постройте график этой зависимости и проанализируйте погрешности измерений на разных его участках.
| 0 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 | 1100 | Нагрузка |
| 0 | 2,1 | 4,2 | 6,3 | 8,5 | 10,6 | 12,6 | 14,6 | 16,6 | 18,6 | 20,5 | 22,3 | Растяжение |
Самостоятельные работы
- Рассмотрите шприц и охарактеризуйте его как измерительный прибор.. Определите погрешность, верхний и нижний пределы его измерений.
- Определите с земли высоту дерева, телеграфного столба или любого другого предмета, имея только небольшую линейку. Предложите несколько способов. Оцените погрешность каждого способа.
- Измерить площадь фигуры неправильной формы и подсчитать погрешность своих измерений.
7/11. Измерение коэффициента упругости пружин различной жесткости с помощью графика.
Графическая зависимость силы упругости от растяжения. Расчет коэффициента упругости с помощью графика.
Демонстрации Измерение растяжения пружин разной жесткости под действием различных сил.
Лабораторные работы и опыты
Измерение коэффициента упругости пружин различной жесткости с помощью графика.
Самостоятельные работы
Начертить график зависимости силы упругости от деформации на миллиметровой бумаге, подсчитать погрешность опыта, построить прямоугольник ошибок и вычислить коэффициент упругости пружины.
8/12. Сила трения. Измерение коэффициента трения.
Сила трения покоя, скольжения, качения. Зависимость силы трения от силы нормального давления. Коэффициент трения. Шероховатости соприкасающихся поверхностей, взаимодействие молекул. Жидкое трение.
Демонстрации
— 9 —
- Трение скольжения, покоя и качения. Равновесие тела на вращающемся диске.
- Смазывание трущихся поверхностей уменьшает трение. Почему же труднее удерживать рукоятку топора сухой рукой, чем влажной?
Лабораторные работы и опыты
Изучение зависимости силы трения скольжения от силы давления. Результат получить аналитически и графически.
Самостоятельные работы
- Карандаш удерживают на столе в вертикальном положении заостренным концом вниз. После того как его отпустили, он начинает падать, как движется при этом острие карандаша в зависимости от коэффициента трения? Оторвется ли острие карандаша от стола (в отличие от случая, когда в результате скольжения место заточки карандаша в конце концов соприкоснется со столом )?
- Карандаш находится в горизонтальном положении, опираясь концами на два моих указательных пальца. Пока я медленно сдвигаю пальцы, чтобы они встретились под центром стержня, он скользит либо по одному, либо по другому пальцу. Почему он так движется?
9/13. Закон инерции. Законы взаимодействия.
Фундаментальные законы взаимодействия. Их значение для становления физики как науки. Связь действующей силы с изменением скорости. Движение с постоянной скоростью.
Демонстрации
- Расположите на столе близко друг к другу два алюминиевых бруска. Свяжите ножки пинцета и поместите его между брусками. Пережгите нить. Почему бруски приходят в движение? Одинаковы ли их скорости? Массы?
- Повторите опыт, взяв бруски одинакового объема, но разных масс. Одинаковы ли их скорости?
- Демонстрация законов инерции.
Приборы и материалы. Бумажная тарелка, ножницы, бумажный шарик.
Ход работы.
- Отрежьте от тарелки одну половину.
- Поместите шарик на кромку отрезанной части.
- Поставьте тарелку на стол и слегка наклоните ее, чтобы шарик быстро покатился по выемке тарелки.
Шарик скатывается с тарелки и удаляется от нее по прямой.
Вывод. Предметы движутся по прямой, если на них не действуют никакие силы.
- Положите лист картона так, чтобы он опирался на две книги. На середину листа положите мешочек с песком. Резко поднимите лист вместе с мешочком. Почему изменилась его форма?
— 10 —
- Действие равно противодействию. Но почему тело движется, ведь какую бы силу мы не приложили, появится противодействующая сила. Где здесь ошибка в рассуждениях?
Лабораторные работы и опыты
- Положите шарик на лист бумаги. Отметьте положение шарика относительно стола. Выдерните лист резким движением. Изменилось ли положение шарика?
- Подвесите алюминиевый и медный цилиндры на нить к лапке штатива. Отклоните их в разные стороны и проследите, что с ними происходит после удара.
- Зацепите крючками два динамометра и слегка разведите их в стороны. Заметьте их показания.
Самостоятельные работы
- Придумайте и проделайте опыты, при помощи которых можно показать проявление инерции у покоящихся и движущихся тел.
- Придумайте опыты, при помощи которых можно показать зависимость инертности тел от массы.
- Висящий на нити, привязанной к потолку каюты, груз отклонился в сторону, хотя на него ничто не действовало. Нет ли здесь противоречия с законом инерции?
- Свойством инерции обладают не только твердые, но также жидкие и газообразные тела. Придумайте и проделайте опыты, при помощи которых можно показать проявление инерции жидких тел.
- Предмет покоится на краю горизонтального стола. Его толкают и он падает с другой стороны стола, ширина которого 1 м, через 2 с. Есть ли у предмета колеса?
10/14. Скорость равномерного движения. Относительность движения.
Мгновенная скорость. Скорость равномерного движения. Относительность движения. Относительная скорость тел. Расчет скорости движения для равномерного движения. Средняя скорость.
Демонстрации
- Самолет, летящий со скоростью 900 км/ч, во время полета заправляется горючим от другого самолета. С какой скоростью движется при этом самолет-заправщик?
- Демонстрация относительности движения на примере тележки и вращающегося диска, установленного на штативе.
- Демонстрация теневой проекции вращения тела, лежащего на горизонтально расположенном диске.
- Автомобиль проехал 60 км за 1 ч, а потом еще 240 км за 5 ч. Какова средняя скорость на всем пути?
- Двигаясь по шоссе, велосипедист проехал 900 м со скоростью 15 м/с, а затем по плохой дороге 400 м со скоростью 10 м/с. С какой средней скоростью он проехал весь путь?
- Минутная стрелка настенных часов вдвое длиннее, чем часовая. В какой момент после полуночи конец минутной стрелки будет удаляться от конца часовой стрелки с наибольшей скоростью?
Лабораторные работы и опыты
- Положите линейку на лист бумаги. Один конец линейки зажмите и с помощью карандаша переместите на некоторый угол. Определите траекторию, скорость и перемещение относительно линейки и листа бумаги.
- Положите деревянный брусок на лист бумаги. Медленно потяните за край листа. В каком состоянии относительно стола находится лист бумаги и брусок? В каком состоянии относительно листа бумаги находился брусок?
— 11 —
- Положите брусок на лист бумаги и резко потяните за край листа. В каком состоянии относительно стола находился лист бумаги? В каком состоянии относительно бумаги находился стол? В каком состоянии относительно стола находился брусок?
- Можно ли сказать, что брусок движется относительно стола в опытах, указанных в предыдущих задачах?
Самостоятельные работы
- Подсчитайте скорость своего подъема по лестнице.
- Определите среднюю скорость движения автобуса между остановками и переведите ее в м/с.
- Определите скорость, с которой перемещается конец минутной стрелки ваших часов.
- Голодный паук приготовился поймать насекомое, если оно окажется в паутинке, которая натянута между ним и стеной. Длина нити 1 м. на нить попала гусеница. Увидев паука, она стала уползать от него к стене со скоростью ν1= 1мм/с относительно нити, а паук , оставаясь на месте, стал вытягивать свой конец нити со скоростью ν0= 1 см/с, считая, что нить может растягиваться без ограничений. Доползет ли гусеница до стены? Как изменится решение предыдущей задачи, если паук не сидит на месте, а удаляется от стены, увлекая за собой конец нити?
11/15. Перемещение при равномерном движении.
Траектория. Перемещение. Путь. Связь пути и перемещения при прямолинейном равномерном движении.
Демонстрации
Сравнить движение стрелок часов; нитяного маятника; равномерное движение тележки, привязанной к грузу, подвешенному к ней через блок. На тележке стоит капельница, с помощью которой отмечаются величины перемещений за равные промежутки времени. Вращение диска с закрепленной осью.
Лабораторные работы и опыты
Расположите резиновую трубку, заполненную водой, вертикально. Перевернув трубку, проследите за движением пузырька воздуха в ней. Отмерив одинаковые расстояния, проследите за тем, соответствуют ли ударам метронома прохождение пузырьком сделанных вами меток.
Самостоятельные работы
- Определите путь и перемещение минутной стрелки часов за 10 минут, 30 минут и 1 час.
- В движущемся вагоне в любой момент времени есть точки, движущиеся в сторону, обратную движению вагона. Какие это точки?
- Две одинаковые шайбы А и В скользят без трения по льду озера. Они соединены легкой, нерастяжимой, но упругой нитью длиной √2L. В момент времени t = 0 шайба А покоится в точке с координатами (0,0), а шайба В, которая находится в точке с координатами (L,0), сообщают скорость v вдоль оси y в положительном направлении. Определите координаты и скорости шайб А и В в моменты времени t1 = 2L/v и t2 = 100L /v.
12/16. Графики зависимости скорости и перемещения от времени.
Научить строить и читать графики равномерного движения.
1. Получены данные о движения автомобиля:
| Длительность движения,ч | 0,1 | 0,4 | 0,2 |
| Скорость, км/ч | 20 | 60 | 20 |
— 12 —
- Какой путь пройдет автомобиль за первый промежуток времени?
- Какова общая длина пути, пройденного автомобилем?
- Постройте график зависимости скорости от времени для этой поездки
- За какое время автомобиль пройдет первые 14 км пути?
- Укажите площадь на вашем графике, соответствующую первым 14 км пути.
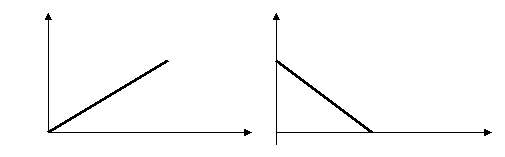
2. Проанализируем графики, приведенные ниже. Какие из них могут соответствовать графикам зависимости перемещения от времени и почему? Какие из них могут соответствовать графикам зависимости скорости равномерного движения от времени и почему?
Лабораторные работы и опыты
Проследим, как движутся пузырьки воздуха со дна водоема. Проанализируем фотографии, сделанные за одинаковые промежутки времени. Измеряя перемещения пузырьков, запишем результаты в таблицу.
| x, cм | ||||
| t, c |
По полученным данным построим график зависимости перемещения от времени.
Самостоятельные работы
На рисунке представлены графики проекций скоростей двух автомобилей, движущихся по одной прямой. Что можно сказать о направлении движения автомобилей? Меняются ли их скорости со временем? Какой из автомобилей движется быстрее?
— 13 —
13/17. Координатный метод описания движения.
Движение-это изменение положения тела относительно данного тела отсчета и связанной с ним системы координат с течением времени. Система отсчета и система координат. Положение тела в одномерной, двумерной и трехмерной системе координат. Угловая система координат.
Демонстрации
- Все вы знаете стихотворение А. С. Пушкина «У лукоморья дуб зеленый…». Что является телом отсчета для описания движения кота?
- Определим координаты люстры в классе, выбрав за тело отсчета входную дверь.
- На рисунке изображено положение двух точек в пространстве относительно координатных осей. Определить:
Цену деления осей
Координаты точки А.
Координаты точки В.
Лабораторные работы и опыты
На рисунке показано положение трех точек А, В и С, соединенных между собой кривой линией. Эта линия является траекторией движения точки из А в С. Определить:
- Цену деления осей координат
- Координаты точек А, В и С.
- Проекции вектора АВ, ВС и АС.
На рисунке изображен график координаты тела от времени. Определите:
- Цену деления осей.
- Время движения по оси ох
- Время остановки
- Время движения против оси ох
- Пройденный путь
- Среднюю скорость движения
- Скорость до остановки
- Скорость после остановки
- Величину перемещения
— 14 —
X,м

Самостоятельные работы
С помощью рулетки или сантиметровой измерительной ленты определите координаты точки подвеса комнатного светильника по отношению к системе отсчета, связанной с одним из нижних углов комнаты. Координаты оси направьте вдоль стен комнаты.
14/18. Движение с ускорением.
Движение с изменяющейся во времени скоростью. Ускорение. Перемещение при прямолинейном равноускоренном движении. Изменение скорости по направлению при вращении стрелок часов.
Демонстрации
1. Видеофильм «Основы кинематики». Элемент технологии критического мышления И.Д.Е.А.Л.
- Формулировка проблемы (все ли тела движутся равномерно)
- Формулировка проблемы в виде вопроса (как можно описать движение тел, отличающихся от равномерного)
- Генерирование как можно большего числа решений вопроса
- Выбор наилучших вариантов
- Характер изменения физические величины при движении со скоростью, меняющейся во времени
Оформление решения проблемы
2. Конический маятник.
3. Проделайте опыт Г.Галилея: убедитесь в том, что пути, проходимые в последовательные равные промежутки времени, относятся как последовательный ряд нечетных чисел. Положив шарик вверху желоба, отпустите его и карандашом отметьте местоположения шарика под удары метронома. Пути, проходимые при равноускоренном движении за последовательные равные промежутки времени, определите по миллиметровой шкале на линейке. Наклонная плоскость должна составлять малый угол с плоскостью стола, для того чтобы шарик скатывался медленно.
Лабораторные работы и опыты
Определите среднюю скорость шарика, скатывающегося с наклонной плоскости. Как она зависит от угла наклона плоскости? От чего зависит точность ваших измерений? Как определить конечную скорость шарика? Как она зависит от угла наклонной плоскости и ее длины?
Самостоятельные работы
Пластиковый пузырек с подкрашенной жидкостью поставить на тележку и открыть отверстие в дне сосуда. Измерить расстояния между каплями, оставленными на бумажной ленте, положенной на демонстрационный стол, при скатывании тележки с наклонной плоскости, а также общее время движения и интервалы времени, соответствующие отметкам на ленте. Подсчитать среднюю скорость движения.
— 15 —
15/19. Свободное падение тел.
Движение тела из состояния покоя под действием силы тяжести. Постоянство ускорения свободного падения для данного места на земной поверхности. Измерение ускорения свободного падения.
Демонстрации
- Определите экспериментально ускорение, с которым шарик скатывается по наклонному желобу. Как изменяется ускорение шарика при увеличении угла наклона желоба?
- Шарик упал со стола. С каким ускорением он двигался? Сколько времени длилось падение шарика? Какой была скорость шарика в момент, когда он коснулся пола? Какова высота стола?
Лабораторные работы и опыты
- Пронаблюдайте за падением тел разной массы, но одинакового объема; разной формы. Сделайте вывод.
- Придумать опыт, доказывающий, что свободно падающий шарик движется по вертикали.
Самостоятельные работы
- Определите ускорение свободного падения, пользуясь отвесом, секундомером и камнями различной формы и объема. Местом проведения опыта может быть высокий мост, глубокий овраг или балкон многоэтажного дома. Возьмите округленный камень небольших размеров и под счет “раз, два, пуск” предоставьте ему возможность падать. Секундомером измерьте время падения камня, а затем по известной формуле найдите ускорение свободного падения. Повторите опыт несколько раз с разными телами и убедитесь в том, что ускорение свободного падения не зависит от массы падающего тела. Как влияет на результат расчета ускорения свободного падения погрешность измерения времени и время реакции человека?
- Маленький шарик В лежит на краю стола высотой 1 м, другой такой же шарик А подвешен на нити длинной 1 м и представляет собой математический маятник. Если нить с шариком А привести в горизонтальное положение и отпустить, то между шариками произойдет упругое столкновение. Рассматривая движение шарика В только до момента его падения на землю, ответьте на вопросы: а) какой шарик дольше находится в движении; б) у какого шарика больше длина траектории?
16/20. График скорости от времени при равноускоренном движении.
График скорости от времени при равномерном движении (повторение). Отличие графика скорости неравномерного движения от графика скорости для равномерного движения. Физический смысл угла наклона графика. График скорости свободно падающего тела. Угол наклона графика скорости тела, движущегося под действием силы тяжести.
Основной материал
- В таблице приведены значения мгновенной скорости автомобиля от времени:
| Время,с | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Скорость, м/с | 10,0 | 12,4 | 14,8 | 17,2 | 19,6 | 22,0 | 24,4 |
Постройте график скорости от времени для этой поездки и ответьте на вопросы:
- С какой скоростью двигался автомобиль в моменты времени 2,6 с и 4,8 с?
- Какой путь прошел автомобиль между этими двумя моментами времени?
2. Дан график скорости от времени.
— 16 —
V,м/c

Разобрать, как меняется скорость движения велосипедиста по графику. Какое время он двигался равномерно? Какое расстояние он проехал, двигаясь с постоянной скоростью, при разгоне и при торможении?
Лабораторные работы и опыты
По графику скорости найдите ускорение и среднюю скорость за первые две секунды его
движения.
Самостоятельные работы

Определите ускорение и среднюю скорость тел, пользуясь графиками скорости от времени.
Pgfplots: краткое руководство
О пакете
Пакет pgfplots представляет собой мощный инструмент, предназначенный для создания научных графиков. Он создан на базе tikz, не менее прекрасного пакета, который позволяет создавать векторную графику прямо на латехе.
Если вы сомневаетесь в необходимости использования pgfplots или tikz, посмотрите на простые графики, созданные с помощью этих пакетов:
Много небольших примеров применения можно посмотреть в галерее pgfplots 1.
Основная идея pgfplots — упрощение включения графиков в документ. Задача пользователя — задать формулу или данные, а остальным занимается pgfplots. Так, код графиков (см. пример на overleaf), приведенных выше (без преамбулы) выглядит так:
% Код первого графика
begin{tikzpicture}
begin{axis}
addplot[color=red]{exp(x)};
end{axis}
end{tikzpicture}% Код второго графика
begin{tikzpicture}
begin{axis}
addplot3[surf] {exp(-x^2-y^2)*x};
end{axis}
end{tikzpicture}Заметьте, от пользователя в простейшем случае не потребовалось практически ничего, кроме задания функции и вида её отображения. Разумеется, можно и вручную задать пределы построения функции и многое
другое.
Оглавление
- 0. Введение в pgfplots
- 0.1. Преамбула
- 0.2. Окружение осей
- 0.3. Пакет standalone: графики в отдельных файлах
- 1. Математика в pgfplots
- 1.1. Стандартные операторы
- 1.2. Стандартные функции
- 1.3. Генерация случайных чисел
- 2. Объявление новых функций
- 2.1. Составление функции Хевисайда. Ступенька произвольной длины
- 3. Настройка осей и сетки
- 3.1. Оси и их подписи. Настройка
- 3.2. «Тики» (метки на осях) и их подписи
- 3.2.1. Дополнительные тики
- 3.2.2. Промежуточные тики (minor ticks)
- 3.3. Максимальные и минимальные значения на графике. Масштаб осей
- 3.4. Сетка. Единицы измерения в LaTeX
- 3.4.1. Сетка через основные и промежуточные тики
- 3.4.2. Сетка через дополнительные (extra) тики
- 4. Легенда графика
- 5. Построение графика
- 5.1. Чтение данных из таблицы
- 5.1.2. Создание новых стоблцов таблицы
- 5.2. Отметки на линии графика (marks)
- 5.3. Прямоугольники ошибок
- 5.3.1. Постоянная абсолютная или относительная погрешность
- 5.3.2. Абсолютная или относительная погрешность из файла
- 5.4. Настройка линии графика
- 5.4.1. Толщина и цвет линии графика
- 5.4.2. Тип линии графика
- 5.1. Чтение данных из таблицы
- 6. Особенности построения графиков
- 6.1. Построение графиков, терпящих бесконечный скачок
- 6.2. Циклы в pgfplots и построение асимптот. Системы координат рисунка
- 6.3. Использование команд TikZ на графиках Pgfplots
- The End. Рекомендуемые источники
0. Введение в pgfplots
0.1. Преамбула
Подключается пакет стандартным образом. Вставьте этот код в преамбулу (до begin{document}):
Так же можно сразу в преамбуле сделать некоторые настройки. Во-первых, можно задать используемую версию pgfplots. Так как пакет динамично развивается, то некоторые вещи становятся несовместимыми от версии к версии. Наиболее разумным является использование текущей версии указанием параметра
pgfplotsset{width=10cm,compat=newest}но после окончания работы неплохо бы указать текущую версию вручную, чтобы если вдруг у вас будет такая функциональность, что не будет работать в следующих версиях, это не помешало бы компилировать график спустя длительное время.
Параметр width задает ширину графика. Также можно задать и высоту height. Надо заметить, что это нововведение по сравнению с tikz: в tikz картинки изменяют свой размер соответственно содержимому, pgfplots же может подогнать содержимое (масштабом осей) под график. Надо заметить, что возможно и обратное — задавать вручную масштаб осей, тогда высота и ширина будут определяться ими и содержимым, а параметры width, height будут игнорироваться.
0.2. Окружение осей
Поскольку pgfplots основан на tikz, график должен находиться в окружении tikzpicture. Сам график строится в осях (полотно графика с системой координат и некоторым масштабом).
Оси задаются окружением begin{axis} ... end{axis}. У осей могут быть свои параметры:
begin{tikzpicture}
begin{axis}[
%axis, % Обычные оси
%semilogxaxis, % По оси x логарифмический масштаб
%semilogyaxis, % По оси y логарифмический масштаб
%loglogaxis, % По обоим осям логарифмический масштаб
enlargelimits=true, % Делать размер осей чуть больше графика
]
addplot[color=red]{ln(x)};
end{axis}
end{tikzpicture}Булев параметр enlargelimits, если он включен, делает размер рисунка немного больше, так, чтобы нарисованные графики не касались края рисунка, а оставалось некоторое расстояние. По умолчанию он включен, и отключать его почти никогда не требуется.
Здесь они закомментированы. Достаточно одного из параметров, причем параметр axis используется по умолчанию, и его можно не указывать.
Чтобы добавить график, используется команда
addplot[color=red]{ln(x)};Внутри квадратных скобок могут быть переданы некоторые параметры, например здесь указан цвет линии графика. Квадратные скобки обязательны, если не передано ни одного параметра, нужно оставить между ними пробел.
Важно, что все команды (эта необходимость тянется из пакета tikz) должны заканчиваться точкой с запятой.
Внутри фигурных скобок размещается функция, задающая график. О её составлении рассказано ниже.
Так же более подробно о настройке осей и сетки см. раздел 3 «Настройка осей и сетки»
Самое подробное описание (на английском) можно найти в мануале по pgfplots 2.
0.3. Пакет standalone: графики в отдельных файлах
Компиляция графиков pgfplots может быть долгой. Особенно это касается случаев, когда строится функция с большим числом точек, уходящая на бесконечность или обрабатываются большие экспериментальные данные из файла.
В таком случае разумно, чтобы сократить время компиляции, создавать каждый рисунок как отдельный pdf-документ, а затем подключать его как картинку. С одной стороны, увеличивается скорость компиляции, с другой, документ становится проще за счет выноса длинного кода в отдельные файлы, а структура документа становится более гибкой: отдельный график можно использовать в других проектах.
Настоятельно рекомендуется использовать именно этот способ. Для него достаточно указать классом документа standalone, и документ будет компилироваться в pdf файл, причем так, что поле документа будет обрезано до размеров графика.
Стоит отметить, что этот пакет конфликтует с пакетом geometry, и последний использовать в документах класса standalone не нужно.
Дочерний документ (например, это файл img/ris1.tex):
documentclass{standalone}
usepackage[utf8]{inputenc}
usepackage{pgfplots}
pgfplotsset{width=10cm,compat=1.9}
begin{document}
begin{tikzpicture}
begin{axis}
addplot[color=red]{exp(x)};
end{axis}
end{tikzpicture}
end{document}Вставка картинки в основной документ:
begin{figure}[h!]
centering
includegraphics[scale=1]{img/ris1}
caption{Наш отдельный график}
label{fig:ris1}
end{figure}1. Математика в pgfplots
Математический аппарат pgfplots-а принадлежит пакету более низкого уровня pgf. Математические возможности pgf достаточно велики, и мы рассмотрим только некоторые аспекты составления сложных функций для построения различных графиков.
1.1. Стандартные операторы
- Без пояснения:
+,-,*,/,^ - Сравнение:
>,>=,<=,==,!= - Оператор факториала:
x!аналогичен вызову функцииfactorial(x)
Отдельно стоит сказать об условном операторе x ? y : z. Он вернет y, если x истина, и z, если ложь. Это можно использовать, например, для построения функций Хевисайда, о чем будет сказано ниже.
1.2. Стандартные функции
div(x,y)— целочисленное делениеmod(x,y)— остаток от деленияsign(x)— знак числа
Также ряд функций, не нуждающихся в объяснениях:
factorial(x),
sqrt(x),
exp(x),
ln(x),
log10(x),
log2(x),
abs(x)
Функции округления
round(x)— округлит до ближайшего целого, большего по модулю чем округляемое, числа: 1.5->2, -1.5->-2floor(x)— округлит х до ближайшего целого числа в большую сторонуceil(x)— округлит х до ближайшего целого числа в меньшую сторонуint(x)— просто вернет целую частьxfrac(x)— вернет дробную частьx
Целочисленные функции
iseven(x),isodd(x)— проверяет четность (нечетность) числа, в случае успеха вернет 1, в случае неудачи 1isprime(x)— проверяет, простое ли число (аналогично вернет 1/0)
Тригонометрические функции
sin,cos,tan,sec,cosec,cot,asin,acos,atan
Важно заметить, что все тригонометрические функции принимают на вход число в градусах, а для перевода из радиан в градусы служит функция deg, а обратно — rad. Это поведение по умолчанию, его можно поменять:
pgfkeys{/pgf/trig format=rad|deg}Кроме того, можно использовать радианы и не изменяя поведение по умолчанию — указать, что аргумент дан в радианах: cos(pi/2 r) ->0.
Гиперболические функции
sinh,cosh,tanh
1.3. Генерация случайных чисел
Присутствует и возможность генерации случайных чисел: вызов rnd вернет случайное число от 0 до 1, rand от -1 до 1.
Более подробно о функциях и операторах можно почитать в руководстве по pgf, 1000-1011 страницы 3.
2. Объявление новых функций
begin{tikzpicture}[
declare function={
myfun(x,t) = (x*t);
}
]
begin{axis}
addplot[color=red, domain=0:4, samples=300]{myfun(x,2)};
end{axis}
end{tikzpicture}Объявляется новая функция для всего рисунка. Все должно быть понятно из примера.
2.1. Составление функции Хевисайда. Ступенька произвольной длины
Используя условный оператор, несложно составить функцию Хевисайда:
Очевидно, она будет равна множителю перед скобкой при x>0 и нулю в отрицательной области. Из двух функций Хевисайда можно составить и прямоугольный импульс:
1*(x>0 ? 1 : 0)-1*(x>1 ? 1 : 0)Это прямоугольный импульс, начинающийся от нуля. Однако, можно создать функцию с аргументами высоты, ширины и начала ступеньки:
Нажмите для просмотра результата
begin{tikzpicture}[
declare function={
impuls(h,w,b,x) = h*((x>b ? 1 : 0)-(x>(b+w) ? 1 : 0));
}
]
begin{axis}
addplot[color=red, domain=0:4, samples=300]{impuls(2,2,1,x)};
end{axis}
end{tikzpicture}Заметим, что в общем случае, например для построения кусочно-гладких функций, необязательно создавать громоздкую функцию, которая будет включать в себя все остальные с помощью условного оператора.
Если заранее известно, что функция будет без скачков (скачок сам по себе можно построить, но особого смысла нет), то можно воспользоваться тем, что команда addplot имеет параметр области построения графика domain=start:end и использовать несколько плотов:
begin{tikzpicture}
begin{axis}
addplot[color=red, domain=0:1, samples=300]{x^2};
addplot[color=red, domain=1:4, samples=300]{2*x};
end{axis}
end{tikzpicture}samples здесь — количество точек графика. График не может строиться абсолютно непрерывно и берется в некотором числе точек, которые соединяются отрезками: чем выше число точек, тем качественнее картинка, но и медленнее её компиляция и отрисовка. Разумно делать это число меньше для медленно меняющихся графиков и много больше для быстро меняющихся, особенно для таких, как в предыдущем примере — со скачком.
По мере чтения руководства читатель может заметить появление новых параметров без объяснения. Предполагается, что они могут быть интуитивно понятны.
3. Настройка осей и сетки
3.1. Оси и их подписи. Заголовок графика.
Рассмотрим базовый пример настройки осей. По умолчанию, вместо координатных осей рисуется прямоугольник координат (axis lines = box), как это часто принято в научных статьях. Однако никто не мешает использовать оси-стрелки, или вообще отключить оси:
begin{tikzpicture}
begin{axis}[
axis lines = middle, % привычные оси со стрелочками с пересечением в нуле
% возможные значения: box, left, middle, center, right, none
xlabel = {$x$}, % подпись оси x
ylabel = {$f(x)$}, % подпись оси y
title={Мой первый график $f(x)=x^2 - 2cdot x - 1$},
]
addplot[domain=-10:10, samples=100, color=red] {x^2 - 2*x - 1};
end{axis}
end{tikzpicture}Обратите внимание на то, что у нас появился параметр title, задающий заголовок графику. Как правило, при использовании пакета standalone, это не нужно — заголовок графика задается командой caption в окружении figure.
Вообще говоря, положение осей можно применять и по отдельности:
axis x line=center,
axis y line=left,Можно задать и определенные правила отрисовки осей, например цвет, или сделать их пунктиром (dashed):
x axis line style ={black!40, dashed},
y axis line style ={red},Заметьте, как здесь указывается цвет. Это обозначение black!40!red означает смешение цветов, в соотношении 40% black 60% red, если цвет справа не указан, то он берется белым: значит, black!40 даст нам серый цвет. Таким образом из базовых цветов можно составить любой цвет.
Также можно перенести подписи осей к стрелкам на осях:
xlabel style={below right},
ylabel style={above left, red, scale=1.5},Здесь появился новый параметр scale, подпись к оси y будет в полтора раза больше, чем к оси x, очевидно.
Подразумевается, что все приведенные выше параметры подставляются в параметры окружения axis.
3.2. «Тики» (метки на осях) и их подписи
Когда график не качественный, важно наиболее удобно показать подписи (числа) к осям. За них отвечают ticks (тики) — маленькие перпендикулярные черты к осям с численной подписью.
Настройка расстояния между тиками:
xtick distance=1,
ytick distance=2Также можно вручную указать список основных тиков:
xtick={0,20,40,60,80,100},
ytick={0,20,40,60,80,100,120}А при необходимости, можно задать и подписи к ним (по умолчанию подпись — это координата тика):
ytick={1.5707,0.7853,1},
yticklabels={$frac{pi}{2},$, $frac{pi}{4}$, 1}, По умолчанию pgfplots пытается подобрать наиболее разумное расположение тиков.
3.2.1. Дополнительные тики
Иногда требуется специально показать положение чего-либо на осях. Для этого можно использовать дополнительные тики, задав им координаты и их подписи:
extra y ticks={-9/16,-6/16}, % положение дополнительных тиков
extra y tick labels={ % их подписи
{$U_{min}$}, {$U_{min}+Delta U$}
}, Для x аналогично.
3.2.2. Промежуточные тики (minor ticks)
Часто кроме основных меток на осях, ставят промежуточные: так, например, на линейке отмечены сантиметры рисками с подписями, а миллиметры просто рисками без подписей.
Такое задается с помощью minor ticks:
Этот параметр задает количество таких тиков (эквидистантных) между основными (major) тиками для обоих осей одинаково. А можно задать и для каждой оси отдельно:
minor x tick num=3,
minor y tick num=8,3.3. Максимальные и минимальные значения на графике. Масштаб осей
Масштаб осей задан в виде <длина орта x> <длина орта y>:
unit vector ratio = 1 1,
xmax = 8,
xmin=-2,
ymax=1.5,
ymin=-0.2,Максимальные и минимальные значения заданы очевидным образом.
3.4. Сетка. Единицы измерения в LaTeX
3.4.1. Сетка через основные и промежуточные тики
Сетка всегда проходит через тики на осях. Она может проходить как через основные (major) так и через промежуточные (minor) тики:
grid=major, % м.б. еще both - и там и там
grid style={dotted, cyan},Причем стиль можно задать как всей сетке (и основной major и промежуточной minor), так и по отдельности:
minor grid style={dashed,red, line width=0.2pt},
major grid style={solid,black, line width=0.1pt},Обратите внимание на используемые единицы измерения. em — это высота одной буквы шрифта 10pt:
pt называется типографским пунктом.
По умолчанию, сетка автоматически проведет линии и через пользовательские (дополнительные) тики, но этот стиль можно модифицировать:
extra tick style={grid=major, grid style={dotted, cyan}},Здесь мы скопировали стиль основных линий сетки и модифицировали его, сделав в точечку (dotted) и голубым (cyan).
4. Легенда графика
Для того, чтобы сопоставить какому-либо графику, который строится с помощью addplot, элемент легенды, есть специальная команда addlegendentry, которую нужно разместить после addplot:
begin{tikzpicture}
begin{axis}[
axis lines = middle,
xlabel = {$x$},
ylabel = {$f(x)$},
title={Мой первый график $f(x)=x^2 - 2cdot x - 1$},
legend pos={south west},
]
addplot[domain=-10:10, samples=100, color=red] {x^2+2*x};
addlegendentry{$x^+2cdot x$};
end{axis}
end{tikzpicture}Здесь появился параметр legend pos, который задает положение легенды на графике:
legend pos=south west|south east|north west|north east5. Построение графика
В самом начале мы рассмотрели и далее неоднократно употребляли построение графика заданной функции (y=f(x)). Однако, часто требуется построить не такой (или не только такой график), а покоординатный график (или, как это говорят математики, функция задана таблично, а не аналитически).
Обычно такая задача возникает при обработке экспериментальных данных. Есть два способа: записать данные непосредественно в график, или записать их в текстовую таблицу (tsv или csv). Рассмотрим такие случаи.
5.1. Чтение данных из таблицы
Важно: для чтения из таблицы нужно подключить пакет:
usepackage{pgfplotstable}Рассмотрим такой пример: пусть у нас есть файл data.tsv, лежащий в той же папке, что и рисунок:
Fr Uin err
15 7.446 0.1
25 7.532 0.1
40 7.512 0.1
100 7.412 0.1
200 7.41 0.1
300 7.32 0.1
400 7.27 0.1
500 7.236 0.1
1000 7.3 0.1
2000 7.282 0.1
3000 7.27 0.1Тогда его можно построить командой:
addplot +[blue, dashed]
plot table [
x=Fr,
y=Uin
]{data.tsv};В этом примере все просто. В первых квадратных скобках пишутся параметры, управляющие отрисованным графиком, построением прямоугольников ошибок и т.п., а во вторых — параметры чтения из таблицы, создание новых столбцов таблицы путем математического выражения, составленного из существующих столбцов, о чем написано ниже.
5.1.2. Создание новых стоблцов таблицы
Рассмотрим простой пример, на основе приведенного выше файла данных. В нем в первой столбце стоит частота в герцах, но допустим, что мы хотим построить график от круговой частоты, т.е. домножить на (2pi):
addplot +[blue, dashed]
plot table [
create on use/omega/.style={
create col/expr={
thisrow{Fr}*2*pi
}
},
x=omega,
y=Uin
]{data.tsv};Здесь видно, как несложно оперировать созданием новых столбцов. При этом применима вся математика, рассмотренная в разделе выше.
5.2. Маркеры на линии графика
Часто требуется не просто соединить экспериментальные точки линией, а указать каждую конкретную точку маркером (mark), а то и вовсе составить график только из маркеров. Для этого предыдущий пример несложно модифицируется:
addplot +[blue, mark=*, mark size=1.5pt, only marks]
plot table [
create on use/omega/.style={
create col/expr={
thisrow{Fr}*2*pi
}
},
x=omega,
y=Uin
]{data.tsv};Параметр only marks принуждает рисовать только маркеры, без линии их соединяющих, mark size размер маркера, mark тип маркера.
Существует достаточно много типов:
Эта картинка взята из руководства по tikz в картинках 4.
Для маркеров можно сразу задать несколько параметров: вместо размера задать масштаб (второй способ изменить размер маркера, иногда более удобный), основной цвет (draw) и цвет заливки (fill
addplot +[
mark=*,
mark options={
scale=2,
fill=blue,
draw=red,
},
only marks
] plot table [
create on use/omega/.style={
create col/expr={
thisrow{Fr}*2*pi
}
},
x=omega,
y=Uin
]{data.tsv};5.3. Прямоугольники ошибок
Для начала рассмотрим простейший случай постоянной ошибки. Параметры прямоугольников ошибок пишутся в параметры команды plot. Рассматривать будем все на примере ошибки по y, по другим осям анологично с точностью до замены y->x,z.
Для включения прямоугольников ошибки и возможности их настройки перед последующими рассмотренными параметрами нужно вставлять параметр error bars/.cd.
5.3.1. Постоянная абсолютная или относительная погрешность
Сначала нужно определить, какая будет ошибка: строго положительная, отрицательная или в обе стороны. За это отвечает параметр y dir=minus|plus|both.
addplot +[
mark=*,
only marks,
] plot[
error bars/.cd,
y dir=both,
y fixed=0.1,
% y fixed relative=0.1,
] table [
x=Fr,
y=Uin
]{data.tsv};Здесь указана сразу абсолютная погрешность для всех значений. Аналогично можно задать сразу относительную параметром y fixed relative.
5.3.2. Абсолютная или относительная погрешность из файла
Необходимо явно указать, что ожидается чтение данных ошибки из файла, указать в каком столбце (y error=err) записана ошибка и тип ошибки:
addplot +[
mark=*,
only marks,
] plot[
error bars/.cd,
y dir=both,
y explicit relative,
] table [
x=Fr,
y=Uin,
y error=err,
]{data.tsv};Для абсолютной ошибки параметр y explicit, для относительной y explicit relative.
5.4. Настройка линии графика
5.4.1. Толщина и цвет линии графика
Толщина линии управляется либо параметром line width=, либо словесными алиасами (рекомендуется использовать именно их):
Цвет линии сам является параметром:
addplot +[
thick,
blue!20!black
] plot table [
x=Fr,
y=Uin,
]{data.tsv};О составлении цветов сказано ранее в разделе ().
5.4.2. Тип линии графика
Как и цвет, тип линии графика сам по себе параметр:
addplot +[
thick,
blue!20!black,
dashed
] plot table [
x=Fr,
y=Uin,
]{data.tsv};Существует несколько типов линий:
6. Особенности построения графиков
6.1. Построение графиков, терпящих бесконечный скачок
Рассмотрим построение графика с бесконечным скачком на примере построения (tan(x)).
Расчет функций, которые уходят на бесконечность, может привести к ошибкам компиляции. Чтобы этого избежать, можно указать в параметрах принудительное вписывание в пределы расчетов: выйдя за эти пределы, математический движок pgf просто будет пропускать эти значения, пока опять не войдет в пределы:
restrict y to domain=-20:20,Разумно выбирать эти пределы немного больше заданного предела осей xmin,xmax,ymin,ymax.
Кроме того, можно сказать pgfplots-у, как вести себя при получении бесконечности в расчетах, и не ограничивая расчет:
unbounded coords=discard|jumpЭтот ключ настраивает, что делать, если одна или несколько координат одной точки неограничена, или, например, при чтении из файла на этом месте стоит nan или ничего не стоит.
discard (по умолчанию) отбрасывает точку завершения, и в логе компиляции выдается предупреждение. При этом график строится, как если бы неограниченная точка не произошла: pgfplots интерполирует между ограниченными ближайшими точками.
jump просто пропустит значения, которые уходят на бесконечность, и график станет с разрывом.
Однако, как это ни странно, в случае тангенса это все не так: для стандартных функций с разрывом разработчики постарались, и они строятся без дополнительных усилий. Но при этом (+infty) и (-infty) точки графика соединяются, что не всегда может быть полезно: например, обычно в этом месте строят линии асимптот.
Все же придется вернуться к первоначальному определению:
documentclass[tikz,10pt]{standalone}
usepackage[T2A]{fontenc}
usepackage[utf8x]{inputenc}
usepackage[russian]{babel}
usepackage{amsmath,amssymb,cmap,pgfplots,pgfplotstable}
usetikzlibrary{arrows,calc,intersections}
pgfplotsset{compat=newest}
begin{document}
begin{tikzpicture}
begin{axis}[
xlabel={$x$},
ylabel={$tg x$},
axis lines=middle,
ymax = 10,
ymin = -10,
enlargelimits=true,
xmin=-4*pi/2,
xmax=4*pi/2,
restrict y to domain=-20:20,
xtick=empty,
ytick=empty,
]
addplot[blue!50,domain={-4*pi/2:4*pi/2},samples=1000] {tan(deg(x))};
pgfplotsinvokeforeach{-2,-1,...,2}{%
draw[dashed, black!20]
({{pi/2+pi*#1},0} |- {rel axis cs:0,0})
-- ({{pi/2+pi*#1},0}|-{rel axis cs:0,1});
}
end{axis}
end{tikzpicture}
end{document}Здесь есть интересный код для построения асимптот. Рассмотрим его подробнее.
6.2. Циклы в pgfplots и построение асимптот. Системы координат рисунка
Стандартный цикл tikz-а, к сожалению, в pgfplots не работает. Приходится использовать его более низкоуровневый аналог:
pgfplotsinvokeforeach{-2,-1,...,2}{%
% Выражение в цикле. Счетчик цикла - #1
}Счетчик пробегает указанные значения. Можно указывать их как список {0,1,2,3},а можно указать первое значение, второе, троеточие, последнее: из первого и второго рассчитается шаг и счетчик пробежит нужные значения. Они могут быть дробными.
Теперь подробнее, как же работает код построения вертикальной асимптоты. В tikz есть интересный способ расчета координаты в угле. Если задана такая координата X: (A -| B), то она находится в точке, которая образована пересечением горизонтальной линии через A и вертикальной через B:
Можно наоборот, (B -| A), соотв. вертикальная через А и горизонтальная через B.
По умолчанию используется система координат осей, в которой начало и орты отвечают нарисованным на графике.
Есть еще так называемая rel axis cs — система координат рисунка: в ней точка (0,0) это левый нижний угол рисунка, а (1,1) — верхний правый.
Со всей этой информацией теперь нетрудно должно быть понять, как работает асимптота через точку x:
({x},0} |- {rel axis cs:0,0}) -- ({x},0}|-{rel axis cs:0,1});6.3. Использование команд TikZ на графиках Pgfplots
Ровно в предыдущем параграфе рассмотрено применение команд tikz для построения асимптот в осях графика.
Часто возникает еще потребность подписать какие-либо точки на кривой. Для этого можно создать ноду на кривой, где положение ноды задается от 0 до 1 — 0 в начале кривой, 1 в конце. Эдакие криволинейные координаты.
addplot[blue!50,domain={-4*pi/2:4*pi/2},samples=1000] {sin(deg(x))}
node[pos=0.3] (1) {}
node[pos=.3,left,black]{$x$};
draw[fill=magenta] (1) circle (1pt);Здесь мы специально создали пустую ноду с координатой (1), в которой потом можно нарисовать точку, а вторая нода уже рисует текст.
Для понимания это может быть затруднено, если вы не изучали tikz. Тогда можно просто использовать этот пример, не заботясь принципами его работы.
На кривую так можно поместить сколько угодно точек, главное, в конце списка должна стоять точка с запятой.
6.3. Качественные графики: удаление меток с осей
Достаточно добавить два параметра к окружению axis:
xtick=empty,
ytick=empty,The End. Рекомендуемые источники
Наконец, прочитав небольшое руководство по использованию pgfplots, вы почти готовы к тому, чтобы применить его для своих работ. В этом нелегком (поначалу) труде смогут помочь некоторые источники.
Методические материалы
ПРАВИЛА СОСТАВЛЕНИЯ ОТЧЁТА ПО ЛАБОРАТОРНОЙ РАБОТЕ
Основные требования к существу отчета:
- Необходимо обращать внимание на чёткую рубрикацию отчета (нумерацию составных частей, выделение заголовков и т.д.).
- Отчет должен содержать следующие элементы:
- полное название лабораторной работы и дату составления отчета;
- кратко сформулированную цель работы;
- перечень приборов, используемых в данной работе, с указанием их марки и класса точности;
- принципиальную схему электрической цепи, на основе которой делаются измерения;
- краткое изложение теории изучаемого в данном эксперименте физического явления с выводом формул, используемых для обработки экспериментальных данных, определениями измеряемых величин и пояснением всех используемых буквенных сокращений;
- краткое изложение методики проведения экспериментальной части работы и измерения требуемых величин;
- «краткое изложение» вовсе не означает, что нужно комбинацией «Копировать»-«Вставить» полностью передрать теоретическую часть из методички, а предполагает сокращённое изложение теории применительно к тем практическим заданиям, которые выполнялись и методикам измерений, которые при этом использовались;
- содержание выполняемых заданий, результаты измерений;
- выводы, в которых результаты измерений и вычислений сравниваются с теоретическими значениями, выясняются причины расхождения опыта и теории и даются рекомендации по их устранению.
- Результаты измерений (прямых и косвенных), оформленные в виде графиков, размещаются в соответствующих местах отчета.
При выборе масштаба графика надо предусмотреть, чтобы результаты измерений полностью и наглядно отразились на графике, не осталось много свободных полей, т.е. кривая не должна быть прижата к одной или другой оси. У осей координат наносят обозначения величин и единиц их измерений. На осях откладывают масштабные единицы, а не координаты экспериментальных точек. На подготовленной таким образом плоскости наносят точки.
Так как и аргумент, и функция определяются на опыте с соответствующими погрешностями, то около экспериментальных точек строят прямоугольники ошибок, стороны которых выражают в данном масштабе величины абсолютных ошибок функции и аргумента. Линию графика проводят не через каждую точку, а плавно и по возможности близко к экспериментальным точкам так, чтобы точки равномерно располагались по обе стороны кривой. Линия графика должна пересекать прямоугольники ошибок или касаться их. Для точек, резко отклоняющихся от кривой, нужно проверить правильность измерения или вычисления их координат. - Расчет погрешностей косвенных измерений. Число значащих цифр в записи результата вычислений косвенно измеряемой величины должно соответствовать погрешности этой величины. Например, если абсолютная погрешность частоты резонанса равна 0,01 МГц, то правильной является запись F=32,17 МГц, а не F=32,1 МГц или F=32,175 МГц.
О погрешностях измерений при проведении лабораторных работ можно кратко почитать в статье «Мерь точно!»», формулы для расчёта погрешности косвенных измерений есть по этой ссылке. Ещё подробнее – в учебном пособии «Методы обработки результатов измерений в лаборатории физпрактикума». - В отчёте должны быть даны ответы на вопросы, если они формулируются в описании соответствующей лабораторной работы.
- Отчёт оформляется в редакторе Word, при необходимости распечатывается. Правила, предъявляемые к оформлению, находятся здесь.
Только, пожалуйста:- не копируйте полностью учебник по электронике или методичку в теоретическую часть отчёта – придётся объяснять всё, что в этом отчёте написано (а при тупом копировании теории это очень трудно, а порой, и невозможно), что займёт времени значительно больше, чем при нормальном написании отчёта;
- не переписывайте у товарища его отчёт, заменив фамилию, и т.д. – преподаватели замечают до 90% таких случаев, а в любом отчёте, даже в сданном, есть ошибки, которые придётся объяснять и исправлять (исправлять чужие ошибки!), а если ещё и протокол измерений у кого-то списан (естественно, опять же с чужими ошибками), то сдать такую работу практически невозможно.
- Сокращение слов в отчете (кроме единиц измерения физических величин) не допускается.
- При сдаче отчёта у студента должен быть протокол выполнения практических заданий по лабораторной работе.
© Кафедра электроники РФ ННГУ им. Н.И. Лобачевского, 2021–2023
Методические рекомендации особенности физических наблюдений.(4 часа)
Подобный материал:
- Методические рекомендации по проведению Единого Всекубанского классного часа, 33.75kb.
- Методические рекомендации «Педагогические особенности использования мультимедиа в образовании», 698.02kb.
- Постановлением Президиума Ростовского областного суда 6 августа 2004 года методические, 89.43kb.
- Методические рекомендации для учителей предметников по использованию цор в своей педагогической, 1201.3kb.
- Методические рекомендации по подготовке проекта муниципального правового акта органа, 154.99kb.
- Методические рекомендации и учебные материалы для проведения единого классного часа, 148.78kb.
- Методика преподавания темы «Многочлены» в профильной школе Методические рекомендации, 72.18kb.
- Основы метрологии в физике, 146.66kb.
- С. И. Сай «17» февраля 2003 года методические рекомендации, 234.96kb.
- Академия оценки и строительства казахстанская республиканская палата оценщиков особенности, 1159.14kb.
6/10. Определение погрешности измерений. Прямоугольник ошибок.
Дать понятие о погрешности измерений, ее влияние на вывод эмпирических зависимостей. Виды погрешностей. Погрешность измерительного прибора. Абсолютная погрешность. Погрешность отсчета. Прямоугольник ошибок.
Демонстрации
- Измерение объема колбы мензурками с разной ценой деления.
- Измерение длины нескольких тетрадных листов одной линейкой и определение среднего значения длины тетрадного листа.
— 8 —
- Определение толщины нити с помощью линейки с миллиметровыми делениями.
- Измерение длины парты линейкой, длина которой не превышает 30 см.
- Определение погрешности скорости равномерного движения математическими методами.
- Погрешность, вызываемая округлением величин.
- Построить график зависимости силы тяжести от массы, определить цену деления динамометра, точность измерения массы и указать на графике прямоугольник ошибок.
Лабораторные работы и опыты
- При измерении длины с помощью ученической линейки может быть допущена ошибка за счет неправильного расположения глаза. Как измерять правильно? Чем вызывается ошибка при таких измерениях?
- Дана таблица измерений приложенной нагрузки от положения конца образца. Постройте график этой зависимости и проанализируйте погрешности измерений на разных его участках.
| 0 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 | 1100 | Нагрузка |
| 0 | 2,1 | 4,2 | 6,3 | 8,5 | 10,6 | 12,6 | 14,6 | 16,6 | 18,6 | 20,5 | 22,3 | Растяжение |
Самостоятельные работы
- Рассмотрите шприц и охарактеризуйте его как измерительный прибор.. Определите погрешность, верхний и нижний пределы его измерений.
- Определите с земли высоту дерева, телеграфного столба или любого другого предмета, имея только небольшую линейку. Предложите несколько способов. Оцените погрешность каждого способа.
- Измерить площадь фигуры неправильной формы и подсчитать погрешность своих измерений.
7/11. Измерение коэффициента упругости пружин различной жесткости с помощью графика.
Графическая зависимость силы упругости от растяжения. Расчет коэффициента упругости с помощью графика.
Демонстрации Измерение растяжения пружин разной жесткости под действием различных сил.
Лабораторные работы и опыты
Измерение коэффициента упругости пружин различной жесткости с помощью графика.
Самостоятельные работы
Начертить график зависимости силы упругости от деформации на миллиметровой бумаге, подсчитать погрешность опыта, построить прямоугольник ошибок и вычислить коэффициент упругости пружины.
8/12. Сила трения. Измерение коэффициента трения.
Сила трения покоя, скольжения, качения. Зависимость силы трения от силы нормального давления. Коэффициент трения. Шероховатости соприкасающихся поверхностей, взаимодействие молекул. Жидкое трение.
Демонстрации
— 9 —
- Трение скольжения, покоя и качения. Равновесие тела на вращающемся диске.
- Смазывание трущихся поверхностей уменьшает трение. Почему же труднее удерживать рукоятку топора сухой рукой, чем влажной?
Лабораторные работы и опыты
Изучение зависимости силы трения скольжения от силы давления. Результат получить аналитически и графически.
Самостоятельные работы
- Карандаш удерживают на столе в вертикальном положении заостренным концом вниз. После того как его отпустили, он начинает падать, как движется при этом острие карандаша в зависимости от коэффициента трения? Оторвется ли острие карандаша от стола (в отличие от случая, когда в результате скольжения место заточки карандаша в конце концов соприкоснется со столом )?
- Карандаш находится в горизонтальном положении, опираясь концами на два моих указательных пальца. Пока я медленно сдвигаю пальцы, чтобы они встретились под центром стержня, он скользит либо по одному, либо по другому пальцу. Почему он так движется?
9/13. Закон инерции. Законы взаимодействия.
Фундаментальные законы взаимодействия. Их значение для становления физики как науки. Связь действующей силы с изменением скорости. Движение с постоянной скоростью.
Демонстрации
- Расположите на столе близко друг к другу два алюминиевых бруска. Свяжите ножки пинцета и поместите его между брусками. Пережгите нить. Почему бруски приходят в движение? Одинаковы ли их скорости? Массы?
- Повторите опыт, взяв бруски одинакового объема, но разных масс. Одинаковы ли их скорости?
- Демонстрация законов инерции.
Приборы и материалы. Бумажная тарелка, ножницы, бумажный шарик.
Ход работы.
- Отрежьте от тарелки одну половину.
- Поместите шарик на кромку отрезанной части.
- Поставьте тарелку на стол и слегка наклоните ее, чтобы шарик быстро покатился по выемке тарелки.
Шарик скатывается с тарелки и удаляется от нее по прямой.
Вывод. Предметы движутся по прямой, если на них не действуют никакие силы.
- Положите лист картона так, чтобы он опирался на две книги. На середину листа положите мешочек с песком. Резко поднимите лист вместе с мешочком. Почему изменилась его форма?
— 10 —
- Действие равно противодействию. Но почему тело движется, ведь какую бы силу мы не приложили, появится противодействующая сила. Где здесь ошибка в рассуждениях?
Лабораторные работы и опыты
- Положите шарик на лист бумаги. Отметьте положение шарика относительно стола. Выдерните лист резким движением. Изменилось ли положение шарика?
- Подвесите алюминиевый и медный цилиндры на нить к лапке штатива. Отклоните их в разные стороны и проследите, что с ними происходит после удара.
- Зацепите крючками два динамометра и слегка разведите их в стороны. Заметьте их показания.
Самостоятельные работы
- Придумайте и проделайте опыты, при помощи которых можно показать проявление инерции у покоящихся и движущихся тел.
- Придумайте опыты, при помощи которых можно показать зависимость инертности тел от массы.
- Висящий на нити, привязанной к потолку каюты, груз отклонился в сторону, хотя на него ничто не действовало. Нет ли здесь противоречия с законом инерции?
- Свойством инерции обладают не только твердые, но также жидкие и газообразные тела. Придумайте и проделайте опыты, при помощи которых можно показать проявление инерции жидких тел.
- Предмет покоится на краю горизонтального стола. Его толкают и он падает с другой стороны стола, ширина которого 1 м, через 2 с. Есть ли у предмета колеса?
10/14. Скорость равномерного движения. Относительность движения.
Мгновенная скорость. Скорость равномерного движения. Относительность движения. Относительная скорость тел. Расчет скорости движения для равномерного движения. Средняя скорость.
Демонстрации
- Самолет, летящий со скоростью 900 км/ч, во время полета заправляется горючим от другого самолета. С какой скоростью движется при этом самолет-заправщик?
- Демонстрация относительности движения на примере тележки и вращающегося диска, установленного на штативе.
- Демонстрация теневой проекции вращения тела, лежащего на горизонтально расположенном диске.
- Автомобиль проехал 60 км за 1 ч, а потом еще 240 км за 5 ч. Какова средняя скорость на всем пути?
- Двигаясь по шоссе, велосипедист проехал 900 м со скоростью 15 м/с, а затем по плохой дороге 400 м со скоростью 10 м/с. С какой средней скоростью он проехал весь путь?
- Минутная стрелка настенных часов вдвое длиннее, чем часовая. В какой момент после полуночи конец минутной стрелки будет удаляться от конца часовой стрелки с наибольшей скоростью?
Лабораторные работы и опыты
- Положите линейку на лист бумаги. Один конец линейки зажмите и с помощью карандаша переместите на некоторый угол. Определите траекторию, скорость и перемещение относительно линейки и листа бумаги.
- Положите деревянный брусок на лист бумаги. Медленно потяните за край листа. В каком состоянии относительно стола находится лист бумаги и брусок? В каком состоянии относительно листа бумаги находился брусок?
— 11 —
- Положите брусок на лист бумаги и резко потяните за край листа. В каком состоянии относительно стола находился лист бумаги? В каком состоянии относительно бумаги находился стол? В каком состоянии относительно стола находился брусок?
- Можно ли сказать, что брусок движется относительно стола в опытах, указанных в предыдущих задачах?
Самостоятельные работы
- Подсчитайте скорость своего подъема по лестнице.
- Определите среднюю скорость движения автобуса между остановками и переведите ее в м/с.
- Определите скорость, с которой перемещается конец минутной стрелки ваших часов.
- Голодный паук приготовился поймать насекомое, если оно окажется в паутинке, которая натянута между ним и стеной. Длина нити 1 м. на нить попала гусеница. Увидев паука, она стала уползать от него к стене со скоростью ν1= 1мм/с относительно нити, а паук , оставаясь на месте, стал вытягивать свой конец нити со скоростью ν0= 1 см/с, считая, что нить может растягиваться без ограничений. Доползет ли гусеница до стены? Как изменится решение предыдущей задачи, если паук не сидит на месте, а удаляется от стены, увлекая за собой конец нити?
11/15. Перемещение при равномерном движении.
Траектория. Перемещение. Путь. Связь пути и перемещения при прямолинейном равномерном движении.
Демонстрации
Сравнить движение стрелок часов; нитяного маятника; равномерное движение тележки, привязанной к грузу, подвешенному к ней через блок. На тележке стоит капельница, с помощью которой отмечаются величины перемещений за равные промежутки времени. Вращение диска с закрепленной осью.
Лабораторные работы и опыты
Расположите резиновую трубку, заполненную водой, вертикально. Перевернув трубку, проследите за движением пузырька воздуха в ней. Отмерив одинаковые расстояния, проследите за тем, соответствуют ли ударам метронома прохождение пузырьком сделанных вами меток.
Самостоятельные работы
- Определите путь и перемещение минутной стрелки часов за 10 минут, 30 минут и 1 час.
- В движущемся вагоне в любой момент времени есть точки, движущиеся в сторону, обратную движению вагона. Какие это точки?
- Две одинаковые шайбы А и В скользят без трения по льду озера. Они соединены легкой, нерастяжимой, но упругой нитью длиной √2L. В момент времени t = 0 шайба А покоится в точке с координатами (0,0), а шайба В, которая находится в точке с координатами (L,0), сообщают скорость v вдоль оси y в положительном направлении. Определите координаты и скорости шайб А и В в моменты времени t1 = 2L/v и t2 = 100L /v.
12/16. Графики зависимости скорости и перемещения от времени.
Научить строить и читать графики равномерного движения.
1. Получены данные о движения автомобиля:
| Длительность движения,ч | 0,1 | 0,4 | 0,2 |
| Скорость, км/ч | 20 | 60 | 20 |
— 12 —
- Какой путь пройдет автомобиль за первый промежуток времени?
- Какова общая длина пути, пройденного автомобилем?
- Постройте график зависимости скорости от времени для этой поездки
- За какое время автомобиль пройдет первые 14 км пути?
- Укажите площадь на вашем графике, соответствующую первым 14 км пути.
2. Проанализируем графики, приведенные ниже. Какие из них могут соответствовать графикам зависимости перемещения от времени и почему? Какие из них могут соответствовать графикам зависимости скорости равномерного движения от времени и почему?
Лабораторные работы и опыты
Проследим, как движутся пузырьки воздуха со дна водоема. Проанализируем фотографии, сделанные за одинаковые промежутки времени. Измеряя перемещения пузырьков, запишем результаты в таблицу.
| x, cм | ||||
| t, c |
По полученным данным построим график зависимости перемещения от времени.
Самостоятельные работы
На рисунке представлены графики проекций скоростей двух автомобилей, движущихся по одной прямой. Что можно сказать о направлении движения автомобилей? Меняются ли их скорости со временем? Какой из автомобилей движется быстрее?
— 13 —
13/17. Координатный метод описания движения.
Движение-это изменение положения тела относительно данного тела отсчета и связанной с ним системы координат с течением времени. Система отсчета и система координат. Положение тела в одномерной, двумерной и трехмерной системе координат. Угловая система координат.
Демонстрации
- Все вы знаете стихотворение А. С. Пушкина «У лукоморья дуб зеленый…». Что является телом отсчета для описания движения кота?
- Определим координаты люстры в классе, выбрав за тело отсчета входную дверь.
- На рисунке изображено положение двух точек в пространстве относительно координатных осей. Определить:
Цену деления осей
Координаты точки А.
Координаты точки В.
Лабораторные работы и опыты
На рисунке показано положение трех точек А, В и С, соединенных между собой кривой линией. Эта линия является траекторией движения точки из А в С. Определить:
- Цену деления осей координат
- Координаты точек А, В и С.
- Проекции вектора АВ, ВС и АС.
На рисунке изображен график координаты тела от времени. Определите:
- Цену деления осей.
- Время движения по оси ох
- Время остановки
- Время движения против оси ох
- Пройденный путь
- Среднюю скорость движения
- Скорость до остановки
- Скорость после остановки
- Величину перемещения
— 14 —
X,м

Самостоятельные работы
С помощью рулетки или сантиметровой измерительной ленты определите координаты точки подвеса комнатного светильника по отношению к системе отсчета, связанной с одним из нижних углов комнаты. Координаты оси направьте вдоль стен комнаты.
14/18. Движение с ускорением.
Движение с изменяющейся во времени скоростью. Ускорение. Перемещение при прямолинейном равноускоренном движении. Изменение скорости по направлению при вращении стрелок часов.
Демонстрации
1. Видеофильм «Основы кинематики». Элемент технологии критического мышления И.Д.Е.А.Л.
- Формулировка проблемы (все ли тела движутся равномерно)
- Формулировка проблемы в виде вопроса (как можно описать движение тел, отличающихся от равномерного)
- Генерирование как можно большего числа решений вопроса
- Выбор наилучших вариантов
- Характер изменения физические величины при движении со скоростью, меняющейся во времени
Оформление решения проблемы
2. Конический маятник.
3. Проделайте опыт Г.Галилея: убедитесь в том, что пути, проходимые в последовательные равные промежутки времени, относятся как последовательный ряд нечетных чисел. Положив шарик вверху желоба, отпустите его и карандашом отметьте местоположения шарика под удары метронома. Пути, проходимые при равноускоренном движении за последовательные равные промежутки времени, определите по миллиметровой шкале на линейке. Наклонная плоскость должна составлять малый угол с плоскостью стола, для того чтобы шарик скатывался медленно.
Лабораторные работы и опыты
Определите среднюю скорость шарика, скатывающегося с наклонной плоскости. Как она зависит от угла наклона плоскости? От чего зависит точность ваших измерений? Как определить конечную скорость шарика? Как она зависит от угла наклонной плоскости и ее длины?
Самостоятельные работы
Пластиковый пузырек с подкрашенной жидкостью поставить на тележку и открыть отверстие в дне сосуда. Измерить расстояния между каплями, оставленными на бумажной ленте, положенной на демонстрационный стол, при скатывании тележки с наклонной плоскости, а также общее время движения и интервалы времени, соответствующие отметкам на ленте. Подсчитать среднюю скорость движения.
— 15 —
15/19. Свободное падение тел.
Движение тела из состояния покоя под действием силы тяжести. Постоянство ускорения свободного падения для данного места на земной поверхности. Измерение ускорения свободного падения.
Демонстрации
- Определите экспериментально ускорение, с которым шарик скатывается по наклонному желобу. Как изменяется ускорение шарика при увеличении угла наклона желоба?
- Шарик упал со стола. С каким ускорением он двигался? Сколько времени длилось падение шарика? Какой была скорость шарика в момент, когда он коснулся пола? Какова высота стола?
Лабораторные работы и опыты
- Пронаблюдайте за падением тел разной массы, но одинакового объема; разной формы. Сделайте вывод.
- Придумать опыт, доказывающий, что свободно падающий шарик движется по вертикали.
Самостоятельные работы
- Определите ускорение свободного падения, пользуясь отвесом, секундомером и камнями различной формы и объема. Местом проведения опыта может быть высокий мост, глубокий овраг или балкон многоэтажного дома. Возьмите округленный камень небольших размеров и под счет “раз, два, пуск” предоставьте ему возможность падать. Секундомером измерьте время падения камня, а затем по известной формуле найдите ускорение свободного падения. Повторите опыт несколько раз с разными телами и убедитесь в том, что ускорение свободного падения не зависит от массы падающего тела. Как влияет на результат расчета ускорения свободного падения погрешность измерения времени и время реакции человека?
- Маленький шарик В лежит на краю стола высотой 1 м, другой такой же шарик А подвешен на нити длинной 1 м и представляет собой математический маятник. Если нить с шариком А привести в горизонтальное положение и отпустить, то между шариками произойдет упругое столкновение. Рассматривая движение шарика В только до момента его падения на землю, ответьте на вопросы: а) какой шарик дольше находится в движении; б) у какого шарика больше длина траектории?
16/20. График скорости от времени при равноускоренном движении.
График скорости от времени при равномерном движении (повторение). Отличие графика скорости неравномерного движения от графика скорости для равномерного движения. Физический смысл угла наклона графика. График скорости свободно падающего тела. Угол наклона графика скорости тела, движущегося под действием силы тяжести.
Основной материал
- В таблице приведены значения мгновенной скорости автомобиля от времени:
| Время,с | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Скорость, м/с | 10,0 | 12,4 | 14,8 | 17,2 | 19,6 | 22,0 | 24,4 |
Постройте график скорости от времени для этой поездки и ответьте на вопросы:
- С какой скоростью двигался автомобиль в моменты времени 2,6 с и 4,8 с?
- Какой путь прошел автомобиль между этими двумя моментами времени?
2. Дан график скорости от времени.
— 16 —
V,м/c

Разобрать, как меняется скорость движения велосипедиста по графику. Какое время он двигался равномерно? Какое расстояние он проехал, двигаясь с постоянной скоростью, при разгоне и при торможении?
Лабораторные работы и опыты
По графику скорости найдите ускорение и среднюю скорость за первые две секунды его
движения.
Самостоятельные работы

Определите ускорение и среднюю скорость тел, пользуясь графиками скорости от времени.
Pgfplots: краткое руководство
О пакете
Пакет pgfplots представляет собой мощный инструмент, предназначенный для создания научных графиков. Он создан на базе tikz, не менее прекрасного пакета, который позволяет создавать векторную графику прямо на латехе.
Если вы сомневаетесь в необходимости использования pgfplots или tikz, посмотрите на простые графики, созданные с помощью этих пакетов:
Много небольших примеров применения можно посмотреть в галерее pgfplots 1.
Основная идея pgfplots — упрощение включения графиков в документ. Задача пользователя — задать формулу или данные, а остальным занимается pgfplots. Так, код графиков (см. пример на overleaf), приведенных выше (без преамбулы) выглядит так:
% Код первого графика
begin{tikzpicture}
begin{axis}
addplot[color=red]{exp(x)};
end{axis}
end{tikzpicture}% Код второго графика
begin{tikzpicture}
begin{axis}
addplot3[surf] {exp(-x^2-y^2)*x};
end{axis}
end{tikzpicture}Заметьте, от пользователя в простейшем случае не потребовалось практически ничего, кроме задания функции и вида её отображения. Разумеется, можно и вручную задать пределы построения функции и многое
другое.
Оглавление
- 0. Введение в pgfplots
- 0.1. Преамбула
- 0.2. Окружение осей
- 0.3. Пакет standalone: графики в отдельных файлах
- 1. Математика в pgfplots
- 1.1. Стандартные операторы
- 1.2. Стандартные функции
- 1.3. Генерация случайных чисел
- 2. Объявление новых функций
- 2.1. Составление функции Хевисайда. Ступенька произвольной длины
- 3. Настройка осей и сетки
- 3.1. Оси и их подписи. Настройка
- 3.2. «Тики» (метки на осях) и их подписи
- 3.2.1. Дополнительные тики
- 3.2.2. Промежуточные тики (minor ticks)
- 3.3. Максимальные и минимальные значения на графике. Масштаб осей
- 3.4. Сетка. Единицы измерения в LaTeX
- 3.4.1. Сетка через основные и промежуточные тики
- 3.4.2. Сетка через дополнительные (extra) тики
- 4. Легенда графика
- 5. Построение графика
- 5.1. Чтение данных из таблицы
- 5.1.2. Создание новых стоблцов таблицы
- 5.2. Отметки на линии графика (marks)
- 5.3. Прямоугольники ошибок
- 5.3.1. Постоянная абсолютная или относительная погрешность
- 5.3.2. Абсолютная или относительная погрешность из файла
- 5.4. Настройка линии графика
- 5.4.1. Толщина и цвет линии графика
- 5.4.2. Тип линии графика
- 5.1. Чтение данных из таблицы
- 6. Особенности построения графиков
- 6.1. Построение графиков, терпящих бесконечный скачок
- 6.2. Циклы в pgfplots и построение асимптот. Системы координат рисунка
- 6.3. Использование команд TikZ на графиках Pgfplots
- The End. Рекомендуемые источники
0. Введение в pgfplots
0.1. Преамбула
Подключается пакет стандартным образом. Вставьте этот код в преамбулу (до begin{document}):
Так же можно сразу в преамбуле сделать некоторые настройки. Во-первых, можно задать используемую версию pgfplots. Так как пакет динамично развивается, то некоторые вещи становятся несовместимыми от версии к версии. Наиболее разумным является использование текущей версии указанием параметра
pgfplotsset{width=10cm,compat=newest}но после окончания работы неплохо бы указать текущую версию вручную, чтобы если вдруг у вас будет такая функциональность, что не будет работать в следующих версиях, это не помешало бы компилировать график спустя длительное время.
Параметр width задает ширину графика. Также можно задать и высоту height. Надо заметить, что это нововведение по сравнению с tikz: в tikz картинки изменяют свой размер соответственно содержимому, pgfplots же может подогнать содержимое (масштабом осей) под график. Надо заметить, что возможно и обратное — задавать вручную масштаб осей, тогда высота и ширина будут определяться ими и содержимым, а параметры width, height будут игнорироваться.
0.2. Окружение осей
Поскольку pgfplots основан на tikz, график должен находиться в окружении tikzpicture. Сам график строится в осях (полотно графика с системой координат и некоторым масштабом).
Оси задаются окружением begin{axis} ... end{axis}. У осей могут быть свои параметры:
begin{tikzpicture}
begin{axis}[
%axis, % Обычные оси
%semilogxaxis, % По оси x логарифмический масштаб
%semilogyaxis, % По оси y логарифмический масштаб
%loglogaxis, % По обоим осям логарифмический масштаб
enlargelimits=true, % Делать размер осей чуть больше графика
]
addplot[color=red]{ln(x)};
end{axis}
end{tikzpicture}Булев параметр enlargelimits, если он включен, делает размер рисунка немного больше, так, чтобы нарисованные графики не касались края рисунка, а оставалось некоторое расстояние. По умолчанию он включен, и отключать его почти никогда не требуется.
Здесь они закомментированы. Достаточно одного из параметров, причем параметр axis используется по умолчанию, и его можно не указывать.
Чтобы добавить график, используется команда
addplot[color=red]{ln(x)};Внутри квадратных скобок могут быть переданы некоторые параметры, например здесь указан цвет линии графика. Квадратные скобки обязательны, если не передано ни одного параметра, нужно оставить между ними пробел.
Важно, что все команды (эта необходимость тянется из пакета tikz) должны заканчиваться точкой с запятой.
Внутри фигурных скобок размещается функция, задающая график. О её составлении рассказано ниже.
Так же более подробно о настройке осей и сетки см. раздел 3 «Настройка осей и сетки»
Самое подробное описание (на английском) можно найти в мануале по pgfplots 2.
0.3. Пакет standalone: графики в отдельных файлах
Компиляция графиков pgfplots может быть долгой. Особенно это касается случаев, когда строится функция с большим числом точек, уходящая на бесконечность или обрабатываются большие экспериментальные данные из файла.
В таком случае разумно, чтобы сократить время компиляции, создавать каждый рисунок как отдельный pdf-документ, а затем подключать его как картинку. С одной стороны, увеличивается скорость компиляции, с другой, документ становится проще за счет выноса длинного кода в отдельные файлы, а структура документа становится более гибкой: отдельный график можно использовать в других проектах.
Настоятельно рекомендуется использовать именно этот способ. Для него достаточно указать классом документа standalone, и документ будет компилироваться в pdf файл, причем так, что поле документа будет обрезано до размеров графика.
Стоит отметить, что этот пакет конфликтует с пакетом geometry, и последний использовать в документах класса standalone не нужно.
Дочерний документ (например, это файл img/ris1.tex):
documentclass{standalone}
usepackage[utf8]{inputenc}
usepackage{pgfplots}
pgfplotsset{width=10cm,compat=1.9}
begin{document}
begin{tikzpicture}
begin{axis}
addplot[color=red]{exp(x)};
end{axis}
end{tikzpicture}
end{document}Вставка картинки в основной документ:
begin{figure}[h!]
centering
includegraphics[scale=1]{img/ris1}
caption{Наш отдельный график}
label{fig:ris1}
end{figure}1. Математика в pgfplots
Математический аппарат pgfplots-а принадлежит пакету более низкого уровня pgf. Математические возможности pgf достаточно велики, и мы рассмотрим только некоторые аспекты составления сложных функций для построения различных графиков.
1.1. Стандартные операторы
- Без пояснения:
+,-,*,/,^ - Сравнение:
>,>=,<=,==,!= - Оператор факториала:
x!аналогичен вызову функцииfactorial(x)
Отдельно стоит сказать об условном операторе x ? y : z. Он вернет y, если x истина, и z, если ложь. Это можно использовать, например, для построения функций Хевисайда, о чем будет сказано ниже.
1.2. Стандартные функции
div(x,y)— целочисленное делениеmod(x,y)— остаток от деленияsign(x)— знак числа
Также ряд функций, не нуждающихся в объяснениях:
factorial(x),
sqrt(x),
exp(x),
ln(x),
log10(x),
log2(x),
abs(x)
Функции округления
round(x)— округлит до ближайшего целого, большего по модулю чем округляемое, числа: 1.5->2, -1.5->-2floor(x)— округлит х до ближайшего целого числа в большую сторонуceil(x)— округлит х до ближайшего целого числа в меньшую сторонуint(x)— просто вернет целую частьxfrac(x)— вернет дробную частьx
Целочисленные функции
iseven(x),isodd(x)— проверяет четность (нечетность) числа, в случае успеха вернет 1, в случае неудачи 1isprime(x)— проверяет, простое ли число (аналогично вернет 1/0)
Тригонометрические функции
sin,cos,tan,sec,cosec,cot,asin,acos,atan
Важно заметить, что все тригонометрические функции принимают на вход число в градусах, а для перевода из радиан в градусы служит функция deg, а обратно — rad. Это поведение по умолчанию, его можно поменять:
pgfkeys{/pgf/trig format=rad|deg}Кроме того, можно использовать радианы и не изменяя поведение по умолчанию — указать, что аргумент дан в радианах: cos(pi/2 r) ->0.
Гиперболические функции
sinh,cosh,tanh
1.3. Генерация случайных чисел
Присутствует и возможность генерации случайных чисел: вызов rnd вернет случайное число от 0 до 1, rand от -1 до 1.
Более подробно о функциях и операторах можно почитать в руководстве по pgf, 1000-1011 страницы 3.
2. Объявление новых функций
begin{tikzpicture}[
declare function={
myfun(x,t) = (x*t);
}
]
begin{axis}
addplot[color=red, domain=0:4, samples=300]{myfun(x,2)};
end{axis}
end{tikzpicture}Объявляется новая функция для всего рисунка. Все должно быть понятно из примера.
2.1. Составление функции Хевисайда. Ступенька произвольной длины
Используя условный оператор, несложно составить функцию Хевисайда:
Очевидно, она будет равна множителю перед скобкой при x>0 и нулю в отрицательной области. Из двух функций Хевисайда можно составить и прямоугольный импульс:
1*(x>0 ? 1 : 0)-1*(x>1 ? 1 : 0)Это прямоугольный импульс, начинающийся от нуля. Однако, можно создать функцию с аргументами высоты, ширины и начала ступеньки:
Нажмите для просмотра результата
begin{tikzpicture}[
declare function={
impuls(h,w,b,x) = h*((x>b ? 1 : 0)-(x>(b+w) ? 1 : 0));
}
]
begin{axis}
addplot[color=red, domain=0:4, samples=300]{impuls(2,2,1,x)};
end{axis}
end{tikzpicture}Заметим, что в общем случае, например для построения кусочно-гладких функций, необязательно создавать громоздкую функцию, которая будет включать в себя все остальные с помощью условного оператора.
Если заранее известно, что функция будет без скачков (скачок сам по себе можно построить, но особого смысла нет), то можно воспользоваться тем, что команда addplot имеет параметр области построения графика domain=start:end и использовать несколько плотов:
begin{tikzpicture}
begin{axis}
addplot[color=red, domain=0:1, samples=300]{x^2};
addplot[color=red, domain=1:4, samples=300]{2*x};
end{axis}
end{tikzpicture}samples здесь — количество точек графика. График не может строиться абсолютно непрерывно и берется в некотором числе точек, которые соединяются отрезками: чем выше число точек, тем качественнее картинка, но и медленнее её компиляция и отрисовка. Разумно делать это число меньше для медленно меняющихся графиков и много больше для быстро меняющихся, особенно для таких, как в предыдущем примере — со скачком.
По мере чтения руководства читатель может заметить появление новых параметров без объяснения. Предполагается, что они могут быть интуитивно понятны.
3. Настройка осей и сетки
3.1. Оси и их подписи. Заголовок графика.
Рассмотрим базовый пример настройки осей. По умолчанию, вместо координатных осей рисуется прямоугольник координат (axis lines = box), как это часто принято в научных статьях. Однако никто не мешает использовать оси-стрелки, или вообще отключить оси:
begin{tikzpicture}
begin{axis}[
axis lines = middle, % привычные оси со стрелочками с пересечением в нуле
% возможные значения: box, left, middle, center, right, none
xlabel = {$x$}, % подпись оси x
ylabel = {$f(x)$}, % подпись оси y
title={Мой первый график $f(x)=x^2 - 2cdot x - 1$},
]
addplot[domain=-10:10, samples=100, color=red] {x^2 - 2*x - 1};
end{axis}
end{tikzpicture}Обратите внимание на то, что у нас появился параметр title, задающий заголовок графику. Как правило, при использовании пакета standalone, это не нужно — заголовок графика задается командой caption в окружении figure.
Вообще говоря, положение осей можно применять и по отдельности:
axis x line=center,
axis y line=left,Можно задать и определенные правила отрисовки осей, например цвет, или сделать их пунктиром (dashed):
x axis line style ={black!40, dashed},
y axis line style ={red},Заметьте, как здесь указывается цвет. Это обозначение black!40!red означает смешение цветов, в соотношении 40% black 60% red, если цвет справа не указан, то он берется белым: значит, black!40 даст нам серый цвет. Таким образом из базовых цветов можно составить любой цвет.
Также можно перенести подписи осей к стрелкам на осях:
xlabel style={below right},
ylabel style={above left, red, scale=1.5},Здесь появился новый параметр scale, подпись к оси y будет в полтора раза больше, чем к оси x, очевидно.
Подразумевается, что все приведенные выше параметры подставляются в параметры окружения axis.
3.2. «Тики» (метки на осях) и их подписи
Когда график не качественный, важно наиболее удобно показать подписи (числа) к осям. За них отвечают ticks (тики) — маленькие перпендикулярные черты к осям с численной подписью.
Настройка расстояния между тиками:
xtick distance=1,
ytick distance=2Также можно вручную указать список основных тиков:
xtick={0,20,40,60,80,100},
ytick={0,20,40,60,80,100,120}А при необходимости, можно задать и подписи к ним (по умолчанию подпись — это координата тика):
ytick={1.5707,0.7853,1},
yticklabels={$frac{pi}{2},$, $frac{pi}{4}$, 1}, По умолчанию pgfplots пытается подобрать наиболее разумное расположение тиков.
3.2.1. Дополнительные тики
Иногда требуется специально показать положение чего-либо на осях. Для этого можно использовать дополнительные тики, задав им координаты и их подписи:
extra y ticks={-9/16,-6/16}, % положение дополнительных тиков
extra y tick labels={ % их подписи
{$U_{min}$}, {$U_{min}+Delta U$}
}, Для x аналогично.
3.2.2. Промежуточные тики (minor ticks)
Часто кроме основных меток на осях, ставят промежуточные: так, например, на линейке отмечены сантиметры рисками с подписями, а миллиметры просто рисками без подписей.
Такое задается с помощью minor ticks:
Этот параметр задает количество таких тиков (эквидистантных) между основными (major) тиками для обоих осей одинаково. А можно задать и для каждой оси отдельно:
minor x tick num=3,
minor y tick num=8,3.3. Максимальные и минимальные значения на графике. Масштаб осей
Масштаб осей задан в виде <длина орта x> <длина орта y>:
unit vector ratio = 1 1,
xmax = 8,
xmin=-2,
ymax=1.5,
ymin=-0.2,Максимальные и минимальные значения заданы очевидным образом.
3.4. Сетка. Единицы измерения в LaTeX
3.4.1. Сетка через основные и промежуточные тики
Сетка всегда проходит через тики на осях. Она может проходить как через основные (major) так и через промежуточные (minor) тики:
grid=major, % м.б. еще both - и там и там
grid style={dotted, cyan},Причем стиль можно задать как всей сетке (и основной major и промежуточной minor), так и по отдельности:
minor grid style={dashed,red, line width=0.2pt},
major grid style={solid,black, line width=0.1pt},Обратите внимание на используемые единицы измерения. em — это высота одной буквы шрифта 10pt:
pt называется типографским пунктом.
По умолчанию, сетка автоматически проведет линии и через пользовательские (дополнительные) тики, но этот стиль можно модифицировать:
extra tick style={grid=major, grid style={dotted, cyan}},Здесь мы скопировали стиль основных линий сетки и модифицировали его, сделав в точечку (dotted) и голубым (cyan).
4. Легенда графика
Для того, чтобы сопоставить какому-либо графику, который строится с помощью addplot, элемент легенды, есть специальная команда addlegendentry, которую нужно разместить после addplot:
begin{tikzpicture}
begin{axis}[
axis lines = middle,
xlabel = {$x$},
ylabel = {$f(x)$},
title={Мой первый график $f(x)=x^2 - 2cdot x - 1$},
legend pos={south west},
]
addplot[domain=-10:10, samples=100, color=red] {x^2+2*x};
addlegendentry{$x^+2cdot x$};
end{axis}
end{tikzpicture}Здесь появился параметр legend pos, который задает положение легенды на графике:
legend pos=south west|south east|north west|north east5. Построение графика
В самом начале мы рассмотрели и далее неоднократно употребляли построение графика заданной функции (y=f(x)). Однако, часто требуется построить не такой (или не только такой график), а покоординатный график (или, как это говорят математики, функция задана таблично, а не аналитически).
Обычно такая задача возникает при обработке экспериментальных данных. Есть два способа: записать данные непосредественно в график, или записать их в текстовую таблицу (tsv или csv). Рассмотрим такие случаи.
5.1. Чтение данных из таблицы
Важно: для чтения из таблицы нужно подключить пакет:
usepackage{pgfplotstable}Рассмотрим такой пример: пусть у нас есть файл data.tsv, лежащий в той же папке, что и рисунок:
Fr Uin err
15 7.446 0.1
25 7.532 0.1
40 7.512 0.1
100 7.412 0.1
200 7.41 0.1
300 7.32 0.1
400 7.27 0.1
500 7.236 0.1
1000 7.3 0.1
2000 7.282 0.1
3000 7.27 0.1Тогда его можно построить командой:
addplot +[blue, dashed]
plot table [
x=Fr,
y=Uin
]{data.tsv};В этом примере все просто. В первых квадратных скобках пишутся параметры, управляющие отрисованным графиком, построением прямоугольников ошибок и т.п., а во вторых — параметры чтения из таблицы, создание новых столбцов таблицы путем математического выражения, составленного из существующих столбцов, о чем написано ниже.
5.1.2. Создание новых стоблцов таблицы
Рассмотрим простой пример, на основе приведенного выше файла данных. В нем в первой столбце стоит частота в герцах, но допустим, что мы хотим построить график от круговой частоты, т.е. домножить на (2pi):
addplot +[blue, dashed]
plot table [
create on use/omega/.style={
create col/expr={
thisrow{Fr}*2*pi
}
},
x=omega,
y=Uin
]{data.tsv};Здесь видно, как несложно оперировать созданием новых столбцов. При этом применима вся математика, рассмотренная в разделе выше.
5.2. Маркеры на линии графика
Часто требуется не просто соединить экспериментальные точки линией, а указать каждую конкретную точку маркером (mark), а то и вовсе составить график только из маркеров. Для этого предыдущий пример несложно модифицируется:
addplot +[blue, mark=*, mark size=1.5pt, only marks]
plot table [
create on use/omega/.style={
create col/expr={
thisrow{Fr}*2*pi
}
},
x=omega,
y=Uin
]{data.tsv};Параметр only marks принуждает рисовать только маркеры, без линии их соединяющих, mark size размер маркера, mark тип маркера.
Существует достаточно много типов:
Эта картинка взята из руководства по tikz в картинках 4.
Для маркеров можно сразу задать несколько параметров: вместо размера задать масштаб (второй способ изменить размер маркера, иногда более удобный), основной цвет (draw) и цвет заливки (fill
addplot +[
mark=*,
mark options={
scale=2,
fill=blue,
draw=red,
},
only marks
] plot table [
create on use/omega/.style={
create col/expr={
thisrow{Fr}*2*pi
}
},
x=omega,
y=Uin
]{data.tsv};5.3. Прямоугольники ошибок
Для начала рассмотрим простейший случай постоянной ошибки. Параметры прямоугольников ошибок пишутся в параметры команды plot. Рассматривать будем все на примере ошибки по y, по другим осям анологично с точностью до замены y->x,z.
Для включения прямоугольников ошибки и возможности их настройки перед последующими рассмотренными параметрами нужно вставлять параметр error bars/.cd.
5.3.1. Постоянная абсолютная или относительная погрешность
Сначала нужно определить, какая будет ошибка: строго положительная, отрицательная или в обе стороны. За это отвечает параметр y dir=minus|plus|both.
addplot +[
mark=*,
only marks,
] plot[
error bars/.cd,
y dir=both,
y fixed=0.1,
% y fixed relative=0.1,
] table [
x=Fr,
y=Uin
]{data.tsv};Здесь указана сразу абсолютная погрешность для всех значений. Аналогично можно задать сразу относительную параметром y fixed relative.
5.3.2. Абсолютная или относительная погрешность из файла
Необходимо явно указать, что ожидается чтение данных ошибки из файла, указать в каком столбце (y error=err) записана ошибка и тип ошибки:
addplot +[
mark=*,
only marks,
] plot[
error bars/.cd,
y dir=both,
y explicit relative,
] table [
x=Fr,
y=Uin,
y error=err,
]{data.tsv};Для абсолютной ошибки параметр y explicit, для относительной y explicit relative.
5.4. Настройка линии графика
5.4.1. Толщина и цвет линии графика
Толщина линии управляется либо параметром line width=, либо словесными алиасами (рекомендуется использовать именно их):
Цвет линии сам является параметром:
addplot +[
thick,
blue!20!black
] plot table [
x=Fr,
y=Uin,
]{data.tsv};О составлении цветов сказано ранее в разделе ().
5.4.2. Тип линии графика
Как и цвет, тип линии графика сам по себе параметр:
addplot +[
thick,
blue!20!black,
dashed
] plot table [
x=Fr,
y=Uin,
]{data.tsv};Существует несколько типов линий:
6. Особенности построения графиков
6.1. Построение графиков, терпящих бесконечный скачок
Рассмотрим построение графика с бесконечным скачком на примере построения (tan(x)).
Расчет функций, которые уходят на бесконечность, может привести к ошибкам компиляции. Чтобы этого избежать, можно указать в параметрах принудительное вписывание в пределы расчетов: выйдя за эти пределы, математический движок pgf просто будет пропускать эти значения, пока опять не войдет в пределы:
restrict y to domain=-20:20,Разумно выбирать эти пределы немного больше заданного предела осей xmin,xmax,ymin,ymax.
Кроме того, можно сказать pgfplots-у, как вести себя при получении бесконечности в расчетах, и не ограничивая расчет:
unbounded coords=discard|jumpЭтот ключ настраивает, что делать, если одна или несколько координат одной точки неограничена, или, например, при чтении из файла на этом месте стоит nan или ничего не стоит.
discard (по умолчанию) отбрасывает точку завершения, и в логе компиляции выдается предупреждение. При этом график строится, как если бы неограниченная точка не произошла: pgfplots интерполирует между ограниченными ближайшими точками.
jump просто пропустит значения, которые уходят на бесконечность, и график станет с разрывом.
Однако, как это ни странно, в случае тангенса это все не так: для стандартных функций с разрывом разработчики постарались, и они строятся без дополнительных усилий. Но при этом (+infty) и (-infty) точки графика соединяются, что не всегда может быть полезно: например, обычно в этом месте строят линии асимптот.
Все же придется вернуться к первоначальному определению:
documentclass[tikz,10pt]{standalone}
usepackage[T2A]{fontenc}
usepackage[utf8x]{inputenc}
usepackage[russian]{babel}
usepackage{amsmath,amssymb,cmap,pgfplots,pgfplotstable}
usetikzlibrary{arrows,calc,intersections}
pgfplotsset{compat=newest}
begin{document}
begin{tikzpicture}
begin{axis}[
xlabel={$x$},
ylabel={$tg x$},
axis lines=middle,
ymax = 10,
ymin = -10,
enlargelimits=true,
xmin=-4*pi/2,
xmax=4*pi/2,
restrict y to domain=-20:20,
xtick=empty,
ytick=empty,
]
addplot[blue!50,domain={-4*pi/2:4*pi/2},samples=1000] {tan(deg(x))};
pgfplotsinvokeforeach{-2,-1,...,2}{%
draw[dashed, black!20]
({{pi/2+pi*#1},0} |- {rel axis cs:0,0})
-- ({{pi/2+pi*#1},0}|-{rel axis cs:0,1});
}
end{axis}
end{tikzpicture}
end{document}Здесь есть интересный код для построения асимптот. Рассмотрим его подробнее.
6.2. Циклы в pgfplots и построение асимптот. Системы координат рисунка
Стандартный цикл tikz-а, к сожалению, в pgfplots не работает. Приходится использовать его более низкоуровневый аналог:
pgfplotsinvokeforeach{-2,-1,...,2}{%
% Выражение в цикле. Счетчик цикла - #1
}Счетчик пробегает указанные значения. Можно указывать их как список {0,1,2,3},а можно указать первое значение, второе, троеточие, последнее: из первого и второго рассчитается шаг и счетчик пробежит нужные значения. Они могут быть дробными.
Теперь подробнее, как же работает код построения вертикальной асимптоты. В tikz есть интересный способ расчета координаты в угле. Если задана такая координата X: (A -| B), то она находится в точке, которая образована пересечением горизонтальной линии через A и вертикальной через B:
Можно наоборот, (B -| A), соотв. вертикальная через А и горизонтальная через B.
По умолчанию используется система координат осей, в которой начало и орты отвечают нарисованным на графике.
Есть еще так называемая rel axis cs — система координат рисунка: в ней точка (0,0) это левый нижний угол рисунка, а (1,1) — верхний правый.
Со всей этой информацией теперь нетрудно должно быть понять, как работает асимптота через точку x:
({x},0} |- {rel axis cs:0,0}) -- ({x},0}|-{rel axis cs:0,1});6.3. Использование команд TikZ на графиках Pgfplots
Ровно в предыдущем параграфе рассмотрено применение команд tikz для построения асимптот в осях графика.
Часто возникает еще потребность подписать какие-либо точки на кривой. Для этого можно создать ноду на кривой, где положение ноды задается от 0 до 1 — 0 в начале кривой, 1 в конце. Эдакие криволинейные координаты.
addplot[blue!50,domain={-4*pi/2:4*pi/2},samples=1000] {sin(deg(x))}
node[pos=0.3] (1) {}
node[pos=.3,left,black]{$x$};
draw[fill=magenta] (1) circle (1pt);Здесь мы специально создали пустую ноду с координатой (1), в которой потом можно нарисовать точку, а вторая нода уже рисует текст.
Для понимания это может быть затруднено, если вы не изучали tikz. Тогда можно просто использовать этот пример, не заботясь принципами его работы.
На кривую так можно поместить сколько угодно точек, главное, в конце списка должна стоять точка с запятой.
6.3. Качественные графики: удаление меток с осей
Достаточно добавить два параметра к окружению axis:
xtick=empty,
ytick=empty,The End. Рекомендуемые источники
Наконец, прочитав небольшое руководство по использованию pgfplots, вы почти готовы к тому, чтобы применить его для своих работ. В этом нелегком (поначалу) труде смогут помочь некоторые источники.
Sometimes, when representing data in a line chart, the data points aren’t points, but intervals, since the magnitude they represent has some kind of error margin.
That’s why those points are drawn as intervals in both X and Y axis, with a size corresponding to the error. That creates on each point something called error rectangles. Here’s a picture of what I’m talking about:
As far as I know, this can be done in Excel, but I don’t know the procedure. Searching for it in Google didn’t return any relevant results. Any ideas?
The rectangles I’m trying to show are going to have the same size on each axis (for example, ±2 in the X axis, and ±3 in Y, for all the points). This means they won’t vary, like in the picture.
Методические материалы
ПРАВИЛА СОСТАВЛЕНИЯ ОТЧЁТА ПО ЛАБОРАТОРНОЙ РАБОТЕ
Основные требования к существу отчета:
- Необходимо обращать внимание на чёткую рубрикацию отчета (нумерацию составных частей, выделение заголовков и т.д.).
- Отчет должен содержать следующие элементы:
- полное название лабораторной работы и дату составления отчета;
- кратко сформулированную цель работы;
- перечень приборов, используемых в данной работе, с указанием их марки и класса точности;
- принципиальную схему электрической цепи, на основе которой делаются измерения;
- краткое изложение теории изучаемого в данном эксперименте физического явления с выводом формул, используемых для обработки экспериментальных данных, определениями измеряемых величин и пояснением всех используемых буквенных сокращений;
- краткое изложение методики проведения экспериментальной части работы и измерения требуемых величин;
- «краткое изложение» вовсе не означает, что нужно комбинацией «Копировать»-«Вставить» полностью передрать теоретическую часть из методички, а предполагает сокращённое изложение теории применительно к тем практическим заданиям, которые выполнялись и методикам измерений, которые при этом использовались;
- содержание выполняемых заданий, результаты измерений;
- выводы, в которых результаты измерений и вычислений сравниваются с теоретическими значениями, выясняются причины расхождения опыта и теории и даются рекомендации по их устранению.
- Результаты измерений (прямых и косвенных), оформленные в виде графиков, размещаются в соответствующих местах отчета.
При выборе масштаба графика надо предусмотреть, чтобы результаты измерений полностью и наглядно отразились на графике, не осталось много свободных полей, т.е. кривая не должна быть прижата к одной или другой оси. У осей координат наносят обозначения величин и единиц их измерений. На осях откладывают масштабные единицы, а не координаты экспериментальных точек. На подготовленной таким образом плоскости наносят точки.
Так как и аргумент, и функция определяются на опыте с соответствующими погрешностями, то около экспериментальных точек строят прямоугольники ошибок, стороны которых выражают в данном масштабе величины абсолютных ошибок функции и аргумента. Линию графика проводят не через каждую точку, а плавно и по возможности близко к экспериментальным точкам так, чтобы точки равномерно располагались по обе стороны кривой. Линия графика должна пересекать прямоугольники ошибок или касаться их. Для точек, резко отклоняющихся от кривой, нужно проверить правильность измерения или вычисления их координат. - Расчет погрешностей косвенных измерений. Число значащих цифр в записи результата вычислений косвенно измеряемой величины должно соответствовать погрешности этой величины. Например, если абсолютная погрешность рассчитанной ёмкости равна ±2 пФ, то правильной является запись C=32,1 пФ, а не C=32 пФ или C=32,17 пФ.
О погрешностях измерений при проведении лабораторных работ можно кратко почитать в статье «Мерь точно!»», формулы для расчёта погрешности косвенных измерений есть по этой ссылке. Ещё подробнее – в учебном пособии «Методы обработки результатов измерений в лаборатории физпрактикума». - В отчёте должны быть даны ответы на вопросы, если они формулируются в описании соответствующей лабораторной работы.
- Отчёт оформляется в редакторе Word, при необходимости распечатывается. Правила, предъявляемые к оформлению, находятся здесь.
Только, пожалуйста:- не копируйте полностью учебник по электронике или методичку в теоретическую часть отчёта – придётся объяснять всё, что в этом отчёте написано (а при тупом копировании теории это очень трудно, а порой, и невозможно), что займёт времени значительно больше, чем при нормальном написании отчёта;
- не переписывайте у товарища его отчёт, заменив фамилию, и т.д. – преподаватели замечают до 90% таких случаев, а в любом отчёте, даже в сданном, есть ошибки, которые придётся объяснять и исправлять (исправлять чужие ошибки!), а если ещё и протокол измерений у кого-то списан (естественно, опять же с чужими ошибками), то сдать такую работу практически невозможно.
- Сокращение слов в отчете (кроме единиц измерения физических величин) не допускается.
- При сдаче отчёта у студента должен быть протокол выполнения практических заданий по лабораторной работе.
© Кафедра электроники РФ ННГУ им. Н.И. Лобачевского, 2021–2023
После корректировки по методу наименьших квадратов ковариационная матрица используется для вычисления среднеквадратических отклонений положения и
.
На следующем рисунке показаны среднеквадратические отклонения, представляющие полуразмеры среднеквадратической 68% вероятности прямоугольника ошибок вокруг каждой точки:
Где:
- t = ориентация эллипса ошибок, направления большой полуоси
- u = большая полуось эллипса ошибок
- v = малая полуось эллипса ошибок
- x = половина ширины прямоугольника ошибок
- у = половина высоты прямоугольника ошибок
- S = среднеквадратическое отклонения положения точки
Pgfplots: краткое руководство
О пакете
Пакет pgfplots представляет собой мощный инструмент, предназначенный для создания научных графиков. Он создан на базе tikz, не менее прекрасного пакета, который позволяет создавать векторную графику прямо на латехе.
Если вы сомневаетесь в необходимости использования pgfplots или tikz, посмотрите на простые графики, созданные с помощью этих пакетов:
Много небольших примеров применения можно посмотреть в галерее pgfplots 1.
Основная идея pgfplots — упрощение включения графиков в документ. Задача пользователя — задать формулу или данные, а остальным занимается pgfplots. Так, код графиков (см. пример на overleaf), приведенных выше (без преамбулы) выглядит так:
% Код первого графика
\begin{tikzpicture}
\begin{axis}
\addplot[color=red]{exp(x)};
\end{axis}
\end{tikzpicture}% Код второго графика
\begin{tikzpicture}
\begin{axis}
\addplot3[surf] {exp(-x^2-y^2)*x};
\end{axis}
\end{tikzpicture}Заметьте, от пользователя в простейшем случае не потребовалось практически ничего, кроме задания функции и вида её отображения. Разумеется, можно и вручную задать пределы построения функции и многое
другое.
Оглавление
- 0. Введение в pgfplots
- 0.1. Преамбула
- 0.2. Окружение осей
- 0.3. Пакет standalone: графики в отдельных файлах
- 1. Математика в pgfplots
- 1.1. Стандартные операторы
- 1.2. Стандартные функции
- 1.3. Генерация случайных чисел
- 2. Объявление новых функций
- 2.1. Составление функции Хевисайда. Ступенька произвольной длины
- 3. Настройка осей и сетки
- 3.1. Оси и их подписи. Настройка
- 3.2. «Тики» (метки на осях) и их подписи
- 3.2.1. Дополнительные тики
- 3.2.2. Промежуточные тики (minor ticks)
- 3.3. Максимальные и минимальные значения на графике. Масштаб осей
- 3.4. Сетка. Единицы измерения в LaTeX
- 3.4.1. Сетка через основные и промежуточные тики
- 3.4.2. Сетка через дополнительные (extra) тики
- 4. Легенда графика
- 5. Построение графика
- 5.1. Чтение данных из таблицы
- 5.1.2. Создание новых стоблцов таблицы
- 5.2. Отметки на линии графика (marks)
- 5.3. Прямоугольники ошибок
- 5.3.1. Постоянная абсолютная или относительная погрешность
- 5.3.2. Абсолютная или относительная погрешность из файла
- 5.4. Настройка линии графика
- 5.4.1. Толщина и цвет линии графика
- 5.4.2. Тип линии графика
- 5.1. Чтение данных из таблицы
- 6. Особенности построения графиков
- 6.1. Построение графиков, терпящих бесконечный скачок
- 6.2. Циклы в pgfplots и построение асимптот. Системы координат рисунка
- 6.3. Использование команд TikZ на графиках Pgfplots
- The End. Рекомендуемые источники
0. Введение в pgfplots
0.1. Преамбула
Подключается пакет стандартным образом. Вставьте этот код в преамбулу (до \begin{document}):
Так же можно сразу в преамбуле сделать некоторые настройки. Во-первых, можно задать используемую версию pgfplots. Так как пакет динамично развивается, то некоторые вещи становятся несовместимыми от версии к версии. Наиболее разумным является использование текущей версии указанием параметра
\pgfplotsset{width=10cm,compat=newest}но после окончания работы неплохо бы указать текущую версию вручную, чтобы если вдруг у вас будет такая функциональность, что не будет работать в следующих версиях, это не помешало бы компилировать график спустя длительное время.
Параметр width задает ширину графика. Также можно задать и высоту height. Надо заметить, что это нововведение по сравнению с tikz: в tikz картинки изменяют свой размер соответственно содержимому, pgfplots же может подогнать содержимое (масштабом осей) под график. Надо заметить, что возможно и обратное — задавать вручную масштаб осей, тогда высота и ширина будут определяться ими и содержимым, а параметры width, height будут игнорироваться.
0.2. Окружение осей
Поскольку pgfplots основан на tikz, график должен находиться в окружении tikzpicture. Сам график строится в осях (полотно графика с системой координат и некоторым масштабом).
Оси задаются окружением \begin{axis} ... \end{axis}. У осей могут быть свои параметры:
\begin{tikzpicture}
\begin{axis}[
%axis, % Обычные оси
%semilogxaxis, % По оси x логарифмический масштаб
%semilogyaxis, % По оси y логарифмический масштаб
%loglogaxis, % По обоим осям логарифмический масштаб
enlargelimits=true, % Делать размер осей чуть больше графика
]
\addplot[color=red]{ln(x)};
\end{axis}
\end{tikzpicture}Булев параметр enlargelimits, если он включен, делает размер рисунка немного больше, так, чтобы нарисованные графики не касались края рисунка, а оставалось некоторое расстояние. По умолчанию он включен, и отключать его почти никогда не требуется.
Здесь они закомментированы. Достаточно одного из параметров, причем параметр axis используется по умолчанию, и его можно не указывать.
Чтобы добавить график, используется команда
\addplot[color=red]{ln(x)};Внутри квадратных скобок могут быть переданы некоторые параметры, например здесь указан цвет линии графика. Квадратные скобки обязательны, если не передано ни одного параметра, нужно оставить между ними пробел.
Важно, что все команды (эта необходимость тянется из пакета tikz) должны заканчиваться точкой с запятой.
Внутри фигурных скобок размещается функция, задающая график. О её составлении рассказано ниже.
Так же более подробно о настройке осей и сетки см. раздел 3 «Настройка осей и сетки»
Самое подробное описание (на английском) можно найти в мануале по pgfplots 2.
0.3. Пакет standalone: графики в отдельных файлах
Компиляция графиков pgfplots может быть долгой. Особенно это касается случаев, когда строится функция с большим числом точек, уходящая на бесконечность или обрабатываются большие экспериментальные данные из файла.
В таком случае разумно, чтобы сократить время компиляции, создавать каждый рисунок как отдельный pdf-документ, а затем подключать его как картинку. С одной стороны, увеличивается скорость компиляции, с другой, документ становится проще за счет выноса длинного кода в отдельные файлы, а структура документа становится более гибкой: отдельный график можно использовать в других проектах.
Настоятельно рекомендуется использовать именно этот способ. Для него достаточно указать классом документа standalone, и документ будет компилироваться в pdf файл, причем так, что поле документа будет обрезано до размеров графика.
Стоит отметить, что этот пакет конфликтует с пакетом geometry, и последний использовать в документах класса standalone не нужно.
Дочерний документ (например, это файл img/ris1.tex):
\documentclass{standalone}
\usepackage[utf8]{inputenc}
\usepackage{pgfplots}
\pgfplotsset{width=10cm,compat=1.9}
\begin{document}
\begin{tikzpicture}
\begin{axis}
\addplot[color=red]{exp(x)};
\end{axis}
\end{tikzpicture}
\end{document}Вставка картинки в основной документ:
\begin{figure}[h!]
\centering
\includegraphics[scale=1]{img/ris1}
\caption{Наш отдельный график}
\label{fig:ris1}
\end{figure}1. Математика в pgfplots
Математический аппарат pgfplots-а принадлежит пакету более низкого уровня pgf. Математические возможности pgf достаточно велики, и мы рассмотрим только некоторые аспекты составления сложных функций для построения различных графиков.
1.1. Стандартные операторы
- Без пояснения:
+,-,*,/,^ - Сравнение:
>,>=,<=,==,!= - Оператор факториала:
x!аналогичен вызову функцииfactorial(x)
Отдельно стоит сказать об условном операторе x ? y : z. Он вернет y, если x истина, и z, если ложь. Это можно использовать, например, для построения функций Хевисайда, о чем будет сказано ниже.
1.2. Стандартные функции
div(x,y)— целочисленное делениеmod(x,y)— остаток от деленияsign(x)— знак числа
Также ряд функций, не нуждающихся в объяснениях:
factorial(x),
sqrt(x),
exp(x),
ln(x),
log10(x),
log2(x),
abs(x)
Функции округления
round(x)— округлит до ближайшего целого, большего по модулю чем округляемое, числа: 1.5->2, -1.5->-2floor(x)— округлит х до ближайшего целого числа в большую сторонуceil(x)— округлит х до ближайшего целого числа в меньшую сторонуint(x)— просто вернет целую частьxfrac(x)— вернет дробную частьx
Целочисленные функции
iseven(x),isodd(x)— проверяет четность (нечетность) числа, в случае успеха вернет 1, в случае неудачи 1isprime(x)— проверяет, простое ли число (аналогично вернет 1/0)
Тригонометрические функции
sin,cos,tan,sec,cosec,cot,asin,acos,atan
Важно заметить, что все тригонометрические функции принимают на вход число в градусах, а для перевода из радиан в градусы служит функция deg, а обратно — rad. Это поведение по умолчанию, его можно поменять:
\pgfkeys{/pgf/trig format=rad|deg}Кроме того, можно использовать радианы и не изменяя поведение по умолчанию — указать, что аргумент дан в радианах: cos(pi/2 r) ->0.
Гиперболические функции
sinh,cosh,tanh
1.3. Генерация случайных чисел
Присутствует и возможность генерации случайных чисел: вызов rnd вернет случайное число от 0 до 1, rand от -1 до 1.
Более подробно о функциях и операторах можно почитать в руководстве по pgf, 1000-1011 страницы 3.
2. Объявление новых функций
\begin{tikzpicture}[
declare function={
myfun(\x,\t) = (\x*\t);
}
]
\begin{axis}
\addplot[color=red, domain=0:4, samples=300]{myfun(x,2)};
\end{axis}
\end{tikzpicture}Объявляется новая функция для всего рисунка. Все должно быть понятно из примера.
2.1. Составление функции Хевисайда. Ступенька произвольной длины
Используя условный оператор, несложно составить функцию Хевисайда:
Очевидно, она будет равна множителю перед скобкой при x>0 и нулю в отрицательной области. Из двух функций Хевисайда можно составить и прямоугольный импульс:
1*(x>0 ? 1 : 0)-1*(x>1 ? 1 : 0)Это прямоугольный импульс, начинающийся от нуля. Однако, можно создать функцию с аргументами высоты, ширины и начала ступеньки:
Нажмите для просмотра результата
\begin{tikzpicture}[
declare function={
impuls(\h,\w,\b,\x) = \h*((\x>\b ? 1 : 0)-(\x>(\b+\w) ? 1 : 0));
}
]
\begin{axis}
\addplot[color=red, domain=0:4, samples=300]{impuls(2,2,1,x)};
\end{axis}
\end{tikzpicture}Заметим, что в общем случае, например для построения кусочно-гладких функций, необязательно создавать громоздкую функцию, которая будет включать в себя все остальные с помощью условного оператора.
Если заранее известно, что функция будет без скачков (скачок сам по себе можно построить, но особого смысла нет), то можно воспользоваться тем, что команда \addplot имеет параметр области построения графика domain=start:end и использовать несколько плотов:
\begin{tikzpicture}
\begin{axis}
\addplot[color=red, domain=0:1, samples=300]{x^2};
\addplot[color=red, domain=1:4, samples=300]{2*x};
\end{axis}
\end{tikzpicture}samples здесь — количество точек графика. График не может строиться абсолютно непрерывно и берется в некотором числе точек, которые соединяются отрезками: чем выше число точек, тем качественнее картинка, но и медленнее её компиляция и отрисовка. Разумно делать это число меньше для медленно меняющихся графиков и много больше для быстро меняющихся, особенно для таких, как в предыдущем примере — со скачком.
По мере чтения руководства читатель может заметить появление новых параметров без объяснения. Предполагается, что они могут быть интуитивно понятны.
3. Настройка осей и сетки
3.1. Оси и их подписи. Заголовок графика.
Рассмотрим базовый пример настройки осей. По умолчанию, вместо координатных осей рисуется прямоугольник координат (axis lines = box), как это часто принято в научных статьях. Однако никто не мешает использовать оси-стрелки, или вообще отключить оси:
\begin{tikzpicture}
\begin{axis}[
axis lines = middle, % привычные оси со стрелочками с пересечением в нуле
% возможные значения: box, left, middle, center, right, none
xlabel = {$x$}, % подпись оси x
ylabel = {$f(x)$}, % подпись оси y
title={Мой первый график $f(x)=x^2 - 2\cdot x - 1$},
]
\addplot[domain=-10:10, samples=100, color=red] {x^2 - 2*x - 1};
\end{axis}
\end{tikzpicture}Обратите внимание на то, что у нас появился параметр title, задающий заголовок графику. Как правило, при использовании пакета standalone, это не нужно — заголовок графика задается командой caption в окружении figure.
Вообще говоря, положение осей можно применять и по отдельности:
axis x line=center,
axis y line=left,Можно задать и определенные правила отрисовки осей, например цвет, или сделать их пунктиром (dashed):
x axis line style ={black!40, dashed},
y axis line style ={red},Заметьте, как здесь указывается цвет. Это обозначение black!40!red означает смешение цветов, в соотношении 40% black 60% red, если цвет справа не указан, то он берется белым: значит, black!40 даст нам серый цвет. Таким образом из базовых цветов можно составить любой цвет.
Также можно перенести подписи осей к стрелкам на осях:
xlabel style={below right},
ylabel style={above left, red, scale=1.5},Здесь появился новый параметр scale, подпись к оси y будет в полтора раза больше, чем к оси x, очевидно.
Подразумевается, что все приведенные выше параметры подставляются в параметры окружения axis.
3.2. «Тики» (метки на осях) и их подписи
Когда график не качественный, важно наиболее удобно показать подписи (числа) к осям. За них отвечают ticks (тики) — маленькие перпендикулярные черты к осям с численной подписью.
Настройка расстояния между тиками:
xtick distance=1,
ytick distance=2Также можно вручную указать список основных тиков:
xtick={0,20,40,60,80,100},
ytick={0,20,40,60,80,100,120}А при необходимости, можно задать и подписи к ним (по умолчанию подпись — это координата тика):
ytick={1.5707,0.7853,1},
yticklabels={$\frac{\pi}{2},$, $\frac{\pi}{4}$, 1}, По умолчанию pgfplots пытается подобрать наиболее разумное расположение тиков.
3.2.1. Дополнительные тики
Иногда требуется специально показать положение чего-либо на осях. Для этого можно использовать дополнительные тики, задав им координаты и их подписи:
extra y ticks={-9/16,-6/16}, % положение дополнительных тиков
extra y tick labels={ % их подписи
{$U_{min}$}, {$U_{min}+\Delta U$}
}, Для x аналогично.
3.2.2. Промежуточные тики (minor ticks)
Часто кроме основных меток на осях, ставят промежуточные: так, например, на линейке отмечены сантиметры рисками с подписями, а миллиметры просто рисками без подписей.
Такое задается с помощью minor ticks:
Этот параметр задает количество таких тиков (эквидистантных) между основными (major) тиками для обоих осей одинаково. А можно задать и для каждой оси отдельно:
minor x tick num=3,
minor y tick num=8,3.3. Максимальные и минимальные значения на графике. Масштаб осей
Масштаб осей задан в виде <длина орта x> <длина орта y>:
unit vector ratio = 1 1,
xmax = 8,
xmin=-2,
ymax=1.5,
ymin=-0.2,Максимальные и минимальные значения заданы очевидным образом.
3.4. Сетка. Единицы измерения в LaTeX
3.4.1. Сетка через основные и промежуточные тики
Сетка всегда проходит через тики на осях. Она может проходить как через основные (major) так и через промежуточные (minor) тики:
grid=major, % м.б. еще both - и там и там
grid style={dotted, cyan},Причем стиль можно задать как всей сетке (и основной major и промежуточной minor), так и по отдельности:
minor grid style={dashed,red, line width=0.2pt},
major grid style={solid,black, line width=0.1pt},Обратите внимание на используемые единицы измерения. em — это высота одной буквы шрифта 10pt:
pt называется типографским пунктом.
По умолчанию, сетка автоматически проведет линии и через пользовательские (дополнительные) тики, но этот стиль можно модифицировать:
extra tick style={grid=major, grid style={dotted, cyan}},Здесь мы скопировали стиль основных линий сетки и модифицировали его, сделав в точечку (dotted) и голубым (cyan).
4. Легенда графика
Для того, чтобы сопоставить какому-либо графику, который строится с помощью \addplot, элемент легенды, есть специальная команда \addlegendentry, которую нужно разместить после \addplot:
\begin{tikzpicture}
\begin{axis}[
axis lines = middle,
xlabel = {$x$},
ylabel = {$f(x)$},
title={Мой первый график $f(x)=x^2 - 2\cdot x - 1$},
legend pos={south west},
]
\addplot[domain=-10:10, samples=100, color=red] {x^2+2*x};
\addlegendentry{$x^+2\cdot x$};
\end{axis}
\end{tikzpicture}Здесь появился параметр legend pos, который задает положение легенды на графике:
legend pos=south west|south east|north west|north east5. Построение графика
В самом начале мы рассмотрели и далее неоднократно употребляли построение графика заданной функции \(y=f(x)\). Однако, часто требуется построить не такой (или не только такой график), а покоординатный график (или, как это говорят математики, функция задана таблично, а не аналитически).
Обычно такая задача возникает при обработке экспериментальных данных. Есть два способа: записать данные непосредественно в график, или записать их в текстовую таблицу (tsv или csv). Рассмотрим такие случаи.
5.1. Чтение данных из таблицы
Важно: для чтения из таблицы нужно подключить пакет:
\usepackage{pgfplotstable}Рассмотрим такой пример: пусть у нас есть файл data.tsv, лежащий в той же папке, что и рисунок:
Fr Uin err
15 7.446 0.1
25 7.532 0.1
40 7.512 0.1
100 7.412 0.1
200 7.41 0.1
300 7.32 0.1
400 7.27 0.1
500 7.236 0.1
1000 7.3 0.1
2000 7.282 0.1
3000 7.27 0.1Тогда его можно построить командой:
\addplot +[blue, dashed]
plot table [
x=Fr,
y=Uin
]{data.tsv};В этом примере все просто. В первых квадратных скобках пишутся параметры, управляющие отрисованным графиком, построением прямоугольников ошибок и т.п., а во вторых — параметры чтения из таблицы, создание новых столбцов таблицы путем математического выражения, составленного из существующих столбцов, о чем написано ниже.
5.1.2. Создание новых стоблцов таблицы
Рассмотрим простой пример, на основе приведенного выше файла данных. В нем в первой столбце стоит частота в герцах, но допустим, что мы хотим построить график от круговой частоты, т.е. домножить на \(2\pi\):
\addplot +[blue, dashed]
plot table [
create on use/omega/.style={
create col/expr={
\thisrow{Fr}*2*pi
}
},
x=omega,
y=Uin
]{data.tsv};Здесь видно, как несложно оперировать созданием новых столбцов. При этом применима вся математика, рассмотренная в разделе выше.
5.2. Маркеры на линии графика
Часто требуется не просто соединить экспериментальные точки линией, а указать каждую конкретную точку маркером (mark), а то и вовсе составить график только из маркеров. Для этого предыдущий пример несложно модифицируется:
\addplot +[blue, mark=*, mark size=1.5pt, only marks]
plot table [
create on use/omega/.style={
create col/expr={
\thisrow{Fr}*2*pi
}
},
x=omega,
y=Uin
]{data.tsv};Параметр only marks принуждает рисовать только маркеры, без линии их соединяющих, mark size размер маркера, mark тип маркера.
Существует достаточно много типов:
Эта картинка взята из руководства по tikz в картинках 4.
Для маркеров можно сразу задать несколько параметров: вместо размера задать масштаб (второй способ изменить размер маркера, иногда более удобный), основной цвет (draw) и цвет заливки (fill
\addplot +[
mark=*,
mark options={
scale=2,
fill=blue,
draw=red,
},
only marks
] plot table [
create on use/omega/.style={
create col/expr={
\thisrow{Fr}*2*pi
}
},
x=omega,
y=Uin
]{data.tsv};5.3. Прямоугольники ошибок
Для начала рассмотрим простейший случай постоянной ошибки. Параметры прямоугольников ошибок пишутся в параметры команды plot. Рассматривать будем все на примере ошибки по y, по другим осям анологично с точностью до замены y->x,z.
Для включения прямоугольников ошибки и возможности их настройки перед последующими рассмотренными параметрами нужно вставлять параметр error bars/.cd.
5.3.1. Постоянная абсолютная или относительная погрешность
Сначала нужно определить, какая будет ошибка: строго положительная, отрицательная или в обе стороны. За это отвечает параметр y dir=minus|plus|both.
\addplot +[
mark=*,
only marks,
] plot[
error bars/.cd,
y dir=both,
y fixed=0.1,
% y fixed relative=0.1,
] table [
x=Fr,
y=Uin
]{data.tsv};Здесь указана сразу абсолютная погрешность для всех значений. Аналогично можно задать сразу относительную параметром y fixed relative.
5.3.2. Абсолютная или относительная погрешность из файла
Необходимо явно указать, что ожидается чтение данных ошибки из файла, указать в каком столбце (y error=err) записана ошибка и тип ошибки:
\addplot +[
mark=*,
only marks,
] plot[
error bars/.cd,
y dir=both,
y explicit relative,
] table [
x=Fr,
y=Uin,
y error=err,
]{data.tsv};Для абсолютной ошибки параметр y explicit, для относительной y explicit relative.
5.4. Настройка линии графика
5.4.1. Толщина и цвет линии графика
Толщина линии управляется либо параметром line width=, либо словесными алиасами (рекомендуется использовать именно их):
Цвет линии сам является параметром:
\addplot +[
thick,
blue!20!black
] plot table [
x=Fr,
y=Uin,
]{data.tsv};О составлении цветов сказано ранее в разделе ().
5.4.2. Тип линии графика
Как и цвет, тип линии графика сам по себе параметр:
\addplot +[
thick,
blue!20!black,
dashed
] plot table [
x=Fr,
y=Uin,
]{data.tsv};Существует несколько типов линий:
6. Особенности построения графиков
6.1. Построение графиков, терпящих бесконечный скачок
Рассмотрим построение графика с бесконечным скачком на примере построения \(\tan(x)\).
Расчет функций, которые уходят на бесконечность, может привести к ошибкам компиляции. Чтобы этого избежать, можно указать в параметрах принудительное вписывание в пределы расчетов: выйдя за эти пределы, математический движок pgf просто будет пропускать эти значения, пока опять не войдет в пределы:
restrict y to domain=-20:20,Разумно выбирать эти пределы немного больше заданного предела осей xmin,xmax,ymin,ymax.
Кроме того, можно сказать pgfplots-у, как вести себя при получении бесконечности в расчетах, и не ограничивая расчет:
unbounded coords=discard|jumpЭтот ключ настраивает, что делать, если одна или несколько координат одной точки неограничена, или, например, при чтении из файла на этом месте стоит nan или ничего не стоит.
discard (по умолчанию) отбрасывает точку завершения, и в логе компиляции выдается предупреждение. При этом график строится, как если бы неограниченная точка не произошла: pgfplots интерполирует между ограниченными ближайшими точками.
jump просто пропустит значения, которые уходят на бесконечность, и график станет с разрывом.
Однако, как это ни странно, в случае тангенса это все не так: для стандартных функций с разрывом разработчики постарались, и они строятся без дополнительных усилий. Но при этом \(+\infty\) и \(-\infty\) точки графика соединяются, что не всегда может быть полезно: например, обычно в этом месте строят линии асимптот.
Все же придется вернуться к первоначальному определению:
\documentclass[tikz,10pt]{standalone}
\usepackage[T2A]{fontenc}
\usepackage[utf8x]{inputenc}
\usepackage[russian]{babel}
\usepackage{amsmath,amssymb,cmap,pgfplots,pgfplotstable}
\usetikzlibrary{arrows,calc,intersections}
\pgfplotsset{compat=newest}
\begin{document}
\begin{tikzpicture}
\begin{axis}[
xlabel={$x$},
ylabel={$\tg x$},
axis lines=middle,
ymax = 10,
ymin = -10,
enlargelimits=true,
xmin=-4*pi/2,
xmax=4*pi/2,
restrict y to domain=-20:20,
xtick=\empty,
ytick=\empty,
]
\addplot[blue!50,domain={-4*pi/2:4*pi/2},samples=1000] {tan(deg(x))};
\pgfplotsinvokeforeach{-2,-1,...,2}{%
\draw[dashed, black!20]
({{pi/2+pi*#1},0} |- {rel axis cs:0,0})
-- ({{pi/2+pi*#1},0}|-{rel axis cs:0,1});
}
\end{axis}
\end{tikzpicture}
\end{document}Здесь есть интересный код для построения асимптот. Рассмотрим его подробнее.
6.2. Циклы в pgfplots и построение асимптот. Системы координат рисунка
Стандартный цикл tikz-а, к сожалению, в pgfplots не работает. Приходится использовать его более низкоуровневый аналог:
\pgfplotsinvokeforeach{-2,-1,...,2}{%
% Выражение в цикле. Счетчик цикла - #1
}Счетчик пробегает указанные значения. Можно указывать их как список {0,1,2,3},а можно указать первое значение, второе, троеточие, последнее: из первого и второго рассчитается шаг и счетчик пробежит нужные значения. Они могут быть дробными.
Теперь подробнее, как же работает код построения вертикальной асимптоты. В tikz есть интересный способ расчета координаты в угле. Если задана такая координата X: (A -| B), то она находится в точке, которая образована пересечением горизонтальной линии через A и вертикальной через B:
Можно наоборот, (B -| A), соотв. вертикальная через А и горизонтальная через B.
По умолчанию используется система координат осей, в которой начало и орты отвечают нарисованным на графике.
Есть еще так называемая rel axis cs — система координат рисунка: в ней точка (0,0) это левый нижний угол рисунка, а (1,1) — верхний правый.
Со всей этой информацией теперь нетрудно должно быть понять, как работает асимптота через точку x:
({x},0} |- {rel axis cs:0,0}) -- ({x},0}|-{rel axis cs:0,1});6.3. Использование команд TikZ на графиках Pgfplots
Ровно в предыдущем параграфе рассмотрено применение команд tikz для построения асимптот в осях графика.
Часто возникает еще потребность подписать какие-либо точки на кривой. Для этого можно создать ноду на кривой, где положение ноды задается от 0 до 1 — 0 в начале кривой, 1 в конце. Эдакие криволинейные координаты.
\addplot[blue!50,domain={-4*pi/2:4*pi/2},samples=1000] {sin(deg(x))}
node[pos=0.3] (1) {}
node[pos=.3,left,black]{$x$};
\draw[fill=magenta] (1) circle (1pt);Здесь мы специально создали пустую ноду с координатой (1), в которой потом можно нарисовать точку, а вторая нода уже рисует текст.
Для понимания это может быть затруднено, если вы не изучали tikz. Тогда можно просто использовать этот пример, не заботясь принципами его работы.
На кривую так можно поместить сколько угодно точек, главное, в конце списка должна стоять точка с запятой.
6.3. Качественные графики: удаление меток с осей
Достаточно добавить два параметра к окружению axis:
xtick=\empty,
ytick=\empty,The End. Рекомендуемые источники
Наконец, прочитав небольшое руководство по использованию pgfplots, вы почти готовы к тому, чтобы применить его для своих работ. В этом нелегком (поначалу) труде смогут помочь некоторые источники.