Раздел 2, все ответы правильные, на «5»
Какое условие должно соблюдаться при определении объемов земляных работ при вертикальной планировке площадок?
Vv = Vп (+/-) P
При какой глубине снимаются Верхняя и нижняя бровки при исполнительной съемке котлованов?
свыше 3 м
При каких условиях осуществляется контроль глубины разработки при помощи визирок?
при сравнительно неглубоких и нешироких котлованах
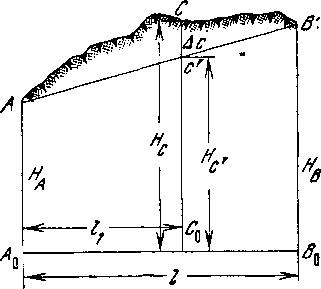
Как определить длину l контрольной визирки рассчитывают по проектной отметке Hо дна котлована и отметке верха постоянных визирок Н?
l= Hв – Hо
Какая документация оформляется после окончания работ по устройству котлована?
все ответы верны
Определить схему контроля тригонометрическим нивелированием при значительных размерах котлована:
(на рис. две пунктирные линии)
Как вычисляют рабочие отметки?
как разность между проектными (красными) и черными отметками
Какое количество временных реперов закладывают на дно котлована при геометрическом нивелировании?
2
Сколько видов допусков точности при разбивке?
два – допуск до точности перенесения на местность проекта зданий относительно пунктов разбивочной основы; допуск до точности во взаимном положении зданий, сооружений и детальной разбивки их точек относительно главных или основных осей
При каких условиях осуществляется контроль глубины разработки тригонометрическим нивелированием?
если котлован имеет значительные размеры
Что означают рабочие отметки со знаком плюс?
указывают на необходимость устройства насыпи
Каким способом производят разбивку контуров котлована?
способами прямоугольных и полярных координат
Какого вида обноски не существует?
металлокаркасная
Как осуществляют перенос осей в котлован?
все ответы верны
Что выступает в качестве исходных данных для выполнения геодезических работ по устройству фундаментов?
все ответы верны
Какой вид работ не входит в состав работ в подземной части, требующих геодезического обеспечения?
устройство внутренней разбивочной сети здания
Какой способ считается основным способом точной передачи отметок в котлован?
способ геометрического нивелирования
Как вычисляют объем грунта в пределах переходных квадратов при относительно небольшом их количестве?
VH(B)=a2/4*(сумма hH(B))2/сумма h
Каким способом не осуществляется перенесение осей здания (сооружения) на дно котлована?
способом редукционных углов
С каким недобором заканчивают выемку грунта в котлованах и траншеях?
на 10-20 см до проектной отметки
Какая операция не относится к основной операции при устройстве котлованов?
нет правильного ответа
Как определяется средняя планировочная отметка?
Нср=Vп/F
Как определяется высота визирования при тригонометрическом нивелировании?
h=d*tgv
Как определяют объемы участков насыпи и выемки переходных квадратов по средней рабочей отметке и площади каждого участка?
Vн=Fнhн м3; Vв=Fвhв
Какие устраиваются котлованы в грунтах естественной влажности с ненарушенной структурой, при отсутствии грунтовых вод и глубине котлована в пределах 1…2 м?
с вертикальными стенками
Добавлено через 19 часов 27 минут
Раздел 3, все ответы правильные, сдано на «5»
Что принято считать исходным горизонтом при при возведении надземной части зданий и сооружений?
плоскость, проходящая через опорные площадки последних по высоте несущих конструкций подземной части перекрытия подвала, бетонная подготовка или блоки фундамента
Какие отклонения определяют при плановой исполнительной съемке панелей?
отклонение оси панели от продольной разбивочной оси в нижнем сечении в двух точках по краям панели
Какое должно быть число опорных точек, передаваемых на монтажные горизонты?
не менее 3
При каком условии точнее определяется угол по измеренным сторонам в трилатерации?
чем острее угол
Сколько монтажных реперов должно быть на монтажном горизонте?
не менее 2
Что происходит с точностью определения пунктов при увеличении числа треугольников в схемах внутренних разбивочных сетей зданий и сооружений?
точность снижается
В каких схемах внутренних разбивочных сетей зданий и сооружений взаимное поперечное положение смежных пунктов определяют с высокой точностью?
в кольцевых и линейных
Как высчитывается отклонение центра колонны от разбивочной оси?
Δн = a — b1н — 0,5 d, где d — толщина колонны, b1н — отсчет по рейке на оси 1-1 в нижнем сечении
Какие отклонения определяют при плановой исполнительной съемке колонн?
отклонения оси колонны от продольной и поперечной осей здания
Какой применяется способ для контроля вертикальности ряда колонн?
способ бокового нивелирования
Как определяют отметку рабочего репера на монтажном горизонте?
Hb = Ha + a + (c2 — c1) — b
Как вычисляются отклонения колонн по высоте?
Δi=Hi-Hn, где Hn — проектная отметка опорной поверхности колонн.
При выверке колонн, какое принимается расстояние теодолита от выверяемой колонны?
расстояние принимают таким, чтобы при максимальном подъеме трубы угол ее наклона не превышал 30-35гр.
Что может служить рабочим репером?
все вышеперечисленные элементы
Какие особенности характерны для кольцевой радиальной сети?
в сети измеряют все стороны и радиусы
Как построить угол заданной величины с повышенной точностью?
ВВ’=OB’*Δb»/p»
Какая схема внутренних разбивочных сетей зданий и сооружений относится к радиально-кольцевым схемам?
(см. схемы в разделе 3.1)
Какие особенности характерны при приближенной оценке точности плановых сетей в виде геодезического четырехугольника?
определяется исходная точка, а определенное направление принято за ось абсцисс
Какие отклонения определяют при высотной исполнительной съемке?
отклонения опорных поверхностей колонны от проектного значения
Как оформляются результаты высотной съемки колонн?
выписывают на схему исполнительной съемки
Как рассчитывается ошибка дирекционного угла?
m(альфа)=(m1/a2)*p»*корень из 2
Определить схему трилатерационных сетей-геодезические четырехугольники
Прямоугольник на пересечении диагоналей которого стоит буква L
2.3.1
Реальная ошибка ( С.К.О.) положения
контурной точки на карте принимается
равной 0.5 мм в масштабе карты :
мм,
предельная
мм
2.3.2
Ошибка в длине линии
,
измеренной по карте в
раз
больше ошибки определения планового
положения точки.
мм,
2.3.3
Для ломаных линий :
,
где
—
число звеньев ломаной линии.
2. Точность определения расстояний и направлений между контурными точками плана
При
подготовке исходных данных для
перенесения проекта в натуру и решении
других задач приходится измерять
расстояния и направления между контурными
точками.
-
Точность
определения расстояний (горизонтальных,
проложений)
между близлежащими контурными точками.
Съемка их проведена
с одной точки съемочного обоснования.
Горизонтальное
проложение
между контурными точками:
,
где
— соответственно координаты концов
линий, определяемые
графически.
С.
к. п.
линии
при условии, что с.к.
п. положения концов линий
.
где
—
коэффициент автокорреляции координат
контурной точки.
Коэффициент
автокорреляции координат для близлежащих
точек :
,
где
и
и
соответственно с.к.п. положения
исходного пункта и контурной точки.
Для
близлежащих контурных точек можно
принять
= 0,4 -0,6.
Погрешность
расстояния
равна
погрешности
положения
контурной
точки лишь при
=
0. Корреляцией
координат контурных точек можно
пренебречь, если
концы линии находятся на значительном
расстоянии
друг от друга или их съемка выполнена
с разных точек съемочной сети.
Таким
образом, при некоррелированных
координатах, (когда
=
0 ) :
Пример
1
При
съемке застроенных территорий с
капитальной застройкой
0,3 мм на плане . При
=
0,6, для близлежащих контурных точек
получим:
на
плане.
С
вероятностью, близкой к 1.0 предельная
погрешность
расстояния между близлежащими точками
капитальных зданий и сооружений
не превысит 0,4 мм на плане.
Пример 2
Для
плана
на незастроенной территории с четкими
очертаниями контуров, погрешность тг
= 0,5мм на
плане; положение точек независимо, так
как их съемка выполнена
с разных точек съемочного обоснования
тогда
мм
на плане.Следовательно,
предельная погрешность расстояния
мм
на
плане.
3.
Средняя квадратическая погрешность
определения направления (дирекционного
угла)
3.1
Дирекционный
угол линии между точками с координатами
,
определяется
по формуле :
.
СКП
определения величины дирекционного
угла
линии
длиной S
между контурными точками, положение
которых некоррелировано, определится
по формуле
Для
близлежащих контурных точек СКП
дирекционного угла:
Формулы
(1.1), (1.2) показывают, что СКП
дирекционного угла уменьшается с
увеличением
расстояния между точками. Поэтому при
привязке проекта
автомобильной дороги к пунктам
геодезического обоснования
за исходное направление принимают
имеющее
большую длину.
Например,
при
8 см
на плане и
мм
на плане,
найдем
Предельная
погрешность определения дирекционного
угла
3.2
СКП измерения дирекционного угла
линии
длиной S
между контурными точками, положение
которых некоррелировано,
определится по формуле
4.
Точность определения высотных параметров
НА плане.
Точность
топографических планов в высотном
отношении
характеризуется
средней квадратической
или
средней
погрешностью
определения по
горизонталям плана высот точек
относительно ближайших пунктов
съемочного
обоснования. Погрешности
и
связаны следующей зависимостью:
=
1,25
,
что следует
учитывать при расчетах точности
крупномасштабных топографических
съемок.
Основным
видом наземных топографических съемок
является тахеометрическая , обладающая
рядом несомненных преимуществ.
Тахеометрическая
съемка производятся
путем набора пикетов, интерполирования
и проведения горизонталей.
Полнота и детальность изображения
рельефа зависят от высоты сечения,
густоты
пикетов и пр. Но
до мельчайших подробностей рельеф
изобразить нельзя,
какой бы ни была высота сечения рельефа,.
Это не позволит
сделать масштаб плана. При съемках
приходится обобщать рельеф, выделяя
главное и отбрасывая второстепенное.
Погрешности,
влияющие на точность положения
горизонталей:.
Первая
группа — погрешности,
влияющие на точность положения
горизонтали по высоте и не
зависящие
от угла наклона топографической
поверхности:
1)
построения съемочного обоснования;
2)
«топографической шероховатости»
поверхности земли (мелкие неровности
земной поверхности); 3) определения
высот пикетов;
4)
обобщения рельефа,
возникающие из-за неоднородности ската
между пикетами;
5)
несовершенства
средств вычисления отметок точек.
Вторая
группа —
погрешности, вызывающие плановое
смещение горизонтали.
Точность высотного положения горизонтали
в этом случае зависит
от угла наклона топографической
поверхности:
1)
построения планового обоснования;
2)
нанесения пикетов на план;
3)
интерполирования и проведения
горизонталей;
4)
вычерчивания горизонталей;.
Точность
положения горизонтали по высоте
зависит
главным образом от погрешностей
обобщения рельефа при съемке. Горизонтали
получают на плане путем линейного
интерполирования
между высотами пикетов. Однако в
результате интерполирования мы
имеем точку
высотой
,
а не точку земной поверхности с высотой
(рис.1).
Разность
назовается
истинной
погрешностью обобщения рельефа
при производстве съемки.
Рис.
1. Обобщение рельефа при съемке
Средняя
квадратическая погрешность
при
съемке вследствие
обобщения рельефа, вычисляется по
формуле
,
где
— коэффициент случайного влияния
обобщения рельефа при съемке,
приведенный к длине в 1
м;
—
расстояние между пикетами,
выраженное в метрах.Величина
коэффициента
зависит
от характера рельефа и колеблется
в пределах 0,01—0,02. Для
промышленно-гражанского
строительства принято
= 0,012.
Из
расчета численных значении
погрешностей, влияющих на точность
положения горизонталей получены
многочисленные
формулы для оценки точности положения
горизонталей по высоте
и определения отметок точек
по плану.
1.
Формула
проф. Н. Г. Видуева
для вычисления средней
квадратической
погрешности ( С.К.П.) положения
горизонтали по высоте:
где
— высота сечения рельефа,
— знаменатель масштаба плана,
— средний уклон
местности.
2.
Формула проф.
В. Д. Большакова
для вычисления (
С.К.П.)
определения
высоты точки по горизонталям плана:
где
—
высота
сечения рельефа,
—
коэффициент случайного влияния обобщения
рельефа при съемке,
—
расстояние между пикетами при съемке
рельефа,
=0,03м;
= 0,7 мм на плане,
—
знаменатель численного
масштаба плана;
— коэффициент, колеблющийся
в пределах 0,010—0,015 для местности с углом
наклона
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Книга найдена на
http://www.geolink-group.com/tourclub/ — спасибо создателям
Вы можете заказать 2CD
с картами Юга России
Содержание книги
1.15.
ИЗМЕРЕНИЕ ДИРЕКЦИОННЫХ УГЛОВ ПО КАРТЕ
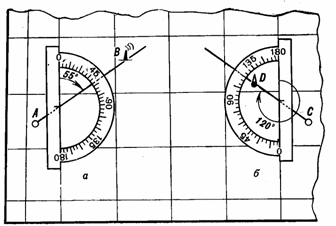
Измерение транспортиром.
Тонко очиненным карандашом, аккуратно по линейке, прочерчивают линию через
главные точки условных знаков исходного пункта и ориентира. Длина
прочерченной линии должна быть больше радиуса транспортира, считая от точки
ее пересечения с вертикальной линией координатной сетки. Затем совмещают
центр транспортира с точкой пересечения и поворачивают его, сообразуясь с
величиной угла, как показано на рис. 27. Отсчет против прочерченной линии
при положении транспортира, указанном на рис. 27, а, будет соответствовать
величине дирекционного угла, а при положении транспортира, указанном на рис.
27,6, к полученному отсчету необходимо прибавить 180°.
При измерении дирекционного угла
необходимо помнить, что дирекционный угол отсчитывается от северного
направления вертикальной линии сетки по ходу часовой стрелки.
Средняя ошибка измерения дирекционного
угла транспортиром, имеющимся на командирской линейке, примерно равна 1°.
Большим транспортиром (с радиусом 8—10 см) угол на карте можно
измерить со средней ошибкой 15′.
Рис.
27. Измерение дирекционных углов транспортиром
/
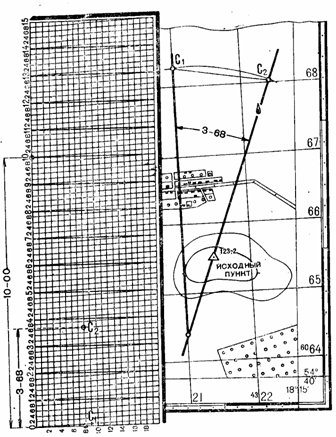
Измерение хордоугломером
(рис. 28). Через главные точки условных знаков исходного пункта и ориентира
проводят на карте тонкую прямую линию длиной не менее 12 см. Из точки
пересечения этой линии с вертикальной линией сетки карты циркулем делают на
них засечки радиусом, равным расстоянию на хордоугло-мере от 0 до 10 больших
делений. Засечки делают на линиях, образующих острый угол.
Затем измеряют хорду — расстояние между
отметками отложенных радиусов. Для этого левую иглу циркуля-измерителя с
отложенной хордой передвигают по крайней левой вертикальной линии шкалы
хордоугломера до тех пор, пока правая игла циркуля не совпадет с каким-либо
пересечением наклонной и горизонтальной линии. При этом правую иглу
необходимо передвигать строго на одном уровне с левой. В таком положении
циркуля производят отсчет против его правой иглы. По верхней части шкалы
отсчитывают большие и десятки малых делений. По левой части шкалы с ценой
делений 0-01 уточняют величину угла. Пример измерения угла хордоугломером
показан на рисунке.
С помощью хордоугломера измеряют острый
угол от ближайшей вертикальной линии координатной сетки, а дирекционный угол
отсчитывают от северного направления линии сетки по ходу часовой стрелки.
Значение дирекционного угла определяют по изме-
Рис.
28. Измерение дирекционого угла хордоугломером
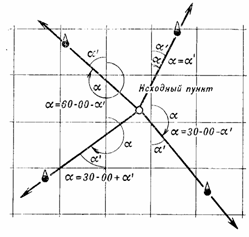
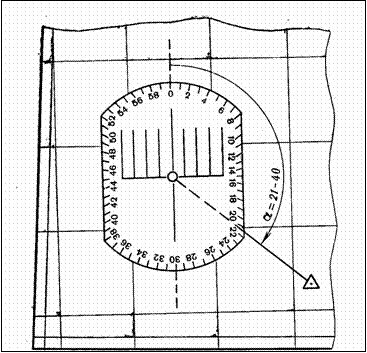
ренному углу в зависимости от четверти,
в которой расположен ориентир. Зависимость между измеренным углом а’
и дирекционным углом а показана на рис. 29.
Углы хордоугломером можно измерить си
средней ошибкой 0-01—0-02 дел. угл.
(4— 8′).
Рис. 29.
Переход от угла а’, измеренного хордоугломером, к дирекционному углу а
Измерение артиллерийским кругом. Центр
круга совмещают с исходным пунктом (главной точкой условного знака) и круг
устанавливают так, чтобы диаметр его 0—30 был параллелен вертикальным линиям
координатной сетки, а нуль направлен на север. Затем масштабную линейку
совмещают с главной точкой условного знака ориентира и на пересечении ребра
линейки со шкалой круга считывают величину угла.
Артиллерийским кругом можно измерить
дирекционный угол и без масштабной линейки (рис. 30). В этом случае
предварительно прочерчивают на карте линию через главные точки условных
знаков исходного пункта и ориентира. Затем артиллерийский круг
устанавливают, как указано выше, и против прочерченной линии считывают по
шкале круга величину дирекционного угла.
Рис. 30.
Измерение дирекционного угла артиллерийским кругом
Артиллерийским кругом дирекционный
угол. можно измерить со средней ошибкой 0-03 дел. угл.
Вы
можете заказать 2CD с картами Юга России
Комментариев нет — Ваш будет первым!
Скачать с Depositfiles
2.5 Вычисление дирекционных углов замкнутого теодолитного хода
Дирекционный угол начальной стороны выбирают из табл.2. Дирекционные углы последующих сторон полигона вычисляют по формуле
(7)
В этой формуле исправленный угол тот, который заключен, между предыдущей и последующей сторонами полигона. Например, для второй стороны полигона, т.е. стороны (II-III) дирекционный угол вычисляется по формуле
Знак «минус» перед третьим членом в первой части формулы берут в том случае, когда сумма двух первых членов превышает 180°.
Если же сумма двух первых членов настолько велика, что после вычитания из нее 180° значение дирекционного угла какой-нибудь стороны полигона окажется больше чем 360°, то в этомслучае следует еще вычесть 360°. Это и будет искомое значение дирекционного угла.
Тан, пользуясь приведенной выше формулой, последовательно переходя от одной стороны к другой, т.е. от предыдущей к последующей, вычисляют дирекционные углы всех сторон полигона.
Вычислив дирекционные углы всех сторон полигона, производят контроль вычислений. Для этого необходимо продолжить вычисления, используя исправленное значение последнего измеренного угла полигона, чтобы получить вторично значение дирекционного угла начальной стороны.
Вычисления считаются безошибочными, если полученное путем вычислений значение дирекционного угла начальной стороны полигона будет в точности (до I») равно заданной величине.Эту величину следует записать в графу «Дирекционные углы» в конце всех вычислений.
2.6 Вычисления приращений координат точек замкнутого хода
Формулы, по которым определяются приращения координат, следующие:
(8)
где и
— приращения координат;
— горизонтальное приложение длины линии;
— дирекционный угол стороны полигона.
Пример
Значения приращений координат в теодолитном ходе вычисляет с округлением до сотых долей метра.
2.7. Вычисление невязок в приращениях координат и их распределение
В замкнутом теодолитной ходе невязки в приращениях координат определяют по формулам:
(9)
где и
— алгебраические суммы приращений координат по координатным осям, соответственно X и Y.
Прежде чем распределить полученные невязки, необходимо убедиться в их допустимости, судя не по каждой отдельной невязке или
, а по невязке в периметре полигона.
Абсолютная линейная невязка в периметре полигона вычисляется по формуле:
(10)
Невязка в полигоне зависит главным образом от периметра полигона. Чем больше периметр, тем большую невязку следует в нем ожидать. Поэтому и допустимость невязки определяют в зависимости от периметра полигона. Невязка в периметре теодолитного полигона
при благоприятных условиях измерения линий считается допустимой,
если она не превышает 1/2000 периметра Р, т.е.
Отношение к периметру хода Р, т.е.
называется относительной невязкой в периметре хода.
Если полученные невязки окажутся больше допустимых, то следует прежде всего проверить правильность вычисления. При отсутствия ошибок в вычислениях следует перемерить в первую очередь длины тех сторон дирекционные углы которых близки к дирекционному углу вычисленному по формуле
Если невязка в периметре оказалась допустимой (табл.6), то невязки по осям координат
и
распределяют с обратным знаком на все приращения (по соответствующей оси) пропорционально длинам сторон полигона.
Поправки в приращения координат вычисляют по формулам:
(11)
……………….……………….
Для упрощения вычислений поправок в приращения координат периметр и длины сторон полигона рекомендуется выражать в сотнях метров. Поправки в приращения вычисляются с точностью до сантиметра.
Пример:
Р=789м=7,9 сотни метров (табл.6)
Сумма поправок должна быть равна невязке с обратным знаком. Если сумма поправок вследствие приближенных вычислений не равна невязке, то некоторые из поправок следует исправить так, чтобы эта сумма равнялась невязке с обратным знаком, т.е.
В том случае, когда невязка в приращениях по какой-либо оси мала» невязку распределяют по I см только на несколько приращений, подученных по наиболее длинным сторонам полигона.
Поправки в приращения координат с их знаком подписывают «над» или «под» вычисленными знаками приращений. Затем производят алгебраическое сложение значений приращений координат. Величины исправленных приращений заносят в графы 9 и 10 табл. 6
Контролем вычислений исправленных приращений служит точное совпадение алгебраической суммы их по каждой из осей в отдельности о теоретической величиной, т.е. эти суммы должны быть равны нулю.
2.8 Вычисление координат вершин полигона
Координаты начальной точки полигона приведены в табл. 1.Координата X иди У последующей вершины полигона равна координате предыдущей вершины плюс (алгебраически) соответствующее исправленное приращение со своим знаком.
………………………
Контролем вычислений координат вершин замкнутого полигона является получение координат первой вершины полигона, которые должны быть равны значениям заданных координат этой вершины. Вычисленные значения координат вершин полигона записывают на самой н… стороне в соответствующих графах ведомости.
Скачать с Depositfiles