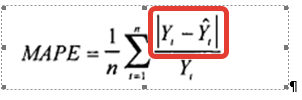Ошибка прогнозирования: виды, формулы, примеры
Ошибка прогнозирования — это такая величина, которая показывает, как сильно прогнозное значение отклонилось от фактического. Она используется для расчета точности прогнозирования, что в свою очередь помогает нам оценивать как точно и корректно мы сформировали прогноз. В данной статье я расскажу про основные процентные «ошибки прогнозирования» с кратким описанием и формулой для расчета. А в конце статьи я приведу общий пример расчётов в Excel. Напомню, что в своих расчетах я в основном использую ошибку WAPE или MAD-Mean Ratio, о которой подробно я рассказал в статье про точность прогнозирования, здесь она также будет упомянута.
В каждой формуле буквой Ф обозначено фактическое значение, а буквой П — прогнозное. Каждая ошибка прогнозирования (кроме последней!), может использоваться для нахождения общей точности прогнозирования некоторого списка позиций, по типу того, что изображен ниже (либо для любого другого подобной детализации):
Алгоритм для нахождения любой из ошибок прогнозирования для такого списка примерно одинаковый: сначала находим ошибку прогнозирования по одной позиции, а затем рассчитываем общую. Итак, основные ошибки прогнозирования!
MPE — Mean Percent Error
MPE — средняя процентная ошибка прогнозирования. Основная проблема данной ошибки заключается в том, что в нестабильном числовом ряду с большими выбросами любое незначительное колебание факта или прогноза может значительно поменять показатель ошибки и, как следствие, точности прогнозирования. Помимо этого, ошибка является несимметричной: одинаковые отклонения в плюс и в минус по-разному влияют на показатель ошибки.
- Для каждой позиции рассчитывается ошибка прогноза (из факта вычитается прогноз) — Error
- Для каждой позиции рассчитывается процентная ошибка прогноза (ошибка прогноза делится на фактический показатель) — Percent Error
- Находится среднее арифметическое всех процентных ошибок прогноза (процентные ошибки суммируются и делятся на количество) — Mean Percent Error
MAPE — Mean Absolute Percent Error
MAPE — средняя абсолютная процентная ошибка прогнозирования. Основная проблема данной ошибки такая же, как и у MPE — нестабильность.
- Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта по модулю) — Absolute Error
- Для каждой позиции рассчитывается абсолютная процентная ошибка прогноза (абсолютная ошибка прогноза делится на фактический показатель) — Absolute Percent Error
- Находится среднее арифметическое всех абсолютных процентных ошибок прогноза (абсолютные процентные ошибки суммируются и делятся на количество) — Mean Absolute Percent Error
Вместо среднего арифметического всех абсолютных процентных ошибок прогноза можно использовать медиану числового ряда (MdAPE — Median Absolute Percent Error), она наиболее устойчива к выбросам.
WMAPE / MAD-Mean Ratio / WAPE — Weighted Absolute Percent Error
WAPE — взвешенная абсолютная процентная ошибка прогнозирования. Одна из «лучших ошибок» для расчета точности прогнозирования. Часто называется как MAD-Mean Ratio, то есть отношение MAD (Mean Absolute Deviation — среднее абсолютное отклонение/ошибка) к Mean (среднее арифметическое). После упрощения дроби получается искомая формула WAPE, которая очень проста в понимании:
- Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта, по модулю) — Absolute Error
- Находится сумма всех фактов по всем позициям (общий фактический объем)
- Сумма всех абсолютных ошибок делится на сумму всех фактов — WAPE
Данная ошибка прогнозирования является симметричной и наименее чувствительна к искажениям числового ряда.
Рекомендуется к использованию при расчете точности прогнозирования. Более подробно читать здесь.
RMSE (as %) / nRMSE — Root Mean Square Error
RMSE — среднеквадратичная ошибка прогнозирования. Примерно такая же проблема, как и в MPE и MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня. Но так как MSE дает расчетные единицы измерения в квадрате, то использовать данную ошибку будет немного неправильно.
- Для каждой позиции рассчитывается квадрат отклонений (разница между фактом и прогнозом, возведенная в квадрат) — Square Error
- Затем рассчитывается среднее арифметическое (сумма квадратов отклонений, деленное на количество) — MSE — Mean Square Error
- Извлекаем корень из полученного результат — RMSE
- Для перевода в процентную или в «нормализованную» среднеквадратичную ошибку необходимо:
- Разделить на разницу между максимальным и минимальным значением показателей
- Разделить на разницу между третьим и первым квартилем значений показателей
- Разделить на среднее арифметическое значений показателей (наиболее часто встречающийся вариант)
MASE — Mean Absolute Scaled Error
MASE — средняя абсолютная масштабированная ошибка прогнозирования. Согласно Википедии, является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени.
Важно! Если предыдущие ошибки прогнозирования мы могли использовать для нахождения точности прогнозирования некого списка номенклатур, где каждой из которых соответствует фактическое и прогнозное значение (как было в примере в начале статьи), то данная ошибка для этого не предназначена: MASE используется для расчета точности прогнозирования одной единственной позиции, основываясь на предыдущих показателях факта и прогноза, и чем больше этих показателей, тем более точно мы сможем рассчитать показатель точности. Вероятно, из-за этого ошибка не получила широкого распространения.
Здесь данная формула представлена исключительно для ознакомления и не рекомендуется к использованию.
Суть формулы заключается в нахождении среднего арифметического всех масштабированных ошибок, что при упрощении даст нам следующую конечную формулу:
Также, хочу отметить, что существует ошибка RMMSE (Root Mean Square Scaled Error — Среднеквадратичная масштабированная ошибка), которая примерно похожа на MASE, с теми же преимуществами и недостатками.
Это основные ошибки прогнозирования, которые могут использоваться для расчета точности прогнозирования. Но не все! Их очень много и, возможно, чуть позже я добавлю еще немного информации о некоторых из них. А примеры расчетов уже описанных ошибок прогнозирования будут выложены через некоторое время, пока что я подготавливаю пример, ожидайте.
Об авторе
HeinzBr
Автор статей и создатель сайта SHTEM.RU
 MAPE – средняя абсолютная ошибка в процентах используется:
MAPE – средняя абсолютная ошибка в процентах используется:
- Для оценки точности прогноза;
- Показывает на сколько велики ошибки в сравнении со значениями ряда;
- Хороша для сравнения 1-й модели для разных рядов;
- Используется для сравнения разных моделей для одного ряда;
- Оценки экономического эффекта, за счет повышения точности прогноза.
В данной статье мы рассмотрим, как рассчитать MAPE в Excel и как ее использовать.
Формула расчета MAPE:
Где:
- Yt – фактический объем продаж за анализируемый период;
- Ŷt — значение прогнозной модели за аналазируемый период;
- n — количество периодов.
Для того, чтобы рассчитать среднюю абсолютную ошибку мы:
- Рассчитываем значение модели прогноза — Ŷt;
- Рассчитываем ошибку прогноза;
- Берем ошибку по модулю;
- Определяем абсолютную ошибку;
- Рассчитываем среднюю абсолютную ошибку в процентах — MAPE.
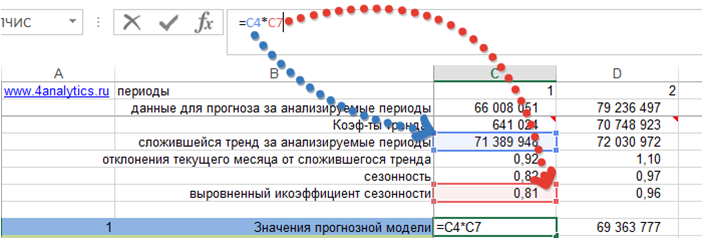
1. Рассчитаем значение модели прогноза — Ŷt
Возьмем модель с трендом и сезонностью. Рассчитаем значение модели для каждого периода, когда нам известны фактические продажи. Для этого сложившийся тренд за анализируемый период умножим на коэффициент сезонности для соответствующего месяца.
Получили значения прогнозной модели для каждого периода времени:
Подробнее о расчете прогноза с помощью тренда и сезонности читайте в статье «Расчет прогноза с помощью тренда и сезонности».
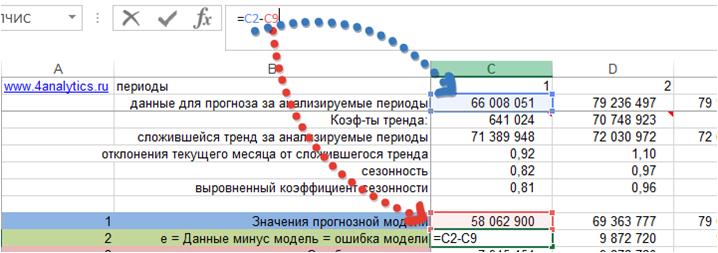
2. Рассчитаем значения ошибки прогноза.
В формуле расчета MAPE – это:
e — Ошибка прогноза — это разность между значениями временного ряда (фактом продаж) и моделью прогноза:
e= Yt — Ŷt
Получили значение ошибки прогноза для каждого момента времени за анализируемый период.
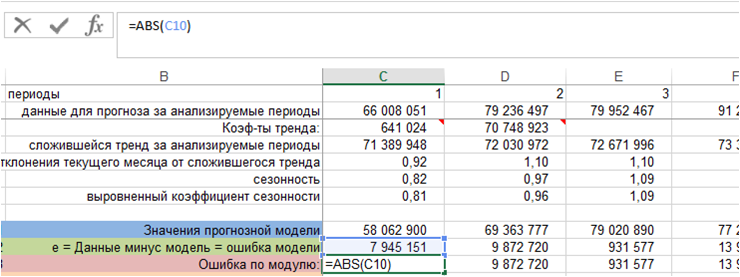
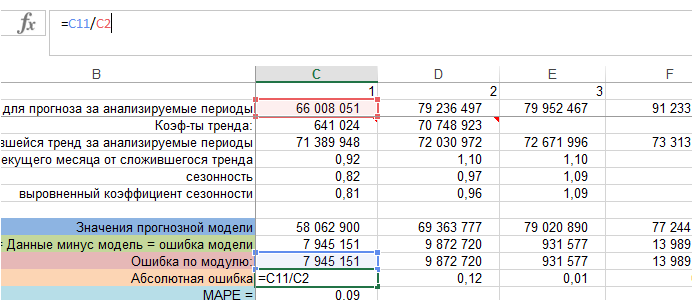
3. Рассчитаем ошибку по модулю.
Для этого воспользуемся функцией Excel =ABC()
4. Определяем абсолютную ошибку.
Для каждого периода ошибку по модулю делим на фактические значения ряда, т.е. на фактический объем продаж:
Получили абсолютную ошибку для каждого периода фактических продаж. В формуле MAPE — это:
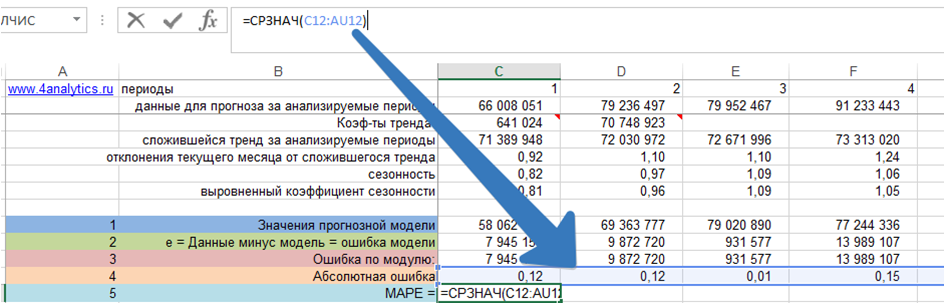
5. Рассчитаем MAPE – среднюю абсолютную ошибку.
Для этого рассчитаем среднее значение абсолютной ошибки за все периоды:
Скачать файл с примером расчета MAPE – средней абсолютной ошибки.
Как рассчитать показатель точность прогноза?
Показатель точность прогноза = 1 –MAPE:
С помощью MAPE вы можете сравнивать различные модели между собой, можете оценивать, как и на сколько модель делает точные прогнозы для разных временных рядов.
А также, что самое главное, можете оценить экономический эффект для компании за счет повышения точности прогноза.
Об этом подробнее можете почитать в нашей статье на сайте http://novoforecast.com/novo-forecast/instruktsiya/item/rost-tochnosti-prognoza-rost-pribyli.html
Если есть вопросы, пожалуйста, пишите в комментариях!
Forecast4AC PRO рассчитает MAPE для каждого временного ряда!
Точных вам прогнозов!
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel.
- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
Зарегистрируйтесь и скачайте решения
Статья полезная? Поделитесь с друзьями
читать 2 мин
Одной из наиболее распространенных метрик, используемых для измерения точности прогнозирования модели, является MAPE , что означает среднюю абсолютную ошибку в процентах .
Формула для расчета MAPE выглядит следующим образом:
MAPE = (1/n) * Σ(|факт – прогноз| / |факт|) * 100
куда:
- Σ — причудливый символ, означающий «сумма».
- n – размер выборки
- фактический – фактическое значение данных
- прогноз – прогнозируемое значение данных
MAPE обычно используется, потому что его легко интерпретировать и легко объяснить. Например, значение MAPE, равное 11,5%, означает, что средняя разница между прогнозируемым значением и фактическим значением составляет 11,5%.
Чем ниже значение MAPE, тем лучше модель способна прогнозировать значения. Например, модель с MAPE 2% более точна, чем модель с MAPE 10%.
Как рассчитать MAPE в Excel
Чтобы рассчитать MAPE в Excel, мы можем выполнить следующие шаги:
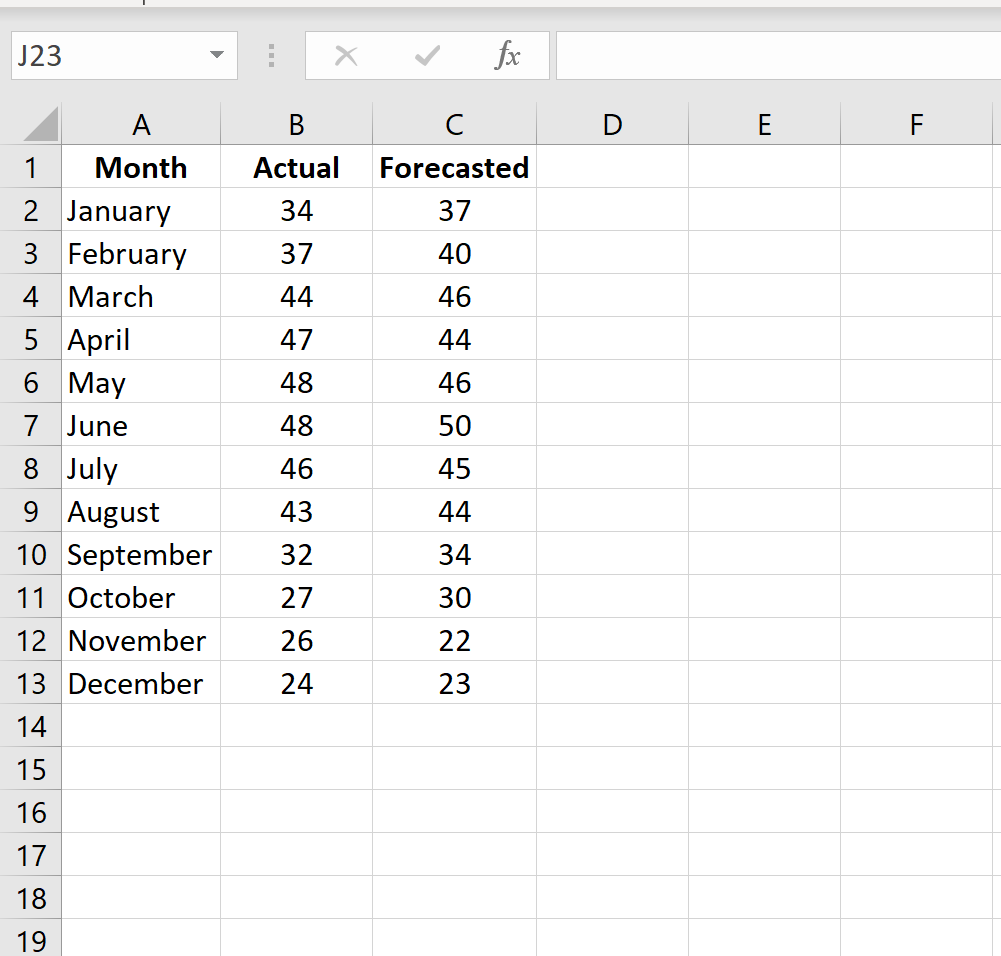
Шаг 1: Введите фактические значения и прогнозируемые значения в два отдельных столбца.
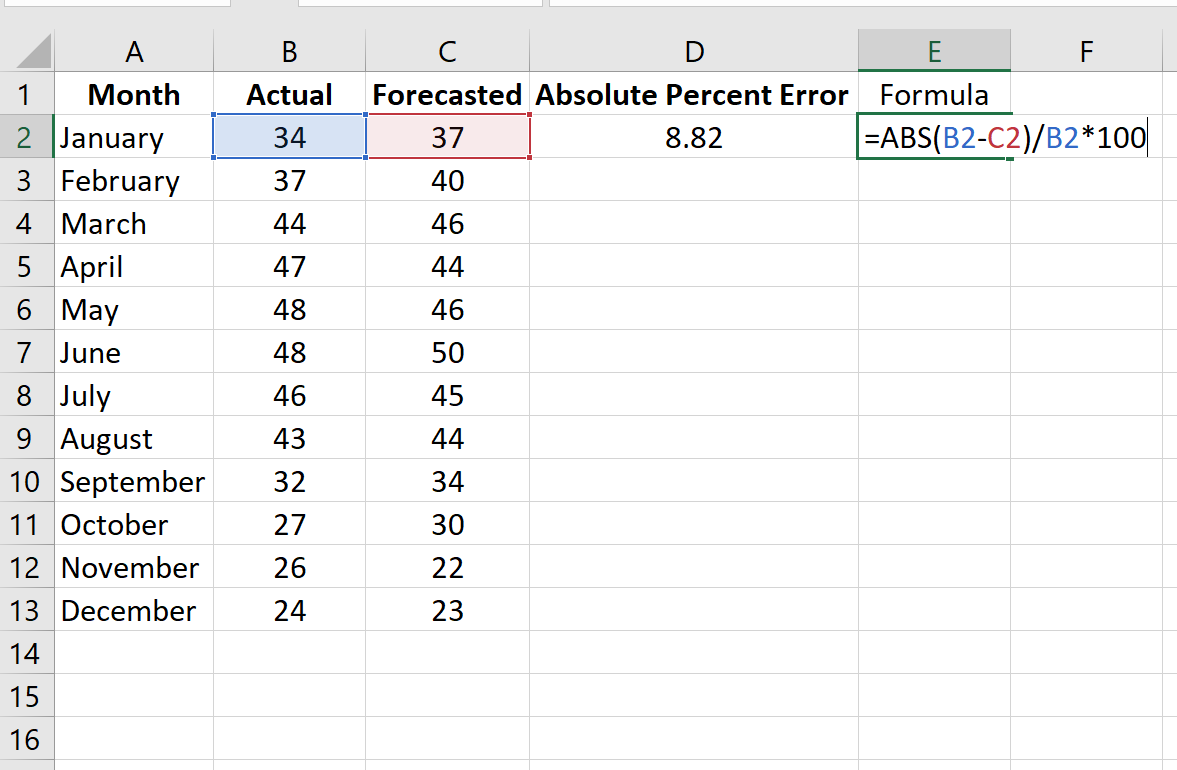
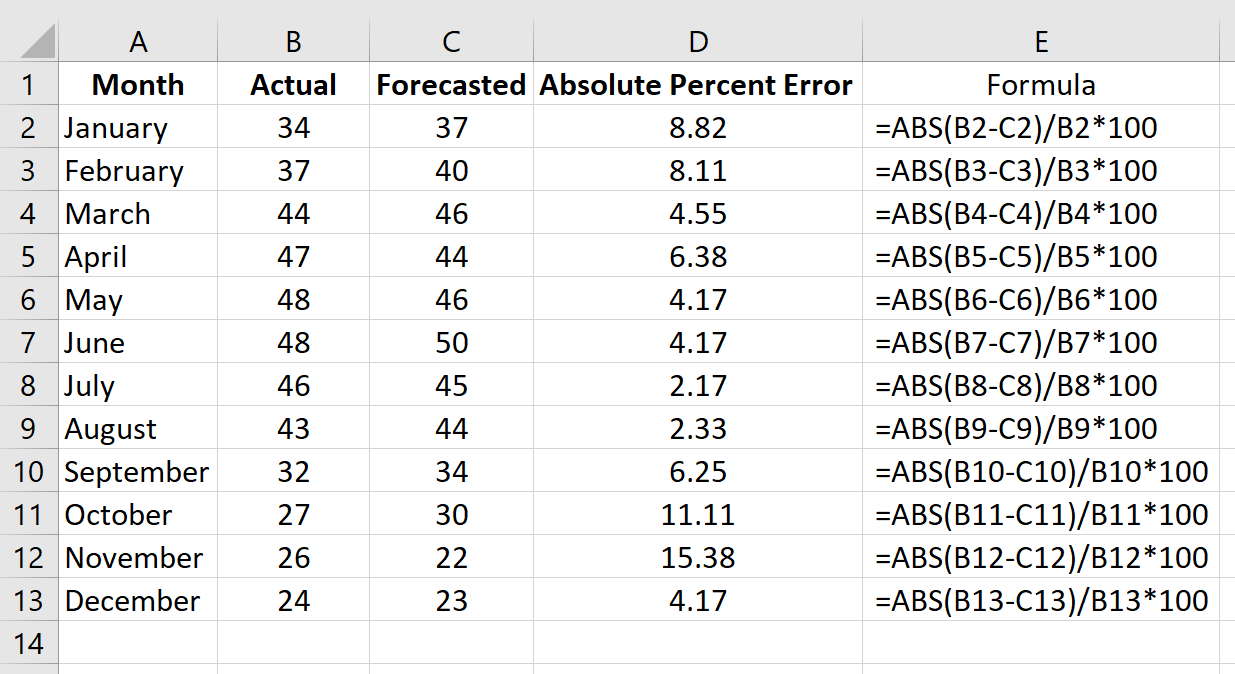
Шаг 2: Рассчитайте абсолютную процентную ошибку для каждой строки.
Напомним, что абсолютная процентная ошибка рассчитывается как: |фактический-прогноз| / |фактическое| * 100. Мы будем использовать эту формулу для расчета абсолютной процентной ошибки для каждой строки.
Столбец D отображает абсолютную процентную ошибку, а столбец E показывает формулу, которую мы использовали:
Повторим эту формулу для каждой строки:
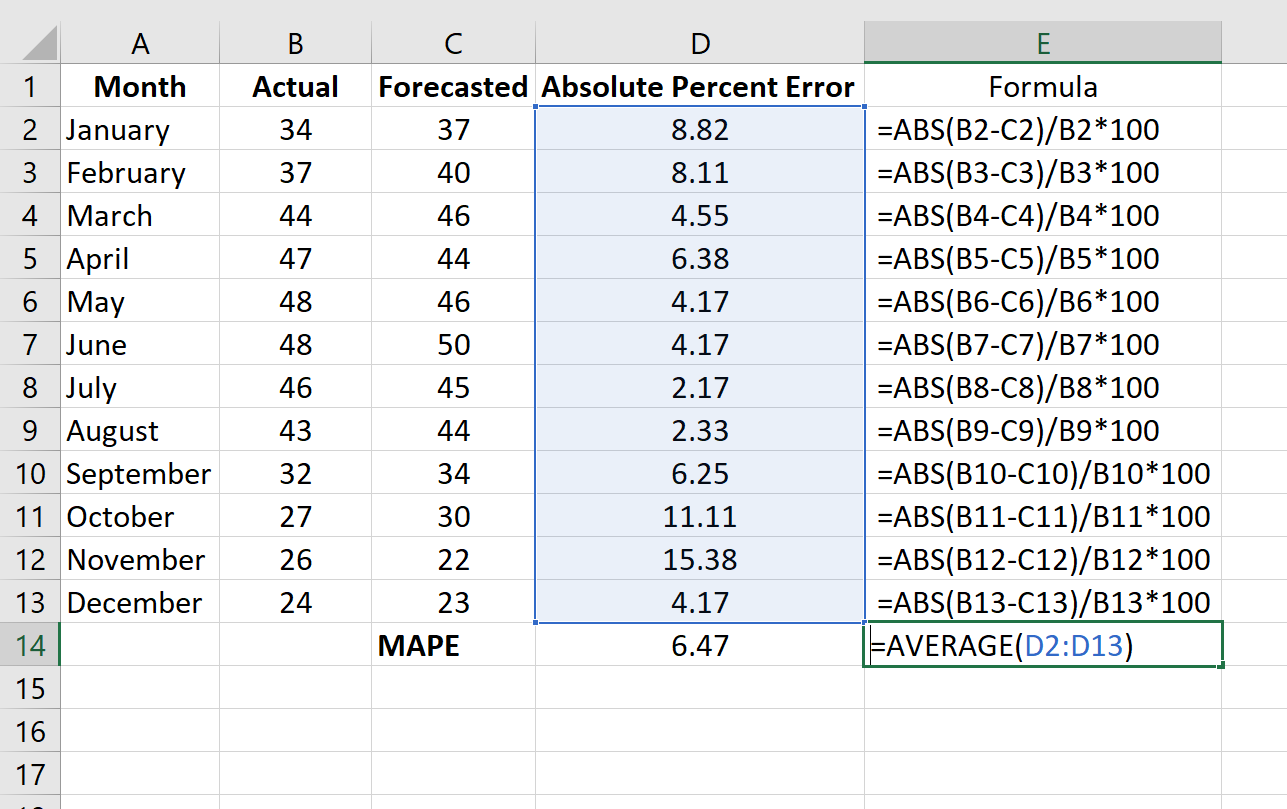
Шаг 3: Рассчитайте среднюю абсолютную ошибку в процентах.
Рассчитайте MAPE, просто найдя среднее значение в столбце D:
MAPE этой модели оказывается равным 6,47% .
Примечание по использованию MAPE
Хотя MAPE легко вычислить и легко интерпретировать, его использование имеет несколько потенциальных недостатков:
1. Поскольку формула для расчета абсолютной процентной ошибки |фактический-прогноз| / |фактическое| это означает, что он будет неопределенным, если какое-либо из фактических значений равно нулю.
2. MAPE не следует использовать с данными небольшого объема. Например, если фактический спрос на какой-либо товар равен 2, а прогноз равен 1, значение абсолютной процентной ошибки будет |2-1| / |2| = 50%, что создает впечатление, что ошибка прогноза довольно высока, несмотря на то, что прогноз отличается всего на одну единицу.
Другим распространенным способом измерения точности прогнозирования модели является MAD — среднее абсолютное отклонение. О том, как посчитать MAD в Excel, читайте здесь .
Дополнительные ресурсы
Что считается хорошей ценностью для MAPE?
Как рассчитать SMAPE в Excel
Как рассчитать MAE в Excel
Перевод
Ссылка на автора
Показатели эффективности прогнозирования по временным рядам дают сводку об умениях и возможностях модели прогноза, которая сделала прогнозы.
Есть много разных показателей производительности на выбор. Может быть непонятно, какую меру использовать и как интерпретировать результаты.
В этом руководстве вы узнаете показатели производительности для оценки прогнозов временных рядов с помощью Python.
Временные ряды, как правило, фокусируются на прогнозировании реальных значений, называемых проблемами регрессии. Поэтому показатели эффективности в этом руководстве будут сосредоточены на методах оценки реальных прогнозов.
После завершения этого урока вы узнаете:
- Основные показатели выполнения прогноза, включая остаточную ошибку прогноза и смещение прогноза.
- Вычисления ошибок прогноза временного ряда, которые имеют те же единицы, что и ожидаемые результаты, такие как средняя абсолютная ошибка.
- Широко используются вычисления ошибок, которые наказывают большие ошибки, такие как среднеквадратическая ошибка и среднеквадратичная ошибка.
Давайте начнем.
Ошибка прогноза (или остаточная ошибка прогноза)
ошибка прогноза рассчитывается как ожидаемое значение минус прогнозируемое значение.
Это называется остаточной ошибкой прогноза.
forecast_error = expected_value - predicted_valueОшибка прогноза может быть рассчитана для каждого прогноза, предоставляя временной ряд ошибок прогноза.
В приведенном ниже примере показано, как можно рассчитать ошибку прогноза для серии из 5 прогнозов по сравнению с 5 ожидаемыми значениями. Пример был придуман для демонстрационных целей.
expected = [0.0, 0.5, 0.0, 0.5, 0.0]
predictions = [0.2, 0.4, 0.1, 0.6, 0.2]
forecast_errors = [expected[i]-predictions[i] for i in range(len(expected))]
print('Forecast Errors: %s' % forecast_errors)При выполнении примера вычисляется ошибка прогноза для каждого из 5 прогнозов. Список ошибок прогноза затем печатается.
Forecast Errors: [-0.2, 0.09999999999999998, -0.1, -0.09999999999999998, -0.2]Единицы ошибки прогноза совпадают с единицами прогноза. Ошибка прогноза, равная нулю, означает отсутствие ошибки или совершенный навык для этого прогноза.
Средняя ошибка прогноза (или ошибка прогноза)
Средняя ошибка прогноза рассчитывается как среднее значение ошибки прогноза.
mean_forecast_error = mean(forecast_error)Ошибки прогноза могут быть положительными и отрицательными. Это означает, что при вычислении среднего из этих значений идеальная средняя ошибка прогноза будет равна нулю.
Среднее значение ошибки прогноза, отличное от нуля, указывает на склонность модели к превышению прогноза (положительная ошибка) или занижению прогноза (отрицательная ошибка). Таким образом, средняя ошибка прогноза также называется прогноз смещения,
Ошибка прогноза может быть рассчитана непосредственно как среднее значение прогноза. В приведенном ниже примере показано, как среднее значение ошибок прогноза может быть рассчитано вручную.
expected = [0.0, 0.5, 0.0, 0.5, 0.0]
predictions = [0.2, 0.4, 0.1, 0.6, 0.2]
forecast_errors = [expected[i]-predictions[i] for i in range(len(expected))]
bias = sum(forecast_errors) * 1.0/len(expected)
print('Bias: %f' % bias)При выполнении примера выводится средняя ошибка прогноза, также известная как смещение прогноза.
Bias: -0.100000Единицы смещения прогноза совпадают с единицами прогнозов. Прогнозируемое смещение нуля или очень маленькое число около нуля показывает несмещенную модель.
Средняя абсолютная ошибка
средняя абсолютная ошибка или MAE, рассчитывается как среднее значение ошибок прогноза, где все значения прогноза вынуждены быть положительными.
Заставить ценности быть положительными называется сделать их абсолютными. Это обозначено абсолютной функциейабс ()или математически показано как два символа канала вокруг значения:| Значение |,
mean_absolute_error = mean( abs(forecast_error) )кудаабс ()делает ценности позитивными,forecast_errorодна или последовательность ошибок прогноза, иимею в виду()рассчитывает среднее значение.
Мы можем использовать mean_absolute_error () функция из библиотеки scikit-learn для вычисления средней абсолютной ошибки для списка прогнозов. Пример ниже демонстрирует эту функцию.
from sklearn.metrics import mean_absolute_error
expected = [0.0, 0.5, 0.0, 0.5, 0.0]
predictions = [0.2, 0.4, 0.1, 0.6, 0.2]
mae = mean_absolute_error(expected, predictions)
print('MAE: %f' % mae)При выполнении примера вычисляется и выводится средняя абсолютная ошибка для списка из 5 ожидаемых и прогнозируемых значений.
MAE: 0.140000Эти значения ошибок приведены в исходных единицах прогнозируемых значений. Средняя абсолютная ошибка, равная нулю, означает отсутствие ошибки.
Средняя квадратическая ошибка
средняя квадратическая ошибка или MSE, рассчитывается как среднее значение квадратов ошибок прогноза. Возведение в квадрат значений ошибки прогноза заставляет их быть положительными; это также приводит к большему количеству ошибок.
Квадратные ошибки прогноза с очень большими или выбросами возводятся в квадрат, что, в свою очередь, приводит к вытягиванию среднего значения квадратов ошибок прогноза, что приводит к увеличению среднего квадрата ошибки. По сути, оценка дает худшую производительность тем моделям, которые делают большие неверные прогнозы.
mean_squared_error = mean(forecast_error^2)Мы можем использовать mean_squared_error () функция из scikit-learn для вычисления среднеквадратичной ошибки для списка прогнозов. Пример ниже демонстрирует эту функцию.
from sklearn.metrics import mean_squared_error
expected = [0.0, 0.5, 0.0, 0.5, 0.0]
predictions = [0.2, 0.4, 0.1, 0.6, 0.2]
mse = mean_squared_error(expected, predictions)
print('MSE: %f' % mse)При выполнении примера вычисляется и выводится среднеквадратическая ошибка для списка ожидаемых и прогнозируемых значений.
MSE: 0.022000Значения ошибок приведены в квадратах от предсказанных значений. Среднеквадратичная ошибка, равная нулю, указывает на совершенное умение или на отсутствие ошибки.
Среднеквадратическая ошибка
Средняя квадратичная ошибка, описанная выше, выражается в квадратах единиц прогнозов.
Его можно преобразовать обратно в исходные единицы прогнозов, взяв квадратный корень из среднего квадрата ошибки Это называется среднеквадратичная ошибка или RMSE.
rmse = sqrt(mean_squared_error)Это можно рассчитать с помощьюSQRT ()математическая функция среднего квадрата ошибки, рассчитанная с использованиемmean_squared_error ()функция scikit-learn.
from sklearn.metrics import mean_squared_error
from math import sqrt
expected = [0.0, 0.5, 0.0, 0.5, 0.0]
predictions = [0.2, 0.4, 0.1, 0.6, 0.2]
mse = mean_squared_error(expected, predictions)
rmse = sqrt(mse)
print('RMSE: %f' % rmse)При выполнении примера вычисляется среднеквадратичная ошибка.
RMSE: 0.148324Значения ошибок RMES приведены в тех же единицах, что и прогнозы. Как и в случае среднеквадратичной ошибки, среднеквадратическое отклонение, равное нулю, означает отсутствие ошибки.
Дальнейшее чтение
Ниже приведены некоторые ссылки для дальнейшего изучения показателей ошибки прогноза временных рядов.
- Раздел 3.3 Измерение прогнозирующей точности, Практическое прогнозирование временных рядов с помощью R: практическое руководство,
- Раздел 2.5 Оценка точности прогноза, Прогнозирование: принципы и практика
- scikit-Learn Metrics API
- Раздел 3.3.4. Метрики регрессии, scikit-learn API Guide
Резюме
В этом руководстве вы обнаружили набор из 5 стандартных показателей производительности временных рядов в Python.
В частности, вы узнали:
- Как рассчитать остаточную ошибку прогноза и как оценить смещение в списке прогнозов.
- Как рассчитать среднюю абсолютную ошибку прогноза, чтобы описать ошибку в тех же единицах, что и прогнозы.
- Как рассчитать широко используемые среднеквадратические ошибки и среднеквадратичные ошибки для прогнозов.
Есть ли у вас какие-либо вопросы о показателях эффективности прогнозирования временных рядов или об этом руководстве?
Задайте свои вопросы в комментариях ниже, и я сделаю все возможное, чтобы ответить.
Для анализа результатов расчета прогноза, в продолжение ряда вы можете рассчитать следующие ошибки:
- MAPE – средняя абсолютная ошибка в % . Ошибка оценивает на сколько велики ошибки в сравнении со значением ряда и с ошибками в соседних рядах.
Подробнее читайте в статье на нашем сайте: http://4analytics.ru/metodi-analiza/mape-%E2%80%93-srednyaya-absolyutnaya-oshibka-praktika-primeneniya.html - MRPE – средняя относительная ошибка в %, оценивает на сколько велика дельта между фактом и прогнозом. Чем ближе к 100%, тем больше ошибка, чем ближе к нулю, тем ошибка меньше.
- MSE – средняя квадратическая ошибка, подчеркивает большие ошибки за счет возведения каждой ошибки в квадрат.
Подробнее читайте в статье на нашем сайте:
http://4analytics.ru/metodi-analiza/mse-%E2%80%93-srednekvadraticheskaya-oshibka-v-excel.html - MPE – средняя процентная ошибка – показывает завышен или занижен прогноз относительно факта. Если ошибка меньше нулю, то прогноз последовательно завышен, если ошибка больше нуля, то прогноз последовательно занижен.
Подробнее читайте в статье на нашем сайте:
http://4analytics.ru/metodi-analiza/mpe-%E2%80%93-srednyaya-procentnaya-oshibka-v-excel.html - MAD – среднее абсолютное отклонение. Используется, когда важно измерить ошибку в тех же единицах, что и исходный ряд.
Подробнее читайте в статье на нашем сайте:
http://4analytics.ru/planirovanie-i-prognozirovanie-praktika/dopolnitelnie-oborotnie-sredstva-za-schet-povisheniya-tochnosti-prognoza.html - A MAPE – ошибка, которая показывает отклонение средних значений ряда к средним значениям модели прогноза. Имеет значение при неравномерном перераспределении значений ряда по периодам.
- S MAPE – ошибка, которая показывает отклонение суммы значения ряда к сумме значений модели прогноза. Имеет значение при неравномерном перераспределении значений ряда по периодам.
А также 2 показателя «Точность прогноза»:
- Точность прогноза = 1 – МАРЕ
- Точность прогноза 2 = 1 – MRPE
Для расчета ошибок одновременно с прогнозом, нажимаем кнопку «Расчет ошибок» в меню «FORECAST»
В открывшемся окне выбираем нужные для расчета ошибки:
Теперь при расчете прогноза, в продолжение ряда, программа автоматически сделает расчет отмеченных Вами ошибок:








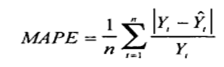 MAPE – средняя абсолютная ошибка в процентах используется:
MAPE – средняя абсолютная ошибка в процентах используется: