Как рассчитать относительную ошибку взвешивания

Метрологические свойства весов

Весы, независимо
от их конструкции, должны иметь такие
метрологические свойства.

Устойчивость
— способность
весов, выведенных из состояния равновесия,
быстро возвращаться к первоначальному
положению.

Устойчивость весов
достигается при условии, если их коромысло
находится в состоянии устойчивого
равновесия. Устойчивость весов зависит
также от отдаленности центра от точки
опоры, причем, чем ниже размещен центр
весов, тем больше устойчивость и тем
труднее их вывести из состояния
равновесия, а соответственно ниже их
чувствительность.

Проверка устойчивости
проводится следующим образом: весы,
находящиеся в равновесии, необходимо
вывести из положения равновесия, слегка
коснувшись чашки. Подсчитать количество
колебаний стрелки весов до возвращения
ее в положение равновесия. Если стрелка
совершила не более 4—6 колебаний, можно
считать, что весы устойчивы.

Постоянство
показаний
— способность
весов показывать одни и те же результаты
при многоразовых определениях массы
тела, проводимых на этих весах в одних
и тех же условиях.

Проверка постоянства
показаний проводится следующим образом:
весы должны находиться в положении
равновесия. На технических аптечных
весах уравновешивают, например, флакон
с массой гирь. Если все 3 раза масса
взвешиваемого тела одна и та же, то весы
обладают постоянством показаний. Если
результаты не совпадают, то это значит,
что острия призм не вполне параллельны,
смещены. Кроме того, на постоянство
показаний большое влияние оказывает
величина трения в подвижных контактах
весов. Затупленность призм и их
загрязненность приводит к нарушению
постоянства показаний весов. Поэтому
весы в нерабочем состоянии должны
храниться так, чтобы избежать затупленности
призм.

Причиной непостоянства
показаний весов является несовершенство
устройства весов (например, незаметное
смещение отдельных частей при пользовании
ими), а также условия, в которых производится
взвешивание (например, одностороннее
нагревание коромысла (электрическая
лампа, солнечные лучи и пр.), вследствие
чего может произойти удлинение одного
плеча).

Чувствительность
— способность
весов показывать минимальное изменение
нагрузки в момент равновесия.

При этом чем меньше
разница в весе гирь, которую можно
определить этими весами, тем выше их
чувствительность и тем точнее результаты
взвешивания.

Чувствительность
весов прямо пропорциональна длине плеча
коромысла и обратно пропорциональна
массе коромысла, нагрузке весов (массе
чашек, груза, перегруза), величине прогиба
коромысла, расстоянию от точки опоры
до центра тяжести коромысла. Чувствительность
весов определяется формулой:

где

S
—
чувствительность, мм/мг;

L
— длина
плеча коромысла, мм;

Р —
масса чашки с грузом, мг;

р —
масса перегруза, выводящего весы из
состояния равновесия, мг;

h
— расстояние
от точки опоры до линии, соединяющей
острия грузоподъемных
и опорной
призм (величина прогиба коромысла), мм;

R
— масса
коромысла, мг;

т. —
расстояние от точки опоры до центра
тяжести коромысла, мм; Z
— длина
стрелки, мм;

X
— цена деления шкалы, мм.

Из формулы следует,
что величины L,
R,
m,
Z,
X
зависят от
конструкции весов.

В наибольшей
степени на величину чувствительности
весов влияет величина прогиба коромысла
h.
Весы с
прямолинейным коромыслом характеризуются
тем, что острия опорной и грузоприемных
призм находятся на одной прямой линии
(прямолинейность весов). При этом величина
h
= 0, а уравнение
принимает вид:

то есть чувствительность
весов становится независимой от величины
нагрузки весов. Это возможно лишь при
взвешивании минимальных количеств. На
практике даже незначительное определение
массы вызывает прогиб коромысла и влияет
на чувствительность весов. С увеличением
нагрузки весов, как следует из формулы,
их чувствительность уменьшается. Прогиб
коромысла при этом может быть недопустимо
большим, а коромысло необратимо
деформироваться, то есть весы выйдут
из рабочего состояния. Во избежание
этого необходимо во время взвешивания
не превышать величины предельно
допустимой нагрузки, обозначенной на
коромысле весов.

Чувствительность
весов зависит от ряда факторов.

От расположения
центра тяжести коромысла по отношению
к точке его опоры. Весы
будут иметь наибольшую чувствительность
при достаточной устойчивости в том
случае, когда центр тяжести коромысла
лежит как можно ближе к точке опоры, но
во всяком случае ниже этой точки.

От массы коромысла.
Чем меньше
масса коромысла, тем большую чувствительность
при всех прочих условиях будут иметь
весы. Для облегчения коромысла в нем
делаются вырезы круглой или иной формы.

От длины плеч
коромысла. Теоретически,
чем больше длина плеч коромысла, тем
больше его чувствительность. Однако
практически нецелесообразно изготовлять
коромысла с длинными плечами, так как
удлинение коромысла ведет к увеличению
его массы, что вызывает уменьшение
чувствительности. Наряду с увеличением
длины коромысла значительно возрастает
прогиб его от действия груза, вследствие
чего понижается центр тяжести коромысла
и чувствительность весов уменьшается.
Поэтому практически коромысла делают
с как можно более короткими плечами.

На чувствительность
весов оказывает влияние величина
трения между призмами и
подушками: чем больше трение, тем меньше
чувствительность, чем острее призмы,
тем чувствительность больше. Поэтому
призмы делают острыми из закаленной
стали. Износ-затупление призм приводит
к увеличению трения, и, следовательно,
к уменьшению чувствительности весов.

Следует отметить,
что большинство весов, служащих для
взвешивания с
большей
точностью (в том числе тарирные и ручные),
имеют длинные стрелки. Это объясняется
тем, что увеличение длины стрелки весов
позволяет наблюдать и отсчитывать
незначительные угловые отклонения
коромысла, так как чем больше радиус
(длина стрелки), тем больше длина дуги,
соответствующей отклонению коромысла
на один и тот же угол.

Проверка
чувствительности весов
проводится
путем определения минимальной нагрузки
(мг), вызывающей стандартное отклонение
стрелки от положения равновесия. За
стандартное отклонение принимают
отклонение стрелки, равное 5 мм (или трем
делениям шкалы) для тарирных весов и
выход стрелки из обоймицы до половины
своей длины с образованием угла, равного
приблизительно 5°, для ручных весов.

Чувствительность,
выраженную абсолютным значением груза,
вызывающего стандартное отклонение
стрелки, называют абсолютной
чувствительностью (<S_a₆_c),
или абсолютной
ошибкой взвешивания.

Чувствительность
ручных и тарирных весов определяют в
трех положениях: нагруженных на 1/10
предельной нагрузки, предельно нагруженных
и ненагруженных. Если груз, соответствующий
величине допустимой погрешности
(установленной ГОСТом) для данного типа
весов (табл. 5), помещенный на одну из
чашек таких весов, вызывает стандартное
отклонение стрелки, то весы считаются
чувствительными .

Так весы технические
ВКТ-1000 имеют следующие величины
погрешностей:

— ненагруженных
— 20 мг;

— с 1/10 максимальной
нагрузки — 60 мг;

— максимально
нагруженные — 100 мг.

При определении
величины чувствительности этих весов
при 1/10 нагрузки поступают так: весы
приводят в состояние равновесия, на
каждую чашку помещают гири массой по
100,0 г, уравновешивают весы, затем
постепенно нагружают правую чашу весов
гирьками (от меньшей к большей). Груз,
вызывающий стандартное отклонение
стрелки, показывает абсолютную
чувствительность. Если величина
дополнительной нагрузки больше допустимой
погрешности (60 мг), например 80 мг, весы
считают нечувствительными. Их изымают
из пользования и направляют на проверку
до срока клеймения. Аналогично проводят
определение чувствительности при
ненагруженных и при предельной нагрузке
весов. Чувствительность весов можно
определить и таким образом: при трех
состояниях весов, приведенных в положение
равновесия, на одну из чашек кладут гирю
массой, соответствующей величине
допустимой погрешности.

Таблица 5
Метрологическая
характеристика ручных и тарирных весов

Типоразмеры весов	Нагрузка, г	Допустимая погрешность, мг
Максимальная	Минимальная	Ненагруженных весов	При 1/10 предельной нагрузки	При максимальной нагрузке
ВР-1	1	0,02	2	3	5
ВР-5	5	0,010	2	4	10
ВР-20	20	1,00	3	6	20
ВР-100	100	5,00	5	10	50
ВКТ-1000	1000	50,00	20	60	100
Т-2-1000	1000	50,00	20	50	200

Если во всех трех
случаях стрелка весов отклонилась на
расстояние 5 мм (или 3 деления по шкале),
то весы обладают достаточной
чувствительностью. Если стрелка
отклонилась на расстояние менее, чем 5
мм, то такие весы недостаточно
чувствительные и ими пользоваться
нельзя.

Что касается
определения чувствительности ручных
весов, то оно осуществляется аналогичным
путем по стандартному отклонению
стрелки. В этих случаях чувствительность
весов выражается числом миллиграммов,
вызывающих необходимое отклонение
стрелки.

На практике большое
значение имеет так называемая относительная
чувствительность, которая может указать
относительную ошибку взвешивания
(точность дозирования).

Относительная
чувствительность весов S_отн может
быть выражена отношением минимального
груза Р, вызывающего заметное отклонение
стрелки от нулевого положения шкалы, к
нагрузке л,
лежащей на
одной чашке весов, потому что
чувствительность весов может немного
варьировать в зависимости от величины
нагрузки:

или

Если, например,
весы нагрузить гирями по 100,0 г на каждую
чашечку и поместить дополнительный
груз, равный 0,05 г, который дает стандартное
отклонение стрелки, то относительная
чувствительность весов равна:

Значит, на этих
весах можно взвешивать груз, равный
100,0 г, с точностью 0,0005 его настоящей
массы, то есть относительная ошибка не
превышает 0,05 % (0,0005 • 100). Такие весы можно
считать достаточно чувствительными.

Определение
ошибки взвешивания.
На одних и
тех лее весах груз можно взвесить с
различной точностью. Наибольшая точность
может быть получена тогда, когда навеска
близка по значению к наибольшей допустимой
нагрузке весов. Ошибка взвешивания
возрастает, если переходят границу
предельной или минимальной нагрузки,
которая обозначена на коромысле данных
весов.

Чтобы сделать
вывод, насколько правильно выбраны весы
для определения массы вещества, надо
установить точность взвешивания или
относительную ошибку (в %).

Например, необходимо
взвесить массу 0,06 г. Какими весами при
этом следует воспользоваться? Для весов
ВР-100 величина 0,06 г близка к ненагруженным
весам, поэтому S_абс
по табл. 5
равна 0,005 г, а S_OTH— 8%:

Для весов ВР-1
величина массы 0,06 г близка к ненагруженным
весам, поэтому S_а6с
(табл. 5) — 0,002 г, а
S _отв
— 3,6 %:

Таким образом, для
взвешивания массы 0,06 г нужно использовать
ручные весы ВР-1.

Расчет относительной
ошибки взвешивания можно осуществить
путем составления соответствующей
пропорции.

Например, рассчитать
относительную ошибку при взвешивании
0,1 г натрия хлорида на ВР-1. По табл. 5
находят ошибку, допустимую при нагрузке
0,1 г. Так как навеска наиболее близка по
значению к 1/10 предельной нагрузки, а не
к предельной нагрузке или к ненагруженным
весам, то допустимая погрешность S_oth
равна 0,003
(3 мг). Составив пропорцию, находят ошибку
взвешивания (х),
которая
составляет ±3 %:

0,1 – 0,003

100 — х

При взвешивании
на этих же весах большего количества
натрия хлорида 0,9 г (навеска наиболее
близка по значению к предельной нагрузке
ВР-1) допустимая погрешность равна 0,005
(5 мг). Относительная ошибка в этом случае
составляет ±0,55 %:

0,9 – 0,005

100 — х

Точность или
правильность
— способность
весов показывать правильное соотношение
между массой взвешиваемого вещества
и соответствующими гирями.

Точность или
правильность весов зависит от таких
факторов:

— от равноплечности
коромысла весов;

—от параллельности
острия опорной и грузопринимающих
призм;

— от положения
центра тяжести весов коромысла, который
должен лежать точно на вертикали,
проходящей через точки опоры, которые
находятся ниже нее;

— от равенства
массы чашек.

Если весы отвечают
указанным требованиям, то их коромысло
должно находиться в горизонтальном
положении, а показчик равновесия
(стрелка) — строго вертикальном как
при пустых, так и при нагруженных
одинаковым грузом чашечках. Вследствие
невозможности обеспечить у весов
абсолютно точное равенство плеч и в
связи с трением, создающимся в опорных
деталях коромысла при его колебаниях,
весы всегда имеют ограниченную точность.
В связи с этим для всех весов установлены
максимально допустимые погрешности и
весы считаются правильными (верными),
если их погрешности не превышают
установленных значений.

Проверка
точности весов
проводится
при 1/10 максимальной нагрузки, при полной
нагрузке и ненагруженных весах.

Например, необходимо
определить точность технических весов
с максимальной нагрузкой 1 кг. Для этого
на левую чашку помещают гирю, равную
1/10 максимальной нагрузки, 100,0 г, а на
правую — тарирный стакан с дробью и
добиваются равновесия. Затем при
нерабочем положении арретира гирю и
груз меняют местами и переводят арретир
в рабочее положение. Стрелка весов при
перемене местами гири и груза должна
прийти в положение равновесия. Если
равновесие восстанавливается, то весы
верны (равноплечи). При отсутствии
равновесия на поднявшуюся чашку весов
добавляют груз-допуск (миллиграммовый
разновес), равный величине погрешности
(см. табл. 5). Это должно привести весы в
состояние равновесия или отклонить
стрелку в противоположную сторону не
более чем на 5 мм. Вес добавленных гирь
в этом случае будет являться величиной
неравноплечно-сти весов. Если этого не
произойдет, весы не обладают достаточной
точностью, они неравноплечи. Неравноплечие
весы применять нельзя, так как они не
будут давать точные показатели массы
взвешиваемого вещества.

Гири и разновес.
Разновес представляет собой набор
гирь. Гири
— это
меры определенно установленной массы
(веса), служащие для измерения массы
тела по весу.

Взвешивая тело,
мы сравниваем его массу с величиной,
принятой за единицу по Международной
метрологической системе мер. За единицу
массы принимается килограмм. В
повседневной аптечной практике основной
единицей измерения массы лекарственного
средства является грамм — тысячная
доля килограмма. Названия низших единиц
долей грамма образуются с помощью
латинских приставок «деци» (0,1), «санти»
(0,01), «милли» (0,001). В рецепте слово «грамм»
или его обозначение «г» опускается.
Всякое число в рецепте, обозначенное
десятичными знаками, целыми или дробными,
принимается за выражение количества
вещества в граммах, если нет других
обозначений.

В зависимости от
назначения различают такие гири:

— образцовые,
изготовляемые из золота, платины и
медных сплавов;

— аналитические,
изготовляемые из медных сплавов и стали
с тщательно отполированной поверхностью,
покрытой золотом, платиной, никелем
или хромом;

— технические
1, 2 и 3-го классов.

В аптечной практике
применяются технические гири 2-го класса
в виде специальных наборов (разновесов):
крупного (граммового), содержащего гири
от 1,0 до 500,0 г, и мелкого (миллиграммового),
содержащего гири от 0,01 до 0,500 г. Граммовый
разновес изготавливают из латуни или
углеродистой стали с никелевым или
хромовым покрытием для предохранения
от окисления. Поверхность гирь должна
быть гладкой, без трещин, царапин и т.
п. Гири имеют форму прямых цилиндров с
головками. Миллиграммовые гири
изготавливают из мельхиора или алюминия
в виде разной формы пластинок:
треугольников, квадратов, шестиугольников.

Для защиты от
внешних влияний и повреждений гири
хранят в специальных коробках с гнездами
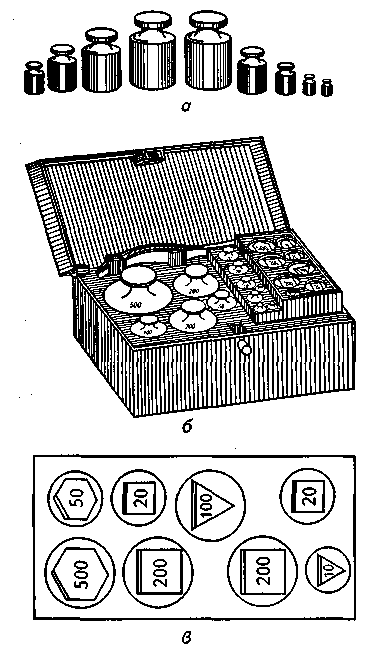
(рис. 15).

Гири должны
содержаться в чистоте, для чего
периодически их очищают от пыли и жира,
промывая в мыльной теплой воде или в
органических растворителях (спирте,
бензине), после чего тщательно вытирают
насухо

Рис. 15. Разновес:
а —
крупный; б
— набор в
футляре; в
— мелкий

мягкой тканью.
Брать их необходимо только пинцетом,
чистить гири
разными
полирующими средствами категорически
запрещается.

Гири и разновесы
подвергаются проверке и клеймению один
раз в год. Исправность весового хозяйства
аптечных учреждений контролируется
представителями местных отделений
Государственного комитета стандартов,
мер и измерительных приборов. При этом
на коромысло ручных и тарирных весов
наносится клеймо с указанием года
проверки (выбивают две последние цифры,
например, цифра 97 означает, что проверка
весов была проведена в 1997 г.).

Правила взвешивания
на технических и ручных равноплечих
весах. Прежде
чем начать взвешивание, нужно проверить
соответствие весов выше указанным
метрологическим свойствам, то есть
убедиться в их точности, чувствительности,
неизменности показаний и устойчивости.
Необходимо придерживаться предельной
и минимальной нагрузок, установленных
для данных весов.

Перед работой
весы следует осмотреть, протереть
марлевой салфеткой, смоченной
спирто-эфирной смесью, убедиться в их
равновесии в ненагруженном состоянии.
Если весы не уравновешены, то их
уравновешивают при помощи регуляторов,
помещенных на концах коромысла.

Как правило (для
удобства), гири помещают на левую чашечку
весов, а взвешиваемое лекарственное
средство — на правую.

При взвешивании
лекарственных и вспомогательных веществ
их названия ассистент читает трижды:
снимая с вертушки, при отвешивании и
возвращении штангласа на место. Подсчет
массы гирь производится дважды — в
начале взвешивания и по окончании.

Порошкообразные
вещества при взвешивании на ручных
весах помещают непосредственно на
чашку весов, а густые — на кружок
пергаментной или фильтровальной бумаги
(предварительно стари-рованный).
Взвешивать какие-либо вещества
непосредственно на чашечке тарирных
весов недопустимо, нужно применять
соответствующую тару (флаконы, банки,
капсулы и др.). Во избежание ошибок не
рекомендуется для тарирования применять
разновес.

Сыпучие вещества
отвешивают непосредственно из штангласа
путем легкого постукивания по нему
указательным пальцем правой руки.
Прибавляют вещество небольшими порциями
так, чтобы нити весов не загрязнялись.
По мере приближения момента равновесия
порции добавляемого вещества уменьшают,
чтобы исключить возможную передозировку
порошка. В случае необходимости вещество
отбирают при помощи пластмассовой или
целлулоидной пластинки. После взвешивания
с весов сначала снимают разновес (и
второй раз проводят подсчет массы
гирь), а затем лекарственное вещество.
После каждого отвешивания лекарственного
вещества из штангласа шейку и пробку
штангласа, а также чашечки весов
тщательно протирают марлевой салфеткой.

Источник

Загрузить PDF

Абсолютная погрешность – это фактическая ошибка, допущенная при измерении какой-либо величины. Относительная погрешность сравнивает абсолютную погрешность со значением измеряемой величины. Чтобы вычислить относительную погрешность, следует найти и абсолютную погрешность. Если вы измеряете предмет, длина которого равна 12 см, и вы допустили ошибку в 6 см, то относительная погрешность будет огромной. Но если длина измеряемого предмета равна 12 м, а ошибка – 6 см, то относительная погрешность будет значительно меньше, даже с учетом того, что абсолютная погрешность (6 см) не изменилась.^[1]

1
Если вам дано ожидаемое значение, вычтите из него полученное вами значение, чтобы вычислить абсолютную погрешность. Как правило, ожидаемое значение находится в ходе тестовых или лабораторных испытаний. Ожидаемое значение является наиболее точным значением некоторой величины, которое используется при различных вычислениях. Чтобы получить абсолютную погрешность, сравните результаты ваших измерений с ожидаемым значением – так вы узнаете, насколько ваши результаты отличаются от ожидаемого значения. Для этого просто вычтите полученное вами значение из ожидаемого. Если разность отрицательная, превратите ее в положительную, проигнорировав знак «минус». Вы получите абсолютную погрешность.^[2]
- Например, вы хотите узнать точность измерения расстояния при помощи шагов. Вы идете от одного дерева к другому, считаете шаги и выясняете, что деревья расположены на расстоянии 5,4 м друг от друга. Это экспериментальное значение. Потом вы берете рулетку и измеряете точное расстояние между деревьями, которое равно 6 м. Это действительное значение. Абсолютная погрешность равна: 6 – 5,4 = 0,6 м = 60 см.^[3]
2
Теперь допустим, что абсолютная погрешность – это наименьшая единица измерения. Например, рулетка имеет миллиметровые деления, то есть ее наименьшей единицей является 1 мм. Таким образом, вы можете измерить расстояние с точностью до ± 1 мм; в этом случае абсолютная погрешность составляет 1 мм.
- Это верно для любых измерительных инструментов или систем. Например, на корпус многих научных инструментов, таких как прецизионные весы и измерительные приборы, наносят маркировку об абсолютной погрешности в виде «± ____».
3

Не забудьте приписать соответствующие единицы измерения. Предположим, что абсолютная погрешность равна 2 м. Такая информация позволит наглядно представить величину ошибки. Но если вы записываете, что погрешность равна 2, то эта цифра ничего не значит. Используйте те же единицы измерения, которыми вы пользовались в ваших измерениях.^[4]
4
Попрактикуйтесь на нескольких примерах. Это наилучший способ научиться вычислять погрешность. Решите следующие задачи (ответы приведены в конце каждой задачи).
- На уроке химии в результате реакции ученик получил вещество массой 32 г. Известно, что действительное значение выхода этой реакции равно 34 г. Абсолютная погрешность равна ± 2 г.
- На уроке химии ученику необходимо 10 мл воды, чтобы вызвать реакцию; при этом погрешность капельницы составляет «± 0,5 мл». В этом случае абсолютная погрешность измерений равна ± 0,5 мл.
5
Уясните, что приводит к появлению погрешности и как ее устранить. Всякое научное исследование подразумевает наличие ошибок – даже в научных работах, за которые вручаются Нобелевские премии, сообщается о допущениях или погрешностях. Но если вы определите причину появления погрешности, вы, возможно, сможете устранить ее.^[5]
- Человеческий фактор – наиболее распространенная причина появления ошибок. Сюда относятся неподобающие условия для проведения измерений и плохо продуманные эксперименты.
- Одной из причин появления ошибок может являться внезапное отключение энергии, недостаточное количество рабочего материала или изменение других условий, например, нехватка воды в результате ее испарения, внезапное изменение температуры окружающей среды и так далее.
- Еще одной причиной является несовершенство оборудования, используемого для измерений или исследований, например, прецизионных инструментов или горелок, которые обеспечивают неравномерное распределение тепла.^[6]
Реклама

1
Разделите абсолютную погрешность на действительное значение исследуемой величины. Так вы вычислите относительную погрешность. Эта формула позволит вам выяснить, насколько полученное вами значение отличается от действительного значения изучаемой величины. Конечно, прекрасно, если относительная погрешность мала. Продолжим рассматривать пример с измерением расстояния между двумя деревьями.
- Абсолютная погрешность равна 0,6 м, а действительное значение равно 6 м.
- 0,6 м / 6 м
- Относительная погрешность равна 0,1 м.^[7]
2
Полученный результат умножьте на 100, чтобы выразить относительную погрешность в процентах. Вы можете представить относительную погрешность в виде обыкновенной дроби, десятичной дроби или в процентах – в этом случае умножьте десятичную дробь на 100. Так вы узнаете, какой процент от полученного вами значения составляет погрешность. Если вы измеряете длину 60 м лодки, а погрешность составляет 0,6 м, то процент ошибки будет значительно меньше, чем при вычислении расстояния между деревьями (6 м) с погрешностью 0,6 м. Погрешность представляет собой небольшой процент от экспериментального значения. ^[8]
- 0,6 м / 6 м = 0,1 м
- 0,1 * 100 = 10% – относительная погрешность.
3
Вычислите относительную погрешность без нахождения абсолютной погрешности. Для этого выражение для вычисления абсолютной погрешности запишите в числителе выражения для нахождения относительной погрешности. Уяснив разницу между абсолютной и относительной погрешностями, нет необходимости отдельно вычислять абсолютную погрешность. Просто замените значение абсолютной погрешности на выражение для ее вычисления. Обратите внимание, что вертикальные черты обозначают абсолютную величину, то есть любое полученное значение нужно превратить в положительное.
- Относительная погрешность: $={\frac {|{\mathrm {E}}-{\mathrm {D}}|}{{\mathrm {D}}}}$ , где Е — экспериментальное значение, D — действительное значение.
- Умножьте это выражение на 100, чтобы выразить относительную погрешность в процентах.^[9]
4

Не забудьте приписать соответствующие единицы измерения. Предположим, что абсолютная погрешность равна 2 м. Такая информация позволит наглядно представить величину ошибки. Но если вы записываете, что погрешность равна 2, то эта цифра ничего не значит. Также не имеет смысла указывать погрешность в виде процентов от ошибки (10% от 0,6 м) – следует писать, например, так: относительная погрешность равна 10%.^[10]

Реклама

Советы

Удостоверьтесь, что экспериментальное значение и действительное значение измеряются в одних единицах измерения. Например, если экспериментальное значение измеряется в сантиметрах, а действительное значение – в миллиметрах, преобразуйте одну из этих единиц измерения в другую.

Предупреждения

Убедитесь, что вы правильно округляете числа.

Об этой статье

Эту страницу просматривали 171 372 раза.

Была ли эта статья полезной?

Источник

5 сообщений в этой теме

Присоединиться к обсуждению

Вы можете ответить сейчас, а зарегистрироваться позже.

Если у вас уже есть аккаунт, войдите, чтобы ответить от своего имени.

Источник

Пример. Определить относительную ошибку взвешивания 100 г хлористого кальция, если в результате взвешивания получено 99,8473 0,0001 г [c.222]

Вычислить относительную ошибку взвешивания осадка ( весовой формы ) при определении 1 г кальция в обоих случаях, если весы позволяют взвешивать с точностью 0,0001 г. [c.67]

Какую наименьшую навеску можно брать на аналитических весах с ценой деления шкалы для стрелки 0,3 мг при допустимой относительной ошибке взвешивания не более 0,3 /о (точку равновесия определяют с точностью 0,5 деления) [c.29]

Взвешивание — это одна из наиболее точных операций анализа. Относительная ошибка взвешивания зависит от взвешиваемой массы. Если взвешивание проводят с точностью до 0,1 мг и взвешивают не менее 100 мг (как это бывает в обычных анализах), то ошибка взвешивания ничтожно мала. [c.299]

Вычислим, с какой точностью определена эта концентрация, если взвешивание проводилось на аналитических весах с точностью до 0,0002 г, а измерение объема раствора содержит ошибку, равную Н-0,5 мл. Относительная ошибка взвешивания в данном случае равна [c.56]

Относительные ошибки взвешивания осадков будут в первом случае [c.176]

Недостатком соды в сравнении с бурой является меньший эквивалентный вес, в связи с чем увеличивается относительная ошибка взвешивания. Кроме того, безводная сода гигроскопична, и перед употреблением ее необходимо прокалить для удаления влаги. [c.330]

Относительными ошибками взвешивания и измерений объемов по бюретке пренебрегаем следовательно, [c.256]

Более точные данные определений получаются с рабочим раствором буры, поскольку эквивалентный вес ее (190,72) в 3,6 раза больше, чем соды (53). При большом эквивалентном весе исходного вещества уменьшается относительная ошибка взвешивания. [c.242]

Например, при повторных взвешиваниях стеклянного фильтра были получены следующие результаты (в г) 10,2375 10,2374 10,2378 10,2375. Определить среднее арифметическое значение, дисперсию, среднюю квадратичную ошибку, среднюю квадратичную ошибку среднего арифметического, коэффициент нормирования отклонений, вероятное квадратичное отклонение среднего арифметического, истинную массу стеклянного фильтра и относительную ошибку взвешивания с надежностью а, равной 0,95. Для удобства вычислений запишем данные в виде таблицы [c.302]

Определение очень малых количеств какого-либо иона выгоднее производить в виде соединения с возможно большим молекулярным весом еще и потому, что здесь будут меньше не только относительные ошибки взвешивания, но и другие ошибки. [c.42]

Из всех условий, обычно предъявляемых к исходным веществам, в микрохимическом анализе особенно желательна работа с веществом, обладающим более высоким грамм-эквивалентом. Чем выше грамм-эквивалент, тем точнее может быть взята его навеска на микровесах. Если необходимо произвести определение с ошибкой до 0,1%, то ошибка в приготовлении раствора исходного вещества, являющаяся частью допустимой ошибки, не должна превышать 0,03%. Если учесть, что на обычных микровесах можно взвешивать со средней ошибкой +0,003 мг, то нетрудно вычислить, что минимальная навеска исходного вещества, при которой относительная ошибка взвешивания не превысит 0,03%, равна 10 мг. На титрование этой навески должно уйти в среднем 4 Л1Л 0,01 н. раствора, т. е. 0,04 мг-экв. Отсюда нетрудно рассчитать, что минимальная величина 1 г-экв должна быть около 250 г [c.162]

В нашей лаборатории применялись ультрамикровесы с нихромовым коромыслом длиною 250 мм и толщиною 0,2 мм для отбора навесок от 20 у ДО 600 т с относительной ошибкой взвешивания не более 3—5%. [c.244]

Иметь достаточно высокую эквивалентную массу. Масса вещества, требующегося для стандартизации или приготовления раствора данной концентрации, тем больше, чем выше его эквивалентная масса. Поскольку прп увеличении массы относительная ошибка взвешивания уменьшается, высокая эквивалентная масса способствует уменьшению ошибок взвешивания. [c.172]

Это означает, что 1 мг 5102 в пробе соответствует более 40 мг осадка крем- немолибденовой соли, что обеспечивает относительную ошибку ( ) взвешивания 1 мг 5Юз не выше 0,5 %, если принять абсолютную погрешность взвешивания на аналитических весах примерно 0,2 мг. [c.26]

Сказанное справедливо, однако, только при условии, если не приходится брать для титрования слишком малых навесок, так как это сильно увеличивает относительную ошибку взвешивания. [c.224]

Относительная ошибка определения мольной доли искусственно введенной примеси не превосходит суммы относительной ошибки взвешивания исследуемого вещества и относительной ошибки взвешивания искусственной примеси. В нашем случае обычно величина навески вещества составляет 1—1,5 г, навеска примеси — 0,01 г, погрешность взвешивания 0,0001 г. Из этого следует, что такой относительной ошибкой взвешивания исследуемого вещества можно пренебречь, так как она будет примерно на два порядка меньше относительной ошибки взвешивания искусственной примеси. Ошибку определения мольной доли искусственной примеси будет определять величина относительной ошибки взвешивания искусственной примеси. Из этого вытекает, что при такой точности взвешивания не следует брать навеску примеси меньше 0,01 г, так как это приведет к значительной ошибке. [c.122]

Считая, что максимальная относительная ошибка взвешивания не должна превышать 0,25—0,337о, можно установить следующую зависимость между чувствительностью весов и минимальной навеской [c.23]

Относительная ошибка взвешивания обычно составляет г0,1°/о. т. е. Д у= =+гО,17о- [c.23]

Отсюда можно заключить, что при прочих равных условиях определение кальция в виде СаС204-Н20 (где фактор пересчета меньший) точнее, так как относительная ошибка взвешивания в этом случае меньше. [c.236]

Фактор пересчета для определения кальция в виде СаО равен 0,7147, а для определения в виде СаС204 Н2О равен 0,2743. Вычислить относительную ошибку взвешивания осадка ( весовой формы ) при определении 1 2 кальция в обоих случаях, если весы позволяют взвешивать с точностью + 0,000 1 г. [c.64]

Можно приблизительно вычислить желательную величину коэфициента пересчета для весового микрохимического анализа. Величина весовой формы определяется по разности двух взвешиваний (например, вес пустого тигля и вес тигля с весовой формой). Средняя ошибка каждого взвешивания на микровесах составляет 0,005 мг значит, ошибка определения веса весовой формы около 0,01мг. При навеске в 10 жг относительная ошибка взвешивания равна 0,1 /о, при 1 мг — достигает 1%. Если коэфициент пересчета равен 0,3, то ошибка весового определения достигает в этих случаях 0,03% и 0,3%, а при коэфициенте пересчета 0,1 ошибки соответственно равны 0,01 % и 0,1 %. Для 1—2мг весовой формы желательно, чтобы коэфициент пересчета не превышал 0,2. [c.42]

На практике широко используются два метода конечного определения масла в органическом растворителе 1) весовой, в основе которого лежит определение масла взвешиванием после испарения органического растворителя, 2) различные варианты спектрального метода, в частности люминесцентный, а также по ИК- и УФ-спектрам поглощения. Весовой метод методически прост и надежен. Однако ои оказывается неэффективным при малом содержании масла в техническом продукте, когда относительные ошибки взвешивания стано-., вятся больщими. Основные требования, которые предт.явля-ются к органическому растворителю в весовом методе,— это нерастворимость технического продукта в экстрагенте и по (ВОЗМОЖНОСТИ низкая температура его кипения. В случае мочевины наиболее полно обоим требованиям удовлетворяет четыреххлористый углерод. [c.29]

Практикум по общей химии Издание 4 (1960) — [

c.15

]

Практикум по общей химии Издание 5 (1964) — [

c.15

]

Источник

Несмотря на технические и научные достижения, доступные современному человеку, до сих пор не существует методов, которые позволили бы с абсолютной точностью проводить измерение физических величин. Исключением не стала и масса тела. Когда проводится взвешивание объекта, то получаемый результат можно назвать случайным, поскольку он будет зависеть от большого количества внешних и внутренних факторов, таких как чувствительность весового оборудования, правильность его установки, условия окружающей среды (влажность, температура), опыт оператора весов и другие. Именно по этим причинам и введено такое понятие, как погрешность.

Погрешность крановых весов, автомобильных или вагонных можно представить, как разность между реальным весом объекта и тем результатом, который был получен в процессе измерения его массы.

Абсолютная и относительная погрешность

Чтобы обозначить погрешность автомобильных весов, крановых или вагонных, могут использоваться разные выражения. Например, когда погрешность вагонных весов выражается в тех же единицах, что и масса взвешиваемого объекта (в килограммах, граммах, тоннах и т. п.), то она называется абсолютной. По абсолютной погрешности сложно делать выводы о точности проведенных измерений. Поэтому гораздо чаще используется относительная погрешность, которая выражается в процентах или долях от результата измерения.

Систематическая и случайная погрешность

Под систематической погрешностью автомобильных весов можно понимать погрешность, которая постоянна по своей величине, или которая изменяется по определенной закономерности при повторных взвешиваниях. Она всегда присутствует в результатах измерений, пока не удастся устранить вызывающие ее причины. В числе факторов, из-за которых появляются систематические погрешности крановых весов, автомобильных или вагонных, можно выделить некорректную установку или монтаж весового оборудования, неисправность отдельных механизмов, изменение температуры, при которой осуществляются измерения, и некоторые другие.

Даже если попытаться полностью устранить описанные факторы, то добиться идентичности показателей при повторном измерении массы одного и того же объекта все равно не удастся. Этому препятствует наличие случайной погрешности вагонных весов. Она не поддается полному исключению из результатов взвешивания, однако путем применения методов математической статистики и вычисления вероятности совпадений можно рассчитать значение результатов измерения, которое будет наиболее близким к истинному весу объекта.

Источник

Метрологические свойства весов

Советы

Предупреждения

Похожие статьи

Об этой статье

Была ли эта статья полезной?

5 сообщений в этой теме

Рекомендуемые сообщения

Ссылка на комментарий

Поделиться на других сайтах

Ссылка на комментарий

Поделиться на других сайтах

Ссылка на комментарий

Поделиться на других сайтах

Ссылка на комментарий

Поделиться на других сайтах

Ссылка на комментарий

Поделиться на других сайтах

Присоединиться к обсуждению

Абсолютная и относительная погрешность

Систематическая и случайная погрешность