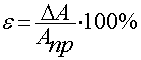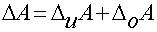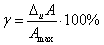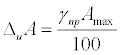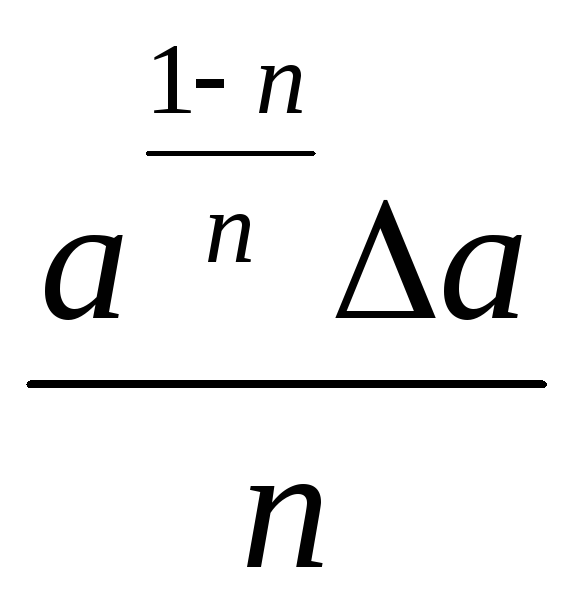Как определять погрешности измерений
Измерение – нахождение значения физической величины
опытным путем с помощью средств измерений.
Прямое
измерение
– определение значения физической
величины непосредственно средствами измерения.
Косвенное
измерение
– определение значения физической
величины по формуле, связывающей ее с другими физическими величинами, определяемыми
прямыми измерениями.
А, В, С, … — физические величины.
Апр. – приближенное значение физической величины.
А – абсолютная погрешность измерения физической
величины.
— относительная погрешность измерения
физической величины.
иА
– абсолютная
инструментальная погрешность, определяемая конструкцией прибора.
оА – абсолютная погрешность отсчета, она равна в
большинстве случаев
половине цены деления; при
измерении времени – цене деления секундомера или часов.
Абсолютную погрешность измерения
обычно округляют до одной значащей цифры:
Численное значение результата
измерений округляют так, чтобы его последняя цифра оказалась в том же разряде,
что и цифра погрешности:
Результат
измерения записывается так:
%
Определение погрешности методом среднего арифметического
При многократных
измерениях величины погрешность можно оценить следующим образом:
1.
Определить среднее
значение величины А:
(при трех
измерениях).
2.Определить отклонение каждого значения от среднего:
3.Определить среднее значение отклонения,
его и принимают за абсолютную погрешность:
4.Определить
относительную погрешность и выразить ее в процентах:
|
|
|
|
|
|
|
1 |
|
|
||
|
2 |
|
|
||
|
3 |
|
|
Многократные измерения
предпочтительнее, так как при их проведении возможна компенсация случайных
факторов, влияющих на результат. Обычно многократные измерения проводят, слегка
изменяя условия опыта, но предполагая, что значение величины А не изменяются
Определение
погрешности косвенных измерений
При косвенных измерениях значение
физической величины находится путем расчетов по формуле.
Относительную погрешность
определяют так, как показано в таблице:
|
Формула величины |
Формула |
|
1. |
|
|
2. 3. |
|
|
4. |
|
Абсолютную погрешность определяют
по формуле:
(
выражается десятичной дробью)
Пример: пусть измеряется сопротивление проводника. 
.
Результаты прямых измерений: 
Тогда 
;
, 
;
, 
;
, 
, 
.
Графическое
представление результатов эксперимента
Правила построения
графиков
выберите соответствующую бумагу;
выберите масштаб по осям координат;
напишите обозначения измеряемых физических величин;
нанесите на график данные;
нанесите на график доверительные интервалы;
проведите кривую через нанесенные точки;
составьте заголовок графика.
Для построения графиков выпускают
специальную бумагу-миллиметровку.
При выборе масштабов по осям
координат следует руководствоваться следующими правилами:
— значение независимой переменной
откладывают вдоль оси абсцисс, функции – вдоль оси ординат;
— цена наименьшего деления масштабной
сетки должна быть сравнимой с величиной погрешности измерения;
— точка пересечения оси абсцисс и оси
ординат не обязательно должна иметь координаты (0,0).
При построении графиков следует
иметь в виду, что по результатам опытов мы получаем не точку, а прямоугольник
со сторонами 
и
.
В
|
|
|||||
|
|
|||||
 |
|||||
 |
0
А
При выполнении простых лабораторных
работ достаточно обвести экспериментальную точку кружком или пометить
крестиком, не указывая доверительных интервалов.
Этот кружок или крестик будут
обозначать, что данная точка получена с каким-то приближением и истинное
значение измеряемой величины лежит где-то в ее окрестности.
Правила
приближенных вычислений
1. Основное
правило округления.
Если первая
отброшенная цифра равна 5 или больше, то последнюю из сохраняемых цифр
увеличивают на единицу; если первая отброшенная цифра меньше 5, то последнюю из
сохраняемых цифр оставляют без изменения, например:
2. При сложении и
вычитании приближенных чисел
в полученном результате сохраняют столько десятичных знаков, сколько их в числе
с наименьшим количеством десятичных знаков, например:
3. При умножении
и делении приближенных чисел
в полученном результате нужно сохранить столько значащих цифр, сколько их имеет
приближенное число с наименьшим количеством значащих цифр, например:
4. При возведении
в квадрат приближенного числа
нужно в результате сохранять столько значащих цифр, сколько их имеет возводимое
в степень число, например:
5. При извлечении
квадратного корня в результате
нужно сохранять столько значащих цифр, сколько их имеет подкоренное число,
например:
6. При вычислении
промежуточных результатов в
них следует сохранять на одну цифру больше, чем требуют правила 2-5. Причем при
подсчете значащих цифр запасные цифры не учитываются. В окончательном
результате запасная цифра отбрасывается по основному правилу округления.
7. При нахождении
углов или тригонометрических функций значение соответствующего угла записывают с точностью до градуса, если
значение тригонометрической функции имеет две значащие цифры; если угол задан с
точностью до градусов, то в значении тригонометрической функции сохраняют две
значащие цифры, например:
1. Как определять погрешности измерений.
Выполнение лабораторных работ связано с измерением различных физических величин и последующей обработкой их результатов.
Измерение — нахождение значения физической величины опытным путем с помощью средств измерений.
Прямое измерение — определение значения физической величины непосредственно средствами измерения.
Косвенное измерение — определение значения физической величины по формуле, связывающей ее с другими физическими величинами, определяемыми прямыми измерениями.
Введем следующие обозначения:
А, В, С, … — физические величины.
Апр — приближенное значение физической величины, т. е. значение, полученное путем прямых или косвенных измерений.
ΔА — абсолютная погрешность измерения физической величины.
ε — относительная погрешность измерения физической величины, равная:
ΔИА — абсолютная инструментальная погрешность, определяемая конструкцией прибора (погрешность средств измерения; см. табл. 1).
Δ0А — абсолютная погрешность отсчета (получающаяся от недостаточно точного отсчета показаний средств измерения); она равна в большинстве случаев половине цены деления, при измерении времени — цене деления секундомера или часов.
Таблица 1
Абсолютные инструментальные погрешности средств измерений
| № | Средства измерения | Предел измерения | Цена деления | Абсолютная инструментальная погрешность |
| 1 | Линейка | |||
| ученическая | до 50 см | 1 мм | ± 1 мм | |
| чертежная | до 50 см | 1 мм | ± 0,2 мм | |
| инструментальная (стальная) | 20 см | 1 мм | ± 0,1 мм | |
| демонстрационная | 100 см | 1 см | ± 0,5 см | |
| 2 | Лента измерительная | 150 см | 0,5 см | ± 0,5 см |
| 3 | Измерительный цилиндр | до 250 мл | 1 мл | ± 1 мл |
| 4 | Штангенциркуль | 150 мм | 0,1 мм | ± 0,05 мм |
| 5 | Микрометр | 25 мм | 0,01 мм | ± 0,005 мм |
| 6 | Динамометр учебный | 4 Н | 0,1 Н | ± 0,05 Н |
| 7 | Весы учебные | 200 г | — | ± 0,01 г |
| 8 | Секундомер | 0-30 мин | 0,2 с | ± 1 с за 30 мин |
| 9 | Барометр-анероид | 720-780 мм рт. ст. | 1 мм рт. ст. | ± 3 мм рт. ст. |
| 10 | Термометр лабораторный | 0-100 0С | 1 0С | ± 1 0С |
| 11 | Амперметр школьный | 2 А | 0,1 А | ± 0,05 А |
| 12 | Вольтметр школьный | 6 В | 0,2 В | ± 0,15 В |
Максимальная абсолютная погрешность прямых измерений складывается из абсолютной инструментальной погрешности и абсолютной погрешности отсчета при отсутствии других погрешностей:
Абсолютную погрешность измерения обычно округляют до одной значащей цифры (ΔА = 0,17 ≈ 0,2); числовое значение результата измерений округляют так, чтобы его последняя цифра оказалась в том же разряде, что и цифра погрешности (А = 10,332 ≈ 10,3).
Результаты повторных измерений физической величины А, проведенных при одних и тех же контролируемых условиях и при использовании достаточно чувствительных и точных (с малыми погрешностями) средств измерения, обычно отличаются друг от друга. В этом случае Апр находят как среднее арифметическое значение всех измерений, а погрешность ΔА (ее называют случайной погрешностью) определяют методами математической статистики.
В школьной лабораторной практике такие средства измерения практически не используются. Поэтому при выполнении лабораторных работ необходимо определять максимальные погрешности измерения физических величин. Для получения результата достаточно одного измерения.
Относительная погрешность косвенных измерений определяется так, как показано в таблице 2.
Таблица 2
Формулы для вычисления относительной погрешности косвенных измерений
| № | Формула для физической величины | Формула для относительной погрешности |
| 1 |  |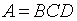
 |
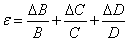| 2 |  |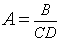
|
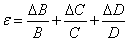| 3 |  |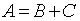
 |
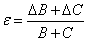| 4 |  |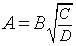
 |
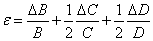Абсолютная погрешность косвенных измерений определяется по формуле ΔА = Апрε (ε выражается десятичной дробью).
2. О классе точности электроизмерительных приборов.
Для определения абсолютной инструментальной погрешности прибора надо знать его класс точности. Класс точности γпр измерительного прибора показывает, сколько процентов составляет абсолютная инструментальная погрешность ΔиА от всей шкалы прибора (Amax):
Класс точности указывают на шкале прибора или в его паспорте (знак % при этом не пишут). Существуют следующие классы точности электроизмерительных приборов: 0,1; 0,2; 0,5; 1; 1,5; 2,5; 4. Зная класс точности прибора (γпр) и всю его шкалу (Аmах), определяют абсолютную погрешность ΔиА измерения физической величины А этим прибором:
3. Как сравнивать результаты измерений.
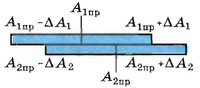
1. Записать результаты измерений в виде двойных неравенств:
А1np — ΔА1 < А1пр < А1пр + ΔА1,
А2пр — ΔА2 < А2пр < А2пр + ΔА2.
2. Сравнить полученные интервалы значений: если интервалы не перекрываются, то результаты неодинаковы; если перекрываются — одинаковы при данной относительной погрешности измерений.
4. Как оформлять отчет о проделанной работе.
- Лабораторная работа № … .
- Наименование работы.
- Цель работы.
- Чертеж (если требуется).
- Формулы искомых величин и их погрешностей.
- Таблица результатов измерений и вычислений.
- Окончательный результат, вывод и пр. (согласно цели работы).
5. Как записывать результат измерения.
А = Апр ± ΔА
е = …%.
Вычисление погрешностей измерений
Выполнение лабораторных работ связано с измерением физических величин, т. е. определением значений величин опытным путём с помощью измерительных приборов (средств измерения), и обработкой результатов измерений.
Различают прямые и косвенные измерения. При этом результат любого измерения является приблизительным, т. е. содержит погрешность измерения. Точность измерения физической величины характеризуют абсолютная и относительная погрешности.
Прямое измерение — определение значения физической величины непосредственно с помощью измерительного прибора.
Абсолютную погрешность прямых измерений определяют суммой абсолютной инструментальной погрешности и абсолютной погрешности отсчёта Δx = Δиx + Δоx при условии, что случайная погрешность и погрешность вычисления или отсутствуют, или незначительны и ими можно пренебречь.
Абсолютная инструментальная погрешность Δиx связана с классом точности прибора. Абсолютные инструментальные погрешности некоторых средств измерений представлены в таблице 1.
| Средства измерений | Диапазон измерений | Абсолютная инструментальная погрешность |
| Линейки: металлические деревянные пластмассовые |
150, 300, 500 мм 400, 500, 750 мм 200, 250, 300 мм |
0,1 мм 0,5 мм 1 мм |
| Лента измерительная | 150 см | 0,5 см |
| Мензурки 2-го класса | 100, 200, 250 см3 | 5 см3 |
| Амперметр школьный | 2 А | 0,05 А |
| Миллиамперметр | от 0 до Imax | 4 % максимального предела измерений Imax |
| Вольтметр школьный | 6 В | 0,15 В |
| Термометр лабораторный | 100 °С | 1 °С |
| Барометр-анероид | 720–780 мм рт. ст. | 3 мм рт. ст. |
| Штангенциркули с ценой деления 0,1; 0,05 мм | 155, 250, 350 мм | 0,1; 0,05 мм в соответствии с ценой деления нониуса |
| Микрометры с ценой деления 0,01 мм | 0–25, 25–50, 50–75 мм | 0,004 мм |
Абсолютная погрешность отсчёта Δоx связана с дискретностью шкалы прибора. Если величину измеряют с точностью до целого деления шкалы прибора, то погрешность отсчёта принимают равной цене деления. Если при измерении значение величины округляют до половины деления шкалы, то погрешность отсчёта принимают равной половине цены деления.
Абсолютная погрешность определяет значение интервала, в котором лежит истинное значение измеренной величины:
Относительную погрешность прямого измерения определяют отношением абсолютной погрешности к значению измеряемой величины:
Относительная погрешность характеризует точность измерения: чем она меньше, тем точность измерения выше.
Косвенное измерение — определение значения физической величины с использованием формулы, связывающей её с другими величинами, измеренными непосредственно с помощью приборов.
Одним из методов определения погрешности косвенных измерений является метод границ погрешностей. Формулы для вычисления абсолютных и относительных погрешностей косвенных измерений методом границ погрешностей представлены в таблице 2.
| Вид функции y | Абсолютная погрешность Δy | Относительная погрешность  |
| x1 + x2 | Δx1 + Δx2 |  |
| x1 − x2 | Δx1 + Δx2 | |
| Cx | CΔx |  |
| x1x2 | |x1| Δx2 + |x2| Δx1 |  |
 |
 |
|
| xn | |n||x|n−1Δx |  |
| lnx | |
 |
| sinx | |cosx| Δx |  |
| cosx | |sinx| Δx | |tgx| Δx |
| tgx |  |
 |
Абсолютную погрешность табличных величин и фундаментальных физических постоянных определяют как половину единицы последнего разряда значения величины.
Расчет погрешности измерений
Измерения
называются прямыми, если значения
величин определяются приборами
непосредственно (например, измерение
длины линейкой, определение времени
секундомером и т. д.). Измерения называютсякосвенными, если значение измеряемой
величины определяется посредством
прямых измерений других величин, которые
связаны с измеряемой определенной
зависимостью.
Случайные погрешности при прямых измерениях
Абсолютная
и относительная погрешность. Пусть
проведеноNизмерений
одной и той же величиныxв отсутствии систематической погрешности.
Отдельные результаты измерений имеют
вид:x1,x2,
…,xN.
В качестве наилучшего выбирается среднее
значение измеренной величины:
.
(1)
Абсолютной
погрешностьюединичного измерения
называется разность вида:
.
Среднее
значение абсолютной погрешности Nединичных измерений:
(2)
называется
средней абсолютной погрешностью.
Относительной
погрешностью называется отношение
средней абсолютной погрешности к
среднему значению измеряемой величины:
.
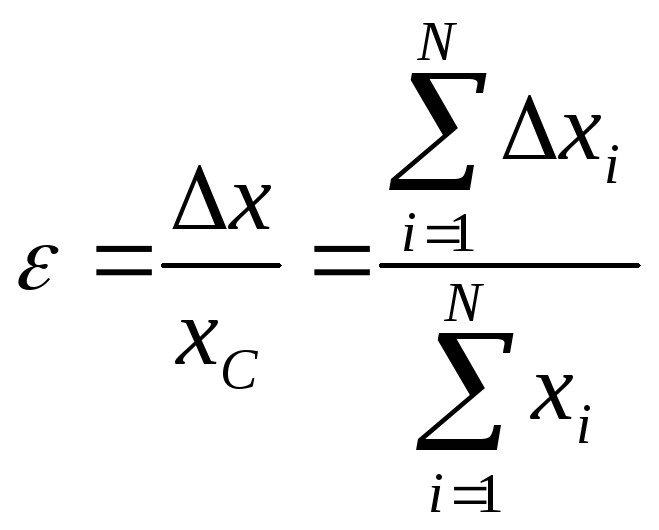
(3)
Приборные погрешности при прямых измерениях
-
Если
нет особых указаний, погрешность прибора
равна половине его цены деления (линейка,
мензурка). -
Погрешность
приборов, снабженных нониусом, равна
цене деления нониуса (микрометр – 0,01
мм, штангенциркуль – 0,1 мм). -
Погрешность
табличных величин равна половине
единицы последнего разряда (пять единиц
следующего порядка за последней значащей
цифрой). -
Погрешность
электроизмерительных приборов
вычисляется согласно классу точности
С,
указанному на шкале прибора:
Например:
и
,
где Umax
и Imax
– предел измерения прибора.
-
Погрешность
приборов с цифровой индикацией равна
единице последнего разряда индикации.
После оценки
случайной и приборной погрешностей в
расчет принимается та, значение которой
больше.
Вычисление погрешностей при косвенных измерениях
Большинство
измерений являются косвенными. В этом
случае искомая величина Х является
функцией нескольких переменных а,
b,
c…,
значения которых можно найти прямыми
измерениями: Х = f(a,b,c…).
Среднее арифметическое
результата косвенных измерений будет
равно:
X
= f(a,b,c…).
Одним из способов
вычисления погрешности является способ
дифференцирования натурального логарифма
функции Х = f(a,b,c…).
Если, например, искомая величина Х
определяется соотношением Х =
,
то после логарифмирования получаем:lnX
= lna
+ lnb
+ ln(c+d).
Дифференциал этого
выражения имеет вид:
.
Применительно к
вычислению приближенных значений его
можно записать для относительной
погрешности в виде:
=
.
(4)
Абсолютная
погрешность при этом рассчитывается
по формуле:
Х = Х(5)
Таким
образом, расчет погрешностей и вычисление
результата при косвенных измерениях
производят в следующем порядке:
1)
Проводят измерения всех величин, входящих
в исходную формулу для вычисления
конечного результата.
2)
Вычисляют средние арифметические
значения каждой измеряемой величины и
их абсолютные погрешности.
3)
Подставляют в исходную формулу средние
значения всех измеренных величин и
вычисляют среднее значение искомой
величины:
X
= f(a,b,c…).
4)
Логарифмируют исходную формулу Х =
f(a,b,c…)
и записывают выражение для относительной
погрешности в виде формулы (4).
5)
Рассчитывают относительную погрешность
=
.
6) Рассчитывают
абсолютную погрешность результата по
формуле (5).
7) Окончательный
результат записывают в виде:
-
Х
= ХсрХ =
…%
Абсолютные
и относительные погрешности простейших
функций приведены в таблице:
|
Функция |
Абсолютная погрешность |
Относительная погрешность |
|
a+b |
a+b |
|
|
a-b |
a+b |
|
|
ab |
ab+ba |
|
|
|
|
|
|
|
|
|
|
sin a |
|
|
|
cos a |
|
|
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
При измерении разных физических величин мы получаем их числовые значения с определенной точностью. Например, при определении размеров листа бумаги (длины, ширины) мы можем указать их с точностью до миллиметра; размеры стола – с точностью до сантиметра, размеры дома, стадиона – с точностью до метра.
Нет необходимости указывать размеры стола с точностью до миллиметра, а размеры стадиона с точностью до сантиметра или миллиметра. Мы сами в каждой ситуации, опыте и эксперименте определяем, с какой точностью нам нужны данные физические величины. Однако очень важно оценивать, насколько точно мы определяем физическую величину, какую ошибку (погрешность) в ее измерении допускаем.
При измерении мы не можем определить истинное значение измеряемой величины, а только пределы, в которых она находится.
Пример:
Измерим ширину стола рулеткой с сантиметровыми и миллиметровыми делениями на ней (рис. 5.1). Значение наименьшего деления шкалы называют ценой деления и обозначают буквой С. Видно, что цена деления рулетки С = 1 мм (или 0,1 см).
Совместим нулевое деление рулетки с краем стола и посмотрим, с каким значением
шкалы линейки совпадает второй край стола (рис. 5.1). Видно, что ширина стола составляет чуть больше 70 см и 6 мм, или 706 мм. Но результат наших измерений мы запишем с точностью до 1 мм, то есть L = 706 мм.
Абсолютная погрешность измерения ∆ (ДЕЛЬТА)
Из рис. 5.1 видно, что мы допускаем определенную погрешность и определить ее «на глаз» достаточно трудно. Эта погрешность составляет не более половины цены деления шкалы рулетки. Эту погрешность называют погрешностью измерения и помечают ∆L («дельта эль»). В данном эксперименте ее можно записать
Сам результат измерения принято записывать таким образом: ширина стола L = (706,0 ± 0,5) мм, читают: 706 плюс-минус 0,5 мм. Эти 0,5 мм в нашем примере называют абсолютной погрешностью. Значения измеряемой величины (706,0 мм) и абсолютной погрешности (0,5 мм) должны иметь одинаковое количество цифр после запятой, то есть нельзя записывать 706 мм ± 0,5 мм.
Такая запись результата измерения означает, что истинное значение измеряемой величины находится между 705,5 мм и 706,5 мм, то есть 705,5 мм ≤ L ≤ 706,5 мм.
Относительная погрешность измерения ε (ЭПСИЛОН)
Иногда важно знать, какую часть составляет наша погрешность от значения
измеряемой величины. Для этого разделим 0,5 мм на 706 мм. В результате получим: 
. То есть наша ошибка составляет 0,0007 долю ширины стола, или 0,0007 · 100% = 0,07%. Это свидетельствует о достаточно высокой точности измерения. Эту погрешность называют относительной и обозначают греческой буквой (эпсилон):
(5.1)
Относительная погрешность измерения свидетельствует о качестве измерения. Если длина какогото предмета равна 5 мм, а точность измерения – плюс-минус 0,5 мм, то относительная погрешность будет составлять уже 10%.
Стандартная запись результата измерений и выводы
Таким образом, абсолютная погрешность в примере 5.1. составляет ∆L = 0,5 мм, а результат измерений следует записать в стандартном виде: L = (706,0 
0,5) мм — Опыт выполнен с относительной погрешностью 0,0007 или 0,07%.
На точность измерения влияет много факторов, в частности:
- При совмещении края стола с делением шкалы рулетки мы неминуемо допускаем погрешность, поскольку делаем это «на глаз» — смотреть можно под разными углами.
- Не вполне ровно установили рулетку.
- Наша рулетка является копией эталона и может несколько отличаться от оригинала.
Все это необходимо учитывать при проведении измерений.
Итоги:
- Измерения в физике всегда неточны, и надо знать пределы погрешности измерений, чтобы понимать, насколько можно доверять результатам.
- Абсолютную погрешность измерения можно определить как половину цены деления шкалы измерительного прибора.
- Относительная погрешность есть частное от деления абсолютной погрешности на значение измеряемой величины:
и указывает на качество измерения. Ее можно выразить в процентах.
Измерительные приборы
Устройства, с помощью которых измеряют физические величины, называют измерительными приборами.
Простейший и хорошо известный вам измерительный прибор — линейка с делениями. На ее примере вы видите, что у измерительного прибора есть шкала, на которой нанесены деления, причем возле некоторых делений написано соответствующее значение физической величины. Так, значения длины в сантиметрах нанесены на линейке возле каждого десятого деления (рис. 3.11). Значения же, соответствующие «промежуточным» делениям шкалы, можно найти с помощью простого подсчета.
Разность значений физической величины, которые соответствуютближайшим делениям шкалы, называют ценой деления прибора. Ёе находят так: берут ближайшие деления, возле которых написаны значения величины, и делят разность этих значений на количество промежутков между делениями, расположенными между ними.
Например, ближайшие сантиметровые деления на линейке разделены на десять промежутков. Значит, цена деления линейки равна 0,1 см = 1 мм.
Как определяют единицы длины и времени
В старину мерами длины служили большей частью размеры человеческого тела и его частей. Дело в том, что собственное тело очень удобно как «измерительный прибор», так как оно всегда «рядом». И вдобавок «человек есть мера всех вещей»: мы считаем предмет большим или малым, сравнивая его с собой.
Так, длину куска ткани измеряли «локтями», а мелкие предметы — «дюймами» (это слово происходит от голландского слова, которое означает «большой палец»).
Однако человеческое тело в качестве измерительного прибора имеет существенный недостаток: размеры тела и его частей у разных людей заметно отличаются. Поэтому ученые решили определить единицу длины однозначно и точно. Международным соглашением было принято, что один метр равен пути, который проходит свет в вакууме за 1/299792458 с. А секунду определяют с помощью атомных часов, которые сегодня являются самыми точными.
Можно ли расстояние измерять годами
Именно так и измеряют очень большие расстояния — например, расстояния между звездами! Но при этом речь идет не о годах как промежутках времени, а о «световых годах». А один световой год — это расстояние, которое проходит свет за один земной год. По нашим земным меркам это очень большое расстояние — чтобы убедиться в этом, попробуйте выразить его в километрах! А теперь вообразите себе, что расстояние от Солнца до ближайшей к нему звезды составляет больше четырех световых лет! И по астрономическим масштабам это совсем небольшое расстояние: ведь с помощью современных телескопов астрономы тщательно изучают звезды, расстояние до которых составляет много тысяч световых лет!
Что надо знать об измерительных приборах
Приступая к измерениям, необходимо, прежде всего, подобрать приборы. Что надо знать об измерительных приборах?
Минимальное (нижний предел) и максимальное (верхний предел) значения шкалы прибора — это пределы измерения. Чаще всего предел измерения один, но может быть и два. Например, линейка имеет один предел — верхний. У линейки на рисунке 32 он равен 25 см. У термометра на рисунке 33 два предела: верхний предел измерения температуры равен +50 °С; нижний -40 °С.
На рисунке 34 изображены три линейки с одинаковыми верхними пределами (25 см). По эти линейки измеряют длину с различной точностью. Наиболее точные результаты измерений дает линейка 7, наименее точные — линейка 3. Что же такое точность измерений и от чего она зависит? Для ответа на эти вопросы рассмотрим сначала понятие цена деления шкалы прибора.
Цена деления — это значение наименьшего деления шкалы прибора.
Как определить цену деления шкалы? Для этого необходимо:
- выбрать на шкале линейки два соседних значения, например 3 см и 4 см;
- подсчитать число делений (не штрихов!) между этими значениями; например, на линейке 1 (см. рис. 34) число делений между значениями 3 см и 4 см равно 10;
- вычесть из большего значения меньшее (4 см — 3 см = 1 см) и результат разделить на число делений.
Полученное значение и будет ценой деления шкалы прибора. Обозначим ее буквой С.
Точно так же можно определить и цену деления шкалы мензурок 1 и 2 (рис. 35). Цена деления шкалы мензурки 1:
Цена деления шкалы мензурки 2:
А какими линейкой и мензуркой можно измерить точнее?
Измерим один и тот же объем мензуркой 1 и мензуркой 2. Но показаниям шкал в мензурке 1 объем воды V = 35 мл; в мензурке 2 — V = 37 мл.
Понятно, что точнее измерен объем воды мензуркой 2, цена деления которой меньше 
Значит, чем меньше цена деления шкалы, тем точнее можно измерить данным прибором. Говорят: мензуркой 1 мы измерили объем с точностью до 5 мл (сравните с ценой деления шкалы 
), мензуркой 2 — с точностью до 1 мл (сравните с ценой деления 
). Точность измерения температуры термометрами 1 и 2 (рис. 36) определите самостоятельно.
Итак, любым прибором, имеющим шкалу, измерить физическую величину можно с точностью, не превышающей цены деления шкалы.
Линейкой 1 (см. рис. 34) можно измерить длину с точностью до 1 мм. Точность измерения длины линейками 2 и 3 определите самостоятельно.
Главные выводы:
- Верхний и нижний пределы измерения — это максимальное и минимальное значения шкалы прибора.
- Цена деления шкалы равна значению наименьшего деления шкалы.
- Чем меньше цена деления шкалы, тем точнее будут проведены измерения данным прибором.
Для любознательных:
В истории науки есть немало случаев, когда повышение точности измерений давало толчок к новым открытиям. Более точные измерения плотности азота, выделенного из воздуха, позволили в 1894 г. открыть новый инертный газ — аргон. Повышение точности измерений плотности воды привело к открытию в 1932 г. одной из разновидностей тяжелых атомов водорода — дейтерия. Позже дейтерий вошел в состав ядерного горючего. Оценить расстояния до звезд и создать их точные каталоги ученые смогли благодаря повышению точности при измерении положения ярких звезд на небе.
- Заказать решение задач по физике
Пример решения задачи
Для измерения величины угла используют транспортир. Определите: 1) цену деления каждой шкалы транспортира, изображенного на рисунке 38; 2) значение угла BАС, используя каждую шкалу; укажите точность измерения угла ВАС в каждом случае.
Решение:
1) Цена деления нижней шкалы:
Цена деления средней шкалы:
Цена деления верхней шкалы:
2) Определенный но нижней шкале с точностью до 10° 
определенный по средней шкале с точностью до 5° 
определенный по верхней шкале с точностью до 1° 
- Определение площади и объема
- Связь физики с другими науками
- Макромир, мегамир и микромир в физике
- Пространство и время
- Как зарождалась физика
- Единая физическая картина мира
- Физика и научно-технический прогресс
- Физические величины и их единицы измерения