Ошибки I и II рода при проверке гипотез, мощность
Общий обзор
Принятие неправильного решения
Мощность и связанные факторы
Проверка множественных гипотез
Общий обзор
Большинство проверяемых гипотез сравнивают между собой группы объектов, которые испытывают влияние различных факторов.
Например, можно сравнить эффективность двух видов лечения, чтобы сократить 5-летнюю смертность от рака молочной железы. Для данного исхода (например, смерть) сравнение, представляющее интерес (например, различные показатели смертности через 5 лет), называют эффектом или, если уместно, эффектом лечения.
Нулевую гипотезу выражают как отсутствие эффекта (например 5-летняя смертность от рака молочной железы одинаковая в двух группах, получающих разное лечение); двусторонняя альтернативная гипотеза будет означать, что различие эффектов не равно нулю.
Критериальная проверка гипотезы дает возможность определить, достаточно ли аргументов, чтобы отвергнуть нулевую гипотезу. Можно принять только одно из двух решений:
- отвергнуть нулевую гипотезу и принять альтернативную гипотезу
- остаться в рамках нулевой гипотезы
Важно: В литературе достаточно часто встречается понятие «принять нулевую гипотезу». Хотелось бы внести ясность, что со статистической точки зрения принять нулевую гипотезу невозможно, т.к. нулевая гипотеза представляет собой достаточно строгое утверждение (например, средние значения в сравниваемых группах равны ).
Поэтому фразу о принятии нулевой гипотезы следует понимать как то, что мы просто остаемся в рамках гипотезы.
Принятие неправильного решения
Возможно неправильное решение, когда отвергают/не отвергают нулевую гипотезу, потому что есть только выборочная информация.
| Верная гипотеза | |||
|---|---|---|---|
| H0 | H1 | ||
| Результат
применения критерия |
H0 | H0 верно принята | H0 неверно принята
(Ошибка второго рода) |
| H1 | H0 неверно отвергнута
(Ошибка первого рода) |
H0 верно отвергнута |
Ошибка 1-го рода: нулевую гипотезу отвергают, когда она истинна, и делают вывод, что имеется эффект, когда в действительности его нет. Максимальный шанс (вероятность) допустить ошибку 1-го рода обозначается α (альфа). Это уровень значимости критерия; нулевую гипотезу отвергают, если наше значение p ниже уровня значимости, т. е., если p < α.
Следует принять решение относительно значения а прежде, чем будут собраны данные; обычно назначают условное значение 0,05, хотя можно выбрать более ограничивающее значение, например 0,01.
Шанс допустить ошибку 1-го рода никогда не превысит выбранного уровня значимости, скажем α = 0,05, так как нулевую гипотезу отвергают только тогда, когда p< 0,05. Если обнаружено, что p > 0,05, то нулевую гипотезу не отвергнут и, следовательно, не допустят ошибки 1-го рода.
Ошибка 2-го рода: не отвергают нулевую гипотезу, когда она ложна, и делают вывод, что нет эффекта, тогда как в действительности он существует. Шанс возникновения ошибки 2-го рода обозначается β (бета); а величина (1-β) называется мощностью критерия.
Следовательно, мощность — это вероятность отклонения нулевой гипотезы, когда она ложна, т.е. это шанс (обычно выраженный в процентах) обнаружить реальный эффект лечения в выборке данного объема как статистически значимый.
В идеале хотелось бы, чтобы мощность критерия составляла 100%; однако это невозможно, так как всегда остается шанс, хотя и незначительный, допустить ошибку 2-го рода.
К счастью, известно, какие факторы влияют на мощность и, таким образом, можно контролировать мощность критерия, рассматривая их.
Мощность и связанные факторы
Планируя исследование, необходимо знать мощность предложенного критерия. Очевидно, можно начинать исследование, если есть «хороший» шанс обнаружить уместный эффект, если таковой существует (под «хорошим» мы подразумеваем, что мощность должна быть по крайней мере 70-80%).
Этически безответственно начинать исследование, у которого, скажем, только 40% вероятности обнаружить реальный эффект лечения; это бесполезная трата времени и денежных средств.
Ряд факторов имеют прямое отношение к мощности критерия.
Объем выборки: мощность критерия увеличивается по мере увеличения объема выборки. Это означает, что у большей выборки больше возможностей, чем у незначительной, обнаружить важный эффект, если он существует.
Когда объем выборки небольшой, у критерия может быть недостаточно мощности, чтобы обнаружить отдельный эффект. Эти методы также можно использовать для оценки мощности критерия для точно установленного объема выборки.
Вариабельность наблюдений: мощность увеличивается по мере того, как вариабельность наблюдений уменьшается.
Интересующий исследователя эффект: мощность критерия больше для более высоких эффектов. Критерий проверки гипотез имеет больше шансов обнаружить значительный реальный эффект, чем незначительный.
Уровень значимости: мощность будет больше, если уровень значимости выше (это эквивалентно увеличению допущения ошибки 1-го рода, α, а допущение ошибки 2-го рода, β, уменьшается).
Таким образом, вероятнее всего, исследователь обнаружит реальный эффект, если на стадии планирования решит, что будет рассматривать значение р как значимое, если оно скорее будет меньше 0,05, чем меньше 0,01.
Обратите внимание, что проверка ДИ для интересующего эффекта указывает на то, была ли мощность адекватной. Большой доверительный интервал следует из небольшой выборки и/или набора данных с существенной вариабельностью и указывает на недостаточную мощность.
Проверка множественных гипотез
Часто нужно выполнить критериальную проверку значимости множественных гипотез на наборе данных с многими переменными или существует более двух видов лечения.
Ошибка 1-го рода драматически увеличивается по мере увеличения числа сравнений, что приводит к ложным выводам относительно гипотез. Следовательно, следует проверить только небольшое число гипотез, выбранных для достижения первоначальной цели исследования и точно установленных априорно.
Можно использовать какую-нибудь форму апостериорного уточнения значения р, принимая во внимание число выполненных проверок гипотез.
Например, при подходе Бонферрони (его часто считают довольно консервативным) умножают каждое значение р на число выполненных проверок; тогда любые решения относительно значимости будут основываться на этом уточненном значении р.
Связанные определения:
p-уровень
Альтернативная гипотеза, альтернатива
Альфа-уровень
Бета-уровень
Гипотеза
Двусторонний критерий
Критерий для проверки гипотезы
Критическая область проверки гипотезы
Мощность
Мощность исследования
Мощность статистического критерия
Нулевая гипотеза
Односторонний критерий
Ошибка I рода
Ошибка II рода
Статистика критерия
Эквивалентные статистические критерии
В начало
Содержание портала
Ошибки первого и второго рода
Выдвинутая гипотеза
может быть правильной или неправильной,
поэтому возникает необходимость её
проверки. Поскольку проверку производят
статистическими методами, её называют
статистической. В итоге статистической
проверки гипотезы в двух случаях может
быть принято неправильное решение, т.
е. могут быть допущены ошибки двух родов.
Ошибка первого
рода состоит в том, что будет отвергнута
правильная гипотеза.
Ошибка второго
рода состоит в том, что будет принята
неправильная гипотеза.
Подчеркнём, что
последствия этих ошибок могут оказаться
весьма различными. Например, если
отвергнуто правильное решение «продолжать
строительство жилого дома», то эта
ошибка первого рода повлечёт материальный
ущерб: если же принято неправильное
решение «продолжать строительство»,
несмотря на опасность обвала стройки,
то эта ошибка второго рода может повлечь
гибель людей. Можно привести примеры,
когда ошибка первого рода влечёт более
тяжёлые последствия, чем ошибка второго
рода.
Замечание 1.
Правильное решение может быть принято
также в двух случаях:
-
гипотеза принимается,
причём и в действительности она
правильная; -
гипотеза отвергается,
причём и в действительности она неверна.
Замечание 2.
Вероятность совершить ошибку первого
рода принято обозначать через
;
её называют уровнем значимости. Наиболее
часто уровень значимости принимают
равным 0,05 или 0,01. Если, например, принят
уровень значимости, равный 0,05, то это
означает, что в пяти случаях из ста
имеется риск допустить ошибку первого
рода (отвергнуть правильную гипотезу).
Статистический
критерий проверки нулевой гипотезы.
Наблюдаемое значение критерия
Для проверки
нулевой гипотезы используют специально
подобранную случайную величину, точное
или приближённое распределение которой
известно. Обозначим эту величину в целях
общности через
.
Статистическим
критерием
(или просто критерием) называют случайную
величину
,
которая служит для проверки нулевой
гипотезы.
Например, если
проверяют гипотезу о равенстве дисперсий
двух нормальных генеральных совокупностей,
то в качестве критерия
принимают отношение исправленных
выборочных дисперсий:
Эта величина
случайная, потому что в различных опытах
дисперсии принимают различные, наперёд
неизвестные значения, и распределена
по закону Фишера – Снедекора.
Для проверки
гипотезы по данным выборок вычисляют
частные значения входящих в критерий
величин и таким образом получают частное
(наблюдаемое) значение критерия.
Наблюдаемым
значением
называют значение критерия, вычисленное
по выборкам. Например, если по двум
выборкам найдены исправленные выборочные
дисперсиии
,
то наблюдаемое значение критерия
Критическая
область. Область принятия гипотезы.
Критические точки
После выбора
определённого критерия множество всех
его возможных значений разбивают на
два непересекающихся подмножества:
одно из них содержит значения критерия,
при которых нулевая гипотеза отвергается,
а другая – при которых она принимается.
Критической
областью называют совокупность значений
критерия, при которых нулевую гипотезу
отвергают.
Областью принятия
гипотезы (областью допустимых значений)
называют совокупность значений критерия,
при которых гипотезу принимают.
Основной принцип
проверки статистических гипотез можно
сформулировать так: если наблюдаемое
значение критерия принадлежит критической
области – гипотезу отвергают, если
наблюдаемое значение критерия принадлежит
области принятия гипотезы – гипотезу
принимают.
Поскольку критерий
— одномерная случайная величина, все её
возможные значения принадлежат некоторому
интервалу. Поэтому критическая область
и область принятия гипотезы также
являются интервалами и, следовательно,
существуют точки, которые их разделяют.
Критическими
точками (границами)
называют точки, отделяющие критическую
область от области принятия гипотезы.
Различают
одностороннюю (правостороннюю или
левостороннюю) и двустороннюю критические
области.
Правосторонней
называют критическую область, определяемую
неравенством
>
,
где— положительное число.
Левосторонней
называют критическую область, определяемую
неравенством
<
,
где— отрицательное число.
Односторонней
называют правостороннюю или левостороннюю
критическую область.
Двусторонней
называют критическую область, определяемую
неравенствами
где
.
В частности, если
критические точки симметричны относительно
нуля, двусторонняя критическая область
определяется неравенствами ( в
предположении, что
>0):
,
или равносильным неравенством
.
Отыскание
правосторонней критической области
Как найти критическую
область? Обоснованный ответ на этот
вопрос требует привлечения довольно
сложной теории. Ограничимся её элементами.
Для определённости начнём с нахождения
правосторонней критической области,
которая определяется неравенством
>
,
где>0.
Видим, что для отыскания правосторонней
критической области достаточно найти
критическую точку. Следовательно,
возникает новый вопрос: как её найти?
Для её нахождения
задаются достаточной малой вероятностью
– уровнем значимости
.
Затем ищут критическую точку,
исходя из требования, чтобы при условии
справедливости нулевой гипотезы
вероятность того, критерийпримет значение, большее
,
была равна принятому уровню значимости:
Р(>
)=
.
Для каждого критерия
имеются соответствующие таблицы, по
которым и находят критическую точку,
удовлетворяющую этому требованию.
Замечание 1.
Когда
критическая точка уже найдена, вычисляют
по данным выборок наблюдаемое значение
критерия и, если окажется, что
>
,
то нулевую гипотезу отвергают; если же<
,
то нет оснований, чтобы отвергнуть
нулевую гипотезу.
Пояснение. Почему
правосторонняя критическая область
была определена, исходя из требования,
чтобы при справедливости нулевой
гипотезы выполнялось соотношение
Р(>
)=
?
(*)
Поскольку вероятность
события
>
мала (
— малая вероятность), такое событие при
справедливости нулевой гипотезы, в силу
принципа практической невозможности
маловероятных событий, в единичном
испытании не должно наступить. Если всё
же оно произошло, т.е. наблюдаемое
значение критерия оказалось больше,
то это можно объяснить тем, что нулевая
гипотеза ложна и, следовательно, должна
быть отвергнута. Таким образом, требование
(*) определяет такие значения критерия,
при которых нулевая гипотеза отвергается,
а они и составляют правостороннюю
критическую область.
Замечание 2.
Наблюдаемое значение критерия может
оказаться большим
не потому, что нулевая гипотеза ложна,
а по другим причинам (малый объём выборки,
недостатки методики эксперимента и
др.). В этом случае, отвергнув правильную
нулевую гипотезу, совершают ошибку
первого рода. Вероятность этой ошибки
равна уровню значимости.
Итак, пользуясь требованием (*), мы с
вероятностьюрискуем совершить ошибку первого рода.
Замечание 3. Пусть
нулевая гипотеза принята; ошибочно
думать, что тем самым она доказана.
Действительно, известно, что один пример,
подтверждающий справедливость некоторого
общего утверждения, ещё не доказывает
его. Поэтому более правильно говорить,
«данные наблюдений согласуются с нулевой
гипотезой и, следовательно, не дают
оснований её отвергнуть».
На практике для
большей уверенности принятия гипотезы
её проверяют другими способами или
повторяют эксперимент, увеличив объём
выборки.
Отвергают гипотезу
более категорично, чем принимают.
Действительно, известно, что достаточно
привести один пример, противоречащий
некоторому общему утверждению, чтобы
это утверждение отвергнуть. Если
оказалось, что наблюдаемое значение
критерия принадлежит критической
области, то этот факт и служит примером,
противоречащим нулевой гипотезе, что
позволяет её отклонить.
Отыскание
левосторонней и двусторонней критических
областей***
Отыскание
левосторонней и двусторонней критических
областей сводится (так же, как и для
правосторонней) к нахождению соответствующих
критических точек. Левосторонняя
критическая область определяется
неравенством
<
(
<0).
Критическую точку находят, исходя из
требования, чтобы при справедливости
нулевой гипотезы вероятность того, что
критерий примет значение, меньшее,
была равна принятому уровню значимости:
Р(<
)=
.
Двусторонняя
критическая область определяется
неравенствами
Критические
точки находят, исходя из требования,
чтобы при справедливости нулевой
гипотезы сумма вероятностей того, что
критерий примет значение, меньшееили большее
,
была равна принятому уровню значимости:
.
(*)
Ясно, что критические
точки могут быть выбраны бесчисленным
множеством способов. Если же распределение
критерия симметрично относительно нуля
и имеются основания (например, для
увеличения мощности) выбрать симметричные
относительно нуля точки (-
)и
(
>0),
то
Учитывая (*), получим
.
Это соотношение
и служит для отыскания критических
точек двусторонней критической области.
Критические точки находят по соответствующим
таблицам.
Дополнительные
сведения о выборе критической области.
Мощность критерия
Мы строили
критическую область, исходя из требования,
чтобы вероятность попадания в неё
критерия была равна
при условии, что нулевая гипотеза
справедлива. Оказывается целесообразным
ввести в рассмотрение вероятность
попадания критерия в критическую область
при условии, что нулевая гипотеза неверна
и, следовательно, справедлива конкурирующая.
Мощностью критерия
называют вероятность попадания критерия
в критическую область при условии, что
справедлива конкурирующая гипотеза.
Другими словами, мощность критерия есть
вероятность того, что нулевая гипотеза
будет отвергнута, если верна конкурирующая
гипотеза.
Пусть для проверки
гипотезы принят определённый уровень
значимости и выборка имеет фиксированный
объём. Остаётся произвол в выборе
критической области. Покажем, что её
целесообразно построить так, чтобы
мощность критерия была максимальной.
Предварительно убедимся, что если
вероятность ошибки второго рода (принять
неправильную гипотезу) равна
,
то мощность равна 1-.
Действительно, если— вероятность ошибки второго рода, т.е.
события «принята нулевая гипотеза,
причём справедливо конкурирующая», то
мощность критерия равна 1 —.
Пусть мощность 1
—
возрастает; следовательно, уменьшается
вероятностьсовершить ошибку второго рода. Таким
образом, чем мощность больше, тем
вероятность ошибки второго рода меньше.
Итак, если уровень
значимости уже выбран, то критическую
область следует строить так, чтобы
мощность критерия была максимальной.
Выполнение этого требования должно
обеспечить минимальную ошибку второго
рода, что, конечно, желательно.
Замечание 1.
Поскольку вероятность события «ошибка
второго рода допущена» равна
,
то вероятность противоположного события
«ошибка второго рода не допущена» равна
1 —,
т.е. мощности критерия. Отсюда следует,
что мощность критерия есть вероятность
того, что не будет допущена ошибка
второго рода.
Замечание 2. Ясно,
что чем меньше вероятности ошибок
первого и второго рода, тем критическая
область «лучше». Однако при заданном
объёме выборки уменьшить одновременно
и
невозможно; если уменьшить
,
тобудет возрастать. Например, если принять
=0,
то будут приниматься все гипотезы, в
том числе и неправильные, т.е. возрастает
вероятностьошибки второго рода.
Как же выбрать
наиболее целесообразно? Ответ на этот
вопрос зависит от «тяжести последствий»
ошибок для каждой конкретной задачи.
Например, если ошибка первого рода
повлечёт большие потери, а второго рода
– малые, то следует принять возможно
меньшее.
Если
уже выбрано, то, пользуясь теоремой Ю.
Неймана и Э.Пирсона, можно построить
критическую область, для которойбудет минимальным и, следовательно,
мощность критерия максимальной.
Замечание 3.
Единственный способ одновременного
уменьшения вероятностей ошибок первого
и второго рода состоит в увеличении
объёма выборок.
Соседние файлы в папке Лекции 2 семестр
- #
- #
- #
- #
Проверка корректности А/Б тестов
Хабр, привет! Сегодня поговорим о том, что такое корректность статистических критериев в контексте А/Б тестирования. Узнаем, как проверить, является критерий корректным или нет. Разберём пример, в котором тест Стьюдента не работает.
Меня зовут Коля, я работаю аналитиком данных в X5 Tech. Мы с Сашей продолжаем писать серию статей по А/Б тестированию, это наша третья статья. Первые две можно посмотреть тут:
-
Стратификация. Как разбиение выборки повышает чувствительность A/Б теста
-
Бутстреп и А/Б тестирование
Корректный статистический критерий
В А/Б тестировании при проверке гипотез с помощью статистических критериев можно совершить одну из двух ошибок:
-
ошибку первого рода – отклонить нулевую гипотезу, когда на самом деле она верна. То есть сказать, что эффект есть, хотя на самом деле его нет;
-
ошибку второго рода – не отклонить нулевую гипотезу, когда на самом деле она неверна. То есть сказать, что эффекта нет, хотя на самом деле он есть.
Совсем не ошибаться нельзя. Чтобы получить на 100% достоверные результаты, нужно бесконечно много данных. На практике получить столько данных затруднительно. Если совсем не ошибаться нельзя, то хотелось бы ошибаться не слишком часто и контролировать вероятности ошибок.
В статистике ошибка первого рода считается более важной. Поэтому обычно фиксируют допустимую вероятность ошибки первого рода, а затем пытаются минимизировать вероятность ошибки второго рода.
Предположим, мы решили, что допустимые вероятности ошибок первого и второго рода равны 0.1 и 0.2 соответственно. Будем называть статистический критерий корректным, если его вероятности ошибок первого и второго рода равны допустимым вероятностям ошибок первого и второго рода соответственно.
Как сделать критерий, в котором вероятности ошибок будут равны допустимым вероятностям ошибок?
Вероятность ошибки первого рода по определению равна уровню значимости критерия. Если уровень значимости положить равным допустимой вероятности ошибки первого рода, то вероятность ошибки первого рода должна стать равной допустимой вероятности ошибки первого рода.
Вероятность ошибки второго рода можно подогнать под желаемое значение, меняя размер групп или снижая дисперсию в данных. Чем больше размер групп и чем ниже дисперсия, тем меньше вероятность ошибки второго рода. Для некоторых гипотез есть готовые формулы оценки размера групп, при которых достигаются заданные вероятности ошибок.
Например, формула оценки необходимого размера групп для гипотезы о равенстве средних:
где и
– допустимые вероятности ошибок первого и второго рода,
– ожидаемый эффект (на сколько изменится среднее),
и
– стандартные отклонения случайных величин в контрольной и экспериментальной группах.
Проверка корректности
Допустим, мы работаем в онлайн-магазине с доставкой. Хотим исследовать, как новый алгоритм ранжирования товаров на сайте влияет на среднюю выручку с покупателя за неделю. Продолжительность эксперимента – одна неделя. Ожидаемый эффект равен +100 рублей. Допустимая вероятность ошибки первого рода равна 0.1, второго рода – 0.2.
Оценим необходимый размер групп по формуле:
import numpy as np
from scipy import stats
alpha = 0.1 # допустимая вероятность ошибки I рода
beta = 0.2 # допустимая вероятность ошибки II рода
mu_control = 2500 # средняя выручка с пользователя в контрольной группе
effect = 100 # ожидаемый размер эффекта
mu_pilot = mu_control + effect # средняя выручка с пользователя в экспериментальной группе
std = 800 # стандартное отклонение
# исторические данные выручки для 10000 клиентов
values = np.random.normal(mu_control, std, 10000)
def estimate_sample_size(effect, std, alpha, beta):
"""Оценка необходимого размер групп."""
t_alpha = stats.norm.ppf(1 - alpha / 2, loc=0, scale=1)
t_beta = stats.norm.ppf(1 - beta, loc=0, scale=1)
var = 2 * std ** 2
sample_size = int((t_alpha + t_beta) ** 2 * var / (effect ** 2))
return sample_size
estimated_std = np.std(values)
sample_size = estimate_sample_size(effect, estimated_std, alpha, beta)
print(f'оценка необходимого размера групп = {sample_size}')оценка необходимого размера групп = 784Чтобы проверить корректность, нужно знать природу случайных величин, с которыми мы работаем. В этом нам помогут исторические данные. Представьте, что мы перенеслись в прошлое на несколько недель назад и запустили эксперимент с таким же дизайном, как мы планировали запустить его сейчас. Дизайн – это совокупность параметров эксперимента, таких как: целевая метрика, допустимые вероятности ошибок первого и второго рода, размеры групп и продолжительность эксперимента, техники снижения дисперсии и т.д.
Так как это было в прошлом, мы знаем, какие покупки совершили пользователи, можем вычислить метрики и оценить значимость отличий. Кроме того, мы знаем, что эффекта на самом деле не было, так как в то время эксперимент на самом деле не запускался. Если значимые отличия были найдены, то мы совершили ошибку первого рода. Иначе получили правильный результат.
Далее нужно повторить эту процедуру с мысленным запуском эксперимента в прошлом на разных группах и временных интервалах много раз, например, 1000.
После этого можно посчитать долю экспериментов, в которых была совершена ошибка. Это будет точечная оценка вероятности ошибки первого рода.
Оценку вероятности ошибки второго рода можно получить аналогичным способом. Единственное отличие состоит в том, что каждый раз нужно искусственно добавлять ожидаемый эффект в данные экспериментальной группы. В этих экспериментах эффект на самом деле есть, так как мы сами его добавили. Если значимых отличий не будет найдено – это ошибка второго рода. Проведя 1000 экспериментов и посчитав долю ошибок второго рода, получим точечную оценку вероятности ошибки второго рода.
Посмотрим, как оценить вероятности ошибок в коде. С помощью численных синтетических А/А и А/Б экспериментов оценим вероятности ошибок и построим доверительные интервалы:
def run_synthetic_experiments(values, sample_size, effect=0, n_iter=10000):
"""Проводим синтетические эксперименты, возвращаем список p-value."""
pvalues = []
for _ in range(n_iter):
a, b = np.random.choice(values, size=(2, sample_size,), replace=False)
b += effect
pvalue = stats.ttest_ind(a, b).pvalue
pvalues.append(pvalue)
return np.array(pvalues)
def print_estimated_errors(pvalues_aa, pvalues_ab, alpha):
"""Оценивает вероятности ошибок."""
estimated_first_type_error = np.mean(pvalues_aa < alpha)
estimated_second_type_error = np.mean(pvalues_ab >= alpha)
ci_first = estimate_ci_bernoulli(estimated_first_type_error, len(pvalues_aa))
ci_second = estimate_ci_bernoulli(estimated_second_type_error, len(pvalues_ab))
print(f'оценка вероятности ошибки I рода = {estimated_first_type_error:0.4f}')
print(f' доверительный интервал = [{ci_first[0]:0.4f}, {ci_first[1]:0.4f}]')
print(f'оценка вероятности ошибки II рода = {estimated_second_type_error:0.4f}')
print(f' доверительный интервал = [{ci_second[0]:0.4f}, {ci_second[1]:0.4f}]')
def estimate_ci_bernoulli(p, n, alpha=0.05):
"""Доверительный интервал для Бернуллиевской случайной величины."""
t = stats.norm.ppf(1 - alpha / 2, loc=0, scale=1)
std_n = np.sqrt(p * (1 - p) / n)
return p - t * std_n, p + t * std_n
pvalues_aa = run_synthetic_experiments(values, sample_size, effect=0)
pvalues_ab = run_synthetic_experiments(values, sample_size, effect=effect)
print_estimated_errors(pvalues_aa, pvalues_ab, alpha)оценка вероятности ошибки I рода = 0.0991
доверительный интервал = [0.0932, 0.1050]
оценка вероятности ошибки II рода = 0.1978
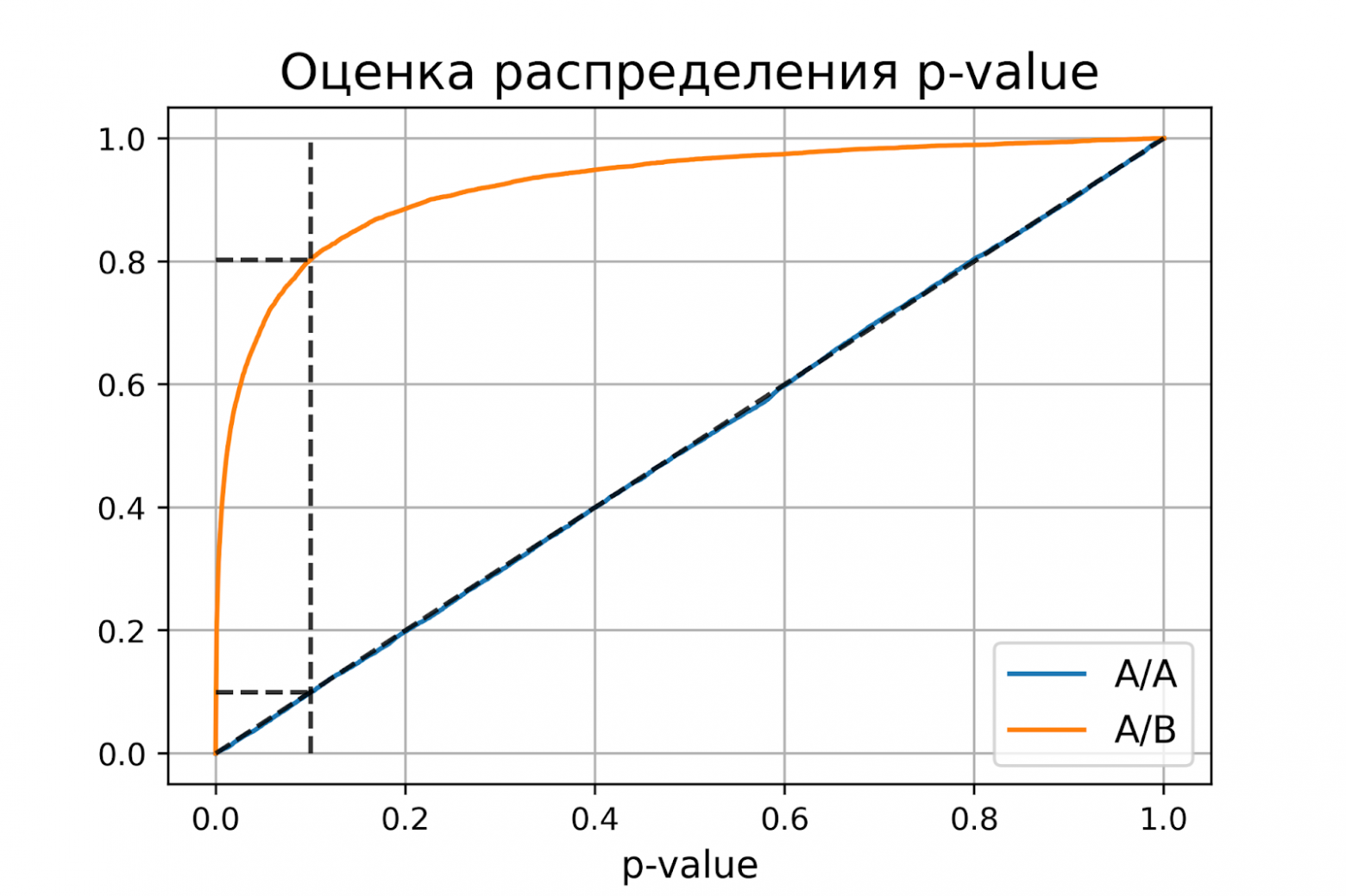
доверительный интервал = [0.1900, 0.2056]Оценки вероятностей ошибок примерно равны 0.1 и 0.2, как и должно быть. Всё верно, тест Стьюдента на этих данных работает корректно.
Распределение p-value
Выше рассмотрели случай, когда тест контролирует вероятность ошибки первого рода при фиксированном уровне значимости. Если решим изменить уровень значимости с 0.1 на 0.01, будет ли тест контролировать вероятность ошибки первого рода? Было бы хорошо, если тест контролировал вероятность ошибки первого рода при любом заданном уровне значимости. Формально это можно записать так:
Для любого выполняется
.
Заметим, что в левой части равенства записано выражение для функции распределения p-value. Из равенства следует, что функция распределения p-value в точке X равна X для любого X от 0 до 1. Эта функция распределения является функцией распределения равномерного распределения от 0 до 1. Мы только что показали, что статистический критерий контролирует вероятность ошибки первого рода на заданном уровне для любого уровня значимости тогда и только тогда, когда при верности нулевой гипотезы p-value распределено равномерно от 0 до 1.
При верности нулевой гипотезы p-value должно быть распределено равномерно. А как должно быть распределено p-value при верности альтернативной гипотезы? Из условия для вероятности ошибки второго рода следует, что
.
Получается, график функции распределения p-value при верности альтернативной гипотезы должен проходить через точку , где
и
– допустимые вероятности ошибок конкретного эксперимента.
Проверим, как распределено p-value в численном эксперименте. Построим эмпирические функции распределения p-value:
import matplotlib.pyplot as plt
def plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta):
"""Рисует графики распределения p-value."""
estimated_first_type_error = np.mean(pvalues_aa < alpha)
estimated_second_type_error = np.mean(pvalues_ab >= alpha)
y_one = estimated_first_type_error
y_two = 1 - estimated_second_type_error
X = np.linspace(0, 1, 1000)
Y_aa = [np.mean(pvalues_aa < x) for x in X]
Y_ab = [np.mean(pvalues_ab < x) for x in X]
plt.plot(X, Y_aa, label='A/A')
plt.plot(X, Y_ab, label='A/B')
plt.plot([alpha, alpha], [0, 1], '--k', alpha=0.8)
plt.plot([0, alpha], [y_one, y_one], '--k', alpha=0.8)
plt.plot([0, alpha], [y_two, y_two], '--k', alpha=0.8)
plt.plot([0, 1], [0, 1], '--k', alpha=0.8)
plt.title('Оценка распределения p-value', size=16)
plt.xlabel('p-value', size=12)
plt.legend(fontsize=12)
plt.grid()
plt.show()
plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta)P-value для синтетических А/А тестах действительно оказалось распределено равномерно от 0 до 1, а для синтетических А/Б тестов проходит через точку .
Кроме оценок распределений на графике дополнительно построены четыре пунктирные линии:
-
диагональная из точки [0, 0] в точку [1, 1] – это функция распределения равномерного распределения на отрезке от 0 до 1, по ней можно визуально оценивать равномерность распределения p-value;
-
вертикальная линия с
– пороговое значение p-value, по которому определяем отвергать нулевую гипотезу или нет. Проекция на ось ординат точки пересечения вертикальной линии с функцией распределения p-value для А/А тестов – это вероятность ошибки первого рода. Проекция точки пересечения вертикальной линии с функцией распределения p-value для А/Б тестов – это мощность теста (мощность = 1 —
).
-
две горизонтальные линии – проекции на ось ординат точки пересечения вертикальной линии с функцией распределения p-value для А/А и А/Б тестов.
График с оценками распределения p-value для синтетических А/А и А/Б тестов позволяет проверить корректность теста для любого значения уровня значимости.
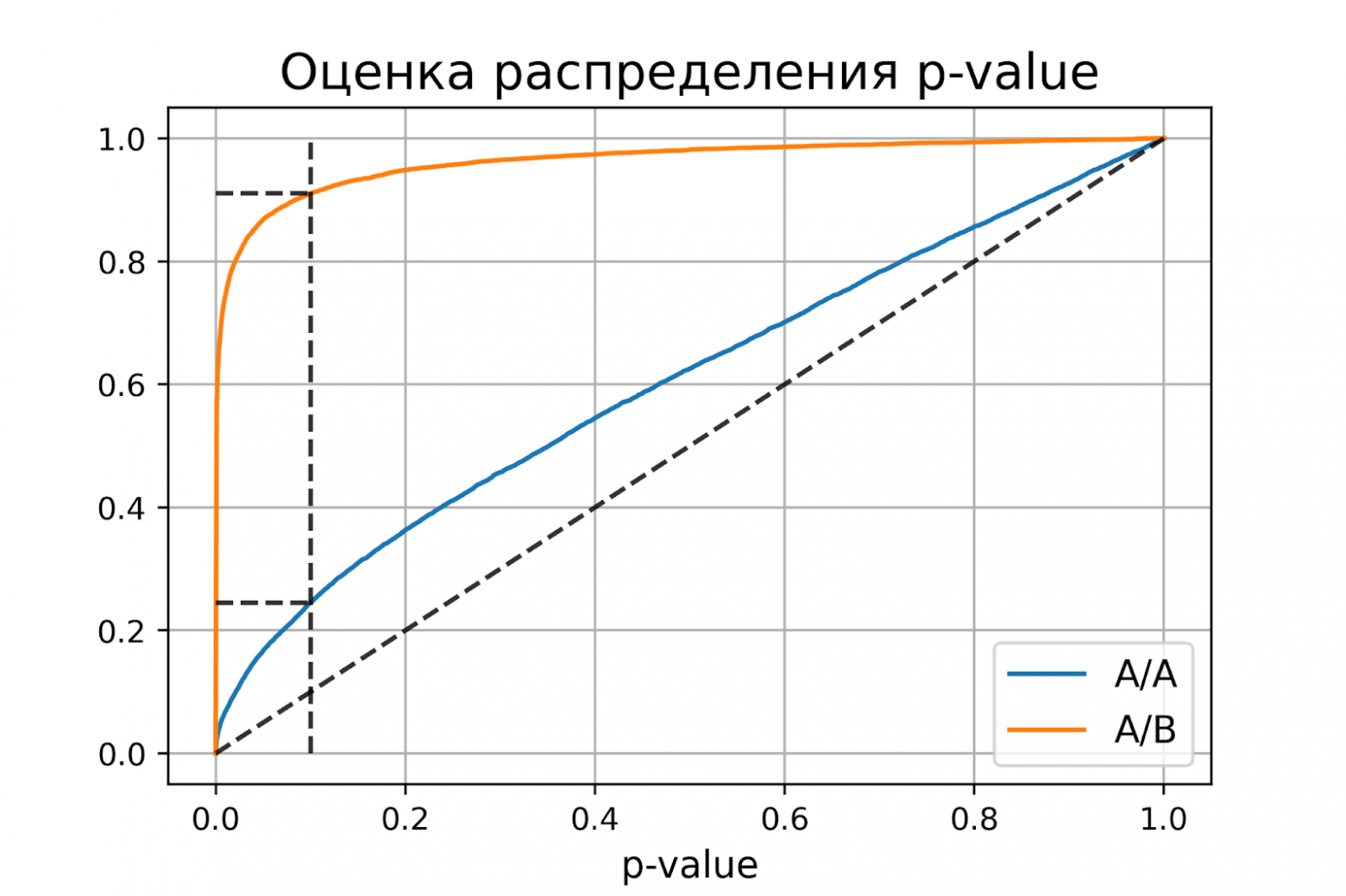
Некорректный критерий
Выше рассмотрели пример, когда тест Стьюдента оказался корректным критерием для случайных данных из нормального распределения. Может быть, все критерии всегда работаю корректно, и нет смысла каждый раз проверять вероятности ошибок?
Покажем, что это не так. Немного изменим рассмотренный ранее пример, чтобы продемонстрировать некорректную работу критерия. Допустим, мы решили увеличить продолжительность эксперимента до 2-х недель. Для каждого пользователя будем вычислять стоимость покупок за первую неделю и стоимость покупок за второю неделю. Полученные стоимости будем передавать в тест Стьюдента для проверки значимости отличий. Положим, что поведение пользователей повторяется от недели к неделе, и стоимости покупок одного пользователя совпадают.
def run_synthetic_experiments_two(values, sample_size, effect=0, n_iter=10000):
"""Проводим синтетические эксперименты на двух неделях."""
pvalues = []
for _ in range(n_iter):
a, b = np.random.choice(values, size=(2, sample_size,), replace=False)
b += effect
# дублируем данные
a = np.hstack((a, a,))
b = np.hstack((b, b,))
pvalue = stats.ttest_ind(a, b).pvalue
pvalues.append(pvalue)
return np.array(pvalues)
pvalues_aa = run_synthetic_experiments_two(values, sample_size)
pvalues_ab = run_synthetic_experiments_two(values, sample_size, effect=effect)
print_estimated_errors(pvalues_aa, pvalues_ab, alpha)
plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta)оценка вероятности ошибки I рода = 0.2451
доверительный интервал = [0.2367, 0.2535]
оценка вероятности ошибки II рода = 0.0894
доверительный интервал = [0.0838, 0.0950]Получили оценку вероятности ошибки первого рода около 0.25, что сильно больше уровня значимости 0.1. На графике видно, что распределение p-value для синтетических А/А тестов не равномерно, оно отклоняется от диагонали. В этом примере тест Стьюдента работает некорректно, так как данные зависимые (стоимости покупок одного человека зависимы). Если бы мы сразу не догадались про зависимость данных, то оценка вероятностей ошибок помогла бы нам понять, что такой тест некорректен.
Итоги
Мы обсудили, что такое корректность статистического теста, посмотрели, как оценить вероятности ошибок на исторических данных и привели пример некорректной работы критерия.
Таким образом:
-
корректный критерий – это критерий, у которого вероятности ошибок первого и второго рода равны допустимым вероятностям ошибок первого и второго рода соответственно;
-
чтобы критерий контролировал вероятность ошибки первого рода для любого уровня значимости, необходимо и достаточно, чтобы p-value при верности нулевой гипотезы было распределено равномерно от 0 до 1.
5.6. Вероятность ошибки р
Если следовать подразделению статистики на описательную и аналитическую, то задача аналитической статистики — предоставить методы, с помощью которых можно было бы объективно выяснить,
например, является ли наблюдаемая разница в средних значениях или взаимосвязь (корреляция) выборок случайной или нет.
Например, если сравниваются два средних значения выборок, то можно сформулировать две предварительных гипотезы:
-
Гипотеза 0 (нулевая): Наблюдаемые различия между средними значениями выборок находятся в пределах случайных отклонений.
-
Гипотеза 1 (альтернативная): Наблюдаемые различия между средними значениями нельзя объяснить случайными отклонениями.
В аналитической статистике разработаны методы вычисления так называемых тестовых (контрольных) величин, которые рассчитываются по определенным формулам на основе данных,
содержащихся в выборках или полученных из них характеристик. Эти тестовые величины соответствуют определенным теоретическим распределениям
(t-pacnpeлелению, F-распределению, распределению X2 и т.д.), которые позволяют вычислить так называемую вероятность ошибки. Это вероятность равна проценту ошибки,
которую можно допустить отвергнув нулевую гипотезу и приняв альтернативную.
Вероятность определяется в математике, как величина, находящаяся в диапазоне от 0 до 1. В практической статистике она также часто выражаются в процентах. Обычно вероятность обозначаются буквой р:
0 < р < 1
Вероятности ошибки, при которой допустимо отвергнуть нулевую гипотезу и принять альтернативную гипотезу, зависит от каждого конкретного случая.
В значительной степени эта вероятность определяется характером исследуемой ситуации. Чем больше требуемая вероятность, с которой надо избежать ошибочного решения,
тем более узкими выбираются границы вероятности ошибки, при которой отвергается нулевая гипотеза, так называемый доверительный интервал вероятности.
Обычно в исследованиях используют 5% вероятность ошибки.
Существует общепринятая терминология, которая относится к доверительным интервалам вероятности:
- Высказывания, имеющие вероятность ошибки р <= 0,05 — называются значимыми.
- Высказывания с вероятностью ошибки р <= 0,01 — очень значимыми,
- А высказывания с вероятностью ошибки р <= 0,001 — максимально значимыми.
В литературе такие ситуации иногда обозначают одной, двумя или тремя звездочками.
| Вероятность ошибки | Значимость | Обозначение |
| р > 0.05 | Не значимая | ns |
| р <= 0.05 | Значимая | * |
| р <= 0.01 | Очень значимая | ** |
| р <= 0.001 | Максимально значимая | *** |
В SPSS вероятность ошибки р имеет различные обозначения; звездочки для указания степени значимости применяются лишь в немногих случаях. Обычно в SPSS значение р обозначается Sig. (Significant).
Времена, когда не было компьютеров, пригодных для статистического анализа, давали практикам по крайней мере одно преимущество. Так как все вычисления надо было выполнять вручную,
статистик должен был сначала тщательно обдумать, какие вопросы можно решить с помощью того или иного теста. Кроме того, особое значение придавалось точной формулировке нулевой гипотезы.
Но с помощью компьютера и такой мощной программы, как SPSS, очень легко можно провести множество тестов за очень короткое время. К примеру, если в таблицу сопряженности свести 50 переменных
с другими 20 переменными и выполнить тест X2, то получится 1000 результатов проверки значимости или 1000 значений р. Некритический подбор значимых величин может
дать бессмысленный результат, так как уже при граничном уровне значимости р = 0,05 в пяти процентах наблюдений, то есть в 50 возможных наблюдениях, можно ожидать значимые результаты.
Этим ошибкам первого рода (когда нулевая гипотеза отвергается, хотя она верна) следует уделять достаточно внимания. Ошибкой второго рода называется ситуация,
когда нулевая гипотеза принимается, хотя она ложна. Вероятность допустить ошибку первого рода равна вероятности ошибки р. Вероятность ошибки второго рода тем меньше, чем больше вероятность ошибки р.
Статистические гипотезы
Определение статистической гипотезы. Нулевая и альтернативная, простая и сложная гипотезы. Ошибки первого и второго рода. Статистический критерий, наблюдаемое значение критерия. Критическая область. Область принятия нулевой гипотезы; критическая точка. Общая методика построения право-, лево- и двухсторонней критических областей
Понятие и определение статистической гипотезы
Проверка статистических гипотез тесно связана с теорией оценивания параметров. В естествознании, технике, экономике для выяснения того или иного случайного факта часто прибегают к высказыванию гипотез, которые можно проверить статистически, т. е. опираясь на результаты наблюдений в случайной выборке. Под статистическими подразумеваются такие гипотезы, которые относятся или к виду, или к отдельным параметрам распределения случайной величины. Например, статистической является гипотеза о том, что распределение производительности труда рабочих, выполняющих одинаковую работу в одинаковых условиях, имеет нормальный закон распределения. Статистической будет также гипотеза о том, что средние размеры деталей, производимые на однотипных, параллельно работающих станках, не различаются.
Статистическая гипотеза называется простой, если она однозначно определяет распределение случайной величины , в противном случае гипотеза называется сложной. Например, простой гипотезой является предположение о том, что случайная величина распределена по нормальному закону с математическим ожиданием, равным нулю, и дисперсией, равной единице. Если высказывается предположение, что случайная величина имеет нормальное распределение с дисперсией, равной единице, а математическое ожидание — число из отрезка , то это сложная гипотеза. Другим примером сложной гипотезы является предположение о том, что непрерывная случайная величина с вероятностью принимает значение из интервала , в этом случае распределение случайной величины может быть любым из класса непрерывных распределений.
Часто распределение величины известно, и по выборке наблюдений необходимо проверить предположения о значении параметров этого распределения. Такие гипотезы называются параметрическими.
Проверяемая гипотеза называется нулевой и обозначается . Наряду с гипотезой рассматривают одну из альтернативных (конкурирующих) гипотез . Например, если проверяется гипотеза о равенстве параметра некоторому заданному значению , то есть , то в качестве альтернативной гипотезы можно рассмотреть одну из следующих гипотез: где — заданное значение, . Выбор альтернативной гипотезы определяется конкретной формулировкой задачи.
Правило, по которому принимается решение принять или отклонить гипотезу , называется критерием . Так как решение принимается на основе выборки наблюдений случайной величины , необходимо выбрать подходящую статистику, называемую в этом случае статистикой критерия . При проверке простой параметрической гипотезы в качестве статистики критерия выбирают ту же статистику, что и для оценки параметра .
Проверка статистической гипотезы основывается на принципе, в соответствии с которым маловероятные события считаются невозможными, а события, имеющие большую вероятность, — достоверными; Этот принцип можно реализовать следующим образом. Перед анализом выборки фиксируется некоторая малая вероятность , называемая уровнем значимости. Пусть — множество значений статистики , а — такое подмножество, что при условии истинности гипотезы вероятность попадания статистики критерия в равна , то есть .
Обозначим выборочное значение статистики , вычисленное по выборке наблюдений. Критерий формулируется так: отклонить гипотезу , если ; принять гипотезу , если . Критерий, основанный на использовании заранее заданного уровня значимости, называют критерием значимости. Множество всех значений статистики критерия , при которых принимается решение отклонить гипотезу , называется критической областью; область называется областью принятия гипотезы .
Уровень значимости определяет размер критической области . Положение критической области на множестве значений статистики зависит от формулировки альтернативной гипотезы . Например, если проверяется гипотеза , а альтернативная гипотеза формулируется как , то критическая область размещается на правом (левом) «хвосте» распределения статистики , т. е. имеет вид неравенства , где — значения статистики , которые принимаются с вероятностями соответственно и при условии, что верна гипотеза . В этом случае критерий называется односторонним (соответственно правосторонним и левосторонним). Если альтернативная гипотеза формулируется как , то критическая область размещается на обоих «хвостах» распределения , то есть определяется совокупностью неравенств и в этом случае критерий называется двухсторонним.
Расположение критической области для различных альтернативных гипотез показано на рис. 30, где — плотность распределения статистики критерия при условии, что верна гипотеза , — область принятия гипотезы, .
Проверку параметрической статистической гипотезы с помощью критерия значимости можно разбить на этапы:
1) сформулировать проверяемую и альтернативную гипотезы;
2) назначить уровень значимости ;
3) выбрать статистику критерия для проверки гипотезы ;
4) определить выборочное распределение статистики при условии, что верна гипотеза ;
5) в зависимости от формулировки альтернативной гипотезы определить критическую область одним из неравенств или совокупностью неравенств и ;
6) получить выборку наблюдений и вычислить выборочные значения статистики критерия;
7) принять статистическое решение: если , то отклонить гипотезу как не согласующуюся с результатами наблюдений; если , то принять гипотезу , т. е. считать, что гипотеза не противоречит результатам наблюдений.
Обычно при выполнении пп. 4-7 используют статистику с нормальным распределением, статистику Стьюдента, Фишера.
Пример 3. По паспортным данным автомобильного двигателя расход топлива на 100 км пробега составляет 10 л. В результате изменения конструкции двигателя ожидается, что расход топлива уменьшится. Для проверки проводятся испытания 25 случайно отобранных автомобилей с модернизированным двигателем, причем выборочное среднее расходов топлива на 100 км пробега по результатам испытаний составило 9,3 л. Предположим, что выборка расходов топлива получена из нормально распределенной генеральной совокупности со средним и дисперсией л². Используя критерий значимости, проверить гипотезу, утверждающую, что изменение конструкции двигателя не повлияло на расход топлива.
Решение. Проверим гипотезу о среднем нормально распределенной генеральной совокупности. Проверку проведем по этапам:
1) проверяемая гипотеза ; альтернативная гипотеза ;
2) уровень значимости ;
3) в качестве статистики критерия используем статистику математического ожидания — выборочное среднее;
4) так как выборка получена из нормально распределенной генеральной совокупности, выборочное среднее также имеет нормальное распределение с дисперсией . При условии, что верна гипотеза , математическое ожидание этого распределения равно 10. Нормированная статистика имеет нормальное распределение;
5) альтернативная гипотеза предполагает уменьшение расхода топлива, следовательно, нужно использовать односторонний критерий. Критическая область определяется неравенством . По прил. 5 находим ;
б) выборочное значение нормированной статистики критерия
7) статистическое решение: так как выборочное значение статистики критерия принадлежит критической области, гипотеза отклоняется: следует считать, что изменение конструкции двигателя привело к уменьшению расхода топлива. Границу критической области для исходной статистики критерия можно получить из соотношения , откуда , т. е. критическая область для статистики определяется неравенством .
Ошибки первого и второго рода
Решение, принимаемое на основе критерия значимости, может быть ошибочным. Пусть выборочное значение статистики критерия попадает в критическую область, и гипотеза , отклоняется в соответствии с критерием. Если, тем не менее, гипотеза верна, то принимаемое решение неверно. Ошибка, совершаемая при отклонении правильной гипотезы if о, называется ошибкой первого рода. Вероятность ошибки первого рода равна вероятности попадания статистики критерия в критическую область при условии, что верна гипотеза , т. е. равна уровню значимости
Ошибка второго рода происходит тогда, когда гипотеза принимается, но в действительности верна гипотеза . Вероятность ошибки второго рода вычисляется по формуле
Пример 4. В условиях примера 3 предположим, что наряду с гипотезой л рассматривается альтернативная гипотеза л. В качестве статистики критерия снова возьмем выборочное среднее . Предположим, что критическая область задана неравенством л. Найти вероятности ошибок первого и второго рода для критерия с такой критической областью.
Решение. Найдем вероятность ошибки первого рода. Статистика критерия при условии, что верна гипотеза л, имеет нормальное распределение с математическим ожиданием, равным 10, и дисперсией, равной . Используя прил. 5, по формуле (11.1) находим
Это означает, что принятый критерий классифицирует примерно 8% автомобилей, имеющих расход 10 л на 100 км пробега, как автомобили, имеющие меньший расход топлива. При условии, что верна гипотеза л, статистика имеет нормальное распределение с математическим ожиданием, равным 9, и дисперсией, равной . Вероятность ошибки второго рода найдем по формуле (11.2):
Следовательно, в соответствии с принятым критерием 13,6% автомобилей, имеющих расход топлива 9 л на 100 км пробега, классифицируются как автомобили, имеющие расход топлива 10 л.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Ошибки первого и второго рода
Выдвинутая гипотеза
может быть правильной или неправильной,
поэтому возникает необходимость её
проверки. Поскольку проверку производят
статистическими методами, её называют
статистической. В итоге статистической
проверки гипотезы в двух случаях может
быть принято неправильное решение, т.
е. могут быть допущены ошибки двух родов.
Ошибка первого
рода состоит в том, что будет отвергнута
правильная гипотеза.
Ошибка второго
рода состоит в том, что будет принята
неправильная гипотеза.
Подчеркнём, что
последствия этих ошибок могут оказаться
весьма различными. Например, если
отвергнуто правильное решение «продолжать
строительство жилого дома», то эта
ошибка первого рода повлечёт материальный
ущерб: если же принято неправильное
решение «продолжать строительство»,
несмотря на опасность обвала стройки,
то эта ошибка второго рода может повлечь
гибель людей. Можно привести примеры,
когда ошибка первого рода влечёт более
тяжёлые последствия, чем ошибка второго
рода.
Замечание 1.
Правильное решение может быть принято
также в двух случаях:
-
гипотеза принимается,
причём и в действительности она
правильная; -
гипотеза отвергается,
причём и в действительности она неверна.
Замечание 2.
Вероятность совершить ошибку первого
рода принято обозначать через
;
её называют уровнем значимости. Наиболее
часто уровень значимости принимают
равным 0,05 или 0,01. Если, например, принят
уровень значимости, равный 0,05, то это
означает, что в пяти случаях из ста
имеется риск допустить ошибку первого
рода (отвергнуть правильную гипотезу).
Статистический
критерий проверки нулевой гипотезы.
Наблюдаемое значение критерия
Для проверки
нулевой гипотезы используют специально
подобранную случайную величину, точное
или приближённое распределение которой
известно. Обозначим эту величину в целях
общности через
.
Статистическим
критерием
(или просто критерием) называют случайную
величину
,
которая служит для проверки нулевой
гипотезы.
Например, если
проверяют гипотезу о равенстве дисперсий
двух нормальных генеральных совокупностей,
то в качестве критерия
принимают отношение исправленных
выборочных дисперсий:
Эта величина
случайная, потому что в различных опытах
дисперсии принимают различные, наперёд
неизвестные значения, и распределена
по закону Фишера – Снедекора.
Для проверки
гипотезы по данным выборок вычисляют
частные значения входящих в критерий
величин и таким образом получают частное
(наблюдаемое) значение критерия.
Наблюдаемым
значением
называют значение критерия, вычисленное
по выборкам. Например, если по двум
выборкам найдены исправленные выборочные
дисперсиии
,
то наблюдаемое значение критерия
Критическая
область. Область принятия гипотезы.
Критические точки
После выбора
определённого критерия множество всех
его возможных значений разбивают на
два непересекающихся подмножества:
одно из них содержит значения критерия,
при которых нулевая гипотеза отвергается,
а другая – при которых она принимается.
Критической
областью называют совокупность значений
критерия, при которых нулевую гипотезу
отвергают.
Областью принятия
гипотезы (областью допустимых значений)
называют совокупность значений критерия,
при которых гипотезу принимают.
Основной принцип
проверки статистических гипотез можно
сформулировать так: если наблюдаемое
значение критерия принадлежит критической
области – гипотезу отвергают, если
наблюдаемое значение критерия принадлежит
области принятия гипотезы – гипотезу
принимают.
Поскольку критерий
— одномерная случайная величина, все её
возможные значения принадлежат некоторому
интервалу. Поэтому критическая область
и область принятия гипотезы также
являются интервалами и, следовательно,
существуют точки, которые их разделяют.
Критическими
точками (границами)
называют точки, отделяющие критическую
область от области принятия гипотезы.
Различают
одностороннюю (правостороннюю или
левостороннюю) и двустороннюю критические
области.
Правосторонней
называют критическую область, определяемую
неравенством
>
,
где— положительное число.
Левосторонней
называют критическую область, определяемую
неравенством
<
,
где— отрицательное число.
Односторонней
называют правостороннюю или левостороннюю
критическую область.
Двусторонней
называют критическую область, определяемую
неравенствами
где
.
В частности, если
критические точки симметричны относительно
нуля, двусторонняя критическая область
определяется неравенствами ( в
предположении, что
>0):
,
или равносильным неравенством
.
Отыскание
правосторонней критической области
Как найти критическую
область? Обоснованный ответ на этот
вопрос требует привлечения довольно
сложной теории. Ограничимся её элементами.
Для определённости начнём с нахождения
правосторонней критической области,
которая определяется неравенством
>
,
где>0.
Видим, что для отыскания правосторонней
критической области достаточно найти
критическую точку. Следовательно,
возникает новый вопрос: как её найти?
Для её нахождения
задаются достаточной малой вероятностью
– уровнем значимости
.
Затем ищут критическую точку,
исходя из требования, чтобы при условии
справедливости нулевой гипотезы
вероятность того, критерийпримет значение, большее
,
была равна принятому уровню значимости:
Р(>
)=
.
Для каждого критерия
имеются соответствующие таблицы, по
которым и находят критическую точку,
удовлетворяющую этому требованию.
Замечание 1.
Когда
критическая точка уже найдена, вычисляют
по данным выборок наблюдаемое значение
критерия и, если окажется, что
>
,
то нулевую гипотезу отвергают; если же<
,
то нет оснований, чтобы отвергнуть
нулевую гипотезу.
Пояснение. Почему
правосторонняя критическая область
была определена, исходя из требования,
чтобы при справедливости нулевой
гипотезы выполнялось соотношение
Р(>
)=
?
(*)
Поскольку вероятность
события
>
мала (
— малая вероятность), такое событие при
справедливости нулевой гипотезы, в силу
принципа практической невозможности
маловероятных событий, в единичном
испытании не должно наступить. Если всё
же оно произошло, т.е. наблюдаемое
значение критерия оказалось больше,
то это можно объяснить тем, что нулевая
гипотеза ложна и, следовательно, должна
быть отвергнута. Таким образом, требование
(*) определяет такие значения критерия,
при которых нулевая гипотеза отвергается,
а они и составляют правостороннюю
критическую область.
Замечание 2.
Наблюдаемое значение критерия может
оказаться большим
не потому, что нулевая гипотеза ложна,
а по другим причинам (малый объём выборки,
недостатки методики эксперимента и
др.). В этом случае, отвергнув правильную
нулевую гипотезу, совершают ошибку
первого рода. Вероятность этой ошибки
равна уровню значимости.
Итак, пользуясь требованием (*), мы с
вероятностьюрискуем совершить ошибку первого рода.
Замечание 3. Пусть
нулевая гипотеза принята; ошибочно
думать, что тем самым она доказана.
Действительно, известно, что один пример,
подтверждающий справедливость некоторого
общего утверждения, ещё не доказывает
его. Поэтому более правильно говорить,
«данные наблюдений согласуются с нулевой
гипотезой и, следовательно, не дают
оснований её отвергнуть».
На практике для
большей уверенности принятия гипотезы
её проверяют другими способами или
повторяют эксперимент, увеличив объём
выборки.
Отвергают гипотезу
более категорично, чем принимают.
Действительно, известно, что достаточно
привести один пример, противоречащий
некоторому общему утверждению, чтобы
это утверждение отвергнуть. Если
оказалось, что наблюдаемое значение
критерия принадлежит критической
области, то этот факт и служит примером,
противоречащим нулевой гипотезе, что
позволяет её отклонить.
Отыскание
левосторонней и двусторонней критических
областей***
Отыскание
левосторонней и двусторонней критических
областей сводится (так же, как и для
правосторонней) к нахождению соответствующих
критических точек. Левосторонняя
критическая область определяется
неравенством
<
(
<0).
Критическую точку находят, исходя из
требования, чтобы при справедливости
нулевой гипотезы вероятность того, что
критерий примет значение, меньшее,
была равна принятому уровню значимости:
Р(<
)=
.
Двусторонняя
критическая область определяется
неравенствами
Критические
точки находят, исходя из требования,
чтобы при справедливости нулевой
гипотезы сумма вероятностей того, что
критерий примет значение, меньшееили большее
,
была равна принятому уровню значимости:
.
(*)
Ясно, что критические
точки могут быть выбраны бесчисленным
множеством способов. Если же распределение
критерия симметрично относительно нуля
и имеются основания (например, для
увеличения мощности) выбрать симметричные
относительно нуля точки (-
)и
(
>0),
то
Учитывая (*), получим
.
Это соотношение
и служит для отыскания критических
точек двусторонней критической области.
Критические точки находят по соответствующим
таблицам.
Дополнительные
сведения о выборе критической области.
Мощность критерия
Мы строили
критическую область, исходя из требования,
чтобы вероятность попадания в неё
критерия была равна
при условии, что нулевая гипотеза
справедлива. Оказывается целесообразным
ввести в рассмотрение вероятность
попадания критерия в критическую область
при условии, что нулевая гипотеза неверна
и, следовательно, справедлива конкурирующая.
Мощностью критерия
называют вероятность попадания критерия
в критическую область при условии, что
справедлива конкурирующая гипотеза.
Другими словами, мощность критерия есть
вероятность того, что нулевая гипотеза
будет отвергнута, если верна конкурирующая
гипотеза.
Пусть для проверки
гипотезы принят определённый уровень
значимости и выборка имеет фиксированный
объём. Остаётся произвол в выборе
критической области. Покажем, что её
целесообразно построить так, чтобы
мощность критерия была максимальной.
Предварительно убедимся, что если
вероятность ошибки второго рода (принять
неправильную гипотезу) равна
,
то мощность равна 1-.
Действительно, если— вероятность ошибки второго рода, т.е.
события «принята нулевая гипотеза,
причём справедливо конкурирующая», то
мощность критерия равна 1 —.
Пусть мощность 1
—
возрастает; следовательно, уменьшается
вероятностьсовершить ошибку второго рода. Таким
образом, чем мощность больше, тем
вероятность ошибки второго рода меньше.
Итак, если уровень
значимости уже выбран, то критическую
область следует строить так, чтобы
мощность критерия была максимальной.
Выполнение этого требования должно
обеспечить минимальную ошибку второго
рода, что, конечно, желательно.
Замечание 1.
Поскольку вероятность события «ошибка
второго рода допущена» равна
,
то вероятность противоположного события
«ошибка второго рода не допущена» равна
1 —,
т.е. мощности критерия. Отсюда следует,
что мощность критерия есть вероятность
того, что не будет допущена ошибка
второго рода.
Замечание 2. Ясно,
что чем меньше вероятности ошибок
первого и второго рода, тем критическая
область «лучше». Однако при заданном
объёме выборки уменьшить одновременно
и
невозможно; если уменьшить
,
тобудет возрастать. Например, если принять
=0,
то будут приниматься все гипотезы, в
том числе и неправильные, т.е. возрастает
вероятностьошибки второго рода.
Как же выбрать
наиболее целесообразно? Ответ на этот
вопрос зависит от «тяжести последствий»
ошибок для каждой конкретной задачи.
Например, если ошибка первого рода
повлечёт большие потери, а второго рода
– малые, то следует принять возможно
меньшее.
Если
уже выбрано, то, пользуясь теоремой Ю.
Неймана и Э.Пирсона, можно построить
критическую область, для которойбудет минимальным и, следовательно,
мощность критерия максимальной.
Замечание 3.
Единственный способ одновременного
уменьшения вероятностей ошибок первого
и второго рода состоит в увеличении
объёма выборок.
Соседние файлы в папке Лекции 2 семестр
- #
- #
- #
- #
Ошибки I и II рода при проверке гипотез, мощность
Общий обзор
Принятие неправильного решения
Мощность и связанные факторы
Проверка множественных гипотез
Общий обзор
Большинство проверяемых гипотез сравнивают между собой группы объектов, которые испытывают влияние различных факторов.
Например, можно сравнить эффективность двух видов лечения, чтобы сократить 5-летнюю смертность от рака молочной железы. Для данного исхода (например, смерть) сравнение, представляющее интерес (например, различные показатели смертности через 5 лет), называют эффектом или, если уместно, эффектом лечения.
Нулевую гипотезу выражают как отсутствие эффекта (например 5-летняя смертность от рака молочной железы одинаковая в двух группах, получающих разное лечение); двусторонняя альтернативная гипотеза будет означать, что различие эффектов не равно нулю.
Критериальная проверка гипотезы дает возможность определить, достаточно ли аргументов, чтобы отвергнуть нулевую гипотезу. Можно принять только одно из двух решений:
- отвергнуть нулевую гипотезу и принять альтернативную гипотезу
- остаться в рамках нулевой гипотезы
Важно: В литературе достаточно часто встречается понятие «принять нулевую гипотезу». Хотелось бы внести ясность, что со статистической точки зрения принять нулевую гипотезу невозможно, т.к. нулевая гипотеза представляет собой достаточно строгое утверждение (например, средние значения в сравниваемых группах равны ).
Поэтому фразу о принятии нулевой гипотезы следует понимать как то, что мы просто остаемся в рамках гипотезы.
Принятие неправильного решения
Возможно неправильное решение, когда отвергают/не отвергают нулевую гипотезу, потому что есть только выборочная информация.
| |
Верная гипотеза | ||
|---|---|---|---|
| H0 | H1 | ||
| Результат применения критерия |
H0 | H0 верно принята | H0 неверно принята (Ошибка второго рода) |
| H1 | H0 неверно отвергнута (Ошибка первого рода) |
H0 верно отвергнута |
Ошибка 1-го рода: нулевую гипотезу отвергают, когда она истинна, и делают вывод, что имеется эффект, когда в действительности его нет. Максимальный шанс (вероятность) допустить ошибку 1-го рода обозначается α (альфа). Это уровень значимости критерия; нулевую гипотезу отвергают, если наше значение p ниже уровня значимости, т. е., если p < α.
Следует принять решение относительно значения а прежде, чем будут собраны данные; обычно назначают условное значение 0,05, хотя можно выбрать более ограничивающее значение, например 0,01.
Шанс допустить ошибку 1-го рода никогда не превысит выбранного уровня значимости, скажем α = 0,05, так как нулевую гипотезу отвергают только тогда, когда p< 0,05. Если обнаружено, что p > 0,05, то нулевую гипотезу не отвергнут и, следовательно, не допустят ошибки 1-го рода.
Ошибка 2-го рода: не отвергают нулевую гипотезу, когда она ложна, и делают вывод, что нет эффекта, тогда как в действительности он существует. Шанс возникновения ошибки 2-го рода обозначается β (бета); а величина (1-β) называется мощностью критерия.
Следовательно, мощность — это вероятность отклонения нулевой гипотезы, когда она ложна, т.е. это шанс (обычно выраженный в процентах) обнаружить реальный эффект лечения в выборке данного объема как статистически значимый.
В идеале хотелось бы, чтобы мощность критерия составляла 100%; однако это невозможно, так как всегда остается шанс, хотя и незначительный, допустить ошибку 2-го рода.
К счастью, известно, какие факторы влияют на мощность и, таким образом, можно контролировать мощность критерия, рассматривая их.
Мощность и связанные факторы
Планируя исследование, необходимо знать мощность предложенного критерия. Очевидно, можно начинать исследование, если есть «хороший» шанс обнаружить уместный эффект, если таковой существует (под «хорошим» мы подразумеваем, что мощность должна быть по крайней мере 70-80%).
Этически безответственно начинать исследование, у которого, скажем, только 40% вероятности обнаружить реальный эффект лечения; это бесполезная трата времени и денежных средств.
Ряд факторов имеют прямое отношение к мощности критерия.
Объем выборки: мощность критерия увеличивается по мере увеличения объема выборки. Это означает, что у большей выборки больше возможностей, чем у незначительной, обнаружить важный эффект, если он существует.
Когда объем выборки небольшой, у критерия может быть недостаточно мощности, чтобы обнаружить отдельный эффект. Эти методы также можно использовать для оценки мощности критерия для точно установленного объема выборки.
Вариабельность наблюдений: мощность увеличивается по мере того, как вариабельность наблюдений уменьшается.
Интересующий исследователя эффект: мощность критерия больше для более высоких эффектов. Критерий проверки гипотез имеет больше шансов обнаружить значительный реальный эффект, чем незначительный.
Уровень значимости: мощность будет больше, если уровень значимости выше (это эквивалентно увеличению допущения ошибки 1-го рода, α, а допущение ошибки 2-го рода, β, уменьшается).
Таким образом, вероятнее всего, исследователь обнаружит реальный эффект, если на стадии планирования решит, что будет рассматривать значение р как значимое, если оно скорее будет меньше 0,05, чем меньше 0,01.
Обратите внимание, что проверка ДИ для интересующего эффекта указывает на то, была ли мощность адекватной. Большой доверительный интервал следует из небольшой выборки и/или набора данных с существенной вариабельностью и указывает на недостаточную мощность.
Проверка множественных гипотез
Часто нужно выполнить критериальную проверку значимости множественных гипотез на наборе данных с многими переменными или существует более двух видов лечения.
Ошибка 1-го рода драматически увеличивается по мере увеличения числа сравнений, что приводит к ложным выводам относительно гипотез. Следовательно, следует проверить только небольшое число гипотез, выбранных для достижения первоначальной цели исследования и точно установленных априорно.
Можно использовать какую-нибудь форму апостериорного уточнения значения р, принимая во внимание число выполненных проверок гипотез.
Например, при подходе Бонферрони (его часто считают довольно консервативным) умножают каждое значение р на число выполненных проверок; тогда любые решения относительно значимости будут основываться на этом уточненном значении р.
Связанные определения:
p-уровень
Альтернативная гипотеза, альтернатива
Альфа-уровень
Бета-уровень
Гипотеза
Двусторонний критерий
Критерий для проверки гипотезы
Критическая область проверки гипотезы
Мощность
Мощность исследования
Мощность статистического критерия
Нулевая гипотеза
Односторонний критерий
Ошибка I рода
Ошибка II рода
Статистика критерия
Эквивалентные статистические критерии
В начало
Содержание портала
Перед тем, как ответить на вопрос о том, как посчитать значение ошибки 1 рода для распределения, необходимо рассмотреть основные понятия и определения, связанные с этим показателем.
Ошибка 1 рода – это ошибка, которая происходит, когда нулевая гипотеза (гипотеза о равенстве средних значений, медиан, дисперсий и т.д. двух выборок) отвергается, когда она на самом деле верна. Ошибка 1 рода также известна как «ложное срабатывание» или «ложная тревога». Она связана с вероятностью попадания в критическую область при проверке статистических гипотез.
Распределение – это функция вероятности, которая определяет, как часто возникают различные значения случайной величины. Распределение может иметь различные формы, включая нормальное распределение, биномиальное распределение, Пуассоново распределение и др.
Теперь, касательно вопроса о том, как посчитать значение ошибки 1 рода для распределения, необходимо отметить, что это можно сделать, используя уровень значимости и критическую область.
Уровень значимости (α) – это вероятность того, что будет допущена ошибка 1 рода. Обычно уровень значимости равен 0,05 или 0,01.
Критическая область – это область на графике распределения, которая определяется, используя значения уровня значимости и степеней свободы, и в которой нулевая гипотеза отвергается в пользу альтернативной гипотезы.
Для расчета значения ошибки 1 рода по распределению, необходимо выполнить следующие шаги:
Шаг 1: Определить уровень значимости (α) и степени свободы (df) для соответствующего распределения.
Шаг 2: Определить критическую область на графике распределения, используя значения уровня значимости и степеней свободы.
Шаг 3: Определить значение ошибки 1 рода, используя следующую формулу:
Ошибка 1 рода = Вероятность того, что нулевая гипотеза верна, но она все равно отвергнута = α
Таким образом, значение ошибки 1 рода по распределению можно рассчитать, используя уровень значимости и критическую область, которые определяются для соответствующего распределения. Ошибка 1 рода может быть уменьшена путем увеличения объема выборки (для уменьшения стандартной ошибки) или уменьшения уровня значимости. Однако, при этом возрастает вероятность допущения ошибки 2 рода (ошибки неотвержения нулевой гипотезы, когда она на самом деле неверна).