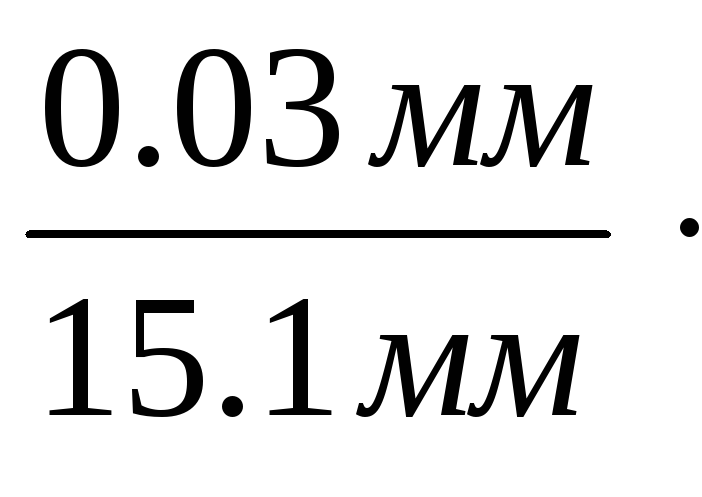Как рассчитать абсолютную ошибку измерений - Решение и исправление самых разных ошибок на TopOshibok.ru

Загрузить PDF

Абсолютная ошибка – это разность между измеренным значением и фактическим значением.^[1] Эта ошибка характеризует точность измерений. Если вам известны фактическое и измеренное значения, можно с легкостью вычислить абсолютную ошибку. Но иногда фактическое значение не дано, поэтому в качестве абсолютной ошибки пользуются максимально возможной ошибкой.^[2] Если даны фактическое значение и относительная ошибка, можно вычислить абсолютную ошибку.

1

Запишите формулу для вычисления абсолютной ошибки. Формула: $\Delta x=x_{{0}}-x$ , где $\Delta x$ – абсолютная ошибка (разность между измеренным и фактическим значениями), $x_{{0}}$ – измеренное значение, – фактическое значение.^[3]
2
Подставьте в формулу фактическое значение. Фактическое значение должно быть дано; в противном случае используйте принятое опорное значение. Фактическое значение подставьте вместо .
- Например, нужно измерить длину футбольного поля. Фактическая длина (принятая опорная длина) футбольного поля равна 105 м (именно такое значение рекомендуется FIFA). Таким образом, фактическое значение равно 105 м: $\Delta x=x_{{0}}-105$ .
3
Подставьте в формулу измеренное значение. Оно будет дано; в противном случае измерьте величину (длину или ширину и так далее). Измеренное значение подставьте вместо $x_{0}$ .
- Например, вы измерили длину футбольного поля и получили значение 104 м. Таким образом, измеренное значение равно 104 м: $\Delta x=104-105$ .
4
Вычтите фактическое значение из измеренного значения. Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».^[4] Так вы вычислите абсолютную ошибку.
- В нашем примере: $\Delta x=104-105=-1$ , то есть абсолютная ошибка измерения равна 1 м.
Реклама

1

Запишите формулу для вычисления относительной ошибки. Формула: $\delta x={\frac {x_{{0}}-x}{x}}$ , где $\delta x$ – относительная ошибка (отношение абсолютной ошибки к фактическому значению), $x_{{0}}$ – измеренное значение, – фактическое значение.^[5]
2
Подставьте в формулу относительную ошибку. Скорее всего, она будет дана в виде десятичной дроби. Относительную ошибку подставьте вместо $\delta x$ .
- Например, если относительная ошибка равна 0,02, формула запишется так: $0,02={\frac {x_{{0}}-x}{x}}$ .
3
Подставьте в формулу фактическое значение. Оно будет дано. Фактическое значение подставьте вместо .
- Например, если фактическое значение равно 105 м, формула запишется так: $0,02={\frac {x_{{0}}-105}{105}}$ .
4

Умножьте обе стороны уравнения на фактическое значение. Так вы избавитесь от дроби.
5

Прибавьте фактическое значение к каждой стороне уравнения. Так вы найдете $x_{{0}}$ , то есть измеренное значение.
6
Вычтите фактическое значение из измеренного значения. Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».^[6] Так вы вычислите абсолютную ошибку.
- Например, если измеренное значение равно 107,1 м, а фактическое значение равно 105 м, вычисления запишутся так: . Таким образом, абсолютная ошибка равна 2,1 м.
Реклама

1
Определите единицу измерения. То есть выясните, было ли значение измерено с точностью до сантиметра, метра и так далее. Возможно, эта информация будет дана (например, «длина поля измерена с точностью до метра»). Чтобы определить единицу измерения, посмотрите на то, как округлено данное значение.^[7]
- Например, если измеренная длина поля равна 106 м, значение было округлено до метров. Таким образом, единица измерения равна 1 м.
2
3
Используйте максимально возможную ошибку в качестве абсолютной ошибки.^[9] Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».^[10] Так вы вычислите абсолютную ошибку.
- Например, если измеренная длина поля равна $106\pm 0,5$ м, то есть абсолютная ошибка равна 0,5 м.
Реклама

Советы

Если фактическое значение не указано, найдите принятое опорное или теоретическое значение.

Об этой статье

Эту страницу просматривали 26 271 раз.

Была ли эта статья полезной?

Источник

Вычисление абсолютной и относительной погрешностей измерений при прямых измерениях

1. Абсолютная погрешность

Оценить отклонение
каждого из результатов измерения от
истинной величины можно лишь при наличии
данных большого числа измерений с
использованием теории вероятности.
Однако на практике, в лабораторных
условиях проводят 3-5 измерений. В этом
случае абсолютная погрешность отдельного
i-го
измерения будет следующей:

|DА_i|
= |А_СР
— А_i|,

где
А_СР
— средняя величина размера А. Средняя
арифметическая величина всех ½DА_i½
значений

называется
абсолютной погрешностью опыта.
Окончательный результат измерения
может быть записан в виде

А = А_СР
±
DА_СР,

где
А — искомая величина, которая лежит
внутри интервала

А_СР
±
DА_СР.

апример, если сделаем несколько
измерений длины заготовки в столярной
мастерской и получим среднее значение
l_СР= 75.5 см, а среднее
арифметическое абсолютной погрешности
l_СР= 0.3 см, то результат
запишется в виде

l
= (75.5 ± 0.3) см.

Это
означает, что истинное значение длины
заготовки лежит в интервале от 75.2 см до
75.8 см. При этом не имеет смысла вычислять
среднее значение с большим числом знаков
после запятой, так как от этого точность
не увеличивается.

2. Относительная погрешность

Абсолютная
погрешность измерения не характеризует
точности проведенных измерений. Поэтому
для того, чтобы сравнить точность
различных измерений и величин разной
размерности, находят среднюю относительную
погрешность результата (Е_А).
Относительная погрешность определяется
отношением абсолютной погрешности к
среднему арифметическому значению
измеряемой величины, которая определяется
в процентах:

Е_А=100%.

Относительная
погрешность показывает, какая часть
абсолютной погрешности приходится на
каждую единицу измеренной величины.
Это дает возможность оценить точность
проведенных измерений, качество работы.

Так,
например, пусть при измерении бруска
длиной l
= 1.51 см была допущена абсолютная
погрешность 0.03 мм, а при измерении
расстояния от Земли до Луны L
= 3.64^.10⁵
км абсолютная погрешность составила
100 км. Может показаться, что первое
измерение выполнено намного точнее
второго. Однако о точности измерения
можно судить по относительной погрешности,
а она показывает, что второе измерение
было выполнено в семь раз точнее первого:

E_l
=

100% = 0.2%

и
Е_L
=
100%
= 0.03%.

Вычисление абсолютных и относительных погрешностей при косвенных2 измерениях

В
большинстве случаев при выполнении
физических экспериментов исследуемая
величина не может быть измерена
непосредственно, а является функцией
одной или нескольких переменных,
измеренных непосредственно. При косвенных
измерениях абсолютная и относительная
погрешности результатов измерений
находятся вычислением через абсолютные
и относительные погрешности непосредственно
измеренных величин.

Использование формул дифференцирования

Для
определения абсолютных и относительных
погрешностей искомой величины при
косвенных измерениях можно воспользоваться
формулами дифференцирования, потому
что абсолютная ошибка функции равна
абсолютной ошибке аргумента, умноженной
на производную этой функции, то есть
полному дифференциалу функции.

Рассмотрим
это более подробно. Допустим, что
физическая величина А является функцией
многих переменных:

A
= f
(x,
y,
z
…).

Правило
I. Вначале
находят абсолютную погрешность величины
А, а затем относительную погрешность.
Для этого необходимо:

1) Найти полный
дифференциал функции

) Заменить бесконечно малые dx, dу,
dz, … соответствующими абсолютными
ошибками аргументовDx,
Dy,
Dz,
… (при этом знаки «минус» в абсолютных
ошибках аргументов заменяют знаками
«плюс», так чтобы величина ошибки
была максимальной):

Применяя
это правило к частным случаям, получим:

—
абсолютная погрешность суммы равна
сумме абсолютных погрешностей слагаемых.
Если X
= a
+ b,
то DX
= Da
+ Db;

—
абсолютная погрешность разности равна
сумме абсолютных погрешностей
уменьшаемого и вычитаемого. Если X
= a
— b,
то DX
= Da
+ Db;

—
абсолютная погрешность произведения
двух сомножителей равна сумме произведений
среднего значения первого множителя
(a_CP)
на абсолютную погрешность второго и
среднего значения второго множителя
(b_CP)
на абсолютную погрешность первого. Если
X
= а 
b,
то DX
= a_CP

Db
+ b_CP
Dа.
Если X
= a ⁿ, то DX
= nа_CPⁿ^-1Dа;

—
абсолютная погрешность дроби равна
сумме произведения знаменателя на
абсолютную погрешность числителя и
числителя на абсолютную погрешность
знаменателя, деленной на квадрат
знаменателя. Если X
=,
то DX=.

3) По определению
найдем относительную погрешность

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
#
#
#
#
#
#
#
#
12.02.2015183.3 Кб27Пример работы по теме ПЕРЕСКАЗ.doc
#

Источник

Вычисление погрешностей измерений

Выполнение лабораторных работ связано с измерением физических величин, т. е. определением значений величин опытным путём с помощью измерительных приборов (средств измерения), и обработкой результатов измерений.

Различают прямые и косвенные измерения. При этом результат любого измерения является приблизительным, т. е. содержит погрешность измерения. Точность измерения физической величины характеризуют абсолютная и относительная погрешности.

Прямое измерение — определение значения физической величины непосредственно с помощью измерительного прибора.

Абсолютную погрешность прямых измерений определяют суммой абсолютной инструментальной погрешности и абсолютной погрешности отсчёта Δx = Δ_иx + Δ_оx при условии, что случайная погрешность и погрешность вычисления или отсутствуют, или незначительны и ими можно пренебречь.

Абсолютная инструментальная погрешность Δ_иx связана с классом точности прибора. Абсолютные инструментальные погрешности некоторых средств измерений представлены в таблице 1.

Таблица 1

Средства измерений	Диапазон измерений	Абсолютная инструментальная погрешность
Линейки: металлические деревянные пластмассовые	150, 300, 500 мм 400, 500, 750 мм 200, 250, 300 мм	0,1 мм 0,5 мм 1 мм
Лента измерительная	150 см	0,5 см
Мензурки 2-го класса	100, 200, 250 см³	5 см³
Амперметр школьный	2 А	0,05 А
Миллиамперметр	от 0 до I_max	4 % максимального предела измерений I_max
Вольтметр школьный	6 В	0,15 В
Термометр лабораторный	100 °С	1 °С
Барометр-анероид	720–780 мм рт. ст.	3 мм рт. ст.
Штангенциркули с ценой деления 0,1; 0,05 мм	155, 250, 350 мм	0,1; 0,05 мм в соответствии с ценой деления нониуса
Микрометры с ценой деления 0,01 мм	0–25, 25–50, 50–75 мм	0,004 мм

Абсолютная погрешность отсчёта Δ_оx связана с дискретностью шкалы прибора. Если величину измеряют с точностью до целого деления шкалы прибора, то погрешность отсчёта принимают равной цене деления. Если при измерении значение величины округляют до половины деления шкалы, то погрешность отсчёта принимают равной половине цены деления.

Абсолютная погрешность определяет значение интервала, в котором лежит истинное значение измеренной величины:

Относительную погрешность прямого измерения определяют отношением абсолютной погрешности к значению измеряемой величины:

$straight epsilon subscript x equals fraction numerator increment x over denominator x subscript изм end fraction times 100 percent sign.$

Относительная погрешность характеризует точность измерения: чем она меньше, тем точность измерения выше.

Косвенное измерение — определение значения физической величины с использованием формулы, связывающей её с другими величинами, измеренными непосредственно с помощью приборов.

Одним из методов определения погрешности косвенных измерений является метод границ погрешностей. Формулы для вычисления абсолютных и относительных погрешностей косвенных измерений методом границ погрешностей представлены в таблице 2.

Таблица 2

Вид функции y	Абсолютная погрешность Δy	Относительная погрешность $fraction numerator bold increment bold y over denominator bold y end fraction$
x₁ + x₂	Δx₁ + Δx₂	$fraction numerator increment x subscript 1 plus increment x subscript 2 over denominator open vertical bar x subscript 1 plus x subscript 2 close vertical bar end fraction$
x₁ − x₂	Δx₁ + Δx₂	$fraction numerator increment x subscript 1 plus increment x subscript 2 over denominator open vertical bar x subscript 1 minus x subscript 2 close vertical bar end fraction$
Cx	CΔx	$fraction numerator increment x over denominator x end fraction$
x₁x₂	\|x₁\| Δx₂ + \|x₂\| Δx₁	$fraction numerator increment x subscript 1 over denominator open vertical bar x subscript 1 close vertical bar end fraction plus fraction numerator increment x subscript 2 over denominator open vertical bar x subscript 2 close vertical bar end fraction$
	$fraction numerator open vertical bar x subscript 1 close vertical bar increment x subscript 2 plus open vertical bar x subscript 2 close vertical bar increment x subscript 1 over denominator x subscript 2 superscript 2 end fraction$	$fraction numerator increment x subscript 1 over denominator open vertical bar x subscript 1 close vertical bar end fraction plus fraction numerator increment x subscript 2 over denominator open vertical bar x subscript 2 close vertical bar end fraction$
xⁿ	\|n\|\|x\|ⁿ⁻¹Δx	$open vertical bar n close vertical bar fraction numerator increment x over denominator open vertical bar x close vertical bar end fraction$
lnx	$fraction numerator increment x over denominator x end fraction$	$fraction numerator increment x over denominator x open vertical bar ln x close vertical bar end fraction$
sinx	\|cosx\| Δx	$fraction numerator increment x over denominator open vertical bar tg x close vertical bar end fraction$
cosx	\|sinx\| Δx	\|tgx\| Δx
tgx	$fraction numerator increment x over denominator cos squared x end fraction$	$fraction numerator 2 increment x over denominator open vertical bar sin 2 x close vertical bar end fraction$

Абсолютную погрешность табличных величин и фундаментальных физических постоянных определяют как половину единицы последнего разряда значения величины.

Источник

Download Article

Absolute error is the difference between the measured value and the actual value.^[1] It is one way to consider error when measuring the accuracy of values. If you know the actual and measured values, calculating the absolute error is a simple matter of subtraction. Sometimes, however, you may be missing the actual value, in which case you should use the maximum possible error as the absolute error.^[2] If you know the actual value and the relative error, you can work backwards to find the absolute error.

1

Set up the formula for calculating the absolute error. The formula is $\Delta x=x_{{0}}-x$ , where $\Delta x$ equals the absolute error (the difference, or change, in the measured and actual value), $x_{{0}}$ equals the measured value, and equals the actual value.^[3]
2
Plug the actual value into the formula. The actual value should be given to you. If not, use a standardly accepted value. Substitute this value for .^[4]
- For example, you might be measuring the length of a football field. You know that the actual, or accepted length of a professional American football field is 360 feet (including both end zones). So, you would use 360 as the actual value: $\Delta x=x_{{0}}-360$ .
Advertisement
3
Find the measured value. This will be given to you, or you should make the measurement yourself. Substitute this value for $x_{{0}}$ .
- For example, if you measure the football field and find that it is 357 feet long, you would use 357 as the measured value: $\Delta x=357-360$ .
4
Subtract the actual value from the measured value. Since absolute error is always positive, take the absolute value of this difference, ignoring any negative signs. This will give you the absolute error.^[5]
- For example, since $\Delta x=357-360=-3$ , the absolute error of your measurement is 3 feet.

1

Set up the formula for relative error. The formula is $\delta x={\frac {x_{{0}}-x}{x}}$ , where $\delta x$ equals the relative error (the ratio of the absolute error to the actual value), $x_{{0}}$ equals the measured value, and equals the actual value.^[6]
2
Plug in the value for the relative error. This will likely be a decimal. Make sure you substitute it for $\delta x$ .
- For example, if you know that the relative error is .025, your formula will look like this: $.025={\frac {x_{{0}}-x}{x}}$ .
3
Plug in the value for the actual value. This information should be given to you. Make sure you substitute this value for .
- For example, if you know that the actual value is 360 ft, your formula will look like this: $.025={\frac {x_{{0}}-360}{360}}$ .
4

Multiply each side of the equation by the actual value. This will cancel out the fraction.
5

Add the actual value to each side of the equation. This will give you the value of $x_{{0}}$ , giving you the measured value.
6
Subtract the actual value from the measured value. Since absolute error is always positive, take the absolute value of this difference, ignoring any negative signs. This will give you the absolute error.^[7]
- For example, if the measured value is 369 ft, and the actual value is 360 feet, you would subtract . So, the absolute error is 9 feet.

1
Determine the measuring unit. This is the “to the nearest” value. This might be explicitly stated (for example, “The building was measured to the nearest foot.”), but it doesn’t have to be. To determine the measuring unit, just look at what place value the measurement is rounded to.
- For example, if the measured length of a building is stated as 357 feet, you know that the building was measured to the nearest foot. So, the measuring unit is 1 foot.
2
3
Use the maximum possible error as the absolute error.^[9] Since absolute error is always positive, take the absolute value of this difference, ignoring any negative signs. This will give you the absolute error.
- For example, if you find the measurement of a building to be $357\pm .5ft$ , the absolute error is .5 ft.

Add New Question

Question

How do I find absolute error of any equation?

An equation does not contain an «absolute error.» Re-read the introduction above.
Question

How do I find the root value of a 6-digit number?
Question

What is the absolute error in 2.11?

As explained above, the concept of «absolute error» involves both a measured value and an «actual» value.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Video

If the actual value is not given, you can look for the accepted or theoretical value.

Thanks for submitting a tip for review!

References

About This Article

Article SummaryX

To calculate the absolute error, use the formula, “Absolute Error = Measured Value — Actual Value.” Begin by plugging the actual value into the formula, which will either be given to you or is the standardly accepted value. Then, make a measurement and put the measured value into the formula. Finally, subtract the actual value from the measure value to calculate the absolute error. If there are any negative signs, ignore them when you record your answer. To learn how to find the absolute error if you don’t have the measured value, keep reading.

Did this summary help you?

Thanks to all authors for creating a page that has been read 210,614 times.

Did this article help you?

Источник