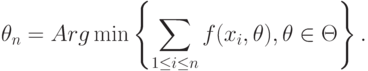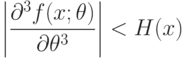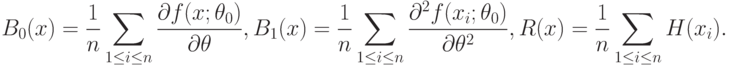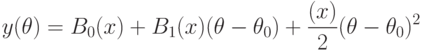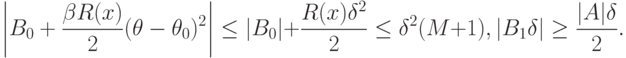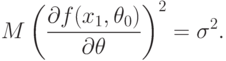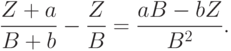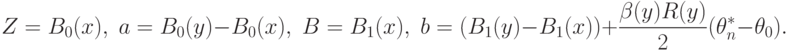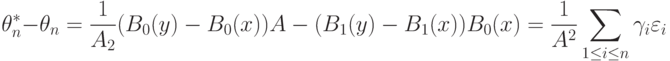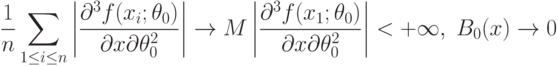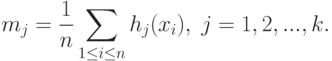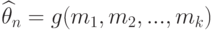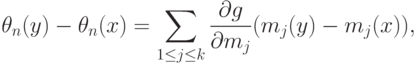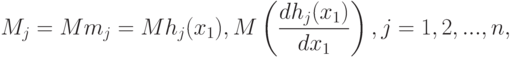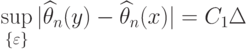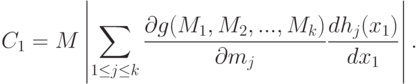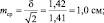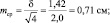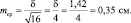Как определить статистическую ошибку - Решение и исправление самых разных ошибок на TopOshibok.ru

Статистические ошибки

Использование
методов биометрии позволяет исследователю
на ограниченном по численности материале
делать заключения о проявлении признака,
его изменчивости и других параметрах
в генеральной совокупности. Но так
как выборочная совокупность — часть
генеральной и ее формируют методом
случайного отбора, то в выборку могут
попасть животные с более низкими
продуктивными качествами, или несколько
лучшие особи. В этом случае вычисленные
значения M, б, C_v и
других биометрических величин будут
отличаться от значений этих величин в
генеральной совокупности, то есть
выборка отражает генеральную совокупность
с ошибкой. Эти ошибки, связанные с
методом выборочности, называются
статистическими и устранить их нельзя.
Ошибки не будет лишь в том случае, когда
в обработку включаются все члены
генеральной совокупности. Величины
статистических ошибок зависят от
изменчивости признаков и объема выборки:
чем более изменчив признак, тем больше
ошибка, и чем больше объем выборки, тем
она меньше. Ошибки статистических
величин в биометрии принято обозначать
буквой m.

Ошибки
имеют все статистические величины.
Вычисляют их по формулам:

Все
ошибки измеряют в тех же единицах, что
и сами показатели, и записывают обычно
рядом с ними.

Статистические
ошибки указывают интервал, в котором
находится величина того или иного
статистического показателя в генеральной
совокупности. Зная среднее значение
признака (М) и его ошибку (m), можно
установить доверительные границы
средней величины в генеральной
совокупности по формуле: М_ген.=М_в. 
tm, где t — нормированное отклонение,
которое зависит от уровня вероятности
и объема выборки. Цифровое значение t
для каждого конкретного случая находят
с помощью специальной таблицы. Например,
нас интересует средняя частота пульса
у овец породы прекос. Для изучения этого
показателя была сформирована выборка
в количестве 50 голов и определена у
этих животных средняя частота пульса.
Оказалось, что этот показатель равен
75 ударов в минуту, изменчивость его б =
12 ударов. Ошибка средней арифметической
величины в этом случае составит:

б
12

m
= ──── = ──── = 1,7 (уд./мин).

n
50

Итоговая
запись будет иметь вид: М 
m или 75 
1,7, то есть частота пульса 75 ударов в
минуту — среднее значение для 50 голов.
Чтобы определить среднюю частоту пульса
в генеральной совокупности животных,
возьмем в качестве доверительной
вероятности P = 0,95. В этом случае, исходя
из таблицы, t = 2,01. Определим доверительные
границы частоты пульса в генеральной
совокупности M 
tm.

75,0
+ 2,01 x 1,7 = 75,0 + 3,4 = 78,4 (уд./мин)

75,0
— 2,01 x 1,7 = 75,0 — 3,4 = 71,6 (уд./мин)

Таким
образом, средняя частота пульса для
генеральной совокупности будет в
пределах от 71,6 до 78,4 ударов в минуту.

Зная
величину статистических ошибок,
устанавливают также, правильно ли
выборочная совокупность отражает тот
или иной параметр генеральной, то есть
устанавливают критерий доверительности
выборочных величин.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Статистическая погрешность — это та неопределенность в оценке истинного значения измеряемой величины, которая возникает из-за того, что несколько повторных измерений тем же самым инструментом дали различающиеся результаты. Возникает она, как правило, из-за того, что результаты измерения в микромире не фиксированы, а вероятностны. Она тесно связана с объемом статистики: обычно чем больше данных, тем меньше статистическая погрешность и тем точнее результат измерения. Среди всех типов погрешностей она, пожалуй, самая безобидная: понятно, как ее считать, и понятно, как с ней бороться.

Статистическая погрешность: чуть подробнее

Предположим, что ваш детектор может очень точно измерить какую-то величину в каждом конкретном столкновении. Это может быть энергия или импульс какой-то родившейся частицы, или дискретная величина (например, сколько мюонов родилось в событии), или вообще элементарный ответ «да» или «нет» на какой-то вопрос (например, родилась ли в этом событии хоть одна частица с импульсом больше 100 ГэВ).

Это конкретное число, полученное в одном столкновении, почти бессмысленно. Скажем, взяли вы одно событие и выяснили, что в нём хиггсовский бозон не родился. Никакой научной пользы от такого единичного факта нет. Законы микромира вероятностны, и если вы организуете абсолютно такое же столкновение протонов, то картина рождения частиц вовсе не обязана повторяться, она может оказаться совсем другой. Если бозон не родился сейчас, не родился в следующем столкновении, то это еще ничего не говорит о том, может ли он родиться вообще и как это соотносится с теоретическими предсказаниями. Для того, чтобы получить какое-то осмысленное число в экспериментах с элементарными частицами, надо повторить эксперимент много раз и набрать статистику одинаковых столкновений. Всё свое рабочее время коллайдеры именно этим и занимаются, они накапливают статистику, которую потом будут обрабатывать экспериментаторы.

В каждом конкретном столкновении результат измерения может быть разный. Наберем статистику столкновений и усредним по ней результат. Этот средний результат, конечно, тоже не фиксирован, он может меняться в зависимости от статистики, но он будет намного стабильнее, он не будет так сильно прыгать от одной статистической выборки к другой. У него тоже есть некая неопределенность (в статистическом анализе она так и называется: «неопределенность среднего»), но она обычно небольшая. Вот эта величина и называется статистической погрешностью измерения.

Итак, когда экспериментаторы предъявляют измерение какой-то величины, то они сообщают результат усреднения этой величины по всей набранной статистике столкновений и сопровождают его статистической погрешностью. Именно такие средние значения имеют физический смысл, только их может предсказывать теория.

Есть, конечно, и иной источник статистической погрешности: недостаточный контроль условий эксперимента при повторном измерении. Если в физике частиц этот источник можно попытаться устранить, по крайней мере, в принципе, то в других разделах естественных наук он выходит на первый план; например, в медицинских исследованиях каждый человек отличается от другого по большому числу параметров.

Как считать статистическую погрешность?

Существует теория расчета статистической погрешности, в которую мы, конечно, вдаваться не будем. Но есть одно очень простое правило, которое легко запомнить и которое срабатывает почти всегда. Пусть у вас есть статистическая выборка из N столкновений и в ней присутствует n событий какого-то определенного типа. Тогда в другой статистической выборке из N событий, набранной в тех же условиях, можно ожидать примерно n ± √n таких событий. Поделив это на N, мы получим среднюю вероятность встретить такое событие и погрешность среднего: n/N ± √n/N. Оценка истинного значения вероятности такого типа события примерно соответствует этому выражению.

Сразу же, впрочем, подчеркнем, что эта простая оценка начинает сильно «врать», когда количество событий очень мало. В науке обсчета маленькой статистики есть много дополнительных тонкостей.

Более серьезное (но умеренно краткое) введение в методы статистической обработки данных в применении к экспериментам на LHC см. в лекциях arXiv.1307.2487.

Именно поэтому эксперименты в физике элементарных частиц стараются оптимизировать не только по энергии, но и по светимости. Ведь чем больше светимость, тем больше столкновений будет произведено — значит, тем больше будет статистическая выборка. И уже это позволит сделать измерения более точными — даже без каких-либо улучшений в эксперименте. Примерная зависимость тут такая: если вы увеличите статистику в k раз, то относительные статистические погрешности уменьшатся примерно в √k раз.

Этот пример — некая симуляция того, как могло бы происходить измерение массы ρ-мезона свыше полувека назад, на заре адронной физики, если бы он был вначале обнаружен в процессе e⁺e^– → π⁺π^–. А теперь перенесемся в наше время.

Сейчас этот процесс изучен вдоль и поперек, статистика набрана огромная (миллионы событий), а значит, и масса ρ-мезона сейчас определена несравнимо точнее. На рис. 3 показано современное состояние дел в этой области масс. Если ранние эксперименты еще имели какие-то существенные погрешности, то сейчас они практически неразличимы глазом. Огромная статистика позволила не только измерить массу (примерно равна 775 МэВ с точностью в десятые доли МэВ), но и заметить очень странную форму этого пика. Такая форма получается потому, что практически в том же месте на шкале масс находится и другой мезон, ω(782), который «вмешивается» в процесс и искажает форму ρ-мезонного пика.

Другой, гораздо более реальный пример влияния статистики на процесс поиска и изучения хиггсовского бозона обсуждался в новости Анимации показывают, как в данных LHC зарождался хиггсовский сигнал.

Источник

From Wikipedia, the free encyclopedia

In statistics and optimization, errors and residuals are two closely related and easily confused measures of the deviation of an observed value of an element of a statistical sample from its «true value» (not necessarily observable). The error of an observation is the deviation of the observed value from the true value of a quantity of interest (for example, a population mean). The residual is the difference between the observed value and the estimated value of the quantity of interest (for example, a sample mean). The distinction is most important in regression analysis, where the concepts are sometimes called the regression errors and regression residuals and where they lead to the concept of studentized residuals.
In econometrics, «errors» are also called disturbances.^[1]^[2]^[3]

Introduction[edit]

Suppose there is a series of observations from a univariate distribution and we want to estimate the mean of that distribution (the so-called location model). In this case, the errors are the deviations of the observations from the population mean, while the residuals are the deviations of the observations from the sample mean.

A statistical error (or disturbance) is the amount by which an observation differs from its expected value, the latter being based on the whole population from which the statistical unit was chosen randomly. For example, if the mean height in a population of 21-year-old men is 1.75 meters, and one randomly chosen man is 1.80 meters tall, then the «error» is 0.05 meters; if the randomly chosen man is 1.70 meters tall, then the «error» is −0.05 meters. The expected value, being the mean of the entire population, is typically unobservable, and hence the statistical error cannot be observed either.

A residual (or fitting deviation), on the other hand, is an observable estimate of the unobservable statistical error. Consider the previous example with men’s heights and suppose we have a random sample of n people. The sample mean could serve as a good estimator of the population mean. Then we have:

The difference between the height of each man in the sample and the unobservable population mean is a statistical error, whereas
The difference between the height of each man in the sample and the observable sample mean is a residual.

Note that, because of the definition of the sample mean, the sum of the residuals within a random sample is necessarily zero, and thus the residuals are necessarily not independent. The statistical errors, on the other hand, are independent, and their sum within the random sample is almost surely not zero.

One can standardize statistical errors (especially of a normal distribution) in a z-score (or «standard score»), and standardize residuals in a t-statistic, or more generally studentized residuals.

In univariate distributions[edit]

If we assume a normally distributed population with mean μ and standard deviation σ, and choose individuals independently, then we have

$X_{1},\dots ,X_{n}\sim N\left(\mu ,\sigma ^{2}\right)\,$

and the sample mean

$\overline{X}={X_1 + \cdots + X_n \over n}$

is a random variable distributed such that:

${\overline {X}}\sim N\left(\mu ,{\frac {\sigma ^{2}}{n}}\right).$

The statistical errors are then

$e_{i}=X_{i}-\mu ,\,$

with expected values of zero,^[4] whereas the residuals are

$r_{i}=X_{i}-{\overline {X}}.$

The sum of squares of the statistical errors, divided by σ², has a chi-squared distribution with n degrees of freedom:

${\frac {1}{\sigma ^{2}}}\sum _{i=1}^{n}e_{i}^{2}\sim \chi _{n}^{2}.$

However, this quantity is not observable as the population mean is unknown. The sum of squares of the residuals, on the other hand, is observable. The quotient of that sum by σ² has a chi-squared distribution with only n − 1 degrees of freedom:

${\frac 1{\sigma ^{2}}}\sum _{{i=1}}^{n}r_{i}^{2}\sim \chi _{{n-1}}^{2}.$

This difference between n and n − 1 degrees of freedom results in Bessel’s correction for the estimation of sample variance of a population with unknown mean and unknown variance. No correction is necessary if the population mean is known.

[edit]

It is remarkable that the sum of squares of the residuals and the sample mean can be shown to be independent of each other, using, e.g. Basu’s theorem. That fact, and the normal and chi-squared distributions given above form the basis of calculations involving the t-statistic:

$T={\frac {{\overline {X}}_{n}-\mu _{0}}{S_{n}/{\sqrt {n}}}},$

where ${\overline {X}}_{n}-\mu _{0}$ represents the errors, $S_{n}$ represents the sample standard deviation for a sample of size n, and unknown σ, and the denominator term $S_n/\sqrt n$ accounts for the standard deviation of the errors according to:^[5]

$\operatorname {Var} \left({\overline {X}}_{n}\right)={\frac {\sigma ^{2}}{n}}$

The probability distributions of the numerator and the denominator separately depend on the value of the unobservable population standard deviation σ, but σ appears in both the numerator and the denominator and cancels. That is fortunate because it means that even though we do not know σ, we know the probability distribution of this quotient: it has a Student’s t-distribution with n − 1 degrees of freedom. We can therefore use this quotient to find a confidence interval for μ. This t-statistic can be interpreted as «the number of standard errors away from the regression line.»^[6]

Regressions[edit]

In regression analysis, the distinction between errors and residuals is subtle and important, and leads to the concept of studentized residuals. Given an unobservable function that relates the independent variable to the dependent variable – say, a line – the deviations of the dependent variable observations from this function are the unobservable errors. If one runs a regression on some data, then the deviations of the dependent variable observations from the fitted function are the residuals. If the linear model is applicable, a scatterplot of residuals plotted against the independent variable should be random about zero with no trend to the residuals.^[5] If the data exhibit a trend, the regression model is likely incorrect; for example, the true function may be a quadratic or higher order polynomial. If they are random, or have no trend, but «fan out» — they exhibit a phenomenon called heteroscedasticity. If all of the residuals are equal, or do not fan out, they exhibit homoscedasticity.

However, a terminological difference arises in the expression mean squared error (MSE). The mean squared error of a regression is a number computed from the sum of squares of the computed residuals, and not of the unobservable errors. If that sum of squares is divided by n, the number of observations, the result is the mean of the squared residuals. Since this is a biased estimate of the variance of the unobserved errors, the bias is removed by dividing the sum of the squared residuals by df = n − p − 1, instead of n, where df is the number of degrees of freedom (n minus the number of parameters (excluding the intercept) p being estimated — 1). This forms an unbiased estimate of the variance of the unobserved errors, and is called the mean squared error.^[7]

Another method to calculate the mean square of error when analyzing the variance of linear regression using a technique like that used in ANOVA (they are the same because ANOVA is a type of regression), the sum of squares of the residuals (aka sum of squares of the error) is divided by the degrees of freedom (where the degrees of freedom equal n − p − 1, where p is the number of parameters estimated in the model (one for each variable in the regression equation, not including the intercept)). One can then also calculate the mean square of the model by dividing the sum of squares of the model minus the degrees of freedom, which is just the number of parameters. Then the F value can be calculated by dividing the mean square of the model by the mean square of the error, and we can then determine significance (which is why you want the mean squares to begin with.).^[8]

However, because of the behavior of the process of regression, the distributions of residuals at different data points (of the input variable) may vary even if the errors themselves are identically distributed. Concretely, in a linear regression where the errors are identically distributed, the variability of residuals of inputs in the middle of the domain will be higher than the variability of residuals at the ends of the domain:^[9] linear regressions fit endpoints better than the middle. This is also reflected in the influence functions of various data points on the regression coefficients: endpoints have more influence.

Thus to compare residuals at different inputs, one needs to adjust the residuals by the expected variability of residuals, which is called studentizing. This is particularly important in the case of detecting outliers, where the case in question is somehow different from the others in a dataset. For example, a large residual may be expected in the middle of the domain, but considered an outlier at the end of the domain.

Other uses of the word «error» in statistics[edit]

The use of the term «error» as discussed in the sections above is in the sense of a deviation of a value from a hypothetical unobserved value. At least two other uses also occur in statistics, both referring to observable prediction errors:

The mean squared error (MSE) refers to the amount by which the values predicted by an estimator differ from the quantities being estimated (typically outside the sample from which the model was estimated).
The root mean square error (RMSE) is the square-root of MSE.
The sum of squares of errors (SSE) is the MSE multiplied by the sample size.

Sum of squares of residuals (SSR) is the sum of the squares of the deviations of the actual values from the predicted values, within the sample used for estimation. This is the basis for the least squares estimate, where the regression coefficients are chosen such that the SSR is minimal (i.e. its derivative is zero).

Likewise, the sum of absolute errors (SAE) is the sum of the absolute values of the residuals, which is minimized in the least absolute deviations approach to regression.

The mean error (ME) is the bias.
The mean residual (MR) is always zero for least-squares estimators.

References[edit]

^ Kennedy, P. (2008). A Guide to Econometrics. Wiley. p. 576. ISBN 978-1-4051-8257-7. Retrieved 2022-05-13.
^ Wooldridge, J.M. (2019). Introductory Econometrics: A Modern Approach. Cengage Learning. p. 57. ISBN 978-1-337-67133-0. Retrieved 2022-05-13.
^ Das, P. (2019). Econometrics in Theory and Practice: Analysis of Cross Section, Time Series and Panel Data with Stata 15.1. Springer Singapore. p. 7. ISBN 978-981-329-019-8. Retrieved 2022-05-13.
^ Wetherill, G. Barrie. (1981). Intermediate statistical methods. London: Chapman and Hall. ISBN 0-412-16440-X. OCLC 7779780.
^ ^a ^b Frederik Michel Dekking; Cornelis Kraaikamp; Hendrik Paul Lopuhaä; Ludolf Erwin Meester (2005-06-15). A modern introduction to probability and statistics : understanding why and how. London: Springer London. ISBN 978-1-85233-896-1. OCLC 262680588.
^ Peter Bruce; Andrew Bruce (2017-05-10). Practical statistics for data scientists : 50 essential concepts (First ed.). Sebastopol, CA: O’Reilly Media Inc. ISBN 978-1-4919-5296-2. OCLC 987251007.
^ Steel, Robert G. D.; Torrie, James H. (1960). Principles and Procedures of Statistics, with Special Reference to Biological Sciences. McGraw-Hill. p. 288.
^ Zelterman, Daniel (2010). Applied linear models with SAS ([Online-Ausg.]. ed.). Cambridge: Cambridge University Press. ISBN 9780521761598.
^ «7.3: Types of Outliers in Linear Regression». Statistics LibreTexts. 2013-11-21. Retrieved 2019-11-22.

Cook, R. Dennis; Weisberg, Sanford (1982). Residuals and Influence in Regression (Repr. ed.). New York: Chapman and Hall. ISBN 041224280X. Retrieved 23 February 2013.
Cox, David R.; Snell, E. Joyce (1968). «A general definition of residuals». Journal of the Royal Statistical Society, Series B. 30 (2): 248–275. JSTOR 2984505.
Weisberg, Sanford (1985). Applied Linear Regression (2nd ed.). New York: Wiley. ISBN 9780471879572. Retrieved 23 February 2013.
«Errors, theory of», Encyclopedia of Mathematics, EMS Press, 2001 [1994]

External links[edit]

Media related to Errors and residuals at Wikimedia Commons

Источник

Метрологические, методические, статистические и вычислительные погрешности. Целесообразно выделить ряд видов погрешностей статистических данных. Погрешности, вызванные неточностью измерения исходных данных, называем метрологическими. Их максимальное значение можно оценить с помощью нотны. Впрочем, выше на примере оценивания параметров гамма-распределения показано, что переход от максимального отклонения к реально имеющемуся в вероятностно-статистической модели не меняет выводы (с точностью до умножения предельных значений погрешностей $\Delta$ или $\delta$ на константы). Как правило, метрологические погрешности не убывают с ростом объема выборки.

Методические погрешности вызваны неадекватностью вероятностно-статистической модели, отклонением реальности от ее предпосылок. Неадекватность обычно не исчезает при росте объема выборки. Методические погрешности целесообразно изучать с помощью «общей схемы устойчивости» [
[
1.15
]
,
[
12.38
]
], обобщающей популярную в теории робастных статистических процедур модель засорения большими выбросами. В настоящей главе методические погрешности не рассматриваются.

Статистическая погрешность — это та погрешность, которая традиционно рассматривается в математической статистике. Ее характеристики — дисперсия оценки, дополнение до 1 мощности критерия при фиксированной альтернативе и т.д. Как правило, статистическая погрешность стремится к 0 при росте объема выборки.

Вычислительная погрешность определяется алгоритмами расчета, в частности, правилами округления. На уровне чистой математики справедливо тождество правых частей формул (22) и (24), задающих выборочную дисперсию s^2 , а на уровне вычислительной математики формула (22) дает при определенных условиях существенно больше верных значащих цифр, чем вторая [
[
12.40
]
, с.51-52].

Выше на примере задачи оценивания параметров гамма-распределения рассмотрено совместное действие метрологических и вычислительных погрешностей, причем погрешности вычислений оценивались по классическим правилам для ручного счета [
[
12.4
]
]. Оказалось, что при таком подходе оценки метода моментов имеют преимущество перед оценками максимального правдоподобия в обширной области изменения параметров. Однако, если учитывать только метрологические погрешности, как это делалось выше в примерах 1-5, то с помощью аналогичных выкладок можно показать, что оценки этих двух типов имеют (при достаточно больших ) одинаковую погрешность.

Вычислительную погрешность здесь подробно не рассматриваем. Ряд интересных результатов о ее роли в статистике получили Н.Н. Ляшенко и М.С. Никулин [
[
12.20
]
].

Проведем сравнение методов оценивания параметров в более общей постановке.

В теории оценивания параметров классической математической статистики установлено, что метод максимального правдоподобия, как правило, лучше (в смысле асимптотической дисперсии и асимптотического среднего квадрата ошибки), чем метод моментов. Однако в интервальной статистике это, вообще говоря, не так, что продемонстрировано выше на примере оценивания параметров гамма-распределения. Сравним эти два метода оценивания в случае интервальных данных в общей постановке. Поскольку метод максимального правдоподобия — частный случай метода минимального контраста, начнем с разбора этого несколько более общего метода.

Оценки минимального контраста. Пусть — пространство, в котором лежат независимые одинаково распределенные случайные элементы .. Будем оценивать элемент пространства параметров $\Theta$ с помощью функции контраста $f:X\times\Theta\rightarrow R^1$ . Оценкой минимального контраста называется

$\theta_n=Arg\min\left\{\sum_{1\le i\le n}f(x_i,\theta),\theta\in\Theta\right\}.$

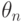
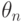
Если множество $\theta_n$ состоит из более чем одного элемента, то оценкой минимального контраста называют также любой элемент $\theta_n$ .

Оценками минимального контраста являются, в частности, многие робастные статистики [
[
1.15
]
,
[
12.45
]
]. Эти оценки широко используются в статистике объектов нечисловой природы [
[
1.15
]
,
[
12.38
]
], поскольку при $X=\Theta$ переходят в эмпирические средние, а если $X=\Theta$ — пространство бинарных отношений — в медиану Кемени.

Пусть в имеется мера $\mu$ (заданная на той же $\sigma$ -алгебре, что участвует в определении случайных элементов x_i ), и $p(x;\theta)$ — плотность распределения x_i по мере $\mu$ . Если

$f(x;\theta)=-\ln p(x;\theta),$

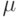
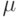
то оценка минимального контраста переходит в оценку максимального правдоподобия.

Асимптотическое поведение оценок минимального контраста в случае пространств и $\Theta$ общего вида хорошо изучено [
[
12.25
]
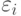
], в частности, известны условия состоятельности оценок. Здесь ограничимся случаем X = R^1 , но при этом введя погрешности измерений $\varepsilon_i$ . Примем также, что $\Theta=(\theta_{min},\theta_{max})\subseteq R^1$ .

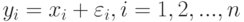
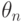
В рассматриваемой математической модели предполагается, что статистику известны лишь искаженные значения $y_i=x_i+\varepsilon_i,i=1,2,...,n$ . Поэтому вместо $\theta_n$ он вычисляет

$\theta_n^*=Arg\min\left\{\sum_{1\le i\le n}f(y_i,\theta),\theta\in\Theta\right\}.$

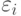
Будем изучать величину $\theta_n^*-\theta_n$ в предположении, что погрешности измерений $\varepsilon_i$ малы. Цель этого изучения — продемонстрировать идеи статистики интервальных данных при достаточно простых предположениях. Поэтому естественно следовать условиям и ходу рассуждений, которые обычно принимаются при изучении оценок максимального правдоподобия [
[
2.10
]
, п.33.3].

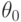
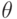
Пусть $\theta_0$ — истинное значение параметра, функция f(x;\theta) трижды дифференцируема по $\theta$ , причем

$\left|\frac{\partial^3 f(x;\theta)}{\partial \theta^3}\right|<H(x)$

при всех $x, \theta$ . Тогда

$\frac{\partial f(x;\theta)}{\partial\theta}=\frac{\partial f(x;\theta_0)}{\partial\theta}= \frac{\partial^2 f(x;\theta_0)}{\partial\theta^2} (\theta-\theta_0)+\frac12\alpha(x)H(x)(\theta-\theta_0)^2,$

(
27)

где $|\alpha(x)|<1$ .

Используя обозначения векторов 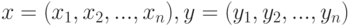, введем суммы

$B_0(x)=\frac{1}{n}\sum_{1\le i\le n}\frac{\partial f(x;\theta_0)}{\partial\theta}, B_1(x)=\frac{1}{n}\sum_{1\le i\le n}\frac{\partial^2 f(x_i;\theta_0)}{\partial\theta^2}, R(x)=\frac{1}{n}\sum_{1\le i\le n}H(x_i).$

Аналогичным образом введем функции , в которых вместо x_i стоят .

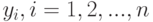
Поскольку в соответствии с теоремой Ферма оценка минимального контраста 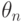$\theta_n$ удовлетворяет уравнению

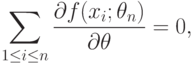$\sum_{1\le i\le n}\frac{\partial f(x_i;\theta_n)}{\partial\theta}=0,$

(
28)

то, подставляя в (27) x_i вместо и суммируя по , получаем, что

$0=B_0(x)+B_1(x)(\theta_n-\theta_0)+\frac{\beta R(x)}{2}(\theta_n-\theta_0)^2,|\beta|<1,$

(
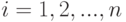
29)

откуда

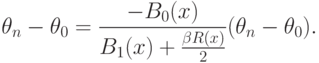$\theta_n-\theta_0=\frac{-B_0(x)}{B_1(x)+\frac{\beta R(x)}{2}}(\theta_n-\theta_0).$

(
30)

Решения уравнения (28) будем также называть оценками минимального контраста. Хотя уравнение (28) — лишь необходимое условие минимума, такое словоупотребление не будет вызывать трудностей.

Теорема 1. Пусть для любого выполнено соотношение (27). Пусть для случайной величины x_1 с распределением, соответствующим значению параметра $\theta=\theta_0$ , существуют математические ожидания

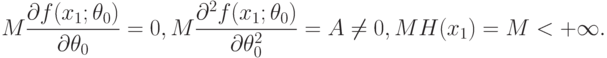$M\frac{\partial f(x_1;\theta_0)}{\partial\theta_0}=0, M\frac{\partial^2 f(x_1;\theta_0)}{\partial\theta_0^2}=A\ne 0, MH(x_1)=M<+\infty.$

(
31)

Тогда существуют оценки минимального контраста 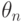$\theta_n$ такие, что $\theta_n\rightarrow\theta_0$ при $n\rightarrow\infty$ (в смысле сходимости по вероятности).

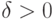
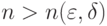
Доказательство. Возьмем $\varepsilon>0$ и $\delta>0$ . В силу закона больших чисел (теорема Хинчина) существует $n(\varepsilon,\delta)$ такое, что для любого $n>n(\varepsilon,\delta)$ справедливы неравенства

$P\{|B_0|\ge\delta^2\}<\varepsilon/3, P\{|B_1|<|A|/2\}<\varepsilon/3, P\{R(x)>2M\}<\varepsilon/3.$

Тогда с вероятностью не менее 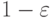$1-\varepsilon$ одновременно выполняются соотношения

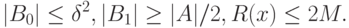$|B_0|\le\delta^2,|B_1|\ge|A|/2,R(x)\le 2M.$

(
32)

При $\theta\in[\theta_0-\delta;\theta_0+\delta]$ рассмотрим многочлен второй степени

$y(\theta)=B_0(x)+B_1(x)(\theta-\theta_0)+\frac{\betaR(x)}{2}(\theta-\theta_0)^2$

(см. формулу (29)). С вероятностью не менее 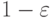$1-\varepsilon$ выполнены соотношения

$\left|B_0+\frac{\beta R(x)}{2}(\theta-\theta_0)^2\right|\le|B_0|+ \frac{R(x)\delta^2}{2}\le\delta^2(M+1),|B_1\delta|\ge\frac{|A|\delta}{2}.$

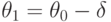
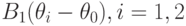
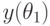
Если $0<2(M+1)\delta<|A|$ , то знак $y(\theta)$ в точках $\theta_1=\theta_0-\delta$ и $\theta_2=\theta_0+\delta$ определяется знаком линейного члена $B_1(\theta_i-\theta_0),i=1,2$ , следовательно, знаки $y(\theta_1)$ и $y(\theta_2)$ различны, а потому существует $\theta_n\in[\theta_0-\delta;\theta_0+\delta]$ такое, что $y(\theta_n)=0$ , что и требовалось доказать.

Теорема 2. Пусть выполнены условия теоремы 1 и, кроме того, для случайной величины x_1 , распределение которой соответствует значению параметра $\theta=\theta_0$ , существует математическое ожидание

$M\left(\frac{\partial f(x_1,\theta_0)}{\partial\theta}\right)^2=\sigma^2.$

Тогда оценка минимального контраста имеет асимптотически нормальное распределение:

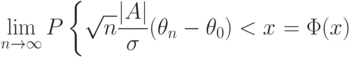$\lim_{n\rightarrow\infty}P\left\{\sqrt{n}\frac{|A|}{\sigma}(\theta_n-\theta_0)<x\right}=\Phi(x)$

(
33)

для любого , где $\Phi(x)$ — функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1.

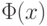
Доказательство. Из центральной предельной теоремы вытекает, что числитель в правой части формулы (30) асимптотически нормален с математическим ожиданием 0 и дисперсией 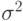$\sigma^2$ . Первое слагаемое в знаменателе формулы (30) в силу условий (31) и закона больших чисел сходится по вероятности к $A\ne 0$ , а второе слагаемое по тем же основаниям и с учетом теоремы 1 — к 0. Итак, знаменатель сходится по вероятности к $A\ne 0$ . Доказательство теоремы 2 завершает ссылка на теорему о наследовании сходимости (4.3 и [
[
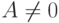
1.15
]
, $\S$ 2.4]).

Нотна оценки минимального контраста. Аналогично (30) нетрудно получить, что

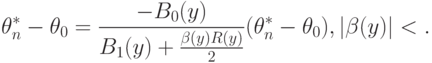$\theta_n^*-\theta_0=\frac{-B_0(y)}{B_1(y)+\frac{\beta(y)R(y)}{2}}(\theta_n^*-\theta_0), |\beta(y)|<.$

(
34)

Следовательно, $\theta_n^*-\theta_n$ есть разность правых частей формул (30) и (34). Найдем максимально возможное значение (т.е. нотну) величины при ограничениях (1) на абсолютные погрешности результатов измерений.

Покажем, что при $\Delta\rightarrow 0$ для некоторого C>0 нотна имеет вид

$N_{\theta_n}(x)=\sup_{\{\varepsilon\}}|\theta_n^*-\theta_n|=C\Delta(1+o(1)).$

(
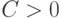
35)

Поскольку 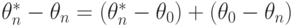$\theta_n^*-\theta_n=(\theta_n^*-\theta_0)+(\theta_0-\theta_n)$ , то из (33) и (35) следует, что

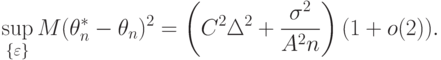$\sup_{\{\varepsilon\}}M(\theta_n^*-\theta_n)^2= \left(C^2\Delta^2+\frac{\sigma^2}{A^2 n}\right)(1+o(2)).$

(
36)

Можно сказать, что наличие погрешностей 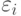$\varepsilon_i$ приводит к появлению систематической ошибки (смещения) у оценки метода максимального правдоподобия, и нотна является максимально возможным значением этой систематической ошибки.

В правой части (36) первое слагаемое — квадрат асимптотической нотны, второе соответствует статистической ошибке. Приравнивая их, получаем рациональный объем выборки

$n_{rat}=\left(\frac{\sigma}{CA\Delta}\right)^2.$

Остается доказать соотношение (35) и вычислить . Укажем сначала условия, при которых $\theta_n^*\rightarrow\theta_0$ (по вероятности) при $n\rightarrow\infty$ одновременно с $\Delta\rightarrow 0$ .

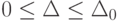
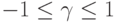
Теорема 3. Пусть существуют константа $\Delta_0$ и функции такие, что при $0\le\Delta\le\Delta_0$ и $-1\le\gamma\le 1$ выполнены неравенства (ср. формулу (27))

$\begin{aligned} &\left|\frac{\partial f(x;\theta_0)}{\partial \theta}- \frac{\partial f(x+\gamma\Delta;\theta_0)}{\partial \theta}\right|\le g_1(x)\Delta, \\ &\left|\frac{\partial^2 f(x;\theta_0)}{\partial \theta^2}- \frac{\partial^2 f(x+\gamma\Delta;\theta_0)}{\partial \theta^2}\right|\le g_2(x)\Delta, \\ &|H(x)-H(x+\gamma\Delta)|\le g_3(x)\Delta \end{aligned}$

(
37)

при всех . Пусть для случайной величины x_1 , распределение которой соответствует $\theta=\theta_0$ , существуют и . Пусть выполнены условия теоремы 1. Тогда $\theta_n^*\rightarrow\theta_0$ (по вероятности) при $\Delta\rightarrow 0,n\rightarrow\infty$ .

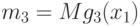
Доказательство проведем по схеме доказательства теоремы 1. Из неравенств (37) вытекает, что

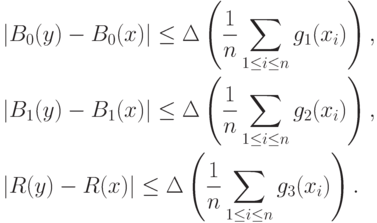$\begin{aligned} &|B_0(y)-B_0(x)|\le\Delta\left(\frac{1}{n}\sum_{1\le i\le n}g_1(x_i)\right), \\ &|B_1(y)-B_1(x)|\le\Delta\left(\frac{1}{n}\sum_{1\le i\le n}g_2(x_i)\right), \\ &|R(y)-R(x)|\le\Delta\left(\frac{1}{n}\sum_{1\le i\le n}g_3(x_i)\right). \end{aligned}$

(
38)

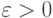
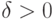
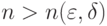
Возьмем $\varepsilon>0$ и $\delta>0$ . В силу закона больших чисел (теорема Хинчина) существует $n(\varepsilon,\delta)$ такое, что для любого $n>n(\varepsilon,\delta)$ справедливы неравенства

$\begin{aligned} &P\left\{|B_0|\ge\frac{\delta^2}{2}\right\}<\frac{\varepsilon}{6}, \left\{|B_1|<\frac{3|A|}{4}\right\}<\frac{\varepsilon}{6}, P\left\{R(x)>\frac{3M}{2}\right\}<\frac{\varepsilon}{6}, \\ &P\left\{\frac{1}{n}\sum_{1\le i\le n}g_j(x_i)>2m_j\right\}<\frac{\varepsilon}{6},j=1,2,3. \end{aligned}$

Тогда с вероятностью не менее 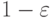$1-\varepsilon$ одновременно выполняются соотношения

$|B_0|<\frac12\delta^2,|B_1\ge\frac{3|A|}{4}|,R(x)\le\frac{3M}{2}, \frac{1}{n}\sum_{1\le i\le n}g_j(x_i)\le 2m_j, j=1,2,3.$

В силу (38) при этом

$|B_0(y)|<\frac12\delta^2+2\Delta m_1, |B_1(y)|\ge\frac{3|A|}{4}-2\Delta m_2, R(y)\le\frac{3M}{2}+2\Delta m_3.$

Пусть

$0\le\Delta\le\min\left\{\frac14\frac{\delta^2}{m_1};\frac18\frac{|A|}{m_2};\frac14\frac{M}{m_3}\right\}.$

Тогда с вероятностью не менее 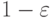$1-\varepsilon$ одновременно выполняются соотношения (ср. (32))

$|B_0(y)|\le\delta^2,|B_1(y)|\ge|A|/2,R(y)\le 2M.$

Завершается доказательство дословным повторением такового в теореме 1, с единственным отличием — заменой в обозначениях на .

Теорема 4. Пусть выполнены условия теоремы 3 и, кроме того, существуют математические ожидания (при $\theta=\theta_0$ )

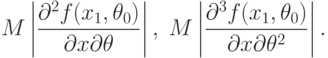$M\left|\frac{\partial^2 f(x_1,\theta_0)}{\partial x\partial\theta}\right|,\; M\left|\frac{\partial^3 f(x_1,\theta_0)}{\partial x\partial\theta^2}\right|.$

(
39)

Тогда выполнено соотношение (35) с

$C=\frac{1}{|A|}M\left|\frac{\partial^2 f(x_1,\theta_0)}{\partial x\partial\theta}\right|.$

(
40)

Доказательство. Воспользуемся следующим элементарным соотношением. Пусть и — бесконечно малые по сравнению с и соответственно. Тогда с точностью до бесконечно малых более высокого порядка

$\frac{Z+a}{B+b}-\frac{Z}{B}=\frac{aB-bZ}{B^2}.$

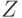
Чтобы применить это соотношение к анализу $\theta_n^*-\theta_n$ в соответствии с (30), (34) и теоремой 2, положим

$Z=B_0(x),\;a=B_0(y)-B_0(x),\;B=B_1(x),\;b=(B_1(y)-B_1(x))+\frac{\beta(y)R(y)}{2}(\theta_n^*-\theta_0).$

В силу условий теоремы 4 при малых 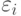$\varepsilon_i$ с точностью до членов более высокого порядка

$B_0(y)-B_0(x)=\frac{1}{n}\sum_{1\le i\le n}\frac{\partial^2 f(x_i,\theta_0)}{\partial x_i\partial\theta_0}\varepsilon_i, B_1(y)-B_1(x)=\frac{1}{n}\sum_{1\le i\le n}\frac{\partial^3 f(x_i,\theta_0)}{\partial x_i\partial\theta_0^2}\varepsilon_i.$

При $\Delta\rightarrow 0$ эти величины бесконечно малы, а потому с учетом сходимости B_1(x) к и теоремы 3

$\theta_n^*-\theta_n=\frac{1}{A_2}{(B_0(y)-B_0(x))A-(B_1(y)-B_1(x))B_0(x)}=\frac{1}{A^2}\sum_{1\le i\le n}\gamma_i\varepsilon_i$

с точностью до бесконечно малых более высокого порядка, где

$\gamma_i=\frac{\partial^2 f(x_i,\theta_0)}{\partial x_i\partial\theta_0}A- \frac{\partial^3 f(x_i,\theta_0)}{\partial x_i\partial\theta_0^2}B_0(x).$

Ясно, что задача оптимизации

$\left\{ \begin{aligned} &\sum_{1\le i\le n}\gamma_i\varepsilon_i\rightarrow\max \\ &|\varepsilon_i|\le\Delta, i=1,2,...,, \end{aligned} \right.$

(
41)

имеет решение

$\varepsilon_i= \left\{ \begin{aligned} &\Delta,&\gamma_i\ge 0, \\ &-\Delta,&\gamma_i<0, \end{aligned} \right.$

при этом максимальное значение линейной формы есть $\Delta\sum_{1\le i\le n}|\gamma_i|$ . Поэтому

$\sup_{\{\varepsilon\}}|\theta_n^*-\theta_n|=\frac{\Delta}{A^2n}\sum_{1\le i\le n}|\gamma_i|.$

(
42)

С целью упрощения правой части (42) воспользуемся тем, что

$\frac{1}{n}\sum_{1\le i\le n}|\gamma_i|=\frac{|A|}{n}\sum_{1\le i\le n}\left|\frac{\partial^2 f(x_i;\theta_0)}{\partial x\partial\theta_0}\right|+ \alpha\frac{|B_0(x)|}{n}\sum_{1\le i\le n}\left|\frac{\partial^3 f(x_i;\theta_0)}{\partial x\partial\theta_0^2}\right|,$

(
43)

где $|\alpha|\le 1$ .

Поскольку при $m\rightarrow\infty$

$\frac{1}{n}\sum_{1\le i\le n}\left|\frac{\partial^3 f(x_i;\theta_0)}{\partial x\partial\theta_0^2}\right|\rightarrow M\left|\frac{\partial^3 f(x_1;\theta_0)}{\partial x\partial\theta_0^2}\right|<+\infty,\;B_0(x)\rightarrow 0$

по вероятности, то второе слагаемое в (43) сходится к 0, а первое в силу закона больших чисел с учетом (39) сходится к CA^2 , где определено в (40). Теорема 4 доказана.

Оценки метода моментов. Пусть 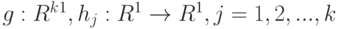$g:R^k\rightarrowR^1,h_j:R^1\rightarrow R^1, j=1,2,...,k$ , — некоторые функции. Рассмотрим аналоги выборочных моментов

$m_j=\frac{1}{n}\sum_{1\le i\le n}h_j(x_i),\;j=1,2,...,k.$

Оценки метода моментов имеют вид

$\widehat{\theta}_n=g(m_1,m_2,...,m_k)$

(функции и h_j должны удовлетворять некоторым дополнительным условиям [
[
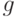
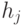
12.3
]
, с.80], которые здесь не приводим). Очевидно, что

$\theta_n(y)-\theta_n(x)=\sum_{1\le j\le k}\frac{\partial g}{\partial m_j}(m_j(y)-m_j(x)),$

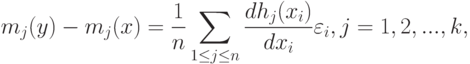$m_j(y)-m_j(x)=\frac{1}{n}\sum_{1\le j\le n}\frac{dh_j(x_i)}{dx_i}\varepsilon_i,j=1,2,...,k,$

(
44)

с точностью до бесконечно малых более высокого порядка, а потому с той же точностью

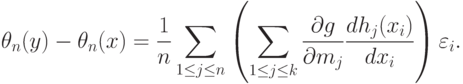$\theta_n(y)-\theta_n(x)=\frac{1}{n}\sum_{1\le j\le n}\left(\sum_{1\le j\le k}\frac{\partial g}{\partial m_j}\frac{dh_j(x_i)}{dx_i}\right)\varepsilon_i.$

(
45)

Теорема 5. Пусть при $\theta=\theta_0$ существуют математические ожидания

$M_j=Mm_j=Mh_j(x_1), M\left(\frac{dh_j(x_1)}{dx_1}\right), j=1,2,...,n,$

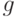
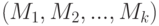
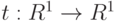
функция дважды непрерывно дифференцируема в некоторой окрестности точки . Пусть существует функция $t:R^1\rightarrow R^1$ такая, что

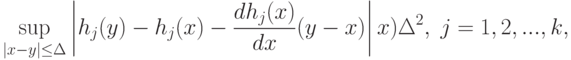$\sup_{|x-y|\le\Delta}\left|h_j(y)-h_j(x)-\frac{dh_j(x)}{dx}(y-x)\right|\let(x)\Delta^2,\;j=1,2,...,k,$

(
46)

причем 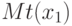Mt(x_1) существует. Тогда

$\sup_{\{\varepsilon\}}|\widehat{\theta}_n(y)-\widehat{\theta}_n(x)|=C_1\Delta$

с точностью до бесконечно малых более высокого порядка, причем

$C_1=M\left|\sum_{1\le j\le k}\frac{\partial g(M_1,M_2,...,M_k)}{\partial m_j}\frac{dh_j(x_1)}{dx_1}\right|.$

Доказательство теоремы 5 сводится к обоснованию проведенных ранее рассуждений, позволивших получить формулу (45). В условиях теоремы 5 собраны предположения, достаточные для такого обоснования. Так, условие (46) дает возможность обосновать соотношения (44); существование $M\left(\frac{dh_j(x_1)}{dx_1}\right)$ обеспечивает существование C_1 , и т.д. Завершает доказательство ссылка на решение задачи оптимизации (41) и применение закона больших чисел.

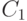
Полученные в теоремах 4 и 5 нотны оценок минимального контраста и метода моментов, асимптотические дисперсии этих оценок (см. теорему 2 и [
[
12.17
]
] соответственно) позволяют находить рациональные объемы выборок, строить доверительные интервалы с учетом погрешностей измерений, а также сравнивать оценки по среднему квадрату ошибки (36). Подобное сравнение было проведено для оценок максимального правдоподобия и метода моментов параметров гамма-распределения. Установлено, что классический вывод о преимуществе оценок максимального правдоподобия [
[
1.7
]
, с.99-100] неверен в случае $\Delta>0$ .

Источник

2.1. Стандартное отклонение среднего выборочного значения (ошибка среднего) и доверительный интервал

Результаты измерений обычно показывают с так называемой «средней статистической ошибкой средней величины» и для нашего случая (см. табл. 1.1) это будет запись: «высота сеянцев в опыте составила 5,0 ± 0,28 см». Словосочетание «средняя статистическая ошибка» обычно сокращают до названия «ошибка среднего» или просто «ошибка», обозначают буквой m и определяют по очень простой формуле. Для итогов упомянутой таблицы, где расчеты по 25 высотам дали значение δ = 1,42 см, эта ошибка составит:

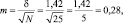
11.wmf (2.1)

где δ –	стандартное отклонение;
N –	число наблюдений или объем выборки, шт.

Если объем выборки взять 100 шт., то ошибка снизится в 2 раза: 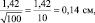12.wmf а если увеличить до 10000 шт., то в 10 раз, до 0,014 см.

Рассмотрим эту «среднюю статистическую ошибку» (далее просто ошибка) подробно, так как именно в ней скрыто понимание того, что называют статистическим мышлением. Интуитивно мы понимаем, что малая выборка дает большую ошибку, т.е. неточное определение среднего значения. Последний термин настолько привычен, что мы даже не задумываемся о том, что его правильное и полное название «среднее выборочное значение», т.е. среднее, определяемое в некоторой выборке. И выборки могут быть очень разные по численности. Начнем с самых малых. Например, что произойдет с ошибкой, если объем выборки сократить до 2 измерений? Такие выборки бывают, например, в почвенных исследованиях, когда каждое измерение достается дорогой ценой. Для этого вернемся к рис. 1.1. На нем стандартное отклонение ±δ, которое отражает разброс значений вокруг среднего в левую и правую сторону в виде холма, наблюдается при объеме выборки 1 шт. В этом случае ошибка среднего выборочного значения будет равна стандартному отклонению: m = δ = 1,42. С увеличением N ошибка уменьшается:

при объеме выборки N = 2 ошибка будет

13.wmf

при объеме выборки N = 4 ошибка будет

14.wmf

при объеме выборки N = 16 ошибка будет

15.wmf

Важно понять, что ряд распределения частот этих выборочных средних будет постепенно как бы съеживаться и приближаться к центру, где находится так называемое «генеральное» среднее. Поясним, что в математике генеральное среднее значение называется математическим ожиданием и его обозначают буквой «М». Например, это может быть средняя высота, рассчитанная по всем измеренным в теплице сеянцам, или среднее число семян в 1 шишке у дерева после подсчета семян во всех собранных с дерева шишках (50, 100, 500 и т.д., т.е. весьма небольшая генеральная совокупность). Распределение частот значений выборочных средних, которых может быть множество, будет иметь форму такого же холма, как и распределение единичных значений на рис. 1.1. При этом, если выборка будет из 1 шт., то холм будет в точности таким же, но при выборках из 2 шт. его форма съежится в 16.wmf = в 1,41 раза; при выборках из 4 шт. –
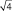
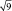
в 17.wmf = в 2 раза; при выборках из 9 шт. – в 18.wmf = в 3 раза и т.д.

Для этих сокращающихся рядов распределения выборочных средних можно рассчитать свое, особое стандартное отклонение. Вероятно, чтобы не путать его со СТАНДОТКЛ, его стали называть по-другому, т.е. «средней статистической ошибкой средней величины». Чем больше по объему выборки, тем короче ряд распределения средних значений этих выборок с его «хвостами» в левую и правую сторону, и тем меньше величина этого особого стандартного отклонения. Закон распределения частот выборочных средних точно такой же, и имеет те же свойства: в пределах ±2m находится 95 % всех значений выборочных средних, в пределах ±3m – 99,5 %, а в пределах ±4m находится 100 % всех значений xср. Форма этого распределения меняется от пологой при малых выборках до очень крутой, вплоть до «схлопывания» в центре при выборках большого объема, когда ошибка среднего стремится к нулю.

Здесь следует пояснить, что, на наш взгляд, словосочетание «средняя статистическая ошибка средней величины», сокращаемое до «ошибки среднего значения» или просто до «ошибки», вводит нас в некоторое заблуждение, так как мы привыкли со школы, что ошибки надобно исправлять. Более правильным, вместо слов «ошибка среднего значения», будет использование слов «стандартное отклонение выборочных средних значений от генерального среднего». Не случайно математики выбрали для обозначения величины этого отклонения букву «m», а для обозначения генерального среднего (математического ожидания) – букву «М». Слова для объяснения этих сложных явлений могут быть разными, но и у математиков, и у биологов есть единодушие в понимании статистического смысла, лежащего за этими буквенными символами. Вообще, лучше было бы ввести некий иной термин вместо слов «ошибка» или «отклонение», так как они изначально имеют в нашем сознании иной смысл; на наш взгляд, более всего подходит слово «скачок» (чем сильнее отскакивает выборочное среднее от генерального среднего, тем реже оно встречается). Но так уж получилось, что не нашлось нейтрального (иностранного) слова, и слово «ошибка» традиционно используют, и мы также будем его использовать; важно понимать его иной, чем в обыденном употреблении, математический и статистический смысл.

Для самого точного определения средней высоты сеянцев нужно измерять все растения в питомнике, и тогда мы получим «генеральное среднее значение». Но так не делают, а измеряют несколько сотен растений в разных местах и этого бывает достаточно для определения среднего выборочного значения с приемлемой точностью. В нашем примере при 100 растениях ошибка его определения составит 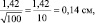19.wmf а ее отнесение к средней высоте сеянцев 5,0 см, выражаемое в %, дает нам так называемую точность опыта: 0,14/5,0×100 = 2,8 %. В биологии точность опыта ±2–3 % считается высокой, ±5 % – достаточной, а ±6–7 % – пониженной, но это весьма упрощенное представление о планировании эксперимента.

Вообще, точность опыта не самоцель; гораздо важнее сократить численность (объем) выборки до минимума. Представим себе, что средняя высота сеянцев xср = 5,0 см, а ее ±δ = 1,42 см, рассмотренные выше, получены при измерении 1000 растений потомства сосны, например, из Кунгура. Поделив ±δ на корень из 1000 получаем ошибку опыта m = ±0,045 см. Далее получаем точность опыта

Р = m/xср×100 = 0,045/5,0×100 = 0,9 %.

Точность получилась очень высокой. Но в питомнике есть потомства и из других мест и такой уровень точности совершенно не нужен, так как нужно узнать еще высоты сеянцев, например, из Очера, Осы, Добрянки и других районов. Если выборку из 1 тыс. растений снижать, то будет увеличиваться ошибка в определении средней высоты. И нужно найти приемлемую величину такой ошибки, которая позволит нам, тем не менее, уверенно утверждать, что это потомство растет быстрее, либо медленнее других. Причем происхождений может быть несколько сотен и минимизация выборок крайне важна, так как масштабы работ ограничены физическими возможностями бригады селекционеров. Следовательно, надо сокращать объем выборки. Как это сделать правильно?

Рассмотрим два потомства. Первое – это упомянутые сеянцы происхождением из Кунгура (хср1), второе – сеянцы из Кизела с хср2 = 6,0 см и δ2 = ± 1,0 см (превышение высоты на 20 %). Надо это превышение доказать. При выборках из 100 растений ранее определенная ошибка m1 была равна 0,14 см, вторая ошибка m2 после расчетов по формуле (2.1) составит 0,1 см. По закону нормального распределения 99,5 % всех возможных значений этих средних хср1 и хср2 будут в пределах «плюс-минус три ошибки», что можно показать графически (рис. 2.1) или в виде формул:

хср1 ± 3m1 = 5,0 ± 3×0,14 = 5,0 ± 0,4 см

хср2 ± 3m2 = 6,0 ± 3×0,1 = 6,0 ± 0,3 см.

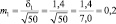
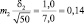
Возможные теоретические значения средних в генеральной совокупности не перекрывают друг друга, значит, различие достоверно. А если сократить выборки до 50 сеянцев? Тогда 20.wmf и 21.wmf и пределы колебаний возможных значений средних будут:

хср1 ± 3m1 = 5,0 ± 3×0,20 = 5,0 ± 0,6 см;

хср2 ± 3m2 = 6,0 ± 3×0,14 = 6,0 ± 0,3 см.

2_1.tif

Рис. 2.1. Средние значения по выборкам из 100 растений и их тройные ошибки (пределы возможных значений выборочных средних в 99,5 % случаев)

Снова вынесем эти пределы на график (рис. 2.2).

2_2.tif

Рис. 2.2. Средние значения при N = 50 растений и их тройные ошибки

Как видим, пределы сблизились и если еще сократить выборки, то они перекроются. Можно ли далее снижать объем выборки?

Можно, но здесь вступает в силу так называемое условие безошибочного прогноза. Мы это условие задали на уровне 99,5 % и для этого взяли ±3m для распределения ошибок. Но можно взять уровень пониже, с пределами ±2δ (уровень 95 %) и даже с пределами ±1,7δ (уровень 90 %).

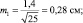
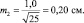
При выборках из 25 штук сеянцев, получаем две ошибки: 22.wmf 23.wmf Тогда пределы значений для этих двух выборочных средних для уровня прогноза в 95 % будут:

хср1 ± 2m1 = 5,0 ± 2×0,28 = 5,0 ± 0,56 см;

хср2 ± 2m2 = 6,0 ± 2×0,20 = 6,0 ± 0,40 см.

Выносим эти пределы опять на график (рис. 2.3).

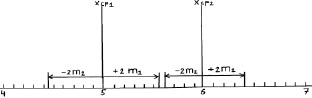
2_3.tif

Рис. 2.3. Средние значения при N = 25 растений и их двойные ошибки (пределы возможных значений средних в 95 % случаев)

Как видим, просвет все еще есть, и поэтому между возможными значениями средних высот сеянцев в других выборках из происхождений Кунгур и Кизел различия будут опять доказаны. Но уровень доказательства понизился до 95 %, и для 5 % оставшихся случаев нет гарантии, что различия будут иметь место при выборке из 25 растений. Их может и не быть, но эту вероятность в 5 % мы допускаем.

Источник

Статистические ошибки

Статистическая погрешность: чуть подробнее

Как считать статистическую погрешность?

Introduction[edit]

In univariate distributions[edit]

[edit]

Regressions[edit]

Other uses of the word «error» in statistics[edit]

See also[edit]

References[edit]

External links[edit]

2.1. Стандартное отклонение среднего выборочного значения (ошибка среднего) и доверительный интервал