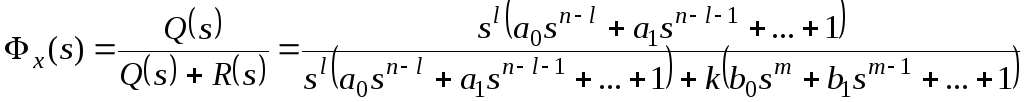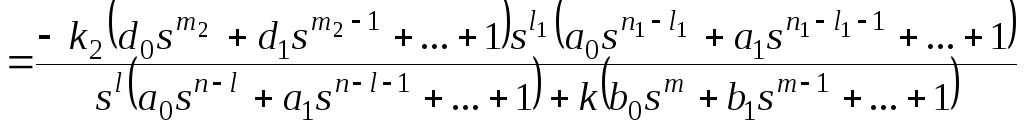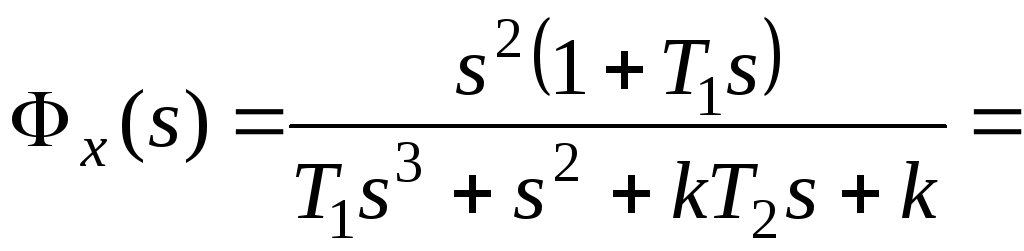Как найти установившуюся ошибку системы

Лекция 17.
Расчет
установившейся ошибки в системах
управления. Структурные признаки
астатизма. Коэффициенты ошибок

Установившейся
(статической) ошибкой называют постоянное
значение сигнала ошибки x(t)=g(t)-y(t),
которое она приобретает по окончании
переходного процесса:
,
рисунок 116.

Очевидно,
установившаяся ошибка зависит от законов
изменения и численных характеристик
входных сигналов системы. Поэтому при
ее определении принято рассматривать
так называемые типовые входные сигналы,
законы изменения которых составляют
степенной ряд относительно времени.
Например, для задающего воздействия:

,

,

и так далее.

При наличии
нескольких воздействий на линейную
систему для определения x_уст
используется принцип суперпозиции –
реакция линейной системы на совокупность
входных сигналов совпадает с алгебраической
суммой ее реакций на каждый из сигналов
в отдельности:

,

где каждое слагаемое,
или составляющая сигнала ошибки,
определяется
для i-го
входного сигнала при условии, что
остальные тождественно равны нулю.
Такой подход полностью соответствует
определению передаточной функции и
позволяет выполнять расчет установившейся
ошибки на основе структурной схемы
системы.

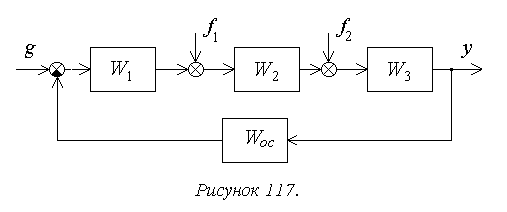
Рассмотрим порядок
расчета установившейся ошибки на
следующем достаточно общем примере
(рисунок 117).

В соответствии с
принципом суперпозиции установившаяся
ошибка будет определяться здесь в виде
суммы трех составляющих
.

Изображение по
Лапласу ошибки от задающего воздействия
получают через передаточную функцию
замкнутой системы по ошибке

при известном изображении задающего
воздействия G(s):

,

где (s)
– основная передаточная функция
замкнутой системы. Для структурной
схемы на рисунке 117

,

где

— передаточная функция разомкнутой
системы, или прямой цепи системы, для
рассматриваемого примера.

Непосредственно
для расчета установившегося значения
ошибки от задающего воздействия
используют теорему о конечном значении
для преобразования Лапласа:

В результате:

.

Изображение по
Лапласу ошибки от возмущающего воздействия
получают через передаточную функцию
замкнутой системы по ошибке от возмущения

при известном изображении возмущающего
воздействия F(s):

,

где _f(s)
–передаточная функция замкнутой системы
по возмущающему воздействию,

;

W_f(s)
– передаточная функция разомкнутой
системы по возмущению (передаточная
функция участка прямой цепи системы от
точки приложения возмущающего воздействия
до выхода системы).

Для структурной
схемы на рисунке 8 необходимо учитывать
два возмущающих воздействия, приложенные
в различные точки системы.

Для f₁:

,

,

.

Для f₂:

,

,

.

Расчет упрощается
для системы с единичной отрицательной
обратной связью (рисунок 118):

,

,

где k=k₁k₂k₃
– коэффициент передачи разомкнутой
системы.

Найдем установившуюся
ошибку для некоторых типовых вариантов
задающего воздействия.

При

получим:

.

При

получим:

.

При

получим:

.

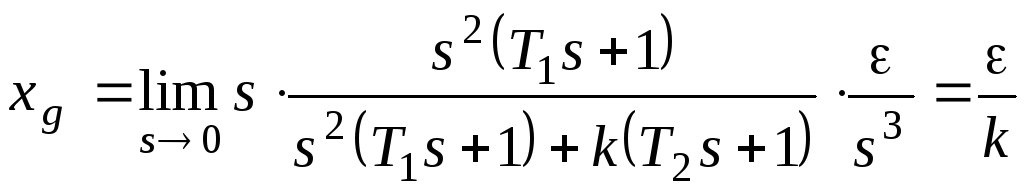
Если установившаяся
ошибка тождественно равна нулю при
каком-либо типовом варианте входного
сигнала, независимо от его численных
характеристик, систему называют
астатической по рассматриваемому
входному сигналу.

Количество типовых
вариантов входного сигнала – членов
степенного ряда, при которых установившаяся
ошибка тождественно равна нулю, определяет
порядок астатизма.

Рассматриваемая
система обладает свойством астатизма
второго порядка по задающему воздействию.

Рассмотрим
установившуюся ошибку от возмущения
f₁:

,

,

где

– коэффициент передачи разомкнутой
системы по возмущению f₁.

При

получим:

.

При

получим:

.

При

получим тот же результат.

Отметим, что по
возмущению f₁
рассматриваемая система не является
астатической. Кроме того, она не в
состоянии отработать два последних
варианта входного сигнала.

Рассмотрим
установившуюся ошибку от возмущения
f₂:

,

,

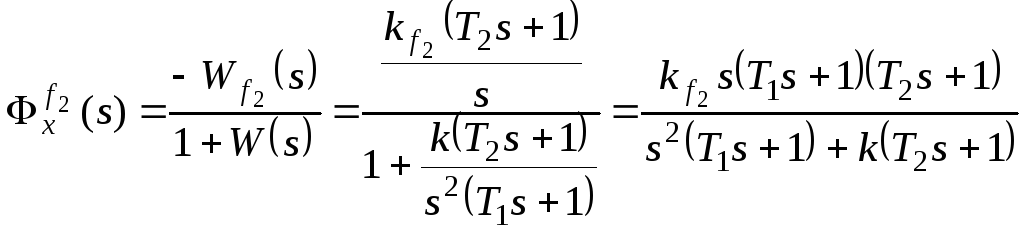
где

– коэффициент передачи разомкнутой
системы по возмущению f₂.

При

получим:

.

При

получим:

.

При

получим:

.

По возмущению f₂
рассматриваемая система имеет астатизм
первого порядка. Она не в состоянии
отработать возмущающее воздействие,
изменяющееся во времени с постоянным
ускорением.

Подведем некоторые
итоги:

1. Наличие и глубина
свойства астатизма зависят от точки
приложения входного сигнала.

2. Постоянные
времени звеньев системы не влияют на
ее точность.

3. Увеличение
значения коэффициента передачи
разомкнутой системы приводит к снижению
величины установившейся ошибки.

Для систем с
единичной отрицательной обратной связью
существуют достаточно простые структурные
признаки астатизма.

Рассмотрим
структуру, показанную на рисунке 119.

В общем случае
передаточная функция разомкнутой
системы может быть представлена в
следующей форме:

,

где l0.

Тогда получим:

и для общего вида
задающего воздействия
,
которому соответствует изображение
,

.

Результат нахождения
этого предела зависит от соотношения
показателей степени:

— при l>v
установившаяся ошибка равна нулю
независимо от остальных параметров, то
есть имеет место астатизм;

— при l=v
получаем константу;

— при l<v
установившаяся ошибка стремится к
бесконечности, то есть система не в
состоянии отработать входной сигнал.

Учитывая, что
минимальное значение v
нулевое, получаем условие астатизма по
задающему воздействию: l>0.

Таким образом,
структурный признак астатизма по
задающему воздействию в системе с
единичной отрицательной обратной связью
состоит в наличии нулевых корней в
знаменателе передаточной функции
разомкнутой системы, или интегрирующих
звеньев в прямой цепи системы.

Нетрудно также
убедиться, что положительное значение
l
совпадает с порядком астатизма.

Для получения
признака астатизма по возмущающему
воздействию представим передаточные
функции на рисунке 10 в форме:

,

,

где l₁+l₂=l,
k₁k₂=k,
m₁+m₂=m,
n₁+n₂=n,
причем

и
.

Тогда получим:

и для общего вида
возмущающего воздействия
,
которому соответствует изображение
,

.

Все вышеприведенные
выводы можно повторить для показателя
степени l₁.

Таким образом,
структурный признак астатизма по
возмущающему воздействию в системе с
единичной отрицательной обратной связью
состоит в наличии нулевых корней в
знаменателе передаточной функции
участка системы до точки приложения
воздействия, или интегрирующих звеньев
на том же участке.

Более общий подход
к оценке точности линейных систем
управления основан на получении и
использовании коэффициентов ошибок.
Рассмотрим его на примере анализа
реакции системы на задающее воздействие.

Если рассматривать
произвольный закон изменения задающего
воздействия g(t),
то эта функция времени может быть
разложена в степенной ряд относительно
аргумента t.
Члены степенного ряда, как известно,
находятся через производные

,
,
…,
,
…

В общем случае ряд
бесконечен. Поэтому с практической
точки зрения рассматривать такое
представление сигнала целесообразно
только при достаточно плавном его
изменении, когда можно ограничиться
конечным числом членов ряда, имея в
виду, что при n
большем некоторого m
можно принять

,
n>m.

Для задачи оценки
установившейся ошибки при

с формулированное допущение вполне
корректно, так как в противном случае
эта задача не имеет смысла.

Коэффициенты
ошибки получают разложением передаточной
функции замкнутой системы по ошибке в
степенной ряд (ряд Тейлора) относительно
аргумента s:

,

где коэффициенты
разложения в общем случае находят как
значения производных в точке s=0:

.

Передаточные
функции, представляющие собой отношения
полиномов, при достаточно высоком
порядке системы могут оказаться слишком
сложными для дифференцирования. Поэтому
на практике коэффициенты их разложения
в ряд чаще находят путем деления полиномов
– числителя на знаменатель.

С учетом разложения
передаточной функции в ряд можно записать
изображение по Лапласу сигнала ошибки
в следующей форме:

.

Отметим, что с
учетом сформулированного выше допущения
такое представление сигнала ошибки
соответствует

или
.

Перейдя к оригиналу
с учетом теоремы дифференцирования
получим:

.

Вернемся к
рассмотренному выше примеру и предположим,
что задающее воздействие изменяется
по произвольному закону, но при достаточно
больших значениях времени этот закон
аппроксимируется выражением
.

Найдем коэффициенты
разложения передаточной функции по
ошибке

в степенной ряд.

Здесь сразу можно
отметить, что номер первого ненулевого
члена ряда определяется низшей степенью
аргумента s
в числителе дроби, то есть первые два
коэффициента c₀
и c₁
здесь получаем тождественно равными
нулю.

Далее получим:

В результате
получаем
,
,
,

и так далее.

Найдем производные
задающего воздействия:

,
,
.

Ясно, что для
определения установившейся ошибки
достаточно первых трех коэффициентов:

.

В заключение
отметим, что порядок астатизма системы
по какому-либо входному сигналу совпадает
с количеством нулевых коэффициентов
ошибки, получаемых в разложении в ряд
передаточной функции по ошибке от
данного входного сигнала.

Соседние файлы в папке Конспект ТАУ

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Шаг за шагом: как определить полную установившуюся ошибку в системе ТАУ?

Введение

Системы технического автоматического управления (ТАУ) используются в различных областях, таких как производство, транспорт, энергетика и т.д. Эти системы работают с различными объектами управления, такими как роботы, конвейеры, двигатели, отопление и т.д. Одним из важных показателей работы системы ТАУ является установившаяся ошибка. Она показывает отклонение выходного сигнала системы от желаемого значения при установившемся режиме работы.

Определение установившейся ошибки

Установившаяся ошибка — это разница между желаемым значением выходного сигнала и фактическим значением выходного сигнала при установившемся режиме работы системы ТАУ. Установившийся режим — это тот момент времени, когда выходной сигнал системы перестает меняться и стабилизируется на определенном значении.

Установившаяся ошибка может быть положительной или отрицательной. Положительная установившаяся ошибка означает, что фактическое значение выходного сигнала больше желаемого значения, а отрицательная — что фактическое значение выходного сигнала меньше желаемого значения.

Шаги для определения установившейся ошибки

Определение установившейся ошибки может быть выполнено в несколько шагов:

1. Задание желаемого значения выходного сигнала. В зависимости от объекта управления и конкретной задачи, желаемое значение выходного сигнала может быть определено как постоянное значение или как функция времени.

2. Настройка системы ТАУ. Этот шаг включает настройку регулятора управления и других параметров системы, чтобы достичь соответствующего уровня устойчивости и точности.

3. Запуск системы. Запустите систему и дождитесь, пока выходной сигнал системы стабилизируется на установившемся значении.

4. Измерение фактического значения выходного сигнала. Измерьте фактическое значение выходного сигнала в установившемся режиме.

5. Вычисление установившейся ошибки. Вычислите разницу между желаемым значением выходного сигнала и фактическим значением выходного сигнала в установившемся режиме.

6. Анализ результатов. Оцените установившуюся ошибку и возможные причины ее появления. В случае необходимости повторите шаги с 2 по 5, чтобы уточнить результаты.

Заключение

Установившаяся ошибка является важным показателем работы системы ТАУ. Она показывает, насколько эффективно система управления достигает заданного значения выходного сигнала в установившемся режиме. Определение установившейся ошибки может помочь выявить проблемы в работе системы ТАУ и улучшить ее производительность и точность.

---

The deviation of the output of control system from desired response during steady state is known as steady state error. It is represented as $e_{ss}$. We can find steady state error using the final value theorem as follows.

$$e_{ss}=\lim_{t \to \infty}e(t)=\lim_{s \to 0}sE(s)$$

Where,

E(s) is the Laplace transform of the error signal, $e(t)$

Let us discuss how to find steady state errors for unity feedback and non-unity feedback control systems one by one.

Steady State Errors for Unity Feedback Systems

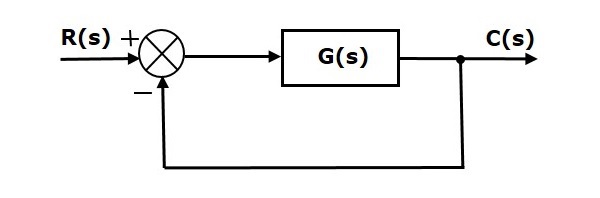
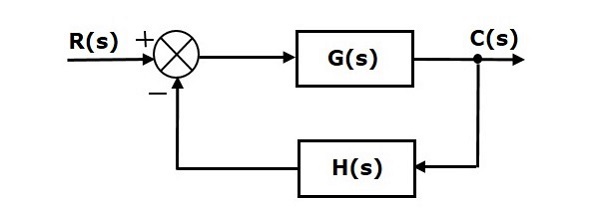
Consider the following block diagram of closed loop control system, which is having unity negative feedback.

Where,

• R(s) is the Laplace transform of the reference Input signal $r(t)$
• C(s) is the Laplace transform of the output signal $c(t)$

We know the transfer function of the unity negative feedback closed loop control system as

$$\frac{C(s)}{R(s)}=\frac{G(s)}{1+G(s)}$$

$$\Rightarrow C(s)=\frac{R(s)G(s)}{1+G(s)}$$

The output of the summing point is —

$$E(s)=R(s)-C(s)$$

Substitute $C(s)$ value in the above equation.

$$E(s)=R(s)-\frac{R(s)G(s)}{1+G(s)}$$

$$\Rightarrow E(s)=\frac{R(s)+R(s)G(s)-R(s)G(s)}{1+G(s)}$$

$$\Rightarrow E(s)=\frac{R(s)}{1+G(s)}$$

Substitute $E(s)$ value in the steady state error formula

$$e_{ss}=\lim_{s \to 0} \frac{sR(s)}{1+G(s)}$$

The following table shows the steady state errors and the error constants for standard input signals like unit step, unit ramp & unit parabolic signals.

Where, $K_p$, $K_v$ and $K_a$ are position error constant, velocity error constant and acceleration error constant respectively.

Note − If any of the above input signals has the amplitude other than unity, then multiply corresponding steady state error with that amplitude.

Note − We can’t define the steady state error for the unit impulse signal because, it exists only at origin. So, we can’t compare the impulse response with the unit impulse input as t denotes infinity.

Example

Let us find the steady state error for an input signal $r(t)=\left( 5+2t+\frac{t^2}{2} \right )u(t)$ of unity negative
feedback control system with $G(s)=\frac{5(s+4)}{s^2(s+1)(s+20)}$

The given input signal is a combination of three signals step, ramp and parabolic. The following table shows the error constants and steady state error values for these three signals.

We will get the overall steady state error, by adding the above three steady state errors.

$$e_{ss}=e_{ss1}+e_{ss2}+e_{ss3}$$

$$\Rightarrow e_{ss}=0+0+1=1$$

Therefore, we got the steady state error $e_{ss}$ as 1 for this example.

Steady State Errors for Non-Unity Feedback Systems

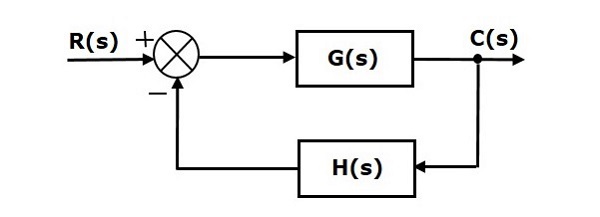
Consider the following block diagram of closed loop control system, which is having nonunity negative feedback.

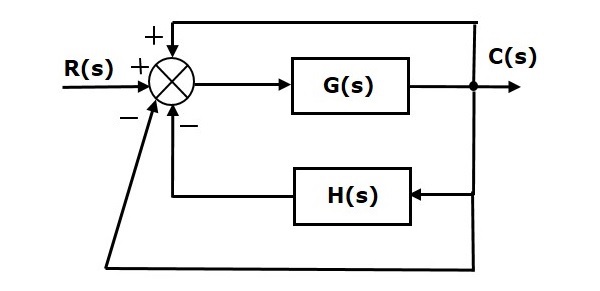
We can find the steady state errors only for the unity feedback systems. So, we have to convert the non-unity feedback system into unity feedback system. For this, include one unity positive feedback path and one unity negative feedback path in the above block diagram. The new block diagram looks like as shown below.

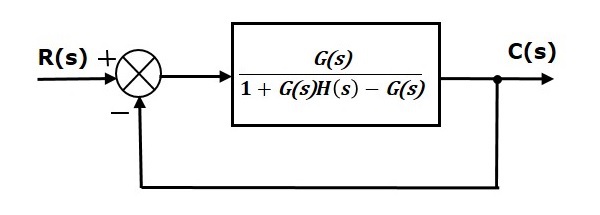
Simplify the above block diagram by keeping the unity negative feedback as it is. The following is the simplified block diagram.

This block diagram resembles the block diagram of the unity negative feedback closed loop control system. Here, the single block is having the transfer function $\frac{G(s)}{1+G(s)H(s)-G(s)}$ instead of $G(s)$. You can now calculate the steady state errors by using steady state error formula given for the unity negative feedback systems.

Note − It is meaningless to find the steady state errors for unstable closed loop systems. So, we have to calculate the steady state errors only for closed loop stable systems. This means we need to check whether the control system is stable or not before finding the steady state errors. In the next chapter, we will discuss the concepts-related stability.

Отклонение выходного сигнала системы управления от желаемого отклика в установившемся режиме известно как steady state error. Он представлен как $ e_ {ss} $. Мы можем найти ошибку установившегося состояния, используя теорему о конечном значении следующим образом.

$$ e_ {ss} = \ lim_ {t \ to \ infty} e (t) = \ lim_ {s \ to 0} sE (s) $$

Куда,

E (s) — преобразование Лапласа сигнала ошибки, $ e (t) $

Давайте обсудим, как по очереди находить стационарные ошибки для систем управления с единичной обратной связью и неединичной обратной связи.

Устойчивые ошибки для систем обратной связи Unity

Рассмотрим следующую блок-схему замкнутой системы управления, имеющей единицу отрицательной обратной связи.

Куда,

• R (ы) представляет собой преобразование Лапласа опорного входного сигнала $ R (T) $
• C (s) — преобразование Лапласа выходного сигнала $ c (t) $

Нам известна передаточная функция замкнутой системы управления с отрицательной обратной связью как

$$ \ frac {C (s)} {R (s)} = \ frac {G (s)} {1 + G (s)} $$

$$ \ Rightarrow C (s) = \ frac {R (s) G (s)} {1 + G (s)} $$

Выход точки суммирования —

$$ E (s) = R (s) -C (s) $$

Подставьте значение $ C (s) $ в приведенное выше уравнение.

$$ E (s) = R (s) — \ frac {R (s) G (s)} {1 + G (s)} $$

$$ \ Rightarrow E (s) = \ frac {R (s) + R (s) G (s) -R (s) G (s)} {1 + G (s)} $$

$$ \ Rightarrow E (s) = \ frac {R (s)} {1 + G (s)} $$

Подставьте значение $ E (s) $ в формулу ошибки установившегося состояния

$$ e_ {ss} = \ lim_ {s \ to 0} \ frac {sR (s)} {1 + G (s)} $$

В следующей таблице показаны ошибки установившегося состояния и константы ошибок для стандартных входных сигналов, таких как единичный шаг, единичное линейное изменение и единичные параболические сигналы.

Входной сигнал	Ошибка устойчивого состояния $ e_ {ss} $	Константа ошибки
единичный шаговый сигнал	$ \ frac {1} {1 + k_p} $	$ K_p = \ lim_ {s \ to 0} G (s) $
сигнал рампы агрегата	$ \ frac {1} {K_v} $	$ K_v = \ lim_ {s \ to 0} sG (s) $
единичный параболический сигнал	$ \ frac {1} {K_a} $	$ K_a = \ lim_ {s \ to 0} s ^ 2G (s) $

Где, $ K_p $, $ K_v $ и $ K_a $ — константа ошибки положения, константа ошибки скорости и константа ошибки ускорения соответственно.

Note — Если какой-либо из вышеуказанных входных сигналов имеет амплитуду, отличную от единицы, умножьте соответствующую ошибку установившегося состояния на эту амплитуду.

Note— Мы не можем определить ошибку установившегося состояния для единичного импульсного сигнала, потому что она существует только в источнике. Таким образом, мы не можем сравнивать импульсную характеристику с единичным импульсным входом, посколькуt обозначает бесконечность.

пример

Найдем установившуюся ошибку для входного сигнала $ r (t) = \ left (5 + 2t + \ frac {t ^ 2} {2} \ right) u (t) $ единичной системы управления с отрицательной обратной связью с $ G (s) = \ frac {5 (s + 4)} {s ^ 2 (s + 1) (s + 20)} $

Данный входной сигнал представляет собой комбинацию трех сигналов: шагового, линейного и параболического. В следующей таблице показаны константы ошибок и значения ошибок устойчивого состояния для этих трех сигналов.

Входной сигнал	Константа ошибки	Ошибка устойчивого состояния
$ r_1 (t) = 5u (t) $	$ K_p = \ lim_ {s \ to 0} G (s) = \ infty $	$ e_ {ss1} = \ frac {5} {1 + k_p} = 0 $
$ r_2 (t) = 2tu (t) $	$ K_v = \ lim_ {s \ to 0} sG (s) = \ infty $	$ e_ {ss2} = \ frac {2} {K_v} = 0 $
$ r_3 (t) = \ frac {t ^ 2} {2} u (t) $	$ K_a = \ lim_ {s \ to 0} s ^ 2G (s) = 1 $	$ e_ {ss3} = \ frac {1} {k_a} = 1 $

Мы получим общую ошибку устойчивого состояния, добавив указанные выше три ошибки устойчивого состояния.

$$ e_ {ss} = e_ {ss1} + e_ {ss2} + e_ {ss3} $$

$$ \ Rightarrow e_ {ss} = 0 + 0 + 1 = 1 $$

Следовательно, мы получили ошибку устойчивого состояния $ e_ {ss} $ как 1 для этого примера.

Устойчивые ошибки для систем с обратной связью, отличных от единства

Рассмотрим следующую блок-схему системы управления с обратной связью, которая не имеет отрицательной обратной связи.

Мы можем найти ошибки установившегося состояния только для систем единой обратной связи. Итак, мы должны преобразовать неединичную систему обратной связи в единую систему обратной связи. Для этого включите в приведенную выше блок-схему один единичный путь положительной обратной связи и один единичный путь отрицательной обратной связи. Новая блок-схема выглядит так, как показано ниже.

Упростите приведенную выше блок-схему, сохранив отрицательную обратную связь единства как есть. Ниже представлена ​​упрощенная блок-схема.

Эта блок-схема напоминает блок-схему замкнутой системы управления с отрицательной обратной связью. Здесь единственный блок имеет передаточную функцию $ \ frac {G (s)} {1 + G (s) H (s) -G (s)} $ вместо $ G (s) $. Теперь вы можете рассчитать ошибки установившегося состояния, используя формулу ошибки установившегося состояния, данную для единых систем отрицательной обратной связи.

Note— Бессмысленно искать ошибки установившегося состояния для нестабильных замкнутых систем. Таким образом, мы должны вычислять ошибки установившегося состояния только для устойчивых систем с замкнутым контуром. Это означает, что нам нужно проверить, является ли система управления стабильной или нет, прежде чем обнаруживать ошибки устойчивого состояния. В следующей главе мы обсудим стабильность, связанную с концепциями.