Как найти стандартную ошибку оценки - Решение и исправление самых разных ошибок на TopOshibok.ru

Загрузить PDF

Стандартная ошибка оценки служит для того, чтобы выяснить, как линия регрессии соответствует набору данных. Если у вас есть набор данных, полученных в результате измерения, эксперимента, опроса или из другого источника, создайте линию регрессии, чтобы оценить дополнительные данные. Стандартная ошибка оценки характеризует, насколько верна линия регрессии.

1

Создайте таблицу с данными. Таблица должна состоять из пяти столбцов, и призвана облегчить вашу работу с данными. Чтобы вычислить стандартную ошибку оценки, понадобятся пять величин. Поэтому разделите таблицу на пять столбцов. Обозначьте эти столбцы так:^[1]
2
Введите данные в таблицу. Когда вы проведете эксперимент или опрос, вы получите пары данных — независимую переменную обозначим как , а зависимую или конечную переменную как . Введите эти значения в первые два столбца таблицы.
- Не перепутайте данные. Помните, что определенному значению независимой переменной должно соответствовать конкретное значение зависимой переменной.
- Например, рассмотрим следующий набор пар данных:
  - (1,2)
  - (2,4)
  - (3,5)
  - (4,4)
  - (5,5)
3
Вычислите линию регрессии. Сделайте это на основе представленных данных. Эта линия также называется линией наилучшего соответствия или линией наименьших квадратов. Расчет можно сделать вручную, но это довольно утомительно. Поэтому рекомендуем воспользоваться графическим калькулятором или онлайн-сервисом, которые быстро вычислят линию регрессии по вашим данным.^[2]
- В этой статье предполагается, что уравнение линии регрессии дано (известно).
- В нашем примере линия регрессии описывается уравнением $y^{{\prime }}=0,6x+2,2$ .
4

Вычислите прогнозируемые значения по линии регрессии. С помощью уравнения линии регрессии можно вычислить прогнозируемые значения «y» для значений «x», которые есть и которых нет в наборе данных.

Реклама

1
Вычислите ошибку каждого прогнозируемого значения. В четвертом столбце таблицы запишите ошибку каждого прогнозируемого значения. В частности, вычтите прогнозируемое значение ( $y^{{\prime }}$ ) из фактического (наблюдаемого) значения ().^[3]
- В нашем примере вычисления будут выглядеть так:
2
Вычислите квадраты ошибок. Возведите в квадрат каждое значение четвертого столбца, а результаты запишите в последнем (пятом) столбце таблицы.
- В нашем примере вычисления будут выглядеть так:
3
Найдите сумму квадратов ошибок. Она пригодится для вычисления стандартного отклонения, дисперсии и других величин. Чтобы найти сумму квадратов ошибок, сложите все значения пятого столбца. ^[4]
- В нашем примере вычисления будут выглядеть так:
4
Завершите расчеты. Стандартная ошибка оценки — это квадратный корень из среднего значения суммы квадратов ошибок. Обычно ошибка оценки обозначается греческой буквой $\sigma$ . Поэтому сначала разделите сумму квадратов ошибок на число пар данных. А потом из полученного значения извлеките квадратный корень.^[5]
- Если рассматриваемые данные представляют всю совокупность, среднее значение находится так: сумму нужно разделить на N (количество пар данных). Если же рассматриваемые данные представляют некоторую выборку, вместо N подставьте N-2.
- В нашем примере, скорее всего, имеет место выборка, потому что мы рассматриваем всего 5 пар данных. Поэтому стандартную ошибку оценки вычислите следующим образом:
5
Интерпретируйте полученный результат. Стандартная ошибка оценки — это статистический показатель, которые оценивает, насколько близко измеренные данные лежат к линии регрессии. Ошибка оценка «0» означает, что каждая точка лежит непосредственно на линии. Чем выше ошибка оценки, тем дальше от линии регрессии лежат точки.^[6]
- В нашем примере выборка достаточно маленькая, поэтому стандартная оценка ошибки 0,894 является довольно низкой и характеризует близко расположенные данные.
Реклама

Об этой статье

Эту страницу просматривали 4986 раз.

Была ли эта статья полезной?

Источник

Download Article

The standard error of estimate is used to determine how well a straight line can describe values of a data set. When you have a collection of data from some measurement, experiment, survey or other source, you can create a line of regression to estimate additional data. With the standard error of estimate, you get a score that describes how good the regression line is.

1

Create a five column data table. Any statistical work is generally made easier by having your data in a concise format. A simple table serves this purpose very well. To calculate the standard error of estimate, you will be using five different measurements or calculations. Therefore, creating a five-column table is helpful. Label the five columns as follows:^[1]
2
Enter the data values for your measured data. After collecting your data, you will have pairs of data values. For these statistical calculations, the independent variable is labeled and the dependent, or resulting, variable is . Enter these values into the first two columns of your data table.^[2]
- The order of the data and the pairing is important for these calculations. You need to be careful to keep your paired data points together in order.
- For the sample calculations shown above, the data pairs are as follows:
  - (1,2)
  - (2,4)
  - (3,5)
  - (4,4)
  - (5,5)
Advertisement
3
Calculate a regression line. Using your data results, you will be able to calculate a regression line. This is also called a line of best fit or the least squares line. The calculation is tedious but can be done by hand. Alternatively, you can use a handheld graphing calculator or some online programs that will quickly calculate a best fit line using your data.^[3]
- For this article, it is assumed that you will have the regression line equation available or that it has been predicted by some prior means.
- For the sample data set in the image above, the regression line is $y^{{\prime }}=0.6x+2.2$ .
4

Calculate predicted values from the regression line. Using the equation of that line, you can calculate predicted y-values for each x-value in your study, or for other theoretical x-values that you did not measure.^[4]

1
Calculate the error of each predicted value. In the fourth column of your data table, you will calculate and record the error of each predicted value. Specifically, subtract the predicted value ( $y^{{\prime }}$ ) from the actual observed value ().^[5]
- For the data in the sample set, these calculations are as follows:
2
Calculate the squares of the errors. Take each value in the fourth column and square it by multiplying it by itself. Fill in these results in the final column of your data table.
- For the sample data set, these calculations are as follows:
3
Find the sum of the squared errors (SSE). The statistical value known as the sum of squared errors (SSE) is a useful step in finding standard deviation, variance and other measurements. To find the SSE from your data table, add the values in the fifth column of your data table.^[6]
- For this sample data set, this calculation is as follows:
4
Finalize your calculations. The Standard Error of the Estimate is the square root of the average of the SSE. It is generally represented with the Greek letter $\sigma$ . Therefore, the first calculation is to divide the SSE score by the number of measured data points. Then, find the square root of that result.^[7]
- If the measured data represents an entire population, then you will find the average by dividing by N, the number of data points. However, if you are working with a smaller sample set of the population, then substitute N-2 in the denominator.
- For the sample data set in this article, we can assume that it is a sample set and not a population, just because there are only 5 data values. Therefore, calculate the Standard Error of the Estimate as follows:
5
Interpret your result. The Standard Error of the Estimate is a statistical figure that tells you how well your measured data relates to a theoretical straight line, the line of regression. A score of 0 would mean a perfect match, that every measured data point fell directly on the line. Widely scattered data will have a much higher score.^[8]
- With this small sample set, the standard error score of 0.894 is quite low and represents well organized data results.

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Video

Thanks for submitting a tip for review!

References

About This Article

Article SummaryX

To calculate the standard error of estimate, create a five-column data table. In the first two columns, enter the values for your measured data, and enter the values from the regression line in the third column. In the fourth column, calculate the predicted values from the regression line using the equation from that line. These are the errors. Fill in the fifth column by multiplying each error by itself. Add together all of the values in column 5, then take the square root of that number to get the standard error of estimate. To learn how to organize the data pairs, keep reading!

Did this summary help you?

Thanks to all authors for creating a page that has been read 196,513 times.

Did this article help you?

Источник

Что такое стандартная ошибка оценки? (Определение и пример)

17 авг. 2022 г.
читать 3 мин

Стандартная ошибка оценки — это способ измерения точности прогнозов, сделанных регрессионной моделью.

Часто обозначаемый σ est , он рассчитывается как:

σ est = √ Σ(y – ŷ) 2 /n

куда:

y: наблюдаемое значение
ŷ: Прогнозируемое значение
n: общее количество наблюдений

Стандартная ошибка оценки дает нам представление о том, насколько хорошо регрессионная модель соответствует набору данных. Особенно:

Чем меньше значение, тем лучше соответствие.
Чем больше значение, тем хуже соответствие.

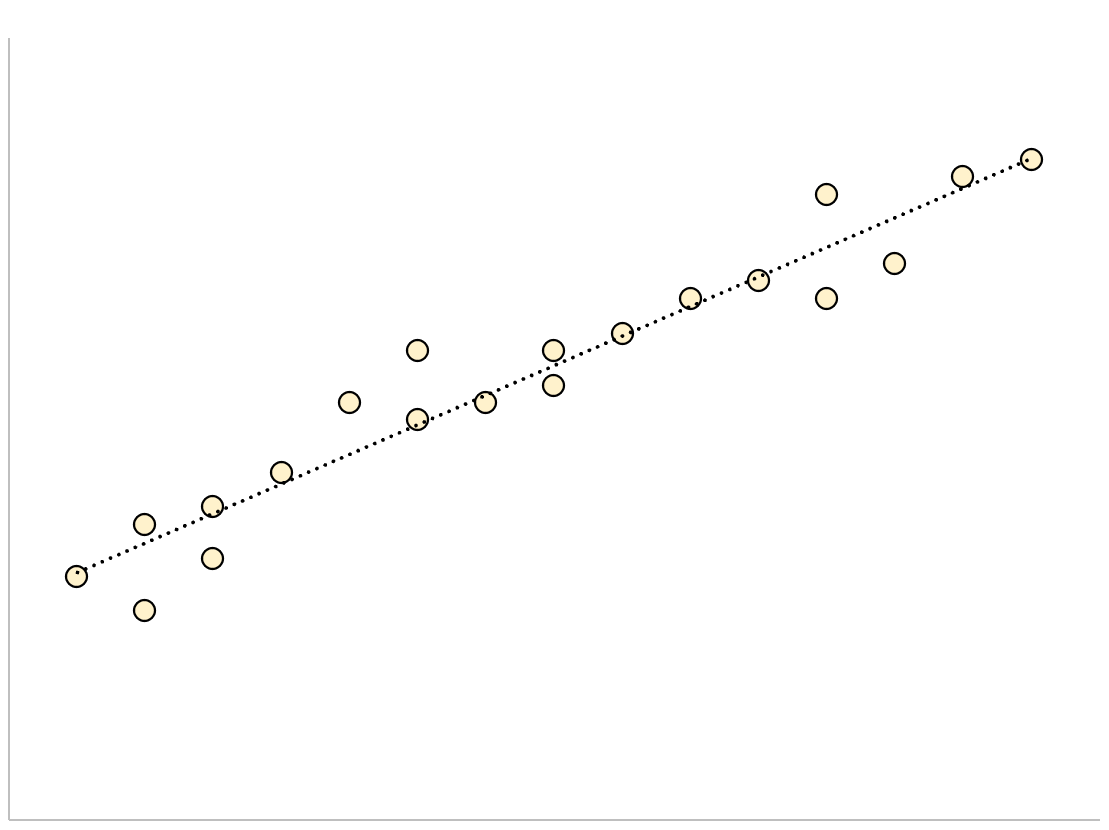
Для регрессионной модели с небольшой стандартной ошибкой оценки точки данных будут плотно сгруппированы вокруг предполагаемой линии регрессии:

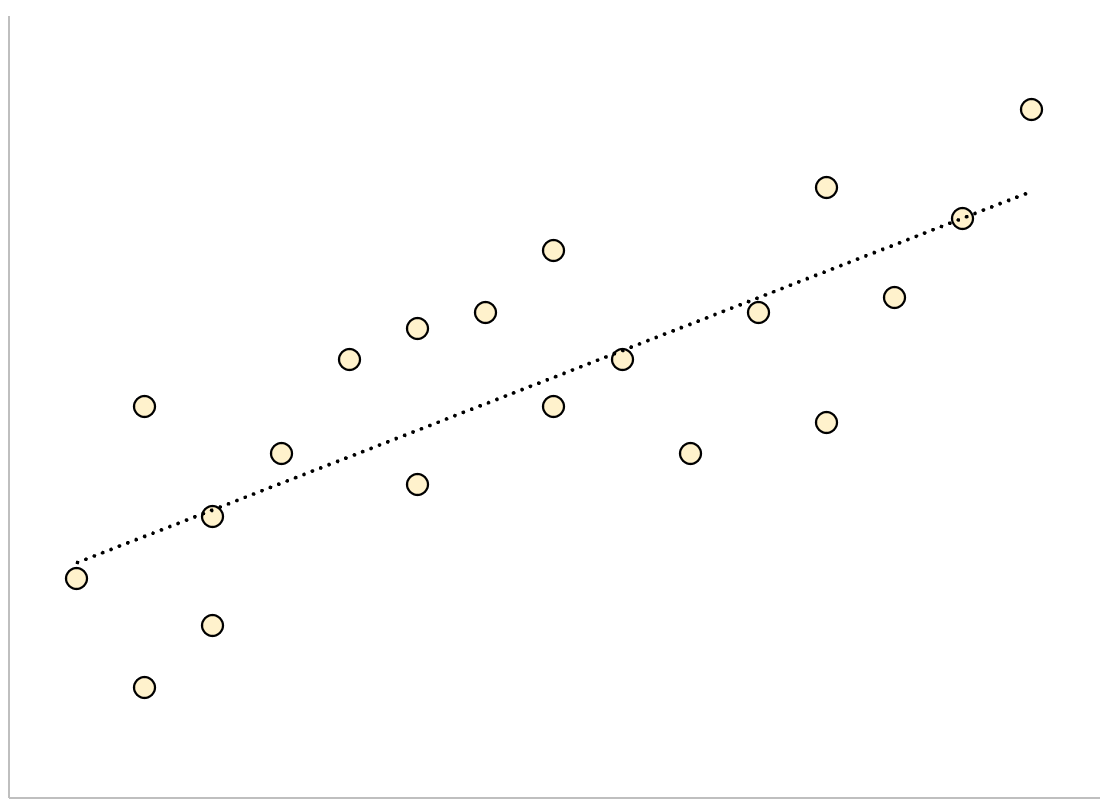
И наоборот, для регрессионной модели с большой стандартной ошибкой оценки точки данных будут более свободно разбросаны по линии регрессии:

В следующем примере показано, как рассчитать и интерпретировать стандартную ошибку оценки для регрессионной модели в Excel.

Пример: стандартная ошибка оценки в Excel

Используйте следующие шаги, чтобы вычислить стандартную ошибку оценки для регрессионной модели в Excel.

Шаг 1: введите данные

Сначала введите значения для набора данных:

Шаг 2: выполните линейную регрессию

Затем щелкните вкладку « Данные » на верхней ленте. Затем выберите параметр « Анализ данных» в группе « Анализ ».

Если вы не видите эту опцию, вам нужно сначала загрузить пакет инструментов анализа .

В появившемся новом окне нажмите « Регрессия », а затем нажмите « ОК ».

В появившемся новом окне заполните следующую информацию:

Как только вы нажмете OK , появится вывод регрессии:

Мы можем использовать коэффициенты из таблицы регрессии для построения оценочного уравнения регрессии:

ŷ = 13,367 + 1,693 (х)

И мы видим, что стандартная ошибка оценки для этой регрессионной модели оказывается равной 6,006.Проще говоря, это говорит нам о том, что средняя точка данных отклоняется от линии регрессии на 6,006 единицы.

Мы можем использовать оценочное уравнение регрессии и стандартную ошибку оценки, чтобы построить 95% доверительный интервал для прогнозируемого значения определенной точки данных.

Например, предположим, что x равно 10. Используя оценочное уравнение регрессии, мы можем предсказать, что y будет равно:

ŷ = 13,367 + 1,693 * (10) = 30,297

И мы можем получить 95% доверительный интервал для этой оценки, используя следующую формулу:

95% ДИ = [ŷ – 1,96*σ расч ., ŷ + 1,96*σ расч .]

Для нашего примера доверительный интервал 95% будет рассчитываться как:

95% ДИ = [ŷ – 1,96*σ расч ., ŷ + 1,96*σ расч .]
95% ДИ = [30,297 – 1,96*6,006, 30,297 + 1,96*6,006]
95% ДИ = [18,525, 42,069]

Дополнительные ресурсы

Как выполнить простую линейную регрессию в Excel
Как выполнить множественную линейную регрессию в Excel
Как создать остаточный график в Excel

Источник

Имея
прямую регрессии, необходимо оценить
насколько сильно точки исходных данных
отклоняются от прямой регрессии. Можно
выполнить оценку разброса, аналогичную
стандартному отклонению выборки. Этот
показатель, называемый стандартной
ошибкой оценки, демонстрирует величину
отклонения точек исходных данных от
прямой регрессии в направлении оси Y.
Стандартная ошибка оценки ()
вычисляется по следующей формуле.

Стандартная
ошибка оценки измеряет степень отличия
реальных значений Y от оцененной величины.
Для сравнительно больших выборок следует
ожидать, что около 67% разностей по модулю
не будет превышать

и около 95% модулей разностей будет не
больше 2.

Стандартная
ошибка оценки подобна стандартному
отклонению. Ее можно использовать для
оценки стандартного отклонения
совокупности. Фактически

оценивает стандартное отклонение

слагаемого ошибки

в статистической модели простой линейной
регрессии. Другими словами,

оценивает общее стандартное отклонение

нормального распределения значений Y,
имеющих математические ожидания

для каждого X.

Малая
стандартная ошибка оценки, полученная
при регрессионном анализе, свидетельствует,
что все точки данных находятся очень
близко к прямой регрессии. Если стандартная
ошибка оценки велика, точки данных могут
значительно удаляться от прямой.

2.3 Прогнозирование величины y

Регрессионную
прямую можно использовать для оценки
величины переменной Y
при данных значениях переменной X. Чтобы
получить точечный прогноз, или предсказание
для данного значения X, просто вычисляется
значение найденной функции регрессии
в точке X.

Конечно
реальные значения величины Y,
соответствующие рассматриваемым
значениям величины X, к сожалению, не
лежат в точности на регрессионной
прямой. Фактически они разбросаны
относительно прямой в соответствии с
величиной
.
Более того, выборочная регрессионная
прямая является оценкой регрессионной
прямой генеральной совокупности,
основанной на выборке из определенных
пар данных. Другая случайная выборка
даст иную выборочную прямую регрессии;
это аналогично ситуации, когда различные
выборки из одной и той же генеральной
совокупности дают различные значения
выборочного среднего.

Есть
два источника неопределенности в
точечном прогнозе, использующем уравнение
регрессии.

Неопределенность,
обусловленная отклонением точек данных
от выборочной прямой регрессии.
Неопределенность,
обусловленная отклонением выборочной
прямой регрессии от регрессионной
прямой генеральной совокупности.

Интервальный
прогноз значений переменной Y
можно построить так, что при этом будут
учтены оба источника неопределенности.

Стандартная
ошибка прогноза

дает меру вариативности предсказанного
значения Y
около истинной величины Y
для данного значения X.
Стандартная ошибка прогноза равна:

Стандартная
ошибка прогноза зависит от значения X,
для которого прогнозируется величина
Y.

минимально, когда
,
поскольку тогда числитель в третьем
слагаемом под корнем в уравнении будет
0. При прочих неизменных величинах
большему отличию соответствует большее
значение стандартной ошибки прогноза.

Если
статистическая модель простой линейной
регрессии соответствует действительности,
границы интервала прогноза величины Y
равны:

где

— квантиль распределения Стьюдента с
n-2 степенями свободы ().
Если выборка велика (),
этот квантиль можно заменить соответствующим
квантилем нормального распределения.
Например, для большой выборки 95%-ный
интервал прогноза задается следующими
значениями:

Завершим
раздел обзором предположений, положенных
в основу статистической модели линейной
регрессии.

Для
заданного значения X генеральная
совокупность значений Y имеет нормальное
распределение относительно регрессионной
прямой совокупности. На практике
приемлемые результаты получаются
и
тогда, когда значения Y имеют
нормальное распределение лишь
приблизительно.
Разброс
генеральной совокупности точек данных
относительно регрессионной прямой
совокупности остается постоянным всюду
вдоль этой прямой. Иными словами, при
возрастании значений X в точках данных
дисперсия генеральной совокупности
не увеличивается и не уменьшается.
Нарушение этого предположения называется
гетероскедастичностью.
Слагаемые
ошибок

независимы между собой. Это предположение
определяет случайность выборки точек
Х-Y.
Если точки данных X-Y
записывались в течение некоторого
времени, данное предположение часто
нарушается. Вместо независимых данных,
такие последовательные наблюдения
будут давать серийно коррелированные
значения.
В
генеральной совокупности существует
линейная зависимость между X и Y.
По аналогии с простой линейной регрессией
может рассматриваться и нелинейная
зависимость между X и У. Некоторые такие
случаи будут обсуждаться ниже.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Стандартная ошибка

Стандартная ошибка — это стандартное отклонение выборочного распределения статистики. Этот термин также может использоваться для оценки (хорошего предположения) этого стандартного отклонения, взятого из выборки всей группы.

Среднее значение некоторой части группы (называемой выборкой) является обычным способом оценки среднего значения для всей группы. Часто бывает слишком сложно или стоит слишком много денег, чтобы измерить всю группу. Но если измерить другую выборку, то ее среднее значение будет немного отличаться от первой выборки. Стандартная ошибка среднего — это способ узнать, насколько близка средняя по выборке к средней по всей группе. Это способ узнать, насколько вы можете быть уверены в среднем значении по выборке.

В реальных измерениях истинное значение стандартного отклонения среднего для всей группы обычно неизвестно. Поэтому термин стандартная ошибка часто используется для обозначения близкого к истинному значению для всей группы. Чем больше измерений в выборке, тем ближе к истинному значению для всей группы.

Для значения, отобранного с несмещенной нормально распределенной ошибкой, выше показана доля выборок, которые будут находиться в пределах 0, 1, 2 и 3 стандартных отклонений выше и ниже фактического значения.

Как найти стандартную ошибку среднего значения

Один из способов найти стандартную ошибку среднего — это множество выборок. Сначала находят среднее значение для каждой выборки. Затем находят среднее и стандартное отклонение этих средних по выборкам. Стандартное отклонение для всех средних по выборке и есть стандартная ошибка среднего. Это может быть большой объем работы. Иногда иметь большое количество образцов слишком сложно или стоит слишком много денег.

Другой способ найти стандартную ошибку среднего — использовать уравнение, для которого нужна только одна выборка. Стандартная ошибка среднего обычно оценивается по стандартному отклонению для выборки из всей группы (стандартное отклонение выборки), деленному на квадратный корень из размера выборки.

S E x ¯ = s n {\displaystyle SE_{\bar {x}}\ ={\frac {s}{\sqrt {n}}}} $SE_{\bar {x}}\ ={\frac {s}{\sqrt {n}}}$

где

s — стандартное отклонение выборки (т.е. выборочная оценка стандартного отклонения популяции), и

n — количество измерений в выборке.

Насколько большой должна быть выборка, чтобы оценка стандартной ошибки среднего была близка к фактической стандартной ошибке среднего для всей группы? В выборке должно быть не менее шести измерений. Тогда стандартная ошибка среднего для выборки будет находиться в пределах 5% от стандартной ошибки среднего, если бы измерялась вся группа.

Исправления для некоторых случаев

Существует еще одно уравнение, которое можно использовать, если количество измерений составляет 5% или более от всей группы:

Существуют специальные уравнения, которые необходимо использовать, если образец имеет менее 20 измерений.

Иногда выборка поступает из одного места, хотя вся группа может быть рассредоточена. Кроме того, иногда выборка может быть сделана за короткий промежуток времени, когда вся группа охватывает более длительный период. В этом случае числа в выборке не являются независимыми. Тогда используются специальные уравнения, чтобы попытаться исправить это.

Полезность

Практический результат: Можно быть более уверенным в среднем значении, если провести больше измерений в выборке. Тогда стандартная ошибка среднего значения будет меньше, поскольку стандартное отклонение делится на большее число. Однако, чтобы сделать неопределенность (стандартную ошибку среднего) среднего значения в два раза меньше, размер выборки (n) должен быть в четыре раза больше. Это происходит потому, что стандартное отклонение делится на квадратный корень из размера выборки. Чтобы сделать неопределенность на одну десятую больше, размер выборки (n) должен быть в сто раз больше!

Стандартные ошибки легко вычисляются и часто используются, потому что:

Если известна стандартная ошибка нескольких отдельных величин, то во многих случаях можно легко рассчитать стандартную ошибку некоторой функции этих величин;
Если вероятностное распределение значения известно, его можно использовать для расчета хорошего приближения к точному доверительному интервалу; и
Если распределение вероятности неизвестно, для оценки доверительного интервала можно использовать другие уравнения
Когда размер выборки становится очень большим, принцип центральной предельной теоремы показывает, что числа в выборке очень похожи на числа во всей группе (они имеют нормальное распределение).

Относительная стандартная ошибка

Относительная стандартная ошибка (RSE) — это стандартная ошибка, деленная на среднее значение. Это число меньше единицы. Умножение его на 100% дает его в процентах от среднего значения. Это помогает показать, является ли неопределенность важной или нет. Например, рассмотрим два исследования доходов домохозяйств, в результате которых среднее значение по выборке составляет $50 000. Если стандартная ошибка одного опроса составляет $10 000, а другого — $5 000, то относительные стандартные ошибки равны 20% и 10% соответственно. Опрос с меньшей относительной стандартной ошибкой лучше, потому что он имеет более точное измерение (неопределенность меньше).

На самом деле, люди, которым необходимо знать средние значения, часто решают, насколько мала должна быть неопределенность, прежде чем они решат использовать информацию. Например, Национальный центр статистики здравоохранения США не сообщает среднее значение, если относительная стандартная ошибка превышает 30%. NCHS также требует не менее 30 наблюдений для того, чтобы оценка была представлена в отчете. ^[]

Пример

Например, в воде Мексиканского залива водится много красной рыбы. Чтобы узнать, сколько в среднем весит красноперка длиной 42 см, невозможно измерить всех красноперок длиной 42 см. Вместо этого можно измерить некоторых из них. Рыба, которую измеряют, называется образцом. В таблице показан вес двух образцов красноперки длиной 42 см. Средний (средний) вес первого образца составляет 0,741 кг. Средний (средний) вес второго образца — 0,735 кг, что немного отличается от первого образца. Каждое из этих средних значений немного отличается от среднего значения, которое было бы получено при измерении каждой красной рыбы длиной 42 см (что в любом случае невозможно).

Неопределенность среднего значения можно использовать для того, чтобы узнать, насколько близки средние значения выборок к среднему значению, которое было бы получено в результате измерения всей группы. Неопределенность среднего оценивается как стандартное отклонение для выборки, деленное на квадратный корень из числа выборок минус один. Из таблицы видно, что неопределенности в средних для двух выборок очень близки друг к другу. Кроме того, относительная неопределенность — это неопределенность среднего значения, деленная на среднее значение, умноженное на 100%. Относительная неопределенность в данном примере составляет 2,38% и 2,50% для двух образцов.

Зная неопределенность среднего, можно узнать, насколько близко выборочное среднее к среднему, которое было бы получено в результате измерения всей группы. Среднее по всей группе находится между а) средним по выборке плюс неопределенность в среднем и б) средним по выборке минус неопределенность в среднем. В данном примере средний вес всей красноперки длиной 42 см в Мексиканском заливе, как ожидается, составит 0,723-0,759 кг по первой выборке и 0,717-0,753 по второй выборке.

Пример красной рыбы (также известной как красный барабан, Sciaenops ocellatus), используемой в примере.

Вопросы и ответы

В: Что такое стандартная ошибка?

О: Стандартная ошибка — это стандартное отклонение выборочного распределения статистики.

В: Можно ли использовать термин стандартная ошибка для оценки стандартного отклонения?

О: Да, термин стандартная ошибка может быть использован для оценки (хорошего предположения) этого стандартного отклонения, взятого из выборки всей группы.

В: Как можно оценить среднее значение для всей группы?

О: Среднее значение некоторой части группы (называемой выборкой) — это обычный способ оценки среднего значения для всей группы.

В: Почему трудно измерить всю группу?

О: Часто бывает слишком трудно или слишком дорого измерить всю группу.

В: Что такое стандартная ошибка среднего, и что она определяет?

О: Стандартная ошибка среднего — это способ узнать, насколько близко среднее значение выборки к среднему значению всей группы. Это способ узнать, насколько можно быть уверенным в среднем значении по выборке.

В: Известно ли обычно истинное значение стандартного отклонения среднего при реальных измерениях?

О: Нет, истинное значение стандартного отклонения среднего для всей группы обычно не известно в реальных измерениях.

В: Как количество измерений в выборке влияет на точность оценки?

О: Чем больше измерений в выборке, тем ближе предположение будет к истинному значению для всей группы.

Источник