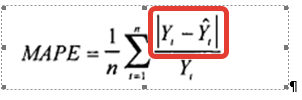Ошибка прогнозирования: виды, формулы, примеры
Ошибка прогнозирования — это такая величина, которая показывает, как сильно прогнозное значение отклонилось от фактического. Она используется для расчета точности прогнозирования, что в свою очередь помогает нам оценивать как точно и корректно мы сформировали прогноз. В данной статье я расскажу про основные процентные «ошибки прогнозирования» с кратким описанием и формулой для расчета. А в конце статьи я приведу общий пример расчётов в Excel. Напомню, что в своих расчетах я в основном использую ошибку WAPE или MAD-Mean Ratio, о которой подробно я рассказал в статье про точность прогнозирования, здесь она также будет упомянута.
В каждой формуле буквой Ф обозначено фактическое значение, а буквой П — прогнозное. Каждая ошибка прогнозирования (кроме последней!), может использоваться для нахождения общей точности прогнозирования некоторого списка позиций, по типу того, что изображен ниже (либо для любого другого подобной детализации):
Алгоритм для нахождения любой из ошибок прогнозирования для такого списка примерно одинаковый: сначала находим ошибку прогнозирования по одной позиции, а затем рассчитываем общую. Итак, основные ошибки прогнозирования!
MPE — Mean Percent Error
MPE — средняя процентная ошибка прогнозирования. Основная проблема данной ошибки заключается в том, что в нестабильном числовом ряду с большими выбросами любое незначительное колебание факта или прогноза может значительно поменять показатель ошибки и, как следствие, точности прогнозирования. Помимо этого, ошибка является несимметричной: одинаковые отклонения в плюс и в минус по-разному влияют на показатель ошибки.
- Для каждой позиции рассчитывается ошибка прогноза (из факта вычитается прогноз) — Error
- Для каждой позиции рассчитывается процентная ошибка прогноза (ошибка прогноза делится на фактический показатель) — Percent Error
- Находится среднее арифметическое всех процентных ошибок прогноза (процентные ошибки суммируются и делятся на количество) — Mean Percent Error
MAPE — Mean Absolute Percent Error
MAPE — средняя абсолютная процентная ошибка прогнозирования. Основная проблема данной ошибки такая же, как и у MPE — нестабильность.
- Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта по модулю) — Absolute Error
- Для каждой позиции рассчитывается абсолютная процентная ошибка прогноза (абсолютная ошибка прогноза делится на фактический показатель) — Absolute Percent Error
- Находится среднее арифметическое всех абсолютных процентных ошибок прогноза (абсолютные процентные ошибки суммируются и делятся на количество) — Mean Absolute Percent Error
Вместо среднего арифметического всех абсолютных процентных ошибок прогноза можно использовать медиану числового ряда (MdAPE — Median Absolute Percent Error), она наиболее устойчива к выбросам.
WMAPE / MAD-Mean Ratio / WAPE — Weighted Absolute Percent Error
WAPE — взвешенная абсолютная процентная ошибка прогнозирования. Одна из «лучших ошибок» для расчета точности прогнозирования. Часто называется как MAD-Mean Ratio, то есть отношение MAD (Mean Absolute Deviation — среднее абсолютное отклонение/ошибка) к Mean (среднее арифметическое). После упрощения дроби получается искомая формула WAPE, которая очень проста в понимании:
- Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта, по модулю) — Absolute Error
- Находится сумма всех фактов по всем позициям (общий фактический объем)
- Сумма всех абсолютных ошибок делится на сумму всех фактов — WAPE
Данная ошибка прогнозирования является симметричной и наименее чувствительна к искажениям числового ряда.
Рекомендуется к использованию при расчете точности прогнозирования. Более подробно читать здесь.
RMSE (as %) / nRMSE — Root Mean Square Error
RMSE — среднеквадратичная ошибка прогнозирования. Примерно такая же проблема, как и в MPE и MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня. Но так как MSE дает расчетные единицы измерения в квадрате, то использовать данную ошибку будет немного неправильно.
- Для каждой позиции рассчитывается квадрат отклонений (разница между фактом и прогнозом, возведенная в квадрат) — Square Error
- Затем рассчитывается среднее арифметическое (сумма квадратов отклонений, деленное на количество) — MSE — Mean Square Error
- Извлекаем корень из полученного результат — RMSE
- Для перевода в процентную или в «нормализованную» среднеквадратичную ошибку необходимо:
- Разделить на разницу между максимальным и минимальным значением показателей
- Разделить на разницу между третьим и первым квартилем значений показателей
- Разделить на среднее арифметическое значений показателей (наиболее часто встречающийся вариант)
MASE — Mean Absolute Scaled Error
MASE — средняя абсолютная масштабированная ошибка прогнозирования. Согласно Википедии, является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени.
Важно! Если предыдущие ошибки прогнозирования мы могли использовать для нахождения точности прогнозирования некого списка номенклатур, где каждой из которых соответствует фактическое и прогнозное значение (как было в примере в начале статьи), то данная ошибка для этого не предназначена: MASE используется для расчета точности прогнозирования одной единственной позиции, основываясь на предыдущих показателях факта и прогноза, и чем больше этих показателей, тем более точно мы сможем рассчитать показатель точности. Вероятно, из-за этого ошибка не получила широкого распространения.
Здесь данная формула представлена исключительно для ознакомления и не рекомендуется к использованию.
Суть формулы заключается в нахождении среднего арифметического всех масштабированных ошибок, что при упрощении даст нам следующую конечную формулу:
Также, хочу отметить, что существует ошибка RMMSE (Root Mean Square Scaled Error — Среднеквадратичная масштабированная ошибка), которая примерно похожа на MASE, с теми же преимуществами и недостатками.
Это основные ошибки прогнозирования, которые могут использоваться для расчета точности прогнозирования. Но не все! Их очень много и, возможно, чуть позже я добавлю еще немного информации о некоторых из них. А примеры расчетов уже описанных ошибок прогнозирования будут выложены через некоторое время, пока что я подготавливаю пример, ожидайте.
Об авторе
HeinzBr
Автор статей и создатель сайта SHTEM.RU
 MAPE – средняя абсолютная ошибка в процентах используется:
MAPE – средняя абсолютная ошибка в процентах используется:
- Для оценки точности прогноза;
- Показывает на сколько велики ошибки в сравнении со значениями ряда;
- Хороша для сравнения 1-й модели для разных рядов;
- Используется для сравнения разных моделей для одного ряда;
- Оценки экономического эффекта, за счет повышения точности прогноза.
В данной статье мы рассмотрим, как рассчитать MAPE в Excel и как ее использовать.
Формула расчета MAPE:
Где:
- Yt – фактический объем продаж за анализируемый период;
- Ŷt — значение прогнозной модели за аналазируемый период;
- n — количество периодов.
Для того, чтобы рассчитать среднюю абсолютную ошибку мы:
- Рассчитываем значение модели прогноза — Ŷt;
- Рассчитываем ошибку прогноза;
- Берем ошибку по модулю;
- Определяем абсолютную ошибку;
- Рассчитываем среднюю абсолютную ошибку в процентах — MAPE.
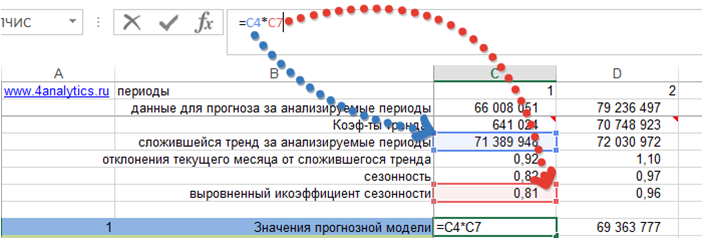
1. Рассчитаем значение модели прогноза — Ŷt
Возьмем модель с трендом и сезонностью. Рассчитаем значение модели для каждого периода, когда нам известны фактические продажи. Для этого сложившийся тренд за анализируемый период умножим на коэффициент сезонности для соответствующего месяца.
Получили значения прогнозной модели для каждого периода времени:
Подробнее о расчете прогноза с помощью тренда и сезонности читайте в статье «Расчет прогноза с помощью тренда и сезонности».
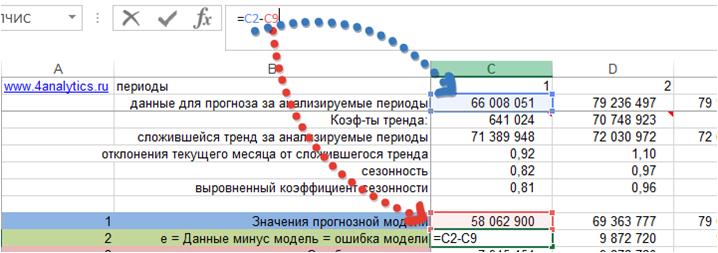
2. Рассчитаем значения ошибки прогноза.
В формуле расчета MAPE – это:
e — Ошибка прогноза — это разность между значениями временного ряда (фактом продаж) и моделью прогноза:
e= Yt — Ŷt
Получили значение ошибки прогноза для каждого момента времени за анализируемый период.
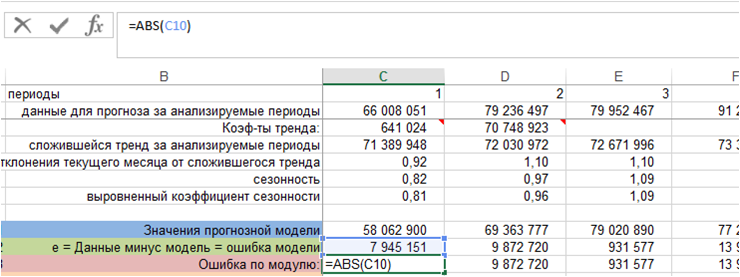
3. Рассчитаем ошибку по модулю.
Для этого воспользуемся функцией Excel =ABC()
4. Определяем абсолютную ошибку.
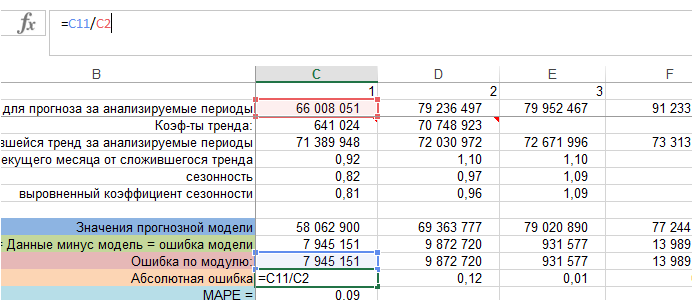
Для каждого периода ошибку по модулю делим на фактические значения ряда, т.е. на фактический объем продаж:
Получили абсолютную ошибку для каждого периода фактических продаж. В формуле MAPE — это:
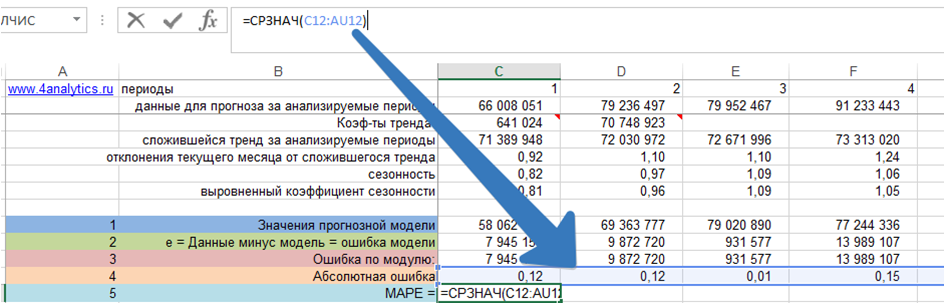
5. Рассчитаем MAPE – среднюю абсолютную ошибку.
Для этого рассчитаем среднее значение абсолютной ошибки за все периоды:
Скачать файл с примером расчета MAPE – средней абсолютной ошибки.
Как рассчитать показатель точность прогноза?
Показатель точность прогноза = 1 –MAPE:
С помощью MAPE вы можете сравнивать различные модели между собой, можете оценивать, как и на сколько модель делает точные прогнозы для разных временных рядов.
А также, что самое главное, можете оценить экономический эффект для компании за счет повышения точности прогноза.
Об этом подробнее можете почитать в нашей статье на сайте http://novoforecast.com/novo-forecast/instruktsiya/item/rost-tochnosti-prognoza-rost-pribyli.html
Если есть вопросы, пожалуйста, пишите в комментариях!
Forecast4AC PRO рассчитает MAPE для каждого временного ряда!
Точных вам прогнозов!
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel.
- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
Зарегистрируйтесь и скачайте решения
Статья полезная? Поделитесь с друзьями
читать 2 мин
Одной из наиболее распространенных метрик, используемых для измерения точности прогнозирования модели, является MAPE , что означает среднюю абсолютную ошибку в процентах .
Формула для расчета MAPE выглядит следующим образом:
MAPE = (1/n) * Σ(|факт – прогноз| / |факт|) * 100
куда:
- Σ — причудливый символ, означающий «сумма».
- n – размер выборки
- фактический – фактическое значение данных
- прогноз – прогнозируемое значение данных
MAPE обычно используется, потому что его легко интерпретировать и легко объяснить. Например, значение MAPE, равное 11,5%, означает, что средняя разница между прогнозируемым значением и фактическим значением составляет 11,5%.
Чем ниже значение MAPE, тем лучше модель способна прогнозировать значения. Например, модель с MAPE 2% более точна, чем модель с MAPE 10%.
Как рассчитать MAPE в Excel
Чтобы рассчитать MAPE в Excel, мы можем выполнить следующие шаги:
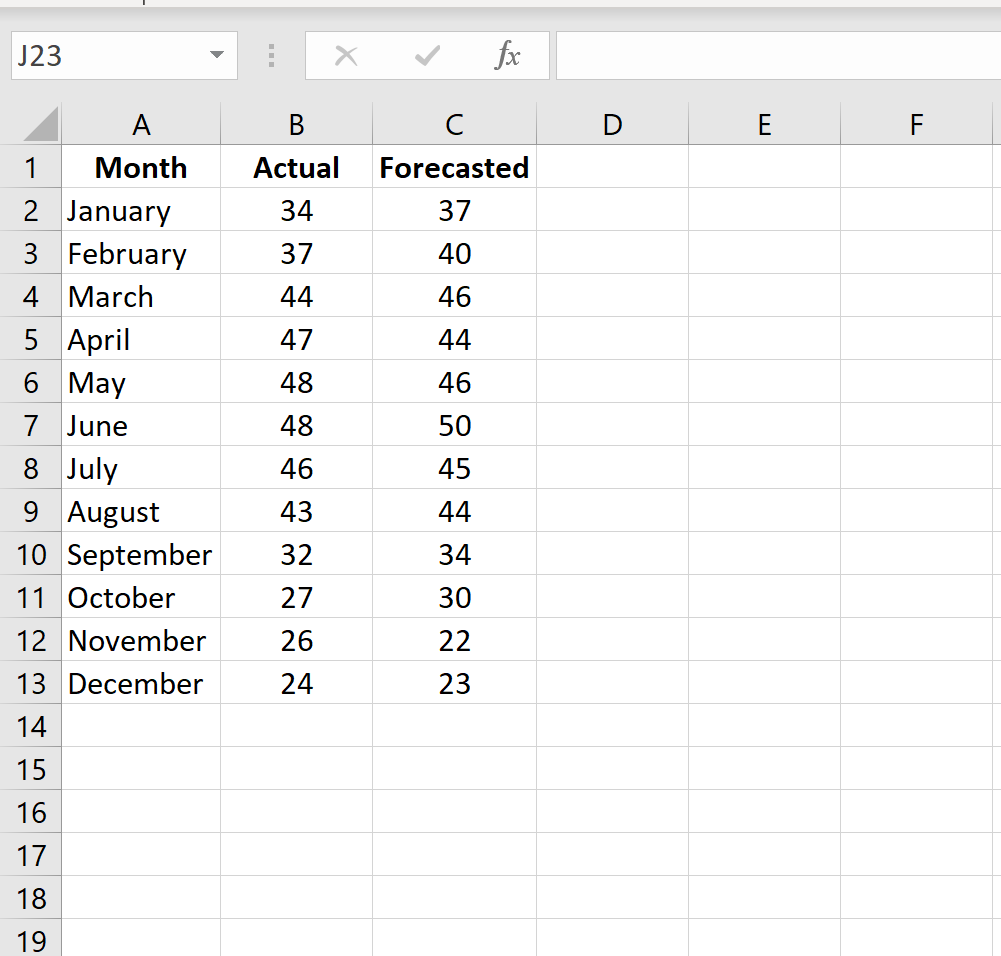
Шаг 1: Введите фактические значения и прогнозируемые значения в два отдельных столбца.
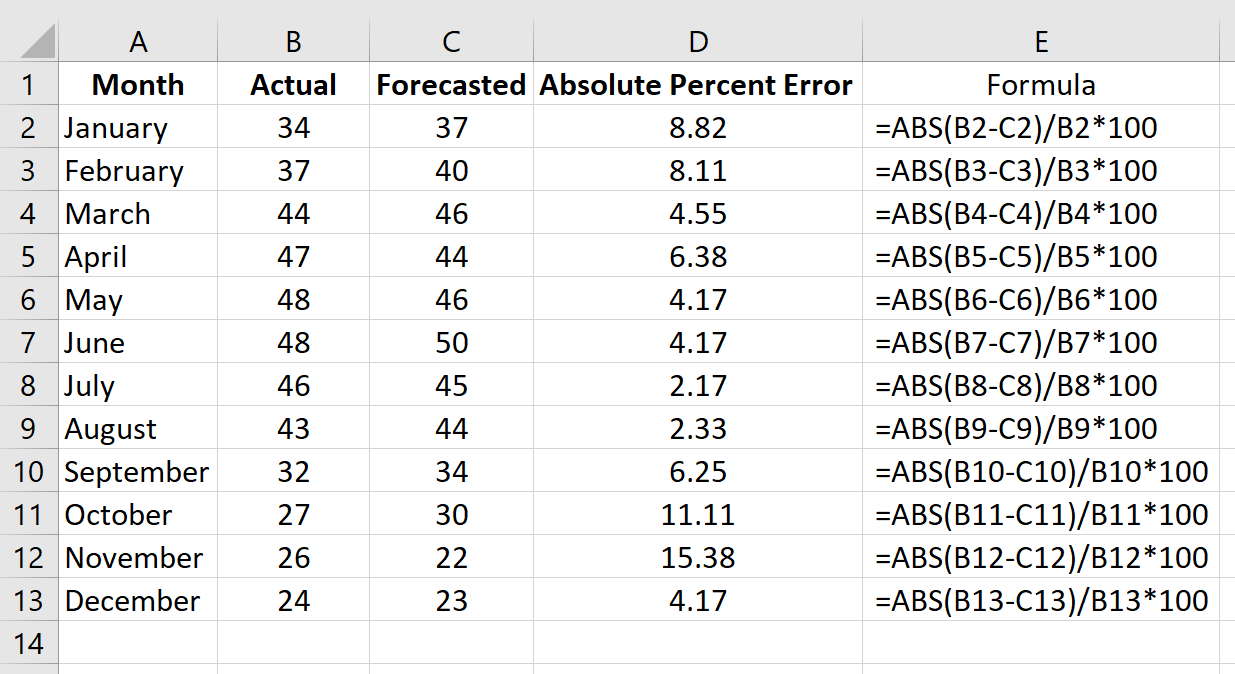
Шаг 2: Рассчитайте абсолютную процентную ошибку для каждой строки.
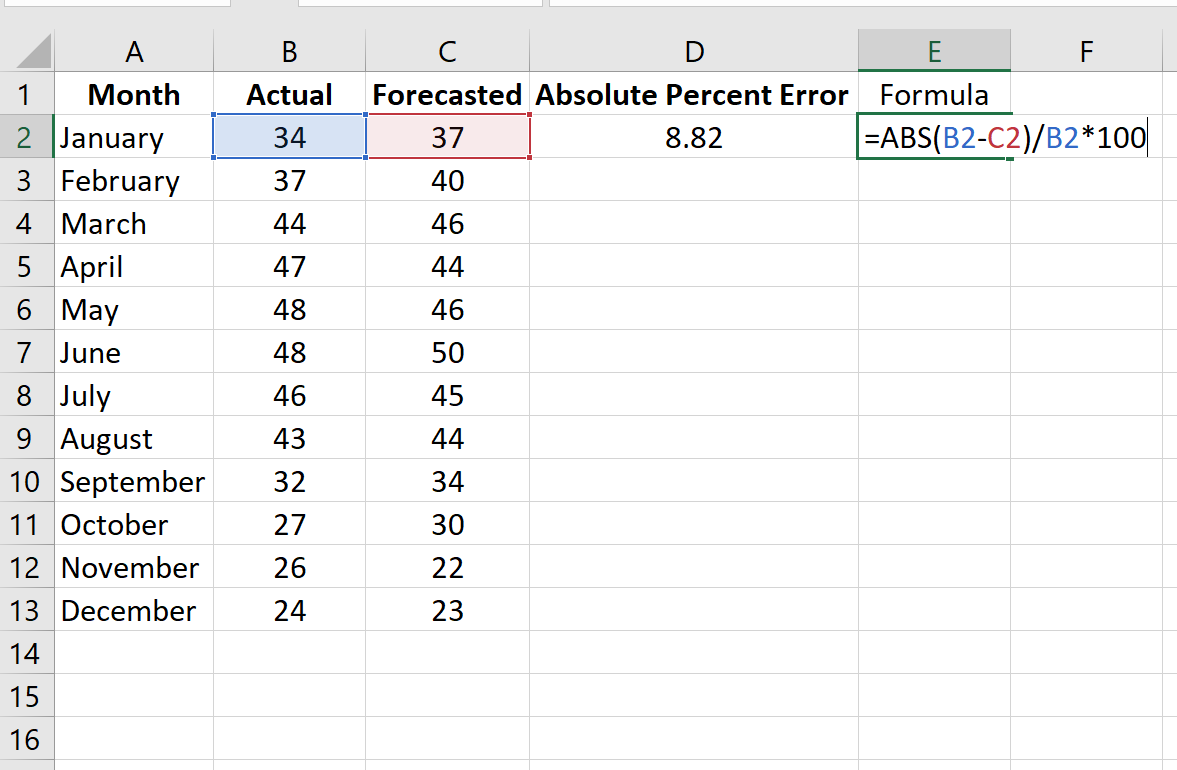
Напомним, что абсолютная процентная ошибка рассчитывается как: |фактический-прогноз| / |фактическое| * 100. Мы будем использовать эту формулу для расчета абсолютной процентной ошибки для каждой строки.
Столбец D отображает абсолютную процентную ошибку, а столбец E показывает формулу, которую мы использовали:
Повторим эту формулу для каждой строки:
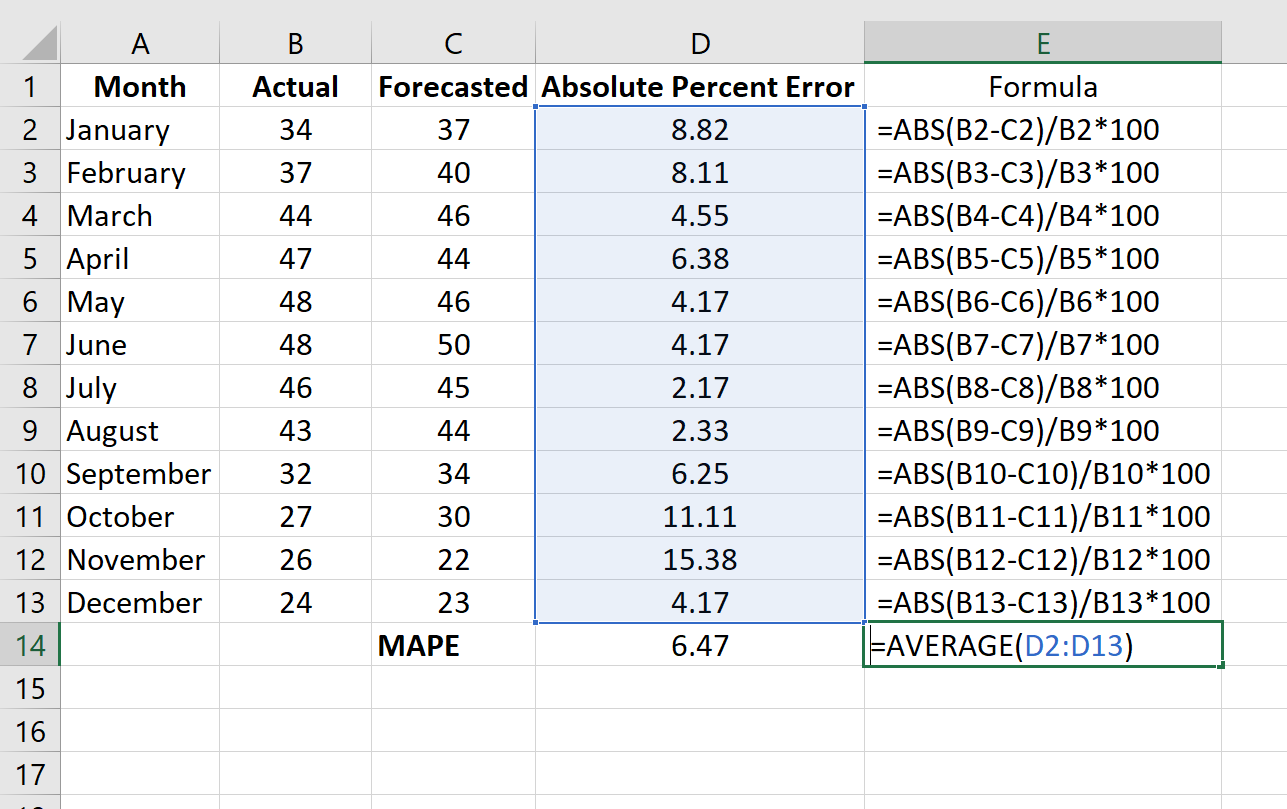
Шаг 3: Рассчитайте среднюю абсолютную ошибку в процентах.
Рассчитайте MAPE, просто найдя среднее значение в столбце D:
MAPE этой модели оказывается равным 6,47% .
Примечание по использованию MAPE
Хотя MAPE легко вычислить и легко интерпретировать, его использование имеет несколько потенциальных недостатков:
1. Поскольку формула для расчета абсолютной процентной ошибки |фактический-прогноз| / |фактическое| это означает, что он будет неопределенным, если какое-либо из фактических значений равно нулю.
2. MAPE не следует использовать с данными небольшого объема. Например, если фактический спрос на какой-либо товар равен 2, а прогноз равен 1, значение абсолютной процентной ошибки будет |2-1| / |2| = 50%, что создает впечатление, что ошибка прогноза довольно высока, несмотря на то, что прогноз отличается всего на одну единицу.
Другим распространенным способом измерения точности прогнозирования модели является MAD — среднее абсолютное отклонение. О том, как посчитать MAD в Excel, читайте здесь .
Дополнительные ресурсы
Что считается хорошей ценностью для MAPE?
Как рассчитать SMAPE в Excel
Как рассчитать MAE в Excel
Для анализа результатов расчета прогноза, в продолжение ряда вы можете рассчитать следующие ошибки:
- MAPE – средняя абсолютная ошибка в % . Ошибка оценивает на сколько велики ошибки в сравнении со значением ряда и с ошибками в соседних рядах.
Подробнее читайте в статье на нашем сайте: http://4analytics.ru/metodi-analiza/mape-%E2%80%93-srednyaya-absolyutnaya-oshibka-praktika-primeneniya.html - MRPE – средняя относительная ошибка в %, оценивает на сколько велика дельта между фактом и прогнозом. Чем ближе к 100%, тем больше ошибка, чем ближе к нулю, тем ошибка меньше.
- MSE – средняя квадратическая ошибка, подчеркивает большие ошибки за счет возведения каждой ошибки в квадрат.
Подробнее читайте в статье на нашем сайте:
http://4analytics.ru/metodi-analiza/mse-%E2%80%93-srednekvadraticheskaya-oshibka-v-excel.html - MPE – средняя процентная ошибка – показывает завышен или занижен прогноз относительно факта. Если ошибка меньше нулю, то прогноз последовательно завышен, если ошибка больше нуля, то прогноз последовательно занижен.
Подробнее читайте в статье на нашем сайте:
http://4analytics.ru/metodi-analiza/mpe-%E2%80%93-srednyaya-procentnaya-oshibka-v-excel.html - MAD – среднее абсолютное отклонение. Используется, когда важно измерить ошибку в тех же единицах, что и исходный ряд.
Подробнее читайте в статье на нашем сайте:
http://4analytics.ru/planirovanie-i-prognozirovanie-praktika/dopolnitelnie-oborotnie-sredstva-za-schet-povisheniya-tochnosti-prognoza.html - A MAPE – ошибка, которая показывает отклонение средних значений ряда к средним значениям модели прогноза. Имеет значение при неравномерном перераспределении значений ряда по периодам.
- S MAPE – ошибка, которая показывает отклонение суммы значения ряда к сумме значений модели прогноза. Имеет значение при неравномерном перераспределении значений ряда по периодам.
А также 2 показателя «Точность прогноза»:
- Точность прогноза = 1 – МАРЕ
- Точность прогноза 2 = 1 – MRPE
Для расчета ошибок одновременно с прогнозом, нажимаем кнопку «Расчет ошибок» в меню «FORECAST»
В открывшемся окне выбираем нужные для расчета ошибки:
Теперь при расчете прогноза, в продолжение ряда, программа автоматически сделает расчет отмеченных Вами ошибок:
Статистика оценки прогнозов с примерами на Python
Если бы мне пришлось выбрать один базовый навык в науке о данных, который был бы наиболее полезным, это было бы прогнозирование временных рядов. Предсказание будущей ценности чего-либо способствует принятию более правильных решений. Поэтому очень важно быть уверенным в том, что вы можете полагаться на прогнозы. Выбор, построение и интерпретация показателей точности прогнозов так же важны, как и составление прогнозов.
Что на самом деле определяет точность прогноза?
Как выбрать статистику оценки
Выбор метода оценки точности часто зависит от предметной области. В своей карьере я сталкивался с ситуацией, когда наспех выбранный показатель вызывал неудовлетворенность клиента результатами прогнозирования, оптимизированными для KPI, несовместимых с конкретным бизнес-кейсом. Например, модель может иметь низкую среднеквадратичную ошибку, но в то же время не предсказывает внезапных отклонений от «повседневных нормальных» значений или изменений тренда.
«🔔 Хотите больше подобных статей? Подпишите здесь.»
Эта статья покажет вам фундаментальную статистику оценки прогнозов, которую вы можете использовать для построения и тестирования своих прогнозных моделей. Мы рассчитаем и интерпретируем их на конкретных примерах: средняя ошибка (ME), среднеквадратичная ошибка (MSE), средняя абсолютная ошибка (MAE), средняя ошибка в процентах (MPE), средняя абсолютная ошибка в процентах (MAPE), и U-статистика Тейла. Мы будем интерпретировать и обсуждать примеры на Python в контексте данных прогнозирования временных рядов.
Примечание. Поскольку в этой статье я сосредоточен на конкретных показателях, я не затрагиваю тему перекрестной проверки и разделения набора данных на обучение и тестирование. Поскольку это важная концепция, я планирую затронуть эту тему в будущих текстах.
Почему?
Представьте, что вы работаете на производителя электроэнергии. Ваша задача — создать модель, которая прогнозирует ежедневное производство электроэнергии на небольшой ветряной электростанции. Это позволит планировать и сокращать производство электроэнергии на обычной электростанции при высокой эффективности из возобновляемых источников.
Вы создали пару моделей прогнозирования. Как выбрать лучшего для выполнения задачи?
Набор данных
Для расчета всей представленной статистики был создан файл CSV.
Эта электронная таблица содержит пример, включающий два месяца наблюдений и четыре альтернативных набора прогнозов (сделанных с помощью наивного, скользящего среднего и двух более сложных методов) интересующей переменной (обозначенной как y).
Технические подробности
Обозначения, используемые ниже, являются довольно стандартными, с yᵢ и fᵢ как переменные, представляющие интерес и прогноз соответственно, и n как количество наблюдений. Полный исходный код, использованный при подготовке этой статьи:
Https://gist.github.com/fischerbach/14e90b32e55b635591934a890ae20f60
Чтобы избежать повторения кода, я набросал простой класс FES, со статическими методами, которые вычисляют каждую статистику. Это делает код более читабельным без риска конфликта имен функций.
Статистика оценки прогнозов
Под «ошибкой» мы понимаем неопределенность в прогнозе или, другими словами, разницу между прогнозируемым значением и реальным значением. Это компонент yᵢ — fᵢ в большинстве следующих формул.
Средняя ошибка
Средняя ошибка — это среднее значение всех ошибок в наборе.
Это очень простая статистика. К сожалению, это предвзятость из-за компенсирующего эффекта положительных и отрицательных ошибок прогноза, которые могут скрыть неточность прогнозов. Из-за этого ME не очень полезен для оценки модели. Однако это очень легко понять даже неспециалисту (это не всегда является преимуществом из-за ограничений, описанных выше). ME может быстро представить симметрию распределения ошибок, что может быть полезно при оценке конкретной модели.
Средняя абсолютная ошибка
Средством исправления неточности средней ошибки является использование средней абсолютной ошибки.
МАЭ использует абсолютные значения ошибок в расчетах, что позволяет преодолеть аннулирование ошибок с противоположными знаками. Он дает нам среднее значение всех ошибок, независимо от того, были они положительными или отрицательными.
Среднеквадратичная ошибка
Так же, как и MAE, среднеквадратичная ошибка преодолевает отмену положительных и отрицательных ошибок.
Кроме того, MSE накладывает больший штраф на большие ошибки прогноза, чем MAE.
Средняя квадратическая ошибка
Среднеквадратичная ошибка — это стандартное отклонение ошибок.
RMSE разделяет преимущества MSE и обычно используется в прогнозировании и регрессионном анализе для проверки экспериментальных результатов. Кроме того, у него есть то преимущество, что у него те же единицы, что и у прогнозируемой переменной, поэтому его легче интерпретировать напрямую.
Средняя процентная ошибка
Средняя процентная ошибка — это среднее процентных ошибок, на которые каждый прогноз отличается от соответствующих реальных наблюдаемых значений.
Эту статистику легко понять, потому что она дает ошибку в процентах. Как и в ME, положительные и отрицательные ошибки прогноза могут компенсировать друг друга, поэтому его можно использовать для измерения систематической ошибки в прогнозах. Недостатком этой статистики является то, что она не подходит для наборов данных, содержащих наблюдаемые значения, которые равны нулю.
Средняя абсолютная ошибка в процентах
Средняя абсолютная процентная ошибка решает проблему смещения ошибок и работает лучше всего, если нет крайних значений для данных (и нет нулей).
Статистика Тейла U
Существует некоторая путаница в отношении коэффициента точности прогноза Тейла, вероятно, вызванная самим Тейлом. Он предложил две разные формулы в разное время под одним и тем же именем, каждая из которых помечена U. Более подробную информацию по этой теме вы найдете в Оценка прогнозов с использованием коэффициентов неравенства Тейла.
U₁
Значения U₁ находятся в диапазоне (0, 1).
Чем выше точность прогноза, тем меньше будет значение U₁.
U₂
U₂ Тейла показывает, насколько более (или менее) точна модель по сравнению с наивным прогнозом.
U₂ имеет нижнюю границу, равную 0 (что указывает на точный прогноз), не имеет верхней границы. Когда значение U₂ thing превышает 1, это означает, что метод прогноза становится хуже, чем наивное прогнозирование.
Оценка модели
Вернемся к нашему набору данных. Он содержит результаты 4 различных моделей прогнозирования.
В таблице ниже представлена вся статистика, описанная в этой статье, рассчитанная для каждой модели.
Стоит отметить, что продвинутый метод имеет квадратную ошибку на порядок меньше, чем любой другой. Он также является лидером по другим статистическим данным.
Выводы
Если основным показателем успеха была способность модели сообщать о внезапных изменениях прогнозируемой переменной, то предпочтительным методом будет «Advanced # 2». Это согласуется с интуицией и визуальной оценкой сюжета. Однако этот метод является наиболее сложным с точки зрения расчета и требует использования внешних переменных. Но в такой важной сфере проблемы, как производство электроэнергии, это приемлемая стоимость.
С другой стороны, «Advanced # 1» и методы скользящих средних подходят для грубых оценок. Вышеупомянутые выводы было бы невозможно сделать без рассмотрения альтернативной статистики, которая показывает, что никакая статистика оценки прогнозов не является избыточной, поскольку каждая из них имеет информацию, которую нужно сообщить.
Описанную статистику я использовал на практике при создании моделей:
использованная литература
Http://www.treasury.act.gov.au/documents/Forecasting%20Accuracy%20-%20ACT%20Budget.pdf
https://www.economicsnetwork.ac.uk/showcase/cook_forecast
https://www.jstor.org/stable/2352722?seq=1
https://stackoverflow.com/questions/54931514/theils-u-1-theils-u -2-формула-коэффициента-прогноза в питоне
https://stats.stackexchange.com/questions/345178/interpretation-of-theils-u2-statistic-forecasting-methods-and-applications
https://docs.oracle.com/cd/E40248_01/epm.1112/cb_statistical/frameset.htm?ch07s02s03s04.html
https://www.statisticshowto.com/mean- ошибка /
https://en.wikipedia.org/wiki/Mean_percentage_error
https://arxiv.org/abs/1905.11744








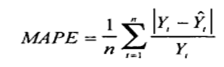 MAPE – средняя абсолютная ошибка в процентах используется:
MAPE – средняя абсолютная ошибка в процентах используется: