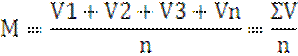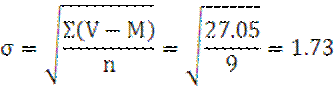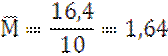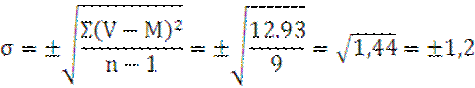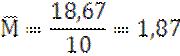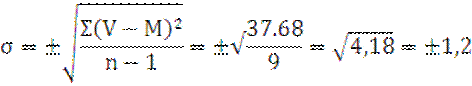Полученные
в результате статистического исследования
средние и относительные величины должны
отражать закономерности, характерные
для всей совокупности. Результаты
исследования обычно тем достовернее,
чем больше сделано наблюдений, и наиболее
точными они являются при сплошном
исследовании (т.е. при изучении генеральной
совокупности). Однако должны быть
достаточно надежные и данные, полученные
путем выборочных исследований, т.е. на
относительно небольшом числе наблюдений.
Различие
результатов выборочного исследования
и результатов, которые могут быть
получены на генеральной совокупности,
представляет собой ошибку выборочного
исследования, которую можно точно
определить математическим путем. Метод
ее оценки основан на закономерностях
случайных вариаций, установленных
теорией вероятности.
1.
Оценка достоверности средней
арифметической.
Средняя
арифметическая, полученная при обработке
результатов научно-практических
исследований, под влиянием случайных
явлений может отличаться от средних,
полученных при проведении повторных
исследований. Поэтому, чтобы иметь
представление о возможных пределах
колебаний средней, о том, с какой
вероятностью возможно перенести
результаты исследования с выборочной
совокупности на всю генеральную
совокупность, определяют степень
достоверности средней величины.
Мерой
достоверности средней является средняя
ошибка средней арифметической (ошибка
репрезентативности – m).
Ошибки репрезентативности возникают
в связи с тем, что при выборочным
наблюдении изучается только часть
генеральной совокупности, которая
недостаточно точно ее представляет.
Фактически ошибка репрезентативности
является разностью между средними,
полученными при выборочном статистическом
наблюдении, и средними, которые были бы
получены при сплошном наблюдении (т.е.
при изучении всей генеральной
совокупности).
Средняя
ошибка средней арифметической вычисляется
по формуле:
—
при числе наблюдений больше 30 (n
> 30):
—
при небольшом числе наблюдений (n
< 30):
Ошибка
репрезентативности прямо пропорциональна
колеблемости ряда (сигме) и обратно
пропорциональна числу наблюдений.
Следовательно,
чем больше
число наблюдений
(т.е. чем ближе по числу наблюдений
выборочная совокупность к генеральной),
тем меньше
ошибка репрезентативности.
Интервал,
в котором с заданным уровнем вероятности
колеблется истинное значение средней
величины или показателя, называется
доверительным
интервалом,
а его границы – доверительными
границами.
Они используются для определения
размеров средней или показателя в
генеральной совокупности.
Доверительные
границы
средней арифметической и показателя в
генеральной совокупности равны:
M
+
tm
P
+
tm,
где
t
– доверительный коэффициент.
Доверительный
коэффициент (t)
– это число, показывающее, во сколько
раз надо увеличить ошибку средней
величины или показателя, чтобы при
данном числе наблюдений с желаемой
степенью вероятности утверждать, что
они не выйдут за полученные таким образом
пределы.
С
увеличением t
степень вероятности возрастает.
Т.к.
известно, что полученная средняя или
показатель при повторных наблюдениях,
даже при одинаковых условиях, в силу
случайных колебаний будут отличаться
от предыдущего результат, теорией
статистики установлена степень
вероятности, с которой можно ожидать,
что колебания эти не выйдут за определенные
пределы. Так, колебания средней
в интервале M
+
1m
гарантируют ее точность с вероятностью
68.3% (такая
степень вероятности не удовлетворяет
исследователей), в
интервале M
+
2m
– 95.5%
(достаточная степень вероятности) и в
интервале M
+
3m
– 99,7% (большая
степень вероятности).
Для
медико-биологических исследований
принята степень вероятности 95% (t
= 2), что соответствует доверительному
интервалу M
+
2m.
Это
означает, что практически
с полной достоверностью (в 95%) можно
утверждать, что полученный средний
результат (М) отклоняется от истинного
значения не больше, чем на удвоенную (M
+
2m) ошибку.
Конечный
результат любого медико-статистического
исследования выражается средней
арифметической и ее параметрами:
2.
Оценка достоверности относительных
величин (показателей).
Средняя
ошибка показателя также служит для
определения пределов его случайных
колебаний, т.е. дает представление, в
каких пределах может находиться
показатель в различных выборках в
зависимости от случайных причин. С
увеличением численности выборки ошибка
уменьшается.
Мерой
достоверности показателя является его
средняя ошибка (m),
которая показывает, на сколько результат,
полученный при выборочным исследовании,
отличается от результата, который был
бы получен при изучении всей генеральной
совокупности.
Средняя
ошибка показателя определяется по
формуле:
,
где mp
– ошибка относительного показателя,
р
– показатель,
q
– величина, обратная показателю (100-p,
1000-р и т.д. в зависимости от того, на какое
основание рассчитан показатель);
n
– число наблюдений.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Представление результатов исследования
В научных публикациях важно представление результатов исследования. Очень часто окончательный результат приводится в следующем виде: M±m, где M – среднее арифметическое, m –ошибка среднего арифметического. Например, 163,7±0,9 см.
Прежде чем разбираться в правилах представления результатов исследования, давайте точно усвоим, что же такое ошибка среднего арифметического.
Ошибка среднего арифметического
Среднее арифметическое, вычисленное на основе выборочных данных (выборочное среднее), как правило, не совпадает с генеральным средним (средним арифметическим генеральной совокупности). Экспериментально проверить это утверждение невозможно, потому что нам неизвестно генеральное среднее. Но если из одной и той же генеральной совокупности брать повторные выборки и вычислять среднее арифметическое, то окажется, что для разных выборок среднее арифметическое будет разным.
Чтобы оценить, насколько выборочное среднее арифметическое отличается от генерального среднего, вычисляется ошибка среднего арифметического или ошибка репрезентативности.
Ошибка среднего арифметического обозначается как m или
Ошибка среднего арифметического рассчитывается по формуле:
где: S — стандартное отклонение, n – объем выборки; Например, если стандартное отклонение равно S=5 см, объем выборки n=36 человек, то ошибка среднего арифметического равна: m=5/6 = 0,833.
Ошибка среднего арифметического показывает, какая ошибка в среднем допускается, если использовать вместо генерального среднего выборочное среднее.
Так как при небольшом объеме выборки истинное значение генерального среднего не может быть определено сколь угодно точно, поэтому при вычислении выборочного среднего арифметического нет смысла оставлять большое число значащих цифр.
Правила записи результатов исследования
- В записи ошибки среднего арифметического оставляем две значащие цифры, если первые цифры в ошибке «1» или «2».
- В остальных случаях в записи ошибки среднего арифметического оставляем одну значащую цифру.
- В записи среднего арифметического положение последней значащей цифры должно соответствовать положению первой значащей цифры в записи ошибки среднего арифметического.
Представление результатов научных исследований
В своей статье «Осторожно, статистика!», опубликованной в 1989 году В.М. Зациорский указал, какие числовые характеристики должны быть представлены в публикации, чтобы она имела научную ценность. Он писал, что исследователь «…должен назвать: 1) среднюю величину (или другой так называемый показатель положения); 2) среднее квадратическое отклонение (или другой показатель рассеяния) и 3) число испытуемых. Без них его публикация научной ценности иметь не будет “с. 52
В научных публикациях в области физической культуры и спорта очень часто окончательный результат приводится в виде: (М±m) (табл.1).
Таблица 1 — Изменение механических свойств латеральной широкой мышцы бедра под воздействием физической нагрузки (n=34)
| Эффективный модуль
упругости (Е), кПа |
Эффективный модуль
вязкости (V), Па с |
|||
| Этап
эксперимента |
Рассл. | Напряж. | Рассл. | Напряж. |
| До ФН | 7,0±0,3 | 17,1±1,4 | 29,7±1,7 | 46±4 |
| После ФН | 7,7±0,3 | 18,7±1,4 | 30,9±2,0 | 53±6 |
Литература
- Высшая математика и математическая статистика: учебное пособие для вузов / Под общ. ред. Г. И. Попова. – М. Физическая культура, 2007.– 368 с.
- Гласс Дж., Стэнли Дж. Статистические методы в педагогике и психологии. М.: Прогресс. 1976.- 495 с.
- Зациорский В.М. Осторожно — статистика! // Теория и практика физической культуры, 1989.- №2.
- Катранов А.Г. Компьютерная обработка данных экспериментальных исследований: Учебное пособие/ А. Г. Катранов, А. В. Самсонова; СПб ГУФК им. П.Ф. Лесгафта. – СПб.: изд-во СПб ГУФК им. П.Ф. Лесгафта, 2005. – 131 с.
- Основы математической статистики: Учебное пособие для ин-тов физ. культ / Под ред. В.С. Иванова.– М.: Физкультура и спорт, 1990. 176 с.
Содержание
1.
Расчет средней арифметической ошибки
2.
Расчет стандартной ошибки при помощи встроенных функций
3.
Решение задачи с помощью опции «Описательная статистика»
Стандартная ошибка появляется при прогнозировании каких-либо данных или арифметических вычислениях, поэтому важно научиться находить этот параметр. В этой публикации разбираем, как найти и исправить стандартную ошибку путем использования инструментов Excel.
Расчет средней арифметической ошибки
В Microsoft Excel цельность и однородность выборки определяется при помощи стандартной ошибки. Стандартная ошибка — это квадратный корень из дисперсии. В приложении предусмотрено два варианта поиска стандартной ошибки: при помощи пакетного анализа и расширенных функций программы.
Чтобы найти значение средней арифметической, необходимо выполнить деление суммарной величины выборки на ее количество в электронной книге.
Расчет стандартной ошибки при помощи встроенных функций
Для того, чтобы правильно вычислять, необходимо изучить пошаговую инструкцию. В этом способе подбор результатов будет осуществляться с помощью комбинированных манипуляций.
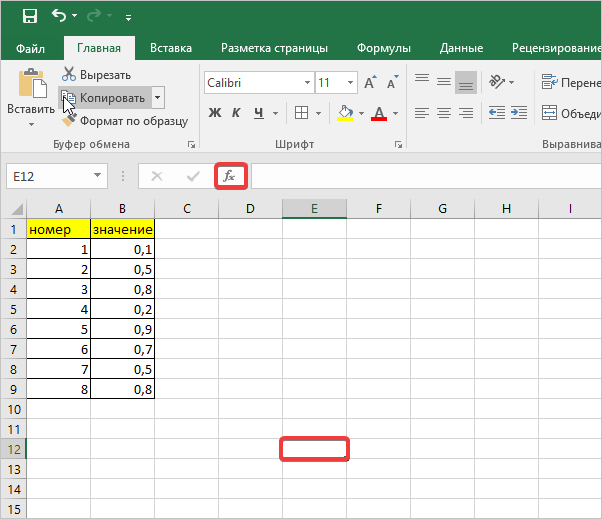
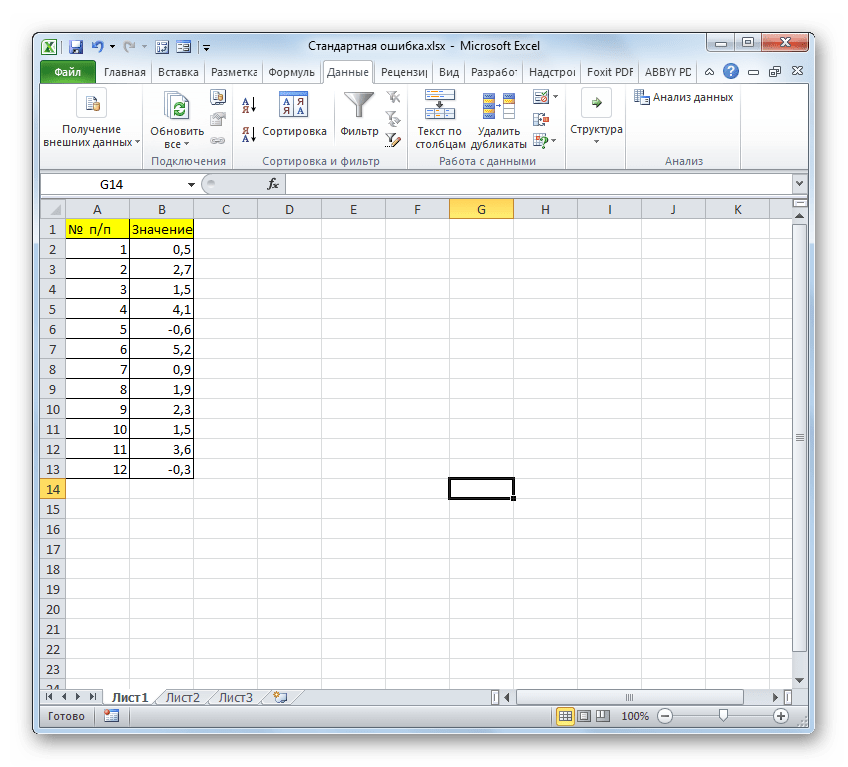
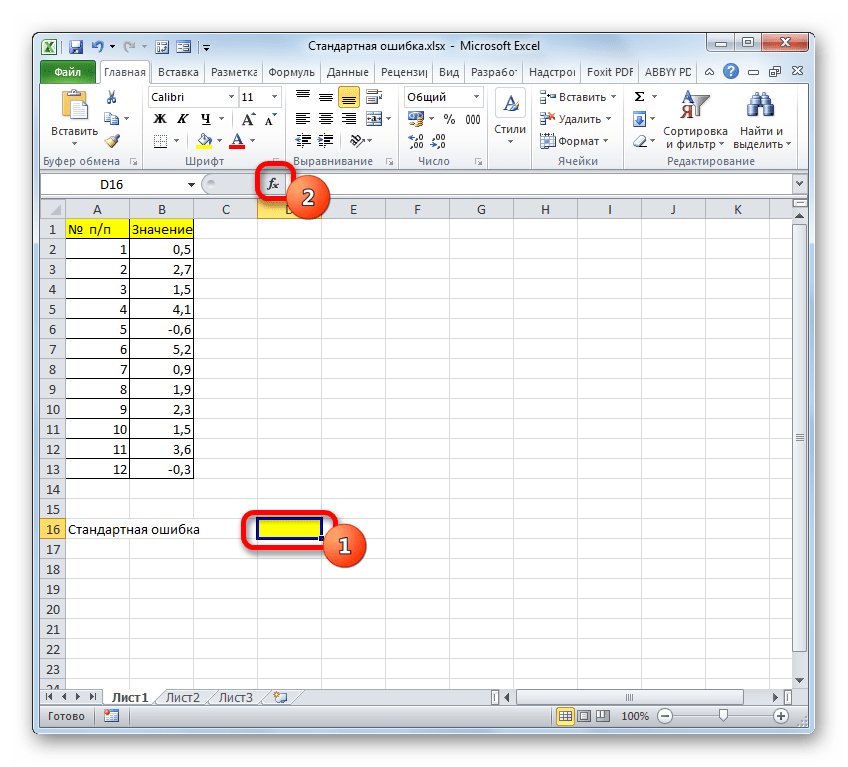
- Для расчетов будем использовать таблицу с выборкой чисел. Кликаем на любой пустой ячейке на листе, где будет отображаться результат. Затем нажимаем кнопку «Вставить функцию.
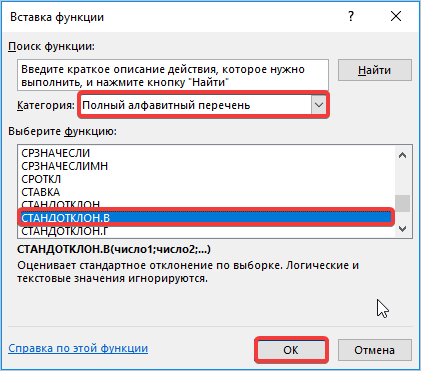
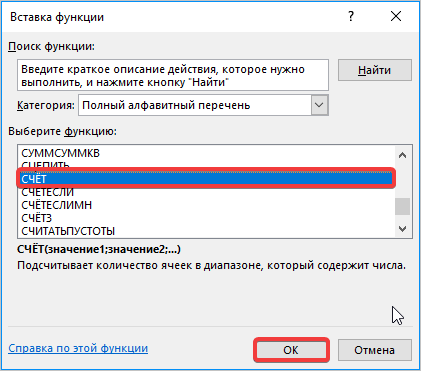
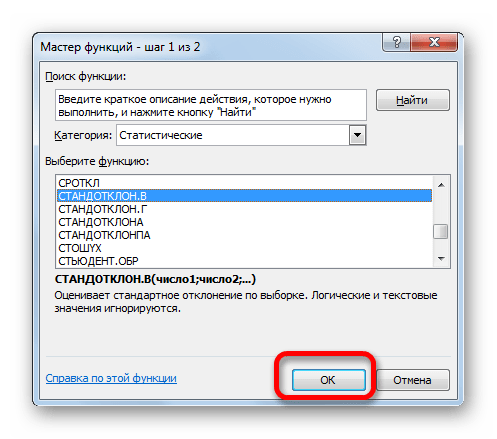
- Далее перед вами открывается диалоговое окно, в котором необходимо использовать «СТАНДОТКЛ.В», для этого в поле «Категория» необходимо выбрать «Полный алфавитный перечень». Затем нажмите кнопку «ОК».
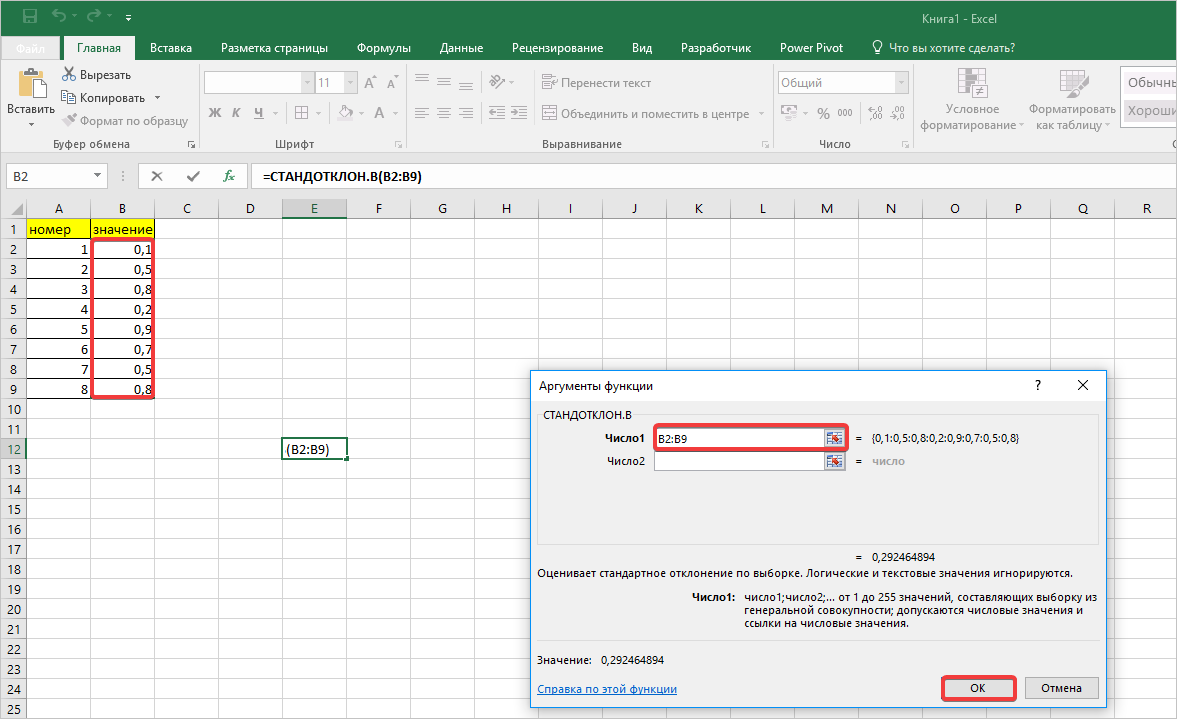
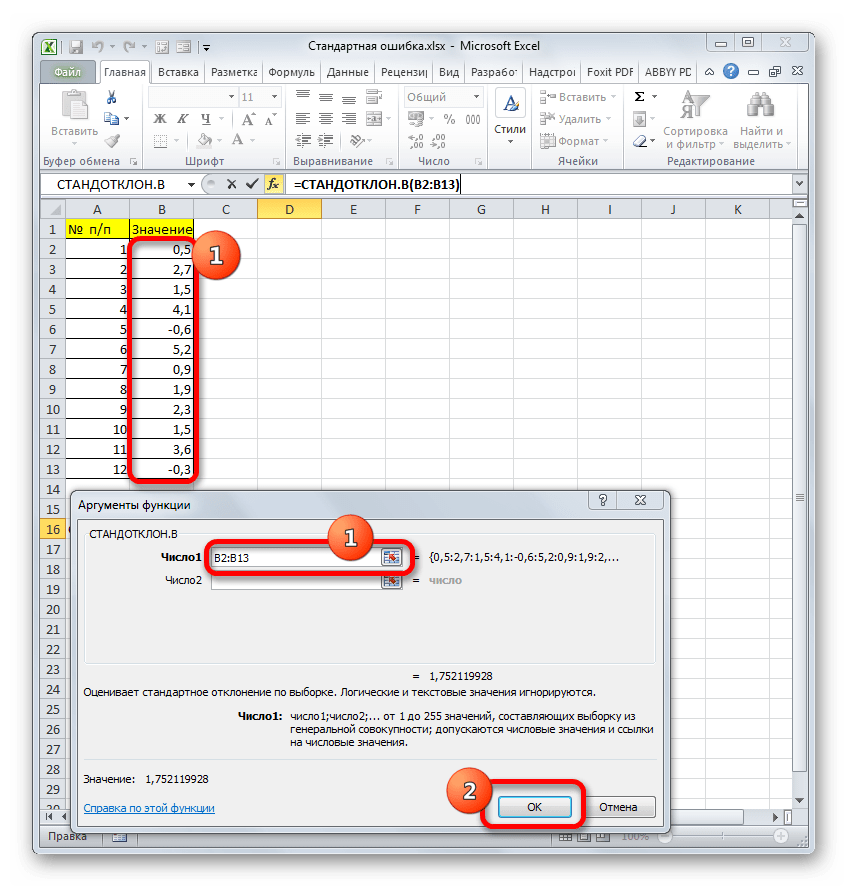
- В окне «Аргументы функции» кликаем в первом поле «Число 1», затем выполняем выделение мышью диапазона ячеек со значениями таблицы и нажимаем кнопку «ОК».
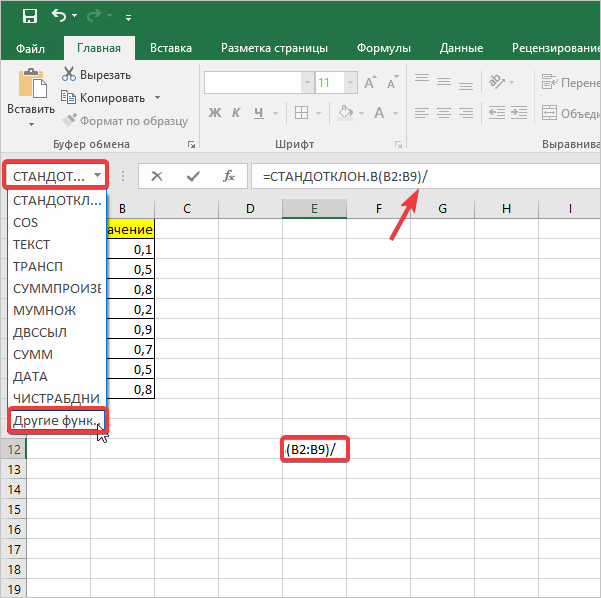
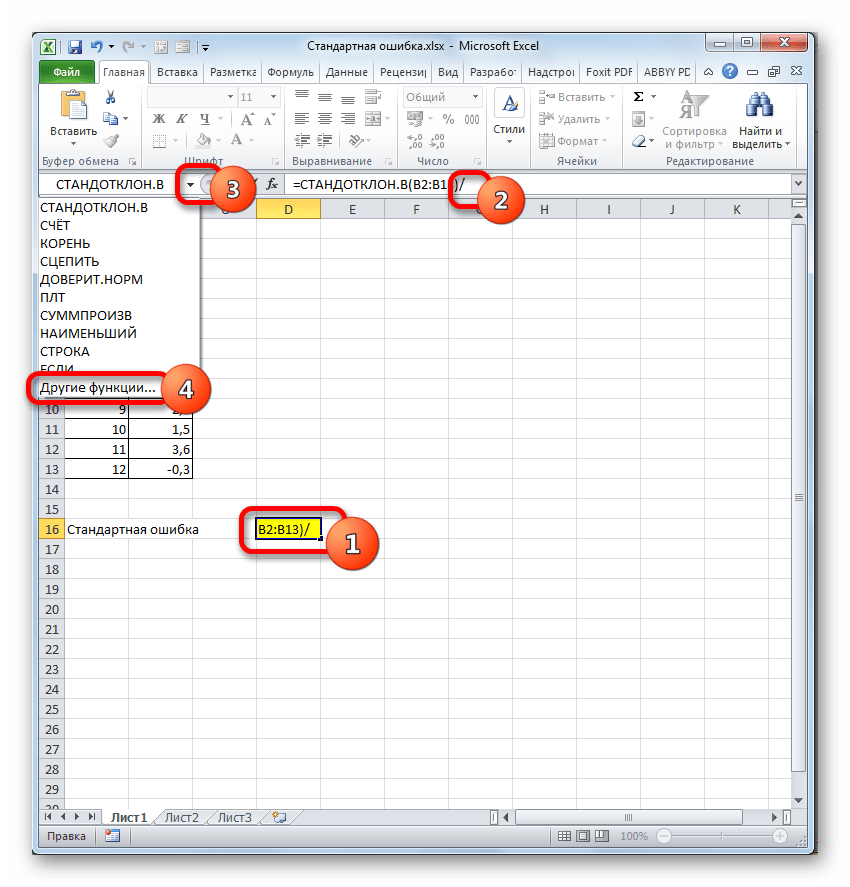
- Далее активируем ячейку с нашими значениями, переходим в строку формулы и ставим после значений наклонную линию. Переходим в поле наименования, кликаем на указывающий вниз флажок, где из списка выбираем «Другие функции».
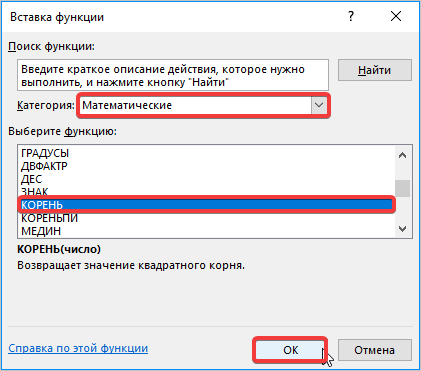
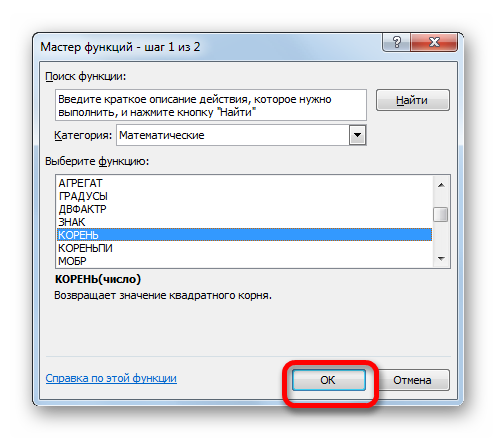
- Снова активируется окно с перечнем функций, в котором необходимо выбрать категорию «Математические», затем функцию «Корень». Далее нажмите кнопку «ОК».
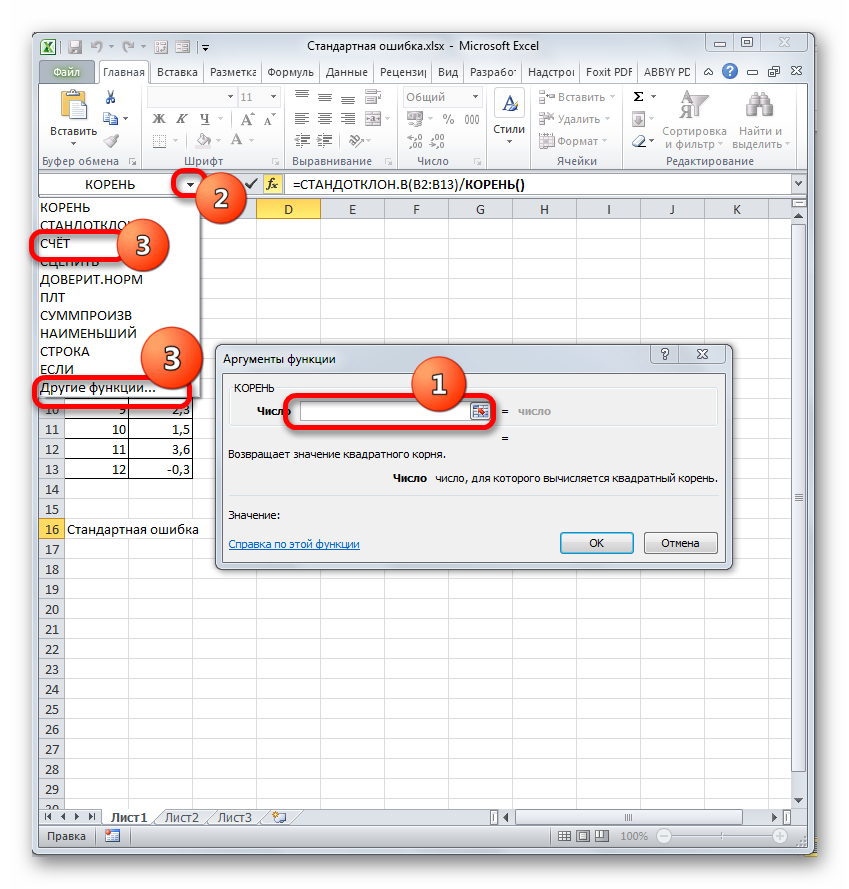
- Далее открывается окно, в котором необходимо заполнить поле с числом. Для этого переходим в поле «Имя», где спускаемся к пункту «Счет». Если его нет, ищите в дополнительных функциях.
После выполнения этих шагов, стандартная ошибка высчитывается автоматически, пользователю остается только сверить их и проверить значение на некорректное отображение.
Для малых и стандартных выборок необходимо использовать разные формулы. В первом случае (если находится до 30 значений), ее необходимо видоизменить.
Решение задачи с помощью опции «Описательная статистика»
Благодаря опции «Описательная статистика» удается выполнить вычисление по различным критериям. По этим правилам удается найти среднюю арифметическую ошибку. Для использования данного метода предварительно нужно запустить «Пакет анализа».
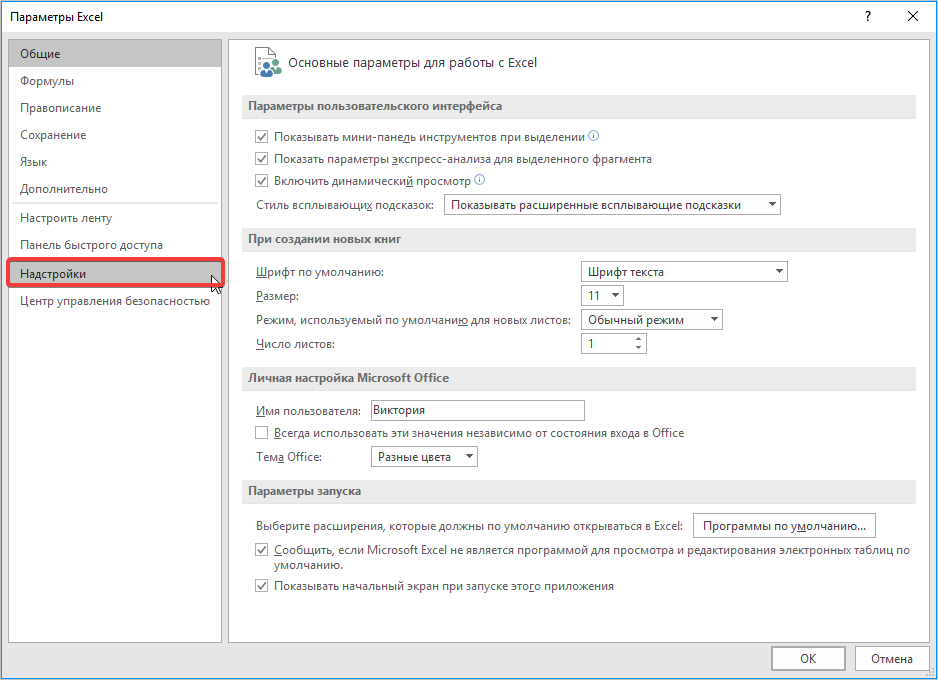
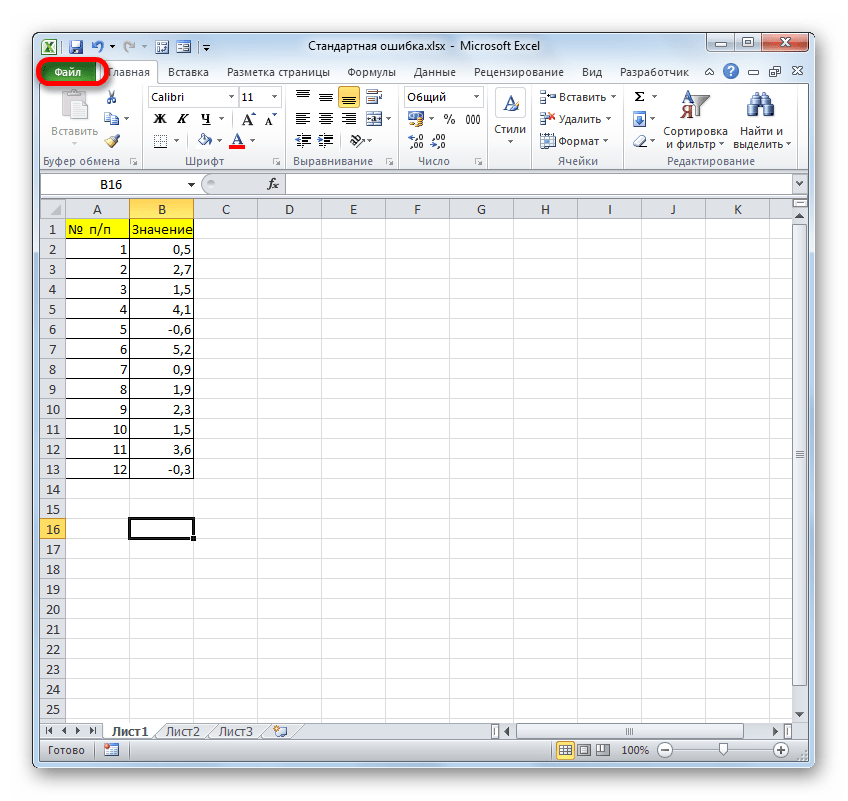
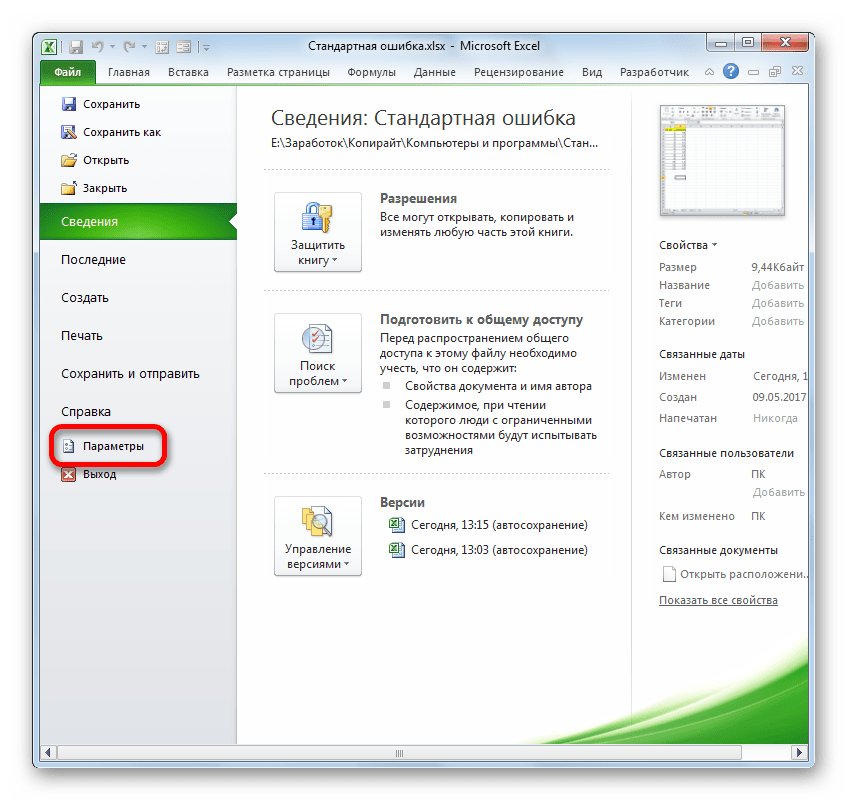
- Переходим во вкладку «Файл», где перемещаемся в пункт «Параметры». Далее нажимаем на запись «Надстройки».
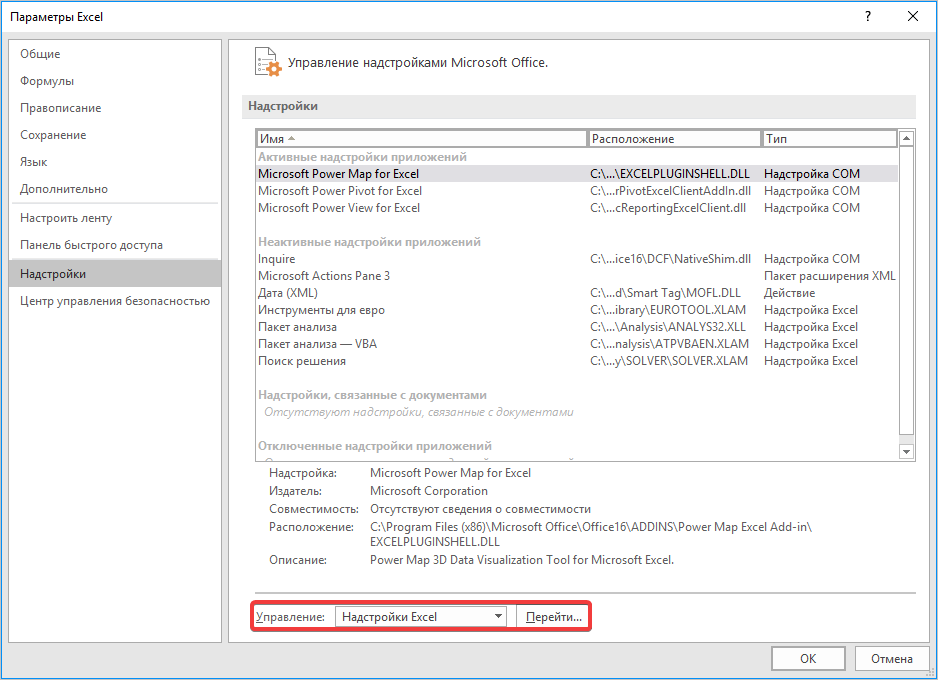
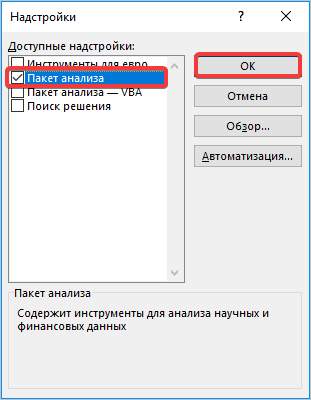
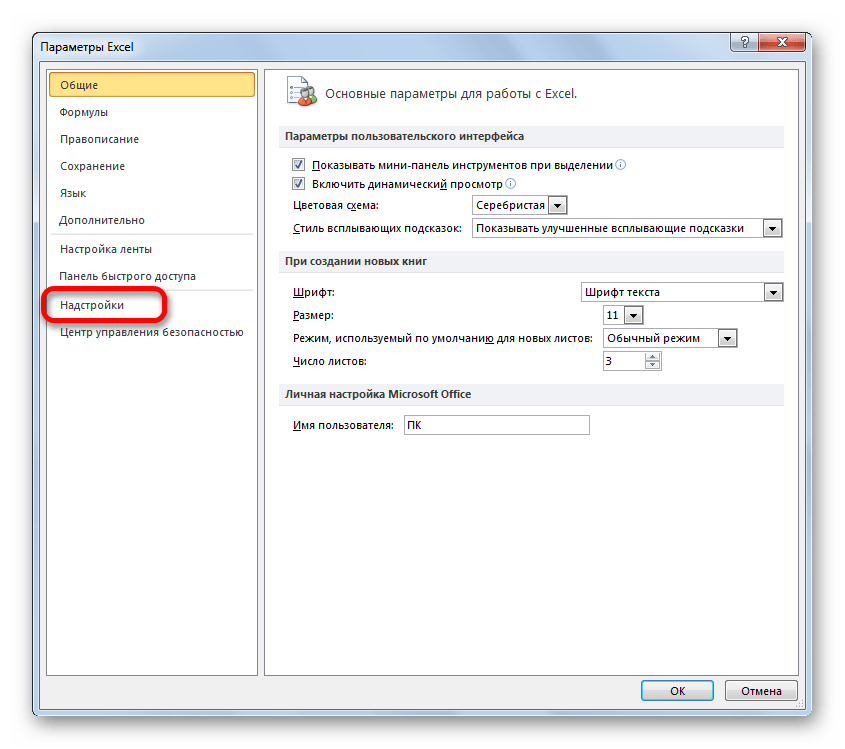
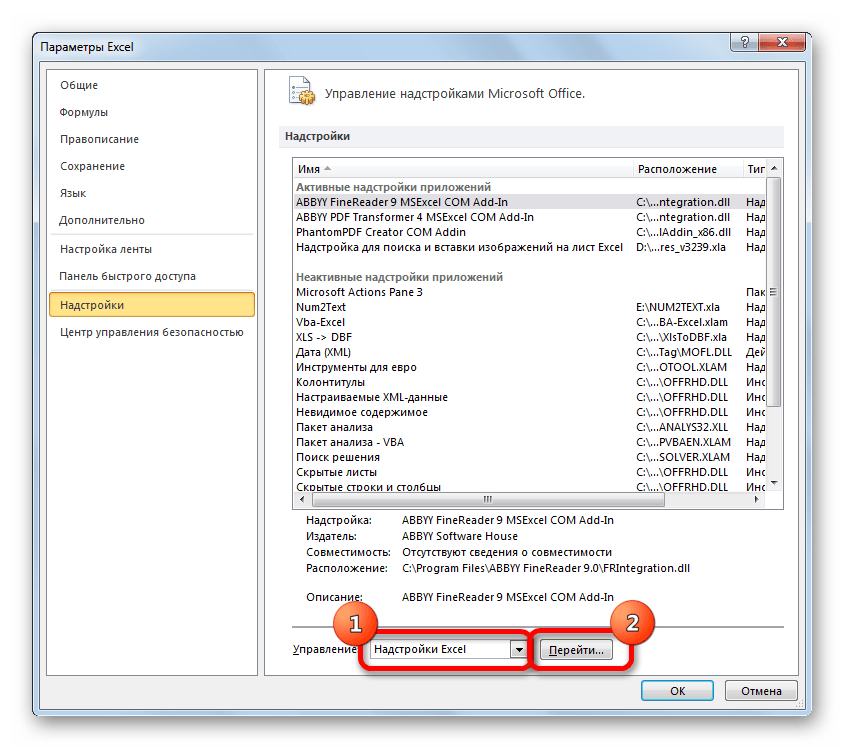
- Открывается окошко, в нем в графе «Управление» должно быть прописано «Надстройки Excel», затем рядом нажимаем кнопку «Параметры».
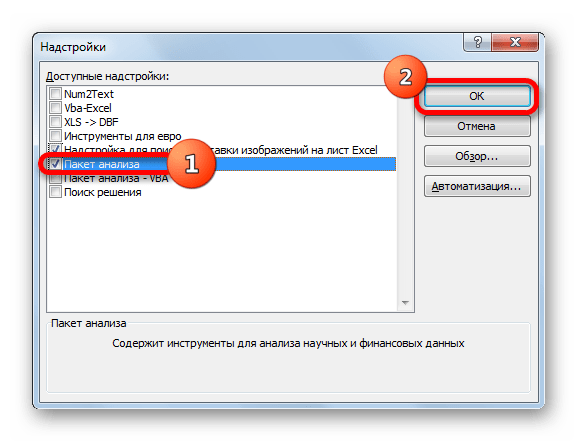
- В появившемся окне находим «Пакет анализа» и нажимаем кнопку «ОК».
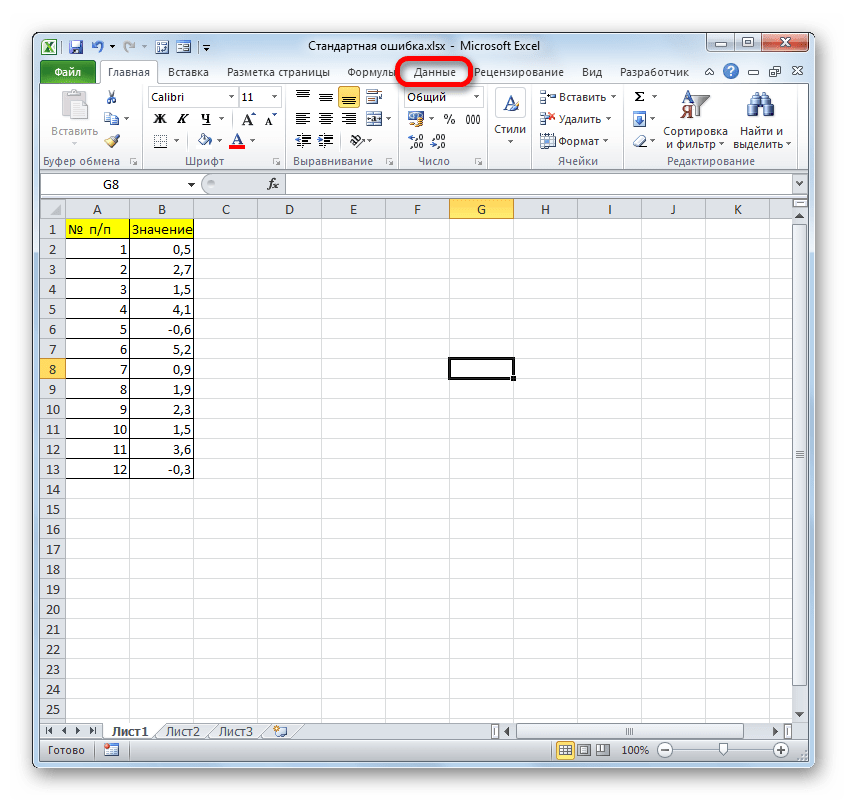
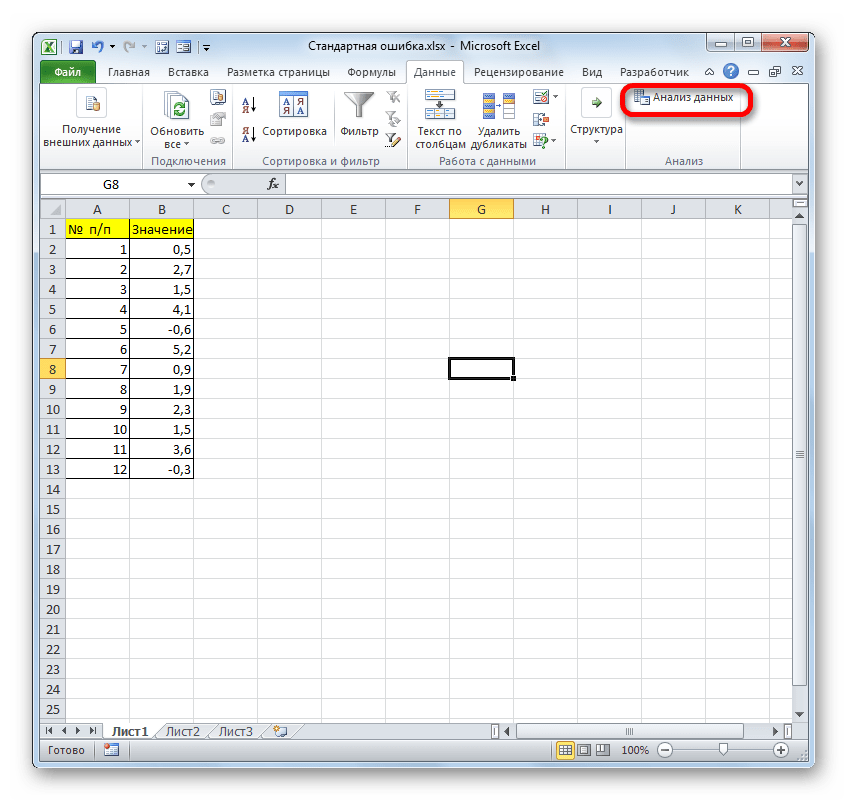
- Далее выбираем любую свободную ячейку, переходим во вкладку «Данные» и нажимаем «Анализ данных» в блоке «Анализ».
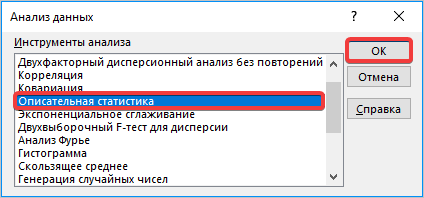
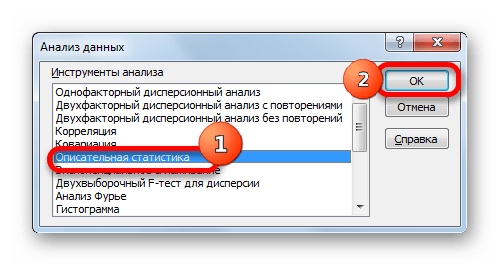
- Происходит запуск вспомогательного окошка, в котором необходимо выбрать из всех инструментов «Описательную статистику» и нажать кнопку «ОК».
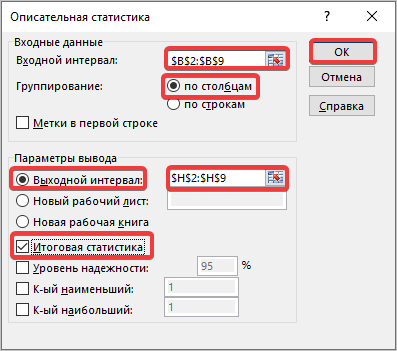
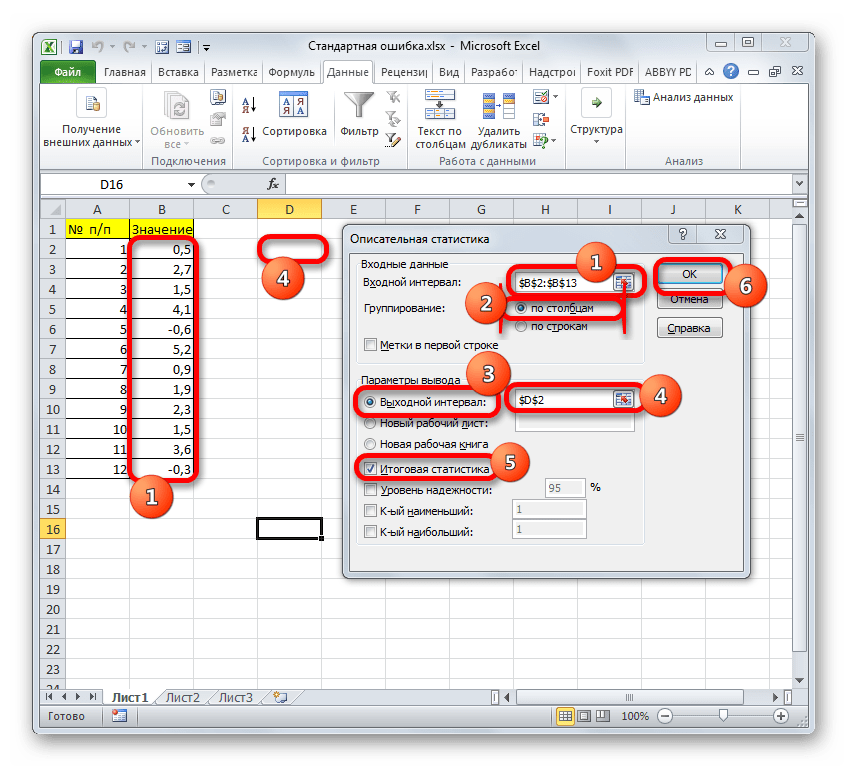
- Открывается новый мастер значений. Здесь нужно вводить данные предельно внимательно. В поле «Входной интервал» вносим адрес диапазона ячеек с выборкой. Затем указываем параметр «Группирование» «По столбцам». Затем выбираем место для «выходного интервала», его должно быть столько же, сколько и «входного». Ставим галочку напротив «Итоговая статистика» и нажимаем кнопку «ОК».
В результате вычислений вы получаете небольшую таблицу, в которой указаны все данные с определенной стандартной ошибкой.
Вычисление среднего арифметического отклонения заболеваемости (летальности, иммунизации)
Страницы работы
Содержание работы
Лабораторное
занятие №7
Тема:
Вычисление среднего арифметического отклонения заболеваемости (летальности,
иммунизации)
Цель
– научиться изучать величину средней арифметической и ее ошибки.
Задачи:
1. Изучить
основные обозначения.
2. Построить
основную и вспомогательную таблицы.
3. Вычислить
величину средней арифметической.
4. Вычислить
величину ошибки средней арифметической.
Вариационная статистика – наука, разрабатывающая изучение метода варьирующего
признака на массовых материалах в различных областях знания. Варьирующими
признаками принято называть такие, которые проявляют определенную
закономерность в изменчивости значений.
В качестве варьирующих могут быть такие показатели развития эпизоотического
процесса, как количество неблагополучных пунктов, коэффициент очаговости,
заболеваемость, летальность, уровень вакцинации животных и так далее. Взятые за
ряд лет по годам и связанные в определенные таблицы.
При переработки показателей эпизоотического процесса, для вычисления средней
арифметической, среднего квадратического отклонения, ошибки средней
арифметической, критерия средней арифметической, критерия достоверности и
вероятности, варьирующие величины обозначаются специальными терминами,
символами, принятыми в вариационной статистике.
Основные
обозначения:
V(X)
– величина варьирующего признака (показатель);
n
– число варьирующих признаков (показателей, участвующих в обработке);
Σ
(большая греческая сигма) – общепринятое обозначение арифметического
действия (суммы);
(
) – среднее арифметическое
варьирующих признаков (показателей участвующих в обработке);
(S) – сигма малая, показатель среднего
квадратического отклонения;
m (Sx) – искомая
ошибка средней арифметической;
n-1=V – число
степеней свободы; (ню)
t – критерий
достоверности (существенности);
P –уровень
вероятности (существенности);
r – коэффициент
парной корреляции;
R – коэффициент
множественной корреляции;
Таблица
28.
Заболеваемость
лептоспирозом крупного рогатого скота в России
в
2001-2010 гг. (количество заболевших животных на 10 тысяч поголовья)
|
Край |
Годы |
Средний показатель за 10 лет M±m |
p |
|||||||||
|
2001 |
2002 |
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
|||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|||
|
Хабаровский |
3,41 |
4,89 |
4,49 |
5,54 |
3,61 |
1,80 |
1,83 |
1,08 |
1,24 |
0,80 |
2,87±0,58 |
<0,001 |
|
Красноярский |
3,44 |
2,0 |
2,63 |
3,33 |
1,83 |
1,19 |
0,91 |
0,43 |
0,36 |
0,28 |
1,69±0,41 |
<0,001 |
|
Краснодарский |
4,33 |
3,58 |
5,95 |
1,91 |
1,03 |
0,32 |
0,28 |
0,51 |
0,12 |
0,64 |
1,86±0,68 |
<0,001 |
Таблица
29.
Разброс
вариационного ряда по заболеваемости крупного рогатого скота лептоспирозом по
Хабаровскому краю
|
n |
V |
V-M |
(V-M)² |
|
1 |
3.41 |
0.54 |
0.29 |
|
2 |
4.89 |
2.02 |
4.08 |
|
3 |
4.49 |
1.62 |
2.62 |
|
4 |
5.54 |
2.67 |
7.13 |
|
5 |
3.61 |
0.74 |
0.55 |
|
6 |
1.80 |
-1.07 |
1.14 |
|
7 |
1.83 |
-1.04 |
1.08 |
|
8 |
1.08 |
-1.79 |
3.20 |
|
9 |
1.24 |
-1.63 |
2.66 |
|
10 |
0.8 |
-2.07 |
4.28 |
|
n=10 |
Σv=28.69 M=2.87 |
Σ(V-M)²=27.05 |
Из приведенного примера видно, что число показателей (n)
равно 10. Следовательно, число вариантов (показателей заболеваемости, анализ за
2001-2010 гг.) также равно 10.
Вычисление средней арифметической (М)
Средняя арифметическая определяется путем деления суммы (ΣV)
вариантов на число вариантов, участвующих в обработке (п) по формуле:
На нашем примере общая сумма вариантов (показателей) ΣV
равна
28,69 откуда средняя арифметическая составит:
М=
Вычисление
среднего квадратического отклонения:
m=±
М±m=2.87±0.58
Таблица
30.
Разброс
вариационного ряда по заболеваемости крупного рогатого скота лептоспирозом в
Красноярском крае
|
№ |
V |
V-M |
(V-M)² |
|
1 |
3,44 |
1,80 |
3,24 |
|
2 |
2,00 |
0,36 |
0,13 |
|
3 |
2,63 |
0,99 |
0,98 |
|
4 |
3,33 |
1,69 |
2,86 |
|
5 |
1,87 |
0,19 |
0,04 |
|
6 |
1,19 |
-0,45 |
0,20 |
|
7 |
0,91 |
-0,73 |
0,53 |
|
8 |
0,43 |
-1,21 |
1,46 |
|
9 |
0,36 |
-1,28 |
1,64 |
|
10 |
0,28 |
-1,36 |
1,85 |
|
n=10 |
Σv M=1,64 |
Σ(V-M)²=12,93 |
m=±
M±m=1.64
± 0.4
Таблица
31.
Разброс
вариационного ряда по заболеваемости крупного рогатого скота лептоспирозом в
Краснодарском крае
|
№ |
V |
V-M |
(V-M)² |
|
1 |
4,33 |
2,46 |
6,05 |
|
2 |
3,58 |
1,71 |
2,92 |
|
3 |
5,95 |
4,08 |
16,65 |
|
4 |
1,91 |
0,04 |
0,01 |
|
5 |
1,03 |
-0,84 |
0,70 |
|
6 |
0,32 |
-1,55 |
2,40 |
|
7 |
0,28 |
-1,59 |
2,53 |
|
8 |
0,51 |
1,36 |
1,85 |
|
9 |
0,12 |
1,75 |
3,06 |
|
10 |
0,64 |
1,23 |
1,51 |
|
n=10 |
Σv=18,67 M=1,87 |
Σ(V-M)²=37,68 |
m=±
M±m=1,87
± 0.68
Вычисление
ошибки средней арифметической (М)
При
малом числе показателей, участвующих в обработке (п<30) ошибку средней
арифметической определяют по формуле:
M=±
а при 30 m
= ±
В
нашем примере: m= ±
Среднюю
арифметическую принято записывать с ее ошибкой:M±m
Ошибка
средней арифметической дает возможность:
1.
Определить
в каких пределах находится средняя величина. Выборочные статистические величины
правильно отражают свойства генеральной совокупности, если ошибка (m)
укладывается в своей средней (М) не менее двух раз.
2.
Выяснить
степень достоверности между двумя сравниваемыми выборочными средними.
Таким образом, в нашем примере средняя арифметическая М=2,87, ошибка средней
арифметической m=±0,58. Средний
показатель за 10 лет при этих данных будет М±m
=
2.87±0.58 (по Хабаровскому краю). Средний показатель заболеваемости крупного
рогатого скота лептоспирозом в Красноярском крае M±m
=
1.64±0.40, Красноярском крае M±m
= 1.64±0.68.
Контрольные
вопросы:
1.
Основные
обозначения величин.
2.
Что
означает средняя арифметическая величина и ее формула.
3.
Вычислить
среднюю арифметическую величину.
4.
Что
означает ошибка средней арифметической, ее формула.
5.
Вычислить
ошибку средней арифметической на конкретном примере.
Похожие материалы
- Сезонность лептоспироза свиней. Сезонность лептоспироза свиней в Хабаровском краев
- Чума плотоядных в г. Благовещенске по данным ветеринарной клиники ИП Чубин
- Определение удельного веса инфекционного заболевания
Информация о работе
Тип:
Отчеты по лабораторным работам
Содержание
- Расчет ошибки средней арифметической
- Способ 1: расчет с помощью комбинации функций
- Способ 2: применение инструмента «Описательная статистика»
- Вопросы и ответы
Стандартная ошибка или, как часто называют, ошибка средней арифметической, является одним из важных статистических показателей. С помощью данного показателя можно определить неоднородность выборки. Он также довольно важен при прогнозировании. Давайте узнаем, какими способами можно рассчитать величину стандартной ошибки с помощью инструментов Microsoft Excel.
Расчет ошибки средней арифметической
Одним из показателей, которые характеризуют цельность и однородность выборки, является стандартная ошибка. Эта величина представляет собой корень квадратный из дисперсии. Сама дисперсия является средним квадратном от средней арифметической. Средняя арифметическая вычисляется делением суммарной величины объектов выборки на их общее количество.
В Экселе существуют два способа вычисления стандартной ошибки: используя набор функций и при помощи инструментов Пакета анализа. Давайте подробно рассмотрим каждый из этих вариантов.
Способ 1: расчет с помощью комбинации функций
Прежде всего, давайте составим алгоритм действий на конкретном примере по расчету ошибки средней арифметической, используя для этих целей комбинацию функций. Для выполнения задачи нам понадобятся операторы СТАНДОТКЛОН.В, КОРЕНЬ и СЧЁТ.
Для примера нами будет использована выборка из двенадцати чисел, представленных в таблице.
- Выделяем ячейку, в которой будет выводиться итоговое значение стандартной ошибки, и клацаем по иконке «Вставить функцию».
- Открывается Мастер функций. Производим перемещение в блок «Статистические». В представленном перечне наименований выбираем название «СТАНДОТКЛОН.В».
- Запускается окно аргументов вышеуказанного оператора. СТАНДОТКЛОН.В предназначен для оценивания стандартного отклонения при выборке. Данный оператор имеет следующий синтаксис:
=СТАНДОТКЛОН.В(число1;число2;…)«Число1» и последующие аргументы являются числовыми значениями или ссылками на ячейки и диапазоны листа, в которых они расположены. Всего может насчитываться до 255 аргументов этого типа. Обязательным является только первый аргумент.
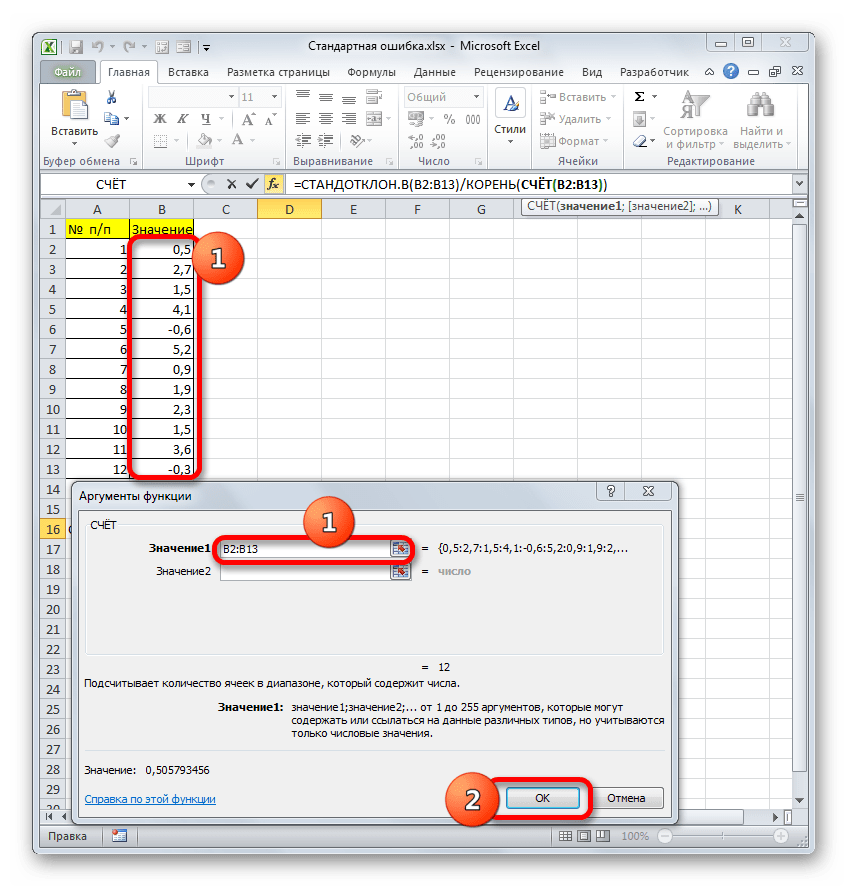
Итак, устанавливаем курсор в поле «Число1». Далее, обязательно произведя зажим левой кнопки мыши, выделяем курсором весь диапазон выборки на листе. Координаты данного массива тут же отображаются в поле окна. После этого клацаем по кнопке «OK».
- В ячейку на листе выводится результат расчета оператора СТАНДОТКЛОН.В. Но это ещё не ошибка средней арифметической. Для того, чтобы получить искомое значение, нужно стандартное отклонение разделить на квадратный корень от количества элементов выборки. Для того, чтобы продолжить вычисления, выделяем ячейку, содержащую функцию СТАНДОТКЛОН.В. После этого устанавливаем курсор в строку формул и дописываем после уже существующего выражения знак деления (/). Вслед за этим клацаем по пиктограмме перевернутого вниз углом треугольника, которая располагается слева от строки формул. Открывается список недавно использованных функций. Если вы в нем найдете наименование оператора «КОРЕНЬ», то переходите по данному наименованию. В обратном случае жмите по пункту «Другие функции…».
- Снова происходит запуск Мастера функций. На этот раз нам следует посетить категорию «Математические». В представленном перечне выделяем название «КОРЕНЬ» и жмем на кнопку «OK».
- Открывается окно аргументов функции КОРЕНЬ. Единственной задачей данного оператора является вычисление квадратного корня из заданного числа. Его синтаксис предельно простой:
=КОРЕНЬ(число)Как видим, функция имеет всего один аргумент «Число». Он может быть представлен числовым значением, ссылкой на ячейку, в которой оно содержится или другой функцией, вычисляющей это число. Последний вариант как раз и будет представлен в нашем примере.
Устанавливаем курсор в поле «Число» и кликаем по знакомому нам треугольнику, который вызывает список последних использованных функций. Ищем в нем наименование «СЧЁТ». Если находим, то кликаем по нему. В обратном случае, опять же, переходим по наименованию «Другие функции…».
- В раскрывшемся окне Мастера функций производим перемещение в группу «Статистические». Там выделяем наименование «СЧЁТ» и выполняем клик по кнопке «OK».
- Запускается окно аргументов функции СЧЁТ. Указанный оператор предназначен для вычисления количества ячеек, которые заполнены числовыми значениями. В нашем случае он будет подсчитывать количество элементов выборки и сообщать результат «материнскому» оператору КОРЕНЬ. Синтаксис функции следующий:
=СЧЁТ(значение1;значение2;…)В качестве аргументов «Значение», которых может насчитываться до 255 штук, выступают ссылки на диапазоны ячеек. Ставим курсор в поле «Значение1», зажимаем левую кнопку мыши и выделяем весь диапазон выборки. После того, как его координаты отобразились в поле, жмем на кнопку «OK».
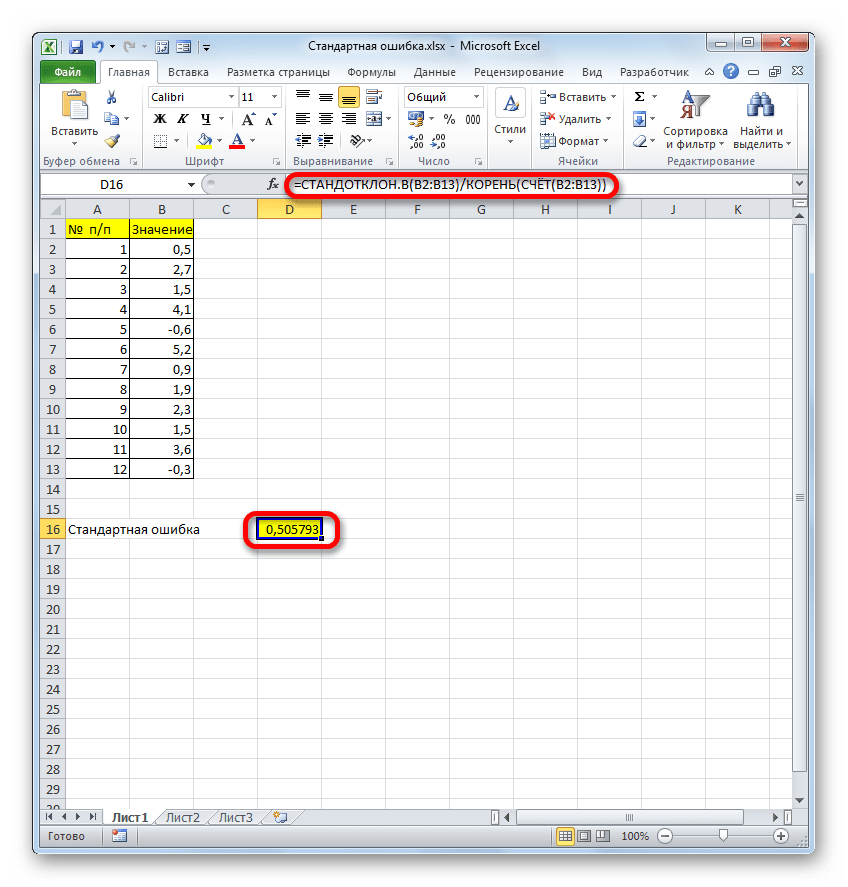
- После выполнения последнего действия будет не только рассчитано количество ячеек заполненных числами, но и вычислена ошибка средней арифметической, так как это был последний штрих в работе над данной формулой. Величина стандартной ошибки выведена в ту ячейку, где размещена сложная формула, общий вид которой в нашем случае следующий:
=СТАНДОТКЛОН.В(B2:B13)/КОРЕНЬ(СЧЁТ(B2:B13))Результат вычисления ошибки средней арифметической составил 0,505793. Запомним это число и сравним с тем, которое получим при решении поставленной задачи следующим способом.
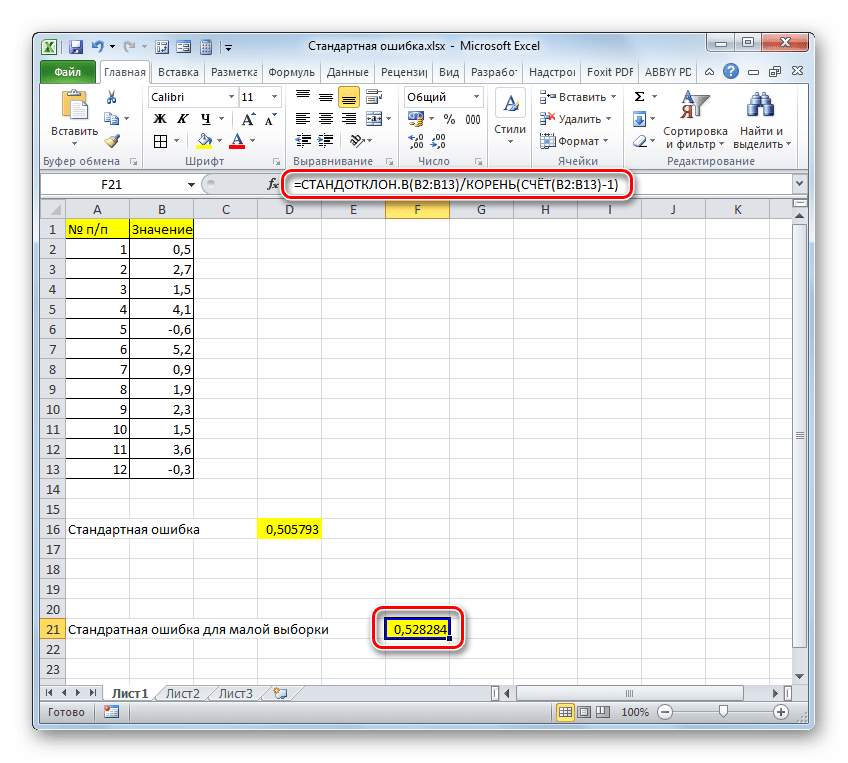
Но дело в том, что для малых выборок (до 30 единиц) для большей точности лучше применять немного измененную формулу. В ней величина стандартного отклонения делится не на квадратный корень от количества элементов выборки, а на квадратный корень от количества элементов выборки минус один. Таким образом, с учетом нюансов малой выборки наша формула приобретет следующий вид:
=СТАНДОТКЛОН.В(B2:B13)/КОРЕНЬ(СЧЁТ(B2:B13)-1)
Урок: Статистические функции в Экселе
Способ 2: применение инструмента «Описательная статистика»
Вторым вариантом, с помощью которого можно вычислить стандартную ошибку в Экселе, является применение инструмента «Описательная статистика», входящего в набор инструментов «Анализ данных» («Пакет анализа»). «Описательная статистика» проводит комплексный анализ выборки по различным критериям. Одним из них как раз и является нахождение ошибки средней арифметической.
Но чтобы воспользоваться данной возможностью, нужно сразу активировать «Пакет анализа», так как по умолчанию в Экселе он отключен.
- После того, как открыт документ с выборкой, переходим во вкладку «Файл».
- Далее, воспользовавшись левым вертикальным меню, перемещаемся через его пункт в раздел «Параметры».
- Запускается окно параметров Эксель. В левой части данного окна размещено меню, через которое перемещаемся в подраздел «Надстройки».
- В самой нижней части появившегося окна расположено поле «Управление». Выставляем в нем параметр «Надстройки Excel» и жмем на кнопку «Перейти…» справа от него.
- Запускается окно надстроек с перечнем доступных скриптов. Отмечаем галочкой наименование «Пакет анализа» и щелкаем по кнопке «OK» в правой части окошка.
- После выполнения последнего действия на ленте появится новая группа инструментов, которая имеет наименование «Анализ». Чтобы перейти к ней, щелкаем по названию вкладки «Данные».
- После перехода жмем на кнопку «Анализ данных» в блоке инструментов «Анализ», который расположен в самом конце ленты.
- Запускается окошко выбора инструмента анализа. Выделяем наименование «Описательная статистика» и жмем на кнопку «OK» справа.
- Запускается окно настроек инструмента комплексного статистического анализа «Описательная статистика».
В поле «Входной интервал» необходимо указать диапазон ячеек таблицы, в которых находится анализируемая выборка. Вручную это делать неудобно, хотя и можно, поэтому ставим курсор в указанное поле и при зажатой левой кнопке мыши выделяем соответствующий массив данных на листе. Его координаты тут же отобразятся в поле окна.
В блоке «Группирование» оставляем настройки по умолчанию. То есть, переключатель должен стоять около пункта «По столбцам». Если это не так, то его следует переставить.
Галочку «Метки в первой строке» можно не устанавливать. Для решения нашего вопроса это не важно.
Далее переходим к блоку настроек «Параметры вывода». Здесь следует указать, куда именно будет выводиться результат расчета инструмента «Описательная статистика»:
- На новый лист;
- В новую книгу (другой файл);
- В указанный диапазон текущего листа.
Давайте выберем последний из этих вариантов. Для этого переставляем переключатель в позицию «Выходной интервал» и устанавливаем курсор в поле напротив данного параметра. После этого клацаем на листе по ячейке, которая станет верхним левым элементом массива вывода данных. Её координаты должны отобразиться в поле, в котором мы до этого устанавливали курсор.
Далее следует блок настроек определяющий, какие именно данные нужно вводить:
- Итоговая статистика;
- К-ый наибольший;
- К-ый наименьший;
- Уровень надежности.
Для определения стандартной ошибки обязательно нужно установить галочку около параметра «Итоговая статистика». Напротив остальных пунктов выставляем галочки на свое усмотрение. На решение нашей основной задачи это никак не повлияет.
После того, как все настройки в окне «Описательная статистика» установлены, щелкаем по кнопке «OK» в его правой части.
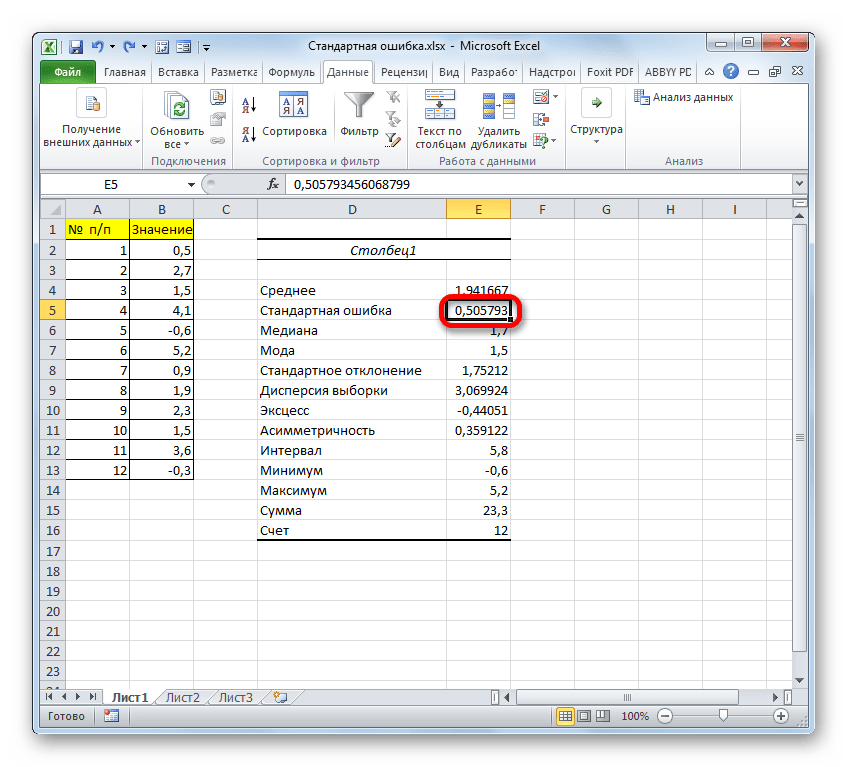
- После этого инструмент «Описательная статистика» выводит результаты обработки выборки на текущий лист. Как видим, это довольно много разноплановых статистических показателей, но среди них есть и нужный нам – «Стандартная ошибка». Он равен числу 0,505793. Это в точности тот же результат, который мы достигли путем применения сложной формулы при описании предыдущего способа.
Урок: Описательная статистика в Экселе
Как видим, в Экселе можно произвести расчет стандартной ошибки двумя способами: применив набор функций и воспользовавшись инструментом пакета анализа «Описательная статистика». Итоговый результат будет абсолютно одинаковый. Поэтому выбор метода зависит от удобства пользователя и поставленной конкретной задачи. Например, если ошибка средней арифметической является только одним из многих статистических показателей выборки, которые нужно рассчитать, то удобнее воспользоваться инструментом «Описательная статистика». Но если вам нужно вычислить исключительно этот показатель, то во избежание нагромождения лишних данных лучше прибегнуть к сложной формуле. В этом случае результат расчета уместится в одной ячейке листа.