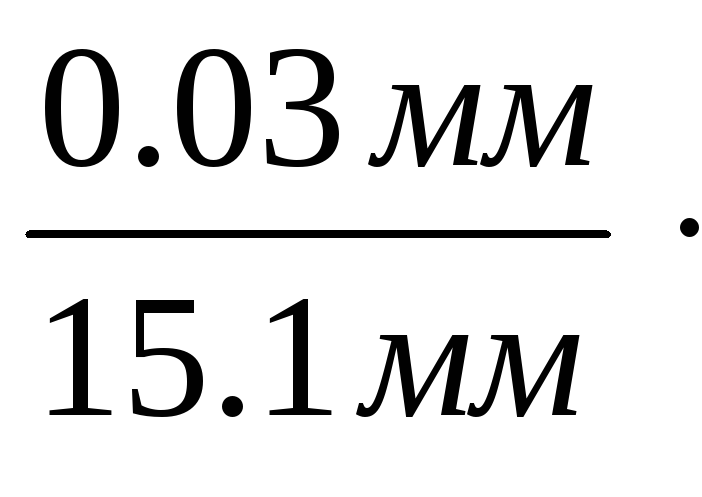Загрузить PDF
Загрузить PDF
Абсолютная погрешность – это фактическая ошибка, допущенная при измерении какой-либо величины. Относительная погрешность сравнивает абсолютную погрешность со значением измеряемой величины. Чтобы вычислить относительную погрешность, следует найти и абсолютную погрешность. Если вы измеряете предмет, длина которого равна 12 см, и вы допустили ошибку в 6 см, то относительная погрешность будет огромной. Но если длина измеряемого предмета равна 12 м, а ошибка – 6 см, то относительная погрешность будет значительно меньше, даже с учетом того, что абсолютная погрешность (6 см) не изменилась.[1]
-
1
Если вам дано ожидаемое значение, вычтите из него полученное вами значение, чтобы вычислить абсолютную погрешность. Как правило, ожидаемое значение находится в ходе тестовых или лабораторных испытаний. Ожидаемое значение является наиболее точным значением некоторой величины, которое используется при различных вычислениях. Чтобы получить абсолютную погрешность, сравните результаты ваших измерений с ожидаемым значением – так вы узнаете, насколько ваши результаты отличаются от ожидаемого значения. Для этого просто вычтите полученное вами значение из ожидаемого. Если разность отрицательная, превратите ее в положительную, проигнорировав знак «минус». Вы получите абсолютную погрешность.[2]
-
Например, вы хотите узнать точность измерения расстояния при помощи шагов. Вы идете от одного дерева к другому, считаете шаги и выясняете, что деревья расположены на расстоянии 5,4 м друг от друга. Это экспериментальное значение. Потом вы берете рулетку и измеряете точное расстояние между деревьями, которое равно 6 м. Это действительное значение. Абсолютная погрешность равна: 6 – 5,4 = 0,6 м = 60 см.[3]
-
Например, вы хотите узнать точность измерения расстояния при помощи шагов. Вы идете от одного дерева к другому, считаете шаги и выясняете, что деревья расположены на расстоянии 5,4 м друг от друга. Это экспериментальное значение. Потом вы берете рулетку и измеряете точное расстояние между деревьями, которое равно 6 м. Это действительное значение. Абсолютная погрешность равна: 6 – 5,4 = 0,6 м = 60 см.[3]
-
2
Теперь допустим, что абсолютная погрешность – это наименьшая единица измерения. Например, рулетка имеет миллиметровые деления, то есть ее наименьшей единицей является 1 мм. Таким образом, вы можете измерить расстояние с точностью до ± 1 мм; в этом случае абсолютная погрешность составляет 1 мм.
- Это верно для любых измерительных инструментов или систем. Например, на корпус многих научных инструментов, таких как прецизионные весы и измерительные приборы, наносят маркировку об абсолютной погрешности в виде «± ____».
-
3
Не забудьте приписать соответствующие единицы измерения. Предположим, что абсолютная погрешность равна 2 м. Такая информация позволит наглядно представить величину ошибки. Но если вы записываете, что погрешность равна 2, то эта цифра ничего не значит. Используйте те же единицы измерения, которыми вы пользовались в ваших измерениях.[4]
-
4
Попрактикуйтесь на нескольких примерах. Это наилучший способ научиться вычислять погрешность. Решите следующие задачи (ответы приведены в конце каждой задачи).
- На уроке химии в результате реакции ученик получил вещество массой 32 г. Известно, что действительное значение выхода этой реакции равно 34 г. Абсолютная погрешность равна ± 2 г.
- На уроке химии ученику необходимо 10 мл воды, чтобы вызвать реакцию; при этом погрешность капельницы составляет «± 0,5 мл». В этом случае абсолютная погрешность измерений равна ± 0,5 мл.
-
5
Уясните, что приводит к появлению погрешности и как ее устранить. Всякое научное исследование подразумевает наличие ошибок – даже в научных работах, за которые вручаются Нобелевские премии, сообщается о допущениях или погрешностях. Но если вы определите причину появления погрешности, вы, возможно, сможете устранить ее.[5]
- Человеческий фактор – наиболее распространенная причина появления ошибок. Сюда относятся неподобающие условия для проведения измерений и плохо продуманные эксперименты.
- Одной из причин появления ошибок может являться внезапное отключение энергии, недостаточное количество рабочего материала или изменение других условий, например, нехватка воды в результате ее испарения, внезапное изменение температуры окружающей среды и так далее.
- Еще одной причиной является несовершенство оборудования, используемого для измерений или исследований, например, прецизионных инструментов или горелок, которые обеспечивают неравномерное распределение тепла.[6]
Реклама
-
1
Разделите абсолютную погрешность на действительное значение исследуемой величины. Так вы вычислите относительную погрешность. Эта формула позволит вам выяснить, насколько полученное вами значение отличается от действительного значения изучаемой величины. Конечно, прекрасно, если относительная погрешность мала. Продолжим рассматривать пример с измерением расстояния между двумя деревьями.
- Абсолютная погрешность равна 0,6 м, а действительное значение равно 6 м.
- 0,6 м / 6 м
- Относительная погрешность равна 0,1 м.[7]
-
2
Полученный результат умножьте на 100, чтобы выразить относительную погрешность в процентах. Вы можете представить относительную погрешность в виде обыкновенной дроби, десятичной дроби или в процентах – в этом случае умножьте десятичную дробь на 100. Так вы узнаете, какой процент от полученного вами значения составляет погрешность. Если вы измеряете длину 60 м лодки, а погрешность составляет 0,6 м, то процент ошибки будет значительно меньше, чем при вычислении расстояния между деревьями (6 м) с погрешностью 0,6 м. Погрешность представляет собой небольшой процент от экспериментального значения. [8]
- 0,6 м / 6 м = 0,1 м
- 0,1 * 100 = 10% – относительная погрешность.
-
3
Вычислите относительную погрешность без нахождения абсолютной погрешности. Для этого выражение для вычисления абсолютной погрешности запишите в числителе выражения для нахождения относительной погрешности. Уяснив разницу между абсолютной и относительной погрешностями, нет необходимости отдельно вычислять абсолютную погрешность. Просто замените значение абсолютной погрешности на выражение для ее вычисления. Обратите внимание, что вертикальные черты обозначают абсолютную величину, то есть любое полученное значение нужно превратить в положительное.
- Относительная погрешность:
, где Е — экспериментальное значение, D — действительное значение.
- Умножьте это выражение на 100, чтобы выразить относительную погрешность в процентах.[9]
- Относительная погрешность:
-
4
Не забудьте приписать соответствующие единицы измерения. Предположим, что абсолютная погрешность равна 2 м. Такая информация позволит наглядно представить величину ошибки. Но если вы записываете, что погрешность равна 2, то эта цифра ничего не значит. Также не имеет смысла указывать погрешность в виде процентов от ошибки (10% от 0,6 м) – следует писать, например, так: относительная погрешность равна 10%.[10]
Реклама
Советы
- Удостоверьтесь, что экспериментальное значение и действительное значение измеряются в одних единицах измерения. Например, если экспериментальное значение измеряется в сантиметрах, а действительное значение – в миллиметрах, преобразуйте одну из этих единиц измерения в другую.
Реклама
Предупреждения
- Убедитесь, что вы правильно округляете числа.
Реклама
Похожие статьи
Об этой статье
Эту страницу просматривали 171 372 раза.
Была ли эта статья полезной?
Вычисление абсолютной и относительной погрешностей измерений при прямых измерениях
1. Абсолютная погрешность
Оценить отклонение
каждого из результатов измерения от
истинной величины можно лишь при наличии
данных большого числа измерений с
использованием теории вероятности.
Однако на практике, в лабораторных
условиях проводят 3-5 измерений. В этом
случае абсолютная погрешность отдельного
i-го
измерения будет следующей:
|DАi|
= |АСР
— Аi|,
где
АСР
— средняя величина размера А. Средняя
арифметическая величина всех ½DАi½
значений
называется
абсолютной погрешностью опыта.
Окончательный результат измерения
может быть записан в виде
А = АСР
±
DАСР,
где
А — искомая величина, которая лежит
внутри интервала
АСР
±
DАСР.
Н
14
апример, если сделаем несколько
измерений длины заготовки в столярной
мастерской и получим среднее значение
lСР
= 75.5 см, а среднее
арифметическое абсолютной погрешности
lСР
= 0.3 см, то результат
запишется в виде
l
= (75.5 ± 0.3) см.
Это
означает, что истинное значение длины
заготовки лежит в интервале от 75.2 см до
75.8 см. При этом не имеет смысла вычислять
среднее значение с большим числом знаков
после запятой, так как от этого точность
не увеличивается.
2. Относительная погрешность
Абсолютная
погрешность измерения не характеризует
точности проведенных измерений. Поэтому
для того, чтобы сравнить точность
различных измерений и величин разной
размерности, находят среднюю относительную
погрешность результата (ЕА).
Относительная погрешность определяется
отношением абсолютной погрешности к
среднему арифметическому значению
измеряемой величины, которая определяется
в процентах:
ЕА=
Относительная
погрешность показывает, какая часть
абсолютной погрешности приходится на
каждую единицу измеренной величины.
Это дает возможность оценить точность
проведенных измерений, качество работы.
Так,
например, пусть при измерении бруска
длиной l
= 1.51 см была допущена абсолютная
погрешность 0.03 мм, а при измерении
расстояния от Земли до Луны L
= 3.64.105
км абсолютная погрешность составила
100 км. Может показаться, что первое
измерение выполнено намного точнее
второго. Однако о точности измерения
можно судить по относительной погрешности,
а она показывает, что второе измерение
было выполнено в семь раз точнее первого:
El
=
100% = 0.2%
и
ЕL
=

= 0.03%.
Вычисление абсолютных и относительных погрешностей при косвенных2 измерениях
В
большинстве случаев при выполнении
физических экспериментов исследуемая
величина не может быть измерена
непосредственно, а является функцией
одной или нескольких переменных,
измеренных непосредственно. При косвенных
измерениях абсолютная и относительная
погрешности результатов измерений
находятся вычислением через абсолютные
и относительные погрешности непосредственно
измеренных величин.
Использование формул дифференцирования
Для
определения абсолютных и относительных
погрешностей искомой величины при
косвенных измерениях можно воспользоваться
формулами дифференцирования, потому
что абсолютная ошибка функции равна
абсолютной ошибке аргумента, умноженной
на производную этой функции, то есть
полному дифференциалу функции.
Рассмотрим
это более подробно. Допустим, что
физическая величина А является функцией
многих переменных:
A
= f
(x,
y,
z
…).
Правило
I. Вначале
находят абсолютную погрешность величины
А, а затем относительную погрешность.
Для этого необходимо:
1) Найти полный
дифференциал функции
.
2
16
) Заменить бесконечно малые dx, dу,
dz, … соответствующими абсолютными
ошибками аргументовDx,
Dy,
Dz,
… (при этом знаки «минус» в абсолютных
ошибках аргументов заменяют знаками
«плюс», так чтобы величина ошибки
была максимальной):
.
Применяя
это правило к частным случаям, получим:
—
абсолютная погрешность суммы равна
сумме абсолютных погрешностей слагаемых.
Если X
= a
+ b,
то DX
= Da
+ Db;
—
абсолютная погрешность разности равна
сумме абсолютных погрешностей
уменьшаемого и вычитаемого. Если X
= a
— b,
то DX
= Da
+ Db;
—
абсолютная погрешность произведения
двух сомножителей равна сумме произведений
среднего значения первого множителя
(aCP)
на абсолютную погрешность второго и
среднего значения второго множителя
(bCP)
на абсолютную погрешность первого. Если
X
= а
b,
то DX
= aCP
Db
+ bCP
Dа.
Если X
= a n
, то DX
= n
аCPn-1
Dа;
—
абсолютная погрешность дроби равна
сумме произведения знаменателя на
абсолютную погрешность числителя и
числителя на абсолютную погрешность
знаменателя, деленной на квадрат
знаменателя. Если X
=,
то DX=.
3) По определению
найдем относительную погрешность
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
12.02.2015183.3 Кб27Пример работы по теме ПЕРЕСКАЗ.doc
- #
Download Article
Download Article
Absolute error is the actual amount you were off, or mistaken by, when measuring something. Relative error compares the absolute error against the size of the thing you were measuring. In order to calculate relative error, you must calculate the absolute error as well. If you tried to measure something that was 12 inches long and your measurement was off by 6 inches, the relative error would be very large. But, if you tried to measure something that was 120 feet long and only missed by 6 inches, the relative error would be much smaller — even though the value of the absolute error, 6 inches, has not changed.
-
1
When given an expected value, subtract the value you got from the expected value to get the Absolute Error. An expected value is usually found on tests and school labs. Basically, this is the most precise, common measurement to come up with, usually for common equations or reactions. You can compare your own results to get Absolute Error, which measures how far off you were from the expected results. To do so, simply subtract the measured value from the expected one. Even if the result is negative, make it positive. This is your absolute error![1]
- Example: You want to know how accurately you estimate distances by pacing them off. You pace from one tree to another and estimate that they’re 18 feet apart. This is the experimental value. Then you come back with a long measuring tape to measure the exact distance, finding out that the trees are in fact 20 feet (6 meters) apart. That is the «real» value. Your absolute error is 20 — 18 = 2 feet (60.96 centimeters).
-
2
Alternatively, when measuring something, assume the absolute error to be the smallest unit of measurement at your disposal. For example, if you’re measuring something with a meter stick, the smallest unit marked on the meter stick is 1 millimeter (mm). So you know that your measurement is accurate to within + or — 1 mm; your absolute error is 1 mm.
- This works for any measurement system. Many scientific tools, like precision droppers and measurement equipment, often has absolute error labeled on the sides as «+/- ____ «
Advertisement
-
3
Always add the appropriate units. Say your Absolute Error was «2 meters.» This tells your viewers exactly how far off your error was. But if you write that your error was simply «2,» this doesn’t tell your audience anything. Use the same unites as the ones in your measurements.
-
4
Practice with several examples. The best way to learn how to calculate error is to go ahead and calculate it. Take a stab at the following problems, then highlight the space after the colon (:) to see your answer.
- Jill is studying chemical reactions. After mixing and matching, her test tube contains 32 grams of substrate. The accepted value for her experiment was 34 grams. Her Absolute Error is: +/- 2 grams
- Clive is testing reactions in chemistry. It takes 10ml drops of water to cause a reaction, but his dropper claims it is «+/- .5ml.» The Absolute Error in his measurements must be: +/- .5ml
-
5
Understand what causes error, and how you can work to eliminate it. No scientific study is ever perfectly error free — even Nobel Prize winning papers and discoveries have a margin or error attached. Still, understanding where error comes from is essential to help try and prevent it:[2]
- Human error is the most common. This is from bad measurements, faulty premises, or mistakes in the lab.
- Incidental energy/material loss, such as the little fluid left in the beaker after pouring, changes in temperature due to the environment, etc.
- Imperfect equipment used either for measurement or studies, such as very small, precise measurements or burners that provide uneven heat.[3]
Advertisement
-
1
Divide the Absolute Error by the Actual Value of the item in question to get Relative Error. The result is the relative error.[4]
-
2
Multiply the answer by 100 to get an easier to understand percentage. Leave the relative error in fraction form, complete the division to render it in decimal form, or multiply the resulting decimal form by 100 to render your answer as a percentage. This tells you what percentage of the final measurement you messed up by. If you are measuring a 200 foot boat, and miss the measurement by 2 feet, your percentage error will be much lower than missing the 20 foot tree measurement by 2 feet. The error is a smaller percentage of the total measurement.[5]
-
3
Calculate Relative Error all at once by turning the numerator (top of fraction) into your Absolute Error equation. Once you understand the difference between Absolute and Relative Error, there is really no reason to do everything all by itself. Simply substitute the equation for Absolute Error in for the actual number. Note that the vertical bars are absolute value signs, meaning anything within them must be positive.[6]
-
Relative Error
- Multiply the whole thing by 100 to get Relative Error Percentage all at once.[7]
-
Relative Error
-
4
Always provide units as context. Let the audience know the units you’re using for measurement. However, the relative error does not employ units of measurement. It is expressed as a fraction or a percentage, such as a relative error of 10%.[8]
Advertisement
Add New Question
-
Question
What does the +/- sign tell about the relative percentage error?
It means the reported or estimated amount could be higher or lower than the true amount.
-
Question
What is the difference between systematic and random errors?
Systematic errors are those which occur according to a certain pattern or system; these errors are due to known reasons. Random errors have no set pattern or cause.
-
Question
If the absolute error was 0.94, then what will the relative error be?
Aditya Kannan
Community Answer
Relative error, as mentioned in the answer, equals (Absolute Error)/(Actual Value). Hence, it isn’t possible to calculate relative error just by knowing the absolute error.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Make sure that your experimental value and real value are all expressed in the same unit of measurement. For example, if your experimental value is in inches but your real value is in feet, you must convert one of them to the other unit of measurement.
Thanks for submitting a tip for review!
Advertisement
-
If taking the regents exam, make sure you round correctly
Advertisement
References
About This Article
Article SummaryX
Before you can calculate relative error, you must calculate the absolute error in your calculations. To do this, subtract your answer from the expected value, or the correct answer. Write the answer as a positive number, even if it’s negative, and add the appropriate units. To get the relative error, divide the absolute error by the actual value of the item in question. If you’d like, you can multiply the answer by 100 to display it as a percentage. To understand when you would need to use relative error, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 477,278 times.
Reader Success Stories
-
Aditya Kannan
Jul 11, 2017
«I’ve got this messed up exam tomorrow. Heck, if wikiHow didn’t exist, Relative Errors would’ve…» more
Did this article help you?
Вычисление погрешностей измерений
Выполнение лабораторных работ связано с измерением физических величин, т. е. определением значений величин опытным путём с помощью измерительных приборов (средств измерения), и обработкой результатов измерений.
Различают прямые и косвенные измерения. При этом результат любого измерения является приблизительным, т. е. содержит погрешность измерения. Точность измерения физической величины характеризуют абсолютная и относительная погрешности.
Прямое измерение — определение значения физической величины непосредственно с помощью измерительного прибора.
Абсолютную погрешность прямых измерений определяют суммой абсолютной инструментальной погрешности и абсолютной погрешности отсчёта Δx = Δиx + Δоx при условии, что случайная погрешность и погрешность вычисления или отсутствуют, или незначительны и ими можно пренебречь.
Абсолютная инструментальная погрешность Δиx связана с классом точности прибора. Абсолютные инструментальные погрешности некоторых средств измерений представлены в таблице 1.
| Средства измерений | Диапазон измерений | Абсолютная инструментальная погрешность |
| Линейки: металлические деревянные пластмассовые |
150, 300, 500 мм 400, 500, 750 мм 200, 250, 300 мм |
0,1 мм 0,5 мм 1 мм |
| Лента измерительная | 150 см | 0,5 см |
| Мензурки 2-го класса | 100, 200, 250 см3 | 5 см3 |
| Амперметр школьный | 2 А | 0,05 А |
| Миллиамперметр | от 0 до Imax | 4 % максимального предела измерений Imax |
| Вольтметр школьный | 6 В | 0,15 В |
| Термометр лабораторный | 100 °С | 1 °С |
| Барометр-анероид | 720–780 мм рт. ст. | 3 мм рт. ст. |
| Штангенциркули с ценой деления 0,1; 0,05 мм | 155, 250, 350 мм | 0,1; 0,05 мм в соответствии с ценой деления нониуса |
| Микрометры с ценой деления 0,01 мм | 0–25, 25–50, 50–75 мм | 0,004 мм |
Абсолютная погрешность отсчёта Δоx связана с дискретностью шкалы прибора. Если величину измеряют с точностью до целого деления шкалы прибора, то погрешность отсчёта принимают равной цене деления. Если при измерении значение величины округляют до половины деления шкалы, то погрешность отсчёта принимают равной половине цены деления.
Абсолютная погрешность определяет значение интервала, в котором лежит истинное значение измеренной величины:
Относительную погрешность прямого измерения определяют отношением абсолютной погрешности к значению измеряемой величины:
Относительная погрешность характеризует точность измерения: чем она меньше, тем точность измерения выше.
Косвенное измерение — определение значения физической величины с использованием формулы, связывающей её с другими величинами, измеренными непосредственно с помощью приборов.
Одним из методов определения погрешности косвенных измерений является метод границ погрешностей. Формулы для вычисления абсолютных и относительных погрешностей косвенных измерений методом границ погрешностей представлены в таблице 2.
| Вид функции y | Абсолютная погрешность Δy | Относительная погрешность |
| x1 + x2 | Δx1 + Δx2 | |
| x1 − x2 | Δx1 + Δx2 | |
| Cx | CΔx | |
| x1x2 | |x1| Δx2 + |x2| Δx1 | |
| xn | |n||x|n−1Δx | |
| lnx | ||
| sinx | |cosx| Δx | |
| cosx | |sinx| Δx | |tgx| Δx |
| tgx |
Абсолютную погрешность табличных величин и фундаментальных физических постоянных определяют как половину единицы последнего разряда значения величины.
Абсолютная и относительная погрешность

4.2
Средняя оценка: 4.2
Всего получено оценок: 2248.
4.2
Средняя оценка: 4.2
Всего получено оценок: 2248.
Абсолютную и относительную погрешность используют для оценки неточности в производимых расчетах с высокой сложностью. Также они используются в различных измерениях и для округления результатов вычислений. Рассмотрим, как определить абсолютную и относительную погрешность.
Опыт работы учителем математики — более 33 лет.
Абсолютная погрешность
Абсолютной погрешностью числа называют разницу между этим числом и его точным значением.
Рассмотрим пример: в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26.
Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.
Существует формула абсолютной погрешности. Обозначим точное число буквой А, а буквой а – приближение к точному числу. Приближенное число – это число, которое незначительно отличается от точного и обычно заменяет его в вычислениях. Тогда формула будет выглядеть следующим образом:
Δа=А-а. Как найти абсолютную погрешность по формуле, мы рассмотрели выше.
На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой. Но если погрешность в 1 см была допущена при измерении стены в 20 метров, это измерение можно считать максимально точным. Поэтому в практике более важное значение имеет определение относительной погрешности измерения.
Записывают абсолютную погрешность числа, используя знак ±. Например, длина рулона обоев составляет 30 м ± 3 см. Границу абсолютной погрешности называют предельной абсолютной погрешностью.
Относительная погрешность
Относительной погрешностью называют отношение абсолютной погрешности числа к самому этому числу. Чтобы рассчитать относительную погрешность в примере с учениками, разделим 26 на 374.
Получим число 0,0695, переведем в проценты и получим 7 %. Относительную погрешность обозначают процентами, потому что это безразмерная величина. Относительная погрешность – это точная оценка ошибки измерений. Если взять абсолютную погрешность в 1 см при измерении длины отрезков 10 см и 10 м, то относительные погрешности будут соответственно равны 10 % и 0,1 %. Для отрезка длиной в 10 см погрешность в 1 см очень велика, это ошибка в 10 %. А для десятиметрового отрезка 1 см не имеет значения, всего 0,1 %.
Различают систематические и случайные погрешности. Систематической называют ту погрешность, которая остается неизменной при повторных измерениях. Случайная погрешность возникает в результате воздействия на процесс измерения внешних факторов и может изменять свое значение.
Правила подсчета погрешностей
Для номинальной оценки погрешностей существует несколько правил:
- при сложении и вычитании чисел необходимо складывать их абсолютные погрешности;
- при делении и умножении чисел требуется сложить относительные погрешности;
- при возведении в степень относительную погрешность умножают на показатель степени.
Приближенные и точные числа записываются при помощи десятичных дробей. Берется только среднее значение, поскольку точное может быть бесконечно длинным. Чтобы понять, как записывать эти числа, необходимо узнать о верных и сомнительных цифрах.
Верными называются такие цифры, разряд которых превосходит абсолютную погрешность числа. Если же разряд цифры меньше абсолютной погрешности, она называется сомнительной. Например, для дроби 3,6714 с погрешностью 0,002 верными будут цифры 3,6,7, а сомнительными – 1 и 4. В записи приближенного числа оставляют только верные цифры. Дробь в этом случае будет выглядеть таким образом – 3,67.
Что мы узнали?
Абсолютные и относительные погрешности используются для оценки точности измерений. Абсолютной погрешностью называют разницу между точным и приближенным числом. Относительная погрешность – это отношение абсолютной погрешности числа к самому числу. На практике используют относительную погрешность, так как она является более точной.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
-
Светлана Лобанова-Асямолова
10/10
-
Валерий Соломин
10/10
-
Анастасия Юшкова
10/10
-
Ксюша Пономарева
7/10
-
Паша Кривов
10/10
-
Евгений Холопик
9/10
-
Guzel Murtazina
10/10
-
Максим Аполонов
10/10
-
Olga Bimbirene
9/10
-
Света Колодий
10/10
Оценка статьи
4.2
Средняя оценка: 4.2
Всего получено оценок: 2248.
А какая ваша оценка?