Как найти ошибку репрезентативности

В
статистике выделяют два основных метода
исследования — сплошной и выборочный.
При проведении выборочного исследования
обязательным является соблюдение
следующих требований: репрезентативность
выборочной совокупности и достаточное
число единиц наблюдений. При выборе
единиц наблюдения возможны ошибки
смещения,
т.е. такие события, появление которых
не может быть точно предсказуемым. Эти
ошибки являются объектив­ными и
закономерными. При определении степени
точности выборочно­го исследования
оценивается величина ошибки, которая
может прои­зойти в процессе выборки
— случайная
ошибка репрезентативности (m)
— является
фактической разностью между средними
или относительными величинами, полученными
при проведении выборочного исследования
и аналогичными величинами, которые были
бы получены при проведении исследования
на гене­ральной совокупности.

Оценка
достоверности результатов исследования
предусматривает определение:

1.
ошибки репрезентативности

2.
доверительных границ средних (или
относительных) величин в генеральной
совокупности

3.
достоверности разности средних (или
относительных) величин (по критерию t)

Расчет
ошибки репрезентативности
(m_м)
средней арифмети­ческой величины
(М):

,
где σ
— среднее квадратическое отклонение; n
— численность выборки (>30).

Расчет
ошибки репрезентативности (m_Р)
относительной величины (Р):

,
где Р — соответствующая относительная
величина (рассчитанная, например, в %);

q
=100 — Ρ%
— величина, обратная Р; n
— численность выборки (n>30)

В
клинических и экспериментальных работах
довольно часто приходится использовать
малую
выборку, когда
число наблюдений меньше или равно 30.
При малой выборке для расчета ошибок
репрезентатив­ности, как средних, так
и относительных величин,
число
наблюде­ний уменьшается на единицу,
т.е.

;
.

Величина
ошибки репрезентативности зависит от
объема выборки: чем больше число
наблюдений, тем меньше ошибка. Для оценки
достоверности выборочного показателя
принят следующий подход: показатель
(или средняя величина) должен в 3 раза
превышать свою ошибку, в этом случае он
считается достоверным.

83. Определение доверительных границ средних и относительных величин.

Знание
величины ошибки недостаточно для того,
чтобы быть уве­ренным в результатах
выборочного исследования, так как
конкрет­ная ошибка выборочного
исследования может быть значительно
больше (или меньше) величины средней
ошибки репрезентативности. Для
оп­ределения точности, с которой
исследователь желает получить ре­зультат,
в статистике используется такое понятие,
как вероят­ность безошибочного
прогноза, которая является характеристикой
надежности результатов выборочных
медико-биологических статистических
исследований. Обычно, при проведении
медико-биологических статистических
исследований используют вероятность
безошибочного прогноза 95% или 99%. В
наиболее ответственных случаях, когда
необходимо сделать особенно важные
выводы в теоретическом или практическом
отношении, используют вероятность
безошибочного прогноза 99,7%

Определенной
степени вероятности безошибочного
прогноза соот­ветствует определенная
величина предельной
ошибки случайной выборки (Δ
— дельта),
которая определяется по формуле:

Δ=t
* m
, где t
— доверительный коэффициент, который
при большой выборке при вероятности
безо­шибочного прогноза 95% равен 2,6;
при вероятности безоши­бочного
прогноза 99% — 3,0; при вероятности
безошибочно­го прогноза 99,7% — 3,3, а при
малой выборке определяется по специальной
таблице значений t
Стьюдента.

Используя
предельную ошибку выборки (Δ),
можно определить до­верительные
границы,
в которых с определенной вероятностью
безо­шибочного прогноза заключено
действительное значение статистичес­кой
величины,
характеризующей
всю генеральную совокупность (сред­ней
или относительной).

Для
определения доверительных границ
используются следующие формулы:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Лекция 2. Ошибка репрезентативности и доверительный интервал для
генерального параметра
Выборочные характеристики, представляющие собой числа (точки на
шкале) называют точечными оценками (существуют также и интервальные
оценки). Оценки должны удовлетворять следующим требованиям: быть
состоятельными, эффективными, несмещенными. Только при удовлетворении
этих требований оценки хорошо представляют соответствующие параметры.
В математической статистике введено понятие статистической ошибки
или ошибки репрезентативности; она связана с точностью, с которой
выборочная оценка представляет, репрезентирует свой параметр.
Когда ошибка оценивания генерального параметра стремится к нулю при
возрастании объема выборки, т.е. значение оценки стремится к значению
параметра, то такая оценка называется состоятельной. Оценка называется
эффективной,
если
она
имеет
наименьшую
дисперсию
выборочного
распределения по сравнению с другими аналогичными оценками.
К примеру,
из трех показателей, описывающих положение центра
нормального распределения (средняя, медиана, мода), наиболее эффективной
является средняя арифметическая, наименее эффективной — мода.
Оценка
ожидание)
называется
ее
несмещенной,
выборочного
если
распределения
среднее
совпадает
(математическое
со
значением
генерального параметра. Выборочная средняя является несмещенной оценкой
генеральной средней, а тогда как выборочная дисперсия представляет собой
смещенную оценку.
Например, чтобы получить несмещенную оценку, надо при вычислении
выборочной дисперсии использовать формулу, где в знаменателе (N — 1):
D=S2=
1
2
( Xi  X )

N 1
Для понимания смысла этих требований нужно рассмотреть понятие
выборочного распределения оценок какого-либо параметра.
Рассмотрим
условный
пример
для
такого
понятия,
как
арифметическое среднее: пусть ГС представляет собой 5 результатов
выполнения некоторого психологического теста: 8 16 20 24 32:
=
8  16  20  24  32
= 20
5
Таким образом, 20 — это значение генерального параметра.
Заменим изучение генеральной совокупности изучением выборок объемом
n = 4. Рассмотрим все возможные варианты таких выборок:
1) 8
16 20 24
 = 17
2) 16 20 24 32
 = 23
3) 8
16 24 32
 = 20
4) 8
16 20 32
 = 19
Из нашего примера видно, что из 5 оценок средних лишь одна совпала
с параметром. Заранее мы не можем знать, как составить (отобрать) выборку,
чтобы оценка параметра по ней была близка к параметру.
Однако очевидно, что чем больше объем выборки, тем меньше вероятность
того, что  , определяемое по выборке, будет значительно отличаться от
генерального среднего (крайние случаи n=N-1 и n=2 ,т.е. N>>n) .
Когда
генеральная совокупность велика и, соответственно, число
возможных выборок велико, то совокупность выборочных оценок средних для
каждой
из
этих
концентрирующееся
выборок
вокруг
«концентрация» (дисперсия)
Дисперсия
образует
генерального
тем
выше,
нормальное
среднего,
чем
больше
распределение,
причем
эта
объемы выборок.
распределения средних имеет особое название, она именуется
ошибкой репрезентативности.
Выше речь шла о распределении выборочных средних.
Это же
рассуждение можно повторить для оценок дисперсии, моды, коэффициентов
корреляции и т.д.
В теории математической статистики доказано, что нормального
распределения при достаточном объеме выборки (на практике n  30),
стандартное отклонение среднего арифметического равно:
Sx =
S
N
; где
S — стандартное отклонение
N — объем выборки.
Эту величину называют также статистической ошибкой или ошибкой
репрезентативности, т.е. это средняя ошибка, которая допускается, когда 
рассматривается как генеральный параметр.
Для других параметров ошиб ки репрезентативности таковы:
Ошибка репрезентативности дисперсии:
Ss2=S2/ 2N
Ошибка репрезентативности стандартного отклонения
Ss=S/ 2N
Ошибка репрезентативности показателя асимметрии:
Sa= 6 / N
Ошибка репрезентативности показателя эксцесса:
Se= 24 / N
Теперь перейдем к понятию доверительного интервала, которое применяется
для любого параметра. Мы рассмотрим его для генеральной средней. По
известным выборочным характеристикам можно построить интервал, в котором
с той или иной степенью вероятности находится генеральное среднее. Понятие
доверительного интервала связано с понятием доверительной вероятности.
Согласно этому принципу, маловероятные события считаются практически
невозможными,
а
события,
вероятность
которых
близка
к
единице,
принимаются за почти достоверные. Обычно в психологии в качестве
доверительных используют вероятности р = 0,95 и р = 0,99. Это означает, что
при оценивании генерального параметра по известной выборочной оценке риск
ошибиться в первом случае — один раз на 20 испытаний, во втором случае 1 раз
на 100 испытаний.
С доверительной вероятностью связано понятие уровня значимости
 = 1- р
Геометрически — это площадь под нормальной кривой выборочного
распределения, выходящая за пределы той его части, которая соответствует
Р%, поскольку в сумме они соответствуют всей площади под кривой. Иначе
говоря,

означает площадь двух хвостов под кривой нормального
распределения. При при р = 0,95 и  = 0, 05 на каждый «хвост» приходится
по 2,5 % площади.
Вероятность того, что  будет находиться в пределах
доверительного интервала x — t SX     + t SX,
описывается
особой функцией, которая сведена в таблице (обычно это таблица 1 в
приложении учебников по математической статистике)
для р= 0,95
t=1,96
для р=0,99
t = 2,58
для p=0, 999 t =3,29
График нормальной кривой
Выбор того или иного уровня доверительной вероятности зависит от
исследователя, от его оценки ответственности за ошибочность выводов
относительно генерального параметра .
Пример: При измерении объема памяти у 100 испытуемых
получено среднее значение числа запоминаемых сигналов
было
= 9 и
стандартное отклонение S = 3. 27. Построить доверительный
интервал для генеральной средней .
Вычисления проводятся по формуле:
x — t SX     + t SX
9 — 1,96
3271
.
327
.
   92+1,96
100
100
или 9+ 0.196  3,27    9 + 1..96  3,27 или 8. 36    9.64.
Таким образом, с вероятностью р = 0.95 генеральный параметр 
находится в интервале 8.36 — 9.64.
95%

2.4. Точность статистического наблюдения

Под точностью статистического наблюдения понимают степень соответствия значения наблюдаемого показателя, вычисленного по материалам обследования, его действительной величине. Расхождение, или разница, между ними называется ошибкой статистического наблюдения.

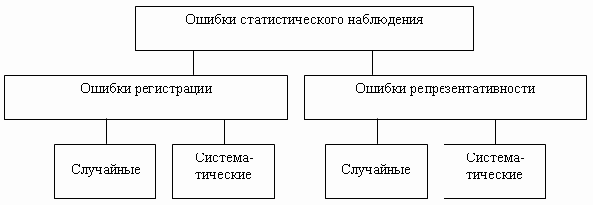
Различают две группы ошибок:

1. ошибки регистрации;
2. ошибки репрезентативности.

Ошибки регистрации присущи любому статистическому наблюдению, как сплошному, так и несплошному. Они делятся на случайные ошибки регистрации и систематические ошибки регистрации.

Случайными ошибками регистрации называют ошибки, возникающие вследствие действия случайных факторов. К ним можно отнести различного рода непреднамеренные описки: например, вместо возраста человека «15 лет» указано «5 лет», у Ивановой Марии Петровны в графе пол отмечен «Мужской» и т. п. Такие ошибки легко выявляются методом логического анализа, например, если человеку 8 лет, но имеется высшее образование, а в графе «Семейное положение» указано «Состоит в браке», то, естественно, следует исправить возраст. Если объем исследуемой совокупности велик или велика доля отбора при выборочном наблюдении, случайные ошибки регистрации имеют тенденцию взаимопогашаться вследствие действия закона больших чисел, поскольку ошибки, как правило, разнонаправлены и искажают статистический показатель как в большую, так и в меньшую сторону. При небольшом объеме наблюдения требуется тщательная выверка его результатов — логический анализ данных.

Систематические ошибки регистрации чаще всего имеют однонаправленные искажения: они либо увеличивают, либо уменьшают статистический показатель, и, что характерно, подобная ситуация повторяется от обследования к обследованию. Так, по результатам переписей (практически всех!) число замужних женщин превышает число женатых мужчин — мужчинам приятнее ощущать себя неженатыми, а для женщины как бы «стыдно» быть не замужем. Другой пример, когда человек округляет свой возраст — вместо 32 лет говорит 30, вместо 79-80 и т. п. (это явление широко известно и даже получило свое название — «аккумуляция возрастов»). Систематические ошибки регистрации могут возникать и из-за неточностей измерительных приборов, если сбор информации проводят путем непосредственного наблюдения.

Ошибки репрезентативности присущи только несплошному обследованию. Они также делятся на случайные и систематические ошибки.

Случайные ошибки репрезентативности возникают из-за того, что обследованию подвергается не вся совокупность в целом, а только ее часть, и, следовательно, при несплошном наблюдении они присутствуют всегда. В теории статистики разработаны специальные методы для оценки величин таких ошибок, на их основе для наблюдаемых показателей строят доверительные интервалы, т.д. эти ошибки вычисляются и находятся как бы «под контролем».

Хуже обстоит дело, если наряду со случайными ошибками имеются и ошибки систематические.

Систематические ошибки репрезентативности возникают, если при несплошном наблюдении кардинально нарушаются технологии отбора единиц из генеральной совокупности объектов, но чаще — если в ходе обследования не удается получить информацию обо всех отобранных для наблюдения единицах, например, вследствие отказа отвечать на вопросы анкеты, или если человека не удалось застать дома и т. п.

Ошибки статистического наблюдения для наглядности можно изобразить в виде схемы (рис. 2.1).

Для повышения точности наблюдения необходимо:

1. правильно разработать формуляр статистического наблюдения: вопросы должны быть четкими, однозначными, не допускающими двойного толкования;
2. иметь хорошо обученный персонал для проведения обследования;
3. строго придерживаться выбранной технологии обследования (если проводится несплошное наблюдение) и помнить, что если не удается опросить какую-то конкретную единицу, отобранную для наблюдения, замена ее на другую единицу может привести к возникновению систематической ошибки репрезентативности;
4. провести логический анализ данных, основанный на логических взаимосвязях показателей, после сбора всей совокупности анкет или формуляров;
5. целесообразно провести и арифметический контроль данных, т.д. заново пересчитать расчетные величины, если какие-либо показатели получаются в результате определенных арифметических действий;
6. предпринять определенные меры по восстановлению данных при наличии незаполненных анкет или формуляров либо при получении результатов обследования сделать поправку на неответы респондентов.