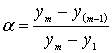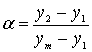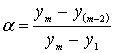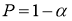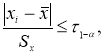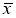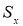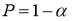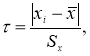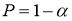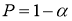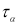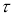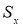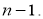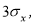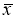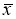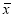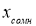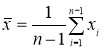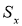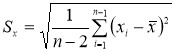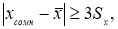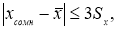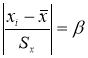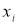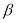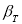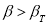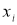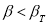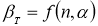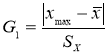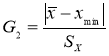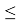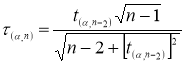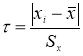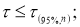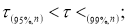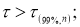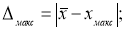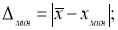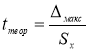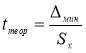При
статистическом анализе экспериментальных
данных для процессов, негативный
результат которых не создает ситуаций,
опасных для жизни людей или утраты
больших материальных ценностей,
доверительная вероятность обычно
принимают равной Р=0,95
Среди
результатов yk
повторностей опыта могут быть результаты,
значительно отличающиеся от других.
Это может быть связано либо с какой-то
грубой ошибкой, либо с неизбежным
случайным влиянием неучтенных факторов
на результат данной повторности опыта.
Признаком
наличия «выделяющегося» результата
среди других является большая величина
отклонения │▲yk│=
yk
– yˉ.
Если
▲yk>yпред,
то такие результаты относятся к грубым
ошибкам. Предельное абсолютное отклонение
определяют в зависимости от сложившейся
ситуации различными методами. Если,
например, проводиться статистический
анализ экспериментальных данных опыта
с эталонным процессом (известно истинное
значение результата опыта и ▲yk=yk-y)
и если исследователь имеет в своем
распоряжении оценку дисперсии S2(yk)
с таким большим числом степеней свободы,
то может принять f→∞
и S2(yk)=σ2,
то для определения грубых ошибок можно
применить правило
«2-х сигм»: все
результаты, абсолютные отклонения
которых по модулю превышают величину
двух среднеквадратичных отклонений с
надежностью 0,95 считаются грубыми
ошибками и исключаются из массива
экспериментальных данных (вероятность
исключения достоверных результатов
равна уровню значимости q=0,05).
Если
доверительная вероятность отличается
от 0,95 то пользуются правилом
«одной сигмы» (Р=0,68)
или правилом
«трех сигм» (Р=0,997),
или по заданной вероятности Р=2Ф(t) –
1 находят Ф(t)
по справочным данным и параметр t,
по которому и рассчитывают абсолютное
отклонение:
Если
в распоряжении исследователя имеется
лишь приближенная оценка дисперсии с
небольшим (конечным) числом степеней
свободы, то применение правила «сигм»
может привести либо к необоснованному
исключению достоверных результатов
либо к необоснованному оставлению
ошибочных результатов.
В
этой ситуации для определения грубых
ошибок можно применить критерий
максимального отклонения
rmax(P,
m),
взятый из соответствующих таблиц. Для
этого rmax
сравнивают
с величиной r,
равной
(22)
Если
r
> rmax,
то данный результат должен исключаться
из дальнейшего анализа, оценка yˉ
должна
быть пересчитана, изменяются абсолютные
отклонения ▲yk
и соответственно оценка дисперсии
S2(yk)
и S2(yˉ).
Анализ на грубые ошибки повторяют при
новых значениях оценок yˉ
и S2(yk),
прекращают его при r
<= rmax.
При
пользовании формулой (22) следует применять
оценку дисперсии, полученную по
результатам повторностей опыта, среди
которых находится сомнительный результат.
Для
определения грубых ошибок существуют
и другие методы, среди которых наиболее
быстрым является метод «по
размаху»,
основанный на оценке максимальных
различий полученных результатов. Анализ
по этому методу проводят в такой
последовательности:
1)
располагают
результаты yk
в упорядоченный ряд, в котором максимальному
результату присваивается номер первый
(y1),
а максимальному – наибольший (ym).
2)
Если
результатом, вызывающим сомнение, будет
ym,
рассчитывают отношение
(23)
если
сомнительным результатом будет y1
– отношение
(24)
3)
при
заданном уровни значимости q
и известном числе повторностей m
по приложению 6 находят табличное
значение критерия αТ.
4)
если
α
> αТ,
то подозреваемый результат является
ошибочным и его следует исключить.
После
исключения грубой ошибки находят по
таблице новую величину αТ
и решают судьбу следующего «подозреваемого»
результата, сравнивая αТ
и рассчитанный для него α.
Если
есть основание предполагать, что 2
наибольших (2 наименьших) результата
являются «промахами», то их можно выявить
в один прием, используя соответствующий
столбец таблицы приложения 6 для
определения αТ
и рассчитывая α
по формуле:
(25)
или
(26)
Средневзвешенные
оценки дисперсии. Анализ однородности
исходных оценок дисперсии
Если
в распоряжении экспериментатора имеются
результаты многократных измерений
величин критерия оптимальности в опытах
при различных условиях ведения процесса,
то появляется возможность расчета
средневзвешенной
оценки дисперсии единичного
результата, единой для всех опытов
эксперимента.
В
каждом из N опытов (номер опыта и
=
1+N)
оценка
дисперсии единичного результата равна
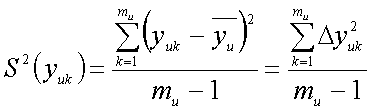
где
ти
– число повторностей и-го опыта.
Средневзвешенная
оценка дисперсии единичного результата
рассчитывается по всем оценкам дисперсии
единичного результата опытов:
а)
при различных ти
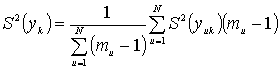
где
—
число
степеней свободы средневзвешенной
оценки дисперсии; ти
–
1 = fu
– «вес» соответствующей и-ой оценки
дисперсии, равный числу степеней свободы
fu;
б)
при
ти
= т = const
где
N
(m-1)=f
– число степеней
свободы средневзвешенной оценки
дисперсии.
Прежде
чем пользоваться соотношениями (28) и
(29) для расчета средневзвешенных
уточненных оценок дисперсии (чем больше
число степеней свободы, тем более точной
будет оценка дисперсии), надо доказать
однородность исходных оценок дисперсии.
Определение
«однородные» в статистике означает
«являющиеся оценкой одного и того же
параметра» (в данном случае – дисперсии
σ
2).
Если
измеряемая случайная величина уик
распределена
по нормальному закону во всем исследуемом
диапазоне, то независимо от значений
и
дисперсия
σ
не будет изменять своей величины и
оценки этой дисперсии должны быть
однородными. Однородность этих оценок
проявляется в том, что они могут отличаться
друг от друга лишь незначительно, в
пределах, зависящих от принятой
вероятности и объема экспериментальных
данных.
Если
ти
= т и f
= const,
то однородность оценок дисперсий можно
проанализировать при помощи критерия
Кохрена Gkp.
Вычисляют
отношение максимальной дисперсии
S2(yuk)max
к
сумме всех дисперсий

и
сравнивают это отношение с величиной
критерия Кохрена Gkp
(P;
f;
N).
Если
G
< Gkp,
то
оценки однородны.
Таблица
значений критерия Кохрена в зависимости
от числа степеней свободы числителя
fu,
числа
сравниваемых дисперсий N и принятого
уровня значимости q
=
1 – Р
дана
в приложении.
Если
число повторностей в опытах различно
(flt
≠ const),
однородность оценок дисперсии можно
проанализировать с помощью критерия
Фишера FТ.
Для
этого из N
оценок
дисперсии выбирают 2: максимальную
S2(yuk)max
и минимальную S2(yuk)min.
Если вычисленное значение F
их
отношения меньше Ft,
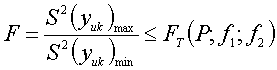
то
все N
оценок
дисперсии будут однородны.
Значения
критерия Фишера FT
даны
в приложении в зависимости от принятого
уровня значимости q
и
числа степеней свободы f1
и
f2
оценок S2(yuk)max
и S2(yuk)min
соответственно.
Если
оценки дисперсии непосредственно
измеряемого параметра у
оказались
неоднородными, т.е. оценками различных
дисперсий, то средневзвешенная оценка
не может быть рассчитана. И кроме того,
величины ук
уже
нельзя считать подчиняющимися нормальному
закону, при котором дисперсия может
быть лишь одной и неизменной при любом
у.
Причиной
нарушения нормального закона распределения
может быть наличие оставшихся грубых
ошибок (анализ на грубые ошибки либо не
проводился, либо проведен недостаточно
тщательно).
Другой
причиной может быть наличие активного
фактора, ошибочно отнесенного
исследователем к неактивным и не
снабженного системой стабилизации.
Поскольку условия изменились, этот
фактор стал значимо влиять на процесс.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Статья рассказывает о грубых и негрубых ошибках, их примерах и последствиях, а также о том, как избежать их.
О чем статья
Введение
В данной лекции мы будем говорить о грубых и негрубых ошибках в русском языке. Ошибки в речи могут быть разного характера и влиять на понимание и восприятие текста. Грубые ошибки являются наиболее серьезными и могут сильно искажать смысл высказывания. Негрубые ошибки, хоть и менее значимы, все равно могут влиять на качество коммуникации. В этой лекции мы рассмотрим примеры грубых и негрубых ошибок, а также узнаем, как их избежать.
Нужна помощь в написании работы?

Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.
Подробнее
Что такое грубые ошибки
Грубые ошибки – это серьезные и очевидные ошибки, которые совершаются при использовании русского языка. Они являются нарушением правил грамматики, пунктуации или орфографии, и могут существенно искажать смысл высказывания.
Грубые ошибки могут включать в себя неправильное использование падежей, склонений, времен глаголов, а также неправильное построение предложений и нарушение правил орфографии и пунктуации.
Эти ошибки легко заметить и исправить, так как они сразу бросаются в глаза и могут вызывать недоумение или непонимание у читателя или слушателя.
Примеры грубых ошибок
Вот несколько примеров грубых ошибок, которые часто встречаются:
Неправильное использование падежей:
– Я видела книгу. (вместо “Я видел книгу”)
– Он дал мне подарок. (вместо “Он дал мне подароку”)
Неправильное использование склонений:
– Моя сестра купила новый компьютер. (вместо “Моя сестра купила нового компьютера”)
– Он пьет чай с сахаром. (вместо “Он пьет чай со сахаром”)
Неправильное использование времен глаголов:
– Я иду в кино вчера. (вместо “Я пошел в кино вчера”)
– Она будет готовить обед завтра. (вместо “Она будет готовить обеды завтра”)
Неправильное построение предложений:
– Я люблю книги, читать и писать. (вместо “Я люблю читать и писать книги”)
– Он ходит в школу, чтобы учиться и друзей. (вместо “Он ходит в школу, чтобы учиться и встречаться с друзьями”)
Нарушение правил орфографии и пунктуации:
– Он пошел гулять, и забыл взять зонт (вместо “Он пошел гулять и забыл взять зонт”)
– Мама сказала, что нужно купить: молоко, хлеб, и яйца. (вместо “Мама сказала, что нужно купить молоко, хлеб и яйца”)
Это лишь некоторые примеры грубых ошибок, которые могут возникать при использовании русского языка. Важно помнить, что правильное использование грамматики, пунктуации и орфографии помогает передать свои мысли и идеи более точно и понятно.
Последствия грубых ошибок
Грубые ошибки в использовании русского языка могут иметь негативные последствия как для говорящего, так и для его аудитории. Вот некоторые из них:
Неправильное понимание
Грубые ошибки могут привести к неправильному пониманию сообщения. Если вы используете неправильные слова, грамматические конструкции или пунктуацию, ваше сообщение может быть непонятным или искаженным. Это может привести к недоразумениям и неправильным выводам со стороны аудитории.
Утрата доверия
Грубые ошибки могут вызвать у аудитории сомнения в вашей компетентности и надежности. Если вы делаете много грубых ошибок в своей речи или письменности, это может создать впечатление, что вы не обладаете достаточными знаниями или навыками в использовании русского языка. Это может привести к утрате доверия со стороны аудитории и снижению вашей репутации.
Проблемы в коммуникации
Грубые ошибки могут привести к проблемам в коммуникации. Если вы не используете правильные грамматические конструкции или не следуете правилам пунктуации, ваше сообщение может быть нечетким или непонятным. Это может затруднить понимание и взаимодействие с вашей аудиторией, особенно если они не знакомы с вашим стилем речи или не говорят на русском языке как родном.
Потеря влияния
Грубые ошибки могут привести к потере вашего влияния и убедительности. Если вы делаете много грубых ошибок в своей речи или письменности, это может снизить вашу способность убедить или влиять на аудиторию. Неправильное использование языка может вызвать сомнения в вашей компетентности и авторитетности, что может привести к отказу аудитории принять ваши идеи или предложения.
В целом, грубые ошибки в использовании русского языка могут иметь серьезные последствия для говорящего и его аудитории. Поэтому важно уделять внимание правильному использованию грамматики, пунктуации и орфографии, чтобы избежать этих негативных последствий.
Как избежать грубых ошибок
Чтобы избежать грубых ошибок в использовании русского языка, следует обратить внимание на несколько важных аспектов:
Изучение правил грамматики
Одним из основных способов избежать грубых ошибок является тщательное изучение правил грамматики русского языка. Это включает в себя знание правильного склонения существительных, спряжения глаголов, правил согласования слов в предложении и т.д. Регулярное повторение и практика помогут закрепить эти правила и избежать ошибок.
Внимательное чтение и анализ текстов
Чтение качественных текстов на русском языке поможет вам улучшить свои навыки и избежать грубых ошибок. Обратите внимание на структуру предложений, использование пунктуации, правильное использование слов и выражений. Анализируйте, как авторы строят свои высказывания и как они используют язык для передачи своих идей.
Проверка и редактирование
После написания текста всегда рекомендуется провести проверку и редактирование. Ошибки могут быть неочевидными, поэтому важно внимательно прочитать свой текст и исправить все грубые ошибки. Обратите внимание на правильность грамматики, пунктуации, орфографии и стилистики.
Обратитесь за помощью
Если вы не уверены в правильности своего текста, не стесняйтесь обратиться за помощью. Попросите кого-то, кто владеет русским языком лучше вас, прочитать ваш текст и указать на возможные ошибки. Иногда взгляд со стороны может помочь заметить ошибки, которые вы сами не заметили.
Следуя этим рекомендациям, вы сможете избежать грубых ошибок в использовании русского языка и улучшить свои навыки коммуникации. Помните, что практика и постоянное самосовершенствование играют важную роль в достижении успеха в овладении русским языком.
Что такое негрубые ошибки
Негрубые ошибки – это ошибки, которые не являются очевидными или серьезными, но все же могут влиять на понимание и качество вашего выражения на русском языке. Они могут быть связаны с грамматикой, пунктуацией, выбором слов или стилем написания.
Негрубые ошибки могут включать неправильное использование временных форм глаголов, неправильное построение предложений, неправильное использование падежей, неправильное употребление запятых и других знаков препинания, неправильный выбор слов или фраз, неправильное использование сленга или неуместное использование иностранных слов.
Хотя негрубые ошибки могут быть менее серьезными, они все равно могут привести к недопониманию или неправильному восприятию вашего сообщения. Поэтому важно стараться избегать таких ошибок и стремиться к более точному и грамотному использованию русского языка.
Для избежания негрубых ошибок рекомендуется обращать внимание на правила грамматики и пунктуации, использовать словари и справочники для проверки правильности слов и фраз, а также просить кого-то, кто владеет русским языком лучше вас, прочитать ваш текст и указать на возможные ошибки. Иногда взгляд со стороны может помочь заметить ошибки, которые вы сами не заметили.
Следуя этим рекомендациям, вы сможете избежать негрубых ошибок в использовании русского языка и улучшить свои навыки коммуникации. Помните, что практика и постоянное самосовершенствование играют важную роль в достижении успеха в овладении русским языком.
Примеры негрубых ошибок
Негрубые ошибки – это ошибки, которые не являются очевидными или серьезными, но все же могут влиять на понимание и качество вашего выражения на русском языке. Вот несколько примеров негрубых ошибок:
Неправильное употребление предлогов
Например, использование предлога “в” вместо “на” или наоборот. Например, “Я живу в Москве” вместо “Я живу на Москве”. Это может привести к неправильному пониманию вашего сообщения.
Неправильное склонение существительных и прилагательных
Например, использование неправильной формы существительного или прилагательного в предложении. Например, “Красивый девушка” вместо “Красивая девушка”. Это может вызвать замешательство у слушателя или читателя.
Неправильное использование временных форм глаголов
Например, неправильное использование прошедшего времени вместо настоящего времени или наоборот. Например, “Я иду в кино вчера” вместо “Я пошел в кино вчера”. Это может привести к неправильному пониманию временных отношений в вашем сообщении.
Неправильное употребление местоимений
Например, использование неправильного местоимения в предложении. Например, “Он сказал, что она придет” вместо “Он сказал, что он придет”. Это может вызвать путаницу в указании на конкретного человека или объект.
Это лишь некоторые примеры негрубых ошибок, которые могут возникнуть при использовании русского языка. Важно помнить, что даже негрубые ошибки могут влиять на понимание и качество вашей коммуникации, поэтому стоит обращать внимание на такие детали при изучении и использовании русского языка.
Последствия негрубых ошибок
Негрубые ошибки в русском языке могут иметь различные последствия, которые могут варьироваться в зависимости от контекста и ситуации. Вот некоторые из возможных последствий:
Неправильное понимание сообщения
Одна из основных проблем негрубых ошибок заключается в том, что они могут привести к неправильному пониманию сообщения. Например, неправильное использование слова или неправильное построение предложения может изменить смысл высказывания и привести к недоразумениям.
Снижение качества коммуникации
Негрубые ошибки могут снизить качество вашей коммуникации. Например, неправильное использование грамматических конструкций или неправильное употребление слов может сделать вашу речь менее четкой и понятной для слушателей или читателей.
Ухудшение впечатления о вас
Негрубые ошибки могут также создать негативное впечатление о вас как о говорящем на русском языке. Например, частые ошибки в грамматике или словарном запасе могут вызвать сомнения в вашей компетентности и профессионализме.
Потеря доверия
Если вы часто делаете негрубые ошибки, это может привести к потере доверия со стороны ваших собеседников или читателей. Они могут начать сомневаться в вашей способности правильно использовать русский язык и, следовательно, в вашей способности передавать информацию точно и надежно.
В целом, негрубые ошибки могут иметь негативные последствия для вашей коммуникации и впечатления о вас. Поэтому важно стремиться к улучшению своих навыков русского языка и избегать таких ошибок.
Как избежать негрубых ошибок
Чтобы избежать негрубых ошибок в использовании русского языка, вам следует обратить внимание на следующие аспекты:
Изучайте правила русской грамматики
Ознакомьтесь с основными правилами русской грамматики, такими как правила согласования слов, правила склонения и спряжения глаголов, а также правила пунктуации. Понимание этих правил поможет вам избежать многих негрубых ошибок.
Читайте и слушайте русскую литературу и речь носителей языка
Чтение и прослушивание русской литературы, статей, новостей и разговоров носителей языка поможет вам улучшить свои навыки в использовании русского языка. Обращайте внимание на правильное использование слов, фраз и грамматических конструкций.
Практикуйте письменную и устную речь
Чем больше вы практикуете письменную и устную речь на русском языке, тем лучше вы становитесь в использовании языка. Пишите эссе, статьи, письма и занимайтесь разговорной практикой с носителями языка. Это поможет вам улучшить свои навыки и избежать негрубых ошибок.
Проверяйте свои тексты на ошибки
Перед отправкой или публикацией своих текстов, всегда проверяйте их на наличие ошибок. Используйте проверяющие программы или попросите кого-то прочитать ваш текст и указать на возможные ошибки. Это поможет вам исправить негрубые ошибки и улучшить качество вашей коммуникации.
Задавайте вопросы и просите обратную связь
Если у вас возникают сомнения или вопросы по поводу правильного использования русского языка, не стесняйтесь задавать вопросы и просить обратную связь. Обратитесь к преподавателю, носителю языка или другим надежным источникам, чтобы получить ясные объяснения и советы.
Следуя этим рекомендациям, вы сможете избежать негрубых ошибок и улучшить свои навыки в использовании русского языка. Помните, что практика и постоянное обучение являются ключевыми факторами в достижении успеха в овладении языком.
Разграничение между грубыми и негрубыми ошибками
В русском языке существуют различные типы ошибок, которые могут быть сделаны при его использовании. Однако, можно выделить две основные категории ошибок: грубые ошибки и негрубые ошибки.
Грубые ошибки
Грубые ошибки – это серьезные нарушения правил русского языка, которые существенно искажают смысл высказывания или делают его непонятным. Такие ошибки могут включать:
- Неправильное склонение или спряжение слов;
- Неправильное использование падежей, времен и лиц;
- Неправильное употребление предлогов;
- Неправильное образование слов;
- Неправильное ударение;
- Неправильное использование знаков препинания.
Грубые ошибки могут существенно влиять на понимание текста и могут вызывать недоумение или неправильное восприятие со стороны читателя или слушателя.
Негрубые ошибки
Негрубые ошибки – это менее серьезные нарушения правил русского языка, которые не искажают смысл высказывания, но все же могут быть замечены и считаться неправильными. Такие ошибки могут включать:
- Неправильное использование запятых, точек с запятой и других знаков препинания;
- Неправильное использование слов или выражений;
- Неправильное употребление синонимов или антонимов;
- Неправильное употребление идиом и фразеологизмов;
- Неправильное употребление сленга или жаргона.
Негрубые ошибки могут быть замечены более опытными носителями языка или людьми, которые обладают хорошим знанием русского языка. Однако, они обычно не приводят к непониманию или неправильному восприятию текста.
Важно отметить, что разграничение между грубыми и негрубыми ошибками может быть субъективным и зависит от контекста и уровня знания русского языка у читателя или слушателя. Однако, стараться избегать как грубых, так и негрубых ошибок является важным аспектом в совершенствовании своих навыков в использовании русского языка.
Заключение
Грубые ошибки – это серьезные и очевидные ошибки, которые могут привести к неправильному пониманию или неправильным результатам. Они должны быть избегнуты, чтобы обеспечить точность и качество работы.
Негрубые ошибки – это менее очевидные и подверженные субъективному толкованию ошибки, которые могут влиять на понимание и качество работы, но не так сильно, как грубые ошибки. Они также должны быть избегнуты, чтобы обеспечить точность и качество работы.
Важно различать между грубыми и негрубыми ошибками, чтобы правильно оценивать и исправлять свою работу. Избегая этих ошибок, мы можем достичь более точных и качественных результатов в изучении русского языка.
Светлана Остапенко
Эксперт по предмету «Русский язык»
преподавательский стаж — 10 лет
Стать автором
Грубые и негрубые ошибки в работах учащихся: вопросы разграничения
В различных работах учащихся встречаются многообразные ошибки: в написании слов, постановке знаков препинания, образовании форм слов, построении синтаксических конструкций, словоупотреблении и проч. Профилактика, а также коррекция ошибок в работах учащихся является частью систематической работы на уроках русского языка по развитию языковой нормы и повышению речевой культуры.
Определение 1
Ошибка – понятие, которое в методике преподавания русского языка используется для обозначения различных типов нарушения языковой нормы при выполнении учебного задания.
Ошибки встречаются в устной и письменной речи учащихся, однако чаще всего ученики имеют дело с орфографическими и пунктуационными ошибками на изученные правила. Вопросы классификации ошибок имеют не только методическую, но и обучающую ценность, поскольку позволяют ученикам осуществлять самопроверку в процессе выполнения учебных заданий.
Педагогу представления об ошибках и их типах необходимы для организации систематической работы по их профилактике, а также корректного оценивания работ учащихся.
Методическое значение имеет разграничение грубых и негрубых ошибок, поскольку их соотношение и количество определяют отметку за работу.
Определение 2
Грубыми считаются ошибки, которые допускаются на уже изученные правила и типы орфограмм, в словарных словах, которые были разобраны и изучены на уроке, а также в словах, написанных на доске, в учебнике и проч.
Определение 3
Негрубые ошибки — это недочеты, допущенные в написании слов на еще не изученные правила, в исключениях, в словарных словах, которые не изучаются на уроке или в школьном курсе языкознания, в употреблении заглавной буквы или в сложных случаях написания, не регулируемых правилами или обусловленных синтаксической позицией слова.
«Грубые и негрубые ошибки в работах учащихся: вопросы разграничения» 👇
Помимо ошибок, следует учитывать, что в работах учащихся также бывают описки — ошибочные написания, не обусловленные знанием или незнанием орфографической нормы. К опискам относят замену и перестановку букв по созвучию, обозначенных ими фонем (например, написание «мемля» вместо «земля», «рорняк» вместо «сорняк»). При этом от описок следует отличать дисграфические ошибки, при которых замена букв или их перестановка является систематической или осуществляется в определенных фонетических позициях.
Помимо орфографических ошибок, в работах также можно обнаружить и пунктуационные ошибки, среди них также выделяются грубые и негрубые. Грубые пунктуационные ошибки касаются замены знаков препинания, пропуска одной из частей парных или сочетающихся знаков. При этом к негрубым обычно относят ошибки в текстах с авторской пунктуацией.
Оценивание работ учащихся с учетом грубых и негрубых ошибок
По отношению к речевым или грамматическим ошибкам определение «грубые» или «негрубые» не применяют. Обычно в работах учитывают их обще количество и оценивают характер их влияния на понимание текста. Если грамматические и речевые недочеты препятствуют пониманию речевого замысла автора текста, то отметки за грамотность и содержание работы (например, в сочинениях, изложениях) снижаются на балл. При проверке итоговых сочинений выпускников при большом количестве речевых ошибок, влияющих на качество речи, ученик может получить отметку «незачет» по критерию «Качество письменной речи».
Грубые ошибки влияют на выставление оценку за работу. Например, при оценивании диктантов работа, в которой содержатся три грубых орфографических ошибки, не может быть оценена отметкой «четыре». При этом при сочетании двух грубых и одной негрубой ошибки возможно выставление отметки «четыре», если в работе нет грубых пунктуационных ошибок. Подробные нормы оценивания устанавливаются в рабочих программах по предмету (в разделе, посвященном оцениванию работ учащихся) или определяются в специальном «Положении о нормах и критериях оценивания по русскому языку и литературе». В основу норм проверки кладутся разработанные методистами и авторами учебных курсов типовые критерии оценивания словарных диктантов, контрольных диктантов, творческих работ, устных ответов, тестов и проч.
Иногда бывает сложно разграничить грубые и негрубые ошибки в работах учащихся, для этого необходимо знать перечень изученных орфограмм, а также те орфограммы, которые еще не пройдены, исключения и некоторые другие случаи правописания, относящиеся к спорным или трудным. Чаще всего к определенным видам упражнений (например, диктантам) учитель составляет таблицу типов орфограмм, в которой отмечает уже изученные или еще не пройденные орфограммы. Необходимо проинформировать учащихся о критериях оценивания, а также о типах ошибок, влияющих на выставление отметки.
Таким образом, знание особенностей разграничения грубых и негрубых ошибок необходимо учителю для проверки работ и выставления отметок, а учащимся – для своевременной коррекции недочетов в различных письменных работах.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
4.2.1. Определение и исключение грубых погрешностей (промахов)
В литературе приведены различные методы оценки и исключения грубых погрешностей. Рассмотрим два наиболее простых для практического использования метода.
Исключение грубых промахов по Q-критерию
При малых выборках с числом измерений п < 10 определение грубых погрешностей лучше оценивать при помощи размаха варьирования по Q-критерию. Для этого составляют отношение:
Q = |х1 – х2|R, (4.11)
|
где х1 – |
подозрительно выделяющийся результат определения (измерения); |
|
х2 – |
результат единичного определения, ближайший по значению к х1; |
|
R – |
размах варьирования, R = хmax –хmin разница между наибольшим и наименьшим значением. |
При малой выборке (n < 10) размах варьирования служит также одной из характеристик рассеяния результатов измерений.
Таблица 4.1
Значения – Q критерия в зависимости от пi и 
|
пi |
Доверительная вероятность |
||
|
0,90 |
0,95 |
0,99 |
|
|
3 |
0,89 |
0,94 |
0,99 |
|
4 |
0,68 |
0,77 |
0,89 |
|
5 |
0,56 |
0,64 |
0,76 |
|
6 |
0,48 |
0,56 |
0,70 |
|
7 |
0,43 |
0,51 |
0,64 |
|
8 |
0,40 |
0,48 |
0,58 |
Вычисленное значение Q сопоставляют с табличным значением Q (

Исключение грубых погрешностей методом вычисления максимального относительного отклонения. Статистический критерий обнаружения грубых погрешностей основан на предположении, что выборка взята из генеральной совокупности, распределенной нормально. Это позволяет использовать распределение наибольшего по абсолютному значению нормированного отклонения:
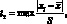
где tт – теоретическое значение квантиля распределения статистики.
Для уровней значимости р = >>0,10; 0,05; 0,01 или доверительной вероятности 1 – р = 0,90; 0,95; 0,99 и п ? 25 значения tт приведены в табл. 4.2. Уровень значимости р = (1 – Р) – максимальная вероятность того, что погрешность превзойдет некое предельное (критическое) значение ±?xkj, т.е. такое значение, что появление этой погрешности можно рассматривать как следствие значимой (неслучайной) причины. На практике обычно используют уровень значимости р = 0,05 (результат получается с 95 %-й доверительной вероятностью).
Для того, чтобы в группе из п наблюдений х1 х2, …, хп отбросить результат хmax (или хmin), надо:
а) вычислить дробь 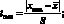
б) по табл. 4.2 найти теоретическое значение tт в зависимости от п и выбранного уровня значимости р;
в) сравнить рассчитанное по п. «а» значение tmax с tт. Если tmax > tт, то результат tmax следует отбросить как промах.
Таблица 4.2
Значения квантилей распределения максимального отклонения, 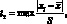
|
n |
Уровни значимости p |
n |
Уровни значимости p |
||||||
|
0,1 |
0,05 |
0,025 |
0,01 |
0,1 |
0,05 |
0,025 |
0,01 |
||
|
3 |
1,41 |
1,41 |
1,41 |
1,41 |
15 |
2,33 |
2,49 |
2,64 |
2,80 |
|
4 |
1,65 |
1,69 |
1,71 |
1,72 |
16 |
2,35 |
2,52 |
2,67 |
2,84 |
|
5 |
1,79 |
1,87 |
1,92 |
1,96 |
17 |
2,38 |
2,55 |
2,70 |
2,87 |
|
6 |
1,89 |
2,00 |
2,07 |
2,13 |
18 |
2,40 |
2,58 |
2,73 |
2,90 |
|
7 |
1,97 |
2,09 |
2,18 |
2,27 |
19 |
2,43 |
2,60 |
2,75 |
2,93 |
|
8 |
2,04 |
2,17 |
2,27 |
2,37 |
20 |
2,45 |
2,62 |
2,78 |
2,96 |
|
9 |
2,10 |
2,24 |
2,35 |
2,46 |
21 |
2,47 |
2,64 |
2,80 |
2;98 |
|
10 |
2,15 |
2,29 |
2,41 |
2,54 |
22 |
2,49 |
2,66 |
2,82 |
3,01 |
|
11 |
2,19 |
2,34 |
2,47 |
2,61 |
23 |
2,50 |
2,68 |
2,84 |
3,03 |
|
12 |
2,23 |
2,39 |
2,52 |
2,66 |
24 |
2,52 |
2,70 |
2,86 |
3,05 |
|
13 |
2,26 |
2,43 |
2,56 |
2,71 |
25 |
2,54 |
2,72 |
2,88 |
3,07 |
|
14 |
2,30 |
2,46 |
2,60 |
2,76 |
Процедуру исключения промахов можно повторить и для следующего по абсолютному значению максимального относительного отклонения, но предварительно необходимо пересчитать 
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
В статье рассмотрены различные критерии отбрасывания грубых погрешностей измерений, применяемые в практической деятельности, на основе рекомендаций ведущих специалистов-метрологов, а также с учетом действующих в настоящий момент нормативных документов.
Приведен пример использования Excel при оценке грубых погрешностей по критериям Стьюдента и Романовского при обработке реальных результатов измерений.
Ключевые слова:
грубые погрешности, критерии согласия, сомнительные значения, уровень значимости, нормальное распределение, критерий согласия Стьюдента, критерий Романовского, выборка, отклонения, Excel.
Одним из важнейших условий правильного применения статистических оценок является отсутствие грубых ошибок при наблюдениях. Поэтому все грубые ошибки должны быть выявлены и исключены из рассмотрения в самом начале обработки наблюдений.
Единственным достаточно надежным способом выявления грубых ошибок является тщательный анализ условий самих испытаний. При этом наблюдения, проводившиеся в нарушенных условиях, должны отбрасываться, независимо от их результата. Например, если при проведении эксперимента, связанного с электричеством, в лаборатории на некоторое время был выключен ток, то весь эксперимент обязательно нужно проводить заново, хотя результат, быть может, не сильно отличается от предыдущих измерений. Точно так же отбрасываются результаты измерений на фотопластинках с поврежденной эмульсией и вообще на любых образцах с обнаруженным позднее дефектом.
На практике, однако, не всегда удается провести подобный анализ условий испытания. Чаще всего приходится иметь дело с окончательным цифровым материалом, в котором отдельные данные вызывают сомнение лишь своим значительным отклонением от остальных. При этом сама «значительность» отклонения во многом субъективна — зачастую приходится сталкиваться со случаями, когда исследователь отбрасывает наблюдения, которые ему не понравились, как ошибочные исключительно по той причине, что они нарушают уже созданную им в воображении картину изучаемого процесса.
Строгий научный анализ готового ряда наблюдений может быть проведен лишь статистическим путем, причем должен быть достаточно хорошо известен характер распределения наблюдаемой случайной величины. В большинстве случаев исследователи исходят из нормального распределения. Каждая грубая ошибка будет соответствовать нарушению этого распределения, изменению его параметров, иными словами, нарушится однородность испытаний (или, как говорят
,
однородность наблюдений), поэтому выявление грубых ошибок можно трактовать как проверку однородности наблюдений.
Промахи, или грубые погрешности, возникают при единичном измерении и обычно устраняются путем повторных измерений. Причиной их возникновения могут быть:
- Объективная реальность (наш реальный мир отличается от идеальной модели мира, которую мы принимаем в данной измерительной задаче);
- Внезапные кратковременные изменения условий измерения (могут быть вызваны неисправностью аппаратуры или источников питания);
- Ошибка оператора (неправильное снятие показаний, неправильная запись и т. п.).
В третьем случае, если оператор в процессе измерения обнаружит промах, он вправе отбросить этот результат и провести повторные измерения.
В настоящее время определение грубой погрешности приведено в ГОСТ Р 8.736–2011: «Грубая погрешность измерения: Погрешность измерения, существенно превышающая зависящие от объективных условий измерений значения систематической и случайной погрешностей» [1, с. 6].
Общие подходы к методам отсеивания грубых погрешностей, как это уже давно принято в практике измерений, заключаются в следующем.
Задаются вероятностью
Р
или уровнем значимости
α
(
) того, что результат наблюдения содержит промах. Выявление сомнительного результата осуществляют с помощью специальных критериев. Операция отбрасывания удаленных от центра выборки сомнительных значений измеряемой величины называется «цензурированием выборки».
Проверяемая гипотеза состоит в утверждении, что результат наблюдения
x
i
не содержит грубой погрешности, т. е. является одним из значений случайной величины
x
с законом распределения Fx(x), статистические оценки параметров которого предварительно определены. Сомнительным может быть в первую очередь лишь наибольший x
max
или наименьший xmin из результатов наблюдений.
Предложим для практического использования наиболее простые методы отсева грубых погрешностей.
Если в распоряжении экспериментатора имеется выборка небольшого объема
n
≤ 25, то можно воспользоваться методом вычисления максимального относительного отклонения [2, с. 149]:
(1)
где
x
i
— крайний (наибольший или наименьший) элемент выборки, по которой подсчитывались оценки среднего значения
и среднеквадратичного отклонения
;
τ
1-
p
— табличное значение статистики
τ
, вычисленной при доверительной вероятности
.
Таким образом, для выделения аномального значения вычисляют значение статистики,
(2)
которое затем сравнивают с табличным значением
τ
1-α
:
τ
≤
τ
1-α
. Если неравенство
τ
≤
τ
1-α
соблюдается, то наблюдение не отсеивают, если не соблюдается, то наблюдение исключают. После исключения того или иного наблюдения или нескольких наблюдений характеристики эмпирического распределения должны быть пересчитаны по данным сокращенной выборки.
Квантили распределения статистики
τ
при уровнях значимости
α
= 0,10; 0,05; 0,025 и 0,01 или доверительной вероятности
=
0,90; 0,95; 0,975 и 0,99 приведены в таблице 1. На практике очень часто используют уровень значимости
α
= 0,05 (результат получается с 95 %-й доверительной вероятностью).
Функции распределения статистики
τ
определяют методами теории вероятностей. По данным таблицы, приведенной в источниках [2, с. 283; 3, с. 184] при заданной доверительной вероятности
или уровне значимости
α
можно для чисел измерения п = 3–25 найти те наибольшие значения
которые случайная величина
может еще принять по чисто случайным причинам.
Процедуру отсева можно повторить и для следующего по абсолютной величине максимального относительного отклонения, но предварительно необходимо пересчитать оценки среднего значения
и среднеквадратичного отклонения
для выборки нового объема
Таблица 1
Квантили распределения максимального относительного отклонения при отсеве грубых погрешностей [2, с. 283]
|
|
Уровень значимости |
|
Уровень значимости |
||||||
|
0,10 |
0,05 |
0,025 |
0,01 |
0,10 |
0,05 |
0,025 |
0,01 |
||
|
3 |
1,41 |
1,41 |
1,41 |
1,41 |
15 |
2,33 |
2,49 |
2,64 |
2,80 |
|
4 |
1,65 |
1,69 |
1,71 |
1,72 |
16 |
2,35 |
2,52 |
2,67 |
2,84 |
|
5 |
1,79 |
1,87 |
1,92 |
1,96 |
17 |
2,38 |
2,55 |
2,70 |
2,87 |
|
6 |
1,89 |
2,00 |
2,07 |
2,13 |
18 |
2,40 |
2,58 |
2,73 |
2,90 |
|
7 |
1,97 |
2,09 |
2,18 |
2,27 |
19 |
2,43 |
2,60 |
2,75 |
2,93 |
|
8 |
2,04 |
2,17 |
2,27 |
2,37 |
20 |
2,45 |
2,62 |
2,78 |
2,96 |
|
9 |
2,10 |
2,24 |
2,35 |
2,46 |
21 |
2,47 |
2,64 |
2,80 |
2,98 |
|
10 |
2,15 |
2,29 |
2,41 |
2,54 |
22 |
2,49 |
2,66 |
2,82 |
3,01 |
|
11 |
2,19 |
2,34 |
2,47 |
2,61 |
23 |
2,50 |
2,68 |
2,84 |
3,03 |
|
12 |
2,23 |
2,39 |
2,52 |
2,66 |
24 |
2,52 |
2,70 |
2,86 |
3,05 |
|
13 |
2,26 |
2,43 |
2,56 |
2,71 |
25 |
2,54 |
2,72 |
2,88 |
3,07 |
|
14 |
2,30 |
2,46 |
2,60 |
2,76 |
|||||
В литературе можно встретить большое количество методических рекомендаций для проведения отсева грубых погрешностей измерений, подробно рассмотренных в [4, с. 25]. Обратим внимание на некоторые из существующих критериев отсеивания грубых погрешностей.
-
Критерий «трех сигм» применяется для случая, когда измеряемая величина
x
распределена по нормальному закону. По этому критерию считается, что с вероятностью
Р
= 0,9973 и значимостью
α
= 0,0027 появление даже одной случайной погрешности, большей, чеммаловероятное событие и ее можно считать промахом, если
−
x
i
> 3
S
x
, где
S
x
—
оценка среднеквадратического отклонения (СКО) измерений. Величиныи
S
x
вычисляют без учета экстремальных значений
x
i
. Данный критерий надежен при числе измерений
n
≥ 20…50 и поэтому он широко применяется. Это правило обычно считается слишком жестким, поэтому рекомендуется назначать границу цензурирования в зависимости от объема выборки: при
6 <
n
≤100 она равна 4
S
x
; при 100 <
n
≤1000 − 4,5
S
x
; при 1000 <
n
≤10000–5
Sx
. Данное правило также используется только при нормальном распределении.
Практические вычисления проводят следующим образом [5, с. 65]:
- Выявляют сомнительное значение измеряемой величины. Сомнительным значением может быть лишь наибольшее, либо наименьшее значение наблюдения измеряемой величины.
-
Вычисляют среднее арифметическое значение выборки
без учета сомнительного значения
измеряемой величины.
(3)
-
Вычисляют оценку СКО выборки
без учета сомнительного значения
измеряемой величины.
(4)
- Вычисляют разность среднеарифметического и сомнительного значения измеряемой величины и сравнивают.
Если
то сомнительное значение отбрасывают, как промах.
Если
то сомнительное значение оставляют как равноправное в ряду наблюдений.
Данный метод «трех сигм» среди метрологов-практиков является самым популярным, достаточно надежным и удобным, так как при этом иметь под рукой какие-то таблицы нет необходимости.
-
Критерий В. И. Романовского применяется, если число измерений невелико,
n
≤ 20. При этом вычисляется соотношение
(5)
где
— результат, вызывающий сомнение,
— коэффициент, предельное значение которого
определяют по таблице 2. Если
, сомнительное значение
исключают («отбрасывают») как промах. Если
,
сомнительное значение оставляют как равноправное в ряду наблюдений [5, с. 65].
Таблица 2
Значение критерия Романовского
|
Уровень значимости, |
Число измерений, |
||||||
|
|
|
|
|
|
|
|
|
|
0,01 |
1,73 |
2,16 |
2,43 |
2,62 |
2,75 |
2,90 |
3,08 |
|
0,02 |
1,72 |
2,13 |
2,37 |
2,54 |
2,66 |
2,80 |
2,96 |
|
0,05 |
1,71 |
2,10 |
2,27 |
2,41 |
2,52 |
2,64 |
2,78 |
|
0,10 |
1,69 |
2,00 |
2,17 |
2,29 |
2,39 |
2,49 |
2,62 |
Несмотря на многообразие существующих и применяемых на практике методов отсеивания грубых погрешностей в настоящее время действует национальный стандарт ГОСТ Р 8.736–2011, который является основным нормативным документом в данной области. В новом стандарте для исключения грубых погрешностей применяется критерий Граббса.
- Статистический критерий Граббса (Смирнова) исключения грубых погрешностей основан на предположении о том, что группа результатов измерений принадлежит нормальному распределению [1, с. 8]. Для этого вычисляют критерии Граббса (Смирнова) G1 и G2, предполагая, что наибольший хmax или наименьший xmin результат измерений вызван грубыми погрешностями.
и
(6)
Сравнивают G1 и G2 с теоретическим значением GT критерия Граббса (Смирнова) при выбранном уровне значимости α. Таблица критических значений критерия Граббса (Смирнова) приведена в приложении к стандарту [1, с. 12]. Следует отметить, что критические значения критерия Граббса (Смирнова) GT отличаются от критических значений критериев
t
-статистик или значений критериев Стьюдента при одних и тех же величинах уровней значимости, что может вызывать некоторые трудности у пользователей при выборе конкретного метода отсеивания погрешностей, соответствующего нормативным документам.
Если G1>GТ, то хmax исключают как маловероятное значение. Если G2>GТ, то xmin исключают как маловероятное значение. Далее вновь вычисляют среднее арифметическое и среднее квадратическое отклонение ряда результатов измерений и процедуру проверки наличия грубых погрешностей повторяют.
Если G1
GТ, то хmax не считают промахом и его сохраняют в ряду результатов измерений. Если G2
GТ, то xmin не считают промахом и его сохраняют в ряду результатов измерений.
Отсев грубых погрешностей можно производить и для больших выборок (
n
= 50…100). Для практических целей лучше всего использовать таблицы распределения Стьюдента. Этот метод исключения аномальных значений для выборок большого объема отличается простотой, а таблицы распределения Стьюдента имеются практически в любой книге по математической статистике, кроме того, распределение Стьюдента реализовано в пакете Excel. Распределение Стьюдента относится к категории распределений, связанных с нормальным распределением. Подробно эти распределения рассмотрены в учебниках по математической статистике [3, с. 24].
Известно, что критическое значение
τ
p
(
p
— процентная точка нормирования выборочного отклонения) выражается через критическое значение распределения Стьюдента
t
α, n-2
[6, с. 26]:
(7)
Учитывая это, можно предложить следующую процедуру отсева грубых погрешностей измерения для больших выборок (
n
= 100):
1) из таблицы наблюдений выбирают наблюдение имеющее наибольшее отклонение;
2)
по формуле
вычисляют значение статистики
τ
;
3)
по таблице (или в программе Excel) находят процентные точки
t
-распределения Стьюдента
t
(
α,
n
-2
)
:
t
(95
%, 98)
= 1,6602, и
t
(
99
%, 98)
= 3,1737;
По предыдущей формуле в программе Excel вычисляют соответствующие точки
t
(95
%, 100)
= 1,66023и
t
(99
%, 100)
=3,17374.
Сравнивают значение расчетной статистики с табличными критическими значениями и принимают решение по отсеву грубых погрешностей.
Рекомендуемый метод отсева грубых погрешностей удобен еще тем, что максимальные относительные отклонения могут быть разделены на три группы: 1)
2)
3)
.
Наблюдения, попавшие в первую группу, нельзя отсеивать ни в коем случае. Наблюдения второй группы можно отсеять, если в пользу этой процедуры имеются еще и другие соображения экспериментатора (например, заключения, сделанные на основе изучения физических, химических и других свойств изучаемого явления). Наблюдения третьей группы, как правило, отсеивают всегда.
Рассмотрим далее пример с использованием средств программного пакета Excel, который позволяет снизить трудоемкость расчетов при осуществлении данной процедуры. К сожалению, в настоящее время средства Excel не позволяют автоматизировать расчеты по всем известным критериям отсеивания грубых погрешностей, поэтому проиллюстрируем рассмотренные методы с использованием доступных в Excel критериев Стьюдента.
Пример 1.
Имеется выборка из 100 шт. резисторов с номинальным сопротивлением
R
н
= (150,0 ± 5 %) кОм, которая используется для оценки качества партии резисторов (генеральная совокупность). Используя критерий Стьюдента, отсеем грубые погрешности (промахи) при измерениях.
- Заносим данные измерений в таблицу Excel в ячейки В2:В101
- Составляем вариационный ряд — располагаем данные в порядке возрастания с помощью функции «Сортировка по возрастанию» в ячейках С2:С101 (рис. 1)
Рис. 1. Фрагмент диалогового окна с данными измерений и вариационного ряда
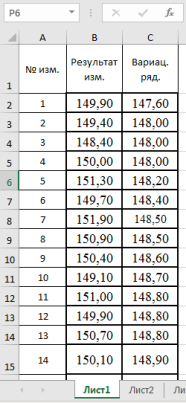
3. Находим среднее значение выборки с помощью мастера функций в категории «Статистические» и функции — СРЗНАЧ, результат в ячейке Н3 (рис. 2).
Рис. 2. Фрагмент диалогового окна при нахождении среднего значения выборки
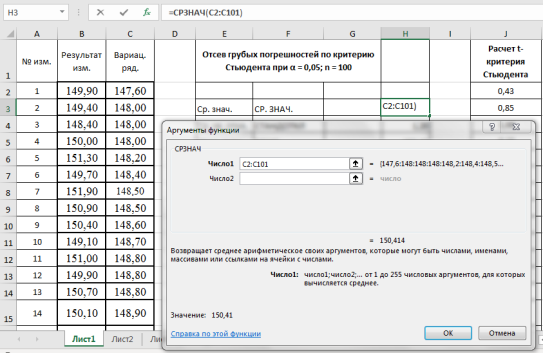
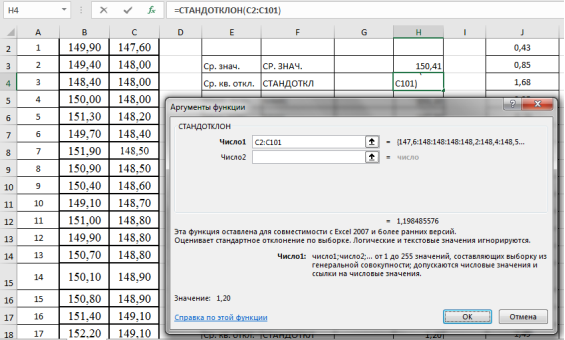
-
Находим среднеквадратическое отклонение —
S
x
. Выделяем ячейку Н4, вызываем «Мастер функций», категория «Статистические», функция — СТАНДОТКЛОН, результат в ячейке Н4–1,20 (рис. 3).
Рис. 3. Фрагмент диалогового окна при нахождении среднего квадратического отклонения
-
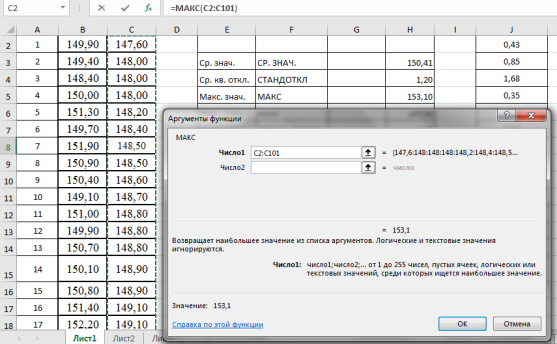
Находим максимальное значение в выборке —
x
макс
. Выделяем ячейку Н5, в категории «Статистические», функция — МАКС, выделяем мышкой вариационный ряд C2:С101, результат в ячейке Н5–153,10 (рис. 4).
Рис. 4. Фрагмент диалогового окна при нахождении максимального значения
-
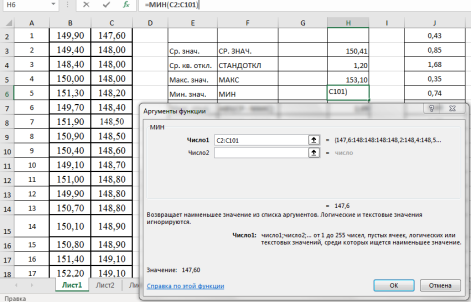
Находим минимальное значение в выборке —
x
мин
. Выделяем ячейку Н6, в категории «Статистические», функция — МИН, выделяем мышкой вариационный ряд C2:С101, результат в ячейке Н6–147,6 (рис. 5).
Рис. 5. Фрагмент диалогового окна при нахождении минимального значения
-
Находим максимальное и минимальное отклонения — Δ
макс
и Δ
мин
. Вводим в ячейки Н7 и Н8 формулы:
-
Находим теоретическое значение —
t
теор
. для максимального и минимального отклонений. Вводим в ячейки Н9 и Н12 формулу
. и
-
Находим табличное значение
t
табл.
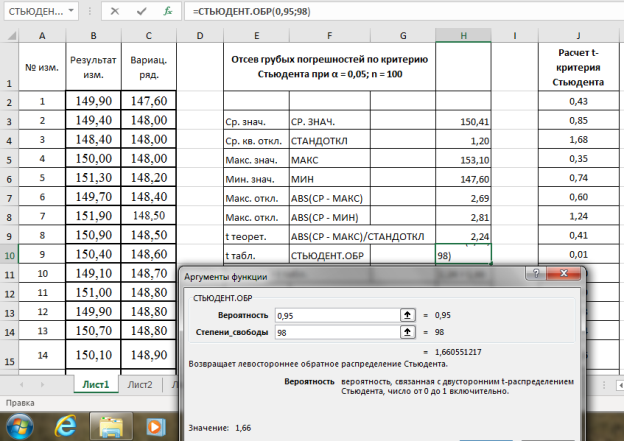
Выделяем ячейку Н10, вызываем в категории «Статистические» функцию — СТЬЮДЕНТ.ОБР, «Вероятность» — 0,95, степени свободы (
n
-2) — 98, результат в ячейке Н10–1,66 (рис. 6).
Рис. 6. Фрагмент диалогового окна при нахождении табличного значения критерия Стьюдента
-
Сравниваем теоретическое значение
t
теор
= 2,24 критерия Стьюдента для максимального значения — 153,1 кОм с табличным значением:
t
табл
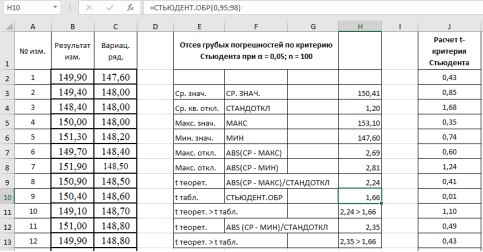
.= 1,6605. - Аналогично п. 9 проверим на наличие грубой погрешности у минимального значения в выборке — 147,6 кОм. Результат в ячейке Н12–2,35 (рис. 7).
Рис. 7. Фрагмент диалогового окна при окончательном анализе данных
- Делаем вывод о наличии грубых ошибок в данных измерениях. Рассмотренная процедура подтвердила наши сомнения относительно достоверности максимального и минимального значений в данной выборке, т. е., указанные результаты могут быть отброшены из результатов измерений, и проверка может быть повторена снова без этих данных.
Пример расчета теоретического критерия Романовского по аналогичным формулам в Excel и диалоговое окно представлены на рис. 8, при условии α = 0,05, число измерений
n
= 20, β
табл
= 2,78 (из таблицы 2).
Рис. 8. Фрагмент диалогового окна при расчете критерия Романовского
Выводы
- Для использования различных критериев отбрасывания грубых погрешностей измерений необходимо учитывать требования действующих нормативных документов.
- Рассмотренный пример показал, что расчеты погрешностей по критерию Стьюдента с использованием таблиц и формул Excel значительно упрощаются, а процесс отбрасывания грубых погрешностей можно осуществить наиболее качественно и быстро.
Литература:
1. ГОСТ Р 8.736–2011 Государственная система обеспечения единства измерений. Измерения прямые многократные. Методы обработки результатов измерений. Основные положения. — М.: ФГУП Стандартинформ, 2013. — 24 с.
2. Пустыльник Е. И. Статистические методы анализа и обработки наблюдений. — М.: Наука, 1968. — 288 с.
3. Львовский Е. Н. Статистические методы построения эмпирических формул: Учеб. пособие. — М.: Высш. школа, 1982. — 224 с.
4. Фаюстов А. А. Ещё раз о критериях отсеивания грубых погрешностей. — Законодательная и прикладная метрология, 2016, № 5, с. 25–30.
5. Сергеев А. Г. Метрология: Учебник. — М.: Логос, 2005. — 272 с.
6. Большев Л. Н., Смирнов Н. В. Таблицы математической статистики. — М.: Наука, Главная редакция физико-математической литературы, 1983. — 416 с.
Основные термины (генерируются автоматически): диалоговое окно, сомнительное значение, уровень значимости, измеряемая величина, погрешность, критерий, нормальное распределение, ячейка, вариационный ряд, минимальное значение.