Результат любого измерения не определён однозначно и имеет случайную составляющую.
Поэтому адекватным языком для описания погрешностей является язык вероятностей.
Тот факт, что значение некоторой величины «случайно», не означает, что
она может принимать совершенно произвольные значения. Ясно, что частоты, с которыми
возникает те или иные значения, различны. Вероятностные законы, которым
подчиняются случайные величины, называют распределениями.
2.1 Случайная величина
Случайной будем называть величину, значение которой не может быть достоверно определено экспериментатором. Чаще всего подразумевается, что случайная величина будет изменяться при многократном повторении одного и того же эксперимента. При интерпретации результатов измерений в физических экспериментах, обычно случайными также считаются величины, значение которых является фиксированным, но не известно экспериментатору. Например смещение нуля шкалы прибора. Для формализации работы со случайными величинами используют понятие вероятности. Численное значение вероятности того, что какая-то величина примет то или иное значение определяется либо как относительная частота наблюдения того или иного значения при повторении опыта большое количество раз, либо как оценка на основе данных других экспериментов.
Замечание.
Хотя понятия вероятности и случайной величины являются основополагающими, в литературе нет единства в их определении. Обсуждение формальных тонкостей или построение строгой теории лежит за пределами данного пособия. Поэтому на начальном этапе лучше использовать «интуитивное» понимание этих сущностей. Заинтересованным читателям рекомендуем обратиться к специальной литературе: [5].
Рассмотрим случайную физическую величину x, которая при измерениях может
принимать непрерывный набор значений. Пусть
P[x0,x0+δx] — вероятность того, что результат окажется вблизи
некоторой точки x0 в пределах интервала δx: x∈[x0,x0+δx].
Устремим интервал
δx к нулю. Нетрудно понять, что вероятность попасть в этот интервал
также будет стремиться к нулю. Однако отношение
w(x0)=P[x0,x0+δx]δx будет оставаться конечным.
Функцию w(x) называют плотностью распределения вероятности или кратко
распределением непрерывной случайной величины x.
Замечание. В математической литературе распределением часто называют не функцию
w(x), а её интеграл W(x)=∫w(x)𝑑x. Такую функцию в физике принято
называть интегральным или кумулятивным распределением. В англоязычной литературе
для этих функций принято использовать сокращения:
pdf (probability distribution function) и
cdf (cumulative distribution function)
соответственно.
Гистограммы.
Проиллюстрируем наглядно понятие плотности распределения. Результат
большого числа измерений случайной величины удобно представить с помощью
специального типа графика — гистограммы.
Для этого область значений x, размещённую на оси абсцисс, разобьём на
равные малые интервалы — «корзины» или «бины» (англ. bins)
некоторого размера h. По оси ординат будем откладывать долю измерений w,
результаты которых попадают в соответствующую корзину. А именно,
пусть k — номер корзины; nk — число измерений, попавших
в диапазон x∈[kh,(k+1)h]. Тогда на графике изобразим «столбик»
шириной h и высотой wk=nk/n.
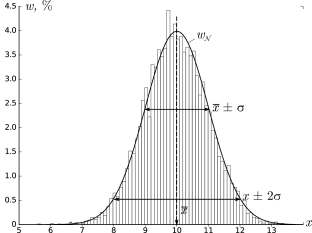
В результате получим картину, подобную изображённой на рис. 2.1.
σ=1,0, h=0,1, n=104)
Высоты построенных столбиков будут приближённо соответствовать значению
плотности распределения w(x) вблизи соответствующей точки x.
Если устремить число измерений к бесконечности (n→∞), а ширину корзин
к нулю (h→0), то огибающая гистограммы будет стремиться к некоторой
непрерывной функции w(x).
Самые высокие столбики гистограммы будут группироваться вблизи максимума
функции w(x) — это наиболее вероятное значение случайной величины.
Если отклонения в положительную и отрицательную стороны равновероятны,
то гистограмма будет симметрична — в таком случае среднее значение ⟨x⟩
также будет лежать вблизи этого максимума. Ширина гистограммы будет характеризовать разброс
значений случайной величины — по порядку величины
она, как правило, близка к среднеквадратичному отклонению sx.
Свойства распределений.
Из определения функции w(x) следует, что вероятность получить в результате
эксперимента величину x в диапазоне от a до b
можно найти, вычислив интеграл:
| Px∈[a,b]=∫abw(x)𝑑x. | (2.1) |
Согласно определению вероятности, сумма вероятностей для всех возможных случаев
всегда равна единице. Поэтому интеграл распределения w(x) по всей области
значений x (то есть суммарная площадь под графиком w(x)) равен единице:
Это соотношение называют условием нормировки.
Среднее и дисперсия.
Вычислим среднее по построенной гистограмме. Если размер корзин
h достаточно мал, все измерения в пределах одной корзины можно считать примерно
одинаковыми. Тогда среднее арифметическое всех результатов можно вычислить как
Переходя к пределу, получим следующее определение среднего значения
случайной величины:
где интегрирование ведётся по всей области значений x.
В теории вероятностей x¯ также называют математическим ожиданием
распределения.
Величину
| σ2=(x-x¯)2¯=∫(x-x¯)2w𝑑x | (2.3) |
называют дисперсией распределения. Значение σ есть
срекднеквадратичное отклонение в пределе n→∞. Оно имеет ту
же размерность, что и сама величина x и характеризует разброс распределения.
Именно эту величину, как правило, приводят как характеристику погрешности
измерения x.
Доверительный интервал.
Обозначим как P|Δx|<δ вероятность
того, что отклонение от среднего Δx=x-x¯ составит величину,
не превосходящую по модулю значение δ:
| P|Δx|<δ=∫x¯-δx¯+δw(x)𝑑x. | (2.4) |
Эту величину называют доверительной вероятностью для
доверительного интервала |x-x¯|≤δ.
2.2 Нормальное распределение
Одним из наиболее примечательных результатов теории вероятностей является
так называемая центральная предельная теорема. Она утверждает,
что сумма большого количества независимых случайных слагаемых, каждое
из которых вносит в эту сумму относительно малый вклад, подчиняется
универсальному закону, не зависимо от того, каким вероятностным законам
подчиняются её составляющие, — так называемому нормальному
распределению (или распределению Гаусса).
Доказательство теоремы довольно громоздко и мы его не приводим (его можно найти
в любом учебнике по теории вероятностей). Остановимся
кратко на том, что такое нормальное распределение и его основных свойствах.
Плотность нормального распределения выражается следующей формулой:
| w𝒩(x)=12πσe-(x-x¯)22σ2. | (2.5) |
Здесь x¯ и σ
— параметры нормального распределения: x¯ равно
среднему значению x, a σ —
среднеквадратичному отклонению, вычисленным в пределе n→∞.
Как видно из рис. 2.1, распределение представляет собой
симметричный
«колокол», положение вершины которого
соответствует x¯ (ввиду симметрии оно же
совпадает с наиболее вероятным значением — максимумом
функции w𝒩(x)).
При значительном отклонении x от среднего величина
w𝒩(x)
очень быстро убывает. Это означает, что вероятность встретить отклонения,
существенно большие, чем σ, оказывается пренебрежимо
мала. Ширина «колокола» по порядку величины
равна σ — она характеризует «разброс»
экспериментальных данных относительно среднего значения.
Замечание. Точки x=x¯±σ являются точками
перегиба графика w(x) (в них вторая производная по x
обращается в нуль, w′′=0), а их положение по высоте составляет
w(x¯±σ)/w(x¯)=e-1/2≈0,61
от высоты вершины.
Универсальный характер центральной предельной теоремы позволяет широко
применять на практике нормальное (гауссово) распределение для обработки
результатов измерений, поскольку часто случайные погрешности складываются из
множества случайных независимых факторов. Заметим, что на практике
для приближённой оценки параметров нормального распределения
случайной величины используются выборочные значения среднего
и дисперсии: x¯≈⟨x⟩, sx≈σx.
x-x0σ2=2w(x)σ1=1
Доверительные вероятности.
Вычислим некоторые доверительные вероятности (2.4) для нормально
распределённых случайных величин.
Замечание. Значение интеграла вида ∫e-x2/2𝑑x
(его называют интегралом ошибок) в элементарных функциях не выражается,
но легко находится численно.
Вероятность того, что результат отдельного измерения x окажется
в пределах x¯±σ оказывается равна
| P|Δx|<σ=∫x¯-σx¯+σw𝒩𝑑x≈0,68. |
Вероятность отклонения в пределах x¯±2σ:
а в пределах x¯±3σ:
Иными словами, при большом числе измерений нормально распределённой
величины можно ожидать, что лишь треть измерений выпадут за пределы интервала
[x¯-σ,x¯+σ]. При этом около 5%
измерений выпадут за пределы [x¯-2σ;x¯+2σ],
и лишь 0,27% окажутся за пределами
[x¯-3σ;x¯+3σ].
Пример. В сообщениях об открытии бозона Хиггса на Большом адронном коллайдере
говорилось о том, что исследователи ждали подтверждение результатов
с точностью «5 сигма». Используя нормальное распределение (2.5)
нетрудно посчитать, что они использовали доверительную вероятность
P≈1-5,7⋅10-7=0,99999943. Такую точность можно назвать фантастической.
Полученные значения доверительных вероятностей используются при
стандартной записи результатов измерений. В физических измерениях
(в частности, в учебной лаборатории), как правило, используется P=0,68,
то есть, запись
означает, что измеренное значение лежит в диапазоне (доверительном
интервале) x∈[x¯-δx;x¯+δx] с
вероятностью 68%. Таким образом погрешность ±δx считается
равной одному среднеквадратичному отклонению: δx=σ.
В технических измерениях чаще используется P=0,95, то есть под
абсолютной погрешностью имеется в виду удвоенное среднеквадратичное
отклонение, δx=2σ. Во избежание разночтений доверительную
вероятность следует указывать отдельно.
Замечание. Хотя нормальный закон распределения встречается на практике довольно
часто, стоит помнить, что он реализуется далеко не всегда.
Полученные выше соотношения для вероятностей попадания значений в
доверительные интервалы можно использовать в качестве простейшего
признака нормальности распределения: в частности, если количество попадающих
в интервал ±σ результатов существенно отличается от 2/3 — это повод
для более детального исследования закона распределения ошибок.
Сравнение результатов измерений.
Теперь мы можем дать количественный критерий для сравнения двух измеренных
величин или двух результатов измерения одной и той же величины.
Пусть x1 и x2 (x1≠x2) измерены с
погрешностями σ1 и σ2 соответственно.
Ясно, что если различие результатов |x2-x1| невелико,
его можно объяснить просто случайными отклонениями.
Если же теория предсказывает, что вероятность обнаружить такое отклонение
слишком мала, различие результатов следует признать значимым.
Предварительно необходимо договориться о соответствующем граничном значении
вероятности. Универсального значения здесь быть не может,
поэтому приходится полагаться на субъективный выбор исследователя. Часто
в качестве «разумной» границы выбирают вероятность 5%,
что, как видно из изложенного выше, для нормального распределения
соответствует отклонению более, чем на 2σ.
Допустим, одна из величин известна с существенно большей точностью:
σ2≪σ1 (например, x1 — результат, полученный
студентом в лаборатории, x2 — справочное значение).
Поскольку σ2 мало, x2 можно принять за «истинное»:
x2≈x¯. Предполагая, что погрешность измерения
x1 подчиняется нормальному закону с и дисперсией σ12,
можно утверждать, что
различие считают будет значимы, если
Пусть погрешности измерений сравнимы по порядку величины:
σ1∼σ2. В теории вероятностей показывается, что
линейная комбинация нормально распределённых величин также имеет нормальное
распределение с дисперсией σ2=σ12+σ22
(см. также правила сложения погрешностей (2.7)). Тогда
для проверки гипотезы о том, что x1 и x2 являются измерениями
одной и той же величины, нужно вычислить, является ли значимым отклонение
|x1-x2| от нуля при σ=σ12+σ22.
Пример. Два студента получили следующие значения для теплоты испарения
некоторой жидкости: x1=40,3±0,2 кДж/моль и
x2=41,0±0,3 кДж/моль, где погрешность соответствует
одному стандартному отклонению. Можно ли утверждать, что они исследовали
одну и ту же жидкость?
Имеем наблюдаемую разность |x1-x2|=0,7 кДж/моль,
среднеквадратичное отклонение для разности
σ=0,22+0,32=0,36 кДж/моль.
Их отношение |x2-x1|σ≈2. Из
свойств нормального распределения находим вероятность того, что измерялась
одна и та же величина, а различия в ответах возникли из-за случайных
ошибок: P≈5%. Ответ на вопрос, «достаточно»
ли мала или велика эта вероятность, остаётся на усмотрение исследователя.
Замечание. Изложенные здесь соображения применимы, только если x¯ и
его стандартное отклонение σ получены на основании достаточно
большой выборки n≫1 (или заданы точно). При небольшом числе измерений
(n≲10) выборочные средние ⟨x⟩ и среднеквадратичное отклонение
sx сами имеют довольно большую ошибку, а
их распределение будет описываться не нормальным законом, а так
называемым t-распределением Стъюдента. В частности, в зависимости от
значения n интервал ⟨x⟩±sx будет соответствовать несколько
меньшей доверительной вероятности, чем P=0,68. Особенно резко различия
проявляются при высоких уровнях доверительных вероятностей P→1.
2.3 Независимые величины
Величины x и y называют независимыми если результат измерения одной
из них никак не влияет на результат измерения другой. Для таких величин вероятность того, что x окажется в некоторой области X, и одновременно y — в области Y,
равна произведению соответствующих вероятностей:
Обозначим отклонения величин от их средних как Δx=x-x¯ и
Δy=y-y¯.
Средние значения этих отклонений равны, очевидно, нулю: Δx¯=x¯-x¯=0,
Δy¯=0. Из независимости величин x и y следует,
что среднее значение от произведения Δx⋅Δy¯
равно произведению средних Δx¯⋅Δy¯
и, следовательно, равно нулю:
| Δx⋅Δy¯=Δx¯⋅Δy¯=0. | (2.6) |
Пусть измеряемая величина z=x+y складывается из двух независимых
случайных слагаемых x и y, для которых известны средние
x¯ и y¯, и их среднеквадратичные погрешности
σx и σy. Непосредственно из определения (1.1)
следует, что среднее суммы равно сумме средних:
Найдём дисперсию σz2. В силу независимости имеем
| Δz2¯=Δx2¯+Δy2¯+2Δx⋅Δy¯≈Δx2¯+Δy2¯, |
то есть:
Таким образом, при сложении независимых величин их погрешности
складываются среднеквадратичным образом.
Подчеркнём, что для справедливости соотношения (2.7)
величины x и y не обязаны быть нормально распределёнными —
достаточно существования конечных значений их дисперсий. Однако можно
показать, что если x и y распределены нормально, нормальным
будет и распределение их суммы.
Замечание. Требование независимости
слагаемых является принципиальным. Например, положим y=x. Тогда
z=2x. Здесь y и x, очевидно, зависят друг от друга. Используя
(2.7), находим σ2x=2σx,
что, конечно, неверно — непосредственно из определения
следует, что σ2x=2σx.
Отдельно стоит обсудить математическую структуру формулы (2.7).
Если одна из погрешностей много больше другой, например,
σx≫σy,
то меньшей погрешностью можно пренебречь, σx+y≈σx.
С другой стороны, если два источника погрешностей имеют один порядок
σx∼σy, то и σx+y∼σx∼σy.
Эти обстоятельства важны при планирования эксперимента: как правило,
величина, измеренная наименее точно, вносит наибольший вклад в погрешность
конечного результата. При этом, пока не устранены наиболее существенные
ошибки, бессмысленно гнаться за повышением точности измерения остальных
величин.
Пример. Пусть σy=σx/3,
тогда σz=σx1+19≈1,05σx,
то есть при различии двух погрешностей более, чем в 3 раза, поправка
к погрешности составляет менее 5%, и уже нет особого смысла в учёте
меньшей погрешности: σz≈σx. Это утверждение
касается сложения любых независимых источников погрешностей в эксперименте.
2.4 Погрешность среднего
Выборочное среднее арифметическое значение ⟨x⟩, найденное
по результатам n измерений, само является случайной величиной.
Действительно, если поставить серию одинаковых опытов по n измерений,
то в каждом опыте получится своё среднее значение, отличающееся от
предельного среднего x¯.
Вычислим среднеквадратичную погрешность среднего арифметического
σ⟨x⟩.
Рассмотрим вспомогательную сумму n слагаемых
Если {xi} есть набор независимых измерений
одной и той же физической величины, то мы можем, применяя результат
(2.7) предыдущего параграфа, записать
| σZ=σx12+σx22+…+σxn2=nσx, |
поскольку под корнем находится n одинаковых слагаемых. Отсюда с
учётом ⟨x⟩=Z/n получаем
Таким образом, погрешность среднего значения x по результатам
n независимых измерений оказывается в n раз меньше погрешности
отдельного измерения. Это один из важнейших результатов, позволяющий
уменьшать случайные погрешности эксперимента за счёт многократного
повторения измерений.
Подчеркнём отличия между σx и σ⟨x⟩:
величина σx — погрешность отдельного
измерения — является характеристикой разброса значений
в совокупности измерений {xi}, i=1..n. При
нормальном законе распределения примерно 68% измерений попадают в
интервал ⟨x⟩±σx;
величина σ⟨x⟩ — погрешность
среднего — характеризует точность, с которой определено
среднее значение измеряемой физической величины ⟨x⟩ относительно
предельного («истинного») среднего x¯;
при этом с доверительной вероятностью P=68% искомая величина x¯
лежит в интервале
⟨x⟩-σ⟨x⟩<x¯<⟨x⟩+σ⟨x⟩.
2.5 Результирующая погрешность опыта
Пусть для некоторого результата измерения известна оценка его максимальной
систематической погрешности Δсист и случайная
среднеквадратичная
погрешность σслуч. Какова «полная»
погрешность измерения?
Предположим для простоты, что измеряемая величина в принципе
может быть определена сколь угодно точно, так что можно говорить о
некотором её «истинном» значении xист
(иными словами, погрешность результата связана в основном именно с
процессом измерения). Назовём полной погрешностью измерения
среднеквадратичное значения отклонения от результата измерения от
«истинного»:
Отклонение x-xист можно представить как сумму случайного
отклонения от среднего δxслуч=x-x¯
и постоянной (но, вообще говоря, неизвестной) систематической составляющей
δxсист=x¯-xист=const:
Причём случайную составляющую можно считать независимой от систематической.
В таком случае из (2.7) находим:
| σполн2=⟨δxсист2⟩+⟨δxслуч2⟩≤Δсист2+σслуч2. | (2.9) |
Таким образом, для получения максимального значения полной
погрешности некоторого измерения нужно квадратично сложить максимальную
систематическую и случайную погрешности.
Если измерения проводятся многократно, то согласно (2.8)
случайная составляющая погрешности может быть уменьшена, а систематическая
составляющая при этом остаётся неизменной:
Отсюда следует важное практическое правило
(см. также обсуждение в п. 2.3): если случайная погрешность измерений
в 2–3 раза меньше предполагаемой систематической, то
нет смысла проводить многократные измерения в попытке уменьшить погрешность
всего эксперимента. В такой ситуации измерения достаточно повторить
2–3 раза — чтобы убедиться в повторяемости результата, исключить промахи
и проверить, что случайная ошибка действительно мала.
В противном случае повторение измерений может иметь смысл до
тех пор, пока погрешность среднего
σ⟨x⟩=σxn
не станет меньше систематической.
Замечание. Поскольку конкретная
величина систематической погрешности, как правило, не известна, её
можно в некотором смысле рассматривать наравне со случайной —
предположить, что её величина была определена по некоторому случайному
закону перед началом измерений (например, при изготовлении линейки
на заводе произошло некоторое случайное искажение шкалы). При такой
трактовке формулу (2.9) можно рассматривать просто
как частный случай формулы сложения погрешностей независимых величин
(2.7).
Подчеркнем, что вероятностный закон, которому подчиняется
систематическая ошибка, зачастую неизвестен. Поэтому неизвестно и
распределение итогового результата. Из этого, в частности, следует,
что мы не можем приписать интервалу x±Δсист какую-либо
определённую доверительную вероятность — она равна 0,68
только если систематическая ошибка имеет нормальное распределение.
Можно, конечно, предположить,
— и так часто делают — что, к примеру, ошибки
при изготовлении линеек на заводе имеют гауссов характер. Также часто
предполагают, что систематическая ошибка имеет равномерное
распределение (то есть «истинное» значение может с равной вероятностью
принять любое значение в пределах интервала ±Δсист).
Строго говоря, для этих предположений нет достаточных оснований.
Пример. В результате измерения диаметра проволоки микрометрическим винтом,
имеющим цену деления h=0,01 мм, получен следующий набор из n=8 значений:
Вычисляем среднее значение: ⟨d⟩≈386,3 мкм.
Среднеквадратичное отклонение:
σd≈9,2 мкм. Случайная погрешность среднего согласно
(2.8):
σ⟨d⟩=σd8≈3,2
мкм. Все результаты лежат в пределах ±2σd, поэтому нет
причин сомневаться в нормальности распределения. Максимальную погрешность
микрометра оценим как половину цены деления, Δ=h2=5 мкм.
Результирующая полная погрешность
σ≤Δ2+σd28≈6,0 мкм.
Видно, что σслуч≈Δсист и проводить дополнительные измерения
особого смысла нет. Окончательно результат измерений может быть представлен
в виде (см. также правила округления
результатов измерений в п. 4.3.2)
d=386±6мкм,εd=1,5%.
Заметим, что поскольку случайная погрешность и погрешность
прибора здесь имеют один порядок величины, наблюдаемый случайный разброс
данных может быть связан как с неоднородностью сечения проволоки,
так и с дефектами микрометра (например, с неровностями зажимов, люфтом
винта, сухим трением, деформацией проволоки под действием микрометра
и т. п.). Для ответа на вопрос, что именно вызвало разброс, требуются
дополнительные исследования, желательно с использованием более точных
приборов.
Пример. Измерение скорости
полёта пули было осуществлено с погрешностью δv=±1 м/c.
Результаты измерений для n=6 выстрелов представлены в таблице:
Усреднённый результат ⟨v⟩=162,0м/с,
среднеквадратичное отклонение σv=13,8м/c, случайная
ошибка для средней скорости
σv¯=σv/6=5,6м/с.
Поскольку разброс экспериментальных данных существенно превышает погрешность
каждого измерения, σv≫δv, он почти наверняка связан
с реальным различием скоростей пули в разных выстрелах, а не с ошибками
измерений. В качестве результата эксперимента представляют интерес
как среднее значение скоростей ⟨v⟩=162±6м/с
(ε≈4%), так и значение σv≈14м/с,
характеризующее разброс значений скоростей от выстрела к выстрелу.
Малая инструментальная погрешность в принципе позволяет более точно
измерить среднее и дисперсию, и исследовать закон распределения выстрелов
по скоростям более детально — для этого требуется набрать
бо́льшую статистику по выстрелам.
Пример. Измерение скорости
полёта пули было осуществлено с погрешностью δv=10 м/c. Результаты
измерений для n=6 выстрелов представлены в таблице:
Усреднённый результат ⟨v⟩=163,3м/с,
σv=12,1м/c, σ⟨v⟩=5м/с,
σполн≈11,2м/с. Инструментальная
погрешность каждого измерения превышает разброс данных, поэтому в
этом опыте затруднительно сделать вывод о различии скоростей от выстрела
к выстрелу. Результат измерений скорости пули:
⟨v⟩=163±11м/с,
ε≈7%. Проводить дополнительные выстрелы при такой
большой инструментальной погрешности особого смысла нет —
лучше поработать над точностью приборов и методикой измерений.
2.6 Обработка косвенных измерений
Косвенными называют измерения, полученные в результате расчётов,
использующих результаты прямых (то есть «непосредственных»)
измерений физических величин. Сформулируем основные правила пересчёта
погрешностей при косвенных измерениях.
2.6.1 Случай одной переменной
Пусть в эксперименте измеряется величина x, а её «наилучшее»
(в некотором смысле) значение равно x⋆ и оно известно с
погрешностью σx. После чего с помощью известной функции
вычисляется величина y=f(x).
В качестве «наилучшего» приближения для y используем значение функции
при «наилучшем» x:
Найдём величину погрешности σy. Обозначая отклонение измеряемой
величины как Δx=x-x⋆, и пользуясь определением производной,
при условии, что функция y(x) — гладкая
вблизи x≈x⋆, запишем
где f′≡dydx — производная фукнции f(x), взятая в точке
x⋆. Возведём полученное в квадрат, проведём усреднение
(σy2=⟨Δy2⟩,
σx2=⟨Δx2⟩), и затем снова извлечём
корень. В результате получим
Пример. Для степенной функции
y=Axn имеем σy=nAxn-1σx, откуда
σyy=nσxx,или εy=nεx,
то есть относительная погрешность степенной функции возрастает пропорционально
показателю степени n.
Пример. Для y=1/x имеем ε1/x=εx
— при обращении величины сохраняется её относительная
погрешность.
Упражнение. Найдите погрешность логарифма y=lnx, если известны x
и σx.
Упражнение. Найдите погрешность показательной функции y=ax,
если известны x и σx. Коэффициент a задан точно.
2.6.2 Случай многих переменных
Пусть величина u вычисляется по измеренным значениям нескольких
различных независимых физических величин x, y, …
на основе известного закона u=f(x,y,…). В качестве
наилучшего значения можно по-прежнему взять значение функции f
при наилучших значениях измеряемых параметров:
Для нахождения погрешности σu воспользуемся свойством,
известным из математического анализа, — малые приращения гладких
функции многих переменных складываются линейно, то есть справедлив
принцип суперпозиции малых приращений:
где символом fx′≡∂f∂x обозначена
частная производная функции f по переменной x —
то есть обычная производная f по x, взятая при условии, что
все остальные аргументы (кроме x) считаются постоянными параметрами.
Тогда пользуясь формулой для нахождения дисперсии суммы независимых
величин (2.7), получим соотношение, позволяющее вычислять
погрешности косвенных измерений для произвольной функции
u=f(x,y,…):
| σu2=fx′2σx2+fy′2σy2+… | (2.11) |
Это и есть искомая общая формула пересчёта погрешностей при косвенных
измерениях.
Отметим, что формулы (2.10) и (2.11) применимы
только если относительные отклонения всех величин малы
(εx,εy,…≪1),
а измерения проводятся вдали от особых точек функции f (производные
fx′, fy′ … не должны обращаться в бесконечность).
Также подчеркнём, что все полученные здесь формулы справедливы только
для независимых переменных x, y, …
Остановимся на некоторых важных частных случаях формулы
(2.11).
Пример. Для суммы (или разности) u=∑i=1naixi имеем
σu2=∑i=1nai2σxi2.
(2.12)
Пример. Найдём погрешность степенной функции:
u=xα⋅yβ⋅…. Тогда нетрудно получить,
что
σu2u2=α2σx2x2+β2σy2y2+…
или через относительные погрешности
εu2=α2εx2+β2εy2+…
(2.13)
Пример. Вычислим погрешность произведения и частного: u=xy или u=x/y.
Тогда в обоих случаях имеем
εu2=εx2+εy2,
(2.14)
то есть при умножении или делении относительные погрешности складываются
квадратично.
Пример. Рассмотрим несколько более сложный случай: нахождение угла по его тангенсу
u=arctgyx.
В таком случае, пользуясь тем, что (arctgz)′=11+z2,
где z=y/x, и используя производную сложной функции, находим
ux′=uz′zx′=-yx2+y2,
uy′=uz′zy′=xx2+y2, и наконец
σu2=y2σx2+x2σy2(x2+y2)2.
Упражнение. Найти погрешность вычисления гипотенузы z=x2+y2
прямоугольного треугольника по измеренным катетам x и y.
По итогам данного раздела можно дать следующие практические рекомендации.
-
•
Как правило, нет смысла увеличивать точность измерения какой-то одной
величины, если другие величины, используемые в расчётах, остаются
измеренными относительно грубо — всё равно итоговая погрешность
скорее всего будет определяться самым неточным измерением. Поэтому
все измерения имеет смысл проводить примерно с одной и той же
относительной погрешностью. -
•
При этом, как следует из (2.13), особое внимание
следует уделять измерению величин, возводимых при расчётах в степени
с большими показателями. А при сложных функциональных зависимостях
имеет смысл детально проанализировать структуру формулы
(2.11):
если вклад от некоторой величины в общую погрешность мал, нет смысла
гнаться за высокой точностью её измерения, и наоборот, точность некоторых
измерений может оказаться критически важной. -
•
Следует избегать измерения малых величин как разности двух близких
значений (например, толщины стенки цилиндра как разности внутреннего
и внешнего радиусов): если u=x-y, то абсолютная погрешность
σu=σx2+σy2
меняется мало, однако относительная погрешность
εu=σux-y
может оказаться неприемлемо большой, если x≈y.
Вычисление дисперсии ошибки исследуемой системы
Структура
исследуемой системы приведена на рис.
4.2.
Рис.
4.2. Структурная схема лабораторной САУ.
Передаточная
функция ошибки от полезного сигнала:
где
Кпе
= КпСп;
Кое
= К0С0;
p
= s
– оператор Лапласа;
Т02=
Ти
— искомый параметр.
Передаточная
функция ошибки от помехи:
Полезный
сигнал представляет собой синусоиду
со случайной фазой
G(t)
= Asin(0t
+ f) ,
у
которой фаза распределена по равномерному
закону
P(f)
= {1/(2)
при | f |
;
0 при | f | > }
Составляющая
ошибки от полезного сигнала может быть
вычислена по формуле (11). Спектральная
плотность синусоидального сигнала
представляет собой сумму двух -функций,
расположенных на частотах 0
и -0:
Sg()
= A2[(
+
0)
+ (
—
0)].
(13)
После
подстановки (13) в выражение (11) получается:
С
учетом свойства -функции
можно
записать
Составляющая
Den
дисперсии De
от помехи N(t)
определяется следующим образом.
Рис.
4.3. Спектральная плотность помехи.
На
рис. 4.3. приведен график спектральной
плотности помехи. Из графика видно, что
математическое ожидание помехи равно
нулю. Величина Sno
определяется
из выражения
Отсюда
Верхняя
n2
и нижняя n1
частоты спектра помехи и среднеквадратичное
отклонение n
заданы.
Дисперсия
ошибки от помехи согласно (12) определяется
следующим образом:
Суммарная
дисперсия ошибки

Выражение
(14) позволяет построить график зависимости
дисперсии ошибки от постоянной времени
Т02.
Характер этой зависимости показан на
рис.4.4. Как видно из графика, функция
De(T02)
имеет минимум при T02опт.
Рис.
4.4. Графики зависимостей дисперсии
ошибки САУ
от
постоянной времени объекта управления.
Определение
оптимального значения постоянной
времени T02опт
является конечной целью данной
лабораторной работы.
Значения
параметров, входящих в формулу (14):
0
= 6 c-1;
n1
= 7,85 c-1;
n2
= 126 c-1;
КпСп
= 0,1; (Cп
= 0,1); К0С0
= 10; (Co = 1); Сnn
= 13; (Сn
= 1); Dn
= n2
— n1
= 118,15;
T02
= 0,011c
— изменяется
в ходе эксперимента.
Экспериментальное определение дисперсии.
В
данной лабораторной работе сигнал
ошибки e(t)
проходит через квадратор, на выходе
которого получается сигнал e2(t).
Затем этот сигнал поступает на вход
апериодического звена с постоянной
времени Т.
Сигнал
на выходе апериодического звена можно
описать функцией:
где
exp(-t/T)/T = L-1{
1/(Tp+1) } — весовая функция апериодического
звена.
При
T
предел функции f(e) определяется следующей
зависимостью:
Положив
верхний предел равным Т
и переобозначив переменную интегрирования,
можно получить
Таким
образом, если постоянная времени
апериодического звена T,
то на его выходе получается значение
дисперсии ошибки De.
Но, так как время наблюдения и постоянная
времени не могут быть бесконечными, то
фактически на выходе апериодического
звена получается приближенная оценка
дисперсии
Если
время наблюдения выбрать равным
постоянной времени Т,
которая определяется из условия
T
50/н,
где
н
— низшая частота спектра случайного
сигнала e2(t),
то точность вычисления дисперсии
составит примерно 2%, что вполне достаточно
для практики. За низшую частоту спектра
принимают частоту полезного сигнала
0
=
6 c-1.
Тогда необходимая постоянная времени
апериодического звена Т
= 10 с,
что и реализовано в лабораторном стенде.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Среднее арифметическое, как известно, используется для получения обобщающей характеристики некоторого набора данных. Если данные более-менее однородны и в них нет аномальных наблюдений (выбросов), то среднее хорошо обобщает данные, сведя к минимуму влияние случайных факторов (они взаимопогашаются при сложении).
Когда анализируемые данные представляют собой выборку (которая состоит из случайных значений), то среднее арифметическое часто (но не всегда) выступает в роли приближенной оценки математического ожидания. Почему приближенной? Потому что среднее арифметическое – это величина, которая зависит от набора случайных чисел, и, следовательно, сама является случайной величиной. При повторных экспериментах (даже в одних и тех же условиях) средние будут отличаться друг от друга.
Для того, чтобы на основе статистического анализа данных делать корректные выводы, необходимо оценить возможный разброс полученного результата. Для этого рассчитываются различные показатели вариации. Но то исходные данные. И как мы только что установили, среднее арифметическое также обладает разбросом, который необходимо оценить и учитывать в дальнейшем (в выводах, в выборе метода анализа и т.д.).
Интуитивно понятно, что разброс средней должен быть как-то связан с разбросом исходных данных. Основной характеристикой разброса средней выступает та же дисперсия.
Дисперсия выборочных данных – это средний квадрат отклонения от средней, и рассчитать ее по исходным данным не составляет труда, например, в Excel предусмотрены специальные функции. Однако, как же рассчитать дисперсию средней, если в распоряжении есть только одна выборка и одно среднее арифметическое?
Расчет дисперсии и стандартной ошибки средней арифметической
Чтобы получить дисперсию средней арифметической нет необходимости проводить множество экспериментов, достаточно иметь только одну выборку. Это легко доказать. Для начала вспомним, что средняя арифметическая (простая) рассчитывается по формуле:
где xi – значения переменной,
n – количество значений.
Теперь учтем два свойства дисперсии, согласно которым, 1) — постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат и 2) — дисперсия суммы независимых случайных величин равняется сумме соответствующих дисперсий. Предполагается, что каждое случайное значение xi обладает одинаковым разбросом, поэтому несложно вывести формулу дисперсии средней арифметической:
Используя более привычные обозначения, формулу записывают как:
где σ2 – это дисперсия, случайной величины, причем генеральная.
На практике же, генеральная дисперсия известна далеко не всегда, точнее совсем редко, поэтому в качестве оной используют выборочную дисперсию:
Стандартное отклонение средней арифметической называется стандартной ошибкой средней и рассчитывается, как квадратный корень из дисперсии.
Формула стандартной ошибки средней при использовании генеральной дисперсии
Формула стандартной ошибки средней при использовании выборочной дисперсии
Последняя формула на практике используется чаще всего, т.к. генеральная дисперсия обычно не известна. Чтобы не вводить новые обозначения, стандартную ошибку средней обычно записывают в виде соотношения стандартного отклонения выборки и корня объема выборки.
Назначение и свойство стандартной ошибки средней арифметической
Стандартная ошибка средней много, где используется. И очень полезно понимать ее свойства. Посмотрим еще раз на формулу стандартной ошибки средней:
Числитель – это стандартное отклонение выборки и здесь все понятно. Чем больше разброс данных, тем больше стандартная ошибка средней – прямо пропорциональная зависимость.
Посмотрим на знаменатель. Здесь находится квадратный корень из объема выборки. Соответственно, чем больше объем выборки, тем меньше стандартная ошибка средней. Для наглядности изобразим на одной диаграмме график нормально распределенной переменной со средней равной 10, сигмой – 3, и второй график – распределение средней арифметической этой же переменной, полученной по 16-ти наблюдениям (которое также будет нормальным).
Судя по формуле, разброс стандартной ошибки средней должен быть в 4 раза (корень из 16) меньше, чем разброс исходных данных, что и видно на рисунке выше. Чем больше наблюдений, тем меньше разброс средней.
Казалось бы, что для получения наиболее точной средней достаточно использовать максимально большую выборку и тогда стандартная ошибка средней будет стремиться к нулю, а сама средняя, соответственно, к математическому ожиданию. Однако квадратный корень объема выборки в знаменателе говорит о том, что связь между точностью выборочной средней и размером выборки не является линейной. Например, увеличение выборки с 20-ти до 50-ти наблюдений, то есть на 30 значений или в 2,5 раза, уменьшает стандартную ошибку средней только на 36%, а со 100-а до 130-ти наблюдений (на те же 30 значений), снижает разброс данных лишь на 12%.
Лучше всего изобразить эту мысль в виде графика зависимости стандартной ошибки средней от размера выборки. Пусть стандартное отклонение равно 10 (на форму графика это не влияет).
Видно, что примерно после 50-ти значений, уменьшение стандартной ошибки средней резко замедляется, после 100-а – наклон постепенно становится почти нулевым.
Таким образом, при достижении некоторого размера выборки ее дальнейшее увеличение уже почти не сказывается на точности средней. Этот факт имеет далеко идущие последствия. Например, при проведении выборочного обследования населения (опроса) чрезмерное увеличение выборки ведет к неоправданным затратам, т.к. точность почти не меняется. Именно поэтому количество опрошенных редко превышает 1,5 тысячи человек. Точность при таком размере выборки часто является достаточной, а дальнейшее увеличение выборки – нецелесообразным.
Подведем итог. Расчет дисперсии и стандартной ошибки средней имеет довольно простую формулу и обладает полезным свойством, связанным с тем, что относительно хорошая точность средней достигается уже при 100 наблюдениях (в этом случае стандартная ошибка средней становится в 10 раз меньше, чем стандартное отклонение выборки). Больше, конечно, лучше, но бесконечно увеличивать объем выборки не имеет практического смысла. Хотя, все зависит от поставленных задач и цены ошибки. В некоторых опросах участие принимают десятки тысяч людей.
Дисперсия и стандартная ошибка средней имеют большое практическое значение. Они используются в проверке гипотез и расчете доверительных интервалов.
Поделиться в социальных сетях:
15. Оценка дисперсии случайной ошибки модели регрессии
При проведении регрессионного анализа основная трудность заключается в том, что генеральная дисперсия случайной ошибки является неизвестной величиной, что вызывает необходимость в расчёте её несмещённой выборочной оценки.
Несмещённой оценкой дисперсии (или исправленной дисперсией) случайной ошибки линейной модели парной регрессии называется величина, рассчитываемая по формуле:
где n – это объём выборочной совокупности;
еi– остатки регрессионной модели:
Для линейной модели множественной регрессии несмещённая оценка дисперсии случайной ошибки рассчитывается по формуле:
где k – число оцениваемых параметров модели регрессии.
Оценка матрицы ковариаций случайных ошибок Cov(?) будет являться оценочная матрица ковариаций:
где In – единичная матрица.
Оценка дисперсии случайной ошибки модели регрессии распределена по ?2(хи-квадрат) закону распределения с (n-k-1) степенями свободы.
Для доказательства несмещённости оценки дисперсии случайной ошибки модели регрессии необходимо доказать справедливость равенства
Доказательство. Примем без доказательства справедливость следующих равенств:
где G2(?) – генеральная дисперсия случайной ошибки;
S2(?) – выборочная дисперсия случайной ошибки;
– выборочная оценка дисперсии случайной ошибки.
Тогда:
т. е.
что и требовалось доказать.
Следовательно, выборочная оценка дисперсии случайной ошибки
является несмещённой оценкой генеральной дисперсии случайной ошибки модели регрессии G2(?).
При условии извлечения из генеральной совокупности нескольких выборок одинакового объёма n и при одинаковых значениях объясняющих переменных х, наблюдаемые значения зависимой переменной у будут случайным образом колебаться за счёт случайного характера случайной компоненты ?. Отсюда можно сделать вывод, что будут варьироваться и зависеть от значений переменной у значения оценок коэффициентов регрессии и оценка дисперсии случайной ошибки модели регрессии.
Для иллюстрации данного утверждения докажем зависимость значения МНК-оценки
от величины случайной ошибки ?.
МНК-оценка коэффициента ?1 модели регрессии определяется по формуле:
В связи с тем, что переменная у зависит от случайной компоненты ? (yi=?0+?1xi+?i), то ковариация между зависимой переменной у и независимой переменной х может быть представлена следующим образом:
Для дальнейших преобразования используются свойства ковариации:
1) ковариация между переменной х и константой С равна нулю: Cov(x,C)=0, C=const;
2) ковариация переменной х с самой собой равна дисперсии этой переменной: Cov(x,x)=G2(x).
Исходя из указанных свойств ковариации, справедливы следующие равенства:
Cov(x,?0)=0 (?0=const);
Cov(x, ?1x)= ?1*Cov(x,x)= ?1*G2(x).
Следовательно, ковариация между зависимой и независимой переменными Cov(x,y) может быть записана как:
Cov(x,y)= ?1G2(x)+Cov(x,?).
В результате МНК-оценка коэффициента ?1 модели регрессии примет вид:
Таким образом, МНК-оценка
может быть представлена как сумма двух компонент:
1) константы ?1, т. е. истинного значения коэффициента;
2) случайной ошибки Cov(x,?), вызывающей вариацию коэффициента модели регрессии.
Однако на практике подобное разложение МНК-оценки невозможно, потому что истинные значения коэффициентов модели регрессии и значения случайной ошибки являются неизвестными. Теоретически данное разложение можно использовать при изучении статистических свойств МНК-оценок.
Аналогично доказывается, что МНК-оценка
коэффициента модели регрессии и несмещённая оценка дисперсии случайной ошибки
могут быть представлены как сумма постоянной составляющей (константы) и случайной компоненты, зависящей от ошибки модели регрессии ?.
Данный текст является ознакомительным фрагментом.
Читайте также
11. Критерии оценки неизвестных коэффициентов модели регрессии
11. Критерии оценки неизвестных коэффициентов модели регрессии
В ходе регрессионного анализа была подобрана форма связи, которая наилучшим образом отражает зависимость результативной переменной у от факторной переменной х:y=f(x).Необходимо оценить неизвестные
14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии
14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии
Помимо метода наименьших квадратов, с помощью которого в большинстве случаев определяются неизвестные параметры модели регрессии, в случае линейной модели парной регрессии
18. Характеристика качества модели регрессии
18. Характеристика качества модели регрессии
Качеством модели регрессии называется адекватность построенной модели исходным (наблюдаемым) данным.Для оценки качества модели регрессии используются специальные показатели.Качество линейной модели парной регрессии
22. Проверка гипотезы о значимости коэффициентов модели парной регрессии
22. Проверка гипотезы о значимости коэффициентов модели парной регрессии
Проверкой статистической гипотезы о значимости отдельных параметров модели называется проверка предположения о том, что данные параметры значимо отличаются от нуля.Необходимость проверки
25. Точечный и интервальный прогнозы для модели парной регрессии
25. Точечный и интервальный прогнозы для модели парной регрессии
Одна из задач эконометрического моделирования заключается в прогнозировании поведения исследуемого явления или процесса в будущем. В большинстве случаев данная задача решается на основе регрессионных
32. Построение частных коэффициентов корреляции для модели множественной регрессии через показатель остаточной дисперсии и коэффициент множественной детерминации
32. Построение частных коэффициентов корреляции для модели множественной регрессии через показатель остаточной дисперсии и коэффициент множественной детерминации
Помимо рекуррентных формул, которые используются для построения частных коэффициентов корреляции для
35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом
35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом
Проверка значимости коэффициентов регрессии означает проверку основной гипотезы об их значимом отличии от нуля.Основная гипотеза состоит в предположении о незначимости
39. Модели регрессии, нелинейные по факторным переменным
39. Модели регрессии, нелинейные по факторным переменным
При исследовании социально-экономических явлений и процессов далеко не все зависимости можно описать с помощью линейной связи. Поэтому в эконометрическом моделировании широко используется класс нелинейных
40. Модели регрессии, нелинейные по оцениваемым коэффициентам
40. Модели регрессии, нелинейные по оцениваемым коэффициентам
Нелинейными по оцениваемым параметрам моделями регрессииназываются модели, в которых результативная переменная yi нелинейно зависит от коэффициентов модели ?0…?n.К моделям регрессии, нелинейными по
41. Модели регрессии с точками разрыва
41. Модели регрессии с точками разрыва
Определение. Моделями регрессии с точками разрыва называются модели, которые нельзя привести к линейной форме, т. е. внутренне нелинейные модели регрессии.Модели регрессии делятся на два класса:1) кусочно-линейные модели регрессии;2)
44. Методы нелинейного оценивания коэффициентов модели регрессии
44. Методы нелинейного оценивания коэффициентов модели регрессии
Функцией потерь или ошибок называется функционал вида
Также в качестве функции потерь может быть использована сумма модулей отклонений наблюдаемых значений результативного признака у от теоретических
46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии
46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии
На нелинейные модели регрессии, которые являются внутренне линейными, т. е. сводимыми к линейному виду, распространяются все
57. Гетероскедастичность остатков модели регрессии
57. Гетероскедастичность остатков модели регрессии
Случайной ошибкой называется отклонение в линейной модели множественной регрессии:?i=yi–?0–?1x1i–…–?mxmiВ связи с тем, что величина случайной ошибки модели регрессии является неизвестной величиной, рассчитывается
60. Устранение гетероскедастичности остатков модели регрессии
60. Устранение гетероскедастичности остатков модели регрессии
Существует множество методов устранения гетероскедастичности остатков модели регрессии. Рассмотрим некоторые из них.Наиболее простым методом устранения гетероскедастичности остатков модели регрессии
63. Устранение автокорреляции остатков модели регрессии
63. Устранение автокорреляции остатков модели регрессии
В связи с тем, что наличие в модели регрессии автокорреляции между остатками модели может привести к негативным результатам всего процесса оценивания неизвестных коэффициентов модели, автокорреляция остатков
67. Модели регрессии с переменной структурой. Фиктивные переменные
67. Модели регрессии с переменной структурой. Фиктивные переменные
При построении модели регрессии может возникнуть ситуация, когда в неё необходимо включить не только количественные, но и качественные переменные (например, возраст, образование, пол, расовую
Пусть
Поскольку
заменяются две величины (
и
),
то это вызывает смещение оценки
:
. (1.22)
Покажем
это .
Известно
что
.
Пусть
Х1,
Х2,…,
Хi
,…,Xn
— независимые случайные величины, каждая
из которых имеет один и тот же закон
распределения с числовыми характеристиками:
и D(Xi)=D0.
Пусть
подставим в (*), тогда:
Найдем
E[Dв]:
Итак
Что и требовалось доказать.
При
больших п
смещение невелико, им можно пренебречь,
но при малых выборках оно существенно.
Таким
образм,
есть несмещенная оценка дисперсии или
.
(1.23)
Тогда
исправленное среднее квадратическое
отклонение имеет вид:
.
(1.24)
Для
интервальной оценки используется
выражение
,
где
находится по формуле (1.24).
Замечание.
Однако для больших выборок можно считать,
что
.
В случае малых выборок (п
< 30) пользуются исправленной дисперсией
по формуле (1.24).
По
закону больших чисел
является состоятельной оценкой для
генеральной дисперсии. А так как множитель
при
,
то
также является состоятельной оценкой
для
.
Оценка
,
строго говоря, не является эффективной
оценкой для
,
однако при наличии нормального
распределения ее можно считать приближенно
эффективной.
Замечание.
Если известно точное значение
математического ожидания «
»
для n
измерений, то E(Xi)
=
где хi
– отдельные измерения. Исправленная
(несмещённая) дисперсия находится по
формуле
(1.25)
Действительно.
,
т.е. E(D*в)
= D0
.
Пример
1.19. В ящике содержатся стержни трех
размеров (N
= 3): 12 см, 14 см и 16 см с соответствующими
долями 0,1; 0,3; 0,6. Производится повторная
выборка двух стержней (n
= 2). Найти
все возможные выборочные распределения
и построить законы распределения для
и
.
Проверить на данном примере справедливость
равенств
.
Решение.
Определим
количество возможных выборок:
.
Закон
распределения генеральной совокупности
представлен в следующей в таблице
|
X |
12 |
14 |
16 |
|
P |
0,1 |
0,3 |
0,6 |
Вычислим
генеральные характеристики :
Все
выборочные законы представлены в
следующей таблице.
|
№ выборки |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
12 12 |
12 14 |
12 16 |
14 12 |
14 14 |
14 16 |
16 12 |
16 14 |
16 16 |
|
|
2 |
1 1 |
1 1 |
1 1 |
2 |
1 1 |
1 1 |
1 1 |
2 |
|
|
12 |
13 |
14 |
13 |
14 |
15 |
14 |
15 |
16 |
|
|
0 |
1 |
4 |
1 |
0 |
1 |
4 |
1 |
0 |
|
|
0,01 |
0,03 |
0,06 |
0,03 |
0,09 |
0,18 |
0,06 |
0,18 |
0,36 |
Проверим,
что
.
По
данным последней таблицы получим строим
законы распределения для
и Dв
и находим соответствующие характеристики.
|
|
12 |
13 |
14 |
15 |
16 |
|
|
P |
0,01 |
0,06 |
0,21 |
0,36 |
0,36 |
1 |
,
|
|
0 |
1 |
4 |
|
|
|
0,46 |
0,42 |
0,12 |
1 |
E[Dв]=0,42+0,48=0.9/
Итак,
,
Откуда
следует:
и
при n
= 2.
Пример
1.20. Даны результаты 6 независимых
измерений одной и той же величины
прибором, не имеющим систематических
ошибок: 36; 37; 32; 43; 39; 41. Найдите несмещенную
оценку дисперсии ошибок измерений,
если истинная длина неизвестна.
Решение.
Представим исходные данные в виде
таблицы:
|
xi |
32 |
36 |
37 |
39 |
41 |
43 |
|
р |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
Вычислим
последовательно
;
Отсюда
Пример
1.21.
В условиях предыдущей задачи найдите
несмещённую оценку дисперсии ошибок
измерений, если истинная величина
известна и равна 37,8.
Решение
В этом случае в формулу подставляется
не выборочное среднее, а истинная
величина:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Несмещенная оценка выборочной дисперсии
Краткая теория
Пусть из генеральной совокупности в результате
независимых наблюдений над количественным
признаком
извлечена повторная выборка объема
:
При этом
Требуется по данным выборки оценить (приближенно найти) неизвестную
генеральную дисперсию
.
Если в качестве оценки генеральной дисперсии принять выборочную дисперсию, то
эта оценка будет приводить в систематическим ошибкам, давая заниженное значение
генеральной дисперсии. Объясняется это тем, что, как можно доказать, выборочная
дисперсия является смещенной оценкой
,
другими словами, математическое ожидание выборочной дисперсии не равно
оцениваемой генеральной дисперсии, а равно:
Легко «исправить» выборочную дисперсию так, чтобы ее математическое
ожидание было равно генеральной дисперсии. Достаточно для этого умножить
на дробь
.
Сделав это, получим исправленную дисперсию, которую обычно обозначают через
:
Исправленная дисперсия является, конечно, несмещенной оценкой
генеральной дисперсии. Действительно:
Итак, в качестве оценки генеральной дисперсии принимают
исправленную дисперсию:
Для оценки среднего квадратического
отклонения генеральной совокупности используют исправленное среднее квадратическое отклонение, которое равно квадратному корню
из исправленной дисперсии:
При достаточно больших значениях
объема выборки выборочная и исправленная
дисперсия отличаются мало. На практике используются исправленной дисперсией,
если примерно
.
Пример решения задачи
Задача
Найти
несмещенную выборочную дисперсию на основании данного распределения выборки.
Решение
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Выборочная дисперсия является смещенной оценкой генеральной дисперсии, поэтому в статистике применяют также исправленную выборочную дисперсию, которая является несмещенной оценкой генеральной дисперсии.
Сумма
частот:
Вычислим
среднюю:
Средняя квадратов:
Несмещенная
выборочная дисперсия:
Ответ:
Кроме этой задачи на другой странице сайта есть
пример расчета исправленной выборочной дисперсии и среднего квадратического отклонения для интервального вариационного ряда
|
Заблокирован |
|
|
1 |
|
Найти несмещенную оценку дисперсии ошибок измерений03.08.2016, 18:54. Показов 7812. Ответов 1
Даны результаты 5 независимых измерений одной и той же величины прибором, не имеющим систематических ошибок: 10, 9, 11, 8, 12. Найти несмещенную оценку дисперсии ошибок измерений, если истинная длина неизвестна. Правильно ли я нашел нужное значение? Несмещенная оценка дисперсии ошибок измерений вычисляется как: Найдем выборочное среднее: Используем формулу для Ответ 2 правильный?
__________________ 0 |
|
1941 / 1050 / 159 Регистрация: 06.12.2012 Сообщений: 4,598 |
|
|
03.08.2016, 19:07 |
2 |
|
1 |
15. Оценка дисперсии случайной ошибки модели регрессии
При проведении регрессионного анализа основная трудность заключается в том, что генеральная дисперсия случайной ошибки является неизвестной величиной, что вызывает необходимость в расчёте её несмещённой выборочной оценки.
Несмещённой оценкой дисперсии (или исправленной дисперсией) случайной ошибки линейной модели парной регрессии называется величина, рассчитываемая по формуле:
где n – это объём выборочной совокупности;
еi– остатки регрессионной модели:
Для линейной модели множественной регрессии несмещённая оценка дисперсии случайной ошибки рассчитывается по формуле:
где k – число оцениваемых параметров модели регрессии.
Оценка матрицы ковариаций случайных ошибок Cov(?) будет являться оценочная матрица ковариаций:
где In – единичная матрица.
Оценка дисперсии случайной ошибки модели регрессии распределена по ?2(хи-квадрат) закону распределения с (n-k-1) степенями свободы.
Для доказательства несмещённости оценки дисперсии случайной ошибки модели регрессии необходимо доказать справедливость равенства
Доказательство. Примем без доказательства справедливость следующих равенств:
где G2(?) – генеральная дисперсия случайной ошибки;
S2(?) – выборочная дисперсия случайной ошибки;
– выборочная оценка дисперсии случайной ошибки.
Тогда:
т. е.
что и требовалось доказать.
Следовательно, выборочная оценка дисперсии случайной ошибки
является несмещённой оценкой генеральной дисперсии случайной ошибки модели регрессии G2(?).
При условии извлечения из генеральной совокупности нескольких выборок одинакового объёма n и при одинаковых значениях объясняющих переменных х, наблюдаемые значения зависимой переменной у будут случайным образом колебаться за счёт случайного характера случайной компоненты ?. Отсюда можно сделать вывод, что будут варьироваться и зависеть от значений переменной у значения оценок коэффициентов регрессии и оценка дисперсии случайной ошибки модели регрессии.
Для иллюстрации данного утверждения докажем зависимость значения МНК-оценки
от величины случайной ошибки ?.
МНК-оценка коэффициента ?1 модели регрессии определяется по формуле:
В связи с тем, что переменная у зависит от случайной компоненты ? (yi=?0+?1xi+?i), то ковариация между зависимой переменной у и независимой переменной х может быть представлена следующим образом:
Для дальнейших преобразования используются свойства ковариации:
1) ковариация между переменной х и константой С равна нулю: Cov(x,C)=0, C=const;
2) ковариация переменной х с самой собой равна дисперсии этой переменной: Cov(x,x)=G2(x).
Исходя из указанных свойств ковариации, справедливы следующие равенства:
Cov(x,?0)=0 (?0=const);
Cov(x, ?1x)= ?1*Cov(x,x)= ?1*G2(x).
Следовательно, ковариация между зависимой и независимой переменными Cov(x,y) может быть записана как:
Cov(x,y)= ?1G2(x)+Cov(x,?).
В результате МНК-оценка коэффициента ?1 модели регрессии примет вид:
Таким образом, МНК-оценка
может быть представлена как сумма двух компонент:
1) константы ?1, т. е. истинного значения коэффициента;
2) случайной ошибки Cov(x,?), вызывающей вариацию коэффициента модели регрессии.
Однако на практике подобное разложение МНК-оценки невозможно, потому что истинные значения коэффициентов модели регрессии и значения случайной ошибки являются неизвестными. Теоретически данное разложение можно использовать при изучении статистических свойств МНК-оценок.
Аналогично доказывается, что МНК-оценка
коэффициента модели регрессии и несмещённая оценка дисперсии случайной ошибки
могут быть представлены как сумма постоянной составляющей (константы) и случайной компоненты, зависящей от ошибки модели регрессии ?.
Данный текст является ознакомительным фрагментом.
Читайте также
11. Критерии оценки неизвестных коэффициентов модели регрессии
11. Критерии оценки неизвестных коэффициентов модели регрессии
В ходе регрессионного анализа была подобрана форма связи, которая наилучшим образом отражает зависимость результативной переменной у от факторной переменной х:y=f(x).Необходимо оценить неизвестные
14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии
14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии
Помимо метода наименьших квадратов, с помощью которого в большинстве случаев определяются неизвестные параметры модели регрессии, в случае линейной модели парной регрессии
18. Характеристика качества модели регрессии
18. Характеристика качества модели регрессии
Качеством модели регрессии называется адекватность построенной модели исходным (наблюдаемым) данным.Для оценки качества модели регрессии используются специальные показатели.Качество линейной модели парной регрессии
22. Проверка гипотезы о значимости коэффициентов модели парной регрессии
22. Проверка гипотезы о значимости коэффициентов модели парной регрессии
Проверкой статистической гипотезы о значимости отдельных параметров модели называется проверка предположения о том, что данные параметры значимо отличаются от нуля.Необходимость проверки
25. Точечный и интервальный прогнозы для модели парной регрессии
25. Точечный и интервальный прогнозы для модели парной регрессии
Одна из задач эконометрического моделирования заключается в прогнозировании поведения исследуемого явления или процесса в будущем. В большинстве случаев данная задача решается на основе регрессионных
32. Построение частных коэффициентов корреляции для модели множественной регрессии через показатель остаточной дисперсии и коэффициент множественной детерминации
32. Построение частных коэффициентов корреляции для модели множественной регрессии через показатель остаточной дисперсии и коэффициент множественной детерминации
Помимо рекуррентных формул, которые используются для построения частных коэффициентов корреляции для
35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом
35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом
Проверка значимости коэффициентов регрессии означает проверку основной гипотезы об их значимом отличии от нуля.Основная гипотеза состоит в предположении о незначимости
39. Модели регрессии, нелинейные по факторным переменным
39. Модели регрессии, нелинейные по факторным переменным
При исследовании социально-экономических явлений и процессов далеко не все зависимости можно описать с помощью линейной связи. Поэтому в эконометрическом моделировании широко используется класс нелинейных
40. Модели регрессии, нелинейные по оцениваемым коэффициентам
40. Модели регрессии, нелинейные по оцениваемым коэффициентам
Нелинейными по оцениваемым параметрам моделями регрессииназываются модели, в которых результативная переменная yi нелинейно зависит от коэффициентов модели ?0…?n.К моделям регрессии, нелинейными по
41. Модели регрессии с точками разрыва
41. Модели регрессии с точками разрыва
Определение. Моделями регрессии с точками разрыва называются модели, которые нельзя привести к линейной форме, т. е. внутренне нелинейные модели регрессии.Модели регрессии делятся на два класса:1) кусочно-линейные модели регрессии;2)
44. Методы нелинейного оценивания коэффициентов модели регрессии
44. Методы нелинейного оценивания коэффициентов модели регрессии
Функцией потерь или ошибок называется функционал вида
Также в качестве функции потерь может быть использована сумма модулей отклонений наблюдаемых значений результативного признака у от теоретических
46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии
46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии
На нелинейные модели регрессии, которые являются внутренне линейными, т. е. сводимыми к линейному виду, распространяются все
57. Гетероскедастичность остатков модели регрессии
57. Гетероскедастичность остатков модели регрессии
Случайной ошибкой называется отклонение в линейной модели множественной регрессии:?i=yi–?0–?1x1i–…–?mxmiВ связи с тем, что величина случайной ошибки модели регрессии является неизвестной величиной, рассчитывается
60. Устранение гетероскедастичности остатков модели регрессии
60. Устранение гетероскедастичности остатков модели регрессии
Существует множество методов устранения гетероскедастичности остатков модели регрессии. Рассмотрим некоторые из них.Наиболее простым методом устранения гетероскедастичности остатков модели регрессии
63. Устранение автокорреляции остатков модели регрессии
63. Устранение автокорреляции остатков модели регрессии
В связи с тем, что наличие в модели регрессии автокорреляции между остатками модели может привести к негативным результатам всего процесса оценивания неизвестных коэффициентов модели, автокорреляция остатков
67. Модели регрессии с переменной структурой. Фиктивные переменные
67. Модели регрессии с переменной структурой. Фиктивные переменные
При построении модели регрессии может возникнуть ситуация, когда в неё необходимо включить не только количественные, но и качественные переменные (например, возраст, образование, пол, расовую
В статистике , то несмещенная оценка дисперсии переменных возмущений , также называется несмещенной оценкой дисперсии ошибки , является точечной оценкой , что обладает свойством качества , что оценивает неизвестные дисперсии переменных возмущений в непредвзято , если предположениях Гаусса-Markow применяются.
Введение в проблему
Дисперсия ошибки , и остаточная дисперсия , экспериментальные ошибки , Störgrößenvarianz , дисперсия возмущений , необъяснимой дисперсии , необъясненные дисперсии называют , являются дисперсией функции регрессии в популяции и дисперсии условий ошибок или помех. Дисперсия ошибки — это неизвестный параметр, который необходимо оценить на основе информации о выборке. Он измеряет отклонения, которые можно проследить до ошибок измерения или переменных возмущений. Первый очевидный подход заключался бы в оценке дисперсии смешивающих переменных, как обычно, с оценкой максимального правдоподобия (см. Классическую линейную модель нормальной регрессии ). Однако эта оценка проблематична, как будет объяснено ниже.
Ожидаемая оценка дисперсии возмущающих переменных
Простая линейная регрессия
Хотя иногда предполагается, что гомоскедастическая дисперсия в генеральной совокупности известна, следует исходить из того, что она неизвестна в большинстве случаев использования (например, при оценке параметров спроса в экономических моделях или производственных функций ). Поскольку дисперсия переменной возмущения имеет неизвестное значение, численные значения дисперсии параметра наклона и абсолютного члена не могут быть оценены, поскольку формулы зависят от этого. Однако эти количества можно оценить по имеющимся данным. Очевидной оценкой переменных возмущения является невязка , которую представляет выборочная функция регрессии . Таким образом, информация, содержащаяся в остатках, может использоваться для оценки дисперсии возмущающей переменной. Из-за того, что , с частотной точки зрения, « среднее значение » равно . Однако размер не может быть соблюден, так как нельзя наблюдать переменные возмущения. Если вместо текущего используется наблюдаемый аналог , это приводит к следующей оценке дисперсии возмущающей переменной


-
,
где остаточная сумма квадратов. Эта оценка представляет собой выборочное среднее оцененных квадратов остатков и может использоваться для оценки смешанной дисперсии . Можно показать, что приведенное выше определение также соответствует оценке максимального правдоподобия ( ). Однако оценщик не соответствует общим критериям качества для точечных оценщиков и поэтому нечасто используется. Например, оценщик не беспристрастный для . Это связано с тем, что ожидаемое значение дает остаточную сумму квадратов и, следовательно, применяется к ожидаемому значению этого средства оценки . В простой линейной регрессии можно показать в предположениях классической модели единственной линейной регрессии, что несмещенная оценка , т.е. .h оценка, которой удовлетворяет

-
,
при условии, что . Эта несмещенная оценка представляет собой средний квадрат остаточной величины , которую иногда называют остаточной дисперсией . Корень квадратный из этого несмещенной оценки или остаточной дисперсии называется стандартной ошибкой регрессии . Остаточная дисперсия может быть интерпретирована как средняя модель оценки ошибка и формирует основу для всех дальнейших расчетов ( доверительных интервалов , стандартных ошибок в параметрах регрессии, и т.д.). Оно отличается от приведенного выше выражения тем, что остаточная сумма квадратов корректируется числом степеней свободы . Эту настройку можно интуитивно объяснить тем фактом, что одна теряет две степени свободы при оценке двух неизвестных параметров регрессии и .
Как упоминалось выше, несмещенная оценка для простой линейной регрессии дается выражением
-
,
где и являются методом наименьших квадратов для и .
Чтобы показать точность математического ожидания, используется свойство, заключающееся в том, что остатки могут быть представлены как функция переменных возмущения как . Кроме того, используется свойство, заключающееся в том, что дисперсия оценки KQ определяется выражением . Следует также отметить, что ожидаемое значение оценки KQ задается и то же самое относится к . Ожидание можно доказать следующим образом:

-
.
Дисперсии оценок KQ также могут быть оценены с помощью несмещенной оценки . Например, можно оценить , заменив на. Предполагаемая дисперсия параметра наклона тогда определяется выражением
-
.
Множественная линейная регрессия
В множественной линейной регрессии несмещенная оценка дисперсии возмущающих переменных или остаточной дисперсии дается выражением
-
,
в котором оценки по методу наименьших квадратов и -й строки из экспериментальной конструкции матрицы представляет. В качестве альтернативы несмещенная оценка дисперсии переменных возмущения в множественном случае может быть представлена как

-
.
Это представление является результатом того факта, что остаточная сумма квадратов может быть записана как . Другое альтернативное представление остаточной дисперсии является результатом того факта, что остаточная сумма квадратов также может быть представлена с использованием порождающей невязки матрицы как . Это приводит к остаточной дисперсии
Эта оценка, в свою очередь, может использоваться для вычисления ковариационной матрицы вектора оценки KQ . Если теперь заменить на , получается вектор оценки KQ для оцененной ковариационной матрицы.
-
.
Регрессия со стохастическими регрессорами
В случае регрессии со стохастическими регрессорами со стохастической матрицей регрессора , основанная на ожидании оценка дисперсии переменных возмущения также дается выражением
-
.
Верность ожиданиям можно показать с помощью закона повторного математического ожидания.
веб ссылки
- Ursa Pantle: Неожиданная оценка дисперсии σ² переменных возмущения. 2003 г., по состоянию на 10 апреля 2019 г. (конспект лекций Ульмского университета ).
Индивидуальные доказательства
- ↑ Людвиг фон Ауэр : Эконометрика. Введение. Springer, ISBN 978-3-642-40209-8 , с 6 по. u. обновленное издание. 2013.
- ↑ Людвиг фон Ауэр: Эконометрика. Введение. Springer, ISBN 978-3-642-40209-8 , с 6 по. u. обновленное издание. 2013. 191 с.
- ↑ Джордж Джадж, Р. Картер Хилл, В. Гриффитс, Гельмут Люткеполь , Т. С. Ли. Введение в теорию и практику эконометрики. 2-е издание. John Wiley & Sons, Нью-Йорк / Чичестер / Брисбен / Торонто / Сингапур 1988, ISBN 0-471-62414-4 , стр.170 .
- ^ Людвиг Фармейр , Томас Кнейб , Стефан Ланг, Брайан Маркс: Регрессия: модели, методы и приложения. Springer Science & Business Media, 2013, ISBN 978-3-642-34332-2 , стр.109.
- ^ Людвиг Фармейр, Томас Кнейб, Стефан Ланг, Брайан Маркс: Регрессия: модели, методы и приложения. Springer Science & Business Media, 2013, ISBN 978-3-642-34332-2 , стр.109.
- ^ Карл Мослер и Фридрих Шмид: расчет вероятности и окончательная статистика. Springer-Verlag, 2011, с. 308.
- ↑ Джеффри Марк Вулдридж: Вводная эконометрика: современный подход. 5-е издание. Нельсон Образование 2015
- ↑ Джеффри Марк Вулдридж : Вводная эконометрика: современный подход. 4-е издание. Nelson Education, 2015, стр. 55.
- ↑ Джеффри Марк Вулдридж: Вводная эконометрика: современный подход. 4-е издание. Nelson Education, 2015, стр. 55.



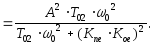


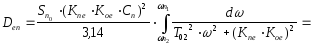

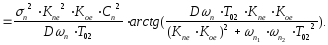



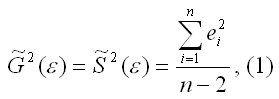
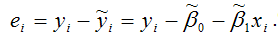
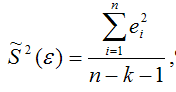
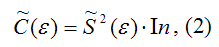
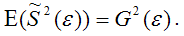
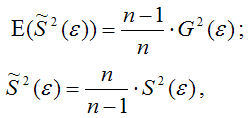
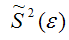
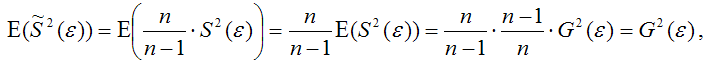
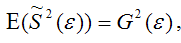
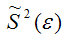
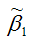
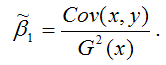
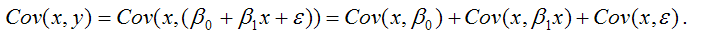
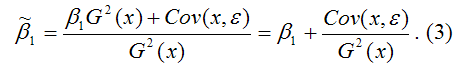
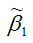
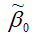
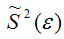
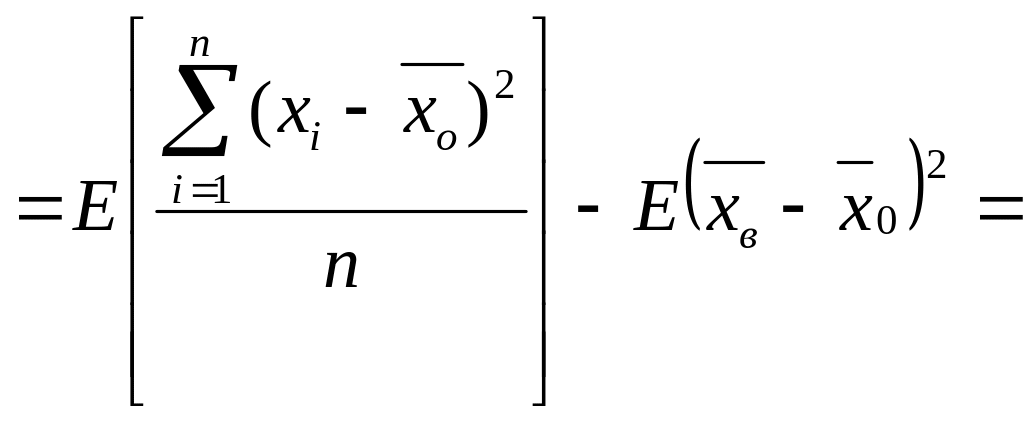
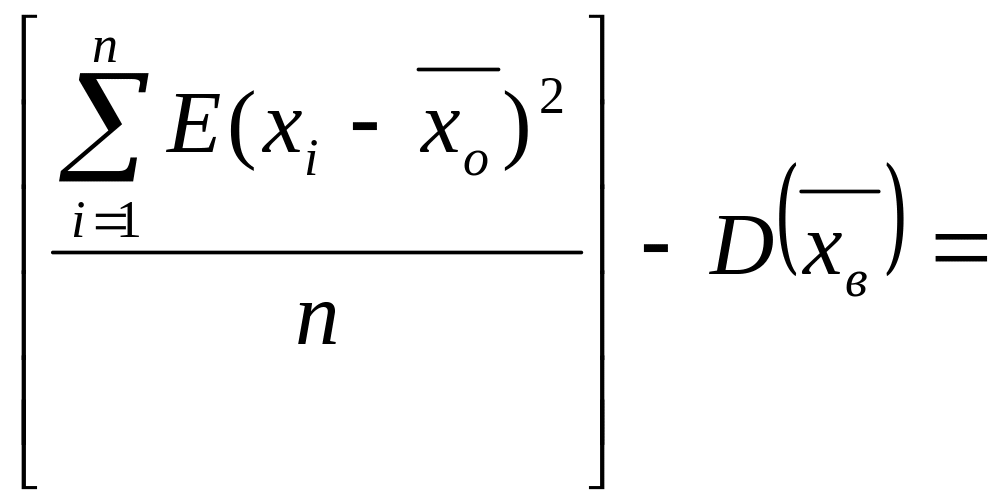
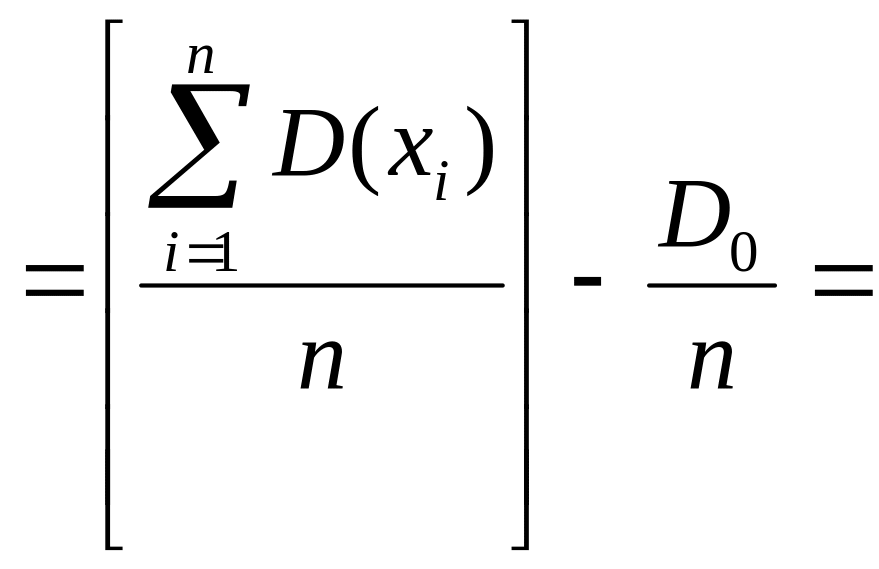
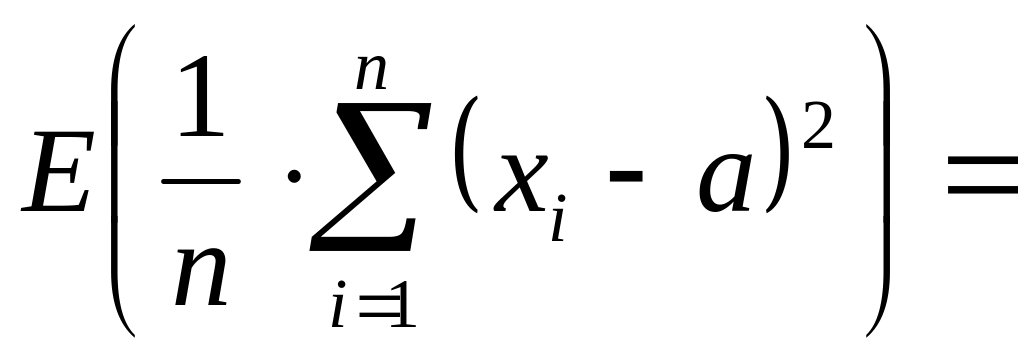
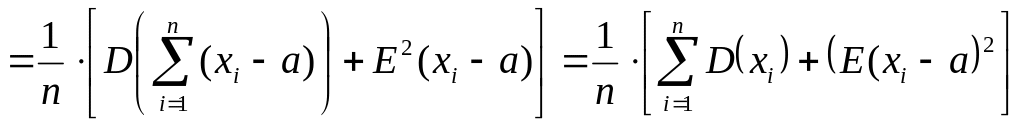
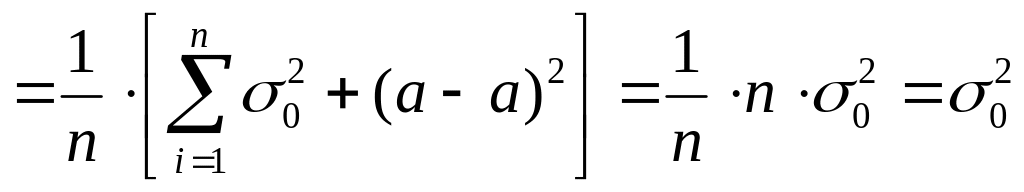
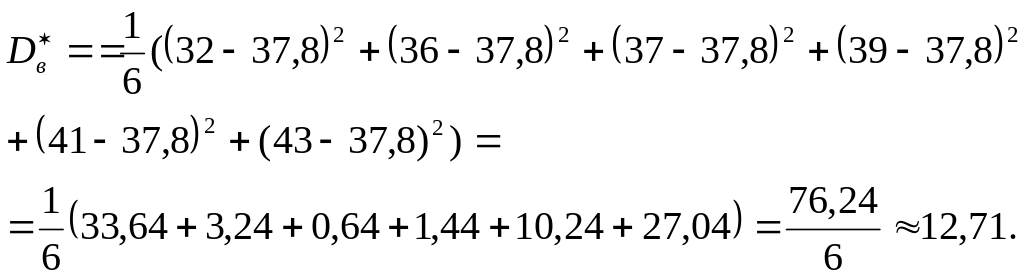
![{ displaystyle sigma ^ {2} = operatorname {E} [( varepsilon _ {i} - operatorname {E} ( varepsilon _ {i})) ^ {2}] quad, i = 1 ldots n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3d3236d5188541aa9126704580731209a9266cc)




































