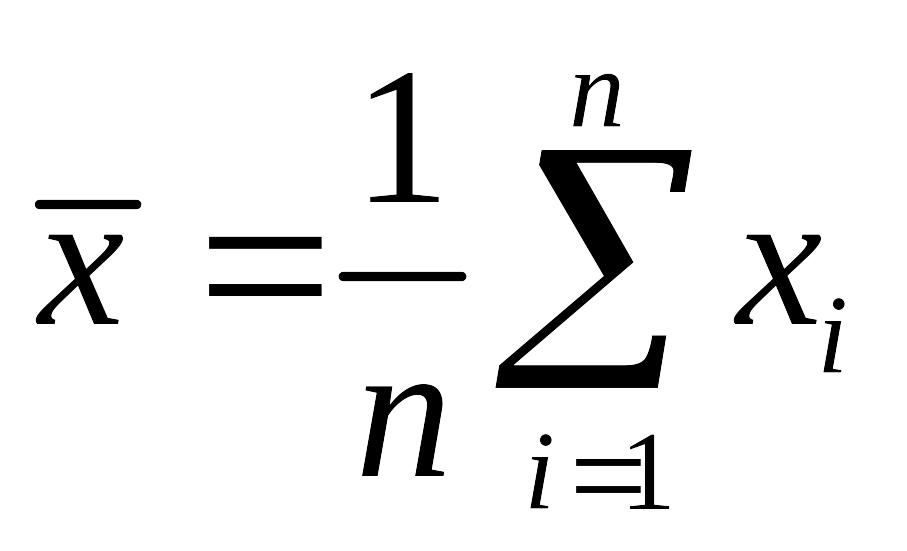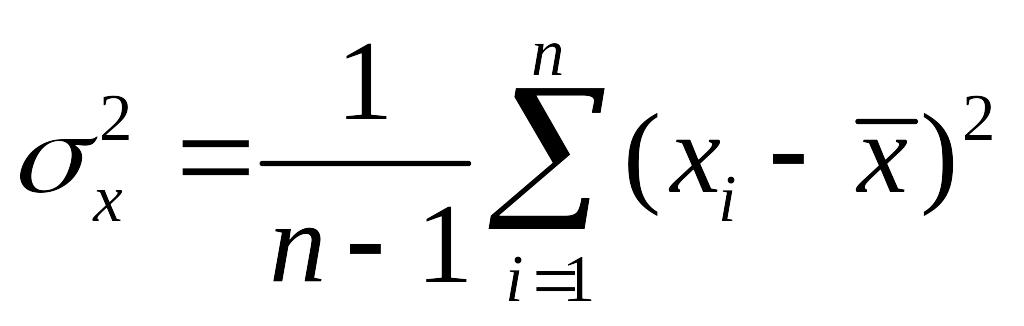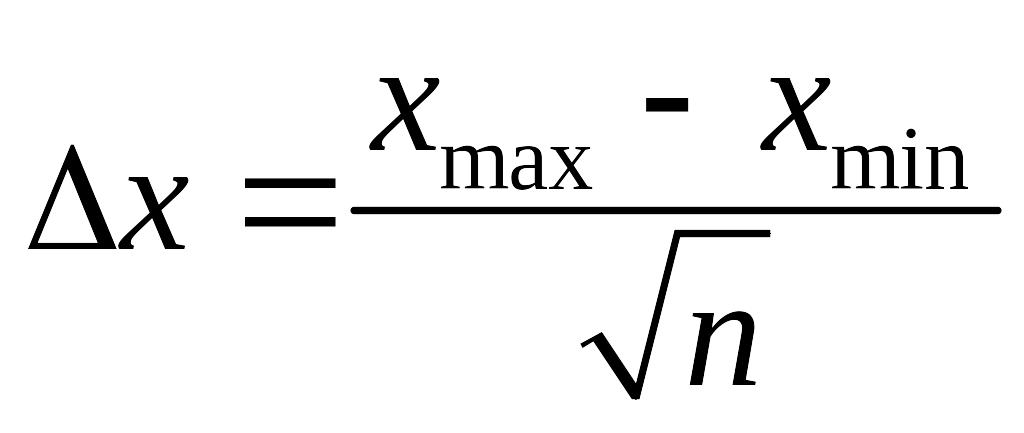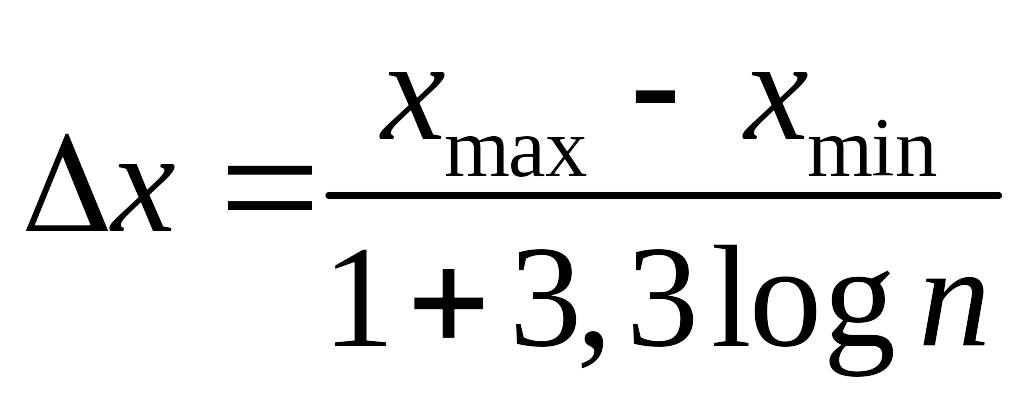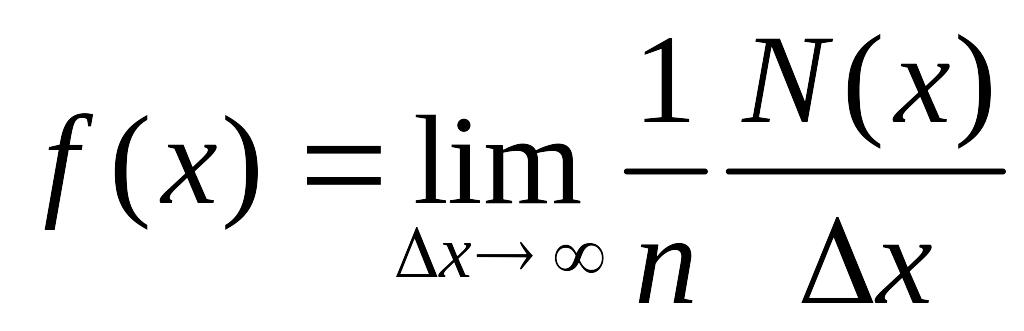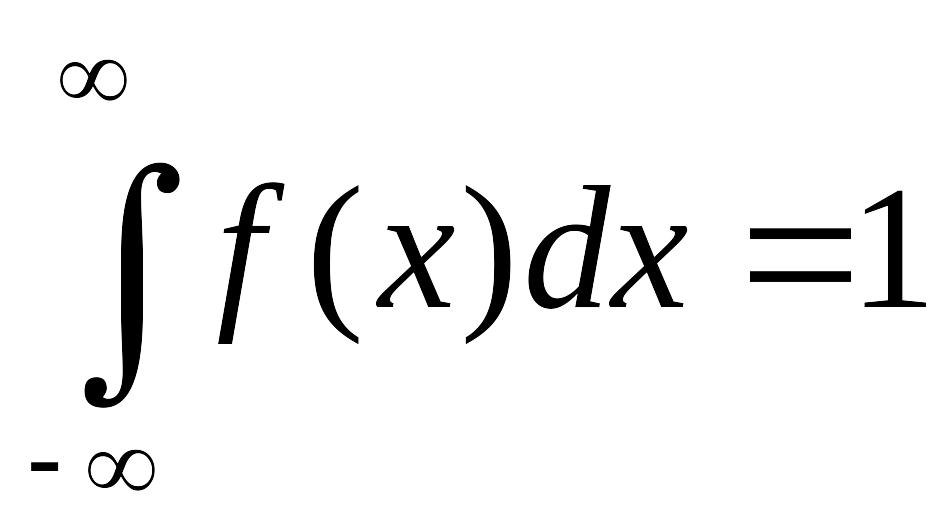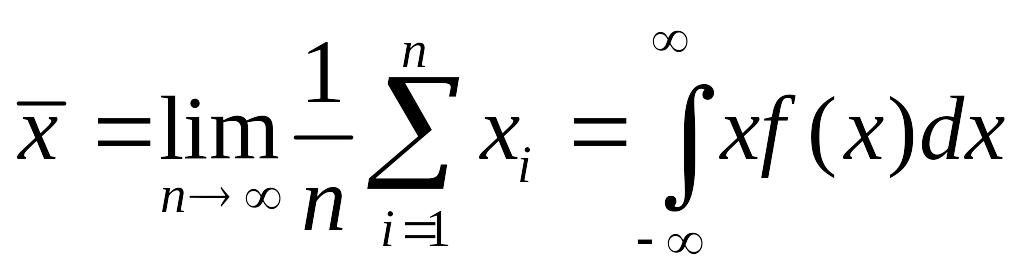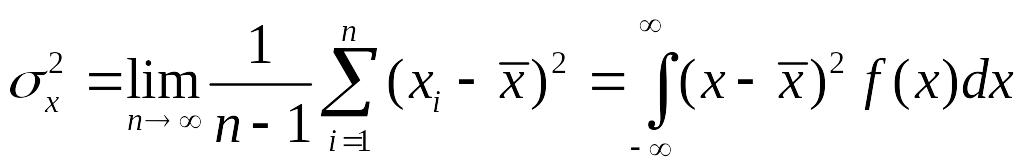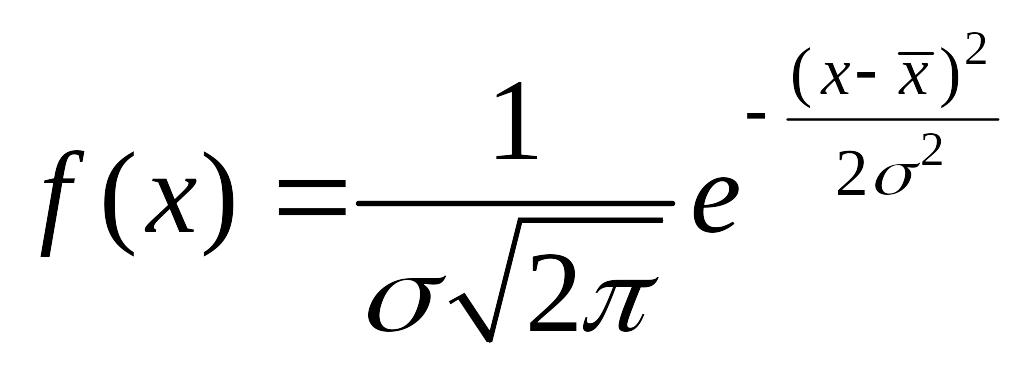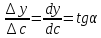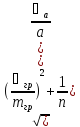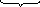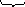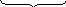Методы исключения систематических погрешностей
Результаты
измерений, содержащие систематическую
погрешность, относятся к неисправленным.
При проведении измерений стремятся
исключить, уменьшить или учесть влияние
систематических погрешностей. Однако
вначале их надо обнаружить.
Постоянные
систематические погрешности можно
обнаружить только путем сравнения
результатов измерений с другими,
полученными с использованием более
точных методов и средств измерения. В
ряде случаев такие погрешности можно
устранить, используя специальные методы
измерений.
Рассмотрим
наиболее известные методы исключения
(существенного уменьшения) постоянных
систематических погрешностей.
Метод замещения
обеспечивает наиболее полное решение
задачи компенсации постоянной
систематической погрешности. Суть
метода состоит в такой замене измеряемой
величины Хи известной величиной А,
получаемой с помощью регулируемой меры,
чтобы показание измерительного прибора
сохранилось неизменным. Значение
измеряемой величины считывается в этом
случае по указателю меры.
При использовании
данного метода погрешность неточного
измерительного прибора устраняется, а
погрешность измерения определяется
только погрешностью самой меры и
погрешностью отсчета измеряемой величины
по указателю меры.
Пример. Измерялось
сопротивление резистора Rx
омметром малой точности. Результат
измерения равен Х = Rx
+ Δс, где Х и Δс — соответственно показание
омметра и систематическая погрешность
измерения. Заменив Rx
магазином сопротивлений и отрегулировав
его так, чтобы сохранилось показание
омметра, получим Х = Rм
+ Δс. Из приведенных двух выражений для
х следует, что Rx
= Rм.
Метод компенсации
погрешности
по знаку
(метод двух отсчетов или изменения знака
систематической погрешности) используется
для устранения постоянной систематической
погрешности, у которой в зависимости
от условий измерения изменяется только
знак. При этом методе выполняют два
измерения, результаты которых должны
быть равны
Х1
= Хи + Δс
и
Х2
= Хи — Δс.
где Хи — измеряемая
величина. Среднее значение из полученных
результатов
(Х1
+ Х2)/2
= Хи
представляет собой
окончательный результат измерения, не
содержащий погрешности ±Δс. Данный
метод часто используется при измерении
экстремальных значений (максимума и
нуля) неизвестной величины.
Пример. Измерить
значение ЭДС потенциометром постоянного
тока, который обладает паразитной
термоЭДС.
Решение.
Уравновесив потенциометр и выполнив
первое измерение, получаем ЭДС U1.
Затем меняем полярность измеряемой
ЭДС, а значит и направление тока в
потенциометре. Снова проводим его
уравновешивание и в результате второго
измерения получаем значение U2.
Если термоЭДС дает погрешность ΔU
и напряжение
U1
= Ux
+ ΔU,
то U2
= Uх
— ΔU.
Отсюда напряжение
Ux
= (U1
+ U2)/2.
Итак, систематическая
погрешность, обусловленная действием
термоЭДС потенциометра, устранена.
Метод
противопоставления
применяется в радиоизмерениях для
уменьшения постоянных систематических
погрешностей при сравнении измеряемой
величины с известной величиной примерно
равного значения, воспроизводимой
соответствующей образцовой мерой. Этот
метод является разновидностью метода
сравнения, при котором измерение
выполняется дважды и проводится так,
чтобы в обоих случаях причина постоянной
погрешности оказывала разные, но
известные по закономерности воздействия
на результаты наблюдений.
Пример. Измерить
сопротивление резистора с помощью
одинарного моста методом противопоставления.
Решение. Сначала
измеряемое сопротивление Rx
уравновешивают образцовой мерой —
известным сопротивлением R1
включенным в плечо сравнения моста. При
этом
Rx
= R1R3/R4,
где R3,
R4
— сопротивления плеч моста. Затем
резисторы Rx
и R1
меняют местами и вновь уравновешивают
мост, регулируя сопротивление образцового
резистора R1
= R’1
В этом случае
Rx
= R’1R3/R4.
Из двух уравнений
для Rx
исключается отношение R3/R4.
Тогда
.
Метод рандомизации
(от англ. random
— случайный, беспорядочный; в переводе
на русский означает: перемешивание,
создание беспорядка, хаоса) основан на
принципе перевода систематических
погрешностей в случайные.
Этот метод
позволяет эффективно уменьшать постоянную
систематическую погрешность (методическую
и инструментальную) путем измерения
некоторой величины рядом однотипных
приборов с последующей оценкой результата
измерений в виде математического
ожидания (среднего арифметического
значения) выполненного ряда наблюдений.
В данном методе при обработке результатов
измерений используются случайные
изменения погрешности от прибора к
прибору. Уменьшение систематической
погрешности достигается и при изменении
случайным образом методики и условий
проведения измерений.
Поясним действие
метода рандомизации простым примером.
Пусть некоторая физическая величина
измеряется n
(число n
достаточно велико) однотипными приборами,
имеющими систематические погрешности
одинакового происхождения. Для одного
прибора эта погрешность — величина
постоянная, но от прибора к прибору она
изменяется случайным образом. Поэтому,
если измерить неизвестную величину n
приборами и затем вычислить математическое
ожидание всех результатов, то значение
погрешности существенно уменьшится
(как и в случае усреднения случайной
погрешности).
Метод введения
поправок.
Довольно часто систематические
погрешности могут быть вычислены и
исключены из результата измерения с
помощью поправки. Поправка С — величина,
одноименная с измеряемой Хи, которая
вводится в результат измерения Х = Хи +
Δс + С с целью исключения систематической
погрешности Δс,.. В случае С = -Δс,
систематическая погрешность полностью
исключается из результата измерения.
Поправки определяются экспериментально
или путем специальных теоретических
исследований и задаются в виде формул,
таблиц или графиков.
Наиболее просто
методом введения поправок исключают
постоянные инструментальные систематические
погрешности, которые обычно выявляют
посредством поверки средства измерения.
Пример. При
измерении напряжения в сети переменного
тока показания вольтметра составили
218 В. В свидетельстве о поверке прибора
указано, что на этой отметке его шкалы
систематическая погрешность вольтметра
составляет -2 В. С учетом поправки
напряжение в сети равно 218 + 2 = 220 В.
Пример. Напряжение
источника ЭДС Ux
измерено вольтметром, сопротивление
которого RV
= 5 кОм
определено с погрешностью ± 0,5 %. Внутреннее
сопротивление источника ЭДС Ri
= 60 ±10 Ом. Показание вольтметра Uv
= 12,50 В. Найти поправку, которую нужно
внести, и показание прибора для определения
действительного значения напряжения
источника.
Решение. Показания
вольтметра соответствуют падению
напряжения на нем:
Относительная
систематическая методическая погрешность,
обусловленная ограниченным значением
сопротивления RV,
Поправка измерения
напряжения равна абсолютной систематической
погрешности, взятой с обратным знаком:
Δс= 12,50-0,012 = 0,15В.
Погрешность
полученного значения поправки определяется
погрешностью, с которой известно
сопротивление Ri
а это Δ = ± 10 Ом. Ее предельное значение
составит
ΔсRi
= 10/60 = 0,167.
Погрешностью
ΔRV
= 0,005 неточности оценки RV
можно пренебречь. Следовательно,
погрешность определения поправки
Δ = ± 0,167 · 0,15 = 0,0251
≈ 0,03 В.
Итак, в показания
вольтметра необходимо ввести поправку:
ΔU=
+ 0,15 В.
Тогда исправленное
значение
= 12,5 + 0,15 = 12,65 В.
Этот результат
имеет определенную погрешность, в том
числе неисключенный остаток систематической
погрешности
Δ = ± 0,03 В
или
δ = ± 0,24 %
из-за потребления
некоторой мощности вольтметром.
Ввод одной
поправки позволяет исключить влияние
только одной составляющей систематической
погрешности. Для устранения всех
составляющих, в результат измерения
приходится вводить ряд поправок.
Рассмотрим далее
некоторые методы, применяющиеся для
обнаружения и уменьшения переменных и
монотонно изменяющихся во времени
систематических погрешностей.
Метод симметричных
наблюдений
весьма эффективен при выявлении и
исключении погрешности, являющейся
линейной функцией соответствующего
аргумента (амплитуды, напряжения,
времени, температуры и т. д.).
Предположим,
что измеряется величина Хи, а результаты
наблюдений Хi
зависят от времени t.
Для выявления характера изменения
погрешности выполняют несколько
наблюдений через равные промежутки
времени Δt.
Пусть выполнено пять наблюдений Х1
… Х5
в моменты времени t1
… t5.
Далее вычисляют средние арифметические
значения двух пар наблюдений
(Х1
+ Х5)/2
и (Х2
+ Х4)/2.
Наблюдения в
этих парах проведены в моменты t1,
t5
и t2,
t4,
симметричные относительно момента t3.
При линейном характере изменения
погрешности, полученные средние значения
должны быть одинаковы. Убедившись в
этом, результаты наблюдений можно
записать в виде
Хi
= Хи + kti
где k
— некоторая постоянная.
Пусть
Х1 = Хи + kt1
и Х2 = Хи + kt2.
Решение системы
этих уравнений дает значение Хи свободное
от переменной систематической погрешности:
Хи = (Х2t1
– X1t2)/(t2
– t1).
Подобным образом
удается исключить погрешности,
обусловленные, например, постепенным
падением уровня напряжения источника
питания (аккумулятора, батареи).
Метод анализа
знаков неисправленных случайных
погрешностей.
Когда знаки неисправленных случайных
погрешностей чередуются с некоторой
закономерностью, имеет место переменная
систематическая погрешность. Если у
случайных погрешностей последовательность
знаков «+» сменяется последовательностью
знаков «-» или наоборот, то присутствует
монотонно изменяющаяся систематическая
погрешность. Если же у случайных
погрешностей группы знаков «+» и «-»
чередуются, то имеет место периодическая
систематическая погрешность.
Графический
метод является
наиболее простым для обнаружения
переменной систематической погрешности
в ряде результатов наблюдений. При этом
методе рекомендуется построить график,
на который нанесены результаты наблюдений
в той последовательности, в какой они
были получены. На графике через точки
наблюдений проводят плавную линию,
которая выражает тенденцию результата
измерения, если она существует. Если
тенденция не прослеживается, то переменную
систематическую погрешность считают
практически отсутствующей.
В заключение
отметим, что при измерениях всегда
остаются неисключенные остатки
систематических погрешностей (НСП).
Вопрос №4
Случайные
погрешности (ошибки)
Случайными
являются такие ошибки, которые меняются
непредсказуемо от одного измерения к
другому при определении одной и той же
физической величины с помощью одной и
той же измерительной системы при
неизменных условиях. Обычно они
обусловлены большим числом факторов,
которые влияют на результат измерения
независимо. Мы не можем скорректировать
случайные ошибки, так как нам неизвестны
их причины и следствием их являются
случайные (непредсказуемые) колебания
результата измерения.
Примерами
случайных ошибок служат:
ошибки наблюдателя;
ошибки регулировки
и настройки Ипри;
ошибки округления
и т. д.
Все, о чем мы
можем говорить, имея дело со случайными
ошибками, это вероятность того, что
ошибка будет той или иной величины.
Теория вероятностей и мат. статистика
дают возможность делать определенные
утверждения при наличии случайных
ошибок.
Можно считать,
что как систематические, так и случайные
ошибки вызываются сигналом помехи,
который накладывается на истинный
сигнал при его измерении. Флюктуация
помехи вызывает случайную ошибку, а
постоянный сигнал помехи является
причиной систематической погрешности.
К сожалению, постоянный характер помехи
делает задачу обнаружения систематических
ошибок более трудной.
Влияние случайных
ошибок можно уменьшить, осуществляя
измерения несколько раз и принимая в
качестве конечного результата среднее
значение результатов отдельных измерений.
Возможно это тогда, когда измеряемая
величина не изменяется на протяжении
всех этих измерений и измерения
выполняются быстро. Среднее значение
результатов
измерений
имеет вид:
.
Среднее
представляет собой лучшую возможную
оценку значения
постоянной ФВ по
результатам измерений. Такой вывод
можно сделать из того факта, что

Таким образом,
сумма всех отклонений
равна нулю. Кроме того, величина
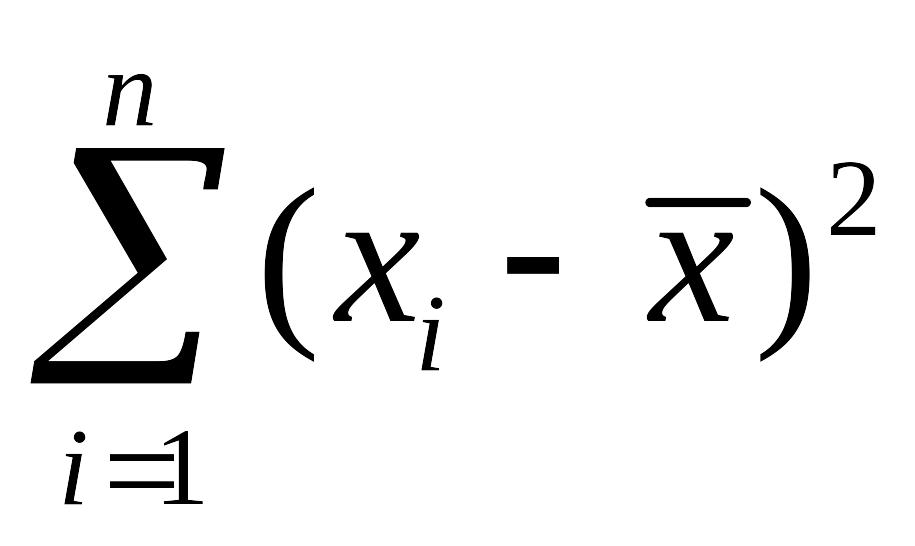
минимальна.
Другими словами,
минимальными являются рассеяние
или разброс выборочных значений
относительно среднего
.
Мерой рассеяния
в окрестности среднего
является дисперсия
(мера концентрированности распределения),
равная по определению,
.
Обычно указывается
квадратный корень из дисперсии; эта
величина называется среднеквадратическим
отклонением
.
Выборки
,
полученные в отдельных измерениях
величины
,
при наличии случайный ошибок, можно
представить на диаграмме в виде столбцов.
Чтобы построить такую диаграмму, нам
следует разбить диапазон всех возможных
значений
,
включающий все выборки
полученные в измерениях, на небольшие
интервалы ширины
,
а затем отложить число выборок
,
попавших в эти небольшие интервалы
,
как функцию от
(см рис.1). Обычно размер мелких интервалов
выбирается по правилу
.
Если
,
то лучшее определить значение
по правилу Старджеса
.
Если ширину
интервала
выбрать слишком малой, то «огибающая»
диаграммы будет сильно изрезанной. При
слишком большом значении
«огибающая» оказывается квантованной
слишком грубо, и форма распределения
проступает не так явно.
Можно построить
нормализованную диаграмму, откладывая
,
а не
.
Тогда по вертикали указывается
относительное число измерений, результаты
которых лежат в данном интервале. В этом
случае можно утверждать, что теперь по
оси ординат отложена вероятность
попадания результата измерения в данный
интервал. Кроме того, можно произвести
нормализацию также и по ширине интервала
,
откладывая
вместо
.
Диаграмму, получающуюся в результате
нормализации, обычно называют
гистограммой.
Рис.1 Гистограммы:
а.
при правильном выборе ширины интервалов
Δх,
на которые разбивается весь диапазон
возможных значений х;
-
при слишком малых
значениях Δх; -
при слишком больших
значениях Δх.
Если число
выборок растет, а диапазон
остается в ограниченных пределах, как
это бывает на практике при измерении
всех физических величин, то число
интервалов, на которые разбивается этот
диапазон, и число столбцов в гистограмме,
увеличиваются, тогда как ширина одного
интервала
уменьшается. При
огибающая гистограммы переходит в
гладкую кривую. Такая (дважды)
нормализованная гистограмма носит
название плотности
распределения вероятностей
.
По определению,
.
Это соотношение
можно также записать в виде:
.
Это означает,
что
есть вероятность того, что значение
выборки попадает в интервал между
и
;
отсюда и следует название: плотность
распределения вероятности.
Из последнего равенства следует, что
.
Интеграл в этом
выражении представляет собой сумму
всех вероятностей
.
Он равен вероятности того, что очередная
выборка попадет в первый интервал ширины
,
или во второй, или в третий и т.д. Так как
результат измерения должен принадлежать
одному из этих интервалов, сумма должна
равняться 1. Последнее соотношение
показывает, что единице равна площадь
под плотностью распределения вероятностей
(что и достигается, главным образом,
путем двукратной нормализации). Зная
плотность распределения вероятностей,
легко найти вероятность того, что
результат очередного измерения окажется
меньше определенного значения а
(см. рис.2).
Обозначая эту вероятность
,
получим
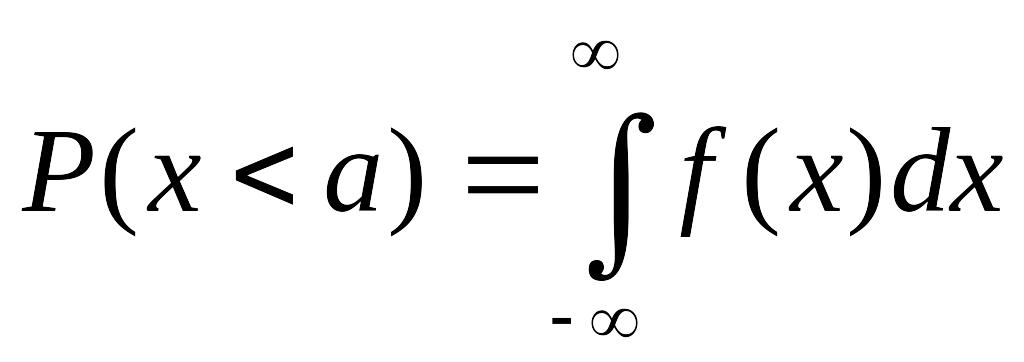
Эта величина в
точности равна площади под
слева от линии х
= а (см. рис.2).
Рис.2 Плотность
распределения вероятностей.
Точно так же при
заданной плотности распределения
можно найти среднее
набора выборочных значений
:
.
Эта величина
получила название
МОЖ случайной
величины и равна сумме бесконечно
большого числа произведений всех
возможных значений случайной величины
на бесконечно малые площади f(x)dx.
Дисперсию, как
меру рассеяния случайной величины,
можно представить в виде:
.
Отметим ещё раз,
что СКО
– это квадратный корень из дисперсии:
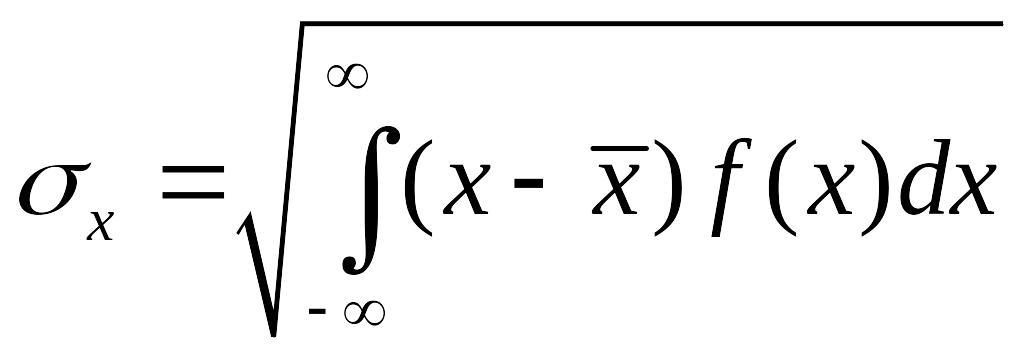
СКО
чаще всего используется для характеристики
рассеяния (степени разбросанности)
случайной величины и имеет ту же
размерность, что и сама случайная
величина.
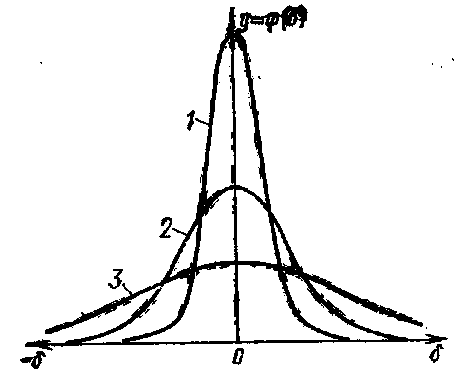
Рис. 3. Кривые
нормального распределения случайных
погрешностей: 1—σ = 0,5а; 2—σ = 1а; 3—σ = 2а,
где а — исходное значение

Рис. 4. Кривая
нормального распределения случайных
погрешностей и среднее квадратическое
отклонение ± σ
На рис.3 указаны
относительные значения среднего
квадратического отклонения σ. Как видим,
чем меньше σ, тем больше вероятность
появления малых погрешностей и меньше
вероятность появления больших
погрешностей. Другими словами, тем
больше сходимость результатов наблюдений.
Среднее
квадратическое отклонение соответствует
характерной точке кривой нормального
распределения. Абсциссам +σ, -σ соответствуют
точки перегиба кривой. Вероятность
того, что случайные погрешности измерения
не выйдут за пределы ±σ составляет
0,6826, приближенно 2/3. На рис.4 это
соответствует попаданию в заштрихованную
площадь, примерно в два раза большую,
чем в незаштрихованную.
Если ошибки,
содержащиеся в результатах измерений,
обусловлены большим числом взаимно
независимых событий, то можно доказать,
что они распределены по вполне
определенному закону: в этом случае
распределение вероятностей является
нормальным
или
гауссовым.
Доказательство
содержится в центральной
предельной теореме теории вероятностей.
Нормальное
распределение плотности вероятности
характерно тем, что, согласно центральной
предельной теореме теории вероятностей,
такое распределение имеет сумма
бесконечно большого числа бесконечно
малых случайных возмущений с любыми
распределениями. Применительно к
измерениям это означает, что нормальное
распределение случайных погрешностей
возникает тогда, когда на результат
измерения действует множество случайных
возмущений, ни одно из которых не является
преобладающим. Практически, суммарное
воздействие даже сравнительно небольшого
числа возмущений приводит к закону
распределения результатов и погрешностей
измерений, близкому к нормальному.
Плотность
вероятности нормального распределения
имеет вид:
;
график такого
распределения показан на рис.5. Вероятности
того, что
или х >
+ а, выражаются
следующими интегралами, соответственно:

и
;
эти интегралы
нельзя представить с помощью элементарных
функций.
Рис.5 Нормальное
или гауссово распределение
Примеры найденных
численно приближенных значений этих
интегралов представлены в табл.1.
«Вероятность того,
что результат измерения, имеющий
нормальное распределение со средним
значением и СКО, лежит вне интервалов
шириной 1
,
2
и 3
с центром в точке
»
Табл.1
|
находится |
Вероятность |
|
|
0,32 |
|
|
0,045 |
|
|
0,0026 |
На рис.6 показан
случай, когда результаты измерений
содержат как случайные, так и систематические
ошибки. Здесь случайные ошибки распределены
по нормальному закону.
Истинное значение
измеряемой величины равно
а.
Систематическая ошибка вызывает сдвиг
среднего значения выборок, которое
равно b.
Полная ошибка (при верояности больших
уклонений 0,14%) равна сумме систематической
ошибки а-b
и
«максимальной случайной ошибки». Этой
полной ошибкой определяется погрешность
измерения. Неопределенность результата
измерения является мера разброса между
выборками, обусловленного только
случайными ошибками. Строго говоря,
неопределенность результата измерения
задается интервалом, в пределах которого
истинное значение измеряемой величины
находится с заданной доверительной
вероятностью.
Рис.6 Случайные и
систематические ошибки
Оценка результата
измерения.
Задача состоит в том, чтобы по полученным
экспериментальным путем результатам
наблюдений, содержащим случайные
погрешности, найти оценку истинного
значения измеряемой величины — результат
измерения. Будем полагать, что
систематические погрешности в результатах
наблюдений отсутствуют или исключены.
К оценкам,
получаемым по статистическим данным,
предъявляются требования состоятельности,
несмещенности и
эффективности.
Оценка называется
состоятельной,
если при увеличении числа наблюдений
она стремится к истинному значению
оцениваемой величины.
Оценка называется
несмещенной,
если ее математическое ожидание равно
истинному значению оцениваемой величины.
В том случае, когда можно найти несколько
несмещенных оценок, лучшей из них
считается та, которая имеет наименьшую
дисперсию. Чем меньше дисперсия оценки,
тем более эффективной считают эту
оценку.
Способы нахождения
оценок результата зависят от вида
функции распределения и от имеющихся
соглашений по этому вопросу, регламентируемых
в рамках законодательной метрологии.
Общие соображения по выбору оценок
заключаются в следующем.
Распределения
погрешностей результатов наблюдений,
как правило, являются симметричными
относительно центра распределения,
поэтому истинное значение измеряемой
величины может быть определено как
координата центра рассеивания Хц, т.е.
центра симметрии распределения случайной
погрешности (при условии, что систематическая
погрешность исключена). Отсюда следует
принятое в метрологии правило оценивания
случайной погрешности в виде интервала,
симметричного относительно результата
измерения (Хц ± Δх). Координата Хц может
быть найдена несколькими способами.
Наиболее общим является определение
центра симметрии из принципа симметрии
вероятностей, т.е. нахождение такой
точки на оси х, слева и справа от которой
вероятности появления различных значений
случайных погрешностей равны между
собой и составляют P1
= Р2
= 0,5. Такое значение Хц называется
медианой.
Координата Хц
может быть определена и как центр тяжести
распределения, т.е. как математическое
ожидание случайной величины.
При ассиметричной
кривой плотности распределения
вероятностей оценкой центра распределения
может служить абсцисса моды распределения,
т.е. координата максимума плотности.
Однако есть распределения, у которых
не существует моды (например, равномерное),
и распределения, у которых не существует
математического ожидания.
В практике
измерений встречаются различные формы
кривой закона распределения, однако
чаще всего имеют дело с нормальным и
равномерным распределением плотности
вероятностей.
Учитывая
многовариантность подходов к выбору
оценок и в целях обеспечения единства
измерений, правила обработки результатов
наблюдений обычно регламентируются
нормативно-техническими документами
(стандартами, методическими указаниями,
инструкциями). Так, в стандарте на методы
обработки результатов прямых измерений
с многократными наблюдениями указывается,
что приведенные в нем методы обработки
установлены для результатов наблюдений,
принадлежащих нормальному распределению.
Если вы устраняете систематическую ошибку модели, то уже слишком поздно
Введение
Машинное обучение — это технологический прорыв, случающийся раз в поколение. Однако с ростом его популярности основной проблемой становятся систематические ошибки алгоритма. Если модели ML не обучаются на репрезентативных данных, у них могут развиться серьёзные систематические ошибки, оказывающие существенный вред недостаточно представленным группам и приводящие к созданию неэффективных продуктов. Мы изучили массив данных CoNLL-2003, являющийся стандартом для создания алгоритмов распознавания именованных сущностей в тексте, и выяснили, что в данных присутствует серьёзный перекос в сторону мужских имён. При помощи наших технологии мы смогли компенсировать эту систематическую ошибку:
- Мы обогатили данные, чтобы выявить сокрытые систематические ошибки
- Дополнили массив данных недостаточно представленными примерами, чтобы компенсировать гендерный перекос
Модель, обученная на нашем расширенном массиве данных CoNLL-2003, характеризуется снижением систематической ошибки и повышенной точностью, и это показывает, что систематическую ошибку можно устранить без каких-либо изменений в модели. Мы выложили в open source наши аннотации Named Entity Recognition для исходного массива данных CoNLL-2003, а также его улучшенную версию, скачать их можно здесь.
Систематическая ошибка алгоритма: слабое место ИИ
Сегодня тысячи инженеров и исследователей создают системы, самостоятельно обучающиеся тому, как достигать существенных прорывов — повышать безопасность на дорогах при помощи беспилотных автомобилей, лечить болезни оптимизированными ИИ процедурами, бороться с изменением климата при помощи управления энергопотреблением.
Однако сила самообучающихся систем является и их слабостью. Так как фундаментом всех процессов машинного обучения являются данные, обучение на несовершенных данных может привести к искажённым результатам.
ИИ-системы имеют большие полномочия, поэтому они могут наносить существенный ущерб. Недавние протесты против полицейской жестокости, приведшей к смертям Джорджа Флойда, Бреонны Тейлор, Филандо Кастиле, Сандры Блэнд и многих других, является важным напоминанием о систематическом неравенстве в нашем обществе, которое не должны усугублять ИИ-системы. Но нам известны многочисленные примеры (закрепляющие гендерные стереотипы результаты поиска картинок, дискриминация чёрных подсудимых в системах управления данными нарушителей и ошибочная идентификация цветных людей системами распознавания лиц), показывающие, что предстоит пройти долгий путь, прежде чем проблема систематических ошибок ИИ будет решена.
Распространённость ошибок вызвана лёгкостью их внесения. Например, они проникают в «золотые стандарты» моделей и массивов данных в open source, ставшие фундаментом огромного объёма работы в сфере ML. Массив данных для определения эмоционального настроя текста word2vec, используемый в построении моделей других языков, искажён по этнической принадлежности, а word embeddings — способ сопоставления слов и значений алгоритмом ML — содержит сильно искажённые допущения о занятиях, с которыми ассоциируются женщины.
Проблема (и, как минимум, часть её решения) лежит в данных. Чтобы проиллюстрировать это, мы провели эксперимент с одним из самых популярных массивов данных для построения систем распознавания именованных сущностей в тексте: CoNLL-2003.
Что такое «распознавание именованных сущностей»?
Распознавание именованных сущностей (Named-Entity Recognition, NER) — один из фундаментальных камней моделей естественных языков, без него были бы невозможны онлайн-поиск, извлечение информации и анализ эмоционального настроя текста.
Миссия нашей компании заключается в ускорении разработки ИИ. Естественный язык — одна из основных сфер наших интересов. Наш продукт Scale Text содержит NER, заключающееся в аннотировании текста согласно заданному списку меток. На практике, среди прочего, это может помочь крупным розничным сетям анализировать онлайн-обсуждение их продуктов.
Многие модели NER обучаются и подвергаются бенчмаркам на CoNLL-2003 — массиве данных из примерно 20 тысяч предложений новостных статей Reuters, аннотированных такими атрибутами, как «PERSON», «LOCATION» и «ORGANIZATION».
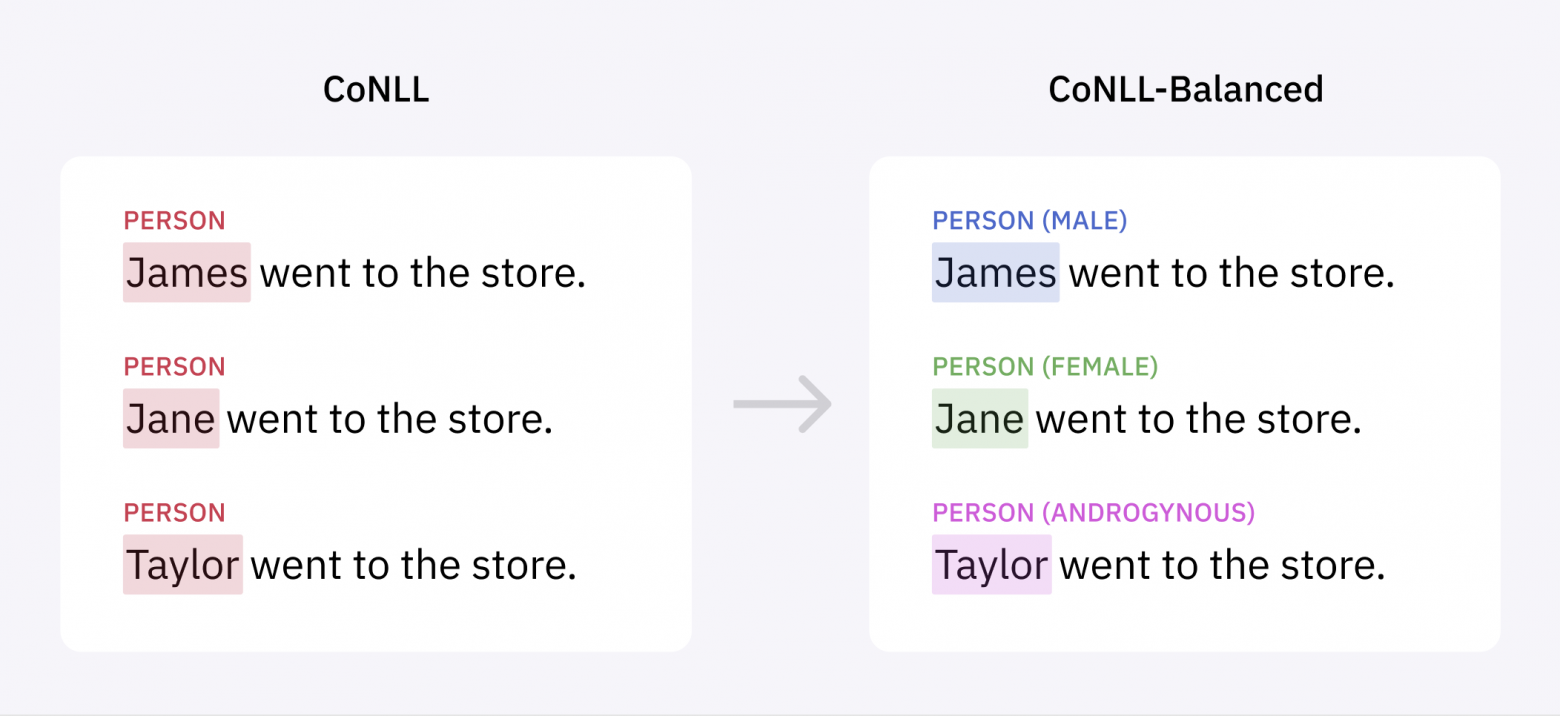
Нам захотелось изучить эти данные на наличие систематических ошибок. Для этого мы воспользовались своим конвейером разметки, чтобы категоризировать все имена в массиве данных, размечая их как мужские, женские или гендерно-нейтральные, исходя из традиционного использования имён.
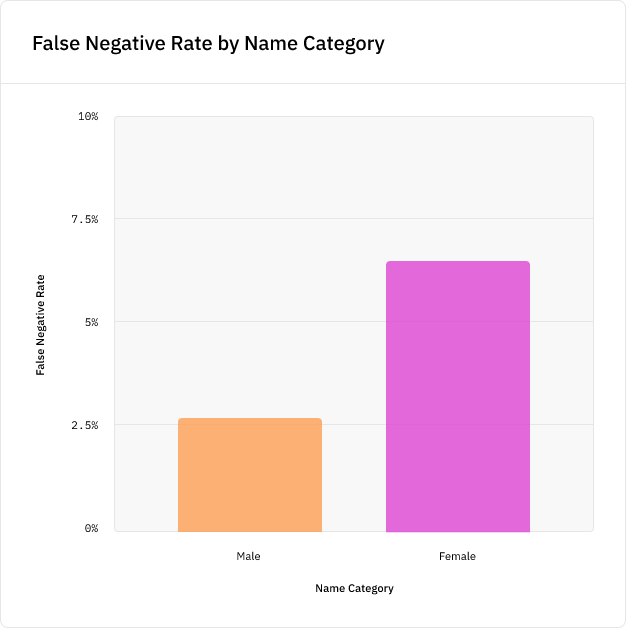
При этом мы выявили существенную разницу. Мужские имена упоминались почти в пять раз чаще женских, и менее 2% имён были гендерно-нейтральными:
Это вызвано тем, что по социальным причинам новостные статьи в основном содержат мужские имена. Однако из-за этого модель NER, обученная на таких данных, лучше будет справляться с выбором мужских имён, чем женских. Например, поисковые движки используют модели NER для классификации имён в поисковых запросах, чтобы выдавать более точные результаты. Но если внедрить модель NER с перекосом, то поисковый движок хуже будет идентифицировать женские имена по сравнению с мужскими, и именно подобная малозаметная распространённая систематическая ошибка может проникнуть во многие системы реального мира.
Новый эксперимент по снижению систематической ошибки
Чтобы проиллюстрировать это, мы обучили модель NER для изучения того, как этот гендерный перекос повлияет на её точность. Был создан алгоритм извлечения имён, выбирающий метки PERSON при помощи популярной NLP-библиотеки spaCy, и на подмножестве данных CoNLL была обучена модель. Затем мы протестировали модель на новых именах из тестовых данных, не присутствовавших в данных обучения, и обнаружили, что модель с вероятностью на 5% больше пропустит новое женское имя, чем новое мужское имя, а это серьёзное расхождение в точности:
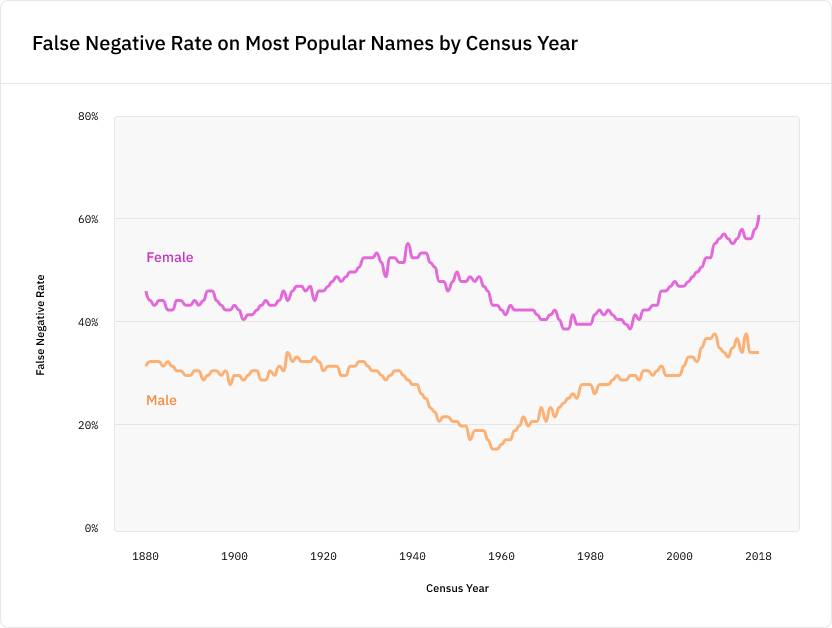
Мы наблюдали схожие результаты, когда применили модель к шаблону «NAME is a person», подставив 100 самых популярных мужских и женских имён на каждый год переписи населения США. Результаты работы модели оказались значительно хуже для женских имён во все года переписи:
Критически важно то, что наличие перекоса в данных обучения приводит к смещению ошибок в сторону недостаточно представленных категорий. Эксперимент с переписями демонстрирует это и другим образом: точность модели существенно деградирует после 1997 года (точки отсечения статей Reuters в массиве данных CoNLL), потому что массив данных больше не является репрезентативным отображением популярности имён каждого последующего года.
Модели обучаются соответствовать трендам данных, на которых они обучены. Нельзя ожидать их хорошей точности в случаях, когда они видели лишь малое количество примеров.
Если вы исправляете систематическую ошибку модели, то уже слишком поздно
Как же это исправить?
Один из способов — попробовать устранить систематическую ошибку модели, например, выполнив постобработку модели или добавив целевую функцию для смягчения перекоса, оставив определение подробностей самой модели.
Но это не лучший подход по множеству причин:
- Справедливость — это очень сложная проблема, и мы не можем ждать, что алгоритм решит её сам. Исследование показало, что обучение алгоритма на одинаковый уровень точности для всех подмножеств населения не обеспечит справедливости и нанесёт вред обучению модели.
- Добавление новых целевых функций может навредить точности модели, приводя к негативному побочному эффекту. Вместо этого лучше обеспечить простоту алгоритма и сбалансированность данных, что повысит точность модели и позволит избежать негативных эффектов.
- Неразумно ожидать, что модель покажет хорошие результаты в случаях, примеров которых она видела очень мало. Наилучший способ обеспечения хороших результатов заключается в повышении разнообразия данных.
- Попытки устранения систематической ошибки при помощи инженерных техник — это дорогой и длительный процесс. Гораздо дешевле и проще изначально обучать модели на данных без перекосов, освободив ресурсы инженеров для работы над реализацией.
Данные — это лишь одна часть проблемы систематических ошибок. Однако эта часть фундаментальна и влияет на всё, что идёт после неё. Именно поэтому мы считаем, что данные содержат ключ к частичному решению, обеспечивая потенциальные систематические улучшения в исходных материалах. Если вы не размечаете критические классы (например, гендер или этническую принадлежность) явным образом, то невозможно сделать так, чтобы эти классы не были источником систематической ошибки.
Такая ситуация контринтуитивна. Кажется, что если нам нужно построить модель, не зависящую от чувствительных характеристик наподобие гендера, возраста или этнической принадлежности, то лучше исключить эти свойства из данных обучения, чтобы модель не могла их учитывать.
Однако принцип «справедливости, реализуемой через неведение» на самом деле усугубляет проблему. Модели ML превосходно справляются с выводом заключений из признаков, они не прекращают делать этого, если мы не разметили эти признаки явным образом. Систематические ошибки просто остаются невыявленными, из-за чего их сложнее устранить.
Единственный надёжный способ решения проблемы заключается в разметке большего количества данных, чтобы сбалансировать распределение имён. Мы использовали отдельную модель ML для идентификации предложений в корпусах Reuters и Brown, с большой вероятностью содержащих женские имена, а затем разметили эти предложения в нашем конвейере NER, чтобы дополнить CoNLL.
Получившийся массив данных, который мы назвали CoNLL-Balanced, содержит на 400 с лишним больше женских имён. После повторного обучения на нём модели NER мы обнаружили, что алгоритм больше не имеет систематической ошибки, приводящей к снижению показателей при распознавании женских имён:
Кроме того, модель улучшила показатели и при распознавании мужских имён.
Это стало впечатляющей демонстрацией важности данных. Благодаря устранению перекоса в исходном материале нам не пришлось вносить никаких изменений в нашу модель ML, что позволило сэкономить на времени разработки. И мы достигли этого без негативного влияния на точность модели; на самом деле, она даже слегка увеличилась.
Чтобы позволить сообществу разработчиков развивать нашу работу и устранять гендерный перекос в моделях, построенных на основе CoNLL-2003, мы выложили на наш веб-сайте дополненный массив данных в open source, в том числе и добавив гендерную информацию.
Сообщество разработчиков ИИ/ML имеет проблемы с культурными различиями, но мы испытываем умеренный оптимизм от этих результатов. Они намекают на то, что мы, возможно, сможем предложить техническое решение насущной социальной проблемы, если займёмся проблемой сразу же, выявим сокрытые систематические ошибки и улучшим точность модели для всех.
Сейчас мы изучаем, как этот подход можно применить к ещё одному критичному атрибуту — этнической принадлежности — чтобы придумать, как создать надёжную систему для устранения перекоса в массивах данных, распространяющегося и на другие охраняемые от дискриминации категории населения.
Кроме того, это показывает, почему наша компания уделяет так много внимания качеству данных. Если нельзя доказать, что данные точны, сбалансированы и лишены систематических ошибок, то нет гарантии того, что создаваемые на их основе модели будут безопасными и точными. А без этого мы не сможем создавать качественно новых ИИ-технологий, идущих на пользу всем людям.
Благодарности
Упоминаемый в этом посте массив данных CoNLL 2003 — это тестовый набор Reuters-21578, Distribution 1.0, доступный для скачивания на странице проекта исходного эксперимента 2003 года: https://www.clips.uantwerpen.be/conll2003/ner/.
From Wikipedia, the free encyclopedia
«Systematic bias» redirects here. For the sociological and organizational phenomenon, see Systemic bias.
Observational error (or measurement error) is the difference between a measured value of a quantity and its true value.[1] In statistics, an error is not necessarily a «mistake». Variability is an inherent part of the results of measurements and of the measurement process.
Measurement errors can be divided into two components: random and systematic.[2]
Random errors are errors in measurement that lead to measurable values being inconsistent when repeated measurements of a constant attribute or quantity are taken. Systematic errors are errors that are not determined by chance but are introduced by repeatable processes inherent to the system.[3] Systematic error may also refer to an error with a non-zero mean, the effect of which is not reduced when observations are averaged.[citation needed]
Measurement errors can be summarized in terms of accuracy and precision.
Measurement error should not be confused with measurement uncertainty.
Science and experiments[edit]
When either randomness or uncertainty modeled by probability theory is attributed to such errors, they are «errors» in the sense in which that term is used in statistics; see errors and residuals in statistics.
Every time we repeat a measurement with a sensitive instrument, we obtain slightly different results. The common statistical model used is that the error has two additive parts:
- Systematic error which always occurs, with the same value, when we use the instrument in the same way and in the same case.
- Random error which may vary from observation to another.
Systematic error is sometimes called statistical bias. It may often be reduced with standardized procedures. Part of the learning process in the various sciences is learning how to use standard instruments and protocols so as to minimize systematic error.
Random error (or random variation) is due to factors that cannot or will not be controlled. One possible reason to forgo controlling for these random errors is that it may be too expensive to control them each time the experiment is conducted or the measurements are made. Other reasons may be that whatever we are trying to measure is changing in time (see dynamic models), or is fundamentally probabilistic (as is the case in quantum mechanics — see Measurement in quantum mechanics). Random error often occurs when instruments are pushed to the extremes of their operating limits. For example, it is common for digital balances to exhibit random error in their least significant digit. Three measurements of a single object might read something like 0.9111g, 0.9110g, and 0.9112g.
Characterization[edit]
Measurement errors can be divided into two components: random error and systematic error.[2]
Random error is always present in a measurement. It is caused by inherently unpredictable fluctuations in the readings of a measurement apparatus or in the experimenter’s interpretation of the instrumental reading. Random errors show up as different results for ostensibly the same repeated measurement. They can be estimated by comparing multiple measurements and reduced by averaging multiple measurements.
Systematic error is predictable and typically constant or proportional to the true value. If the cause of the systematic error can be identified, then it usually can be eliminated. Systematic errors are caused by imperfect calibration of measurement instruments or imperfect methods of observation, or interference of the environment with the measurement process, and always affect the results of an experiment in a predictable direction. Incorrect zeroing of an instrument leading to a zero error is an example of systematic error in instrumentation.
The Performance Test Standard PTC 19.1-2005 “Test Uncertainty”, published by the American Society of Mechanical Engineers (ASME), discusses systematic and random errors in considerable detail. In fact, it conceptualizes its basic uncertainty categories in these terms.
Random error can be caused by unpredictable fluctuations in the readings of a measurement apparatus, or in the experimenter’s interpretation of the instrumental reading; these fluctuations may be in part due to interference of the environment with the measurement process. The concept of random error is closely related to the concept of precision. The higher the precision of a measurement instrument, the smaller the variability (standard deviation) of the fluctuations in its readings.
Sources[edit]
Sources of systematic error[edit]
Imperfect calibration[edit]
Sources of systematic error may be imperfect calibration of measurement instruments (zero error), changes in the environment which interfere with the measurement process and sometimes imperfect methods of observation can be either zero error or percentage error. If you consider an experimenter taking a reading of the time period of a pendulum swinging past a fiducial marker: If their stop-watch or timer starts with 1 second on the clock then all of their results will be off by 1 second (zero error). If the experimenter repeats this experiment twenty times (starting at 1 second each time), then there will be a percentage error in the calculated average of their results; the final result will be slightly larger than the true period.
Distance measured by radar will be systematically overestimated if the slight slowing down of the waves in air is not accounted for. Incorrect zeroing of an instrument leading to a zero error is an example of systematic error in instrumentation.
Systematic errors may also be present in the result of an estimate based upon a mathematical model or physical law. For instance, the estimated oscillation frequency of a pendulum will be systematically in error if slight movement of the support is not accounted for.
Quantity[edit]
Systematic errors can be either constant, or related (e.g. proportional or a percentage) to the actual value of the measured quantity, or even to the value of a different quantity (the reading of a ruler can be affected by environmental temperature). When it is constant, it is simply due to incorrect zeroing of the instrument. When it is not constant, it can change its sign. For instance, if a thermometer is affected by a proportional systematic error equal to 2% of the actual temperature, and the actual temperature is 200°, 0°, or −100°, the measured temperature will be 204° (systematic error = +4°), 0° (null systematic error) or −102° (systematic error = −2°), respectively. Thus the temperature will be overestimated when it will be above zero and underestimated when it will be below zero.
Drift[edit]
Systematic errors which change during an experiment (drift) are easier to detect. Measurements indicate trends with time rather than varying randomly about a mean. Drift is evident if a measurement of a constant quantity is repeated several times and the measurements drift one way during the experiment. If the next measurement is higher than the previous measurement as may occur if an instrument becomes warmer during the experiment then the measured quantity is variable and it is possible to detect a drift by checking the zero reading during the experiment as well as at the start of the experiment (indeed, the zero reading is a measurement of a constant quantity). If the zero reading is consistently above or below zero, a systematic error is present. If this cannot be eliminated, potentially by resetting the instrument immediately before the experiment then it needs to be allowed by subtracting its (possibly time-varying) value from the readings, and by taking it into account while assessing the accuracy of the measurement.
If no pattern in a series of repeated measurements is evident, the presence of fixed systematic errors can only be found if the measurements are checked, either by measuring a known quantity or by comparing the readings with readings made using a different apparatus, known to be more accurate. For example, if you think of the timing of a pendulum using an accurate stopwatch several times you are given readings randomly distributed about the mean. Hopings systematic error is present if the stopwatch is checked against the ‘speaking clock’ of the telephone system and found to be running slow or fast. Clearly, the pendulum timings need to be corrected according to how fast or slow the stopwatch was found to be running.
Measuring instruments such as ammeters and voltmeters need to be checked periodically against known standards.
Systematic errors can also be detected by measuring already known quantities. For example, a spectrometer fitted with a diffraction grating may be checked by using it to measure the wavelength of the D-lines of the sodium electromagnetic spectrum which are at 600 nm and 589.6 nm. The measurements may be used to determine the number of lines per millimetre of the diffraction grating, which can then be used to measure the wavelength of any other spectral line.
Constant systematic errors are very difficult to deal with as their effects are only observable if they can be removed. Such errors cannot be removed by repeating measurements or averaging large numbers of results. A common method to remove systematic error is through calibration of the measurement instrument.
Sources of random error[edit]
The random or stochastic error in a measurement is the error that is random from one measurement to the next. Stochastic errors tend to be normally distributed when the stochastic error is the sum of many independent random errors because of the central limit theorem. Stochastic errors added to a regression equation account for the variation in Y that cannot be explained by the included Xs.
Surveys[edit]
The term «observational error» is also sometimes used to refer to response errors and some other types of non-sampling error.[1] In survey-type situations, these errors can be mistakes in the collection of data, including both the incorrect recording of a response and the correct recording of a respondent’s inaccurate response. These sources of non-sampling error are discussed in Salant and Dillman (1994) and Bland and Altman (1996).[4][5]
These errors can be random or systematic. Random errors are caused by unintended mistakes by respondents, interviewers and/or coders. Systematic error can occur if there is a systematic reaction of the respondents to the method used to formulate the survey question. Thus, the exact formulation of a survey question is crucial, since it affects the level of measurement error.[6] Different tools are available for the researchers to help them decide about this exact formulation of their questions, for instance estimating the quality of a question using MTMM experiments. This information about the quality can also be used in order to correct for measurement error.[7][8]
Effect on regression analysis[edit]
If the dependent variable in a regression is measured with error, regression analysis and associated hypothesis testing are unaffected, except that the R2 will be lower than it would be with perfect measurement.
However, if one or more independent variables is measured with error, then the regression coefficients and standard hypothesis tests are invalid.[9]: p. 187 This is known as attenuation bias.[10]
See also[edit]
- Bias (statistics)
- Cognitive bias
- Correction for measurement error (for Pearson correlations)
- Errors and residuals in statistics
- Error
- Replication (statistics)
- Statistical theory
- Metrology
- Regression dilution
- Test method
- Propagation of uncertainty
- Instrument error
- Measurement uncertainty
- Errors-in-variables models
- Systemic bias
References[edit]
- ^ a b Dodge, Y. (2003) The Oxford Dictionary of Statistical Terms, OUP. ISBN 978-0-19-920613-1
- ^ a b John Robert Taylor (1999). An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements. University Science Books. p. 94, §4.1. ISBN 978-0-935702-75-0.
- ^ «Systematic error». Merriam-webster.com. Retrieved 2016-09-10.
- ^ Salant, P.; Dillman, D. A. (1994). How to conduct your survey. New York: John Wiley & Sons. ISBN 0-471-01273-4.
- ^ Bland, J. Martin; Altman, Douglas G. (1996). «Statistics Notes: Measurement Error». BMJ. 313 (7059): 744. doi:10.1136/bmj.313.7059.744. PMC 2352101. PMID 8819450.
- ^ Saris, W. E.; Gallhofer, I. N. (2014). Design, Evaluation and Analysis of Questionnaires for Survey Research (Second ed.). Hoboken: Wiley. ISBN 978-1-118-63461-5.
- ^ DeCastellarnau, A. and Saris, W. E. (2014). A simple procedure to correct for measurement errors in survey research. European Social Survey Education Net (ESS EduNet). Available at: http://essedunet.nsd.uib.no/cms/topics/measurement Archived 2019-09-15 at the Wayback Machine
- ^ Saris, W. E.; Revilla, M. (2015). «Correction for measurement errors in survey research: necessary and possible» (PDF). Social Indicators Research. 127 (3): 1005–1020. doi:10.1007/s11205-015-1002-x. hdl:10230/28341. S2CID 146550566.
- ^ Hayashi, Fumio (2000). Econometrics. Princeton University Press. ISBN 978-0-691-01018-2.
- ^ Angrist, Joshua David; Pischke, Jörn-Steffen (2015). Mastering ‘metrics : the path from cause to effect. Princeton, New Jersey. p. 221. ISBN 978-0-691-15283-7. OCLC 877846199.
The bias generated by this sort of measurement error in regressors is called attenuation bias.
Further reading[edit]
- Cochran, W. G. (1968). «Errors of Measurement in Statistics». Technometrics. 10 (4): 637–666. doi:10.2307/1267450. JSTOR 1267450.
From Wikipedia, the free encyclopedia
«Systematic bias» redirects here. For the sociological and organizational phenomenon, see Systemic bias.
Observational error (or measurement error) is the difference between a measured value of a quantity and its true value.[1] In statistics, an error is not necessarily a «mistake». Variability is an inherent part of the results of measurements and of the measurement process.
Measurement errors can be divided into two components: random and systematic.[2]
Random errors are errors in measurement that lead to measurable values being inconsistent when repeated measurements of a constant attribute or quantity are taken. Systematic errors are errors that are not determined by chance but are introduced by repeatable processes inherent to the system.[3] Systematic error may also refer to an error with a non-zero mean, the effect of which is not reduced when observations are averaged.[citation needed]
Measurement errors can be summarized in terms of accuracy and precision.
Measurement error should not be confused with measurement uncertainty.
Science and experiments[edit]
When either randomness or uncertainty modeled by probability theory is attributed to such errors, they are «errors» in the sense in which that term is used in statistics; see errors and residuals in statistics.
Every time we repeat a measurement with a sensitive instrument, we obtain slightly different results. The common statistical model used is that the error has two additive parts:
- Systematic error which always occurs, with the same value, when we use the instrument in the same way and in the same case.
- Random error which may vary from observation to another.
Systematic error is sometimes called statistical bias. It may often be reduced with standardized procedures. Part of the learning process in the various sciences is learning how to use standard instruments and protocols so as to minimize systematic error.
Random error (or random variation) is due to factors that cannot or will not be controlled. One possible reason to forgo controlling for these random errors is that it may be too expensive to control them each time the experiment is conducted or the measurements are made. Other reasons may be that whatever we are trying to measure is changing in time (see dynamic models), or is fundamentally probabilistic (as is the case in quantum mechanics — see Measurement in quantum mechanics). Random error often occurs when instruments are pushed to the extremes of their operating limits. For example, it is common for digital balances to exhibit random error in their least significant digit. Three measurements of a single object might read something like 0.9111g, 0.9110g, and 0.9112g.
Characterization[edit]
Measurement errors can be divided into two components: random error and systematic error.[2]
Random error is always present in a measurement. It is caused by inherently unpredictable fluctuations in the readings of a measurement apparatus or in the experimenter’s interpretation of the instrumental reading. Random errors show up as different results for ostensibly the same repeated measurement. They can be estimated by comparing multiple measurements and reduced by averaging multiple measurements.
Systematic error is predictable and typically constant or proportional to the true value. If the cause of the systematic error can be identified, then it usually can be eliminated. Systematic errors are caused by imperfect calibration of measurement instruments or imperfect methods of observation, or interference of the environment with the measurement process, and always affect the results of an experiment in a predictable direction. Incorrect zeroing of an instrument leading to a zero error is an example of systematic error in instrumentation.
The Performance Test Standard PTC 19.1-2005 “Test Uncertainty”, published by the American Society of Mechanical Engineers (ASME), discusses systematic and random errors in considerable detail. In fact, it conceptualizes its basic uncertainty categories in these terms.
Random error can be caused by unpredictable fluctuations in the readings of a measurement apparatus, or in the experimenter’s interpretation of the instrumental reading; these fluctuations may be in part due to interference of the environment with the measurement process. The concept of random error is closely related to the concept of precision. The higher the precision of a measurement instrument, the smaller the variability (standard deviation) of the fluctuations in its readings.
Sources[edit]
Sources of systematic error[edit]
Imperfect calibration[edit]
Sources of systematic error may be imperfect calibration of measurement instruments (zero error), changes in the environment which interfere with the measurement process and sometimes imperfect methods of observation can be either zero error or percentage error. If you consider an experimenter taking a reading of the time period of a pendulum swinging past a fiducial marker: If their stop-watch or timer starts with 1 second on the clock then all of their results will be off by 1 second (zero error). If the experimenter repeats this experiment twenty times (starting at 1 second each time), then there will be a percentage error in the calculated average of their results; the final result will be slightly larger than the true period.
Distance measured by radar will be systematically overestimated if the slight slowing down of the waves in air is not accounted for. Incorrect zeroing of an instrument leading to a zero error is an example of systematic error in instrumentation.
Systematic errors may also be present in the result of an estimate based upon a mathematical model or physical law. For instance, the estimated oscillation frequency of a pendulum will be systematically in error if slight movement of the support is not accounted for.
Quantity[edit]
Systematic errors can be either constant, or related (e.g. proportional or a percentage) to the actual value of the measured quantity, or even to the value of a different quantity (the reading of a ruler can be affected by environmental temperature). When it is constant, it is simply due to incorrect zeroing of the instrument. When it is not constant, it can change its sign. For instance, if a thermometer is affected by a proportional systematic error equal to 2% of the actual temperature, and the actual temperature is 200°, 0°, or −100°, the measured temperature will be 204° (systematic error = +4°), 0° (null systematic error) or −102° (systematic error = −2°), respectively. Thus the temperature will be overestimated when it will be above zero and underestimated when it will be below zero.
Drift[edit]
Systematic errors which change during an experiment (drift) are easier to detect. Measurements indicate trends with time rather than varying randomly about a mean. Drift is evident if a measurement of a constant quantity is repeated several times and the measurements drift one way during the experiment. If the next measurement is higher than the previous measurement as may occur if an instrument becomes warmer during the experiment then the measured quantity is variable and it is possible to detect a drift by checking the zero reading during the experiment as well as at the start of the experiment (indeed, the zero reading is a measurement of a constant quantity). If the zero reading is consistently above or below zero, a systematic error is present. If this cannot be eliminated, potentially by resetting the instrument immediately before the experiment then it needs to be allowed by subtracting its (possibly time-varying) value from the readings, and by taking it into account while assessing the accuracy of the measurement.
If no pattern in a series of repeated measurements is evident, the presence of fixed systematic errors can only be found if the measurements are checked, either by measuring a known quantity or by comparing the readings with readings made using a different apparatus, known to be more accurate. For example, if you think of the timing of a pendulum using an accurate stopwatch several times you are given readings randomly distributed about the mean. Hopings systematic error is present if the stopwatch is checked against the ‘speaking clock’ of the telephone system and found to be running slow or fast. Clearly, the pendulum timings need to be corrected according to how fast or slow the stopwatch was found to be running.
Measuring instruments such as ammeters and voltmeters need to be checked periodically against known standards.
Systematic errors can also be detected by measuring already known quantities. For example, a spectrometer fitted with a diffraction grating may be checked by using it to measure the wavelength of the D-lines of the sodium electromagnetic spectrum which are at 600 nm and 589.6 nm. The measurements may be used to determine the number of lines per millimetre of the diffraction grating, which can then be used to measure the wavelength of any other spectral line.
Constant systematic errors are very difficult to deal with as their effects are only observable if they can be removed. Such errors cannot be removed by repeating measurements or averaging large numbers of results. A common method to remove systematic error is through calibration of the measurement instrument.
Sources of random error[edit]
The random or stochastic error in a measurement is the error that is random from one measurement to the next. Stochastic errors tend to be normally distributed when the stochastic error is the sum of many independent random errors because of the central limit theorem. Stochastic errors added to a regression equation account for the variation in Y that cannot be explained by the included Xs.
Surveys[edit]
The term «observational error» is also sometimes used to refer to response errors and some other types of non-sampling error.[1] In survey-type situations, these errors can be mistakes in the collection of data, including both the incorrect recording of a response and the correct recording of a respondent’s inaccurate response. These sources of non-sampling error are discussed in Salant and Dillman (1994) and Bland and Altman (1996).[4][5]
These errors can be random or systematic. Random errors are caused by unintended mistakes by respondents, interviewers and/or coders. Systematic error can occur if there is a systematic reaction of the respondents to the method used to formulate the survey question. Thus, the exact formulation of a survey question is crucial, since it affects the level of measurement error.[6] Different tools are available for the researchers to help them decide about this exact formulation of their questions, for instance estimating the quality of a question using MTMM experiments. This information about the quality can also be used in order to correct for measurement error.[7][8]
Effect on regression analysis[edit]
If the dependent variable in a regression is measured with error, regression analysis and associated hypothesis testing are unaffected, except that the R2 will be lower than it would be with perfect measurement.
However, if one or more independent variables is measured with error, then the regression coefficients and standard hypothesis tests are invalid.[9]: p. 187 This is known as attenuation bias.[10]
See also[edit]
- Bias (statistics)
- Cognitive bias
- Correction for measurement error (for Pearson correlations)
- Errors and residuals in statistics
- Error
- Replication (statistics)
- Statistical theory
- Metrology
- Regression dilution
- Test method
- Propagation of uncertainty
- Instrument error
- Measurement uncertainty
- Errors-in-variables models
- Systemic bias
References[edit]
- ^ a b Dodge, Y. (2003) The Oxford Dictionary of Statistical Terms, OUP. ISBN 978-0-19-920613-1
- ^ a b John Robert Taylor (1999). An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements. University Science Books. p. 94, §4.1. ISBN 978-0-935702-75-0.
- ^ «Systematic error». Merriam-webster.com. Retrieved 2016-09-10.
- ^ Salant, P.; Dillman, D. A. (1994). How to conduct your survey. New York: John Wiley & Sons. ISBN 0-471-01273-4.
- ^ Bland, J. Martin; Altman, Douglas G. (1996). «Statistics Notes: Measurement Error». BMJ. 313 (7059): 744. doi:10.1136/bmj.313.7059.744. PMC 2352101. PMID 8819450.
- ^ Saris, W. E.; Gallhofer, I. N. (2014). Design, Evaluation and Analysis of Questionnaires for Survey Research (Second ed.). Hoboken: Wiley. ISBN 978-1-118-63461-5.
- ^ DeCastellarnau, A. and Saris, W. E. (2014). A simple procedure to correct for measurement errors in survey research. European Social Survey Education Net (ESS EduNet). Available at: http://essedunet.nsd.uib.no/cms/topics/measurement Archived 2019-09-15 at the Wayback Machine
- ^ Saris, W. E.; Revilla, M. (2015). «Correction for measurement errors in survey research: necessary and possible» (PDF). Social Indicators Research. 127 (3): 1005–1020. doi:10.1007/s11205-015-1002-x. hdl:10230/28341. S2CID 146550566.
- ^ Hayashi, Fumio (2000). Econometrics. Princeton University Press. ISBN 978-0-691-01018-2.
- ^ Angrist, Joshua David; Pischke, Jörn-Steffen (2015). Mastering ‘metrics : the path from cause to effect. Princeton, New Jersey. p. 221. ISBN 978-0-691-15283-7. OCLC 877846199.
The bias generated by this sort of measurement error in regressors is called attenuation bias.
Further reading[edit]
- Cochran, W. G. (1968). «Errors of Measurement in Statistics». Technometrics. 10 (4): 637–666. doi:10.2307/1267450. JSTOR 1267450.
1) Кислотно-основного титриметрического определения уксусной кислоты в уксусной эссенции;
2) Гравиметрического определения хроматов в электролите для хромирования.
Абсолютная погрешность аналитических
весов 0,1мг
Абсолютная погрешность (ошибка)
∆x=xi—xист.
Xi-измеренное
значениеXист-истинное
значение ( если истинное значение не
известно – берется среднее)
Абсолютная погрешность не может ясно
охарактеризовать точность измерения,
так как она не связана с измеренным
значением.
Относительная погрешность (ошибка)
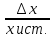
Систематические погрешности (ошибки)– возникают при действии постоянных
причин, их можно выявить устранить или
учесть изменяются по постоянно
действующему закону .
-
Инструментальные погрешности–связанные с инструментами для измерения
аналитического сигнала (весы, посуда)
уменьшить можно периодической проверкой
аналитических приборов. Обычно составляют
небольшую долю . -
Методические ошибки–
обусловлены методом анализа (например
погрешности пробоотбора и пробоподготовки.)
вносят основной вклад в общую погрешность. -
Реактивные– связаны с чистотой
используемых реактивов. -
Оперативные ошибки –зависят
от правильности и точности выполнения
аналитических операций (например,
недостаточное или излишнее промывание
или прокаливания осадков, недостаточное
тщательное перемещение осадка из одной
посуды в другую, неправильный способ
выливания раствора из пипетки и т.д.) -
Индивидуальные ошибки(личные) – это результат некоторых
физических недостатков экспериментатора,
которые мешают ему правильно проводить
известные операции.
Способы выявления систематических
погрешностей
1)варьирование величин пробы
Увеличив размер в кратное число раз
можно обнаружить по изменению найденного
содержания постоянную систематическую
погрешность
2)способ «введено найдено»
Добавить точно известное количество
компонента в той же форме, в которой
находится аналитический объект. Введенная
добавка проводится через все стадии
анализа. Если на конечной стадии
определяется добавка с точностью, то
систематической ошибки нет.
3) сравнение результата анализа с
результатом, полученным другим независимым
методом
4)анализ стандартного образца
Проведение всех стадий анализа, на
стадии обработки сравнивается с
паспортом, если все совпадает , то
систематической ошибки нет.
Типы погрешностей
-
Погрешности известной природы, могут
быть рассчитаны и учтены введение
соответствующей поправки -
Погрешности известной природы, значение
которых может быть оценены в ходе
химического анализа
Релятивизация — способ устранения
систематической погрешности, когда в
идентичных условиях проводят отдельные
аналитические операции таким образом,
что происходит нивелирование
систематической ошибки
-
Погрешность невыясненной природы,
значение который неизвестно, их сложно
выявить и устранить , используют прием
рандомизации
Рандомизация – переведение систематической
ошибки в разряд случайной
Случайные ошибки– обрабатываются
по правилам матемтической статистики,
связаны с влиянием неконтролируемых
параметров, непредвиденны и неучтимы.
Промахи– грубые ошибки, сильно
искажающие результаты анализа (ошибки
при расчётах, неправильный отчёт по
шкале, проливание раствора или просыпание
осадка). Результат с промахом отбрасывается
при выводе среднего значения.
6. Случайные
ошибки. Метрологические характеристики,
отражающие случайные ошибки. Оценка и
критерии воспроизводимости и правильности.
Рассмотрите на примере титриметрического
комплексонометрического определения
меди (II).
Случайные ошибки–отражают
неопределенность результата , присущую
любому измерению, обрабатываются по
правилам матемтической статистики,
связаны с влиянием неконтролируемых
параметров, непредвиденны и неучтимы.
Причины таких погрешностей:
Изменение температуры во время измерения,
ослабление внимания при работе, случайные
потери, загрязнение, использование
разной посуды, весов и тд.
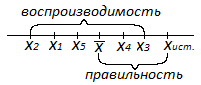
метрологические характеристики:
Правильность— характеризует степень
близости измеренного результата
некоторой величины к её истинному
значению
Воспроизводимость— характеризует
степень близости друг к другу единичный
определений (рассеяние единичных
результатов относительно среднего
значения
Точность— собирательная характеристика
метода или методики , включающая их
правильность и воспроизводимость .
Чувствительность— величина,
определяемая минимальным количеством
вещества, которое можно обнаружить
данным методом
Чувствительность – собирательное
понятие , включающее три характеристики:
1)Коэффициент чувствительности
коэффициент чувствительности sхарактеризует отклик аналитического
сигналаyна содержание
компонентаc,s-
это значение первой производной
градуировочной функции при определенном
содержании компонента, для прямолинейных
градуировочных графиковs– это тангенс угла наклона прямойy=Sc+b
s=
чем больше s, тем меньшие
количества компонента можно обнаружить
, используя один и тот же аналитический
сигнал, чем большеs, тем
точнее можно определить одно и то же
количество вещества
2)предел обнаружения Сminнаименьшее содержание при котором по
данной методике можно обнаружить
присутствие компонента с заданной
доверительной вероятностью, относится
к области качественного анализа и
определяет минимальное содержание
компонента
3)нижняя граница определяемого содержания
Сн
В количественном анализе обычно приводят
интервал определяемых содержаний-
область значений определяемых содержаний,
предусмотренная данной методикой и
ограниченная нижней и верхней границами.
Верхняя граница Свнаибольшее
значение количества или концентрации
компонента, определяемое по данной
методике.
нижняя граница Сн-наименьшее
содержание компонента , определяемое
по данной методике . З нижнюю границу
обычно принимают то минимальное
количество или концентрацию, которые
можно определить с относительным
стандартным отклонением Ϭr≤0,33
Оценка и критерии воспроизводимости
1)Среднее арифметическое

2)Отклонение
di=xi—
3)Медиана— тот единичный результат
, относительно которого число результатов
с большими и меньшими значениями
одинаковое, если количество значений
нечетное, то медиана совпадает с
центральным результатом ранжированной
выборки , если количество значений
четное, то медиана есть среднее
арифметическое между двумя центральными
значениями ранжированной выборки
4)среднее отклонение-среднее
арифметическое единичных отклонений,
без учет знака

5)Дисперсия
Ϭ2илиs2
Ϭ2=
еслиn>10
Ϭ2=
еслиn≤10
6)стандартное отклонениеϬx=
7)Относительное стандартное отклонение
Ϭr=
Титриметрическое комплексонометрическое
определения меди (II).
Выполнение определениея
1)Титрование исследуемого раствора
стандартным раствором ЭДТА
2)расчет граммового содержания меди
Ход анализа:Титрование исследуемого
раствора стандартным раствором ЭДТА.
Анализируемый раствор помещают в мерную
колбу на 100 мл, довдят водой до метки,
тщательно перемешивают. В коническую
колбу дл титрования берут аликвоту,
добавляют индикатор мурексид на кончике
шпателя и титруют раствором ЭДТА сначала
до грязно-розового цвета, натем добавляют
несколько капель 10%-ного раствора аммиака
до появления изумрудной или желтой
окраски раствора и дотитровывают
раствором ЭДТА до перехода окраски в
фиолетовую.
Формула для расчета граммового содержания
меди:
mCu,г=C(

ЭДТА·Mэкв(Cu)·P·10-3
Формула для расчета процентного
содержания меди:
ωCu=
Возможные причины возникновения
случайных ошибокв комплексонометрическом
титровании меди возникают в процессе
измерения объемов: неточное доведение
до метки мерной колбы, использование
разных пипеток, потеря титранта (капнуло
мимо), использование непромытой посуды.
Так же могут возникать ошибки из-за
неточного определения перехода окраски
, но эти ошибки будут относиться к
категории систематических индивидуальных
ошибок.
7. Гравиметрическое
определение бария в минерале альстонит:
этапы определения, возможные формулы
осадителей, осаждаемой и гравиметрической
формы, механизм образования осадка,
возможные варианты загрязнения осадка,
приемы повышения чистоты осадка,
погрешности определения. Условия
аналитического выделения осадков бария.
Минерал альстонит минерал, безводный
двойной карбонат бария и кальция
BaCa(CO3)2
Этапы определения:
1)взятие навески и её растворение
2)расчет количества осадителя
3)приготовление раствора осадителя
4)осаждение
5)фильтрование и промывание
6)высушивание и прокаливание осадка
7)взвешивание осадка, расчёт содержания
бария
Для количественного определения бария
его осаждают в виде сульфата BaSO4
(осаждаемая форма)
BaCO3+H2SO4=
BaSO4+H2CO3
В качестве осадителя, посташика
сульфат-ионов используют серную кислоту
H2SO4(осадитель)
После прокаливания осадка его формула
не меняется и остается так же в виде
сульфата бария BaSO4
(гравиметрическая форма)
Механизм образования осадка:
В процессе образования осадка различают
три стадии :
1)образование зародышей кристаллов
2)рост кристаллов
3)объединение (агрегация) хаотично
ориентированных кристаллов
Насыщение=>пересыщение=>ПКИ>ПР=>
образование мельчайших зародышей
кристаллов
Осаждение происходит при определенной
степени пересыщения раствора
P=


пересыщение,Q-концентрация
кристаллизующегося вещества в растворе
Центром кристалла может служить твердая
частица этого вещества или любая другая
твердая частица, которую мы вносим в
раствор, твердые частицы могут изначально
присутствовать в растворе как примесь.
Если осаждение происходи из разбавленных
растворов, то появление осадка занимает
время-индукцинный период.
В процессе добавления каждой новой
порции осадителя происходит мгновенное
пересыщение раствора, зародыши растут
быстро за счет окружающих их ионов, как
только зародыш дотиг определенного
размера выпадает осадок
Рост кристаллов идет параллельно 1-ой
стадии, происходит за счет диффузии
ионов к поверхности растущего кристалла.
Число и размер частиц осадка (дисперсность
системы кол-во в единицы объёма) зависит
от соотношения скоростей 1-ой и 2-ой
стадий
V1— скорость образования
зародышейV2-скорость
роста кристаллов
V1>>V2-мелкодисперсный
осадокV1<<V2-крупнокристаллический
осадок
Лимитирующую стадию определяет скорость
осаждения и концентрации ионов
При медленном осаждении лимитирующей
стадией является кристаллизация ,
частица окружена однородным слоем
осаждаемый ионов в результате получается
кристалл правильной форм
При высокой концентрации ионов
лимитирующей стадией становится диффузия
, образуются кристаллы не правильной
формы с большой площадью поверхности
Следует отметить, что на скорость
процесса кристаллизации влияет

влияние
зародышей и на скорость роста кристаллов
В случае образования зародышей
V1=k·(
закон
В случае роста кристаллов V2=k·
При высокой степени

мелкодисперсные осадки, при уменьшении
образуются крупнокристаллические
осадки
Агрегация происходит в гетерогенной
системе, в значительной степени
определяется числом центров кристаллизации.
Чем больше центров кристаллизации , тем
в меньшей степени они укрупняются на
второй стадии , тем хуже структура и тем
выше дисперсность осадков.
К аналитическим свойствам осадка
относятся: растворимость, чистота,
фильтруемость.
Лучшими свойствами обладают
крупнокристаллические осадки.
Загрязнение осадков
В гарвиметрическом определении часто
возникают ошибки , вызванные переходом
осадка в раствор или веществ из раствора
в осадок-соосождение
Соосаждение происходит в процессе
образования осадка
Отрицательная роль : загрязнение осадка
Положительная роль :используется для
концентрирования микропримесей
Существует три типа соосаждения:
1)Адсорбция- соосаждение примесей на
поверхности уже сформированного осадка,
происходит в результате нескомпенсированности
зарядов внутри и на поверхности.
Характеризуется ярко выраженной
избирательность, преимущественно
адсорбируются те ионы, которые входят
в структуру осадка, противоионы-примеси
Адсорбция противоионов подчиняется
правилам Панета-Фаянса-Гана
А)при одинаковых концентрациях
адсорбируются многозарядные ионы
Б)при одинаковых зарядах адсорбируются
те, концентрация которых выше
В)при одинаковых концентрациях и
зарядах-те, которые образуют с ионами
решетки менее растворимое соединение
Г)в кислой среде соосаждение ионов
уменьшается в следствии конкурентной
адсорбции H3O+
Количество адсорбируемой примеси
зависит от величины поверхности осадка,
концентрации адсорбируемой примеси и
температуры ( с ↑ поверхности и ↑
концентрации- адсорбция ↑; с ↑ температуры
адсорбция ↓)
2)Окклюзия- загрязнение осадка в результате
захвата примеси внутрь растущего
кристалла, происходит в процессе
формирования осадка.
Различают 2-х видов: абсорбционная и
механическая
Механическа- случайный захват частиц
маточного раствора внутрь твердой фазы
вследствие нарушения механической
структуры
Характерна при выделении аморфных
осадков.
Окклюзированные примеси равномерно
распределены внутри, но не принимают
участие в построении решетки кристалла.
Адсорбционная-возникает при быстром
росте кристалла, когда ионы на поверхности
обратают кристаллизованным веществом.
Протекает вследствии адсорбции примесей
по микротрещинам кристаллической
структуры.
Окклюзия подчиняется тем же правилам,
что и адсорбция
Общие правила понижения окклюзии–замедление процесса выделения твердой
фазы-осаждение при малом пересыщении
, работают с разбавленными растворами
, осадитель добавляют по каплям, при
постоянном перемешивании.
3)изоморфное соосаждение характерно
для изоморфно кристаллизующегося
веществ, которые могут образовывать
смешанные кристаллы, примесь участвует
в построении кристаллической решетки,
наблюдается лишь в тех случаях, когда
вещества сходны по химическим свойствам
или ионы имеют одинаковые кч и радиус.
Совместное осаждение-выделение в твердую
фазу нескольких веществ, для которых в
услових осаждения достигнуты величины
их Kst
Последовательное осаждение- веделение
примеси на поверхности уже сформированного
осадка
Приемы и методы повышения чистоты
осадка
Зависят от типа соосаждения
1)адсорбционные примеси хорошо удаляются
промыванием осадка, более эффективно
многократное промывание малыми порциями
Выбор промывочной жидкости:
Не увеличивает растворимость осадка и
не ухудшает его фильтруемость, водой
промывают осадки с k~10-11/-12,
не подвергаемых пептизации, кристаллические
осадки с конст, растворимости 10-9/-11промывают разбавленным раствором
осадителя, аморфные осадки промывают
разбавленными растворами электролитов
коагуляторов, чтобы избежать пептизации
Промывние кристаллических осадков
проводят холодной промывочной жидкостью,
чтоб не увеличивать растворимость,
аморфные наоборот горячими
2)окклюзированные примеси , для избавления
от них:
Для кристаллических осадков-старение
Для аморфных-переосаждение
Погрешность гравиметрического
метода анализа
Общая погрешность анализа
Ϭ2=


пробоотбораm-число пробn-число параллельных
определений

измерений
Результат находится по формуле
P,%=
Методическая ошибка, обусловлена
неколичественным выпадением осадка,
её устранить нельзя
Qоб=
г/100мл воды,
фильтрата,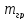
масса гравиметрической формы
Случайные ошибки
Относительное стандартное отклонение


массы гравиметрической формы

гравиметрической формы
Ϭa1-погрешность
взвешивания тары
Ϭa2-погрешность
взвешивания тары с навеской


г Ϭa1= Ϭa2=0,0002г
Суммарная ошибка
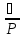
n-число проб
m-число измерений

прибора

измерения
8. Гравиметрическое
определение алюминия в каолине: этапы
определения, возможные формулы осадителей,
осаждаемой и гравиметрической формы,
механизм образования осадка, возможные
варианты загрязнения осадка, приемы
повышения чистоты осадка, погрешности
определения. Преимущества органических
осадителей. Условия аналитического
выделения осадков алюминия.
Механизм образования осадка:
В процессе образования осадка различают
три стадии :
1)образование зародышей кристаллов
2)рост кристаллов
3)объединение (агрегация) хаотично
ориентированных кристаллов
Насыщение=>пересыщение=>ПКИ>ПР=>
образование мельчайших зародышей
кристаллов
Осаждение происходит при определенной
степени пересыщения раствора
P=


пересыщение,Q-концентрация
кристаллизующегося вещества в растворе
Центром кристалла может служить твердая
частица этого вещества или любая другая
твердая частица, которую мы вносим в
раствор, твердые частицы могут изначально
присутствовать в растворе как примесь.
Если осаждение происходи из разбавленных
растворов, то появление осадка занимает
время-индукцинный период.
В процессе добавления каждой новой
порции осадителя происходит мгновенное
пересыщение раствора, зародыши растут
быстро за счет окружающих их ионов, как
только зародыш дотиг определенного
размера выпадает осадок
Рост кристаллов идет параллельно 1-ой
стадии, происходит за счет диффузии
ионов к поверхности растущего кристалла.
Число и размер частиц осадка (дисперсность
системы кол-во в единицы объёма) зависит
от соотношения скоростей 1-ой и 2-ой
стадий
V1— скорость образования
зародышейV2-скорость
роста кристаллов
V1>>V2-мелкодисперсный
осадокV1<<V2-крупнокристаллический
осадок
Лимитирующую стадию определяет скорость
осаждения и концентрации ионов
При медленном осаждении лимитирующей
стадией является кристаллизация ,
частица окружена однородным слоем
осаждаемый ионов в результате получается
кристалл правильной форм
При высокой концентрации ионов
лимитирующей стадией становится диффузия
, образуются кристаллы не правильной
формы с большой площадью поверхности
Следует отметить, что на скорость
процесса кристаллизации влияет

влияние
зародышей и на скорость роста кристаллов
В случае образования зародышей
V1=k·(
закон
В случае роста кристаллов V2=k·
При высокой степени

мелкодисперсные осадки, при уменьшении
образуются крупнокристаллические
осадки
Агрегация происходит в гетерогенной
системе, в значительной степени
определяется числом центров кристаллизации.
Чем больше центров кристаллизации , тем
в меньшей степени они укрупняются на
второй стадии , тем хуже структура и тем
выше дисперсность осадков.
К аналитическим свойствам осадка
относятся: растворимость, чистота,
фильтруемость.
Лучшими свойствами обладают
крупнокристаллические осадки.
Загрязнение осадков
В гарвиметрическом определении часто
возникают ошибки , вызванные переходом
осадка в раствор или веществ из раствора
в осадок-соосождение
Соосаждение происходит в процессе
образования осадка
Отрицательная роль : загрязнение осадка
Положительная роль :используется для
концентрирования микропримесей
Существует три типа соосаждения:
1)Адсорбция- соосаждение примесей на
поверхности уже сформированного осадка,
происходит в результате нескомпенсированности
зарядов внутри и на поверхности.
Характеризуется ярко выраженной
избирательность, преимущественно
адсорбируются те ионы, которые входят
в структуру осадка, противоионы-примеси
Адсорбция противоионов подчиняется
правилам Панета-Фаянса-Гана
А)при одинаковых концентрациях
адсорбируются многозарядные ионы
Б)при одинаковых зарядах адсорбируются
те, концентрация которых выше
В)при одинаковых концентрациях и
зарядах-те, которые образуют с ионами
решетки менее растворимое соединение
Г)в кислой среде соосаждение ионов
уменьшается в следствии конкурентной
адсорбции H3O+
Количество адсорбируемой примеси
зависит от величины поверхности осадка,
концентрации адсорбируемой примеси и
температуры ( с ↑ поверхности и ↑
концентрации- адсорбция ↑; с ↑ температуры
адсорбция ↓)
2)Окклюзия- загрязнение осадка в результате
захвата примеси внутрь растущего
кристалла, происходит в процессе
формирования осадка.
Различают 2-х видов: абсорбционная и
механическая
Механическа- случайный захват частиц
маточного раствора внутрь твердой фазы
вследствие нарушения механической
структуры
Характерна при выделении аморфных
осадков.
Окклюзированные примеси равномерно
распределены внутри, но не принимают
участие в построении решетки кристалла.
Адсорбционная-возникает при быстром
росте кристалла, когда ионы на поверхности
обратают кристаллизованным веществом.
Протекает вследствии адсорбции примесей
по микротрещинам кристаллической
структуры.
Окклюзия подчиняется тем же правилам,
что и адсорбция
Общие правила понижения окклюзии–замедление процесса выделения твердой
фазы-осаждение при малом пересыщении
, работают с разбавленными растворами
, осадитель добавляют по каплям, при
постоянном перемешивании.
3)изоморфное соосаждение характерно
для изоморфно кристаллизующегося
веществ, которые могут образовывать
смешанные кристаллы, примесь участвует
в построении кристаллической решетки,
наблюдается лишь в тех случаях, когда
вещества сходны по химическим свойствам
или ионы имеют одинаковые кч и радиус.
Совместное осаждение-выделение в твердую
фазу нескольких веществ, для которых в
услових осаждения достигнуты величины
их Kst
Последовательное осаждение- веделение
примеси на поверхности уже сформированного
осадка
Приемы и методы повышения чистоты
осадка
Зависят от типа соосаждения
1)адсорбционные примеси хорошо удаляются
промыванием осадка, более эффективно
многократное промывание малыми порциями
Выбор промывочной жидкости:
Не увеличивает растворимость осадка и
не ухудшает его фильтруемость, водой
промывают осадки с k~10-11/-12,
не подвергаемых пептизации, кристаллические
осадки с конст, растворимости 10-9/-11промывают разбавленным раствором
осадителя, аморфные осадки промывают
разбавленными растворами электролитов
коагуляторов, чтобы избежать пептизации
Промывние кристаллических осадков
проводят холодной промывочной жидкостью,
чтоб не увеличивать растворимость,
аморфные наоборот горячими
2)окклюзированные примеси , для избавления
от них:
Для кристаллических осадков-старение
Для аморфных-переосаждение
Погрешность гравиметрического
метода анализа
Общая погрешность анализа
Ϭ2=


пробоотбораm-число пробn-число параллельных
определений

измерений
Результат находится по формуле
P,%=
Методическая ошибка, обусловлена
неколичественным выпадением осадка,
её устранить нельзя
Qоб=
г/100мл воды,
фильтрата,
масса гравиметрической формы
Случайные ошибки
Относительное стандартное отклонение


массы гравиметрической формы

гравиметрической формы
Ϭa1-погрешность
взвешивания тары
Ϭa2-погрешность
взвешивания тары с навеской


г Ϭa1= Ϭa2=0,0002г
Суммарная ошибка

n-число проб
m-число измерений
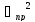
прибора
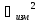
измерения
9. Гравиметрическое
определение железа в руде: этапы
определения, возможные формулы осадителя,
осаждаемой и гравиметрической формулы,
механизм образования коллоидной частицы,
процессы, приводящие к образованию
осадка, возможные варианты загрязнения
осадка, приемы повышения чистоты осадка,
погрешности. Условия аналитического
выделения осадков железа.
Гравиметрическое определение железа(III)
основано на его осаждении в виде
гидроксида железа(III)Fe(OH)3.
Трехвалентное железо осаждают раствором
аммиака, осаждаемой формой являетсяFe(OH)3.
Реакция:Fe(NO3)3+3NH3·H2O=Fe(OH)3+3NH4NO3.
При прокаливании гидроксид железа(III)
превращается в оксид железа(III),
который является гравиметрической
формой:Fe(OH)3=(t°)Fe2O3+3H2O.
Этапы определения:1) взятие навески
и ее растворение; 2) приготовление
раствора осадителя; 3) осаждение; 4)
фильтрование и промывание осадка; 5)
высушивание и прокаливание; 6) взвешивание
осадка, расчет содержания железа.
Расчет ведут по формулам
ωFe2O3=

ωFe
=
Механизм образования коллоидной
частицы:
Fe(NO3)3+3NH4OH(изб.)=Fe(OH)3↓+3NH4NO3
{[Fe(OH)3]m
· nOH—
·(n-x)NH4+}-x
·xNH4+
агрегат плотный слой
диффузный слой Мицелла
Ядро
Коллоидная частица
Вещество в коллоидной системе имеет
большую развитую поверхность и
нескомпенсированный заряд на границе
разлела фаз. Существование
нескомпенсированного силового поля
ведет к адсорбции из раствора молекул
или ионов. Если коллоидная система
возникла в результате проведения
химической реакции осаждения, то частицы
адсорбируют в первую очередь те ионы,
которые могут достраивать кристаллическую
решетку. Адсорбированные ионы сообщают
частице «+» или «-« заряд. Слой
адсорбированных ионов на ядре – это
первичный адсорбционный слой. Заряд,
созданный таким слоем, достаточно высок
и обуславливает электростатическое
взаимодействие с иоами противоположного
знака. В результате образуется слой
противоионов, который выравнивает заряд
первичного слоя. Слой противоионов
имеет диффузный характер. Часть
противоионов, прочно связанных с
первичным слоем – это плотный слой,
остальные противоионы составляют
диффузный слой.
Образование осадкапроисходит
тогда, когда раствор становится
пересыщенным, т.е. [A+]m[B-]n>Ks(ПКИ>ПР). Образование осадков связано
с процессом укрупнения частиц, с
образованием кристаллической решетки
вещества. Этот процесс определяется
числом центров кристаллизации: чем
больше центров, тем в меньшей степени
они укрупняются и тем хуже структура и
выше дисперсность осадка.
Возможные варианты загрязнения:
1)Путем адсорбции ( для конкретного
примера хлорид-ионов на поверхности
осадка); 2)Окклюзия; 3)Изоморфное
соосаждение; 4) Совместное осаждение;
5) Последующее осаждение.
Приемы повышения чистоты осадка:
1) Адсорбированные на поверхности примеси
хорошо удаляются при промывании осадков
на фильтре при помощи промывных жидкостей,
т.к. примеси переходят в промывную
жидкость и уходят через поры фильтра.
Эффективно многократное промывание
небольшими порциями промывной жидкости.
Промывную жидкость выбирают максимально
тщательно, чтобы не увеличивать
растворимость осадка и не ухудшать его
фильтрацию. Кристаллические осадки
промывают холодными промывными
жидкостями, чтобы не увеличить
растворимость осадка, а аморфные –
наоборот горячими. Водой промывают
осадки с низкими константами растворимости
(ниже 10-11-10-12), а также те,
которые не подвергаются пептизации.
Если константа растворимости осадка
10-9-10-11и он кристаллический,
то его промывают разбавленным раствором
осадителя. Аморфные осадки промывают
разбавленными растворами
электролитов-коагулянтов (солиNH4+),
чтобы избежать пептизации(в опыте с
железом осадок промывали растворомNH4NO3).
Повышение температуры также способствует
уменьшению адсорбции (на конкретном
примере горячий раствор, содержащий
10% аммиак разбавляют горячей водой для
уменьшения адсорбции хлорид-ионов на
поверхности осадка). 2) Для очищения
окклюдированных примесей в случае
кристаллических осадков используют
старение, в случае аморфных осадков –
переосаждение.Степень окклюзии в
процессе осаждения можно уменьшить
медленным добавлением осадителя по
каплям, при перемешивании.
Погрешности:
1) Общая погрешность анализа σ2=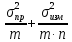
где σпр2– погрешность
пробоотбора, σизм2–
погрешность измерения,m– число проб,n– число
параллельных определений.
2) Методическая ошибка OобOоб=
—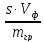
гдеs– растворимость
осадка, г/100 мл воды;Vф
– объем фильтрата и промывных вод,
мл;mгр– масса
полученного осадка, г.
3) Относительное стандартное отклонение


массы гравиметрической формы;mгр– масса гравиметрической формы; σa– дисперсия массы исходной навески;a– масса исходной навески;p– процентное содержание вещества в
исследуемой пробе;n–число
измерений.
4) Погрешность взвешивания тары σa1и тары с навескойσa2σa1=σa2=0,0002
г, σгр=
отклонение с учетом стадий пробоотбора
и пробоподготовки

Fe(OH)3– типичный пример осадка в аморфном
состоянии, легко дающий коллоидный
раствор.
Условия его осаждения следующие:
1)осаждение проводят из горячего раствора
анализируемого вещества горячим
раствором осадителя при перемешивании;
2)осаждение проводят из достаточно
концентрированного исследуемого
раствора концентрированным раствором
осадителя с последующим разбавлением(при
разбавлении устанавливается адсорбционное
равновесие, часть адсорбированных ионов
переходи в раствор, и осадок становится
более чистым); 3)осаждение проводят в
присутствии подходящего
электролита-коагулятора;
4)аморфные осадки почти не требуют
времени для созревания, их необходимо
фильтровать сразу после разбавления
раствора. Аморфные осадки нельзя
оставлять более, чем на несколько минут,
т.к. сильное уплотнение их затрудняет
последующее отмывание примесей, а также
при стоянии увеличивается количество
примесей, адсорбированных поверхностью
осадка.
10. Гравиметрическое определение никеля
в нихромовом сплаве: этапы определения,
возможные формулы осадителей, осаждаемой
и гравиметрической формулы, механизм
образования осадка, возможные варианты
загрязнения осадка, приемы повышения
чистоты осадка, погрешности. Условия
аналитического выделения осадков
никеля.
Гравиметрическое определение никеля
в нихромовом сплаве основано на его
осаждении в виде диметилглиоксимата
никеля Ni(HDMG)2.
Никель осаждают 1 %-ным спиртовым раствором
диметикглиоксимаH2DMG,
осаждаемой формой являетсяNi(HDMG)2.
Реакция:Ni2++2H2DMG=Ni(HDMG)2+2H+.
После высушивания осадка остается сухойNi(HDMG)2,
который является гравиметрической
формой.
Этапы определения:1) взятие навески
и ее растворение; 2) приготовление
раствора осадителя; 3) осаждение; 4)
фильтрование и промывание осадка; 5)
высушивание; 6) взвешивание осадка,
расчет содержания никеля.
Расчет ведут по формуле ωNi=
Механизм образования осадка:в
процессе образования осадка различают
3 параллельных процесса: 1) образование
зародышей кристалла (центров
кристаллизации); 2) рост кристаллов; 3)
объединение (агрегация) хаотично
ориентированных мелких кристаллов. В
начальный момент происходит насыщение
раствора, а затем его пересыщение. В
момент определенной пересыщенности
раствора, начинается выпадение
осадка.Центром кристалла может служить
твердая частица этого вещества или
любая другая твердая частица, которую
мы вносим в раствор, твердые частицы
могут изначально присутствовать в
растворе как примесь.
Если осаждение происходит из разбавленных
растворов, то появление осадка занимает
время-индукционный период.
В процессе добавления каждой новой
порции осадителя происходит мгновенное
пересыщение раствора, зародыши растут
быстро за счет окружающих их ионов, как
только зародыш достиг определенного
размера выпадает осадок.
Рост кристаллов идет параллельно 1-ой
стадии, происходит за счет диффузии
ионов к поверхности растущего кристалла.
Число и размер частиц осадка (дисперсность
системы кол-во в единицы объёма) зависит
от соотношения скоростей 1-ой и 2-ой
стадий (V1— скорость
образования зародышей,V2-скорость
роста кристаллов):V1>>V2-мелкодисперсный
осадок,V1<<V2-крупнокристаллический
осадок. Какая из стадий будет лимитировать
определяет скорость осаждения и
концентрации ионов. При медленном
осаждении лимитирующей стадией является
кристаллизация, частица окружена
однородным слоем осаждаемых ионов в
результате получается кристалл правильной
формы. При высокой концентрации ионов
лимитирующей стадией становится
диффузия, образуются кристаллы
неправильной формы с большой площадью
поверхности. Следует отметить, что на
скорость процесса кристаллизации влияет
влияние
зародышей и на скорость роста кристаллов.
При высокой степени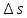
мелкодисперсные осадки, при уменьшении
осадки. Агрегация происходит в гетерогенной
системе, в значительной степени
определяется числом центров
кристаллизации.Чем больше центров
кристаллизации, тем в меньшей степени
они укрупняются на второй стадии, тем
хуже структура и тем выше дисперсность
осадков.
К аналитическим свойствам осадка
относятся: растворимость, чистота,
фильтруемость.Лучшими свойствами
обладают крупнокристаллические осадки.
Возможные варианты загрязнения: 1)
Путем адсорбции ( для конкретного примера
хлорид-ионов на поверхности осадка); 2)
Окклюзия; 3) Изоморфное соосаждение; 4)
Совместное осаждение; 5) Последующее
осаждение.
Приемы повышения чистоты осадка:
1) Адсорбированные на поверхности примеси
хорошо удаляются при промывании осадков
на фильтре при помощи промывных жидкостей,
т.к. примеси переходят в промывную
жидкость и уходят через поры фильтра.
Эффективно многократное промывание
небольшими порциями промывной жидкости.
Промывную жидкость выбирают максимально
тщательно, чтобы не увеличивать
растворимость осадка и не ухудшать его
фильтрацию. Кристаллические осадки
промывают холодными промывными
жидкостями, чтобы не увеличить
растворимость осадка, а аморфные –
наоборот горячими. Водой промывают
осадки с низкими константами растворимости
(ниже 10-11-10-12), а также те,
которые не подвергаются пептизации.
Если константа растворимости осадка
10-9-10-11и он кристаллический,
то его промывают разбавленным раствором
осадителя. Аморфные осадки промывают
разбавленными растворами
электролитов-коагулянтов (солиNH4+),
чтобы избежать пептизации (в опыте с
железом осадок промывали растворомNH4NO3).
Повышение температуры также способствует
уменьшению адсорбции (на конкретном
примере горячий раствор, содержащий
10% аммиак разбавляют горячей водой для
уменьшения адсорбции хлорид-ионов на
поверхности осадка). 2) Для очищения
окклюдированных примесей в случае
кристаллических осадков используют
старение, в случае аморфных осадков –
переосаждение.Степень окклюзии в
процессе осаждения можно уменьшить
медленным добавлением осадителя по
каплям, при перемешивании.
Погрешности:1) Общая погрешность
анализа σ2=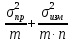
где σпр2– погрешность
пробоотбора, σизм2–
погрешность измерения,m– число проб,n– число
параллельных определений.
2) Методическая ошибка OобOоб=
—
гдеs– растворимость
осадка, г/100 мл воды;Vф
– объем фильтрата и промывных вод,
мл;mгр– масса
полученного осадка, г.
3) Относительное стандартное отклонение


массы гравиметрической формы;mгр– масса гравиметрической формы; σa– дисперсия массы исходной навески;a– масса исходной навески;p– процентное содержание вещества в
исследуемой пробе;n–число
измерений.
4) Погрешность взвешивания тары σa1и тары с навескойσa2σa1=σa2=0,0002
г, σгр=
5) Относительное стандартное отклонение
с учетом стадий пробоотбора и
пробоподготовки


Ni(HDMG)2– кристаллический осадок.
Условия его осаждения следующие:
1) осаждение ведут из достаточно
разбавленного исследуемого раствора
разбавленным раствором осадителя
(концентрации исследуемого раствора и
раствора осадителя должны быть примерно
одинаковыми);
2) раствор осадителя прибавляют медленно,
по каплям, при постоянном перемешивании
стеклянной палочкой (это предотвращает
явление окклюзии);
3) осаждение ведут из подогретого
исследуемого раствора горячим раствором
осадителя (для предотвращения пептизации);
4) к раствору прибавляют вещества,
способствующие повышению растворимости
осадка (увеличивают Iраствора), а затем понижают его
растворимость путем прибавления избытка
осадителя;
5) осадок оставляют на «созревание».
11. Гравиметрическое определение меди:
этапы определения, возможные формулы
осадителей, осаждаемой и гравиметрической
формулы, механизм образования осадка,
возможные варианты загрязнения осадка,
приемы повышения чистоты осадка,
погрешности. Преимущества органических
осадителей. Условия выделения осадков.
При гравиметрическом определении меди
медь из раствора осаждают различными
осадителями: 1) раствор аммиака осаждает
из нагретого раствора осадок Cu(OH)2;
2) Тиокарбонат калияK2CS3осаждает из нагретого раствора осадокCuS, который сушат при
100-110
3) В виде оксалата медь осаждается в
присутствиеCH3COOH;
4) При определении меди в виде
тетророданомеркуриатамедиCu[Hg(SCN)4]
медь осаждают из нагретого до кипения
раствора содержащего серную или азотную
кислоту, действиемK2[Hg(SCN)4].
Метод рекомендован для определения
меди в медных рудах; 5) Соль Рейнеке
(тетрароданодиаминохромат аммония)
NH4[Cr(NH3)2(SCN)4]
является избирательным реагентом для
определения меди в присутствие многих
посторонних ионов. Осаждение проводят
как в кислом, так и в аммиачном растворе
в виде [Cu(NH3)4][Cr(NH3)2(SCN)4]2
после предварительного восстановления
меди до одновалентного состояния
оловом(II). Для осаждения меди используются
также различные органические реагенты:
1) 8- оксихинолин осаждает медь в
уксуснокислом, аммиачном и щелочном
растворах при pH=5.33 — 14.55. Осадок, высушенный
при 105-110°С, соответствует составу
Cu(C9H6ON)2; 2) Медь осаждается
спиртовым раствором β-бензоиноксима в
слабощелочной среде в виде хлопьевидного
зеленого осадка составаCu(C6H5CHOCNOC6H5)2.
Осадок высушивают при 105-110
3) Салицилальдиоксим осаждает Cu (II) в
виде внутрикомплексного соединения
Cu(C7H6O2N)2в
уксуснокислой среде, среде ацетатного
буфера или ацетата аммония; 4) При действии
купферона наCu(II)
образуется купферонат меди (II)
с формулой Cu(C6H5N(NO)O)2;
5) При действии глицина на медь образуется
кристаллический осадок глицината меди
(II)Cu(NH2CH2COO)2.
Рассмотрим гравиметрическое определение
меди на примере осаждения ее
глицином.Реакция:CuO+2NH2CH2COOH=Cu(NH2CH2COO)2+H2OВданном случае глицинNH2CH2COOHявляется
осадителем, глицинат меди (II)Cu(NH2CH2COO)2– осаждаемой формой. При высушивании
получается гравиметрическая форма
сухогоCu(NH2CH2COO)2.
Этапы определения:1) взятие навески
и её растворение;2) приготовление раствора
осадителя;3) осаждение;4) фильтрование
и промывание;5) высушивание осадка;6)
взвешивание осадка, расчёт содержания
меди.
Механизм образования осадка:в
процессе образования осадка различают
3 параллельных процесса: 1) образование
зародышей кристалла (центров
кристаллизации); 2) рост кристаллов; 3)
объединение (агрегация) хаотично
ориентированных мелких кристаллов. В
начальный момент происходит насыщение
раствора, а затем его пересыщение. В
момент определенной пересыщенности
раствора, начинается выпадение осадка.
Центром кристалла может служить твердая
частица этого вещества или любая другая
твердая частица, которую мы вносим в
раствор, твердые частицы могут изначально
присутствовать в растворе как примесь.
Если осаждение происходит из разбавленных
растворов, то появление осадка занимает
время-индукционный период.
В процессе добавления каждой новой
порции осадителя происходит мгновенное
пересыщение раствора, зародыши растут
быстро за счет окружающих их ионов, как
только зародыш достиг определенного
размера выпадает осадок.
Рост кристаллов идет параллельно 1-ой
стадии, происходит за счет диффузии
ионов к поверхности растущего кристалла.
Число и размер частиц осадка (дисперсность
системы кол-во в единицы объёма) зависит
от соотношения скоростей 1-ой и 2-ой
стадий (V1— скорость
образования зародышей,V2-скорость
роста кристаллов):V1>>V2-мелкодисперсный
осадок,V1<<V2-крупнокристаллический
осадок. Какая из стадий будет лимитировать
определяет скорость осаждения и
концентрации ионов. При медленном
осаждении лимитирующей стадией является
кристаллизация, частица окружена
однородным слоем осаждаемых ионов в
результате получается кристалл правильной
формы. При высокой концентрации ионов
лимитирующей стадией становится
диффузия, образуются кристаллы
неправильной формы с большой площадью
поверхности. Следует отметить, что на
скорость процесса кристаллизации влияет
влияние
зародышей и на скорость роста кристаллов.
При высокой степени
мелкодисперсные осадки, при уменьшении
осадки. Агрегация происходит в гетерогенной
системе, в значительной степени
определяется числом центров
кристаллизации.Чем больше центров
кристаллизации, тем в меньшей степени
они укрупняются на второй стадии, тем
хуже структура и тем выше дисперсность
осадков.
К аналитическим свойствам осадка
относятся: растворимость, чистота,
фильтруемость.Лучшими свойствами
обладают крупнокристаллические осадки.
Возможные варианты загрязнения: 1)
Путем адсорбции ( для конкретного примера
хлорид-ионов на поверхности осадка); 2)
Окклюзия; 3) Изоморфное соосаждение; 4)
Совместное осаждение; 5) Последующее
осаждение.
Приемы повышения чистоты осадка:
1) Адсорбированные на поверхности примеси
хорошо удаляются при промывании осадков
на фильтре при помощи промывных жидкостей,
т.к. примеси переходят в промывную
жидкость и уходят через поры фильтра.
Эффективно многократное промывание
небольшими порциями промывной жидкости.
Промывную жидкость выбирают максимально
тщательно, чтобы не увеличивать
растворимость осадка и не ухудшать его
фильтрацию. Кристаллические осадки
промывают холодными промывными
жидкостями, чтобы не увеличить
растворимость осадка, а аморфные –
наоборот горячими. Водой промывают
осадки с низкими константами растворимости
(ниже 10-11-10-12), а также те,
которые не подвергаются пептизации.
Если константа растворимости осадка
10-9-10-11и он кристаллический,
то его промывают разбавленным раствором
осадителя. Аморфные осадки промывают
разбавленными растворами
электролитов-коагулянтов (солиNH4+),
чтобы избежать пептизации (в опыте с
железом осадок промывали растворомNH4NO3).
Повышение температуры также способствует
уменьшению адсорбции (на конкретном
примере горячий раствор, содержащий
10% аммиак разбавляют горячей водой для
уменьшения адсорбции хлорид-ионов на
поверхности осадка). 2) Для очищения
окклюдированных примесей в случае
кристаллических осадков используют
старение, в случае аморфных осадков –
переосаждение.Степень окклюзии в
процессе осаждения можно уменьшить
медленным добавлением осадителя по
каплям, при перемешивании.
Погрешности:1) Общая погрешность
анализа σ2 =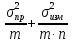
где σпр2– погрешность
пробоотбора, σизм2–
погрешность измерения,m– число проб,n– число
параллельных определений
2) Методическая ошибка OобOоб=
—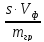
гдеs– растворимость
осадка, г/100 мл воды;Vф
– объем фильтрата и промывных вод,
мл;mгр– масса
полученного осадка, г.
3) Относительное стандартное отклонение


массы гравиметрической формы;mгр– масса гравиметрической формы; σa– дисперсия массы исходной навески;a– масса исходной навески;p– процентное содержание вещества в
исследуемой пробе;n–число
измерений.
4) Погрешность взвешивания тары σa1и тары с навескойσa2σa1=σa2=0,0002
г, σгр=
5) Относительное стандартное отклонение
с учетом стадий пробоотбора и
пробоподготовки


Преимущества органических осадителей:
1. Пользуясь органическими осадителями,
можно осаждать и разделять различные
элементы из очень сложных смесей.
Например, при помощи диметилглиоксима
возможно количественное осаждение
катионов никеля в присутствии многих
других катионов.
2. Осадки, получающиеся с органическими
осадителями, хорошо отфильтровываются
и промываются (например, осадки комплексных
соединений катионов, содержащих в
качестве лигандов пиридин или другие
органические соединения). Это дает
возможность легко отмывать от осадков
примеси, содержащиеся в анализируемом
растворе.
3. Осадки, получающиеся при действии на
катионы или анионы органических
осадителей, отличаются большим
молекулярным весом. Вследствие этого
точность анализа повышается. Например,
определение магния, алюминия и других
катионов проводится с большой точностью
осаждением их в виде оксихинолятов,
обладающих большим молекулярным весом.
4. В составе осадков, являющихся
соединениями неорганических веществ
с органическими компонентами, обычно
содержится мало соосаждающихся пиримесей.
Cu(NH2CH2COO)2– кристаллический осадок, поэтому
условия его выделения следующие:
1) осаждение ведут из достаточно
разбавленного исследуемого раствора
разбавленным раствором осадителя
(концентрации исследуемого раствора и
раствора осадителя должны быть примерно
одинаковыми);
2) раствор осадителя прибавляют медленно,
по каплям, при постоянном перемешивании
стеклянной палочкой (это предотвращает
явление окклюзии);
3) осаждение ведут из подогретого
исследуемого раствора горячим раствором
осадителя (для предотвращения пептизации);
4) к раствору прибавляют вещества,
способствующие повышению растворимости
осадка (увеличивают Iраствора), а затем понижают его
растворимость путем прибавления избытка
осадителя;
5) осадок оставляют на «созревание».
12. Гравиметрическое определение
кремния в силикатных породах: этапы
определения, возможные формулы осадителя,
осаждаемой и гравиметрической формулы,
механизм образования коллоидной частицы,
процессы, приводящие к образованию
осадка, возможные варианты загрязнения
осадка, приемы повышения чистоты осадка,
погрешности. Классификация коллоидных
систем. Условия аналитического выделения
кремнекислоты.
При гравиметрическом определении
кремния растворимый силикат натрия
Na2SiO3,
полученный в результате сплавления не
разлагаемой кремниевой кислоты с содойNa2CO3,
обрабатывается сильной кислотойHCl.
Реакция:Na2SiO3+2HCl=H2SiO3↓+2NaCl.
Осадителем в данном случае являетсяHCl, осаждаемой формой –H2SiO3.
При высушивании и прокаливании получается
гравиметрическая формаSiO2.
Этапы определения:1) взятие навески
и ее растворение; 2) приготовление
раствора осадителя; 3) осаждение; 4)
фильтрование и промывание осадка; 5)
высушивание и прокаливание осадка;; 6)
взвешивание осадка, расчет содержания
кремния.
Механизм образования коллоидной
частицы: Вещество в коллоидной системе
имеет большую развитую поверхность и
нескомпенсированный заряд на границе
разлела фаз. Существование
нескомпенсированного силового поля
ведет к адсорбции из раствора молекул
или ионов. Если коллоидная система
возникла в результате проведения
химической реакции осаждения, то частицы
адсорбируют в первую очередь те ионы,
которые могут достраивать кристаллическую
решетку. Адсорбированные ионы сообщают
частице “+» или “-“ заряд. Слой
адсорбированных ионов на ядре – это
первичный адсорбционный слой. Заряд,
созданный таким слоем, достаточно высок
и обуславливает электростатическое
взаимодействие с иоами противоположного
знака. В результате образуется слой
противоионов, который выравнивает заряд
первичного слоя. Слой противоионов
имеет диффузный характер. Часть
противоионов, прочно связанных с
первичным слоем – это плотный слой,
остальные противоионы составляют
диффузный слой.
Образование осадкапроисходит
тогда, когда раствор становится
пересыщенным, т.е. [A+]m[B-]n>Ks(ПКИ>ПР). Образование осадков связано
с процессом укрупнения частиц, с
образованием кристаллической решетки
вещества. Этот процесс определяется
числом центров кристаллизации: чем
больше центров, тем в меньшей степени
они укрупняются и тем хуже структура и
выше дисперсность осадка.
Возможные варианты загрязнения:1)
Путем адсорбции ( для конкретного примера
хлорид-ионов на поверхности осадка); 2)
Окклюзия; 3) Изоморфное соосаждение; 4)
Совместное осаждение; 5) Последующее
осаждение.
Приемы повышения чистоты осадка:
1) Адсорбированные на поверхности примеси
хорошо удаляются при промывании осадков
на фильтре при помощи промывных жидкостей,
т.к. примеси переходят в промывную
жидкость и уходят через поры фильтра.
Эффективно многократное промывание
небольшими порциями промывной жидкости.
Промывную жидкость выбирают максимально
тщательно, чтобы не увеличивать
растворимость осадка и не ухудшать его
фильтрацию. Кристаллические осадки
промывают холодными промывными
жидкостями, чтобы не увеличить
растворимость осадка, а аморфные –
наоборот горячими. Водой промывают
осадки с низкими константами растворимости
(ниже 10-11-10-12), а также те,
которые не подвергаются пептизации.
Если константа растворимости осадка
10-9-10-11и он кристаллический,
то его промывают разбавленным раствором
осадителя. Аморфные осадки промывают
разбавленными растворами
электролитов-коагулянтов (солиNH4+),
чтобы избежать пептизации (в опыте с
железом осадок промывали растворомNH4NO3).
Повышение температуры также способствует
уменьшению адсорбции (на конкретном
примере горячий раствор, содержащий
10% аммиак разбавляют горячей водой для
уменьшения адсорбции хлорид-ионов на
поверхности осадка). 2) Для очищения
окклюдированных примесей в случае
кристаллических осадков используют
старение, в случае аморфных осадков –
переосаждение.Степень окклюзии в
процессе осаждения можно уменьшить
медленным добавлением осадителя по
каплям, при перемешивании.
Погрешности:
1) Общая погрешность анализа σ2 =
где σпр2– погрешность
пробоотбора, σизм2–
погрешность измерения,m– число проб,n– число
параллельных определений.
2) Методическая ошибка OобOоб=
—
гдеs– растворимость
осадка, г/100 мл воды;Vф
– объем фильтрата и промывных вод,
мл;mгр– масса
полученного осадка, г.
3) Относительное стандартное отклонение


массы гравиметрической формы;mгр– масса гравиметрической формы; σa– дисперсия массы исходной навески;a– масса исходной навески;p– процентное содержание вещества в
исследуемой пробе;n–число
измерений.
4) Погрешность взвешивания тары σa1и тары с навескойσa2σa1=σa2=0,0002
г, σгр=
5) Относительное стандартное отклонение
с учетом стадий пробоотбора и
пробоподготовки


Классификация коллоидных систем. В
зависимости от характера межмолекулярных
сил, которые действуют на границе раздела
фаз коллоидные растворы делят на
лиофильные и лиофобные. Вокруг лиофильной
частицы располагается прочная сольватная
оболочка. В этих оболочках молекулы
ориентированы определенным образом и
образуют более или менее правильные
структуры. Вокруг лиофобной частицы
раствора также имеются сольватные
оболочки, но они непрочные и не предохраняют
молекулы от слипания.
H2SiO3– аморфный осадок, поэтому
условия его осаждения следующие:
1)осаждение проводят из горячего раствора
анализируемого вещества горячим
раствором осадителя при перемешивании;
2)осаждение проводят из достаточно
концентрированного исследуемого
раствора концентрированным раствором
осадителя с последующим разбавлением(при
разбавлении устанавливается адсорбционное
равновесие, часть адсорбированных ионов
переходи в раствор, и осадок становится
более чистым); 3)осаждение проводят в
присутствии подходящего
электролита-коагулятора;
4)аморфные осадки почти не требуют
времени для созревания, их необходимо
фильтровать сразу после разбавления
раствора. Аморфные осадки нельзя
оставлять более, чем на несколько минут,
т.к. сильное уплотнение их затрудняет
последующее отмывание примесей, а также
при стоянии увеличивается количество
примесей, адсорбированных поверхностью
осадка.
Если вы устраняете систематическую ошибку модели, то уже слишком поздно
Время на прочтение
7 мин
Количество просмотров 5.6K
Введение
Машинное обучение — это технологический прорыв, случающийся раз в поколение. Однако с ростом его популярности основной проблемой становятся систематические ошибки алгоритма. Если модели ML не обучаются на репрезентативных данных, у них могут развиться серьёзные систематические ошибки, оказывающие существенный вред недостаточно представленным группам и приводящие к созданию неэффективных продуктов. Мы изучили массив данных CoNLL-2003, являющийся стандартом для создания алгоритмов распознавания именованных сущностей в тексте, и выяснили, что в данных присутствует серьёзный перекос в сторону мужских имён. При помощи наших технологии мы смогли компенсировать эту систематическую ошибку:
- Мы обогатили данные, чтобы выявить сокрытые систематические ошибки
- Дополнили массив данных недостаточно представленными примерами, чтобы компенсировать гендерный перекос
Модель, обученная на нашем расширенном массиве данных CoNLL-2003, характеризуется снижением систематической ошибки и повышенной точностью, и это показывает, что систематическую ошибку можно устранить без каких-либо изменений в модели. Мы выложили в open source наши аннотации Named Entity Recognition для исходного массива данных CoNLL-2003, а также его улучшенную версию, скачать их можно здесь.
Систематическая ошибка алгоритма: слабое место ИИ
Сегодня тысячи инженеров и исследователей создают системы, самостоятельно обучающиеся тому, как достигать существенных прорывов — повышать безопасность на дорогах при помощи беспилотных автомобилей, лечить болезни оптимизированными ИИ процедурами, бороться с изменением климата при помощи управления энергопотреблением.
Однако сила самообучающихся систем является и их слабостью. Так как фундаментом всех процессов машинного обучения являются данные, обучение на несовершенных данных может привести к искажённым результатам.
ИИ-системы имеют большие полномочия, поэтому они могут наносить существенный ущерб. Недавние протесты против полицейской жестокости, приведшей к смертям Джорджа Флойда, Бреонны Тейлор, Филандо Кастиле, Сандры Блэнд и многих других, является важным напоминанием о систематическом неравенстве в нашем обществе, которое не должны усугублять ИИ-системы. Но нам известны многочисленные примеры (закрепляющие гендерные стереотипы результаты поиска картинок, дискриминация чёрных подсудимых в системах управления данными нарушителей и ошибочная идентификация цветных людей системами распознавания лиц), показывающие, что предстоит пройти долгий путь, прежде чем проблема систематических ошибок ИИ будет решена.
Распространённость ошибок вызвана лёгкостью их внесения. Например, они проникают в «золотые стандарты» моделей и массивов данных в open source, ставшие фундаментом огромного объёма работы в сфере ML. Массив данных для определения эмоционального настроя текста word2vec, используемый в построении моделей других языков, искажён по этнической принадлежности, а word embeddings — способ сопоставления слов и значений алгоритмом ML — содержит сильно искажённые допущения о занятиях, с которыми ассоциируются женщины.
Проблема (и, как минимум, часть её решения) лежит в данных. Чтобы проиллюстрировать это, мы провели эксперимент с одним из самых популярных массивов данных для построения систем распознавания именованных сущностей в тексте: CoNLL-2003.
Что такое «распознавание именованных сущностей»?
Распознавание именованных сущностей (Named-Entity Recognition, NER) — один из фундаментальных камней моделей естественных языков, без него были бы невозможны онлайн-поиск, извлечение информации и анализ эмоционального настроя текста.
Миссия нашей компании заключается в ускорении разработки ИИ. Естественный язык — одна из основных сфер наших интересов. Наш продукт Scale Text содержит NER, заключающееся в аннотировании текста согласно заданному списку меток. На практике, среди прочего, это может помочь крупным розничным сетям анализировать онлайн-обсуждение их продуктов.
Многие модели NER обучаются и подвергаются бенчмаркам на CoNLL-2003 — массиве данных из примерно 20 тысяч предложений новостных статей Reuters, аннотированных такими атрибутами, как «PERSON», «LOCATION» и «ORGANIZATION».
Нам захотелось изучить эти данные на наличие систематических ошибок. Для этого мы воспользовались своим конвейером разметки, чтобы категоризировать все имена в массиве данных, размечая их как мужские, женские или гендерно-нейтральные, исходя из традиционного использования имён.
При этом мы выявили существенную разницу. Мужские имена упоминались почти в пять раз чаще женских, и менее 2% имён были гендерно-нейтральными:
Это вызвано тем, что по социальным причинам новостные статьи в основном содержат мужские имена. Однако из-за этого модель NER, обученная на таких данных, лучше будет справляться с выбором мужских имён, чем женских. Например, поисковые движки используют модели NER для классификации имён в поисковых запросах, чтобы выдавать более точные результаты. Но если внедрить модель NER с перекосом, то поисковый движок хуже будет идентифицировать женские имена по сравнению с мужскими, и именно подобная малозаметная распространённая систематическая ошибка может проникнуть во многие системы реального мира.
Новый эксперимент по снижению систематической ошибки
Чтобы проиллюстрировать это, мы обучили модель NER для изучения того, как этот гендерный перекос повлияет на её точность. Был создан алгоритм извлечения имён, выбирающий метки PERSON при помощи популярной NLP-библиотеки spaCy, и на подмножестве данных CoNLL была обучена модель. Затем мы протестировали модель на новых именах из тестовых данных, не присутствовавших в данных обучения, и обнаружили, что модель с вероятностью на 5% больше пропустит новое женское имя, чем новое мужское имя, а это серьёзное расхождение в точности:
Мы наблюдали схожие результаты, когда применили модель к шаблону «NAME is a person», подставив 100 самых популярных мужских и женских имён на каждый год переписи населения США. Результаты работы модели оказались значительно хуже для женских имён во все года переписи:
Критически важно то, что наличие перекоса в данных обучения приводит к смещению ошибок в сторону недостаточно представленных категорий. Эксперимент с переписями демонстрирует это и другим образом: точность модели существенно деградирует после 1997 года (точки отсечения статей Reuters в массиве данных CoNLL), потому что массив данных больше не является репрезентативным отображением популярности имён каждого последующего года.
Модели обучаются соответствовать трендам данных, на которых они обучены. Нельзя ожидать их хорошей точности в случаях, когда они видели лишь малое количество примеров.
Если вы исправляете систематическую ошибку модели, то уже слишком поздно
Как же это исправить?
Один из способов — попробовать устранить систематическую ошибку модели, например, выполнив постобработку модели или добавив целевую функцию для смягчения перекоса, оставив определение подробностей самой модели.
Но это не лучший подход по множеству причин:
- Справедливость — это очень сложная проблема, и мы не можем ждать, что алгоритм решит её сам. Исследование показало, что обучение алгоритма на одинаковый уровень точности для всех подмножеств населения не обеспечит справедливости и нанесёт вред обучению модели.
- Добавление новых целевых функций может навредить точности модели, приводя к негативному побочному эффекту. Вместо этого лучше обеспечить простоту алгоритма и сбалансированность данных, что повысит точность модели и позволит избежать негативных эффектов.
- Неразумно ожидать, что модель покажет хорошие результаты в случаях, примеров которых она видела очень мало. Наилучший способ обеспечения хороших результатов заключается в повышении разнообразия данных.
- Попытки устранения систематической ошибки при помощи инженерных техник — это дорогой и длительный процесс. Гораздо дешевле и проще изначально обучать модели на данных без перекосов, освободив ресурсы инженеров для работы над реализацией.
Данные — это лишь одна часть проблемы систематических ошибок. Однако эта часть фундаментальна и влияет на всё, что идёт после неё. Именно поэтому мы считаем, что данные содержат ключ к частичному решению, обеспечивая потенциальные систематические улучшения в исходных материалах. Если вы не размечаете критические классы (например, гендер или этническую принадлежность) явным образом, то невозможно сделать так, чтобы эти классы не были источником систематической ошибки.
Такая ситуация контринтуитивна. Кажется, что если нам нужно построить модель, не зависящую от чувствительных характеристик наподобие гендера, возраста или этнической принадлежности, то лучше исключить эти свойства из данных обучения, чтобы модель не могла их учитывать.
Однако принцип «справедливости, реализуемой через неведение» на самом деле усугубляет проблему. Модели ML превосходно справляются с выводом заключений из признаков, они не прекращают делать этого, если мы не разметили эти признаки явным образом. Систематические ошибки просто остаются невыявленными, из-за чего их сложнее устранить.
Единственный надёжный способ решения проблемы заключается в разметке большего количества данных, чтобы сбалансировать распределение имён. Мы использовали отдельную модель ML для идентификации предложений в корпусах Reuters и Brown, с большой вероятностью содержащих женские имена, а затем разметили эти предложения в нашем конвейере NER, чтобы дополнить CoNLL.
Получившийся массив данных, который мы назвали CoNLL-Balanced, содержит на 400 с лишним больше женских имён. После повторного обучения на нём модели NER мы обнаружили, что алгоритм больше не имеет систематической ошибки, приводящей к снижению показателей при распознавании женских имён:
Кроме того, модель улучшила показатели и при распознавании мужских имён.
Это стало впечатляющей демонстрацией важности данных. Благодаря устранению перекоса в исходном материале нам не пришлось вносить никаких изменений в нашу модель ML, что позволило сэкономить на времени разработки. И мы достигли этого без негативного влияния на точность модели; на самом деле, она даже слегка увеличилась.
Чтобы позволить сообществу разработчиков развивать нашу работу и устранять гендерный перекос в моделях, построенных на основе CoNLL-2003, мы выложили на наш веб-сайте дополненный массив данных в open source, в том числе и добавив гендерную информацию.
Сообщество разработчиков ИИ/ML имеет проблемы с культурными различиями, но мы испытываем умеренный оптимизм от этих результатов. Они намекают на то, что мы, возможно, сможем предложить техническое решение насущной социальной проблемы, если займёмся проблемой сразу же, выявим сокрытые систематические ошибки и улучшим точность модели для всех.
Сейчас мы изучаем, как этот подход можно применить к ещё одному критичному атрибуту — этнической принадлежности — чтобы придумать, как создать надёжную систему для устранения перекоса в массивах данных, распространяющегося и на другие охраняемые от дискриминации категории населения.
Кроме того, это показывает, почему наша компания уделяет так много внимания качеству данных. Если нельзя доказать, что данные точны, сбалансированы и лишены систематических ошибок, то нет гарантии того, что создаваемые на их основе модели будут безопасными и точными. А без этого мы не сможем создавать качественно новых ИИ-технологий, идущих на пользу всем людям.
Благодарности
Упоминаемый в этом посте массив данных CoNLL 2003 — это тестовый набор Reuters-21578, Distribution 1.0, доступный для скачивания на странице проекта исходного эксперимента 2003 года: https://www.clips.uantwerpen.be/conll2003/ner/.
Таким образом, при значительном уменьшении систематической ошибки относительная случайная ошибка увеличивается по крайней мере в У2 раз. При необходимости этот фактор можно уменьшить многократным повторением измерений и нахождением среднего результата. [c.452]
Для полного (по возможности) исключения артефактов ТСХ используют в данном случае технику спаренных данных , заключающуюся в нанесении образцов стандартного и исследуемых растворов с разным их расположением на нескольких пластинах и вычислении среднего значения величины пика. Подобный прием обеспечивает уменьшение систематической ошибки до 1%. [c.292]
Именно поэтому, проводя серию измерений, в качестве наилучшего берут средний результат. Но заметим, что увеличение числа измерений не может привести к уменьшению систематической ошибки. [c.387]
Систематические ошибки. Систематическими ошибками называют погрешности, одинаковые по знаку, происходящие от определенных причин, влияющих на результат либо в сторону увеличения, либо в сторону уменьшения его. Систематические ошибки можно обычно предусмотреть и устранить их или же ввести соответствующие поправки. Отметим следующие виды систематических ошибок. [c.48]
Мы уже говорили, что если взять среднее арифметическое из ряда измерений, то случайная ошибка этого среднего измерения будет меньше, чем единичного. Поэтому для уменьшения случайной ошибки необходим ряд измерений, причем, как мы увидим дальше, тем больший, чем меньшую случайную ошибку мы хотим получить. Однако, очевидно, что нет смысла в большем числе измерений, чем это необходимо, чтобы систематическая ошибка существенно превышала случайную. [c.47]
Установлено, что в некоторых случаях при калибровке скоростей расходования реагентов по величине падения давления могут возникнуть значительные систематические ошибки из-за адиабатического расширения в колбах с газом, приводящего к слабому уменьшению температуры. [c.300]
Так как включение в модель равновесия (13.3) приводит к небольшому уменьшению дисперсии, то для доказательства существования этого равновесия повторно рассчитывали систематические ошибки. В этом случае получены гораздо более приемлемые поправки (< 3%) к общим концентрациям хлорида (табл. 13.4). Однако эти данные плохо определяют константу равновесия (13.3) (Кз), так как величина стандартного отклонения оказалась близкой к оценке значения самой константы /Сз= (3,5 3,9) Ю»» моль/л. Поэтому существование равновесия [c.243]
Уменьшение случайной ошибки может быть достигнуто выбором в качестве аналитических характеристик суммарных интенсивностей пиков с наименьшими коэффициентами вариации внутри каждой группы соединений [31—33]. Наличие систематической ошибки е а можно обнаружить, анализируя невязки уравнений (2) для большого количества однотипных по качественному составу смесей. Если средние значения невязок в каких-либо уравнениях значимо отличаются от нуля, то имеет место систематическое отклонение калибровочной матрицы А от средней матрицы А. [c.85]
При косвенных методах анализа значительная часть ошибки вносится во время озоления пробы и разбавления золы. Коэффициент вариации результатов прямого озоления работавших масел около 8%. При озолении с коллектором эта ошибка несколько уменьшается. Применение кислотного озоления снижает систематическую ошибку, но не дает заметного уменьшения случайной ошибки. [c.115]
Для устранения такого рода систематических ошибок в практике спектрального анализа геологических образцов необходимо добиваться, чтобы химический состав эталонов был как можно ближе к химическому составу изучаемых образцов. Систематические ошибки всегда должны быть обнаружены и устранены. Только в таком случае можно правильно учесть величину неизбежных в спектральном анализе случайных ошибок. Систематические ошибки всегда действуют в одном направлении либо в сторону уменьшения, либо в сторону увеличения результатов анализа на некоторую величину. Причины систематических ошибок, как правило, зависят от дефектов аппаратуры и несовершенства применяемых методов. [c.153]
Точность результата есть его воспроизводимость, правильность— его близость к истинному значению. Систематическая ошибка вызывает уменьшение правильности, и ее влияние на точность результата определяется тем, постоянной или переменной является ошибка. Случайные ошибки понижают воспроизводимость, но, проводя наблюдение более точно, можно уменьшить рассеяние в такой степени, что это не отразится на правильности. Строго говоря, статистическая обработка может быть применена только к случайным ошибкам. Даже в том случае, когда заранее неизвестно, являются ли ошибки действительно случайными, могут быть [c.570]
Из сопоставления формул (11.18) я (11.20) видно, что к разрешающей способности спектра Af—Be предъявляются противоречащие друг другу требования систематическая ошибка уменьшается с уменьшением величины Af, тогда как случайная ошибка уменьшается с ростом А/. Последнее утверждение справедливо, так как при фиксированной общей длине реализации 7 общ величина прямо пропорциональна разрешающей [c.281]
Разделение ошибок по характеру вызывающих их причин представляет наиболее принципиальный тип классификации ошибок любых измерений. Плодотворность такого подхода состоит в том, что он позволяет наметить общую стратегию уменьшения ошибок путем поэтапной борьбы сначала с систематическими ошибками, причины которых либо заведомо известны, либо могут быть выявлены при детальном анализе процедуры измерения, а потом со случайными ошибками. Вполне естественно, что при этом для борьбы с ошибками разной природы применяются различные приемы и методы математической обработки результатов анализа. Рассмотрим более подробно понятия систематической и случайной ошибок и понятие промаха применительно к химическому анализу. [c.20]
Требование полной идентичности эталонов и образцов естественно невыполнимо, поскольку предполагает априорное знание состава, подлежащего определению, однако максимально доступная близость состава — непременное требование, которое следует соблюдать для уменьшения эталонной ошибки. Широкий набор эталонов разнообразного состава — условие успешной работы химико-аналитической лаборатории. В заключение отметим, что наличие эталона, близко совпадающего по составу с анализируемым образцом, открывает возможность оценки общей и систематической ошибки анализа, а следовательно, правильности анализа в целом. [c.40]
Условимся под ошибкой отдельного измерения понимать величину в — a — X , где х.1 есть результат этого измерения, а а — истинное значение измеряемой величины. Ошибки е,- можно подразделить на систематические и случайные ошибки. Систематические ошибки есть ошибки, обусловленные какой-либо постоянно влияющей причиной, например дефектом аппаратуры, который действует регулярно либо в сторону уменьшения, либо в сторону увеличения результатов измерения на некоторую постоянную величину. Случайные ошибки обусловливаются несовершенством аппаратуры и методов измерений, отклоняющими результат измерений от истинного значения их как в положительную. Так и отрицательную стороны, причём ни те, ни другие отклонения не имеют преимущественного характера. [c.217]
При анализе результатов определения мощности пласта по сланцу и породе способами фотограмметрии и зарисовок была обнаружена систематическая ошибка в сторону увеличения мощности пласта по сланцу. Для устранения этой ошибки и уменьшения трудоемкости работ Институтом сланцев был разработан новый метод определения мощности пласта по сланцу и породе — замер по вертикальным линиям (рис. 1), рекомендуемый для практического применения. [c.44]
Систематические ошибки — одинаковые во всех измерениях, получаемых одним и тем же методом с помощью одних и тех же измерительных приборов. Для уменьшения систематических ошибок учитывают различные поправки, класс точности измерительных приборов и ряд других факторов. [c.340]
Как было отмечено ранее, ошибки анализа могут быть систематическими или случайными. Систематические ошибки влияют на точность определения, т. е. на отклонение среднего значения от истинного значения, тогда как случайные ошибки приводят как к положительным, так и к отрицательным отклонениям от среднего значения, по которым рассчитывается разброс. Ошибки последнего типа обычно распределяются нормально вокруг среднего значения. Кривые нормального распределения хорошо известны экспериментаторам и хорошо изучены их можно получить из гистограмм при неограниченном увеличении числа измерений и уменьшении интервалов разбиения. В силикатном анализе 5 [c.67]
Систематические ошибки анализа, как и в обычных методах, зависят от качества эталонов. Близость химического состава эталонов и проб очень существенна для уменьшения систематических погрешностей. [c.376]
Из приведенных подсчетов можно сделать вывод о том, что при использовании метода корректировки случайная ошибка анализа практически не изменилась, а правильность результатов, характеризуемая уменьшением систематических ошибок, значительно возросла. [c.448]
Однако необходимо иметь в виду, что увеличение числа определений и улучшение воспроизводимости целесообразно проводить только до тех пор, пока общая ошибка измерений не будет определяться систематической ошибкой. Считается, что уменьшение случайной ошибки целесообразно в большинстве случаев до тех пор, пока доверительный интервал, определенный с заданной степенью надежности, не станет меньше систематической ошибки. [c.165]
Точность калибрирования может быть повышена, если увеличить число калибровочных точек, что приводит к уменьшению вероятности случайных ошибок. Если же имеют место систематические ошибки (калибрирование пипетки, измерение длины, определение веса), то они останутся без изменения, независимо от числа точек, полученных в процессе калибрирования. В большинстве случаев точность 0,5% соответствует точности анализа, а иногда точность калибрирования весов бывает даже ниже точности анализа. Поэтому калибрирование следует проводить чрезвычайно тщательно, т. е. так, чтобы все ошибки были по возможности сведены к минимуму. [c.110]
Показано, что метод калибровки катарометра по чистым в-вам приводит к систематическим ошибкам, которые снижаются при уменьшении величины пробы. [c.38]
Некоторые авторы считают, что нерационально проводить измерения в порядке увеличения или уменьшения концентрации и предлагают приготовлять растворы вне кюветы, чтобы не вносить систематическую ошибку [30]. [c.162]
В первую очередь для уменьшения систематической ошибки необходимо правильно подобрать стандартные образцы или так изменить условия проведения анализа, чтобы различия между стандартными образцами и пробами практически не влияли на результаты анализа. Если это по каким-либо причинам оказывается невозможным, нужно произвести химическую или физическую обработку проб и стандартных образцов, приводящую их к единому виду и составу. Например, при анализе порошков и растворов ошибка, связанная со стандартными образцами, снижается игти совсем устраняется при введении буфера во все пробы. При аняли-зе металлов и сплавов ошибку, связанную с неодинаковой термической обработкой проб и стандартных образцов, удается уменьшить ьли устранить переведением всех проб в оксиды или растворением. [c.217]
Систематические ошибки, как указывалось, стремятся к нулю при 0 = 90 , относительная точность промера также резко возрастает при больших 0. Поэтому более точные значения параметров решетки можно получить, откладывая на графике вычисленные значения параметров решетки в зависимости от угла 0 и экстраполируя затем к 90 (экстраполяция по Кеттману). Такой график показан на рис. 21 (из рисунка видно и уменьшение разброса при больших углах). [c.135]
В методических указаниях приведены общие положения и понятия по проведению количественного газохроматографнческого аналнзаа с использованием различных приемов уменьшения случайной и систематической ошибки анализа. Рассмотреены методы внешнего стандарта, внутреннего стандарта, метод стандартной добавки, объединенный метод стандартной добавки и внутреннего стандарта. [c.2]
Ошибка настройки и измерения. Ошибка при калибровке прибора вызывает систематическую пофешность при последующих измерениях. Для уменьшения этой ошибки рекомендуется после калибровки по кон-фольному образцу или другой мере несколько раз повторить измерения и убедиться, что среднеарифметическое значение измеренной толщины близко к истинному. [c.283]
Систематические ошибки могут быть вызваны влиянием постоянно действующих факторов на результаты измерений. Например, неправильно выбраны условия выполнения анализа, неправильно отградуирована шкала измерительного прибора, нарушен режим работы измерительных устройств или систематически- нарушаются условия выполнения анализа изменение температуры,, окраски раствора и др. Результаты измерений при этом отличаются от истинного значения определяемой величины в сторону увеличения или уменьшения, т. е. погрешность измерен1Й имеет знак плюс или минус. Систематические ошибки практически постоянны или закономерно изменяются прн повторных измерениях. Выявление систематических ошибок требует специальных исследований, но как толька они обнаружены, их можно устранить. [c.232]
Точность результата есть его воспроизводимость, правильность— его близость истинной величине. Систематическая ошибка вызывает уменьшение правильности, и ее влияние на точность результата определяется тем, постоянной или переменной является ошибка. Случайные ошибки понижают воспроизводимость, но, проводя наблюдение более точно, можно уменьшить рассеяние в такой степени, что это не отразится на правильности. Строго говоря, статистическая обработка может быть применена только к случайным ошибкам. Даже в том случае, когда заранее неизвестно, являются ли ошибки действительно случайными, то и тогда могут быть применены законы вероятности для того, чтобы определить является ли неслучайность (тенденции, скачки, группы и т. п.) определяюшим фактором или нет. В этом случае необходимо выявлять и корректировать систематические причины. Даже случайные ошибки могут не следовать нормальному закону ошибок, который является основной отправной точкой для анализа данных. И опять-таки статистические исследования можно использовать для того, чтобы определить, имеется ли значительное отклонение от нормального закона, и соответственно этому интерпретировать данные. [c.581]
Точность измерения можно повысить, увеличивая число измерений. Вследствие того, что зависимость выражается корнем квадратным в ур(агЬнении (26-6), существует практический предел улучшения, достигаемого повторными измерениями. Например, уменьшение стандартного отклонения в 10 раз требует увеличения числа наблюдений в 100 раз. Очевидно, что любые систематические ошибки, которые включаются в определенне, не могут быть исключены повторением. Следовательно, практический предел для полезного увеличения числа повторных испытаний достигается тогда, когда стандартное отклонение случайных ошибок среднего значения становится соизмеримым с систематической ошибкой. [c.576]
В каждом отдельно взятом сосуде физическое отставание стремится уменьшить манометрический эффект при переходе от темноты к свету (и наоборот) и тем самым приводит к уменьшению расчетного светового эффекта. Это не значит, однако, что расчетные значения lf также должны быть занижены. Квантовый выход и отношение Qф подсчитаны из световых эффектов в двух сосудах, и величина ошибки при подсчете ( зависит от соотношения двух отставаний. Для двух сосудов, примененных Варбургом и Бёрком, отставание больше в сосуде с большим газовым объемом, и это ведет к завышению расчетной величины квантового выхода. Очень малая систематическая ошибка, вызванная этим различным отставанием (порядка 0,3 мм в 10 мин.), уже вдвое увеличивает расчетную величину [c.545]
Однако химика-аналитика часто не интересует сама по себе оценка величины систематической ошибки, а в большей мере — методы ее устранения и уменьшения. Существует несколько путей для достижения этой цели, с некоторыми из которых мы коротко ознакомимся на примере инструментальных ошибок весового (правиметрического) и объемного (тит-риметри ческого) анализов. [c.26]
Рандомизация систематических ошибок химического анализа. Рандомизация (от англ. random — случайно, наугад) — прием, переводящий систематические ошибки в разряд случайных. Возможность рандомизации основана на том, что систематическая ошибка единичного явления (прибора, процесса, метода, субъекта анализа) при рассмотрении ее в более широком классе однотипных явлений (серия приборов, группа процессов или методов, коллектив аналитиков) становится величиной переменной, т. е. приобретает черты случайной ошибки. Например, каждая единичная бюретка одного класса точности характеризуется своей систематической по-лол итатьной или отрицательной ошибкой. Однако, если проводить объемное определение, используя последовательно не одну, а несколько бюреток, можно надеяться, что результат объемного анализа, усредненный по всем определениям и для всех бюреток, будет отягощен меньшей ошибкой, чем при использовании одной бюретки, за счет того, что при усреднении систематические ошибки разных бюреток частично компенсируют друг друга. Аналогичным образом, если одновременно со сменой бюреток менять пипетки для отбора аликвот, то при З среднении можно рассчитывать на дополнительное уменьшение [c.26]
Проведенный выше раэбор систематических ошибок хими-t e Koro аяализа не претендует на исчерпывающую полноту. Из рассмотрения исключены некоторые виды ошибок, например, ошибка натекания и капельная ошибка в титриметрических методах анализа. Некоторые виды систематических ошибок только упомянуты. Основное внимание и наибольшее количество примеров посвящено ошибкам традиционных методов гравиметрического, титриметрического и фотометрического анализов. Такой стиль изложения оправдан целью данного раздела—дать общее представление о систематических ошибках химического анализа, способах их обнаружения и оценки и методах их уменьшения. Детальный разбор всех известных источников ошибок должен входить как составная часть в теорию и практику каждого отдельного метода химического анализа, ибо каждому методу присущи свои специфические ошибки». Удачным примером в этом плане может служить руководство по (фотоколориметрическим и спектрофотометрическим методам анализа М. И. Булатова и И. П. Калин-кина (Л, Химия , 1976, 376 с.), где этому вопросу уделено большое внимание. Однако сказанное в равной мере относится и к любым другим химическим и физическим методам, [c.48]
Грань, которая отличает систематические ошибки от случайных, носит условный характер. Ошибки, квалифицируемые как систе.матичес кие при рассмотрении в одной выборке, при-, обретают характер случайных в другой выборке большей мощности. С другой стороны, отдельные случайные ошибки могут быть исключены из совокупной ошибки методами, схожими с методами исключения и уменьшения систематических ошибок, например, за счет модернизации отдельных узлов прибора или перехода к более стабильным усл0 виям проведения анализа. [c.50]
Результаты работ Густафсона, проведенных в широкой области концентраций внешнего раствора, двойственны. В большей части случаев им отмечено заметное уменьшение расчетного коэффициента активности электролитов в ионите при уменьшении концен -рации, которое в общем неудивительно, поскольку концентрации внешнего раствора достигали значений 1—4 и. Однако по достижении некоторой -малой концентрации происходило резкое уменьшение коэффициента активности, что, по нашему мнению, может быть объяснено лишь наличием источника систематической ошибки, существенного при малых концентрациях. [c.65]
На основании этих данных были вычислены углы X — Р — X (в предположении, что соответствующие соединения обладают симметрией XgPY) и электронные заряды Zp [при допущении, что соединения характеризуются положительным зарядом на атоме фосфора, меньшим -Ь1 (значения а) и большим +1 (значения б) . Отсутствие каких-либо вспомогательных данных не позволяет сделать определенный выбор между значениями а и б. В первом приближении можнс принять значения а на основании того факта, что группа UF в соединении Vni более электроотрицательна, чем группы, присоединенные к фосфору, в соединениях IX и X. Этим, по-видимому, обусловлено уменьшение заряда Zp от 4-0,91 до +0,89 и +0,88. То же самое относится н к двум другим рядам соединенпй (I—II и III—VII). Другим доводом в пользу выбора значений а является вычисленная величина валентного угла для молекулы хлористого тетра-(окси-метил)-фосфония, который в норме должен был быть близким к 109°28. То обстоятельство, что вычисленные значения не совпадают с этой величиной, может быть обусловлено либо систематической ошибкой в расчетах, либо вкладом -орбиталей атома фосфора в стабилизацию молекулы. В последнем случае отклонение угла С—Р—С от величины, соответствующей чистому SjD -гибриду, может объясняться участием структуры приведенного типа [c.241]
Для учёта и устранения систематических погрешностей применяют методы, которые условно можно разбить на две группы: теоретические и экспериментальные способы.
1. Теоретические способы возможны, когда может быть получено аналитическое выражение для искомой погрешности на основании априорной информации.
2. Экспериментальные способы также предполагают наличие априорной информации, но лишь качественного характера. Для получения количественной оценки необходимо проведение дополнительных исследований.
Для устранения систематических погрешностей применяются следующие методы:
1. Постоянные систематические погрешности.
а) Метод замещения — осуществляется путем замены измеряемой величины известной величиной так, чтобы в состоянии и действии средства измерений не происходило изменений;
б) Метод противопоставления.
Измерения выполняются с двумя наблюдениями, проводимыми так, чтобы причина постоянной погрешности оказывала разные, но известные по закономерности воздействия на результаты наблюдений.
в) Метод компенсации погрешности по знаку.
Измерения также проводятся дважды так, чтобы постоянная систематическая погрешность входила в результат измерения с разными знаками. За результат измерения принимается среднее значение двух измерений.
2. Прогрессирующие систематические погрешности.
а) Метод симметричных наблюдений.
Измерения производят с несколькими наблюдениями, проводимыми через равные интервалы времени, затем обрабатывают результаты, вычисляют среднее арифметическое симметрично расположенных наблюдений. Теоретически эти средние значения должны быть равны. Эти данные позволяют контролировать ход эксперимента, а также устранять систематические погрешности.
б) Метод рандомизации.
Этот метод основан на переводе систематических погрешностей в случайные. При этом измерение некоторой физической величины проводят рядом однотипных приборов с дальнейшей статистической обработкой полученных результатов. Уменьшение систематической погрешности достигается и при изменении случайным образом методики и условий проведения измерений. При определёнии значений систематической погрешности, результаты измерений исправляют, то есть вносят либо поправку, или поправочный множитель, но исправленные результаты обязательно содержат не исключенные остатки систематических погрешностей (НСП)