Статья рассматривает ошибки первого и второго рода в статистическом выводе, их определение, свойства и примеры, а также предлагает способы минимизации этих ошибок.
О чем статья
Введение
В теории вероятности существует понятие ошибок первого и второго рода, которые играют важную роль при принятии решений на основе статистических данных. Ошибки первого рода возникают, когда мы отвергаем верную нулевую гипотезу, а ошибки второго рода – когда мы принимаем неверную нулевую гипотезу. В данной лекции мы рассмотрим определение и свойства ошибок первого и второго рода, а также приведем примеры и способы их минимизации.
Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Заказать работу
Ошибки первого и второго рода
Ошибки первого и второго рода являются важным понятием в теории вероятности и статистике. Они связаны с процессом принятия решений на основе статистических данных и могут иметь серьезные последствия.
Определение ошибок первого и второго рода
Ошибки первого и второго рода связаны с принятием или отвержением нулевой гипотезы в статистическом тестировании. Нулевая гипотеза обычно предполагает отсутствие эффекта или различий между группами или явлениями, альтернативная гипотеза предполагает наличие эффекта или различий.
Ошибка первого рода (также известная как ложное положительное решение) происходит, когда нулевая гипотеза отвергается, хотя она на самом деле верна. То есть, мы делаем вывод о наличии эффекта или различий, когда их на самом деле нет.
Ошибка второго рода (также известная как ложное отрицательное решение) происходит, когда нулевая гипотеза принимается, хотя она на самом деле неверна. То есть, мы не обнаруживаем эффекта или различий, хотя они на самом деле существуют.
Свойства ошибок первого и второго рода
Ошибки первого и второго рода являются взаимоисключающими: если одна ошибка уменьшается, то другая ошибка увеличивается. Это связано с тем, что при установлении более строгих критериев для отвержения нулевой гипотезы (чтобы уменьшить ошибку первого рода), вероятность совершения ошибки второго рода увеличивается, и наоборот.
Примеры ошибок первого и второго рода
Пример ошибки первого рода может быть следующим: при проведении клинического исследования нового лекарства, мы отвергаем нулевую гипотезу о его отсутствии эффекта, хотя на самом деле эффекта нет. Это может привести к неправильному принятию лекарства на рынок и негативным последствиям для пациентов.
Пример ошибки второго рода может быть следующим: при проведении исследования о влиянии нового метода обучения на успеваемость студентов, мы принимаем нулевую гипотезу о его отсутствии эффекта, хотя на самом деле метод действительно улучшает успеваемость. Это может привести к упущению возможности улучшить образовательный процесс.
Как минимизировать ошибки первого и второго рода
Для минимизации ошибок первого и второго рода необходимо выбрать правильный уровень значимости и размер выборки. Уровень значимости определяет, насколько мы готовы рисковать совершением ошибки первого рода. Размер выборки влияет на вероятность совершения ошибки второго рода.
Также важно проводить повторные исследования и репликации результатов, чтобы убедиться в их надежности и избежать ошибок. Кроме того, использование более точных и надежных методов статистического анализа может помочь уменьшить вероятность ошибок первого и второго рода.
Определение ошибок первого и второго рода
Ошибки первого и второго рода являются важными понятиями в теории вероятности и статистике. Они связаны с процессом принятия решений на основе статистических данных и могут влиять на достоверность результатов и выводов.
Ошибки первого рода
Ошибки первого рода, также известные как ложные положительные результаты, возникают, когда нулевая гипотеза отвергается, хотя она на самом деле верна. Вероятность совершения ошибки первого рода обозначается как α (альфа) и называется уровнем значимости.
Нулевая гипотеза обычно формулируется так, чтобы предположить отсутствие эффекта или различий между группами. Ошибка первого рода может привести к неправильному заключению о наличии эффекта или различиях, когда на самом деле их нет.
Ошибки второго рода
Ошибки второго рода, также известные как ложные отрицательные результаты, возникают, когда нулевая гипотеза принимается, хотя она на самом деле неверна. Вероятность совершения ошибки второго рода обозначается как β (бета).
Ошибки второго рода могут привести к неправильному заключению о отсутствии эффекта или различий, когда на самом деле они существуют. Ошибка второго рода связана с мощностью статистического теста, которая определяет способность теста обнаружить наличие эффекта или различий.
Ошибки первого и второго рода являются взаимоисключающими: уменьшение вероятности одной ошибки приводит к увеличению вероятности другой ошибки. Поэтому важно найти баланс между уровнем значимости и мощностью теста, чтобы минимизировать оба типа ошибок.
Свойства ошибок первого и второго рода
Ошибки первого и второго рода являются важными понятиями в теории вероятности и статистике. Они связаны с процессом принятия решений на основе статистических данных и имеют следующие свойства:
Ошибки первого рода
Ошибки первого рода, также известные как ложные положительные результаты, возникают, когда нулевая гипотеза отвергается, хотя она на самом деле верна. Вероятность совершить ошибку первого рода обозначается как α (альфа) и называется уровнем значимости.
Свойства ошибок первого рода:
- Вероятность ошибки первого рода может быть контролируема и выбирается исследователем.
- Уровень значимости α определяет, насколько мы готовы рисковать совершить ошибку первого рода.
- Чем ниже уровень значимости α, тем меньше вероятность ошибки первого рода, но тем больше вероятность ошибки второго рода.
- Ошибки первого рода могут привести к неправильным выводам и неверным заключениям.
Ошибки второго рода
Ошибки второго рода, также известные как ложные отрицательные результаты, возникают, когда нулевая гипотеза принимается, хотя она на самом деле неверна. Вероятность совершить ошибку второго рода обозначается как β (бета).
Свойства ошибок второго рода:
- Вероятность ошибки второго рода зависит от мощности теста.
- Мощность теста определяет способность теста обнаружить наличие эффекта или различий.
- Чем выше мощность теста, тем меньше вероятность ошибки второго рода, но тем больше вероятность ошибки первого рода.
- Ошибки второго рода могут привести к пропуску важных результатов и неверным заключениям.
Важно найти баланс между уровнем значимости и мощностью теста, чтобы минимизировать оба типа ошибок и получить надежные и точные результаты.
Примеры ошибок первого и второго рода
Ошибки первого рода
Ошибки первого рода происходят, когда мы отвергаем нулевую гипотезу, когда она на самом деле верна. То есть, мы делаем ложное положительное заключение.
Например, представьте, что у нас есть новый лекарственный препарат, который, по нашей гипотезе, должен быть эффективным в лечении определенного заболевания. Мы проводим клиническое исследование и получаем статистически значимые результаты, которые позволяют нам отвергнуть нулевую гипотезу и сделать вывод о том, что препарат действительно эффективен. Однако, в действительности, препарат может быть неэффективным, и наши результаты могут быть случайными или искаженными.
Ошибки второго рода
Ошибки второго рода происходят, когда мы принимаем нулевую гипотезу, когда она на самом деле неверна. То есть, мы делаем ложное отрицательное заключение.
Продолжая пример с лекарственным препаратом, представьте, что на самом деле препарат является эффективным, но наше исследование не показывает статистически значимых результатов, и мы не можем отвергнуть нулевую гипотезу. В этом случае мы делаем ошибку второго рода, пропуская возможность использования эффективного лекарства.
Важно понимать, что вероятность ошибки первого и второго рода связана с выбранным уровнем значимости и мощностью теста. Чем ниже уровень значимости, тем меньше вероятность ошибки первого рода, но тем больше вероятность ошибки второго рода.
Как минимизировать ошибки первого и второго рода
Ошибки первого и второго рода являются неизбежной частью статистического анализа и тестирования гипотез. Однако, существуют некоторые методы и стратегии, которые могут помочь минимизировать вероятность этих ошибок.
Минимизация ошибки первого рода:
Ошибку первого рода можно минимизировать, устанавливая более строгий уровень значимости. Уровень значимости определяет, насколько сильные доказательства требуются для отвержения нулевой гипотезы. Чем ниже уровень значимости, тем меньше вероятность ошибки первого рода. Однако, следует помнить, что снижение уровня значимости также может увеличить вероятность ошибки второго рода.
Также, для минимизации ошибки первого рода, необходимо использовать надежные и точные методы сбора данных. Важно убедиться, что выборка достаточно большая и представляет всю популяцию, чтобы избежать искажений результатов.
Минимизация ошибки второго рода:
Ошибку второго рода можно минимизировать, увеличивая мощность теста. Мощность теста определяет способность теста обнаружить наличие эффекта или различия, если они действительно существуют. Чем выше мощность теста, тем меньше вероятность ошибки второго рода.
Для увеличения мощности теста можно использовать большую выборку, что позволит увеличить точность оценки параметров и улучшить способность теста обнаружить различия. Также, можно использовать более чувствительные статистические методы или улучшить качество измерений.
Важно также учитывать контекст и цель исследования при выборе уровня значимости и мощности теста. Необходимо балансировать между минимизацией ошибок первого и второго рода в зависимости от важности исследуемого эффекта и рисков, связанных с принятием неверных решений.
Таблица сравнения ошибок первого и второго рода
| Тип ошибки | Определение | Свойства | Примеры | Минимизация |
|---|---|---|---|---|
| Ошибка первого рода | Отклонение от нулевой гипотезы, когда она на самом деле верна | – Вероятность ошибки первого рода обозначается как α (альфа) – Также известна как уровень значимости – Чем меньше α, тем меньше вероятность ошибки первого рода |
– Отклонение невиновного человека в суде – Отклонение нулевой гипотезы о равенстве средних двух групп, когда на самом деле они равны |
– Установить более строгий уровень значимости – Увеличить объем выборки |
| Ошибка второго рода | Неотклонение от нулевой гипотезы, когда она на самом деле ложна | – Вероятность ошибки второго рода обозначается как β (бета) – Чем меньше β, тем меньше вероятность ошибки второго рода – Связана с мощностью теста |
– Неотклонение виновного человека в суде – Неотклонение нулевой гипотезы о различии средних двух групп, когда на самом деле они различаются |
– Увеличить объем выборки – Использовать более чувствительный статистический тест |
Заключение
Ошибки первого и второго рода являются важным понятием в теории вероятности. Ошибка первого рода происходит, когда мы отвергаем верную нулевую гипотезу, а ошибка второго рода – когда мы принимаем неверную нулевую гипотезу. Обе ошибки имеют свои свойства и могут иметь серьезные последствия. Чтобы минимизировать ошибки первого и второго рода, необходимо правильно выбирать уровень значимости и размер выборки, а также проводить статистические тесты с учетом контекста и целей исследования.
Перенос знаний от выборочной
совокупности к генеральной может быть
осуществлен лишь с некоторой вероятностью
P{Θ},
т.е. суждение о генеральной совокупности
носит вероятностный характер и содержит
элемент риска (1-P{Θ}).
Суждения о свойствах генеральной
совокупности называются статистическими
гипотезами. Их
проверка осуществляется с помощью
статистических
критериев, назначаемых
в зависимости от формулировки гипотезы
H.
Основная выдвинутая
гипотеза называется нуль-гипотеза
(H0).
Противоречащие ей
гипотезы Hi
называют альтернативными,
или конкурирующими.
Нуль-гипотеза
Н0:
между обеими
выборками нет существенной разницы,
обе они принадлежат одной генеральной
совокупности, а имеющиеся различия
обусловлены случайным характером
выборок, например, влиянием случайных
ошибок. В этом случае любые оценки,
рассчитанные по этим двум выборкам,
будут оценками одних и тех же генеральных
(истинных) значений; тогда в большинстве
случаев имеет смысл объединить обе
выборки в одну, увеличив тем самым число
степеней свободы.
Противоположная, или
альтернативная
гипотеза H1
различия объясняются не случайностью,
а существом дела. Выборки относятся к
разным генеральным совокупностям.
Поскольку проверка гипотез
ведется по выборке, то могут возникнуть
ошибки двух родов. Если будет отвергнута
правильная гипотеза,
то совершается ошибка
первого рода, если
будет допущена
неправильная гипотеза,
то совершается ошибка
второго рода.
Вероятность допустить
ошибку первого рода называется уровнем
значимости и
обозначается α.
Область, отвечающая вероятности α,
называется критической, а дополняющая
ее область, вероятность попадания в
некоторую P{Θα}=1-α,
называется областью
правдоподобных
статистических
критериев Cr.
Вероятность ошибки второго
рода обозначается β, а величина P{Θβ}=1-β
называется мощностью
критерия. Чем больше
эта мощность, тем меньше вероятность
совершить ошибку второго рода.
В задачах статистического
моделирования обычно устанавливают
некоторое значение α, и статистический
критерий Cr
выбирают так, чтобы минимизировать β.
Обычная процедура проверки
гипотез заключается в следующем:
1) по выборочным данным
рассчитывается критерий проверки;
2) полученное значение
критерия сравнивают с критическим
значением, находимым из таблиц. Критическое
значение каждого конкретного критерия
определяется уровнем значимости и
числом степеней свободы, по которому
были рассчитаны величины, входящие в
критерий.
Критерий Пирсона χ2.
Для проверки гипотезы о соответствии
эмпирического распределения СВ
теоретическому наиболее часто применяют
критерий Пирсона
χ2.
Суть этой проверки сводится к следующему.
Предположим, что за время испытаний t
выборки объемом n
отказало d
изделий, причем отказы фиксировались
в различные моменты времени испытаний.
Требуется проверить,
согласуются ли экспериментальные данные
с гипотезой о том, что СВ d
имеет данный закон распределения
заданный функцией F(d)
или плотностью вероятности f(d).
Назовем этот закон распределения
«теоретическим».
Зная этот закон, можно
вычислить ожидаемое число отказов
изделия в определенных интервалах, на
которые разбить время испытания.
В результате получим
теоретический ряд
частот в k
интервалах времени
испытаний:

Подсчитаем также число
отказавших изделий в этих же интервалах
в нашем опыте и получим экспериментальный
ряд частот

Для проверки согласованности
теоретического и экспериментального
распределений подсчитывается мера
расхождения χ2.

и число степеней свободы
v=k–f,
где f
– число ограничений. Число ограничений
равно числу параметров распределения,
увеличенному на единицу. Так, например,
для нормального закона распределения
имеет места два параметра распределения
(математическое ожидание и среднеквадратичное
отклонение). Для распределения Пирсона
составлены специальные таблицы. Пользуясь
этими таблицами, можно для каждого
значения критерия Пирсона и числа
степеней свободы v
определить вероятность
P
того, что за счет
случайных причин мера расхождения
теоретического и эмпирического
распределений будет не меньше, чем
фактически наблюдаемое в данной серии
опытов значение χ2.
Если эта вероятность
сравнительно велика (P≥0,05),
то можно признать гипотезу о соответствии
эмпирического распределения теоретическому
правильно.
Если вероятность весьма
мала (P<0,05),
т.е. событие с такой вероятностью можно
считать практически невозможным, то
результат опыта следует считать
противоречащим гипотезе о том, что закон
распределения величины x
(в нашем случае x=d)
есть F(x).
Следовательно, гипотеза
отвергается и следует подобрать другую
теоретическую кривую.
Критерий Колмогорова
λ.
Критерий Пирсона применяют только в
тех случаях, когда число наблюдений
(n≥25).
Если теоретические значения параметров
распределения известны, то лучшим
критерием является критерий Колмогорова.
Для расчета критерия
Колмогорова, как и для критерия Пирсона
определяют теоретический mi
и экспериментальный ряд частот mi/.
Затем рассчитывают накопленные суммы,
которые образуются путем прибавления
последующих частот к сумме предыдущих.
Составляют разность между накопленными
теоретическими и эмпирическими суммами
и находят максимальное значение этой
разности, вычисляя величину D
по формуле:

Где
,
– разность функций экспериментального
и теоретического распределения СВ.
Коэффициент λ
находят по формуле:
.Пользуясь
табличными данными для вычисленного
значения λ, определяют вероятность P(λ)
– вероятность того, что гипотетическая
функция выбрана правильно.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Всякий раз, когда кто-то начинает изучать машинное обучение/статистику, первая концепция, с которой он сталкивается, — это проверка гипотез, которая, конечно же, является наиболее фундаментальной концепцией, от которой зависят все концепции машинного обучения. Я знаю, что это очень сбивает с толку, если только вы не видели болливудский фильм.😊. Кто не любит фильмы Болливуда?
Я понял эту идею проверки гипотез и ее различных ошибок, основанных на сценарии «Судья и преступник». В этой статье говорится о различных сценариях в этой ситуации, является ли обвиняемый преступником или нет, применительно к проверке гипотез.
Прежде чем вы продолжите читать эту статью, я должен сказать вам, что вам нужно иметь немного предварительных знаний о статистической проверке гипотез.
Теперь всегда говорят, что
«Обвиняемый не является преступником, если нет достаточных доказательств, доказывающих его вину (осуждения)». Теперь представьте, что вы судья, назначенный для слушания дела. Можно надеть судейскую фуражку. Все нормально. 😊
Теперь ваша задача собрать достаточно улик, чтобы доказать, что этот парень не преступник. Теперь вопрос, почему вы как судья должны это делать? Я приду к этому ответу сейчас, как показано ниже. Теперь есть 4 возможности. Вы, должно быть, угадали правильно.
Возможно, что обвиняемый может быть преступником или не быть преступником в действительности. Также решение, принятое вами как судьей, может быть в пользу обвиняемого или против обвиняемого.
Теперь справедливость восторжествует, если: (Ситуация I)
1.1. Обвиняемый преступник, и вы осудили его.
1.2. Обвиняемый не преступник, и вы сделали его невиновным.
Но другой плохой вывод, если: (Ситуация II)
2.1. Обвиняемый преступник, но вы освободили его. (Плохая ситуация I)
2.2. Обвиняемый не преступник, но вы осудили его. (Плохая ситуация 2)
Теперь, как судья, вы можете погладить себя, если попадете в ситуацию I. Но, к сожалению, допустим, вы попали в ситуацию II; Как вы думаете, вы сделали ошибку/ошибку? Если да, то какой из двух более опасен, 2.1 или 2.2.
Ситуация 2.2 более опасна. Не так ли?
Более несправедливо осуждать невиновного (2.2), чем освобождать преступника (2.1). Любая судебная система работает на этом понятии, по крайней мере индийская судебная система.😊. Основная идея, по крайней мере, невиновный парень не должен быть осужден. Вы так не думаете?
Теперь мы доведем эту идею до статистической гипотезы и ее ошибок. Сравните картинку выше с картинкой ниже. Это просто обобщение любой случайной ситуации (не то что в сценарии «Судья и преступник»).
В настоящее время,
α означает ошибку, которую вы допустили, отвергнув H0 (нулевую гипотезу/статус-кво), когда в действительности она должна была быть правдой или должна была быть принята.
ß означает ошибку, которую вы допустили, приняв H0 (нулевая гипотеза/статус-кво), хотя на самом деле она должна была быть ложной или должна была быть отвергнута.
Как указывалось ранее, бета более опасна, чем альфа. Не так ли?
Теперь, поскольку статус-кво был отвергнут, поскольку у вас есть достаточно доказательств, чтобы доказать это, хотя на самом деле это правда. Вы говорите это как «уровень значимости». Как правило, он установлен на 0,05, что означает, насколько важно для вас отказаться от статус-кво на основе доказательств. Теперь очевидно, что он должен быть как можно ниже, чтобы отказаться от статус-кво.
Хм… Стоп здесь… Думайте об этом какое-то время, пока это не проникнет в ваш разум.
Помните, что обвиняемый не является преступником (статус-кво), если его не отвергают, он не является преступником. (доказанная судимость)
Теперь возникает вопрос; Как уменьшить количество ошибок α?
Очень простой. Максимально уменьшите уровень α, чтобы быть уверенным, что вы не совершаете ошибок. Посмотрите на нормальное распределение ниже:
Если вы стремитесь уменьшить область отклонения, вы увеличиваете вероятность принятия H0 (нулевая гипотеза/статус-кво). Другими словами, вы увеличиваете вероятность принятия H0. Вы должны делать это, когда хотите быть увереннее, чем просто 95% (95% — общепринятая норма).
Теперь спросите себя, что представляет собой ß?
Что вы думаете? Думайте, что судья осуждает невиновного парня. Вам не кажется, что судья недостаточно все изучил, прежде чем вынести решение?
Если да, не думаете ли вы, что это отражает уровень выступления (в данном случае судьи). На самом деле он недостаточно изучил, вероятно, потому, что не встречал достаточного количества подобных случаев. Возможно, это уникальный для него случай. Если бы он был разоблачен в достаточном количестве подобных случаев, он, возможно, не осудил бы невиновного парня.
Хммм… Стоп здесь… Подумайте об этом какое-то время, пока оно не проникнет в ваш разум.
Теперь возникает вопрос; Как уменьшить число ß-ошибок?
Простой ответ — увеличение пространства выборки. Я еще раз повторю: «Если судья будет сталкиваться с достаточным количеством подобных дел, его работа улучшится».
Так так так…
Возможно, вас ввело в заблуждение мое заявление, когда я сказал, что ß более опасен, чем α. Как я могу это сказать? Ты прав.
Фактический ответ: «Это зависит от того, с каким делом вы имеете дело».
В этом случае «Судья и преступник» опаснее ß, чем α.
Можете ли вы представить себе ситуацию, когда иначе, т. е. α более опасен, чем ß? Ваши мысли приветствуются.
Проверка корректности А/Б тестов
Время на прочтение
8 мин
Количество просмотров 10K
Хабр, привет! Сегодня поговорим о том, что такое корректность статистических критериев в контексте А/Б тестирования. Узнаем, как проверить, является критерий корректным или нет. Разберём пример, в котором тест Стьюдента не работает.
Меня зовут Коля, я работаю аналитиком данных в X5 Tech. Мы с Сашей продолжаем писать серию статей по А/Б тестированию, это наша третья статья. Первые две можно посмотреть тут:
-
Стратификация. Как разбиение выборки повышает чувствительность A/Б теста
-
Бутстреп и А/Б тестирование
Корректный статистический критерий
В А/Б тестировании при проверке гипотез с помощью статистических критериев можно совершить одну из двух ошибок:
-
ошибку первого рода – отклонить нулевую гипотезу, когда на самом деле она верна. То есть сказать, что эффект есть, хотя на самом деле его нет;
-
ошибку второго рода – не отклонить нулевую гипотезу, когда на самом деле она неверна. То есть сказать, что эффекта нет, хотя на самом деле он есть.
Совсем не ошибаться нельзя. Чтобы получить на 100% достоверные результаты, нужно бесконечно много данных. На практике получить столько данных затруднительно. Если совсем не ошибаться нельзя, то хотелось бы ошибаться не слишком часто и контролировать вероятности ошибок.
В статистике ошибка первого рода считается более важной. Поэтому обычно фиксируют допустимую вероятность ошибки первого рода, а затем пытаются минимизировать вероятность ошибки второго рода.
Предположим, мы решили, что допустимые вероятности ошибок первого и второго рода равны 0.1 и 0.2 соответственно. Будем называть статистический критерий корректным, если его вероятности ошибок первого и второго рода равны допустимым вероятностям ошибок первого и второго рода соответственно.
Как сделать критерий, в котором вероятности ошибок будут равны допустимым вероятностям ошибок?
Вероятность ошибки первого рода по определению равна уровню значимости критерия. Если уровень значимости положить равным допустимой вероятности ошибки первого рода, то вероятность ошибки первого рода должна стать равной допустимой вероятности ошибки первого рода.
Вероятность ошибки второго рода можно подогнать под желаемое значение, меняя размер групп или снижая дисперсию в данных. Чем больше размер групп и чем ниже дисперсия, тем меньше вероятность ошибки второго рода. Для некоторых гипотез есть готовые формулы оценки размера групп, при которых достигаются заданные вероятности ошибок.
Например, формула оценки необходимого размера групп для гипотезы о равенстве средних:
где и
– допустимые вероятности ошибок первого и второго рода,
– ожидаемый эффект (на сколько изменится среднее),
и
– стандартные отклонения случайных величин в контрольной и экспериментальной группах.
Проверка корректности
Допустим, мы работаем в онлайн-магазине с доставкой. Хотим исследовать, как новый алгоритм ранжирования товаров на сайте влияет на среднюю выручку с покупателя за неделю. Продолжительность эксперимента – одна неделя. Ожидаемый эффект равен +100 рублей. Допустимая вероятность ошибки первого рода равна 0.1, второго рода – 0.2.
Оценим необходимый размер групп по формуле:
import numpy as np
from scipy import stats
alpha = 0.1 # допустимая вероятность ошибки I рода
beta = 0.2 # допустимая вероятность ошибки II рода
mu_control = 2500 # средняя выручка с пользователя в контрольной группе
effect = 100 # ожидаемый размер эффекта
mu_pilot = mu_control + effect # средняя выручка с пользователя в экспериментальной группе
std = 800 # стандартное отклонение
# исторические данные выручки для 10000 клиентов
values = np.random.normal(mu_control, std, 10000)
def estimate_sample_size(effect, std, alpha, beta):
"""Оценка необходимого размер групп."""
t_alpha = stats.norm.ppf(1 - alpha / 2, loc=0, scale=1)
t_beta = stats.norm.ppf(1 - beta, loc=0, scale=1)
var = 2 * std ** 2
sample_size = int((t_alpha + t_beta) ** 2 * var / (effect ** 2))
return sample_size
estimated_std = np.std(values)
sample_size = estimate_sample_size(effect, estimated_std, alpha, beta)
print(f'оценка необходимого размера групп = {sample_size}')оценка необходимого размера групп = 784Чтобы проверить корректность, нужно знать природу случайных величин, с которыми мы работаем. В этом нам помогут исторические данные. Представьте, что мы перенеслись в прошлое на несколько недель назад и запустили эксперимент с таким же дизайном, как мы планировали запустить его сейчас. Дизайн – это совокупность параметров эксперимента, таких как: целевая метрика, допустимые вероятности ошибок первого и второго рода, размеры групп и продолжительность эксперимента, техники снижения дисперсии и т.д.
Так как это было в прошлом, мы знаем, какие покупки совершили пользователи, можем вычислить метрики и оценить значимость отличий. Кроме того, мы знаем, что эффекта на самом деле не было, так как в то время эксперимент на самом деле не запускался. Если значимые отличия были найдены, то мы совершили ошибку первого рода. Иначе получили правильный результат.
Далее нужно повторить эту процедуру с мысленным запуском эксперимента в прошлом на разных группах и временных интервалах много раз, например, 1000.
После этого можно посчитать долю экспериментов, в которых была совершена ошибка. Это будет точечная оценка вероятности ошибки первого рода.
Оценку вероятности ошибки второго рода можно получить аналогичным способом. Единственное отличие состоит в том, что каждый раз нужно искусственно добавлять ожидаемый эффект в данные экспериментальной группы. В этих экспериментах эффект на самом деле есть, так как мы сами его добавили. Если значимых отличий не будет найдено – это ошибка второго рода. Проведя 1000 экспериментов и посчитав долю ошибок второго рода, получим точечную оценку вероятности ошибки второго рода.
Посмотрим, как оценить вероятности ошибок в коде. С помощью численных синтетических А/А и А/Б экспериментов оценим вероятности ошибок и построим доверительные интервалы:
def run_synthetic_experiments(values, sample_size, effect=0, n_iter=10000):
"""Проводим синтетические эксперименты, возвращаем список p-value."""
pvalues = []
for _ in range(n_iter):
a, b = np.random.choice(values, size=(2, sample_size,), replace=False)
b += effect
pvalue = stats.ttest_ind(a, b).pvalue
pvalues.append(pvalue)
return np.array(pvalues)
def print_estimated_errors(pvalues_aa, pvalues_ab, alpha):
"""Оценивает вероятности ошибок."""
estimated_first_type_error = np.mean(pvalues_aa < alpha)
estimated_second_type_error = np.mean(pvalues_ab >= alpha)
ci_first = estimate_ci_bernoulli(estimated_first_type_error, len(pvalues_aa))
ci_second = estimate_ci_bernoulli(estimated_second_type_error, len(pvalues_ab))
print(f'оценка вероятности ошибки I рода = {estimated_first_type_error:0.4f}')
print(f' доверительный интервал = [{ci_first[0]:0.4f}, {ci_first[1]:0.4f}]')
print(f'оценка вероятности ошибки II рода = {estimated_second_type_error:0.4f}')
print(f' доверительный интервал = [{ci_second[0]:0.4f}, {ci_second[1]:0.4f}]')
def estimate_ci_bernoulli(p, n, alpha=0.05):
"""Доверительный интервал для Бернуллиевской случайной величины."""
t = stats.norm.ppf(1 - alpha / 2, loc=0, scale=1)
std_n = np.sqrt(p * (1 - p) / n)
return p - t * std_n, p + t * std_n
pvalues_aa = run_synthetic_experiments(values, sample_size, effect=0)
pvalues_ab = run_synthetic_experiments(values, sample_size, effect=effect)
print_estimated_errors(pvalues_aa, pvalues_ab, alpha)оценка вероятности ошибки I рода = 0.0991
доверительный интервал = [0.0932, 0.1050]
оценка вероятности ошибки II рода = 0.1978
доверительный интервал = [0.1900, 0.2056]Оценки вероятностей ошибок примерно равны 0.1 и 0.2, как и должно быть. Всё верно, тест Стьюдента на этих данных работает корректно.
Распределение p-value
Выше рассмотрели случай, когда тест контролирует вероятность ошибки первого рода при фиксированном уровне значимости. Если решим изменить уровень значимости с 0.1 на 0.01, будет ли тест контролировать вероятность ошибки первого рода? Было бы хорошо, если тест контролировал вероятность ошибки первого рода при любом заданном уровне значимости. Формально это можно записать так:
Для любого выполняется
.
Заметим, что в левой части равенства записано выражение для функции распределения p-value. Из равенства следует, что функция распределения p-value в точке X равна X для любого X от 0 до 1. Эта функция распределения является функцией распределения равномерного распределения от 0 до 1. Мы только что показали, что статистический критерий контролирует вероятность ошибки первого рода на заданном уровне для любого уровня значимости тогда и только тогда, когда при верности нулевой гипотезы p-value распределено равномерно от 0 до 1.
При верности нулевой гипотезы p-value должно быть распределено равномерно. А как должно быть распределено p-value при верности альтернативной гипотезы? Из условия для вероятности ошибки второго рода следует, что
.
Получается, график функции распределения p-value при верности альтернативной гипотезы должен проходить через точку , где
и
– допустимые вероятности ошибок конкретного эксперимента.
Проверим, как распределено p-value в численном эксперименте. Построим эмпирические функции распределения p-value:
import matplotlib.pyplot as plt
def plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta):
"""Рисует графики распределения p-value."""
estimated_first_type_error = np.mean(pvalues_aa < alpha)
estimated_second_type_error = np.mean(pvalues_ab >= alpha)
y_one = estimated_first_type_error
y_two = 1 - estimated_second_type_error
X = np.linspace(0, 1, 1000)
Y_aa = [np.mean(pvalues_aa < x) for x in X]
Y_ab = [np.mean(pvalues_ab < x) for x in X]
plt.plot(X, Y_aa, label='A/A')
plt.plot(X, Y_ab, label='A/B')
plt.plot([alpha, alpha], [0, 1], '--k', alpha=0.8)
plt.plot([0, alpha], [y_one, y_one], '--k', alpha=0.8)
plt.plot([0, alpha], [y_two, y_two], '--k', alpha=0.8)
plt.plot([0, 1], [0, 1], '--k', alpha=0.8)
plt.title('Оценка распределения p-value', size=16)
plt.xlabel('p-value', size=12)
plt.legend(fontsize=12)
plt.grid()
plt.show()
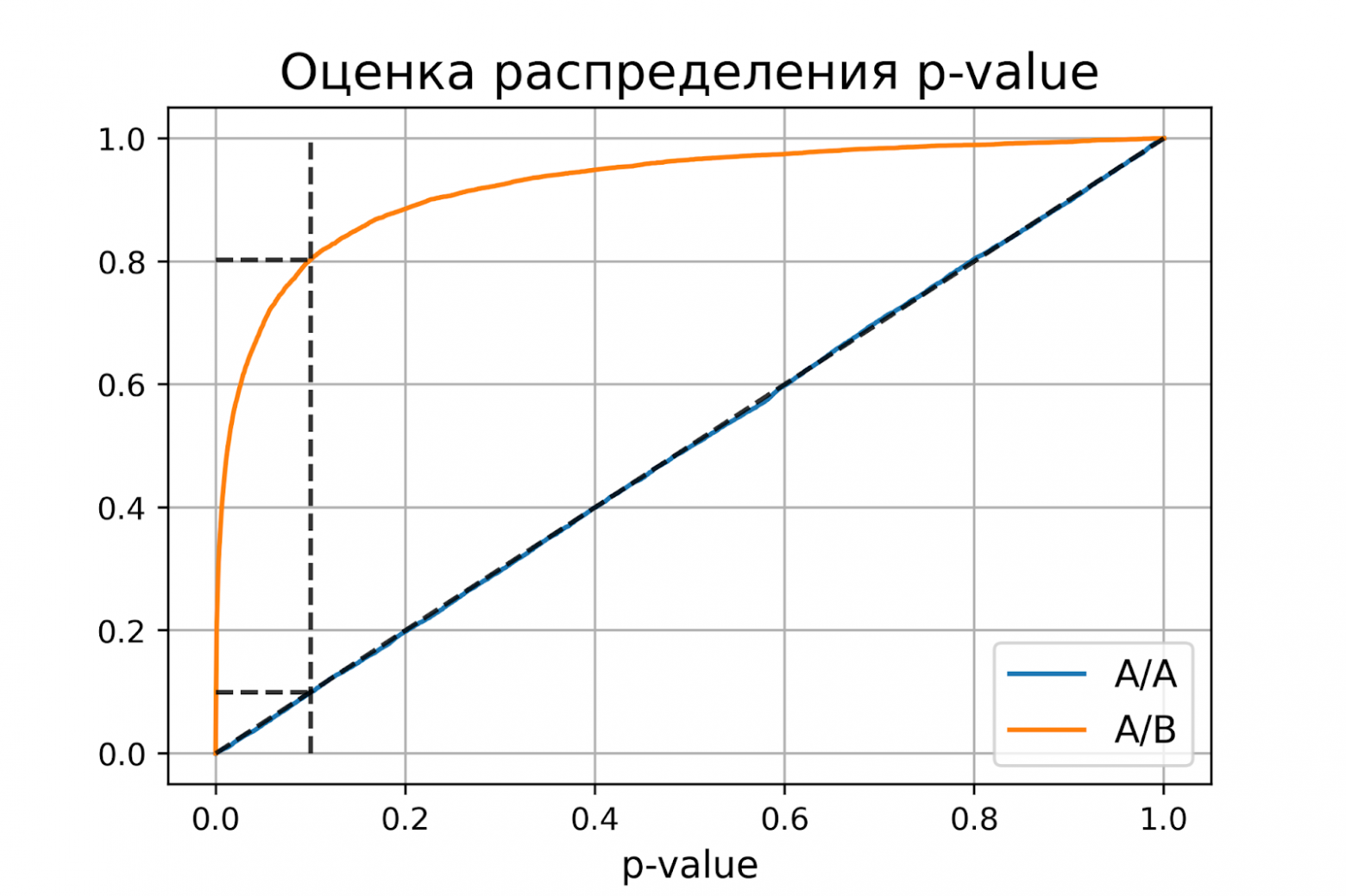
plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta)P-value для синтетических А/А тестах действительно оказалось распределено равномерно от 0 до 1, а для синтетических А/Б тестов проходит через точку .
Кроме оценок распределений на графике дополнительно построены четыре пунктирные линии:
-
диагональная из точки [0, 0] в точку [1, 1] – это функция распределения равномерного распределения на отрезке от 0 до 1, по ней можно визуально оценивать равномерность распределения p-value;
-
вертикальная линия с
– пороговое значение p-value, по которому определяем отвергать нулевую гипотезу или нет. Проекция на ось ординат точки пересечения вертикальной линии с функцией распределения p-value для А/А тестов – это вероятность ошибки первого рода. Проекция точки пересечения вертикальной линии с функцией распределения p-value для А/Б тестов – это мощность теста (мощность = 1 —
).
-
две горизонтальные линии – проекции на ось ординат точки пересечения вертикальной линии с функцией распределения p-value для А/А и А/Б тестов.
График с оценками распределения p-value для синтетических А/А и А/Б тестов позволяет проверить корректность теста для любого значения уровня значимости.
Некорректный критерий
Выше рассмотрели пример, когда тест Стьюдента оказался корректным критерием для случайных данных из нормального распределения. Может быть, все критерии всегда работаю корректно, и нет смысла каждый раз проверять вероятности ошибок?
Покажем, что это не так. Немного изменим рассмотренный ранее пример, чтобы продемонстрировать некорректную работу критерия. Допустим, мы решили увеличить продолжительность эксперимента до 2-х недель. Для каждого пользователя будем вычислять стоимость покупок за первую неделю и стоимость покупок за второю неделю. Полученные стоимости будем передавать в тест Стьюдента для проверки значимости отличий. Положим, что поведение пользователей повторяется от недели к неделе, и стоимости покупок одного пользователя совпадают.
def run_synthetic_experiments_two(values, sample_size, effect=0, n_iter=10000):
"""Проводим синтетические эксперименты на двух неделях."""
pvalues = []
for _ in range(n_iter):
a, b = np.random.choice(values, size=(2, sample_size,), replace=False)
b += effect
# дублируем данные
a = np.hstack((a, a,))
b = np.hstack((b, b,))
pvalue = stats.ttest_ind(a, b).pvalue
pvalues.append(pvalue)
return np.array(pvalues)
pvalues_aa = run_synthetic_experiments_two(values, sample_size)
pvalues_ab = run_synthetic_experiments_two(values, sample_size, effect=effect)
print_estimated_errors(pvalues_aa, pvalues_ab, alpha)
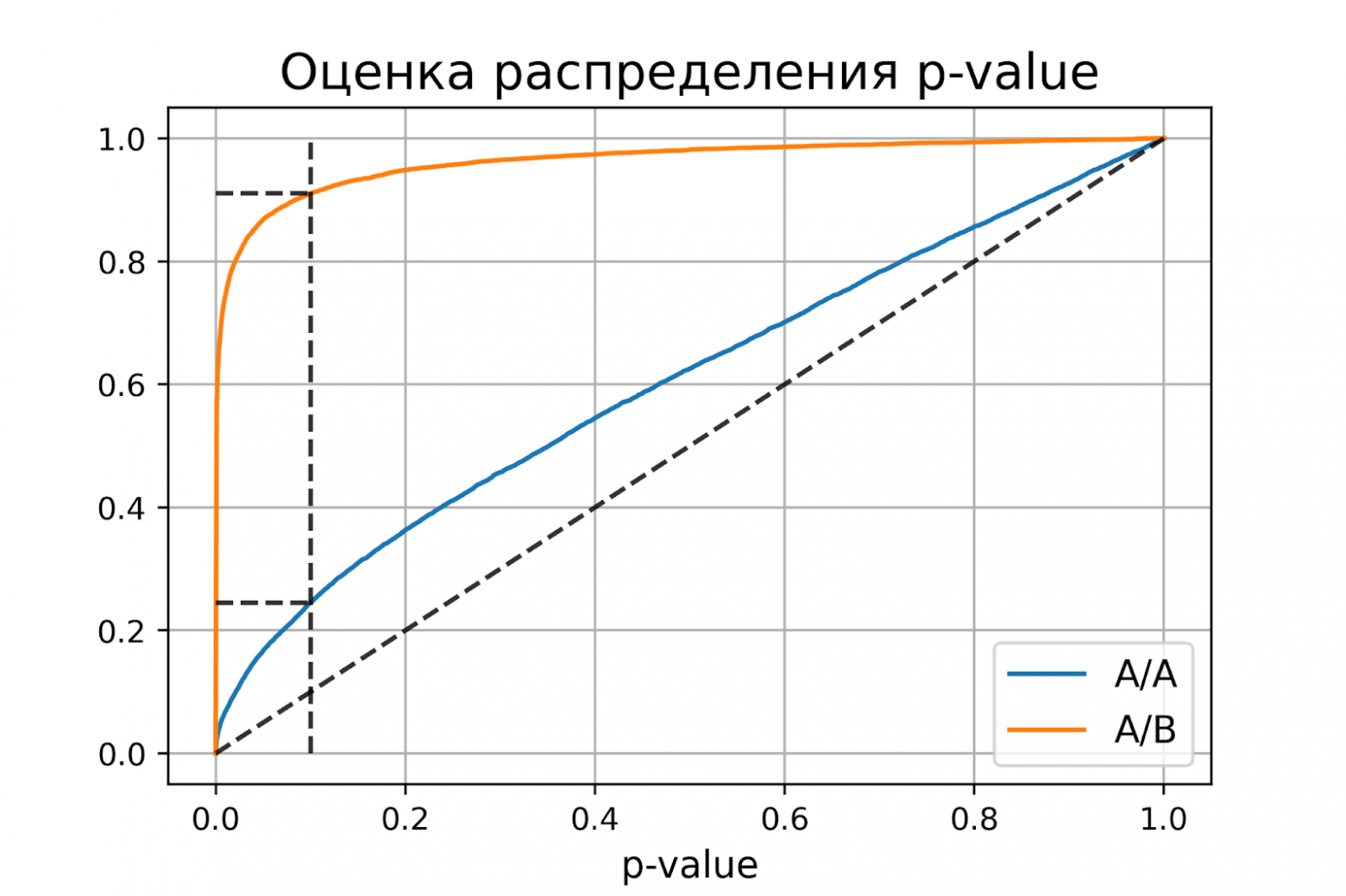
plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta)оценка вероятности ошибки I рода = 0.2451
доверительный интервал = [0.2367, 0.2535]
оценка вероятности ошибки II рода = 0.0894
доверительный интервал = [0.0838, 0.0950]Получили оценку вероятности ошибки первого рода около 0.25, что сильно больше уровня значимости 0.1. На графике видно, что распределение p-value для синтетических А/А тестов не равномерно, оно отклоняется от диагонали. В этом примере тест Стьюдента работает некорректно, так как данные зависимые (стоимости покупок одного человека зависимы). Если бы мы сразу не догадались про зависимость данных, то оценка вероятностей ошибок помогла бы нам понять, что такой тест некорректен.
Итоги
Мы обсудили, что такое корректность статистического теста, посмотрели, как оценить вероятности ошибок на исторических данных и привели пример некорректной работы критерия.
Таким образом:
-
корректный критерий – это критерий, у которого вероятности ошибок первого и второго рода равны допустимым вероятностям ошибок первого и второго рода соответственно;
-
чтобы критерий контролировал вероятность ошибки первого рода для любого уровня значимости, необходимо и достаточно, чтобы p-value при верности нулевой гипотезы было распределено равномерно от 0 до 1.
This article is about erroneous outcomes of statistical tests. For closely related concepts in binary classification and testing generally, see false positives and false negatives.
In statistical hypothesis testing, a type I error is the mistaken rejection of a null hypothesis that is actually true. A type I error is also known as a «false positive» finding or conclusion; example: «an innocent person is convicted». A type II error is the failure to reject a null hypothesis that is actually false. A type II error is also known as a «false negative» finding or conclusion; example: «a guilty person is not convicted».[1] Much of statistical theory revolves around the minimization of one or both of these errors, though the complete elimination of either is a statistical impossibility if the outcome is not determined by a known, observable causal process.
By selecting a low threshold (cut-off) value and modifying the alpha (α) level, the quality of the hypothesis test can be increased.[citation needed] The knowledge of type I errors and type II errors is widely used in medical science, biometrics and computer science.[clarification needed]
Intuitively, type I errors can be thought of as errors of commission (i.e., the researcher unluckily concludes that something is the fact). For instance, consider a study where researchers compare a drug with a placebo. If the patients who are given the drug get better than the patients given the placebo by chance, it may appear that the drug is effective, but in fact the conclusion is incorrect.
In reverse, type II errors are errors of omission. In the example above, if the patients who got the drug did not get better at a higher rate than the ones who got the placebo, but this was a random fluke, that would be a type II error. The consequence of a type II error depends on the size and direction of the missed determination and the circumstances. An expensive cure for one in a million patients may be inconsequential even if it truly is a cure.
Definition[edit]
Statistical background[edit]
In statistical test theory, the notion of a statistical error is an integral part of hypothesis testing. The test goes about choosing about two competing propositions called null hypothesis, denoted by H0 and alternative hypothesis, denoted by H1. This is conceptually similar to the judgement in a court trial. The null hypothesis corresponds to the position of the defendant: just as he is presumed to be innocent until proven guilty, so is the null hypothesis presumed to be true until the data provide convincing evidence against it. The alternative hypothesis corresponds to the position against the defendant. Specifically, the null hypothesis also involves the absence of a difference or the absence of an association. Thus, the null hypothesis can never be that there is a difference or an association.
If the result of the test corresponds with reality, then a correct decision has been made. However, if the result of the test does not correspond with reality, then an error has occurred. There are two situations in which the decision is wrong. The null hypothesis may be true, whereas we reject H0. On the other hand, the alternative hypothesis H1 may be true, whereas we do not reject H0. Two types of error are distinguished: type I error and type II error.[2]
Type I error[edit]
The first kind of error is the mistaken rejection of a null hypothesis as the result of a test procedure. This kind of error is called a type I error (false positive) and is sometimes called an error of the first kind. In terms of the courtroom example, a type I error corresponds to convicting an innocent defendant.
Type II error[edit]
The second kind of error is the mistaken failure to reject the null hypothesis as the result of a test procedure. This sort of error is called a type II error (false negative) and is also referred to as an error of the second kind. In terms of the courtroom example, a type II error corresponds to acquitting a criminal.[3]
Crossover error rate[edit]
The crossover error rate (CER) is the point at which type I errors and type II errors are equal. A system with a lower CER value provides more accuracy than a system with a higher CER value.
False positive and false negative[edit]
In terms of false positives and false negatives, a positive result corresponds to rejecting the null hypothesis, while a negative result corresponds to failing to reject the null hypothesis; «false» means the conclusion drawn is incorrect. Thus, a type I error is equivalent to a false positive, and a type II error is equivalent to a false negative.
Table of error types[edit]
Tabularised relations between truth/falseness of the null hypothesis and outcomes of the test:[4]
| Table of error types | Null hypothesis (H0) is | ||
|---|---|---|---|
| True | False | ||
| Decision about null hypothesis (H0) |
Fail to reject | Correct inference (true negative) (probability = 1−α) |
Type II error (false negative) (probability = β) |
| Reject | Type I error (false positive) (probability = α) |
Correct inference (true positive) (probability = 1−β) |
Error rate[edit]
A perfect test would have zero false positives and zero false negatives. However, statistical methods are probabilistic, and it cannot be known for certain whether statistical conclusions are correct. Whenever there is uncertainty, there is the possibility of making an error. Considering this nature of statistics science, all statistical hypothesis tests have a probability of making type I and type II errors.[citation needed]
- The type I error rate is the probability of rejecting the null hypothesis given that it is true. The test is designed to keep the type I error rate below a prespecified bound called the significance level, usually denoted by the Greek letter α (alpha) and is also called the alpha level. Usually, the significance level is set to 0.05 (5%), implying that it is acceptable to have a 5% probability of incorrectly rejecting the true null hypothesis.[5]
- The rate of the type II error is denoted by the Greek letter β (beta) and related to the power of a test, which equals 1−β.[citation needed]
These two types of error rates are traded off against each other: for any given sample set, the effort to reduce one type of error generally results in increasing the other type of error.[citation needed]
The quality of hypothesis test[edit]
The same idea can be expressed in terms of the rate of correct results and therefore used to minimize error rates and improve the quality of hypothesis test. To reduce the probability of committing a type I error, making the alpha value more stringent is quite simple and efficient. To decrease the probability of committing a type II error, which is closely associated with analyses’ power, either increasing the test’s sample size or relaxing the alpha level could increase the analyses’ power.[citation needed] A test statistic is robust if the type I error rate is controlled.
Varying different threshold (cut-off) value could also be used to make the test either more specific or more sensitive, which in turn elevates the test quality. For example, imagine a medical test, in which an experimenter might measure the concentration of a certain protein in the blood sample. The experimenter could adjust the threshold (black vertical line in the figure) and people would be diagnosed as having diseases if any number is detected above this certain threshold. According to the image, changing the threshold would result in changes in false positives and false negatives, corresponding to movement on the curve.[citation needed]
Example[edit]
Since in a real experiment it is impossible to avoid all type I and type II errors, it is important to consider the amount of risk one is willing to take to falsely reject H0 or accept H0. The solution to this question would be to report the p-value or significance level α of the statistic. For example, if the p-value of a test statistic result is estimated at 0.0596, then there is a probability of 5.96% that we falsely reject H0. Or, if we say, the statistic is performed at level α, like 0.05, then we allow to falsely reject H0 at 5%. A significance level α of 0.05 is relatively common, but there is no general rule that fits all scenarios.
Vehicle speed measuring[edit]
The speed limit of a freeway in the United States is 120 kilometers per hour (75 mph). A device is set to measure the speed of passing vehicles. Suppose that the device will conduct three measurements of the speed of a passing vehicle, recording as a random sample X1, X2, X3. The traffic police will or will not fine the drivers depending on the average speed 

In addition, we suppose that the measurements X1, X2, X3 are modeled as normal distribution N(μ,4). Then, T should follow N(μ,4/3) and the parameter μ represents the true speed of passing vehicle. In this experiment, the null hypothesis H0 and the alternative hypothesis H1 should be
H0: μ=120 against H1: μ>120.
If we perform the statistic level at α=0.05, then a critical value c should be calculated to solve

According to change-of-units rule for the normal distribution. Referring to Z-table, we can get

Here, the critical region. That is to say, if the recorded speed of a vehicle is greater than critical value 121.9, the driver will be fined. However, there are still 5% of the drivers are falsely fined since the recorded average speed is greater than 121.9 but the true speed does not pass 120, which we say, a type I error.
The type II error corresponds to the case that the true speed of a vehicle is over 120 kilometers per hour but the driver is not fined. For example, if the true speed of a vehicle μ=125, the probability that the driver is not fined can be calculated as

which means, if the true speed of a vehicle is 125, the driver has the probability of 0.36% to avoid the fine when the statistic is performed at level α=0.05, since the recorded average speed is lower than 121.9. If the true speed is closer to 121.9 than 125, then the probability of avoiding the fine will also be higher.
The tradeoffs between type I error and type II error should also be considered. That is, in this case, if the traffic police do not want to falsely fine innocent drivers, the level α can be set to a smaller value, like 0.01. However, if that is the case, more drivers whose true speed is over 120 kilometers per hour, like 125, would be more likely to avoid the fine.
Etymology[edit]
In 1928, Jerzy Neyman (1894–1981) and Egon Pearson (1895–1980), both eminent statisticians, discussed the problems associated with «deciding whether or not a particular sample may be judged as likely to have been randomly drawn from a certain population»:[6] and, as Florence Nightingale David remarked, «it is necessary to remember the adjective ‘random’ [in the term ‘random sample’] should apply to the method of drawing the sample and not to the sample itself».[7]
They identified «two sources of error», namely:
- (a) the error of rejecting a hypothesis that should have not been rejected, and
- (b) the error of failing to reject a hypothesis that should have been rejected.
In 1930, they elaborated on these two sources of error, remarking that:
…in testing hypotheses two considerations must be kept in view, we must be able to reduce the chance of rejecting a true hypothesis to as low a value as desired; the test must be so devised that it will reject the hypothesis tested when it is likely to be false.
In 1933, they observed that these «problems are rarely presented in such a form that we can discriminate with certainty between the true and false hypothesis» . They also noted that, in deciding whether to fail to reject, or reject a particular hypothesis amongst a «set of alternative hypotheses», H1, H2…, it was easy to make an error:
…[and] these errors will be of two kinds:
- (I) we reject H0 [i.e., the hypothesis to be tested] when it is true,[8]
- (II) we fail to reject H0 when some alternative hypothesis HA or H1 is true. (There are various notations for the alternative).
In all of the papers co-written by Neyman and Pearson the expression H0 always signifies «the hypothesis to be tested».
In the same paper they call these two sources of error, errors of type I and errors of type II respectively.[9]
[edit]
Null hypothesis[edit]
It is standard practice for statisticians to conduct tests in order to determine whether or not a «speculative hypothesis» concerning the observed phenomena of the world (or its inhabitants) can be supported. The results of such testing determine whether a particular set of results agrees reasonably (or does not agree) with the speculated hypothesis.
On the basis that it is always assumed, by statistical convention, that the speculated hypothesis is wrong, and the so-called «null hypothesis» that the observed phenomena simply occur by chance (and that, as a consequence, the speculated agent has no effect) – the test will determine whether this hypothesis is right or wrong. This is why the hypothesis under test is often called the null hypothesis (most likely, coined by Fisher (1935, p. 19)), because it is this hypothesis that is to be either nullified or not nullified by the test. When the null hypothesis is nullified, it is possible to conclude that data support the «alternative hypothesis» (which is the original speculated one).
The consistent application by statisticians of Neyman and Pearson’s convention of representing «the hypothesis to be tested» (or «the hypothesis to be nullified») with the expression H0 has led to circumstances where many understand the term «the null hypothesis» as meaning «the nil hypothesis» – a statement that the results in question have arisen through chance. This is not necessarily the case – the key restriction, as per Fisher (1966), is that «the null hypothesis must be exact, that is free from vagueness and ambiguity, because it must supply the basis of the ‘problem of distribution,’ of which the test of significance is the solution.»[10] As a consequence of this, in experimental science the null hypothesis is generally a statement that a particular treatment has no effect; in observational science, it is that there is no difference between the value of a particular measured variable, and that of an experimental prediction.[citation needed]
Statistical significance[edit]
If the probability of obtaining a result as extreme as the one obtained, supposing that the null hypothesis were true, is lower than a pre-specified cut-off probability (for example, 5%), then the result is said to be statistically significant and the null hypothesis is rejected.
British statistician Sir Ronald Aylmer Fisher (1890–1962) stressed that the «null hypothesis»:
… is never proved or established, but is possibly disproved, in the course of experimentation. Every experiment may be said to exist only in order to give the facts a chance of disproving the null hypothesis.
— Fisher, 1935, p.19
Application domains[edit]
Medicine[edit]
In the practice of medicine, the differences between the applications of screening and testing are considerable.
Medical screening[edit]
Screening involves relatively cheap tests that are given to large populations, none of whom manifest any clinical indication of disease (e.g., Pap smears).
Testing involves far more expensive, often invasive, procedures that are given only to those who manifest some clinical indication of disease, and are most often applied to confirm a suspected diagnosis.
For example, most states in the USA require newborns to be screened for phenylketonuria and hypothyroidism, among other congenital disorders.
Hypothesis: «The newborns have phenylketonuria and hypothyroidism»
Null Hypothesis (H0): «The newborns do not have phenylketonuria and hypothyroidism»,
Type I error (false positive): The true fact is that the newborns do not have phenylketonuria and hypothyroidism but we consider they have the disorders according to the data.
Type II error (false negative): The true fact is that the newborns have phenylketonuria and hypothyroidism but we consider they do not have the disorders according to the data.
Although they display a high rate of false positives, the screening tests are considered valuable because they greatly increase the likelihood of detecting these disorders at a far earlier stage.
The simple blood tests used to screen possible blood donors for HIV and hepatitis have a significant rate of false positives; however, physicians use much more expensive and far more precise tests to determine whether a person is actually infected with either of these viruses.
Perhaps the most widely discussed false positives in medical screening come from the breast cancer screening procedure mammography. The US rate of false positive mammograms is up to 15%, the highest in world. One consequence of the high false positive rate in the US is that, in any 10-year period, half of the American women screened receive a false positive mammogram. False positive mammograms are costly, with over $100 million spent annually in the U.S. on follow-up testing and treatment. They also cause women unneeded anxiety. As a result of the high false positive rate in the US, as many as 90–95% of women who get a positive mammogram do not have the condition. The lowest rate in the world is in the Netherlands, 1%. The lowest rates are generally in Northern Europe where mammography films are read twice and a high threshold for additional testing is set (the high threshold decreases the power of the test).
The ideal population screening test would be cheap, easy to administer, and produce zero false-negatives, if possible. Such tests usually produce more false-positives, which can subsequently be sorted out by more sophisticated (and expensive) testing.
Medical testing[edit]
False negatives and false positives are significant issues in medical testing.
Hypothesis: «The patients have the specific disease».
Null hypothesis (H0): «The patients do not have the specific disease».
Type I error (false positive): «The true fact is that the patients do not have a specific disease but the physicians judges the patients was ill according to the test reports».
False positives can also produce serious and counter-intuitive problems when the condition being searched for is rare, as in screening. If a test has a false positive rate of one in ten thousand, but only one in a million samples (or people) is a true positive, most of the positives detected by that test will be false. The probability that an observed positive result is a false positive may be calculated using Bayes’ theorem.
Type II error (false negative): «The true fact is that the disease is actually present but the test reports provide a falsely reassuring message to patients and physicians that the disease is absent».
False negatives produce serious and counter-intuitive problems, especially when the condition being searched for is common. If a test with a false negative rate of only 10% is used to test a population with a true occurrence rate of 70%, many of the negatives detected by the test will be false.
This sometimes leads to inappropriate or inadequate treatment of both the patient and their disease. A common example is relying on cardiac stress tests to detect coronary atherosclerosis, even though cardiac stress tests are known to only detect limitations of coronary artery blood flow due to advanced stenosis.
Biometrics[edit]
Biometric matching, such as for fingerprint recognition, facial recognition or iris recognition, is susceptible to type I and type II errors.
Hypothesis: «The input does not identify someone in the searched list of people»
Null hypothesis: «The input does identify someone in the searched list of people»
Type I error (false reject rate): «The true fact is that the person is someone in the searched list but the system concludes that the person is not according to the data».
Type II error (false match rate): «The true fact is that the person is not someone in the searched list but the system concludes that the person is someone whom we are looking for according to the data».
The probability of type I errors is called the «false reject rate» (FRR) or false non-match rate (FNMR), while the probability of type II errors is called the «false accept rate» (FAR) or false match rate (FMR).
If the system is designed to rarely match suspects then the probability of type II errors can be called the «false alarm rate». On the other hand, if the system is used for validation (and acceptance is the norm) then the FAR is a measure of system security, while the FRR measures user inconvenience level.
Security screening[edit]
False positives are routinely found every day in airport security screening, which are ultimately visual inspection systems. The installed security alarms are intended to prevent weapons being brought onto aircraft; yet they are often set to such high sensitivity that they alarm many times a day for minor items, such as keys, belt buckles, loose change, mobile phones, and tacks in shoes.
Here, the null hypothesis is that the item is not a weapon, while the alternative hypothesis is that the item is a weapon.
A type I error (false positive): «The true fact is that the item is not a weapon but the system still alarms».
Type II error (false negative) «The true fact is that the item is a weapon but the system keeps silent at this time».
The ratio of false positives (identifying an innocent traveler as a terrorist) to true positives (detecting a would-be terrorist) is, therefore, very high; and because almost every alarm is a false positive, the positive predictive value of these screening tests is very low.
The relative cost of false results determines the likelihood that test creators allow these events to occur. As the cost of a false negative in this scenario is extremely high (not detecting a bomb being brought onto a plane could result in hundreds of deaths) whilst the cost of a false positive is relatively low (a reasonably simple further inspection) the most appropriate test is one with a low statistical specificity but high statistical sensitivity (one that allows a high rate of false positives in return for minimal false negatives).
Computers[edit]
The notions of false positives and false negatives have a wide currency in the realm of computers and computer applications, including computer security, spam filtering, Malware, Optical character recognition and many others.
For example, in the case of spam filtering the hypothesis here is that the message is a spam.
Thus, null hypothesis: «The message is not a spam».
Type I error (false positive): «Spam filtering or spam blocking techniques wrongly classify a legitimate email message as spam and, as a result, interferes with its delivery».
While most anti-spam tactics can block or filter a high percentage of unwanted emails, doing so without creating significant false-positive results is a much more demanding task.
Type II error (false negative): «Spam email is not detected as spam, but is classified as non-spam». A low number of false negatives is an indicator of the efficiency of spam filtering.
See also[edit]
- Binary classification
- Detection theory
- Egon Pearson
- Ethics in mathematics
- False positive paradox
- False discovery rate
- Family-wise error rate
- Information retrieval performance measures
- Neyman–Pearson lemma
- Null hypothesis
- Probability of a hypothesis for Bayesian inference
- Precision and recall
- Prosecutor’s fallacy
- Prozone phenomenon
- Receiver operating characteristic
- Sensitivity and specificity
- Statisticians’ and engineers’ cross-reference of statistical terms
- Testing hypotheses suggested by the data
- Type III error
References[edit]
- ^ «Type I Error and Type II Error». explorable.com. Retrieved 14 December 2019.
- ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ Sheskin, David (2004). Handbook of Parametric and Nonparametric Statistical Procedures. CRC Press. p. 54. ISBN 1584884401.
- ^ Lindenmayer, David. (2005). Practical conservation biology. Burgman, Mark A. Collingwood, Vic.: CSIRO Pub. ISBN 0-643-09310-9. OCLC 65216357.
- ^ NEYMAN, J.; PEARSON, E. S. (1928). «On the Use and Interpretation of Certain Test Criteria for Purposes of Statistical Inference Part I». Biometrika. 20A (1–2): 175–240. doi:10.1093/biomet/20a.1-2.175. ISSN 0006-3444.
- ^ C.I.K.F. (July 1951). «Probability Theory for Statistical Methods. By F. N. David. [Pp. ix + 230. Cambridge University Press. 1949. Price 155.]». Journal of the Staple Inn Actuarial Society. 10 (3): 243–244. doi:10.1017/s0020269x00004564. ISSN 0020-269X.
- ^ Note that the subscript in the expression H0 is a zero (indicating null), and is not an «O» (indicating original).
- ^ Neyman, J.; Pearson, E. S. (30 October 1933). «The testing of statistical hypotheses in relation to probabilities a priori». Mathematical Proceedings of the Cambridge Philosophical Society. 29 (4): 492–510. Bibcode:1933PCPS…29..492N. doi:10.1017/s030500410001152x. ISSN 0305-0041. S2CID 119855116.
- ^ Fisher, R.A. (1966). The design of experiments. 8th edition. Hafner:Edinburgh.
Bibliography[edit]
- Betz, M.A. & Gabriel, K.R., «Type IV Errors and Analysis of Simple Effects», Journal of Educational Statistics, Vol.3, No.2, (Summer 1978), pp. 121–144.
- David, F.N., «A Power Function for Tests of Randomness in a Sequence of Alternatives», Biometrika, Vol.34, Nos.3/4, (December 1947), pp. 335–339.
- Fisher, R.A., The Design of Experiments, Oliver & Boyd (Edinburgh), 1935.
- Gambrill, W., «False Positives on Newborns’ Disease Tests Worry Parents», Health Day, (5 June 2006). [1] Archived 17 May 2018 at the Wayback Machine
- Kaiser, H.F., «Directional Statistical Decisions», Psychological Review, Vol.67, No.3, (May 1960), pp. 160–167.
- Kimball, A.W., «Errors of the Third Kind in Statistical Consulting», Journal of the American Statistical Association, Vol.52, No.278, (June 1957), pp. 133–142.
- Lubin, A., «The Interpretation of Significant Interaction», Educational and Psychological Measurement, Vol.21, No.4, (Winter 1961), pp. 807–817.
- Marascuilo, L.A. & Levin, J.R., «Appropriate Post Hoc Comparisons for Interaction and nested Hypotheses in Analysis of Variance Designs: The Elimination of Type-IV Errors», American Educational Research Journal, Vol.7., No.3, (May 1970), pp. 397–421.
- Mitroff, I.I. & Featheringham, T.R., «On Systemic Problem Solving and the Error of the Third Kind», Behavioral Science, Vol.19, No.6, (November 1974), pp. 383–393.
- Mosteller, F., «A k-Sample Slippage Test for an Extreme Population», The Annals of Mathematical Statistics, Vol.19, No.1, (March 1948), pp. 58–65.
- Moulton, R.T., «Network Security», Datamation, Vol.29, No.7, (July 1983), pp. 121–127.
- Raiffa, H., Decision Analysis: Introductory Lectures on Choices Under Uncertainty, Addison–Wesley, (Reading), 1968.
External links[edit]
- Bias and Confounding – presentation by Nigel Paneth, Graduate School of Public Health, University of Pittsburgh