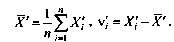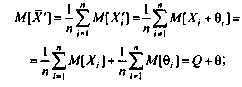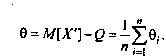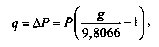Качество измерения характеризующее величину случайных ошибок - TopOshibok.ru - решение и исправление самых разных ошибок

Оценка эффективности методов измерения

вмедицинской диагностике.

•Для оценки эффективности методов измерения в медицинской диагностике, как и в других разделах медицины и биологии, применяют ряд критериев, главными из которых являются:

•точность измерения (accuracy) — соответствие результатов измерения истинному значению определяемой величины. Высокая точность измерения достигается при минимальных рандомизированных

исистематических погрешностях;

•правильность измерения (correctness). Это качество измерения характеризует величину систематических погрешностей. Чем они меньше, тем более правильным оказывается измерение;

Оценка эффективности методов измерения

вмедицинской диагностике.

•сходимость измерений (precision). Данное качество измерений характеризует величину случайных ошибок. Чем они меньше, тем лучше сходимость измерений. Этот критерий показывает, насколько близки друг к другу измерения, выполненные в одинаковых условиях, т.е. в одной и той же лаборатории и на одном и том же приборе;

•воспроизводимость измерений (reliability). Этот критерий показывает, насколько близки между собой результаты измерений, выполненных в различных условиях, т.е. в разных лабораториях и на разных аппаратах. Поэтому в медицинской диагностике существует незыблемое правило — иметь собственный «внутренний» стандарт оценки результатов исследования, естественно с учетом всех имеющихся внешних данных.

Критерии успешности выполнения диагностического исследования.

Ведущими критериями успешности выполнения любого диагностического исследования являются его

1.результативность, 2.действенность (сила),

3.эффективность диагностического метода, 4.доступность диагностического метода.

•.Результативность диагностики (effective, effectiveness) — вероятность

получения успешного результата у индивидуума или популяции в целом в результате осуществления данной технологии в усредненных условиях

ее выполнения.

•.Другими словами, результативность — это следствие того, что делаются

нужные, правильные вещи ( англ. doing the right things).

Критерии успешности выполнения диагностического исследования.

•Эффективность диагностики (efficient, efficiency) — мастерство, с которым используются ресурсы для решения данной проблемы, в частности эффективной считается диагностика, при которой наибольшее число истинно положительных и истинно отрицательных результатов получается при минимальных затратах (финансов, времени, ресурсов).

•Эффективность — это следствие того, что правильно делаются эти самые нужные вещи (англ. doing the things right).

•Реальная эффективность – определяется при использовании данного метода в обычных (усредненных) условиях его применения. Понятно, что эффективность всегда будет ниже, чем сила метода.

•Отметим, что подавляющее большинство врачей работает именно на уровне эффективности процедуры, а фирмы, производящие медицинское оборудование, указывают в рекламных целях его силу..

Критерии успешности выполнения диагностического исследования.

•Действенность (сила) диагностики (efficacy) — это способность диагностического теста, примененного в оптимальных условиях, влиять на решение врача относительно диагностики заболевания и ведения больного (лечения, реабилитации), т.е. влиять на здоровье, как индивидуума, так и населения в целом.

•Термин «сила метода» медицинской диагностики, таким образом, определяет меру успеха данного диагностического теста в идеальных условиях. Этот показатель иногда называют также внутренней оценкой метода исследования, или идеальной эффективностью метода диагностики.

•Понятно, что результативность метода всегда будет ниже, чем его сила, поскольку она зависит от мастерства специалиста, обеспечивающего получение диагностического изображения, а также потому, что инфраструктура в усредненных условиях отнюдь не соответствует таковой в оптимальных условиях.

Требования к организации прав доступа

кэлектронной персональной медицинской записи

иэлектронным медицинским архивам

Права доступа сотрудников могут быть:

—персональными, то есть предоставленными сотруднику лично;

—должностными, то есть предоставленными сотруднику в соответствии с занимаемой им должностью (лечащий врач, зав. отделением и др.);

—ситуационными (ролевыми), то есть отвечающими той ситуации (роли), в которой сотрудник исполняет свои обязанности (например, дежурный врач на время дежурства должен иметь больше прав, чем врач отделения; врач-консультант только при проведении консультации или врач-лаборант при выполнении исследования может получать полный доступ ко всем ЭПМЗ пациента);

—административными, то есть расширенными правами доступа, предоставленными специальному персоналу, осуществляющему администрирование медицинских архивов и ЭПМЗ, обеспечивающему безопасность и разрешение нештатных ситуаций.

Права доступа могут распространяться на отдельные типы записей или записи, относящиеся к определенным пациентам.

Вопросы

•Дайте определение АРМ медицинского работника.

•Перечислите три типа АРМ медицинского работника

•Перечислите 5 основных требований к аппаратно- программному комплексу АРМ медицинского работника

•Перечислите 6 стандартных медицинских документов, подлежащих обязательному переводу в электронный вид.

На сегодня все…

Благодарю за внимание !!!

Соседние файлы в папке Лекция

Источник

ОЦЕНКА СЛУЧАЙНЫХ ПОГРЕШНОСТЕЙ

Глава 2

ПОГРЕШНОСТИ ИЗМЕРЕНИЙ

§ 1. ПОГРЕШНОСТЬ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
И ИСТОЧНИКИ ЕЕ ПОЯВЛЕНИЯ

Процесс познания окружающего нас материального мира, происходящих в нем процессов и явлений осуществляется с помощью определения количественных значений характеризующих их физических величин. Познавая окружающий нас мир, физические предметы и явления, мы стремимся определить истинное значение характеризующих их физических величин. Однако абсолютно точно определить, измерить их значение невозможно. Наше познание будет с той или иной степенью точности приближаться к истинному значению. Точность измерения истинных значений физических величин зависит от метода измерения, от технических средств, с помощью которых проводятся измерения, от условий проведения измерений и от свойств органов чувств наблюдателя. Таким образом, результат измерения складывается из двух величин: истинного значения величины и погрешности ее измерения. Но, как мы уже отмечали, даже пользуясь самыми точными измерительными средствами, выполняя измерения самым тщательным образом, мы все равно не получим истинного значения физической величины. Поэтому при определении погрешности пользуются не истинным, а действительным значением величины.

Согласно ГОСТ 16263-70 под действительным значением физической величины следует понимать такое ее значение, которое найдено экспериментальным путем и настолько приближается к истинному значению, Что для данной цели может быть использовано вместо него. Отклонение результата от действительного значения измеряемой величины называется погрешностью измерения

Следовательно, результат всякого измерения является функцией двух величин: действительной величины и погрешности измерения.

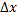
Если действительную величину обозначить а погрешность ее измерения , то результат определиться равенством

(2.1)

откуда

(2.2)

т. е. погрешность представляет собой разность между результатом измерения и действительным значением физической величины.

Так, если измеренный диаметр вала равен а действительное значение диаметра то погрешность измерения

Чтобы определить действительное значение измеряемой величины, необходимо согласно (2.1) из результата вычесть погрешность

т. е. внести поправку в приближенное значение измеряемой величины

Если поправку обозначить через то получим

(2.3)

или

(2.4)

Следовательно, поправка представляет собой погрешность, взятую с обратным знаком. В нашем примере поправка и действительное значение измеряемой величины мм.

Несмотря на огромное количество причин возникновения погрешностей измерении, их можно объединить в следующие группы: методические, инструментальные и субъективные

Методические погрешности являются следствием неточности метода измерения или расчетной формулы, положенной в основу создания прибора. Методические погрешности могут быть также обусловлены тем, что принципиальная схема прибора не обеспечивает точного воспроизведения функциональной зависимости, связывающей измеряемую величину с той, на которую в действительности реагирует чувствительный элемент.

В качестве примера можно привести попытки создания прибора для определения количества воды в нефти (влагомера) по изменению диэлектрической проницаемости. Действительно, диэлектрическая проницаемость воды существенно отличается от диэлектрической проницаемости нефти и изменение количества воды в водонефтяной эмульсии приводит к изменению суммарной диэлектрической проницаемости последней. Однако диэлектрическая проницаемость самой нефти для различных ее сортов различна и несколько изменяется с изменением температуры и количества растворенного в нефти газа. Результаты измерения количества воды в нефти влагомерами, не учитывающими влияния отмеченных факторов, содержали погрешность.

Инструментальные погрешности являются следствием недостатка конструкции прибора, несоблюдения технологии его изготовления, неточности изготовления деталей прибора, недостатков регулировки и сборки прибора, а также следствием его износа или старения. Инструментальные погрешности делят на следующие основные группы: шкаловые погрешности, погрешности трения, погрешности, вызванные наличием зазоров, погрешности остаточной деформации (гистерезиса).

Шкаловые погрешности возникают вследствие смещения шкалы, эксцентриситета круглой шкалы, неточной ее градуировки (если шкала градуируется индивидуально для каждого прибора), неточности установки стрелки при сборке прибора.

Погрешности, вызываемые трением, обусловлены силами (моментами) трения, возникающими в опорах и подвижных соединениях. Силы трения всегда направлены против движения подвижных частей прибора. Поэтому при возрастании измеряемой величины прибор дает заниженные показания, а при убывании — завышенные. Погрешность трения определяют при испытаниях прибора путем сравнения его показаний до и после постукивания по прибору. При этом стрелка прибора смещается на величину, характеризующую погрешность трения.

Погрешности, вызываемые наличием зазоров, возникают в случаях, когда зазоры в опорах и подвижных соединениях не выбираются пружинами. Эти погрешности при статических измерениях могут проявляться в виде непостоянства показаний прибора. Для устранения этих погрешностей зазоры по возможности уменьшают и применяют пружины, выбирающие зазоры.

Погрешности остаточной деформации упругих элементов проявляются в том, что подвижная система не возвращается в исходное положение после прекращения действия измеряемой величины или значения одной и той же измеряемой величины не совпадают при отсчетах, когда измеряемая величина возрастает и убывает. Такие погрешности называют гистерезисом. Для уменьшения погрешности остаточной деформации упругие элементы выполняют из специальных сплавов. При изготовлении упругих элементов необходимо строго соблюдать технологию термической обработки. Но и при этом полностью устранить погрешность остаточной деформации не удается. Поэтому остаточные деформации относят к погрешностям, величина которых устанавливается нормами на так называемое допустимое расхождение в показаниях прибора, а также на невозвращение стрелки к нулю шкалы после снятия нагрузки.

Инструментальные погрешности определяются экспериментально и заносятся в паспорт прибора. Однако определенные однажды, они не остаются неизменными в течение всего срока эксплуатации прибора. Шкаловые погрешности могут изменяться от смещения стрелок. Погрешности трения могут возрасти от засорения механизма прибора пылью, из-за коррозии деталей, нарушения нормальной смазки и т. д. Погрешности остаточной деформации (гестерезис) могут возрасти при работе прибора вблизи крайних точек шкалы. Таким образом, инструментальные погрешности не являются величиной постоянной. Поэтому, чтобы быть уверенным в том, что инструментальные погрешности находятся в допустимых пределах, необходимо периодически поверять приборы, т. е. сравнивать показания рабочих приборов с образцовыми. Такую поверку прибора следует выполнять перед использованием приборов даже в тех случаях, если прибор в течение длительного времени не эксплуатировался.

Субъективные погрешности — это такие погрешности, которые связаны с индивидуальными качествами наблюдателя (исследователя, оператора). Эти погрешности зависят от индивидуальной оценки показаний прибора тем или иным наблюдателем, от опытности его, от положения наблюдателя относительно прибора. По причинам появления погрешности можно разделить на систематические, случайные и грубые.

Систематические погрешности — это погрешности измерения, остающиеся постоянными или закономерно изменяющимися при повторных измерениях одной и той же величины. К систематическим погрешностям относятся: инструментальные, погрешности установки, являющиеся следствием неправильной установки прибора (не по отвесу или уровню), методические. Систематические погрешности можно изучить и определить влияние их на результат измерения, а также устранить. Но даже если все систематические погрешности учтены, т. е. вычислены и введены все поправки, то и в этом случае результаты измерения все же не свободны от случайных погрешностей.

Случайными погрешностями называют погрешности, изменяющиеся случайным образом при повторных измерениях одной и той же величины. Они обнаруживаются при повторных измерениях, выполненных с одинаковой тщательностью. Эти погрешности следуют законам, которые выводятся в теории вероятностей по отношению к случайным величинам. Закономерность случайных погрешностей обнаруживается путем анализа и сравнения большого ряда измерений. Источниками случайных погрешностей являются различные неконтролируемые условия. Случайная погрешность зависит от точости измерительных приборов и тщательности выполнения измерений. Чем выше точность измерения, тем больше учитываются и исключаются факторы, неблагоприятно влияющие на результат измерения; чем тщательнее проводится измерение, тем меньше величина случайной погрешности. Но как бы тщательно измерения ни проводились, какими бы точными приборами для измерений ни пользовались, избежать случайных погрешностей невозможно.

Однако случайные погрешности можно оценить, влияние их на результат измерения свести к минимуму с помощью математических приемов, выработанных теорией вероятностей.

Грубыми погрешностями называют погрешности, явно превышающие по своему значению погрешности, оправданные условиями эксперимента. Причинами грубых погрешностей являются непредусмотренные изменения условий эксперимента, например внезапное изменение напряжения в сети электропитания. К грубым погрешностям (промахам) относят погрешности, зависящие от наблюдателя и связанные с неправильным обращением со средствами измерений, неверным отсчетом показаний или ошибками при записи результатов. Грубые погрешности определяются специальными математическими методами (см. § 4, гл. 2). Наблюдения, содержащие грубые погрешности (промахи), должны быть исключены из дальнейшего рассмотрения.

ОЦЕНКА СЛУЧАЙНЫХ ПОГРЕШНОСТЕЙ

Процесс измерения представляет собой физический эксперимент, при многократном выполнении которого в одних и тех же условиях одними и теми же измерительными средствами и одним и тем же оператором мы получаем результаты, несколько отличающиеся друг от друга и, конечно, от действительного значения измеряемой величины. Получающиеся при этом погрешности носят случайный характер. Закономерности, присущие случайным явлениям и случайным событиям, рассматриваются теорией вероятностей.

Случайные погрешности в большинстве случаев подчинены следующим условиям:

1) равные по абсолютной величине и обратные по знаку погрешности равновероятны;

2) малые по абсолютной величине погрешности более вероятны, нежели большие;

3) вероятность появления погрешностей, превосходящих по величине некоторое определенное число, практически равна нулю (это число обычно называют пределом возможных погрешностей и обозначают Е).

Эти условия позволяют применить для их описания нормальный закон распределения.

Пусть — функция распределения погрешностей, т. е. вероятность того, что погрешность не превосходит величины :

(2.5)

Полагая, что погрешности представляют непрерывную случайную величину, можно определить вероятность того, что погрешность примет значение, заключенное между и с точностью до малых более высокого порядка, чем , т.е.

(2.6)

где — плотность распределения погрешностей.

Функция обладает следующими свойствами.

1. Функция — четная, т. е. . Это следует из того, что равные отклонения в обе стороны одинаково вероятны и поэтому плотности распределения вероятности в точках и равны между собой.

2. Функция при возрастании убывает, так как малые по абсолютной величине погрешности более вероятны, чем большие.

3. Функция при .

Итак, графиком функции _(рис. 2.1) будет непрерывная линия, симметричная относительно оси Оу, имеющая максимум при и случайных величин монотонно убывающая по обе стороны от нуля. При график асимптотически приближается к оси абсцисс. Вероятность того, что погрешность находится в некоторых определенных пределах определить по формуле

(2.7)

Известно, что

Пусть действительное значение измеряемой величины равно Измеренное значение и величины х есть величина случайная, закон распределения которой тесно связан с законом распределения погрешностей. Действительно, поскольку , то вероятность получения в результате измерения ԑ и значения x одна и та же. Если обозначить плотность вероятности величины x через , то . В силу четности функции получим . Это показывает, что графики функций и сдвинуты друг относительно друга на величину Q.Функция имеет максимум при , а функция — при . Из теории вероятности известно, что для нормального закона распределения наиболее вероятным значением искомой величины является среднее арифметическое полученных значений.

(2.8)

где х₁ х₂, …, х_п — значения, полученные при измерении величины X.

Если вычесть среднее значение из измеренных величин получим — называемые к остаточными погрешностями, которые могут быть положительными и отрицательными.

Согласно свойству среднего арифметического при отсутствии погрешностей вычисления должно соблюдаться условие

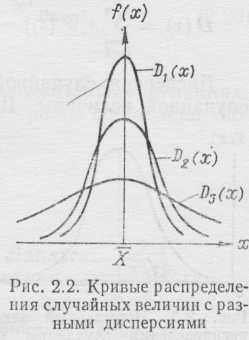
Функция представляет собой закон распределения случайных величин. Однако для практических целей иногда нет необходимости случайные величины характеризовать функцией распределения. Для практических целей оценки погрешностей измерений достаточно указать отдельные так называемые числовые характеристики, определяющие существенные черты распределения случайной величины: среднее значение, около которого группируются возможные значения случайной величины и число, характеризующее степень разбросанности этих значений относительно среднего. Средним значением случайной величины будет математическое ожидание. Если взять случайную величину х, имеющую возможные дискретные значения х₁ х₂, …, х_п с вероятностями Р₁, Р₂, …, Р_п, то при п, стремящемся к бесконечности, среднее арифметическое будет некоторая величина М (х), называемая математическим о ж и д а н и ем

(2.9)

Но из теории вероятности известно, что сумма вероятностей всех возможных значений случайной величины равна единице,

Следовательно,

(2.10)

т. е. математическим ожиданием дискретных значений случайной величины, называется сумма произведений всех возможных значений случайной величины на вероятности этих значений.

Для непрерывных случайных величин с плотностью вероятности математическим ожиданием будет

(2.11)

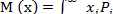
При определении центра группирования эмпирического распределения случайных величин, полученных в результате измерений погрешностей, мы получим величину

(2.12)

где – число полученных значений величины общее число наблюдений.

Выражение (2.12) можно записать в виде

, (2.13)

где —частость, представляющая отношение количества событий, полученного данного результата наблюдений, к общему количеству наблюдений.

Можно считать, что при , следовательно,

, (2.14)

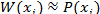
т. е. мы пришли к выводу, что математическое ожидание приблизительно равно среднему арифметическому наблюденных значений.

Точность равенства (2.14) повышается с увеличением числа наблюдений N.

Основными числовыми характеристиками рассеивания случайной величины относительно центра группирования являются дисперсия н среднее квадратическое отклонение.

Дисперсия D(x) служит мерой рассеивания (разбросанности) значений случайной величины х около центра группирования.

На рис. 2.2 изображены кривые распределения случайных величин одного типа с одним центром группирования , но с разными дисперсиями

Дисперсия вычисляется по следующим формулам: для дискретных величин

(2.15)

для непрерывной величин

(2.16)

При вычислении дисперсии распределения случайных величин, полученных в результате опыта, можно заменить математическое ожидание средним арифметическим и вероятности Р(х) — частостями W(х). Тогда дисперсия эмпирического распределения может быть вычислена по формуле

(2.17)

Дисперсия случайной величины имеет размерность квадрата случайной величины. Для наглядности характеристики рассеи наглядности характеристики рассеивания удобней пользоваться величиной, размерность которой совпадает с размерностью случайной величины. Поэтому в качестве меры рассеивания значений случайной величины х чаще всего применяется среднее квадратическое отклонение случайной величины х от центра группирования

(2.18)

Среднее квадратическое отклонение имеет ту же размерность, что и случайная величина, мерой рассеивания которой она является. Величина а является числовой характеристикой качества совокупности измерений, для которых она задана или вычислена. Чем больше а, тем хуже качество измерений. Если случайные погрешности в соответствии с принятыми условиями распределены по нормальному закону, математическое выражение распределения погрешностей имеет вид

(2.19)

где — дисперсия измерений; — центр рассеивания.

Кривая распределения по нормальному закону показана на рис. 2.3. Как видно, кривая симметрична относительно ординаты, соответствующей центру группирования . Ордината, соответствующая центру группирования , имеет максимальное значение

В том случае, _когда центр группирования совпадает с началом координат, т. е. 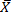= 0, выражение для закона нормального распределения примет вид

Вероятность того, что случайная величина х лежит в пределах от а до b, в этом случае определится равенством

(2.20)

Выражение не интегрируется в элементарных функциях.

Поэтому для вычисления искомых интегралов составлена таблица значений функции

Функция Ф (z) называется функцией Лапласа.

Пользуясь табличными значениями функций, можно найти значение интеграла (2.21).

Для этого необходимо выразить все величины в долях , . Тогда равенство (2.20) запишется так:

(2.22)

Равенство (2.22) позволяет найти интересующие нас вероятности. Значения функции Лапласа Ф (z) приведены в приложении I.

Пример 1. Случайная величина X, распределенная по нормальному закону, представляет собой погрешность измерения ординаты на диаграмме глубинного манометра. При измерении допускается систематическая погрешность в сторону завышения 0,4 мм. Среднее квадратическое отклонение погрешности измерения равно 0,2 мм. Найти вероятности того, что отклонение измеренного значения от истинного не превзойдет по абсолютной величине 0,5 мм.

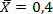
Погрешность измерения представляет собой случайную величину , подчиненную нормальному закону с параметрами и . Нужно найти вероятность попадания этой величины на участок от а = —0,5 до b = +0,5: ; .

По приложению находим Ф (z₁) = — 0,4999, Ф (z₂)=0, 1915.

По формуле (2.22) .

Источник

Качество измерений характеризуется точностью, достоверностью, правильностью, сходимостью, воспроизводимостью и погрешностью измерений.

Точность – это качество измерений, отражающее близость их результатов к истинному значению измеряемой величины. Высокая точность измерений соответсвует малым погрешностям как систематическим, так и случайным. Точность количественно оценивают обратной величиной модуля относительной погрешности. Напремер, если погрешность измерений равна 0,05%, то точность будет равна 1/0,0005 = 2000.

Достоверность измерений характеризует степень доверия к результатам измерений. Достоверность оценки погрешностей определяют на основе законов теории вероятностей и математической статистики. Это дает возможность для каждого конкретного случая выбирать средства и методы измерений, обеспечивающие получение результата, погрешности которого не превышают заданных границ.

Правильность измерений – качество измерений, отражающее близость к нулю систематических погрешностей в результатах измерений.

Сходимость – качество измерений, отражающее близость друг к другу результатов измерений, выполняемых в одинаковых условиях. Сходимость измерений отражает влияние случайных погрешностей.

Воспроизводимость – это такое качество измерений, которое отражает близость друг к другу результатов измерений, выполняемых в различных условиях (в различное время, в различных местах, разными методами и средствами).

Погрешность измерения – отклонение результата измерения от истинного (действительного) значения измеряемой величины. Погрешность измерений представляет собой сумму ряда составляющих, каждая из которых имеет свою причину. Можно выделить слудующие группы причин возникновения погрешностей:

неверная настройка средства измерений или смещение уровня настройки во время эксплуатации;
неверная установка объекта измерения на измерительную позицию;
ошибки в процессе получения, преобразования и выдачи информации в измерительной цепи средства измерений;
внешние воздействия на средство и объект измерений (изменение температуры и давления, влияние электрического и магнитного полей, вибрация и т.п.);
свойства измеряемого объекта;
квалификация и состояние оператора.

Анализируя причины возникновения погрешностей, необходимо в первую очередь выявить те из них, которые оказывают существенное влияние на резульат измерения. Анализ должен проводится в определенной последовательности.

Источник

неверная настройка средства измерений или смещение уровня настройки во время эксплуатации;
неверная установка объекта измерения на измерительную позицию;
ошибки в процессе получения, преобразования и выдачи информации в измерительной цепи средства измерений;
внешние воздействия на средство и объект измерений (изменение температуры и давления, влияние электрического и магнитного полей, вибрация и т.п.);
свойства измеряемого объекта;
квалификация и состояние оператора.

Правильность измерений – это близость среднего арифметического бесконечно большого числа повторно измеренных значений величины к опорному значению величины. Правильность измерений не является величиной и поэтому не может быть выражена численно, однако соответствующие показатели приведены в ISO 5725.

Правильность — степень близости результата измерений к истинному или условно истинному (действительному) значению измеряемой величины или — в случае отсутствия эталона измеряемой величины — степень близости среднего значения, полученного на основании серии результатов измерений, к принятому опорному значению.

Термин ‘ правильность ‘ характеризует степень близости среднего арифметического значения большого числа результатов измерений к истинному или принятому опорному значению, термин ‘прецизионность’ — степень близости результатов измерений друг к другу.

Под качеством измерений понимают совокупность свойств, обусловливающих получение результатов с требуемыми точностными характеристиками, в необходимом виде и в установленные сроки. Качество измерений характеризуется такими показателями, как точность, правильность и достоверность.

ТОЧНОСТЬ ИЗМЕРЕНИЙ ТОЧНОСТЬ ИЗМЕРЕНИЙ характеристика качества измерений, отражающая степень близости результатов измерений к истинному значению измеряемой величины. Чем меньше результат измерения отклоняется от истинного значения величины, т.е. чем меньше его погрешность, тем выше Т.и., независимо от того, является ли погрешность систематической, случайной или содержит ту и другую составляющие (см.

Физический энциклопедический словарь. — М.: Советская энциклопедия, Главный редактор А.М. Прохоров,1983,

Результаты измерения записывают в виде A = a ± Δ a, где A — измеряемая величина, a — средний результат полученных измерений, Δ a — абсолютная погрешность измерений.

точность анализа — analizės tikslumas statusas T sritis Standartizacija ir metrologija apibrėžtis Analizės charakteristika, apibūdinama visų rūšių paklaidų artumu nuliui. atitikmenys: angl. precision of analysis vok. Analyse Genauigkeit, f rus. точность анализа, f Penkiakalbis aiškinamasis metrologijos terminų žodynas точность анализа — analizės tikslumas statusas T sritis fizika atitikmenys: angl. precision of analysis vok. Analyse Genauigkeit, f rus. точность анализа, f pranc. précision de l’analyse, f Fizikos terminų žodynas Точность анализа химического — характеристика результатов качественного анализа (См. Качественный анализ) и количественного анализа (См. Количественный анализ), отражающая влияние на них случайных ошибок метода определения. Точность химических определений зависит от Большая советская энциклопедия Точность (в автоматич. управлении) — Точность системы автоматического управления, одна из важнейших характеристик систем автоматического управления (САУ), определяющая степень приближения реального управляемого процесса (УП) к требуемому. Отклонение УП от требуемого вызывается Большая советская энциклопедия точность фактов — (напр. представленных для анализа аварии на АЭС) Тематики энергетика в целом EN factual accuracy Справочник технического переводчика точность — 3.1.1 точность (accuracy): Степень близости результата измерений к принятому опорному значению. Примечание Термин «точность», когда он относится к серии результатов измерений, включает сочетание случайных составляющих и общей систематической Словарь-справочник терминов нормативно-технической документации Точность — I Точность системы автоматического управления, одна из важнейших характеристик систем автоматического управления (См. Автоматическое управление) (САУ), определяющая степень приближения реального управляемого процесса (УП) к требуемому. Большая советская энциклопедия РМГ 61-2003: Государственная система обеспечения единства измерений. Показатели точности, правильности, прецизионности методик количественного химического анализа. Методы оценки — Терминология РМГ 61 2003: Государственная система обеспечения единства измерений. Показатели точности, правильности, прецизионности методик количественного химического анализа. Методы оценки: 3.12 внутрилабораторная прецизионность: Прецизионность Словарь-справочник терминов нормативно-технической документации РАДИОИНДИКАТОРНЫЕ МЕТОДЫ АНАЛИЗА — (РМА), методы качеств. и количеств. хим. анализа с использованием радионуклидов. Последние могут содержаться в исходном анализируемом в ве (напр., прир. радионуклиды таких элементов, как К, Th, U и др.), м.б. введены на определенном этапе Химическая энциклопедия нормы характеристик погрешности анализа; нормы погрешности — 3.23 нормы характеристик погрешности анализа; нормы погрешности: Значения характеристики погрешности результатов анализа, задаваемые в качестве требуемых или допускаемых. Примечание Нормы погрешности характеризуют требуемую точность анализа.

Каким образом обеспечивается качество результатов измерений?

Правильность результата измерения обеспечивается совпадением среднего значения измерений со значением измеряемой величины. Значение Х — величина случайная, поправка не является случайной, она характеризует относительную погрешность измерения.

Какая бывает погрешность измерений?

Погрешность средств измерения и результатов измерения. Погрешности средств измерений – отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений (создающие так называемые инструментальные ошибки измерений).

Погрешность результата измерения – отклонение результата измерения от действительного (истинного) значения измеряемой величины.
Инструментальные и методические погрешности.
Методическая погрешность обусловлена несовершенством метода измерений или упрощениями, допущенными при измерениях.
Так, она возникает из-за использования приближенных формул при расчете результата или неправильной методики измерений.

Выбор ошибочной методики возможен из-за несоответствия (неадекватности) измеряемой физической величины и ее модели. Причиной методической погрешности может быть не учитываемое взаимное влияние объекта измерений и измерительных приборов или недостаточная точность такого учета.

Например, методическая погрешность возникает при измерениях падения напряжения на участке цепи с помощью вольтметра, так как из-за шунтирующего действия вольтметра измеряемое напряжение уменьшается. Механизм взаимного влияния может быть изучен, а погрешности рассчитаны и учтены. Инструментальная погрешность обусловлена несовершенством применяемых средств измерений.

Причинами ее возникновения являются неточности, допущенные при изготовлении и регулировке приборов, изменение параметров элементов конструкции и схемы вследствие старения. В высокочувствительных приборах могут сильно проявляться их внутренние шумы. Статическая и динамическая погрешности.

Статическая погрешность измерений – погрешность результата измерений, свойственная условиям статического измерения, то есть при измерении постоянных величин после завершения переходных процессов в элементах приборов и преобразователей. Статическая погрешность средства измерений возникает при измерении с его помощью постоянной величины. Если в паспорте на средства измерений указывают предельные погрешности измерений, определенные в статических условиях, то они не могут характеризовать точность его работы в динамических условиях. Динамическая погрешность измерений – погрешность результата измерений, свойственная условиям динамического измерения. Динамическая погрешность появляется при измерении переменных величин и обусловлена инерционными свойствами средств измерений. Динамической погрешностью средства измерений является разность между погрешностью средсва измерений в динамических условиях и его статической погрешностью, соответствующей значению величины в данный момент времени. При разработке или проектировании средства измерений следует учитывать, что увеличение погрешности измерений и запаздывание появления выходного сигнала связаны с изменением условий.

Статические и динамические погрешности относятся к погрешностям результата измерений. В большей части приборов статическая и динамическая погрешности оказываются связаны между собой, поскольку соотношение между этими видами погрешностей зависит от характеристик прибора и характерного времени изменения величины.

Как оценивают точность средств измерений?

1. Оценку точности измерений производят — предварительно до начала измерений путем обработки результатов специально выполненных наблюдений; — после окончания измерений путем обработки результатов наблюдений, выполненных в процессе этих измерений.2. Для оценки точности измерений используют многократные наблюдения параметра в одном из установленных сечений (мест) или двойные наблюдения параметра в разных сечениях (местах) одного или нескольких объектов измерений.

Общее число наблюдений М, необходимое для оценки точности результата измерений, составляет: для предварительной оценки — 20; для оценки точности выполненных измерений — не менее 6. Для уменьшения влияния систематических погрешностей измерения выполняют в соответствии с требованиями настоящего стандарта (ГОСТ 26433.0-85): Наблюдения производят в прямом и обратном направлениях, на разных участках шкалы отсчетного устройства, меняя установку и настройку прибора и соблюдая другие приемы, указанные в инструкции по эксплуатации на средства измерения.

При этом должны быть соблюдены условия равноточности наблюдений (выполнение наблюдений одним наблюдателем, тем же методом, с помощью одного и того же прибора и в одинаковых условиях). Перед началом наблюдений средства измерений следует выдерживать на месте измерений до выравнивания температур этих средств и окружающей среды.3. Таблица 1. Среднюю квадратическую погрешность измерения при многократных наблюдениях параметра определяют по формуле Если при измерениях используются средства и методы, для которых из специально выполненных ранее измерений или из эксплуатационной документации установлена средняя квадратическая погрешность наблюдения, то действительную погрешность измерения определяют по формуле 5. Действительную погрешность результата измерения при двойных наблюдениях параметра в одном из установленных сечений (местах) оценивают по формуле где вычисляемая величина — это абсолютное значение остаточной систематической погрешности, численное значение которой определено из обработки ряда двойных наблюдений.

Как погрешность характеризует качество измерения?

Погре́шность измере́ния — отклонение измеренного значения величины от её истинного (действительного) значения. Погрешность измерения является характеристикой точности измерения. Выяснить с абсолютной точностью истинное значение измеряемой величины, как правило, невозможно, поэтому невозможно и указать величину отклонения измеренного значения от истинного.

Это отклонение принято называть ошибкой измерения, Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов, На практике вместо истинного значения используют действительное значение величины х д, то есть значение физической величины, полученное экспериментальным путём и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него,

Такое значение обычно вычисляется как среднестатистическое значение, полученное при статистической обработке результатов серии измерений. Это полученное значение не является точным, а лишь наиболее вероятным. Поэтому при записи результатов измерений необходимо указывать их точность,

Например, запись T = 2,8 ± 0,1 с; P = 0,95 означает, что истинное значение величины T лежит в интервале от 2,7 с до 2,9 с с доверительной вероятностью 95 %.
Количественная оценка величины погрешности измерения — мера «сомнения в измеряемой величине» — приводит к такому понятию, как « неопределённость измерения ».

В то же время иногда, особенно в физике, термин «погрешность измерения» ( англ. measurement error ) используется как синоним термина «неопределённость измерения» ( англ. measurement uncertainty ),

Что отражает смещение измерений?

смещение, систематическая погрешность 3.1.11 смещение, систематическая погрешность (bias): Разность между математическим ожиданием результатов наблюдений и истинным, или (в его отсутствие) принятым опорным значением. Примечание 1 — Смещение характеризует систематическую ошибку или погрешность в противоположность случайным ошибке или погрешности.

Смещение может иметь одну или несколько составляющих. Большее систематическое отклонение от истинного или принятого опорного значения соответствует большему значению смещения. Примечание 2 — Смещение средства измерений обычно оценивают на основе среднего арифметического погрешностей в показаниях средства измерения, найденных по соответствующему количеству повторных измерений.

Погрешность показаний средства измерений — отклонение измеренного значения входной величины от ее истинного значения. Словарь-справочник терминов нормативно-технической документации, academic.ru,2015,

Что представляет собой средство измерений?

Сре́дство измере́ний — техническое средство, предназначенное для измерений, имеющее нормированные метрологические характеристики, воспроизводящее и (или) хранящее единицу физической величины, размер которой принимают неизменным (в пределах установленной погрешности) в течение известного интервала времени.

Как оценить ошибку измерений?

1.1 Результат измерения — Рассмотрим простейший пример: измерение длины стержня с помощью линейки. Линейка проградуирована производителем с помощью некоторого эталона длины — таким образом, сравнивая длину стержня с ценой деления линейки, мы выполняем косвенное сравнение с общепринятым стандартным эталоном.

Допустим, мы приложили линейку к стержню и увидели на шкале некоторый результат x = x изм, Можно ли утверждать, что x изм — это длина стержня? Во-первых, значение x не может быть задано точно, хотя бы потому, что оно обязательно округлено до некоторой значащей цифры: если линейка «обычная», то у неё есть цена деления ; а если линейка, к примеру, «лазерная» — у неё высвечивается конечное число значащих цифр на дисплее.

Во-вторых, мы никак не можем быть уверенны, что длина стержня на самом деле такова хотя бы с точностью до ошибки округления. Действительно, мы могли приложить линейку не вполне ровно; сама линейка могла быть изготовлена не вполне точно; стержень может быть не идеально цилиндрическим и т.п.

И, наконец, если пытаться хотя бы гипотетически переходить к бесконечной точности измерения, теряет смысл само понятие «длины стержня». Ведь на масштабах атомов у стержня нет чётких границ, а значит говорить о его геометрических размерах в таком случае крайне затруднительно! Итак, из нашего примера видно, что никакое физическое измерение не может быть произведено абсолютно точно, то есть у любого измерения есть погрешность,

Замечание. Также используют эквивалентный термин ошибка измерения (от англ. error). Подчеркнём, что смысл этого термина отличается от общеупотребительного бытового: если физик говорит «в измерении есть ошибка», — это не означает, что оно неправильно и его надо переделать.

Имеется ввиду лишь, что это измерение неточно, то есть имеет погрешность, Количественно погрешность можно было бы определить как разность между измеренным и «истинным» значением длины стержня: δ ⁢ x = x изм — x ист, Однако на практике такое определение использовать нельзя: во-первых, из-за неизбежного наличия погрешностей «истинное» значение измерить невозможно, и во-вторых, само «истинное» значение может отличаться в разных измерениях (например, стержень неровный или изогнутый, его торцы дрожат из-за тепловых флуктуаций и т.д.).

Поэтому говорят обычно об оценке погрешности. Об измеренной величине также часто говорят как об оценке, подчеркивая, что эта величина не точна и зависит не только от физических свойств исследуемого объекта, но и от процедуры измерения. Замечание. Термин оценка имеет и более формальное значение.

Чем отличается погрешность от точности?

Погрешность и точность — Часто понятия погрешность и точность рассматриваются как синонимы. Однако, эти термины имеют совершенно различные значения. Погрешность показывает, насколько близко измеренное значение к его реальной величине, то есть отклонение между измеренным и фактическим значением.

Точность относится к случайному разбросу измеряемых величин. Когда мы проводим некоторое число измерений до момента стабилизации напряжения или же какого-то другого параметра, то в измеренных значениях будет наблюдаться некоторая вариация. Это вызвано тепловым шумом в измерительной цепи измерительного оборудования и измерительной установки.

Ниже, на левом графике показаны эти изменения. Определения неопределенностей. Слева — серия измерений. Справа — значения в виде гистограммы.

Какой показатель является мерой точности измерения?

Погрешность измерения — Оценка отклонения измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения. Поскольку выяснить с абсолютной точностью истинное значение любой величины невозможно, то невозможно и указать величину отклонения измеренного значения от истинного.

Это отклонение принято называть ошибкой измерения. В ряде источников, например, в Большой советской энциклопедии, термины ошибка измерения и погрешность измерения используются как синонимы, но согласно РМГ 29-99 термин ошибка измерения не рекомендуется применять как менее удачный). Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов,

На практике вместо истинного значения используют действительное значение величины х д, то есть значение физической величины, полученное экспериментальным путём и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него,

Такое значение, обычно, вычисляется как среднестатистическое значение, полученное при статистической обработке результатов серии измерений.
Это полученное значение не является точным, а лишь наиболее вероятным.
Поэтому в измерениях необходимо указывать, какова их точность,
Для этого вместе с полученным результатом указывается погрешность измерений.

Например, запись T=2,8±0,1 c. означает, что истинное значение величины T лежит в интервале от 2,7 с. до 2,9 с. с некоторой оговорённой вероятностью (см. доверительный интервал, доверительная вероятность, стандартная ошибка ).

Что такое достоверность результатов измерений?

В нормативных документах по метрологии термин » достоверность измерений » встречается часто, но официально утвержденного определения данному термину не дано. Принято считать, что достоверность измерений — это характеристика, определяющая степень доверия к полученным результатам измерений.

Согласно приведенному определению достоверность может иметь какую либо величину (степень), которая во первых, должна быть оценена на достаточность степени достоверности, во вторых — должны быть разарботаны методики проведения оценки достоверности результатов измерений. Федеральный закон 102-ФЗ от 26.06.2008 г.

«Об обеспечении единства измерений» содержит следующие положения относительно достоверности измерений:

ст.1 п.1 «Целями настоящего федерального закона является:,2) защита прав и законных интересов граждан, общества и государства от отрицательных последствий недостоверных результатов измерений»; 3) обеспечение потребности граждан, общества и государства в получении объективных, достоверных и сопоставимых результатов измерений,»;
ст.2 п.24 «технические требования к средствам измерений — требования, которые определяют особенности конструкции средств измерений (без ограничения их технического совершенствования) в целях сохранения их метрологических характеристик в процессе эксплуатации средств измерений, достижения достоверности результата измерений, предотвращения несанкционированных настройки и вмешательства, а также требования, обеспечивающие безопасность и электромагнитную совместимость средств измерений».

Таким образом, обеспечение достоверности измерений является одной из целей закона «Об обеспечении единства измерений». Процесс обеспечения достоверности измерений требует комплексного подхода, при котором будет обеспечено выполнение всех необходимых для достижения достоверности требований, а именно:

требования к измерениям: — измерения должны проводиться по аттестованным методикам; — применяемые средства измерений должны быть утвержденного типа; — применяемые средства измерений должны подтвердить установленные для них метрологические характеристики (быть поверены); — результаты измерений должны быть выражены в единицах, допущенных к применению в Российской Федерации.

Кроме этого, РМГ 29-2013 содержат следующее определение термина «измерение (величины)»:

«процесс эеспериментального получения одного или более значений величины, которые могут быть обоснованно приписаны величине».

Следовательно результат измерений можно считать достоверным только в случае наличия объективных данных, подтверждающих обоснованность присвоения полученного результата измерений. Основываясь на изложенных выше данных можно сделать следующие выводы:

Достоверность измерений является целью и итогом комплекса действий, включающего в себя методы, средства и способы достижения поставленных целей.
Согласно действующему законодательству предполагается, что при выполнении установленных норм и правил результаты измерений будут достоверными.
Границы погрешности, приписанные результату измерений, не являются параметром, характеризующим его достоверность, но отсутствие сведений о приписанных методике или средству измерений границах погрешности не позволит подтвердить факт достоверности полученных результатов измерений и соответственно достоверности выводов, сделанных на основании результатов измерения.

Что является результатом измерений?

Результат измерения физической величины — значение величины, полученное путем ее измерения – установленное значение величины, характеризующей свойство физического объекта, представляемое действительным числом с принятой размерностью (размерность определяется выбранной единицей измерений );

В чем заключается обработка результатов измерений?

Статистическая обработка результатов измерений – обработка измерительной информации с целью получения достоверных данных. Разнообразие задач, решаемых с помощью измерений, определяет и разнообразие видов статистической обработки их результатов.

Что такое исправленный ряд результатов измерений?

Исправленный результат измерения (англ. corrected result) – полученное при измерении значение величины и уточненное путем введения в него необходимых поправок на действие систематических погрешностей. Сходимость результатов измерений (англ.

Что такое качество измерений? Это способность передать эмпирическую систему отношений числами. Видим (пусть субъективно), Иванов работает лучше Петрова, а это значит, что и зарплата у него должна быть больше. Всё понятно, но как же сложно… Например, в компаниях используется маркетинговая информация. Качество, то есть надёжность и достоверность маркетинговой информации, определить весьма не просто. Ещё большее значение качество играет при измерении показателей компании. Ведь плохое качество измерения показателя дискредитирует всю систему показателей компании. В этой части статьи мы обсудим, от чего зависит надёжность и достоверность измерений.

Незнание теории не освобождает от ответственности.

Надёжность измерений

Надёжность измерений — это широкое понятие. Описанные в теории измерений виды шкал не дают полного представления о свойствах полученных по ним оценок. Необходимо выявить присущие этим оценкам ошибки. Это и называется оценкой надёжности измерения. Данная проблема решается путём выявления трёх свойств измерения:

правильности;
устойчивости;
обоснованности.

Правильность измерения — это приемлемость используемого способа измерения (шкалы или системы шкал). Оно связано с возможностью учёта различного рода систематических ошибок, возникающих в результате измерения. Систематические ошибки измерения имеют некоторую стабильную природу возникновения: они либо постоянные, либо меняются по определённому закону. Возможно, что последующие этапы оценки надёжности измерения окажутся излишними, если в начале выяснится полная неспособность инструмента измерения дифференцировать изучаемую характеристику на требуемом уровне. Самый простой возможный вариант — исследуемую характеристику объекта просто нельзя дифференцировать с нужной точностью. Систематические ошибки в результате измерения также будут, если окажется, что систематически не используется какая-то градация шкалы или вопроса. Например, исследования показывают, что при непосредственном присваивании коэффициентов люди пользуются ограниченным набором чисел [2].

В отличие от правильности и устойчивости, которые в идеале могут быть измерены достаточно строго, критерии обоснованности определяются либо экспертно, на основе логических рассуждений, либо на основе косвенных данных.

Как добиться правильности измерений? Прежде всего, нужно ликвидировать или уменьшить такого рода недостатки шкалы и только затем использовать её в прикладных целях. Например, изменение шкалы оценок, используемой в ВШЭ. Первоначально в ВШЭ использовалась 10-балльная шкала без пояснений к баллам. В результате анализа правильности измерений выяснилось, что есть градации шкалы, которые практически не применяются (оценки 1, 2 и 10). Тогда шкала оценок была заменена на новую 5-балльную — менее информативную, но более надёжную (таблица 5).

Таблица 5. Шкала соответствия оценок ВШЭ.

Французская 20-балльная шкала	10-балльная шкала оценок ВШЭ	Новая 5-балльная шкала оценок ВШЭ
18 и выше	10	«Отлично» — 5
17	9
15 — 16	8
14	7	«Хорошо» — 4
12 — 13	6
11	5	«Удовлетворительно» — 3
9 — 10	4
Менее 9	1 — 3	Неудовлетворительно

Устойчивость измерения характеризует степень совпадения результатов при повторных применениях измерительной процедуры. Она описывается величиной случайной ошибки (чаще всего используется средняя квадратическая ошибка). Устойчивость характеризует постоянство подхода респондента к ответам на одинаковые или подобные вопросы. День на день не приходится, один и тот же человек в разных условиях может дать разные ответы на одинаковый вопрос. Эту неустойчивость оценок при использовании нефинансовых качественных показателей деятельности компании исключать или игнорировать никак нельзя.

Как оценить устойчивость измерений? Существует несколько методов оценки устойчивости измерений:

повторное тестирование;
включение в анкету эквивалентных вопросов, то есть вопросов по той же проблеме, но сформулированных по-другому, и разделение выборки на две части (сравнение ответов на вопросы двух групп респондентов).

Устойчивость может быть измерена статистически достаточно строго и выражена в форме числового показателя. Правда, в системе показателей компании это практически не применяется, и устойчивость оценок остаётся «вещью в себе». Например, на Талнахской горно-обогатительной фабрике начальник может увеличить или уменьшить на 1 балл оценку своему подчинённому при 4-балльной системе измерений. Попробуйте установить устойчивость такой оценки формально. Это не получится.

Тем не менее, этот приём (субъективное увеличение или уменьшение оценки на 1 балл) я оцениваю положительно. Дело в том, что абсолютно объективных оценок не бывает. Всегда надо как-то учесть субъективное мнение. Особенно если добавление (удаление) целого балла прописано и используется в системе как «дамоклов меч», то есть скорее как угроза, исключительная мера, а не система оценок «за голубые глазки» (именно так он используется, например, на Талнахской горно-обогатительной фабрике).

Обоснованность измерения — это доказательство соответствия между тем, что измерено, и тем, что должно было быть измерено. Это наиболее сложный вопрос надёжности измерения. Трудно доказать, что измерено вполне определённое заданное свойство объекта, а не некоторое другое, более или менее на него похожее.

В отличие от правильности и устойчивости, которые в идеале могут быть измерены достаточно строго и иногда даже могут быть выражены в форме числового показателя, критерии обоснованности определяются либо экспертно, на основе логических рассуждений, либо на основе косвенных данных. В социологии обычно применяется сравнение данных одной методики с данными других методик или исследований, однако в системе показателей компании это практически исключено. Остаётся экспертное профессиональное мнение. Однако наши менеджеры уверены, что их шкалы оценки той или иной характеристики верные. Уверяю вас, это очень далеко от истины! Наши руководители сами разрабатывают даже систему мотивации, тогда как на Западе принято отдавать это на аутсорсинг фирмам-профессионалам. Что уж говорить о каких-то показателях. Неудивительно, что нефинансовые показатели используются пока редко.

Четвертый объект лишний? Или третий эксперт?

Иногда при измерении по порядковым шкалам привлечение ещё одного объекта экспертизы меняет отношения порядка при обработке с помощью суммарного балла порядковых измерений. Предположим, трём экспертам дали задание ранжировать 4 объекта. Результаты приведены в таблице:

Объекты измерения	A	B	C	D
Результаты измерений трёх экспертов	1	2	3	4
4	2	1	3
2	3	4	1
Суммарная оценка	7	7	8	8

Вывод: объекты А и В равноценны и лучше, чем С и D, которые тоже равноценны. Теперь уберём объект D и попросим экспертов снова упорядочить между собой объекты А, В и С. Мы вправе ожидать, что предпочтения экспертов, то есть их оценки относительного порядка объектов, не изменятся. Тогда получим следующие результаты:

Объекты измерения	A	B	C	Нет данных
Результаты измерений трёх экспертов	1	2	3	Нет данных
3	2	1	Нет данных
1	2	3	Нет данных
Суммарная оценка	5	6	7	Нет данных

Вывод: объект А лучше объекта В, который, в свою очередь, лучше, чем С. Согласитесь, что выводы различаются. И всё из-за наличия «лишнего» объекта измерений. Значит, достоверность зависит от количества объектов измерения.

Вывод по результатам измерений в порядковой шкале меняется и в зависимости от количества экспертов. Уберём одного эксперта, а предпочтения оставшихся будем считать неизменными. В результате получим:

Объекты измерения	A	B	C	D
Результаты измерений трёх экспертов	1	2	3	4
4	2	1	3
Нет данных	Нет данных	Нет данных	Нет данных
Суммарная оценка	5	4	4	7

Вывод опять изменился: объекты В и С равно хороши и лучше объекта А, который, в свою очередь, лучше, чем объект D. Значит, достоверность измерения зависит от количества экспертов. И не факт, что чем больше экспертов, тем выше достоверность выводов.

Три составляющие измерения. Помимо перечисленного выше, при установлении надёжности следует иметь в виду, что в процессе измерения участвуют три составляющие:

объект измерения;
измеряющие средства, с помощью которых производится отображение свойств объекта на числовую систему;
производящий измерение субъект (интервьюер, оценщик, разработчик ССП и т. д.).

Предпосылки надёжного измерения кроются в каждой отдельной составляющей. Может быть, что способ получения оценки не в состоянии дать максимально точных значений измеряемого свойства. Например, у респондента существует развёрнутая иерархия ценностей, а для получения информации используется шкала с вариациями ответов только «очень важно» и «совсем не важно». Как правило, если используется такая шкала, то все характеристики будут «очень важными», хотя реально у респондента имеется большее число уровней значимости.

Возможно, что субъект, производящий измерение, допускает грубые ошибки; нечётко составлены инструкции к анкете; интервьюер каждый раз по-разному формулирует один и тот же вопрос, используя различную терминологию. На практике это критически важно. Именно поэтому построение системы показателей деятельности сопровождается обучением, разработкой тезауруса, распространением информации, разбором опыта подобных измерений и оценок, приёмами социологии и психологии.

Достоверность измерений

Достоверность характеризует другие аспекты измерений, чем надёжность. Измерение может быть надёжным, но недостоверным. Достоверность характеризует точность измерений по отношению к тому, что существует в реальности. Например, респонденту задали вопрос о целевой месячной выручке. Он её оценивает в 250 000 долларов. Однако, не желая называть интервьюеру истинную цифру, респондент указал «более 100 000 долларов». При повторном тестировании он снова назвал данную цифру, демонстрируя высокий уровень надёжности измерений. То есть измерение надёжно, но недостоверно. Но ложь не является единственной причиной низкого уровня достоверности измерений, её причиной может быть плохое знание респондентом действительности и т. п.

Достоверность — это доверие измерению и оценке, степень уверенности, что в измерении нет ошибки.

Достоверность системы показателей деятельности компании весьма важна. Например, какой вес присвоить одному из двух показателей, сделав его более важным? Точно посчитать вес невозможно, выбирать его придётся субъективно из множества чисел от 0,5 до 1. Но исследования показывают, что при присваивании коэффициентов люди пользуются ограниченным набором чисел, причём используют этот набор крайне неравномерно [2].

Достоверность системы показателей деятельности компании весьма важна. Она характеризует точность измерений по отношению к тому, что существует в реальности.

Отметим некоторые наиболее общие факторы, влияющие на достоверность измерений и не связанные с предметной областью.

Достоверность измерений зависит от шкалы. Наиболее достоверные измерения выполняются в шкале наименований, а наименее достоверные — в абсолютной шкале. Закономерность здесь такова: чем шире класс допустимых преобразований, тем легче оценивать и измерять, то есть давать оценки.
Количество экспериментов или экспертов влияет на достоверность измерений. Этот эффект наглядно показан во врезке «Четвёртый объект лишний? Или третий эксперт?».

Как повысить достоверность измерений? Повышение достоверности измерений может быть связано с разными факторами. Отметим два наиболее общих способа.

Укрупнение градаций шкалы — это такая группировка значений измерения, которая сокращает число значимых оценок, делает измерение более грубым и одновременно более достоверным. Например, такие значения шкалы, как «полностью согласен» и «скорее согласен» объединяются в одно значение «согласен». Достоверность измерений растёт, так как если вы колеблетесь между «полностью согласен» и «скорее согласен», то уж точно в новой шкале с более грубыми градациями ответите «согласен». Но при этом страдает информативность, она падает, поскольку в шкале с более грубыми градациями исчезают оттенки.
Переход к измерениям в шкалах меньшей информативности. Например, количественную шкалу заменить на порядковую. В этом случае достоверность вырастет за счёт понижения информативности измерений.

Отмечу, что в социологии и маркетинге достоверность измерений существенно более сложное понятие, чем то, что описано выше. В социологии достоверность определяют как степень, в которой различия между оценками, полученными по шкале, отражают истинные различия между измеряемыми характеристиками объектов, а не обусловлены случайными и систематическими ошибками.

Полная достоверность — это отсутствие ошибок измерения.

Исследователи разделяют содержательную, критериальную и конструктивную достоверность.

Содержательная достоверность (content validity)1 — субъективная систематическая оценка того, насколько хорошо содержание шкалы соответствует поставленной цели измерения. Например, шкала, разработанная для измерения имиджа магазина, считается неадекватной, если будет опущена одна из существенных характеристик объекта (например, качество и разнообразие (широта и глубина ассортимента) предлагаемой продукции). Оценка содержательной достоверности очевидно субъективна, но в любой системе показателей деятельности субъективизм неизбежен. Однако важно понимать: баллы выбраны и описаны адекватно измеряемому объекту или нет. Хотя выбор балльной шкалы — дело достаточно субъективное.

Критериальная достоверность (criterion validity) отражает, насколько используемая шкала соответствует цели измерений. В зависимости от временных рамок измерения критериальная достоверность может принимать две формы — текущую или прогнозную достоверность. Текущая критериальная достоверность определяется, когда данные, полученные на основе использования шкалы, и сведения о целях измерения (критериальных переменных) собираются одновременно. Для оценки прогнозной критериальной достоверности исследователь собирает измерения по шкале в один период времени, а по целям (критериальным переменным) — в другой. Например, отношение к различным маркам продуктов может использоваться для прогноза будущих объёмов их продаж. У определённой выборки покупателей получают информацию об их отношении к продукту, а затем будущие закупки проверяются по данным исследования. Прогнозные и фактические данные по покупкам сравниваются для оценки прогнозной достоверности шкалы отношения к различным маркам продуктов.

В социологии достоверность определяют как степень, в которой различия между оценками, полученными по шкале, отражают истинные различия между измеряемыми характеристиками объектов, а не обусловлены случайными и систематическими ошибками.

При разработке и эксплуатации системы показателей деятельности компании критериальная достоверность вполне применима. Всем важно знать, как используются их оценки в системе мотивации и при принятии каких решений. Поэтому не лишне иметь представление и о проблеме критериальной достоверности.

Конструктивная достоверность (construct validity) связана с ответами на теоретические вопросы: почему должна использоваться эта шкала и какие выводы можно сделать из лежащей в её основе теории. Конструктивную достоверность понять сложнее, останавливаться на ней здесь мы не будем.

* * *

В следующей части статьи речь пойдёт об информативности измерений. Мы проанализируем приведённую в предыдущей части систему оценок в фигурном катании, а также обсудим использование теории измерений в системе показателей компании.

Систематической погрешностью называется составляющая погрешности измерения, остающаяся постоянной или закономерно меняющаяся при повторных измерениях одной и той же величины. При этом предполагается, что систематические погрешности представляют собой определенную функцию неслучайных факторов, состав которых зависит от физических, конструкционных и технологических особенностей средств измерений, условий их применения, а также индивидуальных качеств наблюдателя. Сложные детерминированные закономерности, которым подчиняются систематические погрешности, определяются либо при создании средств измерений и комплектации измерительной аппаратуры, либо непосредственно при подготовке измерительного эксперимента и в процессе его проведения. Совершенствование методов измерения, использование высококачественных материалом, прогрессивная технология — все это позволяет на практике устранить систематические погрешности настолько, что при обработке результатов наблюдений с их наличием зачастую не приходится считаться.

Систематические погрешности принято классифицировать в зависимости от причин их возникновения и по характеру их проявления при измерениях.

В зависимости от причин возникновения рассматриваются четыре вида систематических погрешностей.

1. Погрешности метода, или теоретические погрешности, проистекающие от ошибочности или недостаточной разработки принятой теории метода измерений в целом или от допущенных упрощений при проведении измерений.

Погрешности метода возникают также при экстраполяции свойства, измеренного на ограниченной части некоторого объекта, на весь объект, если последний не обладает однородностью измеряемого свойства. Так, считая диаметр цилиндрического вала равным результату, полученному при измерении в одном сечении и в одном направлении, мы допускаем систематическую погрешность, полностью определяемую отклонениями формы исследуемого вала. При определении плотности вещества по измерениям массы и объема некоторой пробы возникает систематическая погрешность, если проба содержала некоторое количество примесей, а результат измерения принимается за характеристику данного вещества -вообще.

К погрешностям метода следует отнести также те погрешности, которые возникают вследствие влияния измерительной аппаратуры на измеряемые свойства объекта. Подобные явления возникают, например, при измерении длин, когда измерительное усилие используемых приборов достаточно велико, при регистрации быстропротекаюших процессов недостаточно быстродействующей аппаратурой, при измерениях температур жидкостными или газовыми термометрами и т.д.

2. Инструментальные погрешности, зависящие от погрешностей применяемых средств измерений.. Среди инструментальных погрешностей в отдельную группу выделяются погрешности схемы, не связанные с неточностью изготовления средств измерения и обязанные своим происхождением самой структурной схеме средств измерений. Исследование инструментальных погрешностей является предметом специальной дисциплины — теории точности измерительных устройств.

3. Погрешности, обусловленные неправильной установкой и взаимным расположением средств измерения, являющихся частью единого комплекса, несогласованностью их характеристик, влиянием внешних температурных, гравитационных, радиационных и других полей, нестабильностью источников питания, несогласованностью входных и выходных параметров электрических цепей приборов и т.д.

4. Личные погрешности, обусловленные индивидуальными особенностями наблюдателя. Такого рода погрешности вызываются, например, запаздыванием или опережением при регистрации сигнала, неправильным отсчетом десятых долей деления шкалы, асимметрией, возникающей при установке штриха посередине между двумя рисками.

По характеру своего поведения в процессе измерения систематические погрешности подразделяются на постоянные и переменные.

Постоянные систематические погрешности возникают, например, при неправильной установке начала отсчета, неправильной градуировке и юстировке средств измерения и остаются постоянными при всех повторных наблюдениях. Поэтому, если уж они возникли, их очень трудно обнаружить в результатах наблюдений.

Среди переменных систематических погрешностей принято выделять прогрессивные и периодические.

Прогрессивная погрешность возникает, например, при взвешивании, когда одно из коромысел весов находится ближе к источнику тепла, чем другое, поэтому быстрее нагревается и

удлиняется. Это приводит к систематическому сдвигу начала отсчета и к монотонному изменению показаний весов.

Периодическая погрешность присуща измерительным приборам с круговой шкалой, если ось вращения указателя не совпадает с осью шкалы.

Все остальные виды систематических погрешностей принято называть погрешностями, изменяющимися по сложному закону.

В тех случаях, когда при создании средств измерений, необходимых для данной измерительной установки, не удается устранить влияние систематических погрешностей, приходится специально организовывать измерительный процесс и осуществлять математическую обработку результатов. Методы борьбы с систематическими погрешностями заключаются в их обнаружении и последующем исключении путем полной или частичной компенсации. Основные трудности, часто непреодолимые, состоят именно в обнаружении систематических погрешностей, поэтому иногда приходится довольствоваться приближенным их анализом.

Способы обнаружения систематических погрешностей. Результаты наблюдений, полученные при наличии систематических погрешностей, будем называть неисправленными и в отличие от исправленных снабжать штрихами их обозначения (например, Х1, Х₂ и т.д.). Вычисленные в этих условиях средние арифметические значения и отклонения от результатов наблюдений будем также называть неисправленными и ставить штрихи у символов этих величин. Таким образом,

Поскольку неисправленные результаты наблюдений включают в себя систематические погрешности, сумму которых для каждого /-го наблюдения будем обозначать через 8., то их математическое ожидание не совпадает с истинным значением измеряемой величины и отличается от него на некоторую величину 0, называемую систематической погрешностью неисправленного среднего арифметического. Действительно,

Если систематические погрешности постоянны, т.е. 0_/ = 0, /=1,2, …, п, то неисправленные отклонения могут быть непосредственно использованы для оценки рассеивания ряда наблюдений. В противном случае необходимо предварительно исправить отдельные результаты измерений, введя в них так называемые поправки, равные систематическим погрешностям по величине и обратные им по знаку:

q = -Oi.

Таким образом, для нахождения исправленного среднего арифметического и оценки его рассеивания относительно истинного значения измеряемой величины необходимо обнаружить систематические погрешности и исключить их путем введения поправок или соответствующей каждому конкретному случаю организации самого измерения. Остановимся подробнее на некоторых способах обнаружения систематических погрешностей.

Постоянные систематические погрешности не влияют на значения случайных отклонений результатов наблюдений от средних арифметических, поэтому никакая математическая обработка результатов наблюдений не может привести к их обнаружению. Анализ таких погрешностей возможен только на основании некоторых априорных знаний об этих погрешностях, получаемых, например, при поверке средств измерений. Измеряемая величина при поверке обычно воспроизводится образцовой мерой, действительное значение которой известно. Поэтому разность между средним арифметическим результатов наблюдения и значением меры с точностью, определяемой погрешностью аттестации меры и случайными погрешностями измерения, равна искомой систематической погрешности.

Одним из наиболее действенных способов обнаружения систематических погрешностей в ряде результатов наблюдений является построение графика последовательности неисправленных значений случайных отклонений результатов наблюдений от средних арифметических.

Рассматриваемый способ обнаружения постоянных систематических погрешностей можно сформулировать следующим образом: если неисправленные отклонения результатов наблюдений резко изменяются при изменении условий наблюдений, то данные результаты содержат постоянную систематическую погрешность, зависящую от условий наблюдений.

Систематические погрешности являются детерминированными величинами, поэтому в принципе всегда могут быть вычислены и исключены из результатов измерений. После исключения систематических погрешностей получаем исправленные средние арифметические и исправленные отклонения результатов наблюдении, которые позволяют оценить степень рассеивания результатов.

Для исправления результатов наблюдений их складывают с поправками, равными систематическим погрешностям по величине и обратными им по знаку. Поправку определяют экспериментально при поверке приборов или в результате специальных исследований, обыкновенно с некоторой ограниченной точностью.

Поправки могут задаваться также в виде формул, по которым они вычисляются для каждого конкретного случая. Например, при измерениях и поверках с помощью образцовых манометров следует вводить поправки к их показаниям на местное значение ускорения свободного падения

где Р — измеряемое давление.

Введением поправки устраняется влияние только одной вполне определенной систематической погрешности, поэтому в результаты измерения зачастую приходится вводить очень большое число поправок. При этом вследствие ограниченной точности определения поправок накапливаются случайные погрешности и дисперсия результата измерения увеличивается.

Систематическая погрешность, остающаяся после введения поправок на ее наиболее существенные составляющие включает в себя ряд элементарных составляющих, называемых неисключенными остатками систематической погрешности. К их числу относятся погрешности:

• определения поправок;

• зависящие от точности измерения влияющих величин, входящих в формулы для определения поправок;

• связанные с колебаниями влияющих величин (температуры окружающей среды, напряжения питания и т.д.).

Перечисленные погрешности малы, и поправки на них не вводятся.

Систематическая погрешность

Систематической погрешностью называется составляющая погрешности измерения, остающаяся постоянной или закономерно меняющаяся при повторных измерениях одной и той же величины. При этом предполагается, что систематические погрешности представляют собой определенную функцию неслучайных факторов, состав которых зависит от физических, конструкционных и технологических особенностей средств измерений, условий их применения, а также индивидуальных качеств наблюдателя. Сложные детерминированные закономерности, которым подчиняются систематические погрешности, определяются либо при создании средств измерений и комплектации измерительной аппаратуры, либо непосредственно при подготовке измерительного эксперимента и в процессе его проведения. Совершенствование методов измерения, использование высококачественных материалов, прогрессивная технология — все это позволяет на практике устранить систематические погрешности настолько, что при обработке результатов наблюдений с их наличием зачастую не приходится считаться.

Или: Систематическая погрешность измерения — составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины.

В зависимости от характера измерения систематические погрешности подразделяют на постоянные, прогрессивные и погрешности, изменяющиеся по сложному закону.

В зависимости от причин появления систематические погрешности подразделяют на инструментальные, погрешности метода измерений, субъективные и др.

Свойства физического объекта (явления, процесса) определяются набором
количественных характеристик — физических величин.
Как правило, результат измерения представляет
собой число, задающее отношение измеряемой величины к некоторому эталону.
Сравнение с эталоном может быть как
прямым (проводится непосредственно
экспериментатором), так и косвенным (проводится с помощью некоторого
прибора, которому экспериментатор доверяет).
Полученные таким образом величины имеют размерность, определяемую выбором эталона.

Замечание. Результатом измерения может также служить количество отсчётов некоторого
события, логическое утверждение (да/нет) или даже качественная оценка
(сильно/слабо/умеренно). Мы ограничимся наиболее типичным для физики случаем,
когда результат измерения может быть представлен в виде числа или набора чисел.

Взаимосвязь между различными физическими величинами может быть описана
физическими законами, представляющими собой идеализированную
модель действительности. Конечной целью любого физического
эксперимента (в том числе и учебного) является проверка адекватности или
уточнение параметров таких моделей.

1.1 Результат измерения

Рассмотрим простейший пример: измерение длины стержня
с помощью линейки. Линейка проградуирована производителем с помощью
некоторого эталона длины — таким образом, сравнивая длину
стержня с ценой деления линейки, мы выполняем косвенное сравнение с
общепринятым стандартным эталоном.

Допустим, мы приложили линейку к стержню и увидели на шкале некоторый результат
x=xизм. Можно ли утверждать, что xизм — это длина
стержня?

Во-первых, значение x не может быть задано точно, хотя бы
потому, что оно обязательно округлено до некоторой значащей
цифры: если линейка «обычная», то у неё
есть цена деления; а если линейка, к примеру, «лазерная»
— у неё высвечивается конечное число значащих цифр
на дисплее.

Во-вторых, мы никак не можем быть уверенны, что длина стержня на
самом деле такова хотя бы с точностью до ошибки округления. Действительно,
мы могли приложить линейку не вполне ровно; сама линейка могла быть
изготовлена не вполне точно; стержень может быть не идеально цилиндрическим
и т.п.

Итак, из нашего примера видно, что никакое физическое измерение не может быть
произведено абсолютно точно, то есть
у любого измерения есть погрешность.

Замечание. Также используют эквивалентный термин ошибка измерения
(от англ. error). Подчеркнём, что смысл этого термина отличается от
общеупотребительного бытового: если физик говорит «в измерении есть ошибка»,
— это не означает, что оно неправильно и его надо переделать.
Имеется ввиду лишь, что это измерение неточно, то есть имеет
погрешность.

Количественно погрешность можно было бы определить как разность между
измеренным и «истинным» значением длины стержня:
δ⁢x=xизм-xист. Однако на практике такое определение
использовать нельзя: во-первых, из-за неизбежного наличия
погрешностей «истинное» значение измерить невозможно, и во-вторых, само
«истинное» значение может отличаться в разных измерениях (например, стержень
неровный или изогнутый, его торцы дрожат из-за тепловых флуктуаций и т.д.).
Поэтому говорят обычно об оценке погрешности.

Об измеренной величине также часто говорят как об оценке, подчеркивая,
что эта величина не точна и зависит не только от физических свойств
исследуемого объекта, но и от процедуры измерения.

Замечание.
Термин оценка имеет и более формальное значение. Оценкой называют результат процедуры получения значения параметра или параметров физической модели, а также иногда саму процедуру. Теория оценок является подразделом математической статистики. Некоторые ее положения изложены в главе 3, но для более серьезного понимания следует обратиться к [5].

Для оценки значения физической величины корректно использовать
не просто некоторое фиксированное число xизм, а интервал (или
диапазон) значений, в пределах которого может лежать её
«истинное» значение. В простейшем случае этот интервал
может быть записан как

где δ⁢x — абсолютная величина погрешности.
Эта запись означает, что исследуемая величина лежит в интервале
x∈(xизм-δ⁢x;xизм+δ⁢x)
с некоторой достаточно большой долей вероятности (более подробно о
вероятностном содержании интервалов см. п. 2.2).
Для наглядной оценки точности измерения удобно также использовать
относительную величину погрешности:

Она показывает, насколько погрешность мала по сравнению с
самой измеряемой величиной (её также можно выразить в процентах:
ε=δ⁢xx⋅100%).

Пример. Штангенциркуль —
прибор для измерения длин с ценой деления 0,1⁢мм. Пусть
диаметр некоторой проволоки равен 0,37 мм. Считая, что абсолютная
ошибка составляет половину цены деления прибора, результат измерения
можно будет записать как d=0,40±0,05⁢мм (или
d=(40±5)⋅10-5⁢м).
Относительная погрешность составляет ε≈13%, то
есть точность измерения весьма посредственная — поскольку
размер объекта близок к пределу точности прибора.

О необходимости оценки погрешностей.

Измерим длины двух стержней x1 и x2 и сравним результаты.
Можно ли сказать, что стержни одинаковы или различны?

Казалось бы,
достаточно проверить, справедливо ли x1=x2. Но никакие
два результата измерения не равны друг другу с абсолютной точностью! Таким
образом, без указания погрешности измерения ответ на этот вопрос дать
невозможно.

С другой стороны, если погрешность δ⁢x известна, то можно
утверждать, что если измеренные длины одинаковы
в пределах погрешности опыта, если |x2-x1|<δ⁢x
(и различны в противоположном случае).

Итак, без знания погрешностей невозможно сравнить между собой никакие
два измерения, и, следовательно, невозможно сделать никаких
значимых выводов по результатам эксперимента: ни о наличии зависимостей
между величинами, ни о практической применимости какой-либо теории,
и т. п. В связи с этим задача правильной оценки погрешностей является крайне
важной, поскольку существенное занижение или завышение значения погрешности
(по сравнению с реальной точностью измерений) ведёт к неправильным выводам.

В физическом эксперименте (в том числе лабораторном практикуме) оценка
погрешностей должна проводиться всегда
(даже когда составители задания забыли упомянуть об этом).

1.2 Многократные измерения

Проведём серию из n одинаковых (однотипных) измерений одной
и той же физической величины (например, многократно приложим линейку к стержню) и получим
ряд значений

Что можно сказать о данном наборе чисел и о длине стержня?
И можно ли увеличивая число измерений улучшить конечный результат?

Если цена деления самой линейки достаточно мала, то как нетрудно убедиться
на практике, величины {xi} почти наверняка окажутся
различными. Причиной тому могут быть
самые разные обстоятельства, например: у нас недостаточно остроты
зрения и точности рук, чтобы каждый раз прикладывать линейку одинаково;
стенки стержня могут быть слегка неровными; у стержня может и не быть
определённой длины, например, если в нём возбуждены звуковые волны,
из-за чего его торцы колеблются, и т. д.

В такой ситуации результат измерения интерпретируется как
случайная величина, описываемая некоторым вероятностным законом
(распределением).
Подробнее о случайных величинах и методах работы с ними см. гл. 2.

По набору результатов 𝐱 можно вычислить их среднее арифметическое:

⟨x⟩=x1+x2+…+xnn≡1n⁢∑i=1nxi.

(1.1)

Это значение, вычисленное по результатам конечного числа n измерений,
принято называть выборочным средним. Здесь и далее для обозначения
выборочных средних будем использовать угловые скобки.

Кроме среднего представляет интерес и то, насколько сильно варьируются
результаты от опыта к опыту. Определим отклонение каждого измерения от среднего как

Разброс данных относительно среднего принято характеризовать
среднеквадратичным отклонением:

s=Δ⁢x12+Δ⁢x22+…+Δ⁢xn2n=1n⁢∑i=1nΔ⁢xi2

(1.2)

или кратко

Значение среднего квадрата отклонения s2 называют
выборочной дисперсией.

Будем увеличивать число измерений n (n→∞). Если объект измерения и методика
достаточно стабильны, то отклонения от среднего Δ⁢xi будут, во-первых,
относительно малы, а во-вторых, положительные и отрицательные отклонения будут
встречаться примерно одинаково часто. Тогда при вычислении (1.1)
почти все отклонения Δ⁢xi скомпенсируются и можно ожидать,
что выборочное среднее при n≫1 будет стремиться к некоторому пределу:

Тогда предельное значение x¯ можно отождествить с «истинным» средним
для исследуемой величины.

Предельную величину среднеквадратичного отклонения при n→∞
обозначим как

Замечание. В общем случае указанные пределы могут и не существовать. Например, если измеряемый параметр
меняется во времени или в результате самого измерения, либо испытывает слишком большие
случайные скачки и т. п. Такие ситуации требуют особого рассмотрения и мы на них не
останавливаемся.

Замечание. Если n мало (n<10), для оценки среднеквадратичного отклонения
математическая статистика рекомендует вместо формулы (1.3) использовать
исправленную формулу (подробнее см. п. 5.2):

sn-12=1n-1⁢∑i=1nΔ⁢xi2,

(1.4)

где произведена замена n→n-1. Величину sn-1
часто называют стандартным отклонением.

Итак, можно по крайней мере надеяться на то, что результаты небольшого числа
измерений имеют не слишком большой разброс, так что величина ⟨x⟩
может быть использована как приближенное значение (оценка) истинного значения
⟨x⟩≈x¯,
а увеличение числа измерений позволит уточнить результат.

Многие случайные величины подчиняются так называемому нормальному закону
распределения (подробнее см. Главу 2). Для таких величин
могут быть строго доказаны следующие свойства:

•

при многократном повторении эксперимента бо́льшая часть измерений
(∼68%) попадает в интервал x¯-σ<x<x¯+σ
(см. п. 2.2).
•

выборочное среднее значение ⟨x⟩ оказывается с большей
вероятностью ближе к истинному значению x¯, чем каждое из измерений
{xi} в отдельности. При этом ошибка вычисления среднего
убывает пропорционально корню из числа опытов n
(см. п. 2.4).

Упражнение. Показать, что

s2=⟨x2⟩-⟨x⟩2.

(1.5)

то есть дисперсия равна разности среднего значения квадрата
⟨x2⟩=1n⁢∑i=1nxi2
и квадрата среднего ⟨x⟩2=(1n⁢∑i=1nxi)2.

1.3 Классификация погрешностей

Чтобы лучше разобраться в том, нужно ли многократно повторять измерения,
и в каком случае это позволит улучшить результаты опыта,
проанализируем источники и виды погрешностей.

В первую очередь, многократные измерения позволяют проверить
воспроизводимость результатов: повторные измерения в одинаковых
условиях, должны давать близкие результаты. В противном случае
исследование будет существенно затруднено, если вообще возможно.
Таким образом, многократные измерения необходимы для того,
чтобы убедиться как в надёжности методики, так и в существовании измеряемой
величины как таковой.

При любых измерениях возможны грубые ошибки — промахи
(англ. miss). Это «ошибки» в стандартном
понимании этого слова — возникающие по вине экспериментатора
или в силу других непредвиденных обстоятельств (например, из-за сбоя
аппаратуры). Промахов, конечно, нужно избегать, а результаты таких
измерений должны быть по возможности исключены из рассмотрения.

Как понять, является ли «аномальный» результат промахом? Вопрос этот весьма
непрост. В литературе существуют статистические
критерии отбора промахов, которыми мы, однако, настоятельно не рекомендуем
пользоваться (по крайней мере, без серьезного понимания последствий
такого отбора). Отбрасывание аномальных данных может, во-первых, привести
к тенденциозному искажению результата исследований, а во-вторых, так
можно упустить открытие неизвестного эффекта. Поэтому при научных
исследованиях необходимо максимально тщательно проанализировать причину
каждого промаха, в частности, многократно повторив эксперимент. Лишь
только если факт и причина промаха установлены вполне достоверно,
соответствующий результат можно отбросить.

Замечание. Часто причины аномальных отклонений невозможно установить на этапе
обработки данных, поскольку часть информации о проведении измерений к этому моменту
утеряна. Единственным способ борьбы с этим — это максимально подробное описание всего
процесса измерений в лабораторном журнале. Подробнее об этом
см. п. 4.1.1.

При многократном повторении измерении одной и той же физической величины
погрешности могут иметь систематический либо случайный
характер. Назовём погрешность систематической, если она повторяется
от опыта к опыту, сохраняя свой знак и величину, либо закономерно
меняется в процессе измерений. Случайные (или статистические)
погрешности меняются хаотично при повторении измерений как по величине,
так и по знаку, и в изменениях не прослеживается какой-либо закономерности.

Кроме того, удобно разделять погрешности по их происхождению. Можно
выделить

•

инструментальные (или приборные) погрешности,
связанные с несовершенством конструкции (неточности, допущенные при
изготовлении или вследствие старения), ошибками калибровки или ненормативными
условиями эксплуатации измерительных приборов;
•

методические погрешности, связанные с несовершенством
теоретической модели явления (использование приближенных формул и
моделей явления) или с несовершенством методики измерения (например,
влиянием взаимодействия прибора и объекта измерения на результат измерения);
•

естественные погрешности, связанные со случайным
характером
измеряемой физической величины — они являются не столько
«ошибками» измерения, сколько характеризуют
природу изучаемого объекта или явления.

Замечание. Разделение погрешностей на систематические и случайные
не является однозначным и зависит от постановки опыта. Например, производя
измерения не одним, а несколькими однотипными приборами, мы переводим
систематическую приборную ошибку, связанную с неточностью шкалы и
калибровки, в случайную. Разделение по происхождению также условно,
поскольку любой прибор подвержен воздействию «естественных»
случайных и систематических ошибок (шумы и наводки, тряска, атмосферные
условия и т. п.), а в основе работы прибора всегда лежит некоторое
физическое явление, описываемое не вполне совершенной теорией.

1.3.1 Случайные погрешности

Случайный характер присущ большому количеству различных физических
явлений, и в той или иной степени проявляется в работе всех без исключения
приборов. Случайные погрешности обнаруживаются просто при многократном
повторении опыта — в виде хаотичных изменений (флуктуаций)
значений {xi}.

Если случайные отклонения от среднего в большую или меньшую стороны
примерно равновероятны, можно рассчитывать, что при вычислении среднего
арифметического (1.1) эти отклонения скомпенсируются,
и погрешность результирующего значения ⟨x⟩ будем меньше,
чем погрешность отдельного измерения.

Случайные погрешности бывают связаны, например,

•

с особенностями используемых приборов: техническими
недостатками
(люфт в механических приспособлениях, сухое трение в креплении стрелки
прибора), с естественными (тепловой и дробовой шумы в электрических
цепях, тепловые флуктуации и колебания измерительных устройств из-за
хаотического движения молекул, космическое излучение) или техногенными
факторами (тряска, электромагнитные помехи и наводки);
•

с особенностями и несовершенством методики измерения (ошибка
при отсчёте по шкале, ошибка времени реакции при измерениях с секундомером);
•

с несовершенством объекта измерений (неровная поверхность,
неоднородность состава);
•

со случайным характером исследуемого явления (радиоактивный
распад, броуновское движение).

Остановимся несколько подробнее на двух последних случаях. Они отличаются
тем, что случайный разброс данных в них порождён непосредственно объектом
измерения. Если при этом приборные погрешности малы, то «ошибка»
эксперимента возникает лишь в тот момент, когда мы по своей
воле совершаем замену ряда измеренных значений на некоторое среднее
{xi}→⟨x⟩. Разброс данных при этом
характеризует не точность измерения, а сам исследуемый объект или
явление. Однако с математической точки зрения приборные и
«естественные»
погрешности неразличимы — глядя на одни только
экспериментальные данные невозможно выяснить, что именно явилось причиной
их флуктуаций: сам объект исследования или иные, внешние причины.
Таким образом, для исследования естественных случайных процессов необходимо
сперва отдельно исследовать и оценить случайные инструментальные погрешности
и убедиться, что они достаточно малы.

1.3.2 Систематические погрешности

Систематические погрешности, в отличие от случайных, невозможно обнаружить,
исключить или уменьшить просто многократным повторением измерений.
Они могут быть обусловлены, во-первых, неправильной работой приборов
(инструментальная погрешность), например, сдвигом нуля отсчёта
по шкале, деформацией шкалы, неправильной калибровкой, искажениями
из-за не нормативных условий эксплуатации, искажениями из-за износа
или деформации деталей прибора, изменением параметров прибора во времени
из-за нагрева и т.п. Во-вторых, их причиной может быть ошибка в интерпретации
результатов (методическая погрешность), например, из-за использования
слишком идеализированной физической модели явления, которая не учитывает
некоторые значимые факторы (так, при взвешивании тел малой плотности
в атмосфере необходимо учитывать силу Архимеда; при измерениях в электрических
цепях может быть необходим учет неидеальности амперметров и вольтметров
и т. д.).

Систематические погрешности условно можно разделить на следующие категории.

1.

Известные погрешности, которые могут быть достаточно точно вычислены
или измерены. При необходимости они могут быть учтены непосредственно:
внесением поправок в расчётные формулы или в результаты измерений.
Если они малы, их можно отбросить, чтобы упростить вычисления.
2.

Погрешности известной природы, конкретная величина которых неизвестна,
но максимальное значение вносимой ошибки может быть оценено теоретически
или экспериментально. Такие погрешности неизбежно присутствуют в любом
опыте, и задача экспериментатора — свести их к минимуму,
совершенствуя методики измерения и выбирая более совершенные приборы.

Чтобы оценить величину систематических погрешностей опыта, необходимо
учесть паспортную точность приборов (производитель, как правило, гарантирует,
что погрешность прибора не превосходит некоторой величины), проанализировать
особенности методики измерения, и по возможности, провести контрольные
опыты.
3.

Погрешности известной природы, оценка величины которых по каким-либо
причинам затруднена (например, сопротивление контактов при подключении
электронных приборов). Такие погрешности должны быть обязательно исключены
посредством модификации методики измерения или замены приборов.
4.

Наконец, нельзя забывать о возможности существования ошибок, о
которых мы не подозреваем, но которые могут существенно искажать результаты
измерений. Такие погрешности самые опасные, а исключить их можно только
многократной независимой проверкой измерений, разными методами
и в разных условиях.

В учебном практикуме учёт систематических погрешностей ограничивается,
как правило, паспортными погрешностями приборов и теоретическими поправками
к упрощенной модели исследуемого явления.

Точный учет систематической ошибки возможен только при учете специфики конкретного эксперимента. Особенное внимание надо обратить на зависимость (корреляцию) систематических смещений при повторных измерениях. Одна и та же погрешность в разных случаях может быть интерпретирована и как случайная, и как систематическая.

Пример.
Калибровка электромагнита производится при помощи внесения в него датчика Холла или другого измерителя магнитного потока. При последовательных измерениях с разными токами (и соотственно полями в зазоре) калибровку можно учитыать двумя различными способами:

•

Измерить значение поля для разных токов, построить линейную калибровочную кривую и потом использовать значения, восстановленные по этой кривой для вычисления поля по току, используемому в измерениях.

•

Для каждого измерения проводить допольнительное измерения поля и вообще не испльзовать значения тока.

В первом случае погрешность полученного значения будет меньше, поскльку при проведении прямой, отдельные отклонения усреднятся. При этом погрешность измерения поля будет носить систематический харрактер и при обработке данных ее надо будет учитывать в последний момент. Во втором случае погрешность будет носить статистический (случайный) харрактер и ее надо будет добавить к погрешности каждой измеряемой точки. При этом сама погрешность будет больше. Выбор той или иной методики зависит от конретной ситуации. При большом количестве измерений, второй способ более надежный, поскольку статистическая ошибка при усреднении уменьшается пропорционально корню из количества измерений. Кроме того, такой способ повзоляет избежать методической ошибки, связанной с тем, что зависимость поля от тока не является линейной.

Пример.
Рассмотрим измерение напряжения по стрелочному вольтметру. В показаниях прибора будет присутствовать три типа погрешности:

1.

Статистическая погрешность, связанная с дрожанием стрелки и ошибкой визуального наблюдения, примерно равная половине цены деления.

2.

Систематическая погрешность, связанная с неправильной установкой нуля.

3.

Систематическая погрешность, связанная с неправильным коэффициентом пропорциональности между напряжением и отклонением стрелки. Как правило приборы сконструированы таким образом, чтобы максимальное значение этой погрешности было так же равно половине цены деления (хотя это и не гарантируется).

Источник

Оценка эффективности методов измерения

Оценка эффективности методов измерения

Критерии успешности выполнения диагностического исследования.

Критерии успешности выполнения диагностического исследования.

Критерии успешности выполнения диагностического исследования.

Требования к организации прав доступа

Вопросы

На сегодня все…

ОЦЕНКА СЛУЧАЙНЫХ ПОГРЕШНОСТЕЙ

Каким образом обеспечивается качество результатов измерений?

Какая бывает погрешность измерений?

Как оценивают точность средств измерений?

Как погрешность характеризует качество измерения?

Что отражает смещение измерений?

Что представляет собой средство измерений?

Как оценить ошибку измерений?

Чем отличается погрешность от точности?

Какой показатель является мерой точности измерения?

Что такое достоверность результатов измерений?

Что является результатом измерений?

В чем заключается обработка результатов измерений?

Что такое исправленный ряд результатов измерений?

Надёжность измерений

Четвертый объект лишний? Или третий эксперт?

Достоверность измерений

* * *

Систематическая погрешность

1.1 Результат измерения

О необходимости оценки погрешностей.

1.2 Многократные измерения

1.3 Классификация погрешностей

1.3.1 Случайные погрешности

1.3.2 Систематические погрешности

Интересное по теме: