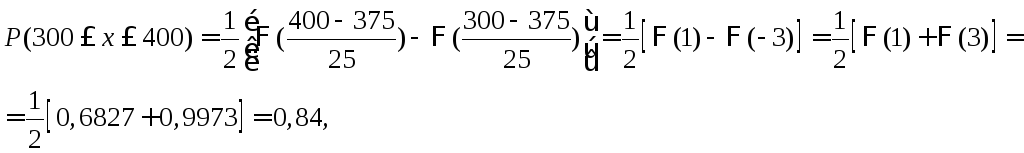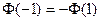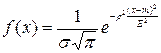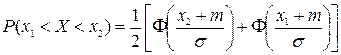Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
stusha |
Заголовок сообщения: Измерительный прибор имеет систематическую ошибку 5 м
|
||
|
Задача на нормальный закон распределения, помогите решить. Измерительный прибор имеет систематическую ошибку 5 м и серединную ошибку 50 м. какая вероятность того, что ошибка измерения не привысит по абсолютной величине 5 м.
|
||
| Вернуться к началу |
|
||
 |
Добавлено: 18 дек 2011, 14:33 
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Прибор состоит из 15 узлов
в форуме Теория вероятностей |
Alexandr42 |
1 |
391 |
05 апр 2017, 15:45 |
|
Прибор состоит из n элементов
в форуме Комбинаторика и Теория вероятностей |
Tatiana_1 |
1 |
99 |
21 сен 2022, 15:50 |
|
Найдите вероятность, что прибор выключен
в форуме Комбинаторика и Теория вероятностей |
Yanchik |
1 |
115 |
31 окт 2022, 19:50 |
|
Где я допустил ошибку?
в форуме Пределы числовых последовательностей и функций, Исследования функций |
Garfield |
8 |
365 |
06 окт 2017, 21:39 |
|
Найти ошибку
в форуме Дифференциальные и Интегральные уравнения |
NERFSD |
2 |
326 |
08 ноя 2017, 19:49 |
|
Найти ошибку
в форуме Аналитическая геометрия и Векторная алгебра |
tanyhaftv |
3 |
232 |
16 фев 2019, 23:37 |
|
Укажите ошибку
в форуме Алгебра |
Andreww |
3 |
309 |
22 фев 2018, 17:19 |
|
Найти ошибку в композиции
в форуме Дискретная математика, Теория множеств и Логика |
ZeGRyX |
1 |
155 |
08 окт 2020, 13:25 |
|
Покажите ошибку в доказательствах
в форуме Комплексный анализ и Операционное исчисление |
sa233091 |
3 |
278 |
11 авг 2016, 21:23 |
|
Помогите найти ошибку
в форуме Дифференциальные и Интегральные уравнения |
Danoldjar |
2 |
451 |
24 сен 2015, 10:54 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 7 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Powered by phpBB © 2000, 2002, 2005, 2007 phpBB Group
Вы можете создать форум бесплатно PHPBB3 на Getbb.Ru, Также возможно сделать готовый форум PHPBB2 на Mybb2.ru
Русская поддержка phpBB
Полученный результат позволяет сформулировать правило «трех сигм»: если случайная величина распределена нормально, то модуль ее отклонения от х = а не превосходит 3σ.
Числовые характеристики
Для вычисления математического ожидания нормально распределенной случайной величины воспользуемся тем, что интеграл Пуассона
|
z2 |
|||||||||||||||||||||||||||||||
|
e 2 dz |
2 . |
||||||||||||||||||||||||||||||
|
1 |
( x a )2 |
x a |
1 |
z2 |
|||||||||||||||||||||||||||
|
) |
|||||||||||||||||||||||||||||||
|
M(X) |
xe 2 2 dx (z |
( z a)e 2 dz |
|||||||||||||||||||||||||||||
|
2 |
2 |
||||||||||||||||||||||||||||||
|
1 |
z2 |
a |
z2 |
a |
|||||||||||||||||||||||||||
|
ze |
2 dz |
e 2 dz |
0 |
2 |
a |
||||||||||||||||||||||||||
|
2 |
2 |
2 |
|||||||||||||||||||||||||||||
(первое слагаемое равно 0, так как подынтегральная функция нечетна, а пределы интегрирования симметричны относительно нуля).
|
1 |
( x a )2 |
||||||||||||||||||||||
|
D(X) |
(x a)2 e 2 2 dx |
||||||||||||||||||||||
|
2 |
|||||||||||||||||||||||
|
2 |
z2 |
z2 |
|||||||||||||||||||||
|
z |
ze 2 |
dz (u |
z, dv ze |
2 ) |
|||||||||||||||||||
|
2 |
|||||||||||||||||||||||
|
2 |
z2 |
z2 |
2 |
||||||||||||||||||||
|
z |
e 2 |
e 2 dz |
0 |
2 |
2 . |
||||||||||||||||||
|
2 |
2 |
||||||||||||||||||||||
.
Следовательно, параметры нормального распределения (а и σ) равны соответственно математическому ожиданию и среднему квадратическому отклонению исследуемой случайной величины.
|
Замечание. Можно показать, что для нормального распределения |
4 |
3 |
, и, |
|
4 |
соответственно, эксцесс Ех = 0. Для кривых с более острой вершиной Ех >0, в случае более плоской вершины Ех < 0.
Показательное распределение
Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью
63
|
f (x) |
0, |
x |
0 |
(8) |
|||
|
e |
x , x |
0. |
|||||
В отличие от нормального распределения, показательный закон определяется только одним параметром λ. В этом его преимущество, так как обычно параметры распределения заранее не известны и их приходится оценивать приближенно. Понятно, что оценить один параметр проще, чем несколько.
Найдем функцию распределения показательного закона:
|
x |
0 |
x |
||
|
F(x) |
f (t)dt |
0 dt |
e t dt 1 e x . |
|
|
0 |
||||
|
Следовательно, |
||||
|
F(x) |
0, |
x |
0 |
|
|
1 e |
x , |
x 0. |
||
Теперь можно найти вероятность попадания показательно распределенной случайной величины в интервал (а, b):
p(a X b) e a e b .
Значения функции е-х можно найти из таблиц.
Функция надежности
Пусть элемент (то есть некоторое устройство) начинает работать в момент времени t0 = 0 и должен проработать в течение периода времени t. Обозначим за Т непрерывную случайную величину – время безотказной работы элемента, тогда функция F(t) = p(T > t) определяет вероятность отказа за время t. Следовательно, вероятность безотказной работы за это же время равна
R(t) = p(T > t) = 1 – F(t).
Эта функция называется функцией надежности.
Показательный закон надежности
Часто длительность безотказной работы элемента имеет показательное распределение, то есть
F(t) = 1 – e— t .
Следовательно, функция надежности в этом случае имеет вид:
R(t) = 1 – F(t) = 1 – (1 – e— t) = e— t .
Определение. Показательным законом надежности называют функцию надежности, определяемую равенством
R(t) = e— t ,
где – интенсивность отказов.
64
Пример 4.
Пусть время безотказной работы элемента распределено по показательному закону с плотностью распределения f(t) = 0,1 e—0,1t при t ≥ 0. Найти вероятность того, что элемент проработает безотказно в течение 10 часов.
Решение.
Так как = 0,1, R(10) = e-0,1·10 = e-1 = 0,368.
Числовые характеристики
Для показательного распределения
|
M(X) |
xe |
xdx |
xe |
x |
e |
xdx |
||||||||||||||
|
0 |
0 |
0 |
||||||||||||||||||
|
1 |
1 |
|||||||||||||||||||
|
e |
x |
; |
||||||||||||||||||
|
0 |
||||||||||||||||||||
|
1 |
1 |
|||||||||||||||||||
|
D(X) |
x2 e xdx |
x2 e x |
2 xe |
xdx |
||||||||||||||||
|
2 |
2 |
|||||||||||||||||||
|
0 |
0 |
0 |
||||||||||||||||||
|
2 |
1 |
1 |
; |
1 |
. |
|||||||||||||||
|
2 |
2 |
2 |
||||||||||||||||||
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1.
Стрелок делает 6 выстрелов по мишени. Вероятность попадания при каждом выстреле равна 0,7. Для случайной величины Х – числа попаданий – найти вероятность того, что Х < 3.
Указание
Случайная величина Х распределена по биномиальному закону. Найдите вероятности того, что Х равна 0, 1 и 2.
Решение
Случайная величина Х распределена по биномиальному закону, поэтому
|
p(X k) |
C6k 0, 7k 0, 36 k |
|||||
|
p(0) |
0, 36 |
0, 000729; |
||||
|
p(1) |
6 |
0, 7 |
0, 35 |
0, 010206; |
||
|
p(2) |
C62 |
0, 49 0, 34 |
0, 059535; |
|||
|
p(X 3) |
p(0) |
p(1) |
p(2) 0, 07047. |
Ответ: 0,07047.
65
Задача 2.
Стрелок делает 6 выстрелов по мишени. Вероятность попадания при каждом выстреле равна 0,7. Для случайной величины Х – числа попаданий – найти дисперсию.
Указание
Случайная величина Х распределена по биномиальному закону, поэтому D(X) = npq.
Решение
D(X) npq 6 0,7 0, 3 1, 26.
Ответ: 1,26.
Задача 3.
Вероятность повреждения изделия при перевозке составляет 2%. Случайная величина Х – число изделий из партии в 100 штук, поврежденных при перевозке. Найти вероятность того, что X < 2 (ответ округлить до третьего знака после запятой).
Указание
Можно считать, что Х распределена по закону Пуассона, то есть
|
p(X k) |
k e |
, |
np |
|
|
k ! |
||||
(здесь п – число изделий, р – вероятность повреждения одного изделия).
Решение
Воспользуемся формулой Пуассона:
|
p(X |
k) |
k e |
, |
np |
|
|
k ! |
|||||
|
2k e 2 |
|||||
|
2, |
p(X |
k) |
k ! . |
||
|
p(X 0) e 2 , p(X 1) 2e 2 , p(X 2) 2e 2 , |
|||||
|
p(X 2) p(X |
0) p(X 1) |
p(X |
2) 5e 2 0, 677. |
Ответ: 0,677.
Задача 4.
Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляют до ближайшего числа на шкале. Полагая, что ошибка измерения Х распределена по равномерному закону, найти дисперсию D(X).
Указание
Воспользуйтесь формулой для вычисления дисперсии равномерно распределенной случайной величины:
66
|
D(X) |
(b a)2 |
. |
|||
|
12 |
|||||
|
Решение |
|||||
|
a 0, b 0, 2, D(X) |
(b a)2 |
0,04 |
1 |
. |
|
|
12 |
12 |
300 |
|||
Ответ: 3001 .
Задача 5.
Измерительный прибор имеет систематическую ошибку 5 м, а случайные ошибки распределены по нормальному закону со средним квадратическим отклонением 75 м. Найти вероятность того, что ошибка измерения не превысит по модулю 5 м.
Указание
Из условия задачи следует, что параметры нормального закона а = 5, = 75. Для определения искомой вероятности воспользуйтесь формулой
|
p( |
X |
) |
a |
a |
. |
|||||
|
Решение |
||||||||||
|
Параметры нормального закона а = 5, |
= 75. Тогда |
|||||||||
|
p( 5 |
X |
5) |
5 |
5 |
5 |
5 |
||||
|
75 |
75 |
|||||||||
|
(0) |
( 0, 133) |
0 0, 053 |
0, 053. |
Ответ: 0,053.
Задача 6.
Какой наименьшей ширины должно быть поле допуска, чтобы с вероятностью не более 0,0027 получалась деталь с контролируемым размером вне поля допуска, если случайные отклонения размера от середины поля допуска распределены по нормальному закону с параметрами а = 0, = 5?
Указание
Используйте «правило трех сигм».
Решение
Если вероятность выхода размера детали из поля допуска равна 0,0027, то вероятность того, что размер попадает в поле допуска, равна 1 – 0,0027 = 0,9973. Именно такова вероятность попадания нормально распределенной случайной величины в интервал (а — 3 , а + 3 ). Следовательно, размеры
67
поля допуска: (0 – 15, 0 + 15) = (-15, 15), а ширина поля допуска – не менее
30.
Ответ: 30.
Задача 7.
Среднее время безотказной работы прибора равно 80 часам. Полагая, что время безотказной работы распределено по показательному закону, найти вероятность того, что в течение 100 часов прибор не выйдет из строя.
|
Указание |
||||
|
Найдите значение параметра |
из условия, что М(Х) = 1/ , и воспользуйтесь |
|||
|
формулой |
||||
|
R(t) |
e |
t . |
||
|
Решение |
||||
|
1 |
1 |
0, 0125; |
||
|
M(X) |
80 |
|||
|
R(100) |
e 0,0125 100 |
e 1,25 0, 286. |
||
|
Ответ: 0,286. |
1.2.4. Двумерные случайные величины. Коррелированность случайных величин
Наряду с одномерными случайными величинами, возможные значения которых определяются одним числом, теория вероятностей рассматривает и многомерные случайные величины. Каждое возможное значение такой величины представляет собой упорядоченный набор нескольких чисел. Геометрической иллюстрацией этого понятия служат точки п-мерного пространства, каждая координата которых является случайной величиной (дискретной или непрерывной), или п-мерные векторы. Поэтому многомерные случайные величины называют еще случайными векторами.
Дискретные двумерные случайные величины
Закон распределения дискретной двумерной случайной величины (Х, Y) имеет вид таблицы с двойным входом, задающей перечень возможных значений каждой компоненты и вероятности p(xi, yj), с которыми величина принимает значение (xi, yj):
68
|
Y |
Х |
||||||
|
x1 |
x2 |
… |
xi |
… |
xn |
||
|
y1 |
p(x1, y1) |
p(x2, y1) |
… |
p(xi, y1) |
… |
p(xn, y1) |
|
|
… |
… |
… |
… |
… |
… |
… |
|
|
yj |
p(x1, yj) |
p(x2, yj) |
… |
p(xi, yj) |
… |
p(xn, yj) |
|
|
… |
… |
… |
… |
… |
… |
… |
|
|
ym |
p(x1, ym) |
p(x2, ym) |
… |
p(xi, ym) |
… |
p(xn, ym) |
При этом сумма вероятностей, стоящих во всех клетках таблицы, равна 1. Зная закон распределения двумерной случайной величины, можно найти законы распределения ее составляющих. Действительно, событие Х = х1 представляется собой сумму несовместных событий (X = x1, Y = y1), (X = x1, Y = y2),…, (X = x1, Y = ym), поэтому
р(Х = х1) = p(x1, y1) + p(x1, y2) +…+ p(x1, ym)
(в правой части находится сумма вероятностей, стоящих в столбце, соответствующем Х = х1). Так же можно найти вероятности остальных возможных значений Х. Для определения вероятностей возможных значений Y нужно сложить вероятности, стоящие в строке таблицы, соответствующей
Y = yj.
Пример 1.
Дан закон распределения двумерной случайной величины:
|
Y |
X |
||
|
-2 |
3 |
6 |
|
|
-0,8 |
0,1 |
0,3 |
0,1 |
|
-0,5 |
0,15 |
0,25 |
0,1 |
Найти законы распределения составляющих.
Решение. Складывая стоящие в таблице вероятности «по столбцам», получим ряд распределения для Х:
Складывая те же вероятности «по строкам», найдем ряд распределения для Y:
Непрерывные двумерные случайные величины
Функцией распределения F(x, y) двумерной случайной величины (X, Y) называется вероятность того, что X < x, a Y < y:
F(x, y) p(X x,Y y). (1)
69
Это означает, что точка (X, Y) попадет в область, заштрихованную на рис. 1, если вершина прямого угла располагается в точке (х, у).
Замечание. Определение функции распределения справедливо как для непрерывной, так и для дискретной двумерной случайной величины.
Свойства функции распределения:
1)0 ≤ F(x, y) ≤ 1 (так как F(x, y) является вероятностью).
2)F(x, y) есть неубывающая функция по каждому аргументу:
F(x2, y) ≥ F(x1, y), если x2 > x1; F(x, y2) ≥ F(x, y1), если y2 > y1.
Доказательство.
F(x2, y) = p(X < x2, Y < y) = p(X < x1, Y < y) + p(x1 ≤ X < x2, Y < y) ≥ ≥ p(X < x1, Y < y) = F(x1, y).
Аналогично доказывается и второе утверждение.
3)Имеют место предельные соотношения:
|
a) |
F( |
, y) |
0; |
|
b) |
F(x, |
) |
0; |
|
c) |
F( |
, |
) 0; |
d)F( , ) 1.
Доказательство.
События а), b) и с) невозможны ( так как невозможно событие
X или Y ),
а событие d) достоверно, откуда следует справедливость приведенных
|
равенств. |
||
|
4) |
При у = |
функция распределения двумерной случайной величины |
|
становится функцией распределения составляющей Х: |
||
|
F(x, ) F1(x). |
||
|
При |
х = |
функция распределения двумерной случайной величины |
становится функцией распределения составляющей Y :
F( , y) F2(y).
70
Доказательство.
Так как событие Y < достоверно, то
F(x, ) p(X x) F1(x).
Аналогично доказывается второе утверждение.
Плотностью совместного распределения вероятностей (двумерной плотностью вероятности) непрерывной двумерной случайной величины называется смешанная частная производная 2-го порядка от функции распределения:
|
f (x, y) |
2F(x, y) |
. |
(2) |
|
|
x y |
||||
Замечание. Двумерная плотность вероятности представляет собой предел отношения вероятности попадания случайной точки в прямоугольник со сторонами х и у к площади этого прямоугольника при х 0, у 0.
Свойства двумерной плотности вероятности:
1) f(x, y) ≥ 0 (см. предыдущее замечание: вероятность попадания точки в прямоугольник неотрицательна, площадь этого прямоугольника положительна, следовательно, предел их отношения неотрицателен).
yx
2)F(x, y) f (x, y)dxdy
(cледует из определения двумерной плотности вероятности).
yx
3)F(x, y) f (x, y)dxdy
(поскольку это вероятность того, что точка попадет на плоскость Оху, то есть достоверного события).
Вероятность попадания случайной точки в произвольную область
Пусть в плоскости Оху задана произвольная область D. Найдем вероятность того, что точка, координаты которой представляют собой систему двух случайных величин (двумерную случайную величину) с плотностью распределения f(x, y), попадет в область D. Разобьем эту область прямыми, параллельными осям координат, на прямоугольники со сторонами х и у. Вероятность попадания в каждый такой прямоугольник равна f ( i , i ) x y,
где ( i , i ) — координаты точки, принадлежащей прямоугольнику. Тогда вероятность попадания точки в область D есть предел интегральной суммы
|
n |
||
|
f ( |
i , i ) x y, , |
|
|
i 1 |
||
|
то есть |
||
|
p((X,Y) D) |
f (x, y)dxdy. |
(3) |
|
D |
71
Отыскание плотностей вероятности составляющих двумерной случайной величины
Выше было сказано, как найти функцию распределения каждой составляющей, зная двумерную функцию распределения. Тогда по определению плотности распределения
|
x |
||||||||
|
d |
f (x, y) |
|||||||
|
f1 |
(x) |
dF1(x) |
dF(x, ) |
f (x, y)dy. (4) |
||||
|
dx |
dx |
dx |
||||||
Аналогично находится
Условные законы распределения составляющих дискретной двумерной случайной величины
Рассмотрим дискретную двумерную случайную величину и найдем закон распределения составляющей Х при условии, что Y примет определенное значение (например, Y = у1). Для этого воспользуемся формулой Байеса, считая гипотезами события Х = х1, Х = х2,…, Х = хп, а событием А – событие Y = у1. При такой постановке задачи нам требуется найти условные вероятности гипотез при условии, что А произошло. Следовательно,
|
р |
(x |
) |
p(xi , y1 ) |
. |
|
y1 i |
p(y1 ) |
|||
Таким же образом можно найти вероятности возможных значений Х при условии, что Y принимает любое другое свое возможное значение:
|
р |
(x ) |
p(xi , y j ) |
. |
(5) |
|
|
y j |
|||||
|
i |
p(y j ) |
||||
Аналогично находят условные законы распределения составляющей Y:
px (y j ) p(xi , y j ) . (5 ) i p(xi )
Пример 2.
Найдем закон распределения Х при условии Y = -0,8 и закон распределения Y при условии Х = 3 для случайной величины, рассмотренной в примере 1.
|
р(x1 /y1 ) |
0, 1 |
1 |
0, 2; р(x2 |
/y1 ) |
0, 3 |
3 |
0, 6; |
||||||
|
0, 5 |
5 |
0, 5 |
5 |
||||||||||
|
р(x3 /y1 ) |
0, 1 |
1 |
0, 2. |
||||||||||
|
0, 5 |
5 |
||||||||||||
|
р(у1 |
/х2 ) |
0, 3 |
6 |
; р(у2 |
/х2 ) |
0, 25 |
5 |
. |
|||||
|
0, 55 |
11 |
0, 55 |
11 |
||||||||||
72
Соседние файлы в папке ТВиМС
- #
- #
- #
- #
Тема. Законы распределения случайных величин
1. Нормальное распределение
Пример 1.Вес вылавливаемых в пруду
рыб подчиняется нормальному закону с
математическим ожиданием, равным 375 г,
и средним квадратическим отклонением
25 г. Определить вероятность того, что
вес одной пойманной рыбы будет заключен
в пределах от 300 до 400г.
Решение.
Дано: М(Х)=а=375 г.,
г.,
с=300г.,d=400г.
Найдем искомую вероятность.
где функции Лапласа Ф(1) = 0,6827, Ф(3) = 0,9973.
Пример 2. Ошибка измерения прибора
подчиняется нормальному распределению.
С вероятностью 0,92 ошибка измерения не
превосходит 4. Найти среднее квадратическое
отклонение ошибки прибора. Систематическая
ошибка отсутствует.
Решение.
Дано:
,
Воспользовавшись второй теоремой о
нормальной случайной величине, найдем
величину
.
Из таблицы Лапласа, зная
, найдемt=1,75.
Тогда
или
Ответ:
.
2. Равномерное распределение
Пример 3. Цена деления шкалы
прибора 0,5 вольт. При измерениях показания
округляются до ближайшего целого
деления. Найти вероятность того, что
при считывании показаний будет сделана
ошибка, не превышающая 0,01 вольт.
Решение.
Дано: Случайная величина Х — истинное
показание прибора имен равномерное
распределение с параметрами а=0 ,в=0,5. Тогда
.
Искомая вероятность – это вероятность
показания х либо на
,
либо на
.
Задания для самостоятельной работы
1) Размер детали подчиняется
нормальному закону распределения со
средней арифметической 15 мм и дисперсией
0,25. Определить ожидаемый процент брака,
если допустимые размеры находятся в
пределах от 14 мм до 17 мм. Найти выражение
интегральной и дифференциальной функции.
2) Изготовленные цехом детали по
размерам диаметра распределяются по
нормальному закону с математическим
ожиданием, равным 4,5 см, и средним
квадратическим отклонением 0,5 см.
Определить вероятность того, что размер
диаметра наудачу взятой детали отклонится
от математического ожидания не более,
чем на 1 см.
3) Математическое ожидание нормально
распределенной случайной величины
равно 15, среднее квадратическое отклонение
равно 5. Определить вероятность того,
что абсолютная величина отклонения
Х-М(Х) будет меньше 10.
4) Ошибка измерения – нормально
распределенная случайная величина с
дисперсией, равной 100. Систематическая
ошибка отсутствует. Найти вероятность
того, что ошибка измерения окажется в
интервале (3;6).
5) Ошибка взвешивания – случайная
нормально распределенная величина с
дисперсией 400. Весы заранее настроены
на обвес 50 г. Найти вероятность того,
что ошибка взвешивания находится в
пределах от 30 до 70 г.
6) Автобус некоторого маршрута идет
с интервалом в десять минут. Пассажир
в какой-то момент подходит к остановке.
Время, в течении которого пассажир
ожидает автобус, представляет случайную
величину, имеющую равномерное
распределение. Определить дифференциальную
функцию распределения этой случайной
величины, ее математическое ожидание
и дисперсию.
7) По данным задачи 6 определить
вероятность того, что пассажир подошедший
к остановке, будет ждать автобус менее
4 минут.
Цена деления шкалы измерительного
прибора равна 0,2. Показания прибора
округляют до ближайшего целого деления.
Найти вероятность того, что при отсчете
будет сделана ошибка:
а) меньшая 0,04;
б) большая 0,05.
9) Минутная стрелка электрических
часов перемещается скачком в конце
каждой минуты. Найти вероятность того,
что в данное мгновение часы покажут
время, которое отличается от истинного
не более чем на 20 сек.
Форма контроля:
Проверка
решений задач и заданий
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Решение типовых задач. Пример 12.1. Измерение дальности до объекта сопровождается систематическими и случайными ошибками
Пример 12.1. Измерение дальности до объекта сопровождается систематическими и случайными ошибками. Систематическая ошибка равна 50 м в сторону занижения дальности. Случайные ошибки подчиняются нормальному закону со средним квадратическим отклонением 
=100 м. Найти:
1) вероятность измерения дальности с ошибкой, не превосходящей по абсолютной величине 150 м,
2) вероятность того, что измеренная дальность не превзойдет истинной.
Обозначим через X суммарную ошибку измерения дальности. Ее систематическая составляющая 
— 50 м. Следовательно, плотность вероятности суммарной ошибки имеет вид
.
1) Согласно общей формуле имеем
.
Интеграл вероятности является функцией нечетной, поэтому
.
;
.
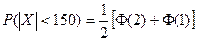
2) Вероятность того, что измеренная дальность не превзойдет истинной,
.
Так как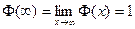 
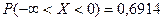
, а из таблицы находим 
, то
.
Пример 12.2. Определить срединную ошибку прибора, если систематических ошибок он не имеет, а случайные распределены по нормальному закону и с вероятностью 0,8 не выходят за пределы ± 20 м.
Из условия задачи следует, что
.
Неизвестное значение срединной ошибки находим как решение уравнения
.
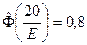
С помощью таблицы получим
,
м.
Дата добавления: 2014-12-23 ; просмотров: 177 ; Нарушение авторских прав
Источник
Занятие 12. Закон нормального распределения.
Краткая теоретическая часть
Плотность вероятности нормально распределенной случайной величины имеет вид
,
где 
— среднее квадратическое отклонение, 
— срединное отклонение (иногда называемое и «вероятным отклонением»), 
Вероятность попадания нормально распределенной случайной величины X в интервал 
вычисляется по одной из следующих формул:
1) 
,
где 
— функция Лапласа (интеграл вероятности);
2) 
,
где 
— приведенная функция Лапласа.
Значения функций 
и 
даны в специальных таблицах.
Во всех задачах данного параграфа ошибки измерения считаются нормальными величинами.
1. Нормальное распределение играет достаточно важную роль в теории вероятностей и среди законов занимает особое положение. Укажите причины, по которым, на Ваш взгляд, это происходит:
а) Это наиболее часто употребляемый во многих приложениях закон распределения
б) Нормальный закон распределения применим как для дискретных, так и для непрерывных случайных величин
в) Нормальный закон распределения является предельным законом, к которому сходятся другие при весьма типичных часто встречающихся условиях
г) Нормальный закон распределения таков, что позволяет характеризовать сравнительную крутость других законов относительно него
2. Плотность вероятности нормально распределенной случайной величины имеет вид:
а)
б)
в) или
г) 
д) 
е) или
3. Параметры 
и 
закона нормального распределения совпадают с математическим ожиданием и среднеквадратическим отклонением нормально распределенной случайной величины соответственно. Следовательно, они определенным образом характеризуют случайную величину. А как? Выберите наиболее точный, на Ваш взгляд, вариант ответа.
а) Характеризуют форму кривой распределения и положение распределения случайной величины на оси абсцисс соответственно
б) Характеризуют положение распределения случайной величины на оси абсцисс и форму кривой распределения соответственно
в) Определяют центр рассеянья и центр симметрии случайной величины соответственно
г) Определяют центр симметрии и центр рассеянья случайной величины соответственно
4. Какой особенностью обладают моменты нормального распределения?
а) Все четные центральные моменты равны нулю.
б) Все нечетные центральные моменты равны нулю.
в) Все центральные моменты равны нулю
5. Одной из формул, по которым можно вычислить вероятность попадания нормально распределенной случайной величины 
в заданный интервал является (здесь — функция Лапласа (интеграл вероятности)):
а) 
б) 
в) 
г) 
6. Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, обладают следующим свойством:
в) равны параметру Пуассона
Решение типовых задач
Пример 12.1. Измерение дальности до объекта сопровождается систематическими и случайными ошибками. Систематическая ошибка равна 50 м в сторону занижения дальности. Случайные ошибки подчиняются нормальному закону со средним квадратическим отклонением =100 м. Найти:
1) вероятность измерения дальности с ошибкой, не превосходящей по абсолютной величине 150 м,
2) вероятность того, что измеренная дальность не превзойдет истинной.
Обозначим через X суммарную ошибку измерения дальности. Ее систематическая составляющая 
— 50 м. Следовательно, плотность вероятности суммарной ошибки имеет вид
.
1) Согласно общей формуле имеем
.
Интеграл вероятности является функцией нечетной, поэтому
.
;
.
2) Вероятность того, что измеренная дальность не превзойдет истинной,
.
Так как 
, а из таблицы находим 
, то
.
Пример 12.2. Определить срединную ошибку прибора, если систематических ошибок он не имеет, а случайные распределены по нормальному закону и с вероятностью 0,8 не выходят за пределы ± 20 м.
Из условия задачи следует, что
.
Неизвестное значение срединной ошибки находим как решение уравнения
.
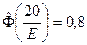
С помощью таблицы получим
,
м.
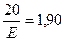
12.4. Задачи для самостоятельной работы
12.1. Измерительный прибор имеет систематическую ошибку 5 м и среднюю квадратическую ошибку 75 м, Какова вероятность того, что ошибка измерения не превзойдет по абсолютной величине 5 м?
(Ответ: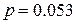 
)
12.2. Систематическая ошибка удержания высоты самолетом +20 м, а случайная ошибка имеет среднее квадратическое отклонение 75 м. Для полета самолета отведен коридор высотой 100 м. Какова вероятность, что самолет будет лететь ниже, внутри и выше коридора, если самолету задана высота, соответствующая середине коридора?
12.3. Срединная ошибка измерения дальности радиолокатором равна 25 м, а систематическая ошибка отсутствует. Определить:
а) дисперсию ошибок измерения дальности;
б) вероятность получения ошибки измерения дальности, по абсолютной величине не превосходящей 20 м.
12.4. Случайное отклонение размера детали от номинала при изготовлении ее на данном станке имеет нулевое математическое ожидание и среднее квадратическое отклонение, равное 5 мк. Сколько необходимо изготовить деталей, чтобы с вероятностью не менее 0,9 среди них была хотя бы одна годная, если для годной детали допустимо отклонение размера от номинала не более, чем на 2 мк?
(Ответ: 
)
12.5. Даны две случайные величины X и Y, имеющие одинаковые дисперсии, но первая распределена нормально,а вторая равномерно. Определить соотношение между их срединными отклонениями.
(Ответ: 
)
12.6. Нормально распределенная случайная величина X имеет математическое ожидание 
м и срединное отклонение 10 м. Вычислить таблицу функции распределения для значений аргумента через каждые 10 м и построить график.
12.7. Систематическая ошибка высотомера равна +20 м, а случайные ошибки распределены по нормальному закону. Какую среднюю квадратическую ошибку должен иметь высотомер, чтобы с вероятностью 0,9 ошибка измерения высоты по абсолютной величине была меньше 100 м?
(Ответ: 
. Получающееся трансцендентное уравнение проще решить графически)
12.8. Найти связь между средним арифметическим отклонением
нормально распределенной случайной величины и ее средним квадратическим отклонением.
(Ответ: 
)
12.9. Определить для нормально распределенной случайной величины X, имеющей М [X] = 0,
1) 
2) (при 
(Ответ: 1) 0,1587; 0,0228; 0,00135; 2) 0,3173; 0,0455; 0,0027)
12.10. Заряд охотничьего пороха отвешивается на весах, имеющих среднюю квадратическую ошибку взвешивания 150 мг. Номинальный вес порохового заряда 2,3 г. Определить вероятность повреждения ружья, если максимально допустимый вес порохового заряда 2,5 г.
(Ответ: 
)
12.11. Производятся два независимых измерения прибором, имеющим среднюю квадратическую ошибку 30м и систематическую ошибку +10м. Какова вероятность того, что обе ошибки измерений, имея разные знаки, по абсолютной величине превзойдут 10 м?
(Ответ: 
)
12.12. На плоскости проведены две параллельные прямые, расстояние между ними L. На эту же плоскость бросается круг радиуса R. Центр рассеивания расположен на расстоянии b от одной из линий во внешнюю сторону. Срединное отклонение центра круга в направлении, перпендикулярном линии, равно Е.
Определить при одном бросании:
а) вероятность накрытия кругом хотя бы одной прямой;
б) вероятность накрытия обеих прямых, если L= 10м, R = 8м, b=5м, E=10м.
12.13. Изделие считается высшего качества, если отклонение его размеров от номинала не превосходит по абсолютной величине 3,45 мм. Случайные отклонения размера изделия от номинала подчиняются нормальному закону со средним квадратическим отклонением, равным 3 мм, а систематические отклонения отсутствуют. Определить среднее число изделий высшего сорта, если изготовляются четыре изделия.
(Ответ: 
изделия)
12.14. Какой ширины должно быть поле допуска, чтобы с вероятностью не более 0,0027 получалась деталь с контролируемым размером вне поля допуска, если случайные отклонения размера от середины поля допуска подчиняются закону нормального распределения с параметрами 
= 0 и = 5 мк
12.15. Какое наибольшее расстояние допустимо между двумя рыболовецкими судами, идущими параллельными курсами, чтобы вероятность обнаружения косяка рыбы, находящегося посередине между ними, была не менее 0,5, если дальность обнаружения косяка для каждого из судов является независимой нормально распределенной случайной величиной с 
км и средним квадратическим отклонением =1,1 км?
12.16. При большом числе измерений установлено, что 75% ошибок
б) не превосходят по абсолютной величине 1,25 мм.
Заменяя частоты появления ошибок их вероятностями, определить в обоих случаях среднее квадратическое отклонение ошибок измерения, считая их нормально распределенными с нулевым математическим ожиданием.
12.17. Случайное отклонение X размера детали от номинала распределено по нормальному закону с математическим ожиданием и средним квадратическим отклонением . Годными деталями являются те, для которых а b.
а) функцию распределения случайных отклонений размеров деталей, подлежащих переделке;
б) функцию распределения случайных отклонений размеров годных деталей.
(Ответ: а) 
) для 
; б) 
для 
)
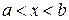
12.18. Нормально распределенная случайная величина X имеет нулевое математическое ожидание. Определить среднее квадратическое отклонение , при котором вероятность 
была бы наибольшей ( 
).
(Ответ: 
)
1. Б.В. Гнеденко. Курс теории вероятностей, Изд. «Наука», 1969.
2. Е.С. Вентцель. Теория вероятностей, Изд. «Наука», 1969.
3. И.В. Дунин – Барковский, Н.В. Смирнов, Теория вероятностей и математическая статистика, ГТТИ, 1965.
4. И.Н. Коваленко, А.А. Филиппова, Теория вероятностей и математическая статистика, «Высшая школа», 1973.
5. Ю.В. Кожевников, Теория вероятностей и математическая статистика, Изд. «Машиностроение», 2002.
6. Сборник задач по теории вероятностей, математической статистике и теории случайных функций. Под редакцией А.А Свешникова, «Наука», 1970.
7. Л.Д. Мешалкин, Сборник задач по теории вероятностей, Изд. «МГУ». М., 1963.
8. Г.В. Емильянов , В.П. Скитович, Задачи по теории вероятностей и математической статистике, Изд. «ЛГУ». Ленинград, 1967.
9. В.В. Скворцов, Теория вероятностей, Изд. «Мир». М., 1993.
10. Руководство для инженеров по решнию задач теории вероятностей. Под редакцией А.А Свешникова, «Судпромгиз». Ленинград, 1962.
Источник