6.1. Определения коэффициента ошибок
6.2. Математическое выражение коэффициента битовых ошибок
6.3. Нормы на параметры ошибок систем передачи
6.4. Принципы построения измерителей ошибок
6.5. Техника измерения коэффициента ошибок
6.1. Определения коэффициента ошибок
Коэффициент ошибок – важнейшая характеристика линейного тракта. Он измеряется как для отдельных участков регенерации, так и для тракта в целом. Определяется коэффициент ошибок kОШ, по формуле:
kОШ = NОШ /N, (6.1)
где N – общее число символов, переданных за интервал измерения; NОШ – число ошибочно принятых символов за интервал измерения.
Измерение коэффициента ошибок носит статистический характер, так как получаемый за конечное время результат является случайной величиной. Относительную погрешность измерения в случае нормального закона распределения числа ошибок, что допустимо при N≥10, можно определить по формуле:
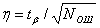
Здесь — коэффициент, зависящий от доверительной вероятности результата измерений:
, (6.3)
где — обратная функция интеграла вероятности
:
. (6.4)
Значение kОШ позволяет оценивать вероятность ошибки pОШ – количественную оценку помехоустойчивости. Область возможных значений оценки, в которой с заданной доверительной вероятностью будет находиться значение pОШ, определяется верхней (pВ) и нижней (pН) доверительными границами. При нормальном законе распределения числа ошибок значения pВ и pН определяются по формулам:
, (6.5)
, (6.6)
Очевидно, что точность оценок вероятности ошибки и коэффициента ошибки растет с увеличением N. Общее число символов цифрового сигнала, переданных за интервал измерения T, зависит от скорости передачи B: N = TB. Отсюда следует, что чем больше скорость передачи, тем быстрее и точнее можно оценить коэффициент ошибок.
6.2. Математическое выражение коэффициента битовых ошибок
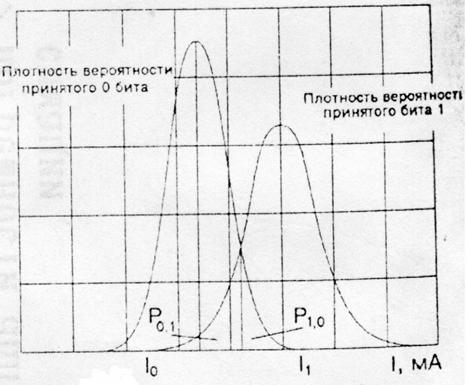
Определим коэффициент битовых ошибок для реальных приёмников, которым свойственно наличие различных источников шумов. При этом будем считать, что приёмник принимает решение, какой бит (0 или 1) был передан в каждом битовом интервале путем стробирования фототока. Очевидно, что из-за наличия шумов данное решение может быть неверным, что приводит к появлению ошибочных битов. Поэтому, чтобы определить коэффициент битовых ошибок, необходимо понять, каким образом приемник принимает решение относительно переданного бита.
Обозначим через I1 и I0 фототоки, стробированные приемником в течение 1 и 0 битов, соответственно, а через s12 и s02 соответствующие шумы. Принимая, что последние имеют гауссовское распределение, проблема установления истинного значения принятого бита имеет следующую математическую формулировку. Фототок для битов 1 и 0 является выборкой гауссовской переменной со средним значением I1 и вариацией s1, а приёмник должен отслеживать этот сигнал и решать, является ли переданный бит 0 или 1. При этом существует много возможных правил принятия решения, которые могут быть реализованы в приёмнике с целью минимизации коэффициента битовых ошибок. Для значения фототока I этим оптимальным решением является наиболее вероятное значение переданного бита, которое определяется путём сравнения текущего значения фототока с пороговым значением Iп, используемым для принятия решения.
Рисунок 6.1. Функция плотности вероятности фототока принятых сигналов
Пусть при I ³ Iп принимается решение о том, что был передан бит 1, в противном случае – бит 0. Когда биты 1 и 0 равновероятны, что и рассматривается в дальнейшем, пороговый ток приблизительно равен:
(6.7)
Геометрически Iп представляет собой значение тока I, для которого две кривые плотности вероятностей (рис. 6.1) пересекаются.
Вероятность того, что I < Iп, т. е. вероятность ошибки при передаче бита 1, обозначим через Р0,1, а вероятность решения для переданного бита 1, когда I ³ Iп при переданном 0, обозначим Р1,0.
Пусть Q(х) обозначает вероятность того, что нулевая средняя вариация гауссовской переменной превышает значение х, тогда:
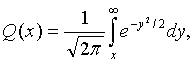
а
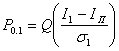
а
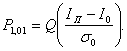
Можно показать [14], что BER определяется,
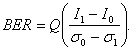
Очень важно отметить, что в ряде случаев эффективным является использование изменяемого в зависимости от уровня сигнала порога принятия решения, как, например, шума оптического усилителя. Многие высокоскоростные приёмники обладают такой особенностью. Однако более простые приемники имеют порог, соответствующий среднему уровню принимаемого тока, а именно (I1 + I0)/2. Такая настройка порогового значения дает большой коэффициент битовых ошибок, определяемый выражением [14].
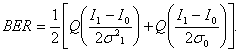
Выражение (6.11) можно использовать для оценки BER, когда известны как мощность полученного сигнала, соответствующего битам 0 и 1, так и статистика шумов.
6.3. Нормы на параметры ошибок систем передачи
Битовые ошибки являются основным источником ухудшения качества связи, проявляющегося в искажении речи в телефонных каналах, недостоверности передачи информации или снижении пропускной способности передачи данных, и характеризуются статистическими параметрами и нормами на них, которые определены соответствующей вероятностью выполнения этих норм. Последние делятся на долговременные и оперативные нормы, первые из которых определяются рекомендациями ITU-T G.821 и G.826, а вторые – М.2100, М.2110 и М.2120, при этом, согласно М.2100, качество цифрового тракта по критерию ошибок делят на три категории:
- нормальное – BER < 10-6;
- пониженное – 10-6 ≤ BER < 10-3 (предаварийное состояние);
- неприемлемое – BER ≥ 10-3 (аварийное состояние).
Так как появление ошибок является следствием совокупности всех текущих условий передачи цифровых сигналов, имеющих случайный характер, то при отсутствии данных о законе распределения ошибок его отдельные элементы могут быть определены с определенной степенью достоверности только по результатам продолжительных измерений. В то же время на практике необходимо, чтобы значения параметров ошибок для ввода в эксплуатацию и технического обслуживания систем передачи основывались на достаточно коротких интервалах времени измерения. Исходя из этого, были определены следующие параметры ошибок [14]:
- секунда с ошибками (error second, ES) – односекундный интервал, содержащий хотя бы один ошибочный бит;
- секунда, пораженная ошибками (severely error second, SES) – односекундный интервал с BER ≥ 10-3.
Данные параметры ошибок должны оцениваться в течение времени готовности (available time), отсчет которого начинается с первой секунды из десяти следующих друг за другом секунд, в каждой из которых BER<10-3. ITU-T M.2100 регламентирует нормы качества (performance objectives, PO) на выраженные максимальным процентом времени параметры ошибок, которые зависят только от скорости передачи и приводятся для условного эталонного соединения (hypothetical reference connection, HRC/HRX/) длиной 27500 км. При этом нормы качества распределяются по участкам соединения соответствующей категории качества. В качестве эталонной модели такого распределения принимается участок высокой категории качества протяженностью 25000 км, которому присваивается 40% от общей нормы качества на параметры ошибок передачи точка-точка, что в пересчете на 1 км, дает 0.0016 %/км.. Остальные 4 участка (2 среднего качества и 2 с приемлемым качеством) длиной 2 х 1250 км расположены по обе стороны от центрального. Поэтому распределение, пропорциональное протяженности L км тракта высокой категории качества, будет определяться, как
AL = 0.0016 · L %/км. (6.13)
Нормы качества на цифровые тракты и каналы подразделяются на настроечные и эксплуатационные, причем вводимые в эксплуатацию впервые или после проведения корректирующих действий они должны сдаваться по настроечным нормам качества, а в процессе эксплуатации должны соответствовать эксплуатационным нормам. Обычно [105] эксплуатационная норма представляется в виде эталонной нормы качества (reference performance objective, RPO)
RPO = A · T · PO, (6.14)
а настроечная, включающая запас на старение, используемая при вводе в эксплуатацию (bringing into service objective, BISO), определяется, как половина RPO, т.е.
BISO = RPO/2. (6.15)
Здесь PO – норма качества оцениваемого параметра, а T = 86400 с (одни сутки) – продолжительность измерений (количество односекундных интервалов).
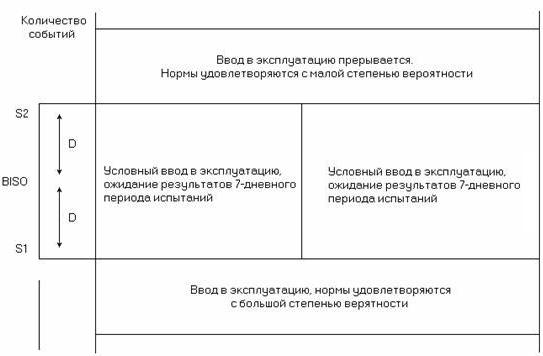
Для анализа результатов, полученных в процессе измерений, используются также предельные значения S1и S2 норм (рисунок 6.2), которые соответствуют числу событий (ES,SES) и определяются, как:
S1 = RPO/2 – D и S2 = RPO/2 + D, (6.16)
где D = 2 — дисперсия оцениваемого параметра.
Рисунок 6.2. Предельные значения и условия ввода в эксплуатацию системы передачи
При соответствии результатов измерений норме S1 цифровой тракт может быть введен в эксплуатацию без всякого сомнения, а при превышении нормы S2 в обязательном порядке требуется повышение качества испытываемого цифрового тракта, т.е. должны быть проведены корректирующие действия с повторными измерениями. Если значение ES или SES лежит в интервале от S1 до S2, цифровой тракт может быть введен в эксплуатацию условно или временно с продолжением измерений в течение 7 суток. Данный подход к оценке качества цифровых систем передачи по параметрам ошибок позволяет сократить время измерений и получить норму цифрового тракта суммированием норм цифровых участков. При этом значения RPO, D, S1 и S2 выражаются в виде числа событий за установленный интервал времени, а не в виде процентов времени.
Для измерения коэффициента ошибок разработан ряд специальных BER анализаторов – измерителей коэффициента ошибок, включающих генераторы псевдослучайных и детерминированных последовательностей передаваемых кодированных символов, а также приемное оборудование, осуществляющее собственно измерение коэффициента ошибок. В случае посимвольного сравнения кодов измерение может быть выполнено с использованием шлейфа, т.е. путем измерения ошибок с одной оконечной станции при установке на противоположном конце шлейфа. Другой метод основан на выделении ошибок благодаря избыточности используемых кодов и используется для измерений от передающей до приемной сторон тракта или участка линии, т.е. когда выделение и фиксация ошибок производятся на ее приемном конце. Очевидно, что в первом случае требуется использование одного комплекта, а во втором – двух комплектов приборов. При этом измеренное значение коэффициента ошибок отражает качество передачи при прохождении сигнала в обоих направлениях и в каждом направлении соответственно.
6.4. Принципы построения измерителей ошибок
В зависимости от скорости передачи контролируемой системы передачи в анализаторе используются различные схемотехнические решения.
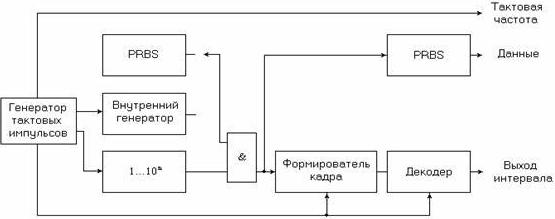
Рисунок 6.3. Генератор низкоскоростного BER анализатора
Низкоскоростной генератор тестовых кодов и детектор ошибок. Используемый в телекоммуникациях анализатор BER, состоящий [106] из генератора тестовых кодов и собственно анализатора ошибок, представлен на рисунках 6.3 и 6.4. Он предназначен для невысоких (до 200 Мбит/с) битовых скоростей, учитывая, что максимальные типовые скорости составляют 44.736 Мбит/с (DS3) в Северной Америке и 139.364 Мбит/с – за пределами Северной Америки.
PRBS с генератором кодовых групп, представленный на рис. 6.16, синхронизируется либо от источника тактового сигнала с фиксированной частотой (согласно G.703), либо от синтезатора, осуществляя тем самым изменение частоты синхронизации. В связи с этим использование данных средств требует задания некоторых определенных частот синхронизации и наличия возможности обеспечения их небольших смещений от ±15 до ±50 ppm. Для повторения тестовых кодов схема PRBS и генератор кодовых групп обычно имеют триггерную схему, управляющую либо выходным усилителем бинарных данных, который обеспечивает данные и данные с сопровождающим синхросигналом, либо выходную схему кодированных данных. Это позволяет создавать цикловую синхронизацию сигнала в соответствии с требованием, например, системы SONET/SDH. Кроме этого, данная схема способствует созданию соответствующего интерфейсного кода для эффективного восстановления тактовой синхронизации. Выходной усилитель обеспечивает необходимый уровень сигнала в соответствии со спецификацией электрического интерфейса, в том числе сигнала с чередованием полярности импульсов.
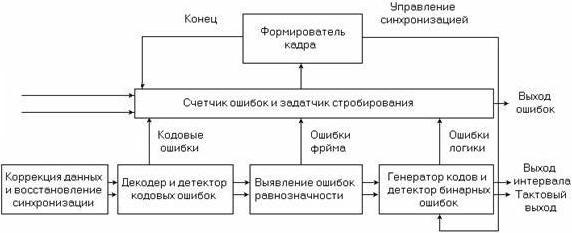
Рисунок 6.4. Низкоскоростной детектор ошибок
Детектор ошибок, показанный на рисунке 6.4, получает стандартный кодированный сигнал, восстанавливает генератор синхросигнала и устраняет кодирование для обеспечения бинарной даты и синхросигналов. Он обнаруживает любые нарушения алгоритма интерфейсного кода и посылает сигналы на счетчик ошибок, что составляет первый уровень процесса обнаружения ошибок. При работе с цикловыми сигналами приемник захватывает любой присутствующий элемент цикловой синхронизации, проверяет наличие цикловых ошибок и декодирует любые встроенные сигналы тревоги, или CRC биты, тем самым обеспечивая возможность измерения.
Наконец, бинарные данные и синхросигнал направляются на детектор ошибок и генератор эталонных тестовых кодов, которые проверяют полученный тестовый код бит за битом на предмет обнаружения логических ошибок. Временная база контролирует пропускание измерения для непрерывного, периодического и ручного режима. Накопленное количество ошибок обрабатывается для получения значения BER и анализа функционирования при наличии ошибок.
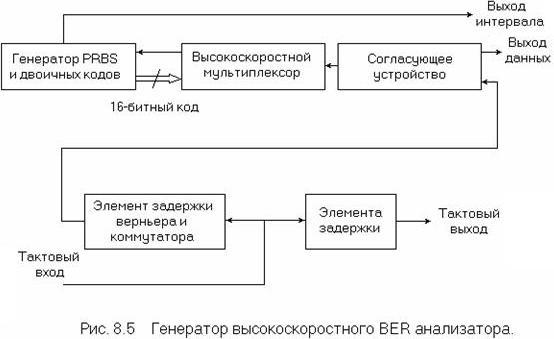
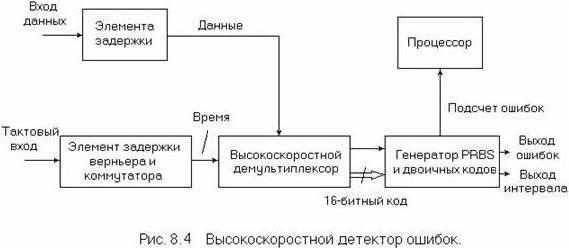
Высокоскоростной генератор тестовых кодов и детектор ошибок. На рисунках 6.5 и 6.6 показаны схемы [14] для 3 Гбит/с генератора тестовых кодов и детектора ошибок. Вследствие высокой битовой скорости генерация последовательных PRBS и кодовых групп на этой скорости не представляется целесообразной. Поэтому тестовые коды генерируются (рисунок 6.5) как параллельные 16-битные кодовые группы при максимальной скорости 200 Мбит/с, используя затем выполненные по биполярной технологии регистраторы смещения и высокоемкостную память. Высокоскоростные схемы обычно выполняются на основе арсенид-галлиевых логических схем, преобразующих параллельные данные в последовательный поток на скорости до 3 Гбит/с.
Согласно данной схеме, вход синхросигнала генерируется синтезатором частоты, согласующее устройство управляется через линию фиксированной задержки, а генератор тестовых кодов и выходной усилитель синхронизируются через схему дискретной и плавно изменяемой задержки, так что фаза синхросигнала/данных может изменяться как в положительном направлении, так и в отрицательном. Дискретные значения задержки составляют 250, 500 и 1000 пс, тогда как диапазон плавной задержки лежит в пределах от 0 до 250 пс с 1 пс инкрементом.
Корректор временной диаграммы, связанный с выходным усилителем, пересинхронизирует данные через триггер D типа для поддержания минимального фазового дрожания. Так как подобный тип тестового устройства обычно используется при проведении лабораторных измерений, выходные уровни синхросигнала и данных и постоянные смещения могут варьироваться для того или иного конкретного случая использования.
Детектор ошибок, показанный на рис. 6.6, имеет простое параллельное соединение, в связи с чем входы синхросигнала и данных проходят через схемы дискретной и плавной задержки, обеспечивая оптимальную настройку при обнаружении ошибок для любой фазы синхросигнала/данных. Действительно, путем настройки под контролем внутреннего процессора решающего порога и фазы синхросигнала условия функционирования детектора ошибок могут быть оптимизированы автоматически. Высокоскоростной демультиплексор преобразует последовательный поток данных в 16-битные параллельные кодовые группы наряду с поделенным на 16 синхросигналом. Параллельно соединенный генератор эталонных тестовых кодов синхронизируется с входными данными и осуществляет сравнение битов, поэтому любая ошибка фиксируется одним из двух счетчиков, первый из которых подсчитывает число ошибок, а второй – общее число битов. Процессор измерения обеспечивает анализ функционирования при наличии ошибок с разрешением до 1 мс.
6.5. Техника измерения коэффициента ошибок
Рассмотрим измерение коэффициента ошибок путем посимвольного сравнения и подсчета ошибочно принятых элементарных импульсов. Для этого вначале (перед измерением) на передающей станции с помощью оптического аттенюатора устанавливают заданный в технических условиях на аппаратуру линейного тракта уровень оптического излучения. Затем на передающем конце подключают генератор испытательных сигналов, а на приемном – измеритель коэффициента ошибок и, изменяя значения уровней средней мощности, измеряют коэффициент ошибок. Время измерения определяют в зависимости от скорости передачи, объема информации и значений коэффициента ошибок Кошi (BERi).
Коэффициент ошибок при заданном уровне оптического излучения вычисляют по формуле [14]
(6.17)
где
,
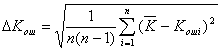
где и
— погрешность и среднее значение коэффициента ошибок при пяти и более измерениях с интервалом 3 мин, соответственно, a — коэффициент, учитывающий наличие погрешности измерения при проведении n измерений.
From Wikipedia, the free encyclopedia
In digital transmission, the number of bit errors is the numbers of received bits of a data stream over a communication channel that have been altered due to noise, interference, distortion or bit synchronization errors.
The bit error rate (BER) is the number of bit errors per unit time. The bit error ratio (also BER) is the number of bit errors divided by the total number of transferred bits during a studied time interval. Bit error ratio is a unitless performance measure, often expressed as a percentage.[1]
The bit error probability pe is the expected value of the bit error ratio. The bit error ratio can be considered as an approximate estimate of the bit error probability. This estimate is accurate for a long time interval and a high number of bit errors.
Example[edit]
As an example, assume this transmitted bit sequence:
1 1 0 0 0 1 0 1 1
and the following received bit sequence:
0 1 0 1 0 1 0 0 1,
The number of bit errors (the underlined bits) is, in this case, 3. The BER is 3 incorrect bits divided by 9 transferred bits, resulting in a BER of 0.333 or 33.3%.
Packet error ratio[edit]
The packet error ratio (PER) is the number of incorrectly received data packets divided by the total number of received packets. A packet is declared incorrect if at least one bit is erroneous. The expectation value of the PER is denoted packet error probability pp, which for a data packet length of N bits can be expressed as
,
assuming that the bit errors are independent of each other. For small bit error probabilities and large data packets, this is approximately
Similar measurements can be carried out for the transmission of frames, blocks, or symbols.
The above expression can be rearranged to express the corresponding BER (pe) as a function of the PER (pp) and the data packet length N in bits:
Factors affecting the BER[edit]
In a communication system, the receiver side BER may be affected by transmission channel noise, interference, distortion, bit synchronization problems, attenuation, wireless multipath fading, etc.
The BER may be improved by choosing a strong signal strength (unless this causes cross-talk and more bit errors), by choosing a slow and robust modulation scheme or line coding scheme, and by applying channel coding schemes such as redundant forward error correction codes.
The transmission BER is the number of detected bits that are incorrect before error correction, divided by the total number of transferred bits (including redundant error codes). The information BER, approximately equal to the decoding error probability, is the number of decoded bits that remain incorrect after the error correction, divided by the total number of decoded bits (the useful information). Normally the transmission BER is larger than the information BER. The information BER is affected by the strength of the forward error correction code.
Analysis of the BER[edit]
The BER may be evaluated using stochastic (Monte Carlo) computer simulations. If a simple transmission channel model and data source model is assumed, the BER may also be calculated analytically. An example of such a data source model is the Bernoulli source.
Examples of simple channel models used in information theory are:
- Binary symmetric channel (used in analysis of decoding error probability in case of non-bursty bit errors on the transmission channel)
- Additive white Gaussian noise (AWGN) channel without fading.
A worst-case scenario is a completely random channel, where noise totally dominates over the useful signal. This results in a transmission BER of 50% (provided that a Bernoulli binary data source and a binary symmetrical channel are assumed, see below).
In a noisy channel, the BER is often expressed as a function of the normalized carrier-to-noise ratio measure denoted Eb/N0, (energy per bit to noise power spectral density ratio), or Es/N0 (energy per modulation symbol to noise spectral density).
For example, in the case of QPSK modulation and AWGN channel, the BER as function of the Eb/N0 is given by:

People usually plot the BER curves to describe the performance of a digital communication system. In optical communication, BER(dB) vs. Received Power(dBm) is usually used; while in wireless communication, BER(dB) vs. SNR(dB) is used.
Measuring the bit error ratio helps people choose the appropriate forward error correction codes. Since most such codes correct only bit-flips, but not bit-insertions or bit-deletions, the Hamming distance metric is the appropriate way to measure the number of bit errors. Many FEC coders also continuously measure the current BER.
A more general way of measuring the number of bit errors is the Levenshtein distance.
The Levenshtein distance measurement is more appropriate for measuring raw channel performance before frame synchronization, and when using error correction codes designed to correct bit-insertions and bit-deletions, such as Marker Codes and Watermark Codes.[3]
Mathematical draft[edit]
The BER is the likelihood of a bit misinterpretation due to electrical noise 





Knowing that the noise has a bilateral spectral density 


and 

Returning to BER, we have the likelihood of a bit misinterpretation 


where 

We can use the average energy of the signal 
±§
Bit error rate test[edit]
BERT or bit error rate test is a testing method for digital communication circuits that uses predetermined stress patterns consisting of a sequence of logical ones and zeros generated by a test pattern generator.
A BERT typically consists of a test pattern generator and a receiver that can be set to the same pattern. They can be used in pairs, with one at either end of a transmission link, or singularly at one end with a loopback at the remote end. BERTs are typically stand-alone specialised instruments, but can be personal computer–based. In use, the number of errors, if any, are counted and presented as a ratio such as 1 in 1,000,000, or 1 in 1e06.
Common types of BERT stress patterns[edit]
- PRBS (pseudorandom binary sequence) – A pseudorandom binary sequencer of N Bits. These pattern sequences are used to measure jitter and eye mask of TX-Data in electrical and optical data links.
- QRSS (quasi random signal source) – A pseudorandom binary sequencer which generates every combination of a 20-bit word, repeats every 1,048,575 words, and suppresses consecutive zeros to no more than 14. It contains high-density sequences, low-density sequences, and sequences that change from low to high and vice versa. This pattern is also the standard pattern used to measure jitter.
- 3 in 24 – Pattern contains the longest string of consecutive zeros (15) with the lowest ones density (12.5%). This pattern simultaneously stresses minimum ones density and the maximum number of consecutive zeros. The D4 frame format of 3 in 24 may cause a D4 yellow alarm for frame circuits depending on the alignment of one bits to a frame.
- 1:7 – Also referred to as 1 in 8. It has only a single one in an eight-bit repeating sequence. This pattern stresses the minimum ones density of 12.5% and should be used when testing facilities set for B8ZS coding as the 3 in 24 pattern increases to 29.5% when converted to B8ZS.
- Min/max – Pattern rapid sequence changes from low density to high density. Most useful when stressing the repeater’s ALBO feature.
- All ones (or mark) – A pattern composed of ones only. This pattern causes the repeater to consume the maximum amount of power. If DC to the repeater is regulated properly, the repeater will have no trouble transmitting the long ones sequence. This pattern should be used when measuring span power regulation. An unframed all ones pattern is used to indicate an AIS (also known as a blue alarm).
- All zeros – A pattern composed of zeros only. It is effective in finding equipment misoptioned for AMI, such as fiber/radio multiplex low-speed inputs.
- Alternating 0s and 1s — A pattern composed of alternating ones and zeroes.
- 2 in 8 – Pattern contains a maximum of four consecutive zeros. It will not invoke a B8ZS sequence because eight consecutive zeros are required to cause a B8ZS substitution. The pattern is effective in finding equipment misoptioned for B8ZS.
- Bridgetap — Bridge taps within a span can be detected by employing a number of test patterns with a variety of ones and zeros densities. This test generates 21 test patterns and runs for 15 minutes. If a signal error occurs, the span may have one or more bridge taps. This pattern is only effective for T1 spans that transmit the signal raw. Modulation used in HDSL spans negates the bridgetap patterns’ ability to uncover bridge taps.
- Multipat — This test generates five commonly used test patterns to allow DS1 span testing without having to select each test pattern individually. Patterns are: all ones, 1:7, 2 in 8, 3 in 24, and QRSS.
- T1-DALY and 55 OCTET — Each of these patterns contain fifty-five (55), eight bit octets of data in a sequence that changes rapidly between low and high density. These patterns are used primarily to stress the ALBO and equalizer circuitry but they will also stress timing recovery. 55 OCTET has fifteen (15) consecutive zeroes and can only be used unframed without violating one’s density requirements. For framed signals, the T1-DALY pattern should be used. Both patterns will force a B8ZS code in circuits optioned for B8ZS.
Bit error rate tester[edit]
A bit error rate tester (BERT), also known as a «bit error ratio tester»[4] or bit error rate test solution (BERTs) is electronic test equipment used to test the quality of signal transmission of single components or complete systems.
The main building blocks of a BERT are:
- Pattern generator, which transmits a defined test pattern to the DUT or test system
- Error detector connected to the DUT or test system, to count the errors generated by the DUT or test system
- Clock signal generator to synchronize the pattern generator and the error detector
- Digital communication analyser is optional to display the transmitted or received signal
- Electrical-optical converter and optical-electrical converter for testing optical communication signals
See also[edit]
- Burst error
- Error correction code
- Errored second
- Pseudo bit error ratio
- Viterbi Error Rate
References[edit]
- ^ Jit Lim (14 December 2010). «Is BER the bit error ratio or the bit error rate?». EDN. Retrieved 2015-02-16.
- ^
Digital Communications, John Proakis, Massoud Salehi, McGraw-Hill Education, Nov 6, 2007 - ^
«Keyboards and Covert Channels»
by Gaurav Shah, Andres Molina, and Matt Blaze (2006?) - ^ «Bit Error Rate Testing: BER Test BERT » Electronics Notes». www.electronics-notes.com. Retrieved 2020-04-11.
This article incorporates public domain material from Federal Standard 1037C. General Services Administration. (in support of MIL-STD-188).
External links[edit]
- QPSK BER for AWGN channel – online experiment
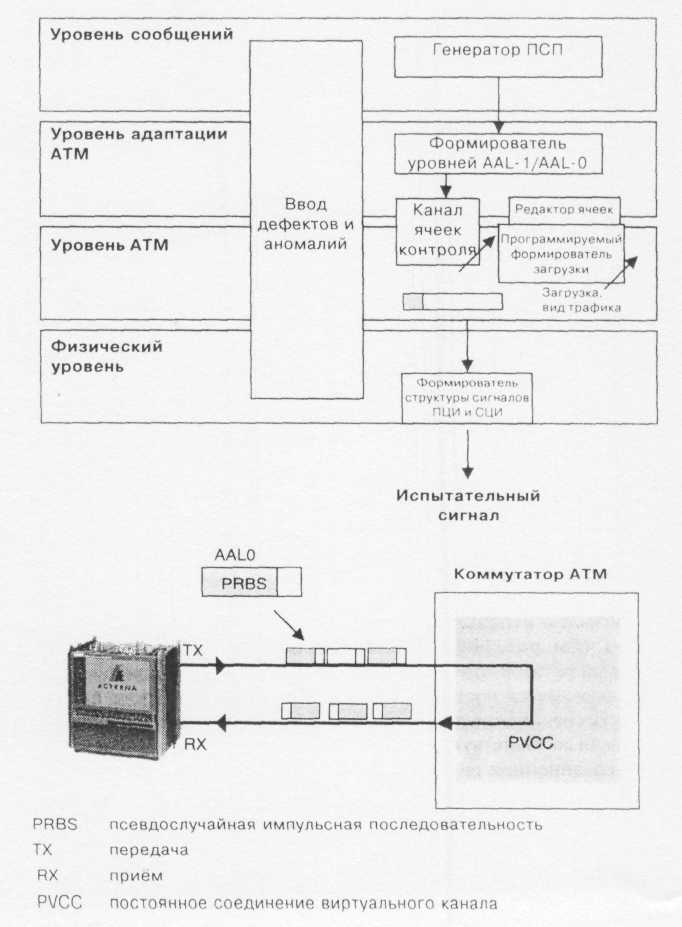
Определение
величины коэффициента битовых ошибок
является основным методом проверки
степени прозрачности сетевых трактов
или проверки конфигурации элементов
сети. Коэффициент битовых ошибок
измеряется в процессе контроля каналов
передачи ячеек путём анализа псевдослучайной
импульсной последовательности, которая
вводится непосредственно в информационные
ячейки сигнала на уровне ATM.
На уровне адаптации AAL-0
псевдослучайным сигналом заполняются
все ячейки. Заполнение таким же сигналом
используется для проверки всего уровня
адаптации AAL-1. (См. рис.
11.11). Постоянное соединение, которое
обеспечивается работой сетевого
оборудования, как это показано на рис.
11.11, называется постоянным соединением
виртуального канала. Если же соединение
производится выбором абонента при
помощи передачи соответствующих
сигналов, оно называется коммутируемым
соединением виртуального канала.
Работа
в режиме транзита
Существует
два варианта организации транзита (см.
рис. 11.12).
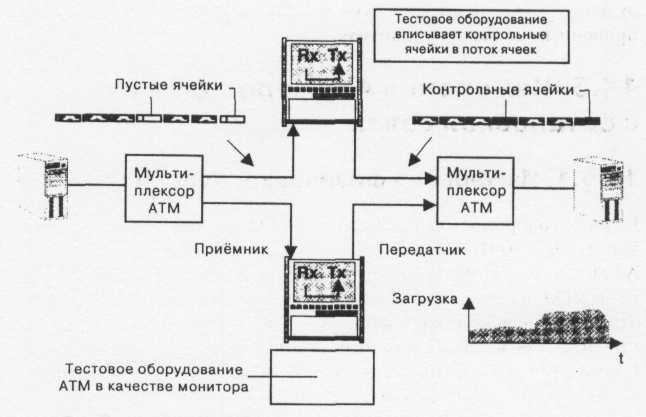
Тестовое
оборудование формирует незаполненные
ячейки и создаёт дополнительной
независимое контрольное соединение со
своими идентификаторами виртуальных
каналов и трактов. Преимущество этого
метода заключается в возможности точного
воспроизведения режима прохождения
ячеек пользователей, так как компоненты
сети не могут отличить тестовые ячейки
от информационных. Метод в основном
используется на этапе лабораторных
испытаний и не входит в стандарты
широкого применения. Причина этого, как
считают многие специалисты, состоит в
возможности изменения характеристик
трафика в режиме транзита.
Проверка соединений
в режиме транзита. Этот вид испытаний
рекомендуется в основном для проведения
долговременного тестирования и построения
гистограмм распределения загрузки во
времени.
В
технологии ATM требования,
предъявляемые к качеству, зависят от
вида сообщений. Для получения достоверной
информации о качестве работы сети
измерения на ней должны проводиться с
использованием испытательных сигналов,
как можно точнее имитирующих реальные
сигналы различных типов. Если информация
о характере трафика отсутствует или
носит слишком общий характер, в процесс
измерения необходимо включить терминальное
оборудование. В этом случае оптимальным
можно считать измерения, проводимые в
режиме транзита.
Рис. 11.11 Измерение
коэффициента битовых ошибок сигнала
АТМ
Рис. 11.12 Работа
в режиме ввода-вывода
12.7.Универсальный сетевой анализатор
Универсальный
сетевой анализатор ANT-20SE
предназначен для определения коэффициента
битовых ошибок (BERT), анализа
рабочих характеристик для DSN-,
PDH-, SONET- и
SDH- сигналов для всех
стандартных скоростей согласно
рекомендациям ITU-T,
анализа характеристик в режиме передачи
от 1,5Мбит/с до 10Гбит/с в соответствии с
рекомендациями 0,172 ITU-T,
анализа ТСМ (Tandem Connection
Monitoring) для SDH-
сетей. ANT-20SE
обеспечивает функции Jitter/Wander
– генератора, имеет автоматизированные
режимы выполнения тестов с применением
генератора ПСП и обеспечивает режимы
автоматического запуска тестов.
Прибор
выполнен в виде модульной конструкции
(четыре слота в компактном корпусе).
Программное обеспечение прибора
позволяет комбинировать и параллельно
производить измерения на всех стандартных
электрических и оптических интерфейсах
от 2Мбит/с до STM-16 (от DS1
до ОС-48) и обеспечивать разрешение
сигнальных структур до уровня 2,5Гбит/с.
Обеспечивается доступ ко всем
стандартизированным кодовым преобразованиям
как для различных методов передачи,
например SDH, SONET,
так и для таких структур, как DS1,
STM-1.
ANT-20
выполнен в настольном формате и работает
на базе встроенного ПК. Прибор может
оснащаться сенсорным дисплеем, специальной
ручкой-стилусом, клавиатурой и всеми
необходимыми разъемами для подключения
внешних устройств и носителей.
Интуитивно-понятное управление и
дружественный интерфейс делают работу
с анализатором доступной даже для
неподготовленного специалиста.
Сетевой
тестер ANT-20SE
(Advanced Network
Tecter) имеет встроенный
Pentium-PC с
графическим представлением результатов
измерений на цветном мониторе (LCD
с сенсорным экраном). С off-line
анализом на внешнем РС с последующей
обработкой результатов тестер производит
измерения рабочих характеристик (анализ
ошибок) согласно рекомендациям G.821;
G.826; G.828; G
829; М.2100 и М.2101, графическое представление
последовательности указателей согласно
G.783 и графический анализ
указателей.
Универсальный
сетевой анализатор ANT-20SE
может адаптироваться к вновь возникающим
потребностям в измерениях с учетом
меняющихся запросов операторов и
производителей современных коммуникационных
сетей. Модульное программное обеспечение
позволяет адаптировать тестовые функции
ANT-20SE для
выполнения новых задач.
Из
наиболее важных задач следует отметить
режим генерации потоков с возможностью
вставок ошибок и аномалий вставок/выделения
отдельных трибутарных потоков, анализ
и генерация джиттера и вандера до уровня
STM-16.
Прибор
ANT-20SE
позволяет значительно повысить качество
работы телекоммуникаций своевременно
реагировать на все аварийные ситуации,
прогнозировать поведение контролируемых
параметров.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
ИССЛЕДОВАНИЕ МЕТОДА ГЛАЗКОВЫХ ДИАГРАММ ДЛЯ ИЗМЕРЕНИЯ КОЭФФИЦИЕНТА БИТОВЫХ ОШИБОК В ЦИФРОВЫХ СИСТЕМАХ СВЯЗИ
В данной статье рассмотрен метод выявления коэффициента ошибок в канале связи с помощью глазковых диаграмм. В программном пакете MATLAB смоделирована схема для измерения коэффициента ошибок.
Ключевые слова: глазковая диаграмма, вероятность ошибки, коэффициент битовой ошибки, помехоустойчивость.
Введение.
Сфера телекоммуникаций является важной частью человечества, поскольку представляет собой возможность общения людей друг с другом. На сегодняшний день это наиболее перспективное направление в науке, которое продолжает развиваться.
Одно из требований к сетям обмена информацией – точность приема этой информации. Сейчас практически все системы связи являются цифровыми. Повышение точности приема информации тесно связано с помехоустойчивостью системы. А, в свою очередь, характеристикой помехоустойчивости является коэффициент битовых ошибок (BER – bit error rate). Вычисление коэффициента ошибок является наиболее эффективным способом для оценки функционирования системы.
Так как радиоканал сети связи является менее защищенным, чем кабельная система передачи информации, вычисление количества ошибок в такой системе будет актуальным.
1. Определение коэффициента ошибок.
Для начала стоит определить, что коэффициент битовых ошибок – это некоторая величина, которая помогает оценить помехоустойчивость системы связи. И чем меньше BER, тем лучше работает система, и тем менее она будет восприимчива к воздействию внешних помех.
По определению коэффициент битовых ошибок является отношением ошибочно принятых битов к общему количеству переданных битов.
BER = n/N (1)
где n – количество ошибок;
N – количество переданных битов.
Как правило, коэффициент битовых ошибок является оценкой вероятности ошибок в приеме бита.
2. Основы метода глазковых диаграмм.
Принцип работы схемы, представленной на рисунке 1, заключается в том, что поток бит подается на осциллограф, пока синхронизация внешней развертки осуществляется от битового потока с частотой fb. Если требуется построение многоуровневых диаграмм, то сигнал дополнительно направляют на многоуровневый конвертер, а синхронизация осуществляется от символьного потока с частотой fs.
Рис. 1. Схема построения глазковых диаграмм
Построение глазковой диаграммы
С точки зрения исследования глазковая диаграмма – это изображение на экране осциллографа в виде результата наложения импульсных сигналов друг на друга, часто с применением режима персистенции (запоминания осциллограмм на некоторое время) и с нормированием масштабов осциллограмм сигналов. В процессе передачи сигнала по каналу связи импульс искажается. И по мере этих искажений можно делать выводы о параметрах канала связи. [1]
Рис. 2. Глазковая диаграмма двухуровневого сигнала
Расстояние B характеризуется, как раскрыв глазковой диаграммы, определяется между двумя ближайшими уровнями реализаций сигнала и соответствует значению коэффициента интенсивности битовых ошибок. Расстояние B/2 является запасом помехоустойчивости регенератора, который равен минимальному дополнительному уровню шума, который может вызывать ошибку. Максимальный запас помехоустойчивости обеспечивается, в случае когда принятие решения о переданном бите информации производится в определенный момент времени iT. [2]
3. Реализация метода глазковых диаграмм.
Целью данной работы являлось моделирование канала связи и определение коэффициента ошибок по методу глазковых диаграмм. Для наглядного представления метода глазковых диаграмм исследование было проведено в программном пакете MATLAB с использованием канала с аддитивным белым гауссовским шумом. В цифровой системе передачи, чтобы описать гауссовский шум, используют распределение Гаусса.
где: µ – математическое ожидание; σ – среднеквадратическое отклонение.
Схема реализации поставленной задачи приведена на рисунке 3.
Рис. 3. Схема исследования в Simulink
В исследуемой схеме сигнал задается генератором случайных последовательностей и преодолевает свой путь, начиная с конвертации в биполярный вид (Unipolar to Bipolar Converter), затем, разделяясь на две ветви, следует на модулятор с минимальным частотным сдвигом (MSK) и с минимальным гауссовским сдвигом (GMSK). Пройдя через модуляторы, сигнал попадает в канал с аддитивным белым гауссовским шумом (AWGN) для имитации условий прохождения сигнала по каналу, близких к реальным. Далее установлены два осциллографа глазковых диаграмм (Eye Diagram), с помощью которых можно оценить интенсивность битовых ошибок. Затем сигнал проходит через демодуляторы и обратно конвертируется в однополярный вид, после чего можно пронаблюдать результат на осциллографах (Time Scope).
Полученные глазковые диаграммы представлены на рисунках ниже (Рис.4, Рис.5).
Рис. 4. Глазковая диаграмма по ветви с GMSK модуляцией

Рис. 5. Глазковая диаграмма по ветви с MSK модуляцией
В идеале глазковая диаграмма, исходя из названия, представляет собой «раскрытый глаз», так как получилось на рисунке 7 при MSK модуляции. На рисунке 6 при другой ветке модуляции видим очевидное наложение волн друг на друга – явление интерференции. Анализируя подобные глазковые диаграммы, можно определить коэффициент интенсивности битовых ошибок, значение которого соответствует расстоянию между низким и высоким глазковыми уровнями. Такое расстояние называется вертикальным глазковым открытием. Обратим внимание, что поставленный блок счетчика ошибок показывает значение 0.28409, что допустимо при передаче сигнала при моделировании на компьютере.
4. Заключение.
Бесперебойная и точная передача данных всегда являлась главной задачей в телекоммуникационной сфере. Однако не всегда нам удается передать данные безошибочно. Для того чтобы регулировать измерение коэффициента ошибок в системе, метод глазковых диаграмм является удобным, нетрудным и неутомительным. Простота реализации с помощью пакета MATLAB является преимуществом перед другими методами выявления ошибок.
Обязательными элементами современных сетей связи являются системы сетевого управления, с помощью которых решаются такие задачи, как реконфигурация сети, непрерывный мониторинг параметров системы связи (например, SIP GSM шлюзов), фиксация аварийных состояний, защитные переключения, хранение и обработка результатов мониторинга и т. д. Все указанные операции выполняются, как правило, автоматически, с помощью встроенных аппаратных и программных средств.
В то же время зачастую при обслуживании сетей связи не удается обойтись без ручных операций с применением портативных измерительных приборов. Классический пример – устранение сложных повреждений металлических кабелей связи, случившихся по причине намокания.
АНАЛИЗ ОШИБОК В ЦИФРОВЫХ СИСТЕМАХ ПЕРЕДАЧИ
Основное преимущество цифровой передачи по сравнению с аналоговой заключается в отсутствии накопления помех вдоль линии. Это достигается за счет восстановления формы передаваемого сигнала на каждом регенерационном участке.
Все факторы, от которых зависит длина участка, можно разделить на внутренние и внешние.
Наиболее важными внутренними считают затухание линии, межсимвольные помехи, нестабильность тактовой частоты системы, вариацию задержки, возрастание уровня шумов вследствие старения системы.
К существенным внешним факторам обычно относят переходные и импульсные помехи, внешние электромагнитные влияния, механические повреждения контактов при вибрации или ударах, ухудшение свойств передающей среды вследствие перепадов температуры.
Все они обычно предопределяют ухудшение самого чувствительного к ошибкам параметра цифровой передачи — соотношения сигнал/шум. Действительно, снижение величины данного соотношения всего на 1 дБ приводит к увеличению обобщенного параметра качества цифровых систем передачи, которым является коэффициент битовых ошибок (Bit Error Rate, BER), по крайней мере на порядок.
Согласно определению, BER представляет собой отношение числа ошибочно принятых битов к общему числу принятых битов. Его величина статистически колеблется около значения среднего коэффициента ошибок за длительный промежуток времени. Разница между непосредственно измеренным коэффициентом ошибок и долговременным средним значением зависит от числа контролируемых бит и тем самым от длительности измерения.
База времени формируется при помощи двух основных методов.
В соответствии с первым из них, на принимающем конце задается фиксированное число наблюдаемых бит и регистрируется соответствующее число бит с ошибками.
Например, если число ошибочно принятых бит оказалось равным 20, а заданное общее число принимаемых бит – 106, то коэффициент ошибок составит 20/106 = 20 x 10-6 = 2 x 10-5 .
Достоинством такого подхода является точно известное время измерения, а недостатком – невысокая надежность измерения при малом числе ошибок.
Согласно второму методу, время измерений определяется заданным числом ошибок. Измерение длится до тех пор, пока, например, не будет зафиксировано 100 ошибок. Затем на основании соответствующего числа битов данных вычисляется коэффициент ошибок.
Его недостаток заключается в том, что неизвестно время измерений, которое при малых коэффициентах ошибок может оказаться очень большим. Кроме того, вполне возможно, что счетчик бит данных заполнится полностью, и измерения прекратятся. Поэтому такой способ используется редко.
На начальном этапе развития цифровых систем передачи они применялись главным образом для передачи аналогового телефонного сигнала, и потому требования к качеству цифровых систем передачи определялись характеристиками этого сигнала.
Ошибка в цифровом сигнале приводит к быстрому изменению величины сигнала АИМ на входе канального демодулятора, и абонент слышит неприятный щелчок на выходе канала ИКМ. Экспериментально установлено, что заметные щелчки возникают только при ошибках в одном из первых двух наибольших по весу символов кодовой группы, что соответствует максимальному (положительному или отрицательному) изменению сигнала АИМ. Качество связи считается удовлетворительным, если в каждом канале наблюдается не более одного щелчка в минуту. При частоте дискретизации, равной 8 кГц, по каналу передается 8000 x 60 = 480 тыс. кодовых групп в минуту, причем опасными в отношении щелчков являются 960 тыс. старших разрядов. Если считать, что вероятность ошибки для любого разряда кодовой группы одинакова, то при допущении одного щелчка в минуту вероятность ошибки в линейном тракте не должна быть более 1/960 000 = 10-6.
С учетом передачи данных, которая более чувствительна к ошибкам передачи, для эталонного международного соединения протяженностью 27 500 км величина BER не должна превышать 10-7.
Ошибки можно обнаружить двумя основными методами.
Во-первых, во время приемки и настройки линий связи, поиске неисправностей и ремонте выполняются измерения с перерывом связи, которые реализуются по трем схемам подключения: точка-точка, шлейф и транзит.
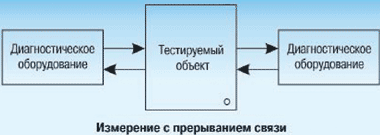
Во-вторых, для мониторинга сети и качественной оценки ее состояния, обнаружения и устранения повреждений используются измерения без перерыва связи.
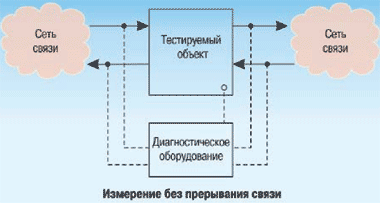
Измерение BER без перерыва связи требует точного знания структуры цифрового сигнала. Таким сигналом в составе цикла, например первичного цифрового сигнала Е-1, является цикловой синхросигнал, занимающий 7 бит нулевого канального интервала (КИ) сигнала E-1.
Цикловой сигнал передается в каждом втором цикле сигнала E-1, причем каждый цикл E-1 содержит 32 КИ и, следовательно, 32 х 8 = 256 бит. Таким образом, относительная доля циклового синхросигнала в сигнале E-1 составляет 7/(256 x 2) < 1,4%. Поэтому достоверность оценки BER с помощью циклового синхросигнала очень низка.
Еще один известный метод оценки качества цифровой передачи основан на обнаружении ошибок кода. Он используется, например, в цифровых трактах T-1/E-1, где применяются коды с чередованием полярности единиц AMI и HDB-3. Однако с помощью измерителя ошибок кода нельзя выявить истинное значение коэффициента битовых ошибок. Отклонения между результатами измерения ошибок кода и обычного измерения ошибок методом побитового сравнения становятся особенно заметными при коэффициентах ошибок более 10-3. Кроме того, нарушение правил кодирования часто распространяется и на нескольких бит, находящихся после бита с ошибкой. Вследствие этого зависящее от содержания сигнала смещение и погрешность при больших коэффициентах ошибок делают невозможным точный анализ распределения ошибок.
Итак, практическая оценка BER возможна только в режиме измерений с перерывом связи и посылкой эталонных испытательных сигналов. При измерении BER испытательный сигнал должен как можно лучше имитировать реальный, т. е. иметь случайный характер. В качестве такого испытательного сигнала обычно используют псевдослучайную последовательность битов (ПСП) с заданной структурой, близкой к настоящему информационному сигналу. Такие последовательности формируются тактируемыми регистрами сдвига с обратной связью.
Цифровой испытательный сигнал заменяет обычно передаваемый информационный сигнал и оценивается на приемном конце измерителем ошибок.
Таким образом, необходимый в условиях нормальной эксплуатации непрерывный мониторинг ошибок цифровой передачи методом BER без перерыва связи практически невозможен.
В настоящее время для оценки качества цифровых систем передачи в эксплуатационных условиях применяется метод измерения блочных ошибок. Как нетрудно догадаться, главное его достоинство состоит в том, что он основан на использовании самого информационного сигнала и выполняется без прерывания связи.
Все методы измерения блочных ошибок предполагают введение избыточности в информационный сигнал, обработку этого вспомогательного сигнала по определенному алгоритму и передачу результата обработки на принимающую сторону, где принятый сигнал обрабатывается по тому же алгоритму, что и при передаче, а итог сравнивается с результатом обработки, полученным от передающей стороны. При их разнице переданный блок считается ошибочным.
Известно несколько способов обнаружения блочных ошибок. Способы поблочного контроля четности и контрольной суммы не позволяют распознать все типы ошибок, тем самым ограничивая их практическую применимость. Пожалуй, единственным универсальным способом измерения ошибок без перерыва связи является контроль при помощи циклического избыточного кода (Cyclical Redundancy Check, CRC).
�
Таблица 1. Измерения в цифровых системах связи и соответствующие им процедуры могут применяться для решения целого ряда задач.
| Область применения измерений | Измерительные процедуры |
| Разработка оборудования | Испытания с применением высокоточного контрольно-измерительного оборудования, отработка и проверка программного обеспечения, анализ результатов |
| Производство оборудования | Оперативные измерения параметров оборудования и сравнение их с эталонными, проверка дистанционного управления, контроль комплектующих изделий |
| Инсталляция и линейные испытания оборудования | Измерения с перерывом связи, долговременный анализ, сохранение результатов, использование высокоточных и стандартных приборов |
| Нормальная эксплуатация и техническое обслуживание при поиске и устранении неисправностей | Измерения с перерывом и без перерыва связи, включая непрерывный мониторинг с помощью встроенных систем тестирования и измерения с помощью стандартных приборов, имитация ошибок и аварийных сигналов, контроль качества каналов |
| Ремонт и калибровка — локализация дефектов монтажа и печатных плат, имитация условий эксплуатации | Лабораторное оборудование для проверки на соответствие нормативной документации, испытательные стенды |



![{\displaystyle p_{e}=1-{\sqrt[{N}]{(1-p_{p})}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5d380e45b0451c45265e199221fae5bd5b84bf9)