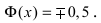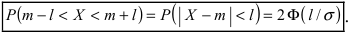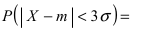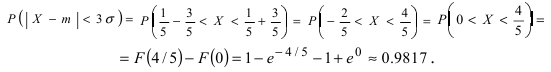Основным
критерием точности результатов измерений
является средняя
квадратическая ошибка
(оценка СКО), определяемая по формуле
|
|
Для
ряда истинных ошибок при известном
формула принимает вид (1.3) и называетсяформулой
Гаусса:
|
|
где
;
.
Средней
ошибкой
называют среднее арифметическое из
абсолютных значений ошибок, т.е.
|
|
Вероятной
ошибкой называют такое значение случайной
ошибки,
больше или меньше которого, по абсолютной
величине, ошибки равновозможны, т.е.
.
На
практике
определяется величиной, которую находят,
расположив все ошибкиi
в ряд в порядке возрастания их абсолютных
величин. Вероятная ошибка будет расположена в середине такого
ряда.
При нормальном
законе распределения случайных ошибок
имеют место соотношения:
|
|
Величины
и
являются оценками параметров и r:
соответственно среднего и вероятного
отклонений (см. раздел I
п. 3.5).
Соотношения
называют критериями нормального закона
(в разделе I
они представлены в виде
;
).
Предельной
ошибкой
называют такую ошибку, больше которой
в ряде измерений ошибок не должно быть.
В качестве предельных выбирают величины,
определяемые по правилу
и
(с
вероятностями 0,954 и 0,997 соответственно).
Перечисленные
выше критерии
,m,
,
,
называютабсолютными
ошибками.
Относительной
ошибкой
называют отношение соответствующей
абсолютной ошибки к значению измеряемой
величины X
(если X
неизвестно, его заменяют результатом
измерения x).
Относительную
ошибку обычно выражают в виде дроби с
числителем, равным 1, например:
—средняя
квадратическая относительная ошибка;
—предельная
относительная ошибка величины X
и
т.д.
Значения
абсолютных ошибок получают с двумя–тремя
значащими цифрами, а знаменатель
относительной ошибки округляют до двух
значащих цифр с нулями.
Например,
при
и
.
.
1.5 Исследование ряда истинных ошибок на нормальное распределение
Для
решения этой первой задачи теории ошибок
используем методику, изложенную в
разделе математической статистики, а
также выполним вычисления по
формулам (1.1–1.5) настоящего раздела.
Задача 1.1.
В таблице 1.1
даны невязки 32‑х треугольников.
Невязки
можно считать истинными ошибками,
так как сумму углов в треугольнике можно
рассматривать как измеренную величину,
истинное значение которой равно
.
Выполнить исследование ряда невязокна нормальный закон распределения.
|
Таблица |
|||||||
|
№ |
невязки i |
№ |
невязки i |
№ |
невязки i |
№ |
невязки i |
|
1 |
–0,76″ |
9 |
+1,29″ |
17 |
+0,71″ |
25 |
+0,22″ |
|
2 |
+1,52″ |
10 |
+0,38″ |
18 |
+1,04″ |
26 |
+0,06″ |
|
3 |
–0,24″ |
11 |
–1,03″ |
19 |
–0,38″ |
27 |
+0,43″ |
|
4 |
+1,31″ |
12 |
+0,00″ |
20 |
+1,16″ |
28 |
–1,28″ |
|
5 |
–1,27″ |
13 |
–1,23″ |
21 |
–0,19″ |
29 |
–0,41″ |
|
6 |
–1,88″ |
14 |
–1,38″ |
22 |
+2,28″ |
30 |
–2,50″ |
|
7 |
+0,01″ |
15 |
–0,25″ |
23 |
+0,07″ |
31 |
+1,92″ |
|
8 |
–0,69″ |
16 |
–0,73″ |
24 |
–0,95″ |
32 |
–0,62″ |
Найдём ряд сумм,
необходимых для дальнейшего исследования:
;
;
;
;
;
;
.
Решение:
-
Вычисление
оценок параметров нормального
распределения
,
,
кривая плотности которого определяется
выражением :


-
Вычисление
средней ошибки
и коэффициента:
;
;
.
-
Определение
вероятной ошибкии коэффициента
.
Располагаем
истинные ошибки в ряд по возрастанию
их абсолютных величин:
+0,00;
+0,01; +0,06;+0,07; –0,19; +0,22; –0,24; –0,25; +0,38; –0,38;
–0,41; +0,43; –0,62; –0,69; +0,71; –0,73; –0,76; –0,95;
–1,03; +1,04; +1,16; –1,23; –1,27; –1,28; +1,29; +1,31;
–1,38; +1,52; -1,88; +1,92; +2,28; –2,50.
Находим:
;
;
.
-
Построение
статистического группированного ряда.
Распределим
невязки (табл. 1.2) в двенадцати
интервалах (длину интервала примем
равной половине средней квадратической
ошибки, т.е.
).
|
Таблица |
|||||||
|
№ п/п |
длины интервалов в m |
длины интервалов в |
число |
частоты |
высоты прямо-угольников |
||
|
1 |
–3,0m |
–2,5m |
–3,30″ |
–2,75″ |
0 |
0,000 |
0,000 |
|
2 |
–2,5m |
–2,0m |
–2,75 |
–2,20 |
1 |
0,031 |
0,056 |
|
3 |
–2,0m |
–1,5m |
–2,20 |
–1,65 |
1 |
0,031 |
0,056 |
|
4 |
–1,5m |
–1,0m |
–1,65 |
–1,10 |
4 |
0,125 |
0,227 |
|
5 |
–1,0m |
–0,5m |
–1,10 |
–0,55 |
6 |
0,188 |
0,342 |
|
6 |
–0,5m |
+0 |
–0,55 |
–0 |
5 |
0,156 |
0,284 |
|
7 |
+0 |
+0,5m |
–0 |
+0,55 |
7 |
0,219 |
0,398 |
|
8 |
+0,5m |
+1,0m |
+0,55 |
+1,10 |
2 |
0,062 |
0,113 |
|
9 |
+1,0m |
+1,5m |
+1,10 |
+1,65 |
4 |
0,125 |
0,227 |
|
10 |
+1,5m |
+2,0m |
+1,65 |
+2,20 |
1 |
0,031 |
0,056 |
|
11 |
+2,0m |
+2,5m |
+2,20 |
+2,75 |
1 |
0,031 |
0,056 |
|
12 |
+2,5m |
+3,0m |
+2,75 |
+3,30 |
0 |
0,000 |
0,000 |
|
∑ |
32 |
1,000 |
― |
||||
|
mi — |
-
Построение
гистограммы и выравнивающей её кривой
распределения.
По
данным таблицы 1.2 (столбцы 2 и 6)
строим гистограмму (рис. 1.1) —
график эмпирического распределения
(на выбор масштаба изображения наложим
лишь условие наглядности).
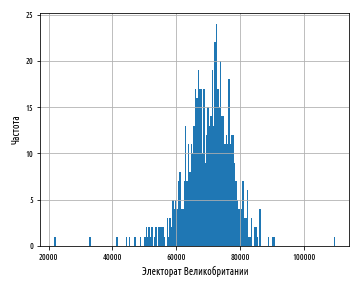
Рис. 1.1 —
Гистограмма и выравнивающая кривая
Вид
гистограммы позволяет действительно
предположить нормальный закон
распределения ошибок i.
Теоретическая кривая, наилучшим образом
выравнивающая (сглаживающая) гистограмму,
определяется уравнением
|
|
где
;
;
;
;

Вычисление
ординат кривой
выполняем,
используя таблицу Приложения A.
Результаты вычислений поместим в
таблице 1.3.
|
Таблица 1.3 |
|||||
|
№ п/п |
левые границы интервалов i |
|
yi |
|
|
|
1 |
0 |
0 |
0,564 |
0,645 |
0,364 |
|
2 |
0,5m |
0,5 |
0,498 |
―»― |
0,321 |
|
3 |
1,0m |
1,0 |
0,342 |
―»― |
0,220 |
|
4 |
1,5m |
1,5 |
0,183 |
―»― |
0,118 |
|
5 |
2,0m |
2,0 |
0,076 |
―»― |
0,049 |
|
6 |
2,5m |
2,5 |
0,025 |
―»― |
0,016 |
|
7 |
3,0m |
3,0 |
0,006 |
―»― |
0,004 |
По
данным таблицы 1.3 (столбцы 2 и 6)
на графике рис. 1.1 наносим ряд точек ,
которые соединяем плавной кривой. Левую
ветвь кривой строим по тем же ординатам.
Как
видно из графика, кривая ()
удовлетворительно сглаживает гистограмму.
-
Применение
критерия 2‑Пирсона.
Для оценки степени
приближения статистического распределения
(гистограммы) к теоретическому нормальному
закону (кривой распределения) вычисляем
величину
|
|
где
|
|
Результаты
вычислений поместим в таблице 1.4.
находят
по таблице Приложения B
для левых границ интервалов ti.
|
Таблица 1.4 |
|||||||
|
№ |
Интервалы ti |
|
pi |
mi |
npi |
|
|
|
1 |
–3,0 |
–2,5 |
–0,5 |
0,0062 |
0 |
0,20 |
0,20 |
|
2 |
–2,5 |
–2,0 |
–0,4938 |
0,0166 |
1 |
0,53 |
0,42 |
|
3 |
–2,0 |
–1,5 |
–0.4772 |
0,0440 |
1 |
1,41 |
0,12 |
|
4 |
–1,5 |
–1,0 |
–0.4332 |
0,0918 |
4 |
2,94 |
0,38 |
|
5 |
–1,0 |
–0,5 |
–0,3414 |
0,1500 |
6 |
4,80 |
0,30 |
|
6 |
–0,5 |
+0 |
–0,1914 |
0,1914 |
5 |
6,12 |
0,20 |
|
7 |
+0 |
+0,5 |
+0 |
0,1914 |
7 |
6,12 |
0,13 |
|
8 |
+0,5 |
+1,0 |
+0,1914 |
0,1500 |
2 |
4,80 |
1,63 |
|
9 |
+1,0 |
+1,5 |
+0,3414 |
0,0918 |
4 |
2,94 |
0,38 |
|
10 |
+1,5 |
+2,0 |
+0,4332 |
0,0440 |
1 |
1,41 |
0,12 |
|
11 |
+2,0 |
+2,5 |
+0,4772 |
0,0166 |
1 |
0,53 |
0,42 |
|
12 |
+2,5 |
+3,0 |
+0,4938 |
0,0062 |
0 |
0,20 |
0,20 |
|
13 |
+3,0 |
+∞ |
+0,5 |
― |
― |
― |
― |
|
|
1,0000 |
32 |
32,00 |
4,50 |
Число
степеней свободы определяется формулой
.
Находим(k —
число
интервалов,
,
так как только один параметроценивался по выборке, а
принято равным нулю).
По
таблице Приложения E
по числу степеней свободы для
находим
вероятность,
а длянаходим
.
Интерполируя, дляполучим
.
-
Вычисление
оценок скошенностии эксцесса
и проверка соотношений:
|
|
которые
являются критериями нормального закона.
Находим:
-
;
-
;
-
;
-
;
-
;
.
Как
видно из вычислений, соотношения
выполняются.
В
результате исследования приходим к
выводу о том, что рассматриваемый ряд
истинных ошибок является действительно
рядом случайных ошибок, подчиняющихся
приближенно нормальному закону, так
как:
-
выполняются
свойства случайных ошибок:
-
среднее
арифметическоепрактически равно нулю,
-
положительные
и отрицательные ошибки, равные по
абсолютной величине (см. гистограмму),
примерно одинаково часто встречаются
в данном ряде, -
малые
по абсолютной величине ошибки встречаются
чаще, чем большие, -
случайные
ошибки
с заданной
вероятностью
не превосходят определенного предела,
равного,
ни одна из ошибок ряда не превышает
предельной ошибки, равной
;
-
коэффициенты
и
совпадают
с их теоретическими значениями (;
);
-
вероятность
велика, так как значительно больше
критического уровня значимости,
равного 0,1; -
величины
скошенности и эксцесса незначительно
отличаются от нуля.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Исследование ряда погрешностей на соответствие нормальному закону распределения
Исследование ряда погрешностей на соответствие нормальному закону
распределения
1.
Теоретические основы выполнения исследований
Обработка результатов
измерений имеет место всегда, когда одна из определяемых величин получена
несколько раз с отличными друг от друга значениями. При этом корректная оценка
полученных результатов возможна, только если известны правила, определяющие
поведение погрешностей измерений ∆. К главным таким правилам относят
законы поведения погрешностей в дифференциальной F(∆)
и интегральной F (∆) формах, их
основные численные характеристики и представления законов в виде графического
материала. Интегральная форма называется функцией распределения погрешностей , дифференциальная форма
— функцией плотности распределения погрешностей . К основным
характеристикам законов относят наиболее вероятное значение определяемой
величины, называемое математическим ожиданием и обозначаемое МО (∆) или
М(∆), или Е(∆); меру рассеивания измерений вокруг математического
ожидания, называемую дисперсией и D(∆)
(чаще используют просто величину σ(∆),
называемую стандартом, так как он не имеет квадратичной размерности как у
дисперсии). К дополнительным характеристикам законов относят меру скошенности
относительно вертикальной оси симметрии, называемую асимметрией и обозначаемую
А или и меру крутости,
называемую эксцессом и обозначаемую Е.
Множество теоретических
и практических исследований показывают, что результаты геодезических измерений
подчиняются нормальному закону распределения (закону Гаусса) и имеют вид
В процессе измерений
часто имеет место наличие грубых погрешностей (погрешностей, больших заданного
допуска) или промахов (т.е. очень сильно отличающихся от других). С другой
стороны, при наблюдениях в результатах могут содержаться и какие-либо
постоянные составляющие, называемые систематическими ошибками.
2.
Предварительные вычисления для исследования
В предварительных вычислениях ряд
исследуется на наличие значимых систематических и грубых погрешностей а также
меры однородности результатов по точности на основе каких-либо критериев.
Определение значимости
систематического влияния. Следует иметь
ввиду, что систематические влияния в рядах присутствуют всегда, но они могут
быть значимы и не значимы. При определении наличия значимых систематических
погрешностей в ряде имеют место два случая:
1) известно истинное значение
определяемой величины Хист и произведено ее измерений х. В этом
случае пользуются зависимостью
Где ∆=X-
=
— средняя квадратическая
погрешность среднего арифметического, m-СКП
одной величины, n — число элементов в
ряде. Величина (квантиль t-распределения Стьюдента) определяется по уровню значимости q (или вероятности р) и числу избыточных измерений (числу степеней
свободы) k = n — 1 и выбирается из
статистических таблиц, или получается из какого либо программного продукта.
Если неравенство (2) выполняется, то с вероятностью р = 1 — q считаем, что значимые систематические погрешности в ряде
измерений отсутствуют.
|
Аббе |
|
|
|
|
|
|
|
|
1 |
-0,06 |
-0,04 |
0,00 |
0,00 |
0,00 |
-1,96 |
3,84 |
|
2 |
-2,02 |
-1,99 |
3,98 |
-7,94 |
15,83 |
1,04 |
1,08 |
|
3 |
-0,98 |
-0,95 |
0,91 |
-0,87 |
0,83 |
1,59 |
2,54 |
|
4 |
0,61 |
0,64 |
0,41 |
0,26 |
0,17 |
-0,67 |
0,45 |
|
5 |
-0,05 |
-0,03 |
0,00 |
0,00 |
0,00 |
-1,06 |
1,13 |
|
6 |
-1,12 |
-1,09 |
1,19 |
-1,30 |
1,42 |
0,49 |
0,24 |
|
7 |
-0,63 |
-0,60 |
0,36 |
-0,21 |
0,13 |
0,88 |
0,77 |
|
8 |
0,25 |
0,28 |
0,08 |
0,02 |
0,01 |
-1,24 |
1,54 |
|
9 |
-0,99 |
-0,97 |
0,93 |
-0,90 |
0,87 |
1,97 |
3,87 |
|
10 |
0,98 |
1,00 |
1,00 |
1,01 |
1,01 |
-1,62 |
2,61 |
|
11 |
-0,64 |
-0,61 |
0,38 |
-0,23 |
0,14 |
2,45 |
6,00 |
|
12 |
1,81 |
1,84 |
3,37 |
6,19 |
11,37 |
-2,89 |
8,35 |
|
13 |
-1,08 |
-1,05 |
1,11 |
-1,17 |
1,23 |
1,28 |
1,64 |
|
14 |
0,20 |
0,23 |
0,05 |
0,01 |
0,00 |
-1,72 |
2,96 |
|
15 |
-1,52 |
-1,49 |
2,23 |
-3,33 |
4,98 |
0,80 |
0,64 |
|
16 |
-0,72 |
-0,70 |
0,48 |
-0,34 |
0,23 |
0,13 |
0,02 |
|
17 |
-0,59 |
-0,57 |
0,32 |
-0,18 |
0,10 |
0,99 |
0,99 |
|
18 |
0,40 |
0,43 |
0,18 |
0,08 |
0,03 |
0,54 |
0,29 |
|
19 |
0,94 |
0,97 |
0,94 |
0,91 |
0,88 |
-0,64 |
0,41 |
|
20 |
0,30 |
0,33 |
0,11 |
0,04 |
0,01 |
-0,67 |
0,45 |
|
21 |
-0,37 |
-0,35 |
0,12 |
-0,04 |
0,01 |
1,19 |
1,41 |
|
22 |
0,82 |
0,84 |
0,71 |
0,60 |
0,50 |
-0,02 |
0,00 |
|
23 |
0,80 |
0,83 |
0,68 |
0,56 |
0,47 |
-0,68 |
0,46 |
|
24 |
0,12 |
0,15 |
0,02 |
0,00 |
0,00 |
0,45 |
0,20 |
|
25 |
0,57 |
0,60 |
0,36 |
0,21 |
0,13 |
-0,16 |
0,03 |
|
26 |
0,41 |
0,44 |
0,19 |
0,09 |
0,04 |
-1,40 |
1,96 |
|
27 |
-0,99 |
-0,96 |
0,92 |
-0,88 |
0,85 |
1,75 |
3,05 |
|
28 |
0,76 |
0,79 |
0,62 |
0,49 |
0,38 |
-1,42 |
2,01 |
|
29 |
-0,66 |
-0,63 |
0,40 |
-0,25 |
0,16 |
0,05 |
0,00 |
|
30 |
-0,60 |
-0,58 |
0,33 |
-0,19 |
0,11 |
0,78 |
0,61 |
|
31 |
0,18 |
0,20 |
0,04 |
0,01 |
0,00 |
-0,48 |
0,23 |
|
32 |
-0,31 |
-0,28 |
0,08 |
-0,02 |
0,01 |
0,18 |
0,03 |
|
33 |
-0,13 |
-0,10 |
0,01 |
0,00 |
0,00 |
0,73 |
0,53 |
|
34 |
0,60 |
0,62 |
0,39 |
0,24 |
0,15 |
0,45 |
0,20 |
|
35 |
1,05 |
1,07 |
1,15 |
1,24 |
1,33 |
-1,24 |
1,55 |
|
36 |
-0,20 |
-0,17 |
0,03 |
0,00 |
0,00 |
0,53 |
0,28 |
|
37 |
0,33 |
0,36 |
0,13 |
0,04 |
0,02 |
-0,57 |
0,32 |
|
38 |
-0,24 |
-0,21 |
0,04 |
-0,01 |
0,00 |
0,47 |
0,22 |
|
39 |
0,23 |
0,26 |
0,07 |
0,02 |
0,00 |
0,21 |
0,04 |
|
40 |
0,44 |
0,47 |
0,22 |
0,10 |
0,05 |
-1,06 |
1,12 |
|
41 |
-0,62 |
-0,59 |
0,35 |
-0,20 |
0,12 |
0,89 |
0,80 |
|
42 |
0,27 |
0,09 |
0,03 |
0,01 |
0,33 |
0,11 |
|
|
43 |
0,60 |
0,63 |
0,39 |
0,25 |
0,16 |
-0,51 |
0,26 |
|
44 |
0,09 |
0,12 |
0,01 |
0,00 |
0,00 |
1,64 |
2,68 |
|
45 |
1,73 |
1,76 |
3,09 |
5,43 |
9,53 |
-2,34 |
5,47 |
|
46 |
-0,61 |
-0,58 |
0,34 |
-0,20 |
0,11 |
-0,13 |
0,02 |
|
47 |
-0,74 |
-0,71 |
0,50 |
-0,36 |
0,25 |
-1,01 |
1,03 |
|
48 |
-1,75 |
-1,72 |
2,97 |
-5,11 |
8,80 |
2,66 |
7,08 |
|
49 |
0,91 |
0,94 |
0,88 |
0,82 |
0,77 |
-0,04 |
0,00 |
|
50 |
0,87 |
0,89 |
0,80 |
0,72 |
0,64 |
2) Исследование
на наличие существенного систематического влияния по критерию Аббе.
Истинное значение величины не известно. Тогда наличие в результатах наблюдений
постоянной составляющей может быть выяснено по наиболее распространенному в
геодезии критерию Аббе [2 и др.]. Для этого выдвигаем гипотезу, что с
вероятностью β в предложенном ряде отсутствует значимое систематическое влияние.
По исследуемым величинам получаем практическую величину
являющуюся отношением двух оценок
дисперсий, средние квадратические ошибки которых получены как
где уклонение i — той
величины от среднего
последовательные
разности
Для сравнения, по
заданной вероятности β
(или уровню значимости q),
числу степеней свободы п и с использованием статистических таблиц критерия Аббе
получают контрольную величину . Тогда, при δ >
принимается гипотеза об
отсутствии систематической ошибки с вероятностью β
=1 — q. В противном случае (δ
< ) следует принять
гипотезу о постоянной составляющей в статистической совокупности и для
корректной оценки исследуемых параметров ее необходимо исключить из ряда
измерений. Для этого получают усредненную величину систематического влияния,
равную среднему арифметическому из всех элементов, которую и исключаем из
измерений, получая новый ряд с уменьшенной по
сравнению с исходным рядом систематической составляющей
По исследуемым величинам получаю
практическую величину:
где
|
|
|
Проверим неравенство (

выполняется , значит модно
утверждать, что в исследуемом ряде отсутствуют существенные систематические
ошибки с вероятностью .
) Исследование ряда
данных на наличие грубых ошибок по критерию Граббса. (В зависимости от
требований задачи существует масса критериев, решающих поставленную задачу:
критерий Граббса, Диксона, Шарлье, Шовенэ и др. В работе для выявления грубых
погрешностей предлагается использовать критерий Граббса. Критерий дает
вероятность выполнения выдвинутой гипотезы о том, что максимальное, или
минимальное значение из ряда не являются грубыми погрешностями. Для этого по
экстремальным значениям выборки Хтах и Xmin,
среднему арифметическому и средней
квадратической погрешности т, вычисляют значения
Если Zвыч < zq, для максимального и минимального значения, то следует принять
гипотезу об отсутствии в ряде грубых погрешностей, так как экстремальные
значения не являются грубыми. Значения теоретической величины критерия zq получают по
заданному аргументу q и числу элементов в выборке п по специальным статистическим
таблицам критерия Граббса для zq. Если же zfвыч > zq, тогда или
наибольшее или наименьшее значение ряда из дальнейшей обработки следует
исключить.
Если не имеется таблиц статистики
критерия Смирнова-Граббса, то её можно достаточно точно получить на основе
формулы
где ta/ 2nn-2 — квантиль t-распределения Стьюдента с уровнем значимости а.
— 2 степенями свободы с п элементами в ряде.
|
Практические величины: |
|
где ,
,
Из статистических таблиц
получим коэффициент
для вероятности и степени свободы
, равный
. Проверяемое
неравенство выполняется для
максимального и минимального значений ошибки:
|
|
|
Следовательно, можно
утверждать, то с вероятностью ни левая, ни правая
крайние в ряде ошибки не являются грубыми.
) Оценки основных
характеристик ряда. Теоретическое значение математического ожидания для
нормального закона распределения Гаусса равно нулю и, следовательно, если
вычисленная его оценка M(X) будет отличаться от нуля на величину не более утроенной
средней квадратической погрешности 3 *m = ∆пред, то это говорит о том, что распределение
исследуемых величин может быть близко к нормальному, но только по критерию
близости теоретического значения математического ожидания к вычисленному значению.
Оценки математического ожидания, дисперсии и стандарта получим по следующим
формулам
Практические значения:
• среднее арифметическое
;
• средняя квадратическая
ошибка ;
• оценка дисперсии ;
5) Приближенные методы
исследования на соответствие нормальному закону. Приближенные
критерии исследования ряда погрешностей на соответствие нормальному закону
распределения используют сравнение некоторых известных теоретических
характеристик нормального закона и их вычисленного по результатам измерений
аналога. Кроме наиболее распространенной средней квадратической погрешности т
используют средние абсолютные v и вероятные (срединные) ошибки r. Между тремя ошибками т, V и r
для нормального закона распределения величин имеются теоретически строгие
соотношения
«Критерий ничтожных влияний»,
гласящий, что величина считается неизменной, если её вариация составляет не
более 11% от самой величины.
Для вычисления средней
абсолютной ошибки пользуются формулами:
Приближённые критерии на основе
коэффициентов
|
|
|
|
|
|
|
|
Не все абсолютные
отклонения между практическими и теоретическими значениями величин меньше
допустимых по критерию ничтожных погрешностей 0,3930. 138,0.712
0. 163,0,284
0.130.
Характеристики будут такими:
|
|
|
Проведём контроль:
Эксцесс — мера «крутости».
|
|
|
Проведем контроль:
|
|
|
Это говорит о том, что эмпирическое
распределение по отношению к теоретическому на допустимую величину скошено
вправо (отрицательное) и на допустимую величину выше нормального (положительное).
6-8) Графический критерий
исследования ряда погрешностей на соответствие нормальному закону распределения
Для дальнейших исследований
погрешностей на соответствие их нормальному закону распределения строят для
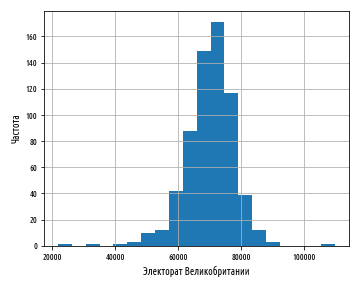
ряда одно из его графических представлений, например, в виде гистограммы или
многоугольника распределения, с нанесенной поверх её теоретической кривой
закона Гаусса с параметрами О и m, называемой огивой. В данной работе предлагается использовать
гистограмму. Построение гистограммы начинают с разбиения ряда погрешностей на
интервалы. Число интервалов к зависит от точности измерений, количества
элементов в выборке и является в некотором смысле произвольным. Основное
требование к количеству и величине интервалов заключается в том, чтобы полученный
на их основе график был наглядным и правдоподобным. Длину интервала Q можно получить, например, используя
следующие формулы
если известно число интервалов к, и
В геодезии чаще всего в такого рода
исследованиях ряд делят на 12 интервалов, каждый из которых должен быть в 0.5 m.
Далее необходимо
подсчитать число n. элементов ряда,
принадлежащих j-му интервалу, и вычислить практические оценки неизвестных
вероятностей (частоты ) по формуле
Вертикальные
составляющие гистограммы, называемые высотами прямоугольников
На этом же графике необходимо
построить теоретическую кривую, соответствующую нормальному закону, которая
наилучшим образом сглаживает данное эмпирическое статистическое распределение.
Кривая строится на основе формулы плотности вероятности для закона Гаусса
Наиболее точный критерий
соответствия исследуемого ряда нормальному закону распределения получу,
используя критерий χ2 Пирсона по формулам:
Здесь — теоретическая
вероятность попаданияслучайной величины в соответствующий интервал.
Таблица построения гистограммы
эмпирического закона распределения
|
Интервал в долях |
Интервал в секундах |
Количество элементов в интервале |
Относит. частота |
Высота прямоугольника |
|
m(t) |
(Ø) |
|
|
|
|
-3m |
-2,50 |
0 |
0 |
0 |
|
-2,5m |
-2,08 |
3 |
0,06 |
0,1441 |
|
-2m |
-1,67 |
3 |
0,06 |
0,1441 |
|
-1,5m |
-1,25 |
6 |
0,12 |
0,2882 |
|
-1m |
-0,83 |
5 |
0,1 |
0,2402 |
|
-0,5m |
-0,42 |
7 |
0,14 |
0,3363 |
|
0m |
0,00 |
7 |
0,14 |
0,3363 |
|
0,5m |
0,42 |
6 |
0,12 |
0,2882 |
|
1m |
0,83 |
4 |
0,08 |
0,1921 |
|
1,5m |
1,25 |
1 |
0,02 |
0,0480 |
|
2m |
1,67 |
2 |
0,04 |
0,0961 |
|
2,5m |
2,08 |
1 |
0,02 |
0,0480 |
|
45 |
0,9 |
При этом сумма элементов по
интервалам должна равняться общему количеству элементов в ряде; сумма частот
равняется единице в пределах ошибки округления; сумма высот прямоугольников
равняется 2/т. Выбрав масштабы по горизонтальной оси для величин интервалов
(например, 0.5т — 1 см), по вертикальной для высот прямоугольников (например,
0.05 от — высоты прямоугольника — 1 см), откладывают по соответствующим
границам вертикальные высоты, которые замыкаются в прямоугольники. Полученный
график и будет называться гистограммой (эмпирическим представлением плотности
закона распределения), площадь которого равна единице
) На этом же графике необходимо
построить теоретическую кривую, соответствующую нормальному закону, которая
наилучшим образом сглаживает (выравнивает) данное эмпирическое статистическое
распределение. Кривая строится на основе формулы плотности вероятности для
закона Гаусса
Обычно величина t изменяется от -3 до 3 через 0.5,
так что вычисления не представляют трудности. Необходимо учитывать, что функция
симметричная, т.е. f(x)= — f(x) Значения функции с m = 1 приведены в любых книгах по статистике или обработке
измерений в виде таблиц и также могут быть использованы при вычислениях.
Значения теоретической функции
плотности на границах интервалов будут равны:
|
t = |
0 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
|
φ(∆)= |
0,48 |
0,42 |
0,29 |
0,16 |
0,06 |
0,02 |
0,01 |
По вычисленным данным строят график
на гистограмме
10) Наиболее точный
критерий соответствия исследуемого ряда нормальному закону распределения
получим используя критерий -Пирсона.
Следует иметь в виду,
что все критерии соответствия являются частными случаями общего алгоритма
статистической проверки гипотез, в основе которой лежат следующие пункты:
) выдвижение с
доверительной вероятностью исходной гипотезы;
) получение
теоретического значения критерия;
) сравнение двух
значений критериев и вывод.
Предположим, что с
вероятностью ряд ошибок распределен
нормально. Из статистических таблиц распределения -Пирсона по числу
степеней свободы находим эталонное
значение .
|
i |
Интервалы |
|||||
|
1 2 3 4 5 6 7 8 9 10 |
-3 -2.5 -2.5 -2.0 |
0.0013 0.0062 |
0.0049 0.0165 |
0 3 |
0.25 |
-0.25 |
|
-2.0 -1.5 -1.5 -1.0 |
0.0228 0.0668 0.1587 0.3085 0.5000 0.6915 0.8413 0.9332 0.9772 |
0.0441 0.0918 0.1499 0.1915 0.1915 0.1499 0.0918 0.0441 0.0165 |
3 6 |
2.2 4.6 |
0.8 |
|
|
∑ |
0.998 |
45 |
49.9 |
На основании проведенных
исследований установлено, что рад является случайным, оценка математического
ожидания в виде среднего арифметического не превосходит утроенной средней
квадратической ошибки, то есть практически равна нулю. Количество положительных
элементов (23) равно количеству отрицательных (27).
В результате вычисления
критерия Аббе и сравнения практических и теоретических значений выявлено, что в
ряду отсутствуют значимые систематические влияния с вероятностью и с этой же вероятностью
крайние значения вариационного ряда не являются грубыми.
Приближённые критерии
соответствия нормальному закону, учитывающие расхождения между теоретическими и
практическими значениями соотношениями между тремя видами ошибок: средней
квадратической, средней абсолютной и вероятной, показывают, что ряд
соответствует нормальному закону. Значениями асимметрии и эксцесса можно
пренебречь.
Визуальный анализ
гистограммы (эмпирическое распределение) и огивы (вид теоретического закона
распределения) показывает недостаточное согласование по форме и величине между
ними, что говорит о недостаточном соответствии нормальному закону
распределения.
Наиболее точные
результаты соответствия исследуемого ряда нормальному закону дает критерий c2 Пирсона, который учитывает расхождение между практическими и
теоретическими частотами по всем выделенным интервалам.
Таким образом, выполненные
исследования ряда ошибок на соответствие нормальному закону распределения дают
по всем использованным критериям положительные результаты, что позволяет
сделать вывод о достаточной близости ряда предполагаемому закону. И сделать
вывод, что мой ряд достаточно хорошо подчиняется нормальному закону
распределения.
погрешность распределение закон
статистический
Основным
критерием точности результатов измерений
является средняя
квадратическая ошибка
(оценка СКО), определяемая по формуле
|
|
Для
ряда истинных ошибок при известном
формула принимает вид (1.3) и называетсяформулой
Гаусса:
|
|
где
;
.
Средней
ошибкой
называют среднее арифметическое из
абсолютных значений ошибок, т.е.
|
|
Вероятной
ошибкой называют такое значение случайной
ошибки,
больше или меньше которого, по абсолютной
величине, ошибки равновозможны, т.е.
.
На
практике
определяется величиной, которую находят,
расположив все ошибкиi
в ряд в порядке возрастания их абсолютных
величин. Вероятная ошибка будет расположена в середине такого
ряда.
При нормальном
законе распределения случайных ошибок
имеют место соотношения:
|
|
Величины
и
являются оценками параметров и r:
соответственно среднего и вероятного
отклонений (см. раздел I
п. 3.5).
Соотношения
называют критериями нормального закона
(в разделе I
они представлены в виде
;
).
Предельной
ошибкой
называют такую ошибку, больше которой
в ряде измерений ошибок не должно быть.
В качестве предельных выбирают величины,
определяемые по правилу
и
(с
вероятностями 0,954 и 0,997 соответственно).
Перечисленные
выше критерии
,m,
,
,
называютабсолютными
ошибками.
Относительной
ошибкой
называют отношение соответствующей
абсолютной ошибки к значению измеряемой
величины X
(если X
неизвестно, его заменяют результатом
измерения x).
Относительную
ошибку обычно выражают в виде дроби с
числителем, равным 1, например:
—средняя
квадратическая относительная ошибка;
—предельная
относительная ошибка величины X
и
т.д.
Значения
абсолютных ошибок получают с двумя–тремя
значащими цифрами, а знаменатель
относительной ошибки округляют до двух
значащих цифр с нулями.
Например,
при
и
.
.
1.5 Исследование ряда истинных ошибок на нормальное распределение
Для
решения этой первой задачи теории ошибок
используем методику, изложенную в
разделе математической статистики, а
также выполним вычисления по
формулам (1.1–1.5) настоящего раздела.
Задача 1.1.
В таблице 1.1
даны невязки 32‑х треугольников.
Невязки
можно считать истинными ошибками,
так как сумму углов в треугольнике можно
рассматривать как измеренную величину,
истинное значение которой равно
.
Выполнить исследование ряда невязокна нормальный закон распределения.
|
Таблица |
|||||||
|
№ |
невязки i |
№ |
невязки i |
№ |
невязки i |
№ |
невязки i |
|
1 |
–0,76″ |
9 |
+1,29″ |
17 |
+0,71″ |
25 |
+0,22″ |
|
2 |
+1,52″ |
10 |
+0,38″ |
18 |
+1,04″ |
26 |
+0,06″ |
|
3 |
–0,24″ |
11 |
–1,03″ |
19 |
–0,38″ |
27 |
+0,43″ |
|
4 |
+1,31″ |
12 |
+0,00″ |
20 |
+1,16″ |
28 |
–1,28″ |
|
5 |
–1,27″ |
13 |
–1,23″ |
21 |
–0,19″ |
29 |
–0,41″ |
|
6 |
–1,88″ |
14 |
–1,38″ |
22 |
+2,28″ |
30 |
–2,50″ |
|
7 |
+0,01″ |
15 |
–0,25″ |
23 |
+0,07″ |
31 |
+1,92″ |
|
8 |
–0,69″ |
16 |
–0,73″ |
24 |
–0,95″ |
32 |
–0,62″ |
Найдём ряд сумм,
необходимых для дальнейшего исследования:
;
;
;
;
;
;
.
Решение:
-
Вычисление
оценок параметров нормального
распределения
,
,
кривая плотности которого определяется
выражением :


-
Вычисление
средней ошибки
и коэффициента:
;
;
.
-
Определение
вероятной ошибкии коэффициента
.
Располагаем
истинные ошибки в ряд по возрастанию
их абсолютных величин:
+0,00;
+0,01; +0,06;+0,07; –0,19; +0,22; –0,24; –0,25; +0,38; –0,38;
–0,41; +0,43; –0,62; –0,69; +0,71; –0,73; –0,76; –0,95;
–1,03; +1,04; +1,16; –1,23; –1,27; –1,28; +1,29; +1,31;
–1,38; +1,52; -1,88; +1,92; +2,28; –2,50.
Находим:
;
;
.
-
Построение
статистического группированного ряда.
Распределим
невязки (табл. 1.2) в двенадцати
интервалах (длину интервала примем
равной половине средней квадратической
ошибки, т.е.
).
|
Таблица |
|||||||
|
№ п/п |
длины интервалов в m |
длины интервалов в |
число |
частоты |
высоты прямо-угольников |
||
|
1 |
–3,0m |
–2,5m |
–3,30″ |
–2,75″ |
0 |
0,000 |
0,000 |
|
2 |
–2,5m |
–2,0m |
–2,75 |
–2,20 |
1 |
0,031 |
0,056 |
|
3 |
–2,0m |
–1,5m |
–2,20 |
–1,65 |
1 |
0,031 |
0,056 |
|
4 |
–1,5m |
–1,0m |
–1,65 |
–1,10 |
4 |
0,125 |
0,227 |
|
5 |
–1,0m |
–0,5m |
–1,10 |
–0,55 |
6 |
0,188 |
0,342 |
|
6 |
–0,5m |
+0 |
–0,55 |
–0 |
5 |
0,156 |
0,284 |
|
7 |
+0 |
+0,5m |
–0 |
+0,55 |
7 |
0,219 |
0,398 |
|
8 |
+0,5m |
+1,0m |
+0,55 |
+1,10 |
2 |
0,062 |
0,113 |
|
9 |
+1,0m |
+1,5m |
+1,10 |
+1,65 |
4 |
0,125 |
0,227 |
|
10 |
+1,5m |
+2,0m |
+1,65 |
+2,20 |
1 |
0,031 |
0,056 |
|
11 |
+2,0m |
+2,5m |
+2,20 |
+2,75 |
1 |
0,031 |
0,056 |
|
12 |
+2,5m |
+3,0m |
+2,75 |
+3,30 |
0 |
0,000 |
0,000 |
|
∑ |
32 |
1,000 |
― |
||||
|
mi — |
-
Построение
гистограммы и выравнивающей её кривой
распределения.
По
данным таблицы 1.2 (столбцы 2 и 6)
строим гистограмму (рис. 1.1) —
график эмпирического распределения
(на выбор масштаба изображения наложим
лишь условие наглядности).
Рис. 1.1 —
Гистограмма и выравнивающая кривая
Вид
гистограммы позволяет действительно
предположить нормальный закон
распределения ошибок i.
Теоретическая кривая, наилучшим образом
выравнивающая (сглаживающая) гистограмму,
определяется уравнением
|
|
где
;
;
;
;

Вычисление
ординат кривой
выполняем,
используя таблицу Приложения A.
Результаты вычислений поместим в
таблице 1.3.
|
Таблица 1.3 |
|||||
|
№ п/п |
левые границы интервалов i |
|
yi |
|
|
|
1 |
0 |
0 |
0,564 |
0,645 |
0,364 |
|
2 |
0,5m |
0,5 |
0,498 |
―»― |
0,321 |
|
3 |
1,0m |
1,0 |
0,342 |
―»― |
0,220 |
|
4 |
1,5m |
1,5 |
0,183 |
―»― |
0,118 |
|
5 |
2,0m |
2,0 |
0,076 |
―»― |
0,049 |
|
6 |
2,5m |
2,5 |
0,025 |
―»― |
0,016 |
|
7 |
3,0m |
3,0 |
0,006 |
―»― |
0,004 |
По
данным таблицы 1.3 (столбцы 2 и 6)
на графике рис. 1.1 наносим ряд точек ,
которые соединяем плавной кривой. Левую
ветвь кривой строим по тем же ординатам.
Как
видно из графика, кривая ()
удовлетворительно сглаживает гистограмму.
-
Применение
критерия 2‑Пирсона.
Для оценки степени
приближения статистического распределения
(гистограммы) к теоретическому нормальному
закону (кривой распределения) вычисляем
величину
|
|
где
|
|
Результаты
вычислений поместим в таблице 1.4.
находят
по таблице Приложения B
для левых границ интервалов ti.
|
Таблица 1.4 |
|||||||
|
№ |
Интервалы ti |
|
pi |
mi |
npi |
|
|
|
1 |
–3,0 |
–2,5 |
–0,5 |
0,0062 |
0 |
0,20 |
0,20 |
|
2 |
–2,5 |
–2,0 |
–0,4938 |
0,0166 |
1 |
0,53 |
0,42 |
|
3 |
–2,0 |
–1,5 |
–0.4772 |
0,0440 |
1 |
1,41 |
0,12 |
|
4 |
–1,5 |
–1,0 |
–0.4332 |
0,0918 |
4 |
2,94 |
0,38 |
|
5 |
–1,0 |
–0,5 |
–0,3414 |
0,1500 |
6 |
4,80 |
0,30 |
|
6 |
–0,5 |
+0 |
–0,1914 |
0,1914 |
5 |
6,12 |
0,20 |
|
7 |
+0 |
+0,5 |
+0 |
0,1914 |
7 |
6,12 |
0,13 |
|
8 |
+0,5 |
+1,0 |
+0,1914 |
0,1500 |
2 |
4,80 |
1,63 |
|
9 |
+1,0 |
+1,5 |
+0,3414 |
0,0918 |
4 |
2,94 |
0,38 |
|
10 |
+1,5 |
+2,0 |
+0,4332 |
0,0440 |
1 |
1,41 |
0,12 |
|
11 |
+2,0 |
+2,5 |
+0,4772 |
0,0166 |
1 |
0,53 |
0,42 |
|
12 |
+2,5 |
+3,0 |
+0,4938 |
0,0062 |
0 |
0,20 |
0,20 |
|
13 |
+3,0 |
+∞ |
+0,5 |
― |
― |
― |
― |
|
|
1,0000 |
32 |
32,00 |
4,50 |
Число
степеней свободы определяется формулой
.
Находим(k —
число
интервалов,
,
так как только один параметроценивался по выборке, а
принято равным нулю).
По
таблице Приложения E
по числу степеней свободы для
находим
вероятность,
а длянаходим
.
Интерполируя, дляполучим
.
-
Вычисление
оценок скошенностии эксцесса
и проверка соотношений:
|
|
которые
являются критериями нормального закона.
Находим:
-
;
-
;
-
;
-
;
-
;
.
Как
видно из вычислений, соотношения
выполняются.
В
результате исследования приходим к
выводу о том, что рассматриваемый ряд
истинных ошибок является действительно
рядом случайных ошибок, подчиняющихся
приближенно нормальному закону, так
как:
-
выполняются
свойства случайных ошибок:
-
среднее
арифметическоепрактически равно нулю,
-
положительные
и отрицательные ошибки, равные по
абсолютной величине (см. гистограмму),
примерно одинаково часто встречаются
в данном ряде, -
малые
по абсолютной величине ошибки встречаются
чаще, чем большие, -
случайные
ошибки
с заданной
вероятностью
не превосходят определенного предела,
равного,
ни одна из ошибок ряда не превышает
предельной ошибки, равной
;
-
коэффициенты
и
совпадают
с их теоретическими значениями (;
);
-
вероятность
велика, так как значительно больше
критического уровня значимости,
равного 0,1; -
величины
скошенности и эксцесса незначительно
отличаются от нуля.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Исследование ряда погрешностей на соответствие нормальному закону распределения
Исследование ряда погрешностей на соответствие нормальному закону
распределения
1.
Теоретические основы выполнения исследований
Обработка результатов
измерений имеет место всегда, когда одна из определяемых величин получена
несколько раз с отличными друг от друга значениями. При этом корректная оценка
полученных результатов возможна, только если известны правила, определяющие
поведение погрешностей измерений ∆. К главным таким правилам относят
законы поведения погрешностей в дифференциальной F(∆)
и интегральной F (∆) формах, их
основные численные характеристики и представления законов в виде графического
материала. Интегральная форма называется функцией распределения погрешностей , дифференциальная форма
— функцией плотности распределения погрешностей . К основным
характеристикам законов относят наиболее вероятное значение определяемой
величины, называемое математическим ожиданием и обозначаемое МО (∆) или
М(∆), или Е(∆); меру рассеивания измерений вокруг математического
ожидания, называемую дисперсией и D(∆)
(чаще используют просто величину σ(∆),
называемую стандартом, так как он не имеет квадратичной размерности как у
дисперсии). К дополнительным характеристикам законов относят меру скошенности
относительно вертикальной оси симметрии, называемую асимметрией и обозначаемую
А или и меру крутости,
называемую эксцессом и обозначаемую Е.
Множество теоретических
и практических исследований показывают, что результаты геодезических измерений
подчиняются нормальному закону распределения (закону Гаусса) и имеют вид
В процессе измерений
часто имеет место наличие грубых погрешностей (погрешностей, больших заданного
допуска) или промахов (т.е. очень сильно отличающихся от других). С другой
стороны, при наблюдениях в результатах могут содержаться и какие-либо
постоянные составляющие, называемые систематическими ошибками.
2.
Предварительные вычисления для исследования
В предварительных вычислениях ряд
исследуется на наличие значимых систематических и грубых погрешностей а также
меры однородности результатов по точности на основе каких-либо критериев.
Определение значимости
систематического влияния. Следует иметь
ввиду, что систематические влияния в рядах присутствуют всегда, но они могут
быть значимы и не значимы. При определении наличия значимых систематических
погрешностей в ряде имеют место два случая:
1) известно истинное значение
определяемой величины Хист и произведено ее измерений х. В этом
случае пользуются зависимостью
Где ∆=X-
=
— средняя квадратическая
погрешность среднего арифметического, m-СКП
одной величины, n — число элементов в
ряде. Величина (квантиль t-распределения Стьюдента) определяется по уровню значимости q (или вероятности р) и числу избыточных измерений (числу степеней
свободы) k = n — 1 и выбирается из
статистических таблиц, или получается из какого либо программного продукта.
Если неравенство (2) выполняется, то с вероятностью р = 1 — q считаем, что значимые систематические погрешности в ряде
измерений отсутствуют.
|
Аббе |
|
|
|
|
|
|
|
|
1 |
-0,06 |
-0,04 |
0,00 |
0,00 |
0,00 |
-1,96 |
3,84 |
|
2 |
-2,02 |
-1,99 |
3,98 |
-7,94 |
15,83 |
1,04 |
1,08 |
|
3 |
-0,98 |
-0,95 |
0,91 |
-0,87 |
0,83 |
1,59 |
2,54 |
|
4 |
0,61 |
0,64 |
0,41 |
0,26 |
0,17 |
-0,67 |
0,45 |
|
5 |
-0,05 |
-0,03 |
0,00 |
0,00 |
0,00 |
-1,06 |
1,13 |
|
6 |
-1,12 |
-1,09 |
1,19 |
-1,30 |
1,42 |
0,49 |
0,24 |
|
7 |
-0,63 |
-0,60 |
0,36 |
-0,21 |
0,13 |
0,88 |
0,77 |
|
8 |
0,25 |
0,28 |
0,08 |
0,02 |
0,01 |
-1,24 |
1,54 |
|
9 |
-0,99 |
-0,97 |
0,93 |
-0,90 |
0,87 |
1,97 |
3,87 |
|
10 |
0,98 |
1,00 |
1,00 |
1,01 |
1,01 |
-1,62 |
2,61 |
|
11 |
-0,64 |
-0,61 |
0,38 |
-0,23 |
0,14 |
2,45 |
6,00 |
|
12 |
1,81 |
1,84 |
3,37 |
6,19 |
11,37 |
-2,89 |
8,35 |
|
13 |
-1,08 |
-1,05 |
1,11 |
-1,17 |
1,23 |
1,28 |
1,64 |
|
14 |
0,20 |
0,23 |
0,05 |
0,01 |
0,00 |
-1,72 |
2,96 |
|
15 |
-1,52 |
-1,49 |
2,23 |
-3,33 |
4,98 |
0,80 |
0,64 |
|
16 |
-0,72 |
-0,70 |
0,48 |
-0,34 |
0,23 |
0,13 |
0,02 |
|
17 |
-0,59 |
-0,57 |
0,32 |
-0,18 |
0,10 |
0,99 |
0,99 |
|
18 |
0,40 |
0,43 |
0,18 |
0,08 |
0,03 |
0,54 |
0,29 |
|
19 |
0,94 |
0,97 |
0,94 |
0,91 |
0,88 |
-0,64 |
0,41 |
|
20 |
0,30 |
0,33 |
0,11 |
0,04 |
0,01 |
-0,67 |
0,45 |
|
21 |
-0,37 |
-0,35 |
0,12 |
-0,04 |
0,01 |
1,19 |
1,41 |
|
22 |
0,82 |
0,84 |
0,71 |
0,60 |
0,50 |
-0,02 |
0,00 |
|
23 |
0,80 |
0,83 |
0,68 |
0,56 |
0,47 |
-0,68 |
0,46 |
|
24 |
0,12 |
0,15 |
0,02 |
0,00 |
0,00 |
0,45 |
0,20 |
|
25 |
0,57 |
0,60 |
0,36 |
0,21 |
0,13 |
-0,16 |
0,03 |
|
26 |
0,41 |
0,44 |
0,19 |
0,09 |
0,04 |
-1,40 |
1,96 |
|
27 |
-0,99 |
-0,96 |
0,92 |
-0,88 |
0,85 |
1,75 |
3,05 |
|
28 |
0,76 |
0,79 |
0,62 |
0,49 |
0,38 |
-1,42 |
2,01 |
|
29 |
-0,66 |
-0,63 |
0,40 |
-0,25 |
0,16 |
0,05 |
0,00 |
|
30 |
-0,60 |
-0,58 |
0,33 |
-0,19 |
0,11 |
0,78 |
0,61 |
|
31 |
0,18 |
0,20 |
0,04 |
0,01 |
0,00 |
-0,48 |
0,23 |
|
32 |
-0,31 |
-0,28 |
0,08 |
-0,02 |
0,01 |
0,18 |
0,03 |
|
33 |
-0,13 |
-0,10 |
0,01 |
0,00 |
0,00 |
0,73 |
0,53 |
|
34 |
0,60 |
0,62 |
0,39 |
0,24 |
0,15 |
0,45 |
0,20 |
|
35 |
1,05 |
1,07 |
1,15 |
1,24 |
1,33 |
-1,24 |
1,55 |
|
36 |
-0,20 |
-0,17 |
0,03 |
0,00 |
0,00 |
0,53 |
0,28 |
|
37 |
0,33 |
0,36 |
0,13 |
0,04 |
0,02 |
-0,57 |
0,32 |
|
38 |
-0,24 |
-0,21 |
0,04 |
-0,01 |
0,00 |
0,47 |
0,22 |
|
39 |
0,23 |
0,26 |
0,07 |
0,02 |
0,00 |
0,21 |
0,04 |
|
40 |
0,44 |
0,47 |
0,22 |
0,10 |
0,05 |
-1,06 |
1,12 |
|
41 |
-0,62 |
-0,59 |
0,35 |
-0,20 |
0,12 |
0,89 |
0,80 |
|
42 |
0,27 |
0,09 |
0,03 |
0,01 |
0,33 |
0,11 |
|
|
43 |
0,60 |
0,63 |
0,39 |
0,25 |
0,16 |
-0,51 |
0,26 |
|
44 |
0,09 |
0,12 |
0,01 |
0,00 |
0,00 |
1,64 |
2,68 |
|
45 |
1,73 |
1,76 |
3,09 |
5,43 |
9,53 |
-2,34 |
5,47 |
|
46 |
-0,61 |
-0,58 |
0,34 |
-0,20 |
0,11 |
-0,13 |
0,02 |
|
47 |
-0,74 |
-0,71 |
0,50 |
-0,36 |
0,25 |
-1,01 |
1,03 |
|
48 |
-1,75 |
-1,72 |
2,97 |
-5,11 |
8,80 |
2,66 |
7,08 |
|
49 |
0,91 |
0,94 |
0,88 |
0,82 |
0,77 |
-0,04 |
0,00 |
|
50 |
0,87 |
0,89 |
0,80 |
0,72 |
0,64 |
2) Исследование
на наличие существенного систематического влияния по критерию Аббе.
Истинное значение величины не известно. Тогда наличие в результатах наблюдений
постоянной составляющей может быть выяснено по наиболее распространенному в
геодезии критерию Аббе [2 и др.]. Для этого выдвигаем гипотезу, что с
вероятностью β в предложенном ряде отсутствует значимое систематическое влияние.
По исследуемым величинам получаем практическую величину
являющуюся отношением двух оценок
дисперсий, средние квадратические ошибки которых получены как
где уклонение i — той
величины от среднего
последовательные
разности
Для сравнения, по
заданной вероятности β
(или уровню значимости q),
числу степеней свободы п и с использованием статистических таблиц критерия Аббе
получают контрольную величину . Тогда, при δ >
принимается гипотеза об
отсутствии систематической ошибки с вероятностью β
=1 — q. В противном случае (δ
< ) следует принять
гипотезу о постоянной составляющей в статистической совокупности и для
корректной оценки исследуемых параметров ее необходимо исключить из ряда
измерений. Для этого получают усредненную величину систематического влияния,
равную среднему арифметическому из всех элементов, которую и исключаем из
измерений, получая новый ряд с уменьшенной по
сравнению с исходным рядом систематической составляющей
По исследуемым величинам получаю
практическую величину:
где
|
|
|
Проверим неравенство (

выполняется , значит модно
утверждать, что в исследуемом ряде отсутствуют существенные систематические
ошибки с вероятностью .
) Исследование ряда
данных на наличие грубых ошибок по критерию Граббса. (В зависимости от
требований задачи существует масса критериев, решающих поставленную задачу:
критерий Граббса, Диксона, Шарлье, Шовенэ и др. В работе для выявления грубых
погрешностей предлагается использовать критерий Граббса. Критерий дает
вероятность выполнения выдвинутой гипотезы о том, что максимальное, или
минимальное значение из ряда не являются грубыми погрешностями. Для этого по
экстремальным значениям выборки Хтах и Xmin,
среднему арифметическому и средней
квадратической погрешности т, вычисляют значения
Если Zвыч < zq, для максимального и минимального значения, то следует принять
гипотезу об отсутствии в ряде грубых погрешностей, так как экстремальные
значения не являются грубыми. Значения теоретической величины критерия zq получают по
заданному аргументу q и числу элементов в выборке п по специальным статистическим
таблицам критерия Граббса для zq. Если же zfвыч > zq, тогда или
наибольшее или наименьшее значение ряда из дальнейшей обработки следует
исключить.
Если не имеется таблиц статистики
критерия Смирнова-Граббса, то её можно достаточно точно получить на основе
формулы
где ta/ 2nn-2 — квантиль t-распределения Стьюдента с уровнем значимости а.
— 2 степенями свободы с п элементами в ряде.
|
Практические величины: |
|
где ,
,
Из статистических таблиц
получим коэффициент
для вероятности и степени свободы
, равный
. Проверяемое
неравенство выполняется для
максимального и минимального значений ошибки:
|
|
|
Следовательно, можно
утверждать, то с вероятностью ни левая, ни правая
крайние в ряде ошибки не являются грубыми.
) Оценки основных
характеристик ряда. Теоретическое значение математического ожидания для
нормального закона распределения Гаусса равно нулю и, следовательно, если
вычисленная его оценка M(X) будет отличаться от нуля на величину не более утроенной
средней квадратической погрешности 3 *m = ∆пред, то это говорит о том, что распределение
исследуемых величин может быть близко к нормальному, но только по критерию
близости теоретического значения математического ожидания к вычисленному значению.
Оценки математического ожидания, дисперсии и стандарта получим по следующим
формулам
Практические значения:
• среднее арифметическое
;
• средняя квадратическая
ошибка ;
• оценка дисперсии ;
5) Приближенные методы
исследования на соответствие нормальному закону. Приближенные
критерии исследования ряда погрешностей на соответствие нормальному закону
распределения используют сравнение некоторых известных теоретических
характеристик нормального закона и их вычисленного по результатам измерений
аналога. Кроме наиболее распространенной средней квадратической погрешности т
используют средние абсолютные v и вероятные (срединные) ошибки r. Между тремя ошибками т, V и r
для нормального закона распределения величин имеются теоретически строгие
соотношения
«Критерий ничтожных влияний»,
гласящий, что величина считается неизменной, если её вариация составляет не
более 11% от самой величины.
Для вычисления средней
абсолютной ошибки пользуются формулами:
Приближённые критерии на основе
коэффициентов
|
|
|
|
|
|
|
|
Не все абсолютные
отклонения между практическими и теоретическими значениями величин меньше
допустимых по критерию ничтожных погрешностей 0,3930. 138,0.712
0. 163,0,284
0.130.
Характеристики будут такими:
|
|
|
Проведём контроль:
Эксцесс — мера «крутости».
|
|
|
Проведем контроль:
|
|
|
Это говорит о том, что эмпирическое
распределение по отношению к теоретическому на допустимую величину скошено
вправо (отрицательное) и на допустимую величину выше нормального (положительное).
6-8) Графический критерий
исследования ряда погрешностей на соответствие нормальному закону распределения
Для дальнейших исследований
погрешностей на соответствие их нормальному закону распределения строят для
ряда одно из его графических представлений, например, в виде гистограммы или
многоугольника распределения, с нанесенной поверх её теоретической кривой
закона Гаусса с параметрами О и m, называемой огивой. В данной работе предлагается использовать
гистограмму. Построение гистограммы начинают с разбиения ряда погрешностей на
интервалы. Число интервалов к зависит от точности измерений, количества
элементов в выборке и является в некотором смысле произвольным. Основное
требование к количеству и величине интервалов заключается в том, чтобы полученный
на их основе график был наглядным и правдоподобным. Длину интервала Q можно получить, например, используя
следующие формулы
если известно число интервалов к, и
В геодезии чаще всего в такого рода
исследованиях ряд делят на 12 интервалов, каждый из которых должен быть в 0.5 m.
Далее необходимо
подсчитать число n. элементов ряда,
принадлежащих j-му интервалу, и вычислить практические оценки неизвестных
вероятностей (частоты ) по формуле
Вертикальные
составляющие гистограммы, называемые высотами прямоугольников
На этом же графике необходимо
построить теоретическую кривую, соответствующую нормальному закону, которая
наилучшим образом сглаживает данное эмпирическое статистическое распределение.
Кривая строится на основе формулы плотности вероятности для закона Гаусса
Наиболее точный критерий
соответствия исследуемого ряда нормальному закону распределения получу,
используя критерий χ2 Пирсона по формулам:
Здесь — теоретическая
вероятность попаданияслучайной величины в соответствующий интервал.
Таблица построения гистограммы
эмпирического закона распределения
|
Интервал в долях |
Интервал в секундах |
Количество элементов в интервале |
Относит. частота |
Высота прямоугольника |
|
m(t) |
(Ø) |
|
|
|
|
-3m |
-2,50 |
0 |
0 |
0 |
|
-2,5m |
-2,08 |
3 |
0,06 |
0,1441 |
|
-2m |
-1,67 |
3 |
0,06 |
0,1441 |
|
-1,5m |
-1,25 |
6 |
0,12 |
0,2882 |
|
-1m |
-0,83 |
5 |
0,1 |
0,2402 |
|
-0,5m |
-0,42 |
7 |
0,14 |
0,3363 |
|
0m |
0,00 |
7 |
0,14 |
0,3363 |
|
0,5m |
0,42 |
6 |
0,12 |
0,2882 |
|
1m |
0,83 |
4 |
0,08 |
0,1921 |
|
1,5m |
1,25 |
1 |
0,02 |
0,0480 |
|
2m |
1,67 |
2 |
0,04 |
0,0961 |
|
2,5m |
2,08 |
1 |
0,02 |
0,0480 |
|
45 |
0,9 |
При этом сумма элементов по
интервалам должна равняться общему количеству элементов в ряде; сумма частот
равняется единице в пределах ошибки округления; сумма высот прямоугольников
равняется 2/т. Выбрав масштабы по горизонтальной оси для величин интервалов
(например, 0.5т — 1 см), по вертикальной для высот прямоугольников (например,
0.05 от — высоты прямоугольника — 1 см), откладывают по соответствующим
границам вертикальные высоты, которые замыкаются в прямоугольники. Полученный
график и будет называться гистограммой (эмпирическим представлением плотности
закона распределения), площадь которого равна единице
) На этом же графике необходимо
построить теоретическую кривую, соответствующую нормальному закону, которая
наилучшим образом сглаживает (выравнивает) данное эмпирическое статистическое
распределение. Кривая строится на основе формулы плотности вероятности для
закона Гаусса
Обычно величина t изменяется от -3 до 3 через 0.5,
так что вычисления не представляют трудности. Необходимо учитывать, что функция
симметричная, т.е. f(x)= — f(x) Значения функции с m = 1 приведены в любых книгах по статистике или обработке
измерений в виде таблиц и также могут быть использованы при вычислениях.
Значения теоретической функции
плотности на границах интервалов будут равны:
|
t = |
0 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
|
φ(∆)= |
0,48 |
0,42 |
0,29 |
0,16 |
0,06 |
0,02 |
0,01 |
По вычисленным данным строят график
на гистограмме
10) Наиболее точный
критерий соответствия исследуемого ряда нормальному закону распределения
получим используя критерий -Пирсона.
Следует иметь в виду,
что все критерии соответствия являются частными случаями общего алгоритма
статистической проверки гипотез, в основе которой лежат следующие пункты:
) выдвижение с
доверительной вероятностью исходной гипотезы;
) получение
теоретического значения критерия;
) сравнение двух
значений критериев и вывод.
Предположим, что с
вероятностью ряд ошибок распределен
нормально. Из статистических таблиц распределения -Пирсона по числу
степеней свободы находим эталонное
значение .
|
i |
Интервалы |
|||||
|
1 2 3 4 5 6 7 8 9 10 |
-3 -2.5 -2.5 -2.0 |
0.0013 0.0062 |
0.0049 0.0165 |
0 3 |
0.25 |
-0.25 |
|
-2.0 -1.5 -1.5 -1.0 |
0.0228 0.0668 0.1587 0.3085 0.5000 0.6915 0.8413 0.9332 0.9772 |
0.0441 0.0918 0.1499 0.1915 0.1915 0.1499 0.0918 0.0441 0.0165 |
3 6 |
2.2 4.6 |
0.8 |
|
|
∑ |
0.998 |
45 |
49.9 |
На основании проведенных
исследований установлено, что рад является случайным, оценка математического
ожидания в виде среднего арифметического не превосходит утроенной средней
квадратической ошибки, то есть практически равна нулю. Количество положительных
элементов (23) равно количеству отрицательных (27).
В результате вычисления
критерия Аббе и сравнения практических и теоретических значений выявлено, что в
ряду отсутствуют значимые систематические влияния с вероятностью и с этой же вероятностью
крайние значения вариационного ряда не являются грубыми.
Приближённые критерии
соответствия нормальному закону, учитывающие расхождения между теоретическими и
практическими значениями соотношениями между тремя видами ошибок: средней
квадратической, средней абсолютной и вероятной, показывают, что ряд
соответствует нормальному закону. Значениями асимметрии и эксцесса можно
пренебречь.
Визуальный анализ
гистограммы (эмпирическое распределение) и огивы (вид теоретического закона
распределения) показывает недостаточное согласование по форме и величине между
ними, что говорит о недостаточном соответствии нормальному закону
распределения.
Наиболее точные
результаты соответствия исследуемого ряда нормальному закону дает критерий c2 Пирсона, который учитывает расхождение между практическими и
теоретическими частотами по всем выделенным интервалам.
Таким образом, выполненные
исследования ряда ошибок на соответствие нормальному закону распределения дают
по всем использованным критериям положительные результаты, что позволяет
сделать вывод о достаточной близости ряда предполагаемому закону. И сделать
вывод, что мой ряд достаточно хорошо подчиняется нормальному закону
распределения.
погрешность распределение закон
статистический
Результат любого измерения не определён однозначно и имеет случайную составляющую.
Поэтому адекватным языком для описания погрешностей является язык вероятностей.
Тот факт, что значение некоторой величины «случайно», не означает, что
она может принимать совершенно произвольные значения. Ясно, что частоты, с которыми
возникает те или иные значения, различны. Вероятностные законы, которым
подчиняются случайные величины, называют распределениями.
2.1 Случайная величина
Случайной будем называть величину, значение которой не может быть достоверно определено экспериментатором. Чаще всего подразумевается, что случайная величина будет изменяться при многократном повторении одного и того же эксперимента. При интерпретации результатов измерений в физических экспериментах, обычно случайными также считаются величины, значение которых является фиксированным, но не известно экспериментатору. Например смещение нуля шкалы прибора. Для формализации работы со случайными величинами используют понятие вероятности. Численное значение вероятности того, что какая-то величина примет то или иное значение определяется либо как относительная частота наблюдения того или иного значения при повторении опыта большое количество раз, либо как оценка на основе данных других экспериментов.
Замечание.
Хотя понятия вероятности и случайной величины являются основополагающими, в литературе нет единства в их определении. Обсуждение формальных тонкостей или построение строгой теории лежит за пределами данного пособия. Поэтому на начальном этапе лучше использовать «интуитивное» понимание этих сущностей. Заинтересованным читателям рекомендуем обратиться к специальной литературе: [5].
Рассмотрим случайную физическую величину x, которая при измерениях может
принимать непрерывный набор значений. Пусть
P[x0,x0+δx] — вероятность того, что результат окажется вблизи
некоторой точки x0 в пределах интервала δx: x∈[x0,x0+δx].
Устремим интервал
δx к нулю. Нетрудно понять, что вероятность попасть в этот интервал
также будет стремиться к нулю. Однако отношение
w(x0)=P[x0,x0+δx]δx будет оставаться конечным.
Функцию w(x) называют плотностью распределения вероятности или кратко
распределением непрерывной случайной величины x.
Замечание. В математической литературе распределением часто называют не функцию
w(x), а её интеграл W(x)=∫w(x)𝑑x. Такую функцию в физике принято
называть интегральным или кумулятивным распределением. В англоязычной литературе
для этих функций принято использовать сокращения:
pdf (probability distribution function) и
cdf (cumulative distribution function)
соответственно.
Гистограммы.
Проиллюстрируем наглядно понятие плотности распределения. Результат
большого числа измерений случайной величины удобно представить с помощью
специального типа графика — гистограммы.
Для этого область значений x, размещённую на оси абсцисс, разобьём на
равные малые интервалы — «корзины» или «бины» (англ. bins)
некоторого размера h. По оси ординат будем откладывать долю измерений w,
результаты которых попадают в соответствующую корзину. А именно,
пусть k — номер корзины; nk — число измерений, попавших
в диапазон x∈[kh,(k+1)h]. Тогда на графике изобразим «столбик»
шириной h и высотой wk=nk/n.
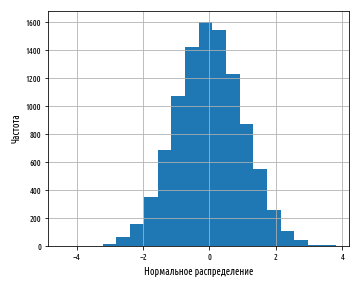
В результате получим картину, подобную изображённой на рис. 2.1.
σ=1,0, h=0,1, n=104)
Высоты построенных столбиков будут приближённо соответствовать значению
плотности распределения w(x) вблизи соответствующей точки x.
Если устремить число измерений к бесконечности (n→∞), а ширину корзин
к нулю (h→0), то огибающая гистограммы будет стремиться к некоторой
непрерывной функции w(x).
Самые высокие столбики гистограммы будут группироваться вблизи максимума
функции w(x) — это наиболее вероятное значение случайной величины.
Если отклонения в положительную и отрицательную стороны равновероятны,
то гистограмма будет симметрична — в таком случае среднее значение ⟨x⟩
также будет лежать вблизи этого максимума. Ширина гистограммы будет характеризовать разброс
значений случайной величины — по порядку величины
она, как правило, близка к среднеквадратичному отклонению sx.
Свойства распределений.
Из определения функции w(x) следует, что вероятность получить в результате
эксперимента величину x в диапазоне от a до b
можно найти, вычислив интеграл:
| Px∈[a,b]=∫abw(x)𝑑x. | (2.1) |
Согласно определению вероятности, сумма вероятностей для всех возможных случаев
всегда равна единице. Поэтому интеграл распределения w(x) по всей области
значений x (то есть суммарная площадь под графиком w(x)) равен единице:
Это соотношение называют условием нормировки.
Среднее и дисперсия.
Вычислим среднее по построенной гистограмме. Если размер корзин
h достаточно мал, все измерения в пределах одной корзины можно считать примерно
одинаковыми. Тогда среднее арифметическое всех результатов можно вычислить как
Переходя к пределу, получим следующее определение среднего значения
случайной величины:
где интегрирование ведётся по всей области значений x.
В теории вероятностей x¯ также называют математическим ожиданием
распределения.
Величину
| σ2=(x-x¯)2¯=∫(x-x¯)2w𝑑x | (2.3) |
называют дисперсией распределения. Значение σ есть
срекднеквадратичное отклонение в пределе n→∞. Оно имеет ту
же размерность, что и сама величина x и характеризует разброс распределения.
Именно эту величину, как правило, приводят как характеристику погрешности
измерения x.
Доверительный интервал.
Обозначим как P|Δx|<δ вероятность
того, что отклонение от среднего Δx=x-x¯ составит величину,
не превосходящую по модулю значение δ:
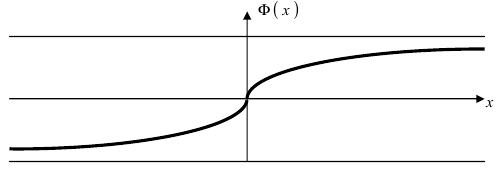
| P|Δx|<δ=∫x¯-δx¯+δw(x)𝑑x. | (2.4) |
Эту величину называют доверительной вероятностью для
доверительного интервала |x-x¯|≤δ.
2.2 Нормальное распределение
Одним из наиболее примечательных результатов теории вероятностей является
так называемая центральная предельная теорема. Она утверждает,
что сумма большого количества независимых случайных слагаемых, каждое
из которых вносит в эту сумму относительно малый вклад, подчиняется
универсальному закону, не зависимо от того, каким вероятностным законам
подчиняются её составляющие, — так называемому нормальному
распределению (или распределению Гаусса).
Доказательство теоремы довольно громоздко и мы его не приводим (его можно найти
в любом учебнике по теории вероятностей). Остановимся
кратко на том, что такое нормальное распределение и его основных свойствах.
Плотность нормального распределения выражается следующей формулой:
| w𝒩(x)=12πσe-(x-x¯)22σ2. | (2.5) |
Здесь x¯ и σ
— параметры нормального распределения: x¯ равно
среднему значению x, a σ —
среднеквадратичному отклонению, вычисленным в пределе n→∞.
Как видно из рис. 2.1, распределение представляет собой
симметричный
«колокол», положение вершины которого
соответствует x¯ (ввиду симметрии оно же
совпадает с наиболее вероятным значением — максимумом
функции w𝒩(x)).
При значительном отклонении x от среднего величина
w𝒩(x)
очень быстро убывает. Это означает, что вероятность встретить отклонения,
существенно большие, чем σ, оказывается пренебрежимо
мала. Ширина «колокола» по порядку величины
равна σ — она характеризует «разброс»
экспериментальных данных относительно среднего значения.
Замечание. Точки x=x¯±σ являются точками
перегиба графика w(x) (в них вторая производная по x
обращается в нуль, w′′=0), а их положение по высоте составляет
w(x¯±σ)/w(x¯)=e-1/2≈0,61
от высоты вершины.
Универсальный характер центральной предельной теоремы позволяет широко
применять на практике нормальное (гауссово) распределение для обработки
результатов измерений, поскольку часто случайные погрешности складываются из
множества случайных независимых факторов. Заметим, что на практике
для приближённой оценки параметров нормального распределения
случайной величины используются выборочные значения среднего
и дисперсии: x¯≈⟨x⟩, sx≈σx.
x-x0σ2=2w(x)σ1=1
Доверительные вероятности.
Вычислим некоторые доверительные вероятности (2.4) для нормально
распределённых случайных величин.
Замечание. Значение интеграла вида ∫e-x2/2𝑑x
(его называют интегралом ошибок) в элементарных функциях не выражается,
но легко находится численно.
Вероятность того, что результат отдельного измерения x окажется
в пределах x¯±σ оказывается равна
| P|Δx|<σ=∫x¯-σx¯+σw𝒩𝑑x≈0,68. |
Вероятность отклонения в пределах x¯±2σ:
а в пределах x¯±3σ:
Иными словами, при большом числе измерений нормально распределённой
величины можно ожидать, что лишь треть измерений выпадут за пределы интервала
[x¯-σ,x¯+σ]. При этом около 5%
измерений выпадут за пределы [x¯-2σ;x¯+2σ],
и лишь 0,27% окажутся за пределами
[x¯-3σ;x¯+3σ].
Пример. В сообщениях об открытии бозона Хиггса на Большом адронном коллайдере
говорилось о том, что исследователи ждали подтверждение результатов
с точностью «5 сигма». Используя нормальное распределение (2.5)
нетрудно посчитать, что они использовали доверительную вероятность
P≈1-5,7⋅10-7=0,99999943. Такую точность можно назвать фантастической.
Полученные значения доверительных вероятностей используются при
стандартной записи результатов измерений. В физических измерениях
(в частности, в учебной лаборатории), как правило, используется P=0,68,
то есть, запись
означает, что измеренное значение лежит в диапазоне (доверительном
интервале) x∈[x¯-δx;x¯+δx] с
вероятностью 68%. Таким образом погрешность ±δx считается
равной одному среднеквадратичному отклонению: δx=σ.
В технических измерениях чаще используется P=0,95, то есть под
абсолютной погрешностью имеется в виду удвоенное среднеквадратичное
отклонение, δx=2σ. Во избежание разночтений доверительную
вероятность следует указывать отдельно.
Замечание. Хотя нормальный закон распределения встречается на практике довольно
часто, стоит помнить, что он реализуется далеко не всегда.
Полученные выше соотношения для вероятностей попадания значений в
доверительные интервалы можно использовать в качестве простейшего
признака нормальности распределения: в частности, если количество попадающих
в интервал ±σ результатов существенно отличается от 2/3 — это повод
для более детального исследования закона распределения ошибок.
Сравнение результатов измерений.
Теперь мы можем дать количественный критерий для сравнения двух измеренных
величин или двух результатов измерения одной и той же величины.
Пусть x1 и x2 (x1≠x2) измерены с
погрешностями σ1 и σ2 соответственно.
Ясно, что если различие результатов |x2-x1| невелико,
его можно объяснить просто случайными отклонениями.
Если же теория предсказывает, что вероятность обнаружить такое отклонение
слишком мала, различие результатов следует признать значимым.
Предварительно необходимо договориться о соответствующем граничном значении
вероятности. Универсального значения здесь быть не может,
поэтому приходится полагаться на субъективный выбор исследователя. Часто
в качестве «разумной» границы выбирают вероятность 5%,
что, как видно из изложенного выше, для нормального распределения
соответствует отклонению более, чем на 2σ.
Допустим, одна из величин известна с существенно большей точностью:
σ2≪σ1 (например, x1 — результат, полученный
студентом в лаборатории, x2 — справочное значение).
Поскольку σ2 мало, x2 можно принять за «истинное»:
x2≈x¯. Предполагая, что погрешность измерения
x1 подчиняется нормальному закону с и дисперсией σ12,
можно утверждать, что
различие считают будет значимы, если
Пусть погрешности измерений сравнимы по порядку величины:
σ1∼σ2. В теории вероятностей показывается, что
линейная комбинация нормально распределённых величин также имеет нормальное
распределение с дисперсией σ2=σ12+σ22
(см. также правила сложения погрешностей (2.7)). Тогда
для проверки гипотезы о том, что x1 и x2 являются измерениями
одной и той же величины, нужно вычислить, является ли значимым отклонение
|x1-x2| от нуля при σ=σ12+σ22.
Пример. Два студента получили следующие значения для теплоты испарения
некоторой жидкости: x1=40,3±0,2 кДж/моль и
x2=41,0±0,3 кДж/моль, где погрешность соответствует
одному стандартному отклонению. Можно ли утверждать, что они исследовали
одну и ту же жидкость?
Имеем наблюдаемую разность |x1-x2|=0,7 кДж/моль,
среднеквадратичное отклонение для разности
σ=0,22+0,32=0,36 кДж/моль.
Их отношение |x2-x1|σ≈2. Из
свойств нормального распределения находим вероятность того, что измерялась
одна и та же величина, а различия в ответах возникли из-за случайных
ошибок: P≈5%. Ответ на вопрос, «достаточно»
ли мала или велика эта вероятность, остаётся на усмотрение исследователя.
Замечание. Изложенные здесь соображения применимы, только если x¯ и
его стандартное отклонение σ получены на основании достаточно
большой выборки n≫1 (или заданы точно). При небольшом числе измерений
(n≲10) выборочные средние ⟨x⟩ и среднеквадратичное отклонение
sx сами имеют довольно большую ошибку, а
их распределение будет описываться не нормальным законом, а так
называемым t-распределением Стъюдента. В частности, в зависимости от
значения n интервал ⟨x⟩±sx будет соответствовать несколько
меньшей доверительной вероятности, чем P=0,68. Особенно резко различия
проявляются при высоких уровнях доверительных вероятностей P→1.
2.3 Независимые величины
Величины x и y называют независимыми если результат измерения одной
из них никак не влияет на результат измерения другой. Для таких величин вероятность того, что x окажется в некоторой области X, и одновременно y — в области Y,
равна произведению соответствующих вероятностей:
Обозначим отклонения величин от их средних как Δx=x-x¯ и
Δy=y-y¯.
Средние значения этих отклонений равны, очевидно, нулю: Δx¯=x¯-x¯=0,
Δy¯=0. Из независимости величин x и y следует,
что среднее значение от произведения Δx⋅Δy¯
равно произведению средних Δx¯⋅Δy¯
и, следовательно, равно нулю:
| Δx⋅Δy¯=Δx¯⋅Δy¯=0. | (2.6) |
Пусть измеряемая величина z=x+y складывается из двух независимых
случайных слагаемых x и y, для которых известны средние
x¯ и y¯, и их среднеквадратичные погрешности
σx и σy. Непосредственно из определения (1.1)
следует, что среднее суммы равно сумме средних:
Найдём дисперсию σz2. В силу независимости имеем
| Δz2¯=Δx2¯+Δy2¯+2Δx⋅Δy¯≈Δx2¯+Δy2¯, |
то есть:
Таким образом, при сложении независимых величин их погрешности
складываются среднеквадратичным образом.
Подчеркнём, что для справедливости соотношения (2.7)
величины x и y не обязаны быть нормально распределёнными —
достаточно существования конечных значений их дисперсий. Однако можно
показать, что если x и y распределены нормально, нормальным
будет и распределение их суммы.
Замечание. Требование независимости
слагаемых является принципиальным. Например, положим y=x. Тогда
z=2x. Здесь y и x, очевидно, зависят друг от друга. Используя
(2.7), находим σ2x=2σx,
что, конечно, неверно — непосредственно из определения
следует, что σ2x=2σx.
Отдельно стоит обсудить математическую структуру формулы (2.7).
Если одна из погрешностей много больше другой, например,
σx≫σy,
то меньшей погрешностью можно пренебречь, σx+y≈σx.
С другой стороны, если два источника погрешностей имеют один порядок
σx∼σy, то и σx+y∼σx∼σy.
Эти обстоятельства важны при планирования эксперимента: как правило,
величина, измеренная наименее точно, вносит наибольший вклад в погрешность
конечного результата. При этом, пока не устранены наиболее существенные
ошибки, бессмысленно гнаться за повышением точности измерения остальных
величин.
Пример. Пусть σy=σx/3,
тогда σz=σx1+19≈1,05σx,
то есть при различии двух погрешностей более, чем в 3 раза, поправка
к погрешности составляет менее 5%, и уже нет особого смысла в учёте
меньшей погрешности: σz≈σx. Это утверждение
касается сложения любых независимых источников погрешностей в эксперименте.
2.4 Погрешность среднего
Выборочное среднее арифметическое значение ⟨x⟩, найденное
по результатам n измерений, само является случайной величиной.
Действительно, если поставить серию одинаковых опытов по n измерений,
то в каждом опыте получится своё среднее значение, отличающееся от
предельного среднего x¯.
Вычислим среднеквадратичную погрешность среднего арифметического
σ⟨x⟩.
Рассмотрим вспомогательную сумму n слагаемых
Если {xi} есть набор независимых измерений
одной и той же физической величины, то мы можем, применяя результат
(2.7) предыдущего параграфа, записать
| σZ=σx12+σx22+…+σxn2=nσx, |
поскольку под корнем находится n одинаковых слагаемых. Отсюда с
учётом ⟨x⟩=Z/n получаем
Таким образом, погрешность среднего значения x по результатам
n независимых измерений оказывается в n раз меньше погрешности
отдельного измерения. Это один из важнейших результатов, позволяющий
уменьшать случайные погрешности эксперимента за счёт многократного
повторения измерений.
Подчеркнём отличия между σx и σ⟨x⟩:
величина σx — погрешность отдельного
измерения — является характеристикой разброса значений
в совокупности измерений {xi}, i=1..n. При
нормальном законе распределения примерно 68% измерений попадают в
интервал ⟨x⟩±σx;
величина σ⟨x⟩ — погрешность
среднего — характеризует точность, с которой определено
среднее значение измеряемой физической величины ⟨x⟩ относительно
предельного («истинного») среднего x¯;
при этом с доверительной вероятностью P=68% искомая величина x¯
лежит в интервале
⟨x⟩-σ⟨x⟩<x¯<⟨x⟩+σ⟨x⟩.
2.5 Результирующая погрешность опыта
Пусть для некоторого результата измерения известна оценка его максимальной
систематической погрешности Δсист и случайная
среднеквадратичная
погрешность σслуч. Какова «полная»
погрешность измерения?
Предположим для простоты, что измеряемая величина в принципе
может быть определена сколь угодно точно, так что можно говорить о
некотором её «истинном» значении xист
(иными словами, погрешность результата связана в основном именно с
процессом измерения). Назовём полной погрешностью измерения
среднеквадратичное значения отклонения от результата измерения от
«истинного»:
Отклонение x-xист можно представить как сумму случайного
отклонения от среднего δxслуч=x-x¯
и постоянной (но, вообще говоря, неизвестной) систематической составляющей
δxсист=x¯-xист=const:
Причём случайную составляющую можно считать независимой от систематической.
В таком случае из (2.7) находим:
| σполн2=⟨δxсист2⟩+⟨δxслуч2⟩≤Δсист2+σслуч2. | (2.9) |
Таким образом, для получения максимального значения полной
погрешности некоторого измерения нужно квадратично сложить максимальную
систематическую и случайную погрешности.
Если измерения проводятся многократно, то согласно (2.8)
случайная составляющая погрешности может быть уменьшена, а систематическая
составляющая при этом остаётся неизменной:
Отсюда следует важное практическое правило
(см. также обсуждение в п. 2.3): если случайная погрешность измерений
в 2–3 раза меньше предполагаемой систематической, то
нет смысла проводить многократные измерения в попытке уменьшить погрешность
всего эксперимента. В такой ситуации измерения достаточно повторить
2–3 раза — чтобы убедиться в повторяемости результата, исключить промахи
и проверить, что случайная ошибка действительно мала.
В противном случае повторение измерений может иметь смысл до
тех пор, пока погрешность среднего
σ⟨x⟩=σxn
не станет меньше систематической.
Замечание. Поскольку конкретная
величина систематической погрешности, как правило, не известна, её
можно в некотором смысле рассматривать наравне со случайной —
предположить, что её величина была определена по некоторому случайному
закону перед началом измерений (например, при изготовлении линейки
на заводе произошло некоторое случайное искажение шкалы). При такой
трактовке формулу (2.9) можно рассматривать просто
как частный случай формулы сложения погрешностей независимых величин
(2.7).
Подчеркнем, что вероятностный закон, которому подчиняется
систематическая ошибка, зачастую неизвестен. Поэтому неизвестно и
распределение итогового результата. Из этого, в частности, следует,
что мы не можем приписать интервалу x±Δсист какую-либо
определённую доверительную вероятность — она равна 0,68
только если систематическая ошибка имеет нормальное распределение.
Можно, конечно, предположить,
— и так часто делают — что, к примеру, ошибки
при изготовлении линеек на заводе имеют гауссов характер. Также часто
предполагают, что систематическая ошибка имеет равномерное
распределение (то есть «истинное» значение может с равной вероятностью
принять любое значение в пределах интервала ±Δсист).
Строго говоря, для этих предположений нет достаточных оснований.
Пример. В результате измерения диаметра проволоки микрометрическим винтом,
имеющим цену деления h=0,01 мм, получен следующий набор из n=8 значений:
Вычисляем среднее значение: ⟨d⟩≈386,3 мкм.
Среднеквадратичное отклонение:
σd≈9,2 мкм. Случайная погрешность среднего согласно
(2.8):
σ⟨d⟩=σd8≈3,2
мкм. Все результаты лежат в пределах ±2σd, поэтому нет
причин сомневаться в нормальности распределения. Максимальную погрешность
микрометра оценим как половину цены деления, Δ=h2=5 мкм.
Результирующая полная погрешность
σ≤Δ2+σd28≈6,0 мкм.
Видно, что σслуч≈Δсист и проводить дополнительные измерения
особого смысла нет. Окончательно результат измерений может быть представлен
в виде (см. также правила округления
результатов измерений в п. 4.3.2)
d=386±6мкм,εd=1,5%.
Заметим, что поскольку случайная погрешность и погрешность
прибора здесь имеют один порядок величины, наблюдаемый случайный разброс
данных может быть связан как с неоднородностью сечения проволоки,
так и с дефектами микрометра (например, с неровностями зажимов, люфтом
винта, сухим трением, деформацией проволоки под действием микрометра
и т. п.). Для ответа на вопрос, что именно вызвало разброс, требуются
дополнительные исследования, желательно с использованием более точных
приборов.
Пример. Измерение скорости
полёта пули было осуществлено с погрешностью δv=±1 м/c.
Результаты измерений для n=6 выстрелов представлены в таблице:
Усреднённый результат ⟨v⟩=162,0м/с,
среднеквадратичное отклонение σv=13,8м/c, случайная
ошибка для средней скорости
σv¯=σv/6=5,6м/с.
Поскольку разброс экспериментальных данных существенно превышает погрешность
каждого измерения, σv≫δv, он почти наверняка связан
с реальным различием скоростей пули в разных выстрелах, а не с ошибками
измерений. В качестве результата эксперимента представляют интерес
как среднее значение скоростей ⟨v⟩=162±6м/с
(ε≈4%), так и значение σv≈14м/с,
характеризующее разброс значений скоростей от выстрела к выстрелу.
Малая инструментальная погрешность в принципе позволяет более точно
измерить среднее и дисперсию, и исследовать закон распределения выстрелов
по скоростям более детально — для этого требуется набрать
бо́льшую статистику по выстрелам.
Пример. Измерение скорости
полёта пули было осуществлено с погрешностью δv=10 м/c. Результаты
измерений для n=6 выстрелов представлены в таблице:
Усреднённый результат ⟨v⟩=163,3м/с,
σv=12,1м/c, σ⟨v⟩=5м/с,
σполн≈11,2м/с. Инструментальная
погрешность каждого измерения превышает разброс данных, поэтому в
этом опыте затруднительно сделать вывод о различии скоростей от выстрела
к выстрелу. Результат измерений скорости пули:
⟨v⟩=163±11м/с,
ε≈7%. Проводить дополнительные выстрелы при такой
большой инструментальной погрешности особого смысла нет —
лучше поработать над точностью приборов и методикой измерений.
2.6 Обработка косвенных измерений
Косвенными называют измерения, полученные в результате расчётов,
использующих результаты прямых (то есть «непосредственных»)
измерений физических величин. Сформулируем основные правила пересчёта
погрешностей при косвенных измерениях.
2.6.1 Случай одной переменной
Пусть в эксперименте измеряется величина x, а её «наилучшее»
(в некотором смысле) значение равно x⋆ и оно известно с
погрешностью σx. После чего с помощью известной функции
вычисляется величина y=f(x).
В качестве «наилучшего» приближения для y используем значение функции
при «наилучшем» x:
Найдём величину погрешности σy. Обозначая отклонение измеряемой
величины как Δx=x-x⋆, и пользуясь определением производной,
при условии, что функция y(x) — гладкая
вблизи x≈x⋆, запишем
где f′≡dydx — производная фукнции f(x), взятая в точке
x⋆. Возведём полученное в квадрат, проведём усреднение
(σy2=⟨Δy2⟩,
σx2=⟨Δx2⟩), и затем снова извлечём
корень. В результате получим
Пример. Для степенной функции
y=Axn имеем σy=nAxn-1σx, откуда
σyy=nσxx,или εy=nεx,
то есть относительная погрешность степенной функции возрастает пропорционально
показателю степени n.
Пример. Для y=1/x имеем ε1/x=εx
— при обращении величины сохраняется её относительная
погрешность.
Упражнение. Найдите погрешность логарифма y=lnx, если известны x
и σx.
Упражнение. Найдите погрешность показательной функции y=ax,
если известны x и σx. Коэффициент a задан точно.
2.6.2 Случай многих переменных
Пусть величина u вычисляется по измеренным значениям нескольких
различных независимых физических величин x, y, …
на основе известного закона u=f(x,y,…). В качестве
наилучшего значения можно по-прежнему взять значение функции f
при наилучших значениях измеряемых параметров:
Для нахождения погрешности σu воспользуемся свойством,
известным из математического анализа, — малые приращения гладких
функции многих переменных складываются линейно, то есть справедлив
принцип суперпозиции малых приращений:
где символом fx′≡∂f∂x обозначена
частная производная функции f по переменной x —
то есть обычная производная f по x, взятая при условии, что
все остальные аргументы (кроме x) считаются постоянными параметрами.
Тогда пользуясь формулой для нахождения дисперсии суммы независимых
величин (2.7), получим соотношение, позволяющее вычислять
погрешности косвенных измерений для произвольной функции
u=f(x,y,…):
| σu2=fx′2σx2+fy′2σy2+… | (2.11) |
Это и есть искомая общая формула пересчёта погрешностей при косвенных
измерениях.
Отметим, что формулы (2.10) и (2.11) применимы
только если относительные отклонения всех величин малы
(εx,εy,…≪1),
а измерения проводятся вдали от особых точек функции f (производные
fx′, fy′ … не должны обращаться в бесконечность).
Также подчеркнём, что все полученные здесь формулы справедливы только
для независимых переменных x, y, …
Остановимся на некоторых важных частных случаях формулы
(2.11).
Пример. Для суммы (или разности) u=∑i=1naixi имеем
σu2=∑i=1nai2σxi2.
(2.12)
Пример. Найдём погрешность степенной функции:
u=xα⋅yβ⋅…. Тогда нетрудно получить,
что
σu2u2=α2σx2x2+β2σy2y2+…
или через относительные погрешности
εu2=α2εx2+β2εy2+…
(2.13)
Пример. Вычислим погрешность произведения и частного: u=xy или u=x/y.
Тогда в обоих случаях имеем
εu2=εx2+εy2,
(2.14)
то есть при умножении или делении относительные погрешности складываются
квадратично.
Пример. Рассмотрим несколько более сложный случай: нахождение угла по его тангенсу
u=arctgyx.
В таком случае, пользуясь тем, что (arctgz)′=11+z2,
где z=y/x, и используя производную сложной функции, находим
ux′=uz′zx′=-yx2+y2,
uy′=uz′zy′=xx2+y2, и наконец
σu2=y2σx2+x2σy2(x2+y2)2.
Упражнение. Найти погрешность вычисления гипотенузы z=x2+y2
прямоугольного треугольника по измеренным катетам x и y.
По итогам данного раздела можно дать следующие практические рекомендации.
-
•
Как правило, нет смысла увеличивать точность измерения какой-то одной
величины, если другие величины, используемые в расчётах, остаются
измеренными относительно грубо — всё равно итоговая погрешность
скорее всего будет определяться самым неточным измерением. Поэтому
все измерения имеет смысл проводить примерно с одной и той же
относительной погрешностью. -
•
При этом, как следует из (2.13), особое внимание
следует уделять измерению величин, возводимых при расчётах в степени
с большими показателями. А при сложных функциональных зависимостях
имеет смысл детально проанализировать структуру формулы
(2.11):
если вклад от некоторой величины в общую погрешность мал, нет смысла
гнаться за высокой точностью её измерения, и наоборот, точность некоторых
измерений может оказаться критически важной. -
•
Следует избегать измерения малых величин как разности двух близких
значений (например, толщины стенки цилиндра как разности внутреннего
и внешнего радиусов): если u=x-y, то абсолютная погрешность
σu=σx2+σy2
меняется мало, однако относительная погрешность
εu=σux-y
может оказаться неприемлемо большой, если x≈y.
Содержание:
Нормальный закон распределения:
Нормальный закон распределения имеет плотность вероятности
где
График функции плотности вероятности (2.9.1) имеет максимум в точке 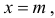

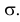
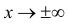
Помимо геометрического смысла, параметры нормального закона распределения имеют и вероятностный смысл. Параметр 
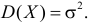
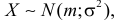

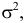
где 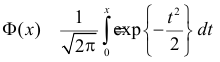
Значения функции 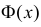
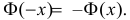
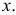
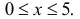
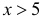
Если 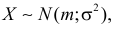
Пример:
Случайная величина X имеет нормальный закон распределения 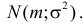
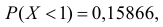
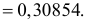
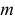
Решение. Воспользуемся формулой (2.9.2):
Так как 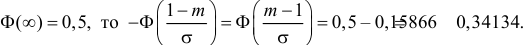
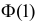
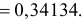
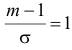
Аналогично 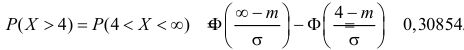
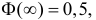
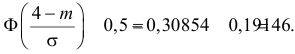
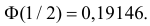
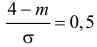
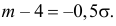
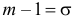
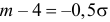
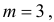
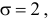
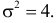
График функции плотности вероятности этого закона распределения изображен на рис. 2.9.3.
Ответ.
Пример:
Ошибка измерения X имеет нормальный закон распределения, причем систематическая ошибка равна 1 мк, а дисперсия ошибки равна 4 мк2. Какова вероятность того, что в трех независимых измерениях ошибка ни разу не превзойдет по модулю 2 мк?
Решение. По условиям задачи 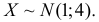
Вычисленная вероятность численно равна заштрихованной площади на рис. 2.9.4.
Каждое измерение можно рассматривать как независимый опыт. Поэтому по формуле Бернулли (2.6.1) вероятность того, что в трех независимых измерениях ошибка ни разу не превзойдет 2 мк, равна
Ответ.
Пример:
Функция плотности вероятности случайной величины X имеет вид
Требуется определить коэффициент 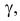
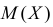
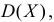
Замечание. Если каждый закон распределения из некоторого семейства законов распределения имеет функцию распределения , 
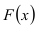
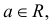
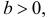
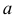
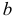
Решение. Так как (2.9.4) функция плотности вероятности, то интеграл от нее по всей числовой оси должен быть равен единице:
Преобразуем выражение в показателе степени, выделяя полный квадрат:
Тогда (2.9.5) можно записать в виде
Сделаем замену переменных так, чтобы 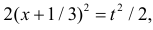
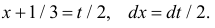
Умножим и разделим левую часть равенства на 
Так как 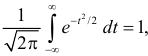
Поэтому
Последняя запись означает, что случайная величина имеет нормальный закон распределения с параметрами 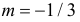
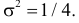
Ответ.
Пример:
Цех на заводе выпускает транзисторы с емкостью коллекторного перехода 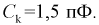
Решение.
Статистическими исследованиями в цеху установлено, что 
Чтобы вычислить количество транзисторов, попадающих в группу 
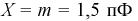
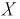
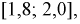
Для расчета этой вероятности надо построить математическую модель. Экспериментальные данные говорят о том, что нормальное распределение можно принять в качестве математической модели. Эмпирическая оценка (установлена статистическими исследованиями в цеху) среднего значения
дает 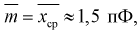
Обозначая 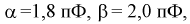
Тогда количество транзисторов 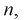
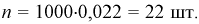
Нормальное распределение и его свойства
Если выйти на улицу любого города и случайным образом выбранных прохожих спросить о том, какой у них рост, вес, возраст, доход, и т.п., а потом построить график любой из этих величин, например, роста… Но не будем спешить, сначала посмотрим, как можно построить такой график.
Сначала, мы просто запишем результаты своего исследования. Потом, мы отсортируем всех людей по группам, так чтобы каждый попал в свой диапазон роста, например, «от 180 до 181 включительно».
После этого мы должны посчитать количество людей в каждой подгруппе-диапазоне, это будет частота попадания роста жителей города в данный диапазон. Обычно эту часть удобно оформить в виде таблички. Если затем эти частоты построить по оси у, а диапазоны отложить по оси х, можно получить так называемую гистограмму, упорядоченный набор столбиков, ширина которых равна, в данном случае, одному сантиметру, а длина будет равна той частоте, которая соответствует каждому диапазону роста. Если
Вам попалось достаточно много жителей, то Ваша схема будет выглядеть примерно так:
Дальше можно уточнить задачу. Каждый диапазон разбить на десять, жителей рассортировать по росту с точностью до миллиметра. Диаграмма станет глаже, но уменьшится по высоте, «оплывет» вниз, т.к. в каждом маленьком диапазоне количество жителей уменьшается. Чтобы избежать этого, просто увеличим масштаб по вертикальной оси в 10 раз. Если гипотетически повторить эту процедуру несколько раз, будет вырисовываться та знаменитая колоколообразная фигура, которая характерна для нормального (или Гауссова) распределения. В результате, относительная частота встречаемости каждого конкретного диапазона роста может быть посчитана как отношение площади «ломтика» кривой, приходящегося на этот диапазон к площади подо всей кривой. Стандартизированные кривые нормального распределения, значения функций которых приводятся в таблицах книг по статистике, всегда имеют суммарную площадь под кривой равную единице. Это связано с тем, что, как Вы помните из курса теории вероятности, вероятность достоверного события всегда равна 100% (или единице), а для любого человека иметь хоть какое-то значение роста — достоверное событие. А вот вероятность того, что рост произвольного человека попадет в определенный выбранный нами диапазон, будет зависеть от трех факторов.
Во-первых, от величины такого диапазона — чем точнее наши требования, тем меньше вероятности, что нам повезет.
Во-вторых, от того, насколько «популярен» выбранный нами рост. Напомним, что мода — самое часто встречающееся значение роста. Кстати для нормального распределения мода, медиана и среднее значение совпадают. Кривая нормального распределения симметрична относительно среднего значения.
И, в-третьих, вероятность попадания роста в определенный диапазон зависит от характеристики рассеивания случайной величины. Отчасти это связано с единицами измерения (представьте, что мы бы измеряли людей в дюймах, а не в миллиметрах, но сами люди и их рост были бы теми же). Но дело не только в этом. Просто некоторые процессы кучнее группируются возле среднего значения, в то время как другие более разбросаны.
Например, рост собак и рост домашних кошек имеют разный разброс значений, их кривые нормального распределения будут выглядеть по-разному (напомним еще раз, что площадь под обеими кривыми будет единичной).
Так, кривая для роста кошек будет более узкой и высокой, а для роста собак кривая будет ниже и шире. Для характеристики разброса конечного ряда данных в прошлом разделе мы использовали величину среднего квадратического отклонения. Аналогичная величина используется для характеристики кривой нормального распределения. Она обозначается буквой s и называется в этом случае стандартным отклонением. Это очень важная величина для кривой нормального распределения. Кривая нормального распределения полностью задана, если известно среднее значение 
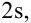
Для вычисления других значений вероятности, которые могут Вам понадобиться, можно воспользоваться приведенной таблицей:
Таблица вероятности попадания случайной величины в отмеченный (заштрихованный) диапазон
Нормальный закон распределения
Нормальный закон распределения случайных величин, который иногда называют законом Гаусса или законом ошибок, занимает особое положение в теории вероятностей, так как 95 % изученных случайных величин подчиняются этому закону. Природа этих случайных величин такова, что их значение в проводимом эксперименте связано с проявлением огромного числа взаимно независимых случайных факторов, действие каждого из которых составляет малую долю их совокупного действия. Например, длина детали, изготавливаемой на станке с программным управлением, зависит от случайных колебаний резца в момент отрезания, от веса и толщины детали, ее формы и температуры, а также от других случайных факторов. По нормальному закону распределения изменяются рост и вес мужчин и женщин, дальность выстрела из орудия, ошибки различных измерений и другие случайные величины.
Определение: Случайная величина X называется нормальной, если она подчиняется нормальному закону распределения, т.е. ее плотность распределения задается формулой
Приведенная дифференциальная функция распределения удовлетворяет всем свойствам плотности вероятности, проверим, например, свойство 4.:
Выясним геометрический смысл параметров 
Рис. 8. Изменение графика плотности вероятности в зависимости от изменения математического ожидания при фиксированном значении средне-квадратичного отклонения. Из рисунка видно, кривая 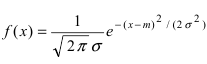
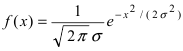
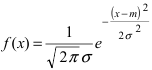
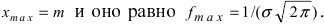
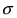
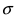
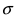
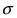
Рис. 9. Изменение графика плотности вероятности в зависимости от изменения средне-квадратичного отклонения при фиксированном значении математического ожидания.
Интегральная функция нормального распределения имеет вид:
График функции распределения имеет вид (Рис. 10):
Рис. 10. Графика интегральной функции распределения нормальной случайной величины.
Вероятность попадания нормальной случайной величины в заданный интервал
Пусть требуется определить вероятность того, что нормальная случайная величина попадает в интервал 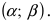
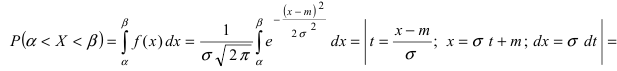
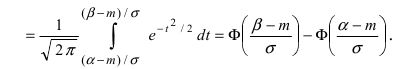
Рассмотрим основные свойства функции Лапласа Ф(х):
- Ф(0) = 0 — график функции Лапласа проходит через начало координат.
- Ф (-х) = — Ф(х) — функция Лапласа является нечетной функцией, поэтому
- таблицы для функции Лапласа приведены только для неотрицательных значений аргумента.
— график функции Лапласа имеет горизонтальные асимптоты
Следовательно, график функции Лапласа имеет вид (Рис. 11):
Рис. 11. График функции Лапласа.
Пример №1
Закон распределения нормальной случайной величины X имеет вид: 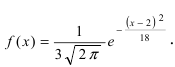
Решение:
Согласно условиям задачи 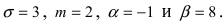
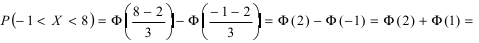
Вычисление вероятности заданного отклонения
Вычисление вероятности заданного отклонения. Правило 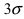
Если интервал, в который попадает нормальная случайная величина X, симметричен относительно математического ожидания 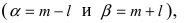
Данная формула показывает, что отклонение случайной величины Х от ее математического ожидания на заданную величину l равна удвоенному значению функции Лапласа от отношения / к среднему квадратичному отклонению. Если положить 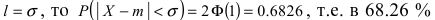
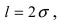
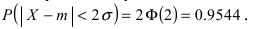
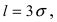
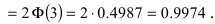
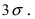
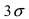
Показательный закон распределения
Определение: Закон распределения, определяемый фу нкцией распределения:
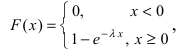
График экспоненциального закона распределения имеет вид (Рис. 12):
Рис. 12. График функции распределения для случая экспоненциального закона.
Дифференциальная функция распределения (плотность вероятности) имеет вид: 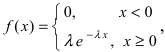
Рис. 13. График плотности вероятности для случая экспоненциального закона.
Пример №2
Случайная величина X подчиняется дифференциальной функции распределения 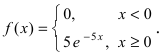
Решение:
Интегральная функция распределения 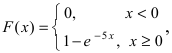
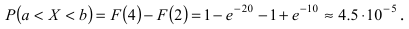
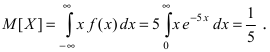
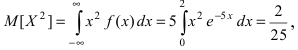
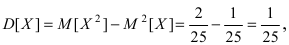
отклонение 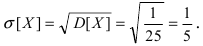
- Основные законы распределения вероятностей
- Асимптотика схемы независимых испытаний
- Функции случайных величин
- Центральная предельная теорема
- Повторные независимые испытания
- Простейший (пуассоновский) поток событий
- Случайные величины
- Числовые характеристики случайных величин
Макеты страниц
Ошибки измерений и способ наименьших квадратов
9.1.21. Ошибки измерений и нормальный закон распределения.
Измерения всегда сопровождаются ошибками. Различают ошибки двух основных видов: систематические и случайные. Систематические ошибки имеют определенные причины, которые искажают измерение всегда в одном направлении и часто на постоянную величину. Они возникают за счет неисправности или плохой регулировки приборов, за счет ошибок в эталонах, из-за плохого выполнения технологии и т. д. Во многих случаях можно найти причины таких ошибок и устранить их.
Случайные ошибки неопределенны, и причина их неизвестна. Свое незнание причины ошибок мы обычно маскируем, говоря, что их порождает случай. А это просто означает, что их можно приписать большому количеству причин, действующих в любом направлении и создающих каждая свою погрешность. Такие случайные ошибки можно учитывать статистическими методами.
Существует еще одна категория ошибок, о которой будет кратко сказано в п. 9.1.27; это категория отдельных промахов, происходящих по однократной вине экспериментатора, например, если он по рассеянности один раз неправильно считает показания со шкалы измерительного прибора. В этом случае мы имеем дело с анормальным результатом измерения. Существует простое правилу, позволяющее исключить из таблицы результатов измерений ошибки этой категории.
Мы займемся в основном категорией случайных ошибок. Допустим, что имеется несколько в одинаковой степени надежных измерений физической величины, истинное значение которой равно 


Это чисто случайные ошибки.
Мы не знаем точного значения величины X и не можем определить ее на опыте, так как всякое измерение, сделанное для ее определения, искажается ошибкой. Обозначим через X наиболее вероятное значение величины 
Рассмотрим величины

Величины 

Положим




где 
Вычертим кривые Гаусса при двух различных значениях мерь; точности 



Вероятность того, что ошибка будет заключаться между 

Пост №2 для начинающих посвящен описательным статистикам, группированию данных и нормальному распределению. Все эти сведения заложат основу для дальнейшего анализа электоральных данных. Предыдущий пост см. здесь.
Описательные статистики
Описательные статистические величины, или статистики, — это числа, которые используются для обобщения и описания данных. В целях демонстрации того, что мы имеем в виду, посмотрим на столбец с данными об электорате Electorate. Он показывает суммарное число зарегистрированных избирателей в каждом избирательном округе:
def ex_1_6():
'''Число значений в поле "Электорат"'''
return load_uk_scrubbed()['Electorate'].count()650Мы уже очистили столбец, отфильтровав пустые значения (nan) из набора данных, и поэтому предыдущий пример должен вернуть суммарное число избирательных округов.
Описательные статистики, так называемые сводные статистики, представляют собой разные подходы к измерению свойств последовательностей чисел. Они помогают охарактеризовать последовательность и способны выступать в качестве ориентира для дальнейшего анализа. Начнем с двух самых базовых статистик, которые мы можем вычислить из последовательности чисел — ее среднее значение и дисперсию (варианс).
-
Среднее значение
Наиболее распространенный способ усреднить набор данных — взять его среднее значение. Среднее значение на самом деле представляет собой один из нескольких способов измерения центра распределения данных.
Среднее значение числового ряда вычисляется на Python следующим образом:
def mean(xs):
'''Среднее значение числового ряда'''
return sum(xs) / len(xs) Мы можем воспользоваться нашей новой функцией mean для вычисления среднего числа избирателей в Великобритании:
def ex_1_7():
'''Вернуть среднее значение поля "Электорат"'''
return mean( load_uk_scrubbed()['Electorate'] )70149.94На самом деле, библиотека pandas уже содержит функцию mean, которая гораздо эффективнее вычисляет среднее значение последовательности. В нашем случае ее можно применить следующим образом:
load_uk_scrubbed()['Electorate'].mean()-
Медиана
Медиана — это еще одна распространенная описательная статистика для измерения центра распределения последовательности. Если Вы упорядочили все данные от меньшего до наибольшего, то медиана — это значение, которое находится ровно по середине. Если в последовательности число точек данных четное, то медиана определяется, как полусумма двух срединных значений.
def median(xs):
'''Медиана числового ряда'''
n = len(xs)
mid = n // 2
if n % 2 == 1:
return sorted(xs)[mid]
else:
return mean( sorted(xs)[mid-1:][:2] )Медианное значение электората Великобритании составляет:
def ex_1_8():
'''Вернуть медиану поля "Электорат"'''
return median( load_uk_scrubbed()['Electorate'] )70813.5Библиотека pandas тоже располагает встроенной функцией для вычисления медианного значения, которая так и называется median.
-
Дисперсия
Среднее арифметическое и медиана являются двумя альтернативными способами описания среднего значения последовательности, но сами по себе они мало что говорят о содержащихся в ней значениях. Например, если известно, что среднее последовательности из девяноста девяти значений равно 50, то мы почти ничего не скажем о том, какого рода значения последовательность содержит.
Она может содержать целые числа от одного до девяноста девяти либо сорок девять нулей и пятьдесят девяносто девяток, а может быть и так, что она девяносто восемь раз содержит отрицательную единицу и одно число 5048, или же вообще все значения могут быть равны 50.
Дисперсия (варианс) последовательности чисел показывает «разброс» данных вокруг среднего значения. К примеру, данные, приведенные выше, имели бы разную дисперсию. На языке математики дисперсия обозначается следующим образом:
где s2 — это математический символ, который часто используют для обозначения дисперсии.
Выражение
def variance(xs):
'''Дисперсия (варианс) числового ряда,
несмещенная дисперсия при n <= 30'''
mu = mean(xs)
n = len(xs)
n = n-1 if n in range(1, 30) else n
square_deviation = lambda x : (x - mu) ** 2
return sum( map(square_deviation, xs) ) / nДля вычисления квадрата выражения используется оператор языка Python возведения в степень **.
-
Стандартное отклонение
Поскольку мы взяли средний квадрат отклонения, т.е. получили квадрат отклонения и затем его среднее, то единицы измерения дисперсии (варианса) тоже будут в квадрате, т.е. дисперсия электората Великобритании будет измеряться «людьми в квадрате». Несколько неестественно рассуждать об избирателях в таком виде. Единицу измерения можно привести к более естественному виду, снова обозначающему «людей», путем извлечения квадратного корня из дисперсии (варианса). В результате получим так называемое стандартное отклонение, или среднеквадратичное отклонение:
def standard_deviation(xs):
'''Стандартное отклонение числового ряда'''
return sp.sqrt( variance(xs) )
def ex_1_9():
'''Стандартное отклонение поля "Электорат"'''
return standard_deviation( load_uk_scrubbed()['Electorate'] )7672.77В библиотеке pandas функции для вычисления дисперсии (варианса) и стандартного отклонения имплементированы соответственно, как var и std. При этом последняя по умолчанию вычисляет несмещенное значение, поэтому, чтобы получить тот же самый результат, нужно применить именованный аргумент ddof=0, который сообщает, что требуется вычислить смещенное значение стандартного отклонения:
load_uk_scrubbed()['Electorate'].std( ddof=0 )-
Квантили
Медиана представляет собой один из способов вычислить срединное значение из списка, т.е. находящееся ровно по середине, дисперсия же предоставляет способ измерить разброс данных вокруг среднего значения. Если весь разброс данных представить на шкале от 0 до 1, то значение 0.5 будет медианным.
Для примера рассмотрим следующую ниже последовательность чисел:
[10 11 15 21 22.5 28 30]Отсортированная последовательность состоит из семи чисел, поэтому медианой является число 21 четвертое в ряду. Его также называют 0.5-квантилем. Мы можем получить более полную картину последовательности чисел, взглянув на 0.0 (нулевой), 0.25, 0.5, 0.75 и 1.0 квантили. Все вместе эти цифры не только показывают медиану, но также обобщают диапазон данных и сообщат о характере распределения чисел внутри него. Они иногда упоминаются в связи с пятичисловой сводкой.
Один из способов составления пятичисловой сводки для данных об электорате Великобритании показан ниже. Квантили можно вычислить непосредственно в pandas при помощи функции quantile. Последовательность требующихся квантилей передается в виде списка.
def ex_1_10():
'''Вычислить квантили:
возвращает значение в последовательности xs,
соответствующее p-ому проценту'''
q = [0, 1/4, 1/2, 3/4, 1]
return load_uk_scrubbed()['Electorate'].quantile(q=q)0.00 21780.00
0.25 65929.25
0.50 70813.50
0.75 74948.50
1.00 109922.00
Name: Electorate, dtype: float64Когда квантили делят диапазон на четыре равных диапазона, как показано выше, то они называются квартилями. Разница между нижним (0.25) и верхним (0.75) квартилями называется межквартильным размахом, или иногда сокращенно МКР. Аналогично дисперсии (варианса) вокруг среднего значения, межквартильный размах измеряет разброс данных вокруг медианы.
Группирование данных в корзины
В целях развития интуитивного понимания в отношении того, что именно все эти расчеты разброса значений измеряют, мы можем применить метод под названием группировка в частотные корзины (binning). Когда данные имеют непрерывный характер, использование специального словаря для подсчета частот Counter (подобно тому, как он использовался при подсчете количества пустых значений в наборе данных об электорате) становится нецелесообразным, поскольку никакие два значения не могут быть одинаковыми. Между тем, общее представление о структуре данных можно все-равно получить, сгруппировав для этого данные в частотные корзины (bins).
Процедура образования корзин заключается в разбиении диапазона значений на ряд последовательных, равноразмерных и меньших интервалов. Каждое значение в исходном ряду попадает строго в одну корзину. Подсчитав количества точек, попадающих в каждую корзину, мы можем получить представление о разбросе данных:
На приведенном выше рисунке показано 15 значений x, разбитых на 5 равноразмерных корзин. Подсчитав количество точек, попадающих в каждую корзину, мы можем четко увидеть, что большинство точек попадают в корзину по середине, а меньшинство — в корзины по краям. Следующая ниже функция Python nbin позволяет добиться того же самого результата:
def nbin(n, xs):
'''Разбивка данных на частотные корзины'''
min_x, max_x = min(xs), max(xs)
range_x = max_x - min_x
fn = lambda x: min( int((abs(x) - min_x) / range_x * n), n-1 )
return map(fn, xs)Например, мы можем разбить диапазон 0-14 на 5 корзин следующим образом:
list( nbin(5, range(15)) )[0, 0, 0, 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4]После того, как мы разбили значения на корзины, мы можем в очередной раз воспользоваться словарем Counter, чтобы подсчитать количество точек в каждой корзине. В следующем ниже примере мы воспользуемся этим словарем для разбиения данных об электорате Великобритании на пять корзин:
def ex_1_11():
'''Разбиmь электорат Великобритании на 5 корзин'''
series = load_uk_scrubbed()['Electorate']
return Counter( nbin(5, series) )Counter({2: 450, 3: 171, 1: 26, 0: 2, 4: 1})Количество точек в крайних корзинах (0 и 4) значительно ниже, чем в корзинах в середине — количества, судя по всему, растут по направлению к медиане, а затем снова снижаются. В следующем разделе мы займемся визуализацией формы этих количеств.
Гистограммы
Гистограмма — это один из способов визуализации распределения одной последовательности значений. Гистограммы попросту берут непрерывное распределение, разбивают его на корзины, и изображают частоты точек, попадающих в каждую корзину, в виде столбцов. Высота каждого столбца гистограммы показывает количество точек данных, которые содержатся в этой корзине.
Мы уже увидели, каким образом можно выполнить разбиение данных на корзины самостоятельно, однако в библиотеке pandas уже содержится функция hist, которая разбивает данные и визуализирует их в виде гистограммы.
def ex_1_12():
'''Построить гистограмму частотных корзин
электората Великобритании'''
load_uk_scrubbed()['Electorate'].hist()
plt.xlabel('Электорат Великобритании')
plt.ylabel('Частота')
plt.show()Приведенный выше пример сгенерирует следующий ниже график:
Число корзин, на которые данные разбиваются, можно сконфигурировать, передав в функцию при построении гистограммы именованный аргумент bins:
def ex_1_13():
'''Построить гистограмму частотных корзин
электората Великобритании с 200 корзинами'''
load_uk_scrubbed()['Electorate'].hist(bins=200)
plt.xlabel('Электорат Великобритании')
plt.ylabel('Частота')
plt.show()Приведенный выше график показывает единственный высокий пик, однако он выражает форму данных довольно грубо. Следующий ниже график показывает мелкие детали, но величина столбцов делает неясной форму распределения, в особенности в хвостах:
При выборе количества корзин для представления данных следует найти точку равновесия — с малым количеством корзин форма данных будет представлена лишь приблизительно, а слишком большое их число приведет к тому, что шумовые признаки могут заслонить лежащую в основании структуру.
def ex_1_14():
'''Построить гистограмму частотных корзин
электората Великобритании с 20 корзинами'''
load_uk_scrubbed()['Electorate'].hist(bins=20)
plt.xlabel('Электорат Великобритании')
plt.ylabel('Частота')
plt.show()Ниже показана гистограмма теперь уже из 20 корзин:
Окончательный график, состоящий из 20 корзин, судя по всему, пока лучше всего представляет эти данные.
Наряду со средним значением и медианой, есть еще один способ измерить среднюю величину последовательности. Это мода. Мода — это значение, встречающееся в последовательности наиболее часто. Она определена исключительно только для последовательностей, имеющих по меньшей мере одно дублирующее значение; во многих статистических распределениях это не так, и поэтому для них мода не определена. Тем не менее, пик гистограммы часто называют модой, поскольку он соответствует наиболее распространенной корзине.
Из графика ясно видно, что распределение вполне симметрично относительно моды, и его значения резко падают по обе стороны от нее вдоль тонких хвостов. Эти данные приближенно подчиняются нормальному распределению.
Нормальное распределение
Гистограмма дает приблизительное представление о том, каким образом данные распределены по всему диапазону, и является визуальным средством, которое позволяет квалифицировать данные как относящиеся к одному из немногих популярных распределений. В анализе данных многие распределения встречаются часто, но ни одно не встречается также часто, как нормальное распределение, именуемое также гауссовым распределением.
Распределение названо нормальным распределением из-за того, что оно очень часто встречается в природе. Галилей заметил, что ошибки в его астрономических измерениях подчинялись распределению, где малые отклонения от среднего значения встречались чаще, чем большие. Вклад великого математика Гаусса в описание математической формы этих ошибок привел к тому, что это распределение стали называть в его честь распределением Гаусса.
Любое распределение похоже на алгоритм сжатия: оно позволяет очень эффективно резюмировать потенциально большой объем данных. Нормальное распределение требует только два параметра, исходя из которых можно аппроксимировать остальные данные. Это среднее значение и стандартное отклонение.
Центральная предельная теорема
Высокая встречаемость нормального распределения отчасти объясняется центральной предельной теоремой. Дело в том, что значения, полученные из разнообразных статистических распределений, при определенных обстоятельствах имеют тенденцию сходиться к нормальному распределению, и мы это покажем далее.
В программировании типичным распределением является равномерное распределение. Оно представлено распределением чисел, генерируемых функцией библиотеки scipy stats.uniform.rvs: в справедливом генераторе случайных чисел все числа имеют равные шансы быть сгенерированными. Мы можем увидеть это на гистограмме, многократно генерируя серию случайных чисел между 0 и 1 и затем построив график с результатами.
def ex_1_15():
'''Показать гистограмму равномерного распределения
синтетического набора данных'''
xs = stats.uniform.rvs(0, 1, 10000)
pd.Series(xs).hist(bins=20)
plt.xlabel('Равномерное распределение')
plt.ylabel('Частота')
plt.show()Обратите внимание, что в этом примере мы впервые использовали тип Series библиотеки pandas для числового ряда данных.
Приведенный выше пример создаст следующую гистограмму:
Каждый столбец гистограммы имеет примерно одинаковую высоту, что соответствует равновероятности генерирования числа, которое попадает в каждую корзину. Столбцы имеют не совсем одинаковую высоту, потому что равномерное распределение описывает теоретический результат, который наша случайная выборка не может отразить в точности. Раздел инференциальной статистики, посвященный проверке статистических гипотез, изучает способы точной количественной оценки расхождения между теорией и практикой, чтобы определить, являются ли расхождения достаточно большими, чтобы обратить на это внимание. В данном случае они таковыми не являются.
Если напротив сгенерировать гистограмму средних значений последовательностей чисел, то в результате получится распределение, которое выглядит совсем непохоже.
def bootstrap(xs, n, replace=True):
'''Вернуть список массивов меньших размеров
по n элементов каждый'''
return np.random.choice(xs, (len(xs), n), replace=replace)
def ex_1_16():
'''Построить гистограмму средних значений'''
xs = stats.uniform.rvs(loc=0, scale=1, size=10000)
pd.Series( map(sp.mean, bootstrap(xs, 10)) ).hist(bins=20)
plt.xlabel('Распределение средних значений')
plt.ylabel('Частота')
plt.show()Приведенный выше пример сгенерирует результат, аналогичный следующей ниже гистограмме:
Хотя величина среднего значения близкая к 0 или 1 не является невозможной, она является чрезвычайно невероятной и становится менее вероятной по мере роста числа усредненных чисел и числа выборочных средних. Фактически, на выходе получается результат очень близкий к нормальному распределению.
Этот результат, когда средний эффект множества мелких случайных колебаний в итоге приводит к нормальному распределению, называется центральной предельной теоремой, иногда сокращенно ЦПТ, и играет важную роль для объяснения, почему нормальное распределение встречается так часто в природных явлениях.
До 20-ого века самого термина еще не существовало, хотя этот эффект был зафиксирован еще в 1733 г. французским математиком Абрахамом де Mуавром, который использовал нормальное распределение, чтобы аппроксимировать число орлов в результате бросания уравновешенной монеты. Исход бросков монеты лучше всего моделировать при помощи биномиального распределения. В отличие от центральной предельной теоремы, которая позволяет получать выборки из приближенно нормального распределения, библиотека scipy содержит функции для эффективного генерирования выборок из самых разнообразных статистических распределений, включая нормальное:
def ex_1_17():
'''Показать гистограмму нормального распределения
синтетического набора данных'''
xs = stats.norm.rvs(loc=0, scale=1, size=10000)
pd.Series(xs).hist(bins=20)
plt.xlabel('Нормальное распределение')
plt.ylabel('Частота')
plt.show()Отметим, что в функции sp.random.normal параметр loc – это среднее значение, scale – дисперсия и size – размер выборки. Приведенный выше пример сгенерирует следующую гистограмму нормального распределения:
По умолчанию среднее значение и стандартное отклонение для получения нормального распределения равны соответственно 0 и 1.
Примеры исходного кода для этого поста находятся в моем репо на Github. Все исходные данные взяты в репозитории автора книги.
Следующая часть, часть 3, серии постов «Python, исследование данных и выборы» посвящена генерированию распределений, их свойствам, а также графикам для их сопоставительного анализа

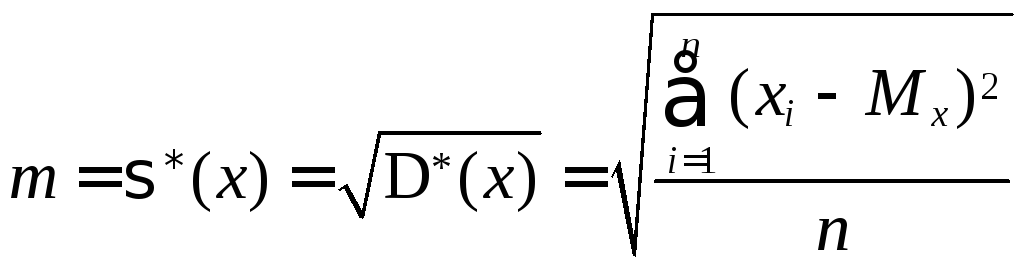 .
. ,
, .
.
 ,
, ,
,
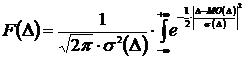
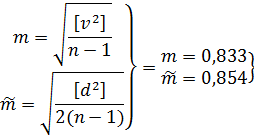
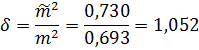
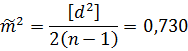
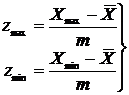
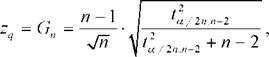
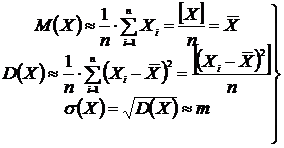
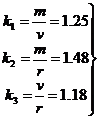
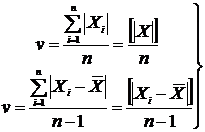
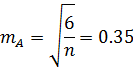
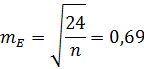
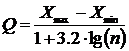
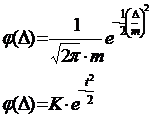
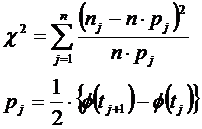
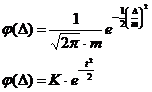
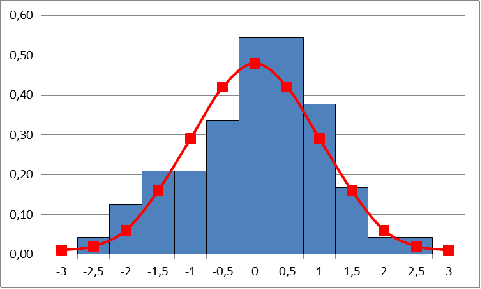
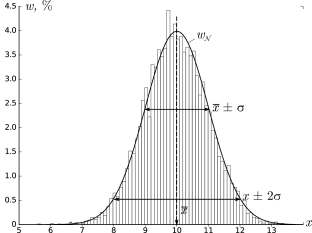
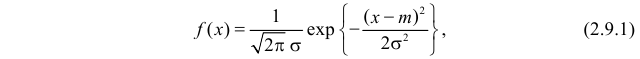
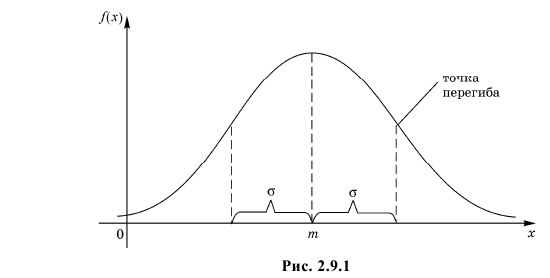
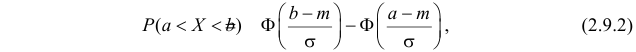
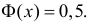
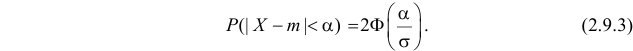
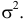
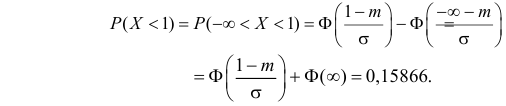
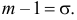
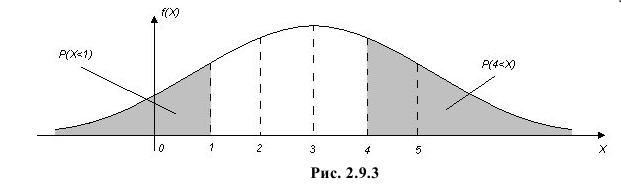
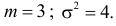
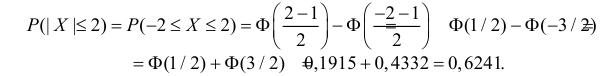
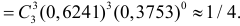
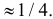
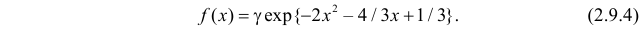
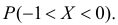
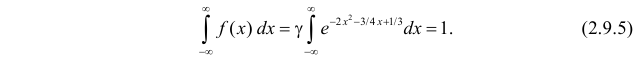
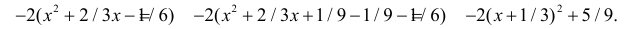
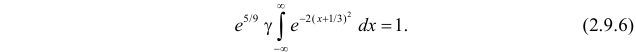

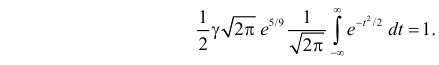

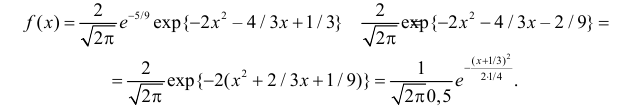
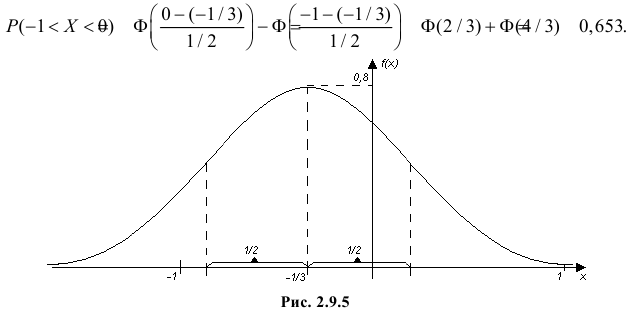
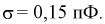
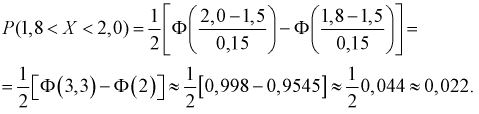
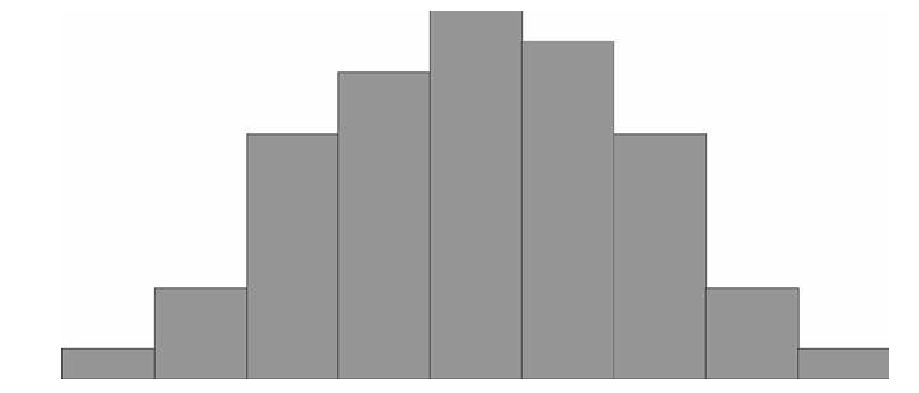
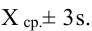
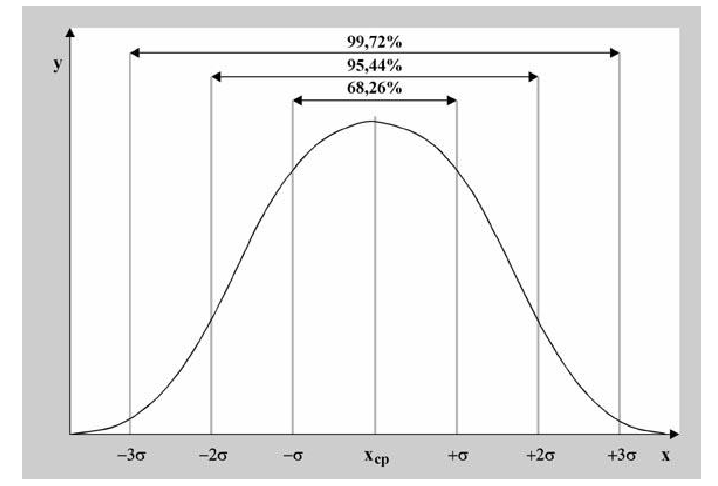
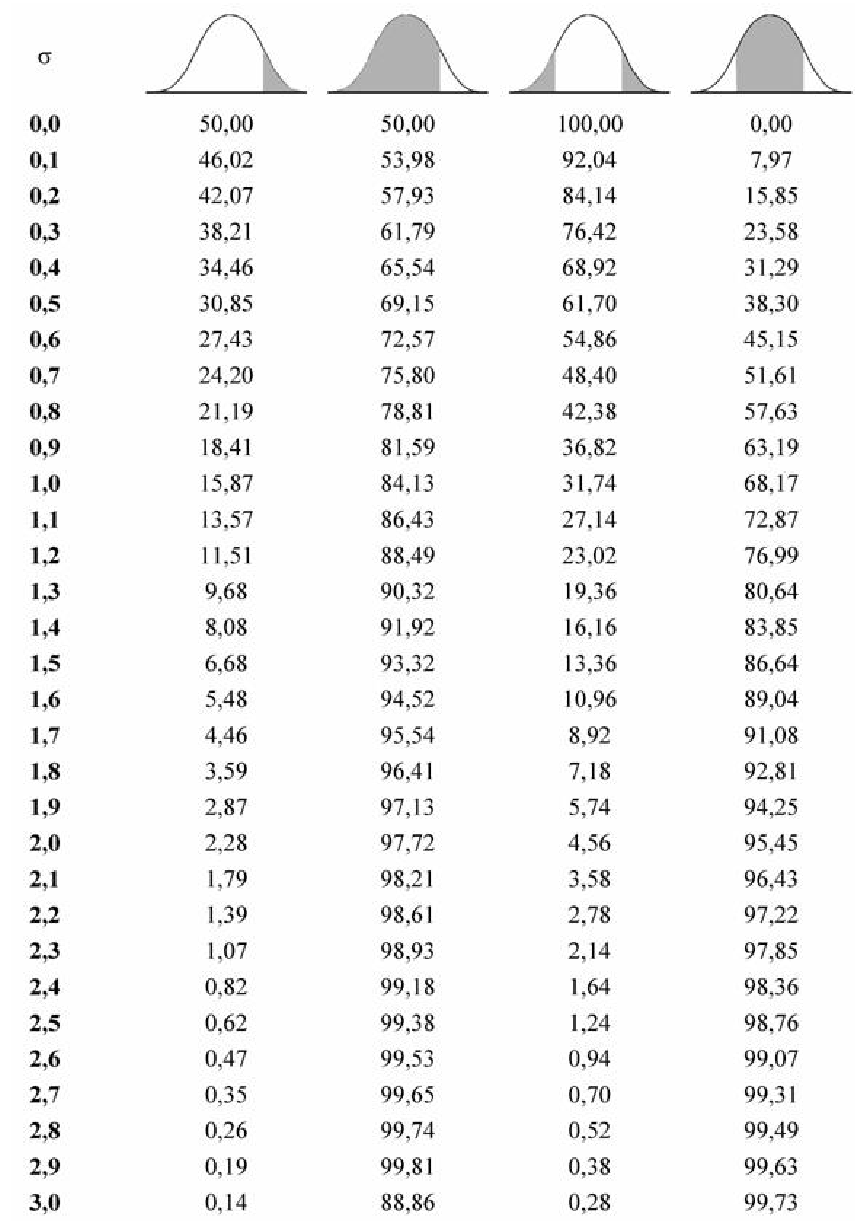
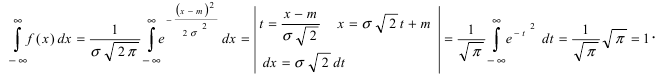
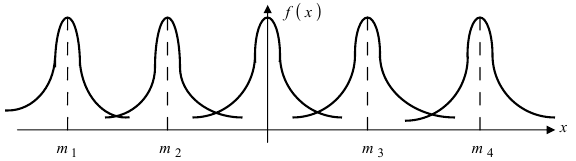
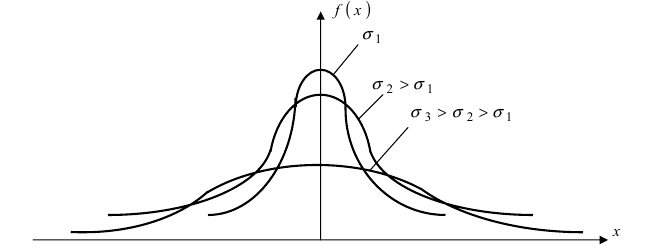
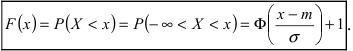
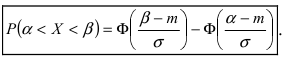
 — график функции Лапласа имеет горизонтальные асимптоты
— график функции Лапласа имеет горизонтальные асимптоты