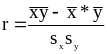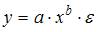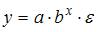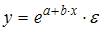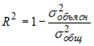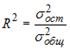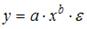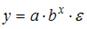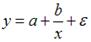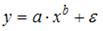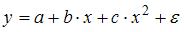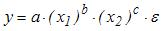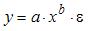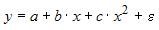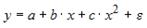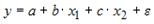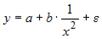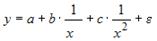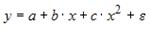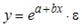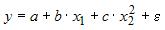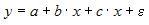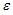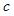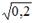Парная регрессия
1.
Коэффициент корреляции, равный нулю,
означает, что между переменными
линейная
связь отсутствует
существует
линейная связь
ситуация
не определена.
2.
Коэффициент корреляции, равный 1,
означает, что между переменными
функциональная
зависимость
линейная
связь отсутствует
ситуация
не определена
3. В
парной обратной
линейной регресии коэффициент корреляции
-1<r<0
r=0
0<r<0
r>0
r<0
4. В
парной прямой
линейной регрессии коэффициент корреляции
0<r<1
r=0
r<0
r>0
-1<r<0
5.
Для парной регресии F- критерий равен:
t2
r2
b
s2
6.
Если в уравнении регрессии имеется
несущественная переменная, то она
обнаруживает себя по низкому значению
t —
статистики
F —
статистики
коэффициента
детерминации
76.
Коэффициент детерминации характеризует
-долю
факторной дисперсии в общей дисперсии
результативного признака
-долю
остаточной дисперсии в общей дисперсии
результативного признака
-соотношение
факторной и остаточной дисперсий
8.
Коэффициент детерминации это
квадрат
множественного коэффициента корреляции
квадрат
частного коэффициента корреляции
квадрат
F
распределения
9.
Табличное значение критерия Стьюдента
зависит
И
от доверительной вероятности, и от
числа факторов, и от длины исходного
рядас
Только
от числа факторов в модели
Только
от длины исходного ряда
Только
от уровня доверительной вероятности и
длины исходного ряда
Только
от уровня доверительной вероятности
10.
Выбор формы связи между переменными
называется:
-спецификацией
-параметризация
-верификацией
11.
Суть МНК состоит в:
-минимизации
суммы квадратов отклонений точек
наблюдений от уравнения регрессии
-минимизации
суммы квадратов коэффициентов регрессии.
-минимизации
суммы квадратов значений зависимой
переменной
-минимизации
суммы квадратов отклонений точек
эмпирического уравнения регрессии от
точек теоретического уравнения регрессии
12.
В производственной функции Кобба-Дугласа
параметр b соответствует коэффициенту:
-эластичности
-корреляции
-детерминации
-вариации
13.
Оценка значимости уравнения регрессии
в целом дается с помощью:
-F-критерия
Фишера
-стандартной
ошибки регрессии
-коэффициента
детерминации
14.
Верификация модели – это:
—
проверка точности модельных данных
—
статистическое оценивание неизвестных
параметров модели
—
формулировка вида модели, состава и
формы входящих в нее связей
—
сбор необходимой статистической
информации
15.
Параметризация модели — это
статистическое
оцениванте неизвестных параметров
модели
формулировка
вида модели, состава и формы входящих
в нее связей
сбор
необходимой информации
проверка
точности модельных данных
16.
Законы распределения случайной величины
необходимы для:
определения
интервальных оценок и проверки
статистических гипотез
определения
интервальных оценок
проверки
статистических гипотез
17.
Какое из уравнений регрессии нельзя
свести к линейному виду?
18.
F-критерий характеризует:
-соотношение
факторной и остаточной дисперсий
-долю
остаточной дисперсии в общей дисперсии
результативного признака
-долю
факторной дисперсии в общей дисперсии
результативного признака
19.
Экспериментальный метод подбора вида
уравнения регрессии основан на:
-сравнении
величины остаточной дисперсии при
разных моделях
-изучении
поля корреляции
-изучении
природы связи признаков
20.
Применим ли метод наименьших квадратов
для расчёта параметров нелинейных
моделей?
применим
после её специального приведения к
линейному виду
нет
да
21.
Статистическая надежность оценки
коэффициентов регрессии увеличивается:
— с
увеличением числа степеней свободы
— не
зависит от числа степеней свободы
— с
уменьшением числа степеней свободы
22.
Пространственные данные фиксируются:
в
один и тот же момент времени по нескольким
объектам
по
одному объекту за период времени
по
нескольким объектам за период времени
23.
Что минимизируется согласно методу
наименьших квадратов?
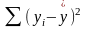
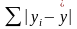
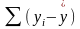
24.
Если фактор не оказывает влияния на
результат, то линия регрессии на графике:
-параллельна
оси ох
-параллельна
оси оу
-является
биссектрисой первой четверти декартовой
системы координат
25.
Для функции
средний
коэффициент эластичности равен
26.
Случайное отклонение приведет к
увеличению дисперсии оценок, если
cov(ei,ej)≠0
cov(xi,ej)=0
D(ei)=D(ej)
27.
Гомоскедастичность подразумевает:
D(ei)=D(ej)
M(ei)=0
cov(xi,ej)=0
28.
Случайное отклонение в среднем не
оказывает влияние на зависимую переменную,
если:
M(ei)=0
cov(ei,ej)
≠0
D(ei)
≠D(xj)
29.
Эмпирическое уравнение регрессии
построено таким образом, что:
∑ei=0
cov(yi,xi)=cov(yi,ei)
r
x,y>0,5
30.
Уравнение регрессии статистически
значимо, если
-«объясненная»
сумма квадратов отклонений значимо
больше остаточной суммы квадратов
отклонений
-остаточная
сумма квадратов отклонений значимо
больше «объясненной» суммы квадратов
отклонений
-«объясненная»
и остаточная суммы квадратов отклонений
равны
31.
Случайное отклонение приведет к
увеличению дисперсии оценок, если
D(ei)
≠D(еj)
cov(ei,ej)=0
cov(xi,ej)=0
32.
Значимая линейная связь между х и у
имеет место, когда:
|t|>3
1<|t|<2
|t|<1
33.
Отсутствие автокорреляции случайных
отклонений влечет соотношение:
cov(ei,ej)=0
cov(xi,ej)=0
D(ei)=D(ej)
34.
С увеличением числа наблюдений n
дисперсии оценок a и b
уменьшаются
увеличивается
не
изменяются
35.
Критерий Стьюдента предназначен для:
-Определения
статистической значимости каждого
коэффициента уравнения
-Определения
экономической значимости модели в
целом.
-Проверки
на гомоскедастичность
-Определения
экономической значимости каждого
коэффициента уравнения
—Проверки
модели на автокорреляцию остатков
36.
Общая сумма квадратов отклонений в
парной регрессии имеет число степеней
свободы, равное:
n-1
1
n-2
37.
Остаточная сумма квадратов отклонений
в парной регрессии имеет число степеней
свободы, равное:
n-2
n-1
1
38.
Остаточная сумма квадратов отклонений
отражает влияние на разброс у:
прочих
факторов
изучаемого
фактора х и прочих факторов
изучаемого
фактора х
39.
Объясненная (факторная) сумма квадратов
отклонений в парной регрессии имеет
число степеней свободы, равное:
1
n-1
n-2
40.
Коэффициент эластичности показывает
-на
сколько % изменится результат при
изменении фактора на 1 %
-на
сколько единиц изменится фактор при
изменении результата на 1 единицу.
-на
сколько единиц изменится результат при
изменении фактора на 1 единицу.
-во
сколько раз изменится результат при
изменении фактора на одну единицу.
-на
сколько %изменится фактор при изменении
результата на 1%.
41.
Коэффициент корреляции является
величиной:
безразмерной
размерной
имеет
ту же единицу измерения, что и случайная
величина
42.
Эмпирическая прямая регрессии обязательно
проходит через точку:
43.
Величина, рассчитанная по формуле
является
оценкой
парного
коэффициента корреляции
множественного
коэффициента корреляции
частного
коэффициента корреляции
коэффициента
детерминации
44.
Аналитический метод подбора вида
уравнения регрессии основан на:
-изучении
природы связи признаков
-сравнении
величины остаточной дисперсии при
разных моделях
-изучении
поля корреляции
45.
Графический метод подбора вида уравнения
регрессии основан на:
-изучении
поля корреляции
-сравнении
величины остаточной дисперсии при
разных моделях
-изучении
природы связи признаков
46.
Если коэффициент детерминации равен
нулю, то:
величина
зависимой переменной Y линейно не зависит
от независимых переменных Xi
нельзя
сделать вывод о линейной зависимости
Y от независимых переменных Xi
величина
зависимой переменной Y линейно зависит
от независимых переменных Xi
47.
Величина коэффициента регрессии
показывает:
-среднее
изменение результата с изменением
фактора на одну единицу
-изменение
результата в процентах с изменением
фактора на один процент
-среднее
изменение результата с изменением
фактора на один процент
48.
Суть коэффициента детерминации
состоит
в следующем:
-коэффициент
определяет долю общего разброса значений
,
объясненного уравнением регрессии
-коэффициент
свидетельствует о значимости коэффициентов
регрессии
-коэффициент
свидетельствует о наличии / отсутствии
автокорреляции
-коэффициент
определяет тесноту связи между признаками
49.
Не является предпосылкой классической
модели предположение:
-факторы
являются случайными величинами
-матрица
факторов содержит все важные факторы,
влияющие на результат
-длина
исходного ряда данных больше, чем
количество факторов
-факторы
экзогенны
50.
Переменные, задаваемые «из вне», в
определенной степени управляемые
(планируемые), называются:
экзогенные
эндогенные
предопределенные
51.
Остаточная сумма квадратов равна нулю
в том случае, когда:
-у
связан с х функционально
-вся
общая дисперсия у обусловлена влиянием
прочих факторов
-значения
у, рассчитанные по уравнению регрессии,
равны среднему значению у
52.
Коэффициент уравнения регрессии
показывает
-на
сколько единиц изменится результат при
изменении фактора на 1 единицу
-на
сколько % изменится результат при
изменении фактора на 1%.
-во
сколько раз изменится результат при
изменении фактора на 1 единицу.
-на
сколько % изменится фактор при изменении
результата на 1%.
на
сколько единиц изменится фактор при
изменении результата на 1 единицу
53.
В регрессионном анализе xj рассматриваются
как
неслучайная
величина
случайная
величина
любая
величина
54.
Переменные, определяемые из уравнений
модели, называются
зависимые
предопределенные
независимые
55.
«Объясненная» сумма квадратов отклонений
отражает влияние на разброс y:
изучаемого
фактора х
прочих
факторов
изучаемого
фактора х и прочих факторов
56.
С увеличением объема выборки:
увеличивается
точность оценок
увеличивается
точность прогноза по модели
уменьшается
коэффициент детерминации
57.
Переменные, задаваемые «из вне», в
определенной степени управляемые
(планируемые), называются:
независимые
предопределенные
зависимые
58.
Эконометрика — это:
наука,
которая дает количественные выражения
взаимосвязей в экономике
учение
о системе показателей, дающих представление
об экономике
различного
рода цифровые данные
59.
Найдите предположение, не
являющееся
предпосылкой классической модели.
-Случайное
отклонение не обладает нормальным
распределением.
-Случайное
отклонение имеет постоянную дисперсию.
-Случайное
отклонение имеет нулевое математическое
ожидание.
-Отсутствует
автокорреляция случайных отклонений.
-Случайное
отклонение независимо от объясняющих
переменных.
60.
Использование парной регрессии вместо
множественной является примером
ошибки
спецификации
ошибки
выборки
ошибки
измерения
61.
С увеличением дисперсии х дисперсия
оценок a и b
уменьшается
увеличивается
не
изменяется
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Использование в эконометрическом моделировании парной регрессии вместо множественной является ошибкой …
- линеаризации
- выборки
- спецификации
- измерения
Тип вопроса: Вопрос с одним правильными вариантом
Ответ на этот вопрос уже получили: 26 раз(а)
Помогли ответы? Ставь лайк 👍
Вопрос задал(а): Анонимный пользователь, 17 Ноябрь 2015 в 06:40
На вопрос ответил(а): Любимов Павел, 17 Ноябрь 2015 в 06:41
Похожие вопросы
Вопрос № 1026216
Установите соответствие между спецификацией модели и видом уравнения:
1) линейное уравнение парной регрессии
%place1%
2) нелинейное уравнение парной регрессии
%place2%
3) линейное уравнение множественной регрессии
%place3%
Вопрос № 1026215
Установите соответствие между спецификацией модели и видом уравнения:
1) линейное уравнение множественной регрессии
%place1%
2) линейное уравнение парной регрессии
%place2%
3) нелинейное уравнение парной регрессии
%place3%
Другие вопросы по предмету Химия
Вопрос № 33605
Типичным примером пищевой цепи в лесной экосистеме является последовательность …
Вопрос № 33607
Под ликвидностью предприятия подразумевается состояние счетов предприятия, гарантирующее…
постоянное покрытие убытков
погашение долгов
независимость от внешних источников
его постоянную платежеспособность
Вопрос № 33608
Лес является …
гидроэкосистемой
агроэкосистемой
урбаэкосистемой
наземной экосистемой
Вопрос № 33610
Вертикальный анализ прибыли от продаж предполагает …
выявление линии тренда
анализ динамики показателей прибыли от продаж за несколько периодов
сравнительный анализ прибыли от продаж с предыдущим периодом
анализ структуры прибыли от продаж
Ошибки спецификации эконометрической модели имеют место вследствие …
Спецификацией модели называется отбор факторов, включаемых в модель, и выбор математической функции для 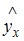
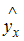
Эконометрика : учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М. : Финансы и статистика, 2005. – С. 45.
Прикладная статистика. Основы эконометрики: Учебник для вузов: В 2 т. 2-е изд., испр. – Т. 2: Айвазян С.А. Основы эконометрики. – М.: ЮНИТИ-ДАНА, 2001. – С. 20–30 .
ответ тест i-exam
Тема 2: Отбор факторов, включаемых в модель множественной регрессии
Тема 1: Спецификация эконометрической модели
1. Ошибки спецификации эконометрической модели имеют место вследствие …
неправильного выбора математической функции или недоучета в уравнении регрессии какого-то существенного фактора
недостоверности или недостаточности исходной информации
неоднородности данных в исходной статистической совокупности
недостаточного количества данных
Решение:
Спецификацией модели называется отбор факторов, включаемых в модель, и выбор математической функции для 

2. Для регрессионной модели вида 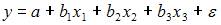
Решение:
Считается, на каждый оцениваемый коэффициент регрессии необходимо не менее 5–7 объектов статистических наблюдений. Так как представленная модель содержит 3 независимые переменные, то на каждый из параметров регрессии при независимой переменной необходимо по 5–7 наблюдений, то есть в совокупности не менее 15–21 наблюдения. Берем нижнюю границу интервала, тогда правильный вариант ответа – «15».
3. Нелинейным по объясняющим переменным, но линейным по параметрам уравнением регрессии является …
Решение:
Из приведенных функций только в функции 
4. В модели вида 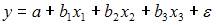
Решение:
Эконометрическая модель уравнения регрессии может быть представлена линейным уравнением множественной регрессии в виде выражения 

5. При идентификации модели множественной регрессии 
Решение:
При оценке модели множественной регрессии 
Тема 2: Отбор факторов, включаемых в модель множественной регрессии
1. В модели множественной регрессии 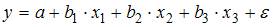






Решение:
Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами. Если факторы не коррелированы между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной. Поскольку все недиагональные элементы 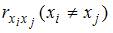

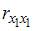
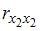
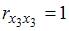
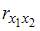
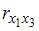
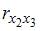
Если между факторами существует полная линейная зависимость и все коэффициенты парной корреляции равны единице, то определитель такой матрицы равен нулю.
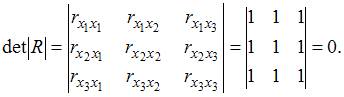
Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.
2. При моделировании линейного уравнения множественной регрессии вида 
Решение:
Эконометрическая модель уравнения регрессии может быть представлена линейным уравнением множественной регрессии в виде выражения 

V7: Система линейных одновременных уравнений
S: При выполнении предпосылок метода наименьших квадратов (МНК) оценки параметров регрессионной модели, рассчитанные с помощью МНК, обладают свойствами
-: состоятельности, смещенности и эффективности
+: состоятельности, несмещенности и эффективности
-: состоятельности, смещенности и неэффективности
-: несостоятельности, смещенности и эффективности
S: Для регрессионной модели вида 
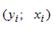
S: Для обнаружения автокорреляции в остатках используется
+: статистика Дарбина – Уотсона
-: критерий Гольдфельда – Квандта
S: Величина 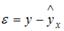
S: Строится эконометрическая модель линейного уравнения множественной регрессии вида
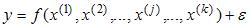

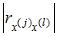
S: Для учета влияния на исследуемую (зависимую) переменную признаков качественного характера используются фиктивные переменные, при этом фиктивной переменной может присваиваться значение
S: В эконометрической модели линейного уравнения регрессии
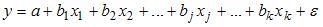
S: Система эконометрических уравнений включает совокупность _________ переменных.
S: Несмещенность оценок параметров регрессии означает, что …
-: дисперсия остатков минимальная
-: точность оценок выборки увеличивается с увеличением объема выборки
+: математическое ожидание остатков равно нулю
-: дисперсия остатков не зависит от величины
S: Дана автокорреляционная функция временного ряда
Верным будет утверждение, что ряд …
-: содержит только тенденцию, и не содержит сезонной компоненты
-: не имеет ни тенденции, ни сезонной компоненты, имеет только случайную компоненту
+: имеет выраженную сезонную компоненту с лагом 4
-: имеет выраженную сезонную компоненту с лагом 6
S: Если параметр эконометрической модели является статистически значимым, то его значение признается …
+: равным коэффициенту парной корреляции
S: Для регрессионной модели вида 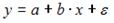
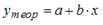

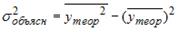

-:
+:
-:
-:
S: Построена эконометрическая модель для зависимости прибыли от реализации единицы продукции (руб., у) от величины оборотных средств предприятия (тыс. р., х1): 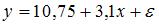
S: Нелинейным по объясняющим переменным, но линейным по параметрам уравнением регрессии является …
-:
-:
-:
+:
S: Примерами фиктивных переменных в эконометрической модели зависимости стоимости 1 м2 жилья не являются …
-: принадлежность тому или иному региону
-: категория жилья: первичное (новое) жилье / вторичное (неновое) жилье
+: площадь жилья (м2)
S: Среди предложенных нелинейных зависимостей нелинейной существенно (внутренне нелинейной) является …
+:
-:
-:
-:
S: При линеаризации нелинейных регрессионных моделей как один из видов преобразований используется логарифмирование уравнения. Указанным способом не может быть линеаризовано уравнение …
-:
-:
-:
+:
S: По результатам проведения исследования торговых точек было построено уравнение нелинейной регрессии 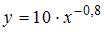
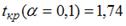
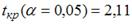
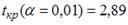
-: при уровне значимости 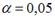
-: при уровне значимости 
-: эластичность спроса по цене составляет –0,8
+: при уровне значимости 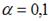
S: По типу функциональной зависимости между переменными эконометрической модели различают _____ уравнения регрессии.
-: стохастические и вероятностные
-: линейные и парные
-: множественные и парные
+: линейные и нелинейные
S: Дана таблица исходных данных для построения эконометрической регрессионной модели:
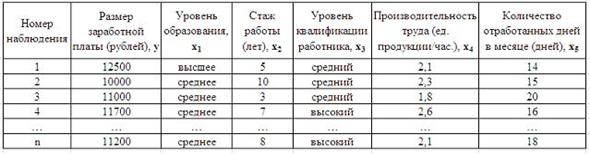
Фиктивными переменными не являются …
-: уровень квалификации работника
S: При моделировании уравнения множественной регрессии проверку тесноты связи между независимыми переменными (объясняющими переменными, регрессорами, факторами) модели осуществляют на основе …
-: коэффициента множественной корреляции
-: показателей существенности параметров модели
+: матрицы парных коэффициентов линейной корреляции
-: системы нормальных уравнений МНК
S: Для регрессионной модели зависимости среднедушевого денежного дохода населения (руб., у) от объема валового регионального продукта (тыс. р., х1) и уровня безработицы в субъекте (%, х2) получено уравнение 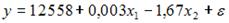
-: увеличится на 1,67
-: изменится на (-1,67)
-: изменится на 0,003
+: уменьшится на (-1,67)
S: В модели вида 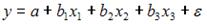
S: В модели множественной регрессии 
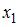
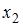
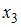
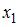
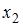
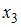
S: В уравнении линейной множественной регрессии: 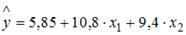
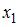
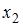
-: на 1 тыс. руб. … уменьшится на 10,8 тыс. руб.
-: на 1% … увеличится на 10,8%
-: на 1 тыс. руб. … увеличится на 10,8%
+: на 1 тыс. руб. … увеличится на 10,8 тыс. руб.
S: Переменная х является нелинейной в уравнении
-:
-:
+:
-:
S: Уравнением нелинейной регрессии, отражающей полиномиальную зависимость y от x, является
-:
-:
+:
-:
S: При линеаризации нелинейных регрессионных моделей как один из видов преобразований используется способ приведения уравнения к обратному виду, то есть к переменной 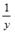
-:
-:
-:
+:
S: Для регрессионной модели парной регрессии рассчитано значение коэффициента детерминации 
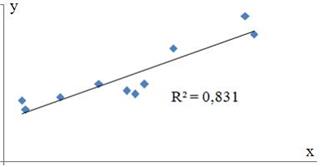
На дисперсию зависимой переменной, объясненную построенным уравнением приходится ________ общей дисперсии зависимой переменной.
S: Пусть 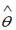




S: Степенной модельюне является регрессионная модель …
-:
+:
-:
-:
S: Нелинейным уравнением множественной регрессии является …
+:
-:
-:
-:
S: Система эконометрических уравнений может состоять из _____ уравнения (-ий) регрессии.
+: бесконечно большого количества
S: В эконометрической модели линейного уравнения регрессии 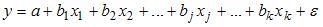
+:
S: Для эконометрической модели линейного уравнения множественной регрессии вида 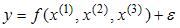
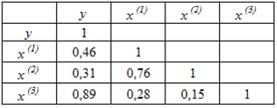
Коллинеарными (тесносвязанными) независимыми (объясняющими) переменными являются …
S: Регрессионная модель вида 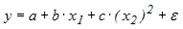
-: переменной
+: переменной
-: параметра
-: переменной
S: Известно, что доля остаточной дисперсии зависимой переменной в ее общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет
-:
-:
S: Обобщенный метод наименьших квадратов применяется для оценки параметров линейных регрессионных моделей с __________ остатками.
-: гомоскедастичными и некоррелированными
+: автокоррелированными и/или гетероскедастичными
S: Метод наименьших квадратов (МНК) может применяться для оценки параметров исходной регрессионной модели в _________ форме.
S: Автокорреляцией уровней ряда называется корреляционная зависимость между …
-: факторами, формирующими уровень ряда
-: уровнями двух рядов
+: последовательными уровнями ряда
-: компонентами, образующими уровни ряда
S: Самым коротким интервалом изменения коэффициента корреляции для уравнения парной линейной регрессии 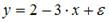
S: Левая часть системы эконометрических уравнений представлена совокупностью _________ переменных.
S: При расчете скорректированного коэффициента множественной детерминации пользуются формулой 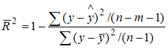
+: n – число наблюдений; m – число факторов, включенных в модель множественной регрессии
-: n – число параметров при независимых переменных; m – число наблюдений
-: n – число параметров при независимых переменных; m – число факторов, включенных в модель множественной регрессии
-: m – число наблюдений; n – число факторов, включенных в модель множественной регрессии
S: Для эконометрической модели вида 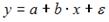


S: Ошибкой спецификации эконометрической модели уравнения регрессии является …
+: использование парной регрессии вместо множественной
-: расчет показателей качества модели
-: учет случайных факторов
-: оценка параметров при помощи МНК
S: В модели множественной регрессии 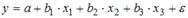
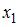
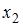
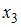
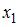
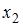
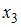
S: Совокупность значений экономического показателя за несколько последовательных моментов (периодов) времени называется …
S: Автокорреляционной функцией временного ряда называется последовательность коэффициентов автокорреляции …
-: между трендовой, сезонной и случайной компонентами
+: первого, второго, третьего и последующих порядков
-: факторов, формирующих уровень ряда
-: между несколькими временными рядами
S: Уровень временного ряда (yt) формируется под воздействием различных факторов – компонент: Т (тенденция), S (циклические и/или сезонные колебания), Е (случайные факторы). Мультипликативную модель временного ряда формируют следующие значения компонент уровня временного ряда …
-: yt = 7; T = 6,5; S = 0; E = 0,5
-: yt = 7; T = -3,5; S = -2; E = -1
+: yt = 7; T = 3,5; S = 2; E = 1
-: yt = 7; T = 3,5; S = -2; E = 1
источники:
http://poisk-ru.ru/s16310t6.html
http://lektsia.com/2×1276.html
- Если коэффициент регрессии является несущественным, то для него выполняются условия ….(несколько правильных ответов)
- стандартная ошибка превышает половину значения параметров
- расчетное значение t- критерия Стьюдента меньше табличного
- Если доверительный интервал для коэффициента регрессии содержит 0, то справедливы следующие утверждения(несколько правильных ответов):
- коэффициент регрессии статистически незначим
- фактическое значение статистики Стьюдента для этого коэффициента по модулю меньше критического (табличного)
- Если статистическая оценка θ*nпараметра θ содержит всю информацию об оцениваемом параметре, она называется…
- достаточной
- Если значение индекса корреляции для нелинейного уравнения регрессии стремится к 1, следовательно нелинейная связь …
- очень тесная
- Использование полинома третьего порядка в качестве регрессионной зависимости для однофакторной модели обусловлено .
- неоднородностью выборки
- Изображение корреляционного поля для парной регрессионной модели относится к статическим графикам, характеризующим …
- тесноту и форму зависимости между признаками
- Какое из этих значений может принимать линейный коэффициент корреляции при прямой связи?
- 0,6
- Коэффициент парной линейной корреляции между признаками Y и X равен 0,9. Следовательно, доля дисперсии результативного признака Y, не объяснённая линейной парной регрессией Y по фактору X, будет равно …
- 10%
- Коэффициент эластичности является постоянной величиной и не зависит от значения факторного признака для …
- степенной функции регрессии
- Линейный коэффициент корреляции
- показывает меру тесноты связи между двумя показателями
- Линейный коэффициент корреляции – это отношение …
- ковариации к произведению средних квадратичных отклонений двух показателей
- Множественный коэффициент линейной корреляции близок к единице. Это означает, что …
- рассматриваются факторы, значимо влияющие на результат
- Свойства оценок параметров эконометрической модели, получаемых при помощи МНК
- коэффициента эластичности
- Если предпосылки метода наименьших квадратов (МНК) не выполняются, то остатки могут характеризоваться …(несколько правильных ответов)
- нулевой средней величиной
- Оценки параметров сверхидентифицируемой системы эконометрических уравнений могут быть найдены с помощью _________ метода наименьших квадратов
- двухшагового
- При увеличении объема выборки дисперсия эффективной оценки параметра становится бесконечно малой величиной. Такая оценка параметра называется
- состоятельной
- Самым распространенным методом оценки параметров регрессии является
МНК
- Систему МНК построенную для оценки параметров линейного управления множественной регрессии можно решить методом…
- определителей
- Параметры управления тренда определяются _____ методом наименьших кадров
- обычным
- Обобщенный метод наименьших квадратов может использоваться для корректировки ________ остатков
- гетероскедастичности
- Обобщенный метод наименьших квадратов подразумевает …(несколько правильных ответов)
- Двухэтапное применение метода наименьших квадратов
- Преобразование переменных
- Проявление гетероскедастичности в остатках удается устранить при помощи метода обобщенного метода наименьших квадратов путем …(несколько правильных ответов)
- преобразования переменных
- введение в выражения для дисперсии остатков коэффициента пропорциональности
- Метод инструментальных переменных применяется в случае корреляции
- эндогенной переменной с регрессором
- Дано уравнение регрессии. Определите спецификацию модели.
- линейное уравнение множественной регрессии
- Дисперсия – это отношение
- среднего квадратичного отклонения к средней арифметической величине.
- Использование в эконометрическом моделировании парной регрессии вместо множественной является ошибкой…
- спецификации
- К ошибкам спецификации относится …
- неправильный выбор той или иной математической функции
- Найти среднее квадратичное отклонение, если дисперсия совокупности равна 12,25.
- 3,5
- Наличие возмущения зависимой переменной, вызванное неоднородностью данных в исходной статистической совокупности, является учетом.
- ошибки выборки
- При анализе взаимосвязи признаков в экономической модели используют корреляционное отношение, подсчитанное на основе
- аналитической группировки
- Расположите модели в возрастающем порядке по степени сложности оценки их параметров.
2Нелинейная модель, линейная относительно параметров
4Нелинейная модель внутренние нелинейные
3Нелинейная модель нелинейная относительно параметров (внутренне линейная)
- Разность фактического и теоретического значений результирующей переменной регрессионной модели называется…
- остатком
- Среднее квадратичное отклонение
- показывает в среднем, на сколько отклоняются значения показателя от среднего значения..
- Средняя арифметическая величина – это отношение
- среднего квадратичного отклонения к средней арифметической величине
- Текущее значение экономического процесса ytпредопределено его предысторией. Пусть εtошибка модели в момент t. f-аналитическая функция. Тогда модель для указанного допущения имеет следующий вид…
- yt = f(yt)
- Укажитевыводы, которые соответствуют графику зависимости остатков от теоретических значений зависимости переменной у (несколько правильных ответов):
- имеет место автокорреляция остатков
- отсутствует закономерность в поведении остатков
- остатки носят случайный характер
1.Термин эконометрика был введен (Фришем)
2.Формулой определяется _________ показателя (средняя арифметическая величина)
3.Часть зависимой переменной в регрессионной модели, которая полностью объясняется значением регрессора (уравнение регрессии)
4.Остаток регрессионной модели представляет собой оценку (случайной ошибки)
5. Экономические модели относятся к классу ___________ экономико-математических моделей (стохастических)
6.Найти среднюю урожайность пшеницы с 1 га за три года: 60ц, 49ц, 41ц. (55)
7.Эконометрика — это . (наука, которая дает количественное выражение взаимосвязей экономических явлений и процессов.)
8.Стохастическая связь между признаками, выраженная в том, что средняя величина одного признака увеличивается с возрастанием другого, называется. ( автокорреляцией)
9 Как изменяется средняя арифметическая, если все веса уменьшить в А раз?( Увеличивается)
10.Основные стадии экономико-статистического исследования включают: а) сбор первичных данных, б) статистическая сводка и группировка данных, в) контроль и управление объектами статистического изучения, г) анализ статистических данных (а, б, г)11.Медиана в ряду распределения с четным числом членов ряда равна (полусумме двух срединных членов)
12.Изображение корреляционного поля для парной регрессионной модели относится к статическим графикам, характеризующим . (тесноту и форму зависимости между признаками)
13.К ошибкам спецификации относится . ( неправильный выбор той или иной математической функции)
14.При использовании метода Монте-Карло результаты наблюдений генерируются с помощью (датчика случайных чисел)
15.По какой формуле производится вычисление средней величины в интервальном ряду? (Средняя арифметическая взвешенная)
16.Назовите основные виды ошибок регистрации: а) случайные; б) систематические; в) ошибки репрезентативности; г) расчетные (а,б,в)
17.Число степеней свободы определяется . (числом свободы независимого варьирования признака (переменной, фактора))
18.Формализация закономерностей общей эконометрической теории является одним из принципов . эконометрической модели (спецификации)
19.Часть зависимой переменной в регрессионной модели, которая не может быть объяснена значением регрессора (случайное возмущение)20.Корреляция подразумевает наличие связи между . (переменными)
21.Принцип спецификации модели, лежащий в основании классификации: экономические модели; эконометрические модели (включение случайных возмущений)
22.Дисперсия — это отношение (среднего квадратичного отклонения к средней арифметической величине)23.Для описания тесноты (силы) связи между зависимой переменной и фактором (факторами) проводят расчет. (коэффициент корреляции)
24.Среднее квадратичное отклонение (показывает в среднем, на сколько отклоняются значения показателя от среднего значения)
25.Значение признака, повторяющееся с наибольшей частотой, называется (модой)
26.Случайная составляющая характеризует ( отклонение модельного значения результирующей переменной от наблюдаемого)
27.Укажите правильные варианты ответов относительно числа переменных включаемых в уравнение регрессии(несколько зависимых и одна не зависимая переменных, одна зависимая и несколько независимых переменных)
28.Коэффициент парной линейной корреляции между признаками Y и X равен 0,9. Следовательно, доля дисперсии результативного признака Y, не объяснённая линейной парной регрессией Y по фактору X, будет равно . ( 10%)
29.Верификация модели заключается в( сопоставлении модельных и реальных данных)
30.Этап параметризации модели включает в себя.. (оценку параметров модели)
31.определяется _________ показателей x и y.( Ковариация)
32.В линейной эконометрической модели наблюдаемое значение результирующей переменной, зависящей от факторов модели, и случайной составляющей равно . (сумме)
33.Один из этапов построения экономической модели, на котором проверяются статистические свойства построенной модели, называется. (верификацией модели.)
34.По отношению к выбранной спецификации модели, все экономические переменные объекта подразделяются на (эндогенные и экзогенные)
35.Коэффициент корреляции это: (относительная мера взаимосвязи переменных)
.Использование полинома третьего порядка в качестве регрессионной зависимости для однофакторной модели обусловлено . (неоднородностью выборки)
37. Использование в эконометрическом моделировании парной регрессии вместо множественной является ошибкой.. (спецификации)
38Средне квадратическое отклонение исчисляется как (корень квадратный из дисперсии)
39.Разность фактического и теоретического значений результирующей переменной регрессионной модели называется. (остатком)
40.Статистический показатель дает оценку свойства изучаемого явления: (количественную)
41.Под верификацией модели понимается (проверка адекватности модели)
42.Выбор списка переменных модели и типа взаимосвязи между ними выполняется на этапе (спецификация модели)
43.Найти среднее квадратичное отклонение, если дисперсия совокупности равна 12,25 (3,5)
44.Наличие возмущения зависимой переменной, вызванное неоднородностью данных в исходной статистической совокупности, является учетом (ошибки выборки)
45.Принцип спецификации модели, лежащий в основании классификации: статические модели; динамические модели (датирование переменных)
46.Средняя арифметическая величина — это отношение( суммы значений показателя к объему совокупности)
47.Экономические модели относятся к классу ___________ экономико-математических моделей (стохастических)
48.Средняя геометрическая — это: (корень из произведения индивидуальных показателей)
49.При анализе взаимосвязи признаков в экономической модели используют корреляционное отношение, подсчитанное на основе( аналитической группировки)
50.Требуется вычислить средний стаж деятельности работников фирмы: 6,5,4,6,3,1,4,5,4,5. Какую формулу Вы примените? (средняя арифметическая)
51.Причинами нарушения предпосылок МНК могут являться .. (наличие неучтенного в уравнении существенного фактора ,наличие в уравнении фиктивных переменных.)
52.Модель, содержащая фиктивную переменную, относится к ____ модели. (Регрессионной)
53.МНК позволяет получить состоятельные и несмещенные оценки параметров системы: (независимых уравнений)
При каком значении линейного коэффициента корреляции связь между признаками Y и X можно считать тесной (сильной)( 0,975)
54.С увеличением объема выборки длина доверительного интервала индивидуального значения эндогенной переменной (уменьшается)
55.Если все наблюдения лежат на линии регрессии, то коэффициент детерминации R 2 для модели парной регрессии равен: (единице)
Задачи и тесты по эконометрике
19.1. Рассматривается следующая модель:
t, =с, + i, + d =ao+a | р+8
где Q- количество товара, р- цена товара, w — заработная плата, 8 и в — случайные отклонения, удовлетворяющие предпосылкам МНК.
Пусть имеются следующие наблюдения:
- а) Какие из переменных являются экзогенными, а какие — эндогенными?; б) Представьте систему в приведенном виде; в) Определите по МНК коэффициенты приведенных уравнений; г) совпадают ли знаки найденных коэффициентов с предполагаемыми теоретически?; д) на основе найденных приведенных коэффициентов по КМНК определите структурные коэффициенты для функции спроса; е) можно ли по МНК оценить структурные коэффициенты для функции предложения? Если да, то как?
- 19.3. Рассматривается следующая система одновременных уравнений:
- а) Выделите экзогенные и эндогенные переменные в данной модели;
- б) Пусть по статистическим данным в момент времени t получены следующие результаты: ?q’=l 10, Xp 2 =5O,Xi 2 =ioo,Xi 2 =ioo,Xq-p=ioo,Xqi=9O,Xpi=ioo.
На основе МНК найдите оценку параметра ар в) Найдите оценку параметра а, на основе КМНК по методу ДМНК. г)Сравнитс найденные оценки.
19.4. К системе уравнений вида
приведен КМНК и для коэффициентов приведенной формы
получены следующие оценки: сц=2,2; Cj 2=0,4; c2i=0,08; с22=-0,5.
Найдите оценки ДМНК, примененного к структурной модели.
19.5. Дана следующая структурная модель:
‘ У2 = ^21У| ^^2зУз + а 22 Х 2
,Уз = ^32^2 “*? Я зН1 + а ЗЗ Х 3
а) Оценить данную систему на идентификацию, б) Исходя из следующей приведенной формы модели
найти структурные коэффициенты модели.
19.6. Изучается модель вида
где yt — валовой национальный доход, yt.i — ВНП предшествующего года, ct — личное потребление, dr конечный спрос.
Имеется информация за девять лет:___________________________________________
Для данной модели была получена система приведенных уравнений:
Требуется: 1) Провести идентификацию модели. 2) Рассчитать параметры первого уравнения структурной модели.
- 19.7. Применив необходимое и достаточное условие идентификации определите идентифицировано ли каждое из уравнений модели. Определите метод оценки параметров и запишите приведенную форму модели:
- 1. Модель денежного рынка:
где R- процентная ставка, Y- ВВП, М-денежная масса, I-внутренние инвестиции, t-текущий период.
2. Макроэкономическая модель (модель Клейна)
где С- потребление, 1-инвестиции, Y-доход, Т-налоги, К-запас капитала.
3. Модель протекционизма Сальватора (упрошенная версия):
Ма ] +Ь12Nt+b 13S t+b 14 Ef. 1 + ?j
где M- доля импорта в ВВП; N- общее число прошений об освобождении от таможенных пошлин; S- число удовлетворительных прошений об освобождении от таможенных пошлин; Е- фиктивная переменная, равная 1 для тех лет, в которую курс доллара на международных валютных рынках был искусственно завышен, и 0 — для всех остальных лет; Y- реальный ВВП, Х-реальный объем чистого экспорта.
4.Гипотетическая модель экономики:
где совокупность потребления, Y-совокупный доход, I-инвсстиции, Т- налоги, G- государственные доходы ( все в период t).
Тесты по эконометрике.
- 1. Использование в эконометрическом моделировании парной регрессии вместо множественной является ошибкой.
- а) измерения; б) выборки; в) линеаризации; г) спецификации.
- 2. Отбор факторов в эконометрическую модель множественной регрессии может быть осуществлена на основе.
- а) значение коэффициентов автокорреляции уровней ряда различных порядков;
- б) матрицы парных коэффициентов корреляции;
- в) сравнения коэффициентов «чистой» регрессии;
- г) сравнения остаточной дисперсии до и после включения фактора в модель.
- ( Укажите не менее двух вариантов)
- 3. Для оценки заработной платы некоторого работника используется следующая модель
стаж его работы на данном предприятии; D— количество лет, потраченных работником на профессиональное обучение ( в том числе и повышение квалификации ); С,- переменная, принимающая значение 1, если у работника есть дети и 0 если нет; S,переменная имеющая значение 1, если работник мужчина и 0, если женщина; W, — количество должностей, который сменил работник на различных предприятиях в течении последнего года. Сколько факторов необходимо представить в модели фиктивными переменными? Выведите ответ.
- 4. Для уравнения множественной регрессииy-a + hix] + b2x2 + Ь3х3 + ?построено частное уравнение видау = а—Ьхх<+Ь2х2 + Ь3х3 + ?,в которомх2и х3.
- а) приравнены к 1; б) закреплены на неизменном уровне; в) являются изменяемыми факторными переменными; не оказывают существенное влияние на у .
- 5. Метод наименьших квадратов применим к уравнениям регрессии.
- а) которые отражают нелинейную зависимость между двумя экономическими показателями, но могут быть приведены к линейному виду;
- б) которые отражают линейную зависимость между двумя экономическими показателями; в) которые отражают нелинейную зависимость между двумя экономическими показателями и не могут быть приведены к линейному виду; г) нелинейного вида.
- 6. Если предпосылки метода наименьших квадратов нарушены, то.
- а) коэффициент регрессии является несущественным; б) полученное уравнение статистически не значимо; в) оценки параметров могут не обладать свойствами эффективности, состоятельности и несмещенности; г) коэффициент корреляции является несущественным.
- 7. Несмещенность оценки характеризуется. (Укажите не менее двух вариантов)
- а) зависимостью от объема выборки значения математического ожидания остатков;
- б) максимальной дисперсией остатков;
- в) отсутствием накопления остатков при большом числе выборочных оцениваний;
- г) равенством нулю математического ожидания остатков.
- 8. Обобщенный МНК применяется в случае.
- а) наличия в модели фиктивных переменных; б) наличия в модели мультиколлинеарности; в) наличия в остатках гстсросксдастичности или автокорреляции; г) наличия в модели незначимых оценок.
- 9. Для значимости спроса на некоторый товар от цены за единицу товара и дохода потребителя получено уравнение регрессии видау = а + Ьх ? хх + Ь, -х2+?.Парными коэффициентами корреляции могут быть
- а) гхх ; б) R ; в) г ; r)7?J .
- 10. Критическое (табличное) значение F-критерия является пороговым значением для определения.
- а) доли дисперсии зависимой переменной, не объясняемой с помощью построения модели, а вызванной влиянием случайных воздействий ;
- б) статистической значимости построения моделей;
- в) доли дисперсии зависимой переменной, объясняемой с помощью построенной модели;
- г) значимости (существенности) моделируемой связи между зависимой переменной и совокупностью независимых переменных эконометрической модели.
- 11. Если коэффициент регрессии является несущественным, то его значение приравнивается
- а) к нулю и соответствующий фактор включается в модель;
- б) к табличному значению и соответствующий фактор не включается в модель;
- в) к нулю и соответствующий фактор не включается в модель;
- г) к единице и не влияет на результат.
- 12. Пусть зависимость выпуска (Y) от затрат капитала (К) и труда (L) описывается функцией Кобба-ДугласаY = АК а L p. Тогда.
- а) эластичность выпуска по затратам труда равна а; б) эластичность выпуска по затратам труда равна 0; в) эластичность выпуска по затратам капитала равна 0; г) эластичность выпуска по затратам капитала равна а.
- (Укажите не менее двух вариантов).
- 13.Установите соответствие между названием модели и видом ее уравнения:
- 1. гипербола а) у = а + Ьх • х, + с • х2 + d • х3 + г
- 2. парабола третьего порядка б) у = a + bx -х + с -х 2 +d -х 3 + ?
- 3. многофакторная в) у = а + Ь-х + ?
4. линейная г) у = al Ь?
- (Укажите соответствие для каждого нумерованного элемента задания).
- 14.Линеаризация экспоненциальной зависимости У = а0-Х 0 ’ ?? (кривой Энгеля,
отражающей зависимость спроса от уровня семейных доходов) основана на.
- а) разложение функции в ряд; б) дифференцирование функции по параметрам;
- в) интегрировании функции по параметрам; г) логарифмировании и замене преобразованной переменной.
- 15. Относительные отклонения расчётных значений результирующего признака от его наблюдаемых значений используются при расчете.
- а) параметров регрессии; б) t-критерия Стыодента; в) средней ошибки аппроксимации;
- г) коэффициента эластичности.
- 16. Факторы, описывающие трендовую компоненту временного ряда характеризуются.
- а) долговременным воздействием на экономический показатель;
- б) периодическим воздействием на величину экономического показателя;
- в) возможностью расчета значения компонента с помощью аналитической функции от времени; г) случайным воздействием на уровень временного ряда.
- (Укажите не менее двух вариантов ответа).
- 17. Область значений автокорреляционной функции представляет собой промежуток.
- а) (-1,1); б) [-1,0]; в) [-1,1]; г) [0,1].
- 18. Построение модели временного ряда может быть осуществлено с использованием.
- а) критерия Дарбина-Уотсона; б) аддитивной модели; в) мультипликативной модели;
- г) метода последовательных разностей.
- 19. При моделировании временных рядов экономических показателей необходимо учитывать характер уровней исследуемых показателей.
- а) конструктивный; б) аналитический; в) независящий от времени; г) стохастичный.
- 20. Для оценки коэффициентов структурной формы моделей не применяют метод
- а) косвенный; б) трёхшаговый; в) двухшаговый; г) обычный.
- 21. Согласно предпосылке теоремы Гаусса-Маркова дисперсии случайных возмущений в уравнениях наблюдений должны быть.
- а) равными; б) различными; в) нулевыми; г) случайными.
- 22. Если справедлива гипотеза //„:b = 0, относительно коэффициентаbмодели парной регрессии, то независимая переменнаяхявляется.
- а) значимой; б) незначимой; в) необходимой; г) желательной.
- 23. Для оценки точности оптимального прогноза зависимой переменной, нужно знать.
- а) прогнозное значение зависимой переменной; б) оценку дисперсии случайного возмущения; в) параметры модели; г) коэффициент детерминации.
- 24. Наличие незначащей объясняющей переменной в функции регрессии влечет.
- а) неадекватность модели; б) неравенство нулю математических ожиданий случайных возмущений;
- в) некоррелированность независимых переменных; г) снижение точности коэффициентов регрессии.
- 25. Если в модели присутствуют лаговые зависимые переменные, то это.
- а) линейная модель; б) нелинейная модель; в) модель со случайными возмущениями; г) динамическая модель.
- 26. Состояние экономики в момент времени t описывается следующими характеристиками: У,- валовой внутренний продукт, С,-уровень потребления, /,-величина инвестиций,G, —
государственные расходы, Т, -величина налогов, Rt -реальная ставка процентов. При этом величина инвестиций зависит от реальной ставки процента в предыдущем периоде, то есть в системе к предопределенным переменным системы относится лаговая экзогенная переменная. Приведенное утверждение справедливо для модели.
а) b o +Ь Y i + Ь 2 R :-l + ? 2
T,) + t ‘ A = Ь 0 +b r Y , +b 2- R ,
В ) i Л = + Ь ‘ К + Ь 2 ‘ R , + ^,-1
источники:http://topuch.ru/dlya-poiska-nujnogo-otveta-najimaem-ctrlf-i-vvodim-nujnij-vopr/index.html
http://ozlib.com/983321/ekonomika/zadachi_testy_ekonometrike
49 вопросов с вариантами ответов
Задания к работе:
1) Использование парной регрессии вместо множественной является примером…
2) Включение в совокупность единиц с «выбросами» данных является примером
49) Имеется следующая модель
Материалы, размещаемые в каталоге, с согласия автора, могут использоваться только в качестве дополнительного инструмента для решения имеющихся у вас задач,
сбора информации и источников, содержащих стороннее мнение по вопросу, его оценку, но не являются готовым решением.
Пользователь вправе по собственному усмотрению перерабатывать материалы, создавать производные произведения,
соглашаться или не соглашаться с выводами, предложенными автором, с его позицией.
| Тема: | ИЭУиП 1) Использование парной регрессии вместо множественной является примером… 2) Включение в совокупность единиц с «выбросами» данных является примером |
| Артикул: | 9602703 |
| Дата написания: | 06.02.2009 |
| Тип работы: | Тестовые вопросы |
| Предмет: | Эконометрика и экономическое моделирование |
| Количество страниц: | 7 |