Интервальная ошибка прогноза

Точечный прогноз
заключается в получении прогнозного
значения уp,
которое определяется путем подстановки
в уравнение регрессии соответствующего
(прогнозного) значения xp:

уp = a + b* xp

Интервальный
прогноз
заключается в построении доверительного
интервала прогноза, т. е. нижней и верхней
границ уpmin,
уpmax интервала,
содержащего точную величину для
прогнозного значения yp
(ypmin < yp <
ypmin) с заданной
вероятностью.

При построении
доверительного интервала прогноза
используется стандартная
ошибка прогноза:

,
где

Строится доверительный
интервал прогноза:

Множественный регрессионный анализ

(слайд
1)
Множественная регрессия применяется
в ситуациях, когда из множества факторов,
влияющих на результативный признак,
нельзя выделить один доминирующий
фактор и необходимо учитывать влияние
нескольких факторов. Например, объем
выпуска продукции определяется величиной
основных и оборотных средств, численностью
персонала, уровнем менеджмента и т. д.,
уровень спроса зависит не только от
цены, но и от имеющихся у населения
денежных средств.

Основная цель
множественной регрессии – построить
модель с несколькими факторами и
определить при этом влияние каждого
фактора в отдельности, а также их
совместное воздействие на изучаемый
показатель.

Таким образом,
множественная регрессия – это уравнение
связи с несколькими независимыми
переменными:

(слайд
2)
Построение уравнения множественной
регрессии

1. Постановка задачи

По имеющимся данным
n наблюдений
(табл. 3.1) за совместным изменением p+1
параметра y
и xj и
((yi,xj,i);
j=1,
2, …, p;
i=1,
2, …, n)
необходимо определить аналитическую
зависимость ŷ
= f(x1,x2,…,xp),
наилучшим образом описывающую данные
наблюдений.

Таблица 3.1

Данные наблюдений

	y	х1	х2	…	хр
1	y1	x11	х21	…	xp1
2	y2	х12	х22	…	xp2
…	…	…	…	…	…
n	yn	х1n	x2n	…	xpn

Каждая строка
таблицы представляет собой результат
одного наблюдения. Наблюдения различаются
условиями их проведения.

Вопрос о том, какую
зависимость следует считать наилучшей,
решается на основе какого-либо критерия.
В качестве такого критерия обычно
используется минимум суммы квадратов
отклонений расчетных значений
результативного показателя ŷi
от наблюдаемых
значений yi:

2. Спецификация модели

(слайд
3)
Спецификация модели включает в себя
решение двух задач:

– отбор факторов,
подлежащих включению в модель;

– выбор формы
уравнения регрессии.

2.1. Отбор факторов при построении множественной регрессии

Включение в
уравнение множественной регрессии того
или иного набора факторов связано прежде
всего с представлениями исследователя
о природе взаимосвязи моделируемого
показателя с другими экономическими
явлениями.

К факторам,
включаемым в модель, предъявляются
следующие требования:

1. Факторы должны
быть количественно измеримы.
Включение фактора в модель должно
приводить к существенному увеличению
доли объясненной части в общей вариации
зависимой переменной. Поскольку данная
величина характеризуется коэффициентом
детерминации,
включение нового фактора в модель должно
приводить к заметному изменению
коэффициента. Если этого не происходит,
то включаемый в анализ фактор не улучшает
модель и является лишним.

Например, если для
регрессии, включающей 5 факторов,
коэффициент детерминации составил
0,85, и включение шестого фактора дало
коэффициент детерминации 0,86, то вряд
ли целесообразно дополнять модель этим
фактором.

Если необходимо
включить в модель качественный фактор,
не имеющий количественной оценки, то
нужно придать ему количественную
определенность. В этом случае в модель
включается соответствующая ему
«фиктивная»
переменная,
имеющая конечное количество формально
численных значений, соответствующих
градациям качественного фактора (балл,
ранг).

Например, если
нужно учесть влияние уровня образования
(на размер заработной платы), то в
уравнение регрессии можно включить
переменную, принимающую значения: 0 –
при начальном образовании, 1 – при
среднем, 2 – при высшем.

Несмотря на то,
что теоретически регрессионная модель
позволяет учесть любое количество
факторов, на практике в этом нет
необходимости, т.к. неоправданное их
увеличение приводит к затруднениям в
интерпретации модели и снижению
достоверности результатов.

2. Факторы не
должны быть взаимно коррелированы
и, тем более, находиться в точной
функциональной связи. Наличие высокой
степени коррелированности между
факторами может привести к неустойчивости
и ненадежности оценок коэффициентов
регрессии, а также к невозможности
выделить изолированное влияние факторов
на результативный показатель. В результате
параметры регрессии оказываются
неинтерпретируемыми.

Пример.
Рассмотрим регрессию себестоимости
единицы продукции (у)
от заработной платы работника (х)
и производительности труда в час (z).

Коэффициент
регрессии при переменной z
показывает, что с ростом производительности
труда на 1 ед-цу в час себестоимость
единицы продукции снижается в среднем
на 10 руб. при постоянном уровне оплаты
труда.

А параметр при х
нельзя интерпретировать как снижение
себестоимости единицы продукции за
счет роста заработной платы. Отрицательное
значение коэффициента регрессии в
данном случае обусловлено высокой
корреляцией между х
и z
(0,95).

(слайд
4)
Считается, что две переменные явно
коллинеарны,
т.е. находятся между собой в линейной
зависимости, если коэффициент
интеркорреляции
(корреляции между двумя объясняющими
переменными) ≥ 0,7. Если факторы явно
коллинеарны, то они дублируют друг друга
и один из них рекомендуется исключить
из уравнения. Предпочтение при этом
отдается не тому фактору, который более
тесно связан с результатом, а тому,
который при достаточно тесной связи с
результатом имеет наименьшую тесноту
связи с другими факторами.

В этом требовании
проявляется специфика множественной
регрессии как метода исследования
комплексного воздействия факторов в
условиях их независимости друг от друга.

Наряду с парной
коллинеарностью может иметь место
линейная зависимость между более чем
двумя переменными – мультиколлинеарность,
т.е. совокупное воздействие факторов
друг на друга.

Наличие
мультиколлинеарности факторов может
означать, что некоторые факторы всегда
будут действовать в унисон. В результате
вариация в исходных данных перестанет
быть полностью независимой, что не
позволит оценить воздействие каждого
фактора в отдельности. Чем сильнее
мультиколлинеарность факторов, тем
менее надежна оценка распределения
суммы объясненной вариации по отдельным
факторам с помощью МНК.

(слайд
5) Включение
в модель мультиколлинеарных факторов
нежелательно по следующим причинам:

затрудняется
интерпретация параметров множественной
регрессии; параметры линейной регрессии
теряют экономический смысл;
оценки параметров
не надежны, имеют большие стандартные
ошибки и меняются с изменением количества
наблюдений (не только по величине, но
и по знаку), что делает модель непригодной
для анализа и прогнозирования.

(слайд
6) Для
оценки мультиколлинеарности используется
определитель
матрицы парных коэффициентов
интеркорреляции:

(!)
Если факторы не коррелируют между собой,
то матрица коэффициентов интеркорреляции
является единичной, поскольку в этом
случае все недиагональные элементы
равны 0. Например, для уравнения с тремя
переменными
матрица коэффициентов интеркорреляции
имела бы определитель, равный 1, посколькуи.

(слайд
7)

(!)
Если между факторами существует полная
линейная зависимость
и все коэффициенты корреляции равны 1,
то определитель такой матрицы равен 0
(Если
две строки матрицы совпадают, то её
определитель равен нулю).

Чем ближе к 0
определитель матрицы коэффициентов
интеркорреляции, тем сильнее
мультиколлинеарность и ненадежнее
результаты множественной регрессии.

Чем ближе к 1
определитель
матрицы коэффициентов интеркорреляции,
тем меньше мультиколлинеарность
факторов.

(слайд

Способы
преодоления мультиколлинеарности
факторов:

1)
исключение из модели одного или нескольких
факторов;

2)
переход к совмещенным уравнениям
регрессии, т.е. к уравнениям, которые
отражают не только влияние факторов,
но и их взаимодействие. Например, если
,
то можно построить следующее совмещенное
уравнение:;

3)
переход к уравнениям приведенной формы
(в уравнение регрессии подставляется
рассматриваемый фактор, выраженный из
другого уравнения).

(слайд
9)
2.2. Выбор формы уравнения регрессии

Различают следующие
виды уравнений
множественной регрессии:

линейные,
нелинейные,
сводящиеся к линейным,
нелинейные, не
сводящиеся к линейным (внутренне
нелинейные).

В первых двух
случаях для оценки параметров модели
применяются методы классического
линейного регрессионного анализа. В
случае внутренне нелинейных уравнений
для оценки параметров применяются
методы нелинейной оптимизации.

Основное требование,
предъявляемое к уравнениям регрессии,
заключается в наличии наглядной
экономической интерпретации модели и
ее параметров. Исходя из этих соображений,
наиболее часто используются линейная
и степенная зависимости.

Линейная
множественная регрессия имеет вид:

Параметры bi
при факторах хi
называются коэффициентами
«чистой» регрессии.
Они показывают, на сколько единиц в
среднем изменится результативный
признак за счет изменения соответствующего
фактора на единицу при неизмененном
значении других факторов, закрепленных
на среднем уровне.

(слайд
10)
Например, зависимость спроса на товар
(Qd) от цены (P) и дохода (I) характеризуется
следующим уравнением:

Qd = 2,5 — 0,12P + 0,23 I.

Коэффициенты
данного уравнения говорят о том, что
при увеличении цены на единицу, спрос
уменьшится в среднем на 0,12 единиц, а при
увеличении дохода на единицу, спрос
возрастет в среднем 0,23 единицы.

Параметр а
не всегда может быть содержательно
проинтерпретирован.

Степенная
множественная регрессия имеет вид:

Параметры bj
(степени факторов хi)
являются коэффициентами эластичности.
Они показывают, на сколько % в среднем
изменится результативный признак за
счет изменения соответствующего фактора
на 1% при неизмененном значении остальных
факторов.

Наиболее широкое
применение этот вид уравнения регрессии
получил в производственных функциях,
а также при исследовании спроса и
потребления.

Например, зависимость
выпуска продукции Y от затрат капитала
K и труда L:
говорит
о том, что увеличение затрат капитала
K на 1% при неизменных затратах труда
вызывает увеличение выпуска продукции
Y на 0,23%. Увеличение затрат труда L на 1%
при неизменных затратах капитала K
вызывает увеличение выпуска продукции
Y на 0,81 %.

Возможны и другие
линеаризуемые функции для построения
уравнения множественной регрессии:

экспонента

;
гипербола

.

Чем сложнее функция,
тем менее интерпретируемы ее параметры.
Кроме того, необходимо помнить о
соотношении между количеством наблюдений
и количеством факторов в модели. Так,
для анализа трехфакторной модели должно
быть проведено не менее 21 наблюдения.

(слайд
11) 3.
Оценка параметров модели

Параметры уравнения
множественной регрессии оцениваются,
как и в парной регрессии, методом
наименьших квадратов,
согласно которому следует выбирать
такие значения
параметров а
и bi,
при которых сумма квадратов отклонений
фактических значений результативного
признака yi
от теоретических
значений ŷ
минимальна,
т. е.:

Если
,
тогдаS
является функцией неизвестных параметров
a,
bi:

Чтобы найти минимум
функции, нужно найти частные производные
по каждому из параметров и приравнять
их к 0:

Отсюда получаем
систему уравнений:

(слайд
12) Ее
решение может быть осуществлено методом
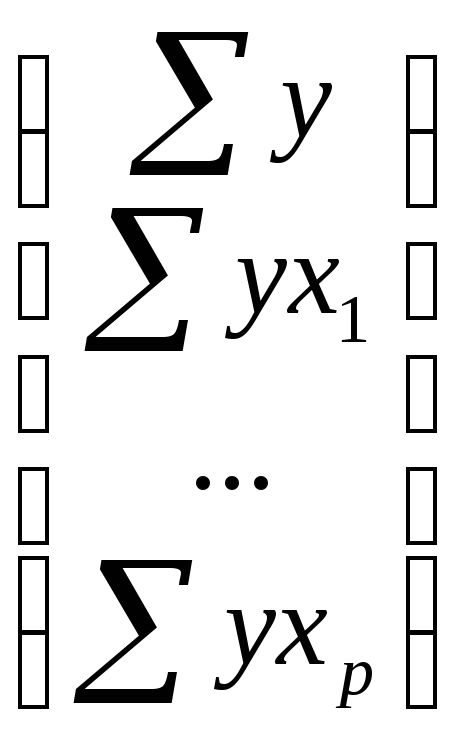
определителей:

где ∆
– определитель системы;

∆a,
∆b1,
∆bp
– частные определители (∆j).

–определитель
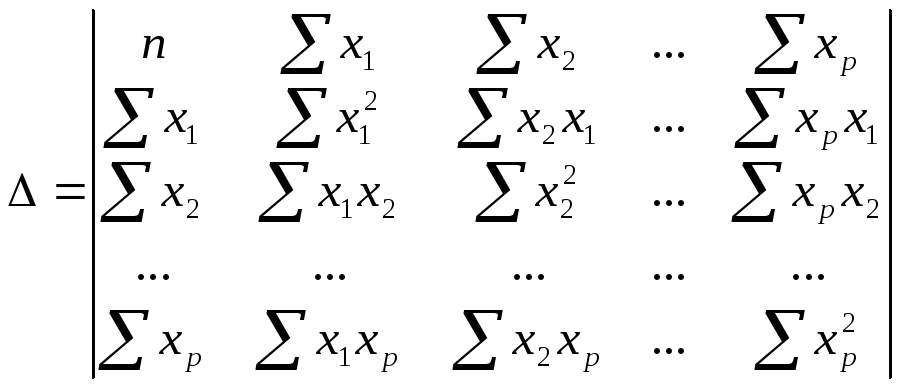
системы,

∆j
– частные
определители, которые получаются из
основного определителя путем замены
j-го столбца на столбец свободных членов
.

При использовании
данного метода возможно возникновение
следующих ситуаций:

1) если основной
определитель системы Δ равен
нулю и все определители Δj
также равны
нулю, то данная система имеет бесконечное
множество решений;

2) если основной
определитель системы Δ равен
нулю и хотя бы один из определителей Δj
также равен
нулю, то система решений не имеет.

(слайд
13) Помимо
классического МНК для определения
неизвестных параметров линейной модели
множественной регрессии используется
метод оценки параметров через
β-коэффициенты
– стандартизованные коэффициенты
регрессии.

Построение
модели множественной регрессии в
стандартизированном, или нормированном,
масштабе
означает, что все переменные, включенные
в модель регрессии, стандартизируются
с помощью специальных формул.

Уравнение
регрессии
в стандартизованном масштабе:

где
,— стандартизованные переменные;

— стандартизованные
коэффициенты регрессии.

Т.е. посредством
процесса стандартизации точкой отсчета
для каждой нормированной переменной
устанавливается ее среднее значение
по выборочной совокупности. При этом в
качестве единицы измерения
стандартизированной переменной
принимается ее среднеквадратическое
отклонение σ.

β-коэффициенты
показывают,
на сколько сигм (средних квадратических
отклонений) изменится в среднем результат
за счет изменения соответствующего
фактора xi
на одну сигму при неизменном среднем
уровне других факторов.

Стандартизованные
коэффициенты регрессии βi
сравнимы
между собой, что позволяет ранжировать
факторы по силе их воздействия на
результат. Большее относительное влияние
на изменение результативной переменной
y оказывает
тот фактор, которому соответствует
большее по модулю значение коэффициента
βi.
В этом основное
достоинство стандартизованных
коэффициентов регрессии,
в отличие от коэффициентов «чистой»
регрессии, которые не сравнимы между
собой.

(слайд
14)
Связь коэффициентов «чистой» регрессии
bi
с коэффициентами βi
описывается соотношением:

,
или

Параметр a
определяется как
.

Коэффициенты
β определяются при помощи
МНК
из следующей системы уравнений
методом определителей:

Для оценки параметров
нелинейных
уравнений множественной регрессии
предварительно осуществляется
преобразование последних в линейную
форму (с помощью замены переменных) и
МНК применяется для нахождения параметров
линейного уравнения множественной
регрессии в преобразованных переменных.
В случае внутренне
нелинейных
зависимостей для оценки параметров
приходится применять методы нелинейной
оптимизации.

(слайд
1) 4.
Проверка качества уравнения регрессии

Практическая
значимость уравнения множественной
регрессии оценивается с помощью
показателя множественной корреляции
и его квадрата – коэффициента детерминации.

Показатель
множественной корреляции
характеризует тесноту связи рассматриваемого
набора факторов с исследуемым признаком,
т.е. оценивает тесноту совместного
влияния факторов на результат.

Независимо от
формы связи показатель
множественной корреляции
рассчитывается по формуле:

Коэффициент
множественной корреляции принимает
значения в диапазоне 0 ≤ R
≤ 1. Чем ближе
он к 1, тем теснее связь результативного
признака со всем набором исследуемых
факторов.

При линейной
зависимости признаков формулу индекса
множественной корреляции можно записать
в виде:

где
—
стандартизованные коэффициенты
регрессии,

—
парные коэффициенты корреляции результата
с каждым фактором.

Данная формула
получила название линейного
коэффициента множественной корреляции,
или совокупного
коэффициента корреляции.

Индекс детерминации
для нелинейных по оцениваемым параметрам
функций принято называть «квази-».Для его
определения по функциям, использующим
логарифмические преобразования
(степенная, экспонента), необходимо
сначала найти теоретические значения
ln
y,
затем трансформировать их через
антилогарифмы (антилогарифм ln
y
= y)
и далее определить индекс детерминации
как «квази-»
по формуле:

Величина «квази-»
не будет совпадать с совокупным
коэффициентом корреляции, который может
быть рассчитан для линейного в логарифмах
уравнения множественной регрессии,
потому что в последнем раскладывается
на факторную и остаточную суммы квадратов
не,
а.

(слайд
2)
Использование коэффициента множественной
детерминации

для оценки качества модели обладает
тем недостатком, что включение в модель
нового фактора (даже несущественного)
автоматически увеличивает величину.
Поэтому при большом количестве факторов
предпочтительней использовать так
называемый скорректированный
(улучшенный) коэффициент множественной
детерминации

,
определяемый соотношением:

где n
– число наблюдений,

m
– число параметров при переменных х
(чем больше величина m,
тем сильнее различия между к-том множ.
детерминации

и скорректированным к-том
).

При заданном объеме
наблюдений и при прочих равных условиях
с увеличением числа независимых
переменных (параметров) скорректированный
к-т множ. детерминации убывает. Его
величина может стать и отрицательной
при слабых связях результата с факторами.
При небольшом числе наблюдений
нескорректированная величина к-та
имеет
тенденцию переоценивать долю вариации
результативного признака, связанную с
влиянием факторов, включенных в
регрессионную модель. Чем
больше объем совокупности, по которой
исчислена регрессия, тем меньше
различаются
и
.

Отметим, что низкое
значение коэффициента множественной
корреляции и коэффициента множественной
детерминации может быть обусловлено
следующими причинами:

– в регрессионную
модель не включены существенные факторы;

– неверно выбрана
форма аналитической зависимости, не
отражающая реальные соотношения между
переменными, включенными в модель.

(слайд
3)
Значимость уравнения множественной
регрессии в целом оценивается с помощью
F—
критерия Фишера:

Выдвигаемая
«нулевая» гипотеза H0 о статистической
незначимости уравнения регрессии
отвергается при выполнении условия F
> Fкрит,
где Fкрит
определяется по таблицам F-критерия
Фишера по двум степеням свободы k1
= m,
k2=
n-m—1
и заданному уровню значимости α.

Значимость одного
и того же фактора может быть различной
в зависимости от последовательности
введения его в модель.

(слайд
4) Мерой
для оценки включения фактора в модель
служит частный
F-критерий
(оценивает статистическую значимость
присутствия каждого из факторов в
уравнении):

где
—
коэффициент множ. детерминации для
модели с полным

набором
факторов;

—
тот же показатель, но без включения в
модель фактора х1;

n
– число наблюдений;

m
– число параметров при переменных х.

Если фактическое
значение F
превышает табличное, то дополнительное
включение в модель фактора xi
статистически оправдано и коэффициент
чистой регрессии bi
при факторе xi
статистически значим.

Если же фактическое
значение F
меньше табличного, то нецелесообразно
включать в модель дополнительный фактор,
поскольку он не увеличивает существенно
долю объясненной вариации результата,
а коэффициент регрессии при данном
факторе статистически не значим.

(слайд
5) Частный
F-критерий
оценивает значимость коэффициентов
чистой регрессии. Зная величину
,
можно определить и t-критерий
Стьюдента:

или

где m_bi
– средняя квадратическая ошибка
коэффициента регрессии b_i,
она может быть определена по формуле:

Величина
стандартной ошибки совместно с
t-распределением Стьюдента при n-m-1
степенях свободы применяется для
проверки значимости коэффициента
регрессии и для расчета его доверительного
интервала.

Соседние файлы в папке Эконометрика

Источник

Интервалы прогнозирования для машинного обучения

Перевод

Ссылка на автора

Прогноз с точки зрения машинного обучения — это единственная точка, которая скрывает неопределенность этого прогноза.

Интервалы прогнозирования дают возможность количественно оценить и сообщить о неопределенности в прогнозе. Они отличаются от доверительных интервалов, которые вместо этого стремятся количественно определить неопределенность в параметре совокупности, таком как среднее или стандартное отклонение. Интервалы прогнозирования описывают неопределенность для одного конкретного результата.

В этом уроке вы узнаете интервал прогнозирования и как рассчитать его для простой модели линейной регрессии.

После завершения этого урока вы узнаете:

Что интервал прогнозирования количественно определяет неопределенность прогнозирования в одной точке.
Эти интервалы прогнозирования могут быть оценены аналитически для простых моделей, но более сложны для нелинейных моделей машинного обучения.
Как рассчитать интервал прогнозирования для простой модели линейной регрессии.

Давайте начнем.

Обзор учебника

Этот урок состоит из 5 частей; они есть:

Что не так с точечной оценкой?
Что такое интервал прогнозирования?
Как рассчитать интервал прогнозирования
Интервал прогнозирования для линейной регрессии
Работал Пример

Зачем рассчитывать интервал прогнозирования?

В прогнозном моделировании прогноз или прогноз — это единичное значение результата с учетом некоторых входных переменных.

Например:

yhat = model.predict(X)

кудаyhatэто предполагаемый результат или прогноз, сделанный обученной моделью для заданных входных данныхИкс,

Это точечный прогноз.

По определению, это оценка или приближение и содержит некоторую неопределенность.

Неопределенность возникает из-за ошибок в самой модели и шума во входных данных. Модель является приближением отношения между входными переменными и выходными переменными.

Учитывая процесс, использованный для выбора и настройки модели, она будет наилучшим приближением, сделанным с учетом доступной информации, но все равно будет допускать ошибки. Данные из домена будут естественным образом скрывать скрытые и неизвестные отношения между входными и выходными переменными. Это затруднит подбор модели, а также вызов модели прогнозирования.

Учитывая эти два основных источника ошибок, их точного прогноза из прогнозирующей модели недостаточно для описания истинной неопределенности прогноза.

Что такое интервал прогнозирования?

Интервал прогнозирования — это количественная оценка неопределенности в прогнозе.

Он обеспечивает вероятностные верхние и нижние границы для оценки переменной результата.

Интервал прогнозирования для одного будущего наблюдения — это интервал, который с заданной степенью достоверности будет содержать будущее случайно выбранное наблюдение из распределения.

— страница 27, Статистические интервалы: руководство для практиков и исследователей, 2017

Интервалы прогнозирования чаще всего используются при создании прогнозов или прогнозов с помощью регрессионной модели, где прогнозируется количество.

Пример представления интервала прогнозирования следующий:

Учитывая прогноз «y» с учетом «x», вероятность того, что диапазон от «a» до «b» охватывает истинный результат, составляет 95%.

Интервал прогнозирования окружает прогноз, сделанный моделью, и, надеюсь, охватывает диапазон истинного результата.

Диаграмма ниже помогает визуально понять взаимосвязь между прогнозом, интервалом прогнозирования и фактическим результатом.

Интервал прогнозирования отличается от доверительного интервала.

Доверительный интервал количественно определяет неопределенность оценочной переменной популяции, такой как среднее значение или стандартное отклонение. Принимая во внимание, что интервал прогнозирования количественно определяет неопределенность одного наблюдения, оцененного по совокупности.

В прогнозном моделировании доверительный интервал может использоваться для количественной оценки неопределенности оцениваемого навыка модели, тогда как интервал прогнозирования может использоваться для количественной оценки неопределенности одного прогноза.

Интервал прогнозирования часто больше доверительного интервала, поскольку он должен учитывать доверительный интервал и прогнозируемую дисперсию выходной переменной.

Интервалы прогнозирования всегда будут шире, чем доверительные интервалы, поскольку они учитывают неопределенность, связанную с e [error], неустранимой ошибкой.

— Страница 103, Введение в статистическое обучение: с приложениями в R, 2013.

Как рассчитать интервал прогнозирования

Интервал прогнозирования рассчитывается как некоторая комбинация оценочной дисперсии модели и дисперсии исходной переменной.

Интервалы прогнозирования легко описать, но на практике их сложно вычислить.

В простых случаях, таких как линейная регрессия, мы можем непосредственно оценить доверительный интервал

В случаях алгоритмов нелинейной регрессии, таких как искусственные нейронные сети, это намного сложнее и требует выбора и реализации специализированных методов. Могут использоваться общие методы, такие как метод повторной выборки при начальной загрузке, но они требуют больших вычислительных затрат.

Бумага » Комплексный обзор интервалов прогнозирования на основе нейронных сетей и новых достижений »Предоставляет сравнительно недавнее исследование интервалов прогнозирования для нелинейных моделей в контексте нейронных сетей. В следующем списке приведены некоторые методы, которые можно использовать для прогнозирования неопределенности для нелинейных моделей машинного обучения:

Дельта-метод из области нелинейной регрессии.
Байесовский метод, из байесовского моделирования и статистики.
Метод оценки среднего отклонения с использованием оценочной статистики.
Метод Bootstrap, использующий повторную выборку данных и разработку множества моделей.

Мы можем сделать расчет прогнозируемого интервала конкретным на проработанном примере в следующем разделе.

Интервал прогнозирования для линейной регрессии

Линейная регрессия — это модель, которая описывает линейную комбинацию входных данных для вычисления выходных переменных.

Например, оценочная модель линейной регрессии может быть записана как:

yhat = b0 + b1 . x

кудаyhatэто прогноз,b0а такжеb1коэффициенты модели, оцененные по данным обучения иИксявляется входной переменной.

Мы не знаем истинных значений коэффициентовb0а такжеb1, Мы также не знаем истинных параметров популяции, таких как среднее значение и стандартное отклонение дляИксили жеY, Все эти элементы должны быть оценены, что вносит неопределенность в использование модели для прогнозирования.

Мы можем сделать некоторые предположения, такие как распределениеИкса такжеYи ошибки прогнозирования, сделанные моделью, называемые невязками, являются гауссовыми.

Интервал прогнозирования вокругyhatможно рассчитать следующим образом:

yhat +/- z * sigma

кудаyhatявляется прогнозируемой величиной,Zявляется критическим значением из распределения Гаусса (например, 1,96 для интервала 95%) исигмастандартное отклонение прогнозируемого распределения.

Мы не знаем на практике. Мы можем рассчитать непредвзятую оценку прогнозируемого стандартного отклонения следующим образом (взяты изПодходы машинного обучения для оценки интервала прогнозирования для выхода модели):

stdev = sqrt(1 / (N - 2) * e(i)^2 for i to N)

кудаSTDEVявляется объективной оценкой стандартного отклонения для прогнозируемого распределения,Nобщие прогнозы, ие (я)это разница между i-м прогнозом и фактическим значением.

Работал Пример

Давайте конкретизируем случай интервалов прогнозирования линейной регрессии на проработанном примере.

Во-первых, давайте определим простой набор данных с двумя переменными, где выходная переменная (Y) зависит от входной переменной (Икс) с некоторым гауссовским шумом.

Пример ниже определяет набор данных, который мы будем использовать для этого примера.

# generate related variables
from numpy import mean
from numpy import std
from numpy.random import randn
from numpy.random import seed
from matplotlib import pyplot
# seed random number generator
seed(1)
# prepare data
x = 20 * randn(1000) + 100
y = x + (10 * randn(1000) + 50)
# summarize
print('x: mean=%.3f stdv=%.3f' % (mean(x), std(x)))
print('y: mean=%.3f stdv=%.3f' % (mean(y), std(y)))
# plot
pyplot.scatter(x, y)
pyplot.show()

При выполнении примера сначала выводятся среднее и стандартное отклонение двух переменных.

x: mean=100.776 stdv=19.620
y: mean=151.050 stdv=22.358

Затем создается набор данных.

Мы можем видеть четкую линейную связь между переменными с разбросом точек, выделяющих шум или случайную ошибку в отношениях.

Далее мы можем разработать простую линейную регрессию, которая задана входной переменнойИкспредскажетYпеременная. Мы можем использовать linregress () функция SciPy соответствовать модели и вернутьb0а такжеb1коэффициенты для модели.

# fit linear regression model
b1, b0, r_value, p_value, std_err = linregress(x, y)

Мы можем использовать коэффициенты для расчета прогнозируемогоYценности, называемыеyhat, для каждой из входных переменных. Полученные точки сформируют линию, которая представляет изученные отношения.

# make prediction
yhat = b0 + b1 * x

Полный пример приведен ниже.

# simple linear regression model
from numpy.random import randn
from numpy.random import seed
from scipy.stats import linregress
from matplotlib import pyplot
# seed random number generator
seed(1)
# prepare data
x = 20 * randn(1000) + 100
y = x + (10 * randn(1000) + 50)
# fit linear regression model
b1, b0, r_value, p_value, std_err = linregress(x, y)
print('b0=%.3f, b1=%.3f' % (b1, b0))
# make prediction
yhat = b0 + b1 * x
# plot data and predictions
pyplot.scatter(x, y)
pyplot.plot(x, yhat, color='r')
pyplot.show()

Выполнение примера соответствует модели и выводит коэффициенты.

b0=1.011, b1=49.117

Коэффициенты затем используются с входными данными из набора данных, чтобы сделать прогноз. Полученные данные и прогнозируемыеY-значения представлены в виде линии сверху графика рассеяния для набора данных.

Мы можем ясно видеть, что модель изучила основные отношения в наборе данных.

Теперь мы готовы сделать прогноз с помощью нашей простой модели линейной регрессии и добавить интервал прогнозирования.

Мы будем соответствовать модели, как и раньше. На этот раз мы возьмем одну выборку из набора данных, чтобы продемонстрировать интервал прогнозирования. Мы будем использовать входные данные, чтобы сделать прогноз, вычислить интервал прогнозирования для прогнозирования и сравнить прогноз и интервал с известным ожидаемым значением.

Сначала давайте определим входные данные, прогноз и ожидаемые значения.

x_in = x[0]
y_out = y[0]
yhat_out = yhat[0]

Далее мы можем оценить стандартное отклонение в направлении прогнозирования.

SE = sqrt(1 / (N - 2) * e(i)^2 for i to N)

Мы можем вычислить это напрямую, используя массивы NumPy следующим образом:

# estimate stdev of yhat
sum_errs = arraysum((y - yhat)**2)
stdev = sqrt(1/(len(y)-2) * sum_errs)

Далее мы можем рассчитать интервал прогнозирования для выбранного нами входа:

interval = z . stdev

Мы будем использовать уровень значимости 95%, который является гауссовым критическим значением 1,96

После того, как интервал рассчитан, мы можем суммировать границы на прогноз для пользователя.

# calculate prediction interval
interval = 1.96 * stdev
lower, upper = yhat_out - interval, yhat_out + interval

Мы можем связать все это вместе. Полный пример приведен ниже.

# linear regression prediction with prediction interval
from numpy.random import randn
from numpy.random import seed
from numpy import power
from numpy import sqrt
from numpy import mean
from numpy import std
from numpy import sum as arraysum
from scipy.stats import linregress
from matplotlib import pyplot
# seed random number generator
seed(1)
# prepare data
x = 20 * randn(1000) + 100
y = x + (10 * randn(1000) + 50)
# fit linear regression model
b1, b0, r_value, p_value, std_err = linregress(x, y)
# make predictions
yhat = b0 + b1 * x
# define new input, expected value and prediction
x_in = x[0]
y_out = y[0]
yhat_out = yhat[0]
# estimate stdev of yhat
sum_errs = arraysum((y - yhat)**2)
stdev = sqrt(1/(len(y)-2) * sum_errs)
# calculate prediction interval
interval = 1.96 * stdev
print('Prediction Interval: %.3f' % interval)
lower, upper = y_out - interval, y_out + interval
print('95%% likelihood that the true value is between %.3f and %.3f' % (lower, upper))
print('True value: %.3f' % yhat_out)
# plot dataset and prediction with interval
pyplot.scatter(x, y)
pyplot.plot(x, yhat, color='red')
pyplot.errorbar(x_in, yhat_out, yerr=interval, color='black', fmt='o')
pyplot.show()

Выполнение примера оцениваетyhatстандартное отклонение, а затем рассчитывает доверительный интервал.

После расчета интервал прогнозирования представляется пользователю для заданной входной переменной. Поскольку мы придумали этот пример, мы знаем истинный результат, который мы также показываем. Мы можем видеть, что в этом случае интервал прогнозирования 95% действительно покрывает истинное ожидаемое значение.

Prediction Interval: 20.204
95% likelihood that the true value is between 160.750 and 201.159
True value: 183.124

Также создается график, показывающий необработанный набор данных в виде точечной диаграммы, прогнозы для набора данных в виде красной линии и интервал прогнозирования и прогнозирования в виде черной точки и линии соответственно.

расширения

В этом разделе перечислены некоторые идеи по расширению учебника, которые вы, возможно, захотите изучить.

Суммируйте разницу между терпимостью, доверием и интервалами прогнозирования.
Разработайте модель линейной регрессии для стандартного набора данных машинного обучения и рассчитайте интервалы прогнозирования для небольшого набора тестов.
Опишите подробно, как работает один метод интервалов нелинейного прогнозирования.

Если вы исследуете какое-либо из этих расширений, я хотел бы знать.

Дальнейшее чтение

Этот раздел предоставляет больше ресурсов по теме, если вы хотите углубиться.

Сообщений

Как сообщить о производительности классификатора с доверительными интервалами
Как рассчитать доверительные интервалы начальной загрузки для результатов машинного обучения в Python
Понимать неопределенность прогноза временных рядов, используя доверительные интервалы с Python
Оцените количество повторений эксперимента для алгоритмов стохастического машинного обучения

книги

Понимание новой статистики: размеры эффектов, доверительные интервалы и метаанализ, 2017
Статистические интервалы: руководство для практиков и исследователей, 2017
Введение в статистическое обучение: с приложениями в R, 2013.
Введение в новую статистику: оценка, открытая наука и не только, 2016
Прогнозирование: принципы и практика, 2013.

документы

Сравнение некоторых оценок ошибок для моделей нейронных сетей 1995
Подходы машинного обучения для оценки интервала прогнозирования для выхода модели, 2006.
Комплексный обзор интервалов прогнозирования на основе нейронных сетей и новых достижений, 2010.

API

API scipy.stats.linregress ()
API matplotlib.pyplot.scatter ()
API matplotlib.pyplot.errorbar ()

статьи

Интервал прогнозирования в Википедии
Интервал прогнозирования начальной загрузки при перекрестной проверке

Резюме

В этом уроке вы обнаружили интервал прогнозирования и способы его расчета для простой модели линейной регрессии.

В частности, вы узнали:

Что интервал прогнозирования количественно определяет неопределенность прогнозирования в одной точке.
Эти интервалы прогнозирования могут быть оценены аналитически для простых моделей, но более сложны для нелинейных моделей машинного обучения.
Как рассчитать интервал прогнозирования для простой модели линейной регрессии.

У вас есть вопросы?
Задайте свои вопросы в комментариях ниже, и я сделаю все возможное, чтобы ответить.

Источник

Тема 8. Доверительные интервалы прогноза. Оценка адекватности и точности моделей

Доверительные интервалы прогноза

Прогнозные значения исследуемого показателя вычисляют путем подстановки в уравнение кривой значений времени t, соответствующих периоду упреждения. Полученный таким образом прогноз называется точечным прогнозом. На практике в дополнение к точечному определяют границы возможного значения прогнозированного показателя, то есть вычисляют интервальный прогноз.

Несовпадение фактических данных с точечным прогнозом может быть вызвано:

1) субъективной ошибочностью выбора вида кривой;

2) погрешностью оценивания параметров кривых;

3) погрешностью, связанной с отклонением отдельных наблюдений от тренда.

Погрешность, связанная со вторым и третьим источником, может быть отражена в виде доверительного интервала прогноза. Доверительный интервал прогноза определяется в следующем виде:

Introduction[edit]

For example, if one makes the parametric assumption that the underlying distribution is a normal distribution, and has a sample set {X₁, …, X_n}, then confidence intervals and credible intervals may be used to estimate the population mean μ and population standard deviation σ of the underlying population, while prediction intervals may be used to estimate the value of the next sample variable, X_n+1.

Alternatively, in Bayesian terms, a prediction interval can be described as a credible interval for the variable itself, rather than for a parameter of the distribution thereof.

The concept of prediction intervals need not be restricted to inference about a single future sample value but can be extended to more complicated cases. For example, in the context of river flooding where analyses are often based on annual values of the largest flow within the year, there may be interest in making inferences about the largest flood likely to be experienced within the next 50 years.

Since prediction intervals are only concerned with past and future observations, rather than unobservable population parameters, they are advocated as a better method than confidence intervals by some statisticians, such as Seymour Geisser,^{[citation needed]} following the focus on observables by Bruno de Finetti.^{[citation needed]}

Normal distribution[edit]

Given a sample from a normal distribution, whose parameters are unknown, it is possible to give prediction intervals in the frequentist sense, i.e., an interval [a, b] based on statistics of the sample such that on repeated experiments, X_n+1 falls in the interval the desired percentage of the time; one may call these «predictive confidence intervals».^[1]

A general technique of frequentist prediction intervals is to find and compute a pivotal quantity of the observables X₁, …, X_n, X_n+1 – meaning a function of observables and parameters whose probability distribution does not depend on the parameters – that can be inverted to give a probability of the future observation X_n+1 falling in some interval computed in terms of the observed values so far, $X_{1},\dots ,X_{n}.$ Such a pivotal quantity, depending only on observables, is called an ancillary statistic.^[2] The usual method of constructing pivotal quantities is to take the difference of two variables that depend on location, so that location cancels out, and then take the ratio of two variables that depend on scale, so that scale cancels out.
The most familiar pivotal quantity is the Student’s t-statistic, which can be derived by this method and is used in the sequel.

Known mean, known variance[edit]

A prediction interval [ℓ,u] for a future observation X in a normal distribution N(µ,σ²) with known mean and variance may be calculated from

$\gamma =P(\ell <X<u)=P\left({\frac {\ell -\mu }{\sigma }}<{\frac {X-\mu }{\sigma }}<{\frac {u-\mu }{\sigma }}\right)=P\left({\frac {\ell -\mu }{\sigma }}<Z<{\frac {u-\mu }{\sigma }}\right),$

where $Z={\frac {X-\mu }{\sigma }}$ , the standard score of X, is distributed as standard normal.

Hence

${\frac {\ell -\mu }{\sigma }}=-z,\quad {\frac {u-\mu }{\sigma }}=z,$

$\ell =\mu -z\sigma ,\quad u=\mu +z\sigma ,$

with z the quantile in the standard normal distribution for which:

$\gamma =P(-z<Z<z).$

or equivalently;

${\tfrac 12}(1-\gamma )=P(Z>z).$

Prediction interval	z
75%	1.15^[3]
90%	1.64^[3]
95%	1.96^[3]
99%	2.58^[3]

Prediction interval (on the y-axis) given from z (the quantile of the standard score, on the x-axis). The y-axis is logarithmically compressed (but the values on it are not modified).

The prediction interval is conventionally written as:

$\left[\mu -z\sigma ,\ \mu +z\sigma \right].$

For example, to calculate the 95% prediction interval for a normal distribution with a mean (µ) of 5 and a standard deviation (σ) of 1, then z is approximately 2. Therefore, the lower limit of the prediction interval is approximately 5 ‒ (2·1) = 3, and the upper limit is approximately 5 + (2·1) = 7, thus giving a prediction interval of approximately 3 to 7.

Diagram showing the cumulative distribution function for the normal distribution with mean (µ) 0 and variance (σ²) 1. In addition to the quantile function, the prediction interval for any standard score can be calculated by (1 − (1 − Φ_µ,σ²(standard score))·2). For example, a standard score of x = 1.96 gives Φ_µ,σ²(1.96) = 0.9750 corresponding to a prediction interval of (1 − (1 − 0.9750)·2) = 0.9500 = 95%.

Estimation of parameters[edit]

For a distribution with unknown parameters, a direct approach to prediction is to estimate the parameters and then use the associated quantile function – for example, one could use the sample mean ${\overline {X}}$ as estimate for μ and the sample variance s² as an estimate for σ². Note that there are two natural choices for s² here – dividing by (n-1) yields an unbiased estimate, while dividing by n yields the maximum likelihood estimator, and either might be used. One then uses the quantile function with these estimated parameters $\Phi _{{\overline {X},s^{2}}}^{{-1}}$ to give a prediction interval.

This approach is usable, but the resulting interval will not have the repeated sampling interpretation^[4] – it is not a predictive confidence interval.

For the sequel, use the sample mean:

$\overline {X}=\overline {X}_{n}=(X_{1}+\cdots +X_{n})/n$

and the (unbiased) sample variance:

$s^{2}=s_{n}^{2}={1 \over n-1}\sum _{i=1}^{n}(X_{i}-{\overline {X}}_{n})^{2}$

Unknown mean, known variance[edit]

Given^[5] a normal distribution with unknown mean μ but known variance 1, the sample mean ${\overline {X}}$ of the observations $X_{1},\dots ,X_{n}$ has distribution $N(\mu ,1/n),$ while the future observation $X_{{n+1}}$ has distribution $N(\mu ,1).$ Taking the difference of these cancels the μ and yields a normal distribution of variance thus

${\frac {X_{{n+1}}-\overline {X}}{{\sqrt {1+(1/n)}}}}\sim N(0,1).$

Solving for $X_{{n+1}}$ gives the prediction distribution $N(\overline {X},1+(1/n)),$ from which one can compute intervals as before. This is a predictive confidence interval in the sense that if one uses a quantile range of 100p%, then on repeated applications of this computation, the future observation $X_{{n+1}}$ will fall in the predicted interval 100p% of the time.

Notice that this prediction distribution is more conservative than using the estimated mean ${\overline {X}}$ and known variance 1, as this uses variance 1+(1/n) , hence yields wider intervals. This is necessary for the desired confidence interval property to hold.

Known mean, unknown variance[edit]

Conversely, given a normal distribution with known mean 0 but unknown variance $\sigma ^{2}$ ,
the sample variance $s^{2}$ of the observations $X_{1},\dots ,X_{n}$ has, up to scale, a $\scriptstyle \chi _{{n-1}}^{2}$ distribution; more precisely:

${\frac {(n-1)s_{n}^{2}}{\sigma ^{2}}}\sim \chi _{{n-1}}^{2}.$

while the future observation $X_{{n+1}}$ has distribution $N(0,\sigma ^{2}).$
Taking the ratio of the future observation and the sample standard deviation^{[clarification needed]} cancels the σ, yielding a Student’s t-distribution with n – 1 degrees of freedom:

${\frac {X_{n+1}}{s}}\sim T^{n-1}.$

Solving for $X_{{n+1}}$ gives the prediction distribution $sT^{{n-1}},$ from which one can compute intervals as before.

Notice that this prediction distribution is more conservative than using a normal distribution with the estimated standard deviation and known mean 0, as it uses the t-distribution instead of the normal distribution, hence yields wider intervals. This is necessary for the desired confidence interval property to hold.

Unknown mean, unknown variance[edit]

Combining the above for a normal distribution $N(\mu ,\sigma ^{2})$ with both μ and σ² unknown yields the following ancillary statistic:^[6]

${\frac {X_{n+1}-{\overline {X}}_{n}}{s_{n}{\sqrt {1+1/n}}}}\sim T^{n-1}$

This simple combination is possible because the sample mean and sample variance of the normal distribution are independent statistics; this is only true for the normal distribution, and in fact characterizes the normal distribution.

Solving for $X_{{n+1}}$ yields the prediction distribution

${\overline {X}}_{n}+s_{n}{\sqrt {1+1/n}}\cdot T^{n-1}$

The probability of $X_{{n+1}}$ falling in a given interval is then:

$\Pr \left(\overline {X}_{n}-T_{a}s_{n}{\sqrt {1+(1/n)}}\leq X_{{n+1}}\leq \overline {X}_{n}+T_{a}s_{n}{\sqrt {1+(1/n)}}\,\right)=p$

where T_a is the 100((1 − p)/2)^th percentile of Student’s t-distribution with n − 1 degrees of freedom. Therefore, the numbers

${\overline {X}}_{n}\pm T_{a}s_{n}{\sqrt {1+(1/n)}}$

are the endpoints of a 100(1 − p)% prediction interval for $X_{{n+1}}$ .

Non-parametric methods[edit]

One can compute prediction intervals without any assumptions on the population; formally, this is a non-parametric method.^[7] If one has a sample of identical random variables {X₁, …, X_n}, then the probability that the next observation X_n+1 will be the largest is 1/(n + 1), since all observations have equal probability of being the maximum. In the same way, the probability that X_n+1 will be the smallest is 1/(n + 1). The other (n − 1)/(n + 1) of the time, X_n+1 falls between the sample maximum and sample minimum of the sample {X₁, …, X_n}. Thus, denoting the sample maximum and minimum by M and m, this yields an (n − 1)/(n + 1) prediction interval of [m, M].

Notice that while this gives the probability that a future observation will fall in a range, it does not give any estimate as to where in a segment it will fall – notably, if it falls outside the range of observed values, it may be far outside the range. See extreme value theory for further discussion. Formally, this applies not just to sampling from a population, but to any exchangeable sequence of random variables, not necessarily independent or identically distributed.

Contrast with other intervals[edit]

Contrast with confidence intervals[edit]

Note that in the formula for the predictive confidence interval no mention is made of the unobservable parameters μ and σ of population mean and standard deviation – the observed sample statistics ${\overline {X}}_{n}$ and $S_{n}$ of sample mean and standard deviation are used, and what is estimated is the outcome of future samples.

Rather than using sample statistics as estimators of population parameters and applying confidence intervals to these estimates, one considers «the next sample» $X_{{n+1}}$ as itself a statistic, and computes its sampling distribution.

In parameter confidence intervals, one estimates population parameters; if one wishes to interpret this as prediction of the next sample, one models «the next sample» as a draw from this estimated population, using the (estimated) population distribution. By contrast, in predictive confidence intervals, one uses the sampling distribution of (a statistic of) a sample of n or n + 1 observations from such a population, and the population distribution is not directly used, though the assumption about its form (though not the values of its parameters) is used in computing the sampling distribution.

Contrast with tolerance intervals[edit]

Applications[edit]

Prediction intervals are commonly used as definitions of reference ranges, such as reference ranges for blood tests to give an idea of whether a blood test is normal or not. For this purpose, the most commonly used prediction interval is the 95% prediction interval, and a reference range based on it can be called a standard reference range.

Regression analysis[edit]

A common application of prediction intervals is to regression analysis.

Suppose the data is being modeled by a straight line regression:

$y_{i}=\alpha +\beta x_{i}+\varepsilon _{i}\,$

where $y_{i}$ is the response variable, $x_{i}$ is the explanatory variable, ε_i is a random error term, and $\alpha$ and $\beta$ are parameters.

Given estimates $\hat \alpha$ and ${\hat {\beta }}$ for the parameters, such as from a simple linear regression, the predicted response value y_d for a given explanatory value x_d is

$\hat{y}_d=\hat\alpha+\hat\beta x_d ,$

(the point on the regression line), while the actual response would be

$y_{d}=\alpha +\beta x_{d}+\varepsilon _{d}.\,$

The point estimate ${\hat {y}}_{d}$ is called the mean response, and is an estimate of the expected value of y_d, $E(y\mid x_{d}).$

A prediction interval instead gives an interval in which one expects y_d to fall; this is not necessary if the actual parameters α and β are known (together with the error term ε_i), but if one is estimating from a sample, then one may use the standard error of the estimates for the intercept and slope ( ${\hat {\alpha }}$ and ${\hat {\beta }}$ ), as well as their correlation, to compute a prediction interval.

In regression, Faraway (2002, p. 39) makes a distinction between intervals for predictions of the mean response vs. for predictions of observed response—affecting essentially the inclusion or not of the unity term within the square root in the expansion factors above; for details, see Faraway (2002).

Bayesian statistics[edit]

Seymour Geisser, a proponent of predictive inference, gives predictive applications of Bayesian statistics.^[8]

In Bayesian statistics, one can compute (Bayesian) prediction intervals from the posterior probability of the random variable, as a credible interval. In theoretical work, credible intervals are not often calculated for the prediction of future events, but for inference of parameters – i.e., credible intervals of a parameter, not for the outcomes of the variable itself. However, particularly where applications are concerned with possible extreme values of yet to be observed cases, credible intervals for such values can be of practical importance.

Notes[edit]

^ Geisser (1993, p. 6): Chapter 2: Non-Bayesian predictive approaches
^ Geisser (1993, p. 7)
^ ^a ^b ^c ^d Table A2 in Sterne & Kirkwood (2003, p. 472)
^ Geisser (1993, p. 8–9)
^ Geisser (1993, p. 7–)
^ Geisser (1993, Example 2.2, p. 9–10)
^ «Prediction Intervals», Statistics @ SUNY Oswego
^ Geisser (1993)

References[edit]

Faraway, Julian J. (2002), Practical Regression and Anova using R (PDF)
Geisser, Seymour (1993), Predictive Inference, CRC Press
Sterne, Jonathan; Kirkwood, Betty R. (2003), Essential Medical Statistics, Blackwell Science, ISBN 0-86542-871-9

t	yt			Условное время	Утеор
1	91,6	—	—	-5	91,64
2	91,5	-0,1	—	-4	91,47
3	91,3	-0,2	-0,1	-3	92,3
4	91,1	-0,2	0	-2	91,13
5	91,0	-0,1	0,1	-1	90,96
6	90,8	-0,2	-0,1	0	90,79
7	90,6	-0,2	0	1	90,62
8	90,4	-0,2	0	2	90,45
9	90,2	-0,2	0	3	90,28
10	90,0	-0,2	0	4	90,11
11	89,9	-0,1	0,1	5	89,94
Итого		-17	0

Месяц	Прогнозное значение	Фактическое значение
1 модель	2 модель
Апрель	35400	36300	36505
Май	41600	Ещё посмотрите лекцию «34 Девиация» по этой теме. 99200	40524
Июнь	45600	43100	45416