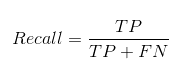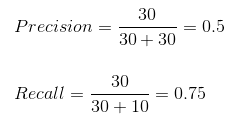Перевод статьи – Understanding Confusion Matrix – Sarang Narkhede
Когда мы получаем данные после очистки, предварительной обработки и обработки данных, первым шагом, который мы делаем, является создание модели и, конечно, получение результатов в вероятностях. Но держись! Как, черт возьми, мы можем измерить эффективность нашей модели? Лучшая эффективность, лучшая производительность и это именно то, что мы хотим. В данном случае мы начинаем использовать матрицу ошибок. Матрица ошибок (Confusion Matrix) – это измерение производительности для классификации машинного обучения.
Содержание
- Этот пост призван ответить на следующие вопросы:
- Что такое матрица ошибок, и зачем она нужна?
- Как вычислить матрицу ошибок для задачи классификации с бинарными классами?
Этот пост призван ответить на следующие вопросы:
- Что такое Матрица ошибок и зачем она нужна?
- Как вычислить матрицу ошибок для задач бинарной классификации?
Сегодня давайте разберемся с матрицей путаницы раз и навсегда.
Что такое матрица ошибок, и зачем она нужна?
Ну, это измерение производительности для задачи классификации машинного обучения, где выходной может быть два или более классов. Это таблица с 4 различными комбинациями прогнозируемых и фактических значений.
Это чрезвычайно полезно для вычисления Полноты, Точности, Специфичность, Точность и, что наиболее важно кривой ошибок AUC-ROC.
Давайте поймем термины TP, FP, FN, TN на примере аналогии с беременностью.
TP — истино-положительное решение:
Интерпретация: Вы предсказали положительное, и это правда.
Вы предсказали, что женщина беременна, и она на самом деле беременна.
TN — истино-отрицательное решение:
Интерпретация: Вы прогнозировали отрицательное значения, и это правда.
Вы предсказали, что мужчина не беременен, а он на самом деле не беременен.
FP — ложно-положительное решение (Ошибка типа 1):
Интерпретация: Вы предсказали положительное значение, и это неверно.
Вы предсказали, что мужчина беременен, но на самом деле это не так.
FN— ложно-отрицательное решение (Ошибка Типа 2):
Интерпретация: Вы предсказали отрицательное значение, и это неверно.
Вы предсказали, что женщина не беременна, но она на самом деле беременная.
Только помните, мы описываем прогнозируемые значения как положительные и отрицательные, а фактические значения как истинные и ложные.
How to Calculate Confusion Matrix for a 2-class classification problem?
Как вычислить матрицу ошибок для задачи классификации с бинарными классами?
Давайте разберемся с матрицей ошибок посредством математик
Полнота Recall
Из всех положительных классов, сколько мы предсказали правильно. Это должно быть как можно выше.
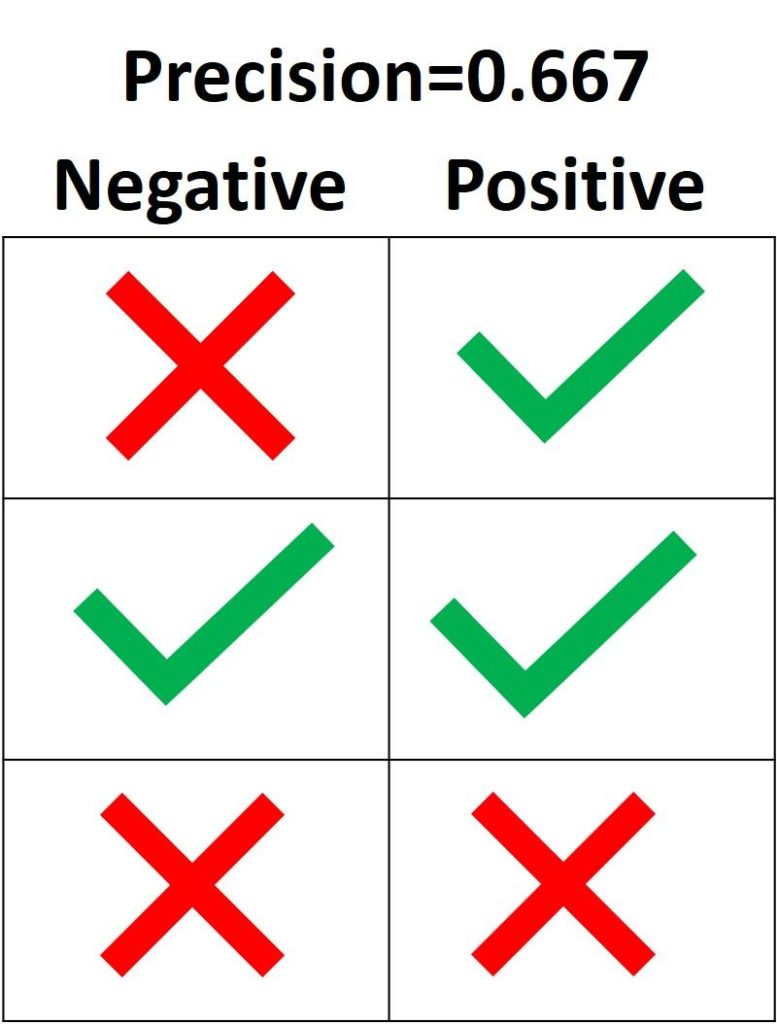
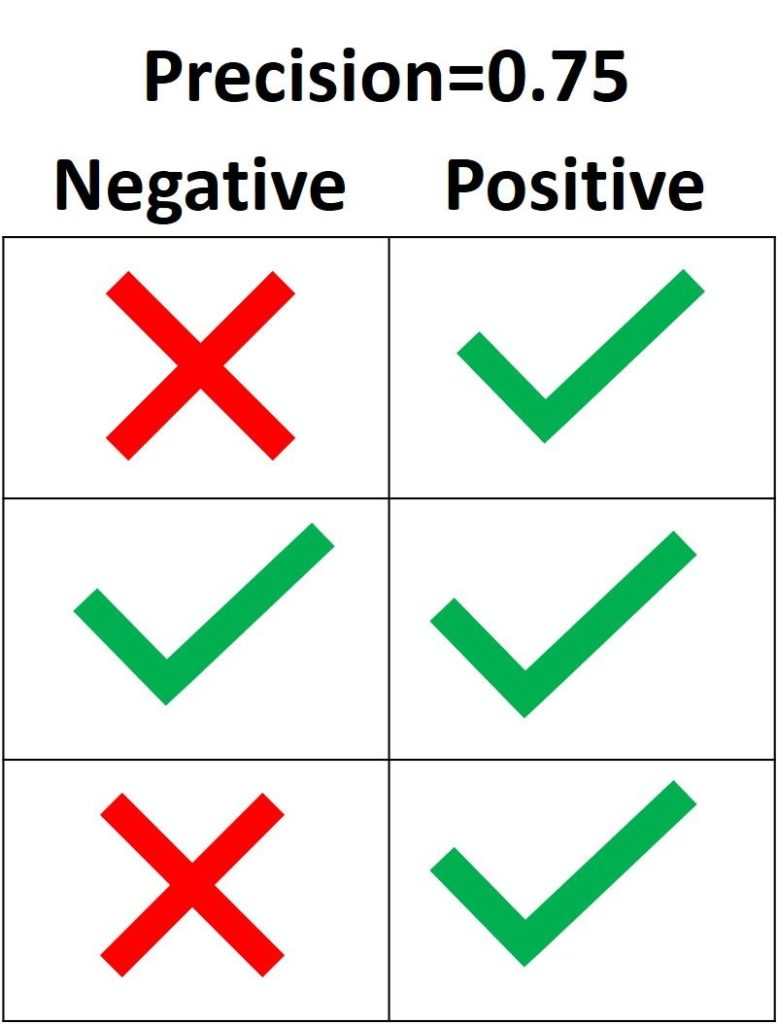
Точность Precision
Из всех классов, сколько мы предсказали правильно. Это должно быть как можно выше.
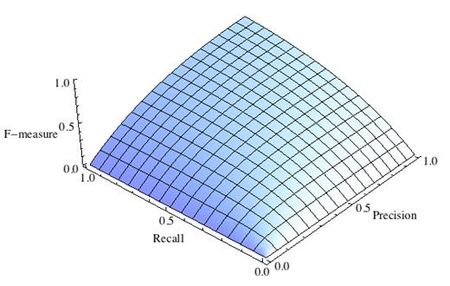
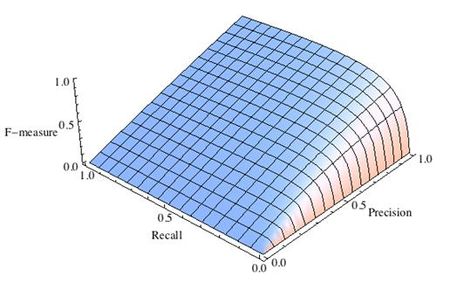
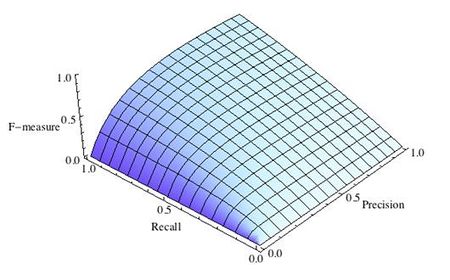
F-мера
Трудно сравнить две модели с низкой точностью и высокой отзывчивостью или наоборот. Поэтому, чтобы сделать их сопоставимыми, мы используем F-меру. F-мера помогает измерять Полноту и Точность одновременно. Она использует гармоническое среднее вместо среднего арифметического, наказывая экстремальные значения больше.
https://towardsdatascience.com/understanding-confusion-matrix-a9ad42dcfd62
Матрица ошибок – это метрика производительности классифицирующей модели Машинного обучения (ML).
Когда мы получаем данные, то после очистки и предварительной обработки, первым делом передаем их в модель и, конечно же, получаем результат в виде вероятностей. Но как мы можем измерить эффективность нашей модели? Именно здесь матрица ошибок и оказывается в центре внимания.
Матрица ошибок – это показатель успешности классификации, где классов два или более. Это таблица с 4 различными комбинациями сочетаний прогнозируемых и фактических значений.
Давайте рассмотрим значения ячеек (истинно позитивные, ошибочно позитивные, ошибочно негативные, истинно негативные) с помощью «беременной» аналогии.
Истинно позитивное предсказание (True Positive, сокр. TP)
Вы предсказали положительный результат, и женщина действительно беременна.
Истинно отрицательное предсказание (True Negative, TN)
Вы предсказали отрицательный результат, и мужчина действительно не беременен.
Ошибочно положительное предсказание (ошибка типа I, False Positive, FN)
Вы предсказали положительный результат (мужчина беременен), но на самом деле это не так.
Ошибочно отрицательное предсказание (ошибка типа II, False Negative, FN)
Вы предсказали, что женщина не беременна, но на самом деле она беременна.
Давайте разберемся в матрице ошибок с помощью арифметики.
Пример. Мы располагаем датасетом пациентов, у которых диагностируют рак. Зная верный диагноз (столбец целевой переменной «Y на самом деле»), хотим усовершенствовать диагностику с помощью модели Машинного обучения. Модель получила тренировочные данные, и на тестовой части, состоящей из 7 записей (в реальных задачах, конечно, больше) и изображенной ниже, мы оцениваем, насколько хорошо прошло обучение.
Модель сделала свои предсказания для каждого пациента и записала вероятности от 0 до 1 в столбец «Предсказанный Y». Мы округляем эти числа, приводя их к нулю или единице, с помощью порога, равного 0,6 (ниже этого значения – ноль, пациент здоров). Результаты округления попадают в столбец «Предсказанная вероятность»: например, для первой записи модель указала 0,5, что соответствует нулю. В последнем столбце мы анализируем, угадала ли модель.
Теперь, используя простейшие формулы, мы рассчитаем Отзыв (Recall), точность результата измерений (Precision), точность измерений (Accuracy), и наконец поймем разницу между этими метриками.
Отзыв
Из всех положительных значений, которые мы предсказали правильно, сколько на самом деле положительных? Подсчитаем, сколько единиц в столбце «Y на самом деле» (4), это и есть сумма TP + FN. Теперь определим с помощью «Предсказанной вероятности», сколько из них диагностировано верно (2), это и будет TP.
$$Отзыв = \frac{TP}{TP + FN} = \frac{2}{2 + 2} = \frac{1}{2}$$
Точность результата измерений (Precision)
В этом уравнении из неизвестных только FP. Ошибочно диагностированных как больных здесь только одна запись.
$$Точность\spaceрезультата\spaceизмерений = \frac{TP}{TP + FP} = \frac{2}{2 + 1} = \frac{2}{3}$$
Точность измерений (Accuracy)
Последнее значение, которое предстоит экстраполировать из таблицы – TN. Правильно диагностированных моделью здоровых людей здесь 2.
$$Точность\spaceизмерений = \frac{TP + TN}{Всего\spaceзначений} = \frac{2 + 2}{7} = \frac{4}{7}$$
F-мера точности теста
Эти метрики полезны, когда помогают вычислить F-меру – конечный показатель эффективности модели.
$$F-мера = \frac{2 * Отзыв * Точность\spaceизмерений}{Отзыв + Точность\spaceизмерений} = \frac{2 * \frac{1}{2} * \frac{2}{3}}{\frac{1}{2} + \frac{2}{3}} = 0,56$$
Наша скромная модель угадывает лишь 56% процентов диагнозов, и такой результат, как правило, считают промежуточным и работают над улучшением точности модели.
SkLearn
С помощью замечательной библиотеки Scikit-learn мы можем мгновенно определить множество метрик, и матрица ошибок – не исключение.
from sklearn.metrics import confusion_matrix
y_true = [2, 0, 2, 2, 0, 1]
y_pred = [0, 0, 2, 2, 0, 2]
confusion_matrix(y_true, y_pred)Выводом будет ряд, состоящий из трех списков:
array([[2, 0, 0],
[0, 0, 1],
[1, 0, 2]])Значения диагонали сверху вниз слева направо [2, 0, 2] – это число верно предсказанных значений.
Фото: @opeleye
Были ли вы в ситуации, когда вы ожидали, что ваша модель машинного обучения должна работать очень хорошо, но у нее была низкая точность? Вы проделали всю тяжелую работу — так где же модель классификации сработала не так? Как это исправить?
Существует множество способов оценить эффективность вашей модели классификации, но ни один из них не выдержал испытания временем, кроме матрицы ошибок. Она помогает нам оценить, как наша модель работала, где она пошла не туда, и предлагает нам рекомендации по исправлению нашего пути.
В этой статье мы рассмотрим, как матрица ошибок дает целостное представление об эффективности вашей модели. И, в отличие от названия, вы поймете, что матрица ошибок — довольно простая, но мощная концепция. Итак, давайте раскроем тайну матрицы ошибок!
Что такое матрица ошибок?
Вопрос на миллион долларов — что такое, в конце концов, матрица ошибок?
Матрица ошибок — это матрица размером N x N, используемая для оценки эффективности модели классификации, где N — количество целевых классов. Матрица сравнивает фактические целевые значения с предсказанными моделью машинного обучения. Это дает нам целостное представление о том, насколько хорошо работает наша классификационная модель и какие ошибки она допускает.
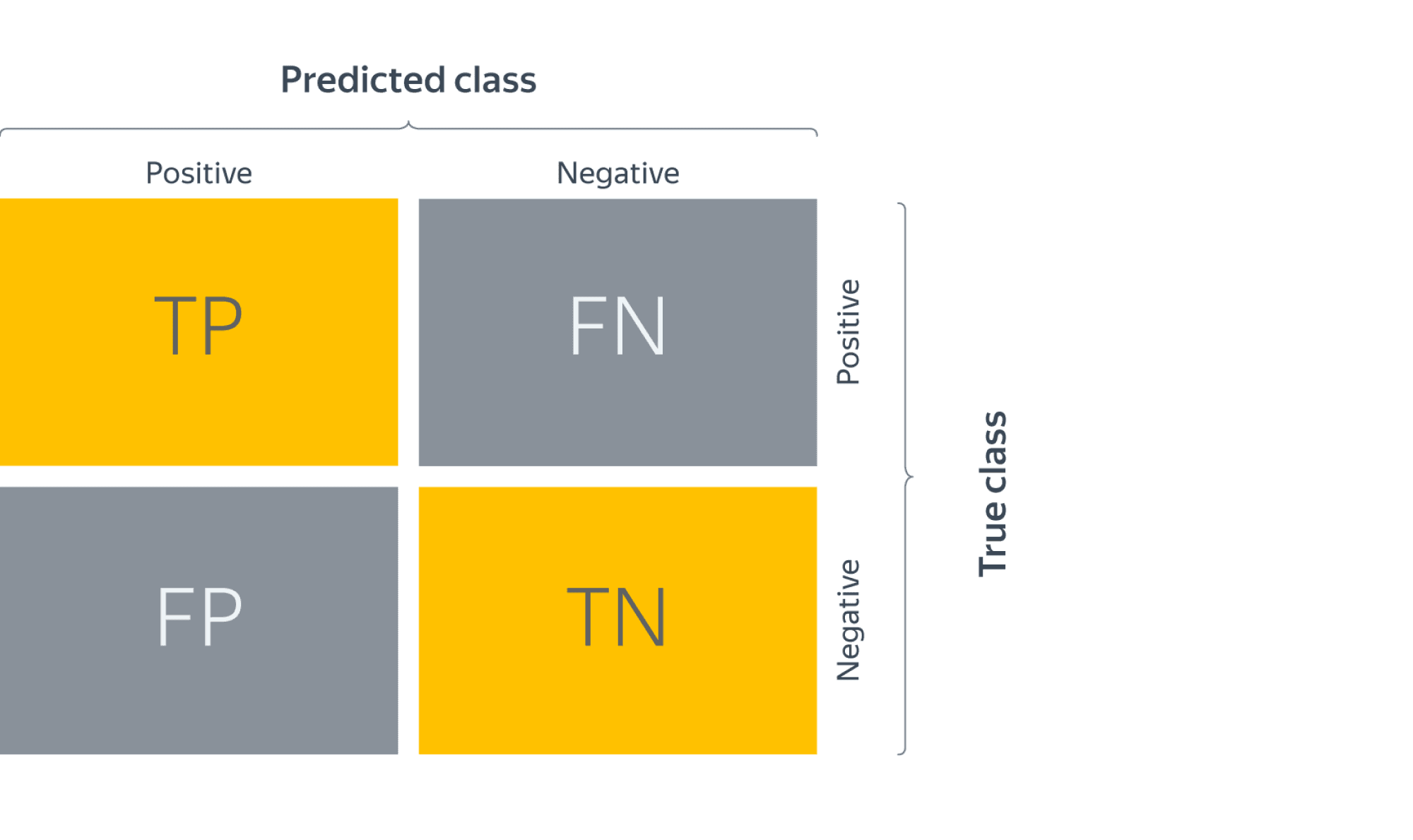
Для задачи двоичной классификации у нас будет матрица 2 x 2, как показано ниже, с 4 значениями:
Расшифруем матрицу:
- Целевая переменная имеет два значения: положительное или отрицательное.
- Столбцы представляют фактические значения целевой переменной.
- Строки представляют собой прогнозируемые значения целевой переменной.
Но подождите — что здесь TP, FP, FN и TN? Это важнейшая часть матрицы ошибок. Давайте разберемся с каждым термином ниже.
Понимание True Positive, True Negative, False Positive и False Negative в матрице ошибок
True Positive (TP)
- Прогнозируемое значение соответствует фактическому значению.
- Фактическое значение было положительным, и модель предсказала положительное значение.
True Negative (TN)
- Прогнозируемое значение соответствует фактическому значению.
- Фактическое значение было отрицательным, и модель предсказала отрицательное значение.
False Positive (FP) — ошибка 1-го типа
- Прогнозируемое значение было предсказано неверно.
- Фактическое значение было отрицательным, но модель предсказала положительное значение.
- Также известна как ошибка 1-го типа.
False Negative (FN) — ошибка 2-го типа
- Прогнозируемое значение было предсказано неверно.
- Фактическое значение было положительным, но модель предсказала отрицательное значение.
- Также известна как ошибка 2-го типа.
Позвольте мне привести пример, чтобы лучше это понять. Предположим, у нас есть набор данных классификации с 1000 точками данных. Мы подгоняем на нем классификатор и получаем следующую матрицу ошибок:
Различные значения матрицы ошибок будут следующими:
- True Positive (TP) = 560; это означает, что 560 положительных точек данных были правильно классифицированы моделью.
- True Negative (TN) = 330; это означает, что 330 отрицательных точек данных были правильно классифицированы моделью.
- False Positive (FP) = 60; это означает, что 60 отрицательных точек данных были неправильно классифицированы моделью как положительные.
- False Negative (FN) = 50; это означает, что 50 положительных точек данных были неправильно классифицированы моделью как отрицательные.
Это оказался довольно приличный классификатор для нашего набора данных, учитывая относительно большее количество истинно положительных и истинно отрицательных значений.
Помните об ошибках 1-го и 2-го типа. Интервьюеры любят спрашивать, в чем разница между ними!
Зачем нам нужна матрица ошибок?
Прежде чем ответить на этот вопрос, давайте подумаем о проблеме гипотетической классификации.
Допустим, вы хотите предсказать, сколько людей инфицировано заразным вирусом, до того, как у них проявятся симптомы, и изолировать их от здорового населения. Двумя значениями для нашей целевой переменной будут: Sick и Not Sick.
Теперь вы, должно быть, задаетесь вопросом — зачем нам матрица ошибок, когда у нас есть наш вечный друг — Точность? Что ж, посмотрим, где точность не работает.
Наш набор данных является примером несбалансированного набора данных. Имеется 947 точек данных для отрицательного класса и 3 точки данных для положительного класса. Вот как мы рассчитаем точность:
Посмотрим, как работает наша модель:
Общие значения результатов:
TP = 30, TN = 930, FP = 30, FN = 10
Итак, точность для нашей модели:
96%! Неплохо!
Но это дает неверное представление о результате. Подумайте об этом.
Наша модель гласит: «Я могу предсказать заболевание в 96% случаев». Однако она делает наоборот. Это предсказание людей, которые не заболеют с точностью 96%, пока больные распространяют вирус!
Как вы думаете, это правильный показатель для нашей модели, учитывая серьезность проблемы? Разве мы не должны измерять, сколько положительных случаев мы можем правильно предсказать, чтобы остановить распространение заразного вируса? Или, из правильно спрогнозированных случаев сколько положительных случаев для проверки надежности нашей модели?
Здесь мы сталкиваемся с двойным понятием «точность (Precision) и полнота (Recall)».
Precision vs. Recall
Точность говорит нам, сколько из правильно предсказанных случаев действительно оказались положительными.
Вот как рассчитать точность:
Это определило бы надежность нашей модели.
Полнота сообщает нам, сколько реальных положительных случаев мы смогли правильно предсказать с помощью нашей модели.
А вот как мы можем рассчитать полноту:
Мы можем легко рассчитать точность и полноту для нашей модели, подставив значения в приведенные выше уравнения:
50% процентов правильно предсказанных случаев оказались положительными. В то время как 75% положительных результатов были успешно предсказаны нашей моделью. Потрясающие!
Точность — полезный показатель в тех случаях, когда ложноположительный результат важнее, чем ложноотрицательный.
Точность важна в системах рекомендаций по музыке или видео, на веб-сайтах электронной коммерции и т. д. Неправильные результаты могут привести к оттоку клиентов и нанести вред бизнесу.
Полнота — полезный показатель в случаях, когда ложноотрицательный результат важнее ложноположительного.
Полнота важна в медицинских случаях, когда не имеет значения, что возникает ложная тревога, но реальные положительные случаи не должны оставаться незамеченными!
В нашем примере полнота была бы лучшим показателем, потому что мы не хотим, чтобы случайно выписали инфицированного человека и позволили ему смешаться со здоровым населением, тем самым распространяя заразный вирус. Теперь вы можете понять, почему точность была плохим показателем для нашей модели.
Но будут случаи, когда нет четкой разницы между тем, что важнее: точность или полнота. Что нам делать в таких случаях? Мы их совмещаем!
F1-Score
На практике, когда мы пытаемся повысить точность нашей модели, полнота снижается, и наоборот. F1-Score отражает обе тенденции в одном значении:
F1-Score представляет собой гармоничное среднее значение точности и полноты, поэтому дает общее представление об этих двух показателях. Оно максимально, когда точность равно полноте.
Но здесь есть одна загвоздка. Интерпретируемость оценки F1 оставляет желать лучшего. Это означает, что мы не знаем, чего добивается наш классификатор — точности или полноты? Итак, мы используем его в сочетании с другими оценочными метриками, что дает нам полную картину результата.
Матрица ошибок с использованием scikit-learn в Python
Вы знаете теорию — теперь давайте применим ее на практике. Давайте запрограммируем матрицу ошибок с помощью библиотеки Scikit-learn (sklearn) на Python.
# confusion matrix in sklearn
from sklearn.metrics import confusion_matrix
3 from sklearn.metrics import classification_report
# actual values
actual = [1,0,0,1,0,0,1,0,0,1]
# predicted values
predicted = [1,0,0,1,0,0,0,1,0,0]
# confusion matrix
matrix = confusion_matrix(actual,predicted, labels=[1,0])
print(‘Confusion matrix : \n’,matrix)
# outcome values order in sklearn
tp, fn, fp, tn = confusion_matrix(actual,predicted,labels=[1,0]).reshape(-1)
print(‘Outcome values : \n’, tp, fn, fp, tn)
# classification report for precision, recall f1-score and accuracy
matrix = classification_report(actual,predicted,labels=[1,0])
print(‘Classification report : \n’,matrix)
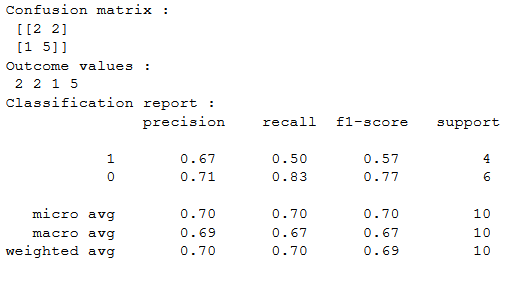
Sklearn имеет две отличные функции: confusion_matrix() и classification_report().
возвращает значения матрицы ошибок. Однако результат немного отличается от того, что мы изучили до сих пор. Она принимает строки как фактические значения, а столбцы как прогнозные значения. В остальном концепция осталась прежней.
выводит точность, полноту и f1-score для каждого целевого класса. В дополнение к этому, она также имеет некоторые дополнительные значения: micro avg, macro avg и weighted avg.
Mirco average — это оценка точности/полноты/f1, рассчитанная для всех классов.
Macro average — это среднее значение точности/полноты/f1-score.
Weighted average — это просто средневзвешенное значение точности/полноты/f1-score.
Матрица ошибок для мультиклассовой классификации
Как матрица ошибок будет работать для задачи классификации нескольких классов? Мы рассмотрим и этот случай.
Давайте нарисуем матрицу ошибок для мультиклассовой задачи, в которой мы должны предсказать, любит ли человек Facebook, Instagram или Snapchat. Матрица ошибок будет иметь вид 3 x 3:
true positive, true negative, false positive и false negative для каждого класса будут вычисляться путем сложения значений ячеек следующим образом:
Вот и все! Вы готовы расшифровать любую матрицу ошибок размером N x N!
Заключение
И вдруг матрица ошибок перестает быть такой запутанной! Эта статья должна дать вам прочную основу для интерпретации и использования матрицы ошибок для алгоритмов классификации в машинном обучении.
Вскоре мы выпустим статью о кривой AUC-ROC и продолжим наше обсуждение там. До этого не теряйте надежды на свою модель классификации, возможно, вы просто используете неправильную метрику оценки!
В случае проблемы классификации наличие только одной точности классификации может не дать вам всей картины. Таким образом, матрица неточностей или матрица ошибок используется для суммирования производительности алгоритма классификации.
Вычисление матрицы неточностей может дать вам представление о том, где правильная модель классификации и какие типы ошибок она допускает.
Матрица неточностей используется для проверки эффективности модели классификации на наборе тестовых данных, для которых известны истинные значения. Большинство показателей эффективности, таких как точность и отзыв, рассчитываются на основе матрицы неточностей.
Эта статья преследует следующие цели:
1. Что такое матрица неточностей и зачем она нужна.
2. Как рассчитать матрицу неточностей для задачи классификации двух классов на примере «кошка-собака». .
3. Как создать матрицу неточностей в Python и R.
4. Резюме и интуиция по различным параметрам: точность, отзыв, точность и специфичность
1. Матрица неточностей:
Матрица неточностей представляет собой сводку прогнозных результатов в задаче классификации. Правильные и неправильные прогнозы сведены в таблицу с их значениями и разбиты по каждому классу.
Мы не можем полагаться на единственное значение точности классификации, когда классы не сбалансированы. Например, у нас есть набор данных из 100 пациентов, из которых 5 страдают диабетом и 95 здоровы. Однако, если наша модель предсказывает только класс большинства, то есть все 100 человек здоровы, даже если точность классификации составляет 95%. Следовательно, нам нужна матрица путаницы.
2. Рассчитайте матрицу неточностей:
Возьмем пример:
Всего у нас 10 кошек и собак, и наша модель предсказывает, кошка это или нет.
Фактические значения = [собака, кошка, собака, кошка, собака, собака, кошка, собака, кошка, собака]
Прогнозируемые значения = [‘собака’, ‘собака’, ‘собака’, ‘кошка’, ‘собака’, ‘собака’, ‘кошка’, ‘кошка’, ‘кошка’, ‘кошка’]
Помните, что мы описываем прогнозируемые значения как положительные / отрицательные, а фактические значения — как истинные / ложные.
Определение терминов:
Истинно-положительный: вы предсказали положительный результат, и это правда. Вы предсказали, что животное — это кошка, и это действительно так.
Истинно-отрицательный: вы предсказали отрицательный результат, и это правда. Вы предсказали, что животное не кошка, и на самом деле это не кошка (это собака).
Ложноположительный результат (ошибка типа 1): вы предсказали положительный результат, но он неверен. Вы предсказали, что животное — кошка, но на самом деле это не так (это собака).
Ложноотрицательный результат (ошибка типа 2): вы предсказали отрицательный результат, но он неверен. Вы предсказали, что животное не кошка, но это действительно так.
Точность классификации:
Точность классификации определяется соотношением:
Отзыв (он же чувствительность):
Отзыв определяется как отношение общего количества правильно классифицированных положительных классов к общему количеству положительных классов. Или, насколько мы правильно предсказали из всех положительных классов. Напоминание должно быть высоким.
Точность:
Точность определяется как отношение общего количества правильно классифицированных положительных классов к общему количеству предсказанных положительных классов. Или, насколько мы правильно предсказали из всех классов положительного прогноза. Точность должна быть высокой.
Помните: Предварительная оценка имеет в знаменателе предварительный результат.
Оценка F или F1:
Трудно сравнить две модели с разной точностью и отзывчивостью. Чтобы сделать их сопоставимыми, мы используем F-Score. Это гармоническое средство точности и вспоминания. По сравнению со средним арифметическим, среднее гармоническое больше наказывает крайние значения. F-оценка должна быть высокой.
Специфичность
. Специфичность определяет долю правильно идентифицированных фактических негативов.
Пример интерпретации матрицы ошибок:
Давайте рассчитаем матрицу ошибок, используя приведенный выше пример с кошками и собаками:
Точность классификации:
Точность = (TP + TN) / (TP + TN + FP + FN) = (3 + 4) / (3 + 4 + 2 + 1) = 0,70.
Напоминание: напоминание дает нам представление о том, когда это на самом деле «да» и как часто оно предсказывает «да».
Напоминание = TP / (TP + FN) = 3 / (3 + 1) = 0,75
Точность: точность сообщает нам, когда она предсказывает «да» и как часто она оказывается правильной.
Точность = TP / (TP + FP) = 3 / (3 + 2) = 0,60
Оценка F:
Оценка F = (2 * Отзыв * Точность) / (Отзыв + Предъявление) = (2 * 0,75 * 0,60) / (0,75 + 0,60) = 0,67
Специфичность:
Специфичность = TN / (TN + FP) = 4 / (4 + 2) = 0,67.
3. Создайте матрицу путаницы в Python & R
Давайте воспользуемся кодами Python и R, чтобы понять приведенный выше пример собаки и кошки, который даст вам лучшее понимание того, что вы узнали о матрице путаницы на данный момент.
PYTHON: сначала возьмем код Python, чтобы создать матрицу путаницы. Мы должны импортировать модуль матрицы путаницы из библиотеки sklearn, которая помогает нам сгенерировать матрицу путаницы.
Ниже представлена реализация приведенного выше объяснения на языке Python:
OUTPUT ->
Confusion Matrix :
[[3 1]
[2 4]]
Accuracy Score : 0.7
Classification Report :
precision recall f1-score support
cat 0.60 0.75 0.67 4
dog 0.80 0.67 0.73 6
micro avg 0.70 0.70 0.70 10
macro avg 0.70 0.71 0.70 10
weighted avg 0.72 0.70 0.70 10
R: Давайте теперь воспользуемся кодом R, чтобы создать матрицу путаницы. Мы будем использовать библиотеку каретки в R для вычисления матрицы путаницы.
OUTPUT ->
Confusion Matrix and Statistics
Reference
Prediction 0 1
0 4 1
1 2 3
Accuracy : 0.7
95% CI : (0.3475, 0.9333)
No Information Rate : 0.6
P-Value [Acc > NIR] : 0.3823
Kappa : 0.4
Mcnemar's Test P-Value : 1.0000
Sensitivity : 0.6667
Specificity : 0.7500
Pos Pred Value : 0.8000
Neg Pred Value : 0.6000
Prevalence : 0.6000
Detection Rate : 0.4000
Detection Prevalence : 0.5000
Balanced Accuracy : 0.7083
'Positive' Class : 0
4. Резюме:
- Точность — это то, насколько вы уверены в своих истинных достоинствах. Вспомните, насколько вы уверены в том, что не упускаете никаких положительных моментов.
- Выберите Отзыв, если появление ложноотрицательных результатов недопустимо / недопустимо. Например, в случае диабета вы предпочли бы иметь несколько дополнительных ложных срабатываний (ложных тревог), а не сохранять некоторые ложноотрицательные результаты.
- Выберите Точность, если вы хотите быть более уверены в своих истинных положительных результатах. Например, в случае спама, вы бы предпочли иметь несколько спам-писем в вашем почтовом ящике, а не несколько обычных писем в вашем ящике для спама. Прежде чем мы поместим его в ящик для спама, вы хотите быть уверены в том, что электронное письмо X является спамом.
- Выберите Специфичность, если вы хотите охватить все истинные негативы, т. Е. это означает, что мы не хотим ложных срабатываний или ложных срабатываний. Например, в случае теста на наркотики, при котором все люди с положительным результатом теста немедленно попадут в тюрьму, вы не захотите, чтобы кто-то без наркотиков попадал в тюрьму.
Можно сделать вывод, что:
- Значение точности 70% означает, что идентификация 3 из каждых 10 кошек неверна, а 7 — верны.
- Значение точности 60% означает, что на этикетке 4 из каждых 10 кошек не указана кошка (т.е. собака), а 6 — кошки.
- Значение отзыва 70% означает, что 3 из каждых 10 кошек на самом деле пропущены нашей моделью, а 7 правильно определены как кошки.
- Значение специфичности 60% означает, что 4 из каждых 10 собак (т. Е. Не кошек) на самом деле неправильно помечены как кошки, а 6 правильно помечены как собаки.
Если у вас есть какие-либо комментарии или вопросы, не стесняйтесь оставлять свои отзывы ниже. Для получения дополнительных статей посетите KeytoDataSicence. Вы всегда можете связаться со мной в LinkedIn.
Классификация — одна из наиболее популярных технологий интеллектуального анализа данных. С необходимостью построения классификаторов рано или поздно сталкивается любой аналитик. Но даже построив модель, необходимо прежде всего убедиться в ее работоспособности. Для этого разработано большое количество мер качества. Наиболее популярные из них рассматриваются в данной статье.
Для классификационных моделей, как и для моделей регрессии, актуальна задача оценки их качества для определения работоспособности моделей и их сравнения. Однако решение этой задачи для моделей классификации вообще, и бинарной классификации в частности, сложнее, чем для регрессии. Связано это с тем, что целевая переменная (метка класса) является категориальным (дискретным) значением, и, следовательно, ошибка классификации не может быть выражена числовым значением.
Поэтому в основе оценки качества классификационных моделей лежит статистика результатов классификации обучающих примеров. С ее помощью вычисляются метрики качества — показатели, которые зависят от результатов классификации и не зависят от внутреннего состояния модели.
Среди наиболее популярных методов оценки качества классификаторов можно выделить следующие:
- Матрица ошибок (Сonfusion matrix).
- Меткость (Accuracy).
- Точность (Precision).
- Полнота (Recall).
- Специфичность (Specificity).
- F1-мера (F1-score).
- Метрика P4 .
- Площадь под ROC-кривой (Area under ROC-curve, AUC-ROC).
- Площадь под кривой полнота-точность (Area under precision-recall curve, AUC-PR).
- Коэффициент корреляции Мэтьюса (Matthews correlation coefficient, MCC).
- Функция потерь логистической регрессии (Logistic loss function, Log Loss).
Матрица ошибок
Прежде чем переходить к описанию собственно метрик качества бинарных классификаторов, рассмотрим методику описания этих метрик в терминах ошибок классификации. Пусть заданы два класса y=left { 0,1 right } и алгоритм, предсказывающий принадлежность каждого объекта одному из классов. Эта задача анализа известна как бинарная классификация.
Приведем пример. Пусть в страховой компании используется аналитическая платформа для поддержки принятия решений о целесообразности страхования того или иного объекта. Если риск наступления страхового события выше определенного порога, то такие объекты страховать нецелесообразно. Именно выявление таких объектов и является целью анализа. Тогда для объектов, страхование которых целесообразно, система должна установить класс 0, а объектам, в страховании которых отказано, — класс 1.
Любой реальный классификатор совершает ошибки. В нашем случае таких ошибок может быть две:
- класс 0 распознается классификатором как класс 1, что можно интерпретировать как «ложную тревогу»;
- класс 1 распознается как класс 0, что можно трактовать как «пропуск цели».
Очевидно, что приведенные ошибки неравноценны по связанным с ними издержкам классификации. В случае «ложной тревоги» компания потеряет только потенциальную страховую премию, т.е. будет иметь место всего лишь упущенная выгода. В случае «пропуска цели» возможна потеря значительной суммы из-за наступления страхового случая. Поэтому важнее не допустить «пропуск цели», чем «ложную тревогу».
Иными словами, важнее правильно определить объект, нежелательный для страхования из-за высокого риска, чем ошибиться в распознавании желательного. Будем называть соответствующий исход классификации положительным (объект не подлежит страхованию y=1), а противоположный — отрицательным (объект подлежит страхованию y=0). Тогда возможны следующие исходы классификации:
- Объект, нежелательный для страхования, классифицирован как нежелательный, т.е. «положительный» класс распознан как положительный. Такой исход классификации (а также пример, для которого он получен) называют истинноположительным.
- Объект, желательный для страхования, распознан как желательный, т.е. «отрицательный» класс распознан как отрицательный. Такой исход классификации называют истинноотрицательными.
- Объект, желаемый для страхования, классифицирован как не желаемый, т.е. имела место ошибка, в результате которой отрицательный класс был распознан как положительный. Данный исход классификации называют ложноположительным, а ошибка классификации называется ошибкой I рода.
- Нежелательный объект распознан как желательный, т.е. имела место ошибка, в результате которой положительный класс был распознан как отрицательный. Такой исход классификации называется ложноотрицательным, а ошибка классификации — ошибкой II рода.
Таким образом, ошибка I рода, или ложноположительный исход классификации, имеет место, когда пример, с которым связано отрицательное событие распознан моделью как положительный. Ошибкой II рода, или ложноотрицательным исходом классификации, называют случай, когда пример, с которым связано положительное событие, распознан как отрицательный. Поясним это с помощью матрицы ошибок классификации, называемой также таблицей сопряженности:
| y=0 | y=1 | |
|---|---|---|
| widehat{y}=0 | Истинноположительный (True Positive — TP) | Ложноположительный (False Positive — FP) |
| widehat{y}=1 | Ложноотрицательный (False Negative — FN) | Истинноотрицательный (True Negative — TN) |
Здесь widehat{y} — отклик модели, а y — фактическое значение. Таким образом, ошибки классификации бывают двух видов: False Negative (FN) и False Positive (FP). В данном случае P означает, что классификатор определяет класс объекта как положительный, а N как — отрицательный. T значит, что класс предсказан правильно, соответственно, F — неправильно. Каждая строка в матрице ошибок представляет предсказанный класс, а каждый столбец — фактически наблюдаемый класс.
Идеальный классификатор, если бы он существовал, выдавал бы только истинноположительные и истинноотрицательные классификации, и его матрица ошибок содержала бы значения, отличные от нуля, только на главной диагонали.
Меткость
Представляет собой долю правильных классификаций модели:
ACC=frac{TP+TN}{TP+TN+FP+FN}.
Несложно увидеть, что сумма в знаменателе формулы представляет собой общее число классифицируемых примеров. Графически это можно интерпретировать следующим образом:
Рисунок 1. Меткость
В английском языке этот термин обозначается как «accuracy», поэтому в интернете он часто упоминается как «аккуратность», хотя это слово и не передает смыслового значения данной величины.
Несмотря на то, что эта мера хорошо интерпретируется, на практике она используется достаточно редко, поскольку плохо работает в случае дисбаланса классов в обучающей выборке.
Поясним это на примере кредитного скоринга. Пусть требуется классифицировать заемщиков на добросовестных (не допустивших просрочку) и недобросовестных (допустивших просрочку). Целью является выявление недобросовестных заемщиков, поскольку связанные с ними издержки выше. Следовательно, классификация заемщика как недобросовестного является положительным событием, а как добросовестного — отрицательным.
Выборка содержит 1000 добросовестных заемщиков, 900 из которых классификатор предсказал правильно (TN=900, FP=100), и 100 недобросовестных, 50 из которых классификатор также определил верно (TP=50, FN=50).
Несложно вычислить, что:
ACC=frac{50+900}{50+900+100+50}=0.866.
Однако, если построить «наивную» модель, которая просто будет классифицировать всех клиентов, как добросовестных (на основании того, что таковых большинство), то меткость такой модели окажется:
ACC=frac{0+1000}{0+1000+0+100}=0.909.
Таким образом, оказалось, что меткость «бесполезной» модели, не имеющей предсказательной силы, выше, чем «рабочей» модели. Это противоречит здравому смыслу. Поэтому на практике стараются использовать альтернативные меры качества.
Точность
Точность равна доле истинноположительных классификаций к общему числу положительных классификаций. Данная величина часто упоминается как positive predictive value (PPV) или положительное прогностическое значение:
Pr=PPV=frac{TP}{TP+FP}.
Поясним данное выражение с помощью рисунка:
Рисунок 2. Точность
Несложно увидеть, что попытка отнести все объекты к одному классу неизбежно приведет к росту FP и уменьшению значения точности.
Полнота
Полнота, известная еще как чувствительность или доля истинноположительных примеров (TPR — true positive rate), определяется как число истинноположительных классификаций относительно общего числа положительных наблюдений:
Re=TPR=frac{TP}{TP+FN}.
Таким образом, полноту можно рассматривать как способность классификатора обнаруживать определенный класс. Графически полноту можно проиллюстрировать с помощью рисунка:
Рисунок 3. Полнота
Точность и полноту для каждого класса легко определять с помощью матрицы ошибок. Точность равна отношению соответствующего диагонального элемента матрицы и суммы элементов всей строки класса, а полнота — отношению диагонального элемента матрицы и суммы элементов всего столбца класса.
PPV_{c}=frac{A_{cc}}{sumlimits_{i=1}^{n}A_{ci}},
TPR_{c}=frac{A_{cc}}{sumlimits_{i=1}^{n}A_{ic}},
где c — класс, n — число элементов столбца (равно числу классов), i — номер элемента в столбце, A — элемент матрицы ошибок.
Специфичность
Специфичность классификатора — это доля истинноотрицательных (True Negative Rate — TNR) классификаций в общем числе отрицательных классификаций:
Sp=TNR=frac{TN}{TN+FP}.
TNR показывает, насколько хорошо модель классифицирует отрицательные примеры. Поясним это с помощью рисунка.
Рисунок 4. Специфичность
Очевидно, что если все отрицательные примеры классифицированы правильно (т.е. число ложноположительных случаев равно 0), то TPR=1.
F1-мера
Точность и полнота, в отличие от меткости, не зависят от соотношения классов и, следовательно, могут применяться в условиях несбалансированных выборок. На практике часто встречается задача поиска оптимального баланса между точностью и полнотой. Действительно, улучшая настройку модели на один класс, например, путем изменения дискриминационного порога, мы тем самым ухудшаем настройку на другой.
Чем выше точность и полнота, тем лучше модель. Но на практике их максимальные значения одновременно недостижимы, поэтому приходится искать баланс между ними. Для этого используется метрика, объединяющая в себе информацию о точности и полноте. Она называется F1-мера и вычисляется следующим образом:
F1=frac{2cdot PPVcdot TPR}{PPV+TPR}=frac{2cdot TP}{2cdot TP+FP+FN}.
В данном выражении точность PPV и полнота TPR имеют одинаковый вес, поэтому при их уменьшении F1-мера сокращается пропорционально.
Однако на практике чаще используется сбалансированная F1-мера, в которой точности и полноте присваиваются разные веса с целью найти оптимальный баланс между данными метриками. Для этого в формулу для F1-меры вводится дополнительный балансировочный параметр, обозначаемый β. Сбалансированная F1-мера вычисляется следующим образом:
F1=frac{(1-beta ^{2})cdot PPVcdot TPR}{beta ^{2}cdot PPV+TPR}.
Если параметр принимает значения из диапазона 0< beta < 1, то приоритет имеет точность, а если beta> 1, то полнота.
Еще одним источником критики F1-меры является отсутствие симметрии. Это означает, что она может изменить свое значение при инверсии положительного и отрицательного классов.
Метрика P4
Метрика P_{4} была разработана как расширение F1-меры, обладающее симметрией относительно инверсии классов. Вычисляется по формуле:
P_{4}=frac{4cdot TPcdot TN}{4cdot TPcdot TN+(TP+TN)cdot (FP+FN)}.
Метрика P_{4} изменяется в диапазоне от 0 до 1. Чем ближе значение метрики к 1, тем лучше работает модель. Очевидно, что значение меры стремится к 0, если хотя бы один из множителей в числителе становится равным нулю, т.е. когда модель теряет способность правильно распознавать положительные или отрицательные примеры.
AUC-ROC
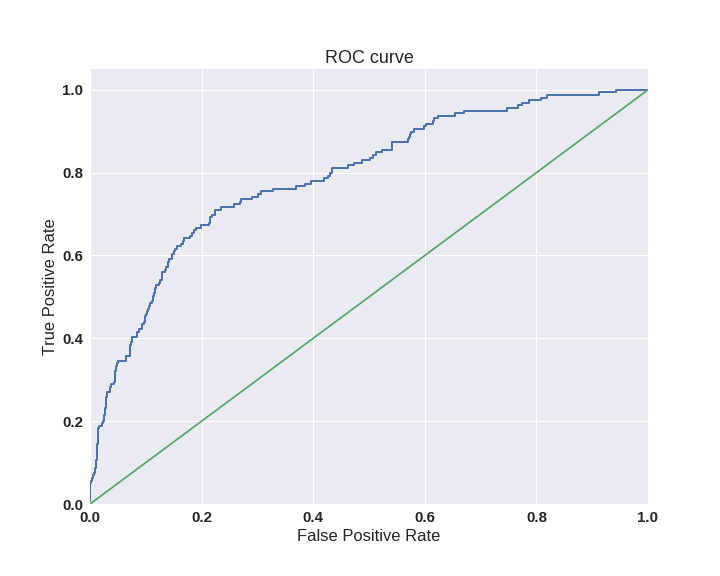
ROC-кривая, или кривая рабочих характеристик приемника (Receiver Operating Characteristics curve), позволяет не только оценить качество работы классификатора, но и исследовать его поведение при различных значениях дискриминационного порога. Технология оценки качества моделей бинарной классификации с помощью ROC-кривых известна как ROC-анализ.
Рассмотрим совместно TPR и TNR классификатора. TPR показывает, насколько хорошо модель классифицирует положительные примеры. Очевидно, что если все положительные примеры классифицированы правильно (т.е. число ложноотрицательных случаев равно 0), то TPR=1. TNR показывает, насколько хорошо модель классифицирует отрицательные примеры. Очевидно, что если все отрицательные примеры классифицированы правильно (т.е. число ложноположительных случаев равно 0), то TPR=1.
Таким образом, по отдельности TPR и TNR характеризуют способность модели распознавать только один из классов. Но их совместное использование помогает создать метрику, которая позволяет выбирать значение дискриминационного порога, который оптимально балансирует модель между способностью распознавать положительные и отрицательные примеры. Именно эта задача и решается с помощью ROC-кривой.
Действительно, если изменять дискриминационный порог от 0 до 1 и наносить по оси абсцисс точки 1−TNR, а по оси ординат TPR, то полученный график и будет ROC-кривой. Величину 1−TNR называют долей ложноположительных классификаций (false positive rate) или показателем ложной тревоги. Она вычисляется следующим образом:
1-TNR=FPR=frac{FP}{FP+TN}.
При пороге, равном 1, все примеры будут классифицированы как отрицательные (FPR=1, TPR=1), а при пороге, равном 0, — как положительные (FPR=0, TPR=0). Поэтому ROC-кривая всегда идет от точки (0,0) до точки (1,1).
Рисунок 5. ROC-кривая
Несложно увидеть, что для идеальной модели ROC-кривая превращается в ломаную, проходящую через точки (0,0), (0,1) и (1,1). При этом площадь под ROC-кривой (AUC — Area Under Curve) окажется равной 1. Площадь под кривой выделена на рисунке светло-серым цветом.
Точка (0,1) соответствует идеальному состоянию модели, в котором и TPR, и TNR одновременно равны 1. Т.е. модель одинаково хорошо «научилась» работать как с положительными, так и с отрицательными примерами при существующем в обучающей выборке балансе классов.
Идеальная модель является скорее гипотетической и на практике, как правило, недостижима. Поэтому обычно приходится иметь дело с ROC-кривыми, которые не проходят через точку (0,1), а приближаются к ней на определенное расстояние. Соответственно и AUC−ROC оказывается меньше 1.
Таким образом показатель AUC−ROC является удобной мерой качества классификатора относительно идеального. Принята следующая шкала оценки качества.
| AUC | Оценка |
|---|---|
| 0.9 — 1 | Отличное |
| 0.8 — 0.9 | Очень хорошее |
| 0.7 — 0.8 | Хорошее |
| 0.6 — 0.7 | Удовлетворительное |
| 0.5 — 0.7 | Плохое |
Если AUC-ROC=0.5, то ROC-кривая превращается в линию, проходящую через точки (0,0) и (1,1), которая соответствует бесполезному классификатору, работающему как случайный предсказатель. Если AUC-ROC< 0.5, то получается модель, которая работает хуже случайного предсказателя и от ее использования следует отказаться.
AUC-PR
PR-кривые определяются аналогично ROC-кривым, но только по оси абсцисс у них откладываются значения полноты, а по оси ординат — точности.
Точность и полнота — две наиболее важные метрики, на которые следует обращать внимание при оценке качества модели бинарной классификации в условиях несбалансированности классов. Они помогают увидеть, какая часть фактически положительных наблюдений была классифицирована правильно, и какие среди классифицированных как положительные, были истинноположительными.
Если точность равна 1, то ложноположительные классификации отсутствуют. Но это ничего не говорит о том, были ли распознаны все положительные примеры. Если полнота равна 1, то все положительные объекты были распознаны правильно, а ложноотрицательные классификации отсутствуют. При этом ничего не говорится о том, сколько было допущено ложноположительных классификаций.
Таким образом, точность и полнота не особенно полезны для оценки качества классификатора, если их использовать по отдельности. В задаче классификации оценка точности, равная 1 для класса C, означает, что каждый элемент, помеченный как принадлежащий классу C, действительно принадлежит к классу C, но ничего не говорит о количестве элементов из класса
C, которые не были правильно классифицированы. Тогда как полнота, равная 1, означает, что каждый элемент из класса C был помечен как принадлежащий к классу C, но ничего не говорит о том, сколько элементов из других классов были также неправильно классифицированы как принадлежащие к классу C.
Обычно показатели точности и полноты не используются по отдельности. Вместо этого либо значения одной меры сравниваются с фиксированным уровнем другой (например, точность на уровне полноты 0.75), либо обе меры объединяются в один показатель. Примерами такой комбинации и является F1-мера — взвешенное гармоническое среднее точности и полноты.
Еще одним способом комбинирования точности и полноты в задаче оценки качества классификации являются так называемые кривые полнота-точность, которые строятся в системе координат, где по оси абсцисс откладывается полнота, а по оси ординат — точность. Кривая точность-полнота показывает, как выбор порога влияет на точность классификатора, а также помогает выбрать лучшее значение дискриминационного порога для определенного баланса классов.
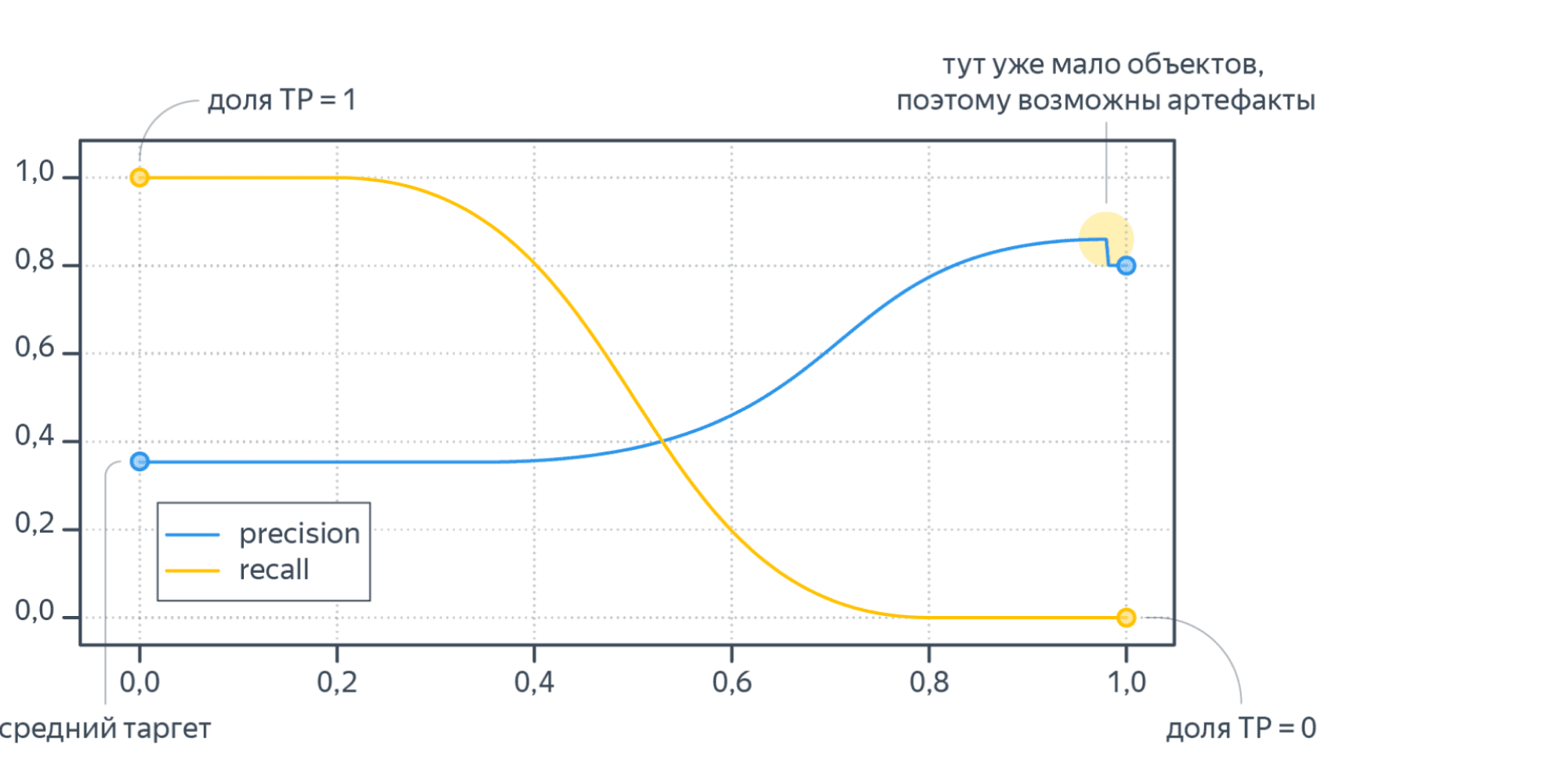
Рисунок 6. Кривая точность-полнота
Каждая точка PR-кривой представляет определенное значение дискриминационного порога, а ее расположение соответствует результирующей точности и полноте, когда этот порог выбран. Точка 1 на рисунке соответствует значению дискриминационного порога, равному 1, а точка 3 — значению порога 0. Точка 2 соответствует идеальному классификатору и совпадает с координатами (1,1), а точка 4 — оптимальному значению порога (точка кривой, наиболее близкая к идеальной точке (1,1)).
Преимущества PR-кривой по сравнению с ROC:
- ROC-кривая, как правило, дает чрезмерно оптимистичную картину в условиях несбалансированности классов.
- При изменении распределения классов ROC-кривая не меняется, а PR-кривая отражает изменение.
Аналогично ROC-кривой, площадь под PR-кривой (для отличия от ROC ее часто называют PR−AUC) отражает качество классификатора и позволяет сравнивать кривые, соответствующие различным балансам классов и значениям порога. Чем выше площадь, тем лучше работает модель.
Пунктирная линия внизу графика соответствует бесполезному классификатору (no-skill model — модель без навыков, или базовая модель), уровень которой изменяется при изменении баланса классов. Такая модель будет присваивать рейтинг 0.5 для любого примера.
На рисунке ниже представлена линия, соответствующая балансу классов, когда положительные примеры составляют 10% от обучающей выборки.
Рисунок 7. Кривая точность-полнота при фиксированном балансе классов
На рисунке точка 1 соответствует порогу 0.5, точка 2 соответствует порогу [0, 0.5). Для порогов (0.5, 1] точность не определена из-за деления на ноль. Можно увидеть, что точность здесь является константой, то есть PPV=0.1 (соответствует доле положительного класса), PR−AUC=0.1.
Таким образом, полнота базовой модели лежит в диапазоне (0.5, 1] независимо от дисбаланса классов, а точность равна доле положительного класса в обучающей выборке.
На следующем рисунке представлена PR-кривая для идеальной модели. На ней точка 1 соответствует порогу (0, 1], точка 2 соответствует порогу 0. Очевидно, что PR−AUC=1.
Рисунок 8. Кривая точность-полнота для идеальной модели
И, наконец, на рисунке ниже отображена PR-кривая (красная линия) для модели, которая работает хуже, чем базовая модель «без навыков» (синяя пунктирная линия). Она расположена ниже линии базовой модели.
Рисунок 9. Кривая точность-полнота для модели хуже бесполезной
Очевидный способ повысить качество «плохой» модели без каких-либо настроек — просто инвертировать классы (класс 0 изменить на класс 1). Это автоматически приведет к повышению точности по сравнению с базовой моделью.
Обычно «плохая» PR-кривая классификатора указывает на то, что в обучающих данных присутствуют проблемы: они содержат шум или классы в них плохо выражены (модель не может выявить закономерность, в соответствии с которой один класс отличается от другого). В этом случае PR−AUC не превышает доли положительных примеров обучающей выборке.
Возможен гибридный случай, когда «плохая» модель работает лучше, чем модель «без навыков», но для определенных пороговых значений.
Коэффициент корреляции Мэтьюса
Коэффициент используется в качестве показателя качества бинарных классификаторов. Он учитывает истинные и ложные классификации и обычно рассматривается как сбалансированная мера, которую можно использовать даже в условиях сильного дисбаланса классов.
MCC, по сути, коэффициент корреляции между фактическими и предсказанными моделью бинарными классификациями. Он изменяется в диапазоне от -1 до 1. MCC=1 указывает на идеальную классификацию, когда фактические и предсказанные классы совпадают для всех обучающих примеров (т.е. ложноположительные и ложноотрицательные классификации отсутствуют). Модель, для которой MCC=0, соответствует случайному предсказателю. MCC=−1 указывает на полное расхождение между фактом и предсказанием (т.е. вместо положительного класса модель всегда предсказывает отрицательный, и наоборот), следовательно, истинноположительные и истинноотрицательные классификации отсутствуют.
Формула для расчета MCC имеет вид:
MCC=frac{TPcdot TN-FPcdot FN}{sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)}}.
Несложно увидеть, что если в этой формуле обнулить все ложные классификации, то MCC=1, что соответствует ранее сделанным заключениям. Если число истинных и ложных классификаций равны, то числитель формулы становится равным 0 и MCC=0. И, наконец, если число истинных классификаций равно нулю, то числитель становится отрицательным, и делает таковым результат формулы.
Если какая-либо из четырех сумм в знаменателе равна нулю, знаменатель можно произвольно установить равным единице, это приводит к нулевому коэффициенту корреляции Мэтьюса.
Функция потерь логистической регрессии (Logistic loss function, Log Loss).
Функция потерь в задачах классификации показывает, какую «цену» придется заплатить за неточность предсказаний классификационной модели. Для логистической регрессии, решающей задачу бинарной классификации, она может быть вычислена следующим образом:
Log Loss=-frac{1}{l}sumlimits_{i=1}^{l}(y_{i}cdot log(widehat{y_{i}})+(1-y_{i})cdot log(1-widehat{y_{i}})),
где l — размер выборки, y_{i}=left { 0,1 right } — бинарная метка класса, заданная в примере, widehat{y_{i}} — предсказание модели.
Несложно увидеть, что функция потерь получается путем суммирования логарифма потерь на каждом примере. Потери на каждом примере определяются следующим образом: если предсказанный класс совпадает с фактическим, то потери равны 0, в противном случае потери равны 1. Очевидно, чем больше будет неправильных классификаций, тем больше будет значение LogLoss и тем хуже будет модель. Таким образом, чтобы получить лучшую модель, нужно минимизировать функцию потерь.
Преимуществом метрики LogLoss является устойчивость к выбросам и аномальным значениям в данных и простота вычисления. Недостатком — сложность интерпретации из-за нелинейного характера.
Сравнение метрик
Подведем итоги, кратко резюмируя преимущества и недостатки рассмотренных мер качества классификационных моделей.
| Мера | Преимущества | Недостатки |
|---|---|---|
| Меткость | Хорошо интерпретируется. | Чувствительна к дисбалансу классов. Неадекватно отражает точность классификации. |
| Точность | Не чувствительна к дисбалансу классов. | Отражает качество классификации только для положительного класса. |
| Полнота | Не чувствительна к дисбалансу классов. | Не учитывает отрицательные классификации. |
| Специфичность | Просто вычисляется и интерпретируется. | Характеризует способность модели распознавать только один класс. |
| F1-мера | Позволяет найти баланс между точностью и полнотой. | Чувствительность к дисбалансу, отсутствие симметрии. |
| P4 | Симметрична относительно инверсии классов. | Чувствительность к дисбалансу классов. |
| AUC-ROC | Наглядна, хорошо интерпретируется. | В условиях дисбаланса классов завышает качество модели. Не отражает изменения баланса классов. |
| AUC-PR | Наглядна, хорошо интерпретируется. | Не учитывает отрицательные классификации. |
| Коэффициент Мэтьюса | Более информативен, поскольку использует все типы результатов классификации. | Не может применяться, если один из множителей в знаменателе обращается в 0. |
| LogLoss | Устойчивость к выбросам в данных, простота вычисления. | Сложность интерпретации из-за нелинейного характера. |
В статье рассмотрены наиболее общие меры оценки качества моделей бинарной классификации, отмечены их преимущества и недостатки. Однако в литературе авторы предлагают и другие подходы, которые показали хорошие результаты при решении конкретных задач и не претендующие на универсальность.
Другие материалы по теме:
Метрики качества линейных регрессионных моделей
Отбор переменных в моделях линейной регрессии
Репрезентативность выборочных данных
Были ли вы в ситуации, когда вы ожидали, что ваша модель машинного обучения должна работать очень хорошо, но у нее была низкая точность? Вы проделали всю тяжелую работу — так где же модель классификации сработала не так? Как это исправить?
Существует множество способов оценить эффективность вашей модели классификации, но ни один из них не выдержал испытания временем, кроме матрицы ошибок. Она помогает нам оценить, как наша модель работала, где она пошла не туда, и предлагает нам рекомендации по исправлению нашего пути.
В этой статье мы рассмотрим, как матрица ошибок дает целостное представление об эффективности вашей модели. И, в отличие от названия, вы поймете, что матрица ошибок — довольно простая, но мощная концепция. Итак, давайте раскроем тайну матрицы ошибок!
Что такое матрица ошибок?
Вопрос на миллион долларов — что такое, в конце концов, матрица ошибок?
Матрица ошибок — это матрица размером N x N, используемая для оценки эффективности модели классификации, где N — количество целевых классов. Матрица сравнивает фактические целевые значения с предсказанными моделью машинного обучения. Это дает нам целостное представление о том, насколько хорошо работает наша классификационная модель и какие ошибки она допускает.
Для задачи двоичной классификации у нас будет матрица 2 x 2, как показано ниже, с 4 значениями:
Расшифруем матрицу:
- Целевая переменная имеет два значения: положительное или отрицательное.
- Столбцы представляют фактические значения целевой переменной.
- Строки представляют собой прогнозируемые значения целевой переменной.
Но подождите — что здесь TP, FP, FN и TN? Это важнейшая часть матрицы ошибок. Давайте разберемся с каждым термином ниже.
Понимание True Positive, True Negative, False Positive и False Negative в матрице ошибок
True Positive (TP)
- Прогнозируемое значение соответствует фактическому значению.
- Фактическое значение было положительным, и модель предсказала положительное значение.
True Negative (TN)
- Прогнозируемое значение соответствует фактическому значению.
- Фактическое значение было отрицательным, и модель предсказала отрицательное значение.
False Positive (FP) — ошибка 1-го типа
- Прогнозируемое значение было предсказано неверно.
- Фактическое значение было отрицательным, но модель предсказала положительное значение.
- Также известна как ошибка 1-го типа.
False Negative (FN) — ошибка 2-го типа
- Прогнозируемое значение было предсказано неверно.
- Фактическое значение было положительным, но модель предсказала отрицательное значение.
- Также известна как ошибка 2-го типа.
Позвольте мне привести пример, чтобы лучше это понять. Предположим, у нас есть набор данных классификации с 1000 точками данных. Мы подгоняем на нем классификатор и получаем следующую матрицу ошибок:
Различные значения матрицы ошибок будут следующими:
- True Positive (TP) = 560; это означает, что 560 положительных точек данных были правильно классифицированы моделью.
- True Negative (TN) = 330; это означает, что 330 отрицательных точек данных были правильно классифицированы моделью.
- False Positive (FP) = 60; это означает, что 60 отрицательных точек данных были неправильно классифицированы моделью как положительные.
- False Negative (FN) = 50; это означает, что 50 положительных точек данных были неправильно классифицированы моделью как отрицательные.
Это оказался довольно приличный классификатор для нашего набора данных, учитывая относительно большее количество истинно положительных и истинно отрицательных значений.
Помните об ошибках 1-го и 2-го типа. Интервьюеры любят спрашивать, в чем разница между ними!
Зачем нам нужна матрица ошибок?
Прежде чем ответить на этот вопрос, давайте подумаем о проблеме гипотетической классификации.
Допустим, вы хотите предсказать, сколько людей инфицировано заразным вирусом, до того, как у них проявятся симптомы, и изолировать их от здорового населения. Двумя значениями для нашей целевой переменной будут: Sick и Not Sick.
Теперь вы, должно быть, задаетесь вопросом — зачем нам матрица ошибок, когда у нас есть наш вечный друг — Точность? Что ж, посмотрим, где точность не работает.
Наш набор данных является примером несбалансированного набора данных. Имеется 947 точек данных для отрицательного класса и 3 точки данных для положительного класса. Вот как мы рассчитаем точность:
Посмотрим, как работает наша модель:
Общие значения результатов:
TP = 30, TN = 930, FP = 30, FN = 10
Итак, точность для нашей модели:
96%! Неплохо!
Но это дает неверное представление о результате. Подумайте об этом.
Наша модель гласит: «Я могу предсказать заболевание в 96% случаев». Однако она делает наоборот. Это предсказание людей, которые не заболеют с точностью 96%, пока больные распространяют вирус!
Как вы думаете, это правильный показатель для нашей модели, учитывая серьезность проблемы? Разве мы не должны измерять, сколько положительных случаев мы можем правильно предсказать, чтобы остановить распространение заразного вируса? Или, из правильно спрогнозированных случаев сколько положительных случаев для проверки надежности нашей модели?
Здесь мы сталкиваемся с двойным понятием «точность (Precision) и полнота (Recall)».
Precision vs. Recall
Точность говорит нам, сколько из правильно предсказанных случаев действительно оказались положительными.
Вот как рассчитать точность:
Это определило бы надежность нашей модели.
Полнота сообщает нам, сколько реальных положительных случаев мы смогли правильно предсказать с помощью нашей модели.
А вот как мы можем рассчитать полноту:
Мы можем легко рассчитать точность и полноту для нашей модели, подставив значения в приведенные выше уравнения:
50% процентов правильно предсказанных случаев оказались положительными. В то время как 75% положительных результатов были успешно предсказаны нашей моделью. Потрясающие!
Точность — полезный показатель в тех случаях, когда ложноположительный результат важнее, чем ложноотрицательный.
Точность важна в системах рекомендаций по музыке или видео, на веб-сайтах электронной коммерции и т. д. Неправильные результаты могут привести к оттоку клиентов и нанести вред бизнесу.
Полнота — полезный показатель в случаях, когда ложноотрицательный результат важнее ложноположительного.
Полнота важна в медицинских случаях, когда не имеет значения, что возникает ложная тревога, но реальные положительные случаи не должны оставаться незамеченными!
В нашем примере полнота была бы лучшим показателем, потому что мы не хотим, чтобы случайно выписали инфицированного человека и позволили ему смешаться со здоровым населением, тем самым распространяя заразный вирус. Теперь вы можете понять, почему точность была плохим показателем для нашей модели.
Но будут случаи, когда нет четкой разницы между тем, что важнее: точность или полнота. Что нам делать в таких случаях? Мы их совмещаем!
F1-Score
На практике, когда мы пытаемся повысить точность нашей модели, полнота снижается, и наоборот. F1-Score отражает обе тенденции в одном значении:
F1-Score представляет собой гармоничное среднее значение точности и полноты, поэтому дает общее представление об этих двух показателях. Оно максимально, когда точность равно полноте.
Но здесь есть одна загвоздка. Интерпретируемость оценки F1 оставляет желать лучшего. Это означает, что мы не знаем, чего добивается наш классификатор — точности или полноты? Итак, мы используем его в сочетании с другими оценочными метриками, что дает нам полную картину результата.
Матрица ошибок с использованием scikit-learn в Python
Вы знаете теорию — теперь давайте применим ее на практике. Давайте запрограммируем матрицу ошибок с помощью библиотеки Scikit-learn (sklearn) на Python.
# confusion matrix in sklearn
from sklearn.metrics import confusion_matrix
3 from sklearn.metrics import classification_report
# actual values
actual = [1,0,0,1,0,0,1,0,0,1]
# predicted values
predicted = [1,0,0,1,0,0,0,1,0,0]
# confusion matrix
matrix = confusion_matrix(actual,predicted, labels=[1,0])
print(‘Confusion matrix : n’,matrix)
# outcome values order in sklearn
tp, fn, fp, tn = confusion_matrix(actual,predicted,labels=[1,0]).reshape(-1)
print(‘Outcome values : n’, tp, fn, fp, tn)
# classification report for precision, recall f1-score and accuracy
matrix = classification_report(actual,predicted,labels=[1,0])
print(‘Classification report : n’,matrix)
Sklearn имеет две отличные функции: confusion_matrix() и classification_report().
возвращает значения матрицы ошибок. Однако результат немного отличается от того, что мы изучили до сих пор. Она принимает строки как фактические значения, а столбцы как прогнозные значения. В остальном концепция осталась прежней.
выводит точность, полноту и f1-score для каждого целевого класса. В дополнение к этому, она также имеет некоторые дополнительные значения: micro avg, macro avg и weighted avg.
Mirco average — это оценка точности/полноты/f1, рассчитанная для всех классов.
Macro average — это среднее значение точности/полноты/f1-score.
Weighted average — это просто средневзвешенное значение точности/полноты/f1-score.
Матрица ошибок для мультиклассовой классификации
Как матрица ошибок будет работать для задачи классификации нескольких классов? Мы рассмотрим и этот случай.
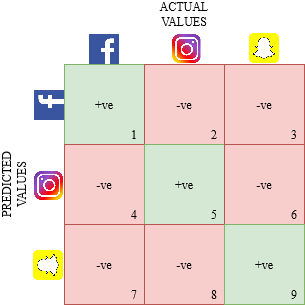
Давайте нарисуем матрицу ошибок для мультиклассовой задачи, в которой мы должны предсказать, любит ли человек Facebook, Instagram или Snapchat. Матрица ошибок будет иметь вид 3 x 3:
true positive, true negative, false positive и false negative для каждого класса будут вычисляться путем сложения значений ячеек следующим образом:
Вот и все! Вы готовы расшифровать любую матрицу ошибок размером N x N!
Заключение
И вдруг матрица ошибок перестает быть такой запутанной! Эта статья должна дать вам прочную основу для интерпретации и использования матрицы ошибок для алгоритмов классификации в машинном обучении.
Вскоре мы выпустим статью о кривой AUC-ROC и продолжим наше обсуждение там. До этого не теряйте надежды на свою модель классификации, возможно, вы просто используете неправильную метрику оценки!
На чтение 3 мин. Опубликовано 13.06.2019
Перевод статьи – Understanding Confusion Matrix – Sarang Narkhede
Когда мы получаем данные после очистки, предварительной обработки и обработки данных, первым шагом, который мы делаем, является создание модели и, конечно, получение результатов в вероятностях. Но держись! Как, черт возьми, мы можем измерить эффективность нашей модели? Лучшая эффективность, лучшая производительность и это именно то, что мы хотим. В данном случае мы начинаем использовать матрицу ошибок. Матрица ошибок (Confusion Matrix) – это измерение производительности для классификации машинного обучения.
Содержание
- Этот пост призван ответить на следующие вопросы:
- Что такое матрица ошибок, и зачем она нужна?
- Как вычислить матрицу ошибок для задачи классификации с бинарными классами?
Этот пост призван ответить на следующие вопросы:
- Что такое Матрица ошибок и зачем она нужна?
- Как вычислить матрицу ошибок для задач бинарной классификации?
Сегодня давайте разберемся с матрицей путаницы раз и навсегда.
Что такое матрица ошибок, и зачем она нужна?
Ну, это измерение производительности для задачи классификации машинного обучения, где выходной может быть два или более классов. Это таблица с 4 различными комбинациями прогнозируемых и фактических значений.
Это чрезвычайно полезно для вычисления Полноты, Точности, Специфичность, Точность и, что наиболее важно кривой ошибок AUC-ROC.
Давайте поймем термины TP, FP, FN, TN на примере аналогии с беременностью.
TP — истино-положительное решение:
Интерпретация: Вы предсказали положительное, и это правда.
Вы предсказали, что женщина беременна, и она на самом деле беременна.
TN — истино-отрицательное решение:
Интерпретация: Вы прогнозировали отрицательное значения, и это правда.
Вы предсказали, что мужчина не беременен, а он на самом деле не беременен.
FP — ложно-положительное решение (Ошибка типа 1):
Интерпретация: Вы предсказали положительное значение, и это неверно.
Вы предсказали, что мужчина беременен, но на самом деле это не так.
FN— ложно-отрицательное решение (Ошибка Типа 2):
Интерпретация: Вы предсказали отрицательное значение, и это неверно.
Вы предсказали, что женщина не беременна, но она на самом деле беременная.
Только помните, мы описываем прогнозируемые значения как положительные и отрицательные, а фактические значения как истинные и ложные.
How to Calculate Confusion Matrix for a 2-class classification problem?
Как вычислить матрицу ошибок для задачи классификации с бинарными классами?
Давайте разберемся с матрицей ошибок посредством математик
Полнота Recall
Из всех положительных классов, сколько мы предсказали правильно. Это должно быть как можно выше.
Точность Precision
Из всех классов, сколько мы предсказали правильно. Это должно быть как можно выше.
F-мера
Трудно сравнить две модели с низкой точностью и высокой отзывчивостью или наоборот. Поэтому, чтобы сделать их сопоставимыми, мы используем F-меру. F-мера помогает измерять Полноту и Точность одновременно. Она использует гармоническое среднее вместо среднего арифметического, наказывая экстремальные значения больше.
https://towardsdatascience.com/understanding-confusion-matrix-a9ad42dcfd62
Матрица ошибок – это метрика производительности классифицирующей модели Машинного обучения (ML).
Когда мы получаем данные, то после очистки и предварительной обработки, первым делом передаем их в модель и, конечно же, получаем результат в виде вероятностей. Но как мы можем измерить эффективность нашей модели? Именно здесь матрица ошибок и оказывается в центре внимания.
Матрица ошибок – это показатель успешности классификации, где классов два или более. Это таблица с 4 различными комбинациями сочетаний прогнозируемых и фактических значений.
Давайте рассмотрим значения ячеек (истинно позитивные, ошибочно позитивные, ошибочно негативные, истинно негативные) с помощью «беременной» аналогии.
Истинно позитивное предсказание (True Positive, сокр. TP)
Вы предсказали положительный результат, и женщина действительно беременна.
Истинно отрицательное предсказание (True Negative, TN)
Вы предсказали отрицательный результат, и мужчина действительно не беременен.
Ошибочно положительное предсказание (ошибка типа I, False Positive, FN)
Вы предсказали положительный результат (мужчина беременен), но на самом деле это не так.
Ошибочно отрицательное предсказание (ошибка типа II, False Negative, FN)
Вы предсказали, что женщина не беременна, но на самом деле она беременна.
Давайте разберемся в матрице ошибок с помощью арифметики.
Пример. Мы располагаем датасетом пациентов, у которых диагностируют рак. Зная верный диагноз (столбец целевой переменной «Y на самом деле»), хотим усовершенствовать диагностику с помощью модели Машинного обучения. Модель получила тренировочные данные, и на тестовой части, состоящей из 7 записей (в реальных задачах, конечно, больше) и изображенной ниже, мы оцениваем, насколько хорошо прошло обучение.
Модель сделала свои предсказания для каждого пациента и записала вероятности от 0 до 1 в столбец «Предсказанный Y». Мы округляем эти числа, приводя их к нулю или единице, с помощью порога, равного 0,6 (ниже этого значения – ноль, пациент здоров). Результаты округления попадают в столбец «Предсказанная вероятность»: например, для первой записи модель указала 0,5, что соответствует нулю. В последнем столбце мы анализируем, угадала ли модель.
Теперь, используя простейшие формулы, мы рассчитаем Отзыв (Recall), точность результата измерений (Precision), точность измерений (Accuracy), и наконец поймем разницу между этими метриками.
Отзыв
Из всех положительных значений, которые мы предсказали правильно, сколько на самом деле положительных? Подсчитаем, сколько единиц в столбце «Y на самом деле» (4), это и есть сумма TP + FN. Теперь определим с помощью «Предсказанной вероятности», сколько из них диагностировано верно (2), это и будет TP.
$$Отзыв = frac{TP}{TP + FN} = frac{2}{2 + 2} = frac{1}{2}$$
Точность результата измерений (Precision)
В этом уравнении из неизвестных только FP. Ошибочно диагностированных как больных здесь только одна запись.
$$Точностьspaceрезультатаspaceизмерений = frac{TP}{TP + FP} = frac{2}{2 + 1} = frac{2}{3}$$
Точность измерений (Accuracy)
Последнее значение, которое предстоит экстраполировать из таблицы – TN. Правильно диагностированных моделью здоровых людей здесь 2.
$$Точностьspaceизмерений = frac{TP + TN}{Всегоspaceзначений} = frac{2 + 2}{7} = frac{4}{7}$$
F-мера точности теста
Эти метрики полезны, когда помогают вычислить F-меру – конечный показатель эффективности модели.
$$F-мера = frac{2 * Отзыв * Точностьspaceизмерений}{Отзыв + Точностьspaceизмерений} = frac{2 * frac{1}{2} * frac{2}{3}}{frac{1}{2} + frac{2}{3}} = 0,56$$
Наша скромная модель угадывает лишь 56% процентов диагнозов, и такой результат, как правило, считают промежуточным и работают над улучшением точности модели.
SkLearn
С помощью замечательной библиотеки Scikit-learn мы можем мгновенно определить множество метрик, и матрица ошибок – не исключение.
from sklearn.metrics import confusion_matrix
y_true = [2, 0, 2, 2, 0, 1]
y_pred = [0, 0, 2, 2, 0, 2]
confusion_matrix(y_true, y_pred)Выводом будет ряд, состоящий из трех списков:
array([[2, 0, 0],
[0, 0, 1],
[1, 0, 2]])Значения диагонали сверху вниз слева направо [2, 0, 2] – это число верно предсказанных значений.
Фото: @opeleye
В компьютерном зрении обнаружение объекта — это проблема определения местоположения одного или нескольких объектов на изображении. Помимо традиционных методов обнаружения, продвинутые модели глубокого обучения, такие как R-CNN и YOLO, могут обеспечить впечатляющие результаты при различных типах объектов. Эти модели принимают изображение в качестве входных данных и возвращают координаты прямоугольника, ограничивающего пространство вокруг каждого найденного объекта.
В этом руководстве обсуждается матрица ошибок и то, как рассчитываются precision, recall и accuracy метрики.
Здесь мы рассмотрим:
- Матрицу ошибок для двоичной классификации.
- Матрицу ошибок для мультиклассовой классификации.
- Расчет матрицы ошибок с помощью Scikit-learn.
- Accuracy, Precision и Recall.
- Precision или Recall?
Матрица ошибок для бинарной классификации
В бинарной классификации каждая выборка относится к одному из двух классов. Обычно им присваиваются такие метки, как 1 и 0, или положительный и отрицательный (Positive и Negative). Также могут использоваться более конкретные обозначения для классов: злокачественный или доброкачественный (например, если проблема связана с классификацией рака), успех или неудача (если речь идет о классификации результатов тестов учащихся).
Предположим, что существует проблема бинарной классификации с классами positive и negative. Вот пример достоверных или эталонных меток для семи выборок, используемых для обучения модели.
positive, negative, negative, positive, positive, positive, negativeТакие наименования нужны в первую очередь для того, чтобы нам, людям, было проще различать классы. Для модели более важна числовая оценка. Обычно при передаче очередного набора данных на выходе вы получите не метку класса, а числовой результат. Например, когда эти семь семплов вводятся в модель, каждому классу будут назначены следующие значения:
0.6, 0.2, 0.55, 0.9, 0.4, 0.8, 0.5На основании полученных оценок каждой выборке присваивается соответствующий класс. Такое преобразование числовых результатов в метки происходит с помощью порогового значения. Данное граничное условие является гиперпараметром модели и может быть определено пользователем. Например, если порог равен 0.5, тогда любая оценка, которая больше или равна 0.5, получает положительную метку. В противном случае — отрицательную. Вот предсказанные алгоритмом классы:
positive (0.6), negative (0.2), positive (0.55), positive (0.9), negative (0.4), positive (0.8), positive (0.5)Сравните достоверные и полученные метки — мы имеем 4 верных и 3 неверных предсказания. Стоит добавить, что изменение граничного условия отражается на результатах. Например, установка порога, равного 0.6, оставляет только два неверных прогноза.
Реальность: positive, negative, negative, positive, positive, positive, negative
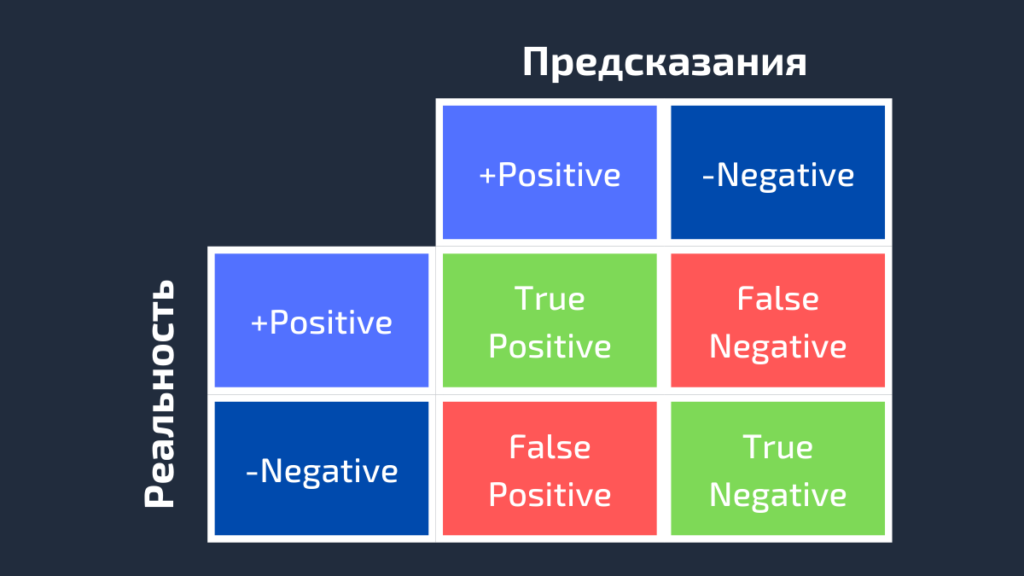
Предсказания: positive, negative, positive, positive, negative, positive, positiveДля получения дополнительной информации о характеристиках модели используется матрица ошибок (confusion matrix). Матрица ошибок помогает нам визуализировать, «ошиблась» ли модель при различении двух классов. Как видно на следующем рисунке, это матрица 2х2. Названия строк представляют собой эталонные метки, а названия столбцов — предсказанные.
Четыре элемента матрицы (клетки красного и зеленого цвета) представляют собой четыре метрики, которые подсчитывают количество правильных и неправильных прогнозов, сделанных моделью. Каждому элементу дается метка, состоящая из двух слов:
- True или False.
- Positive или Negative.
True, если получено верное предсказание, то есть эталонные и предсказанные метки классов совпадают, и False, когда они не совпадают. Positive или Negative — названия предсказанных меток.
Таким образом, всякий раз, когда прогноз неверен, первое слово в ячейке False, когда верен — True. Наша цель состоит в том, чтобы максимизировать показатели со словом «True» (True Positive и True Negative) и минимизировать два других (False Positive и False Negative). Четыре метрики в матрице ошибок представляют собой следующее:
- Верхний левый элемент (True Positive): сколько раз модель правильно классифицировала Positive как Positive?
- Верхний правый (False Negative): сколько раз модель неправильно классифицировала Positive как Negative?
- Нижний левый (False Positive): сколько раз модель неправильно классифицировала Negative как Positive?
- Нижний правый (True Negative): сколько раз модель правильно классифицировала Negative как Negative?
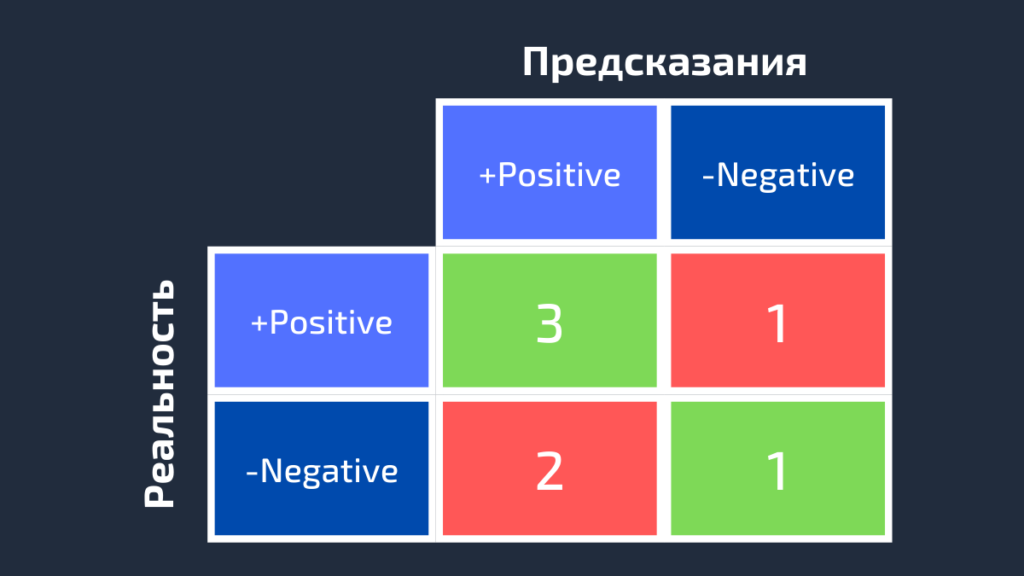
Мы можем рассчитать эти четыре показателя для семи предсказаний, использованных нами ранее. Полученная матрица ошибок представлена на следующем рисунке.
Вот так вычисляется матрица ошибок для задачи двоичной классификации. Теперь посмотрим, как решить данную проблему для большего числа классов.
Матрица ошибок для мультиклассовой классификации
Что, если у нас более двух классов? Как вычислить эти четыре метрики в матрице ошибок для задачи мультиклассовой классификации? Очень просто!
Предположим, имеется 9 семплов, каждый из которых относится к одному из трех классов: White, Black или Red. Вот достоверные метки для 9 выборок:
Red, Black, Red, White, White, Red, Black, Red, WhiteПосле загрузки данных модель делает следующее предсказание:
Red, White, Black, White, Red, Red, Black, White, RedДля удобства сравнения здесь они расположены рядом.
Реальность: Red, Black, Red, White, White, Red, Black, Red, White Предсказания: Red, White, Black, White, Red, Red, Black, White, RedПеред вычислением матрицы ошибок необходимо выбрать целевой класс. Давайте назначим на эту роль класс Red. Он будет отмечен как Positive, а все остальные отмечены как Negative.
Positive, Negative, Positive, Negative, Negative, Positive, Negative, Positive, Negative Positive, Negative, Negative, Negative, Positive, Positive, Negative, Negative, Positive11111111111111111111111После замены остались только два класса (Positive и Negative), что позволяет нам рассчитать матрицу ошибок, как было показано в предыдущем разделе. Стоит заметить, что полученная матрица предназначена только для класса Red.
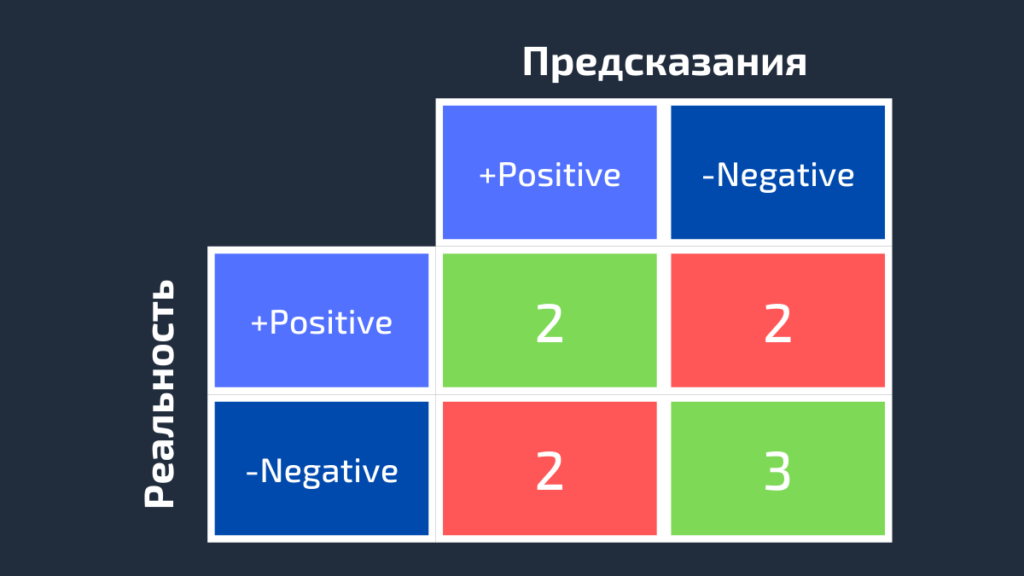
Далее для класса White заменим каждое его вхождение на Positive, а метки всех остальных классов на Negative. Мы получим такие достоверные и предсказанные метки:
Negative, Negative, Negative, Positive, Positive, Negative, Negative, Negative, Positive Negative, Positive, Negative, Positive, Negative, Negative, Negative, Positive, NegativeНа следующей схеме показана матрица ошибок для класса White.
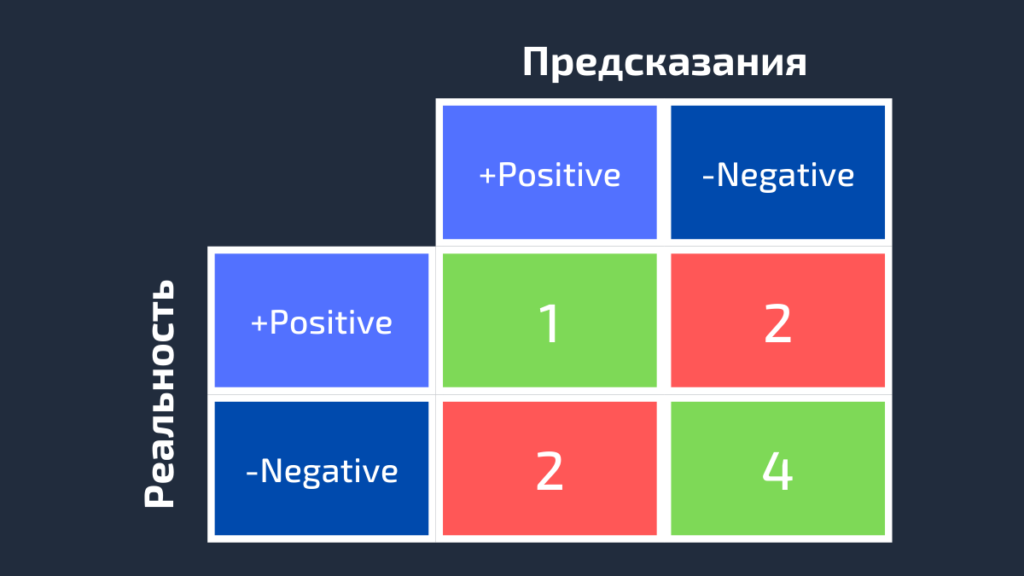
Точно так же может быть получена матрица ошибок для Black.
Расчет матрицы ошибок с помощью Scikit-Learn
В популярной Python-библиотеке Scikit-learn есть модуль metrics, который можно использовать для вычисления метрик в матрице ошибок.
Для задач с двумя классами используется функция confusion_matrix(). Мы передадим в функцию следующие параметры:
y_true: эталонные метки.y_pred: предсказанные метки.
Следующий код вычисляет матрицу ошибок для примера двоичной классификации, который мы обсуждали ранее.
array([[1, 2],
[1, 3]], dtype=int64)Обратите внимание, что порядок метрик отличается от описанного выше. Например, показатель True Positive находится в правом нижнем углу, а True Negative — в верхнем левом углу. Чтобы исправить это, мы можем перевернуть матрицу.
array([[3, 1],
[2, 1]], dtype=int64)Чтобы вычислить матрицу ошибок для задачи с большим числом классов, используется функция multilabel_confusion_matrix(), как показано ниже. В дополнение к параметрам y_true и y_pred третий параметр labels принимает список классовых меток.
array([
[[4 2]
[2 1]]
[[6 1]
[1 1]]
[[3 2]
[2 2]]], dtype=int64)Функция вычисляет матрицу ошибок для каждого класса и возвращает все матрицы. Их порядок соответствует порядку меток в параметре labels. Чтобы изменить последовательность метрик в матрицах, мы будем снова использовать функцию numpy.flip().
# матрица ошибок для класса White
[[1 2]
[2 4]]
# матрица ошибок для класса Black
[[1 1]
[1 6]]
# матрица ошибок для класса Red
[[2 2]
[2 3]]В оставшейся части этого текста мы сосредоточимся только на двух классах. В следующем разделе обсуждаются три ключевых показателя, которые рассчитываются на основе матрицы ошибок.
Как мы уже видели, матрица ошибок предлагает четыре индивидуальных показателя. На их основе можно рассчитать другие метрики, которые предоставляют дополнительную информацию о поведении модели:
- Accuracy
- Precision
- Recall
В следующих подразделах обсуждается каждый из этих трех показателей.
Метрика Accuracy
Accuracy — это показатель, который описывает общую точность предсказания модели по всем классам. Это особенно полезно, когда каждый класс одинаково важен. Он рассчитывается как отношение количества правильных прогнозов к их общему количеству.
Рассчитаем accuracy с помощью Scikit-learn на основе ранее полученной матрицы ошибок. Переменная acc содержит результат деления суммы True Positive и True Negative метрик на сумму всех значений матрицы. Таким образом, accuracy, равная 0.5714, означает, что модель с точностью 57,14% делает верный прогноз.
В модуле sklearn.metrics есть функция precision_score(), которая также может вычислять accuracy. Она принимает в качестве аргументов достоверные и предсказанные метки.
Стоит учесть, что метрика accuracy может быть обманчивой. Один из таких случаев — это несбалансированные данные. Предположим, у нас есть всего 600 единиц данных, из которых 550 относятся к классу Positive и только 50 — к Negative. Поскольку большинство семплов принадлежит к одному классу, accuracy для этого класса будет выше, чем для другого.
Если модель сделала 530 правильных прогнозов из 550 для класса Positive, по сравнению с 5 из 50 для Negative, то общая accuracy равна (530 + 5) / 600 = 0.8917. Это означает, что точность модели составляет 89.17%. Полагаясь на это значение, вы можете подумать, что для любой выборки (независимо от ее класса) модель сделает правильный прогноз в 89.17% случаев. Это неверно, так как для класса Negative модель работает очень плохо.
Precision
Precision представляет собой отношение числа семплов, верно классифицированных как Positive, к общему числу выборок с меткой Positive (распознанных правильно и неправильно). Precision измеряет точность модели при определении класса Positive.
Когда модель делает много неверных Positive классификаций, это увеличивает знаменатель и снижает precision. С другой стороны, precision высока, когда:
- Модель делает много корректных предсказаний класса Positive (максимизирует True Positive метрику).
- Модель делает меньше неверных Positive классификаций (минимизирует False Positive).
Представьте себе человека, который пользуется всеобщим доверием; когда он что-то предсказывает, окружающие ему верят. Метрика precision похожа на такого персонажа. Если она высока, вы можете доверять решению модели по определению очередной выборки как Positive. Таким образом, precision помогает узнать, насколько точна модель, когда она говорит, что семпл имеет класс Positive.
Основываясь на предыдущем обсуждении, вот определение precision:
Precision отражает, насколько надежна модель при классификации Positive-меток.
На следующем изображении зеленая метка означает, что зеленый семпл классифицирован как Positive, а красный крест – как Negative. Модель корректно распознала две Positive выборки, но неверно классифицировала один Negative семпл как Positive. Из этого следует, что метрика True Positive равна 2, когда False Positive имеет значение 1, а precision составляет 2 / (2 + 1) = 0.667. Другими словами, процент доверия к решению модели, что выборка относится к классу Positive, составляет 66.7%.
Цель precision – классифицировать все Positive семплы как Positive, не допуская ложных определений Negative как Positive. Согласно следующему рисунку, если все три Positive выборки предсказаны правильно, но один Negative семпл классифицирован неверно, precision составляет 3 / (3 + 1) = 0.75. Таким образом, утверждения модели о том, что выборка относится к классу Positive, корректны с точностью 75%.
Единственный способ получить 100% precision — это классифицировать все Positive выборки как Positive без классификации Negative как Positive.
В Scikit-learn модуль sklearn.metrics имеет функцию precision_score(), которая получает в качестве аргументов эталонные и предсказанные метки и возвращает precision. Параметр pos_label принимает метку класса Positive (по умолчанию 1).
Вывод: 0.6666666666666666.
Recall
Recall рассчитывается как отношение числа Positive выборок, корректно классифицированных как Positive, к общему количеству Positive семплов. Recall измеряет способность модели обнаруживать выборки, относящиеся к классу Positive. Чем выше recall, тем больше Positive семплов было найдено.
Recall заботится только о том, как классифицируются Positive выборки. Эта метрика не зависит от того, как предсказываются Negative семплы, в отличие от precision. Когда модель верно классифицирует все Positive выборки, recall будет 100%, даже если все представители класса Negative были ошибочно определены как Positive. Давайте посмотрим на несколько примеров.
На следующем изображении представлены 4 разных случая (от A до D), и все они имеют одинаковый recall, равный 0.667. Представленные примеры отличаются только тем, как классифицируются Negative семплы. Например, в случае A все Negative выборки корректно определены, а в случае D – наоборот. Независимо от того, как модель предсказывает класс Negative, recall касается только семплов относящихся к Positive.
Из 4 случаев, показанных выше, только 2 Positive выборки определены верно. Таким образом, метрика True Positive равна 2. False Negative имеет значение 1, потому что только один Positive семпл классифицируется как Negative. В результате recall будет равен 2 / (2 + 1) = 2/3 = 0.667.
Поскольку не имеет значения, как предсказываются объекты класса Negative, лучше их просто игнорировать, как показано на следующей схеме. При расчете recall необходимо учитывать только Positive выборки.
Что означает, когда recall высокий или низкий? Если recall имеет большое значение, все Positive семплы классифицируются верно. Следовательно, модели можно доверять в ее способности обнаруживать представителей класса Positive.
На следующем изображении recall равен 1.0, потому что все Positive семплы были правильно классифицированы. Показатель True Positive равен 3, а False Negative – 0. Таким образом, recall вычисляется как 3 / (3 + 0) = 1. Это означает, что модель обнаружила все Positive выборки. Поскольку recall не учитывает, как предсказываются представители класса Negative, могут присутствовать множество неверно определенных Negative семплов (высокая False Positive метрика).
С другой стороны, recall равен 0.0, если не удается обнаружить ни одной Positive выборки. Это означает, что модель обнаружила 0% представителей класса Positive. Показатель True Positive равен 0, а False Negative имеет значение 3. Recall будет равен 0 / (0 + 3) = 0.
Когда recall имеет значение от 0.0 до 1.0, это число отражает процент Positive семплов, которые модель верно классифицировала. Например, если имеется 10 экземпляров Positive и recall равен 0.6, получается, что модель корректно определила 60% объектов класса Positive (т.е. 0.6 * 10 = 6).
Подобно precision_score(), функция repl_score() из модуля sklearn.metrics вычисляет recall. В следующем блоке кода показан пример ее использования.
Вывод: 0.6666666666666666.
После определения precision и recall давайте кратко подведем итоги:
- Precision измеряет надежность модели при классификации Positive семплов, а recall определяет, сколько Positive выборок было корректно предсказано моделью.
- Precision учитывает классификацию как Positive, так и Negative семплов. Recall же использует при расчете только представителей класса Positive. Другими словами, precision зависит как от Negative, так и от Positive-выборок, но recall — только от Positive.
- Precision принимает во внимание, когда семпл определяется как Positive, но не заботится о верной классификации всех объектов класса Positive. Recall в свою очередь учитывает корректность предсказания всех Positive выборок, но не заботится об ошибочной классификации представителей Negative как Positive.
- Когда модель имеет высокий уровень recall метрики, но низкую precision, такая модель правильно определяет большинство Positive семплов, но имеет много ложных срабатываний (классификаций Negative выборок как Positive). Если модель имеет большую precision, но низкий recall, то она делает высокоточные предсказания, определяя класс Positive, но производит всего несколько таких прогнозов.
Некоторые вопросы для проверки понимания:
- Если recall равен 1.0, а в датасете имеются 5 объектов класса Positive, сколько Positive семплов было правильно классифицировано моделью?
- Учитывая, что recall составляет 0.3, когда в наборе данных 30 Positive семплов, сколько представителей класса Positive будет предсказано верно?
- Если recall равен 0.0 и в датасете14 Positive-семплов, сколько корректных предсказаний класса Positive было сделано моделью?
Precision или Recall?
Решение о том, следует ли использовать precision или recall, зависит от типа вашей проблемы. Если цель состоит в том, чтобы обнаружить все positive выборки (не заботясь о том, будут ли negative семплы классифицированы как positive), используйте recall. Используйте precision, если ваша задача связана с комплексным предсказанием класса Positive, то есть учитывая Negative семплы, которые были ошибочно классифицированы как Positive.
Представьте, что вам дали изображение и попросили определить все автомобили внутри него. Какой показатель вы используете? Поскольку цель состоит в том, чтобы обнаружить все автомобили, используйте recall. Такой подход может ошибочно классифицировать некоторые объекты как целевые, но в конечном итоге сработает для предсказания всех автомобилей.
Теперь предположим, что вам дали снимок с результатами маммографии, и вас попросили определить наличие рака. Какой показатель вы используете? Поскольку он обязан быть чувствителен к неверной идентификации изображения как злокачественного, мы должны быть уверены, когда классифицируем снимок как Positive (то есть с раком). Таким образом, предпочтительным показателем в данном случае является precision.
Вывод
В этом руководстве обсуждалась матрица ошибок, вычисление ее 4 метрик (true/false positive/negative) для задач бинарной и мультиклассовой классификации. Используя модуль metrics библиотеки Scikit-learn, мы увидели, как получить матрицу ошибок в Python.
Основываясь на этих 4 показателях, мы перешли к обсуждению accuracy, precision и recall метрик. Каждая из них была определена и использована в нескольких примерах. Модуль sklearn.metrics применяется для расчета каждого вышеперечисленного показателя.
- Главная
- Вопросы и ответы
Матрица ошибок и расчет показателей точности тематических карт
Дано определение матрицы ошибок (confusion matrix, contingency table, error matrix), приведены примеры использования.
Обсудить в форуме Комментариев — 2
Матрица ошибок представляет собой инструмент, использующий кросс-табуляцию (http://en.wikipedia.org/wiki/Cross-tabulation) для показа того, как соотносятся значения совпадающих классов, полученные из различных источников. В качестве источников могут выступать, например, проверяемый растр (тематическая классификация) и опорный более точный источник данных (растр или набор полевых данных в виде точек). При интерпретации результатов обычно полагается, что проверяемый результат потенциально является неточным, а проверочный растр хорошо отражает реальную ситуацию. В противном случае, если проверочный растр также несовершенен, нельзя говорить об «ошибке», а следует говорить о «разнице» между двумя наборами данных. Для построения матрицы могут использоваться все ячейки растра (пиксели) или выборка ячеек, расположенных случайно, стратифицировано случайно или согласно какому-либо другому распределению.
По одной из осей матрицы записываются названия классов легенды классификации проверяемого набора данных, по второй — классы легенды данных, используемых для проверки.
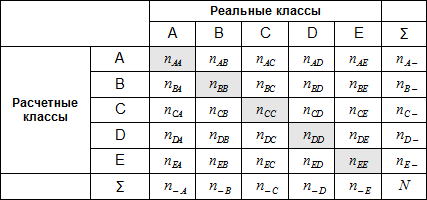
Серым отмечена главная диагональ матрицы, показывающая случаи, где расчетные классы и реальные данные совпадают (правильная классификация). Сумма значений диагональных элементов показывает общее количество правильно классифицированных пикселей, а отношение этого количества к общему количеству пикселей в матрице N называется общей точностью классификации и обычно выражается в процентах:
Для определения точности определенного расчетного класса, необходимо разделить количество правильно классифицированных пикселей этого класса на общее количество пикселей в этом классе согласно проверочным данным. Этот показатель также называют «точностью производителя» (producer’s accuracy), так как он показывает, насколько хорошо результат классификации для этого класса совпадает с проверочными данными. Для класса A:
Похожий показатель может быть вычислен для реального класса, если разделить количество правильно классифицированных пикселей класса на общее количество пикселей в этом классе согласно проверяемым данным. Этот показатель называют «точностью пользователя» (user’s accuracy), так как он показывает пользователю классификации насколько вероятно, что данный класс совпадает с результатами классификации. Для класса A:
Вне-диагональные элементы показывает случаи несовпадения между расчетными и реальными классами (ошибки классификации).
Пример 1 Маска пожаров
Приведем пример реальной ситуации, при желании вы можете повторить все расчеты и вычисления. Допустим, у нас есть классификации, показывающие какая территория сгорела, а какая нет. Одна из этих классификаций сделана на базе данных AVHRR, а другая — MODIS. Например, иллюстрация показывает результат наложения двух классификаций, где:
0 – оба источника определили территорию как не сгоревшую;
1 – AVHRR определил территорию как сгоревшую, MODIS – как не сгоревшую;
2 — MODIS определил территорию как сгоревшую, AVHRR – как не сгоревшую;
3 — оба источника определили территорию как сгоревшую.
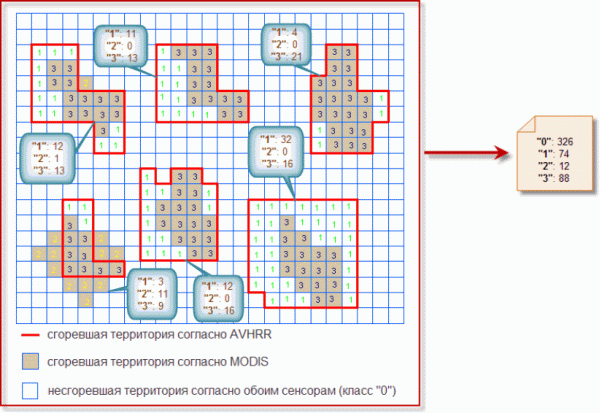
В этом случае, если мы обозначим сгоревшую территорию как «ДА», а не сгоревшую как «НЕТ», наша матрица ошибок будет выглядеть следующим образом:
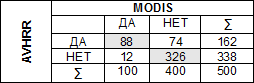
Рассчитаем общую ошибку и ошибки для разных классов.
Общая точность 83%, из рисунка очевидно, что решающую роль в такой высокой точности играет масса территорий, классифицированных как несгоревшие обоими источниками.
Точность производителя (producer’s accuracy) для класса сгоревших территорий – 88%. Высокая точность производителя означает, что в проверяемой классификации мало ошибок омиссии (ommission errors), т.е. мало сгоревших пикселей было пропущено. Другими словами, небольшое количество пикселей, которые были на самом деле (согласно проверочному набору) сгоревшими, были ошибочно классифицированы как несгоревшие.
Точность пользователя (user’s accuracy) для класса сгоревших территорий – 54%. Низкая точность пользователя означает, что в проверяемой классификации много ошибок комиссии (commission errors), т.е. много пикселей, которые не сгорели, но были классифицированы как сгоревшие.
Разберем интерпретацию точностей для класса сгоревших территорий, как целевого класса в данном примере. Как можно видеть, для этого класса точность производителя значительно лучше точности пользователя, что в переводе на человеческий язык означает, что при производстве данного набора данных предпочтение было отдано тому, что «лучше, чтобы все территории которые на самом деле сгорели, были классифицированы как сгоревшие», а не «лучше, чтобы сгоревших территорий было меньше, но все они были точно сгоревшими».
Как видно из примера, ошибки комиссии и омиссии для одного класса часто являются противоположными, высокое значение одной из них часто связано с низким значением другой. Интерпретация качества классификации зависит от ставящихся перед ней задач, обычной стратегией является нахождение максимального значения обоих типов ошибок.
Пример 2
Более сложный пример, с большим количеством классов (источник):
Количество классов q = 5.
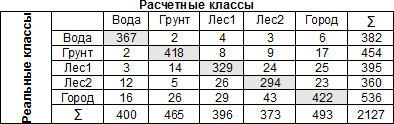
Рассчитаем общую точность, точность производителя и пользователя:

Расчеты всех показателей точности для приведенных выше данных в формате MS Excel XLS.
Обсудить в форуме Комментариев — 2
Последнее обновление: September 09 2021
Дата создания: 06.01.2010
Автор(ы): Денис Рыков
В машинном обучении различают оценки качества для задачи классификации и регрессии. Причем оценка задачи классификации часто значительно сложнее, чем оценка регрессии.
Содержание
- 1 Оценки качества классификации
- 1.1 Матрица ошибок (англ. Сonfusion matrix)
- 1.2 Аккуратность (англ. Accuracy)
- 1.3 Точность (англ. Precision)
- 1.4 Полнота (англ. Recall)
- 1.5 F-мера (англ. F-score)
- 1.6 ROC-кривая
- 1.7 Precison-recall кривая
- 2 Оценки качества регрессии
- 2.1 Средняя квадратичная ошибка (англ. Mean Squared Error, MSE)
- 2.2 Cредняя абсолютная ошибка (англ. Mean Absolute Error, MAE)
- 2.3 Коэффициент детерминации
- 2.4 Средняя абсолютная процентная ошибка (англ. Mean Absolute Percentage Error, MAPE)
- 2.5 Корень из средней квадратичной ошибки (англ. Root Mean Squared Error, RMSE)
- 2.6 Cимметричная MAPE (англ. Symmetric MAPE, SMAPE)
- 2.7 Средняя абсолютная масштабированная ошибка (англ. Mean absolute scaled error, MASE)
- 3 Кросс-валидация
- 4 Примечания
- 5 См. также
- 6 Источники информации
Оценки качества классификации
Матрица ошибок (англ. Сonfusion matrix)
Перед переходом к самим метрикам необходимо ввести важную концепцию для описания этих метрик в терминах ошибок классификации — confusion matrix (матрица ошибок).
Допустим, что у нас есть два класса и алгоритм, предсказывающий принадлежность каждого объекта одному из классов.
Рассмотрим пример. Пусть банк использует систему классификации заёмщиков на кредитоспособных и некредитоспособных. При этом первым кредит выдаётся, а вторые получат отказ. Таким образом, обнаружение некредитоспособного заёмщика () можно рассматривать как «сигнал тревоги», сообщающий о возможных рисках.
Любой реальный классификатор совершает ошибки. В нашем случае таких ошибок может быть две:
- Кредитоспособный заёмщик распознается моделью как некредитоспособный и ему отказывается в кредите. Данный случай можно трактовать как «ложную тревогу».
- Некредитоспособный заёмщик распознаётся как кредитоспособный и ему ошибочно выдаётся кредит. Данный случай можно рассматривать как «пропуск цели».
Несложно увидеть, что эти ошибки неравноценны по связанным с ними проблемам. В случае «ложной тревоги» потери банка составят только проценты по невыданному кредиту (только упущенная выгода). В случае «пропуска цели» можно потерять всю сумму выданного кредита. Поэтому системе важнее не допустить «пропуск цели», чем «ложную тревогу».
Поскольку с точки зрения логики задачи нам важнее правильно распознать некредитоспособного заёмщика с меткой , чем ошибиться в распознавании кредитоспособного, будем называть соответствующий исход классификации положительным (заёмщик некредитоспособен), а противоположный — отрицательным (заемщик кредитоспособен ). Тогда возможны следующие исходы классификации:
- Некредитоспособный заёмщик классифицирован как некредитоспособный, т.е. положительный класс распознан как положительный. Наблюдения, для которых это имеет место называются истинно-положительными (True Positive — TP).
- Кредитоспособный заёмщик классифицирован как кредитоспособный, т.е. отрицательный класс распознан как отрицательный. Наблюдения, которых это имеет место, называются истинно отрицательными (True Negative — TN).
- Кредитоспособный заёмщик классифицирован как некредитоспособный, т.е. имела место ошибка, в результате которой отрицательный класс был распознан как положительный. Наблюдения, для которых был получен такой исход классификации, называются ложно-положительными (False Positive — FP), а ошибка классификации называется ошибкой I рода.
- Некредитоспособный заёмщик распознан как кредитоспособный, т.е. имела место ошибка, в результате которой положительный класс был распознан как отрицательный. Наблюдения, для которых был получен такой исход классификации, называются ложно-отрицательными (False Negative — FN), а ошибка классификации называется ошибкой II рода.
Таким образом, ошибка I рода, или ложно-положительный исход классификации, имеет место, когда отрицательное наблюдение распознано моделью как положительное. Ошибкой II рода, или ложно-отрицательным исходом классификации, называют случай, когда положительное наблюдение распознано как отрицательное. Поясним это с помощью матрицы ошибок классификации:
-
Истинно-положительный (True Positive — TP) Ложно-положительный (False Positive — FP) Ложно-отрицательный (False Negative — FN) Истинно-отрицательный (True Negative — TN)
Здесь — это ответ алгоритма на объекте, а — истинная метка класса на этом объекте.
Таким образом, ошибки классификации бывают двух видов: False Negative (FN) и False Positive (FP).
P означает что классификатор определяет класс объекта как положительный (N — отрицательный). T значит что класс предсказан правильно (соответственно F — неправильно). Каждая строка в матрице ошибок представляет спрогнозированный класс, а каждый столбец — фактический класс.
# код для матрицы ошибок # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import confusion_matrix from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (англ. Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе # Для расчета матрицы ошибок сначала понадобится иметь набор прогнозов, чтобы их можно было сравнивать с фактическими целями y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687], # [ 1891, 3530]])
Безупречный классификатор имел бы только истинно-положительные и истинно отрицательные классификации, так что его матрица ошибок содержала бы ненулевые значения только на своей главной диагонали (от левого верхнего до правого нижнего угла):
import numpy as np
from sklearn.datasets import fetch_openml
from sklearn.metrics import confusion_matrix
mnist = fetch_openml('mnist_784', version=1)
X, y = mnist["data"], mnist["target"]
y = y.astype(np.uint8)
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки
y_test_5 = (y_test == 5)
y_train_perfect_predictions = y_train_5 # притворись, что мы достигли совершенства
print(confusion_matrix(y_train_5, y_train_perfect_predictions))
# array([[54579, 0],
# [ 0, 5421]])
Аккуратность (англ. Accuracy)
Интуитивно понятной, очевидной и почти неиспользуемой метрикой является accuracy — доля правильных ответов алгоритма:
Эта метрика бесполезна в задачах с неравными классами, что как вариант можно исправить с помощью алгоритмов сэмплирования и это легко показать на примере.
Допустим, мы хотим оценить работу спам-фильтра почты. У нас есть 100 не-спам писем, 90 из которых наш классификатор определил верно (True Negative = 90, False Positive = 10), и 10 спам-писем, 5 из которых классификатор также определил верно (True Positive = 5, False Negative = 5).
Тогда accuracy:
Однако если мы просто будем предсказывать все письма как не-спам, то получим более высокую аккуратность:
При этом, наша модель совершенно не обладает никакой предсказательной силой, так как изначально мы хотели определять письма со спамом. Преодолеть это нам поможет переход с общей для всех классов метрики к отдельным показателям качества классов.
# код для для подсчета аккуратности: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import accuracy_score from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) # print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687] # [ 1891, 3530]]) print(accuracy_score(y_train_5, y_train_pred)) # == (53892 + 3530) / (53892 + 3530 + 1891 +687) # 0.9570333333333333
Точность (англ. Precision)
Точностью (precision) называется доля правильных ответов модели в пределах класса — это доля объектов действительно принадлежащих данному классу относительно всех объектов которые система отнесла к этому классу.
Именно введение precision не позволяет нам записывать все объекты в один класс, так как в этом случае мы получаем рост уровня False Positive.
Полнота (англ. Recall)
Полнота — это доля истинно положительных классификаций. Полнота показывает, какую долю объектов, реально относящихся к положительному классу, мы предсказали верно.
Полнота (recall) демонстрирует способность алгоритма обнаруживать данный класс вообще.
Имея матрицу ошибок, очень просто можно вычислить точность и полноту для каждого класса. Точность (precision) равняется отношению соответствующего диагонального элемента матрицы и суммы всей строки класса. Полнота (recall) — отношению диагонального элемента матрицы и суммы всего столбца класса. Формально:
Результирующая точность классификатора рассчитывается как арифметическое среднее его точности по всем классам. То же самое с полнотой. Технически этот подход называется macro-averaging.
# код для для подсчета точности и полноты: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import precision_score, recall_score from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) # print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687] # [ 1891, 3530]]) print(precision_score(y_train_5, y_train_pred)) # == 3530 / (3530 + 687) print(recall_score(y_train_5, y_train_pred)) # == 3530 / (3530 + 1891) # 0.8370879772350012 # 0.6511713705958311
F-мера (англ. F-score)
Precision и recall не зависят, в отличие от accuracy, от соотношения классов и потому применимы в условиях несбалансированных выборок.
Часто в реальной практике стоит задача найти оптимальный (для заказчика) баланс между этими двумя метриками. Понятно что чем выше точность и полнота, тем лучше. Но в реальной жизни максимальная точность и полнота не достижимы одновременно и приходится искать некий баланс. Поэтому, хотелось бы иметь некую метрику которая объединяла бы в себе информацию о точности и полноте нашего алгоритма. В этом случае нам будет проще принимать решение о том какую реализацию запускать в производство (у кого больше тот и круче). Именно такой метрикой является F-мера.
F-мера представляет собой гармоническое среднее между точностью и полнотой. Она стремится к нулю, если точность или полнота стремится к нулю.
Данная формула придает одинаковый вес точности и полноте, поэтому F-мера будет падать одинаково при уменьшении и точности и полноты. Возможно рассчитать F-меру придав различный вес точности и полноте, если вы осознанно отдаете приоритет одной из этих метрик при разработке алгоритма:
где принимает значения в диапазоне если вы хотите отдать приоритет точности, а при приоритет отдается полноте. При формула сводится к предыдущей и вы получаете сбалансированную F-меру (также ее называют ).
-
Рис.1 Сбалансированная F-мера,
-
Рис.2 F-мера c приоритетом точности,
-
Рис.3 F-мера c приоритетом полноты,
F-мера достигает максимума при максимальной полноте и точности, и близка к нулю, если один из аргументов близок к нулю.
F-мера является хорошим кандидатом на формальную метрику оценки качества классификатора. Она сводит к одному числу две других основополагающих метрики: точность и полноту. Имея «F-меру» гораздо проще ответить на вопрос: «поменялся алгоритм в лучшую сторону или нет?»
# код для подсчета метрики F-mera: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier from sklearn.metrics import f1_score mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распознавать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) print(f1_score(y_train_5, y_train_pred)) # 0.7325171197343846
ROC-кривая
Кривая рабочих характеристик (англ. Receiver Operating Characteristics curve).
Используется для анализа поведения классификаторов при различных пороговых значениях.
Позволяет рассмотреть все пороговые значения для данного классификатора.
Показывает долю ложно положительных примеров (англ. false positive rate, FPR) в сравнении с долей истинно положительных примеров (англ. true positive rate, TPR).
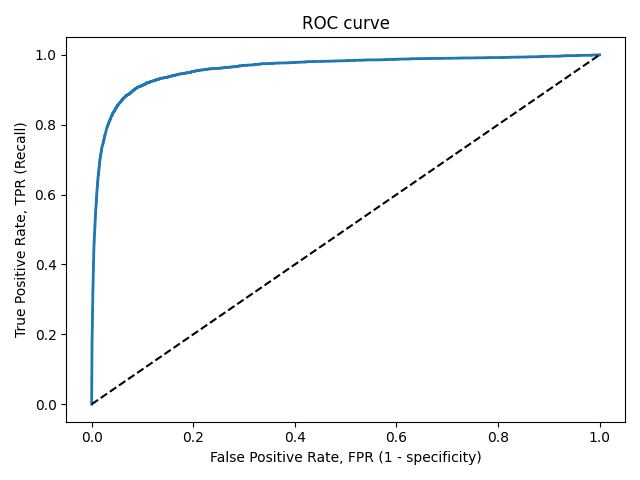
Доля FPR — это пропорция отрицательных образцов, которые были некорректно классифицированы как положительные.
- ,
где TNR — доля истинно отрицательных классификаций (англ. Тrие Negative Rate), представляющая собой пропорцию отрицательных образцов, которые были корректно классифицированы как отрицательные.
Доля TNR также называется специфичностью (англ. specificity). Следовательно, ROC-кривая изображает чувствительность (англ. seпsitivity), т.е. полноту, в сравнении с разностью 1 — specificity.
Прямая линия по диагонали представляет ROC-кривую чисто случайного классификатора. Хороший классификатор держится от указанной линии настолько далеко, насколько это
возможно (стремясь к левому верхнему углу).
Один из способов сравнения классификаторов предусматривает измерение площади под кривой (англ. Area Under the Curve — AUC). Безупречный классификатор будет иметь площадь под ROC-кривой (ROC-AUC), равную 1, тогда как чисто случайный классификатор — площадь 0.5.
# Код отрисовки ROC-кривой # На примере классификатора, способного проводить различие между всего лишь двумя классами # "пятерка" и "не пятерка" из набора рукописных цифр MNIST from sklearn.metrics import roc_curve import matplotlib.pyplot as plt import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function") fpr, tpr, thresholds = roc_curve(y_train_5, y_scores) def plot_roc_curve(fpr, tpr, label=None): plt.plot(fpr, tpr, linewidth=2, label=label) plt.plot([0, 1], [0, 1], 'k--') # dashed diagonal plt.xlabel('False Positive Rate, FPR (1 - specificity)') plt.ylabel('True Positive Rate, TPR (Recall)') plt.title('ROC curve') plt.savefig("ROC.png") plot_roc_curve(fpr, tpr) plt.show()
Precison-recall кривая
Чувствительность к соотношению классов.
Рассмотрим задачу выделения математических статей из множества научных статей. Допустим, что всего имеется 1.000.100 статей, из которых лишь 100 относятся к математике. Если нам удастся построить алгоритм , идеально решающий задачу, то его TPR будет равен единице, а FPR — нулю. Рассмотрим теперь плохой алгоритм, дающий положительный ответ на 95 математических и 50.000 нематематических статьях. Такой алгоритм совершенно бесполезен, но при этом имеет TPR = 0.95 и FPR = 0.05, что крайне близко к показателям идеального алгоритма.
Таким образом, если положительный класс существенно меньше по размеру, то AUC-ROC может давать неадекватную оценку качества работы алгоритма, поскольку измеряет долю неверно принятых объектов относительно общего числа отрицательных. Так, алгоритм , помещающий 100 релевантных документов на позиции с 50.001-й по 50.101-ю, будет иметь AUC-ROC 0.95.
Precison-recall (PR) кривая. Избавиться от указанной проблемы с несбалансированными классами можно, перейдя от ROC-кривой к PR-кривой. Она определяется аналогично ROC-кривой, только по осям откладываются не FPR и TPR, а полнота (по оси абсцисс) и точность (по оси ординат). Критерием качества семейства алгоритмов выступает площадь под PR-кривой (англ. Area Under the Curve — AUC-PR)
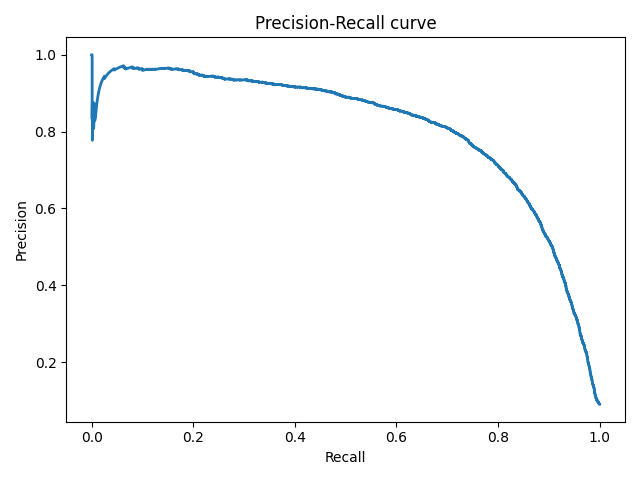
# Код отрисовки Precison-recall кривой # На примере классификатора, способного проводить различие между всего лишь двумя классами # "пятерка" и "не пятерка" из набора рукописных цифр MNIST from sklearn.metrics import precision_recall_curve import matplotlib.pyplot as plt import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function") precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores) def plot_precision_recall_vs_threshold(precisions, recalls, thresholds): plt.plot(recalls, precisions, linewidth=2) plt.xlabel('Recall') plt.ylabel('Precision') plt.title('Precision-Recall curve') plt.savefig("Precision_Recall_curve.png") plot_precision_recall_vs_threshold(precisions, recalls, thresholds) plt.show()
Оценки качества регрессии
Наиболее типичными мерами качества в задачах регрессии являются
Средняя квадратичная ошибка (англ. Mean Squared Error, MSE)
MSE применяется в ситуациях, когда нам надо подчеркнуть большие ошибки и выбрать модель, которая дает меньше больших ошибок прогноза. Грубые ошибки становятся заметнее за счет того, что ошибку прогноза мы возводим в квадрат. И модель, которая дает нам меньшее значение среднеквадратической ошибки, можно сказать, что что у этой модели меньше грубых ошибок.
- и
Cредняя абсолютная ошибка (англ. Mean Absolute Error, MAE)
Среднеквадратичный функционал сильнее штрафует за большие отклонения по сравнению со среднеабсолютным, и поэтому более чувствителен к выбросам. При использовании любого из этих двух функционалов может быть полезно проанализировать, какие объекты вносят наибольший вклад в общую ошибку — не исключено, что на этих объектах была допущена ошибка при вычислении признаков или целевой величины.
Среднеквадратичная ошибка подходит для сравнения двух моделей или для контроля качества во время обучения, но не позволяет сделать выводов о том, на сколько хорошо данная модель решает задачу. Например, MSE = 10 является очень плохим показателем, если целевая переменная принимает значения от 0 до 1, и очень хорошим, если целевая переменная лежит в интервале (10000, 100000). В таких ситуациях вместо среднеквадратичной ошибки полезно использовать коэффициент детерминации —
Коэффициент детерминации
Коэффициент детерминации измеряет долю дисперсии, объясненную моделью, в общей дисперсии целевой переменной. Фактически, данная мера качества — это нормированная среднеквадратичная ошибка. Если она близка к единице, то модель хорошо объясняет данные, если же она близка к нулю, то прогнозы сопоставимы по качеству с константным предсказанием.
Средняя абсолютная процентная ошибка (англ. Mean Absolute Percentage Error, MAPE)
Это коэффициент, не имеющий размерности, с очень простой интерпретацией. Его можно измерять в долях или процентах. Если у вас получилось, например, что MAPE=11.4%, то это говорит о том, что ошибка составила 11,4% от фактических значений.
Основная проблема данной ошибки — нестабильность.
Корень из средней квадратичной ошибки (англ. Root Mean Squared Error, RMSE)
Примерно такая же проблема, как и в MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня.
Cимметричная MAPE (англ. Symmetric MAPE, SMAPE)
Средняя абсолютная масштабированная ошибка (англ. Mean absolute scaled error, MASE)
MASE является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени.
Обратите внимание, что в MASE мы имеем дело с двумя суммами: та, что в числителе, соответствует тестовой выборке, та, что в знаменателе — обучающей. Вторая фактически представляет собой среднюю абсолютную ошибку прогноза. Она же соответствует среднему абсолютному отклонению ряда в первых разностях. Эта величина, по сути, показывает, насколько обучающая выборка предсказуема. Она может быть равна нулю только в том случае, когда все значения в обучающей выборке равны друг другу, что соответствует отсутствию каких-либо изменений в ряде данных, ситуации на практике почти невозможной. Кроме того, если ряд имеет тенденцию к росту либо снижению, его первые разности будут колебаться около некоторого фиксированного уровня. В результате этого по разным рядам с разной структурой, знаменатели будут более-менее сопоставимыми. Всё это, конечно же, является очевидными плюсами MASE, так как позволяет складывать разные значения по разным рядам и получать несмещённые оценки.
Недостаток MASE в том, что её тяжело интерпретировать. Например, MASE=1.21 ни о чём, по сути, не говорит. Это просто означает, что ошибка прогноза оказалась в 1.21 раза выше среднего абсолютного отклонения ряда в первых разностях, и ничего более.
Кросс-валидация
Хороший способ оценки модели предусматривает применение кросс-валидации (cкользящего контроля или перекрестной проверки).
В этом случае фиксируется некоторое множество разбиений исходной выборки на две подвыборки: обучающую и контрольную. Для каждого разбиения выполняется настройка алгоритма по обучающей подвыборке, затем оценивается его средняя ошибка на объектах контрольной подвыборки. Оценкой скользящего контроля называется средняя по всем разбиениям величина ошибки на контрольных подвыборках.
Примечания
- [1] Лекция «Оценивание качества» на www.coursera.org
- [2] Лекция на www.stepik.org о кросвалидации
- [3] Лекция на www.stepik.org о метриках качества, Precison и Recall
- [4] Лекция на www.stepik.org о метриках качества, F-мера
- [5] Лекция на www.stepik.org о метриках качества, примеры
См. также
- Оценка качества в задаче кластеризации
- Кросс-валидация
Источники информации
- [6] Соколов Е.А. Лекция линейная регрессия
- [7] — Дьяконов А. Функции ошибки / функционалы качества
- [8] — Оценка качества прогнозных моделей
- [9] — HeinzBr Ошибка прогнозирования: виды, формулы, примеры
- [10] — egor_labintcev Метрики в задачах машинного обучения
- [11] — grossu Методы оценки качества прогноза
- [12] — К.В.Воронцов, Классификация
- [13] — К.В.Воронцов, Скользящий контроль
Расшифровка матрицы путаницы
Перевод
Ссылка на автора
В случае проблемы классификации, имеющей только одну точность классификации, может не дать вам полную картину. Таким образом, матрица путаницы или матрица ошибок используется для суммирования производительности алгоритма классификации.
Вычисление матрицы путаницы может дать вам представление о том, где модель классификации верна и какие ошибки она допускает.
Путаница путаница используется для проверки производительности модели классификации на наборе тестовых данных, для которых известны истинные значения. Большинство показателей эффективности, таких как точность, отзыв, рассчитываются из матрицы путаницы.
Эта статья направлена на:
1. Что такое матрица путаницы и зачем она нужна?
2. Как рассчитать путаницу для двухклассовой задачи классификации на примере кошки-собаки.
3. Как создать путаницу в Python & R.
4. Краткое изложение и интуиция о различных мерах: точность, отзыв, точность и специфика
1. Матрица путаницы:
Матрица путаницы предоставляет сводку прогнозирующих результатов в задаче классификации. Правильные и неправильные прогнозы суммируются в таблице со своими значениями и разбиваются по каждому классу.
Мы не можем полагаться на одно значение точности в классификации, когда классы не сбалансированы. Например, у нас есть набор данных из 100 пациентов, 5 из которых имеют диабет, а 95 здоровы. Однако, если наша модель только предсказывает класс большинства, то есть все 100 человек здоровы, даже если у нас точность классификации составляет 95%. Поэтому нам нужна матрица путаницы.
2. Рассчитайте матрицу путаницы:
Давайте возьмем пример:
У нас всего 10 кошек и собак, и наша модель предсказывает, кошка это или нет.
Фактические значения = [«собака», «кошка», «собака», «кошка», «собака», «собака», «кошка», «собака», «кошка», «собака» »]
Прогнозируемые значения = [«собака», «собака», «собака», «собака», «собака», «собака», «кошка», «кошка», «кошка», «кошка»]
Помните, мы описываем прогнозируемые значения как положительные / отрицательные, а фактические значения как истинные / ложные.
Определение терминов:
Настоящий позитив: вы предсказали позитив, и это правда. Вы предсказали, что животное — это кошка, и это действительно так.
True Negative: вы предсказали отрицательный результат, и это правда. Вы предсказали, что животное — это не кошка, и на самом деле это не так (это собака).
Ложный положительный результат (ошибка типа 1). Вы предсказали положительный результат, и это неверно. Вы предсказали, что животное — это кошка, но на самом деле это не так (это собака).
Ложное отрицание (ошибка типа 2). Вы прогнозировали отрицательное значение, и оно ложно. Вы предсказали, что животное не кошка, но на самом деле это так.
Точность классификации:
Точность классификации определяется соотношением:
Напомним (Чувствительность ака):
Напомним, определяется как отношение общего количества правильно классифицированных положительных классов к общему количеству положительных классов. Или из всех положительных классов, сколько мы предсказали правильно. Отзыв должен быть высоким.
Точность:
Точность определяется как отношение общего количества правильно классифицированных положительных классов к общему количеству предсказанных положительных классов. Или из всех прогнозирующих положительных классов, сколько мы предсказали правильно. Точность должна быть высокой.
Уловка, чтобы помнить:дозрение имеетдоДиктивные результаты в знаменателе.
F-оценка или F1-оценка:
Сложно сравнивать две модели с разными Precision и Recall. Поэтому, чтобы сделать их сопоставимыми, мы используем F-Score. Это Гармоническое Средство Точности и Вспомнить. По сравнению с арифметическим средним, гармоническое среднее наказывает более экстремальные значения. F-оценка должна быть высокой.
Специфичность:
Специфичность определяет долю фактических негативов, которые правильно определены.
Пример для интерпретации матрицы путаницы:
Давайте вычислим матрицу путаницы, используя приведенный выше пример с кошкой и собакой:
Точность классификации:
Точность = (TP + TN) / (TP + TN + FP + FN) = (3 + 4) / (3 + 4 + 2 + 1) = 0,70
Отзыв:Напомним, дает нам представление о том, когда на самом деле да, как часто он предсказывает да.
Напомним = TP / (TP + FN) = 3 / (3 + 1) = 0,75
Точность:Точность говорит нам о том, когда он предсказывает, да, как часто это правильно.
Точность = TP / (TP + FP) = 3 / (3 + 2) = 0,60
F-оценка:
F-оценка = (2 * Recall * Precision) / (Recall + Presision) = (2 * 0,75 * 0,60) / (0,75 + 0,60) = 0,67
Специфичность:
Специфичность = TN / (TN + FP) = 4 / (4 + 2) = 0,67
3. Создать путаницу в Python & R
Давайте используем и коды Python, и R, чтобы понять приведенный выше пример с собакой и кошкой, который поможет вам лучше понять, что вы узнали о матрице путаницы до сих пор.
ПИТОН:Сначала давайте возьмем код Python для создания матрицы путаницы. Мы должны импортировать модуль матрицы путаницы из библиотеки sklearn, которая помогает нам генерировать матрицу путаницы
Ниже приведена реализация приведенного выше объяснения в Python:
OUTPUT ->Confusion Matrix :
[[3 1]
[2 4]]
Accuracy Score : 0.7
Classification Report :
precision recall f1-score supportcat 0.60 0.75 0.67 4
dog 0.80 0.67 0.73 6micro avg 0.70 0.70 0.70 10
macro avg 0.70 0.71 0.70 10
weighted avg 0.72 0.70 0.70 10
Р:Давайте теперь используем R-код для создания матрицы путаницы. Мы будем использовать библиотеку карет в R для вычисления матрицы путаницы.
OUTPUT ->Confusion Matrix and Statistics Reference
Prediction 0 1
0 4 1
1 2 3Accuracy : 0.7
95% CI : (0.3475, 0.9333)
No Information Rate : 0.6
P-Value [Acc > NIR] : 0.3823Kappa : 0.4Mcnemar's Test P-Value : 1.0000Sensitivity : 0.6667
Specificity : 0.7500
Pos Pred Value : 0.8000
Neg Pred Value : 0.6000
Prevalence : 0.6000
Detection Rate : 0.4000
Detection Prevalence : 0.5000
Balanced Accuracy : 0.7083'Positive' Class : 0
4. Резюме:
- Точность — это насколько вы уверены в своих истинных положительных сторонах. Вспомните, насколько вы уверены, что не пропускаете ни одного позитива.
- выберитеОтзывесли возникновениеложные негативы недопустимы / недопустимы.Например, в случае диабета у вас было бы больше ложных срабатываний (ложных срабатываний) вместо сохранения ложных отрицательных.
- выберитеточностьесли хочешь быть побольшеуверен в своих истинных позитивах, Например, в случае спам-писем вы бы предпочли иметь несколько спам-писем в вашем почтовом ящике, а не обычные электронные письма в вашем ящике для спама. Вы хотели бы быть уверены, что электронная почта X является спамом, прежде чем мы поместим ее в ящик для спама.
- выберитеспецифичностьесли хочешьпокрыть все истинные негативы,то есть мы не хотим ложных срабатываний или ложных срабатываний. Например, в случае теста на наркотики, при котором все люди с положительным тестом немедленно попадут в тюрьму, вы не хотели бы, чтобы кто-либо без наркотиков отправлялся в тюрьму.
Мы можем сделать вывод, что:
- Значение точности 70% означает, что идентификация 3 из каждых 10 кошек неверна, а 7 — правильна.
- Точность 60% означает, что метка 4 из каждых 10 кошек — это не кошка (то есть собака), а 6 — кошки.
- Напомним, что значение 70% означает, что 3 из каждых 10 кошек в действительности пропущены нашей моделью, а 7 правильно определены как кошки.
- Значение специфичности, равное 60%, означает, что 4 из каждых 10 собак (то есть не кошек) в действительности помечены как кошки, а 6 — как собаки.
Если у вас есть какие-либо комментарии или вопросы, не стесняйтесь оставлять свои отзывы ниже. Вы всегда можете связаться со мной по LinkedIn,
Метрики в задачах машинного обучения
Привет, Хабр!
В задачах машинного обучения для оценки качества моделей и сравнения различных алгоритмов используются метрики, а их выбор и анализ — непременная часть работы датасатаниста.
В этой статье мы рассмотрим некоторые критерии качества в задачах классификации, обсудим, что является важным при выборе метрики и что может пойти не так.
Метрики в задачах классификации
Для демонстрации полезных функций sklearn и наглядного представления метрик мы будем использовать датасет по оттоку клиентов телеком-оператора.
Загрузим необходимые библиотеки и посмотрим на данные
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.pylab import rc, plot
import seaborn as sns
from sklearn.preprocessing import LabelEncoder, OneHotEncoder
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier
from sklearn.metrics import precision_recall_curve, classification_report
from sklearn.model_selection import train_test_split
df = pd.read_csv('../../data/telecom_churn.csv')
df.head(5)Предобработка данных
# Сделаем маппинг бинарных колонок
# и закодируем dummy-кодированием штат (для простоты, лучше не делать так для деревянных моделей)
d = {'Yes' : 1, 'No' : 0}
df['International plan'] = df['International plan'].map(d)
df['Voice mail plan'] = df['Voice mail plan'].map(d)
df['Churn'] = df['Churn'].astype('int64')
le = LabelEncoder()
df['State'] = le.fit_transform(df['State'])
ohe = OneHotEncoder(sparse=False)
encoded_state = ohe.fit_transform(df['State'].values.reshape(-1, 1))
tmp = pd.DataFrame(encoded_state,
columns=['state ' + str(i) for i in range(encoded_state.shape[1])])
df = pd.concat([df, tmp], axis=1)Accuracy, precision и recall
Перед переходом к самим метрикам необходимо ввести важную концепцию для описания этих метрик в терминах ошибок классификации — confusion matrix (матрица ошибок).
Допустим, что у нас есть два класса и алгоритм, предсказывающий принадлежность каждого объекта одному из классов, тогда матрица ошибок классификации будет выглядеть следующим образом:
| True Positive (TP) | False Positive (FP) | |
| False Negative (FN) | True Negative (TN) |
Здесь — это ответ алгоритма на объекте, а
— истинная метка класса на этом объекте.
Таким образом, ошибки классификации бывают двух видов: False Negative (FN) и False Positive (FP).
Обучение алгоритма и построение матрицы ошибок
X = df.drop('Churn', axis=1)
y = df['Churn']
# Делим выборку на train и test, все метрики будем оценивать на тестовом датасете
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, test_size=0.33, random_state=42)
# Обучаем ставшую родной логистическую регрессию
lr = LogisticRegression(random_state=42)
lr.fit(X_train, y_train)
# Воспользуемся функцией построения матрицы ошибок из документации sklearn
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm)
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, cm[i, j],
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
font = {'size' : 15}
plt.rc('font', **font)
cnf_matrix = confusion_matrix(y_test, lr.predict(X_test))
plt.figure(figsize=(10, 8))
plot_confusion_matrix(cnf_matrix, classes=['Non-churned', 'Churned'],
title='Confusion matrix')
plt.savefig("conf_matrix.png")
plt.show()
Accuracy
Интуитивно понятной, очевидной и почти неиспользуемой метрикой является accuracy — доля правильных ответов алгоритма:
Эта метрика бесполезна в задачах с неравными классами, и это легко показать на примере.
Допустим, мы хотим оценить работу спам-фильтра почты. У нас есть 100 не-спам писем, 90 из которых наш классификатор определил верно (True Negative = 90, False Positive = 10), и 10 спам-писем, 5 из которых классификатор также определил верно (True Positive = 5, False Negative = 5).
Тогда accuracy:
Однако если мы просто будем предсказывать все письма как не-спам, то получим более высокую accuracy:
При этом, наша модель совершенно не обладает никакой предсказательной силой, так как изначально мы хотели определять письма со спамом. Преодолеть это нам поможет переход с общей для всех классов метрики к отдельным показателям качества классов.
Precision, recall и F-мера
Для оценки качества работы алгоритма на каждом из классов по отдельности введем метрики precision (точность) и recall (полнота).
Precision можно интерпретировать как долю объектов, названных классификатором положительными и при этом действительно являющимися положительными, а recall показывает, какую долю объектов положительного класса из всех объектов положительного класса нашел алгоритм.
Именно введение precision не позволяет нам записывать все объекты в один класс, так как в этом случае мы получаем рост уровня False Positive. Recall демонстрирует способность алгоритма обнаруживать данный класс вообще, а precision — способность отличать этот класс от других классов.
Как мы отмечали ранее, ошибки классификации бывают двух видов: False Positive и False Negative. В статистике первый вид ошибок называют ошибкой I-го рода, а второй — ошибкой II-го рода. В нашей задаче по определению оттока абонентов, ошибкой первого рода будет принятие лояльного абонента за уходящего, так как наша нулевая гипотеза состоит в том, что никто из абонентов не уходит, а мы эту гипотезу отвергаем. Соответственно, ошибкой второго рода будет являться «пропуск» уходящего абонента и ошибочное принятие нулевой гипотезы.
Precision и recall не зависят, в отличие от accuracy, от соотношения классов и потому применимы в условиях несбалансированных выборок.
Часто в реальной практике стоит задача найти оптимальный (для заказчика) баланс между этими двумя метриками. Классическим примером является задача определения оттока клиентов.
Очевидно, что мы не можем находить всех уходящих в отток клиентов и только их. Но, определив стратегию и ресурс для удержания клиентов, мы можем подобрать нужные пороги по precision и recall. Например, можно сосредоточиться на удержании только высокодоходных клиентов или тех, кто уйдет с большей вероятностью, так как мы ограничены в ресурсах колл-центра.
Обычно при оптимизации гиперпараметров алгоритма (например, в случае перебора по сетке GridSearchCV ) используется одна метрика, улучшение которой мы и ожидаем увидеть на тестовой выборке.
Существует несколько различных способов объединить precision и recall в агрегированный критерий качества. F-мера (в общем случае ) — среднее гармоническое precision и recall :
в данном случае определяет вес точности в метрике, и при
это среднее гармоническое (с множителем 2, чтобы в случае precision = 1 и recall = 1 иметь
)
F-мера достигает максимума при полноте и точности, равными единице, и близка к нулю, если один из аргументов близок к нулю.
В sklearn есть удобная функция _metrics.classificationreport, возвращающая recall, precision и F-меру для каждого из классов, а также количество экземпляров каждого класса.
report = classification_report(y_test, lr.predict(X_test), target_names=['Non-churned', 'Churned'])
print(report)
| class | precision | recall | f1-score | support |
|---|---|---|---|---|
| Non-churned | 0.88 | 0.97 | 0.93 | 941 |
| Churned | 0.60 | 0.25 | 0.35 | 159 |
| avg / total | 0.84 | 0.87 | 0.84 | 1100 |
Здесь необходимо отметить, что в случае задач с несбалансированными классами, которые превалируют в реальной практике, часто приходится прибегать к техникам искусственной модификации датасета для выравнивания соотношения классов. Их существует много, и мы не будем их касаться, здесь можно посмотреть некоторые методы и выбрать подходящий для вашей задачи.
AUC-ROC и AUC-PR
При конвертации вещественного ответа алгоритма (как правило, вероятности принадлежности к классу, отдельно см. SVM) в бинарную метку, мы должны выбрать какой-либо порог, при котором 0 становится 1. Естественным и близким кажется порог, равный 0.5, но он не всегда оказывается оптимальным, например, при вышеупомянутом отсутствии баланса классов.
Одним из способов оценить модель в целом, не привязываясь к конкретному порогу, является AUC-ROC (или ROC AUC) — площадь (Area Under Curve) под кривой ошибок (Receiver Operating Characteristic curve ). Данная кривая представляет из себя линию от (0,0) до (1,1) в координатах True Positive Rate (TPR) и False Positive Rate (FPR):
TPR нам уже известна, это полнота, а FPR показывает, какую долю из объектов negative класса алгоритм предсказал неверно. В идеальном случае, когда классификатор не делает ошибок (FPR = 0, TPR = 1) мы получим площадь под кривой, равную единице; в противном случае, когда классификатор случайно выдает вероятности классов, AUC-ROC будет стремиться к 0.5, так как классификатор будет выдавать одинаковое количество TP и FP.
Каждая точка на графике соответствует выбору некоторого порога. Площадь под кривой в данном случае показывает качество алгоритма (больше — лучше), кроме этого, важной является крутизна самой кривой — мы хотим максимизировать TPR, минимизируя FPR, а значит, наша кривая в идеале должна стремиться к точке (0,1).
Код отрисовки ROC-кривой
sns.set(font_scale=1.5)
sns.set_color_codes("muted")
plt.figure(figsize=(10, 8))
fpr, tpr, thresholds = roc_curve(y_test, lr.predict_proba(X_test)[:,1], pos_label=1)
lw = 2
plt.plot(fpr, tpr, lw=lw, label='ROC curve ')
plt.plot([0, 1], [0, 1])
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC curve')
plt.savefig("ROC.png")
plt.show()
Критерий AUC-ROC устойчив к несбалансированным классам (спойлер: увы, не всё так однозначно) и может быть интерпретирован как вероятность того, что случайно выбранный positive объект будет проранжирован классификатором выше (будет иметь более высокую вероятность быть positive), чем случайно выбранный negative объект.
Рассмотрим следующую задачу: нам необходимо выбрать 100 релевантных документов из 1 миллиона документов. Мы намашинлернили два алгоритма:
- Алгоритм 1 возвращает 100 документов, 90 из которых релевантны. Таким образом,
- Алгоритм 2 возвращает 2000 документов, 90 из которых релевантны. Таким образом,
Скорее всего, мы бы выбрали первый алгоритм, который выдает очень мало False Positive на фоне своего конкурента. Но разница в False Positive Rate между этими двумя алгоритмами крайне мала — всего 0.0019. Это является следствием того, что AUC-ROC измеряет долю False Positive относительно True Negative и в задачах, где нам не так важен второй (больший) класс, может давать не совсем адекватную картину при сравнении алгоритмов.
Для того чтобы поправить положение, вернемся к полноте и точности :
- Алгоритм 1
- Алгоритм 2
Здесь уже заметна существенная разница между двумя алгоритмами — 0.855 в точности!
Precision и recall также используют для построения кривой и, аналогично AUC-ROC, находят площадь под ней.
Здесь можно отметить, что на маленьких датасетах площадь под PR-кривой может быть чересчур оптимистична, потому как вычисляется по методу трапеций, но обычно в таких задачах данных достаточно. За подробностями о взаимоотношениях AUC-ROC и AUC-PR можно обратиться сюда.
Logistic Loss
Особняком стоит логистическая функция потерь, определяемая как:
здесь — это ответ алгоритма на
-ом объекте,
— истинная метка класса на
-ом объекте, а
размер выборки.
Подробно про математическую интерпретацию логистической функции потерь уже написано в рамках поста про линейные модели.
Данная метрика нечасто выступает в бизнес-требованиях, но часто — в задачах на kaggle.
Интуитивно можно представить минимизацию logloss как задачу максимизации accuracy путем штрафа за неверные предсказания. Однако необходимо отметить, что logloss крайне сильно штрафует за уверенность классификатора в неверном ответе.
Рассмотрим пример:
def logloss_crutch(y_true, y_pred, eps=1e-15):
return - (y_true * np.log(y_pred) + (1 - y_true) * np.log(1 - y_pred))
print('Logloss при неуверенной классификации %f' % logloss_crutch(1, 0.5))
>> Logloss при неуверенной классификации 0.693147
print('Logloss при уверенной классификации и верном ответе %f' % logloss_crutch(1, 0.9))
>> Logloss при уверенной классификации и верном ответе 0.105361
print('Logloss при уверенной классификации и НЕверном ответе %f' % logloss_crutch(1, 0.1))
>> Logloss при уверенной классификации и НЕверном ответе 2.302585Отметим, как драматически выросла logloss при неверном ответе и уверенной классификации!
Следовательно, ошибка на одном объекте может дать существенное ухудшение общей ошибки на выборке. Такие объекты часто бывают выбросами, которые нужно не забывать фильтровать или рассматривать отдельно.
Всё становится на свои места, если нарисовать график logloss:
Видно, что чем ближе к нулю ответ алгоритма при ground truth = 1, тем выше значение ошибки и круче растёт кривая.
Подытожим:
- В случае многоклассовой классификации нужно внимательно следить за метриками каждого из классов и следовать логике решения задачи, а не оптимизации метрики
- В случае неравных классов нужно подбирать баланс классов для обучения и метрику, которая будет корректно отражать качество классификации
- Выбор метрики нужно делать с фокусом на предметную область, предварительно обрабатывая данные и, возможно, сегментируя (как в случае с делением на богатых и бедных клиентов)
Полезные ссылки
- Курс Евгения Соколова: Семинар по выбору моделей (там есть информация по метрикам задач регрессии)
- Задачки на AUC-ROC от А.Г. Дьяконова
- Дополнительно о других метриках можно почитать на kaggle. К описанию каждой метрики добавлена ссылка на соревнования, где она использовалась
- Презентация Богдана Мельника aka ld86 про обучение на несбалансированных выборках
Благодарности
Спасибо mephistopheies и madrugado за помощь в подготовке статьи.
Были ли вы в ситуации, когда вы ожидали, что ваша модель машинного обучения должна работать очень хорошо, но у нее была низкая точность? Вы проделали всю тяжелую работу — так где же модель классификации сработала не так? Как это исправить?
Существует множество способов оценить эффективность вашей модели классификации, но ни один из них не выдержал испытания временем, кроме матрицы ошибок. Она помогает нам оценить, как наша модель работала, где она пошла не туда, и предлагает нам рекомендации по исправлению нашего пути.
В этой статье мы рассмотрим, как матрица ошибок дает целостное представление об эффективности вашей модели. И, в отличие от названия, вы поймете, что матрица ошибок — довольно простая, но мощная концепция. Итак, давайте раскроем тайну матрицы ошибок!
Что такое матрица ошибок?
Вопрос на миллион долларов — что такое, в конце концов, матрица ошибок?
Матрица ошибок — это матрица размером N x N, используемая для оценки эффективности модели классификации, где N — количество целевых классов. Матрица сравнивает фактические целевые значения с предсказанными моделью машинного обучения. Это дает нам целостное представление о том, насколько хорошо работает наша классификационная модель и какие ошибки она допускает.
Для задачи двоичной классификации у нас будет матрица 2 x 2, как показано ниже, с 4 значениями:
Расшифруем матрицу:
- Целевая переменная имеет два значения: положительное или отрицательное.
- Столбцы представляют фактические значения целевой переменной.
- Строки представляют собой прогнозируемые значения целевой переменной.
Но подождите — что здесь TP, FP, FN и TN? Это важнейшая часть матрицы ошибок. Давайте разберемся с каждым термином ниже.
Понимание True Positive, True Negative, False Positive и False Negative в матрице ошибок
True Positive (TP)
- Прогнозируемое значение соответствует фактическому значению.
- Фактическое значение было положительным, и модель предсказала положительное значение.
True Negative (TN)
- Прогнозируемое значение соответствует фактическому значению.
- Фактическое значение было отрицательным, и модель предсказала отрицательное значение.
False Positive (FP) — ошибка 1-го типа
- Прогнозируемое значение было предсказано неверно.
- Фактическое значение было отрицательным, но модель предсказала положительное значение.
- Также известна как ошибка 1-го типа.
False Negative (FN) — ошибка 2-го типа
- Прогнозируемое значение было предсказано неверно.
- Фактическое значение было положительным, но модель предсказала отрицательное значение.
- Также известна как ошибка 2-го типа.
Позвольте мне привести пример, чтобы лучше это понять. Предположим, у нас есть набор данных классификации с 1000 точками данных. Мы подгоняем на нем классификатор и получаем следующую матрицу ошибок:
Различные значения матрицы ошибок будут следующими:
- True Positive (TP) = 560; это означает, что 560 положительных точек данных были правильно классифицированы моделью.
- True Negative (TN) = 330; это означает, что 330 отрицательных точек данных были правильно классифицированы моделью.
- False Positive (FP) = 60; это означает, что 60 отрицательных точек данных были неправильно классифицированы моделью как положительные.
- False Negative (FN) = 50; это означает, что 50 положительных точек данных были неправильно классифицированы моделью как отрицательные.
Это оказался довольно приличный классификатор для нашего набора данных, учитывая относительно большее количество истинно положительных и истинно отрицательных значений.
Помните об ошибках 1-го и 2-го типа. Интервьюеры любят спрашивать, в чем разница между ними!
Зачем нам нужна матрица ошибок?
Прежде чем ответить на этот вопрос, давайте подумаем о проблеме гипотетической классификации.
Допустим, вы хотите предсказать, сколько людей инфицировано заразным вирусом, до того, как у них проявятся симптомы, и изолировать их от здорового населения. Двумя значениями для нашей целевой переменной будут: Sick и Not Sick.
Теперь вы, должно быть, задаетесь вопросом — зачем нам матрица ошибок, когда у нас есть наш вечный друг — Точность? Что ж, посмотрим, где точность не работает.
Наш набор данных является примером несбалансированного набора данных. Имеется 947 точек данных для отрицательного класса и 3 точки данных для положительного класса. Вот как мы рассчитаем точность:
Посмотрим, как работает наша модель:
Общие значения результатов:
TP = 30, TN = 930, FP = 30, FN = 10
Итак, точность для нашей модели:
96%! Неплохо!
Но это дает неверное представление о результате. Подумайте об этом.
Наша модель гласит: «Я могу предсказать заболевание в 96% случаев». Однако она делает наоборот. Это предсказание людей, которые не заболеют с точностью 96%, пока больные распространяют вирус!
Как вы думаете, это правильный показатель для нашей модели, учитывая серьезность проблемы? Разве мы не должны измерять, сколько положительных случаев мы можем правильно предсказать, чтобы остановить распространение заразного вируса? Или, из правильно спрогнозированных случаев сколько положительных случаев для проверки надежности нашей модели?
Здесь мы сталкиваемся с двойным понятием «точность (Precision) и полнота (Recall)».
Precision vs. Recall
Точность говорит нам, сколько из правильно предсказанных случаев действительно оказались положительными.
Вот как рассчитать точность:
Это определило бы надежность нашей модели.
Полнота сообщает нам, сколько реальных положительных случаев мы смогли правильно предсказать с помощью нашей модели.
А вот как мы можем рассчитать полноту:
Мы можем легко рассчитать точность и полноту для нашей модели, подставив значения в приведенные выше уравнения:
50% процентов правильно предсказанных случаев оказались положительными. В то время как 75% положительных результатов были успешно предсказаны нашей моделью. Потрясающие!
Точность — полезный показатель в тех случаях, когда ложноположительный результат важнее, чем ложноотрицательный.
Точность важна в системах рекомендаций по музыке или видео, на веб-сайтах электронной коммерции и т. д. Неправильные результаты могут привести к оттоку клиентов и нанести вред бизнесу.
Полнота — полезный показатель в случаях, когда ложноотрицательный результат важнее ложноположительного.
Полнота важна в медицинских случаях, когда не имеет значения, что возникает ложная тревога, но реальные положительные случаи не должны оставаться незамеченными!
В нашем примере полнота была бы лучшим показателем, потому что мы не хотим, чтобы случайно выписали инфицированного человека и позволили ему смешаться со здоровым населением, тем самым распространяя заразный вирус. Теперь вы можете понять, почему точность была плохим показателем для нашей модели.
Но будут случаи, когда нет четкой разницы между тем, что важнее: точность или полнота. Что нам делать в таких случаях? Мы их совмещаем!
F1-Score
На практике, когда мы пытаемся повысить точность нашей модели, полнота снижается, и наоборот. F1-Score отражает обе тенденции в одном значении:
F1-Score представляет собой гармоничное среднее значение точности и полноты, поэтому дает общее представление об этих двух показателях. Оно максимально, когда точность равно полноте.
Но здесь есть одна загвоздка. Интерпретируемость оценки F1 оставляет желать лучшего. Это означает, что мы не знаем, чего добивается наш классификатор — точности или полноты? Итак, мы используем его в сочетании с другими оценочными метриками, что дает нам полную картину результата.
Матрица ошибок с использованием scikit-learn в Python
Вы знаете теорию — теперь давайте применим ее на практике. Давайте запрограммируем матрицу ошибок с помощью библиотеки Scikit-learn (sklearn) на Python.
# confusion matrix in sklearn
from sklearn.metrics import confusion_matrix
3 from sklearn.metrics import classification_report
# actual values
actual = [1,0,0,1,0,0,1,0,0,1]
# predicted values
predicted = [1,0,0,1,0,0,0,1,0,0]
# confusion matrix
matrix = confusion_matrix(actual,predicted, labels=[1,0])
print(‘Confusion matrix : n’,matrix)
# outcome values order in sklearn
tp, fn, fp, tn = confusion_matrix(actual,predicted,labels=[1,0]).reshape(-1)
print(‘Outcome values : n’, tp, fn, fp, tn)
# classification report for precision, recall f1-score and accuracy
matrix = classification_report(actual,predicted,labels=[1,0])
print(‘Classification report : n’,matrix)
Sklearn имеет две отличные функции: confusion_matrix() и classification_report().
возвращает значения матрицы ошибок. Однако результат немного отличается от того, что мы изучили до сих пор. Она принимает строки как фактические значения, а столбцы как прогнозные значения. В остальном концепция осталась прежней.
выводит точность, полноту и f1-score для каждого целевого класса. В дополнение к этому, она также имеет некоторые дополнительные значения: micro avg, macro avg и weighted avg.
Mirco average — это оценка точности/полноты/f1, рассчитанная для всех классов.
Macro average — это среднее значение точности/полноты/f1-score.
Weighted average — это просто средневзвешенное значение точности/полноты/f1-score.
Матрица ошибок для мультиклассовой классификации
Как матрица ошибок будет работать для задачи классификации нескольких классов? Мы рассмотрим и этот случай.
Давайте нарисуем матрицу ошибок для мультиклассовой задачи, в которой мы должны предсказать, любит ли человек Facebook, Instagram или Snapchat. Матрица ошибок будет иметь вид 3 x 3:
true positive, true negative, false positive и false negative для каждого класса будут вычисляться путем сложения значений ячеек следующим образом:
Вот и все! Вы готовы расшифровать любую матрицу ошибок размером N x N!
Заключение
И вдруг матрица ошибок перестает быть такой запутанной! Эта статья должна дать вам прочную основу для интерпретации и использования матрицы ошибок для алгоритмов классификации в машинном обучении.
Вскоре мы выпустим статью о кривой AUC-ROC и продолжим наше обсуждение там. До этого не теряйте надежды на свою модель классификации, возможно, вы просто используете неправильную метрику оценки!
Гораздо легче что-то измерить, чем понять, что именно вы измеряете
Джон Уильям Салливан
Задачи машинного обучения с учителем как правило состоят в восстановлении зависимости между парами (признаковое описание, целевая переменная) по данным, доступным нам для анализа. Алгоритмы машинного обучения (learning algorithm), со многими из которых вы уже успели познакомиться, позволяют построить модель, аппроксимирующую эту зависимость. Но как понять, насколько качественной получилась аппроксимация?
Почти наверняка наша модель будет ошибаться на некоторых объектах: будь она даже идеальной, шум или выбросы в тестовых данных всё испортят. При этом разные модели будут ошибаться на разных объектах и в разной степени. Задача специалиста по машинному обучению – подобрать подходящий критерий, который позволит сравнивать различные модели.
Перед чтением этой главы мы хотели бы ещё раз напомнить, что качество модели нельзя оценивать на обучающей выборке. Как минимум, это стоит делать на отложенной (тестовой) выборке, но, если вам это позволяют время и вычислительные ресурсы, стоит прибегнуть и к более надёжным способам проверки – например, кросс-валидации (о ней вы узнаете в отдельной главе).
Выбор метрик в реальных задачах
Возможно, вы уже участвовали в соревнованиях по анализу данных. На таких соревнованиях метрику (критерий качества модели) организатор выбирает за вас, и она, как правило, довольно понятным образом связана с результатами предсказаний. Но на практике всё бывает намного сложнее.
Например, мы хотим:
- решить, сколько коробок с бананами нужно завтра привезти в конкретный магазин, чтобы минимизировать количество товара, который не будет выкуплен и минимизировать ситуацию, когда покупатель к концу дня не находит желаемый продукт на полке;
- увеличить счастье пользователя от работы с нашим сервисом, чтобы он стал лояльным и обеспечивал тем самым стабильный прогнозируемый доход;
- решить, нужно ли направить человека на дополнительное обследование.
В каждом конкретном случае может возникать целая иерархия метрик. Представим, например, что речь идёт о стриминговом музыкальном сервисе, пользователей которого мы решили порадовать сгенерированными самодельной нейросетью треками – не защищёнными авторским правом, а потому совершенно бесплатными. Иерархия метрик могла бы иметь такой вид:
- Самый верхний уровень: будущий доход сервиса – невозможно измерить в моменте, сложным образом зависит от совокупности всех наших усилий;
- Медианная длина сессии, возможно, служащая оценкой радости пользователей, которая, как мы надеемся, повлияет на их желание продолжать платить за подписку – её нам придётся измерять в продакшене, ведь нас интересует реакция настоящих пользователей на новшество;
- Доля удовлетворённых качеством сгенерированной музыки асессоров, на которых мы потестируем её до того, как выставить на суд пользователей;
- Функция потерь, на которую мы будем обучать генеративную сеть.
На этом примере мы можем заметить сразу несколько общих закономерностей. Во-первых, метрики бывают offline и online (оффлайновыми и онлайновыми). Online метрики вычисляются по данным, собираемым с работающей системы (например, медианная длина сессии). Offline метрики могут быть измерены до введения модели в эксплуатацию, например, по историческим данным или с привлечением специальных людей, асессоров. Последнее часто применяется, когда метрикой является реакция живого человека: скажем, так поступают поисковые компании, которые предлагают людям оценить качество ранжирования экспериментальной системы еще до того, как рядовые пользователи увидят эти результаты в обычном порядке. На самом же нижнем этаже иерархии лежат оптимизируемые в ходе обучения функции потерь.
В данном разделе нас будут интересовать offline метрики, которые могут быть измерены без привлечения людей.
Функция потерь $neq$ метрика качества
Как мы узнали ранее, методы обучения реализуют разные подходы к обучению:
- обучение на основе прироста информации (как в деревьях решений)
- обучение на основе сходства (как в методах ближайших соседей)
- обучение на основе вероятностной модели данных (например, максимизацией правдоподобия)
- обучение на основе ошибок (минимизация эмпирического риска)
И в рамках обучения на основе минимизации ошибок мы уже отвечали на вопрос: как можно штрафовать модель за предсказание на обучающем объекте.
Во время сведения задачи о построении решающего правила к задаче численной оптимизации, мы вводили понятие функции потерь и, обычно, объявляли целевой функцией сумму потерь от предсказаний на всех объектах обучающей выборке.
Важно понимать разницу между функцией потерь и метрикой качества. Её можно сформулировать следующим образом:
-
Функция потерь возникает в тот момент, когда мы сводим задачу построения модели к задаче оптимизации. Обычно требуется, чтобы она обладала хорошими свойствами (например, дифференцируемостью).
-
Метрика – внешний, объективный критерий качества, обычно зависящий не от параметров модели, а только от предсказанных меток.
В некоторых случаях метрика может совпадать с функцией потерь. Например, в задаче регрессии MSE играет роль как функции потерь, так и метрики. Но, скажем, в задаче бинарной классификации они почти всегда различаются: в качестве функции потерь может выступать кросс-энтропия, а в качестве метрики – число верно угаданных меток (accuracy). Отметим, что в последнем примере у них различные аргументы: на вход кросс-энтропии нужно подавать логиты, а на вход accuracy – предсказанные метки (то есть по сути argmax логитов).
Бинарная классификация: метки классов
Перейдём к обзору метрик и начнём с самой простой разновидности классификации – бинарной, а затем постепенно будем наращивать сложность.
Напомним постановку задачи бинарной классификации: нам нужно по обучающей выборке ${(x_i, y_i)}_{i=1}^N$, где $y_iin{0, 1}$ построить модель, которая по объекту $x$ предсказывает метку класса $f(x)in{0, 1}$.
Первым критерием качества, который приходит в голову, является accuracy – доля объектов, для которых мы правильно предсказали класс:
$$ color{#348FEA}{text{Accuracy}(y, y^{pred}) = frac{1}{N} sum_{i=1}^N mathbb{I}[y_i = f(x_i)]} $$
Или же сопряженная ей метрика – доля ошибочных классификаций (error rate):
$$text{Error rate} = 1 — text{Accuracy}$$
Познакомившись чуть внимательнее с этой метрикой, можно заметить, что у неё есть несколько недостатков:
- она не учитывает дисбаланс классов. Например, в задаче диагностики редких заболеваний классификатор, предсказывающий всем пациентам отсутствие болезни будет иметь достаточно высокую accuracy просто потому, что больных людей в выборке намного меньше;
- она также не учитывает цену ошибки на объектах разных классов. Для примера снова можно привести задачу медицинской диагностики: если ошибочный положительный диагноз для здорового больного обернётся лишь ещё одним обследованием, то ошибочно отрицательный вердикт может повлечь роковые последствия.
Confusion matrix (матрица ошибок)
Исторически задача бинарной классификации – это задача об обнаружении чего-то редкого в большом потоке объектов, например, поиск человека, больного туберкулёзом, по флюорографии. Или задача признания пятна на экране приёмника радиолокационной станции бомбардировщиком, представляющем угрозу охраняемому объекту (в противовес стае гусей).
Поэтому класс, который представляет для нас интерес, называется «положительным», а оставшийся – «отрицательным».
Заметим, что для каждого объекта в выборке возможно 4 ситуации:
- мы предсказали положительную метку и угадали. Будет относить такие объекты к true positive (TP) группе (true – потому что предсказали мы правильно, а positive – потому что предсказали положительную метку);
- мы предсказали положительную метку, но ошиблись в своём предсказании – false positive (FP) (false, потому что предсказание было неправильным);
- мы предсказали отрицательную метку и угадали – true negative (TN);
- и наконец, мы предсказали отрицательную метку, но ошиблись – false negative (FN). Для удобства все эти 4 числа изображают в виде таблицы, которую называют confusion matrix (матрицей ошибок):
Не волнуйтесь, если первое время эти обозначения будут сводить вас с ума (будем откровенны, даже профи со стажем в них порой путаются), однако логика за ними достаточно простая: первая часть названия группы показывает угадали ли мы с классом, а вторая – какой класс мы предсказали.
Пример
Попробуем воспользоваться введёнными метриками в боевом примере: сравним работу нескольких моделей классификации на Breast cancer wisconsin (diagnostic) dataset.
Объектами выборки являются фотографии биопсии грудных опухолей. С их помощью было сформировано признаковое описание, которое заключается в характеристиках ядер клеток (таких как радиус ядра, его текстура, симметричность). Положительным классом в такой постановке будут злокачественные опухоли, а отрицательным – доброкачественные.
Модель 1. Константное предсказание.
Решение задачи начнём с самого простого классификатора, который выдаёт на каждом объекте константное предсказание – самый часто встречающийся класс.
Зачем вообще замерять качество на такой модели?При разработке модели машинного обучения для проекта всегда желательно иметь некоторую baseline модель. Так нам будет легче проконтролировать, что наша более сложная модель действительно дает нам прирост качества.
from sklearn.datasets
import load_breast_cancer
the_data = load_breast_cancer()
# 0 – "доброкачественный"
# 1 – "злокачественный"
relabeled_target = 1 - the_data["target"]
from sklearn.model_selection import train_test_split
X = the_data["data"]
y = relabeled_target
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
from sklearn.dummy import DummyClassifier
dc_mf = DummyClassifier(strategy="most_frequent")
dc_mf.fit(X_train, y_train)
from sklearn.metrics import confusion_matrix
y_true = y_test y_pred = dc_mf.predict(X_test)
dc_mf_tn, dc_mf_fp, dc_mf_fn, dc_mf_tp = confusion_matrix(y_true, y_pred, labels = [0, 1]).ravel()
| Прогнозируемый класс + | Прогнозируемый класс — | |
|---|---|---|
| Истинный класс + | TP = 0 | FN = 53 |
| Истинный класс — | FP = 0 | TN = 90 |
Обучающие данные таковы, что наш dummy-классификатор все объекты записывает в отрицательный класс, то есть признаёт все опухоли доброкачественными. Такой наивный подход позволяет нам получить минимальный штраф за FP (действительно, нельзя ошибиться в предсказании, если положительный класс вообще не предсказывается), но и максимальный штраф за FN (в эту группу попадут все злокачественные опухоли).
Модель 2. Случайный лес.
Настало время воспользоваться всем арсеналом моделей машинного обучения, и начнём мы со случайного леса.
from sklearn.ensemble import RandomForestClassifier
rfc = RandomForestClassifier()
rfc.fit(X_train, y_train)
y_true = y_test
y_pred = rfc.predict(X_test)
rfc_tn, rfc_fp, rfc_fn, rfc_tp = confusion_matrix(y_true, y_pred, labels = [0, 1]).ravel()
| Прогнозируемый класс + | Прогнозируемый класс — | |
|---|---|---|
| Истинный класс + | TP = 52 | FN = 1 |
| Истинный класс — | FP = 4 | TN = 86 |
Можно сказать, что этот классификатор чему-то научился, т.к. главная диагональ матрицы стала содержать все объекты из отложенной выборки, за исключением 4 + 1 = 5 объектов (сравните с 0 + 53 объектами dummy-классификатора, все опухоли объявляющего доброкачественными).
Отметим, что вычисляя долю недиагональных элементов, мы приходим к метрике error rate, о которой мы говорили в самом начале:
$$text{Error rate} = frac{FP + FN}{ TP + TN + FP + FN}$$
тогда как доля объектов, попавших на главную диагональ – это как раз таки accuracy:
$$text{Accuracy} = frac{TP + TN}{ TP + TN + FP + FN}$$
Модель 3. Метод опорных векторов.
Давайте построим еще один классификатор на основе линейного метода опорных векторов.
Не забудьте привести признаки к единому масштабу, иначе численный алгоритм не сойдется к решению и мы получим гораздо более плохо работающее решающее правило. Попробуйте проделать это упражнение.
from sklearn.svm import LinearSVC
from sklearn.preprocessing import StandardScaler
ss = StandardScaler() ss.fit(X_train)
scaled_linsvc = LinearSVC(C=0.01,random_state=42)
scaled_linsvc.fit(ss.transform(X_train), y_train)
y_true = y_test
y_pred = scaled_linsvc.predict(ss.transform(X_test))
tn, fp, fn, tp = confusion_matrix(y_true, y_pred, labels = [0, 1]).ravel()
| Прогнозируемый класс + | Прогнозируемый класс — | |
|---|---|---|
| Истинный класс + | TP = 50 | FN = 3 |
| Истинный класс — | FP = 1 | TN = 89 |
Сравним результаты
Легко заметить, что каждая из двух моделей лучше классификатора-пустышки, однако давайте попробуем сравнить их между собой. С точки зрения error rate модели практически одинаковы: 5/143 для леса против 4/143 для SVM.
Посмотрим на структуру ошибок чуть более внимательно: лес – (FP = 4, FN = 1), SVM – (FP = 1, FN = 3). Какая из моделей предпочтительнее?
Замечание: Мы сравниваем несколько классификаторов на основании их предсказаний на отложенной выборке. Насколько ошибки данных классификаторов зависят от разбиения исходного набора данных? Иногда в процессе оценки качества мы будем получать модели, чьи показатели эффективности будут статистически неразличимыми.
Пусть мы учли предыдущее замечание и эти модели действительно статистически значимо ошибаются в разную сторону. Мы встретились с очевидной вещью: на матрицах нет отношения порядка. Когда мы сравнивали dummy-классификатор и случайный лес с помощью Accuracy, мы всю сложную структуру ошибок свели к одному числу, т.к. на вещественных числах отношение порядка есть. Сводить оценку модели к одному числу очень удобно, однако не стоит забывать, что у вашей модели есть много аспектов качества.
Что же всё-таки важнее уменьшить: FP или FN? Вернёмся к задаче: FP – доля доброкачественных опухолей, которым ошибочно присваивается метка злокачественной, а FN – доля злокачественных опухолей, которые классификатор пропускает. В такой постановке становится понятно, что при сравнении выиграет модель с меньшим FN (то есть лес в нашем примере), ведь каждая не обнаруженная опухоль может стоить человеческой жизни.
Рассмотрим теперь другую задачу: по данным о погоде предсказать, будет ли успешным запуск спутника. FN в такой постановке – это ошибочное предсказание неуспеха, то есть не более, чем упущенный шанс (если вас, конечно не уволят за срыв сроков). С FP всё серьёзней: если вы предскажете удачный запуск спутника, а на деле он потерпит крушение из-за погодных условий, то ваши потери будут в разы существеннее.
Итак, из примеров мы видим, что в текущем виде введенная нами доля ошибочных классификаций не даст нам возможности учесть неравную важность FP и FN. Поэтому введем две новые метрики: точность и полноту.
Точность и полнота
Accuracy — это метрика, которая характеризует качество модели, агрегированное по всем классам. Это полезно, когда классы для нас имеют одинаковое значение. В случае, если это не так, accuracy может быть обманчивой.
Рассмотрим ситуацию, когда положительный класс это событие редкое. Возьмем в качестве примера поисковую систему — в нашем хранилище хранятся миллиарды документов, а релевантных к конкретному поисковому запросу на несколько порядков меньше.
Пусть мы хотим решить задачу бинарной классификации «документ d релевантен по запросу q». Благодаря большому дисбалансу, Accuracy dummy-классификатора, объявляющего все документы нерелевантными, будет близка к единице. Напомним, что $text{Accuracy} = frac{TP + TN}{TP + TN + FP + FN}$, и в нашем случае высокое значение метрики будет обеспечено членом TN, в то время для пользователей более важен высокий TP.
Поэтому в случае ассиметрии классов, можно использовать метрики, которые не учитывают TN и ориентируются на TP.
Если мы рассмотрим долю правильно предсказанных положительных объектов среди всех объектов, предсказанных положительным классом, то мы получим метрику, которая называется точностью (precision)
$$color{#348FEA}{text{Precision} = frac{TP}{TP + FP}}$$
Интуитивно метрика показывает долю релевантных документов среди всех найденных классификатором. Чем меньше ложноположительных срабатываний будет допускать модель, тем больше будет её Precision.
Если же мы рассмотрим долю правильно найденных положительных объектов среди всех объектов положительного класса, то мы получим метрику, которая называется полнотой (recall)
$$color{#348FEA}{text{Recall} = frac{TP}{TP + FN}}$$
Интуитивно метрика показывает долю найденных документов из всех релевантных. Чем меньше ложно отрицательных срабатываний, тем выше recall модели.
Например, в задаче предсказания злокачественности опухоли точность показывает, сколько из определённых нами как злокачественные опухолей действительно являются злокачественными, а полнота – какую долю злокачественных опухолей нам удалось выявить.
Хорошее понимание происходящего даёт следующая картинка: 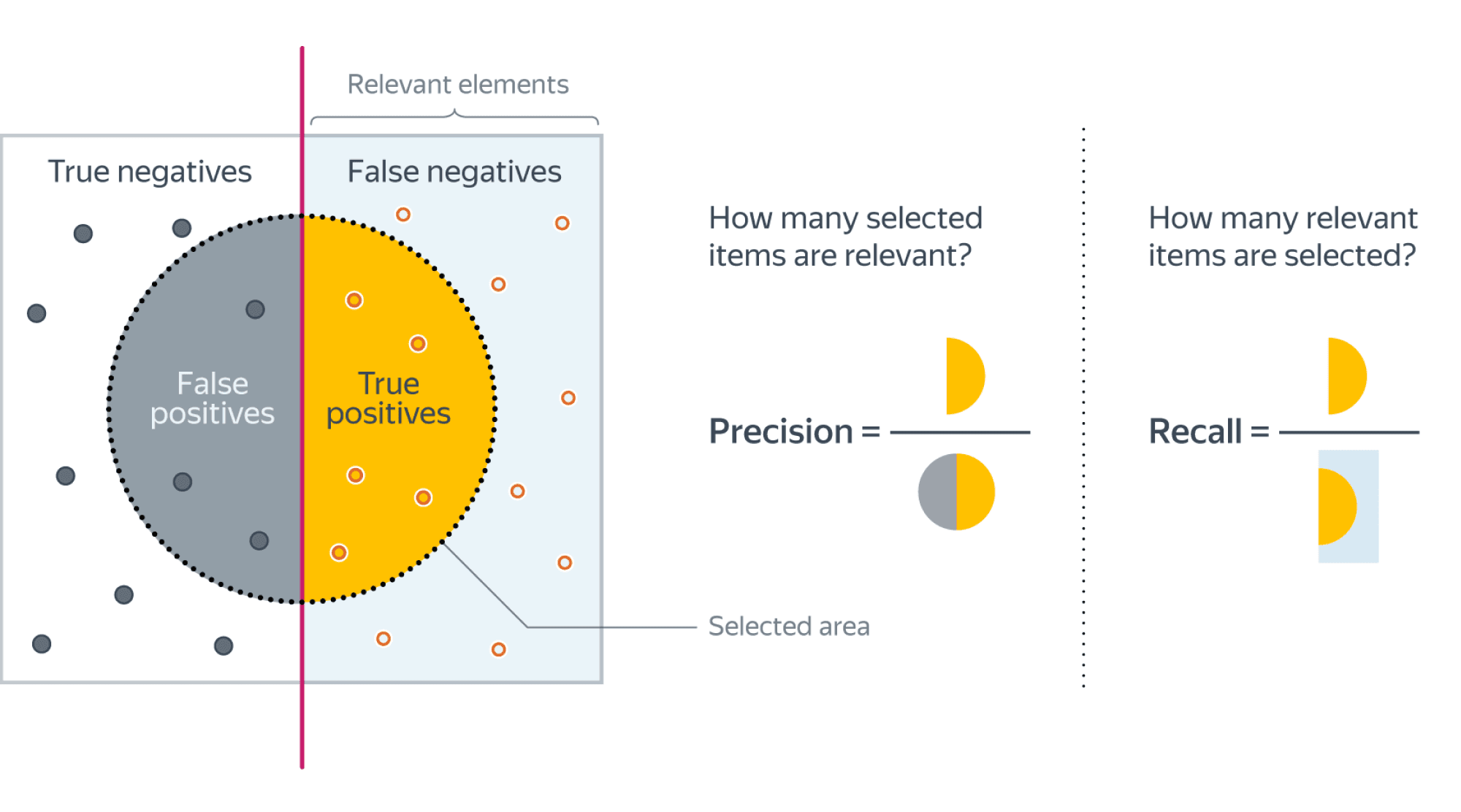
Recall@k, Precision@k
Метрики Recall и Precision хорошо подходят для задачи поиска «документ d релевантен запросу q», когда из списка рекомендованных алгоритмом документов нас интересует только первый. Но не всегда алгоритм машинного обучения вынужден работать в таких жестких условиях. Может быть такое, что вполне достаточно, что релевантный документ попал в первые k рекомендованных. Например, в интерфейсе выдачи первые три подсказки видны всегда одновременно и вообще не очень понятно, какой у них порядок. Тогда более честной оценкой качества алгоритма будет «в выдаче D размера k по запросу q нашлись релевантные документы». Для расчёта метрики по всей выборке объединим все выдачи и рассчитаем precision, recall как обычно подокументно.
F1-мера
Как мы уже отмечали ранее, модели очень удобно сравнивать, когда их качество выражено одним числом. В случае пары Precision-Recall существует популярный способ скомпоновать их в одну метрику — взять их среднее гармоническое. Данный показатель эффективности исторически носит название F1-меры (F1-measure).
$$
color{#348FEA}{F_1 = frac{2}{frac{1}{Recall} + frac{1}{Precision}}} = $$
$$ = 2 frac{Recall cdot Precision }{Recall + Precision} = frac
{TP} {TP + frac{FP + FN}{2}}
$$
Стоит иметь в виду, что F1-мера предполагает одинаковую важность Precision и Recall, если одна из этих метрик для вас приоритетнее, то можно воспользоваться $F_{beta}$ мерой:
$$
F_{beta} = (beta^2 + 1) frac{Recall cdot Precision }{Recall + beta^2Precision}
$$
Бинарная классификация: вероятности классов
Многие модели бинарной классификации устроены так, что класс объекта получается бинаризацией выхода классификатора по некоторому фиксированному порогу:
$$fleft(x ; w, w_{0}right)=mathbb{I}left[g(x, w) > w_{0}right].$$
Например, модель логистической регрессии возвращает оценку вероятности принадлежности примера к положительному классу. Другие модели бинарной классификации обычно возвращают произвольные вещественные значения, но существуют техники, называемые калибровкой классификатора, которые позволяют преобразовать предсказания в более или менее корректную оценку вероятности принадлежности к положительному классу.
Как оценить качество предсказываемых вероятностей, если именно они являются нашей конечной целью? Общепринятой мерой является логистическая функция потерь, которую мы изучали раньше, когда говорили об устройстве некоторых методов классификации (например уже упоминавшейся логистической регрессии).
Если же нашей целью является построение прогноза в терминах метки класса, то нам нужно учесть, что в зависимости от порога мы будем получать разные предсказания и разное качество на отложенной выборке. Так, чем ниже порог отсечения, тем больше объектов модель будет относить к положительному классу. Как в этом случае оценить качество модели?
AUC
Пусть мы хотим учитывать ошибки на объектах обоих классов. При уменьшении порога отсечения мы будем находить (правильно предсказывать) всё большее число положительных объектов, но также и неправильно предсказывать положительную метку на всё большем числе отрицательных объектов. Естественным кажется ввести две метрики TPR и FPR:
TPR (true positive rate) – это полнота, доля положительных объектов, правильно предсказанных положительными:
$$ TPR = frac{TP}{P} = frac{TP}{TP + FN} $$
FPR (false positive rate) – это доля отрицательных объектов, неправильно предсказанных положительными:
$$FPR = frac{FP}{N} = frac{FP}{FP + TN}$$
Обе эти величины растут при уменьшении порога. Кривая в осях TPR/FPR, которая получается при варьировании порога, исторически называется ROC-кривой (receiver operating characteristics curve, сокращённо ROC curve). Следующий график поможет вам понять поведение ROC-кривой.
Желтая и синяя кривые показывают распределение предсказаний классификатора на объектах положительного и отрицательного классов соответственно. То есть значения на оси X (на графике с двумя гауссианами) мы получаем из классификатора. Если классификатор идеальный (две кривые разделимы по оси X), то на правом графике мы получаем ROC-кривую (0,0)->(0,1)->(1,1) (убедитесь сами!), площадь под которой равна 1. Если классификатор случайный (предсказывает одинаковые метки положительным и отрицательным объектам), то мы получаем ROC-кривую (0,0)->(1,1), площадь под которой равна 0.5. Поэкспериментируйте с разными вариантами распределения предсказаний по классам и посмотрите, как меняется ROC-кривая.
Чем лучше классификатор разделяет два класса, тем больше площадь (area under curve) под ROC-кривой – и мы можем использовать её в качестве метрики. Эта метрика называется AUC и она работает благодаря следующему свойству ROC-кривой:
AUC равен доле пар объектов вида (объект класса 1, объект класса 0), которые алгоритм верно упорядочил, т.е. предсказание классификатора на первом объекте больше:
$$
color{#348FEA}{operatorname{AUC} = frac{sumlimits_{i = 1}^{N} sumlimits_{j = 1}^{N}mathbb{I}[y_i < y_j] I^{prime}[f(x_{i}) < f(x_{j})]}{sumlimits_{i = 1}^{N} sumlimits_{j = 1}^{N}mathbb{I}[y_i < y_j]}}
$$
$$
I^{prime}left[f(x_{i}) < f(x_{j})right]=
left{
begin{array}{ll}
0, & f(x_{i}) > f(x_{j}) \
0.5 & f(x_{i}) = f(x_{j}) \
1, & f(x_{i}) < f(x_{j})
end{array}
right.
$$
$$
Ileft[y_{i}< y_{j}right]=
left{
begin{array}{ll}
0, & y_{i} geq y_{j} \
1, & y_{i} < y_{j}
end{array}
right.
$$
Чтобы детальнее разобраться, почему это так, советуем вам обратиться к материалам А.Г.Дьяконова.
В каких случаях лучше отдать предпочтение этой метрике? Рассмотрим следующую задачу: некоторый сотовый оператор хочет научиться предсказывать, будет ли клиент пользоваться его услугами через месяц. На первый взгляд кажется, что задача сводится к бинарной классификации с метками 1, если клиент останется с компанией и $0$ – иначе.
Однако если копнуть глубже в процессы компании, то окажется, что такие метки практически бесполезны. Компании скорее интересно упорядочить клиентов по вероятности прекращения обслуживания и в зависимости от этого применять разные варианты удержания: кому-то прислать скидочный купон от партнёра, кому-то предложить скидку на следующий месяц, а кому-то и новый тариф на особых условиях.
Таким образом, в любой задаче, где нам важна не метка сама по себе, а правильный порядок на объектах, имеет смысл применять AUC.
Утверждение выше может вызывать у вас желание использовать AUC в качестве метрики в задачах ранжирования, но мы призываем вас быть аккуратными.
ПодробнееУтверждение выше может вызывать у вас желание использовать AUC в качестве метрики в задачах ранжирования, но мы призываем вас быть аккуратными.» details=»Продемонстрируем это на следующем примере: пусть наша выборка состоит из $9100$ объектов класса $0$ и $10$ объектов класса $1$, и модель расположила их следующим образом:
$$underbrace{0 dots 0}_{9000} ~ underbrace{1 dots 1}_{10} ~ underbrace{0 dots 0}_{100}$$
Тогда AUC будет близка к единице: количество пар правильно расположенных объектов будет порядка $90000$, в то время как общее количество пар порядка $91000$.
Однако самыми высокими по вероятности положительного класса будут совсем не те объекты, которые мы ожидаем.
Average Precision
Будем постепенно уменьшать порог бинаризации. При этом полнота будет расти от $0$ до $1$, так как будет увеличиваться количество объектов, которым мы приписываем положительный класс (а количество объектов, на самом деле относящихся к положительному классу, очевидно, меняться не будет). Про точность же нельзя сказать ничего определённого, но мы понимаем, что скорее всего она будет выше при более высоком пороге отсечения (мы оставим только объекты, в которых модель «уверена» больше всего). Варьируя порог и пересчитывая значения Precision и Recall на каждом пороге, мы получим некоторую кривую примерно следующего вида:
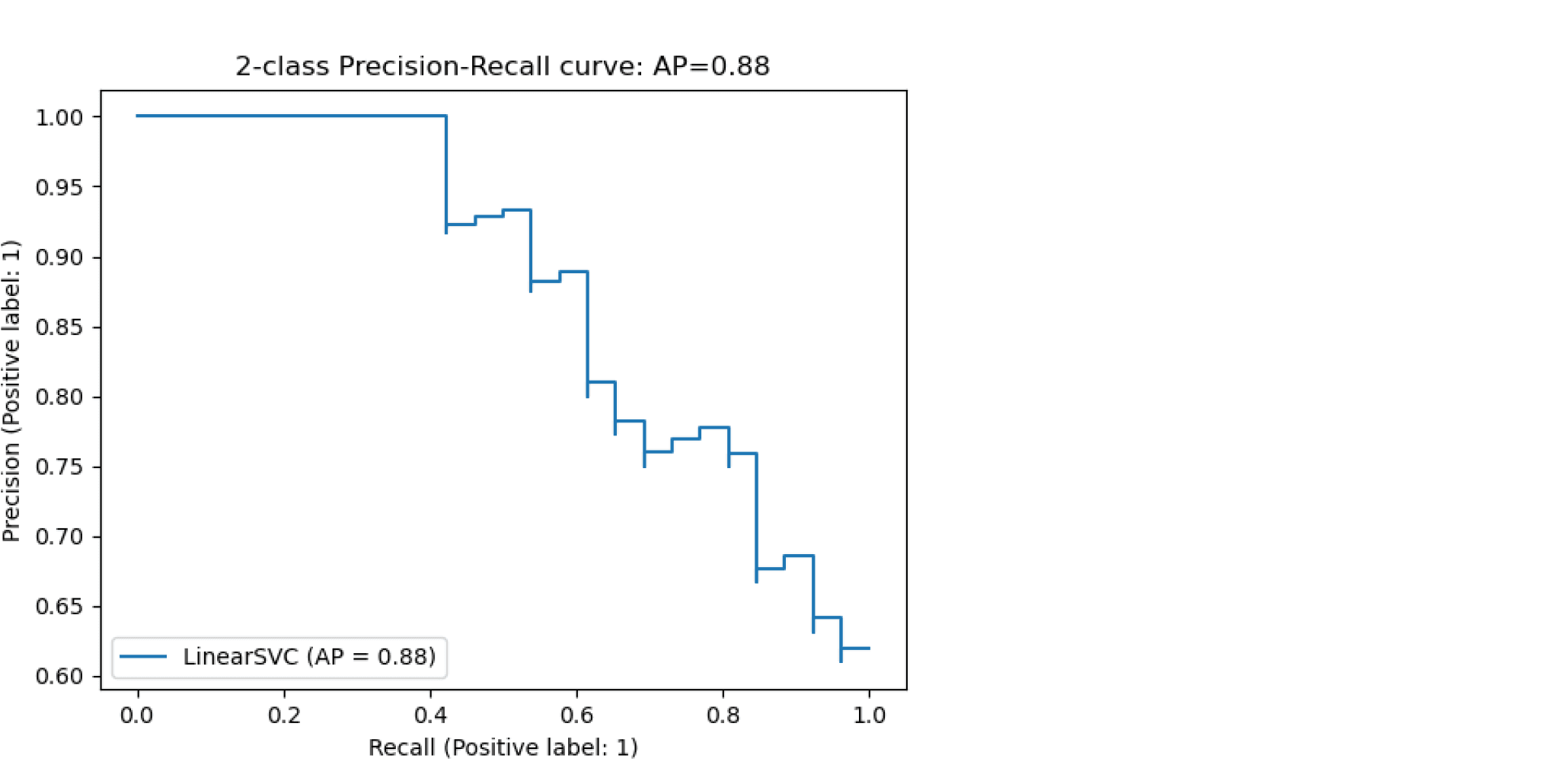
Рассмотрим среднее значение точности (оно равно площади под кривой точность-полнота):
$$ text { AP }=int_{0}^{1} p(r) d r$$
Получим показатель эффективности, который называется average precision. Как в случае матрицы ошибок мы переходили к скалярным показателям эффективности, так и в случае с кривой точность-полнота мы охарактеризовали ее в виде числа.
Многоклассовая классификация
Если классов становится больше двух, расчёт метрик усложняется. Если задача классификации на $K$ классов ставится как $K$ задач об отделении класса $i$ от остальных ($i=1,ldots,K$), то для каждой из них можно посчитать свою матрицу ошибок. Затем есть два варианта получения итогового значения метрики из $K$ матриц ошибок:
- Усредняем элементы матрицы ошибок (TP, FP, TN, FN) между бинарными классификаторами, например $TP = frac{1}{K}sum_{i=1}^{K}TP_i$. Затем по одной усреднённой матрице ошибок считаем Precision, Recall, F-меру. Это называют микроусреднением.
- Считаем Precision, Recall для каждого классификатора отдельно, а потом усредняем. Это называют макроусреднением.
Порядок усреднения влияет на результат в случае дисбаланса классов. Показатели TP, FP, FN — это счётчики объектов. Пусть некоторый класс обладает маленькой мощностью (обозначим её $M$). Тогда значения TP и FN при классификации этого класса против остальных будут не больше $M$, то есть тоже маленькие. Про FP мы ничего уверенно сказать не можем, но скорее всего при дисбалансе классов классификатор не будет предсказывать редкий класс слишком часто, потому что есть большая вероятность ошибиться. Так что FP тоже мало. Поэтому усреднение первым способом сделает вклад маленького класса в общую метрику незаметным. А при усреднении вторым способом среднее считается уже для нормированных величин, так что вклад каждого класса будет одинаковым.
Рассмотрим пример. Пусть есть датасет из объектов трёх цветов: желтого, зелёного и синего. Желтого и зелёного цветов почти поровну — 21 и 20 объектов соответственно, а синих объектов всего 4.
Модель по очереди для каждого цвета пытается отделить объекты этого цвета от объектов оставшихся двух цветов. Результаты классификации проиллюстрированы матрицей ошибок. Модель «покрасила» в жёлтый 25 объектов, 20 из которых были действительно жёлтыми (левый столбец матрицы). В синий был «покрашен» только один объект, который на самом деле жёлтый (средний столбец матрицы). В зелёный — 19 объектов, все на самом деле зелёные (правый столбец матрицы).
Посчитаем Precision классификации двумя способами:
- С помощью микроусреднения получаем $$
text{Precision} = frac{dfrac{1}{3}left(20 + 0 + 19right)}{dfrac{1}{3}left(20 + 0 + 19right) + dfrac{1}{3}left(5 + 1 + 0right)} = 0.87
$$ - С помощью макроусреднения получаем $$
text{Precision} = dfrac{1}{3}left( frac{20}{20 + 5} + frac{0}{0 + 1} + frac{19}{19 + 0}right) = 0.6
$$
Видим, что макроусреднение лучше отражает тот факт, что синий цвет, которого в датасете было совсем мало, модель практически игнорирует.
Как оптимизировать метрики классификации?
Пусть мы выбрали, что метрика качества алгоритма будет $F(a(X), Y)$. Тогда мы хотим обучить модель так, чтобы $F$ на валидационной выборке была минимальная/максимальная. Лучший способ добиться минимизации метрики $F$ — оптимизировать её напрямую, то есть выбрать в качестве функции потерь ту же $F(a(X), Y)$. К сожалению, это не всегда возможно. Рассмотрим, как оптимизировать метрики иначе.
Метрики precision и recall невозможно оптимизировать напрямую, потому что эти метрики нельзя рассчитать на одном объекте, а затем усреднить. Они зависят от того, какими были правильная метка класса и ответ алгоритма на всех объектах. Чтобы понять, как оптимизировать precision, recall, рассмотрим, как расчитать эти метрики на отложенной выборке. Пусть модель обучена на стандартную для классификации функцию потерь (LogLoss). Для получения меток класса специалист по машинному обучению сначала применяет на объектах модель и получает вещественные предсказания модели ($p_i in left(0, 1right)$). Затем предсказания бинаризуются по порогу, выбранному специалистом: если предсказание на объекте больше порога, то метка класса 1 (или «положительная»), если меньше — 0 (или «отрицательная»). Рассмотрим, что будет с метриками precision, recall в крайних положениях порога.
- Пусть порог равен нулю. Тогда всем объектам будет присвоена положительная метка. Следовательно, все объекты будут либо TP, либо FP, потому что отрицательных предсказаний нет, $TP + FP = N$, где $N$ — размер выборки. Также все объекты, у которых метка на самом деле 1, попадут в TP. По формуле точность $text{Precision} = frac{TP}{TP + FP} = frac1N sum_{i = 1}^N mathbb{I} left[ y_i = 1 right]$ равна среднему таргету в выборке. А полнота $text{Recall} = frac{TP}{TP + FN} = frac{TP}{TP + 0} = 1$ равна единице.
- Пусть теперь порог равен единице. Тогда ни один объект не будет назван положительным, $TP = FP = 0$. Все объекты с меткой класса 1 попадут в FN. Если есть хотя бы один такой объект, то есть $FN ne 0$, будет верна формула $text{Recall} = frac{TP}{TP + FN} = frac{0}{0+ FN} = 0$. То есть при пороге единица, полнота равна нулю. Теперь посмотрим на точность. Формула для Precision состоит только из счётчиков положительных ответов модели (TP, FP). При единичном пороге они оба равны нулю, $text{Precision} = frac{TP}{TP + FP} = frac{0}{0 + 0}$то есть при единичном пороге точность неопределена. Пусть мы отступили чуть-чуть назад по порогу, чтобы хотя бы несколько объектов были названы моделью положительными. Скорее всего это будут самые «простые» объекты, которые модель распознает хорошо, потому что её предсказание близко к единице. В этом предположении $FP approx 0$. Тогда точность $text{Precision} = frac{TP}{TP + FP} approx frac{TP}{TP + 0} approx 1$ будет близка к единице.
Изменяя порог, между крайними положениями, получим графики Precision и Recall, которые выглядят как-то так:
Recall меняется от единицы до нуля, а Precision от среднего тагрета до какого-то другого значения (нет гарантий, что график монотонный).
Итого оптимизация precision и recall происходит так:
- Модель обучается на стандартную функцию потерь (например, LogLoss).
- Используя вещественные предсказания на валидационной выборке, перебирая разные пороги от 0 до 1, получаем графики метрик в зависимости от порога.
- Выбираем нужное сочетание точности и полноты.
Пусть теперь мы хотим максимизировать метрику AUC. Стандартный метод оптимизации, градиентный спуск, предполагает, что функция потерь дифференцируема. AUC этим качеством не обладает, то есть мы не можем оптимизировать её напрямую. Поэтому для метрики AUC приходится изменять оптимизационную задачу. Метрика AUC считает долю верно упорядоченных пар. Значит от исходной выборки можно перейти к выборке упорядоченных пар объектов. На этой выборке ставится задача классификации: метка класса 1 соответствует правильно упорядоченной паре, 0 — неправильно. Новой метрикой становится accuracy — доля правильно классифицированных объектов, то есть доля правильно упорядоченных пар. Оптимизировать accuracy можно по той же схеме, что и precision, recall: обучаем модель на LogLoss и предсказываем вероятности положительной метки у объекта выборки, считаем accuracy для разных порогов по вероятности и выбираем понравившийся.
Регрессия
В задачах регрессии целевая метка у нас имеет потенциально бесконечное число значений. И природа этих значений, обычно, связана с каким-то процессом измерений:
- величина температуры в определенный момент времени на метеостанции
- количество прочтений статьи на сайте
- количество проданных бананов в конкретном магазине, сети магазинов или стране
- дебит добывающей скважины на нефтегазовом месторождении за месяц и т.п.
Мы видим, что иногда метка это целое число, а иногда произвольное вещественное число. Обычно случаи целочисленных меток моделируют так, словно это просто обычное вещественное число. При таком подходе может оказаться так, что модель A лучше модели B по некоторой метрике, но при этом предсказания у модели A могут быть не целыми. Если в бизнес-задаче ожидается именно целочисленный ответ, то и оценивать нужно огрубление.
Общая рекомендация такова: оценивайте весь каскад решающих правил: и те «внутренние», которые вы получаете в результате обучения, и те «итоговые», которые вы отдаёте бизнес-заказчику.
Например, вы можете быть удовлетворены, что стали ошибаться не во втором, а только в третьем знаке после запятой при предсказании погоды. Но сами погодные данные измеряются с точностью до десятых долей градуса, а пользователь и вовсе может интересоваться лишь целым числом градусов.
Итак, напомним постановку задачи регрессии: нам нужно по обучающей выборке ${(x_i, y_i)}_{i=1}^N$, где $y_i in mathbb{R}$ построить модель f(x).
Величину $ e_i = f(x_i) — y_i $ называют ошибкой на объекте i или регрессионным остатком.
Весь набор ошибок на отложенной выборке может служить аналогом матрицы ошибок из задачи классификации. А именно, когда мы рассматриваем две разные модели, то, глядя на то, как и на каких объектах они ошиблись, мы можем прийти к выводу, что для решения бизнес-задачи нам выгоднее взять ту или иную модель. И, аналогично со случаем бинарной классификации, мы можем начать строить агрегаты от вектора ошибок, получая тем самым разные метрики.
MSE, RMSE, $R^2$
MSE – одна из самых популярных метрик в задаче регрессии. Она уже знакома вам, т.к. применяется в качестве функции потерь (или входит в ее состав) во многих ранее рассмотренных методах.
$$ MSE(y^{true}, y^{pred}) = frac1Nsum_{i=1}^{N} (y_i — f(x_i))^2 $$
Иногда для того, чтобы показатель эффективности MSE имел размерность исходных данных, из него извлекают квадратный корень и получают показатель эффективности RMSE.
MSE неограничен сверху, и может быть нелегко понять, насколько «хорошим» или «плохим» является то или иное его значение. Чтобы появились какие-то ориентиры, делают следующее:
-
Берут наилучшее константное предсказание с точки зрения MSE — среднее арифметическое меток $bar{y}$. При этом чтобы не было подглядывания в test, среднее нужно вычислять по обучающей выборке
-
Рассматривают в качестве показателя ошибки:
$$ R^2 = 1 — frac{sum_{i=1}^{N} (y_i — f(x_i))^2}{sum_{i=1}^{N} (y_i — bar{y})^2}.$$
У идеального решающего правила $R^2$ равен $1$, у наилучшего константного предсказания он равен $0$ на обучающей выборке. Можно заметить, что $R^2$ показывает, какая доля дисперсии таргетов (знаменатель) объяснена моделью.
MSE квадратично штрафует за большие ошибки на объектах. Мы уже видели проявление этого при обучении моделей методом минимизации квадратичных ошибок – там это проявлялось в том, что модель старалась хорошо подстроиться под выбросы.
Пусть теперь мы хотим использовать MSE для оценки наших регрессионных моделей. Если большие ошибки для нас действительно неприемлемы, то квадратичный штраф за них — очень полезное свойство (и его даже можно усиливать, повышая степень, в которую мы возводим ошибку на объекте). Однако если в наших тестовых данных присутствуют выбросы, то нам будет сложно объективно сравнить модели между собой: ошибки на выбросах будет маскировать различия в ошибках на основном множестве объектов.
Таким образом, если мы будем сравнивать две модели при помощи MSE, у нас будет выигрывать та модель, у которой меньше ошибка на объектах-выбросах, а это, скорее всего, не то, чего требует от нас наша бизнес-задача.
История из жизни про бананы и квадратичный штраф за ошибкуИз-за неверно введенных данных метка одного из объектов оказалась в 100 раз больше реального значения. Моделировалась величина при помощи градиентного бустинга над деревьями решений. Функция потерь была MSE.
Однажды уже во время эксплуатации случилось ч.п.: у нас появились предсказания, в 100 раз превышающие допустимые из соображений физического смысла значения. Представьте себе, например, что вместо обычных 4 ящиков бананов система предлагала поставить в магазин 400. Были распечатаны все деревья из ансамбля, и мы увидели, что постепенно число ящиков действительно увеличивалось до прогнозных 400.
Было решено проверить гипотезу, что был выброс в данных для обучения. Так оно и оказалось: всего одна точка давала такую потерю на объекте, что алгоритм обучения решил, что лучше переобучиться под этот выброс, чем смириться с большим штрафом на этом объекте. А в эксплуатации у нас возникли точки, которые плюс-минус попадали в такие же листья ансамбля, что и объект-выброс.
Избежать такого рода проблем можно двумя способами: внимательнее контролируя качество данных или адаптировав функцию потерь.
Аналогично, можно поступать и в случае, когда мы разрабатываем метрику качества: менее жёстко штрафовать за большие отклонения от истинного таргета.
MAE
Использовать RMSE для сравнения моделей на выборках с большим количеством выбросов может быть неудобно. В таких случаях прибегают к также знакомой вам в качестве функции потери метрике MAE (mean absolute error):
$$ MAE(y^{true}, y^{pred}) = frac{1}{N}sum_{i=1}^{N} left|y_i — f(x_i)right| $$
Метрики, учитывающие относительные ошибки
И MSE и MAE считаются как сумма абсолютных ошибок на объектах.
Рассмотрим следующую задачу: мы хотим спрогнозировать спрос товаров на следующий месяц. Пусть у нас есть два продукта: продукт A продаётся в количестве 100 штук, а продукт В в количестве 10 штук. И пусть базовая модель предсказывает количество продаж продукта A как 98 штук, а продукта B как 8 штук. Ошибки на этих объектах добавляют 4 штрафных единицы в MAE.
И есть 2 модели-кандидата на улучшение. Первая предсказывает товар А 99 штук, а товар B 8 штук. Вторая предсказывает товар А 98 штук, а товар B 9 штук.
Обе модели улучшают MAE базовой модели на 1 единицу. Однако, с точки зрения бизнес-заказчика вторая модель может оказаться предпочтительнее, т.к. предсказание продажи редких товаров может быть приоритетнее. Один из способов учесть такое требование – рассматривать не абсолютную, а относительную ошибку на объектах.
MAPE, SMAPE
Когда речь заходит об относительных ошибках, сразу возникает вопрос: что мы будем ставить в знаменатель?
В метрике MAPE (mean absolute percentage error) в знаменатель помещают целевое значение:
$$ MAPE(y^{true}, y^{pred}) = frac{1}{N} sum_{i=1}^{N} frac{ left|y_i — f(x_i)right|}{left|y_iright|} $$
С особым случаем, когда в знаменателе оказывается $0$, обычно поступают «инженерным» способом: или выдают за непредсказание $0$ на таком объекте большой, но фиксированный штраф, или пытаются застраховаться от подобного на уровне формулы и переходят к метрике SMAPE (symmetric mean absolute percentage error):
$$ SMAPE(y^{true}, y^{pred}) = frac{1}{N} sum_{i=1}^{N} frac{ 2 left|y_i — f(x_i)right|}{y_i + f(x_i)} $$
Если же предсказывается ноль, штраф считаем нулевым.
Таким переходом от абсолютных ошибок на объекте к относительным мы сделали объекты в тестовой выборке равнозначными: даже если мы делаем абсурдно большое предсказание, на фоне которого истинная метка теряется, мы получаем штраф за этот объект порядка 1 в случае MAPE и 2 в случае SMAPE.
WAPE
Как и любая другая метрика, MAPE имеет свои границы применимости: например, она плохо справляется с прогнозом спроса на товары с прерывистыми продажами. Рассмотрим такой пример:
| Понедельник | Вторник | Среда | |
|---|---|---|---|
| Прогноз | 55 | 2 | 50 |
| Продажи | 50 | 1 | 50 |
| MAPE | 10% | 100% | 0% |
Среднее MAPE – 36.7%, что не очень отражает реальную ситуацию, ведь два дня мы предсказывали с хорошей точностью. В таких ситуациях помогает WAPE (weighted average percentage error):
$$ WAPE(y^{true}, y^{pred}) = frac{sum_{i=1}^{N} left|y_i — f(x_i)right|}{sum_{i=1}^{N} left|y_iright|} $$
Если мы предсказываем идеально, то WAPE = 0, если все предсказания отдаём нулевыми, то WAPE = 1.
В нашем примере получим WAPE = 5.9%
RMSLE
Альтернативный способ уйти от абсолютных ошибок к относительным предлагает метрика RMSLE (root mean squared logarithmic error):
$$ RMSLE(y^{true}, y^{pred}| c) = sqrt{ frac{1}{N} sum_{i=1}^N left(vphantom{frac12}log{left(y_i + c right)} — log{left(f(x_i) + c right)}right)^2 } $$
где нормировочная константа $c$ вводится искусственно, чтобы не брать логарифм от нуля. Также по построению видно, что метрика пригодна лишь для неотрицательных меток.
Веса в метриках
Все вышеописанные метрики легко допускают введение весов для объектов. Если мы из каких-то соображений можем определить стоимость ошибки на объекте, можно брать эту величину в качестве веса. Например, в задаче предсказания спроса в качестве веса можно использовать стоимость объекта.
Доля предсказаний с абсолютными ошибками больше, чем d
Еще одним способом охарактеризовать качество модели в задаче регрессии является доля предсказаний с абсолютными ошибками больше заданного порога $d$:
$$frac{1}{N} sum_{i=1}^{N} mathbb{I}left[ left| y_i — f(x_i) right| > d right] $$
Например, можно считать, что прогноз погоды сбылся, если ошибка предсказания составила меньше 1/2/3 градусов. Тогда рассматриваемая метрика покажет, в какой доле случаев прогноз не сбылся.
Как оптимизировать метрики регрессии?
Пусть мы выбрали, что метрика качества алгоритма будет $F(a(X), Y)$. Тогда мы хотим обучить модель так, чтобы F на валидационной выборке была минимальная/максимальная. Аналогично задачам классификации лучший способ добиться минимизации метрики $F$ — выбрать в качестве функции потерь ту же $F(a(X), Y)$. К счастью, основные метрики для регрессии: MSE, RMSE, MAE можно оптимизировать напрямую. С формальной точки зрения MAE не дифференцируема, так как там присутствует модуль, чья производная не определена в нуле. На практике для этого выколотого случая в коде можно возвращать ноль.
Для оптимизации MAPE придётся изменять оптимизационную задачу. Оптимизацию MAPE можно представить как оптимизацию MAE, где объектам выборки присвоен вес $frac{1}{vert y_ivert}$.