| Error function | |
|---|---|

Plot of the error function |
|
| General information | |
| General definition |  |
| Fields of application | Probability, thermodynamics |
| Domain, Codomain and Image | |
| Domain |  |
| Image |  |
| Basic features | |
| Parity | Odd |
| Specific features | |
| Root | 0 |
| Derivative |  |
| Antiderivative |  |
| Series definition | |
| Taylor series |  |
In mathematics, the error function (also called the Gauss error function), often denoted by erf, is a complex function of a complex variable defined as:[1]
Some authors define 

This nonelementary integral is a sigmoid function that occurs often in probability, statistics, and partial differential equations. In many of these applications, the function argument is a real number. If the function argument is real, then the function value is also real.
In statistics, for non-negative values of x, the error function has the following interpretation: for a random variable Y that is normally distributed with mean 0 and standard deviation 1/√2, erf x is the probability that Y falls in the range [−x, x].
Two closely related functions are the complementary error function (erfc) defined as
and the imaginary error function (erfi) defined as
where i is the imaginary unit.
Name[edit]
The name «error function» and its abbreviation erf were proposed by J. W. L. Glaisher in 1871 on account of its connection with «the theory of Probability, and notably the theory of Errors.»[3] The error function complement was also discussed by Glaisher in a separate publication in the same year.[4]
For the «law of facility» of errors whose density is given by
(the normal distribution), Glaisher calculates the probability of an error lying between p and q as:
Plot of the error function Erf(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
Applications[edit]
When the results of a series of measurements are described by a normal distribution with standard deviation σ and expected value 0, then erf (a/σ √2) is the probability that the error of a single measurement lies between −a and +a, for positive a. This is useful, for example, in determining the bit error rate of a digital communication system.
The error and complementary error functions occur, for example, in solutions of the heat equation when boundary conditions are given by the Heaviside step function.
The error function and its approximations can be used to estimate results that hold with high probability or with low probability. Given a random variable X ~ Norm[μ,σ] (a normal distribution with mean μ and standard deviation σ) and a constant L < μ:
where A and B are certain numeric constants. If L is sufficiently far from the mean, specifically μ − L ≥ σ√ln k, then:
so the probability goes to 0 as k → ∞.
The probability for X being in the interval [La, Lb] can be derived as
Properties[edit]
Integrand exp(−z2)
erf z
The property erf (−z) = −erf z means that the error function is an odd function. This directly results from the fact that the integrand e−t2 is an even function (the antiderivative of an even function which is zero at the origin is an odd function and vice versa).
Since the error function is an entire function which takes real numbers to real numbers, for any complex number z:
where z is the complex conjugate of z.
The integrand f = exp(−z2) and f = erf z are shown in the complex z-plane in the figures at right with domain coloring.
The error function at +∞ is exactly 1 (see Gaussian integral). At the real axis, erf z approaches unity at z → +∞ and −1 at z → −∞. At the imaginary axis, it tends to ±i∞.
Taylor series[edit]
The error function is an entire function; it has no singularities (except that at infinity) and its Taylor expansion always converges, but is famously known «[…] for its bad convergence if x > 1.»[5]
The defining integral cannot be evaluated in closed form in terms of elementary functions (see Liouville’s theorem), but by expanding the integrand e−z2 into its Maclaurin series and integrating term by term, one obtains the error function’s Maclaurin series as:
which holds for every complex number z. The denominator terms are sequence A007680 in the OEIS.
For iterative calculation of the above series, the following alternative formulation may be useful:
because −(2k − 1)z2/k(2k + 1) expresses the multiplier to turn the kth term into the (k + 1)th term (considering z as the first term).
The imaginary error function has a very similar Maclaurin series, which is:
which holds for every complex number z.
Derivative and integral[edit]
The derivative of the error function follows immediately from its definition:
From this, the derivative of the imaginary error function is also immediate:
An antiderivative of the error function, obtainable by integration by parts, is
An antiderivative of the imaginary error function, also obtainable by integration by parts, is
Higher order derivatives are given by
where H are the physicists’ Hermite polynomials.[6]
Bürmann series[edit]
An expansion,[7] which converges more rapidly for all real values of x than a Taylor expansion, is obtained by using Hans Heinrich Bürmann’s theorem:[8]
where sgn is the sign function. By keeping only the first two coefficients and choosing c1 = 31/200 and c2 = −341/8000, the resulting approximation shows its largest relative error at x = ±1.3796, where it is less than 0.0036127:
Inverse functions[edit]
Given a complex number z, there is not a unique complex number w satisfying erf w = z, so a true inverse function would be multivalued. However, for −1 < x < 1, there is a unique real number denoted erf−1 x satisfying
The inverse error function is usually defined with domain (−1,1), and it is restricted to this domain in many computer algebra systems. However, it can be extended to the disk |z| < 1 of the complex plane, using the Maclaurin series[9]
where c0 = 1 and
So we have the series expansion (common factors have been canceled from numerators and denominators):
(After cancellation the numerator/denominator fractions are entries OEIS: A092676/OEIS: A092677 in the OEIS; without cancellation the numerator terms are given in entry OEIS: A002067.) The error function’s value at ±∞ is equal to ±1.
For |z| < 1, we have erf(erf−1 z) = z.
The inverse complementary error function is defined as
For real x, there is a unique real number erfi−1 x satisfying erfi(erfi−1 x) = x. The inverse imaginary error function is defined as erfi−1 x.[10]
For any real x, Newton’s method can be used to compute erfi−1 x, and for −1 ≤ x ≤ 1, the following Maclaurin series converges:
where ck is defined as above.
Asymptotic expansion[edit]
A useful asymptotic expansion of the complementary error function (and therefore also of the error function) for large real x is
where (2n − 1)!! is the double factorial of (2n − 1), which is the product of all odd numbers up to (2n − 1). This series diverges for every finite x, and its meaning as asymptotic expansion is that for any integer N ≥ 1 one has
where the remainder is
which follows easily by induction, writing
and integrating by parts.
The asymptotic behavior of the remainder term, in Landau notation, is
as x → ∞. This can be found by
For large enough values of x, only the first few terms of this asymptotic expansion are needed to obtain a good approximation of erfc x (while for not too large values of x, the above Taylor expansion at 0 provides a very fast convergence).
Continued fraction expansion[edit]
A continued fraction expansion of the complementary error function is:[11]
Integral of error function with Gaussian density function[edit]
which appears related to Ng and Geller, formula 13 in section 4.3[12] with a change of variables.
Factorial series[edit]
The inverse factorial series:
converges for Re(z2) > 0. Here
zn denotes the rising factorial, and s(n,k) denotes a signed Stirling number of the first kind.[13][14]
There also exists a representation by an infinite sum containing the double factorial:
Numerical approximations[edit]
Approximation with elementary functions[edit]
- Abramowitz and Stegun give several approximations of varying accuracy (equations 7.1.25–28). This allows one to choose the fastest approximation suitable for a given application. In order of increasing accuracy, they are:
(maximum error: 5×10−4)
where a1 = 0.278393, a2 = 0.230389, a3 = 0.000972, a4 = 0.078108
(maximum error: 2.5×10−5)
where p = 0.47047, a1 = 0.3480242, a2 = −0.0958798, a3 = 0.7478556
(maximum error: 3×10−7)
where a1 = 0.0705230784, a2 = 0.0422820123, a3 = 0.0092705272, a4 = 0.0001520143, a5 = 0.0002765672, a6 = 0.0000430638
(maximum error: 1.5×10−7)
where p = 0.3275911, a1 = 0.254829592, a2 = −0.284496736, a3 = 1.421413741, a4 = −1.453152027, a5 = 1.061405429
All of these approximations are valid for x ≥ 0. To use these approximations for negative x, use the fact that erf x is an odd function, so erf x = −erf(−x).
- Exponential bounds and a pure exponential approximation for the complementary error function are given by[15]
- The above have been generalized to sums of N exponentials[16] with increasing accuracy in terms of N so that erfc x can be accurately approximated or bounded by 2Q̃(√2x), where
In particular, there is a systematic methodology to solve the numerical coefficients {(an,bn)}N
n = 1 that yield a minimax approximation or bound for the closely related Q-function: Q(x) ≈ Q̃(x), Q(x) ≤ Q̃(x), or Q(x) ≥ Q̃(x) for x ≥ 0. The coefficients {(an,bn)}N
n = 1 for many variations of the exponential approximations and bounds up to N = 25 have been released to open access as a comprehensive dataset.[17] - A tight approximation of the complementary error function for x ∈ [0,∞) is given by Karagiannidis & Lioumpas (2007)[18] who showed for the appropriate choice of parameters {A,B} that
They determined {A,B} = {1.98,1.135}, which gave a good approximation for all x ≥ 0. Alternative coefficients are also available for tailoring accuracy for a specific application or transforming the expression into a tight bound.[19]
- A single-term lower bound is[20]
where the parameter β can be picked to minimize error on the desired interval of approximation.
-
- Another approximation is given by Sergei Winitzki using his «global Padé approximations»:[21][22]: 2–3
where
This is designed to be very accurate in a neighborhood of 0 and a neighborhood of infinity, and the relative error is less than 0.00035 for all real x. Using the alternate value a ≈ 0.147 reduces the maximum relative error to about 0.00013.[23]
This approximation can be inverted to obtain an approximation for the inverse error function:
- An approximation with a maximal error of 1.2×10−7 for any real argument is:[24]
with
and
- An approximation of
with a maximum relative error less than
in absolute value is:[25]
for
,
and for
Table of values[edit]
| x | erf x | 1 − erf x |
|---|---|---|
| 0 | 0 | 1 |
| 0.02 | 0.022564575 | 0.977435425 |
| 0.04 | 0.045111106 | 0.954888894 |
| 0.06 | 0.067621594 | 0.932378406 |
| 0.08 | 0.090078126 | 0.909921874 |
| 0.1 | 0.112462916 | 0.887537084 |
| 0.2 | 0.222702589 | 0.777297411 |
| 0.3 | 0.328626759 | 0.671373241 |
| 0.4 | 0.428392355 | 0.571607645 |
| 0.5 | 0.520499878 | 0.479500122 |
| 0.6 | 0.603856091 | 0.396143909 |
| 0.7 | 0.677801194 | 0.322198806 |
| 0.8 | 0.742100965 | 0.257899035 |
| 0.9 | 0.796908212 | 0.203091788 |
| 1 | 0.842700793 | 0.157299207 |
| 1.1 | 0.880205070 | 0.119794930 |
| 1.2 | 0.910313978 | 0.089686022 |
| 1.3 | 0.934007945 | 0.065992055 |
| 1.4 | 0.952285120 | 0.047714880 |
| 1.5 | 0.966105146 | 0.033894854 |
| 1.6 | 0.976348383 | 0.023651617 |
| 1.7 | 0.983790459 | 0.016209541 |
| 1.8 | 0.989090502 | 0.010909498 |
| 1.9 | 0.992790429 | 0.007209571 |
| 2 | 0.995322265 | 0.004677735 |
| 2.1 | 0.997020533 | 0.002979467 |
| 2.2 | 0.998137154 | 0.001862846 |
| 2.3 | 0.998856823 | 0.001143177 |
| 2.4 | 0.999311486 | 0.000688514 |
| 2.5 | 0.999593048 | 0.000406952 |
| 3 | 0.999977910 | 0.000022090 |
| 3.5 | 0.999999257 | 0.000000743 |
[edit]
Complementary error function[edit]
The complementary error function, denoted erfc, is defined as
Plot of the complementary error function Erfc(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
which also defines erfcx, the scaled complementary error function[26] (which can be used instead of erfc to avoid arithmetic underflow[26][27]). Another form of erfc x for x ≥ 0 is known as Craig’s formula, after its discoverer:[28]
This expression is valid only for positive values of x, but it can be used in conjunction with erfc x = 2 − erfc(−x) to obtain erfc(x) for negative values. This form is advantageous in that the range of integration is fixed and finite. An extension of this expression for the erfc of the sum of two non-negative variables is as follows:[29]
Imaginary error function[edit]
The imaginary error function, denoted erfi, is defined as
where D(x) is the Dawson function (which can be used instead of erfi to avoid arithmetic overflow[26]).
Despite the name «imaginary error function», erfi x is real when x is real.
When the error function is evaluated for arbitrary complex arguments z, the resulting complex error function is usually discussed in scaled form as the Faddeeva function:
Cumulative distribution function[edit]
The error function is essentially identical to the standard normal cumulative distribution function, denoted Φ, also named norm(x) by some software languages[citation needed], as they differ only by scaling and translation. Indeed,
the normal cumulative distribution function plotted in the complex plane
or rearranged for erf and erfc:
Consequently, the error function is also closely related to the Q-function, which is the tail probability of the standard normal distribution. The Q-function can be expressed in terms of the error function as
The inverse of Φ is known as the normal quantile function, or probit function and may be expressed in terms of the inverse error function as
The standard normal cdf is used more often in probability and statistics, and the error function is used more often in other branches of mathematics.
The error function is a special case of the Mittag-Leffler function, and can also be expressed as a confluent hypergeometric function (Kummer’s function):
It has a simple expression in terms of the Fresnel integral.[further explanation needed]
In terms of the regularized gamma function P and the incomplete gamma function,
sgn x is the sign function.
Generalized error functions[edit]
grey curve: E1(x) = 1 − e−x/√π
red curve: E2(x) = erf(x)
green curve: E3(x)
blue curve: E4(x)
gold curve: E5(x).
Some authors discuss the more general functions:[citation needed]
Notable cases are:
- E0(x) is a straight line through the origin: E0(x) = x/e√π
- E2(x) is the error function, erf x.
After division by n!, all the En for odd n look similar (but not identical) to each other. Similarly, the En for even n look similar (but not identical) to each other after a simple division by n!. All generalised error functions for n > 0 look similar on the positive x side of the graph.
These generalised functions can equivalently be expressed for x > 0 using the gamma function and incomplete gamma function:
Therefore, we can define the error function in terms of the incomplete gamma function:
Iterated integrals of the complementary error function[edit]
The iterated integrals of the complementary error function are defined by[30]
The general recurrence formula is
They have the power series
from which follow the symmetry properties
and
Implementations[edit]
As real function of a real argument[edit]
- In POSIX-compliant operating systems, the header
math.hshall declare and the mathematical librarylibmshall provide the functionserfanderfc(double precision) as well as their single precision and extended precision counterpartserff,erflanderfcf,erfcl.[31]
- The GNU Scientific Library provides
erf,erfc,log(erf), and scaled error functions.[32]
As complex function of a complex argument[edit]
libcerf, numeric C library for complex error functions, provides the complex functionscerf,cerfc,cerfcxand the real functionserfi,erfcxwith approximately 13–14 digits precision, based on the Faddeeva function as implemented in the MIT Faddeeva Package
See also[edit]
[edit]
- Gaussian integral, over the whole real line
- Gaussian function, derivative
- Dawson function, renormalized imaginary error function
- Goodwin–Staton integral
In probability[edit]
- Normal distribution
- Normal cumulative distribution function, a scaled and shifted form of error function
- Probit, the inverse or quantile function of the normal CDF
- Q-function, the tail probability of the normal distribution
- Standard score
References[edit]
- ^ Andrews, Larry C. (1998). Special functions of mathematics for engineers. SPIE Press. p. 110. ISBN 9780819426161.
- ^ Whittaker, E. T.; Watson, G. N. (1927). A Course of Modern Analysis. Cambridge University Press. p. 341. ISBN 978-0-521-58807-2.
- ^ Glaisher, James Whitbread Lee (July 1871). «On a class of definite integrals». London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4. 42 (277): 294–302. doi:10.1080/14786447108640568. Retrieved 6 December 2017.
- ^ Glaisher, James Whitbread Lee (September 1871). «On a class of definite integrals. Part II». London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4. 42 (279): 421–436. doi:10.1080/14786447108640600. Retrieved 6 December 2017.
- ^ «A007680 – OEIS». oeis.org. Retrieved 2 April 2020.
- ^ Weisstein, Eric W. «Erf». MathWorld.
- ^ Schöpf, H. M.; Supancic, P. H. (2014). «On Bürmann’s Theorem and Its Application to Problems of Linear and Nonlinear Heat Transfer and Diffusion». The Mathematica Journal. 16. doi:10.3888/tmj.16-11.
- ^ Weisstein, Eric W. «Bürmann’s Theorem». MathWorld.
- ^ Dominici, Diego (2006). «Asymptotic analysis of the derivatives of the inverse error function». arXiv:math/0607230.
- ^ Bergsma, Wicher (2006). «On a new correlation coefficient, its orthogonal decomposition and associated tests of independence». arXiv:math/0604627.
- ^ Cuyt, Annie A. M.; Petersen, Vigdis B.; Verdonk, Brigitte; Waadeland, Haakon; Jones, William B. (2008). Handbook of Continued Fractions for Special Functions. Springer-Verlag. ISBN 978-1-4020-6948-2.
- ^ Ng, Edward W.; Geller, Murray (January 1969). «A table of integrals of the Error functions». Journal of Research of the National Bureau of Standards Section B. 73B (1): 1. doi:10.6028/jres.073B.001.
- ^ Schlömilch, Oskar Xavier (1859). «Ueber facultätenreihen». Zeitschrift für Mathematik und Physik (in German). 4: 390–415.
- ^ Nielson, Niels (1906). Handbuch der Theorie der Gammafunktion (in German). Leipzig: B. G. Teubner. p. 283 Eq. 3. Retrieved 4 December 2017.
- ^ Chiani, M.; Dardari, D.; Simon, M.K. (2003). «New Exponential Bounds and Approximations for the Computation of Error Probability in Fading Channels» (PDF). IEEE Transactions on Wireless Communications. 2 (4): 840–845. CiteSeerX 10.1.1.190.6761. doi:10.1109/TWC.2003.814350.
- ^ Tanash, I.M.; Riihonen, T. (2020). «Global minimax approximations and bounds for the Gaussian Q-function by sums of exponentials». IEEE Transactions on Communications. 68 (10): 6514–6524. arXiv:2007.06939. doi:10.1109/TCOMM.2020.3006902. S2CID 220514754.
- ^ Tanash, I.M.; Riihonen, T. (2020). «Coefficients for Global Minimax Approximations and Bounds for the Gaussian Q-Function by Sums of Exponentials [Data set]». Zenodo. doi:10.5281/zenodo.4112978.
- ^ Karagiannidis, G. K.; Lioumpas, A. S. (2007). «An improved approximation for the Gaussian Q-function» (PDF). IEEE Communications Letters. 11 (8): 644–646. doi:10.1109/LCOMM.2007.070470. S2CID 4043576.
- ^ Tanash, I.M.; Riihonen, T. (2021). «Improved coefficients for the Karagiannidis–Lioumpas approximations and bounds to the Gaussian Q-function». IEEE Communications Letters. 25 (5): 1468–1471. arXiv:2101.07631. doi:10.1109/LCOMM.2021.3052257. S2CID 231639206.
- ^ Chang, Seok-Ho; Cosman, Pamela C.; Milstein, Laurence B. (November 2011). «Chernoff-Type Bounds for the Gaussian Error Function». IEEE Transactions on Communications. 59 (11): 2939–2944. doi:10.1109/TCOMM.2011.072011.100049. S2CID 13636638.
- ^ Winitzki, Sergei (2003). «Uniform approximations for transcendental functions». Computational Science and Its Applications – ICCSA 2003. Lecture Notes in Computer Science. Vol. 2667. Springer, Berlin. pp. 780–789. doi:10.1007/3-540-44839-X_82. ISBN 978-3-540-40155-1.
- ^ Zeng, Caibin; Chen, Yang Cuan (2015). «Global Padé approximations of the generalized Mittag-Leffler function and its inverse». Fractional Calculus and Applied Analysis. 18 (6): 1492–1506. arXiv:1310.5592. doi:10.1515/fca-2015-0086. S2CID 118148950.
Indeed, Winitzki [32] provided the so-called global Padé approximation
- ^ Winitzki, Sergei (6 February 2008). «A handy approximation for the error function and its inverse» (Document).
- ^ Numerical Recipes in Fortran 77: The Art of Scientific Computing (ISBN 0-521-43064-X), 1992, page 214, Cambridge University Press.
- ^ Dia, Yaya D. (2023). Approximate Incomplete Integrals, Application to Complementary Error Function. Available at SSRN: https://ssrn.com/abstract=4487559 or http://dx.doi.org/10.2139/ssrn.4487559, 2023
- ^ a b c Cody, W. J. (March 1993), «Algorithm 715: SPECFUN—A portable FORTRAN package of special function routines and test drivers» (PDF), ACM Trans. Math. Softw., 19 (1): 22–32, CiteSeerX 10.1.1.643.4394, doi:10.1145/151271.151273, S2CID 5621105
- ^ Zaghloul, M. R. (1 March 2007), «On the calculation of the Voigt line profile: a single proper integral with a damped sine integrand», Monthly Notices of the Royal Astronomical Society, 375 (3): 1043–1048, Bibcode:2007MNRAS.375.1043Z, doi:10.1111/j.1365-2966.2006.11377.x
- ^ John W. Craig, A new, simple and exact result for calculating the probability of error for two-dimensional signal constellations Archived 3 April 2012 at the Wayback Machine, Proceedings of the 1991 IEEE Military Communication Conference, vol. 2, pp. 571–575.
- ^ Behnad, Aydin (2020). «A Novel Extension to Craig’s Q-Function Formula and Its Application in Dual-Branch EGC Performance Analysis». IEEE Transactions on Communications. 68 (7): 4117–4125. doi:10.1109/TCOMM.2020.2986209. S2CID 216500014.
- ^ Carslaw, H. S.; Jaeger, J. C. (1959), Conduction of Heat in Solids (2nd ed.), Oxford University Press, ISBN 978-0-19-853368-9, p 484
- ^ «math.h — mathematical declarations». opengroup.org. 2018. Retrieved 21 April 2023.
- ^ «Special Functions – GSL 2.7 documentation».
Further reading[edit]
- Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. «Chapter 7». Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 297. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (2007), «Section 6.2. Incomplete Gamma Function and Error Function», Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
- Temme, Nico M. (2010), «Error Functions, Dawson’s and Fresnel Integrals», in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248.
External links[edit]
- A Table of Integrals of the Error Functions
характеристике Переходный
режим вызван тем, что система инерционна
и должна некоторое время приспосабливаться
к поступающим на нее воздействиям. В
этих условиях оценку качества удобно
вести при наиболее тяжелом с точки
зрения воспроизведения системой
воздействии, таком, как ступенчатая
функция А*l(t).
Реакция системы на единичную ступенчатую
функцию является переходным процессом h(t),
по форме которого в простейшем случае
и можно судить о качестве переходного
режима.
На рис.
52.
изображены переходные характеристики
колебательного и монотонного типов,
оценка которых проводится с помощью
локальных критериев, называемых
показателями качества переходной
характеристики.
Рис.
52. Показатели качества переходной
характеристики
Для
характеристик колебательного типа
обычно используются следующие
показатели: Hm —
перерегулирование, которое определяет
относительное максимальное отклонение;
время установления tу —
момент достижения первого максимума;
время регулирования tр,
которое определяет длительность процесса
по уровню + 0,05 относительно установившегося
значения; период колебаний T.
Для
монотонных характеристик наиболее
употребительным является показатель
длительности переходного процесса tр. В
общем случае точное построение переходных
характеристик и, следовательно,
определение качества затруднительно.
Существует ряд методов, позволяющих
приближенно строить переходные
характеристики, однако эти методы сложны
и приводят к громоздким вычислительным
работам. Найти точные значения указанных
выше величин удается только для простейших
систем первого и второго порядков. Для
более сложных следящих систем существуют
приближенные формулы их нахождения.
В
основе формул лежит знание двух
параметров: частоты среза разомкнутой
следящей системы w с
и запаса по фазе. Эти параметры могут
быть найдены аналитически или по
логарифмическим частотным характеристикам.
Сводка вычислительных соотношений
приводится в табл.
П. 2.
2.2.3. Интегральный квадратичный критерий качества переходного режима
Локальные
критерии качества обычно наглядны, но
трудно вычисляются аналитически.
Примером тому служат показатели
переходной характеристики, рассмотренные
выше. Интегральные критерии, особенно
квадратичные, достаточно легко
вычисляются, однако не так наглядны,
как локальные. Обратимся к рис.53,
на котором изображены два монотонных
переходных процесса. Процесс 1 наименьшей
длительности. Об этом может свидетельствовать
такой косвенный фактор, как площадь
между кривой h(t)
и уровнем установившегося значения
выходного процесса. Отсюда для оценки
качества можно ввести критерий
где
через eп (t)
обозначена ошибка переходного режима,
представляющая разность между текущим
и установившемся значениями переходной
характеристики. Чем меньше Q, тем выше
качество САУ.
Причем
подынтегральная квадратичная функция
потерь eп(t)
будет неотрицательной как для монотонных,
так и для колебательных процессов.
Очевидно,
что описанные критерии можно использовать
не только для случая переходной
характеристики, но и при произвольных
воздействиях.
Рис.53.
Сравнение качества переходных
характеристик
Рассмотрим
методику нахождения интегрального
квадратичного критерия переходного
режима для регулярного воздействия x(t).
Изображение
динамической ошибки можно записать в
виде произведения
|
e(p) = |
(29) |
Не
прибегая к нахождению оригинала eх(t), можно
найти установившееся значение ошибки
управления
,
или
.
Если
из полной ошибки eх(t)
вычесть ошибку установившегося
режима eх уст,
то получим составляющую, которая равна
ошибке переходного режима
еп(t) =
eх (t) —
eх уст.
Очевидно,
что
еп(t) 0
при t
,
так как eх (t) eх уст.
Интегральный
квадратичный критерий качества
переходного режима определим как
величину
На
основании известной теоремы Парсеваля,
нахождение интегрального квадратичного
критерия качества Q переходного
режима сводится к вычислению интеграла
Парсеваля
|
|
(30) |
Чтобы
вычислить конкретное значение этого
интеграла, функцию eп(p)
записывают в виде отношения полиномов

Тогда
интеграл будет функцией параметров a ,
и b . Значения функций табулированы
и для n <
4 приведены в табл.
П.3.
Изображение
ошибки переходного режима получаем из
формулы:
где
учтено, что изображение от
постоянной ex уст равно e x уст /p.
Пример.
Найдем
интегральный квадратичный критерий
качества переходного процесса в системе
управления антенной.
Передаточная
функция разомкнутой системы

Передаточная
функция ошибки по задающему воздействию
равна

Так
как рассматривается переходный процесс,
то воздействием является единичная
функция
x(t) = 1 (t)
с
изображением
x(p)=1/p .
Изображение
ошибки управления

Установившееся
значение ошибки
В
итоге получим, что изображение ошибки
переходного режима равно
где
a 0 =
1+K;
a 1 =
T; b 0 =
K; b 1 =
1+K; b 2 =
T.
Согласно
формуле (30)
интегральный квадратичный критерий
качества переходного режима равен
интегралу Парсеваля
Q
= I
[e п (p)].
Используя
данные табл.
П.3. для n =
2, находим значение интеграла

Из
этого результата видно, что изменением
параметров системы можно в широких
пределах изменить величину критерия.
Особенно характерны в этом отношении
два параметра: Rи T.
На
практике для регулировки показателей
переходного процесса широко используют
коэффициент преобразования К элемента,
не охваченного внутренней обратной
связью. В то же время постоянную
времени T усилителя
следует подбирать так, чтобы величина
первого слагаемого критерия не превышала
допустимого уровня.
252
Точность САУ
Точность
САУ оценивается в установившемся режиме
по величине установившейся ошибки при
типовых воздействиях. При анализе
точности систем рассматривается
установившийся режим, так как текущее
значение ошибки резко меняется вследствие
наличия переходных процессов и не может
быть мерой точности.
Рассмотрим
систему представленную на рис. 1.
На
схеме приняты следующие обозначения:
Kу(p)
– передаточная функция устройства
управления; K0(p)
– передаточная функция объекта
управления; f
–
возмущающее воздействие; x
–
задающее воздействие; y
– регулируемая величина.
Ошибка
по задающему воздействию равна (t)
= x(t) – y(t).
Изображение
ошибки равно
(1)
Установившееся
значение ошибки определяется с помощью
теоремы о конечном значении функции
(2)
Ошибка
по возмущению воздействию равна (t)
= – y(t),
т.е. равна изменению регулируемой
величины под действием возмущения при
отсутствии входного воздействия.
В общем
случае как задающее, так и возмущающее
воздействия являются сложными функциями
времени. При определении ошибок пользуются
типовыми воздействиями, которые с одной
стороны соответствуют наиболее тяжелым
режимам работы системы и, вместе с тем,
достаточно просты для аналитических
исследований.
Кроме
того, типовые воздействия удобны для
сравнительного анализа различных
систем, и соответствуют наиболее часто
применяемым законам изменения управляющих
и возмущающих воздействий.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
04.08.2019142.76 Кб022.rtf
- #
- #
- #
- #
- #
- #
04.08.2019112.25 Кб126.rtf
- #
- #
- #
- #
Интегральная квадратичная ошибка
Cтраница 1
Интегральная квадратичная ошибка определяется как интеграл квадратов мгновенных ( текущих) значений рассогласования. При возведении в квадрат текущих значении рассогласования отрицательные величины не компенсируют положительные, поэтому с возрастанием рассогласования интегральная квадратичная ошибка растет очень быстро.
[1]
Эти коэффициенты соответствуют минимуму интегральной квадратичной ошибки между f ( t) и апроксимирующей функцией, что вытекает из (9.81), если Г оо. Полная функция f ( t) подбирается так, чтобы при этом значении Т получить наилучшую апроксимацию.
[2]
В этом разделе в качестве критерия оценки точности апроксимации применяется интегральная квадратичная ошибка. Выбор этого критерия диктуется главным образом удобством его применения; вместе с тем во многих конкретных случаях он служит весьма хорошей оценкой точности апроксимации. В нем одинаково учитываются как положительные, так и отрицательные ошибки. Критерий интегральной квадратичной ошибки достаточно хорошо оценивает большие и длительные ошибки, а малые и кратковременные ошибки слабо сказываются на его величине.
[3]
Экспоненциальные функции не являются ортогональными в любом интервале, так что критерий минимума интегральной квадратичной ошибки к такому ряду функций приложить нелегко.
[4]
С усилением интегрального воздействия ( уменьшение времени интегрирования) процесс из апериодического переходит в колебательный со все более уменьшающейся степенью затухания; при этом динамическая ошибка регулирования уменьшается, а время регулирования и интегральная квадратичная ошибка регулирования возрастают.
[5]
Для выбора наиболее рациональных с точки зрения технологии переходных процессов по каналам регулирования обычно выполняются расчеты для четырех процессов регулирования: без перерегулирования, с 20 % — ным перерегулированием, с минимальным временем регулирования и с минимальной интегральной квадратичной ошибкой.
[7]
Интегральные ошибки этих трех переходных процессов равны, так как настройки диапазона пропорциональности и времени изо-дрома регулятора во всех случаях одинаковы. Интегральная квадратичная ошибка последнего переходного процесса меньше, чем у первых двух, так как он имеет меньшую динамическую ошибку.
[9]
В частности, это имеет место для систем с симметричными и кососимметрич-ньгми матрицами А в силу ортогональности их канонических базисов. Эквивалентные сепаратные системы равноправны с точки зрения квадратичной оценки для системы в целом: значения их интегральных квадратичных ошибок входят в сумму ( ИЗ) с одинаковым весом.
[10]
Интегральная квадратичная ошибка определяется как интеграл квадратов мгновенных ( текущих) значений рассогласования. При возведении в квадрат текущих значении рассогласования отрицательные величины не компенсируют положительные, поэтому с возрастанием рассогласования интегральная квадратичная ошибка растет очень быстро.
[11]
Для большинства методов решения задачи синтеза оптимальных виброзащитных систем характерны следующие принципы: используется линейная динамическая модель с одной степенью свободы; для системы с двумя степенями свободы рассматриваются лишь частные случаи синтеза; учитывается не более одного ограничения; для одной и той же модели изменение спектральной плотности воздействия приводит к необходимости повторения процесса решения задачи. Например, для синтеза оптимальной системы с активным динамическим гасителем колебаний ( судовых механизмов и машин) был выбран метод минимально-квадратичной оптимизации, позволяющий синтезировать системы с наименьшим значением интегральной квадратичной ошибки при учете ограничений, накладываемых объектом.
[12]
На практике наиболее широкое распространение при оценке качества работы ристем регулирования получили интегральная и интегральная квадратичная ошибки. Принципиальное отличие между ними состоит в том, что вторая учитывает абсолютное значение ошибки. Например, две кривые переходного процесса с различными амплитудами колебаний параметра могут иметь одинаковые интегральные ошибки, но разные интегральные квадратичные ошибки.
[13]
В этом разделе в качестве критерия оценки точности апроксимации применяется интегральная квадратичная ошибка. Выбор этого критерия диктуется главным образом удобством его применения; вместе с тем во многих конкретных случаях он служит весьма хорошей оценкой точности апроксимации. В нем одинаково учитываются как положительные, так и отрицательные ошибки. Критерий интегральной квадратичной ошибки достаточно хорошо оценивает большие и длительные ошибки, а малые и кратковременные ошибки слабо сказываются на его величине.
[14]
Страницы:
1
2
Интегральные оценки качества являются интегралами по времени от некоторых функций переходного процесса свободной составляющей выходной величины 



Рис. 4.19

Рис. 4.20
Однако чаще используют моменты 

Простейшей из этих оценок является 









Для 

Сравнивая это выражение с (4.47) для 

Разложим 


Подставим (4.51) в выражение для определения 

Если разложить 

то, сопоставляя (4.52) и (4.53), можно сделать следующее заключение, приравнивая выражения при равных степенях 

Если сравнить результаты (4.50), 


Квадратичные интегральные оценки вычисляются по формулам


где 
Оценки 
Геометрический смысл интегральной квадратичной оценки ояснен на рис. 4.21. Выбирая параметры системы по минимуму квадратичной интегральной оценки 


Методы вычисления этих оценок предложены А. И. Манелыптамом и Н. Д. Папалекси в 1909 г. В 1937 г. акад. А. А. [аркевич применил эту оценку для исследования режимов аботы усилителей, в 1948 г. А. А. Красовский и А. А. Фельдаум использовали ее для исследования качества линейных истем автоматического регулирования.
Рассмотрим методы вычисления квадратичных интегральных оценок 


По теореме о предельных переходах,

педовательно,

Поскольку 



Рис. 4.21
При 



где 

в котором все коэффициенты с меньшим индексом 0 и большим 



Коэффициенты 

Интегральную квадратичную оценку 
Пусть 




где 
Таким образом, по (4.64) и (4.65) можно вычислить 
Существуют таблицы расчета интеграла 






Таблица 4.1

где

При выборе параметров системы по минимуму оценки 

при этом запас устойчивости. В обобщенных квадратичных оценках 










Остановимся на методике расчета системы по минимуму обобщенной квадратичной оценки:

Этот интеграл можно представить в виде суммы двух интегралов:

Если система устойчива, то 

Кроме того, интеграл 

при

Если

то решение дифференциального уравнения (4.68)

является оптимальным по минимуму (экстремальным) переходным процессом (где 
При выборе параметров системы по минимуму 


А. А. Фельдбаумом [10] было показано, что переходный процесс будет отличаться от экстремального на величину, меньшую 

По величине 6 можно оценить отклонение истинного переходного процесса 



Следует заметить, что задача выбора параметров по минимуму 

Рассмотрим примеры выбора оптимального значения какого-либо параметра системы по минимуму 
Пример 4.4. Вычислить значение коэффициента усиления системы, минимизирующие

Рис. 4.22
мизирующее квадратичную интегральную оценку 

где 
Входной сигнал — единичная функция 


где 
Воспользуемся формулами для вычисления 


Определим частную производную:

Определим 


откуда 
Пример 4.5. Определить оптимальное значение коэффициента усиления к, соответствующее минимуму обобщенной квадратичной оценки
Передаточная функция разомкнутой системы 
Входной сигнал — единичная функция 


Изображение отклонения 

где 
Воспользуемся данными табл. 4.1 и определим значение 


Определим изображение производной 

По теореме о предельном переходе,

Тогда 
где 
Теперь можно определить интеграл

пользуясь формулой для 


Итак, 
Определим 


откуда 
Оптимальный переходный процесс описывается в соответствии с формулой (4.69) выражением

Так как 



Интегральные оценки качества широко используются при синтезе оптимальных САУ в качестве критерия оптимальности.
|
|
Макеты страниц
Интегральные оценки имеют целью дать общую оценку быстроты затухания и величины отклонения регулируемой величины в совокупности, без определения того и другого в отдельности. Простейшей интегральной оценкой может служить величина

где 
В устойчивой системе 


Рис. 8.19.
Площадь будет тем меньше, чем быстрее затухает переходный процесс и чем меньше величина отклонения. Поэтому параметры системы рекомендуется выбирать таким образом, чтобы добиваться минимума этой интегральной оценки.
Для вычисления интеграла (8.53) нет необходимости в нахождении 

Отсюда следует, что интеграл (8.53) может быть найден посредством предельного перехода 

Неудобством интегральной оценки вида (8.53) является то, что она годится только для монотонных процессов, когда не меняется знак отклонения 
вычислении интеграла (8.53) площади будут складываться алгебраически 

т. е. сумма абсолютных величин всех площадей по кривой переходного процесса. Но оказалось, что вычисление ее по коэффициентам уравнения затруднительно.
Квадратичная интегральная оценка.
В свете вышесказанного целесообразно перейти к квадратичной интегральной оценке, называемой иногда «квадратичной площадью» регулирования:

которая не зависит от знаков отклонений, а значит, и от формы переходного процесса (монотонной или колебательной).

Рис. 8.20.
Величина I (8.56) будет тем меньше, чем меньше сумма заштрихованных на рис. 8.20 площадей (взятых для квадратов ординат), т. е. чем лучше переходный процесс приближается к идеальному скачку регулируемой величины вслед за скачком задающего или возмущающего воздействия. Ниже будет показано, что такая оценка не всегда является лучшей, но пока остановимся на ней.
Заметим, что оценку (8.56) называют также квадратичной динамической ошибкой регулирования. Ее можно записать в безразмерном виде:

где 


Рассмотрим один из возможных способов вычисления квадратичной интегральной оценки (8.56) при скачкообразном внешнем воздействии.
В общем случае дифференциальное уравнение системы автоматического регулирования (в символической операторной записи) согласно (5.5) имеет вид

где 

Степени многочленов 








Лапласа такого скачка будет 

Изображение регулируемой величины 

Отклонение х регулируемой величины от нового установившегося состояния в переходном процессе, входящее в формулу (8.56), будет

где 
Для изложенных условий при 

где А есть следующий определитель 

На границе устойчивости 
Через 


Коэффициенты 

В определителе (8.62) заменяются нулями все буквы с индексами меньше нуля и больше 

В том случае, когда 

где

При поступлении на вход системы единичного импульса 



В связи с этим квадратичную интегральную оценку при действии единичного импульса можно рассматривать в виде выражения

где 

Таким образом, техника вычисления оценки Г полностью совпадает с вычислением оценки I по формуле (8.61) или (8.65). Совпадает при этом и значение определителя 





Интегральная оценка Г также может использоваться в безразмерном виде аналогично формуле (8.57):

Интегральные оценки 


Вычисление квадратичных интегральных оценок 
Если 







где 

В астатических системах и статических системах с неединичной обратной связью или с масштабированием (см. § 9.3) установившееся значение 

где 
Аналогичным образом для входного задающего воздействия типа единичного импульса 




Рис. 8.21.
Подобные выражения могут быть получены и для входного возмущающего воздействия, если вместо частотной передаточной функции 

Недостатком интегральных оценок является то, что здесь ничем не ограничивается форма кривой переходного процесса. Оказывается, например, что три совершенно различных по форме процесса, изображенных на рис. 8.21, имеют одно и то же значение квадратичной интегральной оценки (8.56).
Часто оказывается, что выбранные по минимуму этой оценки параметры системы соответствуют слишком сильно колебательному процессу, ибо отмечавшееся уже при этом стремление приблизить процесс к идеальному скачку вызывает большую скорость процесса при подходе к установившемуся значению 
Это получается вследствие того, что оценка (8.56) учитывает только величину отклонения и быстроту затухания и никак не учитывает близость системы к колебательной границе устойчивости.
Если, например, подать на вход системы единичный скачок, то ошибка в переходном процессе определится заштрихованной частью на рис. 8.22, а. Очевидно, что величина интегральной оценки (8.56) будет тем меньше, чем ближе будет кривая переходного процесса к ломаной линии 



Рис. 8.22.
Увеличение же начальной скорости может вызвать значительное перерегулирование и, следовательно, малый запас устойчивости.
Поэтому применяется еще другой вид интегральной оценки, в которой ограничение накладывается не только на величину отклонения х, но также и на скорость отклонения х. Эта улучшенная квадратичная интегральная оценка имеет вид

где Т — некоторая постоянная времени.
Выясним, какой вид переходного процесса будет получаться при выборе параметров системы регулирования по минимуму улучшенной интегральной оценки (8.72). Для этого проделаем следующие преобразования:

где 
Наименьшее значение последнего выражения будет при выполнении условия 
Это есть дифференциальное уравнение первого порядка, решение которого имеет вид

где 
Этот процесс изображен на рис. 8.22, б пунктиром. Следовательно, выбирая параметры системы по минимуму улучшенной интегральной оценки (8.72), можно приблизить переходный процесс к заданной экспоненте (8.73) с постоянной времени Г, которая носит в этом случае название экстремали. Из этих соображений можно заранее задаться определенной величиной Т.
Выбор параметров системы по улучшенной квадратичной интегральной оценке приводит к менее колебательным процессам по сравнению с использованием обычной квадратичной интегральной оценки (8.56).
Методика вычисления интеграла (8.72) сводится к тому, что правая его часть разбивается на два слагаемых:

При входном воздействии типа единичной ступенчатой функции первое слагаемое последнего выражения соответствует интегральной оценке 


Улучшенная интегральная оценка 

где 



Недостатком приведенных расчетных формул для вычисления как 


Несколько сложнее вычисляется только определитель 


Удобство интегральных оценок состоит в том, что они дают единый числовой критерий качества. Недостатком является то, что одному и тому же значению интегральной оценки могут отвечать разные формы переходного процесса, что создает недостаточную определенность решения задачи.
В принципе возможно использование более сложных выражений, чем (8.72), в которые кроме первой производной от отклонения будут входить вторая, третья и т. д. производные. Так, например, ограничившись при подаче ступенчатого воздействия 


Эта оценка будет характеризовать приближение переходного процесса к экстремали, определяемой решением дифференциального уравнения

Экстремаль в данном случае будет соответствовать более сложной кривой, чем экспонента, что позволяет точнее задать желаемый вид переходного процесса.
Однако нахождение интегральных оценок вида

к которым сводится вычисление интеграла (8.76), сопряжено со значительными трудностями, что ограничивает их применение.
Определение минимума интегральной оценки.
Пусть требуется, исходя из минимума какой-нибудь интегральной оценки, выбрать два каких-нибудь параметра 


Для определения значений 


с двумя неизвестными 


Функция 
Важно также иметь в виду, что выражение интегральной оценки через выбираемые параметры системы в буквенном виде может в ряде случаев оказаться сложным для исследования в общем виде. В таких случаях можно поступить иначе: задавать несколько числовых значений одного из выбираемых параметров (при жестко заданных всех остальных) и вычислять для каждого из них значения I (или 

В конкретных расчетах всегда надо учитывать, что одновременно с таким выбором параметров нужно, во-первых, обеспечить хорошие статические «свойства системы и, во-вторых, проследить, чтобы оптимальная точка не оказалась слишком близкой к границе устойчивости, так как всегда надо иметь некоторый запас устойчивости.
Рассмотрим в качестве примера дифференциальное уравнение третьего порядка

где 


Установившееся значение регулируемой величины здесь будет 
Вычислим для этого случая интегральную оценку I. Так как 

Далее по выражению (8.62) находим определитель

Для нахождения 


По формуле (8.64) находим единственный коэффициент 
В результате получаем значение интегральной квадратичной оценки:

Это выражение и служит для выбора параметров системы, входящих в коэффициенты 

Построим диаграмму квадратичной интегральной оценки на плоскости параметров Вышнеградского А и В. Согласно § 8.7

Подставив это выражение в (8.78), получим

Найдем безразмерную оценку 


При 

Построенные по этому уравнению кривые постоянных значений оценки 


что

откуда находим 


Этот результат имеет смысл, однако, только в тех случаях, когда 

1
Оглавление
- ПРЕДИСЛОВИЕ
- РАЗДЕЛ I. ОБЩИЕ СВЕДЕНИЯ О СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- § 1.1. Понятие о замкнутых автоматических системах
- § 1.2. Классификация автоматических систем по характеру внутренних динамических процессов
- § 1.3. Примеры непрерывных автоматических систем
- § 1.4. Примеры дискретных и релейных автоматических систем
- ГЛАВА 2. ПРОГРАММЫ И ЗАКОНЫ РЕГУЛИРОВАНИЯ. АДАПТИВНЫЕ СИСТЕМЫ
- § 2.1. Программы регулирования
- § 2.2. Линейные и нелинейные законы регулирования
- § 2.3. Системы с переменной структурой
- § 2.4. Системы с самонастройкой программы (экстремальные системы)
- § 2.5. Системы с самонастройкой параметров (собственно самонастраивающиеся системы)
- § 2.6. Системы с самонастройкой структуры (самоорганизующиеся системы)
- РАЗДЕЛ II. ОБЫКНОВЕННЫЕ ЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- § 3.1. Линеаризация уравнений
- § 3.2. О записи линеаризованных уравнений звеньев
- ГЛАВА 4. ДИНАМИЧЕСКИЕ ЗВЕНЬЯ И ИХ ХАРАКТЕРИСТИКИ
- § 4.2. Временные характеристики
- § 4.3. Частотная передаточная функция и частотные характеристики
- § 4.4. Логарифмические частотные характеристики
- § 4.5. Позиционные звенья
- § 4.6. Интегрирующие звенья
- § 4.7. Дифференцирующие звенья
- § 4.8. Неустойчивые и неминимально-фазовые звенья
- § 4.9. Звенья с модулированным сигналом
- ГЛАВА 5. СОСТАВЛЕНИЕ ИСХОДНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- § 5.1. Общий метод составления исходных уравнений
- § 5.2. Передаточные функции систем автоматического регулирования
- § 5.3. Законы регулирования
- § 5.4. Использование структурных схем и графов
- § 5.5. Многомерные системы регулирования
- § 5.6. Управляемость и наблюдаемость
- § 5.7. Уравнения следящей системы
- ГЛАВА 6. КРИТЕРИИ УСТОЙЧИВОСТИ
- § 6.1. Понятие об устойчивости систем регулирования
- § 6.2. Критерий устойчивости Гурвица
- § 6.3. Критерий устойчивости Михайлова
- § 6.4. Построение областей устойчивости. D-разбиение
- § 6.5. Критерий устойчивости Найквиста
- § 6.6. Определение устойчивости по логарифмическим частотным характеристикам
- § 6.7. Устойчивость двумерных систем с антисимметричными связями
- ГЛАВА 7. ПОСТРОЕНИЕ КРИВОЙ ПЕРЕХОДНОГО ПРОЦЕССА В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- § 7.2. Непосредственное решение исходного дифференциального уравнения
- § 7.3. Сведение неоднородного уравнения к однородному
- § 7.4. Использование преобразований Фурье, Лапласа и Карсона—Хевиеайда
- § 7.5. Использование вещественных частотных характеристик
- § 7.6. Использование вычислительных машин
- ГЛАВА 8. ОЦЕНКА КАЧЕСТВА РЕГУЛИРОВАНИЯ
- § 8.2. Точность в типовых режимах
- § 8.3. Коэффициенты ошибок
- § 8.4. Определение запаса устойчивости и быстродействия по переходной характеристике
- § 8.5. Приближенная оценка вида переходного процесса по вещественной частотной характеристике
- § 8.6. Корневые методы
- § 8.7. Диаграмма Вышнеградского
- § 8.8. Интегральные оценки
- § 8.9. Частотные критерии качества
- § 8.10. Чувствительность систем регулирования
- ГЛАВА 9. ПОВЫШЕНИЕ ТОЧНОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- § 9.2. Теория инвариантности и комбинированное управление
- § 9.3. Неединичные обратные связи
- ГЛАВА 10. УЛУЧШЕНИЕ КАЧЕСТВА ПРОЦЕССА РЕГУЛИРОВАНИЯ
- § 10.2. Последовательные корректирующие звенья
- § 10.3. Параллельные корректирующие звенья
- § 10.4. Обратные связи
- § 10.5. Методы повышения запаса устойчивости
- § 10.6. Примеры
- ГЛАВА 11. СЛУЧАЙНЫЕ ПРОЦЕССЫ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- § 11.2. Случайные процессы
- § 11.3. Стационарные случайные процессы
- § 11.4. Корреляционная функция
- § 11.5. Спектральная плотность стационарных процессов
- § 11.6. Канонические разложения случайных функций
- § 11.7. Прохождение случайного сигнала через линейную систему
- § 11.8. Расчет установившихся ошибок в автоматических системах
- § 11.9. Расчеты по минимуму среднеквадратичной ошибки
- ГЛАВА 12. МЕТОДЫ СИНТЕЗА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- § 12.2. Корневой метод
- § 12.3. Метод корневых годографов
- § 12.4. Метод стандартных переходных характеристик
- § 12.5. Метод логарифмических амплитудных характеристик
- § 12.6. Синтез систем автоматического регулирования на основе частотных критериев качества
- § 12.7. Об оптимальном синтезе
- § 12.8. Использование классических вариационных методов
- § 12.9. Динамическое программирование
- § 12.10. Аналитическое конструирование регуляторов
- РАЗДЕЛ III. ОСОБЫЕ ЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА 13. СИСТЕМЫ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
- § 13.2. Нахождение функции веса и построение переходных процессов
- § 13.3. Передаточные функции
- § 13.4. Устойчивость и качество регулирования
- § 13.5. О синтезе систем с переменными параметрами
- ГЛАВА 14. СИСТЕМЫ С ЗАПАЗДЫВАНИЕМ И СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- § 14.1. Уравнения линейных систем с запаздыванием
- § 14.2. Уравнения линейных систем с распределенными параметрами
- § 14.3. Исследование устойчивости и качества регулирования
- ГЛАВА 15. ИМПУЛЬСНЫЕ СИСТЕМЫ
- § 15.2. Использование z-преобразования
- § 15.3. Передаточные функции
- § 15.4. Устойчивость и качество импульсных систем регулирования
- § 15.5. Случайные процессы в импульсных системах
- РАЗДЕЛ IV. НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА 16. СОСТАВЛЕНИЕ УРАВНЕНИЙ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- § 16.2. Уравнения систем с нелинейностью релейного типа
- § 16.3. Уравнения систем с нелинейностью в виде сухого трения и зазора
- § 16.4. Уравнения систем с нелинейностями других видов
- ГЛАВА 17. ТОЧНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ И АВТОКОЛЕБАНИЙ
- § 17.1. Фазовые траектории и метод точечных преобразований
- § 17.2. Теоремы прямого метода Ляпунова и их применение
- § 17.3. Определение автоколебаний релейных систем методом припасовывания
- § 17.4. Частотный метод В. М. Попова
- § 17.5. Исследование систем с переменной структурой
- ГЛАВА 18. ПРИБЛИЖЕННЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ И АВТОКОЛЕБАНИЙ
- § 18.1. Гармоническая линеаризация нелинейностей
- § 18.2. Алгебраические способы определения автоколебаний и устойчивости в нелинейных системах первого класса
- § 18.3. Примеры исследования нелинейных систем первого класса
- § 18.4. Нелинейные системы второго класса
- § 18.5. Вычисление высших гармоник и уточнение первой гармоники автоколебаний
- § 18.6, Частотный метод определения автоколебаний
- ГЛАВА 19. МЕДЛЕННО МЕНЯЮЩИЕСЯ ПРОЦЕССЫ В АВТОКОЛЕБАТЕЛЬНЫХ СИСТЕМАХ
- § 19.1. Статические и скоростные ошибки автоколебательных систем
- § 19.2. Прохождение медленно меняющихся сигналов в автоколебательных системах
- § 19.3. Гармоническая линеаризация нелинейностей при несимметричных колебаниях
- ГЛАВА 20. ОЦЕНКА КАЧЕСТВА НЕЛИНЕЙНЫХ ПРОЦЕССОВ РЕГУЛИРОВАНИЯ
- § 20.1. Приближенное исследование колебательных переходных процессов
- § 20.2. Примеры исследования колебательных переходных процессов
- § 20.3. Система с нелинейным корректирующим устройством
- § 20.4. Применение логарифмических частотных характеристик для исследования нелинейных законов рзгулирования
- ГЛАВА 21. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
- § 21.1. Симметричные одночастотные вынужденные колебания
- § 21.2. Несимметричные вынужденные колебания с медленно меняющейся составляющей
- § 21.3. Зависимость устойчивости и качества нелинейных систем от внешних вибраций
- ГЛАВА 22. СЛУЧАЙНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ СИСТЕМАХ
- § 22.1. Статистическая линеаризация нелинейностей
- § 22.2. Простейшие случайные процессы в нелинейных системах
- § 22.3. Пример исследования влияния случайных помех на динамику нелинейной системы
- ГЛАВА 23. НЕЛИНЕЙНАЯ ОПТИМИЗАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- § 23.2. Синтез оптимальной системы с использованием принципа максимума
- § 23.3. Последовательная оптимизация на базе нелинейного программирования
- РАЗДЕЛ V. ЦИФРОВЫЕ И АДАПТИВНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- ГЛАВА 24. СИСТЕМЫ РЕГУЛИРОВАНИЯ С ЦИФРОВЫМИ ВЫЧИСЛИТЕЛЬНЫМИ МАШИНАМИ
- § 24.2. О синтезе систем регулирования с ЦВМ
- § 24.3. Дискретная коррекция
- § 24.4. Периодические режимы, обусловленные квантованием по уровню
- ГЛАВА 25. АДАПТИВНЫЕ СИСТЕМЫ
- § 25.1. Системы экстремального регулирования
- § 25.2. Самонастраивающиеся системы
- ПРИЛОЖЕНИЕ 1. ТАБЛИЦА ФУНКЦИЙ
- ПРИЛОЖЕНИЕ 2. ТАБЛИЦА ИНТЕГРАЛОВ
- ЛИТЕРАТУРА
Интегральная квадратичная ошибка
Cтраница 1
Интегральная квадратичная ошибка определяется как интеграл квадратов мгновенных ( текущих) значений рассогласования. При возведении в квадрат текущих значении рассогласования отрицательные величины не компенсируют положительные, поэтому с возрастанием рассогласования интегральная квадратичная ошибка растет очень быстро.
[1]
Эти коэффициенты соответствуют минимуму интегральной квадратичной ошибки между f ( t) и апроксимирующей функцией, что вытекает из (9.81), если Г оо. Полная функция f ( t) подбирается так, чтобы при этом значении Т получить наилучшую апроксимацию.
[2]
В этом разделе в качестве критерия оценки точности апроксимации применяется интегральная квадратичная ошибка. Выбор этого критерия диктуется главным образом удобством его применения; вместе с тем во многих конкретных случаях он служит весьма хорошей оценкой точности апроксимации. В нем одинаково учитываются как положительные, так и отрицательные ошибки. Критерий интегральной квадратичной ошибки достаточно хорошо оценивает большие и длительные ошибки, а малые и кратковременные ошибки слабо сказываются на его величине.
[3]
Экспоненциальные функции не являются ортогональными в любом интервале, так что критерий минимума интегральной квадратичной ошибки к такому ряду функций приложить нелегко.
[4]
С усилением интегрального воздействия ( уменьшение времени интегрирования) процесс из апериодического переходит в колебательный со все более уменьшающейся степенью затухания; при этом динамическая ошибка регулирования уменьшается, а время регулирования и интегральная квадратичная ошибка регулирования возрастают.
[5]
Для выбора наиболее рациональных с точки зрения технологии переходных процессов по каналам регулирования обычно выполняются расчеты для четырех процессов регулирования: без перерегулирования, с 20 % — ным перерегулированием, с минимальным временем регулирования и с минимальной интегральной квадратичной ошибкой.
[7]
Интегральные ошибки этих трех переходных процессов равны, так как настройки диапазона пропорциональности и времени изо-дрома регулятора во всех случаях одинаковы. Интегральная квадратичная ошибка последнего переходного процесса меньше, чем у первых двух, так как он имеет меньшую динамическую ошибку.
[9]
В частности, это имеет место для систем с симметричными и кососимметрич-ньгми матрицами А в силу ортогональности их канонических базисов. Эквивалентные сепаратные системы равноправны с точки зрения квадратичной оценки для системы в целом: значения их интегральных квадратичных ошибок входят в сумму ( ИЗ) с одинаковым весом.
[10]
Интегральная квадратичная ошибка определяется как интеграл квадратов мгновенных ( текущих) значений рассогласования. При возведении в квадрат текущих значении рассогласования отрицательные величины не компенсируют положительные, поэтому с возрастанием рассогласования интегральная квадратичная ошибка растет очень быстро.
[11]
Для большинства методов решения задачи синтеза оптимальных виброзащитных систем характерны следующие принципы: используется линейная динамическая модель с одной степенью свободы; для системы с двумя степенями свободы рассматриваются лишь частные случаи синтеза; учитывается не более одного ограничения; для одной и той же модели изменение спектральной плотности воздействия приводит к необходимости повторения процесса решения задачи. Например, для синтеза оптимальной системы с активным динамическим гасителем колебаний ( судовых механизмов и машин) был выбран метод минимально-квадратичной оптимизации, позволяющий синтезировать системы с наименьшим значением интегральной квадратичной ошибки при учете ограничений, накладываемых объектом.
[12]
На практике наиболее широкое распространение при оценке качества работы ристем регулирования получили интегральная и интегральная квадратичная ошибки. Принципиальное отличие между ними состоит в том, что вторая учитывает абсолютное значение ошибки. Например, две кривые переходного процесса с различными амплитудами колебаний параметра могут иметь одинаковые интегральные ошибки, но разные интегральные квадратичные ошибки.
[13]
В этом разделе в качестве критерия оценки точности апроксимации применяется интегральная квадратичная ошибка. Выбор этого критерия диктуется главным образом удобством его применения; вместе с тем во многих конкретных случаях он служит весьма хорошей оценкой точности апроксимации. В нем одинаково учитываются как положительные, так и отрицательные ошибки. Критерий интегральной квадратичной ошибки достаточно хорошо оценивает большие и длительные ошибки, а малые и кратковременные ошибки слабо сказываются на его величине.
[14]
Страницы:
1
2
Лебедев С.К. Математические основы теории автоматического управления — файл n1.doc
приобрести
Лебедев С.К. Математические основы теории автоматического управления
скачать (2089 kb.)
Доступные файлы (1):
n1.doc
Интегральные оценки качества
Интегральными оценками качества переходного процесса систем управления называют интегралы по времени от некоторых функций переходного процесса изменения ошибки регулирования.
Рассмотрим скалярную линейную систему, показанную на рис. 7. На вход управления системы поступает ступенчатый сигнал с амплитудой , система предназначена для стабилизации заданного значения регулируемой переменной
, на систему так же может действовать скалярное ступенчатое возмущение
стремящееся снизить значение регулируемой переменной.
Рис. 7
Примерный вид графиков переходных процессов регулируемой величины и ошибки регулирования –
,
показаны соответственно на рис. 8 и 9.
Рис. 8
Рис. 9
Основные области применения интегральных оценок в теории автоматического управления:
- Общая оценка быстроты затухания и величины отклонения регулируемой величины в совокупности, без определения того и другого в отдельности.
- Выбор при синтезе параметров систем, обеспечивающих оптимальность переходного процесса с точки зрения достижения минимума интегральных оценок.
Простейшей интегральной оценкой может служить линейная интегральная оценка следующего вида –

Геометрическая интерпретация этого интеграла представляет собой площадь под кривой , как это показано на рис. 10 для переходных процессов изменения ошибки при управлении и возмущении.
Рис. 10
Если система управления устойчива и обладает свойством астатизма, тогда
,
а интеграл стремится к конечному значению, равному площади под кривой
. Параметры системы управления стремятся выбирать таким образом, чтобы добиться минимума
, при этом идеальный переходный процесс будет стремиться к идеальной ступенчатой форма.
Контрольные вопросы и задачи
- Как определить показатель колебательности по АЧХ системы?
- Как определить частоту среза и полосу пропускания по АЧХ?
- Как соотносятся частота среза системы и ее быстродействие?
- Дайте определение линейной интегральной оценке, укажаите ее достоинства и недостатки.
- Почему для интегральных оценок переходного процесса используют график изменения ошибки регулирования?
- По графику АЧХ системы
определить показатель колебательности и частоту среза системы.
Ответ:
Показатель колебательности , частота среза
.
- По графикам АЧХ двух систем: САУ1 –
, САУ2 –
,
определить систему управления, переходные процессы которой имеют большую колебательность.
Ответ:
Большую колебательность переходных процессов имеет система САУ2.
- По графикам АЧХ двух систем: САУ1 –
, САУ2 –
,
определить систему управления, которая имеет большее быстродействие.
Ответ:
Большую колебательность переходных процессов имеет система САУ1.
Лекция 18
Вычисление линейных интегральных оценок
Рассмотрим проблему вычисления интеграла линейной интегральной оценки. Можно сначала решить аналитически дифференциальные уравнения, описывающие систему, долее определить ошибку регулирования, затем подставить выражение для ошибки в интеграл линейной оценки и, взяв его, получить выражение для .
Но можно поступить и иначе.
Пусть свободное движение ошибки регулирования системы описывается уравнением
| (1) |
Проинтегрируем это уравнение –
После интегрирования получаем –
 |
(2) |
Подстановки верхнего предела дают члены следующего вида –
 |
(3) |
так как все производные ошибки в установившемся режиме обращаются в ноль.
Подстановки нижнего предела дают члены вида –
 |
(4) |
которые являются начальными условиями уравнения (1).
Подставив (3) и (4) в (2), получим
 |
(5) |
А так как

окончательно получаем
| (6) |
Решая (6) относительно , получим выражение для вычисления линейной интегральной ошибки –
| (7) |
Теперь мы может определить по коэффициентам характеристического уравнения системы и начальным условиям переходного процесса ошибки.
Для синтеза систем, определения параметров минимизирующих , следует воспользоваться обычными методами исследования функций на экстремум. Следовательно, если мы хотим определить параметр системы, на пример, параметр
, обеспечивающий
, необходимо решить относительно параметра
следующее уравнение –
.
Рассмотрим несколько примеров использования линейной интегральной оценки.
Пример
Система имеет характеристическое уравнение
| (8) |
Определим выражение для , если начальные условия имеют вид –
.
Определим значение параметра , при котором интегральная оценка имеет минимум.
Решение
Обозначим –
.
Используем для нахождения выражение (7) –
| (9) |
Из рассмотрения (9) получаем, что в этом случае не имеет экстремума, а меньшее значение интегральной ошибки мы будем получать при меньшем значении
. Действительно, ведь уравнение (8) является характеристическим уравнением апериодического звена, параметр
– это постоянная времени. Переходный процесс для двух разных постоянных времени будет иметь вид, показанный на рис. 1.
Рис. 1
Пример
Система имеет характеристическое уравнение
.
Определим выражение для , если начальные условия имеют вид –
.
Определим значение параметра , при котором интегральная оценка имеет минимум.
Решение
Обозначим –
.
Используем для нахождения выражение (7) –
.
Если , то процессы монотонные,
обеспечивается при наименьших
и
. Если
, то уменьшение коэффициента затухания уменьшает линейную интегральную оценку, но это приводит к ухудшению переходного процесса, повышению его колебательности.
При колебательных процессах в системах линейная интегральная оценка дает значительную погрешность. При этом минимум оценки может соответствовать процессу с большим числом колебаний со значительной амплитудой, малым быстродействием, так как, по сути, в оценке происходит сложение положительных и отрицательных областей площади под интегральной кривой. Это иллюстрируют рис. 2 и 3, показывая два процесса, которые могут иметь одно и то же значение линейной интегральной оценки.
Рис. 2
Рис. 3
И так как форма переходного процесса при анализе системы автоматического управления часто заранее неизвестна, то применять линейные интегральные оценки на практике нецелесообразно.
Можно попытаться использовать интеграл от модуля ошибки следующего вида –
 |
(10) |
На рис. 4 показан примерный вид кривых изменения ошибки и ее модуля. Но аналитическое вычисление интеграла от модуля ошибки по математической модели системы оказалось весьма громоздким, поэтому эта оценка широкого распространения не получила.
Рис. 4
Квадратичная интегральная оценка
В большинстве случаев, при возможности возникновения в системе колебательного переходного процесса, используют квадратичную интегральную оценку, которая имеет следующий вид –
 |
(11) |
Оценка не зависит от знака отклонений ошибки, а значит и от формы переходного процесса, монотонный, апериодический или колебательный характер он будет иметь. На рис. 5 и 6 показан примерный вид кривых изменения ошибки и квадрата ошибки.
Рис. 5
Рис. 6
Рассмотрим процедуру вычисления квадратичной оценки по математической модели системы. Система управления представляется в виде, показанном на рис. 7.
Рис. 7
Изображение по Лапласу сигнала на выходе системы имеет вид –
| (12) |
где — изображение по Лапласу единичной ступенчатой функции – входного сигнала системы.
Для системы автоматического управления, математическая модель которой приведена к виду (12), интегральная квадратичная ошибка определяется по следующему выражению –
 |
(13) |
где
 |
(14) |
в все элементы с индексами меньше 0 и больше
заменяются 0.
Определители в (13), где
, получаются заменой в определителе
(14) (
)-го столбца столбцом следующего вида –
.
Коэффициенты в выражении (13) определяются следующим образом –
 |
(15) |
при определении коэффициенты, индексы которых меньше 0 и больше
, заменяются 0.
Контрольные вопросы и задачи
- Какие параметры математической модели объекта требуются для вычисления линейной интегральной оценки?
- Почему нельзя использовать линейную интегральную оценку в случае колебательного характера переходных процессов?
- Какие интегральные оценки целесообразно использовать в том случае если в системе возможно наличие колебательных переходных процессов?
- Дайте определение квадратичной интегральной оценке переходного процесса.
- При минимизации квадратичной оценки, к какому виду стремится переходный процесс?
- Какие параметры математической модели объекта требуются для вычисления квадратичной интегральной оценки?
- Объект управления описывается передаточной функцией –
.
Вычислите линейную интегральную оценку переходного процесса при начальном значении ошибки .
Ответ:
Линейная интегральная оценка .
- Объект управления описывается передаточной функцией –
.
Вычислите линейную интегральную оценку переходного процесса при начальном значении ошибки .
Ответ:
Линейная интегральная оценка .
Лекция 19
Квадратичная интегральная оценка с учетом производной
Недостатком квадратичной интегральной оценки , как и предыдущих оценок, является то, что при минимизации оценки не накладываются ограничения на форму переходного процесса. На пример, показанные на рис. 1 графики
– (а, б, в) могут иметь одинаковые значения
существенно при этом отличаясь по форме переходного процесса.
Рис. 1
Кроме того, часто оказывается, что выбранные по параметры системы приводят к существенно колебательному процессу, большим производным из-за стремления приблизить процесс к идеальному скачку.
Поэтому используют еще один вид интегрально квадратичной оценки, в которой ограничение накладывается не только на величину отклонения , но и на скорость его изменения
. Эта оценка имеет следующий вид –
 |
(1) |
где – некоторая постоянная времени.
Разницу между оценками и
можно представить графически, как это показано на рис. 2.
Рис. 2
То есть оптимизированный по переходный процесс стремиться к идеальному скачку, а оптимизированный по
– к кривой экспоненциального вида, которая описывается следующим выражением –
.
Докажем последнее утверждение. Для этого проанализируем выражение (1).

с учетом того, что
,
получаем
 |
(2) |
С учетом того, что последнее слагаемое в (2) является величиной постоянной –
,
квадратичная оценка будет иметь минимум при
| (3) |
Решение дифференциального уравнения (3) имеет вид –
,
а если перейти от ошибок к выходным переменным, то получим –
,
что и требовалось доказать.
Следовательно, выбирая параметры системы по , можно приблизить переходный процесс к экспоненте с заданной постоянной времени
, тем самым вводится ограничение на скорость нарастания выходной величины
.
Методика определения может быть аналогичной методике определения
, рассмотренной выше, если представить квадратичную оценку с учетом производной в следующем виде –

где определяется по формулам для
, но с учетом того, что порядок числителя
–
увеличивается на 1.
В теории автоматического управления используют квадратичные оценки с производными более высокого порядка (до ) для более точного задания желаемой формы переходного процесса, естественно, что при этом усложняется и процесс вычисления оценок.
Вычисление квадратичных интегральных оценок
Рассмотрим вычисление и использование квадратичных ошибок на примере.
Пример
В системе управления с передаточной функцией –
,
зададим :
и сравним переходные процессы для двух этих случаев.
Решение
Получим выражение для . Для этого преобразуем передаточную функцию системы к заданному виду
,
тогда получим
| (4) |
Выражение для принимает вид –
| (5) |
Определим компоненты (5) по параметра передаточной функции системы (4).
 |
(6) |
Для нахождения определим (
), при
,
,
Заменим в выражении (6) для первый столбец столбцом вида

Тогда получаем

Определим –
.
После подстановки полученных компонент в (5) получаем выражение для квадратичной интегральной оценки.
| (5) |
Найдем выражение для частной производной по от выражения (5)
,
приравнивая полученное выражение к нулю получаем уравнение для нахождения оптимального значения .
.
В результате получаем оптимизированное по квадратичной оценке значение –
| (6) |
Передаточная функция системы при примет вид –
.
На рис. 3 покажем вид переходного процесса системы при единичном ступенчатом воздействии и оптимизированным по параметром.
Рис. 3
Таким образом, имеем следующие показатели качества переходного процесса,
| (7) |
Определим по отработанной выше методике для
–
,
выражение для берем из предыдущего случая –
.
Определим теперь . Передаточная функция системы для этого случая имеет вид –
,
тогда получим
| (8) |
Выражение для принимает вид –
| (9) |
Определим компоненты (9) по параметра передаточной функции системы (8).
 |
(10) |
Определим коэффициенты –

не определяем, так как
. Для нахождения
определим (
), при
,
,
Заменим в выражении (10) для второй столбец столбцом вида

Тогда получаем

После подстановки полученных компонент в (9) получаем выражение для квадратичной интегральной оценки.
| (11) |
Окончательно получаем
| (12) |
Найдем выражение для частной производной по от выражения (12)
,
приравнивая полученное выражение к нулю получаем уравнение для нахождения оптимального значения .
.
В результате получаем оптимизированное по квадратичной оценке с учетом производной значение –
| (13) |
Полагаем для определенности , тогда
.
Передаточная функция системы при примет вид –
.
На рис. 3 покажем вид переходного процесса системы при единичном ступенчатом воздействии и оптимизированным по параметром.
Рис. 4
Таким образом, имеем следующие показатели качества переходного процесса,
| (14) |
Сравнивая переходные процессы, видим, что при оптимизации по квадратичной оценке с учетом производной () получили существенно меньшие значения перерегулирования и быстродействия, при более плавном нарастании переменной.
Интегральные оценки качества
| Error function | |
|---|---|

Plot of the error function |
|
| General information | |
| General definition |  |
| Fields of application | Probability, thermodynamics |
| Domain, Codomain and Image | |
| Domain |  |
| Image |  |
| Basic features | |
| Parity | Odd |
| Specific features | |
| Root | 0 |
| Derivative |  |
| Antiderivative |  |
| Series definition | |
| Taylor series |  |
In mathematics, the error function (also called the Gauss error function), often denoted by erf, is a complex function of a complex variable defined as:[1]
This integral is a special (non-elementary) sigmoid function that occurs often in probability, statistics, and partial differential equations. In many of these applications, the function argument is a real number. If the function argument is real, then the function value is also real.
In statistics, for non-negative values of x, the error function has the following interpretation: for a random variable Y that is normally distributed with mean 0 and standard deviation 1/√2, erf x is the probability that Y falls in the range [−x, x].
Two closely related functions are the complementary error function (erfc) defined as
and the imaginary error function (erfi) defined as
where i is the imaginary unit
Name[edit]
The name «error function» and its abbreviation erf were proposed by J. W. L. Glaisher in 1871 on account of its connection with «the theory of Probability, and notably the theory of Errors.»[2] The error function complement was also discussed by Glaisher in a separate publication in the same year.[3]
For the «law of facility» of errors whose density is given by
(the normal distribution), Glaisher calculates the probability of an error lying between p and q as:
Plot of the error function Erf(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
Applications[edit]
When the results of a series of measurements are described by a normal distribution with standard deviation σ and expected value 0, then erf (a/σ √2) is the probability that the error of a single measurement lies between −a and +a, for positive a. This is useful, for example, in determining the bit error rate of a digital communication system.
The error and complementary error functions occur, for example, in solutions of the heat equation when boundary conditions are given by the Heaviside step function.
The error function and its approximations can be used to estimate results that hold with high probability or with low probability. Given a random variable X ~ Norm[μ,σ] (a normal distribution with mean μ and standard deviation σ) and a constant L < μ:
where A and B are certain numeric constants. If L is sufficiently far from the mean, specifically μ − L ≥ σ√ln k, then:
so the probability goes to 0 as k → ∞.
The probability for X being in the interval [La, Lb] can be derived as
Properties[edit]
Integrand exp(−z2)
erf z
The property erf (−z) = −erf z means that the error function is an odd function. This directly results from the fact that the integrand e−t2 is an even function (the antiderivative of an even function which is zero at the origin is an odd function and vice versa).
Since the error function is an entire function which takes real numbers to real numbers, for any complex number z:
where z is the complex conjugate of z.
The integrand f = exp(−z2) and f = erf z are shown in the complex z-plane in the figures at right with domain coloring.
The error function at +∞ is exactly 1 (see Gaussian integral). At the real axis, erf z approaches unity at z → +∞ and −1 at z → −∞. At the imaginary axis, it tends to ±i∞.
Taylor series[edit]
The error function is an entire function; it has no singularities (except that at infinity) and its Taylor expansion always converges, but is famously known «[…] for its bad convergence if x > 1.»[4]
The defining integral cannot be evaluated in closed form in terms of elementary functions, but by expanding the integrand e−z2 into its Maclaurin series and integrating term by term, one obtains the error function’s Maclaurin series as:
which holds for every complex number z. The denominator terms are sequence A007680 in the OEIS.
For iterative calculation of the above series, the following alternative formulation may be useful:
because −(2k − 1)z2/k(2k + 1) expresses the multiplier to turn the kth term into the (k + 1)th term (considering z as the first term).
The imaginary error function has a very similar Maclaurin series, which is:
which holds for every complex number z.
Derivative and integral[edit]
The derivative of the error function follows immediately from its definition:
From this, the derivative of the imaginary error function is also immediate:
An antiderivative of the error function, obtainable by integration by parts, is
An antiderivative of the imaginary error function, also obtainable by integration by parts, is
Higher order derivatives are given by
where H are the physicists’ Hermite polynomials.[5]
Bürmann series[edit]
An expansion,[6] which converges more rapidly for all real values of x than a Taylor expansion, is obtained by using Hans Heinrich Bürmann’s theorem:[7]
where sgn is the sign function. By keeping only the first two coefficients and choosing c1 = 31/200 and c2 = −341/8000, the resulting approximation shows its largest relative error at x = ±1.3796, where it is less than 0.0036127:
Inverse functions[edit]
Given a complex number z, there is not a unique complex number w satisfying erf w = z, so a true inverse function would be multivalued. However, for −1 < x < 1, there is a unique real number denoted erf−1 x satisfying
The inverse error function is usually defined with domain (−1,1), and it is restricted to this domain in many computer algebra systems. However, it can be extended to the disk |z| < 1 of the complex plane, using the Maclaurin series
where c0 = 1 and
So we have the series expansion (common factors have been canceled from numerators and denominators):
(After cancellation the numerator/denominator fractions are entries OEIS: A092676/OEIS: A092677 in the OEIS; without cancellation the numerator terms are given in entry OEIS: A002067.) The error function’s value at ±∞ is equal to ±1.
For |z| < 1, we have erf(erf−1 z) = z.
The inverse complementary error function is defined as
For real x, there is a unique real number erfi−1 x satisfying erfi(erfi−1 x) = x. The inverse imaginary error function is defined as erfi−1 x.[8]
For any real x, Newton’s method can be used to compute erfi−1 x, and for −1 ≤ x ≤ 1, the following Maclaurin series converges:
where ck is defined as above.
Asymptotic expansion[edit]
A useful asymptotic expansion of the complementary error function (and therefore also of the error function) for large real x is
where (2n − 1)!! is the double factorial of (2n − 1), which is the product of all odd numbers up to (2n − 1). This series diverges for every finite x, and its meaning as asymptotic expansion is that for any integer N ≥ 1 one has
where the remainder, in Landau notation, is
as x → ∞.
Indeed, the exact value of the remainder is
which follows easily by induction, writing
and integrating by parts.
For large enough values of x, only the first few terms of this asymptotic expansion are needed to obtain a good approximation of erfc x (while for not too large values of x, the above Taylor expansion at 0 provides a very fast convergence).
Continued fraction expansion[edit]
A continued fraction expansion of the complementary error function is:[9]
Integral of error function with Gaussian density function[edit]
which appears related to Ng and Geller, formula 13 in section 4.3[10] with a change of variables.
Factorial series[edit]
The inverse factorial series:
converges for Re(z2) > 0. Here
zn denotes the rising factorial, and s(n,k) denotes a signed Stirling number of the first kind.[11][12]
There also exists a representation by an infinite sum containing the double factorial:
Numerical approximations[edit]
Approximation with elementary functions[edit]
- Abramowitz and Stegun give several approximations of varying accuracy (equations 7.1.25–28). This allows one to choose the fastest approximation suitable for a given application. In order of increasing accuracy, they are:
(maximum error: 5×10−4)
where a1 = 0.278393, a2 = 0.230389, a3 = 0.000972, a4 = 0.078108
(maximum error: 2.5×10−5)
where p = 0.47047, a1 = 0.3480242, a2 = −0.0958798, a3 = 0.7478556
(maximum error: 3×10−7)
where a1 = 0.0705230784, a2 = 0.0422820123, a3 = 0.0092705272, a4 = 0.0001520143, a5 = 0.0002765672, a6 = 0.0000430638
(maximum error: 1.5×10−7)
where p = 0.3275911, a1 = 0.254829592, a2 = −0.284496736, a3 = 1.421413741, a4 = −1.453152027, a5 = 1.061405429
All of these approximations are valid for x ≥ 0. To use these approximations for negative x, use the fact that erf x is an odd function, so erf x = −erf(−x).
- Exponential bounds and a pure exponential approximation for the complementary error function are given by[13]
- The above have been generalized to sums of N exponentials[14] with increasing accuracy in terms of N so that erfc x can be accurately approximated or bounded by 2Q̃(√2x), where
In particular, there is a systematic methodology to solve the numerical coefficients {(an,bn)}N
n = 1 that yield a minimax approximation or bound for the closely related Q-function: Q(x) ≈ Q̃(x), Q(x) ≤ Q̃(x), or Q(x) ≥ Q̃(x) for x ≥ 0. The coefficients {(an,bn)}N
n = 1 for many variations of the exponential approximations and bounds up to N = 25 have been released to open access as a comprehensive dataset.[15] - A tight approximation of the complementary error function for x ∈ [0,∞) is given by Karagiannidis & Lioumpas (2007)[16] who showed for the appropriate choice of parameters {A,B} that
They determined {A,B} = {1.98,1.135}, which gave a good approximation for all x ≥ 0. Alternative coefficients are also available for tailoring accuracy for a specific application or transforming the expression into a tight bound.[17]
- A single-term lower bound is[18]
where the parameter β can be picked to minimize error on the desired interval of approximation.
-
- Another approximation is given by Sergei Winitzki using his «global Padé approximations»:[19][20]: 2–3
where
This is designed to be very accurate in a neighborhood of 0 and a neighborhood of infinity, and the relative error is less than 0.00035 for all real x. Using the alternate value a ≈ 0.147 reduces the maximum relative error to about 0.00013.[21]
This approximation can be inverted to obtain an approximation for the inverse error function:
- An approximation with a maximal error of 1.2×10−7 for any real argument is:[22]
with
and
Table of values[edit]
| x | erf x | 1 − erf x |
|---|---|---|
| 0 | 0 | 1 |
| 0.02 | 0.022564575 | 0.977435425 |
| 0.04 | 0.045111106 | 0.954888894 |
| 0.06 | 0.067621594 | 0.932378406 |
| 0.08 | 0.090078126 | 0.909921874 |
| 0.1 | 0.112462916 | 0.887537084 |
| 0.2 | 0.222702589 | 0.777297411 |
| 0.3 | 0.328626759 | 0.671373241 |
| 0.4 | 0.428392355 | 0.571607645 |
| 0.5 | 0.520499878 | 0.479500122 |
| 0.6 | 0.603856091 | 0.396143909 |
| 0.7 | 0.677801194 | 0.322198806 |
| 0.8 | 0.742100965 | 0.257899035 |
| 0.9 | 0.796908212 | 0.203091788 |
| 1 | 0.842700793 | 0.157299207 |
| 1.1 | 0.880205070 | 0.119794930 |
| 1.2 | 0.910313978 | 0.089686022 |
| 1.3 | 0.934007945 | 0.065992055 |
| 1.4 | 0.952285120 | 0.047714880 |
| 1.5 | 0.966105146 | 0.033894854 |
| 1.6 | 0.976348383 | 0.023651617 |
| 1.7 | 0.983790459 | 0.016209541 |
| 1.8 | 0.989090502 | 0.010909498 |
| 1.9 | 0.992790429 | 0.007209571 |
| 2 | 0.995322265 | 0.004677735 |
| 2.1 | 0.997020533 | 0.002979467 |
| 2.2 | 0.998137154 | 0.001862846 |
| 2.3 | 0.998856823 | 0.001143177 |
| 2.4 | 0.999311486 | 0.000688514 |
| 2.5 | 0.999593048 | 0.000406952 |
| 3 | 0.999977910 | 0.000022090 |
| 3.5 | 0.999999257 | 0.000000743 |
[edit]
Complementary error function[edit]
The complementary error function, denoted erfc, is defined as
-
Plot of the complementary error function Erfc(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
which also defines erfcx, the scaled complementary error function[23] (which can be used instead of erfc to avoid arithmetic underflow[23][24]). Another form of erfc x for x ≥ 0 is known as Craig’s formula, after its discoverer:[25]
This expression is valid only for positive values of x, but it can be used in conjunction with erfc x = 2 − erfc(−x) to obtain erfc(x) for negative values. This form is advantageous in that the range of integration is fixed and finite. An extension of this expression for the erfc of the sum of two non-negative variables is as follows:[26]
Imaginary error function[edit]
The imaginary error function, denoted erfi, is defined as
Plot of the imaginary error function Erfi(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
where D(x) is the Dawson function (which can be used instead of erfi to avoid arithmetic overflow[23]).
Despite the name «imaginary error function», erfi x is real when x is real.
When the error function is evaluated for arbitrary complex arguments z, the resulting complex error function is usually discussed in scaled form as the Faddeeva function:
Cumulative distribution function[edit]
The error function is essentially identical to the standard normal cumulative distribution function, denoted Φ, also named norm(x) by some software languages[citation needed], as they differ only by scaling and translation. Indeed,
-
the normal cumulative distribution function plotted in the complex plane
or rearranged for erf and erfc:
Consequently, the error function is also closely related to the Q-function, which is the tail probability of the standard normal distribution. The Q-function can be expressed in terms of the error function as
The inverse of Φ is known as the normal quantile function, or probit function and may be expressed in terms of the inverse error function as
The standard normal cdf is used more often in probability and statistics, and the error function is used more often in other branches of mathematics.
The error function is a special case of the Mittag-Leffler function, and can also be expressed as a confluent hypergeometric function (Kummer’s function):
It has a simple expression in terms of the Fresnel integral.[further explanation needed]
In terms of the regularized gamma function P and the incomplete gamma function,
sgn x is the sign function.
Generalized error functions[edit]
Graph of generalised error functions En(x):
grey curve: E1(x) = 1 − e−x/√π
red curve: E2(x) = erf(x)
green curve: E3(x)
blue curve: E4(x)
gold curve: E5(x).
Some authors discuss the more general functions:[citation needed]
Notable cases are:
- E0(x) is a straight line through the origin: E0(x) = x/e√π
- E2(x) is the error function, erf x.
After division by n!, all the En for odd n look similar (but not identical) to each other. Similarly, the En for even n look similar (but not identical) to each other after a simple division by n!. All generalised error functions for n > 0 look similar on the positive x side of the graph.
These generalised functions can equivalently be expressed for x > 0 using the gamma function and incomplete gamma function:
Therefore, we can define the error function in terms of the incomplete gamma function:
Iterated integrals of the complementary error function[edit]
The iterated integrals of the complementary error function are defined by[27]
The general recurrence formula is
They have the power series
from which follow the symmetry properties
and
Implementations[edit]
As real function of a real argument[edit]
- In Posix-compliant operating systems, the header
math.hshall declare and the mathematical librarylibmshall provide the functionserfanderfc(double precision) as well as their single precision and extended precision counterpartserff,erflanderfcf,erfcl.[28] - The GNU Scientific Library provides
erf,erfc,log(erf), and scaled error functions.[29]
As complex function of a complex argument[edit]
libcerf, numeric C library for complex error functions, provides the complex functionscerf,cerfc,cerfcxand the real functionserfi,erfcxwith approximately 13–14 digits precision, based on the Faddeeva function as implemented in the MIT Faddeeva Package
See also[edit]
[edit]
- Gaussian integral, over the whole real line
- Gaussian function, derivative
- Dawson function, renormalized imaginary error function
- Goodwin–Staton integral
In probability[edit]
- Normal distribution
- Normal cumulative distribution function, a scaled and shifted form of error function
- Probit, the inverse or quantile function of the normal CDF
- Q-function, the tail probability of the normal distribution
References[edit]
- ^ Andrews, Larry C. (1998). Special functions of mathematics for engineers. SPIE Press. p. 110. ISBN 9780819426161.
- ^ Glaisher, James Whitbread Lee (July 1871). «On a class of definite integrals». London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4. 42 (277): 294–302. doi:10.1080/14786447108640568. Retrieved 6 December 2017.
- ^ Glaisher, James Whitbread Lee (September 1871). «On a class of definite integrals. Part II». London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4. 42 (279): 421–436. doi:10.1080/14786447108640600. Retrieved 6 December 2017.
- ^ «A007680 – OEIS». oeis.org. Retrieved 2 April 2020.
- ^ Weisstein, Eric W. «Erf». MathWorld.
- ^ Schöpf, H. M.; Supancic, P. H. (2014). «On Bürmann’s Theorem and Its Application to Problems of Linear and Nonlinear Heat Transfer and Diffusion». The Mathematica Journal. 16. doi:10.3888/tmj.16-11.
- ^ Weisstein, Eric W. «Bürmann’s Theorem». MathWorld.
- ^ Bergsma, Wicher (2006). «On a new correlation coefficient, its orthogonal decomposition and associated tests of independence». arXiv:math/0604627.
- ^ Cuyt, Annie A. M.; Petersen, Vigdis B.; Verdonk, Brigitte; Waadeland, Haakon; Jones, William B. (2008). Handbook of Continued Fractions for Special Functions. Springer-Verlag. ISBN 978-1-4020-6948-2.
- ^ Ng, Edward W.; Geller, Murray (January 1969). «A table of integrals of the Error functions». Journal of Research of the National Bureau of Standards Section B. 73B (1): 1. doi:10.6028/jres.073B.001.
- ^ Schlömilch, Oskar Xavier (1859). «Ueber facultätenreihen». Zeitschrift für Mathematik und Physik (in German). 4: 390–415. Retrieved 4 December 2017.
- ^ Nielson, Niels (1906). Handbuch der Theorie der Gammafunktion (in German). Leipzig: B. G. Teubner. p. 283 Eq. 3. Retrieved 4 December 2017.
- ^ Chiani, M.; Dardari, D.; Simon, M.K. (2003). «New Exponential Bounds and Approximations for the Computation of Error Probability in Fading Channels» (PDF). IEEE Transactions on Wireless Communications. 2 (4): 840–845. CiteSeerX 10.1.1.190.6761. doi:10.1109/TWC.2003.814350.
- ^ Tanash, I.M.; Riihonen, T. (2020). «Global minimax approximations and bounds for the Gaussian Q-function by sums of exponentials». IEEE Transactions on Communications. 68 (10): 6514–6524. arXiv:2007.06939. doi:10.1109/TCOMM.2020.3006902. S2CID 220514754.
- ^ Tanash, I.M.; Riihonen, T. (2020). «Coefficients for Global Minimax Approximations and Bounds for the Gaussian Q-Function by Sums of Exponentials [Data set]». Zenodo. doi:10.5281/zenodo.4112978.
- ^ Karagiannidis, G. K.; Lioumpas, A. S. (2007). «An improved approximation for the Gaussian Q-function» (PDF). IEEE Communications Letters. 11 (8): 644–646. doi:10.1109/LCOMM.2007.070470. S2CID 4043576.
- ^ Tanash, I.M.; Riihonen, T. (2021). «Improved coefficients for the Karagiannidis–Lioumpas approximations and bounds to the Gaussian Q-function». IEEE Communications Letters. 25 (5): 1468–1471. arXiv:2101.07631. doi:10.1109/LCOMM.2021.3052257. S2CID 231639206.
- ^ Chang, Seok-Ho; Cosman, Pamela C.; Milstein, Laurence B. (November 2011). «Chernoff-Type Bounds for the Gaussian Error Function». IEEE Transactions on Communications. 59 (11): 2939–2944. doi:10.1109/TCOMM.2011.072011.100049. S2CID 13636638.
- ^ Winitzki, Sergei (2003). «Uniform approximations for transcendental functions». Computational Science and Its Applications – ICCSA 2003. Lecture Notes in Computer Science. Vol. 2667. Springer, Berlin. pp. 780–789. doi:10.1007/3-540-44839-X_82. ISBN 978-3-540-40155-1.
- ^ Zeng, Caibin; Chen, Yang Cuan (2015). «Global Padé approximations of the generalized Mittag-Leffler function and its inverse». Fractional Calculus and Applied Analysis. 18 (6): 1492–1506. arXiv:1310.5592. doi:10.1515/fca-2015-0086. S2CID 118148950.
Indeed, Winitzki [32] provided the so-called global Padé approximation
- ^ Winitzki, Sergei (6 February 2008). «A handy approximation for the error function and its inverse».
- ^ Numerical Recipes in Fortran 77: The Art of Scientific Computing (ISBN 0-521-43064-X), 1992, page 214, Cambridge University Press.
- ^ a b c Cody, W. J. (March 1993), «Algorithm 715: SPECFUN—A portable FORTRAN package of special function routines and test drivers» (PDF), ACM Trans. Math. Softw., 19 (1): 22–32, CiteSeerX 10.1.1.643.4394, doi:10.1145/151271.151273, S2CID 5621105
- ^ Zaghloul, M. R. (1 March 2007), «On the calculation of the Voigt line profile: a single proper integral with a damped sine integrand», Monthly Notices of the Royal Astronomical Society, 375 (3): 1043–1048, Bibcode:2007MNRAS.375.1043Z, doi:10.1111/j.1365-2966.2006.11377.x
- ^ John W. Craig, A new, simple and exact result for calculating the probability of error for two-dimensional signal constellations Archived 3 April 2012 at the Wayback Machine, Proceedings of the 1991 IEEE Military Communication Conference, vol. 2, pp. 571–575.
- ^ Behnad, Aydin (2020). «A Novel Extension to Craig’s Q-Function Formula and Its Application in Dual-Branch EGC Performance Analysis». IEEE Transactions on Communications. 68 (7): 4117–4125. doi:10.1109/TCOMM.2020.2986209. S2CID 216500014.
- ^ Carslaw, H. S.; Jaeger, J. C. (1959), Conduction of Heat in Solids (2nd ed.), Oxford University Press, ISBN 978-0-19-853368-9, p 484
- ^ https://pubs.opengroup.org/onlinepubs/9699919799/basedefs/math.h.html
- ^ «Special Functions – GSL 2.7 documentation».
Further reading[edit]
- Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. «Chapter 7». Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 297. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (2007), «Section 6.2. Incomplete Gamma Function and Error Function», Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
- Temme, Nico M. (2010), «Error Functions, Dawson’s and Fresnel Integrals», in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
External links[edit]
- A Table of Integrals of the Error Functions
| Error function | |
|---|---|

Plot of the error function |
|
| General information | |
| General definition |  |
| Fields of application | Probability, thermodynamics |
| Domain, Codomain and Image | |
| Domain |  |
| Image |  |
| Basic features | |
| Parity | Odd |
| Specific features | |
| Root | 0 |
| Derivative |  |
| Antiderivative |  |
| Series definition | |
| Taylor series |  |
In mathematics, the error function (also called the Gauss error function), often denoted by erf, is a complex function of a complex variable defined as:[1]
This integral is a special (non-elementary) sigmoid function that occurs often in probability, statistics, and partial differential equations. In many of these applications, the function argument is a real number. If the function argument is real, then the function value is also real.
In statistics, for non-negative values of x, the error function has the following interpretation: for a random variable Y that is normally distributed with mean 0 and standard deviation 1/√2, erf x is the probability that Y falls in the range [−x, x].
Two closely related functions are the complementary error function (erfc) defined as
and the imaginary error function (erfi) defined as
where i is the imaginary unit
Name[edit]
The name «error function» and its abbreviation erf were proposed by J. W. L. Glaisher in 1871 on account of its connection with «the theory of Probability, and notably the theory of Errors.»[2] The error function complement was also discussed by Glaisher in a separate publication in the same year.[3]
For the «law of facility» of errors whose density is given by
(the normal distribution), Glaisher calculates the probability of an error lying between p and q as:
Plot of the error function Erf(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
Applications[edit]
When the results of a series of measurements are described by a normal distribution with standard deviation σ and expected value 0, then erf (a/σ √2) is the probability that the error of a single measurement lies between −a and +a, for positive a. This is useful, for example, in determining the bit error rate of a digital communication system.
The error and complementary error functions occur, for example, in solutions of the heat equation when boundary conditions are given by the Heaviside step function.
The error function and its approximations can be used to estimate results that hold with high probability or with low probability. Given a random variable X ~ Norm[μ,σ] (a normal distribution with mean μ and standard deviation σ) and a constant L < μ:
where A and B are certain numeric constants. If L is sufficiently far from the mean, specifically μ − L ≥ σ√ln k, then:
so the probability goes to 0 as k → ∞.
The probability for X being in the interval [La, Lb] can be derived as
Properties[edit]
Integrand exp(−z2)
erf z
The property erf (−z) = −erf z means that the error function is an odd function. This directly results from the fact that the integrand e−t2 is an even function (the antiderivative of an even function which is zero at the origin is an odd function and vice versa).
Since the error function is an entire function which takes real numbers to real numbers, for any complex number z:
where z is the complex conjugate of z.
The integrand f = exp(−z2) and f = erf z are shown in the complex z-plane in the figures at right with domain coloring.
The error function at +∞ is exactly 1 (see Gaussian integral). At the real axis, erf z approaches unity at z → +∞ and −1 at z → −∞. At the imaginary axis, it tends to ±i∞.
Taylor series[edit]
The error function is an entire function; it has no singularities (except that at infinity) and its Taylor expansion always converges, but is famously known «[…] for its bad convergence if x > 1.»[4]
The defining integral cannot be evaluated in closed form in terms of elementary functions, but by expanding the integrand e−z2 into its Maclaurin series and integrating term by term, one obtains the error function’s Maclaurin series as:
which holds for every complex number z. The denominator terms are sequence A007680 in the OEIS.
For iterative calculation of the above series, the following alternative formulation may be useful:
because −(2k − 1)z2/k(2k + 1) expresses the multiplier to turn the kth term into the (k + 1)th term (considering z as the first term).
The imaginary error function has a very similar Maclaurin series, which is:
which holds for every complex number z.
Derivative and integral[edit]
The derivative of the error function follows immediately from its definition:
From this, the derivative of the imaginary error function is also immediate:
An antiderivative of the error function, obtainable by integration by parts, is
An antiderivative of the imaginary error function, also obtainable by integration by parts, is
Higher order derivatives are given by
where H are the physicists’ Hermite polynomials.[5]
Bürmann series[edit]
An expansion,[6] which converges more rapidly for all real values of x than a Taylor expansion, is obtained by using Hans Heinrich Bürmann’s theorem:[7]
where sgn is the sign function. By keeping only the first two coefficients and choosing c1 = 31/200 and c2 = −341/8000, the resulting approximation shows its largest relative error at x = ±1.3796, where it is less than 0.0036127:
Inverse functions[edit]
Given a complex number z, there is not a unique complex number w satisfying erf w = z, so a true inverse function would be multivalued. However, for −1 < x < 1, there is a unique real number denoted erf−1 x satisfying
The inverse error function is usually defined with domain (−1,1), and it is restricted to this domain in many computer algebra systems. However, it can be extended to the disk |z| < 1 of the complex plane, using the Maclaurin series
where c0 = 1 and
So we have the series expansion (common factors have been canceled from numerators and denominators):
(After cancellation the numerator/denominator fractions are entries OEIS: A092676/OEIS: A092677 in the OEIS; without cancellation the numerator terms are given in entry OEIS: A002067.) The error function’s value at ±∞ is equal to ±1.
For |z| < 1, we have erf(erf−1 z) = z.
The inverse complementary error function is defined as
For real x, there is a unique real number erfi−1 x satisfying erfi(erfi−1 x) = x. The inverse imaginary error function is defined as erfi−1 x.[8]
For any real x, Newton’s method can be used to compute erfi−1 x, and for −1 ≤ x ≤ 1, the following Maclaurin series converges:
where ck is defined as above.
Asymptotic expansion[edit]
A useful asymptotic expansion of the complementary error function (and therefore also of the error function) for large real x is
where (2n − 1)!! is the double factorial of (2n − 1), which is the product of all odd numbers up to (2n − 1). This series diverges for every finite x, and its meaning as asymptotic expansion is that for any integer N ≥ 1 one has
where the remainder, in Landau notation, is
as x → ∞.
Indeed, the exact value of the remainder is
which follows easily by induction, writing
and integrating by parts.
For large enough values of x, only the first few terms of this asymptotic expansion are needed to obtain a good approximation of erfc x (while for not too large values of x, the above Taylor expansion at 0 provides a very fast convergence).
Continued fraction expansion[edit]
A continued fraction expansion of the complementary error function is:[9]
Integral of error function with Gaussian density function[edit]
which appears related to Ng and Geller, formula 13 in section 4.3[10] with a change of variables.
Factorial series[edit]
The inverse factorial series:
converges for Re(z2) > 0. Here
zn denotes the rising factorial, and s(n,k) denotes a signed Stirling number of the first kind.[11][12]
There also exists a representation by an infinite sum containing the double factorial:
Numerical approximations[edit]
Approximation with elementary functions[edit]
- Abramowitz and Stegun give several approximations of varying accuracy (equations 7.1.25–28). This allows one to choose the fastest approximation suitable for a given application. In order of increasing accuracy, they are:
(maximum error: 5×10−4)
where a1 = 0.278393, a2 = 0.230389, a3 = 0.000972, a4 = 0.078108
(maximum error: 2.5×10−5)
where p = 0.47047, a1 = 0.3480242, a2 = −0.0958798, a3 = 0.7478556
(maximum error: 3×10−7)
where a1 = 0.0705230784, a2 = 0.0422820123, a3 = 0.0092705272, a4 = 0.0001520143, a5 = 0.0002765672, a6 = 0.0000430638
(maximum error: 1.5×10−7)
where p = 0.3275911, a1 = 0.254829592, a2 = −0.284496736, a3 = 1.421413741, a4 = −1.453152027, a5 = 1.061405429
All of these approximations are valid for x ≥ 0. To use these approximations for negative x, use the fact that erf x is an odd function, so erf x = −erf(−x).
- Exponential bounds and a pure exponential approximation for the complementary error function are given by[13]
- The above have been generalized to sums of N exponentials[14] with increasing accuracy in terms of N so that erfc x can be accurately approximated or bounded by 2Q̃(√2x), where
In particular, there is a systematic methodology to solve the numerical coefficients {(an,bn)}N
n = 1 that yield a minimax approximation or bound for the closely related Q-function: Q(x) ≈ Q̃(x), Q(x) ≤ Q̃(x), or Q(x) ≥ Q̃(x) for x ≥ 0. The coefficients {(an,bn)}N
n = 1 for many variations of the exponential approximations and bounds up to N = 25 have been released to open access as a comprehensive dataset.[15] - A tight approximation of the complementary error function for x ∈ [0,∞) is given by Karagiannidis & Lioumpas (2007)[16] who showed for the appropriate choice of parameters {A,B} that
They determined {A,B} = {1.98,1.135}, which gave a good approximation for all x ≥ 0. Alternative coefficients are also available for tailoring accuracy for a specific application or transforming the expression into a tight bound.[17]
- A single-term lower bound is[18]
where the parameter β can be picked to minimize error on the desired interval of approximation.
-
- Another approximation is given by Sergei Winitzki using his «global Padé approximations»:[19][20]: 2–3
where
This is designed to be very accurate in a neighborhood of 0 and a neighborhood of infinity, and the relative error is less than 0.00035 for all real x. Using the alternate value a ≈ 0.147 reduces the maximum relative error to about 0.00013.[21]
This approximation can be inverted to obtain an approximation for the inverse error function:
- An approximation with a maximal error of 1.2×10−7 for any real argument is:[22]
with
and
Table of values[edit]
| x | erf x | 1 − erf x |
|---|---|---|
| 0 | 0 | 1 |
| 0.02 | 0.022564575 | 0.977435425 |
| 0.04 | 0.045111106 | 0.954888894 |
| 0.06 | 0.067621594 | 0.932378406 |
| 0.08 | 0.090078126 | 0.909921874 |
| 0.1 | 0.112462916 | 0.887537084 |
| 0.2 | 0.222702589 | 0.777297411 |
| 0.3 | 0.328626759 | 0.671373241 |
| 0.4 | 0.428392355 | 0.571607645 |
| 0.5 | 0.520499878 | 0.479500122 |
| 0.6 | 0.603856091 | 0.396143909 |
| 0.7 | 0.677801194 | 0.322198806 |
| 0.8 | 0.742100965 | 0.257899035 |
| 0.9 | 0.796908212 | 0.203091788 |
| 1 | 0.842700793 | 0.157299207 |
| 1.1 | 0.880205070 | 0.119794930 |
| 1.2 | 0.910313978 | 0.089686022 |
| 1.3 | 0.934007945 | 0.065992055 |
| 1.4 | 0.952285120 | 0.047714880 |
| 1.5 | 0.966105146 | 0.033894854 |
| 1.6 | 0.976348383 | 0.023651617 |
| 1.7 | 0.983790459 | 0.016209541 |
| 1.8 | 0.989090502 | 0.010909498 |
| 1.9 | 0.992790429 | 0.007209571 |
| 2 | 0.995322265 | 0.004677735 |
| 2.1 | 0.997020533 | 0.002979467 |
| 2.2 | 0.998137154 | 0.001862846 |
| 2.3 | 0.998856823 | 0.001143177 |
| 2.4 | 0.999311486 | 0.000688514 |
| 2.5 | 0.999593048 | 0.000406952 |
| 3 | 0.999977910 | 0.000022090 |
| 3.5 | 0.999999257 | 0.000000743 |
[edit]
Complementary error function[edit]
The complementary error function, denoted erfc, is defined as
-
Plot of the complementary error function Erfc(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
which also defines erfcx, the scaled complementary error function[23] (which can be used instead of erfc to avoid arithmetic underflow[23][24]). Another form of erfc x for x ≥ 0 is known as Craig’s formula, after its discoverer:[25]
This expression is valid only for positive values of x, but it can be used in conjunction with erfc x = 2 − erfc(−x) to obtain erfc(x) for negative values. This form is advantageous in that the range of integration is fixed and finite. An extension of this expression for the erfc of the sum of two non-negative variables is as follows:[26]
Imaginary error function[edit]
The imaginary error function, denoted erfi, is defined as
Plot of the imaginary error function Erfi(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
where D(x) is the Dawson function (which can be used instead of erfi to avoid arithmetic overflow[23]).
Despite the name «imaginary error function», erfi x is real when x is real.
When the error function is evaluated for arbitrary complex arguments z, the resulting complex error function is usually discussed in scaled form as the Faddeeva function:
Cumulative distribution function[edit]
The error function is essentially identical to the standard normal cumulative distribution function, denoted Φ, also named norm(x) by some software languages[citation needed], as they differ only by scaling and translation. Indeed,
-
the normal cumulative distribution function plotted in the complex plane
or rearranged for erf and erfc:
Consequently, the error function is also closely related to the Q-function, which is the tail probability of the standard normal distribution. The Q-function can be expressed in terms of the error function as
The inverse of Φ is known as the normal quantile function, or probit function and may be expressed in terms of the inverse error function as
The standard normal cdf is used more often in probability and statistics, and the error function is used more often in other branches of mathematics.
The error function is a special case of the Mittag-Leffler function, and can also be expressed as a confluent hypergeometric function (Kummer’s function):
It has a simple expression in terms of the Fresnel integral.[further explanation needed]
In terms of the regularized gamma function P and the incomplete gamma function,
sgn x is the sign function.
Generalized error functions[edit]
Graph of generalised error functions En(x):
grey curve: E1(x) = 1 − e−x/√π
red curve: E2(x) = erf(x)
green curve: E3(x)
blue curve: E4(x)
gold curve: E5(x).
Some authors discuss the more general functions:[citation needed]
Notable cases are:
- E0(x) is a straight line through the origin: E0(x) = x/e√π
- E2(x) is the error function, erf x.
After division by n!, all the En for odd n look similar (but not identical) to each other. Similarly, the En for even n look similar (but not identical) to each other after a simple division by n!. All generalised error functions for n > 0 look similar on the positive x side of the graph.
These generalised functions can equivalently be expressed for x > 0 using the gamma function and incomplete gamma function:
Therefore, we can define the error function in terms of the incomplete gamma function:
Iterated integrals of the complementary error function[edit]
The iterated integrals of the complementary error function are defined by[27]
The general recurrence formula is
They have the power series
from which follow the symmetry properties
and
Implementations[edit]
As real function of a real argument[edit]
- In Posix-compliant operating systems, the header
math.hshall declare and the mathematical librarylibmshall provide the functionserfanderfc(double precision) as well as their single precision and extended precision counterpartserff,erflanderfcf,erfcl.[28] - The GNU Scientific Library provides
erf,erfc,log(erf), and scaled error functions.[29]
As complex function of a complex argument[edit]
libcerf, numeric C library for complex error functions, provides the complex functionscerf,cerfc,cerfcxand the real functionserfi,erfcxwith approximately 13–14 digits precision, based on the Faddeeva function as implemented in the MIT Faddeeva Package
See also[edit]
[edit]
- Gaussian integral, over the whole real line
- Gaussian function, derivative
- Dawson function, renormalized imaginary error function
- Goodwin–Staton integral
In probability[edit]
- Normal distribution
- Normal cumulative distribution function, a scaled and shifted form of error function
- Probit, the inverse or quantile function of the normal CDF
- Q-function, the tail probability of the normal distribution
References[edit]
- ^ Andrews, Larry C. (1998). Special functions of mathematics for engineers. SPIE Press. p. 110. ISBN 9780819426161.
- ^ Glaisher, James Whitbread Lee (July 1871). «On a class of definite integrals». London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4. 42 (277): 294–302. doi:10.1080/14786447108640568. Retrieved 6 December 2017.
- ^ Glaisher, James Whitbread Lee (September 1871). «On a class of definite integrals. Part II». London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4. 42 (279): 421–436. doi:10.1080/14786447108640600. Retrieved 6 December 2017.
- ^ «A007680 – OEIS». oeis.org. Retrieved 2 April 2020.
- ^ Weisstein, Eric W. «Erf». MathWorld.
- ^ Schöpf, H. M.; Supancic, P. H. (2014). «On Bürmann’s Theorem and Its Application to Problems of Linear and Nonlinear Heat Transfer and Diffusion». The Mathematica Journal. 16. doi:10.3888/tmj.16-11.
- ^ Weisstein, Eric W. «Bürmann’s Theorem». MathWorld.
- ^ Bergsma, Wicher (2006). «On a new correlation coefficient, its orthogonal decomposition and associated tests of independence». arXiv:math/0604627.
- ^ Cuyt, Annie A. M.; Petersen, Vigdis B.; Verdonk, Brigitte; Waadeland, Haakon; Jones, William B. (2008). Handbook of Continued Fractions for Special Functions. Springer-Verlag. ISBN 978-1-4020-6948-2.
- ^ Ng, Edward W.; Geller, Murray (January 1969). «A table of integrals of the Error functions». Journal of Research of the National Bureau of Standards Section B. 73B (1): 1. doi:10.6028/jres.073B.001.
- ^ Schlömilch, Oskar Xavier (1859). «Ueber facultätenreihen». Zeitschrift für Mathematik und Physik (in German). 4: 390–415. Retrieved 4 December 2017.
- ^ Nielson, Niels (1906). Handbuch der Theorie der Gammafunktion (in German). Leipzig: B. G. Teubner. p. 283 Eq. 3. Retrieved 4 December 2017.
- ^ Chiani, M.; Dardari, D.; Simon, M.K. (2003). «New Exponential Bounds and Approximations for the Computation of Error Probability in Fading Channels» (PDF). IEEE Transactions on Wireless Communications. 2 (4): 840–845. CiteSeerX 10.1.1.190.6761. doi:10.1109/TWC.2003.814350.
- ^ Tanash, I.M.; Riihonen, T. (2020). «Global minimax approximations and bounds for the Gaussian Q-function by sums of exponentials». IEEE Transactions on Communications. 68 (10): 6514–6524. arXiv:2007.06939. doi:10.1109/TCOMM.2020.3006902. S2CID 220514754.
- ^ Tanash, I.M.; Riihonen, T. (2020). «Coefficients for Global Minimax Approximations and Bounds for the Gaussian Q-Function by Sums of Exponentials [Data set]». Zenodo. doi:10.5281/zenodo.4112978.
- ^ Karagiannidis, G. K.; Lioumpas, A. S. (2007). «An improved approximation for the Gaussian Q-function» (PDF). IEEE Communications Letters. 11 (8): 644–646. doi:10.1109/LCOMM.2007.070470. S2CID 4043576.
- ^ Tanash, I.M.; Riihonen, T. (2021). «Improved coefficients for the Karagiannidis–Lioumpas approximations and bounds to the Gaussian Q-function». IEEE Communications Letters. 25 (5): 1468–1471. arXiv:2101.07631. doi:10.1109/LCOMM.2021.3052257. S2CID 231639206.
- ^ Chang, Seok-Ho; Cosman, Pamela C.; Milstein, Laurence B. (November 2011). «Chernoff-Type Bounds for the Gaussian Error Function». IEEE Transactions on Communications. 59 (11): 2939–2944. doi:10.1109/TCOMM.2011.072011.100049. S2CID 13636638.
- ^ Winitzki, Sergei (2003). «Uniform approximations for transcendental functions». Computational Science and Its Applications – ICCSA 2003. Lecture Notes in Computer Science. Vol. 2667. Springer, Berlin. pp. 780–789. doi:10.1007/3-540-44839-X_82. ISBN 978-3-540-40155-1.
- ^ Zeng, Caibin; Chen, Yang Cuan (2015). «Global Padé approximations of the generalized Mittag-Leffler function and its inverse». Fractional Calculus and Applied Analysis. 18 (6): 1492–1506. arXiv:1310.5592. doi:10.1515/fca-2015-0086. S2CID 118148950.
Indeed, Winitzki [32] provided the so-called global Padé approximation
- ^ Winitzki, Sergei (6 February 2008). «A handy approximation for the error function and its inverse».
- ^ Numerical Recipes in Fortran 77: The Art of Scientific Computing (ISBN 0-521-43064-X), 1992, page 214, Cambridge University Press.
- ^ a b c Cody, W. J. (March 1993), «Algorithm 715: SPECFUN—A portable FORTRAN package of special function routines and test drivers» (PDF), ACM Trans. Math. Softw., 19 (1): 22–32, CiteSeerX 10.1.1.643.4394, doi:10.1145/151271.151273, S2CID 5621105
- ^ Zaghloul, M. R. (1 March 2007), «On the calculation of the Voigt line profile: a single proper integral with a damped sine integrand», Monthly Notices of the Royal Astronomical Society, 375 (3): 1043–1048, Bibcode:2007MNRAS.375.1043Z, doi:10.1111/j.1365-2966.2006.11377.x
- ^ John W. Craig, A new, simple and exact result for calculating the probability of error for two-dimensional signal constellations Archived 3 April 2012 at the Wayback Machine, Proceedings of the 1991 IEEE Military Communication Conference, vol. 2, pp. 571–575.
- ^ Behnad, Aydin (2020). «A Novel Extension to Craig’s Q-Function Formula and Its Application in Dual-Branch EGC Performance Analysis». IEEE Transactions on Communications. 68 (7): 4117–4125. doi:10.1109/TCOMM.2020.2986209. S2CID 216500014.
- ^ Carslaw, H. S.; Jaeger, J. C. (1959), Conduction of Heat in Solids (2nd ed.), Oxford University Press, ISBN 978-0-19-853368-9, p 484
- ^ https://pubs.opengroup.org/onlinepubs/9699919799/basedefs/math.h.html
- ^ «Special Functions – GSL 2.7 documentation».
Further reading[edit]
- Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. «Chapter 7». Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 297. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (2007), «Section 6.2. Incomplete Gamma Function and Error Function», Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
- Temme, Nico M. (2010), «Error Functions, Dawson’s and Fresnel Integrals», in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
External links[edit]
- A Table of Integrals of the Error Functions

В математике функция ошибок (также называемая Функция ошибок Гаусса ), часто обозначаемая erf, является сложной функцией комплексной определяемой как:
- erf z = 2 π ∫ 0 ze — t 2 dt. { displaystyle operatorname {erf} z = { frac {2} { sqrt { pi}}} int _ {0} ^ {z} e ^ {- t ^ {2}} , dt.}
Этот интеграл является особой (не элементарной ) и сигмоидной функцией, которая часто встречается в статистике вероятность, и уравнения в частных производных. Во многих из этих приложений аргумент функции является действительным числом. Если аргумент функции является действительным, значение также является действительным.
В статистике для неотрицательных значений x функция имеет интерпретацию: для случайной величины Y, которая нормально распределена с среднее 0 и дисперсия 1/2, erf x — это вероятность того, что Y попадает в диапазон [-x, x].
Две связанные функции: дополнительные функции ошибок (erfc ), определенная как
- erfc z = 1 — erf z, { displaystyle operatorname {erfc} z = 1- operatorname {erf} z,}
и функция мнимой ошибки (erfi ), определяемая как
- erfi z = — i erf (iz), { displaystyle operatorname {erfi} z = -i operatorname {erf} (iz),}
, где i — мнимая единица.
Содержание
- 1 Имя
- 2 Приложения
- 3 Свойства
- 3.1 Ряд Тейлора
- 3.2 Производная и интеграл
- 3.3 Ряд Бюрмана
- 3.4 Обратные функции
- 3.5 Асимптотическое разложение
- 3.6 Разложение на непрерывную дробь
- 3,7 Интеграл функции ошибок с функцией плотности Гаусса
- 3.8 Факториальный ряд
- 4 Численные приближения
- 4.1 Аппроксимация с элементарными функциями
- 4.2 Полином
- 4.3 Таблица значений
- 5 Связанные функции
- 5.1 функция дополнительных ошибок
- 5.2 Функция мнимой ошибки
- 5.3 Кумулятивная функци я распределения на
- 5.4 Обобщенные функции ошибок
- 5.5 Итерированные интегралы дополнительных функций ошибок
- 6 Реализации
- 6.1 Как действующая функция действительного аргумента
- 6.2 Как комплексная функция комплексного аргумента
- 7 См. Также
- 7.1 Связанные функции
- 7.2 Вероятность
- 8 Ссылки
- 9 Дополнительная литература
- 10 Внешние ссылки
Имя
Название «функция ошибки» и его аббревиатура erf были предложены Дж. В. Л. Глейшер в 1871 г. по причине его связи с «теорией вероятности, и особенно теорией ошибок ». Дополнение функции ошибок также обсуждалось Глейшером в отдельной публикации в том же году. Для «закона удобства» ошибок плотность задана как
- f (x) = (c π) 1 2 e — cx 2 { displaystyle f (x) = left ({ frac {c } { pi}} right) ^ { tfrac {1} {2}} e ^ {- cx ^ {2}}}
(нормальное распределение ), Глейшер вычисляет вероятность ошибки, лежащей между p { displaystyle p}

- (c π) 1 2 ∫ pqe — cx 2 dx = 1 2 (erf (qc) — erf (pc)). { displaystyle left ({ frac {c} { pi}} right) ^ { tfrac {1} {2}} int _ {p} ^ {q} e ^ {- cx ^ {2} } dx = { tfrac {1} {2}} left ( operatorname {erf} (q { sqrt {c}}) — operatorname {erf} (p { sqrt {c}}) right).}
Приложения
Когда результаты серии измерений описываются нормальным распределением со стандартным отклонением σ { displaystyle sigma}

Функции и дополнительные функции ошибок возникают, например, в решениях уравнения теплопроводности, когда граничные ошибки задаются ступенчатой функцией Хевисайда.
Функция ошибок и ее приближения Программу присвоили себе преподавателей, которые получили с высокой вероятностью или с низкой вероятностью. Дана случайная величина X ∼ Norm [μ, σ] { displaystyle X sim operatorname {Norm} [ mu, sigma]}![X sim operatorname {Norm} [ му, sigma]](https://wikimedia.org/api/rest_v1/media/math/render/svg/84024bc6827355ec6d23a062283a26d54b29698d)

- Pr [X ≤ L ] = 1 2 + 1 2 erf (L — μ 2 σ) ≈ A ехр (- B (L — μ σ) 2) { Displaystyle Pr [X Leq L] = { frac {1} {2 }} + { frac {1} {2}} operatorname {erf} left ({ frac {L- mu} {{ sqrt {2}} sigma}} right) приблизительно A exp left (-B left ({ frac {L- mu} { sigma}} right) ^ {2} right)}
где A и B — верх числовые константы. Если L достаточно далеко от среднего, то есть μ — L ≥ σ ln k { displaystyle mu -L geq sigma { sqrt { ln {k}}}}
- Pr [X ≤ L] ≤ A exp (- B ln k) = A К B { displaystyle Pr [X leq L] leq A exp (-B ln {k}) = { frac {A} {k ^ {B}}}}
, поэтому становится вероятность 0 при k → ∞ { displaystyle k to infty}
Свойства
Графики на комплексной плоскости 

Свойство erf (- z) = — erf (z) { displaystyle operatorname {erf} (-z) = — operatorname {erf} (z)}

Для любого комплексное число z:
- erf (z ¯) = erf (z) ¯ { displaystyle operatorname {erf} ({ overline {z}}) = { overline { operatorname {erf} (z)}}}
где z ¯ { displaystyle { overline {z}}}
Подынтегральное выражение f = exp (−z) и f = erf (z) показано в комплексной плоскости z на рисунках 2 и 3. Уровень Im (f) = 0 показан жирным зеленым цветом. линия. Отрицательные целые значения Im (f) показаны жирными красными линиями. Положительные целые значения Im (f) показаны толстыми синими линиями. Промежуточные уровни Im (f) = проявляются тонкими зелеными линиями. Промежуточные уровни Re (f) = показаны тонкими красными линиями для отрицательных значений и тонкими синими линиями для положительных значений.
Функция ошибок при + ∞ равна 1 (см. интеграл Гаусса ). На действительной оси erf (z) стремится к единице при z → + ∞ и к −1 при z → −∞. На мнимой оси он стремится к ± i∞.
Серия Тейлора
Функция ошибок — это целая функция ; у него нет сингулярностей (кроме бесконечности), и его разложение Тейлора всегда сходится, но, как известно, «[…] его плохая сходимость, если x>1».
определяющий интеграл нельзя вычислить в закрытой форме в терминах элементарных функций, но путем расширения подынтегрального выражения e в его ряд Маклорена и интегрирована почленно, можно получить ряд Маклорена функции ошибок как:
- erf (z) = 2 π ∑ n = 0 ∞ (- 1) nz 2 n + 1 n! (2 n + 1) знак равно 2 π (z — z 3 3 + z 5 10 — z 7 42 + z 9 216 — ⋯) { displaystyle operatorname {erf} (z) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n} z ^ {2n + 1}} {n! (2n + 1)}} = { frac {2} { sqrt { pi}}} left (z — { frac {z ^ {3}} {3}} + { frac {z ^ { 5}} {10}} — { frac {z ^ {7}} {42}} + { frac {z ^ {9}} {216}} — cdots right)}
, которое выполняется для каждого комплексного числа г. Члены знаменателя представляют собой последовательность A007680 в OEIS.
Для итеративного вычисления нового ряда может быть полезна следующая альтернативная формулировка:
- erf (z) = 2 π ∑ n = 0 ∞ (z ∏ К знак равно 1 N — (2 К — 1) Z 2 К (2 К + 1)) знак равно 2 π ∑ N = 0 ∞ Z 2 N + 1 ∏ К = 1 N — Z 2 К { Displaystyle OperatorName { erf} (z) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} left (z prod _ {k = 1} ^ {n} { frac {- (2k-1) z ^ {2}} {k (2k + 1)}} right) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {z} {2n + 1}} prod _ {k = 1} ^ {n} { frac {-z ^ {2}} {k}}}
потому что что — (2 k — 1) z 2 k (2 k + 1) { displaystyle { frac {- (2k-1) z ^ {2}} {k (2k + 1))}} }
Функция мнимой ошибки имеет очень похожий ряд Маклорена:
- erfi (z) = 2 π ∑ n = 0 ∞ z 2 n + 1 n! (2 n + 1) знак равно 2 π (z + z 3 3 + z 5 10 + z 7 42 + z 9 216 + ⋯) { displaystyle operatorname {erfi} (z) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {z ^ {2n + 1}} {n! (2n + 1)}} = { frac {2} { sqrt { pi}}} left (z + { frac {z ^ {3}} {3}} + { frac {z ^ { 5}} {10}} + { frac {z ^ {7}} {42}} + { frac {z ^ {9}} {216}} + cdots right)}
, которое выполняется для любого комплексного числа z.
Производная и интеграл
Производная функция ошибок сразу следует из ее определения:
- ddz erf (z) = 2 π e — z 2. { displaystyle { frac {d} {dz}} operatorname {erf} (z) = { frac {2} { sqrt { pi}}} e ^ {- z ^ {2}}.}
Отсюда немедленно вычисляется производная функция мнимой ошибки :
- ddz erfi (z) = 2 π ez 2. { displaystyle { frac {d} {dz}} operatorname {erfi} (z) = { frac {2} { sqrt { pi }}} e ^ {z ^ {2}}.}
первообразная функции ошибок, которые можно получить посредством интегрирования по частям, составляет
- z erf (z) + е — z 2 π. { displaystyle z operatorname {erf} (z) + { frac {e ^ {- z ^ {2}}} { sqrt { pi}}}.}
Первообразная мнимой функции ошибок, также можно получить интегрированием по частям:
- z erfi (z) — ez 2 π. { displaystyle z operatorname {erfi} (z) — { frac {e ^ {z ^ {2}}} { sqrt { pi}}}.}
Производные высшего порядка задаются как
- erf (k) (z) = 2 (- 1) k — 1 π H k — 1 (z) e — z 2 = 2 π dk — 1 dzk — 1 (e — z 2), k = 1, 2, … { Displaystyle operatorname {erf} ^ {(k)} (z) = { frac {2 (-1) ^ {k-1}} { sqrt { pi}}} { mathit {H} } _ {k-1} (z) e ^ {- z ^ {2}} = { frac {2} { sqrt { pi}}} { frac {d ^ {k-1}} {dz ^ {k-1}}} left (e ^ {- z ^ {2}} right), qquad k = 1,2, dots}
где H { displaystyle { mathit {H}}}
ряд Бюрмана
Расширение, которое сходится быстрее для всех реальных значений x { displaystyle x}
- erf (x) = 2 π sgn (x) 1 — e — x 2 (1 — 1 12 ( 1 — e — x 2) — 7 480 (1 — e — x 2) 2 — 5 896 (1 — e — x 2) 3 — 787 276480 (1 — e — x 2)) 4 — ⋯) знак равно 2 π знак (x) 1 — e — x 2 (π 2 + ∑ k = 1 ∞ cke — kx 2). { displaystyle { begin {align} operatorname {erf} (x) = { frac {2} { sqrt { pi}}} operatorname {sgn} (x) { sqrt {1-e ^ {-x ^ {2}}}} left (1 — { frac {1} {12}} left (1-e ^ {- x ^ {2}} right) — { frac {7} {480}} left (1-e ^ {- x ^ {2}} right) ^ {2} — { frac {5} {896}} left (1-e ^ {- x ^ {2 }} right) ^ {3} — { frac {787} {276480}} left (1-e ^ {- x ^ {2}} right) ^ {4} — cdots right) \ [10pt] = { frac {2} { sqrt { pi}}} operatorname {sgn} (x) { sqrt {1-e ^ {- x ^ {2}}}} left ({ frac { sqrt { pi}} {2}} + sum _ {k = 1} ^ { infty} c_ {k} e ^ {- kx ^ {2}} right). end {выровнено}}
Сохраняя только первые два коэффициента и выбирая c 1 = 31 200 { displaystyle c_ {1} = { frac {31} {200}}}



- erf (x) ≈ 2 π sign (x) 1 — e — x 2 (π 2 + 31 200 e — x 2 — 341 8000 e — 2 х 2). { displaystyle operatorname {erf} (x) приблизительно { frac {2} { sqrt { pi}}} operatorname {sgn} (x) { sqrt {1-e ^ {- x ^ {2 }}}} left ({ frac { sqrt { pi}} {2}} + { frac {31} {200}} e ^ {- x ^ {2}} — { frac {341} {8000}} e ^ {- 2x ^ {2}} right).}
Обратные функции
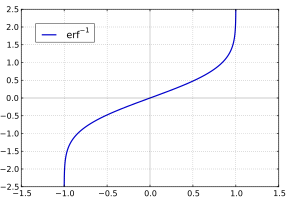
Учитывая комплексное число z, не существует уникального комплексного числа w, удовлетворяющего erf (w) = z { displaystyle operatorname {erf} (w) = z}

- erf (erf — 1 ( х)) = х. { displaystyle operatorname {erf} left ( operatorname {erf} ^ {- 1} (x) right) = x.}
Обратная функция ошибок обычно определяется с помощью домена (- 1,1), и он ограничен этой областью многих систем компьютерной алгебры. Однако его можно продолжить и на диск | z | < 1 of the complex plane, using the Maclaurin series
- erf — 1 (z) знак равно ∑ К знак равно 0 ∞ ck 2 k + 1 (π 2 z) 2 k + 1, { displaystyle operatorname {erf} ^ {- 1} (z) = sum _ {k = 0} ^ { infty} { frac {c_ {k}} {2k + 1}} left ({ frac { sqrt { pi}} {2}} z right) ^ {2k + 1},}
где c 0 = 1 и
- ck = ∑ m = 0 k — 1 cmck — 1 — m (m + 1) (2 m + 1) = {1, 1, 7 6, 127 90, 4369 2520, 34807 16200,…}. { displaystyle c_ {k} = sum _ {m = 0} ^ {k-1} { frac {c_ {m} c_ {k-1-m}} {(m + 1) (2m + 1) }} = left {1,1, { frac {7} {6}}, { frac {127} {90}}, { frac {4369} {2520}}, { frac {34807} {16200}}, ldots right }.}
Итак, у нас есть разложение в ряд (общие множители были удалены из числителей и знаменателей):
- erf — 1 (z) = 1 2 π ( z + π 12 z 3 + 7 π 2 480 z 5 + 127 π 3 40320 z 7 + 4369 π 4 5806080 z 9 + 34807 π 5 182476800 z 11 + ⋯). { displaystyle operatorname {erf} ^ {- 1} (z) = { tfrac {1} {2}} { sqrt { pi}} left (z + { frac { pi} {12} } z ^ {3} + { frac {7 pi ^ {2}} {480}} z ^ {5} + { frac {127 pi ^ {3}} {40320}} z ^ {7} + { frac {4369 pi ^ {4}} {5806080}} z ^ {9} + { frac {34807 pi ^ {5}} {182476800}} z ^ {11} + cdots right). }
(После отмены дроби числителя / знаменателя характерми OEIS : A092676 / OEIS : A092677 в OEIS ; без отмены членов числителя в записи OEIS : A002067.) Значение функции ошибок при ± ∞ равно ± 1.
Для | z | < 1, we have erf (erf — 1 (z)) = z { displaystyle operatorname {erf} left ( operatorname {erf} ^ {- 1} (z) right) = z}
обратная дополнительная функция ошибок определяется как
- erfc — 1 (1 — z) = erf — 1 (z). { displaystyle operatorname {erfc} ^ {- 1} (1-z) = operatorname {erf} ^ {- 1} (z).}
Для действительного x существует уникальное действительное число erfi — 1 (x) { displaystyle operatorname {erfi} ^ {- 1} (x)}


Для любого действительного x, Метод Ньютона можно использовать для вычислений erfi — 1 (x) { displaystyle operatorname {erfi} ^ {- 1} (x)}

- erfi — 1 (z) = ∑ k = 0 ∞ (- 1) ККК 2 К + 1 (π 2 Z) 2 К + 1, { Displaystyle OperatorName {erfi} ^ {- 1} (г) = сумма _ {к = 0} ^ { infty} { гидроразрыва {(-1) ^ {k} c_ {k}} {2k + 1}} left ({ frac { sqrt { pi}} {2}} z right) ^ {2k + 1},}
, где c k определено, как указано выше.
Асимптотическое разложение
Полезным асимптотическим разложением дополнительные функции (и, следовательно, также и функции ошибок) для больших вещественных x
- erfc (x) = e — x 2 x π [1 + ∑ n = 1 ∞ (- 1) n 1 ⋅ 3 ⋅ 5 ⋯ (2 n — 1) (2 x 2) n] = e — x 2 x π ∑ n = 0 ∞ (- 1) п (2 п — 1)! ! (2 х 2) n, { displaystyle operatorname {erfc} (x) = { frac {e ^ {- x ^ {2}}} {x { sqrt { pi}}}} left [1 + sum _ {n = 1} ^ { infty} (- 1) ^ {n} { frac {1 cdot 3 cdot 5 cdots (2n-1)} {(2x ^ {2}) ^ {n}}} right] = { frac {e ^ {- x ^ {2}}} {x { sqrt { pi}}}} sum _ {n = 0} ^ { infty} ( -1) ^ {n} { frac {(2n-1) !!} {(2x ^ {2}) ^ {n}}},}
где (2n — 1) !! — это двойной факториал числа (2n — 1), которое является произведением всех нечетных чисел до (2n — 1). Этот ряд расходуется для любого конечного x, и его значение как асимптотического разложения состоит в том, что для любого N ∈ N { displaystyle N in mathbb {N}}
- erfc (Икс) знак равно е — Икс 2 Икс π ∑ N знак равно 0 N — 1 (- 1) N (2 N — 1)! ! (2 х 2) n + RN (x) { displaystyle operatorname {erfc} (x) = { frac {e ^ {- x ^ {2}}} {x { sqrt { pi}}}} sum _ {n = 0} ^ {N-1} (- 1) ^ {n} { frac {(2n-1) !!} {(2x ^ {2}) ^ {n}}} + R_ {N} (x)}
где остаток в нотации Ландау равен
- RN (x) = O (x 1 — 2 N e — x 2) { displaystyle R_ {N} ( x) = O left (x ^ {1-2N} e ^ {- x ^ {2}} right)}
при x → ∞. { displaystyle x to infty.}
Действительно, точное значение остатка равно
- R N (x): = (- 1) N π 2 1 — 2 N (2 N)! N! ∫ Икс ∞ T — 2 N e — T 2 dt, { Displaystyle R_ {N} (x): = { frac {(-1) ^ {N}} { sqrt { pi}}} 2 ^ { 1-2N} { frac {(2N)!} {N!}} Int _ {x} ^ { infty} t ^ {- 2N} e ^ {- t ^ {2}} , dt,}
который легко следует по индукции, записывая
- e — t 2 = — (2 t) — 1 (e — t 2) ′ { displaystyle e ^ {- t ^ {2}} = — (2t) ^ {- 1} left (e ^ {- t ^ {2}} right) ‘}
и интегрирование по частям.
Для достаточно больших значений x, только первые несколько этих асимптотических разностей необходимы, чтобы получить хорошее приближение erfc (x) (в то время как для не слишком больших значений x приведенное выше разложение Тейлора при 0 обеспечивает очень быструю сходимость).
Расширение непрерывной дроби
A Разложение непрерывной дроби дополнительные функции ошибок:
- erfc (z) = z π e — z 2 1 z 2 + a 1 1 + a 2 z 2 + a 3 1 + ⋯ am = м 2. { displaystyle operatorname {erfc} (z) = { frac {z} { sqrt { pi}}} e ^ {- z ^ {2}} { cfrac {1} {z ^ {2} + { cfrac {a_ {1}} {1 + { cfrac {a_ {2}} {z ^ {2} + { cfrac {a_ {3}} {1+) dotsb}}}}}}}} qquad a_ {m} = { frac {m} {2}}.}
Интеграл функции ошибок с функцией плотности Гаусса
- ∫ — ∞ ∞ erf (ax + б) 1 2 π σ 2 е — (Икс — μ) 2 2 σ 2 dx знак равно erf [a μ + b 1 + 2 a 2 σ 2], a, b, μ, σ ∈ R { displaystyle int _ {- infty} ^ { infty} operatorname {erf} left (ax + b right) { frac {1} { sqrt {2 pi sigma ^ {2}}}} e ^ {- { frac {(x- mu) ^ {2}} {2 sigma ^ {2}}}} , dx = operatorname {erf} left [{ frac {a mu + b } { sqrt {1 + 2a ^ {2} sigma ^ {2}}} right], qquad a, b, mu, sigma in mathbb {R}}
Факториальный ряд
- Обратное:
-
- erfc z = e — z 2 π z ∑ n = 0 ∞ (- 1) n Q n (z 2 + 1) n ¯ = e — z 2 π z (1 — 1 2 1 (z 2 + 1) + 1 4 1 (z 2 + 1) (z 2 + 2) — ⋯) { displaystyle { begin {align} operatorname {erfc} z = { frac {e ^ {- z ^ {2}}} {{ sqrt { pi}} , z}} sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n} Q_ {n}} {{(z ^ {2} + 1)} ^ { ba r {n}}}} \ = { frac {e ^ {- z ^ {2}}} {{ sqrt { pi}} , z}} left ( 1 — { frac {1} {2}} { frac {1} {(z ^ {2} +1)}} + { frac {1} {4}} { frac {1} {(z ^ {2} +1) (z ^ {2} +2)}} — cdots right) end {align}}}
- erfc z = e — z 2 π z ∑ n = 0 ∞ (- 1) n Q n (z 2 + 1) n ¯ = e — z 2 π z (1 — 1 2 1 (z 2 + 1) + 1 4 1 (z 2 + 1) (z 2 + 2) — ⋯) { displaystyle { begin {align} operatorname {erfc} z = { frac {e ^ {- z ^ {2}}} {{ sqrt { pi}} , z}} sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n} Q_ {n}} {{(z ^ {2} + 1)} ^ { ba r {n}}}} \ = { frac {e ^ {- z ^ {2}}} {{ sqrt { pi}} , z}} left ( 1 — { frac {1} {2}} { frac {1} {(z ^ {2} +1)}} + { frac {1} {4}} { frac {1} {(z ^ {2} +1) (z ^ {2} +2)}} — cdots right) end {align}}}
- сходится для Re (z 2)>0. { displaystyle operatorname {Re} (z ^ {2})>0.}
Здесь
- Q n = def 1 Γ (1/2) ∫ 0 ∞ τ (τ — 1) ⋯ ( τ — n + 1) τ — 1/2 е — τ d τ знак равно ∑ К знак равно 0 N (1 2) к ¯ s (n, k), { displaystyle Q_ {n} { stackrel { text {def}} {=}} { frac {1} { Gamma (1/2)}} int _ {0} ^ { infty} tau ( tau -1) cdots ( tau -n + 1) tau ^ {-1/2} e ^ {- tau} d tau = sum _ {k = 0} ^ {n} left ({ frac {1} {2}} right) ^ { bar {k}} s (n, k),}
- Q n = def 1 Γ (1/2) ∫ 0 ∞ τ (τ — 1) ⋯ ( τ — n + 1) τ — 1/2 е — τ d τ знак равно ∑ К знак равно 0 N (1 2) к ¯ s (n, k), { displaystyle Q_ {n} { stackrel { text {def}} {=}} { frac {1} { Gamma (1/2)}} int _ {0} ^ { infty} tau ( tau -1) cdots ( tau -n + 1) tau ^ {-1/2} e ^ {- tau} d tau = sum _ {k = 0} ^ {n} left ({ frac {1} {2}} right) ^ { bar {k}} s (n, k),}
- zn ¯ { displaystyle z ^ { bar {n}}}
обозначает возрастающий факториал, а s (n, k) { displaystyle s (n, k)}
обозначает знаковое число Стирлинга первого рода.
- Представление бесконечной суммой, составляющей двойной факториал :
-
- ERF (Z) знак равно 2 π ∑ N знак равно 0 ∞ (- 2) N (2 N — 1)! (2 N + 1)! Z 2 N + 1 { Displaystyle OperatorName {ERF} (г) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {( -2) ^ {n} (2n-1) !!} {(2n + 1)!}} Z ^ {2n + 1}}
- ERF (Z) знак равно 2 π ∑ N знак равно 0 ∞ (- 2) N (2 N — 1)! (2 N + 1)! Z 2 N + 1 { Displaystyle OperatorName {ERF} (г) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {( -2) ^ {n} (2n-1) !!} {(2n + 1)!}} Z ^ {2n + 1}}
Численные приближения
Приближение элементов сарными функциями
- Абрамовиц и Стегун дают несколько приближений с точностью (уравнения 7.1.25–28). Это позволяет выбрать наиболее быстрое приближение, подходящее для данного приложения. В порядке увеличения точности они следующие:
-
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + a 3 x 3 + a 4 x 4) 4, x ≥ 0 { displaystyle имя оператора {erf} (x) приблизительно 1 — { frac {1} {(1 + a_ {1} x + a_ {2} x ^ {2} + a_ {3} x ^ {3} + a_ { 4} x ^ {4}) ^ {4}}}, qquad x geq 0}
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + a 3 x 3 + a 4 x 4) 4, x ≥ 0 { displaystyle имя оператора {erf} (x) приблизительно 1 — { frac {1} {(1 + a_ {1} x + a_ {2} x ^ {2} + a_ {3} x ^ {3} + a_ { 4} x ^ {4}) ^ {4}}}, qquad x geq 0}
- (максимальная ошибка: 5 × 10)
- , где a 1 = 0,278393, a 2 = 0,230389, a 3 = 0,000972, a 4 = 0,078108
-
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + a 3 t 3) e — x 2, t = 1 1 + px, x ≥ 0 { displaystyle operatorname {erf} (x) приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + a_ {3} t ^ {3}) e ^ {- x ^ {2}}, quad t = { frac {1} {1 + px}}, qquad x geq 0}
(максимальная ошибка: 2,5 × 10)
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + a 3 t 3) e — x 2, t = 1 1 + px, x ≥ 0 { displaystyle operatorname {erf} (x) приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + a_ {3} t ^ {3}) e ^ {- x ^ {2}}, quad t = { frac {1} {1 + px}}, qquad x geq 0}
- где p = 0,47047, a 1 = 0,3480242, a 2 = -0,0958798, a 3 = 0,7478556
-
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + ⋯ + a 6 x 6) 16, x ≥ 0 { displaystyle operatorname {erf} (x) приблизительно 1 — { frac {1} {(1 + a_ {1} x + a _ {2} x ^ {2} + cdots + a_ {6} x ^ {6}) ^ {16}}}, qquad x geq 0}
(максимальная ошибка: 3 × 10)
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + ⋯ + a 6 x 6) 16, x ≥ 0 { displaystyle operatorname {erf} (x) приблизительно 1 — { frac {1} {(1 + a_ {1} x + a _ {2} x ^ {2} + cdots + a_ {6} x ^ {6}) ^ {16}}}, qquad x geq 0}
- , где a 1 = 0,0705230784, a 2 = 0,0422820123, a 3 = 0,0092705272, a 4 = 0,0001520143, a 5 = 0,0002765672, a 6 = 0,0000430638
-
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + ⋯ + a 5 t 5) e — x 2, t = 1 1 + px { displaystyle operatorname {erf} (x) приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + cdots + a_ {5} t ^ {5}) e ^ {- x ^ {2}}, quad t = { frac {1} {1 + px}}}
(максимальная ошибка: 1,5 × 10)
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + ⋯ + a 5 t 5) e — x 2, t = 1 1 + px { displaystyle operatorname {erf} (x) приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + cdots + a_ {5} t ^ {5}) e ^ {- x ^ {2}}, quad t = { frac {1} {1 + px}}}
- , где p = 0,3275911, a 1 = 0,254829592, a 2 = −0,284496736, a 3 = 1,421413741, a 4 = −1,453152027, a 5 = 1,061405429
- Все эти приближения действительны для x ≥ 0 Чтобы использовать эти приближения для отрицательного x, викорируйте тот факт, что erf (x) — нечетная функция, поэтому erf (x) = −erf (−x).
- Экспоненциальные границы и чисто экспоненциальное приближение для дополнительных функций задаются как
-
- erfc (x) ≤ 1 2 e — 2 x 2 + 1 2 e — x 2 ≤ e — x 2, x>0 erfc ( х) ≈ 1 6 е — х 2 + 1 2 е — 4 3 х 2, х>0. { displaystyle { begin {align} operatorname {erfc} (x) leq { frac {1} {2}} e ^ {- 2x ^ {2}} + { frac {1} {2} } e ^ {- x ^ {2}} leq e ^ {- x ^ {2}}, qquad x>0 \ имя оператора {erfc} (x) приблизительно { frac {1} { 6}} e ^ {- x ^ {2}} + { frac {1} {2}} e ^ {- { frac {4} {3}} x ^ {2}}, qquad x>0. end {align}}}
- erfc (x) ≤ 1 2 e — 2 x 2 + 1 2 e — x 2 ≤ e — x 2, x>0 erfc ( х) ≈ 1 6 е — х 2 + 1 2 е — 4 3 х 2, х>0. { displaystyle { begin {align} operatorname {erfc} (x) leq { frac {1} {2}} e ^ {- 2x ^ {2}} + { frac {1} {2} } e ^ {- x ^ {2}} leq e ^ {- x ^ {2}}, qquad x>0 \ имя оператора {erfc} (x) приблизительно { frac {1} { 6}} e ^ {- x ^ {2}} + { frac {1} {2}} e ^ {- { frac {4} {3}} x ^ {2}}, qquad x>0. end {align}}}
-
- erfc (x) ≈ (1 — e — A x) e — x 2 B π х. { displaystyle operatorname {erfc} left (x right) приблизительно { frac { left (1-e ^ {- Ax} right) e ^ {- x ^ {2}}} {B { sqrt { pi}} x}}.}
- erfc (x) ≈ (1 — e — A x) e — x 2 B π х. { displaystyle operatorname {erfc} left (x right) приблизительно { frac { left (1-e ^ {- Ax} right) e ^ {- x ^ {2}}} {B { sqrt { pi}} x}}.}
- Они определили {A, B} = {1.98, 1.135}, { displaystyle {A, B } = {1.98,1.135 },}
, что дает хорошее приближение для всех x ≥ 0. { displaystyle x geq 0.}
- Одноканальная нижняя граница:
-
- erfc (x) ≥ 2 e π β — 1 β е — β Икс 2, Икс ≥ 0, β>1, { Displaystyle OperatorName {erfc} (x) geq { sqrt { frac {2e} { pi}}} { frac { sqrt { beta -1}} { beta}} e ^ {- beta x ^ {2}}, qquad x geq 0, beta>1,}
- erfc (x) ≥ 2 e π β — 1 β е — β Икс 2, Икс ≥ 0, β>1, { Displaystyle OperatorName {erfc} (x) geq { sqrt { frac {2e} { pi}}} { frac { sqrt { beta -1}} { beta}} e ^ {- beta x ^ {2}}, qquad x geq 0, beta>1,}
- где параметр β может быть выбран, чтобы минимизировать ошибку на желаемом интервале приближения.
- Другое приближение дано Сергеем Виницким с использованием его «глобальных приближений Паде»:
-
- erf (x) ≈ sgn (x) 1 — exp (- x 2 4 π + ax 2 1 + ax 2) { displaystyle operatorname {erf} (x) приблизительно Operatorname {sgn} (x) { sqrt {1- exp left (-x ^ {2} { frac {{ frac {4} { pi) })} + ax ^ {2}} {1 + ax ^ {2}}} right)}}}
- erf (x) ≈ sgn (x) 1 — exp (- x 2 4 π + ax 2 1 + ax 2) { displaystyle operatorname {erf} (x) приблизительно Operatorname {sgn} (x) { sqrt {1- exp left (-x ^ {2} { frac {{ frac {4} { pi) })} + ax ^ {2}} {1 + ax ^ {2}}} right)}}}
- где
-
- a = 8 (π — 3) 3 π (4 — π) ≈ 0, 140012. { displaystyle a = { frac {8 ( pi -3)} {3 pi (4- pi)}} приблизительно 0,140012.}
- a = 8 (π — 3) 3 π (4 — π) ≈ 0, 140012. { displaystyle a = { frac {8 ( pi -3)} {3 pi (4- pi)}} приблизительно 0,140012.}
- Это сделано так, чтобы быть очень точным в окрестностях 0 и добавление бесконечности, а относительная погрешность меньше 0,00035 для всех действительных x. Использование альтернативного значения ≈ 0,147 снижает максимальную относительную ошибку примерно до 0,00013.
- Это приближение можно инвертировать, чтобы получить приближение для других функций ошибок:
-
- erf — 1 (x) ≈ sgn (x) (2 π a + ln (1 — x 2) 2) 2 — ln (1 — x 2) a — (2 π a + ln (1 — x 2) 2). { displaystyle operatorname {erf} ^ {- 1} (x) приблизительно operatorname {sgn} (x) { sqrt {{ sqrt { left ({ frac {2} { pi a}} + { frac { ln (1-x ^ {2})} {2}} right) ^ {2} — { frac { ln (1-x ^ {2})} {a}}}} — left ({ frac {2} { pi a}} + { frac { ln (1-x ^ {2})} {2}} right)}}.}
- erf — 1 (x) ≈ sgn (x) (2 π a + ln (1 — x 2) 2) 2 — ln (1 — x 2) a — (2 π a + ln (1 — x 2) 2). { displaystyle operatorname {erf} ^ {- 1} (x) приблизительно operatorname {sgn} (x) { sqrt {{ sqrt { left ({ frac {2} { pi a}} + { frac { ln (1-x ^ {2})} {2}} right) ^ {2} — { frac { ln (1-x ^ {2})} {a}}}} — left ({ frac {2} { pi a}} + { frac { ln (1-x ^ {2})} {2}} right)}}.}
Многочлен
Приближение с максимальной ошибкой 1,2 × 10-7 { displaystyle 1,2 times 10 ^ {- 7}}
- erf ( x) = {1 — τ x ≥ 0 τ — 1 x < 0 {displaystyle operatorname {erf} (x)={begin{cases}1-tau xgeq 0\tau -1x<0end{cases}}}
с
- τ = t ⋅ exp (- x 2 — 1,26551223 + 1,00002368 t + 0,37409196 t 2 + 0,09678418 t 3 — 0,18628806 t 4 + 0,27886807 t 5 — 1,13520398 t 6 + 1,48851587 t 7 — 0,82215223 t 8 + 0,17087277 t 9) { displaystyle { begin {align} tau = t cdot exp left (-x ^ {2} -1,26551223 + 1,00002368 t + 0,37409196t ^ {2} + 0,09678418t ^ {3} -0,18628806t ^ {4} вправо. \ left. qquad qquad qquad + 0,27886807t ^ {5} -1,13520398t ^ {6} + 1,48851587t ^ {7} -0,82215223t ^ {8} + 0,17087 277t ^ {9} right) end {align}}}
и
- t = 1 1 + 0,5 | х |. { displaystyle t = { frac {1} {1 + 0,5 | x |}}.}
Таблица значений
| x | erf(x) | 1-erf (x) |
|---|---|---|
| 0 | 0 | 1 |
| 0,02 | 0,022564575 | 0,977435425 |
| 0,04 | 0,045111106 | 0,954888894 |
| 0,06 | 0,067621594 | 0, 932378406 |
| 0,08 | 0.090078126 | 0,909921874 |
| 0,1 | 0,112462916 | 0,887537084 |
| 0,2 | 0,222702589 | 0,777297411 |
| 0,3 | 0,328626759 | 0,671373241 |
| 0, 4 | 0,428392355 | 0,571607645 |
| 0,5 | 0,520499878 | 0,479500122 |
| 0,6 | 0.603856091 | 0,396143909 |
| 0,7 | 0,677801194 | 0,322198806 |
| 0,8 257> | 0,742100965 | 0,257899035 |
| 0,9 | 0,796908212 | 0,203091788 |
| 1 | 0,842700793 | 0, 157299207 |
| 1,1 | 0,88020507 | 0,11979493 |
| 1,2 | 0,910313978 | 0,089686022 |
| 1,3 | 0,934007945 | 0,065992055 |
| 1,4 | 0.95228512 | 0,04771488 |
| 1,5 | 0, 966105146 | 0,033894854 |
| 1,6 | 0,976348383 | 0,023651617 |
| 1,7 | 0,983790459 | 0,016209541 |
| 1,8 | 0,989090502 | 0,010909498 |
| 1,9 | 0,992790429 | 0,007209571 |
| 2 | 0,995322265<25767> | 0,00477 |
| 2.1 | 0.997020533 | 0.002979467 |
| 2.2 | 0.998137154 | 0,001862846 |
| 2,3 | 0,998856823 | 0,001143177 |
| 2,4 | 0,999311486 | 0,000688514 |
| 2,5 | 0.999593048 | 0.000406952 |
| 3 | 0.99997791 | 0,00002209 |
| 3,5 | 0,999999257 | 0,000000743 |
Связанные функции
Дополнительная функция
дополнительная функция ошибок, обозначается erfc { displaystyle mathrm {erfc}}
- erfc (x) = 1 — erf (x) = 2 π ∫ x ∞ e — t 2 dt знак равно е — Икс 2 erfcx (х), { displaystyle { begin {выровнено} OperatorName {erfc} (x) = 1- operatorname {erf} (x) \ [5p t] = { frac {2} { sqrt { pi}}} int _ {x} ^ { infty} e ^ {- t ^ {2}} , dt \ [5pt] = e ^ {- x ^ {2}} operatorname {erfcx} (x), end {align}}}
, который также определяет erfcx { displaystyle mathrm {erfcx} }


- erfc (x ∣ x ≥ 0) = 2 π ∫ 0 π / 2 exp (- x 2 sin 2 θ) d θ. { displaystyle operatorname {erfc} (x mid x geq 0) = { frac {2} { pi}} int _ {0} ^ { pi / 2} exp left (- { frac {x ^ {2}} { sin ^ {2} theta}} right) , d theta.}
Это выражение действительно только для положительных значений x, но его можно использовать вместе с erfc (x) = 2 — erfc (−x), чтобы получить erfc (x) для отрицательных значений. Эта форма выгодна тем, что диапазон интегрирования является фиксированным и конечным. Расширение этого выражения для erfc { displaystyle mathrm {erfc}}
- erfc (x + y ∣ x, y ≥ 0) = 2 π ∫ 0 π / 2 ехр (- x 2 sin 2 θ — y 2 cos 2 θ) d θ. { displaystyle operatorname {erfc} (x + y mid x, y geq 0) = { frac {2} { pi}} int _ {0} ^ { pi / 2} exp left (- { frac {x ^ {2}} { sin ^ {2} theta}} — { frac {y ^ {2}} { cos ^ {2} theta}} right) , d theta.}
Функция мнимой ошибки
мнимой ошибки, обозначаемая erfi, обозначает ошибки как
- erfi (x) = — i erf (ix) Знак равно 2 π ∫ 0 xet 2 dt знак равно 2 π ex 2 D (x), { displaystyle { begin {align} operatorname {erfi} (x) = — i operatorname {erf} (ix) \ [ 5pt] = { frac {2} { sqrt { pi}}} int _ {0} ^ {x} e ^ {t ^ {2}} , dt \ [5pt] = { frac {2} { sqrt { pi}}} e ^ {x ^ {2}} D (x), end {align}}}
где D (x) — функция Доусона (который можно использовать вместо erfi, чтобы избежать арифметического переполнения ).
Несмотря на название «функция мнимой ошибки», erfi (x) { displaystyle operatorname {erfi} (x)}
Функция Когда ошибки оценивается для произвольных сложных аргументов z, результирующая комплексная функция ошибок обычно обсуждается в масштабированной форме как функция Фаддеева :
- w (z) = e — z 2 erfc (- iz) = erfcx (- iz). { displaystyle w (z) = e ^ {- z ^ {2}} operatorname {erfc} (-iz) = operatorname {erfcx} (-iz).}
Кумулятивная функция распределения
Функция ошибок по существующей стандартной стандартной функции нормального кумулятивного распределения, обозначаемой нормой (x) в некоторых языках программного обеспечения, поскольку они отличаются только масштабированием и переводом. Действительно,
- Φ (x) = 1 2 π ∫ — ∞ xe — t 2 2 dt = 1 2 [1 + erf (x 2)] = 1 2 erfc (- x 2) { displaystyle Phi (x) = { frac {1} { sqrt {2 pi}}} int _ {- infty} ^ {x} e ^ { tfrac {-t ^ {2}} {2}} , dt = { frac {1} {2}} left [1+ operatorname {erf} left ({ frac {x} { sqrt {2}}} right) right] = { frac {1} {2}} operatorname {erfc} left (- { frac {x} { sqrt {2}}} right)}
или переставлен для erf и erfc:
- erf ( x) = 2 Φ (x 2) — 1 erfc (x) = 2 Φ (- x 2) = 2 (1 — Φ (x 2)). { displaystyle { begin {align} operatorname {erf} (x) = 2 Phi left (x { sqrt {2}} right) -1 \ operatorname {erfc} (x) = 2 Phi left (-x { sqrt {2}} right) = 2 left (1- Phi left (x { sqrt {2}} right) right). End {выравнивается} }}
Следовательно, функция ошибок также тесно связана с Q-функцией, которая является вероятностью хвоста стандартного нормального распределения. Q-функция может быть выражена через функцию ошибок как
- Q (x) = 1 2 — 1 2 erf (x 2) = 1 2 erfc (x 2). { displaystyle Q (x) = { frac {1} {2}} — { frac {1} {2}} operatorname {erf} left ({ frac {x} { sqrt {2}}) } right) = { frac {1} {2}} operatorname {erfc} left ({ frac {x} { sqrt {2}}} right).}
Обратное значение из Φ { displaystyle Phi}
- пробит (p) = Φ — 1 (p) = 2 erf — 1 (2 p — 1) = — 2 erfc — 1 (2 p). { displaystyle operatorname {probit} (p) = Phi ^ {- 1} (p) = { sqrt {2}} operatorname {erf} ^ {- 1} (2p-1) = — { sqrt {2}} operatorname {erfc} ^ {- 1} (2p).}
Стандартный нормальный cdf чаще используется в вероятности и статистике, а функция ошибок чаще используется в других разделах математики.
Функция ошибки является частным случаем функции Миттаг-Леффлера и может также быть выражена как сливающаяся гипергеометрическая функция (функция Куммера):
- erf (х) знак равно 2 х π M (1 2, 3 2, — х 2). { displaystyle operatorname {erf} (x) = { frac {2x} { sqrt { pi}}} M left ({ frac {1} {2}}, { frac {3} {2 }}, — x ^ {2} right).}
Он имеет простое выражение в терминах интеграла Френеля.
В терминах регуляризованной гамма-функции P и неполная гамма-функция,
- erf (x) = sgn (x) P (1 2, x 2) = sgn (x) π γ (1 2, x 2). { displaystyle operatorname {erf} (x) = operatorname {sgn} (x) P left ({ frac {1} {2}}, x ^ {2} right) = { frac { operatorname {sgn} (x)} { sqrt { pi}}} gamma left ({ frac {1} {2}}, x ^ {2} right).}
sgn (x) { displaystyle operatorname {sgn} (x)}
Обобщенные функции ошибок

π { displaystyle scriptstyle { sqrt { pi}}}

Некоторые авторы обсуждают более общие функции:
- E n (x) = n! π ∫ 0 Икс е — Т N д т знак равно N! π ∑ п знак равно 0 ∞ (- 1) п Икс N п + 1 (N п + 1) п!. { displaystyle E_ {n} (x) = { frac {n!} { sqrt { pi}}} int _ {0} ^ {x} e ^ {- t ^ {n}} , dt = { frac {n!} { sqrt { pi}}} sum _ {p = 0} ^ { infty} (- 1) ^ {p} { frac {x ^ {np + 1}} {(np + 1) p!}}.}
Примечательные случаи:
- E0(x) — прямая линия, проходящая через начало координат: E 0 (x) = xe π { displaystyle textstyle E_ {0} (x) = { dfrac {x} {e { sqrt { pi}}}}}
- E2(x) — функция, erf (x) ошибки.
После деления на n!, все E n для нечетных n выглядят похожими (но не идентичными) друг на друга. Аналогично, E n для четного n выглядят похожими (но не идентичными) друг другу после простого деления на n!. Все обобщенные функции ошибок для n>0 выглядят одинаково на положительной стороне x графика.
Эти обобщенные функции могут быть эквивалентно выражены для x>0 с помощью гамма-функции и неполной гамма-функции :
- E n (x) = 1 π Γ (n) (Γ (1 n) — Γ (1 n, xn)), x>0. { displaystyle E_ {n} (x) = { frac {1} { sqrt { pi}}} Gamma (n) left ( Gamma left ({ frac {1} {n}} right) — Gamma left ({ frac {1} {n}}, x ^ {n} right) right), quad quad x>0.}
Следовательно, мы можем определить ошибку функция в терминах неполной гамма-функции:
- erf (x) = 1 — 1 π Γ (1 2, x 2). { displaystyle operatorname {erf} (x) = 1 — { frac {1} { sqrt { pi}}} Gamma left ({ frac {1} {2}}, x ^ {2} right).}
Итерированные интегралы дополнительных функций
Повторные интегралы дополнительные функции ошибок определения как
- inerfc (z) = ∫ z ∞ in — 1 erfc (ζ) d ζ i 0 erfc (z) = erfc (z) i 1 erfc (z) = ierfc (z) знак равно 1 π е — z 2 — z erfc (z) я 2 erfc (z) = 1 4 [erfc (z) — 2 z ierfc (z)] { displaystyle { begin {align } operatorname {i ^ {n} erfc} (z) = int _ {z} ^ { infty} operatorname {i ^ {n-1} erfc} ( zeta) , d zeta \ имя оператора {i ^ {0} erfc} (z) = operatorname {erfc} (z) \ operatorname {i ^ {1} erfc} (z) = operat orname {ierfc} (z) = { frac { 1} { sqrt { pi}}} e ^ {- z ^ {2}} — z operatorname {erfc} (z) \ operatorname {i ^ {2} erfc} (z) = { frac {1} {4}} left [ operatorname {erfc} (z) -2z operatorname {ierfc} (z) right] \ end {выровнено}}
Общая рекуррентная формула:
- 2 ninerfc (z) = in — 2 erfc (z) — 2 цинк — 1 erfc (z) { displaystyle 2n operatorname {i ^ {n} erfc} (z) = operatorname {i ^ { n-2} erfc} (z) -2z operatorname {i ^ {n-1} erfc} (z)}
У них есть степенной ряд
- в erfc (z) = ∑ j = 0 ∞ (- Z) J 2 N — JJ! Γ (1 + N — J 2), { displaystyle i ^ {n} operatorname {erfc} (z) = sum _ {j = 0} ^ { infty} { frac {(-z) ^ { j}} {2 ^ {nj} j! Gamma left (1 + { frac {nj} {2}} right)}},}
из следуют свойства симметрии
- i 2 m ERFC (- Z) знак равно — я 2 m ERFC (Z) + ∑ Q знак равно 0 мZ 2 д 2 2 (м — д) — 1 (2 д)! (м — д)! { displaystyle i ^ {2m} operatorname {erfc} (-z) = — i ^ {2m} operatorname {erfc} (z) + sum _ {q = 0} ^ {m} { frac {z ^ {2q}} {2 ^ {2 (mq) -1} (2q)! (Mq)!}}}
и
- i 2 m + 1 erfc (- z) = i 2 m + 1 erfc (г) + ∑ ä знак равно 0 ìZ 2 ä + 1 2 2 ( м — д) — 1 (2 д + 1)! (м — д)!. { displaystyle i ^ {2m + 1} operatorname {erfc} (-z) = i ^ {2m + 1} operatorname {erfc} (z) + sum _ {q = 0} ^ {m} { гидроразрыва {z ^ {2q + 1}} {2 ^ {2 (mq) -1} (2q + 1)! (mq)!}}.}
Реализации
Как действительная функция вещественного аргумента
- В операционных системах, совместимых с Posix, заголовок math.h должен являть, а математическая библиотека libm должна быть функция erf и erfc (двойная точность ), а также их одинарная точность и расширенная точность аналоги erff, erfl и erfc, erfcl.
- Библиотека GNU Scientific предоставляет функции erf, erfc, log (erf) и масштабируемые функции ошибок.
Как сложная функция комплексного аргумента
- libcerf, числовая библиотека C для сложных функций, предоставляет комплексные функции cerf, cerfc, cerfcx и реальные функции erfi, erfcx с точностью 13–14 цифр на основе функции Фаддеева, реализованной в пакете MIT Faddeeva Package
См. также
Связанные ции
- интеграл Гаусса, по всей действительной прямой
- функция Гаусса, производная
- функция Доусона, перенормированная функция мнимой ошибки
- интеграл Гудвина — Стона
по вероятности
- Нормальное распределение
- Нормальная кумулятивная функция распределения, масштабированная и сдвинутая форма функций ошибок
- Пробит, обратная или квантильная функция нормального CDF
- Q-функция, вероятность хвоста нормального распределения
Ссылки
Дополнительная литература
- Abramowitz, Milton ; Стегун, Ирен Энн, ред. (1983) [июнь 1964]. «Глава 7». Справочник по математическим функциям с формулами, графики и математическими таблицами. Прикладная математика. 55 (Девятое переиздание с дополнительными исправлениями; десятое оригинальное издание с исправлениями (декабрь 1972 г.); первое изд.). Вашингтон.; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Dover Publications. п. 297. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- Press, William H.; Теукольский, Саул А.; Веттерлинг, Уильям Т.; Фланнери, Брайан П. (2007), «Раздел 6.2. Неполная гамма-функция и функция ошибок », Числовые рецепты: Искусство научных вычислений (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN 978-0-521- 88068-8
- Темме, Нико М. (2010), «Функции ошибок, интегралы Доусона и Френеля», в Олвер, Фрэнк У. Дж. ; Лозье, Даниэль М.; Бойсверт, Рональд Ф.; Кларк, Чарльз В. (ред.), Справочник NIST по математическим функциям, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
Внешние ссылки
- MathWorld — Erf
- Таблица интегралов функций ошибок
В математике функция ошибок (также называемая функцией ошибок Гаусса ), часто обозначаемая erf, является сложной функцией комплексной переменной, определяемой как:
Этот интеграл представляет собой специальную ( неэлементарную ) сигмовидную функцию, которая часто встречается в уравнениях вероятности, статистики и дифференциальных уравнений в частных производных . Во многих из этих приложений аргумент функции является действительным числом. Если аргумент функции является действительным, то значение функции также является действительным.
В статистике для неотрицательных значений x функция ошибок имеет следующую интерпретацию: для случайной величины Y, которая нормально распределена со средним значением 0 и стандартным отклонением
1/√ 2, erf x — вероятность того, что Y попадает в диапазон [- x, x ] .
Две тесно связанные функции — это дополнительная функция ошибок ( erfc ), определяемая как
и функция мнимой ошибки ( erfi ), определяемая как
где i — мнимая единица .
Имя
Название «функция ошибок» и ее сокращение erf были предложены Дж. В. Л. Глейшером в 1871 г. в связи с его связью с «теорией вероятности и, в частности, теорией ошибок ». Дополнение к функции ошибок также обсуждалось Глейшером в отдельной публикации в том же году. Для «закона удобства» ошибок, плотность которых определяется как
( нормальное распределение ), Глейшер вычисляет вероятность ошибки, лежащей между p и q, как:
Приложения
Когда результаты серии измерений описываются нормальным распределением со стандартным отклонением σ и ожидаемым значением 0, тогда erf (а/σ √ 2) — вероятность того, что ошибка единичного измерения находится между — a и + a для положительного a . Это полезно, например, при определении частоты ошибок по битам в цифровой системе связи.
Ошибки и дополнительные функции ошибок возникают, например, в решениях уравнения теплопроводности, когда граничные условия задаются ступенчатой функцией Хевисайда .
Функция ошибок и ее приближения могут использоваться для оценки результатов, которые имеют высокую или низкую вероятность. Дана случайная величина X ~ Norm [ μ, σ ] (нормальное распределение со средним μ и стандартным отклонением σ ) и константа L < μ :
где A и B — некоторые числовые константы. Если L достаточно далеко от среднего, а именно μ — L ≥ σ √ ln k, то:
поэтому вероятность стремится к 0 при k → ∞ .
Вероятность того, что X находится в интервале [ L a, L b ], может быть получена как
Характеристики
Интегрируем exp (- z 2 )
erf z
Свойство erf (- z ) = −erf z означает, что функция ошибок является нечетной функцией . Это напрямую связано с тем, что подынтегральное выражение e — t 2 является четной функцией (интегрирование четной функции дает нечетную функцию и наоборот).
Для любого комплексного числа z :
где г представляет собой комплексно сопряженное из г .
Подынтегральное выражение f = exp (- z 2 ) и f = erf z показано на комплексной плоскости z на рисунках справа с раскраской области .
Функция ошибок при + ∞ равна 1 (см. Интеграл Гаусса ). На действительной оси erf z стремится к единице при z → + ∞ и −1 при z → −∞ . На мнимой оси он стремится к ± i ∞ .
Серия Тейлора
Функция ошибок — это целая функция ; у него нет сингулярностей (кроме бесконечности), и его разложение Тейлора всегда сходится, но, как известно, «[…] его плохая сходимость, если x > 1 ».
Определяющий интеграл не может быть вычислен в замкнутой форме в терминах элементарных функций, но, раскладывая подынтегральное выражение e — z 2 в его ряд Маклорена и интегрируя член за членом, можно получить ряд Маклорена функции ошибок как:
которое выполняется для любого комплексного числа z . Члены знаменателя — это последовательность (последовательность A007680 в OEIS ) в OEIS .
Для итеративного расчета вышеуказанного ряда может быть полезна следующая альтернативная формулировка:
потому что — (2 к — 1) z 2/к (2 к + 1)выражает множитель для превращения k- го члена в ( k + 1) -й член (считая z первым членом).
Функция мнимой ошибки имеет очень похожий ряд Маклорена, а именно:
которое выполняется для любого комплексного числа z .
Производная и интеграл
Производная функции ошибок сразу следует из ее определения:
Отсюда немедленно вычисляется производная мнимой функции ошибок:
Первообразная функции ошибки, получаемый путем интегрирования по частям, является
Первообразной функции мнимой ошибки, которую также можно получить интегрированием по частям, является
Производные высшего порядка даются формулами
где H — полиномы Эрмита физиков .
Серия Bürmann
Разложение, которое сходится быстрее для всех действительных значений x, чем разложение Тейлора, получается с помощью теоремы Ганса Генриха Бюрмана :
где sgn — знаковая функция . Сохраняя только первые два коэффициента и выбирая c 1 =31 год/200и c 2 = —341/8000, полученное приближение показывает свою наибольшую относительную ошибку при x = ± 1,3796, где она меньше 0,0036127:
Обратные функции
Для комплексного числа z не существует уникального комплексного числа w, удовлетворяющего erf w = z, поэтому истинная обратная функция будет многозначной. Однако для −1 < x <1 существует уникальное действительное число, обозначенное erf −1 x, удовлетворяющее
Функция обратной ошибки обычно определяется с помощью области (-1,1), и она ограничена этой областью во многих системах компьютерной алгебры. Однако его можно распространить на диск | z | <1 комплексной плоскости, используя ряд Маклорена
где c 0 = 1 и
Итак, у нас есть расширение в ряд (общие множители из числителей и знаменателей удалены):
(После отмены дроби числителя / знаменателя представляют собой записи OEIS : A092676 / OEIS : A092677 в OEIS ; без отмены члены числителя приведены в записи OEIS : A002067 .) Значение функции ошибок при ± ∞ равно ± 1 .
Для | z | <1, имеем erf (erf −1 z ) = z .
Обратная дополнительная функция ошибок определяются как
Для действительного x существует уникальное действительное число erfi −1 x, удовлетворяющее erfi (erfi −1 x ) = x . Функция обратной мнимой ошибки определяется как erfi −1 x .
Для любого вещественного х, метод Ньютона может быть использован для вычисления ЕрФИ -1 х, а для -1 ≤ х ≤ 1, следующие сходится ряд Маклорена:
где c k определено, как указано выше.
Асимптотическое разложение
Полезное асимптотическое разложение дополнительной функции ошибок (и, следовательно, также функции ошибок) для больших действительных x :
где (2 n — 1) !! — двойной факториал числа (2 n — 1), который является произведением всех нечетных чисел до (2 n — 1) . Этот ряд расходится для любого конечного x, и его смысл как асимптотического разложения состоит в том, что для любого целого числа N ≥ 1 выполняется
где остаток в обозначениях Ландау равен
при x → ∞ .
Действительно, точное значение остатка равно
что легко следует по индукции, записывая
и интеграция по частям.
Для достаточно больших значений x необходимы только первые несколько членов этого асимптотического разложения, чтобы получить хорошее приближение erfc x (в то время как для не слишком больших значений x приведенное выше разложение Тейлора при 0 обеспечивает очень быструю сходимость).
Непрерывное расширение фракции
Цепная дробь расширение дополнительной функции ошибок является:
Интеграл функции ошибок с функцией плотности Гаусса
которая, по-видимому, связана с Нг и Геллером, формула 13 в разделе 4.3 с заменой переменных.
Факторный ряд
Обратный факторный ряд :
сходится при Re ( z 2 )> 0 . Здесь
z n обозначает возрастающий факториал, а s ( n, k ) обозначает число Стирлинга первого рода со знаком . Также существует представление бесконечной суммой, содержащее двойной факториал :
Численные приближения
Приближение с элементарными функциями
- Абрамовиц и Стегун дают несколько приближений с различной точностью (уравнения 7.1.25–28). Это позволяет выбрать наиболее быстрое приближение, подходящее для данного приложения. В порядке увеличения точности это:
(максимальная ошибка: 5 × 10 −4 )
где a 1 = 0,278393, a 2 = 0,230389, a 3 = 0,000972, a 4 = 0,078108
(максимальная ошибка: 2,5 × 10 −5 )
где p = 0,47047, a 1 = 0,3480242, a 2 = −0,0958798, a 3 = 0,7478556
(максимальная ошибка: 3 × 10 −7 )
где a 1 = 0,0705230784, a 2 = 0,0422820123, a 3 = 0,0092705272, a 4 = 0,0001520143, a 5 = 0,0002765672, a 6 = 0,0000430638
(максимальная ошибка: 1,5 × 10 −7 )
где p = 0,3275911, a 1 = 0,254829592, a 2 = −0,284496736, a 3 = 1,421413741, a 4 = −1,453152027, a 5 = 1,061405429.
Все эти приближения верны для x ≥ 0 . Чтобы использовать эти приближения для отрицательного x, используйте тот факт, что erf x — нечетная функция, поэтому erf x = −erf (- x ) .
- Экспоненциальные границы и чисто экспоненциальное приближение для дополнительной функции ошибок даются формулами
- Вышеупомянутое было обобщено до сумм из N экспонент с возрастающей точностью в терминах N, так что erfc x может быть точно аппроксимирован или ограничен величиной 2 Q̃ ( √ 2 x ), где
В частности, существует систематическая методология решения числовых коэффициентов {( a n, b n )}N
n = 1которые дают минимаксное приближение или оценку для тесно связанной Q-функции : Q ( x ) ≈ Q̃ ( x ), Q ( x ) ≤ Q̃ ( x ) или Q ( x ) ≥ Q̃ ( x ) для x ≥ 0 . Коэффициенты {( a n, b n )}N
n = 1для многих вариаций экспоненциальных приближений и границ до N = 25 были выпущены в открытый доступ в виде исчерпывающего набора данных. - Точная аппроксимация дополнительной функции ошибок для x ∈ [0, ∞) дана Karagiannidis & Lioumpas (2007), которые показали для соответствующего выбора параметров { A, B }, что
Они определили { A, B } = {1.98,1.135}, что дает хорошее приближение для всех x ≥ 0 . Также доступны альтернативные коэффициенты для настройки точности для конкретного приложения или преобразования выражения в жесткую границу.
- Одноканальная нижняя граница
где параметр β может быть выбран так, чтобы минимизировать ошибку на желаемом интервале аппроксимации.
-
- Другое приближение дает Сергей Виницкий, используя свои «глобальные приближения Паде»:
куда
Это сделано так, чтобы быть очень точным в окрестности 0 и в окрестности бесконечности, а относительная ошибка меньше 0,00035 для всех действительных x . Использование альтернативного значения a ≈ 0,147 снижает максимальную относительную ошибку примерно до 0,00013.
Это приближение можно инвертировать, чтобы получить приближение для обратной функции ошибок:
- Приближение с максимальной погрешностью 1,2 × 10 −7 для любого действительного аргумента:
с участием
а также
Таблица значений
| Икс | erf x | 1 — эрф х |
|---|---|---|
| 0 | 0 | 1 |
| 0,02 | 0,022 564 575 | 0,977 435 425 |
| 0,04 | 0,045 111 106 | 0,954 888 894 |
| 0,06 | 0,067 621 594 | 0,932 378 406 |
| 0,08 | 0,090 078 126 | 0,909 921 874 |
| 0,1 | 0,112 462 916 | 0,887 537 084 |
| 0,2 | 0,222 702 589 | 0,777 297 411 |
| 0,3 | 0,328 626 759 | 0,671 373 241 |
| 0,4 | 0,428 392 355 | 0,571 607 645 |
| 0,5 | 0,520 499 878 | 0,479 500 122 |
| 0,6 | 0,603 856 091 | 0,396 143 909 |
| 0,7 | 0,677 801 194 | 0,322 198 806 |
| 0,8 | 0,742 100 965 | 0,257 899 035 |
| 0,9 | 0,796 908 212 | 0,203 091 788 |
| 1 | 0,842 700 793 | 0,157 299 207 |
| 1.1 | 0,880 205 070 | 0,119 794 930 |
| 1.2 | 0,910 313 978 | 0,089 686 022 |
| 1.3 | 0,934 007 945 | 0,065 992 055 |
| 1.4 | 0,952 285 120 | 0,047 714 880 |
| 1.5 | 0,966 105 146 | 0,033 894 854 |
| 1.6 | 0,976 348 383 | 0,023 651 617 |
| 1,7 | 0,983 790 459 | 0,016 209 541 |
| 1,8 | 0,989 090 502 | 0,010 909 498 |
| 1.9 | 0,992 790 429 | 0,007 209 571 |
| 2 | 0,995 322 265 | 0,004 677 735 |
| 2.1 | 0,997 020 533 | 0,002 979 467 |
| 2.2 | 0,998 137 154 | 0,001 862 846 |
| 2.3 | 0,998 856 823 | 0,001 143 177 |
| 2,4 | 0,999 311 486 | 0,000 688 514 |
| 2,5 | 0,999 593 048 | 0,000 406 952 |
| 3 | 0,999 977 910 | 0,000 022 090 |
| 3.5 | 0,999 999 257 | 0,000 000 743 |
Дополнительная функция ошибок
Дополнительная функция ошибок, обозначаемая ERFC, определяется как
который также определяет erfcx, масштабированную дополнительную функцию ошибок (которую можно использовать вместо erfc, чтобы избежать арифметического переполнения ). Другая форма erfc x для x ≥ 0 известна как формула Крейга в честь ее первооткрывателя:
Это выражение действительно только для положительных значений x, но его можно использовать вместе с erfc x = 2 — erfc (- x ) для получения erfc ( x ) для отрицательных значений. Эта форма выгодна тем, что диапазон интегрирования является фиксированным и конечным. Расширение этого выражения для erfc суммы двух неотрицательных переменных выглядит следующим образом:
Функция мнимой ошибки
Функция мнимой ошибки, обозначаемая erfi, определяется как
где D ( x ) — функция Доусона (которую можно использовать вместо erfi, чтобы избежать арифметического переполнения ).
Несмотря на название «мнимая функция ошибок», erfi x реально, когда x реально.
Когда функция ошибок оценивается для произвольных комплексных аргументов z, результирующая комплексная функция ошибок обычно обсуждается в масштабированной форме как функция Фаддеева :
Кумулятивная функция распределения
Функция ошибок по существу идентична стандартной нормальной кумулятивной функции распределения, обозначаемой Φ, также называемой нормой ( x ) в некоторых языках программного обеспечения, поскольку они различаются только масштабированием и преобразованием. Действительно,
или переставил для erf и erfc :
Следовательно, функция ошибок также тесно связана с Q-функцией, которая является вероятностью хвоста стандартного нормального распределения. Q-функция может быть выражена через функцию ошибок как
Обратное из Ф называется нормальной функции квантиль, или пробит функции и могут быть выражены в терминах функции обратной ошибки как
Стандартный нормальный cdf чаще используется в вероятностях и статистике, а функция ошибок чаще используется в других разделах математики.
Функция ошибок является частным случаем функции Миттаг-Леффлера и также может быть выражена как конфлюэнтная гипергеометрическая функция ( функция Куммера):
Он имеет простое выражение в терминах интеграла Френеля .
С точки зрения регуляризованном гамма — функции P и неполной гамма — функции ,
sgn x — знаковая функция .
Обобщенные функции ошибок
График обобщенных функций ошибок E n ( x ) :
серая кривая: E 1 ( x ) =1 — е — х/√ π
красная кривая: E 2 ( x ) = erf ( x )
зеленая кривая: E 3 ( x )
синяя кривая: E 4 ( x )
золотая кривая: E 5 ( x ) .
Некоторые авторы обсуждают более общие функции:
Известные случаи:
- E 0 ( x ) — прямая линия, проходящая через начало координат: E 0 ( x ) =Икс/е √ π
- E 2 ( x ) — функция ошибок, erf x .
После деления на п ! , все E n для нечетных n похожи (но не идентичны) друг на друга. Точно так же E n для четного n выглядят похожими (но не идентичными) друг на друга после простого деления на n ! . Все обобщенные функции ошибок для n > 0 выглядят одинаково на положительной стороне графика x .
Эти обобщенные функции могут быть эквивалентно выражены для x > 0 с использованием гамма-функции и неполной гамма-функции :
Следовательно, мы можем определить функцию ошибок в терминах неполной гамма-функции:
Итерированные интегралы дополнительной функции ошибок
Повторные интегралы дополнительной функции ошибок определяются как
Общая рекуррентная формула
У них есть степенной ряд
откуда следуют свойства симметрии
а также
Реализации
Как реальная функция реального аргумента
- В Posix -совместимый операционных систем, заголовок math.h возвестят и математическая библиотека libm должна обеспечивать функции
erfиerfc( двойной точности ), а также их одинарной точности и повышенной точности аналоговerff,erflиerfcf,erfcl. - GNU Scientific Library предоставляет
erf,erfc,log(erf), и масштабируемые функции ошибок.
Как сложная функция сложного аргумента
-
libcerf, цифровая библиотека C для сложных функций ошибок, обеспечивает комплексные функции
cerf,cerfc,cerfcxи реальные функцииerfi,erfcxпримерно с 13-14 точностью цифр, на основе функции Фаддеева, как реализовано в MIT Фаддеевого пакете
Смотрите также
- Гауссовский интеграл по всей действительной прямой
- Функция Гаусса, производная
- Функция Доусона, перенормированная функция мнимой ошибки
- Интеграл Гудвина – Стэтона
По вероятности
- Нормальное распределение
- Нормальная кумулятивная функция распределения, масштабированная и сдвинутая форма функции ошибок
- Пробит, обратная или квантильная функция нормального CDF
- Q-функция, хвостовая вероятность нормального распределения
использованная литература
дальнейшее чтение
- Абрамовиц, Милтон ; Стегун, Ирен Энн, ред. (1983) [июнь 1964]. «Глава 7» . Справочник по математическим функциям с формулами, графиками и математическими таблицами . Прикладная математика. 55 (Девятое переиздание с дополнительными исправлениями, десятое оригинальное издание с исправлениями (декабрь 1972 г.); первое изд.). Вашингтон; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Dover Publications. п. 297. ISBN. 978-0-486-61272-0. LCCN 64-60036 . Руководство по ремонту 0167642 . LCCN 65-12253 .
- Press, William H .; Teukolsky, Saul A .; Веттерлинг, Уильям Т .; Фланнери, Брайан П. (2007), «Раздел 6.2. Неполная гамма-функция и функция ошибок», Численные рецепты: Искусство научных вычислений (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN 978-0-521-88068-8
- Темме, Нико М. (2010), «Функции ошибок, интегралы Доусона и Френеля», в Olver, Frank WJ ; Lozier, Daniel M .; Бойсверт, Рональд Ф .; Кларк, Чарльз В. (ред.), Справочник по математическим функциям NIST, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
внешние ссылки
- MathWorld — Эрф
- Таблица интегралов функций ошибок
3.3.Температурное
поле непрерывного неподвижного точечного
источника в неограниченной среде.
Функция ошибок Гаусса (функция erf(x)).
Если в точке с
координатами x‘,
y‘,
z‘
в интервале времени от t‘
= 0 до t‘
= t
работает источник тепла мощностью
W,
то температурное поле этого источника,
как указано выше, может быть найдено
интегрированием фундаментального
решения по t‘
от 0 до t
(т.е. от момента включения до момента
выключения источника). Поместим начало
координат в точку, где находится источник
тепла. Тогда x’
= y’
= z’
= 0, и формула
для температуры принимает вид:
,
(3.3.1)
где r2
= (x — x’)2
+ (y — y’)2
+ (z — z’)2
= x2
+ y2
+ z2
— квадрат расстояния от источника до
точки наблюдения.
Произведем в
интеграле (3.3.1) замену переменных:
r2/[4a(t
— t’)] = 2.
Тогда: (t —
t’)3/2
= r3/(8a3/23),
dt’ = r2d/(2a3),
пределы интегрирования: t’
= 0
,
t’ = t
= ,
и формула (3.3.1) принимает вид:
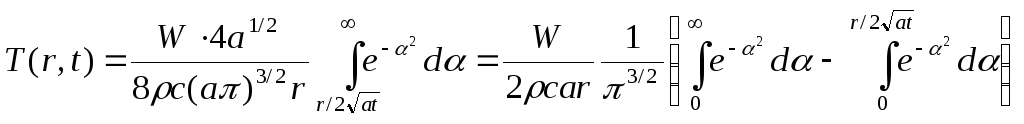
(3.3.2)
Первый интеграл,
стоящий в скобках, известен из курса
высшей математики:
(интеграл
Пуассона),
а второй интеграл
через элементарные функции не выражается
и определяет специальную функцию,
которая называется функцией
ошибок Гаусса,
или интегралом
вероятностей,
или функцией эрфектум:
(3.3.3)
(читается «эрфектум»
или сокращенно: «эрф»). Через эту
функцию выражаются решения многих
задач в теории теплопроводности, да и
в других областях физики она играет
важную роль.
Из определения
(3.3.3) видно, что erf(0)
= 0, а erf()
= 1, т.е. erf(x)
— это монотонно возрастающая
функция, вид которой изображен
на Рис.3.3. Функция erf(x)
табулирована, и ее значения
приводятся в различных
справочниках; в таблице 3.1 приведены
несколько значений этой функции. В
библиотеках некоторых
языков программирования имеются
готовые подпрограммы для
вычисления функции erf(x).
Если готовой подпрограммы
нет, функцию erf(x)
можно
вычислить с помощью степенного
ряда. «Стандартное»
разложение этой функции в
степенной ряд, которое обычно
приводится в математических
справочниках, имеет вид:
.
(3.3.4)
Э
ряд удобен для анализа свойств функции,
но для практических расчетов он неудобен,
т.к. является знакопеременным, что
при вычислениях приводит к потере
точности. Более удобен следующий
ряд:
,
(3.3.5)
где
,
.
С
Рис. 3.3.
помощью этого ряда легко составить
программу вычисления erf(x)
на любом языке программирования
и даже на программируемом
микрокалькуляторе. Суммирование
надо прекращать, когда при
добавлении очередного an-го
слагаемого сумма перестанет меняться
(будет достигнута «машинная
точность»).
Если большой
точности не требуется, то можно
использовать приближенную формулу:
erf(x)
[1 — exp(-4x2/)]1/2.
(3.3.6)
Формула (3.3.6) дает
значения, абсолютная погрешность которых
не более 6.310-3,
а относительная погрешность
не более 0.71%.
Иногда требуется
определить erf(x)
в области отрицательных значений x.
Из формулы (3.3.3) очевидно, что erf(-x)
= — erf(x).
Заметим, что хотя
функция erf(x)
не является «элементарной», с точки
зрения ее свойств и способов
вычисления она проще, чем многие
«элементарные» функции, например,
тригонометрические.
С функцией erf(x)
связано еще несколько функций, часто
встречающихся в теплофизических
задачах. Это прежде всего дополнительный
интеграл вероятностей:
,
(3.3.7)
который встречается
настолько часто, что для него используется
специальное обозначение: erfc(x)
(сокращенно читается «эрфик»). Вид
этой функции также приведен на рис.3.3.
Довольно часто
функцию erf(x)
приходится дифференцировать и
интегрировать. Из определения
(3.3.3) следует, что
,
(3.3.8)
а интеграл от
erfc(x)
(обозначается как ierfc(x))
равен:
.
(3.3.9)
Вернемся к формуле
(3.3.2). Замечая, что ca
= ,
запишем эту формулу в виде:
.
(3.3.10)
При t
значение функции
0,
1, и формула (3.3.10), как и должно быть,
совпадает с формулой для
стационарного решения (если T0
принять за начало отсчета
температуры), т.к. при t
достигается стационарное
распределение температуры
в безграничной среде.
Таблица 3.1.
Некоторые значения функции erf(x).
|
x |
erf(x) |
x |
erf(x) |
x |
erf(x) |
x |
erf(x) |
x |
erf(x) |
|
0.0 |
0.0 |
0.3 |
0.32863 |
0.6 |
0.60386 |
0.9 |
0.79691 |
2.0 |
0.99532 |
|
0.1 |
0.11246 |
0.4 |
0.42839 |
0.7 |
0.67780 |
1.0 |
0.84270 |
2.5 |
0.99959 |
|
0.2 |
0.22270 |
0.5 |
0.52050 |
0.8 |
0.74210 |
1.5 |
0.96611 |
Соседние файлы в папке КраткийКонспектЛекций
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Функция ошибок (также называемая функция ошибок Гаусса) — не элементарная функция, возникающая в теории вероятностей, статистике и теории дифференциальных уравнений в частных производных. Она определяется как
- [math]displaystyle{ operatorname{erf},x = frac{2}{sqrt{pi}}intlimits_0^x e^{-t^2},mathrm dt }[/math].
Дополнительная функция ошибок, обозначаемая [math]displaystyle{ operatorname{erfc},x }[/math] (иногда применяется обозначение [math]displaystyle{ operatorname{Erf},x }[/math]), определяется через функцию ошибок:
- [math]displaystyle{ operatorname{erfc},x = 1-operatorname{erf},x = frac{2}{sqrt{pi}} intlimits_x^{infty} e^{-t^2},mathrm dt }[/math].
Комплексная функция ошибок, обозначаемая [math]displaystyle{ w(x) }[/math], также определяется через функцию ошибок:
- [math]displaystyle{ w(x) = e^{-x^2}operatorname{erfc},(-ix) }[/math].
Свойства
- Функция ошибок нечётна:
-
- [math]displaystyle{ operatorname{erf},(-x) = -operatorname{erf},x. }[/math]
- Для любого комплексного [math]displaystyle{ x }[/math] выполняется
-
- [math]displaystyle{ operatorname{erf},bar{x} = overline{operatorname{erf},x} }[/math]
- где черта обозначает комплексное сопряжение числа [math]displaystyle{ x }[/math].
- Функция ошибок не может быть представлена через элементарные функции, но, разлагая интегрируемое выражение в ряд Тейлора и интегрируя почленно, мы можем получить её представление в виде ряда:
-
- [math]displaystyle{ operatorname{erf},x= frac{2}{sqrt{pi}}sum_{n=0}^infinfrac{(-1)^n x^{2n+1}}{n! (2n+1)} =frac{2}{sqrt{pi}} left(x-frac{x^3}{3}+frac{x^5}{10}-frac{x^7}{42}+frac{x^9}{216}- cdotsright) }[/math]
- Это равенство выполняется (и ряд сходится) как для любого вещественного [math]displaystyle{ x }[/math], так и на всей комплексной плоскости, согласно признаку Д’Аламбера. Последовательность знаменателей образует последовательность A007680 в OEIS.
- Для итеративного вычисления элементов ряда полезно представить его в альтернативном виде:
-
- [math]displaystyle{ operatorname{erf},x= frac{2}{sqrt{pi}}sum_{n=0}^infinleft(x prod_{i=1}^n{frac{-(2i-1) x^2}{i (2i+1)}}right) = frac{2}{sqrt{pi}} sum_{n=0}^infin frac{x}{2n+1} prod_{i=1}^n frac{-x^2}{i} }[/math]
- поскольку [math]displaystyle{ frac{-(2i-1) x^2}{i (2i+1)} }[/math] — сомножитель, превращающий [math]displaystyle{ i }[/math]-й член ряда в [math]displaystyle{ (i+1) }[/math]-й, считая первым членом [math]displaystyle{ x }[/math].
- Функция ошибок на бесконечности равна единице; однако это справедливо только при приближении к бесконечности по вещественной оси, так как:
- При рассмотрении функции ошибок в комплексной плоскости точка [math]displaystyle{ z=infty }[/math] будет для неё существенно особой.
- Производная функции ошибок выводится непосредственно из определения функции:
-
- [math]displaystyle{ frac{d}{dx},operatorname{erf},x=frac{2}{sqrt{pi}},e^{-x^2}. }[/math]
- Первообразная функции ошибок, получаемая способом интегрирования по частям:
-
- [math]displaystyle{ F(x)=xoperatorname{erf}(x) + frac{e^{-x^2}}{sqrt{pi}}. }[/math]
- Обратная функция ошибок представляет собой ряд
-
- [math]displaystyle{ operatorname{erf}^{-1},x=sum_{k=0}^infinfrac{c_k}{2k+1}left (frac{sqrt{pi}}{2}xright )^{2k+1}, }[/math]
- где c0 = 1 и
- [math]displaystyle{ c_k=sum_{m=0}^{k-1}frac{c_m c_{k-1-m}}{(m+1)(2m+1)} = left{1,1,frac{7}{6},frac{127}{90},ldotsright}. }[/math]
- Поэтому ряд можно представить в следующем виде (заметим, что дроби сокращены):
- [math]displaystyle{ operatorname{erf}^{-1},x=frac{1}{2}sqrt{pi}left (x+frac{pi x^3}{12}+frac{7pi^2 x^5}{480}+frac{127pi^3 x^7}{40320}+frac{4369pi^4 x^9}{5806080}+frac{34807pi^5 x^{11}}{182476800}+dotsright ). }[/math][1]
- Последовательности числителей и знаменателей после сокращения — A092676 и A132467 в OEIS; последовательность числителей до сокращения — A002067 в OEIS.
Дополнительная функция ошибок
Применение
Если набор случайных величин подчиняется нормальному распределению со стандартным отклонением [math]displaystyle{ sigma }[/math], то вероятность, что величина отклонится от среднего не более чем на [math]displaystyle{ a }[/math], равна [math]displaystyle{ operatorname{erf},frac{a}{sigma sqrt{2}} }[/math].
Функция ошибок и дополнительная функция ошибок встречаются в решении некоторых дифференциальных уравнений, например, уравнения теплопроводности с начальными условиями, описываемыми функцией Хевисайда («ступенькой»).
В системах цифровой оптической коммуникации, вероятность ошибки на бит также выражается формулой, использующей функцию ошибок.
Асимптотическое разложение
При больших [math]displaystyle{ x }[/math] полезно асимптотическое разложение для дополнительной функции ошибок:
- [math]displaystyle{ operatorname{erfc},x = frac{e^{-x^2}}{xsqrt{pi}}left [1+sum_{n=1}^infty (-1)^n frac{1cdot3cdot5cdots(2n-1)}{(2x^2)^n}right ]=frac{e^{-x^2}}{xsqrt{pi}}sum_{n=0}^infty (-1)^n frac{(2n)!}{n!(2x)^{2n}}. }[/math]
Хотя для любого конечного [math]displaystyle{ x }[/math] этот ряд расходится, на практике первых нескольких членов достаточно для вычисления [math]displaystyle{ operatorname{erfc},x }[/math] с хорошей точностью, в то время как ряд Тейлора сходится очень медленно.
Другое приближение даётся формулой
- [math]displaystyle{ (operatorname{erf},x)^2approx 1-expleft(-x^2frac{4/pi+ax^2}{1+ax^2}right) }[/math]
где
- [math]displaystyle{ a = frac{8}{3pi}frac{pi — 3}{4 — pi}. }[/math]
Родственные функции
С точностью до масштаба и сдвига, функция ошибок совпадает с нормальным интегральным распределением, обозначаемым [math]displaystyle{ Phi(x) }[/math]
- [math]displaystyle{ Phi(x) = frac{1}{2}biggl(1+operatorname{erf},frac{x}{sqrt{2}}biggl). }[/math]
Обратная функция к [math]displaystyle{ Phi }[/math], известная как нормальная квантильная функция, иногда обозначается [math]displaystyle{ operatorname{probit} }[/math] и выражается через нормальную функцию ошибок как
- [math]displaystyle{
operatorname{probit},p = Phi^{-1}(p) = sqrt{2},operatorname{erf}^{-1}(2p-1).
}[/math]
Нормальное интегральное распределение чаще применяется в теории вероятностей и математической статистике, в то время как функция ошибок чаще применяется в других разделах математики.
Функция ошибок является частным случаем функции Миттаг-Леффлера, а также может быть представлена как вырожденная гипергеометрическая функция (функция Куммера):
- [math]displaystyle{ operatorname{erf},x=
frac{2x}{sqrt{pi}},_1F_1left(frac{1}{2},frac{3}{2},-x^2right). }[/math]
Функция ошибок выражается также через интеграл Френеля. В терминах регуляризованной неполной гамма-функции P и неполной гамма-функции,
- [math]displaystyle{ operatorname{erf},x=operatorname{sign},x,Pleft(frac{1}{2}, x^2right)={operatorname{sign},x over sqrt{pi}}gammaleft(frac{1}{2}, x^2right). }[/math]
Обобщённые функции ошибок
График обобщённых функций ошибок [math]displaystyle{ E_n(x) }[/math]:
серая линия: [math]displaystyle{ E_1(x)=(1-e^{-x})/sqrt{pi} }[/math]
красная линия: [math]displaystyle{ E_2(x)=operatorname{erf},x }[/math]
зелёная линия: [math]displaystyle{ E_3(x) }[/math]
синяя линия: [math]displaystyle{ E_4(x) }[/math]
жёлтая линия: [math]displaystyle{ E_5(x) }[/math].
Некоторые авторы обсуждают более общие функции
- [math]displaystyle{ E_n(x) = frac{n!}{sqrt{pi}} intlimits_0^x e^{-t^n},mathrm dt
=frac{n!}{sqrt{pi}}sum_{p=0}^infin(-1)^pfrac{x^{np+1}}{(np+1)p!},. }[/math]
Примечательными частными случаями являются:
- [math]displaystyle{ E_0(x) }[/math] — прямая линия, проходящая через начало координат: [math]displaystyle{ E_0(x)=frac{x}{e sqrt{pi}} }[/math]
- [math]displaystyle{ E_2(x) }[/math] — функция ошибок [math]displaystyle{ operatorname{erf},x }[/math].
После деления на [math]displaystyle{ n! }[/math] все [math]displaystyle{ E_n }[/math] с нечётными [math]displaystyle{ n }[/math] выглядят похоже (но не идентично), это же можно сказать про [math]displaystyle{ E_n }[/math] с чётными [math]displaystyle{ n }[/math]. Все обобщённые функции ошибок с [math]displaystyle{ ngt 0 }[/math] выглядят похоже на полуоси [math]displaystyle{ xgt 0 }[/math].
На полуоси [math]displaystyle{ xgt 0 }[/math] все обобщённые функции могут быть выражены через гамма-функцию:
- [math]displaystyle{ E_n(x) = frac{Gamma(n)left(Gammaleft(frac{1}{n}right)-Gammaleft(frac{1}{n},x^nright)right)}{sqrtpi},
quad quad
xgt 0 }[/math]
Следовательно, мы можем выразить функцию ошибок через гамма-функцию:
- [math]displaystyle{ operatorname{erf},x = 1 — frac{Gammaleft(frac{1}{2},x^2right)}{sqrtpi} }[/math]
Повторные интегралы дополнительной функции ошибок
Повторные интегралы [math]displaystyle{ operatorname{I^n erfc} }[/math] дополнительной функции ошибок определяются как[1]
- [math]displaystyle{ operatorname{I^0 erfc},z = operatorname{erfc},z }[/math],
- [math]displaystyle{ operatorname{I^n erfc},z = intlimits_z^infty operatorname{I^{n-1}erfc},zeta,dzeta, }[/math] для [math]displaystyle{ ngt 0 }[/math].
Их можно разложить в ряд:
- [math]displaystyle{
operatorname{I^nerfc},z
=
sum_{j=0}^infty frac{(-z)^j}{2^{n-j}j!,Gamma left( 1 + frac{n-j}{2}right)},,
}[/math]
откуда следуют свойства симметрии
- [math]displaystyle{
operatorname{I^{2m}erfc},(-z)
= -operatorname{I^{2m}erfc},z
+ sum_{q=0}^m frac{z^{2q}}{2^{2(m-q)-1}(2q)!(m-q)!}
}[/math]
и
- [math]displaystyle{
operatorname{I^{2m+1}erfc},(-z)
=operatorname{I^{2m+1}erfc},z
+ sum_{q=0}^m frac{z^{2q+1}}{2^{2(m-q)-1}(2q+1)! (m-q)!},.
}[/math]
Реализации
В стандарте языка Си (ISO/IEC 9899:1999, пункт 7.12.8) предусмотрены функция ошибок [math]displaystyle{ operatorname{erf} }[/math] и дополнительная функция ошибок [math]displaystyle{ operatorname{erfc} }[/math]. Функции объявлены в заголовочных файлах math.h (для Си) или cmath (для C++). Там же объявлены пары функций erff(), erfcf() и erfl(), erfcl(). Первая пара получает и возвращает значения типа float, а вторая — значения типа long double. Соответствующие функции также содержатся в библиотеке Math проекта «Boost».
В языке Java стандартная библиотека математических функций java.lang.Math не содержит[2] функцию ошибок. Класс Erf можно найти в пакете org.apache.commons.math.special из не стандартной библиотеки, поставляемой[3] Apache Software Foundation.
Системы компьютерной алгебры Maple[2], Matlab[3], Mathematica и Maxima[4] содержат обычную и дополнительную функции ошибок, а также обратные к ним функции.
В языке Python функция ошибок доступна[4] из стандартной библиотеки math, начиная с версии 2.7. Также функция ошибок, дополнительная функция ошибок и многие другие специальные функции определены в модуле Special проекта SciPy[5].
В языке Erlang функция ошибок и дополнительная функция ошибок доступны из стандартного модуля math[5].
В Excel функция ошибок представлена, как ФОШ и ФОШ.ТОЧН[6]
См. также
- Функция Гаусса
- Функция Доусона
- Гауссов интеграл
Примечания
- ↑ Carslaw, H. S. & Jaeger, J. C. (1959), Conduction of Heat in Solids (2nd ed.), Oxford University Press, ISBN 978-0-19-853368-9, p 484
- ↑ Math (Java Platform SE 6). Дата обращения: 28 марта 2008. Архивировано 29 августа 2009 года.
- ↑ Архивированная копия (недоступная ссылка). Дата обращения: 28 марта 2008. Архивировано 9 апреля 2008 года.
- ↑ 9.2. math — Mathematical functions — Python 2.7.10rc0 documentation
- ↑ Язык Erlang. Описание Архивная копия от 20 июня 2012 на Wayback Machine функций стандартного модуля
math. - ↑ Функция ФОШ. support.microsoft.com. Дата обращения: 15 ноября 2021. Архивировано 15 ноября 2021 года.
Литература
- Press, William H.; Teukolsky, Saul A.; Vetterling, William T. & Flannery, Brian P. (2007), Section 6.2. Incomplete Gamma Function and Error Function, Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
- Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. — New York: Dover, 1972. — Т. 7.
- Nikolai G. Lehtinen. Error functions (April 2010). Дата обращения: 25 мая 2019.
Ссылки
- MathWorld — Erf
- Онлайновый калькулятор Erf и много других специальных функций (до 6 знаков)
- Онлайновый калькулятор, вычисляющий в том числе Erf
График функции ошибок
В математике функция ошибок — это неэлементарная функция, возникающая в теории вероятностей, статистике и теории дифференциальных уравнений в частных производных. Она определяется как
.
Дополнительная функция ошибок, обозначаемая 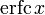
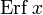
.
Комплексная функция ошибок, обозначаемая w(x), также определяется через функцию ошибок:
.
Содержание
- 1 Свойства
- 2 Применение
- 3 Асимптотическое разложение
- 4 Родственные функции
- 4.1 Обобщённые функции ошибок
- 4.2 Итерированные интегралы дополнительной функции ошибок
- 5 Реализация
- 6 См. также
- 7 Литература
- 8 Внешние ссылки
Свойства
- Функция ошибок нечётна:
- Для любого комплексного x выполняется
где черта обозначает комплексное сопряжение числа x.
- Функция ошибок не может быть представлена через элементарные функции, но, разлагая интегрируемое выражение в ряд Тейлора и интегрируя почленно, мы можем получить её представление в виде ряда:
Это равенство выполняется (и ряд сходится) как для любого вещественного x, так и на всей комплексной плоскости. Последовательность знаменателей образует последовательность A007680 в OEIS.
- Для итеративного вычисления элементов ряда полезно представить его в альтернативном виде:
поскольку 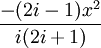
- Функция ошибок на бесконечности равна единице; однако это справедливо только при приближении к бесконечности по вещественной оси, так как:
- При рассмотрении функции ошибок в комплексной плоскости точка
будет для неё существенно особой.
- Производная функции ошибок выводится непосредственно из определения функции:
- Обратная функция ошибок представляет собой ряд
где c0 = 1 и
Поэтому ряд можно представить в следующем виде (заметим, что дроби сокращены):
[1]
Последовательности числителей и знаменателей после сокращения — A092676 и A132467 в OEIS; последовательность числителей до сокращения — A002067 в OEIS.
Дополнительная функция ошибок
Применение
Если набор случайных чисел подчиняется нормальному распределению со стандартным отклонением σ, то вероятность, что число отклонится от среднего не более чем на a, равна 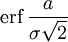
Функция ошибок и дополнительная функция ошибок встречаются в решении некоторых дифференциальных уравнений, например, уравнения теплопроводности с граничными условиями описываемыми функцией Хевисайда («ступенькой»).
В системах цифровой оптической коммуникации, вероятность ошибки на бит также выражается формулой, использующей функцию ошибок.
Асимптотическое разложение
При больших x полезно асимптотическое разложение для дополнительной функции ошибок:
Хотя для любого конечного x этот ряд расходится, на практике первых нескольких членов достаточно для вычисления 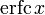
Другое приближение даётся формулой
где
Родственные функции
С точностью до масштаба и сдвига, функция ошибок совпадает с нормальным интегральным распределением, обозначаемым Φ(x)
Обратная функция к Φ, известная как нормальная квантильная функция, иногда обозначается 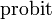
Нормальное интегральное распределение чаще применяется в теории вероятностей и математической статистике, в то время как функция ошибок чаще применяется в других разделах математики.
Функция ошибок является частным случаем функции Миттаг-Леффлера, а также может быть представлена как вырожденная гипергеометрическая функция (функция Куммера):
Функция ошибок выражается также через интеграл Френеля. В терминах регуляризованной неполной гамма-функции P и неполной гамма-функции,
Обобщённые функции ошибок
График обобщённых функций ошибок En(x):
серая линия:
красная линия:
зелёная линия: E3(x)
синяя линия: E4(x)
жёлтая линия: E5(x).
Некоторые авторы обсуждают более общие функции
Примечательными частными случаями являются:
После деления на n! все En с нечётными n выглядят похоже (но не идентично). Все En с чётными n тоже выглядят похоже, но не идентично, после деления на n!. Все обощённые функции ошибок с n > 0 выглядят похоже на полуоси x > 0.
На полуоси x > 0 все обобщённые функции могут быть выражены через гамма-функцию:
Следовательно, мы можем выразить функцию ошибок через гамма-функцию:
Итерированные интегралы дополнительной функции ошибок
Итерированные интегралы дополнительной функции ошибок определяются как
Их можно разложить в ряд:
откуда следуют свойства симметрии
и
Реализация
В стандартах языков Си и C++ функция ошибок 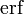
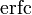
double erf(double x) и double erfc(double x). Функции находятся в заголовочных файлах math.h или cmath. Там же есть пары функций erff(),erfcf() и erfl(),erfcl(). Первая пара получает и возвращает значения типа float, а вторая — значения типа long double. Соответствующие функции также содержатся в библиотеке Math проекта Boost.
В языке [2]. Класс Erf есть в пакете org.apache.commons.math.special от [3]. Однако эта библиотека не является одной из стандартных библиотек Java 6.
Matlab[4] и
В языке Special проекта scipy [5].
См. также
- Функция Гаусса
Литература
- Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972. (См. часть 7)
Внешние ссылки
- MathWorld — Erf
- Онлайновый калькулятор Erf и много других специальных функций (до 6 знаков)
- Онлайновый калькулятор, вычисляющий в том числе Erf
Wikimedia Foundation.
2010.
Функция ошибок
| Аргумент функции ошибок erf(x) |
| Функция ошибок |
| Дополнительная функция ошибок |
Функция ошибок, она же функция Лапласа, он же интеграл вероятности — все это одна и та же сущность, которая выражается функцией
и используется в статистике и теории вероятностей.
Функция неэлементарная, то есть её нельзя представить в виде элементарных (тригонометрических и алгебраических) функций.
Для расчета в нашем калькуляторе, мы используем связь с неполной гамма функцией
Кроме этого мы сможем здесь же вычислить, дополнительную функцию ошибок, обозначаемую 

В приницпе это все, что можно сказать о ней.
Калькулятор высчитывает результат как в вещественном так и комплексном поле.
Замечание: Функция прекрасно работает на всем поле комплексных чисел при условии если аргумент ( фаза) меньше 180 градусов. Это связано с особенностью вычисления этой функции, неполной гамма функции, интегральной показательной функцией через непрерывные дроби.
Отсюда следует вывод, что при отрицательных вещественных аргументах, функция будет выдавать неверные решения. Но при всех положительных, а также отрицательных комплексных аргументах функция ошибок выдает верный ответ.
Несколько примеров:

В математике функция ошибок (также называемая Функция ошибок Гаусса ), часто обозначаемая erf, является сложной функцией комплексной определяемой как:
- erf z = 2 π ∫ 0 ze — t 2 dt. {\ displaystyle \ operatorname {erf} z = {\ frac {2} {\ sqrt {\ pi}}} \ int _ {0} ^ {z} e ^ {- t ^ {2}} \, dt.}
Этот интеграл является особой (не элементарной ) и сигмоидной функцией, которая часто встречается в статистике вероятность, и уравнения в частных производных. Во многих из этих приложений аргумент функции является действительным числом. Если аргумент функции является действительным, значение также является действительным.
В статистике для неотрицательных значений x функция имеет интерпретацию: для случайной величины Y, которая нормально распределена с среднее 0 и дисперсия 1/2, erf x — это вероятность того, что Y попадает в диапазон [-x, x].
Две связанные функции: дополнительные функции ошибок (erfc ), определенная как
- erfc z = 1 — erf z, {\ displaystyle \ operatorname {erfc} z = 1- \ operatorname {erf} z,}
и функция мнимой ошибки (erfi ), определяемая как
- erfi z = — i erf (iz), {\ displaystyle \ operatorname {erfi} z = -i \ operatorname {erf} (iz),}
, где i — мнимая единица.
Содержание
- 1 Имя
- 2 Приложения
- 3 Свойства
- 3.1 Ряд Тейлора
- 3.2 Производная и интеграл
- 3.3 Ряд Бюрмана
- 3.4 Обратные функции
- 3.5 Асимптотическое разложение
- 3.6 Разложение на непрерывную дробь
- 3,7 Интеграл функции ошибок с функцией плотности Гаусса
- 3.8 Факториальный ряд
- 4 Численные приближения
- 4.1 Аппроксимация с элементарными функциями
- 4.2 Полином
- 4.3 Таблица значений
- 5 Связанные функции
- 5.1 функция дополнительных ошибок
- 5.2 Функция мнимой ошибки
- 5.3 Кумулятивная функци я распределения на
- 5.4 Обобщенные функции ошибок
- 5.5 Итерированные интегралы дополнительных функций ошибок
- 6 Реализации
- 6.1 Как действующая функция действительного аргумента
- 6.2 Как комплексная функция комплексного аргумента
- 7 См. Также
- 7.1 Связанные функции
- 7.2 Вероятность
- 8 Ссылки
- 9 Дополнительная литература
- 10 Внешние ссылки
Имя
Название «функция ошибки» и его аббревиатура erf были предложены Дж. В. Л. Глейшер в 1871 г. по причине его связи с «теорией вероятности, и особенно теорией ошибок ». Дополнение функции ошибок также обсуждалось Глейшером в отдельной публикации в том же году. Для «закона удобства» ошибок плотность задана как
- f (x) = (c π) 1 2 e — cx 2 {\ displaystyle f (x) = \ left ({\ frac {c } {\ pi}} \ right) ^ {\ tfrac {1} {2}} e ^ {- cx ^ {2}}}
(нормальное распределение ), Глейшер вычисляет вероятность ошибки, лежащей между p {\ displaystyle p}

- (c π) 1 2 ∫ pqe — cx 2 dx = 1 2 (erf (qc) — erf (pc)). {\ displaystyle \ left ({\ frac {c} {\ pi}} \ right) ^ {\ tfrac {1} {2}} \ int _ {p} ^ {q} e ^ {- cx ^ {2} } dx = {\ tfrac {1} {2}} \ left (\ operatorname {erf} (q {\ sqrt {c}}) — \ operatorname {erf} (p {\ sqrt {c}}) \ right).}
Приложения
Когда результаты серии измерений описываются нормальным распределением со стандартным отклонением σ {\ displaystyle \ sigma}

Функции и дополнительные функции ошибок возникают, например, в решениях уравнения теплопроводности, когда граничные ошибки задаются ступенчатой функцией Хевисайда.
Функция ошибок и ее приближения Программу присвоили себе преподавателей, которые получили с высокой вероятностью или с низкой вероятностью. Дана случайная величина X ∼ Norm [μ, σ] {\ displaystyle X \ sim \ operatorname {Norm} [\ mu, \ sigma]}![X \ sim \ operatorname {Norm} [\ му, \ sigma]](https://wikimedia.org/api/rest_v1/media/math/render/svg/84024bc6827355ec6d23a062283a26d54b29698d)

- Pr [X ≤ L ] = 1 2 + 1 2 erf (L — μ 2 σ) ≈ A ехр (- B (L — μ σ) 2) {\ Displaystyle \ Pr [X \ Leq L] = {\ frac {1} {2 }} + {\ frac {1} {2}} \ operatorname {erf} \ left ({\ frac {L- \ mu} {{\ sqrt {2}} \ sigma}} \ right) \ приблизительно A \ exp \ left (-B \ left ({\ frac {L- \ mu} {\ sigma}} \ right) ^ {2} \ right)}
где A и B — верх числовые константы. Если L достаточно далеко от среднего, то есть μ — L ≥ σ ln k {\ displaystyle \ mu -L \ geq \ sigma {\ sqrt {\ ln {k}}}}
- Pr [X ≤ L] ≤ A exp (- B ln k) = A К B {\ displaystyle \ Pr [X \ leq L] \ leq A \ exp (-B \ ln {k}) = {\ frac {A} {k ^ {B}}}}
, поэтому становится вероятность 0 при k → ∞ {\ displaystyle k \ to \ infty}
Свойства
Графики на комплексной плоскости 

Свойство erf (- z) = — erf (z) {\ displaystyle \ operatorname {erf} (-z) = — \ operatorname {erf} (z)}

Для любого комплексное число z:
- erf (z ¯) = erf (z) ¯ {\ displaystyle \ operatorname {erf} ({\ overline {z}}) = {\ overline {\ operatorname {erf} (z)}}}
где z ¯ {\ displaystyle {\ overline {z}}}
Подынтегральное выражение f = exp (−z) и f = erf (z) показано в комплексной плоскости z на рисунках 2 и 3. Уровень Im (f) = 0 показан жирным зеленым цветом. линия. Отрицательные целые значения Im (f) показаны жирными красными линиями. Положительные целые значения Im (f) показаны толстыми синими линиями. Промежуточные уровни Im (f) = проявляются тонкими зелеными линиями. Промежуточные уровни Re (f) = показаны тонкими красными линиями для отрицательных значений и тонкими синими линиями для положительных значений.
Функция ошибок при + ∞ равна 1 (см. интеграл Гаусса ). На действительной оси erf (z) стремится к единице при z → + ∞ и к −1 при z → −∞. На мнимой оси он стремится к ± i∞.
Серия Тейлора
Функция ошибок — это целая функция ; у него нет сингулярностей (кроме бесконечности), и его разложение Тейлора всегда сходится, но, как известно, «[…] его плохая сходимость, если x>1».
определяющий интеграл нельзя вычислить в закрытой форме в терминах элементарных функций, но путем расширения подынтегрального выражения e в его ряд Маклорена и интегрирована почленно, можно получить ряд Маклорена функции ошибок как:
- erf (z) = 2 π ∑ n = 0 ∞ (- 1) nz 2 n + 1 n! (2 n + 1) знак равно 2 π (z — z 3 3 + z 5 10 — z 7 42 + z 9 216 — ⋯) {\ displaystyle \ operatorname {erf} (z) = {\ frac {2} { \ sqrt {\ pi}}} \ sum _ {n = 0} ^ {\ infty} {\ frac {(-1) ^ {n} z ^ {2n + 1}} {n! (2n + 1)}} = {\ frac {2} {\ sqrt {\ pi}}} \ left (z — {\ frac {z ^ {3}} {3}} + {\ frac {z ^ { 5}} {10}} — {\ frac {z ^ {7}} {42}} + {\ frac {z ^ {9}} {216}} — \ cdots \ right)}
, которое выполняется для каждого комплексного числа г. Члены знаменателя представляют собой последовательность A007680 в OEIS.
Для итеративного вычисления нового ряда может быть полезна следующая альтернативная формулировка:
- erf (z) = 2 π ∑ n = 0 ∞ (z ∏ К знак равно 1 N — (2 К — 1) Z 2 К (2 К + 1)) знак равно 2 π ∑ N = 0 ∞ Z 2 N + 1 ∏ К = 1 N — Z 2 К {\ Displaystyle \ OperatorName { erf} (z) = {\ frac {2} {\ sqrt {\ pi}}} \ sum _ {n = 0} ^ {\ infty} \ left (z \ prod _ {k = 1} ^ {n} {\ frac {- (2k-1) z ^ {2}} {k (2k + 1)}} \ right) = {\ frac {2} {\ sqrt {\ pi}}} \ sum _ {n = 0} ^ {\ infty} {\ frac {z} {2n + 1}} \ prod _ {k = 1} ^ {n} {\ frac {-z ^ {2}} {k}}}
потому что что — (2 k — 1) z 2 k (2 k + 1) {\ displaystyle {\ frac {- (2k-1) z ^ {2}} {k (2k + 1))}} }
Функция мнимой ошибки имеет очень похожий ряд Маклорена:
- erfi (z) = 2 π ∑ n = 0 ∞ z 2 n + 1 n! (2 n + 1) знак равно 2 π (z + z 3 3 + z 5 10 + z 7 42 + z 9 216 + ⋯) {\ displaystyle \ operatorname {erfi} (z) = {\ frac {2} { \ sqrt {\ pi}}} \ sum _ {n = 0} ^ {\ infty} {\ frac {z ^ {2n + 1}} {n! (2n + 1)}} = {\ frac {2} {\ sqrt {\ pi}}} \ left (z + {\ frac {z ^ {3}} {3}} + {\ frac {z ^ { 5}} {10}} + {\ frac {z ^ {7}} {42}} + {\ frac {z ^ {9}} {216}} + \ cdots \ right)}
, которое выполняется для любого комплексного числа z.
Производная и интеграл
Производная функция ошибок сразу следует из ее определения:
- ddz erf (z) = 2 π e — z 2. {\ displaystyle {\ frac {d} {dz}} \ operatorname {erf} (z) = {\ frac {2} {\ sqrt {\ pi}}} e ^ {- z ^ {2}}.}
Отсюда немедленно вычисляется производная функция мнимой ошибки :
- ddz erfi (z) = 2 π ez 2. {\ displaystyle {\ frac {d} {dz}} \ operatorname {erfi} (z) = {\ frac {2} {\ sqrt {\ pi }}} e ^ {z ^ {2}}.}
первообразная функции ошибок, которые можно получить посредством интегрирования по частям, составляет
- z erf (z) + е — z 2 π. {\ displaystyle z \ operatorname {erf} (z) + {\ frac {e ^ {- z ^ {2}}} {\ sqrt {\ pi}}}.}
Первообразная мнимой функции ошибок, также можно получить интегрированием по частям:
- z erfi (z) — ez 2 π. {\ displaystyle z \ operatorname {erfi} (z) — {\ frac {e ^ {z ^ {2}}} {\ sqrt {\ pi}}}.}
Производные высшего порядка задаются как
- erf (k) (z) = 2 (- 1) k — 1 π H k — 1 (z) e — z 2 = 2 π dk — 1 dzk — 1 (e — z 2), k = 1, 2, … {\ Displaystyle \ operatorname {erf} ^ {(k)} (z) = {\ frac {2 (-1) ^ {k-1}} {\ sqrt {\ pi}}} {\ mathit {H} } _ {k-1} (z) e ^ {- z ^ {2}} = {\ frac {2} {\ sqrt {\ pi}}} {\ frac {d ^ {k-1}} {dz ^ {k-1}}} \ left (e ^ {- z ^ {2}} \ right), \ qquad k = 1,2, \ dots}
где H {\ displaystyle {\ mathit {H}}}
ряд Бюрмана
Расширение, которое сходится быстрее для всех реальных значений x {\ displaystyle x}
- erf (x) = 2 π sgn (x) 1 — e — x 2 (1 — 1 12 ( 1 — e — x 2) — 7 480 (1 — e — x 2) 2 — 5 896 (1 — e — x 2) 3 — 787 276480 (1 — e — x 2)) 4 — ⋯) знак равно 2 π знак (x) 1 — e — x 2 (π 2 + ∑ k = 1 ∞ cke — kx 2). {\ displaystyle {\ begin {align} \ operatorname {erf} (x) = {\ frac {2} {\ sqrt {\ pi}}} \ operatorname {sgn} (x) {\ sqrt {1-e ^ {-x ^ {2}}}} \ left (1 — {\ frac {1} {12}} \ left (1-e ^ {- x ^ {2}} \ right) — {\ frac {7} {480}} \ left (1-e ^ {- x ^ {2}} \ right) ^ {2} — {\ frac {5} {896}} \ left (1-e ^ {- x ^ {2 }} \ right) ^ {3} — {\ frac {787} {276480}} \ left (1-e ^ {- x ^ {2}} \ right) ^ {4} — \ cdots \ right) \\ [10pt] = {\ frac {2} {\ sqrt {\ pi}}} \ operatorname {sgn} (x) {\ sqrt {1-e ^ {- x ^ {2}}}} \ left ({ \ frac {\ sqrt {\ pi}} {2}} + \ sum _ {k = 1} ^ {\ infty} c_ {k} e ^ {- kx ^ {2}} \ right). \ end {выровнено}}
Сохраняя только первые два коэффициента и выбирая c 1 = 31 200 {\ displaystyle c_ {1} = {\ frac {31} {200}}}



- erf (x) ≈ 2 π sign (x) 1 — e — x 2 (π 2 + 31 200 e — x 2 — 341 8000 e — 2 х 2). {\ displaystyle \ operatorname {erf} (x) \ приблизительно {\ frac {2} {\ sqrt {\ pi}}} \ operatorname {sgn} (x) {\ sqrt {1-e ^ {- x ^ {2 }}}} \ left ({\ frac {\ sqrt {\ pi}} {2}} + {\ frac {31} {200}} e ^ {- x ^ {2}} — {\ frac {341} {8000}} e ^ {- 2x ^ {2}} \ right).}
Обратные функции

Учитывая комплексное число z, не существует уникального комплексного числа w, удовлетворяющего erf (w) = z {\ displaystyle \ operatorname {erf} (w) = z}

- erf (erf — 1 ( х)) = х. {\ displaystyle \ operatorname {erf} \ left (\ operatorname {erf} ^ {- 1} (x) \ right) = x.}
Обратная функция ошибок обычно определяется с помощью домена (- 1,1), и он ограничен этой областью многих систем компьютерной алгебры. Однако его можно продолжить и на диск | z | < 1 of the complex plane, using the Maclaurin series
- erf — 1 (z) знак равно ∑ К знак равно 0 ∞ ck 2 k + 1 (π 2 z) 2 k + 1, {\ displaystyle \ operatorname {erf} ^ {- 1} (z) = \ sum _ {k = 0} ^ {\ infty} {\ frac {c_ {k}} {2k + 1}} \ left ({\ frac {\ sqrt {\ pi}} {2}} z \ right) ^ {2k + 1},}
где c 0 = 1 и
- ck = ∑ m = 0 k — 1 cmck — 1 — m (m + 1) (2 m + 1) = {1, 1, 7 6, 127 90, 4369 2520, 34807 16200,…}. {\ displaystyle c_ {k} = \ sum _ {m = 0} ^ {k-1} {\ frac {c_ {m} c_ {k-1-m}} {(m + 1) (2m + 1) }} = \ left \ {1,1, {\ frac {7} {6}}, {\ frac {127} {90}}, {\ frac {4369} {2520}}, {\ frac {34807} {16200}}, \ ldots \ right \}.}
Итак, у нас есть разложение в ряд (общие множители были удалены из числителей и знаменателей):
- erf — 1 (z) = 1 2 π ( z + π 12 z 3 + 7 π 2 480 z 5 + 127 π 3 40320 z 7 + 4369 π 4 5806080 z 9 + 34807 π 5 182476800 z 11 + ⋯). {\ displaystyle \ operatorname {erf} ^ {- 1} (z) = {\ tfrac {1} {2}} {\ sqrt {\ pi}} \ left (z + {\ frac {\ pi} {12} } z ^ {3} + {\ frac {7 \ pi ^ {2}} {480}} z ^ {5} + {\ frac {127 \ pi ^ {3}} {40320}} z ^ {7} + {\ frac {4369 \ pi ^ {4}} {5806080}} z ^ {9} + {\ frac {34807 \ pi ^ {5}} {182476800}} z ^ {11} + \ cdots \ right). }
(После отмены дроби числителя / знаменателя характерми OEIS : A092676 / OEIS : A092677 в OEIS ; без отмены членов числителя в записи OEIS : A002067.) Значение функции ошибок при ± ∞ равно ± 1.
Для | z | < 1, we have erf (erf — 1 (z)) = z {\ displaystyle \ operatorname {erf} \ left (\ operatorname {erf} ^ {- 1} (z) \ right) = z}
обратная дополнительная функция ошибок определяется как
- erfc — 1 (1 — z) = erf — 1 (z). {\ displaystyle \ operatorname {erfc} ^ {- 1} (1-z) = \ operatorname {erf} ^ {- 1} (z).}
Для действительного x существует уникальное действительное число erfi — 1 (x) {\ displaystyle \ operatorname {erfi} ^ {- 1} (x)}


Для любого действительного x, Метод Ньютона можно использовать для вычислений erfi — 1 (x) {\ displaystyle \ operatorname {erfi} ^ {- 1} (x)}

- erfi — 1 (z) = ∑ k = 0 ∞ (- 1) ККК 2 К + 1 (π 2 Z) 2 К + 1, {\ Displaystyle \ OperatorName {erfi} ^ {- 1} (г) = \ сумма _ {к = 0} ^ {\ infty} {\ гидроразрыва {(-1) ^ {k} c_ {k}} {2k + 1}} \ left ({\ frac {\ sqrt {\ pi}} {2}} z \ right) ^ {2k + 1},}
, где c k определено, как указано выше.
Асимптотическое разложение
Полезным асимптотическим разложением дополнительные функции (и, следовательно, также и функции ошибок) для больших вещественных x
- erfc (x) = e — x 2 x π [1 + ∑ n = 1 ∞ (- 1) n 1 ⋅ 3 ⋅ 5 ⋯ (2 n — 1) (2 x 2) n] = e — x 2 x π ∑ n = 0 ∞ (- 1) п (2 п — 1)! ! (2 х 2) n, {\ displaystyle \ operatorname {erfc} (x) = {\ frac {e ^ {- x ^ {2}}} {x {\ sqrt {\ pi}}}} \ left [1 + \ sum _ {n = 1} ^ {\ infty} (- 1) ^ {n} {\ frac {1 \ cdot 3 \ cdot 5 \ cdots (2n-1)} {(2x ^ {2}) ^ {n}}} \ right] = {\ frac {e ^ {- x ^ {2}}} {x {\ sqrt {\ pi}}}} \ sum _ {n = 0} ^ {\ infty} ( -1) ^ {n} {\ frac {(2n-1) !!} {(2x ^ {2}) ^ {n}}},}
где (2n — 1) !! — это двойной факториал числа (2n — 1), которое является произведением всех нечетных чисел до (2n — 1). Этот ряд расходуется для любого конечного x, и его значение как асимптотического разложения состоит в том, что для любого N ∈ N {\ displaystyle N \ in \ mathbb {N}}
- erfc (Икс) знак равно е — Икс 2 Икс π ∑ N знак равно 0 N — 1 (- 1) N (2 N — 1)! ! (2 х 2) n + RN (x) {\ displaystyle \ operatorname {erfc} (x) = {\ frac {e ^ {- x ^ {2}}} {x {\ sqrt {\ pi}}}} \ sum _ {n = 0} ^ {N-1} (- 1) ^ {n} {\ frac {(2n-1) !!} {(2x ^ {2}) ^ {n}}} + R_ {N} (x)}
где остаток в нотации Ландау равен
- RN (x) = O (x 1 — 2 N e — x 2) {\ displaystyle R_ {N} ( x) = O \ left (x ^ {1-2N} e ^ {- x ^ {2}} \ right)}
при x → ∞. {\ displaystyle x \ to \ infty.}
Действительно, точное значение остатка равно
- R N (x): = (- 1) N π 2 1 — 2 N (2 N)! N! ∫ Икс ∞ T — 2 N e — T 2 dt, {\ Displaystyle R_ {N} (x): = {\ frac {(-1) ^ {N}} {\ sqrt {\ pi}}} 2 ^ { 1-2N} {\ frac {(2N)!} {N!}} \ Int _ {x} ^ {\ infty} t ^ {- 2N} e ^ {- t ^ {2}} \, dt,}
который легко следует по индукции, записывая
- e — t 2 = — (2 t) — 1 (e — t 2) ′ {\ displaystyle e ^ {- t ^ {2}} = — (2t) ^ {- 1} \ left (e ^ {- t ^ {2}} \ right) ‘}
и интегрирование по частям.
Для достаточно больших значений x, только первые несколько этих асимптотических разностей необходимы, чтобы получить хорошее приближение erfc (x) (в то время как для не слишком больших значений x приведенное выше разложение Тейлора при 0 обеспечивает очень быструю сходимость).
Расширение непрерывной дроби
A Разложение непрерывной дроби дополнительные функции ошибок:
- erfc (z) = z π e — z 2 1 z 2 + a 1 1 + a 2 z 2 + a 3 1 + ⋯ am = м 2. {\ displaystyle \ operatorname {erfc} (z) = {\ frac {z} {\ sqrt {\ pi}}} e ^ {- z ^ {2}} {\ cfrac {1} {z ^ {2} + {\ cfrac {a_ {1}} {1 + {\ cfrac {a_ {2}} {z ^ {2} + {\ cfrac {a_ {3}} {1+) \ dotsb}}}}}}}} \ qquad a_ {m} = {\ frac {m} {2}}.}
Интеграл функции ошибок с функцией плотности Гаусса
- ∫ — ∞ ∞ erf (ax + б) 1 2 π σ 2 е — (Икс — μ) 2 2 σ 2 dx знак равно erf [a μ + b 1 + 2 a 2 σ 2], a, b, μ, σ ∈ R {\ displaystyle \ int _ {- \ infty} ^ {\ infty} \ operatorname {erf} \ left (ax + b \ right) {\ frac {1} {\ sqrt {2 \ pi \ sigma ^ {2}}}} e ^ {- {\ frac {(x- \ mu) ^ {2}} {2 \ sigma ^ {2}}}} \, dx = \ operatorname {erf} \ left [{\ frac {a \ mu + b } {\ sqrt {1 + 2a ^ {2} \ sigma ^ {2}}} \ right], \ qquad a, b, \ mu, \ sigma \ in \ mathbb {R}}
Факториальный ряд
- Обратное:
-
- erfc z = e — z 2 π z ∑ n = 0 ∞ (- 1) n Q n (z 2 + 1) n ¯ = e — z 2 π z (1 — 1 2 1 (z 2 + 1) + 1 4 1 (z 2 + 1) (z 2 + 2) — ⋯) {\ displaystyle {\ begin {align} \ operatorname {erfc} z = {\ frac {e ^ {- z ^ {2}}} {{\ sqrt {\ pi}} \, z}} \ sum _ {n = 0} ^ {\ infty} {\ frac {(-1) ^ {n} Q_ {n}} {{(z ^ {2} + 1)} ^ {\ ba r {n}}}} \\ = {\ frac {e ^ {- z ^ {2}}} {{\ sqrt {\ pi}} \, z}} \ left ( 1 — {\ frac {1} {2}} {\ frac {1} {(z ^ {2} +1)}} + {\ frac {1} {4}} {\ frac {1} {(z ^ {2} +1) (z ^ {2} +2)}} — \ cdots \ right) \ end {align}}}
- erfc z = e — z 2 π z ∑ n = 0 ∞ (- 1) n Q n (z 2 + 1) n ¯ = e — z 2 π z (1 — 1 2 1 (z 2 + 1) + 1 4 1 (z 2 + 1) (z 2 + 2) — ⋯) {\ displaystyle {\ begin {align} \ operatorname {erfc} z = {\ frac {e ^ {- z ^ {2}}} {{\ sqrt {\ pi}} \, z}} \ sum _ {n = 0} ^ {\ infty} {\ frac {(-1) ^ {n} Q_ {n}} {{(z ^ {2} + 1)} ^ {\ ba r {n}}}} \\ = {\ frac {e ^ {- z ^ {2}}} {{\ sqrt {\ pi}} \, z}} \ left ( 1 — {\ frac {1} {2}} {\ frac {1} {(z ^ {2} +1)}} + {\ frac {1} {4}} {\ frac {1} {(z ^ {2} +1) (z ^ {2} +2)}} — \ cdots \ right) \ end {align}}}
- сходится для Re (z 2)>0. {\ displaystyle \ operatorname {Re} (z ^ {2})>0.}
Здесь
- Q n = def 1 Γ (1/2) ∫ 0 ∞ τ (τ — 1) ⋯ ( τ — n + 1) τ — 1/2 е — τ d τ знак равно ∑ К знак равно 0 N (1 2) к ¯ s (n, k), {\ displaystyle Q_ {n} {\ stackrel {\ text {def}} {=}} {\ frac {1} {\ Gamma (1/2)}} \ int _ {0} ^ {\ infty} \ tau (\ tau -1) \ cdots (\ tau -n + 1) \ tau ^ {-1/2} e ^ {- \ tau} d \ tau = \ sum _ {k = 0} ^ {n} \ left ({\ frac {1} {2}} \ right) ^ {\ bar {k}} s (n, k),}
- Q n = def 1 Γ (1/2) ∫ 0 ∞ τ (τ — 1) ⋯ ( τ — n + 1) τ — 1/2 е — τ d τ знак равно ∑ К знак равно 0 N (1 2) к ¯ s (n, k), {\ displaystyle Q_ {n} {\ stackrel {\ text {def}} {=}} {\ frac {1} {\ Gamma (1/2)}} \ int _ {0} ^ {\ infty} \ tau (\ tau -1) \ cdots (\ tau -n + 1) \ tau ^ {-1/2} e ^ {- \ tau} d \ tau = \ sum _ {k = 0} ^ {n} \ left ({\ frac {1} {2}} \ right) ^ {\ bar {k}} s (n, k),}
- zn ¯ {\ displaystyle z ^ {\ bar {n}}}
обозначает возрастающий факториал, а s (n, k) {\ displaystyle s (n, k)}
обозначает знаковое число Стирлинга первого рода.
- Представление бесконечной суммой, составляющей двойной факториал :
-
- ERF (Z) знак равно 2 π ∑ N знак равно 0 ∞ (- 2) N (2 N — 1)! (2 N + 1)! Z 2 N + 1 {\ Displaystyle \ OperatorName {ERF} (г) = {\ frac {2} {\ sqrt {\ pi}}} \ sum _ {n = 0} ^ {\ infty} {\ frac {( -2) ^ {n} (2n-1) !!} {(2n + 1)!}} Z ^ {2n + 1}}
- ERF (Z) знак равно 2 π ∑ N знак равно 0 ∞ (- 2) N (2 N — 1)! (2 N + 1)! Z 2 N + 1 {\ Displaystyle \ OperatorName {ERF} (г) = {\ frac {2} {\ sqrt {\ pi}}} \ sum _ {n = 0} ^ {\ infty} {\ frac {( -2) ^ {n} (2n-1) !!} {(2n + 1)!}} Z ^ {2n + 1}}
Численные приближения
Приближение элементов сарными функциями
- Абрамовиц и Стегун дают несколько приближений с точностью (уравнения 7.1.25–28). Это позволяет выбрать наиболее быстрое приближение, подходящее для данного приложения. В порядке увеличения точности они следующие:
-
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + a 3 x 3 + a 4 x 4) 4, x ≥ 0 {\ displaystyle \ имя оператора {erf} (x) \ приблизительно 1 — {\ frac {1} {(1 + a_ {1} x + a_ {2} x ^ {2} + a_ {3} x ^ {3} + a_ { 4} x ^ {4}) ^ {4}}}, \ qquad x \ geq 0}
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + a 3 x 3 + a 4 x 4) 4, x ≥ 0 {\ displaystyle \ имя оператора {erf} (x) \ приблизительно 1 — {\ frac {1} {(1 + a_ {1} x + a_ {2} x ^ {2} + a_ {3} x ^ {3} + a_ { 4} x ^ {4}) ^ {4}}}, \ qquad x \ geq 0}
- (максимальная ошибка: 5 × 10)
- , где a 1 = 0,278393, a 2 = 0,230389, a 3 = 0,000972, a 4 = 0,078108
-
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + a 3 t 3) e — x 2, t = 1 1 + px, x ≥ 0 {\ displaystyle \ operatorname {erf} (x) \ приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + a_ {3} t ^ {3}) e ^ {- x ^ {2}}, \ quad t = {\ frac {1} {1 + px}}, \ qquad x \ geq 0}
(максимальная ошибка: 2,5 × 10)
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + a 3 t 3) e — x 2, t = 1 1 + px, x ≥ 0 {\ displaystyle \ operatorname {erf} (x) \ приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + a_ {3} t ^ {3}) e ^ {- x ^ {2}}, \ quad t = {\ frac {1} {1 + px}}, \ qquad x \ geq 0}
- где p = 0,47047, a 1 = 0,3480242, a 2 = -0,0958798, a 3 = 0,7478556
-
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + ⋯ + a 6 x 6) 16, x ≥ 0 {\ displaystyle \ operatorname {erf} (x) \ приблизительно 1 — {\ frac {1} {(1 + a_ {1} x + a _ {2} x ^ {2} + \ cdots + a_ {6} x ^ {6}) ^ {16}}}, \ qquad x \ geq 0}
(максимальная ошибка: 3 × 10)
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + ⋯ + a 6 x 6) 16, x ≥ 0 {\ displaystyle \ operatorname {erf} (x) \ приблизительно 1 — {\ frac {1} {(1 + a_ {1} x + a _ {2} x ^ {2} + \ cdots + a_ {6} x ^ {6}) ^ {16}}}, \ qquad x \ geq 0}
- , где a 1 = 0,0705230784, a 2 = 0,0422820123, a 3 = 0,0092705272, a 4 = 0,0001520143, a 5 = 0,0002765672, a 6 = 0,0000430638
-
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + ⋯ + a 5 t 5) e — x 2, t = 1 1 + px {\ displaystyle \ operatorname {erf} (x) \ приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + \ cdots + a_ {5} t ^ {5}) e ^ {- x ^ {2}}, \ quad t = {\ frac {1} {1 + px}}}
(максимальная ошибка: 1,5 × 10)
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + ⋯ + a 5 t 5) e — x 2, t = 1 1 + px {\ displaystyle \ operatorname {erf} (x) \ приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + \ cdots + a_ {5} t ^ {5}) e ^ {- x ^ {2}}, \ quad t = {\ frac {1} {1 + px}}}
- , где p = 0,3275911, a 1 = 0,254829592, a 2 = −0,284496736, a 3 = 1,421413741, a 4 = −1,453152027, a 5 = 1,061405429
- Все эти приближения действительны для x ≥ 0 Чтобы использовать эти приближения для отрицательного x, викорируйте тот факт, что erf (x) — нечетная функция, поэтому erf (x) = −erf (−x).
- Экспоненциальные границы и чисто экспоненциальное приближение для дополнительных функций задаются как
-
- erfc (x) ≤ 1 2 e — 2 x 2 + 1 2 e — x 2 ≤ e — x 2, x>0 erfc ( х) ≈ 1 6 е — х 2 + 1 2 е — 4 3 х 2, х>0. {\ displaystyle {\ begin {align} \ operatorname {erfc} (x) \ leq {\ frac {1} {2}} e ^ {- 2x ^ {2}} + {\ frac {1} {2} } e ^ {- x ^ {2}} \ leq e ^ {- x ^ {2}}, \ qquad x>0 \\\ имя оператора {erfc} (x) \ приблизительно {\ frac {1} { 6}} e ^ {- x ^ {2}} + {\ frac {1} {2}} e ^ {- {\ frac {4} {3}} x ^ {2}}, \ qquad x>0. \ end {align}}}
- erfc (x) ≤ 1 2 e — 2 x 2 + 1 2 e — x 2 ≤ e — x 2, x>0 erfc ( х) ≈ 1 6 е — х 2 + 1 2 е — 4 3 х 2, х>0. {\ displaystyle {\ begin {align} \ operatorname {erfc} (x) \ leq {\ frac {1} {2}} e ^ {- 2x ^ {2}} + {\ frac {1} {2} } e ^ {- x ^ {2}} \ leq e ^ {- x ^ {2}}, \ qquad x>0 \\\ имя оператора {erfc} (x) \ приблизительно {\ frac {1} { 6}} e ^ {- x ^ {2}} + {\ frac {1} {2}} e ^ {- {\ frac {4} {3}} x ^ {2}}, \ qquad x>0. \ end {align}}}
-
- erfc (x) ≈ (1 — e — A x) e — x 2 B π х. {\ displaystyle \ operatorname {erfc} \ left (x \ right) \ приблизительно {\ frac {\ left (1-e ^ {- Ax} \ right) e ^ {- x ^ {2}}} {B {\ sqrt {\ pi}} x}}.}
- erfc (x) ≈ (1 — e — A x) e — x 2 B π х. {\ displaystyle \ operatorname {erfc} \ left (x \ right) \ приблизительно {\ frac {\ left (1-e ^ {- Ax} \ right) e ^ {- x ^ {2}}} {B {\ sqrt {\ pi}} x}}.}
- Они определили {A, B} = {1.98, 1.135}, {\ displaystyle \ {A, B \} = \ {1.98,1.135 \ },}
, что дает хорошее приближение для всех x ≥ 0. {\ displaystyle x \ geq 0.}
- Одноканальная нижняя граница:
-
- erfc (x) ≥ 2 e π β — 1 β е — β Икс 2, Икс ≥ 0, β>1, {\ Displaystyle \ OperatorName {erfc} (x) \ geq {\ sqrt {\ frac {2e} {\ pi}}} {\ frac {\ sqrt {\ beta -1}} {\ beta}} e ^ {- \ beta x ^ {2}}, \ qquad x \ geq 0, \ beta>1,}
- erfc (x) ≥ 2 e π β — 1 β е — β Икс 2, Икс ≥ 0, β>1, {\ Displaystyle \ OperatorName {erfc} (x) \ geq {\ sqrt {\ frac {2e} {\ pi}}} {\ frac {\ sqrt {\ beta -1}} {\ beta}} e ^ {- \ beta x ^ {2}}, \ qquad x \ geq 0, \ beta>1,}
- где параметр β может быть выбран, чтобы минимизировать ошибку на желаемом интервале приближения.
- Другое приближение дано Сергеем Виницким с использованием его «глобальных приближений Паде»:
-
- erf (x) ≈ sgn (x) 1 — exp (- x 2 4 π + ax 2 1 + ax 2) { \ displaystyle \ operatorname {erf} (x) \ приблизительно \ Operatorname {sgn} (x) {\ sqrt {1- \ exp \ left (-x ^ {2} {\ frac {{\ frac {4} {\ pi) })} + ax ^ {2}} {1 + ax ^ {2}}} \ right)}}}
- erf (x) ≈ sgn (x) 1 — exp (- x 2 4 π + ax 2 1 + ax 2) { \ displaystyle \ operatorname {erf} (x) \ приблизительно \ Operatorname {sgn} (x) {\ sqrt {1- \ exp \ left (-x ^ {2} {\ frac {{\ frac {4} {\ pi) })} + ax ^ {2}} {1 + ax ^ {2}}} \ right)}}}
- где
-
- a = 8 (π — 3) 3 π (4 — π) ≈ 0, 140012. {\ displaystyle a = {\ frac {8 (\ pi -3)} {3 \ pi (4- \ pi)}} \ приблизительно 0,140012.}
- a = 8 (π — 3) 3 π (4 — π) ≈ 0, 140012. {\ displaystyle a = {\ frac {8 (\ pi -3)} {3 \ pi (4- \ pi)}} \ приблизительно 0,140012.}
- Это сделано так, чтобы быть очень точным в окрестностях 0 и добавление бесконечности, а относительная погрешность меньше 0,00035 для всех действительных x. Использование альтернативного значения ≈ 0,147 снижает максимальную относительную ошибку примерно до 0,00013.
- Это приближение можно инвертировать, чтобы получить приближение для других функций ошибок:
-
- erf — 1 (x) ≈ sgn (x) (2 π a + ln (1 — x 2) 2) 2 — ln (1 — x 2) a — (2 π a + ln (1 — x 2) 2). {\ displaystyle \ operatorname {erf} ^ {- 1} (x) \ приблизительно \ operatorname {sgn} (x) {\ sqrt {{\ sqrt {\ left ({\ frac {2} {\ pi a}} + {\ frac {\ ln (1-x ^ {2})} {2}} \ right) ^ {2} — {\ frac {\ ln (1-x ^ {2})} {a}}}} — \ left ({\ frac {2} {\ pi a}} + {\ frac {\ ln (1-x ^ {2})} {2}} \ right)}}.}
- erf — 1 (x) ≈ sgn (x) (2 π a + ln (1 — x 2) 2) 2 — ln (1 — x 2) a — (2 π a + ln (1 — x 2) 2). {\ displaystyle \ operatorname {erf} ^ {- 1} (x) \ приблизительно \ operatorname {sgn} (x) {\ sqrt {{\ sqrt {\ left ({\ frac {2} {\ pi a}} + {\ frac {\ ln (1-x ^ {2})} {2}} \ right) ^ {2} — {\ frac {\ ln (1-x ^ {2})} {a}}}} — \ left ({\ frac {2} {\ pi a}} + {\ frac {\ ln (1-x ^ {2})} {2}} \ right)}}.}
Многочлен
Приближение с максимальной ошибкой 1,2 × 10-7 {\ displaystyle 1,2 \ times 10 ^ {- 7}}
- erf ( x) = {1 — τ x ≥ 0 τ — 1 x < 0 {\displaystyle \operatorname {erf} (x)={\begin{cases}1-\tau x\geq 0\\\tau -1x<0\end{cases}}}
с
- τ = t ⋅ exp (- x 2 — 1,26551223 + 1,00002368 t + 0,37409196 t 2 + 0,09678418 t 3 — 0,18628806 t 4 + 0,27886807 t 5 — 1,13520398 t 6 + 1,48851587 t 7 — 0,82215223 t 8 + 0,17087277 t 9) {\ displaystyle {\ begin {align} \ tau = t \ cdot \ exp \ left (-x ^ {2} -1,26551223 + 1,00002368 t + 0,37409196t ^ {2} + 0,09678418t ^ {3} -0,18628806t ^ {4} \ вправо. \\ \ left. \ qquad \ qquad \ qquad + 0,27886807t ^ {5} -1,13520398t ^ {6} + 1,48851587t ^ {7} -0,82215223t ^ {8} + 0,17087 277t ^ {9} \ right) \ end {align}}}
и
- t = 1 1 + 0,5 | х |. {\ displaystyle t = {\ frac {1} {1 + 0,5 | x |}}.}
Таблица значений
| x | erf(x) | 1-erf (x) |
|---|---|---|
| 0 | 0 | 1 |
| 0,02 | 0,022564575 | 0,977435425 |
| 0,04 | 0,045111106 | 0,954888894 |
| 0,06 | 0,067621594 | 0, 932378406 |
| 0,08 | 0.090078126 | 0,909921874 |
| 0,1 | 0,112462916 | 0,887537084 |
| 0,2 | 0,222702589 | 0,777297411 |
| 0,3 | 0,328626759 | 0,671373241 |
| 0, 4 | 0,428392355 | 0,571607645 |
| 0,5 | 0,520499878 | 0,479500122 |
| 0,6 | 0.603856091 | 0,396143909 |
| 0,7 | 0,677801194 | 0,322198806 |
| 0,8 257> | 0,742100965 | 0,257899035 |
| 0,9 | 0,796908212 | 0,203091788 |
| 1 | 0,842700793 | 0, 157299207 |
| 1,1 | 0,88020507 | 0,11979493 |
| 1,2 | 0,910313978 | 0,089686022 |
| 1,3 | 0,934007945 | 0,065992055 |
| 1,4 | 0.95228512 | 0,04771488 |
| 1,5 | 0, 966105146 | 0,033894854 |
| 1,6 | 0,976348383 | 0,023651617 |
| 1,7 | 0,983790459 | 0,016209541 |
| 1,8 | 0,989090502 | 0,010909498 |
| 1,9 | 0,992790429 | 0,007209571 |
| 2 | 0,995322265<25767> | 0,00477 |
| 2.1 | 0.997020533 | 0.002979467 |
| 2.2 | 0.998137154 | 0,001862846 |
| 2,3 | 0,998856823 | 0,001143177 |
| 2,4 | 0,999311486 | 0,000688514 |
| 2,5 | 0.999593048 | 0.000406952 |
| 3 | 0.99997791 | 0,00002209 |
| 3,5 | 0,999999257 | 0,000000743 |
Связанные функции
Дополнительная функция
дополнительная функция ошибок, обозначается erfc {\ displaystyle \ mathrm {erfc}}
- erfc (x) = 1 — erf (x) = 2 π ∫ x ∞ e — t 2 dt знак равно е — Икс 2 erfcx (х), {\ displaystyle {\ begin {выровнено} \ OperatorName {erfc} (x) = 1- \ operatorname {erf} (x) \\ [5p t] = {\ frac {2} {\ sqrt {\ pi}}} \ int _ {x} ^ {\ infty} e ^ {- t ^ {2}} \, dt \\ [5pt] = e ^ {- x ^ {2}} \ operatorname {erfcx} (x), \ end {align}}}
, который также определяет erfcx {\ displaystyle \ mathrm {erfcx} }


- erfc (x ∣ x ≥ 0) = 2 π ∫ 0 π / 2 exp (- x 2 sin 2 θ) d θ. {\ displaystyle \ operatorname {erfc} (x \ mid x \ geq 0) = {\ frac {2} {\ pi}} \ int _ {0} ^ {\ pi / 2} \ exp \ left (- {\ frac {x ^ {2}} {\ sin ^ {2} \ theta}} \ right) \, d \ theta.}
Это выражение действительно только для положительных значений x, но его можно использовать вместе с erfc (x) = 2 — erfc (−x), чтобы получить erfc (x) для отрицательных значений. Эта форма выгодна тем, что диапазон интегрирования является фиксированным и конечным. Расширение этого выражения для erfc {\ displaystyle \ mathrm {erfc}}
- erfc (x + y ∣ x, y ≥ 0) = 2 π ∫ 0 π / 2 ехр (- x 2 sin 2 θ — y 2 cos 2 θ) d θ. {\ displaystyle \ operatorname {erfc} (x + y \ mid x, y \ geq 0) = {\ frac {2} {\ pi}} \ int _ {0} ^ {\ pi / 2} \ exp \ left (- {\ frac {x ^ {2}} {\ sin ^ {2} \ theta}} — {\ frac {y ^ {2}} {\ cos ^ {2} \ theta}} \ right) \, d \ theta.}
Функция мнимой ошибки
мнимой ошибки, обозначаемая erfi, обозначает ошибки как
- erfi (x) = — i erf (ix) Знак равно 2 π ∫ 0 xet 2 dt знак равно 2 π ex 2 D (x), {\ displaystyle {\ begin {align} \ operatorname {erfi} (x) = — i \ operatorname {erf} (ix) \\ [ 5pt] = {\ frac {2} {\ sqrt {\ pi}}} \ int _ {0} ^ {x} e ^ {t ^ {2}} \, dt \\ [5pt] = {\ frac {2} {\ sqrt {\ pi}}} e ^ {x ^ {2}} D (x), \ end {align}}}
где D (x) — функция Доусона (который можно использовать вместо erfi, чтобы избежать арифметического переполнения ).
Несмотря на название «функция мнимой ошибки», erfi (x) {\ displaystyle \ operatorname {erfi} (x)}
Функция Когда ошибки оценивается для произвольных сложных аргументов z, результирующая комплексная функция ошибок обычно обсуждается в масштабированной форме как функция Фаддеева :
- w (z) = e — z 2 erfc (- iz) = erfcx (- iz). {\ displaystyle w (z) = e ^ {- z ^ {2}} \ operatorname {erfc} (-iz) = \ operatorname {erfcx} (-iz).}
Кумулятивная функция распределения
Функция ошибок по существующей стандартной стандартной функции нормального кумулятивного распределения, обозначаемой нормой (x) в некоторых языках программного обеспечения, поскольку они отличаются только масштабированием и переводом. Действительно,
- Φ (x) = 1 2 π ∫ — ∞ xe — t 2 2 dt = 1 2 [1 + erf (x 2)] = 1 2 erfc (- x 2) {\ displaystyle \ Phi (x) = {\ frac {1} {\ sqrt {2 \ pi}}} \ int _ {- \ infty} ^ {x} e ^ {\ tfrac {-t ^ {2}} {2}} \, dt = {\ frac {1} {2}} \ left [1+ \ operatorname {erf} \ left ({\ frac {x} {\ sqrt {2}}} \ right) \ right] = {\ frac {1} {2}} \ operatorname {erfc} \ left (- {\ frac {x} {\ sqrt {2}}} \ right)}
или переставлен для erf и erfc:
- erf ( x) = 2 Φ (x 2) — 1 erfc (x) = 2 Φ (- x 2) = 2 (1 — Φ (x 2)). {\ displaystyle {\ begin {align} \ operatorname {erf} (x) = 2 \ Phi \ left (x {\ sqrt {2}} \ right) -1 \\\ operatorname {erfc} (x) = 2 \ Phi \ left (-x {\ sqrt {2}} \ right) = 2 \ left (1- \ Phi \ left (x {\ sqrt {2}} \ right) \ right). \ End {выравнивается} }}
Следовательно, функция ошибок также тесно связана с Q-функцией, которая является вероятностью хвоста стандартного нормального распределения. Q-функция может быть выражена через функцию ошибок как
- Q (x) = 1 2 — 1 2 erf (x 2) = 1 2 erfc (x 2). {\ displaystyle Q (x) = {\ frac {1} {2}} — {\ frac {1} {2}} \ operatorname {erf} \ left ({\ frac {x} {\ sqrt {2}}) } \ right) = {\ frac {1} {2}} \ operatorname {erfc} \ left ({\ frac {x} {\ sqrt {2}}} \ right).}
Обратное значение из Φ {\ displaystyle \ Phi}
- пробит (p) = Φ — 1 (p) = 2 erf — 1 (2 p — 1) = — 2 erfc — 1 (2 p). {\ displaystyle \ operatorname {probit} (p) = \ Phi ^ {- 1} (p) = {\ sqrt {2}} \ operatorname {erf} ^ {- 1} (2p-1) = — {\ sqrt {2}} \ operatorname {erfc} ^ {- 1} (2p).}
Стандартный нормальный cdf чаще используется в вероятности и статистике, а функция ошибок чаще используется в других разделах математики.
Функция ошибки является частным случаем функции Миттаг-Леффлера и может также быть выражена как сливающаяся гипергеометрическая функция (функция Куммера):
- erf (х) знак равно 2 х π M (1 2, 3 2, — х 2). {\ displaystyle \ operatorname {erf} (x) = {\ frac {2x} {\ sqrt {\ pi}}} M \ left ({\ frac {1} {2}}, {\ frac {3} {2 }}, — x ^ {2} \ right).}
Он имеет простое выражение в терминах интеграла Френеля.
В терминах регуляризованной гамма-функции P и неполная гамма-функция,
- erf (x) = sgn (x) P (1 2, x 2) = sgn (x) π γ (1 2, x 2). {\ displaystyle \ operatorname {erf} (x) = \ operatorname {sgn} (x) P \ left ({\ frac {1} {2}}, x ^ {2} \ right) = {\ frac {\ operatorname {sgn} (x)} {\ sqrt {\ pi}}} \ gamma \ left ({\ frac {1} {2}}, x ^ {2} \ right).}
sgn (x) {\ displaystyle \ operatorname {sgn} (x)}
Обобщенные функции ошибок

π {\ displaystyle \ scriptstyle {\ sqrt {\ pi}}}

Некоторые авторы обсуждают более общие функции:
- E n (x) = n! π ∫ 0 Икс е — Т N д т знак равно N! π ∑ п знак равно 0 ∞ (- 1) п Икс N п + 1 (N п + 1) п!. {\ displaystyle E_ {n} (x) = {\ frac {n!} {\ sqrt {\ pi}}} \ int _ {0} ^ {x} e ^ {- t ^ {n}} \, dt = {\ frac {n!} {\ sqrt {\ pi}}} \ sum _ {p = 0} ^ {\ infty} (- 1) ^ {p} {\ frac {x ^ {np + 1}} {(np + 1) p!}}.}
Примечательные случаи:
- E0(x) — прямая линия, проходящая через начало координат: E 0 (x) = xe π {\ displaystyle \ textstyle E_ {0} (x) = {\ dfrac {x} {e {\ sqrt {\ pi}}}}}
- E2(x) — функция, erf (x) ошибки.
После деления на n!, все E n для нечетных n выглядят похожими (но не идентичными) друг на друга. Аналогично, E n для четного n выглядят похожими (но не идентичными) друг другу после простого деления на n!. Все обобщенные функции ошибок для n>0 выглядят одинаково на положительной стороне x графика.
Эти обобщенные функции могут быть эквивалентно выражены для x>0 с помощью гамма-функции и неполной гамма-функции :
- E n (x) = 1 π Γ (n) (Γ (1 n) — Γ (1 n, xn)), x>0. {\ displaystyle E_ {n} (x) = {\ frac {1} {\ sqrt {\ pi}}} \ Gamma (n) \ left (\ Gamma \ left ({\ frac {1} {n}} \ right) — \ Gamma \ left ({\ frac {1} {n}}, x ^ {n} \ right) \ right), \ quad \ quad x>0.}
Следовательно, мы можем определить ошибку функция в терминах неполной гамма-функции:
- erf (x) = 1 — 1 π Γ (1 2, x 2). {\ displaystyle \ operatorname {erf} (x) = 1 — {\ frac {1} { \ sqrt {\ pi}}} \ Gamma \ left ({\ frac {1} {2}}, x ^ {2} \ right).}
Итерированные интегралы дополнительных функций
Повторные интегралы дополнительные функции ошибок определения как
- inerfc (z) = ∫ z ∞ in — 1 erfc (ζ) d ζ i 0 erfc (z) = erfc (z) i 1 erfc (z) = ierfc (z) знак равно 1 π е — z 2 — z erfc (z) я 2 erfc (z) = 1 4 [erfc (z) — 2 z ierfc (z)] {\ displaystyle {\ begin {align } \ operatorname {i ^ {n} erfc} (z) = \ int _ {z} ^ {\ infty} \ operatorname {i ^ {n-1} erfc} (\ zeta) \, d \ zeta \\\ имя оператора {i ^ {0} erfc} (z) = \ operatorname {erfc} (z) \\\ operatorname {i ^ {1} erfc} (z) = \ operat orname {ierfc} (z) = {\ frac { 1} {\ sqrt {\ pi}}} e ^ {- z ^ {2}} — z \ operatorname {erfc} (z) \\\ operatorname {i ^ {2} erfc} (z) = {\ frac {1} {4}} \ left [\ operatorname {erfc} (z) -2z \ operatorname {ierfc} (z) \ right] \\\ end {выровнено}}
Общая рекуррентная формула:
- 2 ninerfc (z) = in — 2 erfc (z) — 2 цинк — 1 erfc (z) {\ displaystyle 2n \ operatorname {i ^ {n} erfc} (z) = \ operatorname {i ^ { n-2} erfc} (z) -2z \ operatorname {i ^ {n-1} erfc} (z)}
У них есть степенной ряд
- в erfc (z) = ∑ j = 0 ∞ (- Z) J 2 N — JJ! Γ (1 + N — J 2), {\ displaystyle i ^ {n} \ operatorname {erfc} (z) = \ sum _ {j = 0} ^ {\ infty} {\ frac {(-z) ^ { j}} {2 ^ {nj} j! \ Gamma \ left (1 + {\ frac {nj} {2}} \ right)}},}
из следуют свойства симметрии
- i 2 m ERFC (- Z) знак равно — я 2 m ERFC (Z) + ∑ Q знак равно 0 мZ 2 д 2 2 (м — д) — 1 (2 д)! (м — д)! {\ displaystyle i ^ {2m} \ operatorname {erfc} (-z) = — i ^ {2m} \ operatorname {erfc} (z) + \ sum _ {q = 0} ^ {m} {\ frac {z ^ {2q}} {2 ^ {2 (mq) -1} (2q)! (Mq)!}}}
и
- i 2 m + 1 erfc (- z) = i 2 m + 1 erfc (г) + ∑ ä знак равно 0 ìZ 2 ä + 1 2 2 ( м — д) — 1 (2 д + 1)! (м — д)!. {\ displaystyle i ^ {2m + 1} \ operatorname {erfc} (-z) = i ^ {2m + 1} \ operatorname {erfc} (z) + \ sum _ {q = 0} ^ {m} {\ гидроразрыва {z ^ {2q + 1}} {2 ^ {2 (mq) -1} (2q + 1)! (mq)!}}.}
Реализации
Как действительная функция вещественного аргумента
- В операционных системах, совместимых с Posix, заголовок math.h должен являть, а математическая библиотека libm должна быть функция erf и erfc (двойная точность ), а также их одинарная точность и расширенная точность аналоги erff, erfl и erfc, erfcl.
- Библиотека GNU Scientific предоставляет функции erf, erfc, log (erf) и масштабируемые функции ошибок.
Как сложная функция комплексного аргумента
- libcerf, числовая библиотека C для сложных функций, предоставляет комплексные функции cerf, cerfc, cerfcx и реальные функции erfi, erfcx с точностью 13–14 цифр на основе функции Фаддеева, реализованной в пакете MIT Faddeeva Package
См. также
Связанные ции
- интеграл Гаусса, по всей действительной прямой
- функция Гаусса, производная
- функция Доусона, перенормированная функция мнимой ошибки
- интеграл Гудвина — Стона
по вероятности
- Нормальное распределение
- Нормальная кумулятивная функция распределения, масштабированная и сдвинутая форма функций ошибок
- Пробит, обратная или квантильная функция нормального CDF
- Q-функция, вероятность хвоста нормального распределения
Ссылки
Дополнительная литература
- Abramowitz, Milton ; Стегун, Ирен Энн, ред. (1983) [июнь 1964]. «Глава 7». Справочник по математическим функциям с формулами, графики и математическими таблицами. Прикладная математика. 55 (Девятое переиздание с дополнительными исправлениями; десятое оригинальное издание с исправлениями (декабрь 1972 г.); первое изд.). Вашингтон.; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Dover Publications. п. 297. ISBN 978-0-486-61272-0 . LCCN 64-60036. MR 0167642. LCCN 65-12253.
- Press, William H.; Теукольский, Саул А.; Веттерлинг, Уильям Т.; Фланнери, Брайан П. (2007), «Раздел 6.2. Неполная гамма-функция и функция ошибок », Числовые рецепты: Искусство научных вычислений (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN 978-0-521- 88068-8
- Темме, Нико М. (2010), «Функции ошибок, интегралы Доусона и Френеля», в Олвер, Фрэнк У. Дж. ; Лозье, Даниэль М.; Бойсверт, Рональд Ф.; Кларк, Чарльз В. (ред.), Справочник NIST по математическим функциям, Cambridge University Press, ISBN 978-0-521-19225-5 , MR 2723248
Внешние ссылки
- MathWorld — Erf
- Таблица интегралов функций ошибок






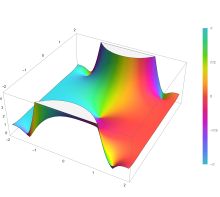
![{\displaystyle {\begin{aligned}\Pr[X\leq L]&={\frac {1}{2}}+{\frac {1}{2}}\operatorname {erf} {\frac {L-\mu }{{\sqrt {2}}\sigma }}\\&\approx A\exp \left(-B\left({\frac {L-\mu }{\sigma }}\right)^{2}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3cb760eaf336393db9fd0bb12c4465655a27de8)
![{\displaystyle \Pr[X\leq L]\leq A\exp(-B\ln {k})={\frac {A}{k^{B}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2baadea015e20a45d1034fd88eed861e7fcce178)
![{\displaystyle {\begin{aligned}\Pr[L_{a}\leq X\leq L_{b}]&=\int _{L_{a}}^{L_{b}}{\frac {1}{{\sqrt {2\pi }}\sigma }}\exp \left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)\,\mathrm {d} x\\&={\frac {1}{2}}\left(\operatorname {erf} {\frac {L_{b}-\mu }{{\sqrt {2}}\sigma }}-\operatorname {erf} {\frac {L_{a}-\mu }{{\sqrt {2}}\sigma }}\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd2214f0db2c1d36075815825b616501175c6283)
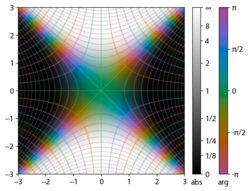


![{\displaystyle {\begin{aligned}\operatorname {erf} z&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{2n+1}}{n!(2n+1)}}\\[6pt]&={\frac {2}{\sqrt {\pi }}}\left(z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{10}}-{\frac {z^{7}}{42}}+{\frac {z^{9}}{216}}-\cdots \right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c80541f305af070bb0510625c584fe1559a0cd2c)
![{\displaystyle {\begin{aligned}\operatorname {erf} z&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }\left(z\prod _{k=1}^{n}{\frac {-(2k-1)z^{2}}{k(2k+1)}}\right)\\[6pt]&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {z}{2n+1}}\prod _{k=1}^{n}{\frac {-z^{2}}{k}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dca22e8e7dee0297e87a455249c282c6b92fedcb)
![{\displaystyle {\begin{aligned}\operatorname {erfi} z&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {z^{2n+1}}{n!(2n+1)}}\\[6pt]&={\frac {2}{\sqrt {\pi }}}\left(z+{\frac {z^{3}}{3}}+{\frac {z^{5}}{10}}+{\frac {z^{7}}{42}}+{\frac {z^{9}}{216}}+\cdots \right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ff91095cd6825137cc951ec0a786db0b7f68fac)





![{\displaystyle {\begin{aligned}\operatorname {erf} x&={\frac {2}{\sqrt {\pi }}}\operatorname {sgn} x\cdot {\sqrt {1-e^{-x^{2}}}}\left(1-{\frac {1}{12}}\left(1-e^{-x^{2}}\right)-{\frac {7}{480}}\left(1-e^{-x^{2}}\right)^{2}-{\frac {5}{896}}\left(1-e^{-x^{2}}\right)^{3}-{\frac {787}{276480}}\left(1-e^{-x^{2}}\right)^{4}-\cdots \right)\\[10pt]&={\frac {2}{\sqrt {\pi }}}\operatorname {sgn} x\cdot {\sqrt {1-e^{-x^{2}}}}\left({\frac {\sqrt {\pi }}{2}}+\sum _{k=1}^{\infty }c_{k}e^{-kx^{2}}\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/164e7f029977edb47c83845b04abfe5b2d28b837)







![{\displaystyle {\begin{aligned}\operatorname {erfc} x&={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\left(1+\sum _{n=1}^{\infty }(-1)^{n}{\frac {1\cdot 3\cdot 5\cdots (2n-1)}{\left(2x^{2}\right)^{n}}}\right)\\[6pt]&={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\sum _{n=0}^{\infty }(-1)^{n}{\frac {(2n-1)!!}{\left(2x^{2}\right)^{n}}},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35a11e2e5b22ca898c74f2e913d276c9ac11124a)































![{\displaystyle {\begin{aligned}\operatorname {erfc} x&=1-\operatorname {erf} x\\[5pt]&={\frac {2}{\sqrt {\pi }}}\int _{x}^{\infty }e^{-t^{2}}\,\mathrm {d} t\\[5pt]&=e^{-x^{2}}\operatorname {erfcx} x,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4acd0062271e2a19c209a02c8cc33d44a28af7cc)



![{\displaystyle {\begin{aligned}\operatorname {erfi} x&=-i\operatorname {erf} ix\\[5pt]&={\frac {2}{\sqrt {\pi }}}\int _{0}^{x}e^{t^{2}}\,\mathrm {d} t\\[5pt]&={\frac {2}{\sqrt {\pi }}}e^{x^{2}}D(x),\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfd2dd94cd6d0325224d412f6b5e5ed63ca81d4a)

![{\displaystyle {\begin{aligned}\Phi (x)&={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{x}e^{\tfrac {-t^{2}}{2}}\,\mathrm {d} t\\[6pt]&={\frac {1}{2}}\left(1+\operatorname {erf} {\frac {x}{\sqrt {2}}}\right)\\[6pt]&={\frac {1}{2}}\operatorname {erfc} \left(-{\frac {x}{\sqrt {2}}}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89a9e9eaaddcd7a91ade15a41b8d1e272d437559)
![{\displaystyle {\begin{aligned}\operatorname {erf} (x)&=2\Phi \left(x{\sqrt {2}}\right)-1\\[6pt]\operatorname {erfc} (x)&=2\Phi \left(-x{\sqrt {2}}\right)\\&=2\left(1-\Phi \left(x{\sqrt {2}}\right)\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86c84a4d2d79631fe9996e30f1d6c0da3089bfe2)







![{\displaystyle {\begin{aligned}\operatorname {i} ^{n}\!\operatorname {erfc} z&=\int _{z}^{\infty }\operatorname {i} ^{n-1}\!\operatorname {erfc} \zeta \,\mathrm {d} \zeta \\[6pt]\operatorname {i} ^{0}\!\operatorname {erfc} z&=\operatorname {erfc} z\\\operatorname {i} ^{1}\!\operatorname {erfc} z&=\operatorname {ierfc} z={\frac {1}{\sqrt {\pi }}}e^{-z^{2}}-z\operatorname {erfc} z\\\operatorname {i} ^{2}\!\operatorname {erfc} z&={\tfrac {1}{4}}\left(\operatorname {erfc} z-2z\operatorname {ierfc} z\right)\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3e7b953efaa4d730a5479bd61a2c378c8f761dc)




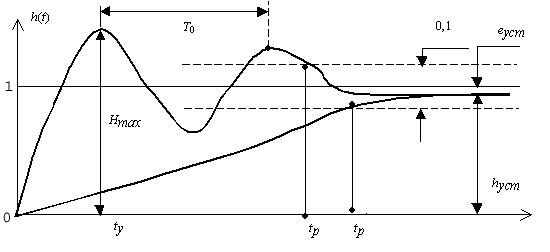


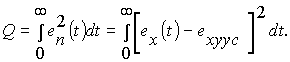

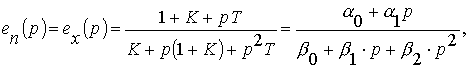
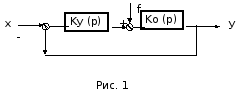
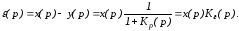

























![{ displaystyle Pr [X leq L ] = { frac {1} {2}} + { frac {1} {2}} operatorname {erf} left ({ frac {L- mu} {{ sqrt {2}} sigma }} right) приблизительно A exp left (-B left ({ frac {L- mu} { sigma}} right) ^ {2} right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a72302c46832449e128a4d4e1adb28b514131270)









![{ displaystyle { begin {align} operatorname {erf} (x) = { frac {2} { sqrt { pi}}} operatorname {sgn} (x) { sqrt {1-e ^ {- x ^ {2}}}} left (1 - { frac {1} {12}} left (1 -e ^ {- x ^ {2}} right) - { frac {7} {480}} left (1-e ^ {- x ^ {2}} right) ^ {2} - { frac {5} {896}} left (1-e ^ {- x ^ {2}} right) ^ {3} - { frac {787} {276480}} left (1-e ^ {- x ^ {2 }} right) ^ {4} - cdots right) \ [10pt] = { frac {2} { sqrt { pi}}} operatorname {sgn} (x) { sqrt {1 -e ^ {- x ^ {2}}}} left ({ frac { sqrt { pi}} {2}} + sum _ {k = 1} ^ { infty} c_ {k} e ^ {- kx ^ {2}} right). end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24ddba05e595a553fee25644a3542188281bd844)







![{ displaystyle operatorname {erfc} (x) = { frac {e ^ {- x ^ {2}}} {x { sqrt { pi}}}} left [1+ sum _ {n = 1} ^ { infty} (-1) ^ {n} { frac {1 cdot 3 cdot 5 cdots (2n-1)} {(2x ^ {2}) ^ { n}}} right] = { frac {e ^ {-x ^ {2}}} {x { sqrt { pi}}}} sum _ {n = 0} ^ { infty} (- 1) ^ {n} { frac {(2n-1) !!} {(2x ^ {2}) ^ {n}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fc8c3aefff3ba787b080c5186dd3aec8ec76ef9)





![{ displaystyle int _ {- infty} ^ { infty} operatorname {erf} left (ax + b right) { frac {1} { sqrt {2 pi sigma ^ {2}}}} e ^ {- { frac {(x- mu) ^ {2}} {2 sigma ^ {2}}}} , dx = operatorname {erf} left [{ frac {a mu + b} { sqrt {1 + 2a ^ {2} sigma ^ {2}}} right], qquad a, b, му, sigma in mathbb {R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b6adc2c661b24b44dc1e3d7e16be70023daacd8)

 обозначает возрастающий факториал, а s (n, k) { displaystyle s (n, k)}
обозначает возрастающий факториал, а s (n, k) { displaystyle s (n, k)} обозначает знаковое число Стирлинга первого рода.
обозначает знаковое число Стирлинга первого рода.

 (максимальная ошибка: 2,5 × 10)
(максимальная ошибка: 2,5 × 10) (максимальная ошибка: 3 × 10)
(максимальная ошибка: 3 × 10) (максимальная ошибка: 1,5 × 10)
(максимальная ошибка: 1,5 × 10)

 , что дает хорошее приближение для всех x ≥ 0. { displaystyle x geq 0.}
, что дает хорошее приближение для всех x ≥ 0. { displaystyle x geq 0.}





![{ displaystyle { begin {align} operatorname {erfc} (x) = 1- operatorname {erf} (x) \ [5pt ] = { frac {2} { sqrt { pi}}} int _ {x} ^ { infty} e ^ {- t ^ {2}} , dt \ [5pt] = e ^ {- x ^ {2}} operatorname {erfcx} (x), end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8808e6f3ad9aab23f14d55db707a39388d256788)


![{ displaystyle { begin {align} operatorname {erfi} (x) = - i operatorname {erf} (ix) \ [5pt] = { frac {2} { sqrt { pi}}} int _ {0} ^ {x} e ^ {t ^ {2 }} , dt \ [5pt] = { frac {2} { sqrt { pi}}} e ^ {x ^ {2}} D (x), end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4480a8ec17e274a7ad6b8ef25cc76234d48c0433)
![{ displaystyle Phi (x) = { frac {1} { sqrt {2 pi}}} int _ {- infty} ^ {x } e ^ { tfrac {-t ^ {2}} {2}} , dt = { frac {1} {2}} left [1+ operatorname {erf} left ({ frac {x } { sqrt {2}}} right) right] = { frac {1} {2}} operatorname {erfc} left (- { frac {x} { sqrt {2}}} справа)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e19dc7206f8b3b571e81153816c478abd91a679e)








![{ displaystyle { begin {align} operatorname { i ^ {n} erfc} (z) = int _ {z} ^ { infty} operatorname {i ^ {n-1} erfc} ( zeta) , d zeta \ имя оператора {i ^ {0} erfc} (z) = operatorname {erfc} (z) \ operatorname {i ^ {1} erfc} (z) = operatorname {ierfc} (z) = { frac {1} { sqrt { pi}}} e ^ {- z ^ {2}} - z operatorname {erfc} (z) \ operatorname {i ^ {2} erfc} (z) = { frac { 1} {4}} left [ operatorname {erfc} (z) -2z operatorname {ierfc} (z) right] \ конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66b57abb0a01139b31a14f5a8d651e4aa2e5f4f2)





![{ displaystyle { begin {align} Pr [L_ {a} leq X leq L_ {b}] & = int _ {L_ {a}} ^ {L_ {b}} { frac {1} {{ sqrt {2 pi}} sigma}} exp left (- { frac {(x- mu) ^ {2}} {2 sigma ^ {2}}} right) , dx \ & = { frac {1} {2}} left ( operatorname {erf} { frac {L_ {b} - mu} {{ sqrt {2}} sigma}} - operatorname {erf} { frac {L_ {a} - mu} {{ sqrt {2}} sigma}} right). end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1b3e43d593e389ed348ff56374118ab644fcec8)



![{ displaystyle { begin {align} operatorname {erfc} x & = 1- operatorname {erf} x \ [5pt] & = { frac {2} { sqrt { pi}}} int _ { x} ^ { infty} e ^ {- t ^ {2}} , dt \ [5pt] & = e ^ {- x ^ {2}} operatorname {erfcx} x, end {выровнено}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/582ae24086ba008f0466a71991c48c405c8248ad)


![{ displaystyle { begin {align} operatorname {erfi} x & = - i operatorname {erf} ix \ [5pt] & = { frac {2} { sqrt { pi}}} int _ { 0} ^ {x} e ^ {t ^ {2}} , dt \ [5pt] & = { frac {2} { sqrt { pi}}} e ^ {x ^ {2}} D (х), конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/937f1aaa2801d245f8056cad15f727ccee0ba1a7)
![{ displaystyle { begin {align} Phi (x) & = { frac {1} { sqrt {2 pi}}} int _ {- infty} ^ {x} e ^ { tfrac { -t ^ {2}} {2}} , dt \ [6pt] & = { frac {1} {2}} left (1+ operatorname {erf} { frac {x} { sqrt {2}}} right) \ [6pt] & = { frac {1} {2}} operatorname {erfc} left (- { frac {x} { sqrt {2}}} right ) конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c70647a7aa4dea3272cb7d90888444e1928c401)
![{ displaystyle { begin {align} operatorname {i} ^ {n} ! operatorname {erfc} z & = int _ {z} ^ { infty} operatorname {i} ^ {n-1} ! operatorname {erfc} zeta , d zeta \ [6pt] operatorname {i} ^ {0} ! operatorname {erfc} z & = operatorname {erfc} z \ operatorname {i} ^ {1} ! Operatorname {erfc} z & = operatorname {ierfc} z = { frac {1} { sqrt { pi}}} e ^ {- z ^ {2}} - z operatorname {erfc } z \ operatorname {i} ^ {2} ! operatorname {erfc} z & = { tfrac {1} {4}} left ( operatorname {erfc} z-2z operatorname {ierfc} z вправо) \ конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39d9046debe25c6cb2fa3709a961ac6a9715a37f)

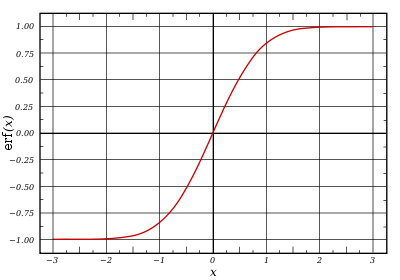
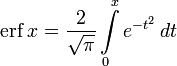 .
.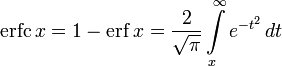 .
.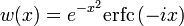 .
.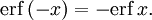

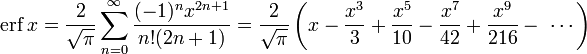
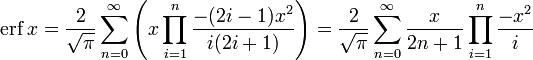
 будет для неё существенно особой.
будет для неё существенно особой.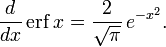
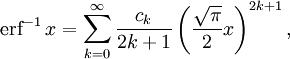

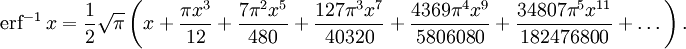 [1]
[1]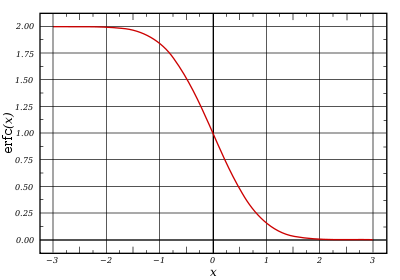
![operatorname{erfc},x = frac{e^{-x^2}}{xsqrt{pi}}left [1+sum_{n=1}^infty (-1)^n frac{1cdot3cdot5cdots(2n-1)}{(2x^2)^n}right ]=frac{e^{-x^2}}{xsqrt{pi}}sum_{n=0}^infty (-1)^n frac{(2n)!}{n!(2x)^{2n}}.,](https://dic.academic.ru/pictures/wiki/files/50/2d5fe0b0f05b66753a4dc4d68612c2e1.png)
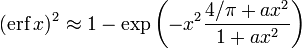

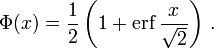

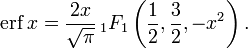
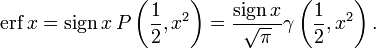
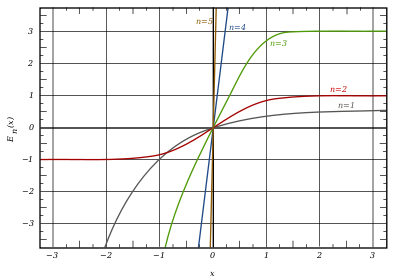


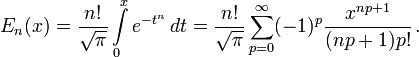
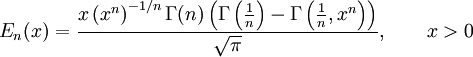
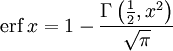
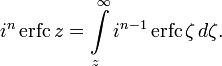
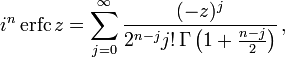
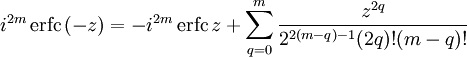
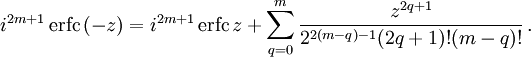

}{{\sqrt%20%20\pi%20}}})
