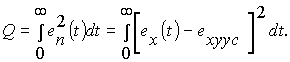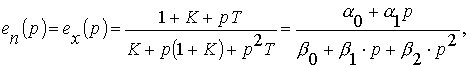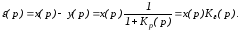Интегральная квадратичная ошибка
Cтраница 1
Интегральная квадратичная ошибка определяется как интеграл квадратов мгновенных ( текущих) значений рассогласования. При возведении в квадрат текущих значении рассогласования отрицательные величины не компенсируют положительные, поэтому с возрастанием рассогласования интегральная квадратичная ошибка растет очень быстро.
[1]
Эти коэффициенты соответствуют минимуму интегральной квадратичной ошибки между f ( t) и апроксимирующей функцией, что вытекает из (9.81), если Г оо. Полная функция f ( t) подбирается так, чтобы при этом значении Т получить наилучшую апроксимацию.
[2]
В этом разделе в качестве критерия оценки точности апроксимации применяется интегральная квадратичная ошибка. Выбор этого критерия диктуется главным образом удобством его применения; вместе с тем во многих конкретных случаях он служит весьма хорошей оценкой точности апроксимации. В нем одинаково учитываются как положительные, так и отрицательные ошибки. Критерий интегральной квадратичной ошибки достаточно хорошо оценивает большие и длительные ошибки, а малые и кратковременные ошибки слабо сказываются на его величине.
[3]
Экспоненциальные функции не являются ортогональными в любом интервале, так что критерий минимума интегральной квадратичной ошибки к такому ряду функций приложить нелегко.
[4]
С усилением интегрального воздействия ( уменьшение времени интегрирования) процесс из апериодического переходит в колебательный со все более уменьшающейся степенью затухания; при этом динамическая ошибка регулирования уменьшается, а время регулирования и интегральная квадратичная ошибка регулирования возрастают.
[5]
Для выбора наиболее рациональных с точки зрения технологии переходных процессов по каналам регулирования обычно выполняются расчеты для четырех процессов регулирования: без перерегулирования, с 20 % — ным перерегулированием, с минимальным временем регулирования и с минимальной интегральной квадратичной ошибкой.
[7]
Интегральные ошибки этих трех переходных процессов равны, так как настройки диапазона пропорциональности и времени изо-дрома регулятора во всех случаях одинаковы. Интегральная квадратичная ошибка последнего переходного процесса меньше, чем у первых двух, так как он имеет меньшую динамическую ошибку.
[9]
В частности, это имеет место для систем с симметричными и кососимметрич-ньгми матрицами А в силу ортогональности их канонических базисов. Эквивалентные сепаратные системы равноправны с точки зрения квадратичной оценки для системы в целом: значения их интегральных квадратичных ошибок входят в сумму ( ИЗ) с одинаковым весом.
[10]
Интегральная квадратичная ошибка определяется как интеграл квадратов мгновенных ( текущих) значений рассогласования. При возведении в квадрат текущих значении рассогласования отрицательные величины не компенсируют положительные, поэтому с возрастанием рассогласования интегральная квадратичная ошибка растет очень быстро.
[11]
Для большинства методов решения задачи синтеза оптимальных виброзащитных систем характерны следующие принципы: используется линейная динамическая модель с одной степенью свободы; для системы с двумя степенями свободы рассматриваются лишь частные случаи синтеза; учитывается не более одного ограничения; для одной и той же модели изменение спектральной плотности воздействия приводит к необходимости повторения процесса решения задачи. Например, для синтеза оптимальной системы с активным динамическим гасителем колебаний ( судовых механизмов и машин) был выбран метод минимально-квадратичной оптимизации, позволяющий синтезировать системы с наименьшим значением интегральной квадратичной ошибки при учете ограничений, накладываемых объектом.
[12]
На практике наиболее широкое распространение при оценке качества работы ристем регулирования получили интегральная и интегральная квадратичная ошибки. Принципиальное отличие между ними состоит в том, что вторая учитывает абсолютное значение ошибки. Например, две кривые переходного процесса с различными амплитудами колебаний параметра могут иметь одинаковые интегральные ошибки, но разные интегральные квадратичные ошибки.
[13]
В этом разделе в качестве критерия оценки точности апроксимации применяется интегральная квадратичная ошибка. Выбор этого критерия диктуется главным образом удобством его применения; вместе с тем во многих конкретных случаях он служит весьма хорошей оценкой точности апроксимации. В нем одинаково учитываются как положительные, так и отрицательные ошибки. Критерий интегральной квадратичной ошибки достаточно хорошо оценивает большие и длительные ошибки, а малые и кратковременные ошибки слабо сказываются на его величине.
[14]
Страницы:
1
2
характеристике Переходный
режим вызван тем, что система инерционна
и должна некоторое время приспосабливаться
к поступающим на нее воздействиям. В
этих условиях оценку качества удобно
вести при наиболее тяжелом с точки
зрения воспроизведения системой
воздействии, таком, как ступенчатая
функция А*l(t).
Реакция системы на единичную ступенчатую
функцию является переходным процессом h(t),
по форме которого в простейшем случае
и можно судить о качестве переходного
режима.
На рис.
52.
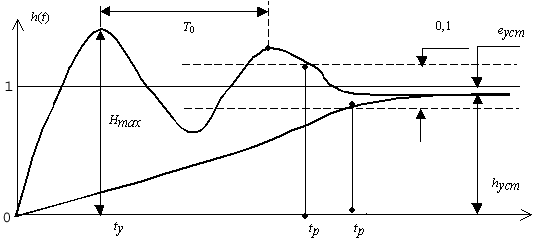
изображены переходные характеристики
колебательного и монотонного типов,
оценка которых проводится с помощью
локальных критериев, называемых
показателями качества переходной
характеристики.
Рис.
52. Показатели качества переходной
характеристики
Для
характеристик колебательного типа
обычно используются следующие
показатели: Hm —
перерегулирование, которое определяет
относительное максимальное отклонение;
время установления tу —
момент достижения первого максимума;
время регулирования tр,
которое определяет длительность процесса
по уровню + 0,05 относительно установившегося
значения; период колебаний T.
Для
монотонных характеристик наиболее
употребительным является показатель
длительности переходного процесса tр. В
общем случае точное построение переходных
характеристик и, следовательно,
определение качества затруднительно.
Существует ряд методов, позволяющих
приближенно строить переходные
характеристики, однако эти методы сложны
и приводят к громоздким вычислительным
работам. Найти точные значения указанных
выше величин удается только для простейших
систем первого и второго порядков. Для
более сложных следящих систем существуют
приближенные формулы их нахождения.
В
основе формул лежит знание двух
параметров: частоты среза разомкнутой
следящей системы w с
и запаса по фазе. Эти параметры могут
быть найдены аналитически или по
логарифмическим частотным характеристикам.
Сводка вычислительных соотношений
приводится в табл.
П. 2.
2.2.3. Интегральный квадратичный критерий качества переходного режима
Локальные
критерии качества обычно наглядны, но
трудно вычисляются аналитически.
Примером тому служат показатели
переходной характеристики, рассмотренные
выше. Интегральные критерии, особенно
квадратичные, достаточно легко
вычисляются, однако не так наглядны,
как локальные. Обратимся к рис.53,
на котором изображены два монотонных
переходных процесса. Процесс 1 наименьшей
длительности. Об этом может свидетельствовать
такой косвенный фактор, как площадь
между кривой h(t)
и уровнем установившегося значения
выходного процесса. Отсюда для оценки
качества можно ввести критерий
где
через eп (t)
обозначена ошибка переходного режима,
представляющая разность между текущим
и установившемся значениями переходной
характеристики. Чем меньше Q, тем выше
качество САУ.
Причем
подынтегральная квадратичная функция
потерь eп(t)
будет неотрицательной как для монотонных,
так и для колебательных процессов.
Очевидно,
что описанные критерии можно использовать
не только для случая переходной
характеристики, но и при произвольных
воздействиях.
Рис.53.
Сравнение качества переходных
характеристик
Рассмотрим
методику нахождения интегрального
квадратичного критерия переходного
режима для регулярного воздействия x(t).
Изображение
динамической ошибки можно записать в
виде произведения
|
e(p) = |
(29) |
Не
прибегая к нахождению оригинала eх(t), можно
найти установившееся значение ошибки
управления
,
или
.
Если
из полной ошибки eх(t)
вычесть ошибку установившегося
режима eх уст,
то получим составляющую, которая равна
ошибке переходного режима
еп(t) =
eх (t) —
eх уст.
Очевидно,
что
еп(t) 
0
при t 
,
так как eх (t) 
eх уст.
Интегральный
квадратичный критерий качества
переходного режима определим как
величину
На
основании известной теоремы Парсеваля,
нахождение интегрального квадратичного
критерия качества Q переходного
режима сводится к вычислению интеграла
Парсеваля
|
|
(30) |
Чтобы
вычислить конкретное значение этого
интеграла, функцию eп(p)
записывают в виде отношения полиномов
.
Тогда
интеграл будет функцией параметров a ,
и b . Значения функций табулированы
и для n <
4 приведены в табл.
П.3.
Изображение
ошибки переходного режима получаем из
формулы:
где
учтено, что изображение от
постоянной ex уст равно e x уст /p.
Пример.
Найдем
интегральный квадратичный критерий
качества переходного процесса в системе
управления антенной.
Передаточная
функция разомкнутой системы
,
Передаточная
функция ошибки по задающему воздействию
равна
.
Так
как рассматривается переходный процесс,
то воздействием является единичная
функция
x(t) = 1 (t)
с
изображением
x(p)=1/p .
Изображение
ошибки управления
.
Установившееся
значение ошибки
В
итоге получим, что изображение ошибки
переходного режима равно
где
a 0 =
1+K;
a 1 =
T; b 0 =
K; b 1 =
1+K; b 2 =
T.
Согласно
формуле (30)
интегральный квадратичный критерий
качества переходного режима равен
интегралу Парсеваля
Q
= I
[e п (p)].
Используя
данные табл.
П.3. для n =
2, находим значение интеграла
.
Из
этого результата видно, что изменением
параметров системы можно в широких
пределах изменить величину критерия.
Особенно характерны в этом отношении
два параметра: Rи T.
На
практике для регулировки показателей
переходного процесса широко используют
коэффициент преобразования К элемента,
не охваченного внутренней обратной
связью. В то же время постоянную
времени T усилителя
следует подбирать так, чтобы величина
первого слагаемого критерия не превышала
допустимого уровня.
252
Точность САУ
Точность
САУ оценивается в установившемся режиме
по величине установившейся ошибки при
типовых воздействиях. При анализе
точности систем рассматривается
установившийся режим, так как текущее
значение ошибки резко меняется вследствие
наличия переходных процессов и не может
быть мерой точности.
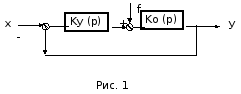
Рассмотрим
систему представленную на рис. 1.
На
схеме приняты следующие обозначения:
Kу(p)
– передаточная функция устройства
управления; K0(p)
– передаточная функция объекта
управления; f
–
возмущающее воздействие; x
–
задающее воздействие; y
– регулируемая величина.
Ошибка
по задающему воздействию равна (t)
= x(t) – y(t).
Изображение
ошибки равно
(1)
Установившееся
значение ошибки определяется с помощью
теоремы о конечном значении функции
(2)
Ошибка
по возмущению воздействию равна (t)
= – y(t),
т.е. равна изменению регулируемой
величины под действием возмущения при
отсутствии входного воздействия.
В общем
случае как задающее, так и возмущающее
воздействия являются сложными функциями
времени. При определении ошибок пользуются
типовыми воздействиями, которые с одной
стороны соответствуют наиболее тяжелым
режимам работы системы и, вместе с тем,
достаточно просты для аналитических
исследований.
Кроме
того, типовые воздействия удобны для
сравнительного анализа различных
систем, и соответствуют наиболее часто
применяемым законам изменения управляющих
и возмущающих воздействий.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
04.08.2019142.76 Кб022.rtf
- #
- #
- #
- #
- #
- #
04.08.2019112.25 Кб126.rtf
- #
- #
- #
- #
Интегральная квадратичная ошибка
Cтраница 1
Интегральная квадратичная ошибка определяется как интеграл квадратов мгновенных ( текущих) значений рассогласования. При возведении в квадрат текущих значении рассогласования отрицательные величины не компенсируют положительные, поэтому с возрастанием рассогласования интегральная квадратичная ошибка растет очень быстро.
[1]
Эти коэффициенты соответствуют минимуму интегральной квадратичной ошибки между f ( t) и апроксимирующей функцией, что вытекает из (9.81), если Г оо. Полная функция f ( t) подбирается так, чтобы при этом значении Т получить наилучшую апроксимацию.
[2]
В этом разделе в качестве критерия оценки точности апроксимации применяется интегральная квадратичная ошибка. Выбор этого критерия диктуется главным образом удобством его применения; вместе с тем во многих конкретных случаях он служит весьма хорошей оценкой точности апроксимации. В нем одинаково учитываются как положительные, так и отрицательные ошибки. Критерий интегральной квадратичной ошибки достаточно хорошо оценивает большие и длительные ошибки, а малые и кратковременные ошибки слабо сказываются на его величине.
[3]
Экспоненциальные функции не являются ортогональными в любом интервале, так что критерий минимума интегральной квадратичной ошибки к такому ряду функций приложить нелегко.
[4]
С усилением интегрального воздействия ( уменьшение времени интегрирования) процесс из апериодического переходит в колебательный со все более уменьшающейся степенью затухания; при этом динамическая ошибка регулирования уменьшается, а время регулирования и интегральная квадратичная ошибка регулирования возрастают.
[5]
Для выбора наиболее рациональных с точки зрения технологии переходных процессов по каналам регулирования обычно выполняются расчеты для четырех процессов регулирования: без перерегулирования, с 20 % — ным перерегулированием, с минимальным временем регулирования и с минимальной интегральной квадратичной ошибкой.
[7]
Интегральные ошибки этих трех переходных процессов равны, так как настройки диапазона пропорциональности и времени изо-дрома регулятора во всех случаях одинаковы. Интегральная квадратичная ошибка последнего переходного процесса меньше, чем у первых двух, так как он имеет меньшую динамическую ошибку.
[9]
В частности, это имеет место для систем с симметричными и кососимметрич-ньгми матрицами А в силу ортогональности их канонических базисов. Эквивалентные сепаратные системы равноправны с точки зрения квадратичной оценки для системы в целом: значения их интегральных квадратичных ошибок входят в сумму ( ИЗ) с одинаковым весом.
[10]
Интегральная квадратичная ошибка определяется как интеграл квадратов мгновенных ( текущих) значений рассогласования. При возведении в квадрат текущих значении рассогласования отрицательные величины не компенсируют положительные, поэтому с возрастанием рассогласования интегральная квадратичная ошибка растет очень быстро.
[11]
Для большинства методов решения задачи синтеза оптимальных виброзащитных систем характерны следующие принципы: используется линейная динамическая модель с одной степенью свободы; для системы с двумя степенями свободы рассматриваются лишь частные случаи синтеза; учитывается не более одного ограничения; для одной и той же модели изменение спектральной плотности воздействия приводит к необходимости повторения процесса решения задачи. Например, для синтеза оптимальной системы с активным динамическим гасителем колебаний ( судовых механизмов и машин) был выбран метод минимально-квадратичной оптимизации, позволяющий синтезировать системы с наименьшим значением интегральной квадратичной ошибки при учете ограничений, накладываемых объектом.
[12]
На практике наиболее широкое распространение при оценке качества работы ристем регулирования получили интегральная и интегральная квадратичная ошибки. Принципиальное отличие между ними состоит в том, что вторая учитывает абсолютное значение ошибки. Например, две кривые переходного процесса с различными амплитудами колебаний параметра могут иметь одинаковые интегральные ошибки, но разные интегральные квадратичные ошибки.
[13]
В этом разделе в качестве критерия оценки точности апроксимации применяется интегральная квадратичная ошибка. Выбор этого критерия диктуется главным образом удобством его применения; вместе с тем во многих конкретных случаях он служит весьма хорошей оценкой точности апроксимации. В нем одинаково учитываются как положительные, так и отрицательные ошибки. Критерий интегральной квадратичной ошибки достаточно хорошо оценивает большие и длительные ошибки, а малые и кратковременные ошибки слабо сказываются на его величине.
[14]
Страницы:
1
2
Интегральные оценки качества являются интегралами по времени от некоторых функций переходного процесса свободной составляющей выходной величины 
или ошибки 
Цель использования таких критериев состоит в том, чтобы получить общую оценку быстродействия и отклонения регулируемой величины от установившегося значения. Широко используются линейные и квадратичные интегральные оценки. Линейные оценки вычисляются по формуле
Рис. 4.19
Рис. 4.20
Однако чаще используют моменты 
порядка, т. е. оценки вида
Простейшей из этих оценок является 
Если система устойчива, то 
интеграл 
стремится к конечному значению, равному площади под кривой 
(рис. 4.19). Чем выше быстродействие системы, тем меньше величина 
поэтому параметры системы следует выбирать так, чтобы 
стремился к минимуму, т. е. 
где А — варьируемый параметр системы. Недостатком этой оценки является то, что она применима к монотонным или апериодическим процессам. При колебательном процессе (рис. 4.20) площади, ограниченные 
складывают алгебраически и минимуму 
может соответствовать процесс с большим числом колебаний 
т. е., с малым быстродействием и даже с незатухающими колебаниями.
Для 
изображение по Лапласу
Сравнивая это выражение с (4.47) для 
можно записать
Разложим 
в ряд по степеням 
Подставим (4.51) в выражение для определения 
т. е.
Если разложить 
степеням s в ряд:
то, сопоставляя (4.52) и (4.53), можно сделать следующее заключение, приравнивая выражения при равных степенях 
Если сравнить результаты (4.50), 
с коэффициентами ошибок, приведенными в § 4.2, то 
где 
коэффициенты ошибок.
Квадратичные интегральные оценки вычисляются по формулам
где 
— постоянные величины.
Оценки 
называют обобщенными квадратичными ценками.
Геометрический смысл интегральной квадратичной оценки ояснен на рис. 4.21. Выбирая параметры системы по минимуму квадратичной интегральной оценки 
приближаем кривую 
к осям 
Методы вычисления этих оценок предложены А. И. Манелыптамом и Н. Д. Папалекси в 1909 г. В 1937 г. акад. А. А. [аркевич применил эту оценку для исследования режимов аботы усилителей, в 1948 г. А. А. Красовский и А. А. Фельдаум использовали ее для исследования качества линейных истем автоматического регулирования.
Рассмотрим методы вычисления квадратичных интегральных оценок 
По определению, 
По теореме о предельных переходах,
педовательно,
Поскольку 
— дробно-ациональная функция, то и 
можно записать в виде дробно-рациональной функции:
Рис. 4.21
При 
оценку 
можно вычислить, используя коэффициенты 
по формулам, приведенным ниже без вывода [4]:
где 
— определитель Гурвица, составленный из коэффициентов:
в котором все коэффициенты с меньшим индексом 0 и большим 
заменяют нулями. Определители 
получают из (4.62) заменой столбца 
столбцом 
.
Коэффициенты 
определяют как
Интегральную квадратичную оценку 
можно вычислять по заданной частотной характеристике замкнутой системы.
Пусть 
— изображение Фурье для функции 
на основании теоремы свертки в комплексной области для 
можно записать [7] при 
где 
комплексный коэффициент усиления замкнутой системы.
Таким образом, по (4.64) и (4.65) можно вычислить 
Выражение (4.64) есть формула Рэлея.
Существуют таблицы расчета интеграла 
в функции коэффициентов 
изображения по Лапласу сигнала ошибки 
для 
и до 
. В табл. 4.1 приведены формулы для 
при 
Таблица 4.1
где
При выборе параметров системы по минимуму оценки 
часто получают нежелательную колебательность процесса, так как приближение процесса 
к идеальному скачку вызывает резкое увеличение начальной скорости, что, в свою очередь, может вызвать высокое перерегулирование, уменьшив
при этом запас устойчивости. В обобщенных квадратичных оценках 
накладывают ограничение не только на величину отклонения 
но и на скорость отклонения 
а также и на производные второго, третьего и высших порядков в 
что означает приближение кривой не к ступенчатой функций, а к экспоненте в случае 
и к более плавной, но сложной кривой в случае использования 
При выборе параметров САУ по минимуму 
существен выбор постоянных 
определяющих вес производных в обобщенных квадратичных оценках (4.58), (4.59). Значительное увеличение 
приводит к отсутствию перерегулирования, но увеличивает время регулирования. При малых 
уменьшение колебательности будет незначительным. Выбор 
осуществляется с учетом постоянной времени экстремали, к которой целесообразно приближать процесс.
Остановимся на методике расчета системы по минимуму обобщенной квадратичной оценки:
Этот интеграл можно представить в виде суммы двух интегралов:
Если система устойчива, то 
тогда
Кроме того, интеграл 
будет иметь минимально возможное значение
при
Если
то решение дифференциального уравнения (4.68)
является оптимальным по минимуму (экстремальным) переходным процессом (где 
— постоянная времени этого процесса).
При выборе параметров системы по минимуму 
обычно имеет место отклонение 
от наименьшего значения 
А. А. Фельдбаумом [10] было показано, что переходный процесс будет отличаться от экстремального на величину, меньшую 
, т. е.
По величине 6 можно оценить отклонение истинного переходного процесса 
от экстремального (рис. 4.22). При увеличении порядка системы увеличивается и ширина зоны 
при этом уменьшается точность оценки качества системы (приближения переходного процесса к экстремали); во избежание этого используют оценки вида (4.59). Величину 
задают по требуемому времени регулирования 
Следует заметить, что задача выбора параметров по минимуму 
или 
решается аналитически лишь в несложных случаях для САУ невысокого порядка. В противном случае расчеты существенно усложняются и задачу следует решать численно на ЦВМ.
Рассмотрим примеры выбора оптимального значения какого-либо параметра системы по минимуму 
Пример 4.4. Вычислить значение коэффициента усиления системы, минимизирующие
Рис. 4.22
мизирующее квадратичную интегральную оценку 
Известна передаточная, функция разомкнутой системы
где 
Входной сигнал — единичная функция 
Изображение отклонения 
по Лапласу
где 
Воспользуемся формулами для вычисления 
приведенными в табл. 4.1 для 
Определим частную производную:
Определим 
из 
Подставляя числовые значения коэффициентов, получим
откуда 
Пример 4.5. Определить оптимальное значение коэффициента усиления к, соответствующее минимуму обобщенной квадратичной оценки
Передаточная функция разомкнутой системы 
.
Входной сигнал — единичная функция 
Можно представить 
в виде суммы:
Изображение отклонения 
по Лапласу
где 
Воспользуемся данными табл. 4.1 и определим значение 
для 
Определим изображение производной 
из свойства преобразований Лапласа:
По теореме о предельном переходе,
Тогда 
где 
Теперь можно определить интеграл
пользуясь формулой для 
из табл. 4.1 для 
Итак, 
Определим 
из 
т. е.
откуда 
Оптимальный переходный процесс описывается в соответствии с формулой (4.69) выражением
Так как 
то по (4.66) наименьшее значение оценки 
Следовательно 
Согласно 
(рис. 4.2).
Интегральные оценки качества широко используются при синтезе оптимальных САУ в качестве критерия оптимальности.
Широкое
распространение среди косвенных методов
исследования качества процессов
регулирования получили интегральные
оценки. Это оценки качества переходной
характеристики, а именно: быстроты
затухания ее колебаний и величины
отклонения регулируемого параметра от
установившегося значения. Рассмотрим
наиболее употребительные интегральные
оценки.
Недостатки двух первых
интегральных оценок преодолеваютсяквадратичной
интегральной оценкой(формула
Рэлея)
На
рис.5.6 представлена геометрическая
интерпретация квадратичной интегральной
оценки качества, численно равная площади
, заключенной между осью времени и
квадратом динамической ошибки
регулирования e2(t).
Этот
интеграл находится также по виду
передаточной функции замкнутой САУ.
Целесообразность же ее применения
обусловлена тем, что существуют готовые
формулы для расчета численных значений
I2.
Следует однако заметить, что
минимизация оценки I2приближает
кривую переходного процесса к 1(t), что,
в свою очередь, вызывает значительное
увеличение скорости отработки сигнала
в начальный момент времени. Чтобы
получить быстро затухающий и достаточно
плавный процесс, вводятулучшенные
квадратичные интегральные оценки
качества, например
где
τ назначается в соответствии с заданием
желаемых свойств переходного процесса.
В этом случает предельной переходной
характеристикой будет экспонента е+τ
=0
с желаемой постоянной времени τ,
получившая название экстремаль. Удобство
интегральных оценок состоит в том, что
они дают единый числовой критерий
качества. Недостатком является то, что
одному и тому же значению интегральной
оценки могут отвечать разные формы
переходного процесса, что создает
недостаточную определенность решения
задачи.
Квадратичная
интегральная оценка
.
Может
применяться для оценки как монотонных,
так и колебательных переходных процессов.
Если
выбирать параметры системы исходя из
минимума квадратичной интегральной
оценки
,
то переходный процесс может оказатьсясильноколебательным.
Данный факт ограничивает использование
квадратичных интегральных оценок при
анализе и синтезе систем автоматического
управления
11 Метод гармонической линеаризации
Метод
гармонической линеаризации является
приближенным методом исследования
режима автоколебаний нелинейных систем.
Этим методом можно определить условия
возникновения и параметры автоколебаний,
как в системах второго порядка, так и в
более сложных системах.
Метод
заключается в замене существенно
нелинейного элемента с
характеристикой 
эквивалентным
линейным звеном с коэффициентом
.
В замкнутой автоматической системе,
работающей в режиме автоколебаний,
условием эквивалентности служит
равенство амплитуд и фаз выходного
сигнала эквивалентного звена и первой
гармоники выходного сигнала реального
нелинейного элемента. При этом
предполагается, что сигнал на входе
нелинейного элемента является
синусоидальным. Такое предположение
справедливо во всех случаях, когда
линейная часть системы достаточно
инерционна и не пропускает высшие
гармоники.
12
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Широкое
распространение среди косвенных методов
исследования качества процессов
регулирования получили интегральные
оценки. Это оценки качества переходной
характеристики, а именно: быстроты
затухания ее колебаний и величины
отклонения регулируемого параметра от
установившегося значения. Рассмотрим
наиболее употребительные интегральные
оценки.
Недостатки двух первых
интегральных оценок преодолеваютсяквадратичной
интегральной оценкой(формула
Рэлея)
На
рис.5.6 представлена геометрическая
интерпретация квадратичной интегральной
оценки качества, численно равная площади
, заключенной между осью времени и
квадратом динамической ошибки
регулирования e2(t).
Этот
интеграл находится также по виду
передаточной функции замкнутой САУ.
Целесообразность же ее применения
обусловлена тем, что существуют готовые
формулы для расчета численных значений
I2.
Следует однако заметить, что
минимизация оценки I2приближает
кривую переходного процесса к 1(t), что,
в свою очередь, вызывает значительное
увеличение скорости отработки сигнала
в начальный момент времени. Чтобы
получить быстро затухающий и достаточно
плавный процесс, вводятулучшенные
квадратичные интегральные оценки
качества, например
где
τ назначается в соответствии с заданием
желаемых свойств переходного процесса.
В этом случает предельной переходной
характеристикой будет экспонента е+τ=0
с желаемой постоянной времени τ,
получившая название экстремаль. Удобство
интегральных оценок состоит в том, что
они дают единый числовой критерий
качества. Недостатком является то, что
одному и тому же значению интегральной
оценки могут отвечать разные формы
переходного процесса, что создает
недостаточную определенность решения
задачи.
Квадратичная
интегральная оценка.
Может
применяться для оценки как монотонных,
так и колебательных переходных процессов.
Если
выбирать параметры системы исходя из
минимума квадратичной интегральной
оценки
,
то переходный процесс может оказатьсясильноколебательным.
Данный факт ограничивает использование
квадратичных интегральных оценок при
анализе и синтезе систем автоматического
управления
11 Метод гармонической линеаризации
Метод
гармонической линеаризации является
приближенным методом исследования
режима автоколебаний нелинейных систем.
Этим методом можно определить условия
возникновения и параметры автоколебаний,
как в системах второго порядка, так и в
более сложных системах.
Метод
заключается в замене существенно
нелинейного элемента с
характеристикой эквивалентным
линейным звеном с коэффициентом.
В замкнутой автоматической системе,
работающей в режиме автоколебаний,
условием эквивалентности служит
равенство амплитуд и фаз выходного
сигнала эквивалентного звена и первой
гармоники выходного сигнала реального
нелинейного элемента. При этом
предполагается, что сигнал на входе
нелинейного элемента является
синусоидальным. Такое предположение
справедливо во всех случаях, когда
линейная часть системы достаточно
инерционна и не пропускает высшие
гармоники.
12
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Интегральная квадратичная ошибка
Cтраница 1
Интегральная квадратичная ошибка определяется как интеграл квадратов мгновенных ( текущих) значений рассогласования. При возведении в квадрат текущих значении рассогласования отрицательные величины не компенсируют положительные, поэтому с возрастанием рассогласования интегральная квадратичная ошибка растет очень быстро.
[1]
Эти коэффициенты соответствуют минимуму интегральной квадратичной ошибки между f ( t) и апроксимирующей функцией, что вытекает из (9.81), если Г оо. Полная функция f ( t) подбирается так, чтобы при этом значении Т получить наилучшую апроксимацию.
[2]
В этом разделе в качестве критерия оценки точности апроксимации применяется интегральная квадратичная ошибка. Выбор этого критерия диктуется главным образом удобством его применения; вместе с тем во многих конкретных случаях он служит весьма хорошей оценкой точности апроксимации. В нем одинаково учитываются как положительные, так и отрицательные ошибки. Критерий интегральной квадратичной ошибки достаточно хорошо оценивает большие и длительные ошибки, а малые и кратковременные ошибки слабо сказываются на его величине.
[3]
Экспоненциальные функции не являются ортогональными в любом интервале, так что критерий минимума интегральной квадратичной ошибки к такому ряду функций приложить нелегко.
[4]
С усилением интегрального воздействия ( уменьшение времени интегрирования) процесс из апериодического переходит в колебательный со все более уменьшающейся степенью затухания; при этом динамическая ошибка регулирования уменьшается, а время регулирования и интегральная квадратичная ошибка регулирования возрастают.
[5]
Для выбора наиболее рациональных с точки зрения технологии переходных процессов по каналам регулирования обычно выполняются расчеты для четырех процессов регулирования: без перерегулирования, с 20 % — ным перерегулированием, с минимальным временем регулирования и с минимальной интегральной квадратичной ошибкой.
[7]
Интегральные ошибки этих трех переходных процессов равны, так как настройки диапазона пропорциональности и времени изо-дрома регулятора во всех случаях одинаковы. Интегральная квадратичная ошибка последнего переходного процесса меньше, чем у первых двух, так как он имеет меньшую динамическую ошибку.
[9]
В частности, это имеет место для систем с симметричными и кососимметрич-ньгми матрицами А в силу ортогональности их канонических базисов. Эквивалентные сепаратные системы равноправны с точки зрения квадратичной оценки для системы в целом: значения их интегральных квадратичных ошибок входят в сумму ( ИЗ) с одинаковым весом.
[10]
Интегральная квадратичная ошибка определяется как интеграл квадратов мгновенных ( текущих) значений рассогласования. При возведении в квадрат текущих значении рассогласования отрицательные величины не компенсируют положительные, поэтому с возрастанием рассогласования интегральная квадратичная ошибка растет очень быстро.
[11]
Для большинства методов решения задачи синтеза оптимальных виброзащитных систем характерны следующие принципы: используется линейная динамическая модель с одной степенью свободы; для системы с двумя степенями свободы рассматриваются лишь частные случаи синтеза; учитывается не более одного ограничения; для одной и той же модели изменение спектральной плотности воздействия приводит к необходимости повторения процесса решения задачи. Например, для синтеза оптимальной системы с активным динамическим гасителем колебаний ( судовых механизмов и машин) был выбран метод минимально-квадратичной оптимизации, позволяющий синтезировать системы с наименьшим значением интегральной квадратичной ошибки при учете ограничений, накладываемых объектом.
[12]
На практике наиболее широкое распространение при оценке качества работы ристем регулирования получили интегральная и интегральная квадратичная ошибки. Принципиальное отличие между ними состоит в том, что вторая учитывает абсолютное значение ошибки. Например, две кривые переходного процесса с различными амплитудами колебаний параметра могут иметь одинаковые интегральные ошибки, но разные интегральные квадратичные ошибки.
[13]
В этом разделе в качестве критерия оценки точности апроксимации применяется интегральная квадратичная ошибка. Выбор этого критерия диктуется главным образом удобством его применения; вместе с тем во многих конкретных случаях он служит весьма хорошей оценкой точности апроксимации. В нем одинаково учитываются как положительные, так и отрицательные ошибки. Критерий интегральной квадратичной ошибки достаточно хорошо оценивает большие и длительные ошибки, а малые и кратковременные ошибки слабо сказываются на его величине.
[14]
Страницы:
1
2