Main Content
Syntax
Description
example
erfinv( computesX)
the inverse
error function of X. If X is
a vector or a matrix, erfinv(X) computes the inverse
error function of each element of X.
Examples
Inverse Error Function for Floating-Point and Symbolic Numbers
Depending on its arguments, erfinv can
return floating-point or exact symbolic results.
Compute the inverse error function for these numbers. Because
these numbers are not symbolic objects, you get floating-point results:
A = [erfinv(1/2), erfinv(0.33), erfinv(-1/3)]
A =
0.4769 0.3013 -0.3046
Compute the inverse error function for the same numbers converted
to symbolic objects. For most symbolic (exact) numbers, erfinv returns
unresolved symbolic calls:
symA = [erfinv(sym(1)/2), erfinv(sym(0.33)), erfinv(sym(-1)/3)]
symA = [ erfinv(1/2), erfinv(33/100), -erfinv(1/3)]
Use vpa to approximate symbolic results
with the required number of digits:
d = digits(10); vpa(symA) digits(d)
ans = [ 0.4769362762, 0.3013321461, -0.3045701942]
Inverse Error Function for Variables and Expressions
For most symbolic variables and expressions, erfinv returns
unresolved symbolic calls.
Compute the inverse error function for x and sin(x). For most symbolic variables and expressions,
+ x*exp(x)erfinv returns
unresolved symbolic calls:
syms x f = sin(x) + x*exp(x); erfinv(x) erfinv(f)
ans = erfinv(x) ans = erfinv(sin(x) + x*exp(x))
Inverse Error Function for Vectors and Matrices
If the input argument is a vector or a matrix, erfinv returns
the inverse error function for each element of that vector or matrix.
Compute the inverse error function for elements of matrix M and
vector V:
M = sym([0 1 + i; 1/3 1]); V = sym([-1; inf]); erfinv(M) erfinv(V)
ans = [ 0, NaN] [ erfinv(1/3), Inf] ans = -Inf NaN
Special Values of Inverse Complementary Error Function
erfinv returns special
values for particular parameters.
Compute the inverse error function for x =
–1, x =
0, and x =
1. The inverse error function has special values
for these parameters:
[erfinv(-1), erfinv(0), erfinv(1)]
Handling Expressions That Contain Inverse Complementary Error Function
Many functions, such as diff and int,
can handle expressions containing erfinv.
Compute the first and second derivatives of the inverse error
function:
syms x diff(erfinv(x), x) diff(erfinv(x), x, 2)
ans = (pi^(1/2)*exp(erfinv(x)^2))/2 ans = (pi*exp(2*erfinv(x)^2)*erfinv(x))/2
Compute the integral of the inverse error function:
ans = -exp(-erfinv(x)^2)/pi^(1/2)
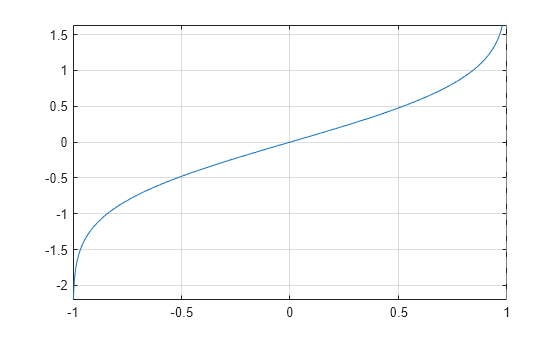
Plot Inverse Error Function
Plot the inverse error function on the interval from -1 to 1.
syms x fplot(erfinv(x),[-1,1]) grid on
Input Arguments
collapse all
X — Input
symbolic number | symbolic variable | symbolic expression | symbolic function | symbolic vector | symbolic matrix
Input, specified as a symbolic number, variable, expression,
or function, or as a vector or matrix of symbolic numbers, variables,
expressions, or functions.
More About
collapse all
Inverse Error Function
The inverse error function is defined as erf -1(x), such that erf(erf -1(x)) = erf -1(erf(x)) = x. Here
is the error function.
Tips
-
Calling
erfinvfor a number that
is not a symbolic object invokes the MATLAB®erfinvfunction. This function accepts
real arguments only. If you want to compute the inverse error function
for a complex number, usesymto
convert that number to a symbolic object, and then callerfinvfor
that symbolic object. -
If x < –1 or x > 1, or if x is
complex, thenerfinv(x)returnsNaN.
Algorithms
The toolbox can simplify expressions that contain error functions
and their inverses. For real values x, the toolbox
applies these simplification rules:
-
erfinv(erf(x)) = erfinv(1 - erfc(x)) = erfcinv(1
- erf(x)) = erfcinv(erfc(x)) = x -
erfinv(-erf(x)) = erfinv(erfc(x) - 1) = erfcinv(1
+ erf(x)) = erfcinv(2 - erfc(x)) = -x
For any value x, the toolbox applies these
simplification rules:
-
erfcinv(x) = erfinv(1 - x) -
erfinv(-x) = -erfinv(x) -
erfcinv(2 - x) = -erfcinv(x) -
erf(erfinv(x)) = erfc(erfcinv(x)) = x -
erf(erfcinv(x)) = erfc(erfinv(x)) = 1 - x
References
[1] Gautschi, W. “Error Function and Fresnel Integrals.” Handbook
of Mathematical Functions with Formulas, Graphs, and Mathematical
Tables. (M. Abramowitz and I. A. Stegun, eds.). New York:
Dover, 1972.
Version History
Introduced in R2012a
- Trial Software
- Trial Software
- Product Updates
- Product Updates
Системы
MatLabSciLab обладают большими возможностями
программирования и визуализации
результатов научных исследований при
решении задач вычислительной математики.
Численные методы в этих системах
предлагаются уже в виде готового
инструментария — набора функций, их
реализующих. Задачей данной работы
является ознакомление с наиболее часто
встречающимися на практике численными
методами, которые используются при
решении нелинейных уравнений, при
аппроксимации и интегрировании функций.
Приближѐнное вычисление определѐнных
интегралов. С вычислением определѐнных
интегралов самого общего вида:

приходится
сталкиваться при решении многих задач
математики, физики, химии и т.д. Как
правило, на практике получить первообразную
аналитически и затем воспользоваться
формулой Ньютона-Лейбница удаѐтся
крайне редко. В этих случаях интеграл
вычисляется приближѐнно с помощью
одного из методов численного интегрирования.
В методе трапеций используется линейная
интерполяция, т.е. подынтегральная
функция заменяется кусочно-линейной,
а еѐ график представляется в виде
ломаной, соединяющей отдельные точки
yi
= f(xi),
где xi
– координаты узлов сетки, введѐнной
на интервале интегрирования. При этом,
очевидно, на каждом из интервалов от
xi
до xi+1
искомые площади вычисляются как площади
обычных трапеций, после чего суммируются.
В итоге формула трапеций при постоянном
шаге сетки h
= xi+1
— xi
= (b
— a)/n
(n
– число интервалов разбиения сетки)
принимает вид:

Эта
схема интегрирования чрезвычайно проста
для реализации и имеет 2-ой порядок
точности относительно шага сетки. Тем
не менее, для экономии времени пользователя
в MatLab
еѐ реализовали в виде функции trapz(x,
y),
а в SciLab
– inttrap(x,
y).
Здесь x
и y
– массивы одного и того же размера 1хn,
содержащие, соответственно, координаты
узлов выбранной сетки и значения функции
в этих узлах. Не многим сложнее
оказывается формула Симпсона 4-го
порядка точности, получаемая при кусочной
интерполяции подынтегрального выражения
с помощью парабол:

В
MatLab формула Симпсона реализуется
функцией quad(fun, a, b [,tol]), где fun –
подынтегральная функция, a, b – концы
интервала интегрирования, tol – требуемая
точность (необязательный параметр).
Подынтегральная функция может быть
предварительно определена в m-файле,
тогда еѐ имя следует указать с дескриптором
@, или еѐ можно указать непосредственно
при вызове quad в виде текстовой строки,
заключѐнной в одинарные кавычки.
Например, вызов quad(@myfun, 0, 1, 1e-3) вычислит
интеграл от myfun(x) на интервале [0, 1] с
точностью 0.001. Файл функции myfun может
быть примерно следующим: function m = myfun(x)
m
= x.*x;
return
Аналогично,
производится интегрирование при
непосредственном задании функции,
например: quad(‘x.*x’,
0, 1, 1e-3).
Примечание: не забывайте, что операции
умножения, деления и возведения в степень
необходимо указывать в форме с «.», т.к.
они производятся над массивами.
Интегрирование
методом трапеций.
Приведенные
ниже функции выполняют численное
интегрирование хорошо известным методом
трапеций и методом трапеций с накоплением.
•
trapz(Y)
возвращает определенный интеграл,
используя интегрирование методом
трапеций с единичным шагом между
отсчетами. Если Y
– вектор, то trapz(Y)
возвращает интеграл элементов вектора
Y,
если Y
– матрица, то trapz(Y)
возвращает векторстроку, содержащую
интегралы каждого столбца этой матрицы.
•
trapz(X,Y)
возвращает интеграл от функции Y
по переменной X,
используя метод трапеций (пределы
интегрирования в этом случае задаются
начальным и конечным элементами вектора
X).
•
trapz(…,dim)
возвращает интеграл по строкам или по
столбцам для входной матрицы, в зависимости
от значения переменной dim.
Примеры:
>>
y=[1,2,3,4]
y
= 1 2 3 4
>>
trapz(y)
ans
= 7.5000
>>
X=0:pi/70:pi/2; Y=cos(X); Z = trapz(Y)
Z
= 22.2780
•
cumtrapz(Y)
возвращает численное значение
определенного интеграла для функции,
заданной ординатами в векторе или
матрице Y
с шагом интегрирования, равным единице
(интегрирование методом трапеций с
накоплением). В случае когда шаг отличен
от единицы, но постоянен, вычисленный
интеграл достаточно умножить на величину
шага. Для векторов эта функция возвращает
вектор, содержащий результат интегрирования
с накоплением элементов вектора Y.
Для матриц – возвращает матрицу того
же размера, что и Y,
содержащую результаты интегрирования
с накоплением для каждого столбца
матрицы Y.
cumtrapz(X,Y)
выполняет интегрирование с накоплением
от Y
по переменной X,
используя метод трапеций. X
и Y
должны быть векторами одной и той же
длины, или X
должен быть векторомстолбцом, а Y
– матрицей. cumtrapz(…,
dim)
выполняет интегрирование с накоплением
элементов по размерности, точно
определенной скаляром dim.
Длина вектора X
должна быть равна size(Y,dim).
Интегрирование
методом квадратур
Метод
трапеций обеспечивает невысокую точность
при заданном числе шагов или дает слишком
большое число шагов при вычислениях с
заданной погрешностью. Приведенные
ниже функции осуществляют интегрирование
и двойное интегрирование, используя
более точную квадратурную формулу
Симпсона или метод Гаусса–Лобатто.
Квадратура – численный метод нахождения
площади под графиком функции f(x),
то есть вычисление определенного
интеграла вида. В приведенных ниже
формулах подынтегральное выражение
fun
обычно задается или в прямых апострофах,
или в форме handleфункции.
Функции quad
и quadl
используют два различных алгоритма
квадратуры для вычисления определенного
интеграла. Функция quad
выполняет интегрирование по методу
низкого порядка, используя рекурсивное
правило Симпсона. Но она может быть
более эффективной при негладких
подынтегральных функциях или при низкой
требуемой точности вычислений. Алгоритм
quad
в MATLAB
6 изменен по сравнению с предшествовавшими
версиями, точность по умолчанию по
сравнению с версиями 5.3x
повышена в 1000 раз (с 10–3 до 10–6). Новая
функция quad1
(квадратура Лобатто) использует адаптивное
правило квадратуры Гаусса–Лобатто
очень высокого порядка. Устаревшая
функция quad8
выполняла интегрирование, используя
квадратурные формулы Ньютона–Котеса
8-го порядка. Достижимая точность
интегрирования гладких функций в MATLAB
6 поэтому также значительно выше, чем в
предшествующих версиях. quad(fun,a,b)
возвращает численное значение
определенного интеграла от заданной
функции @fun
на отрезке [a
b].
Используется значительно усовершенствованный
в MATLAB
6 адаптивный метод Симпсона. quad(fun,a,b,tol)
возвращает численное значение
определенного интеграла с заданной
относительной погрешностью tol.
По умолчанию tol=1.e–6.
Можно также использовать вектор,
состоящий из двух элементов tol
=[rel_tol
abs_tol],
чтобы точно определить комбинацию
относительной и абсолютной погрешностей.
quad(fun,a,b,tol,trace)
возвращает численное значение
определенного интеграла и при значении
trace,
не равном нулю, строит график, показывающий
ход вычисления интеграла.
quad(fun,a,b,tol,trace,P1,P2,…)
возвращает численное значение
определенного интеграла по подынтегральной
функции fun,
использует дополнительные аргументы
P1,
P2,
…, которые напрямую передаются в
подынтегральную функцию: G=fun(X,P1,P2,…).
Вычисления
двойных и тройных интегралов
Для
вычисления двойных интегралов служит
следующая функция:
•
dblquad(fun,inmin,inmax,outmin,outmax)
вычисляет и возвращает значение двойного
интеграла для подынтегральной функции
fun(inner,outer),
по умолчанию используя квадратурную
функцию quad.
inner
– внутренняя переменная, изменяющаяся
от inmin
до inmax,
а outer
– внешняя переменная, изменяющаяся от
outmin
до outmax.
Первый аргумент @fun
– строка, описывающая подынтегральную
функцию. Эта функция должна быть функцией
двух переменных вида fout=fun
(inner,outer).
Функция должна брать вектор inner
и скаляр outer
и возвращать вектор fout,
который является функцией, вычисленной
в outer
и в каждом значении inner.
•
dblquad(fun,inmin,inmax,outmin,outmax,tol,trace)
передает в функцию dblquad
параметры tol
и trace.
Смотрите справку по функции quad
для получения информации о параметрах
tol
и trace.
•
dblquad(fun,inmin,inmax,outmin,outmax,tol,trace,order)
передает параметры tol
и trace
для функции quad
или quadl
в зависимости от значения строки order.
Допустимые значения для параметра order
– @quad
, @quadl
или имя любого определенного пользователем
квадратурного метода с таким же вызовом
и такими же возвращаемыми параметрами,
как у функций quad
и quadl.
(Например, при проверке старых программ
можно использовать @quad8
для большей совместимости с прежними
версиями MATLAB).
По умолчанию (без параметра order)
вызывается @quad,
поскольку подынтегральные функции
могут быть не гладкими.
Пример:
пусть mфайл
integ1.m
описывает функцию 2*y*sin(x)+x/2*cos(y),
тогда вычислить двойной интеграл от
этой функции можно следующим образом:
>>
result = dblquad(@integ1,pi,2*pi,0,2*pi)
result
= -78.9574
В
систему MATLAB
6.5 была введена новая функция для
вычисления тройных интегралов. Она
имеет четыре формы записи:
triplequad(fun,xmin,xmax,ymin,ymax,zmin,zmax)
triplequad(fun,xmin,xmax,ymin,ymax,zmin,zmax,tol)
triplequad(fun,xmin,xmax,ymin,ymax,zmin,zmax,tol,method)
triplequad(fun,xmin,xmax,ymin,ymax,zmin,zmax,tol,method,p1,p2,…)
Параметры
этой функции уже были определены выше
(добавлены только пределы для новой
переменной z).
Пример:
>>
Q
= triplequad(‘x+y*z’,0,pi,0,1,-1,1,0.001)
Q
= 9.8696
К
сожалению, проверка данной функции на
ряде тройных интегралов показала, что
она не всегда обеспечивает вычисления.
Возможны ситуации, когда данная функция
выводит ряд сообщений об ошибках даже
для берущихся интегралов.
Интегрирование
Если f символьное выражение, затем
попытки найти другое символьное выражение, F, так, чтобы diff(F) = f. Таким образом, int(f) возвращает неопределенный интеграл или антипроизводную f (если каждый существует в закрытой форме). Подобно дифференцированию,
использует символьный объект v когда переменная интегрирования, а не переменная определяется symvar. Смотрите как int работает путем рассмотрения этой таблицы.
|
Математическая операция |
MATLAB® Команда |
|---|---|
|
∫xndx={log(x)если n=−1xn+1n+1в противном случае. |
|
|
∫0π/2sin(2x)dx=1 |
|
|
g = because(at + b) ∫g(t)dt=sin(at+b)/a |
|
|
∫J1(z)dz=−J0(z) |
|
В отличие от дифференцирования, символьное интегрирование является более сложной задачей. Много трудностей могут возникнуть в вычислении интеграла:
-
Антипроизводная,
F, может не существовать в закрытой форме. -
Антипроизводная может задать незнакомую функцию.
-
Антипроизводная может существовать, но программное обеспечение не может найти его.
-
Программное обеспечение могло найти антипроизводную на более крупном компьютере, но заканчивается время или память на доступной машине.
Тем не менее, во многих случаях, MATLAB может выполнить символьное интегрирование успешно. Например, создайте символьные переменные
Следующая таблица иллюстрирует интегрирование выражений, содержащих те переменные.
|
f |
int (f) |
|---|---|
syms x n f = x^n; |
int(f) ans = piecewise(n == -1, log(x), n ~= -1,... x^(n + 1)/(n + 1)) |
syms y f = y^(-1); |
int(f) ans = log(y) |
syms x n f = n^x; |
int(f) ans = n^x/log(n) |
syms a b theta f = sin(a*theta+b); |
int(f) ans = -cos(b + a*theta)/a |
syms u f = 1/(1+u^2); |
int(f) ans = atan(u) |
syms x f = exp(-x^2); |
int(f) ans = (pi^(1/2)*erf(x))/2 |
В последнем примере, exp(-x^2), нет никакой формулы для интеграла включающих стандартных выражений исчисления, таких как тригонометрические и показательные функции. В этом случае MATLAB дает ответ в терминах функции ошибок erf.
Если MATLAB не может найти ответ на интеграл функционального f, это только возвращает int(f).
Определенное интегрирование также возможно.
|
Определенный интеграл |
Команда |
|---|---|
|
∫abf(x)dx |
|
|
∫abf(v)dv |
|
Вот некоторые дополнительные примеры.
|
f |
a, B |
int (f, a, b) |
|---|---|---|
syms x f = x^7; |
a = 0; b = 1; |
int(f, a, b) ans = 1/8 |
syms x f = 1/x; |
a = 1; b = 2; |
int(f, a, b) ans = log(2) |
syms x f = log(x)*sqrt(x); |
a = 0; b = 1; |
int(f, a, b) ans = -4/9 |
syms x f = exp(-x^2); |
a = 0; b = inf; |
int(f, a, b) ans = pi^(1/2)/2 |
syms z f = besselj(1,z)^2; |
a = 0; b = 1; |
int(f, a, b) ans =
hypergeom([3/2, 3/2],...
[2, 5/2, 3], -1)/12
|
Для Функции Бесселя (besselj) пример, возможно вычислить числовое приближение к значению интеграла, с помощью double функция. Команды
syms z a = int(besselj(1,z)^2,0,1)
возврат
a = hypergeom([3/2, 3/2], [2, 5/2, 3], -1)/12
и команда
возвращается
Интеграция с действительными параметрами
Одна из тонкости, вовлеченной в символьное интегрирование, является “значением” различных параметров. Например, если a является каким-либо положительным вещественным числом, выражением
положительная, кривая, имеющая форму звонка, которая стремится к 0, как x стремится к ± ∞. Можно создать пример этой кривой для a = 1/2.
syms x
a = sym(1/2);
f = exp(-a*x^2);
fplot(f)
Однако, при попытке вычислить интеграл
не присваивая значение a, MATLAB принимает, что a представляет комплексное число, и поэтому дает кусочный ответ, который зависит от аргумента a. Если вы только интересуетесь случаем, когда a является положительным вещественным числом, используйте assume установить предположение на a:
Теперь можно вычислить предыдущий интеграл с помощью команд
syms x f = exp(-a*x^2); int(f, x, -inf, inf)
Это возвращается
Интеграция с комплексными параметрами
Вычислить интеграл
для комплексных чисел a, войти
syms a x f = 1/(a^2 + x^2); F = int(f, x, -inf, inf)
Используйте syms очистить все предположения на переменных. Для получения дополнительной информации о символьных переменных и предположениях на них, смотрите, Удаляют Символьные Объекты и Их Предположения.
Предыдущие команды производят комплексный выход
Функция signIm задан как:
Оценивать F в a = 1 + i, войти
Численное интегрирование высокой точности Используя арифметику Переменной Точности
Численное интегрирование высокой точности реализовано в vpaintegral функция Symbolic Math Toolbox™. vpaintegral арифметика переменной точности использования в отличие от MATLAB integral функция, которая использует арифметику с двойной точностью.
Интегрируйте besseli(5,25*u).*exp(-u*25) при помощи обоих integral и vpaintegral. integral функция возвращает NaN и выдает предупреждение в то время как vpaintegral возвращает правильный результат.
syms u f = besseli(5,25*x).*exp(-x*25); fun = @(u)besseli(5,25*u).*exp(-u*25); usingIntegral = integral(fun, 0, 30) usingVpaintegral = vpaintegral(f, 0, 30)
Warning: Infinite or Not-a-Number value encountered. usingIntegral = NaN usingVpaintegral = 0.688424
Для получения дополнительной информации смотрите vpaintegral.
Системы
MatLabSciLab обладают большими возможностями
программирования и визуализации
результатов научных исследований при
решении задач вычислительной математики.
Численные методы в этих системах
предлагаются уже в виде готового
инструментария — набора функций, их
реализующих. Задачей данной работы
является ознакомление с наиболее часто
встречающимися на практике численными
методами, которые используются при
решении нелинейных уравнений, при
аппроксимации и интегрировании функций.
Приближѐнное вычисление определѐнных
интегралов. С вычислением определѐнных
интегралов самого общего вида:

приходится
сталкиваться при решении многих задач
математики, физики, химии и т.д. Как
правило, на практике получить первообразную
аналитически и затем воспользоваться
формулой Ньютона-Лейбница удаѐтся
крайне редко. В этих случаях интеграл
вычисляется приближѐнно с помощью
одного из методов численного интегрирования.
В методе трапеций используется линейная
интерполяция, т.е. подынтегральная
функция заменяется кусочно-линейной,
а еѐ график представляется в виде
ломаной, соединяющей отдельные точки
yi
= f(xi),
где xi
– координаты узлов сетки, введѐнной
на интервале интегрирования. При этом,
очевидно, на каждом из интервалов от
xi
до xi+1
искомые площади вычисляются как площади
обычных трапеций, после чего суммируются.
В итоге формула трапеций при постоянном
шаге сетки h
= xi+1
— xi
= (b
— a)/n
(n
– число интервалов разбиения сетки)
принимает вид:

Эта
схема интегрирования чрезвычайно проста
для реализации и имеет 2-ой порядок
точности относительно шага сетки. Тем
не менее, для экономии времени пользователя
в MatLab
еѐ реализовали в виде функции trapz(x,
y),
а в SciLab
– inttrap(x,
y).
Здесь x
и y
– массивы одного и того же размера 1хn,
содержащие, соответственно, координаты
узлов выбранной сетки и значения функции
в этих узлах. Не многим сложнее
оказывается формула Симпсона 4-го
порядка точности, получаемая при кусочной
интерполяции подынтегрального выражения
с помощью парабол:

В
MatLab формула Симпсона реализуется
функцией quad(fun, a, b [,tol]), где fun –
подынтегральная функция, a, b – концы
интервала интегрирования, tol – требуемая
точность (необязательный параметр).
Подынтегральная функция может быть
предварительно определена в m-файле,
тогда еѐ имя следует указать с дескриптором
@, или еѐ можно указать непосредственно
при вызове quad в виде текстовой строки,
заключѐнной в одинарные кавычки.
Например, вызов quad(@myfun, 0, 1, 1e-3) вычислит
интеграл от myfun(x) на интервале [0, 1] с
точностью 0.001. Файл функции myfun может
быть примерно следующим: function m = myfun(x)
m
= x.*x;
return
Аналогично,
производится интегрирование при
непосредственном задании функции,
например: quad(‘x.*x’,
0, 1, 1e-3).
Примечание: не забывайте, что операции
умножения, деления и возведения в степень
необходимо указывать в форме с «.», т.к.
они производятся над массивами.
Интегрирование
методом трапеций.
Приведенные
ниже функции выполняют численное
интегрирование хорошо известным методом
трапеций и методом трапеций с накоплением.
•
trapz(Y)
возвращает определенный интеграл,
используя интегрирование методом
трапеций с единичным шагом между
отсчетами. Если Y
– вектор, то trapz(Y)
возвращает интеграл элементов вектора
Y,
если Y
– матрица, то trapz(Y)
возвращает векторстроку, содержащую
интегралы каждого столбца этой матрицы.
•
trapz(X,Y)
возвращает интеграл от функции Y
по переменной X,
используя метод трапеций (пределы
интегрирования в этом случае задаются
начальным и конечным элементами вектора
X).
•
trapz(…,dim)
возвращает интеграл по строкам или по
столбцам для входной матрицы, в зависимости
от значения переменной dim.
Примеры:
>>
y=[1,2,3,4]
y
= 1 2 3 4
>>
trapz(y)
ans
= 7.5000
>>
X=0:pi/70:pi/2; Y=cos(X); Z = trapz(Y)
Z
= 22.2780
•
cumtrapz(Y)
возвращает численное значение
определенного интеграла для функции,
заданной ординатами в векторе или
матрице Y
с шагом интегрирования, равным единице
(интегрирование методом трапеций с
накоплением). В случае когда шаг отличен
от единицы, но постоянен, вычисленный
интеграл достаточно умножить на величину
шага. Для векторов эта функция возвращает
вектор, содержащий результат интегрирования
с накоплением элементов вектора Y.
Для матриц – возвращает матрицу того
же размера, что и Y,
содержащую результаты интегрирования
с накоплением для каждого столбца
матрицы Y.
cumtrapz(X,Y)
выполняет интегрирование с накоплением
от Y
по переменной X,
используя метод трапеций. X
и Y
должны быть векторами одной и той же
длины, или X
должен быть векторомстолбцом, а Y
– матрицей. cumtrapz(…,
dim)
выполняет интегрирование с накоплением
элементов по размерности, точно
определенной скаляром dim.
Длина вектора X
должна быть равна size(Y,dim).
Интегрирование
методом квадратур
Метод
трапеций обеспечивает невысокую точность
при заданном числе шагов или дает слишком
большое число шагов при вычислениях с
заданной погрешностью. Приведенные
ниже функции осуществляют интегрирование
и двойное интегрирование, используя
более точную квадратурную формулу
Симпсона или метод Гаусса–Лобатто.
Квадратура – численный метод нахождения
площади под графиком функции f(x),
то есть вычисление определенного
интеграла вида. В приведенных ниже
формулах подынтегральное выражение
fun
обычно задается или в прямых апострофах,
или в форме handleфункции.
Функции quad
и quadl
используют два различных алгоритма
квадратуры для вычисления определенного
интеграла. Функция quad
выполняет интегрирование по методу
низкого порядка, используя рекурсивное
правило Симпсона. Но она может быть
более эффективной при негладких
подынтегральных функциях или при низкой
требуемой точности вычислений. Алгоритм
quad
в MATLAB
6 изменен по сравнению с предшествовавшими
версиями, точность по умолчанию по
сравнению с версиями 5.3x
повышена в 1000 раз (с 10–3 до 10–6). Новая
функция quad1
(квадратура Лобатто) использует адаптивное
правило квадратуры Гаусса–Лобатто
очень высокого порядка. Устаревшая
функция quad8
выполняла интегрирование, используя
квадратурные формулы Ньютона–Котеса
8-го порядка. Достижимая точность
интегрирования гладких функций в MATLAB
6 поэтому также значительно выше, чем в
предшествующих версиях. quad(fun,a,b)
возвращает численное значение
определенного интеграла от заданной
функции @fun
на отрезке [a
b].
Используется значительно усовершенствованный
в MATLAB
6 адаптивный метод Симпсона. quad(fun,a,b,tol)
возвращает численное значение
определенного интеграла с заданной
относительной погрешностью tol.
По умолчанию tol=1.e–6.
Можно также использовать вектор,
состоящий из двух элементов tol
=[rel_tol
abs_tol],
чтобы точно определить комбинацию
относительной и абсолютной погрешностей.
quad(fun,a,b,tol,trace)
возвращает численное значение
определенного интеграла и при значении
trace,
не равном нулю, строит график, показывающий
ход вычисления интеграла.
quad(fun,a,b,tol,trace,P1,P2,…)
возвращает численное значение
определенного интеграла по подынтегральной
функции fun,
использует дополнительные аргументы
P1,
P2,
…, которые напрямую передаются в
подынтегральную функцию: G=fun(X,P1,P2,…).
Вычисления
двойных и тройных интегралов
Для
вычисления двойных интегралов служит
следующая функция:
•
dblquad(fun,inmin,inmax,outmin,outmax)
вычисляет и возвращает значение двойного
интеграла для подынтегральной функции
fun(inner,outer),
по умолчанию используя квадратурную
функцию quad.
inner
– внутренняя переменная, изменяющаяся
от inmin
до inmax,
а outer
– внешняя переменная, изменяющаяся от
outmin
до outmax.
Первый аргумент @fun
– строка, описывающая подынтегральную
функцию. Эта функция должна быть функцией
двух переменных вида fout=fun
(inner,outer).
Функция должна брать вектор inner
и скаляр outer
и возвращать вектор fout,
который является функцией, вычисленной
в outer
и в каждом значении inner.
•
dblquad(fun,inmin,inmax,outmin,outmax,tol,trace)
передает в функцию dblquad
параметры tol
и trace.
Смотрите справку по функции quad
для получения информации о параметрах
tol
и trace.
•
dblquad(fun,inmin,inmax,outmin,outmax,tol,trace,order)
передает параметры tol
и trace
для функции quad
или quadl
в зависимости от значения строки order.
Допустимые значения для параметра order
– @quad
, @quadl
или имя любого определенного пользователем
квадратурного метода с таким же вызовом
и такими же возвращаемыми параметрами,
как у функций quad
и quadl.
(Например, при проверке старых программ
можно использовать @quad8
для большей совместимости с прежними
версиями MATLAB).
По умолчанию (без параметра order)
вызывается @quad,
поскольку подынтегральные функции
могут быть не гладкими.
Пример:
пусть mфайл
integ1.m
описывает функцию 2*y*sin(x)+x/2*cos(y),
тогда вычислить двойной интеграл от
этой функции можно следующим образом:
>>
result = dblquad(@integ1,pi,2*pi,0,2*pi)
result
= -78.9574
В
систему MATLAB
6.5 была введена новая функция для
вычисления тройных интегралов. Она
имеет четыре формы записи:
triplequad(fun,xmin,xmax,ymin,ymax,zmin,zmax)
triplequad(fun,xmin,xmax,ymin,ymax,zmin,zmax,tol)
triplequad(fun,xmin,xmax,ymin,ymax,zmin,zmax,tol,method)
triplequad(fun,xmin,xmax,ymin,ymax,zmin,zmax,tol,method,p1,p2,…)
Параметры
этой функции уже были определены выше
(добавлены только пределы для новой
переменной z).
Пример:
>>
Q
= triplequad(‘x+y*z’,0,pi,0,1,-1,1,0.001)
Q
= 9.8696
К
сожалению, проверка данной функции на
ряде тройных интегралов показала, что
она не всегда обеспечивает вычисления.
Возможны ситуации, когда данная функция
выводит ряд сообщений об ошибках даже
для берущихся интегралов.
If f is a symbolic expression, then
attempts to find another symbolic expression, F, so that
diff(F) = f. That is,
int(f) returns the indefinite integral or antiderivative of
f (provided one exists in closed form). Similar to
differentiation,
uses the symbolic object v as the variable of integration, rather than
the variable determined by symvar. See how int works by
looking at this table.
|
Mathematical Operation |
MATLAB® Command |
|---|---|
|
∫xndx={log(x)if n=−1xn+1n+1otherwise. |
|
|
∫0π/2sin(2x)dx=1 |
|
|
g = cos(at + ∫g(t)dt=sin(at+b)/a |
|
|
∫J1(z)dz=−J0(z) |
|
In contrast to differentiation, symbolic integration is a more complicated task. A number
of difficulties can arise in computing the integral:
-
The antiderivative,
F, may not exist in closed form. -
The antiderivative may define an unfamiliar function.
-
The antiderivative may exist, but the software can’t find it.
-
The software could find the antiderivative on a larger computer, but runs out of time
or memory on the available machine.
Nevertheless, in many cases, MATLAB can perform symbolic integration successfully. For example, create the symbolic
variables
The following table illustrates integration of expressions containing those
variables.
|
f |
int(f) |
|---|---|
syms x n f = x^n; |
int(f) ans = piecewise(n == -1, log(x), n ~= -1,... x^(n + 1)/(n + 1)) |
syms y f = y^(-1); |
int(f) ans = log(y) |
syms x n f = n^x; |
int(f) ans = n^x/log(n) |
syms a b theta f = sin(a*theta+b); |
int(f) ans = -cos(b + a*theta)/a |
syms u f = 1/(1+u^2); |
int(f) ans = atan(u) |
syms x f = exp(-x^2); |
int(f) ans = (pi^(1/2)*erf(x))/2 |
In the last example, exp(-x^2), there is no formula for the integral
involving standard calculus expressions, such as trigonometric and exponential functions. In
this case, MATLAB returns an answer in terms of the error function erf.
If MATLAB is unable to find an answer to the integral of a function f,
it just returns int(f).
Definite integration is also possible.
|
Definite Integral |
Command |
|---|---|
|
∫abf(x)dx |
|
|
∫abf(v)dv |
|
Here are some additional examples.
|
f |
a, b |
int(f, a, b) |
|---|---|---|
syms x f = x^7; |
a = 0; b = 1; |
int(f, a, b) ans = 1/8 |
syms x f = 1/x; |
a = 1; b = 2; |
int(f, a, b) ans = log(2) |
syms x f = log(x)*sqrt(x); |
a = 0; b = 1; |
int(f, a, b) ans = -4/9 |
syms x f = exp(-x^2); |
a = 0; b = inf; |
int(f, a, b) ans = pi^(1/2)/2 |
syms z f = besselj(1,z)^2; |
a = 0; b = 1; |
int(f, a, b) ans =
hypergeom([3/2, 3/2],...
[2, 5/2, 3], -1)/12
|
For the Bessel function (besselj) example, it is possible to compute a
numerical approximation to the value of the integral, using the double function. The commands
syms z a = int(besselj(1,z)^2,0,1)
return
a = hypergeom([3/2, 3/2], [2, 5/2, 3], -1)/12
and the command
returns
Integration with Real Parameters
One of the subtleties involved in symbolic integration is the “value” of
various parameters. For example, if a is any positive real number, the
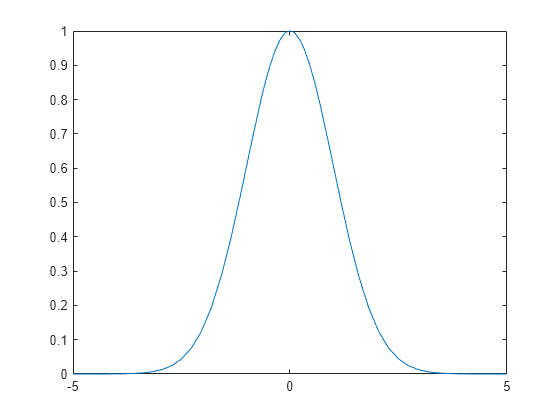
expression
is the positive, bell shaped curve that tends to 0 as x tends to ±∞. You can create an example of this curve, for a = 1/2.
syms x
a = sym(1/2);
f = exp(-a*x^2);
fplot(f)
However, if you try to calculate the integral
without assigning a value to a, MATLAB assumes that a represents a complex number, and therefore
returns a piecewise answer that depends on the argument of a. If you are
only interested in the case when a is a positive real number, use
assume to set an assumption on a:
Now you can calculate the preceding integral using the commands
syms x f = exp(-a*x^2); int(f, x, -inf, inf)
This returns
Integration with Complex Parameters
To calculate the integral
for complex values of a, enter
syms a x f = 1/(a^2 + x^2); F = int(f, x, -inf, inf)
Use syms to clear all the assumptions on variables. For more
information about symbolic variables and assumptions on them, see Use Assumptions on Symbolic Variables.
The preceding commands produce the complex output
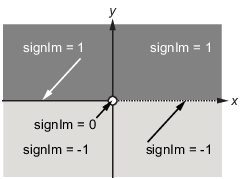
The function signIm is defined as:
To evaluate F at a = 1 + i, enter
High-Precision Numerical Integration Using Variable-Precision Arithmetic
High-precision numerical integration is implemented in the vpaintegral function of the Symbolic Math Toolbox™. vpaintegral uses variable-precision arithmetic in
contrast to the MATLAB
integral function, which uses
double-precision arithmetic.
Integrate besseli(5,25*u).*exp(-u*25) by using both
integral and vpaintegral. The
integral function returns NaN and issues a
warning while vpaintegral returns the correct result.
syms u f = besseli(5,25*x).*exp(-x*25); fun = @(u)besseli(5,25*u).*exp(-u*25); usingIntegral = integral(fun, 0, 30) usingVpaintegral = vpaintegral(f, 0, 30)
Warning: Infinite or Not-a-Number value encountered. usingIntegral = NaN usingVpaintegral = 0.688424
For more information, see vpaintegral.
See Also
int | diff | vpaintegral
External Websites
- Calculus Integrals (MathWorks Teaching Resources)