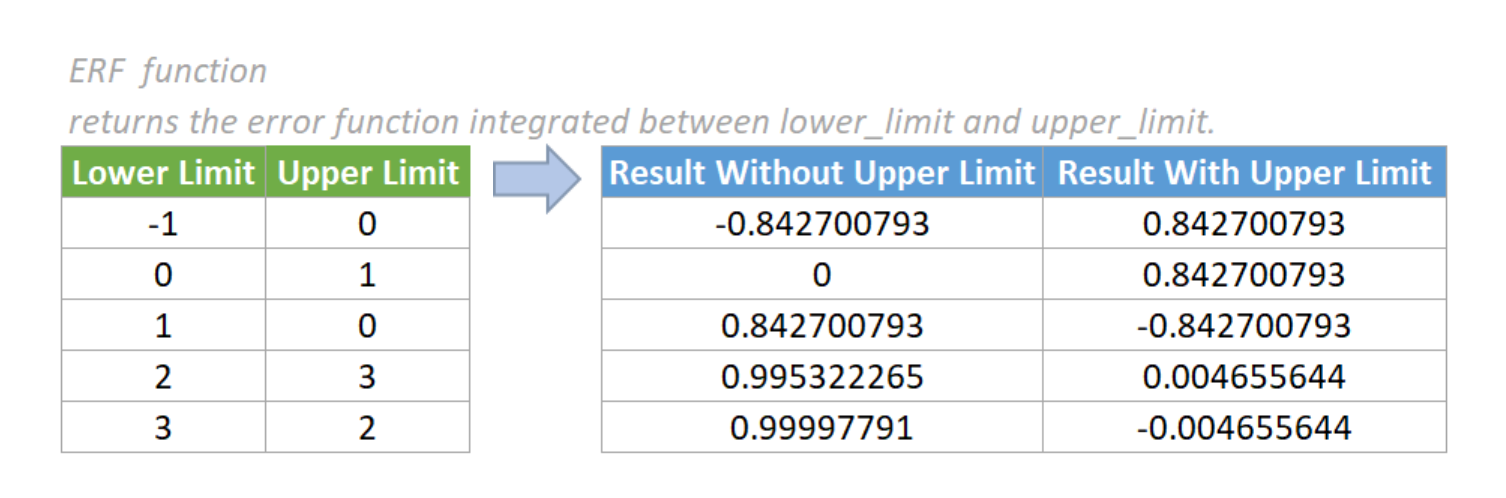
Функция ФОШ возвращает функцию ошибки, проинтегрированную от значения аргумента «нижний_предел» до значения аргумента «верхний_предел».
Описание функции ФОШ
Возвращает функцию ошибки, проинтегрированную от значения аргумента «нижний_предел» до значения аргумента «верхний_предел».
Синтаксис
=ФОШ(нижний_предел; [верхний_предел])Аргументы
нижний_пределверхний_предел
Обязательный аргумент. Нижний предел интегрирования ФОШ.
Необязательный аргумент. Верхний предел интегрирования ФОШ. Если аргумент «верхний_предел» опущен, функция ФОШ выполняет интегрирование в пределах от 0 до значения аргумента «нижний_предел».
Замечания
- Если аргумент «нижний_предел» не является числом, функция ФОШ возвращает значение ошибки #ЗНАЧ!.
- Если аргумент «верхний_предел» не является числом, функция ФОШ возвращает значение ошибки #ЗНАЧ!.
Пример
Функция ERF возвращает функцию ошибки, интегрированную между нижним_пределом и верхним_пределом.
Синтаксис
=ERF (lower_limit, [upper_limit])
аргументы
- Нижний предел (обязательно): Нижний предел интегрирования.
- Верхний предел (необязательно): Верхний предел интегрирования. Если опущено, будет возвращена интеграция между 0 и нижним_пределом.
Возвращаемое значение
Функция ERF возвращает числовое значение.
Примечания к функциям
- Функция ERF была улучшена в Excel 2010, и теперь она может вычислять отрицательные значения.
В Excel 2007 функция ERF принимает только положительные значения. Если какой-либо из предоставленных аргументов имеет отрицательное значение, функция ERF вернет ошибку #ЧИСЛО! значение ошибки. - Значение! значение ошибки возникает, если какой-либо из предоставленных аргументов не является числовым.
- Когда верхний_предел опущен, ERF интегрируется между нулем (значение нижнего_предела) и нижним_пределом (значение верхнего_предела). Следовательно, когда нижний предел положительный, ERF возвращает положительный результат. Наоборот.
Более того, когда нижний_предел больше верхнего_предела, ERF возвращает отрицательный результат. Наоборот. - Результирующий диапазон, возвращаемый функцией ERF, находится между -1 и 1.
- Уравнение функции ошибки:
Примеры
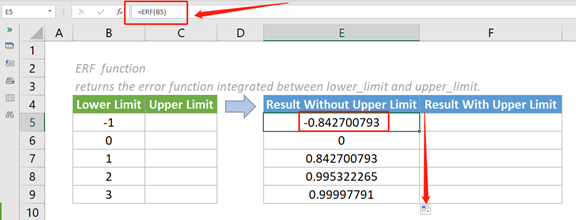
Пример первый: результат без верхнего предела
В этом случае мы хотим вычислить функцию ошибки, когда аргумент upper_limit опущен. Это означает, что функция ERF интегрируется между нулем и нижним_пределом. Пожалуйста, сделайте следующее.
1. Пожалуйста, скопируйте приведенную ниже формулу в ячейку E5, затем нажмите клавишу Enter, чтобы получить результат.
=ERF (B5)
2. Выберите эту ячейку результатов и перетащите ее маркер автозаполнения вниз, чтобы получить остальные результаты.
Заметки:
- Как показано на приведенном выше снимке экрана, когда единственный аргумент нижний_лимит отрицательный, возвращаемый результат также отрицательный. Наоборот.
- Когда единственный аргумент нижний_предел равен нулю (0), ERF возвращает в качестве результата ноль (0).
- Аргумент в каждой из приведенных выше формул предоставляется в виде ссылки на ячейку, содержащей числовое значение.
- Мы также можем напрямую ввести значение в формулу. Например, формулу в ячейке E5 можно изменить на:
=ERF (-1)
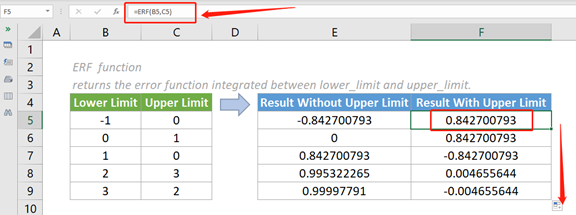
Пример второй: результат с верхним пределом
В этом случае мы хотим вычислить функцию ошибки, когда предоставлены аргументы lower_limit и upper_limit. Пожалуйста, сделайте следующее.
1. Пожалуйста, скопируйте приведенную ниже формулу в ячейку F5, затем нажмите клавишу Enter, чтобы получить результат.
=ERF (B5, C5)
2. Выберите эту ячейку результатов и перетащите ее маркер автозаполнения вниз, чтобы получить остальные результаты.
Заметки:
- Как видно из приведенного выше снимка экрана, когда верхний_предел больше нижнего_предела, ERF возвращает положительный результат. Наоборот.
- Аргументы в каждой из приведенных выше формул предоставляются в виде ссылок на ячейки, содержащих числовые значения.
- Мы также можем напрямую вводить значения в формулу. Например, формулу в ячейке F5 можно изменить на:
=ERF (-1, 0)
Относительные функции:
-
Excel EVEN Функция
Функция EVEN округляет числа от нуля до ближайшего четного целого числа.
-
Excel EXP Функция
Функция EXP возвращает результат возведения константы e в энную степень.
Лучшие инструменты для работы в офисе
Kutools for Excel — поможет вам выделиться из толпы
Хотите быстро и качественно выполнять свою повседневную работу? Kutools for Excel предлагает мощные расширенные функции 300 (объединение книг, суммирование по цвету, разделение содержимого ячеек, преобразование даты и т. д.) и экономит для вас 80% времени.
- Разработан для 1500 рабочих сценариев, помогает решить 80% проблем с Excel.
- Уменьшите количество нажатий на клавиатуру и мышь каждый день, избавьтесь от усталости глаз и рук.
- Станьте экспертом по Excel за 3 минуты. Больше не нужно запоминать какие-либо болезненные формулы и коды VBA.
- 30-дневная неограниченная бесплатная пробная версия. 60-дневная гарантия возврата денег. Бесплатное обновление и поддержка 2 года.
Вкладка Office — включение чтения и редактирования с вкладками в Microsoft Office (включая Excel)
- Одна секунда для переключения между десятками открытых документов!
- Уменьшите количество щелчков мышью на сотни каждый день, попрощайтесь с рукой мыши.
- Повышает вашу продуктивность на 50% при просмотре и редактировании нескольких документов.
- Добавляет эффективные вкладки в Office (включая Excel), точно так же, как Chrome, Firefox и новый Internet Explorer.
Комментарии (0)
Оценок пока нет. Оцените первым!
Оставляйте свои комментарии
The ERF function is an Engineering formula that calculates and returns the error function, integrated between specified lower and upper limits. In this guide, we’re going to show you how to use the ERF function, and also go over some tips and error handling methods.
Supported versions
- All Excel versions (The function was improved in Excel 2010 to include support for negative numbers.)
ERF Function Syntax
ERF(lower_limit, [upper_limit])
Arguments
| lower_limit | The lower bound of the integration. |
| [upper_limit] | Optional. The upper bound of the integral. If omitted, ERF returns the integration between 0 and the lower_limit. |
Examples
Lower limit only
The lower_limit is the only required argument for the ERF function. If you want to calculate the integral between 0 and a numeric value. You only need to enter a lower_limit value The ERF function accepts negative numerical values in Excel 2010 and newer versions. Below is an example set,
=ERF(1) integrates between 0 and 1
Lower Limit and Upper Limit
Enter an [upper_limit] argument to set both lower and upper limits to be used in the error function. The [upper_limit] argument is very similar to the lower_limit as it accepts numerical values without a sign (in Excel 2010 and later). Here is how you can use the ERF function with both arguments:
=ERF(1,2) integrates between 1 and 2
If you look at the screenshots, you can see ERF(1) and ERF(0,1) returns same value.
Download Workbook
Tips
- Other related Excel functions:
- ERF.PRECISE returns the error function between 0 and the entered argument.
- ERFC and ERFC.PRECISE functions return complementary error function integrated between x and infinity. (Both functions work similarly. The ERFC.PRECISE function was added to provide consistency between function names.)
- You can find further details on Wikipedia’s Error Function page.
Issues
- If the lower_limit is non-numeric, the ERF returns the #VALUE! error value.
- If the [upper_limit] is non-numeric, the ERF returns the #VALUE! error value.
- The ERF function returns the #NUM! error value if one or both of the arguments are negative in Excel 2007 or earlier versions.
The ERF function is an Engineering formula that calculates and returns the error function, integrated between specified lower and upper limits. In this guide, we’re going to show you how to use the ERF function, and also go over some tips and error handling methods.
Supported versions
- All Excel versions (The function was improved in Excel 2010 to include support for negative numbers.)
ERF Function Syntax
ERF(lower_limit, [upper_limit])
Arguments
| lower_limit | The lower bound of the integration. |
| [upper_limit] | Optional. The upper bound of the integral. If omitted, ERF returns the integration between 0 and the lower_limit. |
Examples
Lower limit only
The lower_limit is the only required argument for the ERF function. If you want to calculate the integral between 0 and a numeric value. You only need to enter a lower_limit value The ERF function accepts negative numerical values in Excel 2010 and newer versions. Below is an example set,
=ERF(1) integrates between 0 and 1
Lower Limit and Upper Limit
Enter an [upper_limit] argument to set both lower and upper limits to be used in the error function. The [upper_limit] argument is very similar to the lower_limit as it accepts numerical values without a sign (in Excel 2010 and later). Here is how you can use the ERF function with both arguments:
=ERF(1,2) integrates between 1 and 2
If you look at the screenshots, you can see ERF(1) and ERF(0,1) returns same value.
Download Workbook
Tips
- Other related Excel functions:
- ERF.PRECISE returns the error function between 0 and the entered argument.
- ERFC and ERFC.PRECISE functions return complementary error function integrated between x and infinity. (Both functions work similarly. The ERFC.PRECISE function was added to provide consistency between function names.)
- You can find further details on Wikipedia’s Error Function page.
Issues
- If the lower_limit is non-numeric, the ERF returns the #VALUE! error value.
- If the [upper_limit] is non-numeric, the ERF returns the #VALUE! error value.
- The ERF function returns the #NUM! error value if one or both of the arguments are negative in Excel 2007 or earlier versions.
3.3.Температурное
поле непрерывного неподвижного точечного
источника в неограниченной среде.
Функция ошибок Гаусса (функция erf(x)).
Если в точке с
координатами x‘,
y‘,
z‘
в интервале времени от t‘
= 0 до t‘
= t
работает источник тепла мощностью
W,
то температурное поле этого источника,
как указано выше, может быть найдено
интегрированием фундаментального
решения по t‘
от 0 до t
(т.е. от момента включения до момента
выключения источника). Поместим начало
координат в точку, где находится источник
тепла. Тогда x’
= y’
= z’
= 0, и формула
для температуры принимает вид:
,
(3.3.1)
где r2
= (x — x’)2
+ (y — y’)2
+ (z — z’)2
= x2
+ y2
+ z2
— квадрат расстояния от источника до
точки наблюдения.
Произведем в
интеграле (3.3.1) замену переменных:
r2/[4a(t
— t’)] = 2.
Тогда: (t —
t’)3/2
= r3/(8a3/23),
dt’ = r2d/(2a3),
пределы интегрирования: t’
= 0
,
t’ = t
= ,
и формула (3.3.1) принимает вид:
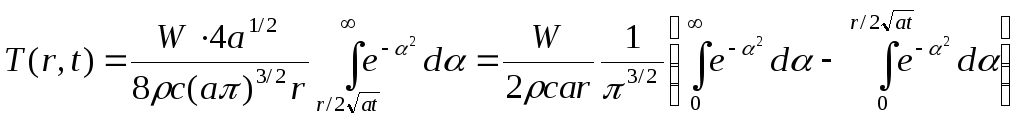
(3.3.2)
Первый интеграл,
стоящий в скобках, известен из курса
высшей математики:
(интеграл
Пуассона),
а второй интеграл
через элементарные функции не выражается
и определяет специальную функцию,
которая называется функцией
ошибок Гаусса,
или интегралом
вероятностей,
или функцией эрфектум:
(3.3.3)
(читается «эрфектум»
или сокращенно: «эрф»). Через эту
функцию выражаются решения многих
задач в теории теплопроводности, да и
в других областях физики она играет
важную роль.
Из определения
(3.3.3) видно, что erf(0)
= 0, а erf()
= 1, т.е. erf(x)
— это монотонно возрастающая
функция, вид которой изображен
на Рис.3.3. Функция erf(x)
табулирована, и ее значения
приводятся в различных
справочниках; в таблице 3.1 приведены
несколько значений этой функции. В
библиотеках некоторых
языков программирования имеются
готовые подпрограммы для
вычисления функции erf(x).
Если готовой подпрограммы
нет, функцию erf(x)
можно
вычислить с помощью степенного
ряда. «Стандартное»
разложение этой функции в
степенной ряд, которое обычно
приводится в математических
справочниках, имеет вид:
.
(3.3.4)
Э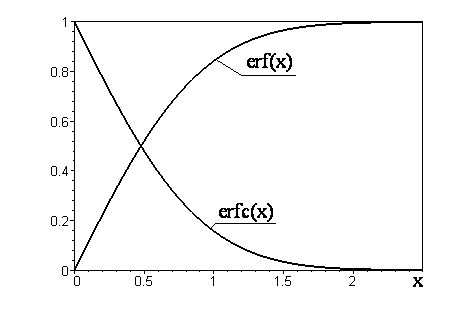
ряд удобен для анализа свойств функции,
но для практических расчетов он неудобен,
т.к. является знакопеременным, что
при вычислениях приводит к потере
точности. Более удобен следующий
ряд:
,
(3.3.5)
где
,
.
С
Рис. 3.3.
помощью этого ряда легко составить
программу вычисления erf(x)
на любом языке программирования
и даже на программируемом
микрокалькуляторе. Суммирование
надо прекращать, когда при
добавлении очередного an-го
слагаемого сумма перестанет меняться
(будет достигнута «машинная
точность»).
Если большой
точности не требуется, то можно
использовать приближенную формулу:
erf(x)
[1 — exp(-4x2/)]1/2.
(3.3.6)
Формула (3.3.6) дает
значения, абсолютная погрешность которых
не более 6.310-3,
а относительная погрешность
не более 0.71%.
Иногда требуется
определить erf(x)
в области отрицательных значений x.
Из формулы (3.3.3) очевидно, что erf(-x)
= — erf(x).
Заметим, что хотя
функция erf(x)
не является «элементарной», с точки
зрения ее свойств и способов
вычисления она проще, чем многие
«элементарные» функции, например,
тригонометрические.
С функцией erf(x)
связано еще несколько функций, часто
встречающихся в теплофизических
задачах. Это прежде всего дополнительный
интеграл вероятностей:
,
(3.3.7)
который встречается
настолько часто, что для него используется
специальное обозначение: erfc(x)
(сокращенно читается «эрфик»). Вид
этой функции также приведен на рис.3.3.
Довольно часто
функцию erf(x)
приходится дифференцировать и
интегрировать. Из определения
(3.3.3) следует, что
,
(3.3.8)
а интеграл от
erfc(x)
(обозначается как ierfc(x))
равен:
.
(3.3.9)
Вернемся к формуле
(3.3.2). Замечая, что ca
= ,
запишем эту формулу в виде:
.
(3.3.10)
При t
значение функции
0,
1, и формула (3.3.10), как и должно быть,
совпадает с формулой для
стационарного решения (если T0
принять за начало отсчета
температуры), т.к. при t
достигается стационарное
распределение температуры
в безграничной среде.
Таблица 3.1.
Некоторые значения функции erf(x).
|
x |
erf(x) |
x |
erf(x) |
x |
erf(x) |
x |
erf(x) |
x |
erf(x) |
|
0.0 |
0.0 |
0.3 |
0.32863 |
0.6 |
0.60386 |
0.9 |
0.79691 |
2.0 |
0.99532 |
|
0.1 |
0.11246 |
0.4 |
0.42839 |
0.7 |
0.67780 |
1.0 |
0.84270 |
2.5 |
0.99959 |
|
0.2 |
0.22270 |
0.5 |
0.52050 |
0.8 |
0.74210 |
1.5 |
0.96611 |
Соседние файлы в папке КраткийКонспектЛекций
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

Функция ошибок (также называемая функция ошибок Гаусса) — неэлементарная функция (b) , возникающая в теории вероятностей (b) , статистике (b) и теории дифференциальных уравнений в частных производных (b) . Она определяется как
- .
Дополнительная функция ошибок, обозначаемая (иногда применяется обозначение ), определяется через функцию ошибок:
- .
Комплексная функция ошибок, обозначаемая , также определяется через функцию ошибок:
- .
Свойства
- Функция ошибок нечётна (b) :
- Для любого комплексного выполняется
- где черта обозначает комплексное сопряжение (b) числа .
- Функция ошибок не может быть представлена через элементарные функции (b) , но, разлагая интегрируемое выражение в ряд Тейлора (b) и интегрируя почленно, мы можем получить её представление в виде ряда:
- Это равенство выполняется (и ряд сходится) как для любого вещественного (b) , так и на всей комплексной плоскости (b) , согласно признаку Д’Аламбера (b) . Последовательность знаменателей образует последовательность A007680 в OEIS (b) .
- Для итеративного вычисления элементов ряда полезно представить его в альтернативном виде:
- поскольку — сомножитель, превращающий -й член ряда в -й, считая первым членом .
- Функция ошибок на бесконечности равна единице; однако это справедливо только при приближении к бесконечности по вещественной оси, так как:
- При рассмотрении функции ошибок в комплексной плоскости точка будет для неё существенно особой.
- Производная функции ошибок выводится непосредственно из определения функции:
- Первообразная (b) функции ошибок, получаемая способом интегрирования по частям (b) :
- Обратная функция ошибок представляет собой ряд
- где c0 = 1 и
- Поэтому ряд можно представить в следующем виде (заметим, что дроби сокращены):
- Последовательности числителей и знаменателей после сокращения — A092676 и A132467 в OEIS; последовательность числителей до сокращения — A002067 в OEIS.
Применение
Если набор случайных величин подчиняется нормальному распределению (b) со стандартным отклонением (b) , то вероятность, что величина отклонится от среднего не более чем на , равна .
Функция ошибок и дополнительная функция ошибок встречаются в решении некоторых дифференциальных уравнений, например, уравнения теплопроводности (b) с начальными условиями, (b) описываемыми функцией Хевисайда (b) («ступенькой»).
В системах цифровой оптической коммуникации, вероятность ошибки на бит также выражается формулой, использующей функцию ошибок.
Асимптотическое разложение
При больших полезно асимптотическое разложение (b) для дополнительной функции ошибок:
Хотя для любого конечного этот ряд расходится, на практике первых нескольких членов достаточно для вычисления с хорошей точностью, в то время как ряд Тейлора сходится очень медленно.
Другое приближение даётся формулой
где
Родственные функции
С точностью до масштаба и сдвига, функция ошибок совпадает с нормальным интегральным распределением, обозначаемым
Обратная функция (b) к , известная как нормальная квантильная функция (b) , иногда обозначается (b) и выражается через нормальную функцию ошибок как
Нормальное интегральное распределение чаще применяется в теории вероятностей и математической статистике, в то время как функция ошибок чаще применяется в других разделах математики.
Функция ошибок является частным случаем функции Миттаг-Леффлера (b) , а также может быть представлена как вырожденная гипергеометрическая функция (функция Куммера (b) ):
Функция ошибок выражается также через интеграл Френеля (b) . В терминах регуляризованной неполной гамма-функции P (b) и неполной гамма-функции (b) ,
Обобщённые функции ошибок
серая линия:
красная линия:
зелёная линия:
синяя линия:
жёлтая линия: .
Некоторые авторы обсуждают более общие функции
Примечательными частными случаями являются:
- — прямая линия, проходящая через начало координат:
- — функция ошибок .
После деления на все с нечётными выглядят похоже (но не идентично), это же можно сказать про с чётными . Все обобщённые функции ошибок с выглядят похоже на полуоси .
На полуоси все обобщённые функции могут быть выражены через гамма-функцию (b) :
Следовательно, мы можем выразить функцию ошибок через гамма-функцию:
Повторные интегралы дополнительной функции ошибок
Повторные интегралы дополнительной функции ошибок определяются как[1]
- ,
- для .
Их можно разложить в ряд:
откуда следуют свойства симметрии
и
Реализации
В стандарте языка Си (b) (ISO/IEC 9899:1999, пункт 7.12.8) предусмотрены функция ошибок и дополнительная функция ошибок . Функции объявлены в заголовочных файлах math.h (b) (для Си (b) ) или cmath (для C++ (b) ). Там же объявлены пары функций erff(), erfcf() и erfl(), erfcl(). Первая пара получает и возвращает значения типа float, а вторая — значения типа long double. Соответствующие функции также содержатся в библиотеке Math проекта «Boost (b) ».
В языке Java (b) стандартная библиотека математических функций java.lang.Math (b) не содержит[2] функцию ошибок. Класс Erf можно найти в пакете org.apache.commons.math.special из не стандартной библиотеки, поставляемой[3]Apache Software Foundation (b) .
Системы компьютерной алгебры (b) Maple (b) , Matlab (b) , Mathematica (b) и Maxima (b) содержат обычную и дополнительную функции ошибок, а также обратные к ним функции.
В языке Python (b) функция ошибок доступна[4] из стандартной библиотеки math, начиная с версии 2.7. Также функция ошибок, дополнительная функция ошибок и многие другие специальные функции определены в модуле Special проекта SciPy (b) .
В языке Erlang (b) функция ошибок и дополнительная функция ошибок доступны из стандартного модуля math[5].
В Excel функция ошибок представлена, как ФОШ и ФОШ.ТОЧН[6]
См. также
- Функция Гаусса (b)
- Функция Доусона (b)
- Гауссов интеграл (b)
Примечания
- ↑ Carslaw, H. S. (b) & Jaeger, J. C. (b) (1959), Conduction of Heat in Solids (2nd ed.), Oxford University Press, ISBN 978-0-19-853368-9, p 484
- ↑ Math (Java Platform SE 6). Дата обращения: 28 марта 2008. Архивировано 29 августа 2009 года.
- ↑ Архивированная копия. Дата обращения: 28 марта 2008. Архивировано из оригинала 9 апреля 2008 года.
- ↑ 9.2. math — Mathematical functions — Python 2.7.10rc0 documentation
- ↑ Язык Erlang (b) . ОписаниеАрхивная копия от 20 июня 2012 на Wayback Machine (b) функций стандартного модуля
math. - ↑ Функция ФОШ. support.microsoft.com. Дата обращения: 15 ноября 2021. Архивировано 15 ноября 2021 года.
Литература
- Press, William H.; Teukolsky, Saul A.; Vetterling, William T. & Flannery, Brian P. (2007), Section 6.2. Incomplete Gamma Function and Error Function, Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
- Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. — New York: Dover, 1972. — Т. 7.
- Nikolai G. Lehtinen. Error functions (апрель 2010). Дата обращения: 25 мая 2019.
Ссылки
- MathWorld — Erf
- Онлайновый калькулятор Erf и много других специальных функций (до 6 знаков)
- Онлайновый калькулятор, вычисляющий в том числе Erf
Функция ГАУСС, подлежащая применению в версиях Excel начиная от 2013 года или новее. Она позволяет вычислить такую вероятность, с которой элемент стандартной нормальной совокупности будет находиться в интервале между средними и стандартными отклонениями от среднего.
Синтаксис рассматриваемой функции не представляет из себя ничего сложного, ведь функции ГАУСС присущ всего один обязательный аргумент – Z – возвращающий число.
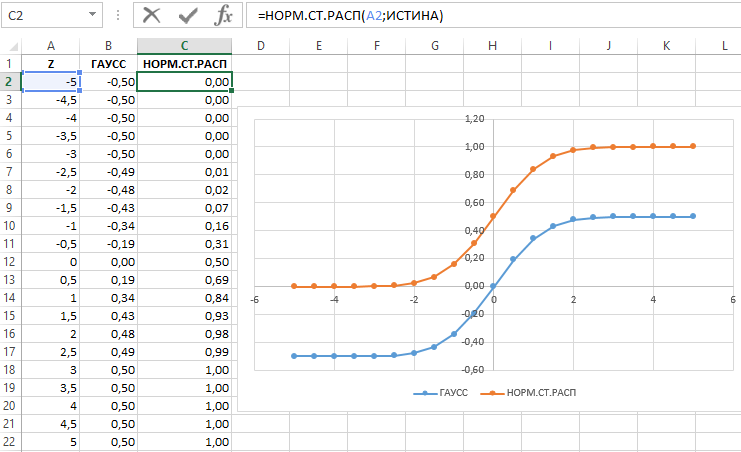
Важно отметить, что существует определенная связь между функцией ГАУСС и такой статистической функцией, как стандартное нормальное распределение, иначе говоря – НОРМ.СТ.РАСП.
Итак, всегда функция НОРМ.СТ.РАСП (0; Истина) делает возврат 0,5, тогда как ГАУСС (z) имеет в результате значение меньше на 0,5, чем результат функции НОРМ.СТ.РАСП. На рисунке, расположенном ниже, приведен пример использования данных статистических функций для возвращения числа 1,5.
Для наглядности продемонстрируем зависимость между значениями функций графическим способом. Для этого – сформируем таблицу с выборкой чисел, например на интервале от -5 до 5 с шагом 0,5, а затем по имеющимся данным построим график:
На графике четко прослеживается пропорциональная корреляция результатов вычислений функций ГАУСС и НОРМ.СТ.РАСП.
Решение системы вероятности методом ГАУССА в Excel
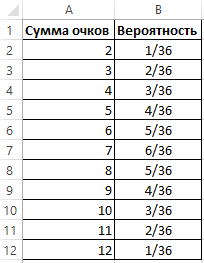
Задача представляет собой вычисление вероятности возможных значений при бросании двух костей.
Пример с игрой в кости является наиболее наглядным, так как мы имеем ограниченный набор данных, которые соответствуют вероятностям. Так, вероятность имеет значение от нуля до единицы, к которому стремится наблюдаемая частота при бесконечно большой выборке или повторении эксперимента.
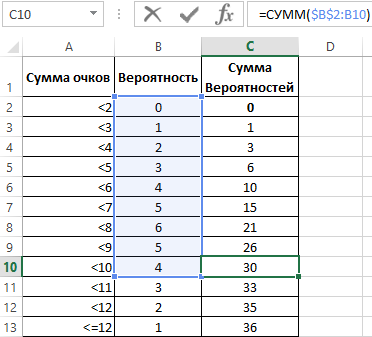
Существует 36 возможных комбинаций. При этом, вероятность того, что при бросании двух костей выпадет 2 очка равна 1/36, а 7 очков – 1/6. Отобразим перечень возможных значений бросания двух игральных костей в таблице, приведя при этом все вероятности к общему знаменателю.
Однако, такой ряд данных не дает возможности для выявления полного распределения, поэтому следует отобразить данные об отдельных вероятностях в рассчитанную по функции распределения. Так необходимо, все вероятности просуммировать последовательно (1+2+3+4+5+6+5+4+3+2+1).
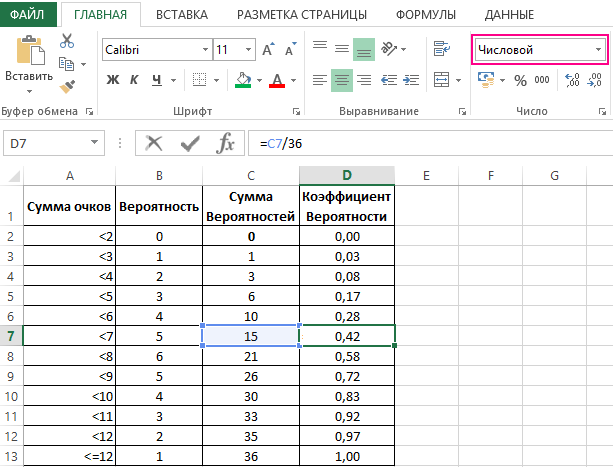
Теперь определяем коэффициент вероятности разделив по отдельности последовательную сумму вероятностей на максимально возможное количество комбинаций 36.
В первом случае нами были рассмотрены отдельные вероятности, во втором – сумма вероятностей от первого возможного значения до заданного.
Необходимо преобразовать диапазон ячеек D2:D13 в числовой формат данных, иначе при обращении на них функции ГАУСС будет иметь место ошибка.
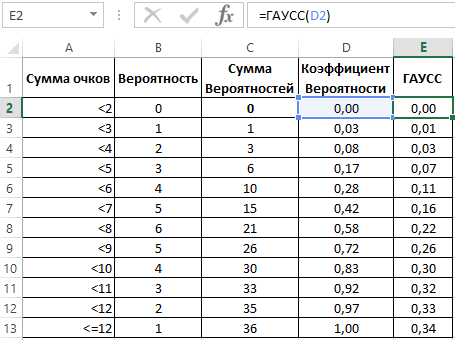
В созданный рядом с первоначальной таблицей столбец E введем формулу, которая в качестве аргумента делает обращение к ячейке D2.
Далее, протянем формулу вниз по столбцу, и получим ряд вероятностей с использованием функции ГАУСС.
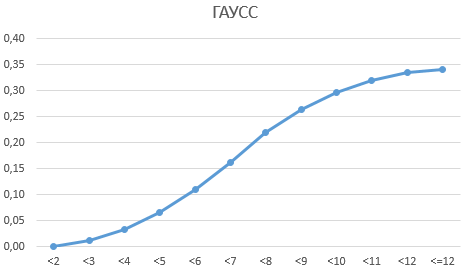
Для более наглядной визуализации, построим график вероятности:
Решение вероятности методом распределения кривой Гаусса в Excel
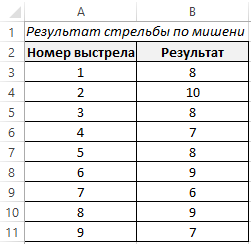
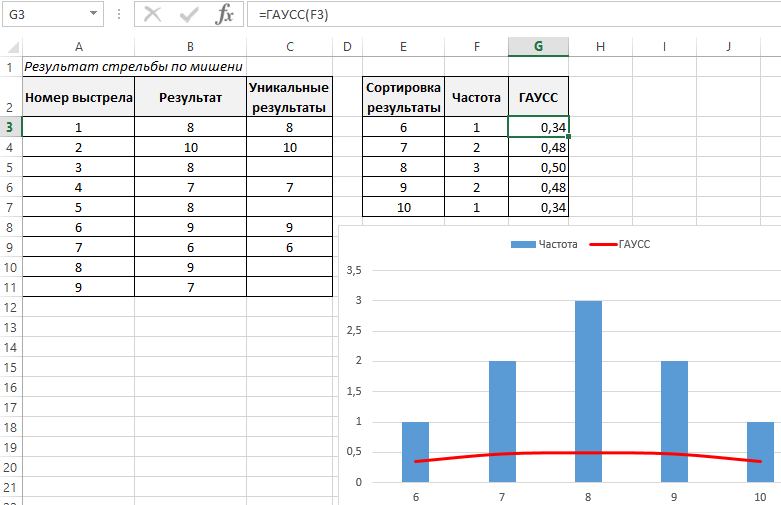
Теперь в качестве примера нормального распределения с помощью функции ГАУСС решим задачу о вероятностном соотношении результатов стрельбы по мишени.
Для этого построим базовую таблицу, которая отражает результаты стрельбы по мишени в девяти подходах.
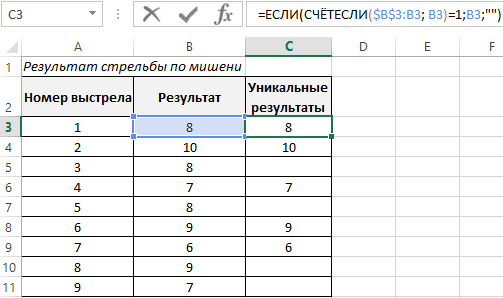
Затем, выберем только уникальные результаты, для этого используем хитрую формулу:
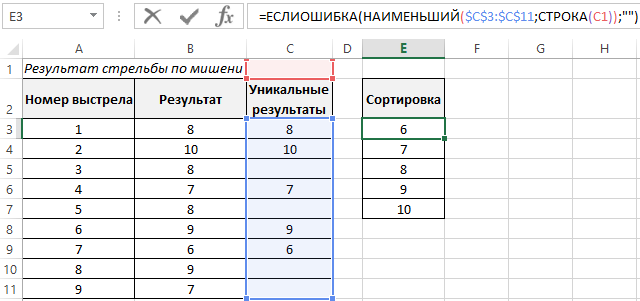
Делаем сортировку формулой для результатов по возрастанию и выводим в отдельную табличку:
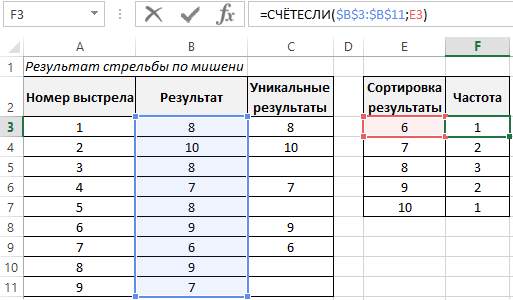
После чего определим частоту встречающихся только для уникальных результатов:
Далее применим функцию ГАУСС к значениям ячеек с частотой встречаемости. Отразим результаты вычислений на графике:
На графике красной линией определено нормальное распределение кривой Гаусса.
Erf x, или функция ошибок, является одной из фундаментальных функций математической статистики. Она широко применяется в решении различных задач, связанных с вероятностным анализом и статистикой. В данной статье мы подробно рассмотрим основные понятия, принципы работы и примеры использования функции ошибок Erf x.
Функция ошибок Erf x связана с распределением Гаусса (нормальным распределением) и позволяет вычислять вероятность возникновения случайной величины в заданном диапазоне. Это делает ее незаменимым инструментом для аналитиков данных, ученых и статистиков, которые занимаются анализом и интерпретацией больших объемов информации. Кроме того, функция ошибок Erf x активно используется в решении задач оптимизации, теории управления и других областях науки и техники.
Чтобы правильно использовать функцию ошибок Erf x, необходимо понимать ее математическую сущность и принципы работы. В следующих разделах мы расскажем об основных свойствах функции ошибок, ее производных, алгоритмах вычисления и примерах применения в решении математических задач.
Содержание
- Что такое Erf x и зачем он нужен?
- Определение и область применения Erf x
- Определение
- Область применения
- Что такое функция Erf x?
- Примеры использования Erf x в математике и статистике
- Как вычислить Erf x?
- Вопрос-ответ
- Что такое функция Эрф x и зачем она нужна?
- Как рассчитать значение функции Эрф x?
- Как связана функция Эрф x с плотностью вероятности нормального распределения?
- Как использовать функцию Эрф x для анализа данных?
- Как использовать функцию Эрф x для вычисления интегралов?
Что такое Erf x и зачем он нужен?
Erf x — это математическая функция, которая используется для вычисления вероятности событий в статистике и физике. Она также называется функцией ошибок ввиду ее свойств, связанных с интегралами ошибок.
При анализе данных часто возникают случаи, когда нужно определить, какую долю выборки составляют значения, находящиеся в определенном интервале. Например, вероятность, что случайно выбранный элемент превысит определенный уровень, может быть вычислена с использованием функции Erf. Это может быть полезно для принятия решений в области финансов, экономики, медицины и других областях.
Также Erf x нашла применение в теоретической физике, в частности, при описании ядерных реакций, распространения света в оптике и других областях, где требуется оценить вероятность наступления определенных событий.
- В общем, функция ошибок является важным инструментом для работы с вероятностными распределениями и статистическими моделями.
- Ее вычисление может помочь принять правильное решение на основе анализа данных.
- В физике и других естественных науках Erf x используется для описания реальных явлений и расчетов.
Определение и область применения Erf x
Определение
Erf x — математическая функция, которая является интегралом от стандартного нормального распределения на интервале от 0 до x. Эта функция используется для определения вероятности случайной величины, имеющей нормальное распределение.
Область применения
Erf x широко используется в различных областях, связанных с математикой, физикой, статистикой и инженерией. Она находит применение в решении задач по статистике, теории вероятности, теплопроводности, электродинамике, квантовой механике и многих других областях.
Erf x может быть полезна при расчете вероятности, что данные находятся в определенном интервале, при предсказании будущих значений на основе имеющихся данных, а также при моделировании систем, где важно учитывать случайные факторы.
Благодаря своей широкой области применения, Erf x является важным инструментом для исследователей и практиков в различных областях знания.
Что такое функция Erf x?
Функция Erf x — это математическая функция ошибок, которая описывает вероятность того, что случайная величина будет попадать в определенный диапазон значений. Она часто используется в статистических расчетах и анализе данных, а также в физике и инженерии.
Если случайная величина x имеет нормальное распределение, то ее функция ошибок может быть выражена через интеграл Гаусса. Эта функция является четной и монотонно возрастающей, и ее значение изменяется от -1 до 1.
Значение функции Erf x может быть вычислено с помощью математических таблиц или с помощью программных библиотек, таких как Math в языке программирования Java или scipy в языке программирования Python.
Функция Erf x может быть использована для решения различных задач, таких как вычисление вероятности при определенных условиях и анализ экспериментальных данных. Она также может быть полезна для определения оптимальных значений параметров в системах управления и проектированиях инженерных конструкций.
Примеры использования Erf x в математике и статистике
Функция Erf x нашла широкое применение в математике и статистике. Она используется для решения различных задач, связанных с вероятностными распределениями. Некоторые примеры ее использования:
- При нахождении вероятности того, что случайная величина, имеющая нормальное распределение, примет значение в определенном интервале. В этом случае Erf x используется для нахождения значения стандартной нормальной функции распределения.
- При аппроксимации других функций. Например, функция Erf x может быть использована для приближения функции ошибок, значения которой не всегда могут быть вычислены точно.
- При измерении амплитуды и фазы ультразвуковых волн. В этом случае функция Erf x используется для нахождения производной от акустического давления, которая определяет амплитуду и фазу колебаний.
Таким образом, функция Erf x имеет множество применений в математике и статистике. Она позволяет решить многие задачи, связанные с вероятностными распределениями, а также приблизить другие функции, что делает ее необходимой инструментальной функцией для многих областей науки и техники.
Как вычислить Erf x?
Функция Erf x представляет собой интегральную функцию нормального распределения вероятностей и очень часто используется в математических расчетах и анализе данных. Если вам необходимо вычислить Erf x, то можно воспользоваться специальными математическими программами, которые имеют функцию Эрмита. Например, вы можете воспользоваться такими программами, как Wolfram Mathematica или Matlab.
Также можно вычислить Erf x при помощи таблиц математических функций, которые содержат значения интегральных функций для различных аргументов. В таких таблицах, как правило, приводится значения функции Erф(x) для нескольких десятков значений аргумента x от -4 до 4 с шагом 0,1. Таким образом, если вы знаете значение аргумента x, то можно найти соответствующее значение функции Erf x в таблице и использовать его в расчетах.
Кроме того, можно вычислить Erf x при помощи специальных математических алгоритмов, которые основаны на приближенных методах расчета интегралов. Такие алгоритмы эффективны при вычислении функций, которые не могут быть выражены аналитически, например, при вычислении интегральных функций с большим числом переменных. Однако для этого необходимо обладать достаточными знаниями в области математики и программирования.
Вопрос-ответ
Что такое функция Эрф x и зачем она нужна?
Функция Эрф x (эрф-функция) — это математическая функция, которая используется для вычисления вероятности нормального распределения. Она имеет множество применений в физике, статистике и науке о данных. Например, она может использоваться для анализа данных из эксперимента или прогнозирования результата в бизнесе.
Как рассчитать значение функции Эрф x?
Значение функции Эрф x можно рассчитать с помощью специальных таблиц или калькуляторов. Также в Python можно использовать модуль math с функцией erf(). Например, чтобы рассчитать значение функции для x = 0.5, нужно вызвать функцию erf(0.5), и результат будет равен 0.520499876
Как связана функция Эрф x с плотностью вероятности нормального распределения?
Функция Эрф x связана с плотностью вероятности нормального распределения через интеграл. Если x — это случайная величина, распределенная нормально с математическим ожиданием mu и стандартным отклонением sigma, то функция плотности вероятности будет равна (1/(sigma * sqrt(2*pi))) * exp(-(x-mu)^2/(2*sigma^2)), а функция Эрф x можно рассчитать по формуле: erf(x) = 2 / sqrt(pi) * integral from 0 to x of e^(-t^2) dt.
Как использовать функцию Эрф x для анализа данных?
Функция Эрф x может использоваться для анализа данных, если значения распределены нормально. Например, если нужно оценить, сколько процентов людей в определенной группе имеют рост от 170 до 180 см, можно использовать функцию Эрф x. Для этого нужно рассчитать значения функции при x = (180-среднее значение роста) / стандартное отклонение и x = (170-среднее значение роста) / стандартное отклонение, а затем вычислить разность между ними и умножить на 100%.
Как использовать функцию Эрф x для вычисления интегралов?
Функция Эрф x может использоваться для вычисления интегралов, связанных с нормальным распределением. Например, интеграл от функции плотности вероятности может быть рассчитан с помощью функции Эрф x. Для этого нужно произвести замену переменной и выразить интеграл через функцию Эрф x. Например, интеграл от exp(-x^2) можно рассчитать как (sqrt(pi)/2) * erf(x).
Функция ERF возвращает функцию ошибки, интегрированную между нижним_пределом и верхним_пределом.
Синтаксис
=ERF (lower_limit, [upper_limit])
аргументы
- Нижний предел (обязательно): Нижний предел интегрирования.
- Верхний предел (необязательно): Верхний предел интегрирования. Если опущено, будет возвращена интеграция между 0 и нижним_пределом.
Возвращаемое значение
Функция ERF возвращает числовое значение.
Примечания к функциям
- Функция ERF была улучшена в Excel 2010, чтобы он мог рассчитывать отрицательные значения.
In Excel С 2007 года функция ERF принимает только положительные значения. Если какой-либо из предоставленных аргументов имеет отрицательное значение, функция ERF вернет #NUM! значение ошибки. - Значение! значение ошибки возникает, если какой-либо из предоставленных аргументов не является числовым.
- Когда верхний_предел опущен, ERF интегрируется между нулем (значение нижнего_предела) и нижним_пределом (значение верхнего_предела). Следовательно, когда нижний предел положительный, ERF возвращает положительный результат. Наоборот.
Более того, когда нижний_предел больше верхнего_предела, ERF возвращает отрицательный результат. Наоборот. - Результирующий диапазон, возвращаемый функцией ERF, находится между -1 и 1.
- Уравнение функции ошибки:
Примеры
Пример первый: результат без верхнего предела
В этом случае мы хотим вычислить функцию ошибки, когда аргумент upper_limit опущен. Это означает, что функция ERF интегрируется между нулем и нижним_пределом. Пожалуйста, сделайте следующее.
1. Пожалуйста, скопируйте приведенную ниже формулу в ячейку E5, затем нажмите клавишу Enter, чтобы получить результат.
=ЭРФ (B5)
2. Выберите эту ячейку результатов и перетащите ее маркер автозаполнения вниз, чтобы получить остальные результаты.
Заметки:
- Как показано на приведенном выше снимке экрана, когда единственный аргумент нижний_лимит отрицательный, возвращаемый результат также отрицательный. Наоборот.
- Когда единственный аргумент нижний_предел равен нулю (0), ERF возвращает в качестве результата ноль (0).
- Аргумент в каждой из приведенных выше формул предоставляется в виде ссылки на ячейку, содержащей числовое значение.
- Мы также можем напрямую ввести значение в формулу. Например, формулу в ячейке E5 можно изменить на:
=ЭРФ (-1)
Пример второй: результат с верхним пределом
В этом случае мы хотим вычислить функцию ошибки, когда предоставлены аргументы lower_limit и upper_limit. Пожалуйста, сделайте следующее.
1. Пожалуйста, скопируйте приведенную ниже формулу в ячейку F5, затем нажмите клавишу Enter, чтобы получить результат.
=ЭРФ (B5, C5)
2. Выберите эту ячейку результатов и перетащите ее маркер автозаполнения вниз, чтобы получить остальные результаты.
Заметки:
- Как видно из приведенного выше снимка экрана, когда верхний_предел больше нижнего_предела, ERF возвращает положительный результат. Наоборот.
- Аргументы в каждой из приведенных выше формул предоставляются в виде ссылок на ячейки, содержащих числовые значения.
- Мы также можем напрямую вводить значения в формулу. Например, формулу в ячейке F5 можно изменить на:
=ЭРФ (-1, 0)
Относительные функции:
-
Excel EVEN Функция
Функция EVEN округляет числа от нуля до ближайшего четного целого числа.
-
Excel EXP Функция
Функция EXP возвращает результат возведения константы e в энную степень.
Лучшие инструменты для работы в офисе
Kutools for Excel — Помогает вам выделиться из толпы
Хотите быстро и качественно выполнять свою повседневную работу? Kutools for Excel предлагает 300 мощных расширенных функций (объединение книг, суммирование по цвету, разделение содержимого ячеек, преобразование даты и т. д.) и экономит для вас 80 % времени.
- Рассчитан на 1500 рабочих сценариев, помогает решить 80% Excel проблемы.
- Уменьшите количество нажатий на клавиатуру и мышь каждый день, избавьтесь от усталости глаз и рук.
- Стать Excel эксперт за 3 минуты. Больше не нужно запоминать мучительные формулы и коды VBA.
- 30-дневная неограниченная бесплатная пробная версия. 60-дневная гарантия возврата денег. Бесплатное обновление и поддержка 2 года.
Office Tab — Включите чтение и редактирование с вкладками в Microsoft Office (включая Excel)
- Одна секунда для переключения между десятками открытых документов!
- Уменьшите количество щелчков мышью на сотни каждый день, попрощайтесь с рукой мыши.
- Повышает вашу продуктивность на 50% при просмотре и редактировании нескольких документов.
- Добавляет эффективные вкладки в Office (включая Excel), Точно так же, как Chrome, Firefox и новый Internet Explorer.
Comments (0)
No ratings yet. Be the first to rate!
Please leave your comments in English
Функция ошибок
| Аргумент функции ошибок erf(x) |
| Функция ошибок |
| Дополнительная функция ошибок |
Функция ошибок, она же функция Лапласа, он же интеграл вероятности — все это одна и та же сущность, которая выражается функцией
и используется в статистике и теории вероятностей.
Функция неэлементарная, то есть её нельзя представить в виде элементарных (тригонометрических и алгебраических) функций.
Для расчета в нашем калькуляторе, мы используем связь с неполной гамма функцией
Кроме этого мы сможем здесь же вычислить, дополнительную функцию ошибок, обозначаемую 

В приницпе это все, что можно сказать о ней.
Калькулятор высчитывает результат как в вещественном так и комплексном поле.
Замечание: Функция прекрасно работает на всем поле комплексных чисел при условии если аргумент ( фаза) меньше 180 градусов. Это связано с особенностью вычисления этой функции, неполной гамма функции, интегральной показательной функцией через непрерывные дроби.
Отсюда следует вывод, что при отрицательных вещественных аргументах, функция будет выдавать неверные решения. Но при всех положительных, а также отрицательных комплексных аргументах функция ошибок выдает верный ответ.
Несколько примеров:

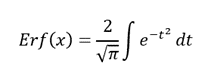














}{{\sqrt%20%20\pi%20}}})
