Интеграл ошибок excel - Решение и исправление самых разных ошибок на TopOshibok.ru

Функция ФОШ возвращает функцию ошибки, проинтегрированную от значения аргумента «нижний_предел» до значения аргумента «верхний_предел».

Описание функции ФОШ

Возвращает функцию ошибки, проинтегрированную от значения аргумента «нижний_предел» до значения аргумента «верхний_предел».

Синтаксис

=ФОШ(нижний_предел; [верхний_предел])

Аргументы

нижний_пределверхний_предел

Обязательный аргумент. Нижний предел интегрирования ФОШ.

Необязательный аргумент. Верхний предел интегрирования ФОШ. Если аргумент «верхний_предел» опущен, функция ФОШ выполняет интегрирование в пределах от 0 до значения аргумента «нижний_предел».

Замечания

Если аргумент «нижний_предел» не является числом, функция ФОШ возвращает значение ошибки #ЗНАЧ!.
Если аргумент «верхний_предел» не является числом, функция ФОШ возвращает значение ошибки #ЗНАЧ!.

Пример

Источник

Erf x, или функция ошибок, является одной из фундаментальных функций математической статистики. Она широко применяется в решении различных задач, связанных с вероятностным анализом и статистикой. В данной статье мы подробно рассмотрим основные понятия, принципы работы и примеры использования функции ошибок Erf x.

Функция ошибок Erf x связана с распределением Гаусса (нормальным распределением) и позволяет вычислять вероятность возникновения случайной величины в заданном диапазоне. Это делает ее незаменимым инструментом для аналитиков данных, ученых и статистиков, которые занимаются анализом и интерпретацией больших объемов информации. Кроме того, функция ошибок Erf x активно используется в решении задач оптимизации, теории управления и других областях науки и техники.

Чтобы правильно использовать функцию ошибок Erf x, необходимо понимать ее математическую сущность и принципы работы. В следующих разделах мы расскажем об основных свойствах функции ошибок, ее производных, алгоритмах вычисления и примерах применения в решении математических задач.

Содержание

Что такое Erf x и зачем он нужен?
Определение и область применения Erf x
Определение
Область применения
Что такое функция Erf x?
Примеры использования Erf x в математике и статистике
Как вычислить Erf x?
Вопрос-ответ
Что такое функция Эрф x и зачем она нужна?
Как рассчитать значение функции Эрф x?
Как связана функция Эрф x с плотностью вероятности нормального распределения?
Как использовать функцию Эрф x для анализа данных?
Как использовать функцию Эрф x для вычисления интегралов?

Что такое Erf x и зачем он нужен?

Erf x — это математическая функция, которая используется для вычисления вероятности событий в статистике и физике. Она также называется функцией ошибок ввиду ее свойств, связанных с интегралами ошибок.

При анализе данных часто возникают случаи, когда нужно определить, какую долю выборки составляют значения, находящиеся в определенном интервале. Например, вероятность, что случайно выбранный элемент превысит определенный уровень, может быть вычислена с использованием функции Erf. Это может быть полезно для принятия решений в области финансов, экономики, медицины и других областях.

Также Erf x нашла применение в теоретической физике, в частности, при описании ядерных реакций, распространения света в оптике и других областях, где требуется оценить вероятность наступления определенных событий.

В общем, функция ошибок является важным инструментом для работы с вероятностными распределениями и статистическими моделями.
Ее вычисление может помочь принять правильное решение на основе анализа данных.
В физике и других естественных науках Erf x используется для описания реальных явлений и расчетов.

Определение и область применения Erf x

Определение

Erf x — математическая функция, которая является интегралом от стандартного нормального распределения на интервале от 0 до x. Эта функция используется для определения вероятности случайной величины, имеющей нормальное распределение.

Область применения

Erf x широко используется в различных областях, связанных с математикой, физикой, статистикой и инженерией. Она находит применение в решении задач по статистике, теории вероятности, теплопроводности, электродинамике, квантовой механике и многих других областях.

Erf x может быть полезна при расчете вероятности, что данные находятся в определенном интервале, при предсказании будущих значений на основе имеющихся данных, а также при моделировании систем, где важно учитывать случайные факторы.

Благодаря своей широкой области применения, Erf x является важным инструментом для исследователей и практиков в различных областях знания.

Что такое функция Erf x?

Функция Erf x — это математическая функция ошибок, которая описывает вероятность того, что случайная величина будет попадать в определенный диапазон значений. Она часто используется в статистических расчетах и анализе данных, а также в физике и инженерии.

Если случайная величина x имеет нормальное распределение, то ее функция ошибок может быть выражена через интеграл Гаусса. Эта функция является четной и монотонно возрастающей, и ее значение изменяется от -1 до 1.

Значение функции Erf x может быть вычислено с помощью математических таблиц или с помощью программных библиотек, таких как Math в языке программирования Java или scipy в языке программирования Python.

Функция Erf x может быть использована для решения различных задач, таких как вычисление вероятности при определенных условиях и анализ экспериментальных данных. Она также может быть полезна для определения оптимальных значений параметров в системах управления и проектированиях инженерных конструкций.

Примеры использования Erf x в математике и статистике

Функция Erf x нашла широкое применение в математике и статистике. Она используется для решения различных задач, связанных с вероятностными распределениями. Некоторые примеры ее использования:

При нахождении вероятности того, что случайная величина, имеющая нормальное распределение, примет значение в определенном интервале. В этом случае Erf x используется для нахождения значения стандартной нормальной функции распределения.
При аппроксимации других функций. Например, функция Erf x может быть использована для приближения функции ошибок, значения которой не всегда могут быть вычислены точно.
При измерении амплитуды и фазы ультразвуковых волн. В этом случае функция Erf x используется для нахождения производной от акустического давления, которая определяет амплитуду и фазу колебаний.

Таким образом, функция Erf x имеет множество применений в математике и статистике. Она позволяет решить многие задачи, связанные с вероятностными распределениями, а также приблизить другие функции, что делает ее необходимой инструментальной функцией для многих областей науки и техники.

Как вычислить Erf x?

Функция Erf x представляет собой интегральную функцию нормального распределения вероятностей и очень часто используется в математических расчетах и анализе данных. Если вам необходимо вычислить Erf x, то можно воспользоваться специальными математическими программами, которые имеют функцию Эрмита. Например, вы можете воспользоваться такими программами, как Wolfram Mathematica или Matlab.

Также можно вычислить Erf x при помощи таблиц математических функций, которые содержат значения интегральных функций для различных аргументов. В таких таблицах, как правило, приводится значения функции Erф(x) для нескольких десятков значений аргумента x от -4 до 4 с шагом 0,1. Таким образом, если вы знаете значение аргумента x, то можно найти соответствующее значение функции Erf x в таблице и использовать его в расчетах.

Кроме того, можно вычислить Erf x при помощи специальных математических алгоритмов, которые основаны на приближенных методах расчета интегралов. Такие алгоритмы эффективны при вычислении функций, которые не могут быть выражены аналитически, например, при вычислении интегральных функций с большим числом переменных. Однако для этого необходимо обладать достаточными знаниями в области математики и программирования.

Вопрос-ответ

Что такое функция Эрф x и зачем она нужна?

Функция Эрф x (эрф-функция) — это математическая функция, которая используется для вычисления вероятности нормального распределения. Она имеет множество применений в физике, статистике и науке о данных. Например, она может использоваться для анализа данных из эксперимента или прогнозирования результата в бизнесе.

Как рассчитать значение функции Эрф x?

Значение функции Эрф x можно рассчитать с помощью специальных таблиц или калькуляторов. Также в Python можно использовать модуль math с функцией erf(). Например, чтобы рассчитать значение функции для x = 0.5, нужно вызвать функцию erf(0.5), и результат будет равен 0.520499876

Как связана функция Эрф x с плотностью вероятности нормального распределения?

Функция Эрф x связана с плотностью вероятности нормального распределения через интеграл. Если x — это случайная величина, распределенная нормально с математическим ожиданием mu и стандартным отклонением sigma, то функция плотности вероятности будет равна (1/(sigma * sqrt(2*pi))) * exp(-(x-mu)^2/(2*sigma^2)), а функция Эрф x можно рассчитать по формуле: erf(x) = 2 / sqrt(pi) * integral from 0 to x of e^(-t^2) dt.

Как использовать функцию Эрф x для анализа данных?

Функция Эрф x может использоваться для анализа данных, если значения распределены нормально. Например, если нужно оценить, сколько процентов людей в определенной группе имеют рост от 170 до 180 см, можно использовать функцию Эрф x. Для этого нужно рассчитать значения функции при x = (180-среднее значение роста) / стандартное отклонение и x = (170-среднее значение роста) / стандартное отклонение, а затем вычислить разность между ними и умножить на 100%.

Как использовать функцию Эрф x для вычисления интегралов?

Функция Эрф x может использоваться для вычисления интегралов, связанных с нормальным распределением. Например, интеграл от функции плотности вероятности может быть рассчитан с помощью функции Эрф x. Для этого нужно произвести замену переменной и выразить интеграл через функцию Эрф x. Например, интеграл от exp(-x^2) можно рассчитать как (sqrt(pi)/2) * erf(x).

Источник

Функция ERF возвращает функцию ошибки, интегрированную между нижним_пределом и верхним_пределом.

Синтаксис

=ERF (lower_limit, [upper_limit])

аргументы

Нижний предел (обязательно): Нижний предел интегрирования.
Верхний предел (необязательно): Верхний предел интегрирования. Если опущено, будет возвращена интеграция между 0 и нижним_пределом.

Возвращаемое значение

Функция ERF возвращает числовое значение.

Примечания к функциям

Функция ERF была улучшена в Excel 2010, чтобы он мог рассчитывать отрицательные значения.
In Excel С 2007 года функция ERF принимает только положительные значения. Если какой-либо из предоставленных аргументов имеет отрицательное значение, функция ERF вернет #NUM! значение ошибки.
Значение! значение ошибки возникает, если какой-либо из предоставленных аргументов не является числовым.
Когда верхний_предел опущен, ERF интегрируется между нулем (значение нижнего_предела) и нижним_пределом (значение верхнего_предела). Следовательно, когда нижний предел положительный, ERF возвращает положительный результат. Наоборот.
Более того, когда нижний_предел больше верхнего_предела, ERF возвращает отрицательный результат. Наоборот.
Результирующий диапазон, возвращаемый функцией ERF, находится между -1 и 1.
Уравнение функции ошибки:

Примеры

Пример первый: результат без верхнего предела

В этом случае мы хотим вычислить функцию ошибки, когда аргумент upper_limit опущен. Это означает, что функция ERF интегрируется между нулем и нижним_пределом. Пожалуйста, сделайте следующее.

1. Пожалуйста, скопируйте приведенную ниже формулу в ячейку E5, затем нажмите клавишу Enter, чтобы получить результат.

=ЭРФ (B5)

2. Выберите эту ячейку результатов и перетащите ее маркер автозаполнения вниз, чтобы получить остальные результаты.

Заметки:

Как показано на приведенном выше снимке экрана, когда единственный аргумент нижний_лимит отрицательный, возвращаемый результат также отрицательный. Наоборот.
Когда единственный аргумент нижний_предел равен нулю (0), ERF возвращает в качестве результата ноль (0).
Аргумент в каждой из приведенных выше формул предоставляется в виде ссылки на ячейку, содержащей числовое значение.
Мы также можем напрямую ввести значение в формулу. Например, формулу в ячейке E5 можно изменить на:
=ЭРФ (-1)

Пример второй: результат с верхним пределом

В этом случае мы хотим вычислить функцию ошибки, когда предоставлены аргументы lower_limit и upper_limit. Пожалуйста, сделайте следующее.

1. Пожалуйста, скопируйте приведенную ниже формулу в ячейку F5, затем нажмите клавишу Enter, чтобы получить результат.

=ЭРФ (B5, C5)

Заметки:

Как видно из приведенного выше снимка экрана, когда верхний_предел больше нижнего_предела, ERF возвращает положительный результат. Наоборот.
Аргументы в каждой из приведенных выше формул предоставляются в виде ссылок на ячейки, содержащих числовые значения.
Мы также можем напрямую вводить значения в формулу. Например, формулу в ячейке F5 можно изменить на:
=ЭРФ (-1, 0)

Относительные функции:

Excel EVEN Функция
Функция EVEN округляет числа от нуля до ближайшего четного целого числа.

Excel EXP Функция
Функция EXP возвращает результат возведения константы e в энную степень.

Лучшие инструменты для работы в офисе

Kutools for Excel — Помогает вам выделиться из толпы

Хотите быстро и качественно выполнять свою повседневную работу? Kutools for Excel предлагает 300 мощных расширенных функций (объединение книг, суммирование по цвету, разделение содержимого ячеек, преобразование даты и т. д.) и экономит для вас 80 % времени.

Рассчитан на 1500 рабочих сценариев, помогает решить 80% Excel проблемы.
Уменьшите количество нажатий на клавиатуру и мышь каждый день, избавьтесь от усталости глаз и рук.
Стать Excel эксперт за 3 минуты. Больше не нужно запоминать мучительные формулы и коды VBA.
30-дневная неограниченная бесплатная пробная версия. 60-дневная гарантия возврата денег. Бесплатное обновление и поддержка 2 года.

Office Tab — Включите чтение и редактирование с вкладками в Microsoft Office (включая Excel)

Одна секунда для переключения между десятками открытых документов!
Уменьшите количество щелчков мышью на сотни каждый день, попрощайтесь с рукой мыши.
Повышает вашу продуктивность на 50% при просмотре и редактировании нескольких документов.
Добавляет эффективные вкладки в Office (включая Excel), Точно так же, как Chrome, Firefox и новый Internet Explorer.

Comments (0)

No ratings yet. Be the first to rate!

Please leave your comments in English

Источник

Функция ошибок

Аргумент функции ошибок erf(x)

Функция ошибок

Дополнительная функция ошибок

Функция ошибок, она же функция Лапласа, он же интеграл вероятности — все это одна и та же сущность, которая выражается функцией

$\operatorname {erf}\,x={\frac {2}{{\sqrt {\pi }}}}\int \limits _{0}^{x}e^{{-t^{2}}}\,{\mathrm d}t$

и используется в статистике и теории вероятностей.

Функция неэлементарная, то есть её нельзя представить в виде элементарных (тригонометрических и алгебраических) функций.

Для расчета в нашем калькуляторе, мы используем связь с неполной гамма функцией

$\operatorname {erf}\,x=1-{\frac {\Gamma \left({\frac {1}{2}},x^{2}\right)}{{\sqrt \pi }}}$

Кроме этого мы сможем здесь же вычислить, дополнительную функцию ошибок, обозначаемую $\operatorname {erfc} \,x$ (иногда применяется обозначение $\operatorname {Erf} \,x$ ) и определяется через функцию ошибок:

$\operatorname {erfc}\,x=1-\operatorname {erf}\,x={\frac {2}{{\sqrt {\pi }}}}\int \limits _{x}^{{\infty }}e^{{-t^{2}}}\,{\mathrm d}t$

В приницпе это все, что можно сказать о ней.

Калькулятор высчитывает результат как в вещественном так и комплексном поле.

Замечание: Функция прекрасно работает на всем поле комплексных чисел при условии если аргумент ( фаза) меньше 180 градусов. Это связано с особенностью вычисления этой функции, неполной гамма функции, интегральной показательной функцией через непрерывные дроби.

Отсюда следует вывод, что при отрицательных вещественных аргументах, функция будет выдавать неверные решения. Но при всех положительных, а также отрицательных комплексных аргументах функция ошибок выдает верный ответ.

Несколько примеров:

Источник

При стремлении постичь нечто сложное, громоздкое, непонятное следует «разбить» его на как можно большее количество простых, мелких, понятных частей, изучить их с помощью существующих инструментов, а затем «сложить» эти результаты и получить итоговый ответ.

Формулировка в предыдущем предложении определяет сущность понятия интегрирования.

Интеграл чего-либо – это сумма всех малых частей этого чего-либо. Чем больше количество этих малых частей, тем точнее значение интеграла соответствует действительности, определяя признак изучаемого объекта.

Интегрирование применимо для изучения свойств физических и философских объектов при условии, что эти свойства остаются неизменными как для «мелкой» части, так и для всего объекта в целом.

Функция – это описание зависимости некоторого признака или свойства объекта от аргумента.

Объект – плоская фигура между графиком функции и осью абсцисс.

Признак (значение функции) – высота фигуры.

Аргумент (независимая переменная) – ширина фигуры.

Функция – описание зависимости высоты от ширины.

Определенный интеграл функции – площадь фигуры. Площадь тоже является признаком фигуры, но зависит от двух переменных – высоты и ширины – и представляет собой качественно иной новый признак.

Теория.

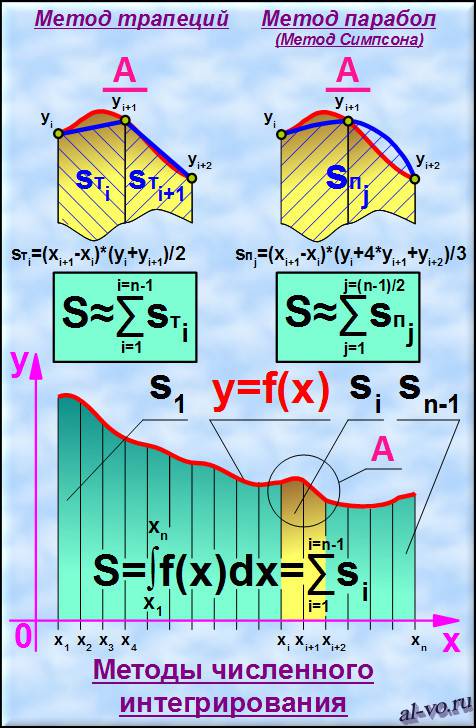
Подробно рассмотрим два наиболее точных метода численного интегрирования функции одной переменной – метод трапеций и метод парабол или метод Симпсона. Есть еще метод прямоугольников, но мы его проигнорируем из-за невысокой точности.

Все, что требуется для понимания и применения метода трапеций и метода Симпсона на практике представлено далее на рисунке.

Площадь под кривой y = f ( x ) разбиваем на n-1 криволинейных трапеций, у которых три стороны – это прямые линии, а одна сторона – участок кривой y =f ( x ). Суммарная площадь под графиком функции на участке от x₁ до x_n – это и есть искомая величина, которая является определенным интегралом функции на этом участке и находится как сумма площадей всех криволинейных трапеций.

Точно вычислить аналитически площадь криволинейной трапеции бывает сложно или даже невозможно.

Для приближенного вычисления площади криволинейной трапеции можно заменить участок кривой прямой линией и, получив простую фигуру – обычную трапецию, найти по известной формуле ее площадь. В этом суть метода трапеций.

Если участок кривой линии над двумя криволинейными трапециями заменить параболой, проведенной через три характерные точки, то получим новую криволинейную трапецию с одной из сторон в виде параболы. Количество новых фигур будет в два раза меньше, чем количество исходных трапеций. Площадь этих новых фигур вычисляется по простой формуле. В этом смысл метода Симпсона.

Идею замены участка любой кривой участком параболы высказывал Исаак Ньютон, но первым вывел формулу английский математик Томас Симпсон. Метод Симпсона для вычисления интегралов является самым точным из приближенных численных методов.

Если вычисление интегралов методом трапеций не имеет ограничений, то для того, чтобы реализовать метод Симпсона необходимо выполнить два условия.

1. Разбить площадь на четное количество частей, то есть n должно быть нечетным числом!

2. Расстояния между точками по оси x должны быть одинаковыми!

Практика вычисления интегралов в Excel.

Определенной сложностью является связать вычисление интегралов с реальными задачами из жизни. Рассмотрение примеров – лучший способ устранения подобных препятствий.

Определение тепловой энергии.

Мой знакомый из города Улан-Удэ Алексей Пыкин проводит испытания воздушных солнечных PCM-коллекторов производства КНР. Воздух из помещения подается вентилятором в коллекторы, нагревается от солнца и поступает назад в помещение. Каждую минуту измеряется и записывается температура воздуха на входе в коллекторы и на выходе при постоянном воздушном потоке. Требуется определить количество тепловой энергии полученной в течение суток.

Более подробно о преобразовании солнечной энергии в тепловую и электрическую и об экспериментах Алексея я постараюсь рассказать в отдельной статье. Следите за анонсами, многим, я думаю, это будет интересно.

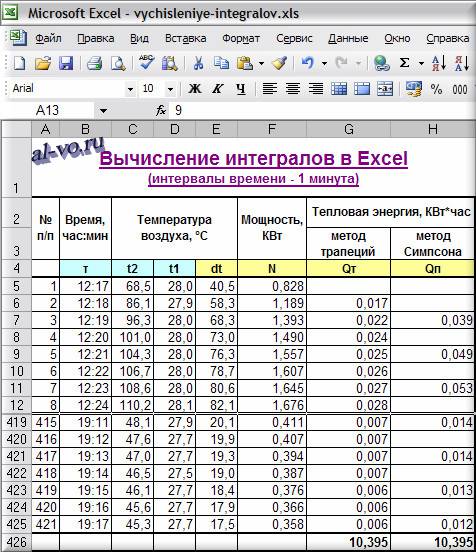
Запускаем MS Excel и начинаем работу – выполняем вычисление интеграла.

1. В столбец B вписываем время проведения измерения τ_i .

2. В столбец C заносим температуры нагретого воздуха t_2i , измеренные на выходе из коллекторов в градусах Цельсия.

3. В столбец D записываем температуры холодного воздуха t_1i , поступающего на вход коллекторов.

4. В столбце E вычисляем разности температур dt_i на выходе и входе

5. Зная удельную теплоемкость воздуха c =1005 Дж/(кг*К) и его постоянный массовый расход (измеренная производительность вентилятора) G =0,02031 кг/с, определяем мощность установки N_i в КВт в каждый из моментов времени в столбце F

N_i = c * G * dt_i

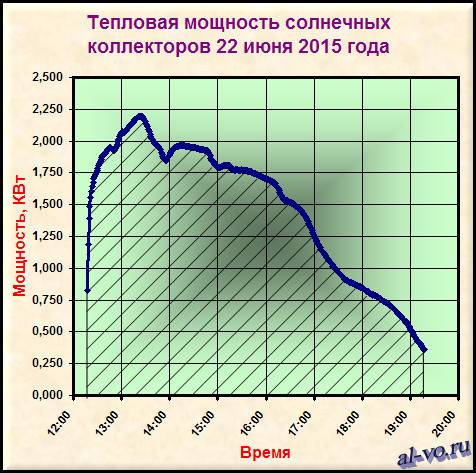
На графике ниже показана экспериментальная кривая зависимости мощности, развиваемой коллекторами, от времени.

Количество тепловой энергии, выработанной за промежуток времени – это интеграл этой функции, и значение интеграла – это заштрихованная площадь под кривой.

6. Вычисляем в ячейках столбца G площади трапеций, суммируем их и находим общее количество энергии, выработанной за день

Q =Σ Q_i =10,395 КВт*час

7. Рассчитываем в ячейках столбца H элементарные площади по методу парабол, суммируем их и находим общее количество энергии по методу Симпсона

Q =Σ Q_j =10,395 КВт*час

Как видим, значения не отличаются друг от друга. Оба метода демонстрируют одинаковые результаты!

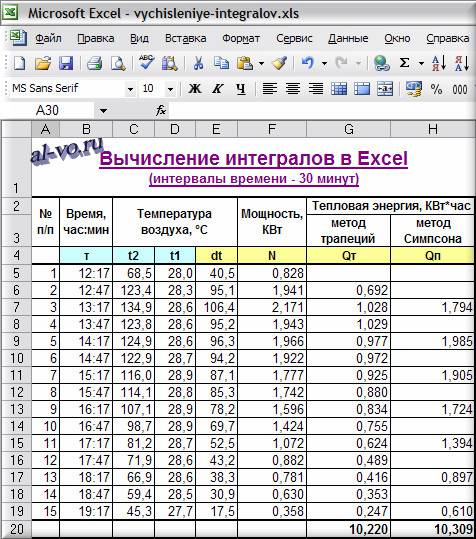
Исходная таблица содержит 421 строку. Давайте уменьшим её в 30 раз и оставим всего 15 строк, увеличив тем самым интервалы между замерами с 1 минуты до 30 минут.

По методу трапеций: Q =10,220 КВт*час (-1,684%)

По методу Симпсона: Q =10,309 КВт*час (-0,827%)

Не смотря на оставшуюся неожиданно весьма высокую точность полученных результатов, метод трапеций дает в данном случае относительную ошибку в 2 раза большую, чем метод Симпсона.

Общие выводы.

Вычисление интегралов численными методами в Excel позволяет эффективно и быстро решать сложные практические задачи, обеспечивая очень высокую точность результатов.

Так как мы существуем в пространстве и времени, то и всё окружающее нас изменяется или в пространстве или во времени. Это означает, что аргументом x функций y интересующих нас процессов или объектов чаще всего являются длина или время. Например, пройденный путь – это интеграл функции скорости (аргумент – время), площадь плотины – это интеграл функции высоты (аргумент – длина), и т.д.

Понимание сути интегрального исчисления и умение использовать его на практике вооружает вас, как специалиста, мощным оружием в осознанном изучении окружающего мира!

Отзывы и комментарии к статье, уважаемые читатели, пишите в блоке, расположенном ниже статьи.

Чтобы получать информацию о выходе новых статей на блоге подпишитесь на анонсы в окне, расположенном вверху страницы или сразу после статьи. Введите адрес своей электронной почты, нажмите на кнопку «Получать анонсы статей» и подтвердите подписку кликом по ссылке в письме, которое придет к вам на указанную почту. С этого момента к вам на почтовый ящик будет пару раз в месяц приходить небольшое уведомление о появлении на моем блоге новой статьи.

Прошу УВАЖАЮЩИХ труд автора скачать файл ПОСЛЕ ПОДПИСКИ на анонсы статей.

Ссылка на скачивание файла с примером: vychisleniye-integralov (xls 216,0KB).

Примеры интегрирования по частям логарифма и обратных тригонометрических функций

Интегрирование функций рационально зависящих от тригонометрических функций

1. Интегралы вида ∫ sin n xdx , ∫ cos n xdx , n>0
a) Если n нечётное, то одну степень sinx (либо cosx ) следует внести под знак дифференциала, а от оставшейся чётной степени следует перейти к противоположной функции.
б) Если n чётное, то пользуемся формулами понижения степени
2sin 2 x=1-cos2x , 2cos 2 x=1+cos2x .
2. Интегралы вида ∫ tg n xdx , ∫ ctg n xdx , где n – целое.
Необходимо использовать формулы

3. Интегралы вида ∫ sin n x·cos m x dx
а) Пусть m и n разной чётности. Применяем подстановку t=sin x , если n – нечётное либо t=cos x , если m – нечётное.
б) Если m и n чётные, то пользуемся формулами понижения степени
2sin 2 x=1-cos2x , 2cos 2 x=1+cos2x .
4. Интегралы вида
3. Интегралы вида ∫ sin n x·cos m x dx
а) Пусть m и n разной чётности. Применяем подстановку t=sin x , если n – нечётное либо t=cos x , если m – нечётное.
б) Если m и n чётные, то пользуемся формулами понижения степени
2sin 2 x=1-cos2x , 2cos 2 x=1+cos2x .
4. Интегралы вида
Если числа m и n одинаковой чётности, то используем подстановку t=tg x . Часто бывает удобным применить приём тригонометрической единицы.
5. ∫ sin(nx)·cos(mx)dx , ∫ cos(mx)·cos(nx)dx , ∫ sin(mx)·sin(nx)dx

Воспользуемся формулами преобразования произведения тригонометрических функций в их сумму:

sin α·cos β = ½(sin(α+β)+sin(α-β))
cos α·cos β = ½(cos(α+β)+cos(α-β))
sin α·sin β = ½(cos(α-β)-cos(α+β))

Решение онлайн
Видеоинструкция

Примеры
1. Вычислить интеграл ∫ cos 4 x·sin 3 xdx .
Делаем замену cos(x)=t . Тогда ∫ cos 4 x·sin 3 xdx =
2. Вычислить интеграл .
Делая замену sin x=t , получаем

3. Найти интеграл .
Делаем замену tg(x)=t . Подставляя, получаем

Основные тригонометрические формулы

Ниже приведены некоторые тригонометрические формулы, которые могут понадобится при интегрировании тригонометрических функций.

sin 2 a + cos 2 a = 1

sin ( a+b ) = sin a cos b + cos a sin b
cos ( a+b ) = cos a cos b – sin a sin b
sin 2 a = 2 sin a cos a
cos 2 a = cos 2 a – sin 2 a = 2 cos 2 a – 1 = 1 – 2 sin 2 a

Примеры интегрирования тангенса и котангенса

Пример 1. Найти интеграл от тангенса tan(4*x).
Вычисления: Применяем приведенную выше методику для интегрирования тангенса

Здесь в скобках мы сначала вычисляем дифференциал от косинуса, а дальше выделяем значение, которое нам нужно достать. Далее интегрирования сводим к логарифму.
Таким образом можем записать обобщенную формулу для интеграла tan(k*x)
Int(tan(k*x),x)=-1/k*(log(cos(x)).
По этой формуле интеграл от тангенса двойного угла равен логарифму косинуса двойного угла умноженному на -0,5 .
Для тангенса половины угла tan (phi / 2) интеграл равен -2 умножить на логарифм косинуса половины угла
По индукции получим формулу интеграла для тангенса одной третьей угла tan(phi/3)

Пример 2. Проинтегрировать котангенс двойного угла
Вычисления: По аналогии с формулами для тангенса мы могли бы выписать готовую формулу, но лучше выполнить промежуточные переходы чтобы Вы лучше поняли и заучили методику внесения под дифференциал

Таким образом, если имеем котангенс тройного угла то перед интегралом получим множителем 1/3
Интегралы от котангенса половины и трети угла будут иметь множителями перед логарифмом соответственно двойку и тройку
При нахождении первоначальной от тангенса и котангенса следует справа добавить постоянную
Зная данную методику, Вы знаете как найти интеграл от тангенса, аргумент которого содержит множителем произвольное число.
Вычисления определенных интегралов от тангенса и котангенса в данной статье рассматривать не будем. Если Вы вычисляли такие интегралы от простых функций то, зная синусы и косинусы углов найти определенный интеграл от тангенса или котангенса сможете без проблем.

Вычисление площадей отдельных трапеций

Теперь нужно найти площади трапеций за каждый промежуток времени. В столбце “E” будем вычислять по приведённой выше формуле площади трапеций. Полусумма оснований – это половина суммы двух последовательных мощностей дозы из столбца “D”. Так как данные идут с периодом 1 раз в минуту, а мы берём интеграл по времени, выраженному в минутах, то высота каждой трапеции будет равна единице (разница времени между каждыми двумя последовательными измерениями, например, 17ч31мин — 17ч30мин = 0ч1мин = 1мин).

Получаем формулу в ячейке “E3”: =1/2*(D3+D2)*1. Понятно, что “×1” в этой формуле можно не писать. И аналогично, с помощью маркера заполнения, распространяем формулу на весь столбец. Теперь в каждой ячейке столбца “Е” посчитана накопленная доза за 1 минуту полёта.

Вычисление площадей прямоугольных трапеций за каждый промежуток времени

Если бы данные шли не через 1 минуту, то нам нужно было бы написать формулу так:
=1/2*(D3+D2)*(МИНУТЫ(A3) – МИНУТЫ(A2)).
Правда при этом, если есть переход на следующий час, то получится отрицательное значение. Чтобы этого не произошло, впишем в формулу часы:
=1/2*(D3+D2)*(ЧАС(A3)*60+МИНУТЫ(A3)) – (ЧАС(A2)*60+МИНУТЫ(A2)).
Если переходим на следующие сутки, то нужно будет уже добавлять даты, и т.д.

Теория.

Точно вычислить аналитически площадь криволинейной трапеции бывает сложно или даже невозможно.

1. Разбить площадь на четное количество частей, то есть n должно быть нечетным числом!

2. Расстояния между точками по оси x должны быть одинаковыми!

Стандартные подстановки при интегрировании тригонометрических функций

Здесь мы рассмотрим стандартные подстановки, с помощью которых, в большинстве случаев, выполняется интегрирование тригонометрических функций.

Применение знаний, формирование умений и навыков

Практическое задание «Вычисление определенных интегралов методом трапеции в среде Microsoft Excel.»

Состав задания:

Ознакомиться с теоретической частью задания;
Провести расчет для своего варианта индивидуального задания в Microsoft Excel
Оформить презентацию в Ms PowerPoint, включающую:
– постановку задачи;
– алгоритм расчета;
– таблицу с расчетом из Ms Excel, график исходной функции;
– результат расчета и его анализ.

Индивидуальное расчетное задание:

Найдите приближенное значение интеграла заданной функции f(x)= 1/(1+x 4 ) 1/2 на отрезке [0; 4]
по формуле трапеций, разбивая отрезок [0; 4] на 8 равных частей. Оцените погрешность приближенного вычисления интеграла при таком разбиении отрезка.
Представьте графически поставленную задачу.

Постановка задачи:

Найти: приближенное значение интеграла заданной функции по формуле трапеций, приняв предельное значение погрешности приближенного вычисления интеграла равным ε=0,02.

Таблица Исходная информация

Представление в Excel

Анализ заданной функции и результаты вычислений в Ms Excel

Расчет площади

f(xi)

Коэффициенты формулы трапеций

Вычисление Ci*f(xi)

N=2

N=4

N=8

N=2

N=4

N=8

N=2

N=4

N=8

Ответ: приближенное значение интеграла заданной функции по формуле трапеций равна 1,60кв.мм, значение погрешности приближенного вычисления интеграла равным ε=0,008.

Задания для индивидуальной работы студентов по вариантам:

Найдите приближенное значение интеграла заданной функции f(x) на отрезке [a; b] (см. таблицу ) по формуле трапеций, разбивая отрезок [a; b] на 8 равных частей. Оцените погрешность приближенного вычисления интеграла при таком разбиении отрезка.

Представьте графически поставленную задачу.

отрезок [a; b]

Функция f(x)

(х 4 /(1+x 4 ) 1/2 ) 1/2

(х 5 /(1+x 4 ) 1/2 ) 1/2

На сегодняшнем занятии мы отработали навыки вычисления определенных интегралов методом трапеции в среде электронных таблиц MS Excel. Выработали умения применять теоретические знания в практических расчетах.

Распространенные примеры интегрирования косинуса

Пример 1. Найти интеграл от cos(5*x).
Решение: По формуле интегрируем косинус

Пример 2. Вычислить интеграл от cos(7*x).
Решение: Выполняем интегрирование

Пример 3. Проинтегрировать выражение cos (11*x).
Решение: Вычисляем неопределенный интеграл

Пример 4. Найти интеграл функции y= cos (x/5).
Решение: Записываем неопределенный интеграл

Пример 5. Найти интеграл функции y= cos (x/6) .
Решение: Проинтегрируем по приведенной выше формуле
Как только Вы освоите методику интегрирования на простых примерах, смело можете переходить к определенным интегралам и первообразным. Для отискания определенного интеграла проводим интегрирование, а дальше подставляем пределы интегрирования и находим изменение первообразной функции.

Пример 6. Проинтегрировать косинус двойного угла y = cos (2 * x) от 0 до 45 градусов.
Решение: Находим указанный интеграл от косинуса

Пример 7. Найти интеграл от косинуса y = cos (x) от 0 до 60 градусов.
Решение: Вычисляем интеграл и подставляем пределы интегрирования

Пример 8. Найти первоначальную от cos (x), которая при 30 градусах равна 1 .
Решение: Находим первоначальную
С наложенного условия на первоначальную вычисляем постоянную
sin(Pi/6)+C=1; C=1-
sin(Pi/6)=1-0,5=0,5.
Подставляем полученную постоянную в уравнение
На этом задача решена. На таких простых примерах Вы четко должны знать, чему равный интеграл от косинуса.
Далее полученные знания можно применять для вычисления площадей криволинейных трапеций. Это достаточно абстрактное понятие, но с помощью интегрирования находить площадь фигур достаточно просто и быстро. Следует только помнить, что площадь всегда принимает положительное значение, в то время как определенный интеграл может принимать отрицательное значение.
Например вычислим площадь и интеграл от косинуса, если переменная принадлежит интервалу от 0 до 2*Pi.
По физическому содержанию площадь равна заштрихованным поверхностям.
Находим определенный интеграл в указанных пределах
Он равен нулю. Что касается площади, то сначала следует найти точки пересечения с осью абсцисс на этом интервале
Таким образом площадь необходимо искать на трех промежутках
Ось абсцисс можем записать функцией y = 0 . Таким образом на первом промежутке площадь равна интегралу от косинуса,
на втором 0-cos (x) = – cos (x) от минус косинуса и на третьем от косинуса. Все при вычислении площади зависит от того, какая функция принимает большее значение по оси ординат (Oy) . Вычисляем площадь интегрированием в указаных пределах
Таким образом искомая площадь равна 4. Если иметь график функции перед глазами, то данное значение можно получить как 4 площади косинус функции, которые периодически повторяются
На этом знакомство с интегрированием косинуса завершается. Приведенная методика интегрирования позволяет вычислить 80% основных задач на интегрирование косинуса. Остальные 20% Вы научитесь после изучения способов нахождения интегралов от функций вида
Мы научим Вас, какие свертки и замены переменных следует использовать, в каких случаях целесообразно интегрировать по частям.
Интегралы от других тригонометрических и обратных к ним функций Вы найдете в категории “ Интегрирование функций “.

Интегрирование обратных тригонометрических функций

Интегралы, содержащие обратные тригонометрические функции
arcsin φ , arctg φ , и т.д., где φ – некоторая алгебраическая функция от x , нередко интегрируются по частям, полагая u = arcsin φ , u = arctg φ , и т.д.

Общий подход

Вначале, если это необходимо, подынтегральное выражение нужно преобразовать, чтобы тригонометрические функции зависели от одного аргумента, который совпадал бы с переменной интегрирования.

Например, если подынтегральное выражение зависит от sin( x+a ) и cos( x+b ) , то следует выполнить преобразование:
cos ( x+b ) = cos ( x+a – ( a–b ) ) = cos ( x+a ) cos ( b–a ) + sin ( x+a ) sin ( b–a ) .
После чего сделать замену z = x+a . В результате, тригонометрические функции будут зависеть только от переменной интегрирования z .

Когда тригонометрические функции зависят от одного аргумента, совпадающим с переменной интегрирования (допустим это z ), то есть подынтегральное выражение состоит только из функций типа sin z , cos z , tg z , ctg z , то нужно сделать подстановку
.
Такая подстановка приводит к интегрированию рациональных или иррациональных функций (если есть корни) и позволяет вычислить интеграл, если он интегрируется в элементарных функциях.

Однако, часто можно найти другие методы, которые позволяют вычислить интеграл более коротким способом, основываясь на специфике подынтегрального выражения. Ниже дано изложение основных таких методов.

Методика вычисленияопределённого интеграла

Вычислять интеграл мы будем самым простым, но довольно точным методом – методом трапеций. Напомню, площадь фигуры под графиком любой кривой можно разделить на прямоугольные трапеции. Сумма площадей этих трапеций и будет искомым значением определённого интеграла.

Площадь трапеции определяется как полусумма оснований, умноженная на высоту: S_трап = (A + B) / 2 × h Основания в нашем случае – это табличные измеренные значения мощности дозы за 2 последовательных промежутка времени, а высота – это разница времени между двумя измерениями.

Метод трапеций для вычисления значения определённого интеграла

Интегрирование выражений вида R(sinx, cosx)

Пример №1 . Вычислить интегралы:

Решение.
а) Интегрирование выражений вида R(sinx, cosx) , где R — рациональная функция от sin x и cos x , преобразуются в интегралы от рациональных функций с помощью универсальной тригонометрической подстановки tg(x/2) = t .
Тогда имеем

Универсальная тригонометрическая подстановка дает возможность перейти от интеграла вида ∫ R(sinx, cosx) dx к интегралу от дробно-рациональной функции, но часто такая замена ведет к громоздким выражениям. При определенных условиях эффективными оказываются более простые подстановки:

Если выполняется равенство R(-sin x, cos x) = -R(sin x, cos x)dx , то применяется подстановка cos x = t .
Если выполняется равенство R(sin x, -cos x) = -R(sin x, cos x)dx , то подстановка sin x = t .
Если выполняется равенство R(-sin x, -cos x) = R(sin x, cos x)dx , то подстановка tgx = t или ctg x = t .

В данном случае для нахождения интеграла
применим универсальную тригонометрическую подстановку tg(x/2) = t .
Тогда

Так как дробь неправильная, то, выделяя целую часть, получим

Возвращась к исходной переменной будем иметь

b) Во втором примере рассмотрим важный частный случай, когда общее выражение ∫ R(sinx, cosx) dx имеет вид ∫ sin m x·cos n xdx . В этом частном случае, если m нечетно, следует применить подстановку cos x = t . Если нечетно n , следует применить подстановку sin x = t . Если оба показателя тип — четные неотрицательные числа (в частности, одно из них может быть равным нулю), то выполняют замену по известным тригонометрическим формулам:
В данном случае

Вычисление определенных интегралов методом трапеции в среде Microsoft Excel

Цель урока: Совершенствование умений и навыков по теме «Численное интегрирование», применяя возможности MS Excel по вычисление определенных интегралов методом трапеции. Отработать практическое освоение соответствующих умений и навыков.

Задачи урока:

Образовательные – совершенствование умений студентов при вычисление определенных интегралов методом трапеции в среде электронных таблиц MS Excel. Выработать умение применять теоретические знания в практических расчетах;
Развивающие – познакомить студентов с применением компьютеров в качестве помощников при решении уравнений. Развивать у студентов математическую речь: создать ситуацию для применения основных понятий в речи; творческого мышления через создание условий для самореализации творческого потенциала обучающихся;
Воспитательные – выработать у студентов умение рационально использовать время и возможности компьютерных технологий при решении задач. Воспитывать интерес к предмету через ситуацию успеха и взаимодоверия.

Тип урока: комбинированный урок.

Вид урока: практическое занятие, продолжительность – 2 часа.

Оборудование урока:

Компьютеры с OS MS Windows;
Программа Microsoft Excel;
Презентация по теме, выполненная в программе PowerPoint;
Карточки с заданиями для самостоятельной работы.

Структура урока:

1.Актуализация знаний:
1.1. Мобилизующее начало, постановка целей и задач на урок;
1.2.Фронтальный опрос с целью выявления основных этапов решения задач интегрирования и методики решения;
1.3. Постановка задачи с целью повторения алгоритма вычисления определенных интегралов методом трапеции;
1.4.Подведение итогов 1 этапа урока.
2.Применение знаний, формирование умений и навыков:
2.1.Беседа с целью формулировки задания для самостоятельной работы и инструктажа по ее организации;
2.2.Самостоятельная работа в группах по выполнению задания вычисления определенных интегралов методом трапеции в среде Microsoft Excel.
2.3.Подведение итога урока.

В данном уроке особое внимание уделено визуальному представлению информации – в ходе урока с помощью проектора демонстрируются слайды, подготовленные в пакете презентационной графики Microsoft PowerPoint.

ХОД УРОКА

1. Актуализация знаний

1.1. Мобилизующее начало, постановка целей и задач на урок.

На прошлых уроках мы с Вами изучили приближенное вычисление определенных интегралов, выделили методы их решения и решали данные интегралы ручным счетом. А на сегодняшнем занятии мы будем совершенствовать умения и навыки при вычислении определенных интегралов методом трапеции в среде Microsoft Excel.

— В чем заключается вычисление интеграла?

— Важным средством вычисления определенных интегралов является формула Ньютона-Лейбница . Ее применение на практике связано с существенными трудностями, возникающими при нахождении первообразной в случае подынтегральной функции. Поэтому применяют численные методы, позволяющие найти приближенное значение исходного интеграла с заданной точностью.
— Общий подход к ее решению состоит в том, чтобы аппроксимировать функцию какой-либо другой функцией , для которой интеграл вычисляется аналитически.

— Тогда для решения задачи строим с оценкой погрешности , и приближенно с очевидной оценкой погрешности .

— Введем на отрезке сетку , , где , и таблицу значений , .

— Рассмотрим простой вариант построения функции , приводящий к формуле трапеций.

— При этом функция строится как кусочно-линейная интерполяция значений , на равномерной сетке с шагом .

— Формулы такого рода () называют механическими квадратурами, – коэффициентами (весами) квадратуры, – ее узлами.

Точность формулы трапеций зависит от гладкости функции . Если она на имеет первую производную, ограниченную числом , то , и погрешность формулы трапеций не превосходит . Если на имеет вторую производную, ограниченную числом , то погрешность формулы итераций не превосходит , поскольку .

Теоретические оценки погрешностей не всегда применяются. Если требуется вычислить интеграл с погрешностью , то мало кто сначала оценит третью производную функции и вычислит шаг сетки . Эта оценка и значение константы завышены. Кроме того, само вычисление может быть трудным, особенно если задана некоторым сложным образом.

Поэтому, вычисляя интеграл с небольшим числом узлов , получают его значение ; вычисляя интеграл с удвоенным , получают . Если модуль (где ε – предельное допустимое значение погрешности расчета), то задачу считают решенной. В противном случае вычисляют и т.д. Для гладких функций часто интеграл вычисляется очень точно при малом числе узлов.

— Объясните алгоритм вычисления интеграла различными методами?

2. Применение знаний, формирование умений и навыков

Практическое задание «Вычисление определенных интегралов методом трапеции в среде Microsoft Excel.»

Состав задания:

Ознакомиться с теоретической частью задания;
Провести расчет для своего варианта индивидуального задания в Microsoft Excel
Оформить презентацию в Ms PowerPoint, включающую:
— постановку задачи;
— алгоритм расчета;
— таблицу с расчетом из Ms Excel, график исходной функции;
— результат расчета и его анализ.

Индивидуальное расчетное задание:

Найдите приближенное значение интеграла заданной функции f(x)= 1/(1+x 4 ) 1/2 на отрезке [0; 4]
по формуле трапеций, разбивая отрезок [0; 4] на 8 равных частей. Оцените погрешность приближенного вычисления интеграла при таком разбиении отрезка.
Представьте графически поставленную задачу.

Постановка задачи:

Источник