4.1. Понятие об измерениях
Измерение
– это процесс сравнения измеряемой
величины с величиной принятой за единицу
сравнения, в результате которого
получается именованное число, называемоерезультатом измерения.
Различают:
прямые,илинепосредственныеикосвенныеизмерения.
Непосредственными
называют такие измерения, когда
определяемые величины получают прямо
из измерений, в результате непосредственного
сравнения их с единицей измерений.
Примеры непосредственных измерений –
определение расстояний мерной лентой,
измерение угла теодолитом.
Косвеннымиявляются такие измерения, при которых
определяемые величины получают как
функции непосредственно измеренных
величин. Косвенный метод предполагает
вычисление значения искомой величины.
Например, превышение при тригонометрическом
нивелировании является функцией
расстояния и угла наклона, измеренных
непосредственно на местности.
Результаты
измерений разделяют на равноточныеинеравноточные.
Равноточныминазывают результаты измерения однородных
величин, полученные при многократных
измерениях в сходных условиях (одним
наблюдателем одним и тем же прибором,
одним методом и при одних и тех же
условиях окружающей среды).
При
нарушении даже одного из перечисленных
условий результаты измерений относят
к неравноточным.
При
математической обработке результатов
топографо-геодезических измерений
определенное значение имеют понятия о
необходимом иизбыточномчисле
измерений. В общем случае для решения
любой топографической задачи необходимо
измерить некоторое минимальное число
величин, обеспечивающее решение задачи.
Эти измерения называютчислом
необходимых измерений t.Разностьkпри вычитании числа необходимых измеренийtиз числа всех измеренных величинn, называют числом избыточных
величин k = n – t.Избыточные измерения
величины позволяют обнаружить ошибки
в результатах измерений и вычислений
и повысить точность определяемых
величин.
4.2. Классификация ошибок измерений
Результаты
измерений отличаются от истинного
значения измеряемой величины. Разность
между результатом измерения lи
истинным значением измеряемой величиныхназывается абсолютной ошибкой
(погрешностью) результата измерения Δ.
Δ = l –
x.
По
характеру действия и свойствам ошибки
подразделяются на: грубые, систематические
и случайные.
Грубые
ошибки, или промахи происходят в
результате невнимательности исполнителя
работ. К грубым относятся ошибки, которые
превышают допустимую величину. Для
исключения грубых ошибок выполняются
повторные измерения.
Систематические
ошибкивозникают по определенным
причинам и характеризуются постоянством
своей величины и знака (+ или –). Делятся
на постоянные (неизменные по знаку и
величине) ипеременные(изменяющие
величину по определенному закону).
Причинами их появления могут быть
инструментальные ошибки (неточности в
юстировке измерительных приборов,
нарушение геометрических условий
приборов и др.) и условия среды (изменение
температуры прибора).
Величина
и знак систематических ошибок
устанавливается путем компарированияприбора,т. е. сравнения показаний
рабочего прибора с показаниями прибора,
принятого в качестве эталона.Систематические ошибки должны быть
обнаружены, изучены и исключены из
результатов измерений путем введенияпоправокили использования
соответствующей методики измерений.
Под
случайными понимаются ошибки, знак
и размер которых не имеют закономерности
своего появления, их возникновение не
подчиняется определенным математическим
законам, т. е. носят случайный характер.
Они подчиняются статистическим
закономерностям массовых случайных
величин. Поэтому от случайных ошибок
нет возможности полностью освободить
результаты измерений.
Соседние файлы в папке Топографическая
- #
- #
- #
Содержание ▲
- ТЕМА ЛЕКЦИИ:
«ОБЩИЕ ПОНЯТИЯ ТЕОРИИ ОШИБОК… - СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Маслов А.В.…
- Задачи теории ошибок измерений.
Задачи теории… - 1. Задачи теории ошибок измерений.…
- Теория ошибок измерений решает
Теория ошибок… - 2. Сущность и виды измерений.
Измерения…
- Непосредственными или прямыми называ-ются…
- Под равноточными понимают измерения, полученные…
- Необходимыми считаются измерения, которые…
- Зависимыми называют измерения, имеющие некоторые…
- 3. Ошибки измерений, их классификация и…
- Причинами возникновения ошибок являются…
- В теории ошибок более важное значение имеет…
- Систематические ошибки подразделяются на…
- Случайными называются ошибки, которые не связаны…
- Случайные ошибки основного типа обладают…
- 4. Понятие о законах распределения ошибок.
4.… - Распределение случайных ошибок измерений наиболее…
- График функции (3) называется кривой нормального…
- Есть ошибки, которые подчиняются закону…
- Основными характеристиками распределения…
- Для непрерывной случайной величины с плотностью…
- Дисперсией случайной величины Х называ-ется…
- Положительное значение квадратного корня из…
- Для случайных ошибок измерений, как уже…
- 5.Числовые характеристики точности измерений.…
- При большом значении n
При большом значении… - Оценку точности измерений характеризуют также…
- Обычно для τ принимают значения 3, 2.5, или 2.…
- При нормальном распределении средняя ошибка v…
-
СПАСИБО ЗА ВНИМАНИЕ.
… - Скачать
- Похожие презентации
Вы можете ознакомиться и скачать презентацию на
тему ОБЩИЕ ПОНЯТИЯ ТЕОРИИ ОШИБОК ИЗМЕРЕНИЙ.
Доклад-сообщение содержит 31 слайдов.
Презентации для любого класса можно скачать бесплатно.
Если материал и наш сайт презентаций Mypresentation Вам понравились – поделитесь
им с друзьями с помощью социальных кнопок и добавьте в закладки в своем
браузере.
Слайды и текст этой презентации
Слайд 1
Описание слайда:
ТЕМА ЛЕКЦИИ:
«ОБЩИЕ ПОНЯТИЯ ТЕОРИИ ОШИБОК ИЗМЕРЕНИЙ»
Слайд 2
Описание слайда:
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Маслов А.В. Геодезия: учеб. и уч. пособие для вузов/ А.В. Маслов, А.В. Гордеев, Ю.Г. Батраков: – М.: Колос, 2006. – 598 с.
Маслов А.В. Геодезические работы при землеустройстве: учеб. пособие для вузов / А.В. Маслов, А.Г. Юнусов, Г.И. Горохов 2-е изд., перераб. и доп. — М.: Недра, 1990. – 215 с. .
Неумывакин Ю.К. Геодезическое обеспечение землеустроительных и кадастровых работ: справ. пособие/ Ю.К.Неумывакин, М.И. Перский: – М.: «Картгеоцентр» — «Геодезиздат», 1996. – 344 с.
Геодезия: учеб.-метод. комплекс / БГСХА; сост. С.И. Помелов, Д.А. Чиж. – Горки, 2006. – 256 с.
Практикум по геодезии / Под ред.Бакановой В.В. – М.: Недра, 1989 .
Слайд 3
Описание слайда:
Задачи теории ошибок измерений.
Задачи теории ошибок измерений.
Сущность и виды измерений.
Ошибки измерений, их классификация и свойства.
Понятие о законах распределения ошибок.
Числовые характеристики точности измерений.
Слайд 4
Описание слайда:
1. Задачи теории ошибок измерений.
Геодезические работы связаны с различными методами измерений длин линий, углов, превышений, площадей и пр. Любые измерения, как бы тщательно они не выполнялись, сопровождаются неизбежными ошибками (погрешностями) поэтому измеренные значения величин будут отклоняться от истинных.
На практике измерения выполняют так, чтобы получить результаты с некоторой заданной точностью. Для обоснования необходимой и достаточной точности измерений надо знать причины возникновения ошибок измерений и их свойства. Эти вопросы рассматриваются в теории ошибок измерений, которая в свою очередь основывается на теории вероятностей и математической статистики.
Слайд 5
Описание слайда:
Теория ошибок измерений решает
Теория ошибок измерений решает
четыре основные задачи:
1. Изучение законов возникновения и распределения ошибок измерений и вычислений.
2. Оценка точности результатов измерений и их функций.
З. Отыскание наиболее надёжного значения определяемой величины и характеристики точности.
4. Установление допусков, ограничивающих использование результатов измерений в заданных пределах точности, т. е. критериев указывающих на наличие грубых ошибок.
Слайд 6
Описание слайда:
2. Сущность и виды измерений.
Измерения различают на непосредственные (прямые), посредственные (косвенные), равноточные, неравноточные, необходимые, дополнительные (избыточные), зависимые и независимые.
Под измерением данной физической величины понимается процесс сравнения ее с другой физической величиной того же рода, принятой за единицу измерения.
Полученное именованное число называется результатом измерения.
Слайд 7
Описание слайда:
Непосредственными или прямыми называ-ются измерения, при которых измеряемая величина непосредственно сравнивается с единицей меры.
Непосредственными или прямыми называ-ются измерения, при которых измеряемая величина непосредственно сравнивается с единицей меры.
Например, измерения линий лентой, углов транспортиром и т.д.
Посредственными или косвенными называются измерения, когда искомая величина находится путем измерения других величин.
Например, определение неприступных расстояний.
Слайд 8
Описание слайда:
Под равноточными понимают измерения, полученные одним и тем же прибором (или различными приборами одного класса точности), одним и тем же или равноценны-ми методами, одинаковым числом приемов и в одинаковых условиях.
Под равноточными понимают измерения, полученные одним и тем же прибором (или различными приборами одного класса точности), одним и тем же или равноценны-ми методами, одинаковым числом приемов и в одинаковых условиях.
Пример: измерения углов теодолитами одинаковой точности.
Если указанные условия не соблюдаются, то результаты измерений будут неравноточ-ными. Например, измерение углов теодо-литами разной точности или одним теодо-литом, но разным числом приемов.
Слайд 9
Описание слайда:
Необходимыми считаются измерения, которые позволяют получить искомую величину только один раз.
Необходимыми считаются измерения, которые позволяют получить искомую величину только один раз.
Если одна величина измерена n-раз, то одно измерение будет необходимым, а остальные n–1 — избыточными.
Например, для определения всех сторон и углов в треугольнике необходимо знать не менее трех его элементов, в т.ч. хотя бы одну сторону. Если измерены все углы и стороны, то три величины будут избыточными.
Избыточные измерения нужны для контроля и повышения точности определения искомых величин, а также оценки точности искомых величин.
Слайд 10
Описание слайда:
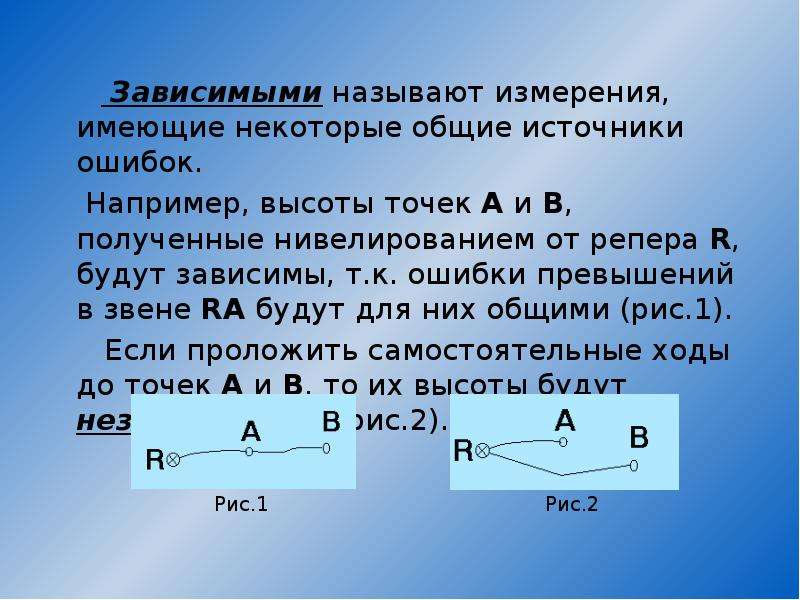
Зависимыми называют измерения, имеющие некоторые общие источники ошибок.
Зависимыми называют измерения, имеющие некоторые общие источники ошибок.
Например, высоты точек А и В, полученные нивелированием от репера R, будут зависимы, т.к. ошибки превышений в звене RA будут для них общими (рис.1).
Если проложить самостоятельные ходы до точек А и В, то их высоты будут независимыми (рис.2).
Слайд 11
Описание слайда:
3. Ошибки измерений, их классификация и свойства.
Ошибкой результата измерения называется разность между результатом измерения и точным (истинным) значением измеряемой величины, т.е.
∆= l–x, (1)
где ∆ – ошибка измерения (иcтинная ошибка);
l – результат измерения;
x – точное значение величины.
Слайд 12
Описание слайда:
Причинами возникновения ошибок являются неточности в изготовлении и юстировке приборов, влияние внешних условий, неточности выполнения операций наблюдателем, изменения самого объекта измерения и несовершенство метода измерений.
Причинами возникновения ошибок являются неточности в изготовлении и юстировке приборов, влияние внешних условий, неточности выполнения операций наблюдателем, изменения самого объекта измерения и несовершенство метода измерений.
В соответствии с источниками возникновения различают ошибки:
1) приборов;
2) внешние;
3) личные;
4) объекта;
5) метода измерений.
Приведенная классификация ошибок по источникам возникновения имеет большое значение при изучении приборов и методов измерений.
Слайд 13
Описание слайда:
В теории ошибок более важное значение имеет классификация ошибок по закономерностям их появления. По характеру действия на конечный результат ошибки делятся на грубые, систематические и случайные.
В теории ошибок более важное значение имеет классификация ошибок по закономерностям их появления. По характеру действия на конечный результат ошибки делятся на грубые, систематические и случайные.
Грубые ошибки (промахи) вызываются невнима-тельностью наблюдателя или неисправностью прибора. Они превосходят по абсолютной величине некоторый предел, установленный для данных условий измерений.
Измерения, содержащие грубые ошибки, бракуются и заменяются новыми. Для выявления грубых ошибок производятся избыточные измерения (линии измеряют дважды, в треугольнике измеряют все три угла и т. п.).
Слайд 14
Описание слайда:
Систематические ошибки подразделяются на постоянные, переменные и односторонне действующие.
Систематические ошибки подразделяются на постоянные, переменные и односторонне действующие.
Постоянные систематические ошибки при измерении одной и той же величины несколько раз, всякий раз появляются с одним знаком и одинаковые по величине. Например, ошибки за счет неточного центрирования теодолита при измерении углов несколькими приемами будут одинаковыми в каждом приеме.
Переменные систематические ошибки меняются от приема к приему, следуя определённому закону. Например, ошибки в направлениях, обусловленные эксцентриситетом алидады, или ошибками нанесения штрихов лимба теодолита.
Односторонне действующие систематические ошибки изменяются случайным образом, но сохраняют знак. Например, ошибка в длине линии из-за отклонения мерной ленты от створа.
Слайд 15
Описание слайда:
Случайными называются ошибки, которые не связаны функциональной зависимостью с какими-либо факторами. Ни величину, ни знак случайной ошибки заранее предсказать нельзя. В последовательности появления ошибок тоже нет никакой закономерности. Однако, если рассматривать их в большом количестве, то выявляются определенные статистические закономерности.
Случайными называются ошибки, которые не связаны функциональной зависимостью с какими-либо факторами. Ни величину, ни знак случайной ошибки заранее предсказать нельзя. В последовательности появления ошибок тоже нет никакой закономерности. Однако, если рассматривать их в большом количестве, то выявляются определенные статистические закономерности.
Слайд 16
Описание слайда:
Случайные ошибки основного типа обладают следующими вероятными свойствами:
Случайные ошибки основного типа обладают следующими вероятными свойствами:
1. По абсолютной величине ошибки не превосходят некоторого предела.
2. Положительные и отрицательные ошибки, равные по абсолютной величине, имеют равные вероятности, т.е. встречаются одинаково часто.
З. Чем больше ошибка по абсолютной величине, тем меньше ее вероятность появления.
4. Среднее арифметическое из значений случайных ошибок при неограниченном возрастании числа измерений одной и той же величины имеет пределом нуль, т. е. математическое ожидание ошибки равно нулю
.
Слайд 17
Описание слайда:
4. Понятие о законах распределения ошибок.
4. Понятие о законах распределения ошибок.
Свойства случайных ошибок являются проявлением закона их распределения.
В общем случае закон распределения ошибок отражает связь между размером ошибки и вероятностью ее появления.
PΔ= f(Δ)dΔ, (2)
где Р∆ – вероятность появления ошибки в интервале (∆, ∆+d∆);
∆ – случайная ошибка;
f(∆) – плотность распределения ошибок.
Слайд 18
Описание слайда:
Распределение случайных ошибок измерений наиболее точно описывается законом нормального распределения.
Распределение случайных ошибок измерений наиболее точно описывается законом нормального распределения.
Плотность нормального распределения выражается формулой
(3)
где σ – среднее квадратическое отклонение случайной ошибки.
Слайд 19
Описание слайда:
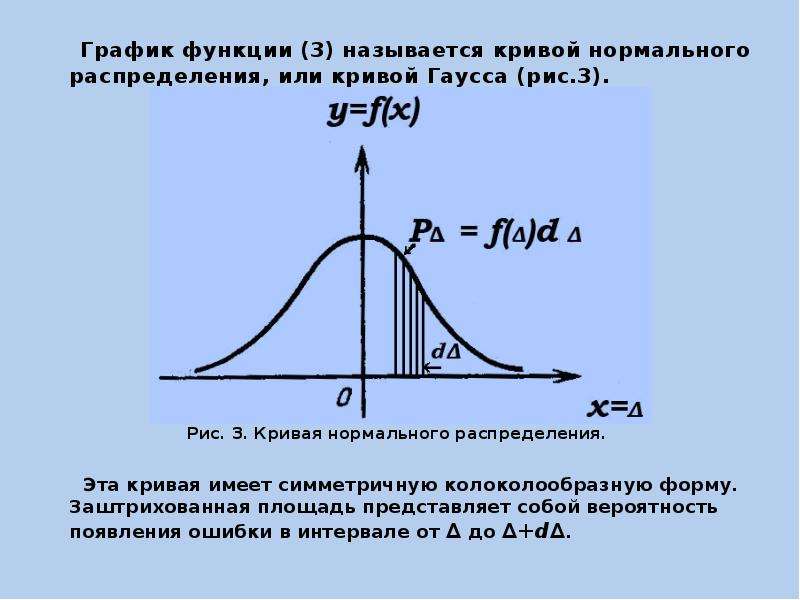
График функции (3) называется кривой нормального распределения, или кривой Гаусса (рис.3).
График функции (3) называется кривой нормального распределения, или кривой Гаусса (рис.3).
Рис. 3. Кривая нормального распределения.
Эта кривая имеет симметричную колоколообразную форму. Заштрихованная площадь представляет собой вероятность появления ошибки в интервале от ∆ до ∆+d∆.
Слайд 20
Описание слайда:
Есть ошибки, которые подчиняются закону равномерного или равновероятного распределения, к примеру, ошибки округления. Плотность распределения их выражается формулой:
Есть ошибки, которые подчиняются закону равномерного или равновероятного распределения, к примеру, ошибки округления. Плотность распределения их выражается формулой:
(4)
где α – наибольшее значение ошибки.
Слайд 21
Описание слайда:
Основными характеристиками распределения случайной величины являются математическое ожидание и дисперсия.
Основными характеристиками распределения случайной величины являются математическое ожидание и дисперсия.
Математическим ожиданием дискретной случайной величины х называют сумму произведений всех возможных значений случайной величины на соответствующие им вероятности р
. (5)
Слайд 22
Описание слайда:
Для непрерывной случайной величины с плотностью распределения f(x) матема-тическое ожидание определяется по формуле:
Для непрерывной случайной величины с плотностью распределения f(x) матема-тическое ожидание определяется по формуле:
. (6)
Слайд 23
Описание слайда:
Дисперсией случайной величины Х называ-ется число, определяемое по формуле:
Дисперсией случайной величины Х называ-ется число, определяемое по формуле:
. (7)
Слайд 24
Описание слайда:
Положительное значение квадратного корня из дисперсии называют стандартом или средним квадратическим отклонением
Положительное значение квадратного корня из дисперсии называют стандартом или средним квадратическим отклонением
. (8)
Слайд 25
Описание слайда:
Для случайных ошибок измерений, как уже отмечалось, математическое ожидание равно нулю =0. Поэтому
Для случайных ошибок измерений, как уже отмечалось, математическое ожидание равно нулю =0. Поэтому
, (9)
или
(10)
при n стремящемуся к бесконечности.
Слайд 26
Описание слайда:
5.Числовые характеристики точности измерений.
В качестве теоретической характеристики точности измерений обычно пользуются средним квадратическим отклонением σ.
Поскольку величина σ не известна, практически пользуются ее приближенным значением – средней квадратической ошибкой (СКО), определяемой по формуле:
, (11)
где ∆1, ∆2, …, ∆n – истинные ошибки измерений.
Слайд 27
Описание слайда:
При большом значении n
При большом значении n
m ≈ σ. (12)
При ограниченном числе измерений величина m будет характеризовать величину σ с некоторой ошибкой. Для оценки точности определения самой средней квадратической ошибки существует формула:
(13)
Слайд 28
Описание слайда:
Оценку точности измерений характеризуют также предельной ошибкой, вычисляемой по формуле:
Оценку точности измерений характеризуют также предельной ошибкой, вычисляемой по формуле:
∆пр= τm, (14)
где τ – коэффициент, значение которого прини-мают таким, чтобы была мала вероятность появления ошибки больше вероятной.
Слайд 29
Описание слайда:
Обычно для τ принимают значения 3, 2.5, или 2.
Обычно для τ принимают значения 3, 2.5, или 2.
В дальнейшем при решении задач по оценке точности измерений будем пользоваться формулой
∆пр= 3m.
Для оценки точности иногда пользуются средней ошибкой v и вероятной ошибкой r. Средняя ошибка вычисляется по формуле
(15)
Слайд 30
Описание слайда:
При нормальном распределении средняя ошибка v связана со средней квадратичеcкой ошибкой m примерным соотношением
При нормальном распределении средняя ошибка v связана со средней квадратичеcкой ошибкой m примерным соотношением
(16)
Если все ошибки расположить в ряд по возрастанию абсолютных значений, то ошибка оказавшаяся в середине ряда будет вероятной. Со средней квадратической ошибкой она связана соотношением
(17)
Ошибка, выраженная в единицах измерения, называется абсолютной. Отношение ее к измеренной величине называется относительной ошибкой.
Слайд 31
Описание слайда:
СПАСИБО ЗА ВНИМАНИЕ.
Содержание статьи:
Именованные числа простыми словами для детей
Определение. Именованные числа — это числа, полученные при измерении величин и сопровождающиеся названием единицы.
Сегодня было представление. Перед его началом Бим уже стоял около двери с огромной линейкой.
К нему подошел Бом и спросил:
— Привет! А что это ты тут делаешь? Зачем тебе понадобилась эта длинная планка?
— Мне сказали, что существуют именованные числа, которые связаны с единицей измерения, — весело ответил Бим. — Вот я и измеряю рост каждого зрителя. А это не планка, а линейка.
— Ну да. Я тоже читал про это в учебнике. Именованные числа для определения роста сопровождаются названиями: миллиметры, сантиметры, дециметры, метры или километры. — уточнил Бом. — Хотя… километрами обычно измеряют большие расстояния. И рост, и расстояние имеют одно общее название — длина.
— Правильно. А здесь на линейке как раз и есть миллиметры, сантиметры и даже метры отмечены.
— А также можно измерять и вес детей в граммах, килограммах, центнерах, тоннах. — добавил Бом. — Нет, центнеры и тонны — это очень большие единицы веса, в них лучше измерять вес слонят и слонов. Кстати, по-другому эта величина еще называется масса.
Тут Бим отдал линейку Бому:
— Точно! Давай ты пока измеришь рост ребят, а я побегу за весами! — предложил он. — Будем еще и вес наших зрителей измерять. Возьму весы у нашей буфетчицы — те, которыми можно взвешивать до 100 кг.
— А что еще можно измерять? — задумчиво спросил Бом.
— Время! То есть, сколько ты тратишь времени на каждое измерение.
— Вот еще! Я не собираюсь тратить время. Я помогаю ребятам узнать свой рост и вес и познакомиться с именованными числами. — обиделся Бом.
Но Бим его уже не слышал. Он побежал за весами.
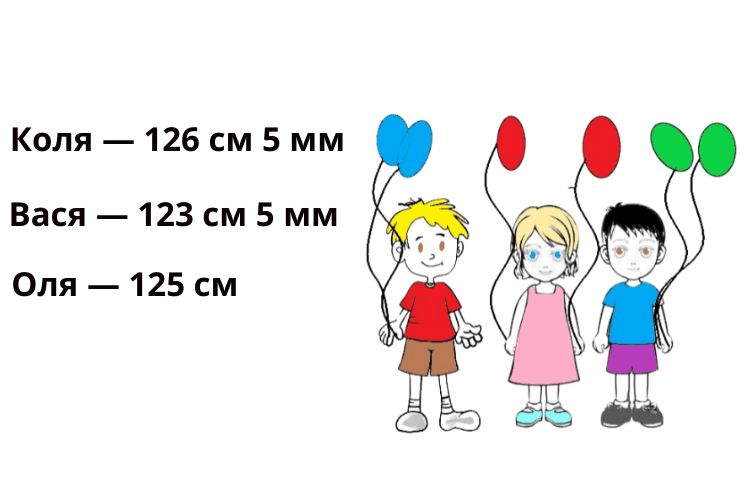
Бом достал часы. И тут подошли наши старые знакомые: Коля, Оля и Вася.
Бом измерил рост ребят и записал на листочке:
- Оля — 125 см, время измерения 18 с;
- Коля — 126 см 5 мм, время 22 с;
- Вася — 123 см 5 мм, время 21 с;
Простые и составные именованные числа — это
Определение. Простыми именованными числами называются именованные числа, в которые входит только одна единица измерения величины.
Определение. Составными именованными числами называются числа, в которые входит несколько единиц измерения величины.
— Мне мама недавно измеряла рост и сказала, что он у меня 1 метр 25 сантиметров, — заметила Оля. — И она внесла в свои записи отметку 1 м 25 см.
— А я записал твой рост как простое именованное число. В нем есть только одна единица измерения — сантиметр, — ответил Бом. — Получилось 125 см.
— Получается, что 1 м 25 см = 125 см? — спросила Оля.
— Да. — подтвердил Бом. — А еще можно записать в метрах, дециметрах и сантиметрах. Мы знаем, что
1 дм = 10 см.
Если мы найдем неполное частное и остаток от деления 125 см на 10, то получим выражение в дециметрах и сантиметрах:
125 см :10 = 12 дм 5 см.
Если знать, что в 1 м = 10 дм, то можно разделить 12 дм на 10. Тогда мы получим неполное частное в метрах, а остаток в дециметрах. Ещё нужно дописать 5 см, которые уже были:
(12дм :10)+5 см = 125 см = 1 м 2 дм 5 см.
Можно 125 см разделить на 100, будет 1 м 25 см. Тогда неполное частное у нас будет в метрах, а остаток в сантиметрах. И это уже будет составное именованное число. Так как в нём мы уже видим несколько единиц измерения.
| (дм):10 = (см):100 | (см):10 | Величина именованного числа | Примечание | |
| м | дм | см | ||
| 125 см | 125 см | простое | ||
| 12 дм | 5 см | 12 дм 5 см | составное | |
| 1 м | 2 дм | 5 см | 1м 2 дм 5 см | составное |
| 1 м | 25 см | 1 м 25 см | составное |
В ячейке, где ничего не написано, стоит 0, ноль мы не пишем.
Превращение (укрупнение) именованного числа — это
Определение. Превращение (укрупнение) именованного числа — это запись именованного числа через какие-нибудь бо́льшие единицы измерения.
Правило. Для того чтобы превратить (укрупнить) именованное число из меньшей единицы измерения в бо́льшую, нужно:
- Разделить именованное число на коэффициент перевода этих единиц измерения из бо́льшей в меньшую.
- Затем неполное частное поставить с бо́льшей единицей измерения, а остаток оставить с меньшей единицей измерения.
При этом числа при меньших единицах измерения остаются без изменения.
Таблица коэффициентов перевода единиц измерений для длины
| 1 км = 1000 м | 1 м = 10 дм | 1 дм = 10 см | 1 см = 10 мм. |
| 1 км = 10 000 дм | 1 м = 100 см | 1дм = 100 мм | |
| 1 км = 100 000 см | 1м = 1 000 мм | ||
| 1 км = 1000 000 мм |
Таблица перевода единиц измерения для массы
| 1 т = 10 ц = 1000 кг = 1 000 000 г | 1 ц = 100 кг = 100 000 г | 1 кг = 1 000 г |
Таблица перевода единиц измерения для времени
| 1 сутки = 24 час = 1440 мин = 8640 с | 1 час = 60 мин = 3600 с | 1 мин = 60 с |
— Интересно, а наш рост — простое или составное именованное число и как можно это число раздробить или укрупнить? — спросили Коля и Вася.
— Позже мы разберем правило раздробления, — ответил Бом. — А пока запишем все в одну таблицу.
Для роста Коли:
126 см 5 мм = (126 х 10) мм + 5мм = 1265 мм — раздробленное число.
Превращение (укрупнение) этого числа запишем в виде таблиц:
- выражаем в метрах, дециметрах, сантиметрах и миллиметрах
| (дм):10 | (см):10 | (мм):10 | Именованное число | примечание | |
| м | дм | см | мм | ||
| 1265 мм | 1265 мм | простое | |||
| 126 см частное | 5 мм остаток | 126 см 5 мм | составное | ||
| 12 дм частное | 6 см остаток | 5 мм | 12 дм 6 см 5 мм | составное | |
| 1 м частное | 2 дм остаток | 6 см | 5 мм | 1м 2 дм 6 см 5 мм | составное |
- выражаем в метрах, сантиметрах и миллиметрах
| (см) : 100 | (мм):10 | Именованное число | примечание | |
| м | см | мм | ||
| 1265 мм | 1265 мм | простое | ||
| 126 см частное | 5 мм остаток | 126 см 5 мм | составное | |
| 1 м частное | 26 см остаток | 5 мм | 1 м 26 см 5 мм | составное |
- выражаем в метрах и миллиметрах
| (мм) : 1000 | Величина именованного числа | примечание | |
| м | мм | ||
| 1265 мм | 1265 мм | простое | |
| 1 м частное | 265 мм остаток | 1м 265 мм | составное |
Для меня самое удобное представление 1 м 26 см 5 мм. Но иногда бывают нужны именованные числа в разных единицах измерения. В таких случаях придется самому сообразить, какое представление больше подходит.
Рост Васи — тоже составное число:
123 см 5 мм = 1 м 2 дм 3 см 5 мм, или 123 см 5 мм =1 м 23 см 5 мм
(читается: 1 метр 23 сантиметра 5 миллиметров).
Все это один и тот же рост, но записанный числами с разными размерностями величины — длины.
А теперь — задание. Хорошо, если у вас получится самим написать такие таблицы для роста Васи и Оли. Выразить рост в разных единицах измерения.
Подошел Бим, который вез на тележке весы.
— А вот и весы! Надеюсь, вам не пришлось меня долго ждать?
— Все хорошо. — ответил Бом. — Мы как раз измерили рост всех ребят — и даже научились укрупнять именованные числа. А теперь — все взвешиваемся!
— Погодите! — вбежала со всех ног буфетчица. — Осторожнее с весами, взвешивать буду я!
— Только сначала дайте, пожалуйста, определение, что такое именованные числа. И как вы будете их использовать?
— Я умею работать с граммами, килограммами, тоннами, центнерами, — ответила буфетчица. — Знаю, что 1 литр воды весит один килограмм. Но вот определения именованных чисел я не знаю. Помогите, ребята.
Ребята дружно ответили:
— Именованные числа — это числа, полученные при измерении величин и сопровождающиеся названиями единицы измерения. Вы работаете с именованными числами для веса (или массы).
— Правда? Если я измеряю в разных единицах измерения ваш вес, так я уже работаю с именованными числами? — удивилась буфетчица?
— Да, — подтвердил Бом.
— И получается, что я всегда работала с именованными числами для веса? Вот это да!
— Ну конечно! — ответил Бим.
Буфетчица начала взвешивать ребят.
— Оля — 23 кг 300 г, Коля — 25 кг 700 г, Вася — 24 кг.
— Быстро же у вас получается! — воскликнул Бим. — Вы потратили по 15 с на Олю и Колю, и 14 с на Васю!
Раздробление именованного числа — это
Определение. Раздробление именованного числа — это запись именованного числа через низшие единицы измерения.
Правило. Для того чтобы раздробить именованное число, нужно:
- Найти наименьшую единицу размерности в именованном числе.
- Значения для остальных единиц измерения из именованного числа умножить на коэффициент перевода в наименьшую единицу размерности в данном именованном числе.
- Сложить полученные числа. Результат получается в самых маленьких единицах размерности числа.
— Теперь я раздроблю полученные числа до граммов и узнаю ваш вес в граммах. — продолжила буфетчица. — Так,
- вес Оли: 23 кг 300 г =23х1000 г + 300 г = 23300 г;
- вес Коли: 25кг 700 г =25х1000 г +700 г= 25700 г;
- вес Васи: 24 кг = 24 х 1000 г = 24000 г.
Сложение и вычитание именованных чисел
Правило. Для сложения и вычитания именованных чисел необходимо выразить оба слагаемых в одинаковых единицах измерения. Сложение и вычитания можно выполнять по соответствующим величинам размерности как обыкновенных чисел в столбик, затем полученное именованное число укрупняют.
— А сейчас, — продолжила буфетчица, — проверим, сколько вы все вместе весите 2-мя способами:
23 кг 300 г +25 кг 700 г + 24 кг = (23+25+24) кг + (300+700) г = 73 кг
— Но Вы же раздробили вес до грамм, — недоумевал Бим. – И куда же эти граммы исчезли?
— Совершенно верно! — ответила буфетчица. — Вес и был до граммов. Но ведь
23 кг+25 кг + 24 кг =72 кг, 300 г + 700 г = 1000 г.
И я-то знаю, что 1000 г = 1 кг. Поэтому
23 кг 300 г +25 кг 700 г + 24 кг = (23+25+24) кг + (300+700) г = 72 кг + 1000 г = 72 кг + 1 кг = 73 кг.
Можно сделать и другим способом. Все веса сложить вместе в граммах, а потом укрупнить:
23300 г + 25700 г + 24000 г = 73000 г.
Это число делится на 1000 и получаем
73000 г : 1000 = 73 кг.
Ответы для первого и второго способов совпадают.
Неожиданно зазвонил телефон. Буфетчица подняла трубку:
— Мне надо срочно отойти, привезли бананы в буфет и для наших обезьян, пойду взвешу их. Бим, помоги вернуть весы назад!
Когда Бим с буфетчицей ушли, Бом продолжил упражнения с именованными числами:
— Теперь давайте узнаем, какой общий рост всех ребят.
125 см +126 см 5 мм + 123 см 5 мм = (125 + 126 + 123) см + (5+5) мм = =374 см + 10 мм = 374 см + 1 см = 375 см.
Укрупняем
375 см = 300 см + 70 см + 5 см = 3 м +7 дм + 5 см = 3 м 7 дм 5 см.
Можно сразу взять ваш рост в превращенных единицах измерения, складывая числа при одинаковых единицах измерения, тогда рост Оли и Коли, рост Коли и Васи будут:
Можно также сложить рост всех ребят через раздробление чисел. Находим самую маленькую единицу для всех величин, которые складываем:
- в величине роста Оли — сантиметры;
- в величине роста Коли и Васи — миллиметры.
Один миллиметр меньше одного сантиметра. Значит, все будем вычислять в миллиметрах.
1 м 2 дм 5 см= (1х100+ 2 х10 + 5) см = 125 см = 125 х 10 мм = 1250 мм,
1 м 2 дм 6 см 5 мм = (1 х 1000 + 2 х 100 + 6 х 10 + 5) мм = 1265 мм,
1 м 2 дм 3 см 5 мм = (1 х 1000 + 2 х 100 + 3 х 10 + 5) мм = 1235 мм
Теперь все сложим и получим
1250 мм + 1265 мм + 1235 мм = 3750 мм.
Укрупняем
3750 мм = (3 х 1000 + 7х 100 + 5 х 10) мм = 3 х1000 мм + 7 х 100 мм + 5 х 10 мм = 3 м + 7 дм + 5 см.
Вернулся Бим и посмотрел на все то, что успел записать Бом.
— Ага, высота нашего цирка 25 м. Значит ребята, даже если встанут друг на друга, не достанут до потолка. Вычисляем
— Получается, что не достанут, — согласился Бом.
Умножение и деление именованных чисел
Правило. При умножении и делении составных именованных чисел нужно:
- Заменить составные числа простыми, выполнить вычисление.
- В случае, если полученный результат — простое именованное число, его превращают в составное.
Потом было представление. Бом с обезьянками выступал просто великолепно.
Пяти обезьянкам в антракте досталось по 2 банана. Буфетчица попросила ребят посчитать, сколько весили бананы, которые съели обезьянки, если один банан весит 180 г. Ребята запросто решили такую задачу:
Обезьянкам дали 5х2=10 (шт.) бананов. Если один банан весит 180 г, то всего обезьянки съели:
180 г х 10 = 1800 г
Затем Оля, Коля и Вася превратили простые именованные числа в составные и получили, что
1800 г = 1 кг 800 г — вес бананов, которые съели обезьянки.
Дальше ребята помогли выяснить, надолго ли хватит бананов, если на сутки нужно 6 кг бананов, а всего привезли 1 ц 99 кг 800 г:
1ц 98 кг = 100 кг + 98 кг =198 кг
198 кг : 6 кг = 33 (суток).
Сравнение именованных чисел
Правило. Два именованных числа можно сравнивать, начиная с наибольшей величины размерности двух чисел по правилам сравнения обыкновенных чисел, следуя от высшей размерности к низшей. Если нет числа в какой-то из размерностей, надо считать, что там стоит 0.
Другой способ. Раздробить именованные числа до наименьшей размерности из двух чисел и сравнить их раздробление, дальше действовать по правилу сравнения обыкновенных чисел.
Известно, что в следующий раз бананы привезут через 720 часов. Хватит ли бананов до следующего их привоза в цирк?
Нам надо раздробить 33 суток до величины измерения часы. В сутках 24 часа, значит всего в 33 сутках
33х 24 ч = 792 ч.
Теперь, когда оба числа выражены в одинаковых единицах измерения — часах, мы сравним значения этих величин
792 ч > 720 ч,
то есть обезьянки все время смогут есть бананы и не быть голодными.
Можно для сравнения превратить (укрупнить) именованное число 720 ч. По правилам укрупнения мы должны часы 720 ч разделить на количество часов в сутках — 24 ч. Получим через сколько суток привезут бананы
720 ч : 24 ч = 30 (суток)
30 суток < 33 суток. Обезьянкам хватит бананов!
Выводы
Для закрепления темы давайте запишем вопросы для именованных чисел и дадим ответы на них. — подытожил Бим.
Что такое именованные числа?
Определение. Именованные числа — это числа, полученные при измерении величин и сопровождающиеся названием единицы.
Что такое простое и составное именованное число?
Определение. Простыми именованными числами называются именованные числа, в которые входит только одна единица измерения величины.
Определение. Составными именованными числами называются числа, в которые входит несколько единиц измерения величины.
Что такое укрупнение и раздробление именованного числа?
Определение. Превращение (укрупнение) именованного числа — это запись именованного числа через какие-нибудь бо́льшие единицы измерения.
Определение. Раздробление именованного числа — это запись именованного числа через низшие единицы измерения.
Правило. Для того чтобы раздробить именованное число, нужно:
1. Найти наименьшую единицу размерности в именованном числе.
2. Значения для остальных единиц измерения из именованного числа умножить на коэффициент перевода в наименьшую единицу размерности в данном именованном числе.
3. Сложить полученные числа. Результат получается в самых маленьких единицах размерности числа.
Операции сложения и вычитания именованных чисел
Правило. Для сложения и вычитания именованных чисел необходимо выразить оба слагаемых в одинаковых единицах измерения. Сложение и вычитания можно выполнять по соответствующим величинам размерности как обыкновенных чисел в столбик, затем полученное именованное число укрупняют.
Операции умножения и деления для именованных чисел.
Правило. При умножении и делении составных именованных чисел надо
1. Заменить составные числа простыми, выполнить вычисление.
2. В случае, если полученный результат — простое именованное число, его превращают в составное.
Сравнение именованных чисел.
Правило. Два именованных числа можно сравнивать начиная с наибольшей величины размерности двух чисел по правилам сравнения обыкновенных чисел, следуя от высшей размерности к низшей. Если нет числа в какой— то из размерностей надо считать, что там стоит 0.
Другой способ. Раздробить именованные числа до наименьшей размерности из двух чисел и сравнить их раздробление, дальше действовать по правилу сравнения обыкновенных чисел.
Мы постарались подробно разобрать, что такое именованные числа и какие они бывают. А также как их складывать и вычитать, умножать и делить, сравнивать между собой.
Оригинальная идея подачи материала принадлежит Стуловой Лилии Валериевне (преподаватель математики от 5 лет и старше).
Не забудьте оценить наши старания! Комментарии приветствуются. По желанию подписывайтесь на нас в Яндекс.Дзен и в других социальных сетях!!!)))
Свойства физического объекта (явления, процесса) определяются набором
количественных характеристик — физических величин.
Как правило, результат измерения представляет
собой число, задающее отношение измеряемой величины к некоторому эталону.
Сравнение с эталоном может быть как
прямым (проводится непосредственно
экспериментатором), так и косвенным (проводится с помощью некоторого
прибора, которому экспериментатор доверяет).
Полученные таким образом величины имеют размерность, определяемую выбором эталона.
Замечание. Результатом измерения может также служить количество отсчётов некоторого
события, логическое утверждение (да/нет) или даже качественная оценка
(сильно/слабо/умеренно). Мы ограничимся наиболее типичным для физики случаем,
когда результат измерения может быть представлен в виде числа или набора чисел.
Взаимосвязь между различными физическими величинами может быть описана
физическими законами, представляющими собой идеализированную
модель действительности. Конечной целью любого физического
эксперимента (в том числе и учебного) является проверка адекватности или
уточнение параметров таких моделей.
1.1 Результат измерения
Рассмотрим простейший пример: измерение длины стержня
с помощью линейки. Линейка проградуирована производителем с помощью
некоторого эталона длины — таким образом, сравнивая длину
стержня с ценой деления линейки, мы выполняем косвенное сравнение с
общепринятым стандартным эталоном.
Допустим, мы приложили линейку к стержню и увидели на шкале некоторый результат
x=xизм. Можно ли утверждать, что xизм — это длина
стержня?
Во-первых, значение x не может быть задано точно, хотя бы
потому, что оно обязательно округлено до некоторой значащей
цифры: если линейка «обычная», то у неё
есть цена деления; а если линейка, к примеру, «лазерная»
— у неё высвечивается конечное число значащих цифр
на дисплее.
Во-вторых, мы никак не можем быть уверенны, что длина стержня на
самом деле такова хотя бы с точностью до ошибки округления. Действительно,
мы могли приложить линейку не вполне ровно; сама линейка могла быть
изготовлена не вполне точно; стержень может быть не идеально цилиндрическим
и т.п.
И, наконец, если пытаться хотя бы гипотетически переходить к бесконечной
точности измерения, теряет смысл само понятие «длины стержня». Ведь
на масштабах атомов у стержня нет чётких границ, а значит говорить о его
геометрических размерах в таком случае крайне затруднительно!
Итак, из нашего примера видно, что никакое физическое измерение не может быть
произведено абсолютно точно, то есть
у любого измерения есть погрешность.
Замечание. Также используют эквивалентный термин ошибка измерения
(от англ. error). Подчеркнём, что смысл этого термина отличается от
общеупотребительного бытового: если физик говорит «в измерении есть ошибка»,
— это не означает, что оно неправильно и его надо переделать.
Имеется ввиду лишь, что это измерение неточно, то есть имеет
погрешность.
Количественно погрешность можно было бы определить как разность между
измеренным и «истинным» значением длины стержня:
δx=xизм-xист. Однако на практике такое определение
использовать нельзя: во-первых, из-за неизбежного наличия
погрешностей «истинное» значение измерить невозможно, и во-вторых, само
«истинное» значение может отличаться в разных измерениях (например, стержень
неровный или изогнутый, его торцы дрожат из-за тепловых флуктуаций и т.д.).
Поэтому говорят обычно об оценке погрешности.
Об измеренной величине также часто говорят как об оценке, подчеркивая,
что эта величина не точна и зависит не только от физических свойств
исследуемого объекта, но и от процедуры измерения.
Замечание.
Термин оценка имеет и более формальное значение. Оценкой называют результат процедуры получения значения параметра или параметров физической модели, а также иногда саму процедуру. Теория оценок является подразделом математической статистики. Некоторые ее положения изложены в главе 3, но для более серьезного понимания следует обратиться к [5].
Для оценки значения физической величины корректно использовать
не просто некоторое фиксированное число xизм, а интервал (или
диапазон) значений, в пределах которого может лежать её
«истинное» значение. В простейшем случае этот интервал
может быть записан как
где δx — абсолютная величина погрешности.
Эта запись означает, что исследуемая величина лежит в интервале
x∈(xизм-δx;xизм+δx)
с некоторой достаточно большой долей вероятности (более подробно о
вероятностном содержании интервалов см. п. 2.2).
Для наглядной оценки точности измерения удобно также использовать
относительную величину погрешности:
Она показывает, насколько погрешность мала по сравнению с
самой измеряемой величиной (её также можно выразить в процентах:
ε=δxx⋅100%).
Пример. Штангенциркуль —
прибор для измерения длин с ценой деления 0,1мм. Пусть
диаметр некоторой проволоки равен 0,37 мм. Считая, что абсолютная
ошибка составляет половину цены деления прибора, результат измерения
можно будет записать как d=0,40±0,05мм (или
d=(40±5)⋅10-5м).
Относительная погрешность составляет ε≈13%, то
есть точность измерения весьма посредственная — поскольку
размер объекта близок к пределу точности прибора.
О необходимости оценки погрешностей.
Измерим длины двух стержней x1 и x2 и сравним результаты.
Можно ли сказать, что стержни одинаковы или различны?
Казалось бы,
достаточно проверить, справедливо ли x1=x2. Но никакие
два результата измерения не равны друг другу с абсолютной точностью! Таким
образом, без указания погрешности измерения ответ на этот вопрос дать
невозможно.
С другой стороны, если погрешность δx известна, то можно
утверждать, что если измеренные длины одинаковы
в пределах погрешности опыта, если |x2-x1|<δx
(и различны в противоположном случае).
Итак, без знания погрешностей невозможно сравнить между собой никакие
два измерения, и, следовательно, невозможно сделать никаких
значимых выводов по результатам эксперимента: ни о наличии зависимостей
между величинами, ни о практической применимости какой-либо теории,
и т. п. В связи с этим задача правильной оценки погрешностей является крайне
важной, поскольку существенное занижение или завышение значения погрешности
(по сравнению с реальной точностью измерений) ведёт к неправильным выводам.
В физическом эксперименте (в том числе лабораторном практикуме) оценка
погрешностей должна проводиться всегда
(даже когда составители задания забыли упомянуть об этом).
1.2 Многократные измерения
Проведём серию из n одинаковых (однотипных) измерений одной
и той же физической величины (например, многократно приложим линейку к стержню) и получим
ряд значений
Что можно сказать о данном наборе чисел и о длине стержня?
И можно ли увеличивая число измерений улучшить конечный результат?
Если цена деления самой линейки достаточно мала, то как нетрудно убедиться
на практике, величины {xi} почти наверняка окажутся
различными. Причиной тому могут быть
самые разные обстоятельства, например: у нас недостаточно остроты
зрения и точности рук, чтобы каждый раз прикладывать линейку одинаково;
стенки стержня могут быть слегка неровными; у стержня может и не быть
определённой длины, например, если в нём возбуждены звуковые волны,
из-за чего его торцы колеблются, и т. д.
В такой ситуации результат измерения интерпретируется как
случайная величина, описываемая некоторым вероятностным законом
(распределением).
Подробнее о случайных величинах и методах работы с ними см. гл. 2.
По набору результатов 𝐱 можно вычислить их среднее арифметическое:
| ⟨x⟩=x1+x2+…+xnn≡1n∑i=1nxi. | (1.1) |
Это значение, вычисленное по результатам конечного числа n измерений,
принято называть выборочным средним. Здесь и далее для обозначения
выборочных средних будем использовать угловые скобки.
Кроме среднего представляет интерес и то, насколько сильно варьируются
результаты от опыта к опыту. Определим отклонение каждого измерения от среднего как
Разброс данных относительно среднего принято характеризовать
среднеквадратичным отклонением:
| s=Δx12+Δx22+…+Δxn2n=1n∑i=1nΔxi2 | (1.2) |
или кратко
Значение среднего квадрата отклонения s2 называют
выборочной дисперсией.
Будем увеличивать число измерений n (n→∞). Если объект измерения и методика
достаточно стабильны, то отклонения от среднего Δxi будут, во-первых,
относительно малы, а во-вторых, положительные и отрицательные отклонения будут
встречаться примерно одинаково часто. Тогда при вычислении (1.1)
почти все отклонения Δxi скомпенсируются и можно ожидать,
что выборочное среднее при n≫1 будет стремиться к некоторому пределу:
Тогда предельное значение x¯ можно отождествить с «истинным» средним
для исследуемой величины.
Предельную величину среднеквадратичного отклонения при n→∞
обозначим как
Замечание. В общем случае указанные пределы могут и не существовать. Например, если измеряемый параметр
меняется во времени или в результате самого измерения, либо испытывает слишком большие
случайные скачки и т. п. Такие ситуации требуют особого рассмотрения и мы на них не
останавливаемся.
Замечание. Если n мало (n<10), для оценки среднеквадратичного отклонения
математическая статистика рекомендует вместо формулы (1.3) использовать
исправленную формулу (подробнее см. п. 5.2):
sn-12=1n-1∑i=1nΔxi2,
(1.4)
где произведена замена n→n-1. Величину sn-1
часто называют стандартным отклонением.
Итак, можно по крайней мере надеяться на то, что результаты небольшого числа
измерений имеют не слишком большой разброс, так что величина ⟨x⟩
может быть использована как приближенное значение (оценка) истинного значения
⟨x⟩≈x¯,
а увеличение числа измерений позволит уточнить результат.
Многие случайные величины подчиняются так называемому нормальному закону
распределения (подробнее см. Главу 2). Для таких величин
могут быть строго доказаны следующие свойства:
-
•
при многократном повторении эксперимента бо́льшая часть измерений
(∼68%) попадает в интервал x¯-σ<x<x¯+σ
(см. п. 2.2). -
•
выборочное среднее значение ⟨x⟩ оказывается с большей
вероятностью ближе к истинному значению x¯, чем каждое из измерений
{xi} в отдельности. При этом ошибка вычисления среднего
убывает пропорционально корню из числа опытов n
(см. п. 2.4).
Упражнение. Показать, что
s2=⟨x2⟩-⟨x⟩2.
(1.5)
то есть дисперсия равна разности среднего значения квадрата
⟨x2⟩=1n∑i=1nxi2
и квадрата среднего ⟨x⟩2=(1n∑i=1nxi)2.
1.3 Классификация погрешностей
Чтобы лучше разобраться в том, нужно ли многократно повторять измерения,
и в каком случае это позволит улучшить результаты опыта,
проанализируем источники и виды погрешностей.
В первую очередь, многократные измерения позволяют проверить
воспроизводимость результатов: повторные измерения в одинаковых
условиях, должны давать близкие результаты. В противном случае
исследование будет существенно затруднено, если вообще возможно.
Таким образом, многократные измерения необходимы для того,
чтобы убедиться как в надёжности методики, так и в существовании измеряемой
величины как таковой.
При любых измерениях возможны грубые ошибки — промахи
(англ. miss). Это «ошибки» в стандартном
понимании этого слова — возникающие по вине экспериментатора
или в силу других непредвиденных обстоятельств (например, из-за сбоя
аппаратуры). Промахов, конечно, нужно избегать, а результаты таких
измерений должны быть по возможности исключены из рассмотрения.
Как понять, является ли «аномальный» результат промахом? Вопрос этот весьма
непрост. В литературе существуют статистические
критерии отбора промахов, которыми мы, однако, настоятельно не рекомендуем
пользоваться (по крайней мере, без серьезного понимания последствий
такого отбора). Отбрасывание аномальных данных может, во-первых, привести
к тенденциозному искажению результата исследований, а во-вторых, так
можно упустить открытие неизвестного эффекта. Поэтому при научных
исследованиях необходимо максимально тщательно проанализировать причину
каждого промаха, в частности, многократно повторив эксперимент. Лишь
только если факт и причина промаха установлены вполне достоверно,
соответствующий результат можно отбросить.
Замечание. Часто причины аномальных отклонений невозможно установить на этапе
обработки данных, поскольку часть информации о проведении измерений к этому моменту
утеряна. Единственным способ борьбы с этим — это максимально подробное описание всего
процесса измерений в лабораторном журнале. Подробнее об этом
см. п. 4.1.1.
При многократном повторении измерении одной и той же физической величины
погрешности могут иметь систематический либо случайный
характер. Назовём погрешность систематической, если она повторяется
от опыта к опыту, сохраняя свой знак и величину, либо закономерно
меняется в процессе измерений. Случайные (или статистические)
погрешности меняются хаотично при повторении измерений как по величине,
так и по знаку, и в изменениях не прослеживается какой-либо закономерности.
Кроме того, удобно разделять погрешности по их происхождению. Можно
выделить
-
•
инструментальные (или приборные) погрешности,
связанные с несовершенством конструкции (неточности, допущенные при
изготовлении или вследствие старения), ошибками калибровки или ненормативными
условиями эксплуатации измерительных приборов; -
•
методические погрешности, связанные с несовершенством
теоретической модели явления (использование приближенных формул и
моделей явления) или с несовершенством методики измерения (например,
влиянием взаимодействия прибора и объекта измерения на результат измерения); -
•
естественные погрешности, связанные со случайным
характером
измеряемой физической величины — они являются не столько
«ошибками» измерения, сколько характеризуют
природу изучаемого объекта или явления.
Замечание. Разделение погрешностей на систематические и случайные
не является однозначным и зависит от постановки опыта. Например, производя
измерения не одним, а несколькими однотипными приборами, мы переводим
систематическую приборную ошибку, связанную с неточностью шкалы и
калибровки, в случайную. Разделение по происхождению также условно,
поскольку любой прибор подвержен воздействию «естественных»
случайных и систематических ошибок (шумы и наводки, тряска, атмосферные
условия и т. п.), а в основе работы прибора всегда лежит некоторое
физическое явление, описываемое не вполне совершенной теорией.
1.3.1 Случайные погрешности
Случайный характер присущ большому количеству различных физических
явлений, и в той или иной степени проявляется в работе всех без исключения
приборов. Случайные погрешности обнаруживаются просто при многократном
повторении опыта — в виде хаотичных изменений (флуктуаций)
значений {xi}.
Если случайные отклонения от среднего в большую или меньшую стороны
примерно равновероятны, можно рассчитывать, что при вычислении среднего
арифметического (1.1) эти отклонения скомпенсируются,
и погрешность результирующего значения ⟨x⟩ будем меньше,
чем погрешность отдельного измерения.
Случайные погрешности бывают связаны, например,
-
•
с особенностями используемых приборов: техническими
недостатками
(люфт в механических приспособлениях, сухое трение в креплении стрелки
прибора), с естественными (тепловой и дробовой шумы в электрических
цепях, тепловые флуктуации и колебания измерительных устройств из-за
хаотического движения молекул, космическое излучение) или техногенными
факторами (тряска, электромагнитные помехи и наводки); -
•
с особенностями и несовершенством методики измерения (ошибка
при отсчёте по шкале, ошибка времени реакции при измерениях с секундомером); -
•
с несовершенством объекта измерений (неровная поверхность,
неоднородность состава); -
•
со случайным характером исследуемого явления (радиоактивный
распад, броуновское движение).
Остановимся несколько подробнее на двух последних случаях. Они отличаются
тем, что случайный разброс данных в них порождён непосредственно объектом
измерения. Если при этом приборные погрешности малы, то «ошибка»
эксперимента возникает лишь в тот момент, когда мы по своей
воле совершаем замену ряда измеренных значений на некоторое среднее
{xi}→⟨x⟩. Разброс данных при этом
характеризует не точность измерения, а сам исследуемый объект или
явление. Однако с математической точки зрения приборные и
«естественные»
погрешности неразличимы — глядя на одни только
экспериментальные данные невозможно выяснить, что именно явилось причиной
их флуктуаций: сам объект исследования или иные, внешние причины.
Таким образом, для исследования естественных случайных процессов необходимо
сперва отдельно исследовать и оценить случайные инструментальные погрешности
и убедиться, что они достаточно малы.
1.3.2 Систематические погрешности
Систематические погрешности, в отличие от случайных, невозможно обнаружить,
исключить или уменьшить просто многократным повторением измерений.
Они могут быть обусловлены, во-первых, неправильной работой приборов
(инструментальная погрешность), например, сдвигом нуля отсчёта
по шкале, деформацией шкалы, неправильной калибровкой, искажениями
из-за не нормативных условий эксплуатации, искажениями из-за износа
или деформации деталей прибора, изменением параметров прибора во времени
из-за нагрева и т.п. Во-вторых, их причиной может быть ошибка в интерпретации
результатов (методическая погрешность), например, из-за использования
слишком идеализированной физической модели явления, которая не учитывает
некоторые значимые факторы (так, при взвешивании тел малой плотности
в атмосфере необходимо учитывать силу Архимеда; при измерениях в электрических
цепях может быть необходим учет неидеальности амперметров и вольтметров
и т. д.).
Систематические погрешности условно можно разделить на следующие категории.
-
1.
Известные погрешности, которые могут быть достаточно точно вычислены
или измерены. При необходимости они могут быть учтены непосредственно:
внесением поправок в расчётные формулы или в результаты измерений.
Если они малы, их можно отбросить, чтобы упростить вычисления. -
2.
Погрешности известной природы, конкретная величина которых неизвестна,
но максимальное значение вносимой ошибки может быть оценено теоретически
или экспериментально. Такие погрешности неизбежно присутствуют в любом
опыте, и задача экспериментатора — свести их к минимуму,
совершенствуя методики измерения и выбирая более совершенные приборы.Чтобы оценить величину систематических погрешностей опыта, необходимо
учесть паспортную точность приборов (производитель, как правило, гарантирует,
что погрешность прибора не превосходит некоторой величины), проанализировать
особенности методики измерения, и по возможности, провести контрольные
опыты. -
3.
Погрешности известной природы, оценка величины которых по каким-либо
причинам затруднена (например, сопротивление контактов при подключении
электронных приборов). Такие погрешности должны быть обязательно исключены
посредством модификации методики измерения или замены приборов. -
4.
Наконец, нельзя забывать о возможности существования ошибок, о
которых мы не подозреваем, но которые могут существенно искажать результаты
измерений. Такие погрешности самые опасные, а исключить их можно только
многократной независимой проверкой измерений, разными методами
и в разных условиях.
В учебном практикуме учёт систематических погрешностей ограничивается,
как правило, паспортными погрешностями приборов и теоретическими поправками
к упрощенной модели исследуемого явления.
Точный учет систематической ошибки возможен только при учете специфики конкретного эксперимента. Особенное внимание надо обратить на зависимость (корреляцию) систематических смещений при повторных измерениях. Одна и та же погрешность в разных случаях может быть интерпретирована и как случайная, и как систематическая.
Пример.
Калибровка электромагнита производится при помощи внесения в него датчика Холла или другого измерителя магнитного потока. При последовательных измерениях с разными токами (и соотственно полями в зазоре) калибровку можно учитыать двумя различными способами:
•
Измерить значение поля для разных токов, построить линейную калибровочную кривую и потом использовать значения, восстановленные по этой кривой для вычисления поля по току, используемому в измерениях.
•
Для каждого измерения проводить допольнительное измерения поля и вообще не испльзовать значения тока.
В первом случае погрешность полученного значения будет меньше, поскльку при проведении прямой, отдельные отклонения усреднятся. При этом погрешность измерения поля будет носить систематический харрактер и при обработке данных ее надо будет учитывать в последний момент. Во втором случае погрешность будет носить статистический (случайный) харрактер и ее надо будет добавить к погрешности каждой измеряемой точки. При этом сама погрешность будет больше. Выбор той или иной методики зависит от конретной ситуации. При большом количестве измерений, второй способ более надежный, поскольку статистическая ошибка при усреднении уменьшается пропорционально корню из количества измерений. Кроме того, такой способ повзоляет избежать методической ошибки, связанной с тем, что зависимость поля от тока не является линейной.
Пример.
Рассмотрим измерение напряжения по стрелочному вольтметру. В показаниях прибора будет присутствовать три типа погрешности:
1.
Статистическая погрешность, связанная с дрожанием стрелки и ошибкой визуального наблюдения, примерно равная половине цены деления.
2.
Систематическая погрешность, связанная с неправильной установкой нуля.
3.
Систематическая погрешность, связанная с неправильным коэффициентом пропорциональности между напряжением и отклонением стрелки. Как правило приборы сконструированы таким образом, чтобы максимальное значение этой погрешности было так же равно половине цены деления (хотя это и не гарантируется).