График ошибки тау - Решение и исправление самых разных ошибок на TopOshibok.ru

Если
функция
дифференцируема и после окончания
переходного процесса существенное
значение имеет только конечное числоi
ее производных, то установившуюся ошибку
можно определить следующим образом.

Положим
для простоты, что возмущающее воздействие
отсутствует
.
В соответствии с выражением (2.126) запишем
изображение ошибки:

.
(2.218)

Разложим
передаточную функцию замкнутой системы
относительно ошибки по задающему
воздействию
в ряд Тэйлора, тогда выражение (2.218)
принимает вид

,
(2.219)

где
,,
…,– коэффициенты ошибок.

Переходя от
изображения ошибки (2.219) к оригиналу,
получим

.
(2.220)

Коэффициенты
ошибок можно определить следующими
способами.

I.
Воспользоваться известными формулами:

;
(2.221)

;
(2.222)

;
(2.223)

……………………..;

.
(2.224)

Рассмотрим
в качестве примера простейшую САУ,
структурная схема которой приведена
на рисунке 2.83.

Рисунок
2.83

Передаточная
функция прямой цепи рассматриваемой
системы

.
(2.225)

Тогда передаточная
функция замкнутой системы относительно
ошибки по задающему воздействию имеет
вид

.
(2.226)

Определим
коэффициенты
,,.
Согласно выражению (2.221), величинабудет

.
(2.227)

Для
расчета коэффициента
возьмем первую производную от передаточной
функции (2.226):

.
(2.228)

В
соответствии с формулой (2.213) коэффициент
будет

.
(2.229)

Для
определения коэффициента
возьмем вторую производную от передаточной
функции (2.226):

.
(2.230)

Тогда
на основании формулы (2.223) коэффициент
будет

.
(2.231)

II.
Если
является дробно-рациональной функцией
вида (2.3), то ее разложение в ряд Тэйлора
с последующим выделением коэффициентов
ошибок можно осуществить простым
делением полинома числителя на полином
знаменателя, располагая члены полиномов
в порядке возрастания степеней.

Разделим полином
числителя (2.226) на полином знаменателя:

(2.232)

Сравнивая (2.232) и
(2.219), получим

,
(2.233)

,
(2.234)

.
(2.235)

Из
формулы (2.235) следует

.
(2.236)

Покажем,
как можно определить
с помощью коэффициентов ошибок на
примере САУ (см. рис. 2.83).

Пусть на вход
системы подается задающее воздействие
вида

.
(2.237)

В
соответствии с формулой (2.220) необходимо
взять первую производную от задающего
воздействия (2.237)

.
(2.238)

Тогда,
согласно формуле (2.220), величина
установившейся ошибки

,
(2.239)

или

.
(2.240)

Учитывая
выражения (2.233) и (2.234), окончательно
получим

.
(2.241)

Полученный
результат подтверждает вывод, сделанный
в пп. 2.9.2: если
степень временной функции задающего
воздействия
m
(в рассмотренном
примере m
= 1) больше
порядка астатизма системы
(),
то с течением времени ошибка неограниченно
возрастает:

.

Так,
на рисунке 2.84 приведены графики изменения
во времени задающего воздействия
(2.237), выходной величины
и ошибки регулированияв системе (см. рис. 2.83).

Рисунок
2.84

Данное
обстоятельство (неограниченный рост
ошибки при
)
необходимо учитывать при проектировании
систем управления соответствующим
выбором порядка астатизма САУ.

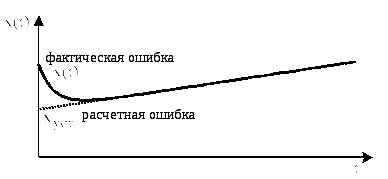
Отметим,
что результат вычисления установившейся
ошибки
с помощью формулы (2.220) справедлив только
после окончания переходного процесса
в системе (рис. 2.85).

Рисунок
2.85

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Время на прочтение
7 мин

Количество просмотров 17K

Продолжаем публикацию лекций по курсу «Управление в Технических Системах» автор — Олег Степанович Козлов на кафедре Э7 МГТУ им. Н.Э. Баумана.

Данные лекции готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется. В предыдущих сериях:

1. Введение в теорию автоматического управления.
2. Математическое описание систем автоматического управления 2.1 — 2.3, 2.3 — 2.8, 2.9 — 2.13.
3. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ РЕГУЛИРОВАНИЯ.
3.1. Амплитудно-фазовая частотная характеристика: годограф, АФЧХ, ЛАХ, ФЧХ. 3.2. Типовые звенья систем автоматического управления регулирования. Классификация типовых звеньев. Простейшие типовые звенья. 3.3. Апериодическое звено 1–го порядка инерционное звено. На примере входной камеры ядерного реактора. 3.4. Апериодическое звено 2-го порядка. 3.5. Колебательное звено. 3.6. Инерционно-дифференцирующее звено. 3.7. Форсирующее звено. 3.8. Инерционно-интегрирующее звено (интегрирующее звено с замедлением). 3.9. Изодромное звено (изодром). 3.10 Минимально-фазовые и не минимально-фазовые звенья. 3.11 Математическая модель кинетики нейтронов в «точечном» реакторе «нулевой» мощности. 4 Структурные преобразования систем автоматического регулирования.

Будет как всегда позновательной увлекательно и жестко

5.1. Главная передаточная функция. Передаточные функции по возмущающему воздействию и для ошибки (рассогласования)

Используя структурные преобразования (см. раздел 4), структурную схему практически любой линейной или линеаризованной САР (САУ) можно привести к виду:

Рисунок 5.1.1 Типовая струкутура САР

Где функции по времени:

— управляющее воздействие;

– регулируемая величина (выходное воздействие);

– возмущающее воздействие;

Или в изображениях:

$\left \{ \begin{align}x(t)&\rightarrow X(s)\\y(t)&\rightarrow Y(s)\\ f(t)& \rightarrow F(s) \\ \epsilon(t)&\rightarrow E(s) \end{align} \right.$

Определение: Если единичная обратная связь охватывает все элементы (звенья) САР – она называется главной.

Определение: Если главная обратная связь отсутствует — САР считается разомкнутой.

Передаточная функция может быть любой сложности (т.е. содержать местные обратные связи, параллельные и последовательные цепи и т.д.).

Возмущающих воздействий может быть несколько и приложены они могут быть в любом месте структурной схемы.

Передаточную функцию которую в Теории Управления называют передаточной функцией разомкнутой САР, будем представлять в следующем виде (для единообразия):

$W(s)=\frac{K\cdot N(s)}{L(s)} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5.1)}$

где – общий коэффициент усиления; – полиномы по степеням переменной , причем свободные члены в них равны 1 (единице).

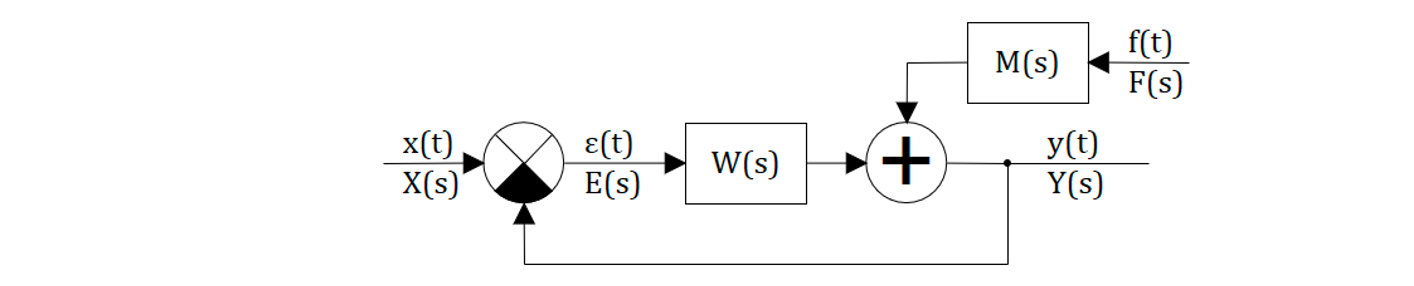
Учитывая, что САР линейна или линеаризована, разделим на структурной схеме каналы прохождения управляющего и возмущающего воздействий. Выделим в отдельное звено (может быть и очень сложное) ту часть системы, через которую проходит возмущающее воздействие $f(t)\Rightarrow$ обозначим ее через $M(s)\Rightarrow$ Структурная схема САР принимает вид:

Рисунок 5.1.2 Структурная схема общего вида с передаточной функцией и внешним воздействием

где: $y_1(t)\rightarrow Y_1(s); \ \ y_2(t)\rightarrow Y_2(s); \ \ y(t)=y_1(t)+y_2(t); \ \ Y(s)=Y_1(s)+Y_2(s).$

В Теории Управления используют 3 основных передаточных функций замкнутой САР:

главная передаточная функция $\Phi(s)$ ;
передаточная функция по возмущающему воздействию $\Phi_f(s)$ ;
передаточная функция для ошибки (рассогласования) $\Phi_\varepsilon(s).$

Рассмотрим более подробно вышеупомянутые передаточные функции.

Главная передаточная функция

Главная передаточная функция -передаточная функция по управляющему воздействию математическое определение этой передаточной функции:

$\Phi(s) =\frac{Y(s)}{X(s)} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5.2)}$

выведем формулу при условии если возмущеющие воздействие равно $f(t)=0, \Rightarrow y(t)=y_1(t)$ . «Обойдем» структурную схемв по контуру:

$Y(s)= E(s)\cdot W(s)=\left[ X(s)-Y(s)\right]\cdot W(s)\Rightarrow\\Y(s)=X(s)\cdot W(s)-Y(s)\cdot W (s) \Rightarrow\\Y(s)+Y(s)\cdot W(s)=X(s)\cdot W(s)\Rightarrow\\ \frac{Y(s)}{X(s)}=\frac{W(s)}{1+W(s)};$ $\Phi(s)=\frac{W(s)}{1+W(s)} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5.3)}$

Примечание. Формула (5.3) совпадает с формулой для передаточной функции цепи с местной единичной обратной связью (см. раздел 4 – «Структурные преобразования»).

Подставляя вместо ее выражение через полиномы и $L(s) \Rightarrow$

$\Phi(s)=\frac{K\cdot N(s)/L(s)}{1+K\cdot N(s)/L(s)}=\frac{K\cdot N(s)}{L(s)+K\cdot N(s)}=\frac{K\cdot N(s)}{D(s)}\ \ \ \ \ \ \mathbf{(5.4)}$

где: $D(s)=L(s)+K\cdot N(s)$

Анализ выражения (5.4) показывает, что свойства главной передаточной функции замкнутой САР однозначно определяются свойствами разомкнутой САР, т.е. через полиномы и .

Передаточная функция замкнутой САР по внешнему возмущающему воздействию

Дадим математическое определение рассматриваемой передаточной функции если управляющие воздействи , а возмущеющие воздействие отличное от нуля $f(x)\neq 0$ . В этом случае (см. рисунок 5.1.2) получается:

$y(t)=y_1(t)+y_2(t)\\ x(t)=0\Rightarrow \varepsilon(t)=0-y(t)=-y(t);$

Перрейдем к изображением и «обойдем» схему (см. рис. 5.1.2) по контуру

$Y(s)=Y_1(s)+Y_2(s) =E(s)\cdot W(s)+F(s)\cdot M(s)=\\=-Y(s)\cdot W(s)+F(s)\cdot M(s) \Rightarrow\\Y(s)\cdot[1+W(s)]=F(s)\cdot M(s)\Rightarrow \frac{Y(s)}{F(s)}=\frac{M(s)}{1+W(s)};$ $\Phi_f=\frac{Y(s)}{F(s)} =\frac{M(s)}{1+W(s)}$

Подставляя вместо ее выражение через полиномы и получаем:

$\Phi_f=\frac{M(s)}{1+K\cdot N(s)/L(s)}=\frac{M(s)\cdot L(s)}{L(s)+K(s)\cdot N(s)}=\frac{R(s)}{D(s)}\ \ \ \ \ \ \ \ \mathbf{(5.6)}$

где: $R(s) =M(s)\cdot L(s)$ — вид данного полинома зависит от места приложения возмущающего воздействия;

Формулы 5.4 и 5.6 имеют общий занаменатель $D(s)=L(s)+K\cdot N(s)$

Передаточная функция замкнутой САР для ошибки (рассогласования)

Дадим математическое определение рассматриваемой передаточной функции если управляющие воздействиt отлично от 0 $x(t) \neq0$ , а возмущеющие воздействие равно 0 . В этом случае для передаточной функции получается (см. рис. 5.1.2):

$\Phi_\varepsilon(s)=\frac{E(s)}{X(s)}$

Сделаем вывод соответствующих формул, выполнив «обход» по контуру схемы (см. рис. 5.1.2) $\Rightarrow$

$E(s)=X(s)-Y(s)=X(s)-E(s)\cdot W(s)\Rightarrow \\ E(s)\cdot(1+W(s))=X(s) \Rightarrow \frac{E(s)}{X(s)}=\frac{1}{1+W(s)}$ $\Phi_\varepsilon(s)=\frac{1}{1+W(s)} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5.7)}$

Учитывая формулу для главной передаточной функции $\Phi(s)=\frac{W(s)}{1+W(s)}$ можно записать выражения для передаточной функции рассоглаосвания:

$\Phi_\varepsilon(s)=1-\Phi(s)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5.8)}$

Подставляя вместо ее выражение через полиномы и получаем:

$\Phi_\varepsilon(s)=\frac{1}{1+K\cdot N(s)/L(s)}=\frac{L(s)}{L(s)+K\cdot N(s)}=\frac{L(s)}{D(s)}\ \ \ \ \ \mathbf{(5.9)}$

где: $D(s)=L(s)+K\cdot N(s)$

Опять замечаем, что знаменатель передаточной функции $\Phi_\varepsilon$ равен полиному следовательно, характерным признаком передаточных функций замкнутой САР является общность знаменателей ! ! !

В Теории Управления выражение $D(s)=L(s)+K\cdot N(s)$ имеет «собственное» название: характеристический полином замкнутой САР.

5.2 Уравнения динамики замкнутой САР

Как указывалось в подразделе 5.1, любую замкнутую САР можно привести к виду представленному на рисунке 5.2.1:

Рисунок 5.2.1 Общая схема замкнутой САР с возмущающим воздействием

Выведены соотношения для 3-х основных передаточных функций замкнутой САР позволяют записать выражения для регулируемой величины в изображениях:

$Y(s)=\underbrace{\Phi(s)\cdot X(s)}_{Y_x(s)}+\underbrace{\Phi_f(s)\cdot F(s)}_{Y_f(s)}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5.2.1)}$

Подставляя значения $\Phi_s(s)$ и $\Phi_f(s)$ через полиномы и разомкнутой САР получаем:

$Y(s)=\frac{K\cdot N(s)}{L(s)+K\cdot N(s)}\cdot X(s)+\frac{R(s)}{L(s)+K\cdot N(s)}\cdot F(s)$

подставим значения для характеристического полинома $D(s)=L(s)+K\cdot N(s)$ получим выражение для динамического уравнения замкнутой САР в изображениях:

$D(s)\cdot Y(s)=K\cdot N(s)\cdot X(s)+R(s)\cdot F(s)\ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5.2.2)}$

Переходя к оригиналам получаем символическую форму записи обыкновенного дифференциального уравнения замкнутой САР:

$D(p)\cdot y(t)=K\cdot N(p) x(t)+R(p)f(t) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5.2.3)}$

Решение диференциального уравнения состоит из двух частей:

$y(t)= y_{соб.}(t)+y_{вын.}(t)$

где: $y_{соб.}(t)$ — собственная часть, решение однородного дифференциального уравнения ;

$y_{вын.}$ — вынужденная часть решения (частное решение), определяемая правой частью уравнения ( 5.2.3 ).

Решения однородного уравнения замкнутой САР:

$D(p)y(t)=0 \Rightarrow a_n\cdot y^{(n)}+a_{n-1}\cdot y^{n-1}+...+a_1\cdot y^1+a_0\cdot y=0$

записываем соответствующее характеристическое уравнение:

$D(\lambda)=0 \Rightarrow a_n\cdot\lambda^n+a_{n-1}\cdot \lambda^{n-1}+...+a_1\cdot \lambda+a_0=0 \Rightarrow$

находим корни степенного уравнения $\lambda_j$ если все корни уравнения разные:

$Y_{соб}(t)=\sum_{j=1}^nC_j\cdot e^{\lambda\cdot j},$

Если есть совпадающие корни характеристического уравнения, то формула для $Y_{соб}(t)$ изменится (см. Математическое описание систем автоматического управления).

Обычно $y_{вын.}$ находят по виду правой части уравнения (5.2.3) или, используя другие методы (например, метод вариаций постоянных).

Необходимо отметить, что порядок дифференциального уравнения (5.2.3) равен «n», т.е. такой же, как и у разомкнутой САР $\Rightarrow$

$L(p)y(t)=K\cdot N(p)x(t)$

если нет возмущающего воздействия, т.к. порядок дифференциального оператора L(p) обычно значительно выше, чем N(p).

По аналогии с выводом уравнения (5.2.3) можно получить уравнение динамики для рассогласования $\varepsilon(t)$ :

$E(s)=\Phi_\varepsilon(s)\cdot X(s)-\Phi_f(s)\cdot F(s) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5.2.4)}$

подставляя значения $\Phi_\varepsilon$ и $\Phi_f$ (см. 5.6 и 5.9) получаем:

$E(s)=\frac{L(s)}{D(s)}\cdot X(s)-\frac{R(s)}{D(s)}\cdot F(s) \Rightarrow$ $D(s)\cdot E(s)=L(s)\cdot X(s)-R(s)\cdot F(s)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5.2.5)}$

Уравнение (5.2.5)- уравнение динамики замкнутой САР в ихображениях для рассогласования (ошибки) при наличии управляющего и возмущающего воздействий.

Особенностью данного уравнения (5.2.5) является то, что левая часть его практически совпадает с левой частью (5.2.2), в то время, как порядок правой части заметно выше , т.к. порядок многочленов D (s) и L (s) — одинаков, а порядок N(s) меньше L(s).

Это означает, что внешние воздействия и влияют на $\varepsilon(t)$ более сильным образом.

Дифференциальное уравнение замкнутой САР для ошибки:

$D(p)\varepsilon(t)=L(p)x(t)-R(p)f(t)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5.2.6)}$

Способы решения уравнения ( 5.2.6 ) такие же, как и для уравнения ( 5.2.3 ) .

5.3. Частотные характеристики замкнутой САР.

Наибольший интерес при анализе замкнутых САР имеет АФЧХ замкнутой САР по управляющему воздействию:

$\Phi(s)_{s=i\cdot\omega}=\Phi(i\cdot\omega)=\frac{W(i\cdot\omega)}{1+W(i\cdot \omega)} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5.3.1)}$

где передаточная функция:

$W(i\cdot\omega)=\frac{K\cdot N(i\cdot\omega)}{L(i\cdot \omega)}$

Учитывая, что $W(i\cdot\omega)=u(\omega)+i\cdot v(\omega)$ — комплексное число, по аналогии имеем:

$\Phi(i\cdot\omega)=P(\omega)+ i\cdot Q(\omega) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5.3.2)}$

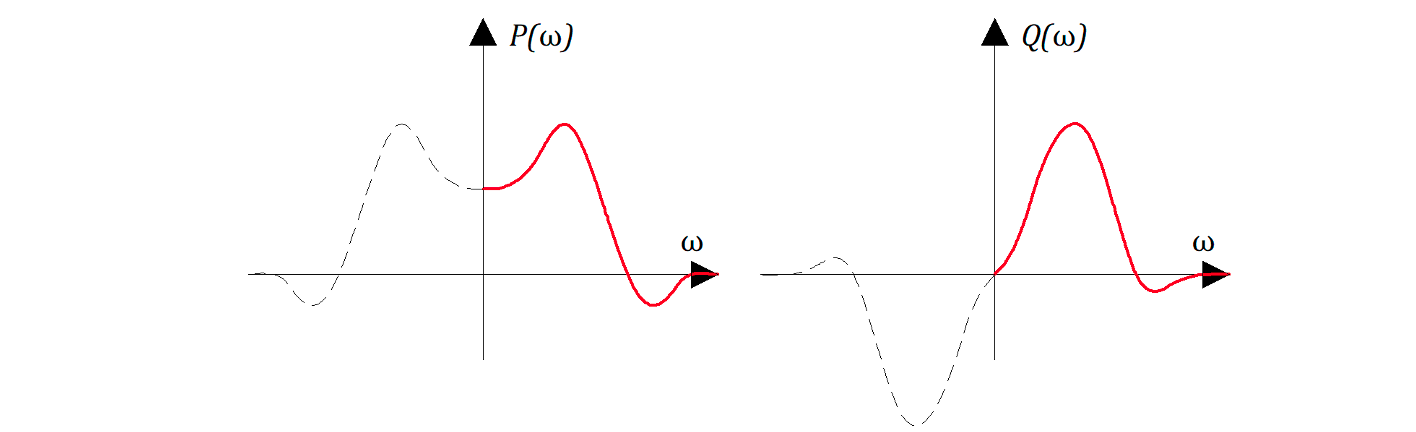
Где $P(\omega)=Re(\Phi_s)$ — вещественная часть функции, $Q(\omega)=Im(\Phi_s)$ — мнимая часть функиции.

Рисунок 5.3.1 Пример зависмостей P и Q

На этих рисунках представлен «примерный» вид зависимостей P (w)и Q(w) для «какой-то» замкнутой САР причем P(w) — четная функция, т.е. P(w) = P(-w); Q(w) — нечетная функция, т.е. Q(w) = — Q(-w).

Если известны частотные свойства разомкнутой САР, то можно определить частотные свойства замкнутой САР. Воспользуемся показательной формой для АФЧХ

$W(i\cdot\omega) = A(\omega)\cdot e^{i\cdot \varphi(\omega)}$

Где $A(\omega)$ — амплитуда (модуль), $\varphi(\omega)$ — сдвиг фазы (фаза). Подставляя это в (5.3.1), имеем получаем:

$\Phi(i\cdot\omega) = A_{з}(\omega)\cdot e^{i\cdot\varphi_з(\omega)}=\frac{A(\omega)\cdot e^{i\cdot \varphi(\omega)}}{1+A(\omega)\cdot e^{i\cdot \varphi(\omega)}}\Rightarrow$ $\Rightarrow 1+A(\omega)\cdot e^{i\cdot\varphi(\omega)}=\frac{A(\omega)\cdot e^{i\cdot \varphi(\omega)}}{A_{з}\cdot e^{i\cdot \varphi_з(\omega)}}\Rightarrow$ $\Rightarrow \frac{e^{-i\cdot \varphi_3(\omega)}}{A_з(\omega)}=1+\frac{e^{-i\cdot \varphi(\omega)}}{A(\omega)}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5.3.3)}$

Учитывая, что $e^{-i\cdot \varphi}=cos(\varphi)-i\cdot sin(\varphi) \Rightarrow$

$\frac{cos[\varphi_з(\omega)]}{A_з(\omega)}-i\cdot\frac{sin[\varphi_З(\omega)]}{A_з(\omega)}=1+\frac{cos[\varphi(\omega)]}{A(\omega)}-i\cdot\frac{sin[\varphi(\omega)]}{A(\omega)}\ \ \ \ \ \ \ \mathbf{(5.3.4)}$

Приравнивая чисто вещественные и чисто мнимые части, имеем $\Rightarrow$

$\left \{ \begin {align}\frac{cos[\varphi_з(\omega)]}{A_з(\omega)}&=1+\frac{cos[\varphi(\omega)]}{A(\omega)} \ \ \ \ \ (1)\\ \frac{sin[\varphi_з(\omega)]}{A_з(\omega)}&=\frac{sin[\varphi(\omega)]}{A(\omega)} \ \ \ \ \ \ \ \ \ \ \ \ (2). \end{align} \right. \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5.3.5)}$

Для нахождения амплитуды $A_з(\omega)$ и сдвига фазы $\varphi_з(\omega)$ замкнутой передаточной функции как функции от амплитуды $A(\omega)$ и сдвига фазы $\varphi (\omega)$ разомкнутой системы. Разделив (2) на (1) получим:

$tg[\varphi_з(\omega)]=\frac{sin[\varphi(\omega)]}{A(\omega)+cos[\varphi(\omega)]} \Rightarrow$

Сдвиг фазы замкнутой системы через характеристики разомкнутой системы:

$\varphi_з(\omega) = arctg \left[ \frac{sin[\varphi(\omega)]}{A(\omega)+cos[\varphi(\omega)]}\right] - \pi\cdot j \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5.3.6)}$

Для получения амплитуды замкнутоей системы возведем оба уравнения системы (5.3.5) в квадрат: $\Rightarrow$

$\left \{ \begin {align}\frac{cos^2[\varphi_з(\omega)]}{A^2_з(\omega)}&=1+\frac{cos^2[\varphi(\omega)]}{A^2(\omega)}+2 \cdot\frac{cos[\varphi(\omega)]}{A(\omega)} ;\\ \frac{sin^2[\varphi_з(\omega)]}{A_з^2(\omega)}&=\frac{sin^2[\varphi(\omega)]}{A^2(\omega)} . \end{align} \right.$

складываем эти два уравнения:

$\frac{1}{A^2_з(\omega)}\left[\underbrace{cos^2\varphi_з(\omega)+sin^2\varphi_з(\omega)}_1\right]=1+\frac{1}{A^2(\omega)}\left[\underbrace{cos^2\varphi(\omega)+sin^2\varphi(\omega)}_1\right]+\dots\\\dots+2\frac{cos[\varphi(\omega]}{A(\omega)}$ $\frac{1}{A^2_з(\omega)}=\frac{A^2(\omega)+2\cdot A\cdot cos[\varphi(\omega)]+1}{A^2(\omega)}\Rightarrow$ $A_з(\omega)=\frac{A(\omega)}{\sqrt{A^2(\omega)+2\cdot A(\omega)\cdot cos[\varphi(\omega)]+1}} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(5.3.7)}$

Аналогичным образом можно выразить, например, P(w) и Q(w) — характеристики замкнутой САР через u(w) и u(w) — характеристики разомкнутой САР.

Пример

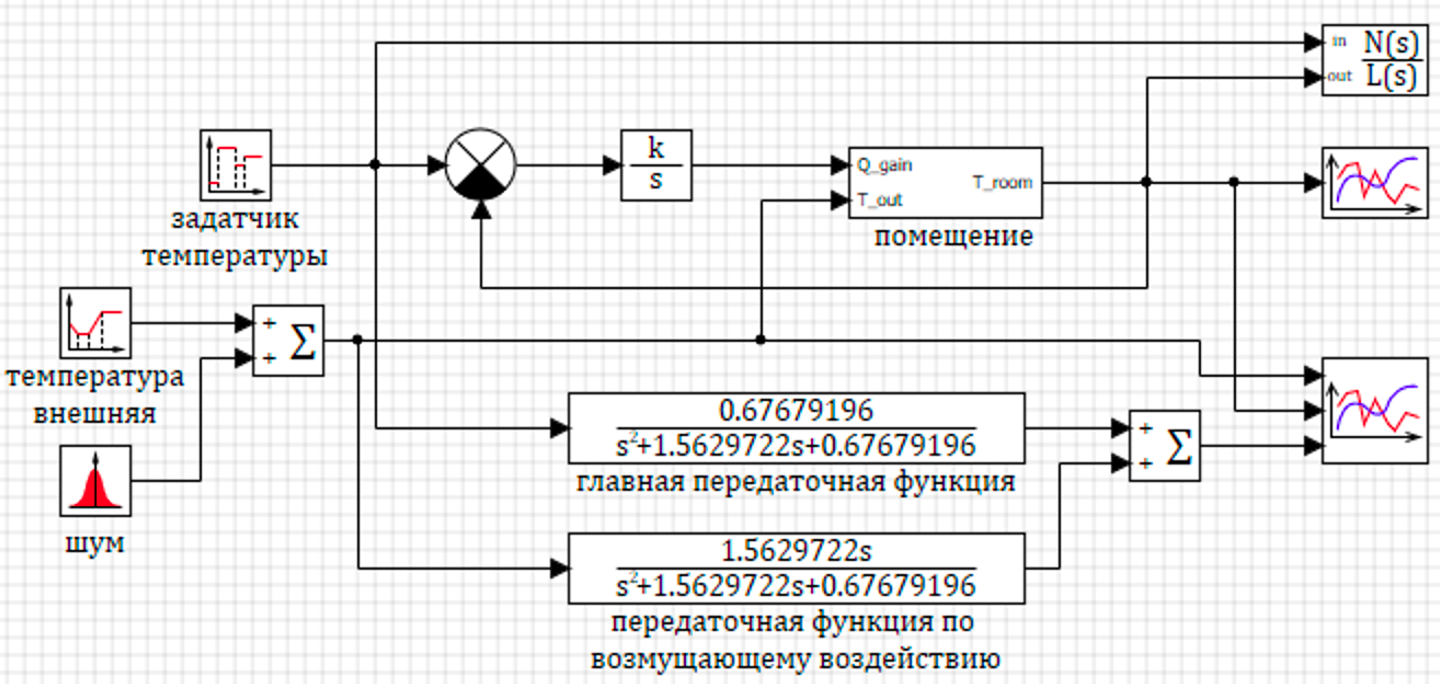
В качестве примера на рисунке 5.4.1 приведена модель помещения, в котором с помощью интегрирующего звена обеспечивается подвод тепла для поддержания температуры. Температура задается в виде ступенчатой функции. В качестве внешнего воздействия используется внешняя температура.

5.4.1 Рисунок сравнение физической модели и передаточных функций

Передаточные функции построены средтвами автоматического анализа. Видно, что знаменатель главной передаточной функции и знаменатель передаточной функции по возмущающиму воздействию одинаковы.

5.4.2 Результаты моделирования.

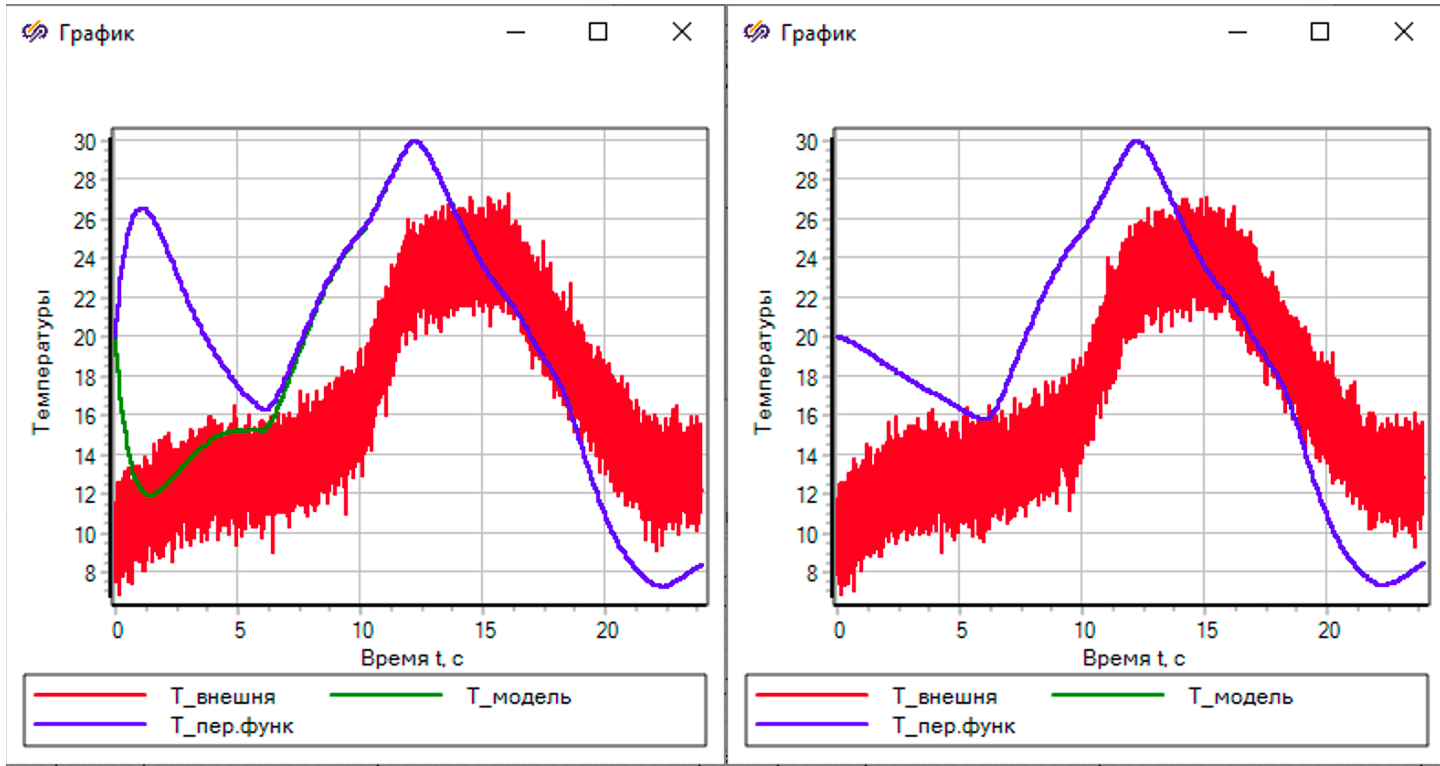
График справа показывает расхождение результаты модели (зеленая линия) и передаточных функций (синит линя) в начале расчета, но потом функции сходятся. Расхождение объясняются разными начальными условиями по производным. Слева тот же самый график, но в это случае начальное состояние определено с помощю загрузки стационарного состояния, полученного предварительным моделированием. В этом случае совпадение модели и передаточных функций полное.

Ссылку на модель примера можено взять здесь…

Источник

1. Тема 8. Анализ показателей качества переходных процессов

1/18
Тема 8.
Анализ показателей качества
переходных процессов
ТАУ. Тема 8: Анализ показателей качества переход
Юркевич В.Д.

2.

2/18
Обсуждаемые вопросы
1.
2.
3.
4.
5.
6.
7.
Показатели качества переходных процессов
Анализ ошибки в установившемся режиме для
статической системы
Анализ ошибки в установившемся режиме
для астатической системы
Скоростная ошибка
Корневой метод анализа показателей
качества переходных процессов
Диаграмма Вышнеградского
Форма начального участка переходной
функции динамического звена
ТАУ. Тема 8: Анализ показателей качества переход
Юркевич В.Д.

3. Показатели качества переходных процессов

3/18
Показатели качества переходных процессов
ТАУ. Тема 8: Анализ показателей качества переход
Юркевич В.Д.

4. Анализ ошибки в установившемся режиме для статической системы

ТАУ. Тема 8: Анализ показателей качества переход
4/18
Юркевич В.Д.

5. Ошибка в установившемся режиме

5/18
Ошибка в установившемся режиме
ТАУ. Тема 8: Анализ показателей качества переход
Юркевич В.Д.

6. Относительная ошибка

6/18
Относительная ошибка
ТАУ. Тема 8: Анализ показателей качества переход
Юркевич В.Д.

7.

7/18
ТАУ. Тема 8: Анализ показателей качества переход
Юркевич В.Д.

8. Анализ ошибки в установившемся режиме для астатической системы с интегратором на входе

ТАУ. Тема 8: Анализ показателей качества переход
8/18
Юркевич В.Д.

9. Скоростная ошибка по задающему воздействию

ТАУ. Тема 8: Анализ показателей качества переход
9/18
Юркевич В.Д.

10. Скоростная ошибка по возмущению

10/18
Скоростная ошибка по возмущению
ТАУ. Тема 8: Анализ показателей качества переход
Юркевич В.Д.

11. Анализ ошибки в установившемся режиме для астатической системы с интегратором на выходе

ТАУ. Тема 8: Анализ показателей качества переход
11/18
Юркевич В.Д.

12. Корневой метод анализа показателей качества переходных процессов

ТАУ. Тема 8: Анализ показателей качества переход
12/18
Юркевич В.Д.

13.

13/18
ТАУ. Тема 8: Анализ показателей качества переход
Юркевич В.Д.

14. Диаграмма Вышнеградского

ТАУ. Тема 8: Анализ показателей качества переход
14/18
Юркевич В.Д.

15. Линии равных значений степени устойчивости

15/18
Линии равных значений степени устойчивости
ТАУ. Тема 8: Анализ показателей качества переход
Юркевич В.Д.

16. Линии равных значений колебательности

ТАУ. Тема 8: Анализ показателей качества переход
16/18
Юркевич В.Д.

17. Свойства динамического звена на высоких частотах

17/18
Вывод: В области низких частот свойства
динамического приближаются к свойствам
пропорционального звена
Вывод: В области высоких частот свойства
динамического звена приближаются к
свойствам (n-m) последовательносоединенных интегрирующих звеньев
ТАУ. Тема 8: Анализ показателей качества переход
Юркевич В.Д.

18. Форма начального участка переходной функции динамического звена

ТАУ. Тема 8: Анализ показателей качества переход
18/18
Юркевич В.Д.

19. Тема 9. Частотные методы анализа показателей качества переходных процессов

19/18
Тема 9.
Частотные методы анализа
показателей качества переходных
процессов
ТАУ. Тема 8: Анализ показателей качества переход
Юркевич В.Д.

Источник

Точность систем автоматического управления

1. Точность САУ

Точность САУ оценивается в установившемся режиме по величине установившейся ошибки при типовых воздействиях. При анализе точности систем рассматривается установившийся режим, так как текущее значение ошибки резко меняется вследствие наличия переходных процессов и не может быть мерой точности.

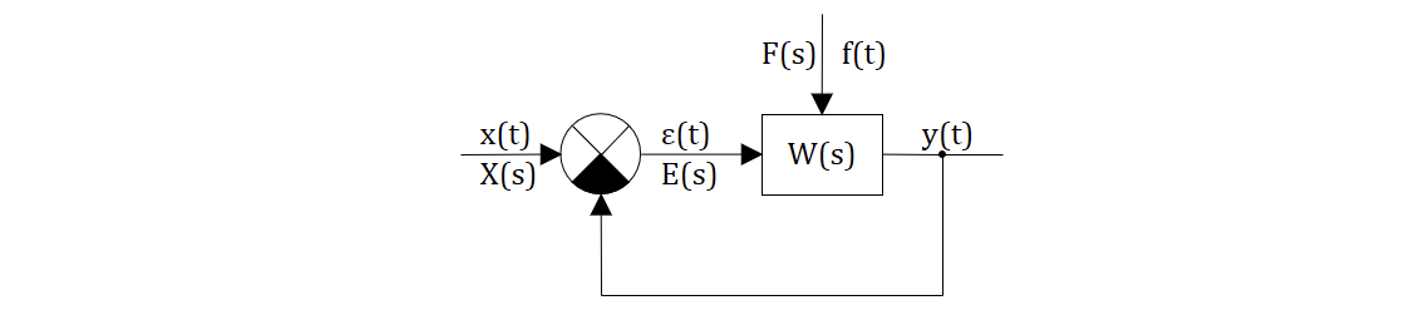
Рассмотрим систему представленную на рис. 1.

На схеме приняты следующие обозначения: K_у(p) – передаточная функция устройства управления; K₀(p) – передаточная функция объекта управления; f – возмущающее воздействие; x – задающее воздействие; y – регулируемая величина.

Ошибка по задающему воздействию равна (t) = x(t) – y(t).

Изображение ошибки равно

(1)

Установившееся значение ошибки определяется с помощью теоремы о конечном значении функции

(2)

Ошибка по возмущению воздействию равна (t) = – y(t), т.е. равна изменению регулируемой величины под действием возмущения при отсутствии входного воздействия.

В общем случае как задающее, так и возмущающее воздействия являются сложными функциями времени. При определении ошибок пользуются типовыми воздействиями, которые с одной стороны соответствуют наиболее тяжелым режимам работы системы и, вместе с тем, достаточно просты для аналитических исследований.

Кроме того, типовые воздействия удобны для сравнительного анализа различных систем, и соответствуют наиболее часто применяемым законам изменения управляющих и возмущающих воздействий.

2. Типы ошибок

Различают следующие типы ошибок:

– статическая ошибка (ошибка по положению) – ошибка, возникающая в системе при отработке единичного воздействия;

– кинетическая ошибка (ошибка по скорости) – ошибка, возникающая в системе при отработке линейно – возрастающего воздействия;

– инерционная ошибка (ошибка по ускорению) – ошибка, возникающая в системе при отработке квадратичного воздействия.

С точки зрения ошибок, системы можно классифицировать на статические и астатические.

Передаточная функция статической системы имеет вид

(3)

Передаточная функция астатической системы имеет вид

(4)

где K*(p) – передаточная функция, не содержащая интегрирующих звеньев а s – порядок астатизма.

Рассмотрим статическую систему (s = 0). Определим выражения для соответствующих ошибок.

1. Статическая ошибка определяется следующим соотношением

(5)

2. Кинетическая ошибка определяется следующим соотношением

(6)

3. Инерционная ошибка определяется следующим соотношением

(7)

Эта система не может быть использована как синхронно – следящая, так как кинетическая ошибка стремится к бесконечности.

Пример 1. Для заданной системы (рис. 2) определить установившиеся ошибки

x y

—

Рис. 2

Решение: Определим установившиеся ошибки.

1. Статическая ошибка определяется следующим соотношением

Кинетическая ошибка определяется следующим соотношением

Инерционная ошибка определяется следующим соотношением

На графиках это можно изобразить следующим образом (рис. 3)

Рассмотрим астатическую систему первого порядка (s = 1).

Определим выражения для установившихся ошибок.

Статическая ошибка определяется следующим соотношением

(8)

Кинетическая ошибка определяется следующим соотношением

(9)

Инерционная ошибка определяется следующим соотношением

(10)

Эта система может быть использована как синхронно – следящая, так как кинетическая ошибка равна нулю.

Пример 2. Для заданной системы (рис. 4) определить ошибки

Решение: Определим выражения для ошибок.

Статическая ошибка определяется следующим соотношением

2. Кинетическая ошибка определяется следующим соотношением

Т.е. ошибка является функцией скорости изменения входного воздействия и коэффициента усиления системы.

3. Инерционная ошибка определяется следующим соотношением

Графики изменения ошибок приведены на рис. 5.

а) b) c)

Рис. 5

ассмотрим астатическую систему второго порядка (s = 2).

Определим выражения для ошибок.

1. Статическая ошибка определяется следующим соотношением

(11)

Кинетическая ошибка определяется следующим соотношением

(12)

Инерционная ошибка определяется следующим соотношением

(13)

Инерционная ошибка является функцией ускорения изменения входного воздействия и коэффициента усиления системы.

Эта система может быть использована как синхронно – следящая, так как кинетическая ошибка равна нулю.

Пример 3. Для заданной системы (рис. 6) определить установившиеся ошибки

x y

—

Рис. 6

Решение: Определим выражения для ошибок.

1. Статическая ошибка определяется следующим соотношением

Кинетическая ошибка определяется следующим соотношением

3. Инерционная ошибка определяется следующим соотношением

На графиках это можно изобразить следующим образом (рис. 7)

b) c)

Рис. 7

Для повышения точности САУ необходимо увеличивать коэффициент усиления системы и порядок астатизма, но это может привести к неустойчивости, т.е. требования по точности и устойчивости противоречивы.

Определение ошибок по виду частотных характеристик САУ

О характере ошибок можно судить по низкочастотной ветви любой частотной характеристики (АФХ, ЛАЧХ, ФЧХ), так как низкочастотная ветвь характеризует статику системы. Частотные характеристики систем с различным порядком астатизма приведены в таблице 1.

Таблица 1

	АФХ	ЛАЧХ	ФЧХ
s = 0; _c= x₀/(1+k); _к= ; _и= .	+j -1 +
s = 1; _c= 0; _к= v/k_v; _и= .	+j -1 +
s = 1; _c= 0; _к= 0; _и= /k.	+j -1 +

3. Ошибки по возмущению

Установившаяся ошибка по возмущению равна

(14)

Рассмотрим примеры

Пример 4. Для заданной системы (рис. 9) со статическим регулятором определить ошибку по возмущению.

Решение: Пусть f(p) = f₀ /p, при этом ошибка равна

При статическом регуляторе установившаяся ошибка по возмущению зависит от амплитуды воздействия и коэффициента усиления регулятора т.е. _f= f(f₀, k₁).

Пример 5. Для заданной системы (рис. 10) с астатическим регулятором, определить ошибку по возмущению.

Решение: Пусть f(p) = f₀ /p, при этом ошибка равна

При астатическом регуляторе ошибка по возмущению равна нулю.

Литература

Вероятностные методы в вычислительной технике. Под ред. А.Н. Лебедева и Е.А. Чернявского – М.: Высш. Шк., 1986. -312 с.
Зайцев Г.Ф. Теория автоматического управления и регулирования. – 2-е изд., перераб. и доп. Киев, Издательство Выща школа Головное издательство, 198
Справочник по теории автоматического управления. /Под ред. А.А. Красовского – М.: Наука, 1987. – 712 с.
Теория автоматического управления: Учебник для вузов. Ч1 / Под ред. А.А. Воронова – М.: Высш. Шк., 1986. – 367 с.
Теория автоматического управления: Учебник для вузов. Ч2 / Под ред. А.А. Воронова – М.: Высш. Шк., 1986. -504 с.
Шандров Б.В. Технические средства автоматизации: учебник для студентов высших учебных заведений. Москва, Издательский центр «Академия», 2007.

Источник