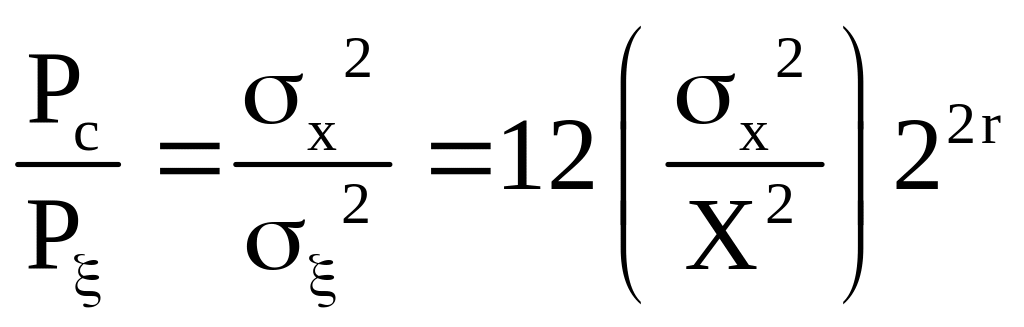Когда я был в Питере, и мы сидели в кабаке, у нас с товарищами 



Поскольку дельта икс у нас совершенно чёткая, или скорее равная отрезкам оцифровки, то производная значения снятого с АЦП будет нынешнее значение минус предыдущее, делённое на период квантования: df/dt=(f(t1) -f(t2))/(t1 -t2). Для опытов я выбрал функцию гармонического синуса sin(x). В дальнейшем проверил и на остальных функциях, но это самая красивая и в нашем случае самая актуальная.
Изначальный график для экспериментов
Для начала я составил таблицу, над которой начал издеваться. Первая строчка [ t= ] — это время от старта работы условного АЦП, который наращивается с шагом квантования (последняя строчка). Вторая — [ SIN(t) ]синус вычесленный от этого кванта времени, формула которого примитивна: =SIN(B1). Третья — [ dSIN(t)/dt ] это численное нахождение производной. Формула её проста: =(C2-B2)/C5 (первая ячейка). Предпоследняя строчка это [ COS(t) ], это нахождения косинуса от перменной t. Она нужна для того, чтобы сравнивать с истинным значением косинуса вычисленную производную (если помните, производная синуса — это косинус). Последняя строка — это квантование, т.е. проще говоря шаг изменения t. Внизу строиться график, который строит гибкую линию по точкам. Сейчас у нас выбран самый оптимальный шаг квантования 0,5 . Здесь всё ясно, дальше я двух разделах покажу сначала ошибки квантования, и следственные ошибки производных, затем ошибки дифференцирования при ошибочных входных данных. Если ваш мозг не вспух и вы готовы дальше пуститься в дебри математики и электроники,
Ошибки квантования
Как видно из самой первой картинки, производная практически полностью соответствует графику косинуса. Если мы ещё уменьшим «частоту дискретизации», или в нашем случае шаг до dt=0,1, то получим вообще практически совпадающие кривые, которые я проиллюстрирую ниже:
Полученный график с шагом 0,1
Как видно, при этом шаге квантования график производной (фиолетовая кривая), практически полностью совпадает с графиком косинуса (красная кривая). Маркерами показанны точки квантования. В этом случае всё ясно, но давайте увеличим шаг, от 0,5 до 1
Полученный график с шагом 1
Видно, что производная, да и все графики начинают «плыть».
Продолжим увеличение квантования до 2:
Полученный график с шагом 2
Всё начинает плыть и уходить, но ещё отдалённо напоминает синус. Однако уже видно, что численно рассчитанная производная СОВЕРШЕННО не соответствует своему значению. Да и вообще находится в противофазе. Напоследок возьмём квантование равное 5 (в 10 раз больше исходного).
Полученный график с шагом 10
Видно что в этом случае мы наблюдаем полную ересь. И в данном случае можно сказать, что высокие частоты и шумы, могут хорошо подпортить реальное значение производной. Теперь же посмотрим как влияет погрешность снятого сигнала, на численный рассчёт производной.
Численное вычисление производной, при неточности снятого сигнала (шумах, наводках, высших гармониках)
Добавим теперь в формулу вычисления синуса некоторую погрешность снятия сигнала, для этого прибавим к формуле вычисления синуса некоторое случайное число: =SIN(C1)+СЛЧИС()*0,1 . Данная формула внесёт 10% погрешность от амплитудного значения в вычисление сигнала, просто добавляя некоторое случайное число от нуля до 0,1. Я покажу несколько вариантов с разной погрешностью. Сначала покажем сигнал с 5% погрешностью:
Полученный график с погрешностью 5%
Как видно из графика, ни на синус, ни на производную такая погрешность не оказывает должного влияния. Возьмём тогда погрешность в 10%
Полученный график с погрешностью 10%
Вот, ярко видно, что на графике синуса погрешность сказалось мало. А вот на графике производной очень даже, в особенности хорошо раскорячило её концы. На последок покажу что будет если построить график производной с 20% погрешностью:
Полученный график с погрешностью 20%
График отдалённо напоминает косинус. Видно куча убеганий и прочего. Надо учитывать, что это ПСЕВДОслучайная велечина, в реальной жизни всё может быть гораздо хуже. Но всё же лучше смоделировать данные фишки, чтобы представлять себе что же может твориться на АЦП.
Вывод: Считать численно производную по снятым значениям с АЦП можно и нужно. Но необходимо оценивать уровень внешних помех, которые могут влиять на сигнал, и очень сильно его портить. Желательно использовать фильтрацию сигнала, выделяя полезный сигнал. Филтрация может быть как аналоговая, так цифровая. Мне даже показали прекрасную формульную замену аналоговой фильтрацией прекрасной програмкой на си. И разумеется мы должны себе ЧЁТКО представлять какой сигнал цифруем, и не цифровать сигнал на пределах возможностей АЦП. 5 точек на период, как показала практика — не самый плохой вариант!
Операция
квантования
сводится к тому, что всем отсчетам
входного сигнала x,
попавшим в некоторый интервал,
приписывается одно и то же значение
,
выражаемое двоичной кодовой комбинацией.
Если
кодовая комбинация содержит r
разрядов, то число дискретных уровней
выходного сигнала квантователя равно
.
Для
взаимно однозначного соответствия весь
диапазон изменения входного сигнала
X
= x
max
– x
min
должен быть разбит на такое же количество
уровней.
Величина
интервала разбиения – шаг
квантования
– представляет собой значение аналоговой
величины, на которую отличаются уровни
входного сигнала, представленные двумя
соседними кодовыми комбинациями.
При
наиболее распространенном равномерном
квантовании шаг квантования равен
(1.12)
Характеристикой
квантования
называется зависимость квантованного
значения
от значения непрерывной величины x.
Типичная
характеристика
квантователя
с постоянном шагом квантования
приведена на рисунке 1.16.

Рисунок 1.16 –
Характеристика квантования при постоянном
шаге квантования
На
рисунке 1.17 приведена временная диаграмма
работы квантователя, где точками отмечены
квантованные значения, и временная
диаграмма ошибки квантования
.
Временная последовательность ошибок
квантования случайного сигнала
представляет собой случайный процесс
с равномерным законом распределения.
Этот случайный процесс называют шумом
квантования.

Рисунок
1.17 – Временные зависимости сигналов
на входе (x)
и выходе (
)
квантователя
и
ошибки квантования
Из
рисувнка видно, что абсолютное значение
ошибки квантования не превышает Δ/2.
Закон
распределения этого случайного процесса
приведен на рисунке 1.18.

Рисунок 1.18 –
Плотность вероятности шума квантования
Определим дисперсию шума квантования

После подстановки
(2.1) в последнее соотношение получим
(1.13)
Из
(1.13) следует, что дисперсия шума квантования
зависит от характеристик квантователя
и не зависит от уровня сигнала.
Определим отношение сигнал/шум на выходе квантователя
,
где
Pc—
мощность сигнала,
–
мощность шума,
—
среднеквадратическое значение сигнала.
Это отношение в
децибелах равно
(1.14)
Из последнего соотношения
видно, что
-
каждое
добавление одного разряда в кодовом
слове увеличивает отношение сигнал/шум
на 6 дБ. -
с
уменьшением уровня входного сигнала
отношение сигнал/шум уменьшается.
1.6.
Квантователи с переменным шагом
квантования
(нелинейные
квантователи)
Недостаток
линейного квантователя, связанный с
уменьшением отношения сигнал/шум
квантования при уменьшении уровня
сигнала, можно устранить, если уменьшать
шаг квантования по мере уменьшения
уровня сигнала.
Характеристика
квантования с переменным шагом квантования
приведена на рисунке 1.19.
Такую
характеристику можно получить, если
последовательно включить нелинейный
преобразователь и линейный квантователь
(рисунок 1.19)
Чтобы
устранить нелинейные искажения,
обусловленные введением нелинейного
преобразователя, после квантователя
используют второй нелинейный
преобразователь квантованного сигнала
с характеристикой, обратной характеристике
первого. С помощью первого осуществляют
компрессию сигнала, а с помощью второго
– его экспандирование. В целом описанная
операция называется компандированием.
Результирующая сквозная характеристика
системы «компрессор-экспандер» остается
линейной.
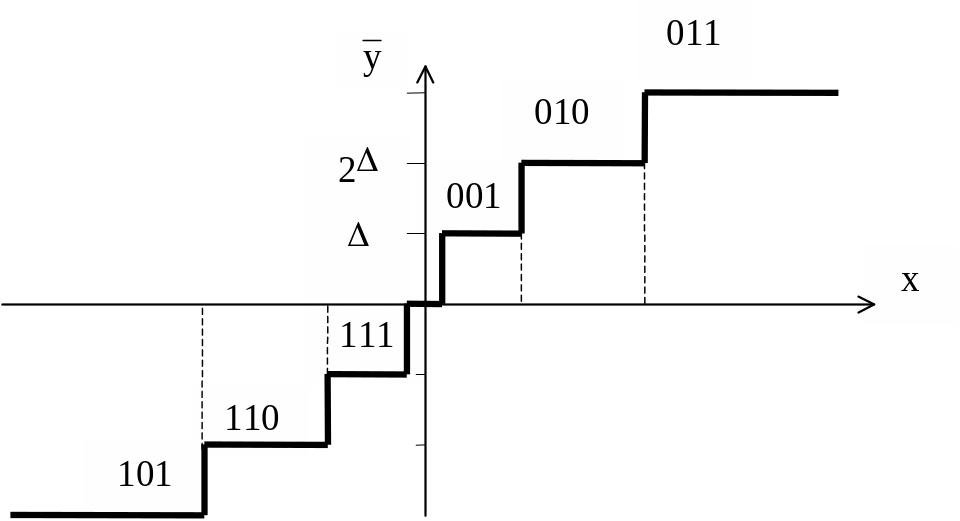
Рисунок
1.19 – Характеристика квантования при
переменном шаге квантования
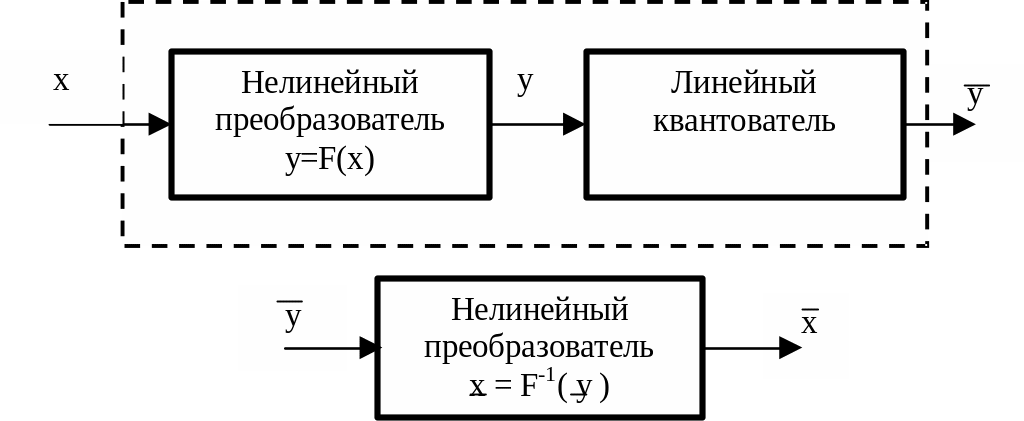
Рисунок
1.20 –Система «компрессор-экспандер»
В настоящее время
используются два закона компандирования:
μ-закон
(1.15) и А – закон (1.16):
(1.15)
где
=255,
,
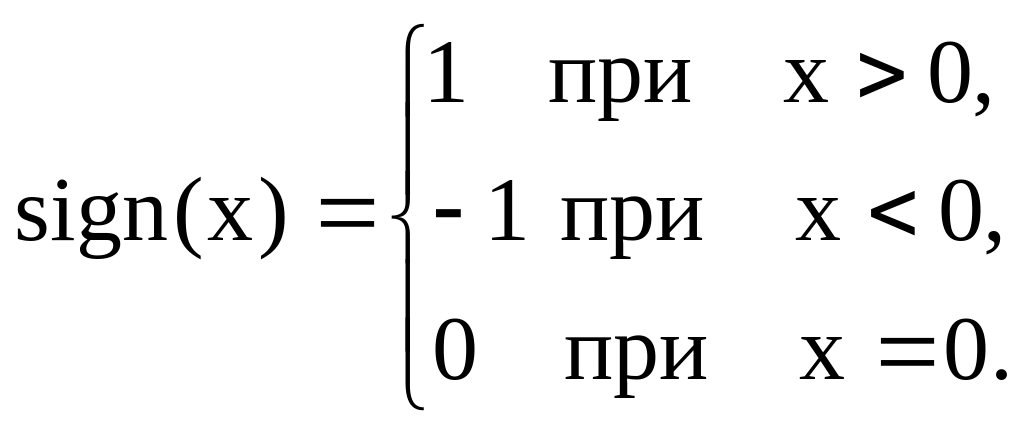
(1.16)
где
A
= 87.6.
Заключение
При дискретизации
аналогового сигнала возникают два
эффекта, касающиеся спектра сигнала:
-
Эффект
размножения спектра аналогового
сигнала, -
Эффект
наложения сгустков спектра дискретного
сигнала друг на друга.
Эффект
наложения спектров приводит к искажению
дискретного сигнала и невозможности
точного восстановления аналогового
сигнала из дискретного.
Спектр дискретного
сигнала представляет собой периодическую
функцию частоты, период которой равен
частоте дискретизации.
Если дискретизации
подвергается периодический аналоговый
сигнал с линейчатым спектром, то
размножение спектра осуществляется по
закону:
при
где
F
– частота спектральной составляющей
аналогового сигнала.
Амплитуды
спектральных составляющих дискретного
сигнала пропорциональны соответствующим
составляющим спектра аналогового
сигнала.
Размножение
спектра апериодического аналогового
сигнала осуществляется по этому же
закону, если рассматривать в качестве
F
характерные частоты непрерывного
спектра аналогового сигнала.
Эффект
наложения спектров при дискретизации
отсутствует, если выполняется условие
,
где
Fmax
– максимальная частота спектра
аналогового сигнала.
Если
дискретизации подвергается узкополосный
модулированный сигнал, а результатом
последующей цифровой обработки должно
быть выделение модулирующего сигнала,
то частота дискретизации может быть
выбрана существенно меньше, чем 2Fmax.
В этом случае
необходимо выполнить условия:
,
где
—
ширина спектра аналогового сигнала,
,
где
,
а f0
– частота несущей аналогового сигнала.
При
выполнении последнего условия частота
несущей, приведенная в интервал частот
от нуля до половины частоты дискретизации
(интервал Котельникова), равна четверти
частоты дискретизации.
Необходимость
квантования дискретного сигнала связана
с тем, что в вычислительных устройствах
значение сигнала должно быть представлено
числом конечной разрядности.
Операция
квантования
сводится к тому, что всем отсчетам
входного сигнала x,
попавшим в некоторый интервал,
приписывается одно и то же значение
,
выражаемое двоичной кодовой комбинацией.
Разность
между квантованным значением и значением
отсчета дискретного сигнала называется
ошибкой квантования. Временная
последовательность ошибок квантования
случайного сигнала представляет собой
случайный процесс с равномерным законом
распределения. Этот случайный процесс
называют шумом
квантования.
В
квантователе с постоянным шагом
квантования (линейном квантователе)
отношение сигнал/шум квантования зависит
от количества разрядов квантователя,
уровня сигнала и диапазона квантователя.
Каждое
добавление одного разряда в кодовом
слове увеличивает отношение сигнал/шум
на 6 дБ.
С
уменьшением уровня входного сигнала
отношение сигнал/шум уменьшается.
Последнее
обстоятельство является недостатком
линейного квантователя, который
устраняется в квантователе с переменным
шагом квантования (нелинейном квантователе)
за счет уменьшения шага квантования по
мере уменьшения абсолютного значения
уровня входного сигнала квантователя.
Контрольные
вопросы и задачи по теме №1:
1.
Что такое дискретизация аналогового
сигнала? Начертите временные диаграммы
синусоидального сигнала на входе и
выходе дискретизатора в случае, когда
частота синусоидального колебания
меньше половины частоты дискретизации.
2. Начертите
спектральные диаграммы синусоидального
сигнала на входе и выходе дискретизатора
в случае, когда частота синусоидального
колебания меньше половины частоты
дискретизации.
3.В
чем сущность эффекта наложения спектров?
Каким образом можно уменьшить ошибку
наложения?
4.Начертите
амплитудный спектр дискретной синусоиды,
если частота аналогового синусоидального
колебания на входе дискретизатора выше
частоты дискретизации.
5.
Из каких условий выбирается частота
дискретизации модулированного колебания,
если результатом последующей цифровой
обработки должно быть выделение
модулирующего колебания?
6.
Дискретизация синусоидального колебания
,
где f0=20МГц,
осуществляется с частотой FД
= 16 МГц. Чему равна частота дискретной
синусоиды?
7.
На входе аналогового ФНЧ действует
последовательность прямоугольных
импульсов. АЧХ фильтра показана на
рисунке 1.21. Выходной сигнал фильтра
подается на дискретизатор. Частота
дискретизации равна 20 кГц. Возникнет
ли эффект наложения спектров при
дискретизации?

8.
На входе дискретизатора действует
сигнал
,
где
F1=1
МГц, F2
= 2 МГц.
Частота дискретизации FД
= 8 МГц. Чему равен максимальный частотный
разнос между соседними составляющими
спектра дискретного сигнала?
9.
На входе дискретизатора действует
сигнал
,
где F=1
МГц, f0
= 15 МГц.
Частота дискретизации FД
= 12 МГц. Чему равен минимальный частотный
разнос между соседними составляющими
спектра дискретного сигнала?
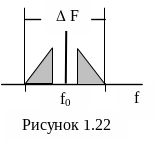
10.На
рисунке 1.22 приведен спектр аналогового
сигнала. Начертите в относительном
масштабе спектр сигнала после дискретизации
в пределах интервала Котельникова (от
0 до половины частоты дискретизации),
если f0=28МГц,
fmin=25МГц,
fmax=31МГц,
а частота дискретизации равна FД=
16 МГц.
11.
На входе демодулятора действует
модулированный аналоговый сигнал,
спектр которого симметричен относительно
частоты несущей f0
= 445кГц (рисунок 1.22). Ширина спектра
.
При каком из двух значений частоты
дискретизации отсутствует эффект
наложения спектров: FД=20кГц,
FД=21кГц?
12. Поясните
сущность операции квантования дискретных
сигналов. Что такое шаг квантования?
Как зависит шаг квантования при
равномерном (линейном) квантовании от
количества разрядов и диапазона
квантователя?
13.
Дайте определение характеристике
квантования. Начертите характеристику
линейного квантователя.
14. Поясните механизм
возникновения шума квантования. Начертите
график вероятностного распределения
шума квантования. Как связана дисперсия
шума квантования с шагом квантования
и количеством разрядов квантователя
при равномерном квантовании?
15.
Как зависит отношение сигнал/шум на
выходе равномерного квантователя от
количества разрядов, диапазона
квантователя и среднеквадратичного
уровня входного сигнала?
16.
Начертите характеристику квантования
квантователя с неравномерным шагом
квантования (нелинейного квантователя).
17.Поясните сущность
алгоритма функционирования нелинейного
квантователя, состоящего из входного
нелинейного преобразователя и линейного
квантователя. Каким образом устраняются
нелинейные искажения выходного сигнала
при использовании нелинейного
квантователя?
18.Чем
отличается зависимость отношения
сигнал/шум на выходе нелинейного
квантователя от среднеквадратичного
уровня входного сигнала от аналогичной
зависимости для линейного квантователя?
19.
Отношение сигнал/шум на выходе линейного
квантователя равно 40 дБ. Каким станет
это отношение, если количество разрядов
увеличить на два при неизменном уровне
входного сигнала и неизменном диапазоне
квантователя?
Контрольная
карта ответов
Номер
ответа соответствует номеру контрольного
вопроса в предыдущем разделе.
6.
F
= f0
–FД
= 20-16 = 4 МГц
7.
FД
= 20 кГц, Fmax
= 8 кГц. Так как FД>
2 Fmax,
то эффект наложения не возникнет.
8.
Максимальный частотный разнос между
соседними составляющими спектра
дискретного сигнала равен 4 МГц
9.
Минимальный частотный разнос между
соседними составляющими спектра
дискретного сигнала равен 2 МГц.
10.

11.
Эффект наложения отсутствует при частоте
дискретизации FД
=20 кГц.
19.
Отношение сигнал/шум станет равным 52
дБ.
Список
литературы по теме № 1:
1.
В.Г.Иванова, А.И.Тяжев. Цифровая обработка
сигналов и сигнальные процессоры / Под
редакцией д.т.н., профессора Тяжева А.И.
— Самара, 2008г.
2.Куприянов
М.С., Матюшкин Б.Д. Цифровая обработка
сигналов: процессоры, алгоритмы, средства
проектирования. –2-е изд., перераб. и
доп.- СПб.: Политехника, 1999. –592с.
:
ил.
3.Л.Р.Рабинер,
Р.В.Шафер. Цифровая обработка речевых
сигналов. – М.: Радио и связь, 1981. – 495с.:
ил.
4.
А.И. Солонина, Д.А.
Улахович, С.М. Арбузов, Е.Б. Соловьёва.
Основы цифровой обработки сигналов.-
Изд. 2-е испр. и перераб. – СПб.: БХВ-Петербург,
2005.-768с.: ил.
5.А.Б.
Сергиенко. Цифровая обработка сигналов.
– СПб.: Питер, 2002.-2002.-608с.: ил.
24
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
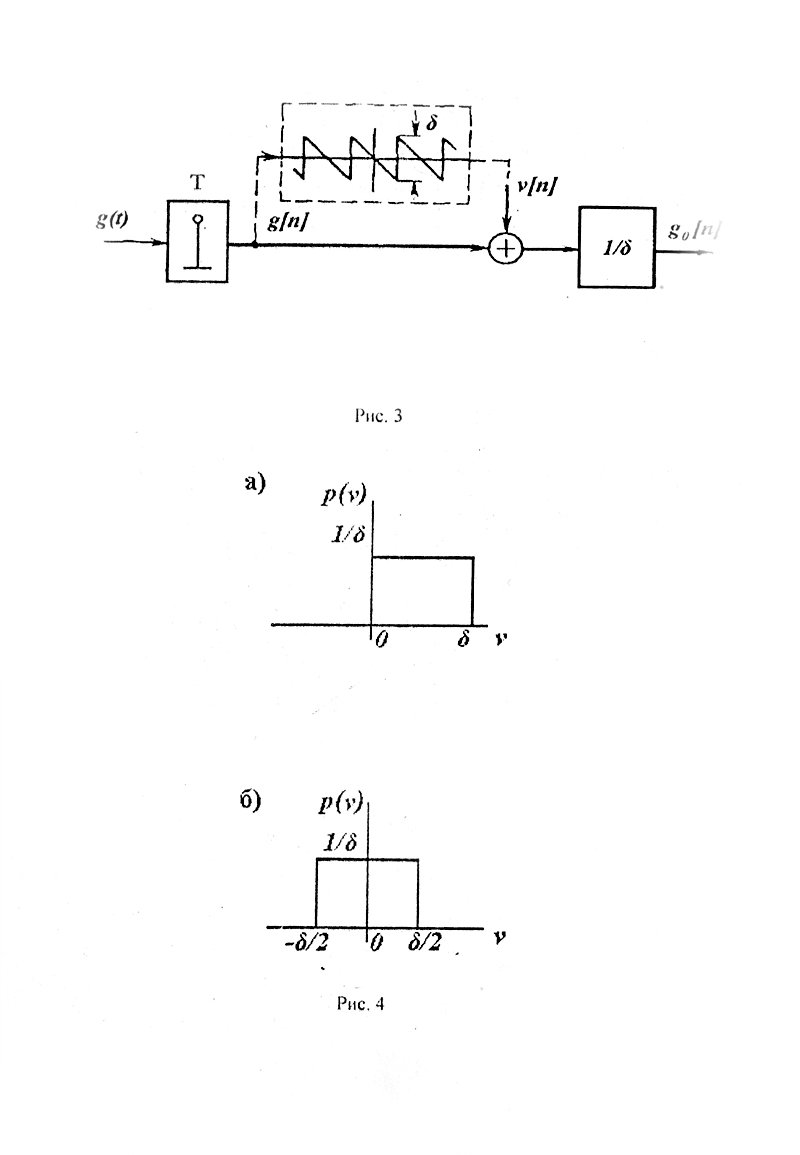
Максимальное значение шума квантования при
округлении составляет . Дисперсия этого шума, если
допустить, что уровень его плотности вероятности в
интервале от до
постоянен,
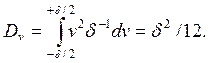
(2)
Корреляционная функция шума квантования затухает тем быстрее, чем меньше величина
по сравнению со среднеквадратичным
приращением (изменением) входного сигнала за время, равное периоду дискретности
. Можно показать, что при выполнении
условия
(3)
где — среднеквадратичное
значение производной входного процесса, корреляционная функция отлична от нуля практически только при
, так как уже при
ее
значение пренебрежимо мало и составляет . Тогда
для корреляционной функции шума квантования справедливо выражение
(4)
где — единичная импульсная
решетчатая функция.
Решетчатый случайный процесс с полученной
корреляционной функцией называют дискретным белым шумом. Его спектральная плотность
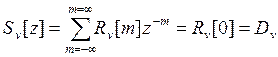
(5)
Аналогичные результаты можно получить и
для случая усечения.
Таким образом, при выполнении условия (3) шум
квантования по уровню во входном АЦП можно считать дискретным белым шумом с
равномерной спектральной плотностью.
На рис.4, а и рис.4, б представлены
графики функций распределения ошибки (шума) квантования для случаев усечения и
округления соответственно. Очевидно, что при одинаковой дисперсии
математические ожидания различны и составляет соответственно и
.
2.
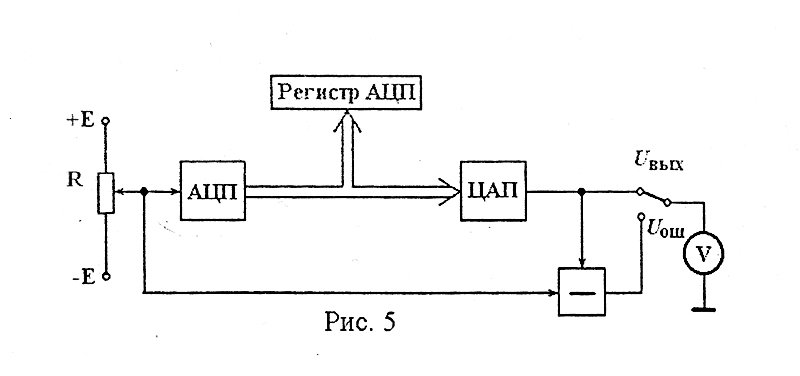
ОПИСАНИЕ ЛАБОРАТОРНОГО МАКЕТА
Схема лабораторного макета представлена на
рис.5.
В качестве объекта для исследования в
данной лабораторной работе предлагается аналого-цифровой преобразователь,
выполненный на интегральной микросхеме 1108ПВ1.
Входной сигнал представляет собой
постоянное напряжение, величина и полярность которого зависит от положения
движка потенциометра (величина этого напряжения
контролируется с помощью потенциометра ).
Выходной сигнал (код) АЦП представляется на светодиодном индикаторе в верхней
части макета, а также поступает на цифро-аналоговый преобразователь (ЦАП).
Выходной сигнал ЦАП может либо поступать
прямо на вольтметр , либо сравниваться на вычитающем
устройстве с входным сигналом АЦП. В последнем случае сигнал на выходе
вычитающего устройства представляет собой ошибку преобразования.
Указанная ошибка включает в себя как
ошибку преобразования «непрерывная величина – код», так и ошибку преобразования
«код – непрерывная величина». Поэтому для исследования ошибки собственно АЦП
рекомендуется искусственно ограничить его точность, принимая во внимание
несколько (четыре-пять) старших разрядов. Поскольку для цифро-аналогового
преобразования при этом используются все разряды, ошибка ЦАП будет значительно
меньше и не окажет существенного влияния на результаты исследований.
- ПОРЯДОК
ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ
- Ознакомиться с
особенностями работы АЦП как элемента ЦАС. - Снять зависимость выходного сигнала (кода) АЦП и
выходного сигнала ЦАП от величины входного напряжения. При этом следует
ограничить число принимаемых во внимание разрядов преобразователя до
четырех. - Снять зависимость напряжения ошибки квантования
от величины входного сигнала.
4.
СОДЕРЖАНИЕ ОТЧЕТА
- Структурная
схема ЦАС. - Схема лабораторной
установки - Результаты измерений и
график характеристики квантования АЦП. - Определенные по результатам
измерений значения цены единицы младшего разряда преобразователя и
коэффициента передачи линеаризованного АЦП. - График зависимости ошибки
квантования от входного напряжения. - Выводы по проделанной
работе.
Библиографический список
1.
Коновалов Г.ф. Радиоавтоматика. –
М. Высшая школа, 1990.
2.
Радиоавтоматика./ Под ре. В.А.
Бесекерского. – М. Высшая школа, 1985.
3.
Микропроцессорные системы
автоматического управления. / Под ре. В.А. Бесекерского – Л.: Машиностроение,
1988
4.
Бесекерский В.А., Изранцев В.В.
Системы автоматического управления с микро-ЭВМ. М.: Наука, 1987.
Ошибки квантования
В реальных
устройствах цифровой обработки сигналов
необходимо учитывать
эффекты, обусловленные квантованием
входных сигналов
и конечной разрядностью всех регистров.
Источниками ошибок
в процессах обработки сигналов являются
округление (усечение)
результатов арифметических операций,
шум аналого-цифрового квантования
входных аналоговых сигналов, неточность
реализации характеристик цифровых
фильтров из-за округления их коэффициентов
(параметров). В дальнейшем с целью
упрощения анализа предполагается, что
вес источники ошибок независимы и не
коррелируют с входным сигналом (хотя
мы и рассмотрим явление предельных
циклов, обусловленных коррелированным
шумом округления).
Эффект квантования
приводят в конечном итоге к погрешностями выходных сигналах цифровых фильтров
(ЦФ), а в некоторыхслучаяхи к неустойчивым
режимам. Выходную ошибку ЦФ будем
рассчитыватькаксуперпозицию ошибок, обусловленных
каждым независимымисточником.
Квантование
чисел– нелинейная операция;m-разрядное
двоичное числоА
представляетсяb-разрядным
двоичнымчислом
B=F(A),
причем b
< m. В
результате квантования число А
представляется
с ошибкой
е
=B–А= F(А)
–А.
Шаг квантования
Q
=
2–b
определяется весом младшего
числовогоразряда.
При квантовании
используется усечение или округление.
Усечение
числаА
состоит в отбрасываниит
– b
младших разрядов числа, при этом
ошибка усечения
eус=
Fус(А) –А.
Оценим величину
ошибки в предположении m
» b.
Для положительных чисел при любом
способе кодирования –2–b
<еус
0. Для
отрицательных чисел при использовании
прямого и обратного кодов ошибка усечения
неотрицательна: 0еус
< 2–b,
а в дополнительном коде эта ошибка
неположительна: 0еус
> –2–b.
Таким образом, во всех случаях
абсолютное значение ошибки усечения
не превосходит шага квантования:maxeус
< 2–b
=Q.
Округление
m-разрядного
числаA
доb
разрядов (b «
m)b-й
разряд остается неизменным или
увеличивается на единицув
зависимости от соотношения (больше –
меньше) между отбрасываемой дробью
0,аb+1…ат
и величиной
,
гдеаi–i-й
разряд числаA;
i =
b+1,
…,m.
Округление можно практически выполнить
путемприбавления
единицы к (b+1)-му
разряду и усечения полученного числа
до b разрядов.
В таком случае ошибка округления еoк
=
fок(А)–
А
при всех способах кодирования лежит в
пределах
–2–(b+1)
<
еoк
< 2–(b+1)
(1.11)
и, следовательно,
max<2–b
= Q/2.
(1.12)
В задачах ЦОС
ошибки квантования чисел рассматриваются
как стационарный
шумоподобный процесс с равномерным
распределением
вероятности по диапазону распределения
ошибок квантования.
(nT)
x(nT)
e(nT)
Рис. 3. Линейная модель квантования
сигналов:
(nT) —дискретный
или m-разрядный
цифровой сигнал (m
> b);
x(nT) —квантованный
b-разрядный
цифровой сигнал;
e(nT)
= x(nT)
–f(nT)
— ошибка
квантования.
Квантование
дискретных сигналов состоит в
представлении отсчета
(выборки сигнала) числамиx(nT),
содержащими b
числовых разрядов. Квантование сигналов,
как и квантование
чисел – нелинейная операция. Однако
при анализе процессов в ЦФ целесообразно
использовать линейную модель квантования
сигналов – рис. 3.
Верхнее значение ошибки квантования
определяетсясоотношением
(1.11) или (1.12).
Вероятностные
оценки ошибок квантования основаны на
предположениях о том, что
последовательностье(пТ)являетсястационарным
случайным процессом с равномерным
распределением вероятности по
диапазону ошибок квантования ие(пТ)
не коррелирован
с f(nT).
Математическое
ожидание (среднее значение) e
и дисперсия
ошибки квантованияе
определяются
по формулам:
=E(е)
=,
=
=
=E(е2)
–,
где ре
— плотность вероятности ошибки. По
этим формуламвычисляются
математическое ожидание и дисперсия
для ошибок
округления и усечения:
=
=
В логарифмическоммасштабе
=
Лекция 2
Вычислите ошибку квантования
В этом примере показано, как вычислить и сравнить статистику ошибки квантования сигнала при использовании различных методов округления.
Во-первых, случайный сигнал создается, который порождает линейную оболочку столбцов квантизатора.
Затем сигнал квантуется, соответственно, с округлением методов ‘фиксируют’, ‘ставят в тупик’, ‘перекрывают’, ‘самый близкий’, и ‘конвергентный’, и статистические данные сигнала оцениваются.
Теоретическая функция плотности вероятности ошибки квантования будет вычислена с ERRPDF, теоретическое среднее значение ошибки квантования будет вычислено с ERRMEAN, и теоретическое отклонение ошибки квантования будет вычислено с ERRVAR.
Равномерно распределенный случайный сигнал
Сначала мы создаем равномерно распределенный случайный сигнал, который охватывает область-1 к 1 из квантизаторов фиксированной точки, на которые мы посмотрим.
q = quantizer([8 7]);
r = realmax(q);
u = r*(2*rand(50000,1) - 1); % Uniformly distributed (-1,1)
xi=linspace(-2*eps(q),2*eps(q),256);
Фиксация: вокруг по направлению к нулю.
Заметьте, что с округлением ‘фиксации’, функция плотности вероятности вдвое более широка, чем другие. Поэтому отклонение в четыре раза больше чем это других.
q = quantizer('fix',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 3 % Theoretical mean = 0 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -46.8586 Theoretical error variance (dB) = -46.9154 Estimated mean = 7.788e-06 Theoretical mean = 0
Пол: вокруг к минус бесконечность.
Пол, округляющийся, часто называется усечением, когда используется с целыми числами и числами фиксированной точки, которые представлены в дополнении two. Это — наиболее распространенный режим округления процессоров DSP, потому что это требует, чтобы никакое оборудование не реализовало. Пол не производит квантованные значения, которые являются как близко к истинным значениям, когда ROUND будет, но это имеет то же отклонение, и маленькие сигналы, которые варьируются по знаку, будут обнаружены, тогда как в ROUND они будут потеряны.
q = quantizer('floor',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = -eps(q)/2 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9148 Theoretical error variance (dB) = -52.936 Estimated mean = -0.0038956 Theoretical mean = -0.0039062
Потолок: вокруг к плюс бесконечность.
q = quantizer('ceil',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = eps(q)/2 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9148 Theoretical error variance (dB) = -52.936 Estimated mean = 0.0039169 Theoretical mean = 0.0039062
Вокруг: вокруг к самому близкому. Вничью, вокруг к самой большой величине.
Вокруг более точно, чем пол, но все значения, меньшие, чем eps (q), округлены, чтобы обнулить и потеряны — также.
q = quantizer('nearest',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = 0 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9579 Theoretical error variance (dB) = -52.936 Estimated mean = -2.212e-06 Theoretical mean = 0
Конвергентный: вокруг к самому близкому. Вничью, вокруг к даже.
Конвергентное округление устраняет смещение, введенное обычным «раундом», вызванным, всегда округляя связь в том же направлении.
q = quantizer('convergent',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = 0 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9579 Theoretical error variance (dB) = -52.936 Estimated mean = -2.212e-06 Theoretical mean = 0
Сравнение самых близких по сравнению с конвергентным
Функция плотности вероятности появления ошибки для конвергентного округления затрудняет, чтобы различать от того из раунда-к-самому-близкому путем рассмотрения графика.
Ошибка p.d.f. из конвергентных
f(err) = 1/eps(q), for -eps(q)/2 <= err <= eps(q)/2, and 0 otherwise
в то время как ошибка p.d.f. из раунда
f(err) = 1/eps(q), for -eps(q)/2 < err <= eps(q)/2, and 0 otherwise
Обратите внимание на то, что ошибка p.d.f. из конвергентных симметрично, в то время как вокруг немного склоняется к положительному.
Единственной разницей является направление округления вничью.
x=(-3.5:3.5)'; [x convergent(x) nearest(x)]
ans =
-3.5000 -4.0000 -3.0000
-2.5000 -2.0000 -2.0000
-1.5000 -2.0000 -1.0000
-0.5000 0 0
0.5000 0 1.0000
1.5000 2.0000 2.0000
2.5000 2.0000 3.0000
3.5000 4.0000 4.0000
Постройте функцию помощника
Функция помощника, которая использовалась, чтобы сгенерировать графики в этом примере, описана ниже.
type(fullfile(matlabroot,'toolbox','fixedpoint','fidemos','+fidemo','qerrordemoplot.m')) %#ok<*NOPTS>
function qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
%QERRORDEMOPLOT Plot function for QERRORDEMO.
% QERRORDEMOPLOT(Q,F_T,XI,MU_T,V_T,ERR) produces the plot and display
% used by the example function QERRORDEMO, where Q is the quantizer
% whose attributes are being analyzed; F_T is the theoretical
% quantization error probability density function for quantizer Q
% computed by ERRPDF; XI is the domain of values being evaluated by
% ERRPDF; MU_T is the theoretical quantization error mean of quantizer Q
% computed by ERRMEAN; V_T is the theoretical quantization error
% variance of quantizer Q computed by ERRVAR; and ERR is the error
% generated by quantizing a random signal by quantizer Q.
%
% See QERRORDEMO for examples of use.
% Copyright 1999-2014 The MathWorks, Inc.
v=10*log10(var(err));
disp(['Estimated error variance (dB) = ',num2str(v)]);
disp(['Theoretical error variance (dB) = ',num2str(10*log10(v_t))]);
disp(['Estimated mean = ',num2str(mean(err))]);
disp(['Theoretical mean = ',num2str(mu_t)]);
[n,c]=hist(err);
figure(gcf)
bar(c,n/(length(err)*(c(2)-c(1))),'hist');
line(xi,f_t,'linewidth',2,'color','r');
% Set the ylim uniformly on all plots
set(gca,'ylim',[0 max(errpdf(quantizer(q.format,'nearest'),xi)*1.1)])
legend('Estimated','Theoretical')
xlabel('err'); ylabel('errpdf')
Дорогие читатели, меня зовут Феликс Арутюнян. Я студент, профессиональный скрипач. В этой статье хочу поделиться с Вами отрывком из моей презентации, которую я представил в университете музыки и театра Граца по предмету прикладная акустика.
Рассмотрим теоретические аспекты преобразования аналогового (аудио) сигнала в цифровой.
Статья не будет всеохватывающей, но в тексте будут гиперссылки для дальнейшего изучения темы.
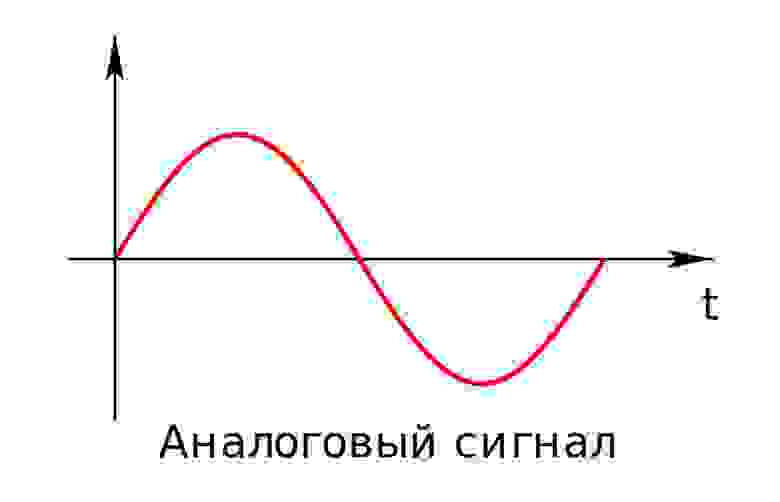
Чем отличается цифровой аудиосигнал от аналогового?
Аналоговый (или континуальный) сигнал описывается непрерывной функцией времени, т.е. имеет непрерывную линию с непрерывным множеством возможных значений (рис. 1).
рис. 1
Цифровой сигнал — это сигнал, который можно представить как последовательность определенных цифровых значений. В любой момент времени он может принимать только одно определенное конечное значение (рис. 2).
рис. 2
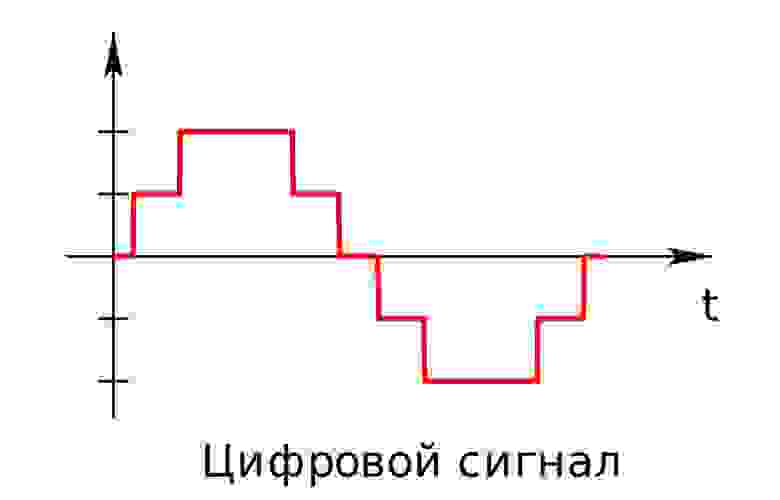
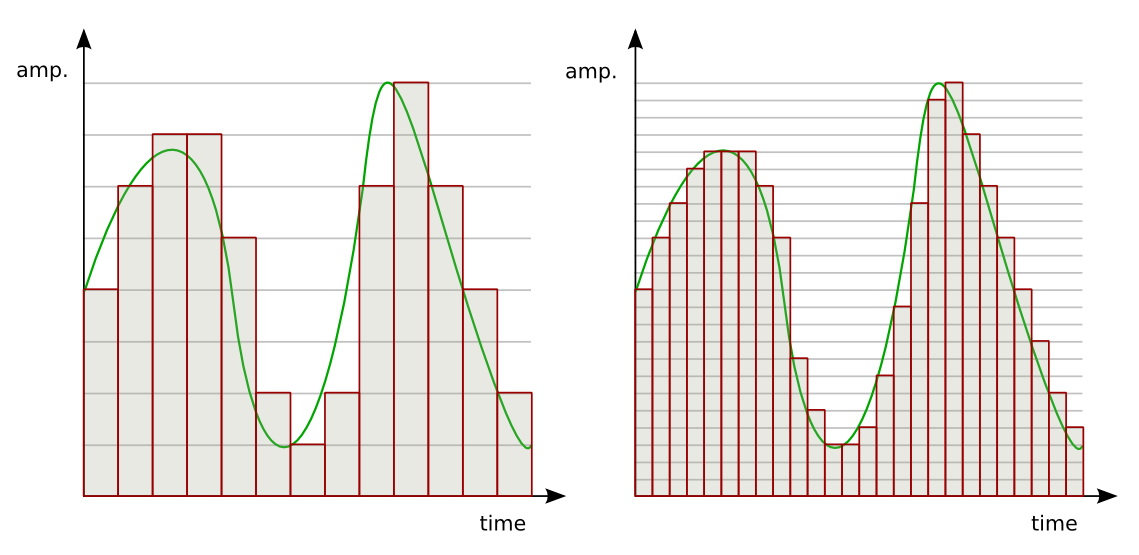
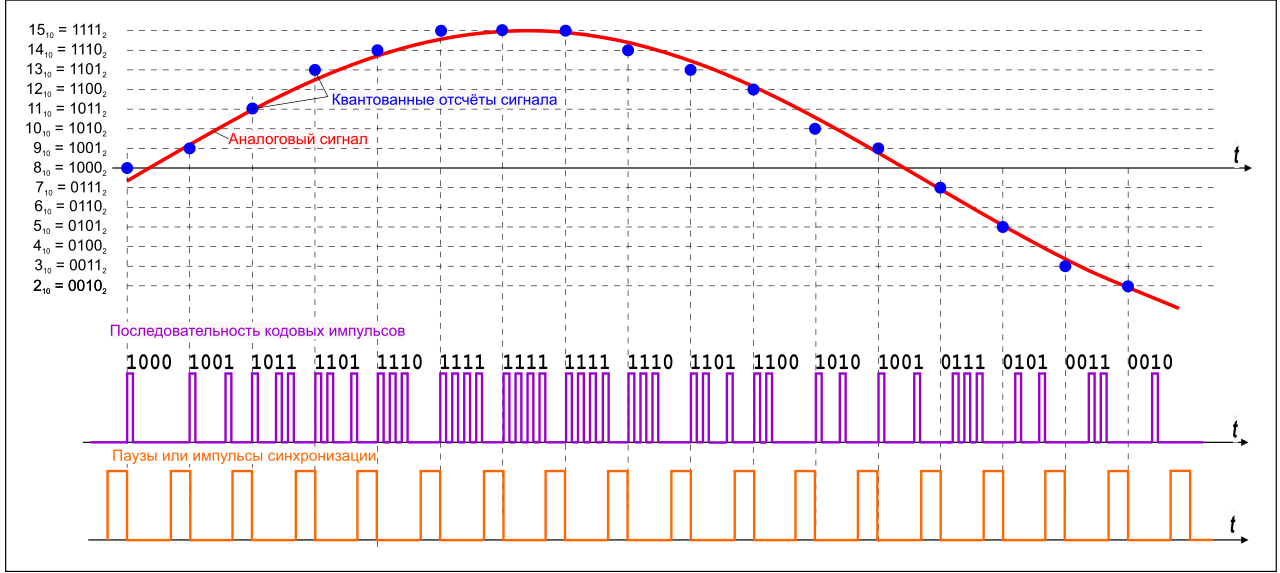
Аналоговый сигнал в динамическом диапазоне может принимать любые значения. Аналоговый сигнал преобразуется в цифровой с помощью двух процессов — дискретизация и квантование. Очередь процессов не важна.
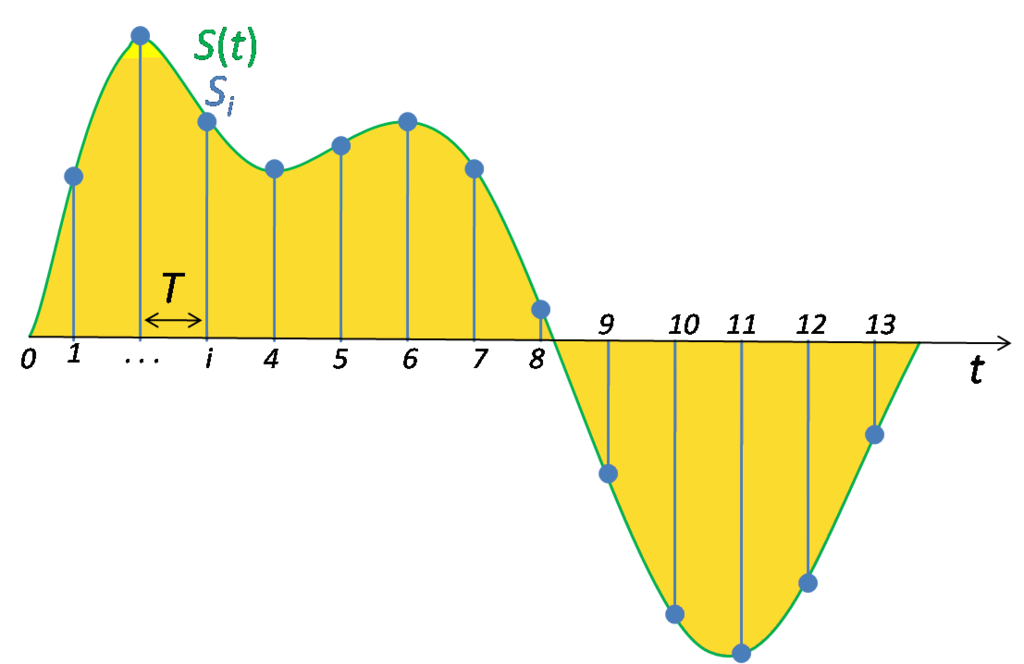
Дискретизацией называется процесс регистрации (измерения) значения сигнала через определенные промежутки (обычно равные) времени (рис. 3).
рис. 3
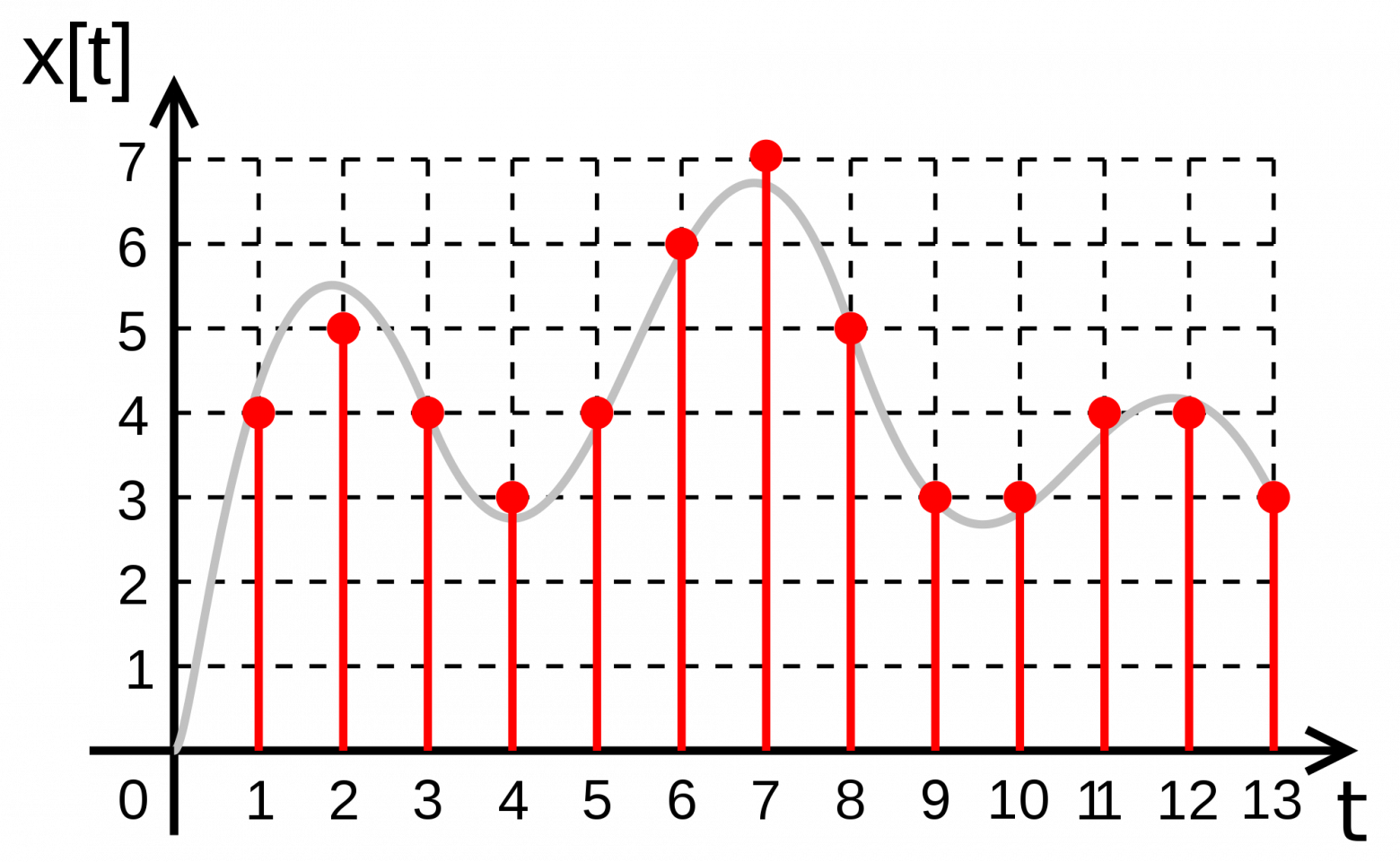
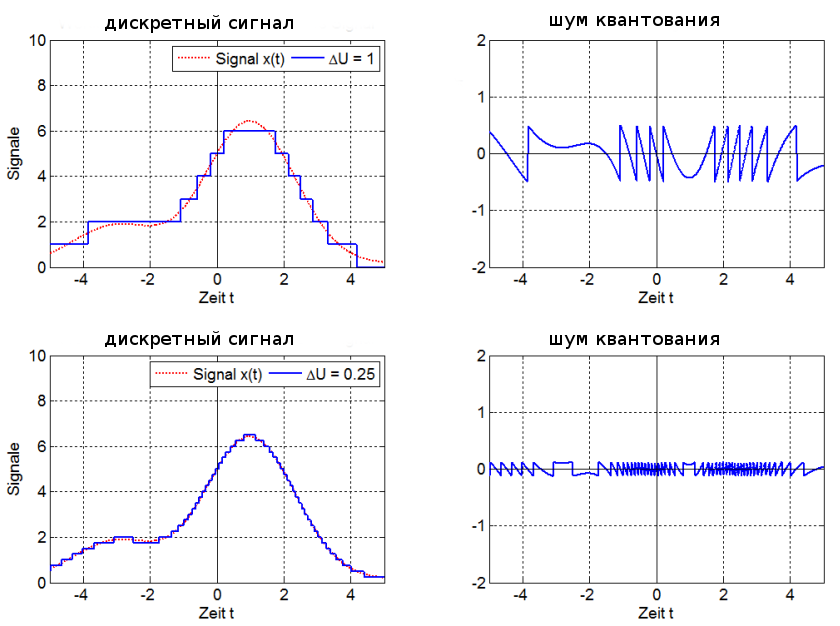
Квантование — это процесс разбиения диапазона амплитуды сигнала на определенное количество уровней и округление значений, измеренных во время дискретизации, до ближайшего уровня (рис. 4).
рис. 4
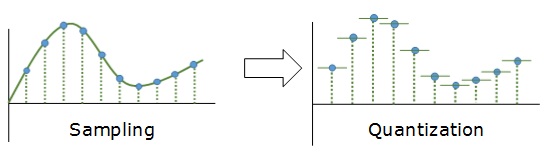
Дискретизация разбивает сигнал по временной составляющей (по вертикали, рис. 5, слева).
Квантование приводит сигнал к заданным значениям, то есть округляет сигнал до ближайших к нему уровней (по горизонтали, рис. 5, справа).
рис. 5
Эти два процесса создают как бы координатную систему, которая позволяет описывать аудиосигнал определенным значением в любой момент времени.
Цифровым называется сигнал, к которому применены дискретизация и квантование. Оцифровка происходит в аналого-цифровом преобразователе (АЦП). Чем больше число уровней квантования и чем выше частота дискретизации, тем точнее цифровой сигнал соответствует аналоговому (рис. 6).
рис. 6
Уровни квантования нумеруются и каждому уровню присваивается двоичный код. (рис. 7)
рис. 7
Количество битов, которые присваиваются каждому уровню квантования называют разрядностью или глубиной квантования (eng. bit depth). Чем выше разрядность, тем больше уровней можно представить двоичным кодом (рис. 8).
рис. 8.
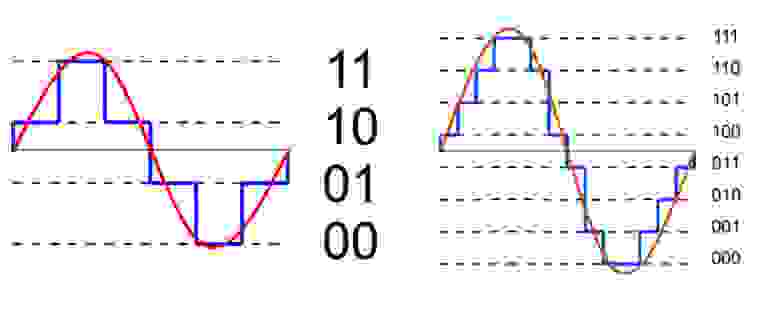
Данная формула позволяет вычислить количество уровней квантования:
Если N — количество уровней квантования,
n — разрядность, то
Обычно используют разрядности в 8, 12, 16 и 24 бит. Несложно вычислить, что при n=24 количество уровней N = 16,777,216.
При n = 1 аудиосигнал превратится в азбуку Морзе: либо есть «стук», либо нету. Существует также разрядность 32 бит с плавающей запятой. Обычный компактный Аудио-CD имеет разрядность 16 бит. Чем ниже разрядность, тем больше округляются значения и тем больше ошибка квантования.
Ошибкой квантований называют отклонение квантованного сигнала от аналогового, т.е. разница между входным значением и квантованным значением
(
)
Большие ошибки квантования приводят к сильным искажениям аудиосигнала (шум квантования).
Чем выше разрядность, тем незначительнее ошибки квантования и тем лучше отношение сигнал/шум (Signal-to-noise ratio, SNR), и наоборот: при низкой разрядности вырастает шум (рис. 9).
рис. 9
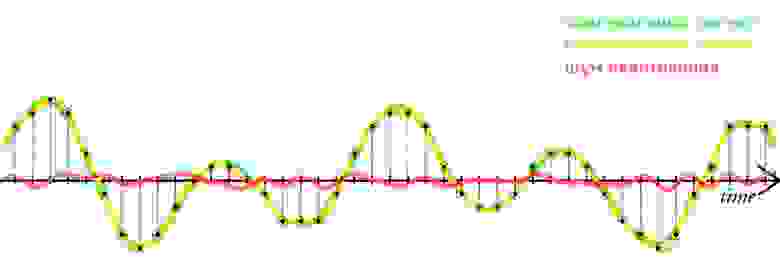
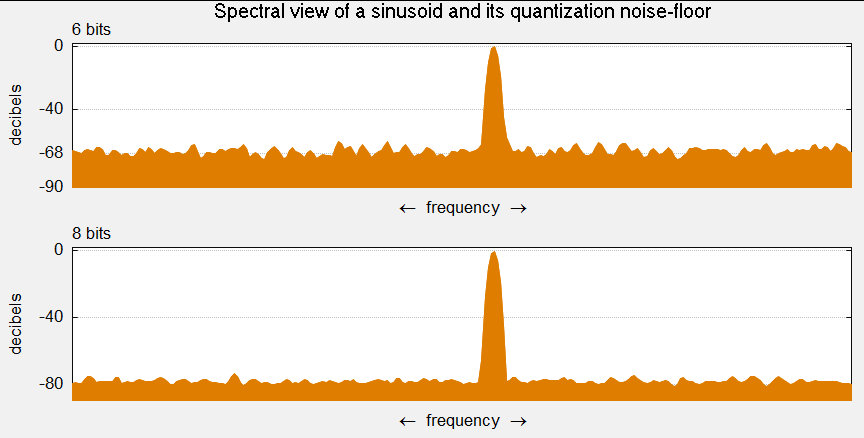
Разрядность также определяет динамический диапазон сигнала, то есть соотношение максимального и минимального значений. С каждым битом динамический диапазон вырастает примерно на 6dB (Децибел) (6dB это в 2 раза; то есть координатная сетка становиться плотнее, возрастает градация).
рис. 10. Интенсивность шумов при разрядности 6 бит и 8 бит
Ошибки квантования (округления) из-за недостаточного количество уровней не могут быть исправлены.
шум квантования
амплитуда сигнала при разрядности 1 бит (сверху) и 4 бит
Аудиопример 1: 8bit/44.1kHz, ~50dB SNR
примечание: если аудиофайлы не воспроизводятся онлайн, пожалуйста, скачивайте их.
Аудиопример 1
Аудиопример 2: 4bit/48kHz, ~25dB SNR
Аудиопример 2
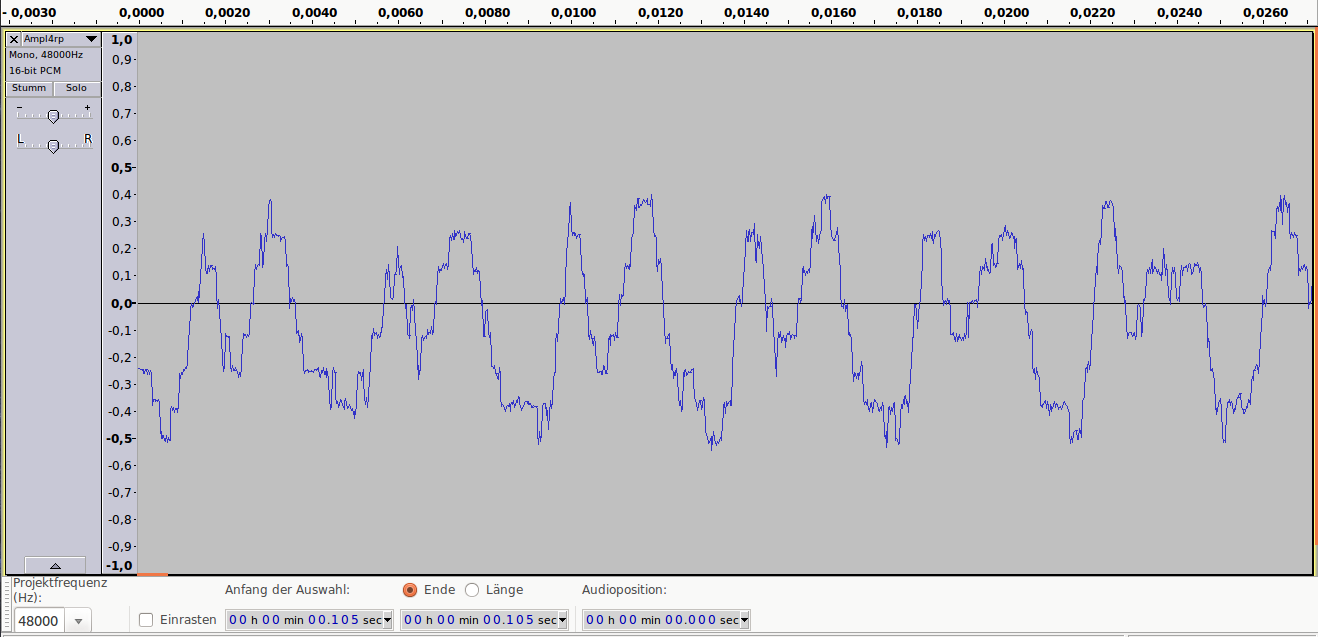
Аудиопример 3: 1bit/48kHz, ~8dB SNR
Аудиопример 3
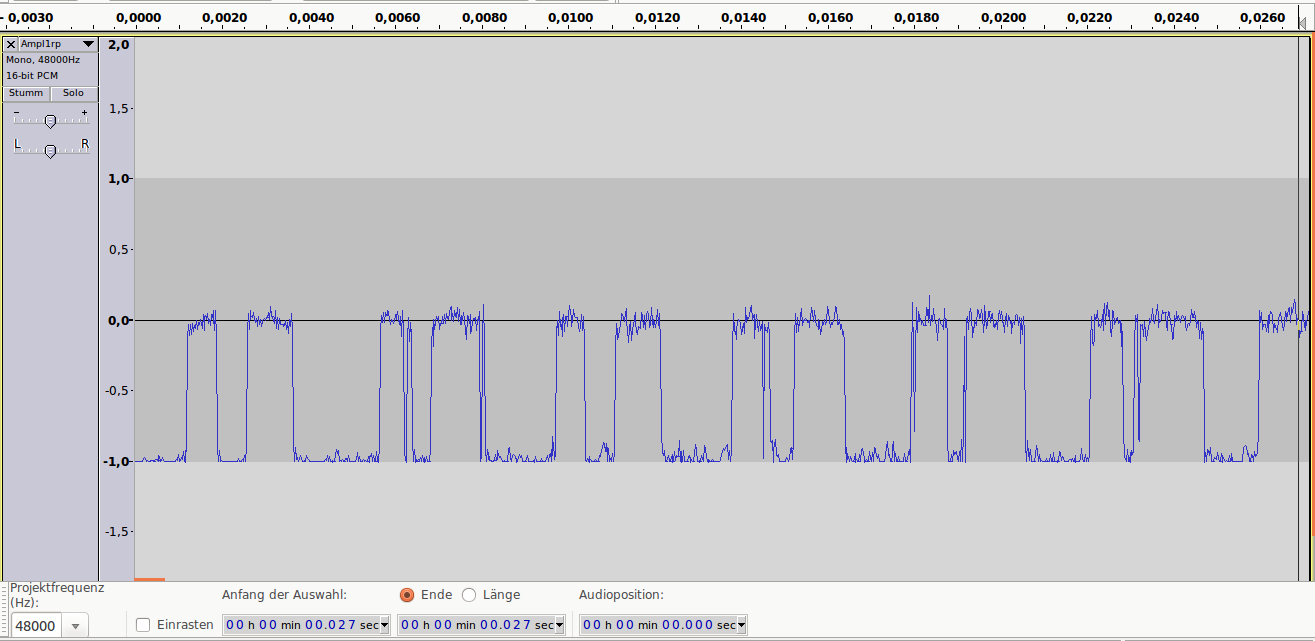
Теперь о дискретизации.
Как уже говорили ранее, это разбиение сигнала по вертикали и измерение величины значения через определенный промежуток времени. Этот промежуток называется периодом дискретизации или интервалом выборок. Частотой выборок, или частотой дискретизации (всеми известный sample rate) называется величина, обратная периоду дискретизации и измеряется в герцах. Если
T — период дискретизации,
F — частота дискретизации, то
Чтобы аналоговый сигнал можно было преобразовать обратно из цифрового сигнала (точно реконструировать непрерывную и плавную функцию из дискретных, «точечных» значении), нужно следовать теореме Котельникова (теорема Найквиста — Шеннона).
Теорема Котельникова гласит:
Если аналоговый сигнал имеет финитный (ограниченной по ширине) спектр, то он может быть восстановлен однозначно и без потерь по своим дискретным отсчетам, взятым с частотой, строго большей удвоенной верхней частоты.
Вам знакомо число 44.1kHz? Это один из стандартов частоты дискретизации, и это число выбрали именно потому, что человеческое ухо слышит только сигналы до 20kHz. Число 44.1 более чем в два раза больше чем 20, поэтому все частоты в цифровом сигнале, доступные человеческому уху, могут быть преобразованы в аналоговом виде без искажении.
Но ведь 20*2=40, почему 44.1? Все дело в совместимости с стандартами PAL и NTSC. Но сегодня не будем рассматривать этот момент. Что будет, если не следовать теореме Котельникова?
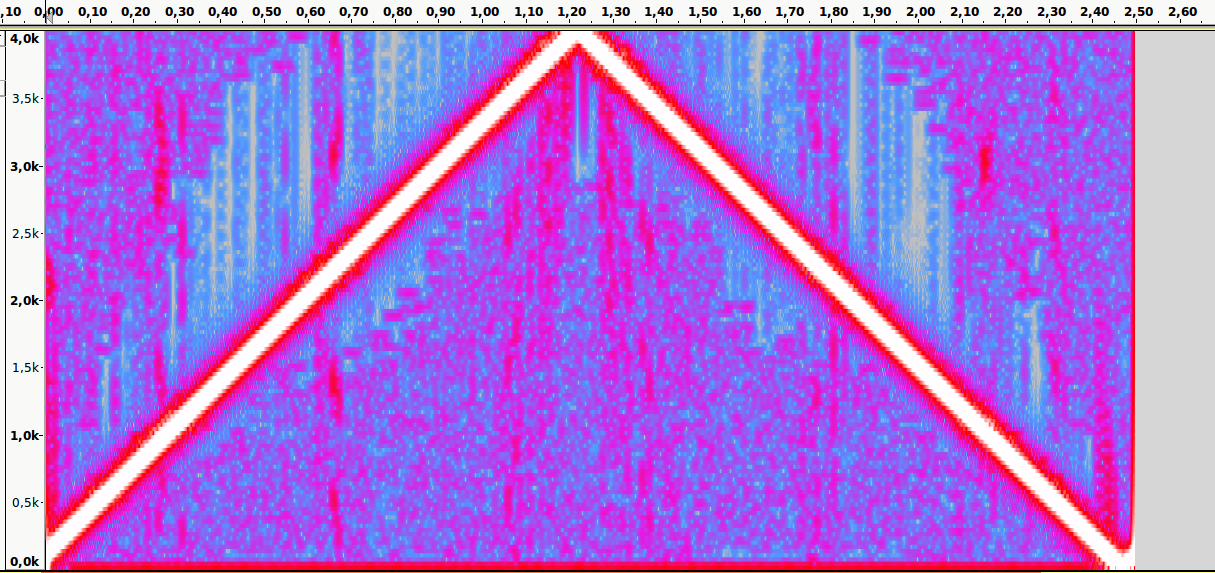
Когда в аудиосигнале встречается частота, которая выше чем 1/2 частоты дискретизации, тогда возникает алиасинг — эффект, приводящий к наложению, неразличимости различных непрерывных сигналов при их дискретизации.
Алиасинг
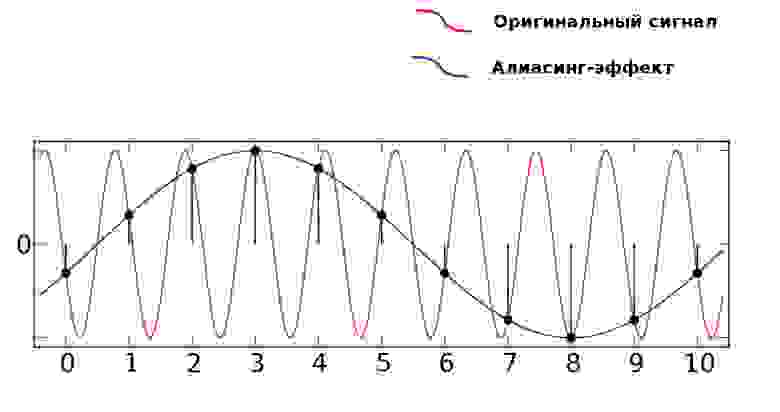
Как видно из предыдущей картинки, точки дискретизации расположены так далеко друг от друга, что при интерполировании (т.е. преобразовании дискретных точек обратно в аналоговый сигнал) по ошибке восстанавливается совершенно другая частота.
Аудиопример 4: Линейно возрастающая частота от ~100 до 8000Hz. Частота дискретизации — 16000Hz. Нет алиасинга.
Спектральный анализ
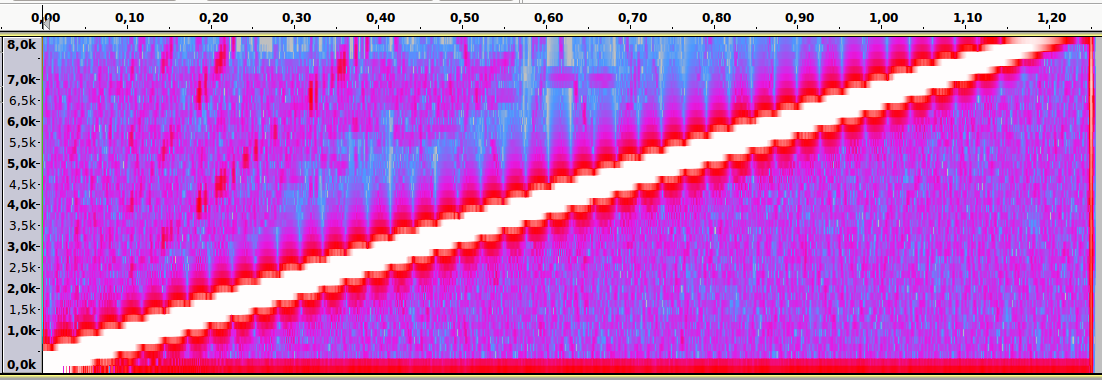
Аудиопример 5: Тот же файл. Частота дискретизации — 8000Hz. Присутствует алиасинг
Спектральный анализ
Пример:
Имеется аудиоматериал, где пиковая частота — 2500Hz. Значит, частоту дискретизации нужно выбрать как минимум 5000Hz.
Следующая характеристика цифрового аудио это битрейт. Битрейт (bitrate) — это объем данных, передаваемых в единицу времени. Битрейт обычно измеряют в битах в секунду (Bit/s или bps). Битрейт может быть переменным, постоянным или усреднённым.
Следующая формула позволяет вычислить битрейт (действительна только для несжатых потоков данных):
Битрейт = Частота дискретизации * Разрядность * Количество каналов
Например, битрейт Audio-CD можно рассчитать так:
44100 (частота дискретизации) * 16 (разрядность) * 2 (количество каналов, stereo)= 1411200 bps = 1411.2 kbit/s
При постоянном битрейте (constant bitrate, CBR) передача объема потока данных в единицу времени не изменяется на протяжении всей передачи. Главное преимущество — возможность довольно точно предсказать размер конечного файла. Из минусов — не оптимальное соотношение размер/качество, так как «плотность» аудиоматериала в течении музыкального произведения динамично изменяется.
При кодировании переменным битрейтом (VBR), кодек выбирает битрейт исходя из задаваемого желаемого качества. Как видно из названия, битрейт варьируется в течение кодируемого аудиофайла. Данный метод даёт наилучшее соотношение качество/размер выходного файла. Из минусов: точный размер конечного файла очень плохо предсказуем.
Усреднённый битрейт (ABR) является частным случаем VBR и занимает промежуточное место между постоянным и переменным битрейтом. Конкретный битрейт задаётся пользователем. Программа все же варьирует его в определенном диапазоне, но не выходит за заданную среднюю величину.
При заданном битрейте качество VBR обычно выше чем ABR. Качество ABR в свою очередь выше чем CBR: VBR > ABR > CBR.
ABR подходит для пользователей, которым нужны преимущества кодирования VBR, но с относительно предсказуемым размером файла. Для ABR обычно требуется кодирование в 2 прохода, так как на первом проходе кодек не знает какие части аудиоматериала должны кодироваться с максимальным битрейтом.
Существуют 3 метода хранения цифрового аудиоматериала:
- Несжатые («сырые») данные
- Данные, сжатые без потерь
- Данные, сжатые с потерями
Несжатый (RAW) формат данных
содержит просто последовательность бинарных значений.
Именно в таком формате хранится аудиоматериал в Аудио-CD. Несжатый аудиофайл можно открыть, например, в программе Audacity. Они имеют расширение .raw, .pcm, .sam, или же вообще не имеют расширения. RAW не содержит заголовка файла (метаданных).
Другой формат хранения несжатого аудиопотока это WAV. В отличие от RAW, WAV содержит заголовок файла.
Аудиоформаты с сжатием без потерь
Принцип сжатия схож с архиваторами (Winrar, Winzip и т.д.). Данные могут быть сжаты и снова распакованы любое количество раз без потери информации.
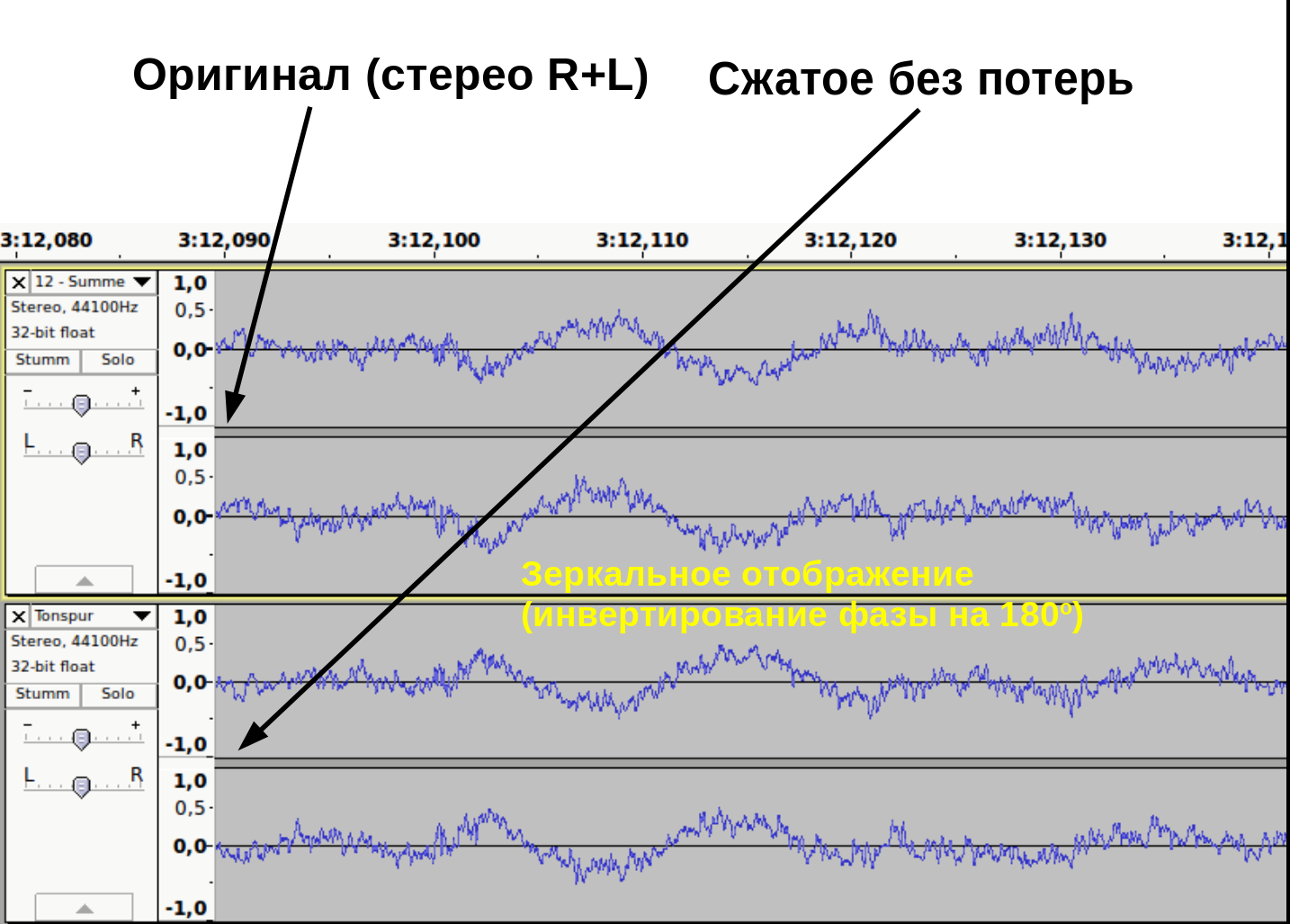
Как доказать, что при сжатии без потерь, информация действительно остаётся не тронутой? Это можно доказать методом деструктивной интерференции. Берем две аудиодорожки. В первой дорожке импортируем оригинальный, несжатый wav файл. Во второй дорожке импортируем тот же аудиофайл, сжатый без потерь. Инвертируем фазу одного из дорожек (зеркальное отображение). При проигрывании одновременно обеих дорожек выходной сигнал будет тишиной.
Это доказывает, что оба файла содержат абсолютно идентичные информации (рис. 11).
рис. 11
Кодеки сжатия без потерь: flac, WavPack, Monkey’s Audio…
При сжатии с потерями
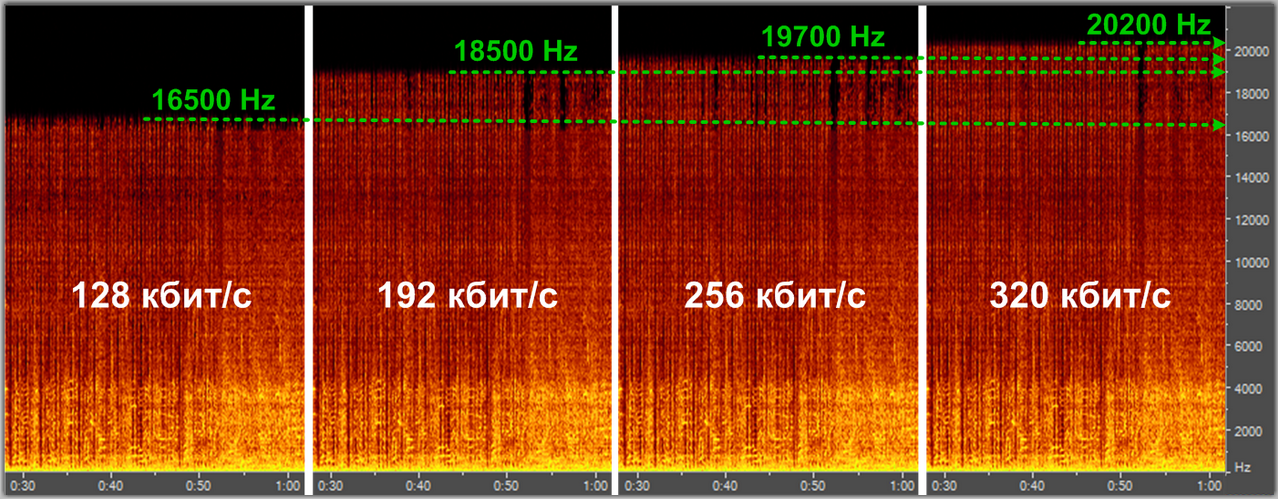
акцент делается не на избежание потерь информации, а на спекуляцию с субъективными восприятиями (Психоакустика). Например, ухо взрослого человек обычно не воспринимает частоты выше 16kHz. Используя этот факт, кодек сжатия с потерями может просто жестко срезать все частоты выше 16kHz, так как «все равно никто не услышит разницу».
Другой пример — эффект маскировки. Слабые амплитуды, которые перекрываются сильными амплитудами, могут быть воспроизведены с меньшим качеством. При громких низких частотах тихие средние частоты не улавливаются ухом. Например, если присутствует звук в 1kHz с уровнем громкости в 80dB, то 2kHz-звук с громкостью 40dB больше не слышим.
Этим и пользуется кодек: 2kHz-звук можно убрать.
Спектральный анализ кодека mp3 с разными уровнями компрессии
Кодеки сжатия с потерям: mp3, aac, ogg, wma, Musepack…
Спасибо за внимание.
UPD:
Если по каким-либо причинам аудиофайлы не загружаются, можете их скачать здесь: cloud.mail.ru/public/HbzU/YEsT34i4c
Когда я был в Питере, и мы сидели в кабаке, у нас с товарищами 



Поскольку дельта икс у нас совершенно чёткая, или скорее равная отрезкам оцифровки, то производная значения снятого с АЦП будет нынешнее значение минус предыдущее, делённое на период квантования: df/dt=(f(t1) -f(t2))/(t1 -t2). Для опытов я выбрал функцию гармонического синуса sin(x). В дальнейшем проверил и на остальных функциях, но это самая красивая и в нашем случае самая актуальная.
Изначальный график для экспериментов
Для начала я составил таблицу, над которой начал издеваться. Первая строчка [ t= ] — это время от старта работы условного АЦП, который наращивается с шагом квантования (последняя строчка). Вторая — [ SIN(t) ]синус вычесленный от этого кванта времени, формула которого примитивна: =SIN(B1). Третья — [ dSIN(t)/dt ] это численное нахождение производной. Формула её проста: =(C2-B2)/C5 (первая ячейка). Предпоследняя строчка это [ COS(t) ], это нахождения косинуса от перменной t. Она нужна для того, чтобы сравнивать с истинным значением косинуса вычисленную производную (если помните, производная синуса — это косинус). Последняя строка — это квантование, т.е. проще говоря шаг изменения t. Внизу строиться график, который строит гибкую линию по точкам. Сейчас у нас выбран самый оптимальный шаг квантования 0,5 . Здесь всё ясно, дальше я двух разделах покажу сначала ошибки квантования, и следственные ошибки производных, затем ошибки дифференцирования при ошибочных входных данных. Если ваш мозг не вспух и вы готовы дальше пуститься в дебри математики и электроники,
Ошибки квантования
Как видно из самой первой картинки, производная практически полностью соответствует графику косинуса. Если мы ещё уменьшим «частоту дискретизации», или в нашем случае шаг до dt=0,1, то получим вообще практически совпадающие кривые, которые я проиллюстрирую ниже:
Полученный график с шагом 0,1
Как видно, при этом шаге квантования график производной (фиолетовая кривая), практически полностью совпадает с графиком косинуса (красная кривая). Маркерами показанны точки квантования. В этом случае всё ясно, но давайте увеличим шаг, от 0,5 до 1
Полученный график с шагом 1
Видно, что производная, да и все графики начинают «плыть».
Продолжим увеличение квантования до 2:
Полученный график с шагом 2
Всё начинает плыть и уходить, но ещё отдалённо напоминает синус. Однако уже видно, что численно рассчитанная производная СОВЕРШЕННО не соответствует своему значению. Да и вообще находится в противофазе. Напоследок возьмём квантование равное 5 (в 10 раз больше исходного).
Полученный график с шагом 10
Видно что в этом случае мы наблюдаем полную ересь. И в данном случае можно сказать, что высокие частоты и шумы, могут хорошо подпортить реальное значение производной. Теперь же посмотрим как влияет погрешность снятого сигнала, на численный рассчёт производной.
Численное вычисление производной, при неточности снятого сигнала (шумах, наводках, высших гармониках)
Добавим теперь в формулу вычисления синуса некоторую погрешность снятия сигнала, для этого прибавим к формуле вычисления синуса некоторое случайное число: =SIN(C1)+СЛЧИС()*0,1 . Данная формула внесёт 10% погрешность от амплитудного значения в вычисление сигнала, просто добавляя некоторое случайное число от нуля до 0,1. Я покажу несколько вариантов с разной погрешностью. Сначала покажем сигнал с 5% погрешностью:
Полученный график с погрешностью 5%
Как видно из графика, ни на синус, ни на производную такая погрешность не оказывает должного влияния. Возьмём тогда погрешность в 10%
Полученный график с погрешностью 10%
Вот, ярко видно, что на графике синуса погрешность сказалось мало. А вот на графике производной очень даже, в особенности хорошо раскорячило её концы. На последок покажу что будет если построить график производной с 20% погрешностью:
Полученный график с погрешностью 20%
График отдалённо напоминает косинус. Видно куча убеганий и прочего. Надо учитывать, что это ПСЕВДОслучайная велечина, в реальной жизни всё может быть гораздо хуже. Но всё же лучше смоделировать данные фишки, чтобы представлять себе что же может твориться на АЦП.
Вывод: Считать численно производную по снятым значениям с АЦП можно и нужно. Но необходимо оценивать уровень внешних помех, которые могут влиять на сигнул, и очень сильно его портить. Желательно использовать фильтрацию сигнала, выделяя полезный сигнал. Филтрация может быть как аналоговая, так цифровуя. Мне даже показали прекрасную формульную замену аналоговой фильтрацией прекрасной програмкой на си. И разумеется мы должны себе ЧЁТКО представлять какой сигнал цифруем, и не цифровать сигнал на пределах возможностей АЦП. 5 точек на период, как показала практика — не самый плохой вариант!
Операция
квантования
сводится к тому, что всем отсчетам
входного сигнала x,
попавшим в некоторый интервал,
приписывается одно и то же значение
,
выражаемое двоичной кодовой комбинацией.
Если
кодовая комбинация содержит r
разрядов, то число дискретных уровней
выходного сигнала квантователя равно
.
Для
взаимно однозначного соответствия весь
диапазон изменения входного сигнала
X
= x
max
– x
min
должен быть разбит на такое же количество
уровней.
Величина
интервала разбиения – шаг
квантования
– представляет собой значение аналоговой
величины, на которую отличаются уровни
входного сигнала, представленные двумя
соседними кодовыми комбинациями.
При
наиболее распространенном равномерном
квантовании шаг квантования равен
(1.12)
Характеристикой
квантования
называется зависимость квантованного
значения
от значения непрерывной величины x.
Типичная
характеристика
квантователя
с постоянном шагом квантования
приведена на рисунке 1.16.

Рисунок 1.16 –
Характеристика квантования при постоянном
шаге квантования
На
рисунке 1.17 приведена временная диаграмма
работы квантователя, где точками отмечены
квантованные значения, и временная
диаграмма ошибки квантования
.
Временная последовательность ошибок
квантования случайного сигнала
представляет собой случайный процесс
с равномерным законом распределения.
Этот случайный процесс называют шумом
квантования.

Рисунок
1.17 – Временные зависимости сигналов
на входе (x)
и выходе (
)
квантователя
и
ошибки квантования
Из
рисувнка видно, что абсолютное значение
ошибки квантования не превышает Δ/2.
Закон
распределения этого случайного процесса
приведен на рисунке 1.18.

Рисунок 1.18 –
Плотность вероятности шума квантования
Определим дисперсию шума квантования

После подстановки
(2.1) в последнее соотношение получим
(1.13)
Из
(1.13) следует, что дисперсия шума квантования
зависит от характеристик квантователя
и не зависит от уровня сигнала.
Определим отношение сигнал/шум на выходе квантователя
,
где
Pc—
мощность сигнала,
–
мощность шума,
—
среднеквадратическое значение сигнала.
Это отношение в
децибелах равно
(1.14)
Из последнего соотношения
видно, что
-
каждое
добавление одного разряда в кодовом
слове увеличивает отношение сигнал/шум
на 6 дБ. -
с
уменьшением уровня входного сигнала
отношение сигнал/шум уменьшается.
1.6.
Квантователи с переменным шагом
квантования
(нелинейные
квантователи)
Недостаток
линейного квантователя, связанный с
уменьшением отношения сигнал/шум
квантования при уменьшении уровня
сигнала, можно устранить, если уменьшать
шаг квантования по мере уменьшения
уровня сигнала.
Характеристика
квантования с переменным шагом квантования
приведена на рисунке 1.19.
Такую
характеристику можно получить, если
последовательно включить нелинейный
преобразователь и линейный квантователь
(рисунок 1.19)
Чтобы
устранить нелинейные искажения,
обусловленные введением нелинейного
преобразователя, после квантователя
используют второй нелинейный
преобразователь квантованного сигнала
с характеристикой, обратной характеристике
первого. С помощью первого осуществляют
компрессию сигнала, а с помощью второго
– его экспандирование. В целом описанная
операция называется компандированием.
Результирующая сквозная характеристика
системы «компрессор-экспандер» остается
линейной.

Рисунок
1.19 – Характеристика квантования при
переменном шаге квантования

Рисунок
1.20 –Система «компрессор-экспандер»
В настоящее время
используются два закона компандирования:
μ-закон
(1.15) и А – закон (1.16):
(1.15)
где
=255,
,
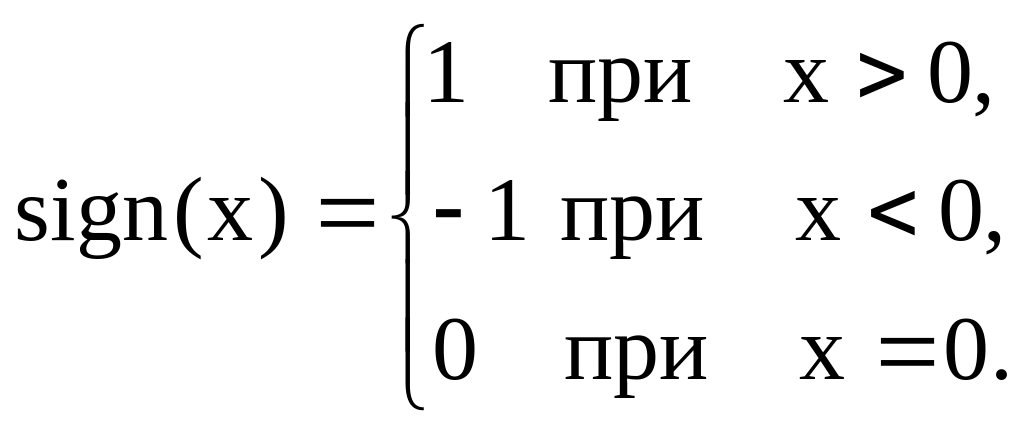
(1.16)
где
A
= 87.6.
Заключение
При дискретизации
аналогового сигнала возникают два
эффекта, касающиеся спектра сигнала:
-
Эффект
размножения спектра аналогового
сигнала, -
Эффект
наложения сгустков спектра дискретного
сигнала друг на друга.
Эффект
наложения спектров приводит к искажению
дискретного сигнала и невозможности
точного восстановления аналогового
сигнала из дискретного.
Спектр дискретного
сигнала представляет собой периодическую
функцию частоты, период которой равен
частоте дискретизации.
Если дискретизации
подвергается периодический аналоговый
сигнал с линейчатым спектром, то
размножение спектра осуществляется по
закону:
при
где
F
– частота спектральной составляющей
аналогового сигнала.
Амплитуды
спектральных составляющих дискретного
сигнала пропорциональны соответствующим
составляющим спектра аналогового
сигнала.
Размножение
спектра апериодического аналогового
сигнала осуществляется по этому же
закону, если рассматривать в качестве
F
характерные частоты непрерывного
спектра аналогового сигнала.
Эффект
наложения спектров при дискретизации
отсутствует, если выполняется условие
,
где
Fmax
– максимальная частота спектра
аналогового сигнала.
Если
дискретизации подвергается узкополосный
модулированный сигнал, а результатом
последующей цифровой обработки должно
быть выделение модулирующего сигнала,
то частота дискретизации может быть
выбрана существенно меньше, чем 2Fmax.
В этом случае
необходимо выполнить условия:
,
где
—
ширина спектра аналогового сигнала,
,
где
,
а f0
– частота несущей аналогового сигнала.
При
выполнении последнего условия частота
несущей, приведенная в интервал частот
от нуля до половины частоты дискретизации
(интервал Котельникова), равна четверти
частоты дискретизации.
Необходимость
квантования дискретного сигнала связана
с тем, что в вычислительных устройствах
значение сигнала должно быть представлено
числом конечной разрядности.
Операция
квантования
сводится к тому, что всем отсчетам
входного сигнала x,
попавшим в некоторый интервал,
приписывается одно и то же значение
,
выражаемое двоичной кодовой комбинацией.
Разность
между квантованным значением и значением
отсчета дискретного сигнала называется
ошибкой квантования. Временная
последовательность ошибок квантования
случайного сигнала представляет собой
случайный процесс с равномерным законом
распределения. Этот случайный процесс
называют шумом
квантования.
В
квантователе с постоянным шагом
квантования (линейном квантователе)
отношение сигнал/шум квантования зависит
от количества разрядов квантователя,
уровня сигнала и диапазона квантователя.
Каждое
добавление одного разряда в кодовом
слове увеличивает отношение сигнал/шум
на 6 дБ.
С
уменьшением уровня входного сигнала
отношение сигнал/шум уменьшается.
Последнее
обстоятельство является недостатком
линейного квантователя, который
устраняется в квантователе с переменным
шагом квантования (нелинейном квантователе)
за счет уменьшения шага квантования по
мере уменьшения абсолютного значения
уровня входного сигнала квантователя.
Контрольные
вопросы и задачи по теме №1:
1.
Что такое дискретизация аналогового
сигнала? Начертите временные диаграммы
синусоидального сигнала на входе и
выходе дискретизатора в случае, когда
частота синусоидального колебания
меньше половины частоты дискретизации.
2. Начертите
спектральные диаграммы синусоидального
сигнала на входе и выходе дискретизатора
в случае, когда частота синусоидального
колебания меньше половины частоты
дискретизации.
3.В
чем сущность эффекта наложения спектров?
Каким образом можно уменьшить ошибку
наложения?
4.Начертите
амплитудный спектр дискретной синусоиды,
если частота аналогового синусоидального
колебания на входе дискретизатора выше
частоты дискретизации.
5.
Из каких условий выбирается частота
дискретизации модулированного колебания,
если результатом последующей цифровой
обработки должно быть выделение
модулирующего колебания?
6.
Дискретизация синусоидального колебания
,
где f0=20МГц,
осуществляется с частотой FД
= 16 МГц. Чему равна частота дискретной
синусоиды?
7.
На входе аналогового ФНЧ действует
последовательность прямоугольных
импульсов. АЧХ фильтра показана на
рисунке 1.21. Выходной сигнал фильтра
подается на дискретизатор. Частота
дискретизации равна 20 кГц. Возникнет
ли эффект наложения спектров при
дискретизации?

8.
На входе дискретизатора действует
сигнал
,
где
F1=1
МГц, F2
= 2 МГц.
Частота дискретизации FД
= 8 МГц. Чему равен максимальный частотный
разнос между соседними составляющими
спектра дискретного сигнала?
9.
На входе дискретизатора действует
сигнал
,
где F=1
МГц, f0
= 15 МГц.
Частота дискретизации FД
= 12 МГц. Чему равен минимальный частотный
разнос между соседними составляющими
спектра дискретного сигнала?
10.На
рисунке 1.22 приведен спектр аналогового
сигнала. Начертите в относительном
масштабе спектр сигнала после дискретизации
в пределах интервала Котельникова (от
0 до половины частоты дискретизации),
если f0=28МГц,
fmin=25МГц,
fmax=31МГц,
а частота дискретизации равна FД=
16 МГц.

11.
На входе демодулятора действует
модулированный аналоговый сигнал,
спектр которого симметричен относительно
частоты несущей f0
= 445кГц (рисунок 1.22). Ширина спектра
.
При каком из двух значений частоты
дискретизации отсутствует эффект
наложения спектров: FД=20кГц,
FД=21кГц?

12. Поясните
сущность операции квантования дискретных
сигналов. Что такое шаг квантования?
Как зависит шаг квантования при
равномерном (линейном) квантовании от
количества разрядов и диапазона
квантователя?
13.
Дайте определение характеристике
квантования. Начертите характеристику
линейного квантователя.
14. Поясните механизм
возникновения шума квантования. Начертите
график вероятностного распределения
шума квантования. Как связана дисперсия
шума квантования с шагом квантования
и количеством разрядов квантователя
при равномерном квантовании?
15.
Как зависит отношение сигнал/шум на
выходе равномерного квантователя от
количества разрядов, диапазона
квантователя и среднеквадратичного
уровня входного сигнала?
16.
Начертите характеристику квантования
квантователя с неравномерным шагом
квантования (нелинейного квантователя).
17.Поясните сущность
алгоритма функционирования нелинейного
квантователя, состоящего из входного
нелинейного преобразователя и линейного
квантователя. Каким образом устраняются
нелинейные искажения выходного сигнала
при использовании нелинейного
квантователя?
18.Чем
отличается зависимость отношения
сигнал/шум на выходе нелинейного
квантователя от среднеквадратичного
уровня входного сигнала от аналогичной
зависимости для линейного квантователя?
19.
Отношение сигнал/шум на выходе линейного
квантователя равно 40 дБ. Каким станет
это отношение, если количество разрядов
увеличить на два при неизменном уровне
входного сигнала и неизменном диапазоне
квантователя?
Контрольная
карта ответов
Номер
ответа соответствует номеру контрольного
вопроса в предыдущем разделе.
6.
F
= f0
–FД
= 20-16 = 4 МГц
7.
FД
= 20 кГц, Fmax
= 8 кГц. Так как FД>
2 Fmax,
то эффект наложения не возникнет.
8.
Максимальный частотный разнос между
соседними составляющими спектра
дискретного сигнала равен 4 МГц
9.
Минимальный частотный разнос между
соседними составляющими спектра
дискретного сигнала равен 2 МГц.
10.

11.
Эффект наложения отсутствует при частоте
дискретизации FД
=20 кГц.
19.
Отношение сигнал/шум станет равным 52
дБ.
Список
литературы по теме № 1:
1.
В.Г.Иванова, А.И.Тяжев. Цифровая обработка
сигналов и сигнальные процессоры / Под
редакцией д.т.н., профессора Тяжева А.И.
— Самара, 2008г.
2.Куприянов
М.С., Матюшкин Б.Д. Цифровая обработка
сигналов: процессоры, алгоритмы, средства
проектирования. –2-е изд., перераб. и
доп.- СПб.: Политехника, 1999. –592с.
:
ил.
3.Л.Р.Рабинер,
Р.В.Шафер. Цифровая обработка речевых
сигналов. – М.: Радио и связь, 1981. – 495с.:
ил.
4.
А.И. Солонина, Д.А.
Улахович, С.М. Арбузов, Е.Б. Соловьёва.
Основы цифровой обработки сигналов.-
Изд. 2-е испр. и перераб. – СПб.: БХВ-Петербург,
2005.-768с.: ил.
5.А.Б.
Сергиенко. Цифровая обработка сигналов.
– СПб.: Питер, 2002.-2002.-608с.: ил.
24
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Когда я был в Питере, и мы сидели в кабаке, у нас с товарищами 



Поскольку дельта икс у нас совершенно чёткая, или скорее равная отрезкам оцифровки, то производная значения снятого с АЦП будет нынешнее значение минус предыдущее, делённое на период квантования: df/dt=(f(t1) -f(t2))/(t1 -t2). Для опытов я выбрал функцию гармонического синуса sin(x). В дальнейшем проверил и на остальных функциях, но это самая красивая и в нашем случае самая актуальная.
Изначальный график для экспериментов
Для начала я составил таблицу, над которой начал издеваться. Первая строчка [ t= ] — это время от старта работы условного АЦП, который наращивается с шагом квантования (последняя строчка). Вторая — [ SIN(t) ]синус вычесленный от этого кванта времени, формула которого примитивна: =SIN(B1). Третья — [ dSIN(t)/dt ] это численное нахождение производной. Формула её проста: =(C2-B2)/C5 (первая ячейка). Предпоследняя строчка это [ COS(t) ], это нахождения косинуса от перменной t. Она нужна для того, чтобы сравнивать с истинным значением косинуса вычисленную производную (если помните, производная синуса — это косинус). Последняя строка — это квантование, т.е. проще говоря шаг изменения t. Внизу строиться график, который строит гибкую линию по точкам. Сейчас у нас выбран самый оптимальный шаг квантования 0,5 . Здесь всё ясно, дальше я двух разделах покажу сначала ошибки квантования, и следственные ошибки производных, затем ошибки дифференцирования при ошибочных входных данных. Если ваш мозг не вспух и вы готовы дальше пуститься в дебри математики и электроники,
Ошибки квантования
Как видно из самой первой картинки, производная практически полностью соответствует графику косинуса. Если мы ещё уменьшим «частоту дискретизации», или в нашем случае шаг до dt=0,1, то получим вообще практически совпадающие кривые, которые я проиллюстрирую ниже:
Полученный график с шагом 0,1
Как видно, при этом шаге квантования график производной (фиолетовая кривая), практически полностью совпадает с графиком косинуса (красная кривая). Маркерами показанны точки квантования. В этом случае всё ясно, но давайте увеличим шаг, от 0,5 до 1
Полученный график с шагом 1
Видно, что производная, да и все графики начинают «плыть».
Продолжим увеличение квантования до 2:
Полученный график с шагом 2
Всё начинает плыть и уходить, но ещё отдалённо напоминает синус. Однако уже видно, что численно рассчитанная производная СОВЕРШЕННО не соответствует своему значению. Да и вообще находится в противофазе. Напоследок возьмём квантование равное 5 (в 10 раз больше исходного).
Полученный график с шагом 10
Видно что в этом случае мы наблюдаем полную ересь. И в данном случае можно сказать, что высокие частоты и шумы, могут хорошо подпортить реальное значение производной. Теперь же посмотрим как влияет погрешность снятого сигнала, на численный рассчёт производной.
Численное вычисление производной, при неточности снятого сигнала (шумах, наводках, высших гармониках)
Добавим теперь в формулу вычисления синуса некоторую погрешность снятия сигнала, для этого прибавим к формуле вычисления синуса некоторое случайное число: =SIN(C1)+СЛЧИС()*0,1 . Данная формула внесёт 10% погрешность от амплитудного значения в вычисление сигнала, просто добавляя некоторое случайное число от нуля до 0,1. Я покажу несколько вариантов с разной погрешностью. Сначала покажем сигнал с 5% погрешностью:
Полученный график с погрешностью 5%
Как видно из графика, ни на синус, ни на производную такая погрешность не оказывает должного влияния. Возьмём тогда погрешность в 10%
Полученный график с погрешностью 10%
Вот, ярко видно, что на графике синуса погрешность сказалось мало. А вот на графике производной очень даже, в особенности хорошо раскорячило её концы. На последок покажу что будет если построить график производной с 20% погрешностью:
Полученный график с погрешностью 20%
График отдалённо напоминает косинус. Видно куча убеганий и прочего. Надо учитывать, что это ПСЕВДОслучайная велечина, в реальной жизни всё может быть гораздо хуже. Но всё же лучше смоделировать данные фишки, чтобы представлять себе что же может твориться на АЦП.
Вывод: Считать численно производную по снятым значениям с АЦП можно и нужно. Но необходимо оценивать уровень внешних помех, которые могут влиять на сигнал, и очень сильно его портить. Желательно использовать фильтрацию сигнала, выделяя полезный сигнал. Филтрация может быть как аналоговая, так цифровая. Мне даже показали прекрасную формульную замену аналоговой фильтрацией прекрасной програмкой на си. И разумеется мы должны себе ЧЁТКО представлять какой сигнал цифруем, и не цифровать сигнал на пределах возможностей АЦП. 5 точек на период, как показала практика — не самый плохой вариант!
Максимальное значение шума квантования при
округлении составляет . Дисперсия этого шума, если
допустить, что уровень его плотности вероятности в
интервале от до
постоянен,
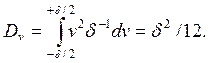
(2)
Корреляционная функция шума квантования затухает тем быстрее, чем меньше величина
по сравнению со среднеквадратичным
приращением (изменением) входного сигнала за время, равное периоду дискретности
. Можно показать, что при выполнении
условия
(3)
где — среднеквадратичное
значение производной входного процесса, корреляционная функция отлична от нуля практически только при
, так как уже при
ее
значение пренебрежимо мало и составляет . Тогда
для корреляционной функции шума квантования справедливо выражение
(4)
где — единичная импульсная
решетчатая функция.
Решетчатый случайный процесс с полученной
корреляционной функцией называют дискретным белым шумом. Его спектральная плотность
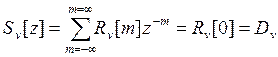
(5)
Аналогичные результаты можно получить и
для случая усечения.
Таким образом, при выполнении условия (3) шум
квантования по уровню во входном АЦП можно считать дискретным белым шумом с
равномерной спектральной плотностью.
На рис.4, а и рис.4, б представлены
графики функций распределения ошибки (шума) квантования для случаев усечения и
округления соответственно. Очевидно, что при одинаковой дисперсии
математические ожидания различны и составляет соответственно и
.
2.
ОПИСАНИЕ ЛАБОРАТОРНОГО МАКЕТА
Схема лабораторного макета представлена на
рис.5.
В качестве объекта для исследования в
данной лабораторной работе предлагается аналого-цифровой преобразователь,
выполненный на интегральной микросхеме 1108ПВ1.
Входной сигнал представляет собой
постоянное напряжение, величина и полярность которого зависит от положения
движка потенциометра (величина этого напряжения
контролируется с помощью потенциометра ).
Выходной сигнал (код) АЦП представляется на светодиодном индикаторе в верхней
части макета, а также поступает на цифро-аналоговый преобразователь (ЦАП).
Выходной сигнал ЦАП может либо поступать
прямо на вольтметр , либо сравниваться на вычитающем
устройстве с входным сигналом АЦП. В последнем случае сигнал на выходе
вычитающего устройства представляет собой ошибку преобразования.
Указанная ошибка включает в себя как
ошибку преобразования «непрерывная величина – код», так и ошибку преобразования
«код – непрерывная величина». Поэтому для исследования ошибки собственно АЦП
рекомендуется искусственно ограничить его точность, принимая во внимание
несколько (четыре-пять) старших разрядов. Поскольку для цифро-аналогового
преобразования при этом используются все разряды, ошибка ЦАП будет значительно
меньше и не окажет существенного влияния на результаты исследований.
- ПОРЯДОК
ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ
- Ознакомиться с
особенностями работы АЦП как элемента ЦАС. - Снять зависимость выходного сигнала (кода) АЦП и
выходного сигнала ЦАП от величины входного напряжения. При этом следует
ограничить число принимаемых во внимание разрядов преобразователя до
четырех. - Снять зависимость напряжения ошибки квантования
от величины входного сигнала.
4.
СОДЕРЖАНИЕ ОТЧЕТА
- Структурная
схема ЦАС. - Схема лабораторной
установки - Результаты измерений и
график характеристики квантования АЦП. - Определенные по результатам
измерений значения цены единицы младшего разряда преобразователя и
коэффициента передачи линеаризованного АЦП. - График зависимости ошибки
квантования от входного напряжения. - Выводы по проделанной
работе.
Библиографический список
1.
Коновалов Г.ф. Радиоавтоматика. –
М. Высшая школа, 1990.
2.
Радиоавтоматика./ Под ре. В.А.
Бесекерского. – М. Высшая школа, 1985.
3.
Микропроцессорные системы
автоматического управления. / Под ре. В.А. Бесекерского – Л.: Машиностроение,
1988
4.
Бесекерский В.А., Изранцев В.В.
Системы автоматического управления с микро-ЭВМ. М.: Наука, 1987.
Цифровое представление аналогового аудиосигнала. Краткий ликбез
Время на прочтение
7 мин
Количество просмотров 43K
Дорогие читатели, меня зовут Феликс Арутюнян. Я студент, профессиональный скрипач. В этой статье хочу поделиться с Вами отрывком из моей презентации, которую я представил в университете музыки и театра Граца по предмету прикладная акустика.
Рассмотрим теоретические аспекты преобразования аналогового (аудио) сигнала в цифровой.
Статья не будет всеохватывающей, но в тексте будут гиперссылки для дальнейшего изучения темы.
Чем отличается цифровой аудиосигнал от аналогового?
Аналоговый (или континуальный) сигнал описывается непрерывной функцией времени, т.е. имеет непрерывную линию с непрерывным множеством возможных значений (рис. 1).
рис. 1

Цифровой сигнал — это сигнал, который можно представить как последовательность определенных цифровых значений. В любой момент времени он может принимать только одно определенное конечное значение (рис. 2).
рис. 2

Аналоговый сигнал в динамическом диапазоне может принимать любые значения. Аналоговый сигнал преобразуется в цифровой с помощью двух процессов — дискретизация и квантование. Очередь процессов не важна.
Дискретизацией называется процесс регистрации (измерения) значения сигнала через определенные промежутки (обычно равные) времени (рис. 3).
рис. 3

Квантование — это процесс разбиения диапазона амплитуды сигнала на определенное количество уровней и округление значений, измеренных во время дискретизации, до ближайшего уровня (рис. 4).
рис. 4

Дискретизация разбивает сигнал по временной составляющей (по вертикали, рис. 5, слева).
Квантование приводит сигнал к заданным значениям, то есть округляет сигнал до ближайших к нему уровней (по горизонтали, рис. 5, справа).
рис. 5

Эти два процесса создают как бы координатную систему, которая позволяет описывать аудиосигнал определенным значением в любой момент времени.
Цифровым называется сигнал, к которому применены дискретизация и квантование. Оцифровка происходит в аналого-цифровом преобразователе (АЦП). Чем больше число уровней квантования и чем выше частота дискретизации, тем точнее цифровой сигнал соответствует аналоговому (рис. 6).
рис. 6

Уровни квантования нумеруются и каждому уровню присваивается двоичный код. (рис. 7)
рис. 7

Количество битов, которые присваиваются каждому уровню квантования называют разрядностью или глубиной квантования (eng. bit depth). Чем выше разрядность, тем больше уровней можно представить двоичным кодом (рис. 8).
рис. 8.

Данная формула позволяет вычислить количество уровней квантования:
Если N — количество уровней квантования,
n — разрядность, то
Обычно используют разрядности в 8, 12, 16 и 24 бит. Несложно вычислить, что при n=24 количество уровней N = 16,777,216.
При n = 1 аудиосигнал превратится в азбуку Морзе: либо есть «стук», либо нету. Существует также разрядность 32 бит с плавающей запятой. Обычный компактный Аудио-CD имеет разрядность 16 бит. Чем ниже разрядность, тем больше округляются значения и тем больше ошибка квантования.
Ошибкой квантований называют отклонение квантованного сигнала от аналогового, т.е. разница между входным значением и квантованным значением
(
)
Большие ошибки квантования приводят к сильным искажениям аудиосигнала (шум квантования).
Чем выше разрядность, тем незначительнее ошибки квантования и тем лучше отношение сигнал/шум (Signal-to-noise ratio, SNR), и наоборот: при низкой разрядности вырастает шум (рис. 9).
рис. 9

Разрядность также определяет динамический диапазон сигнала, то есть соотношение максимального и минимального значений. С каждым битом динамический диапазон вырастает примерно на 6dB (Децибел) (6dB это в 2 раза; то есть координатная сетка становиться плотнее, возрастает градация).
рис. 10. Интенсивность шумов при разрядности 6 бит и 8 бит

Ошибки квантования (округления) из-за недостаточного количество уровней не могут быть исправлены.
шум квантования

амплитуда сигнала при разрядности 1 бит (сверху) и 4 бит

Аудиопример 1: 8bit/44.1kHz, ~50dB SNR
примечание: если аудиофайлы не воспроизводятся онлайн, пожалуйста, скачивайте их.
Аудиопример 1

Аудиопример 2: 4bit/48kHz, ~25dB SNR
Аудиопример 2

Аудиопример 3: 1bit/48kHz, ~8dB SNR
Аудиопример 3

Теперь о дискретизации.
Как уже говорили ранее, это разбиение сигнала по вертикали и измерение величины значения через определенный промежуток времени. Этот промежуток называется периодом дискретизации или интервалом выборок. Частотой выборок, или частотой дискретизации (всеми известный sample rate) называется величина, обратная периоду дискретизации и измеряется в герцах. Если
T — период дискретизации,
F — частота дискретизации, то
Чтобы аналоговый сигнал можно было преобразовать обратно из цифрового сигнала (точно реконструировать непрерывную и плавную функцию из дискретных, «точечных» значении), нужно следовать теореме Котельникова (теорема Найквиста — Шеннона).
Теорема Котельникова гласит:
Если аналоговый сигнал имеет финитный (ограниченной по ширине) спектр, то он может быть восстановлен однозначно и без потерь по своим дискретным отсчетам, взятым с частотой, строго большей удвоенной верхней частоты.
Вам знакомо число 44.1kHz? Это один из стандартов частоты дискретизации, и это число выбрали именно потому, что человеческое ухо слышит только сигналы до 20kHz. Число 44.1 более чем в два раза больше чем 20, поэтому все частоты в цифровом сигнале, доступные человеческому уху, могут быть преобразованы в аналоговом виде без искажении.
Но ведь 20*2=40, почему 44.1? Все дело в совместимости с стандартами PAL и NTSC. Но сегодня не будем рассматривать этот момент. Что будет, если не следовать теореме Котельникова?
Когда в аудиосигнале встречается частота, которая выше чем 1/2 частоты дискретизации, тогда возникает алиасинг — эффект, приводящий к наложению, неразличимости различных непрерывных сигналов при их дискретизации.
Алиасинг

Как видно из предыдущей картинки, точки дискретизации расположены так далеко друг от друга, что при интерполировании (т.е. преобразовании дискретных точек обратно в аналоговый сигнал) по ошибке восстанавливается совершенно другая частота.
Аудиопример 4: Линейно возрастающая частота от ~100 до 8000Hz. Частота дискретизации — 16000Hz. Нет алиасинга.
Спектральный анализ

Аудиопример 5: Тот же файл. Частота дискретизации — 8000Hz. Присутствует алиасинг
Спектральный анализ

Пример:
Имеется аудиоматериал, где пиковая частота — 2500Hz. Значит, частоту дискретизации нужно выбрать как минимум 5000Hz.
Следующая характеристика цифрового аудио это битрейт. Битрейт (bitrate) — это объем данных, передаваемых в единицу времени. Битрейт обычно измеряют в битах в секунду (Bit/s или bps). Битрейт может быть переменным, постоянным или усреднённым.
Следующая формула позволяет вычислить битрейт (действительна только для несжатых потоков данных):
Битрейт = Частота дискретизации * Разрядность * Количество каналов
Например, битрейт Audio-CD можно рассчитать так:
44100 (частота дискретизации) * 16 (разрядность) * 2 (количество каналов, stereo)= 1411200 bps = 1411.2 kbit/s
При постоянном битрейте (constant bitrate, CBR) передача объема потока данных в единицу времени не изменяется на протяжении всей передачи. Главное преимущество — возможность довольно точно предсказать размер конечного файла. Из минусов — не оптимальное соотношение размер/качество, так как «плотность» аудиоматериала в течении музыкального произведения динамично изменяется.
При кодировании переменным битрейтом (VBR), кодек выбирает битрейт исходя из задаваемого желаемого качества. Как видно из названия, битрейт варьируется в течение кодируемого аудиофайла. Данный метод даёт наилучшее соотношение качество/размер выходного файла. Из минусов: точный размер конечного файла очень плохо предсказуем.
Усреднённый битрейт (ABR) является частным случаем VBR и занимает промежуточное место между постоянным и переменным битрейтом. Конкретный битрейт задаётся пользователем. Программа все же варьирует его в определенном диапазоне, но не выходит за заданную среднюю величину.
При заданном битрейте качество VBR обычно выше чем ABR. Качество ABR в свою очередь выше чем CBR: VBR > ABR > CBR.
ABR подходит для пользователей, которым нужны преимущества кодирования VBR, но с относительно предсказуемым размером файла. Для ABR обычно требуется кодирование в 2 прохода, так как на первом проходе кодек не знает какие части аудиоматериала должны кодироваться с максимальным битрейтом.
Существуют 3 метода хранения цифрового аудиоматериала:
- Несжатые («сырые») данные
- Данные, сжатые без потерь
- Данные, сжатые с потерями
Несжатый (RAW) формат данных
содержит просто последовательность бинарных значений.
Именно в таком формате хранится аудиоматериал в Аудио-CD. Несжатый аудиофайл можно открыть, например, в программе Audacity. Они имеют расширение .raw, .pcm, .sam, или же вообще не имеют расширения. RAW не содержит заголовка файла (метаданных).
Другой формат хранения несжатого аудиопотока это WAV. В отличие от RAW, WAV содержит заголовок файла.
Аудиоформаты с сжатием без потерь
Принцип сжатия схож с архиваторами (Winrar, Winzip и т.д.). Данные могут быть сжаты и снова распакованы любое количество раз без потери информации.
Как доказать, что при сжатии без потерь, информация действительно остаётся не тронутой? Это можно доказать методом деструктивной интерференции. Берем две аудиодорожки. В первой дорожке импортируем оригинальный, несжатый wav файл. Во второй дорожке импортируем тот же аудиофайл, сжатый без потерь. Инвертируем фазу одного из дорожек (зеркальное отображение). При проигрывании одновременно обеих дорожек выходной сигнал будет тишиной.
Это доказывает, что оба файла содержат абсолютно идентичные информации (рис. 11).
рис. 11

Кодеки сжатия без потерь: flac, WavPack, Monkey’s Audio…
При сжатии с потерями
акцент делается не на избежание потерь информации, а на спекуляцию с субъективными восприятиями (Психоакустика). Например, ухо взрослого человек обычно не воспринимает частоты выше 16kHz. Используя этот факт, кодек сжатия с потерями может просто жестко срезать все частоты выше 16kHz, так как «все равно никто не услышит разницу».
Другой пример — эффект маскировки. Слабые амплитуды, которые перекрываются сильными амплитудами, могут быть воспроизведены с меньшим качеством. При громких низких частотах тихие средние частоты не улавливаются ухом. Например, если присутствует звук в 1kHz с уровнем громкости в 80dB, то 2kHz-звук с громкостью 40dB больше не слышим.
Этим и пользуется кодек: 2kHz-звук можно убрать.
Спектральный анализ кодека mp3 с разными уровнями компрессии

Кодеки сжатия с потерям: mp3, aac, ogg, wma, Musepack…
Спасибо за внимание.
UPD:
Если по каким-либо причинам аудиофайлы не загружаются, можете их скачать здесь: cloud.mail.ru/public/HbzU/YEsT34i4c