Гомоскедастичность ошибок это

From Wikipedia, the free encyclopedia

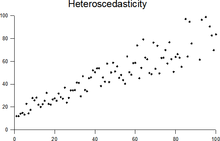
In statistics, a sequence (or a vector) of random variables is homoscedastic () if all its random variables have the same finite variance; this is also known as homogeneity of variance. The complementary notion is called heteroscedasticity, also known as heterogeneity of variance. The spellings homoskedasticity and heteroskedasticity are also frequently used.^[1][2][3]
Assuming a variable is homoscedastic when in reality it is heteroscedastic () results in unbiased but inefficient point estimates and in biased estimates of standard errors, and may result in overestimating the goodness of fit as measured by the Pearson coefficient.

The existence of heteroscedasticity is a major concern in regression analysis and the analysis of variance, as it invalidates statistical tests of significance that assume that the modelling errors all have the same variance. While the ordinary least squares estimator is still unbiased in the presence of heteroscedasticity, it is inefficient and inference based on the assumption of homoskedasticity is misleading. In that case, generalized least squares (GLS) was frequently used in the past.^[4][5] Nowadays, standard practice in econometrics is to include Heteroskedasticity-consistent standard errors instead of using GLS, as GLS can exhibit strong bias in small samples if the actual Skedastic function is unknown.^[6]

Because heteroscedasticity concerns expectations of the second moment of the errors, its presence is referred to as misspecification of the second order.^[7]

The econometrician Robert Engle was awarded the 2003 Nobel Memorial Prize for Economics for his studies on regression analysis in the presence of heteroscedasticity, which led to his formulation of the autoregressive conditional heteroscedasticity (ARCH) modeling technique.^[8]

Definition[edit]

Consider the linear regression equation where the dependent random variable equals the deterministic variable times coefficient plus a random disturbance term that has mean zero. The disturbances are homoscedastic if the variance of is a constant ; otherwise, they are heteroscedastic. In particular, the disturbances are heteroscedastic if the variance of depends on or on the value of . One way they might be heteroscedastic is if (an example of a scedastic function), so the variance is proportional to the value of .

More generally, if the variance-covariance matrix of disturbance across has a nonconstant diagonal, the disturbance is heteroscedastic.^[9] The matrices below are covariances when there are just three observations across time. The disturbance in matrix A is homoscedastic; this is the simple case where OLS is the best linear unbiased estimator. The disturbances in matrices B and C are heteroscedastic. In matrix B, the variance is time-varying, increasing steadily across time; in matrix C, the variance depends on the value of . The disturbance in matrix D is homoscedastic because the diagonal variances are constant, even though the off-diagonal covariances are non-zero and ordinary least squares is inefficient for a different reason: serial correlation.

Examples[edit]

Heteroscedasticity often occurs when there is a large difference among the sizes of the observations.

A classic example of heteroscedasticity is that of income versus expenditure on meals. A wealthy person may eat inexpensive food sometimes and expensive food at other times. A poor person will almost always eat inexpensive food. Therefore, people with higher incomes exhibit greater variability in expenditures on food.

At a rocket launch, an observer measures the distance traveled by the rocket once per second. In the first couple of seconds, the measurements may be accurate to the nearest centimeter. After five minutes, the accuracy of the measurements may be good only to 100 m, because of the increased distance, atmospheric distortion, and a variety of other factors. So the measurements of distance may exhibit heteroscedasticity.

Consequences[edit]

One of the assumptions of the classical linear regression model is that there is no heteroscedasticity. Breaking this assumption means that the Gauss–Markov theorem does not apply, meaning that OLS estimators are not the Best Linear Unbiased Estimators (BLUE) and their variance is not the lowest of all other unbiased estimators.
Heteroscedasticity does not cause ordinary least squares coefficient estimates to be biased, although it can cause ordinary least squares estimates of the variance (and, thus, standard errors) of the coefficients to be biased, possibly above or below the true of population variance. Thus, regression analysis using heteroscedastic data will still provide an unbiased estimate for the relationship between the predictor variable and the outcome, but standard errors and therefore inferences obtained from data analysis are suspect. Biased standard errors lead to biased inference, so results of hypothesis tests are possibly wrong. For example, if OLS is performed on a heteroscedastic data set, yielding biased standard error estimation, a researcher might fail to reject a null hypothesis at a given significance level, when that null hypothesis was actually uncharacteristic of the actual population (making a type II error).

Under certain assumptions, the OLS estimator has a normal asymptotic distribution when properly normalized and centered (even when the data does not come from a normal distribution). This result is used to justify using a normal distribution, or a chi square distribution (depending on how the test statistic is calculated), when conducting a hypothesis test. This holds even under heteroscedasticity. More precisely, the OLS estimator in the presence of heteroscedasticity is asymptotically normal, when properly normalized and centered, with a variance-covariance matrix that differs from the case of homoscedasticity. In 1980, White proposed a consistent estimator for the variance-covariance matrix of the asymptotic distribution of the OLS estimator.^[2] This validates the use of hypothesis testing using OLS estimators and White’s variance-covariance estimator under heteroscedasticity.

Heteroscedasticity is also a major practical issue encountered in ANOVA problems.^[10]
The F test can still be used in some circumstances.^[11]

However, it has been said that students in econometrics should not overreact to heteroscedasticity.^[3] One author wrote, «unequal error variance is worth correcting only when the problem is severe.»^[12] In addition, another word of caution was in the form, «heteroscedasticity has never been a reason to throw out an otherwise good model.»^[3][13] With the advent of heteroscedasticity-consistent standard errors allowing for inference without specifying the conditional second moment of error term, testing conditional homoscedasticity is not as important as in the past.^[6]

For any non-linear model (for instance Logit and Probit models), however, heteroscedasticity has more severe consequences: the maximum likelihood estimates (MLE) of the parameters will usually be biased, as well as inconsistent (unless the likelihood function is modified to correctly take into account the precise form of heteroscedasticity or the distribution is a member of the linear exponential family and the conditional expectation function is correctly specified).^[14][15] Yet, in the context of binary choice models (Logit or Probit), heteroscedasticity will only result in a positive scaling effect on the asymptotic mean of the misspecified MLE (i.e. the model that ignores heteroscedasticity).^[16] As a result, the predictions which are based on the misspecified MLE will remain correct. In addition, the misspecified Probit and Logit MLE will be asymptotically normally distributed which allows performing the usual significance tests (with the appropriate variance-covariance matrix). However, regarding the general hypothesis testing, as pointed out by Greene, “simply computing a robust covariance matrix for an otherwise inconsistent estimator does not give it redemption. Consequently, the virtue of a robust covariance matrix in this setting is unclear.”^[17]

Correction[edit]

There are several common corrections for heteroscedasticity. They are:

• A stabilizing transformation of the data, e.g. logarithmized data. Non-logarithmized series that are growing exponentially often appear to have increasing variability as the series rises over time. The variability in percentage terms may, however, be rather stable.
• Use a different specification for the model (different X variables, or perhaps non-linear transformations of the X variables).
• Apply a weighted least squares estimation method, in which OLS is applied to transformed or weighted values of X and Y. The weights vary over observations, usually depending on the changing error variances. In one variation the weights are directly related to the magnitude of the dependent variable, and this corresponds to least squares percentage regression.^[18]
• Heteroscedasticity-consistent standard errors (HCSE), while still biased, improve upon OLS estimates.^[2] HCSE is a consistent estimator of standard errors in regression models with heteroscedasticity. This method corrects for heteroscedasticity without altering the values of the coefficients. This method may be superior to regular OLS because if heteroscedasticity is present it corrects for it, however, if the data is homoscedastic, the standard errors are equivalent to conventional standard errors estimated by OLS. Several modifications of the White method of computing heteroscedasticity-consistent standard errors have been proposed as corrections with superior finite sample properties.
• Wild bootstrapping can be used as a Resampling method that respects the differences in the conditional variance of the error term. An alternative is resampling observations instead of errors. Note resampling errors without respect for the affiliated values of the observation enforces homoskedasticity and thus yields incorrect inference.
• Use MINQUE or even the customary estimators (for independent samples with observations each), whose efficiency losses are not substantial when the number of observations per sample is large (), especially for small number of independent samples.^[19]

Testing[edit]

Residuals can be tested for homoscedasticity using the Breusch–Pagan test,^[20] which performs an auxiliary regression of the squared residuals on the independent variables. From this auxiliary regression, the explained sum of squares is retained, divided by two, and then becomes the test statistic for a chi-squared distribution with the degrees of freedom equal to the number of independent variables.^[21] The null hypothesis of this chi-squared test is homoscedasticity, and the alternative hypothesis would indicate heteroscedasticity. Since the Breusch–Pagan test is sensitive to departures from normality or small sample sizes, the Koenker–Bassett or ‘generalized Breusch–Pagan’ test is commonly used instead.^{[22][additional citation(s) needed]} From the auxiliary regression, it retains the R-squared value which is then multiplied by the sample size, and then becomes the test statistic for a chi-squared distribution (and uses the same degrees of freedom). Although it is not necessary for the Koenker–Bassett test, the Breusch–Pagan test requires that the squared residuals also be divided by the residual sum of squares divided by the sample size.^[22] Testing for groupwise heteroscedasticity can be done with the Goldfeld–Quandt test.^[23]

Due to the standard use of heteroskedasticity-consistent Standard Errors and the problem of Pre-test, econometricians nowadays rarely use tests for conditional heteroskedasticity.^[6]

List of tests[edit]

Although tests for heteroscedasticity between groups can formally be considered as a special case of testing within regression models, some tests have structures specific to this case.

Generalisations[edit]

Homoscedastic distributions[edit]

Two or more normal distributions, are both homoscedastic and lack Serial correlation if they share the same diagonals in their covariance matrix, and their non-diagonal entries are zero. Homoscedastic distributions are especially useful to derive statistical pattern recognition and machine learning algorithms. One popular example of an algorithm that assumes homoscedasticity is Fisher’s linear discriminant analysis.
The concept of homoscedasticity can be applied to distributions on spheres.^[27]

Multivariate data[edit]

The study of homescedasticity and heteroscedasticity has been generalized to the multivariate case, which deals with the covariances of vector observations instead of the variance of scalar observations. One version of this is to use covariance matrices as the multivariate measure of dispersion. Several authors have considered tests in this context, for both regression and grouped-data situations.^[28][29] Bartlett’s test for heteroscedasticity between grouped data, used most commonly in the univariate case, has also been extended for the multivariate case, but a tractable solution only exists for 2 groups.^[30] Approximations exist for more than two groups, and they are both called Box’s M test.

See also[edit]

• Heterogeneity
• Spherical error
• Heteroskedasticity-consistent standard errors

References[edit]

Further reading[edit]

Most statistics textbooks will include at least some material on homoscedasticity and heteroscedasticity. Some examples are:

• Asteriou, Dimitros; Hall, Stephen G. (2011). Applied Econometrics (Second ed.). Palgrave MacMillan. pp. 109–147. ISBN 978-0-230-27182-1.
• Davidson, Russell; MacKinnon, James G. (1993). Estimation and Inference in Econometrics. New York: Oxford University Press. pp. 547–582. ISBN 978-0-19-506011-9.
• Dougherty, Christopher (2011). Introduction to Econometrics. New York: Oxford University Press. pp. 280–299. ISBN 978-0-19-956708-9.
• Gujarati, Damodar N.; Porter, Dawn C. (2009). Basic Econometrics (Fifth ed.). New York: McGraw-Hill Irwin. pp. 365–411. ISBN 978-0-07-337577-9.
• Kmenta, Jan (1986). Elements of Econometrics (Second ed.). New York: Macmillan. pp. 269–298. ISBN 978-0-02-365070-3.
• Maddala, G. S.; Lahiri, Kajal (2009). Introduction to Econometrics (Fourth ed.). New York: Wiley. pp. 211–238. ISBN 978-0-470-01512-4.

External links[edit]

• Econometrics lecture (topic: heteroscedasticity) on YouTube by Mark Thoma

Гетероскедастичность

Случайной ошибкой
называется отклонение в линейной модели
множественной регрессии:

εi=yi–β0–β1x1i–…–βmxmi

В связи с тем, что
величина случайной ошибки модели
регрессии является неизвестной величиной,
рассчитывается выборочная оценка
случайной ошибки модели регрессии по
формуле:

где ei – остатки
модели регрессии.

Термин
гетероскедастичность в широком смысле
понимается как предположение о дисперсии
случайных ошибок модели регрессии.

При построении
нормальной линейной модели регрессии
учитываются следующие условия, касающиеся
случайной ошибки модели регрессии:

6) математическое
ожидание случайной ошибки модели
регрессии равно нулю во всех наблюдениях:

7) дисперсия случайной
ошибки модели регрессии постоянна для
всех наблюдений:

между значениями
случайных ошибок модели регрессии в
любых двух наблюдениях отсутствует
систематическая взаимосвязь, т. е.
случайные ошибки модели регрессии не
коррелированны между собой (ковариация
случайных ошибок любых двух разных
наблюдений равна нулю):

Второе условие

означает
гомоскедастичность (homoscedasticity – однородный
разброс) дисперсий случайных ошибок
модели регрессии.

Под гомоскедастичностью
понимается предположение о том, что
дисперсия случайной ошибки βi является
известной постоянной величиной для
всех наблюдений.

Но на практике
предположение о гомоскедастичности
случайной ошибки βi или остатков модели
регрессии ei выполняется не всегда.

Под гетероскедастичностью
(heteroscedasticity – неоднородный разброс)
понимается предположение о том, что
дисперсии случайных ошибок являются
разными величинами для всех наблюдений,
что означает нарушение второго условия
нормальной линейной модели множественной
регрессии:

Гетероскедастичность
можно записать через ковариационную
матрицу случайных ошибок модели
регрессии:

Тогда можно
утверждать, что случайная ошибка модели
регрессии βi подчиняется нормальному
закону распределения с нулевым
математическим ожиданием и дисперсией
G2Ω:

εi~N(0; G2Ω),

где Ω – матрица
ковариаций случайной ошибки.

Если дисперсии
случайных ошибок

модели регрессии
известны заранее, то проблема
гетероскедастичности легко устраняется.
Однако в большинстве случаев неизвестными
являются не только дисперсии случайных
ошибок, но и сама функция регрессионной
зависимости y=f(x), которую предстоит
построить и оценить.

Для обнаружения
гетероскедастичности остатков модели
регрессии необходимо провести их анализ.
При этом проверяются следующие гипотезы.

Основная гипотеза
H0 предполагает постоянство дисперсий
случайных ошибок модели регрессии, т.
е. присутствие в модели условия
гомоскедастичности:

Альтернативная
гипотеза H1 предполагает непостоянство
дисперсиий случайных ошибок в различных
наблюдениях, т. е. присутствие в модели
условия гетероскедастичности:

Гетероскедастичность
остатков модели регрессии может привести
к негативным последствиям:

1) оценки неизвестных
коэффициентов нормальной линейной
модели регрессии являются несмещёнными
и состоятельными, но при этом теряется
свойство эффективности;

2) существует большая
вероятность того, что оценки стандартных
ошибок коэффициентов модели регрессии
будут рассчитаны неверно, что конечном
итоге может привести к утверждению
неверной гипотезы о значимости
коэффициентов регрессии и значимости
модели регрессии в целом.

Гомоскедастичность

Гомоскедастичность
остатков означает, что дисперсия каждого
отклонения одинакова для всех значений
x. Если это условие не соблюдается, то
имеет место гетероскедастичность.
Наличие гетероскедастичности можно
наглядно видеть из поля корреляции.

Т.к. дисперсия
характеризует отклонение то из рисунков
видно, что в первом случае дисперсия
остатков растет по мере увеличения x, а
во втором – дисперсия остатков достигает
максимальной величины при средних
значениях величины x и уменьшается при
минимальных и максимальных значениях
x. Наличие гетероскедастичности будет
сказываться на уменьшении эффективности
оценок параметров уравнения регрессии.
Наличие гомоскедастичности или
гетероскедастичности можно определять
также по графику зависимости остатков
от теоретических значений
.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Время на прочтение
20 мин

Количество просмотров 4.5K

Мы школа онлайн-образования, которая уже три года делает курсы по Data Science и разработке. Одна из наших целей — собрать коммьюнити классных специалистов и делиться крутыми и неочевидными знаниями. Так был рождён Симулятор ML — место, в котором начинающие и опытные специалисты решают задачи разной сложности, разрабатывают проекты в командах, осваивают новые инструменты, развивают продуктовое мышление и постоянно растут в профессии.

А, как это свойственно коммьюнити, горящему идеей, студенты и авторы хотят делиться своими инсайтами и открытиями, которые дадут свежий взгляд на устоявшиеся практики. Сегодня хотим поделиться статьей автора Симулятора ML Богдана Печёнкина о том, как лучше использовать анализ ошибок для разработки ML систем.

Введение

Всем привет! Меня зовут Богдан Печёнкин. Я Senior ML Engineer в компании BrandsGoDigital и больше всего известен как автор Симулятора ML.

Мой первый пост на Хабре посвящался 10 первым ошибкам в карьере ML-инженера, что тесно связано с сегодняшней темой. Анализируя свои и чужие ошибки, Я пришёл к выводу, что один из самых недооценённых этапов в построении ML систем — это, как ни странно, анализ ошибок. Он даёт глубокое понимание не только наших моделей, но и данных и метрик, с которыми мы работаем. Сегодня Я хочу поделиться с вами тем, почему анализ ошибок так важен, каким образом его проводить и как он может помочь вам в дизайне и разработке более надёжных и эффективных ML продуктов.

Данная статья написана по мотивам главы «Error Analysis» из книги «Machine Learning System Design with end-2-end examples», которую Я писал вместе с Валерой Бабушкиным и Арсением Кравченко, авторами книги.

^{Certainly, coming up with new ideas is important.
But even more important, to understand the results.
— Ilya Sutskever, сооснователь OpenAI}

Что такое анализ ошибок?

Каждая модель машинного обучения несовершенна и имеет свои границы применимости: на одних данных она работает лучше, на других хуже, а где-то — совсем плохо.

^{All models are wrong, but some are useful.
– George Box, британский статистик}

Определяя, как ведёт себя текущая модель в каждом отдельном кейсе, «в какую сторону» ошибается, мы получаем неоценимые подсказки, какие новые признаки нам нужны, какие преобразования целевой переменной попробовать, каких данных нам не хватает и так далее. Таким образом, анализ ошибок — это важнейший этап построения модели перед проведением A/B экспериментов, её тестированием в боевых условиях.

Но почему нам мало обычной кросс-валидации?

Когда мы считаем метрику на отложенной выборке, мы, по сути, агрегируем ошибки со всех объектов в одно число. Если у нас кросс-валидация вместо отложенной выборки и несколько метрик вместо одной, мы всё ещё агрегируем разного рода ошибки со всех объектов в некую «среднюю температуру по больнице».

Например, считаем MAE, WAPE, wQL в регрессии, или LogLoss в классификации. 

Aгрегированная метрика не показывает, как ошибка распределяется по разным объектам, какое у неё распределение, а тем более — что нужно поменять в собранной ML системе, чтобы скорректировать ошибку (какие у метрики «драйверы роста»?). 

Метрики сообщают нам, что стало либо «хуже», либо «лучше», но подсказок, что делать дальше, из-за чего результат именно такой и что надо менять в ML системе, они не дадут.

Анализ ошибок — процесс прямо противоположный подсчёту метрики: агрегированную метрику мы разбиваем на компоненты — и анализируем их в совокупности. Это даёт нам полную картину: где и как система проявляет себя и какие встречаются паттерны в разных сегментах объектов отложенной выборки.

Мне нравится проводить параллель с алгоритмом back-propagation: мы пробрасываем градиент ошибки от самых последних слоёв нейросети к самым первым, соответствующим образом обновляя каждый компонент сети. Анализ ошибок — это ровно такое же «взятие градиента метрики», но на этот раз для всего ML пайлпайна.

План рассказа

1. Введение в остатки и псевдоостатки

• Определение понятий «остатков» и «псевдоостатков» в контексте регрессии и классификации.

1. Визуальный и статистический анализ остатков

• Методы визуализации распределения остатков.

• Применение статистических тестов для оценки смещения, гетероскедастичности и нормальности остатков.

• Что такое fairness и его роль при принятии решения о деплое модели.

1. Анализ кейсов работы модели

• Разбор наилучших, наихудших и крайних сценариев работы модели.

• Моделирование ошибок с помощью Adversarial Validation

1. Анализ ошибок в нестандартных задачах машинного обучения

• Как проводится анализ ошибок в других областях машинного обучения, отличных от стандартных регрессии и классификации.

Остатки и псевдоостатки

Остатки (residuals)

Что формально мы имеем в виду, говоря «ошибки»? Введём понятие «остатков».

Остатки регрессии представляют собой разницу между фактическим значением целевой переменной и предсказанным значением:

residuals = y_true – y_pred

Остаток — это буквально «то, что осталось недопредсказанным», часть значения таргета, которую модель не смогла объяснить с учётом имеющихся признаков.

Псевдоостатки в классификации

Что может служить остатками в бинарной классификации? Да, мы можем также смотреть на разницу между предсказанной вероятностью (скажем, 0.42) и метками класса 0 и 1. Мы уже упорядочим объекты по размеру их ошибки, но будет ли это самым информативным способом их анализа? Более естественно оперировать слагаемыми LogLoss, поскольку так мы учитываем ещё и вклад каждой ошибки в общую метрику, её вес.

То слагаемые (y log(p) + (1−y) log(1−p)) представляют собой псевдоостатки. Так мы не просто считаем недопредсказанную часть целевой переменной, но ещё и «взвешиваем» объекты пропорционально их влиянию на метрику.

Псевдоостатки в общем случае

Если задуматься, большинство метрик, которые мы используем в машинном обучении (и абсолютно все лоссы) — представляют собой усреднение ошибок по каждому объекту, посчитанных тем или иным образом (вспомните, какие есть исключения из правила?).

• Mean Squared Error (MSE):
  ∑ (y_true — y_pred)2 → sign(y_true – y_pred) * (y_true – y_pred)2

• Mean Absolute Error (MAE):
  ∑ |y_true — y_pred| → y_true – y_pred

• Mean Absolute Percentage Error (MAPE):
  ∑ |y_true — y_pred| / y_true → 1 – y_pred / y_true

Часто возникает путаница между остатками и псевдоостатками, особенно у начинающих специалистов на первых собеседованиях, когда разговор заходит о том, на что обучаются деревья в градиентном бустинге и почему он, собственно, градиентный.

Правильный ответ: каждое дерево ансамбля обучается на градиент функции потерь, или, иначе говоря, на градиент псевдоостатков.

Визуализация остатков

Распределение остатков

Допустим, мы рассчитали остатки. Основываясь на них, какие выводы мы можем сделать? (Примечание: здесь и далее будем использовать термины «остатки», «псевдоостатки» и «ошибки» как взаимозаменяемые). 

Для начала мы анализируем их в совокупности — смотрим на их распределение. Распределение остатков позволяет нам «проверить на прочность» наши базовые предположения (assumptions) относительно данных, модели и других компонентов системы.

К примеру, вот наш коллега обучил модель прогноза спроса, визуализировал распределение остатков.

import seaborn as sns
import matplotlib.pyplot as plt


plt.figure()
sns.histplot(residuals, kde=True)
plt.title('Distribution of Residuals')
plt.xlabel('Residuals')
plt.ylabel('Frequency')
plt.show()

И увидел один из графиков ниже:

Какие выводы сделал бы наш коллега, посмотрев на эти три картинки?

• Остатки распределены практически нормально (как мы и хотели):
  ✓ assumptions are met!

• Распределение нормальное, но с большим хвостом влево (недопредсказания):
  ✗ assumptions are not met!

• Распределение не нормальное и имеет две моды:
  ✗ assumptions are not met!

Какие шаги по улучшению модели он бы предпринял дальше?

1. В первом случае, наш коллега, вероятно, оставил бы модель без изменений, однако для полной уверенности перешёл бы к статистическим тестам и проверке скедастичности.

2. Здесь наш коллега возможно бы использовал логарифмирование таргета перед квантильной регрессией, чтобы минимизировать влияние больших значений.

3. В этом случае, возможно, стоит перейти к более сложным методам, таким как бустинг, чтобы уловить пропущенные моделью паттерны.

Обычно мы предполагаем, что остатки, если они в точности не подчиняются нормальному распределению, как минимум должны быть унимодальными и с центром вокруг нуля (не иметь выраженного сдвига: перепредсказания или недопредсказания). Кроме того, мы стремимся избегать ситуаций, когда остатки имеют сильно вытянутые хвосты, что обычно указывает на наличие существенных выбросов.

Ясно, что мы не хотим проверять эти свойства каждый раз вручную, изучая графики распределений глазами. Автоматизировать проверку остатков помогут статистические тесты, которые можно запускать после каждого запуска обучающего пайплайна. Так, в случае возникновения проблем (например, отвалился источник данных, либо новая версия модели оказалась выраженно хуже предыдущей).

Статистические гипотезы

Свойства распределения можно формулировать в виде статистических гипотез. Так, чтобы оценить наличие или отсутствие смещения (bias), мы сравниваем среднее у распределения остатков с нулём, используя t-тест для одной выборки. Тест учтёт их разброс и отвергнет гипотезу о несмещённости остатков, только если наблюдаемое смещение выходит за рамки погрешности.

Подобным образом, мы можем оценить нормальность распределения, используя критерий Колмогорова-Смирнова. Очевидно, здесь глаз человека даже менее надёжен, чем стат. тест, сравнивающий «отклонение» от нормального распределения численно.

На выходе статистического критерия мы получаем p-value — вероятность встретить наблюдаемое значение статистики или более экстремальное при условии, что нулевая гипотеза верна.

• В случае смещения нулевая гипотеза: остатки не имеют смещения.

• В случае нормальности нулевая гипотеза: остатки распределены нормально.

Для принятия решения мы руководствуемся уровнем значимости α (например, 5%) или, иначе, уровнем ошибки I рода. Уровень значимости сообщает, начиная с какой степени «невероятности» нулевой гипотезы мы её отвергнем.

Гетероскедастичность

Ещё два свойства распределения, которые мы можем оценивать, — гомоскедастичность и гетероскедастичность. Гомоскедастичность (homo + scedasticity) — буквально «одинаковый разброс». Соответственно, гетероскедастичность (hetero + scedasticity) — «разный разброс».

О чём речь в случае остатков? Мы хотим знать, насколько сильно дисперсия остатков варьируется для разных значений целевой переменной. Наблюдаем ли мы, что на малых значениях остатки маленькие, а с ростом таргета они растут (или наоборот)? Наблюдаем ли мы, что на малых и больших значениях таргета (на краях) остатки имеют больший разброс, чем в середине (в основной массе распределения таргетов)? Или остатки везде однородные?

Обратите внимание, что скедастичность остатков (и псевдоостатков) может кардинально отличаться при переходе от одной метрики к другой (например, от разностей таргетов и предиктов — к квадратам разностей), поскольку каждая метрика по-своему взвешивает разные ошибки в зависимости от их знака и величины.

Для гомоскедастичности существует несколько статистических тестов: 

• Bartlett’s test

• Levene’s test

• Fligner-Killeen’s test

Все они доступны в пакете scipy.stats. Это семейство тестов называют ANOVA-тестами (ANalysis Of VAriance). Каждый них принимает на вход набор подвыборок и оценивает, насколько валидно предположение, что каждая из подвыборок имеет одну и ту же дисперсию. 

Для нас подвыборками будут служить бины из остатков, разбитых по мере увеличения таргета. Например, бьём таргет на 5 бинов по пороговым квантилям: 0.2, 0.4, 0.6, 0.8.

Diagnostic Plots

Diagnostic Plots представляют собой ещё один метод для анализа распределения остатков в дополнение к статистическим тестам. Это набор специфических визуализаций остатков и предсказаний целевой переменной в разных разрезах.

Чаще всего эти визуализации используются в линейных моделях для проверки их основных предположений: несмещённости, нормальности и гомоскедастичности.

1. Residuals vs. Fitted

На этом графике мы визуализируем остатки против предсказанных значений целевой переменной. Он позволяет понять характер смещения: распределено ли оно равномерно по всем предсказаниям (тогда наблюдаем прямую линию, см. левый график внизу), либо имеет значимую неравномерность (например, на втором графике ниже — остатки на очень больших и очень маленьких прогнозах резко отрицательные).

2. Normal Q-Q Plot

Q-Q Plot — это способ визуализации отклонения от заданного распределения. Для его отрисовки мы визуализируем, какие теоретические квантили были бы у нашей выборки (остатков), будь она взята из предполагаемого распределения, и какие квантили на самом деле, поэтому график называется Q-Q (Quantile-Quantile) Plot.

Чем больше реальные значения отклоняются от прямой линии, тем менее вероятно, что выборка взята из этого распределения. Частным случаем служит Normal Q-Q Plot, где мы сравниваем выборку с нормальным распределением (ещё один способ оценить, распределены ли остатки нормально — и, если нет, в каких конкретно значениях).

3. Scale-Location Plot

Scale-Location Plot помогает в оценке скедастичности распределения (гетероскедастичности либо гомоскедастичности, с которыми мы уже успели познакомиться). Для его отрисовки мы берём предсказания против корня модуля стандартизированных остатков. 

Если распределение одинаково для всех предсказаний (иметь одного масштаба отклонение), то остатки считаются гомоскедастичными относительно предсказанного значения. Если мы видим растущий или убывающий тренд, другую неоднородность — значит, присутствует гетероскедастичность.

4. Cook’s Distance Plot

Cook’s Distance является мерой влияния каждого отдельного наблюдения на модель в целом. Она помогает выявить наиболее влиятельные объекты в данных, что может быть полезно при проверке модели на наличие аномалий или выбросов, которые могут сильно искажать её предсказания.

Для построения Cook’s Distance Plot визуализируются предсказанные значения против расстояния Кука. В каждой точке графика расстояние Кука представляет собой сумму отклонений предсказаний, полученных при удалении данного наблюдения, к предсказаниям, полученным на всем наборе данных.

Таким образом, если какие-то наблюдения имеют высокое значение расстояния Кука, это означает, что удаление этих точек может значительно изменить модель, поэтому они могут считаться влиятельными.

Diagnostic Plots

Эти четыре типа графиков часто используются вместе для полного визуального анализа остатков и проверки предположений модели. Они помогают понять, хорошо ли модель работает, есть ли какие-либо систематические ошибки, а также позволяют определить возможные проблемы с распределением остатков и наличием выбросов.

Существуют готовые пакеты отрисовки всех четырёх графиков. Например, в языке программирования R они входят в стандартную библиотеку и доступны вызовом функции plot на уже обученной линейной модели.

Fairness

Когда мы улучшаем модель, мы не хотим, чтобы метрика росла на одних сегментах пользователей и падала на других (даже если в среднем она оказывается выше). Бенефиты от прироста метрики легко могут быть перечёркнуты негативным User Experience «пострадавшей» группы пользователей — и за счёт совсем других метрик.

Чтобы этого избежать, мы должны смотреть не только на то, выросла ли метрика или упала, но и на то, как она размазана по всем объектам (например, по всем пользователям или по всем товарам). Для этого вводят концепт Fairness (в переводе с английского, «справедливость»).

Идеализированный пример:

Два ML инженера разрабатывали улучшение бейзлайн-модели. Оба из них получили сокращение MAE (Mean Absolute Error) на 20%. Как их рассудить? Чью модель выкатывать на A/B тест? Первая модель дала небольшой равномерный прирост для всех объектов. Вторая модель сильно сократила ошибку на половине объектов и немного увеличила на другой половиние.

Как мы видим из примера, одного и того же улучшения метрики можно добиться разными способами. Мы предпочтём скорее, чтобы метрика везде выросла понемногу, нежели чтобы где-то она сильно выроста, а где-то просела. Поэтому даже если суммарная метрика выросла, этого ещё не достаточно, чтобы принять решение, что новая модель лучше и её нужно катить в прод!

Аналогично можно представить, что неравномерный прирост (unfair uplift) был получен по ключевой онлайн-метрике и во время A/B теста (эксперимента на реальных пользователях), что также может послужить сигналом, что данную модель не стоит раскатывать на остальном трафике.

Gini Index

В экономике для количественной оценки «справедливости» распределения часто используют Gini-индекс, особенно при анализе распределения доходов населения определённой страны.

Gini-индекс варьируется от 0 до 1, где 0 обозначает идеальное равенство (т. е. все значения равны), а 1 обозначает максимальное неравенство (одно значение максимально, все остальные минимальны). Чем выше индекс Gini, тем более несправедливым считается распределение.

То же касается и распределения ошибок. Встретить случай, когда малое число объектов вносит львиную долю вклада в ошибку, для нас нежелательно. Почти во всех случаях для нас предпочтительнее «размазать» ошибку по разным объектам (или, скажем, для некой группы особых объектов построить отдельную модель), чем встретить явный перекос.

Достичь полностью равномерного распределения ошибок невозможно, и к этому нет смысла стремиться как к самоцели, так же как и к равномерному распределению доходов. Однако, кроме точности предсказания, оценивать, что Gini Index не снижаеся более чем на X%, — это полезно. Здесь нам главное избегать вырожденных случаев.

Кроме того, мы можем добавить и более простые эвристики, которые в лоб считают, на какой доле объектов мы увеличили качество, на какой просадили (по разнице знаков остатков).

Best Case / Worse Case / Corner Case

Изучив остатки в их совокупности и проанализировав их верхнеуровневые свойства, мы спускаемся на один уровень ниже. А именно начинаем искать в них паттерны. Так мы понимаем, «в какую сторону» нужно корректировать модель или остальные компоненты пайплайна обучения, когда что-то сломалось.

Best Case & Worst Case

Зная остатки, можно проанализировать поведение модели в лучших и худших сценариях. Для этого мы выводим топ-20, топ-50, топ-100 объектов по величине остатков и ищем в них общие паттерны.

• Например, если мы прогнозируем число заказов в приложении доставки и видим, что наша модель систематически недооценивает спрос на веганскую и вегетарианскую еду, а также на блюда, которые попадали под промоакции. Мы пришли к выводу, что в качестве признаков нужно добавить «тип кухни» и, кроме того, подключить источник данных, содержащий «промо календарь».

• Другой случай: мы попробовали построить модель прогноза на Трансформерах, распределение её остатков принципиально отличается от текущей модели в проде. Метрика лучше. Мы хотим с нуля проанализировать, на каких блюдах и на каких пользователях прогноз спроса точнее всего. Где пролегает текущая «граница применимости» текущей модели, чтобы раскатить её в первую очередь на той части данных, где она чувствует себя лучше всего. Для этого мы выводим топ-1000, топ-5000, топ-10,000 объектов с наименьшей ошибкой.

Одним из наилучших методов является автоматическое сохранение объектов с наибольшими ошибками (debug samples) в качестве артефактов при каждом запуске обучения. Благодаря этому мы сможем быстро и легко заметить общие паттерны (сходу получаем багаж идей для улучшения пайплайна) и в будущем проследить, как менялся характер ошибки по мере выкатки новых улучшений и добавления новых признаков.

Corner Case Analysis

В то время как анализ лучших и худших случаев направлен на выявление общих паттернов на основе остатков, corner case analysis фокусируется на том, какие остатки характерны для объектов с конкретными особенностями.

• Так, если у остатков разный разброс на разных по масштабу таргетах (например, мы предсказываем выручку и наибольший вклад делают ошибки в предсказании наименьших значений выручки, близких к нулю), тогда нам стоит вывести группу объектов с наименьшими таргетами, посмотреть на их остатки.

• Аналогично, нам может быть любопытно, какие ошибки в районах или ресторанах, которые недавно подключены к нашему сервису (так называемся «проблема холодного старта»: например, как заполнять пропуски в товарах, для которых нет достаточной истории продаж?).

• Или какие ошибки на пользователях из определённого сегмента, например, присоединившиеся в наш сервис после того, как увидели рекламу на маркетплейсе KarpovExpress; или какие ошибки предсказания у самых популярных ресторанов и блюд. Во всех этих случаях нам нужно отфильтровать нужную подвыборку данных и проанализировать её остатки в изоляции.

Случай из жизни: когда мы строили сервис динамического ценообразования в одном крупном маркетплейсе, то столкнулись с забавной проблемой, которую удалось оперативно решить благодаря анализу ошибок. 

Наша система работала по следующему принципу: ML-модель учится предсказывать спрос для товаро-дня с учётом множества факторов, среди которых есть факторы цены и их производные (скидки, наценки, разницы с ценами конкурентов и т.д.). Для дальнейшего использования модели, мы подставляли разные цены (досчитывая зависимые от цены факторы) и оценивали спрос для каждого прайс-поинта. 

Например, -10%, -9%, -8%, …, +9%, +10% от последней наценки.

Чтобы понять, делает ли обученная модель осмысленные предсказания, мы смотрим на графики кривой эластичности по каждому товару. Если не вдаваться в детали, эластичность – это и есть зависимость спроса от цены, которую мы получаем подставляя цены и делая прогноз для новой точки. 

Ожидаемое поведение: чем выше цена, тем ниже спрос, и наоборот. Эластичные товары имеют “более крутую” кривую: малейшее увеличение цены ведёт к сильному спаду спроса, и наоборот. Неэластичные имеют более “плоскую” зависимость: мы можем наглеть в цене, а спрос – не сильно упадёт (значит, заработаем больше денег).

Однако, начав анализ первых графиков эластичности, мы обнаружили вот какую картину:

Как вы понимаете, это вообще вышло за рамки нашего ожидания. Из-за чего так произошло? Есть ли у вас догадки?

Дело в том, что в качестве модели прогноза у нас был CatBoost и обучался он на большом числе товаров. Как мы знаем, градиентный бустинг (начиная с LightGBM) делает квантизацию всех признаков перед обучением (разбивая на бины +- одинаковых размеров), таким образом, с десятков уникальных значений по каждому признаку мы переходим, например, к 256 или 512 значениям. Это обеспечивает ускорение обучения за счёт потери части сигнала в признаках.

Таким образом, даже несмотря на то, что цена и признаки на основе цены выходили в топ по важности, тем не менее, модель была физически «нечувствительна» к малым вариациям цены, на которых мы затем её хотели применять.

Решение: повысить гранулярность квантизации (скажем, до 4096 или 8192). В результате мы получили графики с уже осмысленным «гладким» возрастанием спроса по мере уменьшением цены.

Моделируем ошибку

Но вернёмся к worst-case анализу.

Допустим, мы выделили группу объектов, на которых модель показала наихудшие результаты. Как нам это знание использовать для определения «градиента» ML системы, поиска наискорейшего шага её улучшения? Смотреть на ошибки, конечно, можно и вручную, особенно когда признаков мало, а объектов выделено немного. Но что если того и того становится слишком много?

Наверняка, есть пути автоматизировать и этот процесс, ведь мы инженеры…

И такой приём действительно есть: Что, если использовать одну модель машинного обучения для предсказания ошибок другой модели машинного обучения?

Adversarial Validation

Adversarial Validation — приём, который мы сегодня применим для выделения паттернов в ошибках. Он происходит от соревнований по машинному обучению на Kaggle. В соревнованиях участники стремятся улучшить качество своих моделей, используя наиболее умные и сложные методы. Часто они сталкиваются с проблемой, когда их модели хорошо работают на обучающем наборе данных, но плохо на отложенной выборке (тестовом наборе данных, целевые переменные, для которых надо предсказать). 

Почему так происходит?

1. Первая возможная причина: модели могут переобучаться на обучающем наборе данных (особенно если не предусмотреть надёжную валидацию, на основе которой мы не просто смотрим, подросла ли метрика или нет, но и учитываем чувствительность выбранной схемы.

2. Вторая возможная причина: и от этого куда труднее спастись — тестовый набор данных может существенно отличаться от обучающего набора данных. Именно это называется «расхождением распределений».

Чтобы оценить, насколько два распределения похожи или не похожи (и в каких признаках именно), мы можем обучить отдельную модель-классификатор. Все объекты обучающей выборки примут класс 0, а все объекты тестовой — класс 1.

Если разница между выборками несущественна (например, ROC-AUC ≈ 0.5), это означает, что распределения обучающего и тестового набора данных схожи.

Если между выборками большая разница (например, ROC-AUC > 0.6), тогда выборки уже различимы, мы можем из обучающей выборки выделить самые похожие на тест объекты и использовать их как отложенную валидационную выборку.

Именно это и называется Adversarial Validation.

Граница применимости модели

Если задуматься, этот подход можно применить к любым двум выборкам, чтобы выявить между ними отличия. Более того, поняв, что две группы объектов различимы, мы можем заглянуть в Feature Importance модели (а выбор подходящей модели для анализа ошибок — отдельный разговор) и узнать, в каких именно признаках различие между выборками себя выдаёт.

Как Adversarial Validation «завести» для анализа ошибок? Какие две выборки у нас есть?

1. Отбираем топ ошибок модели (например, топ-1000 или топ-10%). Это наши worst-cases.

2. Присваиваем им класс 1, а всем остальным («здоровым») объектам — класс 0.
   Наши выборки: «хорошо прогнозируемые» и «плохо прогнозируемые».

3. Строим вспомогательную модель-классификатор, которая пытается предсказать, является ли объект «плохо прогнозируемым». Эта модель будет использовать признаки объектов (возможно даже куда больший набор, чем тот, на основе которого мы обучаем основную модель), чтобы понять, чем так отличаются «плохие объекты».

4. Если модель классифицирует «хорошо прогнозируемые» и «плохо прогнозируемые» объекты с достаточной точностью (ROC-AUC > 0.6), то это говорит о том, что ошибка модели зависит от значений некоторых признаков.

5. Анализируем важность признаков в этой модели (например, по SHAP-values), чтобы определить, какие признаки сильнее всего влияют на ошибки основной модели. 

Это подскажет, паттерны в каких признаках сейчас основная модель не понимает чаще всего. Это направляет вектор нашего поиска новых признаков (и их трансформаций), обогащения датасета и, возможно, модификацией loss-функции или процесса предобработки целевых переменных.

Анализ ошибок за пределами регрессии и классификации

Анализ ошибок не ограничивается простыми задачами классификации или регрессии и столь же активно используется в других областях машинного обучения. Давайте посмотрим шире не то, что может играть роль остатков в других доменах.

1. Сегментация изображений (Image Segmentation). В области компьютерного зрения задача сегментации изображений заключается в выделении определенных областей или объектов на изображении, соответствующих определённым классам. «Остатками» здесь является разница предсказанной маски сегментации (контура объекта) и истинной. С помощью наложения масок или использование цветовых карт, мы можем быстро определить области изображения, где модель допускает ошибки (например, плохо отделяет мелкие детали, волосы или ошибочно выделяет зеркальное отражение). 

С другой стороны, мы можем оперировать не пикселями, а самими картинками: просматривать топ-N изображений с самой большой ошибкой после обучения и анализировать, есть ли в них какой-либо паттерн. Так, например, модель может некорректно работать на картинках с тёмным освещением, с зеркалами, с большим количеством объектов или на специфическом фоне. Обнаруженные закономерности подсказывают, каких данных (на какие паттерны) нужно добавить в выборку больше, либо как нужно модифицировать loss-функцию (чтобы модель была внимательнее на границах масок сегментации).

2. Генерация звука (Voice Cloning). В задачах генерации аудио, таких как генерация голоса или Text-to-Speech (TTS), важным элементом анализа ошибок является использование Attention Plots. Они показывают, на какие части исходного текста модель обращала особое внимание при генерации каждого отдельного звука. Это позволяет выявить неправильные соответствия и улучшить качество генерации. 

Кроме того, существует подход Guided Attention, который дополнительно штрафует модель за отклонение от линейного отображения позиции символа в позицию звука. Как мы помним, анализ ошибок служит в том числе и для проверки на прочность наших предположений о модели (model assumptions).

3. Рекомендательные и поисковые движки. Ещё пример — рекомендательные системы. Вместо предсказанной одной цифры, как в классификации и регрессии, мы имеем рейтинг объектов, которые мы порекомендовали бы пользователю. Существует несколько метрик, сравнивающих гипотетическую выдачу и то, что пользователь реально кликал/покупал/смотрел.

Одна из таких метрик — NDCG. Несмотря на отличный от регрессии и классификации формат «предсказаний», эта метрика усредняет качество рекомендации по всем объектам. Значит, ничего не мешает посмотреть на best/worst/corner кейсы по аналогии с регрессией и классификацией: узнать, какие запросы наша система «понимает» хуже всего; как ведёт себя на пользователях с длинной и короткой историей запросов (или просмотров); нет ли очевидных проблем, например, зацикливания на том, что пользователь уже покупал или смотрел?

Вывод

Как мы увидели, анализ ошибок играет ключевую роль в процессе создания и оптимизации ML системы. Это не просто этап «для галочки» перед деплоем, который можно пропустить. Напротив, анализ ошибок стоит в самом начале итеративного цикла улучшения и усложнения модели. 

Когда мы создали baseline с минимальным датасетом, анализ ошибок позволяет нам определить её сильные и слабые стороны, а также выявить моменты, которые требуют оптимизации (что далеко не всегда требует сразу заводить бустинги или BERTы). Этот анализ даёт нам понимание о том, какие улучшения модели следует внести в следующем цикле. Так, на каждой итерации, мы заменяем модель на более сложную, добавляем новые факторы в датасет, анализируем ошибки и сравниваем их с ошибками предыдущей версии. 

Этот цикл дотошного анализа текущих результатов для определения вектора следующего наискорейшего шага в улучшении ML системы – и, непосредственно, внесения изменений в пайплайн — вот, из чего состоит реальная работа ML инженера на практике.

Анализ ошибок — это лишь часть задач инженера по машинному обучению. Кроме анализа ошибок в повседневной работе мы разрабатываем метрики, собираем датасеты, обучаем сами модели, деплоим и тестируем ML-сервисы, проводим A/B-тесты и много чего ещё, порой выходящего за рамки теоретического понимания, как работают модели машинного обучения. 

Гомоскедастичность – допущение линейной регрессии об «одинаковости» Дисперсии (Variance). Иными словами, разность между реальным Y_pred и предсказанным Y_actual значениями, скажем, Линейной регрессии (Linear Regresion) остается в определенном известном диапазоне, что позволяет в принципе использовать такую Модель (Model). В случае такого единообразия ошибок Наблюдения (Observation) с большими значениями будут иметь то же влияние на предсказывающий Алгоритм (Algorithm), что и наблюдения с меньшими значениями:

Линейная регрессия базируется на предположении, что для всех случаев ошибки будут одинаковыми и с очень малой дисперсией.

Пример. У нас есть две переменные – высота дерева навскидку и реальный его рост. Естественно, по мере увеличения оценочной высоты реальные тоже растут. Итак, мы подбираем модель линейной регрессии и видим, что ошибки имеют одинаковую дисперсию:

Прогнозы почти совпадают с линейной регрессией и имеют одинаковую известную дисперсию повсюду. Кроме того, если мы нанесем эти остатки на ось X, мы увидим их вдоль прямой линии, параллельной оси X. Это явный признак гомоскедастичности.

Когда это условие нарушается, в модели присутствует Гетероскедастичность (Heteroscedasticity). Предположим, что для деревьев с меньшей приблизительной высотой разность между прогнозируемым и реальным значением меньше, чем для высоких представителей флоры. По мере увеличения высоты дисперсия в прогнозах увеличивается, что приводит к увеличению значения ошибки или Остатка (Residual). Когда мы снова построим график остатков, то увидим типичную коническую кривую, которая четко указывает на наличие гетероскедастичности в модели:

Гетероскедастичность – это систематическое увеличение или уменьшение дисперсии остатков в диапазоне независимых переменных. Это проблема, потому нарушается базовое предположение о линейной регрессии: все ошибки должны иметь одинаковую дисперсию.

Как узнать, присутствует ли гетероскедастичность?

Проще говоря, самый простой способ узнать, присутствует ли гетероскедастичность, – построить график остатков. Если вы видите какую-либо закономерность, значит, есть гетероскедастичность. Обычно значения увеличиваются, образуя конусообразную кривую.

Причины гетероскедастичности

• Есть большая разница в переменной. Другими словами, когда наименьшее и наибольшее значения переменной слишком экстремальны. Это также могут быть Выбросы (Outlier).
• Мы выбираем неправильную модель. Если вы подгоните модель линейной регрессии к нелинейным данным, это приведет к гетероскедастичности.
• Когда масштаб значений в переменной некорректен (например, стоит рассматривать данные по сезонам, а не по дням).
• Когда для регрессии используется неправильное преобразование данных.
• Когда в данных присутствует Скошенность (Skewness).

Чистая и нечистая гетероскедастичности

Когда мы подбираем правильную модель (линейную или нелинейную) и все же есть видимый образец в остатках, это называется чистой гетероскедастичностью.

Однако, если мы подбираем неправильную модель, а затем наблюдаем закономерность в остатках, то это случай нечистой гетероскедастичности. В зависимости от типа гетероскедастичности необходимо принять меры для ее преодоления. Это зависит и от сферы, в которой мы работаем.

Эффекты гетероскедастичности в Машинном обучении

Как мы обсуждали ранее, модель линейной регрессии делает предположение о наличии гомоскедастичности в данных. Если это предположение неверно, мы не сможем доверять полученным результатам.

Наличие гетероскедастичности делает коэффициенты менее точными, и, следовательно, правильные находятся дальше от значения Генеральной совокупности (Population).

Как лечить гетероскедастичность?

Если мы обнаружили гетероскедастичность, есть несколько способов справиться с ней. Во-первых, давайте рассмотрим пример, в котором у нас есть две переменные: население города и количество заражений COVID-19.

В этом примере будет огромная разница в количестве заражений в крупных мегаполисах по сравнению с небольшими городами. Переменная «Количество инфекций» будет Целевой переменной (Target Variable), а «Население города» – Предиктором (Predictor Variable). Мы знаем, что в модели присутствует гетероскедастичность, и ее необходимо исправить.

В нашем случае, источник проблемы – это переменная с большой дисперсией (Население). Есть несколько способов справиться с подобным неоднообразием остатков, мы же рассмотрим три таких метода.

Управление переменными

Мы можем внести некоторые изменения в имеющиеся переменные, чтобы уменьшить влияние этой большой дисперсии на прогнозы модели. Один из способов сделать это – осуществить Нормализацию (Normalization), то есть привести значения Признака (Feature) к диапазону от 0 до 1. Это заставит признаки передавать немного другую информацию. От проблемы и данных будет зависеть, можно ли реализовать такой подход.

Этот метод требует минимальных модификаций и часто помогает решить проблему, а в некоторых случаях даже повысить производительность модели.

В нашем случае, мы изменим параметр «Количество инфекций» на «Скорость заражения». Это поможет уменьшить дисперсию, поскольку совершенно очевидно, что число инфекций в городах с большой численностью населения будет большим.

Взвешенная регрессия

Взвешенная регрессия – это модификация нормальной регрессии, при которой точкам данных присваиваются определенные Веса (Weights) в соответствии с их дисперсией. Те, у которых есть бо́льшая дисперсия, получают небольшой вес, а те, у которых меньшая дисперсия, получают бо́льший вес.

Таким образом, когда веса возведены в квадрат, это позволяет снизить влияние остатков с большой дисперсией.

Когда используются правильные веса, гетероскедастичность заменяется гомоскедастичностью. Но как найти правильный вес? Один из быстрых способов – использовать инверсию этой переменной в качестве веса (население города превратится в дробь 1/n, где n – число жителей).

Трансформация

Преобразование данных – последнее средство, поскольку при этом вы теряете интерпретируемость функции. Это означает, что вы больше не сможете легко объяснить, что показывает признак. Один из способов – взятие логарифма. Воспринять новые значения высоты дерева (например, 16 метров превратятся в ≈2.772) будет сложнее.

Фото: @sorasagano

Автор оригинальной статьи: Pavan Vadapalli