Калькулятор функции ошибки
О Калькулятор функции ошибки
Калькулятор функции ошибки используется для расчета функции ошибки для заданного числа.
Функция ошибки
В математике функция ошибок — это специальная (нефундаментальная) функция сигмовидной формы, которая встречается в теории вероятностей, статистике и уравнениях в частных производных. Она также известна как функция ошибки Гаусса или интеграл вероятности.
Функция ошибки определяется как:
Таблица функций ошибок
Ниже приведена таблица функций ошибок и дополнительных функций ошибок, в которой показаны значения erf(x) и erfc(x) для x в диапазоне от 0 до 3,5 с шагом 0,01.
| X | ЭРФ(х) | ЭРФК(х) |
|---|---|---|
| 0.0 | 0.0 | 1.0 |
| 0.01 | 0.011283416 | 0.988716584 |
| 0.02 | 0.022564575 | 0.977435425 |
| 0.03 | 0.033841222 | 0.966158778 |
| 0.04 | 0.045111106 | 0.954888894 |
| 0.05 | 0.056371978 | 0.943628022 |
| 0.06 | 0.067621594 | 0.932378406 |
| 0.07 | 0.07885772 | 0.92114228 |
| 0.08 | 0.090078126 | 0.909921874 |
| 0.09 | 0.101280594 | 0.898719406 |
| 0.1 | 0.112462916 | 0.887537084 |
| 0.11 | 0.123622896 | 0.876377104 |
| 0.12 | 0.134758352 | 0.865241648 |
| 0.13 | 0.145867115 | 0.854132885 |
| 0.14 | 0.156947033 | 0.843052967 |
| 0.15 | 0.167995971 | 0.832004029 |
| 0.16 | 0.179011813 | 0.820988187 |
| 0.17 | 0.189992461 | 0.810007539 |
| 0.18 | 0.200935839 | 0.799064161 |
| 0.19 | 0.211839892 | 0.788160108 |
| 0.2 | 0.222702589 | 0.777297411 |
| 0.21 | 0.233521923 | 0.766478077 |
| 0.22 | 0.244295912 | 0.755704088 |
| 0.23 | 0.2550226 | 0.7449774 |
| 0.24 | 0.265700059 | 0.734299941 |
| 0.25 | 0.27632639 | 0.72367361 |
| 0.26 | 0.286899723 | 0.713100277 |
| 0.27 | 0.297418219 | 0.702581781 |
| 0.28 | 0.307880068 | 0.692119932 |
| 0.29 | 0.318283496 | 0.681716504 |
| 0.3 | 0.328626759 | 0.671373241 |
| 0.31 | 0.33890815 | 0.66109185 |
| 0.32 | 0.349125995 | 0.650874005 |
| 0.33 | 0.359278655 | 0.640721345 |
| 0.34 | 0.369364529 | 0.630635471 |
| 0.35 | 0.379382054 | 0.620617946 |
| 0.36 | 0.389329701 | 0.610670299 |
| 0.37 | 0.399205984 | 0.600794016 |
| 0.38 | 0.409009453 | 0.590990547 |
| 0.39 | 0.4187387 | 0.5812613 |
| 0.4 | 0.428392355 | 0.571607645 |
| 0.41 | 0.43796909 | 0.56203091 |
| 0.42 | 0.447467618 | 0.552532382 |
| 0.43 | 0.456886695 | 0.543113305 |
| 0.44 | 0.466225115 | 0.533774885 |
| 0.45 | 0.47548172 | 0.52451828 |
| 0.46 | 0.48465539 | 0.51534461 |
| 0.47 | 0.493745051 | 0.506254949 |
| 0.48 | 0.502749671 | 0.497250329 |
| 0.49 | 0.511668261 | 0.488331739 |
| 0.5 | 0.520499878 | 0.479500122 |
| 0.51 | 0.52924362 | 0.47075638 |
| 0.52 | 0.53789863 | 0.46210137 |
| 0.53 | 0.546464097 | 0.453535903 |
| 0.54 | 0.55493925 | 0.44506075 |
| 0.55 | 0.563323366 | 0.436676634 |
| 0.56 | 0.571615764 | 0.428384236 |
| 0.57 | 0.579815806 | 0.420184194 |
| 0.58 | 0.5879229 | 0.4120771 |
| 0.59 | 0.595936497 | 0.404063503 |
| 0.6 | 0.603856091 | 0.396143909 |
| 0.61 | 0.611681219 | 0.388318781 |
| 0.62 | 0.619411462 | 0.380588538 |
| 0.63 | 0.627046443 | 0.372953557 |
| 0.64 | 0.634585829 | 0.365414171 |
| 0.65 | 0.642029327 | 0.357970673 |
| 0.66 | 0.649376688 | 0.350623312 |
| 0.67 | 0.656627702 | 0.343372298 |
| 0.68 | 0.663782203 | 0.336217797 |
| 0.69 | 0.670840062 | 0.329159938 |
| 0.7 | 0.677801194 | 0.322198806 |
| 0.71 | 0.68466555 | 0.31533445 |
| 0.72 | 0.691433123 | 0.308566877 |
| 0.73 | 0.698103943 | 0.301896057 |
| 0.74 | 0.704678078 | 0.295321922 |
| 0.75 | 0.711155634 | 0.288844366 |
| 0.76 | 0.717536753 | 0.282463247 |
| 0.77 | 0.723821614 | 0.276178386 |
| 0.78 | 0.730010431 | 0.269989569 |
| 0.79 | 0.736103454 | 0.263896546 |
| 0.8 | 0.742100965 | 0.257899035 |
| 0.81 | 0.748003281 | 0.251996719 |
| 0.82 | 0.753810751 | 0.246189249 |
| 0.83 | 0.759523757 | 0.240476243 |
| 0.84 | 0.765142711 | 0.234857289 |
| 0.85 | 0.770668058 | 0.229331942 |
| 0.86 | 0.776100268 | 0.223899732 |
| 0.87 | 0.781439845 | 0.218560155 |
| 0.88 | 0.786687319 | 0.213312681 |
| 0.89 | 0.791843247 | 0.208156753 |
| 0.9 | 0.796908212 | 0.203091788 |
| 0.91 | 0.801882826 | 0.198117174 |
| 0.92 | 0.806767722 | 0.193232278 |
| 0.93 | 0.811563559 | 0.188436441 |
| 0.94 | 0.816271019 | 0.183728981 |
| 0.95 | 0.820890807 | 0.179109193 |
| 0.96 | 0.82542365 | 0.17457635 |
| 0.97 | 0.829870293 | 0.170129707 |
| 0.98 | 0.834231504 | 0.165768496 |
| 0.99 | 0.83850807 | 0.16149193 |
| 1.0 | 0.842700793 | 0.157299207 |
| 1.01 | 0.846810496 | 0.153189504 |
| 1.02 | 0.850838018 | 0.149161982 |
| 1.03 | 0.854784211 | 0.145215789 |
| 1.04 | 0.858649947 | 0.141350053 |
| 1.05 | 0.862436106 | 0.137563894 |
| 1.06 | 0.866143587 | 0.133856413 |
| 1.07 | 0.869773297 | 0.130226703 |
| 1.08 | 0.873326158 | 0.126673842 |
| 1.09 | 0.876803102 | 0.123196898 |
| 1.1 | 0.88020507 | 0.11979493 |
| 1.11 | 0.883533012 | 0.116466988 |
| 1.12 | 0.88678789 | 0.11321211 |
| 1.13 | 0.88997067 | 0.11002933 |
| 1.14 | 0.893082328 | 0.106917672 |
| 1.15 | 0.896123843 | 0.103876157 |
| 1.16 | 0.899096203 | 0.100903797 |
| 1.17 | 0.902000399 | 0.097999601 |
| 1.18 | 0.904837427 | 0.095162573 |
| 1.19 | 0.907608286 | 0.092391714 |
| 1.2 | 0.910313978 | 0.089686022 |
| 1.21 | 0.912955508 | 0.087044492 |
| 1.22 | 0.915533881 | 0.084466119 |
| 1.23 | 0.918050104 | 0.081949896 |
| 1.24 | 0.920505184 | 0.079494816 |
| 1.25 | 0.922900128 | 0.077099872 |
| 1.26 | 0.925235942 | 0.074764058 |
| 1.27 | 0.927513629 | 0.072486371 |
| 1.28 | 0.929734193 | 0.070265807 |
| 1.29 | 0.931898633 | 0.068101367 |
| 1.3 | 0.934007945 | 0.065992055 |
| 1.31 | 0.936063123 | 0.063936877 |
| 1.32 | 0.938065155 | 0.061934845 |
| 1.33 | 0.940015026 | 0.059984974 |
| 1.34 | 0.941913715 | 0.058086285 |
| 1.35 | 0.943762196 | 0.056237804 |
| 1.36 | 0.945561437 | 0.054438563 |
| 1.37 | 0.947312398 | 0.052687602 |
| 1.38 | 0.949016035 | 0.050983965 |
| 1.39 | 0.950673296 | 0.049326704 |
| 1.4 | 0.95228512 | 0.04771488 |
| 1.41 | 0.953852439 | 0.046147561 |
| 1.42 | 0.955376179 | 0.044623821 |
| 1.43 | 0.956857253 | 0.043142747 |
| 1.44 | 0.95829657 | 0.04170343 |
| 1.45 | 0.959695026 | 0.040304974 |
| 1.46 | 0.96105351 | 0.03894649 |
| 1.47 | 0.9623729 | 0.0376271 |
| 1.48 | 0.963654065 | 0.036345935 |
| 1.49 | 0.964897865 | 0.035102135 |
| 1.5 | 0.966105146 | 0.033894854 |
| 1.51 | 0.967276748 | 0.032723252 |
| 1.52 | 0.968413497 | 0.031586503 |
| 1.53 | 0.969516209 | 0.030483791 |
| 1.54 | 0.97058569 | 0.02941431 |
| 1.55 | 0.971622733 | 0.028377267 |
| 1.56 | 0.972628122 | 0.027371878 |
| 1.57 | 0.973602627 | 0.026397373 |
| 1.58 | 0.974547009 | 0.025452991 |
| 1.59 | 0.975462016 | 0.024537984 |
| 1.6 | 0.976348383 | 0.023651617 |
| 1.61 | 0.977206837 | 0.022793163 |
| 1.62 | 0.978038088 | 0.021961912 |
| 1.63 | 0.97884284 | 0.02115716 |
| 1.64 | 0.97962178 | 0.02037822 |
| 1.65 | 0.980375585 | 0.019624415 |
| 1.66 | 0.981104921 | 0.018895079 |
| 1.67 | 0.981810442 | 0.018189558 |
| 1.68 | 0.982492787 | 0.017507213 |
| 1.69 | 0.983152587 | 0.016847413 |
| 1.7 | 0.983790459 | 0.016209541 |
| 1.71 | 0.984407008 | 0.015592992 |
| 1.72 | 0.985002827 | 0.014997173 |
| 1.73 | 0.9855785 | 0.0144215 |
| 1.74 | 0.986134595 | 0.013865405 |
| 1.75 | 0.986671671 | 0.013328329 |
| 1.76 | 0.987190275 | 0.012809725 |
| 1.77 | 0.987690942 | 0.012309058 |
| 1.78 | 0.988174196 | 0.011825804 |
| 1.79 | 0.988640549 | 0.011359451 |
| 1.8 | 0.989090502 | 0.010909498 |
| 1.81 | 0.989524545 | 0.010475455 |
| 1.82 | 0.989943156 | 0.010056844 |
| 1.83 | 0.990346805 | 0.009653195 |
| 1.84 | 0.990735948 | 0.009264052 |
| 1.85 | 0.99111103 | 0.00888897 |
| 1.86 | 0.991472488 | 0.008527512 |
| 1.87 | 0.991820748 | 0.008179252 |
| 1.88 | 0.992156223 | 0.007843777 |
| 1.89 | 0.992479318 | 0.007520682 |
| 1.9 | 0.992790429 | 0.007209571 |
| 1.91 | 0.99308994 | 0.00691006 |
| 1.92 | 0.993378225 | 0.006621775 |
| 1.93 | 0.99365565 | 0.00634435 |
| 1.94 | 0.993922571 | 0.006077429 |
| 1.95 | 0.994179334 | 0.005820666 |
| 1.96 | 0.994426275 | 0.005573725 |
| 1.97 | 0.994663725 | 0.005336275 |
| 1.98 | 0.994892 | 0.005108 |
| 1.99 | 0.995111413 | 0.004888587 |
| 2.0 | 0.995322265 | 0.004677735 |
| 2.01 | 0.995524849 | 0.004475151 |
| 2.02 | 0.995719451 | 0.004280549 |
| 2.03 | 0.995906348 | 0.004093652 |
| 2.04 | 0.99608581 | 0.00391419 |
| 2.05 | 0.996258096 | 0.003741904 |
| 2.06 | 0.996423462 | 0.003576538 |
| 2.07 | 0.996582153 | 0.003417847 |
| 2.08 | 0.996734409 | 0.003265591 |
| 2.09 | 0.996880461 | 0.003119539 |
| 2.1 | 0.997020533 | 0.002979467 |
| 2.11 | 0.997154845 | 0.002845155 |
| 2.12 | 0.997283607 | 0.002716393 |
| 2.13 | 0.997407023 | 0.002592977 |
| 2.14 | 0.997525293 | 0.002474707 |
| 2.15 | 0.997638607 | 0.002361393 |
| 2.16 | 0.997747152 | 0.002252848 |
| 2.17 | 0.997851108 | 0.002148892 |
| 2.18 | 0.997950649 | 0.002049351 |
| 2.19 | 0.998045943 | 0.001954057 |
| 2.2 | 0.998137154 | 0.001862846 |
| 2.21 | 0.998224438 | 0.001775562 |
| 2.22 | 0.998307948 | 0.001692052 |
| 2.23 | 0.998387832 | 0.001612168 |
| 2.24 | 0.998464231 | 0.001535769 |
| 2.25 | 0.998537283 | 0.001462717 |
| 2.26 | 0.998607121 | 0.001392879 |
| 2.27 | 0.998673872 | 0.001326128 |
| 2.28 | 0.998737661 | 0.001262339 |
| 2.29 | 0.998798606 | 0.001201394 |
| 2.3 | 0.998856823 | 0.001143177 |
| 2.31 | 0.998912423 | 0.001087577 |
| 2.32 | 0.998965513 | 0.001034487 |
| 2.33 | 0.999016195 | 0.000983805 |
| 2.34 | 0.99906457 | 0.00093543 |
| 2.35 | 0.999110733 | 0.000889267 |
| 2.36 | 0.999154777 | 0.000845223 |
| 2.37 | 0.99919679 | 0.00080321 |
| 2.38 | 0.999236858 | 0.000763142 |
| 2.39 | 0.999275064 | 0.000724936 |
| 2.4 | 0.999311486 | 0.000688514 |
| 2.41 | 0.999346202 | 0.000653798 |
| 2.42 | 0.999379283 | 0.000620717 |
| 2.43 | 0.999410802 | 0.000589198 |
| 2.44 | 0.999440826 | 0.000559174 |
| 2.45 | 0.99946942 | 0.00053058 |
| 2.46 | 0.999496646 | 0.000503354 |
| 2.47 | 0.999522566 | 0.000477434 |
| 2.48 | 0.999547236 | 0.000452764 |
| 2.49 | 0.999570712 | 0.000429288 |
| 2.5 | 0.999593048 | 0.000406952 |
| 2.51 | 0.999614295 | 0.000385705 |
| 2.52 | 0.999634501 | 0.000365499 |
| 2.53 | 0.999653714 | 0.000346286 |
| 2.54 | 0.999671979 | 0.000328021 |
| 2.55 | 0.99968934 | 0.00031066 |
| 2.56 | 0.999705837 | 0.000294163 |
| 2.57 | 0.999721511 | 0.000278489 |
| 2.58 | 0.9997364 | 0.0002636 |
| 2.59 | 0.999750539 | 0.000249461 |
| 2.6 | 0.999763966 | 0.000236034 |
| 2.61 | 0.999776711 | 0.000223289 |
| 2.62 | 0.999788809 | 0.000211191 |
| 2.63 | 0.999800289 | 0.000199711 |
| 2.64 | 0.999811181 | 0.000188819 |
| 2.65 | 0.999821512 | 0.000178488 |
| 2.66 | 0.999831311 | 0.000168689 |
| 2.67 | 0.999840601 | 0.000159399 |
| 2.68 | 0.999849409 | 0.000150591 |
| 2.69 | 0.999857757 | 0.000142243 |
| 2.7 | 0.999865667 | 0.000134333 |
| 2.71 | 0.999873162 | 0.000126838 |
| 2.72 | 0.999880261 | 0.000119739 |
| 2.73 | 0.999886985 | 0.000113015 |
| 2.74 | 0.999893351 | 0.000106649 |
| 2.75 | 0.999899378 | 0.000100622 |
| 2.76 | 0.999905082 | 9.4918e-05 |
| 2.77 | 0.99991048 | 8.952e-05 |
| 2.78 | 0.999915587 | 8.4413e-05 |
| 2.79 | 0.999920418 | 7.9582e-05 |
| 2.8 | 0.999924987 | 7.5013e-05 |
| 2.81 | 0.999929307 | 7.0693e-05 |
| 2.82 | 0.99993339 | 6.661e-05 |
| 2.83 | 0.99993725 | 6.275e-05 |
| 2.84 | 0.999940898 | 5.9102e-05 |
| 2.85 | 0.999944344 | 5.5656e-05 |
| 2.86 | 0.999947599 | 5.2401e-05 |
| 2.87 | 0.999950673 | 4.9327e-05 |
| 2.88 | 0.999953576 | 4.6424e-05 |
| 2.89 | 0.999956316 | 4.3684e-05 |
| 2.9 | 0.999958902 | 4.1098e-05 |
| 2.91 | 0.999961343 | 3.8657e-05 |
| 2.92 | 0.999963645 | 3.6355e-05 |
| 2.93 | 0.999965817 | 3.4183e-05 |
| 2.94 | 0.999967866 | 3.2134e-05 |
| 2.95 | 0.999969797 | 3.0203e-05 |
| 2.96 | 0.999971618 | 2.8382e-05 |
| 2.97 | 0.999973334 | 2.6666e-05 |
| 2.98 | 0.999974951 | 2.5049e-05 |
| 2.99 | 0.999976474 | 2.3526e-05 |
| 3.0 | 0.99997791 | 2.209E-05 |
| 3.01 | 0.999979261 | 2.0739e-05 |
| 3.02 | 0.999980534 | 1.9466e-05 |
| 3.03 | 0.999981732 | 1.8268e-05 |
| 3.04 | 0.999982859 | 1.7141e-05 |
| 3.05 | 0.99998392 | 1.608e-05 |
| 3.06 | 0.999984918 | 1.5082e-05 |
| 3.07 | 0.999985857 | 1.4143e-05 |
| 3.08 | 0.99998674 | 1.326e-05 |
| 3.09 | 0.999987571 | 1.2429e-05 |
| 3.1 | 0.999988351 | 1.1649e-05 |
| 3.11 | 0.999989085 | 1.0915e-05 |
| 3.12 | 0.999989774 | 1.0226e-05 |
| 3.13 | 0.999990422 | 9.578e-06 |
| 3.14 | 0.99999103 | 8.97e-06 |
| 3.15 | 0.999991602 | 8.398e-06 |
| 3.16 | 0.999992138 | 7.862e-06 |
| 3.17 | 0.999992642 | 7.358e-06 |
| 3.18 | 0.999993115 | 6.885e-06 |
| 3.19 | 0.999993558 | 6.442e-06 |
| 3.2 | 0.999993974 | 6.026e-06 |
| 3.21 | 0.999994365 | 5.635e-06 |
| 3.22 | 0.999994731 | 5.269e-06 |
| 3.23 | 0.999995074 | 4.926e-06 |
| 3.24 | 0.999995396 | 4.604e-06 |
| 3.25 | 0.999995697 | 4.303e-06 |
| 3.26 | 0.99999598 | 4.02e-06 |
| 3.27 | 0.999996245 | 3.755e-06 |
| 3.28 | 0.999996493 | 3.507e-06 |
| 3.29 | 0.999996725 | 3.275e-06 |
| 3.3 | 0.999996942 | 3.058e-06 |
| 3.31 | 0.999997146 | 2.854e-06 |
| 3.32 | 0.999997336 | 2.664e-06 |
| 3.33 | 0.999997515 | 2.485e-06 |
| 3.34 | 0.999997681 | 2.319e-06 |
| 3.35 | 0.999997838 | 2.162e-06 |
| 3.36 | 0.999997983 | 2.017e-06 |
| 3.37 | 0.99999812 | 1.88E-06 |
| 3.38 | 0.999998247 | 1.753e-06 |
| 3.39 | 0.999998367 | 1.633e-06 |
| 3.4 | 0.999998478 | 1.522E-06 |
| 3.41 | 0.999998582 | 1.418e-06 |
| 3.42 | 0.999998679 | 1.321e-06 |
| 3.43 | 0.99999877 | 1.23E-06 |
| 3.44 | 0.999998855 | 1.145e-06 |
| 3.45 | 0.999998934 | 1.066e-06 |
| 3.46 | 0.999999008 | 9.92e-07 |
| 3.47 | 0.999999077 | 9.23e-07 |
| 3.48 | 0.999999141 | 8.59e-07 |
| 3.49 | 0.999999201 | 7.99e-07 |
| 3.5 | 0.999999257 | 7.43e-07 |
Общие инструменты
-
калькулятор золотого прямоугольника
-
двоичный калькулятор
-
Калькулятор доходности облигаций
-
Калькулятор выборки среднего
-
Калькулятор коэффициента вариации
-
футы дюймы в сантиметры
-
калькулятор гипотенузы
-
Генератор случайных цветов
-
конвертер метров в футы
-
Калькулятор срока погашения доходности облигаций
-
калькулятор жима лежа
-
Калькулятор квадратного корня (высокая точность)
-
калькулятор натуральных логарифмов
-
случайный выбор
-
калькулятор выборочной дисперсии
-
конвертер футов в метры
-
список простых чисел
-
Конвертер римских цифр
-
Калькулятор бета-функции
-
Калькулятор функции ошибки
-
генератор случайных букв
-
конвертер кг в фунты
-
конвертер см в футы и дюймы
-
конвертер фунтов в кг
-
Калькулятор Фаренгейта в Цельсия

В математике функция ошибок (также называемая Функция ошибок Гаусса ), часто обозначаемая erf, является сложной функцией комплексной определяемой как:
- erf z = 2 π ∫ 0 ze — t 2 dt. {\ displaystyle \ operatorname {erf} z = {\ frac {2} {\ sqrt {\ pi}}} \ int _ {0} ^ {z} e ^ {- t ^ {2}} \, dt.}
Этот интеграл является особой (не элементарной ) и сигмоидной функцией, которая часто встречается в статистике вероятность, и уравнения в частных производных. Во многих из этих приложений аргумент функции является действительным числом. Если аргумент функции является действительным, значение также является действительным.
В статистике для неотрицательных значений x функция имеет интерпретацию: для случайной величины Y, которая нормально распределена с среднее 0 и дисперсия 1/2, erf x — это вероятность того, что Y попадает в диапазон [-x, x].
Две связанные функции: дополнительные функции ошибок (erfc ), определенная как
- erfc z = 1 — erf z, {\ displaystyle \ operatorname {erfc} z = 1- \ operatorname {erf} z,}
и функция мнимой ошибки (erfi ), определяемая как
- erfi z = — i erf (iz), {\ displaystyle \ operatorname {erfi} z = -i \ operatorname {erf} (iz),}
, где i — мнимая единица.
Содержание
- 1 Имя
- 2 Приложения
- 3 Свойства
- 3.1 Ряд Тейлора
- 3.2 Производная и интеграл
- 3.3 Ряд Бюрмана
- 3.4 Обратные функции
- 3.5 Асимптотическое разложение
- 3.6 Разложение на непрерывную дробь
- 3,7 Интеграл функции ошибок с функцией плотности Гаусса
- 3.8 Факториальный ряд
- 4 Численные приближения
- 4.1 Аппроксимация с элементарными функциями
- 4.2 Полином
- 4.3 Таблица значений
- 5 Связанные функции
- 5.1 функция дополнительных ошибок
- 5.2 Функция мнимой ошибки
- 5.3 Кумулятивная функци я распределения на
- 5.4 Обобщенные функции ошибок
- 5.5 Итерированные интегралы дополнительных функций ошибок
- 6 Реализации
- 6.1 Как действующая функция действительного аргумента
- 6.2 Как комплексная функция комплексного аргумента
- 7 См. Также
- 7.1 Связанные функции
- 7.2 Вероятность
- 8 Ссылки
- 9 Дополнительная литература
- 10 Внешние ссылки
Имя
Название «функция ошибки» и его аббревиатура erf были предложены Дж. В. Л. Глейшер в 1871 г. по причине его связи с «теорией вероятности, и особенно теорией ошибок ». Дополнение функции ошибок также обсуждалось Глейшером в отдельной публикации в том же году. Для «закона удобства» ошибок плотность задана как
- f (x) = (c π) 1 2 e — cx 2 {\ displaystyle f (x) = \ left ({\ frac {c } {\ pi}} \ right) ^ {\ tfrac {1} {2}} e ^ {- cx ^ {2}}}
(нормальное распределение ), Глейшер вычисляет вероятность ошибки, лежащей между p {\ displaystyle p}

- (c π) 1 2 ∫ pqe — cx 2 dx = 1 2 (erf (qc) — erf (pc)). {\ displaystyle \ left ({\ frac {c} {\ pi}} \ right) ^ {\ tfrac {1} {2}} \ int _ {p} ^ {q} e ^ {- cx ^ {2} } dx = {\ tfrac {1} {2}} \ left (\ operatorname {erf} (q {\ sqrt {c}}) — \ operatorname {erf} (p {\ sqrt {c}}) \ right).}
Приложения
Когда результаты серии измерений описываются нормальным распределением со стандартным отклонением σ {\ displaystyle \ sigma}

Функции и дополнительные функции ошибок возникают, например, в решениях уравнения теплопроводности, когда граничные ошибки задаются ступенчатой функцией Хевисайда.
Функция ошибок и ее приближения Программу присвоили себе преподавателей, которые получили с высокой вероятностью или с низкой вероятностью. Дана случайная величина X ∼ Norm [μ, σ] {\ displaystyle X \ sim \ operatorname {Norm} [\ mu, \ sigma]}![X \ sim \ operatorname {Norm} [\ му, \ sigma]](https://wikimedia.org/api/rest_v1/media/math/render/svg/84024bc6827355ec6d23a062283a26d54b29698d)

- Pr [X ≤ L ] = 1 2 + 1 2 erf (L — μ 2 σ) ≈ A ехр (- B (L — μ σ) 2) {\ Displaystyle \ Pr [X \ Leq L] = {\ frac {1} {2 }} + {\ frac {1} {2}} \ operatorname {erf} \ left ({\ frac {L- \ mu} {{\ sqrt {2}} \ sigma}} \ right) \ приблизительно A \ exp \ left (-B \ left ({\ frac {L- \ mu} {\ sigma}} \ right) ^ {2} \ right)}
где A и B — верх числовые константы. Если L достаточно далеко от среднего, то есть μ — L ≥ σ ln k {\ displaystyle \ mu -L \ geq \ sigma {\ sqrt {\ ln {k}}}}
- Pr [X ≤ L] ≤ A exp (- B ln k) = A К B {\ displaystyle \ Pr [X \ leq L] \ leq A \ exp (-B \ ln {k}) = {\ frac {A} {k ^ {B}}}}
, поэтому становится вероятность 0 при k → ∞ {\ displaystyle k \ to \ infty}
Свойства
Графики на комплексной плоскости 

Свойство erf (- z) = — erf (z) {\ displaystyle \ operatorname {erf} (-z) = — \ operatorname {erf} (z)}

Для любого комплексное число z:
- erf (z ¯) = erf (z) ¯ {\ displaystyle \ operatorname {erf} ({\ overline {z}}) = {\ overline {\ operatorname {erf} (z)}}}
где z ¯ {\ displaystyle {\ overline {z}}}
Подынтегральное выражение f = exp (−z) и f = erf (z) показано в комплексной плоскости z на рисунках 2 и 3. Уровень Im (f) = 0 показан жирным зеленым цветом. линия. Отрицательные целые значения Im (f) показаны жирными красными линиями. Положительные целые значения Im (f) показаны толстыми синими линиями. Промежуточные уровни Im (f) = проявляются тонкими зелеными линиями. Промежуточные уровни Re (f) = показаны тонкими красными линиями для отрицательных значений и тонкими синими линиями для положительных значений.
Функция ошибок при + ∞ равна 1 (см. интеграл Гаусса ). На действительной оси erf (z) стремится к единице при z → + ∞ и к −1 при z → −∞. На мнимой оси он стремится к ± i∞.
Серия Тейлора
Функция ошибок — это целая функция ; у него нет сингулярностей (кроме бесконечности), и его разложение Тейлора всегда сходится, но, как известно, «[…] его плохая сходимость, если x>1».
определяющий интеграл нельзя вычислить в закрытой форме в терминах элементарных функций, но путем расширения подынтегрального выражения e в его ряд Маклорена и интегрирована почленно, можно получить ряд Маклорена функции ошибок как:
- erf (z) = 2 π ∑ n = 0 ∞ (- 1) nz 2 n + 1 n! (2 n + 1) знак равно 2 π (z — z 3 3 + z 5 10 — z 7 42 + z 9 216 — ⋯) {\ displaystyle \ operatorname {erf} (z) = {\ frac {2} { \ sqrt {\ pi}}} \ sum _ {n = 0} ^ {\ infty} {\ frac {(-1) ^ {n} z ^ {2n + 1}} {n! (2n + 1)}} = {\ frac {2} {\ sqrt {\ pi}}} \ left (z — {\ frac {z ^ {3}} {3}} + {\ frac {z ^ { 5}} {10}} — {\ frac {z ^ {7}} {42}} + {\ frac {z ^ {9}} {216}} — \ cdots \ right)}
, которое выполняется для каждого комплексного числа г. Члены знаменателя представляют собой последовательность A007680 в OEIS.
Для итеративного вычисления нового ряда может быть полезна следующая альтернативная формулировка:
- erf (z) = 2 π ∑ n = 0 ∞ (z ∏ К знак равно 1 N — (2 К — 1) Z 2 К (2 К + 1)) знак равно 2 π ∑ N = 0 ∞ Z 2 N + 1 ∏ К = 1 N — Z 2 К {\ Displaystyle \ OperatorName { erf} (z) = {\ frac {2} {\ sqrt {\ pi}}} \ sum _ {n = 0} ^ {\ infty} \ left (z \ prod _ {k = 1} ^ {n} {\ frac {- (2k-1) z ^ {2}} {k (2k + 1)}} \ right) = {\ frac {2} {\ sqrt {\ pi}}} \ sum _ {n = 0} ^ {\ infty} {\ frac {z} {2n + 1}} \ prod _ {k = 1} ^ {n} {\ frac {-z ^ {2}} {k}}}
потому что что — (2 k — 1) z 2 k (2 k + 1) {\ displaystyle {\ frac {- (2k-1) z ^ {2}} {k (2k + 1))}} }
Функция мнимой ошибки имеет очень похожий ряд Маклорена:
- erfi (z) = 2 π ∑ n = 0 ∞ z 2 n + 1 n! (2 n + 1) знак равно 2 π (z + z 3 3 + z 5 10 + z 7 42 + z 9 216 + ⋯) {\ displaystyle \ operatorname {erfi} (z) = {\ frac {2} { \ sqrt {\ pi}}} \ sum _ {n = 0} ^ {\ infty} {\ frac {z ^ {2n + 1}} {n! (2n + 1)}} = {\ frac {2} {\ sqrt {\ pi}}} \ left (z + {\ frac {z ^ {3}} {3}} + {\ frac {z ^ { 5}} {10}} + {\ frac {z ^ {7}} {42}} + {\ frac {z ^ {9}} {216}} + \ cdots \ right)}
, которое выполняется для любого комплексного числа z.
Производная и интеграл
Производная функция ошибок сразу следует из ее определения:
- ddz erf (z) = 2 π e — z 2. {\ displaystyle {\ frac {d} {dz}} \ operatorname {erf} (z) = {\ frac {2} {\ sqrt {\ pi}}} e ^ {- z ^ {2}}.}
Отсюда немедленно вычисляется производная функция мнимой ошибки :
- ddz erfi (z) = 2 π ez 2. {\ displaystyle {\ frac {d} {dz}} \ operatorname {erfi} (z) = {\ frac {2} {\ sqrt {\ pi }}} e ^ {z ^ {2}}.}
первообразная функции ошибок, которые можно получить посредством интегрирования по частям, составляет
- z erf (z) + е — z 2 π. {\ displaystyle z \ operatorname {erf} (z) + {\ frac {e ^ {- z ^ {2}}} {\ sqrt {\ pi}}}.}
Первообразная мнимой функции ошибок, также можно получить интегрированием по частям:
- z erfi (z) — ez 2 π. {\ displaystyle z \ operatorname {erfi} (z) — {\ frac {e ^ {z ^ {2}}} {\ sqrt {\ pi}}}.}
Производные высшего порядка задаются как
- erf (k) (z) = 2 (- 1) k — 1 π H k — 1 (z) e — z 2 = 2 π dk — 1 dzk — 1 (e — z 2), k = 1, 2, … {\ Displaystyle \ operatorname {erf} ^ {(k)} (z) = {\ frac {2 (-1) ^ {k-1}} {\ sqrt {\ pi}}} {\ mathit {H} } _ {k-1} (z) e ^ {- z ^ {2}} = {\ frac {2} {\ sqrt {\ pi}}} {\ frac {d ^ {k-1}} {dz ^ {k-1}}} \ left (e ^ {- z ^ {2}} \ right), \ qquad k = 1,2, \ dots}
где H {\ displaystyle {\ mathit {H}}}
ряд Бюрмана
Расширение, которое сходится быстрее для всех реальных значений x {\ displaystyle x}
- erf (x) = 2 π sgn (x) 1 — e — x 2 (1 — 1 12 ( 1 — e — x 2) — 7 480 (1 — e — x 2) 2 — 5 896 (1 — e — x 2) 3 — 787 276480 (1 — e — x 2)) 4 — ⋯) знак равно 2 π знак (x) 1 — e — x 2 (π 2 + ∑ k = 1 ∞ cke — kx 2). {\ displaystyle {\ begin {align} \ operatorname {erf} (x) = {\ frac {2} {\ sqrt {\ pi}}} \ operatorname {sgn} (x) {\ sqrt {1-e ^ {-x ^ {2}}}} \ left (1 — {\ frac {1} {12}} \ left (1-e ^ {- x ^ {2}} \ right) — {\ frac {7} {480}} \ left (1-e ^ {- x ^ {2}} \ right) ^ {2} — {\ frac {5} {896}} \ left (1-e ^ {- x ^ {2 }} \ right) ^ {3} — {\ frac {787} {276480}} \ left (1-e ^ {- x ^ {2}} \ right) ^ {4} — \ cdots \ right) \\ [10pt] = {\ frac {2} {\ sqrt {\ pi}}} \ operatorname {sgn} (x) {\ sqrt {1-e ^ {- x ^ {2}}}} \ left ({ \ frac {\ sqrt {\ pi}} {2}} + \ sum _ {k = 1} ^ {\ infty} c_ {k} e ^ {- kx ^ {2}} \ right). \ end {выровнено}}
Сохраняя только первые два коэффициента и выбирая c 1 = 31 200 {\ displaystyle c_ {1} = {\ frac {31} {200}}}



- erf (x) ≈ 2 π sign (x) 1 — e — x 2 (π 2 + 31 200 e — x 2 — 341 8000 e — 2 х 2). {\ displaystyle \ operatorname {erf} (x) \ приблизительно {\ frac {2} {\ sqrt {\ pi}}} \ operatorname {sgn} (x) {\ sqrt {1-e ^ {- x ^ {2 }}}} \ left ({\ frac {\ sqrt {\ pi}} {2}} + {\ frac {31} {200}} e ^ {- x ^ {2}} — {\ frac {341} {8000}} e ^ {- 2x ^ {2}} \ right).}
Обратные функции
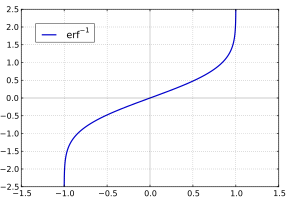
Учитывая комплексное число z, не существует уникального комплексного числа w, удовлетворяющего erf (w) = z {\ displaystyle \ operatorname {erf} (w) = z}

- erf (erf — 1 ( х)) = х. {\ displaystyle \ operatorname {erf} \ left (\ operatorname {erf} ^ {- 1} (x) \ right) = x.}
Обратная функция ошибок обычно определяется с помощью домена (- 1,1), и он ограничен этой областью многих систем компьютерной алгебры. Однако его можно продолжить и на диск | z | < 1 of the complex plane, using the Maclaurin series
- erf — 1 (z) знак равно ∑ К знак равно 0 ∞ ck 2 k + 1 (π 2 z) 2 k + 1, {\ displaystyle \ operatorname {erf} ^ {- 1} (z) = \ sum _ {k = 0} ^ {\ infty} {\ frac {c_ {k}} {2k + 1}} \ left ({\ frac {\ sqrt {\ pi}} {2}} z \ right) ^ {2k + 1},}
где c 0 = 1 и
- ck = ∑ m = 0 k — 1 cmck — 1 — m (m + 1) (2 m + 1) = {1, 1, 7 6, 127 90, 4369 2520, 34807 16200,…}. {\ displaystyle c_ {k} = \ sum _ {m = 0} ^ {k-1} {\ frac {c_ {m} c_ {k-1-m}} {(m + 1) (2m + 1) }} = \ left \ {1,1, {\ frac {7} {6}}, {\ frac {127} {90}}, {\ frac {4369} {2520}}, {\ frac {34807} {16200}}, \ ldots \ right \}.}
Итак, у нас есть разложение в ряд (общие множители были удалены из числителей и знаменателей):
- erf — 1 (z) = 1 2 π ( z + π 12 z 3 + 7 π 2 480 z 5 + 127 π 3 40320 z 7 + 4369 π 4 5806080 z 9 + 34807 π 5 182476800 z 11 + ⋯). {\ displaystyle \ operatorname {erf} ^ {- 1} (z) = {\ tfrac {1} {2}} {\ sqrt {\ pi}} \ left (z + {\ frac {\ pi} {12} } z ^ {3} + {\ frac {7 \ pi ^ {2}} {480}} z ^ {5} + {\ frac {127 \ pi ^ {3}} {40320}} z ^ {7} + {\ frac {4369 \ pi ^ {4}} {5806080}} z ^ {9} + {\ frac {34807 \ pi ^ {5}} {182476800}} z ^ {11} + \ cdots \ right). }
(После отмены дроби числителя / знаменателя характерми OEIS : A092676 / OEIS : A092677 в OEIS ; без отмены членов числителя в записи OEIS : A002067.) Значение функции ошибок при ± ∞ равно ± 1.
Для | z | < 1, we have erf (erf — 1 (z)) = z {\ displaystyle \ operatorname {erf} \ left (\ operatorname {erf} ^ {- 1} (z) \ right) = z}
обратная дополнительная функция ошибок определяется как
- erfc — 1 (1 — z) = erf — 1 (z). {\ displaystyle \ operatorname {erfc} ^ {- 1} (1-z) = \ operatorname {erf} ^ {- 1} (z).}
Для действительного x существует уникальное действительное число erfi — 1 (x) {\ displaystyle \ operatorname {erfi} ^ {- 1} (x)}


Для любого действительного x, Метод Ньютона можно использовать для вычислений erfi — 1 (x) {\ displaystyle \ operatorname {erfi} ^ {- 1} (x)}

- erfi — 1 (z) = ∑ k = 0 ∞ (- 1) ККК 2 К + 1 (π 2 Z) 2 К + 1, {\ Displaystyle \ OperatorName {erfi} ^ {- 1} (г) = \ сумма _ {к = 0} ^ {\ infty} {\ гидроразрыва {(-1) ^ {k} c_ {k}} {2k + 1}} \ left ({\ frac {\ sqrt {\ pi}} {2}} z \ right) ^ {2k + 1},}
, где c k определено, как указано выше.
Асимптотическое разложение
Полезным асимптотическим разложением дополнительные функции (и, следовательно, также и функции ошибок) для больших вещественных x
- erfc (x) = e — x 2 x π [1 + ∑ n = 1 ∞ (- 1) n 1 ⋅ 3 ⋅ 5 ⋯ (2 n — 1) (2 x 2) n] = e — x 2 x π ∑ n = 0 ∞ (- 1) п (2 п — 1)! ! (2 х 2) n, {\ displaystyle \ operatorname {erfc} (x) = {\ frac {e ^ {- x ^ {2}}} {x {\ sqrt {\ pi}}}} \ left [1 + \ sum _ {n = 1} ^ {\ infty} (- 1) ^ {n} {\ frac {1 \ cdot 3 \ cdot 5 \ cdots (2n-1)} {(2x ^ {2}) ^ {n}}} \ right] = {\ frac {e ^ {- x ^ {2}}} {x {\ sqrt {\ pi}}}} \ sum _ {n = 0} ^ {\ infty} ( -1) ^ {n} {\ frac {(2n-1) !!} {(2x ^ {2}) ^ {n}}},}
где (2n — 1) !! — это двойной факториал числа (2n — 1), которое является произведением всех нечетных чисел до (2n — 1). Этот ряд расходуется для любого конечного x, и его значение как асимптотического разложения состоит в том, что для любого N ∈ N {\ displaystyle N \ in \ mathbb {N}}
- erfc (Икс) знак равно е — Икс 2 Икс π ∑ N знак равно 0 N — 1 (- 1) N (2 N — 1)! ! (2 х 2) n + RN (x) {\ displaystyle \ operatorname {erfc} (x) = {\ frac {e ^ {- x ^ {2}}} {x {\ sqrt {\ pi}}}} \ sum _ {n = 0} ^ {N-1} (- 1) ^ {n} {\ frac {(2n-1) !!} {(2x ^ {2}) ^ {n}}} + R_ {N} (x)}
где остаток в нотации Ландау равен
- RN (x) = O (x 1 — 2 N e — x 2) {\ displaystyle R_ {N} ( x) = O \ left (x ^ {1-2N} e ^ {- x ^ {2}} \ right)}
при x → ∞. {\ displaystyle x \ to \ infty.}
Действительно, точное значение остатка равно
- R N (x): = (- 1) N π 2 1 — 2 N (2 N)! N! ∫ Икс ∞ T — 2 N e — T 2 dt, {\ Displaystyle R_ {N} (x): = {\ frac {(-1) ^ {N}} {\ sqrt {\ pi}}} 2 ^ { 1-2N} {\ frac {(2N)!} {N!}} \ Int _ {x} ^ {\ infty} t ^ {- 2N} e ^ {- t ^ {2}} \, dt,}
который легко следует по индукции, записывая
- e — t 2 = — (2 t) — 1 (e — t 2) ′ {\ displaystyle e ^ {- t ^ {2}} = — (2t) ^ {- 1} \ left (e ^ {- t ^ {2}} \ right) ‘}
и интегрирование по частям.
Для достаточно больших значений x, только первые несколько этих асимптотических разностей необходимы, чтобы получить хорошее приближение erfc (x) (в то время как для не слишком больших значений x приведенное выше разложение Тейлора при 0 обеспечивает очень быструю сходимость).
Расширение непрерывной дроби
A Разложение непрерывной дроби дополнительные функции ошибок:
- erfc (z) = z π e — z 2 1 z 2 + a 1 1 + a 2 z 2 + a 3 1 + ⋯ am = м 2. {\ displaystyle \ operatorname {erfc} (z) = {\ frac {z} {\ sqrt {\ pi}}} e ^ {- z ^ {2}} {\ cfrac {1} {z ^ {2} + {\ cfrac {a_ {1}} {1 + {\ cfrac {a_ {2}} {z ^ {2} + {\ cfrac {a_ {3}} {1+) \ dotsb}}}}}}}} \ qquad a_ {m} = {\ frac {m} {2}}.}
Интеграл функции ошибок с функцией плотности Гаусса
- ∫ — ∞ ∞ erf (ax + б) 1 2 π σ 2 е — (Икс — μ) 2 2 σ 2 dx знак равно erf [a μ + b 1 + 2 a 2 σ 2], a, b, μ, σ ∈ R {\ displaystyle \ int _ {- \ infty} ^ {\ infty} \ operatorname {erf} \ left (ax + b \ right) {\ frac {1} {\ sqrt {2 \ pi \ sigma ^ {2}}}} e ^ {- {\ frac {(x- \ mu) ^ {2}} {2 \ sigma ^ {2}}}} \, dx = \ operatorname {erf} \ left [{\ frac {a \ mu + b } {\ sqrt {1 + 2a ^ {2} \ sigma ^ {2}}} \ right], \ qquad a, b, \ mu, \ sigma \ in \ mathbb {R}}
Факториальный ряд
- Обратное:
-
- erfc z = e — z 2 π z ∑ n = 0 ∞ (- 1) n Q n (z 2 + 1) n ¯ = e — z 2 π z (1 — 1 2 1 (z 2 + 1) + 1 4 1 (z 2 + 1) (z 2 + 2) — ⋯) {\ displaystyle {\ begin {align} \ operatorname {erfc} z = {\ frac {e ^ {- z ^ {2}}} {{\ sqrt {\ pi}} \, z}} \ sum _ {n = 0} ^ {\ infty} {\ frac {(-1) ^ {n} Q_ {n}} {{(z ^ {2} + 1)} ^ {\ ba r {n}}}} \\ = {\ frac {e ^ {- z ^ {2}}} {{\ sqrt {\ pi}} \, z}} \ left ( 1 — {\ frac {1} {2}} {\ frac {1} {(z ^ {2} +1)}} + {\ frac {1} {4}} {\ frac {1} {(z ^ {2} +1) (z ^ {2} +2)}} — \ cdots \ right) \ end {align}}}
- erfc z = e — z 2 π z ∑ n = 0 ∞ (- 1) n Q n (z 2 + 1) n ¯ = e — z 2 π z (1 — 1 2 1 (z 2 + 1) + 1 4 1 (z 2 + 1) (z 2 + 2) — ⋯) {\ displaystyle {\ begin {align} \ operatorname {erfc} z = {\ frac {e ^ {- z ^ {2}}} {{\ sqrt {\ pi}} \, z}} \ sum _ {n = 0} ^ {\ infty} {\ frac {(-1) ^ {n} Q_ {n}} {{(z ^ {2} + 1)} ^ {\ ba r {n}}}} \\ = {\ frac {e ^ {- z ^ {2}}} {{\ sqrt {\ pi}} \, z}} \ left ( 1 — {\ frac {1} {2}} {\ frac {1} {(z ^ {2} +1)}} + {\ frac {1} {4}} {\ frac {1} {(z ^ {2} +1) (z ^ {2} +2)}} — \ cdots \ right) \ end {align}}}
- сходится для Re (z 2)>0. {\ displaystyle \ operatorname {Re} (z ^ {2})>0.}
Здесь
- Q n = def 1 Γ (1/2) ∫ 0 ∞ τ (τ — 1) ⋯ ( τ — n + 1) τ — 1/2 е — τ d τ знак равно ∑ К знак равно 0 N (1 2) к ¯ s (n, k), {\ displaystyle Q_ {n} {\ stackrel {\ text {def}} {=}} {\ frac {1} {\ Gamma (1/2)}} \ int _ {0} ^ {\ infty} \ tau (\ tau -1) \ cdots (\ tau -n + 1) \ tau ^ {-1/2} e ^ {- \ tau} d \ tau = \ sum _ {k = 0} ^ {n} \ left ({\ frac {1} {2}} \ right) ^ {\ bar {k}} s (n, k),}
- Q n = def 1 Γ (1/2) ∫ 0 ∞ τ (τ — 1) ⋯ ( τ — n + 1) τ — 1/2 е — τ d τ знак равно ∑ К знак равно 0 N (1 2) к ¯ s (n, k), {\ displaystyle Q_ {n} {\ stackrel {\ text {def}} {=}} {\ frac {1} {\ Gamma (1/2)}} \ int _ {0} ^ {\ infty} \ tau (\ tau -1) \ cdots (\ tau -n + 1) \ tau ^ {-1/2} e ^ {- \ tau} d \ tau = \ sum _ {k = 0} ^ {n} \ left ({\ frac {1} {2}} \ right) ^ {\ bar {k}} s (n, k),}
- zn ¯ {\ displaystyle z ^ {\ bar {n}}}
обозначает возрастающий факториал, а s (n, k) {\ displaystyle s (n, k)}
обозначает знаковое число Стирлинга первого рода.
- Представление бесконечной суммой, составляющей двойной факториал :
-
- ERF (Z) знак равно 2 π ∑ N знак равно 0 ∞ (- 2) N (2 N — 1)! (2 N + 1)! Z 2 N + 1 {\ Displaystyle \ OperatorName {ERF} (г) = {\ frac {2} {\ sqrt {\ pi}}} \ sum _ {n = 0} ^ {\ infty} {\ frac {( -2) ^ {n} (2n-1) !!} {(2n + 1)!}} Z ^ {2n + 1}}
- ERF (Z) знак равно 2 π ∑ N знак равно 0 ∞ (- 2) N (2 N — 1)! (2 N + 1)! Z 2 N + 1 {\ Displaystyle \ OperatorName {ERF} (г) = {\ frac {2} {\ sqrt {\ pi}}} \ sum _ {n = 0} ^ {\ infty} {\ frac {( -2) ^ {n} (2n-1) !!} {(2n + 1)!}} Z ^ {2n + 1}}
Численные приближения
Приближение элементов сарными функциями
- Абрамовиц и Стегун дают несколько приближений с точностью (уравнения 7.1.25–28). Это позволяет выбрать наиболее быстрое приближение, подходящее для данного приложения. В порядке увеличения точности они следующие:
-
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + a 3 x 3 + a 4 x 4) 4, x ≥ 0 {\ displaystyle \ имя оператора {erf} (x) \ приблизительно 1 — {\ frac {1} {(1 + a_ {1} x + a_ {2} x ^ {2} + a_ {3} x ^ {3} + a_ { 4} x ^ {4}) ^ {4}}}, \ qquad x \ geq 0}
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + a 3 x 3 + a 4 x 4) 4, x ≥ 0 {\ displaystyle \ имя оператора {erf} (x) \ приблизительно 1 — {\ frac {1} {(1 + a_ {1} x + a_ {2} x ^ {2} + a_ {3} x ^ {3} + a_ { 4} x ^ {4}) ^ {4}}}, \ qquad x \ geq 0}
- (максимальная ошибка: 5 × 10)
- , где a 1 = 0,278393, a 2 = 0,230389, a 3 = 0,000972, a 4 = 0,078108
-
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + a 3 t 3) e — x 2, t = 1 1 + px, x ≥ 0 {\ displaystyle \ operatorname {erf} (x) \ приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + a_ {3} t ^ {3}) e ^ {- x ^ {2}}, \ quad t = {\ frac {1} {1 + px}}, \ qquad x \ geq 0}
(максимальная ошибка: 2,5 × 10)
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + a 3 t 3) e — x 2, t = 1 1 + px, x ≥ 0 {\ displaystyle \ operatorname {erf} (x) \ приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + a_ {3} t ^ {3}) e ^ {- x ^ {2}}, \ quad t = {\ frac {1} {1 + px}}, \ qquad x \ geq 0}
- где p = 0,47047, a 1 = 0,3480242, a 2 = -0,0958798, a 3 = 0,7478556
-
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + ⋯ + a 6 x 6) 16, x ≥ 0 {\ displaystyle \ operatorname {erf} (x) \ приблизительно 1 — {\ frac {1} {(1 + a_ {1} x + a _ {2} x ^ {2} + \ cdots + a_ {6} x ^ {6}) ^ {16}}}, \ qquad x \ geq 0}
(максимальная ошибка: 3 × 10)
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + ⋯ + a 6 x 6) 16, x ≥ 0 {\ displaystyle \ operatorname {erf} (x) \ приблизительно 1 — {\ frac {1} {(1 + a_ {1} x + a _ {2} x ^ {2} + \ cdots + a_ {6} x ^ {6}) ^ {16}}}, \ qquad x \ geq 0}
- , где a 1 = 0,0705230784, a 2 = 0,0422820123, a 3 = 0,0092705272, a 4 = 0,0001520143, a 5 = 0,0002765672, a 6 = 0,0000430638
-
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + ⋯ + a 5 t 5) e — x 2, t = 1 1 + px {\ displaystyle \ operatorname {erf} (x) \ приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + \ cdots + a_ {5} t ^ {5}) e ^ {- x ^ {2}}, \ quad t = {\ frac {1} {1 + px}}}
(максимальная ошибка: 1,5 × 10)
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + ⋯ + a 5 t 5) e — x 2, t = 1 1 + px {\ displaystyle \ operatorname {erf} (x) \ приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + \ cdots + a_ {5} t ^ {5}) e ^ {- x ^ {2}}, \ quad t = {\ frac {1} {1 + px}}}
- , где p = 0,3275911, a 1 = 0,254829592, a 2 = −0,284496736, a 3 = 1,421413741, a 4 = −1,453152027, a 5 = 1,061405429
- Все эти приближения действительны для x ≥ 0 Чтобы использовать эти приближения для отрицательного x, викорируйте тот факт, что erf (x) — нечетная функция, поэтому erf (x) = −erf (−x).
- Экспоненциальные границы и чисто экспоненциальное приближение для дополнительных функций задаются как
-
- erfc (x) ≤ 1 2 e — 2 x 2 + 1 2 e — x 2 ≤ e — x 2, x>0 erfc ( х) ≈ 1 6 е — х 2 + 1 2 е — 4 3 х 2, х>0. {\ displaystyle {\ begin {align} \ operatorname {erfc} (x) \ leq {\ frac {1} {2}} e ^ {- 2x ^ {2}} + {\ frac {1} {2} } e ^ {- x ^ {2}} \ leq e ^ {- x ^ {2}}, \ qquad x>0 \\\ имя оператора {erfc} (x) \ приблизительно {\ frac {1} { 6}} e ^ {- x ^ {2}} + {\ frac {1} {2}} e ^ {- {\ frac {4} {3}} x ^ {2}}, \ qquad x>0. \ end {align}}}
- erfc (x) ≤ 1 2 e — 2 x 2 + 1 2 e — x 2 ≤ e — x 2, x>0 erfc ( х) ≈ 1 6 е — х 2 + 1 2 е — 4 3 х 2, х>0. {\ displaystyle {\ begin {align} \ operatorname {erfc} (x) \ leq {\ frac {1} {2}} e ^ {- 2x ^ {2}} + {\ frac {1} {2} } e ^ {- x ^ {2}} \ leq e ^ {- x ^ {2}}, \ qquad x>0 \\\ имя оператора {erfc} (x) \ приблизительно {\ frac {1} { 6}} e ^ {- x ^ {2}} + {\ frac {1} {2}} e ^ {- {\ frac {4} {3}} x ^ {2}}, \ qquad x>0. \ end {align}}}
-
- erfc (x) ≈ (1 — e — A x) e — x 2 B π х. {\ displaystyle \ operatorname {erfc} \ left (x \ right) \ приблизительно {\ frac {\ left (1-e ^ {- Ax} \ right) e ^ {- x ^ {2}}} {B {\ sqrt {\ pi}} x}}.}
- erfc (x) ≈ (1 — e — A x) e — x 2 B π х. {\ displaystyle \ operatorname {erfc} \ left (x \ right) \ приблизительно {\ frac {\ left (1-e ^ {- Ax} \ right) e ^ {- x ^ {2}}} {B {\ sqrt {\ pi}} x}}.}
- Они определили {A, B} = {1.98, 1.135}, {\ displaystyle \ {A, B \} = \ {1.98,1.135 \ },}
, что дает хорошее приближение для всех x ≥ 0. {\ displaystyle x \ geq 0.}
- Одноканальная нижняя граница:
-
- erfc (x) ≥ 2 e π β — 1 β е — β Икс 2, Икс ≥ 0, β>1, {\ Displaystyle \ OperatorName {erfc} (x) \ geq {\ sqrt {\ frac {2e} {\ pi}}} {\ frac {\ sqrt {\ beta -1}} {\ beta}} e ^ {- \ beta x ^ {2}}, \ qquad x \ geq 0, \ beta>1,}
- erfc (x) ≥ 2 e π β — 1 β е — β Икс 2, Икс ≥ 0, β>1, {\ Displaystyle \ OperatorName {erfc} (x) \ geq {\ sqrt {\ frac {2e} {\ pi}}} {\ frac {\ sqrt {\ beta -1}} {\ beta}} e ^ {- \ beta x ^ {2}}, \ qquad x \ geq 0, \ beta>1,}
- где параметр β может быть выбран, чтобы минимизировать ошибку на желаемом интервале приближения.
- Другое приближение дано Сергеем Виницким с использованием его «глобальных приближений Паде»:
-
- erf (x) ≈ sgn (x) 1 — exp (- x 2 4 π + ax 2 1 + ax 2) { \ displaystyle \ operatorname {erf} (x) \ приблизительно \ Operatorname {sgn} (x) {\ sqrt {1- \ exp \ left (-x ^ {2} {\ frac {{\ frac {4} {\ pi) })} + ax ^ {2}} {1 + ax ^ {2}}} \ right)}}}
- erf (x) ≈ sgn (x) 1 — exp (- x 2 4 π + ax 2 1 + ax 2) { \ displaystyle \ operatorname {erf} (x) \ приблизительно \ Operatorname {sgn} (x) {\ sqrt {1- \ exp \ left (-x ^ {2} {\ frac {{\ frac {4} {\ pi) })} + ax ^ {2}} {1 + ax ^ {2}}} \ right)}}}
- где
-
- a = 8 (π — 3) 3 π (4 — π) ≈ 0, 140012. {\ displaystyle a = {\ frac {8 (\ pi -3)} {3 \ pi (4- \ pi)}} \ приблизительно 0,140012.}
- a = 8 (π — 3) 3 π (4 — π) ≈ 0, 140012. {\ displaystyle a = {\ frac {8 (\ pi -3)} {3 \ pi (4- \ pi)}} \ приблизительно 0,140012.}
- Это сделано так, чтобы быть очень точным в окрестностях 0 и добавление бесконечности, а относительная погрешность меньше 0,00035 для всех действительных x. Использование альтернативного значения ≈ 0,147 снижает максимальную относительную ошибку примерно до 0,00013.
- Это приближение можно инвертировать, чтобы получить приближение для других функций ошибок:
-
- erf — 1 (x) ≈ sgn (x) (2 π a + ln (1 — x 2) 2) 2 — ln (1 — x 2) a — (2 π a + ln (1 — x 2) 2). {\ displaystyle \ operatorname {erf} ^ {- 1} (x) \ приблизительно \ operatorname {sgn} (x) {\ sqrt {{\ sqrt {\ left ({\ frac {2} {\ pi a}} + {\ frac {\ ln (1-x ^ {2})} {2}} \ right) ^ {2} — {\ frac {\ ln (1-x ^ {2})} {a}}}} — \ left ({\ frac {2} {\ pi a}} + {\ frac {\ ln (1-x ^ {2})} {2}} \ right)}}.}
- erf — 1 (x) ≈ sgn (x) (2 π a + ln (1 — x 2) 2) 2 — ln (1 — x 2) a — (2 π a + ln (1 — x 2) 2). {\ displaystyle \ operatorname {erf} ^ {- 1} (x) \ приблизительно \ operatorname {sgn} (x) {\ sqrt {{\ sqrt {\ left ({\ frac {2} {\ pi a}} + {\ frac {\ ln (1-x ^ {2})} {2}} \ right) ^ {2} — {\ frac {\ ln (1-x ^ {2})} {a}}}} — \ left ({\ frac {2} {\ pi a}} + {\ frac {\ ln (1-x ^ {2})} {2}} \ right)}}.}
Многочлен
Приближение с максимальной ошибкой 1,2 × 10-7 {\ displaystyle 1,2 \ times 10 ^ {- 7}}
- erf ( x) = {1 — τ x ≥ 0 τ — 1 x < 0 {\displaystyle \operatorname {erf} (x)={\begin{cases}1-\tau x\geq 0\\\tau -1x<0\end{cases}}}
с
- τ = t ⋅ exp (- x 2 — 1,26551223 + 1,00002368 t + 0,37409196 t 2 + 0,09678418 t 3 — 0,18628806 t 4 + 0,27886807 t 5 — 1,13520398 t 6 + 1,48851587 t 7 — 0,82215223 t 8 + 0,17087277 t 9) {\ displaystyle {\ begin {align} \ tau = t \ cdot \ exp \ left (-x ^ {2} -1,26551223 + 1,00002368 t + 0,37409196t ^ {2} + 0,09678418t ^ {3} -0,18628806t ^ {4} \ вправо. \\ \ left. \ qquad \ qquad \ qquad + 0,27886807t ^ {5} -1,13520398t ^ {6} + 1,48851587t ^ {7} -0,82215223t ^ {8} + 0,17087 277t ^ {9} \ right) \ end {align}}}
и
- t = 1 1 + 0,5 | х |. {\ displaystyle t = {\ frac {1} {1 + 0,5 | x |}}.}
Таблица значений
| x | erf(x) | 1-erf (x) |
|---|---|---|
| 0 | 0 | 1 |
| 0,02 | 0,022564575 | 0,977435425 |
| 0,04 | 0,045111106 | 0,954888894 |
| 0,06 | 0,067621594 | 0, 932378406 |
| 0,08 | 0.090078126 | 0,909921874 |
| 0,1 | 0,112462916 | 0,887537084 |
| 0,2 | 0,222702589 | 0,777297411 |
| 0,3 | 0,328626759 | 0,671373241 |
| 0, 4 | 0,428392355 | 0,571607645 |
| 0,5 | 0,520499878 | 0,479500122 |
| 0,6 | 0.603856091 | 0,396143909 |
| 0,7 | 0,677801194 | 0,322198806 |
| 0,8 257> | 0,742100965 | 0,257899035 |
| 0,9 | 0,796908212 | 0,203091788 |
| 1 | 0,842700793 | 0, 157299207 |
| 1,1 | 0,88020507 | 0,11979493 |
| 1,2 | 0,910313978 | 0,089686022 |
| 1,3 | 0,934007945 | 0,065992055 |
| 1,4 | 0.95228512 | 0,04771488 |
| 1,5 | 0, 966105146 | 0,033894854 |
| 1,6 | 0,976348383 | 0,023651617 |
| 1,7 | 0,983790459 | 0,016209541 |
| 1,8 | 0,989090502 | 0,010909498 |
| 1,9 | 0,992790429 | 0,007209571 |
| 2 | 0,995322265<25767> | 0,00477 |
| 2.1 | 0.997020533 | 0.002979467 |
| 2.2 | 0.998137154 | 0,001862846 |
| 2,3 | 0,998856823 | 0,001143177 |
| 2,4 | 0,999311486 | 0,000688514 |
| 2,5 | 0.999593048 | 0.000406952 |
| 3 | 0.99997791 | 0,00002209 |
| 3,5 | 0,999999257 | 0,000000743 |
Связанные функции
Дополнительная функция
дополнительная функция ошибок, обозначается erfc {\ displaystyle \ mathrm {erfc}}
- erfc (x) = 1 — erf (x) = 2 π ∫ x ∞ e — t 2 dt знак равно е — Икс 2 erfcx (х), {\ displaystyle {\ begin {выровнено} \ OperatorName {erfc} (x) = 1- \ operatorname {erf} (x) \\ [5p t] = {\ frac {2} {\ sqrt {\ pi}}} \ int _ {x} ^ {\ infty} e ^ {- t ^ {2}} \, dt \\ [5pt] = e ^ {- x ^ {2}} \ operatorname {erfcx} (x), \ end {align}}}
, который также определяет erfcx {\ displaystyle \ mathrm {erfcx} }


- erfc (x ∣ x ≥ 0) = 2 π ∫ 0 π / 2 exp (- x 2 sin 2 θ) d θ. {\ displaystyle \ operatorname {erfc} (x \ mid x \ geq 0) = {\ frac {2} {\ pi}} \ int _ {0} ^ {\ pi / 2} \ exp \ left (- {\ frac {x ^ {2}} {\ sin ^ {2} \ theta}} \ right) \, d \ theta.}
Это выражение действительно только для положительных значений x, но его можно использовать вместе с erfc (x) = 2 — erfc (−x), чтобы получить erfc (x) для отрицательных значений. Эта форма выгодна тем, что диапазон интегрирования является фиксированным и конечным. Расширение этого выражения для erfc {\ displaystyle \ mathrm {erfc}}
- erfc (x + y ∣ x, y ≥ 0) = 2 π ∫ 0 π / 2 ехр (- x 2 sin 2 θ — y 2 cos 2 θ) d θ. {\ displaystyle \ operatorname {erfc} (x + y \ mid x, y \ geq 0) = {\ frac {2} {\ pi}} \ int _ {0} ^ {\ pi / 2} \ exp \ left (- {\ frac {x ^ {2}} {\ sin ^ {2} \ theta}} — {\ frac {y ^ {2}} {\ cos ^ {2} \ theta}} \ right) \, d \ theta.}
Функция мнимой ошибки
мнимой ошибки, обозначаемая erfi, обозначает ошибки как
- erfi (x) = — i erf (ix) Знак равно 2 π ∫ 0 xet 2 dt знак равно 2 π ex 2 D (x), {\ displaystyle {\ begin {align} \ operatorname {erfi} (x) = — i \ operatorname {erf} (ix) \\ [ 5pt] = {\ frac {2} {\ sqrt {\ pi}}} \ int _ {0} ^ {x} e ^ {t ^ {2}} \, dt \\ [5pt] = {\ frac {2} {\ sqrt {\ pi}}} e ^ {x ^ {2}} D (x), \ end {align}}}
где D (x) — функция Доусона (который можно использовать вместо erfi, чтобы избежать арифметического переполнения ).
Несмотря на название «функция мнимой ошибки», erfi (x) {\ displaystyle \ operatorname {erfi} (x)}
Функция Когда ошибки оценивается для произвольных сложных аргументов z, результирующая комплексная функция ошибок обычно обсуждается в масштабированной форме как функция Фаддеева :
- w (z) = e — z 2 erfc (- iz) = erfcx (- iz). {\ displaystyle w (z) = e ^ {- z ^ {2}} \ operatorname {erfc} (-iz) = \ operatorname {erfcx} (-iz).}
Кумулятивная функция распределения
Функция ошибок по существующей стандартной стандартной функции нормального кумулятивного распределения, обозначаемой нормой (x) в некоторых языках программного обеспечения, поскольку они отличаются только масштабированием и переводом. Действительно,
- Φ (x) = 1 2 π ∫ — ∞ xe — t 2 2 dt = 1 2 [1 + erf (x 2)] = 1 2 erfc (- x 2) {\ displaystyle \ Phi (x) = {\ frac {1} {\ sqrt {2 \ pi}}} \ int _ {- \ infty} ^ {x} e ^ {\ tfrac {-t ^ {2}} {2}} \, dt = {\ frac {1} {2}} \ left [1+ \ operatorname {erf} \ left ({\ frac {x} {\ sqrt {2}}} \ right) \ right] = {\ frac {1} {2}} \ operatorname {erfc} \ left (- {\ frac {x} {\ sqrt {2}}} \ right)}
или переставлен для erf и erfc:
- erf ( x) = 2 Φ (x 2) — 1 erfc (x) = 2 Φ (- x 2) = 2 (1 — Φ (x 2)). {\ displaystyle {\ begin {align} \ operatorname {erf} (x) = 2 \ Phi \ left (x {\ sqrt {2}} \ right) -1 \\\ operatorname {erfc} (x) = 2 \ Phi \ left (-x {\ sqrt {2}} \ right) = 2 \ left (1- \ Phi \ left (x {\ sqrt {2}} \ right) \ right). \ End {выравнивается} }}
Следовательно, функция ошибок также тесно связана с Q-функцией, которая является вероятностью хвоста стандартного нормального распределения. Q-функция может быть выражена через функцию ошибок как
- Q (x) = 1 2 — 1 2 erf (x 2) = 1 2 erfc (x 2). {\ displaystyle Q (x) = {\ frac {1} {2}} — {\ frac {1} {2}} \ operatorname {erf} \ left ({\ frac {x} {\ sqrt {2}}) } \ right) = {\ frac {1} {2}} \ operatorname {erfc} \ left ({\ frac {x} {\ sqrt {2}}} \ right).}
Обратное значение из Φ {\ displaystyle \ Phi}
- пробит (p) = Φ — 1 (p) = 2 erf — 1 (2 p — 1) = — 2 erfc — 1 (2 p). {\ displaystyle \ operatorname {probit} (p) = \ Phi ^ {- 1} (p) = {\ sqrt {2}} \ operatorname {erf} ^ {- 1} (2p-1) = — {\ sqrt {2}} \ operatorname {erfc} ^ {- 1} (2p).}
Стандартный нормальный cdf чаще используется в вероятности и статистике, а функция ошибок чаще используется в других разделах математики.
Функция ошибки является частным случаем функции Миттаг-Леффлера и может также быть выражена как сливающаяся гипергеометрическая функция (функция Куммера):
- erf (х) знак равно 2 х π M (1 2, 3 2, — х 2). {\ displaystyle \ operatorname {erf} (x) = {\ frac {2x} {\ sqrt {\ pi}}} M \ left ({\ frac {1} {2}}, {\ frac {3} {2 }}, — x ^ {2} \ right).}
Он имеет простое выражение в терминах интеграла Френеля.
В терминах регуляризованной гамма-функции P и неполная гамма-функция,
- erf (x) = sgn (x) P (1 2, x 2) = sgn (x) π γ (1 2, x 2). {\ displaystyle \ operatorname {erf} (x) = \ operatorname {sgn} (x) P \ left ({\ frac {1} {2}}, x ^ {2} \ right) = {\ frac {\ operatorname {sgn} (x)} {\ sqrt {\ pi}}} \ gamma \ left ({\ frac {1} {2}}, x ^ {2} \ right).}
sgn (x) {\ displaystyle \ operatorname {sgn} (x)}
Обобщенные функции ошибок

π {\ displaystyle \ scriptstyle {\ sqrt {\ pi}}}

Некоторые авторы обсуждают более общие функции:
- E n (x) = n! π ∫ 0 Икс е — Т N д т знак равно N! π ∑ п знак равно 0 ∞ (- 1) п Икс N п + 1 (N п + 1) п!. {\ displaystyle E_ {n} (x) = {\ frac {n!} {\ sqrt {\ pi}}} \ int _ {0} ^ {x} e ^ {- t ^ {n}} \, dt = {\ frac {n!} {\ sqrt {\ pi}}} \ sum _ {p = 0} ^ {\ infty} (- 1) ^ {p} {\ frac {x ^ {np + 1}} {(np + 1) p!}}.}
Примечательные случаи:
- E0(x) — прямая линия, проходящая через начало координат: E 0 (x) = xe π {\ displaystyle \ textstyle E_ {0} (x) = {\ dfrac {x} {e {\ sqrt {\ pi}}}}}
- E2(x) — функция, erf (x) ошибки.
После деления на n!, все E n для нечетных n выглядят похожими (но не идентичными) друг на друга. Аналогично, E n для четного n выглядят похожими (но не идентичными) друг другу после простого деления на n!. Все обобщенные функции ошибок для n>0 выглядят одинаково на положительной стороне x графика.
Эти обобщенные функции могут быть эквивалентно выражены для x>0 с помощью гамма-функции и неполной гамма-функции :
- E n (x) = 1 π Γ (n) (Γ (1 n) — Γ (1 n, xn)), x>0. {\ displaystyle E_ {n} (x) = {\ frac {1} {\ sqrt {\ pi}}} \ Gamma (n) \ left (\ Gamma \ left ({\ frac {1} {n}} \ right) — \ Gamma \ left ({\ frac {1} {n}}, x ^ {n} \ right) \ right), \ quad \ quad x>0.}
Следовательно, мы можем определить ошибку функция в терминах неполной гамма-функции:
- erf (x) = 1 — 1 π Γ (1 2, x 2). {\ displaystyle \ operatorname {erf} (x) = 1 — {\ frac {1} { \ sqrt {\ pi}}} \ Gamma \ left ({\ frac {1} {2}}, x ^ {2} \ right).}
Итерированные интегралы дополнительных функций
Повторные интегралы дополнительные функции ошибок определения как
- inerfc (z) = ∫ z ∞ in — 1 erfc (ζ) d ζ i 0 erfc (z) = erfc (z) i 1 erfc (z) = ierfc (z) знак равно 1 π е — z 2 — z erfc (z) я 2 erfc (z) = 1 4 [erfc (z) — 2 z ierfc (z)] {\ displaystyle {\ begin {align } \ operatorname {i ^ {n} erfc} (z) = \ int _ {z} ^ {\ infty} \ operatorname {i ^ {n-1} erfc} (\ zeta) \, d \ zeta \\\ имя оператора {i ^ {0} erfc} (z) = \ operatorname {erfc} (z) \\\ operatorname {i ^ {1} erfc} (z) = \ operat orname {ierfc} (z) = {\ frac { 1} {\ sqrt {\ pi}}} e ^ {- z ^ {2}} — z \ operatorname {erfc} (z) \\\ operatorname {i ^ {2} erfc} (z) = {\ frac {1} {4}} \ left [\ operatorname {erfc} (z) -2z \ operatorname {ierfc} (z) \ right] \\\ end {выровнено}}
Общая рекуррентная формула:
- 2 ninerfc (z) = in — 2 erfc (z) — 2 цинк — 1 erfc (z) {\ displaystyle 2n \ operatorname {i ^ {n} erfc} (z) = \ operatorname {i ^ { n-2} erfc} (z) -2z \ operatorname {i ^ {n-1} erfc} (z)}
У них есть степенной ряд
- в erfc (z) = ∑ j = 0 ∞ (- Z) J 2 N — JJ! Γ (1 + N — J 2), {\ displaystyle i ^ {n} \ operatorname {erfc} (z) = \ sum _ {j = 0} ^ {\ infty} {\ frac {(-z) ^ { j}} {2 ^ {nj} j! \ Gamma \ left (1 + {\ frac {nj} {2}} \ right)}},}
из следуют свойства симметрии
- i 2 m ERFC (- Z) знак равно — я 2 m ERFC (Z) + ∑ Q знак равно 0 мZ 2 д 2 2 (м — д) — 1 (2 д)! (м — д)! {\ displaystyle i ^ {2m} \ operatorname {erfc} (-z) = — i ^ {2m} \ operatorname {erfc} (z) + \ sum _ {q = 0} ^ {m} {\ frac {z ^ {2q}} {2 ^ {2 (mq) -1} (2q)! (Mq)!}}}
и
- i 2 m + 1 erfc (- z) = i 2 m + 1 erfc (г) + ∑ ä знак равно 0 ìZ 2 ä + 1 2 2 ( м — д) — 1 (2 д + 1)! (м — д)!. {\ displaystyle i ^ {2m + 1} \ operatorname {erfc} (-z) = i ^ {2m + 1} \ operatorname {erfc} (z) + \ sum _ {q = 0} ^ {m} {\ гидроразрыва {z ^ {2q + 1}} {2 ^ {2 (mq) -1} (2q + 1)! (mq)!}}.}
Реализации
Как действительная функция вещественного аргумента
- В операционных системах, совместимых с Posix, заголовок math.h должен являть, а математическая библиотека libm должна быть функция erf и erfc (двойная точность ), а также их одинарная точность и расширенная точность аналоги erff, erfl и erfc, erfcl.
- Библиотека GNU Scientific предоставляет функции erf, erfc, log (erf) и масштабируемые функции ошибок.
Как сложная функция комплексного аргумента
- libcerf, числовая библиотека C для сложных функций, предоставляет комплексные функции cerf, cerfc, cerfcx и реальные функции erfi, erfcx с точностью 13–14 цифр на основе функции Фаддеева, реализованной в пакете MIT Faddeeva Package
См. также
Связанные ции
- интеграл Гаусса, по всей действительной прямой
- функция Гаусса, производная
- функция Доусона, перенормированная функция мнимой ошибки
- интеграл Гудвина — Стона
по вероятности
- Нормальное распределение
- Нормальная кумулятивная функция распределения, масштабированная и сдвинутая форма функций ошибок
- Пробит, обратная или квантильная функция нормального CDF
- Q-функция, вероятность хвоста нормального распределения
Ссылки
Дополнительная литература
- Abramowitz, Milton ; Стегун, Ирен Энн, ред. (1983) [июнь 1964]. «Глава 7». Справочник по математическим функциям с формулами, графики и математическими таблицами. Прикладная математика. 55 (Девятое переиздание с дополнительными исправлениями; десятое оригинальное издание с исправлениями (декабрь 1972 г.); первое изд.). Вашингтон.; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Dover Publications. п. 297. ISBN 978-0-486-61272-0 . LCCN 64-60036. MR 0167642. LCCN 65-12253.
- Press, William H.; Теукольский, Саул А.; Веттерлинг, Уильям Т.; Фланнери, Брайан П. (2007), «Раздел 6.2. Неполная гамма-функция и функция ошибок », Числовые рецепты: Искусство научных вычислений (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN 978-0-521- 88068-8
- Темме, Нико М. (2010), «Функции ошибок, интегралы Доусона и Френеля», в Олвер, Фрэнк У. Дж. ; Лозье, Даниэль М.; Бойсверт, Рональд Ф.; Кларк, Чарльз В. (ред.), Справочник NIST по математическим функциям, Cambridge University Press, ISBN 978-0-521-19225-5 , MR 2723248
Внешние ссылки
- MathWorld — Erf
- Таблица интегралов функций ошибок
Приложение А. Обзор анализа Фурье
А.1. Сигналы, спектры и линейные системы
А.2. Применение методов Фурье к анализу линейных систем
А.2.1. Разложение в ряд Фурье
А.2.2. Спектр последовательности импульсов
А.2.3. Представление в виде интеграла Фурье
А.3. Свойства преобразования Фурье
А.3.1. Сдвиг во времени
А.3.2. Сдвиг по частоте
А.4. Полезные функции
А.4.1. Дельта-функция
А.4.2. Спектр синусоиды
А.5. Свертка
А.5.1. Графическая иллюстрация свертки
А.5.2. Свертка по времени
А.5.3. Свертка по частоте
А.5.4. Свертка функции с единичным импульсом
А.5.5. Применение свертки при демодуляции
А.6. Таблицы Фурье-образов и свойств преобразования Фурье
Приложение Б. Основы теории принятия статистических решений
Б.1. Теорема Байеса
Б.1.1. Дискретная форма теоремы Байеса
Б.1.2. Теорема Байеса в смешанной форме
Б.2. Теория принятия решений
Б.2.1. Элементы задачи теории принятия решений
Б.2.2. Проверка методом отношения правдоподобий и критерий максимума апостериорной вероятности
Б.2.3. Критерий максимального правдоподобия
Б.3. Пример обнаружения сигнала
Б.3.1. Двоичное решение по принципу максимального правдоподобия
Б.3.2. Вероятность битовой ошибки
Приложение В. Отклик корреляторов на белый шум
Приложение Г. Полезные соотношения
Приложение Д. S-область, z-область и цифровая фильтрация
Д.1. Преобразование Лапласа
Д.1.1. Стандартное преобразование Лапласа
Д.1.2. Свойства преобразования Лапласа
Д.1.3. Использование преобразования Лапласа
Д.1.4. Передаточная функция
Д.1.5. Фильтрация нижних частот в RС-цепи
Д.1.6. Полюсы и нули
Д.1.7. Устойчивость линейных систем
Д.2. z-преобразование
Д.2.1. Вычисление z-преобразования
Д.2.2. Обратное z-преобразование
Д.3. Цифровая фильтрация
Д.3.1. Передаточная функция цифрового фильтра
Д.3.2. Устойчивость однополюсного фильтра
Д.3.3. Устойчивость произвольного фильтра
Д.3.4. Диаграмма полюсов-нулей и единичная окружность
Д.3.5. Дискретное преобразование Фурье импульсной характеристики цифрового фильтра
Д.4. Фильтры с конечной импульсной характеристикой
Д.4.1. Структура фильтра с конечной импульсной характеристикой
Д.4.2. Дифференциатор с конечной импульсной характеристикой
Д.5. Фильтры с бесконечной импульсной характеристикой
Д.5.1. Оператор левосторонней разности
Д.5.2. Использование билинейного преобразования для создания фильтров с бесконечной импульсной характеристикой
Д.5.3. Интегратор с бесконечной импульсной характеристикой
Приложение Е. Перечень символов
Приложение А. Обзор анализа Фурье
А.1. Сигналы, спектры и линейные системы
Электрические сигналы связи — это меняющиеся со временем сигналы напряжения или тока, обычно описываемые во временной области. С другой стороны, подобные сигналы также удобно описывать в частотной области, где описание сигнала называется его спектром. Спектральные понятия достаточно важны при анализе и проектировании систем связи; они могут описывать сигнал через его среднюю мощность или энергетическое содержание на различных частотах и показывают, какую часть (полосы) электромагнитного спектра занимает сигнал. Федеральная комиссия по средствам связи США (Federal Communications Commission — FCC) требует, чтобы теле- и радиостанции работали на выделенных им частотах при крайне малых промежутках между полосами, занятыми различными станциями. Например, амплитудно-модулированные радиоканалы разделены полосой 10 кГц, а телевизионные каналы — полосой 6 МГц. Так что наш интерес к спектрам и анализу Фурье объясняется реальными требованиями помещения сигнала в точно заданные границы.
Частотные спектральные характеристики можно приписать как к собственно сигналам, так и электрическим схемам. Если говорится, что конкретный спектр описывает сигнал, подразумевается, что один из способов описания сигнала — это задать его амплитуду и фазу как функции частоты. В то же время, когда мы говорим о спектральных параметрах схемы, имеем в виду передаточную функцию (или частотную характеристику), связывающую выход схемы с ее входом; другими словами, схема характеризуется тем, какая часть спектра входного сигнала пройдет на выход.
А.2. Применение методов Фурье к анализу линейных систем
Методы Фурье используются для анализа линейных схем или систем: (1) для предсказания реакции (отклика) системы; (2) для определения динамики системы (передаточной функции) и (3) для оценки или интерпретации результатов тестов. Предсказание реакции системы (1) схематически проиллюстрировано на рис. А.1. Пусть на вход системы подается произвольный периодический сигнал с периодом Т0секунд. Методы Фурье-анализа, как показано на рисунке, позволяют описать подобный вход как сумму синусоидальных сигналов. Наименьшая (или собственная) частота этих сигналов — 1/Т Гц; остальные частоты кратны данной (2/Т0, 3/Т0, …) и называются гармониками. Важной особенностью линейной системы является принцип суперпозиции — реакция на сумму сигналов равна сумме откликов на каждый сигнал. Фактически это свойство используется как определение линейности. Математически система линейна, если для всех a, b, x1(t) и х2(t)
y1(t) — реакция системы на x1(t);
y2(t) — реакция системы на x2(t);
ay1(t) + by2(t) — реакция системы на ax1(t) + bx2(t).
Рис. А. 1. Предсказание реакции системы
Данное определение свидетельствует о том, что выходной отклик линейной системы с входными синусоидальными сигналами должен составляться из синусоидальных сигналов с теми же частотами, что и у входных сигналов; обычно подобная система задается частотной передаточной функцией (частотной характеристикой), описывающей изменение амплитуды и фазы сигнала в зависимости от частоты, как показано на рис. А.2. На рис. А.2, а представлена характерная зависимость амплитуды сигнала от частоты; подобным образом на рис. А.2, б показана зависимость фазы сигнала от частоты.
Передаточная функция является рабочей характеристикой системы, т.е. описывает отклик системы на каждую синусоиду. Следовательно, имея передаточную функцию системы, можно предсказать каждый выходной компонент. С помощью принципа суперпозиции эти выходные компоненты суммируются, что дает реакцию системы на любой входной сигнал (рис. А.1). Подобным образом, зная входной и выходной сигналы, можно определить передаточную функцию системы.
Развитие методов Фурье-анализа оказало большое влияние на анализ линейных систем; оно позволило связать переходные процессы и методы работы с гармоническими функциями, а также упростило анализ линейных систем при их активизации произвольным входным сигналом. Как логарифм позволяет превратить операцию умножения в операцию сложения, так и методы Фурье-анализа позволяют заменить сложные сигналы гармоническими составляющими и методами работы с гармоническими функциями.
Рис. А.2. Передаточная функция системы:
а) амплитудная характеристика;
б) фазовая характеристика
А.2.1. Разложение в ряд Фурье
Периодические сигналы с конечной энергией, передаваемой за период, можно представить в виде ряда Фурье. Произвольный периодический сигнал x() выражается через бесконечное число гармоник с возрастающими частотами.
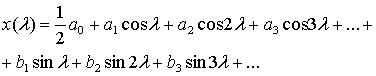
Члены cos и sin
, называются основными; члены cos n
и sin n
при n > 1, где п — целое, именуются гармоническими. Члены апи bn представляют коэффициенты гармоник, а
— это постоянный член или составляющая постоянного тока.
Период функции х() должен равняться 2
или кратной величине; кроме того, функция х(
) должна быть однозначной. Ряд Фурье можно рассматривать как «рецепт приготовления» любого периодического сигнала из синусоидальных составляющих. Чтобы данный ряд имел практическое значение, он должен сходиться, т.е. частичные суммы ряда должны иметь предел.
Процесс создания произвольного периодического сигнала из коэффициентов, описывающих смешивание гармоник, называется синтезом. Обратный процесс вычисления коэффициентов именуется анализом. Вычисление коэффициентов облегчается тем, что среднее от перекрестных произведений синусоиды на косинусоиду (а также средние любой синусоиды или косинусоиды) равно нулю. Ниже приводятся формулы, иллюстрирующие основные свойства средних от гармонических функций.
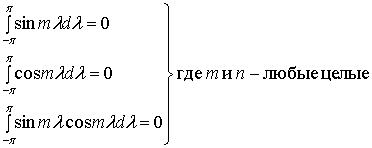
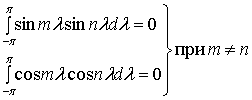
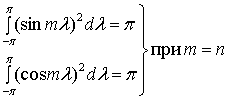
Рассмотрим, как вычисляются значения коэффициентов аn или bn в формуле (А.1). Например, для вычисления коэффициента а3 обе стороны формулы (А. 1) можно умножить на cos 3d
, а затем проинтегрировать.
Полученный вывод можно обобщить.
(A.5)
(А.6)
Коэффициент а0 находится из (А.5) при n = 0. В результате получаем следующее.
(A.7)
Данное выражение — это член нулевой частоты, или среднее значение периодического сигнала. Процесс синтеза уравнения (А.1) можно записать в более компактной форме.
(A.8)
Существует несколько способов выражения пары преобразований (анализа и синтеза) Фурье. Наиболее распространенная форма — это выражение синуса и косинуса через экспоненты с комплексным показателем.
(А.9)
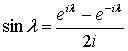
Периодическая функциях c периодом Т0секунд имеет следующие частотные компоненты — ,
,
, …, где f0 = 1/Т0называется собственной частотой. Иногда частотные компоненты записывают как
, 2
, 3
, …, где
именуется собственной угловой частотой; частота f измеряется в герцах, частота w — в радианах в секунду. Заменим п
в аргументах гармонических функций в формулах (А.5)-(А.8) на
, где n— целое. При n = 1, пf0 представляет собственную частоту, а при п>1 — гармоники собственной частоты. Используя формулы (А.8)-(А.10), можно записать x(t) в экспоненциальной форме.
(A.11)
Обозначим через спкомплексные коэффициенты, или спектральные компоненты x(t), связанные с коэффициентами апи bn следующим образом.
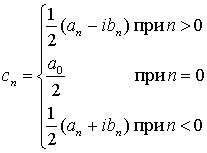
Теперь формулу (А. 11) можно упростить.
(A.13)
Здесь коэффициенты экспоненциальных гармоник определяются следующим образом.
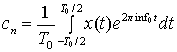
Для проверки справедливости формулы (А. 14) умножим обе части выражения (А. 13) на, проинтегрируем по промежутку (
) и используем следующую формулу.
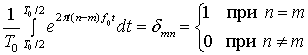
Здесь называется дельта-функцией Кронекера. После выполнения указанных действий получаем
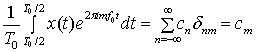
для всех целых т. В общем случае коэффициент сn — комплексное число, выразить которое можно следующим образом.
(А.17)
,
(А.18)
где
(А.19)
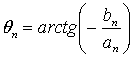
Значение |сn| определяет амплитуду n-й гармоники периодического сигнала, так что график зависимости |сn| от частоты, называемой амплитудным спектром, дает амплитуду каждой из n дискретных гармоник сигнала. Подобным образом график зависимости от частоты, именуемой фазовым спектром, дает фазу каждой гармоники сигнала. Коэффициенты Фурье вещественной периодической по времени функции обладают следующим свойством.
(А.21)
где — комплексно сопряженное сn. Таким образом, получаем следующее.
(А.22)
Амплитудный спектр является четной функцией частоты. Подобным образом фазовый спектр — это нечетная функция частоты, поскольку из формулы (А.20) следует, что
. (А.23)
Итак, как отмечалось выше, ряды Фурье особенно полезны при описании произвольных периодических сигналов с конечной энергией каждого периода. Кроме того, они могут использоваться для описания непериодических сигналов, имеющих конечную энергию за конечный интервал. Впрочем, для таких сигналов более удобным является представление в виде интеграла Фурье (см. раздел А.2.3).
А.2.2. Спектр последовательности импульсов
В цифровой связи весьма важным сигналом является идеальная периодическая последовательность прямоугольных импульсов, показанная на рис. А.З. Для коэффициентов ряда Фурье последовательности импульсов xp(t) с периодом T0 (каждый импульс имеет амплитуду А и длительность T) справедливо следующее выражение (проверить справедливость можно с помощью формул (А. 14) и (А.10)).
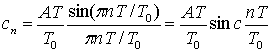
Рис. А.З. Последовательность импульсов
В данном выражении
Функция sinc, как показано на рис. А.4, достигает максимума (единицы) при у=0 и стремится к нулю при у, осциллируя с постепенно уменьшающейся амплитудой. Через нуль она проходит в точках у = ±1, ±2, …. На рис. А.5, а как функция отношения п/Т0показан амплитудный спектр последовательности импульсов |сп|, а на рис. А.5, б изображен фазовый спектр
. Следует отметить, что положительные и отрицательные частоты двустороннего спектры — это весьма полезный способ математического выражения спектра; очевидно, что в лабораторных условиях воспроизвести можно только положительные частоты.
Рис. А.4. Функция sinc
Рис. А.5. Спектр последовательности импульсов:
а) амплитудный; б) фазовый
Синтез выполняется посредством подстановки коэффициентов из формулы (А.24) в формулу (А.13). Получаемый ряд представляет исходную последовательность импульсов xр(t), синтезированную из составных элементов.
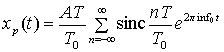
Идеальная периодическая последовательность импульсов включает все гармоники, кратные собственной частоте. В системах связи часто предполагается, что значительная часть мощности или энергии узкополосного сигнала приходится на частоты от нуля до первого нуля амплитудного спектра (рис. А.5, а). Таким образом, в качестве меры ширины полосы последовательности импульсов часто используется величина 1/Т (где Т — длительность импульса). Отметим, что ширина полосы обратно пропорциональна длительности импульса; чем меньше импульсы, тем более широкая полоса с ними связана. Отметим также, что расстояние между спектральными линиями обратно пропорционально периоду импульсов; при увеличении периода линии располагаются ближе друг к другу.
А.2.3. Представление в виде интеграла Фурье
В системах связи часто встречаются непериодические сигналы, имеющие конечную энергию в конечном интервале и нулевую энергию за пределами этого интервала. Подобные сигналы удобно описывать, используя представление в виде интеграла Фурье, или просто Фурье-образ. Непериодический сигнал можно описать как периодический в предельном смысле. Рассмотрим, например, последовательность импульсов, показанную на рис. А.З. Если Т0стремится к бесконечности, последовательность импульсов превращается в отдельный импульс x(t), число спектральных линий стремится к бесконечности, а график спектра превращается в гладкий спектр частот Х(f). Для данного предельного случая можно определить пару интегральных преобразований Фурье.
(A.26)
и
, (A.27)
где f — частота, измеряемая в герцах. Данную пару преобразований можно использовать при описании частотно-временных соотношений непериодических сигналов.
С этого момента применение преобразования Фурье будем обозначать , а обратное преобразование —
. Связь частотной и временной областей будем указывать с использованием знака
.
Данная запись означает, что X(f) получается в результате применения преобразования Фурье к x(t), а х(t) — в результате применения обратного преобразования Фурье к X(f). В контексте систем связи x(t) — вещественная функция, a X(f) — комплексная функция, имеющая действительный и мнимый компоненты; в полярной форме спектр X(f) можно задать через его амплитудную и фазовую характеристики.
(А.28)
Свойства X(f), спектра непериодического сигнала, подобны свойствам периодического сигнала, представленным в формулах (А.17)-(А.23); т.е. если x(t) принимает вещественные значения,
(А.29)
, (А.30)
где X* — комплексно сопряженное X. Амплитудный спектр |X(f)| — это четная функция f, а фазовый спектр — нечетная функция f. Во многих случаях функция X(f) имеет или только действительную часть, или только мнимую, так что для ее описания достаточно одного графика.
А.3. Свойства преобразования Фурье
Существует множество хороших справочников, в которых подробно рассмотрены преобразования Фурье и их свойства [1-4]. В данном приложении внимание акцентируется на свойствах, представляющих интерес в теории связи. Некоторыми ключевыми особенностями передач в системах связи являются временная задержка, сдвиг фазы, перемножение с другими сигналами, трансляция частоты, свертка сигнала и свертка спектра. Остановимся подробнее на свойствах преобразования Фурье (сдвиг и свертка), необходимых для описания данных особенностей.
А.3.1. Сдвиг во времени
Если , то
(A.31)
Пусть , тогда
Если сигнал запаздывает во времени, амплитуда его частотного спектра не меняется, а фазовый спектр сдвигается по фазе. Сдвиг на время t0 во временной области эквивалентен умножению на (сдвигу фазы на
) во временной области.
А.3.2. Сдвиг по частоте
Если , то
(A.32)
Выше приведено свойство трансляции частоты, которое описывает смещенный спектр, возникающий при умножении сигнала на . Используя формулу (А.32) вместе с формулой (А.9), можно получить выражения для Фурье-образа сигнала, умноженного на косинусоиду.
(А.33)
Данное свойство также называется теоремой о модуляции (или смешивании). Умножение произвольного сигнала на синусоиду частоты f0 приводит к трансляции исходного спектра сигнала на f0 и —f0.
А.4. Полезные функции
А.4.1. Дельта-функция
Полезной функцией в теории связи является так называемая дельта-функция Дирака, или единичный импульс, . Импульсную функцию можно определить из любой фундаментальной функции (например, прямоугольного или треугольного импульса). В любом случае импульсная функция определяется в пределе (амплитуда импульса стремится к бесконечности, длительность импульса — к нулю, а площадь импульса равна единице) [5]. Единичная импульсная функция имеет следующие свойства.
(А.34)
(А.35)
не ограничена в точке t = 0 (А.36)
(А.37)
(A.38)
Формула (А.38) представляет просеивающее (или выборочное) свойство; результат интегрирования функции x(t) с дельта-функцией — выборка функции x(t) в точке t = t0.
В некоторых задачах полезными бывают следующие представления дельта-функции в частотной и временной областях.
(А.39)
(A.40)
A.4.2. Спектр синусоиды
Для нахождения Фурье-образа синусоидального сигнала Необходимо предположить, что данный сигнал существует только в интервале (). При таком условии функция будет иметь Фурье-образ, пока Т0будет конечно. В пределе Т0предполагается очень большим, но конечным. Спектр сигнала x(t) =
можно найти, используя формулы (А.9) и (А.26).
Как видно из формулы (А.40), данное интегральное выражение можно записать через следующие единичные импульсные функции.
(А.41)
Подобным образом можно показать, что спектр синусоидального сигнала равен следующему.
(А.42)
Спектр косинусоидального сигнала показан на рис. А.6, а спектр синусоидального сигнала — на рис. А.7. Все дельта-функции на этих рисунках изображены как пики с весовыми коэффициентами А/2 или -А/2.
Рис. А.6. Спектр сигнала x(t) =
А.5. Свертка
В конце XIX века Оливер Хевисайд (Oliver Heaviside) использовал свертку для вычисления тока на выходе электрической схемы, на вход которой подан сигнал, описываемый сложной функцией напряжения. Использование методов Хевисайда предшествовало применению аналитических методов, разработанных Фурье и Лапласом (хотя публикации Фурье и Лапласа вышли раньше).
Рис. A.7. Спектр сигнала
Отклик схемы на входное импульсное возмущение называется импульсной характеристикой и обозначается h(t), как показано на рис. А.8, т.е. это просто выходное напряжение, полученное при подаче на вход дельта-функции. Хевисайд аппроксимировал произвольный сигнал, подобный показанному на рис. А.9, а, набором равноотстоящих импульсов. Подобные импульсы конечной высоты и ненулевой длительности показаны на рис. А.9, б. В пределе при длительности импульса
каждый импульс стремится к дельта-функции с весовым коэффициентом, равным площади импульса. Далее будем считать, что данные равноотстоящие импульсы имеют нулевую длительность, хотя строго они являются такими только в пределе.
Рис. А.8. Импульсная характеристика линейной системы
Поскольку нас интересует как время подачи импульсов на вход, так и время наблюдения реакции на них на выходе, следует весьма аккуратно относиться к записи времени. Поэтому определим две различные временные последовательности; начнем с использования следующей формы записи.
1. Время на входе будем обозначать через , так что входные импульсы напряжения будут записываться как
,
, …,
.
2. Время на выходе будем обозначать через t, так что выходные функции тока будут записываться как i(t1), i(t2), …, i(tN).
Хевисайд нашел отклик схемы (или ток на выходе) для каждого входного импульса; после этого он сложил эти токи и получил общий ток на выходе. Весовой коэффициент прямоугольного импульса, поданного в момент — это произведение
. Если устремить
к нулю, последовательность импульсов будет аппроксимировать произвольное входное напряжение настолько точно, насколько это нужно. Снова отметим, что момент подачи импульса на вход — это
, а момент определения реакции системы — ti, где
— переменная входного времени, a t — переменная выходного времени, i = 1, …, N.
б)
Рис. А.9. Аппроксимация произвольного входного сигнала:
а) входной сигнал; б) аппроксимация входного сигнала
На рис. А.10 показана выходная реакция i(t) = A1h(t—) на импульс с весовым коэффициентом
. Поскольку входной импульс в момент
не является единичным, он умножается на весовой коэффициент — интенсивность (или площадь)
. В некоторый момент времени t1 где
, выходная реакция на импульс
, как показано на рис. А.10, выражается следующим образом.
при
Рис. А. 10. Реакция на импульс в момент
При наличии нескольких входных импульсов общий выходной отклик линейной системы — это просто сумма отдельных откликов. На рис. А.11 показан отклик сети на два единичных импульса. При N импульсах на входе ток на выходе, измеренный в момент времени t1, можно записать следующим образом.
Рис. А. 11. Реакция на два импульса
i(t1) = +
+ …+
,
где импульсы подаются в моменты ,
, …,
и где
.
Все импульсы, поданные на вход после момента t1, не учитываются, поскольку они не дают вклада в i(t1). Это согласуется с требованием причинности физически реализуемых систем — отклик системы должен быть нулевым до применения возмущения. Итак, можно записать ток на выходе в любой момент времени t следующим образом.
i(t) = +
+ …+
или, поскольку весовой коэффициент импульса в момент времени равен
,
(A.43)
Когда стремится к нулю, сумма входных импульсов — к действительному напряжению
,
можно заменить
, при этом сумма переходит в интеграл свертки.
(А.44,а)
или
(A.44,б)
В сокращенной записи
(A.45)
Итак, i(t) — это сумма реакций на отдельные импульсные возмущения, произведенные в некоторый входной момент , причем каждый импульс умножается на весовой коэффициент — интенсивность.
А.5.1. Графическая иллюстрация свертки
Рассмотрим квадратный импульс v(t), подаваемый на вход линейной сети, импульсная характеристика которой равна h(t) (рис. А. 12, а). Отклик на выходе описывается интегралом свертки, представленным в формуле (А.44).
Рис. А. 12. Графическая иллюстрация свертки
Независимой переменной в интеграле свертки является . На рис. А. 12, б показаны функции
и
. Отметим, что
получается отображением
относительно оси
. Член
представляет функцию
, смещенную на t секунд вдоль положительного направления оси
. На рис. А. 12, в показана функция
. Значение интеграла свертки в момент времени t=t1 получается из формулы (А.44), в которой положено t = tl. Это просто площадь под кривой произведения
на
, показанного на рис. А. 12, г. Подобным образом интеграл свертки, взятый в момент t = t2, равен заштрихованной области на рис. А. 12, д. На рис. А. 12, е приведен график отклика на выходе схемы при квадратном импульсе на входе, показанном на рис. А. 12, а. Каждое вычисление интеграла свертки для некоторого момента времени t1 дает одну точку i(ti) графика на рис. А.12, е.
А.5.2. Свертка по времени
Если и
, то
Для линейных систем порядок интегрирования можно изменить.
(A.46)
С помощью свойства сдвига во времени второе интегральное выражение правой части можно заменить на .
(A.47)
Следовательно, операцию свертки во временной области можно заменить умножением в частотной области.
А.5.3. Свертка по частоте
Можно показать, что, вследствие симметрии пары преобразований Фурье (формулы (А.26) и (А.27)), умножение во временной области переходит в свертку в частотной области.
(A.48)
Данный переход умножения в одной области в свертку в другой весьма удобен, поскольку, как правило, одну из этих операций выполнить значительно проще, чем другую. Например, ранее говорилось, что Хевисайд использовал свертку для нахождения тока на выходе линейной системы при подаче на вход произвольного переменного напряжения. Подобные методы часто включают вычисление (иногда трудоемкое) свертки входного сигнала с импульсной характеристикой системы. Поскольку, как видно из формулы (А.47), свертка во временной области переходит в умножение в частотной, для линейной системы входной сигнал можно просто умножить на передаточную функцию системы. Выходной сигнал затем получается путем применения к произведению обратного преобразования Фурье.
(А.49)
Вычислить выражение (А.49) часто намного проще, чем (А.45). В то же время, при определенных обстоятельствах, операция свертки настолько проста, что ее можно выполнить графически, просто внимательно изучив соответствующий график. Предположим, что некоторый произвольный сигнал необходимо умножить на косинусоиду фиксированной частоты, например несущую (если речь идет о модуляции). С помощью формулы (А.48) спектр произвольного сигнала можно свернуть со спектром косинусоиды, что, как показывается в следующем разделе, выполняется довольно просто.
А.5.4. Свертка функций с единичным импульсом
При использовании свойства, представленного в формуле (А.47), очевидно, что если
и
,
то
. (А.50)
Также должно быть очевидно, что
(A.51)
и
(A.52)
Следовательно, можно сделать вывод, что свертка функции с единичным импульсом дает исходную функцию. Простое развитие формулы (А.52) дает следующее.
(A.53)
На рис. А. 13 показано, насколько просто производится свертка спектра произвольного сигнала со спектром косинусоиды. На рис. А. 13, а представлен спектр X(f) произвольного узкополосного сигнала. На рис. А.13, б показан спектр . Выход Z(f) = Х(f)*Y(f) на рис. А.13, в получается при свертке спектра сигнала с импульсной функцией Y(f), согласно формуле (А.53), где импульсы действуют как стробирующие функции. Следовательно, в данном простом примере свертку можно выполнить графически, заметая стробирующие импульсы через спектр сигнала. Умножение на импульсные функции на каждом шаге заметания приводит к повторению спектра сигнала. Результат, показанный на рис. А.13, в, — это версия исходного спектра X(f), смещенная к месторасположению импульсных функций, изображенных на рис. А.13, б.
А.5.5. Применение свертки при демодуляции
В разделе А.5.4 рассматривался сигнал, умноженный на . Было показано, как в частотной области выглядит свертка спектра сигнала со спектром косинусоиды. В данном разделе рассматривается обратный процесс. Необходимо демодулировать сигнал, умноженный на
(сигнал нужно восстановить в его изначальном диапазоне частот).
Рис. А.13. Свертка спектра сигнала со спектром косинусоиды
На рис. А. 14, а представлен спектр, Z(f), сигнала, смещенного вверх по частоте.
Можно демодулировать данный смещенный сигнал и восстановить исходный сигнал, умножив данный сигнал на . Вместо этого мы можем проиллюстрировать процесс обнаружения в частотной области, свернув Z(f) со спектром несущей,
, показанным на рис. А. 14, б.
Рис. А.14. Применение демодуляции
Использование формул (А.52) и (А.53) позволяет записать следующее.
(A.54)
Следовательно, результат демодуляции X(f)=Z(f)*Y(f) получаем в результате применения формулы (А. 54). Получающийся спектр сигнала — это спектр исходного сигнала плюс компоненты, центрированные на частотах ±2f0, как показано на рис. А. 14, в. Как и в предыдущем разделе, свертку можно выполнить графически. На рис. А. 14, в отображены следующие члены.
=
=
+=
= (А.55)
Отметим, что результат — это спектр исходного сигнала плюс члены, связанные с высокочастотными компонентами. Данный результат типичен для процесса обнаружения; высокочастотные члены отфильтровываются и отбрасываются, оставляя спектр демодулированного исходного сигнала.
А.6. Таблицы Фурье-образов и свойств преобразования Фурье
В табл. А.1 и А.2 приведены Фурье-образы наиболее часто встречающихся функций и некоторые свойства преобразования Фурье.
Таблица А. 1. Фурье-образы
|
|
|
|
1. |
1 |
|
2. 1 |
|
|
3. |
|
|
4. |
|
|
5. |
|
|
6. |
|
|
7. |
|
|
8. |
|
|
9. |
|
|
10. |
|
|
11. |
|
|
12. |
|
|
13. |
|
|
14. |
|
|
15. |
|
|
16. |
|
Примечание: rect(f/2W) = 1 для —W<f< W и 0 для | f | > W; sinc x = (sin)/
.
Таблица A. 2. Свойства преобразования Фурье
|
Действие |
|
|
|
1. Изменение масштаба |
x(at) |
|
|
2. Сдвиг во времени |
|
|
|
3. Сдвиг по частоте |
|
|
|
4. Дифференцирование по времени |
|
|
|
5. Дифференцирование по частоте |
|
|
|
6. Интегрирование по времени |
|
|
|
7. Свертка по времени |
|
|
|
8. Свертка по частоте |
|
|
Литература
1. Papoulis A. Signal Analysis. McGraw-Hill Book Company, New York, 1977.
2. Panter P. F. Modulation, Noise, and Spectral Analysis. McGraw-Hill Book Company, New York, 1965.
3. Bracewell R. The Fourier Transfer and Its Applications. McGraw-Hill Book Company, New York, 1978.
4. Haykin S. Communications Systems. John Wiley & Sons, Inc., New York, 1983.
5. Schwartz M. Information, Transmission, Modulation, and Noise. McGraw-Hill Book Company, New York, 1980.
Приложение Б. Основы теории принятия статистических решений
Б.1. Теорема Байеса
Математические основы проверки гипотез базируются на теореме Байеса, которая следует из определения отношения между условной вероятностью и совместной вероятностью случайных переменных A и В.
Р(А|В)Р(В) = Р(В|А)Р(А) = Р(А,В) (Б.1)
Теорема формулируется следующим образом.
Р(А|В)= (Б.2)
Теорема Байеса позволяет выводить условную вероятность Р(А|В) из условной вероятности Р(В|А).
Б. 1.1. Дискретная форма теоремы Байеса
Теорему Байеса можно записать в дискретной форме следующим образом.
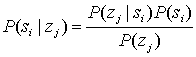
В приложениях связи si — это i-й класс сигнала из набора М классов, a zj — j—я выборка принятого сигнала. Уравнение (Б.З) можно рассматривать как описание эксперимента, в котором задействована принятая выборка и некоторые статистические знания о классах сигнала, к которым может принадлежать эта принятая выборка. До эксперимента вероятность появления i—гo класса сигнала P(si) называется априорной. В результате изучения конкретной принятой выборки zj из плотности условной вероятности P(zj|si) можно найти статистическую меру правдоподобия принадлежности zj к классу si. После эксперимента можно вычислить апостериорную вероятность P(si|zj), которую можно рассматривать как «уточнение» наших априорных знаний. Таким образом, к эксперименту мы приступаем, имея некоторые априорные знания, касающиеся вероятности состояния природы, а после изучения выборочного сигнала получаем апостериорную («после свершения») вероятность. Параметр P(zj) — это вероятность принятой выборкиzj, во всем пространстве классов сигналов. Этот термин, P(zj), можно рассматривать как масштабный множитель, поскольку его значение одинаково для всех классов сигнала.
Пример Б.1. Использование (дискретной формы) теоремы Байеса
Имеется два ящика деталей. Ящик 1 содержит 1000 деталей, 10% из которых неисправны, а ящик 2 — 2000 деталей, из которых неисправными являются 5%. Если в результате случайного выбора ящика и детали из него деталь оказывается исправной, то чему равна вероятность того, что данная деталь взята из ящика 1?
Решение
P (ящик 1|ИД) = Р(ИД | ящик 1)/Р(ИД),
где ИД означает «исправная деталь».
Р(ИД) = Р(ИД | ящик 1)Р(ящик 1) + Р(ИД | ящик 2)Р(ящик 2) =
= (0,90)(0,5) + (0,95)(0,5) = 0,450 + 0,475 = 0,925
Р(ящик 1| ИД) == 0,486
До эксперимента априорные вероятности выбора ящика 1 или 2 равны. После получения исправной детали вычисления, проведенные согласно теореме Байеса, могут рассматриваться как способ «точной подстройки» нашего представления о том, что Р(ящик 1) = 0,5, в результате которой возникает апостериорная вероятность 0,486. Теорема Байеса — это просто формализация здравого смысла. Если была получена исправная деталь, то не кажется ли вам (интуитивно), что она с большей вероятностью могла быть взята из ящика с более высокой концентрацией исправных деталей и с меньшей — из ящика с меньшей концентрацией? Теорема Байеса уточняет априорную статистику выбора ящиков, порождая апостериорную статистику.
Пример Б.2. Применение теории принятия решений в теории игр
В ящике находится три монеты: обычная, с двумя орлами и с двумя решками. Вам предлагается случайным образом вытянуть одну монету, взглянуть на одну ее сторону и угадать, что находится на другой стороне. Какой стратегии лучше всего придерживаться?
Решение
Данную задачу можно рассматриваться как задачу обнаружения сигнала. Сигнал передается, но вследствие шума канала принятый сигнал не совсем отчетлив. Невозможность взглянуть на обратную сторону монеты равносильна приему сигнала, возмущенного шумом. Пусть Hi представляет гипотезу (i = П, О, Р), где индексы П, О и Р обозначают правильную монету, монету с двумя орлами и монету с двумя решками.
НП = О,Р (правильная монета)
НО = О,О (монета с двумя орлами)
НР= Р, Р (монета с двумя решками)
Пусть zj представляет принятую выборку (j=O,P), где zO — орел, аzO — решка. Пусть априорные вероятности гипотез равновероятны, так что Р(НП) = =Р(НО) = Р(НР) = 1/3. Используем теорему Байеса.
Нам необходимо вычислить вероятности всех гипотез для всех классов сигнала. Следовательно, нам нужно изучить результаты шести вычислений, после чего мы сможем установить оптимальную стратегию принятия решения. В каждом случае значение можно вычислить из условных вероятностей, изображенных на рис. Б.1. Пусть мы выбрали монету и увидели орел (zO), тогда вычисление трех апостериорных вероятностей дает следующие результаты.
P(HP / zO) = 0
Если принятой выборкой является решка (zP), вычисления дают следующее.
Рис. Б.1. Условная вероятность :
а) для правильной монеты; б) для монеты с двумя орлами;
в) для монеты с двумя решками
Таким образом, оптимальной стратегией принятия решения является следующая: если принят орел (zO), выбрать гипотезу НO (соответствующую монете с двумя орлами); если принята решка (zP), выбрать гипотезу HP (соответствующую монете с двумя решками).
Б.1.2. Теорема Байеса в смешанной форме
Для большинства приложений связи, представляющих практический интерес, возможные значения принятой выборки принадлежат непрерывному диапазону (причина — наличие в канале связи аддитивного гауссового шума). Следовательно, наиболее полезная форма теоремы Байеса содержит плотность вероятности с непрерывными, а не дискретными значениями. Изменим соответствующим образом формулу (Б.З).
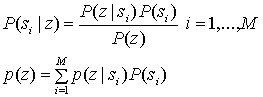
Здесь — плотность условной вероятности принятой выборки z (принимающей значения из непрерывного диапазона) при условии принадлежности к классу si.
Пример Б.З. Наглядное представление теоремы Байеса
Даны два класса сигнала s1 и s2, которые описываются треугольными функциями плотности условной вероятности и
, показанными на рис. Б.2. Принят некоторый сигнал; он может иметь любое значение по оси z. Если функции плотности вероятности не перекрываются, сигнал можно классифицировать однозначно. В данном же примере, приведенном на рис. Б.2, нам требуется правило, которое позволит классифицировать принятые сигналы, поскольку некоторые из них попадут в область перекрывающихся функций плотности вероятности. Рассмотрим принятый сигнал za. Пусть два класса сигналов s1 и s2 являются равновероятными. Нужно вычислить две возможные апостериорные вероятности и предложить правило принятия решений, которое следует использовать при определении принадлежности сигнала za к определенному классу. То же самое нужно сделать для сигнала zb.
Рис. Б.2. Наглядное представление теоремы Байеса
Решение
Из рис. Б.2 видим, что = 0,5 и
= 0,3. Следовательно,
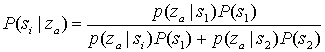
=
и
Одно из возможных правил — определять принятый сигнал к классу с максимальной апостериорной вероятностью (классу S1). Эквивалентное правило, для равных априорных вероятностей, — это исследовать значение функции плотности вероятности, обусловленной каждым классом сигналов (называемой правдоподобием класса сигналов), и выбрать класс с максимальным значением. Рассмотрим рис. Б.2 и отметим, что правило максимального правдоподобия соответствует нашей интуиции. Правдоподобие принадлежности сигналаza к каждому классу сигналов соответствует обведенной кружком точке на каждой функции плотности вероятности. Правило максимального правдоподобия заключается в выборе класса сигналов, дающего максимальную условную вероятность из всех имеющихся. Повторим вычисления для принятого сигнала zb.
Как и ранее, правило максимального правдоподобия указывает нам выбрать класс сигналов s1. Заметим, что при принятии выборки zb, мы более уверены в точности нашего выбора, по сравнению с принятием, сигнала za. Это объясняется тем, что отношение к
существенно больше отношения
к
.
Б.2. Теория принятия решений
Б.2.1. Элементы задачи теории принятия решений
После того как мы описали проверку гипотез на основе статистики Байеса, перейдем к рассмотрению элементов задачи теории принятия решений в контексте системы связи, как показано на рис. Б.З. Источник сигнала в передатчике состоит из множества {si(t)}, i = 1, …, М сигналов (или гипотез). Принимается сигнал r(t) = si(t) + n(t), где n(t) — присутствующий в канале аддитивный белый гауссов шум (additive white Gaussian noise — AWGN). В приемнике сигнал сокращается до единственного числа z (t = T), которое может принимать любое значение. Поскольку шум является гауссовым процессом и приемник предполагается линейным, выход z(t) также есть гауссовым процессом [1], а число z(T) — случайной переменной, принимающей значения из непрерывного диапазона.
z(T) = ai(T) + n0(T) (Б.5)
Выборка z(T) составляется из сигнального компонента аi(Т) и шумового компонента п0(Т). Время Т — это длительность символа. В каждый момент времени kT, где k — целое, приемник использует правило принятия решения для определения принадлежности принятого сигнала к определенному классу сигнала. Для простоты записи выражение (Б.5) иногда используют в виде z = ai + n0, где функциональная зависимость от T не выражается явно.
Рис. Б.3. Элементы задачи теории принятия решений в контексте системы связи
Б.2.2. Проверка методом отношения правдоподобий и критерий максимума апостериорной вероятности
При определении правила принятия решения для двух классов сигналов разумно начать со следующего соотношения.
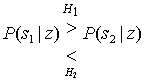
Выражение (Б.6) — это сокращенная запись следующего утверждения: «выбрать гипотезу H1 если апостериорная вероятность P(s1|z) больше апостериорной вероятности P(s2|z); в противном случае выбрать гипотезу H2«.
Апостериорные вероятности в формуле (Б.6) можно заменить эквивалентными выражениями, полученными вследствие использования теоремы Байеса (уравнение (Б.4)), что дает следующее.
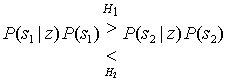
Итак, у нас есть правило принятия решения, выраженное через плотности вероятности (правдоподобия). Если переписать выражение (Б.7) и привести его к следующему виду
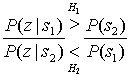
то отношение в левой части будет называться отношением правдоподобий, а все выражение часто именуют критерием отношения правдоподобий. Выражение (Б.8) — это принятие решений на основе сравнения принятого сигнала с порогом. Поскольку проверка опирается на выбор класса сигналов с максимальной апостериорной вероятностью, критерий принятия решения часто называется критерием максимума апостериорной вероятности (maximum a posteriori — MAP). Другое название — критерий минимума ошибки, поскольку в среднем он дает минимальное количество неверных решений. Стоит отметить, что данный критерий является оптимальным, только если ошибки всех типов наносят одинаковый вред (или имеют равную цену). Если ошибки некоторых типов обходятся дороже других, необходимо применять критерий, который учитывал бы относительные стоимости ошибок [1].
Б.2.3. Критерий максимального правдоподобия
Довольно часто сведения об априорных вероятностях гипотез или классов сигналов отсутствуют. Даже при наличии такой информации ее точность иногда вызывает сомнения. В таких случаях решения обычно принимаются исходя из предположения о возможности наиболее выгодной априорной вероятности; иными словами, значения априорных вероятностей выбираются так, чтобы классы были равновероятными. Если выбран такой подход, то критерий принятия решения является критерием максимального правдоподобия, и выражение (Б.8) записывается в следующем виде.
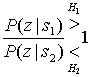
Отметим, что критерий максимального правдоподобия, приведенный в выражении (Б.9), аналогичен правилу максимального правдоподобия, описанному в примере Б.З.
Б.3. Пример обнаружения сигнала
Б.3.1. Двоичное решение по принципу максимального правдоподобия
В наглядном представлении процесса принятия решения (пример Б.З) фигурировали треугольные функции плотности вероятности. На рис. Б.4 приведены функции плотностей условных вероятностей для двоичных выходных сигналов, искаженных шумом: z(T) = а1+ п0 и z(T) = а2 + n0. Сигналы а1и а2взаимно независимы и равновероятны. Шум n0 предполагается независимой гауссовой случайной переменной с нулевым средним, дисперсией и плотностью вероятности, описываемой следующей формулой.
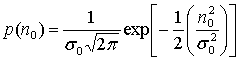
Следовательно, отношение правдоподобий, выраженное в формуле (Б.8), можно записать следующим образом.
=
=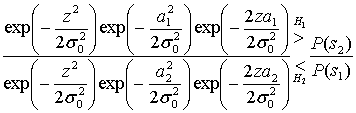
=
Здесь a1 — сигнальный компонент на выходе приемника при переданном s1(t), а а2— сигнальный компонент на выходе приемника при переданном s2(t). Неравенство (Б. 11) сохраняется при любом монотонно возрастающем (или убывающем) преобразовании.
Рис. Б.4. Плотности условных вероятностей для типичного двоичного приемника
Следовательно, для упрощения выражения (БЛ1) от его обеих частей можно взять натуральный логарифм, что даст логарифмическое отношение правдоподобий.
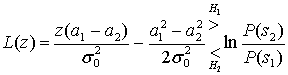
Если классы равновероятны, то
так что
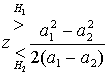
Для антиподных сигналов s1(t) = — s2(t) и a1 = -а2, так что можем записать следующее.
(Б.14)
Следовательно, правило максимального правдоподобия для равновероятных антиподных сигналов заключается в сравнении принятой выборки с нулевым порогом, что равносильно выбору s1(t), если выборка положительна, и выбору s2(t) — если она отрицательна.
Б.3.2. Вероятность битовой ошибки
Для двоичного примера, приведенного в разделе Б.3.1, рассчитаем вероятность битовой ошибки РВс помощью правила принятия решений из формулы (Б.13). Вероятность ошибки вычисляется путем суммирования вероятностей различных возможностей появления ошибки.
PB = P(H2|sl)P(sl) + P(H1|s2)P(s2) (Б.15)
Другими словами, при переданном сигнале s1(t) ошибка произойдет, если будет выбрана гипотеза H2; или ошибка произойдет, если при переданном сигнале s2(t) будет выбрана гипотеза H1. Для частного случая симметричных функций плотности вероятности и для P(s1) = P(s2) = 0,5 можем записать следующее.
PB = P(H2|sl) = P(H1|s2) (Б.16)
Вероятность ошибки РВравна вероятности принятия неверной гипотезы Н1при переданном сигнале s2(t) или принятия неверной гипотезы Н2при переданном сигнале s1(t). Следовательно, РB численно равна площади под хвостом любой функции плотности вероятности, или
, «заползающим» на неверную сторону порога. Таким образом, РВмы можем вычислить, проинтегрировав
от
до
или
от
до
.
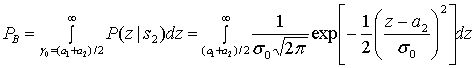
Пусть
Тогда и
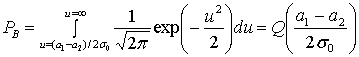
где Q(x), именуемая гауссовым интегралом ошибок [1], протабулирована в табл. Б.1.
Таблица Б.1. Гауссов интеграл ошибок
|
Q(x) |
||||||||||
|
x |
0,00 |
0,01 |
0,02 |
0,03 |
0,04 |
0,05 |
0,06 |
0,07 |
0,08 |
0,09 |
|
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0 3,1 3,2 3,3 3,4 |
0,5000 0,4602 0,4207 0,3821 0,3446 0,3085 0,2743 0,2420 0,2169 0,1841 0,1587 0,1357 0,1151 0,0968 0,0808 0,0668 0,0548 0,0446 0,0359 0,0287 0,0228 0,0179 0,0139 0,0107 0,0082 0,0062 0,0047 0,0035 0,0026 0,0019 0,0013 0,0010 0,0007 0,0005 0,0003 |
0,4960 0,4562 0,4168 0,3783 0,3409 0,3050 0,2709 0,2389 0,2090 0,1814 0,1562 0,1355 0,1131 0,0951 0,0793 0,0655 0,0537 0,0436 0,0351 0,0281 0,0222 0,0174 0,0136 0,0104 0,0080 0,0060 0,0045 0,0034 0,0025 0,0018 0,0013 0,0009 0,0007 0,0005 0,0003 |
0,4920 0,4522 0,4129 0,3745 0,3372 0,3015 0,2676 0,2358 0,2061 0,1788 0,1539 0,1314 0,1112 0,0934 0,0778 0,0643 0,0526 0,0427 0,0344 0,0274 0,0217 0,0170 0,0132 0,0102 0,0078 0,0059 0,0044 0,0033 0,0024 0,0018 0,0013 0,0009 0,0006 0,0005 0,0003 |
0,4880 0,4483 0,4090 0,3707 0,3336 0,2981 0,2643 0,2327 0,2033 0,1762 0,1515 0,1292 0,1093 0,0918 0,0764 0,0630 0,0516 0,0418 0,0336 0,0268 0,0212 0,0166 0,0129 0,0099 0,0075 0,0057 0,0043 0,0032 0,0023 0,0017 0,0012 0,0008 0,0006 0,0004 0,0003 |
0,4840 0,4443 0,4052 0,3669 0,3300 0,2946 0,2611 0,2296 0,2005 0,1736 0,1492 0,1271 0,1075 0,0901 0,0749 0,0618 0,0505 0,0409 0,0329 0,0262 0,0207 0,0162 0,0125 0,0096 0,0073 0,0055 0,0041 0,0031 0,0023 0,0016 0,0012 0,0008 0,0006 0,0004 0,0003 |
0,4801 0,4404 0,4013 0,3632 0,3264 0,2912 0,2578 0,2266 0,1997 0,1711 0,1469 0,1251 0,1056 0,0885 0,0735 0,0606 0,0495 0,0401 0,0322 0,0256 0,0202 0,0158 0,0122 0,0094 0,0071 0,0054 0,0040 0,0030 0,0022 0,0016 0,0011 0,0008 0,0006 0,0004 0,0003 |
0,4761 0,4364 0,3974 0,3594 0,3228 0,2877 0,2546 0,2236 0,1949 0,1685 0,1446 0,1230 0,1038 0,0869 0,0721 0,0594 0,0485 0,0392 0,0314 0,0250 0,0197 0,0154 0,0119 0,0091 0,0069 0,0052 0,0039 0,0029 0,0021 0,0015 0,0011 0,0008 0,0006 0,0004 0,0003 |
0,4721 0,4625 0,3936 0,3557 0,3192 0,2843 0,2514 0,2206 0,1922 0,1660 0,1423 0,1210 0,1020 0,0853 0,0708 0,0582 0,0475 0,0384 0,0307 0,0244 0,0192 0,0150 0,0116 0,0089 0,0068 0,0051 0,0038 0,0028 0,0021 0,0015 0,0011 0,0008 0,0005 0,0004 0,0003 |
0,4681 0,4286 0,3897 0,3520 0,3156 0,2810 0,2483 0,2168 0,1894 0,1635 0,1401 0,1190 0,1003 0,0838 0,0694 0,0571 0,0465 0,0375 0,0301 0,0239 0,0188 0,0146 0,0113 0,0087 0,0066 0,0049 0,0037 0,0027 0,0020 0,0014 0,0010 0,0007 0,0005 0,0004 0,0003 |
0,4641 0,4247 0,3859 0,3483 0,3121 0,2776 0,2451 0,2148 0,1867 0,1611 0,1379 0,1170 0,0985 0,0823 0,0681 0,0599 0,455 0,0367 0,0294 0,0233 0,0183 0,0143 0,0110 0,0084 0,0064 0,0048 0,0036 0,0026 0,0019 0,0014 0,0010 0,0007 0,0005 0,0003 0,0002 |
Еще одной часто используемой формой гауссова интеграла ошибок является следующая.
(Б.19)
Функции Q(x) и erfc(x) связаны следующим образом.
erfc(x) = 2Q(x) (Б.20)
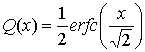
Литература
1. Van Trees H. L. Detection, Estimation, and Modulation Theory. Part 1, John Wiley & Sons. Inc., New York, 1968.
2. Papoulis A. Probability, Random Variables, and Stochastic Processes. McGraw-Hill Book Company, New York, 1965.
Приложение В. Отклик корреляторов на белый шум
На вход группы из N корреляторов подается белый гауссов процесс шума n(t) с нулевым средним и двусторонней спектральной плотностью мощности N0/2. Выходом каждого коррелятора в момент времени t = Т является гауссова случайная переменная, определяемая следующим образом.
(B.1)
Здесь сигналы {} формируют ортонормированное множество. Поскольку переменная nj является гауссовой, она полностью определяется средним и дисперсией. Среднее nj равно
, (В.2)
где — оператор математического ожидания. Дисперсия nj равна
(В.З)
= (В.4)
= (В.5)
Поскольку n(t) — это процесс с нулевым средним,
Е{n(t)} = 0. (В.6)
Отсюда следует
(В.7)
Автокорреляционная функция процесса n(t) равна следующему.
(В.8)
Если шум n(t) предполагать стационарным, то Rn(t,s) зависит только от разности времен t = — s. Из уравнения (В.5) получаем следующее.
(B.9)
Для стационарного случайного процесса спектральная плотность мощности Gn(f) и автокорреляционная функция являются Фурье-образами друг друга. Таким образом, можем записать следующее.
(В.10)
Поскольку n(t) — это белый шум, его спектральная плотность мощности Gn(f) равна для всех f, и предыдущее выражение можно переписать следующим образом.
(B.11)
где — единичная импульсная функция, определенная в разделе А.4.1. Подставляя выражение (В. 11) в (В.9), получаем следующее.
(В.12)
= (B.13)
Здесь было использовано просеивающее свойство единичной импульсной функции (см. раздел А.4.1) и то, что функции {}, j= 1, …,N, составляют ортонормированное множество. Таким образом, для белого гауссова шума с двусторонней спектральной плотностью мощности
Вт/Гц, мощность шума на выходе каждого из N корреляторов равна
Вт.
Приложение Г. Полезные соотношения
|
|
(Г.1) |
|
|
(Г.2) |
|
|
(Г.3) |
|
|
(Г.4) |
|
|
(Г.5) |
|
|
(Г.6) |
|
|
(Г.7) |
|
|
(Г.8) |
|
|
(Г.9) |
|
|
(Г.10) |
|
|
(Г.11) |
|
|
(Г.12) |
|
|
(Г.13) |
|
|
(Г.14) |
|
|
(Г.15) |
|
|
(Г.16) |
Доказательство
Замена i = (j-1)
Таким образом (j=2) переходит в (i=1), а (j=n) – в (i=n-1).
=
=
=
Приложение Д. S-область, z-область и цифровая фильтрация
Д.1. Преобразование Лапласа
Напомним преобразование Фурье, приведенное в формуле (А.26) приложения А.
или
, (Д.1)
где .
Определим новую функцию v(t), равную x(t), умноженному на , где
— вещественное число, т.е. v(t) = x(t)
. Фурье-образ функции v(t) будет выглядеть следующим образом.
(Д.2)
Таким образом, можно переписать формулу (Д.1).
(Д.3)
Пусть s — комплексная частота, s =, тогда Фурье-образ временного сигнала x(t) можно определить следующим образом.
, (Д.4)
где s — переменная Лапласа. Перепишем обратное преобразование Фурье, приведенное в формуле (А.27), через угловую частоту ; тогда
и
(Д.5)
Поскольку , из этого следует, что ds/dw = i, и мы можем определить обратное преобразование Лапласа следующим образом.
(Д.6)
Формулы (Д.4) и (Д.6) представляют пару преобразований Лапласа , или, более точно, пару двусторонних преобразований Лапласа. Если (разумно) предположить, что до момента t = 0 сигнал не существует (т.е. является причинным), то преобразование можно назвать односторонним, что записывается следующим образом.
(Д.7)
Обратное одностороннее преобразование Лапласа аналогично преобразованию, приведенному в формуле (Д.6). Таким образом, формулы (Д.6) и (Д.7) можно называть парой односторонних преобразований Лапласа.
Д. 1.1. Стандартное преобразование Лапласа
В табл. Д.1 приведены некоторые стандартные односторонние преобразования Лапласа. Отметим, что (двустороннее) преобразование Лапласа, приведенное в формуле (Д.4), идентично преобразованию Фурье, приведенному в формуле (А.26), при s=iw, где . Для создания преобразования Лапласа x(t) умножается на «множитель сходимости»
, где
— любое вещественное число. Таким образом, при фактическом вычислении значений интегралов преобразование Лапласа может существовать для многих функций, для которых отсутствует соответствующее преобразование Фурье. Одним из ключевых преимуществ преобразования Лапласа является возможность преобразования функций, не являющихся абсолютно интегрируемыми.
Таблица Д.1. Преобразования Лапласа
|
Тип сигнала |
Временная функция |
Преобразование Лапласа |
| Импульс |
|
|
|
Единичная ступенчатая функция (Хевисайда) |
|
|
| Линейно растущая функция |
|
|
| Экспоненциальные функции |
|
|
| Синусоида |
|
|
| Косинусоида |
|
|
| Затухающая синусоида |
|
|
| Затухающая косинусоида |
|
|
Д.1.2. Свойства преобразования Лапласа
Можно показать, что если известна пара преобразований Лапласа y(t)Y(s), то для запаздывающей версии сигнала, которая записывается как y(t —t0), справедливо следующее.
(Д.8)
Данное свойство называется свойством смешения во времени. Другие свойства-преобразования Лапласа приведены в табл. Д.2. Их справедливость можно проверить путем простой подстановки в интегральное выражение, описывающее соответствующее преобразование. Отметим, что соотношение между преобразованиями Фурье и Лапласа означает, что существует простой эквивалентный переход между преобразованиями, приведенными в табл. Д.1 и А.1, и свойствами, указанными в табл. Д.2 и А.2.
Таблица Д.2. Свойства преобразования Лапласа
|
Свойство |
Временная функция |
Преобразование Лапласа |
|
Произвольная функция |
|
|
|
Произвольная функция |
|
|
|
Линейность |
|
|
|
Сдвиг во времени ( |
|
|
|
Масштабирование времени |
|
|
|
Модуляция |
|
|
|
Дифференцирование |
|
|
|
Интегрирование |
|
|
|
Свертка |
|
|
Д.1.3. Использование преобразования Лапласа
Преобразования Лапласа полезны, когда требуется решать дифференциальные (по времени) уравнения или выполнять операцию свертки. Например, для нахождения тока i(t) простой RС-цепи, показанной на рис. Д.1, отметим, что сумма напряжений на конденсаторе и сопротивлении равна входному напряжению.
(Д.9)
Если входное напряжение — это единичная ступенчатая функция , a, q — заряд конденсатора (в кулонах), то, применяя к обеим частям формулы (Д.9) преобразование Лапласа и используя табл. Д.1 и Д.2, получаем следующее.
откуда следует
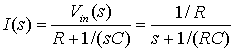
в)
Рис. Д.1. Использование преобразования Лапласа:
а) КС-контур; б) представление с помощью преобразования Лапласа;
в) амплитудная характеристика
(Для единичной ступенчатой функции Vin(s) = 1/s.) Затем, возвращаясь во временную область (и снова используя таблицы свойств преобразования Лапласа), получаем следующее.
(Д.11)
Д.1.4. Передаточная функция
С помощью преобразования Лапласа можно определить (через переменную s) передаточную функцию линейной системы. Из уравнения (Д. 10) при нулевом сопротивлении R= 0 импеданс конденсатора можно вычислить следующим образом.
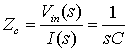
Входное и выходное напряжения (в s-области) можно записать следующим образом.
и
(Д.13)
Таким образом, (в s-области) передаточную функцию можно определить следующим образом.
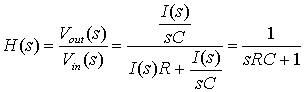
Д.1.5. Фильтрация нижних частот в RC-цепи
Пусть на вход RС-цепи подается комплексная синусоида . Используя сказанное выше, можем перейти к преобразованию Фурье, положив s = iw, где
. Таким образом, из передаточной функции можно получить частотную характеристику цепи.
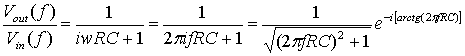
Для малых значений ; а для больших значений
. Если
, то |H(f)|
. Отметим, что
дБ; следовательно, f0 — это частота по уровню -3дБ, когда выходное напряжение вдвое меньше входного. Следовательно, формула (Д.15) задает тот же фильтр нижних частот, что и формула (1.63). Низкие частоты проходят через фильтр, а высокие — подавляются; данная ситуация показана на рис. Д.1, в.
Д.1.6. Полюсы и нули
Линейные системы, а, следовательно, и (линейные) аналоговые фильтры, можно представить через дифференциальные уравнения во временной области. Рассмотрим, например, следующее уравнение второго порядка.
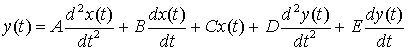
Реализация дифференцирования и/или интегрирования различных порядков происходит с использованием емкостей и индуктивностей вместе с усилителями с обратной связью, имеющими нужный порядок [2]. Применяя преобразование Лапласа к обеим частям уравнения (Д. 16), получаем более удобное (с точки зрения математики и формы записи) уравнение Лапласа.
Y(s) = As2X(s) + BsX(s) + CX(s) + Ds2Y(s) + EsY(s) (Д.17)
Передаточная функция записывается в следующем виде.
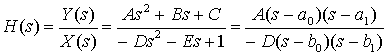
Корни числителя называются нулями, а корни знаменателя
— полюсами. Отметим, что если А, В и С — вещественны, нули
являются комплексно-сопряженными.
Д.1.7. Устойчивость линейных систем
Рассмотрим однополюсное уравнение, соответствующее некоторой линейной системе.
(Д.19)
Импульсную характеристику данной системы можно (используя табл. Д.1) найти как обратное преобразование Лапласа выражения (Д.19); если , то импульсная характеристика выглядит следующим образом.
(Д.20)
Видим, что Re[] =
; если
>0, импульсная характеристика расходится с увеличением t (времени). В то же время, если
<0, импульсная характеристика сходится с увеличением t. Член
— это комплексная (осциллирующая) синусоида (см. раздел А.2.1). Используя формулировку, несколько отличающуюся от применяемых ранее, можно сказать, что система устойчива, если все полюса в s-области имеют отрицательную действительную часть.
Таким образом, если изобразить полюса на комплексной s-плоскости, все они должны располагаться в ее левой части. На рис. Д.2 показана область устойчивости и приведен пример устойчивой передаточной функции третьего порядка, все полюса которой попадают в левую часть комплексной s-плоскости, т.е. имеют отрицательную действительную часть. Отметим, что нули функции могут быть в левой или правой части s-плоскости, и это не влияет на устойчивость.
Нули в точках s = 0,1, 0,2-0,2i, 0,2+0,2i
Полюсы в точках s= —1, -0,5-0,5i, -0,5+0,5i
Рис. Д.2. Нули и полюса передаточной функции, изображенные в s-области
Если цепь имеет более одного полюса, передаточную функцию можно рассматривать как последовательность однополюсных функций.
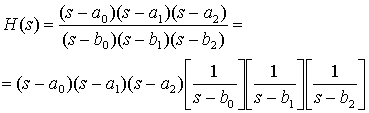
Для устойчивости все полюсы должны находиться в левой части комплексной плоскости. Отметим, что для реальных схем с вещественными коэффициентами Лапласа (т.е. в уравнении (Д. 16) а, В, С, D и Е — вещественные) полюсы и нули будут вещественными или будут разбиты на пары комплексно-сопряженных величин, как показано на рис. Д.2.
Для нашего предыдущего примера RС-цепи передаточная функция в формуле (Д.14) является безусловно устойчивой, поскольку — это всегда положительная величина, что, разумеется, является ожидаемым результатом. Неустойчивость в линейных системах возникает только при наличии в них обратной связи (рекурсии), например, при использовании фильтров с инвертирующими или неинвертирующими усилителями.
Д.2. z-преобразование
По сути, z-преобразование — это дискретный эквивалент преобразования Лапласа. Оно делает возможным удобный математический анализ (стационарный анализ и анализ переходных процессов) и манипулирование сигналами и спектрами. Возможно, наиболее распространенным современным применением z-преобразования является описание дискретных систем и анализ их устойчивости.
z-преобразование позволяет вычислять свертку входного сигнала и характеристики дискретной линейной системы в математически удобном виде. Кроме того, могут определяться нули и полюса системы, что позволяет извлекать информацию о динамическом поведении и устойчивости дискретной системы. Следует отметить, что нули и полюса z-преобразования отличаются от нулей и полюсов преобразования Лапласа.
Д.2.1. Вычисление z-преобразования
z-преобразование можно вывести непосредственно из преобразования Лапласа, определенного в формуле (Д.4), рассмотрев для этого сигнал x(t), выборка которого производится каждые T секунд. Таким образом, сигнал будет представлен как функция дискретного времени: x(0), х(Т), х(2Т), …= {x(kT)}. Дискретные данные представляют множество взвешенных и смещенных дельта-функций, применение к которым преобразования Лапласа дает следующий результат (использовано свойство сдвига во времени).
(Д.22)
Введем параметр z = и заменим дискретное время kT номером выборки k. В результате получаем следующее.
(Д.23)
Приведем в качестве примера результат применения z-преобразования к единичной ступенчатой функции (Хевисайда).
(Д.24)
Выше при суммировании геометрической прогрессии было использовано предположение |z| < 1 (область сходимости). В табл. Д.З и Д.4 приведены, соответственно, примеры применения z-преобразования к некоторым распространенным функциям и представлены полезные свойства данного преобразования.
Таблица Д.3. z-преобразование некоторых функций
|
Тип сигнала |
Временная функция |
z-преобразование |
| Импульс |
|
|
| Задержанный импульс |
|
|
| Единичная ступенчатая функция (Хевисайда) |
|
|
| Линейно растущая функция |
|
|
| Экспоненциальная функция |
|
|
| Синусоида |
|
|
| Косинусоида |
|
|
Таблица Д.4. Свойства z-преобразования
|
Свойство |
Временная функция |
Преобразование Лапласа |
| Произвольная функция |
|
|
| Произвольная функция |
|
|
| Линейность |
|
|
| Сдвиг во времени |
|
|
| Модуляция |
|
|
| Экспоненциальное масштабирование |
|
|
| Линейное масштабирование |
|
|
| Свертка |
|
|
Д.2.2. Обратное z-преобразование
Переход из z-области во временную область выполняется посредством обратного z-преобразования [2].
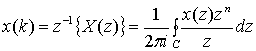
Здесь интегрирование в комплексной области проводится по любому простому контуру в области сходимости X(z), включающему точку z = 0. Как правило, вычисление обратного z-преобразования сложнее вычисления прямого. Обычно приходится раскладывать подынтегральное выражение на сумму рациональных дробей, делить полиномы, использовать теорему о вычетах и составлять разностные уравнения. Поэтому большая часть z-преобразований и обратных z-преобразований вычисляется с использованием таблиц интегралов и их свойств, так что явного вычисления выражения (Д.25) обычно удается избежать. При современном анализе цифровых сигналов и систем используются программные пакеты, подобные SystemView [1], а z-преобразование большей частью представляет собой просто аналитическую форму записи, удобную для определения устойчивости дискретных сигналов и систем.
Д.З. Цифровая фильтрация
С помощью подходящих аналоговых и цифровых компонентов цифровой фильтр можно настроить на выполнение селекции желаемой частоты или модификации фазы. На рис. Д.З показаны компоненты, необходимые для создания цифрового фильтра, дающего фильтрованную последовательность y(k) при входной последовательности x(k) [2].Выходной сигнал фильтра y(k) создается из взвешенной суммы предыдущих входных сигналов x(k) и предыдущих выходных сигналов y(k-п), где п>0. На рис. Д.4 показан поточный граф сигнала (состоит только из сумматоров, умножителей и схем задержки выборки) для цифрового фильтра с четырьмя весовыми коэффициентами прямой связи и тремя весовыми коэффициентами обратной связи. (Задержка, длительность которой равна длительности одной выборки, обозначена символом . Довольно часто подобные графы изображаются с использованием обозначений временной области и z-области, где для представления задержки применяется запись z-1; несмотря на широкое распространение такой формы записи, она не является строгой.)
Рис. Д.3. Уравнения цифрового фильтра реализуются на устройстве цифровой обработки сигналов, преобразовывающем входной дискретный информационный сигнал в выходной информационный сигнал
Рис. Д.4. Общая схема цифрового фильтра
Выход данного фильтра описывается следующим выражением.
y(k) = a0x(k) + alx(k-1) + a2x(k-2) + a3x(k-3) + b1у(k —1) + b2у(k — 2) + b3у(k —3) =
= (Д.26)
Применение z-преобразования к формуле (Д.26) даёт следующий результат.
Y(z)=a0X(z)+alX(z)z-1+a2X(z)z-2+a3X(z)z-3+b1Y(z)z-1+b2Y(z)z-2+b3Y(z)z-3 (Д.27)
Д.3.1. Передаточная функция цифрового фильтра
Передаточная функция цифрового фильтра, изображенного на рис. Д.4, получается после преобразования выражения (Д.27) и выглядит следующим образом.
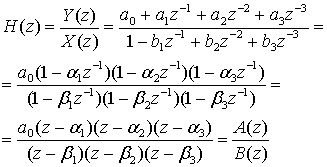
Здесь через обозначены нули, а через
— полюса z-области, которые находятся как корни полинома числителя A(z) и полинома знаменателя B(z). Для цифрового фильтра, подобного изображенному на рис. Д.4, но имеющего N весовых коэффициентов прямой связи и М-1 коэффициентов обратной связи, полиномы числителя и знаменателя в передаточной функции, Приведенной в формуле (Д.28), будут иметь, соответственно, порядок N к М.
Д.3.2. Устойчивость однополюсного фильтра
Вследствие наличия в потоковом графе множественных обратных связей, цифровой фильтр может быть (численно) неустойчивым. Рассмотрим, например, фильтр с одним весовым коэффициентом обратной связи, изображенный на рис. Д.5.
y(k)= x(k) + by(k—1) (Д.29)
Импульсная характеристика данного фильтра (т.е. подача на вход единичного импульса плюс применение принципов свертки, описанных в разделе А.5) имеет следующий вид.
h(k) = bk (Д.30)
Если |b|<1, импульсная характеристика фильтра сходится (устойчива); если |b|>1, импульсная характеристика фильтра расходится (неустойчива). На рис. Д.5 показана сходящаяся импульсная характеристика с |b|< 1; более точно, -1<b<1. Применение z-преобразования к выражению (Д. 29) дает следующее.
Рис. Д.5. Потоковый граф фильтра с одной обратной связью:
а) во временной области; б) в z-области
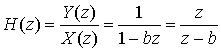
Используя формулу (Д.31), получаем потоковый граф в z-области (рис. Д.5, б), соответствующий потоковому графу во временной области, изображенному на рис. Д.5, а. Элемент задержки (который на рис. Д.5, а обозначен через А) теперь представляется как , а вход и выход заданы как z-образы Х(z) и Y(z). Отметим, впрочем, что общая топология двух графов одинакова. (Это частично объясняет то, что потоковые графы цифровых фильтров часто изображаются с использованием обозначений временной области и z-области.) Критерий устойчивости |b|<1) можно сформулировать следующим образом: система устойчива, если полюсы (или корни полинома знаменателя) передаточной функции цифрового фильтра меньше единицы.
Д.3.3. Устойчивость произвольного фильтра
При изучении факторизованной передаточной функции, приведенной в формуле (Д.28), поточный граф, представленный на рис. Д.4 для временной области, можно преобразовать в поточный граф в z-области (рис. Д.6). Последний граф — это, фактически, графическое представление формулы (Д.28), переписанной в следующем виде.
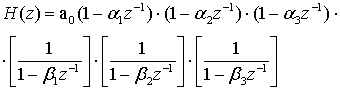
Рис. Д.6. Цифровой фильтр как последовательность каскадов прямой и обратной связи первого порядка
В данном выражении (и на рисунке) обособлены все блоки первого порядка, описываемые нулями и полюсами фильтра. Чтобы фильтр был устойчивым, модули всех полюсов каскада должны быть меньше 1. Если хотя бы один блок первого порядка неустойчив (или расходится), неустойчивым является и весь каскад. Как отмечалось для преобразования Лапласа, полюса (и нули) z-области могут быть комплексными, поэтому в качестве критерия устойчивости используется их абсолютная величина, а не амплитуда. (Стоит сказать, что реализация поточного графа, представленная на рис. Д.6, — это всего лишь иллюстрация принципов анализа; реальный цифровой фильтр никогда не реализуется в подобной факторизованной форме, поскольку в этом случае некоторые множители могут быть комплексными, а это может повлечь за собой ненужное усложнение вычислительных требований фильтров.)
Д.3.4. Диаграмма полюсов-нулей и единичная окружность
Если комплексные нули и полюса фильтра или линейной системы изобразить на плоскости с действительной и мнимой осями, данную плоскость можно будет назвать z-плоскостью (или комплексной плоскостью). Система является устойчивой, если все ее полюса находятся внутри единичной окружности. На рис. Д.7 показан вид z—плоскости для следующей передаточной функции.
Рис. Д. 7. Полюсы и нули, изображенные на z-плоскости
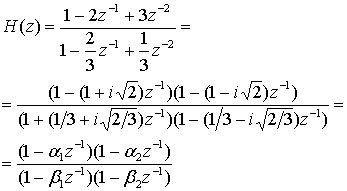
Нули данной функции — и
, полюсы —
и
. Поскольку все полюсы лежат внутри единичной окружности, данный фильтр является устойчивым.
Д.3.5. Дискретное преобразование Фурье импульсной характеристики цифрового фильтра
Частотная характеристика цифрового фильтра вычисляется из дискретного преобразования Фурье (discrete Fourier transform — DFT, ДПФ) импульсной характеристики фильтра. Напомним вид преобразования Фурье, приведенного в формуле (А.26).
(Д.34)
Данную формулу можно использовать для вычисления Фурье-образа импульсной характеристики фильтра. Ее можно упростить, полагая, что используется дискретная версия сигнала x(t), причем выборка сигнала производится каждые Тs = секунд.
(Д.35)
Разумеется, импульсная характеристика цифрового фильтра является причинной, и первая выборка импульсной характеристики производится в момент k = 0, а последняя — в момент k = N— 1, что в сумме дает N выборок на одно преобразование. Таким образом, для данного конечного числа выборок можно переписать формулу (Д.25), использовав не явное время kTs, а число выборок k.
(Д.36)
Отметим, что значение выражения (Д.36) вычисляется для непрерывной частотной переменной f. В действительности же нам требуется знать это значение для некоторых определенных частот — нулевой частоты (постоянной составляющей) и гармоник «собственной» частоты; всего N дискретных; частот: 0, f0, 2f0 и так до f5, где .
для n от 0 до N—1 (Д.37)
Выражение выше можно упростить, использовав только временной индекс k и частотный индекс п. В результате получаем дискретное преобразование Фурье (discrete Fourier transform — DFT, ДПФ).
для n от 0 до N—1 (Д.38)
Поскольку частота дискретизации сигнала x(k) равна fs выборок/с, сигнал включает налагающиеся (или дублирующиеся) компоненты на частотах свыше . Следовательно, при вычислении значения выражения (Д.38) достаточно ограничиться частотами до
. Отметим, что формула (Д.38) аналогична формуле (Д.23), если положить
для последовательности длиной N выборок.
Д.4. Фильтры с конечной импульсной характеристикой
На настоящий момент наиболее распространенный тип цифровых фильтров — это фильтры с конечной импульсной характеристикой (КИХ), имеющие, как понятно из названия, импульсную характеристику конечной длительности. Данные фильтры не имеют весовых коэффициентов обратной связи (см. рис. Д.4); следовательно, можно сделать вывод об их безусловной устойчивости. Выход фильтра с конечной импульсной характеристикой, приведенного на рис. Д.8, описывается следующим выражением.
Рис. Д.8. Цифровой фильтр с конечной импульсной характеристикой
(Д.39)
Таким образом, передаточная функция фильтра имеет только нули и не имеет полюсов.
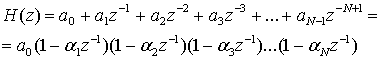
По сути, работа фильтра с конечной импульсной характеристикой — это вычисление текущего среднего; когда выход — это взвешенное среднее N последних входных выборок. Таким образом, фильтры данного типа часто называются фильтрами скользящего среднего (moving average filter). Кроме того, их еще называют линиями задержки с отводами (tapped delay line) и трансверсальными фильтрами (transversal filter).
Д.4.1. Структура фильтра с конечной импульсной характеристикой
В настоящее время цифровые фильтры с конечной импульсной характеристикой разрабатываются с использованием современного программного обеспечения, такого как SystemView [1]. При этом в основе разработки лежит график амплитудной характеристики, на котором указываются допустимые отклонения и пользовательские требования (рис. Д.9). Затем используются классические методы разработки фильтров, такие как метод Паркса-Мак-Леллана (Parks, McLellan), замена Ремеза (Remez Exchange), окно Кайзера и др. [4], в результате чего создается фильтр с подходящей частотной характеристикой, имеющей минимальное число весовых коэффициентов. Если не оговорено противное, большинство фильтров с конечной импульсной характеристикой разрабатывается в расчете на линейное изменение фазы или постоянную групповую задержку (что соответствует симметричной импульсной характеристике).
Рис. Д.9. Типичная амплитудная характеристика фильтра нижних частот. Чем строже требования к затуханию в полосе заграждения и полосе перехода и чем ниже допустимая неравномерность в полосе пропускания, тем больше требуется весовых коэффициентов
На рис. Д.10 показаны импульсная и частотная характеристики цифрового фильтра со следующими параметрами: частота среза = 1000Гц, затухание в полосе заграждения = 20дБ, неравномерность в полосе пропускания = 3дБ, полоса перехода = 500Гц, частота дискретизации, fs = 10000Гц. Если нужен фильтр с более строгими требованиями к частотной характеристике (например, нужно более сильное затухание в полосе заграждения), то, скорее всего, на стадии проектирования фильтра с конечной импульсной характеристикой обнаружится, что требуется больше весовых коэффициентов [4].
Д.4.2. Дифференциатор с конечной импульсной характеристикой
Рассмотрим простой цифровой дифференциатор, показанный на рис. Д.11. После изучения выхода для входных синусоид с высокой и низкой частотами, интуитивно можно предположить, что данный дифференциатор — это фильтр верхних частот. Выходная последовательность данного фильтра описывается следующим выражением.
(Д.41)
Применение z-преобразования к обеим частям формулы, (Д.41) приводит к следующему результату.
(Д.42)
Рис. Д.10. Импульсная характеристика h(n) = wn и частотная харак-теристика Н(f) фильтра нижних частот с 15 весовыми коэффициентами; частота дискретизации = 10 000Гц, частота среза = 1000Гц
Рис. Д. 11. Дифференциатор/фильтр верхних частот
Следовательно, передаточная функция имеет следующий вид.
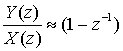
На рис. Д.12 показано, почему данная схема действует как фильтр верхних частот. По сути, выход фильтра — это разность двух последних выборок. Если разность последовательных выборок мала (как для случая низкой частоты), выход будет небольшим. Если разность велика (как для высоких частот), выход будет большим. Если на вход подать сигнал постоянного тока, то выходная амплитуда будет нулевой, т.е. будет происходить бесконечное затухание. Частотную характеристику также можно найти как Фурье-образ импульсной характеристики.
Рис. Д.12. Цифровой дифференциатор, действующий как фильтр верхних частот
Если весовые коэффициенты фильтра изменить с {1, -1} на {1/Т, -1/Т}, где частота дискретизации fs=1/Т, то для входных низкочастотных сигналов выход, у(k), — это приблизительно дифференциал входа.
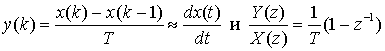
Д.5. Фильтры с бесконечной импульсной характеристикой
Фильтры с бесконечной импульсной характеристикой (infinite impulse response — IIR, БИХ) обычно создаются из аналоговых прототипов с использованием отображения из s—плоскости в z-плоскости. Как понятно из названия, импульсная характеристика таких фильтров (предполагая арифметику бесконечной точности) может иметь бесконечную длительность. Данные фильтры имеют весовые коэффициенты и прямой, и обратной связи, подобно тому, как показано на рис. Д.4. Вследствие рекурсивной природы поточного графа, данные фильтры могут иметь весьма длительные импульсные характеристики (до нескольких весовых коэффициентов). Следовательно, фильтры с бесконечной импульсной характеристикой могут создаваться с меньшим числом весовых коэффициентов, чем фильтры с конечной импульсной характеристикой при аналогичных функциональных амплитудных характеристиках. В общем случае в цифровых фильтрах с бесконечной импульсной характеристикой фаза изменяется нелинейно.
Д.5.1. Оператор левосторонней разности
Уравнение (Д.44) позволяет связать переменную преобразования Лапласа s (непрерывное время) и переменную z-преобразования z (дискретное время). Известно, что при преобразовании Лапласа дифференцирование по времени (d/dt) переходит в умножение на переменную s.
(Д.45)
Возьмем, например, следующую характеристику фильтра Баттерворта.
(Д.46)
Данную аналоговую схему (фильтр нижних частот) можно аппроксимировать дискретно, подставив приближение
(Д.47)
в уравнение (Д.46). Это дает следующее уравнение в z-области.
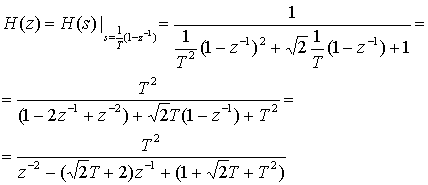
При низких частотах, когда приближение (Д.47) является «хорошим», данное преобразование может давать «разумный» цифровой эквивалент аналогового фильтра нижних частот. (Уравнение (Д.47) иногда называется «оператором левосторонней разности».) К сожалению, данное отображение является очень плохим при высоких частотах, а, следовательно, оно не может использоваться при создании фильтров верхних частот. Таким образом, на практике оно применяется редко.
Д.5.2. Использование билинейного преобразования для создания фильтров с бесконечной импульсной характеристикой
Билинейное преобразование получается при замене s следующим приближением.
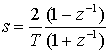
Данная подстановка приводит к отображению, сохраняющему устойчивость аналогового прототипа и дающему фильтры, значительно лучшие по своим характеристикам, чем в предыдущем случае (уравнение (Д.47)) [2]. В SystemView [1] билинейное преобразование используется для создания цифровых фильтров из стандартных аналоговых прототипов, таких как фильтры Баттерворта, эллиптические фильтры и фильтры Чебышева. Отметим, что билинейное преобразование всегда дает фильтр, имеющий нули и полюсы; следовательно, данные фильтры имеют бесконечную импульсную характеристику (БИХ).
Д.5.3. Интегратор с бесконечной импульсной характеристикой
Цифровой интегратор — это, по сути, БИХ-фильтр с одним весовым коэффициентом.
(Д.50)
В z-области передаточная функция дискретного интегратора получается из соотношения
Y(z) = X(z) + z-1Y(z), (Д.51)
которое дает следующее.
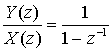
Реализация простого цифрового интегратора и графическое представление связи с интегрированием по непрерывному времени показаны на рис. Д.13.
Рис. Д. 13. Однополюсный фильтр, действующий как интегратор. В контур обратной связи часто вводится весовой коэффициент, немного меньший 1, который обеспечивает «забывание » интегратора
Если в контур обратной связи вводится весовой коэффициент, меньший 1 (скажем, 0,99), интегратор часто называют квазиинтегратором (leaky integrator). При рассмотрении в частотной области, характеристики (квази) интегратора и фильтра нижних частот не отличаются.
Литература
1. SystemViev DSP Communications Software. Elanix, Westlake Village, CA, 2000.
2. Porat. B. A Course in Digital Signal Processing. John Wiley & Cons, 1997.
3. Moon T. K., Stirling W. C. Mathematical Methods and Algorithms for Digital Signal Processing. Prentice Hall, 2000.
4. Stewart R. W. The DSPedia: A Multimedia Resource for DSP. BlueBox Multimedia, UK, 2000.
Приложение Е. Перечень символов
|
|
Коэффициент j-й базисной функции |
|
|
Сигнальный компонент на выходе j—го коррелятора |
|
|
Максимальная амплитуда сигнала |
|
|
Эффективная площадь поверхности (антенны) |
|
|
Односторонняя ширина полосы контура |
|
|
Скорость света = |
|
|
Пропускная способность канала |
|
|
Электрическая емкость |
|
|
Отношение средней мощности несущей к спектральной плотности мощности шума |
|
|
Расстояние |
|
|
Эталонное расстояние |
|
|
Просвет |
|
|
Минимальное расстояние |
|
|
Время задержки (сообщения) |
|
|
Избыточность языка |
|
|
Преобразование дешифрования |
|
|
Основание натурального логарифма |
|
е |
Вектор ошибочной комбинации |
|
|
Сигнал ошибки |
|
|
Полином ошибочной комбинации |
|
|
Преобразование шифрования |
|
|
Энергия сигнала x(t) Математическое ожидание случайной переменной X |
|
|
Эффективная излучённая мощность относительно изотропного источника |
|
|
Отношение энергии бита к спектральной плотности мощности станции-постановщика помех |
|
|
Отношение энергии бита к спектральной плотности мощности шума |
|
|
Отношение энергии канального символа к спектральной плотности мощности шума |
|
|
Частота (герц) |
|
|
Частота несущей волны |
|
|
Максимальная частота |
|
|
Ширина полосы когерентности |
|
|
Доплеровское расширение полосы частот |
|
|
Нижняя частота среза фильтра |
|
|
Верхняя частота среза фильтра |
|
|
Шум-фактор |
|
|
Фурье-преобразование функции x(t) |
|
|
Обратное Фурье-преобразование функции X(f) |
|
|
Поле |
|
|
Конечное поле |
|
|
Псевдослучайная кодовая функция |
|
|
Полиномиальный генератор (для циклического кода) |
|
|
Коэффициент усиления антенны |
|
|
Эффективность кодирования |
|
|
Матрица генератора (для линейных блочных кодов) |
|
|
Нормированный объем информации |
|
|
Коэффициент расширения спектра |
|
|
Спектральная плотность мощности сигнала x(t) |
|
|
Импульсная характеристика сети |
|
|
Импульсная характеристика канала |
|
|
Матрица проверки четности для кода |
|
|
i—я гипотеза |
|
|
Матрица Адамара |
|
|
Частотная передаточная функция сети |
|
|
Оптимальная частотная передаточная функция |
|
|
Энтропия информационного источника X |
|
|
Условная энтропия (энтропия X при условии Y) |
|
|
Форма кривой электрического тока |
|
|
Электрический ток |
|
|
Модифицированная функция Бесселя первого рода нулевого порядка |
|
|
Самоинформация информационного источника X |
|
|
Средняя принятая мощность станции-постановщика помех |
|
|
Спектральная плотность мощности станции-постановщика помех |
|
|
Отношение средней принятой мощности станции-постановщика помех к средней мощности сигнала |
|
|
Число бит в М-арном множестве сигналов |
|
|
Степень кодирования (отношение длины исходного блока информации к длине его кодированного представления) |
|
|
Длина кодового ограничения сверточного кодера |
|
|
Ключ, определяемый схемой шифрования или преобразованием дешифрования |
|
|
Число бит квантования |
|
|
Правдоподобие информационного бита dk |
|
|
Длина упреждения в сверточком декодировании с обратной связью |
|
|
Число ответвляющихся слов в последовательности |
|
|
Число уровней квантования |
|
|
Логарифмическое отношение правдоподобий информационного бита |
|
|
Внешнее логарифмическое отношение правдоподобий |
|
|
Потери в свободном пространстве |
|
|
Другие потери |
|
|
Потери в тракте связи |
|
|
Время наблюдения |
|
|
Время наблюдения для ISI, введенной каналом |
|
|
Время наблюдения для контролируемой ISI |
|
|
Канальное логарифмическое отношение правдоподобий |
|
|
Вектор сообщения |
|
|
Полином сообщения |
|
|
Бит данных |
|
|
Резерв |
|
|
Размер множества сигналов |
|
|
Маркировка кода, где п — общее число бит, a k — число бит в кодовом слове |
|
|
Среднее число бит на символ |
|
|
Переменная случайного шума на выходе коррелятора в момент t = Т |
|
|
Гауссов процесс шума |
|
|
Мощность шума |
|
|
Расстояние единственности |
|
|
Уровень односторонней спектральной плотности мощности белого шума |
|
|
Отношение средней мощности шума к средней мощности сигнала |
|
|
Вероятность ошибки в канальном символе |
|
|
Бит четности |
|
|
Мгновенная мощность |
|
|
Функция плотности вероятности непрерывной случайной переменной |
|
|
Функция плотности вероятности х при условии у |
|
|
Массив четности |
|
|
Вероятность битовой ошибки |
|
|
Вероятность символьной ошибки |
|
|
Вероятность ложной тревоги |
|
|
Вероятность несоответствия |
|
|
Вероятность блочной ошибки или ошибки сообщения |
|
|
Вероятность необнаруженной ошибки |
|
|
Отношение средней принятой мощности сигнала к спектральной плотности мощности шума |
|
|
Полином остатка |
|
|
Вероятность дискретной случайной переменной |
|
|
Средняя мощность сигнала x(t) |
|
|
Шаг квантования |
|
|
Полином частного |
|
|
Гауссов интеграл ошибок |
|
|
Коэффициент сглаживания фильтра |
|
|
Истинная интенсивность языка |
|
|
Абсолютная интенсивность языка |
|
|
Принятый сигнал |
|
|
Скорость передачи данных (бит/с) |
|
|
Корреляционная функция разнесения частоты |
|
|
Корреляционная функция разнесения времени |
|
|
Скорость передачи кодовых или канальных бит (кодовых бит/с) |
|
|
Скорость передачи элементарных сигналов (элементарных сигналов/с) |
|
|
Скорость передачи символов (символов/с) |
|
|
Автокорреляционная функция сигнала x(t) |
|
|
Электрическое сопротивление |
|
|
Сигнал |
|
|
Оценка сигнала |
|
|
Доплеровская спектральная плотность мощности |
|
|
Профиль интенсивности при многолучевом распространении |
|
|
Вектор сигнала |
|
|
Знаковая функция х |
|
|
Состояние в момент k |
|
|
Мощность сигнала |
|
|
Вектор синдрома |
|
|
Отношение средней мощности сигнала к средней мощности помех |
|
|
Отношение средней мощности сигнала к средней мощности шума |
|
|
Отношение мощности сигнала к мощности шума |
|
|
Фурье-образ сигнала s(t) |
|
|
Полином синдрома |
|
|
Число исправимых ошибок в коде коррекции ошибок |
|
|
Независимая переменная времени |
|
|
Временная задержка |
|
|
Объем информации, переданной от i к j |
|
|
Длительность импульса |
|
|
Длительность символа |
|
|
Передаточная функция или производящая функция сверточного кода |
|
|
Время передачи на одной частоте |
|
|
Длительность перехода |
|
|
Интервал дискретизации |
|
|
Температура |
|
|
Температура антенны |
|
|
Эффективная температура линии связи |
|
|
Задержка многолучевого распространения (максимальная) |
|
|
Время когерентности |
|
|
Эффективная температура приемника |
|
|
Температура системы |
|
|
Время синхронизации |
|
|
Кодовый символ |
|
|
Единичная ступенчатая функция |
|
|
Вектор кодового слова |
|
|
Полином кодового слова |
|
|
Относительная скорость |
|
|
Форма кривой электрического напряжения |
|
|
Дисперсия случайной переменной X |
|
|
Скорость |
|
|
Сигнал станции-постановщика помех |
|
|
Ширина полосы |
|
|
Ширина полосы фильтра |
|
|
Двусторонняя ширина полосы |
|
|
Ширина полосы шумового эквивалента |
|
|
Ширина полосы расширения спектра |
|
|
Выход согласованного фильтра или коррелятора |
|
|
Прямая метрика состояния в момент k |
|
|
Обратная метрика состояния в момент k |
|
|
Отношение SNR, усредненное по подъемам и спадам замирания |
|
|
Метрика состояния для состояния а |
|
|
Порог (принятия) решения |
|
|
Оптимальный порог |
|
|
Правдоподобие кодового слова |
|
|
Фракционный уход частоты за день |
|
|
Метрика ветви в момент k |
|
|
Дельта-функция Кронекера |
|
|
Импульсная функция (дельта-функция Дирака) |
|
|
Ошибка |
|
|
Характеристика демпфирования контура (контур второго порядка) |
|
|
Эффективность антенны |
|
|
Переменная фаза |
|
|
Фурье-образ |
|
|
Постоянная Больцмана, |
|
|
Отношение правдоподобий бита данных dk |
|
|
Совместная вероятность |
|
|
Длина волны |
|
|
Скорость поступления пакетов |
|
|
Число «пи», 3,14159 |
|
|
Часть полосы частот, подвергающаяся воздействию помех |
|
|
Часть времени, в течение которого «включены» помехи |
|
|
Нормированное отношение сигнал/шум контура |
|
|
Нормированная пропускная способность сообщений |
|
|
Число исправимых стираний в коде коррекции ошибок |
|
|
Коэффициент временной корреляции |
|
|
Значение |
|
|
Среднеквадратическое распространение задержки |
|
|
Среднеквадратическое отклонение случайной переменной X |
|
|
Дисперсия случайной переменной X |
|
|
Ширина импульса |
|
|
Сдвиг во времени (независимая переменная автокорреляционной функции) |
|
|
Базисная функция |
|
|
Спектральная плотность энергии сигнала x(t) |
|
|
Угловая частота (радиан в секунду) |
| Error function | |
|---|---|

Plot of the error function |
|
| General information | |
| General definition |  |
| Fields of application | Probability, thermodynamics |
| Domain, Codomain and Image | |
| Domain |  |
| Image |  |
| Basic features | |
| Parity | Odd |
| Specific features | |
| Root | 0 |
| Derivative |  |
| Antiderivative |  |
| Series definition | |
| Taylor series |  |
In mathematics, the error function (also called the Gauss error function), often denoted by erf, is a complex function of a complex variable defined as:[1]
Some authors define 

This nonelementary integral is a sigmoid function that occurs often in probability, statistics, and partial differential equations. In many of these applications, the function argument is a real number. If the function argument is real, then the function value is also real.
In statistics, for non-negative values of x, the error function has the following interpretation: for a random variable Y that is normally distributed with mean 0 and standard deviation 1/√2, erf x is the probability that Y falls in the range [−x, x].
Two closely related functions are the complementary error function (erfc) defined as
and the imaginary error function (erfi) defined as
where i is the imaginary unit.
Name[edit]
The name «error function» and its abbreviation erf were proposed by J. W. L. Glaisher in 1871 on account of its connection with «the theory of Probability, and notably the theory of Errors.»[3] The error function complement was also discussed by Glaisher in a separate publication in the same year.[4]
For the «law of facility» of errors whose density is given by
(the normal distribution), Glaisher calculates the probability of an error lying between p and q as:
Plot of the error function Erf(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
Applications[edit]
When the results of a series of measurements are described by a normal distribution with standard deviation σ and expected value 0, then erf (a/σ √2) is the probability that the error of a single measurement lies between −a and +a, for positive a. This is useful, for example, in determining the bit error rate of a digital communication system.
The error and complementary error functions occur, for example, in solutions of the heat equation when boundary conditions are given by the Heaviside step function.
The error function and its approximations can be used to estimate results that hold with high probability or with low probability. Given a random variable X ~ Norm[μ,σ] (a normal distribution with mean μ and standard deviation σ) and a constant L < μ:
where A and B are certain numeric constants. If L is sufficiently far from the mean, specifically μ − L ≥ σ√ln k, then:
so the probability goes to 0 as k → ∞.
The probability for X being in the interval [La, Lb] can be derived as
Properties[edit]
Integrand exp(−z2)
erf z
The property erf (−z) = −erf z means that the error function is an odd function. This directly results from the fact that the integrand e−t2 is an even function (the antiderivative of an even function which is zero at the origin is an odd function and vice versa).
Since the error function is an entire function which takes real numbers to real numbers, for any complex number z:
where z is the complex conjugate of z.
The integrand f = exp(−z2) and f = erf z are shown in the complex z-plane in the figures at right with domain coloring.
The error function at +∞ is exactly 1 (see Gaussian integral). At the real axis, erf z approaches unity at z → +∞ and −1 at z → −∞. At the imaginary axis, it tends to ±i∞.
Taylor series[edit]
The error function is an entire function; it has no singularities (except that at infinity) and its Taylor expansion always converges, but is famously known «[…] for its bad convergence if x > 1.»[5]
The defining integral cannot be evaluated in closed form in terms of elementary functions (see Liouville’s theorem), but by expanding the integrand e−z2 into its Maclaurin series and integrating term by term, one obtains the error function’s Maclaurin series as:
which holds for every complex number z. The denominator terms are sequence A007680 in the OEIS.
For iterative calculation of the above series, the following alternative formulation may be useful:
because −(2k − 1)z2/k(2k + 1) expresses the multiplier to turn the kth term into the (k + 1)th term (considering z as the first term).
The imaginary error function has a very similar Maclaurin series, which is:
which holds for every complex number z.
Derivative and integral[edit]
The derivative of the error function follows immediately from its definition:
From this, the derivative of the imaginary error function is also immediate:
An antiderivative of the error function, obtainable by integration by parts, is
An antiderivative of the imaginary error function, also obtainable by integration by parts, is
Higher order derivatives are given by
where H are the physicists’ Hermite polynomials.[6]
Bürmann series[edit]
An expansion,[7] which converges more rapidly for all real values of x than a Taylor expansion, is obtained by using Hans Heinrich Bürmann’s theorem:[8]
where sgn is the sign function. By keeping only the first two coefficients and choosing c1 = 31/200 and c2 = −341/8000, the resulting approximation shows its largest relative error at x = ±1.3796, where it is less than 0.0036127:
Inverse functions[edit]
Given a complex number z, there is not a unique complex number w satisfying erf w = z, so a true inverse function would be multivalued. However, for −1 < x < 1, there is a unique real number denoted erf−1 x satisfying
The inverse error function is usually defined with domain (−1,1), and it is restricted to this domain in many computer algebra systems. However, it can be extended to the disk |z| < 1 of the complex plane, using the Maclaurin series[9]
where c0 = 1 and
So we have the series expansion (common factors have been canceled from numerators and denominators):
(After cancellation the numerator/denominator fractions are entries OEIS: A092676/OEIS: A092677 in the OEIS; without cancellation the numerator terms are given in entry OEIS: A002067.) The error function’s value at ±∞ is equal to ±1.
For |z| < 1, we have erf(erf−1 z) = z.
The inverse complementary error function is defined as
For real x, there is a unique real number erfi−1 x satisfying erfi(erfi−1 x) = x. The inverse imaginary error function is defined as erfi−1 x.[10]
For any real x, Newton’s method can be used to compute erfi−1 x, and for −1 ≤ x ≤ 1, the following Maclaurin series converges:
where ck is defined as above.
Asymptotic expansion[edit]
A useful asymptotic expansion of the complementary error function (and therefore also of the error function) for large real x is
where (2n − 1)!! is the double factorial of (2n − 1), which is the product of all odd numbers up to (2n − 1). This series diverges for every finite x, and its meaning as asymptotic expansion is that for any integer N ≥ 1 one has
where the remainder is
which follows easily by induction, writing
and integrating by parts.
The asymptotic behavior of the remainder term, in Landau notation, is
as x → ∞. This can be found by
For large enough values of x, only the first few terms of this asymptotic expansion are needed to obtain a good approximation of erfc x (while for not too large values of x, the above Taylor expansion at 0 provides a very fast convergence).
Continued fraction expansion[edit]
A continued fraction expansion of the complementary error function is:[11]
Integral of error function with Gaussian density function[edit]
which appears related to Ng and Geller, formula 13 in section 4.3[12] with a change of variables.
Factorial series[edit]
The inverse factorial series:
converges for Re(z2) > 0. Here
zn denotes the rising factorial, and s(n,k) denotes a signed Stirling number of the first kind.[13][14]
There also exists a representation by an infinite sum containing the double factorial:
Numerical approximations[edit]
Approximation with elementary functions[edit]
- Abramowitz and Stegun give several approximations of varying accuracy (equations 7.1.25–28). This allows one to choose the fastest approximation suitable for a given application. In order of increasing accuracy, they are:
(maximum error: 5×10−4)
where a1 = 0.278393, a2 = 0.230389, a3 = 0.000972, a4 = 0.078108
(maximum error: 2.5×10−5)
where p = 0.47047, a1 = 0.3480242, a2 = −0.0958798, a3 = 0.7478556
(maximum error: 3×10−7)
where a1 = 0.0705230784, a2 = 0.0422820123, a3 = 0.0092705272, a4 = 0.0001520143, a5 = 0.0002765672, a6 = 0.0000430638
(maximum error: 1.5×10−7)
where p = 0.3275911, a1 = 0.254829592, a2 = −0.284496736, a3 = 1.421413741, a4 = −1.453152027, a5 = 1.061405429
All of these approximations are valid for x ≥ 0. To use these approximations for negative x, use the fact that erf x is an odd function, so erf x = −erf(−x).
- Exponential bounds and a pure exponential approximation for the complementary error function are given by[15]
- The above have been generalized to sums of N exponentials[16] with increasing accuracy in terms of N so that erfc x can be accurately approximated or bounded by 2Q̃(√2x), where
In particular, there is a systematic methodology to solve the numerical coefficients {(an,bn)}N
n = 1 that yield a minimax approximation or bound for the closely related Q-function: Q(x) ≈ Q̃(x), Q(x) ≤ Q̃(x), or Q(x) ≥ Q̃(x) for x ≥ 0. The coefficients {(an,bn)}N
n = 1 for many variations of the exponential approximations and bounds up to N = 25 have been released to open access as a comprehensive dataset.[17] - A tight approximation of the complementary error function for x ∈ [0,∞) is given by Karagiannidis & Lioumpas (2007)[18] who showed for the appropriate choice of parameters {A,B} that
They determined {A,B} = {1.98,1.135}, which gave a good approximation for all x ≥ 0. Alternative coefficients are also available for tailoring accuracy for a specific application or transforming the expression into a tight bound.[19]
- A single-term lower bound is[20]
where the parameter β can be picked to minimize error on the desired interval of approximation.
-
- Another approximation is given by Sergei Winitzki using his «global Padé approximations»:[21][22]: 2–3
where
This is designed to be very accurate in a neighborhood of 0 and a neighborhood of infinity, and the relative error is less than 0.00035 for all real x. Using the alternate value a ≈ 0.147 reduces the maximum relative error to about 0.00013.[23]
This approximation can be inverted to obtain an approximation for the inverse error function:
- An approximation with a maximal error of 1.2×10−7 for any real argument is:[24]
with
and
- An approximation of
with a maximum relative error less than
in absolute value is:[25]
for
,
and for
Table of values[edit]
| x | erf x | 1 − erf x |
|---|---|---|
| 0 | 0 | 1 |
| 0.02 | 0.022564575 | 0.977435425 |
| 0.04 | 0.045111106 | 0.954888894 |
| 0.06 | 0.067621594 | 0.932378406 |
| 0.08 | 0.090078126 | 0.909921874 |
| 0.1 | 0.112462916 | 0.887537084 |
| 0.2 | 0.222702589 | 0.777297411 |
| 0.3 | 0.328626759 | 0.671373241 |
| 0.4 | 0.428392355 | 0.571607645 |
| 0.5 | 0.520499878 | 0.479500122 |
| 0.6 | 0.603856091 | 0.396143909 |
| 0.7 | 0.677801194 | 0.322198806 |
| 0.8 | 0.742100965 | 0.257899035 |
| 0.9 | 0.796908212 | 0.203091788 |
| 1 | 0.842700793 | 0.157299207 |
| 1.1 | 0.880205070 | 0.119794930 |
| 1.2 | 0.910313978 | 0.089686022 |
| 1.3 | 0.934007945 | 0.065992055 |
| 1.4 | 0.952285120 | 0.047714880 |
| 1.5 | 0.966105146 | 0.033894854 |
| 1.6 | 0.976348383 | 0.023651617 |
| 1.7 | 0.983790459 | 0.016209541 |
| 1.8 | 0.989090502 | 0.010909498 |
| 1.9 | 0.992790429 | 0.007209571 |
| 2 | 0.995322265 | 0.004677735 |
| 2.1 | 0.997020533 | 0.002979467 |
| 2.2 | 0.998137154 | 0.001862846 |
| 2.3 | 0.998856823 | 0.001143177 |
| 2.4 | 0.999311486 | 0.000688514 |
| 2.5 | 0.999593048 | 0.000406952 |
| 3 | 0.999977910 | 0.000022090 |
| 3.5 | 0.999999257 | 0.000000743 |
[edit]
Complementary error function[edit]
The complementary error function, denoted erfc, is defined as
Plot of the complementary error function Erfc(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
which also defines erfcx, the scaled complementary error function[26] (which can be used instead of erfc to avoid arithmetic underflow[26][27]). Another form of erfc x for x ≥ 0 is known as Craig’s formula, after its discoverer:[28]
This expression is valid only for positive values of x, but it can be used in conjunction with erfc x = 2 − erfc(−x) to obtain erfc(x) for negative values. This form is advantageous in that the range of integration is fixed and finite. An extension of this expression for the erfc of the sum of two non-negative variables is as follows:[29]
Imaginary error function[edit]
The imaginary error function, denoted erfi, is defined as
where D(x) is the Dawson function (which can be used instead of erfi to avoid arithmetic overflow[26]).
Despite the name «imaginary error function», erfi x is real when x is real.
When the error function is evaluated for arbitrary complex arguments z, the resulting complex error function is usually discussed in scaled form as the Faddeeva function:
Cumulative distribution function[edit]
The error function is essentially identical to the standard normal cumulative distribution function, denoted Φ, also named norm(x) by some software languages[citation needed], as they differ only by scaling and translation. Indeed,
the normal cumulative distribution function plotted in the complex plane
or rearranged for erf and erfc:
Consequently, the error function is also closely related to the Q-function, which is the tail probability of the standard normal distribution. The Q-function can be expressed in terms of the error function as
The inverse of Φ is known as the normal quantile function, or probit function and may be expressed in terms of the inverse error function as
The standard normal cdf is used more often in probability and statistics, and the error function is used more often in other branches of mathematics.
The error function is a special case of the Mittag-Leffler function, and can also be expressed as a confluent hypergeometric function (Kummer’s function):
It has a simple expression in terms of the Fresnel integral.[further explanation needed]
In terms of the regularized gamma function P and the incomplete gamma function,
sgn x is the sign function.
Generalized error functions[edit]
grey curve: E1(x) = 1 − e−x/√π
red curve: E2(x) = erf(x)
green curve: E3(x)
blue curve: E4(x)
gold curve: E5(x).
Some authors discuss the more general functions:[citation needed]
Notable cases are:
- E0(x) is a straight line through the origin: E0(x) = x/e√π
- E2(x) is the error function, erf x.
After division by n!, all the En for odd n look similar (but not identical) to each other. Similarly, the En for even n look similar (but not identical) to each other after a simple division by n!. All generalised error functions for n > 0 look similar on the positive x side of the graph.
These generalised functions can equivalently be expressed for x > 0 using the gamma function and incomplete gamma function:
Therefore, we can define the error function in terms of the incomplete gamma function:
Iterated integrals of the complementary error function[edit]
The iterated integrals of the complementary error function are defined by[30]
The general recurrence formula is
They have the power series
from which follow the symmetry properties
and
Implementations[edit]
As real function of a real argument[edit]
- In POSIX-compliant operating systems, the header
math.hshall declare and the mathematical librarylibmshall provide the functionserfanderfc(double precision) as well as their single precision and extended precision counterpartserff,erflanderfcf,erfcl.[31]
- The GNU Scientific Library provides
erf,erfc,log(erf), and scaled error functions.[32]
As complex function of a complex argument[edit]
libcerf, numeric C library for complex error functions, provides the complex functionscerf,cerfc,cerfcxand the real functionserfi,erfcxwith approximately 13–14 digits precision, based on the Faddeeva function as implemented in the MIT Faddeeva Package
See also[edit]
[edit]
- Gaussian integral, over the whole real line
- Gaussian function, derivative
- Dawson function, renormalized imaginary error function
- Goodwin–Staton integral
In probability[edit]
- Normal distribution
- Normal cumulative distribution function, a scaled and shifted form of error function
- Probit, the inverse or quantile function of the normal CDF
- Q-function, the tail probability of the normal distribution
- Standard score
References[edit]
- ^ Andrews, Larry C. (1998). Special functions of mathematics for engineers. SPIE Press. p. 110. ISBN 9780819426161.
- ^ Whittaker, E. T.; Watson, G. N. (1927). A Course of Modern Analysis. Cambridge University Press. p. 341. ISBN 978-0-521-58807-2.
- ^ Glaisher, James Whitbread Lee (July 1871). «On a class of definite integrals». London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4. 42 (277): 294–302. doi:10.1080/14786447108640568. Retrieved 6 December 2017.
- ^ Glaisher, James Whitbread Lee (September 1871). «On a class of definite integrals. Part II». London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4. 42 (279): 421–436. doi:10.1080/14786447108640600. Retrieved 6 December 2017.
- ^ «A007680 – OEIS». oeis.org. Retrieved 2 April 2020.
- ^ Weisstein, Eric W. «Erf». MathWorld.
- ^ Schöpf, H. M.; Supancic, P. H. (2014). «On Bürmann’s Theorem and Its Application to Problems of Linear and Nonlinear Heat Transfer and Diffusion». The Mathematica Journal. 16. doi:10.3888/tmj.16-11.
- ^ Weisstein, Eric W. «Bürmann’s Theorem». MathWorld.
- ^ Dominici, Diego (2006). «Asymptotic analysis of the derivatives of the inverse error function». arXiv:math/0607230.
- ^ Bergsma, Wicher (2006). «On a new correlation coefficient, its orthogonal decomposition and associated tests of independence». arXiv:math/0604627.
- ^ Cuyt, Annie A. M.; Petersen, Vigdis B.; Verdonk, Brigitte; Waadeland, Haakon; Jones, William B. (2008). Handbook of Continued Fractions for Special Functions. Springer-Verlag. ISBN 978-1-4020-6948-2.
- ^ Ng, Edward W.; Geller, Murray (January 1969). «A table of integrals of the Error functions». Journal of Research of the National Bureau of Standards Section B. 73B (1): 1. doi:10.6028/jres.073B.001.
- ^ Schlömilch, Oskar Xavier (1859). «Ueber facultätenreihen». Zeitschrift für Mathematik und Physik (in German). 4: 390–415.
- ^ Nielson, Niels (1906). Handbuch der Theorie der Gammafunktion (in German). Leipzig: B. G. Teubner. p. 283 Eq. 3. Retrieved 4 December 2017.
- ^ Chiani, M.; Dardari, D.; Simon, M.K. (2003). «New Exponential Bounds and Approximations for the Computation of Error Probability in Fading Channels» (PDF). IEEE Transactions on Wireless Communications. 2 (4): 840–845. CiteSeerX 10.1.1.190.6761. doi:10.1109/TWC.2003.814350.
- ^ Tanash, I.M.; Riihonen, T. (2020). «Global minimax approximations and bounds for the Gaussian Q-function by sums of exponentials». IEEE Transactions on Communications. 68 (10): 6514–6524. arXiv:2007.06939. doi:10.1109/TCOMM.2020.3006902. S2CID 220514754.
- ^ Tanash, I.M.; Riihonen, T. (2020). «Coefficients for Global Minimax Approximations and Bounds for the Gaussian Q-Function by Sums of Exponentials [Data set]». Zenodo. doi:10.5281/zenodo.4112978.
- ^ Karagiannidis, G. K.; Lioumpas, A. S. (2007). «An improved approximation for the Gaussian Q-function» (PDF). IEEE Communications Letters. 11 (8): 644–646. doi:10.1109/LCOMM.2007.070470. S2CID 4043576.
- ^ Tanash, I.M.; Riihonen, T. (2021). «Improved coefficients for the Karagiannidis–Lioumpas approximations and bounds to the Gaussian Q-function». IEEE Communications Letters. 25 (5): 1468–1471. arXiv:2101.07631. doi:10.1109/LCOMM.2021.3052257. S2CID 231639206.
- ^ Chang, Seok-Ho; Cosman, Pamela C.; Milstein, Laurence B. (November 2011). «Chernoff-Type Bounds for the Gaussian Error Function». IEEE Transactions on Communications. 59 (11): 2939–2944. doi:10.1109/TCOMM.2011.072011.100049. S2CID 13636638.
- ^ Winitzki, Sergei (2003). «Uniform approximations for transcendental functions». Computational Science and Its Applications – ICCSA 2003. Lecture Notes in Computer Science. Vol. 2667. Springer, Berlin. pp. 780–789. doi:10.1007/3-540-44839-X_82. ISBN 978-3-540-40155-1.
- ^ Zeng, Caibin; Chen, Yang Cuan (2015). «Global Padé approximations of the generalized Mittag-Leffler function and its inverse». Fractional Calculus and Applied Analysis. 18 (6): 1492–1506. arXiv:1310.5592. doi:10.1515/fca-2015-0086. S2CID 118148950.
Indeed, Winitzki [32] provided the so-called global Padé approximation
- ^ Winitzki, Sergei (6 February 2008). «A handy approximation for the error function and its inverse» (Document).
- ^ Numerical Recipes in Fortran 77: The Art of Scientific Computing (ISBN 0-521-43064-X), 1992, page 214, Cambridge University Press.
- ^ Dia, Yaya D. (2023). Approximate Incomplete Integrals, Application to Complementary Error Function. Available at SSRN: https://ssrn.com/abstract=4487559 or http://dx.doi.org/10.2139/ssrn.4487559, 2023
- ^ a b c Cody, W. J. (March 1993), «Algorithm 715: SPECFUN—A portable FORTRAN package of special function routines and test drivers» (PDF), ACM Trans. Math. Softw., 19 (1): 22–32, CiteSeerX 10.1.1.643.4394, doi:10.1145/151271.151273, S2CID 5621105
- ^ Zaghloul, M. R. (1 March 2007), «On the calculation of the Voigt line profile: a single proper integral with a damped sine integrand», Monthly Notices of the Royal Astronomical Society, 375 (3): 1043–1048, Bibcode:2007MNRAS.375.1043Z, doi:10.1111/j.1365-2966.2006.11377.x
- ^ John W. Craig, A new, simple and exact result for calculating the probability of error for two-dimensional signal constellations Archived 3 April 2012 at the Wayback Machine, Proceedings of the 1991 IEEE Military Communication Conference, vol. 2, pp. 571–575.
- ^ Behnad, Aydin (2020). «A Novel Extension to Craig’s Q-Function Formula and Its Application in Dual-Branch EGC Performance Analysis». IEEE Transactions on Communications. 68 (7): 4117–4125. doi:10.1109/TCOMM.2020.2986209. S2CID 216500014.
- ^ Carslaw, H. S.; Jaeger, J. C. (1959), Conduction of Heat in Solids (2nd ed.), Oxford University Press, ISBN 978-0-19-853368-9, p 484
- ^ «math.h — mathematical declarations». opengroup.org. 2018. Retrieved 21 April 2023.
- ^ «Special Functions – GSL 2.7 documentation».
Further reading[edit]
- Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. «Chapter 7». Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 297. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (2007), «Section 6.2. Incomplete Gamma Function and Error Function», Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
- Temme, Nico M. (2010), «Error Functions, Dawson’s and Fresnel Integrals», in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248.
External links[edit]
- A Table of Integrals of the Error Functions

В математике функция ошибок (также называемая Функция ошибок Гаусса ), часто обозначаемая erf, является сложной функцией комплексной определяемой как:
- erf z = 2 π ∫ 0 ze — t 2 dt. { displaystyle operatorname {erf} z = { frac {2} { sqrt { pi}}} int _ {0} ^ {z} e ^ {- t ^ {2}} , dt.}
Этот интеграл является особой (не элементарной ) и сигмоидной функцией, которая часто встречается в статистике вероятность, и уравнения в частных производных. Во многих из этих приложений аргумент функции является действительным числом. Если аргумент функции является действительным, значение также является действительным.
В статистике для неотрицательных значений x функция имеет интерпретацию: для случайной величины Y, которая нормально распределена с среднее 0 и дисперсия 1/2, erf x — это вероятность того, что Y попадает в диапазон [-x, x].
Две связанные функции: дополнительные функции ошибок (erfc ), определенная как
- erfc z = 1 — erf z, { displaystyle operatorname {erfc} z = 1- operatorname {erf} z,}
и функция мнимой ошибки (erfi ), определяемая как
- erfi z = — i erf (iz), { displaystyle operatorname {erfi} z = -i operatorname {erf} (iz),}
, где i — мнимая единица.
Содержание
- 1 Имя
- 2 Приложения
- 3 Свойства
- 3.1 Ряд Тейлора
- 3.2 Производная и интеграл
- 3.3 Ряд Бюрмана
- 3.4 Обратные функции
- 3.5 Асимптотическое разложение
- 3.6 Разложение на непрерывную дробь
- 3,7 Интеграл функции ошибок с функцией плотности Гаусса
- 3.8 Факториальный ряд
- 4 Численные приближения
- 4.1 Аппроксимация с элементарными функциями
- 4.2 Полином
- 4.3 Таблица значений
- 5 Связанные функции
- 5.1 функция дополнительных ошибок
- 5.2 Функция мнимой ошибки
- 5.3 Кумулятивная функци я распределения на
- 5.4 Обобщенные функции ошибок
- 5.5 Итерированные интегралы дополнительных функций ошибок
- 6 Реализации
- 6.1 Как действующая функция действительного аргумента
- 6.2 Как комплексная функция комплексного аргумента
- 7 См. Также
- 7.1 Связанные функции
- 7.2 Вероятность
- 8 Ссылки
- 9 Дополнительная литература
- 10 Внешние ссылки
Имя
Название «функция ошибки» и его аббревиатура erf были предложены Дж. В. Л. Глейшер в 1871 г. по причине его связи с «теорией вероятности, и особенно теорией ошибок ». Дополнение функции ошибок также обсуждалось Глейшером в отдельной публикации в том же году. Для «закона удобства» ошибок плотность задана как
- f (x) = (c π) 1 2 e — cx 2 { displaystyle f (x) = left ({ frac {c } { pi}} right) ^ { tfrac {1} {2}} e ^ {- cx ^ {2}}}
(нормальное распределение ), Глейшер вычисляет вероятность ошибки, лежащей между p { displaystyle p}

- (c π) 1 2 ∫ pqe — cx 2 dx = 1 2 (erf (qc) — erf (pc)). { displaystyle left ({ frac {c} { pi}} right) ^ { tfrac {1} {2}} int _ {p} ^ {q} e ^ {- cx ^ {2} } dx = { tfrac {1} {2}} left ( operatorname {erf} (q { sqrt {c}}) — operatorname {erf} (p { sqrt {c}}) right).}
Приложения
Когда результаты серии измерений описываются нормальным распределением со стандартным отклонением σ { displaystyle sigma}

Функции и дополнительные функции ошибок возникают, например, в решениях уравнения теплопроводности, когда граничные ошибки задаются ступенчатой функцией Хевисайда.
Функция ошибок и ее приближения Программу присвоили себе преподавателей, которые получили с высокой вероятностью или с низкой вероятностью. Дана случайная величина X ∼ Norm [μ, σ] { displaystyle X sim operatorname {Norm} [ mu, sigma]}![X sim operatorname {Norm} [ му, sigma]](https://wikimedia.org/api/rest_v1/media/math/render/svg/84024bc6827355ec6d23a062283a26d54b29698d)

- Pr [X ≤ L ] = 1 2 + 1 2 erf (L — μ 2 σ) ≈ A ехр (- B (L — μ σ) 2) { Displaystyle Pr [X Leq L] = { frac {1} {2 }} + { frac {1} {2}} operatorname {erf} left ({ frac {L- mu} {{ sqrt {2}} sigma}} right) приблизительно A exp left (-B left ({ frac {L- mu} { sigma}} right) ^ {2} right)}
где A и B — верх числовые константы. Если L достаточно далеко от среднего, то есть μ — L ≥ σ ln k { displaystyle mu -L geq sigma { sqrt { ln {k}}}}
- Pr [X ≤ L] ≤ A exp (- B ln k) = A К B { displaystyle Pr [X leq L] leq A exp (-B ln {k}) = { frac {A} {k ^ {B}}}}
, поэтому становится вероятность 0 при k → ∞ { displaystyle k to infty}
Свойства
Графики на комплексной плоскости 

Свойство erf (- z) = — erf (z) { displaystyle operatorname {erf} (-z) = — operatorname {erf} (z)}

Для любого комплексное число z:
- erf (z ¯) = erf (z) ¯ { displaystyle operatorname {erf} ({ overline {z}}) = { overline { operatorname {erf} (z)}}}
где z ¯ { displaystyle { overline {z}}}
Подынтегральное выражение f = exp (−z) и f = erf (z) показано в комплексной плоскости z на рисунках 2 и 3. Уровень Im (f) = 0 показан жирным зеленым цветом. линия. Отрицательные целые значения Im (f) показаны жирными красными линиями. Положительные целые значения Im (f) показаны толстыми синими линиями. Промежуточные уровни Im (f) = проявляются тонкими зелеными линиями. Промежуточные уровни Re (f) = показаны тонкими красными линиями для отрицательных значений и тонкими синими линиями для положительных значений.
Функция ошибок при + ∞ равна 1 (см. интеграл Гаусса ). На действительной оси erf (z) стремится к единице при z → + ∞ и к −1 при z → −∞. На мнимой оси он стремится к ± i∞.
Серия Тейлора
Функция ошибок — это целая функция ; у него нет сингулярностей (кроме бесконечности), и его разложение Тейлора всегда сходится, но, как известно, «[…] его плохая сходимость, если x>1».
определяющий интеграл нельзя вычислить в закрытой форме в терминах элементарных функций, но путем расширения подынтегрального выражения e в его ряд Маклорена и интегрирована почленно, можно получить ряд Маклорена функции ошибок как:
- erf (z) = 2 π ∑ n = 0 ∞ (- 1) nz 2 n + 1 n! (2 n + 1) знак равно 2 π (z — z 3 3 + z 5 10 — z 7 42 + z 9 216 — ⋯) { displaystyle operatorname {erf} (z) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n} z ^ {2n + 1}} {n! (2n + 1)}} = { frac {2} { sqrt { pi}}} left (z — { frac {z ^ {3}} {3}} + { frac {z ^ { 5}} {10}} — { frac {z ^ {7}} {42}} + { frac {z ^ {9}} {216}} — cdots right)}
, которое выполняется для каждого комплексного числа г. Члены знаменателя представляют собой последовательность A007680 в OEIS.
Для итеративного вычисления нового ряда может быть полезна следующая альтернативная формулировка:
- erf (z) = 2 π ∑ n = 0 ∞ (z ∏ К знак равно 1 N — (2 К — 1) Z 2 К (2 К + 1)) знак равно 2 π ∑ N = 0 ∞ Z 2 N + 1 ∏ К = 1 N — Z 2 К { Displaystyle OperatorName { erf} (z) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} left (z prod _ {k = 1} ^ {n} { frac {- (2k-1) z ^ {2}} {k (2k + 1)}} right) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {z} {2n + 1}} prod _ {k = 1} ^ {n} { frac {-z ^ {2}} {k}}}
потому что что — (2 k — 1) z 2 k (2 k + 1) { displaystyle { frac {- (2k-1) z ^ {2}} {k (2k + 1))}} }
Функция мнимой ошибки имеет очень похожий ряд Маклорена:
- erfi (z) = 2 π ∑ n = 0 ∞ z 2 n + 1 n! (2 n + 1) знак равно 2 π (z + z 3 3 + z 5 10 + z 7 42 + z 9 216 + ⋯) { displaystyle operatorname {erfi} (z) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {z ^ {2n + 1}} {n! (2n + 1)}} = { frac {2} { sqrt { pi}}} left (z + { frac {z ^ {3}} {3}} + { frac {z ^ { 5}} {10}} + { frac {z ^ {7}} {42}} + { frac {z ^ {9}} {216}} + cdots right)}
, которое выполняется для любого комплексного числа z.
Производная и интеграл
Производная функция ошибок сразу следует из ее определения:
- ddz erf (z) = 2 π e — z 2. { displaystyle { frac {d} {dz}} operatorname {erf} (z) = { frac {2} { sqrt { pi}}} e ^ {- z ^ {2}}.}
Отсюда немедленно вычисляется производная функция мнимой ошибки :
- ddz erfi (z) = 2 π ez 2. { displaystyle { frac {d} {dz}} operatorname {erfi} (z) = { frac {2} { sqrt { pi }}} e ^ {z ^ {2}}.}
первообразная функции ошибок, которые можно получить посредством интегрирования по частям, составляет
- z erf (z) + е — z 2 π. { displaystyle z operatorname {erf} (z) + { frac {e ^ {- z ^ {2}}} { sqrt { pi}}}.}
Первообразная мнимой функции ошибок, также можно получить интегрированием по частям:
- z erfi (z) — ez 2 π. { displaystyle z operatorname {erfi} (z) — { frac {e ^ {z ^ {2}}} { sqrt { pi}}}.}
Производные высшего порядка задаются как
- erf (k) (z) = 2 (- 1) k — 1 π H k — 1 (z) e — z 2 = 2 π dk — 1 dzk — 1 (e — z 2), k = 1, 2, … { Displaystyle operatorname {erf} ^ {(k)} (z) = { frac {2 (-1) ^ {k-1}} { sqrt { pi}}} { mathit {H} } _ {k-1} (z) e ^ {- z ^ {2}} = { frac {2} { sqrt { pi}}} { frac {d ^ {k-1}} {dz ^ {k-1}}} left (e ^ {- z ^ {2}} right), qquad k = 1,2, dots}
где H { displaystyle { mathit {H}}}
ряд Бюрмана
Расширение, которое сходится быстрее для всех реальных значений x { displaystyle x}
- erf (x) = 2 π sgn (x) 1 — e — x 2 (1 — 1 12 ( 1 — e — x 2) — 7 480 (1 — e — x 2) 2 — 5 896 (1 — e — x 2) 3 — 787 276480 (1 — e — x 2)) 4 — ⋯) знак равно 2 π знак (x) 1 — e — x 2 (π 2 + ∑ k = 1 ∞ cke — kx 2). { displaystyle { begin {align} operatorname {erf} (x) = { frac {2} { sqrt { pi}}} operatorname {sgn} (x) { sqrt {1-e ^ {-x ^ {2}}}} left (1 — { frac {1} {12}} left (1-e ^ {- x ^ {2}} right) — { frac {7} {480}} left (1-e ^ {- x ^ {2}} right) ^ {2} — { frac {5} {896}} left (1-e ^ {- x ^ {2 }} right) ^ {3} — { frac {787} {276480}} left (1-e ^ {- x ^ {2}} right) ^ {4} — cdots right) [10pt] = { frac {2} { sqrt { pi}}} operatorname {sgn} (x) { sqrt {1-e ^ {- x ^ {2}}}} left ({ frac { sqrt { pi}} {2}} + sum _ {k = 1} ^ { infty} c_ {k} e ^ {- kx ^ {2}} right). end {выровнено}}
Сохраняя только первые два коэффициента и выбирая c 1 = 31 200 { displaystyle c_ {1} = { frac {31} {200}}}



- erf (x) ≈ 2 π sign (x) 1 — e — x 2 (π 2 + 31 200 e — x 2 — 341 8000 e — 2 х 2). { displaystyle operatorname {erf} (x) приблизительно { frac {2} { sqrt { pi}}} operatorname {sgn} (x) { sqrt {1-e ^ {- x ^ {2 }}}} left ({ frac { sqrt { pi}} {2}} + { frac {31} {200}} e ^ {- x ^ {2}} — { frac {341} {8000}} e ^ {- 2x ^ {2}} right).}
Обратные функции

Учитывая комплексное число z, не существует уникального комплексного числа w, удовлетворяющего erf (w) = z { displaystyle operatorname {erf} (w) = z}

- erf (erf — 1 ( х)) = х. { displaystyle operatorname {erf} left ( operatorname {erf} ^ {- 1} (x) right) = x.}
Обратная функция ошибок обычно определяется с помощью домена (- 1,1), и он ограничен этой областью многих систем компьютерной алгебры. Однако его можно продолжить и на диск | z | < 1 of the complex plane, using the Maclaurin series
- erf — 1 (z) знак равно ∑ К знак равно 0 ∞ ck 2 k + 1 (π 2 z) 2 k + 1, { displaystyle operatorname {erf} ^ {- 1} (z) = sum _ {k = 0} ^ { infty} { frac {c_ {k}} {2k + 1}} left ({ frac { sqrt { pi}} {2}} z right) ^ {2k + 1},}
где c 0 = 1 и
- ck = ∑ m = 0 k — 1 cmck — 1 — m (m + 1) (2 m + 1) = {1, 1, 7 6, 127 90, 4369 2520, 34807 16200,…}. { displaystyle c_ {k} = sum _ {m = 0} ^ {k-1} { frac {c_ {m} c_ {k-1-m}} {(m + 1) (2m + 1) }} = left {1,1, { frac {7} {6}}, { frac {127} {90}}, { frac {4369} {2520}}, { frac {34807} {16200}}, ldots right }.}
Итак, у нас есть разложение в ряд (общие множители были удалены из числителей и знаменателей):
- erf — 1 (z) = 1 2 π ( z + π 12 z 3 + 7 π 2 480 z 5 + 127 π 3 40320 z 7 + 4369 π 4 5806080 z 9 + 34807 π 5 182476800 z 11 + ⋯). { displaystyle operatorname {erf} ^ {- 1} (z) = { tfrac {1} {2}} { sqrt { pi}} left (z + { frac { pi} {12} } z ^ {3} + { frac {7 pi ^ {2}} {480}} z ^ {5} + { frac {127 pi ^ {3}} {40320}} z ^ {7} + { frac {4369 pi ^ {4}} {5806080}} z ^ {9} + { frac {34807 pi ^ {5}} {182476800}} z ^ {11} + cdots right). }
(После отмены дроби числителя / знаменателя характерми OEIS : A092676 / OEIS : A092677 в OEIS ; без отмены членов числителя в записи OEIS : A002067.) Значение функции ошибок при ± ∞ равно ± 1.
Для | z | < 1, we have erf (erf — 1 (z)) = z { displaystyle operatorname {erf} left ( operatorname {erf} ^ {- 1} (z) right) = z}
обратная дополнительная функция ошибок определяется как
- erfc — 1 (1 — z) = erf — 1 (z). { displaystyle operatorname {erfc} ^ {- 1} (1-z) = operatorname {erf} ^ {- 1} (z).}
Для действительного x существует уникальное действительное число erfi — 1 (x) { displaystyle operatorname {erfi} ^ {- 1} (x)}


Для любого действительного x, Метод Ньютона можно использовать для вычислений erfi — 1 (x) { displaystyle operatorname {erfi} ^ {- 1} (x)}

- erfi — 1 (z) = ∑ k = 0 ∞ (- 1) ККК 2 К + 1 (π 2 Z) 2 К + 1, { Displaystyle OperatorName {erfi} ^ {- 1} (г) = сумма _ {к = 0} ^ { infty} { гидроразрыва {(-1) ^ {k} c_ {k}} {2k + 1}} left ({ frac { sqrt { pi}} {2}} z right) ^ {2k + 1},}
, где c k определено, как указано выше.
Асимптотическое разложение
Полезным асимптотическим разложением дополнительные функции (и, следовательно, также и функции ошибок) для больших вещественных x
- erfc (x) = e — x 2 x π [1 + ∑ n = 1 ∞ (- 1) n 1 ⋅ 3 ⋅ 5 ⋯ (2 n — 1) (2 x 2) n] = e — x 2 x π ∑ n = 0 ∞ (- 1) п (2 п — 1)! ! (2 х 2) n, { displaystyle operatorname {erfc} (x) = { frac {e ^ {- x ^ {2}}} {x { sqrt { pi}}}} left [1 + sum _ {n = 1} ^ { infty} (- 1) ^ {n} { frac {1 cdot 3 cdot 5 cdots (2n-1)} {(2x ^ {2}) ^ {n}}} right] = { frac {e ^ {- x ^ {2}}} {x { sqrt { pi}}}} sum _ {n = 0} ^ { infty} ( -1) ^ {n} { frac {(2n-1) !!} {(2x ^ {2}) ^ {n}}},}
где (2n — 1) !! — это двойной факториал числа (2n — 1), которое является произведением всех нечетных чисел до (2n — 1). Этот ряд расходуется для любого конечного x, и его значение как асимптотического разложения состоит в том, что для любого N ∈ N { displaystyle N in mathbb {N}}
- erfc (Икс) знак равно е — Икс 2 Икс π ∑ N знак равно 0 N — 1 (- 1) N (2 N — 1)! ! (2 х 2) n + RN (x) { displaystyle operatorname {erfc} (x) = { frac {e ^ {- x ^ {2}}} {x { sqrt { pi}}}} sum _ {n = 0} ^ {N-1} (- 1) ^ {n} { frac {(2n-1) !!} {(2x ^ {2}) ^ {n}}} + R_ {N} (x)}
где остаток в нотации Ландау равен
- RN (x) = O (x 1 — 2 N e — x 2) { displaystyle R_ {N} ( x) = O left (x ^ {1-2N} e ^ {- x ^ {2}} right)}
при x → ∞. { displaystyle x to infty.}
Действительно, точное значение остатка равно
- R N (x): = (- 1) N π 2 1 — 2 N (2 N)! N! ∫ Икс ∞ T — 2 N e — T 2 dt, { Displaystyle R_ {N} (x): = { frac {(-1) ^ {N}} { sqrt { pi}}} 2 ^ { 1-2N} { frac {(2N)!} {N!}} Int _ {x} ^ { infty} t ^ {- 2N} e ^ {- t ^ {2}} , dt,}
который легко следует по индукции, записывая
- e — t 2 = — (2 t) — 1 (e — t 2) ′ { displaystyle e ^ {- t ^ {2}} = — (2t) ^ {- 1} left (e ^ {- t ^ {2}} right) ‘}
и интегрирование по частям.
Для достаточно больших значений x, только первые несколько этих асимптотических разностей необходимы, чтобы получить хорошее приближение erfc (x) (в то время как для не слишком больших значений x приведенное выше разложение Тейлора при 0 обеспечивает очень быструю сходимость).
Расширение непрерывной дроби
A Разложение непрерывной дроби дополнительные функции ошибок:
- erfc (z) = z π e — z 2 1 z 2 + a 1 1 + a 2 z 2 + a 3 1 + ⋯ am = м 2. { displaystyle operatorname {erfc} (z) = { frac {z} { sqrt { pi}}} e ^ {- z ^ {2}} { cfrac {1} {z ^ {2} + { cfrac {a_ {1}} {1 + { cfrac {a_ {2}} {z ^ {2} + { cfrac {a_ {3}} {1+) dotsb}}}}}}}} qquad a_ {m} = { frac {m} {2}}.}
Интеграл функции ошибок с функцией плотности Гаусса
- ∫ — ∞ ∞ erf (ax + б) 1 2 π σ 2 е — (Икс — μ) 2 2 σ 2 dx знак равно erf [a μ + b 1 + 2 a 2 σ 2], a, b, μ, σ ∈ R { displaystyle int _ {- infty} ^ { infty} operatorname {erf} left (ax + b right) { frac {1} { sqrt {2 pi sigma ^ {2}}}} e ^ {- { frac {(x- mu) ^ {2}} {2 sigma ^ {2}}}} , dx = operatorname {erf} left [{ frac {a mu + b } { sqrt {1 + 2a ^ {2} sigma ^ {2}}} right], qquad a, b, mu, sigma in mathbb {R}}
Факториальный ряд
- Обратное:
-
- erfc z = e — z 2 π z ∑ n = 0 ∞ (- 1) n Q n (z 2 + 1) n ¯ = e — z 2 π z (1 — 1 2 1 (z 2 + 1) + 1 4 1 (z 2 + 1) (z 2 + 2) — ⋯) { displaystyle { begin {align} operatorname {erfc} z = { frac {e ^ {- z ^ {2}}} {{ sqrt { pi}} , z}} sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n} Q_ {n}} {{(z ^ {2} + 1)} ^ { ba r {n}}}} = { frac {e ^ {- z ^ {2}}} {{ sqrt { pi}} , z}} left ( 1 — { frac {1} {2}} { frac {1} {(z ^ {2} +1)}} + { frac {1} {4}} { frac {1} {(z ^ {2} +1) (z ^ {2} +2)}} — cdots right) end {align}}}
- erfc z = e — z 2 π z ∑ n = 0 ∞ (- 1) n Q n (z 2 + 1) n ¯ = e — z 2 π z (1 — 1 2 1 (z 2 + 1) + 1 4 1 (z 2 + 1) (z 2 + 2) — ⋯) { displaystyle { begin {align} operatorname {erfc} z = { frac {e ^ {- z ^ {2}}} {{ sqrt { pi}} , z}} sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n} Q_ {n}} {{(z ^ {2} + 1)} ^ { ba r {n}}}} = { frac {e ^ {- z ^ {2}}} {{ sqrt { pi}} , z}} left ( 1 — { frac {1} {2}} { frac {1} {(z ^ {2} +1)}} + { frac {1} {4}} { frac {1} {(z ^ {2} +1) (z ^ {2} +2)}} — cdots right) end {align}}}
- сходится для Re (z 2)>0. { displaystyle operatorname {Re} (z ^ {2})>0.}
Здесь
- Q n = def 1 Γ (1/2) ∫ 0 ∞ τ (τ — 1) ⋯ ( τ — n + 1) τ — 1/2 е — τ d τ знак равно ∑ К знак равно 0 N (1 2) к ¯ s (n, k), { displaystyle Q_ {n} { stackrel { text {def}} {=}} { frac {1} { Gamma (1/2)}} int _ {0} ^ { infty} tau ( tau -1) cdots ( tau -n + 1) tau ^ {-1/2} e ^ {- tau} d tau = sum _ {k = 0} ^ {n} left ({ frac {1} {2}} right) ^ { bar {k}} s (n, k),}
- Q n = def 1 Γ (1/2) ∫ 0 ∞ τ (τ — 1) ⋯ ( τ — n + 1) τ — 1/2 е — τ d τ знак равно ∑ К знак равно 0 N (1 2) к ¯ s (n, k), { displaystyle Q_ {n} { stackrel { text {def}} {=}} { frac {1} { Gamma (1/2)}} int _ {0} ^ { infty} tau ( tau -1) cdots ( tau -n + 1) tau ^ {-1/2} e ^ {- tau} d tau = sum _ {k = 0} ^ {n} left ({ frac {1} {2}} right) ^ { bar {k}} s (n, k),}
- zn ¯ { displaystyle z ^ { bar {n}}}
обозначает возрастающий факториал, а s (n, k) { displaystyle s (n, k)}
обозначает знаковое число Стирлинга первого рода.
- Представление бесконечной суммой, составляющей двойной факториал :
-
- ERF (Z) знак равно 2 π ∑ N знак равно 0 ∞ (- 2) N (2 N — 1)! (2 N + 1)! Z 2 N + 1 { Displaystyle OperatorName {ERF} (г) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {( -2) ^ {n} (2n-1) !!} {(2n + 1)!}} Z ^ {2n + 1}}
- ERF (Z) знак равно 2 π ∑ N знак равно 0 ∞ (- 2) N (2 N — 1)! (2 N + 1)! Z 2 N + 1 { Displaystyle OperatorName {ERF} (г) = { frac {2} { sqrt { pi}}} sum _ {n = 0} ^ { infty} { frac {( -2) ^ {n} (2n-1) !!} {(2n + 1)!}} Z ^ {2n + 1}}
Численные приближения
Приближение элементов сарными функциями
- Абрамовиц и Стегун дают несколько приближений с точностью (уравнения 7.1.25–28). Это позволяет выбрать наиболее быстрое приближение, подходящее для данного приложения. В порядке увеличения точности они следующие:
-
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + a 3 x 3 + a 4 x 4) 4, x ≥ 0 { displaystyle имя оператора {erf} (x) приблизительно 1 — { frac {1} {(1 + a_ {1} x + a_ {2} x ^ {2} + a_ {3} x ^ {3} + a_ { 4} x ^ {4}) ^ {4}}}, qquad x geq 0}
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + a 3 x 3 + a 4 x 4) 4, x ≥ 0 { displaystyle имя оператора {erf} (x) приблизительно 1 — { frac {1} {(1 + a_ {1} x + a_ {2} x ^ {2} + a_ {3} x ^ {3} + a_ { 4} x ^ {4}) ^ {4}}}, qquad x geq 0}
- (максимальная ошибка: 5 × 10)
- , где a 1 = 0,278393, a 2 = 0,230389, a 3 = 0,000972, a 4 = 0,078108
-
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + a 3 t 3) e — x 2, t = 1 1 + px, x ≥ 0 { displaystyle operatorname {erf} (x) приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + a_ {3} t ^ {3}) e ^ {- x ^ {2}}, quad t = { frac {1} {1 + px}}, qquad x geq 0}
(максимальная ошибка: 2,5 × 10)
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + a 3 t 3) e — x 2, t = 1 1 + px, x ≥ 0 { displaystyle operatorname {erf} (x) приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + a_ {3} t ^ {3}) e ^ {- x ^ {2}}, quad t = { frac {1} {1 + px}}, qquad x geq 0}
- где p = 0,47047, a 1 = 0,3480242, a 2 = -0,0958798, a 3 = 0,7478556
-
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + ⋯ + a 6 x 6) 16, x ≥ 0 { displaystyle operatorname {erf} (x) приблизительно 1 — { frac {1} {(1 + a_ {1} x + a _ {2} x ^ {2} + cdots + a_ {6} x ^ {6}) ^ {16}}}, qquad x geq 0}
(максимальная ошибка: 3 × 10)
- erf (x) ≈ 1 — 1 (1 + a 1 x + a 2 x 2 + ⋯ + a 6 x 6) 16, x ≥ 0 { displaystyle operatorname {erf} (x) приблизительно 1 — { frac {1} {(1 + a_ {1} x + a _ {2} x ^ {2} + cdots + a_ {6} x ^ {6}) ^ {16}}}, qquad x geq 0}
- , где a 1 = 0,0705230784, a 2 = 0,0422820123, a 3 = 0,0092705272, a 4 = 0,0001520143, a 5 = 0,0002765672, a 6 = 0,0000430638
-
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + ⋯ + a 5 t 5) e — x 2, t = 1 1 + px { displaystyle operatorname {erf} (x) приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + cdots + a_ {5} t ^ {5}) e ^ {- x ^ {2}}, quad t = { frac {1} {1 + px}}}
(максимальная ошибка: 1,5 × 10)
- erf (x) ≈ 1 — (a 1 t + a 2 t 2 + ⋯ + a 5 t 5) e — x 2, t = 1 1 + px { displaystyle operatorname {erf} (x) приблизительно 1- (a_ {1} t + a_ {2} t ^ {2} + cdots + a_ {5} t ^ {5}) e ^ {- x ^ {2}}, quad t = { frac {1} {1 + px}}}
- , где p = 0,3275911, a 1 = 0,254829592, a 2 = −0,284496736, a 3 = 1,421413741, a 4 = −1,453152027, a 5 = 1,061405429
- Все эти приближения действительны для x ≥ 0 Чтобы использовать эти приближения для отрицательного x, викорируйте тот факт, что erf (x) — нечетная функция, поэтому erf (x) = −erf (−x).
- Экспоненциальные границы и чисто экспоненциальное приближение для дополнительных функций задаются как
-
- erfc (x) ≤ 1 2 e — 2 x 2 + 1 2 e — x 2 ≤ e — x 2, x>0 erfc ( х) ≈ 1 6 е — х 2 + 1 2 е — 4 3 х 2, х>0. { displaystyle { begin {align} operatorname {erfc} (x) leq { frac {1} {2}} e ^ {- 2x ^ {2}} + { frac {1} {2} } e ^ {- x ^ {2}} leq e ^ {- x ^ {2}}, qquad x>0 имя оператора {erfc} (x) приблизительно { frac {1} { 6}} e ^ {- x ^ {2}} + { frac {1} {2}} e ^ {- { frac {4} {3}} x ^ {2}}, qquad x>0. end {align}}}
- erfc (x) ≤ 1 2 e — 2 x 2 + 1 2 e — x 2 ≤ e — x 2, x>0 erfc ( х) ≈ 1 6 е — х 2 + 1 2 е — 4 3 х 2, х>0. { displaystyle { begin {align} operatorname {erfc} (x) leq { frac {1} {2}} e ^ {- 2x ^ {2}} + { frac {1} {2} } e ^ {- x ^ {2}} leq e ^ {- x ^ {2}}, qquad x>0 имя оператора {erfc} (x) приблизительно { frac {1} { 6}} e ^ {- x ^ {2}} + { frac {1} {2}} e ^ {- { frac {4} {3}} x ^ {2}}, qquad x>0. end {align}}}
-
- erfc (x) ≈ (1 — e — A x) e — x 2 B π х. { displaystyle operatorname {erfc} left (x right) приблизительно { frac { left (1-e ^ {- Ax} right) e ^ {- x ^ {2}}} {B { sqrt { pi}} x}}.}
- erfc (x) ≈ (1 — e — A x) e — x 2 B π х. { displaystyle operatorname {erfc} left (x right) приблизительно { frac { left (1-e ^ {- Ax} right) e ^ {- x ^ {2}}} {B { sqrt { pi}} x}}.}
- Они определили {A, B} = {1.98, 1.135}, { displaystyle {A, B } = {1.98,1.135 },}
, что дает хорошее приближение для всех x ≥ 0. { displaystyle x geq 0.}
- Одноканальная нижняя граница:
-
- erfc (x) ≥ 2 e π β — 1 β е — β Икс 2, Икс ≥ 0, β>1, { Displaystyle OperatorName {erfc} (x) geq { sqrt { frac {2e} { pi}}} { frac { sqrt { beta -1}} { beta}} e ^ {- beta x ^ {2}}, qquad x geq 0, beta>1,}
- erfc (x) ≥ 2 e π β — 1 β е — β Икс 2, Икс ≥ 0, β>1, { Displaystyle OperatorName {erfc} (x) geq { sqrt { frac {2e} { pi}}} { frac { sqrt { beta -1}} { beta}} e ^ {- beta x ^ {2}}, qquad x geq 0, beta>1,}
- где параметр β может быть выбран, чтобы минимизировать ошибку на желаемом интервале приближения.
- Другое приближение дано Сергеем Виницким с использованием его «глобальных приближений Паде»:
-
- erf (x) ≈ sgn (x) 1 — exp (- x 2 4 π + ax 2 1 + ax 2) { displaystyle operatorname {erf} (x) приблизительно Operatorname {sgn} (x) { sqrt {1- exp left (-x ^ {2} { frac {{ frac {4} { pi) })} + ax ^ {2}} {1 + ax ^ {2}}} right)}}}
- erf (x) ≈ sgn (x) 1 — exp (- x 2 4 π + ax 2 1 + ax 2) { displaystyle operatorname {erf} (x) приблизительно Operatorname {sgn} (x) { sqrt {1- exp left (-x ^ {2} { frac {{ frac {4} { pi) })} + ax ^ {2}} {1 + ax ^ {2}}} right)}}}
- где
-
- a = 8 (π — 3) 3 π (4 — π) ≈ 0, 140012. { displaystyle a = { frac {8 ( pi -3)} {3 pi (4- pi)}} приблизительно 0,140012.}
- a = 8 (π — 3) 3 π (4 — π) ≈ 0, 140012. { displaystyle a = { frac {8 ( pi -3)} {3 pi (4- pi)}} приблизительно 0,140012.}
- Это сделано так, чтобы быть очень точным в окрестностях 0 и добавление бесконечности, а относительная погрешность меньше 0,00035 для всех действительных x. Использование альтернативного значения ≈ 0,147 снижает максимальную относительную ошибку примерно до 0,00013.
- Это приближение можно инвертировать, чтобы получить приближение для других функций ошибок:
-
- erf — 1 (x) ≈ sgn (x) (2 π a + ln (1 — x 2) 2) 2 — ln (1 — x 2) a — (2 π a + ln (1 — x 2) 2). { displaystyle operatorname {erf} ^ {- 1} (x) приблизительно operatorname {sgn} (x) { sqrt {{ sqrt { left ({ frac {2} { pi a}} + { frac { ln (1-x ^ {2})} {2}} right) ^ {2} — { frac { ln (1-x ^ {2})} {a}}}} — left ({ frac {2} { pi a}} + { frac { ln (1-x ^ {2})} {2}} right)}}.}
- erf — 1 (x) ≈ sgn (x) (2 π a + ln (1 — x 2) 2) 2 — ln (1 — x 2) a — (2 π a + ln (1 — x 2) 2). { displaystyle operatorname {erf} ^ {- 1} (x) приблизительно operatorname {sgn} (x) { sqrt {{ sqrt { left ({ frac {2} { pi a}} + { frac { ln (1-x ^ {2})} {2}} right) ^ {2} — { frac { ln (1-x ^ {2})} {a}}}} — left ({ frac {2} { pi a}} + { frac { ln (1-x ^ {2})} {2}} right)}}.}
Многочлен
Приближение с максимальной ошибкой 1,2 × 10-7 { displaystyle 1,2 times 10 ^ {- 7}}
- erf ( x) = {1 — τ x ≥ 0 τ — 1 x < 0 {displaystyle operatorname {erf} (x)={begin{cases}1-tau xgeq 0tau -1x<0end{cases}}}
с
- τ = t ⋅ exp (- x 2 — 1,26551223 + 1,00002368 t + 0,37409196 t 2 + 0,09678418 t 3 — 0,18628806 t 4 + 0,27886807 t 5 — 1,13520398 t 6 + 1,48851587 t 7 — 0,82215223 t 8 + 0,17087277 t 9) { displaystyle { begin {align} tau = t cdot exp left (-x ^ {2} -1,26551223 + 1,00002368 t + 0,37409196t ^ {2} + 0,09678418t ^ {3} -0,18628806t ^ {4} вправо. left. qquad qquad qquad + 0,27886807t ^ {5} -1,13520398t ^ {6} + 1,48851587t ^ {7} -0,82215223t ^ {8} + 0,17087 277t ^ {9} right) end {align}}}
и
- t = 1 1 + 0,5 | х |. { displaystyle t = { frac {1} {1 + 0,5 | x |}}.}
Таблица значений
| x | erf(x) | 1-erf (x) |
|---|---|---|
| 0 | 0 | 1 |
| 0,02 | 0,022564575 | 0,977435425 |
| 0,04 | 0,045111106 | 0,954888894 |
| 0,06 | 0,067621594 | 0, 932378406 |
| 0,08 | 0.090078126 | 0,909921874 |
| 0,1 | 0,112462916 | 0,887537084 |
| 0,2 | 0,222702589 | 0,777297411 |
| 0,3 | 0,328626759 | 0,671373241 |
| 0, 4 | 0,428392355 | 0,571607645 |
| 0,5 | 0,520499878 | 0,479500122 |
| 0,6 | 0.603856091 | 0,396143909 |
| 0,7 | 0,677801194 | 0,322198806 |
| 0,8 257> | 0,742100965 | 0,257899035 |
| 0,9 | 0,796908212 | 0,203091788 |
| 1 | 0,842700793 | 0, 157299207 |
| 1,1 | 0,88020507 | 0,11979493 |
| 1,2 | 0,910313978 | 0,089686022 |
| 1,3 | 0,934007945 | 0,065992055 |
| 1,4 | 0.95228512 | 0,04771488 |
| 1,5 | 0, 966105146 | 0,033894854 |
| 1,6 | 0,976348383 | 0,023651617 |
| 1,7 | 0,983790459 | 0,016209541 |
| 1,8 | 0,989090502 | 0,010909498 |
| 1,9 | 0,992790429 | 0,007209571 |
| 2 | 0,995322265<25767> | 0,00477 |
| 2.1 | 0.997020533 | 0.002979467 |
| 2.2 | 0.998137154 | 0,001862846 |
| 2,3 | 0,998856823 | 0,001143177 |
| 2,4 | 0,999311486 | 0,000688514 |
| 2,5 | 0.999593048 | 0.000406952 |
| 3 | 0.99997791 | 0,00002209 |
| 3,5 | 0,999999257 | 0,000000743 |
Связанные функции
Дополнительная функция
дополнительная функция ошибок, обозначается erfc { displaystyle mathrm {erfc}}
- erfc (x) = 1 — erf (x) = 2 π ∫ x ∞ e — t 2 dt знак равно е — Икс 2 erfcx (х), { displaystyle { begin {выровнено} OperatorName {erfc} (x) = 1- operatorname {erf} (x) [5p t] = { frac {2} { sqrt { pi}}} int _ {x} ^ { infty} e ^ {- t ^ {2}} , dt [5pt] = e ^ {- x ^ {2}} operatorname {erfcx} (x), end {align}}}
, который также определяет erfcx { displaystyle mathrm {erfcx} }


- erfc (x ∣ x ≥ 0) = 2 π ∫ 0 π / 2 exp (- x 2 sin 2 θ) d θ. { displaystyle operatorname {erfc} (x mid x geq 0) = { frac {2} { pi}} int _ {0} ^ { pi / 2} exp left (- { frac {x ^ {2}} { sin ^ {2} theta}} right) , d theta.}
Это выражение действительно только для положительных значений x, но его можно использовать вместе с erfc (x) = 2 — erfc (−x), чтобы получить erfc (x) для отрицательных значений. Эта форма выгодна тем, что диапазон интегрирования является фиксированным и конечным. Расширение этого выражения для erfc { displaystyle mathrm {erfc}}
- erfc (x + y ∣ x, y ≥ 0) = 2 π ∫ 0 π / 2 ехр (- x 2 sin 2 θ — y 2 cos 2 θ) d θ. { displaystyle operatorname {erfc} (x + y mid x, y geq 0) = { frac {2} { pi}} int _ {0} ^ { pi / 2} exp left (- { frac {x ^ {2}} { sin ^ {2} theta}} — { frac {y ^ {2}} { cos ^ {2} theta}} right) , d theta.}
Функция мнимой ошибки
мнимой ошибки, обозначаемая erfi, обозначает ошибки как
- erfi (x) = — i erf (ix) Знак равно 2 π ∫ 0 xet 2 dt знак равно 2 π ex 2 D (x), { displaystyle { begin {align} operatorname {erfi} (x) = — i operatorname {erf} (ix) [ 5pt] = { frac {2} { sqrt { pi}}} int _ {0} ^ {x} e ^ {t ^ {2}} , dt [5pt] = { frac {2} { sqrt { pi}}} e ^ {x ^ {2}} D (x), end {align}}}
где D (x) — функция Доусона (который можно использовать вместо erfi, чтобы избежать арифметического переполнения ).
Несмотря на название «функция мнимой ошибки», erfi (x) { displaystyle operatorname {erfi} (x)}
Функция Когда ошибки оценивается для произвольных сложных аргументов z, результирующая комплексная функция ошибок обычно обсуждается в масштабированной форме как функция Фаддеева :
- w (z) = e — z 2 erfc (- iz) = erfcx (- iz). { displaystyle w (z) = e ^ {- z ^ {2}} operatorname {erfc} (-iz) = operatorname {erfcx} (-iz).}
Кумулятивная функция распределения
Функция ошибок по существующей стандартной стандартной функции нормального кумулятивного распределения, обозначаемой нормой (x) в некоторых языках программного обеспечения, поскольку они отличаются только масштабированием и переводом. Действительно,
- Φ (x) = 1 2 π ∫ — ∞ xe — t 2 2 dt = 1 2 [1 + erf (x 2)] = 1 2 erfc (- x 2) { displaystyle Phi (x) = { frac {1} { sqrt {2 pi}}} int _ {- infty} ^ {x} e ^ { tfrac {-t ^ {2}} {2}} , dt = { frac {1} {2}} left [1+ operatorname {erf} left ({ frac {x} { sqrt {2}}} right) right] = { frac {1} {2}} operatorname {erfc} left (- { frac {x} { sqrt {2}}} right)}
или переставлен для erf и erfc:
- erf ( x) = 2 Φ (x 2) — 1 erfc (x) = 2 Φ (- x 2) = 2 (1 — Φ (x 2)). { displaystyle { begin {align} operatorname {erf} (x) = 2 Phi left (x { sqrt {2}} right) -1 operatorname {erfc} (x) = 2 Phi left (-x { sqrt {2}} right) = 2 left (1- Phi left (x { sqrt {2}} right) right). End {выравнивается} }}
Следовательно, функция ошибок также тесно связана с Q-функцией, которая является вероятностью хвоста стандартного нормального распределения. Q-функция может быть выражена через функцию ошибок как
- Q (x) = 1 2 — 1 2 erf (x 2) = 1 2 erfc (x 2). { displaystyle Q (x) = { frac {1} {2}} — { frac {1} {2}} operatorname {erf} left ({ frac {x} { sqrt {2}}) } right) = { frac {1} {2}} operatorname {erfc} left ({ frac {x} { sqrt {2}}} right).}
Обратное значение из Φ { displaystyle Phi}
- пробит (p) = Φ — 1 (p) = 2 erf — 1 (2 p — 1) = — 2 erfc — 1 (2 p). { displaystyle operatorname {probit} (p) = Phi ^ {- 1} (p) = { sqrt {2}} operatorname {erf} ^ {- 1} (2p-1) = — { sqrt {2}} operatorname {erfc} ^ {- 1} (2p).}
Стандартный нормальный cdf чаще используется в вероятности и статистике, а функция ошибок чаще используется в других разделах математики.
Функция ошибки является частным случаем функции Миттаг-Леффлера и может также быть выражена как сливающаяся гипергеометрическая функция (функция Куммера):
- erf (х) знак равно 2 х π M (1 2, 3 2, — х 2). { displaystyle operatorname {erf} (x) = { frac {2x} { sqrt { pi}}} M left ({ frac {1} {2}}, { frac {3} {2 }}, — x ^ {2} right).}
Он имеет простое выражение в терминах интеграла Френеля.
В терминах регуляризованной гамма-функции P и неполная гамма-функция,
- erf (x) = sgn (x) P (1 2, x 2) = sgn (x) π γ (1 2, x 2). { displaystyle operatorname {erf} (x) = operatorname {sgn} (x) P left ({ frac {1} {2}}, x ^ {2} right) = { frac { operatorname {sgn} (x)} { sqrt { pi}}} gamma left ({ frac {1} {2}}, x ^ {2} right).}
sgn (x) { displaystyle operatorname {sgn} (x)}
Обобщенные функции ошибок

π { displaystyle scriptstyle { sqrt { pi}}}

Некоторые авторы обсуждают более общие функции:
- E n (x) = n! π ∫ 0 Икс е — Т N д т знак равно N! π ∑ п знак равно 0 ∞ (- 1) п Икс N п + 1 (N п + 1) п!. { displaystyle E_ {n} (x) = { frac {n!} { sqrt { pi}}} int _ {0} ^ {x} e ^ {- t ^ {n}} , dt = { frac {n!} { sqrt { pi}}} sum _ {p = 0} ^ { infty} (- 1) ^ {p} { frac {x ^ {np + 1}} {(np + 1) p!}}.}
Примечательные случаи:
- E0(x) — прямая линия, проходящая через начало координат: E 0 (x) = xe π { displaystyle textstyle E_ {0} (x) = { dfrac {x} {e { sqrt { pi}}}}}
- E2(x) — функция, erf (x) ошибки.
После деления на n!, все E n для нечетных n выглядят похожими (но не идентичными) друг на друга. Аналогично, E n для четного n выглядят похожими (но не идентичными) друг другу после простого деления на n!. Все обобщенные функции ошибок для n>0 выглядят одинаково на положительной стороне x графика.
Эти обобщенные функции могут быть эквивалентно выражены для x>0 с помощью гамма-функции и неполной гамма-функции :
- E n (x) = 1 π Γ (n) (Γ (1 n) — Γ (1 n, xn)), x>0. { displaystyle E_ {n} (x) = { frac {1} { sqrt { pi}}} Gamma (n) left ( Gamma left ({ frac {1} {n}} right) — Gamma left ({ frac {1} {n}}, x ^ {n} right) right), quad quad x>0.}
Следовательно, мы можем определить ошибку функция в терминах неполной гамма-функции:
- erf (x) = 1 — 1 π Γ (1 2, x 2). { displaystyle operatorname {erf} (x) = 1 — { frac {1} { sqrt { pi}}} Gamma left ({ frac {1} {2}}, x ^ {2} right).}
Итерированные интегралы дополнительных функций
Повторные интегралы дополнительные функции ошибок определения как
- inerfc (z) = ∫ z ∞ in — 1 erfc (ζ) d ζ i 0 erfc (z) = erfc (z) i 1 erfc (z) = ierfc (z) знак равно 1 π е — z 2 — z erfc (z) я 2 erfc (z) = 1 4 [erfc (z) — 2 z ierfc (z)] { displaystyle { begin {align } operatorname {i ^ {n} erfc} (z) = int _ {z} ^ { infty} operatorname {i ^ {n-1} erfc} ( zeta) , d zeta имя оператора {i ^ {0} erfc} (z) = operatorname {erfc} (z) operatorname {i ^ {1} erfc} (z) = operat orname {ierfc} (z) = { frac { 1} { sqrt { pi}}} e ^ {- z ^ {2}} — z operatorname {erfc} (z) operatorname {i ^ {2} erfc} (z) = { frac {1} {4}} left [ operatorname {erfc} (z) -2z operatorname {ierfc} (z) right] end {выровнено}}
Общая рекуррентная формула:
- 2 ninerfc (z) = in — 2 erfc (z) — 2 цинк — 1 erfc (z) { displaystyle 2n operatorname {i ^ {n} erfc} (z) = operatorname {i ^ { n-2} erfc} (z) -2z operatorname {i ^ {n-1} erfc} (z)}
У них есть степенной ряд
- в erfc (z) = ∑ j = 0 ∞ (- Z) J 2 N — JJ! Γ (1 + N — J 2), { displaystyle i ^ {n} operatorname {erfc} (z) = sum _ {j = 0} ^ { infty} { frac {(-z) ^ { j}} {2 ^ {nj} j! Gamma left (1 + { frac {nj} {2}} right)}},}
из следуют свойства симметрии
- i 2 m ERFC (- Z) знак равно — я 2 m ERFC (Z) + ∑ Q знак равно 0 мZ 2 д 2 2 (м — д) — 1 (2 д)! (м — д)! { displaystyle i ^ {2m} operatorname {erfc} (-z) = — i ^ {2m} operatorname {erfc} (z) + sum _ {q = 0} ^ {m} { frac {z ^ {2q}} {2 ^ {2 (mq) -1} (2q)! (Mq)!}}}
и
- i 2 m + 1 erfc (- z) = i 2 m + 1 erfc (г) + ∑ ä знак равно 0 ìZ 2 ä + 1 2 2 ( м — д) — 1 (2 д + 1)! (м — д)!. { displaystyle i ^ {2m + 1} operatorname {erfc} (-z) = i ^ {2m + 1} operatorname {erfc} (z) + sum _ {q = 0} ^ {m} { гидроразрыва {z ^ {2q + 1}} {2 ^ {2 (mq) -1} (2q + 1)! (mq)!}}.}
Реализации
Как действительная функция вещественного аргумента
- В операционных системах, совместимых с Posix, заголовок math.h должен являть, а математическая библиотека libm должна быть функция erf и erfc (двойная точность ), а также их одинарная точность и расширенная точность аналоги erff, erfl и erfc, erfcl.
- Библиотека GNU Scientific предоставляет функции erf, erfc, log (erf) и масштабируемые функции ошибок.
Как сложная функция комплексного аргумента
- libcerf, числовая библиотека C для сложных функций, предоставляет комплексные функции cerf, cerfc, cerfcx и реальные функции erfi, erfcx с точностью 13–14 цифр на основе функции Фаддеева, реализованной в пакете MIT Faddeeva Package
См. также
Связанные ции
- интеграл Гаусса, по всей действительной прямой
- функция Гаусса, производная
- функция Доусона, перенормированная функция мнимой ошибки
- интеграл Гудвина — Стона
по вероятности
- Нормальное распределение
- Нормальная кумулятивная функция распределения, масштабированная и сдвинутая форма функций ошибок
- Пробит, обратная или квантильная функция нормального CDF
- Q-функция, вероятность хвоста нормального распределения
Ссылки
Дополнительная литература
- Abramowitz, Milton ; Стегун, Ирен Энн, ред. (1983) [июнь 1964]. «Глава 7». Справочник по математическим функциям с формулами, графики и математическими таблицами. Прикладная математика. 55 (Девятое переиздание с дополнительными исправлениями; десятое оригинальное издание с исправлениями (декабрь 1972 г.); первое изд.). Вашингтон.; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Dover Publications. п. 297. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- Press, William H.; Теукольский, Саул А.; Веттерлинг, Уильям Т.; Фланнери, Брайан П. (2007), «Раздел 6.2. Неполная гамма-функция и функция ошибок », Числовые рецепты: Искусство научных вычислений (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN 978-0-521- 88068-8
- Темме, Нико М. (2010), «Функции ошибок, интегралы Доусона и Френеля», в Олвер, Фрэнк У. Дж. ; Лозье, Даниэль М.; Бойсверт, Рональд Ф.; Кларк, Чарльз В. (ред.), Справочник NIST по математическим функциям, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
Внешние ссылки
- MathWorld — Erf
- Таблица интегралов функций ошибок
3.3.Температурное
поле непрерывного неподвижного точечного
источника в неограниченной среде.
Функция ошибок Гаусса (функция erf(x)).
Если в точке с
координатами x‘,
y‘,
z‘
в интервале времени от t‘
= 0 до t‘
= t
работает источник тепла мощностью
W,
то температурное поле этого источника,
как указано выше, может быть найдено
интегрированием фундаментального
решения по t‘
от 0 до t
(т.е. от момента включения до момента
выключения источника). Поместим начало
координат в точку, где находится источник
тепла. Тогда x’
= y’
= z’
= 0, и формула
для температуры принимает вид:
,
(3.3.1)
где r2
= (x — x’)2
+ (y — y’)2
+ (z — z’)2
= x2
+ y2
+ z2
— квадрат расстояния от источника до
точки наблюдения.
Произведем в
интеграле (3.3.1) замену переменных:
r2/[4a(t
— t’)] = 2.
Тогда: (t —
t’)3/2
= r3/(8a3/23),
dt’ = r2d/(2a3),
пределы интегрирования: t’
= 0
,
t’ = t
= ,
и формула (3.3.1) принимает вид:
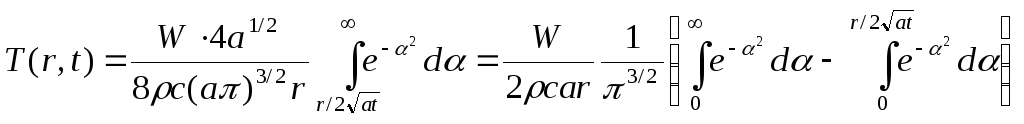
(3.3.2)
Первый интеграл,
стоящий в скобках, известен из курса
высшей математики:
(интеграл
Пуассона),
а второй интеграл
через элементарные функции не выражается
и определяет специальную функцию,
которая называется функцией
ошибок Гаусса,
или интегралом
вероятностей,
или функцией эрфектум:
(3.3.3)
(читается «эрфектум»
или сокращенно: «эрф»). Через эту
функцию выражаются решения многих
задач в теории теплопроводности, да и
в других областях физики она играет
важную роль.
Из определения
(3.3.3) видно, что erf(0)
= 0, а erf()
= 1, т.е. erf(x)
— это монотонно возрастающая
функция, вид которой изображен
на Рис.3.3. Функция erf(x)
табулирована, и ее значения
приводятся в различных
справочниках; в таблице 3.1 приведены
несколько значений этой функции. В
библиотеках некоторых
языков программирования имеются
готовые подпрограммы для
вычисления функции erf(x).
Если готовой подпрограммы
нет, функцию erf(x)
можно
вычислить с помощью степенного
ряда. «Стандартное»
разложение этой функции в
степенной ряд, которое обычно
приводится в математических
справочниках, имеет вид:
.
(3.3.4)
Э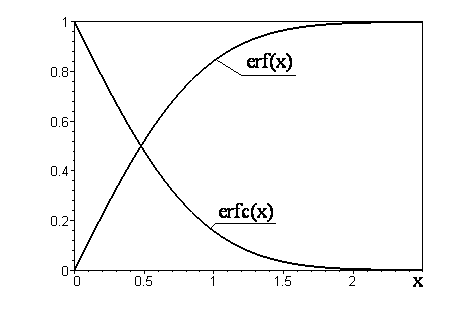
ряд удобен для анализа свойств функции,
но для практических расчетов он неудобен,
т.к. является знакопеременным, что
при вычислениях приводит к потере
точности. Более удобен следующий
ряд:
,
(3.3.5)
где
,
.
С
Рис. 3.3.
помощью этого ряда легко составить
программу вычисления erf(x)
на любом языке программирования
и даже на программируемом
микрокалькуляторе. Суммирование
надо прекращать, когда при
добавлении очередного an-го
слагаемого сумма перестанет меняться
(будет достигнута «машинная
точность»).
Если большой
точности не требуется, то можно
использовать приближенную формулу:
erf(x)
[1 — exp(-4x2/)]1/2.
(3.3.6)
Формула (3.3.6) дает
значения, абсолютная погрешность которых
не более 6.310-3,
а относительная погрешность
не более 0.71%.
Иногда требуется
определить erf(x)
в области отрицательных значений x.
Из формулы (3.3.3) очевидно, что erf(-x)
= — erf(x).
Заметим, что хотя
функция erf(x)
не является «элементарной», с точки
зрения ее свойств и способов
вычисления она проще, чем многие
«элементарные» функции, например,
тригонометрические.
С функцией erf(x)
связано еще несколько функций, часто
встречающихся в теплофизических
задачах. Это прежде всего дополнительный
интеграл вероятностей:
,
(3.3.7)
который встречается
настолько часто, что для него используется
специальное обозначение: erfc(x)
(сокращенно читается «эрфик»). Вид
этой функции также приведен на рис.3.3.
Довольно часто
функцию erf(x)
приходится дифференцировать и
интегрировать. Из определения
(3.3.3) следует, что
,
(3.3.8)
а интеграл от
erfc(x)
(обозначается как ierfc(x))
равен:
.
(3.3.9)
Вернемся к формуле
(3.3.2). Замечая, что ca
= ,
запишем эту формулу в виде:
.
(3.3.10)
При t
значение функции
0,
1, и формула (3.3.10), как и должно быть,
совпадает с формулой для
стационарного решения (если T0
принять за начало отсчета
температуры), т.к. при t
достигается стационарное
распределение температуры
в безграничной среде.
Таблица 3.1.
Некоторые значения функции erf(x).
|
x |
erf(x) |
x |
erf(x) |
x |
erf(x) |
x |
erf(x) |
x |
erf(x) |
|
0.0 |
0.0 |
0.3 |
0.32863 |
0.6 |
0.60386 |
0.9 |
0.79691 |
2.0 |
0.99532 |
|
0.1 |
0.11246 |
0.4 |
0.42839 |
0.7 |
0.67780 |
1.0 |
0.84270 |
2.5 |
0.99959 |
|
0.2 |
0.22270 |
0.5 |
0.52050 |
0.8 |
0.74210 |
1.5 |
0.96611 |
Соседние файлы в папке КраткийКонспектЛекций
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
| Error function | |
|---|---|

Plot of the error function |
|
| General information | |
| General definition |  |
| Fields of application | Probability, thermodynamics |
| Domain, Codomain and Image | |
| Domain |  |
| Image |  |
| Basic features | |
| Parity | Odd |
| Specific features | |
| Root | 0 |
| Derivative |  |
| Antiderivative |  |
| Series definition | |
| Taylor series |  |
In mathematics, the error function (also called the Gauss error function), often denoted by erf, is a complex function of a complex variable defined as:[1]
This integral is a special (non-elementary) sigmoid function that occurs often in probability, statistics, and partial differential equations. In many of these applications, the function argument is a real number. If the function argument is real, then the function value is also real.
In statistics, for non-negative values of x, the error function has the following interpretation: for a random variable Y that is normally distributed with mean 0 and standard deviation 1/√2, erf x is the probability that Y falls in the range [−x, x].
Two closely related functions are the complementary error function (erfc) defined as
and the imaginary error function (erfi) defined as
where i is the imaginary unit
Name[edit]
The name «error function» and its abbreviation erf were proposed by J. W. L. Glaisher in 1871 on account of its connection with «the theory of Probability, and notably the theory of Errors.»[2] The error function complement was also discussed by Glaisher in a separate publication in the same year.[3]
For the «law of facility» of errors whose density is given by
(the normal distribution), Glaisher calculates the probability of an error lying between p and q as:
Plot of the error function Erf(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
Applications[edit]
When the results of a series of measurements are described by a normal distribution with standard deviation σ and expected value 0, then erf (a/σ √2) is the probability that the error of a single measurement lies between −a and +a, for positive a. This is useful, for example, in determining the bit error rate of a digital communication system.
The error and complementary error functions occur, for example, in solutions of the heat equation when boundary conditions are given by the Heaviside step function.
The error function and its approximations can be used to estimate results that hold with high probability or with low probability. Given a random variable X ~ Norm[μ,σ] (a normal distribution with mean μ and standard deviation σ) and a constant L < μ:
where A and B are certain numeric constants. If L is sufficiently far from the mean, specifically μ − L ≥ σ√ln k, then:
so the probability goes to 0 as k → ∞.
The probability for X being in the interval [La, Lb] can be derived as
Properties[edit]
Integrand exp(−z2)
erf z
The property erf (−z) = −erf z means that the error function is an odd function. This directly results from the fact that the integrand e−t2 is an even function (the antiderivative of an even function which is zero at the origin is an odd function and vice versa).
Since the error function is an entire function which takes real numbers to real numbers, for any complex number z:
where z is the complex conjugate of z.
The integrand f = exp(−z2) and f = erf z are shown in the complex z-plane in the figures at right with domain coloring.
The error function at +∞ is exactly 1 (see Gaussian integral). At the real axis, erf z approaches unity at z → +∞ and −1 at z → −∞. At the imaginary axis, it tends to ±i∞.
Taylor series[edit]
The error function is an entire function; it has no singularities (except that at infinity) and its Taylor expansion always converges, but is famously known «[…] for its bad convergence if x > 1.»[4]
The defining integral cannot be evaluated in closed form in terms of elementary functions, but by expanding the integrand e−z2 into its Maclaurin series and integrating term by term, one obtains the error function’s Maclaurin series as:
which holds for every complex number z. The denominator terms are sequence A007680 in the OEIS.
For iterative calculation of the above series, the following alternative formulation may be useful:
because −(2k − 1)z2/k(2k + 1) expresses the multiplier to turn the kth term into the (k + 1)th term (considering z as the first term).
The imaginary error function has a very similar Maclaurin series, which is:
which holds for every complex number z.
Derivative and integral[edit]
The derivative of the error function follows immediately from its definition:
From this, the derivative of the imaginary error function is also immediate:
An antiderivative of the error function, obtainable by integration by parts, is
An antiderivative of the imaginary error function, also obtainable by integration by parts, is
Higher order derivatives are given by
where H are the physicists’ Hermite polynomials.[5]
Bürmann series[edit]
An expansion,[6] which converges more rapidly for all real values of x than a Taylor expansion, is obtained by using Hans Heinrich Bürmann’s theorem:[7]
where sgn is the sign function. By keeping only the first two coefficients and choosing c1 = 31/200 and c2 = −341/8000, the resulting approximation shows its largest relative error at x = ±1.3796, where it is less than 0.0036127:
Inverse functions[edit]
Given a complex number z, there is not a unique complex number w satisfying erf w = z, so a true inverse function would be multivalued. However, for −1 < x < 1, there is a unique real number denoted erf−1 x satisfying
The inverse error function is usually defined with domain (−1,1), and it is restricted to this domain in many computer algebra systems. However, it can be extended to the disk |z| < 1 of the complex plane, using the Maclaurin series
where c0 = 1 and
So we have the series expansion (common factors have been canceled from numerators and denominators):
(After cancellation the numerator/denominator fractions are entries OEIS: A092676/OEIS: A092677 in the OEIS; without cancellation the numerator terms are given in entry OEIS: A002067.) The error function’s value at ±∞ is equal to ±1.
For |z| < 1, we have erf(erf−1 z) = z.
The inverse complementary error function is defined as
For real x, there is a unique real number erfi−1 x satisfying erfi(erfi−1 x) = x. The inverse imaginary error function is defined as erfi−1 x.[8]
For any real x, Newton’s method can be used to compute erfi−1 x, and for −1 ≤ x ≤ 1, the following Maclaurin series converges:
where ck is defined as above.
Asymptotic expansion[edit]
A useful asymptotic expansion of the complementary error function (and therefore also of the error function) for large real x is
where (2n − 1)!! is the double factorial of (2n − 1), which is the product of all odd numbers up to (2n − 1). This series diverges for every finite x, and its meaning as asymptotic expansion is that for any integer N ≥ 1 one has
where the remainder, in Landau notation, is
as x → ∞.
Indeed, the exact value of the remainder is
which follows easily by induction, writing
and integrating by parts.
For large enough values of x, only the first few terms of this asymptotic expansion are needed to obtain a good approximation of erfc x (while for not too large values of x, the above Taylor expansion at 0 provides a very fast convergence).
Continued fraction expansion[edit]
A continued fraction expansion of the complementary error function is:[9]
Integral of error function with Gaussian density function[edit]
which appears related to Ng and Geller, formula 13 in section 4.3[10] with a change of variables.
Factorial series[edit]
The inverse factorial series:
converges for Re(z2) > 0. Here
zn denotes the rising factorial, and s(n,k) denotes a signed Stirling number of the first kind.[11][12]
There also exists a representation by an infinite sum containing the double factorial:
Numerical approximations[edit]
Approximation with elementary functions[edit]
- Abramowitz and Stegun give several approximations of varying accuracy (equations 7.1.25–28). This allows one to choose the fastest approximation suitable for a given application. In order of increasing accuracy, they are:
(maximum error: 5×10−4)
where a1 = 0.278393, a2 = 0.230389, a3 = 0.000972, a4 = 0.078108
(maximum error: 2.5×10−5)
where p = 0.47047, a1 = 0.3480242, a2 = −0.0958798, a3 = 0.7478556
(maximum error: 3×10−7)
where a1 = 0.0705230784, a2 = 0.0422820123, a3 = 0.0092705272, a4 = 0.0001520143, a5 = 0.0002765672, a6 = 0.0000430638
(maximum error: 1.5×10−7)
where p = 0.3275911, a1 = 0.254829592, a2 = −0.284496736, a3 = 1.421413741, a4 = −1.453152027, a5 = 1.061405429
All of these approximations are valid for x ≥ 0. To use these approximations for negative x, use the fact that erf x is an odd function, so erf x = −erf(−x).
- Exponential bounds and a pure exponential approximation for the complementary error function are given by[13]
- The above have been generalized to sums of N exponentials[14] with increasing accuracy in terms of N so that erfc x can be accurately approximated or bounded by 2Q̃(√2x), where
In particular, there is a systematic methodology to solve the numerical coefficients {(an,bn)}N
n = 1 that yield a minimax approximation or bound for the closely related Q-function: Q(x) ≈ Q̃(x), Q(x) ≤ Q̃(x), or Q(x) ≥ Q̃(x) for x ≥ 0. The coefficients {(an,bn)}N
n = 1 for many variations of the exponential approximations and bounds up to N = 25 have been released to open access as a comprehensive dataset.[15] - A tight approximation of the complementary error function for x ∈ [0,∞) is given by Karagiannidis & Lioumpas (2007)[16] who showed for the appropriate choice of parameters {A,B} that
They determined {A,B} = {1.98,1.135}, which gave a good approximation for all x ≥ 0. Alternative coefficients are also available for tailoring accuracy for a specific application or transforming the expression into a tight bound.[17]
- A single-term lower bound is[18]
where the parameter β can be picked to minimize error on the desired interval of approximation.
-
- Another approximation is given by Sergei Winitzki using his «global Padé approximations»:[19][20]: 2–3
where
This is designed to be very accurate in a neighborhood of 0 and a neighborhood of infinity, and the relative error is less than 0.00035 for all real x. Using the alternate value a ≈ 0.147 reduces the maximum relative error to about 0.00013.[21]
This approximation can be inverted to obtain an approximation for the inverse error function:
- An approximation with a maximal error of 1.2×10−7 for any real argument is:[22]
with
and
Table of values[edit]
| x | erf x | 1 − erf x |
|---|---|---|
| 0 | 0 | 1 |
| 0.02 | 0.022564575 | 0.977435425 |
| 0.04 | 0.045111106 | 0.954888894 |
| 0.06 | 0.067621594 | 0.932378406 |
| 0.08 | 0.090078126 | 0.909921874 |
| 0.1 | 0.112462916 | 0.887537084 |
| 0.2 | 0.222702589 | 0.777297411 |
| 0.3 | 0.328626759 | 0.671373241 |
| 0.4 | 0.428392355 | 0.571607645 |
| 0.5 | 0.520499878 | 0.479500122 |
| 0.6 | 0.603856091 | 0.396143909 |
| 0.7 | 0.677801194 | 0.322198806 |
| 0.8 | 0.742100965 | 0.257899035 |
| 0.9 | 0.796908212 | 0.203091788 |
| 1 | 0.842700793 | 0.157299207 |
| 1.1 | 0.880205070 | 0.119794930 |
| 1.2 | 0.910313978 | 0.089686022 |
| 1.3 | 0.934007945 | 0.065992055 |
| 1.4 | 0.952285120 | 0.047714880 |
| 1.5 | 0.966105146 | 0.033894854 |
| 1.6 | 0.976348383 | 0.023651617 |
| 1.7 | 0.983790459 | 0.016209541 |
| 1.8 | 0.989090502 | 0.010909498 |
| 1.9 | 0.992790429 | 0.007209571 |
| 2 | 0.995322265 | 0.004677735 |
| 2.1 | 0.997020533 | 0.002979467 |
| 2.2 | 0.998137154 | 0.001862846 |
| 2.3 | 0.998856823 | 0.001143177 |
| 2.4 | 0.999311486 | 0.000688514 |
| 2.5 | 0.999593048 | 0.000406952 |
| 3 | 0.999977910 | 0.000022090 |
| 3.5 | 0.999999257 | 0.000000743 |
[edit]
Complementary error function[edit]
The complementary error function, denoted erfc, is defined as
-
Plot of the complementary error function Erfc(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
which also defines erfcx, the scaled complementary error function[23] (which can be used instead of erfc to avoid arithmetic underflow[23][24]). Another form of erfc x for x ≥ 0 is known as Craig’s formula, after its discoverer:[25]
This expression is valid only for positive values of x, but it can be used in conjunction with erfc x = 2 − erfc(−x) to obtain erfc(x) for negative values. This form is advantageous in that the range of integration is fixed and finite. An extension of this expression for the erfc of the sum of two non-negative variables is as follows:[26]
Imaginary error function[edit]
The imaginary error function, denoted erfi, is defined as
Plot of the imaginary error function Erfi(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
where D(x) is the Dawson function (which can be used instead of erfi to avoid arithmetic overflow[23]).
Despite the name «imaginary error function», erfi x is real when x is real.
When the error function is evaluated for arbitrary complex arguments z, the resulting complex error function is usually discussed in scaled form as the Faddeeva function:
Cumulative distribution function[edit]
The error function is essentially identical to the standard normal cumulative distribution function, denoted Φ, also named norm(x) by some software languages[citation needed], as they differ only by scaling and translation. Indeed,
-
the normal cumulative distribution function plotted in the complex plane
or rearranged for erf and erfc:
Consequently, the error function is also closely related to the Q-function, which is the tail probability of the standard normal distribution. The Q-function can be expressed in terms of the error function as
The inverse of Φ is known as the normal quantile function, or probit function and may be expressed in terms of the inverse error function as
The standard normal cdf is used more often in probability and statistics, and the error function is used more often in other branches of mathematics.
The error function is a special case of the Mittag-Leffler function, and can also be expressed as a confluent hypergeometric function (Kummer’s function):
It has a simple expression in terms of the Fresnel integral.[further explanation needed]
In terms of the regularized gamma function P and the incomplete gamma function,
sgn x is the sign function.
Generalized error functions[edit]
Graph of generalised error functions En(x):
grey curve: E1(x) = 1 − e−x/√π
red curve: E2(x) = erf(x)
green curve: E3(x)
blue curve: E4(x)
gold curve: E5(x).
Some authors discuss the more general functions:[citation needed]
Notable cases are:
- E0(x) is a straight line through the origin: E0(x) = x/e√π
- E2(x) is the error function, erf x.
After division by n!, all the En for odd n look similar (but not identical) to each other. Similarly, the En for even n look similar (but not identical) to each other after a simple division by n!. All generalised error functions for n > 0 look similar on the positive x side of the graph.
These generalised functions can equivalently be expressed for x > 0 using the gamma function and incomplete gamma function:
Therefore, we can define the error function in terms of the incomplete gamma function:
Iterated integrals of the complementary error function[edit]
The iterated integrals of the complementary error function are defined by[27]
The general recurrence formula is
They have the power series
from which follow the symmetry properties
and
Implementations[edit]
As real function of a real argument[edit]
- In Posix-compliant operating systems, the header
math.hshall declare and the mathematical librarylibmshall provide the functionserfanderfc(double precision) as well as their single precision and extended precision counterpartserff,erflanderfcf,erfcl.[28] - The GNU Scientific Library provides
erf,erfc,log(erf), and scaled error functions.[29]
As complex function of a complex argument[edit]
libcerf, numeric C library for complex error functions, provides the complex functionscerf,cerfc,cerfcxand the real functionserfi,erfcxwith approximately 13–14 digits precision, based on the Faddeeva function as implemented in the MIT Faddeeva Package
See also[edit]
[edit]
- Gaussian integral, over the whole real line
- Gaussian function, derivative
- Dawson function, renormalized imaginary error function
- Goodwin–Staton integral
In probability[edit]
- Normal distribution
- Normal cumulative distribution function, a scaled and shifted form of error function
- Probit, the inverse or quantile function of the normal CDF
- Q-function, the tail probability of the normal distribution
References[edit]
- ^ Andrews, Larry C. (1998). Special functions of mathematics for engineers. SPIE Press. p. 110. ISBN 9780819426161.
- ^ Glaisher, James Whitbread Lee (July 1871). «On a class of definite integrals». London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4. 42 (277): 294–302. doi:10.1080/14786447108640568. Retrieved 6 December 2017.
- ^ Glaisher, James Whitbread Lee (September 1871). «On a class of definite integrals. Part II». London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4. 42 (279): 421–436. doi:10.1080/14786447108640600. Retrieved 6 December 2017.
- ^ «A007680 – OEIS». oeis.org. Retrieved 2 April 2020.
- ^ Weisstein, Eric W. «Erf». MathWorld.
- ^ Schöpf, H. M.; Supancic, P. H. (2014). «On Bürmann’s Theorem and Its Application to Problems of Linear and Nonlinear Heat Transfer and Diffusion». The Mathematica Journal. 16. doi:10.3888/tmj.16-11.
- ^ Weisstein, Eric W. «Bürmann’s Theorem». MathWorld.
- ^ Bergsma, Wicher (2006). «On a new correlation coefficient, its orthogonal decomposition and associated tests of independence». arXiv:math/0604627.
- ^ Cuyt, Annie A. M.; Petersen, Vigdis B.; Verdonk, Brigitte; Waadeland, Haakon; Jones, William B. (2008). Handbook of Continued Fractions for Special Functions. Springer-Verlag. ISBN 978-1-4020-6948-2.
- ^ Ng, Edward W.; Geller, Murray (January 1969). «A table of integrals of the Error functions». Journal of Research of the National Bureau of Standards Section B. 73B (1): 1. doi:10.6028/jres.073B.001.
- ^ Schlömilch, Oskar Xavier (1859). «Ueber facultätenreihen». Zeitschrift für Mathematik und Physik (in German). 4: 390–415. Retrieved 4 December 2017.
- ^ Nielson, Niels (1906). Handbuch der Theorie der Gammafunktion (in German). Leipzig: B. G. Teubner. p. 283 Eq. 3. Retrieved 4 December 2017.
- ^ Chiani, M.; Dardari, D.; Simon, M.K. (2003). «New Exponential Bounds and Approximations for the Computation of Error Probability in Fading Channels» (PDF). IEEE Transactions on Wireless Communications. 2 (4): 840–845. CiteSeerX 10.1.1.190.6761. doi:10.1109/TWC.2003.814350.
- ^ Tanash, I.M.; Riihonen, T. (2020). «Global minimax approximations and bounds for the Gaussian Q-function by sums of exponentials». IEEE Transactions on Communications. 68 (10): 6514–6524. arXiv:2007.06939. doi:10.1109/TCOMM.2020.3006902. S2CID 220514754.
- ^ Tanash, I.M.; Riihonen, T. (2020). «Coefficients for Global Minimax Approximations and Bounds for the Gaussian Q-Function by Sums of Exponentials [Data set]». Zenodo. doi:10.5281/zenodo.4112978.
- ^ Karagiannidis, G. K.; Lioumpas, A. S. (2007). «An improved approximation for the Gaussian Q-function» (PDF). IEEE Communications Letters. 11 (8): 644–646. doi:10.1109/LCOMM.2007.070470. S2CID 4043576.
- ^ Tanash, I.M.; Riihonen, T. (2021). «Improved coefficients for the Karagiannidis–Lioumpas approximations and bounds to the Gaussian Q-function». IEEE Communications Letters. 25 (5): 1468–1471. arXiv:2101.07631. doi:10.1109/LCOMM.2021.3052257. S2CID 231639206.
- ^ Chang, Seok-Ho; Cosman, Pamela C.; Milstein, Laurence B. (November 2011). «Chernoff-Type Bounds for the Gaussian Error Function». IEEE Transactions on Communications. 59 (11): 2939–2944. doi:10.1109/TCOMM.2011.072011.100049. S2CID 13636638.
- ^ Winitzki, Sergei (2003). «Uniform approximations for transcendental functions». Computational Science and Its Applications – ICCSA 2003. Lecture Notes in Computer Science. Vol. 2667. Springer, Berlin. pp. 780–789. doi:10.1007/3-540-44839-X_82. ISBN 978-3-540-40155-1.
- ^ Zeng, Caibin; Chen, Yang Cuan (2015). «Global Padé approximations of the generalized Mittag-Leffler function and its inverse». Fractional Calculus and Applied Analysis. 18 (6): 1492–1506. arXiv:1310.5592. doi:10.1515/fca-2015-0086. S2CID 118148950.
Indeed, Winitzki [32] provided the so-called global Padé approximation
- ^ Winitzki, Sergei (6 February 2008). «A handy approximation for the error function and its inverse».
- ^ Numerical Recipes in Fortran 77: The Art of Scientific Computing (ISBN 0-521-43064-X), 1992, page 214, Cambridge University Press.
- ^ a b c Cody, W. J. (March 1993), «Algorithm 715: SPECFUN—A portable FORTRAN package of special function routines and test drivers» (PDF), ACM Trans. Math. Softw., 19 (1): 22–32, CiteSeerX 10.1.1.643.4394, doi:10.1145/151271.151273, S2CID 5621105
- ^ Zaghloul, M. R. (1 March 2007), «On the calculation of the Voigt line profile: a single proper integral with a damped sine integrand», Monthly Notices of the Royal Astronomical Society, 375 (3): 1043–1048, Bibcode:2007MNRAS.375.1043Z, doi:10.1111/j.1365-2966.2006.11377.x
- ^ John W. Craig, A new, simple and exact result for calculating the probability of error for two-dimensional signal constellations Archived 3 April 2012 at the Wayback Machine, Proceedings of the 1991 IEEE Military Communication Conference, vol. 2, pp. 571–575.
- ^ Behnad, Aydin (2020). «A Novel Extension to Craig’s Q-Function Formula and Its Application in Dual-Branch EGC Performance Analysis». IEEE Transactions on Communications. 68 (7): 4117–4125. doi:10.1109/TCOMM.2020.2986209. S2CID 216500014.
- ^ Carslaw, H. S.; Jaeger, J. C. (1959), Conduction of Heat in Solids (2nd ed.), Oxford University Press, ISBN 978-0-19-853368-9, p 484
- ^ https://pubs.opengroup.org/onlinepubs/9699919799/basedefs/math.h.html
- ^ «Special Functions – GSL 2.7 documentation».
Further reading[edit]
- Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. «Chapter 7». Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 297. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (2007), «Section 6.2. Incomplete Gamma Function and Error Function», Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
- Temme, Nico M. (2010), «Error Functions, Dawson’s and Fresnel Integrals», in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
External links[edit]
- A Table of Integrals of the Error Functions
| Error function | |
|---|---|

Plot of the error function |
|
| General information | |
| General definition |  |
| Fields of application | Probability, thermodynamics |
| Domain, Codomain and Image | |
| Domain |  |
| Image |  |
| Basic features | |
| Parity | Odd |
| Specific features | |
| Root | 0 |
| Derivative |  |
| Antiderivative |  |
| Series definition | |
| Taylor series |  |
In mathematics, the error function (also called the Gauss error function), often denoted by erf, is a complex function of a complex variable defined as:[1]
This integral is a special (non-elementary) sigmoid function that occurs often in probability, statistics, and partial differential equations. In many of these applications, the function argument is a real number. If the function argument is real, then the function value is also real.
In statistics, for non-negative values of x, the error function has the following interpretation: for a random variable Y that is normally distributed with mean 0 and standard deviation 1/√2, erf x is the probability that Y falls in the range [−x, x].
Two closely related functions are the complementary error function (erfc) defined as
and the imaginary error function (erfi) defined as
where i is the imaginary unit
Name[edit]
The name «error function» and its abbreviation erf were proposed by J. W. L. Glaisher in 1871 on account of its connection with «the theory of Probability, and notably the theory of Errors.»[2] The error function complement was also discussed by Glaisher in a separate publication in the same year.[3]
For the «law of facility» of errors whose density is given by
(the normal distribution), Glaisher calculates the probability of an error lying between p and q as:
Plot of the error function Erf(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
Applications[edit]
When the results of a series of measurements are described by a normal distribution with standard deviation σ and expected value 0, then erf (a/σ √2) is the probability that the error of a single measurement lies between −a and +a, for positive a. This is useful, for example, in determining the bit error rate of a digital communication system.
The error and complementary error functions occur, for example, in solutions of the heat equation when boundary conditions are given by the Heaviside step function.
The error function and its approximations can be used to estimate results that hold with high probability or with low probability. Given a random variable X ~ Norm[μ,σ] (a normal distribution with mean μ and standard deviation σ) and a constant L < μ:
where A and B are certain numeric constants. If L is sufficiently far from the mean, specifically μ − L ≥ σ√ln k, then:
so the probability goes to 0 as k → ∞.
The probability for X being in the interval [La, Lb] can be derived as
Properties[edit]
Integrand exp(−z2)
erf z
The property erf (−z) = −erf z means that the error function is an odd function. This directly results from the fact that the integrand e−t2 is an even function (the antiderivative of an even function which is zero at the origin is an odd function and vice versa).
Since the error function is an entire function which takes real numbers to real numbers, for any complex number z:
where z is the complex conjugate of z.
The integrand f = exp(−z2) and f = erf z are shown in the complex z-plane in the figures at right with domain coloring.
The error function at +∞ is exactly 1 (see Gaussian integral). At the real axis, erf z approaches unity at z → +∞ and −1 at z → −∞. At the imaginary axis, it tends to ±i∞.
Taylor series[edit]
The error function is an entire function; it has no singularities (except that at infinity) and its Taylor expansion always converges, but is famously known «[…] for its bad convergence if x > 1.»[4]
The defining integral cannot be evaluated in closed form in terms of elementary functions, but by expanding the integrand e−z2 into its Maclaurin series and integrating term by term, one obtains the error function’s Maclaurin series as:
which holds for every complex number z. The denominator terms are sequence A007680 in the OEIS.
For iterative calculation of the above series, the following alternative formulation may be useful:
because −(2k − 1)z2/k(2k + 1) expresses the multiplier to turn the kth term into the (k + 1)th term (considering z as the first term).
The imaginary error function has a very similar Maclaurin series, which is:
which holds for every complex number z.
Derivative and integral[edit]
The derivative of the error function follows immediately from its definition:
From this, the derivative of the imaginary error function is also immediate:
An antiderivative of the error function, obtainable by integration by parts, is
An antiderivative of the imaginary error function, also obtainable by integration by parts, is
Higher order derivatives are given by
where H are the physicists’ Hermite polynomials.[5]
Bürmann series[edit]
An expansion,[6] which converges more rapidly for all real values of x than a Taylor expansion, is obtained by using Hans Heinrich Bürmann’s theorem:[7]
where sgn is the sign function. By keeping only the first two coefficients and choosing c1 = 31/200 and c2 = −341/8000, the resulting approximation shows its largest relative error at x = ±1.3796, where it is less than 0.0036127:
Inverse functions[edit]
Given a complex number z, there is not a unique complex number w satisfying erf w = z, so a true inverse function would be multivalued. However, for −1 < x < 1, there is a unique real number denoted erf−1 x satisfying
The inverse error function is usually defined with domain (−1,1), and it is restricted to this domain in many computer algebra systems. However, it can be extended to the disk |z| < 1 of the complex plane, using the Maclaurin series
where c0 = 1 and
So we have the series expansion (common factors have been canceled from numerators and denominators):
(After cancellation the numerator/denominator fractions are entries OEIS: A092676/OEIS: A092677 in the OEIS; without cancellation the numerator terms are given in entry OEIS: A002067.) The error function’s value at ±∞ is equal to ±1.
For |z| < 1, we have erf(erf−1 z) = z.
The inverse complementary error function is defined as
For real x, there is a unique real number erfi−1 x satisfying erfi(erfi−1 x) = x. The inverse imaginary error function is defined as erfi−1 x.[8]
For any real x, Newton’s method can be used to compute erfi−1 x, and for −1 ≤ x ≤ 1, the following Maclaurin series converges:
where ck is defined as above.
Asymptotic expansion[edit]
A useful asymptotic expansion of the complementary error function (and therefore also of the error function) for large real x is
where (2n − 1)!! is the double factorial of (2n − 1), which is the product of all odd numbers up to (2n − 1). This series diverges for every finite x, and its meaning as asymptotic expansion is that for any integer N ≥ 1 one has
where the remainder, in Landau notation, is
as x → ∞.
Indeed, the exact value of the remainder is
which follows easily by induction, writing
and integrating by parts.
For large enough values of x, only the first few terms of this asymptotic expansion are needed to obtain a good approximation of erfc x (while for not too large values of x, the above Taylor expansion at 0 provides a very fast convergence).
Continued fraction expansion[edit]
A continued fraction expansion of the complementary error function is:[9]
Integral of error function with Gaussian density function[edit]
which appears related to Ng and Geller, formula 13 in section 4.3[10] with a change of variables.
Factorial series[edit]
The inverse factorial series:
converges for Re(z2) > 0. Here
zn denotes the rising factorial, and s(n,k) denotes a signed Stirling number of the first kind.[11][12]
There also exists a representation by an infinite sum containing the double factorial:
Numerical approximations[edit]
Approximation with elementary functions[edit]
- Abramowitz and Stegun give several approximations of varying accuracy (equations 7.1.25–28). This allows one to choose the fastest approximation suitable for a given application. In order of increasing accuracy, they are:
(maximum error: 5×10−4)
where a1 = 0.278393, a2 = 0.230389, a3 = 0.000972, a4 = 0.078108
(maximum error: 2.5×10−5)
where p = 0.47047, a1 = 0.3480242, a2 = −0.0958798, a3 = 0.7478556
(maximum error: 3×10−7)
where a1 = 0.0705230784, a2 = 0.0422820123, a3 = 0.0092705272, a4 = 0.0001520143, a5 = 0.0002765672, a6 = 0.0000430638
(maximum error: 1.5×10−7)
where p = 0.3275911, a1 = 0.254829592, a2 = −0.284496736, a3 = 1.421413741, a4 = −1.453152027, a5 = 1.061405429
All of these approximations are valid for x ≥ 0. To use these approximations for negative x, use the fact that erf x is an odd function, so erf x = −erf(−x).
- Exponential bounds and a pure exponential approximation for the complementary error function are given by[13]
- The above have been generalized to sums of N exponentials[14] with increasing accuracy in terms of N so that erfc x can be accurately approximated or bounded by 2Q̃(√2x), where
In particular, there is a systematic methodology to solve the numerical coefficients {(an,bn)}N
n = 1 that yield a minimax approximation or bound for the closely related Q-function: Q(x) ≈ Q̃(x), Q(x) ≤ Q̃(x), or Q(x) ≥ Q̃(x) for x ≥ 0. The coefficients {(an,bn)}N
n = 1 for many variations of the exponential approximations and bounds up to N = 25 have been released to open access as a comprehensive dataset.[15] - A tight approximation of the complementary error function for x ∈ [0,∞) is given by Karagiannidis & Lioumpas (2007)[16] who showed for the appropriate choice of parameters {A,B} that
They determined {A,B} = {1.98,1.135}, which gave a good approximation for all x ≥ 0. Alternative coefficients are also available for tailoring accuracy for a specific application or transforming the expression into a tight bound.[17]
- A single-term lower bound is[18]
where the parameter β can be picked to minimize error on the desired interval of approximation.
-
- Another approximation is given by Sergei Winitzki using his «global Padé approximations»:[19][20]: 2–3
where
This is designed to be very accurate in a neighborhood of 0 and a neighborhood of infinity, and the relative error is less than 0.00035 for all real x. Using the alternate value a ≈ 0.147 reduces the maximum relative error to about 0.00013.[21]
This approximation can be inverted to obtain an approximation for the inverse error function:
- An approximation with a maximal error of 1.2×10−7 for any real argument is:[22]
with
and
Table of values[edit]
| x | erf x | 1 − erf x |
|---|---|---|
| 0 | 0 | 1 |
| 0.02 | 0.022564575 | 0.977435425 |
| 0.04 | 0.045111106 | 0.954888894 |
| 0.06 | 0.067621594 | 0.932378406 |
| 0.08 | 0.090078126 | 0.909921874 |
| 0.1 | 0.112462916 | 0.887537084 |
| 0.2 | 0.222702589 | 0.777297411 |
| 0.3 | 0.328626759 | 0.671373241 |
| 0.4 | 0.428392355 | 0.571607645 |
| 0.5 | 0.520499878 | 0.479500122 |
| 0.6 | 0.603856091 | 0.396143909 |
| 0.7 | 0.677801194 | 0.322198806 |
| 0.8 | 0.742100965 | 0.257899035 |
| 0.9 | 0.796908212 | 0.203091788 |
| 1 | 0.842700793 | 0.157299207 |
| 1.1 | 0.880205070 | 0.119794930 |
| 1.2 | 0.910313978 | 0.089686022 |
| 1.3 | 0.934007945 | 0.065992055 |
| 1.4 | 0.952285120 | 0.047714880 |
| 1.5 | 0.966105146 | 0.033894854 |
| 1.6 | 0.976348383 | 0.023651617 |
| 1.7 | 0.983790459 | 0.016209541 |
| 1.8 | 0.989090502 | 0.010909498 |
| 1.9 | 0.992790429 | 0.007209571 |
| 2 | 0.995322265 | 0.004677735 |
| 2.1 | 0.997020533 | 0.002979467 |
| 2.2 | 0.998137154 | 0.001862846 |
| 2.3 | 0.998856823 | 0.001143177 |
| 2.4 | 0.999311486 | 0.000688514 |
| 2.5 | 0.999593048 | 0.000406952 |
| 3 | 0.999977910 | 0.000022090 |
| 3.5 | 0.999999257 | 0.000000743 |
[edit]
Complementary error function[edit]
The complementary error function, denoted erfc, is defined as
-
Plot of the complementary error function Erfc(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
which also defines erfcx, the scaled complementary error function[23] (which can be used instead of erfc to avoid arithmetic underflow[23][24]). Another form of erfc x for x ≥ 0 is known as Craig’s formula, after its discoverer:[25]
This expression is valid only for positive values of x, but it can be used in conjunction with erfc x = 2 − erfc(−x) to obtain erfc(x) for negative values. This form is advantageous in that the range of integration is fixed and finite. An extension of this expression for the erfc of the sum of two non-negative variables is as follows:[26]
Imaginary error function[edit]
The imaginary error function, denoted erfi, is defined as
Plot of the imaginary error function Erfi(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
where D(x) is the Dawson function (which can be used instead of erfi to avoid arithmetic overflow[23]).
Despite the name «imaginary error function», erfi x is real when x is real.
When the error function is evaluated for arbitrary complex arguments z, the resulting complex error function is usually discussed in scaled form as the Faddeeva function:
Cumulative distribution function[edit]
The error function is essentially identical to the standard normal cumulative distribution function, denoted Φ, also named norm(x) by some software languages[citation needed], as they differ only by scaling and translation. Indeed,
-
the normal cumulative distribution function plotted in the complex plane
or rearranged for erf and erfc:
Consequently, the error function is also closely related to the Q-function, which is the tail probability of the standard normal distribution. The Q-function can be expressed in terms of the error function as
The inverse of Φ is known as the normal quantile function, or probit function and may be expressed in terms of the inverse error function as
The standard normal cdf is used more often in probability and statistics, and the error function is used more often in other branches of mathematics.
The error function is a special case of the Mittag-Leffler function, and can also be expressed as a confluent hypergeometric function (Kummer’s function):
It has a simple expression in terms of the Fresnel integral.[further explanation needed]
In terms of the regularized gamma function P and the incomplete gamma function,
sgn x is the sign function.
Generalized error functions[edit]
Graph of generalised error functions En(x):
grey curve: E1(x) = 1 − e−x/√π
red curve: E2(x) = erf(x)
green curve: E3(x)
blue curve: E4(x)
gold curve: E5(x).
Some authors discuss the more general functions:[citation needed]
Notable cases are:
- E0(x) is a straight line through the origin: E0(x) = x/e√π
- E2(x) is the error function, erf x.
After division by n!, all the En for odd n look similar (but not identical) to each other. Similarly, the En for even n look similar (but not identical) to each other after a simple division by n!. All generalised error functions for n > 0 look similar on the positive x side of the graph.
These generalised functions can equivalently be expressed for x > 0 using the gamma function and incomplete gamma function:
Therefore, we can define the error function in terms of the incomplete gamma function:
Iterated integrals of the complementary error function[edit]
The iterated integrals of the complementary error function are defined by[27]
The general recurrence formula is
They have the power series
from which follow the symmetry properties
and
Implementations[edit]
As real function of a real argument[edit]
- In Posix-compliant operating systems, the header
math.hshall declare and the mathematical librarylibmshall provide the functionserfanderfc(double precision) as well as their single precision and extended precision counterpartserff,erflanderfcf,erfcl.[28] - The GNU Scientific Library provides
erf,erfc,log(erf), and scaled error functions.[29]
As complex function of a complex argument[edit]
libcerf, numeric C library for complex error functions, provides the complex functionscerf,cerfc,cerfcxand the real functionserfi,erfcxwith approximately 13–14 digits precision, based on the Faddeeva function as implemented in the MIT Faddeeva Package
See also[edit]
[edit]
- Gaussian integral, over the whole real line
- Gaussian function, derivative
- Dawson function, renormalized imaginary error function
- Goodwin–Staton integral
In probability[edit]
- Normal distribution
- Normal cumulative distribution function, a scaled and shifted form of error function
- Probit, the inverse or quantile function of the normal CDF
- Q-function, the tail probability of the normal distribution
References[edit]
- ^ Andrews, Larry C. (1998). Special functions of mathematics for engineers. SPIE Press. p. 110. ISBN 9780819426161.
- ^ Glaisher, James Whitbread Lee (July 1871). «On a class of definite integrals». London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4. 42 (277): 294–302. doi:10.1080/14786447108640568. Retrieved 6 December 2017.
- ^ Glaisher, James Whitbread Lee (September 1871). «On a class of definite integrals. Part II». London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4. 42 (279): 421–436. doi:10.1080/14786447108640600. Retrieved 6 December 2017.
- ^ «A007680 – OEIS». oeis.org. Retrieved 2 April 2020.
- ^ Weisstein, Eric W. «Erf». MathWorld.
- ^ Schöpf, H. M.; Supancic, P. H. (2014). «On Bürmann’s Theorem and Its Application to Problems of Linear and Nonlinear Heat Transfer and Diffusion». The Mathematica Journal. 16. doi:10.3888/tmj.16-11.
- ^ Weisstein, Eric W. «Bürmann’s Theorem». MathWorld.
- ^ Bergsma, Wicher (2006). «On a new correlation coefficient, its orthogonal decomposition and associated tests of independence». arXiv:math/0604627.
- ^ Cuyt, Annie A. M.; Petersen, Vigdis B.; Verdonk, Brigitte; Waadeland, Haakon; Jones, William B. (2008). Handbook of Continued Fractions for Special Functions. Springer-Verlag. ISBN 978-1-4020-6948-2.
- ^ Ng, Edward W.; Geller, Murray (January 1969). «A table of integrals of the Error functions». Journal of Research of the National Bureau of Standards Section B. 73B (1): 1. doi:10.6028/jres.073B.001.
- ^ Schlömilch, Oskar Xavier (1859). «Ueber facultätenreihen». Zeitschrift für Mathematik und Physik (in German). 4: 390–415. Retrieved 4 December 2017.
- ^ Nielson, Niels (1906). Handbuch der Theorie der Gammafunktion (in German). Leipzig: B. G. Teubner. p. 283 Eq. 3. Retrieved 4 December 2017.
- ^ Chiani, M.; Dardari, D.; Simon, M.K. (2003). «New Exponential Bounds and Approximations for the Computation of Error Probability in Fading Channels» (PDF). IEEE Transactions on Wireless Communications. 2 (4): 840–845. CiteSeerX 10.1.1.190.6761. doi:10.1109/TWC.2003.814350.
- ^ Tanash, I.M.; Riihonen, T. (2020). «Global minimax approximations and bounds for the Gaussian Q-function by sums of exponentials». IEEE Transactions on Communications. 68 (10): 6514–6524. arXiv:2007.06939. doi:10.1109/TCOMM.2020.3006902. S2CID 220514754.
- ^ Tanash, I.M.; Riihonen, T. (2020). «Coefficients for Global Minimax Approximations and Bounds for the Gaussian Q-Function by Sums of Exponentials [Data set]». Zenodo. doi:10.5281/zenodo.4112978.
- ^ Karagiannidis, G. K.; Lioumpas, A. S. (2007). «An improved approximation for the Gaussian Q-function» (PDF). IEEE Communications Letters. 11 (8): 644–646. doi:10.1109/LCOMM.2007.070470. S2CID 4043576.
- ^ Tanash, I.M.; Riihonen, T. (2021). «Improved coefficients for the Karagiannidis–Lioumpas approximations and bounds to the Gaussian Q-function». IEEE Communications Letters. 25 (5): 1468–1471. arXiv:2101.07631. doi:10.1109/LCOMM.2021.3052257. S2CID 231639206.
- ^ Chang, Seok-Ho; Cosman, Pamela C.; Milstein, Laurence B. (November 2011). «Chernoff-Type Bounds for the Gaussian Error Function». IEEE Transactions on Communications. 59 (11): 2939–2944. doi:10.1109/TCOMM.2011.072011.100049. S2CID 13636638.
- ^ Winitzki, Sergei (2003). «Uniform approximations for transcendental functions». Computational Science and Its Applications – ICCSA 2003. Lecture Notes in Computer Science. Vol. 2667. Springer, Berlin. pp. 780–789. doi:10.1007/3-540-44839-X_82. ISBN 978-3-540-40155-1.
- ^ Zeng, Caibin; Chen, Yang Cuan (2015). «Global Padé approximations of the generalized Mittag-Leffler function and its inverse». Fractional Calculus and Applied Analysis. 18 (6): 1492–1506. arXiv:1310.5592. doi:10.1515/fca-2015-0086. S2CID 118148950.
Indeed, Winitzki [32] provided the so-called global Padé approximation
- ^ Winitzki, Sergei (6 February 2008). «A handy approximation for the error function and its inverse».
- ^ Numerical Recipes in Fortran 77: The Art of Scientific Computing (ISBN 0-521-43064-X), 1992, page 214, Cambridge University Press.
- ^ a b c Cody, W. J. (March 1993), «Algorithm 715: SPECFUN—A portable FORTRAN package of special function routines and test drivers» (PDF), ACM Trans. Math. Softw., 19 (1): 22–32, CiteSeerX 10.1.1.643.4394, doi:10.1145/151271.151273, S2CID 5621105
- ^ Zaghloul, M. R. (1 March 2007), «On the calculation of the Voigt line profile: a single proper integral with a damped sine integrand», Monthly Notices of the Royal Astronomical Society, 375 (3): 1043–1048, Bibcode:2007MNRAS.375.1043Z, doi:10.1111/j.1365-2966.2006.11377.x
- ^ John W. Craig, A new, simple and exact result for calculating the probability of error for two-dimensional signal constellations Archived 3 April 2012 at the Wayback Machine, Proceedings of the 1991 IEEE Military Communication Conference, vol. 2, pp. 571–575.
- ^ Behnad, Aydin (2020). «A Novel Extension to Craig’s Q-Function Formula and Its Application in Dual-Branch EGC Performance Analysis». IEEE Transactions on Communications. 68 (7): 4117–4125. doi:10.1109/TCOMM.2020.2986209. S2CID 216500014.
- ^ Carslaw, H. S.; Jaeger, J. C. (1959), Conduction of Heat in Solids (2nd ed.), Oxford University Press, ISBN 978-0-19-853368-9, p 484
- ^ https://pubs.opengroup.org/onlinepubs/9699919799/basedefs/math.h.html
- ^ «Special Functions – GSL 2.7 documentation».
Further reading[edit]
- Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. «Chapter 7». Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 297. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (2007), «Section 6.2. Incomplete Gamma Function and Error Function», Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
- Temme, Nico M. (2010), «Error Functions, Dawson’s and Fresnel Integrals», in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
External links[edit]
- A Table of Integrals of the Error Functions
В математике функция ошибок (также называемая функцией ошибок Гаусса ), часто обозначаемая erf , является сложной функцией комплексной переменной, определяемой как:
Этот интеграл представляет собой специальную ( неэлементарную ) сигмовидную функцию, которая часто встречается в уравнениях вероятности , статистики и дифференциальных уравнений в частных производных . Во многих из этих приложений аргумент функции является действительным числом. Если аргумент функции является действительным, то значение функции также является действительным.
В статистике для неотрицательных значений x функция ошибок имеет следующую интерпретацию: для случайной величины Y, которая нормально распределена со средним значением 0 и стандартным отклонением
1/√ 2, erf x — вероятность того, что Y попадает в диапазон [- x , x ] .
Две тесно связанные функции — это дополнительная функция ошибок ( erfc ), определяемая как
и функция мнимой ошибки ( erfi ), определяемая как
где i — мнимая единица .
Имя
Название «функция ошибок» и ее сокращение erf были предложены Дж. В. Л. Глейшером в 1871 г. в связи с его связью с «теорией вероятности и, в частности, теорией ошибок ». Дополнение к функции ошибок также обсуждалось Глейшером в отдельной публикации в том же году. Для «закона удобства» ошибок, плотность которых определяется как
( нормальное распределение ), Глейшер вычисляет вероятность ошибки, лежащей между p и q, как:
Приложения
Когда результаты серии измерений описываются нормальным распределением со стандартным отклонением σ и ожидаемым значением 0, тогда erf (а/σ √ 2) — вероятность того, что ошибка единичного измерения находится между — a и + a для положительного a . Это полезно, например, при определении частоты ошибок по битам в цифровой системе связи.
Ошибки и дополнительные функции ошибок возникают, например, в решениях уравнения теплопроводности, когда граничные условия задаются ступенчатой функцией Хевисайда .
Функция ошибок и ее приближения могут использоваться для оценки результатов, которые имеют высокую или низкую вероятность. Дана случайная величина X ~ Norm [ μ , σ ] (нормальное распределение со средним μ и стандартным отклонением σ ) и константа L < μ :
где A и B — некоторые числовые константы. Если L достаточно далеко от среднего, а именно μ — L ≥ σ √ ln k , то:
поэтому вероятность стремится к 0 при k → ∞ .
Вероятность того, что X находится в интервале [ L a , L b ], может быть получена как
Характеристики
Интегрируем exp (- z 2 )
erf z
Свойство erf (- z ) = −erf z означает, что функция ошибок является нечетной функцией . Это напрямую связано с тем, что подынтегральное выражение e — t 2 является четной функцией (интегрирование четной функции дает нечетную функцию и наоборот).
Для любого комплексного числа z :
где г представляет собой комплексно сопряженное из г .
Подынтегральное выражение f = exp (- z 2 ) и f = erf z показано на комплексной плоскости z на рисунках справа с раскраской области .
Функция ошибок при + ∞ равна 1 (см. Интеграл Гаусса ). На действительной оси erf z стремится к единице при z → + ∞ и −1 при z → −∞ . На мнимой оси он стремится к ± i ∞ .
Серия Тейлора
Функция ошибок — это целая функция ; у него нет сингулярностей (кроме бесконечности), и его разложение Тейлора всегда сходится, но, как известно, «[…] его плохая сходимость, если x > 1 ».
Определяющий интеграл не может быть вычислен в замкнутой форме в терминах элементарных функций , но, раскладывая подынтегральное выражение e — z 2 в его ряд Маклорена и интегрируя член за членом, можно получить ряд Маклорена функции ошибок как:
которое выполняется для любого комплексного числа z . Члены знаменателя — это последовательность (последовательность A007680 в OEIS ) в OEIS .
Для итеративного расчета вышеуказанного ряда может быть полезна следующая альтернативная формулировка:
потому что — (2 к — 1) z 2/к (2 к + 1)выражает множитель для превращения k- го члена в ( k + 1) -й член (считая z первым членом).
Функция мнимой ошибки имеет очень похожий ряд Маклорена, а именно:
которое выполняется для любого комплексного числа z .
Производная и интеграл
Производная функции ошибок сразу следует из ее определения:
Отсюда немедленно вычисляется производная мнимой функции ошибок:
Первообразная функции ошибки, получаемый путем интегрирования по частям , является
Первообразной функции мнимой ошибки, которую также можно получить интегрированием по частям, является
Производные высшего порядка даются формулами
где H — полиномы Эрмита физиков .
Серия Bürmann
Разложение, которое сходится быстрее для всех действительных значений x, чем разложение Тейлора, получается с помощью теоремы Ганса Генриха Бюрмана :
где sgn — знаковая функция . Сохраняя только первые два коэффициента и выбирая c 1 =31 год/200и c 2 = —341/8000, полученное приближение показывает свою наибольшую относительную ошибку при x = ± 1,3796 , где она меньше 0,0036127:
Обратные функции
Для комплексного числа z не существует уникального комплексного числа w, удовлетворяющего erf w = z , поэтому истинная обратная функция будет многозначной. Однако для −1 < x <1 существует уникальное действительное число, обозначенное erf −1 x, удовлетворяющее
Функция обратной ошибки обычно определяется с помощью области (-1,1) , и она ограничена этой областью во многих системах компьютерной алгебры. Однако его можно распространить на диск | z | <1 комплексной плоскости, используя ряд Маклорена
где c 0 = 1 и
Итак, у нас есть расширение в ряд (общие множители из числителей и знаменателей удалены):
(После отмены дроби числителя / знаменателя представляют собой записи OEIS : A092676 / OEIS : A092677 в OEIS ; без отмены члены числителя приведены в записи OEIS : A002067 .) Значение функции ошибок при ± ∞ равно ± 1 .
Для | z | <1 , имеем erf (erf −1 z ) = z .
Обратная дополнительная функция ошибок определяются как
Для действительного x существует уникальное действительное число erfi −1 x, удовлетворяющее erfi (erfi −1 x ) = x . Функция обратной мнимой ошибки определяется как erfi −1 x .
Для любого вещественного х , метод Ньютона может быть использован для вычисления ЕрФИ -1 х , а для -1 ≤ х ≤ 1 , следующие сходится ряд Маклорена:
где c k определено, как указано выше.
Асимптотическое разложение
Полезное асимптотическое разложение дополнительной функции ошибок (и, следовательно, также функции ошибок) для больших действительных x :
где (2 n — 1) !! — двойной факториал числа (2 n — 1) , который является произведением всех нечетных чисел до (2 n — 1) . Этот ряд расходится для любого конечного x , и его смысл как асимптотического разложения состоит в том, что для любого целого числа N ≥ 1 выполняется
где остаток в обозначениях Ландау равен
при x → ∞ .
Действительно, точное значение остатка равно
что легко следует по индукции, записывая
и интеграция по частям.
Для достаточно больших значений x необходимы только первые несколько членов этого асимптотического разложения, чтобы получить хорошее приближение erfc x (в то время как для не слишком больших значений x приведенное выше разложение Тейлора при 0 обеспечивает очень быструю сходимость).
Непрерывное расширение фракции
Цепная дробь расширение дополнительной функции ошибок является:
Интеграл функции ошибок с функцией плотности Гаусса
которая, по-видимому, связана с Нг и Геллером, формула 13 в разделе 4.3 с заменой переменных.
Факторный ряд
Обратный факторный ряд :
сходится при Re ( z 2 )> 0 . Здесь
z n обозначает возрастающий факториал , а s ( n , k ) обозначает число Стирлинга первого рода со знаком . Также существует представление бесконечной суммой, содержащее двойной факториал :
Численные приближения
Приближение с элементарными функциями
- Абрамовиц и Стегун дают несколько приближений с различной точностью (уравнения 7.1.25–28). Это позволяет выбрать наиболее быстрое приближение, подходящее для данного приложения. В порядке увеличения точности это:
(максимальная ошибка: 5 × 10 −4 )
где a 1 = 0,278393 , a 2 = 0,230389 , a 3 = 0,000972 , a 4 = 0,078108
(максимальная ошибка: 2,5 × 10 −5 )
где p = 0,47047 , a 1 = 0,3480242 , a 2 = −0,0958798 , a 3 = 0,7478556
(максимальная ошибка: 3 × 10 −7 )
где a 1 = 0,0705230784 , a 2 = 0,0422820123 , a 3 = 0,0092705272 , a 4 = 0,0001520143 , a 5 = 0,0002765672 , a 6 = 0,0000430638
(максимальная ошибка: 1,5 × 10 −7 )
где p = 0,3275911 , a 1 = 0,254829592 , a 2 = −0,284496736 , a 3 = 1,421413741 , a 4 = −1,453152027 , a 5 = 1,061405429.
Все эти приближения верны для x ≥ 0 . Чтобы использовать эти приближения для отрицательного x , используйте тот факт, что erf x — нечетная функция, поэтому erf x = −erf (- x ) .
- Экспоненциальные границы и чисто экспоненциальное приближение для дополнительной функции ошибок даются формулами
- Вышеупомянутое было обобщено до сумм из N экспонент с возрастающей точностью в терминах N, так что erfc x может быть точно аппроксимирован или ограничен величиной 2 Q̃ ( √ 2 x ) , где
В частности, существует систематическая методология решения числовых коэффициентов {( a n , b n )}N
n = 1которые дают минимаксное приближение или оценку для тесно связанной Q-функции : Q ( x ) ≈ Q̃ ( x ) , Q ( x ) ≤ Q̃ ( x ) или Q ( x ) ≥ Q̃ ( x ) для x ≥ 0 . Коэффициенты {( a n , b n )}N
n = 1для многих вариаций экспоненциальных приближений и границ до N = 25 были выпущены в открытый доступ в виде исчерпывающего набора данных. - Точная аппроксимация дополнительной функции ошибок для x ∈ [0, ∞) дана Karagiannidis & Lioumpas (2007), которые показали для соответствующего выбора параметров { A , B }, что
Они определили { A , B } = {1.98,1.135} , что дает хорошее приближение для всех x ≥ 0 . Также доступны альтернативные коэффициенты для настройки точности для конкретного приложения или преобразования выражения в жесткую границу.
- Одноканальная нижняя граница
где параметр β может быть выбран так, чтобы минимизировать ошибку на желаемом интервале аппроксимации.
-
- Другое приближение дает Сергей Виницкий, используя свои «глобальные приближения Паде»:
куда
Это сделано так, чтобы быть очень точным в окрестности 0 и в окрестности бесконечности, а относительная ошибка меньше 0,00035 для всех действительных x . Использование альтернативного значения a ≈ 0,147 снижает максимальную относительную ошибку примерно до 0,00013.
Это приближение можно инвертировать, чтобы получить приближение для обратной функции ошибок:
- Приближение с максимальной погрешностью 1,2 × 10 −7 для любого действительного аргумента:
с участием
а также
Таблица значений
| Икс | erf x | 1 — эрф х |
|---|---|---|
| 0 | 0 | 1 |
| 0,02 | 0,022 564 575 | 0,977 435 425 |
| 0,04 | 0,045 111 106 | 0,954 888 894 |
| 0,06 | 0,067 621 594 | 0,932 378 406 |
| 0,08 | 0,090 078 126 | 0,909 921 874 |
| 0,1 | 0,112 462 916 | 0,887 537 084 |
| 0,2 | 0,222 702 589 | 0,777 297 411 |
| 0,3 | 0,328 626 759 | 0,671 373 241 |
| 0,4 | 0,428 392 355 | 0,571 607 645 |
| 0,5 | 0,520 499 878 | 0,479 500 122 |
| 0,6 | 0,603 856 091 | 0,396 143 909 |
| 0,7 | 0,677 801 194 | 0,322 198 806 |
| 0,8 | 0,742 100 965 | 0,257 899 035 |
| 0,9 | 0,796 908 212 | 0,203 091 788 |
| 1 | 0,842 700 793 | 0,157 299 207 |
| 1.1 | 0,880 205 070 | 0,119 794 930 |
| 1.2 | 0,910 313 978 | 0,089 686 022 |
| 1.3 | 0,934 007 945 | 0,065 992 055 |
| 1.4 | 0,952 285 120 | 0,047 714 880 |
| 1.5 | 0,966 105 146 | 0,033 894 854 |
| 1.6 | 0,976 348 383 | 0,023 651 617 |
| 1,7 | 0,983 790 459 | 0,016 209 541 |
| 1,8 | 0,989 090 502 | 0,010 909 498 |
| 1.9 | 0,992 790 429 | 0,007 209 571 |
| 2 | 0,995 322 265 | 0,004 677 735 |
| 2.1 | 0,997 020 533 | 0,002 979 467 |
| 2.2 | 0,998 137 154 | 0,001 862 846 |
| 2.3 | 0,998 856 823 | 0,001 143 177 |
| 2,4 | 0,999 311 486 | 0,000 688 514 |
| 2,5 | 0,999 593 048 | 0,000 406 952 |
| 3 | 0,999 977 910 | 0,000 022 090 |
| 3.5 | 0,999 999 257 | 0,000 000 743 |
Дополнительная функция ошибок
Дополнительная функция ошибок , обозначаемая ERFC , определяется как
который также определяет erfcx , масштабированную дополнительную функцию ошибок (которую можно использовать вместо erfc, чтобы избежать арифметического переполнения ). Другая форма erfc x для x ≥ 0 известна как формула Крейга в честь ее первооткрывателя:
Это выражение действительно только для положительных значений x , но его можно использовать вместе с erfc x = 2 — erfc (- x ) для получения erfc ( x ) для отрицательных значений. Эта форма выгодна тем, что диапазон интегрирования является фиксированным и конечным. Расширение этого выражения для erfc суммы двух неотрицательных переменных выглядит следующим образом:
Функция мнимой ошибки
Функция мнимой ошибки , обозначаемая erfi , определяется как
где D ( x ) — функция Доусона (которую можно использовать вместо erfi, чтобы избежать арифметического переполнения ).
Несмотря на название «мнимая функция ошибок», erfi x реально, когда x реально.
Когда функция ошибок оценивается для произвольных комплексных аргументов z , результирующая комплексная функция ошибок обычно обсуждается в масштабированной форме как функция Фаддеева :
Кумулятивная функция распределения
Функция ошибок по существу идентична стандартной нормальной кумулятивной функции распределения , обозначаемой Φ , также называемой нормой ( x ) в некоторых языках программного обеспечения, поскольку они различаются только масштабированием и преобразованием. Действительно,
или переставил для erf и erfc :
Следовательно, функция ошибок также тесно связана с Q-функцией , которая является вероятностью хвоста стандартного нормального распределения. Q-функция может быть выражена через функцию ошибок как
Обратное из Ф называется нормальной функции квантиль , или пробит функции и могут быть выражены в терминах функции обратной ошибки как
Стандартный нормальный cdf чаще используется в вероятностях и статистике, а функция ошибок чаще используется в других разделах математики.
Функция ошибок является частным случаем функции Миттаг-Леффлера и также может быть выражена как конфлюэнтная гипергеометрическая функция ( функция Куммера):
Он имеет простое выражение в терминах интеграла Френеля .
С точки зрения регуляризованном гамма — функции P и неполной гамма — функции ,
sgn x — знаковая функция .
Обобщенные функции ошибок
График обобщенных функций ошибок E n ( x ) :
серая кривая: E 1 ( x ) =1 — е — х/√ π
красная кривая: E 2 ( x ) = erf ( x )
зеленая кривая: E 3 ( x )
синяя кривая: E 4 ( x )
золотая кривая: E 5 ( x ) .
Некоторые авторы обсуждают более общие функции:
Известные случаи:
- E 0 ( x ) — прямая линия, проходящая через начало координат: E 0 ( x ) =Икс/е √ π
- E 2 ( x ) — функция ошибок, erf x .
После деления на п ! , все E n для нечетных n похожи (но не идентичны) друг на друга. Точно так же E n для четного n выглядят похожими (но не идентичными) друг на друга после простого деления на n ! . Все обобщенные функции ошибок для n > 0 выглядят одинаково на положительной стороне графика x .
Эти обобщенные функции могут быть эквивалентно выражены для x > 0 с использованием гамма-функции и неполной гамма-функции :
Следовательно, мы можем определить функцию ошибок в терминах неполной гамма-функции:
Итерированные интегралы дополнительной функции ошибок
Повторные интегралы дополнительной функции ошибок определяются как
Общая рекуррентная формула
У них есть степенной ряд
откуда следуют свойства симметрии
а также
Реализации
Как реальная функция реального аргумента
- В Posix -совместимый операционных систем, заголовок math.h возвестят и математическая библиотека libm должна обеспечивать функции
erfиerfc( двойной точности ), а также их одинарной точности и повышенной точности аналоговerff,erflиerfcf,erfcl. - GNU Scientific Library предоставляет
erf,erfc,log(erf), и масштабируемые функции ошибок.
Как сложная функция сложного аргумента
-
libcerf , цифровая библиотека C для сложных функций ошибок, обеспечивает комплексные функции
cerf,cerfc,cerfcxи реальные функцииerfi,erfcxпримерно с 13-14 точностью цифр, на основе функции Фаддеева , как реализовано в MIT Фаддеевого пакете
Смотрите также
- Гауссовский интеграл по всей действительной прямой
- Функция Гаусса , производная
- Функция Доусона , перенормированная функция мнимой ошибки
- Интеграл Гудвина – Стэтона
По вероятности
- Нормальное распределение
- Нормальная кумулятивная функция распределения , масштабированная и сдвинутая форма функции ошибок
- Пробит , обратная или квантильная функция нормального CDF
- Q-функция , хвостовая вероятность нормального распределения
использованная литература
дальнейшее чтение
- Абрамовиц, Милтон ; Стегун, Ирен Энн , ред. (1983) [июнь 1964]. «Глава 7» . Справочник по математическим функциям с формулами, графиками и математическими таблицами . Прикладная математика. 55 (Девятое переиздание с дополнительными исправлениями, десятое оригинальное издание с исправлениями (декабрь 1972 г.); первое изд.). Вашингтон; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Dover Publications. п. 297. ISBN. 978-0-486-61272-0. LCCN 64-60036 . Руководство по ремонту 0167642 . LCCN 65-12253 .
- Press, William H .; Teukolsky, Saul A .; Веттерлинг, Уильям Т .; Фланнери, Брайан П. (2007), «Раздел 6.2. Неполная гамма-функция и функция ошибок» , Численные рецепты: Искусство научных вычислений (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN 978-0-521-88068-8
- Темме, Нико М. (2010), «Функции ошибок, интегралы Доусона и Френеля» , в Olver, Frank WJ ; Lozier, Daniel M .; Бойсверт, Рональд Ф .; Кларк, Чарльз В. (ред.), Справочник по математическим функциям NIST , Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
внешние ссылки
- MathWorld — Эрф
- Таблица интегралов функций ошибок
Список литературы
1.Росляков Г.В., Князев Б.А. Методы обработки экспериментальных данных. Новосибирск: НГУ, 1985. 5
2.Князев Б.А., Кругляков Э.П., Воробьев В.В., Капитонов В.А. Постоянная Керра воды ЖПМТФ. 1976. (1):157–160. 7, 9
3.Сквайрс Дж. Практическая физика. М.: Мир, 1971. 31, 32
4.Кунце Х.-И. Методы физических измерений. М.: Мир, 1989. 39
5.Зайдель А.Н. Ошибки измерений физических величин. Л.: Наука, 1974.
6.Худсон Д. Статистика для физиков. М.: Мир, 1967. 30
7.Тейлор Дж. Введение в теорию ошибок. М.: Мир, 1985. 39
8.Румшисский Л.З. Математическая обработка результатов эксперимента. М.: Наука, 1971.
9.Вильямс А., Кэмпион П.Дж., Барнс Д.Е. Практическое руководство по представлению результатов измерений. М.: Атомиздат, 1979.
10.Агекян Т.А. Основы теории ошибок для астрономов и физиков. М.: Наука, 1968.
11.Маркин Н.С. Основы теории обработки результатов измерений. М.: Изд. стандартов, 1991.
12.Секей Г. Парадоксы в теории вероятностей и в математической статистике. М.: Мир, 1990.
13.Мантуров О.В. Курс высшей математики. М.: Выс.школа, 1991. 7, 22
14.Корн Т., Корн Г. Справочник по математике для научных работников и инженеров. М.: Наука, 1968. 16
15.Сирая Т.Н., Грановский В.А. Методы обработки экспериментальных данных при измерениях. Л.: Энергоатомиздат, 1990. 28
16.Дойников А.С., Брянский Л.Н. Краткий справочник метролога. М.: Стандарты, 1991. 28






![{\ displaystyle \ Pr [X \ leq L ] = {\ frac {1} {2}} + {\ frac {1} {2}} \ operatorname {erf} \ left ({\ frac {L- \ mu} {{\ sqrt {2}} \ sigma }} \ right) \ приблизительно A \ exp \ left (-B \ left ({\ frac {L- \ mu} {\ sigma}} \ right) ^ {2} \ right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a72302c46832449e128a4d4e1adb28b514131270)
![{\ displaystyle \ Pr [X \ leq L] \ leq A \ exp (-B \ ln {k}) = {\ frac {A} {k ^ {B}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2baadea015e20a45d1034fd88eed861e7fcce178)









![{\ displaystyle {\ begin {align} \ operatorname {erf} (x) = {\ frac {2} {\ sqrt {\ pi}}} \ operatorname {sgn} (x) {\ sqrt {1-e ^ {- x ^ {2}}}} \ left (1 - {\ frac {1} {12}} \ left (1 -e ^ {- x ^ {2}} \ right) - {\ frac {7} {480}} \ left (1-e ^ {- x ^ {2}} \ right) ^ {2} - {\ frac {5} {896}} \ left (1-e ^ {- x ^ {2}} \ right) ^ {3} - {\ frac {787} {276480}} \ left (1-e ^ {- x ^ {2 }} \ right) ^ {4} - \ cdots \ right) \\ [10pt] = {\ frac {2} {\ sqrt {\ pi}}} \ operatorname {sgn} (x) {\ sqrt {1 -e ^ {- x ^ {2}}}} \ left ({\ frac {\ sqrt {\ pi}} {2}} + \ sum _ {k = 1} ^ {\ infty} c_ {k} e ^ {- kx ^ {2}} \ right). \ end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24ddba05e595a553fee25644a3542188281bd844)







![{\ displaystyle \ operatorname {erfc} (x) = {\ frac {e ^ {- x ^ {2}}} {x {\ sqrt {\ pi}}}} \ left [1+ \ sum _ {n = 1} ^ {\ infty} (-1) ^ {n} {\ frac {1 \ cdot 3 \ cdot 5 \ cdots (2n-1)} {(2x ^ {2}) ^ { n}}} \ right] = {\ frac {e ^ {-x ^ {2}}} {x {\ sqrt {\ pi}}}} \ sum _ {n = 0} ^ {\ infty} (- 1) ^ {n} {\ frac {(2n-1) !!} {(2x ^ {2}) ^ {n}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fc8c3aefff3ba787b080c5186dd3aec8ec76ef9)






![{\ displaystyle \ int _ {- \ infty} ^ {\ infty} \ operatorname {erf} \ left (ax + b \ right) {\ frac {1} {\ sqrt {2 \ pi \ sigma ^ {2}}}} e ^ {- {\ frac {(x- \ mu) ^ {2}} {2 \ sigma ^ {2}}}} \, dx = \ operatorname {erf} \ left [{\ frac {a \ mu + b} {\ sqrt {1 + 2a ^ {2} \ sigma ^ {2}}} \ right], \ qquad a, b, \ му, \ sigma \ in \ mathbb {R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b6adc2c661b24b44dc1e3d7e16be70023daacd8)


 обозначает возрастающий факториал, а s (n, k) {\ displaystyle s (n, k)}
обозначает возрастающий факториал, а s (n, k) {\ displaystyle s (n, k)} обозначает знаковое число Стирлинга первого рода.
обозначает знаковое число Стирлинга первого рода.

 (максимальная ошибка: 2,5 × 10)
(максимальная ошибка: 2,5 × 10) (максимальная ошибка: 3 × 10)
(максимальная ошибка: 3 × 10) (максимальная ошибка: 1,5 × 10)
(максимальная ошибка: 1,5 × 10)

 , что дает хорошее приближение для всех x ≥ 0. {\ displaystyle x \ geq 0.}
, что дает хорошее приближение для всех x ≥ 0. {\ displaystyle x \ geq 0.}







![{\ displaystyle {\ begin {align} \ operatorname {erfc} (x) = 1- \ operatorname {erf} (x) \\ [5pt ] = {\ frac {2} {\ sqrt {\ pi}}} \ int _ {x} ^ {\ infty} e ^ {- t ^ {2}} \, dt \\ [5pt] = e ^ {- x ^ {2}} \ operatorname {erfcx} (x), \ end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8808e6f3ad9aab23f14d55db707a39388d256788)


![{\ displaystyle {\ begin {align} \ operatorname {erfi} (x) = - i \ operatorname {erf} (ix) \\ [5pt] = {\ frac {2} {\ sqrt {\ pi}}} \ int _ {0} ^ {x} e ^ {t ^ {2 }} \, dt \\ [5pt] = {\ frac {2} {\ sqrt {\ pi}}} e ^ {x ^ {2}} D (x), \ end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4480a8ec17e274a7ad6b8ef25cc76234d48c0433)

![{\ displaystyle \ Phi (x) = {\ frac {1} {\ sqrt {2 \ pi}}} \ int _ {- \ infty} ^ {x } e ^ {\ tfrac {-t ^ {2}} {2}} \, dt = {\ frac {1} {2}} \ left [1+ \ operatorname {erf} \ left ({\ frac {x } {\ sqrt {2}}} \ right) \ right] = {\ frac {1} {2}} \ operatorname {erfc} \ left (- {\ frac {x} {\ sqrt {2}}} \ справа)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e19dc7206f8b3b571e81153816c478abd91a679e)









![{\ displaystyle {\ begin {align} \ operatorname { i ^ {n} erfc} (z) = \ int _ {z} ^ {\ infty} \ operatorname {i ^ {n-1} erfc} (\ zeta) \, d \ zeta \\\ имя оператора {i ^ {0} erfc} (z) = \ operatorname {erfc} (z) \\\ operatorname {i ^ {1} erfc} (z) = \ operatorname {ierfc} (z) = {\ frac {1} {\ sqrt {\ pi}}} e ^ {- z ^ {2}} - z \ operatorname {erfc} (z) \\\ operatorname {i ^ {2} erfc} (z) = {\ frac { 1} {4}} \ left [\ operatorname {erfc} (z) -2z \ operatorname {ierfc} (z) \ right] \\\ конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66b57abb0a01139b31a14f5a8d651e4aa2e5f4f2)




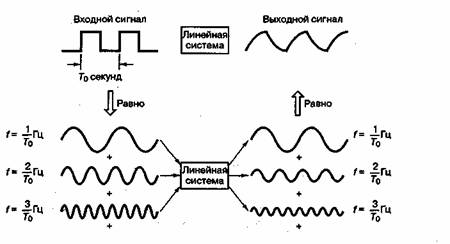
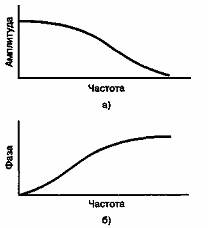
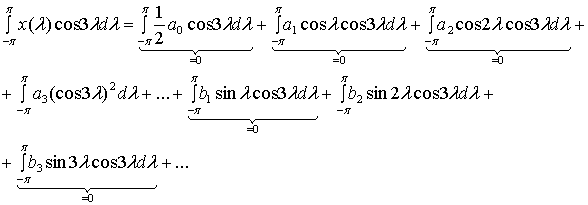
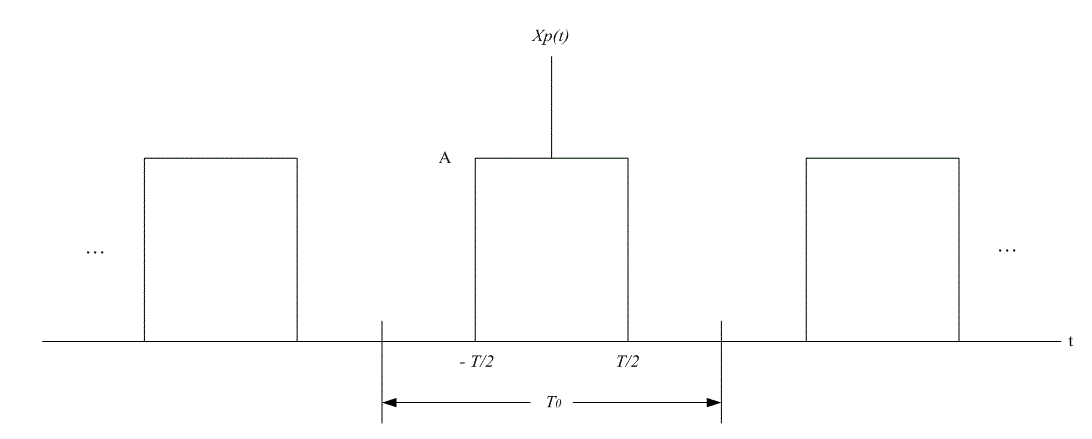
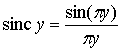
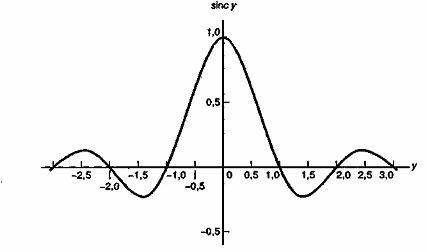
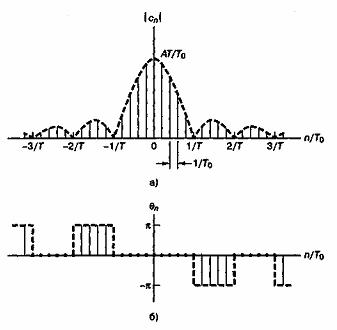
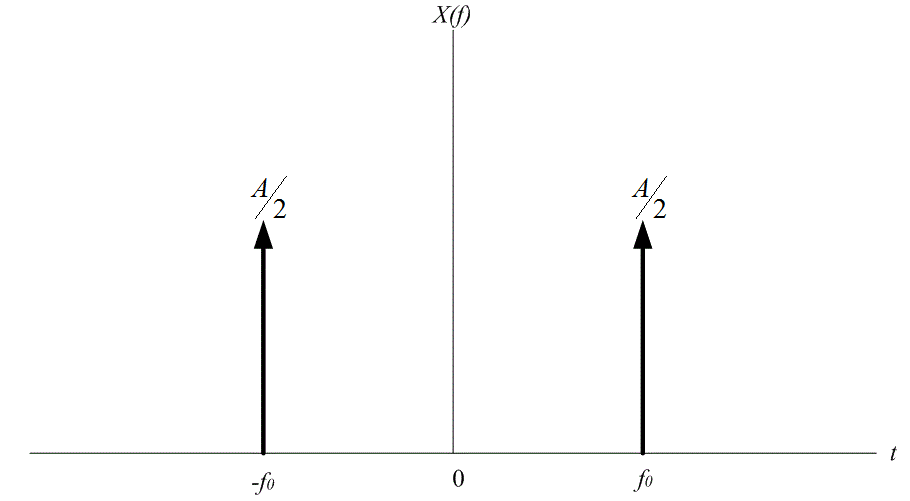
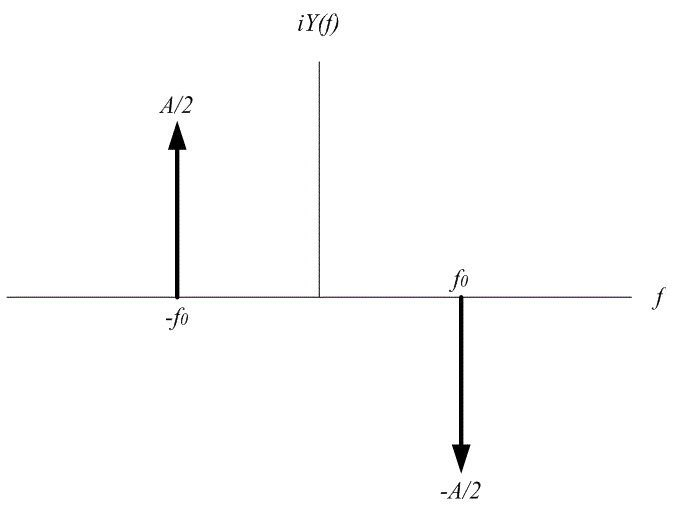
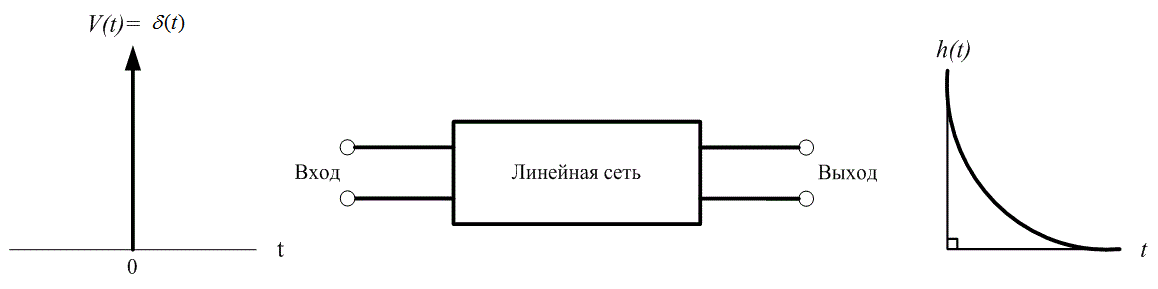
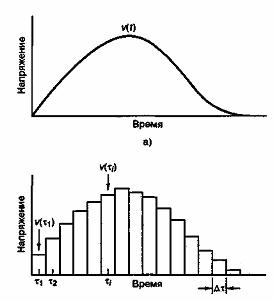
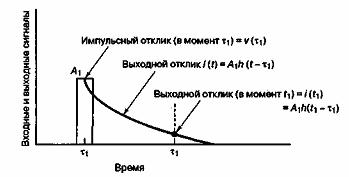
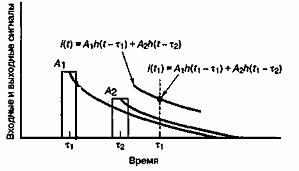
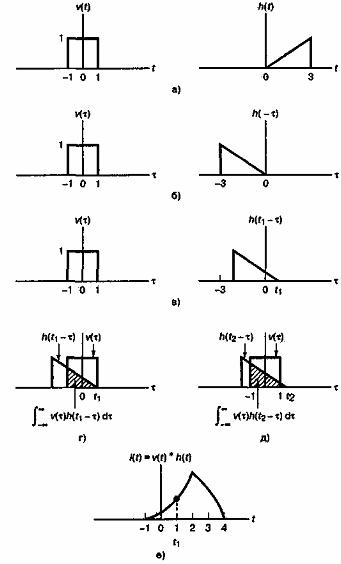
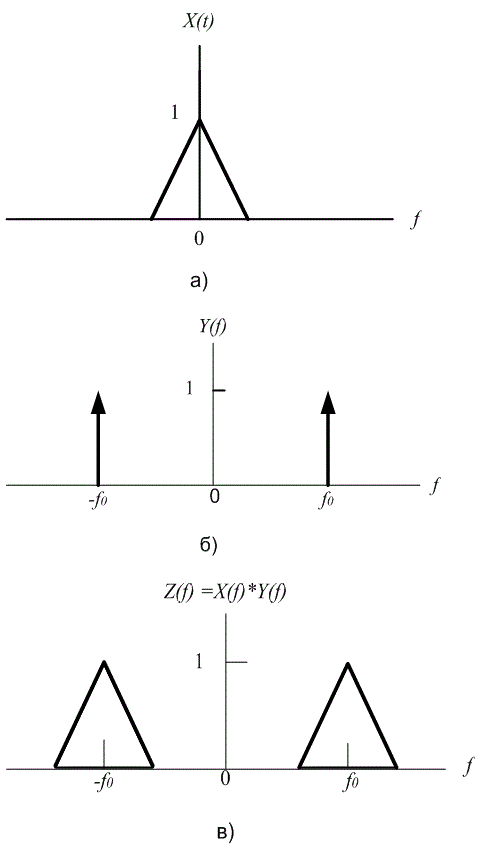
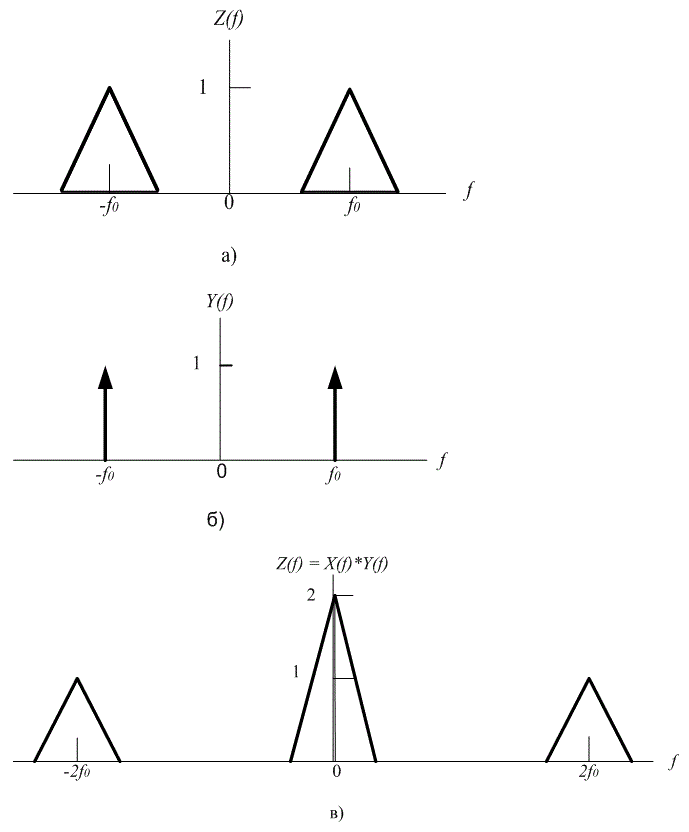
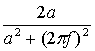
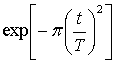
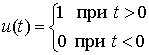
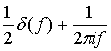
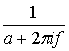
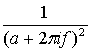
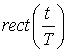
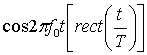
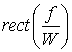
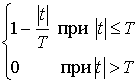
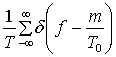
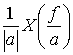
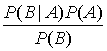
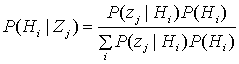
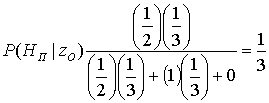
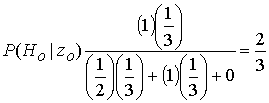
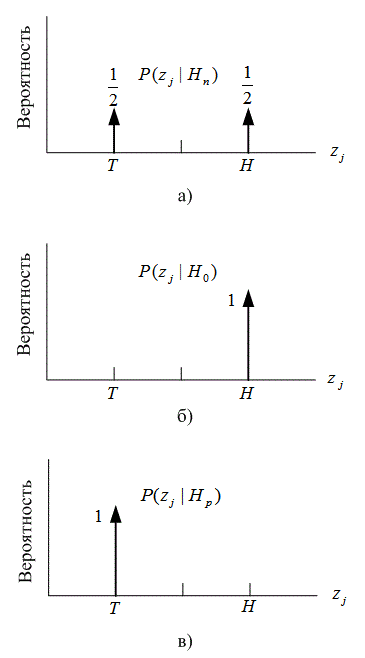
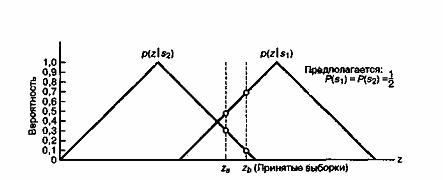
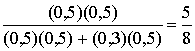
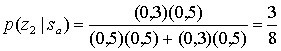
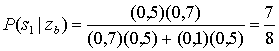
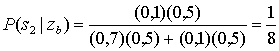
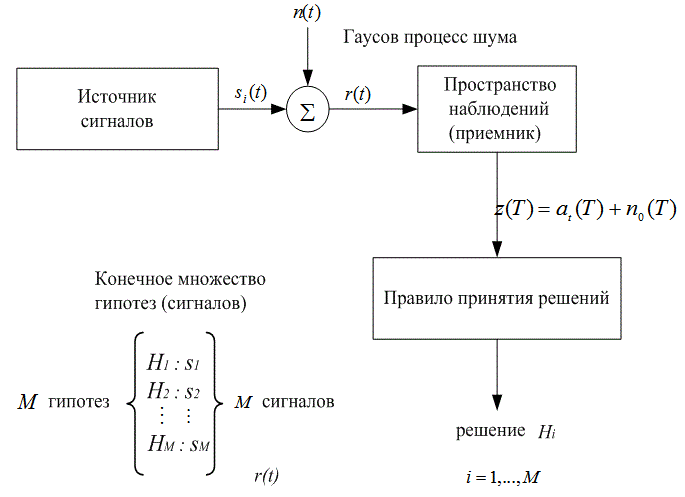
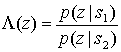
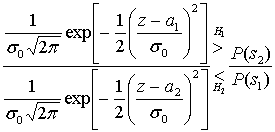
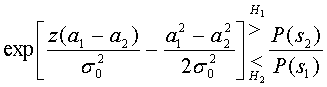
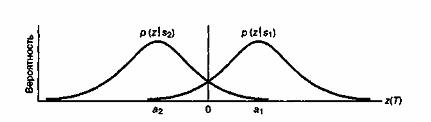
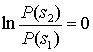
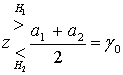
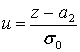
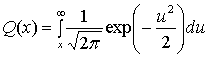
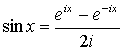
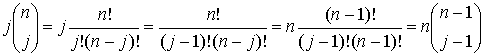
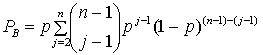
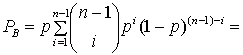
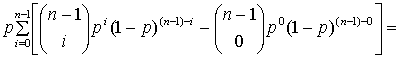
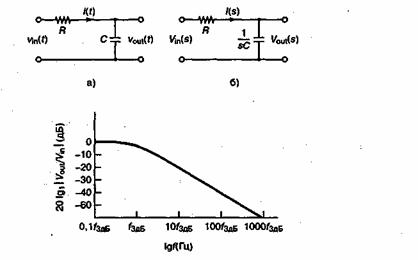
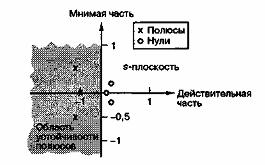
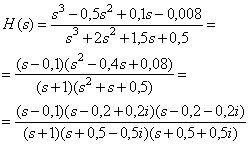
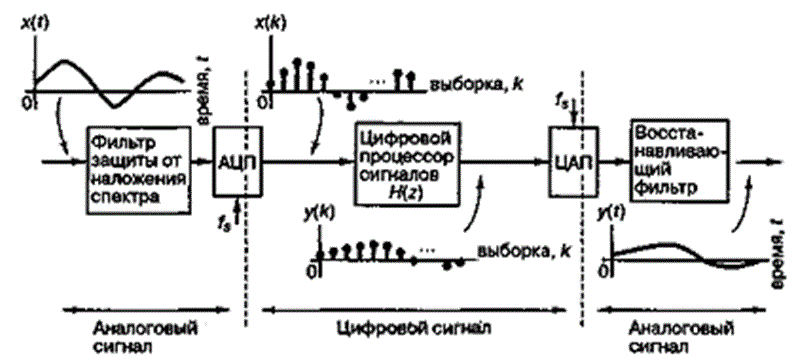
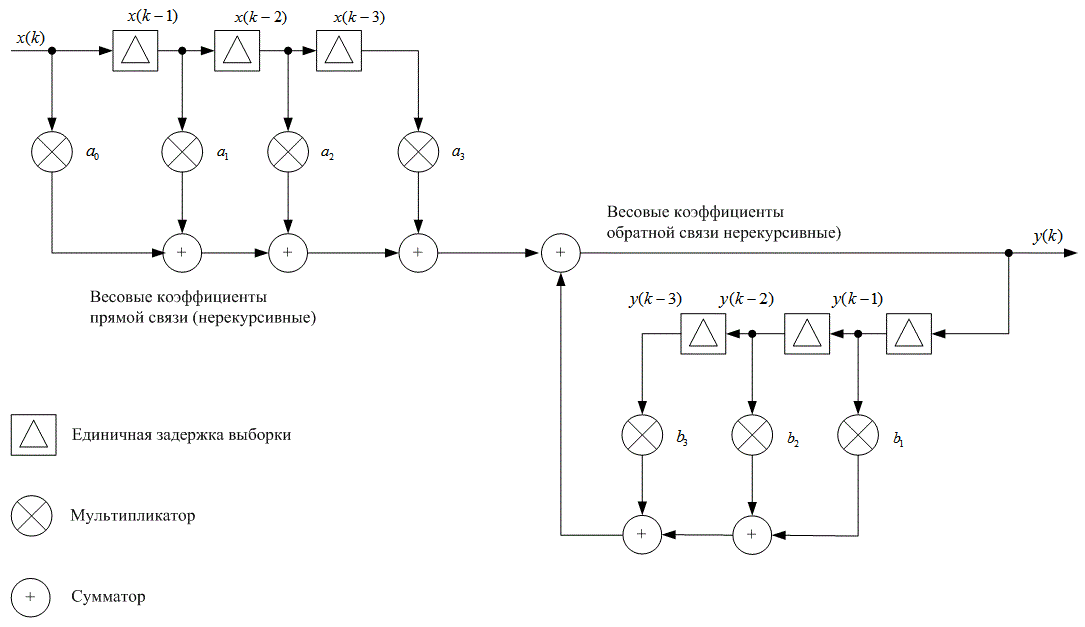
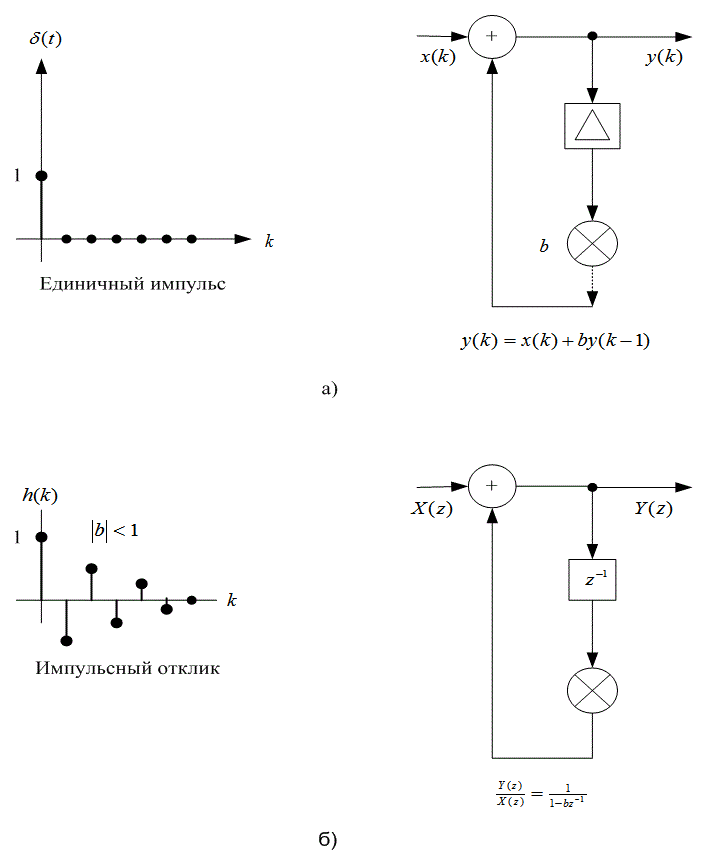
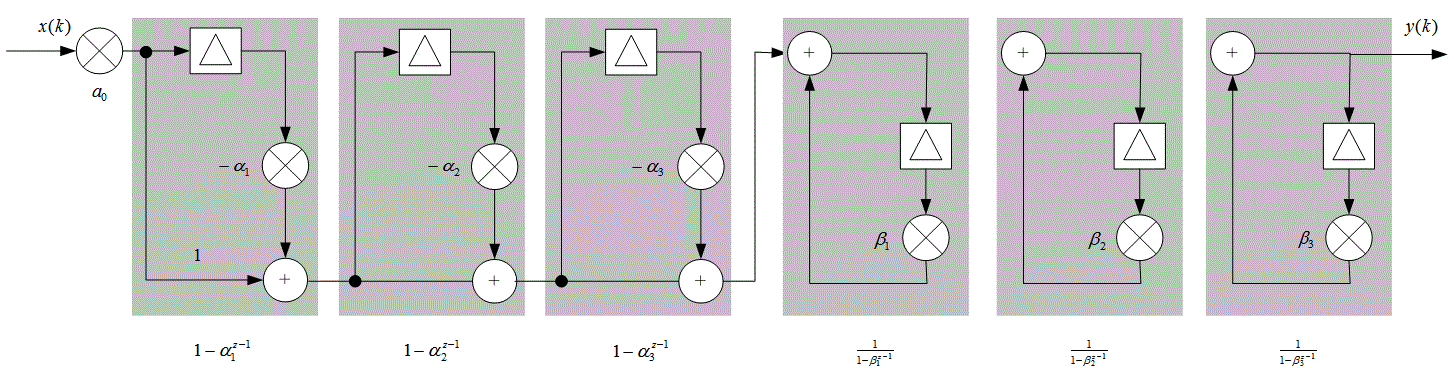
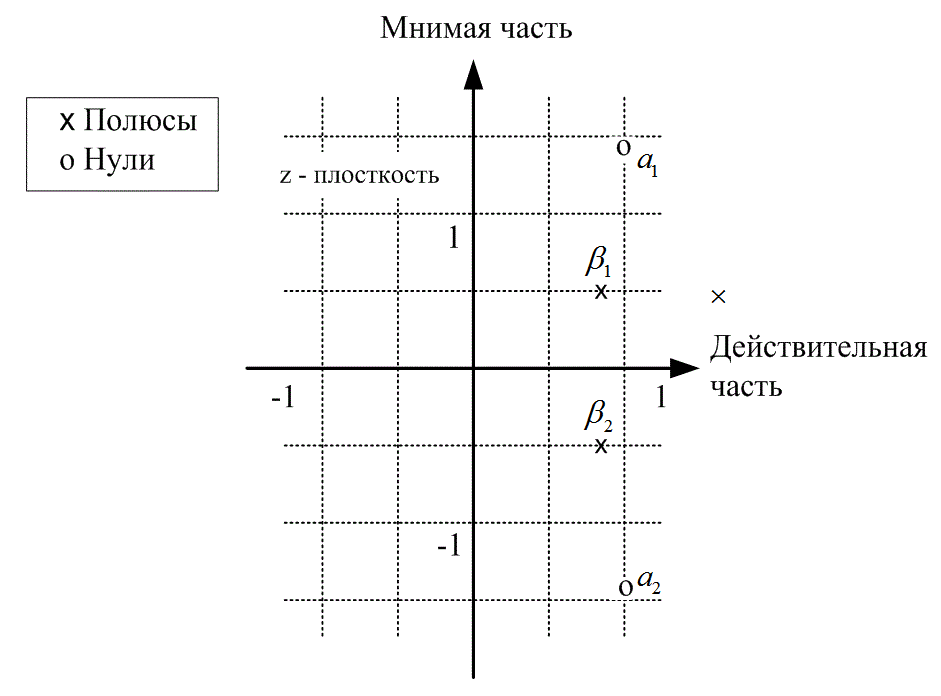
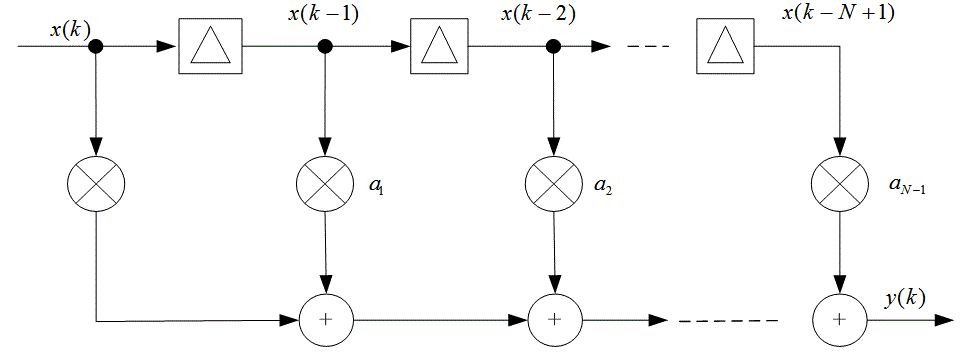
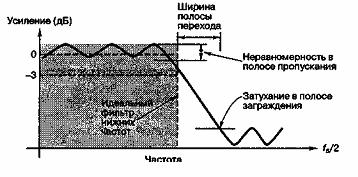


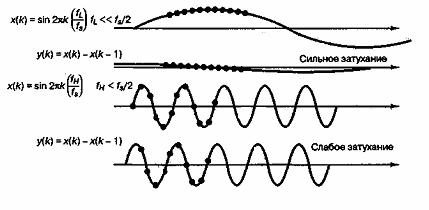
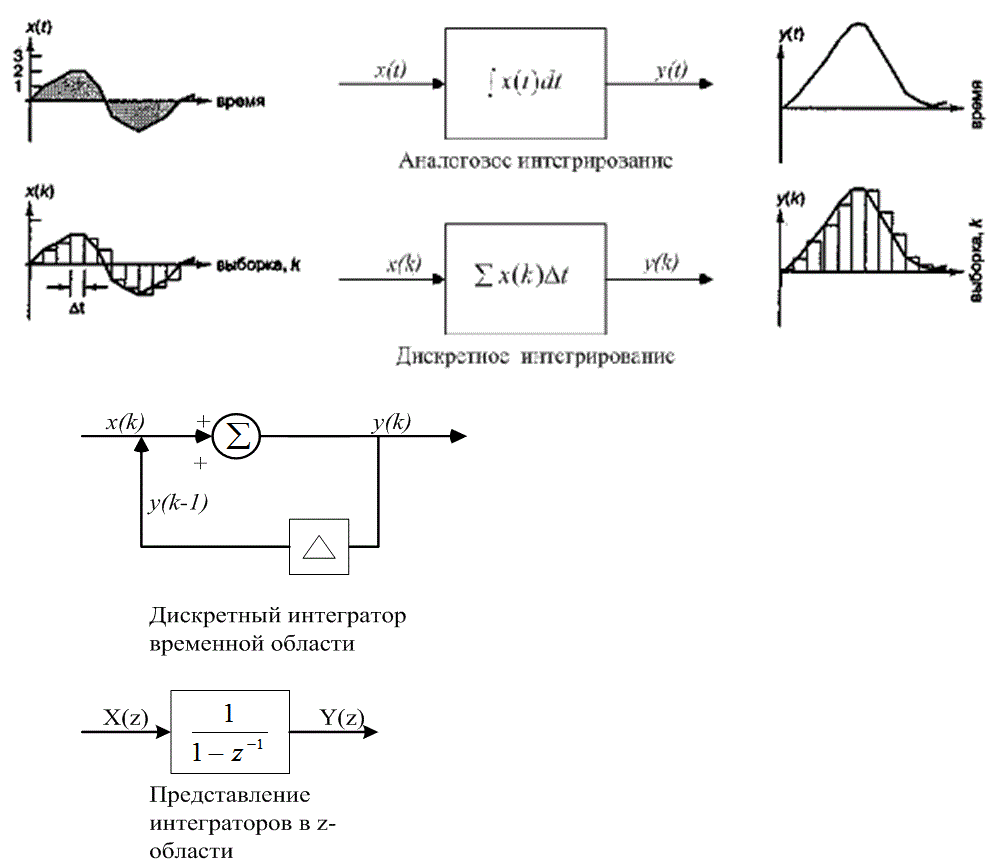




![{\displaystyle {\begin{aligned}\Pr[X\leq L]&={\frac {1}{2}}+{\frac {1}{2}}\operatorname {erf} {\frac {L-\mu }{{\sqrt {2}}\sigma }}\\&\approx A\exp \left(-B\left({\frac {L-\mu }{\sigma }}\right)^{2}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3cb760eaf336393db9fd0bb12c4465655a27de8)
![{\displaystyle {\begin{aligned}\Pr[L_{a}\leq X\leq L_{b}]&=\int _{L_{a}}^{L_{b}}{\frac {1}{{\sqrt {2\pi }}\sigma }}\exp \left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)\,\mathrm {d} x\\&={\frac {1}{2}}\left(\operatorname {erf} {\frac {L_{b}-\mu }{{\sqrt {2}}\sigma }}-\operatorname {erf} {\frac {L_{a}-\mu }{{\sqrt {2}}\sigma }}\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd2214f0db2c1d36075815825b616501175c6283)


![{\displaystyle {\begin{aligned}\operatorname {erf} z&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{2n+1}}{n!(2n+1)}}\\[6pt]&={\frac {2}{\sqrt {\pi }}}\left(z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{10}}-{\frac {z^{7}}{42}}+{\frac {z^{9}}{216}}-\cdots \right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c80541f305af070bb0510625c584fe1559a0cd2c)
![{\displaystyle {\begin{aligned}\operatorname {erf} z&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }\left(z\prod _{k=1}^{n}{\frac {-(2k-1)z^{2}}{k(2k+1)}}\right)\\[6pt]&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {z}{2n+1}}\prod _{k=1}^{n}{\frac {-z^{2}}{k}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dca22e8e7dee0297e87a455249c282c6b92fedcb)
![{\displaystyle {\begin{aligned}\operatorname {erfi} z&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {z^{2n+1}}{n!(2n+1)}}\\[6pt]&={\frac {2}{\sqrt {\pi }}}\left(z+{\frac {z^{3}}{3}}+{\frac {z^{5}}{10}}+{\frac {z^{7}}{42}}+{\frac {z^{9}}{216}}+\cdots \right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ff91095cd6825137cc951ec0a786db0b7f68fac)





![{\displaystyle {\begin{aligned}\operatorname {erf} x&={\frac {2}{\sqrt {\pi }}}\operatorname {sgn} x\cdot {\sqrt {1-e^{-x^{2}}}}\left(1-{\frac {1}{12}}\left(1-e^{-x^{2}}\right)-{\frac {7}{480}}\left(1-e^{-x^{2}}\right)^{2}-{\frac {5}{896}}\left(1-e^{-x^{2}}\right)^{3}-{\frac {787}{276480}}\left(1-e^{-x^{2}}\right)^{4}-\cdots \right)\\[10pt]&={\frac {2}{\sqrt {\pi }}}\operatorname {sgn} x\cdot {\sqrt {1-e^{-x^{2}}}}\left({\frac {\sqrt {\pi }}{2}}+\sum _{k=1}^{\infty }c_{k}e^{-kx^{2}}\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/164e7f029977edb47c83845b04abfe5b2d28b837)







![{\displaystyle {\begin{aligned}\operatorname {erfc} x&={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\left(1+\sum _{n=1}^{\infty }(-1)^{n}{\frac {1\cdot 3\cdot 5\cdots (2n-1)}{\left(2x^{2}\right)^{n}}}\right)\\[6pt]&={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\sum _{n=0}^{\infty }(-1)^{n}{\frac {(2n-1)!!}{\left(2x^{2}\right)^{n}}},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35a11e2e5b22ca898c74f2e913d276c9ac11124a)



























![{\displaystyle {\begin{aligned}\operatorname {erfc} x&=1-\operatorname {erf} x\\[5pt]&={\frac {2}{\sqrt {\pi }}}\int _{x}^{\infty }e^{-t^{2}}\,\mathrm {d} t\\[5pt]&=e^{-x^{2}}\operatorname {erfcx} x,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4acd0062271e2a19c209a02c8cc33d44a28af7cc)



![{\displaystyle {\begin{aligned}\operatorname {erfi} x&=-i\operatorname {erf} ix\\[5pt]&={\frac {2}{\sqrt {\pi }}}\int _{0}^{x}e^{t^{2}}\,\mathrm {d} t\\[5pt]&={\frac {2}{\sqrt {\pi }}}e^{x^{2}}D(x),\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfd2dd94cd6d0325224d412f6b5e5ed63ca81d4a)
![{\displaystyle {\begin{aligned}\Phi (x)&={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{x}e^{\tfrac {-t^{2}}{2}}\,\mathrm {d} t\\[6pt]&={\frac {1}{2}}\left(1+\operatorname {erf} {\frac {x}{\sqrt {2}}}\right)\\[6pt]&={\frac {1}{2}}\operatorname {erfc} \left(-{\frac {x}{\sqrt {2}}}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89a9e9eaaddcd7a91ade15a41b8d1e272d437559)
![{\displaystyle {\begin{aligned}\operatorname {erf} (x)&=2\Phi \left(x{\sqrt {2}}\right)-1\\[6pt]\operatorname {erfc} (x)&=2\Phi \left(-x{\sqrt {2}}\right)\\&=2\left(1-\Phi \left(x{\sqrt {2}}\right)\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86c84a4d2d79631fe9996e30f1d6c0da3089bfe2)






![{\displaystyle {\begin{aligned}\operatorname {i} ^{n}\!\operatorname {erfc} z&=\int _{z}^{\infty }\operatorname {i} ^{n-1}\!\operatorname {erfc} \zeta \,\mathrm {d} \zeta \\[6pt]\operatorname {i} ^{0}\!\operatorname {erfc} z&=\operatorname {erfc} z\\\operatorname {i} ^{1}\!\operatorname {erfc} z&=\operatorname {ierfc} z={\frac {1}{\sqrt {\pi }}}e^{-z^{2}}-z\operatorname {erfc} z\\\operatorname {i} ^{2}\!\operatorname {erfc} z&={\tfrac {1}{4}}\left(\operatorname {erfc} z-2z\operatorname {ierfc} z\right)\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3e7b953efaa4d730a5479bd61a2c378c8f761dc)





![{ displaystyle { begin {align} Pr [L_ {a} leq X leq L_ {b}] & = int _ {L_ {a}} ^ {L_ {b}} { frac {1} {{ sqrt {2 pi}} sigma}} exp left (- { frac {(x- mu) ^ {2}} {2 sigma ^ {2}}} right) , dx \ & = { frac {1} {2}} left ( operatorname {erf} { frac {L_ {b} - mu} {{ sqrt {2}} sigma}} - operatorname {erf} { frac {L_ {a} - mu} {{ sqrt {2}} sigma}} right). end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1b3e43d593e389ed348ff56374118ab644fcec8)



![{ displaystyle { begin {align} operatorname {erfc} x & = 1- operatorname {erf} x \ [5pt] & = { frac {2} { sqrt { pi}}} int _ { x} ^ { infty} e ^ {- t ^ {2}} , dt \ [5pt] & = e ^ {- x ^ {2}} operatorname {erfcx} x, end {выровнено}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/582ae24086ba008f0466a71991c48c405c8248ad)


![{ displaystyle { begin {align} operatorname {erfi} x & = - i operatorname {erf} ix \ [5pt] & = { frac {2} { sqrt { pi}}} int _ { 0} ^ {x} e ^ {t ^ {2}} , dt \ [5pt] & = { frac {2} { sqrt { pi}}} e ^ {x ^ {2}} D (х), конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/937f1aaa2801d245f8056cad15f727ccee0ba1a7)
![{ displaystyle { begin {align} Phi (x) & = { frac {1} { sqrt {2 pi}}} int _ {- infty} ^ {x} e ^ { tfrac { -t ^ {2}} {2}} , dt \ [6pt] & = { frac {1} {2}} left (1+ operatorname {erf} { frac {x} { sqrt {2}}} right) \ [6pt] & = { frac {1} {2}} operatorname {erfc} left (- { frac {x} { sqrt {2}}} right ) конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c70647a7aa4dea3272cb7d90888444e1928c401)
![{ displaystyle { begin {align} operatorname {i} ^ {n} ! operatorname {erfc} z & = int _ {z} ^ { infty} operatorname {i} ^ {n-1} ! operatorname {erfc} zeta , d zeta \ [6pt] operatorname {i} ^ {0} ! operatorname {erfc} z & = operatorname {erfc} z \ operatorname {i} ^ {1} ! Operatorname {erfc} z & = operatorname {ierfc} z = { frac {1} { sqrt { pi}}} e ^ {- z ^ {2}} - z operatorname {erfc } z \ operatorname {i} ^ {2} ! operatorname {erfc} z & = { tfrac {1} {4}} left ( operatorname {erfc} z-2z operatorname {ierfc} z вправо) \ конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39d9046debe25c6cb2fa3709a961ac6a9715a37f)