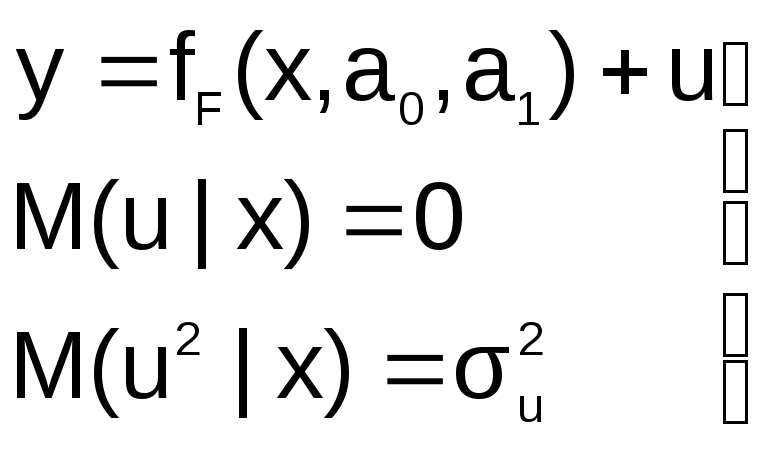Построение
экономической модели включает в себя
спецификацию ее соотношений, выбор
переменных, входящих в соотношение,
определение математической функции,
входящей в каждое соотношение. В данном
пункте мы рассмотрим второй элемент.
Если точно известно,
какая переменная должна быть включена
в уравнение, то наша задача состоит в
определении коэффициентов, построении
доверительных интервалов, проверке
различных гипотез. На практике мы никогда
не можем быть уверены, что уравнение
специфицировано правильно. Что случится,
если мы включим в уравнение переменные,
которых там быть не должно, и что случится,
если мы не включим в уравнение переменные,
которые там должны присутствовать.
Свойства оценок коэффициентов в
значительной степени зависят от
правильности спецификации модели.
Ошибки спецификации
бывают двух видов:
-
невключение
в уравнение существенной объясняющей
переменной; -
включение
в уравнение переменной, которая не
должна там присутствовать.
3)
неправильный выбор формы зависимости
между переменными, мы предположили, что
модель линейная, а она может быть более
сложной.
1.
Влияние отсутствия в уравнении переменной,
которая должна быть включена.
Рассмотрим ситуацию
для случая двух переменных.
Истинная модель
выглядит следующим образом:
.
Но мы не уверены в значимостиZ,
поэтому оцениваем «короткую» модель:.
По методу наименьших квадратов вычисляем:
— несмещенная
оценка , еслиM=. Посчитаем, чему
равноM:
Таким образом,
получаем в числителе:
Итак,
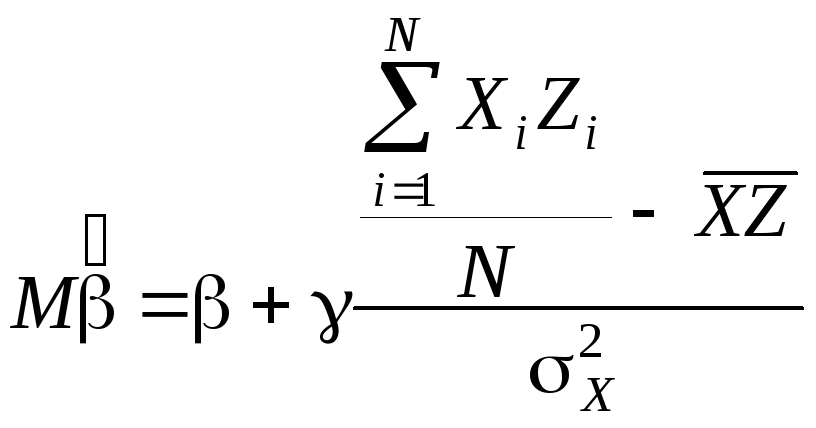
Таким
образом, мы получили смещенную оценку.
Оценка будет несмещенной в двух случаях:
-
;
-
XиZстатистически
независимы.
Наша
оценка будет завышать или занижать
истинное значение коэффициента в
зависимости от знака смещения.
Интуитивное
объяснение.
Предположим, что
иположительны, аXиZположительно коррелированны, тогда с
увеличениемX
-
Yбудет иметь тенденцию к росту, посколькуположителен;
-
Zбудет иметь тенденцию к увеличению,
посколькуXиZположительно коррелированны; -
Yполучит дополнительное ускорение из-за
увеличенияZ, посколькуположительно.
Другими словами,
изменение Yбудет
преувеличивать влияние текущих значенийX, т. к. отчасти они
будут связаны с изменениямиZ.
Т.е. часть измененияYза
счет измененияZбудет
приписаноX.
Однако
смещение оценок коэффициентов здесь –
не единственная неприятность. Что будет
с оценками дисперсий?
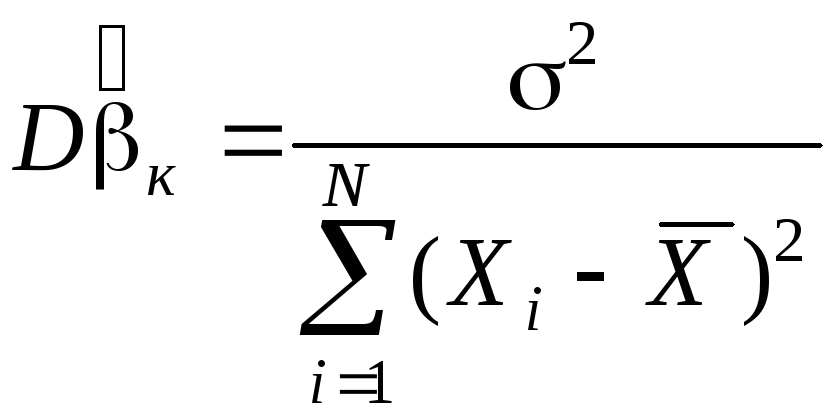
регрессии (без доказательства).
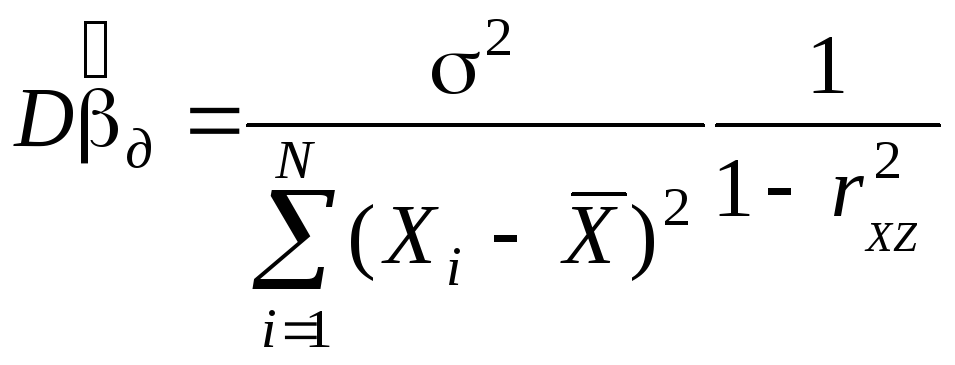
(без доказательства).
Таким образом,
,
т. е.— смещенная оценка, но обладает меньшей
дисперсией.
Что будет с оценкой
—
?
Оказывается, что в случае, если мы не
включаем в регрессию существенную
переменную, эта оценка будет смещенной.
Поскольку
участвует во многих статистических
тестах, то используя их для проверки
гипотез, мы можем получить ложные выводы.
Итак, в случае
невключения объясняющих переменных,
МНК-оценка короткой регрессии смещена,
и обладает меньшей дисперсией, чем у
оценки в длинной регрессии. Оценка
дисперсии ошибки имеет неотрицательное
смещение.
2. Включение
несущественных переменных.
Теперь у нас
ситуация противоположная предыдущей.
Истинная модель выглядит следующим
образом:
,
а мы оцениваем «длинную» регрессию.
Таким образом, включая в уравнение
несущественную переменную, мы не
учитываем информацию о том, что коэффициент
приZравен нулю.
Следует всегда ожидать, что неучитывание
всей информации о модели потере
эффективности оценок. Т. е. в нашем случае
дисперсия оценки в «длинной» регрессии
будет больше, чем дисперсия оценки
коэффициента приХв истинной модели,
поскольку мы вынуждены по тем же самым
наблюдениям оценивать два параметра
вместо одного. Тем не менее, оценки
«длинной» регрессии останутся
несмещенными.
Потеря эффективности
не случится, если переменные ХиZнекоррелированны. Потеря эффективности
приводит к тому, что мы с большей
трудностью отвергаем гипотезу о
незначимости коэффициента, тем не менее
оценка дисперсииостанется несмещенной.
Выводы здесь мы
приводить не будем.
и
— несмещенные оценки, но ее дисперсия
больше, чем в правильной модели, т. е.
точность оценки ухудшается.
Рисунок с графиками
плотностей распределения.
3. Неправильный
выбор функциональной зависимости.
Еще одна ошибка
спецификации происходит, когда
исследователь решает оценить линейную
модель, в то время как истинная
регрессионная модель нелинейная. Пример:
,
а оцениваем мы модель.
Приведенная выше ситуация является
частным случаем ситуации с пропущенными
переменными. Выбор линейной модели, в
то время как истинная модель нелинейная
может привести к смещенности и
несостоятельности оценок регрессии.
Поэтому исследователи часто используют
полиномиальную регрессию как тест на
нелинейность в объясняющих переменных.
Итак, мы с вами
рассмотрели теоретические аспекты
включения лишних или невключения нужных
переменных в уравнение. Что же делать
на практике, когда мы никогда точно не
знаем, какие переменные входят в модель,
а какие нет. В таких ситуациях используют
различные эвристические процедуры
отбора регрессоров.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
4.
Использование
предварительной информации о значениях некоторых параметров. Иногда значения некоторых неизвестных параметров
модели могут быть определены по пробным выборочным наблюдениям, тогда
мультиколлинеарность может быть устранена путем установления значений параметра
у одной коррелирующих переменных. Ограниченность метода – в сложности получения
предварительных значений параметров с высокой точностью.
5.
Преобразование переменных. Для устранения мультиколлинеарности можно
преобразовать переменные, например, путем линеаризации или получения
относительных показателей, а также перехода от номинальных к реальным
показателям (особенно в макроэкономических исследованиях).
При построении модели множественной регрессии с точки
зрения обеспечения ее высокого качества возникают следующие вопросы:
1.
Каковы признаки качественной
модели?
2.
Какие ошибки спецификации могут
быть?
3.
Каковы последствия ошибок
спецификации?
4.
Какие существуют методы
обнаружения и устранения ошибок спецификации?
Рассмотрим основные признаки качественной модели
множественной регрессии:
1.
Простота. Из двух моделей примерно одинаковых статистических
свойств более качественной является та, которая содержит меньше переменных, или
же более простая по аналитической форме.
2.
Однозначность. Метод вычисления коэффициентов должен быть одинаков
для любых наборов данных.
3.
Максимальное соответствие. Этот признак говорит о том, что основным критерием
качества модели является коэффициент детерминации, отражающий объясненную
моделью вариацию зависимой переменной. Для практического использования выбирают
модель, для которой расчетное значение F-критерия для
коэффициента детерминации б четыре раза больше табличного.
4.
Согласованность с теорией. Получаемые значения коэффициентов должны быть
интерпретируемы с точки зрения экономических явлений и процессов. К примеру,
если строится линейная регрессионная модель спроса на товар, то соответствующий
коэффициент при цене товара должен быть отрицательным.
5.
Хорошие прогнозные качества.
Обязательным условием построения
качественной модели является возможность ее использования для прогнозирования.
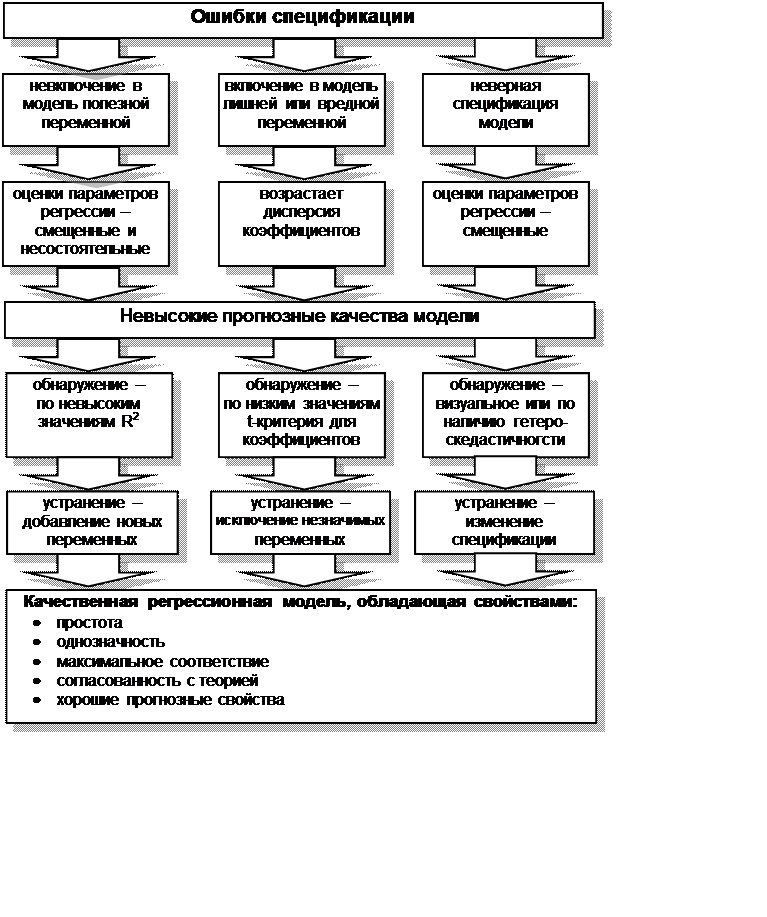
Одной из основных ошибок, допускаемых при построении
регрессионной модели, является ошибка спецификации (рис. 4.3).
Под ошибкой спецификации понимается неправильный выбор функциональной формы
модели или набора объясняющих переменных.
Различают следующие виды ошибок спецификации:
1.
Невключение в модель полезной
(значимой) переменной.
2.
Добавление в модель лишней
(незначимой) переменной
3.
Выбор неправильной функциональной
формы модели
Последствия ошибки первого вида (невключение в
модель значимой переменной) заключаются в том, что полученные по МНК оценки
параметров являются смещенными и несостоятельными, а значение коэффициента
детерминации значительно снижаются.
При добавлении в модель лишней переменной
(ошибка второго вида) ухудшаются статистические свойства оценок
коэффициентов, возрастают их дисперсии, что ухудшает прогнозные качества модели
и затрудняет содержательную интерпретацию параметров, однако по сравнению с
другими ошибками ее последствия менее серьезны.
Если же осуществлен неверный выбор
функциональной формы модели, то есть допущена ошибка третьего вида, то
получаемые оценки будут смещенными, качество модели в целом и отдельных
коэффициентов будет невысоким. Это может существенно сказаться на прогнозных
качествах модели.
Ошибки спецификации первого вида можно обнаружить только
по невысокому качеству модели, низким значениям R2.
Обнаружение ошибок спецификации второго вида, если лишней
является только одна переменная, осуществляется на основе расчета t — статистики для коэффициентов. При лишней переменной коэффициент
будет статистически незначим.
Рис. 4.3 Ошибки спецификации и свойства качественной
регрессионной модели
Доверительные интервалы для машинного обучения
Перевод
Ссылка на автора
Большая часть машинного обучения включает оценку производительности алгоритма машинного обучения на невидимых данных.
Доверительные интервалы являются способом количественной оценки неопределенности оценки. Их можно использовать для добавления границ или вероятности по параметру совокупности, например среднему значению, оцененному из выборки независимых наблюдений из совокупности.
В этом руководстве вы узнаете доверительные интервалы и узнаете, как на практике рассчитывать доверительные интервалы.
После завершения этого урока вы узнаете:
- Этот доверительный интервал является границей оценки параметра совокупности.
- Что доверительный интервал для оцененного навыка метода классификации может быть вычислен напрямую.
- Что доверительный интервал для любой произвольной статистики населения может быть оценен без распределения с использованием начальной загрузки.
Давайте начнем.
- Обновление июнь / 2018: Исправлена опечатка в части выборки примера кода начальной загрузки.
Обзор учебника
Этот урок разделен на 3 части; они есть:
- Что такое доверительный интервал?
- Интервал для точности классификации
- Непараметрический доверительный интервал
Что такое доверительный интервал?
Доверительный интервал — это границы оценки переменной популяции. Это интервальная статистика, используемая для количественной оценки неопределенности в оценке.
Доверительный интервал, содержащий неизвестную характеристику популяции или процесса. Интересующее количество может быть свойством населения или «параметром», таким как среднее или стандартное отклонение населения или процесса.
— Страница 3, Статистические интервалы: руководство для практиков и исследователей, 2017
Доверительный интервал отличается от допустимого интервала, который описывает границы данных, выбранных из распределения. Он также отличается от интервала прогнозирования, который описывает границы одного наблюдения. Вместо этого доверительный интервал предоставляет границы для параметра совокупности, такого как среднее значение, стандартное отклонение или подобное.
В прикладном машинном обучении мы можем пожелать использовать доверительные интервалы при представлении навыка прогнозирующей модели.
Например, доверительный интервал может использоваться при представлении навыка модели классификации, который может быть сформулирован как:
Учитывая выборку, существует 95% вероятность того, что диапазон от x до y покрывает истинную точность модели.
или же
Точность модели составляла x +/- y при уровне достоверности 95%.
Доверительные интервалы могут также использоваться при представлении ошибки модели прогнозирования регрессии; например:
Существует 95% вероятность того, что диапазон от x до y покрывает истинную ошибку модели.
или же
Ошибка модели была x +/- y при уровне достоверности 95%.
Выбор 95% достоверности очень распространен при представлении доверительных интервалов, хотя используются и другие, менее распространенные значения, такие как 90% и 99,7%. На практике вы можете использовать любое значение, которое вы предпочитаете.
95% доверительный интервал (ДИ) — это диапазон значений, рассчитанный по нашим данным, который, скорее всего, включает в себя истинное значение того, что мы оцениваем в отношении населения.
— Страница 4, Введение в новую статистику: оценка, открытая наука и не только, 2016
Значение доверительного интервала — это его способность количественно оценить неопределенность оценки. Он обеспечивает как нижнюю, так и верхнюю границы и вероятность. Взятый как мера радиуса, доверительный интервал часто называют пределом погрешности и может использоваться для графического отображения неопределенности оценки на графиках с использованием бары ошибок,
Часто, чем больше выборка, из которой была получена оценка, тем точнее оценка и тем меньше (лучше) доверительный интервал.
- Меньший доверительный интервал: Более точная оценка
- Большой доверительный интервал: Менее точная оценка.
Мы также можем сказать, что CI говорит нам, насколько точной может быть наша оценка, и предел погрешности является нашей мерой точности. Короткий CI означает небольшой предел погрешности и что мы имеем относительно точную оценку […] Длинный CI означает большой предел погрешности и что мы имеем низкую точность
— Страница 4, Введение в новую статистику: оценка, открытая наука и не только, 2016
Доверительные интервалы относятся к области статистики, называемой оценочной статистикой, которая может использоваться для представления и интерпретации экспериментальных результатов вместо или в дополнение к тестам статистической значимости.
Оценка дает более информативный способ анализа и интерпретации результатов. […] Знание и размышление о величине и точности эффекта более полезно для количественной науки, чем размышление о вероятности наблюдения данных, по крайней мере, этой конечности, при условии, что они абсолютно не влияют.
— Оценка статистики должна заменить значимость тестирования, 2016
Доверительные интервалы могут быть предпочтительны на практике по сравнению с использованием тестов статистической значимости.
Причина в том, что практикующим специалистам и заинтересованным сторонам проще связываться непосредственно с доменом. Их также можно интерпретировать и использовать для сравнения моделей машинного обучения.
Эти оценки неопределенности помогают двумя способами. Во-первых, интервалы дают потребителям модели понимание того, насколько хорошей или плохой может быть модель. […] Таким образом, доверительный интервал помогает оценить вес доказательств, доступных при сравнении моделей. Второе преимущество доверительных интервалов заключается в облегчении компромиссов между моделями. Если доверительные интервалы для двух моделей существенно перекрываются, это указывает на (статистическую) эквивалентность между этими двумя моделями и может послужить причиной для выбора менее сложной или более интерпретируемой модели.
— Страница 416, Прикладное прогнозное моделирование, 2013.
Теперь, когда мы знаем, что такое доверительный интервал, давайте рассмотрим несколько способов, которыми мы можем рассчитать их для прогностических моделей.
Интервал для точности классификации
Проблемы классификации — это те, где метка или переменная результата класса предсказываются с учетом некоторых входных данных.
Обычно используется точность классификации или ошибка классификации (обратная точность), чтобы описать умение модели прогнозирования классификации. Например, модель, которая делает правильные предсказания переменной результата класса 75% времени, имеет точность классификации 75%, рассчитанную как:
accuracy = total correct predictions / total predictions made * 100Эта точность может быть рассчитана на основе набора данных об удержании, не видимого моделью во время обучения, такого как набор данных для проверки или тестирования.
Точность классификации или ошибка классификации доля или соотношение. Он описывает пропорцию правильных или неправильных прогнозов, сделанных моделью. Каждый прогноз — это двоичное решение, которое может быть правильным или неправильным. Технически это называется Испытание Бернулли, названный в честь Джейкоба Бернулли. Пропорции в испытании Бернулли имеют специфическое распределение, называемое биномиальное распределение, К счастью, при больших размерах выборки (например, более 30) мы можем приблизить распределение по Гауссу.
В статистике последовательность независимых событий, которые либо преуспевают, либо проваливаются, называются процессом Бернулли. […] Для больших N распределение этой случайной величины приближается к нормальному распределению.
— Страница 148, Data Mining: практические инструменты и методы машинного обучения, Второе издание, 2005.
Мы можем использовать предположение о гауссовском распределении пропорции (то есть точности классификации или ошибки), чтобы легко вычислить доверительный интервал.
В случае ошибки классификации радиус интервала можно рассчитать как:
interval = z * sqrt( (error * (1 - error)) / n)В случае точности классификации радиус интервала можно рассчитать как:
interval = z * sqrt( (accuracy * (1 - accuracy)) / n)Где интервал — это радиус доверительного интервала, ошибка и точность — это ошибка классификации и точность классификации соответственно, n — размер выборки, sqrt — функция квадратного корня, а z — критическое значение из распределения Гаусса. Технически это называется доверительным интервалом биномиальной пропорции.
Обычно используемые критические значения из гауссовского распределения и их соответствующий уровень значимости следующие:
- 1,64 (90%)
- 1,96 (95%)
- 2,33 (98%)
- 2,58 (99%)
Рассмотрим модель с ошибкой 20% или 0,2 (ошибка = 0,2) для набора данных проверки с 50 примерами (n = 50). Мы можем рассчитать 95% доверительный интервал (z = 1,96) следующим образом:
# binomial confidence interval
from math import sqrt
interval = 1.96 * sqrt( (0.2 * (1 - 0.2)) / 50)
print('%.3f' % interval)Запустив пример, мы видим рассчитанный радиус доверительного интервала, рассчитанный и напечатанный.
0.111Затем мы можем предъявить претензии, такие как:
- Ошибка классификации модели составляет 20% +/- 11%
- Истинная ошибка классификации модели, вероятно, составляет от 9% до 31%.
Мы можем видеть влияние размера выборки на точность оценки в терминах радиуса доверительного интервала.
# binomial confidence interval
interval = 1.96 * sqrt( (0.2 * (1 - 0.2)) / 100)
print('%.3f' % interval)Выполнение примера показывает, что доверительный интервал падает примерно до 7%, что повышает точность оценки навыка модели.
0.078Помните, что доверительный интервал является вероятностью в диапазоне. Истинное умение модели может лежать за пределами диапазона.
Фактически, если бы мы повторяли этот эксперимент снова и снова, каждый раз рисуя новую выборку S, содержащую […] новые примеры, мы обнаружили бы, что приблизительно для 95% этих экспериментов вычисленный интервал будет содержать истинную ошибку. По этой причине мы называем этот интервал оценкой доверительного интервала 95%.
— страница 131, Машинное обучение, 1997.
ratio_confint () функция statsmodels реализация биноминальной пропорции доверительного интервала.
По умолчанию он делает гауссовское предположение для биномиального распределения, хотя поддерживаются и другие более сложные варианты расчета. Функция принимает количество успехов (или неудач), общее количество испытаний и уровень значимости в качестве аргументов и возвращает нижнюю и верхнюю границы доверительного интервала.
Пример ниже демонстрирует эту функцию в гипотетическом случае, когда модель сделала 88 правильных прогнозов из набора данных со 100 экземплярами, и нас интересует 95% доверительный интервал (предоставленный функции как значение 0,05).
from statsmodels.stats.proportion import proportion_confint
lower, upper = proportion_confint(88, 100, 0.05)
print('lower=%.3f, upper=%.3f' % (lower, upper))При выполнении примера печатается нижняя и верхняя границы точности классификации модели.
lower=0.816, upper=0.944Непараметрический доверительный интервал
Часто мы не знаем распределение для выбранного показателя эффективности. С другой стороны, мы можем не знать аналитический способ вычисления доверительного интервала для оценки навыка.
Предположения, лежащие в основе параметрических доверительных интервалов, часто нарушаются. Прогнозируемая переменная иногда не распределяется нормально, и даже в этом случае дисперсия нормального распределения может быть не одинаковой на всех уровнях переменной-предиктора.
— страница 326, Эмпирические методы для искусственного интеллекта 1995
В этих случаях метод повторной выборки при начальной загрузке может использоваться как непараметрический метод для расчета доверительных интервалов, номинально называемых доверительными интервалами при начальной загрузке.
Бутстрап — это метод имитации Монте-Карло, в котором выборки берутся из фиксированного конечного набора данных с заменой, и для каждой выборки оценивается параметр. Эта процедура приводит к надежной оценке истинного параметра популяции посредством выборки.
Мы можем продемонстрировать это следующим псевдокодом.
statistics = []
for i in bootstraps:
sample = select_sample_with_replacement(data)
stat = calculate_statistic(sample)
statistics.append(stat)Процедура может использоваться для оценки навыка прогнозирующей модели путем подбора модели для каждой выборки и оценки навыка модели на тех выборках, которые не включены в выборку. Среднее или срединное умение модели затем может быть представлено как оценка умения модели при оценке по невидимым данным.
К этой оценке могут быть добавлены доверительные интервалы путем выбора наблюдений из выборки баллов навыков с определенными процентилями.
Напомним, что процентиль — это значение наблюдения, полученное из отсортированной выборки, где процент наблюдений в выборке падает. Например, 70-й процентиль образца указывает, что 70% образцов находятся ниже этого значения. 50-й процентиль — это медиана или середина распределения.
Во-первых, мы должны выбрать уровень значимости для уровня достоверности, например 95%, представленный как 5,0% (например, 100 — 95). Поскольку доверительный интервал симметричен относительно медианы, мы должны выбрать наблюдения с 2,5-го процентиля и 97,5-го процентиля, чтобы получить полный диапазон.
Мы можем сделать расчет доверительного интервала начальной загрузки конкретным на проработанном примере.
Предположим, у нас есть набор данных из 1000 наблюдений значений между 0,5 и 1,0, взятых из равномерного распределения.
# generate dataset
dataset = 0.5 + rand(1000) * 0.5Мы выполним процедуру начальной загрузки 100 раз и возьмем образцы из 1000 наблюдений из набора данных с заменой. Мы оценим среднее количество населения как статистику, которую мы рассчитаем на выборках начальной загрузки. Это может быть просто оценка модели.
# bootstrap
scores = list()
for _ in range(100):
# bootstrap sample
indices = randint(0, 1000, 1000)
sample = dataset[indices]
# calculate and store statistic
statistic = mean(sample)
scores.append(statistic)Как только мы получим образец статистики начальной загрузки, мы сможем вычислить центральную тенденцию. Мы будем использовать медиану или 50-й процентиль, поскольку не предполагаем никакого распределения.
print('median=%.3f' % median(scores))Затем мы можем рассчитать доверительный интервал как средние 95% наблюдаемых статистических значений с центром вокруг медианы.
# calculate 95% confidence intervals (100 - alpha)
alpha = 5.0Сначала желаемый нижний процентиль вычисляется на основе выбранного доверительного интервала. Затем наблюдение на этом процентиле извлекается из выборки статистики начальной загрузки.
# calculate lower percentile (e.g. 2.5)
lower_p = alpha / 2.0
# retrieve observation at lower percentile
lower = max(0.0, percentile(scores, lower_p))Мы делаем то же самое для верхней границы доверительного интервала.
# calculate upper percentile (e.g. 97.5)
upper_p = (100 - alpha) + (alpha / 2.0)
# retrieve observation at upper percentile
upper = min(1.0, percentile(scores, upper_p))Полный пример приведен ниже.
# bootstrap confidence intervals
from numpy.random import seed
from numpy.random import rand
from numpy.random import randint
from numpy import mean
from numpy import median
from numpy import percentile
# seed the random number generator
seed(1)
# generate dataset
dataset = 0.5 + rand(1000) * 0.5
# bootstrap
scores = list()
for _ in range(100):
# bootstrap sample
indices = randint(0, 1000, 1000)
sample = dataset[indices]
# calculate and store statistic
statistic = mean(sample)
scores.append(statistic)
print('50th percentile (median) = %.3f' % median(scores))
# calculate 95% confidence intervals (100 - alpha)
alpha = 5.0
# calculate lower percentile (e.g. 2.5)
lower_p = alpha / 2.0
# retrieve observation at lower percentile
lower = max(0.0, percentile(scores, lower_p))
print('%.1fth percentile = %.3f' % (lower_p, lower))
# calculate upper percentile (e.g. 97.5)
upper_p = (100 - alpha) + (alpha / 2.0)
# retrieve observation at upper percentile
upper = min(1.0, percentile(scores, upper_p))
print('%.1fth percentile = %.3f' % (upper_p, upper))Выполнение примера суммирует распределение выборочной статистики начальной загрузки, включая 2,5-й, 50-й (медиана) и 97,5-й процентиль.
50th percentile (median) = 0.750
2.5th percentile = 0.741
97.5th percentile = 0.757Затем мы можем использовать эти наблюдения, чтобы заявить о распределении выборки, например:
Существует 95% вероятность того, что диапазон от 0,741 до 0,757 покрывает истинное среднее статистическое значение.
расширения
В этом разделе перечислены некоторые идеи по расширению учебника, которые вы, возможно, захотите изучить.
- Протестируйте каждый метод доверительного интервала на ваших собственных маленьких надуманных тестовых наборах данных
- Найдите 3 исследовательские работы, которые демонстрируют использование метода каждого доверительного интервала.
- Разработайте функцию для вычисления доверительного интервала начальной загрузки для данной выборки баллов навыков машинного обучения.
Если вы исследуете какое-либо из этих расширений, я хотел бы знать.
Дальнейшее чтение
Этот раздел предоставляет больше ресурсов по теме, если вы хотите углубиться
Сообщений
- Как сообщить о производительности классификатора с доверительными интервалами
- Как рассчитать доверительные интервалы начальной загрузки для результатов машинного обучения в Python
- Понимать неопределенность прогноза временных рядов, используя доверительные интервалы с Python
книги
- Понимание новой статистики: размеры эффектов, доверительные интервалы и метаанализ 2011
- Введение в новую статистику: оценка, открытая наука и не только, 2016
- Статистические интервалы: руководство для практиков и исследователей, 2017
- Прикладное прогнозное моделирование, 2013.
- Машинное обучение, 1997.
- Data Mining: практические инструменты и методы машинного обучения, Второе издание, 2005.
- Введение в Bootstrap, 1996.
- Эмпирические методы для искусственного интеллекта 1995
документы
- Оценка статистики должна заменить значимость тестирования, 2016
- Начальные доверительные интервалы, статистическая наука, 1996.
API
- API statsmodels.stats.proportion.proportion_confint ()
- API numpy.random.rand ()
- API numpy.random.randint ()
- API numpy.random.seed ()
- API numpy.percentile ()
- API numpy.median ()
статьи
- Интервальная оценка в Википедии
- Доверительный интервал в Википедии
- Биноминальная пропорция доверительного интервала в Википедии
- Доверительный интервал RMSE на перекрестной проверке
- Начальная загрузка в Википедии
Резюме
В этом руководстве вы узнали о доверительных интервалах и о том, как рассчитать доверительные интервалы на практике.
В частности, вы узнали:
- Этот доверительный интервал является границей оценки параметра совокупности.
- Что доверительный интервал для оцененного навыка метода классификации может быть вычислен напрямую.
- Что доверительный интервал для любой произвольной статистики населения может быть оценен без распределения с использованием начальной загрузки.
У вас есть вопросы?
Задайте свои вопросы в комментариях ниже, и я сделаю все возможное, чтобы ответить.
Возможные ошибки спецификации модели:
1. Неправильный выбор вида уравнения
регрессии
2. В уравнение регрессии включена лишняя
(незначимая) переменная
3. В уравнении регрессии пропущена
значимая переменная
-
Неправильный выбор вида функции в
уравнении
Пусть на первом этапе была сделана
спецификация модели в виде:
в
которой функция fF(x,a0,a1)
выбрана не верно. Предположим, что
yT=fT(x,a0,a1)+v
– правильный вид функции регрессии.
Тогда справедливо выражение:
И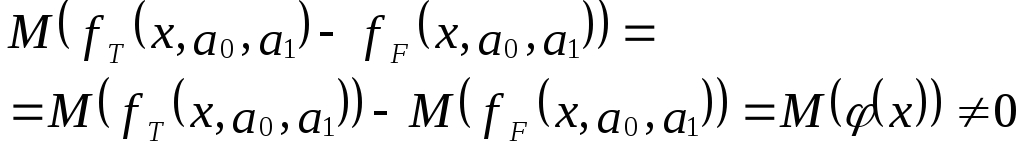
выражения следует:
Иными словами, математические ожидания
эндогенной переменной, полученные с
помощью функций fT
и fF
не совпадают, т.е. первая предпосылка
теоремы Гаусса-Маркова M(ulx)=0
не выполняется
Следовательно, в результате оценивания
такой модели параметры а0 и а1
будут смещенными
Симптомы наличия ошибки спецификации
первого типа:
1. Несоответствие диаграммы рассеяния,
построенной по имеющейся выборке виду
функции, принятой в спецификации
2. В динамических моделях длительно
сохраняется знак значений оценок
случайных возмущений у смежных (по
номеру t ) уравнений
наблюдений
Именно этот симптом и улавливается
статистикой DW Дарбина–Уотсона!
В силу данного обстоятельства тесту
Дарбина–Уотсона в эконометрике придается
большое значение.
Способ устранения: выбор другой формы
спецификации модели. Например, нелинейная
вместо линейной и т.д.
2. В уравнение регрессии включена
лишняя переменная
П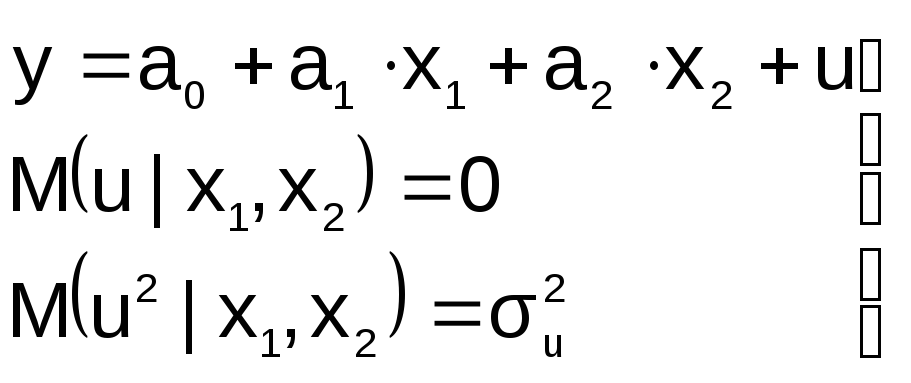
на этапе спецификации в модель включена
«лишняя» переменная, например, X2
«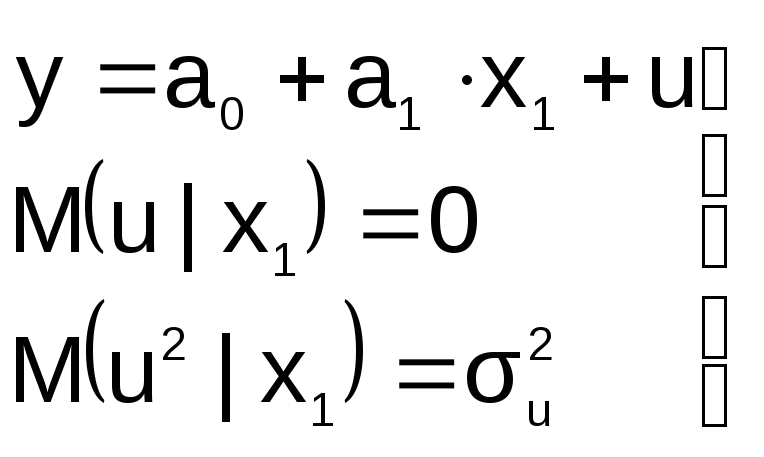
спецификация должна иметь вид:
Последствия:
1.
Оценки параметров а0, а1, а2
останутся несмещенными, но потеряют
свою эффективность (точность)
2. Увеличивается ошибка прогноза по
модели
как за счет ошибок оценок коэффициентов
и σu,
так и за счет последнего слагаемого.
Это особенно опасно при больших абсолютных
значениях регрессора
Диагностика:
В моделях множественной регрессии
необходимо для каждого коэффициента
уравнения проверять статистическую
гипотезу H0: ai=0.
Вспомним, что для этого достаточно
оценить дробь Стьюдента и сравнить ее
значение с критическим значением
распределения Стьюдента, которое
вычисляется по значению доверительной
вероятности и значению степени свободы
n2 = n – (k+1)
3.
В модели не достает важной переменной
Последствия такие же, как и в первом
случае: получаем смещенные оценки
параметров модели
Для устранения необходимо вернуться к
изучению особенностей поведения
экономического объекта, выявить опущенные
переменные и дополнить ими модель
29. Фиктивные переменные и особенности их использования в моделях.
На практике приходится учитывать в
моделях факторы, носящие качественный
характер, значения которых в наблюдениях
не возможно измерить с помощью числовой
шкалы.
Примеры.
Моделирование влияния пола специалистов
на уровень зарплаты.
Моделирование доходов граждан от типа
учебного заведения, в котором он получил
образование (государственное, частное,
специализированное,…)
Модель инфляции с учетом различных
видов регулирования со стороны государства
Возможны два подхода к решению задачи:
— построить несколько моделей отдельно
для каждого значения (градации)
качественной переменной
— учесть влияние качественного фактора
в одной модели
Второй способ представляется более
прогрессивным, т.к в этом случае появляется
возможность оценить статистическую
значимость влияния данного фактора на
поведение эндогенной переменной на
фоне других факторов, внесенных в
спецификацию модели
Пример. Изучается зависимость
расходов на образование «С» в «обычных»
и «специализированных» школах в
зависимости от числа учащихся N
Предположим:
-
Зависимость затрат на обучение от
количества учащихся N в
обоих типах школ одинакова
2. Разница в затратах объясняется
необходимостью приобретения
специализированного оборудования для
обучения специальным дисциплинам
Тогда если строить различные модели
для каждого типа школ, то спецификацию
моделей можно записать в виде:
Yo
= a0 +
a1N +u
Ys
= b0 +
a1N +
v
О
модели можно объединить, если ввести
переменную d, область
определения которой два целых числа :
0 и 1. При этом:
Спецификация такой модели имеет вид:
Y = a0
+ a1N
+ δd + u
Тогда при d=0 получим Yo
= a0 + a1N
+ u
при d=1 получим Ys
= (a0+δ)
+a1N +
v
d – фиктивная переменная
сдвига
Фиктивные переменные часто применяются
при построении динамических моделей,
когда с определенного момента времени
начинает действовать какой-либо
качественный фактор
Пусть некоторый качественный фактор
имеет несколько градаций (более 2-х)
Введение в модель фиктивных переменных
с несколькими градациями рассмотрим
на примере шанхайских школ, где имеются
4 категории школ: общеобразовательные,
технические, ПТУ и специализированные
Казалось достаточно ввести фиктивную
переменную сдвига d, придав
ей четыре различных значения и проблема
будет решена
Такой подход мало эффективен, т.к не
удается оценить статистическую значимость
влияния каждой градации на значения
эндогенной переменной
В этом случае имеет смысл ввести отдельную
переменную для каждой градации фактора
Н
Однако, если взять спецификацию модели
в виде:
Y=a0
+ a1d1+a2d2+a3d3+a4d4+a5N+u
при этом всегда верно тождество
d1+d2+d3+d4=1
Это означает, что матрица Х коэффициентов
системы уравнений наблюдений будет
коллинеарной т.к в ней присутствует
столбец из 1, и как следствие отсутствует
возможность применения МНК для оценки
параметров модели.
Предлагается в спецификацию ввести
(к-1) фиктивную переменную (к- кол-во
градаций), сделав одну из градаций
базовой, относительно которой изучать
влияние остальных градаций. Проблемы
мультиколинеарности в этом случае не
возникает
Для учета возможного изменения наклона
графика модели при изменении градации
качественного фактора предлагается
ввести в спецификацию модели еще одно
слагаемое вида «d умноженное
на x»
Вернемся к примеру изучения зависимости
расходов на образование в различных
школах. Для простоты ограничимся лишь
двумя градациями фактора «тип школы»:
d=0 – обычная школа;
d=1 – профессиональная
школа
Спецификацию модели следует записать
в виде:
Y = a0
+ a1N
+ a2*d
+ a3dN
+U
50
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
анастасия александровна янченко
Эксперт по предмету «Эконометрика»
Задать вопрос автору статьи
Проблема спецификации эконометрической модели
Проблема спецификации эконометрической модели предполагает определение:
- конечной цели моделирования;
- набора эндогенных и экзогенных переменных;
- состава и структуры системы уравнений, набора переменных;
- первоначальных ограничений стохастических составляющих.
Спецификация в эконометрике является важнейшим этапом исследования, эффективность решения влияет на успех исследования в целом. В основе спецификации — имеющиеся теории, интуиция и специальные знания.
Проблема идентифицируемости
В эконометрике проблема идентифицируемости сводится к следующему: нас интересует такие эндогенные переменные, которые относятся к случайным величинам.
Уравнение структурной формы является точно идентифицируемым тогда, когда каждый участвующий неизвестный коэффициент однозначно восстанавливается по коэффициентам приведенной формы, не ограничивая значения последних.

Учим создавать игры
Создавай 3D-графику и концепты, придумывай персонажей, учись программировать с нуля
Записаться на курс
Определение 1
Эконометрическую модель можно назвать точно идентифицируемой, если каждое уравнение ее структурной формы является точно идентифицируемым.
Если какой-либо коэффициент не может быть восстановлен, не идентифицируемо и уравнение, и модель. Проблемы идентификации сводятся к «настройкам» модели по реальным статистическим данным.
Проблема верификации
Замечание 1
Проблема верификации применительно к эконометрическим моделям заключается в разрешении вопросов относительно возможностей использования модели.
Иными словами эта проблема сводится к точности имитационных и прогнозных расчетов. Верификация подразумевает статистическую проверку гипотез и анализ параметров точности оценки. Зачастую применяется ретроспективный расчет: исходные данные делятся на части: обучающая выборка и экзаменующая выборка.
«Проблемы эконометрики» 👇
Обучающая выборка позволяет определить значения неизвестных параметров и получить модельные значения для экзаменующей выборки, которые затем подлежат сравнению с реальными значениями.
Недостаточный набор данных
Замечание 2
Проблема недостаточности данных заключается в том, что имеющиеся данные могут быть недостаточны для определения функциональной связи между переменными, или они мало варьируются для выявления отличий влияния одних факторов от влияния других.
Последнюю проблему в эконометрическом моделировании часто называют «мультиколлинеарностью».
В отличие от экспериментальной науки, отдельный исследователь, изучающий экономические процессы обычно не имеет возможности заметно повлиять на них.
Для восполнения недостатка данных, исследователь должен принимать определенные априорные допущения, которые часто могут быть недостаточно обоснованными.
Обычно функциональная форма эконометрической модели неизвестна заранее. В таком случае целесообразно использовать непараметрические методы оценивания. Но применение подобных методов требует достаточно значительного набора данных. На практике поэтому, как правило, предполагается, что зависимость двумя переменных линейна. Это связано с тем, что линейная зависимость подразумевает хороший уровень аппроксимации гладкой зависимости в определенной окрестности. Однако нет никаких гарантий, что истинная зависимость не будет нелинейной в интервале, к которому отнесены данные.
В случае применении методов эконометрики следует понимать, что обычно постулируемые свойства имеют асимптотический характер, или проявляются при стремлении числа наблюдений к бесконечности. Например, если линейная регрессия подразумевает использование в качестве регрессоров лагов (запаздывания) зависимых переменных, то, даже при выполнении стандартных предположений регрессионного анализа, итоговые оценки будут смещенными, но состоятельными.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Шпоры по эконометрике.
№ 1. СПЕЦИФИКАЦИЯ МОДЕЛИ
Простая регрессия представляет собой регрессию между двумя переменными у и х, т.е. модель вида , где у результативный признак; х — признак-фактор.
Множественная регрессия представляет собой регрессию результативного признака с двумя и большим числом факторов, т. е. модель вида
Спецификация модели — формулировка вида модели, исходя из соответствующей теории связи между переменными. В уравнении регрессии корреляционная по сути связь признаков представляется в виде функциональной связи, выраженной соответствующей математической функцией. где yj фактическое значение результативного признака;
yxj -теоретическое значение результативного признака.
случайная величина, характеризующая отклонения реального значения результативного признака от теоретического.
Случайная величина ε называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения.
От правильно выбранной спецификации модели зависит величина случайных ошибок: они тем меньше, чем в большей мере теоретические значения результативного признака подходят к фактическим данным у.
К ошибкам спецификации относятся неправильный выбор той или иной математической функции для, и недоучет в уравнении регрессии какого-либо существенного фактора, т. е. использование парной регрессии вместо множественной.
Ошибки выборки — исследователь чаще всего имеет дело с выборочными данными при установлении закономерной связи между признаками.
Ошибки измерения практически сводят на нет все усилия по количественной оценке связи между признаками. Основное внимание в эконометрических исследованиях уделяется ошибкам спецификации модели.
В парной регрессии выбор вида математической функции может быть осуществлен тремя методами: графическим, аналитическим и экспериментальным.
Графический метод основан на поле корреляции. Аналитический метод основан на изучении материальной природы связи исследуемых признаков.
Экспериментальный метод осуществляется путем сравнения величины остаточной дисперсии Dост, рассчитанной при разных моделях. Если фактические значения результативного признака совпадают с теоретическими у =, то Docm =0. Если имеют место отклонения фактических данных от теоретических (у ) то .
Чем меньше величина остаточной дисперсии, тем лучше уравнение регрессии подходит к исходным данным. Число наблюдений должно в 6 7 раз превышать число рассчитываемых параметров при переменной х.
№ 2 ЛИНЕЙНАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ: СМЫСЛ И ОЦЕНКА ПАРАМЕТРОВ.
Линейная регрессия сводится к нахождению уравнения вида или .
Уравнение вида позволяет по заданным значениям фактора x иметь теоретические значения результативного признака, подставляя в него фактические значения фактора х.
Построение линейной регрессии сводится к оценке ее параметров а и в.
Оценки параметров линейной регрессии могут быть найдены разными методами.
1.
2.
Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу.
Формально а значение у при х = 0. Если признак-фактор
не имеет и не может иметь нулевого значения, то вышеуказанная
трактовка свободного члена, а не имеет смысла. Параметр, а может
не иметь экономического содержания. Попытки экономически
интерпретировать параметр, а могут привести к абсурду, особенно при а < 0.
Интерпретировать можно лишь знак при параметре а. Если а > 0, то относительное изменение результата происходит медленнее, чем изменение фактора.
Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции rxy. Существуют разные модификации формулы линейного коэффициента корреляции.
Линейный коэффициент корреляции находится и границах: -1≤.rxy ≤ 1. При этом чем ближе r к 0 тем слабее корреляция и наоборот чем ближе r к 1 или -1, тем сильнее корреляция, т.е. зависимость х и у близка к линейной. Если r в точности =1или -1 все точки лежат на одной прямой. Если коэф. регрессии b>0 то 0 ≤.rxy ≤ 1 и наоборот при b<0 -1≤.rxy ≤0. Коэф. корреляции отражает степени линейной зависимости м/у величинами при наличии ярко выраженной зависимости др. вида.
Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции , называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака y, объясняемую регрессией. Соответствующая величина характеризует долю дисперсии у, вызванную влиянием остальных не учтенных в модели факторов.
№ 3. МНК.
МНК позволяет получить такие оценки параметров а и b, которых сумма квадратов отклонений фактических значений результативного признака (у) от расчетных (теоретических) минимальна:
Иными словами, из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной. Решается система нормальных уравнений
№ 4. ОЦЕНКА СУЩЕСТВЕННОСТИ ПАРАМЕТРОВ ЛИНЕЙНОЙ РЕГРЕССИИ И КОРРЕЛЯЦИИ.
Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера. При этом выдвигается нулевая гипотеза, что коэффициент регрессии равен нулю, т. е. b = 0, и следовательно, фактор х не оказывает влияния на результат у.
Непосредственному расчету F-критерия предшествует анализ дисперсии. Центральное место в нем занимает разложение общей суммы квадратов отклонений переменной у от средне го значения у на две части — «объясненную» и «необъясненную»:
— общая сумма квадратов отклонений
— сумма квадратов отклонения объясненная регрессией — остаточная сумма квадратов отклонения.
Любая сумма квадратов отклонений связана с числом степеней свободы, т. е. с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности nис числом определяемых по ней констант. Применительно к исследуемой проблеме число cтепеней свободы должно показать, сколько независимых отклонений из п возможных требуется для образования данной суммы квадратов.
Дисперсия на одну степень свободы D.
F-отношения (F-критерий):
Ecли нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга. Для Н0 необходимо опровержение, чтобы факторная дисперсия превышала остаточную в несколько раз. Английским статистиком Снедекором разработаны таблицы критических значений F-отношений при разных уровнях существенности нулевой гипотезы и различном числе степеней свободы. Табличное значение F-критерия это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы. Вычисленное значение F-отношения признается достоверным, если о больше табличного. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи: Fфакт > Fтабл Н0 отклоняется.
Если же величина окажется меньше табличной Fфакт ‹, Fтабл , то вероятность нулевой гипотезы выше заданного уровня и она не может быть отклонена без серьезного риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически незначимым. Но не отклоняется.
Стандартная ошибка коэффициента регрессии
Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т. е. определяется фактическое значение t-критерия Стьюдентa: которое
затем сравнивается с табличным значением при определенном уровне значимости и числе степеней свободы (n- 2).
Стандартная ошибка параметра а:
Значимость линейного коэффициента корреляции проверяется на основе величины ошибки коэффициента корреляции тr:
Общая дисперсия признака х:
Коэф. регрессии Его величина показывает ср. изменение результата с изменением фактора на 1 ед.
Ошибка аппроксимации:
№ 5. ИНТЕРВАЛЫ ПРОГНОЗА ПО ЛИНЕЙНОМУ УРАВНЕНИЮ
РЕГРЕССИИ
Оценка стат. значимости параметров регрессии проводится с помощью t статистики Стьюдента и путем расчета доверительного интервала для каждого из показателей. Выдвигается гипотеза Н0 о статистически значимом отличие показателей от 0 a = b = r = 0. Рассчитываются стандартные ошибки параметров a,b, r и фактич. знач. t критерия Стьюдента.
Определяется стат. значимость параметров.
ta ›Tтабл — a стат. значим
tb ›Tтабл — b стат. значим
Находятся границы доверительных интервалов.
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что п